Metaheuristic algorithms for PID controller parameters tuning: review, approaches and open problems

Abstract

The simplicity, transparency, reliability, high efficiency and robust nature of PID controllers are some of the reasons for their high popularity and acceptance for control in process industries around the world today. Tuning of PID control parameters has been a field of active research and still is. The primary objectives of PID control parameters are to achieve minimal overshoot in steady state response and lesser settling time. With exception of two popular conventional tuning strategies (Ziegler Nichols closed loop oscillation and Cohen-Coon's process reaction curve) several other methods have been employed for tuning. This work accords a thorough review of state-of-the-art and classical strategies for PID controller parameters tuning using metaheuristic algorithms. Methods appraised are categorized into classical and metaheuristic optimization methods for PID parameters tuning purposes. Details of some metaheuristic algorithms, methods of application, equations and implementation flowcharts/algorithms are presented. Some open problems for future research are also presented. The major goal of this work is to proffer a comprehensive reference source for researchers and scholars working on PID controllers.

PID controller; Tuning; Metaheuristic algorithm; Softcomputing; Machine learning

1. Introduction

Over the years, feedback control mechanisms have established a very strong impact in the fields of manufacturing, robotics, aviation and process control. Several efficient, robust and adaptive controllers (Brogliato and Lozano, 1994; Grimm et al., 2007; Kaloust and Qu, 1997; Lazar and Heemels, 2009; Rakovic et al., 2006) have been proposed aside proportional-integral-derivative (PID) controller. However, the acceptance and reputation of PID controllers in control systems is incomparable and supreme. PID control system can be implemented or applied in different modes (proportional only (P-mode), proportional and integral (PI mode), proportional and derivative (PD-mode) and proportional, integral and derivative (PID mode)) depending on process requirement (Lipták, 2002; Bharat et al., 2019). Several works have reported applications of typical PID controllers for different systems (Ramachandran et al., 2018; Elsrogy et al., 2013; Prasad et al., 2014; Wang, 2011).

PID controllers have been in use for many years in industries for process control applications. The use of PID controllers can be dated back to 1890s. Despite its long time of existence, PID controllers still remain the most popular controllers in both process and manufacturing industries today. Furthermore, research on PID controllers indicates that about ninety percent (90%) of process industries employ PID as controllers (Bansal et al., 2012; Abbasi and Naghavi, 2017). This popularity is as a result of their robustness, simplicity and ease of retuning control parameters (Åström and Hägglund, 1995; Abbasi and Naghavi, 2017). PID controller has been conventionally regarded as the best controller in the absence of fundamental process knowledge (Abbasi and Naghavi, 2017; Bennett, 1993). Despite these advantages of PID controllers, they are also faced with some shortcomings which include: unwanted speed overshoot and sluggish response as a result of unexpected variation in load torque and sensitivity to controller gains $K_I$ and $K_P$ as identified by Kushwah and Patra (2014). The success of PID controller bases on accuracy of system models and variables.

Controller tuning is a long standing and important aspect of feedback controllers. Hence, making the area of controller tuning a significant area of research both in academics and industries. The exploration and investigation of dynamic systems to create efficient, reliable and promising controllers are related to control engineering. After the development of PID control, numerous interests on tuning techniques that assure excellent performance of PID controllers sprang up. Furthermore, drawbacks of PID control strategy typically for nonlinear systems, include: challenges in choosing suitable and correct controller gains, and process termed tuning. The challenges commonly lie in choosing appropriate controller gains if set less than required, the control objective may never be achieved. While using excessively large controller gains may cause system instability, it is a viable option (Abbasi and Naghavi, 2017).

The first PID controller parameters tuning rules was introduced by Ziegler and Nichols (1942), several other tuning rules were proposed later. Though, some of these proposals focused on linear systems stabilization (Åström and Hägglund, 1995), which are not appropriate for nonlinear dynamic models. Conversely, some of these techniques encompass nonlinear systems (Lozano et al., 1999) with the goal of obtaining control variables that satisfy stability criteria. Conversely, the latter strategies do not assure definite response characteristics. Thus, one major difficulties and concern in control engineering area is appropriate controller parameters tuning. Controller variables are tuned to stabilize closed-loop control system and to achieve objectives which are related to stability, durability, performance tracking, performance measurement, noise reduction, disturbance rejection and robustness against environmental uncertainties.

Given a set of objectives, there are several types of tuning strategies for PID controller. Several authors and scholars presented different classifications of PID tuning strategies. Moradi (2003) and Johnson and Moradi (2005) classified PID tuning strategies relying on availability of a process model and model type. These classifications are grouped into four (4) subgroups namely:

• i.Model free methods: In these methods, there is no existence of a model or particular points of process identified. Hence, do not apply explicit identification important model points or parametric model as such.
• ii.Non-parametric model methods: These methods employ only a partial modeling information normally, steady state representation and critical frequency locations. The techniques are most appropriate for online application. They are typically used without needing extensive a priori plant information.
• iii.In-depth data methods: These techniques are midway amid parametric and non-parametric strategies. They use process data for tuning as used in subspace strategy or grey knowledge in fuzzy logic systems.
• iv.Parametric model methods: These methods require availability of model data, and can be obtained using standard offline or online identification process. They need a linear model of the system and its transfer function matrix/space model. These techniques are more appropriate for offline PID tuning. The parametric strategies can be classified into Non-Optimal Parametric, optimal (Restricted Structure control) and optimal (control signal matching) Methods.

A more comprehensive, detail discussion and application strategies of this classification can be obtained in Moradi (2003); Johnson and Moradi (2005).

Also, another classification of PID parameters tuning can be found in Bansal et al. (2012). These methods can be generally categorized into classical and computational techniques as presented in Bansal et al. (2012):

• i.Classical Techniques: These methods are centered on making some assumptions about plant model and required output. They try to extract some system features analytically or graphically, which are then utilized to pick controller settings. These methods are simple to use, computationally efficient, and can be used as a first step in parameter adjustment. However, the controller settings often give desired results directly, this is as a result of assumptions made. Hence, further tuning is required. Some of these classical tuning methods include Ziegler and Nichols, 1942, Ziegler and Nichols, 1993 method and Cohen (1953) method.
• ii.
  Computational or Optimization Techniques: These techniques involve the use of data modeling and optimization of a cost function strategies to tune PID parameters. These methods of controller parameters depend on a cost function which they attempt to minimize. There are six (6) generally used cost functions for PID controller parameters tuning. These commonly used cost functions are:

  • (a)
    Integral Absolute Error (IAE) defined as

    $$\text{IAE}=\underset{0}{\overset{\tau }{\int }}|e(t)|.$$ (1)
  • (b)
    Integral Square Error (ISE) expressed by

    $$\text{ISE}=\underset{0}{\overset{\tau }{\int }}|e(t){|}^2.$$ (2)
  • (c)
    Integral Time Absolute Error (ITAE) represented as

    $$\text{ITAE}=\underset{0}{\overset{\tau }{\int }}t|e(t)|.$$ (3)
  • (d)
    Integral Time Square Error (ITSE) denoted as

    $$\text{ITSE}=\underset{0}{\overset{\tau }{\int }}t|e(t){|}^2.$$ (4)
  • (e)
    Mean Square Error (MSE) defined as

    $$\text{MSE}=\frac{{\int }_0^{\tau }e{(t)}^2}{t}.$$ (5)
  • (f)
    Integral Error (IE) given as

    $$\text{IE}=\underset{0}{\overset{\tau }{\int }}e(t).$$ (6)

Some examples of computational or optimisation techniques are Artificial Immune System algorithm (Kim et al., 2002; Shatnawi and Quwaider, 2019; Quwaider and Shatnawi, 2020), Simulated annealing (Haber et al., 2007) and Particle Swarm Optimization (PSO) (Bassi et al., 2011). Computational strategies are employed for self tuning or automatic tuning of PID controller parameters. While a broader classification based on nature and usage can be classified in five (5) categories (the composition can be found in Rodríguez-Molina et al. (2020); Villarreal-Cervantes and Alvarez-Gallegos (2016); Ang et al. (2005)):

• i.Analytical methods: These methods involve analysis of closed loop model to attain stability. It involves computation of relationship between a given plant model and the set objective to determine appropriate PID parameters. Examples of these strategies may include Lyapunov (Li et al., 2009) and root locus approaches (Baker, 2011), where the latter is employed for linear systems and the former is used for nonlinear systems or frequency response. Other analytical methods include internal model control or lambda method.
• ii.Heuristic methods: Heuristic strategy of PID tuning is progressed with practical experience where controller variables are manually selected reliant on experimental knowledge of a professional designer who utilizes information of controlled variable estimates to set up correct variable-performance relationships. The heuristic method can also serve as a formula or a rule base for online tuning habitually with tradeoff in design goals or objectives. The most popular of these methods are the conventional Ziegler–Nichols and Cohen–Coon as depicted in (Rodríguez-Molina et al., 2020; Kumar et al., 2015; Ho et al., 1996).
• iii.Frequency response methods: These methods for PID parameter tuning are habitually offline and popular in the academic arena. The technique is based on the characteristics of target process or system such as loop shaping as reported in Ang et al. (2005). Natarajan and Gilbert (1997) and Wang et al. (1999) presented the use of frequency response for tuning PID controller parameters. Hagglund and Astrom presented adaptive techniques on frequency response to tune PID controller in Hägglund and Åström (1991).
• iv.Optimization methods: These strategies of PID controller tuning can be considered as an exceptional style of feedback optimal control system. PID variables are acquired on impromptu basis using an offline mathematical programming or numerical optimization technique for singular objective. The computation can also be implemented using computerized heuristics or evolutionary algorithms for multiple design objectives. The process involves stating a mathematical programming problem (MPP) for a targeted plant and employing optimization techniques to solve it. The main attribute of these methods is that control parameters are fixed and acquired by the solution of an offline numerical optimization method. Offline numerical optimization technique uses the derived state vector of plant by simulation or the real plant vectors. The obtained fixed control parameters are then added to a closed-loop system. This review fall to this class of tuning. Some recent optimization techniques for PID tuning may include; Firefly algorithm (dos Santos Coelho and Mariani, 2012), chaotic optimization (dos Santos Coelho, 2009), evolutionary multi-objective optimization (Nisi et al., 2019), PSO (Azar et al., 2019) and glow-worm optimization (Pilla et al., 2019).
• v.Adaptive tuning methods: The adaptive tuning strategies are online real-time tuning methods which involve the use of automated online mechanisms to tune PID controller parameters gains. The key feature of these techniques is that control parameters vary over preset time interval in the closed-loop system. Application of this technique can be found in (Pirabakaran and Becerra, 2001; Kim and Cho, 2005; Chang et al., 2003).

The complexity of plant dynamics depicts the effort or difficulty of tuning the controller parameters (Bernstein, 2002). Plant dynamics can be equipped with nonlinearity behavior, several tunable variables, and enormous numbers of input and output variables (Rodríguez-Molina et al., 2020). Furthermore, difficulties can be as a result of environmental and or operational uncertainties and perturbations. These features contribute to the difficulty of obtaining appropriate or suitable controller parameters geared towards achievement of set performance objectives. Additionally, existing applications require meeting numerous performance conditions/requirements at once, and are usually in conflict (Boyd et al., 1990). Some of these performance requirements may include: high performance accuracy, efficiency in energy consumption, low cost just to mention a few among others. Hence, tuning of controller parameters becomes a significant task since the level of satisfaction is determined by controller parameter settings.

Problems associated with several demand controller calibration can be handled as a multi-objective mathematical programming problem which can be solved using optimization or adaptive-optimization tuning approaches. This method permits the use of multi-objective optimization strategies to obtain a set of accurate controller settings with diverse trade-offs. These trade-offs are as a result of their compatibility with tuning performance conditions. As such operators, designers or decision makers need to select suitable configurations in accordance with the application demands depending on preferences.

The intricacy of multi-objective mathematical programming problems, otherwise termed as Multi-Objective Problem (MOP) with regards to controller parameters tuning function, has necessitated the employment of Computational Intelligence (CI) or soft computing approaches (Ruano et al., 2014). The implementation of CI for multi-objective optimization in control engineering is termed intelligent control (Rodríguez-Molina et al., 2020). Metaheuristic algorithms have been intensively employed to resolve several optimization problems in different fields of endeavor today. Some of these applications can be seen in Mathematics (Stojanović et al., 2017), robotics (Cruz-Bernal, 2013), agricultural engineering (Qi and Altinakar, 2011), structural design (Mirjalili and Lewis, 2016), greenhouse gas emission (Geem, 2011), medicine (Dey and Ashour, 2018), image processing (Alsmadi, 2018) and telecommunication (Kumar and Vidyarthi, 2016). The acceptance and popularity of metaheuristic algorithms can be attributed to their concurrent and quite simple implementation, their ability to handle large complex problems at a reduced computational cost, and their wide usage in different areas of endeavor (Gogna and Tayal, 2013; Talbi, 2009). These aforementioned qualities of metaheuristic algorithms make them appropriate substitutes for controller parameters tuning problem. Metaheuristic algorithms have a track record of outstanding performance and superiority in controller parameters tuning.

The diversity of various assortments of existing dynamic models and controller structures or architectures necessitates a wide range of distinct tuning MOP(s). These problems entail the application of diverse kinds of metaheuristics algorithms with specific search mechanisms to acquire the most appropriate or right controller settings. Thus, based on these assertions, this study seeks to give a comprehensive review on metaheuristic algorithms used for PID controller parameters tuning. Furthermore, in specific terms, the contribution of this work include:

• i.Comprehensive evolutionary background study of PID controller, its most important features, the evolution, developments and application strategies.
• ii.Detailed background of metaheuristic algorithms and their classification, application flowcharts and implementation processes.
• iii.Survey of PID controller tuning methods and their limitations.
• iv.Presented an elaborate study of several techniques applied to PID tuning and a phenomenal review of literatures on PID controller parameters tuning using metaheuristic algorithm over a period of 2000–2020.
• v.Exposed researchers to some powerful metaheuristic algorithms that are not yet explored in PID parameters tuning.
• vi.Identification of PID configuration problems.

The remainder of the paper is laid out as follows: Section 2 gives a succinct account of previous reviews, Section 3 is the background discussion, Section 4 describes the performance measures for evaluating the effectiveness of PID parameters tuning, Section 5 explains the metaheuristic algorithms that have found application in PID tuning, Section 6 is the comparative studies of existing tuning techniques used in PID tuning, Section 7 unveils open research problems in metaheuristic algorithms for PID tuning and future direction before concluding in Section 8.

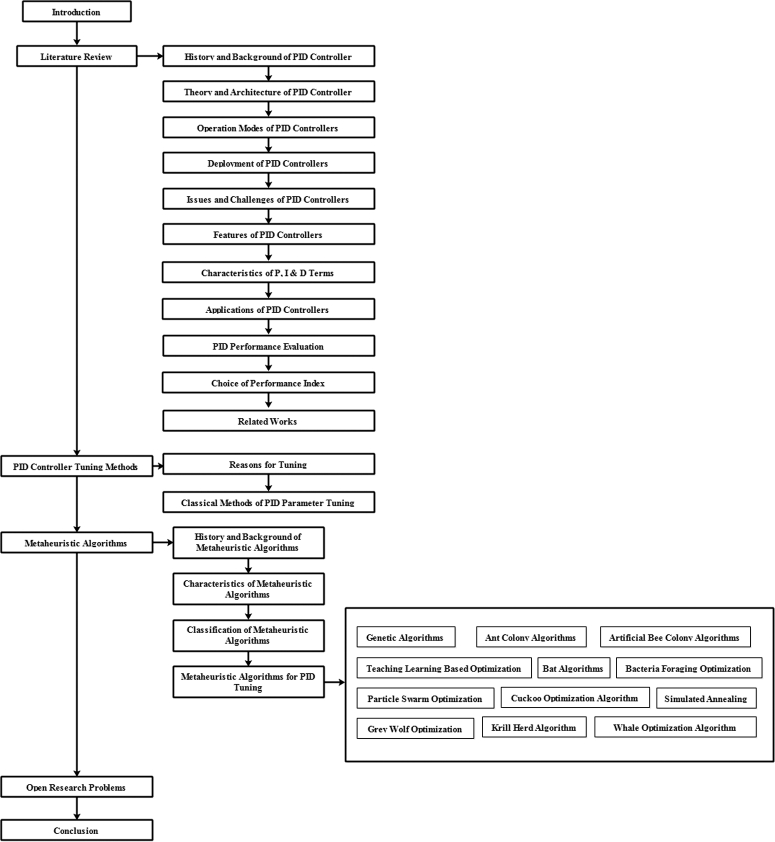
To increase readability of manuscript and also enhance understanding of readers, the structure of this paper is depicted in Fig. 1.

Figure 1.

Pictorial representation of paper structure.

2. Literature review

This section presents a brief history and background of PID controller, architecture (block diagram), equations, issues and application areas.

2.1. Theory and architecture of PID controller

The PID controller is so called due to its output summation of three variables: proportional, integral and derivative terms which are denoted as $K_P$, $K_I$ and $K_D$. These parameters $K_P$, $K_I$ and $K_D$ are reliant on error term e between input and output parameters. Correct tuning of these variables will enhance the dynamic reaction of a system, decrease overshoot, eradicate steady state error and increase stability of the process Saad et al. (2012). This relationship is described in Equation (7).

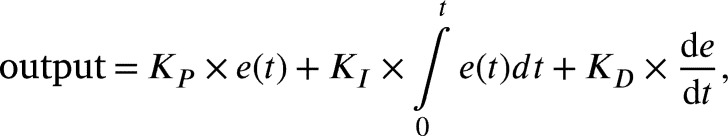(7)

where $K_P,K_I$ and $K_D$ are P, I and D parameters respectively. $K_I$ and $K_D$ can be represented by Equation (8).

$$K_I=K_P\times T_i,K_D=K_P\times \frac{1}{T_d},$$ (8)

where $T_i$ and $T_d$ are reset time and derivative time, respectively. The reset and derivative times are responsible for a systems response type. The controller variables P, I and D properties are briefly presented and discussed as follows:

• i.
  Proportional term (P): The proportional parameter facilitates the reaction as closed loop time constant declines with proportional parameter nonetheless ensures no alteration in system order as the output is just proportional to the input. The proportional parameter reduces nevertheless does not eradicate steady state error, or offset. The main task of the proportional element is to examine the magnitude of error and the PID controller response proportionally. In proportional term P is denoted by Equation (9) as

  $$P_{out}=K_{P}e,$$ (9)

  where

  $P_{out}$: proportional part of controller output,

  $K_P$: proportional gain,

  e: error term.

• ii.
  Integral term (I): This parameter removes offset as it rises the nature and order of the system by 1. This parameter also rises the system reaction speed, but at the cost of continued oscillations. The integral control attempts to mitigate the issues of the proportional control. It studies the error over time and adjust (increase) a small error with time. Reset rate, which is a time factor, is used to denote adjustment of integral control.

  $$I_{out}=\frac{1}{T_i}\int edt=K_I\int edt,$$ (10)

  where

  $I_{out}$: is the integral part of controller output,

  $T_i$: reset time or integral time,

  $K_I$: integral gain, e: error term.

• iii.
  Derivative term (D): This setting essentially reduces the system's oscillatory reaction. It has no effect on the offset, and has no effect on the system's nature and order. It investigates the error signal's rate of variation. A bigger system reaction to a rapid pace of change is caused by the derivative. The derivative term is adjusted with time. Too much of derivative term may cause an erratic control or overshoot. It is denoted by Equation (11).

  (11)

  where

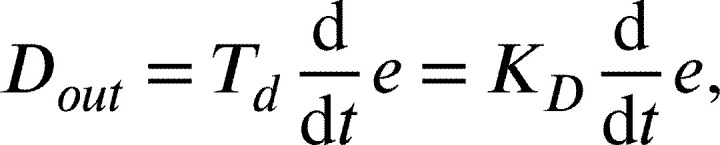
  $D_{out}$: is the derivative part of controller output,

  $T_d$: derivative time,

  $K_D$: derivative gain, e: error term.

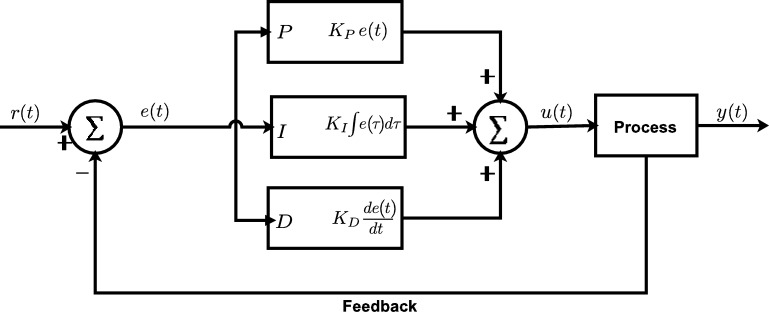
Fig. 2 depicts the standard configuration of a PID control system. When the set value $r(t)$ changes, the error term $e(t)$ between the set value and the actual output is recalculated. The $e(t)$ error signal or term is utilized to construct the $K_P$, $K_I$, and $K_D$ parameter actions, with the resulting signals weighted and summed to make the $u(t)$ control signal applied to the plant model. The output signal $y(t)$ is obtained as a result. The controller will receive this updated genuine signal, and the error signal will be recalculated. The plant receives the newly received control signal, $u(t)$. This process will run indefinitely until it encounters a steady-state mistake.

Figure 2.

Fundamental PID control structure.

The PID control technique is a typical approach to control that uses a proportional factor (P), integrative action (I), and differential action (D) to convert error signals into input signals. The error signal is calculated by comparing the states to their corresponding references (set points). To improve the speed of the system's response to its defect, the error signal is amplified with proportional gain $(K_P)$ and understood as current error term (Muliadi and Kusumoputro, 2018). The error signal is also integrated with the integral gain $(K_I)$ as the accumulation of the past error term and differentiated with the derivative gain $(K_D)$ as the prediction of future error term in parallel (Mange et al., 2015). These gains are fine-tuned using tuning methods based on a linear mathematical model of the system's dynamics. For systems with a modest amount of nonlinearity and perfect uncoupling between the modes of their dynamics, the PID gains can be simply modified.

2.2. Operation modes of PID controllers

The PID controller is a widely used industrial control structure with a common control loop feedback mechanism. PID controllers are the most generally used feedback controllers (Kushwah and Patra, 2014). It is worthy to note that majority of PID controllers are operated in either manual or automated state.

• i.Manual Mode: Here, the output of controller is manipulated by an experienced who manipulates the controller parameters by pushing buttons which will either increase or decrease the controller output.
• ii.Automatic Mode: Controller parameters can be attuned during operation by the use of algorithms.

When variations in modes and terms are observed, it is imperative to stop changing transients. Meanwhile, PID controllers are dynamic systems, hence essential to ascertain state of the scheme is accurate before changing modes of operation. In automatic state, PID algorithm yields a control variable which may be distinct from manually created variable. Consequently, it is essential for operator(s) to ascertain both control terms match during switching. This process is referred to as bumpless transfer. Details of switching from one mode to another can be found in Anthony and Ho (2020).

2.3. PID performance evaluation

The acceptance and wide use of PID controllers has led to an explosion in methods of tuning its parameters. In the past decades, numerous proposals on PID parameters tuning have been published. Some of these proposals are focused on stable processes (Cohen, 1953; Zhuang and Atherton, 1993), integrating and unstable processes Tan et al. (1999) and multivariate processes (Luyben, 1986). Based on this, a natural question emanated: how can PID setting from different strategies be compared? In other words, what is the performance of a controller to be examined or measured? To answer this question, several researchers and authors have proposed and presented different measures to address the issue of performance measurements.

In the past decades, minimum variance (Huang and Shah, 1999; Harris, 1989), as a standard, have been used as criteria in process control to assess closed loop performance (Tan et al., 2004). A comprehensive review and assessment on minimum variance can be seen in Qin (1998); Huang et al. (1997).

Although minimum variance is a highly prized metric of system performance, it pays little heed to traditional metrics like setpoint tracking and disturbance rejection. Furthermore, another vital and important aspect of system performance, robustness, is not directly addressed. Obviously, a benchmark that can be used for single- and/or multi-loop processes that are stable, integrating, or unstable would be quite useful. The benchmark should include both time domain and frequency domain robustness requirements (Tan et al., 2004).

Tan et al. (2004) further suggested the use of integral error as a good measure for single loop process and gain-phase margin for robustness measure. However, these methods are not suitable for multi-loop processes. The use of integral error and gain-phase measure with different tuning methods can be seen in Huang and Shah (1999).

The most commonly used performance indices or measures employed in control system applications are Integral Absolute Error (IAE) (Equation (1)), Integral Square Error (ISE) (Equation (2)), Integral Time Absolute Error (ITAE) (Equation (3)), Integral Time Square Error (ITSE) (Equation (4)), Mean Square Error (MSE) (Equation (5)) and Integral Error (Equation (6)). The application of ITAE for PID tuning can be seen in Martins (2005); da Silva et al. (2019). Jin et al. (2018) evaluated disturbance rejection performance for multiple objectives using IAE to estimate time response of process. Soni and Bhatt (2013) used ISE, IAE, IATE and MSE indices with BF-PSO to optimize PID controller. The performance and robustness trade-offs of PID control using IE and IAE can be seen in Garpinger et al. (2014). A comparison of ISE, IAE, ITAE and MSE using a heating tank was presented in Hussain et al. (2014).

2.4. Related works

There is still a rapid increase in the interest being shown by the academic and global research communities on PID parameter tuning. This segment presents related reviews that have been presented in literature on same subject area. This format is adopted to enhance articulation of issues (gaps) yet to be addressed or not fully addressed and to highlight differences with current review.

Bhawana and Neelu (2017) presented an appraisal of traditional as well as present methods employed for tuning PID controller parameters. The work presented different PID controller tuning procedures existing in literature and gave assessment of some methods. These methods can be typically grouped as classical methods and optimization methods. The methods appraised are classified into either traditional methods designed for tuning PID controller or heuristic methods of tuning. The methods proposed for tuning PID controller for processes like coupled tank system, trajectory tracking of Unmanned Aerial Vehicle (UAV), quadrotor stabilization are as well appraised.

Gholap et al. (2017) presented a review paper comparing different algorithms based on time domain analysis, acquired tuned parameters, iteration number and fitness function values. Two distinct process plants were considered based on ITAE and time domain analysis as objective functions. Variations in values of tuning parameters were considered using two systems and cost functions. Tuning parameters were obtained for both systems using Genetic Algorithm (GA), Particle Swarm Optimization (PSO), and Simulated Annealing (SA). Assessment for all the three algorithms was conducted with gotten tuning variables, time domain analysis, number of iterations, and value of cost functions. Closed loop responses of individual arrangements were plotted. Process with SA-PID variables settles down fast compared to PSO and GA, however its peak overshoot is higher. PSO-PID tuned system variables highest overshoot is least. PSO and SA out performed GA system with GA settling slowly with more overshoot and larger minimum cost function value. PSO algorithm converges fast as compared to SA, also cost minimization is better in PSO. Different algorithms may not yield the same results after implementing with same system and objective function.

In this paper (Srinivas et al., 2014), the results of the GA-PID controller for different tuning techniques employing three tank level process control systems were compared to the classic PID controller. Using computer simulation, this comparison analysis was performed for set point tracking of process plant procedures. Using Matlab, the optimal tuning variables of a PID controller were evaluated using six tuning methodologies (Z-N technique, C-C technique, ISE, IAE, IATE, and genetic algorithm centered PID methodology). The GA-PID controller produces a rapid reaction with less peak overshoot and integral square error, according to simulation results. Furthermore, this technique has a fine capacity to modify tuning variables for system dynamics variations. In conclusion, the GA-PID controller has been shown to be a reliable solution for controlling three tank levels. This method can also be used in a variety of nonlinear process control systems with long transportation lags.

Emmanuel and Inyiama (2015) conducted a survey on robot manipulator controller design strategies that can function optimally in harsh environs. PID controller tuning approaches like the conventional Ziegler Nichol's (ZN) software tool, fuzzy logic, GA, and Artificial Neural Network (ANN) approaches were studied. The study concluded that it is challenging to attain optimal performance using conventional and ZN technique. Fuzzy logic, GA and ANN approaches can be employed to attain anticipated optimal performance but they lack factors to calculate disturbance elimination settling time which aids to measure how fast the system can cancel or reject disturbance in harsh environments. Conversely, software tool scheme using PID tuner can be utilized to attain anticipated performance and good disturbance rejection settling time which satisfies the goal of design.

Fister et al. (2016) did a study on two reactive evolutionary algorithms (differential evolution and genetic algorithm), and four reactive, swarm intelligence-based algorithms (bat, hybrid bat, PSO and Cuckoo Search (CS)), were employed to tune PID controller in the comparative study. Only ten individuals and ten iterations (generations) were utilized in order to choose the most suitable optimization algorithm for fast tuning of controller parameters. The results were compared using statistical analysis and showed that PSO is the best option for such a task.

A survey on PSO and automated voltage regulators for synchronous generators was presented by Dixit and Pragati Joshi (2016). The generator is utilized to maintain electrical appliance control and stability. Automatic Voltage Regulators (AVR) employ a variety of ways. Diverse controllers are also utilized to improve robustness, overshoot, rise time, and voltage control, however the issue is with the AVR survey. According to several research paper analyses, assessment studies focusing on PID Controller are conducted to demonstrate rise time, overshoot, and undershoot.

Kim and Cho (2006) suggests a hybrid technique for adjusting a PID controller for an AVR that combines GAs and Bacterial Foraging (BF). The proposed method was first demonstrated using four test functions, and the algorithm's outcome was evaluated with a focus on mutation, crossover, step size variation, chemotactic steps, and bacteria life duration. Furthermore, the proposed algorithm was used to calibrate an AVR's PID controller. GA, PSO, GA-BF, and GA-PSO are among the algorithms compared.

Nagaraj et al. (2008) presents a survey on how PID controller variables are tuned for DC motor armature control. The performance of conventional procedures such as the continuous cycle approach and the ZN step response methodology was compared and analyzed with intelligent tuning strategies such as the GA, Evolutionary Programming (EP), and PSO. Tuning methods based on GA, EP, and PSO have demonstrated their superiority by achieving better results. They increased the performance indices and steady state characteristics.

Zulu and John (2014) reviewed some conventional control algorithms used on quadrotors in studies. Clearly, no single algorithm can provide the greatest of all essential features, as evidenced by the evaluation. It has been determined that achieving superior performance often demands hybrid control structures with the best combination of robustness, adaptability, optimality, simplicity, tracking ability, fast reaction, and disturbance rejection, among other things. However, such hybrid structures do not guarantee the optimal performance; consequently, for any control application, a compromise must be found as to which of the components is the most appropriate. The assessors are still undecided on which mathematical model will provide the best overall performance. PID, Linear Quadratic Regulator (LQR), Sliding mode, Backstepping, Feedback linearization, Adaptive, Robust, Optimal, L1, ${\text{H}}_{\infty }$, Fuzzy logic, and ANN have all been appraised after a brief description of the system. The article concludes with a recommendation to examine hybrid systems, which integrate advantages from many control paradigms.

Divya and Nirmalkumar (2018) in their paper titled “A Survey on Tuning of PID Controller for Industrial Process Using Soft Computing Techniques” presented a review of some soft computing methods for PID controller parameters tuning. The review considered five (5) soft computing techniques, namely Neural Networks (NN), EP, GA, PSO and Ant Colony Optimization (ACO) methods. The survey gave some basic highlights of selected algorithms and presented their flowcharts. Details of implementation of selected algorithms were not presented.

Bharat et al. (2019) presented a review of PID tuning method. The paper presented a survey on works related to PID controller tuning methods using fuzzy-logic and GA. Also, a comparison of conventional two methods (ZN and process reaction curve) and fuzzy-logic based tuning methods was presented. A brief review of tuning methods like Fuzzy Set-Point Weight (FSPW), GA, fuzzy logic, ZN, and PRC were presented.

A review on tuning techniques for PID controllers was presented in Bansal et al. (2012). The work presented a review on current and classical technique for PID tuning. The work gave a brief description of two main classifications of tuning strategies namely classical and computational or optimization techniques. On classical method, Ziegler and Nichols method, and Cohen Coon method were presented. Artificial Immune Systems (AIS), ACO, Bacteria Forage Technique (BFT), GA, Differential Evolution (DE), EP, ANN, SA, Support Vector Machine (SVM), PSO, Fuzzy logic, and Response Surface Method (RSM) were among the topics discussed. The work presented relevant equations, algorithms and flowcharts for every algorithm considered in the study. A good number of works implementing such algorithms for PID tuning was also presented.

Kushwah and Patra (2014) presented a review on tuning techniques using soft computing strategies. The study was focused on DC motor speed control using PID controller. The study gave a brief discussion on PID controller, its pictorial representations and parametric equations. The review was focused on GA, PSO, and fuzzy logic soft computing techniques for DC motor speed control. The paper only briefly highlighted on a few works that implemented the selected algorithms.

The study in Jain et al. (2012) titled “A Review of Soft Computing Techniques for PID Controller Tuning” presented a review of three soft computing algorithms (GA, ACO, and PSO) for tuning PID parameters. The study presented algorithms for each technique and also gave a little background information on the three algorithms chosen.

A review of how swarm intelligence computation algorithms can be used to tune PID controllers was presented in Ghosal et al. (2012). The study highlighted on different structures of PID controller and presented a survey on swam intelligence computation. The study further listed the advantages of intelligence, and also gave reviews on tuning PID parameters using ACO, PSO and Bacterial Foraging Optimization (BFOA). A comparative analysis of four (4) tuning methods (ZN, PSO, BFO and GA) using MATLAB was presented. Their analysis reported that BFOA gave a better result compared to others.

Despite the significance of metaheuristic algorithms in PID tuning, there is no comprehensive, complete and methodical review about their classification. Additionally, future problems and significant role of metaheuristic algorithms in PID tuning problem have not been itemized properly. In summary, reviewed papers have some shortcomings:

• i.Only a few literatures have been investigated.
• ii.Details of algorithms implementation are not explicitly defined.
• iii.Future studies and unanswered issues are not properly expressed.
• iv.Few qualitative and recent papers were cited.
• v.In some cases, only a few metaheuristic algorithms were explored.
• vi.Classification of studied techniques has not been adequately presented.
• vii.Advantages and disadvantages of selected works not clearly presented.

Further readings on metaheuristic algorithms reviews and taxonomies on other subject matters like: scheduling techniques in cloud computing (Kalra and Singh, 2015), vehicle routing problem and its variants (Elshaer and Awad, 2020), optimizing 3D well-path designs (Biswas et al., 2020), reactive power planning problem (Shaheen et al., 2018), optimization of Service-Level Agreement (SLA) violation costs for dynamic execution of cloud services (Kumar and Bawa, 2020), multi-objective virtual machine placement mechanisms in cloud computing (Donyagard Vahed et al., 2019), applications on PV cell parameter identification (Yang et al., 2020), solving grouping problems (Ramos-Figueroa et al., 2020) and hydropower energy optimization (Azad et al., 2020). A summary of related works is presented in Table 1.

Table 1.

Summary of previous related surveys.

S/No	References	No of study referenced	Focus of review	Number of algorithms reviewed	Taxonomy (classification)
1	Bhawana and Neelu (2017)	33	Classical and Optimisation techniques used for PID tuning	9	Yes
2	Gholap et al. (2017)	10	PID controller tuning parameters, time domain analysis, number of iterations, and value of cost functions using GA, PSO, and SA.	3	No
3	Srinivas et al. (2014)	16	Optimum tuning parameters of PID controller are estimated by six tuning methods (Z-N method, C-C method, ISE, IAE, IATE and GA based PID method) for three tank level process for using Matlab/Simulink	8
4	Emmanuel and Inyiama (2015)	32	PID controller tuning methods such as the manual, Ziegler Nichols, software tool, fuzzy logic, Genetic Algorithm (GA), and the Artificial Neural Network (ANN)
5	Fister et al. (2016)	32	PID controller tuning methods reactive using differential evolution, genetic algorithm, bat, hybrid bat, particle swarm optimization and cuckoo search	6	Yes
6	Dixit and Pragati Joshi (2016)	8	PID Controller tuning for Automatic Voltage Regulator using PSO and GA	2	No
7	Kim and Cho (2006)	29	PID controller of an AVR. using GA, PSO, GA-BF, GA-PSO	4	No
8	Nagaraj et al. (2008)	9	PID controller are tuned for controlling the armature controlled DC motor using Z-N (step response), Kappa-Tau Continuous cycling, EP, GA and PSO.	6	No
9	Zulu and John (2014)	34	PID control tuning for quadrotors using Linear Quadratic Regulator (LQR), Sliding mode, Backstepping, Feedback linearization, Adaptive, Robust, Optimal, L1, H∞, Fuzzy logic and Artificial neutral networks.	12	Yes
10	Divya and Nirmalkumar (2018)	13	Soft Computing Techniques for PID tuning using Neural Networks (NN), Evolutionary Programming (EP), Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO).	5	No
11	Bharat et al. (2019)	15	Techniques for PID tuning using Fuzzy Logic (FL), Genetic Algorithm (GA).	2	No
12	Bansal et al. (2012)	64	Review of tuning Techniques for PID parameters classification of tuning strategies using 14 methods (Z-N method, C-C method, AIS,ACO, BFO, DE, EP, ANN, SA, SVM, PSO, FL and RSM based PID method)	14	No
13	Kushwah and Patra (2014)	43	Speed control of DC motor using for PID controller using three tuning strategies GA, PSO, and fuzzy logic algorithms	14	No
14	Ghosal et al. (2012)	51	Swam intelligence computation for PID controller using four tuning strategies ZN, BFO, PSO, and GA	4	No

3. PID controller tuning methods

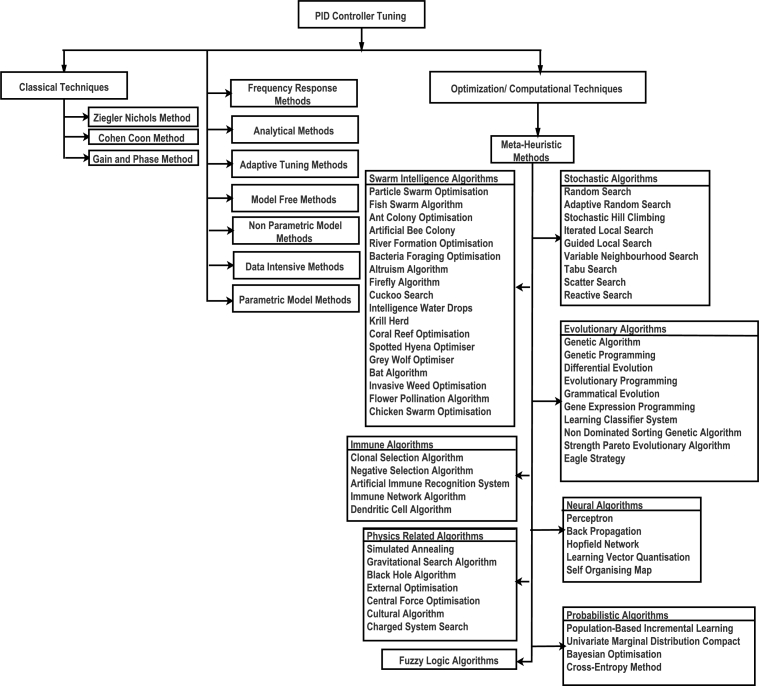
A summary of tuning methods for PID controller is depicted in Fig. 3.

Figure 3.

Summary of PID tuning methods.

3.1. Classical methods of PID parameters tuning

This class of tuning strategy attempts to derive controller configurations for common models. To compute the dynamics of these systems, step response of systems is obtained (Bansal et al., 2012). This response is characterized by diverse equations, which leads to development of different classical approaches.

Before tuning PID parameters, it is crucial to obtain configuration using traditional approaches since the gains of controllers rely on transfer function variables. Although traditional PID tuning approaches are broadly used, oftentimes their behaviors do not match the set desired goal or objective (Reis et al., 2016).

• i.Ziegler-Nichols tuning method: Ziegler and Nichols proposed the most fundamental acknowledged and popular tuning technique in 1942 (Åström and Hägglund, 2004). Ziegler and Nichols conducted multiple studies and proposed rules for calculating $K_P$, $K_I$, and $K_D$ values based on a plant's transient step reaction. They presented two methods: closed-loop and open-loop. Process basic features such as process gain $(K_P)$, process time constant $(Tp)$, and process dead time $(Lp)$ are obtained using the ZN tuning approach. Ziegler and Nichols suggested using the values of $K_P$, $T_I$ and $T_D$ for closed and open loops using different rules. The tables and equations can be seen in (Shahrokhi and Zomorrodi, 2013; Sorensen, 2007; Hahn, 2006).
• ii.Cohen-Coon tuning method: Cohen and Coon (Cohen, 1953) proposed a technique with PID controller parameters obtained through First Order Plus Time Delay (FOLPD) model. The key design condition is elimination of load turbulence. The controller parameter configuration is presented in (Cohen, 1953), while some application examples can be seen in Hambali et al. (2014); Azman et al. (2017). Regardless of a superior model, results of Cohen and Coon technique are not much superior than Ziegler Nichols approach.
• iii.Gain and Phase Method:Åström and Hägglund (1984) suggested a test that, in terms of ease of use in automatic loop tuners, was a significant improvement over the ZN test. They proposed replacing the variable proportional gain with a nonlinear function, with relay nonlinearity as the function.

  Åström and Hägglund (1984) proposed a gain and phase strategy for getting specific spots on the Nyquist curve to aid in determining controller pretuning parameters to overcome the Z-N technique's trail by error limitation. The tuning method is based on the ability to move the critical point on the process Nyquist curve to a specific location. On the Nyquist plot, Åström and Hägglund (1984) proposed that this point be situated at unity gain and a phase of ${\varphi }_m-180$, where ${\varphi }_m$ denotes the predicted phase margin and $A_m$ represents the desired gain margin. A control system's phase and gain margins are a measure of how close the system's polar plot is to the $(-1+j0)$ point.

There are other varieties or modifications of ZN tuning methods suggested by other researchers. Åström and Hägglund (2004) proposed an improved method of Ziegler and Nichols tuning with robust loop shaping strategy (McFarlane and Glover, 1992). Chien, Hrones, and Reswick (CHR) technique was created from original ZN Open Loop technique. It offers swiftest response without overshoot and also with 20% overshoot. This technique has capability for tuning the set point and disturbance. Details and application of CHR can be found in Sen et al. (2015). A comparison of several tuning strategies can be seen in Shahrokhi and Zomorrodi (2012).

4. Metaheuristic algorithms

Metaheuristic based strategies (Talbi, 2009) deals with problems by providing near optimal solutions within reasonable time. Due to its efficiency and effectiveness in solving vast and complicated issues, metaheuristics have exploded in popularity in recent years. Metaheuristics are a type of heuristic that performs better than simple heuristics. Meta implies “beyond” or “higher level”. Every metaheuristic algorithm employs a particular mix of local and global search. Different results are often realized through randomization. There is no standard or verifiable definition of heuristics and metaheuristics in the literature, regardless of whether metaheuristics are accepted. A number of academics and researchers utilize heuristics and metaheuristics interchangeably. Current developments, however, appear to apply to all stochastic algorithms that use randomization and global exploration as metaheuristics. This assessment will also adopt same convention.

4.1. Classification of metaheuristic algorithms

This section briefly explores and summarizes a comprehensive review of metaheuristic algorithms and their emergence. Metaheuristic algorithms can be categorized in several forms, depending on selected characteristics or features that distinguish them. Different authors and scholars classify metaheuristic algorithms considering different features or characteristics. The categorization could also be dependent or centered on objectives or goals of research.

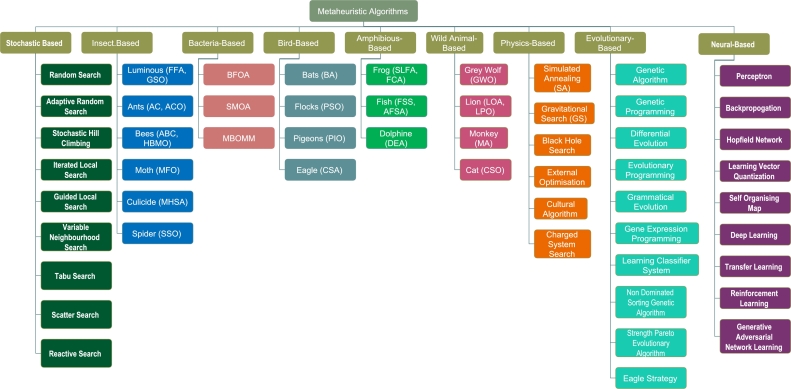
Examples of this category may be found in Blum and Roli (2003) which divides metaheuristics into two categories: nature-inspired and non-nature-inspired. Whether it is a population or a single point search, whether the objective function is dynamic or static, memory utilization or memory-less approaches algorithm and one or more neighborhood structures, Mirjalili and Lewis in Mirjalili and Lewis (2016) classified metaheuristic algorithms into: evolutionary, physics-based, swarm-based and human-based algorithms. A further classification based on population is presented in Beheshti and Shamsuddin (2013); Nojhan (2007). Another classification can be seen in Jackson et al. (2018), metaheuristics can be divided into two types: single-solution and multiple-solution problems.

Several other taxonomies of metaheuristic algorithms can be seen in Kumar and Bawa (2018); Shaheen et al. (2018); DrEO et al. (2007); Beheshti and Shamsuddin (2013); Gogna and Tayal (2013); Hussien et al. (2020); Kumar and Bawa (2020); Abdel-Basset et al. (2018). Fig. 4 presents a summary of meta-heuristics algorithms classification/taxonomy. Furthermore, it is worthy to note that metaheuristic algorithms can be conveniently implemented for global optimization (BoussaïD et al., 2013).

Figure 4.

Summary of metaheuristic classification based on operational procedure.

4.2. Metaheuristic algorithms for PID tuning

Though analytical classical PID tuning techniques are extensively used, occasionally, their performance does not match to the desired results (Ribeiro et al., 2017; Reis et al., 2016). When an optimization approach is used to tune controllers, it is feasible to achieve controller gains to reach as quick as possible responses with reduced overshoot, resulting in errors in the steady-state regime that are close to zero (Ribeiro et al., 2017). It is legal to say that these algorithms are heuristic techniques, which means that they produce acceptable results even if they are not the best. Many controller gains can be discovered in the same system by simply restarting the study.

According to recent literature, heuristic algorithm-based optimization strategies have emerged as a potent tool for solving a variety of control engineering difficulties (Latha et al., 2013). Metaheuristic algorithms are extensively utilized in process control due to their architectural simplicity, good optimization capability, and fast response. When compared to traditional optimization approaches, metaheuristic algorithms are more efficient in solving higher-dimensional optimization problems. They can easily adapt to existing classical controller design methodologies because of their resiliency. Metaheuristic algorithms, regardless of model order, can be used as a basic mechanism for creating traditional and improved structured controllers for a group of unstable operational models.

In order to produce effective engineering applications, controllers are mechanisms that are utilized to govern the performance of dynamic systems. The main purpose of controllers is to ensure that the feedback of a dynamic system is balanced. Despite the fact that controllers are designed to create stability in principle, the way the system stabilizes in practice is determined by a collection of variables. These variables can be adjusted to satisfy a variety of performance requirements, such as shortening the stabilization time (Lequin et al., 1999), permitting recovery of stability under unpredictability or perturbation (Freeman et al., 1998), smoothing transition to stability (Hang et al., 1991).

Controller tuning, or the precise synchronization of controller variables, is a difficult process that is highly reliant on application needs. The common controller tuning challenge entails identifying a collection of controller variables that stabilizes dynamic system reactivity under a defined performance condition that meets the specified parameters (performance criteria). Engineering applications are becoming increasingly difficult with time, in the sense that they demand dynamic systems to meet a variety of competing needs (i.e., one requirement cannot be satisfied completely devoid of harming the achievement of others). As a result, fine-tuning controllers for complex and dynamic systems become a challenging effort or requirement. A GA for controller tuning involves:

• i.Evaluate plant characteristics: This is done to obtain a model for simulation, such as the number of inputs and outputs, nature of performance (linear or nonlinear), and appropriate sort of job it accomplishes.
• ii.Choose controller structure: It is feasible to select an optimal controller configuration that successfully balances plant operation based on the derived plant model.
• iii.Identify tunable controller variables: It has a collection of variables that directly compromise the controller process and plant reaction, regardless of the specified controller configuration. The designer must determine which of these variables are used for tuning and which are set to a fixed value.
• iv.Establish needed performance goals: Designers must describe conflicting performance settings or criteria for controller tuning based on application requirements. These criteria are concerned with the minimization or maximization of quantitative indicators connected to system responsiveness, which officially define a multi-objective optimization issue.
• v.Analyze various sets of controller variables: Due to the difficulties of obtaining analytical answers for engineering optimization problems like controller tuning, various solutions (candidate group of controller variables) must be recommended and tested in simulation to determine their degree of compliance with the application requirements.
• vi.Choose most appropriate set of controller variables: A collection of solutions with outstanding (non-dominated) performance trade-offs is discovered using the degree of compliance of each solution. Then, from among the options, one is chosen to be implemented in the final application.

Automatic PID tuning algorithms have received lots of attention because of their importance in the industry. This has been particularly true in the last two decades (Fraga-Gonzalez et al., 2017). Some methods applied include metaheuristic techniques such as GA, PSO and SA, among others. A comprehensive list of some popular metaheuristic algorithms are presented in Table 2, Table 3. In the following paragraphs, an overview of some of these algorithms and applications for PID tuning will be presented.

Table 2.

Comprehensive list of some popular metaheuristic algorithms (1975–2014).

No.	Year of creation	Name of algorithm	Reference
1.	1975	Genetic Algorithm (GA).	Holland (1975)
2.	1977	Scatter Search (SS).	Cordón et al. (2006)
3.	1980	Genetic Programming.	Abraham et al. (2006)
4.	1983	Simulated Annealing (SA).	Kirkpatrick et al. (1983)
5.	1986	Tabu Search (TS).	Glover (1997)
6.	1986	Artificial Immune System (AIS).	Farmer et al. (1986)
7.	1989	Moscato presented Memetic Algorithm.	Qasem and Shamsuddin (2011)
8.	1992	Ant Colony Algorithm (ACO).	Dorigo et al. (1996)
9.	1993	Multi-Objective GA (MOGA).	Fonseca and Fleming (1993)
10.	1994	Reactive Search Optimization (RSO)	Battiti and Tecchiolli (1994)
11.	1995	Particle Swarm Optimization (PSO).	Eberhart and Kennedy (1995)
12.	1997	Differential Evolution (DE).	Storn and Price (1997)
13.	1997	Cross Entropy Method (CEM).	Rubinstein (1997)
14.	1999	Partial Optimization Metaheuristic Under Special Intensification Conditions (POPMUSIC)	Taillard and Voss (2002)
15.	2001	Harmony Search (HS).	Geem et al. (2001)
16.	2001	Bootstrap Algorithm (BA).	Hanseth and Aanestad (2003)
17.	2002	Evolution strategies	Beyer and Schwefel (2002)
18.	2004	Bees Optimization (BO).	Nakrani and Tovey (2004)
19.	2005	Glowworm Swarm Optimization (GSO).	Krishnanand and Ghose (2005)
20.	2005	Artificial Bee Colony Algorithm (ABC).	Karaboga (2005)
21.	2006	Invasive Weed Optimization (IWO)	Mehrabian and Lucas (2006)
22.	2006	Honey-bee Mating Optimization (HMO).	Haddad et al. (2006)
23.	2006	Cat swarm optimization	Chu et al. (2006)
24.	2007	Intelligent Water Drops (IWD).	Hosseini (2007)
25.	2007	Imperialist Competitive Algorithm (ICA).	Atashpaz-Gargari and Lucas (2007)
26.	2008	Water Drop Optimization (WDO)	Shah-Hosseini (2008)
27.	2007	Monkey Search (MS).	Mucherino and Seref (2007)
28.	2009	Firefly Algorithm (FA).	Yang (2009)
29.	2008	Plant Growth Optimization	Wang and Cheng (2008)
30.	2008	Biogeography - Based Optimization (BBO)	Simon (2008)
31.	2009	League Championship Algorithm (LCA).	Kashan (2009)
32.	2009	Gravitational Search Algorithm (GSA)	Rashedi et al. (2009)
33.	2009	Cuckoo Search (CS).	Yang and Deb (2009)
34.	2010	Bat Algorithm (BA).	Yang (2010)
35.	2010	Fireworks algorithm	Tan and Zhu (2010)
36.	2010	Chemical Reaction Algorithm	Ramaswamy and Sbalzarini (2010)
37.	2011	Galaxy-based Search Algorithm (GbSA).	Shah-Hosseini (2011)
38	2011	Spiral Optimization (SO).	Tamura and Yasuda (2011)
39.	2011	Teaching-Learning-Based Optimization (TLBO) Algorithm.	Rao et al. (2011)
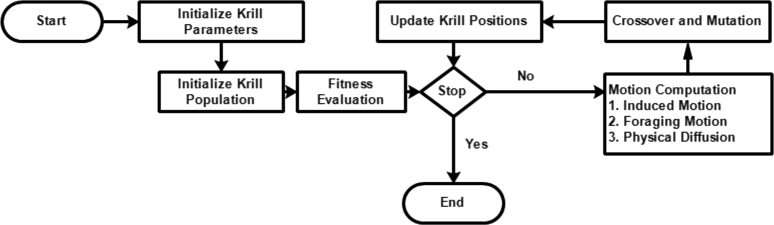
40.	2012	Krill Herd (KH) Algorithm.	Gandomi and Alavi (2012)
41.	2012	Flower Pollination Algorithm (FPA)	Yang (2012b)
42.	2012	Differential Search Algorithm (DSA).	Civicioglu (2012)
43.	2013	Firefly Algorithm (FA) with chaos	Gandomi et al. (2013)
44.	2014	Colliding Bodies Optimization (CBO)	Kaveh and Mahdavi (2014)
45.	2014	Animal Migration Optimization	Li et al. (2014c)
46.	2014	Centripetal Accelerated Particle Swarm Optimization (CAPSO)	Beheshti and Shamsuddin (2014)
47.	2014	Grey Wolf optimization (GWO)	Mirjalili et al. (2014)
48.	2014	Bumble Bees Mating Optimization	Marinakis and Marinaki (2014)
49.	2014	Crisscross Optimization Algorithm (COA)	Meng et al. (2014)

Table 3.

Comprehensive list of some popular metaheuristic algorithms (2015–2020).

No.	Year of creation	Name of algorithm	Reference
50.	2015	Water Wave Optimization	Zheng (2015)
51.	2015	Ions Motion Algorithm	Javidy et al. (2015)
52.	2015	Social Spider Algorithm (SSA)	James and Li (2015)
53.	2015	Bull Optimization Algorithm	FINDIK (2015)
54.	2015	Elephant Herding Optimization	Wang et al. (2015)
55.	2016	Jaya Algorithm	Rao (2016)
56.	2016	Raven Roosting Optimization Algorithm	Brabazon et al. (2016)
57.	2016	FIFA World Cup Competitions Algorithm	Razmjooy et al. (2016)
58.	2016	Spider Monkey Optimization (SMO)	Al-Azza et al. (2016)
59.	2017	Smart Structured Algorithm (SSA)	Salmani and Eshghi (2017)
60.	2017	Opposition-Based Water Wave Optimization	Wu et al. (2017)
61.	2017	Primal-Dual Asynchronous Particle Swarm Optimization (pdAPSO)	Dada et al. (2017)
62.	2018	Primal-Dual Particle Swarm Optimization (pdPSO)	Dada and Ramlan (2018)
63.	2018	Farm Fertility.	Shayanfar and Gharehchopogh (2018)
64.	2018	Coyote Optimization Algorithm (COA).	Pierezan and Coelho (2018)
65.	2019	Wolf Pack Search and Local Search (WPS-LS).	Dong et al. (2019)
66.	2019	Chaotic Dolphin Swarm Algorithm (CDSA)	Qiao and Yang (2019)
67.	2019	Emperor Penguins Colony (EPC).	Harifi et al. (2019)
68.	2019	Pathfinder Algorithm (PFA)	Yapici and Cetinkaya (2019)
69.	2019	Squirrel Search Algorithm (SSA)	Jain et al. (2019)
70.	2019	Algorithm of the Innovative Gunner (AIG).	Pijarski and Kacejko (2019)
71.	2020	Butterfly Optimization Algorithm (BOA).	Arora and Singh (2019)
72.	2020	Levy Flight Distribution (LFD).	Houssein et al. (2020)
73.	2020	Shuffled Shepherd Optimization Algorithm (SSOA).	Kaveh and Zaerreza (2020)

4.3. Genetic algorithms

Genetic Algorithms are search and optimization approaches motivated by two biological philosophies termed as procedure of natural selection and mechanism of natural genetics (Krishnakumar and Goldberg, 1992). GA (Sreekanth and Hari, 2016; Man et al., 1996) is a stochastic global search approach that mimics the natural evolution process or procedure. GA is a class of probabilistic optimization techniques that uses natural selection and genetic inheritance to solve problems. GA avoids local minima and converging to suboptimal solutions by starting at multiple distinct points and searching in parallel (Wang et al., 2003; Skogestad, 2001). As a result, GA has been shown to be effective in locating high performance space in complicated domains while avoiding the issues associated with high dimensionality that other approaches, such as gradient decent techniques that rely on derivative information, may encounter (Goldenberg, 1989).

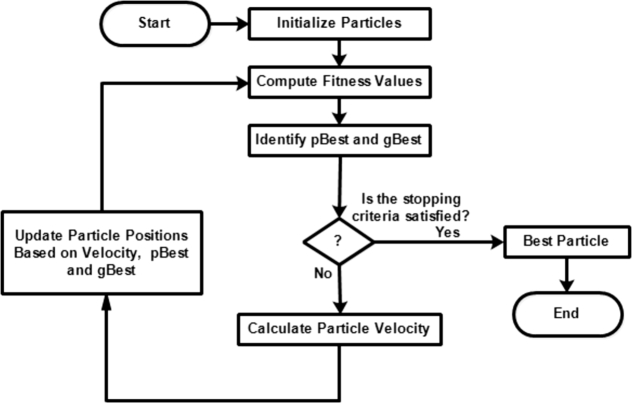
The stages of GA implementation are summarized in a flowchart as shown in Fig. 5. Details of GA implementation for PID tuning can be seen in Meena and Devanshu (2017).

Figure 5.

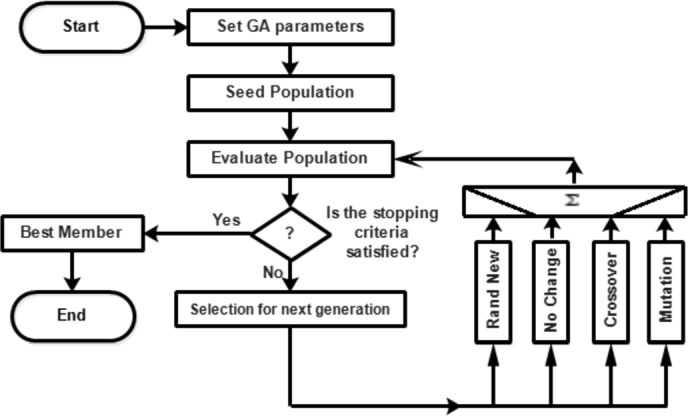
Genetic algorithm process flowchart.

4.3.1. Genetic algorithm for PID tuning

Currently, GA has been getting a good deal of attention and further studies have been done to research its implementation. Implementation in Control Engineering has advanced greatly. Despite the fact that performance, system stability, static and dynamic index, and system robustness must all be considered while designing a control system, PID parameters have been fine-tuned using GAs for various processes or plants. El-Deen et al. (2015) and Joseph and Emmanuel (2018) discussed the best way to tune PID settings for DC motor speed control. The GA controlled PID controller is designed for synchronous generators to promote damping and maintain power system stability, as presented in Mohammed et al. (2014). GA based design of PID controller for cascade control process is presented in Patil and Lakhekar (2017). An investigation on applicability of genetic algorithms for automatic tuning of PID controller parameters is presented in Amaral et al. (2018).

4.4. Ant colony optimization

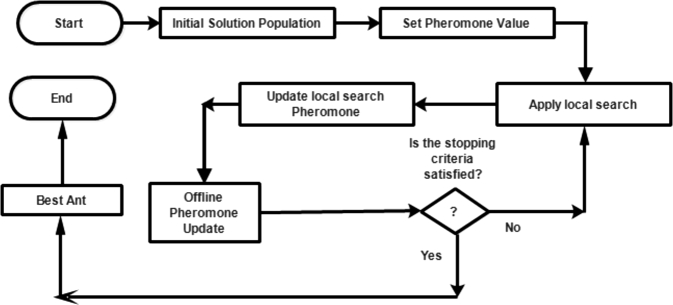
The ant colony optimization (ACO) algorithm is a distinct method inspired by insect swarm behavior and was designed for combinatorial issues at first. ACO is a stochastic based metaheuristic method for solving combinatorial optimization issues that employs artificial ants. ACO's goal is to find shorter routes from their nests to food sources. Ants leave behind a chemical compound called a pheromone that allows them to communicate with other ants. When an ant moves, it leaves a consistent amount of pheromone behind that other ants can detect. Every ant travels in its own unique way, but when it comes across a pheromone trail, it must decide whether or not to follow it. If one ant follows the trail, its own pheromone strengthens it, and an increase in pheromone enhances the likelihood that the next ant will follow it. As a result, the more ants that go along a path, the more appealing it becomes to succeeding ants. In addition, an ant who takes a shorter route to a food source will return to the nest sooner.

Dorigo suggested the fundamental ant structure, an earlier version of ACO, in his PhD thesis in 1992. (Dorigo, 1992). Dorigo devised a difficult optimization algorithm based on both simple and complex foraging ant features, which sparked widespread interest in the 1990s and beyond. Dorigo and others introduced a number of alterations and hybrids. Offline pheromone updates and pheromone evaporation were demonstrated in particular, which led to more widespread of ACO in 1999 (Cooper and Smeresky, 2020; Dorigo et al., 2006). In Adubi and Misra (2014), an overview of the many types of ACO algorithms, their applications, and a comparative study of a few selected versions are presented. The navigation of ant is represented by the following probability Equation (12) in Sundareswaran and Nayak (2012):

$$P_j^{(k)}=\frac{{\tau }_j^{(k)}}{\sum _{j=1}^n{\tau }_j^{(k)}}.$$ (12)

A high level algorithmic concept of ACO is presented in Fig. 6.

Figure 6.

Ant colony optimization search algorithm flowchart.

4.4.1. ACO for PID tuning

The parameters of a PID controller for DC motor of a robotic arm was tuned using ACO in Sandoval et al. (2015). The findings were compared to typical tuning techniques, and ACO-PID performed better than ZN tuned PID. As demonstrated in Priyambodo et al. (2015), a PID controller is utilized for quadrotor stabilization utilizing the ACO method. An application of optimization method based on artificial ants colonies (ACO) for the synthesis of an optimal PID regulator for human heart control is presented in Aabid et al. (2017). Load Frequency Control (LFC) of a single area re-heat thermal power system is one of the other PID tuning applications that uses ACO (Kaliannan et al., 2016), Autonomous Underwater Vehicle (AUV) control system (Herlambang et al., 2019), Single Machine Infinite Bus control (Yunus and Djalal, 2019), position control operation of a DC motor (Şimşek et al., 2019) and multi objective ACO for PID can be found in Chiha et al. (2012).

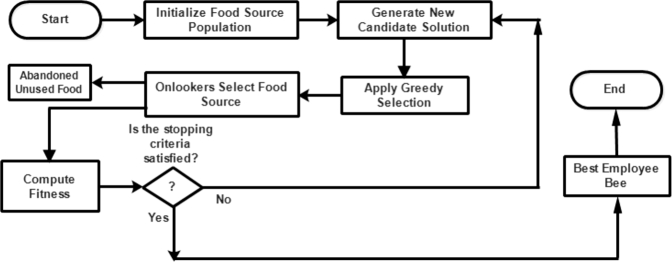
4.5. Artificial bee colony optimization

Karaboga proposed the Artificial Bee Colony (ABC) metaheuristic optimization technique in 2005. Honey bees' clever foraging habit served as inspiration. The method is based on the model for honey bee colony foraging behavior presented by Karaboga (2005). Working and unemployed foraging bees, as well as food sources, are the three main components of the concept. The employed and unemployed foraging bees in the first two components look for ample food sources close to their hive, which is the third component. Forager recruitment to rich food sources, which results in positive feedback, and forager desertion of low food sources, which results in negative feedback, are two fundamental behaviors required for self-organization and collective intelligence, according to the concept. A comprehensive discussion and application strategy of ABC can be seen in Karaboga (2010).

The ABC optimization algorithm, like the ant colony optimization algorithm, was created to solve a combinatorial problem in which several solutions can be discretized into an array of building blocks that can be rearranged and mutated to find the best answer. The ABC approach was also utilized to optimize the trajectory (Murrieta-Mendoza et al., 2018), parameter optimization (Zhong et al., 2014; Ding et al., 2015), and remote sensing applications (Jayanth et al., 2015; Fu et al., 2020). Applications, overview and relevant equations can be seen in Xu et al. (2013); Kumar et al. (2017); Abu-Mouti and El-Hawary (2012). An illustration of ABC application flowchart is presented in Fig. 7.

Figure 7.

Phases of artificial bee colony algorithm flowchart.

4.5.1. ABC for PID tuning

The ABC method outperformed earlier population-based algorithms in numerical tests, with the extra bonus of fewer control settings (Liao et al., 2014). Apart from the usual population-based control parameters like population size or colony size (SN) and maximum generation number or maximum cycle number, the ABC algorithm's basic version only has one control parameter called limit (MCN). Because of its simplicity and ease of implementation, the ABC technique has sparked a lot of attention, and it has been utilized to solve a variety of real optimization problems. One of these practical challenges is the setting of PID controller parameters.

ABC is used to tune PID settings to perfection. Some benchmark functions are used to test the algorithm. For the computation of PID parameters, the test functions were used. On the basis of overshoot, settling time, and minimal error, the performance is compared to that of other approaches (Abachizadeh et al., 2010). ABC algorithm was proposed in El-Telbany (2013) for tuning the regulation parameters of PID controller for DC motor. The optimum parameters of PID controller were obtained using ABC algorithm for higher order oscillatory systems in Bagis and Senberber (2017). Other plants controlled using PID controllers and tuned by ABC algorithm include: fractional order systems (Senberber and Bagis, 2017), hub motion and end point vibration suppression of double-link flexible robotic manipulator (Annisa et al., 2018), bench scaled nonlinear dynamical system (NLDS) (Valluru and Singh, 2017) and single phase inverter (Zhi, 2019).

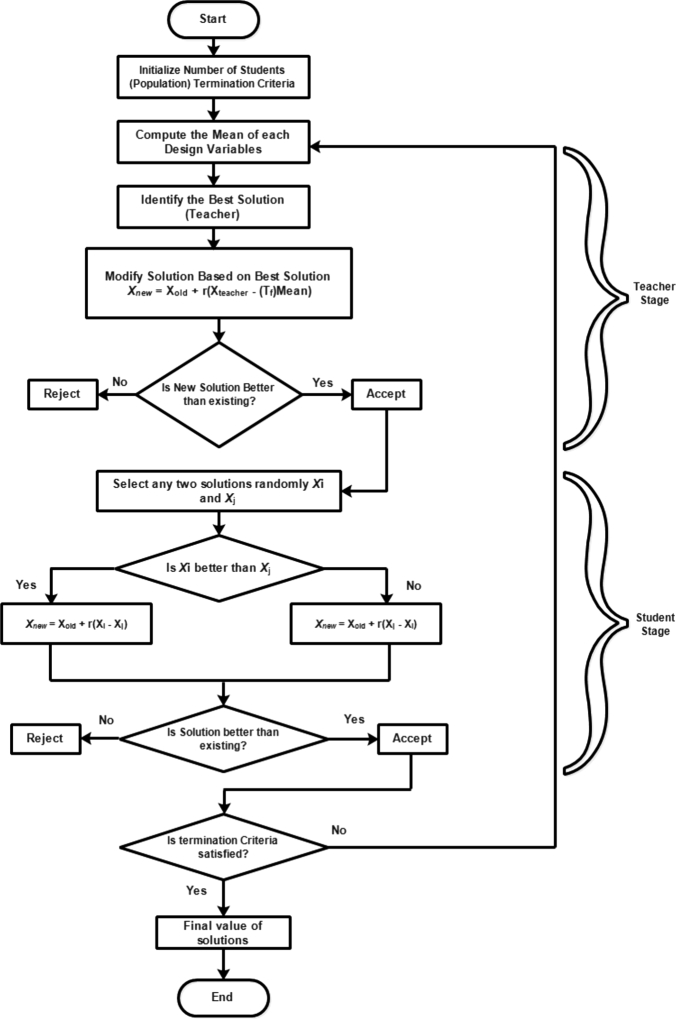
4.6. Teaching learning based optimization

This technique was suggested by Rao et al. (2012) and Rao and Kalyankar (2013) to find the worldwide solution to mechanical design difficulties using large-scale non-linear optimization problems TLBO (Teaching-Learning-Based Optimization) is a population-based metaheuristic search algorithm that mimics a typical class's teaching and learning methods Rao et al. (2012). A group of students is called a solution in TLBO, and the fitness of solutions is called results or grades. The TLBO algorithm adjusts each learner's or student's grade in class by learning from the teacher and learning from student engagement.

The algorithm procedure is divided into two stages or actions: the instructor stage and the learner stage. In the teacher stage, the instructor is seen as the best solution in the entire group, and the teacher shares his or her knowledge with the students in order to improve the class's mean outcome. The equations and details of implementation can be seen in Rao et al. (2012). The application flowchart for TLBO is presented in Fig. 8.

Figure 8.

Descriptive flow chart for Teaching–Learning-Based Optimization (TLBO).

4.6.1. TLBO for PID tuning

TLBO has gained a lot of attention, and has been adjusted to capture limited data due to its appealing properties such as simple concept, lack of exact algorithm variables, simple implementation, and fast convergence (Yu et al., 2016b), multiobjective (Patel and Savsani, 2016; Rao and Patel, 2014), large-scale (Biswas et al., 2012), and dynamic optimization problems (Chen et al., 2018a). TLBO has also been effectively applied to a variety of scientific and engineering sectors (Chen et al., 2018b).

While in the case of PID parameter tuning, TLBO has been employed to adjust the variables of PID for different processes. Some of these include: automatic voltage regulator (AVR) processes, Automatic Generation Control (AGC) in power systems (Sahu et al., 2016), automatic voltage regulator (AVR) (Chatterjee and Mukherjee, 2016; Priyambada et al., 2014), improve performance of the magnetic levitation system (Yadav et al., 2018).

With the help of TLBO, a fuzzy PID controller is proposed for automatic generation control (AGC) of a thermal system (Sahu et al., 2015). There are two degrees of freedom: one and two. Using a teaching learning based approach, a PID controller design is used on an AVR device (Rajinikanth and Satapathy, 2015). The fuzzy-PID controller was proposed by Sahu et al. (2015) for the AGC of a two unequal area interconnected thermal system. For the first time in this sector, the TLBO technique is employed to obtain parameters for the proposed fuzzy-PID controller. The design challenge is formulated as an optimization problem, and the fuzzy-PID controller's parameters are optimized via TLBO. When the proposed method's results are compared to those of several recently published approaches, such as the Lozi Map-based Chaotic Optimization Algorithm (LCOA), GA, Pattern Search (PS), and Simulated Algorithm (SA) based PID controller, the proposed method clearly wins for the same system and objective function. The TLBO optimized fuzzy-PID controller has superior dynamic performance in terms of settling time, frequency overshoot and undershoot, and tie-line power deviation when compared to LCOA, GA, PS, and SA based PID controllers.

4.7. Bat algorithm (BA)

The Bat Algorithm (BA) is a metaheuristic algorithm derived from natural bats' sound waves activity to find prey and differentiate between various kinds of insects even in dark environment (Yang, 2010). BA was recently introduced by Yang (2010), which was influenced by the sonar of microbats. Each bat in the original population updates its position in a correlated fashion using echolocation. Bat echolocation uses a sequence of powerful ultra-sound pulses to generate echoes, which are then received with latencies and different sound frequencies, qualifying bats to identify the exact prey. In natural world, echolocation can last only a few thousandths of a second (up to around 8–10 ms) and also have a varying amplitude in the range of 25–150 kHz, which corresponds to air wavelengths of 2–14 mm (Gandomi and Yang, 2014).

Microbats typically use sound waves to locate prey. Microbats transmit small signals when traveling; nonetheless, when a possible prey is nearby, their transmitted pulse rates increase and the frequency is tuned up. The addition of frequency, also known as frequency tuning, in combination with the speed of pulse emission will reduce the wavelength of echolocations and hence improve detection precision (Gandomi and Yang, 2014). An application illustration flowchart for BA is presented in Fig. 9.

Figure 9.

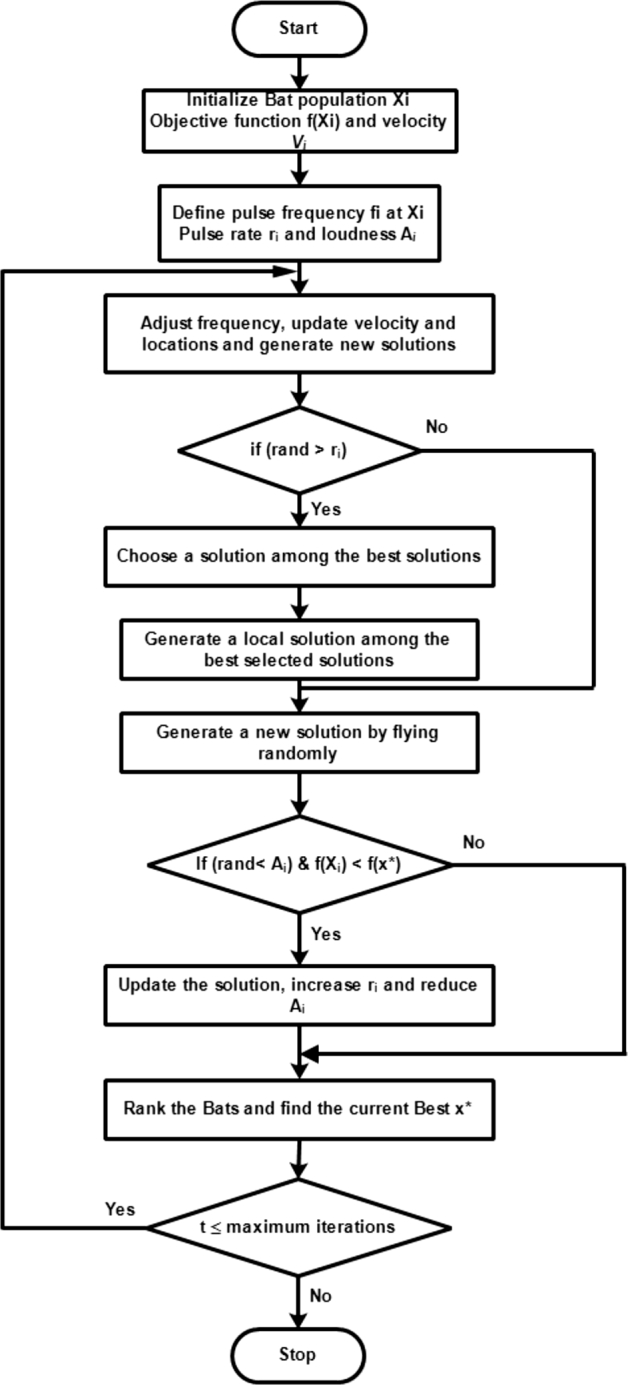
Generic flowchart for Bat algorithm.

Further details, readings or consultation on BAs can be seen in Yang (2012a); Chaib et al. (2017); Gandomi and Yang (2014); Yang and Gandomi (2012); Singh et al. (2015); Al-Betar et al. (2018).

4.7.1. BAT for PID tuning

BA was used to solve realistic real-world problems because it is a suitable metaheuristic algorithm with unique ability to handle hard optimization problems. A few of these classifications are presented in Jayabarathi et al. (2018): structural Optimization, classification and feature selection, electrical power systems, aerospace engineering, petroleum engineering, and nuclear engineering. Furthermore, BA has been implemented in control engineering where PID tuning is an aspect.

The BA for optimizing PID parameters has been used in a variety of process plants with encouraging results. In Katal et al. (2014), BA was utilized to fine-tune the PID controller parameters for a connected tank liquid level control system, which is widely used in the mineral oil, food manufacturing, and water purification companies. BA in Kotteeswaran and Sivakumar (2013) was used to fine-tune the settings of a centrally controlled PI controller for a coal gas turbine, which is a non-linear multidimensional process with complex relationships across control loops. Singh et al. (2015) used BA for tuning the parameters of PID controller of a servo motor. Other implementations of BA for PID tuning include, speed control of brushless direct current drive (Premkumar and Manikandan, 2016), bio-inspired robot manipulator (Rahmani et al., 2016) and control of microelectromechanical systems (MEMS) gyroscopes (Rahmani et al., 2018).

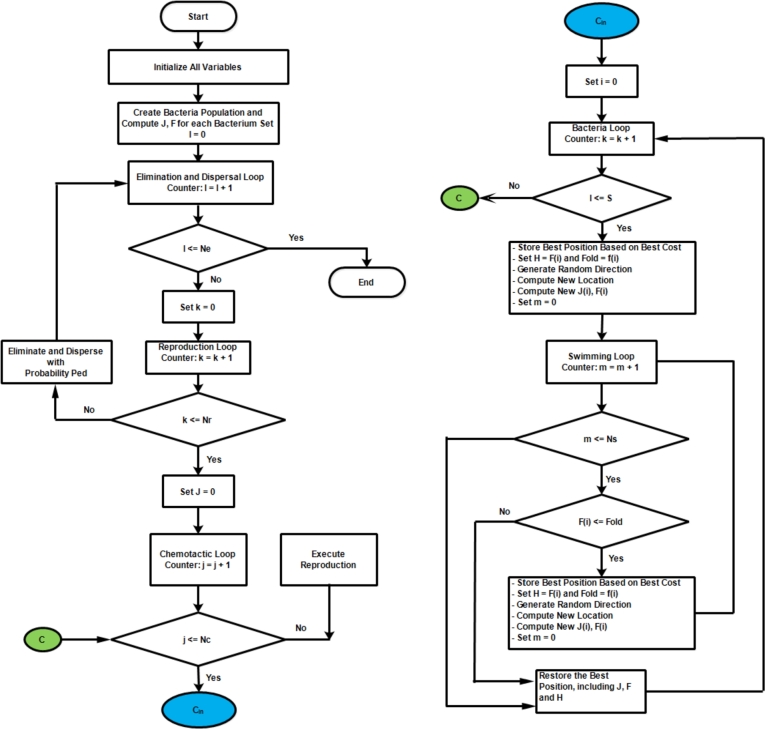
4.8. Bacterial foraging optimization (BFO)

Passino (2002) presented the Bacteria Foraging Optimization (BFO) algorithm, which is a member of the family of nature-inspired optimization algorithms. BFO imitates a swarm of Escherichia coli bacteria's searching strategy. Bacteria look for nourishment in a way that maximizes the amount of energy they get per unit of time. By sending signals, each bacterium communicates with each other. After comparing various prior factors, a bacterium makes foraging decisions. Chemotaxis is the mechanism by which a bacterium moves by taking little steps while looking for nutrition, and a key principle of BFO is to simulate chemotactic motion of artificial bacteria in the problem search space.

Specifics on these processes, as well as the BFO implementation steps, can be found in Das et al. (2009); Datta and Nandakumar (2017); Jhankal and Adhyaru (2011). A flowchart showing the flow of BFO algorithm is depicted in Fig. 10. The BFO variables to be defined for applications include: number of bacteria S, swimming length Nn, number of chemotaxis steps Nc, number of reproduction steps Nr, number of elimination and dispersal events Ne, and the probability of elimination/dispersal Ped. Step size of swimming C for bacteria is a vector $M\times 1$ corresponding to vector θ. Initial values of $\theta (i),i=1,2,\dots ,S$ which are boundaries of parameters randomly created. The functions $J(i)$ and $F(i)$ are defined to evaluate cost and fitness of $i^{th}$ bacterium respectively. Details of application flow diagram can be seen in Huynh et al. (2020).

Figure 10.

Generic flow diagram for BFO algorithm.

For further readings, variants and applications of BFO can be seen in Agrawal et al. (2012); Niu et al. (2010); Tang and Wu (2009); Rani and Kumar (2015).

BFO has piqued the interest of scholars from several disciplines of study since its debut, owing to its biological purpose and beautiful shape. Researchers are attempting to combine BFO with a variety of other algorithms in order to investigate both its local and global search features. It has previously been used to solve a variety of real-world problems, and has been found to be effective over a wide range of GA and PSO types (Jhankal and Adhyaru, 2011).

4.8.1. BFO for PID tuning

The BFO algorithm is a new swarm intelligence system inspired by the foraging behavior of Escherichia coli (E.coli) in human intestines. After significant research over the previous few years, BFO has demonstrated good performance in a range of application domains (Niu et al., 2010). Lately, BFO has gotten a lot of interest, and it offers a lot of promising industrial applications and information processing. Few models that simulate bacterial foraging behavior have been devised and used to solve actual challenges (Bayoumi and Salem, 2012). The BFO method, like other SI algorithms, has been used to solve problems in a wide range of fields. Communication systems, communications engineering, intelligent control engineering systems (Niu et al., 2010) are some of the application sectors in which PID is used.

BFO has been employed for suitable tuning of PID controller settings to overcome difficulties that numerous industrial machinery are regularly troubled with, such as high order and uncertainties. The BF-PID controller was optimized and tuned using BFO in Niu et al. (2006). BF-PID has a faster settling time, little or no overshoot, and greater resilience than GA-PID. Compared with GA-PID, BF-PID have a quicker settling time, little or without overshoot and higher robustness. Similarly, dos Santos Coelho and da Costa Silveira (2006) provided an improved BFO for PID optimization in a robotic manipulator system. To adjust the C constant in basic BFO, the new technique was tested with a chemotactic step parameter (C) variable speed based on Uniform, Gaussian, and Cauchy probability distributions. The BFO approach was used in Ali and Majhi (2006) to improve PID parameters by reducing the integral of time error squared (ISTE) condition. Also, addressing the challenge of PID controller tuning, Korani et al. (2009) coupled bacteria foraging actions with PSO. Rajinikanth and Latha have suggested utilizing BFO to tune PID controller parameters for unstable process models in Rajinikanth and Latha (2012). The results demonstrate that utilizing the bacterium foraging algorithm to tune PID parameters is a viable option.

Monitoring a moving target along an unpredictable route by a mobile robot is another application of BFO for tuning PID controllers (Benbouabdallah and Zhu, 2013; Huynh et al., 2020), speed controller of a permanent magnet synchronous motor (Agarwal et al., 2017), position control of Direct Current (DC) servo motor (Jasim, 2018) and tuning PID parameters for Multi-variable Input and Multi-variable Output (MIMO) systems (Sivakumar et al., 2016).

4.9. Particle swarm optimization (PSO)

Kennedy and Eberhart (1995) proposed the PSO algorithm, which is a metaheuristic algorithm based on the principle of swarm intelligence and capable of solving complicated mathematics problems encountered in engineering (de Almeida and Leite, 2019). The social activities of birds, fish shoals, and even humans inspired the PSO algorithm (Ribeiro et al., 2017). In PSO, it is assumed that each individual has their own experience and can assess its quality. Because the algorithm is based on social behavior, each individual is aware of what their neighbors are going through.

The PSO algorithm is based on these two perspectives (Ribeiro et al., 2017). The individual's actions are influenced by its past performance and its surroundings. A culture's adjustment process can be divided into three categories: assess, compare, and mimic. Every individual have the ability to assess their surroundings and predict their behavior, as well as compare their outcomes to those of their peers. It can detect flaws and advantages in each action and duplicate the important events produced by their neighbors. It indicates that mental talents are acquired and maintained (Ribeiro et al., 2017).

Detail information about the evaluation of the implementation can be found in de Almeida and Leite (2019); Kennedy and Eberhart (1995). The flow diagram for basic PSO algorithm is shown in Fig. 11.

Figure 11.

Flow diagram for basic PSO algorithm.

4.9.1. PSO for PID tuning

PSO has recently received increased interest from researchers because of its suitability for realization and promising optimization capability in a variety of applications (Song and Gu, 2004). PSO's application to various domains of effort is based on two factors. The first is to increase PSO performance by changing parameters, boosting population diversity, and combining it with other optimization methods. The second is PSO's use in various domains such as multi-objective optimization, electronics, neural network training, network security and mute selection, medicine, and emergent system identification, to name a few.

Because of its intelligible performance and ease of use, PSO has been extensively used to a variety of domains of endeavor (Hajihassani et al., 2018). PSO is a popular optimization technique, and because of its versatility, it has a wide range of applications in fields such as medicine (Eshtay et al., 2018), financial (Shie et al., 2012), economics (Lee and Park, 2006), security and military (Cho et al., 2010; Cheng et al., 2008), biological, system identification etc. (Khare and Rangnekar, 2013).

PSO was used by many academics to tackle difficulties in the disciplines of structural, hydrological, and geotechnical civil engineering (Hajihassani et al., 2018). PSO has recently been used to solve problems in operations research (Yu et al., 2016a; Xia and Li, 2017). Some applications are also closely linked to mechanical engineering (Chen et al., 2013), and PSO algorithms have been used to solve problems in operations research (Che et al., 2012). Academic researchers have also used PSO to address optimization problems in the field of electronics and communication engineering (Ganguly et al., 2013). Liu et al. (2013), Liu et al. created a job scheduling model for cloud computing based on the PSO algorithm to reduce energy usage and enhance profit. Zhang et al. (2015) contains a detailed overview of the implementation of PSO techniques. Swarm robotics flocking motion is another domain where PSO has been successfully utilized (Dada and Ramlan, 2015; Dada and Ramlana, 2013).

PSO has been used in various applications of automatic control systems that heavily rely on PID controllers. In Štimac et al. (2014), PSO was used to tune the settings of a PID controller employing an active magnetic bearing that suspends a rotating shaft and keeps it suspended using regulated electromagnetic forces on the rotor in radial and axial directions. Chang and Chen (2014) designed a PID control system for MIMO activities. In MIMO control systems, an improved version of the PSO algorithm was utilized to tune PID control gains. Particle swam optimization approach was used in Rajesh and Ananda (2015) to optimize settings of PID controllers in order to modify the location of the camera in an Unmanned Aerial Vehicle (UAV). The findings were compared to those of a traditional PID controller. PSO approach was used to calibrate PID controllers for various transitory circumstances of Permanent Magnet DC motor in Medewar and Munje (2015). The proposed approach increased both noise immunity and steady state detection accuracy, according to the results of experiments. PSO has also been used to tune PID control variables for the control of an inverted pendulum in the past (Joseph and Dada, 2018), and speed control of a DC motor in Bassi et al. (2011).

4.10. Cuckoo optimization algorithm

Yang and Deb (2009) developed the Cuckoo Search (CS) metaheuristic evolutionary optimization algorithm in 2009. The cuckoo is a bird species that inspired the concept of CS. Cuckoos are appealing birds, not only because of their wonderful songs, but rather because of their proactive breeding approach. Cuckoos lay their eggs in the nests of other host birds or species when they are grown. Compel brood parasitism is the term for this type of parasitism. The ability of a single cuckoo to lay an egg that may duplicate, or resemble, host nest eggs in such a way that the host nest mother bird cannot distinguish the cuckoo egg from her own is crucial. The cuckoo's egg will hatch before the host egg, confirming the cuckoo's control in the nest and so extending their lifespan.

The concept of Cuckoo Optimization Algorithm (COA) is depicted in Fig. 12. The pseudocode, equations and application details for CS can be seen in Yang and Deb (2009); Bhandari et al. (2014); Shair et al. (2015); Mamizadeh et al. (2018); Rajabioun (2011).

Figure 12.

Application flow diagram for Cuckoo search algorithm.

4.10.1. Cuckoo search algorithm for PID tuning

Recently, CS has been applied in almost every area and domain of function optimization (Fister et al., 2014), engineering optimization (Yang and Deb, 2010), image processing (Brajevic and Tuba, 2014), scheduling (Burnwal and Deb, 2013), planning (Akbarzadeh and Shadkam, 2015), feature selection (Abd El Aziz and Hassanien, 2018), forecasting (Wu et al., 2019), and real-world applications (Expósito-Izquierdo and Expósito-Márquez, 2017). Engineering optimization appears to be just one of the many uses. CS and its derivatives have been used in nearly every field of research, technology, and manufacturing.

CS techniques have been used to tune PID controller parameters in many studies. Kumar et al. (2014) presents PID parameter tuning for inverted pendulum monitoring, experimental validation of Van der Pol oscillator, and stability study of capsizing problem as an example of nonlinear systems employing cuckoo optimization approach. Bingul and Karahan (2018) presents a new tuning approach for PID parameters in the AVR system utilizing the CS algorithm and a new frequency-domain performance benchmark. In their paper, a new way for designing PID controllers utilizing the CS optimization algorithm was provided in order to improve the performance of buck-boost converters in LED driver circuits (Verma et al., 2016; Nimisha and Senthilkumar, 2018). The CS optimization approach was recently used to optimize the PID parameters for various different industrial plants. Maximum Power Point Tracking (MPPT) of PV systems (Mosaad et al., 2019b), Speed of induction motor regulation (Peram et al., 2018), and optimization of complicated stability radius via single objective constrained optimization are instances of such plants (Solihin and Akmeliawati, 2018).

4.11. Simulated annealing

In 1953, Metropolis et al. (1953) was the first to propose a Simulated Annealing (SA) approach. It resembles the rearranging of particles in a body to a crystalline state, which is accompanied by a drop in temperature. The constituents of a body wander laterally within a region whose amplitude is defined by its temperature. As long as cooling is gradual enough, atoms or particles can position themselves in lower and lower energy levels, finally reaching the lowest energy state (crystalline state) (Baselga, 2011). SA is based on the Monte-Carlo iterative approach (Jia and Lichti, 2017).

The flowchart for SA is presented in Fig. 13. Further readings and descriptive algorithms on SA can be found in Fouskakis and Draper (2002); Suman and Kumar (2006); Eglese (1990).

Figure 13.

Flowchart for Simulated annealing algorithm.

4.11.1. Simulated annealing for PID tuning

SA is a method for proffering solution to difficult optimization problems with satisfactory outcomes. Over the years, South Africa has attracted a lot of attention and interest. Kirkpatrick et al. (1983) and Černỳ (1985) sparked the current interest. These papers showed how to use a model for simulating solid annealing provided by Metropolis et al. (1953) to tackle optimization issues where the objective function to be minimized relates to the energy of the solid's states.

SA has been used to solve problems in a variety of fields, including computer VLSI design (Wong et al., 2012), image processing (Tavares et al., 2019), molecular physics (Wu et al., 2016), chemistry (Hernandez et al., 2019), process optimization (Sibalija, 2018), and job shop scheduling (Cruz-Chávez et al., 2017). There has also been development on theoretical results from a mathematical examination of the method, as well as several computing studies evaluate the effectiveness of SA with the effectiveness of other techniques for a variety of situations.

Since the SA algorithm selects control parameters in its own evolutionary process and does not need any rule of thumb, it has diffused rapidly into many application areas. Recently, some researchers have used SA algorithm in tuning of PID control parameters. An intelligent concept for PID controller parameters tuning is suggested using SA for multi-objective problem and its results was compared with basic PID which shows SA to be better than conventional or basic PID controller in terms of tuning PID parameters (Bansal et al., 2014). Suman et al. (2010) introduces a novel multi-objective optimization approach based on SA dubbed Orthogonal Simulated Annealing (OSA).

Yachen and Yueming (2008) used SA algorithm for tuning different PID controllers in practical applications. SA was used to tune PID parameters for motion control system having constant disturbance. The experimented results were compared, showing that different controller was superior in different control requirement. Each controller has its own advantage and proper scope.

SA was recently employed to fine-tune the characteristics of a permanent magnet brushless dc motor (PMBLDCMPID)'s controller (Shatnawi and Bayoumi, 2019). The response parameters index, maximum overshoot, rise time, and settling time for each controller are tuned to reduce the controller's parameters. The SA optimization approach is used to tune the system. The technique determines the best PID/PI controller parameter for fixed-structure PID/PI controllers.

SA has been applied for tuning PID parameters of different processes like AVR system (Lahcene et al., 2017), attitude control system for a re-entry capsule (Vijay and Banu, 2016) and DC-DC power converters (Alqudah et al., 2014). Further readings on application of SA can be seen in Siddique and Adeli (2016); Suman and Kumar (2006); Sibalija (2018); Varty (2017).

4.12. Grey wolf optimizer

Grey Wolf Optimization (GWO) is a recently proposed metaheuristic optimization algorithm (Mirjalili et al., 2014). Grey wolves' social structure and intelligent hunting tactics motivate GWO. Grey wolves are generally at the top of the hierarchy in their habitats. Grey wolves usually dwell in groups of 5–12 people. Grey wolves, in particular, have a well-defined social hierarchy. The grey wolf social hierarchy and duties are depicted in Fig. 14. The main distinction between GWO and other metaheuristic optimization algorithms is the social dominant hierarchy, whose primary goal is to develop the candidate solution during each iteration. As a result, GWO imitates grey wolf hunting behavior as regards locating and attacking prey (Goldbogen et al., 2013).

Figure 14.

Social hierarchy of grey wolves and their responsibilities.

Muro et al. (2011) stated the major stages of grey wolves hunting actions as follows:

• i.Trailing, pursuing, and advancing the prey.
• ii.Following, encircling, and harassing the prey until it stops moving.
• iii.Attacking in the direction of prey.

4.12.1. GWO for PID tuning

The remarkable advantages of GWO has led to tremendous research applications from several critical research domains. These application domains can be categorized into: machine learning (Emary et al., 2016, Emary et al., 2015; Al-Tashi et al., 2019), engineering (Kohli and Arora, 2018; Yıldız and Yıldız, 2018), wireless sensor network (Kaushik et al., 2019; Rajakumar et al., 2017), environmental modeling (Tikhamarine et al., 2020; Sweidan et al., 2016), medical and bio informatics (Sharma et al., 2019, Sharma et al., 2020) and image processing (Khairuzzaman and Chaudhury, 2017; Li et al., 2017a).

In control engineering, there has been an explosion in amount of publications that explore application of GWO algorithm for tuning PID controller parameters. The work in Li et al. (2017b) proposed GWO scheme to tune variables of a PI controller for a closed-loop condenser pressure control mechanism. Results of performance demonstrated the efficacy of Grey Wolf (GW) optimizer compared to GA and PSO. Also in Yadav et al. (2016), parameters of a basic PID controller was tuned using GWO algorithm for a magnetic levitation system. Likened to basic ZN tuning scheme, GW optimizer demonstrated superior results. The study in Das et al. (2015) investigated the application GW optimizer to tune the control variables of a PID controller for the regulation of speed of a second order DC motor system. Improved values of transient reaction stipulations were attained in comparison to PSO, ABC and ZN approaches. Regulation of control variables of PID controller for DC motor was similarly explored in Madadi and Motlagh (2014). Results of performance evaluation demonstrated superiority of GWO over PSO, by improving the dynamic performance of the system.

Some other applications of GWO for PID tuning include robotics (Şen and Kalyoncu, 2018), speed control of DC motor (Agarwal et al., 2018), inverted pendulum (Yadav et al., 2020), voltage regulation (Verma and Nagar, 2018) and wind turbine (Sule et al., 2020). A generic flowchart illustrating GWO algorithm is presented in Fig. 15.

Figure 15.

Grey wolf optimization application flowchart.

4.13. Krill herd algorithm

The herding behavior of krill individuals inspired the Krill Herd (KH) algorithm. It is a new swarm intelligent algorithm that has outperformed conventional swarm intelligent algorithms. Gandomi and Alavi (2012) proposes a novel biologically motivated approach for tackling optimization issues called KH. The KH algorithm is based on the herding of krill swarms in response to biological and environmental events. Almost all of the necessary coefficients for using the KH method are determined from real-world experiments. Each krill's fitness function is defined by its remoteness from food and maximal concentration of swarm.

KH's entire optimization technique may be broken down into three simple steps. These three acts are taken into account while updating each krill. The distance between the food position and the krill's location defines the objective function. Because of its remarkable application performance, KH has gotten a lot of attention from academics, experts, and scientists. Further details on KH algorithm can be seen in Gandomi and Alavi (2012). Fig. 16 presents basic KH application flow diagram. Other variants of KH algorithm can be seen in Li et al. (2014a); Yaghoobi and Mojallali (2016); Wang et al. (2019).

Figure 16.

Basic Krill Head application flow diagram.

4.13.1. KH algorithm for PID tuning

KH algorithm has been employed to solve several engineering problems. These engineering applications of KH algorithm as grouped by Wang et al. (2019) include; continuous optimization, combinatorial optimization, constrained optimization, multi-objective optimization, dynamic and noisy environment applications. Supplementary specific application areas of KH include: electric and power systems (Bulbul et al., 2018), wireless and network systems (Kalaiselvi and Radhakrishnan, 2015; Karthick and Palanisamy, 2019), neural network training (Kowalski and Łukasik, 2016), robotics (Rao et al., 2018), clustering (Abualigah et al., 2017) and medicine (Kumari and Arumugam, 2015). Also, KH has been used for design of industrial controllers. An example of such can be seen in Younesi and Tohidi (2015).

The KH algorithm has been shown to be stable and robust in the tuning of PID settings. The KH method was used to propose optimal tuning of PID controller parameters for frequency stability in an isolated wind-diesel power system (Shayanfar et al., 2015). The simulation was run in four different scenarios: a step change in diesel side load, a step change in wind speed, a random change in diesel side load, and a random change in wind speed. The Bee Colony algorithm was used to compare the outcomes of the KH technique. When compared to BC-based PID controllers (BC-PID), the results showed that KH-based PID controllers (KH-PID) perform better. Optimal tuning of PID parameters for First Order Plus Dead Time system (FOPDT) and fourth order system in Alikhani et al. (2013). The results suggest that the KH algorithm is beneficial for controller tuning. The PID-KH algorithm was used to propose and illustrate optimal control of a state microgrid system (Regad et al., 2020). An objective function is used to optimize the gains of PID controllers. The simulation results were shown, and using the KH algorithm improves the system's performance in comparison to the GA and PSO focusing on PID. The efficiency of the system has improved. Other PID-controlled factories that use KH are: Power System Stabilizer (Mukherjee et al., 2019), Power System Restoration (PSR) Indices (Chandrasekar et al., 2017), load frequency load control (Alam et al., 2016).

Furthermore, several other variants of KH algorithm have also been implemented for PID controller tuning. Some of such proposals can be seen in Yaghoobi and Mojallali (2016).

4.14. Whale optimization algorithm

Mirjalili and Lewis (2016) proposed the Whale Optimization Algorithm (WOA) in 2016. It is a stochastic metaheuristic algorithm. WOA was inspired by the hunting activity or tactic of humpback whales. WOA's methodology treats each and every solution as a whale. In this method, a whale tries to fill a new place in a search region that is thought to be the group's best component. Whales use two search tactics to locate prey and attack. Prey encirclement and the development of bubble nets are two of these search techniques. In terms of optimization, as whales look for prey, they explore the search space, and exploitation happens during attack activity. Whales, like humans, have spindle cells that control emotions, judgment, and social behavior (Hof and Van der Gucht, 2007).

The implementation flow diagram for WOA is presented in Fig. 17. Whale optimization algorithm is formulated based on the following steps:

• i.Initialization of population number, maximum iteration number and design variables.
• ii.For every design variable, compute fitness function for each search agent and pick up best solution (optimum) and other search agent tries to update their position to the best one.
• iii.Update the position for each search agent.

Figure 17.

Whale optimization implementation flow diagram.

Further readings and details of WOA can be seen in Mirjalili and Lewis (2016); Gharehchopogh and Gholizadeh (2019); Adhirai et al. (2018); Mirjalili et al. (2020); Mohammed et al. (2019).

4.14.1. Whale optimization algorithm for PID tuning

WOA is employed effectively to backup applications of several areas of study. An example of area of application includes engineering optimization problems. Articulating appropriate problems and defining suitable parameters and objective functions are the main concerns that can aid effectual problem solving while handling engineering applications. Appropriate usage of operators, variable settings, and population illustration are the major concerns regarding optimization algorithms.

WOA applications in engineering are classified into: Electrical engineering (Mirjalili et al., 2020), Civil Engineering (Kaveh and Rastegar Moghaddam, 2018), Classification, Clustering, Image Processing, Mechanical Engineering (Algabalawy et al., 2018), Robotics (Elhosseini et al., 2019), Computer Networks (Pham et al., 2020), Industrial Engineering (Khalilpourazari et al., 2019), Task Scheduling (Chen et al., 2020), and Control Engineering (Saha and Saikia, 2017), applications.

Though controllers may overcome some stability glitches nonetheless they do not resolve the problems of nonlinear loads, variable operating points and time delays. Optimization methods are used to overcome these problems through tuning the controller parameters. One of such techniques is WOA. Tuning of PID controller parameters using WOA for Load Frequency Control (LFC) of two-area interconnected non-reheat thermal power systems in order to maintain the system frequency at a prescheduled value in the presence of disturbances was presented in Bhatt et al. (2019). In Debnath et al. (2018), the parameters of a non-integer type PID controller was successfully tunes using Whale Optimization technique for the adjustment of frequency and interline power oscillations in multi-generation type unified system. Whale optimizer algorithm to regulate PID parameters for tracking control of 2-DOF robot manipulator was presented in Loucif et al. (2020). The results obtained witness the efficacy of WOA-PID in terms settling time, errors, and convergence time as well as its robustness for tuning parameters PID controller for robot tracking control with or without disturbances. Other plants controlled by PID and tuned with WOA include; AVR system (Mosaad et al., 2019a), DC-DC buck converter design (Hekimoğlu et al., 2018) and high-performance drilling machine (Kumar and Kumar, 2018).

5. Open research problems

Notwithstanding the accomplishments of modern metaheuristic algorithms, a number of important concerns remain unresolved. Heuristic algorithms' operating principles are well understood, although comprehending why they operate is only partially understood. Unfortunately, it is difficult to mathematically explain why these algorithms are so successful, despite some interesting previous efforts (Yang, 2011). These are, in fact, unsolved open research problems. To the best of our knowledge, except for mathematical study of SA and PSO, the convergence of any other methods has not been proven using mathematical models. As a result, any mathematical examination will provide important insight into algorithms. This will be useful for advancing more effective variants of these algorithms or demonstrating inventive approaches of constructing new algorithms.

Furthermore, it is only poorly understood why distinct components of heuristics and metaheuristics interact in an intelligent and stable manner to produce effective algorithms that aggregate under specified conditions. Why, for example, does a well-balanced mix of randomization and determinism produce a far more effective algorithm (than a pure deterministic or random algorithm)? How do you tell whether you have reached a state of stability? How can you demonstrate that memory usage can significantly improve an algorithm's search efficiency? What are the circumstances? It can be demonstrated from the well-known No-Free-Lunch assertions of 1997 (Wolpert et al., 1997) that they have been validated for single-objective optimization, but not for multiobjective optimization. What are the implications for algorithm design if they are proven to be true (or not) for multiobjective optimization?

Similarly, there is no universally accepted metric for comparing the performance of diverse algorithms; nonetheless, the assumed absolute objective value and the number of functional evaluations are two commonly used measures. The attempt to provide a universal framework was made by Shilane et al. (2008). A formal theoretical investigation, on the other hand, has yet to be formed (Chiarandini et al., 2007). This could be a fantastic place for students or scholars to conduct further investigation.

Natural World has a nearly infinite number of problem-solving strategies. Individuals are undoubtedly urged to design more powerful and efficient new generation algorithms through diligent observation. In nature, intelligence is a result of biological evolution. In the future, some intelligent algorithms (or systems) may originate, evolve, and modify appropriately to provide efficient and intelligent solutions to NP-hard optimization problems. Furthermore, a current trend is to use simple metaheuristic algorithms to solve difficult optimization problems. Possibly the need for more complicated metaheuristic algorithms that can genuinely mirror the exact operational technique of some natural or biological systems motivates the development of self-regulating, self-evolving, and fully intelligent metaheuristics in the long term.

Although the essential components of most algorithms are well understood, how they interact to achieve efficiency remains a secret, motivating further intensive research. Convergence analysis of a small number of algorithms, such as PSO, demonstrates some knowledge; nevertheless, common mathematical analysis of metaheuristic algorithms remains unsolved and is an important research area. The choice and precise use of a suitable algorithm is required for the solution of an optimization issue. The nature of the optimization problem is largely determined by the algorithm chosen. There is no defined policy as to how and what to choose for large-scale nonlinear global optimization issues. Indeed, it is not definite if an effective algorithm exists, which is especially true for NP-hard problems, which represent the majority of real-world problems.

In summary some of these open research problems include:

• i.Some metaheuristic algorithms, such as GWO, can be improved as their fundamental deficiency, notwithstanding their capacity to handle vast numbers of variables and evading local solutions when dealing with complex problems.
• ii.A hybrid metaheuristic algorithm can be created by combining memetic algorithms to solve several of their individual weaknesses.
• iii.To handle dynamic optimization challenges, certain recently proposed metaheuristic algorithms have to be changed.
• iv.A neutral trade-off between local amplification and global heterogeneity is required (Yang, 2011; Blum and Roli, 2003).
• v.When solving optimization problems, the parameters of metaheuristic algorithms have to be fine-tuned (Dokeroglu et al., 2019).
• vi.Metaheuristic algorithms with no parameters have to be developed.
• vii.Statistical analysis approaches for evaluating the performance of metaheuristic algorithms have to be developed.
• viii.To improve performance and resilience in solving emerging problems and cases, transfer learning is incorporated into metaheuristic algorithms (Talbi, 2020).
• ix.Speeding up execution time (process time) of metaheuristic algorithms. Some metaheuristic algorithms like population-based are slow solvers (Alba et al., 2013).
• x.Theoretical and mathematical models are needed for metaheuristic components like exploration versus exploitation, convergence, searching ability and local optimum versus global optimum (Hussain et al., 2019).
• xi.Development of a self-adapting, self-tuning, and self-evolving scalable metaheuristic algorithm. This is to allow algorithms to deal with the complicated and highly unbalanced landscapes of large optimization problems with a large number of decision variables (Hussain et al., 2019).
• xii.How can awareness about the traits and attributes of particular optimization problem classes and cases be acquired, articulated, and evaluated? (Sala and Müller, 2020).
• xiii.How to exploit knowledge or assumptions on particular properties of problem sub-sets or classes, in the selection or development of effective optimization strategies? (Sala and Müller, 2020).

6. Conclusion

This research provides an in-depth look at metaheuristic algorithms and their application to PID controller tuning. An overview of the current state-of-the-art metaheuristic algorithms employed for parameter tuning of PID controllers is provided. The efforts made by different scholars and researchers to solving tuning problems of PID controller parameters using metaheuristic algorithms were discussed. The evolution of metaheuristic algorithms over the years for optimization problems solving was examined. The basic architecture of PID controller and procedures involved tuning its parameters were looked into. The study surveyed some issues related to PID controller tuning and performance metrics utilized to measure effectiveness of tuning approaches for PID control. The challenges of metaheuristic optimization algorithms in efficiently handling issues of tuning was presented. A highlight of some open research problems associated with metaheuristic algorithms was offered. In general, the figure and volume of literature we reviewed revealed that significant progress have been made and will still be made in this area. Having presented open problems on metaheuristic algorithms, further research to improve the effectiveness of metaheuristic algorithms need to be done. This will make the development of metaheuristic algorithms remain an active research area for academicians and industrial practitioners researching metaheuristic optimization approaches for effective optimization and controller tuning. The goal and aspiration of this research is that researchers and students will use this study as a spring board or background for qualitative research in this field.

Declarations

Author contribution statement

All authors listed have significantly contributed to the development and the writing of this article.

Funding statement

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Data availability statement

No data was used for the research described in the article.

Declaration of interests statement

The authors declare no conflict of interest.

Additional information

No additional information is available for this paper.