Decoding motor expertise from fine‐tuned oscillatory network organization

Abstract

Can motor expertise be robustly predicted by the organization of frequency‐specific oscillatory brain networks? To answer this question, we recorded high‐density electroencephalography (EEG) in expert Tango dancers and naïves while viewing and judging the correctness of Tango‐specific movements and during resting. We calculated task‐related and resting‐state connectivity at different frequency‐bands capturing task performance (delta [δ], 1.5–4 Hz), error monitoring (theta [θ], 4–8 Hz), and sensorimotor experience (mu [μ], 8–13 Hz), and derived topographical features using graph analysis. These features, together with canonical expertise measures (i.e., performance in action discrimination, time spent dancing Tango), were fed into a data‐driven computational learning analysis to test whether behavioral and brain signatures robustly classified individuals depending on their expertise level. Unsurprisingly, behavioral measures showed optimal classification (100%) between dancers and naïves. When considering brain models, the task‐based classification performed well (~73%), with maximal discrimination afforded by theta‐band connectivity, a hallmark signature of error processing. Interestingly, mu connectivity during rest outperformed (100%) the task‐based approach, matching the optimal classification of behavioral measures and thus emerging as a potential trait‐like marker of sensorimotor network tuning by intense training. Overall, our findings underscore the power of fine‐tuned oscillatory network signatures for capturing expertise‐related differences and their potential value in the neuroprognosis of learning outcomes.

In the present study, we use a data‐driven multi‐feature approach to evaluate the power of task and resting‐state oscillatory networks in predicting motor expertise. We show that theta (4–8 Hz) and mu (8–13 Hz) connectivity features indexing anticipatory motor error processing and sensorimotor experience, respectively, are robust markers for classifying individuals depending on their expertise. Strikingly, mu connectivity during rest outperformed the task‐based approach, pointing to its role as a trait‐like marker of plastic reorganization underlying motor training. Overall, our findings underscore the power of fine‐tuned oscillatory network signatures for capturing expertise‐related individual differences and their potential value in the neuroprognosis of learning outcomes.

1. INTRODUCTION

From mirror neurons to extended action observation networks (AONs), it is well‐known that executing and observing others' actions activates similar brain regions (Caspers, Zilles, Laird, & Eickhoff, 2010; Hardwick, Caspers, Eickhoff, & Swinnen, 2018; Rizzolatti & Craighero, 2004). Such sensorimotor activations are stronger for actions within the observer's expert motor repertoire (Calvo‐Merino, Glaser, Grezes, Passingham, & Haggard, 2005; Calvo‐Merino, Grezes, Glaser, Passingham, & Haggard, 2006), likely reflecting anticipatory resonant mechanisms rather than passive responses to visual stimuli (Aglioti, Cesari, Romani, & Urgesi, 2008; Chen, Chang, Huang, & Yen, 2020; Tomeo, Cesari, Aglioti, & Urgesi, 2013). This aligns with current predictive accounts of action processing (Avenanti, Paracampo, Annella, Tidoni, & Aglioti, 2018; Kilner, Friston, & Frith, 2007; Paracampo, Montemurro, de Vega, & Avenanti, 2018; Urgen & Saygin, 2020; Urgesi et al., 2010; Wilson & Knoblich, 2005), suggesting that we use our sensorimotor system to predict other's forthcoming actions. Yet, a crucial question remains unanswered: can prior experience with perceived actions be robustly decoded from brain activity? Here, we used a multi‐feature approach considering task‐related and resting‐state brain connectivity in critical frequency bands (sensitive to task performance, error anticipation, and motor expertise) and trained a machine learning classifier to evaluate whether such signals could discriminate between expert Tango dancers and naïves.

Focusing on system‐level measures such as brain network connectivity has many advantages. Given their uniqueness and stability across brain states, individual patterns of functional connectivity can be seen as trait‐like markers of different cognitive and personality aspects (van den Heuvel, Stam, Kahn, & Hulshoff Pol, 2009). Network fingerprints also differ in individuals depending on their level of motor expertise (Amoruso et al., 2017; Muraskin et al., 2016; Pinho, de Manzano, Fransson, Eriksson, & Ullen, 2014; Wang et al., 2016) and other forms of individual experience (Birba et al., 2020), suggesting that long‐lasting training triggers plastic network reorganization. Nevertheless, the role of neural networks as predictors of motor expertise remains poorly understood. In particular, little is known about the role of specific markers in expertise decoding, especially when compared with signatures of domain‐general processes. To bridge this gap, we recorded high‐density electroencephalography (hdEEG) signals (a) as participants judged the correctness of Tango steps in naturalistic videos and (b) while they underwent a resting‐state condition.

In electroencephalography (EEG) research, error processing during action observation is canonically indexed by mid‐frontal theta (4–8 Hz) modulations, with error magnitude being fine‐graded mapped by this activity (Pezzetta, Nicolardi, Tidoni, & Aglioti, 2018; Spinelli, Tieri, Pavone, & Aglioti, 2018). On the other hand, action observation has been linked to mu suppression (8–13 Hz) (Coll, Press, Hobson, Catmur, & Bird, 2017; Debnath, Salo, Buzzell, Yoo, & Fox, 2019; Pineda, 2005), an effect sensitive to expertise with observed movements (Denis, Rowe, Williams, & Milne, 2017). Finally, more domain‐general functions across multiple tasks have been related to delta activity (1.5–4 Hz) (Harmony, 2013), possibly indexing task engagement and attention. Here, we capitalized on these EEG markers and calculated graph‐theory metrics of task‐related and resting‐state connectivity in theta (θ), mu (μ), and delta (δ) to predict different components of motor expertise. Overall, we sought to identify specific network fingerprints of anticipatory error processing and sensorimotor knowledge to decode expertise (while considering behavioral performance as a canonical control predictor).

Based on previous evidence (Amoruso et al., 2014), we reasoned that behavioral features would robustly classify individuals based on their expertise. Furthermore, we anticipated that accurate classification would also be yielded by expertise‐sensitive brain network metrics. Specifically, we hypothesized that task‐based classification would reflect a mixture of expertise and domain‐general brain processes, while resting‐state data would capture pure trait‐like sensorimotor expertise networks less vulnerable to potential confounds associated to task‐performance. In particular, we predicted that these selective processes would be captured by specific oscillations, with theta reflecting anticipatory error processing during action observation, mu indexing sensorimotor expertise with Tango dancing, and delta involving task domain‐general aspects. By testing these hypotheses, we aimed to elucidate whether brain network signatures can predict distinct aspects of motor expertise and, thus, potentially contribute to the neuroprognosis of learning outcomes (Gabrieli, Ghosh, & Whitfield‐Gabrieli, 2015).

2. MATERIALS AND METHODS

2.1. Participants

The study comprised 44 right‐handed participants, as defined by the Edinburgh Inventory (Oldfield, 1971), all from Argentina. Twenty‐one were expert Tango dancers (M = 30.95 years old, SD = 5.7; 12 females) and 23 were naïve participants (M = 28.74 years old, SD = 5.65; 12 females). The expert Tango dancers were recruited from three top Tango Schools in Buenos Aires: DNI, Flor de Milonga, and Divino Estudio del Abasto. Participants completed a standardized, self‐administered Tango expertise questionnaire (Amoruso et al., 2014; Amoruso et al., 2017) with questions quantifying different domains, such as Tango training, dance practice, and Tango teaching. Key questions within the Tango training domain tapped on the amount of intense practice time and monthly hours spent dancing Tango—two reliable proxies of motor expertise as compared to daily and weekly training hours, which can greatly vary across dancers (Calmels, 2020). Immediately after the EEG recording session, participants also completed a debriefing questionnaire to evaluate their motor expertise (i.e., frequency with which participants performed the Tango figures observed during the task) and visual familiarity (i.e., level of visual knowledge of the Tango figures observed during the task). Importantly, on average, Tango dancers reported executing the observed figures almost every day, while naïves reported never having performed them. Similarly, dancers reported knowing all the observed Tango figures, whereas naïves reported ignoring them all. Thus, these measures further confirmed differences in motor and visual expertise among dancers and naïves. Detailed information about participants' expertise profiles and comparisons between groups are shown in Table 1.

TABLE 1.

Participants' expertise profiles and statistical comparisons

			Experts M(SD)	Naïves M(SD)	Experts versus naïves
Tango training	Do you currently dance tango?	Yes/no	All yes	All no	X 2 = 44, p = <.001
	For how long have you been dancing tango?	Specified in months	106.85 (53.8)	0	t‐value = 9.5, p = <.001
	How many hours per month do you dance tango?	1 = <10 hr/2 = 10 hr/3 = 20 hr/4 = 30 hr/5 = 40 hr/6 = >40 hr	5.5 (0.74)	0	t‐value = 35.3, p = <.001
	Have you ever received formal Tango instruction?	Yes/no	All yes	All no	X 2 = 44, p = <.001
	For how long have you received formal Tango instruction?	Specified in months	85.76 (54.6)	0	t‐value = 7.54, p = <.001
Dance practicing	Do you dance for hobby (at discos, parties, etc.)?	Yes/no	17 yes/4 no	18 yes/5 no	X 2 = 0.048, p = 0.82
	How many hours per week do you dance for hobby?	1—never/2—few times a year/3—few times a month/4—few times a week/5—everyday	3.14 (1.5)	1.95 (0.6)	t‐value = 3.41, p = .001
Tango teaching	Do you teach others to dance Tango?	Yes/no	19 yes/2 no	All no	X 2 = 36, p = <.001
	How many hours per week do you teach tango?	1—never/2—few times a year/3—few times a month/4—few times a week/5—everyday	4.09 (1.9)	0	t‐value = 7.73, p = <.001
	Does your main income derive from teaching tango?	Yes/no	13 yes/8 no	All no	X 2 = 20, p = <.001
	Do you consider yourself as a professional Tango dancer?	Yes/no	16 yes/5 no	All no	X 2 = 27.5, p = <.001
Familiarity with observed videos	Which is the degree of familiarity that you have with the Tango steps previously observed in the videos?	1—none/2—know 1 or 2/3—know half of the steps/4—know most of the steps/5—know all the steps	4.8 (0.4)	1	t‐value = 45.4, p = <.001
	How often do you execute the Tango steps previously observed in the videos?	1—never/2—few times a year/3—few times a month/4—few times a week/5—everyday	5	1	t‐value = 24.1, p = <.001
	How well do you know Tango salon style?	1—not at all/2—very little/3—moderately 4—pretty well/5—perfectly well	4.14 (0.65)	1	t‐value = 23, p = <.001

Note: Descriptive statistics are provided for (a) the self‐rating questionnaire evaluating participants' expertise in Tango training, dance practice, and Tango teaching; and (b) the debriefing questionnaire evaluating visual and motor expertise with the observed action videos. Contrasts between groups are also provided, including independent t‐tests in the case of numerical variables and Pearson χ ² test statistics in the case of categorical variables.

The two groups were matched for age, education, and sex. In addition, we assessed dance‐related relevant cognitive skills (Jola, Abedian‐Amiri, Kuppuswamy, Pollick, & Grosbras, 2012; Noguera, Carmona, Rueda, Fernandez, & Cimadevilla, 2020), including executive functions and empathy levels in both groups by means of a standard frontal executive screening (Torralva, Roca, Gleichgerrcht, Lopez, & Manes, 2009) and the Interpersonal Reactivity Index (Davis, 1980), respectively. The groups' demographic and neurocognitive characteristics are summarized in Table 2. All participants possessed normal or corrected‐to‐normal vision and reported no history of neurological or psychiatric disease. After receiving a complete description of the study, participants provided written informed consent in agreement with the Declaration of Helsinki and the Institutional Ethics' Committee.

TABLE 2.

Demographic and cognitive profiles of Tango dancers and naïves

		Experts (25) M(SD)	Naïves (28) M(SD)	p‐value
Demographics	Age (years)	30.95 (5.7)	28.74 (5.6)	.203
	Gender (M: F)	9:12	11:12	.74
	Education (years)	18.38 (3.59)	17.95 (3.48)	.693
IRI	Perspective taking	27 (3.6)	25.13 (5.18)	3.606
	Fantasy	23.62 (4.65)	23.96 (6.56)	.845
	Empathy	31.95 (4.01)	30.83 (4.2)	.369
	Personal distress	14.05 (3.35)	14.96 (4.06)	.425
Executive functions	IFS global score	26.5 (2.02)	26.43 (2.15)	.918
	Motor series	2.85 (0.35)	2.82 (0.65)	.848
	Conflicting instructions	2.95 (0.21)	2.91 (0.28)	.615
	Go/no go	2.9 (0.3)	2.95 (0.2)	.508
	Backward digits span	4.28 (0.9)	4.26 (1.21)	.939
	Verbal working memory	1.9 (0.3)	1.95 (1.06)	.833
	Spatial working memory	3.38 (0.66)	3.0 (0.8)	.095
	Abstraction capacity	2.78 (0.33)	2.91 (0.35)	.233
	Verbal inhibitory control	5.42 (0.81)	5.73 (0.61)	.159

Note: Descriptive statistics and comparisons between groups. Mean (M), standard deviations (SD), and p‐values for demographics, empathy, and executive function scores obtained in experts and naïves.

2.2. EEG recordings and preprocessing

Figure 1 shows the experimental design and overall analysis pipeline. HdEEG signals were recorded in a Faraday cage with a Biosemi Active Two 128‐channel 24‐bit resolution system (Amsterdam, NLD), with active electrodes, digitalized at 1024 Hz, and band‐pass filtered between 0.1 and 100 Hz. During recording, the reference was set as default to link mastoids. Two bipolar derivations monitored vertical and horizontal ocular movements. Data were obtained while participants performed a Tango dance‐based action observation task (Amoruso et al., 2014; Amoruso et al., 2017) and during a 10‐min eyes‐closed resting period in which participants sat on a reclining chair in a sound‐attenuated room with a dim light.

FIGURE 1.

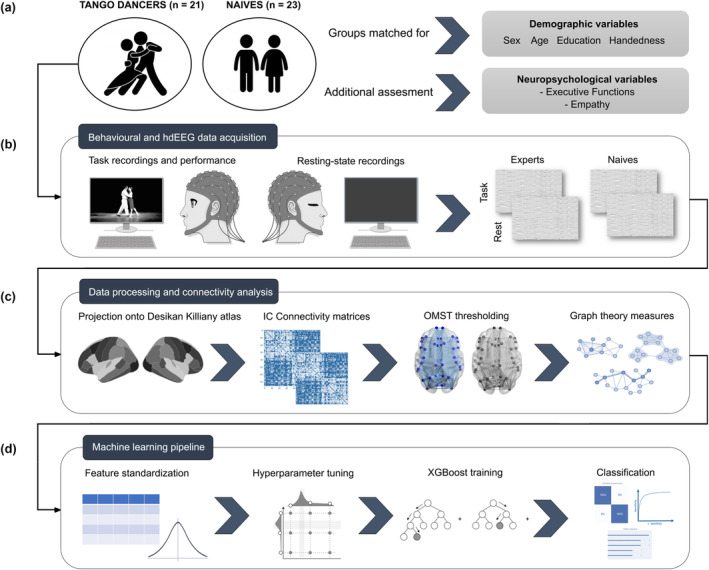
Preprocessing, data analysis, and machine learning pipeline. (a) Samples and neuropsychological assessment. Tango dancers and controls were matched for demographical variables (sex, age, education, and handedness). In addition, we also acquired measures of empathy and executive functions. (b) Behavioral and hdEEG data acquisition. Electroencephalography (EEG) activity was recorded under two conditions (action observation task and resting‐state session). In the task, participants watched videos of correctly or incorrectly executed Tango figures and classified them. After the task, they remained at rest for ~10 m with their eyes closed. (c) Data processing and connectivity analysis. We employed a source‐based approach to connectivity. We estimated EEG sources using MNE and projected activity onto the 68 anatomical regions of the Desikan Killiany atlas. Source‐based whole‐brain connectivity was calculated using the Imaginary part of Coherency (IC) in the delta (δ = 1.5–4 Hz), theta (θ = 4‐8 Hz), and mu (μ = 8–13 Hz) rhythms. Adjacency matrices were built based on orthogonal minimal spanning trees (OMST) method. Finally, standard graph theory connectivity measures at the different frequency‐bands in the task and rest conditions were estimated and fed into machine learning classifiers. (d) Machine learning pipeline. After feature standardization, we used a k‐fold validation grid search scheme for hyper‐parameter tuning to obtain trained XGBoost models. Then we tested our classification by employing the ROC curve, confusion matrices and a feature importance analysis

After acquisition, signals were down‐sampled off‐line to 512 Hz and re‐referenced to the average of all electrodes. Then, the task‐related and resting‐state recordings were segmented into 4‐s trials. Segments containing nonstereotyped artifacts and residual artifacts larger than 100 μV were manually removed by visual inspection based on their scalp topographies, time courses, and activation spectra using Brainstorm (Tadel, Baillet, Mosher, Pantazis, & Leahy, 2011). Segments containing stereotyped artifacts (e.g., eye blinks, muscle activity) were detected and corrected by means of the Signal‐Space Projection (SSP) method (Uusitalo & Ilmoniemi, 1997). A minimum of 60 artifact‐free segments per subject was retained for analysis. Importantly, no significant differences were observed (all p‐values >.05) between conditions or groups in terms of the number of trials used in the task‐related (experts: M = 103.43, SD = 32.26; naïves: M = 101.14, SD = 33.45) and resting‐state (experts: M = 109.45, SD = 31.44; naïves: M = 113.17, SD = 27.06) analyses.

2.3. Experimental stimuli and task procedure

Stimuli were naturalistic action videos (lasting ~5,000 ms) showing a couple of Tango dancers performing Tango Salon figures in a correct or incorrect fashion. In the latter case, errors could be either gross or subtle. Gross errors (e.g., stepping on the other's feet) were exaggerated disruptions that could be noticed by any person irrespective of their experience with Tango dance. Subtle errors, on the other hand, were mistakes representing step violations in the structure of the figure (e.g., an incorrect close position of the feet) and thus presupposed Tango knowledge for accurate recognition. Of note, we used the same stimuli and action observation task originally reported in Amoruso et al. (2014), where videos were statistically validated. Briefly, in the pilot study, 10 professional Tango dancers (6 females, mean age = 26.7, SD = 1.7) with a mean of ~8.8 years of Tango Salón (classic Tango dance style) training and 22 naïves (15 females, mean age = 21.1, SD = 2.3) were asked to rate 330 original videos depicting Tango steps. Participants were instructed to classify them as “correct,” “masculine incorrect” or “feminine incorrect” by selecting one of those possible options in a forced‐choice questionnaire. In addition, using a 7‐point Liker scale (1‐totally correct to 7‐totally incorrect), they rated the degree of correctness of each video. Videos were selected based on the following criteria: high accuracy (>80%) and high degree of correctness (<2) in both experts and naïves for the congruent condition. The gross error condition included those videos with high accuracy (>80%) and a very low degree of correctness (> 5) in both groups. Finally, the subtle error condition was built by selecting those videos with high accuracy (>80%) and a moderate low degree of correctness (<4) only considering judgments from the Tango dancers group. This yielded 150 videos (i.e., 50 per condition). A one‐way ANOVA (F _(4,14) = 1,193.9, p <.001) on this selection further confirmed the appropriate manipulation of action correctness, with congruent actions judged as being more correctly performed than incongruent ones and, in this latter case, with the subtle error condition judged more correct than the gross one (all p‐values <.001).

The final 150 videos were presented twice for a total of 300 trials (i.e., 100 per condition). Importantly, errors always involved leg/foot actions and occurred ~200 ms before video offset, the time at which the last step to close the Tango figure began. When using this task in Amoruso et al. (2014), we found expertise‐related differences in an ongoing wave indexing anticipatory activity (i.e., error anticipation) starting ~4,600 ms after video onset. Thus, we performed our task‐based analysis (see below) by selecting segments of −2,000 ms before error onset, to include the timing in which those action prediction differences were previously captured.

In a two‐alternative forced‐choice task, participants watched the Tango steps and classified them into correct or incorrect as quickly and accurately as possible. Performance in detecting gross and subtle errors as well as correct video identification were further used as behavioral features to feed the machine learning classifier (Table 3).

TABLE 3.

Behavioral, task‐based, and resting‐state features

Features	Category	RFE approach
Motor and visual expertise
Hours spent by month dancing tango	B	✓
Frequency in performing the observed tango figure	B	✓
Familiarity with observed tango figures	B	✓
Performance in tango figures classification
Detection of subtle errors in tango steps	B	✓
Detection of gross errors in tango steps	B	✓
Detection of correct tango steps	B	✓
Overall performance in error detection	B	✓
Neuropsychological scores
Perspective taking	B
Fantasy	B
Empathy	B
Distress	B
IRI total score	B
Conflicting instructions	B
Go‐no go	B
Digit span	B
Verbal working memory	B	✓
Spatial working memory	B	✓
Abstraction capacity	B	✓
Verbal inhibitory control	B	✓
IFS total score	B	✓
Task‐based hdEEG connectivity measures
CPL for correct steps (δ θ μ)	T
GE for correct steps (δ θ μ)	T
C for correct steps (δ θ μ)	T
LE for correct steps (δ θ μ)	T
BC for correct steps (δ θ μ)	T
PC for correct steps (δ θ μ)	T
CPL for incorrect steps with gross errors (δ θ μ)	T	✓ (θ)
GE for incorrect steps with gross errors (δ θ μ)	T
C for incorrect steps with gross errors (δ θ μ)	T
LE for incorrect steps with gross errors (δ θ μ)	T	✓ (μ)
BC for incorrect steps with gross errors (δ θ μ)	T
PC for incorrect steps with gross errors (δ θ μ)	T
CPL for incorrect steps with subtle errors (δ θ μ)	T	✓ (θ)
GE for incorrect steps with subtle errors (δ θ μ)	T
C for incorrect steps with subtle errors (δ θ μ)	T	✓ (μ)
LE for incorrect steps with subtle errors (δ θ μ)	T
BC for incorrect steps with subtle errors (δ θ μ)	T
PC for incorrect steps with subtle errors (δ θ μ)	T
Resting‐state hdEEG connectivity measures
CPL (δ θ μ)	R	✓ (μ)
GE (δ θ μ)	R
C (δ θ μ)	R
LE (δ θ μ)	R
BC (δ θ μ)	R
PC (δ θ μ)	R

Note: All original features included in our machine learning pipeline are shown. In addition, the optimal features selected by means of the recursive feature elimination cross‐validation (RFECV) approach included in the final models are highlighted with a tick. B, behavioral; R, resting‐state; T, task‐related.

2.4. Source reconstruction

We developed a source‐based approach to connectivity. To estimate the neural EEG sources, we selected 68 anatomical regions of interest (ROI) derived from the Desikan Killiany atlas (Desikan et al., 2006), implemented in Brainstorm software. Source activity was estimated by using this toolbox's default brain anatomy, which consisted of the segmented cortical surface (15,000 vertices) of the MNI/Colin27 brain. The head modeling was computed through the Open MEEG Boundary Elements Method (BEM head model; Gramfort, Papadopoulo, Olivi, & Clerc, 2010). Next, a noise covariance matrix was calculated to estimate noise level in the recordings. The solution space was constrained to the cerebral cortex, modeled as a three‐dimensional grid of 15,000 fixed dipoles oriented normally to the cortical surface. Then, the inverse solution was estimated with the weighted minimum norm estimation (wMNE; Hamalainen & Ilmoniemi, 1994). Finally, we extracted the time series from the 68 ROIs as the average of all dipole's signals within each area of the abovementioned atlas.

2.5. EEG functional connectivity

The Imaginary part of Coherency (IC) was used to measure functional connectivity between all 68 brain regions in the delta (1.5–4 Hz), theta (4–8 Hz), and mu (8–13 Hz) rhythms. The use of IC was originally proposed by (Nolte et al., 2004) to remove the spuriousness caused by the volume conduction in EEG sensor‐space coherence analysis. The rationale behind this method is that “self‐interactions” caused by volume conduction are minimized, facilitating the interpretation of this connectivity measure in terms of interactions within the brain. IC is only sensitive to synchronizations of two processes which are time‐lagged to each other. If volume conduction does not cause a time‐lag, IC is hence insensitive to artifactual “self‐interaction.” Thus, using the IC, the zero‐lag effect can be suppressed, because the real part is the one mostly affected by this aspect.

Furthermore, to avoid problems related to volume conduction, we first estimated the source‐level (rather than sensor‐level) activity via wMNE (Shahbazi Avarvand et al., 2012). This allowed us to reduce the effect of volume conduction together with the IC.

The IC was calculated with the following Equation (1):

$$I_{\mathit{xy}}\left(f\right)=\left|\mathit{Im}\frac{{\sum }_{k=1}^k{X}_k\left(f\right)Y_k^{*}\left(f\right)}{\sqrt{\sum _{k=1}^k{\left|X_k\left(f\right)\right|}^2\sum _{k=1}^k{\left|Y_k\left(f\right)\right|}^2}}\right|$$ (1)

where I _xy (f) is the imaginary coherence between a given paired‐ROIs for each frequency, Im is the imaginary part of the complex production, X _k and Y _k are the source‐based spectrums from two ROIs, * denotes the complex conjugate, and K is the number of 4 s length segments (Hsiao et al., 2013).

Adjacency matrices were built based on orthogonal minimal spanning trees (OMST) method (Dimitriadis, Antonakakis, Simos, Fletcher, & Papanicolaou, 2017). OMST is a topological thresholding technique with a novel proposed data‐driven scheme, which attempts to maximize the information flow over the network vs. the cost. Briefly, OMST is based on the notion of sampling the full‐weighted brain matrix over consecutive rounds of minimum spanning trees (Stam, 2014) that are orthogonal to each other. With this iterative approach, OMSTs and topologically filtering brain networks are obtained by optimizing the global efficiency of the network constrained by the cost.

2.6. Graph‐theory analysis

Graph‐theory metrics provide powerful tools for quantifying low‐dimensional properties at the network level (Bullmore & Sporns, 2009). Beyond the overall improvement that these metrics provide to understand brain network architecture, they are particularly promising in informing the mechanisms underpinning motor expertise (Calmels, 2020). Indeed, graph theory‐based network approaches have been proposed to facilitate the identification, interpretation, and comparison of expertise‐related connectivity patterns across studies (Calmels, 2020).

Thus, to describe the architecture of participants' task‐related and resting‐based functional brain networks, we used graph theory connectivity features and estimated them by means of the BCT toolbox (Rubinov & Sporns, 2010). Six measures were selected based on previous literature (Wang et al., 2016) exploring differences in the functional network organization of motor experts (i.e., world class gymnasts) and controls. Briefly, in this study, the features selected to measure integration and segregation properties were the characteristic path length, the global and local efficiency, and the clustering coefficient. Of note, all these functional topographical measures showed significant differences between experts and controls. In addition, we added two centrality measures also previously used to capture expertise‐related network organization (Wang et al., 2013), namely, betweenness centrality and participation coefficient. All six measures were computed in the delta (1.5–4 Hz), theta (4–8 Hz), and mu (8–13 Hz) frequency ranges. A detailed definition of each measure is listed below.

1. Integration measures: “Characteristic path length” (CPL), which is the average shortest path length between all pairs of nodes in the network; and the “Global efficiency” (GE), which is related to the previous one and is defined as the average inverse shortest path length in the network. Both are measures of global connectedness, and give an estimation of how efficiently information is integrated across the network;

2. Segregation measures: “Clustering coefficient” (C), which quantifies the number of connections that exist between the nearest neighbors of a node as a ratio of the maximum number of possible connections, providing information about the level of local connectedness within a network; and “Local efficiency” (LE), which reflects the GE computed in the neighborhood of the node; given an estimation of how efficient the communication is between neighbors of a node;

3. Centrality measures: “Betweenness centrality” (B), which measures how many of the shortest paths between all other node pairs in the network pass through a given node and basically shows which nodes act like bridges between nodes in a network; and “Participation coefficient” (PC), an index of internetwork connections which quantifies the diversity of a node's links across network communities, reflecting how well a node integrates information and coordinates connectivity between communities.

These graph‐derived metrics were computed for all participants in both task‐related and resting‐state networks at each frequency band, for a total of 54 and 18 features, respectively. These features were further entered in the recursive feature elimination cross‐validation (RFECV) pipeline of the machine learning classification, resulting in the selection of four optimal task‐related connectivity metrics and one optimal resting‐state connectivity metric (Table 3).

2.7. Machine learning analysis

We used a supervised machine learning classification approach to evaluate whether behavioral and brain signatures derived from task‐based and resting‐state connectivity could successfully decode individuals according to their level of motor expertise in Tango dancing. Specifically, we tested three classifiers—each trained with a distinct set of features (i.e., behavioral, task‐related, and resting‐state features, respectively)—, and evaluated their performance in decoding motor expertise based on individual differences. A complete list of the features fed into each classifier is shown in Table 3.

Following state‐of‐the‐art machine‐learning analysis guidelines (Poldrack, Huckins, & Varoquaux, 2020), we split the dataset into training (75%) and test (25%) subsets using random partition, to further evaluate for model generalizability without employing the testing subset during the validation phase. We standardized features via z‐score (i.e., so that each feature had a mean centered around zero and standard deviation of one). Within the training sample, we first ran preliminary classifiers by considering the entire feature sets (i.e., all behavioral, task‐related, and rest‐derived features were fed into each of the three classifiers, respectively). During this phase, parameters for the classifiers were optimized by a grid search function and, following best practices (Poldrack et al., 2020), we employed a k‐fold cross‐validation procedure (k = 10) to evaluate the models. Second, we used recursive feature elimination cross‐validation (RFECV, k = 10) to eliminate redundant features and avoid potential overfitting problems (Saeys, Inza, & Larranaga, 2007).

In all cases, we used the Extreme Gradient Boosting (XGBoost) algorithm (Chen & Guestrin, 2016), which creates and combines individually weak but complementary strong classifiers, to produce a robust estimator. XGBoost provides parallel computation tree boosting for fast and accurate predictions, and regularized boosting to reduce overfitting and improve generalization (Torlay, Perrone‐Bertolotti, Thomas, & Baciu, 2017). XGBoost was implemented using the Scikit‐learn (v. 0.22.1) machine learning library on Python.

In keeping with current guidelines to report ML results (Uddin, Khan, Hossain, & Moni, 2019), classification accuracy values for the all‐feature and feature‐reduction approaches in the behavioral, task‐related, and resting‐state models were calculated together with the area under the curve (AUC) of the receiver operating characteristic (ROC) curve. Confusion matrices capturing the sensitivity and specificity of each classification were also calculated to estimate which model performed better. Finally, to establish which features were most relevant in each final classification, we employed the feature importance technique built into the XGBoost ML algorithm.

2.8. Prediction of task‐performance and expertise differences based on brain activity: A multiple regression approach

Finally, to further estimate the robustness and specificity of oscillatory topographical features in predicting error processing and motor expertise, we ran multiple regression analyses to evaluate two different brain models, one based on task‐related activity and the other based on resting‐state activity. For the task‐related model, we entered as the dependent variable the performance in error detection. For the resting‐state model, we used the hours spent by month in dancing Tango, since this is one of the best proxies to tackle motor expertise. Predictors in each model constituted the three most important features in the delta, theta, and mu rhythms identified by our all‐features classifiers. This analysis allowed us to disentangle whether the features captured by our machine learning approach in the different frequency bands were specifically associated with behavioral measures in error processing and motor experience in Tango dancing, as originally hypothesized.

Specifically, we reasoned that if theta activity is involved in error monitoring during action observation (Pezzetta et al., 2018; Spinelli et al., 2018), then the contribution of this predictor to the total variation explained in the model should be greater. In a similar vein, since mu‐rhythm is a hallmark of motor expertise (Denis et al., 2017), we expected that this predictor should be the one mostly contributing to explain motor expertise variability. We followed standard procedures for assessing multicollinearity and confirmed that tolerance (all values <1) and variance inflation factors (all <1.06) were low, indicating that multicollinearity did not affect our statistical analysis (see Table 4).

TABLE 4.

Multiple regression analysis results

	Coefficients	B	SE	Beta	t‐value	p‐value	Collinearity statistics
							Tolerance	VIF
Task model	CPL incorrect steps with gross errors θ	−0.107	0.024	−.58	−4.36	<.0001	0.91	1.09
	CPL correct steps δ	0.012	0.027	.06	0.45	.65	0.99	1.01
	CPL incorrect steps with gross errors μ	−0.002	0.02	−.01	−0.12	.9	0.91	1.09
Rest model	CPL μ	0.08	0.006	.9	12.75	<.0001	0.95	1.05
	B δ	−0.01	0.02	−.03	−0.47	.64	0.97	1.03
	B θ	−0.004	0.01	−.03	−0.41	.68	0.94	1.05

Note: Unstandardized and standardized coefficient values and significance levels for the task‐based and resting‐state models together with measures of collinearity.

p‐values marked with bold indicate statistically significant results.

3. RESULTS

3.1. Decoding expertise with behavioral and oscillatory network features

3.1.1. Skill‐related behavioral features

The machine learning classification between Tango dancers and naïves that included all 20 behavioral features yielded 100% accuracy. The ROC curve showed an AUC of 0.1, with 100% precision and 100% recall. When applying the feature‐reduction approach, behavioral data yielded an optimal number of 12 features with equal levels of accuracy and ROC‐AUC as in the all‐features approach. The confusion matrix in both cases showed a balanced profile between false positives and false negatives, with a precision of 100% and a recall of 100%. Among the 12 features selected by the RFECV approach, the most important features in classifying individuals according to their level of expertise were performance in detecting gross errors, familiarity with observed Tango steps, and hours spent by month in dancing Tango. To a lesser extent, frequency in performing the observed Tango steps and overall performance in error detection also showed relevance (Figure 2a).

FIGURE 2.

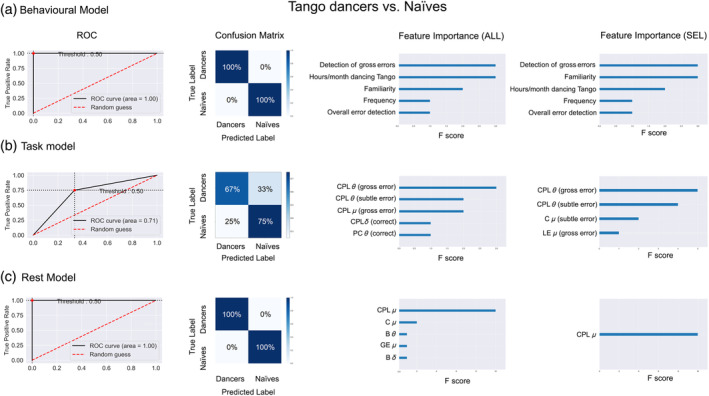
Machine learning results. Classification analysis (Tango dancers vs. Naïves) based on behavioral (a), task (b), and rest (c) functional connectivity features. On the left side, we plot the ROC curve and area under the curve (AUC) for each model. In the center, we provide the confusion matrix for each classifier. On the right side, we list the main features in order of importance for both classification analysis, with the approach including all the features (ALL) and the one including only those selected (SEL) based on the Recursive Feature Elimination (RFE) approach. B, betweenness centrality; C, clustering coefficient; CPL, characteristic path length; GE, global efficiency; LE, local efficiency; PC, participation coefficient; δ: delta (1.5–4 Hz); θ: theta (4–8 Hz); μ: mu (8–13 Hz)

3.1.2. Task‐related brain networks

Classification based on all 54 task‐based connectivity features yielded 72.73% accuracy. The ROC curve showed an AUC of 0.71, with 85.7% precision and 75% recall. The RFECV approach revealed an optimal number of four features, with classification showing equal levels of accuracy, ROC‐AUC, precision, and recall as those exhibited by the all‐features approach. The most important features included the CPL in theta for the gross and subtle error conditions, the C in mu for the subtle error condition, and the LE in mu for the gross error condition (Figure 2b). See Figure 3a for spatial topography distribution of brain network organization showing maximal strength difference between groups (Tango dancers > naïves) in δ, θ, and μ.

FIGURE 3.

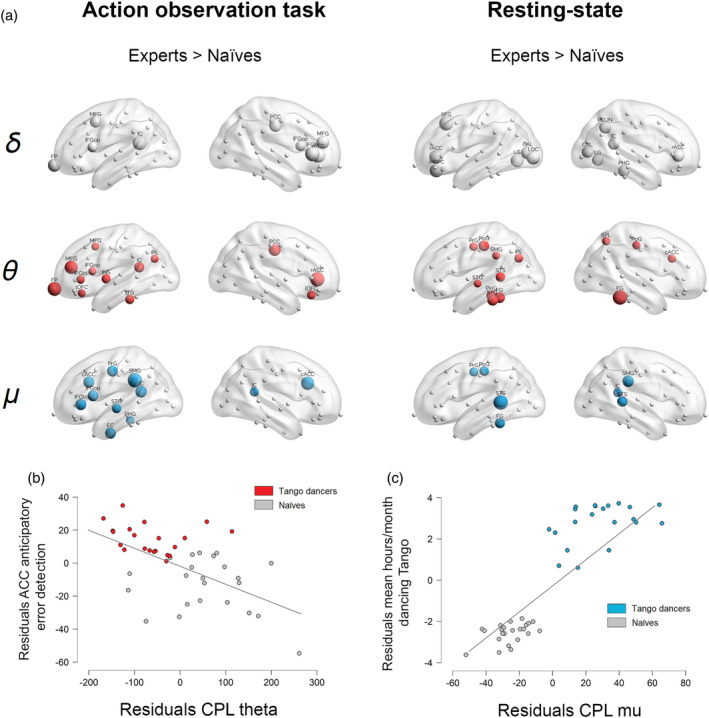
Task‐related and resting‐state network differences between Tango dancers and naïves and multiple regression results. (a) Spatial distribution of the brain network nodes showing maximal strength difference between groups (Tango dancers > naïves) in delta (δ = 1.5–4 Hz in gray), theta (θ = 4–8 Hz in red), and mu (μ = 8–13 Hz in blue) rhythms. For visualization purposes, critical nodes have been defined as those scoring 1 SD above the mean of the strength difference in each condition and frequency band. Node size is proportional to the strength difference between groups. (b) Individual coefficient plot for the main effect of theta CPL on action error discrimination performance, controlling for all other predictors. (c) Individual coefficient plot for the main effect of mu CPL on the amount of time spent in dancing Tango per month, controlling for all other predictors. Please note, that the top‐ranked graph feature in the ML approach (i.e., CPL) only provides one single score per participant (i.e., and not a score per brain region, which is a necessary requisite to plot neural networks). Thus, we used strength to visualize the networks, as this metric provides a more general estimate of the degree of functional connectivity of the whole network

3.1.3. Resting‐state brain networks

Finally, classification using all 18 resting‐state connectivity features reached 100% accuracy. The ROC curve showed an AUC of 0.1, with 100% precision and 100% recall. After RFECV, only one optimal feature was selected, namely CPL in mu, with classification showing equal levels of accuracy and ROC‐AUC as in the all‐features approach (Figure 2a). The confusion matrix in both cases (i.e., all and selected features) showed a balanced profile between false positives and false negatives, with a precision of 100% and a recall of 100% (Figure 2c).

3.2. Fine‐tuned oscillatory networks predict motor expertise

We ran a multiple regression analysis to estimate the robustness and specificity of the selected oscillatory properties of brain networks in predicting expertise. Briefly, we were interested in exploring whether the top‐ranked features highlighted by our all‐features machine learning approach, based on task‐related and resting‐state data, were specifically associated with behavioral measures of error detection and motor experience in Tango dancing.

Overall, the task‐based model explained a significant proportion of error detection variability (adjusted R ² = 30%; F = 7.04; p <.0001). In particular, theta connectivity (Beta = −.58, p <.0001) significantly predicted error processing (see Figure 3b), while delta (Beta = .06, p = .64) and mu (Beta = −.01, p = .9) connectivity did not.

On the other hand, the resting‐state model explained a large proportion of variability in Tango motor expertise (adjusted R ² = 79%; F = 56.04; p <.0001). Only the top‐ranked mu connectivity feature was a significant predictor of motor expertise (Beta = .9, p <.0001, see Figure 3c), with theta (Beta = −0.03, p = .68) and delta (Beta = −.03, p = .64) features showing nonsignificant regression coefficients. See Table 4 for further details.

4. DISCUSSION

Can motor expertise be finely decoded by brain network organization in specific frequency bands? To answer this question, we implemented a data‐driven multi‐feature approach considering task‐related and resting‐state connectivity features associated to task‐performance, error processing, and sensorimotor expertise and tested their power in classifying individuals with different levels of Tango expertise.

Unsurprisingly, behavioral measures showed an excellent classification (100%) between dancers and naïves. When considering brain network signatures, task connectivity measures were also good predictors, although to a lesser extent (~73%). The most discriminative feature during error anticipation was theta connectivity, a hallmark signature of error processing. Perhaps more strikingly, resting‐state connectivity in mu, an index of sensorimotor engagement, was as strong as behavioral features in predicting motor expertise, suggesting that prior knowledge of skilled actions can be sharply captured as a trait‐like fingerprint. Finally, the regression analysis confirmed the one‐to‐one associations between behavior and brain oscillations, with theta and mu connectivity predicting performance in anticipatory error detection and time spent in Tango dancing, respectively. Altogether, these findings underscore the power of oscillatory network measures in decoding fine‐grade signatures of expertise, highlighting the potential role of EEG markers in capturing neurodiversity for predicting skilled action acquisition.

4.1. Neurocognitive decoding of expertise

Behavioral results robustly classified individuals (100%). The most important features were anticipatory detection of gross errors, monthly hours spent dancing Tango, and familiarity with Tango steps. This finding was not surprising given that these questionnaire‐based measures were originally intended to estimate Tango expertise (Amoruso et al., 2014), with participant's performance reflecting a direct validation of our experimental design. Indeed, gross inconsistencies in Tango steps were better detected by experts than naïves (~90% and ~66%, respectively). Furthermore, while skilled participants reported >40 hr per month devoted to Tango dancing, naïves reported 0 hr. Additionally, dancers reported being familiarized with all steps shown in the videos, while naïves did not. This proxy measure of familiarity aimed at controlling for a match between the style danced by the participants and the one used as stimuli, namely, Tango Salon. Thus, the robust classification yielded in the behavioral model validates our design and reflects that individuals were reliably allocated into one or other group depending on their expertise level.

On the other hand, neuropsychological features reflecting empathy and executive functions did not distinguish among individuals. While previous evidence indicates that expert dancers can show differential behavioral and physiological sensitivity to others' affective body movement (Christensen, Gomila, Gaigg, Sivarajah, & Calvo‐Merino, 2016), this nonreplicated result may reflect the lack of significant between‐group differences in their profiles (i.e., individuals from both groups were balanced in terms of empathic and executive abilities). Indeed, when selecting the optimal features by means of RFECV, neuropsychological variables were removed from the model, indicating their weak/irrelevant role in between‐group classification.

4.2. Brain network metrics sensitive to expertise

Neurophysiological evidence (Pezzetta et al., 2018; Spinelli et al., 2018) suggests that theta activity constitutes a hallmark signature of error processing during action observation. Consistent with this evidence, we found that task‐related theta connectivity features were those better capturing individual differences in error processing. The most important feature was CPL for gross error anticipation. These errors constitute exaggerated disruptions in Tango steps more easily noticeable than subtle ones and, likely, more accurately anticipated based on ongoing kinematics. Indeed, in our previous study (Amoruso et al., 2014), anticipatory ongoing responses for gross errors started earlier in fronto‐central channels and showed higher amplitudes than subtle ones.

At the network level, areas showing maximal theta strength difference between groups were the medial frontal and anterior cingulate cortex, which have been linked to the observation and prediction of other's erroneous actions (Alexander & Brown, 2011; de Bruijn, de Lange, von Cramon, & Ullsperger, 2009; van Schie, Mars, Coles, & Bekkering, 2004).

We also predicted that sensorimotor expertise, indexed by mu‐rhythms, would discriminate individuals during action observation. This rhythm is modulated by participant's expertise with dance (Orgs, Dombrowski, Heil, & Jansen‐Osmann, 2008) and sport (Denis et al., 2017), with skilled participants showing greater mu‐desynchronization while anticipating known actions. Consistent with this view, mu features were those showing higher importance after theta ones. In this case, maximal mu strength differences were localized in classical AON nodes including the inferior parietal, precentral gyrus, and IFG (Caspers et al., 2010; Rizzolatti & Craighero, 2004).

Finally, delta connectivity features did not show relevance in the reduced‐features approach (and only a marginal one when using all features). Since this rhythm in involved in domain‐general aspects of task‐performance (i.e., attentional demands; Harmony, 2013), this finding possibly suggests that all participants, independently of their expertise level, were similarly engaged during the task.

Even though the task‐based classifier yielded a good accuracy rate, its performance was lower than the resting‐state classifier (see below), potentially due to the heterogeneous combination of processes captured by task‐related networks.

On the other hand, the resting‐state classifier proved to be as robust as the behavioral one (100%). While the all‐features classification underscored two top‐ranked mu attributes, the RFECV highlighted one unique mu feature (CPL), which offered the best discrimination between dancers and naïves. This suggests that mu‐rhythm can successfully capture individual differences in sensorimotor experience even when participants are resting, highlighting its role as a trait‐like marker of motor expertise. Nevertheless, it is also true that since we did not control for other sensorimotor experiences in the participants (e.g., sports practicing), we cannot completely rule out that this latter aspect may have influenced our results.

In keeping with EEG‐fMRI resting‐state evidence (Yin, Liu, & Ding, 2016), areas showing maximal mu strength difference were observed in classical sensorimotor regions and social cognition areas (e.g., STS).

The graph‐measure showing higher predictive value in task and rest approaches was CPL, with higher scores for experts than naïves. This finding aligns well with evidence from other motor domains (Wang et al., 2016), showing that world‐class gymnasts exhibit longer CPL than controls. Longer CPL indicates that neural information transfer proves more effortful (i.e., greater processing cost). This suggests that as individuals become skilled in a given action, increased connections between various brain areas/system may take place, thus requiring more steps while integrating meaningful information. Furthermore, for those network parameters showing significant between‐group differences, Wang et al. computed the ROC‐AUC to determine which of them better distinguished among groups. In line with our results, the parameter showing best performance was CPL (AUC = 0.77).

Importantly, the regression analysis provided robust complementary evidence by showing that the oscillatory features that were most discriminative of individuals in the task and rest models (namely, CPL in theta and mu) were also the most predictive of performance and sensorimotor expertise, respectively.

These findings also support a predictive coding view of action processing (Amoruso, Finisguerra, & Urgesi, 2016; Kilner et al., 2007; Urgen & Miller, 2015) in which prior sensorimotor knowledge is used to predict other's actions based on observed movement kinematics. Indeed, task‐based network connectivity was derived from those EEG‐segments in which participants were anticipating the unfolding of Tango steps based on ongoing kinematic information from dancers' feet. Our results suggest that this anticipatory resonance mechanism, known to be fine‐tuned in motor experts (Aglioti et al., 2008), can be sharply captured by distinct network signatures, with theta connectivity tracking individual differences in error anticipation and mu connectivity fine‐grained differences in the observers' motor system.

Furthermore, given the contextual nature of the experimental design (i.e., body coordination between couples and their movements unfolding in time), we suggests that participants were able to anticipate action errors based not only on their previous motor experience but also on the contextual information provided by the Tango step sequence being observed. This is compatible with a predictive coding framework highlighting that actions are not performed in isolation but rather context‐embedded, and thus for a role of contextual cues in shaping predictive process via establishing which motor intentions likely underpin an observed action (Amoruso & Finisguerra, 2019; Amoruso, Finisguerra, & Urgesi, 2018; Amoruso & Urgesi, 2016; Baez, Garcia, & Ibanez, 2017; Betti, Finisguerra, Amoruso, & Urgesi, 2021; Ibanez & Manes, 2012; Kilner, 2011; Maranesi, Livi, Fogassi, Rizzolatti, & Bonini, 2014).

4.3. Limitations

The present study is not without limitations. First, our sample size was rather small, although not smaller than those reported in similar EEG studies using oscillatory features for binary classification of individuals varying in their learning style (Jawed, Amin, Malik, & Faye, 2019) and other traits (Stevens & Zabelina, 2020). A recent state‐of‐the‐art comparison of classification algorithms (Zhang, Liu, Zhang, & Almpanidis, 2017) has shown that XGBoost, the algorithm implemented here, can be effective with small and large training sets, outperforming in all cases other more popular classifiers. Our findings were consistent across analyses (all‐features vs. reduced‐features approaches), with the number of selected attributes being considerably fewer than the number of samples/observations. Furthermore, by using a grid‐search approach, we tuned critical hyperparameters to control for potential overfitting (e.g., restricting the maximum depth of trees to low values of 3 and making the model conservative via high gamma values of 2). Thus, although future studies with larger sample sizes are needed to strengthen our conclusions, these considerations likely suggest that our findings were not biased by our “small data” approach.

Second, the order of EEG recordings was not counterbalanced across participants—that is, all participants completed the action observation task first and the resting‐state session afterward. Thus, we cannot completely rule out the potential effect of reentrant‐reverberant visual information of action stimuli in the resting‐state networks. This issue should be clarified by future research assessing resting‐state connectivity before and after action observation.

Third, our results are circumscribed to Tango dancing. However, generalizability is a key requisite of robust brain markers and future studies should test the predictive power of our models not only in an independent larger sample of participants, but also in other motor domains, including other dance styles and sports.

Finally, the present study does not address the relative performance and predictive power of different classification approaches (e.g., ML in comparison with more simple logistic regression methods). While this aspect goes beyond the scope of the study, we believe that using a ML framework has several advantages. For instance, ML requires minimal assumptions and proves more robust than parametric approaches regarding data heterogeneity (Makridakis, Spiliotis, & Assimakopoulos, 2018; Poldrack et al., 2020). Importantly, classification can be performed even in a set of variables with nonlinear interactions whereas logistic regression can only handle linear solutions (Bzdok, Altman, & Krzywinski, 2018; Bzdok, Krzywinski, & Altman, 2017). Combining ML with progressive feature elimination can identify main predictors, enhance classification, and provide a top assortment of features to classify outcomes (Montavon, Samek, & Müller, 2018; Nicholls et al., 2020). Indeed, by using an XGBoost ML approach combined with RFECV, we were able to identify the main behavioral and neurophysiological contributors explaining individual differences in motor expertise with a high predictive value, which was actually the main goal of this work. Nevertheless, future studies better suited to compare different classification approaches, should test this interpretation in deep.

5. CONCLUSIONS

Our findings show that motor expertise can be decoded at a fine‐grained level from network organization in specific frequency bands, with theta and mu connectivity indexing anticipatory error processing and sensorimotor expertise, respectively. Strikingly, participants' level of Tango expertise was predicted by resting‐state connectivity in mu with similar maximum power than behavioral measures, suggesting that this brain rhythm serves as a trait‐like fingerprint of network reorganization triggered by long‐lasting training. Promisingly, we show that EEG represents an affordable robust method to develop oscillatory markers for the evaluation of learning/training outcomes in healthy participants and, as a potential clinical avenue, in the prospective detection of motor‐related disorders.

CONFLICT OF INTEREST

The authors declare no potential conflict of interest.

ETHICS STATEMENT

The present study was approved by the Ethics Committee of the Institute of Cognitive Neurology (INECO).

Amoruso, L. , Pusil, S. , García, A. M. , & Ibañez, A. (2022). Decoding motor expertise from fine‐tuned oscillatory network organization. Human Brain Mapping, 43(9), 2817–2832. 10.1002/hbm.25818

DATA AVAILABILITY STATEMENT

All the data that support the findings of this study as well as the code for data preprocessing and analysis are available on request from the corresponding author.