Mapping the human connectome using diffusion MRI at 300 mT/m gradient strength: Methodological advances and scientific impact

Abstract

Tremendous efforts have been made in the last decade to advance cutting-edge MRI technology in pursuit of mapping structural connectivity in the living human brain with unprecedented sensitivity and speed. The first Connectom 3T MRI scanner equipped with a 300 mT/m whole-body gradient system was installed at the Massachusetts General Hospital in 2011 and was specifically constructed as part of the Human Connectome Project. Since that time, numerous technological advances have been made to enable the broader use of the Connectom high gradient system for diffusion tractography and tissue microstructure studies and leverage its unique advantages and sensitivity to resolving macroscopic and microscopic structural information in neural tissue for clinical and neuroscientific studies. The goal of this review article is to summarize the technical developments that have emerged in the last decade to support and promote large-scale and scientific studies of the human brain using the Connectom scanner. We provide a brief historical perspective on the development of Connectom gradient technology and the efforts that led to the installation of three other Connectom 3T MRI scanners worldwide – one in the United Kingdom in Cardiff, Wales, another in continental Europe in Leipzig, Germany, and the latest in Asia in Shanghai, China. We summarize the key developments in gradient hardware and image acquisition technology that have formed the backbone of Connectom-related research efforts, including the rich array of high-sensitivity receiver coils, pulse sequences, image artifact correction strategies and data preprocessing methods needed to optimize the quality of high-gradient strength diffusion MRI data for subsequent analyses. Finally, we review the scientific impact of the Connectom MRI scanner, including advances in diffusion tractography, tissue microstructural imaging, ex vivo validation, and clinical investigations that have been enabled by Connectom technology. We conclude with brief insights into the unique value of strong gradients for diffusion MRI and where the field is headed in the coming years.

I. Introduction

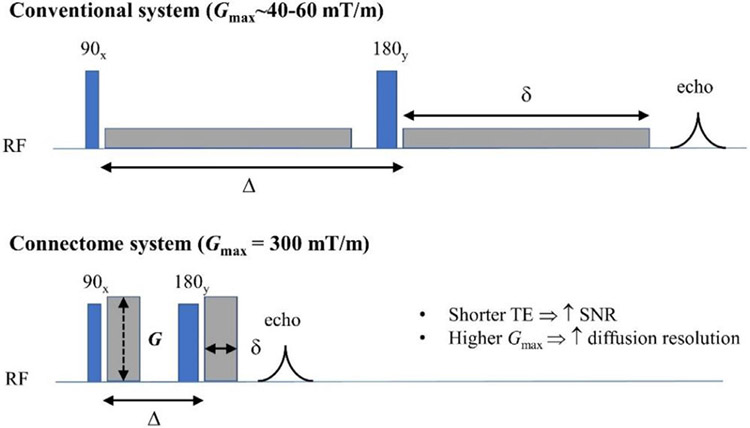
Since its launch in 2010, the Human Connectome Project (HCP) has attracted tremendous attention in the scientific community. Two consortia were awarded in the first phase of the HCP: one led by Washington University, the University of Minnesota, and Oxford University (the WU-Minn-Ox HCP consortium) [see (Elam et al., 2021 ) for details], and the other by Massachusetts General Hospital (MGH) and University of Southern California (USC) (the MGH-USC HCP consortium). The 3T Connectome MRI scanner¹ equipped with a 300 mT/m gradient system was one of the key hardware outcomes achieved in the HCP, led by the MGH-USC consortium. This “super” scanner, whose maximum gradient strength is seven times stronger than what was then considered the clinical standard, was purposely designed for pushing the limits of diffusion MRI (dMRI) and its capability to reconstruct white matter fiber connections in the living human brain. Descriptions of the system design (Setsompop et al., 2013) and initial demonstrations of its unprecedented capabilities (McNab et al., 2013a) were reported in the first special issue of the journal NeuroImage devoted to human connectomics (https://www.sciencedirect.com/journal/neuroimage/vol/80). An obvious advantage of high gradient strengths for dMRI is the improved signal-to-noise ratio (SNR) due to the much shorter echo times (TE) afforded by more efficient diffusion encoding, resulting in less signal loss incurred by T2 relaxation (Fig. 1). Strong diffusion-encoding gradients also enable the use of shorter diffusion-encoding gradient pulses (δ) and shorter diffusion times (Δ), which increase the sensitivity of the dMRI signal to smaller diffusion displacements, thereby encoding information regarding tissue microstructure at shorter length scales (~microns) (Fig. 2). The resulting increase in “diffusion resolution” also serves to sensitize the diffusion of water molecules to complex white matter structures. One of the major benefits to dMRI that the MGH-USC consortium set out to demonstrate using the Connectom scanner was the improved ability to resolve crossing fibers within a voxel using high b-value acquisitions acquired with reasonable SNR in the living human brain.

Fig. 1. Benefits of strong gradients for diffusion MRI.

High gradient amplitudes up to 300 mT/m on the Connectome system (bottom) achieve a given diffusion-encoding gradient area in less time compared to conventional gradient systems (top), as illustrated through the pulsed gradient spin echo diffusion MRI sequence. Benefits of strong diffusion-encoding gradients include shortening the entire diffusion-encoding period and echo time (TE), and hence increasing the signal-to-noise ratio (SNR) by reducing signal loss due to T2 decay. The larger gradient amplitudes also enable stronger diffusion encoding (i.e., larger diffusion-encoding gradient areas, larger q- values and b-values) to be achieved with shorter diffusion times, providing higher “diffusion resolution” to improve the capability of resolving smaller length-scales for probing tissue microstructure and for resolving complex white matter structures such as crossing fibers. RF = radiofrequency, δ = diffusion-encoding gradient pulse duration, Δ = diffusion time.

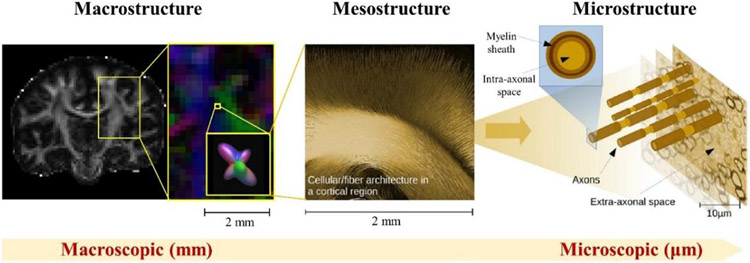
Fig. 2. Illustration of the different length scales accessible by diffusion MRI in the brain.

Macrostructure refers to structures on the whole-brain and regional level, while microstructure refers to structures on the microscopic level, e.g., cells and axons. Mesostructure resides in the intermediate, millimeter to sub-millimeter regime, on the order of the typical MRI voxel size. Figure contents adapted from (Reisert et al., 2017).

A number of excellent review articles on high gradient dMRI and the burgeoning field of in vivo tissue microstructural imaging enabled by such technology have been published in the last few years (Afzali et al., 2021b; Alexander et al., 2019; Duval et al., 2016; Henriques et al., 2021b; Jelescu et al., 2020; Jones et al., 2018; Kiselev, 2021; Nilsson et al., 2018; Novikov, 2021a, 2021b; Novikov et al., 2019, 2018; Palombo et al., 2018; Szczepankiewicz et al., 2021; Xu, 2021). In particular, the review by (Jones et al., 2018) focused on the topic of imaging tissue microstructure in the context of the opportunities and challenges introduced by this ground-breaking scanner and gradient system. The goal of this review article is to summarize the technical developments and advances that have emerged in the last decade to support and enable large-scale and scientific studies of the human brain using the Connectom scanner. We start from the engineering core – developments in gradient coil hardware, radiofrequency coil technology, image acquisition techniques, and data preprocessing methods – that is, the key elements of the imaging chain, from scanner to image. We then focus on the analytical studies that have been performed on and/or utilized data acquired from the Connectom scanner, which will provide insight into the unique value of strong gradients for dMRI and where the field is headed in the coming years.

II. Engineering core: Hardware, sequences and preprocessing

In this section, we discuss the engineering aspects of Connectom-related efforts, which have enabled the neuroscientific investigations that will be described in subsequent sections. The engineering advances include a description of the gradient hardware and scanner design, considerations of peripheral nerve stimulation, advances in acquisition techniques including RF coil development and innovations in imaging sequences and reconstruction, as well as strategies to control artifacts that are specific to the Connectom system, such as eddy currents and gradient nonlinearity.

1. Gradient hardware and scanner design

The rationale, design considerations, and optimization of the gradient coil and MGH Connectome scanner are described in detail in the article by Setsompop et al. (Setsompop et al., 2013). Here, we summarize the design process and specifications of the Connectom gradient coil, which targeted a maximum gradient amplitude of 300 mT/m and maximum slew rate of 200 T/m/s.

Engineering efforts for the MGH Connectome scanner began as a joint collaboration between MGH and Siemens. Initial design studies based on the Siemens SC72 whole-body gradient supported a maximum gradient strength of 100 mT/m and slew rate of 200 T/m/s. The design projections indicated that by reducing the linearity constraints, a maximum gradient strength of 150 mT/m could be reached with a single gradient power amplifier. Due to the large volume encompassed by the whole-body gradient coil with a 56 cm patient bore diameter, the number of current density layers and thereby the gradient amplitude could be doubled to achieve 300 mT/m, at the cost of a four-fold increase in coil inductance due to mutual coupling of the primary and secondary layers. To drive this large inductance at the high slew rate needed for EPI readout, a new gradient system concept involving multiple gradient amplifiers was created. In order to achieve the targeted slew rate of 200 T/m/s, each of the three physical gradient axes (G_x, G_y, and G_z) was divided into four independently driven segments, with each primary and shield pair driven by a separate gradient amplifier, yielding a total of 12 gradient amplifiers (four 900A drivers at 2250 V each per physical axis). Cooling layers were also increased by four-fold for efficient heat dissipation. The operation of this whole-body segmented gradient coil was anchored by the development of an MR control system capable of driving four sets of gradient amplifiers separately. When powered together, these amplifiers drove a gradient coil wound to attain a maximum gradient amplitude of 300 mT/m for high sensitivity dMRI at a maximum slew rate of 200 T/m/s for high-efficiency EPI image encoding. While peripheral nerve stimulation prevents the use of both high gradient strength and high slew rate simultaneously (see Section II.2: Peripheral nerve stimulation and safety considerations), these capabilities can be utilized during different portions of the dMRI sequence, with the diffusion encoding module using the maximum gradient strength but limited slew rate and the EPI image encoding utilizing modest gradient strengths and high slew rates.

The choice of scanner field strength (3T versus 7T) was made based on a number of considerations. Firstly, dMRI contrast is dictated by the displacement of water molecules in the presence of a magnetic field gradient and is independent of field strength. The image SNR is field strength-dependent, but the shorter T2 relaxation times at 7T partially offset the higher SNR afforded by higher field strength. Finally, magnet-gradient interactions were simpler to deal with at the lower field strength, including torques and forces as well as magnet heating effects. The gradient coil was built with a second-order shim set along its outer layer, with a final constructed weight of ~1400 kg. The high mass and stiffness of the finished gradient coil were advantageous as they served to lower acoustic noise and decrease vibrations.

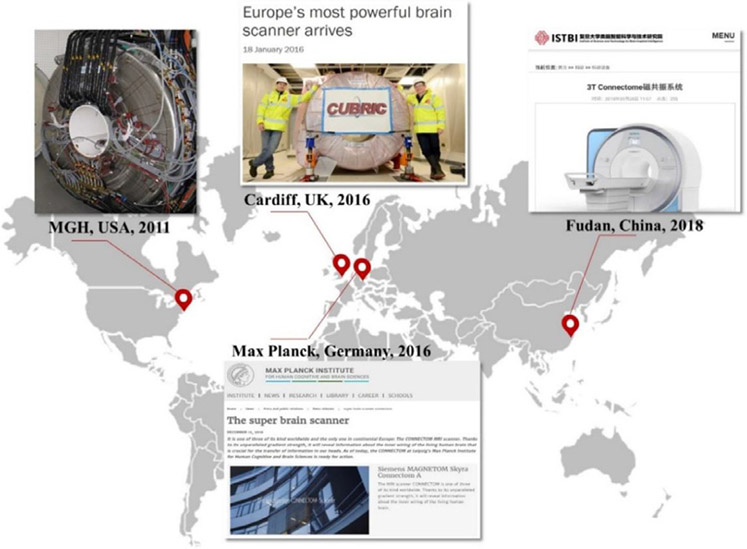
The first Connectome scanner installed at MGH in 2011 was intended to be a one-of-a-kind system built expressly for the HCP. The success of the engineering and technical development efforts, combined with the demonstrated promise and potential of high-gradient dMRI measurements for characterizing human brain structure, motivated the manufacturing and delivery of other Connectom MRI systems to select sites worldwide (Fig. 3). To date, these sites include: the Cardiff University Brain Research Imaging Center (CUBRIC) at Cardiff University in the United Kingdom; the Max Planck Institute for Human Cognitive and Brain Sciences in Leipzig, Germany; and the Zhangjiang International Brain Imaging Center (ZIC) supported by the Shanghai Municipal Government and Fudan University in Shanghai, China.

Fig. 3. Distribution of the four 300 mT/m gradient strength MRI systems installed worldwide.

Figure contents adapted from news announcements for the Cardiff University,² Max Planck Institute for Human Cognitive and Brain Sciences,³ and Fudan University.⁴

Beyond the whole-body design of the original Connectom system, head-only gradient designs have been advanced by several separate research projects in an effort to achieve high G_max and fast slew rates. For example, the MAGNUS (Microstructure Anatomy Gradient for Neuroimaging with Ultrafast Scanning) was developed as part of the Congressional Directed Medical Research Programs (CDMRP) supported by the U.S. Department of Defense. MAGNUS achieves up to G_max of 200 mT/m and 500 T/m/s slew rate (Foo et al., 2020). The 7T Impulse gradient (Feinberg et al., 2021), developed by Siemens Healthineers in collaboration with the University of California, Berkeley, and MGH is also specifically designed as a head gradient for brain imaging. The Impulse gradient is capable of up to 200 mT/m maximum gradient strength with a maximum slew rate of 900 T/m/s per axis. In addition, a next-generation human Connectome MRI scanner (Connectome 2.0) targeting a maximum gradient strength of 500 mT/m and 600 T/m/s is being engineered with a head-only design in collaboration with Siemens Healthineers and will be brought online to replace the current Connectome scanner at MGH (Huang et al., 2021b; Yendiki et al., 2020). In comparison to the body gradient design, the head-only design offers several advantages from an engineering perspective. First, head-only gradients allow for higher gradient performance due to the smaller bore size. Less stringent constraints arising from peripheral and cardiac nerve stimulation are expected due to less exposure of the body to the gradient field. Moreover, head-only gradients can be developed to be synergistic with higher field strengths by taking advantage of the smaller bore sizes and higher SNR afforded by stronger static magnetic fields. As an emerging trend, the head-only design represents a promising long-term direction for the development of future high gradient strength systems.

As a fruitful byproduct of gradient hardware development for the HCP, the strengths of the gradient systems delivered on commercial MRI scanners have continued to increase over the last decade. For example, the Siemens MAGNETOM Prisma 3T scanner and the GE Premier 3T scanner provide up to 80 mT/m and have been installed worldwide for clinical and research use.⁵ Philips developed the high-performance Quasar Dual gradient system (maximum gradient strength of 80 mT/m), which has been installed on different models, including the Achieva 3T system in 2006⁶ and the more recent Ingenia 3T CX model in 2017.⁷ The Vantage Centurian 3T system by Canon provides up to 100 mT/m gradient strength.⁸ Most recently, United Imaging announced the release of the μMR 890 3T system, which is equipped with a gradient system capable of up to 120 mT/m strength.⁹ The advances in gradient technology inspired by the HCP and related efforts have informed and crossed beyond the boundaries of academic inquiry and scientific research into commercially available clinical scanners, illustrating the far-reaching impact of the Connectome scanner and other high-gradient systems in healthcare and clinical practice.

2. Peripheral nerve stimulation and safety considerations

An important biological factor that was considered in the gradient coil design for the Connectome scanner was peripheral nerve stimulation (PNS), especially given the high gradient strengths employed in the diffusion-sensitizing gradient waveforms. PNS is a perceivable sensation generated by the rapid switching of MRI gradient coils (Glover, 2009; Schaefer et al., 2000). The rapid switching induces electric fields (E-fields) in the body powerful enough to evoke unwanted action potentials in peripheral nerves, leading to muscle contractions or tactile perceptions. PNS can render significant portions of the gradient hardware operational parameter space inaccessible to the user and is thus an important factor to consider in the design of high-performance gradient coils. As a whole-body gradient coil, the Connectome gradient system is substantially limited by PNS. In head-only gradient coils, the body is not exposed to the magnetic field as much, but in the latest generation of head-only gradient coils, the PNS effects are also becoming an acute limitation (Davids et al., 2021a; Tan et al., 2020a; Weiger et al., 2018).

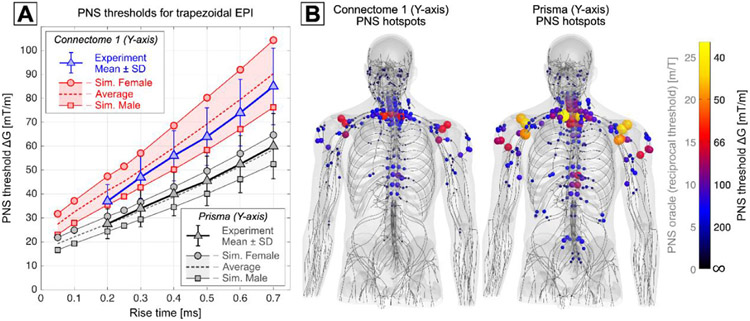
The PNS thresholds of an MRI gradient are typically given in terms of minimum stimulating gradient amplitude ΔG as a function of gradient slew period t_rise. In the range of rise times most relevant to MRI (100 – 2000 μs), the relationship between PNS thresholds and rise times is approximately linear, allowing the characterization of a given experimental setup by the y-axis intercept threshold ΔG_min (PNS threshold at zero rise-time). The exact threshold characteristics of a given coil geometry depend on various design aspects, including the coil geometry, the gradient axis (i.e., X, Y, or Z axis), and properties of the field of view (FOV), including the diameter and gradient linearity (Zhang et al., 2003). For example, decreasing the size of the FOV or tolerating a larger gradient non-linearity decreases the peak B-field excursion in the body, thus leading to lower induced E-fields and higher PNS thresholds. This relationship was utilized in the Connectome whole-body gradient coil by using a comparably small 20 cm FOV with a 6% gradient non-linearity (McNab et al., 2013a; Setsompop et al., 2013). This led to increased PNS thresholds compared to a more typical whole-body coil such as the Siemens Prisma gradient with a 50 cm FOV (Fig. 4A). Note that while the maximum gradient in EPI readout is still PNS limited despite the threshold gains from the small FOV, the peak amplitude of the gradient can be utilized in diffusion imaging when longer rise times are employed to prevent PNS.

Fig. 4. Peripheral Nerve Stimulation (PNS) Simulations.

A: Experimental and simulated PNS threshold curves given as minimum stimulating gradient amplitude AG as a function of rise time for the y-axis of the Connectome gradient (experiments in blue, simulation in red) and the Prisma gradient (in grayscale). PNS thresholds were obtained for a trapezoidal bipolar train with 0.5 ms flat top duration. B: Simulated activation maps plotted as PNS oracle hot-spots (reciprocal PNS thresholds) in the male model for a head-imaging position and for a trapezoidal rise time of 0.5 ms. The overall nerve activation induced by the Connectome y-axis gradient was substantially lower than that of the Prisma y-axis gradient. The activation hot-spots in both coils occurred in the shoulders (suprascapular nerve) and close to the cervical spine (intercostal nerves).

Recent advances in modeling PNS effects using electromagnetic-neurodynamic body models are helping to gain a better understanding of the “where and why” questions surrounding PNS and developing strategies to mitigate PNS (Davids et al., 2020, 2017, 2019; Davids et al., 2022). PNS models can predict threshold curves (similar to those typically obtained in experimental studies) as well as nerve activation maps. Figs. 4A and B show predicted PNS threshold curves and activation maps for the Connectome and Prisma gradients (y-axes), demonstrating good agreement between experimental and predicted PNS thresholds. PNS predictions can be used to inform the design phase of new gradient coils, either by directly including PNS metrics in the numeric boundary element method coil design algorithm (Davids et al., 2021b) or by manually analyzing candidate coil winding patterns. In both cases, the coil windings are iteratively adjusted to minimize PNS effects while satisfying the many other design constraints (i.e., field linearity and efficiency, shielding, coil inductance, wire spacing, power dissipation, etc.). Building on the insights gained from developing the MGH Connectome scanner, a similar approach is currently being used in the design phase of the Connectome 2.0 gradient system, see (Huang et al., 2021b) in this special issue for more details.

3. Advances in RF coils

With the advances in the highly parallel imaging acquisition technology such as SENSE (Pruessmann et al., 1999), GRAPPA (Griswold et al., 2002) and SMS (Setsompop et al., 2012), phased-array receiver coils are widely used nowadays and have played an important role in not only accelerating the image encoding but also improving reception sensitivity as well. Several dedicated multichannel coils have been developed as a result of the HCP efforts (Fig. 5), including a 32-channel head array coil, a 60-channel head-neck coil (Keil et al., 2011) for extended FOV brain and cervical spine dMRI acquisitions (Fig. 6) and a 64-channel brain only array coil (Keil et al., 2013). With more readily available large-volume three-dimensional (3D) printing techniques, as well as digital surface modeling and simulation tools (keil and wald, 2013), a 60-channel ex vivo brain slab array coil (Gruber et al., 2014) was designed to resemble a panini sandwich press to accommodate 1 to 5 cm thick brain slices and achieved a boost in SNR by a factor of 3.5, enabling focused acquisitions of brain slabs up to 350 μm isotropic spatial resolution and diffusion weighting of up to b = 30,000 s/mm² (Wieseotte et al., 2015). More recently, a close-fitting 48-channel ex vivo whole brain coil (Scholz et al., 2021) has been developed for imaging ex vivo whole brain specimens at sub-millimeter spatial resolution with high SNR (Ramos-Llorden et al., 2021).

Fig. 5. Select array coils developed for the Connectome MRI scanner.

Starting in 2011 with a 32-channel head coil, Connectome coil technology has evolved from a 60-channel head-neck array, a 64-channel brain array, and a 48-channel ex vivo brain coil all the way to a 64-channel head coil with an integrated field monitoring system in 2021. Figure adapted from (Gruber et al., 2014; Keil et al., 2013; Mahmutovic et al., 2021; Scholz et al., 2021).

Fig. 6. Combined brain and cervical-spine tractography.

Data was obtained from 1.5 mm isotropic diffusion acquisition using the 60-channel head-neck array coil.

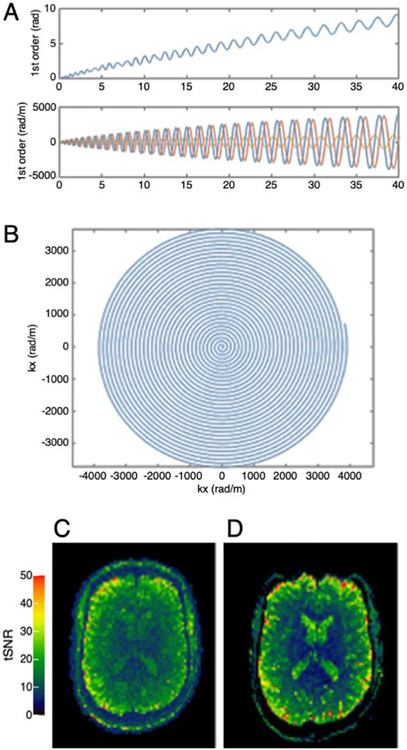
While the dual roles of the Connectome receiver coils in signal detection and image encoding have been successfully implemented, the current goal for the next generation of array coils for Connectome scans centers on embedding a third role into the receiver coil: namely, to incorporate probes that will enable dedicated field monitoring. Such field cameras are being used to concurrently monitor the field perturbations induced by higher-order eddy currents produced by the strong diffusion-sensitizing gradients on the Connectom scanner (Mahmutovic et al., 2021; Ramos-Llorden et al., 2022). The measured field can then be incorporated into the image reconstruction to correct for residual eddy current effects during the image readout and mitigate image artifacts (Barmet et al., 2008; Wilm et al., 2011, 2015). To create state-of-the-art highly parallel RF coil technology with an integrated field monitoring system (Mahmutovic et al., 2021), a 64-channel brain array coil with an integrated 16-channel field monitoring system (Skope Magnetic Resonance Technologies AG, Zurich, Switzerland) was developed that concurrently measures the spatiotemporal magnetic field dynamics during the acquisition (Fig. 7). Substantial reduction of blurring, aliasing, and distortions were observed in the resulting images. Although building high-density receiver arrays with a set of close-fitting field camera probes is challenging, the synergies between advances in gradient and receive coil technology ensure that these technologies will continue to evolve together for high-resolution dMRI in a productive way.

Fig. 7. Illustration of spiral image reconstruction using concurrent field monitoring.

(A) Zero-order phase and higher-order dynamic field effects; (B) first-order read trajectory. Examples of temporal SNR (tSNR) maps (calculated from a series of 20 repetitions) obtained with the 64-ch coil using (C) spiral and (D) EPI acquisitions. Images reconstructed from the spiral acquisitions using concurrently monitored field information do not show evident distortions. Figure adapted from (Mahmutovic et al., 2021).

4. Innovations in pulse sequences and image reconstruction

The dramatic advances in phased array receiver coil technology for dMRI have directly benefitted parallel imaging methodology development by enabling higher SNR and providing more flexibility in sequence design and image reconstruction. Owing to its ability to encode an imaging slice typically within 200 ms, EPI has been the dominant readout strategy in dMRI. In large-scale neuroimaging studies including Adolescent Brain Cognitive Development (ABCD) (Casey et al., 2018), UK Biobank (Miller et al., 2016) and especially the HCP, high angular and spatial resolution have provided increased sensitivity to crossing fibers and improved specificity to hard-to-image tracts (Sotiropoulos et al., 2013b). While EPI has high per-slice imaging efficiency, the need for high angular and spatial resolution dMRI with whole brain coverage has rendered these acquisitions extremely encoding intensive and created a need for additional efficiencies to be built in. To address this need, the HCP projects employed multiband (MB) acceleration (Feinberg et al., 2010; Larkman et al., 2001; Moeller et al., 2010), which reduces the repetition time (TR) by the number of simultaneously excited slices. As part of the MGH-USC Connectome project, blipped controlled aliasing (blipped-CAIPI) emerged as a popular encoding strategy (Setsompop et al., 2012). Blipped-CAIPI simultaneous multislice (SMS) imaging creates FOV shifts between the excited slices to better distribute the image aliasing. Since high acceleration leads to g-factor noise amplification, which is less tolerable in SNR-starved diffusion acquisitions, large-scale studies limited the MB factor to 3–4-fold in dMRI (Casey et al., 2018; Harms et al., 2018; Miller et al., 2016; Sotiropoulos et al., 2013b).

To push the limits of spatial resolution for dMRI, an important strategy is volumetric encoding. This approach either performs multiple 2D acquisitions with thin slabs and employs super-resolution reconstruction to resolve thin-slice information, or utilizes 3D phase encoding in the partition (kz) direction. There are three important commonalities between these approaches: (i) the entire volume is often divided into several slabs, (ii) they benefit from simultaneous multi-slab (SMSlab) encoding where a few slabs are excited together (analogous to the standard SMS strategy), and (iii) they have to estimate and eliminate phase differences due to motion across each slab’s encoding. An exemplary approach to the 2D, thin-slab acquisitions is gSlider (Setsompop et al., 2018), in which multiple acquisitions are made with different RF profiles to encode thin-slice information. Typically, a slab is five times thicker than its constituent slices, e.g., for 1 mm slice resolution, a 5 mm thick slab is excited. The RF profile is modulated across five different acquisitions, thereby performing Hadamard-like encoding (Oh et al., 1984; Saritas et al., 2014; Souza et al., 1988). The encoding matrix formed by the RF profiles is designed to have a small condition number. This ensures minimal noise amplification during the matrix inversion required for super-resolution reconstruction, through which thin-slice information is estimated. gSlider lends itself to SMSlab encoding, where as many as 10 thin slices (5 × from gSlider, 2 × from SMSlab) are excited simultaneously to provide volumetric noise averaging benefits. Phase differences between RF encodes are estimated and removed from interim blipped-CAIPI reconstructions for each shot, prior to super-resolution reconstruction. Hardware imperfections (e.g. B1 ⁺ nonuniformity) and T1 relaxation can be incorporated into the RF encoding matrix to mitigate potential slab boundary artifacts (Liao et al., 2020).

The gSlider acquisition has recently been employed to create a publicly-available reference Connectome diffusion dataset at 760 μm isotropic resolution across 1260 q-space samples, in which data were acquired on a single subject scanned across 9 two-hour sessions (Wang et al., 2021). gSlider can also be combined with multishot EPI (msEPI) encoding in the in-plane direction. This enables pushing the resolution to an unprecedented 600 μm isotropic resolution for in vivo dMRI, and is facilitated by high in-plane acceleration that reduces distortion, blurring and TE (Liao et al., 2021).

Spiral imaging provides efficient k-space transversal and presents a favorable alternative to EPI (Li et al., 1999; Liu et al., 2004), particularly in light of recent innovations in field-probe monitoring (Barmet et al., 2008) and expanded encoding model reconstruction, which have been shown to effectively mitigate the detrimental B0 and eddy-current blurring artifacts in spiral imaging to achieve high-quality diffusion imaging (Wilm et al., 2017). Spiral acquisitions can have significant SNR-benefit over EPI for diffusion imaging (Lee et al., 2021b). With its center-out readout strategy, a much shorter TE can be achieved when compared to EPI, which acts to reduce T2-related signal loss. Moreover, in accelerated acquisitions, spiral image encoding typically incurs a lower g-factor SNR penalty than EPI, thanks to its more favorable spreading rather than folding aliasing pattern (Lee et al., 2021b). Nonetheless, spiral acquisitions at high resolutions can suffer from significant T2* decay related image blurring, caused by the slower k_r transversal at the outer edges of k-space when compared to EPI. Multi-shot strategies can be employed to mitigate this issue (Liu et al., 2004; Truong and Guidon, 2014). Moreover, high-performance gradients can also be used to provide a faster k-space transversal and reduced blurring, while at the same time allowing for faster diffusion encoding to further reduce TE (Mueller et al., 2019b; Wilm et al., 2020). Using a custom-built high performance head gradient system (G_max 200 mT/m, S_max 600 T/m/s), high quality diffusion imaging with an in-plane resolution of 0.68 mm and b-value of 1000s/mm² was demonstrated via single-shot spiral acquisitions at an impressively short TE of 19 ms (Wilm et al., 2020). Analogous efforts are now underway on the Connectom MRI system to achieve shorter TEs beyond what is afforded by the strong gradients for diffusion-encoding and potentially enhance the sensitivity of the dMRI signal not only to diffusion but also myelin content (Mueller et al., 2019a).

5. Challenges posed by eddy currents & concomitant field terms

With the use of strong gradients on the Connectom system, eddy currents are generally more prominent than those observed on most clinical systems. Eddy current-induced magnetic fields [see Appendix for detailed formulation] produce geometric distortions in the acquired images (Jezzard et al., 1998) and may complicate the diffusion-encoding process in certain circumstances (Szczepankiewicz et al., 2020, 2019). As such, eddy currents and strategies to mitigate their negative effects have received considerable attention from investigators working on Connectom studies.

To compensate for eddy current effects on the Connectom system, typical hardware approaches, such as active shielding (Mansfield and Chapman, 1987; Roemer et al., 1986) and gradient pre-emphasis (Ahn and Cho, 1991; Jehenson et al., 1990; Morich et al., 1988; Van Vaals and Bergman, 1990), as illustrated in (Fig. 8a and b), were implemented. To compensate for the residual eddy current effects caused by the use of strong diffusion encoding gradients, additional approaches were also taken, which can be largely divided into three categories: image processing methods, image reconstruction methods that incorporate the measured and/or predicted eddy current effects, and methods that tailor the shape of diffusion encoding gradients to minimize the generation of eddy currents.

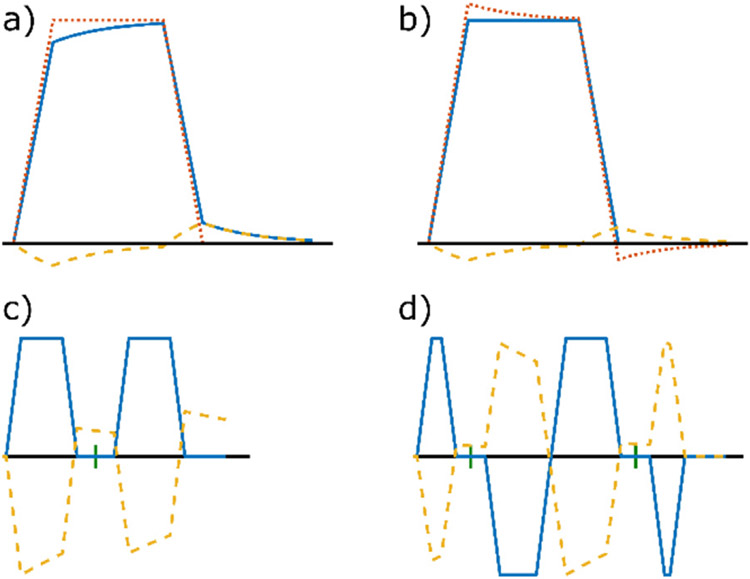
Fig. 8. Schematic illustration of diffusion-encoding gradients and induced eddy currents.

In the following diagrams, the x-axis represents time and the y-axis represents gradient strength. a) If the nominal temporal gradient profile (red dotted line) follows the desired shape, the actual gradient profile (blue continuous line) is distorted by eddy currents (yellow dashed line). b) This can be compensated by gradient pre-emphasis, i.e., overshooting the gradient profile. For demonstration purposes, the eddy current amplitude is exaggerated. c) Stejskal-Tanner diffusion encoding with eddy currents for a single time constant (with rescaled amplitude for better visibility). The short vertical dash between the two diffusion encoding lobes indicates the position of a 180° pulse. d) Twice refocused spin echo diffusion encoding with timing optimized to null the eddy current of this time constant. This method requires two RF pulses to achieve a high b-value and eddy current reduction.

Image processing methods correct for distortions after the images are acquired and are by far the most common approach to eddy current correction due to their ease of use and accessibility. In the case of strong eddy currents due to the use of strong diffusion-encoding gradients, the simplest affine registration-based algorithms (Haselgrove and Moore, 1996; Jezzard et al., 1998) may not be sufficient (Sotiropoulos et al., 2013b). Modern correction methods, such as the EDDY tool from the FMRIB Software Library (Andersson and Sotiropoulos, 2015, 2016), have advanced to accommodate for the distortions induced by higher-order eddy currents. EDDY makes use of the redundancy in the shell-sampled diffusion data, and adopts a Gaussian Process (GP) predictor to make predictions of data based on the fact that diffusion-encoding gradients of opposite polarities generate opposite eddy current effects. It iteratively solves for the model of eddy current-induced magnetic fields up to third order, which is then used to correct for image distortions. These methods were mainly developed for EPI and are not applicable to non-Cartesian sequences (e.g., spiral readouts).

For non-Cartesian readouts, the actual k-space trajectories need to be measured, either by phantom experiments (Brodsky et al., 2013; Duyn et al., 1998; Latta et al., 2007; Rahmer et al., 2019) or using field probes (Barmet et al., 2008, 2009; Dietrich et al., 2016). The nominal k-space trajectory is then replaced with the measured one in the image reconstruction step to compensate for the eddy current effects. This approach has been shown to be effective not only for non-Cartesian readouts corrupted by strong eddy currents (Edwards et al., 2021b; Lee et al., 2021b; Wilm et al., 2017, 2020) but also for EPI (Wilm et al., 2011, 2015).

Alternatively, eddy current effects can be counterbalanced by purposely designing temporal gradient profiles of opposite polarities, as illustrated for the classic Stejskal-Tanner encoding in (Fig. 8c). Similar strategies are also applicable to double diffusion-encoding scenarios (Mueller et al., 2017). This approach has the advantage that it can be combined with more flexible diffusion-encoding gradient schemes such as the free gradient waveforms used for b-tensor encoding (Yang and McNab, 2019). The main drawback arises from the concomitant field-induced dephasing that is caused by the non-symmetric gradient waveforms – that is, a purely linear gradient field is not compatible with the Maxwell equations, giving rise to higher order field distributions:

$$B_C=\frac{1}{2B_0}\left({\left(G_{x}z-\frac{G_{z}x}{2}\right)}^2+{\left(G_{y}z-\frac{G_{z}y}{2}\right)}^2\right)+higherorderterms$$

These fields grow with the square of the gradient amplitude, can become prohibitively large for twice refocused spin-echo scheme on the Connectome scanner (Setsompop et al., 2013) and can cause artifactually large and spatially varying b-values (Szczepankiewicz et al., 2020). The concomitant fields need to be considered explicitly in designing the gradient waveforms, and strategies to compensate for Maxwell terms in designing asymmetric gradient waveforms have also been explored and demonstrated (Szczepankiewicz et al., 2021, 2019).

6. Data preprocessing

In addition to eddy currents, the acquisition of dMRI data on the Connectom system faces several other challenges that may affect the data quality, thereby necessitating preprocessing of the data in order to ensure that the effects on downstream analyses are minimized. In this section, we discuss these challenges, their causes, manifestations and approaches to correction. We also refer readers to a separate review article included in this special issue (Tax et al., 2022) for a more general coverage of dMRI data preprocessing.

6.1. Gradient nonlinearity

By design, the gradient field on the Connectome MRI scanner is less linear than conventional systems (see Section II.1: Gradient hardware and scanner design). As a result, the gradient nonlinearity on the Connectom scanner induces noticeable spatially varying deviations from the expected gradient direction and intensity, resulting in marked distortions away from the center of the image. The 300 mT/m whole-body gradient coil has a tighter-fitting architecture with a much thicker shell compared to conventional gradient coils. The linear region of the gradient is therefore relatively small, and gradient nonlinearities may become apparent even within the brain itself. Nonlinearity in the imaging gradients results in image distortions, which may be moderated by reducing the FOV or corrected in the post-processing using the spherical harmonics description of the gradient profile provided by the vendor (Jovicich et al., 2006).

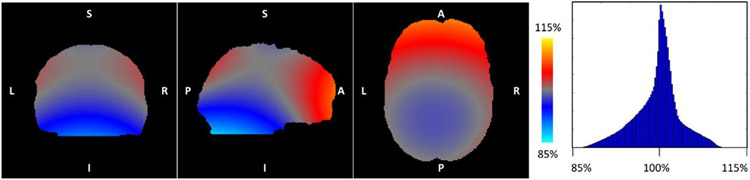
In addition to its impact on image encoding, gradient nonlinearity influences the diffusion encoding by modifying the b-values and directions of the applied diffusion gradients at each voxel. The impact of gradient nonlinearity on the diffusion weighting is particularly pronounced at high gradient strengths, since the b-value is proportional to the square of gradient amplitude. Gradient nonlinearity can result in deviations in the local effective b-value of up to ±15% for the Connectom gradient (Fig. 9) (Eichner et al., 2019). The adverse effects of gradient nonlinearity-induced variations in the b-values and b-vectors for diffusion model fitting (Mesri et al., 2020), fiber orientation estimation and tractography (Guo et al., 2021; Morez et al., 2021), b-tensor encoding (Paquette et al., 2020b) and Maxwell compensation when using asymmetric gradient waveforms (Szczepankiewicz et al., 2020) have been thoroughly studied, and consistent conclusions have been drawn among these studies that the impact of gradient nonlinearity on diffusion encoding cannot be neglected and must be corrected for, especially when using high gradient amplitudes.

Fig. 9. Maps of the deviation in diffusion encoding from the nominal prescribed b-value and corresponding histogram of the calculated variance across the whole brain volume.

The diffusion gradient direction [1, 0, 0] was used to generate the map. Figure adapted from (Eichner et al., 2019).

The impact of gradient nonlinearity on diffusion encoding can be compensated for by correcting the b-values and b-vectors using a spatially varying gradient coil tensor that calculates the actual gradient field produced by the coil using the known gradient profile (Bammer et al., 2003). For analyses in which the b-values for each diffusion-encoding direction are explicitly described in an analytical form, such as diffusion tensor imaging and diffusion kurtosis imaging (DKI), the correction for gradient nonlinearity is straightforward and simply uses the corrected b-values and b-vectors for the model fitting. If descriptions of the gradient profile are not available from the vendor, calibrations on phantoms can be used for corrections (Mohammadi et al., 2012). For spherical deconvolution (Tournier et al., 2007, 2004) and spherical mean technique (SMT) based approaches (Fan et al., 2020; Kaden et al., 2016a, 2016b), accounting for gradient nonlinearity in the diffusion gradients may require additional calculations (Paquette et al., 2019). Moreover, the gradient coil tensor is not only spatially varying but also temporally varying if the head position in the scanner changes due to motion. The spatiotemporal tracking of b-values and b-vectors has been demonstrated to produce the most consistent parameter estimates in the presence of large gradient nonlinearities (Rudrapatna et al., 2021), in which each voxel in every DWI volume is characterized by a distinct b-values and b-vector.

6.2. Susceptibility

Susceptibility-induced off-resonance fields lead to spatially varying image distortions in EPI images. These distortions will challenges in co-registering the diffusion data and anatomical data for subsequent connectome-related analyses, such as cortico-cortical diffusion tractography that relies upon cortical masks derived from T1-weighted images, or surface-based analysis (McNab et al., 2013b) that relies upon the cortical surfaces derived from the T1-weighted image. Image processing-based correction approaches often estimate the susceptibility-induced field from a pair of non-diffusion weighted images acquired with reversed phase encoding directions to compensate for the field inhomogeneity (Andersson et al., 2003). Modern correction methods have evolved to estimate the spatially varying field by tracking head movement and correcting for susceptibility-induced distortions (Andersson et al., 2018). More recently, approaches that utilize non-linear co-registration between distorted images and anatomical images without distortions (Bhushan et al., 2015; Schilling et al., 2020) have also been demonstrated.

6.3. Preprocessing pipeline

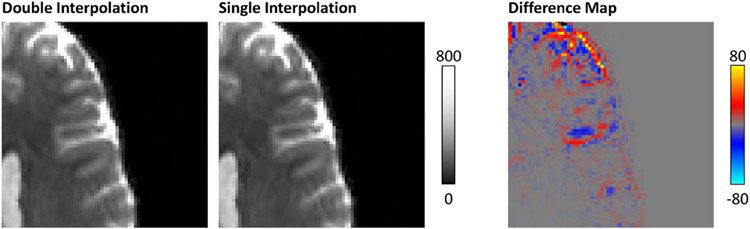
The order in which eddy currents, B₀ inhomogeneity, and gradient nonlinearity corrections are performed in the preprocessing pipeline have been found to impact the model fitting results significantly (Rudrapatna et al., 2021). Two distinct diffusion preprocessing pipelines have been proposed by the MGH-USC and WU-Minn-Ox HCP consortia. The MGH-USC pipeline corrects for the gradient nonlinearity first, followed by eddy current correction (Fan et al., 2016), while the WU-Minn-Ox pipeline adopts the opposite order, i.e., correcting for B₀ inhomogeneity and eddy currents first and finally gradient nonlinearity (Glasser et al., 2013). The performance of each pipeline depends on the amount of gradient nonlinearity and/or motion present in the data. In (Rudrapatna et al., 2021), comparisons were made between different orders of preprocessing steps (as in that of the MGH-USC pipeline versus the WU-Minn-Ox pipeline) using a dataset acquired on the Connectom system installed at Cardiff. They found that there is no obvious preference for the ordering of the preprocessing steps, and the performance of the preprocessing pipeline depends on the specific characteristics of the data and acquisition parameters. For example, in cases where the gradient nonlinearity was more severe, performing gradient nonlinearity correction first followed by simultaneous eddy current and susceptibility correction gave the best results. On the other hand, when extensive motion was present, EDDY+TOPUP followed by gradient nonlinearity correction performed better. Moreover, combining the interpolations from multiple intermediate preprocessing steps into a single step will avoid unnecessary image blurring and loss of structural details arising from multiple successive interpolation steps (Eichner et al., 2019). The negative effect is most pronounced at tissue boundaries, where signal differences on the order of ±10% can be observed (Fig. 10).

Fig. 10. Effects of distortion correction with double versus single interpolation.

The left and middle panels compare enlarged views of a b = 0 image corrected using two successive interpolation steps versus a single concatenated interpolation. Adapted from (Eichner et al., 2019).

6.4. Other considerations

In addition, preprocessing steps that are not particular to the Connectom gradients also benefit the subsequent model fitting and analysis (Ades-Aron et al., 2018; Cieslak et al., 2021), such as B₀ drift correction (Vos et al., 2017), noise reduction and noise level estimation (Veraart et al., 2016b, 2016c), as well as correction for Gibbs ringing artifact (Kellner et al., 2016; Veraart et al., 2016a) and partial-Fourier acquired data (Lee et al., 2021a; Muckley et al., 2021). It is worthwhile to mention that typical image data, which consist of the magnitude of complex values, follow a Rician distribution. This introduces a noise floor for high b-value Connectom data and can bias subsequent model fitting (Fan et al., 2020; Veraart et al., 2020). One solution is to correct this bias in magnitude data, based on the noise level estimated from repeated experiments (Koay and Basser, 2006). Another solution is to acquire both the magnitude and phase data and compute the real vcomponents of the complex data, which is characterized by Gaussian-distributed noise and can provide true signal averaging with significantly reduced noise bias (Eichner et al., 2015). Noise reduction algorithms such as Marchenko-Pastur principal component analysis (MPPCA) (Veraart et al., 2016b, 2016c) have also been adapted to complex data to suppress the effects of Rician noise (Lemberskiy et al., 2019, 2021; Moeller et al., 2021, 2017). In addition, the SENSE1 coil combine method (Sotiropoulos et al., 2013c) is an effective approach to reducing the noise floor in the magnitude data by incorporating coil sensitivity profiles when the images from individual receiver coil elements are combined.

III. Scientific impact

The advances in hardware, acquisition technology and preprocessing techniques developed for the Connectom MRI system provide the technical framework upon which scientific investigations can be launched. In this section, we first discuss the data resources made available by Connectom research efforts, starting with the data-sharing component of the MGH-USC Connectome project. We then review how high-gradient systems have been broadly utilized in the pursuit of comprehensive mapping of structural connectivity and tissue microstructure in the living human brain. Such use cases include identifying complex fiber configurations to improve diffusion tractography, resolving tissue microstructure by leveraging the enhanced diffusion resolution afforded by high gradient strengths, developing ex vivo dMRI as a tool for mapping connectional anatomy at mesoscopic resolutions, and investigating potential non-invasive biomarkers of tissue integrity in a variety of neurological disorders.

1. Dissemination of connectom data

Direct access to the in vivo acquisition capabilities afforded by 300 mT/m gradient strengths has thus far been limited, since only four Connectom scanners have been installed worldwide, lending a unique importance and role to data-sharing efforts. The MGH-USC Connectome project took a first step toward this goal in 2014 by releasing a dataset from 35 healthy adults scanned at this unique facility (Fan et al., 2016) to the broader scientific research community. In subsequent years, as new image acquisition methods were developed and greater experience was accrued on Connectom systems worldwide, the imaging data resources that were disseminated improved in both quality and quantity. Indeed, a growing number of datasets have been made accessible in the past few years, either in perpetual data repositories (Fan et al., 2018b, 2016; Koller et al., 2021; Tian et al., 2022; Wang et al., 2021) or through organizing computational competitions such as the International Symposium on Biomedical Imaging (ISBI) challenge on white matter modeling (Ferizi et al., 2017) and Medical Image Computing and Computer Assisted Intervention (MICCAI) challenges on cross-scanner and cross-protocol diffusion data harmonization (Ning et al., 2020a; Tax et al., 2019) . Each of these datasets was acquired with a unique focus (Table 1) and hence different imaging parameters, such as spatial resolution and b-value. Both high spatial resolution and b-value are desired characteristics in diffusion MRI data, but there is a fundamental trade-off between the two due to the SNR limit (Fan et al., 2017), and the actual choice of the balance depends on the goal of the study and what specific information is of most interest. Although sub-millimeter resolution has been demonstrated on the system (Setsompop et al., 2018), most of the shared datasets used higher gradient strengths and compromised on spatial resolution (typically ~2 mm), as listed in Table 1. This was especially the case for datasets tailored to microstructural modeling, where the high gradient strength of the Connectom system is critical for achieving diffusion resolution and sensitivity to axonal sizes that go beyond what other high-end commercial gradients can offer (Veraart et al., 2019).

Table 1.

Representative Connectom datasets disseminated through data repositories or challenge competitions.

Datasets (References)	Site of Acquisition	Data Repository	Data Description in Brief
MGH HCP Adult Diffusion (Fan et al., 2016)	MGH	ConnectomeDB https://db.humanconnectome.org, or Laboratory of Neuro Imaging Image Data Archive (LONI IDA) https://ida.loni.usc.edu	35 healthy adults b-values = 1000, 3000, 5000, 10,000 s/mm2 voxel size = 1.5 mm isotropic
ISBI 2015 Challenge on White Matter Modeling (Ferizi et al., 2017)	MGH	The Challenge Website: http://cmic.cs.ucl.ac.uk/wmmchallenge	1 healthy adult 48 shells acquired (36 for training, 12 for testing) b-value up to 45,900 s/mm2 voxel size = 2 × 2 × 4 mm
MICCAI 2017 & 2018 Challenge on Data Harmonization (Tax et al., 2019) (Ning et al., 2019)	Cardiff	CUBRIC Center https://www.cardiff.ac.uk/cardiff-university-brain-research-imaging-center/research/projects/cross-scanner-and-cross-protocol-diffusion-MRI-data-harmonization	15 healthy adults, across 3 scanners and 5 acquisition protocols b-value up to 5000 s/mm2 voxel size down to 1.2 mm isotropic
Taxon phantom (Fan et al., 2018b)	MGH	XNAT Central database https://central.xnat.org (ProjectID: dMRI_Phant_MGH)	Biomimetic phantom, b-values up to 18,250 s/mm2 Δ = 20, 30, 40, 50 ms voxel size = 2 mm isotropic
gSlider diffusion data (Wang et al., 2021)	MGH	Dryad https://doi.org/10.5061/dryad.nzs7h44q2 (Part I) https://doi.org/10.5061/dryad.rjdfn2z8g (Part II)	1 healthy adult, 9 two-hour sessions b-values = 1000, 2500s/mm2 voxel size = 760 μm
MICRA (Koller et al., 2021)	Cardiff	Open Science Framework https://osf.io/z3mkn/	6 healthy adults, each with 5 repetitions b-value up to 6000 s/mm2 voxel size = 2 mm isotropic Relaxometry and Quantitative Magnetization Transfer (QMT) data also available
MGH Connectome Diffusion Microstructure Dataset (CDMD) (Tian et al., 2022)	MGH	FigShare https://doi.org/10.6084/m9.figshare.c.5315474.v1	26 healthy adults b-value up to 17,800 s/mm2 Δ = 19, 49 ms; 8 b-values per Δ voxel size = 2 mm isotropic

The dissemination of Connectom data has facilitated research in the broader scientific community from various perspectives, including improving methods of q-space signal representations (Sun et al., 2019; Tian et al., 2019; Varela-Mattatall et al., 2020; Yeh and Verstynen, 2016), noise management (Dela Haije et al., 2020; St-Jean et al., 2020a), data harmonization (Moyer et al., 2020; Ning et al., 2020a; St-Jean et al., 2020b; Tax et al., 2019), resolving multiple fiber bundles (Morez et al., 2021; Shakya et al., 2017; Shi et al., 2021; Tristan-Vega and Aja-Fernandez, 2021), improving diffusion tractography (Benou et al., 2019; Farooq et al., 2019; Girard et al., 2017; Horn et al., 2017; Maffei et al., 2018, 2019; Makris et al., 2016; Ou et al., 2021; Safadi et al., 2018; Siless et al., 2018; Tang et al., 2019; Uesaki et al., 2018; Wang et al., 2019, 2020; Wegmayr et al., 2019; Zhang, 2018), advancing efforts to understand diffusion signal characteristics and parameter estimation (Aja-Fernández et al., 2020; Ferizi et al., 2015; Fick et al., 2016; Harms et al., 2017; Henriques et al., 2021a; Lanzafame et al., 2016; Li et al., 2018, 2019a; Li et al., 2019b; Mozumder et al., 2019; Palombo et al., 2020; Qin et al., 2021), as well as serving as benchmark training data for artificial intelligence-mediated artifact removal (Ding et al., 2019; Schilling et al., 2020) and image reconstruction (Antun et al., 2021; Koonjoo et al., 2021; Xu et al., 2019; Zhu et al., 2018). Other studies have used these data to investigate whether a dMRI protocol with very high b-values offers advantages over the more widely available b_max = 3000 s/mm² HCP protocol of (Harms et al., 2017). For example, (Maffei et al., 2019) found probabilistic tractography to be most reliable with the highest b-value, while (Li et al., 2019a) found that $\overline{S}$ was more specific to the intra-cellular signal component at high b-values (b ≥ 3000 s/mm²). Finally, the Connectom data of Fan et al. (2016) have been used to develop a comprehensive white-matter tract atlas that is distributed freely as part of the FreeSurfer software suite (https://dmri.mgh.harvard.edu/tract-atlas/). When these manually annotated tracts are used as training data for global probabilistic tractography, they allow the same tracts to be reconstructed automatically and with high accuracy from much lower quality dMRI data (Maffei et al., 2021). This is an example of how the benefits of a Connectom system can be extended to studies that collect data with much more widely available scanners.

2. Fiber orientation estimation and diffusion tractography

Taking advantage of the unique capabilities of Connectom systems to improve inference of fiber orientations and reconstruction of white-matter pathways is an active area of research. On the one hand, the reduced TE and thus increased SNR per unit b-value that can be achieved with higher gradient strengths enables dMRI acquisitions with higher spatial resolution, which enables the resolution of smaller white-matter bundles (Jones et al., 2018). Increased spatial resolution is also helpful in mitigating the signal bias toward white matter near the boundary between cerebral cortex and white matter, yielding more accurate fiber orientation estimates close to that boundary. On the other hand, higher gradient strength also enables acquisitions with higher b-values, which have been shown experimentally to yield sharper orientation distribution functions and are thus beneficial in areas of fiber crossings (Fan et al., 2014). However, there is a trade-off between the spatial resolution and b-value achievable for a given SNR level. Thus, early work focused on fusing data acquired with high spatial resolution or with high b-values, to take advantage of their complimentary benefits. Resolutions Unified for Bayesian Inference of X-ings (RubiX) is a method for data fusion of lower- and higher-resolution dMRI scans (Sotiropoulos et al., 2016, 2013a). It was applied to fuse HCP data acquired at 3T (1.25 mm, b_max = 3000 s/mm²) and 7T (1.05 mm, b_max = 2000s/mm²) (Sotiropoulos et al., 2016, 2013a). For data collected with a Connectom system, the HIgh B-value and high Resolution Diffusion Integrated Diffusion (HIBRID) method was proposed to fuse data acquired with a high b-value (2 mm, b = 8000 s/mm²) and data acquired with high spatial resolution (1 mm, b = 1500s/mm²), allowing high-definition imaging of fiber orientations in both white matter and cortex (Fan et al., 2017, 2015).

The nonlinearity of the Connectom gradient coil is a confound for fiber orientation distribution estimation algorithms such as spherical deconvolution (Anderson, 2005; Jeurissen et al., 2014; Tournier et al., 2004), as the applied b-value depends on the spatial location and the diffusion-encoding direction (also see II.6.1: Gradient nonlinearity). Recent work extended the conventional spherical deconvolution approaches by replacing the second-order tensor with more complex response functions, which depend on both the direction and the strength of the diffusion-encoding gradient (Guo et al., 2021; Morez et al., 2021). This was shown to yield more accurate fiber orientation estimates in the presence of gradient nonlinearities, as well as for data collected with non-shell q-space sampling schemes.

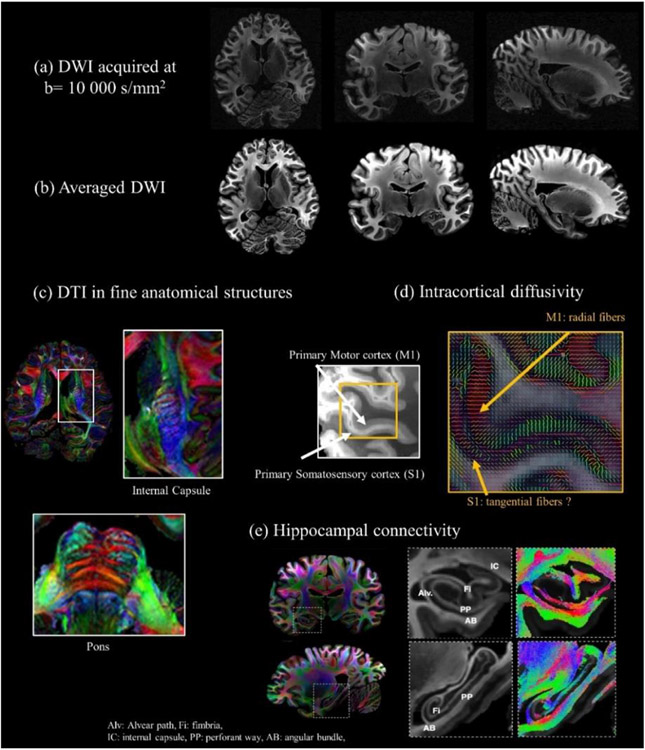
The unprecedented spatial and angular resolution of dMRI data collected with high-gradient systems has enabled the reconstruction of small white matter pathways that were previously impossible to resolve with in vivo dMRI. These pathways include, but are not limited to, the acoustic radiation (Maffei et al., 2018), Meyer’s loop of the optic radiation (Chamberland et al., 2018), brainstem pathways (Edlow et al., 2016; McNab et al., 2013a), projections of Brodmann area 6 to the pyramidal tract (Wang et al., 2019), the subthalamic nucleus (STN)-cerebellum pathway (Wang et al., 2020), the fornix (Perea et al., 2018), and short association fibers in the visual pathway (Movahedian Attar et al., 2020). After these pathways are reconstructed from Connectom data, they can be used to build high-definition atlases (Maffei et al., 2021, 2019; Shan et al., 2019) to train algorithms for reconstructing the same pathways automatically in lower-quality dMRI data (Maffei et al., 2021, 2019; Shan et al., 2019), or to study structure-function relationships with greater specificity (Movahedian Attar et al., 2020).

A major challenge in determining whether these advances have improved the accuracy of fiber orientation estimation or tractography in the brain is that the ground truth of brain circuitry is not fully known. A detailed discussion of post mortem microscopy methods that have been used to validate dMRI, and the key findings of those validation studies, is provided elsewhere in this issue (Yendiki et al., 2021). Here we refer to studies that have compared single- or multi-shell sampling schemes that would be feasible with widely available human scanners (the equivalent of b_max = 3000 s/mm² in vivo) to a denser sampling of q-space that would only be feasible with Connectom scanners (the equivalent of b_max = 10,000 s/mm² in vivo). These validation studies have shown a modest but consistent advantage of ultra-high b-values in terms of the accuracy of fiber orientation estimates (Jones et al., 2020, 2021) or tractography (Grisot et al., 2021; Maffei et al., 2021). A possible explanation for why this advantage is not greater may be that current approaches to the inference of fiber orientations cannot take advantage of the information content in ultra-high b-value data. Specifically, the aforementioned validation studies show that the white-matter areas where errors occur consistently involve complex fiber configurations that go beyond crossings, such as branching, fanning, and turning. Conventional methods for inferring fiber orientations involve antipodally symmetric orientation distribution functions, which were designed to model fiber crossings. This points to a need for methods that can resolve fiber configurations with antipodal asymmetry.

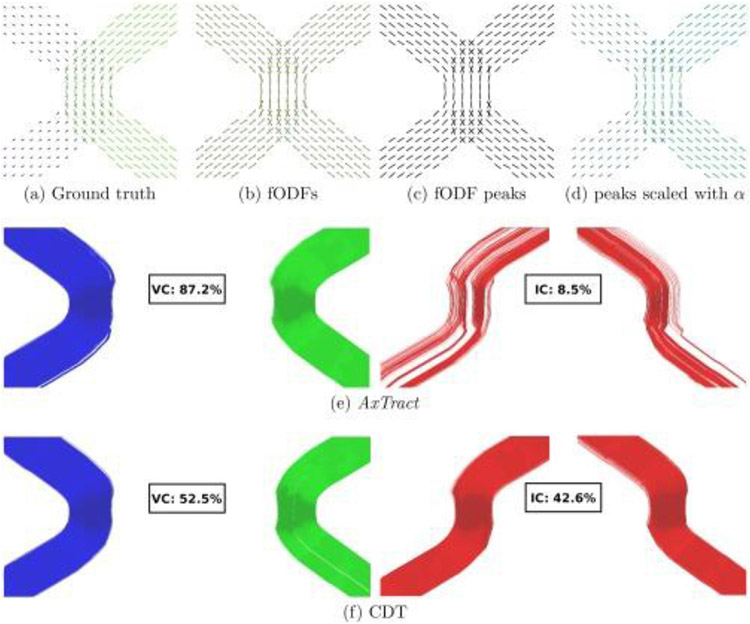
Certain methods have attempted to resolve antipodally asymmetric fanning configurations, either by modeling (Savadjiev et al., 2008) or by using information from neighboring voxels (Bastiani et al., 2017; Reisert et al., 2012). Another approach to overcoming the ambiguities in antipodally symmetric orientation distribution functions is microstructure-informed tractography. One such example is the AxTract framework (Girard et al., 2017) (Fig. 11), in which tractography was informed by microstructure such as the apparent distribution of axon diameters within fascicles (see (Daducci et al., 2016) for an in-depth discussion of microstructure informed tractography). As the diffusion resolution in microstructural imaging also critically depends on gradient strength, Connectom systems have the potential to increase the accuracy of in vivo white matter tract reconstruction through the integration of advanced microstructure imaging and tractography.

Fig. 11. Illustration of the AxTract framework.

(a) Ground truth directions used to generate the data with their lengths scaled by the axon diameter index α. (b) Estimated fiber ODFs (fODFs), (c) fiber ODF peaks and (d) fiber ODF peaks with their lengths scaled by α, (e) show valid connections (VC) and invalid connections (IC) for AxTract. (f) VC and IC for conventional deterministic tractography (CDT) are provided for comparison. Figure adapted from (Girard et al., 2017).

3. Tissue microstructure

Beyond mapping the macroscopic connectome, the high gradient strengths available on the Connectom scanner have introduced the possibility of probing tissue microstructure in the living human brain. Traditionally, histology has been considered the gold standard approach for gleaning information about tissue structure at the microscopic scale, including information regarding cell size and morphology. However, histology is limited to ex vivo assessment in fixed tissue. Diffusion MRI is sensitive to the restriction of membrane structures in neural tissue that is beyond the nominal spatial resolution of dMRI (~millimeters), offering a powerful non-invasive tool to infer tissue microstructural properties such as axon diameter and relative compartmental volume fractions in vivo, and thus provides a bridge between the macroscopic scale tissue features at the whole-brain level and the microscopic cellular details seen under a light or electron microscope (see (Weiskopf et al., 2021) for a review on the topic of quantitative MRI and in vivo histology).

The main advantages of high gradient strengths for assessing tissue microstructure lie in the high diffusion resolution and high SNR / low TE per b-value and voxel size. Diffusion resolution is the minimum length-scale that can be resolved in dMRI experiments and is critically limited by the maximum gradient amplitude G_max and the minimum detectable percentage of signal change (Nilsson et al., 2017) – that is, the higher the G_max and SNR, the smaller the resolution limit. Many applications were made possible for in vivo human imaging by the high gradient strengths on the Connectom scanner, which were previously only feasible in NMR experiments (Callaghan, 1993) or on pre-clinical systems. Axon diameter mapping is one of the most prominent examples and will be discussed in greater detail here.

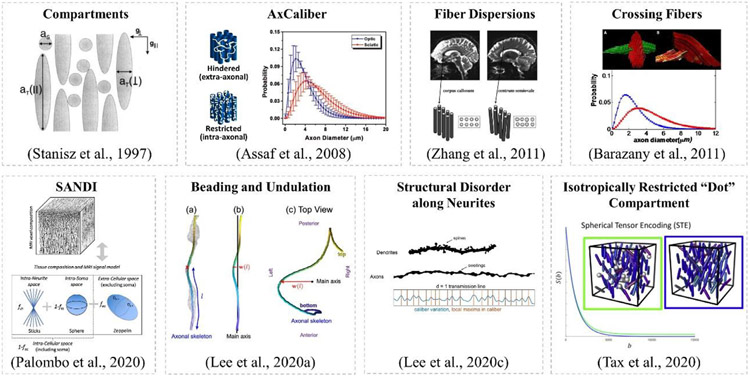
Measuring pore size using dMRI dates back to earlier experiments in MR microscopy (Callaghan, 1993; Callaghan et al., 1979; Cory and Garroway, 1990). The concept of decomposing the MRI signal into various tissue compartments was first proposed by (Stanisz et al., 1997), where the short axis of an ellipsoid was associated with axon diameter (Fig. 12a). More recent models of white matter represent axons as straight, impermeable cylinders. The AxCaliber model (Fig. 12b) (Assaf et al., 2008) was developed and demonstrated using porcine sciatic and optic nerves and porcine spinal cord on preclinical platforms, where a single fiber orientation was assumed to be known, and the diffusion weighting was only applied in the direction perpendicular to the fiber orientation. A gamma distribution was used to model the distribution of axon diameters. The first in vivo AxCaliber experiment was performed in the corpus callosum of a rat brain (Barazany et al., 2009) and in vivo in the human corpus callosum (McNab et al., 2013a) and spinal cord (Duval et al., 2015) on the MGH Connectome scanner. In particular, high gradient strengths were found to be beneficial for gaining greater sensitivity to axonal diameter in empirical studies performed in humans on the Connectome scanner (Huang et al., 2015b) and in ex vivo animal brains on small-bore scanners (Dyrby et al., 2013; Sepehrband et al., 2016). In such models, multiple diffusion times are important for differentiating between restricted and hindered water compartments. High gradient strength systems enable shorter diffusion times compared to conventional systems.

Fig. 12.

Illustration of diffusion models and key concepts. The concept of compartmentalization was initially proposed by Stanisz et al. (a), following which the AxCaliber aims to estimate the diameter distribution of the restricted water compartment (b). Variations of the AxCaliber model was proposed, such as modifications to account for fiber dispersions (c) and crossings (d). Realistic axons are very different from ideal cylinders, instead, there are plenty of beadings and undulations (f) and structural disorder are commonly seen along neurites (g). In gray matter, a sphere (e) or dot (h) compartment is incorporated into the physical model to account for additional signal component present in the measurement. Figure adapted from the papers labeled therein.

To generalize the estimation of axon diameter to fibers of arbitrary orientation, methods like ActiveAx (Alexander et al., 2010) and Tract-Caliber (Huang et al., 2015a, 2020) were developed for axon diameter mapping in the living human brain, in which shelled diffusion data were acquired to sample the diffusion signal decay irrespective of the fiber orientation, and a single apparent axon diameter was fitted to the data instead of a gamma distribution. Modifications to the AxCaliber model were also made to account for fiber dispersion (Fig. 12c) (Zhang et al., 2011) and crossings (Fig. 12d) (Barazany et al., 2011). Later, the powder average or Spherical Mean Technique (SMT) was adopted to integrate out the dependence on fiber orientation distribution and generalize such analyses to the whole brain (Fan et al., 2020; Veraart et al., 2018a, 2019, 2020, 2021).

Despite the dramatic improvements in hardware and software for dMRI in the last decade, validation of tissue microstructural measures is crucial before axon diameter mapping methods can be used and appropriately interpreted for neuroscientific studies. Progressive efforts have been made to validate the estimation of axonal size by dMRI using the Connectom scanner, including studies in bio-mimetic phantoms (Fan et al., 2018b; Huang et al., 2021a) and ex vivo tissue samples (Veraart et al., 2020), which have compared the estimated pore sizes against parameters obtained using orthogonal measures such as manufactured parameters or histological findings from electron microscopy (EM). The work by Veraart et al. (Veraart et al., 2020) performed both ex vivo and in vivo MRI experiments in animal and human brains, respectively, and found that although the MR signal is strongly weighted by the larger axons in the tail of the axon diameter distribution, the apparent axon diameters derived from the Connectom dMRI data agree quantitatively with histology after accounting for the “MR-effective” volume weighting. Correlations to other forms of non-imaging data such as the variability of conduction velocity (CV) in the human brain have also been carried out, and plausible estimates of CV were obtained for regions of the brain in which the axon diameter is sufficiently large (Drakesmith et al., 2019; Mancini et al., 2021). In addition, the scan-rescan repeatability of axon diameter estimates has been evaluated in the human spinal cord (Duval et al., 2018) and brain (Fan et al., 2021; Veraart et al., 2021) to assess variability within and across individuals, and between sites (Veraart et al., 2021), providing essential knowledge to inform on the feasibility of apparent axon diameter mapping in future neuroscientific investigations.

Although there is plenty of research showing the feasibility of axon diameter mapping using Connectom gradient strengths, there are also some works that have placed these findings in question. Paquette et al. (Paquette et al., 2020a) showed that, for the estimation of mean axon diameter, resolving the simplest situations including multiple diameters is infeasible even with diameters much bigger than the resolution limit. Andersson et al., (Andersson et al., 2020) found that the variation in axon diameter correlates with mean diameter, contesting the value of precise diameter determination in larger axons. Lee et al., (Lee et al., 2019) showed that fiber orientation dispersion estimated from MRI should be relatively stable, while the "apparent" axonal diameters are sensitive to experimental settings and cannot be modeled by perfectly straight cylinders. Further, Lee et al., (Lee et al., 2020b) illustrated that dMRI is sensitive to the micrometer-scale variations in axon caliber or pathological beading, by identifying a signature power-law in diffusivity time-dependence along axons. Finally, Brabec et al. (Brabec et al., 2020) investigated frequency-dependent diffusion in thin undulating fibers and its impact on axon diameter estimation. And Lee et al., (Lee et al., 2020a) developed the theory of intra-axonal diffusion transverse to the realistic axon with caliber variations (beading) and micro-dispersion (undulation) along each axon (Fig. 12f), and demonstrated how axon diameter estimation is confounded by these cellular features based on the 3D diffusion coarse graining and numerical simulations in realistic axons.

In addition to the vast literature focused on the modeling of white matter microstructure, Zhu et al. (Zhu et al., 2021) observed time-dependent kurtosis in the human cortical gray matter based on in vivo dMRI data acquired on the Connectom scanner, and attributed the observation to the neurite and soma architecture. Lee et al. (Lee et al., 2020c) observed diffusivity and kurtosis time-dependence in the in vivo human cortical gray matter and argued that structural disorder along neurites (Fig. 12g) was mainly responsible for the observed time dependence. Palombo et al. (Palombo et al., 2020) introduced a compartment-based model for apparent cell body (namely soma) and neurite density imaging (SANDI) (Fig. 12e), which has mainly been developed for modeling gray matter microstructure (Palombo et al., 2020). Maps of soma and neurite signal fractions were shown using the MGH-USC HCP data that remarkably mirror the contrast seen on histological images of brain cyto- and myelo-architecture. Genc et al. studied the repeatability of SANDI estimates using the MICRA data and found that measures of soma density, neurite density and apparent soma size were highly reliable across cortical areas (Genc et al., 2021).

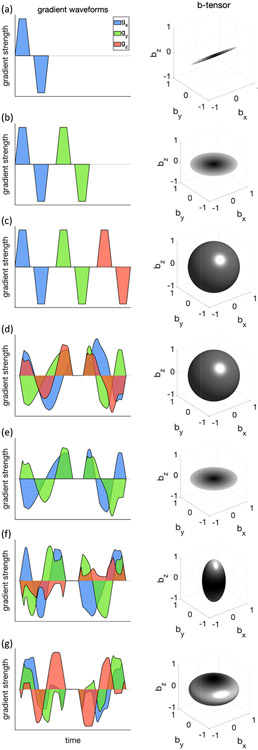
More advanced diffusion encoding schemes (Fig. 13) beyond the conventional Stejskal-Tanner experimental paradigm have also received much attention recently. For example, different combinations of b-tensor encoding for fitting SANDI was proposed (Afzali et al., 2021a). To estimate the soma size using SANDI, the Gaussian phase approximation of intra-soma diffusion for b-tensor encoding was applied to account for the ill-defined diffusion time in optimized b-tensor encoding waveforms. Their results showed that different combinations of linear, planar, and spherical tensor encoding stabilized the fitting and improved the precision of parameter estimation. In another study, Afzali et al. (Afzali et al., 2021a) identified three main challenges in SANDI model fitting, such as the Rician noise floor in magnitude data, the empirical lower bound on the spherical signal fraction and pore-size, and finally, the entanglement of intra-cellular diffusivity time-dependence in spheres and cylinders. Tax et al. (Tax et al., 2020) combined the asymmetric spherical tensor encoding with ultra-strong diffusion gradients to achieve high diffusion-weightings with high SNR, while suppressing signal arising from anisotropic water compartments. The remaining signal at high b-values has the potential to serve as a novel marker for isotropically-restricted water compartments (Fig. 12h). Apparent diffusivities and sphere sizes were further characterized in the cerebellar gray matter and were consistent across healthy volunteers.

Fig. 13. Illustration of various diffusion encoding schemes.

In each row, an exemplary diffusion weighting gradient waveform was shown on the left (x, y, and z components are shown in blue, green, and red, respectively) and its corresponding b-tensor shape was shown on the right. The diffusion encoding schemes shown here include: a) single diffusion encoding (SDE) (standard Stejskal-Tanner), b) double diffusion encoding (DDE), c) tiple diffusion encoding (TDE), (d-g) q-vector trajectory encoding, d) spherical tensor encoding (STE) or isotropic encoding, e) planar tensor encoding, f) prolate encoding, g) oblate encoding.

For stick-like structures (e.g., axons), the $1∕\sqrt{b}$ power-law scaling of orientationally averaged diffusion-weighted signals over each b-shell was investigated using conventional Stejskal-Tanner encoding (Jespersen et al., 2013; Kaden et al., 2016b; McKinnon et al., 2017; Veraart et al., 2019, 2020). Afzali et al. (Afzali et al., 2020) generalized this idea to more advanced encoding schemes including planar tensor encoding (PTE). They found that only three specific forms of encoding result in a power-law dependency, pure linear and pure PTE when the tissue geometry is "stick-like" and pure LTE when the tissue geometry is "pancake-like."

In contrast to the model-based approaches discussed above, where the diffusion signals are related to the underlying tissue microstructure through assumptions about the structural geometries or physical compartments of the microenvironment (i.e., a simplification of the realistic tissue), the signal representation approach aims to identify the best way to represent the measured signal using a mathematical form and does not rely upon any specific assumptions or physical models. For example, Tian et al. (Tian et al., 2016) studied q-space truncation and sampling in diffusion spectrum imaging (DSI) using data acquired on the MGH Connectome scanner. They showed the minimum required q-space sampling density corresponds to a FOV approximately equal to twice the mean displacement distance in the tissue. They found that the 11 × 11 × 11 grid was suitable for both ex vivo and in vivo DSI experiments.

The availability of high gradients on the Connectom scanner has enabled the measurement of the full range of diffusion tensors and their distribution, rather than just averaged diffusion properties that are typically reported on standard clinical dMRI. In addition, the high SNR and advances in image acquisition technology available on the Connectome scanner are crucial for obtaining data with many b-values within a reasonable scan time. In a preliminary study, high quality data were acquired as part of a multi-diffusion time, multi-b-value acquisition to obtain a model-free diffusion tensor distribution (FDTD) in order to characterize and distinguish different classes of tissue in the healthy adult brain. In comparison to previous work on diffusion tensor distribution (DTD) analyses (Magdoom et al., 2021; Topgaard, 2019), FDTD expands the range of diffusion tensors and does not constrain the symmetry of the tensors, hence achieving a model-free approach.

Mapping tissue microstructure using dMRI, even with high gradient strengths, is challenging, primarily due to the limited SNR and image resolution, and some issues regarding the validity of model assumptions that remain open questions. However, with the insights accumulated through the above-mentioned efforts, we are gaining more confidence in obtaining a better understanding of these issues and are motivated to push further on the gradient strength, see (Huang et al., 2021b) in this special issue for further details. With the better technology, including innovations in hardware, image acquisition, diffusion encoding schemes, data analysis frameworks, and validation, we will continue to gain a more in-depth understanding of what we are measuring and how to further improve the measurements in the future.

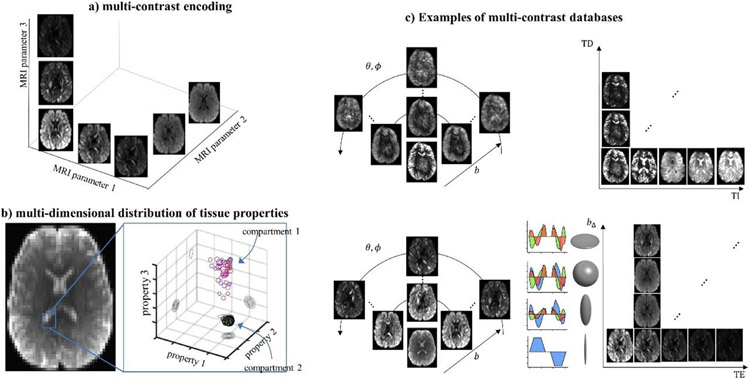
4. Complementing diffusion experiments with additional contrasts

One of the strengths of MRI over other medical imaging modalities arises from the numerous contrasts enabled by different MRI sequences. This diverse range of contrasts can complement each other to reflect tissue properties from distinct perspectives. Specific to high performance gradient systems, the shortened TE and increased SNR provide additional flexibility on the encoding of tissue properties into the MR signal in addition to the diffusion contrast. Correlating diffusion MRI with relaxation times T1, T2 and T2* has gained great interest for its ability to provide additional information from the perspective of molecular interactions of the system of spins in the microenvironment (Tax, 2020). T1 and T2-diffusion correlation experiments have shown to be useful in improving prostate tissue classification (Yu et al., 2017). Relaxation information has been demonstrated to be helpful in resolving distinct signal components arising from nervous tissue in early in vitro NMR experiments (Andrews et al., 2006; Beaulieu et al., 1998; Peled et al., 1999; Stanisz and Henkelman, 1998), and animal MRI experiments (Benjamini and Basser, 2017; De Santis et al., 2016a, 2016b; Does and Gore, 2000; Kim et al., 2017; Qin et al., 2009). More recently, similar MRI experiments have also been carried out in humans (Attar et al., 2019; de Almeida Martins et al., 2021; De Santis et al., 2016c; Kleban et al., 2020; Lemberskiy et al., 2018; Lin et al., 2018; Mulkern et al., 2000; Nam et al., 2015).

The multi-compartmental model is a common approach to interpret water diffusion in neuronal tissues; however, under the typical low SNR in dMRI, more than one solution of parameters yields similar diffusion signals due to the flatness or inherent degeneracy in the fitting parameter landscape (Jelescu et al., 2016; Novikov et al., 2019). Solving such degeneracy in parameter estimations requires additional measurements orthogonal to the conventional pulsed-gradient dMRI. For example, Veraart et al. (Veraart et al., 2018b) performed the TE dependent Diffusion Imaging (TEdDI) to break the degeneracy in parameter estimation and robustly estimate the intra- and extra-axonal water T2 relaxation time. In addition to the relaxation, adding orthogonal measurements of diffusion time-dependence (Lee et al., 2018a) or b-tensor encoding waveforms (Afzali et al., 2019; de Almeida Martins and Topgaard, 2016a; Dhital et al., 2015, 2018b; Fieremans et al., 2018; Szczepankiewicz et al., 2016) also help to lift the degeneracy in parameter estimations. Furthermore, the sensitivity of diffusion signals to intra-axonal diffusion was achieved by adding orthogonal acquisitions suppressing extra-neurite signals via linear (Skinner et al., 2017) or planar (Dhital et al., 2019) diffusion weightings. Similarly, the isotropically restricted compartment in the brain was detected by adding spherical encoding weightings (Dhital et al., 2018a; Tax et al., 2020). Finally, the diffusion properties of myelin water in-between myelin sheaths were estimated by combining dMRI with either double inversion recovery (Andrews et al., 2006) or magnetization transfer preparation to distinguish myelin water signals (Avram et al., 2010).

The “hybrid” type of experiment that measures diffusion and other contrasts such as relaxation simultaneously provides advantages over measuring them separately, because a multi-parametric (i.e., multidimensional) space is naturally laid out (Fig. 13), and the association between various dimensions can be directly analyzed. The advantage of high gradients is to enable a much wider spectrum of multi-contrast imaging parameters (Fig. 13a), such as b-value, TE, diffusion time, diffusion encoding schemes (Lampinen et al., 2020; Reymbaut et al., 2020a), and even spectroscopy (Jenkins et al., 2020), in addition to the diffusion encoding direction (Fig. 13c), to provide sufficient data for multi-dimensional tissue parameter mapping (Fig. 13b). Assuming a single T2 and an axially symmetric tensor per micro-environment, a five-dimensional diffusion-relaxation distribution in living human brain could be resolved using a hybrid diffusion-T2 experiment (de Almeida Martins et al., 2021; Tax et al., 2018), where the five dimensions are the T2 value, the polar and azimuthal angles, and the axial and radial diffusivities of the tensor. Clustering of different tissue types could be observed in this parameter space of high dimensionality, where the relaxation dimension provides additional information. Strong gradients are fostering the translation of NMR experiments into studies of living human brain (de Almeida Martins et al., 2020).

However, solving a nonlinear inverse problem of such a high dimensionality is nontrivial, especially given the limited SNR at the range of imaging parameters. Non-parametric inversion algorithms have been adopted with strategies to sample sparsely and perturb solutions to accelerate the computation (de Almeida Martins and Topgaard, 2016b). In model-based approaches, various strategies were used to reduce the dimensionality of the parameter space to be estimated, such as using powder-average or spherical mean to get rid of the dependence on diffusion direction (Lasič et al., 2014; Veraart et al., 2018a, 2020, 2021), or split and conquer the fiber orientation and tissue property estimations in separate steps (De Santis et al., 2016c). The Markov Chain Monte Carlo (MCMC) framework can be used to quantify the uncertainty in the estimated parameters (Alexander, 2008; Alexander et al., 2010; Fan et al., 2018a; Huang et al., 2015b; Sotiropoulos et al., 2013a).

“Hybrid” experiments can also be thought of as using one contrast as a filter for the other, which can dial up or down the signal weighting from different tissue compartments (Ning et al., 2020b; Palombo et al., 2018). Compartmental relaxation properties can, e.g., be disentangled by diffusion anisotropy/restriction or directionality of diffusion (Reymbaut et al., 2020a; Tax et al., 2021a). The former has been leveraged to investigate the T2 of the intra- and extra-axonal space (Lampinen et al., 2020; McKinnon and Jensen, 2019; Tax et al., 2017, 2021a; Veraart et al., 2018b), T2* and susceptibility effects (Kleban et al., 2020), and orientation-dependence of T2 on the direction of the main magnetic field with a tiltable receiver coil (Tax et al., 2021a). The latter has been used to reveal differences in T2 between different fascicles (Barakovic et al., 2021; Reymbaut et al., 2020b).

Multi-contrast diffusion experiments are challenged by noise, long acquisition times and stringent requirements on hardware that are impractical for clinical applications, as well as limitations arising from model assumptions. Despite these challenges, preliminary experimental results have already demonstrated the great potential of the diffusion-relaxation correlation approach in providing a more complete picture of tissue microstructure than its one-dimensional counterparts. Advances in efficient experiment design in a model-based (e.g., (Lampinen et al., 2020)) or data-driven (e.g., (Grussu et al., 2020; Tax et al., 2021b)) fashion will facilitate the adoption of multi-contrast experiments in clinical research studies.

5. Utilization of the Connectom system for post-mortem tissue acquisitions

In validating the emerging techniques of human connectome mapping using the high gradient system discussed in earlier sections, postmortem dMRI has become an essential tool for probing human brain structure at the mesoscopic level (Liu et al., 2020; Roebroeck et al., 2019). This is especially due to its capability of achieving substantially higher spatial resolutions (i.e., sub-millimeter isotropic voxel sizes) than typically achievable in vivo using long scan times and volumetric encoding strategies (Fritz et al., 2019; McNab et al., 2013a; Miller et al., 2011). High-resolution postmortem dMRI data may help to develop detailed models of brain circuitry, including macro-anatomy and tissue microstructure. Postmortem dMRI provides a mesoscopic bridge between in vivo dMRI and the ground truth that can be obtained from microscopy.

One challenge in the acquisition of postmortem dMRI data stems from the generally altered tissue properties resulting from tissue fixation (Roebroeck et al., 2019). The reduced diffusivity requires substantially stronger diffusion weightings in order to generate a similar diffusion contrast as observed under in vivo conditions. Compared to clinical devices, the Connectom gradient strength of G_max = 300 mT/m allows substantially reduced echo times, and hence elevated SNR to enable much higher resolution diffusion MRI (Jones et al., 2018; Setsompop et al., 2013). Compared to small-bore preclinical devices, the Connectom system has a substantially larger magnet bore, which also allows for imaging of entire human brains.

The initial utilization of the 300 mT/m gradient system for high resolution postmortem dMRI data acquisition was presented in (McNab et al., 2013a), where a complete human brain was scanned with an isotropic resolution of 0.6 mm using a highly accelerated, segmented 3D EPI sequence. In a recent study, the temporal efficiency and SNR of postmortem dMRI data were further improved using multi-echo acquisitions (Eichner et al., 2020). For this purpose, the typically employed rapid, segmented dMRI spin echo EPI train was extended to include several additional segmented gradient echoes at various TEs. This Multi-Echo dMRI (ME-dMRI) sequence was subsequently used for whole brain dMRI acquisitions of non-human primates with up to 500 μm isotropic resolution and b = 5000 s/mm² (Eichner et al., 2021). The developed ME-dMRI sequence was further leveraged to jointly describe white matter anisotropies in diffusion and susceptibility, using a combination of HARDI dMRI and high-angle-resolution susceptibility tensor imaging (STI) (Gkotsoulias et al., 2021). The influence of gradient nonlinearities on the Connectom scanner (also see section II.6.1) for postmortem recordings has been shown recently and should not be disregarded in dMRI reconstruction (Edwards et al., 2021a). With the 48-channel whole brain ex vivo coil built expressly for the MGH Connectome MRI scanner (Scholz et al., 2021) and designed to surround the brain tightly from all sides (see section II.3 and Fig. 5), the substantial SNR gain allows acquisitions of postmortem dMRI data with 550 μm isotropic voxel size and maximum diffusion weighting of b = 10,000 s/mm² or higher (Ramos-Llorden et al., 2021) (Fig. 14). We expect that dedicated postmortem coils will advance dMRI validation efforts on the Connectom system.

Fig. 14. The concept of the multi-contrast diffusion experiments.

(a) Illustration of the concept of multi-contrast encoding space with each MRI parameter as one dimension; (b) the distribution of different tissue types in the multi-dimensional space of tissue properties (figure adapted from de Almeida Martins et al., 2020, permission pending); (c) examples of the contrast dimensions include, but are not limited to, diffusion weighting directions, b-value, TE, delay time (TD), inversion time (TI), diffusion encoding schemes, etc. Figure adapted from (Tax et al., 2021b).

Fig. 15

Fig. 15. Whole-brain ex-vivo diffusion MRI at 550 micrometer isotropic resolution using b-values up to 10000s/mm².

Axial, coronal, and sagittal views of a given diffusion direction are shown in (a), and the corresponding averaged DWI are displayed in (b). High-quality submillimeter diffusion MRI allows mapping diffusivity with unprecedented quality in fine anatomical structures often inaccessible in in-vivo settings, as seen in the internal capsule and transverse fibers in the pons (c), and anisotropic diffusivity in the primary and somatosensory cortex (d). Resolving fiber architecture of the hippocampus is achievable using this high-quality, high-spatial-resolution dataset, as can be seen in (e). Adapted from (Ramos-Llorden et al., 2021).

6. Clinical investigations

The availability of strong gradients up to 300 mT/m on human MRI scanners has enabled new classes of dMRI measurements to be performed in living patients. The use of strong diffusion-encoding gradients promises to offer greater sensitivity to key aspects of tissue microstructure in various neurological diseases. The feasibility of detecting even individual-subject anomalies was recently shown with high b-value data (Chamberland et al., 2021). In particular, high gradient amplitudes have been shown to benefit the estimation of tissue microstructural properties by dMRI such as axon diameter (Alexander et al., 2010; Assaf et al., 2008; Dyrby et al., 2013; Fan et al., 2018b; Huang et al., 2015b) and the dimensions of the extracellular space (Lee et al., 2018b).

Axon diameter mapping using high-gradient diffusion MRI has been applied to study changes in axonal structure and packing density in multiple sclerosis (MS) and the aging brain. Axon diameter mapping in the corpus callosum of relapsing-remitting and progressive MS patients has revealed increased axon diameter and decreased axon density in lesions and the normal-appearing white matter (Huang et al., 2016; Ngamsombat et al., 2020; Yu et al., 2019), in keeping with findings on histopathology, which show decreased axon density and an overall increase in axon diameter in postmortem MS brain tissue (Evangelou et al., 2000). The observed increase in axon diameter as measured by high-gradient dMRI is also a strong predictor of disability and cognitive dysfunction (Huang et al., 2019), particularly in tests of interhemispheric processing speed and working memory, which rely on the corpus callosum as the major white matter fiber tract mediating these processes.

The application of axon diameter mapping to the aging brain has uncovered significant increases in axon diameter with advancing age in the anterior white matter (Fan et al., 2019), with changes most pronounced in the genu of the corpus callosum and forceps minor. These alterations in axon diameter are consistent with previously reported regional decreases in fractional anisotropy within the frontal white matter (Salat et al., 2005) and parallel decreases in corpus callosum area and regional gray matter volume with age. In teenagers, (Genc et al., 2020) showed that with increasing b-values, diffusion MR signal has higher specificity to intra-axonal spaces and hence improved estimations of the apparent fiber density and an increased sensitivity to developmental age relationships.

The availability of strong gradients for dMRI has also enabled the translation of novel diffusion-encoding paradigms to probe brain tissue microstructure in patients, including oscillating-gradient waveforms (Tan et al., 2020b), double-diffusion encoding (Yang et al., 2018), and q-space trajectory imaging (Westin et al., 2016). One recent study combined isotropic diffusion encoding with strong diffusion gradients to achieve high diffusion-weighting in highly restricted, spherical compartments (the so-called “dot compartment”) in the cerebellar gray matter while suppressing signal arising from anisotropic water within axons (Tax et al., 2020). By gaining greater specificity to cellular signatures in the cerebellum, spherical tensor encoding performed with high gradient strengths may enable the earlier identification of cerebellar gray matter loss in patients with hereditary ataxias such as spinocerebellar ataxia type 2, which selectively affects the granule and Purkinje cells. The ability to probe microscopic diffusion anisotropy in brain tumors using q-space trajectory imaging may enable the differentiation of brain tumors such as meningiomas from high-grade glial tumors based on their cellular morphology and composition (Szczepankiewicz et al., 2015).

The results of clinical research studies demonstrate the potential of high-gradient dMRI to uncover changes in axonal and cellular microstructure and motivate the continued development, application and dissemination of high-gradient technology for use in commercially available human MRI scanners.

IV. Conclusion

The high gradient strengths on the Connectom MRI scanner have remarkably expanded the range of diffusion-encoding parameters accessible for studies of the living human brain, providing a veritable playground for the development of new dMRI methods and the investigation of their potential significance in clinical and neuroscientific studies. Much progress has been made since the first special issue on “Advances in Mapping the Connectome” published by NeuroImage in 2013. We are aware that many of the methodologies covered in this article are just emerging, not fully validated and possibly even controversial, yet the field is thriving and expanding rapidly. Connectom MRI scanners equipped with up to 300 mT/m gradient strength are not yet readily available for direct translation to clinical care, but the impact of the related technical development and validation efforts can be seen in the incorporation of gradient systems with ever higher gradient strengths into commercially available MRI scanners. We anticipate this trend will continue into the foreseeable future, thereby providing much hope for the eventual translation of high-gradient dMRI techniques into key technology that will inform and inspire the next-generation of dMRI applications for improving everyday clinical practice.

Appendix. The eddy current induced magnetic fields

Eddy current induced magnetic fields can be expressed as a sum of decaying exponentials with corresponding decay times (from under 1 ms to seconds) and amplitudes. They are not only produced in the gradient direction but also in the other directions (cross-terms) and with more complicated spatial configurations (higher order terms). The magnetic field caused by the eddy currents can be written as (Van Vaals and Bergman, 1990):

$$\begin{gathered} B_{EC}(x,y,z,t)= \\ \underset{{\mathrm{B}}_0\text{eddy currents}}{\underbrace{E_{x\to 0}(t)+E_{y\to 0}(t)+E_{z\to 0}(t)}} \\ +\underset{\text{linear self}-\text{terms}}{\underbrace{E_{x\to x}(t)x+E_{y\to y}(t)y+E_{z\to z}(t)z}} \\ +\underset{\text{linear cross}-\text{terms}}{\underbrace{E_{x\to y}(t)y+E_{x\to z}(t)z+E_{y\to x}(t)x+E_{y\to z}(t)z+E_{z\to x}(t)x+E_{z\to y}(t)y}} \\ +\underset{\text{higher order terms}}{\underbrace{E_{x\to xy}(t)xy+E_{x\to yz}(t)yz+E_{x\to x^2+y^2}(t)(x^2+y^2)+\dots ,}} \end{gathered}$$

where

$$E_{i\to j}(t)=-\frac{\mathrm{d}{G}_i}{\mathrm{d}t}\ast \left(H(t)\sum _k{\alpha }_{ijk}{\mathrm{e}}^{-\frac{t}{{\tau }_{ijk}}}\right).$$

τ_ijk and α_ijk are the decay time and corresponding amplitude. The notation i → j indicates that a gradient pulse (G_i) in direction i (x, y or z) causes a magnetic field with spatial dependency j. H(t) is the Heaviside step function which is 0 for t < 0 and 1 otherwise. The * indicates a convolution. For the higher order terms, we use spherical harmonics here but other bases are possible (Xu et al., 2013).