Spinning Driven Dynamic Nuclear Polarization with Optical Pumping

Abstract

We propose a new, more efficient, and potentially cost effective, solid-state nuclear spin hyperpolarization method combining the Cross Effect mechanism and electron spin optical hyperpolarization in rotating solids. We first demonstrate optical hyperpolarization in the solid state at low temperature and low field, and then investigate its field dependence to obtain the optimal condition for high-field electron spin hyperpolarization. The results are then incorporated into advanced Magic Angle Spinning Dynamic Nuclear Polarization (MAS-DNP) numerical simulations that show that optically pumped MAS-DNP could yield breakthrough enhancements at very high magnetic fields. Based on these investigations, enhancements greater than the ratio of electron to nucleus magnetic moments (>658 for ¹H) are possible without microwave irradiation. This could solve at once the MAS-DNP performance decrease with increasing field and the high cost of MAS-DNP instruments at very high fields.

1. Introduction

MAS-DNP is a powerful solid-state NMR (ssNMR) method that reduces the duration of ssNMR experiments by orders of magnitude.¹ In short, the high polarization of paramagnetic species stemming from microwave (μw) irradiation at the Larmor frequency, can be transferred to nuclei to enable molecular-level characterization even when the isotope of interest is in low concentration or has low receptivity.^2-5 Over the past two decades, there has been significant progress in the development of hardware^6-11, sample preparation methods,^12-16 paramagnetic species used as sources for DNP^17-22 and the theoretical understanding of MAS-DNP.^23-26 MAS-DNP most commonly uses biradicals²⁷ to generate the nuclear hyperpolarization via the Cross Effect (CE) mechanism, which involves fast energy level anti-crossing.^23-26,28,29

As in conventional ssNMR, very high field MAS-DNP (>14.1 T/600 MHz) enables higher resolution, but faces multiple challenges, such as reduced efficiency of the CE with the field^30,31 and significant microwave absorption at high frequencies,¹¹ which reduce the large electron polarization difference and the concomitant nuclear polarization enhancement.^25,30,32,33 Finally, the significant cost of high-field MAS-DNP instrumentation limits widespread availability.

In parallel to DNP developments, optical irradiation has been used to improve NMR sensitivity. For example, nuclear hyperpolarization in ssNMR experiments via photo-CIDNP was observed in certain systems.^34-40 Furthermore, optical electron spin hyperpolarization offers a promising approach for carrying out solid state and liquid-state Overhauser DNP^41,42 and hyperpolarized triplet state has been combined with Integrated Solid-Effect at low field to generate nuclear spin hyperpolarization.^43-49

In this article, we propose a novel method that can provide much higher hyperpolarization than traditional MAS-DNP at high fields, in addition to addressing the issues listed above via the use of optical electron spin hyperpolarization in the solid state. The concept, dubbed optically pumped MAS-DNP (MAS-OPDNP), uses optical irradiation to photophysically generate the electron spin polarization difference required for the CE mechanism and build on the effect of the sample’s rotation to hyperpolarize the nuclei. This concept enables nuclear spin hyperpolarization that is not restricted to the ratio of electron to nucleus magnetic moments, while potentially using affordable hardware. Finally, the method is expected to be field independent, and therefore, it should be easily added to most modern ssNMR spectrometers.

The present work first demonstrates experimentally, in the solid state and X-band (low field), that optically driven electron spin hyperpolarization is possible for nitroxides commonly used for MAS-DNP.^27,50,51 We subsequently investigate the field dependence of optical electron spin hyperpolarization and its characteristic time scales. Based on these results, we propose a Chromophore-Radical-Radical Polarizing Agent and present simulations that were conducted with a high-performance MAS-DNP numerical tool,^25,52 to explore the potential of the CE MAS-DNP mechanism at high magnetic field using optical electron spin hyperpolarization. The results are then discussed in lights of experimental considerations.

2. Method

2.1. Experimental details

Steady-state and time-resolved EPR spectra were recorded in a laboratory-built X-band EPR spectrometer.⁵³ For the time-resolved EPR, the exciting source was the 3^rd harmonic of an Nd:YAG laser (Quantel Model: YG-981C, wavelength: 355 nm, repetition rate: 15 Hz, energy at the sample: 1-4 mJ/pulse). Because of the extremely strong spin polarized EPR signals, the laser energy was reduced to its lowest output value. The absorbance of all the solutions at the exciting wavelength was less than 1. The samples, ANCOOT and Anq1Pr were dissolved in Toluene and placed in a quartz tube (O.D.: 4 mm, I.D.: ~ 3 mm, Wilmad Glass, USA), then degassed by three cycles of freeze-pump-thaw under a vacuum of 105 mbar. The low temperature experiments were performed by passing cold N₂ gas through a Dewar that contained the sample tube. The temperature at the sample tube was calibrated by inserting a thermocouple inside the cavity. Additional experimental details are available in the Supporting Information.

2.2. Numerical simulations

The simulation models of the Reverse Quartet Mechanism at high field is based on previously published results⁵⁴ and the input parameters are detailed in the Supporting Information.

The MAS-OPDNP simulations are based on a previously published MAS-DNP simulations method.^25,52 The model simulates biradicals in a box to account for the inter-biradical interactions thus accounting for the biradicals concentration. The model was modified to account for the optical electron spin hyperpolarization. Details about the modifications and the parameters used can be found in the Supporting Information.

3. Results

3.1. Photophysical electron spin hyperpolarization

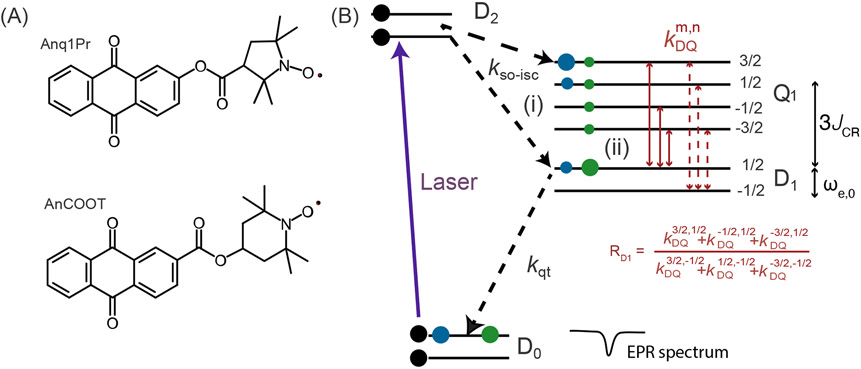
Optically pumped electron spin hyperpolarization can be generated in chromophore-radical (CR) systems during photophysical quenching processes.^55-63 The electron hyperpolarization generation in CR systems is well understood in the liquid state.^64-68 two mechanisms contribute to the electron hyperpolarization (see energy diagram in Scheme 1): (i) the Spin-Orbit induced Inter-System-Crossing (SO-ISC)^68,69 and (ii) the D₁-Q₁ conversion via the Reverse Quartet Mechanism (RQM).⁵⁴ The first mechanism is due to the spin-orbit coupling, while the second involves the large Zero-Field Splitting (ZFS), D_ZFS, both in the excited triplet state of the chromophore.

Scheme 1:

(A) Structures and acronyms of the molecules examined in this study. (B) Key processes involved in electron spin hyperpolarization in a Chromophore-Radical adduct at low magnetic field (~ 0.3 T). The laser pulse excites the molecule from the D₀ to the D₂ state (termed sing doublet),^62,70 which then decays from D₂ to Q₁/D₁ (mixing of triplet and doublet) via SO-ISC, followed by the quenching of D₁ state (termed trip-doublet) to D₀ at a rate of k_qt. Two mechanisms lead to hyperpolarization in the D₀ state: (i) the selective transition of the SO-ISC and (ii) the reversible transitions between D₁ and Q₁ states (RQM). Black dots represent the initial photoexcited populations, the blue and green dots denote the population redistributions after process (i) and (ii), respectively. For process (ii), after decay via SO-ISC, the populations in the Q₁ state are equilibrated via longitudinal relaxation and driven by the RQM pathway via the D₁→Q₁ transitions thanks to cross-relaxation, with rates defined by the $k_{\text{DQ}}^{m,n}$ between ${\mathrm{Q}}_1^m$ and ${\mathrm{D}}_1^n$ (red arrows) to generate hyperpolarization in the D₀ state. The ratio of rates $R_{D1}=\sum k_{\text{DQ}}^{m,1∕2}∕\sum k_{\text{DQ}}^{m,-1∕2}$ (red solid and red dashed arrows) quantifies the selective polarization in the D₁ states. ω_e,0 represents the Zeeman Larmor frequency and 3J_CR (< 0) represents the magnitude of the exchange splitting between the Q₁ and D₁ states.

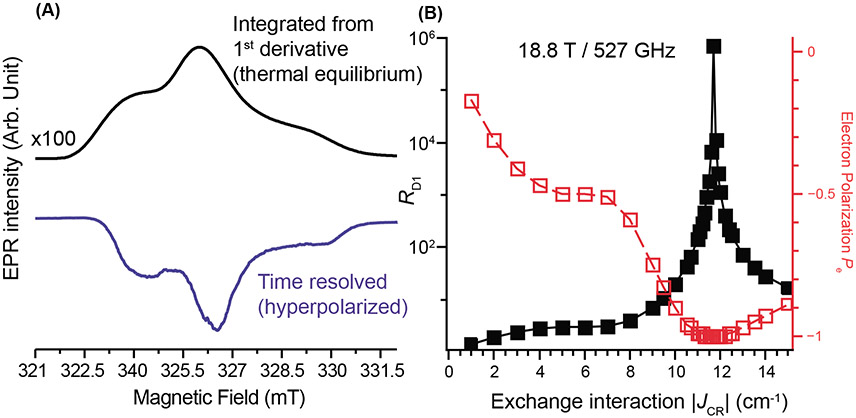
Recently, ANCOOT and Anq1PR (Scheme 1A), two efficient CR-systems, were reported to generate a large electron hyperpolarization in solution.^66,71 We examined their hyperpolarization efficiency in the solid state as a preliminary assessment for MAS-DNP applications. Fig. 1A shows the EPR spectra of ANCOOT in toluene at 100 K in thermal equilibrium (black curve) and hyperpolarized (blue curve) states. The hyperpolarized EPR spectrum is emissive and a near mirror image of the thermal equilibrium one, without any signature of the quartet EPR spectrum. From the signal intensity ratio, we estimated the electron polarization enhancement to be about −100 times the thermal spin polarization (~ −30 % polarization, see SI for details on the evaluation of experimental hyperpolarization). The hyperpolarization is generated on a very fast time-scale < 100 ns (the instrument response time is 100 ns), which is important for applications in MAS-DNP.

Fig. 1:

(A) Experimental EPR spectrum (integrated from the first derivative) of ANCOOT in toluene at 100K (black line) and its hyperpolarized EPR spectrum recorded for 2.5 μs after a 355 nm laser pulse (blue line) and integrated using a boxcar averager over 0.3 μs (see SI for experimental details). The gain factor of −100 for the Boltzmann signal represents the ESP enhancement obtained from time resolved experiments (TREPR), see appendix 4. (B) Plot of the RQM selectivity factor, R_D1 (black squares), and the corresponding values of P_e (red squares) as a function of the exchange parameter, ∣J_CR∣ (J_CR<0), for the case of pure RQM, i.e., process (ii) (scheme 1). N.B. solid black and dashed red interpolating lines are provided as guides to the eye.

The solid state hyperpolarized EPR spectrum and its time dependence for the anthraquinione-nitroxides are determined by the SO-ISC and RQM mechanisms. Their relative contributions at X-band frequencies are beyond the scope of the current work and will be described in a future publication.

At high magnetic fields the SO-ISC mechanism may become less efficient as the net (rotationally invariant) component of the polarization generated during the ISC has an inverse field dependence (see eq. S10).^58,72 It is therefore suspected that the SO-ISC induced hyperpolarization would likely decrease by orders of magnitude at high magnetic field (18.8 T). Thus, at high field and low temperature (~100 K), the RQM is likely the only mechanism that can generate the electron hyperpolarization needed to observed OPDNP.

The polarization generated by the RQM is determined by the rates $k_{\text{DQ}}^{m,n}$ (see Eq. (1), Scheme 1 and Appendix 2, eq. (S11)) which depends on the ZFS and exchange interaction (J_CR) between chromophore and radical in the excited D₁-Q₁ state.^65,73 Due to the solid state nature of the sample, $k_{\text{DQ}}^{m,n}$ would also depend on the orientation of the ZFS tensor with respect to the magnetic field. However, the ZFS (~0.3 cm⁻¹) is relatively small compared to the electron Zeeman term at high fields (>5 cm⁻¹), and the exchange interaction. Thus, the manifestation of anisotropy in k_dq is expected to be weak. Furthermore, since the CR is dissolved in a glass matrix, all crystal orientations are present in the matrix, we thus used average RQM rates, as it is done in the liquid state:⁵⁴

$$k_{DQ}^{mn}\propto \frac{\overline{\langle {\mathrm{Q}}_1^m\mid H_{ZFS}\mid {\mathrm{D}}_1^{\mathrm{n}}{\rangle }^2}}{\Delta E({\mathrm{Q}}_1^m,{\mathrm{D}}_1^{\mathrm{n}}{)}^2}$$ Eq.(1)

where $m\in \left[-\frac{3}{2},-\frac{1}{2},\frac{1}{2},\frac{3}{2}\right]$, $n\in \left[-\frac{1}{2},\frac{1}{2}\right]$, and $\Delta E({\mathrm{Q}}_1^m,{\mathrm{D}}_1^n)$ is the energy difference between states ${\mathrm{Q}}_1^m$ and ${\mathrm{D}}_1^n$. An estimate of $k_{DQ}^{mn}$ at a low temperature was obtained by numerical fitting of the time resolved EPR time profile of ANCOOT recorded at 100 K (see Eq. S7).

At high fields, $k_{\text{DQ}}^{mn}$ can be tuned by adjusting $\Delta E({\mathrm{Q}}_1^{\mathrm{m}},{\mathrm{D}}_1^{\mathrm{n}})\approx 3J_{\text{CR}}+(m-n){\omega }_{e,0}$, which is dominated by J_CR and the Larmor frequency of the electron ω_e,0. The optimal value of J_CR to maximize the efficiency of the RQM can be determined through the selectivity factor, R_D1, which is the ratio of the sum of all the rates from Q₁ levels to the ${\mathrm{D}}_1^{1∕2}$ and the ${\mathrm{D}}_1^{-1∕2}$ energy levels, written as:

$$R_{D1}=\frac{k_{DQ}^{{\mathrm{Q}}_1^{+3∕2}{\mathrm{D}}_1^{+1∕2}}+k_{DQ}^{{\mathrm{Q}}_1^{-1∕2}{\mathrm{D}}_1^{+1∕2}}+k_{DQ}^{{\mathrm{Q}}_1^{-3∕2}{\mathrm{D}}_1^{+1∕2}}}{k_{DQ}^{{\mathrm{Q}}_1^{+3∕2}{\mathrm{D}}_1^{-1∕2}}+k_{DQ}^{{\mathrm{Q}}_1^{+1∕2}{\mathrm{D}}_1^{-1∕2}}+k_{DQ}^{{\mathrm{Q}}_1^{-3∕2}{\mathrm{D}}_1^{-1∕2}}}$$ Eq (2)

R_D1 quantifies how the spin populations redistribute itself within the D₁ states, which ultimately dictate the nitroxide hyperpolarization (see Appendix 3 in the SI). R_D1 was calculated at 18.8T (a typical high field for MAS-DNP) and the resulting plot (Fig. 1B) reveals a large RQM efficiency for ∣J_CR∣ in the range of 9 - 14 cm⁻¹. It is maximum at ~ 12 cm⁻¹ where $\Delta E({\mathrm{Q}}_1^{-3∕2},{\mathrm{D}}_1^{1∕2})=0$. In this case, the ${\mathrm{D}}_1^{1∕2}\leftrightarrow {\mathrm{Q}}_1^{-3∕2}$ transition becomes the dominant RQM pathway, as the mixing rate constants originating from the other D₁-Q₁ transitions are too small to have an effect (see figure S3). This special case enables a selective enhancement of the population of D₁^1/2 state and the generation of a very large electron hyperpolarization in the D₀ state via the D₁→D₀ pathway.

The model predicts an electron hyperpolarization level after laser irradiation, P_e (red curve, Fig.1B, see SI for derivation), that can reach −1 at the optimal J_CR; however, it also shows that smaller exchange interactions (i.e., 4-8 cm⁻¹) already yield significant hyperpolarization P_e ≈ −0.5. Such exchange interactions can be attained in existing CR systems given that earlier studies on the chromophore TEMPO showed J_CR values in the range of 1-5 cm⁻¹.⁵⁴

Hence, we conclude that solid state optical electron spin hyperpolarization is possible at X-band frequencies (Fig. 1). In addition, at high fields, a strong electron hyperpolarization in the solid state can be obtained via an “RQM-only” mechanism, provided that the J_CR falls within a favorable range. In turn, this allows us to explore the potential of MAS-DNP using optically pumped hyperpolarized nitroxides.

3.2. Optically Pumped Cross-Effect for MAS-DNP.

From the mechanistic analysis of the photophysical hyperpolarization, it is now possible to assess how optical pumping could benefit CE under MAS-DNP. CE MAS-DNP requires the use of biradicals, i.e., molecules with two coupled unpaired electrons in their ground state.

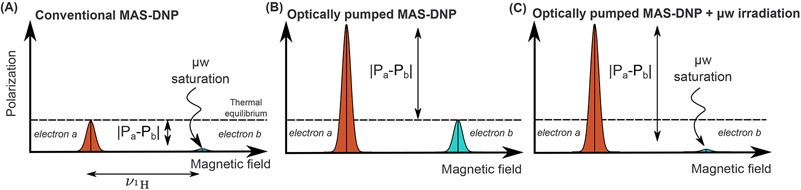
Scheme 2 shows an ideal CE biradical model with two interacting moieties (a) and (b) with electron Larmor frequencies, ν_a(b), and difference matching the Larmor frequency of the proximate nuclear spins,^33,74,75 ν_n, such that ∣ν_a − ν_b∣ ~ ∣ν_n∣. When an electron spin polarization difference, ∣P_e,a − P_e,b∣, is generated, this results in nuclear hyperpolarization.^32,33 Under DNP, it is the μw irradiation that generates ∣P_e,a − P_e,b∣ (Scheme 2A). The nuclear polarization, ∣P_n∣, in a steady state, is related to ∣P_e,a − P_e,b∣ by³²

$$\mid {\mathrm{P}}_{e,a}-{\mathrm{P}}_{e,b}\mid \ge \mid {\mathrm{P}}_n\mid$$ Eq.(3)

Scheme 2:

Schematics of the proton CE MAS-DNP mechanism in the ideal case of a biradical with two non-overlapping EPR spectra separated by the proton Larmor frequency. (A) Conventional MAS-DNP where the spins of electron b are saturated, while the spins of the electron a are at thermal equilibrium. The proposed optically pumped hyperpolarization method in which the polarization of electron spin a is increased while the electron b is at thermal equilibrium (B) or saturated by microwave irradiation (C).

If instead a is hyperpolarized via optical means, two other cases can be envisioned: (i) a is hyperpolarized, and b is at thermal equilibrium (Scheme 2B); or (ii) a is hyperpolarized, and b is saturated with a microwave irradiation (Scheme 2C).

To realize the concept presented in Scheme 2B and 2C, we need a molecule comprised of a chromophore and biradical CR_a-R_b where C and R_a are much closer to each other than C and R_b, such that in the excited state ∣J_CRa∣ ~ 5-14 cm⁻¹ and J_CRb ~ 0 cm⁻¹. In addition, in the ground state, the biradical, R_a-R_b, should have similar properties to typical biradicals that are used as MAS-DNP polarizing agents. For example, biradicals comprised of Trityl and nitroxide moieties are known to be efficient for MAS-DNP^21,74,76. The three cases in Scheme 2 were simulated using a fictitious “CR_a-R_b = Chromophore-TEMPO-Trityl” molecule represented at the top of Fig. 2 (herein, electron “a” stands for the nitroxide and “b” for the Trityl, unless otherwise specified).

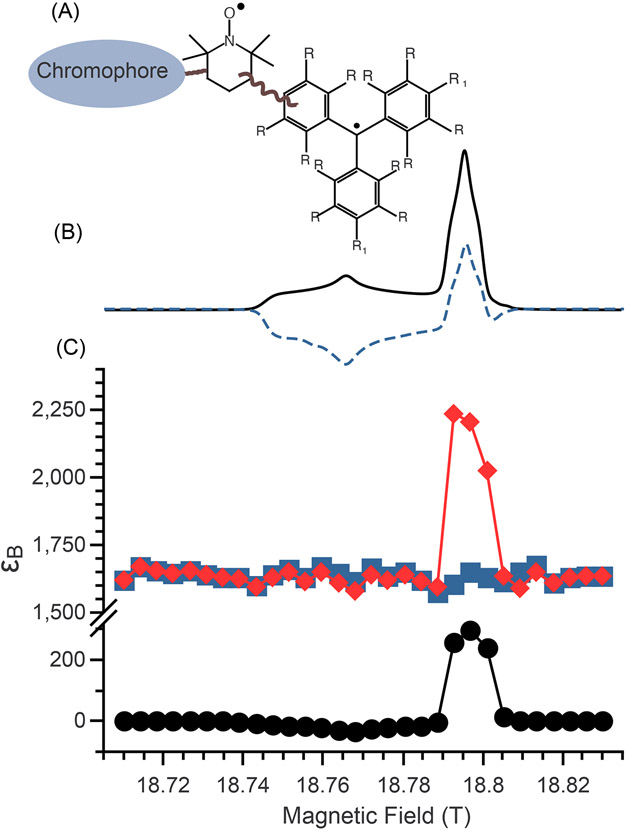
Fig. 2:

(A) Fictitious “Chromophore-TEMPO-Trityl” CR_a-R_b molecule. The wavy line represents unspecified bonds. (B) Simulated EPR spectra of CR_a-R_b in thermal equilibrium (solid black line) with laser irradiation assuming P_e,a = −0.25 (dashed blue line). (C) simulations of the MAS-DNP field profiles using the modified Box model for conventional MAS-DNP (black dots), optically hyperpolarized MAS-DNP (blue squares), and combined μw and optical irradiated hyperpolarization (red diamonds). In all simulations, the optical hyperpolarization leads to P_e,a → −0.75, and for clarity we plot ϵ_B = −f(B₀). Details about the spin system are given in the SI.

Under MAS, this spin system undergoes fast energy level anti-crossings (or rotor-events)³² because the EPR spectra of Trityl and TEMPO are anisotropic, and therefore overlap with one another. This means that the nuclear hyperpolarization results from CE rotor events that transfer the polarization from the electron pair to the nuclei. These rotor-events are active due to MAS, and it is important to note that they can perturb the nuclear spin polarization even in absence of μw irradiation.^77,78 In addition, because the EPR spectra overlap, the dipolar/exchange rotor events are active. This type of rotor event is key for maintaining the electron polarization difference and ensures that the transfer of polarization to the nuclei has a constant sign, allowing for large polarization buildups.^32,33

The complexity of this mechanism and its dependence on relaxation properties requires treatment with numerical simulations. Therefore, we used the “Box model”, which accounts for multiple three-spin systems {2 electron spins – 1 proton spin} distributed in a bounded space that has been extensively tested and validated.^25,52,79 This model treats the inter-biradical interactions to mimic those of a 10 mM biradical solution (see SI), thus faithfully represents the spin dynamics of the electrons²⁵. The model is modified to account for the optical hyperpolarization by assuming that under continuous (or pulsed) laser irradiation nitroxide hyperpolarization is generated on a time scale faster than the MAS period, as determined by the RQM analysis (see SI for details).

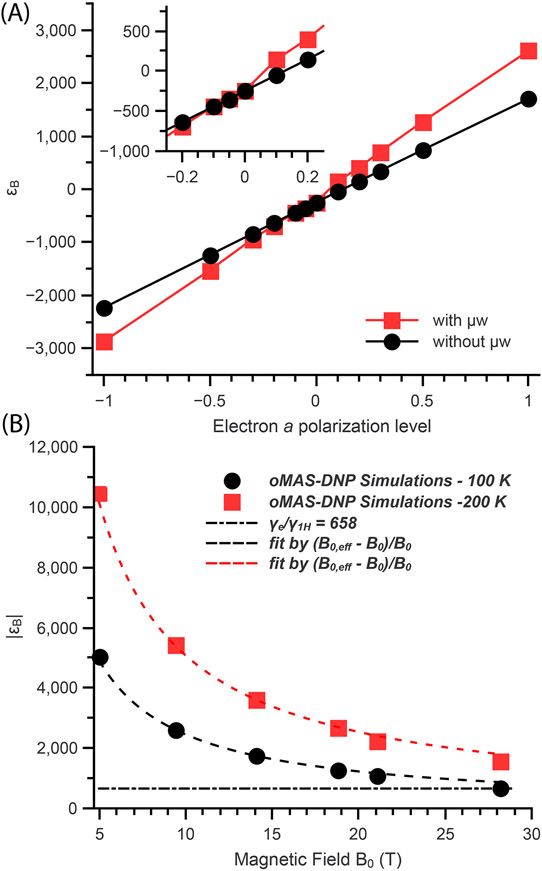
Fig. 2C displays the nuclear spin polarization gain as function of the magnetic field (see SI for calculation details) for conventional MAS-DNP (black dots), optical hyperpolarization (blue squares), and optical hyperpolarization combined with μw irradiation (red diamonds). The field profile calculated for conventional MAS-DNP spans the entire EPR spectra of the Trityl-TEMPO (shown in Fig. 2B) and has a sharp feature at the Trityl Larmor resonant frequency ^21,74,76. In this case, the maximum polarization gain is ϵ_B ≈ 295 with the chosen simulation parameters (see SI). On the other hand, the field profile in the presence of both optical and μw irradiation is very similar in shape but present now a staggering maximum value, ∣ϵ_B∣ ≈ 2200.

While this result is outstanding, the curve with blue squares, which reports ϵ_B in the case of optical hyperpolarization (only) is also very encouraging: it predicts ∣ϵ_B∣ ≈ 1700. This is seven times higher than in the conventional MAS-DNP case and also corresponds to the baseline of the optical and μw irradiation cases. This enhancement is the result of the CE mechanism being always active under MAS.^23,33 In absence of μw irradiation, this can gives rise to nuclear depolarization^77,78 for bis-nitroxides as ∣P_e,a − P_e,b∣_μW,off ≤ ∣P_n∣_eq, while Trityl-nitroxides do not depolarize significantly, i.e., ∣P_e,a − P_e,b∣_μW,off ≈ ∣P_n∣_eq. The centers of mass for the Trityl and nitroxide EPR spectra are separated by the proton Larmor frequency, leading to little depolarization (ϵ_B ≈ 1), as seen outside of the EPR resonant field (Fig. 2C, black dots)²¹. For the CR_a-R_b, this separation of the centers of mass of the EPR spectra is key for efficient DNP with optical hyperpolarization, enabling the existence of an electron spin polarization difference. At B₀ = 18.8 T and 100 K, the thermal equilibrium polarization of the Trityl is $P_{e,b}^{\text{eq}}\approx 0.12$, thus with electron hyperpolarization of the nitroxide (Fig. 2, blue square and red diamonds) we have:

$$\mid {\mathrm{P}}_{e,a}-{\mathrm{P}}_{e,b}^{\text{eq}}\mid \gg \mid {\mathrm{P}}_n{\mid }_{\text{eq}}$$ Eq.(4)

which explains the large ∣ϵ_B∣.

A broad range of scenarios were explored, which report ϵ_B as a function of the nitroxide hyperpolarization level with and without μw (Fig. 3A). Both sets of simulations display linear trends, with a steeper slope when biradicals are under μw irradiation (due to the larger ∣P_e,a − P_e,b∣). Enhancements ∣ϵ_B∣ larger than the ratio of electron to proton magnetic moments (~658) can be achieved for P_e,a → 0 or ${\mathrm{P}}_{e,a}\to 2P_{e,b}^{\text{eq}}=0.24$. However, with the chosen parameters, the nitroxide electron hyperpolarization must be lower than −0.3 or higher than 0.4, as shown Fig. 3A. These values are larger than the ideal case, because ∣P_e,a − P_e,b∣ is affected by the inter-biradical interactions. Under MAS, they tend to equilibrate the polarization among all the Trityls and the nitroxides contained in the Box,^25,77 thereby affecting the average electron spin polarization difference. This effect is spin-system dependent; therefore, different slopes (Fig 3A) are obtained for different electron relaxation times, magnetic fields, radical concentrations and/or temperatures (see examples in SI). The enhancement can also be calculated as a function of the magnetic field. For a given P_e,a, using (see SI for full derivation):

$${ϵ}_B=\frac{B_{\text{eff}}-B_0}{B_0}$$ Eq.(5)

where B_eff is an effective magnetic field.

Fig. 3:

(A) Calculated MAS-DNP polarization gain, ϵ_B, for a Trityl-nitroxide biradical using the modified Box model, with μw irradiation (red squares), and without (black dots) as a function of the nitroxide hyperpolarization. (B) Calculated ∣ϵ_B∣ as function of magnetic field without μw irradiation, assuming a nitroxide hyperpolarization of P_e,a → −0.75 at 100 K (black dots) and 200 K (red squares). All other simulation parameters were kept constant. Dashed lines: best fits using Eq. (5).

Fig. 3B displays ∣ϵ_B∣ as function of the field with P_e,a → −0.75 and without μw irradiation, which confirms ∣ϵ_B∣ > 658. The simulations carried out at 100 and 200 K perfectly fit with Eq. (5). At higher temperatures, the significantly larger ∣ϵ_B∣ is the result of the lower equilibrium polarizations for both Trityl electrons and the protons. This illustrates yet another potential benefits of MAS-OPDNP: better efficiency at higher temperature. Of course, this would depend on the relaxation times at higher temperature, where the CE mechanism may not be as efficient in terms of total nuclear polarization. Finally, the MAS-OPDNP simulations of a bis-nitroxide with a structure equivalent to “AMUPol”⁵² are reported in the SI. While the EPR spectra of R_a and R_b have the same centers of mass, the resulting ∣ϵ_B∣ is on the order of 200 at 14.1 T, which is very similar to the conventional MAS-DNP for AMUPol.⁵²

4. Discussion

The low field (0.3 T) EPR experiments showed that significant electron spin hyperpolarization is achievable in at 100 K with a chromophore covalently bonded to a nitroxide molecule and dissolved in a glass-forming matrix (toluene). The analysis of the hyperpolarization mechanism indicates that a very large exchange interaction between the chromophore and the nitroxide is needed to yield high electron spin hyperpolarization at very high field, as the SO-ISC mechanism becomes weaker with field.^58,72 The strength of the interaction between C and Ra must be of the order of the electron Larmor frequency to favor the RQM mechanism, i.e. ~ 10-12 cm⁻¹, which favors the selective transition ${\mathrm{D}}_1^{1∕2}\leftrightarrow {\mathrm{Q}}_1^{-3∕2}$ at 18.8 T. In addition, the analysis of the hyperpolarization transfer mechanism and the numerical simulations of the MAS-OPDNP reveals that the success of this proposed concept requires the synthesis of new CR_a-R_b molecules possessing the appropriate exchange interactions in the excited state and in the ground state. For successful MAS-OPDNP experiment, the design of such molecule must enable both a very strong C-R_a (∣J_CRa∣ ~ 4-12 cm⁻¹) and a weak C-R_b interaction (∣J_CRb∣ < 1 cm⁻¹) in the excited state, while leading to significant R_a-R_b, (i.e. a dipolar coupling D_a,b ~ 30 MHz and an exchange interaction ∣J_a,b∣ ~ 10s MHz). This design remains possible. A large C-Ra interaction in the excited state can be achieved by tuning the bridge between the chromophore and the nitroxide, i.e. reducing the number of bonds and favoring resonant structures.^59,80 The coupling in between the nitroxide and the Trityl (used in the simulations as an example), must be longer, typically of the order of 5-6 bonds.⁷⁶ For a successful MAS-OPDNP, the Ra-Rb bridge should avoid conjugated bonds in order to prevent large C-Rb couplings in the excited state. Current bridges used in MAS-DNP with Trityl-Nitoxides^20,76,81 already possess the right properties which illustrates the viability of the approach.

The chromophore used to hyperpolarize the nitroxide in the solid-state is only compatible with organic solvents and requires sample that are transparent in the near UV region (355 nm). In the first development stages of the method, toluene could be used to prove the viability of the approach. Application to aqueous samples may be a challenge but recent progress indicate that chromophore modifications could make it possible.⁴⁴ In addition, water soluble anthraquinones can also be examined for the hyperpolarization generation.

Lastly, the sample irradiation could be achieved with a pulsed or a CW laser source. Setup using irradiation under MAS has been demonstrated experimentally in CIDNP experiments, using continuous waves UV sources and (UV transparent) sapphire rotors.^38,39 The approach could be adapted to carry out MAS-OPDNP at cryogenic temperatures using a commercial MAS-DNP probe to enable good temperature control.⁸² A decay of chromophore (bleaching) could occur under CW UV irradiation and thus a pulsed laser should avoid both the decay of the chromophore yield high average electron spin hyperpolarization. The ANCOOT and Anq1pr have demonstrated experimentally a significant stability in toluene and pulsed laser irradiation, with very little decay over time which may make them good molecules to begin exploring MAS-OPDNP as a mixture with Trityl molecules.

5. Conclusions

In conclusion, the MAS-OPDNP simulations demonstrate that even moderate nitroxide hyperpolarization could theoretically lead to ∣ϵ_B∣ > 658. This new concept might also work at higher temperatures, which may be beneficial for samples that require higher peak resolutions.

However, this innovative approach removes the need for expensive high power μw sources and “sweepable” high-field NMR magnets. Instead, MAS-OPDNP would rely on much more affordable high-power lasers that are currently commercially available and sample spinning. Finally, the MAS-OPDNP concept has the potential to be a paradigm shift for high-field MAS-DNP, which will have broad impacts on characterization of numerous materials and potentially biological molecules.