Abstract
Objective:
Kilovoltage computed tomography (kVCT) is the cornerstone of radiotherapy treatment planning for delineating tissues and towards dose calculation. For the former, kVCT provides excellent contrast and signal-to-noise ratio. For the latter, kVCT may have greater uncertainty in determining relative electron density (ρe) and proton stopping power ratio (SPR). Conversely, megavoltage CT (MVCT) may result in superior dose calculation accuracy. The purpose of this work was to convert kVCT HU to MVCT HU using deep learning to obtain higher accuracy ρe and SPR.
Approach:
Tissue-mimicking phantoms were created to compare kVCT- and MVCT-determined ρe and SPR to physical measurements. Using 100 head-and-neck datasets, an unpaired deep learning model was trained to learn the relationship between kVCTs and MVCTs, creating synthetic MVCTs (sMVCTs). Similarity metrics were calculated between kVCTs, sMVCTs, and MVCTs in 20 test datasets. An anthropomorphic head phantom containing bone-mimicking material with known composition was scanned to provide an independent determination of ρe and SPR accuracy by sMVCT.
Main results:
In tissue-mimicking bone, ρe errors were 2.20% versus 0.19% and SPR errors were 4.38% versus 0.22%, for kVCT versus MVCT, respectively. Compared to MVCT, in vivo mean difference (MD) values were 11 and 327 HU for kVCT and 2 and 3 HU for sMVCT in soft tissue and bone, respectively. ρe MD decreased from 1.3% to 0.35% in soft tissue and 2.9% to 0.13% in bone, for kVCT and sMVCT, respectively. SPR MD decreased from 1.8% to 0.24% in soft tissue and 6.8% to 0.16% in bone, for kVCT and sMVCT, respectively. Relative to physical measurements, ρe and SPR error in anthropomorphic bone decreased from 7.50% and 7.48% for kVCT to <1% for both MVCT and sMVCT.
Significance:
Deep learning can be used to map kVCT to sMVCT, suggesting higher accuracy ρe and SPR is achievable with sMVCT versus kVCT.
Keywords: kVCT, MVCT, generative adversarial learning, electron density, proton stopping power
1. INTRODUCTION
Kilovoltage computed tomography (kVCT) scans have been the primary imaging modality used in imaging-based radiation therapy treatment planning. In the treatment planning stage of radiation therapy, kVCT scans serve two main purposes: 1) for contouring of normal and diseased tissues and 2) for calculation of relative electron densities and/or stopping power ratios required for dose calculation. For the former purpose, kVCT scans possess favorable characteristics in terms of soft and bony tissue contrast relative to noise and imaging dose. The favorable contrast in soft and bony tissue observed in kVCT scans is due to the dominance of the photoelectric effect at low x-ray energy and to its higher-order dependence on atomic number (Z). This greater dependence on atomic number, however, causes a degenerate relationship between kVCT Hounsfield Unit (HU) and electron density. This degeneracy prevents accurate determinations of relative electron density (ρe) and stopping power ratio (SPR), which is predominantly dependent on electron density.
While not strictly linear, the relationships between CT HU and both ρe and SPR are often modeled as piecewise linear functions with two or more linear regions (for example, lower density in lung and soft tissue, and higher density in bone). As there’s an explicit atomic number dependence in this relationship, it is known that for a given HU there may be multiple possible solutions for electron density1–3. In other words, as these three types of tissues exhibit different physical/mass densities, any solution to explicitly resolve relative electron density from CT HU necessitates an understanding of the atomic composition of the material or at least some knowledge of the magnitude of its effect on the CT HU. With only a standard single kVCT scan, there is not enough additional information to correct for this atomic number dependence. While a lesser concern for x-ray/photon-based dose calculation where there is a smaller dosimetric impact of these uncertainties, even small inaccuracies in the translation of CT HU to SPR can result in over- or under-dosing of the target volume and nearby organs at risk 2,4. In clinical practice, these uncertainties are typically accounted for by adding an additional margin of 2.5–3.5% to each proton beam’s range5,6. In efforts to address this issue, many groups have proposed solutions involving the incorporation of additional information provided by CT scans of differing energy, known as dual energy CT (DECT). This method considers that multiple CT scans, each taken at a different energy, will have differential responses/intensities due to different atomic numbers and density values, which can be used to solve for the effective atomic number and electron density. Results from prior studies7–11 have shown great promise for high accuracy determination of both quantities. However, practical limitations of DECT include the necessity for two separate scans (on single-source scanners), beam hardening artifacts, and greater nominal noise12–14 relative to single energy kVCT scanners.
At higher photon energies (for example, megavoltage (MV) photon energy), the predominant mechanism of photon interaction is Compton scattering, which is directly dependent on the electron density of the medium rather than its atomic number. Therefore, HU in MVCT images are directly dependent on electron density, with MVCT having demonstrated sufficient accuracy for photon dose calculation15,16. In bony tissue, for example, errors in estimating physical and relative electron density have been reduced from 3.6% and 2.6%, respectively, using kVCT to <1% using MVCT17. Furthermore, in contrast to DECT (and lower energy x-ray methods in general), images acquired at a higher energy spectrum are naturally less susceptible to beam hardening and photon starvation effects. With these advantages in terms of electron density linearity and resistance to beam hardening effects18–22, MVCT imaging would seem to be more favorable than lower energy kVCT techniques for dose calculation. Yet disadvantages such as lower image contrast, greater noise (due to increased Compton scatter interactions relative to photoelectric interactions)23, and reduced availability (due to the potentially cost prohibitive higher energy x-ray accelerator requirements of an MV fan beam CT scanner), have limited clinical implementation of MVCT scans into the radiation oncology clinic to the special case of on-treatment adaptation. Interest in overcoming these limitations has resulted in the development of technologies such as intermediate energy orthovoltage CT (OCT) imaging24 although, to date, no clinical system is available. In the case of proton therapy, proton CT provides a direct map of SPR25,26, however, its primary limitations are the high proton energy required to image a patient27 and low resolution due to multiple coulomb scattering28. In terms of dose calculation accuracy, a methodology to create a more accurate relationship between kVCT HU and relative electron density (in the case of photon radiotherapy) or SPR (in the case of proton therapy), while mitigating these mentioned disadvantages would be ideal.
In recent years, new image processing techniques have been developed to translate the characteristics of one scan to mimic the characteristics of another. In particular, machine learning techniques involving convolutional neural networks (CNNs) have grown in prominence and popularity. Involving radiation oncology volumetric scans for dose calculation, two main use cases have emerged: conversion of MR data to kVCT HU data29–31 for MRI-only radiotherapy planning and improving the image quality of cone-beam CT (CBCT) images from kVCT data32–34. Generally, these deep learning techniques have found that achievable errors may be low (as low as 20–50 HU mean absolute error) with results improving with incremental developments in machine learning technology. In both discussed use cases, the imaging dataset that is being translated towards is fan beam kVCT HU. As there does not exist a one-to-one relationship between single scan kVCT HU and relative electron density or SPR, it is expected that translation of imaging data to synthesize kVCT HU will include any of the inherent relative electron density or SPR uncertainties in this process. As kVCTs exhibit more contrast and less noise than MVCTs, we hypothesized that it was possible to accurately translate (through deep machine learning) trends in HU values from kVCT to MVCT. In doing so, we anticipated that synthetic MVCT (sMVCT) images would naturally exhibit higher accuracy mapping of relative electron density and stopping power ratio, thus promising improvements for dose calculation accuracy. In this work, we report on the first known application of deep machine learning to reduce uncertainty in the relationship between kVCT HU and ρe and SPR through learning of MVCT HU data.
After creation of the CycleGAN machine learning model, the clinical workflow proposed through this work requires only subsequent kVCT data for the conversion to sMVCT data, potentially alleviating the need for an MVCT scanner. In this workflow, we propose that the original kVCT images, with the high contrast and low noise intrinsic to kV imaging, be leveraged for localization and contouring of normal and diseased tissues while the sMVCT generated from the machine learning model be used for dose calculation, as shown in Figure 1.
Figure 1.
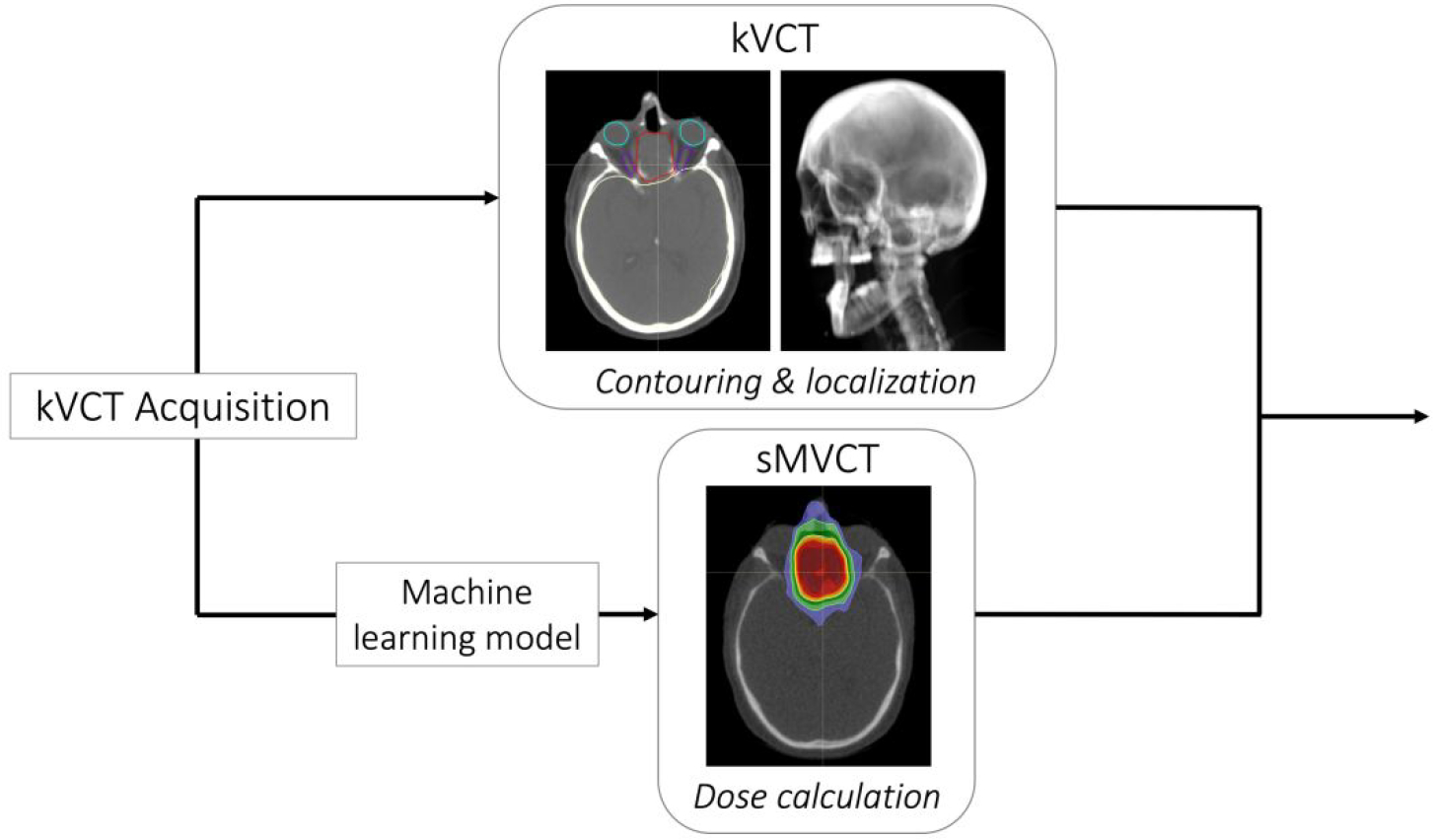
The proposed clinical workflow requires a single kVCT scan, which is subsequently used for contouring and localization (top panel) and converted into a sMVCT using the machine learning model for dose calculation (bottom panel).
2. MATERIALS AND METHODS
In this manuscript, we present an approach to convert kVCT HU data to sMVCT HU data and, in doing so, produce more accurate maps of ρe and SPR. A tissue-mimicking phantom was created to compare physical measurements of ρe and SPR with those determined from kV and MV CT imaging, thus demonstrating the increased accuracy of ρe and SPR provided by our method. A CycleGAN deep learning model was employed to learn the relationship between kVCT HU and MVCT HU from in vivo patient scans and to create sMVCT datasets. Patient kVCT and sMVCT data were compared with MVCT data as the reference. Separately, an anthropomorphic head phantom containing synthetic bone of known material composition and density (and therefore known ρe and SPR values) was tested with CycleGAN model to assess the accuracy of ρe and SPR values calculated from the kVCT, MVCT, and sMVCT versus physical measurements.
2.A. CT imaging and HU-to-ρe and HU-to-SPR calibration curves
In this study, a Siemens Somatom CT scanner (Somatom; Siemens, Munich) was used to create kVCT images of phantoms and patients. Scans were acquired at 120kVp using a helical acquisition at an approximate resolution of 1×1×3mm3 in the axial plane (512×512 matrix). MVCT imaging (3.5MV) of phantoms and patients were completed on an Accuray TomoTherapy system (TomoHD; Sunnyvale, CA) using the “coarse” pitch mode with reconstructed slices of 1×1×3mm3 in the axial plane (512×512 matrix). For the purposes of generating CT calibration curves, a CIRS (180 mm diameter) tissue characterization phantom (Model 062; CIRS, Norfolk, VA) containing nine tissue-surrogate plugs was scanned with both imaging modalities. This diameter phantom was chosen to better mimic scatter and beam hardening effects for the head and neck region studied. Electron density, ρe, was calculated for each type of tissue surrogate material using vendor provided batch number specific elemental compositions and mass density. HU-to-ρe calibration curves from the CIRS tissue surrogate phantom are shown in Figure 2a and were used in subsequent HU-to-ρe conversions.
Figure 2.
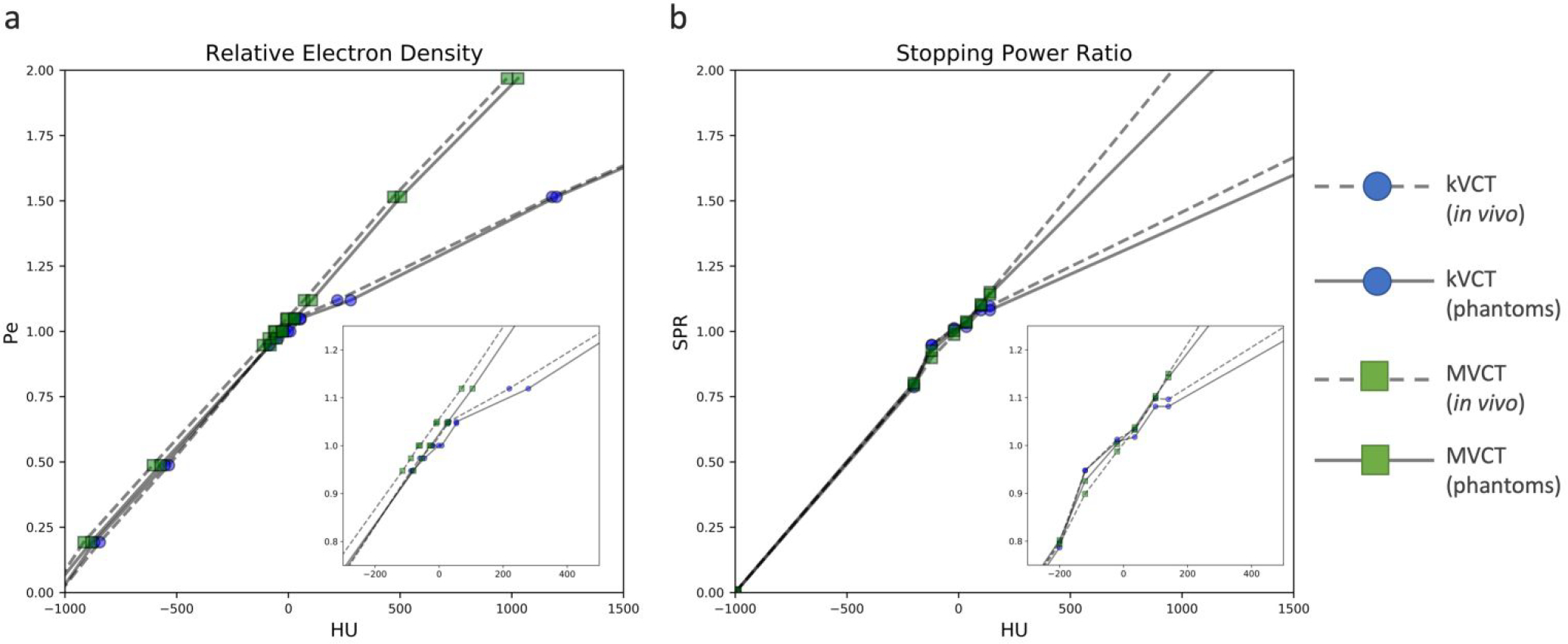
HU plotted against ρe (a) and SPR (b) derived from kVCT and MVCT scans. The HU-vs-ρe curves were derived using vendor-provided relative electron density values with corresponding HU values for each tissue surrogate material. Both kVCT and MVCT curves were interpolated from nine points, one for each tissue surrogate plug in the CIRS phantom. Note that in both kVCT curves, one point extends beyond 1500 HU and is not shown for figure clarity. The HU-vs-SPR curves were derived using a linear regression fit to theoretical HU values calculated for 64 human tissues provided in the literature. Both kVCT and MVCT curves contain six points, one for each node at HU values of −200, −120, −20, +35, +100, and +140. For both HU-to-ρe and HU-to-SPR curves, note the typical bilinear distribution for kVCT, contrasted by the linear distribution for MVCT. All calibration curves were generated twice: one for the phantom data and one for the in vivo data, which was acquired retrospectively two years prior to the phantom data.
HU-to-SPR calibration curves were created according to the stoichiometric method described by Schneider et al35. To this end, scanner-specific coefficients Kph, Kcoh, and KKN characterizing the photoelectric effect, coherent scattering, and incoherent scattering cross-sections, respectively, were computed using a linear regression fit and used to calculate theoretical HU values for 64 human tissues provided in the literature36,37 using elemental mean ionization (Im) values optimized for use with the Bragg additivity rule38. Three separate plots of HU versus SPR were generated for reference tissues classified as organ-like, fat-like, and bone-like, with the final stoichiometric curve constructed from separate fits with nodes at HU values of −200, −120, −20, +35, +100, and +140 as previously described3. All SPR calculations were performed using a fixed proton energy of 115MeV to minimize consequences of energy variability in practice2. In total, two types of stoichiometric CT calibrations were performed: one for the kVCT scanner used in this study (120kVp, 1mm slice thickness) and the other for the MVCT scanner used in this study (3.5MV, 1mm slice thickness). Details regarding stoichiometric calibrations for kV and MV energies is described in the literature by De Marzi et al39. Of note, they compared the traditional Jackson and Hawke’s40 formalism (generally used at diagnostic energies and disregards contributions of pair production) to the Midgley41 formalism (encompassing the total attenuation coefficient spanning energies 6keV to 125MeV) to demonstrate that these methods show good agreement with one another. In other words, the conventional stoichiometric method (which uses the Jackson and Hawke’s formalism) can be accurately applied to a higher energy (e.g. maximum 3.5MeV) spectrum. HU-to-SPR calibration curves are shown in Figure 2b and were used in subsequent HU-to-SPR conversions. HU-vs-ρe and HU-vs-SPR calibration curves for both energies were generated twice: one used for the phantom data and one used for the in vivo data, which was acquired retrospectively two years prior. Curves were generated using CT data of the CIRS phantom acquired within 6 months of image acquisition.
For both ρe and SPR calibration curves, it is noted that there are trends in non-linearity for kVCT between soft tissue, liquid water, and bone materials. On the other hand, MVCT calibration curves are linear with ρe and SPR, with minimal differences in linearity across soft tissue, liquid water, and bone tissues. This trend is in line with the finding by Das et al42 where they found that as kVp increases, the relationship between HU and relative electron density becomes more linear.
2.B. Tissue mimicking phantom
An in-house tissue mimicking phantom with known mass density and elemental composition was created to replicate properties of skin, muscle, adipose and spongiosa bone based on each tissue’s molecular composition provided in the literature36,43. Details on how this phantom was developed and fabricated have been previously published by our group44. Briefly, tissues were created using homogeneous mixtures of distilled water, protein (gelatin), fat (coconut oil), and/or bone (hydroxyapatite powder). Elemental composition of each tissue-mimicking material was determined via carbon, hydrogen, nitrogen, and oxygen (CHNO) combustion analysis at a specialized microanalytic facility. For each tissue type, elemental composition measured by CHNO combustion analysis and mass density measured using a high precision scale (Practum313–1S, Sartorius Biotech, Germany) were used to calculate “measured” values of ρe (Equation 1) and SPR (Equation 2: the Bethe-Bloch equation and Equation 3: the Bragg Additivity Rule) for each tissue type.
| (1) |
| (2) |
| (3) |
In Equations 1–3, for each element i composing material m, w is the fraction by weight, Z is the atomic number, A is the atomic mass, I is the mean ionization potential, ρe is the electron density of the medium relative to water, ρ is the mass density, me is electron mass, c is the speed of light, and β is the proton velocity relative to c. All calculations were performed using a fixed proton energy of 115MeV as previously described.
2.C. Human imaging data, pre-processing, and machine learning
The kVCT and MVCT images of 120 head and neck (H&N) cancer patients treated on an Accuray TomoHD system were retrospectively recruited into this study. This study and its experimental protocols were approved by the University of California, San Francisco Institutional Review Board (IRB) (#14-15452). All methods were carried out in accordance with relevant guidelines and regulations. Informed consent was waived by the IRB due to the retrospective, de-identified nature of the study. One hundred patient scans were used for training and validation while 20 patient scans were used for testing. Each patient received a kVCT simulation scan approximately two weeks prior to treatment (and their first MVCT scan). A simulation scan is a scan in which a patient is positioned in the treatment position to “simulate” the treatment anatomic position. This CT simulation scan is then used for all subsequent delineation of patient anatomy (normal and diseased tissues) as well as calculation of radiation treatment plans and dose distributions. Following treatment planning and during their treatments, each patient was imaged daily by MVCT on the TomoHD immediately prior to treatment. The MVCT scan closest in time to their kVCT simulation scan was included in this study to minimize differences in patient anatomy through potential changes in weight gain or loss and tumor growth or shrinkage. Each kVCT scan volume was co-registered to the space of their respective MVCT scan volume in MIM (MIM Software Inc, v 6.8.3 Cleveland, OH) using the automated 3D rigid registration algorithm to produce a match across the entire scan volume. These kVCT images were then resampled and saved while maintaining a 512×512 matrix. As the deep machine learning algorithm chosen (CycleGAN) would naturally learn from unpaired images, rigid registration was preferred to minimize the introduction of additional registration and intensity errors. Following registration, the kVCT field of view (FOV) was, in general, reduced to match the smaller FOV of MVCT scans. This FOV reduction was to mitigate “hallucinations” whereby unintended features such as FOV differences are learned in the process. Both kVCT and MVCT dataset image intensities were then renormalized to [−1, 1]. During final conversion and analysis, data were rescaled back to HU and then converted to relative electron density and stopping power ratio using the CT calibration data shown in Figure 2. Objects outside the body were ignored by the algorithm through the creation of a body mask that was applied to all images prior to model training.
While efforts were made to best match MVCT and kVCT images, minor changes in patient positioning and anatomy were observed. To mitigate the learning of these subtle changes, an unpaired cycle-consistent generative adversarial network (CycleGAN) machine learning strategy45 was preferred versus other paired pixel-to-pixel machine learning algorithms. The CycleGAN machine learning model consists of a pair of parallel opposed generative adversarial networks (GANs) to learn the relationship from image A to image B and from image B to image A. These two GANs work in opposition to each other to generate and detect increasingly more accurate synthetic images. The role of the generator is to generate data that as closely as possible matches the real data while the discriminator’s role is to accurately distinguish between real and synthetic data produced by the generator. In general, the roles of the generator and discriminator are in competition with each other as the generator learns to produce increasingly realistic images that the discriminator learns to distinguish as synthetic for the purpose of model improvement. The learning of both GANs are coupled with a cyclic loss which penalizes the degree to which the composed forward and backward transformation varied from the identity function. If G:A→B is the generator producing MVCT images from kVCT images and F:B→A is the generator producing kVCT images from MVCT images, then the cyclic loss can be written as
| (4) |
where ‖ · ‖1 is the L1 norm of a vector, xi is an kVCT training example, and yi is a MVCT training example.
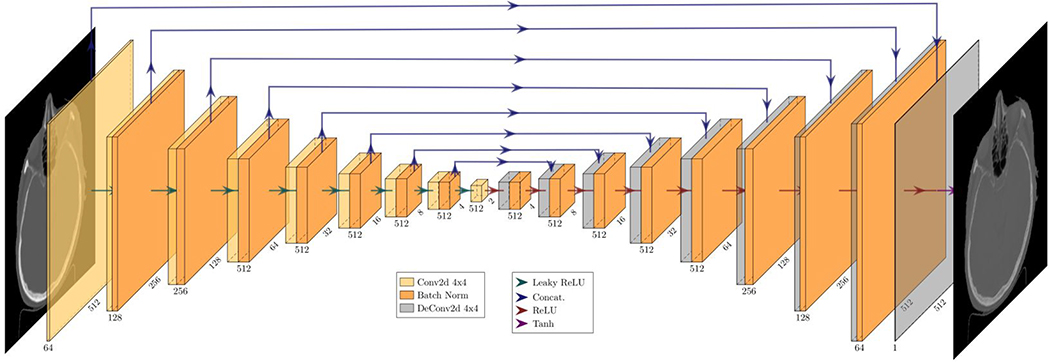
We implemented a version of the CycleGAN deep learning algorithm using PyTorch45. A U-Net architecture with a 2×2 bottleneck was used for the generators and a four-layer PatchGAN discriminator with a patch output of 30×30 with an effective receptive field of 142×142 for a total of 900 patches. This type of discriminator is shallower than modern classifier CNNs but learns faster and captures local style characteristics better than conventional discriminator CNNs46. Approximately 3940 2D CT images were used for training, composed of 100 datasets containing approximately 40 CT slices per patient. Our model was trained using the Adam optimizer with a learning rate of 0.00025, β1 of 0.5, and ϵ of 1.0 × 10−8. Training was run for 210 epochs as it was found, during validation, that going past this point negligibly improved generator expressivity while adding to adversarial noise and potential overtraining. Our methodology is analogous to prior CycleGAN machine learning studies of CT and on-board treatment machine CT imaging47,48. The U-Net architecture used for both is visualized in Figure 3.
Figure 3.
Schematic diagram of the U-Net generator architecture45 used in this work. This figure shows the image transformation pipeline from kVCT to sMVCT image.
2.D. Post-processing and evaluation
Within the twenty test patient datasets, additional processing and analysis was completed to assess the changes that occurred through the deep learning synthetic MVCT (sMVCT) creation process. Tissue segmentation was implemented to compare relative electron density and stopping power ratio accuracy for soft tissue and bony tissue at standard HU thresholds. A total of three tissue masks were created from the kVCT data: a body mask, a bony tissue mask, and a soft tissue mask. The body mask was created by truncating all HU values less than −400 and then segmenting the different connected regions. The largest of these connected regions was defined to be the body region. The body region was refined to a mask through a binary fill operation which preserved any cavities (including nasal and sinus cavities) as well as the lungs of the body. All voxels inside the body mask with HU values greater than 150 HU were included in the bony tissue mask. The set subtraction between body mask and bony tissue mask produced the soft tissue mask.
In this manuscript, mean error metrics were calculated to assess differences between the imaging datasets at the voxel level. Letting N denote the total number of voxels shared between source image X and target image Y while Xi and Yi denote the intensity values of the ith voxel at the source and target images, mean difference (MD) and mean absolute difference (MAD) can be expressed as
| (5) |
| (6) |
Data from all twenty test patients are included in the sums of (5) and (6) and only voxels within the body were included. Signal-to-noise-ratio (SNR), peak signal-to-noise ratio (PSNR), root mean square difference (RMSD), and a structural similarity index measure (SSIM) were also calculated and defined as
| (7) |
| (8) |
| (9) |
| (10) |
where is the mean of source X at slice k and is the mirror case for another source Y such that the noise on slice k is given by the variable, σ(k), σxy is the covariance of x and y, c1 = (k1Imax)2, c2 = (k2Imax)2, k1 = 0.01, and k2 = 0.03.
2.E. Anthropomorphic head phantom
To independently verify the accuracy of bone relative electron density and SPR of kVCT, MVCT, and synthetic MVCT images produced by the developed CycleGAN model, relative electron density and SPR were analyzed in an anthropomorphic head phantom (RS-108, Radiologic Support Devices Inc., Long Beach, CA) containing bone-mimicking material. The phantom material was analyzed using both CHNO combustion analysis and energy dispersive x-ray spectroscopy. Because the model was trained on in vivo human data, phantom materials in this study were selected based on their similarity to values of in vivo tissues provided in the literature36,43,49. Elemental composition, physical density, relative electron density (calculated from Equation 1), and stopping power ratio (calculated from Equations 2 and 3) were compared between phantom tissues and literature in vivo human tissues to ensure the phantom was a reasonable surrogate. Of the phantom materials, bone closely matched composition, density, and SPR values from the literature (as shown in Table 1) and was selected for analysis in this study. Other materials meant to generically mimic tissues in this head phantom did not mimic the typical mass density or elemental compositions found in human tissues49 and were not further investigated.
Table 1:
Tabulated physical parameters for atomic composition, physical density, relative electron density, and stopping power ratio derived from physical measurements of the bone phantom material versus in vivo bone tissue composition from ICRU Report 4422 and ICRP Report 23.23
|
|
||||||||
|---|---|---|---|---|---|---|---|---|
| Phantom Physical Measurements | Literature Values | |||||||
|
|
||||||||
| % composition | Density (g/cc) | ρe | SPR | % composition | Density (g/cc) | ρe | SPR | |
|
| ||||||||
| Bone | H: 6 C: 46 N: 4 O: 31 Ca: 12 Trace < 1 |
1.18 | 1.12 | 1.125 | H: 5–9 C: 40–60 N: 2–4 O: 30–45 Ca: 8–20 |
1.14 – 1.2 | 1.12 – 1.18 | 1.12 – 1.18 |
kVCT and MVCT images were acquired of the head phantom using the same protocols as described for the in vivo data. The kVCT data was run through the CycleGAN model to generate a synthetic MVCT scan. HU values (mean and standard deviation) for cortical bone were extracted and mapped to corresponding ρe and SPR values using the CT calibration curves shown in Figure 2. Values of ρe and SPR estimated from kVCT, MVCT, and sMVCT were compared to the physical measurements tabulated in Table 1.
3. RESULTS
3.A. Tissue mimicking phantom: physical measurements of ρe and SPR versus kVCT and MVCT
Results of relative electron density and stopping power ratio for the four tissue-mimicking phantoms that were measured and calculated through kV and MV CT calibration curves are shown in Table 2. Percent differences between kV and MV imaging and physical measurements (% diff) are also shown. Relative electron density values computed using MVCT were within 0.29%, 0.19%, 0.84%, and −0.19% versus those computed using kVCT of −2.10%, −2.61%, −0.84%, and 2.20% for skin, muscle, adipose, and spongiosa, respectively. In the case of stopping power ratio, both kVCT and MVCT provided accuracy to within 1% for skin and muscle tissues. In the case of adipose, physical measurements of SPR differed by 2.58% for kVCT and 1.70% for MVCT. In the case of bone, SPR values computed with MVCT were within 0.22% of physical measurements while kVCT deviated by more than 4%.
Table 2.
Results of ρe and SPR values calculated using the kV and MV CT calibration curves for skin, muscle, adipose, and spongiosa tissue mimicking phantoms.
|
|
||||||
|---|---|---|---|---|---|---|
| Relative electron density | Stopping power ratio (115 MeV) | |||||
|
|
||||||
| Measured | kVCT (% diff) | MVCT (% diff) | Measured | kVCT (% diff) | MVCT (% diff) | |
|
| ||||||
| Skin | 1.048 ± 0.002 | 1.026 ± 0.004 (−2.10) | 1.051 ± 0.004 (0.29) | 1.049 ± 0.002 | 1.055 ± 0.004 (0.62) | 1.052 ± 0.004 (0.29) |
| Muscle | 1.036 ± 0.002 | 1.009 ± 0.004 (−2.61) | 1.038 ± 0.004 (0.19) | 1.036 ± 0.002 | 1.038 ± 0.004 (0.13) | 1.037 ± 0.004 (0.11) |
| Adipose | 0.955 ± 0.002 | 0.947 ± 0.004 (−0.84) | 0.963 ± 0.005 (0.84) | 0.953 ± 0.002 | 0.978 ± 0.004 (2.58) | 0.970 ± 0.005 (1.70) |
| Spongiosa | 1.044 ± 0.002 | 1.067 ± 0.002 (2.20) | 1.042 ± 0.003 (−0.19) | 1.044 ± 0.002 | 1.090 ± 0.002 (4.38) | 1.042 ± 0.003 (−0.22) |
3.B. In vivo trends in HU, ρe, and SPR
CycleGAN machine learning of kVCT images to MVCT images was used to learn the relationship between kVCT HU and MVCT HU in a dataset containing images of the head and neck. Figure 4 shows exemplar images for kVCT HU, sMVCT HU, MVCT HU, and difference heatmaps of kVCT HU and sMVCT HU compared to MVCT HU for four different subject scans from the test group. In the difference heatmaps (two rightmost columns), there exhibits some trends in value differences between different tissue types. As expected from the tissue mimicking phantom results, bony tissues exhibit the largest difference between kVCT and MVCT, with kVCT images exhibiting higher HU values than those exhibited by corresponding MVCT images. Overall, there appears to be learning of some characteristics of MVCT images beyond its tissue-independent relationship to electron density. sMVCT images exhibit increased noise compared with equivalent kVCT images, an unintended consequence of the learning process.
Figure 4.
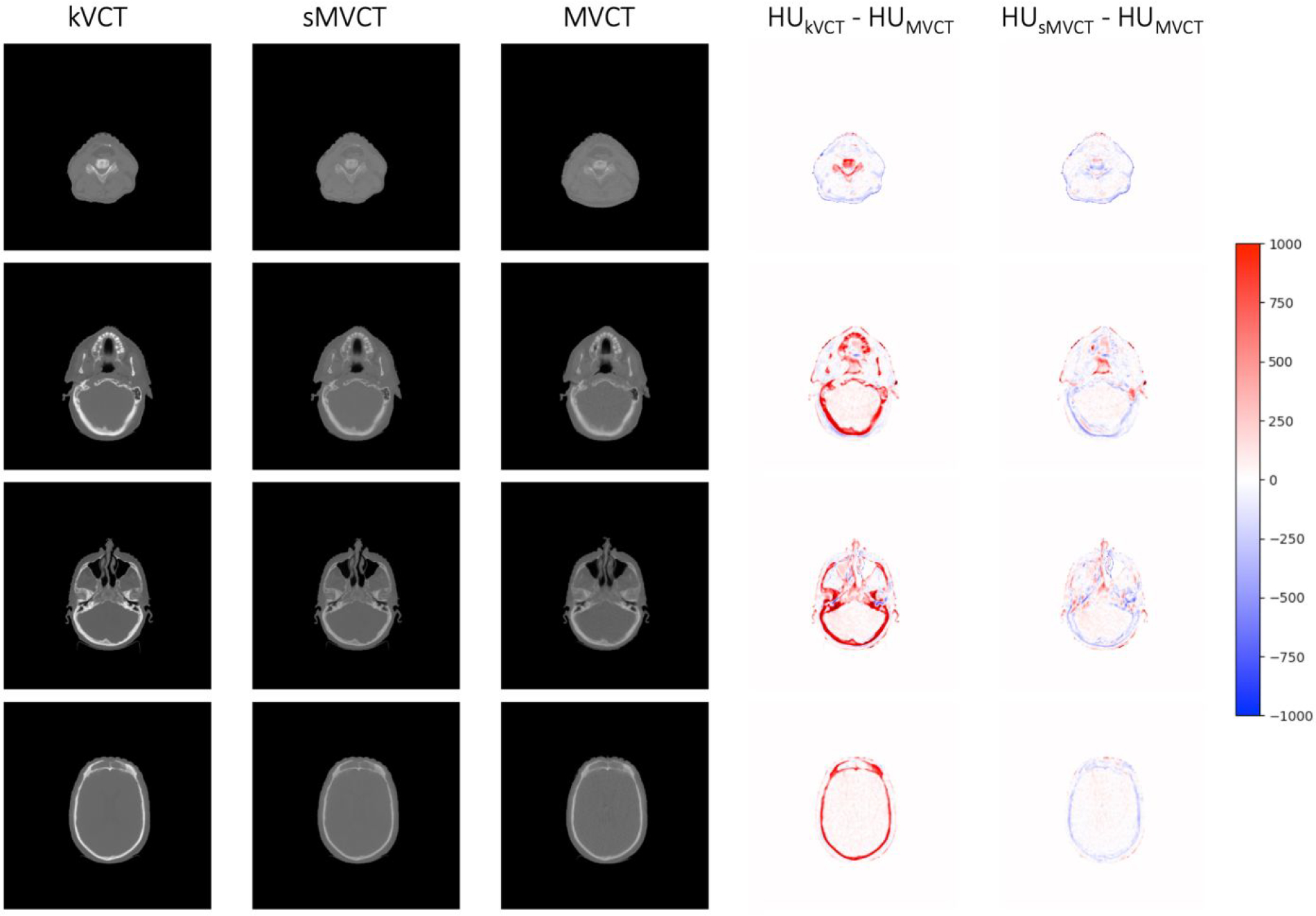
Exemplar images from four different subject scans of kVCT HU (1st column), sMVCT HU (2nd column), MVCT HU (3rd column), and HU difference heat maps for kVCT versus MVCT (4th column) and for sMVCT versus MVCT (5th column). The HU scale used in the difference maps is shown on the right.
Quantitatively, we see a similar trend between kVCT/sMVCT HU and MVCT HU values as was seen in qualitative results shown in Figure 4. A summary of similarity metrics between kVCT HU, sMVCT HU and MVCT HU are presented in Table 3. Following CycleGAN learning, sMVCT HU values were markedly more similar to MVCT HU values than kVCT values. In particular, mean difference (MD) and root mean square difference (RMSD) HU values improved for both soft tissue and bone with the largest improvement in bone. Mean absolute difference (MAD) HU values did not numerically show this same improvement with only bone MAD HU between sMVCT and MVCT showing a large decrease. A potential reason for MAD values not improving may be due to the large amount of noise inherent in MVCT and sMVCT scans. To estimate the contribution of noise on MAD, the voxel MVCT HU data of a center ROI within a uniform water container was measured and the data fit to a Gaussian distribution (R2 = 0.96) with standard deviation of 55 HU. Assuming a Gaussian distribution for the soft tissue/water CT noise, the MAD due to only CT noise would then be equivalent to the mean of a half-normal distribution,. For an MVCT HU Gaussian noise distribution of 55 HU (1σ), the lowest achievable MAD would then be 44 HU assuming only noise. While the kVCT scans do not possess significant noise (< 10HU for 1σ), sMVCT scans will attempt to mimic both the contrast and noise profile of MVCT scans. To estimate the noise properties of these synthetic scans, SNR values for kVCT and sMVCT divided by the respective MVCT SNR values were calculated and tabulated in Table 3. Generally, kVCT SNR values were roughly an order of magnitude higher than MVCT SNR values. sMVCT SNR values were similar (albeit slightly lower) to MVCT SNR values. Thus, the lowest achievable MAE for two scans with MVCT like noise (in soft tissue/water) rises to 62 HU assuming uncorrelated noise between the scans. This estimate illustrates that in both cases, noise would be a dominant contributor to MAE values with a noisier sMVCT (relative to kVCT) potentially overshadowing improvements.
Table 3.
Similarity metrics for kVCT, and sMVCT (CycleGAN) versus MVCT.
| kVCT | sMVCT (CycleGAN) | |
|---|---|---|
|
| ||
| MD soft tissue (HU) | 11 ± 117 | 2 ± 104 |
| MD bone (HU) | 327 ± 269 | 3 ± 160 |
| MAD soft tissue (HU) | 66 ± 97 | 61 ± 85 |
| MAD bone (HU) | 340 +252 | 97 ± 123 |
| RMSD soft tissue (HU) | 118 | 105 |
| RMSD bone (HU) | 270 | 160 |
| MD soft tissue (ρe) | −0.013 ± 0.097 (1.3%) | −0.0035 ± 0.098 (0.35%) |
| MD bone (ρe) | 0.044 ± 0.148 (2.9%) | 0.0020 ± 0.155 (0.13%) |
| MAD soft tissue (ρe) | 0.060 ± 0.080 | 0.057 ± 0.081 |
| MAD bone (ρe) | 0.096 ± 0.124 | 0.095 ± 0.119 |
| RMSD soft tissue (ρe) | 0.16 | 0.10 |
| RMSD bone (ρe) | 0.35 | 0.13 |
| MD soft tissue (SPR) | 0.018 ± 0.106 (1.8%) | 0.0024 ± 0.107 (0.24%) |
| MD bone (SPR) | 0.103 ± 0.158 (6.8%) | 0.0024 ± 0.166 (0.16%) |
| MAD soft tissue (SPR) | 0.063 ± 0.086 | 0.062 ± 0.087 |
| MAD bone (SPR) | 0.129 ± 0.137 | 0.106 ± 0.128 |
| RMSD soft tissue (SPR) | 0.11 | 0.11 |
| RMSD bone (SPR) | 0.16 | 0.16 |
| SNR vs MVCT SNR soft tissue (ratio) | 9.1 | 0.95 |
| SNR vs MVCT SNR bone (ratio) | 11.1 | 0.95 |
| SSIM | 0.856 | 0.862 |
| PSNR | 25.8 | 29.8 |
A heatmap plot (Figure 5) of HU, ρe, and SPR values at each voxel in a given kVCT or sMVCT scan were plotted against corresponding values at the same voxel in the equivalent MVCT image. In this type of plot, comparing two identical images would produce HU values along a 45° diagonal line. In reality, differences in patient positioning and anatomy between the two scans along with intrinsic voxel level specific noise creates a spread away from this line even if there were no inherent systematic differences in HU values. Furthermore, because HU values between kVCT and MVCT images differ due to the fundamental differences in physics interactions at kV versus MV energy, a large deviation from the 45° diagonal line is expected, particularly in bone where the largest HU differences exist.
Figure 5.
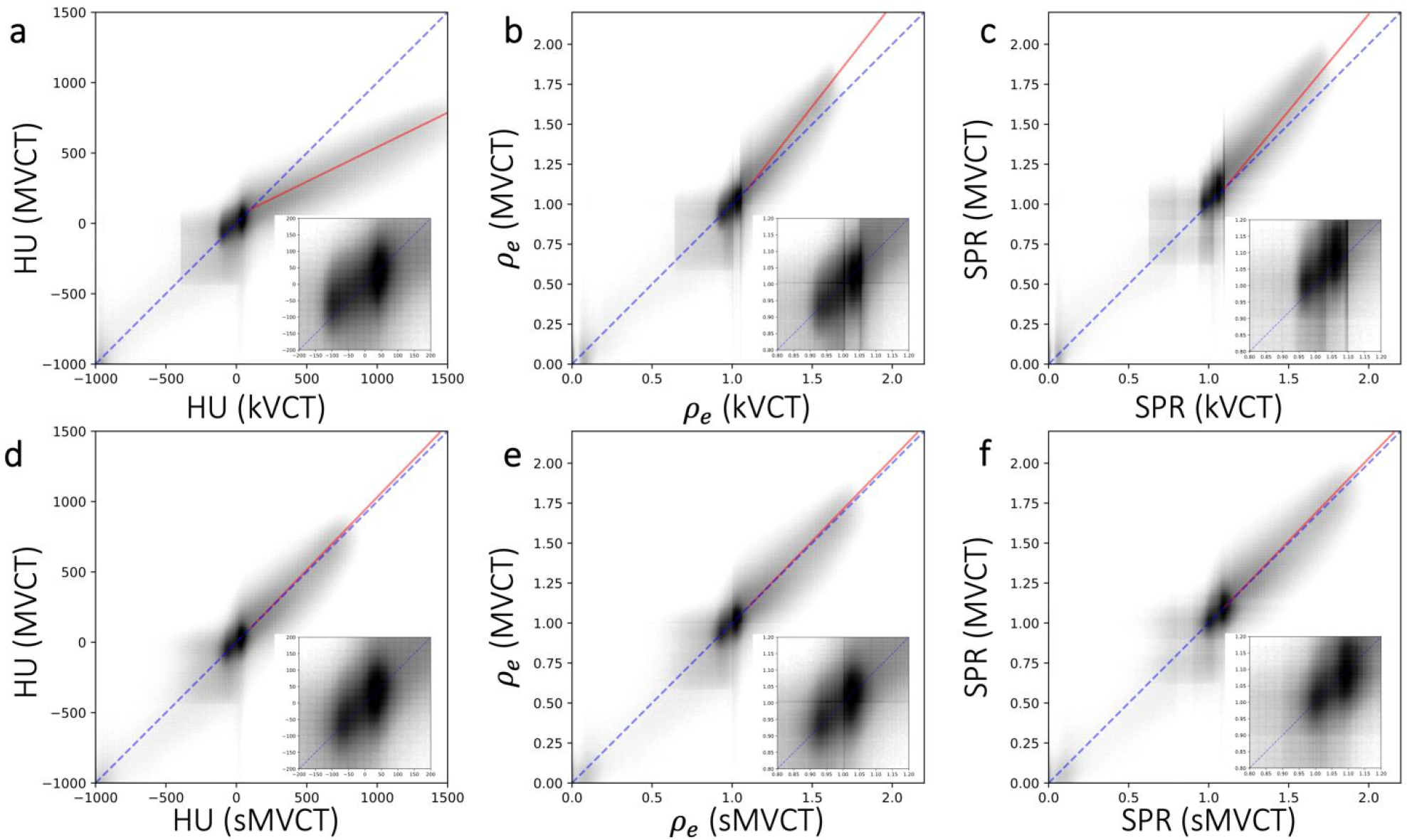
A heatmap plot of HU (left column), ρe (middle column), and SPR (right column) values at each voxel in a given CT scan plotted against HU values at the same voxel in a different CT scan for kVCT vs MVCT (top row) and b) sMVCT vs MVCT (bottom row). Grey scale values were plotted on a log scale with numbers of voxel. The dotted blue diagonal line in each panel represents a 45° reference line. The solid red line represents a linear fit of the bone data between the two image sets. In the lower righthand corner of each panel is an inset image of the −200 to 200 HU, 0.8 to 1.2 ρe values, and 0.8 to 1.2 SPR values expanded for greater clarity.
As predicted, the relationship between kVCT HU and MVCT HU (as in Figure 5a) is non-linear with what appears to be at least 3 distinct regions with differing slopes: 1) low density tissues, 2) soft tissues, and 3) bony tissues. For the bony region, the deviation away from the reference line is about 19° (shown as a solid red line in the figure). Qualitatively, the relationship between kVCT HU and MVCT HU resembles that of the kVCT calibration curve from Figure 2a. In Figure 5d, sMVCT HU value are plotted against MVCT HU values and appear to agree closely with one another, as indicated by the coincidence between red and blue lines, demonstrating that kVCT HU can be mapped to a corresponding sMVCT HU map that agrees well with MVCT HU. In the bony region, the deviation away from the reference line is minimal (< 1°) relative to the 19° deviation seen for kVCT images and is shown as a solid red line in the figure. The overall trend in the data is consistent with there being an atomic number (Z) dependent effect, as in vivo tissues with higher Z will exhibit a higher HU on kVCT and a lower HU on MVCT.
HU values from each kVCT or MVCT scan were converted to ρe with the HU-to-relative electron density calibration curve depicted in Figure 2a. Heatmap plots of ρe (figure 5, middle column) at each voxel in a given kVCT or sMVCT scan were plotted against corresponding ρe values at the same voxel in the analogous MVCT scan (equivalent slice). In Figure 5b (middle, top), we see noticeable differences between ρe values of kVCT versus MVCT. Specifically, ρe(kVCT) values differ from ρe(MVCT) the most for higher density bone with this deviation appearing to increase with increasing relative electron density values. Quantitatively, soft tissues with ρe between 0.95 and 1.05 exhibited an average deviation of < 0.01. For higher density tissues, there appears to be a large jump in the average deviation away from the 45° reference line. In the bony region, the red fit line in Figure 5b shows a 7° deviation away from the 45° reference line as ρe increases. MD values (tabulated in Table 1) between ρe(kVCT) and ρe(MVCT) were −0.013 (1.3%) for soft tissues and 0.044 (2.9%) for bone. MAD values (tabulated in Table 1) between ρe(kVCT) and ρe(MVCT) were 0.060 for soft tissues and 0.096 for bone. RMSD values (tabulated in Table 1) between ρe(kVCT) and ρe(MVCT) were 0.16 and 0.35 for soft tissue and bone, respectively. In Figure 5e, ρe (sMVCT) values were plotted against ρe (MVCT) values, representing the ability of the developed CycleGAN machine learning model to accurately convert kVCT scans to synthetic MVCT scans. As expected, there is uniform and marked improvement in the alignment of ρe (sMVCT) values with ρe (MVCT) values. As a whole, the heatmap appears to better align with the 45° reference line than in Figure 5b. In the bony region, the red fit line in Figure 5b shows a < 1° deviation away from the 45° reference line. Quantitatively, average deviations of ρe were all < 0.01. MD values (tabulated in Table 3) between ρe(sMVCT) and ρe(MVCT) were considerably lower at −0.0035 (0.35%) for soft tissues and 0.0020 (0.13%) for bone. MAD values (tabulated in Table 3) between ρe(sMVCT) and ρe (MVCT) were 0.044 for soft tissues and 0.095 for bone. RMSD values (tabulated in Table 3) between ρe(sMVCT) and ρe(MVCT) improved, relative to ρe(kVCT), to 0.10 and 0.13 for soft tissue and bone, respectively.
HU values from each kVCT or MVCT scan were converted to SPR with the HU-to-SPR calibration curve depicted in Figure 2b. Heatmap plots of SPR (Figure 5, right column) at each voxel in a given kVCT or sMVCT scan were plotted against corresponding SPR values at the same voxel in the analogous MVCT scan (equivalent slice). In Figure 5c (right, top), we see noticeable differences between SPR values of kVCT versus MVCT. Specifically, SPR (kVCT) values differ from SPR (MVCT) the most for higher density bone with this deviation appearing to increase with increasing SPR values. Quantitatively, soft tissues with SPR between 0.95 and 1.05 exhibited an average deviation of < 0.01. Similar to the trends seen for ρe, for higher density tissues there appears to be a large jump in the average deviation away from the 45° reference line. In the bony region, the red fit line in Figure 5b shows a >5° deviation away from the 45° reference line as SPR increases. MD values (tabulated in Table 3) between SPR (kVCT) and SPR (MVCT) were 0.018 (1.8%) for soft tissues and 0.103 (6.8%) for bone. MAD values (tabulated in Table 3) between SPR (kVCT) and SPR (MVCT) were 0.063 for soft tissues and 0.129 for bone. RMSD values (tabulated in Table 3) between SPR (kVCT) and SPR (MVCT) were 0.11 and 0.16 for soft tissue and bone, respectively. In Figure 5f, SPR (sMVCT) values were plotted against SPR (MVCT) values, representing the ability of the developed CycleGAN machine learning model to accurately convert kVCT scans to synthetic MVCT scans. As expected, there is uniform and marked improvement in the alignment of SPR (sMVCT) values with SPR (MVCT) values. The heatmap, as a whole, appears to better align with the 45° reference line than in Figure 5c. In the bony region, the red fit line in Figure 5b shows a < 1° deviation away from the 45° reference line. Quantitatively, average deviations of SPR were all < 0.01. MD values (tabulated in Table 3) between SPR (sMVCT) and SPR (MVCT) were considerably lower at 0.0024 (0.24%) for soft tissues and 0.0024 (0.16%) for bone. MAD values (tabulated in Table 3) between SPR (sMVCT) and SPR (MVCT) were 0.062 for soft tissues and 0.106 for bone. RMSD values (tabulated in Table 3) between SPR (sMVCT) and SPR (MVCT) were 0.11 and 0.16 for soft tissue and bone, respectively.
3.C. Anthropomorphic head phantom
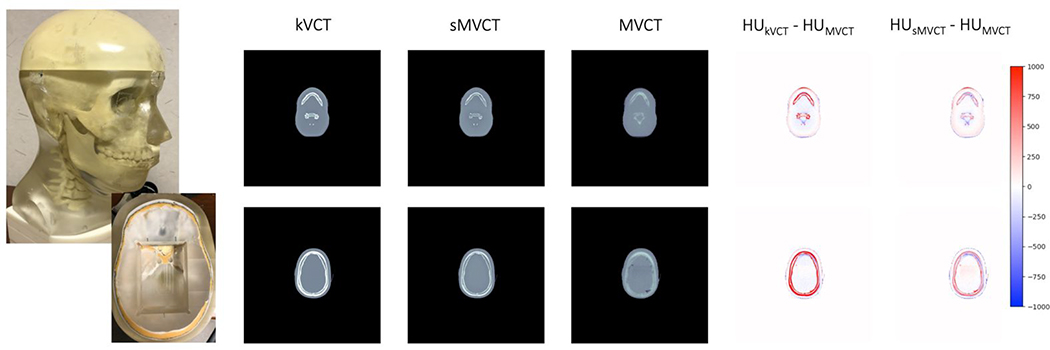
Figure 6 shows exemplar images for kVCT HU, sMVCT HU, MVCT HU, and difference heatmaps of kVCT HU and sMVCT HU compared to MVCT HU for axial planes at the level of the jaw and skull for the anthropomorphic head phantom. Qualitatively, trends seen in the head phantom were similar to in vivo data, where the largest differences were seen between kVCT and MVCT in bony tissues. As expected, kVCT images exhibited higher HU values than those by corresponding MVCT images. On the other hand, sMVCT images appeared qualitatively more similar to MVCT images, particularly in bony tissues, as shown in the 5th and 6th columns of Figure 6.
Figure 6.
Exemplar images of the anthropomorphic head phantom (1st column) imaged using kVCT (2nd column), sMVCT HU (3rd column), MVCT HU (4th column), and HU difference heat maps for kVCT versus MVCT (5th column) and sMVCT versus MVCT (6th column) shown at axial levels of the skull (top row) and jaw (bottom row). The HU scale used in the difference maps is shown on the right.
Quantitative results of relative electron density and stopping power ratio calculated from physical measurements and estimated through kV and MV CT calibration curves for bone material in the anthropomorphic head phantom are shown in Table 4. Percent differences between kV and MV imaging and physical measurements (% diff) are also shown. These results were consistent with those seen in the tissue mimicking phantom. Relative electron density values of the bone computed from kVCT images deviated from physical measurements by 7.5%. This deviation decreased to 0.80% and 0.98% when estimated from MVCT and sMVCT, respectively. Stopping power ratio values of the bone computed from kVCT images deviated from physical measurements by 7.48%. This deviation decreased to 0.78% and 0.96% when estimated from MVCT and sMVCT, respectively.
Table 4:
Tabulated physical parameters for atomic composition, physical density, relative electron density, and stopping power ratio derived from physical measurements of bone phantom versus real bone tissue composition from ICRU Report 4422 and ICRP Report 23.23
|
|
||||||||
|---|---|---|---|---|---|---|---|---|
| Relative electron density | Stopping power ratio (115 MeV) | |||||||
|
|
||||||||
| Measured | kVCT (% diff) | MVCT (% diff) | sMVCT (% diff) | Measured | kVCT (% diff) | MVCT (% diff) | sMVCT (% diff) | |
|
| ||||||||
| Bone (Head Phantom) | 1.120 | 1.204 ± 0.10 (7.50%) | 1.129 ± 0.13 (0.80%) | 1.131 ± 0.20 (0.98%) | 1.125 | 1.207 ± 0.09 (7.48%) | 1.129 ± 0.11 (0.78%) | 1.131 ± 0.17 (0.96%) |
4. DISCUSSION
The relationships between kVCT HU and ρe or SPR have historically been modeled as piecewise linear. In reality, the relationships between kVCT HU and ρe or SPR are more complicated due to the intrinsic non-linearity and no explicit one-to-one relationship between these values when imaged at kV energies. In this manuscript, we used a tissue mimicking phantom to demonstrate that higher accuracy mapping between HU to ρe or HU to SPR can be achieved when using MVCT instead of kVCT. We then used a method to empirically learn the relationship between kVCT HU and MVCT HU through CycleGAN deep learning. In doing so, we intrinsically linearize and improve the accuracy of the relationship between kVCT HU with ρe and kVCT HU with SPR through an MVCT surrogate. Finally, the cycleGAN model was independently validated in an anthropomorphic head phantom containing a tissue mimicking human bone material.
For in vivo data, the ρe value differences between the two scans (kVCT and MVCT) were spatially and organ/tissue dependent with MD values of 0.013 (1.3%) and 0.044 (2.9%) for soft tissue and dense bone, respectively. The ρe values for tissues with high water content (such as orbits and parotids) exhibited little change in ρe (< 0.01) from kVCT to sMVCT with ρe values being close (within 0.005) to the expected value of 1.0 in both cases. It is possible that because liquid water was a material used for generating CT calibration curves that these exact HU-to-ρe and SPR relationships may have reduced uncertainty associated with them. Similarly, subcutaneous fat tended to have, on average, subtle changes in ρe (< 0.01) from kVCT to sMVCT. In contrast, a significant portion of soft tissues/organs with higher protein levels such as skin exhibited relatively larger negative changes in ρe of about −0.03 (from kVCT to sMVCT). For kVCT HU > 0, we see that there is greater uncertainty in the relationship between kVCT HU and ρe (as in Figure 5b) and kVCT HU and SPR (as in Figure 5c) with increasing non-linearity in this region in both curves. Similarity metrics (shown in Table 3) for MD, MAD, RMSD, SNR, PSNR, and SSIM showed overall improvements in agreement with MVCT compared with initial kVCT. In our work, SSIM and PSNR values were found to be 0.862 and 29.8, respectively. Our unpaired results are comparable to the work of Liang et al47 who achieved 0.85 and 30.65 for SSIM and PSNR, respectively, for kV cone-beam CT to kVCT image translation.
In this study, we used a tissue mimicking phantom to evaluate the accuracy in predicting ρe and SPR from MVCT HU conversion compared to kVCT HU conversion. For all tissue mimicking phantom materials examined in this work, MVCT derived ρe and SPR values agreed with physical measurements to within 1%, with the exception of SPR in adipose which differed by 1.7%. While still more accurate than kVCT-derived SPR (which differed by 2.58%), both kV and MV SPR errors in adipose were higher than their corresponding ρe errors. In the Bethe-Bloch equation there are only two parameters that are tissue specific: ρe and Im. In cases where ρe is accurate but SPR is inaccurate, there is the implication that uncertainties in Im are the cause. In our prior work using the same tissue mimicking phantom44, stoichiometric calibration curves were created using Im values published in 198250. More recently, Im values optimized for use with the Bragg additivity rule were published by Bär et al38 and differed from previous values by ~3% in adipose tissues and ~4.5% in bone. This work demonstrated that outdated Im values may lead to overestimation of range uncertainty and should be reassessed in clinical practice. This finding is consistent with the work of Paganetti et al4 which reported that Im was a major contributor to the uncertainties in SPR determination, with uncertainty of Im values lowering the achievable accuracy of CT derived SPR.
In bony tissues specifically we see the largest differences in kVCT relative to MVCT. In the spongiosa bone phantom, errors in ρe were reduced from 2.20% to 0.19% for kVCT and MVCT, respectively. Errors in SPR were reduced from 4.38% to 0.22% for kVCT and MVCT, respectively. These findings are also in line with the bony tissue errors found in the anthropomorphic head phantom whereby ρe and SPR values significantly improved in accuracy from kVCT to sMVCT. This finding is consistent other groups who have investigated the uncertainty in proton therapy dose calculation due to kVCT-based SPR predictions, whereby they found that SPR in bone exhibited greater uncertainty than SPR in soft tissue2. It is also in line with our group’s finding17 that ambiguities in the elemental and molecular composition of bone relative to nominal tissues would lead to greater uncertainties in the prediction of ρe and SPR based on the conversion of kVCT HU. As this error/uncertainty in bone is systematic and increases with ρe and SPR, it is possible that the composition of the bone tissue surrogate materials may not closely mimic that of our subject population. As adults age, there is an age dependent bone change that results in increasing mineral content with decreasing protein content51 potentially accounting for this difference. Additional possible explanations for the large difference between kVCT and MVCT predicted ρe and SPR may be due to a systematic bias in the overall elemental composition of the bone tissue surrogate used in our study. In the work of Woodard and White52, they found that bone composition varies significantly across bone type. White et al37 further showed that even within just cortical bone, the composition varies across age. Within the reference material provided by tissue surrogate manufacturer, it is noted that the cortical bone reference is based on ICRU 4449. It is likely that the bone composition of tissue surrogates is compositionally different in terms of atomic composition from adult cancer patient head and neck bones, and possibly biased towards the composition of other bones in the body or for other age groups.
Uncertainties in SPR are especially important for charged particle therapies such as proton therapy, where the particle range uncertainty is directly proportional to the SPR uncertainty. For the in vivo human data, we showed that kVCT SPR on average deviated from MVCT SPR by 0.018 (1.8%) and 0.103 (6.8%) for soft and bony tissues, respectively, which would directly translate to charged particle range uncertainties of 1.8% and 6.8%. These results are consistent with the clinical range uncertainty budgets (typically an average over all tissue types of 2.5–3.5% the proton beam range) used by proton therapy groups to account for these kVCT-to-SPR uncertainties, In comparison, sMVCT SPR deviated from MVCT SPR with substantially lower MD value differences of 0.0024 (0.24%) and 0.0024 (0.16%) for soft and bony tissues, respectively. In the case of prostate proton therapy treatments, a range uncertainty margin of as much as 1cm is typical when using kVCT-based SPR prediction methods. Utilizing the proposed method to reduce CT-based SPR prediction errors from 2.5–3.5% to <0.5% could result in significant reductions in normal tissue irradiations and potentially allow for dose escalation of tumors. With respect to margins used for prostate radiotherapy, results from Bortfelt et al53 suggest that total safety margins can be reduced to about 6mm when using DECT-based SPR predictions in treatment planning. With a mean range prediction accuracy of 0.0%±0.5% demonstrated using their DECT-based technique, we would expect similar margin reductions using our approach. Overall, our proposed methodology provides a unique perspective into areas of greater SPR uncertainty and potentially increased accuracy of SPR determination when using sMVCT, though a comprehensive validation of SPR estimation using MVCT in a diversity of biological and non-biological materials is required prior to clinical implementation.
Imaging with kVCT can cause severe streaking artifacts in areas near bone, teeth, and/or metalic implants54 and, in some cases, has resulted in sever under- or overdosing of target due to proton range errors55. MVCT, on the other hand, has been demonstrated to reduce proton range uncertainty for large metallic implants through comparisons of kVCT and MVCT treatment plans56 and may be preferred due to its potential to increase SPR accuracy while reducing beam hardening artifacts caused by high-Z materials. Reducing these artifacts could have significant benefits for proton therapy given that dosimetric impacts caused by artifacts or metallic objects can cause more pronounced uncertainties54,57. In Figure 7, we show example images (MVCT, sMVCT, and kVCT) from a patient with dental implants. The sMVCT image better mimics the MVCT image in that there is a reduced streaking artifact in both the dental area itself and in the surrounding soft tissue. Of note, because dental artifacts were not found in all patient scans, it is possible that this behavior was observed in the training dataset but not fully learned, resulting in only partial reduction of beam hardening/streaking artifacts in the sMVCT images. While the machine learning code could be further optimized to better correct for streaking artifacts, this development is outside the scope of the current work.
Figure 7.
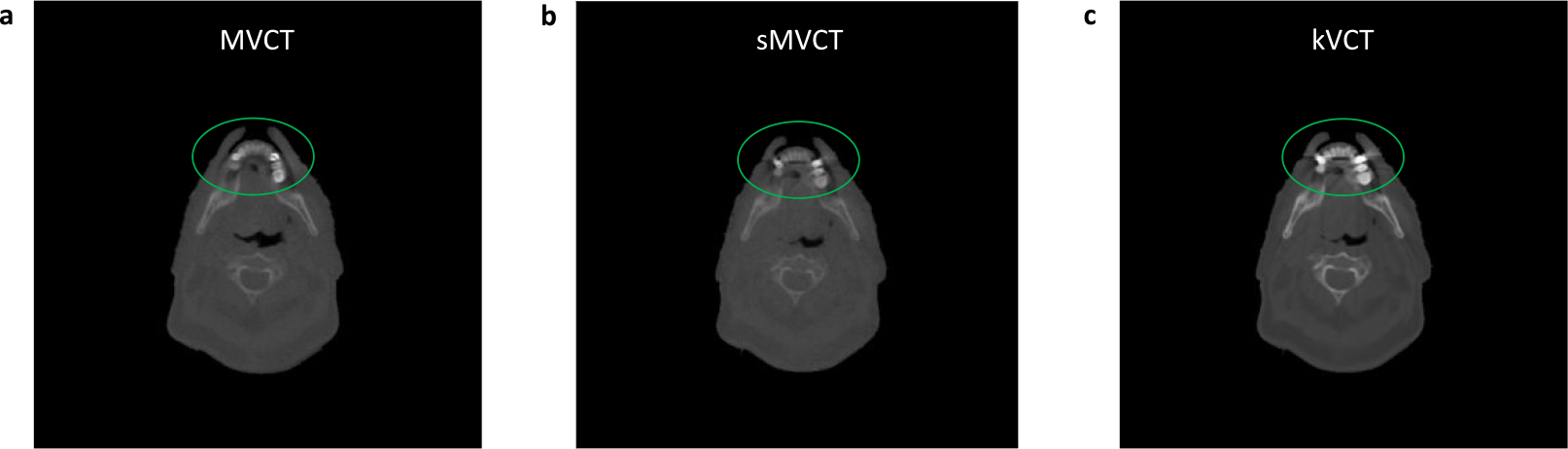
Exemplar images of a streaking/beam hardening artifact around a dental implant in (a) MVCT HU (1st column), (b) sMVCT HU (2nd column), and (c) kVCT HU (3rd column. A linear grayscale colormap was used with −1000 HU as the minimum (black) and the maximum HU of the kVCT image as the maximum (white) and applied to the kVCT, MVCT, and sMVCT images.
Unlike with kVCT scans for which kVp, mAs, and reconstruction filters can be altered by the user, there is limited flexibility in adjusting MVCT parameters on the TomoTherapy system. Beam energy and intensity are fixed with the only user adjusted parameters being collimator width (affecting beam spectrum and, thus, reconstruction kernel), pitch, and reconstruction matrix. Though all three parameters remined fixed in this work, more comprehensive MVCT image performance characterization has been reported in the literature. Held et al23 found that while MVCTs were ~6x noisier than fan beam kVCT, they produced spatially stable image values regardless of image protocol and object size. Meeks et al18 characterized MVCT performance with noise, uniformity, contrast, and spatial resolution and reported comparable image uniformity and spatial resolution to diagnostic fan beam kVCT and contrast linearity with respect to material electron density. As expected, MVCT images demonstrated reduced contrast resolution and signal-to-noise ratio. However, they were still able to provide sufficient contrast to delineate bone and soft tissue structures and deemed adequate for image guidance and dose calculation given linearity between contrast and electron density. Specific to stoichiometric CT calibrations, Ainsley et al58 found that for a given phantom size, kVCT calibration curves are largely independent of plug placement within the scanner field-of-view, which we expect to remain true for MVCT given lower impact of beam hardening artifacts. However, with kVCT, significant deviations have been shown to occur between different phantom sizes, necessitating multiple calibration curves corresponding to the size of relevant anatomy. While all subjects imaged in this study (in vivo and phantoms) were approximately the size of an adult head, additional studies should be performed to characterize MVCT properties across multiple anatomies in both children and adults.
There are some additional considerations for groups considering clinical implementation of this method for kVCT HU-to-ρe or HU-to-SPR conversion. Currently, non-Monte Carlo treatment planning systems (TPS) accept CT HU as input for dose calculation with conversion of these HU values to ρe or SPR through calibration curves similar to those shown in Figure 2. This process could be further simplified if the input datasets were direct maps of ρe or SPR rather than HU. With our methodology, no modification would have been necessary in our learning process to accomplish this. During the pre-processing stage of machine learning, all CT images (both kV and MV) were scaled from HU to values between [−1, 1]. As MVCT HU values were converted to ρe or SPR using a linear scale, the learning process would have been identical (as they would have scaled to equivalent values in this [−1, 1] scale). On the post-learning end, we could have created a linear mapping from [−1, 1] directly to ρe or SPR values. Within the TPS, the calibration curve would then be a simple linear mapping. Another consideration for clinical implementation of this method is generalizability of a developed model across kVCT models, scanner protocols, and kVCT energies. In general, developed CycleGAN models converting from kVCT HU to sMVCT ρe and SPR would be most accurate if created for a specific center/kVCT scanner and for a specific imaging protocol. For centers with a machine capable of creating MVCT scans and kVCT scans, it would be possible to create a dataset of matched patient kVCT and MVCT scans. This matched dataset could be used with deep learning (as in this work) to learn the relationship between kVCT and sMVCT ρe and SPR. For centers without MVCT capabilities, implementation of this methodology may be less straightforward as the created deep learning model would likely be specific (and therefore most accurate) for a given kVCT scanner and/or energy spectrum. As our patient population only received kVCT scans from a specific CT scanner, we were not able to test the effect of scanner model/energy spectrum variability. Future work in this area should include tests on generalizability and stability across scanner/energy spectrum of the created CycleGAN model. A similar approach to this work could be applied to Monte Carlo TPSs by applying the described techniques to mass density instead of relative electron density and/or stopping power ratio.
5. CONCLUSIONS
In this study, we used deep learning to understand the relationship between kVCT HU and MVCT HU and developed an approach to calculate accurate values of ρe and SPR based on MVCT HU. The accuracy of ρe and SPR values calculated using MVCT and kVCT were quantified using tissue mimicking phantoms of known material composition. The deep learning model was also validated using an anthropomorphic head phantom with physical characteristics closely resembling human bone. Synthetic MVCT scans generated by our method appear to closely mimic acquired MVCT scans with even some mitigation of beam hardening artifacts. SPR values estimated from sMVCT data produced by the deep learning model resulted in substantially lower mean error values for soft and bony tissues versus kVCT data. If sMVCT scans are used in conjunction with the originally acquired kVCT, they, together, allow for an appealing scenario in which the advantages of each modality can be fully utilized.
Acknowledgements
Research reported in this manuscript was partially supported by the NIBIB of the National Institutes of Health under award number R21EB026086. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- 1.Huizenga H, Storchi PR. The use of computed tomography numbers in dose calculations for radiation therapy. Acta Radiol Oncol Nov-Dec 1985;24(6):509–19. doi: 10.3109/02841868509134425 [DOI] [PubMed] [Google Scholar]
- 2.Yang M, Zhu XR, Park PC, et al. Comprehensive analysis of proton range uncertainties related to patient stopping-power-ratio estimation using the stoichiometric calibration. Phys Med Biol. Jul 07 2012;57(13):4095–115. doi: 10.1088/0031-9155/57/13/4095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ainsley CG, Yeager CM. Practical considerations in the calibration of CT scanners for proton therapy. J Appl Clin Med Phys. May 8 2014;15(3):4721. doi: 10.1120/jacmp.v15i3.4721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Paganetti H Range uncertainties in proton therapy and the role of Monte Carlo simulations. Phys Med Biol. Jun 07 2012;57(11):R99–117. doi: 10.1088/0031-9155/57/11/R99 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schaffner B, Pedroni E. The precision of proton range calculations in proton radiotherapy treatment planning: experimental verification of the relation between CT-HU and proton stopping power. Phys Med Biol. Jun 1998;43(6):1579–92. [DOI] [PubMed] [Google Scholar]
- 6.Moyers MF, Sardesai M, Sun S, Miller DW. Ion stopping powers and CT numbers. Med Dosim Autumn 2010;35(3):179–94. doi: 10.1016/j.meddos.2009.05.004 [DOI] [PubMed] [Google Scholar]
- 7.Han D, Siebers JV, Williamson JF. A linear, separable two-parameter model for dual energy CT imaging of proton stopping power computation. Med Phys. Jan 2016;43(1):600. doi: 10.1118/1.4939082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hunemohr N, Krauss B, Dinkel J, et al. Ion range estimation by using dual energy computed tomography. Z Med Phys. Dec 2013;23(4):300–13. doi: 10.1016/j.zemedi.2013.03.001 [DOI] [PubMed] [Google Scholar]
- 9.Taasti VT, Petersen JB, Muren LP, Thygesen J, Hansen DC. A robust empirical parametrization of proton stopping power using dual energy CT. Med Phys. Oct 2016;43(10):5547. doi: 10.1118/1.4962934 [DOI] [PubMed] [Google Scholar]
- 10.Tsukihara M, Noto Y, Hayakawa T, Saito M. Conversion of the energy-subtracted CT number to electron density based on a single linear relationship: an experimental verification using a clinical dual-source CT scanner. Phys Med Biol. May 7 2013;58(9):N135–44. doi: 10.1088/0031-9155/58/9/N135 [DOI] [PubMed] [Google Scholar]
- 11.Yang M, Virshup G, Clayton J, Zhu XR, Mohan R, Dong L. Theoretical variance analysis of single- and dual-energy computed tomography methods for calculating proton stopping power ratios of biological tissues. Phys Med Biol. Mar 7 2010;55(5):1343–62. doi: 10.1088/0031-9155/55/5/006 [DOI] [PubMed] [Google Scholar]
- 12.Bar E, Lalonde A, Royle G, Lu HM, Bouchard H. The potential of dual-energy CT to reduce proton beam range uncertainties. Med Phys. Jun 2017;44(6):2332–2344. doi: 10.1002/mp.12215 [DOI] [PubMed] [Google Scholar]
- 13.Lee HHC, Li B, Duan X, Zhou L, Jia X, Yang M. Systematic analysis of the impact of imaging noise on dual-energy CT-based proton stopping power ratio estimation. Med Phys. May 2019;46(5):2251–2263. doi: 10.1002/mp.13493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li B, Lee HC, Duan X, et al. Comprehensive analysis of proton range uncertainties related to stopping-power-ratio estimation using dual-energy CT imaging. Phys Med Biol. Aug 9 2017;62(17):7056–7074. doi: 10.1088/1361-6560/aa7dc9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Mackie TR, Holmes T, Swerdloff S, et al. Tomotherapy: a new concept for the delivery of dynamic conformal radiotherapy. Medical physics. 1993;20(6):1709–1719. [DOI] [PubMed] [Google Scholar]
- 16.Langen K, Meeks S, Poole D, et al. The use of megavoltage CT (MVCT) images for dose recomputations. Physics in Medicine & Biology. 2005;50(18):4259. [DOI] [PubMed] [Google Scholar]
- 17.Sudhyadhom A. On the molecular relationship between Hounsfield Unit (HU), mass density, and electron density in computed tomography (CT). PLoS One. 2020;15(12):e0244861. doi: 10.1371/journal.pone.0244861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Meeks SL, Harmon JF Jr., Langen KM, Willoughby TR, Wagner TH, Kupelian PA. Performance characterization of megavoltage computed tomography imaging on a helical tomotherapy unit. Med Phys. Aug 2005;32(8):2673–81. doi: 10.1118/1.1990289 [DOI] [PubMed] [Google Scholar]
- 19.Langen KM, Meeks SL, Poole DO, et al. The use of megavoltage CT (MVCT) images for dose recomputations. Phys Med Biol. Sep 21 2005;50(18):4259–76. doi: 10.1088/0031-9155/50/18/002 [DOI] [PubMed] [Google Scholar]
- 20.Ruchala KJ, Olivera GH, Schloesser EA, Hinderer R, Mackie TR. Calibration of a tomotherapeutic MVCT system. Phys Med Biol. Apr 2000;45(4):N27–36. doi: 10.1088/0031-9155/45/4/404 [DOI] [PubMed] [Google Scholar]
- 21.Yadav P, Tolakanahalli R, Rong Y, Paliwal BR. The effect and stability of MVCT images on adaptive TomoTherapy. J Appl Clin Med Phys. Jul 2 2010;11(4):3229. doi: 10.1120/jacmp.v11i4.3229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Paudel MR, Mackenzie M, Fallone BG, Rathee S. Evaluation of metal artifacts in MVCT systems using a model based correction method. Med Phys Oct 2012;39(10):6297–308. doi: 10.1118/1.4754647 [DOI] [PubMed] [Google Scholar]
- 23.Held M, Cremers F, Sneed PK, et al. Assessment of image quality and dose calculation accuracy on kV CBCT, MV CBCT, and MV CT images for urgent palliative radiotherapy treatments. Journal of applied clinical medical physics. 2016;17(2):279–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yang M, Virshup G, Mohan R, Shaw CC, Zhu XR, Dong L. Improving accuracy of electron density measurement in the presence of metallic implants using orthovoltage computed tomography. Med Phys. May 2008;35(5):1932–41. doi: 10.1118/1.2905030 [DOI] [PubMed] [Google Scholar]
- 25.Schulte RW, Penfold SN. Proton CT for Improved Stopping Power Determination in Proton Therapy, invited. Trans Am Nucl Soc. 2012;106:55–58. [PMC free article] [PubMed] [Google Scholar]
- 26.Schneider U, Pedroni E. Proton radiography as a tool for quality control in proton therapy. Med Phys. Apr 1995;22(4):353–63. doi: 10.1118/1.597470 [DOI] [PubMed] [Google Scholar]
- 27.Schulte R, Bashkirov V, Li T, et al. Conceptual design of a proton computed tomography system for applications in proton radiation therapy. IEEE Transactions on Nuclear Science. 2004;51(3):866–872. [Google Scholar]
- 28.Collins-Fekete C-A, Dikaios N, Royle G, Evans PM. Statistical limitations in proton imaging. Physics in Medicine & Biology. 2020;65(8):085011. [DOI] [PubMed] [Google Scholar]
- 29.Li W, Li Y, Qin W, et al. Magnetic resonance image (MRI) synthesis from brain computed tomography (CT) images based on deep learning methods for magnetic resonance (MR)-guided radiotherapy. Quant Imaging Med Surg Jun 2020;10(6):1223–1236. doi: 10.21037/qims-19-885 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Florkow MC, Zijlstra F, Willemsen K, et al. Deep learning-based MR-to-CT synthesis: The influence of varying gradient echo-based MR images as input channels. Magn Reson Med. Apr 2020;83(4):1429–1441. doi: 10.1002/mrm.28008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Torrado-Carvajal A, Vera-Olmos J, Izquierdo-Garcia D, et al. Dixon-VIBE Deep Learning (DIVIDE) Pseudo-CT Synthesis for Pelvis PET/MR Attenuation Correction. J Nucl Med. Mar 2019;60(3):429–435. doi: 10.2967/jnumed.118.209288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Barateau A, De Crevoisier R, Largent A, et al. Comparison of CBCT-based dose calculation methods in head and neck cancer radiotherapy: from Hounsfield unit to density calibration curve to deep learning. Med Phys Jul 12 2020;doi: 10.1002/mp.14387 [DOI] [PubMed] [Google Scholar]
- 33.Chen L, Liang X, Shen C, Jiang S, Wang J. Synthetic CT generation from CBCT images via deep learning. Med Phys Mar 2020;47(3):1115–1125. doi: 10.1002/mp.13978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lei Y, Tang X, Higgins K, et al. Learning-based CBCT correction using alternating random forest based on auto-context model. Med Phys Feb 2019;46(2):601–618. doi: 10.1002/mp.13295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Schneider U, Pedroni E, Lomax A. The calibration of CT Hounsfield units for radiotherapy treatment planning. Phys Med Biol. Jan 1996;41(1):111–24. [DOI] [PubMed] [Google Scholar]
- 36.International Commission on Radiological Protection. Task Group on Reference Man. Report of the Task Group on Reference Man : a report. ICRP publication. Pergamon Press; 1975:xix, 480 p. [Google Scholar]
- 37.White DR, Widdowson EM, Woodard HQ, Dickerson JW. The composition of body tissues (II). Fetus to young adult. Br J Radiol. Feb 1991;64(758):149–59. doi: 10.1259/0007-1285-64-758-149 [DOI] [PubMed] [Google Scholar]
- 38.Bär E, Andreo P, Lalonde A, Royle G, Bouchard H. Optimized I-values for use with the Bragg additivity rule and their impact on proton stopping power and range uncertainty. Physics in Medicine & Biology. 2018;63(16):165007. [DOI] [PubMed] [Google Scholar]
- 39.De Marzi L, Lesven C, Ferrand R, Sage J, Boule T, Mazal A. Calibration of CT Hounsfield units for proton therapy treatment planning: use of kilovoltage and megavoltage images and comparison of parameterized methods. Phys Med Biol. Jun 21 2013;58(12):4255–76. doi: 10.1088/0031-9155/58/12/4255 [DOI] [PubMed] [Google Scholar]
- 40.Jackson DF, Hawkes DJ. X-ray attenuation coefficients of elements and mixtures. Physics Reports. 1981;70(3):169–233. [Google Scholar]
- 41.Midgley SM. A parameterization scheme for the x-ray linear attenuation coefficient and energy absorption coefficient. Physics in Medicine & Biology. 2004;49(2):307. [DOI] [PubMed] [Google Scholar]
- 42.Das IJ, Cheng CW, Cao M, Johnstone PA. Computed tomography imaging parameters for inhomogeneity correction in radiation treatment planning. J Med Phys. Jan-Mar 2016;41(1):3–11. doi: 10.4103/0971-6203.177277 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.White DR, Booz J, Griffith RV, Spokas JJ, Wilson IJ. Report 44. Journal of the International Commission on Radiation Units and Measurements. 1989;os23(1):NP–NP. doi: 10.1093/jicru/os23.1.Report44 [DOI] [Google Scholar]
- 44.Scholey JE, Chandramohan D, Naren T, Liu W, Larson PEZ, Sudhyadhom A. Technical Note: A methodology for improved accuracy in stopping power estimation using MRI and CT. Med Phys Oct 27 2020;doi: 10.1002/mp.14555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhu JY, Park T, Isola P, Efros AA. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks. 2017:
- 46.Kearney V, Ziemer BP, Perry A, et al. Attention-Aware Discrimination for MR-to-CT Image Translation Using Cycle-Consistent Generative Adversarial Networks. Radiology: Artificial Intelligence. 2020;2(2):e190027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liang X, Chen L, Nguyen D, et al. Generating synthesized computed tomography (CT) from cone-beam computed tomography (CBCT) using CycleGAN for adaptive radiation therapy. Phys Med Biol. Jun 10 2019;64(12):125002. doi: 10.1088/1361-6560/ab22f9 [DOI] [PubMed] [Google Scholar]
- 48.Vinas L, Scholey J, Descovich M, Kearney V, Sudhyadhom A. Improved contrast and noise of megavoltage computed tomography (MVCT) through cycle-consistent generative machine learning. Med Phys Nov 24 2020;doi: 10.1002/mp.14616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.ICRU. Tissue substitutes in radiation dosimetry and measurement. ICRU report. International Commission on Radiation Units and Measurements; 1989:vii, 189 p. [Google Scholar]
- 50.Janni JF. Energy Loss, range, path length, time-of-flight, straggling, multiple scatting, and nuclear interaction probability: In Two Parts. Part I. For 63 Compounds Part 2. For Elements 1<Z<92. Atomic Data and Nuclear Data Tables. 1982;27(4–5):341–529. [Google Scholar]
- 51.Boskey AL, Coleman R. Aging and bone. J Dent Res. Dec 2010;89(12):1333–48. doi: 10.1177/0022034510377791 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Woodard HQ, White DR. Bone models for use in radiotherapy dosimetry. Br J Radiol. Apr 1982;55(652):277–82. doi: 10.1259/0007-1285-55-652-277 [DOI] [PubMed] [Google Scholar]
- 53.Berthold J, Khamfongkhruea C, Petzoldt J, et al. First-In-Human Validation of CT-Based Proton Range Prediction Using Prompt Gamma Imaging in Prostate Cancer Treatments. International Journal of Radiation Oncology* Biology* Physics. 2021; [DOI] [PubMed] [Google Scholar]
- 54.Jäkel O, Reiss P. The influence of metal artefacts on the range of ion beams. Physics in Medicine & Biology. 2007;52(3):635. [DOI] [PubMed] [Google Scholar]
- 55.Wei J, Sandison GA, Hsi W-C, Ringor M, Lu X. Dosimetric impact of a CT metal artefact suppression algorithm for proton, electron and photon therapies. Physics in Medicine & Biology. 2006;51(20):5183. [DOI] [PubMed] [Google Scholar]
- 56.Newhauser WD, Giebeler A, Langen KM, Mirkovic D, Mohan R. Can megavoltage computed tomography reduce proton range uncertainties in treatment plans for patients with large metal implants? Physics in Medicine & Biology. 2008;53(9):2327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jäkel O Ranges of ions in metals for use in particle treatment planning. Physics in Medicine & Biology. 2006;51(9):N173. [DOI] [PubMed] [Google Scholar]
- 58.Ainsley CG, Yeager CM. Practical considerations in the calibration of CT scanners for proton therapy. Journal of applied clinical medical physics. 2014;15(3):202–220. [DOI] [PMC free article] [PubMed] [Google Scholar]