Dynamic Functional Continuous Time Bayesian Networks for Prediction and Monitoring of the Impact of Patients’ Modifiable Lifestyle Behaviors on the Emergence of Multiple Chronic Conditions

Abstract

More than a quarter of all Americans are estimated to have multiple chronic conditions (MCC). It is known that shared modifiable lifestyle behaviors account for many common MCC. What is not precisely known is the dynamic effect of changes in lifestyle behaviors on the trajectories of MCC emergence. This paper proposes dynamic functional continuous time Bayesian networks to effectively formulate the dynamic effect of patients’ modifiable lifestyle behaviors and their interaction with non-modifiable demographics and preexisting conditions on the emergence of MCC. The proposed method considers the parameters of the conditional dependencies of MCC as a nonlinear state-space model and develops an extended Kalman filter to capture the dynamics of the modifiable risk factors on the MCC evolution. It also develops a tensor-based control chart based on the integration of multilinear principal component analysis and multivariate exponentially weighted moving average chart to monitor the effect of changes in the modifiable risk factors on the risk of new MCC. We validate the proposed method based on a combination of simulation and a real dataset of 385 patients from the Cameron County Hispanic Cohort. The dataset examines the emergence of 5 chronic conditions (Diabetes, Obesity, Cognitive Impairment, Hyperlipidemia, Hypertension) based on 4 modifiable lifestyle behaviors representing (Diet, Exercise, Smoking Habits, Drinking Habits) and 3 non-modifiable demographic risk factors (Age, Gender, Education). For the simulated study, the proposed algorithm shows a run-length of 4 samples (4 months) to identify behavioral changes with significant impacts on the risk of new MCC. For the real data study, the proposed algorithm shows a run-length of one sample (one year) to identify behavioral changes with significant impacts on the risk of new MCC. The results demonstrate the sensitivity of the proposed methodology for dynamic prediction and monitoring of the risk of MCC emergence in individual patients.

I. INTRODUCTION

A. MOTIVATION

The evolution of multiple chronic conditions (MCC) follows a complex stochastic process. This path of evolution is often influenced by several factors, including inter-relationship of preexisting conditions, patient-level modifiable and non-modifiable risk factors [1]. MCCs are associated with 66% of the total healthcare costs in the United States, and approximately one in four Americans and 75% of Americans aged 65 years are burdened with MCC [2], [3]. Furthermore, people with MCCs have an increased risk of mortality [4]. What makes MCC one of the biggest challenges of the 21^st century in healthcare [5], is the complex dynamic nature of MCC which is affected not only by the preexisting chronic conditions and non-modifiable demographic risk factors, such as age, gender, ethnicity, etc., but also the modifiable lifestyle behavioral risk factors, such as diet, exercise, etc.

B. BACKGROUND AND PROBLEM STATEMENT

Several aspects of MCC have been studied in literature over the years. Lippa et al. [6] conducted a structured clinical interview of a sample of 255 previously deployed Post-9/11 service members and veterans. They found over 90% of them suffer from psychiatric conditions. Approximately half of them had three or more conditions, and 76.9% of them suffered from four clinically relevant psychiatric and lifestyle behavioral factors, including deployment trauma, somatic, anxiety, and substance abuse. Alaeddini et al. [7] identified major transitions of four MCC that include hypertension (HTN), depression, PTSD, and back pain in a cohort of 601,805 Iraq and Afghanistan war Veterans (IAVs). They also developed a Latent Regression Markov Mixture Clustering (LRMCL) algorithm that can predict the exact status of comorbidities about 48% of the time. In a separate study, Cai et al. [8] developed algorithms to identify the relationships between factors influencing hepatocellular carcinoma after hepatectomy. Lappenschaar et al. [9] and Faruqui et al. [10] separately used a large dataset to develop a multilevel temporal Bayesian network (MTBN) to model the progression of MCCs. Several studies have also covered the prevalence of MCC and their rate of increase [11]–[20]; health consequences of MCC and their complications [21]–[25]; cost and quality of life [26]–[32]; patient support, intervention and complications [33], [34]; and assessment, prediction, and decision making [7], [10], [35], [36]. However, most of the preexisting literature is cross-sectional, considers single chronic conditions, or studies a short period of time. Moreover, while these methods describe general comorbidity phenotypes, they do not provide insight into the complex interactions between preexisting MCC, non-modifiable demographic risk factors, and modifiable lifestyle behaviors of an individual patient on the complex evolution pathway of MCC. In particular, they do not effectively capture the impact of modifiable lifestyle behaviors of individual patients on dynamics of MCC emergence, and progression [10].

C. PROPOSED APPROACH

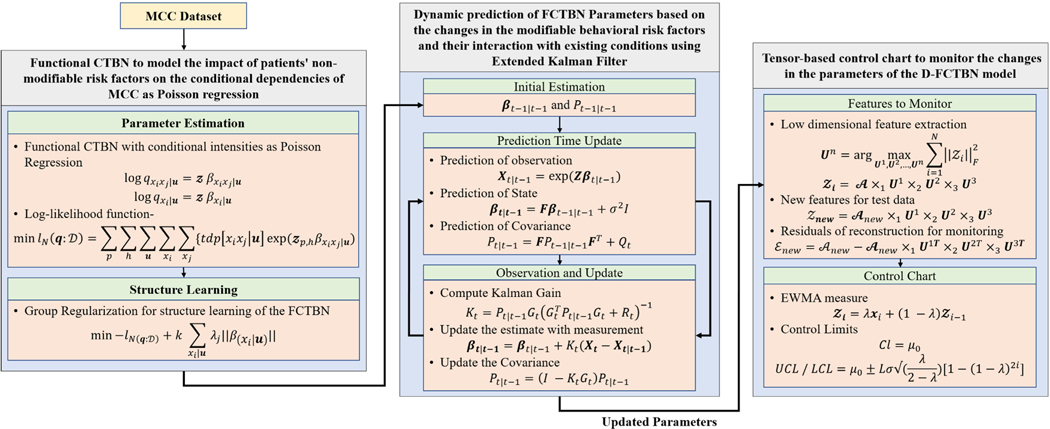
In this study, we first represent the complex stochastic relationship between MCC as a functional continuous time Bayesian network (FCTBN) [37] to take into account the impact of the patients’ risk factors on the MCC emergence and progression (Figure 1-First Component: Functional CTBN to model the impact of patients’ non-modifiable risk factors on the conditional dependencies of MCC as Poisson regression). We then develop a dynamic FCTBN (D-FCTBN) to capture the dynamic impact of modifiable risk factors and their interaction with preexisting conditions on the emergence of new MCC. This is done by formulating the conditional dependencies of FCTBN using a non-linear state-space model based on Extended Kalman Filter (EKF) (Figure 1-Second Component: Dynamic prediction of FCTBN parameters based on the changes in the modifiable lifestyle behavioral risk factors and their interaction with preexisting conditions using extended Kalman filter (EKF)). Next, we develop a tensor-based control chart to monitor the changes in the estimated parameters of the proposed D-FCTBN model, which may have a potentially significant impact on the risk of developing a new MCC (Figure 1 Third Component: Tensor-based control chart to monitor the changes in the parameters of the DFCTBN model). Finally, we validate the proposed approach using a combination of simulation and real data from the Cameron County Hispanic Cohort (CCHC). The overall schema for the proposed method is shown in Figure 1.

FIGURE 1.

The overall scheme of the proposed approach for dynamic prediction and monitoring of the emergence and progression of MCC. The proposed scheme has three major components: (1) A Functional CTBN (FCTBN) to take into account the impact of the patients’ non-modifiable risk factors on the MCC emergence and progression, (2) a dynamic FCTBN (D-FCTB) for prediction of FCTBN parameters based on the changes in the modifiable lifestyle behavioral risk factors using Extended Kalman Filter, and (3) A tensor-based control chart for monitoring the changes in the D-FCTBN parameters.

The proposed methodology has the following contributions:

1. We propose to formulate the conditional dependencies of FCTBN as a non-linear state space model based on EKF to create a dynamic FCTBN (D-FCTBN) that captures the dynamics of modifiable lifestyle behavioral risk factors on the structure and parameters of the MCC network.

2. We propose a tensor-based control chart to proactively monitor the evolution of the D-FCTBN network parameters over time, and signal when there is a significant change in the estimated parameters of the MCC network, which can result in an increased risk of developing new chronic conditions.

3. We validate the proposed methodology for dynamic prediction and monitoring of the emergence of multiple chronic conditions based on a combination of simulation and a real dataset from the Cameron County Hispanic Cohort (CCHC).

The remainder of the paper is structured as follows. Section II presents the preliminaries and background for the CTBN and FCTBN. Specifically, Section II-A describes the details of the CTBN, and Section II-B explains the functional CTBN and the regularized regression model for learning its structure and parameters. Section III details the proposed approach for developing the Dynamic FCTBN (D-FCTBN) and the tensor-based control chart for monitoring the evolution of D-FCTBN. In particular, Section III-A describes the details of the proposed EKF model for modeling the dynamics of edges of the D-FCTBN based on the changes in the modifiable risk factors and their interaction with preexisting conditions. Also, Section III-B describes the building blocks of the proposed tensor-based control chart for monitoring the estimated parameters of the proposed D-FCTBN. Section IV presents the study population, the resulting model structure and parameters, and the tensor-based control chart to detect network changes. Finally, Section V provides the concluding remarks.

II. RELEVANT BACKGROUND

In this section, we review some of the major components of the proposed approach, including the CTBN for modeling MCC evolution as a finite-state continuous time conditional Markov process over a factored state [38]–[40], and functional CTBN (FCTBN) [37] for extending CTBN edges based on Poisson regression of some exogenous risk factors.

A. CONTINUOUS TIME BAYESIAN NETWORK (CTBN)

1). CTBN COMPONENTS

Continuous time Bayesian networks (CTBNs) are Bayesian networks that models time explicitly by defining a graphical structure over continuous time Markov processes [38]. Let $X=\left\{x_1,x_2,\dots ,x_n\right\}$ denotes the state space of a set of random variables with discrete states $x_i=\{1,\dots ,l\}$, such as MCC like Diabetes, Obesity, Hypertension, Heyperlipidemia, and Cognitive Impairment. A CTBN consists of a set of conditional intensity matrices (CIM) under a given graph structure [38], [41]. The components of a CTBN are -

1. An initial distribution $\left(P_x^0\right)$, which formulates the structure of the (conditional) relationship among the random variables and is specified as a Bayesian network, where each edge $X_i\to x_j$ on the network implies the impact of the parent condition x_i on the child condition x_j.

2. A state transition model $\left(Q_{X_i\mid \mathbf{u}}\right)$, which describes the transient behavior of each variable $x_i\in X$ given the state of parent variables u, and is specified based on CIMs -

   $${\mathbf{Q}}_{X\mid \mathbf{u}}=\left[\begin{array}{cccc}-q_{x_1\mid \mathbf{u}}& q_{x_1{x}_2\mid \mathbf{u}}& \cdots & q_{x_1{x}_n\mid \mathbf{u}}\\ q_{x_2{x}_1\mid \mathbf{u}}& -q_{x_2\mid \mathbf{u}}& \cdots & q_{x_2{x}_n\mid \mathbf{u}}\\ ⋮& ⋮& \ddots & ⋮\\ q_{x_n{x}_1\mid \mathbf{u}}& q_{x_n{x}_2\mid \mathbf{u}}& \cdots & -q_{x_n\mid \mathbf{u}}\end{array}\right]$$

where $q_{x_i{x}_j\mid \mathbf{u}}$ represents the intensity of the transition from state x_i to state x_j given a parent set of node u, and $q_{x_i}=\sum _{j\ne i}{q}_{x_i{x}_j}$. Conditioning the transitions on parent conditions sparsifies the intensity matrix considerably, which is especially helpful for modeling large state spaces. When no parent variable is present, the CIM will be the same as the classic intensity matrix.

The probability density function (f) and the probability distribution function (F) for staying at the same state (say, x_i), which is exponentially distributed with parameter q_xi, are calculated as-

$$f\left(q_x,t\right)=q_{x_i}\mathit{exp}\left(-q_{x_i}t\right),t\ge 0$$ (1)

$$F\left(q_x,t\right)=1-\mathit{exp}\left(-q_{x_i}t\right),t\ge 0$$ (2)

After transitioning, which takes an expected transition time of $\frac{1}{q_{x_i}}$, the variable X shifts to state x_j with probability ${\theta }_{x_i{x}_j}=\frac{q_{x_i{x}_j}}{q_{x_i}}$. While a Markov process provides a straightforward framework for modeling the temporal behavior of a random variable with finite states, it doesn’t scale up well for large state spaces i.e. the size of intensity matrix, Q_X grows exponentially with the number of variables.

2). CTBN PARAMETER ESTIMATION

Given a dataset $\mathcal{D}=\left\{{\tau }_{h=1},{\tau }_{h=2},\dots ,{\tau }_{h=H}\right\}$ of H observed transitions, where ${\tau }_h$ represents the time at which the h^th transition has occurred, and $\mathcal{G}$ is a Bayesian network defining the structure of the (conditional) relationship among variables, we can use maximum likelihood estimation (MLE) (equation (3)) to estimate parameters of the as defined in Nodelman et al [38], [40]-

$$L_x\left(q_{x\mid \mathbf{u}}:\mathcal{D}\right)=\prod _{\mathbf{u}}\prod _x{q}_{x\mid \mathbf{u}}^{M[x\mid \mathbf{u}]}\mathit{exp}\left(-q_{x\mid \mathbf{u}}T[x\mid \mathbf{u}]\right)$$ (3)

where, T[x|u] is the total time X spends in the same state x, and M[x|u] the total number of time X transits out of state x given, $x=x^{\prime }$. The log-likelihood function can be then written as-

$$l_x\left(q_{x\mid \mathbf{u}}:\mathcal{D}\right)=\sum _{\mathbf{u}}\sum _{x}M[x\mid \mathbf{u}]\mathit{ln}\left(q_{x\mid \mathbf{u}}\right)-q_{x\mid \mathbf{u}}T[x\mid \mathbf{u}]$$ (4)

Maximizing Equation 4, provides the maximum likelihood estimate (MLE) of the conditional intensities as shown in Equation 5-

$${\widehat{q}}_{x\mid \mathbf{u}}=\frac{M[x\mid \mathbf{u}]}{T[x\mid \mathbf{u}]}$$ (5)

The above estimation is true for the cases with complete data. For the cases including incomplete dataset, the expectation maximization (EM) algorithms can be used [39], [42].

B. FUNCTIONAL CTBN (FCTBN)

1). FCTBN WITH CONDITIONAL INTENSITIES AS POISSON REGRESSION

In reality, the progression of state variables, such as chronic conditions, not only depends on the state of their parents, such as preexisting chronic conditions but some exogenous variables, such as patient level risk factors like age, gender, etc.

Using Poisson regression to represent the impact of exogenous variables on the conditional dependencies, the rate of transition between any pair of MCC states can be derived as [37]-

$$\log q_{x_i,x_j\mid \mathbf{u}}={\beta }_{0_{x_i,x_j|\mathbf{u}}}+z_1{\beta }_{1_{x_i,x_j\mid \mathbf{u}}}+\dots \dots +z_m{\beta }_{m_{x_i,x_j\mid \mathbf{u}}}$$ (6a)

$$=\mathit{z}{\mathit{\beta }}_{{\mathbf{x}}_i,{\mathbf{x}}_j\mid \mathbf{u}}$$ (6b)

where, $\mathbf{z}=\left\{z_1,z_2,\dots ,z_m\right\}$ is the set of exogenous variables (e.g. patient-level risk factors such as age, gender, race, education, marital status, etc.), and ${\beta }_{k_{x_i\mid \mathbf{u}}}={\sum }_{j\ne i}{\beta }_{k_{x_i{x}_j\mid \mathbf{u}}},k=0,\mathrm{...},m$ is the set of coefficients (parameters) associated with the exogenous variables.

Also, the rate of staying in the same state is modeled as-

$$\log q_{x_i\mid \mathbf{u}}={\beta }_{0_{x_i|\mathbf{u}}}+z_1{\beta }_{1_{x_i\mid \mathbf{u}}}+\dots \dots +z_m{\beta }_{m,x_i\mid \mathbf{u}}$$ (7a)

$$=\mathit{z}{\mathit{\beta }}_{{\mathbf{x}}_i\mid \mathbf{u}}$$ (7b)

When the state space of the random variables is binary, as in our case study on MCC transitions, where MCC states include having/not having each of the conditions, the conditional intensities in ${\mathbf{Q}}_{x_i\mid {\mathbf{u}}_i}$, can be estimated just using Equation 7a because for Markov processes with binary states $q_{x_i\mid \mathbf{u}}=-{\sum }_{j\ne i}{q}_{\left(x_i{x}_j\mid \mathbf{u}\right)}$. This feature considerably simplifies the estimation of the functional CTBN conditional intensity matrix based on Poisson regression.

2). PARAMETER ESTIMATION

Having the dataset $D=\left\{{\tau }_{(p=1,h=1)},\dots ,{\tau }_{(P,H)}\right\}$ of MCC trajectories, where ${\tau }_{(p,h)}$ represents the time at which the h^th (MCC) transition of the p^th patient has occurred, we use maximum likelihood estimation to estimate parameters of the proposed FCTBN. The likelihood of D can be decomposed as the product of the likelihood for individual transitions. Let $d=\langle \mathbf{z},\mathbf{u},x_i\left|\mathbf{u},t_d,x_j\right|\mathbf{u}\rangle$ be the transition of patient p with risk factors z and preexisting conditions u, who made the transition to state $x_{j\mid \mathbf{u}}$ after spending the amount of time $t_d={\tau }_{(p,h)}-{\tau }_{(p,h-1)}$ in state $x_{i\mid \mathbf{u}}$. By multiplying the likelihoods of all conditional transitions during the entire trajectory for all patients p = 1,...,P, and taking the log, we obtain the overall log-likelihood function as-

$$\begin{gathered} l_N(\mathbf{q}:\mathcal{D})=\sum _p\sum _h\sum _{\mathbf{u}}\sum _{x_j}\sum _{x_i} \\ \left\{t_{dp}\left[x_i{x}_j\mid \mathbf{u}\right]\exp \left(z_{p,h}{\mathit{\beta }}_{x_i{x}_j\mid \mathbf{u}}\right)\right\} \end{gathered}$$ (8)

which is a convex function and can be maximized efficiently using a convex optimization algorithm such as Newton-Raphson to estimate parameters ${\beta }_{x_i\mid \mathbf{u}}$. Given the structure of the functional CTBN, i.e. the parent set for each variable (node), the maximum number of parameters to be estimated in Equation 8 will be $\overline{\overline{\mathbf{x}}}\times \overline{\overline{\mathbf{z}}}\times 2^{max(\overline{\overline{\mathbf{u}}})+1}$, where $\overline{\overline{\mathbf{x}}}$ is the number of state variables (conditions), $\overline{\overline{\mathbf{z}}}$ is the number of exogenous variables (risk factors) presents in the system, and max($\overline{\overline{\mathbf{u}}}$) is the maximum number of parents considered (preexisting diseases for each condition). Therefore, as in classical Bayesian networks, the number of parents has a direct and exponential influence on the computational efficiency of the estimation process and should be limited to a small number. We propose to assume the conditional effect of parents is multiplicative, i.e. $q_{x_i\mid u_1,u_2}=q_{x_i\mid u_1}\cdot q_{x_i\mid u_2}$, to make the conditional effect of the risk factors additive given the set of parents, i.e. ${\mathit{\beta }}_{x_i{x}_j\mid \mathbf{u}=u_1,\dots u_k}={\mathit{\beta }}_{x_i{x}_j\mid u_1}+\dots +{\mathit{\beta }}_{x_i{x}_j\mid u_k}$. This assumption, which is on a par with the Noisy-OR [43], [44] and the CT-NOR [45], reduces the maximum number of parameters to be estimated to $\overline{\overline{\mathbf{x}}}\times \overline{\overline{\mathbf{z}}}\times 2\times (max(\overline{\overline{\mathbf{u}}})+1))$. Further details of FCTBN model can be found in [37].

3). ADAPTIVE GROUP REGULARIZATION FOR STRUCTURE LEARNING OF THE FCTBN

The parameter estimation approach presented above requires the parent set of each condition to be known, which is equivalent to knowing the Bayesian network structure. Given that FCTBN has a special structure based on a conditional intensity matrix that allows for cycles, group regularization can be used to penalize groups of parameters pertaining to each specific conditional transition (each edge) [37] as-

$$\min -l_N(\mathbf{q}:\mathcal{D})+k\sum _{x_i\mid \mathbf{u}}{\lambda }_j\Vert {\mathit{\beta }}_{x_i\mid \mathbf{u}}\Vert$$ (9)

where, $\Vert {\mathit{\beta }}_{x_i\mid \mathbf{u}}\Vert =\sqrt{\sum _{\mathbf{\text{u}}}\sum _{x_i}({\mathit{\beta }}_{x_i\mid \mathbf{u}}\cdot {\mathit{\beta }}_{x_i\mid \mathbf{u})}^T}$ is the L₁-norm of the group of parameters associated with each conditional transition. k is the groups size which is based on the number of coefficients in the Poisson regression for each conditional intensity. ${\lambda }_j=\lambda {\Vert {\tilde{\mathit{\beta }}}_j\Vert }^{-1}$ is the tuning parameters (of the adaptive group regularization) that control the amount of shrinkage, where λ is inversely weighted based on the unpenalized estimated value of the regression coefficients ${\tilde{\mathit{\beta }}}_j$ [46].

III. PROPOSED APPROACH

In this section, we first propose an extended Kalman filter to capture the effects of the dynamics of modifiable risk factors on the parameters, edges, and structure of the FCTBN (D-FCTBN). Next, we develop a tensor-based control chart to monitor the evolution of the dynamic FCTBN (D-FCTBN).

A. AN EXTENDED KALMAN FILTER FOR DYNAMIC PREDICTION OF FCTBN PARAMETERS

The conditional dependencies (edges) of FCTBN provide the rate of transitioning from one state to another given the parents’ state and exogenous variables, i.e., the rate of a new chronic condition such as obesity emergence during the next t years given the preexisting conditions such as diabetes and patient’s level risk factors such as gender, age, etc. However, in reality, conditional dependencies dynamically change based on a person’s modifiable lifestyle behavioral risk factors, i.e., diet, exercise, and interaction with non-modifiable risk factors and preexisting conditions. To capture the dynamics of the changes in the conditional intensities (risk) of MCC, we propose to transform the parameters (coefficients) of the regression functions, which represent the edges of the MCC (FCTBN) network, into an extended Kalman filter (EKF) [47].

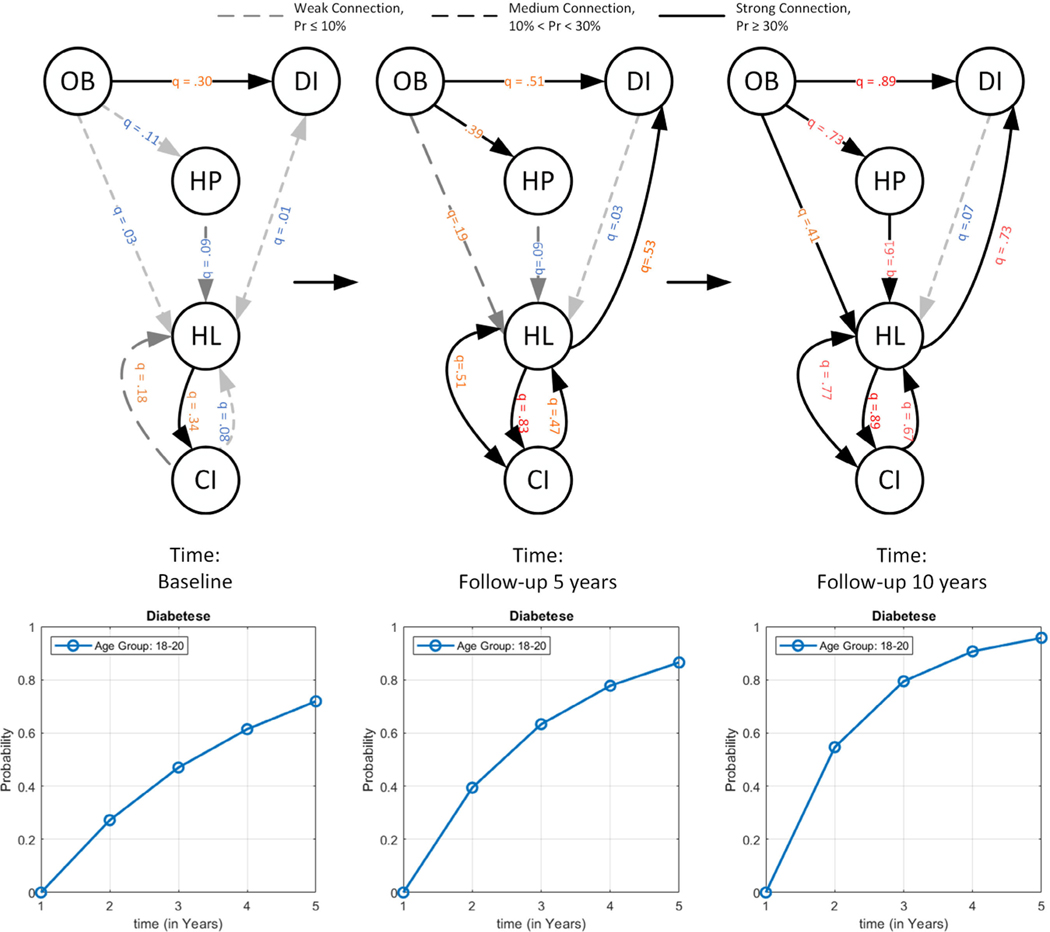
EKF consists of an observation equation and a state transition equation. The observation equation describes the most recent observation of state variables using system dynamics, namely Poisson regression coefficients associated with the emergence and progression of MCC. The transition equation predicts how the state variables evolve to the next period, namely how the coefficients associated with MCC will progress/emerge in the next period (See Fig. 2).

FIGURE 2.

Illustration of the impact of lifestyle behavioral risk factors dynamics on the conditional intensities/dependencies and risk trajectory of developing new MCC conditions, i.e. Diabetes, at three time points, including baseline, 5-year follow up, and 10-year follow up, using extended Kalman filter; The nodes with thick outlines represent the preexisting or developed conditions over time. (The nodes, OB: Obesity, HP: High Blood Pressure, DI: Diabetes, HL: Hyperlipidemia, and CI: Cognitive Impairment).

1). OBSERVATION EQUATION

Each edge/connecting in the MCC FCTBN network represents, the rate of occurrence of a chronic condition such as diabetes, based on a Poisson regression function with parameters. ${\left[{\beta }_{x_i{x}_j\mid u}\right]}_t$. We consider ${\left[{\beta }_{x_i{x}_j\mid u}\right]}_t$ as the state variables of the dynamical system which describe the (noisy) sequences of MCC observations. This results in the observation equation given by-

$${\left[q_{x_i\mid \mathbf{u}}\right]}_t=exp\left(z_t{\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_t\right)$$ (10)

The observation equation (10) is non-linear and thus we will employ the extended Kalman filter (EKF) [48] instead of general Kalman filters (KF) [49]. EKFs similar to KF follows a recursive procedure where it performs predictions based on a given observation and updates the estimates iteratively [48].

2). STATE TRANSITION EQUATION

As a patient changes her lifestyle behaviors, the state variables of the proposed dynamical model evolve in time to best predict the MCC emergence and progression. This results in a state transition equation given by-

$${\left[{\beta }_{x_i\mid \mathbf{u}}\right]}_t=\mathit{F}{\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t-1}+{\epsilon }_t$$ (11)

where F is the state transition matrix, and ε_t is the white noise assumed to follow a Gaussian distribution with mean zero and covariance σ²I. The transition matrix F can be approximated from stream of data ${\mathbf{X}}_{i\mid t}$ utilizing the FCTBN model evaluated at different point in time or by utilizing some system identification techniques [50].

3). DYNAMIC PREDICTION via EKF

EKF takes the most recent estimate of the state variables with information of changes in the (modifiable) lifestyle behavioral risk factors up to time t and uses the system dynamics to predict the future state of the variables and prediction of the MCC as [48]-

$${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}=\mathit{F}{\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t-1\mid t-1}+{\sigma }^{2}I$$ (12)

$$P_{t\mid t-1}=\mathit{F}{\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t-1\mid t-1}{\mathit{F}}^T+Q_t$$ (13)

where ${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}$ and $P_{t\mid t-1}$ are the extended Kalman prediction of the matrix of estimated coefficients and their covariance respectively given a set of observations X_i,t. The observation equation is linearized using the Taylor Expansion to achieve a sub-optimal estimate of the state value.

4). DYNAMIC ESTIMATION via EKF

When new observations of MCC are obtained, the error between the observation and the EKF predictions is used to update the posterior mean of the state variable as-

$${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}={\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}+K_t\left({\mathit{X}}_{x_i\mid \mathbf{u},t}-{\mathit{X}}_{x_i|\mathbf{u},t|t-1}\right)$$ (14)

where K_t is the Kalman gain and calculated using the following equations-

$$P_{t\mid t-1}=\left(I-K_t{G}_t\right)P_{t\mid t-1}$$ (15)

$$K_t=P_{t\mid t-1}{G}_t{\left(G_t^T{P}_{t\mid t-1}{G}_t+R_t\right)}^{-1}$$ (16)

where, G_t denotes the Jacobian of g evaluated at ${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}$ i.e. $G_t={\frac{\partial g}{\partial {\left[{\mathit{\beta }}_{x_j\mid \mathbf{u}}\right]}_t}|}_{{\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}}={\mathit{Z}}_t^{T}diag\left(exp\left({\mathit{Z}}_t{\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}\right)\right)$, redand R_t represents the variance of observations and is estimated based on the underlying network distribution and the observation prediction. The estimated parameter ${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t}$ provides a sub-optimal estimate of the network parameters at time t [48]. The proposed D-FCTBN Algorithm is shown in Algorithm 1.

Algorithm 1.

Dynamic Functional Continuous Time Bayesian Network (D-FCTBN)

Input:
Attribute Data, ${\mathcal{D}}_x=X_1,X_2,\dots ,X_n$
Risk Factor Data, ${\mathcal{D}}_z=z_1,z_2,\dots ,z_n$
Tuning Parameter, λj
Group Size, m
1:	Procedure: Learn Structure and Parameters of FCTBN [37] $\left({\mathcal{D}}_x,{\mathcal{D}}_z,{\lambda }_j,m\right)$
2:	Initialisation → β
3:	for i to p do
4:	for j to h do
5:	for k to u do
6:	for l to x do
7:	$\begin{array}{l}J(\mathit{\beta }):={\sum }_p{\sum }_h{\sum }_{\mathbf{u}}{\sum }_{x_i}\left({\mathbf{z}}_p{\mathit{\beta }}_{x_i\mathbf{u}}\right)-\\ {\sum }_p{\sum }_h{\sum }_{\mathbf{u}}{\sum }_{x_i}\left\{t_{d_p}^h\left[x_i\mid \mathbf{u}\right]exp\left({\mathbf{z}}_p{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right)\right\}+\\ m{\sum }_{x_i\mid \mathbf{u}}\lambda \Vert {\mathit{\beta }}_{x_i\mid \mathbf{u}}\Vert \end{array}$
8:	${\mathit{\beta }}_m:={\mathit{\beta }}_m-\frac{\partial J(\mathit{\beta })}{\partial {\mathit{\beta }}_m}$
9:	end for
10:	end for
11:	end for
12:	end for
13:	DAG ← GMM_Mixture(βm)
14:	Procedure: Dynamic estimation of parameters of FCTBN (D-FCTB) (β, DAG, ${\mathcal{D}}_z$)
15:	for i to N do
16:	${\mathit{X}}_{x_i|\mathbf{u},t|t-1}=exp\left(z_t{\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_t\right)$
17:	${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}=\mathit{F}{\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t-1\mid t-1}+{\sigma }^{2}I$
18:	$P_{t\mid t-1}=\mathit{F}{\left[{\mathit{\beta }}_{x_i\mathbf{u}}\right]}_{t-1\mid t-1}{\mathit{F}}^T+Q_t$
19:	$K_t=P_{t\mid t-1}{G}_t{\left(G_t^T{P}_{t\mid t-1}{G}_t+R_t\right)}^{-1}$
20:	${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}={\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}+K_t\left({\mathit{X}}_{x_i\mid \mathbf{u},t}-{\mathit{X}}_{x_i|\mathbf{u},t|t-1}\right)$
21:	$P_{t\mid t-1}=\left(I-K_t{G}_t\right)P_{t\mid t-1}$
22:	end for
Output: Updated β

B. MONITORING OF EVENTS

In this section, we propose a monitoring scheme to determine meaningful changes in the exogenous variables (modifiable risk factors) that can have an impact on the risk of developing new chronic conditions. For this purpose, we propose a statistical control chart that automatically signals when there is a meaningful change in the predicted value of the coefficients associated with the patient level (modifiable) risk factors, namely ${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}$, which is dynamically updated by the D-FCTBN. The idea behind monitoring the ${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}$ is that the predicted value of the risk factors coefficients are directly related to the network edges (conditional intensities) and the risk of developing new MCC conditions.

Given the dynamic prediction of D-FCTBN (MCC network) parameters for a time point t|t − 1, the coefficients form a 3-dimensional tensor including the parents, children, and risk factors dimensions (modes). To effectively monitor the tensor of predicted coefficients for any potential changes, we propose to use multilinear principal component analysis (MPCA) [51] to extract the most salient features of the data for building the control chart. Compared with some of the alternative methods such as PCA [52], Unfolded MPCA (UMPCA) [53], [54], Robust MPCA (RMPCA) [55], [56], and Non-negative MPCA (NMPCA) [57], MPCA provides an appealing combination of ease of implementation, computational efficiency, and acceptable performance. For classic PCA, it is not directly applicable to our study data which are in the form of a 3-dimensional tensor. For UMPCA, it does not preserve the local structure and correlation in the data [52]. For RMPCA, it removes possible outliers, which our control chart is designed to monitor [56]. For NMPCA, it enforces non-negativity constraints which may affect the extracted pattern from the tensor [58], due to the nature of the problem. Interested readers may also refer to Kruger et al [52], Lu et al [51], and Paynabar et al [58] for comprehensive reviews of tensor feature extraction methods.

1). MULTILINEAR PRINCIPAL COMPONENT ANALYSIS

Lu et al. [51] introduce the MPCA framework for tensor feature extraction. They decompose the original tensor into a series of multiple projection sub-problems and solves them iteratively.

For an in-control training set of N-th order tensor denoted as $\mathcal{A}\in {ℝ}^{I_1\times I_2,\times I_3,\dots \dots ,\times I_N}$, the MPCA projection can be denoted by $y\in {ℝ}^{I_1\times I_2\times I_3}$, where $n=1,2,\dots \dots ,N$, I₁, I₂ and I₃ are the dimensions of the coefficient tensor and N is the number of updated coefficients attained from EKF. Lu et al. [51] find the set of orthogonal transformation matrices ${\mathbf{U}}^n\in R^{I_n\times P_n},n=1,2,3,\dots ,N$, where the dimensionality $P_n\left(P_n\le I_n\right)$ for each mode is predetermined or known for the application of interest. They have also developed methods for adaptive determination of P_n in case it’s not pre-determined. The transformation is performed such that it captures the most variations of the original tensor. To keep the original estimated values of the coefficients, in this work we utilized the non-centered version of the MPCA. Therefore, the low dimensional features after applying MPCA will be,

$${\mathbf{U}}^n=\arg \underset{{\mathbf{U}}^{(1)},{\mathbf{U}}^{(2)},\dots ,{\mathbf{U}}^{(N)}}{\max }\sum _{i=1}^N{\Vert {\mathcal{Z}}_i\Vert }_F^2$$ (17)

where, $n=1,2,3,{\mathcal{Z}}_i=\mathcal{A}{\times }_1{\mathbf{U}}^{(1)}\times 2{\mathbf{U}}^{(2)}{\times }_3{\mathbf{U}}^{(3)}$ and $\mathcal{A}$ is non-centered tensor data. In case of centered data, $\mathcal{A}$ can be replaced with $\tilde{\mathcal{A}}$, where $\tilde{\mathcal{A}}=\mathcal{A}-\overline{\mathcal{A}}$. For a new feature tensor, $A_{new}\in {ℝ}^{I_1\times I_2,\times I_3}$, the features are calculated as,

$${\mathcal{Z}}_{new}={\mathcal{A}}_{new}{\times }_1{\mathbf{U}}^{(1)}{\times }_2{\mathbf{U}}^{(2)}{\times }_3{\mathbf{U}}^{(3)}$$ (18)

and residuals of reconstruction can be calculated as

$${\mathcal{E}}_{\mathit{\text{new}}}={\mathcal{A}}_{\mathit{\text{new}}}-{\mathcal{Z}}_{\mathit{\text{new}}}{\times }_1{\mathbf{U}}^{(1)T}{\times }_2{\mathbf{U}}^{(2)T}{\times }_3{\mathbf{U}}^{(3)T}$$ (19)

The errors at every time step can also be vectorized by calculating the norm of all the data, i.e. ${\mathcal{E}}_{new\text{\_}vector}={\Vert {\mathcal{E}}_{new}\Vert }_2$.

Algorithm 2.

Monitoring of D-FCTBN Parameters

Input:
Parameter Data, βt
Tuning Parameter, λ, L
1:	z ← MPCA(βt)
2:	Phase I: Building the Control Chart
3:	for i to M do
4:	# Low Dimensional Feature Extraction
5:	${\mathbf{U}}^n=\arg {\max }_{{\mathbf{U}}^{(1)},{\mathbf{U}}^{(2)},\dots ,{\mathbf{U}}^{(N)}}{\sum }_{i=1}^N{\Vert {\mathcal{Z}}_i\Vert }_F^2$
6:	${\mathcal{Z}}_i=\mathcal{A}{\times }_1{\mathbf{U}}^{(1)}\times 2{\mathbf{U}}^{(2)}{\times }_3{\mathbf{U}}^{(3)}$
7:	end for
8:	$z_i=\lambda {\mathbf{x}}_i+(1-\lambda )z_i-1$
9:	# Control Limit
10:	$CL=\mu \left(z_i\right)$
11:	$UCL=CL+L\sigma \sqrt{\frac{\lambda }{(2-\lambda )}\left[1-{(1-\lambda )}^{2i}\right]}$
12:	$UCL=CL-L\sigma \sqrt{\frac{\lambda }{(2-\lambda )}\left[1-{(1-\lambda )}^{2i}\right]}$
13:	Phase II: Monitoring
14:	for i to T do
15:	# New Feature for the Test Data
16:	$z_{new}={\mathcal{A}}_{new}{\times }_1{\mathbf{U}}^{(1)}{\times }_2{\mathbf{U}}^{(2)}{\times }_3{\mathbf{U}}^{(3)}$
17:	# Residuals of reconstruction for monitoring
18:	${\mathcal{E}}_{new}={\mathcal{A}}_{new}-{\mathcal{Z}}_{new}{\times }_1{\mathbf{U}}^{(1)T}{\times }_2{\mathbf{U}}^{(2)T}\times {\times }_3{\mathbf{U}}^{(3)T}$
19:	if ${\mathcal{E}}_{new}\ge \text{UCL or}{\mathcal{E}}_{new}\le \text{LCL}$ then
20:	${\mathcal{E}}_{new}$ ← Out-of-control Signal
21:	end if
22:	end for
Output: Detection of Out-of-Control Signal

2). MONITORING SCHEME

Here, we propose a tensor-based control chart to monitor the changes in the D-FCTBN network edges caused by changes in the patient modifiable risk factors, namely lifestyle behavioral changes. Given the estimate of FCTBN parameters σ²I and ${\left[{\mathit{\beta }}_{x_i\mid \mathbf{u}}\right]}_{t\mid t-1}$ based on Section II-B, for any new observation of patients (modifiable and non modifiable) risk factors and MCC conditions, the tensor of new network parameters (risk factors’ coefficients) are predicted using the EKF detailed in Section III-A, and the relevant features are extracted using MPCA discussed in Section III-B1.

When there is no significant change in the patients’ lifestyle behaviors, the reconstruction error in Equation 19 will be small, as patients’ historical/past behavior can accurately estimate the D-FCTBN parameters. However, when there is a significant change in the patients’ lifestyle behaviors, the distribution of reconstruction error will change, and the observed value will supposedly increase. Therefore, for new predictions of the D-FCTBN parameters, ${\left[{\mathit{\beta }}_{x_i\mid u}\right]}_{t+1\mid t}\approx {\mathcal{A}}_{\mathit{\text{new}}}\in {ℝ}^{I_1\times I_2,\times I_3}$, the reconstruction error can be used to identify potential high-impact changed in patients modifiable risk factors. The proposed monitoring scheme is based on a Multivariate Exponential Weighted Moving Average (MEWMA) [59] control chart of the vectorized reconstruction error:

$${\mathbf{Z}}_i=\lambda {\mathbf{x}}_i+(1-\lambda ){\mathbf{Z}}_{i-1}$$ (21)

where $0\le \lambda \le 1$ and ${\mathbf{Z}}_0=0$. In case of MEWMA the quantity plotted on the control chart is -

$$T_i^2={\mathbf{Z}}_i^T{S}_I^{-1}{\mathbf{Z}}_i$$ (21)

where the covariance matrix is,

$$S_I^{-1}=\frac{\lambda }{2-\lambda }\left[1-{(1-\lambda )}^{2i}\right]S$$ (22)

which is equivalent to the variance of the univariate EWMA, and S is the sample covariance matrix calculated of the features estimated by N in-control samples [60]. The control limits of control chart can be calculated as follows (for the univariate case)-

$$\begin{gathered} UCL={\mu }_0+L\sigma \sqrt{\frac{\lambda }{(2-\lambda )}\left[1-{(1-\lambda )}^{2i}\right]} \\ CL={\mu }_0 \\ LCL={\mu }_0-L\sigma \sqrt{\frac{\lambda }{(2-\lambda )}\left[1-{(1-\lambda )}^{2i}\right]} \end{gathered}$$ (23)

Where, L is the width of the control limits, σ² is the variance of the data, and i represents the observation number in the MEWMA statistics. The factor $\frac{\lambda }{(2-\lambda )}\left[1-{(1-\lambda )}^{2i}\right]$ approaches $\frac{\lambda }{(2-\lambda )}$ as i increases per iteration. Therefore, for Phase I analysis of the MEWMA control chart, a few samples are required until the control limit approaches their steady-state values. It is also to be mentioned, a small choice of λ provides more sensitivity in detecting subtle changes in the lifestyle behavioral risk factors. Any observations that fall outside the control limits are considered out-of-control signals. The proposed algorithm for monitoring the parameters of the D-FCTBN is shown below2.

IV. RESULTS AND DISCUSSION

Long-lasting diseases, otherwise known as chronic conditions, can be considered a degradation process that progresses over time and contributes to the development of other new chronic conditions. The presence of two or more chronic medical conditions in an individual is commonly defined as multimorbidity, or multiple chronic conditions (MCC) [10], [35]. Here, we use the proposed dynamic FCTBN (D-FCTBN) to find the impact of patient level risk factors, specifically lifestyle behaviors, on the conditional dependencies of MCC over time. In addition, we use the proposed tensor-based control chart to monitor the risk of new MCC emergence based on the dynamics of patients’ lifestyle behaviors.

A. STUDY POPULATION AND DEMOGRAPHICS

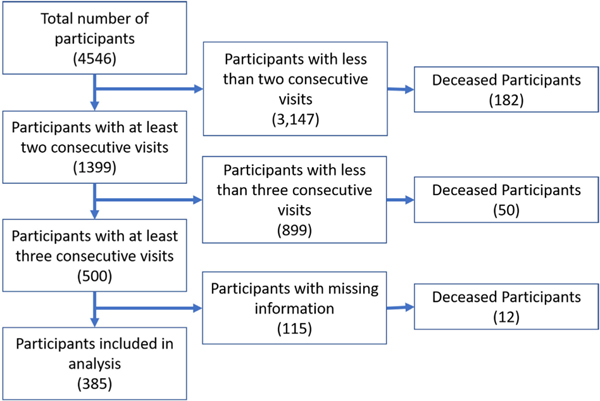
Our case study is based on the Cameron County Hispanic Cohort (CCHC) dataset for comorbidity analyses. The CCHC is a cohort study comprised of mainly Mexican Americans (98% of cohort) randomly recruited from a population with severe health disparities on the Texas-Mexico border and started in 2004. The CCHC is employinga rolling recruitment strategy and currently numbers 4,546 adults. Inclusion criteria: (1) participating in the study between 2004 and 2020, (2) having at least three 5-year follow up visits during that period. 385 patients met these criteria, which include the dataset of our study (see Figure 4). The survey includes participants’ socio-demographic factors (age, gender, marital status, education, etc.) and lifestyle behavioral factors (diet, exercise, tobacco use, alcohol use, etc.).

FIGURE 4.

Flow diagram of sample selection and the final number of patients included in the analysis.

B. DIAGNOSED HEALTH CONDITION AND PATIENTASSOCIATED RISK FACTORS

For this study, we considered some of the most common MCCs present in the Hispanic community, including diabetes, obesity, hypertension, hyperlipidemia, and mild cognitive impairment. The positive criteria (considering the condition to be active) for the conditions selected as below-

• Diabetes: Fasting Glucose >=126 mg/dL, HbA1c>=6.5%, or take diabetes medication [61].

• Obesity: Body mass index (BMI, kg/m2)>=30 [62].

• Hypertension: Systolic blood pressure (BP)>= 130mmHg, Diastolic BP>=80 mmHg, or take antihypertensive medication [63].

• Hyperlipidemia: Total cholesterol > 200 mg/dL, triglycerides >=150 mg/dLl, HDLC < 40 mg/dL (for male)/HDLC < 50 mg/dL (for female), LDLC >=130 mg/dL, or take medication for hyperlipidemia [64].

• Mild Cognitive Impairment: Mini-Mental State Score < 23 (out of 30) [65].

For the risk factors, the dataset includes the participant’s non-modifiable risk factors based on socio-demographic information (age, gender, and education history) and modifiable risk factors based on lifestyle behavioral risk factors (diet, exercise, tobacco use, alcohol use). Diet and exercise are categorized according to the U.S. Healthy Eating Guideline, and U.S Physical Activity Guideline [66].

C. FCTBN STRUCTURE AND PARAMETER LEARNING

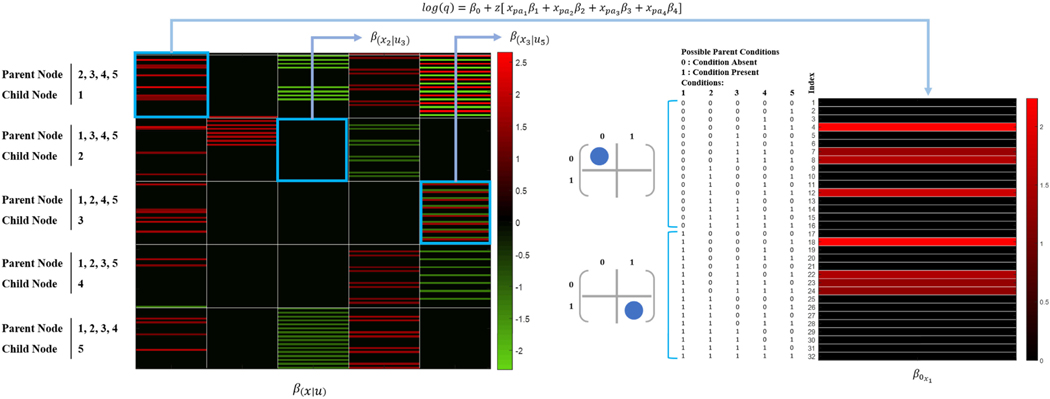
To identify the optimal value of the tuning parameter (λ) of the adaptive group regularization method for FCTBN structure and parameter learning, we use cross-validation error based on several λ values. We attain the structure of FCTBN and the parameters using the optimal value of λ = 10². Figure 5 provides the heatmap of the estimated parameters for the based FCTBN model. These learned parameters will be used as the initial parameters of EKF for estimating the dynamic FTCBN and monitoring possible changes in the risk of acquiring a new MCC condition.

FIGURE 5.

The estimated parameters of FCTBN based on the optimal value of tuning parameters. The matrix contains all the possible combinations of parent and child interaction. For example, the first row set (first 32 rows) of the matrix represents the parameters learned child node 1 while considering the parents’ node are 2, 3, 4, and 5. The right side of the Figure shows all the possible condition possible (1 for the presence of a condition and 0 for no presence of no condition).

D. D-FCTBN DYNAMIC ESTIMATION AND PREDICTION USING EKF

The estimated parameters of FCTBN provide the baseline/initial values of the D-FCTBN. As new (dynamic) observations of patient’s (modifiable) risk factors and MCC status are made available, we use EKF to capture the dynamics of a patient’s modifiable risk factors and MCC update, as detailed in Section III-A. Figure IV-D, visualizes the changes in estimated parameter of the D-FCTNB for time, t + 1 given the parameter information at time t and base parameter, β_{t + 1|t} using the proposed EKF module for 5 patients over 11 consecutive year. The proposed model provides a near-optimal approach to estimate and update the D-FCTBN parameters, which are shown as heatmaps, given the dynamics of patient’s modifiable lifestyle risk factors.

1). STABILITY ANALYSIS OF EKF FOR ESTIMATING PARAMETERS OF FCTBN

In this section, we will discuss the stability of the EKF model derived in Section III-A. For the measurement error, $\mathbf{e}={\mathbf{X}}_t-{\mathbf{X}}_{t\mid t-1}$Konrad et al. [67] showed that the estimation error remains bounded if the following conditions hold-

1. $\Vert \mathbf{F}\left({\mathbf{X}}_t\right)\Vert \le \alpha$, $\Vert G_t\left({\mathbf{X}}_t\right)\Vert \le \beta$, where, $\alpha ,\beta \ge 0$ positive real number for each, t.

2. F is non-singular for every t.

3. The estimation error, e is exponentially bounded in mean square error. This also bounds the probability to one. This is only true when the estimates satisfy the condition $\Vert \mathbf{e}\Vert \le ϵ$ and the covariance matrices of the noise terms are bounded via, ${\sigma }^{2}I\le \delta I$ and $QI\le \delta I$, where $\delta ,ϵ>0$.

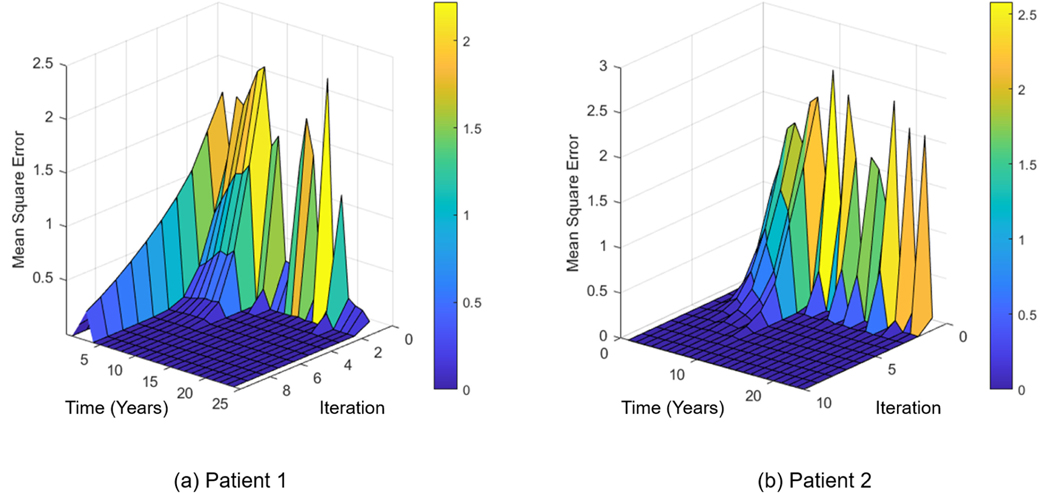
EKF model generally needs additional steps to correct the estimation of the future state. These additional steps are necessary to make sure estimated parameters do not diverge over time. We consider mean squared error (MSE) for stability analysis of EKF. Figure 7 shows the stability check for the proposed EKF model of D-FCTBN parameters. As shown in the Figure, the mean square error rapidly decreases with respect to the time and iterations, showing an acceptable level of stability for the analysis.

FIGURE 7.

The stability check of the D-FCTBN model for estimating the model parameters in the presence of new data. The Figure shows the MSE of predictions for two patients. The time axis shows the parameters estimated at each time step, and the iteration axis shows the steps to minimize the error at each time step.

2). PREDICTIVE ANALYSIS OF D-FCTBN

We use the area under the curve (AUC) of the receiver Operatic Characteristic (ROC) function to evaluate the performance of the proposed D-FCTBN model against CTBN and FCTBN using the CCHC study data. Considering the patients’ preexisting MCC and risk factors in the base year, which can be any combination of the 5 MCC (including no condition), 5 socio-demographic factors, and 4 lifestyle behaviors, each of the comparing methods is used to predict the future combinations of conditions 5 years from the baseline. Table 1 illustrates the AUC performance of the comparing methods for each of the five conditions (presented in the columns) for the 5th year from the baseline (presented in the row).

TABLE 1.

The AUC performance (of ROC) of the Dynamic FCTBN (D-FCTBN) model for predicting the future in comparison to FCTBN.

Year	Method	Diabetes	Obesity	Cognitive Impairment	Hyperlipidemia	High Blood Pressure
Year 5	CTBN	50.41%	77.20%	45.83%	52.63%	53.53%
	FCTBN	50.06%	85.25%	49.81%	52.63%	53.26%
	D-FCTBN	66.10%	73.03%	50.01%	48.29%	59.83%

As can be seen from the table, the proposed D-FCTBN generally provides competitive accuracy compared to CTBN and FCTBN for 3 out of the 5 conditions (Diabetes, Cognitive Impairment, and High Blood Pressure). However, it shows less predictive power in predicting Obesity and High Blood Pressure. This drop-in model performance can be explained from the perspective of the availability of patient level data. Since only two follow up observations have been available in the CCHC dataset for most patients, we believe for some of the conditions such as Obesity and Hyperlipidemia; the proposed D-FCTBN didn’t have a sufficient number of observations to capture the dynamics of patients MCC with respect to the changes in the modifiable lifestyle behavioral risk factors.

E. MONITORING EVENTS IN A D-FCTBN

To demonstrate the effectiveness of the proposed tensor-based control chart for event detection for a change in D-FCTBN model parameter discussed in Section III-B2, we setup two experiments, (1) a simulated experiment, where the patient’s data and the lifestyle behavioral data are synthetically generated to represent similar characteristics of the actual data, and (2) a real experiment, where we use the previously introduced data. In the model setup, we have three non-modifiable demographic conditions (age, gender, and years of education) and four modifiable lifestyle behavioural risk factors (healthy diet, exercise, smoking habits, and drinking habits). We conducted the experiments in two stages. We utilize the data generated (the estimated β_t coefficients) to build Phase I of the control chart. During this period, the lifestyle behavioral risk factors are controlled (for the simulated data). In Phase II, out-of-control samples are randomly generated for the simulated data (by altering the modifiable factors). For each sample, the monitoring features and the residuals are calculated. The error features are then plotted on the corresponding control charts. To demonstrate the generative capability of the proposed approach, for simulated experiments, we consider/generate monthly data/observations. However, for the real experiments, we consider yearly time intervals, given the availability of data. For the simulated experiments, two scenarios are considered. In the first scenario, we change only one of the lifestyle behavioral risk factors, and in the second scenario, we change two lifestyle behavioral risk factors simultaneously. Meanwhile, for real experiments, we consider the case where two lifestyle behavioral risk factors change.

1). SIMULATED CASE STUDY: CHANGING ONE OF THE LIFESTYLE BEHAVIORAL RISK FACTORS

We consider the following setup for estimation of the parameters of the control chart (Phase I). The patient is considered to have diabetes as the prior chronic condition. The falls in the age range of 31–35 and is male. The lifestyle behaviors during the in-control Phase are [Healthy Diet, Exercise, Smoke, Drink] = [Yes, Yes, No, No]. We assume no extreme behavioral change during the Phase I period (12 months) and utilize the proposed D-FCTBN (as explained in Section III-A) to generate the (updated) coefficients. Next, we use MPCA (as explained in Section III-B) to generate the control statistics (equation 19) for the MEWMA control chart. the control statistics are then used to generate the Phase I control chart. Phase I provides the control limits of the MEWMA chart to be used for Phase II. Any point outside these limits is considered as an out-of-control point in Phase II.

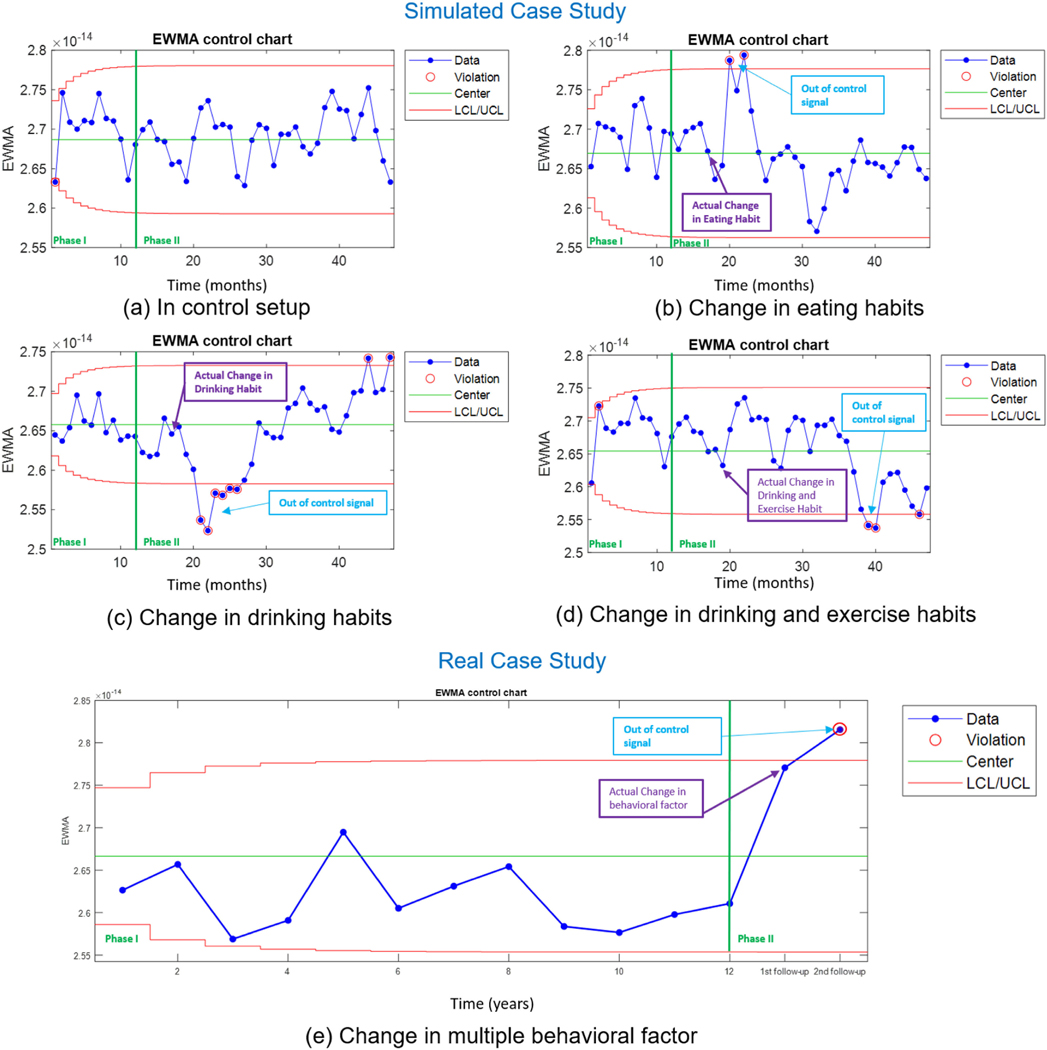
To evaluate the performance of the control chart (Phase II) (after the first 12 months), we modify one or more of the lifestyle behavioral risk factor/s of the patients at some (random) points in time. Phase II follows the same steps as Phase I for generating the control statistic. The control statistic is compared against the control limits (estimated from Phase I) to check for any out-of-control signal. Figure 8(a-c) shows the control chart’s performance for the case studies (simulated and real data), where the control chart parameters are set to λ =.15 and L = 1.5, which is determined based on extensive simulation analysis. Next, we provide a detailed explanation of each of the case studies.

FIGURE 8.

MEWMA Control chart of the reconstruction error obtained from the proposed model. (a) In-control control chart (simulation case) (b-c) shows case 1 where only one of the lifestyle behavioral risk factors are modified (simulation case), (d) shows case 2 where we randomly change more than one lifestyle behavioral risk factor (simulation case), and (e) shows (uncontrolled) changes in more than one lifestyle behavioral risk factor (real case)).

Case (a): In-control behavior:

Figure 8(a) shows the control chart for an in-control case where there is no lifestyle behavioral change in either Phase I or Phase II (in 48 months). As a result, the control chart doesn’t produce any out-of-control signal, which verifies its low type I error.

Case (b): Change in eating habits:

Figure 8(b) represents the case, where the patient changes his diet from healthy eating to unhealthy eating, i.e. [Healthy Diet, Exercise, Smoke, Drink] = [No, Yes, No, No]. We introduce this change in the eating habit in the 17th month. The out-of-control events can be noticed in the control chart after three observations (in month 20). The quick diagnosis of the change in the lifestyle behaviors by the control chart can be attributed to the significant effect of eating habits on the parameters of the D-FCTBN.

Case (c): Change in drinking habits:

For the next out-of-control scenario (Figure 8(c)), we assume the patient picks up drinking alcoholic beverages i.e. [Healthy Diet, Exercise, Smoke, Drink] = [Yes, Yes, No, Yes]. This change was made on 17th month. The control chart picks up this change after four observations (around the 21st month). Similar to eating habits, the quick detection of the change in the drinking habits by the control chart can be related to the significant effect of eating habits on the parameters of the D-FCTBN.

2). SIMULATED CASE STUDY: CHANGING MORE THAN ONE LIFESTYLE BEHAVIORAL RISK FACTORS

Case (d): Change in drinking and exercise habits:

Here, we consider the same lifestyle behavioral risk factors and set up as the Phase I analysis mentioned in Section IV-E1.

Meanwhile, for Phase II analysis, we modify two lifestyle behavioral risk factors (instead of one) simultaneously at on 19th month. The factors considered for change are [Healthy Diet, Exercise, Smoke, Drink] = [No, Yes, No, Yes]. As shown in Figure 8(d), the first out-of-control signal is produced by the control chart in month 39 (after 20 months). This prolonged time for diagnosis can be because of the complex interaction between the modifiable risk factors, which have changed in the opposite directions (stop the exercise and stop drinking simultaneously).

3). REAL CASE STUDY: CHANGE IN TWO LIFESTYLE BEHAVIORAL RISK FACTORS

For the real case study, we consider the patients’ data presented in Section IV-D. Due to the limited number of consecutive visits data available, we conducted this experiment in a hybrid setting. The considered patient has Hyperlipidemia and Obesity as a prior chronic condition/s. The lifestyle behaviors during the in-control Phase are [Healthy Diet, Exercise, Smoke, Drink] = [No, Yes, No, Not Provided]. We estimate the statistics for 12 years using the initial learned model and design the MEWMA control chart limits using the Phase I data. Next, we utilize the patients’ lifestyle behavioral changes in their follow up visits for phase II analysis.

Case (e): Real lifestyle behavioral change:

Figure 8(e) shows the control chart with the real patient data in Phase II. The figure shows the patient’s behavioral change in year 13 to [Healthy Diet, Exercise, Smoke, Drink] = [No, No, Yes, Not Provided]. Consequently, the chart produces an out-of-control signal after one observation (at year 14), which shows the sensitivity of the proposed control scheme when a significant lifestyle behavioral change or multiple changes in the same (negative/positive) direction occurs.

V. CONCLUSION

This study proposes a dynamic functional continuous time Bayesian network (D-FCTBN) for dynamic estimation and monitoring of the impact of patients’ modifiable lifestyle behaviors on the emergence of multiple chronic conditions. For dynamic estimation, the proposed method formulates the conditional dependencies of FCTBN as a nonlinear state space model using an extended Kalman filter (D-FCTBN). For monitoring, the proposed method first utilizes a low-rank tensor decomposition method based on multilinear principal component analysis (MPCA) to extract main features of the D-FCTBN parameters, which form a three-dimensional tensor, and then develops a multivariate exponentially weighted moving average (MEWMA) control chart to monitor the reconstruction error. We hypothesize that any out-of-control signal from the proposed MEWMA control chart, resulting from a large reconstruction error, accounts for a change in the patient’s modifiable risk factors that significantly change the risk of developing a new MCC. The prediction accuracy of the proposed D-FCTBN and the sensitivity of the proposed tensor-based MEWMA control chart has been validated using both real data from Cameron County Hispanic Cohort (CCHC) and simulations. The results demonstrate the effectiveness of the proposed D-FCTBN and tensor-based control chart for dynamic prediction and monitoring of the impact of patients’ modifiable lifestyle behaviors on the emergence of multiple chronic conditions. The proposed D-FCTBN method provides a dynamic (vs. static) platform for estimation of MCC progression and the emergence and can be personalized for individual patients given their non-modifiable demographic and modifiable lifestyle risk factors. The proposed tensor-based MEWMA control charts can also provide a proactive (vs. reactive) framework for monitoring the meaningful changes in patients’ lifestyles that increase or decrease the risk of developing new chronic conditions. Future research will aim to find early intervention strategies when the control charts detect an out-of-control situation, which increases the risk of new chronic condition development.

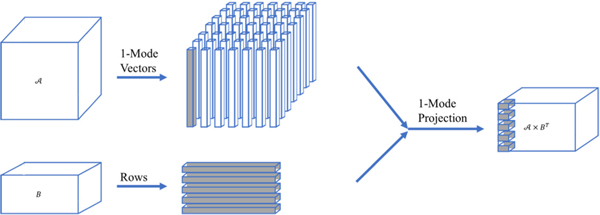
FIGURE 3.

Visual illustration of multilinear projection; projection in the 1-mode vector space.

FIGURE 6.

A visualization of the estimated parameters of the proposed D-FCTBN using EKF for 5 patients over 11 consecutive periods. The illustration shows the changes in learned parameters/coefficients with respect to base year (t = 0) as estimated using D-FCTBN Algorithm (The block of coefficients in Figure 5).

Biographies

SYED HASIB AKHTER FARUQUI received the M.Sc. degree in mechanical engineering from The University of Texas at San Antonio, in 2016, and the Ph.D. degree in mechanical engineering from The University of Texas at San Antonio. His research interests include probabilistic graphical models, scalable graph mining, and time series modeling. His research application is in the area of health care and manufacturing.

ADEL ALAEDDINI received the Ph.D. degree in industrial and systems engineering from Wayne State University. He is currently an Associate Professor of mechanical engineering with The University of Texas at San Antonio. He is also a Postdoctoral Researcher at the University of Michigan, Ann Arbor, MI, USA. He has contributed to over 40 peer-reviewed publications in journals, such as IISE Transactions, Production and Operations Management (POMS), and Information Sciences. His main research interests include statistical learning in systems modeling, control and optimization, and data analytics in health care, manufacturing, and energy. He is also serving as an Associate Editor for the Journal of Applied Statistics, Healthcare Management Science, and IISE Transactions on Healthcare Systems Engineering.

JING WANG is currently the Deananda Professor with the Florida State University College of Nursing. Previously, she was the Hugh Roy Cullen Professor and the Vice Dean for Research at the University of Texas Health Science Center at San Antonio School of Nursing. She is also the Founding Director of an inter-professional Center on Smart and Connected Health Technologies that features an aging-in-place lab, South Texas Connected Health Living Laboratory, and tele-health training and simulation. Her research uses mobile and connected technology to optimize behavioral lifestyle interventions and improve patient-centered outcomes in chronically ill and aging populations, especially among the under-served and minority populations. She is a fellow of the American Academy of Nursing, 2013 Robert Wood Johnson Foundation Nurse Faculty Scholar, 2015 TEDMED Scholar, and 2016 Josiah Macy Jr. Foundation Macy Faculty Scholar. She is also the Editor-in-Chief of JMIR Aging.

SUSAN P. FISHER-HOCH received the Ph.D. degree in epidemiology from London University with the Royal College of Pathology membership in virology. After a long career at the Centers for Disease Control and Prevention working with viral hemorrhagic fevers in poor communities in developing countries, she designed and directed the French Biosafety 4 Level principally for Ebola and Lassa fever studies which she received the Légion d’Honneur. She is a Trained Physician. She joined the Brownsville Campus of the School of Public Health to work in health disparity population health, in 2001. In 2004, she helped found the Cameron County Hispanic Cohort (n=5000), which she directs. This is a randomly selected community-based cohort of health disparity Mexican Americans. Using these data, she has collaborative programs in diabetes, cardiovascular disease, and cancers understudied minorities with a wide range of collaborators from major institutions across the country, funded by several NIH and CPRIT grants, and produced more than 60 publications.

JOSEPH B. MCCORMICK graduated in chemistry and mathematics from Florida Southern College. He received the M.S. degree from Harvard University, in 1970, under Dr. Weller (Nobel Laureate 1954), and the M.D. degree from Duke University, in 1971. He attended Free University, Brussels, in preparation for teaching sciences and mathematics in French in the Congo, where he was also introduced to medicine. He led several initiatives and investigations over the years (Meningitis outbreaks of 1974–6, CDC Lassa Fever Project in Sierra Leone, in 1977, Ebola epidemic 1976 and 1979, AIDS investigation in Africa in 1983, to name a few). He founded the UT Houston School of Public Health Campus in Brownsville, in 2001. The campus has published over 300 peer-reviewed articles characterizing the extraordinary level of health disparities in the region. He was instrumental in bringing in over $100 million in external funding. His current research involves chronic and infectious diseases in the LRGV in a cohort of 5000 people with over 30 research collaborators. He has been featured in several books for the lay reader, such as The Coming Plague and The Hot Zone. He and Sue Fisher-Hoch wrote a popular account (Level 4, Virus Hunters of the CDC) of their professional adventures, which is translated into seven languages.