BEHAVIORAL HAZARD IN HEALTH INSURANCE

Abstract

A fundamental implication of standard moral hazard models is overuse of low-value medical care because copays are lower than costs. In these models, the demand curve alone can be used to make welfare statements, a fact relied on by much empirical work. There is ample evidence, though, that people misuse care for a different reason: mistakes, or “behavioral hazard.” Much high-value care is underused even when patient costs are low, and some useless care is bought even when patients face the full cost. In the presence of behavioral hazard, welfare calculations using only the demand curve can be off by orders of magnitude or even be the wrong sign. We derive optimal copay formulas that incorporate both moral and behavioral hazard, providing a theoretical foundation for value-based insurance design and a way to interpret behavioral “nudges.” Once behavioral hazard is taken into account, health insurance can do more than just provide financial protection — it can also improve health care efficiency.

1. Introduction

Moral hazard is central to how we understand health insurance. Because the insured pay less for health care than it costs, they may overuse it (Arrow 1963; Pauly 1968; Zeckhauser 1970; Cutler and Zeckhauser 2000). In the standard moral hazard model, the demand curve alone is enough to quantify the inefficiency generated by insurance. We can draw welfare conclusions about changes in copays without measuring changes in health: if people optimize, health benefits equal copays at the margin. A large body of empirical work relies on this “sufficient statistic” property to make welfare calculations and policy recommendations, equating evidence of moral hazard with evidence of the price-sensitivity of demand for medical care (Feldstein 1973; Manning et al. 1987; Newhouse 1993; see Finkelstein, 2014 for a review). Yet, when it comes to health care choices, people may fail to optimize so perfectly. This paper develops a richer model of health insurance that allows people to make mistakes and implies that relying on demand data alone can lead to highly misleading welfare calculations.

Many patterns of health care use are hard to reconcile with a world in which moral hazard alone drives misutilization. Many patients underuse care with health benefits that substantially exceed costs (even accounting for possible side-effects or other non-monetary costs).¹ Diabetes medications, for example, increase life span, reduce the risk of limb loss or blindness, and improve quality of life, but estimates of adherence are usually under 70% (DiMatteo 2004). There is similarly low adherence for medications that help manage other chronic conditions and for treatments such as prenatal and post-transplant care (van Dulmen et al. 2007; Osterberg and Blaschke 2005). Nor does moral hazard explain all overutilization: patients sometimes demand care that does not benefit them – or may even be harmful (Schwartz et al. 2014). For example, patients seek out antibiotics with clear risks and unclear benefits for ear infections (Spiro et al. 2006). It is hard to explain this kind of overuse solely by private benefits exceeding private costs.

This evidence is consistent with a simple narrative. People misuse care not just because the price is below the social marginal cost, but also because they make mistakes. We call this kind of misutilization behavioral hazard. Many psychologies can contribute to behavioral hazard. People may overweight salient symptoms (Bordalo, Gennaioli, and Shleifer 2012, 2013) such as back pain or underweight non-salient ones such as high blood pressure or high blood sugar (Osterberg and Blaschke 2005). They may be present-biased (Laibson 1997; O’Donoghue and Rabin 1999) and overweight the immediate costs of care, such as copays and hassle-costs of setting up appointments or filling prescriptions (Newhouse 2006). They may simply forget to take their medications or refill their prescriptions. Or they may have false beliefs about the efficacy of care (Pauly and Blavin 2008). Section 2 builds on Mullainathan, Schwartzstein and Congdon (2012) by introducing a model of behavioral hazard that nests such biases, as well as others within a broad class.

Behavioral hazard means that welfare calculations can no longer be made from demand data alone. Consider the “marginal” insurees—those who respond to a copay change. In the standard model, these consumers are trading off health benefits against the copay. Because they are optimizing, their indifference means these benefits equal the copay.² But Section 3 shows that with behavioral hazard, this inference fails when insurees misvalue care. For example, we would not want to conclude falsely that diabetes medications are ineffective because a modest copay reduces adherence (e.g., based on Goldman et al.’s [2004] estimates), or that breast cancer patients place little value on conserving breast tissue because a modest copay induces them to switch from equally-effective breast-conserving lumpectomy to breast-removing mastectomy (e.g., based on Einav, Finkelstein, and Williams’s [2015] estimates).³ Behavioral hazard means that agents can be marginal in their choices even when health benefits far exceed the copay.

This is more than an abstract concern. First, we show that low-value and high-value care have surprisingly similar price elasticities. Second, we reexamine the results of a large-scale field experiment that eliminated some drug copays for recent heart attack victims and found large increases in drug use (Choudhry et al. 2011). Looking only at this demand response would suggest significant moral hazard and overuse of low-value drugs. But there were also substantial reductions in mortality and improvements in health. While traditional analysis would imply that eliminating drug copays led to a welfare cost, taking behavioral hazard into account implies a much larger welfare gain.

The fact that the demand curve is not a sufficient statistic also has implications for the optimal design of insurance. We show in Section 4 that the optimal copay formula now depends on both demand and health responses.⁴ This provides a formal foundation for “value-based insurance design” with lower cost-sharing for higher value care (Chernew, Rosen, and Fendrick 2007; Liebman and Zeckhauser 2008; and Chandra et al. 2010). Our model nests a more specific result of Pauly and Blavin (2008) that applies to the case of uninformed consumers. Perhaps surprisingly, we show that the health value of treatment should be taken into account even when behavioral hazard is unsystematic and averages to zero across the population, so long as it is variable. Once behavioral hazard is taken into account, health insurance does not just provide financial protection: it can also create incentives for more efficient treatment decisions.

Factoring in behavioral hazard can have a large effect. In Section 5 we compare the optimal copay when behavioral hazard is incorporated to that in the neo-classical model when it is not. The neo-classical model underestimates the optimal copay whenever behavioral hazard systematically drives people to overuse, and overestimates the optimal copay whenever behavioral hazard systematically drives people to underuse.⁵ In fact, we show that when behavioral hazard is extreme, the situations in which a neo-classical model generates particularly low copays are precisely those in which copays should be particularly high, and vice versa.

In addition to changing the calculus around optimal copays, our framework also has implications for the optimal use of nudges (such as defaults and reminders; Thaler and Sunstein 2009) to mitigate misuse or to calibrate the degree of behavioral hazard. Section 6 discusses this as well as other extensions of the basic analysis, including how we might estimate the degree of behavioral hazard when measuring health responses is difficult and what we might expect the market to deliver in equilibrium. While we focus on the patient side, clearly physicians also play an important role in determining the care that is ultimately received. We briefly discuss areas where combining patient and physician behavior into one framework could be fruitful (see also Frank [2004]). Section 7 concludes with a discussion of directions for future work.

2. A Model of Behavioral and Moral Hazard

2.1. Moral Hazard

We begin with a stylized model of health insurance. Consider an individual with wealth y. Insurance has price, or premium, P. When healthy, she has utility U(y − P) if she buys insurance. With probability q ∈ (0, 1), she can fall sick with a specific condition with varying degree of severity s that is her private information. For example, individuals may be afflicted with diabetes that varies in how much it debilitates. Assume s ~ F(s), where F has support on $\mathcal{S}=[\underset{\_}{s},\overline{s}]\subset {ℝ}^{+}$ and $\underset{\_}{s}<\overline{s}$. Assume further that F(s) has strictly positive density f(s) on $\mathcal{S}$. Severity is measured in monetary terms so that the sick agent receives utility U(y − P − s) absent treatment.

Treatment can lessen the impact of the disease. Treatment costs society c, and its benefit b(s; γ) depends on severity, where $\gamma \in ℝ$ is a parameter that allows for heterogeneity across people in treatment benefits conditional on disease severity, and is also private information.⁶ The more severe the disease, the greater the benefits: b_s > 0. We assume b(0; γ) = 0 for all γ (the unaffected get no benefit) and b_s ≤ 1 (the treatment cannot make people better off than not having the disease). The benefits are put in monetary terms. It is efficient for some but not all of the sick to get treated: $b(\underset{\_}{s};\gamma )<c<b(\overline{s};\gamma )$ for all γ. We assume that the insured individual pays price or “copay” p for treatment. While the copay implicitly depends on the disease and treatment, it is independent of s and γ; we assume that both disease severity and treatment benefits cannot be contracted over because the insurer cannot perfectly measure them. The interpretation is that the copay is conditional on all information known to the insurer, but the individual may have some residual private information.⁷ In this way, we nest the traditional moral hazard model. An insured individual who receives treatment for his disease gets utility U(y − P − s + b(s; γ) − p).

We evaluate insurance contracts from the perspective of a benevolent social planner ranking contracts based on social welfare.⁸ Welfare as a function of the copay and the premium equals expected utility:

$$W(p,P)=(1-q)U(y-P)+q\mathbb{E}[U(y-P-s+m(p)(b-p))\mid \text{ sick }],$$ (1)

where m(p) ∈ {0, 1} represents an individual’s demand for care at a given price and equals 1 if and only if the person demands treatment. The first term is the utility if individuals do not get sick with a specific condition: they simply pay the premium. The second term is the utility if they do get sick: the expected utility (depending on disease severity and other stochastic parameters, described in more detail below) that includes the loss due to being sick (−s) as well as the benefits of care net of costs to individuals (b − p) for the times they choose to use care (m(p) = 1). We assume that insurance must be self-funding: P = P(p) = M(p)(c − p), where $M(p)=\mathbb{E}[m(p)]$ equals the per-capita aggregate demand at a given copay. As a result, we can rewrite welfare solely as a function of the copay: with some abuse of notation, W(p) ≡ W(p, P(p)).

In this simple setup, the choice to receive treatment when insured is easy: the rational person gets treated whenever benefits exceed price, or b > p. This decision is the source of moral hazard. While the insurance value in insurance comes from setting price below true cost, or p < c, this subsidized price means that while individuals should efficiently get treated whenever b > c (benefits exceed social costs), they get treated whenever b > p (benefits exceed private costs), generating inefficient utilization when c > b > p. Figure I provides an illustration, where individuals are arrayed on the line according to treatment benefits. Those to the right of the cost c should receive treatment and do so. Those to the left of the price p should not receive treatment and do not. The middle region represents the problem: those individuals should not receive treatment but they do. The price subsidy inherent to insurance is the source of misutilization: Raising the price individuals face would diminish overutilization, but come at the cost of diminished insurance value.⁹

Figure I:

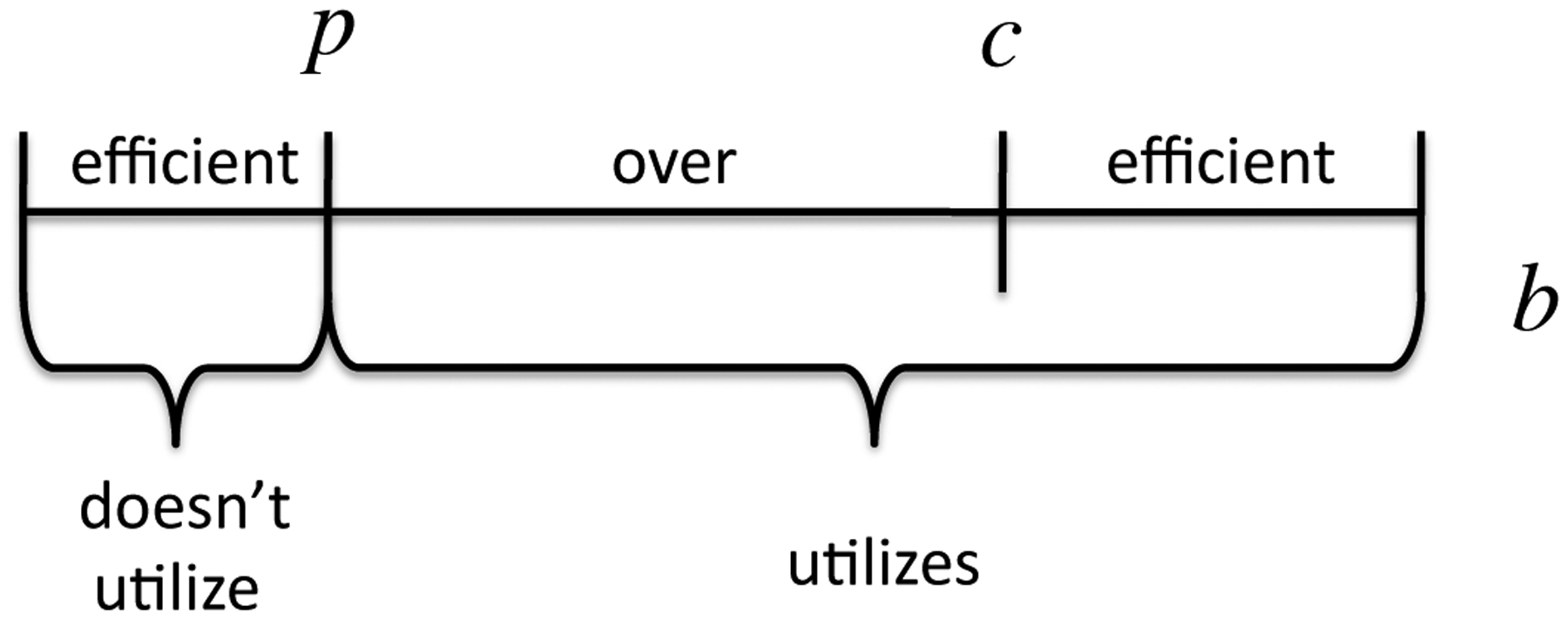
Model with Only Moral Hazard

2.2. Behavioral Hazard

There is, however, ample evidence of misutilization that is difficult to interpret as a rational person’s response to subsidized prices. We incorporate behavioral hazard through a simple modification of the original model. Instead of deciding by comparing true benefits to copays, evaluating whether b(s; γ) > p, people choose according to whether b(s; γ) + ε(s; θ) > p, where ε is positive in the case of positive behavioral hazard (for example, seeking an ineffective treatment for back pain) and negative in the case of negative behavioral hazard (for example, not adhering to effective diabetes treatment). The parameter $\theta \in ℝ$ allows for heterogeneity across people in the degree of behavioral hazard and is not observable to the insurer. We assume that b(s; γ) + ε(s; θ) is differentiable and strictly increasing in s for all (γ, θ). The parameters (γ, θ) are distributed independently from s, according to joint distribution G(γ, θ). We let Q(s, γ, θ) = F(s)G(γ, θ) denote the joint distribution of all the possibly stochastic parameters. All expectations are taken with respect to this distribution unless otherwise noted. When U is non-linear, it will be useful to consider a “normalized” version of the behavioral error,

$${\epsilon }^{\prime }(s;\theta )=\frac{U(y-P-s)-U(y-P-s-\epsilon (s;\theta ))}{\mathbb{E}\left[U^{\prime }(C)\right]},$$

which essentially puts ε in utility units. (Note that ε = ε′ for linear U, so we have the approximation ε ≈ ε′ if we take U to be approximately linear).

This formulation builds on Mullainathan, Schwartzstein and Congdon (2012) and implicitly captures a divide between preference as revealed by choice and utility as it is experienced, or between “decision utility” and “experienced utility” (Kahneman et al. 1997). In our framework, b − p affects the experienced utility of taking the action. Individuals instead choose as if b + ε − p affects this utility.

This framework nests behavioral models where people misbehave because of mistakes. What it is not designed to capture are models of non-standard preferences. For example, anticipation and anxiety may alter how individuals experience benefits (Koszegi 2003): benefits will vary depending on whether taking the action (such as getting an HIV test) leads to anxiety in anticipating the outcome. In these kinds of situations, the behavioral factor may not be a bias affecting ε, but rather a force that affects the mapping between outcomes (such as getting a diagnostic test) and benefits b.

Three examples of behavioral biases that our formulation nests are presented here and summarized in Table I: present-bias, symptom salience, and false beliefs.¹⁰

Table I:

Examples of Biases Underlying Behavioral Hazard

	Present-Bias	Symptom Salience	False Beliefs
Treatment Rule	−k(s; γ) + βθ · υ(s) > p	b(αθυ + μθn + o; γ) > p	$\widehat{b}(s;\gamma ,\theta )<p$
Expression for ε	−(1 – βθ)υ(s)	b(αθυ + μθn + o; γ) – b(s; γ)	$\widehat{b}(s;\gamma ,\theta )-b(s;\gamma )$

Present-bias can be important because the benefits of medical care are often in the distant future while the costs appear now (Newhouse 2006). Take the canonical (β, δ) model of presentbias (Laibson 1996; O’Donoghue and Rabin 1999), where, for simplicity, δ = 1. Suppose each treatment is associated with an immediate cost but a delayed benefit. Specifically, b(s; γ) = −k(s; γ)+v(s), where k(s; γ) represents immediate costs, for example side effects, which can vary across the population even conditional on disease severity, and v(s) represents delayed benefits, which for simplicity are assumed to depend only on disease severity. The notation and language suggest that v > 0 and k > 0, but we also allow for v < 0 and k < 0, with benefits of treatment in the present and costs delayed. For example, taking a medication may lead to immediate benefits and more delayed side effects. While standard agents (for simplicity) are assumed not to discount future benefits, present-biased agents discount these benefits by factor β ∈ (0, 1). Instead of getting treated whenever b(s; γ) = −k(s; γ) + v(s) > p, present-biased agents get treated whenever −k(s; γ) + β_θ · v(s) > p ⇔ b(s; γ) − (1 − β_θ)v(s) > p, where here θ allows for heterogeneity in the degree to which people are present-biased. Defining ε^PB(s; θ) ≡ −(1 − β_θ)v(s), the present-biased agent has a propensity to underuse treatment relative to what is privately optimal whenever ε^PB(s; θ) < 0 (corresponding to delayed treatment benefits, v > 0) and overuse whenever ε^PB(s; θ) > 0 (corresponding to delayed costs, v < 0).

Symptom salience can be important. Individuals appear to overweight salient symptoms and underweight less salient ones (Osterberg and Blaschke 2005), driving overuse or underuse. For example, diabetics’ symptoms of elevated glucose levels are often not salient (Rubin 2005), and it is easy to undervalue the health benefits of taking a pill whose effects cumulate slowly over time. Patients at the symptomatic stages of HIV/AIDS are more likely to be adherent to their treatment regimens than patients at the asymptomatic stage (Gao et al. 2000). Most tuberculosis treatment regimens are at least six months long, but effective therapy leads to improved symptoms after the first four weeks and there is a concurrent drop-off in adherence. Pain, on the other hand, is clearly highly salient, and patients may overweight the current pain and seek expensive treatments with potential adverse effects in the future. Stories in the popular press highlight the role of symptom salience: a recent report noted the death of an uninsured patient with a tooth infection who was prescribed an antibiotic and a painkiller and who spent his limited resources to fill the painkiller prescription rather than the potentially life-saving antibiotic (Gann, ABC News 2011).

Economists in recent years have introduced rich models to study the impact of salience on behavior (e.g., Bordalo, Gennaioli and Shleifer 2012, 2013; Koszegi and Szeidl 2013). We use a modified version of DellaVigna’s (2009) empirical model of limited attention. Suppose the severity of symptoms is the sum of three components: the severity of highly visible or painful symptoms, v, the severity of opaque or non-painful symptoms, n, and other symptoms, o, or

$$s=v+n+o.$$ (2)

The inattentive agent overweights the painful symptoms and underweights non-painful symptoms, so he acts not on true disease severity s, but on “decision severity”

$$\widehat{s}={\alpha }_{\theta }v+{\mu }_{\theta }n+o,$$ (3)

where α_θ ≥ 1 and μ_θ ≤ 1. The magnitudes |1 − α_θ| and |1 − μ_θ| can be thought of as parameterizing the degree to which the agent misbehaves due to symptom salience, where he acts according to the standard model when α_θ = μ_θ = 1. The person gets treated if

$$b\left({\alpha }_{\theta }v+{\mu }_{\theta }n+o;\gamma \right)>p\iff b(s;\gamma )+\left[b\left({\alpha }_{\theta }v+{\mu }_{\theta }n+o;\gamma \right)-b(v+n+o;\gamma )\right]>p.$$ (4)

Defining ε^SS(s; θ) = b(α_θv + μ_θn + o; γ) − b(v + n + o; γ), where we assume the right-hand-side is constant in γ, the person has a propensity to underuse treatment relative to what is privately optimal whenever ε^SS(s; θ) < 0, where non-painful symptoms are sufficiently prominent (i.e., n > v(α_θ − 1)/(1 − μ_θ) for μ_θ ≠ 1), and has a propensity to overuse treatment relative to what is privately optimal whenever ε^SS(s; θ) > 0, where painful symptoms are sufficiently prominent (i.e., v > n(1 − μ_θ)/(α_θ − 1) for α_θ ≠ 1).

False beliefs can also play a role (e.g., Pauly and Blavin 2008).¹¹ Tuberculosis patients may stop taking their antibiotics halfway through their drug regimen not just because salient symptoms have abated, but also because they believe the disease has disappeared. People may falsely attribute treatment benefits as well, such as when they buy an herbal medicine with no known efficacy.¹² Instead of getting treated when b(s; γ) > p, agents with false beliefs get treated when $\widehat{b}(s;\gamma ,\theta )>p\iff b(s;\gamma )+[\widehat{b}(s;\gamma ,\theta )-b(s;\gamma )]>p$, where $\widehat{b}$ is the decision benefit to getting treated. Defining ${\epsilon }^{\text{FB}}(s;\theta )=\widehat{b}(s;\gamma ,\theta )-b(s;\gamma )$, which for simplicity we assume is constant in γ, the person with false beliefs has a propensity to underuse treatment whenever ε^FB(s; θ) < 0, where they undervalue treatment $(\widehat{b}(s;\gamma ,\theta )<b(s;\gamma ))$, and has a propensity to overuse treatment whenever ε^FB(s; θ) > 0, where they overvalue treatment $(\widehat{b}(s;\gamma ,\theta )>b(s;\gamma ))$.

2.3. Misutilization with Behavioral Hazard

No matter the psychological micro-foundation, behavioral hazard changes how we think about the demand for treatment. We illustrate this in Figure II. We have now added a second axis to form a square instead of a line, where the vertical axis represents b + ε, which can vary by individual. The horizontal line separates the region where b + ε > p, while the vertical line separates the region where b > c. We see the ranges of misutilization are no longer clear. The people in the bottom left corner (where b + ε < p and b < c) are efficient non-users. Those in the top right corner (where b + ε > p and b > c) are efficient users. But there are now three other regions.

Figure II:

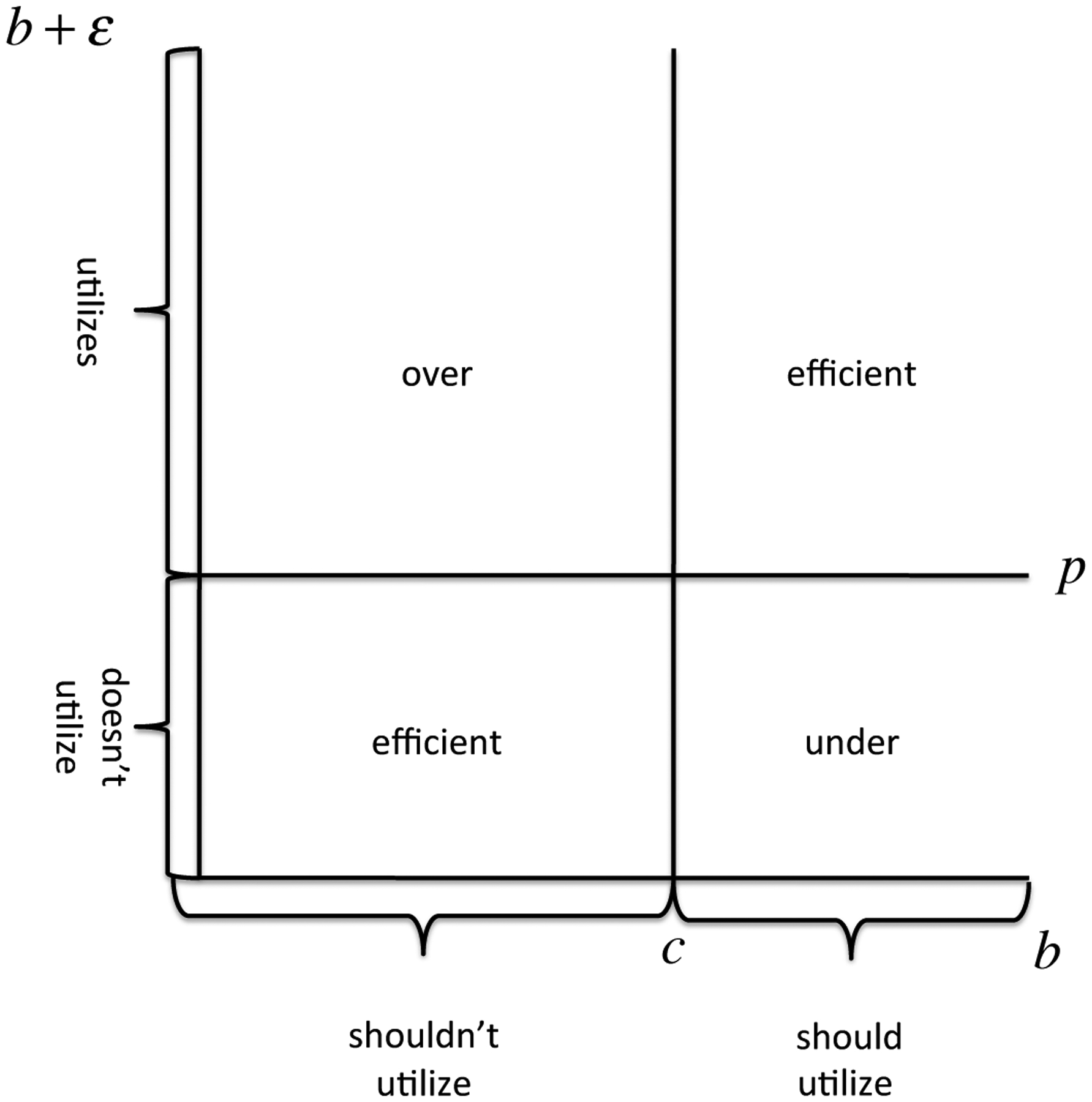
Model with Behavioral Hazard

The bottom right area is a region of underutilization. People fail to consume care in this region because b + ε < p, but the actual benefits exceed social cost. When there is behavioral hazard, underutilization is a concern, not just overutilization due to moral hazard. Examples such as the lack of adherence to drugs treating chronic conditions, like diabetes, hypertension, and high cholestorol, illustrate such underutilization, and Online Appendix Table 1 provides further examples and references.¹³

The top left area illustrates overutilization. In this area, benefits of care are below cost so b < c, and the efficient outcome is for the individual not to get treated. Yet because b + ε > p the behavioral agent receives care. This area can be broken down further, according to whether b + ε > c. When this inequality holds, decision benefits are above cost even though true benefits are below cost. In this case, overutilization will not be solved by setting price at true cost. Examples such as people demanding ineffective (or possibly harmful) antibiotics for sinus or ear infections, the overtreatment of prostate cancer, and the extremely high demand for MRIs for back pain may illustrate such overutilization. Finally, the area of overutilization when b + ε ≤ c illustrates traditional overutilization due to moral hazard.

Misutilization is not solely a consequence of health insurance when there is behavioral hazard. Underuse, not just overuse, is a concern, and overuse may not be eliminated by setting prices at true cost. We next turn to the implications of these findings for the interpretation of observed demand elasticities.

3. Moral Hazard Cannot be Inferred From the Demand Curve Alone

Behavioral hazard dramatically alters standard intuitions for how we think about the welfare impact of copay changes. Reducing a copay that is less than cost has two effects. First, it raises utility for people who are sick enough that they demand treatment, generating insurance value. Second, it may lead people to choose to consume more care. The welfare impact of this increase depends on the magnitude and direction of behavioral hazard.

For a simple illustration, assume people are risk-neutral and consider the effect of reducing the copay from cost (c) to zero in Panel (a) of Figure III, which compares the welfare impact of the change in utilization when there is only moral hazard to when there is also underuse from negative behavioral hazard. The dark grey area represents the standard deadweight loss triangle — the moral hazard cost of insurance. This area is positive because people who get treated only when the price is below marginal cost must have a willingness to pay below this cost. It is also greater the flatter the demand curve: more elastic demand means a greater moral hazard cost of insurance.

Figure III:

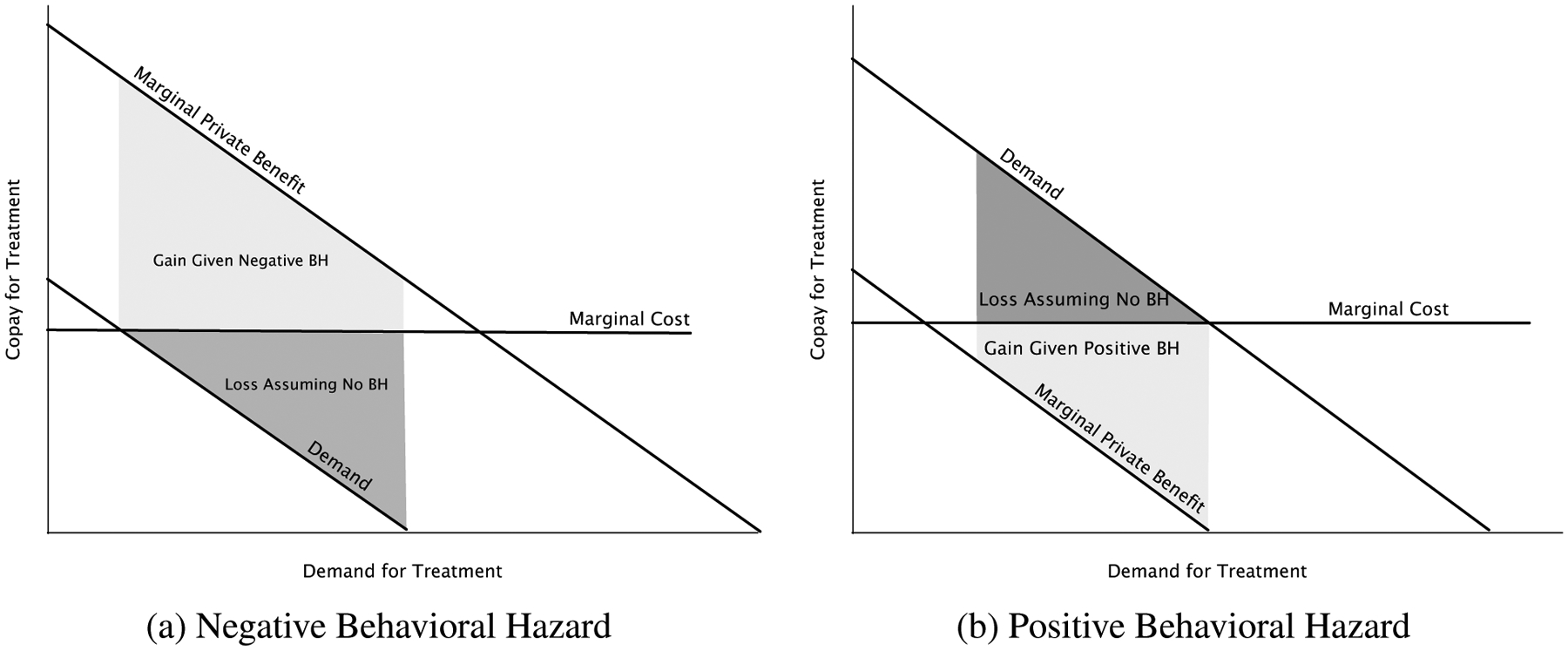
Welfare Impact of a Copay Change: Behavioral Hazard vs. Moral Hazard Alone

Notes: Panel (a) considers the welfare impact of reducing the copay to zero when there is only moral hazard to when there is also negative behavioral hazard. Panel (b) considers the welfare impact of increasing the copay above cost when there is only moral hazard to when there is also positive behavioral hazard.

An often implicit assumption underlying the standard approach is that we can equate demand or willingness to pay with the true marginal benefit of treatment. Behavioral hazard drives a wedge between these objects. For example, Panel (a) illustrates the case where all people have a propensity to underuse because of negative behavioral hazard and share the same ε < 0. In this case, the marginal benefit curve lies above the demand curve and the vertical difference equals |ε|. When the magnitude of negative behavioral hazard (|ε|) is sufficiently large, the marginal benefit of treatment outweighs the marginal cost even when the copay equals zero. In this case, reducing the copay to zero no longer generates a welfare cost of increased utilization, but rather a welfare benefit equal to the light grey area in the figure. This area is greater the flatter is demand: more elastic demand now means a greater benefit of insurance.

Panel (b) illustrates the case where all people share the same ε > 0 and shows how overuse due to behavioral hazard has different implications than overuse due to moral hazard. In particular, consider raising the copay above cost. While absent behavioral hazard this would lead to the standard deadweight loss triangle equal to the dark grey area, with positive behavioral hazard it leads to a welfare gain equal to the light grey area. When people overuse due to behavioral hazard, failing to cover or even penalizing the use of treatments can be beneficial. We next formalize the intuitions from the graphical analysis.

3.1. Analysis

With behavioral hazard, the marginal person does not necessarily value treatment at the copay

Differentiate W with respect to p subject to the break-even constraint, and convert into a money metric by normalizing the increase in welfare by the welfare gain from increasing income by 1. The following proposition details the resulting formula:

Proposition 1. The welfare impact of a marginal copay change is given by

$$\underset{\mathit{\text{Total Welfare Impact }}}{\underbrace{{\tilde{W}}^{\prime }(p)\equiv \frac{\partial W}{\partial p}/\frac{\partial W}{\partial y}}}=\underset{\mathit{\text{Impact from Change in Behavior }}}{\underbrace{-M^{\prime }(p)\cdot \left(c-p+{\epsilon }^{avg}(p)\right)}}-\underset{\mathit{\text{Impact from Change in Insurance Value }}}{\underbrace{I(p)\cdot M(p)}},$$ (5)

where

$$I(p)=\frac{\mathbb{E}\left[U^{\prime }(C)\mid m=1\right]-\mathbb{E}\left[U^{\prime }(C)\right]}{\mathbb{E}\left[U^{\prime }(C)\right]}$$

equals the insurance value to consumers (C = y − P − s + m · (b − p)), defined to equal 0 when M(p) = 0, and

$${\epsilon }^{avg}(p)=\mathbb{E}\left[{\epsilon }^{\prime }\mid b+\epsilon =p\right]$$

equals the average size of marginal behavioral hazard at copay p.

Proof. All proofs are in Online Appendix B. ■

To interpret Proposition 1, first consider the standard model with just moral hazard, where ε^avg(p) = 0 for all p. In this case, the first term of (5), −M′(p)(c − p), represents the welfare gain from reducing moral hazard: it can be thought of as the number of people who are at the margin multiplied by the difference between the social cost and social value of their treatment—the marginal inefficiency—(c − p) > 0. Note that the sensitivity of demand, M′(p), is a sufficient statistic for measuring this gain, since the marginal social value is a known function of the copay when people are rational. The second term represents the reduction in insurance value for all treated individuals, where our assumptions guarantee that I(p) > 0 for all p > 0 when individuals are rational.

Behavioral hazard alters the first term because it changes who is at the margin: with behavioral hazard, the welfare impact of lower utilization equals −M′(p)(c − p + ε^avg(p)), which can be thought of as the number of people who are at the margin multiplied by the difference between the social cost and social value of their treatment, (c − (p − ε^avg(p))). As we saw in the graphical example above, the sign of this term becomes ambiguous. When behavioral hazard is on average positive at the margin, ε^avg(p) ≥ 0, this term is greater than with moral hazard alone: increasing the copay from an amount less than cost has an even greater benefit of decreasing overutilization. On the other hand, when behavioral hazard is on average negative at the margin, ε^avg(p) < 0, this term may be negative: increasing the copay can have the cost of increasing underutilization.^{14 15}

With behavioral hazard, demand responses do not measure the extent of moral hazard

Proposition 1 also formalizes the standard intuition that when there is merely moral hazard, the overall demand response is a powerful tool for measuring the welfare impact of the changes in utilization driven by copay changes. Indeed, −M′(p) · (c − p) is necessarily increasing in |M′(p)| when p < c. But it shows that with behavioral hazard, this composite response is harder to interpret: looking at demand responses alone may provide a misleading impression, since −M′(p)·(c − p+ε^avg(p)) is not necessarily increasing in |M′(p)|. A high response might indicate a great deal of moral hazard (and hence a cost of providing insurance), or could indicate a great deal of negative behavioral hazard or price-responsive underutilization (and hence an additional benefit to insurance).

In practice, researchers effectively ignore behavioral hazard by focusing on aggregate demand responses in calculating the welfare impact of copay changes. For example, researchers calculated a welfare loss of $291 per person from moral hazard in 1984 dollars based on evidence from the RAND Health Insurance Experiment suggesting a demand elasticity of roughly −.2 (Manning et al. 1987; Feldman and Dowd 1991). While recent economic research has questioned whether such a single elasticity can accurately summarize how people respond to changes in non-linear health insurance contracts (Aron-Dine, Einav, and Finkelstein 2013), there has been less emphasis on reexamining the basic assumption that the price sensitivity of demand meaningfully captures the degree of moral hazard. In a recent review article of developments in the study of moral hazard in health insurance since Arrow’s (1963) original article, Finkelstein (2014) equates evidence of moral hazard with evidence of the price sensitivity of demand for medical care. Our analysis suggests this can be misleading, as does a closer look at available evidence.

Table II summarizes evidence indicating that demand for “effective care” is often as elastic as demand for “ineffective care”. Analysis of the RAND health insurance experiment found that cost-sharing induced the same 40% reduction in demand for beta blockers as it did for cold remedies—with reductions for drugs deemed “essential” on average quite similar to those for drugs deemed “less essential” (Lohr et al. 1986).¹⁶ Goldman et al. (2006) estimate that a $10 increase in copayments drives similar reductions in use of cholestorol-lowering medications among those with high risk (and thus presumably those with high health benefits) as those with much lower risk. A quasi-experimental study of the effects of small increases in copayments (rising from around $1 to around $8) among retirees in California by Chandra, Gruber, and McKnight (2010) suggests that HMO enrollees’ elasticity for “lifestyle drugs” such as cold remedies and acne medication is virtually the same as for acute care drugs such as anti-convulsants and critical disease management drugs such as beta-blockers and statins — all clustered around −0.15 (unpublished details provided by authors). To take a particularly striking example, which we discuss in greater detail below, relatively small reductions in copayments even after an event as salient as a heart attack still produce improvements in adherence (Choudhry et al. 2011). The evidence strongly suggests that the degree of moral hazard cannot be inferred from aggregate demand responses.¹⁷

Table II:

Demand Responses Often not Related to Value of Care

Study	Price Change	Change in Use
		Higher Value	Lower Value
Lohr et al. (1986)	Cost-sharing vs. none in RAND	21% ↓ in use of highly effective care; 40% ↓ in beta blockers, 44% ↓ in insulin	26% ↓ in less effective care; 6% ↓ in hayfever treatment, 40% ↓ in cold remedies, 31% ↓ in antacids
Goldman et al. (2006)	$10 ↑ in copay (from $10 to $20)	Compliance with cholestorol meds among high risk ↓ from 62% to 53%	Compliance with cholestorol meds among low risk ↓ from 52% to 46%; medium ↓ from 59% to 49%
Selby et al. (1996)	Introduction of $25–$35 ER copay	9.6% ↓ in visits for emergency conditions	21% ↓ in visits for non-emergency conditions
Johnson et al. (1997)	↑ from 50% coinsurance with $25 max to 70% coinsurance with $30 max	40% ↓ in use of antiasthmatics; 61% ↓ in thyroid hormones	40% ↓ in non-opiate analgesics; 22% ↓ in topical anti-inflammatories
Tamblyn et al. (2001)	Introduction of 25% coinsurance, $100 deductible, $200–$750 max for Rx (elderly population)	9.1% ↓ in essential drugs	15.1% ↓ in non-essential drugs
Chandra et al. (2010)	$7 ↑ in drug copay (from ~$1 to ~$8)	Elasticity of around .15 for acute care and chronic care Rx	Elasticity of around .15 for “lifestyle” Rx

Sources: Authors’ summary of literature (see bibliography)

So how can we systematically distinguish between behavioral hazard and moral hazard? One method is to measure health responses.

With behavioral hazard, measuring health responses helps characterize who is at the margin

Let $H(p)=\mathbb{E}[m(p)\cdot b-s]$ equal the aggregate level of health given copay p, which represents the expected value of disease severity post treatment decisions at copay level p in income-equivalent units. We have the following result:

Proposition 2. Consider a copay p at which demand is price-sensitive, so M′(p) < 0, and let U be linear. The welfare impact of a marginal copay change is

$$\tilde{W}\prime (p)=-M\prime (p)\cdot \left(c-\frac{H\prime (p)}{M\prime (p)}\right).$$

Further, H′(p)/M′(p) = p if and only if ε^avg(p) = 0 and, more generally, ε^avg(p) = p − H′(p)/M′(p).

The first part of this proposition indicates that, all else equal, the welfare impact of a copay increase inversely depends on the marginal health value of care.¹⁸ This is true not only when there is behavioral hazard, but also in the rational model. Intuitively, a copay increase is less desirable when it discourages high-value care rather than low-value care. The second part clarifies why standard formulas for the welfare impact of copay changes are not expressed in terms of health responses: Absent behavioral hazard, we can equate the health response with the copay since being marginal reveals indifference. But it goes on to show that we cannot do this when there is the possibility of marginal behavioral hazard: Rather, we can infer the degree of marginal behavioral hazard from the deviation between the copay and the marginal health value of treatment.

In some of the cases described above, there are indications that the copay changes are associated with large health implications, providing further suggestive evidence for behavioral hazard in such cases. As summarized in Table III, the copay increase studied by Chandra et al. (2010) was associated with an increase in subsequent hospitalizations and Hsu et al. (2006) similarly find that the imposition of a cap on Medicare drug benefits lead to an greater nonelective hospital use. Choudhry et al. (2011) find that providing post-heart attack medications for free is associated with a reduced rate of subsequent major vascular events to an extent that, as we will discuss below, is inconsistent with plausible parameters under the standard model.

Table III:

Responses to Price Changes Can Have Large Health Implications

Study	Price Change	Use Change	Health Value [illustrative fact]
Chandra et al. (2010)	$7 ↑ in drug copay (from ~$1 to ~$8)	Elasticities: .15 for essential drugs; .23 for asthma meds, .12 for cholesterol meds, .22 for depression meds	Offsetting 6% ↑ in hospitalization
Hsu et al. (2006)	Imposition of $1000 annual Rx cap	↑ in non-adherence to antihypertensives, statins, diabetes drugs by ~30%	13% ↑ in nonelective hospital use; 3% ↑ in high blood pressure (among hypertensives); 9% ↑ in high cholesterol (among hyperlipidemics); 16% ↓ in glycemic control (among diabetics)
Lohr et al. (1986)	Cost-sharing vs. none in RAND	↓ in use of insulin by 44%, beta blockers by 40%, antidepressants by 36%	[Consistent filling of diabetic med prescriptions ↓ hospitalization risk from 20–30% down to 13% (Sokol et al. 2005)]
Selby et al. (1996)	Introduction of $25–$35 ER copay	9.6% ↓ in visits for emergency conditions	Emergency conditions included coronary arrest, heart attack, appendicitis, respiratory failure, etc.
Choudhry et al. (2011)	Elimination of Rx copays for post-heart attack patients	4–6 percentage point ↑ in medication adherence	Rates of total major vascular events ↓ by 1.8 ppt, heart attacks by 1.1 ppt

Sources: Authors’ summary of literature (see bibliography); additional unpublished detail provided by Chandra et al. Notes: Health value comes from same study when available. [“Illustrative facts” come from other studies.]

A challenge to using data on health responses to calibrate the degree of behavioral hazard is that the health response may be difficult to observe or to map to hedonic benefits. It may be possible to estimate how much a pill reduces mortality risk and translate this into (money-metric) utility; it may be more difficult to estimate the unpleasantness of side-effects or the inconvenience of treatment. In some instances, however, we may have enough information to confidently bound the unobservable component, in which case we can still say something about the sign and possibly the magnitude of behavioral hazard.¹⁹ This is more likely in the case of highly effective treatments with few side effects than in treatments with non-pecuniary costs that may be experienced quite differently across people (e.g., colonoscopies). Section 6 shows that good prior knowledge of the psychology underlying behavioral hazard can help estimate the marginal degree of behavioral hazard in the latter situations.

3.2. An Illustration

We illustrate the potential importance of taking behavioral hazard into account by further drawing on Choudhry et al.’s (2011) work on the effects of eliminating copays for recent heart attack victims.²⁰ They randomly assigned patients discharged after heart attacks to a control group with usual coverage (with copayments in the $12-$20 range) or a treatment group with no copayments for statins, beta blockers, and ACE inhibitors (drugs of known efficacy), and tracked adherence rates and clinical outcomes over the next year. Faced with lower prices, consumers used more drugs: the full coverage group was significantly more adherent to their medications, using on average $106 more worth of cardiovascular-specific prescription drugs.

Under the moral hazard model, this fact alone tells us the health consequences of eliminating copays. Rational patients forgo only care with marginal value less than their out-of-pocket price. The average patient share under usual coverage in the Choudry data is about 25%, implying that the extra care consumed when copays are eliminated has a monetized health value of at most $.25 on the dollar. Given the $106 increase in spending, the moral hazard model then predicts a health impact of at most $106 · .25 = $26.50 per patient. This in turn implies a moral hazard welfare loss from eliminating copayments of at least $106(1 − .25) = $79.50 per person. In other words, the $106 increase in spending is comprised of $26.50 of health value plus $79.50 of excess utilization. This is the kind of exercise routinely performed with demand data.²¹

But Choudhry et al. (2011) collected data on health impacts, which we can use to gauge the performance of the moral hazard model by comparing the implied health benefits with the observed ones. The increase in prescription drug use was associated with significantly improved clinical outcomes: patients in the full coverage group had lower rates of vascular events (1.8 percentage points), myocardial infarction (1.1 percentage points), and death from cardiovascular causes (.3 percentage points). We apply the commonly used estimate of a $1 million value of a statistical life to the reduction in the mortality to get a measure of the dollar value of health improvements.²² This implies that the elimination of copays leading to a .3 percentage point reduction in mortality generates a value of $3,000. This $3,000 improvement substantially exceeds the standard model’s prediction of $26.50, suggesting large negative behavioral hazard. Applying the traditional moral hazard calculus in this situation would imply that people place an unrealistically low valuation on their life and health.²³

For welfare calculations, the theoretical analysis above highlights the need to use an estimate of the marginal private health benefit in the presence of behavioral hazard. As a rough back-of-the-envelope calculation, the $3,000 improvement in mortality minus the $106 increase in spending generates a surplus of $2,894 per person (a gross return of $28 per dollar spent). The presence of behavioral hazard thus reverses how we interpret the demand response to eliminating copayments: moral hazard implies a welfare loss, while behavioral hazard implies a gain that is over 30 times larger.²⁴

4. Implications for Optimal Copays

We have seen that behavioral hazard can influence whether changing copays from existing levels is good policy. This section describes some features of the optimal insurance plan when behavioral hazard is taken into account.

Consider again Equation (5), which gives us the welfare impact of a marginal copay increase. Setting this equal to zero yields a candidate for the optimal copay. To limit the number of cases, we focus attention on the standard situation where some but not all sick people are treated at the optimum: an optimal copay p^B satisfies M′(p^B) < 0 and M(p^B) > 0. This is true under our assumptions, for example, when people are not too risk averse, i.e., when −U″/U′ is sufficiently small over the relevant range of C. For presentational simplicity, we also focus on the situation where the optimal copay is unique. Defining p^min = inf {p : M(p) < q} to equal the lowest copay where not every sick person demands treatment and p^max = sup{p : M(p) > 0} to equal the highest copay where some sick person demands treatment, we assume the following.

Assumption 1. The optimal copay is unique and satisfies p^B ∈ (p^min, p^max).

Proposition 3. Assuming p^B ≠ 0, the optimal copay satisfies

$$\frac{c-p^B}{p^B}=\frac{I}{\eta }-\frac{{\epsilon }^{avg}}{p^B},$$ (6)

where η = −M′(p)p/M(p) equals the elasticity of demand for treatment, I the insurance value, and ε^avg the average size of marginal behavioral hazard, all evaluated at p^B.

Proposition 3 expresses the optimal copay in terms of reduced-form elasticities as well as the degree of behavioral hazard and the curvature of the utility function. It says that, fixing insurance value and the cost of treatment, the optimal copay is increasing in the demand elasticity and the degree to which behavioral hazard is positive. This simple formula illustrates a number of ways in which behavioral hazard fundamentally changes how we think about optimal copays.

Optimal copays can substantially deviate from cost even when coverage generates little or no insurance value

A simple implication of Equation (6) is that health “insurance” can provide more than financial protection: it can also improve healthcare efficiency. Even when individuals are risk-neutral and there is no value to financial insurance (I = 0), Equation (6) indicates that the optimal copay can differ from cost to provide insurees with incentives for more efficient utilization decisions. In fact, when consumers are risk-neutral, the extent of behavioral hazard (at the margin) fully determines the optimal copay. In this case, the optimal copay formula reduces to p^B = c+ε^avg(p^B): the optimal copay acts like a Pigouvian tax to induce marginal insurees to fully internalize their “internality”. Unlike in the standard model, there is no clear incentive-insurance tradeoff.

Optimal copays can be extreme: It can be optimal to fully cover treatments that are ineffective for some insurees or not to cover treatments that benefit insurees

A related implication is that optimal copays can be more extreme than in a model with only moral hazard. Absent behavioral hazard, the optimal copay lies strictly between the value that provides full insurance (i.e., the value that makes I(p) = 0) and cost when insurees are risk averse and demand is elastic. Intuitively, without behavioral hazard, slightly raising the copay from the amount that provides full insurance has only a second order cost through reducing insurance value but a first order benefit through controlling moral hazard; slightly reducing the copay from cost has a second order cost through inducing moral hazard but a first order benefit through increasing insurance value. In the standard model, it cannot be optimal to deny coverage of treatments that benefit some risk averse individuals and it cannot be optimal to fully cover or subsidize treatments when people are price-sensitive at the full coverage copay.

Behavioral hazard alters these prescriptions. When behavioral hazard is sufficiently positive, the optimal copay can be above cost even when the individual is risk-averse: it can be good to let insurers discriminate against certain treatments, as suggested by Panel (b) of Figure III. When behavioral hazard is sufficiently negative, the optimal copay can be below the level that provides full financial protection, even if demand is price-sensitive at this copay: paying people to get treated can be optimal, as illustrated in Panel (a) of Figure III. In this spirit, some insurers have begun to experiment with paying patients to take their medications (Belluck 2010; Volpp et al. 2009).

Optimal copays depend on health value, not just demand elasticities

Optimal copays likely vary more across treatments than in a model with only moral hazard. The standard model says that, fixing insurance value, copays should be higher the larger the cost and elasticity of demand (Zeckhauser 1970), as can be seen from plugging ε^avg = 0 into Equation (6). That model suggests, for example, that copays should be lower for emergency care (where demand is less elastic) than for regular doctor’s office visits (where it is presumably more price sensitive). However, it also leads to some counterintuitive prescriptions: It suggests that copays should be similar across broad categories of drugs with similar price elasticities, even if they have very different efficacies.

Behavioral hazard alters these prescriptions as well. To see this, make the approximation ε(s; θ) ≈ ε′(s; θ) ∀ (s, θ) and plug ε^avg(p) ≈ p − H′(p)/M′(p) (Proposition 2 establishes that the second approximation follows from the first) into (6), yielding

$$\frac{c-p^B}{p^B}\approx \frac{I}{\eta }+\left(\frac{H\prime \left(p^B\right)}{p^{B}M\prime \left(p^B\right)}-1\right).$$ (7)

From Equation (7), all else equal copays should be decreasing in the net return to the last private dollar spent on treatment, |H′(p)|/(p|M′(p)|) − 1, so the value of treatment now enters into the determination of the optimal copay insofar as it influences H′(p). For a given demand response to copays, copays should be lower when this demand response has greater adverse effects on health.

This connects to value-based insurance design proposals (Chernew, Rosen and Fendrick 2007) where, all else equal, cost sharing should be lower for higher value care. While the marginal rather than the average value of care appears in Equation (7), knowledge of the average health value of care can provide a useful signal about the marginal health value. Consider a case where the demand curve slopes down only because of behavioral hazard: V ar(ε) > 0, but V ar(b) = 0. Then the marginal individual at any copay where demand is price-sensitive must have a marginal health value equal to the average value b, which also can be expressed as (H(p^min)−H(p^max))/(M(p^min)−M(p^max)). (Recall that p^min equals the lowest copay where some of the sick do not demand treatment and p^max equals the largest copay where some people still demand treatment.) Generalizing this example to allow for heterogeneity in private benefits in addition to heterogeneity in behavioral hazard yields the following result.

Proposition 4. Assume U is linear, M′(c) ≠ 0, and the distribution Q(s, θ, γ) is such that b(s; γ) and ε(s; θ) are independently distributed according to symmetric and quasiconcave densities with V ar(ε) > 0.

1. p^B > c if $\frac{H\left(p^{\text{min}}\right)-H\left(p^{\text{max}}\right)}{M\left(p^{\text{min}}\right)-M\left(p^{\text{max}}\right)}<c$ and $\mathbb{E}[\epsilon ]\ge 0$.

2. p^B = c if and $\frac{H\left(p^{\text{min}}\right)-H\left(p^{\text{max}}\right)}{M\left(p^{\text{min}}\right)-M\left(p^{\text{max}}\right)}=c$ and $\mathbb{E}[\epsilon ]=0$.

3. p^B < c if and $\frac{H\left(p^{\text{min}}\right)-H\left(p^{\text{max}}\right)}{M\left(p^{\text{min}}\right)-M\left(p^{\text{max}}\right)}>c$ and $\mathbb{E}[\epsilon ]\le 0$.

This shows that with behavioral hazard, the average value of care provides a useful signal for the optimal copay. So long as there is some variability in behavioral hazard across people and behavioral hazard does not systematically push people to privately overuse high-value treatments or privately underuse low-value treatments, then the optimal copay is above cost whenever the treatment is not socially beneficial on average and is below cost whenever the treatment is socially beneficial on average. Take the case where $\mathbb{E}[\epsilon ]=0$. The average value of care signals the expected direction of behavioral hazard at the margin, since—as is familiar from standard signal-extraction arguments—the marginal patient’s expected valuation lies between the copay (his “revealed” valuation if there is no behavioral hazard) and the unconditional average valuation (his valuation if being marginal was independent of true valuation).²⁵ The marginal degree of behavioral hazard is then negative at copays below the expected value of treatment and positive at copays above the expected value of treatment. Returning to the example where V ar(b) = 0, the marginal degree of behavioral hazard satisfies b + ε = p ⇒ ε = p − b, which clearly is negative if and only if the copay is below the expected value of treatment.

These results suggest that optimal copays should depend on the value of treatment in addition to the demand response. For example, we might expect that we should have high copays for procedures that are not recommended but sought by the patient nonetheless and low copays in situations where people have asymptomatic chronic diseases for which there are effective drug regimens. While advocated by some health researchers—for example, Chernew et al. (2007)—such differential cost-sharing is uncommon in practice; we return to some possible reasons in Section 6 below.²⁶

5. The Pitfalls of Ignoring Behavioral Hazard

Behavioral hazard modifies the central insights of the standard model. The goal of this section is to give a sense of how important it is to take behavioral hazard into account – how wrong would the analyst be if he ignored behavioral hazard?

While the optimal copay, p^B, satisfies $\tilde{W}\prime \left(p^B\right)=0$, where $\tilde{W}$ is defined in Equation (5), a candidate for the “neo-classical optimal copay”, p^N, satisfies the following condition.

Definition 1. p^N is a candidate for the neo-classical optimal copay when

$$\partial {\tilde{W}}^N\left(p^N\right)/\partial p\equiv -M^{\prime }(p)\cdot (c-p)-I(p)\cdot M(p)=0$$

and (i) $\partial {\tilde{W}}^N/\partial p\ge 0$ in a left neighborhood of p^N, (ii) $\partial {\tilde{W}}^N/\partial p\le 0$ in a right neighborhood of p^N, and (iii) at least one of the inequalities in (i) or (ii) is strict for some p in the relevant neighborhoods.

In other words, p^N is a copay that an analyst applying the standard model to estimates of the demand and insurance value schedules, (M(·), I(·)), thinks could be optimal. The neo-classical optimal and true optimal copays will clearly coincide when ε(s; θ) = 0 ∀ s, θ. The direction of the deviation between these copays is also intuitive. As established in Online Appendix A, there is a welfare benefit to raising the copay from the neo-classical optimum whenever behavioral hazard is on average positive for people at the margin, and there is a welfare benefit to reducing the copay from the neo-classical optimum whenever behavioral hazard is on average negative for people at the margin.²⁷ Less obvious, the deviation between the neoclassical optimal and true optimal copays can be huge:

Proposition 5. Suppose U is strictly concave, $\epsilon (s;\theta )=\tilde{\epsilon }\in ℝ$, and b(s; γ) = s ∀ (s, γ, θ).

1. If $\tilde{\epsilon }$ is sufficiently large then the neo-classical analyst believes p^N = 0 is a candidate for the optimal copay but the optimal copay in fact satisfies p^B ≥ c.

2. If $\tilde{\epsilon }$ is sufficiently low then the neo-classical analyst believes p^N = c is a candidate for the optimal copay but the optimal copay in fact satisfies p^B ≤ 0.

When behavioral hazard is extreme, the neo-classical optimal copay is exactly wrong: the situations in which the neo-classical analyst believes that copays should be really low are precisely those situations where copays should be really high and vice versa.²⁸ In the case of very positive behavioral hazard, almost everybody gets treated at p ≈ c, so the neo-classical analyst thinks there is no benefit to controlling moral hazard but there is an insurance value to reducing copays, suggesting to him an optimal copay of at most zero. In reality, however, many people who demand treatment at p = c are inefficiently doing so, yielding a large benefit to controlling behavioral hazard by raising the copay above cost. So long as people are not extremely risk averse, a copay above cost is better than any copay below cost. In the case of very negative behavioral hazard, almost nobody gets treated at p ≈ c, so the neo-classical analyst sees a huge benefit to controlling moral hazard since nobody appears to value the treatment as much as it costs. So long as people are not extremely risk averse, the neo-classical analyst believes the copay should roughly equal cost. In reality, however, even at a copay of zero, people at the margin of getting treated have a benefit above cost. There is no benefit to controlling behavior by raising the copay above zero, but there is an insurance value cost, making the optimal copay at most zero.

An immediate corollary of Proposition 5 is the following:

Corollary 1. Suppose U is strictly concave, b(s; γ) = s, $\epsilon (s;\theta )=\tilde{\epsilon }\in ℝ\forall (s,\gamma ,\theta )$, and

$$\tilde{\epsilon }=\{\begin{array}{ll}e\hfill & \mathit{\text{with}}\text{ex ante}\mathit{\text{probability }}\rho \in (0,1)\hfill \\ -e\hfill & \mathit{\text{with}}\text{ex ante}\mathit{\text{probability }}1-\rho .\hfill \end{array}$$

For sufficiently large e: p^B ≥ c or p^B ≤ 0, where (i) p^B ≥ c if p^N = 0 (but not p^N = c) is a candidate for the neo-classical optimal copay and (ii) p^B ≤ 0 if p^N = c (but not p^N = 0) is a candidate for the neo-classical optimal copay.

This corollary essentially restates Proposition 5 to say that when behavioral hazard is extreme, knowing that the neo-classical analyst believes that the copay should be very low signals that it should be very high and knowing that he believes the copay should be very high signals that it should be very low. For example, when the neo-classical optimal copay is 0, i.e. full insurance, the optimal copay is above c, i.e., no insurance.²⁹

For a numerical illustration, take the case where utility is quadratic, s is uniformly distributed, getting treated returns a person to full health, and the degree of behavioral hazard is constant across the population. Table IV details a resulting calculation for parameter values described in the notes. This example highlights several points. First, p^B > p^N whenever behavioral hazard is positive, and p^B < p^N whenever behavioral hazard is negative. Second, the optimal copay p^B is increasing in $\tilde{\epsilon }$. Third, the neo-classical optimal copay p^N is instead decreasing in $\tilde{\epsilon }$. Fourth, and as a result of the fact that p^B and p^N move in opposite directions as $\tilde{\epsilon }$ moves away from 0, the deviation between p^B and p^N can be huge.³⁰

Table IV:

Numerical Illustration Comparing the Neo-classical Optimal Copay to the Optimal Copay

	Neo-classical Optimal Copay (pN)	Optimal Copay (pB)
$\tilde{\epsilon }=-99$	99.98	.02
$\tilde{\epsilon }=0$	97.95	97.95
$\tilde{\epsilon }=99$	0	197.82

Notes: U(C) = αC − βC² for α = 7000, β = 1/2; $s~U[0,\overline{s}]$ for $\overline{s}=200$; b(s; γ) = s for all (s, γ); and $\epsilon (s;\theta )=\tilde{\epsilon }$ for all (s; θ). We use the following values for the calculations: y = 2500, q = .1, c = 100, and $\tilde{\epsilon }\in \{-99,0,99\}$. There is a unique candidate for the neo-classical optimal copay in all cases. Note that since c = 100, the copay coincides with the coinsurance rate in percentage units.

These results illustrate that setting copays under the assumption that the demand response signals the degree of moral hazard leads to very wrong policy conclusions when behavioral hazard is extreme. The example of Choudhry et al. (2011) on eliminating copays for recent heart attack victims dramatically illustrates this for the case of negative behavioral hazard: given the sizable demand response to eliminating copayments for statins, beta blockers, and ACE inhibitors, a neoclassical analyst could mistakenly conclude that this reduces welfare. There are also examples consistent with mistaken conclusions in the other direction, where the traditional model suggests low copays because insurees exhibit little price-sensitivity, while incorporating behavioral hazard might suggest higher copays because the evidence signals persistent overuse. An example is the case of low price elasticities among the elderly for drugs deemed “inappropriate” for their conditions (Costa Font et al. 2011).

6. Further Issues and Extensions

6.1. Applying Information on Psychological Underpinnings

We have drawn out the implications of behavioral hazard generally, without distinguishing among various psychologies that could underlie it. This section describes two ways in which making such distinctions can be helpful in applied work. First, it can allow us to predict the degree of behavioral hazard in situations where measuring health responses is infeasible. Second, it can suggest new policy instruments that would usefully target specific psychologies.

When it is difficult to use evidence on health responses to measure the degree of behavioral hazard, knowledge of the psychology underlying behavioral hazard can be useful (Beshears et al. 2008, Mullainathan, Schwartzstein and Congdon 2012). For example, in the case of present-bias, knowing the degree to which treament benefits or costs are delayed can predict behavioral hazard and thereby suggest which treatments should have higher or lower copays. Gruber and Koszegi (2001) follow this sort of approach in estimating the marginal internality for the case of cigarette purchase decisions.

Identifying the specific psychologies can also motivate the use of non-financial instruments or “nudges” to change behavior (Thaler and Sunstein 2008). There is substantial evidence, for example, that reminders or framing can affect utilization (Schroeder et al. 2004; Schedlbauer et al. 2010; Strandbygaard et al. 2010; Long et al. 2012).³¹ To incorporate such instruments into the framework, suppose there is a set $\mathcal{N}$ of nudges available to the insurer, where a nudge is modeled as affecting demand through influencing the behavioral error ε, so for $n\in \mathcal{N}$, we have ε = ε_n(s; θ). The direct cost to the insurer of nudge n is ψ(n) ≥ 0, where we suppose there is a “default nudge” $n=0\in \mathcal{N}$ with ψ(0) = 0. So far we have implicitly assumed that the insurer sets the default nudge and have notationally suppressed the relationship between the nudge and the behavioral error.

We can sometimes use responses to nudges to measure the magnitude of behavioral hazard, though we have to be careful in our interpretation. It is tempting to say that responses to reminders, for example, reveal the extent of inattention. But as Bordolo, Gennaioli and Shleifer (2015) point out, this inference may not be valid because people may overreact to such nudges. Nudges can be a useful tool for calibrating the degree of behavioral hazard when we have a precise sense for how nudges affect the error—that is, how ε_n varies in n. Proposition A.2 in Online Appendix A describes conditions under which the degree of marginal behavioral hazard can be calibrated by comparing the demand response to nudges to the demand response to prices.³² Heuristically, if we find that a nudge believed to lead to better decisions increases demand for treatment more than a $d decrease in the copay, that suggests that agents are undervaluing treatment by at least $d at the margin.³³ Relatedly, if we have information that some people are likely more biased than others, we could in principle bound the degree of behavioral hazard by comparing the demand curves of the more and less biased groups.³⁴

It is difficult to perform this exercise rigorously with existing data because few studies estimate the impact of nudges and copays simultaneously. However, the limited evidence on the effects of nudges on adherence suggests that behavioral hazard can be significant. For example, Long et al. (2012) compare peer mentoring and financial incentives to improve glucose control among African American veterans. While they did not measure impacts on drug adherence, they find that a peer mentoring program improved blood sugar control more than a $100-$200 incentive did, which is suggestive of negative behavioral hazard. (Also see Online Appendix C for evidence on the impact of nudges on hypertension.)

Nudges are also potentially useful policy tools for counteracting behavioral hazard when we know that they are reducing errors overall, since they can target behavioral hazard better than copays can. For example, if some fraction of the population exhibits negative behavioral hazard under the default nudge, ε₀(s; θ) < 0 ∀s, while some fraction acts unbiased, then there does not exist a copay that leads to first-best utilization: while p = c leads to first-best utilization for the unbiased, it leads to underuse among those with negative behavioral hazard. Similarly, while some p < c may lead to efficient utilization in the population with negative behavioral hazard, it leads to overuse among the unbiased. On the other hand, if there is a “perfectly de-biasing nudge” n* that eliminates behavioral hazard, ε_n*(s; θ) = 0 ∀(s, θ), then using that nudge leads to first-best utilization when p = c.³⁵ Of course, it is implausible that a perfectly de-biasing nudge exists, and it is unclear how effective many nudges are at reducing behavioral hazard. Studying the optimal mix of nudges and copays in the design of health insurance, taking such uncertainty into account, is an interesting topic for future research.

6.2. Incorporating Testing Decisions

The existence of behavioral hazard can have system-level ripple effects, particularly if early utilization such as diagnostic testing has cascade effects for downstream care. In the traditional model, the additional information yielded by low-cost tests should only improve patient welfare, but with behavioral hazard, subsequent misbehavior can add large costs. We briefly extend the model to allow for a testing stage that reveals s, and suppose the person gets treated only if he is tested. To illustrate through a specific example, further suppose that U″ = 0, s ~ U[0, 1], c = 3/4, and ε = 3/4 for everybody. Without testing, nobody gets treated and welfare is $\mathbb{E}[-s]=-1/2\cdot q$. With testing, everybody gets treated if p ≤ c, and welfare equals −3/4 · q < −1/2 · q. So tests have a substantially negative return if behavioral hazard is uncontrolled (p = p^N = c) and it is better not to test: the return on testing equals (−3/4 − (−1/2)) · q = (−1/4) · q. But if behavioral hazard is perfectly counteracted (say, in this example, with copay p^B = c + ε), then tests would have a positive return: the return on testing is then (−15/32 − (−1/2)) · q = (1/32) · q. So taking health responses into account in setting copays for treatment decisions can be doubly beneficial: not only does it lead to better decisions at the treatment stage, but it can feed back to better policy at the testing stage.

The medical community has designed testing guidelines that implicitly acknowledge the imperfections in the downstream decision-making of patients and physicians alike. The “Choosing Wisely” initiative launched by internal medicine physicians makes blanket recommendations against some common screenings and tests, not because the tests themselves are cost-ineffective conditional on optimal downstream care, but explicitly because of the probability of downstream care that is likely to harm patient health but is delivered nonetheless (Morden et al. 2014). These tests yield useful information that should be acted upon for a subset of identifiable patients, but many other patients end up receiving care (whether because of the disutility of “doing nothing” or mistaken beliefs about efficacy) that is at best useless and at worst harmful, making the expected value of performing the test negative.³⁶ This downstream sub-optimal care is of course the product of both patient and physician decision-making, and there may be ample parallel opportunity to redesign physician incentives to take into account the psychology of their decision-making (as well as train them to help take into account the behavioral decision-making of their patients).³⁷

6.3. Analyzing What the Market Will Provide

Given the welfare benefits of counteracting behavioral hazard, one question is why existing plans do not seem to do so. As shown in Online Appendix Table 2, typical health insurance plans have a copay structure that varies little within broad categories of treatments (e.g., physician office visits, inpatient services, branded drugs, generic drugs), while counteracting behavioral hazard requires a more nuanced structure where copayments are a function of the health benefit associated with the care for a particular patient. In an earlier version of this paper (Baicker, Mullainathan and Schwartzstein 2013) we extend the model to consider what a competitive market will provide in equilibrium under the simplifying assumption of a representative insuree, which requires additional assumptions on the degree to which insurees are sophisticated about behavioral hazard. We show how even though optimal insurance could reduce behavioral hazard, market-provided insurance may not. If enrollees were sophisticated, perfectly predicting their behavioral hazard and insuring accordingly, then market-provided insurance would be optimally designed to counteract behavioral hazard. But with naive enrollees, insurers have less incentive to mitigate underuse since naive consumers will not fully value copays designed to counteract their biases.³⁸ These problems are especially severe when insurers have nudges as well as copays available and when enrollees may be insured with them for limited time horizons (and thus insurers do not bear the full cost of current enrollees’ future health care use). In particular, if insurees do not appreciate the impact of nudges, then we would expect the insurer to supply nudges that minimize costs rather than maximize surplus.

Thus, with naive insurees, insurers only have an incentive to counteract biases when it saves them money. The gains from reducing copays for antidiabetics, beta blockers, and other care prone to negative behavioral hazard may not accrue to insurers, limiting their incentive to incorporate behavioral hazard into their copayment structures.³⁹ For example, Beaulieu et al. (2003) estimate that investment in diabetes disease management produces very small monetary gains for insurers over a 10 year horizon, but would produce $30,000 per patient in improved quality of life and longevity.⁴⁰ The potential for market failure suggests that government interventions may be welfare-improving over market outcomes even in the absence of selection or externalities.⁴¹ An important direction for future work is to develop a better understanding of how sophisticated consumers are about their own behavioral hazard, and how the government could intervene to help counteract behavioral hazard.

7. Discussion

There is ample evidence that moral hazard alone cannot explain the patterns of misutilization observed throughout the health care system. We build a framework for analyzing the relationship between insurance coverage and health care consumption that includes behavioral hazard. With only moral hazard, lowering copays increases the insurance value of a plan but reduces its efficiency by generating overuse. With the addition of behavioral hazard, lowering copays may potentially both increase insurance value and increase efficiency by reducing underuse. Having an estimate of the demand response is no longer enough to set optimal copays; the health response needs to be considered as well. This provides a theoretical foundation for value-based insurance design, where copays should be lower both when price changes have small effects on demand and when they have large effects on health. Ignoring behavioral hazard can lead to welfare estimates that are both wrong in sign and off by an order of magnitude.

The finding that optimal insurance features depend crucially on how prices affect both demand and health highlights the value of having empirical estimates of both responses (see also Lee et al. 2013). There is limited data linking insurance to clinical outcomes—and performing an exhaustive list of experiments and calculations would certainly be daunting—but a small number of conditions account for a large share of health spending. Patients with circulatory system conditions like high blood pressure and high cholesterol are responsible for 17% of total health care spending; mental health conditions like depression for another 9%; respiratory conditions like asthma another 6%; and endocrine conditions like diabetes another 4% (Roehrig et al. 2009). Studies that link changes in price, demand, and health would thus be particularly valuable—and a limited number could go a long way.⁴²

This framework is amenable to a number of extensions. While our model is static, it could be extended to consider how behavioral hazard affects optimal copays for preventive care, where initial underuse could generate expensive future overuse. Further exploration of consumer sophistication and intertemporal incentives for insurers may help explain insurance offerings and the potential role of public policy. Work could also draw out more nuanced implications for the use of nudges versus copayments. And while we highlight that the main results do not depend on the underlying psychological forces generating behavioral hazard, greater understanding of those forces could help estimate the degree of behavioral hazard in different settings and inform the optimal design of nudges. Finally, physicians are of course important drivers of the health care that is ultimately delivered, and, like patients, their choices are driven by both financial incentives and behavioral biases; future work could analyze the interplay of these channels.

Failing to incorporate behavioral hazard into models of health insurance can not only generate very wrong answers – but very wrong answers with substantial import for millions of people. Much of our health spending is on care that is sensitive to copay changes, and much of that care seems to have an impact on health that differs from what is implied by moral hazard alone. Simply assuming that the demand curve reveals the health value of care can generate misleading policy prescriptions; incorporating both moral hazard and behavioral hazard can inform insurance designs that better balance insurance protection with efficient resource use.