A multicountry, multicommodity stochastic game theory network model of competition for medical supplies inspired by the Covid-19 pandemic

Abstract

In this paper, we construct the first stochastic Generalized Nash Equilibrium model for the study of competition among countries for limited supplies of medical items (PPEs, ventilators, etc.) in the disaster preparedness and response phases in the Covid-19 pandemic. The government of each country is faced with a two-stage stochastic optimization problem in which the first stage is prior to the pandemic declaration and the second stage is post the pandemic declaration. We provide the theoretical constructs, a qualitative analysis, and an algorithm, accompanied by convergence results. Both illustrative examples are presented as well as algorithmically solved numerical examples, inspired by the need for N95 masks and ventilators. The results reveal that, in addition to the preparedness of countries before the pandemic declaration, their ability to adapt to the conditions in different scenarios has a significant impact on their overall success in the management of the pandemic crisis. The framework can capture competition for other medical supplies, including Covid-19 vaccines and possible treatments, with modifications to handle perishability.

1. Introduction

Every year, many countries face a variety of disasters and related crises that threaten people's lives and properties, some being unpredictable, with others predictable, but with differing degrees of certainty (Nagurney and Qiang (2009); FEMA (2020)). With advances in science and technology, preparation for and response to many disasters by governments have improved, especially in the developed world. Furthermore, although devastating, major natural disasters such as Hurricane Katrina in 2005, the earthquake in Haiti in 2010, the triple disaster in Fukushima in 2011, and hurricanes Harvey, Irma, and Maria in 2017, never became a global challenge because of such disasters' limitations in both time and space. In contrast, starting in 2020, the world has been faced with a healthcare disaster in the form of a global pandemic that has affected all countries at the same time; has stopped the wheel of the world's economy from spinning, and everyone is anxiously awaiting the light at the end of this tunnel. Raker, Zacher, and Lowe (2020) have called the pandemic “a disaster of unprecedented scale and scope.”

1.1. Background and motivation

On December 31, 2019, a case of pneumonia with unknown cause was detected in Wuhan, China and reported to the World Health Organization (WHO) Country Office in China (WHO (2020)). This was the beginning of the Covid-19 pandemic. Covid-19 is the disease caused by the novel coronavirus that has symptoms such as: a cough, fever, shortness of breath, muscle aches, sore throat, unexplained loss of taste or smell, diarrhea, and headache. Covid-19 cases can be severe, with some resulting in death (Johns Hopkins Medicine (2021)). On January 11, 2020, the first death caused by the coronavirus was announced by the Wuhan Municipal Health Commission. On January 21, the first case on US soil was confirmed by officials (CNN (2021)), and nine days later, WHO declared a Public Health Emergency of International Concern (WHO (2020)). The first death due to the illness in the United States was announced on February 29. Finally, on March 11, WHO declared the novel coronavirus outbreak a pandemic, and, two days later, a national emergency was declared in the United States (Secon et al. (2020); CNN (2021)). As of January 12, 2021, globally, authorities reported 91,374,370 confirmed cases of Covid-19, with the number of deaths reaching 1,956,635 with 379,444 of them having occurred in the US, the country with the most cases and deaths due to Covid-19 as of that date. 50,537,714 individuals have recovered from the disease globally (Johns Hopkins Medicine (2021); Johns Hopkins Coronavirus Resource Center (2021)).

Disaster management consists of the four main phases: mitigation, preparedness, response, and recovery. In the current pandemic, the mitigation phase was especially challenging due to many flights between countries, and other transportation connections, as well as many unknowns about the novel virus. With the onset of the outbreak in China, some countries, such as New Zealand, Australia, Iceland, and Denmark responded more quickly and more effectively than others (Kamal et al. (2020); Lafortune (2020); Gilbert et al. (2020)). The coronavirus spreads mainly through droplets of saliva or discharge from the nose when an infected person coughs, sneezes, or speaks with even asymptomatic people being able to spread it. Although several vaccines have recently been authorized for emergency use (Zimmer et al. (2021)), less than ten million shots have been given in the US to date (The New York Times (2021)). As officials have warned, it is not going to be a light switch and there is still a long way to go before communities become immune to the disease (Scipioni (2020)). Hence, governments have been trying to reduce the spread of the virus by testing and isolating, by minimizing social contacts and emphasizing social distancing (Ferguson et al. (2020); Greenstone and Nigam (2020)), by banning group gatherings, closing schools and nonessential businesses, and implementing travel restrictions (CDC (2021a; 2021b); Anderson et al. (2020)).

1.2. Importance of medical supplies and supply chain networks

One of the most effective ways in decreasing the spread of the virus is to use Personal Protective Equipment (PPE), which is essential for healthcare workers (CDC (2020); Herron et al. (2020)). Also, because the virus may cause severe respiratory problems in certain individuals, doctors and hospitals called out for the urgent need for ventilators (Gelles and Petras (2020); Namendys-Silva (2020)). Therefore, very soon, many national governments began clamoring for such (and other) medical supplies. This meant the beginning of an intense competition among different countries over items that had never before experienced such demand (Goudie et al. (2020); Pifer (2020); Kamdar (2020)). At the same time, the production capacity was far below the level of immediate need (SCCM (2020); Schlanger (2020)).

In terms of disaster preparedness of the United States and the world for pandemics, the lack of PPEs has always been seen as an important issue (Lopez (2020a)). Different estimates of the required number of ventilators during this pandemic, in turn, are from hundreds of thousands to one million. The number of these devices available in the United States is estimated at between 60,000 and 160,000, and the national strategic reserves are insignificant compared to the expected needs (Ranney et al. (2020)). In today's world, every product has a path from production to demand points, and, in some cases, it goes through several countries. PPEs are no exception, and their production process depends not only on the capacity of the factories, but also on raw materials (UNICEF (2020)). For example, paper needed to produce protective gowns has become so scarce that a company had to approach five different countries to find it to keep its supply chain open (Diaz et al. (2020)). As the President of the American Medical Association (AMA) states, the constant shortage of PPEs has disrupted the healthcare system and has consistently weakened the ability of medical staff in the front lines to deal with the surges of Covid-19 cases (Bailey (2020)). The lives of doctors and nurses have been at risk due to the lack of proper masks, gowns, and eye gear; some health centers, such as The Open Cities Community Health Center in St. Paul, Minnesota, have considered shutting down because they do not have enough face masks (Jacobs et al. (2020)). Lack of PPEs makes it harder to flatten the curve. Moreover, the capacity of the healthcare system is not constant, and it will not be easy to handle even the flatter curve if medical staff get sick or refuse to work due to the PPE shortage (Lopez (2020a)).

On March 3, 2020, WHO claimed that it had distributed approximately half a million sets of PPE to 47 countries; at the same time, it raised concerns over the rapid depletion of the global supply. WHO estimates that in order to meet rising global demand, manufacturing must increase by 40 percent (WHO (2020)). The United States Strategic National Stockpile had approximately 12 million N95 masks and 30 million surgical masks while the Department of Health and Human Services had projected that the country would need 3.5 billion face masks in the event of a year-long pandemic (Jacobs et al. (2020)). Lack of proper national planning and coordination has led in some cases low-population regions receiving large amounts of PPEs per the number of cases they have, and in other areas to shortages, and eventually leading state governments to compete with each other and even with federal government and foreign governments to procure the goods they need (Bailey (2020)). At the time of that report, the US federal government's Strategic National Stockpile had almost emptied, and some companies that used to buy from other countries, such as China, said that their previous relationships with manufacturers no longer matter and that they have to compete with other buyers (Diaz et al. (2020)).

China historically has produced half of the world's face masks, and, when the virus outbreak started there, it began to use its own supply for its citizens. Subsequently, the rest of the world bought as much as it could, and, in some cases, such as Germany, even banned the export of many of PPEs (Lopez (2020a)). The fierce competition over PPEs has led to a sharp rise in the price of these items, with some prices rising by more than 1000 percent, according to the report by the Society for Healthcare Organization Procurement Professional. For example, the price of N95 masks grew from $0.38 to $5.75 each (a 1413% increase); the price of vinyl exam gloves went from $0.02 to $0.06 (a 200% increase), and isolation gowns have faced a price increase from $0.25 to $5.00 (a 1900% increase), with the cost of reusable face shields going from $0.50 to $4 (a 700% increase) (Diaz et al. (2020); Berklan (2020)). To increase production capacity and to respond to the sudden increase in demand for ventilators, several companies such as Ford, General Motors, and Tesla announced that they would dedicate their manufacturing facilities and capability to the production of these devices (O'Kane (2020); Morrison (2020)). Even fashion companies have been producing masks. In this regard, President Trump invoked the historic Defense Production Act to expedite the supply and distribution of such essential items during this pandemic (Kelley (2020)).

As Paul et al. (2019) note in their research on manufacturers' recovery models after supply chain disruptions, a number of factors in the supply chain can cause a disruption, from the supplier's side to production plants as well as sudden changes in demand. However, with proper planning, the negative effects can be minimized. Supply chain networks must be investigated from multiple perspectives in order to address the challenges of essential goods procurement in order to meet the needs of people in times of crises such as major epidemics. For example, Dasaklis et al. (2017) argue that implementing a large-scale vaccination program requires rapid and vital decisions about logistics. The number and capacity of warehouses, their location, inventory policies, distribution methods and shipping modes, and many other factors are among the decisions that need to be made, and it is not possible without a regular and optimal plan. Ivanov and Dolgui (2020) state that, in facing a disaster on the scale of the present pandemic, we are dealing with intertwined supply networks (ISNs). The integrity of ISNs and their viability is the focus of their study to ensure that the service and goods sectors can continue to operate in critical situations. As Dasaklis et al. (2012) point out, logistics play a significant role in dealing with epidemic disasters, and in research that has been done, not enough attention has been paid to stochasticity, while many of the relevant parameters are uncertain.

1.3. Research questions

The research questions that we address in this paper include:

• 1.What are the characteristics of competition among countries for essential goods; specifically, medical supplies, in preparation and response to the pandemic?
• 2.What factors affect the competition?
• 3.What are the optimal strategies of governments in achieving their objectives, and can these be determined quantitatively through rigorous modeling and computations?

In this paper, we take up the challenge of constructing a stochastic game theory network model that captures the competition among countries for multiple medical supplies in the setting of the Covid-19 pandemic in order to address the above research questions.

The specific contributions in this paper are delineated below.

1.4. Our contributions

In this paper, we address the vital issue of multicountry competition for multicommodity medical items in the pandemic. We consider governmental decisions and strategies made both before and after the declaration of a pandemic. Hence, this paper builds on the work of Nagurney et al. (2020) but with the following significant extensions/modifications:

Competition among multiple countries under uncertainty: This paper examines the competition of several national governments for medical supplies. The competition arises as each government faces a two-stage stochastic optimization problem for pre- and post-pandemic disaster management in its country.

Multiple medical items: We consider that, in times of a healthcare pandemic disaster, demand is not limited to a single medical item. Governments must identify their optimal strategies in procuring the different medical products, such as PPEs and ventilators. It is also important to note that, unlike in previously noted disasters, the essential goods that have suffered severe shortages in the Covid-10 pandemic are, in fact, medical supplies.

Limited supplies of medical items: The countries compete with one another for the limited medical supplies, leading to a Generalized Nash Equilibrium. This is only the second paper that constructs a two-stage stochastic Generalized Nash Equilibrium model for disaster relief and is actually the first one focused on healthcare in terms of medical supplies.

Penalties on the shortages of medical items: A distinct penalty is assessed by each country on the unmet demand for each medical item.

2. Literature review

With the onset of the Covid-19 pandemic and the emergence of severe disruptions in supply chains, researchers play a critical role in informing decision-makers. Although not much research has been published on this subject yet, Queiroz et al. (2020) mapped out a research agenda by providing a structured literature review of current Covid-19 related research and supply chain research on previous epidemics. Ivanov (2020a) conducted simulation-based research to investigate the possible impact of the Covid-19 pandemic on global supply chains. He found that the extent of these effects depends on the timing of the closing and opening of the facilities at different supply chain tiers, and on the lead-time, the pandemic transmission speed, and the upstream and downstream disruption periods. The impacts that the Covid-19 pandemic and the supply chains have on one other are pervasive; for example, Choi (2020) discusses the effects of this crisis on changing the way businesses operate in order to survive. He argues that the innovative “bring-service-near-your-home” mobile service operation (MSO) is one way for businesses to continue during the time that people no longer visit stores because of their safety concerns. Focusing on demand management, Govindan et al. (2020) propose a decision support system that would help better manage the healthcare supply chain situation by categorizing community members during an outbreak such as the Covid-19 pandemic. In another study, Ivanov (2020b) discusses the viability of the supply chain, an issue that has become increasingly important since the onset of the Covid-19 pandemic. Various aspects of the supply chain, including resilience, sustainability, and digitalization need to be addressed so that the decision-makers can design a network that is stable even in times of crisis and severe global disruption. Ivanov and Dolgui (2021) provide managerial insights for dealing with the ripple effect in supply chain networks in the Covid-19 pandemic. They find that the most important feature for sustainable network management in a pandemic disaster is the supply chain's adaptability. Dolgui, Ivanov, and Sokolov (2020), in turn, in researching supply chain networks and their status in vulnerable environments that humans will encounter, addressed the integrity of digitalization, resilience, sustainability, and leagility in the Reconfigurable Supply Chain (RSC). The authors introduced two new concepts: dynamic supply chain meta-structures and dynamic autonomous services, in the RSC that can be operational in vulnerable environments such as natural disasters.

Earlier, Chick, Mamani, and Simchi-Levi (2008) constructed the first integrated supply chain/health economics model for the distribution of the influenza vaccine. In this model, two players have key roles, the government and the manufacturer, and coordination between them has a significant impact on the outcome of the operation for both players. Liu and Zhang (2016) constructed a dynamic logistics model to study the medical resource allocation in response to epidemic diffusion. Büyüktahtakın, des-Border, and Kibis (2018) presented an epidemic-logistics model to be used in the control of an Ebola epidemic. The objective of their mixed-integer programming model was to minimize the total number of infections and fatalities by determining the optimal amount, timing, and location of resources. Anparasan and Lejeune (2018) worked on the important issue of disasters in developing countries. Using GPS and population data, they were able to provide a good dataset on the cholera epidemic in Haiti after the 2010 earthquake. Later, Anparasan and Lejeune (2019) developed a resource allocation model based on the 2010 cholera outbreak in Haiti to support emergency response to an epidemic outbreak in resource-limited countries. In a two-stage model, Long et al. (2018) investigated the allocation of resources in the event of an epidemic. In the first stage, the model predicts how the epidemic moves between the neighboring areas, and, in the second stage, the necessary resources are allocated to intervene in the epidemic. Enayati and Ozaltin (2020) presented a vaccine distribution model for influenza transmission that minimizes the number of vaccines necessary to control an emerging pandemic in its initial stages. Their model also incorporates transmission dynamics and isolation.

2.1. Game theory related literature

Using a game theory model, Mamani et al. (2013) showed that lack of coordination can lead to unbalanced distribution and shortage or excess of influenza vaccine in different regions. In this study, the use of cost-sharing contracts that increased coordination between different players improved global vaccine allocation. Gupta, Ivanov, and Choi (2020), in their game-theoretical study, investigated the competitive pricing for substitute goods and provided insights that could help managers in choosing ordering strategies and contracts with the aim of reducing the risk in time of crisis and supply chain disruptions. Regarding competition among different organizations for resources in a disaster relief setting, Nagurney et al. (2016) presented the first Generalized Nash Equilibrium (GNE) model that combined financial aspects and the logistics challenges of relief operations after a disaster. In the GNE model, the utility function of each player depended not only on his own strategies but also on the strategies of the other players, and the underlying feasible sets did as well. Removal of the common/shared constraints from the problem, in turn, yields classical Nash Equilibrium model (Nash (1950; 1951)). Subsequently, Nagurney et al. (2018) provided an extension to the previous game theory model by introducing more general logistical cost, financial, and altruism functions, which, unlike in the previous model, did not allow an optimization reformulation. Specifically, the authors used the concept of a Variational Equilibrium to reformulate the GNE conditions as a variational inequality. Nagurney, Salarpour, and Daniele (2019) provided the option of relief items to be purchased from purchasing locations with different features along with the selection of different freight service providers for the humanitarian organizations. In addition, budget constraints were incorporated for the humanitarian organizations to further highlight the need for resource planning and management.

2.2. Stochastic optimization relevant literature

The game theory models discussed above were, nevertheless, focused on the response phase of disaster management and were deterministic. When it comes to integrated disaster preparedness and response, an important feature to consider is the uncertainty of possible scenarios. In problems where the decision-maker has to make some decisions before becoming aware of the value of uncertain variables, stochastic programming with recourse is used (cf. Mulvey and Vladimirou (1992); Dantzig and Madansky (1961); Barbarosoǧlu and Arda (2004)). For a survey on two-stage stochastic optimization applied to disaster relief see Grass and Fischer (2016). Sabbaghtorka, Battaa, and He (2020) also review recent research works in the area of location and allocation of assets and supplies in disaster management and identify the research gaps. They categorize papers based on their area of work and the methods they utilize, but among them a few of papers are mentioned as strong ones (see, e.g., Rawls and Turnquist (2010); Tofighi et al. (2016); Alem et al. (2016)).

Rawls and Turnquist (2010) provided a stochastic mixed-integer programming model that determines the emergency supplies pre-positioning strategies while dealing with the demand uncertainty. Mete and Zabinsky (2010) developed a stochastic programming model for location and allocation of medical supply. In their model, the location of warehouses and their inventory level is determined in the first stage, and in the second stage, based on the scenario, the amount of supplies that must be transported to hospitals is determined. Nagurney et al. (2020) addressed the issue of uncertainty but with the consideration of multiple, competing decision-makers in the first Stochastic Generalized Nash Equilibrium model for disaster relief. In that model, relief organizations compete for existing resources before and after the disaster, and adjust their decisions based on the probability of different scenarios. Each organization is faced with a two-stage stochastic optimization problem where it can buy and store relief items before a disaster occurrence, and may purchase additional items based on the circumstances after the disaster, or utilize their warehouse reserves to meet the demand.

2.3. Two-stage stochastic game theory and organization of this paper

In this paper, we construct a two-stage stochastic game theory model with consideration of the unique characteristics of the Covid-19 pandemic in order to examine the behavior of national governments in this healthcare disaster and their competition for essential medical supplies in both the preparation and response phases.

We emphasize that we believe that game theory is quite relevant to many healthcare issues in the Covid-19 pandemic. For example, recently, Nagurney and Dutta (2020) introduced an equilibrium donor model for convalescent plasma. The model captures the competition between nonprofit and for-profit organizations seeking convalescent plasma donations, which is a characteristic of this new market. Convalescent plasma is now being investigated as a treatment for Covid-19 and there have been documented instances of enhanced patient survival after transfusions. Nagurney et al. (2021) constructed a GNE model with stochastic demands in which healthcare organizations competed for medical supplies in the pandemic but that model, in contrast to the model in this paper, is a single-stage model.

This paper is organized as follows. In Section 3, we develop the pandemic stochastic game theory network model for medical supplies. We describe how the national governments compete for the medical supplies to minimize their respective expected loss/disutility from the pandemic disaster in terms of their individual two-stage stochastic optimization problems. We construct the Stochastic Generalized Nash Equilibrium, define the Variational Equilibrium, and derive alternative variational inequality formulations. We also present illustrative examples. In Section 4, we outline an algorithm, which resolves the variational inequality problem into subproblems yielding closed-form expressions for each of the medical supply flows and the Lagrange multipliers associated with the supply capacities at a given iteration. In Section 5, we compute solutions to numerical examples inspired by the Covid-19 pandemic, and, in Section 6, we provide a summary of the paper along with the conclusions.

3. The pandemic stochastic game theory network model for medical supplies

In this Section, we construct the multicountry, multicommodity stochastic game theory network model for medical supplies in the Covid-19 pandemic. The notation is presented in Table 1 . The vectors are all column vectors.

Table 1.

Notation for the pandemic stochastic game theory network model.

Notation	Parameters
$\omega \in \text{Ω}$	the disaster scenarios.
$p_{\omega }$	the probability of disaster scenario ω in stage 2; $\forall \omega \in \text{Ω}$.
$S_{j,k}^1$	the supply of medical item k in country j in stage 1; $j=1,\dots ,I$; $k=1,\dots ,K$.
$S_{j,k}^{2,\omega }$	the supply of medical item k in country j when scenario ω occurs in stage 2; $j=1,\dots ,I$; $k=1,\dots ,K$; $\omega \in \text{Ω}$.
$d_{i,k}^{2,\omega }$	the demand for medical item k in country i when scenario ω occurs in stage 2; $i=1,\dots ,I$; $k=1,\dots ,K$; $\omega \in \text{Ω}$.
${\beta }_{i,k}$	the unit penalty encumbered by country i on the unmet demand of medical item k; $i=1,\dots ,I$; $k=1,\dots ,K$.
${\rho }_{j,k}$	the unit price of medical item k at country j before the pandemic; $j=1,\dots ,I$; $k=1,\dots ,K$.
${\rho }_{j,k}^{\omega }$	the unit price of medical item k at country j when the scenario ω occurs in stage 2; $j=1,\dots ,I$; $k=1,\dots ,K$; $\omega \in \text{Ω}.$
Notation	Variables
$q_{ij,k}^1$	the amount of medical item k purchased by country i from country j in stage 1. We group all the j and k elements into the vector $q_i^1$ and then group such vectors for all i into the vector $q^1$.
$q_{ij,k}^{2,\omega }$	the amount of medical item k purchased by country i from country j when the scenario ω occurs in stage 2. We group all the j and k elements into the vector $q_i^{2,\omega }$ and then group such vectors for all i into the vector $q^{2,\omega }$. Finally, we group these vectors for all ω into the vector $q^2$. We group the $q^1$ and $q^2$ vectors into the vector $q\in R_{+}^{IIK+\left|\text{Ω}\right|\left(IIK\right)}$.
Notation	Cost Functions
$c_{ji,k}^1\left(q^1\right)$	the total transportation cost that country i pays to have the medical items k delivered from country j where the items are purchased before the pandemic hits the country.
$c_{ji,k}^{2,\omega }\left(q^{2,\omega }\right)$	the total transportation cost that country i pays to have medical items k delivered from country j when the scenario ω occurs in stage 2.

As mentioned in the Introduction, not enough attention has been paid to stochasticity in logistics problems for epidemic disasters (Dasaklis et al. (2012)). In order to fill this research gap, we need to tackle one of the most important issues in disasters, and that is the uncertainty of different parameters. Severity of the disaster, supply chain network status, and demand levels are among those parameters. Decision-makers and managers, in the pre-crisis preparation phase, need to consider several scenarios with different probabilities so as not to be surprised in the response phase, and to minimize the potential losses. As a result, a two-stage stochastic optimization model can well demonstrate a government's efforts to provide essential goods in times of crisis. Furthermore, as evidenced by the Covid-19 pandemic, there are multiple governments that are competing for medical supplies, and, therefore, this generalization also merits serious investigation, which we undertake in this paper.

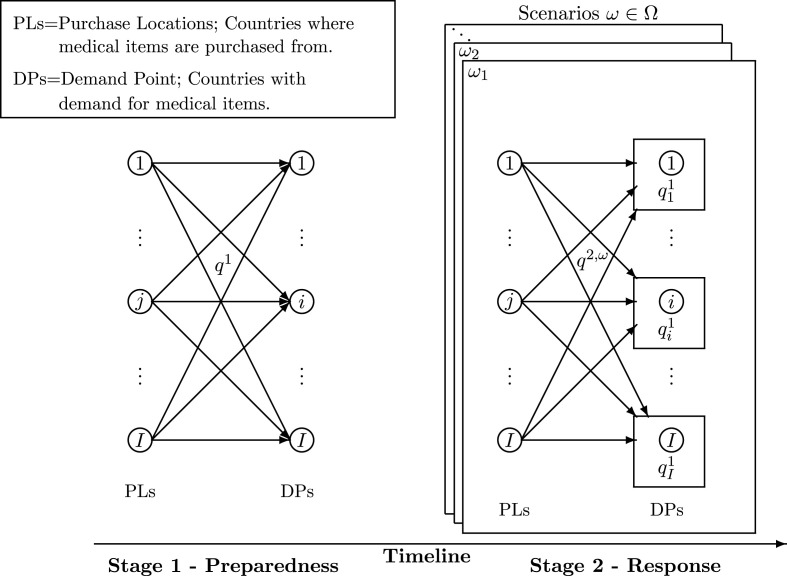
The two stages are displayed in Fig. 1 . There are I national governments of countries with a typical one denoted by i; $i=1,\dots ,I$. Each of these countries requires the acquisition of medical items as they face the pandemic. We have I possible countries where the items are purchased from with a typical one denoted by j; $j=1,\dots ,I$. There are K different medical items with a typical one denoted by k. In the first stage, before the pandemic occurs, the government of country i can purchase medical supplies from its own country and/or from the other countries. After the declaration of the pandemic, and better information as to the demand, the governments procure needed medical supplies to meet the demand as closely as possible; again, either domestically or from other countries, but now under different supply characteristics.

Fig. 1.

The timeline of the pandemic disaster preparedness and response.

3.1. The countries’ two-stage stochastic optimization problems

Faced with a pandemic, the primary goal of each of the national governments is to save lives by having the demands for medical supplies be met as closely as possible. However, it can be challenging as well as expensive to procure such items since a pandemic is global in nature. The objective function that each government seeks to minimize in this model consists of the expected diutility caused by the shortages of medical items and the associated purchasing and logistical costs. The actions that the government takes in the first stage, before the pandemic, and the cost of these actions, are deterministic and, hence, are included in the model deterministically. However, a national government's recourse actions in stage 2, once the pandemic has been declared, depend on the possible scenarios and the realization of the uncertain parameters.

Therefore, each national government is faced with the following two-stage stochastic optimization model in which they minimize the expected disutility:

$$\text{Minimize}\sum _{j=1}^I\sum _{k=1}^K{\rho }_{j,k}{q}_{ij,k}^1+\sum _{j=1}^I\sum _{k=1}^K{c}_{ji,k}^1\left(q^1\right)+E_{\text{Ω}}\left[Q_i^2\left(q^2,\omega \right)\right]$$ (1)

subject to:

$$\sum _{i=1}^I{q}_{ij,k}^1\le S_{j,k}^1,j=1,\dots ,I;k=1,\dots ,K,$$ (2)

$$q_{ij,k}^1\ge 0,j=1,\dots ,I;k=1,\dots ,K.$$ (3)

The first two terms in the objective function (1) indicate the deterministic costs that government i incurs before the pandemic is declared to meet part of the country's needs of medical items in the pandemic and to prepare for it. The first term in the objective function (1) indicates the cost of purchasing the medical items, and the second term represents the total transportation cost that country i pays to have the purchased items delivered. In stage 1, before the pandemic is declared, governments face important constraints, those of supply availability in each country of each medical item. The constraints in (2) capture the supply availability of medical item k in country j for each k and each j. The constraints in (3) guarantee that the medical item purchases/shipments in the first stage are nonnegative.

The last term in the objective function (1) is the expected value of the loss to country i in stage 2, including the procurement costs and the consequences of unmet demand: $E_{\text{Ω}}\left[Q_i^2\left(q^2,\omega \right)\right]=\sum _{\omega \in \text{Ω}}{p}_{\omega }\left[Q_i^2\left(q^2,\omega \right)\right]$, where the loss in scenario ω, for each country i, is obtained by solving the following second stage optimization problem:

$$\text{Minimize}{Q}_i^2\left(q^2,\omega \right)\equiv \sum _{j=1}^I\sum _{k=1}^K{\rho }_{j,k}^{\omega }{q}_{ij,k}^{2,\omega }+\sum _{j=1}^I\sum _{k=1}^K{c}_{ji,k}^{2,\omega }\left(q^{2,\omega }\right)+\sum _{k=1}^K{\beta }_{i,k}[d_{i,k}^{2,\omega }-\sum _{j=1}^I\left(q_{ij,k}^1+q_{ij,k}^{2,\omega }\right)]$$ (4)

subject to:

$$\sum _{i=1}^I{q}_{ij,k}^{2,\omega }\le S_{j,k}^{2,\omega },j=1,\dots ,I;k=1,\dots ,K,$$ (5)

$$q_{ij,k}^{2,\omega }\ge 0,j=1,\dots ,I;k=1,\dots ,K.$$ (6)

In stage 2, when the information about the severity of the pandemic and the level of demand for medical items are revealed, national government i completes its stage 1's efforts by taking the recourse actions. It does this by minimizing the total logistical costs and the damage caused by the unmet demand. The first two terms in objective/recourse function (4) are the costs associated with, respectively, the purchase of the medical items, and the cost of transportation of the items to the country when the disaster scenario ω occurs. The last term in objective function (4) represents the consequences of shortages of the medical items and the losses that the country will suffer from not satisfying the demand for the various medical items.

After the declaration of the pandemic, which may result in disruptions to the medical supply chains, the supply availabilities for the medical items also can be expected to change. In some cases, due to a shortage of raw materials, worker illnesses, and/or factory closures, production capability may be severely reduced. On the other hand, in some cases, governments may increase the production capacity of these items and, thus, the supply of medical items, by invoking different laws and, with the cooperation of large companies, may have greater capacity. Constraints in (5) indicate the supply availability of each medical item k at each country j in stage 2 when scenario ω occurs. Constraints in (6) are the nonnegativity assumptions on the shipments in stage 2.

Our model can assist the national governments in making the best decisions about procuring medical supplies before the onset of the pandemic in their countries. It also gives the optimal response strategies for possible scenarios in the second stage, when the pandemic is declared, so that the governments can act quickly to respond to the healthcare disaster as soon as the uncertain parameters are realized.

Based on standard stochastic programming theory (see the excellent books by Birge and Louveaux (1997) and Shapiro et al. (2009)), the first- and second-stage problems together form the following minimization problem for each country i:

$$\text{Minimize}\sum _{j=1}^I\sum _{k=1}^K{\rho }_{j,k}{q}_{ij,k}^1+\sum _{j=1}^I\sum _{k=1}^K{c}_{ji,k}^1\left(q^1\right)$$

$$+\sum _{\omega \in \text{Ω}}{p}_{\omega }[\sum _{j=1}^I\sum _{k=1}^K{\rho }_{j,k}^{\omega }{q}_{ij,k}^{2,\omega }+\sum _{j=1}^I\sum _{k=1}^K{c}_{ji,k}^{2,\omega }\left(q^{2,\omega }\right)+\sum _{k=1}^K{\beta }_{i,k}[d_{i,k}^{2,\omega }-\sum _{j=1}^I\left(q_{ij,k}^1+q_{ij,k}^{2,\omega }\right)]]$$ (7)

subject to:

$$\sum _{i=1}^I{q}_{ij,k}^1\le S_{j,k}^1,j=1,\dots ,I;k=1,\dots ,K,$$ (8)

$$\sum _{i=1}^I{q}_{ij,k}^{2,\omega }\le S_{j,k}^{2,\omega },j=1,\dots ,I;k=1,\dots ,K;\forall \omega \in \text{Ω},$$ (9)

$$q_{ij,k}^1\ge 0,j=1,\dots ,I;k=1,\dots ,K,$$ (10)

$$q_{ij,k}^{2,\omega }\ge 0,j=1,\dots ,I;k=1,\dots ,K;\forall \omega \in \text{Ω}.$$ (11)

We now define the necessary feasible sets. Let feasible set ${\mathcal{K}}_i$ correspond to country i. It depends only on the strategy vector of country i, where ${\mathcal{K}}_i\equiv \left\{q_i\text{such that}\left(10\right)\text{and}\left(11\right)\text{hold}\right\}$, where recall that $q_i$ is the vector of country i's medical item flows. Define ${\mathcal{K}}^1\equiv {\prod }_{i=1}^I{\mathcal{K}}_i$. Also, let $\mathcal{S}$ denote the feasible set of shared constraints: $\mathcal{S}\equiv \left\{q|\left(8\right)\text{and}\left(9\right)\text{hold}\right\}$, where q is the vector of all countries' medical item flows, and the feasible set. ${\mathcal{K}}^2\equiv {\mathcal{K}}^1\cap \mathcal{S}.$

We refer to objective function (7) as the Expected Disutility $E\left(D{U}_i\right)$ for $i=1,\dots ,I$. Assuming that the cost functions for each country are convex and continuously differentiable, we can state:

Definition 1

Stochastic Generalized Nash Equilibrium for the Countries

A strategy vector $q^{\text{*}}\in {\mathcal{K}}^2$ is a Stochastic Generalized Nash Equilibrium if for each country i; $i=1,\dots ,I$:

$$E\left(D{U}_i\left(q_i^{\text{*}},\widehat{q_i^{\text{*}}}\right)\right)\le E\left(D{U}_i\left(q_i,\widehat{q_i^{\text{*}}}\right)\right),\forall q_i\in {\mathcal{K}}_i\cap \mathcal{S},$$ (12)

where $\widehat{q_i^{\text{*}}}\equiv \left(q_1^{\text{*}},\dots ,q_{i-1}^{\text{*}},q_{i+1}^{\text{*}},\dots ,q_I^{\text{*}}\right)$.

Each government wishes to minimize its expected disutility. The above definition states that no government, given the circumstances and the strategies of the other national governments, at equilibrium, is willing unilaterally to change its vector of strategies, because it may end up with a higher expected disutility. We observe that the expected disutility of each country depends not only on the decisions of its government, but also on the strategies of other countries. Also, their feasible sets are interconnected because of the shared constraints. The latter condition makes the problem a Generalized Nash Equilibrium model (Debreu (1952)).

Generalized Nash Equilibrium problems can be formulated as quasivariational inequality problems (cf. Fischer et al. (2014)). However, the algorithms for the solution of such problems are not as advanced as those for variational inequality problems. As noted in Nagurney et al. (2017) and in Nagurney et al. (2019), we can define a Variational Equilibrium, which is a refinement and a specific type of GNE (cf. Kulkarni and Shanbhag (2012)), and enables a variational inequality formulation. It was used for the first time in Nagurney et al. (2020) in a stochastic setting for disaster relief.

Definition 2

Variational Equilibrium

A medical item flow vector $q^{\text{*}}$ is a Variational Equilibrium of the above Stochastic Generalized Nash Equilibrium problem if $q^{\text{*}}\in {\mathcal{K}}^2$ is a solution to the following variational inequality:

$$\sum _{i=1}^I⟨{\nabla }_{q_i}E\left[D{U}_i\left(q^{\text{*}}\right)\right],q_i-q_i^{\text{*}}⟩\ge 0,\forall q\in {\mathcal{K}}^2,$$ (13)

where $⟨\cdot ,\cdot ⟩$ denotes the inner product in $IIK+\left|\text{Ω}\right|\left(IIK\right)$-dimensional Euclidean space.

Note that the variational equilibrium guarantees that the Lagrange multipliers associated with the common constraints are the same for all the countries. This feature provides a helpful fairness and equity interpretation, and it makes perfect sense for countries involved in disaster management.

Hence, we can utilize the well-developed theory of variational inequalities (see Nagurney (1999) and the references therein). Expanding variational inequality (13), we have:

$$\sum _{i=1}^I\sum _{j=1}^I\sum _{k=1}^K\left[{\rho }_{j,k}+\sum _{r=1}^I\sum _{s=1}^K\frac{\partial c_{ri,s}^1\left(q^{1\text{*}}\right)}{\partial q_{ij,k}^1}-{\beta }_{i,k}\right]\times \left[q_{ij,k}^1-q_{ij,k}^{1\text{*}}\right]$$

$$+\sum _{\omega \in \text{Ω}}{p}_{\omega }\sum _{i=1}^I\sum _{j=1}^I\sum _{k=1}^K\left[{\rho }_{j,k}^{\omega }+\sum _{r=1}^I\sum _{s=1}^K\frac{\partial c_{ri,s}^{2,\omega }\left(q^{2,\omega \text{*}}\right)}{\partial q_{ij,k}^{2,\omega }}-{\beta }_{i,k}\right]\times [q_{ij,k}^{2,\omega }-q_{ij,k}^{2,\omega \text{*}}]\ge 0,\forall q\in {\mathcal{K}}^2.$$ (14)

We now put variational inequality (13) into standard variational inequality form (see Nagurney (1999)), that is: determine vector $X^{\text{*}}\in \mathcal{K}$, such that:

$$⟨F\left(X^{\text{*}}\right),X-X^{\text{*}}⟩\ge 0,\forall X\in \mathcal{K},$$ (15)

where $\mathcal{K}$ is a closed, convex set. In order to put VI (13) into the standard form, we define $X\equiv q$, $F\left(X\right)\equiv \left(F^1\left(X\right),F^2\left(X\right)\right)$, and $\mathcal{K}\equiv {\mathcal{K}}^2$ where:

$$F_{ij,k}^1\left(X\right)\equiv \left[{\rho }_{j,k}+\sum _{r=1}^I\sum _{s=1}^K\frac{\partial c_{ri,s}^1\left(q^1\right)}{\partial q_{ij,k}^1}-{\beta }_{i,k}\right],\forall i,j,k,$$

$$F_{ij,k}^{2,\omega }\left(X\right)\equiv p_{\omega }\left[{\rho }_{j,k}^{\omega }+\sum _{r=1}^I\sum _{s=1}^K\frac{\partial c_{ri,s}^{2,\omega }\left(q^{2,\omega }\right)}{\partial q_{ij,k}^{2,\omega }}-{\beta }_{i,k}\right],\forall i,j,k,\omega .$$ (16)

Under the imposed conditions, the function $F\left(X\right)$ that enters variational inequality problem (13) is continuous, and the feasible set ${\mathcal{K}}^2$ is compact; therefore, the existence of a solution to variational inequality (13) is guaranteed from the classical theory of variational inequalities (cf. Kinderlehrer and Stampacchia (1980)).

3.2. Illustrative examples

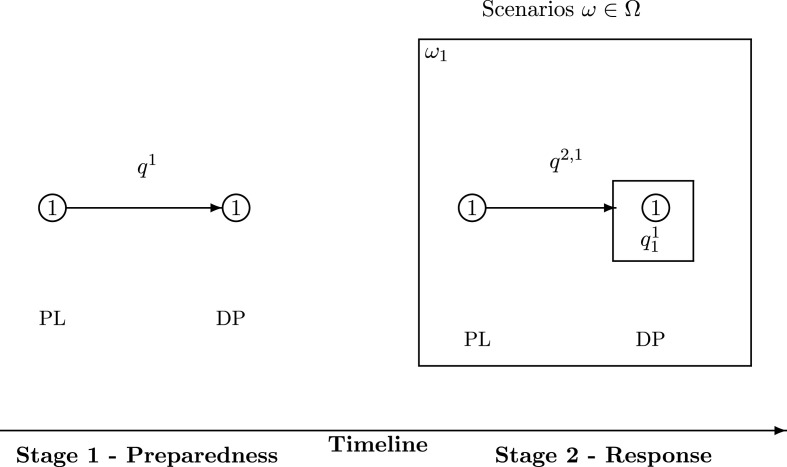
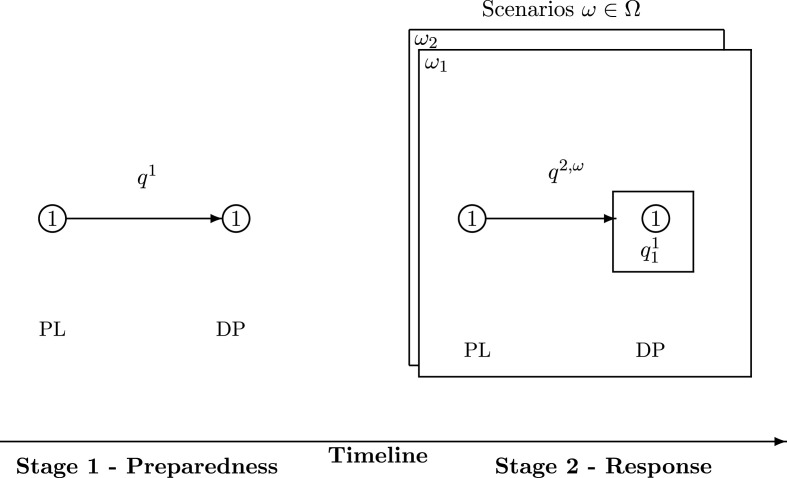
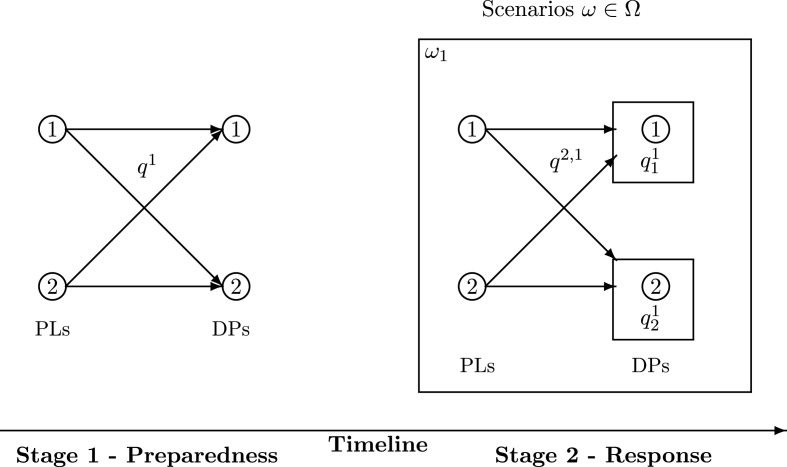
In this Subsection, we provide three illustrative examples that help to illuminate the model. The corresponding network figure depictions are given, respectively, in Fig. 2, Fig. 3, Fig. 4 . Henceforth, in this paper, in our notation for the superscripts, we utilize 1 for ${\omega }_1$, 2 for ${\omega }_2$, and so forth.

Fig. 2.

The timeline of illustrative example 1.

Fig. 3.

The timeline of the illustrative example 2.

Fig. 4.

The timeline of the illustrative example 3.

Illustrative Example 1: One National Government and One Scenario

In the first example, we have a single national government that is facing a pandemic with demand for N95 masks, a form of PPE. Also, the country will be faced with scenario ${\omega }_1=1$ with $p_{{\omega }_1}=1$. The data for this example are: ${\rho }_{\mathrm{1,1}}=2$, ${\rho }_{\mathrm{1,1}}^1=25$, ${\beta }_{\mathrm{1,1}}=3000$, $c_{\mathrm{11,1}}^1={\left(q_{\mathrm{11,1}}^1\right)}^2$, $c_{\mathrm{11,1}}^{\mathrm{2,1}}=2{\left(q_{\mathrm{11,1}}^{\mathrm{2,1}}\right)}^2$. The supply and the demand data are: $S_{\mathrm{1,1}}^1=2000$, $S_{\mathrm{1,1}}^{\mathrm{2,1}}=500$, and $d_{\mathrm{1,1}}^{\mathrm{2,1}}=3000$.

We can rewrite variational inequality (13); equivalently, variational inequality (14), for this example as: determine $q_{\mathrm{11,1}}^{1\ast }$ and $q_{\mathrm{11,1}}^{\mathrm{2,1}\ast }$, where $q_{\mathrm{11,1}}^{1\ast }\le 2000$ and $q_{\mathrm{11,1}}^{\mathrm{2,1}\ast }\le 500$, such that:

$$\left[2+2\left(q_{\mathrm{11,1}}^{1\ast }\right)-3000\right]\times \left[q_{\mathrm{11,1}}^1-q_{\mathrm{11,1}}^{1\ast }\right]+\left(1\right)\left[25+4\left(q_{\mathrm{11,1}}^{\mathrm{2,1}\ast }\right)-3000\right]\times \left[q_{\mathrm{11,1}}^{\mathrm{2,1}}-q_{\mathrm{11,1}}^{\mathrm{2,1}\ast }\right]\ge 0,$$ (17)

for all $q_{\mathrm{11,1}}^1$ and $q_{\mathrm{11,1}}^{\mathrm{2,1}}$ such that

$$q_{\mathrm{11,1}}^1\le 2000,q_{\mathrm{11,1}}^{\mathrm{2,1}}\le 500.$$

We denote by A the expression in (17) preceding the greater than or equal to sign. A can be rewritten as:

$$A=B\times B^{\prime }+C\times C^{″}.$$

Using A, we observe that

$$\begin{array}{l}\text{If }{q}_{\mathrm{11,1}}^{1\ast }=0\Rightarrow \text{always}B\times B^{\prime }\le 0;\\ \text{If }{q}_{\mathrm{11,1}}^{1\ast }=2000\Rightarrow \text{always }B\times B^{\prime }\le 0;\\ \text{If }0<q_{\mathrm{11,1}}^{1\ast }<2000\Rightarrow B^{\prime }\text{is unrestricted}\\ \Rightarrow \text{we desire that}B=0\Rightarrow q_{\mathrm{11,1}}^{1\ast }=1499\\ \text{Since}{q}_{\mathrm{11,1}}^{\mathrm{2,1}}\le 500\Rightarrow \text{always }C<0\Rightarrow \text{we desire that}{C}^{\prime }\le 0\Rightarrow q_{\mathrm{11,1}}^{\mathrm{2,1}\ast }=500.\end{array}$$

Therefore, we conclude that the solution to the associated variational inequality for this example is:

$$q_{\mathrm{11,1}}^{1\ast }=1499,q_{\mathrm{11,1}}^{\mathrm{2,1}\ast }=500.$$

We now demonstrate that variational inequality (14) is, indeed, satisfied. We note that this solution lies in the feasible set ${\mathcal{K}}^2$. Also, substitution of the values into A yields:

$$[2+2\left(1499\right)-3000]\times [q_{\mathrm{11,1}}^1-1499]+\left(1\right)[25+4\left(500\right)-3000]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-500]$$

$$=\left[0\right]\times [q_{\mathrm{11,1}}^1-1499]+[-975]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-500]$$

$$=\mathrm{487,500}-975\times q_{\mathrm{11,1}}^{\mathrm{2,1}},$$

which is clearly greater than or equal to zero since $q_{\mathrm{11,1}}^{\mathrm{2,1}}\le 500$.

We observe that the government purchases a total of 1999.00 items in two stages, with 1499.00 units purchased in the first stage, which can be placed in the national stockpile, and 500 items in the second stage. However, it still faces a shortage of 1001.00 N95 masks and that is because of the high logistical costs in stage 1 and the supply capacity in stage 2. The government's expected disutility under this solution is: $E\left(D{U}_1\left(q^{\text{*}}\right)\right)=\mathrm{5,765,499.00}$. The national government may wish to invest in enhancing production capacity in stage 2.

Illustrative Example 2: One National Government and Two Scenarios

In this example, in addition to the scenario ${\omega }_1=1$ from Example 1, the government predicts another scenario with a greater severity in stage 2. The probability of occurrence of these two scenarios according to government estimates are: $p_{{\omega }_1}=0.3$, $p_{{\omega }_2}=0.7$. In scenario ${\omega }_2=2$, due to the severity of the pandemic, demand increases sharply to $d_{\mathrm{1,1}}^{\mathrm{2,2}}=\mathrm{5,000}$ and the price of the medical item is raised to ${\rho }_{\mathrm{1,1}}^2=80$. The domestic PPE supply $S_{\mathrm{1,1}}^{\mathrm{2,2}}=\mathrm{1,000}$ in stage 2 in scenario ${\omega }_2$ and the transportation cost functions are similar in the two scenarios, $c_{\mathrm{11,1}}^1={\left(q_{\mathrm{11,1}}^1\right)}^2$, $c_{\mathrm{11,1}}^{\mathrm{2,1}}=2{\left(q_{\mathrm{11,1}}^{\mathrm{2,1}}\right)}^2$, $c_{\mathrm{11,1}}^{\mathrm{2,2}}=2{\left(q_{\mathrm{11,1}}^{\mathrm{2,2}}\right)}^2$.

We can rewrite variational inequality (13); equivalently, variational inequality (14), for this example as: determine $q_{\mathrm{11,1}}^{1\text{*}}$, $q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}$, and $q_{\mathrm{11,1}}^{\mathrm{2,2}\text{*}}$ such that

$$q_{\mathrm{11,1}}^{1\text{*}}\le 2000,q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}\le 500,q_{\mathrm{11,1}}^{\mathrm{2,2}\text{*}}\le 1000$$

and

$$[2+2\left(q_{\mathrm{11,1}}^{1\text{*}}\right)-3000]\times [q_{\mathrm{11,1}}^1-q_{\mathrm{11,1}}^{1\text{*}}]+\left(0.3\right)[25+4\left(q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}\right)-3000]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}]$$

$$+\left(0.7\right)[80+4\left(q_{\mathrm{11,1}}^{\mathrm{2,2}\text{*}}\right)-3000]\times [q_{\mathrm{11,1}}^{\mathrm{2,2}}-q_{\mathrm{11,1}}^{\mathrm{2,2}\text{*}}]\ge 0,$$

for all $q_{\mathrm{11,1}}^1$, $q_{\mathrm{11,1}}^{\mathrm{2,1}}$, and $q_{\mathrm{11,1}}^{\mathrm{2,2}}$ satisfying:

$$q_{\mathrm{11,1}}^1\le 2000,q_{\mathrm{11,1}}^{\mathrm{2,1}}\le 500,q_{\mathrm{11,1}}^{\mathrm{2,2}}\le 1000.$$

Proceeding in a similar manner as that in Example 1, yields:

$$q_{\mathrm{11,1}}^{1\text{*}}=\mathrm{1,499.00},q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}=500.00,q_{\mathrm{11,1}}^{\mathrm{2,2}\text{*}}=730.00,$$

Indeed, substitution of the above medical item pattern into the variational inequality yields:

$$[2+2\left(1499\right)-3000]\times [q_{\mathrm{11,1}}^1-1499]+\left(0.3\right)[25+4\left(500\right)-3000]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-500]$$

$$+\left(0.7\right)[80+4\left(730\right)-3000]\times [q_{\mathrm{11,1}}^{\mathrm{2,2}}-730]$$

$$=\left[0\right]\times [q_{\mathrm{11,1}}^1-1499]+[-292.5]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-500]+\left[0\right]\times [q_{\mathrm{11,1}}^{\mathrm{2,2}}-730]$$

$$=146250-292.5q_{\mathrm{11,1}}^{\mathrm{2,1}},$$

which is greater than or equal to zero since $q_{\mathrm{11,1}}^{\mathrm{2,1}}\le 500$.

The expected disutility increases to $E\left(D{U}_1\left(q^{\text{*}}\right)\right)=\mathrm{9,910,689.00}$ in Example 2. We observe that with the addition of a severe disaster scenario, the government ends up in a much worse situation than in Example 1. Despite the higher supply availability, the country continues to face severe shortages: 1001 items under scenario ${\omega }_1$ and 2771 items under scenario ${\omega }_2$.

Illustrative Example 3: Two National Governments and One Scenario

This example is constructed from the first example, with the difference that now there are two governments trying to procure N95 masks for their countries and competing over limited supplies. The data for the second country are: ${\rho }_{\mathrm{2,1}}=2$, ${\rho }_{\mathrm{2,1}}^1=120$, ${\beta }_{\mathrm{2,1}}=3000$, $S_{\mathrm{2,1}}^1=2000$, $S_{\mathrm{2,1}}^{\mathrm{2,1}}=500$, $d_{\mathrm{2,1}}^{\mathrm{2,1}}=5000$, $c_{\mathrm{22,1}}^1={\left(q_{\mathrm{22,1}}^1\right)}^2$, $c_{\mathrm{22,1}}^{\mathrm{2,1}}=2{\left(q_{\mathrm{22,1}}^{\mathrm{2,1}}\right)}^2$. Also, the transportation cost functions between the two countries are as follows:

$$c_{\mathrm{21,1}}^1\left(q^1\right)=2{\left(q_{\mathrm{12,1}}^1\right)}^2+5q_{\mathrm{12,1}}^1,c_{\mathrm{21,1}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=12{\left(q_{\mathrm{12,1}}^{\mathrm{2,1}}\right)}^2+5q_{\mathrm{12,1}}^{\mathrm{2,1}},$$

$$c_{\mathrm{12,1}}^1\left(q^1\right)=2{\left(q_{\mathrm{21,1}}^1\right)}^2+5q_{\mathrm{21,1}}^1,c_{\mathrm{12,1}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=6{\left(q_{\mathrm{21,1}}^{\mathrm{2,1}}\right)}^2+5q_{\mathrm{21,1}}^{\mathrm{2,1}}.$$

Making use of the variational inequality (14), it is straightforward to determine that the equilibrium solution for this example is:

$$q_{\mathrm{11,1}}^{1\text{*}}=\mathrm{1,334.17},q_{\mathrm{12,1}}^{1\text{*}}=665.83,q_{\mathrm{21,1}}^{1\text{*}}=665.83,q_{\mathrm{22,1}}^{1\text{*}}=\mathrm{1,334.17},$$

$$q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}=375.31,q_{\mathrm{12,1}}^{\mathrm{2,1}\text{*}}=71.25,q_{\mathrm{21,1}}^{\mathrm{2,1}\text{*}}=124.69,q_{\mathrm{22,1}}^{\mathrm{2,1}\text{*}}=428.75.$$

The above solution is feasible and satisfies variational inequality (14). Indeed, observe that:

$$[2+2\left(1334.17\right)-3000]\times [q_{\mathrm{11,1}}^1-1334.17]+[2+4\left(665.83\right)+5-3000]\times [q_{\mathrm{12,1}}^1-665.83]$$

$$+[2+4\left(665.83\right)+5-3000]\times [q_{\mathrm{21,1}}^1-665.83]+[2+2\left(1334.17\right)-3000]\times [q_{\mathrm{22,1}}^1-1334.17]$$

$$+[25+4\left(375.31\right)-3000]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-375.31]+[120+24\left(71.25\right)+5-3000]\times [q_{\mathrm{12,1}}^{\mathrm{2,1}}-71.25]$$

$$+[25+12\left(124.69\right)+5-3000]\times [q_{\mathrm{21,1}}^{\mathrm{2,1}}-124.69]+[120+4\left(428.75\right)-3000]\times [q_{\mathrm{22,1}}^{\mathrm{2,1}}-428.75]$$

$$=[-329.66]\times [q_{\mathrm{11,1}}^1-1334.17]+[-329.66]\times [q_{\mathrm{12,1}}^1-665.83]$$

$$+[-329.66]\times [q_{\mathrm{21,1}}^1-665.83]+[-329.66]\times [q_{\mathrm{22,1}}^1-1334.17]$$

$$+[-1473.72]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-375.31]+[-1165]\times [q_{\mathrm{12,1}}^{\mathrm{2,1}}-71.25]$$

$$+[-1473.72]\times [q_{\mathrm{21,1}}^{\mathrm{2,1}}-124.69]+[-1165]\times [q_{\mathrm{22,1}}^{\mathrm{2,1}}-428.75]$$

$$=2638000-329.66\times \left(q_{\mathrm{11,1}}^1+q_{\mathrm{12,1}}^1+q_{\mathrm{21,1}}^1+q_{\mathrm{22,1}}^1\right)$$

$$-1473.72\times \left(q_{\mathrm{11,1}}^{\mathrm{2,1}}+q_{\mathrm{21,1}}^{\mathrm{2,1}}\right)-1165\times \left(q_{\mathrm{12,1}}^{\mathrm{2,1}}+q_{\mathrm{22,1}}^{\mathrm{2,1}}\right),$$

which is greater than or equal to zero for any feasible medical item shipments.

In the first stage, both national governments manage to procure 2000 items and utilize all their domestic supplies. Observe that each government makes more purchases domestically, which is due to lower logistical costs than buying from the other country. However, in stage 2, the prices of the N95 masks in both countries have risen sharply. Country 2, which has a higher demand than country 1, has a higher price than country 1. Also, the cost of transporting the masks from country 2 to country 1 after the pandemic declaration is much higher than the cost on the opposite route. As a result, in stage 2, country 1 adds 446.56 medical items, while country 2 purchases 553.44 items. We can see the effect of a sharp increase in the transportation cost from country 2, which has led to most of its mask supply being purchased by country 2.

Country 1 faces a shortage of 553.44 medical items and its expected disutility is equal to $E\left(D{U}_1\left(q^{\text{*}}\right)\right)=\mathrm{4,695,240.86}$. Country 2 faces a severe shortage of 2446.56 medical items while the expected disutility of country 2 is $E\left(D{U}_2\left(q^{\text{*}}\right)\right)=\mathrm{10,529,807.32}$. An interesting and significant point in Example 3 is that country 1 has a lower shortage than what it was dealing with in Example 1. The reason is the addition of another country with supplies gives governments more options. In times of disaster, having more suppliers can help and, unlike in Examples 1 and 2, there is no unsold capacity Example 3. The national governments purchase all the available medical supplies to reduce the shortages of N95 masks in their countries.

4. The algorithm and alternative variational inequality formulation

Before presenting the algorithm, we define the necessary Lagrange multipliers related to the constraints and provide an alternative variational inequality to variational inequality (14), which we utilize here to derive the closed form expressions for the variables at each iteration of the proposed algorithmic scheme. We associate Lagrange multiplier ${\alpha }_{j,k}^1$ with the supply constraint (8) on the availability of medical item k in country j, for each j and each k. We also let ${\gamma }_{j,k}^{2,\omega }$ be the Lagrange multiplier associated with supply constraint (9) on medical item k in country j when scenario ω occurs, for each j and k. We gather these Lagrange multipliers into the respective vectors: ${\alpha }^1\in R_{+}^{IK}$ and ${\gamma }^2\in R_{+}^{\left|\text{Ω}\right|\left(IK\right)}$.

Therefore, variational inequality (14) can be reformulated as the following variational inequality (cf. arguments in Nagurney et al. (2019)): determine $\left(q^{\text{*}},{\alpha }^{1\text{*}},{\gamma }^{2\text{*}}\right)\in R_{+}^{IIK+\left|\text{Ω}\right|\left(IIK\right)+IK+\left|\text{Ω}\right|\left(IK\right)}$ such that

$$\sum _{i=1}^I\sum _{j=1}^I\sum _{k=1}^K\left[{\rho }_{j,k}+\sum _{r=1}^I\sum _{s=1}^K\frac{\partial c_{ri,s}^1\left(q^{1\text{*}}\right)}{\partial q_{ij,k}^1}-{\beta }_{i,k}+{\alpha }_{j,k}^{1\text{*}}\right]\times [q_{ij,k}^1-q_{ij,k}^{1\text{*}}]$$

$$+\sum _{\omega \in \text{Ω}}{p}_{\omega }\sum _{i=1}^I\sum _{j=1}^I\sum _{k=1}^K\left[{\rho }_{j,k}^{\omega }+\sum _{r=1}^I\sum _{s=1}^K\frac{\partial c_{ri,s}^{2,\omega }\left(q^{2,\omega \text{*}}\right)}{\partial q_{ij,k}^{2,\omega }}-{\beta }_{i,k}+{\gamma }_{j,k}^{2,\omega \text{*}}\right]\times [q_{ij,k}^{2,\omega }-q_{ij,k}^{2,\omega \text{*}}]$$

$$\begin{array}{l}+\sum _{j=1}^I\sum _{k=1}^K\left[S_{j,k}^1-\sum _{i=1}^I{q}_{ij,k}^{1\text{*}}\right]\times [{\alpha }_{j,k}^1-{\alpha }_{j,k}^{1\text{*}}]+\\ \sum _{\omega \in \text{Ω}}\sum _{j=1}^I\sum _{k=1}^K\left[S_{j,k}^{2,\omega }-\sum _{i=1}^I{q}_{ij,k}^{2,\omega \text{*}}\right]\times \left[{\gamma }_{j,k}^{2,\omega }-{\gamma }_{j,k}^{2,\omega \text{*}}\right]\ge 0,\\ \forall \left(q,{\alpha }^1,{\gamma }^2\right)\in R_{+}^{IIK+\left|\text{Ω}\right|\left(IIK\right)+IK+\left|\text{Ω}\right|\left(IK\right)}.\end{array}$$ (18)

4.1. Revisiting examples 1 through 3

Accordingly, we can construct functions in VI (18) using data in Example 1 as below, where ${\alpha }_{\mathrm{1,1}}^{1\text{*}}=0$ and ${\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}=975$:

$$[2+2\left(1499\right)-3000+0]\times [q_{\mathrm{11,1}}^1-1499]+\left(1\right)[25+4\left(500\right)-3000+975]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-500]$$

$$+[2000-1499]\times [{\alpha }_{\mathrm{1,1}}^1-0]+[500-500]\times [{\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}}-975].$$

Noting that the first, second, and fourth terms in the above expression are equal to zero and the third term is greater than or equal to zero for nonnegative ${\alpha }_{\mathrm{1,1}}^1$, VI (17) holds for Example 1.

In Example 2, the full supply capacity is not used in stage 1 and in scenario 2 of stage 2. Hence, the associated Lagrange multipliers, ${\alpha }_{\mathrm{1,1}}^{1\text{*}}$, and ${\gamma }_{\mathrm{1,1}}^{\mathrm{2,2}\text{*}}$, are equal to zero. However, the country government utilizes all the supply in scenario 1 of stage 2, with ${\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}=975$. Using the above and the equilibrium medical iten flow solution of Example 2 in VI (17), we obtain:

$$[2+2\left(1499\right)-300+0]\times [q_{\mathrm{11,1}}^1-1499]+\left(0.3\right)[25+4\left(500\right)-3000+975]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-500]$$

$$+\left(0.7\right)[80+4\left(730\right)-3000+0]\times [q_{\mathrm{11,1}}^{\mathrm{2,2}}-730]$$

$$+[2000-1499]\times [{\alpha }_{\mathrm{1,1}}^1-0]+[500-500]\times [{\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}}-975]+[5000-730]\times [{\gamma }_{\mathrm{1,1}}^{\mathrm{2,2}}-0].$$

All terms in the expression above are equal to zero except for the fourth and final ones, which are both greater than or equal to zero, respectively, for any nonnegative ${\alpha }_{\mathrm{1,1}}^1$ and ${\gamma }_{\mathrm{1,1}}^{\mathrm{2,2}}$. Hence, clearly, VI (18) holds.

In Example 3, all the available supplies of the medical item are purchased and the supply constraints are, therefore, binding. The associated Lagrange multipliers are all positive with values at equilibrium as below:

$${\alpha }_{\mathrm{1,1}}^{1\text{*}}=329.66,{\alpha }_{\mathrm{2,1}}^{1\text{*}}=329.66,{\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}=1473.72,{\gamma }_{\mathrm{2,1}}^{\mathrm{2,1}\text{*}}=1165.00,$$

Indeed, using the data from Example 3, we can construct the function F(X) that enters VI (18) for Example 3 as:

$$[2+2q_{\mathrm{11,1}}^{1\text{*}}-3000+{\alpha }_{\mathrm{1,1}}^{1\text{*}}]\times [q_{\mathrm{11,1}}^1-q_{\mathrm{11,1}}^{1\text{*}}]+[2+4q_{\mathrm{12,1}}^{1\text{*}}+5-3000+{\alpha }_{\mathrm{2,1}}^{1\text{*}}]\times [q_{\mathrm{12,1}}^1-q_{\mathrm{12,1}}^{1\text{*}}]$$

$$+[2+4q_{\mathrm{21,1}}^{1\text{*}}+5-3000+{\alpha }_{\mathrm{1,1}}^{1\text{*}}]\times [q_{\mathrm{21,1}}^1-q_{\mathrm{21,1}}^{1\text{*}}]+[2+2q_{\mathrm{22,1}}^{1\text{*}}-3000+{\alpha }_{\mathrm{2,1}}^{1\text{*}}]\times [q_{\mathrm{22,1}}^1-q_{\mathrm{22,1}}^{1\text{*}}]$$

$$+[25+4q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}-3000+{\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}]\times [q_{\mathrm{11,1}}^{\mathrm{2,1}}-q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}]+[120+24q_{\mathrm{12,1}}^{\mathrm{2,1}\text{*}}+5-3000+{\gamma }_{\mathrm{2,1}}^{\mathrm{2,1}\text{*}}]\times [q_{\mathrm{12,1}}^{\mathrm{2,1}}-q_{\mathrm{12,1}}^{\mathrm{2,1}\text{*}}]$$

$$+[25+12q_{\mathrm{21,1}}^{\mathrm{2,1}\text{*}}+5-3000+{\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}]\times [q_{\mathrm{21,1}}^{\mathrm{2,1}}-q_{\mathrm{21,1}}^{\mathrm{2,1}\text{*}}]+[120+4q_{\mathrm{22,1}}^{\mathrm{2,1}\text{*}}-3000+{\gamma }_{\mathrm{2,1}}^{\mathrm{2,1}\text{*}}]\times [q_{\mathrm{22,1}}^{\mathrm{2,1}}-q_{\mathrm{22,1}}^{\mathrm{2,1}\text{*}}]$$

$$+[2000-q_{\mathrm{11,1}}^{1\text{*}}-q_{\mathrm{21,1}}^{1\text{*}}]\times [{\alpha }_{\mathrm{1,1}}^1-{\alpha }_{\mathrm{1,1}}^{1\text{*}}]+[2000-q_{\mathrm{12,1}}^{1\text{*}}-q_{\mathrm{22,1}}^{1\text{*}}]\times [{\alpha }_{\mathrm{2,1}}^1-{\alpha }_{\mathrm{2,1}}^{1\text{*}}]$$

$$+[500-q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}-q_{\mathrm{21,1}}^{\mathrm{2,1}\text{*}}]\times [{\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}}-{\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}]+[500-q_{\mathrm{12,1}}^{\mathrm{2,1}\text{*}}-q_{\mathrm{22,1}}^{\mathrm{2,1}\text{*}}]\times [{\gamma }_{\mathrm{2,1}}^{\mathrm{2,1}}-{\gamma }_{\mathrm{2,1}}^{\mathrm{2,1}\text{*}}].$$

Substituting the above values for the Lagrange multipliers as well as the product flows reported for Example 3 in Section 3.2, we obtain:

$$\left(2+2\left(1334.17\right)-3000+329.66\right)\times \left(q_{\mathrm{11,1}}^1-1334.17\right)+\left(2+4\left(665.83\right)+5-3000+329.66\right)\times \left(q_{\mathrm{12,1}}^1-665.83\right)$$

$$+\left(2+4\left(665.83\right)+5-3000+329.66\right)\times \left(q_{\mathrm{21,1}}^1-665.83\right)+\left(2+2\left(1334.17\right)-3000+329.66\right)\times \left(q_{\mathrm{22,1}}^1-1334.17\right)$$

$$+\left(25+4\left(375.31\right)-3000+1473.72\right)\times \left(q_{\mathrm{11,1}}^{\mathrm{2,1}}-375.31\right)+\left(120+24\left(71.25\right)+5-3000+1165\right)\times \left(q_{\mathrm{12,1}}^{\mathrm{2,1}}-71.25\right)$$

$$+\left(25+12\left(124.69\right)+5-3000+1473.72\right)\times \left(q_{\mathrm{21,1}}^{\mathrm{2,1}}-124.69\right)+\left(120+4\left(428.75\right)-3000+1165\right)\times \left(q_{\mathrm{22,1}}^{\mathrm{2,1}}-428.75\right).$$

But the above expression can be rewritten as:

$${\epsilon }^1\times \left(q_{\mathrm{11,1}}^1-1334.17\right)+{\tau }^1\times \left(q_{\mathrm{12,1}}^1-665.83\right)+{\epsilon }^1\times \left(q_{\mathrm{21,1}}^1-665.83\right)+{\tau }^1\times \left(q_{\mathrm{22,1}}^1-1334.17\right)$$

$$+{\epsilon }^2\times \left(q_{\mathrm{11,1}}^{\mathrm{2,1}}-375.31\right)+{\tau }^2\times \left(q_{\mathrm{12,1}}^{\mathrm{2,1}}-71.25\right)+{\epsilon }^2\times \left(q_{\mathrm{21,1}}^{\mathrm{2,1}}-124.69\right)+{\tau }^2\times \left(q_{\mathrm{22,1}}^{\mathrm{2,1}}-428.75\right),$$

or

$${\epsilon }^1\times \left(q_{\mathrm{11,1}}^1+q_{\mathrm{21,1}}^1-2000\right)+{\tau }^1\times \left(q_{\mathrm{12,1}}^1+q_{\mathrm{22,1}}^1-2000\right)+{\epsilon }^2\times \left(q_{\mathrm{11,1}}^{\mathrm{2,1}}+q_{\mathrm{21,1}}^{\mathrm{2,1}}-500\right)+{\tau }^2\times \left(q_{\mathrm{12,1}}^{\mathrm{2,1}}+q_{\mathrm{22,1}}^{\mathrm{2,1}}-500\right).$$

We know that ${\epsilon }^1={\epsilon }^2={\tau }^1={\tau }^2=0$. Therefore, VI (18) holds and the above is, indeed, the Generalized Nash Equilibrium solution.

4.2. The algorithm

In this Subsection, we present the algorithm to solve the variational inequality (18). The algorithm that we utilize to compute the solutions of the numerical examples in the next section is the modified projection method (see Korpelevich (1977) and Nagurney (1999)). This algorithm is guaranteed to converge if the function F(X) that enters the variational inequality is monotone and Lipschitz continuous, and that a solution exists (see Nagurney (1999)).

The Modified Projection Method.

Step 0: Initialization.

Initialize with $X^0\in \mathcal{K}$. Set $\tau :=1$ and select ψ, such that $0<\psi \le \frac{1}{L}$, where L is the Lipschitz continuity constant for $F\left(X\right)$.

Step 1: Construction and Computation.

Compute ${\bar{X}}^{\tau -1}$ by solving the variational inequality subproblem:

$$⟨{\bar{X}}^{\tau -1}+\left(\psi F\left(X^{\tau -1}\right)-X^{\tau -1}\right),X-{\bar{X}}^{\tau -1}⟩\ge 0,\forall X\in \mathcal{K}.$$ (19)

Step 2: Adaptation.

Compute $X^{\tau }$ by solving the variational inequality subproblem:

$$⟨X^{\tau }+\left(\psi F\left({\bar{X}}^{\tau -1}\right)-X^{\tau -1}\right),X-X^{\tau }⟩\ge 0,\forall X\in \mathcal{K}.$$ (20)

Step 3: Convergence Verification.

If $|X^{\tau }-X^{\tau -1}|\le \epsilon$, with $\epsilon >0$, a pre-specified tolerance, then stop; otherwise set $\tau :=\tau +1$, and go to Step 1.

Steps 1 and 2 of the modified projection method (cf. (18) and (19)) result in explicit formulae for the computation of the medical supply flows and the Lagrange multipliers at each iteration of the algorithm. In particular, at each iteration of the algorithm, we have the following explicit formulae for Step 1. Similar explicit formulae can be determined accordingly for Step 2.

Explicit Formulae for Step 1 for the Medical Supply Flows in Stage 1.

For each $i,j,k$, compute

$${\left({\bar{q}}_{ij,k}^1\right)}^{\tau }=\text{max}\left\{0,{\left(q_{ij,k}^1\right)}^{\tau -1}-\psi \left({\rho }_{j,k}+\sum _{r=1}^I\sum _{s=1}^K\frac{\partial c_{ri,s}^1\left({\left(q^1\right)}^{\tau -1}\right)}{\partial q_{ij,k}^1}-{\beta }_{i,k}+{\left({\alpha }_{j,k}^1\right)}^{\tau -1}\right)\right\};$$ (21)

Explicit Formulae for Step 1 for the Medical Supply Flows in Stage 2.

For each $\omega ,i,j,k$, compute

$${\left({\bar{q}}_{ij,k}^{2,\omega }\right)}^{\tau }=\text{max}\left\{0,{\left(q_{ij,k}^{2,\omega }\right)}^{\tau -1}-\psi p_{\omega }\left({\rho }_{j,k}^{\omega }+\sum _{r=1}^I\sum _{s=1}^K\frac{\partial c_{ri,s}^{2,\omega }\left({\left(q^{2,\omega }\right)}^{\tau -1}\right)}{\partial q_{ij,k}^{2,\omega }}-{\beta }_{i,k}+{\left({\gamma }_{j,k}^{2,\omega }\right)}^{\tau -1}\right)\right\};$$ (22)

Explicit Formulae for Step 1 the Lagrange Multipliers Associated with the Supply Constraints in Stage 1.

For each $j,k$, compute

$${\left({\bar{\alpha }}_{j,k}^1\right)}^{\tau }=\text{max}\left\{0,{\left({\alpha }_{j,k}^1\right)}^{\tau -1}-\psi \left(S_{j,k}^1-\sum _{i=1}^I{\left(q_{ij,k}^1\right)}^{\tau -1}\right)\right\};$$ (23)

Explicit Formulae for Step 1 for the Lagrange Multipliers Associated with the Supply Constraints in Stage 2.

For each $\omega ,j,k$, compute

$${\left({\bar{\gamma }}_{j,k}^{2,\omega }\right)}^{\tau }=\text{max}\left\{0,{\left({\gamma }_{j,k}^{2,\omega }\right)}^{\tau -1}-\psi \left(S_{j,k}^{2,\omega }-\sum _{i=1}^I{\left(q_{ij,k}^{2,\omega }\right)}^{\tau -1}\right)\right\}.$$ (24)

5. Numerical examples

The examples in this section are inspired by the Covid-19 pandemic. When the global outbreak occurred, the demand for PPEs was much higher than the inventory and production capacities; for example, the United States, before the pandemic, needed about 50 million N95 masks annually, but during the Covid-19 pandemic, the demand increased significantly to about 140 million face masks during a 90-day peak-use period (Lopez (2020b)). Italy, another country that was hit severely by the pandemic, had a monthly demand of over 90 million masks during the crisis, and most of this requirement was met by imports from China (GlobeNewswire (2020)). But China itself, which has almost 38 million healthcare, transportation, and manufacturing industries staff, would require 238 million masks every day (Xie (2020)).

Disruptions in the supply chain also added to the shortage crisis of medical supplies. Over 90% of international PPE shipments have been disrupted in some way. For example, the air freight delivery time from China to the United States, which used to be about 4–6 days, has now reached 8–14 days. Also, the cost of shipping PPEs from China has gone up to 3–4 times of the pre-pandemic rates; additionally, an increase in the price of masks plus transportation disruptions have resulted in the growth in cargo insurance rates as well (C.H. Robinson (2020)). Although the production process has been disrupted in many areas, some governments and companies made every effort to increase production capacity. The U.S. Department of Defense intends to increase the production capacity to 450 million masks a year by October and to have a total domestic production of over a billion masks per year starting 2021 (Lopez (2020b)). China, where half of the world's masks were made before the pandemic, has significantly increased its daily production capacity from around 10 million to 116 million (Xie (2020)).

5.1. Numerical examples detailed

We utilize the information about the current pandemic in the following examples to investigate the competition for medical supplies under different scenarios. The modified projection method was implemented in MATLAB and the computer system used was a Microsoft Windows 10 system. We initialized the algorithm so that all the medical item flows and the Lagrange multipliers were set to 0.00. The convergence tolerance for all the examples was that the absolute value of each of the computed variable values at two successive iterations was less than or equal to 0.0001. We set the ψ parameter in the modified projection method to 0.1.

Numerical Example 1: Two Countries, One Type of Medical Supply, Two Scenarios.

In the first numerical example, there are two countries and two scenarios. The medical item is the N95 mask. In the first scenario, ${\omega }_1=1$, the pandemic is severe and the demand for such PPEs in both countries is very high. The second scenario, ${\omega }_2=2$, is one in which the consequences of the pandemic are less and the countries have a lower demand. As a result, the national governments in both countries take action in two stages, before and after the pandemic declaration, to purchase the PPEs. They purchase the N95 masks in large bulks of 1000 masks each; therefore, $q_{ij,1}^1$ represents 1000 of N95 masks purchased by country i from country j in stage 1. Both countries have supplies of N95 masks. The example's data are as follows.

$$p_{{\omega }_1}=0.7,p_{{\omega }_2}=0.3,$$

$${\rho }_{\mathrm{1,1}}=\mathrm{1,000},S_{\mathrm{1,1}}^1=\mathrm{20,000}{\rho }_{\mathrm{1,1}}^1=\mathrm{5,000},S_{\mathrm{1,1}}^{\mathrm{2,1}}=\mathrm{7,000},{\rho }_{\mathrm{1,1}}^2=\mathrm{2,000},S_{\mathrm{1,1}}^{\mathrm{2,2}}=\mathrm{20,000},$$

$${\rho }_{\mathrm{2,1}}=\mathrm{1,000},S_{\mathrm{2,1}}^1=\mathrm{25,000}{\rho }_{\mathrm{2,1}}^1=\mathrm{2,500},S_{\mathrm{2,1}}^{\mathrm{2,1}}=\mathrm{25,000},{\rho }_{\mathrm{2,1}}^2=\mathrm{2,000},S_{\mathrm{2,1}}^{\mathrm{2,2}}=\mathrm{40,000},$$

$${\beta }_{\mathrm{1,1}}={\beta }_{\mathrm{2,1}}=\mathrm{100,000},d_{\mathrm{1,1}}^{\mathrm{2,1}}=d_{\mathrm{2,1}}^{\mathrm{2,1}}=\mathrm{80,000},d_{\mathrm{1,1}}^{\mathrm{2,2}}=d_{\mathrm{2,1}}^{\mathrm{2,2}}=\mathrm{55,000},$$

$$c_{\mathrm{11,1}}^1=2{\left(q_{\mathrm{11,1}}^1\right)}^2,c_{\mathrm{22,1}}^1=2{\left(q_{\mathrm{22,1}}^1\right)}^2,$$

$$c_{\mathrm{21,1}}^1\left(q^1\right)=5{\left(q_{\mathrm{12,1}}^1\right)}^2+3q_{\mathrm{12,1}}^1,c_{\mathrm{12,1}}^1\left(q^1\right)=5{\left(q_{\mathrm{21,1}}^1\right)}^2+3q_{\mathrm{21,1}}^1,$$

$$c_{\mathrm{11,1}}^{\mathrm{2,1}}=5{\left(q_{\mathrm{11,1}}^{\mathrm{2,1}}\right)}^2,c_{\mathrm{22,1}}^{\mathrm{2,1}}=3{\left(q_{\mathrm{22,1}}^{\mathrm{2,1}}\right)}^2,$$

$$c_{\mathrm{21,1}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=9{\left(q_{\mathrm{12,1}}^{\mathrm{2,1}}\right)}^2+6q_{\mathrm{12,1}}^{\mathrm{2,1}},c_{\mathrm{12,1}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=9{\left(q_{\mathrm{21,1}}^{\mathrm{2,1}}\right)}^2+6q_{\mathrm{21,1}}^{\mathrm{2,1}},$$

$$c_{\mathrm{11,1}}^{\mathrm{2,2}}=2{\left(q_{\mathrm{11,1}}^{\mathrm{2,2}}\right)}^2,c_{\mathrm{22,1}}^{\mathrm{2,2}}=2{\left(q_{\mathrm{22,1}}^{\mathrm{2,2}}\right)}^2,$$

$$c_{\mathrm{21,1}}^{\mathrm{2,2}}\left(q^{\mathrm{2,2}}\right)=5{\left(q_{\mathrm{12,1}}^{\mathrm{2,2}}\right)}^2+3q_{\mathrm{12,1}}^{\mathrm{2,2}},c_{\mathrm{12,1}}^{\mathrm{2,2}}\left(q^{\mathrm{2,2}}\right)=5{\left(q_{\mathrm{21,1}}^{\mathrm{2,2}}\right)}^2+3q_{\mathrm{21,1}}^{\mathrm{2,2}}.$$

The computed equilibrium solution via the modified projection method for this example is:

$$q_{\mathrm{11,1}}^{1\text{*}}=\mathrm{14,285.92},q_{\mathrm{12,1}}^{1\text{*}}=\mathrm{7,142.64},q_{\mathrm{21,1}}^{1\text{*}}=\mathrm{5,714.07},q_{\mathrm{22,1}}^{1\text{*}}=\mathrm{17,857.35},$$

$$q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}=\mathrm{4,500.22},q_{\mathrm{12,1}}^{\mathrm{2,1}\text{*}}=\mathrm{5,416.33},q_{\mathrm{21,1}}^{\mathrm{2,1}\text{*}}=\mathrm{2,499.78},q_{\mathrm{22,1}}^{\mathrm{2,1}\text{*}}=\mathrm{16,250.00},$$

$$q_{\mathrm{11,1}}^{\mathrm{2,2}\text{*}}=\mathrm{14,285.92},q_{\mathrm{12,1}}^{\mathrm{2,2}\text{*}}=\mathrm{9,799.70},q_{\mathrm{21,1}}^{\mathrm{2,2}\text{*}}=\mathrm{5,714.07},q_{\mathrm{22,1}}^{\mathrm{2,2}\text{*}}=\mathrm{24,500.00},$$

$${\alpha }_{\mathrm{1,1}}^{1\text{*}}=\mathrm{41,856.28},{\alpha }_{\mathrm{2,1}}^{1\text{*}}=\mathrm{27,570.57},$$

$${\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}=\mathrm{49,997.79},{\gamma }_{\mathrm{2,1}}^{\mathrm{2,1}\text{*}}=0.00,{\gamma }_{\mathrm{1,1}}^{\mathrm{2,2}\text{*}}=\mathrm{40,856.28},{\gamma }_{\mathrm{2,1}}^{\mathrm{2,2}\text{*}}=0.00.$$

We observe that country 1 is very vulnerable in the face of scenario 1. The available supply of the masks in the country have been drastically reduced, while the transportation costs have also increased due to the pandemic. As a result, country 1 faces a shortage of 48,654.87 units, which is equal to $\mathrm{48,654,870}$ N95 masks. On the other hand, the government of country 2 has a higher supply of masks available in the country in scenario 1 and is in a better position than country 1. However, due to insufficient total available supply, country 2 also faces a large shortage of 37,678.78 units. In scenario 2, where the consequences of the pandemic are less severe, both countries have better conditions than in scenario 1, but country 2, with a significantly greater supply in its country, faces a much smaller shortage than country 1.

Both countries are not prepared sufficiently to respond to the pandemic, but country 2, which has greater flexibility and resilience in terms of its country's supply, performs better in reducing the shortage of face masks post the disaster. Another noteworthy point is that country 2 expends a lot of money to purchase and transport the PPEs, which leads to almost equal expected disutilities for the two countries, $E\left(D{U}_1\left(q^{\text{*}}\right)\right)=\mathrm{1,318,107,953.24}$, $E\left(D{U}_2\left(q^{\text{*}}\right)\right)=\mathrm{1,337,948,865.88}.$

Numerical Example 2: Two Countries, Two Types of Medical Supplies, Two Scenarios.

In Numerical Example 2, in addition to the face masks, the countries are also trying to meet their demand for ventilators. The need for these devices is less than the demand for the face masks, but the value of a ventilator in saving lives in this pandemic is very high. Also, these devices are expensive, especially once the pandemic occurs. The additional data needed for this example are:

$${\rho }_{\mathrm{1,2}}=\mathrm{10,000},S_{\mathrm{1,2}}^1=\mathrm{2,000}{\rho }_{\mathrm{1,2}}^1=\mathrm{45,000},S_{\mathrm{1,2}}^{\mathrm{2,1}}=\mathrm{2,000},{\rho }_{\mathrm{1,2}}^2=\mathrm{20,000},S_{\mathrm{1,2}}^{\mathrm{2,2}}=\mathrm{2,000},$$

$${\rho }_{\mathrm{2,2}}=\mathrm{10,000},S_{\mathrm{2,2}}^1=\mathrm{10,000}{\rho }_{\mathrm{2,2}}^1=\mathrm{20,000},S_{\mathrm{2,2}}^{\mathrm{2,1}}=\mathrm{10,000},{\rho }_{\mathrm{2,2}}^2=\mathrm{15,000},S_{\mathrm{2,2}}^{\mathrm{2,2}}=\mathrm{20,000},$$

$${\beta }_{\mathrm{1,2}}={\beta }_{\mathrm{2,2}}=\mathrm{1,000,000},d_{\mathrm{1,2}}^{\mathrm{2,1}}=d_{\mathrm{2,2}}^{\mathrm{2,1}}=\mathrm{50,000},d_{\mathrm{1,2}}^{\mathrm{2,2}}=d_{\mathrm{2,2}}^{\mathrm{2,2}}=\mathrm{25,000},$$

$$c_{\mathrm{11,2}}^1=2{\left(q_{\mathrm{11,2}}^1\right)}^2,c_{\mathrm{22,2}}^1=2{\left(q_{\mathrm{22,2}}^1\right)}^2,$$

$$c_{\mathrm{21,2}}^1\left(q^1\right)=5{\left(q_{\mathrm{12,2}}^1\right)}^2+3q_{\mathrm{12,2}}^1,c_{\mathrm{12,2}}^1\left(q^1\right)=5{\left(q_{\mathrm{21,2}}^1\right)}^2+3q_{\mathrm{21,2}}^1,$$

$$c_{\mathrm{11,2}}^{\mathrm{2,1}}=5{\left(q_{\mathrm{11,2}}^{\mathrm{2,1}}\right)}^2,c_{\mathrm{22,2}}^{\mathrm{2,1}}=3{\left(q_{\mathrm{22,2}}^{\mathrm{2,1}}\right)}^2,$$

$$c_{\mathrm{21,2}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=9{\left(q_{\mathrm{12,2}}^{\mathrm{2,1}}\right)}^2+6q_{\mathrm{12,2}}^{\mathrm{2,1}},c_{\mathrm{12,2}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=9{\left(q_{\mathrm{21,2}}^{\mathrm{2,1}}\right)}^2+6q_{\mathrm{21,2}}^{\mathrm{2,1}},$$

$$c_{\mathrm{11,2}}^{\mathrm{2,2}}=2{\left(q_{\mathrm{11,2}}^{\mathrm{2,2}}\right)}^2,c_{\mathrm{22,2}}^{\mathrm{2,2}}=2{\left(q_{\mathrm{22,2}}^{\mathrm{2,2}}\right)}^2,$$

$$c_{\mathrm{21,2}}^{\mathrm{2,2}}\left(q^{\mathrm{2,2}}\right)=5{\left(q_{\mathrm{12,2}}^{\mathrm{2,2}}\right)}^2+3q_{\mathrm{12,2}}^{\mathrm{2,2}},c_{\mathrm{12,2}}^{\mathrm{2,2}}\left(q^{\mathrm{2,2}}\right)=5{\left(q_{\mathrm{21,2}}^{\mathrm{2,2}}\right)}^2+3q_{\mathrm{21,2}}^{\mathrm{2,2}}.$$

The computed equilibrium solution for this example is:

$$q_{\mathrm{11,1}}^{1\text{*}}=\mathrm{14,285.92},q_{\mathrm{12,1}}^{1\text{*}}=\mathrm{7,142.64},q_{\mathrm{21,1}}^{1\text{*}}=\mathrm{5,714.07},q_{\mathrm{22,1}}^{1\text{*}}=\mathrm{17,857.35},$$

$$q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}=\mathrm{4,500.22},q_{\mathrm{12,1}}^{\mathrm{2,1}\text{*}}=\mathrm{5,416.33},q_{\mathrm{21,1}}^{\mathrm{2,1}\text{*}}=\mathrm{2,499.78},q_{\mathrm{22,1}}^{\mathrm{2,1}\text{*}}=\mathrm{16,250.00},$$

$$q_{\mathrm{11,1}}^{\mathrm{2,2}\text{*}}=\mathrm{14,285.92},q_{\mathrm{12,1}}^{\mathrm{2,2}\text{*}}=\mathrm{9,799.70},q_{\mathrm{21,1}}^{\mathrm{2,2}\text{*}}=\mathrm{5,714.07},q_{\mathrm{22,1}}^{\mathrm{2,2}\text{*}}=\mathrm{24,500.00},$$

$$q_{\mathrm{11,2}}^{1\text{*}}=\mathrm{1,428.78},q_{\mathrm{12,2}}^{1\text{*}}=\mathrm{2,856.92},q_{\mathrm{21,2}}^{1\text{*}}=571.21,q_{\mathrm{22,2}}^{1\text{*}}=\mathrm{7,143.07},$$

$$q_{\mathrm{11,2}}^{\mathrm{2,1}\text{*}}=\mathrm{1,285.93},q_{\mathrm{12,2}}^{\mathrm{2,1}\text{*}}=\mathrm{2,499.75},q_{\mathrm{21,2}}^{\mathrm{2,1}\text{*}}=714.07,q_{\mathrm{22,2}}^{\mathrm{2,1}\text{*}}=\mathrm{7,500.25},$$

$$q_{\mathrm{11,2}}^{\mathrm{2,2}\text{*}}=\mathrm{1,428.78},q_{\mathrm{12,2}}^{\mathrm{2,2}\text{*}}=\mathrm{5,714.07},q_{\mathrm{21,2}}^{\mathrm{2,2}\text{*}}=571.21,q_{\mathrm{22,2}}^{\mathrm{2,2}\text{*}}=\mathrm{14,285.92},$$

$${\alpha }_{\mathrm{1,1}}^{1\text{*}}=\mathrm{41,856.28},{\alpha }_{\mathrm{2,1}}^{1\text{*}}=\mathrm{27,570.57},{\alpha }_{\mathrm{1,2}}^{1\text{*}}=\mathrm{984,284.85},{\alpha }_{\mathrm{2,2}}^{1\text{*}}=\mathrm{961,427.71},$$

$${\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}=\mathrm{49,997.79},{\gamma }_{\mathrm{2,1}}^{\mathrm{2,1}\text{*}}=0.00,{\gamma }_{\mathrm{1,1}}^{\mathrm{2,2}\text{*}}=\mathrm{40,856.28},{\gamma }_{\mathrm{2,1}}^{\mathrm{2,2}\text{*}}=0.00,$$

$${\gamma }_{\mathrm{1,2}}^{\mathrm{2,1}\text{*}}=\mathrm{942,140.65},{\gamma }_{\mathrm{2,2}}^{\mathrm{2,1}\text{*}}=\mathrm{934,998.49},{\gamma }_{\mathrm{1,2}}^{\mathrm{2,2}\text{*}}=\mathrm{974,284.85},{\gamma }_{\mathrm{2,2}}^{\mathrm{2,2}\text{*}}=\mathrm{927,856.28}.$$

Country 2 has a much higher supply of the ventilators than country 1 even before the pandemic declaration, and this helps them a lot in doing a much better than country 1 in both scenarios. On the other hand, country 1, which is not able to increase the supply of these relatively complex and vital devices, is faced with a severe shortage. This important and significant advantage of country 2 in accessing the supply of a life-saving device leads to a much lower expected disutility for this country than that for country 1, $E\left(D{U}_1\right(q^{\text{*}})=\mathrm{5,640,364,039.56}$, $E\left(D{U}_2\left(q^{\text{*}}\right)\right)=\mathrm{2,529,423,007.30}$.

Numerical Example 3: Two Countries, Two Types of Medical Supplies, Two Scenarios, Conservative Strategies.

In Numerical Example 3, we address the key issue of restrictions on the export of vital medical supplies in times of a pandemic. We have seen that, in some cases, the import of essential medical items from foreign countries has become very difficult or expensive for various reasons, such as the severe disruptions in international transportation and/or the enactment of laws by governments. In this example, we examine the effects of such restriction on countries’ strategies by increasing the international transportation rates as compared to the previous example. The data for this example are:

$$c_{\mathrm{21,1}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=25{\left(q_{\mathrm{12,1}}^{\mathrm{2,1}}\right)}^2+10q_{\mathrm{12,1}}^{\mathrm{2,1}},c_{\mathrm{12,1}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=25{\left(q_{\mathrm{21,1}}^{\mathrm{2,1}}\right)}^2+10q_{\mathrm{21,1}}^{\mathrm{2,1}},$$

$$c_{\mathrm{21,1}}^{\mathrm{2,2}}\left(q^{\mathrm{2,2}}\right)=25{\left(q_{\mathrm{12,1}}^{\mathrm{2,2}}\right)}^2+10q_{\mathrm{12,1}}^{\mathrm{2,2}},c_{\mathrm{12,1}}^{\mathrm{2,2}}\left(q^{\mathrm{2,2}}\right)=25{\left(q_{\mathrm{21,1}}^{\mathrm{2,2}}\right)}^2+10q_{\mathrm{21,1}}^{\mathrm{2,2}},$$

$$c_{\mathrm{21,2}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=25{\left(q_{\mathrm{12,2}}^{\mathrm{2,1}}\right)}^2+10q_{\mathrm{12,2}}^{\mathrm{2,1}},c_{\mathrm{12,2}}^{\mathrm{2,1}}\left(q^{\mathrm{2,1}}\right)=25{\left(q_{\mathrm{21,2}}^{\mathrm{2,1}}\right)}^2+10q_{\mathrm{21,2}}^{\mathrm{2,1}},$$

$$c_{\mathrm{21,2}}^{\mathrm{2,2}}\left(q^{\mathrm{2,2}}\right)=25{\left(q_{\mathrm{12,2}}^{\mathrm{2,2}}\right)}^2+10q_{\mathrm{12,2}}^{\mathrm{2,2}},c_{\mathrm{12,2}}^{\mathrm{2,2}}\left(q^{\mathrm{2,2}}\right)=25{\left(q_{\mathrm{21,2}}^{\mathrm{2,2}}\right)}^2+10q_{\mathrm{21,2}}^{\mathrm{2,2}}.$$

The computed equilibrium solution for this example is:

$$q_{\mathrm{11,1}}^{1\text{*}}=\mathrm{14,285.92},q_{\mathrm{12,1}}^{1\text{*}}=\mathrm{7,142.64},q_{\mathrm{21,1}}^{1\text{*}}=\mathrm{5,714.07},q_{\mathrm{22,1}}^{1\text{*}}=\mathrm{17,857.35},$$

$$q_{\mathrm{11,1}}^{\mathrm{2,1}\text{*}}=\mathrm{5,833.50},q_{\mathrm{12,1}}^{\mathrm{2,1}\text{*}}=\mathrm{1,949.80},q_{\mathrm{21,1}}^{\mathrm{2,1}\text{*}}=\mathrm{1,166.50},q_{\mathrm{22,1}}^{\mathrm{2,1}\text{*}}=\mathrm{16,250.00},$$

$$q_{\mathrm{11,1}}^{\mathrm{2,2}\text{*}}=\mathrm{18,518.70},q_{\mathrm{12,1}}^{\mathrm{2,2}\text{*}}=\mathrm{1,959.80},q_{\mathrm{21,1}}^{\mathrm{2,2}\text{*}}=\mathrm{1,481.298},q_{\mathrm{22,1}}^{\mathrm{2,2}\text{*}}=\mathrm{24,500.00},$$

$$q_{\mathrm{11,2}}^{1\text{*}}=\mathrm{1,428.78},q_{\mathrm{12,2}}^{1\text{*}}=\mathrm{2,856.92},q_{\mathrm{21,2}}^{1\text{*}}=571.21,q_{\mathrm{22,2}}^{1\text{*}}=\mathrm{7,143.07},$$

$$q_{\mathrm{11,2}}^{\mathrm{2,1}\text{*}}=\mathrm{1,666.84},q_{\mathrm{12,2}}^{\mathrm{2,1}\text{*}}=\mathrm{1,071.25},q_{\mathrm{21,2}}^{\mathrm{2,1}\text{*}}=333.16,q_{\mathrm{22,2}}^{\mathrm{2,1}\text{*}}=\mathrm{8,928.75},$$

$$q_{\mathrm{11,2}}^{\mathrm{2,2}\text{*}}=\mathrm{1,852.03},q_{\mathrm{12,2}}^{\mathrm{2,2}\text{*}}=\mathrm{1,481.29},q_{\mathrm{21,2}}^{\mathrm{2,2}\text{*}}=147.96,q_{\mathrm{22,2}}^{\mathrm{2,2}\text{*}}=\mathrm{18,518.70},$$

$${\alpha }_{\mathrm{1,1}}^{1\text{*}}=\mathrm{41,856.28},{\alpha }_{\mathrm{2,1}}^{1\text{*}}=\mathrm{27,570.57},{\alpha }_{\mathrm{1,2}}^{1\text{*}}=\mathrm{984,284.85},{\alpha }_{\mathrm{2,2}}^{1\text{*}}=\mathrm{961,427.71},$$

$${\gamma }_{\mathrm{1,1}}^{\mathrm{2,1}\text{*}}=\mathrm{36,664.99},{\gamma }_{\mathrm{2,1}}^{\mathrm{2,1}\text{*}}=0.00,{\gamma }_{\mathrm{1,1}}^{\mathrm{2,2}\text{*}}=\mathrm{23,925.18},{\gamma }_{\mathrm{2,1}}^{\mathrm{2,2}\text{*}}=0.00,$$

$${\gamma }_{\mathrm{1,2}}^{\mathrm{2,1}\text{*}}=\mathrm{938,331.50},{\gamma }_{\mathrm{2,2}}^{\mathrm{2,1}\text{*}}=\mathrm{926,427.49},{\gamma }_{\mathrm{1,2}}^{\mathrm{2,2}\text{*}}=\mathrm{972,591.85},{\gamma }_{\mathrm{2,2}}^{\mathrm{2,2}\text{*}}=\mathrm{910,925.18}.$$

Comparing the results with the previous example's results, we see that the difficulties in imports have increased the relative shortage of face masks in both countries, but still country 2 is less affected than country 1. However, the situation is quite different in the case of ventilators. Country 2, which dominates the supply of these vital devices, has benefited greatly from the disruption in exchanges between the two countries. Most of the country's supply is allocated to its own demand and the country's competitor has received a very small share. On the other hand, country 1, which has access to very limited resources of these devices domestically, is faced with severe shortages and cannot find another source to meet its needs. The impact of the disruption on the trade exchanges between the two countries is also easily visible in their expected disutility values. Country 2, a country that is a leader in the supply of a strategic medical supply, has drastically reduced its expected disutility to 1,577,985,084.63, while country 1 is faced with a serious crisis and its expected disutility increases to 6,809,140,792.95.

5.2. Additional discussion of the results

As stated in the Introduction and, based on what we have seen in past research, it is important to pay attention to both disaster preparedness and to response when we are planning for a pandemic. This is something that was observed in the solution of our model in the above examples. Since governments cannot easily predict what level of crisis they will face, they must be prepared for different scenarios. In the examples, we saw that, in the event of a low-severity pandemic scenario, countries may not face serious shortages and prices at home and abroad will not change much. However, in the event of a severe crisis in countries, harsh global supply shortages and rising prices significantly affect countries with low domestic production capacity. This finding is consistent with what we have seen in reality in the efforts of various governments to address the Covid-19 pandemic crisis. Countries that were able to increase their domestic production earlier faced fewer problems than countries that were dependent on imports of essential commodities and had to pay huge prices.

Maintaining readiness for a sudden increase in supply is one of the most important strategies that managers and policy-makers should pay special attention to. Firstly, in many cases, it is not possible to predict the occurrence of a crisis in the long run, and, secondly, it is not easy to store and maintain many goods in large volumes; hence, as revealed in the examples, the ability to increase supply in the short term is the most important strength of successful countries in this competition. On the other hand, unlike many previous studies that considered only one product, our model can capture competition for several types of products. We also saw in the examples that a government must maintain its readiness to supply all kinds of medical supplies. Some products, such as face masks, are less expensive and needed in large numbers, whereas others, such as ventilators, are needed in smaller numbers but are more expensive and they have different effects on controlling the crisis. Decision-makers should consider and analyze the effects of different types of medical products on the amount of damage that might be incurred by the society and take the necessary actions to procure these products before and after the occurrence of a possible disaster, such as the pandemic.

The results above emphasize the importance of both the preparedness and the response stages in disaster management and the consideration of uncertainty, and further reinforce the results in the studies of Mete and Zabinsky (2010) and Rawls and Turnquist (2010). The results also support the findings of Anparasan and Lejeune (2019), who pointed out in their study that the optimal strategies for preparation and allocation of vital goods are of particular relevance, given the severity of the disaster. Similar to the research of Long et al. (2018), we showed how having access to critical resources and a proper strategy can help to reduce the damage. However, our study is the first to address not only the stages of preparedness and response, along with the uncertainty, but also the critical issue of resource competition among countries, which was not investigated in previous studies on epidemic crises. Also, most previous research has considered the occurrence of an epidemic to be limited to a single region or, ultimately, to one country, and, as a result, the issue of global supply shortages in a pandemic has not been addressed through game theory and variational inequality theory before.

6. Summary and conclusions

With the spread of the novel coronavirus around the globe and the official declaration of the Covid-19 pandemic in March 2020, it soon became apparent that many countries were not prepared to deal with this healthcare disaster. The sudden increase in demand for medical supplies, including PPEs for essential workers, such as healthcare workers, and ventilators for patients, added to the crisis. The supply levels of these products were much lower than the level of demand and initiated an intense competition among different countries in procuring such items. Meanwhile, some countries had more supply resources than other countries before the pandemic declaration, and some were able to increase the supply of products within their countries by enacting laws after the pandemic declaration.

Taking into account the specific features of the current pandemic, we examine countries’ competition over the purchase of medical supplies under limited availability in our stochastic Generalized Nash Equilibrium model. Specific features of the model include: the uncertainty of the scenarios, the supply capacities of the medical items, and the fluctuating prices before and after the pandemic declaration, as well as disruptions to the global supply chains. We formulate the model as a variational inequality problem applying the concept of a Variational Equilibrium. Also, we utilize an alternative variational inequality formulation with Lagrange multipliers associated with the medical item supply capacities in each country. We study the model both qualitatively and quantitatively. In this regard, we provided illustrative examples and numerical examples, with the former solved analytically, and the latter, algorithmically.

The results reveal that countries that have more flexibility and resilience in increasing their domestic supply after the pandemic declaration are better at dealing with the pandemic disaster and meeting the need for medical supplies. In times of crisis, uncertainty in many cases, including the supply chain status, plays a key role in a country's success or failure in disaster management. Hence, countries must be ready to supply strategic medical supplies domestically. This study adds to the literature on game theory and two-stage stochastic models in disaster management with the focus on specific features of the Covid-19 pandemic. This model has the potential to be extended in future research. For example, we are still in the midst of this pandemic, and every day we see new changes and decisions by governments. Recently, a limited number of vaccines have received emergency use permits, and some countries are in the early stages of vaccine distribution and the administering of them. Many others are still waiting to receive the vaccine from the pharmaceutical manufacturers, and some are waiting for other vaccines to be approved. But what is clear is the fierce competition among the countries to obtain the vaccines delivered to their people as soon as possible, which requires comprehensive and careful planning. Certainly, the competition among different countries over the procurement of vaccines for their own people also has special features that can be examined in a related model, and such a model must include features to capture the perishability aspect of the vaccines and the required cold chains. Similarly, the quest for suitable treatments, with convalescent plasma being quite promising as well as remesdivir for Covid-19 patients, is also leading to competition with specific nuances and features. Expanding the model in this paper to incorporate additional information about the current pandemic and solving examples using data from real experience of countries managing this pandemic disaster is another future research opportunity.