Novel eGZ-motif formed by regularly extruded guanine bases in a left-handed Z-DNA helix as a major motif behind CGG trinucleotide repeats

Abstract

The expansion of d(CGG) trinucleotide repeats (TRs) lies behind several important neurodegenerative diseases. Atypical DNA secondary structures have been shown to trigger TR expansion: their characterization is important for a molecular understanding of TR disease. CD spectroscopy experiments in the last decade have unequivocally demonstrated that CGG runs adopt a left-handed Z-DNA conformation, whose features remain uncertain because it entails accommodating GG mismatches. In order to find this missing motif, we have carried out molecular dynamics (MD) simulations to explore all the possible Z-DNA helices that potentially form after the transition from B- to Z-DNA. Such helices combine either CpG or GpC Watson-Crick steps in Z-DNA form with GG-mismatch conformations set as either intrahelical or extrahelical; and participating in BZ or ZZ junctions or in alternately extruded conformations. Characterization of the stability and structural features (especially overall left-handedness, higher-temperature and steered MD simulations) identified two novel Z-DNA helices: the most stable one displays alternately extruded Gs, and is followed by a helix with symmetrically extruded ZZ junctions. The G-extrusion favors a seamless stacking of the Watson-Crick base pairs; extruded Gs favor syn conformations and display hydrogen-bonding and stacking interactions. Such conformations could have the potential to hijack the MMR complex, thus triggering further expansion.

INTRODUCTION

The comparison of genome sequences indicates that the expansion of simple sequence repeats (SSRs) represents a sophisticated evolutionary device. The incidence of specific sorts of SSRs and their position in genes varies greatly between different genomes, underscoring the vital role of SSRs in genome evolution (1,2). It has been estimated that the rate of repeat number mutations in some SSRs is about 10⁵ times higher than that of a point mutation (3). This can lead to frequent polymorphism in the genes that aids natural selection by rapidly generating new alleles. Unfortunately the expansion phenomena that plays such essential role in the evolution of eukaryotic genomes comes at a price, as SSRs—and in particular, trinucleotide repeats (TRs)—are associated with 50 expandable SSR diseases (4–18). Many of these belong to the category of ‘genetic anticipation’ diseases, caused by the intergenerational expansion of SSRs: After a certain threshold in repeat number, the probability of further expansion and the severity of the disease increase with the repeat number. In particular, the dynamic mutations in human genes associated with most TRs (but not all) cause severe neurodegenerative and neuromuscular disorders, known as Trinucleotide (or triplet) repeat expansion diseases (TREDs) (13–19).

The mechanisms underlying TREDs are extremely complex, and in many ways particular to each disease. Yet, there seems to be a universal trigger behind the expansion reflected in the recognition that the pivotal step in all models of repeat instability is the transient formation of atypical, non-B DNA stable secondary structures in the expandable repeats (17,20–23). In this work, we explore new atypical structures for the CGG TRs, which—along with the complementary sequence CCG TRs—are overexpressed in the exons of the human genome. In particular, CGG TRs are present in the 5′-untranslated region (5′-UTR) of the fragile X mental retardation gene (FMR1) (24). In a normal population, the typical range of the CGG TRs repeats is 5-54 (25,26); repeats in the range of 55–200 leads to male fragile X-associated tremor ataxia syndrome (FXTAS) (27), and female premature ovarian failure (28); and repeats in excess of 200 result in the inherited fragile X mental retardation syndrome (29). In addition, a GGC repeat expansion and methylation of exon 1 in the XYLT1 gene are a common pathogenic variant in the Baratela-Scott syndrome (30).

Experimentally, considerable information about the SSR structures is obtained in an indirect manner, through in vitro experiments such as CD, UV absorbance, NMR, electrophoretic mobility assay, and chemical or enzymatic digestion (31). The results show a general trend to formation of duplexes and hairpins, depending on the sequence length and environmental conditions. An important consideration regarding possible TR conformations is the nature of the Watson-Crick (WC) pairs that surround the mismatches (32,33): homoduplexes of sequences 5′-(CGG)_n-3′ (paired ends, without strand slipping) exhibit GpC steps between the WC base pairs, while homoduplexes of sequence 5′-(GGC)_n-3′ (without strand slipping) exhibit CpG steps between the WC base pairs. In addition to the above experimental approaches, crystallographic studies for short RNA duplexes provide valuable atomic detail, but these studies generally are limited to RNA and to only one type of step. In this sense, atomistic molecular dynamics (MD) represent an invaluable tool to explore the conformations and dynamics of both DNA and RNA, with different type of steps, in different environments, their associated free energies as well as the different transition mechanisms associated with these repeats. This is particularly crucial for DNA, where the original expansion arises. In our previous studies, we have focused on DNA and RNA homoduplexes, hybrid duplexes, triplexes, quadruplexes and hairpins conformations associated with the most common TRs (CAG, GAC, CGG, CCG, GAA, TTC) and with hexanucleotide repeats (GGGGCC, GGCCCC and GGGCCT) (34–40). In particular, the complementary coupling of smFRET experiments and MD provided new insights on the roles of sequence parity and trinucleotide interrupts on the dynamics of DNA CAG hairpins (39).

G-rich and C-rich DNA SSRs have been found to display a wealth of secondary structures, including homoduplexes (35,38), e-motifs (35,37), i-motifs (41) and G-quadruplexes (36,42), with the resulting structure depending very much on the environment. This dependence has been documented for RNA, where experiments involving CD, optical melting and 1D ¹H NMR spectroscopy, combined with chemical and enzymatic probing of an r(GGGGCC) repeat expansion point to a general scenario where the repeat expansion adopts a hairpin structure with GG mismatches in equilibrium with a quadruplex structure (43,44). The equilibrium is temperature dependent, and controlled by the type of ions involved, and their ionic strength, with the larger K⁺ ions favoring G-quadruplexes and the smaller Na⁺ ions favoring hairpins (43). In low salt solution, CGG and GGC sequences can form hairpins and homoduplexes that generally exhibit a B-DNA conformation (32,33) (in the stems, in the case of the hairpins), with the G·G mismatches inside the helical core in anti–syn conformation, and with some unwinding in CG/GG steps in CGG sequences and in GC/GG steps in GGC sequences (38).

Under high salt concentration, on the other hand, CD spectroscopy experiments (45,46) unequivocally demonstrated that CGG runs adopt a non-B DNA conformation—a left-handed Z-DNA (47), whose likelihood of formation increases with increasing number of repeats. The authors of this work also showed that CGG repeats only form quadruplexes at low pH, in the presence of high concentrations of KCl and other non-physiological conditions (45,48). In addition, the ability to form quadruplexes dramatically decreased with the number of repeats; and the presence of AGG interrupts, known to discourage expansions, actually increased the stability of quadruplexes (48). Thus, the authors concluded that a quadruplex cannot be the structure responsible for the expansion of CGG sequences. Although high salt concentrations are used to stabilize Z-DNA in vitro, Z-DNA formation can occur under physiological conditions: mainly by cytosine methylation in CpG islands, by superhelical stress, or by organic solvents that simulate the crowded cell environment. This leaves hairpins as the only viable secondary structure motif, with stems either in B-DNA form as studied in our previous work (38); or in Z-DNA form which is the focus of the present study, given that the combination of CD spectroscopy, UV absorbance and electrophoretic mobility assay cannot reveal the actual molecular conformation of this as yet unknown CGG TR motif. Thus, we set out to construct and study through MD simulations a wide collection of DNA helices that combine either CpG or GpC WC steps in Z-DNA form with different conformations of the GG mismatches, which we set as either intrahelical or extrahelical; and either in local B-DNA conformations (thus, forming a series of BZ junctions (49)) or in local Z-DNA conformations (thus, forming a series of ZZ junctions (50,51)). We characterized the conformations and relative stability of these helices, and found evidence for a new structural motif, which for simplicity we term extruded-G Z-DNA motif, or eGZ-motif. Essentially, the eGZ-motif consists of extruded Gs in a left-handed Z-DNA helix. As will be discussed in the text, there are actually two ways in which mismatched Gs extrude out of the Z-DNA core: in the most stable helix, the Gs extrude in an alternating fashion; in the second most stable helix, Gs belonging to the same mismatch extrude symmetrically out of the helical core. These novel extruded motifs are somewhat reminiscent of the so-called e-motif previously identified experimentally (52,53) and theoretically (37) in d(GCC)_n trinucleotide repeat homoduplexes; and in d(CCCGGC)_n hexanucleotide repeat (HR) homoduplexes (35,37). These homoduplexes correspond to right-handed, B-like DNA helices, where the mismatched cytosines symmetrically flip out in the minor groove, pointing their base moieties towards the 5′-direction in each strand. Out of the two non-equivalent d(GCC)_n and d(CCG)_n TR homoduplexes and the three non-equivalent d(CCCGGC)_n, d(CGGCCC)_n, d(CCCCGG)_n HR homoduplexes, the e-motif is only stable in d(GCC)_n (with CpG WC base steps) and d(CCCGGC)_n homoduplexes due to the favorable stacking of pseudo GpC steps and the formation of hydrogen bonds between the mismatched cytosine at position i and the cytosine (TRs) or guanine (HRs) at position i − 2 along the same strand. In the extended e-motif, where all mismatched cytosines are extruded, their extra-helical stacking additionally stabilizes the homoduplexes.

The present conformation studies do not address the transition from B-DNA to Z-DNA, a study that we have carried out in detail in the past for CG repeats (54). This transition involves crossing a free energy barrier that is sequence and repeat-length dependent. Experimentally, the transitions reported on Refs. (45,46) took hours to days. One of the advantages of MD is that simulations can start in any minimum of the free energy, independently of the complexity of the transition that took the molecule there. Finally, a word with respect to our notation: the TR behind the pathological expansion is generally denoted as CGG. Since CGG strands can slip with respect to each other, they can give rise to either GpC steps (called frame 1 in the notation of Darlow and Leach (32,33)) or CpG steps (frame 2 in the same notation). For simplicity, we denote as CGG the (non-slipped) homoduplex helices that are in frame 1 and GGC those that are in frame 2.

MATERIALS AND METHODS

Normally, left-handed Z-DNA is formed by dinucleotide repeats and occurs in sequences that alternate a purine-pyrimidine repeat, mainly CG (or GC). The anti–syn alternation of these base pairs underlies the zig-zag backbone pattern (that gives Z-DNA its name) and is due to the rotation of the guanine residue around its glycosidic bond resulting in a syn conformation while the cysteine residue retains its anti conformation. The challenge here is how to accommodate the GG mismatches in CGG/GGC sequences.

Molecular dynamics for DNA helices: BZ junctions, ZZ junctions and alternately extruded guanines

We carried out regular Molecular Dynamics (MD) for homoduplexes with a varying number of TRs. In all cases, the initial G-C WC base pairs were built in a Z-DNA form. The GG mismatches were in either B-form or Z-form, such that the resulting helical duplexes encompass a series of DNA BZ or ZZ junctions; or added in alternately extruded conformations. These simulations included (i) GGC sequences (CpG WC steps) with 4 or 8 repeats in BZ- or ZZ-junction conformations, with the GG mismatches starting all in or all out; (ii) CGG sequences (GpC WC steps) with 4 repeats, in full Z-DNA form, and with the GG mismatches starting all in or all out; and (iii) GGC (=CGG) sequences with 4 repeats, in full Z-DNA form with alternately extruded Gs in each GGC(=CGG) unit. A summary of the sequences, force fields (FF), and main results of the simulations is presented in Table 1. A schematic of the sequences and the in/out nature of the mismatches is shown in Figure 1.

Table 1.

Summary of main MD results for the different DNA helices considered. All WC base pairs are in Z-DNA form. Considering the TRs, these sequences describe homoduplexes, except for the terminal bases (when present) that are bonded to their WC counterpart. For example, the sequence 5′-C(GGC)₄G-3′ has as complementary strand, 5′-C(GGC)₄G-3′. The ‘ZZ’ or ‘BZ’ subindices in the structural labels indicate that that GG mismatches are in Z-DNA form, i.e., forming ZZ junctions; or in B-DNA form, i.e, forming BZ junctions with the adjacent WC pairs. ‘Ribbon’-DNA indicates a DNA that is unwinding such that its strands become nearly parallel, as it would occur in a B-to-Z DNA transition. All simulations results presented here were obtained in a 5M NaCl salt environment. Additional low salt (0M and 150mM) simulations were all unstable, and are not explicitly noted here. Interaction notation: base-stacking ‘::’, Hbonds between Gs in the same mismatch ‘·’, and Hbonds between mismatched Gs in different pairs ‘:’

Label	Sequence	Force fields	Stability	Long-lived stackings
GGC4BZ, in, GGC4ZZ, in	C(GGC)4G	BSC0, BSC1	Unstable. Ribbon-DNA forms very fast
GGC4BZ, out	C(GGC)4G	BSC0	Stable
GGC4ZZ, out	C(GGC)4G	BSC0, BSC1, OL15	BSC0 and OL15 stable, BSC1 unstable
GGC8BZ, out	(GGC)8	BSC0, BSC1, OL15	Stable. Mismatches remain out for all three FFs. All (BSC0) or many (BSC1, OL15) mismatches align towards their 5′-end, sometimes forming H-bonds with the backbone	BSC1: G35:G8, G35::G38; OL15: G14::G17, G14::G41, G14::G38::G41, G11::G35
GGC8ZZ, out	(GGC)8	BSC0, BSC1, OL15	Stable. Many mismatches align towards their 5′-end, sometimes forming H-bonds with the backbone. G11·G38 flipped inside the core in BSC1	BSC1: G20::G32; G17::G26; G38::G41
GGC8BZ, in	(GGC)8	BSC0, BSC1, OL15	Unstable. Bent structures lose helical shape and deform
GGC8ZZ, in	(GGC)8	BSC0, BSC1, OL15	Semi-stable. All the mismatched GG residues stay inside the helical core, helices tend to bend. Ribbon-DNA forms: Bases show half a turn (180°) after 24 base pairs, i.e. ∼7.5° twist per base pair
CGG4ZZ, in	G(CGG)4C	BSC0, BSC1, OL15	Stable. All the mismatched GG residues stay inside the helical core, G9·G20 flip out in BSC1
CGG4ZZ, out	G(CGG)4C	BSC0, BSC1, OL15	Unstable, various bases flip back in, a trend that increases with simulation time
GGC4ZZ, alt	(GGC)4G	BSC0, BSC1, OL15	Stable. All the single Gs remain extruded far enough so that the whole become symmetric and stable	BSC1: G8::G24; OL15: G8::G24

Figure 1.

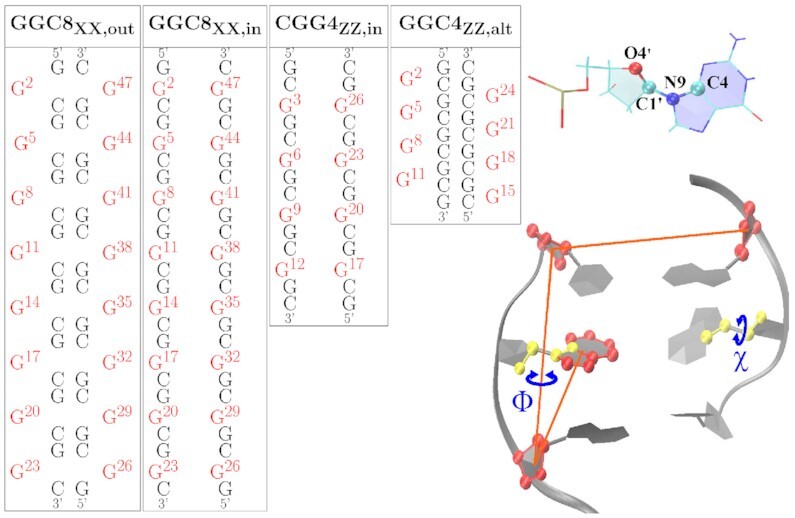
Left: Sequence maps for the initial Z-DNA helices considered in this study, with G mismatched bases in red. The ‘XX’ subindex indicates either BZ or ZZ junction. The GGC4 sequences are not shown. Right: The glycosidic torsion angle χ, O4′-C1′-N9-C4, characterizes the relative base/sugar orientation, and the center-of-mass pseudo-dihedral angle Φ, as defined by the centers of mass of four atom groups, quantifies the base unstacking of a mismatched G.

The initial structures for (i) and (ii) were obtained by using the BIOVIA Discovery Studio (55) v. 2019 software to create the initial structures. First, we created a short d(5′-CG-3′) duplex for GGC sequences ( or a d(5′-GC-3′) duplex for CGG sequences ) in Z-DNA form. We then added a middle CG or GC WC base pair in either B-DNA or Z-DNA conformation, and then added the final d(5′-CG-3′) (or d(5′-GC-3′)) Z-DNA helix. If the middle base pair is in Z-DNA conformation, we have a fully Z-DNA helix; if it is in B-DNA conformation we have to adjust the backbone angles using the Discovery Studio in order to create two BZ junctions due to the mismatch. Finally, we mutated the C in the CG or GC middle WC base pair to G in order to obtain the GG mismatch. The resulting helix was then elongated in this fashion until the desired length was reached. In the GGC helices, the terminal WC base pairs were cut. The initial extruded motif was constructed from the previous helices via the Steered MD (SMD) (56) protocol discussed in detail in SI.

Finally, for case (iii) corresponding to the GGC_{ZZ, alt} helix (Figure 1), we built a standard Z-DNA segment of four periodic repeat units by using the Discovery Studio package; we then cut the O–P–O bonds at the desired locations for the insertion of the additional G bases. These were inserted by enlarging the distance between the oxygen and phosphate atoms and appropriately adjusting the position of the G or C residues in the Z-DNA segment. Finally, we connected the new G residues to the broken Z-DNA segment by adjusting the atomic distances of the related residues within a pseudo GpC or CpG step and then reconnecting the backbones.

The simulations were carried out using the PMEMD module of the AMBER v.20 (57) software package with FF ff99 BSC0 (58), BSC1 (59) and OL15 (60). The TIP3P water model (61) was used for the explicit waters. The simulations were performed with periodic boundary conditions in a truncated octahedron water box. To neutralize the nucleic acid charges, an appropriate number of Na⁺ ions were added with standard ion parameters (62). In addition, both 150 mM and 5 M NaCl salt were added, and some runs were also performed with 0.20 M NaCl and 20 mM NiCl₂ excess salt. Electrostatic interactions were computed with the PME method (63) with a 9 Å cutoff. The cutoff for van der Waals interactions was set as 9 Å as well. Production runs used Langevin dynamics with a coupling parameter 1.0 ps⁻¹. The SHAKE algorithm (64) was applied to all bonds involving hydrogen atoms. Starting conformations for MD calculations were obtained as follows. We first minimized the energy for the initial conformations obtained after modeling: first, by keeping the nucleic acid and ions fixed; then, by allowing them to move. Subsequently, the temperature was gradually raised using constant volume simulations from 0 to 300 K over 200 ps runs with a 1 fs time step, followed by another 200 ps run at constant volume at 300K. Then a 600 ps run was used to gradually reduce the restraining harmonic constants for nucleic acids and ions. During the above minimization and equilibrium steps the hydrogen bonds in the WC base pairs , and the χ values were restrained. After we obtained the starting conformations, we performed MD runs for times that vary between 1 and 3 μs with a 2 fs time step. The pressure of the system was maintained at 1 bar using the Berendsen barostat, with isotropic position scaling and relaxation time of 1 ps. Conformations were saved every 10 ps. In the MD runs, only weak constraints of 1 kcal/mol on hydrogen bonds for the end bases were used in order to reduce artificial. To obtain fully equilibrated results, we used MD results from BSC0 (after around 1 μs MD) as starting configurations for BSC1 and OL15 FFs.

Free energy maps for a single GGC trinucleotide repeat

To investigate the most favorable mismatch conformations, we investigated sequences of the form 5′-GC-(GGC)-GC-3′ which contain a single GG mismatch within a single GGC TR. The initial GG mismatch was set either in the B- or Z-form, giving rise to two BZ junctions or two ZZ junctions; the guanine mismatches were set to be either inside in or outside out of the helical core. The state of the glycosyl χ dihedral angle was carefully chosen as to preserve the symmetry of the sequence and the constraints associated with Z-DNA (i.e. for each WC base pair, G is in syn and C in an anti conformation).

We then calculated the free energy of the mismatch using the Adaptively Biased Molecular Dynamics (ABMD) method (65,66), which is a nonequilibrium MD method that belongs to the general category of umbrella sampling methods with a history-dependent biasing potential. ABMD calculates free energy landscapes (or more correctly the potential of mean force) as a function of a set of collective variables or reaction coordinates that were carefully chosen as to reflect the underlying physics of the problem. ABMD has been implemented with multiple walkers (both noninteracting (67) and interacting walkers, with the latter interacting by means of a selection algorithm (68)), replica exchange molecular dynamics (REMD) (69), and ‘well tempered’ (WT) extensions (70). We choosed WT metadynamics as an enhanced sampling technique due to its effectiveness and ability to assess convergence of sampling. WT metadynamics is widely used to reconstruct the free energies during simulations (71–76). The collective variables chosen were the glycosyl torsion angle χ and the center-of-mass pseudo-dihedral angle Φ, as illustrated in Figure 1. The Φ angle enables the flipping of the mismatch in and out of the helical core. Specifically, we define Φ₄ (for mismatch G4) as given by the centers-of-mass of four atom groups: C12 (C1′, C2′, C3′, C4′, O4′), G3 (C1′, C2′, C3′, C4′, O4′), C5 (C1′, C2′, C3′, C4′, O4′), and G4 (N9 C8 N7 C5 C6 N1 C2 N3 C4); and Φ₁₁ (for mismatch G11) as given by the center-of-mass of four atom groups: G3 (C1′, C2′, C3′, C4′, O4′), C12 (C1′, C2′, C3′, C4′, O4′), G10 (C1′, C2′, C3′, C4′, O4′), and G11 (N9 C8 N7 C5 C6 N1 C2 N3 C4). The χ angle, which specifies the base sugar orientation of the mismatches, is defined as the dihedral angle, O4′-C1′-N9-C4, for residues G4 (χ₄) and G11 (χ₁₁). The rest of the technical details of the simulations are given in the SI.

Steered molecular dynamics for selected helices

In order to investigate the relative stabilities of the GGC4_{ZZ, out}, GGC4_{ZZ, alt} and CGG4_{ZZ, in} structures, we used an SMD (56) pulling protocol. Essentially, we steered the average structure as obtained from the last 200 ns of the MD simulations to a final ‘straight’ structure with the two strands almost parallel to each other. During this process, we monitored the cumulative work performed by pulling the duplexes from their equilibrium configurations to their final stretched state. The amount of work needed to stretch and deform the helices is indicative of the relative structural stability. For the steering process, we used the end-to-end distance d_end as the collective variable in such a way that the atomic center-of-mass of the terminus base pair remained fixed, while the center-of-mass of the other terminus was stretched via a biasing potential of the form 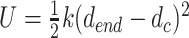, where k = 100 kcal/(mol/Ų) and d_c are the force constant and the harmonic center. The harmonic center d_c was gradually increased by ∼17 Å(from original length of helices), which represents the longest distance that the shortest helix, i.e. GGC4_{ZZ, alt} can be stretched without breaking. The SMD runs were carried out at a constant volume with explicit waters with both neutralizing sodium cations and 150 mM of additional salt (NaCl) at 300 K. Each simulation lasted 20 ns and was repeated 20 times. The average cumulative work performed <W > by pulling the duplexes from their initial equilibrium configurations to their final stretched state was given by: 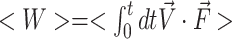, where <> represents average over the 20 independent simulations, 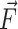is the pulling force, and  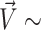17 Å/20ns is the pulling speed.

RESULTS

Free energy maps for a single GGC TR

Before embarking on extended MD simulations, we explored the conformational free energy landscape available to a single GG mismatch. To this end, we considered a Z-DNA homoduplex sequence d(5′-GC-GGC-GC-3′), with every base WC paired except for the single GG mismatch; in this structure all WC G’s were in a syn and C’s in an anti conformation. In this short homoduplex, the GG mismatch is more restricted than in the extended TR sequences used in the MD simulations, as it is sandwiched on both sides by three strong WC base pairs and—in contrast to the case of extruded G’s in a long TR sequence—there are no other extruded G’s that could potential interact with the mismatched G’s. Thus, we do not expect the relative depth of the conformational minima of the GG mismatches to be necessarily the same, but we would expect the minima observed in the short sequence with one TR to still be present in the multiple TR sequence d(5′-(GGC)_n-3′), and the minima not observed in a single GG mismatch to be of higher energy (when present) in multiple GG mismatches.

As described in the Methods section, we used the angles (Φ₄, Φ₁₁) and (χ₄, χ₁₁) as collective variables. Values of Φ between −75° to 75° are considered to be inside the helical core, while larger magnitudes are outside. Values of χ in the range of of −90° to +90° are referred to as syn conformations, with the rest corresponding to anti conformations. Free energy maps are presented in Figure 2 and Supplementary Figures S1–S3. On these maps, the global minimum is set to zero and the free energy of others are quoted relative to this value; the most prominent minima are labeled with capital letters. Since the two mismatched bases are completely equivalent, one can expect fully converged free energy landscapes to display mirror symmetry across the diagonal. This feature is generally observed. Note that labels of symmetry related minima are primed.

Figure 2.

Two-dimensional free energy maps for a single G4–G11 mismatch, and two sample conformations. The capital letters on the maps identify the local minima, listed in Table 2. Top panels show free energy landscapes as a function of the center-of-mass pseudo-dihedral angle Φ with mismatches in (A) B-form and rr Z-form. For an inner base, Φ falls between 30° and 60°, and for an extruded base it falls between 120° and 180°. Panel (D) shows sample conformations at the minima A,A′ (inner bases) and (B) (extruded bases) of the Φ₄–Φ₁₁ ZZ map. The mismatched Gs and WC bases are colored gold and green, respectively. Panel (C) shows the free energy map as a function of glycosidic χ angles, with both G4 and G11 bases restrained to the inside of the helix.

For the (Φ₄, Φ₁₁) free energy map, the dihedral χ angles of the mismatches were restrained to syn–syn, anti–anti or anti–syn conformations. Figure 2, obtained for anti–anti conformations, shows that both in and out GG conformations are possible, whether the GG mismatch is in B-form (Figure 2 A) or Z-form (Figure 2 B). The in conformations are ∼6 kcal/mol (GG in B form) and 5 kcal/mol (GG in Z form) more stable than the extruded conformations (Table 2). Additional free energy diagrams for initial anti–syn and syn–syn B-form conformations are included in Supplementary Figure S1. These landscapes closely resemble those in Figure 2 and confirm an absolute in minimum and an accessible out minimum, very close to the ones displayed in Figure 2. It is interesting that in this single-mismatch duplex sandwiched between three strong Watson-Crick base pairs on each side, there is still an out relative minimum of accessible energy. Such conformations could be expected to become more prominent as the number of mismatches increases. Sample conformations corresponding to in and out minima for the ZZ junction are shown in Figure 2(D).

Table 2.

Summary of main minima identified on the (Φ₄, Φ₁₁) and (χ₄, χ₁₁) (in degrees) free energy landscapes (in kcal/mol) for a short sequence with a single mismatch. Relative energies are measured with respect to the identified global minimum on each map

	(Φ4, Φ11) BZ junction	(Φ4, Φ11) ZZ junction	(χ4, χ11) OL15 FF
Approximate location of (A)	(45, 60)	(38, 56)	(60, –118)
Relative energy	0.0	0.0	0.0
Approximate location of (A′)	(60, 41)	(56, 41)	(–114, 63)
Relative energy	0.18	0.22	0.0
Approximate location of (B)	(147, 136)	(125, 114)	(63, 63)
Relative energy	6.27	5.42	4.06

Further insight into the in/out states can be obtained by computing the free energy barrier to transition from an inner conformation to an extruded conformation. With this aim, we carried out a simple experiment to see how barriers are affected by salt concentration. In this calculation, we used the sequence (GGC)₈ with inner ZZ junctions (GGC8_{ZZ, in} in Table 1). For this sequence, we kept all bases restrained inside the helical core and used a one-dimensional collective variable (1D-CV), the center-of-mass dihedral angle, to flip out a middle base. The results are shown in Supplementary Figure S2. In spite of constraining the other mismatches to the interior of the helix, and of having only one CV, the minimum for the extruded base around 160° with respect to the inner base at 0° is lower than those computed in the previous sequence: 3.5 kcal/mol at 0.15 M NaCl or 1 kcal/mol at 5 M NaCl. The transition occurs through base flipping toward the minor groove, in a two-step process that involves a 3.5 kcal/mol (0.15 M) or 2 kcal/mol (5 M) barrier for the first minimum at ∼40°, which represents breaking the hydrogen bonds between mismatches and loosening the base stacking; and then a 2.5 kcal/mol (0.15 M) or 1.5 kcal/mol (5 M) barrier. We should note that this calculation most probably overestimates the free energy barriers due to hidden degrees of freedom orthogonal to the single reaction coordinate. For example, in the particular case of base flipping, it was clearly shown that 2D-CV biasing results in lower free energy barriers than those obtained with 1D CVs (77). Thus, our 1D results clearly suggest that there are no major constraints against base extrusion at high salt concentration, a result that is confirmed by our unbiased MD simulations, where we occasionally see a base flipping in or out of the helical core.

To explore GG conformations when the mismatches are restrained to remain inside the helical core, we calculated the (χ₄, χ₁₁) free energy landscape (when the mismatches are extruded they can rotate more freely and thus vary the value of their angle χ). Results for the OL15 FF are shown in Figure 2C, while the corresponding map for BSC1 FF is given in the Supplementary Figure S3; numerical values of the relative free energies are given in Table 2. The results indicate that the anti–syn (marked A,A’) minima is the deepest, followed by the syn–syn minima (marked B) and lastly the anti–anti (marked C,C’) minima. In terms of structure, the OL15 anti–syn conformations are characterized by two hydrogen bonds (N1–O6) while the syn–syn and anti–anti conformations have only a single hydrogen bond—(N1/N2-O6) and (N2/N7), respectively. Schematics of these structures are shown in Supplementary Figure S4.

General MD results and relative stability

We focus on (GGC)_n and (CGG)_n homoduplexes, where the number of TRs n is either 4 or 8. The GG mismatches are initialized as all inside or all outside the helical core. The timing of individual runs varied between 1 μs and 3 μs (after 1 ns of minimization and equilibrium). The BSC0, BSC1 and OL15 AMBER FFs were used with varying salt concentrations. As described in the Methods section, all the WC base pairs have a Z-DNA form; the GG mismatches are initially prepared in either a B-DNA or Z-DNA form such that the resulting helix consists of a series of BZ or ZZ junctions. In addition, we considered a configuration in which the Gs are alternatingly extruding out of a Z-DNA helix (Figure 1). We note that full B-DNA CGG and GGC helices have been previously described and characterized (38); here, we are specifically interested in exploring the experimental findings that suggest that GGC repeats can form Z-DNA helices with GG mismatches (46) under various experimental conditions.

First, we ran various duplexes C(GGC)₄G without salt and with 150 mM NaCl (FFs BSC0, BSC1; results not shown), and we found that they were all unstable. The fact that these Z-DNA homoduplexes are not stable at zero or low salt environments is not surprising; previous studies show that CGG and GGC homoduplexes are stable in B-DNA form under these conditions. In general, the left-handed Z-DNA requires a higher salt concentrations for stability, and for structures with mismatches that is very much the case. This is in agreement with experimental work (46). In many simulations, we added 20 mM NiCl₂ (used in some of the experiments (46)). However, we observed that this salt appeared not to make a difference in the DNA structure. This is perhaps due to an inadequate Ni^{2 +} parametrization (78), or perhaps because the action of this salt is to primarily decrease the transition barriers between B- and Z-DNA. Given that our simulations already begin with a Z-DNA conformation, we believe that this salt is not explicitly required. The remainder of the simulations, unless otherwise specified, were therefore carried out with a salt concentration of 5 M NaCl.

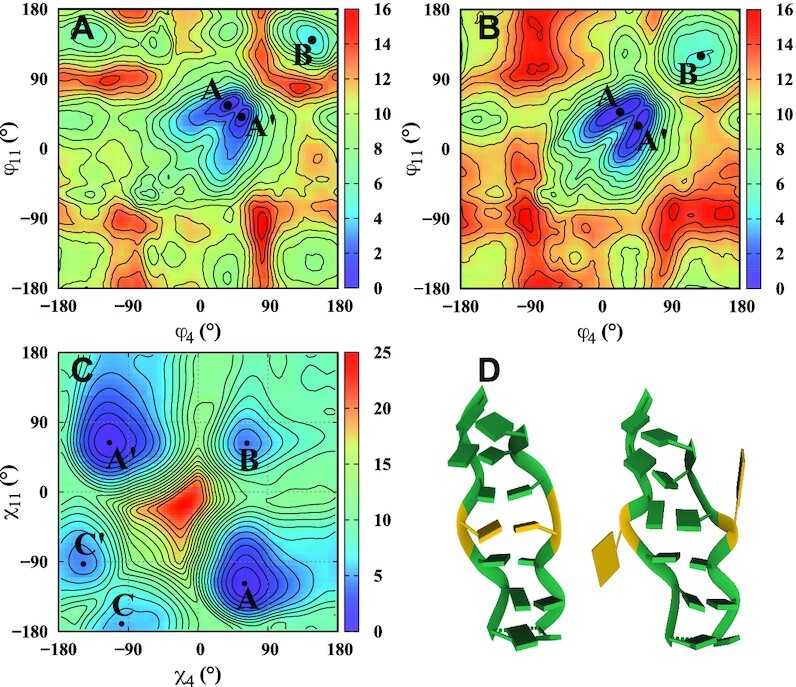
Table 1 summarizes the main results of our MD simulations and Figures 3 and 4 show final conformations for the various sequences and FFs. In addition, Supplementary Figures S5–S9 show the RMSD of backbone atoms with respect to the average frame of the last 200 ns. Convergence of the simulations is confirmed by explicitly checking that the results from different time windows coincide. Results are different according to whether we consider GGC sequences (with CpG steps between the WC base pairs) or CGG sequences (with GpC steps between the WC base pairs). The GG mismatches, especially when inside the helical core, affect the base stacking of adjacent WC bases. Also, the repeating helical unit is not two base pairs, as in regular Z-DNA, but the 3 base pairs in one GGC or CGG TR. For the GGC sequences, we find that four TRs, GGC4, with inner mismatches are not stable; and GGC4 with mismatches symmetrically flipped outwards are stable for BSC0 and OL15, but not for BSC1. This indicates that four TRs are perhaps not enough to stabilize either the BZ- or ZZ-junction helices. Hence, we doubled the number of TRs and found that GGC8 sequences with mismatches outside the helix core are stable, whether the helices are of a BZ or ZZ junction form. GGC8 helices with mismatches inside the helical core tend to be unstable (BZ junction), or long-lived (ZZ junction) as the strands of the helices slowly unwind and become ribbon-like. For the CGG sequences, we found that the BZ junctions are not stable (results not shown), but that four TRs are enough to stabilize the Z-DNA helix when the mismatches are inside the helical core; they are, however, unstable even with the BSC0 FF, if the mismatches are extruded. Interestingly, they tend to flip back inside the helical core and the strands unwind to form a ribbon structure.

Figure 3.

Snapshot of final conformations of the GGC8 helices. The mismatched Gs and WC bases are colored gold and green, respectively.

Figure 4.

Snapshot of final conformations of CGG4_{ZZ, in} and GGC4_{ZZ, alt} helices. The mismatched Gs and WC bases are colored gold and green, respectively.

In summary, GGC sequences can stabilize either the BZ junctions or ZZ junctions, and favor mismatches outside the helical core; CGG sequences can stabilize ZZ junctions as long as the mismatches are inside the helical core. The alternating GGC/CGG sequences, where the Gs are extruded in an alternate fashion, are also remarkably stable: the Gs are completely extruded so that the helix becomes an effective classical Z-DNA helix, with alternating GpC and CpG steps. We note that both CGG and GGC sequences, which result in different WC steps when the mismatches are symmetrically flipped out, converge to the same helix when the Gs are extruded in alternating fashion as shown in the sketch in Figure 1.

GG mismatches outside the helical core tend to stack for long times and thus bend the helices. To characterize the helices independently of these persistent stackings and the associated bending, as well as of end effects, we carried out the rest of our analysis (unless otherwise specified) for the inner four TRs of the GGC8 helices, while we make use the full GGC4 and CGG4 helices. Note that we have carried out simulations of two extruded, ZZ-junction DNA helices: GGC4_{ZZ, out} and GGC8_{ZZ, out}, which only differ in the number of residues. GGC4_{ZZ, out} did not seem very stable in BSC1 and in order to compare structural features for all FFs, we use the inner residues of GGC8_{ZZ, out} (which are structurally consistent with GGC4_{ZZ, out}). After determining that OL15 is the best FF for the description of the helices, we use GGC4_{ZZ, out} for the melting simulations because it is of the same length as the other two helices employed.

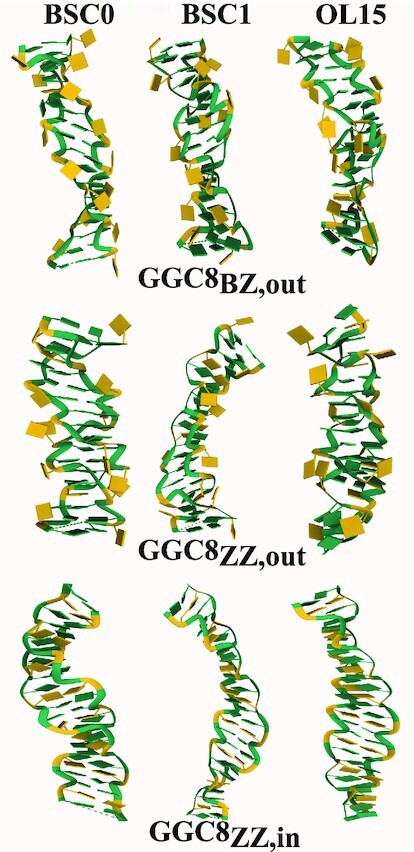
Quantification of the left-handedness and compactness of the helices

Collective variables such as handedness and radius of gyration as introduced in (54) represent a useful way to investigate Z-DNA structures. Handedness (whose definition is given in the SI, see Supplementary Figure S10) is by construction positive for right-handed helices and negative for left-handed helices. The overall handness of a helix is length dependent and involves summing over all the turns of a given helix. Hence, a fair comparison of the handedness between different helices requires the same number of helical turns. In the computation of handedness special care must be given to the treatment of mismatches.

In particular, as the sketch in Figure 5 shows, if the mismatches are fully outside the helical core, they do not contribute to handedness: the mathematical computation of handedness gives zero for their contribution. This is the case for the fully alternatingly extruded G helices GGC4_{ZZ, alt}, as observed in Figures 5B and 6. In addition, if the backbone is locally unwound (i.e. parallel strands) at the inner mismatches, then their contribution is also zero. Since exactly the same number of terms in the definition of handedness must be considered, the completely extruded mismatches in well stacked helices should not be counted, as they do not participate in the helical structure (this can be assessed by using Figure 6 and comparing with the corresponding helical conformations). In the opposite case, when mismatches are fully inside the helical core, they must be considered in the calculation as they represent another base-pair step in the helix. Figure 5 shows the distribution of handedness during the last 1 μs of MD simulations. For comparison, a simple CG Z-DNA with the same number of turns (11 terms in Eq. 1 in SI) is included. The overall handedness stays negative for all helices during the entire simulation time indicating the structures remain left-handed. The following clear tendencies are observed: The GGC8_{ZZ, in} DNA helices have the smallest magnitude of handedness for both BSC1 and OL15 FFs, as these helices are unwinding and becoming more ribbon-like. When mismatches are excluded from the calculation, both the BZ and ZZ GGC8 junctions have almost the same handedness, with the OL15 helices more left-handed than the BSC1 ones. In Figure 5A, we observe that both CGG4_{ZZ, in} and GGC4_{ZZ, alt} have comparable or even larger handedness than regular GC Z-DNA. The rather large left-handedness observed in BSC1 CGG4_{ZZ, in} is due to the fact that the pair G9-G20 in BSC1 are flipped out causing a temporary increase in the magnitude of the left-handedness for the inner residues of the helix. Figure 6 shows the distribution of handedness computed with and without the GG mismatches during the final 1 μs of MD simulations for the OL15 and some of the BSC1 helices (the remainder for BSC1 are included in the Supplementary Figure S11). In order to compute the distribution, the same number of internal base pairs (10 in number) where used for all the helices (C9–G40 to C18–G31 in all GGC8 structures; C2–G27 to C11–G18 in CGG4_{ZZ, in}; and C3–G25 to C12–G16 in GGC4_{ZZ, alt}). Excluding the GG mismatches resulted in 11 terms, while including them resulted in 19 terms in the definition. For extruded bases, this plot provides an indirect way of quantifying the effects of bases flipping out. Figure 6 shows that for GGC4_{ZZ, alt} helices, as explained above, the alternately extruded Gs contribute zero to handedness, which clearly indicates that the G’s are completely extruded from the new helix. The opposite situation is given by GGC8_{ZZ, in}. Since the mismatches are now inside the core of the helix, this means that there is local unwinding at the GG mismatches and thus they are not contributing to helicity but are resulting in parallel strands. This is consistent with the ribbon-like DNA observed in the conformations. For the other three cases, including the GG mismatches in the calculation increases the value of handedness. For the two extruded cases GGC8_{BZ, out} and GGC8_{ZZ, out}, this also implies that the mismatches are not fully extruded and their backbones are therefore contributing to the overall helical structure. Not surprisingly, this effect is larger for the ZZ case. Locating the center of the distributions and dividing by the number of terms, one obtains an average measure of the contribution of each turn to the handedness of the structures. For regular Z-DNA: –3.4/11 (x-axis) ≃ –5.7/19 (y-axis) ≃ –0.30. For GGC4_{ZZ, alt} (Gs completely extruded, only x-axis should be considered) –4.0/11 ≃ –0.36. For GGC8_{ZZ, in} (Gs completely inside the core, only y-axis should be considered) –1.5/19 ≃ –0.08. For GGC8_{BZ, out}: –2.9/11 (x-axis) ≃ –5.0/19 (y-axis) ≃ –0.26. For GGC8_{ZZ, out}: –2.8/11 (x-axis) ≃ –0.25 and –5.6/19 (y-axis) ≃ –0.29. Finally, for CGG4_{ZZ, in} (only y-axis) –5.7/19 ≃ –0.30. Thus, a quick ‘rating’ of left-handedness (for OL15) gives: GGC4_{ZZ, alt} (–0.36) > CGG4_{ZZ, in} ≃ Z-DNA (–0.30) > GGC8_{ZZ, out} ≃ GGC8_{BZ, out} (–0.26) > GGC8_{ZZ, in} (–0.08).

Figure 5.

(A) Distribution of handedness for the different helices, with data taken from the last 1 μs of the simulations. Red: GGC8_{BZ, out}; blue: GGC8_{ZZ, out}; green: GGC8_{ZZ, in}; purple CGG4_{ZZ, in}; orange: GGC4_{ZZ, alt}; black: GC6_Z-DNA. Solid and dashed lines denote OL15 and BSC1 FFs respectively. The data is based on results taken from the middle residues: mismatches out of the helical core are ignored and inner mismatches are considered; the number of turns in the definition of handedness is the same (11) for all helices. (B) Snapshot of the two cases where mismatches contribute zero to handedness: a fully extruded mismatch (left), and inner mismatches in locally parallel strands (right). Phosphorous atoms are shown as grey spheres. Red and blue arrows represent the vectors involved in definition of handedness. The cross product of these vectors is zero as they are parallel and thus do not contribute to handedness. See the SI for more details on the definition and calculation of handedness.

Figure 6.

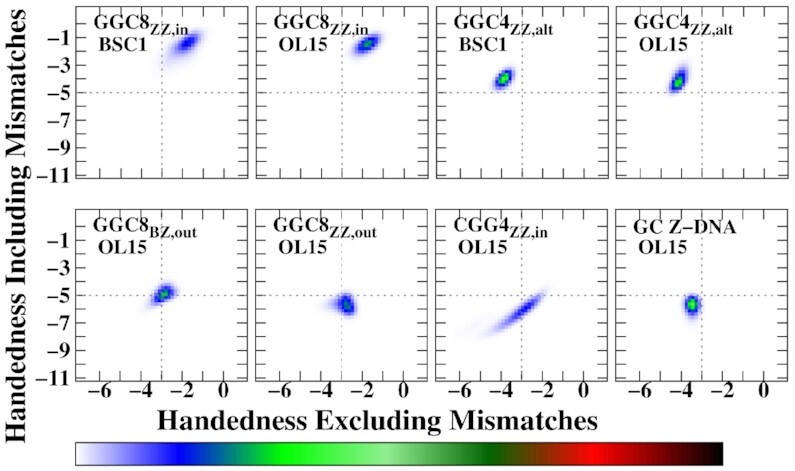
Two-dimensional histograms of handedness including mismatches versus handedness excluding mismatches. The data are based on calculations obtained from the middle residues during the last 1 μs simulation time for each helix. The total number of considered residues is constant for all calculations, which means that handedness with mismatches includes a larger number of terms (19) than handedness calculation without any mismatches (11).

Related to global handedness is the local twist step parameter. Figure 7 shows the average twist angle during the last 200 ns of the simulations for the OL15 FF. The figure shows all the steps for the CGG4_{ZZ, in} and GGC_{ZZ, alt} helices and the inner steps for the GGC8 helices, with the corresponding sequence that identifies the step mapped below each panel. The twist has been computed without the mismatches in the extruded cases in the upper panels, and with the inner mismatches on the lower panels. In the upper panels, GpC are pseudo-steps for both GGC8_{BZ, out} and GGC8_{ZZ, out}; the omission of the GG mismatches leads to the apparently larger value of twist (compared to regular Z-DNA) at the GpC pseudo-steps. The twist for GGC4_{ZZ, alt}, where both CpG and GpC are pseudo-steps, is remarkably close to that of regular Z-DNA, and is consistent with the large value of handedness for this helix. For the internal G’s, the twist parameter reflects the TR unit. In agreement with the small values of handedness, GGC8_{ZZ, in} displays rather small values of twist. Finally, CGG4_{ZZ, in} has a twist profile remarkably similar to that of regular Z-DNA, in spite of the three-step periodicity.

Figure 7.

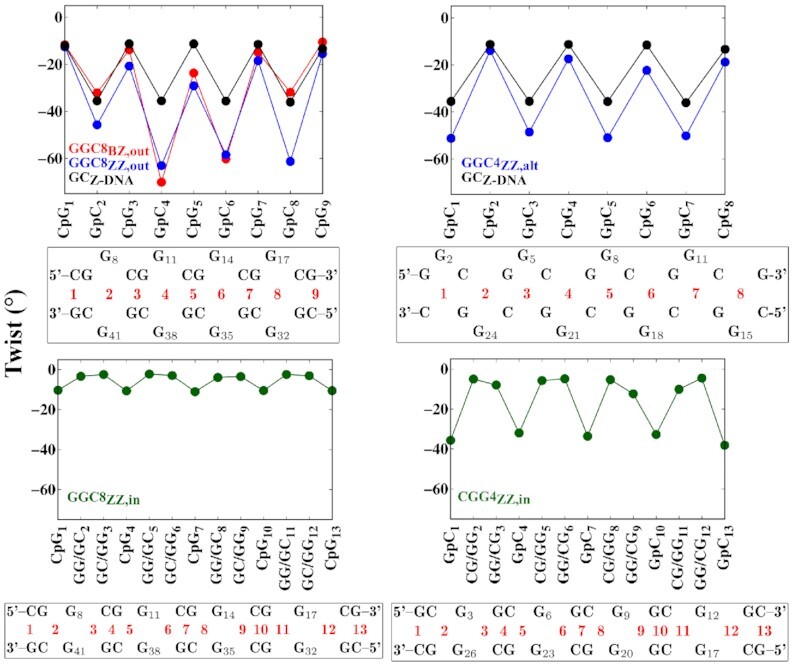
Average twist angle as obtained from the last 200 ns of the simulations with the OL15 FF. Considered here are nucleotides 6–19 on one strand and the complementary nucleotides 30–43 on the other in GGC8 helices; and all residues in the shorter CGG4_{ZZ, in} and GGC_{ZZ, alt} helices. Below each figure, a sequence map specifically identifies the steps considered in the corresponding figure. As the map indicates, the twist has been computed without the mismatches in the extruded cases in the upper panels, and with the inner mismatches on the lower panels. In the upper panels, GpC are pseudo-steps for both GGC8_{BZ, out} and GGC8_{ZZ, out}; and both CpG and GpC are pseudo-steps for GGC4_{ZZ, alt}. The black line represents the twist of standard Z-DNA helix based on a sequence of GC repeats.

The radius of gyration is used as a global measure to determine the compactness of polymers. Supplementary Table S1 compares the initial, final, and average radius of gyration of the helices during the simulations. Not surprisingly, helices with inner mismatches display larger radii of gyration. In the extruded cases, if one base flips inside (as in BSC1 GGC8_{ZZ, out}) then the corresponding radius of gyration increases. A local measure of compactness is given by the step rise parameter. Table 3 lists the average rise values for the different steps and the corresponding van der Waals energies. Although there are many components to the final free energy of the helix, the van der Waals energies for the steps provide a measure of the stacking between these steps. For the GGC8_out helices, both in BZ and ZZ junctions, CpG steps are standard WC steps while GpC are pseudo-steps formed by the stacking of the helix upon extrusion of the mismatches. For GGC4_{ZZ, alt}, CpG are also pseudo-steps. The GpC pseudo-steps in the junctions have equal or slightly smaller rise than the real CpG steps (except BSC1 GGC8_{ZZ, out}, where one base pair flips back inside the helix), which indicates good helix stacking. For the extruded cases, GpC pseudo-steps have higher van der Waals energies than the CpG WC steps (or CpG pseudo-steps in the case of GGC4_{ZZ, alt}). The stacking energies in the GG/GC and GC/GG steps in GGC8_{ZZ, in} are so much larger than those of the CpG steps that they drive the unwinding of the helix, as the stacking involving the GGs is maximized. Instead, for CGG4_{ZZ, in}, the van der Waals energy of the GpC steps is larger than that of the CG/GG and GG/CG steps, which better enables the helical conformation. In a regular, ideal helix the stacking energy also has the periodicity of the sequence, and thus for the dinucleotide step in regular Z-DNA, the ratio of the energies for CpG and GpC steps should be constant on average. For regular Z-DNA this ratio is about 0.73 for both OL15 and BSC1 FFs (Table 3). For the BZ junction, GGC8_{BZ, out}, and the ZZ junction, GGC8_{ZZ, out}, the OL15 ratios are 0.72 and 0.71 respectively, for the alternately extruded helix it is 0.74; the three of them are in remarkable agreement with Z-DNA. In the two intrahelical cases three steps, instead of two, come into play. While consecutive ratios of the stacking energies of CpG and GpC steps in regular Z-DNA give (0.73, 1.37), consecutive ratios of the step van der Waals energies give (1.08, 0.84, 1.10) for CGG4_{ZZ, in} and (1.0, 2.0, 0.5) for GGC8_{ZZ, in}, which are rather different from those of Z-DNA. Finally, GGC4_{ZZ, alt} shows a series of alternating pseudo GpC and CpG steps with the smallest rise giving rise to the most compact of all the helices.

Table 3.

Average van der Waals energy (kcal/mol) and rise (Å) in the GpC, CpG, CG/GG, GG/CG, GG/GC, GC/GG steps measured over last 200ns of the simulations. For each structure, the top and bottom rows represent the average van der Waals energy and the rise between the steps in a given helix, respectively. Numbers in black (blue) represent data obtained from OL15 (BSC1) FF calculations

Structure	GpC	CpG	CG/GG	GG/CG	GG/GC	GC/GG
GGC8BZ, out	–6.99, –7.19	–5.06, –4.73	–	–	–	–
	3.52, 3.35	3.53, 3.81	–	–	–	–
GGC8ZZ, out	–7.18, –5.46	–5.07, –5.07	–	–	–	–
	3.45, 3.90	3.46, 3.84	–	–	–	–
GGC8ZZ, in	–	–4.89, –4.66	–	–	–9.36, –9.29	–9.35, –9.31
	–	4.31, 4.41	–	–	3.16, 3.19	3.15, 3.18
CGG4ZZ, in	–7.84, –8.15	–	–7.08, –6.38	–6.56, –6.50	–	–
	3.11, 3.47	–	3.49, 2.68	3.52, 2.73	–	–
GGC4ZZ, alt	–6.38, –6.44	–4.75, –4.75	–	–	–	–
	3.02, 3.72	3.37, 2.95	–	–	–	–
GC6Z-DNA	–7.22,–7.55	–5.29, –5.54	–	–	–	–
	3.25, 3.29	3.70, 3.82	–	–	–	–

Other structural parameters

Torsion backbone angles such as α, β, γ, δ, ε and ζ differ in purine and pyrimidine bases indicating the zig-zag pattern of the Z-DNA backbone. For instance, Figure 8 shows the conformational parameter β for the different helices, clearly highlighting the three nucleotide periodicity. Next, we consider the glycosidic torsion angle χ that characterizes the relative base/sugar orientation. The WC C–G base pairs are generally in anti–syn or anti-(high-syn) conformations, except for some terminal G’s that tend to fluctuate more. However, some BSC1 helices have some G’s in WC base pairs falling in the anti range. The RMSD of WC bases has been compared with a standard WC Z-DNA (not shown), and indeed all the WC base pairs remain in Z-form, with 2–3 hydrogen bonds. The χ angle distribution of the mismatches is shown in SI, Supplementary Figures S12–S16. The χ angles of extruded mismatches vary greatly due to the fact that these residues tend to bond to the backbone or stack on each other. In BSC1 GGC8_{BZ, out}, two GG pairs are anti–syn and two pairs are syn–syn; in OL15 GGC8_{BZ, out}, all mismatched pairs are syn–syn or on the boundary at χ = −90°. In BSC1 GGC8_{ZZ, out}, one pair is anti–anti, one anti–syn, and two pairs are syn–syn; in OL15 GGC8_{ZZ, out}, three mismatched pairs are syn–syn (or at the boundary χ = −90°) and one pair is anti–syn. In BSC1 GGC8_{ZZ, in}, χ ranges between 60° and 120° with an average around 80°. In OL15 GGC8_{ZZ, in}, all pairs display syn–syn symmetry with an average χ angle around 60°. In CGG4_{ZZ, in}, all pairs are syn–syn (or at the boundary χ = ±90°) except for one G in BSC1 that takes occasional anti values. Finally, for GGC4_{ZZ, alt}anti–syn conformations prevail in BSC1, while syn–syn conformations are present in OL15. Notice that the syn–syn minimum for internal mismatches is the second minimum in the phase diagram for a single mismatch surrounded by three WC G–C base pairs on either side. The MD results for OL15 show that when there are multiple mismatches in a helix, they prefer the syn–syn conformation, as it recovers the original symmetry of the sequence.

Figure 8.

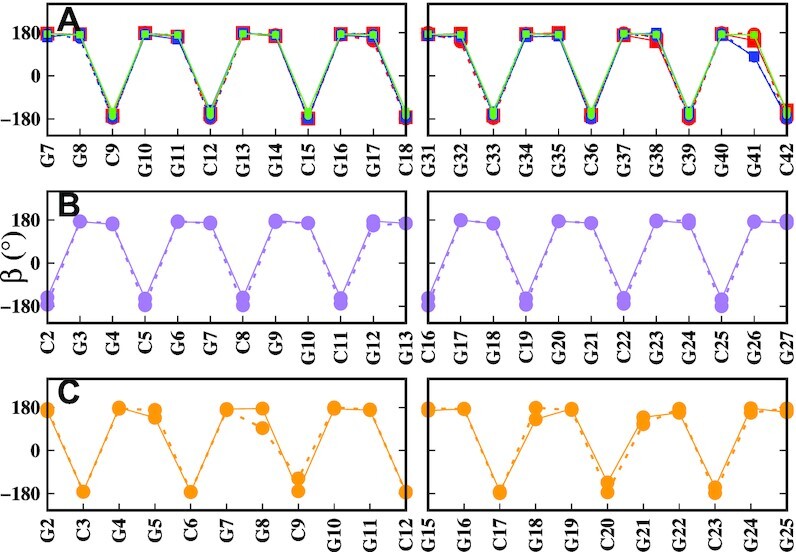
Average β (P–O5′–C5′–C4’) backbone angle for (A) inner-GGC8, (B) CGG4_{ZZ, in}, and (C) GGC4_{ZZ, alt}. Red: GGC8_{BZ, out}; blue: GGC8_{ZZ, out}; green: GGC8_{ZZ, in}; purple CGG4_{ZZ, in}; orange: GGC4_{ZZ, alt}. Solid and dashed lines specify OL15 and BSC1 FFs respectively. The curves are based on data taken from the last 200 ns of the simulations for each helix.

Dynamical characterization and mismatched G interactions

In order to identify the major conformational changes and atomic displacements of the helices we have used principal components analysis (PCA) (79), as applied to the backbone atoms over the last 200 ns. The contribution of the first eigenvector corresponds to the largest positional fluctuations of the helices and accounts for more than 45% (BSC1) and 30% (OL15) of the motions in GGC8_{BZ, out}; 35% (BSC1) and 25% (OL15) in GGC8_{ZZ, out}; 50% (BSC1) and 60% (OL15) in GGC8_{ZZ, in}; 35% (BSC1) and 45% (OL15) in CGG4_{ZZ, in}; and finally 34% (BSC1) and 33% (OL15) in GGC4_{ZZ, alt}. Visual examination of trajectories created by PCA finds that the dominant dynamic modes in GGC8_{BZ, out} and GGC8_{ZZ, out} are bending and twisting; while in GGC8_{ZZ, in} they correspond to bending and stretching, which causes helical deformation. The BSC1 CGG4_{ZZ, in} helix shows twisting, mostly due to motions at the termini, and the corresponding OL15 helix shows bending and stretching motions with smaller amplitude than those in inner-GGC8_{ZZ, in} (4 inner TRs). The BSC1 GGC4_{ZZ, alt} helix also exhibits bending and twisting motions, while OL15 GGC4_{ZZ, alt} primarily displays twisting, especially at the terminating bases. Porcupine plots of these motions are shown in Figure 9. The normalized histograms of motions projected onto the first principal component are given in Supplementary Figures S17 and S18.

Figure 9.

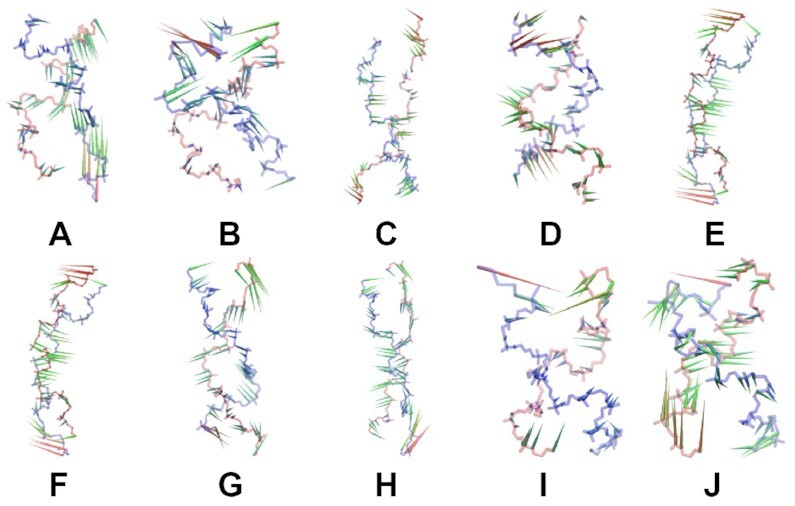
Porcupine plot of first principal component for: (A) BSC1 inner-GGC8_{BZ, out}, (B) OL15 inner-GGC8_{BZ, out}, (C) BSC1 inner-GGC8_{ZZ, out}, (D) OL15 inner-GGC8_{ZZ, out}, (E) BSC1 GGC8_{ZZ, in}, (F) OL15 GGC8_{ZZ, in}, (G) BSC1 CGG4_{ZZ, in}, (H) OL15 CGG4_{ZZ, in}, (I) BSC1 GGC4_{ZZ, alt} and (J) OL15 GGC4_{ZZ, alt}. Only movements of heavy backbone atoms, i.e. P,O3′,O5′, are shown. The helices have different number of residues and are not shown to scale.

Transitions between in and out states have been observed, especially in the less stable helices, e.g. the pair G11–G38 flipped inside the helical core in the GGC8_{ZZ, out} BSC1 helix; and in the CGG4_{ZZ, out} helices the initially extruded bases flip inside the helical core (Table 1). The cooperative effect of mismatches impacts interactions and bonding. In particular, we considered the hydrogen bond interactions associated with mismatched Gs between a polar hydrogen atom and a nearby (<3.0 Å) acceptor atom.

We have observed five types of interactions for the mismatched residues, which are listed in full detail in Supplementary Tables S3–S6. (i) Hydrogen bonds within a mismatch pair inside the helical core. This type of interaction is shown in Figure 10A where the mismatches are in anti–syn conformation and form two H-bonds (only in CGG4_{ZZ, in}), and Figure 10B where mismatches are in syn–syn conformation and form a single H-bond (both in CGG4_{ZZ, in} and GGC8_{ZZ, in}); (ii) hydrogen bonding with the backbone of closest cytosine in the 5′ direction outside the helical core of GGC8_{ZZ, out} and GGC8_{BZ, out} helices, as shown in Figure 10 C; (iii) long-lived base stacking outside the helical core as shown in Figure 10 D, examples of which with their corresponding van der Waals energies are given in Supplementary Table S2; (iv) hydrogen bonding with other mismatches outside the helical core, either on the same strand (intra-strand, short-lived, not shown) or on the other strand (inter-strand, as shown in Figure 10E and F), (iv) short-life interactions with ions (major or minor groove atoms: O6,N7,N3 and Na⁺) as well as salt bridges (not shown). In particular, the OL15 GGC4_{ZZ, out}, GGC8_{ZZ, out} and GGC4_{ZZ, alt} helices tend to make inter-strand, diagonal hydrogen bonds, and also long-lived inter-strand stacking between extruded Gs and occasional intra-strand stackings.

Figure 10.

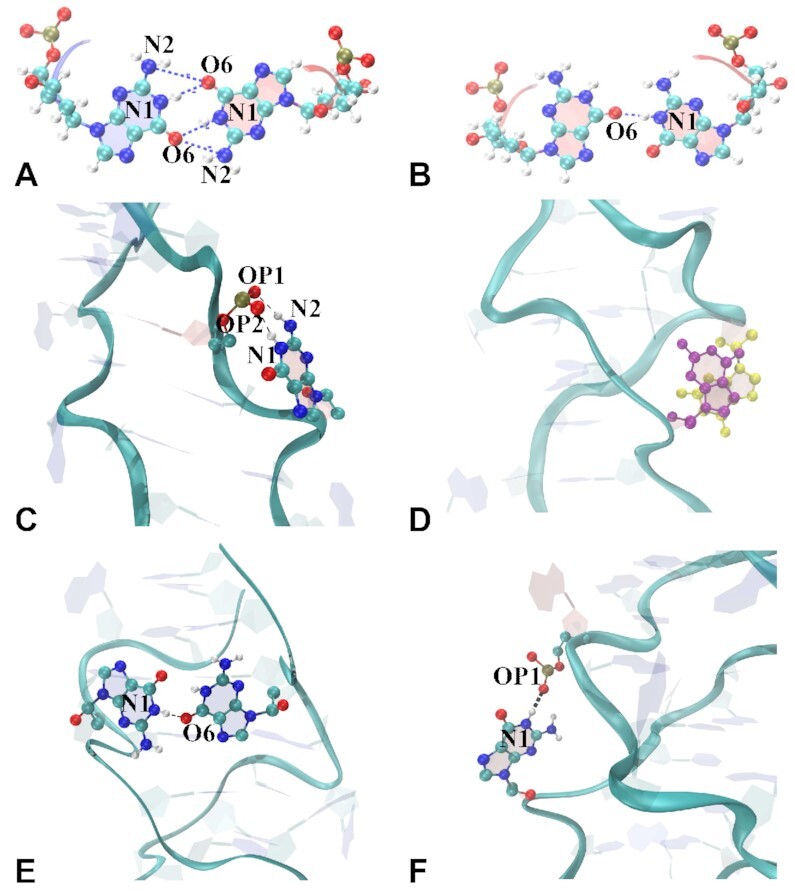
Snapshots of mismatches interacting via hydrogen bonds or base stacking. (A) Hbonds between O6 and N1/N2 when mismatches are inside the helical core in anti–syn conformations; (B) syn–syn conformation; (C) Hbonds between G_i:N1/N2 and C_{(i − 2)}:(phosphate group); (D) base stacking by two mismatches; (E) inter-strand Hbonds between two mismatched bases; (F) inter-strand Hbonds between two mismatches via N1:OP1. O, N, C and H atoms are shown in red, blue, cyan, and white colors, respectively.

Force field comparison

Empirical FF for nucleic acids are constantly under revision and new refinements are periodically introduced. In this work we have used three AMBER FFs: an older force field BSC0 (58) and two new FFs, BSC1 (59) and OL15 (ff99bsc0-εζ_OL1χ_OL4β_OL1) (60) that are considered state-of-the-art. OL15 has been shown to significantly improve the overall description of sugar-phosphate backbone equilibria, particularly in Z-DNA molecules (60,80). Moreover, the BSC1 FF can exhibit different behavior than OL15, as has been reported previously (81). Encouragingly, in our simulations the three FF gave primarily the same results with respect to the relative stability of the various homoduplexes although they differed in the particulars. We also found that OL15 performs better than BSC1. In particular, we observed some G’s in the BSC1 FF switch from syn to anti even though they are part of WC base pairs (see for instance Supplementary Figure S19). This problem probably arises due to imbalances in the ZI/ZII parameters and other backbone substates (60) in BSC1. We quantified important differences in the results between OL15 and BSC1 through carefully obtained free energy maps, as shown for OL15 in Figure 2 and for BSC1 in Supplementary Figure S3. The (A, A′) deepest minima in the BSC1 map correspond to (105°, −90°) and (−90°, 105°), which resemble anti–syn configurations, but are different from the clearly anti–syn configurations in the equivalent positions on the OL15 map. Moreover, there are also other spurious minima that break the diagonal symmetry. The pairs (C,C′), (D,D′) and (B,B′) (the latter on the diagonal itself) in the BSC1 free energy map display an inversion symmetry with respect to origin (0,0). This suggests that the χ’s are strongly correlated, and it is very costly to deviate from this correlation. The syn–syn configurations reflected in points (B, B′) are close to ±90 and have higher free energy value than the corresponding configuration B in OL15. The minima C′ and D′ correspond to the anti–anti configurations that are 1–2 kcal/mol higher in energy. These type of anti–anti configurations form two hydrogen bonds, and exhibit different sugar-phosphate backbone torsion angles, particularly β angles, which leads to different χ. The C and D minima form a single hydrogen bond in anti–syn configurations again 1–2 kcal/mol higher in energy.

Comparison of stability for the CGG4_{ZZ, in}, GGC4_{ZZ, out} and GGC4_{ZZ, alt} helices

The experimental results from CD spectroscopy (46) found strong left-handedness in the generic CGG sequences. Of all the extruded cases that we considered, GGC4_{ZZ, alt} proved to be the one with better left-handedness, stacking interactions and compactness. The GGC4_{ZZ, out} helices were stable for BSC0 and OL15 FFs, but unstable for BSC1 FF. Increasing the number of repeats stabilize the GGC sequences with extruded mismatches for all three BSC0, BSC1, and OL15 FFs. For the inner mismatches, the only stable helix is CGG4_{ZZ, in} as the GGC counterpart tends to unwind. Thus, we set out to compare the relative stability of these three helices by employing an assortment of methods and simulations, detailed below. All the results in this section correspond to OL15, the best performing FF according to our previous discussion.

1. Higher-temperature MD at lower salt: As a first test of stability, we carried out higher-temperature MD simulations at low salt (neutralizing Na⁺ ions and 200 mM NaCl salt). Final configurations at 303 K were chosen as a start for these 1μs simulations which entail 0–200 ns at 303 K, 201–400 ns at 323 K, 401–600 ns at 343 K and 6001–1000 ns at 363 K. Interestingly, all three duplexes were stable under low salt condition up to 363 K when they began to melt. Supplementary Figures S20 and S21 show the RMSD of the backbone atoms for the higher temperatures with respect to the initial 303 K conformations, and the percentage of WC hydrogen bonds versus time. The CGG4_{ZZ, in} duplex seems to undergo more fluctuations and perhaps some conformational instability compared to GGC4_{ZZ, alt} and GGC4_{ZZ, out} as the temperature increases. With respect to the extruded mismatches, the RMSD and the percentage of WC hydrogen bonds results for the higher-temperature simulations indicate comparable stability for GGC4_{ZZ, alt} and GGC4_{ZZ, out}.

2. Work Function: We also performed constant velocity pulling simulations for GGC4_{ZZ, alt}, GGC4_{ZZ, out} and CGG4_{ZZ, in} using the SMD (56) simulation protocol (described in the Materials and Methods section). According to the Jarzynski equality (82), the non-equilibrium work performed on the system during the SMD simulation can be related to the free energy difference, exp(− βΔF) = <exp( − βW)>. SMD is particularly useful for examining select pathways and mechanisms between two equilibrium states (83,84), as well as estimating the transition rates for these reactions (85–87). Since our purpose was to compare the relative stabilities of the GGC4_{ZZ, alt}, GGC4_{ZZ, out} and CGG4_{ZZ, in} helices, we simply calculated the average cumulative work to stretch the duplexes up to the breaking point. Figure 11 shows the average cumulative work versus the extension length. The difference between the three duplexes is appreciable and confirms the results from the higher-temperature MD. The average cumulative works to stretch both GGC4_{ZZ, alt} and GGC4_{ZZ, out} helices are larger than for CGG4_{ZZ, in} by about 14 kcal/mol and 8 kcal/mol respectively. The work required to stretch either GGC4_{ZZ, alt} and GGC4_{ZZ, out} not only is larger than that for CGG4_{ZZ, in}, but also almost linearly increases, while the one for CGG4_{ZZ, in} is almost zero up to 4 Å. In other words, the GGC4_{ZZ, alt} and GGC4_{ZZ, out} duplexes generate significantly more dissipative work than CGG4_{ZZ, in}, which indicates they are more difficult to stretch and therefore more stable. With respect to the relative stability between GGC4_{ZZ, alt} and GGC4_{ZZ, out}, we note that GGC4_{ZZ, alt} needs around 6 kcal/mol more work than GGC4_{ZZ, out}, while its sequence has two fewer residues, thus these calculations indicate that the GGC4_{ZZ, alt} DNA duplex is more stable than the GGC4_{ZZ, out} one.

Figure 11.

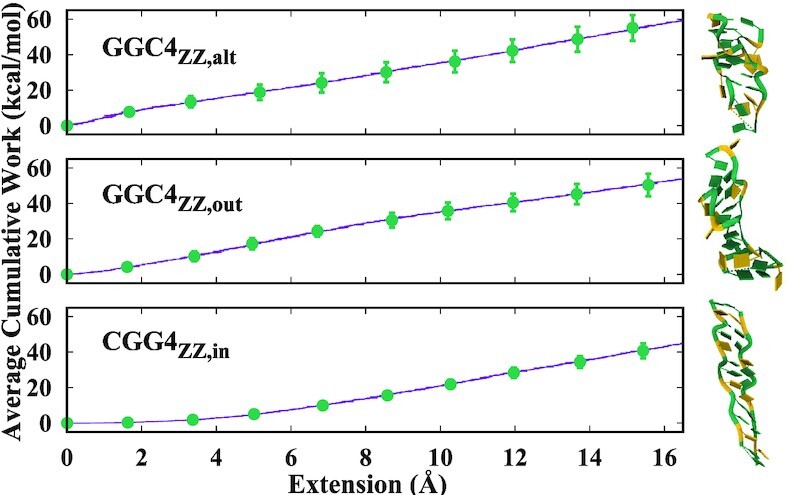
Average cumulative work required to stretch the helices as a function of the end-to-end distance. A snapshot of the final stretched helices is shown on the right.

In summary, these results indicate a better stability for the extruded mismatches, especially for the DNA eGZ-motif motif, GGC4_{ZZ, alt}, particularly at higher salt concentration.

DISCUSSION

Experimental background and motivation

Experimental work (45,46) based on CD spectroscopy, UV absorbance and electrophoretic mobility assays unequivocally demonstrate that CGG runs adopt a non-B DNA conformation – a left-handed Z-DNA, whose likelihood of formation increases with increasing number of repeats. The authors discarded a G-quadruplex as the motif behind CGG expansion because it only forms at low pH, in the presence of high concentrations of KCl and other non-physiological conditions (45,48). Furthermore, these quadruplexes gain additional stability in the presence of AGG interrupts that are supposed to destabilize the expansion by destabilizing the secondary motifs associated with it. Instead, the AGG interrupts destabilize the left-handed hairpins. Although high salt concentrations are used to stabilize Z-DNA in vitro, Z-DNA formation can occur under physiological conditions: mainly by cytosine methylation in CpG islands, by superhelical stress, or by mimicry of a crowded cell environment. CD spectroscopy is extremely sensitive to the formation of Z-DNA: after formation of Z-DNA the typical B-DNA CD spectrum is flipped into a nearly inverse curve (45). Indeed, the left-handed form of DNA was identified (88) nearly a decade before its crystal structure (47).

Previous experiments carried by the same group on CAG and GAC expansions (89) showed that homoduplexes and hairpins associated with GAC repeats that only display CpG WC steps can form Z-DNA, while CAG repeats (with GpC steps) cannot form Z-DNA. Thus, the authors concluded that the CGG sequences can form DNA when in frame 2 (32,33), i.e., when the two strands are aligned such that only CpG steps are present. The authors speculated that the resulting Z-DNA might contain a non-canonical, intrahelical G_syn·G_anti pair or the GG mismatches might be extruded in symmetric pairs. We notice that the evidence for the CpG steps is indirect, made by analogy with GAC and CAG repeats and by the evidence that indeed CG repeats form Z-DNA at shorter lengths than GC repeats. Compared to CAG/GAC, the CGG/GGC sequences are ‘degenerate’ in the sense that slipping between the strands can result in either CpG or GpC steps between the mismatches. Thus, before this work, the exact conformation of these left-handed duplexes was still unknown. Interestingly, an older NMR study of (CGG)₃ homoduplexes at low-salt concentrations (0.1M NaCl) reported right-handed helices with highly mobile mismatched Gs that do not appear to form stable base pairs (53). Moreover, the authors found that the strands of the homoduplexes slipped with respect to each other in such a way that the resulting helix was clearly in frame 2.

MD simulations setup and goals

In order to identify this missing motif, we set out to construct and study through MD simulations an exhaustive collection of DNA helices with Z-DNA WC base pairs. The experiments nucleated Z-DNA by jumping over high free-energy barriers with very slow kinetics: to achieve the characteristic Z-DNA spectra took several hours, and even days, in solution with 5M NaCl and additional NiCl₂ salt to facilitate the barrier crossing. Our studies do not consider the transition between B-DNA and Z-DNA (which we have extensively studied in the past (54)) but focus on all possible left-handed helices that could result from such a transition. Such helices combine either CpG or GpC WC steps in Z-DNA form with different conformations of the GG mismatches, which we set as either intrahelical or extrahelical; and participating in (i) BZ junctions; (ii) ZZ junctions or (iii) alternately extruded conformations. These structures were unstable at low salt (0 and 150mM NaCl), and for most simulations we used the same high salt concentration as experiments (5 M). We used three AMBER FF: an older FF BSC0 (58) and two new FF, BSC1 (59) and OL15 (60), considered state-of-the-art. Encouragingly, the main results of our simulations were consistent with the three FF, although they differed in the particulars. Through carefully mapping free energies and through structural analysis of Z-DNA (especially the more standard WC base pairs) we found that OL15 performs better than BSC1. This is in agreement with systematic, focused studies that have shown that OL15 significantly improves the overall description of sugar-phosphate backbone equilibria, particularly in Z-DNA molecules (60,80).

DNA BZ and ZZ junctions

The BZ junctions were constructed as a ‘thought’ experiment. Although BZ junctions can be obtained experimentally (49), from the point of view of free energies, neither Z-DNA nor B-DNA favor the nucleation of a pair of opposite handedness in the middle of a duplex (54). However, a base pair disruption can result in a nucleation event. Indeed, an experimentally observed BZ junction displays two bases extruded at the junction that favor the stacking of the B- and Z-DNA helices (49). In good agreement with these results, we observed that the series of BZ junctions (where only the GG mismatches are in B-DNA form) for GGC sequences (CpG WC steps) were not stable when inside the helix, but resulted in an stable helix when the mismatches were located outside of its core. The effect was also length-dependent, with (GGC)₄ being unstable but (GGC)₈ being stable. Of course, the nucleation of consecutive BZ junctions is highly improbable: this thought experiment was carried out to check how the helix can readjust in order to maximize stacking, with the symmetric extrusion of the mismatches turning out to be the favored helical conformation.

Next, we moved to ZZ junctions: a ZZ junction is formed when the characteristic purine-pyrimidine dinucleotide repeat of Z-DNA is interrupted by insertions (in our case, the GG mismatches) or deletions that bring the neighboring helices out of phase (50,51,90,91). The conformations of ZZ junctions depend on the environment around the helix. Thus, two studies, one involving chemical probing and modeling (50) and the other based on NMR (51), suggested that the mismatches remain intrahelical. Another study based on fluorescence spectroscopy with fluorescent modified bases at the junction indicated that the bases are extruded (90). Yet, another study where the DNA molecule is bound by Zα, the Z-DNA binding domain of the RNA editing enzyme ADAR1, showed limited extrusion of one of the bases in the mismatch, and non-continuous stacking between the two helices (91). Our simulations reflect this pool of conformations. First, we found that GGC sequences (CpG WC base pairs) favor extruded mismatches, forming well stacked helices with measures of left-handedness, rise and van der Waals energies between steps very close to that of Z-DNA. On the contrary, GGC helices with internal mismatches tend to unwind and become ribbon-like, in a slow process reminiscent of the stretch-collapse mechanism in a Z- to B-DNA transition (54). The main reason for this unwinding is the strong stacking due to GG/GC and GC/GG steps, which completely overwhelms the CpG steps. Exactly the inverse situation happened with CGG sequences (GpC WC base pairs): helices with extruded mismatches were unstable, flipping back in as the simulation progressed, while helices with intrahelical mismatches were stable, with comparable handedness to Z-DNA. This is interesting because these helices contain GpC WC steps: experiments with CAG TRs cannot reproduce the Z-form (89). We believe that this is partly due to large nucleation barriers in the experiments that our system do not need to cross, as the helices are already started in the Z-form. In addition, the interplay between the GpC steps and the CG/GG and GG/CG steps favors rise and van der Waals energies between steps (Table 3) and a twist profile (Figure 7) very close to that of regular Z-DNA. Ultimately, the complementary simulations carried out on these helices showed them to be less stable than the extruded G counterparts.

Alternately extruded Gs

Finally, we considered the case of alternately extruded Gs, GGC4_{ZZ, alt}, where the Gs are completely extruded in an alternating fashion, so that the helix becomes an effective classical Z-DNA helix, with alternating GpC and CpG steps. Notice that both CGG and GGC sequences, which result in different WC steps when the mismatches are symmetrically extruded, converge to the same helix when the Gs are extruded in alternating fashion, as shown in the sketch in Figure 1. Structural analysis for GGC4_{ZZ, alt} revealed that this helix has strong left-handedness, stacking interactions, and compactness, similarly to GGC4_{ZZ, out}. This motif as well as the consecutive ZZ-junction motif are new. We have found in the literature two cases which resemble the alternately extruded motif. The use of two GC-selective intercalator actinomycin D molecules in the GG mismatches causes DNA rearrangements resulting in either a right-handed Z-DNA structure with a sharp kink in a d(TTGGCGAA) duplex (92); or a sharp bend with a local left-handed twist in a d(ATGCGGCAT) duplex (93), with unwinding of the helix. In both cases, the Gs are extruded towards the minor groove, almost perpendicularly to the long axis of the flanking WC base pairs, and pointing slightly in the 5′ direction. These helical structures are induced by the intercalation of the ActD molecules and by mutual stacking interactions with the flipped Gs of other symmetry-equivalent duplexes in the crystal, and do not result in left-handed Z-DNA. However, they still lend encouragement to the existence of the motifs found here.

Comparison between the most stable DNA duplexes, CGG4_{ZZ, in}, GGC4_{ZZ, out} and GGC4_{ZZ, alt} helices

The experimental results from CD spectroscopy (46) found very strong left-handedness in the generic CGG sequences. Thus, a structural analysis seeking to quantify this particular conformational feature can readily select DNA helices that satisfy the experimental findings. As explained in the Results section, we originally started with nine possible non-equivalent helices, but MD simulations quickly identified unstable helices. After that, a geometrical definition of global left-handedness both visually and numerically provided a rating of helical duplexes in terms of decreasing left-handedness: GGC4_{ZZ, alt} (–0.36) > CGG4_{ZZ, in} ≃ Z-DNA (-0.30) > GGC8_{ZZ, out} ≃ GGC8_{BZ, out} (–0.26) > GGC8_{ZZ, in} (–0.08). These findings are consistent with the local definition of step twist, as shown in Figure 7. Discarding the unlikely BZ junctions, these measurements reduce the number of possible helices from nine to three candidates: CGG4_{ZZ, in}, GGC4_{ZZ, out} and GGC4_{ZZ, alt}. In addition to twist and handedness, one can consider other quantities, such as the average van der Waals energies for the different steps in a helix, which gives a measure of stacking for those steps. In a regular, ideal helix the stacking energy also has the periodicity of the sequence, and thus for the dinucleotide step in regular (CG) Z-DNA, the ratio of the energies for CpG and GpC steps should be constant on average. For regular (CG) Z-DNA this ratio is about 0.73 for both OL15 and BSC1 FFs (Table 3). For the BZ junction, GGC8_{BZ, out}, and the ZZ junction, GGC8_{ZZ, out}, the OL15 ratios are 0.72 and 0.71 respectively, for the alternately extruded helix it is 0.74; the three of them are in remarkable agreement with Z-DNA. The comparison becomes less clear for the intrahelical CGG4_{ZZ, in} case because three steps, instead of two, come into play.

The sturdiness of the three candidate helices was further tested with simulations at both higher temperature and lower salt, and the three helices proved quite robust with CGG4_{ZZ, in} undergoing more degradation at 363K. Finally, we employed SMD simulations to calculate the average cumulative work to stretch the duplexes. We found that the average cumulative work to stretch both GGC4_{ZZ, alt} and GGC4_{ZZ, out} helices is larger than for CGG4_{ZZ, in} by about 14 kcal/mol and 8 kcal/mol respectively (Figure 11). The work required to stretch CGG4_{ZZ, in} not only is smaller than that for GGC4_{ZZ, alt} and GGC4_{ZZ, out}, but also is non-linear in shape, since it is almost zero up to 4 Å. In other words, the GGC4_{ZZ, alt} and GGC4_{ZZ, out} duplexes generate significantly more dissipation work than CGG4_{ZZ, in}, which indicates they are more difficult to stretch and therefore more stable. In spite of its sequence being a base pair shorter, GGC4_{ZZ, alt} needs around 6 kcal/mol more work than GGC4_{ZZ, out} in order to be stretched to the same length. Gathering all these results, the evidence indicates that GGC4_{ZZ, alt} DNA duplex is more stable than the GGC4_{ZZ, out} duplex, and both of them are more stable than the CGG4_{ZZ, in} duplex. Finally, a word about some common structural features. In the OL15 FF, the extruded guanines in both GGC4_{ZZ, out} (or GGC8_{ZZ, out}) and GGC4_{ZZ, alt} statistically favor syn conformations (or are at the boundary of χ = −90°); are extruded towards the minor groove slightly in the 5′ direction and display a host of interactions, involving inter-strand hydrogen-bonding (with both base and backbone atoms), diagonal inter-strand stacking, and occasional intra-strand stacking.

In summary, our results have led us to identify two novel secondary structure motifs for GCC/CCG TRs. These are left-handed Z-DNA helices with standard WC base pairs alternating with extruded GG mismatches. The most stable helix corresponds to the alternately extruded eGZ-motif, GGC4_{ZZ, alt}. This is closely followed by the other extruded case, the symmetrically extruded ZZ junction. The CD experiments that inspired this work showed that cytosine methylation further stabilized the left-handed signature of the repeats (46). Perhaps one of the most interesting recent developments towards the understanding of TREDs has been the recognition that the DNA mismatch repair (MMR) protein complex is the major driving force of disease-associated repeat expansions. Under normal circumstances, DNA MMR recognizes and repairs erroneous insertion, deletion, and base mismatches that arise during DNA replication and recombination. However, mammalian MMR has been found to trigger the expansion of TRs (94,95). This was initially shown for the expansion mutations of disease-associated (CAG)·(CTG) TRs (96), but more recently it has been found that MMR (particularly MSH2 and MSH3) also triggers expansion of (CGG)·(CCG) TRs, in spite of the fact that single GG mismatches are recognized with high efficiency by MMR (97). As stated by Schmidt and Pearson (95): ‘These findings reinforce the need to examine unusual structures formed by (CGG)·(CCG)...(and other)... expanded repeats, and the ability for MMR, and other proteins to process these structures, and their combined effects on repeat instability ...’ It is our belief that the structural study presented here will further the understanding of these complex issues.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Institute of Health [NIH-R01GM118508]. Funding for open access charge: NC State Physics Department.

Conflict of interest statement. None declared.