Abstract
In this study, Rosa damascena leaf powder was evaluated as a biosorbent for the removal of copper from aqueous solutions. Process variables such as the biosorbent dose, pH, and initial copper concentration were optimized using response surface methodology. A quadratic model was established to relate the factors to the response based on the Box–Behnken design. Analysis of variance (ANOVA) was used to assess the experimental data, and multiple regression analysis was used to fit it to a second-order polynomial equation. A biosorbent dose of 4.0 g/L, pH of 5.5, and initial copper concentration of 55 mg/L were determined to be the best conditions for copper removal. The removal of Cu2+ ions was 88.7% under these optimal conditions, indicating that the experimental data and model predictions were in good agreement. The biosorption data were well fitted to the pseudo-second-order and Elovich kinetic models. The combination of film and intra-particle diffusion was found to influence Cu2+ biosorption. The Langmuir and Dubinin–Radushkevich isotherm models best fit the experimental data, showing a monolayer isotherm with a qmax value of 25.13 mg/g obtained under optimal conditions. The thermodynamic parameters showed the spontaneity, feasibility and endothermic nature of adsorption. Scanning electron microscopy, energy-dispersive X-ray spectroscopy, and Fourier transform infrared spectroscopy were used to characterize the biosorbent before and after Cu2+ biosorption, revealing its outstanding structural characteristics and high surface functional group availability. In addition, immobilized R. damascena leaves adsorbed 90.7% of the copper from aqueous solution, which is more than the amount adsorbed by the free biosorbent (85.3%). The main mechanism of interaction between R. damascena biomass and Cu2+ ions is controlled by both ion exchange and hydrogen bond formation. It can be concluded that R. damascena can be employed as a low-cost biosorbent to remove heavy metals from aqueous solutions.
Subject terms: Biotechnology, Plant sciences, Environmental sciences
Introduction
With the development of agriculture, industrial activities, and other human activities, various heavy metals have been released into water, and water resources have been severely contaminated1. Heavy metal pollution has been a commonly researched topic for a long time because heavy metals are difficult to remove and are highly toxic2. Copper and its composites are the most frequent heavy metal contaminants in the environment, according to the Environmental Protection Agency3. Wastewater from mining companies, tanneries, metal plating plants and refineries is the most prevalent source of copper4.
Copper is a trace metal that numerous enzymes require for catalysis in living organisms. High quantities of copper, however, may be highly poisonous and cause major health concerns. Ingestion of high levels of copper causes the copper to accumulate in the liver, which can lead to anemia, gastrointestinal issues, and renal difficulties5. As a result, research into low-cost alternatives to presently available processes has been required by the need for safe, more effective and less expensive approaches for removing copper ions from wastewater. Several strategies for the removal of heavy metals from wastewaters have been developed in recent years. Some of these approaches include solvent extraction, membrane filtration, chemical reduction and precipitation, coagulation and ion exchange. The primary drawbacks of these procedures include the need for significant amounts of chemicals, residual metal solubility, costly capital investment, high operating costs, and the formation of a large quantity of sludge6. Adsorption is a potential approach to processing and treating wastewater due to its cost and efficiency7. Recent research has shown that a variety of typical agricultural waste products, microorganisms, algae, and natural polymers are excellent biosorbents for heavy metal removal8–10. Different parts of plants and their wastes are available and are more affordable than chemically modified products. As a result, the majority of adsorption research has focused on untreated plant products and wastes11,12.
Roses are shrubs that are commonly cultivated worldwide. These decorative plants are also utilized in medicine, fragrances, and scented products. Rose water, rose oil, and rose waste biomass are the three major products of rose distillation13. Rose flower biomass has been examined as a biosorbent after distillation in a number of studies13–16.
However, to the best of our knowledge, rose leaves have not been reported for use as waste biomass for the biosorption of copper ions. Therefore, in this study, Rosa damascena leaf powder was employed as a cost effective biosorbent to examine its efficiency in removing copper ions from aqueous solutions. A response surface methodology (RSM) was used to optimize the process variables and to analyze the influences of different factors on the examined response, providing significant advantages, as this methodology saved time, effort, and resources. In addition, RSM is more applicable since it can be used to predict and evaluate the interactive influences of different factors and depict their influence on a process17–19. Three independent factors, including biosorbent dose, pH, and initial Cu2+ concentration, were optimized to maximize copper removal by Rosa damascena leaf powder. Furthermore, we assessed the efficiency of immobilized Rosa damascena biomass as a Cu2+ ion biosorbent. Kinetic, equilibrium, and thermodynamic investigations were carried out to study the nature of the biosorbent and the biosorption process. The biosorbent was characterized by SEM, EDX and FTIR.
Results and discussion
Effect of metal concentration
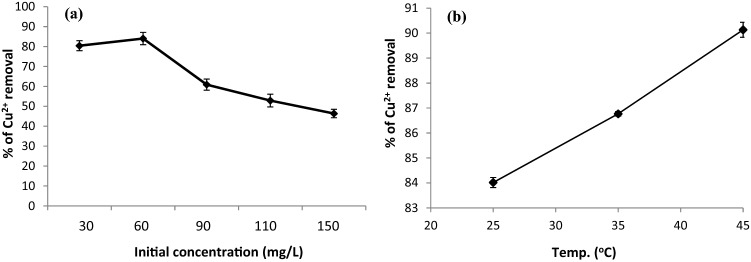
The initial metal concentration is a critical factor that influences the driving force of biosorption systems17. The data in Fig. 1a depict the influence of different metal concentrations (30–150 mg/L) on Cu2+ biosorption of onto the R. damascena biomass. The data showed that as the concentrations of Cu2+ increased from 60 to 150 mg/L, the copper removal declined from 84.0 to 46.3% (Fig. 1a) because at low Cu2+ concentrations, all active sites on the surface of R. damascena are vacant, but at high concentrations of Cu2+ ions, the number of binding sites is restricted. These binding sites are filled quickly, resulting in a significant reduction in Cu2+ biosorption. Several researchers have reported similar findings20,21.
Figure 1.
Effect of (a) Initial Cu2+ concentration, and (b) Temperature on the biosorption of Cu2+ ions onto R. damascena leaves. Data is presented as average ± SE of three replicates.
Effect of temperature
The influence of temperature on Cu2+ ion removal by R. damascena leaf biomass was studied at three different temperatures (25, 35, and 45 °C; Fig. 1b). The data show that the removal of Cu2+ ions increased from 84.0 to 90.1% as the temperature was increased, showing that the biosorption process is endothermic. The highest removal of Cu2+ (90.1%) occurred at a high temperature (45 °C), which may be regarded as optimal for Cu2+ biosorption. Increases in adsorbate affinity for the surface of adsorbent, increases in adsorbent pore size, and increases in driving force to overcome the mass transfer resistance of the adsorbate between the adsorbent surface and aqueous solution may all contribute to the increased biosorption at higher temperatures22.
Box–Behnken experimental design
A Box–Behnken design (BBD) was utilized to decrease the number of tests and predict the best conditions for copper removal by R. damascena leaf powder. Seventeen experiments were carried out using a BBD with varied combinations of three parameters at three levels to maximize the removal of Cu2+ ions from aqueous solution. Table 1 illustrates the actual and predicted removal percentages of Cu2+ for the 17 runs of the design matrix. The results showed that the copper removal varied greatly depending on the independent parameters. The copper removal by R. damascena leaves varied between 44.25 and 87.68%. In run 4, with a biosorbent dose of 5 g/L, pH of 6, and initial Cu2+ concentration of 60 mg/L, the maximum copper removal was obtained with a value of 87.68%. Based on the Box–Behnken design results, a second-order polynomial equation was created to characterize the relationship between the independent parameters and the response, and the final model generated by backward elimination of insignificant parameters is as follows (Eq. (1)):
| 1 |
where A, B and C are the biosorbent dose, pH and initial concentration of copper ions, respectively.
Table 1.
Box–Behnken design factors with coded and un-coded factors and data of the experimental response.
| Run | Factor 1 A: biosorbent dose (g/L) | Factor 2 B: pH | Factor 3 C: initial Cu2+ conc. (mg/L) | Response: Cu2+ removal (%) | Predicted values |
|---|---|---|---|---|---|
| 1 | 1 (− 1) | 2 (− 1) | 60 (0) | 44.25 | 47.28 |
| 2 | 5 (+ 1) | 2 (− 1) | 60 (0) | 64.03 | 68.36 |
| 3 | 1 (− 1) | 6 (+ 1) | 60 (0) | 51.67 | 57.53 |
| 4 | 5 (+ 1) | 6 (+ 1) | 60 (0) | 87.68 | 78.62 |
| 5 | 1 (− 1) | 4 (0) | 30 (− 1) | 56.80 | 57.22 |
| 6 | 5 (+ 1) | 4 (0) | 30 (− 1) | 77.90 | 78.31 |
| 7 | 1 (− 1) | 4 (0) | 90 (+ 1) | 56.90 | 47.58 |
| 8 | 5 (+ 1) | 4 (0) | 90 (+ 1) | 64.34 | 68.67 |
| 9 | 3 (0) | 2 (− 1) | 30 (− 1) | 62.97 | 56.93 |
| 10 | 3 (0) | 6 (+ 1) | 30 (− 1) | 68.43 | 67.18 |
| 11 | 3 (0) | 2 (− 1) | 90 (+ 1) | 50.91 | 47.29 |
| 12 | 3 (0) | 6 (+ 1) | 90 (+ 1) | 55.39 | 57.54 |
| 13–17* | 3 (0) | 4 (0) | 60 (0) | 60.20 | 57.24 |
*Mean value of five center point assays.
Table 2 summarizes the results of the analysis of variance (ANOVA) of the established model. The model was highly statistically significant, as evidenced by the high F value (10.26) and low p value (˂ 0.001). Furthermore, the F value of the lack of fit was 1.69, suggesting that the lack of fit is not significant (as the p value is larger than 0.05) in comparison to the true error, so the model validity may be affirmed23.
Table 2.
Analysis of variance (ANOVA) of the response surface quadratic model of the biosorption of Cu2+ ions onto R. damascena.
| Source | SS | df | MS | F value |
p value Prob > F |
|---|---|---|---|---|---|
| Model | 1423.4 | 4 | 355.8 | 10.26 | 0.0008* |
| Residual | 416.4 | 12 | 34.70 | – | – |
| Lack of fit | 321.4 | 8 | 40.18 | 1.69 | 0.321** |
| Pure error | 95.0 | 4 | 23.74 | – | – |
| Correlation total | 1839.8 | 16 | – | – | – |
| R2 = 0.87 | Adj. R2 = 0.80 | Pred. R2 = 0.70 | Adeq. precision = 9.8 | CV% = 8.83 | Mean = 59.92 |
Df degree of freedom, SS squares sum, MS mean sum of squares, CV Coefficient of variation.
*Significant at p ˂ 0.05.
**Not significant at p > 0.05.
The determination coefficient (R2) and adjusted R2 were used to assess the model’s fit. The R2 values ranged between 0 and 1.0, with values of approximately 1.0 indicating that the model is more accurate. However, under certain conditions, a larger R2 value indicates that the model has a large number of insignificant variables, which indicates a poor response. As a result, the adjusted R2 was developed, which adjusts the value of R2 based on the number of variables and sample size in the model. The high R2 value (0.87; Table 2) in this investigation implies that the actual and expected values are well correlated, and the model can explain 87.0% of the variability in the response. The adjusted R2 of 0.80 agrees well with the R2 value of 0.87, indicating that the model is valid. The actual and expected results were highly correlated, with the adjusted R2 value being high and close to the predicted R2 value (Table 2).
Moreover, the value of the variation coefficient as an estimate of the standard error was less than 10%, indicating that the model was reproducible24. The signal-to-noise ratio indicated adequate precision. In this investigation, a ratio of 9.8 (higher than 4) was found to be sufficient25. As a result, the model may be utilized to explore the design space. Therefore, biosorption studies may be conducted using this model.
Effect of interactive variables
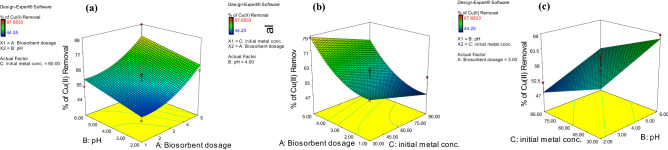
In order to understand the impacts of the interactions of factors on the investigated response, 3-D response surface plots were made using the second-order Eq. (1) (Fig. 2). Each plot depicts the impact of two independent factors on the response within the examined ranges, while all other factors were held constant.
Figure 2.
3-D response surface plots for Cu2+ removal showing the interaction influences of (a) biosorbent dose and pH, (b) biosorbent dose and initial copper concentration, and (c) pH and initial copper concentration.
In Fig. 2a, 3-D plots depict the reciprocal interaction between the biosorbent dose and pH on Cu2+ removal by R. damascena leaf biomass. The data revealed that raising the biosorbent dose and pH improved Cu2+ biosorption by R. damascena leaves. The ANOVA findings also demonstrated that the biosorbent dose was significant and had a positive influence on the efficiency of copper removal (p = 0.0003; Table 3) in linear term. The number of active binding sites for the biosorption process is determined by the biosorbent dose26. As the biosorbent dose was increased, the number of binding sites on the surface of R. damascena leaves rises, resulting in a higher percentage of copper removal26. The elimination of copper by R. damascena leaves is also pH-dependent. The speciation of ions in aqueous solution and the dissociation state of biosorbent’s superficial functional groups are both affected by pH17. The pH exhibited a significant positive influence on the removal of copper by R. damascena leaves in linear term, according to the ANOVA results (Table 3). When the pH was raised from 2.0 to 6.0, the biosorption of Cu2+ increased. However, copper biosorption onto R. damascena leaves was minimal at lower pH. However, when the pH was 6.0, the maximum removal efficiency was observed because the surface charge of the biomass is positive at lower pH, which limits cation biosorption. Additionally, H+ ions compete with copper ions for active sites, leading to reduced biosorption. The competitive impact of H+ ions and electrostatic repulsions between cations and surface sites reduced as the pH was increased. As a result, metal biosorption also increased27. Fawzy20 stated that a pH of 5.0 was the most effective pH for copper removal by Codium vermilara.
Table 3.
Analysis of variance (ANOVA) for the coefficients of the quadratic model of the biosorption of Cu2+ ions onto R. damascena.
| Model term | CE | df | SE | F value |
p value Prob > F |
|---|---|---|---|---|---|
| Intercept | 57.24 | 1 | 1.96 | – | – |
| A-Biosorbent dose | 10.54 | 1 | 2.08 | 25.63 | 0.0003 |
| B-pH | 5.13 | 1 | 2.08 | 6.06 | 0.03 |
| C-initial Cu2+ conc. | − 4.82 | 1 | 2.08 | 5.36 | 0.039 |
| A2 | 5.71 | 1 | 2.86 | 3.98 | 0.069 |
CE coefficient estimate, df degree of freedom, SE standard error.
Figure 2b depicts the mutual impacts of the biosorbent dose and initial copper concentration on the effectiveness of copper removal by R. damascena leaves.
When the biosorbent dose was increased from 1 to 5 g/L, the copper removal efficiency increased. More binding sites on the surface of R. damascena leaves become available to the copper ions as the biosorbent dose increases, resulting in enhanced removal efficiency. At a biosorbent dose of 5 g/L, the optimal removal effectiveness of 79% could be achieved. Generally, a higher biosorbent dose and lower copper concentrations improved the biosorption process28.
As a result, raising the concentration of copper ions had a significant negative impact on Cu2+ ion removal (Table 3). Because more copper ions from the solution connected with the binding sites at lower copper concentrations, the biosorption of Cu2+ ions gradually increased; however, as the concentrations of copper were increased, biosorption was reduced due to biosorbent site saturation, and a large number of ions competed for the residual binding sites in the biosorbent.
The joint influence of pH and initial Cu2+ concentrations on metal ion removal was also investigated in the pH range of 2–6 and initial copper concentrations of 30–90 mg/L, as shown in Fig. 2c. The findings revealed that the removal of copper ions decreases as the pH is decreased. ANOVA revealed that the biosorbent dose was the most statistically significant factor that influenced the removal of copper (p = 0.0003), followed by pH (p = 0.03) and initial copper concentration (p˂ 0.05; Table 3).
Validation of the optimized variables
The goal of the optimization was to optimize the independent parameters of Cu2+ ion elimination by R. damascena leaf powder. The aim was to optimize the copper removal efficiency to achieve the maximum rate of Cu2+ removal. The average Cu2+ removal efficiency was compared to the expected value through experiments conducted in triplicate under optimized conditions. With a biosorbent dose of 4.0 g/L, pH of 5.5, and initial copper concentration of 55 mg/L, the highest expected Cu2+ elimination by R. damascena biomass was achieved. The experimentally observed copper removal efficiency (88.7%) was found to be in accordance with the expected value (87.4%) calculated by the design expert software, implying that the optimized conditions were ideal.
Effect of contact time and kinetic models
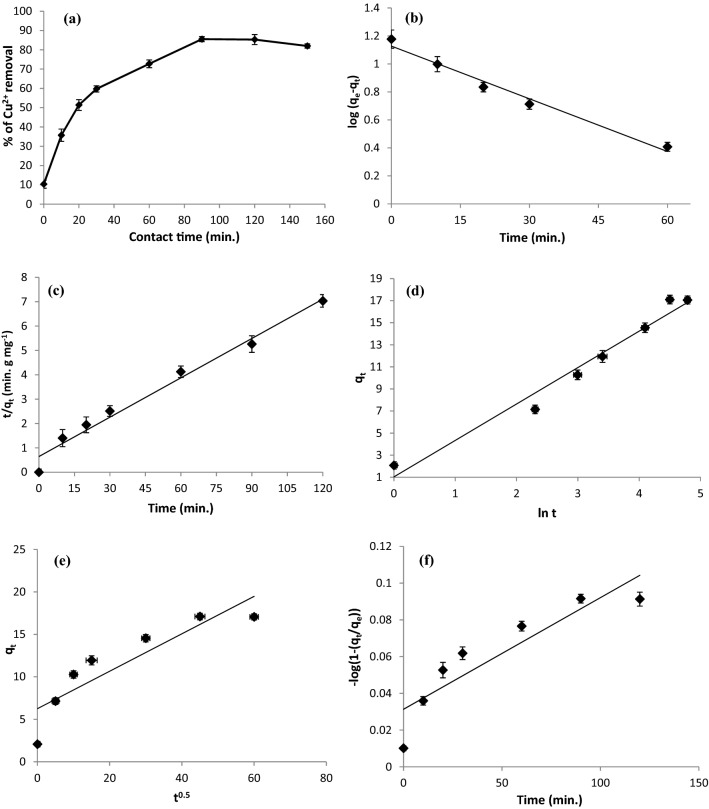
The impact of contact time on Cu2+ ion biosorption was used to evaluate the kinetics. Copper biosorption was examined under the optimal conditions of a 4.0 g/L biosorbent dose, pH 5.5, and an initial Cu2+ concentration of 55 mg/L by varying the biosorption time from 0 to 150 min (Fig. 3a). In the first 30 min, the rate of Cu2+ ion elimination was obviously fast. However, after equilibrium was reached, the biosorption efficiency increased until it was steady, and within 90 min, over 85.5% of the total metal was eliminated. The rates of adsorption and desorption were in dynamic equilibrium, and no additional biosorption was observed after this optimal equilibrium duration29. Because copper ions came into contact with unoccupied surface biosorption sites, the biosorption of copper was initially quicker; however, after adsorption proceeded at equilibrium for 90 min, the biosorption sites became saturated, and no further biosorption occurred30.
Figure 3.
(a) Effect of contact time, (b) Pseudo-first-order plot, (c) Pseudo-second-order plot, (d) Elovich plot, (e) Intra-particle diffusion plot, and (f) film diffusion plot for the biosorption of Cu2+ ions onto R. damascena leaves. Data is presented as average ± SE of three replicates.
Various kinetic models can be used to explain the mechanism and rate of metal ion sorption31. The biosorption kinetics of copper ions on R. damascena leaf biomass was studied using the pseudo-first-order, pseudo-second-order, Elvoish, intra-particle and film diffusion models.
Pseudo-first-order kinetic model
This model describes the adsorption of one adsorbate molecule onto one active site of the biosorbent. It is expressed as follows:
| 2 |
where qe and qt (mg/g) represent the quantity of copper ions absorbed by the biomass of R. damascena at equilibrium and at any time, respectively, and K1 (min−1) represents the rate constant of the pseudo-first-order model.
The constants K1 and qe were estimated from the slope and intercept by plotting log (qe − qt) vs. time, respectively (Fig. 3b).
The high value of the determination coefficient (R2 = 0.980) indicates that the experimental results accurately fit the pseudo-first-order model for describing copper ion biosorption kinetics. However, high ∆qe and X2 values (23.3 and 1.02, respectively; Table 4) suggested that the pseudo-first-order kinetic model does not exhibit good regression. In addition, the difference between the copper ion quantity biosorbed onto the R. damascena surface estimated by experiments (qe exp.; 17.1 mg/g) and the modeled value (qe calc.; 13.4 mg/g) were larger. This result suggests that the biosorption process involved both the copper ions and biosorbent32. Therefore, the pseudo-first-order model is unable to describe the experimental data of Cu2+ biosorption onto the R. damascena biomass. The sorption kinetics of various metal ions onto various adsorbents has been described with similar findings15,33,34.
Table 4.
Kinetic model parameters of the biosorption of Cu2+ ions onto R. damascena.
| Parameters | Values | |
|---|---|---|
| Experimental data | qe (exp.) (mg/g) | 17.1 |
| Pseudo-first order | qe (cal.) (mg/g) | 13.4 |
| k1 (min−1) | 0.029 | |
| ∆qe | 23.3 | |
| X2 | 1.02 | |
| R2 | 0.980 | |
| Pseudo-second order | qe (cal.) (mg/g) | 18.6 |
| k2 (g/mg min) | 0.005 | |
| h (g/mg min) | 1.55 | |
| ∆qe | 12.25 | |
| X2 | 0.12 | |
| R2 | 0.983 | |
| Elovich | α (g/mg min) | 1.30 |
| β (g/mg) | 0.303 | |
| ∆qe | 3.53 | |
| X2 | 0.192 | |
| R2 | 0.971 | |
| Intra-particle diffusion | Ki (mg/g min0.5) | 0.22 |
| Ci (mg/g) | 6.25 | |
| R2 | 0.801 | |
| Film diffusion | Df | 0.001 |
| R2 | 0.821 | |
The rate constant of pseudo-first-order (K1 = 0.029 min−1; Table 4) is not a quantifiable value that can clarify the rapid equilibrium of the biosorption of Cu2+ ions onto the R. damascena leaf surface reported within 30 min. As a result, this model was shown to be inadequate for accurately modeling copper biosorption by R. damascena biomass.
Pseudo-second-order kinetic model
In the pseudo-second-order kinetic model, chemical adsorption, which includes the exchange or sharing of electrons between the adsorbate and the adsorbent, controls the process of adsorption. This model can be described as follows:
| 3 |
where K2 is the pseudo-second-order rate constant (g/mg min), which may be used to calculate the initial rate of biosorption (h; g/mg min).
| 4 |
The kinetic constants K2 and qe were calculated from the intercept and slope of t/qt against t plot, respectively (Fig. 3c).
The rate constant of pseudo-second-order (K2) and the initial rate of adsorption (h) were 0.005 and 1.55 g/mg min, respectively (Table 4). At the beginning of the biosorption process, the h value indicated the rapid biosorption of copper ions. The high determination coefficient (R2 = 0.983) and the low values of ∆qe and X2 (12.25 and 0.12, respectively; Table 4) indicated that the pseudo-second-order model best fit the experimental data for Cu2+ ion biosorption on the R. damascena leaf surface. Additionally, the experimental qe (17.1 mg/g) was relatively similar to the calculated qe (18.6 mg/g). Therefore, the pseudo-second-order model was chosen because it had the best fit, demonstrating significant interactions between the adsorbate and the adsorbent and indicating the occurrence of copper chemisorption on the surface of the R. damascena leaves. The results of several studies support the pseudo-second-order model for the adsorption of copper ions onto different biosorbents, including studies on the adsorption of Cu2+ onto activated rubber wood sawdust35, Tectona grandis leaf36, sour orange residue37, banana trunk fiber38, sulfur-modified bamboo powder39, and Platanus orientalis leaf powder40.
Elovich model
The Elovich model is utilized to explain the kinetics of chemical adsorption of a gas onto solid adsorbents, but it has been proven to be effective in describing various types of adsorption. The Elovich model can be represented by the following equation:
| 5 |
where α (mg/g min) represents the initial rate of sorption, and β (g/mg) is a constant that represents desorption.
To study the mechanism of Cu2+ biosorption, the experimental data were fitted to the Elovich kinetic model (Fig. 3d). A graph of qt versus lnt was plotted, and the Elovich constants (α and β) were determined from the intercept and slope, respectively. The extent of chemisorption is proportional to the value of α. The high value of the Elovich constant (α = 1.3 g/mg min; Table 4) implies that chemisorption is the rate-limiting stage and biosorption proceeded via a pseudo-second-order mechanism.
The lower the value of the Elovich constant β is, the lower the chemisorption activation energy, implying that adsorption occurs quickly41. In the current investigation, the β value was fairly low (0.303 g/mg), suggesting a low activation energy of chemical adsorption. In addition, the high value of the determination coefficient (R2 = 0.971) and the low ∆qe and X2 values (3.53 and 0.192, respectively; Table 4) show that the experimental data fit the Elovich kinetic model well.
From the previous data, it can be concluded that, the ∆qe and X2 values were found to be smaller for the pseudo-second-order and Elovich kinetic models; with higher R2 values than to those of the pseudo-first-order. Thus, the pseudo-second-order and Elovich kinetic models are the best fit models for the biosorption of copper ion onto the R. damascena leaves.
Intra-particle and film diffusion models
The mechanism of diffusion influencing the Cu2+ biosorption process was also evaluated by intra-particle and film diffusion models42.
The intra-particle diffusion kinetic model is related to adsorbate diffusion to the inner pores as the rate-controlling step, which is represented by Eq. (6):
| 6 |
where Ki denotes the intra-particle diffusion rate constant (mg/g min0.5) and Ci denotes the intercept.
The film diffusion model is represented by the following Eq. (7):
| 7 |
where Df is the film diffusion rate constant (min-1).
The trendline of the linear plot in Fig. 3e does not pass through the origin, proposing that intra-particle diffusion is not the sole rate-limiting stage of biosorption. Figure 3e also exhibited the multilinearity of the plot, which has two sections. The first section shows that Cu2+ ions are transferred from the solution to the external surface of the R. damascena biomass via film diffusion. Moreover, the film diffusion plot of − log (1 − (qt/qe)) against time (Fig. 3f) nearly passes through the origin with an intercept of approximately zero, demonstrating that film diffusion plays a significant role in Cu2+ ion biosorption onto the surface of R. damascena leaves. The second part describes the additional Cu2+ ion biosorption on the internal pores of the R. damascena leaf surface, where intra-particle diffusion is the rate-limiting stage43. This result revealed that external diffusion in the film controls the biosorption of copper ions onto R. damascena biomass, followed by the intra-particle diffusion model. The high value of the intercept (Ci, 6.25 mg/g; Table 4) might be due to increased boundary layer thickness, increased internal mass transfer, and reduced external mass transfer30.
Equilibrium isotherms
Under certain experimental conditions, the adsorption isotherm represents the equilibrium correlation between the amounts of ions adsorbed by the biosorbent and the metal ion concentration in the solution44.
Biosorption equilibrium isotherms were obtained under optimized conditions by BBD. The Langmuir, Freundlich, Temkin, Dubinin–Radushkevich and Jovanovic isotherm models were used to describe and estimate the experimental data of copper biosorption.
Langmuir model
This model implies that metal ions are adsorbed by monolayer adsorption on a homogeneous surface with no interaction between the adsorbed metal ions. The Langmuir model is represented in linear form as follows:
| 8 |
where qmax is the maximal sorption quantity (mg/g) required to produce full monolayer coverage on R. damascena’s surface at a high ion equilibrium concentration (Ceq; mg/L) and b is the constant of the Langmuir model, which is associated with binding site affinity45.
The high value of R2 (0.979; Table 5) indicates that the Langmuir model suitably describes the biosorption process, which is based on the homogeneous distribution of active sites on the surface of the R. damascena leaf.
Table 5.
Isotherm model parameters of the biosorption of Cu2+ ions onto R. damascena.
| Isotherms | Parameters | Values |
|---|---|---|
| Langmuir | qmax (mg/g) | 25.13 |
| b (L/mg) | 0.095 | |
| RL | 0.062–0.201 | |
| R2 | 0.979 | |
| Freundlich | 1/n | 0.313 |
| Kf (L/mg) | 5.98 | |
| R2 | 0.735 | |
| Temkin | A (L/mg) | 1.9 |
| b (J/mol) | 551.4 | |
| R2 | 0.807 | |
| Dubinin–Radushkevich | qo (mg/g) | 21.1 |
| β × 10–6(mol2/J2) | 6.0 | |
| E (KJ/mol) | 9.13 | |
| R2 | 0.926 | |
| Jovanovic | qmax (mg/g) | 11.17 |
| KJ (L/g) | 0.01 | |
| R2 | 0.589 |
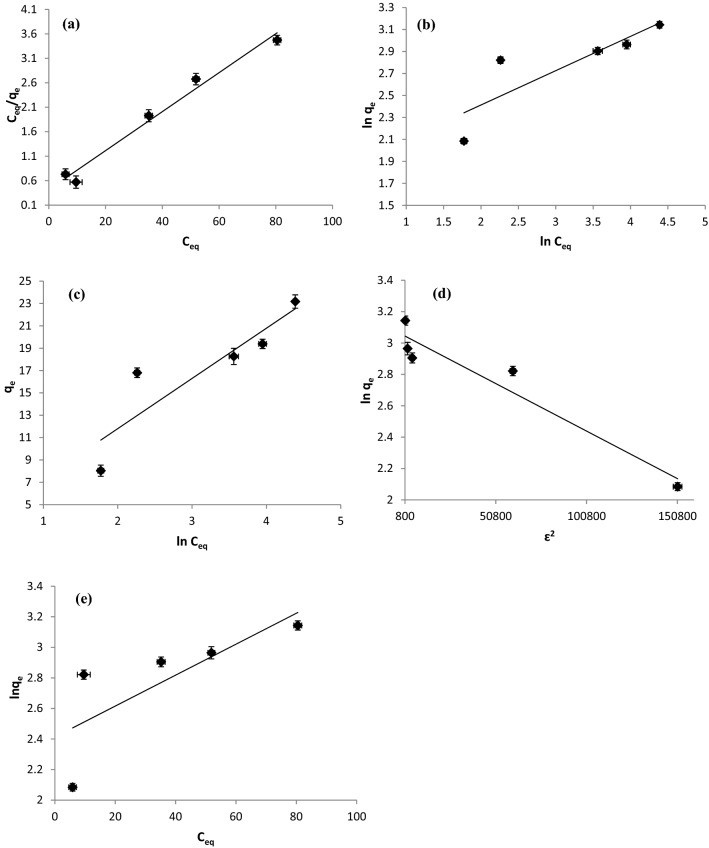
When Ceq/qe was plotted versus Ceq, a straight line was formed, and the slope and intercept were used to determine the qmax and b values, respectively (Fig. 4a). The greater value of the Langmuir constant (b = 0.095 L/mg) suggested a stronger interaction with the functional groups on the R. damascena leaf surface. Furthermore, R. damascena biomass had a maximum biosorption capacity (qmax) of 25.13 mg/g. A similar pattern was achieved by using numerous equilibrium isotherm models, with the Langmuir model having the best fit34,46.
Figure 4.
Biosorption isotherms of copper ions onto R. damascena leaves, including (a) Langmuir, (b) Freundlich, (c) Temkin, (d) Dubinin–Radushkevich and (e) Jovanovic models. Data is presented as average ± SE of three replicates.
A dimensionless separation factor (RL) may be used to determine the shape and favorability of the biosorption process, which can be computed using Eq. (9):
| 9 |
where Co is the metal ion concentration (mg/L). The type of Langmuir isotherm was determined by the RL value, which was either unfavorable (RL > 1), linear (RL = 1), irreversible (RL = 0) or favorable (0 ˂ RL ˂ 1)40. A value of RL between 0 and 1 indicates that adsorption is favorable. In the current study, the RL value was determined to be 0.062–0.201, showing that copper biosorption onto the leaves of R. damascena is favorable (Table 5).
Freundlich isotherm model
The adsorption of ions on an energetically heterogeneous surface is described by the Freundlich isotherm model. The following equation represents the linearized Freundlich model (10):
| 10 |
where Kf is the Freundlich isotherm constant, which reflects the sorption capacity, and n is the Freundlich constant correlated to the adsorption intensity.
The intercept and slope of the plotting of ln qe against lnCeq are used to calculate the Kf and 1/n values, respectively (Fig. 4b). The greater the Kf value, the more biosorbent may be loaded. In addition, adsorption is favorable when the 1/n value is between 0.1 and 1.047. In this study, the value of 1/n was lower than 1.0 (0.313; Table 5), indicating that biosorption of copper ions by R. damascena leaves is favorable. The low value of the determination coefficient (R2 = 0.735) suggested that the Freundlich model is not appropriate for describing the experimental data of the biosorption process (Table 5).
Temkin model
The Temkin model represents adsorption with a uniform distribution of binding energies up to the maximal binding energy, as shown in the following equation48.
| 11 |
| 12 |
where A (L/mg) represents the equilibrium binding constant, b (J/mol) is the constant of the Temkin isotherm model, and B (J/mol) is the heat of sorption constant.
The Temkin model constants (A and b) were determined using the intercept and slope of the qe versus lnCeq plot (Fig. 4c). The high b value (551.4 J/mol; Table 5) indicates that the adsorbate and biosorbent surface interact strongly49. The Temkin model fails to fit the results reported for copper biosorption by R. damascena leaves, as the R2 value was low (0.807; Table 5).
Dubinin–Radushkevich model (D–R)
The D–R model describes whether biosorption occurs via a chemical or physical process and the mean sorption energy of the process. The D–R model is calculated from the following equations:
| 13 |
| 14 |
| 15 |
where qo is the theoretical maximum capacity (mg/g), β is the constant of the D–R model associated with the mean free energy (mol2/J2), ε is the Polanyi potential, T (K) is the absolute temperature, R (8.314 J/mol K) is the gas constant, and E (kJ/mol) is the mean adsorption energy.
Table 5 shows the values of the D–R model parameters. The mean adsorption energy of the system (E) was determined using the parameter β (Eq. (15)). In addition, the chemical and physical characteristics of the adsorption process may be assessed by the mean adsorption energy.
Physical sorption is defined as a value of E less than 8 kJ/mol, whereas chemical sorption is defined as a value of 8 to 16 kJ/mol30. The value of E (9.13 kJ/mol) indicates that R. damascena removed copper ions mostly by chemisorption. This result is also consistent with predictions from the pseudo-second-order and Elovich kinetic models. D–R isotherm model may best describe the experimental data of copper ion biosorption onto the R. damascena leaf surface, according to the R2 value (0.926; Fig. 4d; Table 5).
Jovanovic model
The Jovanovic model is an approximation for localized monolayer adsorption without lateral contacts that is comparable to the Langmuir model. This model is determined as follows:
| 16 |
where KJ: the Jovanovic isotherm constant. The values of qmax and KJ were calculated from the intercept and slope of linear plot of lnqe versus Ceq (Fig. 4e).
The maximum biosorption capacity determined from the Jovanovic equation (qmax = 11.17 mg/g; Table 5) differs from the experimentally measured value (qmax = 23.18). Furthermore, the lower determination coefficient (R2 = 0.589) found in this investigation revealed that there is a lateral interaction and no mechanical contact between the R. damascena leaf biomass and Cu2+ ions. As a result, Jovanovic isotherm model has a lower approach to saturation compared to Langmuir model as stated by Al-Ghouti and Da’ana50.
Thermodynamic studies
The Gibbs free energy (∆G), enthalpy (∆H) and entropy (∆S) are all thermodynamic parameters that describe the spontaneity of a biphasic adsorption process51.
The following equations demonstrate the relationship between the thermodynamic parameters and the absolute temperature (T)52.
| 17 |
| 18 |
| 19 |
where Kc is the thermodynamic equilibrium constant.
At the experimental temperatures, the values of ∆G were negative (Table 6), indicating that biosorption was feasible and spontaneous50. Furthermore, a reduction in the values of ∆G with rising temperature indicates that adsorption became more feasible, resulting in the strengthening of bonds established between the binding sites on the R. damascena leaf surface and the Cu2+ ions19.
Table 6.
Thermodynamic values of Cu2+ ion biosorption onto R. damascena.
| Temperature (K) | ΔG (KJ/mol) | ΔH (KJ/mol) | ΔS (KJ/mol) | R2 |
|---|---|---|---|---|
| 298 | − 1.39 | 21.7 | 0.077 | 0.982 |
| 308 | − 2.00 | |||
| 318 | − 2.94 |
The changes in enthalpy and entropy were evaluated from the slope and intercept of the ln K versus 1/T plot, respectively (Fig. 5).
Figure 5.
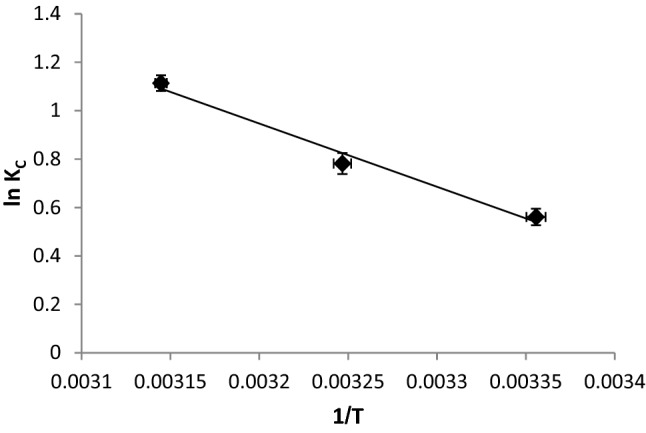
Plot of 1/T against lnK for copper ion biosorption onto R. damascena.
The positive ∆H of 21.7 kJ/mol for copper biosorption by R. damascena leaves indicates that the biosorption process was endothermic. This result indicates that higher temperatures promote biosorption. In addition, the positive ∆S indicated that the biosorption of copper ions onto the R. damascena leaf surface occurred as a result of randomization at the adsorbate-biosorbent interface53.
Characterization of R. damascena leaf surface
Scanning electron microscopy (SEM)
The morphology of the R. damascena leaf surface before and after Cu2+ biosorption was examined by SEM (Fig. 6). SEM micrographs demonstrated that the surface morphology of the R. damascena leaf before and after Cu2+ biosorption was different.
Figure 6.

SEM images of R. damascena leaves (a) before and (b) after Cd2+ biosorption.
The SEM micrographs of the R. damascena leaf surface before copper biosorption revealed a rough surface with substantial porosity (Fig. 6a). This rough flaky surface allowed copper ions to adhere more easily, improving biosorption. The biosorbent's porosity also enables it to interact with the adsorbate more quickly54. However, the SEM images collected after the biosorption of copper revealed a flatter biosorbent surface, appearance of discrete lumps and fewer large spaces (Fig. 6b). These morphological alterations verified the interaction of copper ions with the functional groups on the R. damascena leaf surface20.
Energy dispersive X-ray spectroscopy (EDX)
EDX analysis was used to determine the adsorbent surface composition and to confirm the presence of copper ions on the R. damascena leaf surface. Figure 7 displays the EDX spectra of R. damascena biomass. The EDX spectra showed that the R. damascena leaves consist mostly of C and O, with traces of additional elements, including Na, Mg, Cl, K, Si and Ca that were exchanged or removed during biosorption (Fig. 7a,b). This result shows that the biosorption of Cu2+ ions was caused by ion exchange. After biosorption, the EDX spectra of R. damascena biomass exhibited an additional Cu2+ peak (1.09%) on the R. damascena leaf surface, demonstrating that the biomass of R. damascena participates in the biosorption of Cu2+ ions from solution (Fig. 7b). In this regard, El-Naggar et al.55 observed that a distinctive copper peak appeared following contact with copper.
Figure 7.
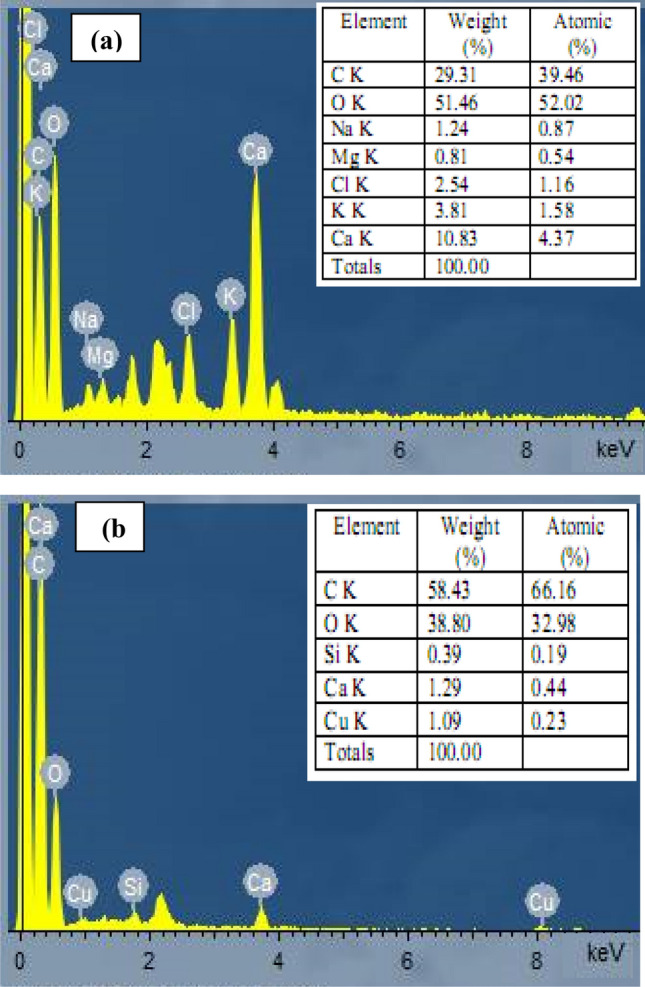
EDX images of R. damascena leaves (a) before and (b) after Cd2+ biosorption.
Analysis of the Fourier transform infrared spectra (FT-IR)
The functional groups found on the surface of biosorbent biomass play a significant role in the process of adsorption. Heavy metal biosorption has been related to various functional groups, such as sulfonate, sulfhydryl, amine, carboxyl, hydroxyl, carbonyl, and others56. Figure 8a,b displays the FT-IR spectra of R. damascena leaves before and after copper biosorption.
Figure 8.
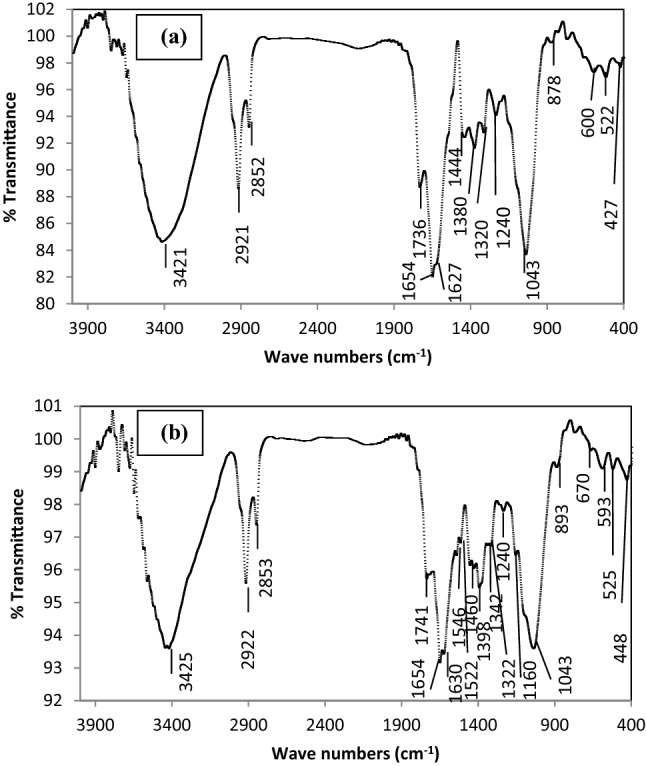
FTIR spectra of R. damascena leaves (a) before and (b) after Cd2+ biosorption.
The presence of a wide absorption peak at approximately 3421–3425 cm−1 is allocated to O–H stretching of hydroxyl radicals of polysaccharides or water57 and to N–H stretching of proteins (amide A)58. Functional groups such as O–H and N–H are commonly present in natural cellulose and proteins found in plant cell walls59. The O–H stretching vibration of the carboxylic acid might be represented by the bands at 2921 cm−1 and 2922 cm−159. These bands indicate the presence of an acidic group, such as –COOH, in the biosorbent cell wall; this group serves as a hyperchemical group for the adsorption of various multivalent metal ions60. The absorption bands at 2852 cm−1 and 2853 cm−1 are attributed to stretching of C–H, more specifically to the C–H stretching vibrations of lipids61. The C=O stretching of amide I, which is related to proteins, is shown by the absorption peak at approximately 1654 cm−162. The appearance of new absorption bands at 1546 cm−1 and 1460 cm−1 after copper was biosorbed onto the surface of the R. damascena leaf might be due to C=O stretching vibrations of different carboxylic and amide (I, II) groups, respectively63. The protein band spectrum identified at 1240 cm−1 on the leaf surface was caused by the P=O asymmetric stretching vibration64. The absorption peak at approximately 1160 cm−1 detected only on the R. damascena leaf surface following copper biosorption is related to C–O–C stretching of polysaccharides from carbohydrates57. Furthermore, after copper biosorption, the peak at 878 cm−1 shifted to 893 cm−1, indicating the binding of copper ions to the amine group on the leaf surface. The bands found only at 670 and 593 cm−1 on the R. damascena leaf surface after copper biosorption may be associated with the compounds of organic halide56. From Fig. 7, it can be observed that the R. damascena leaf biomass included several functional chemical groups, such as carbonyl groups, acids, phosphates, amides, hydroxyl groups, halides, carboxyl groups, and amine groups. They might compensate for the biosorption of copper ions from the aqueous solution onto the R. damascena leaf surface.
Copper removal by immobilized R. damascena biomass
The results in Fig. 9 show that the Ca-alginate-immobilized R. damascena leaves removed 90.7% of copper ions after 120 min under the conditions optimized by BBD, including the biosorbent dose (4 g/L), pH (5.5) and initial copper concentration (55 mg/L); this removal was higher than the removal achieved when a nonimmobilized biosorbent was used (85.3%). Various studies have found that immobilized biosorbents are a more straightforward approach for recovering and removing heavy metals from wastewater than free biosorbents65,66. For example, Ansari et al.15 reported that immobilized rose waste is more effective at absorbing Pb2+ from aqueous solutions than free biomass. Ca-alginate-immobilized Fucus vesiculosus is also an effective biosorbent for copper, lead, and cadmium according to Mata et al.67, and it occasionally has greater biosorption efficacy than free alga or even alginate alone. According to Davis et al.68, the metal ion affinity for alginate is proportional to the quantity of guluronic acid and other uronic acids present. These acids are responsible for the biosorption of heavy metals since they include the majority of the carboxyl groups in alginate. Furthermore, the “egg-box” structure of the gels, as well as the crosslinking between the carboxyl groups and metal ions, have been linked to alginate’s metal selectivity. This selectivity is determined by the stereochemical environment created by the structure of the gel. Therefore, R. damascena immobilized in Ca-alginate has great potential to adsorb heavy metals from wastewater.
Figure 9.
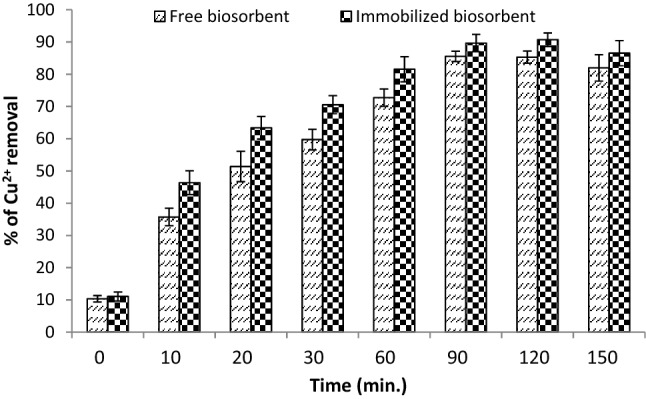
Copper ion removal by Ca–alginate-immobilized R. damascena.
Mechanisms of biosorption
The mechanisms of biosorption for heavy metals include surface precipitation, chelation, complexation, ion exchange, electrostatic interaction, or a combination of these mechanisms depending on the biosorbent used and the conditions of solution69. Ion exchange was suggested as a main mechanism for copper ion biosorption onto the R. damascena biomass70. Light metal ions such as Ca2+, Mg2+, Na+ and K+ were described to be involved in the process of ion exchange owing to a poor connection with the biomass of R. damascena in comparison to the heavy metals70. Moreover, functional groups containing oxygen and/or nitrogen, such as COOH, OH, and NH2, help biosorb Cu2+ ions by forming hydrogen bonds between the surface of R. damascena biomass and Cu2+ ions. These findings were supported by the FT-IR analysis because of the shift in the wavenumbers of the COOH, OH, and NH2 groups following Cu2+ ion biosorption (Fig. 8a,b). The intermolecular hydrogen bonding between the biomass of R. damascena and Cu2+ ions enhances the biosorption process. The formation of complexes with functional groups on the biosorbent through electrostatic interactions and ion exchange is also a possible mechanism for the biosorption of Cu2+ on R. damascena biomass.
SEM and EDX analyses were obtained after adsorption to acquire a better understanding of the Cu2+ biosorption mechanism by the biomass of R. damascena. The SEM analysis displays that the biomass of R. damascena is porous with numerous rough pores. The biosorption of Cu2+ takes place in the pores of the R. damascena biomass. In a comparison of the EDX analyses of R. damascena before and after Cu2+ ion biosorption (Fig. 7a,b), significant alterations were found along with the appearance of an additional Cu2+ peak, indicating that the R. damascena biomass was transformed after adsorption. As a result, all of these findings suggest that the biosorption of Cu2+ onto R. damascena biomass can be accomplished by ion exchange and hydrogen bond formation mechanisms.
Comparison of biosorption capacity
The maximum biosorption capacity of Cu2+ ions by various biosorbents was compared with that observed in the current investigation. Table 7 shows that R. damascena leaves have a higher biosorption capacity for copper removal than most of the biosorbents previously described in the literature20,34,71–77. The wide availability of Rosa damascena leaf wastes and their low cost are added advantages for their selection by numerous industries.
Table 7.
Maximum biosorption capacity of Cu2+ ion by low-cost sorbents.
| Biosorbent used for Cu(II) | qmax (mg/g) | References |
|---|---|---|
| Codium vermilara | 14.4 | 20 |
| Bael flowers | 23.14 | 34 |
| Sago waste | 12.4 | 71 |
| Myriophyllum spicatum | 10.37 | 72 |
| Wheat shell | 10.84 | 73 |
| Caulerpa lentillifera | 5.57 | 74 |
| Lentil shell | 8.98 | 75 |
| Cinnamomum camphora | 16.76 | 76 |
| Coconut shell | 19.89 | 77 |
| Neem leaves | 17.49 | 77 |
| Rosa damascena leaves | 25.13 | Present study |
Conclusions
Heavy metals, such as copper, are present in high concentrations in certain industrial effluents, posing serious health and environmental risks. Biosorption is a biotechnological approach to heavy metal ion removal from contaminated aquatic environments. The aim of the current investigation was to optimize the process variables for maximal copper removal from aqueous solution using statistical design. The Box–Behnken experimental design combined with response surface methodology has been shown to be an effective method for maximizing the removal of copper ions from solution using R. damascena leaves because they require a decreased number of experimental tests, result in the most efficient conditions, and maintain the accuracy of the predicted response. ANOVA, with its low P value, high F value, and determination coefficient, showed that the developed model represents the experimental data with high accuracy. The maximum removal percentage of Cu2+ ions (88.7%) was reached under the optimal conditions of a biosorbent dose of 4.0 g/L, pH of 5.5, and initial copper content of 55 mg/L. The pseudo-second-order and Elovich kinetic models were best fit to the experimental data. In addition, the liquid film diffusion model initially describes copper biosorption onto the R. damascena surface, followed by the intra-particle diffusion model. Equilibrium isotherm studies demonstrated that the Langmuir and D–R isotherm models could describe Cu2+ biosorption better than the Freundlich, Temkin and Jovanovic models, with the highest monolayer biosorption capacity of 25.13 mg/g, suggesting chemical interactions between the metal ions and biosorbent. Thermodynamic parameters such as Gibbs free energy, enthalpy, and entropy showed that the biosorption process is spontaneous, feasible and endothermic. After biosorption, SEM and EDX spectroscopy indicated noticeable alterations in the properties of the R. damascena leaf surface. In addition, FT-IR spectroscopy revealed the existence of functional groups, such as carbonyl groups, acids, phosphates, amides, hydroxyl groups, halides, carboxyl groups, and amine groups, in the R. damascena leaf biomass, all of which are likely to be involved in the biosorption of copper ions. Immobilization was shown to be a promising method for producing efficient adsorbents that can be used to sequester metal ions from wastewater. Therefore, R. damascena leaves can be used as a low-cost biosorbent to remove copper ions from aqueous solutions.
Materials and methods
Preparation of biosorbent
Rosa damascena Miller var. trigintipetala Dieck was collected from Taif rose farms in the Al-Shafa highland, Taif region, Saudi Arabia. Voucher specimens were deposited and identified by staff members of the herbarium at Taif University, Taif, Saudi Arabia. The rose leaves were removed from the plants, washed under running water to eliminate any impurities or pollutants, and then dried at room temperature for two weeks. Until further investigation, the leaves were crushed into a fine powder and stored in an airtight container.
Preparation of copper solutions
Approximately 3.93 g of copper sulfate (CuSO4·5H2O) was dissolved in 1000 mL distilled water to prepare the Cu2+ stock solution. All of the chemicals used in this investigation were of analytical grade and obtained from Sigma–Aldrich, including CuSO4·5H2O, HCl, NaOH, Na-alginate and CaCl2.
Batch biosorption experiments
Impact of individual factors
The impact of different variables on biosorption by R. damascena leaf biomass was investigated using batch experiments. The effect of the initial Cu2+ concentration (30–150 mg/L), temperature (25–45 °C) and contact time (0–150 min) was examined. The biosorption tests were carried out in 250 mL conical flasks with 100 mL of copper solution, and the mixture was agitated at 170 rpm in a shaker. Deionized water was used to prepare the solutions, and the pH was adjusted using 0.1 M HCl or 0.1 M NaOH.
Each experiment was repeated three times, with the average results provided. The biosorbent was removed from the solutions at the end of the biosorption procedure by centrifugation for 5 min at 4000 rpm.
The concentration of copper in the filtrate was determined by inductively coupled plasma–optical emission spectrometry (ICP–OES) (Perkin Elmer Optima 2000 DV). The following equation was used to calculate the biosorption of copper ions onto R. damascena leaf biomass (qe; mg/g).
| 20 |
where Ci and Ceq (mg/L) are the copper ion concentrations before and after the equilibrium contact time, V (mL) is the volume of copper solution, and W (g) is the weight of R. damascena leaf powder.
The removal percentage of Cu2+ ions by R. damascena leaves was calculated by Eq. (21):
| 21 |
Optimization of Cu2+ removal by Box–Behnken statistical design (BBD)
Response surface methodology is a multivariable optimization approach that fits experimental results to a second-order equation to determine the optimal response of a process that is a function of numerous independent factors. Designing an experimental matrix, developing a mathematical model, and optimizing the response are the three key processes of RSM78. Experiments were developed to determine the optimal copper biosorption onto R. damascena leaves using Box–Behnken Design and RSM (Stat-Ease Inc., Minneapolis, USA). The design included 17 runs with three independent factors, biosorbent dose (1, 3, 5 g/L), pH (2, 4, 6) and initial copper concentration (30, 60, 90 mg/L), at three coded levels (− 1, 0, + 1) (Table 1).
The sorption experiments were carried out with a fixed contact time of 90 min at 25 °C and 180 rpm, and the remaining concentration of Cu2+ ions was then determined as previously described.
The following equation is a second-order polynomial equation that includes the independent factors and the dependent response.
| 22 |
where Y is the expected response, β0 is the intercept term, βi, βii and βij are the linear, quadratic, and interaction impacts, respectively, Xi and Xj are the independent variables, and ε is the error.
The optimized conditions obtained from BBD were used to determine the kinetic biosorption models at various time periods (0–150 min) and to estimate isothermal models at various initial Cu2+ concentrations (30, 60, 90, 120 and 150 mg/L) and a contact time of 90 min at 25 °C. Thermodynamic investigations of Cu2+ ion biosorption were also examined, with the biosorption process being tested under optimal conditions at different temperatures (25, 35, and 45 °C).
Validity of kinetics models
The applicability and validity of the biosorption kinetic models was established by determining the normalized standard deviation (NSD) and chi-square (X2).
The lower the NSD and X2 values for a given kinetic model are, the more likely the experimental data are to be valid79.
The mathematical equations of NSD and X2 are given as follows:
| 23 |
| 24 |
where N is the number of data points.
Statistical analysis of the data
It has been stated that three-dimensional response surface plots can be used to analyze the principal and interaction impacts of two parameters while all other variables are held constant. The regression model was used to produce the 3D response surface plots for the copper removal percentage by keeping one factor at the center level. The experimental design and statistical analysis were performed in Design Expert version 7. Multiple regression analysis and ANOVA were used to assess the experimental data, and significance was determined at probability levels using the F test (p ≤ 0.05). The Duncan’s multiple range tests were performed to compare the means using the SPSS statistical package (version 16.0).
Characterization of R. damascena leaves
A scanning electron microscope (SEM-JEOL JSM-6510 L. V operated at 30 kV) with energy-dispersive X-ray spectroscopy (EDX, JEOL JEM-2100 (HRTEM) operated at a voltage of 200 kV) was used to examine the surface morphology of the R. damascena leaves. The functional groups on the R. damascena leaf surface were determined using Fourier transform infrared radiation spectroscopy (FTIR, Thermo Fisher Scientific model FT-IR is 10, USA) before and after biosorption process.
Biosorbent immobilization
Rosa damascena leaves were immobilized for 30 min at 60 °C under continuous stirring by the dissolution of 4 g of Na-alginate in 100 mL distilled water80. In the Na-alginate solution, 4 g/L R. damascena leaf powder was added. This mixture was then added to a 2% CaCl2 solution using a 3 mL syringe to form beads. For full gelation, the spherical beads (3 mm) were maintained for 2 h in a 2% calcium chloride solution. The beads were then rinsed in distilled water to eliminate any excess CaCl2 and stored in the refrigerator until they were needed again. The biosorption experiment was performed as previously described using immobilized R. damascena leaves and non-immobilized biosorbent as a control under the optimum conditions obtained by BBD at a temperature of 25 °C and over various time intervals (0–150 min).
All methods were performed in accordance with relevant guidelines and regulations.
Acknowledgements
The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through Project Number 1-441-129.
Author contributions
M.A.F.: Investigation, formal analysis, writing—original draft. H.M.A., T.M.G.: Writing—original draft, supervision, project administration, funding acquisition, writing—review & editing. M.A.F., R.Z.H., T.G.A.: Methodology, supervision, writing—review & editing. S.H.A.H., E.F.A.: Methodology, writing—review & editing.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Yu S, et al. Macroscopic, spectroscopic, and theoretical investigation for the interaction of phenol and naphthol on reduced graphene oxide. Environ. Sci. Technol. 2017;51(6):3278–3286. doi: 10.1021/acs.est.6b06259. [DOI] [PubMed] [Google Scholar]
- 2.Banerjee M, Basu RK, Das SK. Cu (II) removal using green adsorbents: kinetic modeling and plant scale-up design. Environ. Sci. Pollut. Res. 2019;26(12):11542–11557. doi: 10.1007/s11356-018-1930-5. [DOI] [PubMed] [Google Scholar]
- 3.Dulla JB, Tamana MR, Boddu S, Pulipati K, Srirama K. Biosorption of copper (II) onto spent biomass of Gelidiella acerosa (brown marine algae): Optimization and kinetic studies. Appl. Water Sci. 2020;10(2):1–10. doi: 10.1007/s13201-019-1125-3. [DOI] [Google Scholar]
- 4.Calero M, Iáñez-Rodríguez I, Pérez A, Martín-Lara MA, Blázquez G. Neural fuzzy modelization of copper removal from water by biosorption in fixed-bed columns using olive stone and pinion shell. Bioresour. Technol. 2018;252:100–109. doi: 10.1016/j.biortech.2017.12.074. [DOI] [PubMed] [Google Scholar]
- 5.Al-Homaidan AA, Al-Houri HJ, Al-Hazzani AA, Elgaaly G, Moubayed NM. Biosorption of copper ions from aqueous solutions by Spirulina platensis biomass. Arab. J. Chem. 2014;7(1):57–62. doi: 10.1016/j.arabjc.2013.05.022. [DOI] [Google Scholar]
- 6.Chen H, Wang A. Kinetic and isothermal studies of lead ion adsorption onto palygorskite clay. J. Colloid Interface Sci. 2007;307:309–316. doi: 10.1016/j.jcis.2006.10.054. [DOI] [PubMed] [Google Scholar]
- 7.Bagheri R, Ghaedi M, Asfaram A, Dil EA, Javadian H. RSM-CCD design of malachite green adsorption onto activated carbon with multimodal pore size distribution prepared from Amygdalus scoparia: Kinetic and isotherm studies. Polyhedron. 2019;171:464–472. doi: 10.1016/j.poly.2019.07.037. [DOI] [Google Scholar]
- 8.Fawzy MA. Process optimization and modeling of Cd2+ biosorption onto the free and immobilized Turbinaria ornata using Box–Behnken experimental design. Sci. Rep. 2022;12(1):1–18. doi: 10.1038/s41598-022-07288-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fawzy MA, Hifney AF, Adam MS, Al-Badaani AA. Biosorption of cobalt and its effect on growth and metabolites of Synechocystis pevalekii and Scenedesmus bernardii: Isothermal analysis. Environ. Technol. Innov. 2020;19:100953. doi: 10.1016/j.eti.2020.100953. [DOI] [Google Scholar]
- 10.Asemave K, Thaddeus L, Tarhemba PT. Lignocellulosic based sorbents: A review. Sustain. Chem. 2021;2:271–285. doi: 10.3390/suschem2020016. [DOI] [Google Scholar]
- 11.Alia RM, Hamada HA, Hussein MM, Malash GF. Potential of using green adsorbent of heavy metal removal from aqueous solutions: Adsorption kinetics, isotherm, thermodynamic, mechanism and economic analysis. Ecol. Eng. 2016;91:317–332. doi: 10.1016/j.ecoleng.2016.03.015. [DOI] [Google Scholar]
- 12.Medhi H, Chowdhury PR, Baruah PD, Bhattacharyya KG. Kinetics of aqueous Cu(II) biosorption onto Thevetia peruviana leaf powder. ACS Omega. 2020;5(23):13489–13502. doi: 10.1021/acsomega.9b04032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nasir MH, Nadeem R, Akhtar K, Hanif MA, Khalid AM. Efficacy of modified distillation sludge of rose (Rosa centifolia) petals for lead (II) and zinc (II) removal from aqueous solutions. J. Hazard. Mater. 2007;147(3):1006–1014. doi: 10.1016/j.jhazmat.2007.01.131. [DOI] [PubMed] [Google Scholar]
- 14.Iftikhar AR, Bhatti HN, Hanif MA, Nadeem R. Kinetic and thermodynamic aspects of Cu (II) and Cr (III) removal from aqueous solutions using rose waste biomass. J. Hazard. Mater. 2009;161(2–3):941–947. doi: 10.1016/j.jhazmat.2008.04.040. [DOI] [PubMed] [Google Scholar]
- 15.Ansari TM, et al. Immobilization of rose waste biomass for uptake of Pb (II) from aqueous solutions. Biotechnol. Res. Int. 2011 doi: 10.4061/2011/685023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aman A, Ahmed D, Asad N, Masih R, Abd ur Rahman HM. Rose biomass as a potential biosorbent to remove chromium, mercury and zinc from contaminated waters. Int. J. Environ. Stud. 2018;75(5):774–787. doi: 10.1080/00207233.2018.1429130. [DOI] [Google Scholar]
- 17.Dil EA, Ghaedi M, Ghezelbash GR, Asfaram A, Ghaedi AM, Mehrabi F. Modeling and optimization of Hg2+ ion biosorption by live yeast Yarrowia lipolytica 70562 from aqueous solutions under artificial neural network-genetic algorithm and response surface methodology: Kinetic and equilibrium study. RSC Adv. 2016;6(59):54149–54161. doi: 10.1039/C6RA11292G. [DOI] [Google Scholar]
- 18.Dil EA, Ghaedi M, Asfaram A, Mehrabi F, Sadeghfar F. Efficient adsorption of Azure B onto CNTs/Zn: ZnO@ Ni2P-NCs from aqueous solution in the presence of ultrasound wave based on multivariate optimization. J. Ind. Eng. Chem. 2019;74:55–62. doi: 10.1016/j.jiec.2018.12.050. [DOI] [Google Scholar]
- 19.Sharifpour E, Alipanahpour Dil E, Asfaram A, Ghaedi M, Goudarzi A. Optimizing adsorptive removal of malachite green and methyl orange dyes from simulated wastewater by Mn-doped CuO-nanoparticles loaded on activated carbon using CCD-RSM: Mechanism, regeneration, isotherm, kinetic, and thermodynamic studies. Appl. Organomet. Chem. 2019;33(3):e4768. doi: 10.1002/aoc.4768. [DOI] [Google Scholar]
- 20.Fawzy MA. Biosorption of copper ions from aqueous solution by Codium vermilara: Optimization, kinetic, isotherm and thermodynamic studies. Adv. Powder Technol. 2020;31(9):3724–3735. doi: 10.1016/j.apt.2020.07.014. [DOI] [Google Scholar]
- 21.Shen Z, Hou D, Jin F, Shi J, Fan X, Tsang DC, Alessi DS. Effect of production temperature on lead removal mechanisms by rice straw biochars. Sci. Total Environ. 2019;655:751–758. doi: 10.1016/j.scitotenv.2018.11.282. [DOI] [PubMed] [Google Scholar]
- 22.Liu Y, Cao Q, Luo F, Chen J. Biosorption of Cd2+, Cu2+, Ni2+ and Zn2+ ions from aqueous solutions by pretreated biomass of brown algae. J. Hazard. Mater. 2009;163(2–3):931–938. doi: 10.1016/j.jhazmat.2008.07.046. [DOI] [PubMed] [Google Scholar]
- 23.Dil EA, Ghaedi M, Asfaram A, Mehrabi F, Bazrafshan AA, Tayebi L. Synthesis and application of Ce-doped TiO2 nanoparticles loaded on activated carbon for ultrasound-assisted adsorption of Basic Red 46 dye. Ultrason. Sonochem. 2019;58:104702. doi: 10.1016/j.ultsonch.2019.104702. [DOI] [PubMed] [Google Scholar]
- 24.Fawzy MA. Fatty acid characterization and biodiesel production by the marine microalga Asteromonas gracilis: Statistical optimization of medium for biomass and lipid enhancement. Mar. Biotechnol. 2017;19(3):219–231. doi: 10.1007/s10126-017-9743-y. [DOI] [PubMed] [Google Scholar]
- 25.Fawzy MA, Alharthi S. Use of response surface methodology in optimization of biomass, lipid productivity and fatty acid profiles of marine microalga Dunaliella parva for biodiesel production. Environ. Technol. Innov. 2021;22:101485. doi: 10.1016/j.eti.2021.101485. [DOI] [Google Scholar]
- 26.Alharbi NK, et al. Kinetic, isotherm and thermodynamic aspects of Zn2+ biosorption by Spirulina platensis: optimization of process variables by response surface methodology. Life. 2022;12(4):585. doi: 10.3390/life12040585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen X, Tian Z, Cheng H, Xu G, Zhou H. Adsorption process and mechanism of heavy metal ions by different components of cells, using yeast (Pichia pastoris) and Cu2+ as biosorption models. RSC Adv. 2021;11(28):17080–17091. doi: 10.1039/D0RA09744F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Dehghani HM, et al. Response surface modeling, isotherm, thermodynamic and optimization study of arsenic (V) removal from aqueous solutions using modified bentonite-chitosan (MBC) Korean J. Chem. Eng. 2016;32:1–11. [Google Scholar]
- 29.Bibi A, Naz S, Uroos M. Evaluating the effect of ionic liquid on biosorption potential of peanut waste: Experimental and theoretical studies. ACS Omega. 2021;6:22259–22271. doi: 10.1021/acsomega.1c02957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fawzy MA, Alharthi S. Cellular responses and phenol bioremoval by green alga Scenedesmus abundans: Equilibrium, kinetic and thermodynamic studies. Environ. Technol. Innov. 2021;22:101463. doi: 10.1016/j.eti.2021.101463. [DOI] [Google Scholar]
- 31.Ghasemi M, Naushad M, Ghasemi N, Khosravi-Fard Y. Adsorption of Pb (II) from aqueous solution using new adsorbents prepared from agricultural waste: Adsorption isotherm and kinetic studies. J. Ind. Eng. Chem. 2014;20(4):2193–2199. doi: 10.1016/j.jiec.2013.09.050. [DOI] [Google Scholar]
- 32.Meitei MD, Prasad MNV. Adsorption of Cu(II), Mn(II) and Zn(II) by Spirodela polyrhiza (L.) Schleiden: Equilibrium, kinetic and thermodynamic studies. Ecol. Eng. 2014;71:308–317. doi: 10.1016/j.ecoleng.2014.07.036. [DOI] [Google Scholar]
- 33.Fawzy MA, Gomaa M. Use of algal biorefinery waste and waste office paper in the development of xerogels: A low cost and eco-friendly biosorbent for the effective removal of congo red and Fe (II) from aqueous solutions. J. Environ. Manage. 2020;262:110380. doi: 10.1016/j.jenvman.2020.110380. [DOI] [PubMed] [Google Scholar]
- 34.Thanthri SHP, Ranaweera KH, Perera BA. Adsorption study of Cu2+ ions from aqueous solutions by bael flowers (Aegle marmelos) Biointerface Res. Appl. Chem. 2021;11(4):11891–11904. [Google Scholar]
- 35.Kalavathy MH, Karthikeyan T, Rajgopal S, Miranda LR. Kinetic and isotherm studies of Cu(II) adsorption onto H-activated rubber wood sawdust. J. Colloid Interface Sci. 2005;292:354–362. doi: 10.1016/j.jcis.2005.05.087. [DOI] [PubMed] [Google Scholar]
- 36.King P, Srinivas P, Kumar YP, Prasad VSRK. Sorption of copper (II) ion from aqueous solution by Tectona grandis L.f. (teak leaves powder) J. Hazard. Mater. 2006;136:560–566. doi: 10.1016/j.jhazmat.2005.12.032. [DOI] [PubMed] [Google Scholar]
- 37.Khormaei M, Nasernejad B, Edrisi M, Eslamzadeh T. Copper biosorption from aqueous solutions by sour orange residue. J. Hazard. Mater. 2007;149:269–274. doi: 10.1016/j.jhazmat.2007.03.074. [DOI] [PubMed] [Google Scholar]
- 38.Sathasivam K, Haris MRHM. Banana trunk fibers as an efficient biosorbent for the removal of Cd(II), Cu(II), Fe(II) and Zn(II) from aqueous solutions. J. Chil. Chem. Soc. 2010;55:278–282. doi: 10.4067/S0717-97072010000200030. [DOI] [Google Scholar]
- 39.Ai T, et al. Equilibrium, kinetic and mechanism studies on the biosorption of Cu2+ and Ni2+ by sulfur-modified bamboo powder. Korean J. Chem. Eng. 2015;32:342–349. doi: 10.1007/s11814-014-0227-8. [DOI] [Google Scholar]
- 40.Abadian S, Rahbar-Kelishami A, Norouzbeigi R, Peydayesh M. Cu(II) adsorption onto Platanus orientalis leaf powder: Kinetic, isotherm, and thermodynamic studies. Res. Chem. Intermed. 2015;41:7669–7681. doi: 10.1007/s11164-014-1851-y. [DOI] [Google Scholar]
- 41.Vasudevan S, Lakshmi J. The adsorption of phosphate by graphene from aqueous solution. RSC Adv. 2012;2:5234–5242. doi: 10.1039/c2ra20270k. [DOI] [Google Scholar]
- 42.Ocampo-Perez R, Leyva-Ramos R, Mendoza-Barron J, GuerreroCoronado RM. Adsorption rate of phenol from aqueous solution onto organobentonite: Surface diffusion and kinetic models. J. Colloid Interface Sci. 2011;364:195–204. doi: 10.1016/j.jcis.2011.08.032. [DOI] [PubMed] [Google Scholar]
- 43.Kumar N, Mittal H, Alhassan SM, Ray SS. Bionanocomposite hydrogel for the adsorption of dye and reusability of generated waste for the photodegradation of ciprofloxacin: A demonstration of the circularity concept for water purification. ACS Sustain. Chem. Eng. 2018;6:17011–17025. doi: 10.1021/acssuschemeng.8b04347. [DOI] [Google Scholar]
- 44.Malamis S, Katsou E. A review on zinc and nickel adsorption on natural and modified zeolite, bentonite and vermiculite: Examination of process parameters, kinetics and isotherms. J. Hazard. Mater. 2013;252:428–461. doi: 10.1016/j.jhazmat.2013.03.024. [DOI] [PubMed] [Google Scholar]
- 45.Langmuir I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918;40:1361–1403. doi: 10.1021/ja02242a004. [DOI] [Google Scholar]
- 46.Lopičić ZR, et al. Effects of different mechanical treatments on structural changes of lignocellulosic waste biomass and subsequent Cu (II) removal kinetics. Arab. J. Chem. 2019;12(8):4091–4103. doi: 10.1016/j.arabjc.2016.04.005. [DOI] [Google Scholar]
- 47.Bazargan-Lari R, Zafarani HR, Bahrololoom ME, Nemati A. Removal of Cu(II) ions from aqueous solutions by low-cost natural hydroxyapatite/chitosan composite: Equilibrium, kinetic and thermodynamic studies. J. Taiwan Inst. Chem. Eng. 2014;45:1642–1648. doi: 10.1016/j.jtice.2013.11.009. [DOI] [Google Scholar]
- 48.Vijayaraghavan K, Padmesh TVN, Palanivelu K, Velan M. Biosorption of nickel(II) ions onto Sargassum wightii: Application of two-parameter and three-parameter isotherm models. J. Hazard. Mater. 2006;133:304–308. doi: 10.1016/j.jhazmat.2005.10.016. [DOI] [PubMed] [Google Scholar]
- 49.Khan TA, Mukhlif AA, Khan EA, Sharma DK. Isotherm and kinetics modeling of Pb(II) and Cd(II) adsorptive uptake from aqueous solution by chemically modified green algal biomass. Model. Earth Syst. Environ. 2016;2(3):1–13. doi: 10.1007/s40808-016-0264-x. [DOI] [Google Scholar]
- 50.Al-Ghouti MA, Da'ana DA. Guidelines for the use and interpretation of adsorption isotherm models: A review. J. Hazard. Mater. 2020;393:122383. doi: 10.1016/j.jhazmat.2020.122383. [DOI] [PubMed] [Google Scholar]
- 51.Gupta V, Rastogi A. Biosorption of hexavalent chromium by raw and acidtreated green alga Oedogonium hatei from aqueous solutions. J. Hazard. Mater. 2009;163:396–402. doi: 10.1016/j.jhazmat.2008.06.104. [DOI] [PubMed] [Google Scholar]
- 52.Bermúdez YG, Rico ILR, Guibal E, de Hoces MC, Lara MAM. Biosorption of hexavalent chromium from aqueous solution by Sargassum muticum brown alga. Application of statistical design for process optimization. Chem. Eng. J. 2012;183:68–76. doi: 10.1016/j.cej.2011.12.022. [DOI] [Google Scholar]
- 53.Hodaifa G, Alami SBD, Ochando-Pulido JM, Victor-Ortega MD. Iron removal from liquid effluents by olive stones on adsorption column: Breakthrough curves. Ecol. Eng. 2014;73:270–275. doi: 10.1016/j.ecoleng.2014.09.049. [DOI] [Google Scholar]
- 54.Asim AM, Uroos M, Naz S, Muhammad N. Pyridinium protic ionic liquids: Effective solvents for delignification of wheat straw. J. Mol. Liq. 2021;325:115013. doi: 10.1016/j.molliq.2020.115013. [DOI] [Google Scholar]
- 55.El-Naggar NEA, Hamouda RA, Saddiq AA, Alkinani MH. Simultaneous bioremediation of cationic copper ions and anionic methyl orange azo dye by brown marine alga Fucus vesiculosus. Sci. Rep. 2021;11(1):1–19. doi: 10.1038/s41598-020-79139-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Pradhan D, Sukla LB, Mishra BB, Devi N. Biosorption for removal of hexavalent chromium using microalgae Scenedesmus sp. J. Clean. Prod. 2019;209:617–629. doi: 10.1016/j.jclepro.2018.10.288. [DOI] [Google Scholar]
- 57.Grace CEE, et al. Biomolecular transitions and lipid accumulation in green microalgae monitored by FTIR and Raman analysis. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2020;224:117382. doi: 10.1016/j.saa.2019.117382. [DOI] [PubMed] [Google Scholar]
- 58.Ponnuswamy I, Madhavan S, Shabudeen S. Isolation and characterization of green microalgae for carbon sequestration, waste water treatment and bio-fuel production. Int. J. Bio-Sci. Bio-Technol. 2013;5:17–26. [Google Scholar]
- 59.Dittert IM, et al. Adding value to marine macro-algae Laminaria digitata through its use in the separation and recovery of trivalent chromium ions from aqueous solution. Chem. Eng. J. 2012;193:348–357. doi: 10.1016/j.cej.2012.04.048. [DOI] [Google Scholar]
- 60.Bertagnolli C, daSilva MGC, Guibal E. Chromium biosorption using the residue of alginate extraction from Sargassum filipendula. Chem. Eng. J. 2014;237:362–371. doi: 10.1016/j.cej.2013.10.024. [DOI] [Google Scholar]
- 61.Al-Zaban MI, et al. Experimental Modeling Investigations on the Biosorption of Methyl Violet 2B Dye by the Brown Seaweed Cystoseira tamariscifolia. Sustainability. 2022;14(9):5285. doi: 10.3390/su14095285. [DOI] [Google Scholar]
- 62.Stehfest K, Toepel J, Wilhelm C. The application of micro-FTIR spectroscopy to analyze nutrient stress-related changes in biomass composition of phytoplankton algae. Plant Physiol. Biochem. 2005;43:717–726. doi: 10.1016/j.plaphy.2005.07.001. [DOI] [PubMed] [Google Scholar]
- 63.Elangovan R, Philip L, Chandraraj K. Biosorption of hexavalent and trivalent chromium by palm flower (Borassus aethiopum) Chem. Eng. J. 2008;141:99–111. doi: 10.1016/j.cej.2007.10.026. [DOI] [Google Scholar]
- 64.Sultana N, et al. Experimental study and parameters optimization of microalgae based heavy metals removal process using a hybrid response surface methodology-crow search algorithm. Sci. Rep. 2020;10:15068. doi: 10.1038/s41598-020-72236-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Barquilha CER, Cossich ES, Tavares CRG, Silva EA. Biosorption of nickel (II) and copper (II) ions in batch and fixed-bed columns by free and immobilized marine algae Sargassum sp. J. Clean. Prod. 2017;150:58–64. doi: 10.1016/j.jclepro.2017.02.199. [DOI] [Google Scholar]
- 66.Tan KF, Chu KH, Hashim MA. Continuous packed bed biosorption of copper by immobilized seaweed biomass. Eur. J. Min. Proc. Environ. Prot. 2002;2:246–252. [Google Scholar]
- 67.Mata YN, Blázquez ML, Ballester A, González F, Munoz JA. Biosorption of cadmium, lead and copper with calcium alginate xerogels and immobilized Fucus vesiculosus. J. Hazard. Mater. 2009;163(2–3):555–562. doi: 10.1016/j.jhazmat.2008.07.015. [DOI] [PubMed] [Google Scholar]
- 68.Davis TA, Ramirez M, Mucci A, Larsen B. Extraction, isolation and cadmium binding of alginate from Sargassum spp. J. Appl. Phycol. 2004;16(4):275–284. doi: 10.1023/B:JAPH.0000047779.31105.ec. [DOI] [Google Scholar]
- 69.Cheng SY, Show PL, Lau BF, Chang JS, Ling TC. New prospects for modified algae in heavy metal adsorption. Trends Biotechnol. 2019;37:1255–1268. doi: 10.1016/j.tibtech.2019.04.007. [DOI] [PubMed] [Google Scholar]
- 70.Verma VK, Tewari S, Rai JPN. Ion exchange during heavy metal bio-sorption from aqueous solution by dried biomass of macrophytes. Bioresour. Technol. 2008;99(6):1932–1938. doi: 10.1016/j.biortech.2007.03.042. [DOI] [PubMed] [Google Scholar]
- 71.Quek SY, Wase DAJ, Forster CF. The use of sago waste for the sorption of lead and copper. Water Sa. 1998;24(3):251–256. [Google Scholar]
- 72.Keskinkan OL, Goksu MZ, Yuceer AH, Basibuyuk MF, Forster CF. Heavy metal adsorption characteristics of a submerged aquatic plant (Myriophyllum spicatum) Process Biochem. 2003;39(2):179–183. doi: 10.1016/S0032-9592(03)00045-1. [DOI] [Google Scholar]
- 73.Basci N, Kocadagistan E, Kocadagistan B. Biosorption of copper (II) from aqueous solutions by wheat shell. Desalination. 2004;164:135–140. doi: 10.1016/S0011-9164(04)00172-9. [DOI] [Google Scholar]
- 74.Pavasant P, et al. Biosorption of Cu2+, Cd2+, Pb2+, and Zn2+ using dried marine green macroalga Caulerpa lentillifera. Bioresour. Technol. 2006;97(18):2321–2329. doi: 10.1016/j.biortech.2005.10.032. [DOI] [PubMed] [Google Scholar]
- 75.Aydın H, Bulut Y, Yerlikaya Ç. Removal of copper (II) from aqueous solution by adsorption onto low-cost adsorbents. J. Environ. Manage. 2008;87(1):37–45. doi: 10.1016/j.jenvman.2007.01.005. [DOI] [PubMed] [Google Scholar]
- 76.Chen H, Dai G, Zhao J, Zhong A, Wu J, Yan H. Removal of copper(II) ions by a biosorbent-Cinnamomum camphora leaves powder. J. Hazard. Mater. 2010;177:228–236. doi: 10.1016/j.jhazmat.2009.12.022. [DOI] [PubMed] [Google Scholar]
- 77.Singha B, Das SK. Adsorptive removal of Cu(II) from aqueous solution and industrial effluent using natural/agricultural wastes. Colloids Surf. B. 2013;107:97–106. doi: 10.1016/j.colsurfb.2013.01.060. [DOI] [PubMed] [Google Scholar]
- 78.Sadhu K, Mukherjee A, Shukla SK, Adhikari K, Datta S. Adsorptive removal of phenol from coke-oven waste water using Gondwana shale, India: Experiment, modeling and optimization. Desalin. Water Treat. 2014;52(34–36):6492–6504. doi: 10.1080/19443994.2013.815581. [DOI] [Google Scholar]
- 79.Zamri KA, Munaim MS, Wahid ZA. Regression analysis for the adsorption isotherms of natural dyes onto bamboo yarn. Int. Res. J. Eng. Technol. 2017;4:1699–1703. [Google Scholar]
- 80.Kumar SS, Saramma AV. Nitrate and phosphate uptake by immobilized cells of Gloeocapsa gelatinosa. J. Mar. Biol. Assoc. India. 2012;54:119–122. [Google Scholar]