Statistical methods for Mendelian randomization in genome-wide association studies: A review

Graphical abstract

Abstract

Genome-wide association studies have yielded thousands of associations for many common diseases and disease-related complex traits. The identified associations made it possible to identify the causal risk factors underlying diseases and investigate the causal relationships among complex traits through Mendelian randomization. Mendelian randomization is a form of instrumental variable analysis that uses SNP associations from genome-wide association studies as instruments to study and uncover causal relationships between complex traits. By leveraging SNP genotypes as instrumental variables, or proxies, for the exposure complex trait, investigators can tease out causal effects from observational data, provided that necessary assumptions are satisfied. We discuss below the development of Mendelian randomization methods in parallel with the growth of genome-wide association studies. We argue that the recent availability of GWAS summary statistics for diverse complex traits has motivated new Mendelian randomization methods with relaxed causality assumptions and that this area continues to offer opportunities for robust biological discoveries.

1. Introduction

Great interest has developed in inferring causal relationships between complex traits, i.e., traits that seemingly are not inherited in a Mendelian fashion, in observational human genetics studies. Discovery of such relationships is crucial to enhancing our understanding of the biology of health and disease. Inferring causal relationship in genetics is often carried out through Mendelian randomization (MR) analysis. MR analysis is a form of instrumental variable analysis in which genetic markers, typically single nucleotide polymorphisms (SNPs), serve as instruments, or proxies, for inferring causal effects of an exposure variable on an outcome variable [1], [2], [3], [4], [5], [6], [7].

MR analysis is facilitated by the development of genome-wide association studies (GWAS), which present unique opportunities for discovery of causal relationships via MR [8]. A GWAS interrogates millions of single nucleotide polymorphisms (SNPs) to infer which are associated with the trait [9], [10]. In the nearly 17 years since publication of early studies, researchers have reported thousands of novel SNP-trait associations from GWAS [10], [11], [12], [13]. Ever larger sample sizes in GWAS have enhanced statistical power to detect associations and have refined our understanding of human health and disease. The association results from many large-scale GWAS are nowadays readily available, often in the form of summary statistics that include the marginal SNP p-values and/or their effect size estimates and standard errors [14]. The identified SNP associations are used as the main input for MR analysis and thus the wide availability of GWAS summary statistics clear the way for effective MR analysis in complex genetics studies.

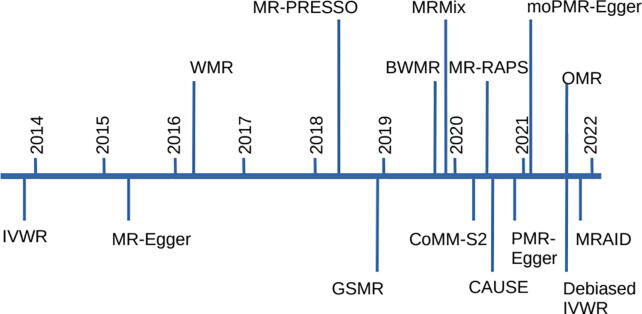
Effective MR analyses are enabled by many MR methods developed in recent years. Methods for and uses of MR have appeared at a rapid and accelerating pace since the publication of the early GWAS (Fig. 1). The overall trend of the methodology development is in the direction of increasingly sophisticated modeling of horizontal pleiotropy including both independent and correlated horizontal pleiotropy while attempting to maintain scalability and computational efficiency in the presence of multiple correlated SNPs.

Fig. 1.

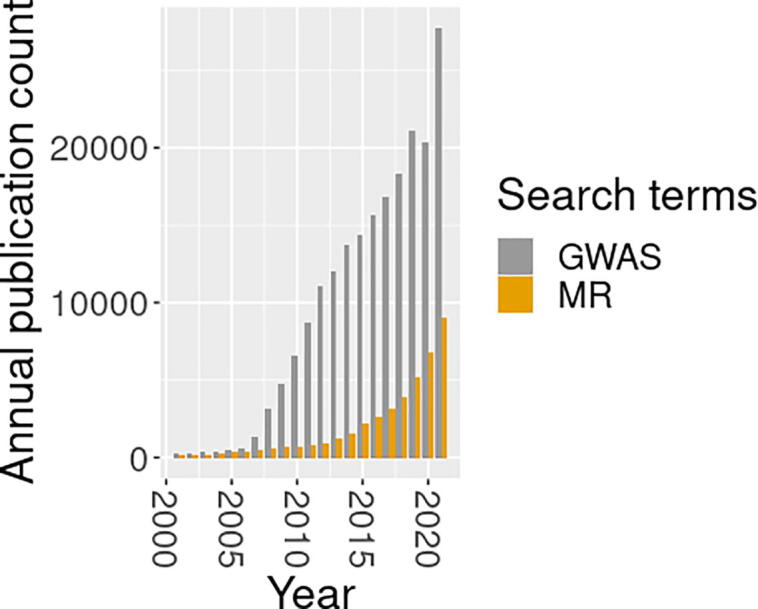
Upward trend in article counts by year for Google Scholar keyword searches: 1. Mendelian randomization and 2. Genome-wide association study.

Here, we present a comprehensive review on 47 MR methods, primarily in the context of GWAS summary statistics, to help practitioners to choose which MR methods to use in applied data analysis. We discuss the basics form of MR analysis, the causality assumptions in MR, and how recent MR methods are developed to ensure robust results in the presence of assumption violations. We discuss in detail methods advances before briefly summarizing applications and directions for future research. Different from existing MR reviews [15], [16], [17], we discuss in detail recent methods developments that enable modeling of horizontal pleiotropy and correlated horizontal pleiotropy and place these developments in the larger context of MR analysis with GWAS data. We present these recent methods developments for an audience of both statisticians and epidemiologists. We hope our review will facilitate the further advance of MR methods and their wide application on GWAS data.

2. Assumptions of Mendelian randomization

Mendelian randomization uses genetic markers in the form of SNP genotypes as the proxy (“instrument” or “instrumental variable”) for the “exposure,” a complex trait, and asks whether the “exposure” variable is causal for the “outcome” variable, which is typically a second complex trait. The exposure and outcome variables can be binary, a count, a time to event, or a continuous variable. For brevity and simplicity, we focus on continuous exposures and outcomes before considering other classes of outcome variables in a later section. Most MR studies use the “two-sample” MR design, in which one cohort of subjects has measurements for the exposure, while a second cohort has measurements for the outcome, with both cohorts sharing the same set of SNP instruments [18]. We focus on the two-sample MR design before considering the one-sample design and the partial two-sample design where samples are partially overlapped between the two cohorts.

MR aims to infer the causal effect of the exposure variable on the outcome variable in observational studies. The proper causal interpretation in an MR study requires the SNP instruments to satisfy three causality assumptions. The first assumption states that SNP instruments are associated with the exposure. If the first assumption, about the association between the SNP instruments and the exposure, holds, but this association is weak, then an amplification of biases, such as those due to violations of assumptions 2 and 3, may result [19]. Indeed, bias in causal estimates can increase with decreases in the strength of association between the SNP instrument and exposure [20]. The second assumption requires independence, conditional on the exposure and all measured and unmeasured confounders, between the SNP instruments and the outcome. The second MR assumption, often termed the exclusion restriction assumption, can also be stated as the need for the SNP instruments to affect the outcome only through the exposure. In a causal diagram, this means that the only path from the SNP instruments to the outcome is that containing the exposure. The last of the three assumptions states that the SNP instruments are independent of all (measured and unmeasured) confounders of the relationship between exposure and outcome. The third assumption ensures that the SNP instruments are independent of all confounders of the exposure-outcome relationship.

When the three MR assumptions hold, one may use instrumental variable statistical methods, with the genetic marker data, the exposure data, and the outcome data, to estimate and to test the causal effect of the exposure on the outcome [7], [21], [22]. In practice, careful evaluation of the assumptions is needed. Because assumptions 2 and 3, which involve absence of certain types of confounding, can’t be verified, practitioners must be cautious when planning MR analyses. Sensitivity analysis is highly recommended as a way to assess robustness of estimates in the presence of possible assumption violations [19]. We will discuss these sensitivity analyses in more detail in a later section and consider their evaluation in MR studies [19].

The causal assumptions of MR also help one to understand the origin of the term “Mendelian randomization.” Recall Mendel’s inheritance laws [23], under the assumption that alleles segregate randomly from parent to offspring, the offspring genotypes are unlikely to be associated with confounders of the exposure-outcome relationship. Additionally, reverse causation from the outcome or exposure to the genotypes is unanticipated since germ-line genotypes are fixed at conception and, thus, precede realization of other observed variables. Therefore, using SNP instruments in the instrumental variable analysis is often referred to as Mendelian randomization.

3. Statistical models and methods for MR with one instrument

We begin our discussion of Mendelian randomization in GWAS data by considering the simplest case, where there is a single SNP instrument and a single outcome variable. Approaches to MR with one SNP instrument can be classified into four categories: ratio of coefficients method, two-stage methods, likelihood-based methods, and semiparametric methods [15]. We discuss each of these before turning to methods that leverage multiple SNP instruments.

3.1. Ratio of coefficients method

The ratio of coefficients method, also known as the Wald method, estimates the causal effect of the exposure X on the outcome Y by using a single SNP instrument [24]. For a continuous outcome, the causal effect estimator, (1).

$${\widehat{\gamma }}_{\mathit{Wald}}=\frac{{\widehat{\beta }}_{\mathit{YZ}}}{{\widehat{\beta }}_{\mathit{XZ}}}$$

In Eq. (1), ${\widehat{\beta }}_{\mathit{YZ}}$ and ${\widehat{\beta }}_{\mathit{XZ}}$ are the slope estimates from the regressions of the outcome and exposure, respectively, on the SNP instrument. Since the Wald method requires only the regression coefficients, it can be used with summary data. However, the Wald method doesn’t accommodate multiple SNP instruments, which limits its direct use in the GWAS setting as will be discussed later.

3.2. Two-stage methods

A two-stage statistical model involves two regression models [15], [25]. For a continuous outcome, one may perform “two-stage least squares,” which involves two linear regressions. First, the exposure variable is regressed on the instrument (i.e., the SNP genotypes) (Equation (2)). We denote each subject’s exposure variable value as $x_i$ in Equation (2), while ${\alpha }_0$ denotes an intercept term and ${\alpha }_1$ is the slope. $z_i$ denotes the SNP instrument genotype for subject $i$, while ${∊}_i$, the error term, is assumed to be independent among subjects and normally distributed with a shared common variance and mean zero.

The resulting fitted values for the exposure variable from Eq. (2) are the independent variable in the second linear regression, where the outcome is the dependent variable. The causal effect estimate, then, is the coefficient ${\widehat{\beta }}_1$ obtained from the second regression analysis (Eq. (3)). Note also that the random errors in Eq. (3) are assumed independent of those in Eq. (2). Like the ${∊}_i$ in Eq. (2), the ${\tau }_i$ are assumed independent and identically distributed normal random errors.

$$x_i={\alpha }_0+{\alpha }_1{z}_i+{∊}_i$$

$$y_i={\beta }_0+{\beta }_1{\widehat{x}}_i+{\tau }_i$$

Note that the uncertainty in the fitted values from the first regression is not considered when performing the second regression. For this reason, the variance of the estimator is incorrect in two-stage calculations [15], [26]. This and other observations led researchers to develop likelihood-based MR methods.

3.3. Likelihood-based methods

Likelihood-based MR methods, unlike two-stage methods, provide maximum likelihood estimates with their many desirable properties [27]. Limited information maximum likelihood from econometrics is the earliest approach for likelihood-based inference in MR [28], [29]. Limited information maximum likelihood with a single SNP instrument is modeled with two equations (Eqs. (4) and (5)), where the random errors follow a bivariate normal distribution [15].

$$x_i={\alpha }_0+{\alpha }_1{z}_{i1}+{∊}_{\mathit{Xi}}$$

$$y_i={\beta }_0+{\beta }_1{x}_i+{∊}_{\mathit{Yi}}$$

Limited information maximum likelihood is sometimes called the maximum likelihood counterpart of two-stage least squares, and it yields the same causal estimate as two-stage least squares and the ratio method when used with a single SNP instrument. Additionally, the limited information maximum likelihood framework can accommodate more than one SNP instrument by replacing ${\alpha }_1{z}_{i1}$ with the sum ${\sum }_{k=1}^K{\alpha }_k{z}_{\mathit{ik}}$.

One may also use Bayesian methods to obtain likelihood-based estimators [30]. Kleibergen [31] examined a model that is similar to that from the limited information maximum likelihood framework (Eq. (6)). The Bayesian model differs from the limited information maximum likelihood model in that the causal effect parameter, ${\beta }_1$ represents the effect between the true means for the exposure and the outcome. In the limited information maximum likelihood model, the causal effect is that of the measured effect on the measured outcome.

$$\begin{array}{c}\left(\begin{array}{c}{X}_i\\ Y_i\end{array}\right)\sim N_2\left(\left(\begin{array}{c}{\xi }_i\\ {\eta }_i\end{array}\right),\mathrm{\Sigma }\right)\\ {\xi }_i={\alpha }_0+{\alpha }_1{z}_{i1}\\ {\eta }_i={\beta }_0+{\beta }_1{\xi }_i\end{array}$$

For each subject $i$, the exposure and outcome values come from a bivariate normal distribution. The mean of the exposure distribution is assumed linear in the SNP instrument, and the mean of the outcome distribution is linear in the mean exposure [15], [32]. Kleibergen [31] demonstrated that the Bayesian model, with weak instruments, outperforms the limited information maximum likelihood model in terms of frequentist coverage levels.

3.4. Semiparametric methods

Semiparametric instrumental variable methods, which feature parametric and nonparametric components, typically assume a parametric model connecting the exposure and outcome, but don’t impose distributional assumptions on the errors [15]. Compared to fully parametric models, semiparametric models often are more robust to model misspecification [15], [33]. We follow Burgess [15] by discussing three semiparametric strategies, generalized method of moments, continuous updating estimator, and G-estimation of structural mean models.

Generalized method of moments can be viewed as a more flexible form of two-stage least squares that handles heteroscedastic errors and nonlinearity in the two regressions [15]. Before specifying the model, we introduce notation. $E\left(Y\vee \text{do}\left(X=x\right)\right)$ is the conditional expectation of $Y$ if we forced $X$ to take value $x$ for every subject [34]. The generalized method of moments equations, with a single SNP instrument, then, can be written as in Eq. (7).

$$\begin{array}{c}{\sum }_i\left(y_i-f\left(x_i;\beta \right)\right)=0\\ {\sum }_i{z}_i\left(y_i-f\left(x_i;\beta \right)\right)=0\end{array}$$

The GMM estimate is the value of the vector $\beta$ that satisfies Eq. (7), where $f\left(x_i;\beta \right)=E\left(Y\vee \text{do}\left(X=x\right)\right)$. Pearl [35] developed numerical methods for obtaining estimates from Eq. (7).

Another semiparametric estimation method is G-estimation of a structural mean model [15], [36], [37]. We follow Burgess [15] by defining the potential outcome $Y\left(x\right)$ as the outcome value that we would have observed had we set the exposure value $X$ to $x$. For example, $Y\left(0\right)$ denotes the observed outcome had we set the exposure to zero instead of its observed value $x$. The structural mean model for a continuous outcome is displayed in Eq. (8).

$$E\left(Y\left(x\right)-Y\left(0\right)|X=x,Z=z\right)={\beta }_{1}x$$

The causal effect parameter is ${\beta }_1$. Burgess [15] derives the estimating equations for ${\beta }_1$, after noting that the conditional expectation, $E\left(Y\left(0\right)|X=x,Z=z\right)$ is independent of $Z$ and reasoning that the causal effect is that value of ${\beta }_1$ that yields zero covariance between $Z$ and $E\left(Y\left(0\right)\vee X=x,Z=z\right)$ (Eq. (9)).

$${\sum }_i\left(z_{\mathit{ik}}-z_k\right)\left(y_i-{\beta }_1{x}_i\right)=0$$

Note that $k$ indexes SNP instruments and ranges from $1$ to $K$ in Eq. (9).

3.5. Mendelian randomization with multiple independent SNP instruments

While using a single SNP instrument for MR analysis can be effective, Greenland [38] recognized that many genetic variants individually explain a small proportion of the variation in a trait, and, thus, sufficient statistical power of MR analysis with a single SNP instrument would require sample sizes in the tens of thousands [39], [40]. Schatzkin [41] resolved this issue by proposing use of multiple SNP instruments in MR analysis. In particular, Palmer [42] reasoned that a single causal estimate derived from a collection of causal SNPs would have greater precision than an estimate derived from only one SNP [39]. Recognition of complex traits’ diverse genetic architectures has thus fueled development of two-sample MR methods with multiple SNP instruments [42], [43], [44], [45].

There are two important considerations for MR analysis with multiple SNP instruments. The first consideration is how to choose a subset of the available SNPs to serve as instruments. The solution to this task differs among published methods and majority of MR methods chose a set of independent SNPs as instruments [46], [47]. The independent SNPs may be selected through linkage disequilibrium (LD) clumping [48]. The second consideration is how to make use of GWAS summary statistics for MR analysis, as sharing of GWAS summary statistics was encouraged and became a common practice [49]. [50] recognized that one could calculate the Wald ratio estimate of the causal effect from GWAS summary statistics, and [39] devised a strategy for determining a single causal effect from summary statistics for a collection of independent SNPs. Below, we discuss a number of MR methods that make use of multiple independent SNP instruments.

4. Statistical models and methods for MR with multiple instruments

4.1. Methods with Individual-level data

One approach to integrating multiple SNP instruments into a MR framework is through calculation of allele scores [51]. Harbord [51] calculate an unweighted score as the number of exposure-increasing alleles in the subject’s genotypes. They also calculate a weighted allele score by using the exposure effects as weights. For example, a subject with $g_k$ copies of exposure-increasing alleles for SNP $k$ has an unweighted allele score $z={\sum }_{k=1}^K{g}_k$ and a weighted allele score $z={\sum }_{k=1}^K{w}_k{g}_k$. Harbord [51] found that when weights are obtained from external data or from cross-validation or jackknife approaches applied to the analysis data, the allele score functions as a single instrumental variable and greatly diminishes the bias compared to that of the two-stage least squares estimator [15], [52].

Angrist [53] developed a LASSO-based method, sisVIVE, to identify invalid SNP instruments [54]. sisVIVE’s advantage over earlier methods is that it doesn’t require the analyst to know which SNP instruments are valid. Instead, it requires that at least 50% of the instruments be valid. sisVIVE outperforms two-stage least squares in many ways and performs similar to oracle two-stage least squares. Simulations and data analysis results reveal that sisVIVE is robust to possibly invalid instruments.

Tibshirani [55], building on the research from [53], implemented an adaptive LASSO-based estimator after recognizing that sisVIVE misclassifies valid SNP instruments as invalid when the invalid SNP instruments have strong effects on the exposure. Consistent selection of invalid SNP instruments, they found, depends on SNP instrument correlations. To address this issue, Tibshirani [55] proposed a median estimator with consistency that doesn’t depend on SNP instrument-exposure association strength or the SNP instrument correlation structure. They then applied methods from Windmeijer [56] to achieve a consistent estimator with the same asymptotic distribution as the oracle two-stages least squares. One important limitation of this thread of research is that both Angrist [53] and Tibshirani [55] require individual-level data.

Zou [57], working with individual-level GWAS data, share naive and smoothed constrained instrumental variable methods. Central to their work is the proposal to create a new instrumental variable as a linear combination of genotype data from a collection of SNP instruments. They require that the new instrumental variable be standardized to have norm 1 and be orthogonal to potentially vertically pleiotropic traits. For a collection of SNPs, they choose the $K$-vector that meets these criteria and maximizes the correlation with the exposure. To obtain their second estimator, Zou [57] apply a $l_0$ penalty to constrain the number of SNP instruments that are given nonzero weights in the calculation of the new instrumental variable. They then compare their method with sisVIVE and allele score methods. Zou [57] find that both the smoothed version of their estimator and the allele score method are unbiased in their simulation settings.

Jiang [58] and Spiller [59] present a method, MR-GxE, that exploits gene by environment interactions to detect and to adjust for bias due to horizontal pleiotropy. Spiller [59] treat a SNP-covariate interaction as an instrumental variable, and, by so doing, they impose assumptions on that interaction. Together, these assumptions require that MR-GxE assume that horizontal pleiotropy effects are constant across the study cohort. The authors devise a three-step inferential procedure for two-sample MR with GWAS summary statistics. First, they estimate the SNP-exposure and SNP-outcome associations at a range of covariate values. Second, they regress the SNP-outcome estimated associations on the SNP-exposure estimated associations. Third, they treat the resulting slope as the causal effect estimate and the intercept as the mean horizontal pleiotropy effect.

4.2. Methods with summary data

The proliferation of publicly available GWAS data accelerates the development of MR methods with multiple SNP instruments that make use of GWAS summary statistics for model fitting. Our timeline highlights some of the many multi-instrument MR methods with GWAS summary statistics, with an increasing density of methods over time in the last three years (Fig. 2). These methods include the inverse variance weighted MR [39], MR-Egger [43], weighted median estimation [60], Bayesian weighted MR [61], robust adjusted profile score [62], MRMix [63], CAUSE [64], and MRAID [65]. These methods differ in their approaches to three considerations that include instrument selection (from among the available SNPs), modeling and controlling for horizontal pleiotropy, and statistical inference procedure. We summarize some of these MR methods that use independent or correlated SNP instruments below. We will cover the remaining MR methods that model horizontal pleiotropy in a later section.

Fig. 2.

Two-sample MR with GWAS summary statistics methods publications density increases over time.

Smith [39] termed their method “inverse variance weighting” (IVW) because each causal SNP’s effect is weighted by the inverse of the variance of the ratio estimator, and the overall causal effect is the sum of the weighted SNP causal effects. Specifically, Smith [39] combined causal effect ratio estimates from independent SNPs by using Eq. (10).

$${\hat{\beta }}_{\mathit{IVW}}=\frac{{\sum }_{j=1}^M{\hat{\theta }}_{j}Var{\left({\hat{\theta }}_j\right)}^{-1}}{{\sum }_{j=1}^{M}Var{\left({\hat{\theta }}_j\right)}^{-1}}$$

Spiller [60], noting that consistency with IVW MR is not robust to invalid instrument use, developed a method for consistent MR analysis with weighted median-based estimators, building on research from [66]. Its breakdown point is 50%, meaning that up to 50% of SNP instruments can be invalid while maintaining consistency in estimation [67]. Specifically, let ${\stackrel{\sim }{\beta }}_j$ denote the $j^{\mathit{th}}$ ordered ratio estimate statistic, from least to greatest. If an odd number, say $2K=1$, of SNP instruments is used, then the simple median estimator is defined as the $K+1$ ordered ratio estimate. For an even number, say $2K$, number of SNP instruments, choose the midpoint between the two middle-ranking ordered ratio estimates, $\frac{{\stackrel{\sim }{\beta }}_K+{\stackrel{\sim }{\beta }}_{K+1}}{2}$.

Due to the inefficiency of the simple median estimator, Spiller [60] define the weighted median estimator. To construct this estimator, order the ratio estimates from least to greatest, as with the simple median estimator. The weighted median estimator, then is the median of a distribution defined by having ${\stackrel{\sim }{\beta }}_j$ as the $p_j=100$ percentile, where $w_j$ is the weight assigned to the $j^{\mathit{th}}$ ordered ratio estimate. In this setting, the simple median estimator is seen to be the weighted median estimator when all weights are equal.

Spiller [60] also studied the penalized weighted median estimator. They defined the penalized weights, $w^i=w_j\text{'}\times \text{min}\left(1,20q_j\right)$, where $q_j$ is the p-value resulting from the comparison of $Q_j=w_j\text{'}{\left({\stackrel{\sim }{\beta }}_j-{\widehat{\beta }}_{\mathit{IVW}}\right)}^2$ to a ${\chi }_1^2$ distribution [60], [68]. The penalized weighted median estimator leaves most variants unaffected, but downweights those with outlying Wald ratio estimates. While the above MR methods all use independent SNP instruments, using independent instruments may not be ideal when there are multiple causal SNPs in linkage disequilibrium with each other. In this setting, discarding some of the causal SNPs may only capture a small proportion of trait variance explained by the exposure and lead to a power loss in MR [15], [39], [69], [70]. Consequently, many MR methods have been recently developed to model multiple correlated instruments.

Cochran [69] developed methods for using correlated SNPs in IVW MR by inserting a covariance matrix into the standard IVW formulation. However, many MR methods use a set of pre-selected SNPs as instruments. Typically, these SNPs are selected to be statistically independent. This restriction to independent SNPs is needed for valid inference in methods like standard inverse variance weighting MR [39].

4.3. Assumption violations and sensitivity analysis

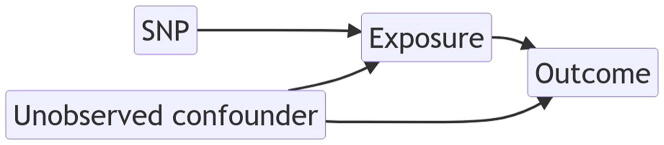
It is worthwhile to consider ways in which the standard MR assumptions may be violated and strategies for identifying such violations. Let’s first consider the exclusion restriction assumption (assumption 2 above). It states that the SNP instrument must affect the outcome only through the exposure (Fig. 3B). The causal diagram in Fig. 3A illustrates a scenario that violates this assumption [19]. Bias in causal effect estimation would result. However, if the intermediate is measured and treated as the exposure, then an unbiased estimate of causal effect is possible, since the intermediate captures the two pathways, intermediate -> outcome and intermediate -> exposure -> outcome, through which the SNP instrument affects the outcome Y [19].

Fig. 3.

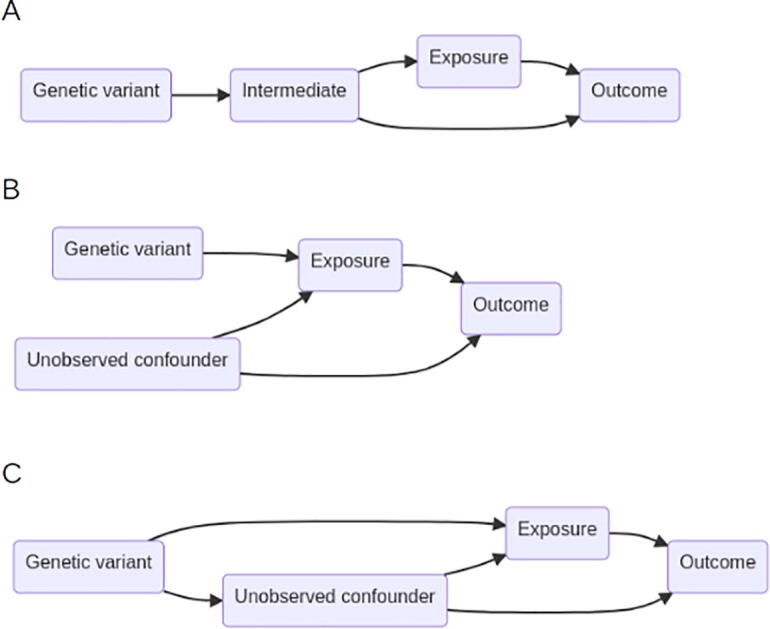
Causal diagrams for MR. A. Scenario where the genetic variant affects an intermediate variable on the pathway to the exposure. Because the intermediate affects the outcome through a pathway that doesn’t involve exposure, this scenario violates the exclusion restriction assumption. B. Scenario where the genetic variant affects an exposure, which in turn affects an outcome, possibly in the presence of unmeasured confounding. C. Correlated horizontal pleiotropy occurs when the genetic variant affects the exposure, which in turn affects the outcome, and the genetic variant affects the unobserved confounder, which in turn affects the exposure and the outcome independently.

Recognition of the many ways that the MR assumptions may be violated has inspired methods advances that enable assumption relaxations and has motivated use of sensitivity analysis to quantify the impact of possible assumption violations. Sensitivity analysis is recommended and widely used in MR studies because of the inability to verify the three MR assumptions with observational data. The goal of a sensitivity analysis is to gain insight into how the results might differ if the assumptions be violated. Because not all confounding variables are known or measured, assumptions 2 and 3 are not fully verifiable in MR studies. Recognition of this fact has inspired the development of sensitivity analysis tools. While we can’t assess whether a SNP instrument is associated with every confounder of the exposure-outcome association, it is possible to examine the associations of the SNP instrument with the measured covariates. While absence of such associations doesn’t guarantee satisfaction of the assumption, presence of SNP-covariate associations must be investigated carefully, as they may constitute assumption violations [71].

Burgess [71] considered a collection of sensitivity analysis methods when working with GWAS summary statistics. Burgess [71] presented methods for both assessing the MR assumptions, to the extent possible, and performing robust analyses. For example, they used measured covariates to assess for possible associations with the SNP instruments. While they can’t rule out the possibility of unmeasured confounding, they can study the possibility of measured covariates serving as confounders.

To illustrate their approach, Burgess [71] shared a case study in which they examined the causal effect of C-reactive protein (CRP) levels on coronary artery disease risk with four genetic variants in the CRP gene region and 17 other genetic variants that affect coronary artery disease risk. They used measured covariates to probe for SNP-covariate associations, and followed it up with scatter plots and Cochran’s Q test on the causal estimates to inquire about whether the SNP instruments all identify the same causal parameter [72], [73], [74]. Additionally, Burgess [71] suggested using a funnel plot, like those in the meta-analysis literature, to visualize possible evidence of directional pleiotropy, where the average pleiotropic effects of the SNP instruments is nonzero [75]. Additionally, Egger regression can be useful in this setting [43], [76], [77], [78].

Spiller [59] point out that MR-GxE can be used as a sensitivity analysis tool to choose a set of valid SNP instruments from a collection of SNPs in settings where there may be a violation of the constant pleiotropy assumption.

MR-GENIUS is a framework for two-sample MR analysis when individual-level data are available [79]. Bowden [79] focused efforts on relaxing the exclusion restriction assumption and building on existing G-estimation methods to create an estimator that is robust to violations of the exclusion restriction and to additive unmeasured confounding [80]. They observe that their estimator, in some settings, reduces to that of [81], which is widely used in econometrics, but not in the MR literature.

4.4. Explicit modeling of horizontal pleiotropy

Besides sensitivity analysis, several methods have been developed to directly model horizontal pleiotropy to ensure the validity of MR assumptions. Pleiotropy, where a single genetic variant affects multiple traits, has a long history of study in genetics and complex traits [82], [83], [84]. In MR setting, horizontal pleiotropy occurs when a SNP instrument affects the outcome through at least one pathway that bypasses the exposure variable [46]. The presence of horizontal pleiotropy constitutes a violation of the standard MR assumptions and can lead to biased causal effect estimates and diminished statistical power. Watanabe [46] documented widespread horizontal pleiotropy in GWAS. We discuss approaches to modeling and accounting for horizontal pleiotropy below.

In the short time since publication of [46], researchers have recognized two types of horizontal pleiotropy [65]. The first occurs via exposure-independent paths. The resulting horizontal pleiotropic effects are independent of the SNP-exposure relationships. The second type of horizontal pleiotropy manifests in the presence of unobserved exposure-outcome confounding. It induces correlation between horizontal pleiotropic effects and SNP-exposure effects. Both types of horizontal pleiotropy violate standard MR modeling assumptions and can bias causal effect estimates and can increase false discoveries [65]. Early MR analyses avoided confounding from horizontal pleiotropy by discarding instrumental SNPs that might be associated with the outcome [46], [47]. More recent methods have attempted to model horizontal pleiotropy [64], [65], [85]. CAUSE [64] and MRMix [63] both use a mixture of normal distributions to control for both types of horizontal pleiotropy. Modeling both types of horizontal pleiotropy is particularly challenging because the MR model likelihood often involves an integral that can’t be solved analytically. Because of this issue with the model likelihood, both MRMix and CAUSE use other, non-likelihood-based methods for inference.

Pierce [43] adapted Egger regression, originally developed to detect bias in meta-analyses, to detect bias from horizontal pleiotropy in two-sample MR studies with GWAS summary statistics or individual-level data [76]. Their approach is termed MR-Egger. They formulate their model as

$$\begin{array}{c}{X}_i={\sum }_{j=1}^J{\gamma }_j{G}_{\mathit{ij}}+U_i+{∊}_{\mathit{Xi}}\\ Y_i={\sum }_{j=1}^J{\alpha }_j{G}_{\mathit{ij}}+\beta X_i+U_i+{∊}_{\mathit{Yi}}\end{array}$$

where $U$ designates confounders, $X$ and $Y$ denote the exposure and outcome, respectively, $G$ is a SNP instrument, and ${∊}_X$ and ${∊}_Y$ are the zero-mean, normally distributed random errors.

Pierce [43] then write the outcome in terms of the SNP instrument $j$ and the effects defined in Eq. (11) and define the new parameter ${\mathrm{\Gamma }}_j={\alpha }_j+\beta {\gamma }_j$ (Eq. (12)).

$$\begin{array}{c}{Y}_i=\left({\alpha }_j+\beta {\gamma }_j\right)G_{\mathit{ij}}+∊{\text{'}}_{\mathit{Yij}}\\ ={\mathrm{\Gamma }}_j{G}_{\mathit{ij}}+∊{\text{'}}_{\mathit{Yij}}\end{array}$$

In Eq. (12), ${\alpha }_j=0$ when SNP $j$ is a valid instrument.

MR-Egger fits the regression model in Eq. (13).

$${\widehat{\mathrm{\Gamma }}}_j={\beta }_{0E}+{\beta }_E{\widehat{\gamma }}_j$$

The notation in Eq. (13) could be a little misleading. The independent and dependent variables are ${\widehat{\gamma }}_j$ and ${\widehat{\mathrm{\Gamma }}}_j$, respectively, while the regression parameters are ${\beta }_{0E}$ and ${\beta }_E$.

The slope coefficient ${\widehat{\beta }}_E$ estimates the causal effect of the exposure on the outcome. Under the assumption that the SNP-exposure relationship is independent of the SNP’s pleiotropic effects, Egger’s test offers a valid test of the null causal hypothesis and consistently estimates the causal effect, even if all SNPs are invalid instruments [43]. In efforts to detect the presence of horizontal pleiotropy in two-sample MR studies with GWAS summary data, [72] developed the between-instrument heterogeneity test. In a meta-analysis of MR Wald ratio estimates, one per SNP instrument, they calculate $Q$ in Eq. (14).

$$Q={\sum }_{k=1}^K{w}_k{\left({\widehat{\beta }}_{\mathit{XY}}^{\left(k\right)}-{\mu }_F\right)}^2$$

In Eq. (14), $w_k$ is the inverse variance of the Wald estimator, and ${\mu }_F=\frac{{\sum }_{k=1}^K{w}_k{\widehat{\beta }}_{\mathit{XY}}^{\left(k\right)}}{{\sum }_{k=1}^K{w}_k}$.

While the $Q$ test tends to be conservative in small sample sizes, its power increases with increasing sample size and increasing degree of pleiotropy [72].

Yuan [86], working in the setting of two-sample MR with summary GWAS data, recognized that measurement error in outcome and exposure can give misleading results with the inferred causal arrow in the wrong direction. To work around this issue, they extended MR with a method that infers the causal direction between two traits. Specifically, Yuan [86] adapt Steiger’s Z test for a difference in correlations [87] to assess which of the two traits in an analysis has the stronger correlation with the SNP instrument. That with the stronger correlation is treated as the exposure. Yuan [86] applied their test in a study of DNA methylation and gene expression, where either direction of causality is plausible, and found that many methylation traits cause changes in gene expression.

Steiger [88] developed a weighted mode-based MR causal effect estimation method for two-sample MR analysis with GWAS summary data. They first calculate Wald ratio estimates for every instrumental SNP. They then apply smoothing to the empirical distribution of ratio estimates. The mode of this smoothed distribution is the simple mode-based estimate of the causal effect [88]. The inverse variance-weighted mode-based estimate is obtained by weighting the empirical distribution of ratio estimates by the inverse variance of each estimate. Steiger [88] compared their weighted and unweighted mode-based estimators with weighted and unweighted median-based estimators, MR Egger regression, and IVW. They found that their mode-based estimators demonstrated less bias and lower type I error rates than other estimators in some simulation settings. The mode-based estimators possessed lower statistical power to detect a causal effect compared to the IVW and weighted median-based methods, but their power exceeded that of MR Egger regression [88]. The mode-based estimators consistently estimated the causal effect when the mode across SNP instruments of the horizontal pleiotropy effects was zero [88]. In this manner, the mode-based estimators demonstrated a greater robustness to horizontal pleiotropy than did the other estimators.

Hartwig [89] approached the challenge of horizontal pleiotropy by developing three new methods for two-sample MR analysis with GWAS summary data: robust regression, penalized weights, and LASSO penalization. The first two can be viewed as modifications of MR-Egger and IVW methods. Together, they offer three strategies for downweighting or excluding variants with heterogeneous causal estimates. Recall that MR-Egger offers consistent causal effect estimates when there is no horizontal pleiotropy or when the horizontal pleiotropy effects adhere to the “Instrument Strength Independent of Direct Effect” (InSIDE) assumption [43]. The InSIDE assumption is satisfied when there is no correlation between the pleiotropic SNP instrument-outcome effects and the SNP instrument-exposure effects. Hartwig [89] uses MM estimation, which is one technique for robust linear regression [90], to formulate an estimator with high breakdown point and high efficiency. The second estimation method, with penalized weights, is much like the penalized median estimator, from above, except that the second argument in the minimum function is, instead of the above. Finally the LASSO-based method fashions an estimator by applying a penalty to the objective function from MR-Egger to get Eq. (15) as the objective function.

$${\sum }_{j}Var{\left({\hat{\beta }}_j\right)}^{-1}{\left({\hat{\beta }}_{\mathit{Yj}}-{\theta }_{0j}-{\theta }_1{\hat{\beta }}_{1j}\right)}^2+\lambda {\sum }_j\left|{\theta }_{0j}\right|$$

Hartwig [89] studied two procedures for choosing $\lambda$: a heterogeneity stopping rule and a cross-validation rule. Taken together, these three methods offer additional contributions to a suite of sensitivity analysis tools that practitioners should consider.

Koller [91] introduced the contamination mixture method for robust and efficient MR analysis with hundreds of SNPs, some of which may be invalid instruments by violating one or more of the three core MR assumptions. Working in the setting of two-sample MR with GWAS data, they begin by considering a collection of candidate SNP instruments, which may contain some invalid SNP instruments. For each candidate SNP instrument, they calculate the Wald ratio estimate of the causal effect. With the collection of Wald ratio estimates, Koller [91] reason that the set of valid SNP instruments have Wald ratio estimates that arise from a normal distribution centered on the true causal parameter with variance equal to that of the Wald ratio estimator. The invalid instruments, however, are assumed to follow a normal distribution centered at zero with a variance greater than that of the Wald ratio estimator. They then work with profile log likelihood over a grid of causal parameter values to make inferences.

Zhao [62] presented MR-RAPS, a method that leverages a robust adjusted profile score to accomplish statistical inference in two-sample MR analyses with GWAS summary data. Dividing pleiotropic effects into systematic and idiosyncratic, they model the systematic pleiotropy with random effects. In so doing, no SNP satisfies the exclusion restriction assumption. Adjusting their profile likelihood estimator from the setting without pleiotropy, [62] obtain an estimator with consistency and asymptotic normality [92]. Idiosyncratic pleiotropy is addressed through robustification of the adjusted profile score [93]. They then demonstrate the properties of their estimator by analyzing simulated and real data [62].

Huber [94], working with a collection of SNP instruments, reasoned that if all three MR assumptions are satisfied, then the collection of Wald ratio estimates should be homogeneous; thus, any departures from homogeneity may signal a violation of one or more assumptions. They reported modified weights, in addition to studying weights derived from first order and second order approximations to the variance. Their modified weights lead to an estimator that is useful for quantifying heterogeneity and detecting outliers.

Bowden [95] developed the MR-TRYX framework for exploiting horizontal pleiotropy to identify alternative causal pathways. They did this by positing that, for a collection of putative SNP instruments, any heterogeneity in the Wald ratio estimates may be due to horizontal pleiotropy. Once they identify a SNP with outlying ratio estimates, they search GWAS results by querying the MR-Base database to identify complex traits (in other studies) that associate with the outlying SNP [96]. They follow up promising trait associations to account for their observations with multiple causal pathways.

Hemani [97] recognized that in some MR studies, the Wald ratio estimates for different SNP instruments may form clusters, and these clusters may represent distinct causal mechanisms and may identify the SNPs that are involved in them. They devised a method to detect these clusters in the collection of Wald ratio estimates and found SNP instruments that point to distinct causal pathways of biological importance [97].

Fang [98] sought a probabilistic model that accounts for both linkage disequilibrium among SNP instruments and horizontal pleiotropy. They termed their method MR-LDP. Using an approach from [99], [98] derived an approximate likelihood for their regression models of the exposure and outcome on the SNP instruments. Incorporation of a random effect into their models accounted for the variance in causal effect estimates due to horizontal pleiotropy. They situate inference within an empirical Bayesian framework and present a parameter-expanded variational Bayes expectation–maximization algorithm for estimation [100]. By jointly modeling the distribution of GWAS summary statistics and causal effects, [98] efficiently accommodates multiple SNP instruments in linkage disequilibrium. One limitation of MR-LDP is its reliance on the InSIDE assumption and resulting inability to accommodate correlated horizontal pleiotropy.

Liu [101] present IMRP, a method for causal effect estimation and horizontal pleiotropy detection. They describe a test to distinguish vertical pleiotropy from horizontal pleiotropy. By combining this test with two-sample MR analysis of GWAS summary statistics, they develop an iterative procedure for estimating the causal effect of exposure on outcome and test for presence of horizontal pleiotropy in the SNP instruments. The iterative procedure alternates between 1) updating the estimate of the causal effect and 2) testing for horizontal pleiotropy with the included SNP instruments. At each test for horizontal pleiotropy, some SNP instruments may be discarded if they demonstrate evidence of horizontal pleiotropic effects. The procedure ends when there remain only SNP instruments that don’t exhibit horizontal pleiotropy. In the authors’ simulations and data analysis sections, their new method performs about as well as GSMR, IVW, and MR-PRESSO in the settings with and without balanced pleiotropy and with and without satisfaction of the InSIDE assumption [101]. Finally, the authors note that IMRP is three orders of magnitude faster than simulations-based MR-PRESSO.

Zhu [102] build on research from Grant [103] to present a method that applies a ${\mathcal{l}}_1$ penalty to coefficients of covariates in two-sample MR with GWAS summary statistics. Importantly, their method doesn’t penalize the SNP-exposure association. Instead, it shrinks towards zero those coefficients for covariates that demonstrate little pleiotropy. In so doing, they extend work from [104], [105] to get a causal effect estimator that needs no valid SNP instruments and is robust to measured vertical pleiotropy and more statistically efficient than previous MR methods.

Burgess [106] consider two classes of horizontal pleiotropy with their method, MRCIP. They partition horizontal pleiotropic effects into correlated or idiosyncratic horizontal pleiotropy. Idiosyncratic horizontal pleiotropy is that with a large effect size, while correlated horizontal pleiotropy, like its definition elsewhere in our manuscript, refers to correlation between the effects of the SNP instruments on the exposure and the effects of the SNP instruments on the outcome. MRCIP relaxes both the exclusion restriction assumption and the InSIDE assumption by directly modeling the correlated horizontal pleiotropy with random effects. Furthermore, to accommodate the idiosyncratic pleiotropy, the authors downweight SNP instruments that demonstrate strong direct effects on the outcome. They find that their MRCIP provides valid causal inference even when there are no valid SNP instruments (i.e., when all SNP instruments are invalid) and when the InSIDE assumption is violated [106]. Their PRW-EM algorithm adds a reweighting step to the traditional expectation maximization algorithm to estimate the causal effect parameter in MR analysis [107]. Finally, they compare MRCIP to other MR methods with both simulated and real data sets [106], like the developers of MR-RAPS, assume that the horizontal pleiotropy is balanced, i.e., that the mean horizontal pleiotropic effect is zero. One direction for future study is to augment MRCIP to permit unbalanced horizontal pleiotropy.

Dempster [108] build on other research using mixture models in the two-sample MR setting with GWAS summary statistics. Like MR-Clust, MR-PATH, as the method from [108] is called, works with the Wald ratio estimates from multiple SNP instruments. Coining the term “mechanistic heterogeneity” to refer to the distribution of Wald ratio estimates due to SNP involvement in distinct causal pathways, [108] specify a $J$-component normal mixture model. They use an expectation maximization algorithm to fit the model parameters (the component weights and the parameters for each of the $J$ normal distributions) and suggest a Bayesian information criterion-based approach to choosing $J$ [109].

Schwarz [110] propose causal effect test statistics that are robust under weak instrument asymptotics [111]. Specifically, they extend three econometric methods to two-sample MR with GWAS summary statistics [112], [113], [114] and study the theoretical properties and the performance in applications. Schwarz [110] extend their methods to demonstrate conditions under which their estimators are equivalent to those in works from [62], [55], and [94].

Moreira [115] developed BayesMR, a Bayesian framework for two-sample MR with individual-level data and discuss an approximation for use with GWAS summary statistics. Unlike many MR methods, BayesMR both aims to control for horizontal pleiotropy and to quantitatively assess the possibility of reverse causation, where the putative exposure is actually caused by the putative outcome. For independent SNP instruments, Moreira [115] permit each SNP instrument to have both a direct effect on the exposure and a horizontally pleiotropic direct effect on the outcome. Instrument effects and horizontally pleiotropic effects are assumed independent. Note that this is the Bayesian analog of the InSIDE assumption. After specifying the model, they present a nested sampling scheme [116], [117], [118] that simultaneously computes the model evidence for both causal directions (i.e., exposure causes outcome and outcome causes exposure) and acquires samples from the posterior distribution for Bayesian statistical inferences.

Handley [119] present BMRE, a Bayesian implementation of MR Egger. They apply weakly informative priors to the horizontal pleiotropy effect estimator in efforts to increase statistical power to detect a nonzero slope, i.e., the coefficient of the SNP instrument. They develop their method for two-sample MR with individual-level data. Simulations demonstrate that BMRE outperforms the MR Egger method while maintaining type I error rates in the examined scenarios. The authors emphasize a potential role for BMRE in MR sensitivity analysis.

Schmidt [120] found that multivariable MR, where multiple exposures jointly cause an outcome, consistently estimates the effect of the exposures on the outcome. They examined multivariable MR with both individual-level data and GWAS summary statistics. Schmidt [120] also develop a generalized version of Cochran’s Q test for quantifying SNP instrument strength and validity. However, this test requires knowledge of the covariances between the effects of the SNP instruments on the exposures. While these covariances could be estimated from individual-level data, such data are often unavailable in the GWAS setting. Importantly, the authors note that the estimands for multivariable MR and MR differ; multivariable MR estimates the direct causal effects of each exposure on the outcome, while MR estimates the total causal effect of an exposure on the outcome.

MR-link, reported by Sanderson [121], aims to account for unobserved pleiotropy and linkage disequilibrium by using individual-level data on the outcome variable and summary statistics for the exposure. MR-link uses a three-step procedure to estimate causal effects.

• Use GCTA-COJO to obtain SNP instruments [122].

• Prune all SNPs in linkage disequilibrium with the SNP instruments to obtain a set of “tag” SNPs with correlations less than 0.95.

• Solve for the causal effect estimate with ridge regression of the outcome on the matrix resulting from concatenation of the SNP instrument genotypes matrix and the tag SNPs genotypes matrix.

Note that in step 3, ridge regression is preferred to ordinary least squares due to the limited statistical power of ordinary least squares in this setting. Presumably, this is due to collinearity in the matrix of tag SNP genotypes.

4.5. Correlated horizontal pleiotropy

The second type of horizontal pleiotropy, from above, is sometimes called “correlated horizontal pleiotropy.” Correlated horizontal pleiotropy occurs when a SNP affects both the exposure and a variable that confounds the relationship between exposure and outcome (Fig. 3C). CAUSE and MRAID are two methods that aim to model correlated horizontal pleiotropy [64], [65]. Their approaches to modeling correlated horizontal pleiotropy differ in important ways that ultimately affect performance. CAUSE allows for a proportion of SNPs to exhibit correlated pleiotropy, which [64] models as an effect on a shared, unobserved factor. The remaining SNPs are independent of this unobserved factor. Every SNP can have a nonzero pleiotropic effect on the outcome, and these pleiotropic effects are uncorrelated with the variant effects on the exposure. The model, then, is written as a mixture of biavariate normal distributions, and inference proceeds by borrowing ideas on adaptive shrinkage from [123]. Finally, [64] compares two models to determine whether the GWAS summary statistics are consistent with a causal effect of the exposure on the outcome. Specifically, they estimate the difference in the expected log pointwise posterior density for the model with causal effect fixed at zero and the model that permits a nonzero causal effect [124].

Morrison [65] found that MRMix is not robust to misspecification of SNP effect sizes and often is biased. CAUSE, they found, yields overly conservative p-values [65]. These observations motivated [65] to develop a new method, MRAID. MRAID accommodates both individual-level data and GWAS summary statistics [65]. We focus on the approach that uses GWAS summary statistics. Two equations are central to MRAID modeling (Eqs. (16) and (17)).

$$\widehat{{\beta }_X}={\mathrm{\Sigma }}_1\beta +e_x$$

$$\widehat{{\beta }_Y}=\alpha {\mathrm{\Sigma }}_2\beta +{\mathrm{\Sigma }}_2{\eta }_0+{\mathrm{\Sigma }}_2{\eta }_1+e_y$$

The estimated marginal effects for the $p$ SNP instruments on the exposure are denoted by ${\widehat{\beta }}_X$, while ${\widehat{\beta }}_Y$ represents the estimated effects of the same SNPs on the outcome. The $p$ by $p$ SNP instrument correlation matrices for the exposure and outcome are written as ${\mathrm{\Sigma }}_1$ and ${\mathrm{\Sigma }}_2$, respectively. ${\mathrm{\Sigma }}_1$ and ${\mathrm{\Sigma }}_2$ can be estimated with 1000 Genomes Project data, for example, by choosing a subset of 1000 Genomes Project subjects that have similar ancestry [125]. The $p$-vector error terms, $e_x$ and $e_y$, follow multivariate normal distributions with mean zero and variances ${\mathrm{\Sigma }}_1\frac{{\sigma }_X^2}{n_1-1}$ and ${\mathrm{\Sigma }}_2\frac{{\sigma }_Y^2}{n_2-1}$, respectively. Morrison [65] then constructs a Gibbs sampler to make likelihood-based inferences [126]. To facilitate computations, the investigators make several assumptions about the collection of SNPs:

• Relatively small proportion of SNPs have nonzero effects on the exposure

• A relatively small proportion of SNPs demonstrate horizontal pleiotropy.

• The chosen instrumental SNPs are more likely to display horizontal pleiotropy than are non-instrumental SNPs.

• Those SNPs that display horizontal pleiotropy are more likely to demonstrate uncorrelated horizontal pleiotropy than correlated horizontal pleiotropy.

By encoding these assumptions in prior distributions, Morrison [65] enables the inferential procedures to accommodate the observed data in the context of the assumptions on SNPs.

4.6. Binary, count, and time-to-event outcomes and exposures

While we’ve focused above on continuous outcomes and continuous exposures, some data are more naturally treated as binary, count, or time-to-event variables. MR methods for non-continuous outcomes and exposures is an active area of research. Kleibergen [31] and Geman [127] developed MR strategies for binary exposures and binary outcomes. Kleibergen [31] extended methods from Mendel [24] by fitting two logistic regressions, one for the outcome and one for the exposure. They then calculated the causal effect estimator as the ratio of the two logistic regression coefficient estimators. Geman [127] devised a new MR method for binary outcome and binary exposure by drawing on [128] and treating the exposure and outcome as correlated binary random variables. They implemented an iterative optimization algorithm to simultaneously infer the causal effect parameter and other parameters.

Researchers have also leveraged other generalized linear models for analysis in MR studies [129]. However, this area is relatively unexplored. Nelder et al. [130] treated hospitalizations as a count variable and modeled it with quasi-Poisson methods. Hazewinkel et al. [131] characterized statistical properties, including bias and power, with simulations of count random variables and binary random variables. With growing interest in modeling counts in biomedical data, where molecular phenotyping technologies now acquire RNA molecule counts and protein abundances, there may be opportunities for methods innovations in a generalized linear models framework for MR studies [132], [133], [134], [135].

Recently, multiple teams of investigators have analyzed time-to-event traits in MR studies [136], [137], [138], [139], [140]. He et al. [140], for example, studied post-diagnosis survival time in women with breast cancer. They treated survival as a time-to-event outcome, which enabled them to model it with a proportional hazards model [141] in two-stage MR with individual-level data. Similarly, Tikkanen [139], in a study of cardiovascular disease, applied proportional hazards regression when examining time to stroke as an outcome variable. In very recent work, Bowden [79] reported methods, MR GENIUS, that are robust to violations of the exclusion restriction assumption (under many assumed MR data generating processes). They considered binary, continuous, and time-to-event outcomes within their framework. We are unaware of MR studies that treat the exposure variable as a time-to-event, but it’s conceivable that future research will consider time-to-event traits as exposures in MR analyses.

5. Recent findings

5.1. Omnigenic MR

Recent research on the omnigenic hypothesis, which posits that every SNP’s effect on a trait is nonzero, has informed MR methods development [142]. Boyle [143] recognized the limitations of previous MR methods in the context of the omnigenic hypothesis. In response, Boyle [143] developed a MR method that uses all genome-wide SNPs as instruments. Using GWAS summary statistics as inputs, their method relies on a composite likelihood framework for scalable computation and allows for horizontal pleiotropy. Boyle [143] used extensive simulations, including those with model misspecifications, to characterize their method’s statistical power and robustness. Finally, they applied the new method to identify multiple complex traits that affect coronary artery disease and asthma. These causal relationships highlight the important roles of plasma lipids, blood pressure, and the immune system in CAD susceptibility and those of obesity and the immune system in asthma development.

5.2. Sample overlap in biobanks

The issue of overlapping samples in the two-sample MR with GWAS summary data has recently received attention in the published literature. Hemani [97], working with data from the UK Biobank, found that SNP instruments derived from overlapping samples explained a higher proportion of the variance compared to those derived from non-overlapping samples. They argue that block jackknife resampling MR enables causal inference while avoiding bias due to overlapping samples. Wang [144] analyzed 2514 traits from the UK Biobank and evaluated the impact of winner’s curse on MR analysis. Winner’s curse, they found, amplifies weak instrument bias without inflating the false discovery rate. This finding led the authors to design a pseudoreplication process that reduces bias in MR studies. Sadreev [145] proposed a Bayesian approach for one-sample MR analysis where SNP instruments are permitted to exhibit pleiotropic effects on the outcome. Working in the setting of one-sample MR with individual-level data, they construct their model with a shrinkage prior, so that many SNP instruments have no horizontal pleiotropic effects. Their method relaxes the exclusion restriction assumption to permit horizontal pleiotropy (for some SNP instruments) and permits correlated SNP instruments, unlike many frequentist methods. Posterior inference proceeds by Markov chain Monte Carlo sampling. They also elaborate their model for a univariate exposure into that for a bivariate exposure to analyze the causal effects of body mass index and serum phenylalanine levels on blood pressure.

5.3. Bi-directional causal inference with MR to account for reverse causation

Reverse causation occurs when the outcome at an early time point has a causal effect on the exposure variable. While reverse causation is often assumed to not occur in MR study designs, [146] points out several scenarios where this assumption may not hold [147]. In recognition of this observation, [148] developed a framework, GRAPPLE, for performing two-sample MR with weak and strong instruments. Using GWAS summary statistics as inputs, GRAPPLE extends MR-RAPS and can detect presence of horizontally pleiotropic pathways, infer the causal direction, and perform multivariable MR. Central to the GRAPPLE framework is the observation that a horizontally pleiotropic pathway often gives rise to an additional mode in the profile likelihood. GRAPPLE uses the presence of multiple profile likelihood modes to diagnose horizontal pleiotropy with effects that are grouped by pathway. GRAPPLE facilitates identification of SNP instruments that contribute to the additional profile likelihood modes. A researcher using GRAPPLE may then recognize a confounding factor for each mode. With additional GWAS summary data with traits that reflect the confounding factors, GRAPPLE can fit multivariable MR models when the InSIDE assumption holds for the remaining horizontally pleiotropic effects [148].

5.4. Practice recommendations

We now turn attention to the question of how to choose among the MR methods for a given analysis. We focus on the two-sample setting where only GWAS summary statistics are available. The large number of two-sample MR methods with summary statistics may challenge a practitioner seeking to develop an analysis plan. Early considerations include:

• assessing the plausibility of the MR assumptions

• determining which questions to address with sensitivity analysis

• assessing causal directionality between exposure and outcome variables

Detailed examples may be found in [149], [150], and [151]. In some settings, a practitioner may address these questions by a careful study of the relevant scientific literature. For example, there may be experimental studies that suggest a causal direction for the relationship between exposure and outcome. If both causal directions are plausible, then a bidirectional MR analysis may be needed. If the bidirectional MR analysis (and supporting scientific evidence) is consistent with a single causal direction, then a practitioner may proceed with unidirectional MR methods. Given the pervasive nature of horizontal pleiotropy and its potential impact on MR, we recommend using one or more MR methods explicitly model horizontal pleiotropy. Recent methods, such as CAUSE and MRAID, go a step further by modeling correlated horizontal pleiotropy [64], [65].

Other MR methods can be used in sensitivity analysis to assess robustness of findings to possible violations of MR assumptions. Methods like MR-clust have the potential to reveal additional relationships among genes that share a biological pathway [152]. The STROBE-MR statement has additional practice recommendations [153].

6. Summary and outlook

Open research questions remain in the MR field. We have highlighted above three recent findings: omnigenic MR, methods for sample overlap in biobanks, and methods for bidirectional causal inference. While we discussed initial findings in these three areas, many opportunities for methods enhancements remain. For example, as biobank sizes grow in number of subjects and number of measured traits, there is increasing demand for MR methods that scale efficiently with large sample sizes. Development of methods for two-sample MR with overlapping samples opens opportunities to study rich biobank data, and we anticipate that this question - how to accommodate overlapping samples – will continue to be an active area of research.

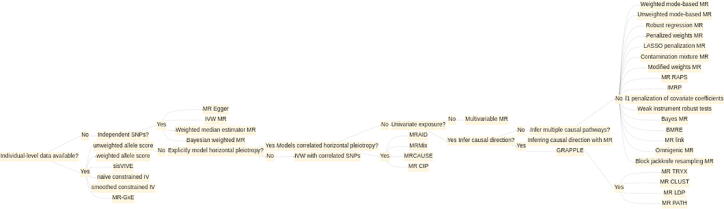
In summary, we have presented a comprehensive review on 47 methods for MR analysis in GWAS (Fig. 4). The overall trend of the methodology development for MR analysis is in the direction of increasingly sophisticated modeling of horizontal pleiotropy including both independent and correlated horizontal pleiotropy while attempting to maintain scalability and computational efficiency in the presence of multiple correlated SNPs. We hope our detailed review would benefit both methodology developers and applied analysts to further advance the development of MR methods and aid in their applications towards large, biobank-scale datasets, thus offering the possibility of discovering even more causal relationships among complex traits [154].

Fig. 4.

Decision tree diagram for choosing among multiple-SNP MR methods.

CRediT authorship contribution statement

Frederick J. Boehm: Conceptualization, Investigation, Writing – original draft, Writing – review & editing, Visualization. Xiang Zhou: Conceptualization, Investigation, Writing – original draft, Writing – review & editing, Visualization, Supervision, Project administration.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.