Abstract
Cerebral small vessel disease (SVD) is considered a disconnection syndrome, which can be quantified using structural brain network analysis obtained from diffusion MRI. Network analysis is a demanding analysis approach and the added benefit over simpler diffusion MRI analysis is largely unexplored in SVD. In this pre-registered study, we assessed the clinical and technical validity of network analysis in two non-overlapping samples of SVD patients from the RUN DMC study (n = 52 for exploration and longitudinal analysis and n = 105 for validation). We compared two connectome pipelines utilizing single-shell or multi-shell diffusion MRI, while also systematically comparing different node and edge definitions. For clinical validation, we assessed the added benefit of network analysis in explaining processing speed and in detecting short-term disease progression. For technical validation, we determined test-retest repeatability.
Our findings in clinical validation show that structural brain networks provide only a small added benefit over simpler global white matter diffusion metrics and do not capture short-term disease progression. Test-retest reliability was excellent for most brain networks. Our findings question the added value of brain network analysis in clinical applications in SVD and highlight the utility of simpler diffusion MRI based markers.
Keywords: Cerebral small vessel disease, connectome, diffusion MRI, network analysis, quantitative MRI marker
Introduction
Cerebral small vessel disease (SVD) is a leading cause of vascular cognitive impairment and loss of independence in the elderly. Sporadic SVD, related to increased age and arterial hypertension, is particularly common with a prevalence up to 50% in individuals over the age of 70.1,2 While neuroimaging features currently used in clinical routine are typically based on visible lesions – such as white matter hyperintensities, lacunes, and microbleeds 3 – there is a move towards quantitative markers for measuring disease burden and progression. Measures based on diffusion MRI, such as diffusion tensor imaging, have shown high potential as quantitative markers. They allow detecting subtle white matter changes, are strongly associated with clinical deficits and provide excellent reliability.4,5
Diffusion MRI analysis approaches differ substantially in their complexity, both in terms of data acquisition and subsequent processing. 6 Because SVD is considered a disconnection syndrome, 7 brain networks based on tractography and graph theoretical analysis of network structure are regarded as a compelling approach for quantifying clinically relevant brain network alterations in SVD. These structural brain networks are based on fiber tractography and pre-defined regions-of-interest, i.e. the nodes, which are connected via white matter tracts, i.e. the edges. The corresponding network architecture is quantified with graph-informed measures, such as global efficiency, 8 which has proven to be the most sensitive graph measure to capture brain alterations in SVD. 9 Several studies suggest a high potential of structural network analysis for characterizing SVD burden, for exploring the underpinnings of symptoms or for predicting the disease course.10–12
There are, however, several critical knowledge gaps that are considered major roadblocks for further application in research and clinical routine. Network analysis is a highly demanding diffusion MRI analysis approach, and the added benefit over simpler diffusion MRI analysis has so far not been systematically assessed. Also, connectome pipelines depend on arbitrary choices, especially in terms of tractography algorithm and the definition of nodes and edges. Of particular interest are more elaborate tractography algorithms, which better model the complex fiber architecture of the brain, but typically rely on a more demanding data acquisition, such as multi-shell diffusion imaging and high-angular resolution. 13 These different choices have so far not been systematically compared in SVD. Previous studies suggest that most graph metrics capturing structural network architecture show good to excellent test-retest reliability in healthy young volunteers. 14 Importantly, the reliability of the network analysis approach in SVD is largely unknown, but is a crucial factor for clinical application.
The goal of this pre-registered study was a systematic clinical and technical validation of structural brain network analysis in SVD. We applied two different connectome pipelines, utilizing single-shell or multi-shell diffusion MRI data, while also systematically comparing different node and edge definitions. For exploration and independent validation, we used two non-overlapping patient samples with state-of-the-art diffusion MRI from the RUN DMC study.1,15
For clinical validation, we assessed the added benefit of structural brain network analysis in explaining processing speed deficits, the main cognitive deficit in SVD, and in detecting disease progression over time. Our pre-specified hypotheses were that i) compared with simpler global white matter diffusion metrics, brain network analysis better explains processing speed deficits and better captures disease progression over time, and ii) a more elaborate connectome pipeline using multi-shell data and constrained-spherical deconvolution-based tractography outperforms a simpler deterministic connectome pipeline using single-shell data. For technical validation, we assessed test-retest repeatability in a high-frequency serial imaging longitudinal dataset.
Material and methods
Our study design, analysis plan, and hypotheses were pre-registered and are available at https://aspredicted.org/382ha.pdf.
Participants
We included data from SVD patients participating in the RUN DMC study. 15 For exploration, we used data from the RUN DMC – InTENse sub-study (Radboud University Nijmegen Diffusion tensor and Magnetic resonance imaging Cohort – Investigating The origin and EvolutioN of cerebral small vessel disease). 1 In this sub-study, 54 patients from the main study were invited to a baseline MRI assessment, used for the cross-sectional analysis, and a total of 9 monthly follow-up MRI scans, used for the longitudinal analysis. For the cross-sectional exploratory analysis, two patients were excluded because of confounding neuropsychological test results, 5 which resulted in a final sample of 52 sporadic SVD patients.
For independent validation of the cross-sectional results, we used a non-overlapping sample from the 3rd follow-up visit of the RUN DMC main study (n = 183). Some patients had to be excluded due to missing DWI data (n = 2), non-SVD infarcts (n = 6), MRI protocol violation (n = 1), missing neuropsychological data (n = 16), or insufficient image quality (n = 5). To ensure that results were not driven by outlier observations, we excluded five patients with Trail Making Test (TMT) compound scores qualifying as outlier according to the interquartile range criterion (i.e., scores outside the range defined by the cut-points of the first and third quartile plus 1.5 times the interquartile range above and below). Since the InTENse sub-study deliberately included a subset of patients with higher lesion load, we restricted the main study sample to SVD patients above 70 years of age to keep disease severity roughly similar across both samples (Table 1). This resulted in a final sample of 105 SVD patients for validation.
Table 1.
Sample characteristics.
| RUN DMC – InTENse sub-study n = 52 | RUN DMC main study n = 105 | p-value | |
|---|---|---|---|
| Demographic characteristics | |||
| Age [years], median (IQR) | 68.50 (8.25) | 77.15 (8.19) | <0.0001 |
| Female, n (%) | 18 (35) | 48 (46) | 0.2484 |
| Vascular risk factors, n (%) | |||
| Hypertension | 43 (83) | 75 (72)a | 0.2102 |
| Hypercholesterolemia | 25 (50) | 62 (60)a | 0.3318 |
| Diabetes | 6 (12) | 16 (15)a | 0.6843 |
| Current or past smoking | 37 (71) | 72 (69) | 0.8835 |
| Clinical scores, median (IQR) | |||
| Processing speed z-score | −0.15 (1.16) | −0.18 (1.55) | 0.6265 |
| Barthel scale score | 100 (5) | 100 (5)a | 0.8930 |
| SVD imaging markers, median (IQR) | |||
| WMH volumeb [%] | 0.35 (0.59) | 0.31 (0.74) | 0.7984 |
| Lacune count | 0 (0) | 0 (1) | 0.3648 |
| Microbleed count | 0 (1) | 0 (1) | 0.8816 |
| Brain volumeb [%] | 77.73 (5.35) | 72.51 (4.79) | <0.0001 |
IQR= interquartile range; WMH = white matter hyperintensity.
aBased on n = 104 due to missing data for one patient.
bNormalized by intracranial volume.
For the longitudinal analysis, we split the sample from the RUN DMC – InTENse sub-study into an exploration (n = 27) and validation group (n = 26) while accounting for a similar number of visits and disease severity (i.e. WMH volume) across groups. A few visits had to be excluded from the longitudinal analysis due to insufficient data quality, of which some only became apparent during tractography (n = 7). Only patients with at least 3 MRI visits were included for the longitudinal analysis, rendering the sample size to 25 patients for exploration and 26 patients for validation with a median of 9 (range 3–10) MRIs per participant.
Study protocols were in accordance with the declaration of Helsinki and approved by the medical research ethics committee (CMO Arnhem-Nijmegen). Written informed consent was obtained from all participants prior to the start of the study.
Neuropsychological testing
Neuropsychological testing was performed following identical protocols in both samples. We pre-specified to focus on the core deficit in SVD, i.e. processing speed, which was assessed by the time to complete Trail Making Test matrix A and B. We derived age- and education-corrected z-scores for matrix A and B separately as based on healthy subjects4,5,16 and next calculated the average to derive an established compound score. Patients were further characterized with respect to vascular risk factors (arterial hypertension, hypercholesterolemia, diabetes, smoking status) and activities of daily living (Barthel scale score).
MRI acquisition and conventional SVD imaging markers
MRI scans were performed on a single 3 Tesla scanner (Magnetom Prisma with 32-channel head coil; Siemens Healthineers, Erlangen, Germany). Imaging protocols in both studies were largely similar and included 3D T1-weighted, 3D fluid-attenuated inversion recovery (3D-FLAIR), and 3D gradient echo (T2*-weighted) sequences. The diffusion MRI protocol was identical in both samples and comprised a multi-band echo planar imaging multi-shell diffusion-weighted imaging sequence (repetition time 3220 ms, echo time 74 ms, diffusion-encoding directions 30 × b = 1000 s/mm2 and 60 × b = 3000 s/mm2, 10 × b = 0 images, multi-band factor 3). One b = 0 image with inverted phase-encoding direction was acquired for correction of susceptibility-induced distortions during preprocessing. A complete description of all sequence parameters can be found in Table e1.
Conventional SVD imaging markers (white matter hyperintensity [WMH] volume, lacune count, microbleed count, brain volume) were quantified according to the STRIVE consensus criteria. 3 All volumes were normalized to the intracranial volume. Details on the calculation of conventional SVD imaging markers have been described previously. 17
Diffusion MRI preprocessing
Preprocessing steps included visual quality control, Marchenko-Pastur principal component analysis-based denoising, Gibbs artefact removal, and correction for susceptibility-induced distortions, eddy current-induced distortions, as well as head motion. This was done using tools from MRtrix3 (www.mrtrix.org/, version 3.0.0, dwidenoise,18–21 mrdegibbs21,22) and the Functional Magnetic Resonance Imaging of the Brain (FMRIB) Software Library (FSL; version 5.0.10 (RUN DMC – InTENse), version 6.0.1 (RUN DMC main), topup23,24 eddy 25 ).
Skeleton-based, global white matter diffusion markers
To assess the added benefit of structural brain network analysis, we included measures of global white matter integrity as reference, that were based on diffusion tensor imaging (DTI) and diffusion kurtosis imaging (DKI) metrics. DTI metrics were calculated using ‘dtifit’ in FSL (using only b = 0 and b = 1000 s/mm2 images) and DKI metrics using the Diffusional Kurtosis Estimator (www.nitrc.org/projects/dke). 26
For DTI, we included the most commonly used diffusion metrics fractional anisotropy and mean diffusivity. 27 For DKI, we included mean kurtosis and radial kurtosis as reference metrics, since these showed the highest association with processing speed in a previous study. 5
Global white matter measures of these metrics were derived as average over a skeleton of the major white matter tracts, as implemented in the tract-based spatial statistics (TBSS) pipeline in FSL. 27 The TBSS-based registration to standard space and projections onto the white matter skeleton was estimated from fractional anisotropy images and then applied to all other diffusion metrics. Prior to averaging, we applied a custom mask to remove all areas from the skeleton that are typically susceptible to cerebrospinal fluid partial volume effects in SVD patients. 4 The resulting global white matter diffusion metrics will be referred to as ‘skeleton-based’ diffusion markers.
Overview of the structural brain network analysis
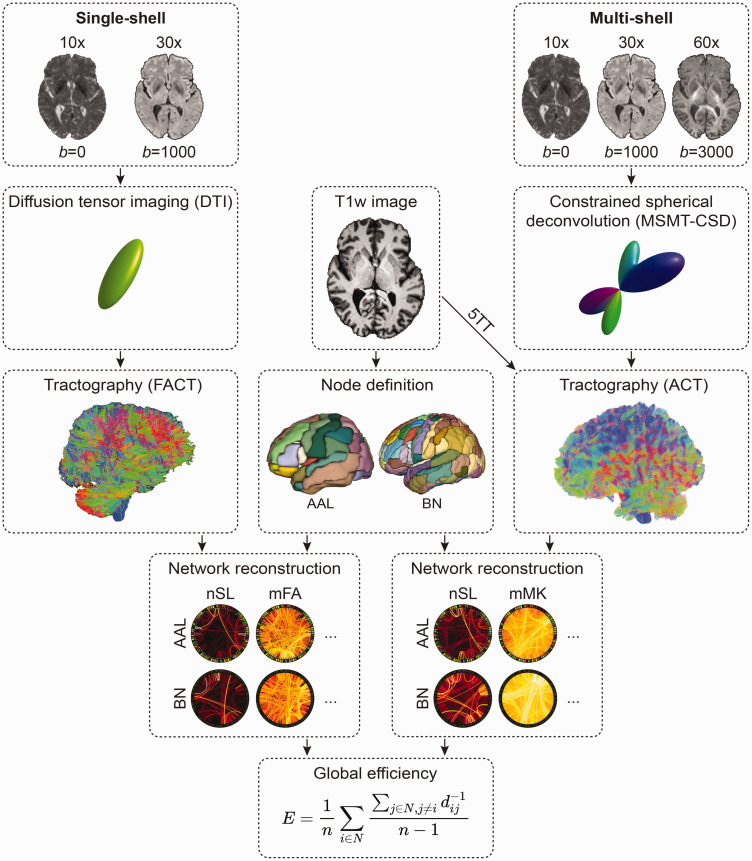
We applied two brain network pipelines (described in detail in the following sections), using either single-shell or multi-shell data as starting point. The key difference between these two brain network pipelines was the tractography approach. In the single-shell pipeline (Figure 1, left), streamlines were tracked by following the main direction of the diffusion tensor per voxel. The multi-shell data (Figure 1, right) enabled a more advanced tractography approach based on constrained-spherical deconvolution (CSD), which reconstructs complex fiber orientation distributions of multiple fiber populations within a voxel. As such, CSD-based tractography allows to track crossing fibers, which occur in most white matter regions. 28 In addition to CSD, we improved the biological accuracy of the streamline reconstruction by introducing anatomical constraints (i.e. streamlines followed white matter fiber orientation distributions, were terminated when entering cortical grey matter and rejected when entering fluid-filled regions; for full algorithm details see original publication). 29
Figure 1.
Overview of the two connectome pipelines (single-shell left, multi-shell right). The single-shell pipeline relies on diffusion tensor imaging and tractography using the FACT algorithm. The multi-shell pipeline relies on MSMT-CSD and anatomically constrained tractography. For both pipelines, we applied the node definition according to the AAL or Brainnetome atlas. After network reconstruction, each structural brain network was summarized by the global efficiency metric (E). N is the set of all nodes in the network, and n is the number of nodes, whereas d(i,j) is the weighted distance between nodes i and j,(i,j ∈ N).
AAL: automated anatomical labelling; ACT: anatomically constrained tractography; BN: Brainnetome; DTI: diffusion tensor imaging; FACT: fiber assignment through continuous tracking; mFA: mean of fractional anisotropy of streamlines; mMK: mean of mean kurtosis of streamlines; MSMT-CSD: multi-shell multi-tissue constrained spherical deconvolution; nSL: number of streamlines; T1w: T1-weighted image; 5TT: five tissue-type image.
We then applied a brain parcellation to the reconstructed streamlines to form structural networks, which are defined by a set of nodes (i.e., brain regions) and edges connecting these nodes. Across both pipelines, we defined the nodes based on the AAL atlas (automated anatomical labelling, 90 ROIs in total, after excluding cerebellar regions) and the Brainnetome atlas with a higher number of smaller regions (246 ROIs in total). Several commonly used edge definitions were used to calculate edge weights (details are given below for each pipeline).
Finally, we derived the global efficiency as a well-established network marker of SVD burden from each structural network (Figure 1, center bottom). Efficiency between two regions is expressed as the inverse of the shortest path length between two regions, 8 where the length of each possible path is equal to the sum of the lengths of all edges in that path. Global efficiency of the network is then defined as the average efficiency across all node pairs. To assess whether some nodes within the global network disconnect faster than others over time, we also calculated local efficiency for each node of the structural network that showed the highest clinical and technical validity in the longitudinal dataset (i.e. highest effect sizes in regression analyses, highest added benefit in random forest regression and highest intraclass correlation coefficient [ICC]).
Single-shell pipeline
For single-shell networks, streamlines were reconstructed based on the diffusion tensor using the fiber assignment by continuous tracking (FACT) algorithm (‘dti_tracker’, Diffusion Toolkit, version 0.6.4.1). In short, the algorithm started at the center of all voxels with fractional anisotropy >0.2 and terminated if the streamlines left the brain mask, encountered voxels with fractional anisotropy <0.2 or when the turning angle exceeded 45°. Reconstructed streamlines were filtered and smoothed requiring a step length of 1 voxel (‘spline_filter’, Diffusion Toolkit). Two nodes were considered connected if the endpoints of the reconstructed streamlines lay within both nodes. Atlas parcellations were registered to diffusion space, applying a series of linear and non-linear registrations, leading from the MNI template space, through T1-weighted and FLAIR space, to the diffusion space. All registrations were estimated and concatenated with the Advanced Normalization Tools (ANTs). 30 For the longitudinal data, as previously described in detail, 31 baseline T1-weighted images were indirectly normalized into MNI space via an intermediate custom template, and follow-up scans were normalized by concatenating this normalization with the registration between baseline and follow-up T1-weighted images.
Five commonly used edge weights were applied in the single-shell pipeline: number of streamlines (nSL), number of streamlines weighted by the mean length (mLen), number of streamlines weighted by the inverse of the streamline length (invLen), 32 mean fractional anisotropy over all streamlines (mFA), number of streamlines weighted by the mean fractional anisotropy (wFA). Each edge was further normalized by the average volume of the connected nodes to correct for the different volumes of the nodes and for different brain sizes.
For each of the resulting 10 (2 node definitions × 5 edge definitions) weighted undirected networks, we calculated the global efficiency using the Brain Connectivity Toolbox. 8
Multi-shell pipeline
For the advanced multi-shell networks, streamlines were reconstructed using a multi-shell multi-tissue constrained spherical deconvolution tractography pipeline using tools from MRtrix3. 21 To limit false positives and improve biological accuracy, 25 tractography was anatomically-constrained to white matter by using a 5-tissue-type image generated from T1-weighted images. WMH masks were set as the fifth volume (i.e., pathological tissue) of the 5-tissue-type image to allow tracking within these regions, which are often is misclassified as grey matter, leading the tracking algorithm to terminate prematurely. Importantly, WMH segmentations were performed on each time point in the longitudinal dataset. The remaining steps were: response function estimation (‘dhollander’ algorithm), estimation of the fiber orientation distributions, 33 multi-tissue informed log-domain intensity normalization, modelling 10 million streamlines using anatomically constrained streamlines tractography, dynamic seeding and cropping at the GMWM-interface, as well as SIFT2 filtering of the streamlines. 34
Consistent with the single-shell pipeline, nodes were defined either according to the AAL atlas or Brainnetome atlas.
Seven different edges were applied in the multi-shell pipeline: number of streamlines (nSL), number of streamlines weighted by the length of each streamline (mLen), number of streamlines weighted by the inverse length of each streamline (invLen), 35 mean of the mean kurtosis of streamlines (mMK), number of streamlines weighted by the mean of the mean kurtosis (wMK), mean fractional anisotropy of streamlines (mFA), number of streamlines weighted by the mean fractional anistropy (wFA). While fractional anisotropy maps were calculated on single-shell diffusion data, edges based on fractional anisotropy were also included here to allow a more direct comparison of the two pipelines. Again, we calculated global efficiency for the 14 (2 node definitions x 7 edge definitions) networks.
Statistical analysis
All statistical analyses were performed in R (version 3.6.1). 36 The statistical
significance level was set at α < 0.05. Since we mainly focused on the effect sizes when interpreting the results, we did not correct for multiple comparisons.
To compare sample characteristics between RUN DMC – InTENse and RUN DMC main, we used chi-squared (χ2) tests (for categorical variables) and non-parametric Wilcoxon rank sum tests (for numeric variables), as appropriate.
Subsequent analyses were conducted completely independently for both samples. The processing speed compound scores were power-transformed using the Yeo-Johnson transformation to approximate a normal distribution. 37
Four main analyses were conducted to examine clinical and technical validation of structural brain network analysis in SVD.
First, we performed simple linear regression analyses between global efficiency of structural brain networks (independent variable) and processing speed performance (i.e., TMT compound score, dependent variable). We used the adjusted R2 to quantify and compare associations. Second, we assessed the added benefit for each marker on top of conventional SVD imaging markers (i.e., normalized WMH volume, lacune count, microbleeds and normalized brain volume). We used multivariable random forest regression with conditional inference trees (R package ‘party’, version 1.3.3) to overcome the problem of multicollinearity, which is a critical aspect since SVD imaging markers and diffusion markers are intercorrelated. We constructed one random forest regression model with conventional SVD imaging markers only (number of trees = 1501, mtry = 3), and additional models adding respectively one of the diffusion-based markers. Prediction accuracy was calculated for each random forest regression model as the root-mean-square error (RMSE) between observed and predicted values using leave-one-out cross-validation. The added benefit of each diffusion-based marker for prediction of processing speed was quantified by the difference of the RMSE between the model with and without that diffusion-based marker. 5 We repeated random forest regression for each model (with cross-validation) 100 times to determine a point estimate and 95% confidence interval for the RMSE.
Third, to assess the ability of structural brain networks to capture change over time, we calculated linear mixed effects models in the split exploration and validation longitudinal samples. Brain network and skeleton-based diffusion markers were first normalized individually for each patient to the baseline score and then centered and scaled (by subtracting the mean and dividing by the standard deviation). Time of MRI visits (relative to baseline visit) was modelled as fixed effect. To account for patient-specific variation, we included a random intercept for each patient in the model architecture, but models with random slopes per patient did not converge. The fixed effect reflects the mean change in the structural brain network over time, marginal R2 reflects the explained variance by the fixed effect. The following R packages were used for estimation of linear mixed models: ‘lme4' (version 1.1.21), 38 ‘lmerTest' (version 3.1.2), 39 ‘boot' (version 1.3.22), 40 ‘MuMIn’ (version 1.43.15). 41
For technical validation, we assessed the test-retest reliability of structural brain networks as our fourth analysis within the same exploration and validation sample used for the longitudinal analysis. Intraclass correlation coefficients (1,1) 42 were calculated with the R package ‘psych’ (version 1.9.12.31). 31
Deviations from the pre-registered analysis protocol
For parts of this investigation, we had to follow an unplanned path for valid reasons. First, for the independent validation sample of the cross-sectional analysis, we originally planned to randomly sample one hundred subjects from a subset of the UK Biobank with matching range of the WMH volume and age of the RUN DMC – InTENse subjects. However, when calculating the established TMT compound score, we noticed implausibly low z-scores in many UK Biobank subjects due to extremely low reaction times. This might have resulted from a key difference in task administration, since in the UK Biobank study the TMT was performed using a computer mouse, whereas the norm data was based on the paper-pencil version. 16 Since the TMT data was pre-specified as the clinical endpoint for the cross-sectional analyses, we did not want to deviate from this aspect, but instead chose a different validation sample.
Second, we pre-registered to normalize global efficiency values by the global efficiency of random networks using the Brain Connectivity Toolbox. However, after revisiting the literature, we noticed that in most brain network studies in SVD - if not all - global efficiency values were not normalized. This might result in important consequences of the interpretation of these global efficiency values per se (see discussion), however, to ensure comparability with previous studies, we chose to follow the established procedure for brain networks in SVD.
Third, we planned to compare a random forest regression model with skeleton-based DTI/DKI metrics only as a comparison model, but since we were interested in the added benefit of brain networks compared with skeleton-based diffusion markers – and not in the added benefit of brain networks on top of skeleton-based diffusion markers – we revised our random forest regression approach accordingly.
Data availability
Anonymized data will be made available upon request to the corresponding author.
Results
Sample characteristics are presented in Table 1. SVD patients of the RUN DMC – InTENse sub-study were younger and presented with higher brain volumes compared to patients from the RUN DMC main study (p < 0.0001).
Clinical validation: Associations with processing speed performance
Associations with processing speed performance as assessed by simple regression greatly varied depending on node, edge, and tractography pipeline (Figure 2(a); Table e2).
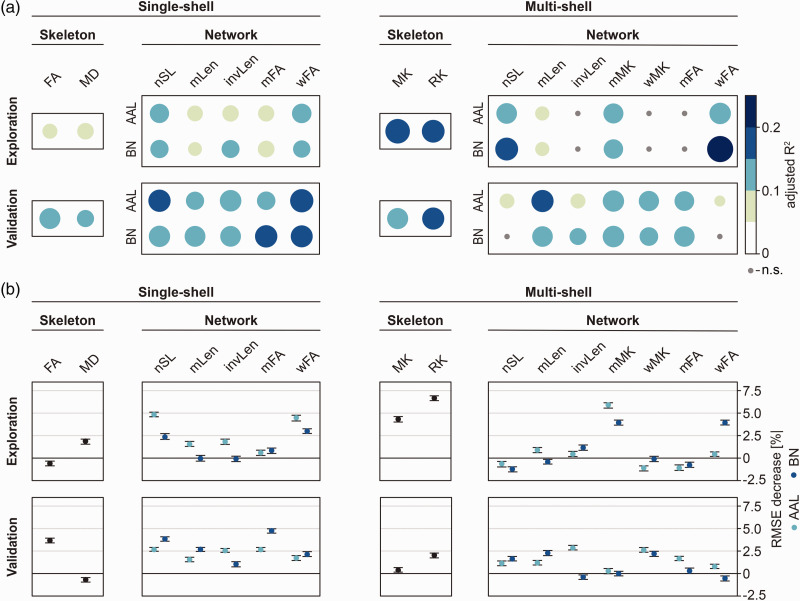
Figure 2.
Associations between diffusion MRI markers (skeleton- or network-based) and processing speed. Analyses were performed in an exploration (RUN DMC – InTENse) and validation sample (RUN DMC main study). (a) Simple linear regression between each diffusion marker and processing speed. Color and circle size depict explained variance (adjusted R2). (b) Multivariable random forest regression assessing the added benefit of each diffusion marker on top of conventional SVD markers. Plots indicate point estimate and 95% confidence interval for the change in model accuracy as assessed by the RMSE decrease.
AAL: automated anatomical labelling; BN: Brainnetome; FA: fractional anisotropy; invLen: number of streamlines weighted by the inverse length of each streamline; MD: mean diffusivity; mFA: mean of fractional anisotropy of streamlines; MK: mean kurtosis; mMK: mean of mean kurtosis of streamlines; mLen: mean length of streamlines; nSL: number of streamlines; RK : radial kurtosis; RMSE: root mean squared error; wFA: number of streamlines weighted by fractional anisotropy; wMK: number of streamlines weighted by mean kurtosis.
In the exploratory sample, brain networks defined by nSL/wFA edges and AAL nodes explained the highest variance of processing speed deficits (R2=11%) in the single-shell pipeline. Thus, this combination performed slightly better than the simple, skeleton-based diffusion marker mean diffusivity (R2=8%). Explained variance was overall higher for the multi-shell pipeline. Brain networks defined by the wFA edge and Brainnetome nodes best explained processing speed deficits (R2=20%), followed by skeleton-based mean kurtosis (R2=18%) and radial kurtosis (R2=15%).
In line with the findings in the exploration sample, brain networks defined by nSL/wFA edges and AAL nodes yielded the strongest associations with processing speed deficits (up to R2=16%) in the validation sample, explaining more variance than the best-performing skeleton-based diffusion marker fractional anisotropy (R2=13%). In contrast with the exploratory sample, explained variance was barely higher for the multi-shell pipeline. Only brain networks defined by the mLen edge performed as well as the skeleton-based diffusion marker radial kurtosis (R2=14%).
To assess an added benefit in explaining processing speed deficits on top of conventional SVD imaging markers (normalized WMH volume, lacune count, microbleed count, normalized brain volume), we performed multivariable random forest regression analyses (Figure 2(b)). In the exploratory sample, brain networks based on the nSL/wFA edges and AAL nodes showed the highest added benefit (RMSE decrease 5%), whereas the skeleton-based diffusion markers only showed a small added benefit (RMSE decrease 2.5%), or even no benefit (i.e., skeleton-based fractional anisotropy). In the multi-shell pipeline, skeleton-based radial kurtosis added the highest benefit in explaining processing speed deficits (RMSE decrease 7%), followed by brain networks based on the wMK edge (RMSE decrease 6%).
In the validation sample, skeleton-based fractional anisotropy added the highest benefit on top of conventional SVD imaging markers (RMSE decrease 4%), but brain networks with the wFA/mFA edge and the Brainnetome nodes showed a similar benefit. Results from the multi-shell pipeline showed a mixed pattern in the validation sample, with no consistent difference between skeleton-based diffusion markers and most structural brain networks.
Clinical validation: Tracking short-term disease progression in serial MRIs
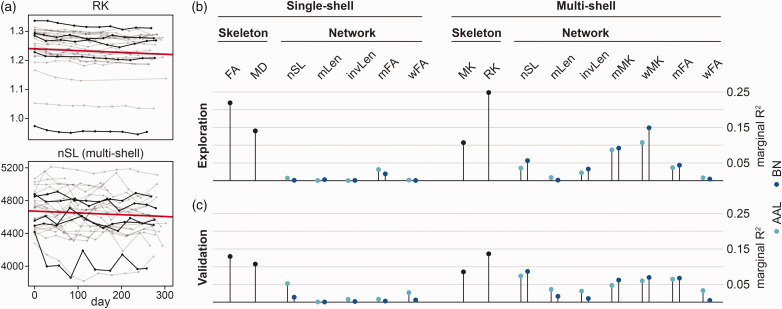
To assess the ability of brain networks to monitor short-term disease progression, we used data from high-frequency serial imaging and linear mixed effects models (Figure 3(a) and (b); Table e3). In the exploratory sample and using the single-shell pipeline, the brain network based on the mFA edge was the only network parameter demonstrating a significant change over time. A change over time was more evident for skeleton-based diffusion markers (all p < 0.05), as indicated by substantially larger marginal R2. Most brain networks derived from the multi-shell pipeline showed a change over time. However, also in this pipeline, the simpler, skeleton-based diffusion markers outperformed brain networks in the ability to capture short-term disease progression.
Figure 3.
Short-term disease progression analysis using linear mixed effects models. (a) Single subject data from the exploration sample. Skeleton-based RK (top) and structural brain networks with AAL node and nSL edge definition (bottom) plotted against time as examples. For better visibility, five subjects are depicted in black and the fixed effect of time is depicted in red. (b) Marginal R2 (variance explained by time) from the linear mixed-effects models in the exploration and (c) validation sample.
AAL: automated anatomical labelling; BN: brainnetome; FA: fractional anisotropy; invLen: number of streamlines weighted by the inverse length of each streamline; MD: mean diffusivity; mFA: mean of fractional anisotropy of streamlines; MK: mean kurtosis; mLen: mean length of streamlines; mMK: mean of mean kurtosis of streamlines; nSL: number of streamlines; RK: radial kurtosis; wFA: number of streamlines weighted by fractional anisotropy; wMK: number of streamlines weighted by mean kurtosis.
This pattern was replicated in the validation sample (Figure 3(c)).
To assess regional changes over time, we calculated local efficiency of each node of the structural brain network weighted by the mFA and defined by the AAL atlas, since this was the network with the largest change over time among global networks. Only four out of 90 nodes showed a significant change over time, but effect sizes were extremely small (fixed effects <0.002, marginal R2 < 0.02).
Technical validation: Test-retest repeatability
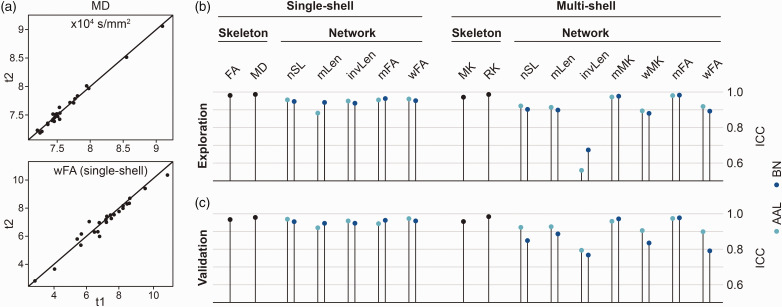
For technical validation, we used intraclass correlation coefficients to estimate test-retest repeatability in the serial MRI dataset. Most networks from the single-shell pipeline showed excellent test-retest repeatability with intraclass correlation coefficients higher than 93% in the exploratory sample (Figure 4(a) and (b); Table e4). Only brain networks based on the AAL node and mLen edge definition were less reliable (ICC < 89%). Still, skeleton-based diffusion markers demonstrated a better test-retest repeatability (ICC > 98%). Some brain networks derived from the multi-shell pipeline showed also high test-retest repeatability, in particular those based on a mMK or mFA edge definition were in the range of the skeleton-based diffusion markers (ICC > 97%). The remaining brain networks of the multi-shell pipeline were less reliable. Especially the invLen edge showed intraclass correlation coefficients below 60%, indicating the worst technical validity of all assessed brain networks. Again, this pattern was replicated in the validation sample (Figure 4(c)).
Figure 4.
Test-retest repeatability of diffusion markers. (a) Scatterplots showing the consistency of diffusion markers illustrated using the first two visits (time points t1 and t2) for skeleton-based MD (top) and wFA structural brain networks (bottom) as examples. In case of perfect test-retest repeatability, all points would lie on the diagonal. (b) Intraclass correlation coefficients of diffusion markers assessed in the exploration and (c) validation sample.
AAL: automated anatomical labelling; BN: Brainnetome; FA: fractional anisotropy; ICC: intraclass correlation coefficient; invLen: number of streamlines weighted by the inverse length of each streamline; MD: mean diffusivity; mFA: mean of fractional anisotropy of streamlines; MK: mean kurtosis; mMK: mean of mean kurtosis of streamlines; mLen: mean length of streamlines; nSL: number of streamlines; RK: radial kurtosis; wFA: number of streamlines weighted by fractional anisotropy; wMK: number of streamlines weighted by mean kurtosis.
Discussion
We systematically assessed the clinical and technical validity of brain network analysis as a marker for SVD. Our main findings are that i) for explaining processing speed, structural brain networks provide only a small added benefit over simpler, global white matter diffusion markers; ii) structural brain networks do not capture short-term disease progression over time; iii) multi-shell imaging does not improve the clinical validity of structural networks; iv) most structural brain networks show excellent test-retest reliability and thus a high technical validity and v) node and edge definitions have a substantial effect on brain network analysis results, highlighting the need for standardization to facilitate comparisons between studies.
Markers from diffusion MRI are well-established quantitative markers for SVD, both for cross-sectional and longitudinal use.4,5 While global white matter markers, e.g. obtained as average over the entire fiber tract skeleton, offer a straightforward implementation, they do not account for the complex network structure of the human brain. Brain network analysis leverages this complex information for additional mechanistic insight, but its implementation is more demanding and subject to arbitrary decisions, such as node and edge definitions. In our pre-registered analysis and systematic comparison, we did not find a substantial advantage of brain network analysis over simpler, skeleton-based diffusion MRI markers. Importantly, for capturing change over time in the longitudinal dataset, the simple markers were clearly superior. Thus, our findings question the added value of brain network analysis over simpler methods for clinical applications in SVD.
Diffusion MRI excels especially for longitudinal studies of SVD due to excellent test-retest reliability and high sensitivity to subtle white matter changes. Previous studies have shown that diffusion MRI markers (i.e. global skeleton-based markers) yield the smallest sample size estimates for assessing treatment effects over time, thus offering great potential to facilitate phase II randomized controlled trials.4,43 While brain networks were also very reliable in terms of test-retest repeatability, they failed to capture short-term disease progression over time. However, brain topology changes might only become visible throughout long-term disease progression reflecting secondary degeneration. 44 Still, tracking short-term progression is of particular interest for clinical trials with typically limited study duration. Thus, skeleton-based markers can be considered the first choice for application in clinical trials. Nonetheless, network analysis might still be useful for gaining pathomechanistic insights. As such, previous work has shown that especially connections between rich club nodes (i.e., nodes that are highly interconnected) decline in SVD. 45 The development of targeted intervention strategies might benefit from such mechanistic insights. Also, while global diffusion markers are mostly determined by SVD – not Alzheimer’s disease pathology 46 – in memory clinical patients, regional brain network analysis might offer the possibility to disentangle the contribution of different pathologies.
Given that the brain’s white matter contains more than 80% of crossing fibers, 28 we expected the more elaborate connectome pipeline with modelling of multiple fiber populations within a voxel via constrained spherical deconvolution to better depict SVD burden. Surprisingly, networks based on the multi-shell pipeline did not show an advantage over those based on the single-shell pipeline, although the latter method completely neglects the issue of crossing fibers.
Overall, we can only speculate why there was no clear added benefit of structural network analysis over simpler, skeleton-based diffusion markers. A potential explanation might be that the complex algorithms needed to construct the networks were developed on brains of young, healthy volunteers. The marked alterations of white matter microstructure 2 in SVD might interfere with or violate model assumptions, e.g. of tractography algorithms. Furthermore, small vessel disease is now recognized as a global brain disease and thus, a simple global marker, such as the skeleton-based markers, might be sufficient to capture disease burden. Similar to the tractography algorithm, the more elaborate Brainnetome atlas with a finer parcellation and better representation of the functional organization of the cortex was not superior to the AAL parcellation, which has a rather coarse, purely anatomically based parcellation. In conclusion, the simpler connectome pipeline, which was used in most previous brain network studies in SVD, performed best among the different combinations. Along the same theme that simpler measures perform better than more complex methods, and contrary to our previous study, 5 we did not observe a benefit of the diffusion kurtosis model in the validation sample.
In line with previous work on brain networks in SVD,10,11 we did not normalize the brain networks by the global efficiency of random networks. We also did not threshold the corresponding networks to a certain density and refer to previous work suggesting that – at least in the multi-shell pipeline – it might not be necessary to do so. 47 In addition, others have already reported the effect of density thresholding and concluded that networks weighted by fractional anisotropy might be less prone to network density effects. 48 Still, global efficiency measures might be influenced by the density of the structural network and should thus not be understood as the “efficiency” of the brain network, but rather be interpreted as a global diffusion marker of the brain network. However, to not add another level of complexity, we decided a priori against trying out different arbitrary density thresholds.
Several limitations of our study need to be discussed. First, we only focused on global efficiency as the core graph metric of structural networks in SVD, even though other graph metrics might have been suitable as well. However, others have reported global efficiency to be the most sensitive graph measure of cognitive impairment in SVD, 9 which is why we decided a priori on using this graph measure to reduce the complexity of the study. Also, we did not normalize the global efficiency measure against null-models. Consequently, global efficiency might be heavily influenced by the density of the structural network. However, to facilitate a comparison with previous work, 11 we decided against this normalization step. Second, while the exploration and validation sample were non-overlapping in terms of study participants, they were collected at the same center with identical protocols and might therefore not be considered as fully independent. Accordingly, we cannot estimate how our results would generalize to a dataset with a different acquisition protocol. On the other hand, this can also be regarded as a strength, since observed differences between results in the exploration and validation sample are unlikely to originate from technical differences. Third, to identify the optimal imaging marker, we did not test for significance between different markers. However, since this is methodologically non-straightforward, we decided to focus on the comparison of effect sizes and included two non-overlapping samples for replication of findings and to further facilitate the interpretation of results. A main strength of the study is its pre-registration. To our knowledge, this is the first brain network study in SVD using a fully pre-specified analysis plan. As demonstrated here, results highly depend on arbitrary choices during analysis, which is why pre-specifying the analysis plan is of great importance to improve the transparency and quality of research on network analysis in SVD.
New diffusion analysis techniques are constantly emerging. Evaluating the benefit of a novel method over established techniques as well as technical validation are indispensable for evaluating the utility in research and clinical use. 49 The structural network approach is compelling as it captures the complex network structure of the human brain. But when in need of disease burden or progression markers, network analysis did not show an advantage over the simpler skeletonized approach. Because skeleton-based markers are more straightforward to implement, even with fully automated processing, we conclude that skeleton-based diffusion markers are currently better suited for clinical research, trials and potentially also routine use.
Supplemental Material
Supplemental material, sj-pdf-1-jcb-10.1177_0271678X211069228 for Systematic validation of structural brain networks in cerebral small vessel disease by Anna Dewenter, Benno Gesierich, Annemieke ter Telgte, Kim Wiegertjes, Mengfei Cai, Mina A Jacob, José P Marques, David G Norris, Nicolai Franzmeier, Frank-Erik de Leeuw, Anil M Tuladhar and Marco Duering in Journal of Cerebral Blood Flow & Metabolism
Footnotes
Funding: The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: Mengfei Cai was supported by the China Scholarship Council (201706100189). Nicolai Franzmeier was supported by the Hertie Foundation for clinical neurosciences.
Declaration of conflicting interests: The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
| Name | Contribution |
|---|---|
| Anna Dewenter, MSc | Study concept and design, statistical analysis, interpretation of data, drafting and revising the manuscript |
| Benno Gesierich, PhD | Analysis and interpretation of data, revising the manuscript |
| Annemieke ter Telgte, PhD | Study design, acquisition and interpretation of data, revising the manuscript |
| Kim Wiegertjes, PhD | Acquisition and interpretation of data, revising the manuscript |
| Mengfei Cai, MD | Acquisition and interpretation of data, revising the manuscript |
| Mina A. Jacob, MD | Acquisition and interpretation of data, revising the manuscript |
| José P. Marques, PhD | MRI protocol design, acquisition of data, interpretation of data, revising the manuscript |
| David G. Norris, PhD | MRI protocol design, interpretation of data, revising the manuscript |
| Nicolai Franzmeier, PhD | Interpretation of data, revising the manuscript |
| Frank-Erik de Leeuw, MD, PhD | Study design and supervision, interpretation of data, revising the manuscript |
| Anil M. Tuladhar, MD, PhD | Study design and supervision, analysis, interpretation of data, revising the manuscript |
| Marco Duering, MD | Study concept, design and supervision, analysis and interpretation of data, drafting and revising the manuscript |
Supplemental material: Supplemental material for this article is available online.
ORCID iDs: Anna Dewenter https://orcid.org/0000-0002-5636-196X
Kim Wiegertjes https://orcid.org/0000-0001-7480-1482
David G Norris https://orcid.org/0000-0002-3699-6917
Marco Duering https://orcid.org/0000-0003-2302-3136
References
- 1.ter Telgte A, Wiegertjes K, Tuladhar AM, et al. Investigating the origin and evolution of cerebral small vessel disease: the RUN DMC – InTENse study. Eur Stroke J 2018; 3: 369–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wardlaw JM, Smith C, Dichgans M. Small vessel disease: mechanisms and clinical implications. Lancet Neurol 2019; 18: 684–696. [DOI] [PubMed] [Google Scholar]
- 3.Wardlaw JM, Smith EE, Biessels GJ, et al.; STandards for ReportIng Vascular changes on nEuroimaging (STRIVE v1). Neuroimaging standards for research into small vessel disease and its contribution to ageing and neurodegeneration. Lancet Neurol 2013; 12: 822–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Baykara E, Gesierich B, Adam R, et al.; Alzheimer's Disease Neuroimaging Initiative. A novel imaging marker for small vessel disease based on skeletonization of white matter tracts and diffusion histograms. Ann Neurol 2016; 80: 581–592. [DOI] [PubMed] [Google Scholar]
- 5.Konieczny MJ, Dewenter A, ter Telgte A, et al. Multi-shell diffusion MRI models for white matter characterization in cerebral small vessel disease. Neurology 2021; 96: e698–e708. [DOI] [PubMed] [Google Scholar]
- 6.Tournier J-D. Diffusion MRI in the brain – theory and concepts. Prog Nucl Magn Reson Spectrosc 2019; 112–113: 1–16. [DOI] [PubMed] [Google Scholar]
- 7.ter Telgte A, van Leijsen EMC, Wiegertjes K, et al. Cerebral small vessel disease: from a focal to a global perspective. Nat Rev Neurol 2018; 14: 387–398. [DOI] [PubMed] [Google Scholar]
- 8.Rubinov M, Sporns O. Complex network measures of brain connectivity: Uses and interpretations. NeuroImage 2010; 52: 1059–1069. [DOI] [PubMed] [Google Scholar]
- 9.Boot EM, Mc van Leijsen E, Bergkamp MI, et al. Structural network efficiency predicts cognitive decline in cerebral small vessel disease. NeuroImage Clin 2020; 27: 102325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Reijmer YD, Fotiadis P, Martinez-Ramirez S, et al. Structural network alterations and neurological dysfunction in cerebral amyloid angiopathy. Brain 2015; 138: 179–188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tuladhar AM, Tay J, Leijsen E, van, et al. Structural network changes in cerebral small vessel disease. J Neurol Neurosurg Psychiatry 2020; 91: 196–203. [DOI] [PubMed] [Google Scholar]
- 12.Xu X, Lau KK, Wong YK, et al. The effect of the total small vessel disease burden on the structural brain network. Sci Rep 2018; 8: 7442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jeurissen B, Leemans A, Tournier J-D, et al. Investigating the prevalence of complex fiber configurations in white matter tissue with diffusion magnetic resonance imaging. Hum Brain Mapp 2013; 34: 2747–2766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Welton T, Kent DA, Auer DP, et al. Reproducibility of graph-theoretic brain network metrics: a systematic review. Brain Connect 2015; 5: 193–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.van Norden AG, de Laat KF, Gons RA, et al. Causes and consequences of cerebral small vessel disease. The RUN DMC study: a prospective cohort study. Study rationale and protocol. BMC Neurol 2011; 11: 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tombaugh TN. Trail making test a and B: Normative data stratified by age and education. Arch Clin Neuropsychol 2004; 19: 203–214. [DOI] [PubMed] [Google Scholar]
- 17.Telgte A, Wiegertjes K, Gesierich B, et al. The contribution of acute infarcts to cerebral small vessel disease progression. Ann Neurol 2019; 86: 582–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Veraart J, Novikov DS, Christiaens D, et al. Denoising of diffusion MRI using random matrix theory. NeuroImage 2016; 142: 394–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Veraart J, Fieremans E, Novikov DS. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med 2016; 76: 1582–1593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cordero-Grande L, Christiaens D, Hutter J, et al. Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage 2019; 200: 391–404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tournier J-D, Smith R, Raffelt D, et al. MRtrix3: a fast, flexible and open software framework for medical image processing and visualisation. NeuroImage 2019; 202: 116137. [DOI] [PubMed] [Google Scholar]
- 22.Kellner E, Dhital B, Kiselev VG, et al. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn Reson Med 2016; 76: 1574–1581. [DOI] [PubMed] [Google Scholar]
- 23.Andersson JLR, Skare S, Ashburner J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. NeuroImage 2003; 20: 870–888. [DOI] [PubMed] [Google Scholar]
- 24.Smith SM, Jenkinson M, Woolrich MW, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage 2004; 23: S208–S219. [DOI] [PubMed] [Google Scholar]
- 25.Andersson JLR, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. NeuroImage 2016; 125: 1063–1078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tabesh A, Jensen JH, Ardekani BA, et al. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn Reson Med 2011; 65: 823–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Smith SM, Jenkinson M, Johansen-Berg H, et al. Tract-based spatial statistics: voxelwise analysis of multi-subject diffusion data. NeuroImage 2006; 31: 1487–1505. [DOI] [PubMed] [Google Scholar]
- 28.Tournier J-D, Calamante F, Connelly A. MRtrix: diffusion tractography in crossing fiber regions. Int J Imaging Syst Technol 2012; 22: 53–66. [Google Scholar]
- 29.Smith RE, Tournier J-D, Calamante F, et al. Anatomically-constrained tractography: Improved diffusion MRI streamlines tractography through effective use of anatomical information. NeuroImage 2012; 62: 1924–1938. [DOI] [PubMed] [Google Scholar]
- 30.Avants BB, Tustison NJ, Song G, et al. A reproducible evaluation of ANTs similarity metric performance in brain image registration. NeuroImage 2011; 54: 2033–2044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gesierich B, Tuladhar AM, Telgte A, ter, et al. Alterations and test–retest reliability of functional connectivity network measures in cerebral small vessel disease. Hum Brain Mapp 2020; 41: 2629–2641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hagmann P, Kurant M, Gigandet X, et al. Mapping human whole-brain structural networks with diffusion MRI. Plos One 2007; 2: e597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Jeurissen B, Tournier J-D, Dhollander T, et al. Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data. NeuroImage 2014; 103: 411–426. [DOI] [PubMed] [Google Scholar]
- 34.Smith RE, Tournier J-D, Calamante F, et al. SIFT2: enabling dense quantitative assessment of brain white matter connectivity using streamlines tractography. NeuroImage 2015; 119: 338–351. [DOI] [PubMed] [Google Scholar]
- 35.Hagmann P, Cammoun L, Gigandet X, et al. Mapping the structural core of human cerebral cortex. PLOS Biol 2008; 6: e159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.R Core Team. R: a language and environment for statistical computing. Found Stat Comput. Vienna: Author, 2016. [Google Scholar]
- 37.Yeo I, Johnson RA. A new family of power transformations to improve normality or symmetry. Biometrika 2000; 87: 954–959. [Google Scholar]
- 38.Bates D, Mächler M, Bolker B, et al. Fitting linear mixed-effects models using lme4. ArXiv14065823 Stat, http://arxiv.org/abs/1406.5823. 2014.
- 39.Kuznetsova A, Brockhoff PB, Christensen RHB. lmerTest package: tests in linear mixed effects models. J Stat Softw 2017; 82: 1–26. [Google Scholar]
- 40.Canty AJ, Ripley B. boot: Bootstrap R (S-Plus) Functions: R Package Version 1.3-11. The R Package for Statistical Reporting: 2014.
- 41.Barton K, Barton MK. Package ‘Mu-MIn’: Multi-model inference Version 1. The R Package for Statistical Reporting: 2019.
- 42.Shrout PE, Fleiss JL. Intraclass correlations: Uses in assessing rater reliability. Psychol Bull 1979; 86: 420–428. [DOI] [PubMed] [Google Scholar]
- 43.Benjamin P, Zeestraten E, Lambert C, et al. Progression of MRI markers in cerebral small vessel disease: sample size considerations for clinical trials. J Cereb Blood Flow Metab off J Tab 2016; 36: 228–240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Tiedt S, Duering M, Barro C, et al. Serum neurofilament light: a biomarker of neuroaxonal injury after ischemic stroke. Neurology 2018; 91: e1338–e1347. [DOI] [PubMed] [Google Scholar]
- 45.Tuladhar AM, Lawrence A, Norris DG, et al. Disruption of rich club organisation in cerebral small vessel disease. Hum Brain Mapp 2017; 38: 1751–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Finsterwalder S, Vlegels N, Gesierich B, et al.’ Utrecht VCI study group. Small vessel disease more than Alzheimer’s disease determines diffusion MRI alterations in memory clinic patients. Alzheimers Dement 2020; 16: 1504–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Civier O, Smith RE, Yeh C-H, et al. Is removal of weak connections necessary for graph-theoretical analysis of dense weighted structural connectomes from diffusion MRI? NeuroImage 2019; 194: 68–81. [DOI] [PubMed] [Google Scholar]
- 48.de Brito Robalo BM, Vlegels N, Meier J, et al.; Utrecht VCI Study Group. Effect of fixed-density thresholding on structural brain networks: a demonstration in cerebral small vessel disease. Brain Connect 2020; 10: 121–133. [DOI] [PubMed] [Google Scholar]
- 49.Smith EE, Biessels GJ, De Guio F, et al. Harmonizing brain magnetic resonance imaging methods for vascular contributions to neurodegeneration. Alzheimers Dement (Amst) 2019; 11: 191–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental material, sj-pdf-1-jcb-10.1177_0271678X211069228 for Systematic validation of structural brain networks in cerebral small vessel disease by Anna Dewenter, Benno Gesierich, Annemieke ter Telgte, Kim Wiegertjes, Mengfei Cai, Mina A Jacob, José P Marques, David G Norris, Nicolai Franzmeier, Frank-Erik de Leeuw, Anil M Tuladhar and Marco Duering in Journal of Cerebral Blood Flow & Metabolism
Data Availability Statement
Anonymized data will be made available upon request to the corresponding author.