Correlation Imputation for Single-Cell RNA-seq

Abstract

Recent advances in single-cell RNA sequencing (scRNA-seq) technologies have yielded a powerful tool to measure gene expression of individual cells. One major challenge of the scRNA-seq data is that it usually contains a large amount of zero expression values, which often impairs the effectiveness of downstream analyses. Numerous data imputation methods have been proposed to deal with these “dropout” events, but this is a difficult task for such high-dimensional and sparse data. Furthermore, there have been debates on the nature of the sparsity, about whether the zeros are due to technological limitations or represent actual biology. To address these challenges, we propose Single-cell RNA-seq Correlation completion by ENsemble learning and Auxiliary information (SCENA), a novel approach that imputes the correlation matrix of the data of interest instead of the data itself. SCENA obtains a gene-by-gene correlation estimate by ensembling various individual estimates, some of which are based on known auxiliary information about gene expression networks. Our approach is a reliable method that makes no assumptions on the nature of sparsity in scRNA-seq data or the data distribution. By extensive simulation studies and real data applications, we demonstrate that SCENA is not only superior in gene correlation estimation, but also improves the accuracy and reliability of downstream analyses, including cell clustering, dimension reduction, and graphical model estimation to learn the gene expression network.

1. INTRODUCTION

RNA sequencing reveals RNA information of biological samples at a given moment, using high-throughput technology. Traditional bulk RNA-seq can only provide the average gene expression levels across all cells and fails to distinguish various cell types within the sample. The advanced technology single-cell RNA sequencing (scRNA-seq) untangles the drawbacks of bulk RNA-seq by measuring the gene expression of each individual cell. Such improvement in technology allows researchers to identify the critical differences among cells from the same organism, and enables the discovery of rare and new cells. With the superior advantages, scRNA-seq technology has become an important and powerful tool in transcriptome analysis (Kolodziejczyk et al., 2015).

However, scRNA-seq sacrifices some measurement accuracy to identify the gene expression of individual cells. The data quality of scRNA-seq is less reliable due to its high level of sparsity. There has been a debate on the reasons behind such sparsity (Silverman et al., 2020). Some argue that the zeros are biologically meaningful and no correction is necessary (Wang et al., 2018; Townes et al., 2019; Svensson, 2020). Yet, several others refer the large number of zeros as dropouts, which are technical artifacts where genes erroneously appear to have zero expression due to sequencing inefficiency (Chen et al., 2018; Gong et al., 2018; Huang et al., 2018; Zhu et al., 2018; Tracy et al., 2019; Jeong and Liu, 2020). The loss of information is believed to cause major problems in downstream analyses.

Numerous imputation methods have been developed to fill in the dropout values in the scRNA-seq data. For example, the model-based imputation method SAVER (Huang et al., 2018) predicts gene expressions under the assumption that the measured gene expressions follow Poisson-Gamma distributions, where the latent Gamma random variables are the true gene expressions. Moreover, smooth-based imputations, such as drImpute (Gong et al., 2018) and PRIME (Jeong and Liu, 2020), impute the dropouts of a cell by using the gene expressions of the cells belonging to the same cluster. Furthermore, the low-rank matrix-based method scRMD methodology (Chen et al., 2018) infers the gene expressions of cells by robust matrix decomposition, where the dropouts are encoded in a sparse matrix, and the matrix of true gene expressions has low rank. Plenty of other widely used imputation approaches have been compared in Hou et al. (2020).

However, effective imputation of the missing values in scRNA-seq data can be difficult and biased because the data are sparse and contains tens-of-thousands of cells and genes. Moreover, researchers are in fact interested in discovering gene-to-gene connections and interactions, identifying cell types, and visualizing the scRNA-seq data in a lower dimensional space. Such analyses require a good estimate of the correlation matrix of the gene expressions. Then, why not directly correct the correlation matrix of the data of interest? If so, how do we make assumptions about the zeros in the data matrix? Unfortunately, the presence of dropouts still generates several challenges.

On the one hand, the sample correlation would be corrupted if all zeros are assumed to be true values; on the other hand, with the assumption that all zeros are missing values, the Pearson correlation of two genes may be computed empirically only if there are enough pairwise-complete observations, otherwise it is infeasible. That is, the presence of dropouts can cause missingness in the sample covariance matrix. Even though plenty of covariance matrix completion methodologies can be implemented here (Ledoit and Wolf, 2003; Lounici, 2014; Hastie et al., 2015; Cai and Zhang, 2016; Josse et al., 2016; Zamanighomi et al., 2016; Pavez and Ortega, 2020), ideal performance is only guaranteed under strict assumptions, for example, low-rankness, similar to data imputation methods.

So, one may ask: can we effectively impute the correlation matrix, without further strict assumptions on either dropout events or the underlying model of gene expression? In this article, we solve this problem by using auxiliary information, which can be any additional information beyond the data of interest. Indeed, improvements in estimation performance due to the use of auxiliary information have been observed in various contexts (Ferkingstad et al., 2008; Hecker et al., 2009; Lin and Lee, 2010; Gao and Wang, 2011; Li and Jackson, 2015; Van De Wiel et al., 2016; Novianti et al., 2017; Liang et al., 2019). For instance, in scRNA-seq analysis, SCRABBLE (Peng et al., 2019) utilizes bulk data as a constraint to reduce bias during imputation.

Hecker et al. (2009) discuss improvements in network inference allowed by the incorporation of genome sequence and protein–DNA interaction data. Moreover, Lin and Lee (2010) study age-related macular degeneration by incorporating prior knowledge from previous linkage and association studies. Furthermore, Gao and Wang (2011) and Li and Jackson (2015) use information about Gene Ontology annotation to improve network estimation. Finally, Novianti et al. (2017) use gene pathway databases and genomic annotations to improve prediction accuracy, and Liang et al. (2019) use auxiliary information about gene length and test statistics from microarray studies for the analysis of differential expression of genes.

In this article, we propose a novel approach, Single-cell RNA-seq Correlation completion by ENsemble learning and Auxiliary information (SCENA), which estimates the gene-by-gene correlation matrix by ensemble learning and the incorporation of auxiliary information (Section 2). Specifically, we seek to generate a reliable and accurate correlation estimation from scRNA-seq data so as to enable effective downstream analyses, including dimension reduction, cell clustering, and graphical modeling, to learn gene expression networks. We achieve these goals using additional auxiliary information about the underlying biological connections and other data sources together with the dropout-corrupted scRNA-seq data of interest.

To implement SCENA, the first step is to obtain various single correlation estimates by (1) calculating the sample correlation matrix of the data of interest, under different assumptions on the nature of sparsity; (2) converting all auxiliary data sources into approximate correlation matrices; and (3) recovering correlations through existing data imputation and matrix completion strategies. We then ensemble all obtained single correlation matrices into a final gene-by-gene correlation matrix estimate by model stacking. We test our novel method and compare it with existing data imputation approaches through extensive simulations (Section 3) and several real data case studies (Section 4). Our results show that SCENA outperforms other existing methods in terms of correlation matrix completion, dimension reduction, clustering, and graphical modeling.

2. SINGLE-CELL RNA-SEQ CORRELATION COMPLETION BY ENSEMBLE LEARNING AND AUXILIARY INFORMATION

Let X_s be an $N\times M$ scRNA-seq data matrix of gene expressions of N genes measured over M cells. The challenge raised is that the data matrix X_s typically contains a large proportion of zeros (usually 80%), and it is difficult to distinguish between the true zero gene expression and the dropout events. These missing values might significantly influence the reliability of the further downstream analyses. Traditional imputation methods aim to recover the underlying dropout-free data matrix X by imputing the missing entries (Chen et al., 2018; Gong et al., 2018; Huang et al., 2018; Zhu et al., 2018; Tracy et al., 2019; Jeong and Liu, 2020), with different assumptions on the data. However, the accuracy of the imputed data as well as further analyses rely on the appropriateness of assumptions.

One may ask: is there any way to integrate different assumptions on both the nature of zeros and the distribution of gene expression? Before we answer this question, note that most of the downstream analyses require a reliable gene-to-gene correlation matrix. Then why not directly correct the corrupted correlation matrix instead? In this study, we propose a novel approach to generate more accurate correlation estimates and improve the accuracy of further downstream procedures by directly imputing the gene-by-gene correlation matrix instead of the data matrix itself.

Our proposed method, SCENA offers three major methodological innovations that yield better correlation estimates, and dramatically higher accuracy in further analyses, including dimension reduction, clustering, and graphical model. Our first innovation is to impute the estimated correlation matrix of X_s, instead of the data itself, which is unseen in the scRNA-seq imputation literature so far. In this way, we are able to integrate different assumptions on the distribution of the underlying gene expressions and can reduce additional bias created from the imputation process.

Second, rather than solely relying on the data of interest, SCENA estimates the correlations using numerous sources of auxiliary information. These auxiliary quantities can be any kind of data beyond the scRNA-seq data of interest, including gene networks and other relevant RNA-seq data. The incorporation of additional information derived from various sources can provide more insights into the underlying gene-to-gene biological connections, so as to better approximate the correlation matrix. Improvements on estimation performance using auxiliary information have also been shown in the genomics literature (Ferkingstad et al., 2008; Hecker et al., 2009; Lin and Lee, 2010; Gao and Wang, 2011; Li and Jackson, 2015; Van De Wiel et al., 2016; Novianti et al., 2017; Liang et al., 2019; Peng et al., 2019).

Next, one may ask how to optimally incorporate the different sources of auxiliary information with the data of interest to generate an ultimate reliable estimate of the gene-by-gene correlation matrix. Our approach builds upon a strikingly simple but powerful idea: model stacking. After converting auxiliary information into single correlation matrices through various techniques, SCENA generates a final estimate by ensembling all the single correlation matrices. Superior performance can be achieved as ensemble learning is able to reduce noise and bias of each single estimate, and improve predictive power (Opitz and Maclin, 1999; Polikar, 2006; Rokach, 2010). In Section 2.1 we describe the derivation of single correlation matrix estimates, and in Section 2.2 we present the model stacking algorithm for final estimates. In the rest of the article, gene expressions are transformed according to $x{log}_2\left(1+x\right)$ before computing correlations.

2.1. Single correlation matrix estimates

Our first step is to construct numerous single correlation estimates of the data of interest with auxiliary information. There has been a debate on the nature of the sparsity in scRNA-seq data. Some argue that the large quantity of zeros are due to technical inefficiency (Chen et al., 2018; Gong et al., 2018; Huang et al., 2018; Zhu et al., 2018; Tracy et al., 2019; Jeong and Liu, 2020), whereas others believe that the zeros are actually biologically meaningful rather than “dropouts,” and corrections to scRNA-seq data are unnecessary (Wang et al., 2018; Townes et al., 2019; Svensson, 2020). To integrate such controversy, we build several kinds of correlation estimates using different assumptions on the sparsity of scRNA-seq, along with various types of auxiliary information.

These single estimates can be divided into the following four groups: (1) blind correlation estimates, (2) data-imputed estimates, (3) correlation estimates based on auxiliary data, and (4) skeptical correlation estimates. Our first type of single correlation estimate is constructed by simply assuming all zeros in the scRNA-seq data matrix X_s are true gene expressions, referred as the blind correlation estimate. Second, with the assumption that some zeros are dropouts that require corrections, we can construct correlation estimates utilizing the existing data imputation methods (Chen et al., 2018; Gong et al., 2018; Huang et al., 2018; Jeong and Liu, 2020). Then single estimates are calculated as the sample correlation matrices of imputed scRNA-seq data.

Third, auxiliary information that can reflect the underlying biological connections among genes is used to approximate correlation matrices. For example, the bulk cell RNA-seq data can be considered as one type of auxiliary data because it is free from the dropout issue, and numerous resources on the bulk cell experiments are available. Another helpful auxiliary quantity is a new scRNA-seq data set of the same tissue as the data of interest. It is possible that another scRNA-seq data set $X_s^{\ast }$ presents fewer dropouts for some of the genes in the main data matrix X_s, so the lost information of those genes might be found in the new data. For both kinds of auxiliary RNA-seq data, the sample gene-by-gene correlation matrix is calculated as a single correlation estimate. In this article, we include bulk cell RNA-seq data of 39 different tissues from the Encyclopedia of DNA Elements (ENCODE) (Consortium et al., 2012), and other scRNA-seq data collected from cells of the same type of organism as the scRNA-seq data set of interest (Yan et al., 2013; Lake et al., 2018).

Another kind of auxiliary information is biological networks. By providing gene or protein connections, this network information can also significantly help us approximate single correlation estimates. However, the networks are usually not in the shape of correlations, so some preprocessing steps are required to convert them into approximate correlation matrices. For instance, the gene pathway database from the Kyoto Encyclopedia of Genes and Genomes (KEGG) (Kanehisa et al., 2016) provides information about $n=6860$ genes and $c=239$ gene pathways which can be summarized in an $n\times c$ matrix $K=\left[K_{ij}\right]$ where $K_{ij}=1$ if gene i is in pathway j, $K_{ij}=0$ otherwise. Then we can compute the $n\times n$ sample correlation matrix of K.

From the gene interaction networks from the Biological General Repository for Interaction Datasets (BioGRID) (Stark et al., 2010), we extract an adjacency matrix $A\in {\left\{0,1\right\}}^{N\times N}$ of gene connections, and obtain the correlation matrix 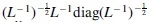, where L is the Laplacian matrix $L=D-A$, and D is a diagonal matrix with $D_{ii}={\sum }_{j=1}^N{A}_{ji}$, that is, the degree of gene i. Another network auxiliary network is the protein–protein interaction networks from STRING (Szklarczyk et al., 2016). We construct a correlation matrix by treating gene-by-gene combined connection scores as correlations. In this way, we are able to obtain correlation estimates of genes from different auxiliary networks using the corresponding preprocessing procedures.

Finally, we assume all zeros in the scRNA-seq are dropouts. We obtain the matrix $X_s^{NA}$ which corresponds to X_s with all zeros replaced by missing values (NAs). From this matrix, it is possible to compute the pairwise complete sample correlation matrix ${\widehat{\Sigma }}_O$, which contains missing entries for gene pairs with no jointly nonzero measured scRNA-seq expressions. However, how do we fill up the missing values in ${\widehat{\Sigma }}_O$? In this study, we propose several methods to obtain completed skeptical correlation versions. Our first method is to produce a complete correlation matrix by existing low rank matrix completion strategies (Lounici, 2014), denoted as cor${}_{shrink}$.

Second, since we already have plenty of single correlation estimates from auxiliary data, why not correct the missing values in ${\widehat{\Sigma }}_O$ using those complete correlation matrices? One simple solution is to construct a convex combination of the incomplete correlation ${\widehat{\Sigma }}_O$ and the single estimates, say ${\widehat{\Sigma }}_{aux}$. In this way, we can simply fill up the missing values utilizing the auxiliary information in a time-efficient manner. One idea to integrate the two correlation matrices is simply replacing all the missing values in ${\widehat{\Sigma }}_O$ by the corresponding entries in the ${\widehat{\Sigma }}_{aux}$. Another approach is to generate a new correlation estimate by a weighted sum of the two matrices.

To be specific, we will put more weight on ${\widehat{\Sigma }}_{O,ij}$ if genes $i,j$ have a higher signal-to-noise ratio, which is calculated as the proportion of cells where two genes have jointly nonzero read counts in the data matrix X_s. This approach is reasonable because the pairwise complete correlation between two genes is more reliable if they are more jointly observed in the main scRNA-seq data. Formally, we can obtain a completed version of the pairwise complete scRNA-seq sample correlation matrix ${\widehat{\Sigma }}_O$ as $\dot{\Sigma }=\alpha \odot {\widehat{\Sigma }}_O^{\ast }+\left(1-\alpha \right)\odot {\widehat{\Sigma }}_{aux}$, where ${\widehat{\Sigma }}_O^{\ast }$ is a version of ${\widehat{\Sigma }}_O$ with all NA's replaced by zeros, and $\alpha =\left[{\alpha }_{ij}\right]$ is a $N\times N$ weight matrix. We consider two types of weights:

1. Simple replacement

2. Signal-to-noise ratio

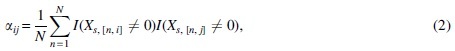
where N denotes the number of cells and $X_{s,\left[n,i\right]}$ denotes gene i^’s expression in cell n. And ${\alpha }_{ij}$ is the proportion of cells where genes i and j have jointly nonzero read counts.

2.2. Model stacking

One may ask how do we unify the single estimates. Before we try to construct a final estimate, one challenge raised in integrating a series of gene-by-gene correlation matrices is that the genes available in each source of auxiliary information might be different. For example, the KEGG pathway database contains pathway information of only 6860 genes, whereas the scRNA-seq data usually has >10,000 genes. For simplicity, we consider only the genes that all the auxiliary data have in common. Now that we have a series of correlation matrices of the same genes and same dimensions, how do we optimally combine them? As ensemble methods are widely used in machine learning and known to have predictive advantages (Opitz and Maclin, 1999; Polikar, 2006; Rokach, 2010), we propose to address this question through a simple and powerful approach: model stacking. Let ${\dot{\Sigma }}_1,\dots ,{\dot{\Sigma }}_p$ be the single correlation estimates derived in Section 2.1. We aim to obtain a final correlation matrix estimate $\tilde{\Sigma }$ by model stacking in the form

where $F:{ℛ}^{N\times N}\to {ℛ}^{N\times N}$ is an invertible mapping, and ${\beta }_1,\dots ,{\beta }_q\in ℛ$.

The next question is: how to choose function F to ensure an accurate correlation estimate? The simplest choice of F is the identity mapping $F\left(A\right)=A,\forall A\in {ℛ}^{N\times N}$. However, $\tilde{\Sigma }$ is not guaranteed to be a positive semidefinite correlation matrix, even if all single estimates ${\dot{\Sigma }}_1,\dots ,{\dot{\Sigma }}_p$ are positive semidefinite correlation matrices, unless we impose appropriate constraints on ${\beta }_1,\dots ,{\beta }_q$. For instance, a sufficient condition is ${\beta }_q>0,\forall q$, with ${\sum }_q{\beta }_q=1$, which specifies a convex linear combination. Another possible mapping is $F\left(A\right)=A^{-1}$, requiring ${\dot{\Sigma }}_p\succ 0,\forall p$. To satisfy the positive semidefinite requirement, we propose to replace $\tilde{\Sigma }$ with the nearest correlation matrix (Higham, 2002) as per $\tilde{\Sigma }:=arg{min}_{\Psi \in C}\parallel \tilde{\Sigma }-\Psi {\parallel }_F$, where C is the set of positive semidefinite correlation matrices. In this way, we are able to obtain a proper correlation matrix without much sacrifice in accuracy.

Then the next major step is to properly specify Equation (2.2) with optimal parameters ${\beta }_q,q=1,..,p$. The first possible solution we propose is a simple average of all the single correlation estimates. The simple average solution SCENA_average is obtained by setting F to be the identity mapping and ${\beta }_q=\frac{1}{p}$, for all q, yielding the convex linear combination

One major benefit of this approach is its obvious computational advantage. Since the weights are prespecified as $\frac{1}{p}$, we have no additional tuning or validation steps required. Another advantage of the simple average approach is that, $\tilde{\Sigma }$ here is guaranteed to be a positive semidefinite correlation matrix if all the single estimates ${\dot{\Sigma }}_1,\dots ,{\dot{\Sigma }}_p$ are all positive semidefinite.

Besides simple averaging, we propose to estimate the parameters ${\beta }_q,q=1,..,p$ by a regression model. First, we assume a linear relationship between the true underlying correlation and the single correlation estimates,

where $f:\left(-1,1\right)\to ℛ$ is an invertible function, for example, the Fisher transformation $f\left(x\right)=\frac{1}{2}log\left(\left(1+x\right)∕\left(1-x\right)\right)$, and ${\delta }_{ij}$ is an error component. Then we are able to estimate the vector of coefficients 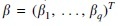is then estimated by solving the penalized optimization problem

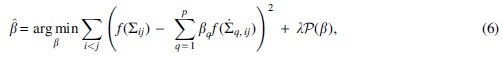
where $P$ is a penalty. We are able to select the hyper-parameter $\lambda \ge 0$ through cross-validation, which is implemented by creating multiple held-out data subsets that are iteratively removed from training and used instead to validate prediction accuracy. There are many possibilities to specify the penalty function, and here we propose to set $P\left(\beta \right)={\sum }_{q=1}^p{\beta }_q^2$ to produce the ridge estimator, which is known to protect from overfitting with regularization (Hoerl and Kennard, 1970). We denote the resulting final correlation matrix $\tilde{\Sigma }$ as SCENA_ridge. Of course, the challenge here is that we do not know ${\Sigma }_{ij}$ in Equation (2.2). So, to estimate the parameters, we develop a reference-downsampling method to construct a small simulation of the sparse data and thus approximate the ridge estimates.

In the scRNA-seq data of interest, we are able to identify a small subset of genes and cells, which we may assume to contain very few dropouts and could give us reliable estimates of ${\Sigma }_{ij}$, referred as a “reference data,” as presented in Algorithm 1. Then we assume that gene expressions follow Poisson-Gamma distributions, where the latent Gamma random variables are the true gene expressions. We are able to construct a downsampled version of the reference data by creating artificial dropouts as Algorithm 2. In this way, ridge parameters can be estimated using the reference data as response and the single estimates of the downsampled data as predictors. Finally, a final correlation estimate of the scRNA-seq is obtained using the resulting ridge coefficients. The full procedure is summarized in Algorithm 3.

Algorithm 1: Reference data selection
Input: $N\times M$ data matrix X; parameter vector a.
1. Filter out cells with library size greater than a1-th percentile.
2. Remove genes with mean expression less than a2-th percentile.
3. Remove genes with less than a3-th percentile nonzero cells.
4. Keep cells with library size greater than the a4-th percentile.
5. Keep genes with nonzero proportion greater than a5-th percentile.
The default parameter values are$a_1=95,a_2=25,a_3=15,a_4=5,a_5=50$.
Output: $N\prime \times M\prime$ reference data matrix Y.

Algorithm 2: Poisson-Gamma downsampling
Input: $N\times M$ data matrix X; parameters $s,r>0$;
1. Draw $Z_1,\dots ,Z_M{\sim }^{i.i.d.}\Gamma \left(s,r\right)$.
2. Draw ${\tilde{X}}_{ij}\sim Poisson\left(X_{ij}{Z}_j\right)$, for $i=1,\dots ,N$ and $j=1,\dots ,M$.
Output: $N\times M$ downsampled data matrix $\tilde{X}$.

Algorithm 3: Stacking regression validation

Both SCENA_ridge and SCENA_average combine the same single correlation matrices through model stacking. But the difference is that the weighting coefficients of SCENA_ridge are calibrated for the optimal recovery of the true correlation structure of the corrupted gene expression data, whereas SCENA_average simply assigns uniform weights, presumably upweighting auxiliary biological network structures that are more informative about cell characteristics. Besides, SCENA_average is computationally cheaper than SCENA_ridge, because the estimation of the weighting coefficients of SCENA_ridge involves multiple additional imputation and optimization steps that are computationally expensive.

3. SIMULATION

In this section, we present an extensive simulation study showing that SCENA is superior to other methods in terms of correlation matrix completion, dimensionality reduction, clustering, and graphical modeling of gene expression network recovery. In Section 3.1 we describe how we generate realistic artificial scRNA-seq data based on real data sets. Specifically, given a real scRNA-seq data set, we first extract a reference data set, a subset of data where all zeros can be safely assumed to be true values and not dropouts. Then, we generate downsampled data by creating dropouts in the reference scRNA-seq data according to the Poisson-Gamma scheme in Algorithm 2. Finally, in Section 3.2 we assess the performance of SCENA and other existing methods at recovering the correlation structure of the reference data based on the corrupted downsampled data and other available auxiliary data.

3.1. Generating scRNA-seq data

3.1.1. Original data sets

We use three human scRNA-seq data sets in this simulation study:

• 1.chu: human embryonic stem cells (Chu et al., 2016).
• 2.chu_time: human definitive endoderm cells (time-series sequencing) (Chu et al., 2016).
• 3.darmanis: human brain cells (Darmanis et al., 2015).

The number of cells and number of cell types are reported in Table 1 (genes with zero expression in all cells are removed).

Table 1.

Human scRNA-seq Data Sets Used in Simulations

	chu	chu_time	darmanis
Tissue	Embryonic stem cells	Definitive endoderm cell	Brain cell
No. of cell types	7	6	5
No. of cells	1018	758	366
No. of genes	21,413	18,294	17,738
% zeros	47.43%	51.15%	80.06%
No. of reference cells	951	689	332
No. of reference genes	2522	2160	2306
Source	Chu et al. (2016)	Chu et al. (2016)	Darmanis et al. (2015)
GEO accession code	GSE75748	GSE75748	GSE67835

GEO, gene expression omnibus; scRNA-seq, single-cell RNA sequencing.

3.1.2. Reference data sets

For each of the three data sets, we first match the genes with those available in the auxiliary data (Section 2.1), and then apply Algorithm 1 to perform quality control by filtering out low-quality genes and cells, and finally extract reference data. All values in the reference data are treated as true gene expressions, that is, the reference data is free from dropouts. The dimensions of the three resulting reference data sets are reported in Table 1.

3.1.3. Simulated data

For each of the three reference data sets, we apply Algorithm 2 to generate downsampled versions of the reference data. We set $s=10$, and $r=3000,1000,1000$ for chu, chu_time and darmanis data, respectively, to ensure the expected percentage of zeros in the simulated downsample data to be similar to the percentage of zeros in the original scRNA-seq data (Table 1). We refer the simulated downsample data as X_s.

3.2. Models comparison

In this section, we assess the performance of SCENA and other existing methods at recovering the correlation structure of the reference data based on the corrupted downsampled data and other available auxiliary data. Although there are many imputation methods for scRNA-seq data, we choose to compare SCENA with the most popular ones, including SAVER (Huang et al., 2018), drImpute (Gong et al., 2018), scRMD (Chen et al., 2018), and PRIME (Jeong and Liu, 2020) methods. And SAVER is demonstrated to outperform other existing methods consistently according to the systematic comparisons on the data imputation methods by Hou et al. (2020). We show that SCENA_average and SCENA_ridge (Section 2.2) outperform SAVER, drImpute, scRMD, and PRIME in terms of correlation matrix completion, dimension reduction, clustering, and graphical modeling. The results shown are averaged across multiple downsampled data sets.

3.2.1. Correlation completion

We measure the similarity between the correlation matrix estimators considered and the reference correlation matrix ${\widehat{\Sigma }}_{ref}$ in terms of mean squared error (MSE) and average correlation matrix distance (CMD) (Herdin et al., 2005). Table 2 shows that SCENA outperforms all other data imputation methods in terms of both MSE and CMD. The baseline is the MSE and CMD between ${\widehat{\Sigma }}_{ref}$ and the sample correlation of the downsampled data (blind estimate ${\widehat{\Sigma }}_s$, Section 2.1), treating all 0s as true gene expressions. SCENA_ridge has the lowest MSE and CMD among all methods as well as the baseline in chu_time and darmanis data. SCENA_average is also better in correlation completion than SAVER and PRIME.

Table 2.

Correlation Completion Accuracy

	MSE	chu_time	darmanis	CMD	chu_time	darmanis
	chu			chu
Blind estimate	0.01008	0.00796	0.00804	0.21217	0.15855	0.22897
SAVER	0.01949	0.01850	0.01476	0.44604	0.40991	0.52235
drImpute	0.01181	0.00796	0.01371	0.23595	0.16050	0.33769
scRMD	0.01125	0.00868	0.00879	0.23598	0.17621	0.26170
PRIME	0.03707	0.03508	0.02661	0.47846	0.42137	0.33218
SCENA_average	0.01285	0.01119	0.01313	0.27283	0.21596	0.42946
SCENA_ridge	0.01212	0.00708	0.00513	0.20497	0.12942	0.12474

MSE and CMD between the reference correlation and the estimated correlation derived from various methods. SCENA_ridge has the lowest MSE and CMD among imputation methods in chu_time and darmanis data, and is lower than the baseline (“Downsample”), which is the sample correlation matrix of the downsampled data. All other imputation approaches perform worse than the baseline.

CMD, correlation matrix distance; MSE, mean squared error.

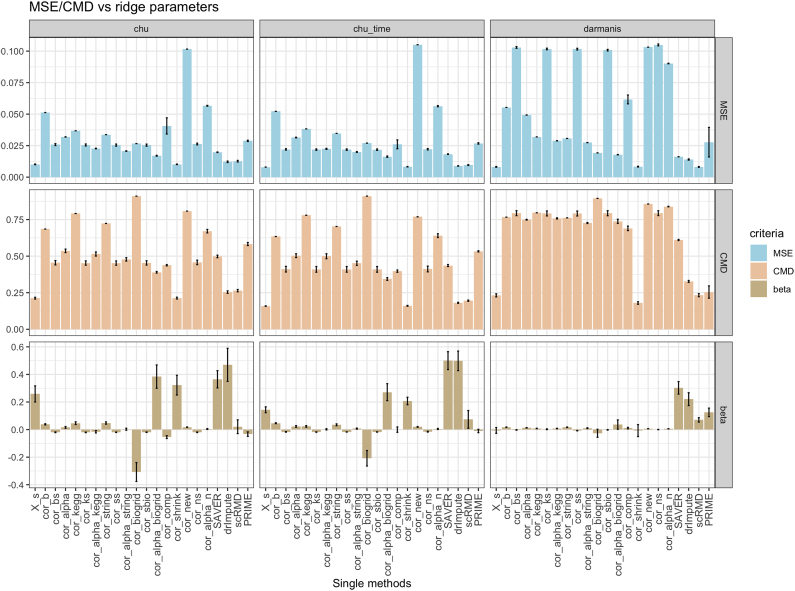
Besides, the correlation accuracy of single estimates, which are the input of SCENA_ridge regression demonstrate consistent patterns with the resulting ridge coefficients. Same as before, the accuracy is measured by MSE and CMD between reference correlation and each single correlation. The single estimates with lower(higher) MSE and CMD tend to have higher(lower) ridge coefficients and thus contribute more(less) to the construction of final estimates, as shown in Figure 1. Therefore, SCENA_ridge can accurately recover the reference correlation by allocating more weights to those single correlations with better performance.

FIG. 1.

Correlation accuracy and estimated parameters of SCENA_ridge of single estimates. It presents a consistent pattern between lower MSE/CMD and higher ridge parameters. cor_shrink (Lounici, 2014) has relatively lower MSE and CMD with the reference correlation in all three data sets, which is consistent with its higher ridge coefficients. CMD, correlation matrix distance; MSE, mean squared error.

3.2.2. Dimension reduction

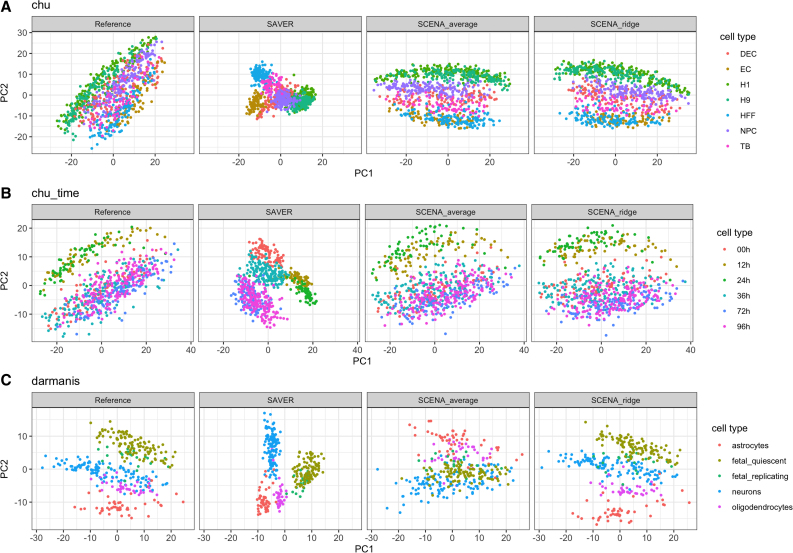
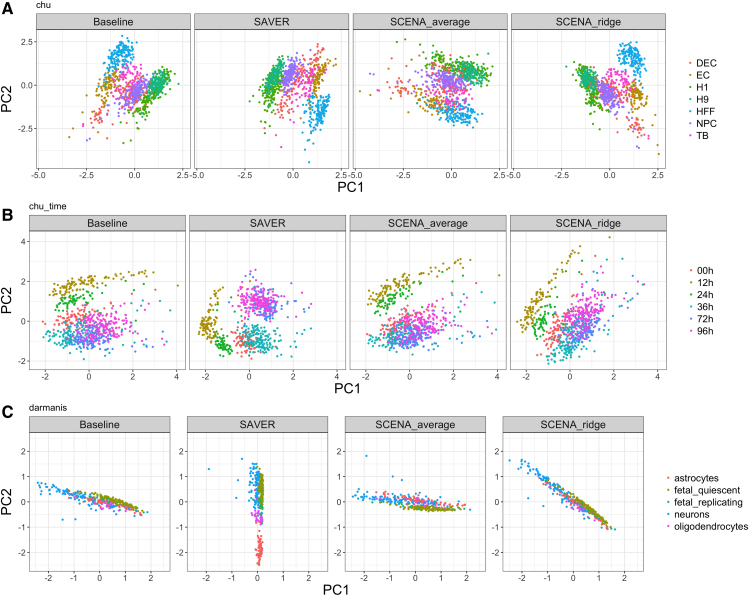
For each correlation matrix estimate from imputed data and SCENA, we compute the matrix of eigenvectors V, and obtain the principal component scores $U=Z^{T}V$, where Z is a standardized version of the $log$ transformed simulated data X_s. In Figure 2, we compare the scatterplots of the top two principal component (PC) scores of the cells against each other. The plots are colored by cell type labels, and PCs are derived from sample correlations of reference data, SAVER imputed data, and correlation estimations of SCENA_ridge and SCENA_average. Both SCENA_ridge and SCENA_average recover the reference data structure better than data imputation, and yield scatterplots with clear separation among different types of cells indicated by the cell type labels.

FIG. 2.

Dimension reduction accuracy. Scatterplots of the top two PC scores of the cells colored by cell type. Both SCENA_ridge and SCENA_average appear to recover the reference data structure better than SAVER, yielding scatterplots with a clear separation among different types of cells. PC, principal component.

3.2.3. Clustering

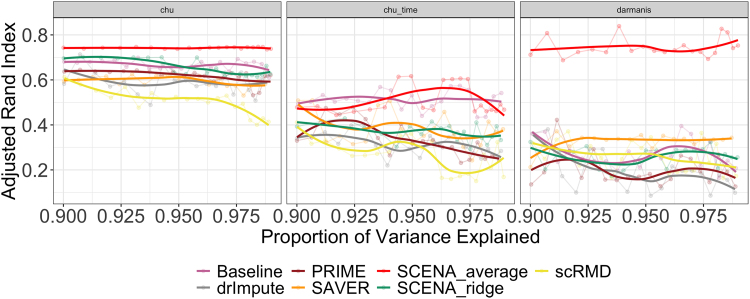
We perform hierarchical cells clustering (Ward's minimum variance method with Manhattan distance; Friedman et al., 2001) based on the standardized principal components of the downsample scRNA-seq data obtained from the different approaches considered (quantities U computed in Section 3.2.2). For each method, we use the top PCs with the proportion of variance explained within the range (90%,99%), and set the number of clusters equal to the number of true cell labels in the scRNA-seq data.

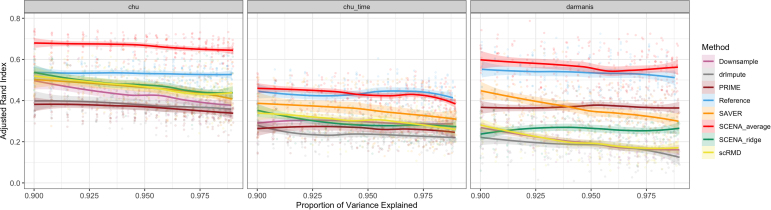
To assess clustering performance, we measure the similarity between cluster assignments and true cell labels by calculating the adjusted rand index (ARI) (Rand, 1971). This metric takes values in the interval $\left[0,1\right]$, with large values indicating stronger similarity. In Figure 3 we can see that SCENA_average yields the best clustering performance over all other methods in all three data sets. Interestingly, in the chu data, SCENA_average has even better performance than the clustering obtained from reference data, in accordance with the fact that SCENA exploits auxiliary information besides the scRNA-seq data.

FIG. 3.

Clustering performance. ARI (higher is better) of cell type grouping through hierarchical clustering after dimension reduction through PCA explaining various proportions of variance. SCENA_average yields the best clustering performance over all other methods in all data sets, and even better than the clustering obtained from the reference data in the chu data. ARI, adjusted rand index.

3.2.4. Graphical model of gene expression network

Gene expression network recovery in the case where several pairs of variables are never observed jointly is a major statistical problem that has gained strong interest recently. A thorough theoretical investigation of the so-called graph quilting problem can be found in Vinci et al. (2019). Such problem is strictly related to ours, where an extremely large number of gene pairs have no reliable empirical correlation estimates. In this study, we investigate the graph recovery performance based on the various correlation matrix estimates through simulations. Specifically, we plug the correlation matrix estimates into the graphical lasso (Yuan and Lin, 2007) to obtain a gene-by-gene network estimate through sparse precision matrix estimation.

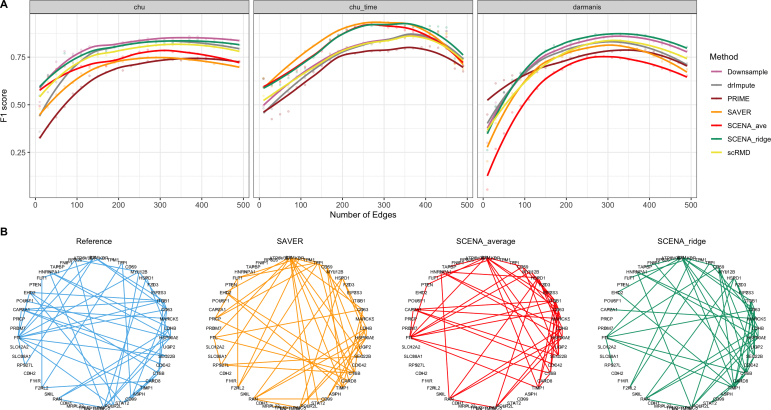
For simplicity, we compute graphs about only the top 50 most variable genes among cell types, identified by applying analysis of variance (ANOVA) to gene expression of reference data. To evaluate the graph recovery performance of the methods, we compute the F1-score with respect to the graph estimated from reference data. In Figure 4A we plot F1-score versus the number of graph edges for all methods and data sets. SCENA_ridge is superior in recovering the reference graph than other methods in chu and darmanis data, and it produces a similarly high F1-score in chu_time data as SAVER method. For illustration, in Figure 4B we also display gene expression network relative to the chu data with 50 edges.

FIG. 4.

Genetic graph recovery. (A) F1 score (higher is better) quantifying the performance of methods at recovering the reference gene expression network of 50 most variable genes for various numbers of edges. SCENA_ridge exhibits strong performance for all data sets, whereas other methods' performance dramatically changes across different data sets. (B) Gene expression network of chu data, setting the number of edges to 50.

4. APPLICATION TO scRNA-seq DATA

We now apply the methods to the analysis of the three data sets (Table 1), where the chu data set contains the gene expression of 6038 genes (largest genes set that matched available auxiliary information) measured in 1018 human embryonic stem cells, chu_time data set contains 5863 genes measured in 1018 human definitive endoderm cells, and darmanis contains 6001 genes measured in 366 human brain cells.

In Figure 5 we plot the first two principal components based on SCENA_average and SCENA_ridge, whereas in Figure 6 we compare the cell clustering performance of SCENA with other methods in terms of ARI. The hierarchical clustering based on SCENA_average performs the best at recovering true cell type labels, in accordance with simulation results (Section 3.2.3).

FIG. 5.

Dimension reduction accuracy of real data applications. Scatterplots of the top two PC scores of the cells colored by cell type. Both SCENA_ridge and SCENA_average yield scatterplots with a clear separation among different types of cells.

FIG. 6.

Clustering performance of real data applications. ARI of cell type grouping through hierarchical clustering after dimension reduction using PCA explaining various proportions of variance. SCENA_average yields the best clustering performance over all other methods in all three data sets.

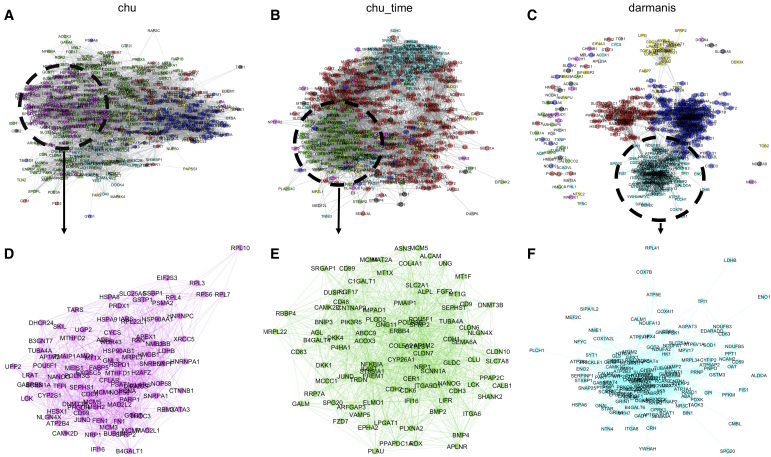
Finally, in Figure 7 we display the gene expression network (graphical lasso; Yuan and Lin, 2007) of the 500 most variable genes among cell types (ANOVA criterion as in Section 3.2.4) based on SCENA_ridge, with number of edges selected through Extended Bayesian Information Criterion (Foygel and Drton, 2010). Gene-level communities can be detected by edge betweenness score (Newman and Girvan, 2004), and the darmanis data set shows a clear separation among the detected clusters. With the hypothesis that genes that belong to the same cluster might share similar biological functions, we find that the main communities are enriched in biologically meaningful pathways.

FIG. 7.

Gene Expression Network Estimation. (A,B,C) Gene expression network (graphical lasso; number of edges selected through EBIC) estimate based on SCENA_ridge correlation estimate, colored by community detected through edge betweenness score. (D,E,F) Zoomed-in communities, which are enriched in biologically meaningful KEGG terms “DNA replication,” “Cell adhesion molecules,” and “GABAergic synapse” pathways, respectively. EBIC, extended Bayesian information criterion; KEGG, Kyoto Encyclopedia of Genes and Genomes.

For instance, in the darmanis data set, there are three main communities enriched in the KEGG terms, metabolic pathways, GABAergic synapse, and PI3K-Akt signaling pathway, which either contribute to fundamental cellular functions or are significant in the mammalian central nervous system (Kanehisa et al., 2016). Besides, the hub gene with the largest number of edges SDC4 (408 edges) encodes the transmembrane (type I) heparan sulfate proteoglycan, which is significant in intracellular signaling (Ridgway et al., 2010). In addition, the enriched pathways in the chu data set of embryonic stem cell are also biologically meaningful, including KEGG terms Regulation of actin cytoskeleton, DNA replication, and Focal adhesion.

A top hub node protein coding gene DNMT3B is a catalytically active DNA methyltransferase (Liao et al., 2015), and is specifically expressed in totipotent embryonic stem cells (Watanabe et al., 2002). Moreover, DNMT3B is one of the pluripotency markers with high level of expression in the cell type H1, as demonstrated by Chu et al. (2016). Besides, genes IFI16 (Hurst et al., 2019) and HAND1 (Wagh et al., 2014) are marker genes in cell type EC and cell type TB, respectively, and correspondingly have relatively large numbers of connections. Also, the main communities detected in chu_time data include Cysteine and methionine metabolism, Cell adhesion molecules, and Ribosome, which also control important biological functions in endoderm cells (Kanehisa et al., 2016).

5. DISCUSSION

We have proposed and studied SCENA, a novel methodology for gene-by-gene correlation matrix estimation from dropout-corrupted scRNA-seq data. SCENA builds upon the strikingly simple but powerful idea of optimally combining multiple gene-by-gene correlation matrices derived from various sources of information, besides the scRNA-seq data of interest. This combination is implemented efficiently through model stacking techniques.

We have demonstrated that SCENA can provide superior estimation performance compared with traditional data imputation methods. In our analyses, SCENA_ridge remarkably recovered the information underlying the corrupted scRNA-seq data in terms of correlation completion, dimension reduction, and graphical modeling, whereas the hierarchical clustering based on SCENA_average yielded cell groupings that best reflected true cell type heterogeneity in terms of ARI.

Indeed, although both variants combine the same single correlation matrices through model stacking, the weighting coefficients of SCENA_ridge are calibrated for the optimal recovery of the true correlation structure of the corrupted gene expression data, whereas SCENA_average simply assigns uniform weights, presumably upweighting auxiliary biological network structures that are more informative about cell characteristics. SCENA_average is computationally cheaper than SCENA_ridge, because the estimation of the weighting coefficients of SCENA_ridge involves multiple additional imputation and optimization steps that are computationally expensive.

For instance, in the application presented in Section 4, the model stacking step for SCENA_ridge took about 40 minutes, whereas only about 30 seconds for SCENA_average, on a laptop with 16 GB of RAM (2133 MHz) and dual-core processor (3.1 GHz). Given all these considerations, we recommend to use SCENA_average for the analysis of massive scRNA-seq data sets.

Although we have demonstrated our approach using specific auxiliary sources, SCENA is general and conducive to many different types of correlation imputation approaches and additional sources of auxiliary information on genetic interactions. In addition, our approach can be further optimized using different machine learning approaches to model stacking and ensemble learning. Overall, we expect SCENA to become an important instrument for downstream analyses of massive scRNA-seq data that powerfully incorporates known auxiliary information on genetic interactions.

AUTHOR DISCLOSURE STATEMENT

The authors declare they have no conflicting financial interests.

FUNDING INFORMATION

L.G., G.V., and G.A. are supported by NSF DMS-1554821, NSF NeuroNex-1707400, and NIH 1R01GM140468. G.V. is additionally supported by a Rice Academy Postdoctoral Fellowship and the Dan L. Duncan Foundation.