Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2022 May 24.
Published in final edited form as: J Biomech. 2012 Jun 29;45(12):2084–2091. doi: 10.1016/j.jbiomech.2012.05.039

Effects of Perturbation Magnitude on Dynamic Stability When Walking in Destabilizing Environments ✰

Emily H Sinitksi 1, Kevin Terry 1,2, Jason M Wilken 1, Jonathan B Dingwell 2,*
PMCID: PMC9128720  NIHMSID: NIHMS1805277  PMID: 22749389

Abstract

External perturbations applied to the walking surface or visual field can challenge an individual’s ability to maintain stability during walking. Accurately quantifying and predicting changes in stability during walking will further our understanding of how individuals respond to challenges encountered during daily life and guide the development of assessments and rehabilitation interventions for individuals at increased risk of falling. This study is the first to determine how orbital and local dynamic stability metrics, including maximum Floquet multipliers and local divergence exponents, change in response to continuous medial-lateral visual and surface perturbations of different amplitudes. Eleven healthy individuals walked in a fully immersive virtual environment. Participants completed two 3-min walking trials each under the following nine conditions: no perturbations, surface perturbations at each of 3 amplitudes, and visual perturbations at each of 5 amplitudes. All perturbations were applied as continuous pseudo-random oscillations. During both surface and visual perturbations, individuals were significantly more orbitally and locally unstable compared to un-perturbed walking. As walking surface perturbation amplitudes increased, individuals were more orbitally (but not locally) unstable. As visual perturbation amplitudes increased, individuals were more locally (but not orbitally) unstable between lower and higher amplitudes. Overall, these dynamic stability metrics were much less sensitive to changes in perturbation amplitudes than to differences between un-perturbed and perturbed walking, or to differences between mechanical and visual perturbations. This suggests that the type of perturbation(s) applied has a far greater impact than the magnitude of those perturbations in determining the response that will be elicited.

Introduction

To effectively identify individuals with increased fall risk, we must first determine how humans maintain stability during walking. Dynamic walking stability is the ability to respond to external (e.g., irregular surface) or internal (e.g., neuromuscular noise) perturbations without falling (Dingwell and Kang, 2007). Imposing external perturbations can challenge a person’s ability to maintain stability while they walk. Accurately quantifying and predicting these changes is critical to understanding how individuals respond to challenges encountered during daily life, and can help guide development of assessments and interventions for individuals with increased fall risk.

Maximum Floquet multipliers (that quantify “orbital” stability) and local divergence exponents (that quantify “local” stability) each quantify the sensitivity of gait trajectories to very small perturbations (Dingwell and Cusumano, 2000; Dingwell and Kang, 2007) and have yielded a number of significant insights. Among other findings, healthy elderly are more locally unstable than young (Kang and Dingwell, 2008) and elderly fallers are less orbitally stable than non-fallers (Granata and Lockhart, 2008; Hamacher et al., 2011). Patients with knee osteoarthritis exhibit greater local instability before corrective surgery, but not after (Yakhdani et al., 2010). Importantly, elderly (Kang and Dingwell, 2008) and patients with diabetic neuropathy (Dingwell et al., 2000; Manor et al., 2008) can improve their local dynamic stability by walking slower (Dingwell and Marin, 2006; England and Granata, 2007), even though slower speeds simultaneously lead to increased gait variability (Dingwell and Marin, 2006; Kang and Dingwell, 2008). However, none of these studies imposed external perturbations during walking.

While these dynamic stability metrics are mathematically well defined, there is no theoretical guarantee responses to infinitesimally small perturbations will predict responses to larger perturbations. Thus, the extent to which these measures can predict actual fall risk is still being determined. Recent modeling studies provide both indirect (Bruijn et al., 2012) and direct (Roos and Dingwell, 2011) support for using short-term local divergence exponents to predict fall risk. In healthy humans, local divergence exponents differentiated walking on compliant surfaces versus rigid surfaces (Chang et al., 2010) and walking with or without galvanic vestibular stimulation (Sloot et al., 2011; van Schooten et al., 2011). These studies, however, imposed only very subtle perturbations. Conversely, McAndrew et al. (2010; 2011) imposed constantly-varying side-to-side movements of either the visual field or walking surface. Those perturbations mimicked typical mechanical perturbations, like walking across loose rocks (Gates et al., 2012), or visual perturbations, like walking along a crowded sidewalk or hallway. However, McAndrew et al. (2010; 2011) imposed only one perturbation amplitude of each type, making it difficult to assess the sensitivity of individuals’ responses to those perturbations. O’Conner and Kuo (2009) applied continuous mediolateral sinusoidal translations of the visual field using multiple amplitudes. However, they only examined visual field translations and only quantified variability of step lengths and step widths during walking.

Currently, no published studies have investigated how systematic changes in perturbation amplitude affect the dynamic stability of human walking. However, different perturbations of different amplitudes may be more or less challenging to different individuals, and/or to different patient populations (e.g., elderly, stroke, amputation, etc.) than to appropriate control groups. Therefore, the present study applied continuous mediolateral visual and walking surface perturbations of different amplitudes to quantify how sensitive these metrics are to larger versus smaller perturbations. We hypothesized that both types of perturbations would lead to larger maximum Floquet multipliers (i.e., less linearly stable) and larger local divergence exponents (i.e., locally more unstable) compared to un-perturbed walking. We also hypothesized that larger perturbation amplitudes would further destabilize participants, thus inducing even larger values of both measures. Testing these hypotheses is critical to developing assessment tools that can allow us to predict patients’ risk of falling without having to actually make them fall.

Methods

Subjects and Experimental Protocol

Eleven healthy individuals (8 M / 3 F; age 26 ± 7 years; height 1.73 ± 0.09 m; body mass 78 ± 16 kg) with no history of lower extremity injury, surgery, or neurological impairments volunteered to participate. This study was approved by the Institutional Review Boards at Brooke Army Medical Center, Ft. Sam Houston, TX, and The University of Texas at Austin. All participants provided written, informed consent.

All subjects walked on a treadmill in a Computer Assisted Rehabilitation Environment (CAREN) virtual reality system (Motek, Amsterdam, Netherlands; Fig. 1). The protocols used here were similar those previously described in (McAndrew et al., 2010; 2011). Walking speed (v) was scaled to each subject’s leg length (l):v=0.40×g⋅l, resulting in a speed of approximately 1.25 m/s for a subject with l = 1 m (Vaughan and O'Malley, 2005). Participants completed a 6-min acclimation period followed by two trials of each of the following walking conditions: no perturbations (NP), mediolateral walking surface (platform) perturbations at each of 3 amplitudes (P1-3), or mediolateral visual perturbations at each of five amplitudes (V1-5). Each walking trial was 3 minutes long. The order of presentation of these conditions was randomized for each individual, but within each condition trials were presented consecutively. Rest breaks were provided between conditions or at the participant’s request. Only mediolateral perturbations were applied because humans are more unstable in the mediolateral direction while walking (Kuo, 1999; Bauby and Kuo, 2000; Dean et al., 2007; O'Connor and Kuo, 2009; McAndrew et al., 2011).

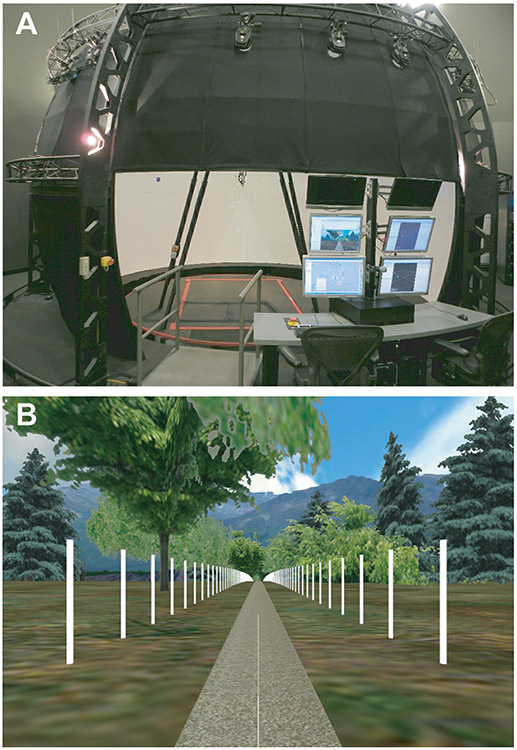
Figure 1. Computer Assisted Rehabilitation ENvironment (CAREN):

Figure 1.

Open in a new tab

A) The CAREN system consists of a 7m diameter dome with a virtual environment projected 300° around the subject from 40° below eye level to 60° above eye level on the inside of the dome. At the base of the dome is a 2m × 3m instrumented treadmill embedded in a 4m diameter platform capable of motion with 6 degrees-of-freedom. B) The virtual reality scene depicted a path through a forest with mountains in the background. The path was lined on both sides with 2.4 m tall white posts spaced every 3 m to enhance motion parallax.

During NP trials, participants walked at constant speed with no perturbations and normal visual optic flow where the scene movement matched the treadmill belt speed. Following McAndrew et al. (2010; 2011), all mediolateral perturbations were applied as a pseudo-random signal consisting of a sum of 4 sine waves (Eq. 1) with incommensurate frequencies (0.16, 0.21, 0.24, and 0.49 Hz):

A(t)=AW[1.0sin(0.16⋅2πt)+0.8sin(0.21⋅2πt)+1.4sin(0.24⋅2πt)+0.5sin(0.49⋅2πt)], (1)

where A(t) was the perturbation amplitude in meters, Aw was a weighting factor (Table 1) in meters and t was time in seconds. Maximum amplitudes selected for each condition (i.e., P3 and V5) here were the same as in McAndrew et al. (2010; 2011). During platform perturbation trials, the treadmill surface translated continuously while participants walked with normal visual optic flow. During visual perturbation trials, the platform remained stationary and mediolateral translations of the visual field were added to the normal visual optic flow.

Table 1:

Amplitude weighting factors, Aw, and the corresponding maximum ± peak-to-peak mediolateral displacements, A(t), for each platform and visual perturbation condition.

Platform:
Condition Amplitude
(Aw)		 Maximum
A(t) (cm)
NP 0.00 ± 0.0
P1 0.03 ± 9.3
P2 0.04 ± 12.5
P3 0.05 ± 15.6
Visual:
Condition Amplitude
(Aw)		 Maximum
A(t) (cm)
NP 0.00 ± 0.0
V1 0.30 ± 93
V2 0.35 ± 110
V3 0.40 ± 125
V4 0.45 ± 140
V5 0.50 ± 156
Open in a new tab

Data Collection and Processing

To represent trunk movements, a marker on the C7 vertebra (Dingwell and Marin, 2006) was recorded at 60 samples/sec using a 24-camera motion capture system (VICON Peak, Oxford, UK). Kinematic data were analyzed using Nexus (VICON Peak, Oxford, UK), Visual3D (C-Motion Inc., Germantown, MD), and Matlab (The Mathworks, Natick, MA). For the analyses presented here, only the mediolateral component of these C7 marker movements was analyzed. Heel strikes were determined using a velocity-based detection algorithm (Zeni et al., 2008) and the first 150 strides for each trial were used for subsequent analyses. C7 marker velocity data were analyzed to remove non-stationarities associated with drifting of the subjects relative to the treadmill (Dingwell and Marin, 2006). For platform perturbation trials, however, the recorded marker data included the movements of both the subject and the platform. Therefore, the platform displacements were subtracted from the C7 marker displacements prior to calculating C7 marker velocity.

Following standard methods (Dingwell and Cusumano, 2000; Gates and Dingwell, 2009), delay embedded state spaces were constructed from the mediolateral velocity (vML) of the C7 marker and its time delayed copies (Fig. 2):

SML(t)=[vML(t),vML(t+τ),vML(t+2τ),vML(t+3τ),vML(t+4τ)]∈ℜ5, (2)

where SML(t) was the 5-dimensional state vector, vML(t) was the original 1-dimensional time series, and τ was the time delay. Time delays were selected using the Average Mutual Information function (Fraser and Swinney, 1986) for each subject. The average time delay computed across subjects (τ = 20 samples = 0.333 sec) was used to reconstruct all final state spaces. Embedding dimensions were determined using Global False Nearest Neighbors analysis (Kennel et al., 1992), yielding an embedding dimension of 5 for all walking conditions (Dingwell and Cusumano, 2000; Dingwell and Marin, 2006).

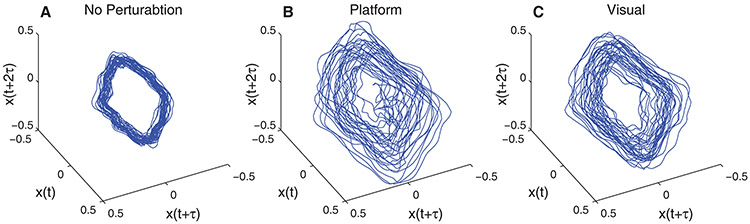
Figure 2. Typical Trunk Movements During Walking:

Figure 2.

Open in a new tab

Examples of 3-dimensional projections of the 5-dimensional time-delay state spaces of the medial-lateral velocity of the C7 marker. Conditions shown include A) no perturbation, B) platform perturbation amplitude P2, and C) visual perturbation amplitude V4. Data shown are for 1 typical subject. State spaces were reconstructed using a time delay of 20 samples (i.e., 333 ms).

Dynamic Stability Analyses

Dynamic stability of these C7 velocity state spaces was quantified using two approaches: maximum Floquet multipliers (maxFM) and local divergence exponents (short-term, λ*S, and long-term, λ*L). MaxFM quantifies the rate at which all trajectories diverge or converge from the average trajectory after one complete stride. In contrast, λ*S and λ*L assess dynamic walking stability within consecutive strides and describe how quickly infinitesimally close initial conditions diverge over time (Rosenstein et al., 1993; Dingwell and Cusumano, 2000). Floquet theory assumes purely periodic dynamics, whereas local divergence exponents assume strongly aperiodic system. Because human walking is neither strictly periodic nor strongly aperiodic, both measures provide complimentary estimates of dynamic walking stability (Dingwell and Cusumano, 2000; Dingwell and Kang, 2007).

To compute maxFM, the state space data were first divided into individual strides. Data for each stride were normalized to 0-100% gait cycle (Dingwell and Kang, 2007). At each percent of the gait cycle, a Poincaré map was defined to determine how small perturbations from the average trajectory grew or diminished between consecutive strides (Nayfeh and Balachandran, 1995; Donelan et al., 2004; Kang and Dingwell, 2008). The magnitude of maxFM for each Poincaré section was calculated and averaged over the gait cycle. MaxFM < 1 indicates that trajectories on average converge over consecutive strides and the system is orbitally stable. If maxFM increases, but remains < 1, the system is less orbitally stable (Kang and Dingwell, 2008).

To compute λ*S and λ*L, prior to state space construction, the 150 continuous strides of data were first re-sampled to 15,000 total data points, or an average of 100 data points per stride (England and Granata, 2007; Bruijn et al., 2009). For each nearest neighbor in state space, the logarithmic distance between neighboring trajectories was calculated for 10 subsequent strides. The resulting average logarithmic distance for all nearest neighbors was used to determine the divergence exponents. A least-square fit was used to estimate the slope of the mean log divergence curve between 0-1 stride (λ*S) and 4-10 strides (λ*L) (Dingwell and Cusumano, 2000; Kang and Dingwell, 2008). Positive exponents indicate that perturbations diverge over time and that the system is locally unstable. Larger positive exponents indicate greater local instability.

Statistical Analyses

For each dependent measure (maxFM, λ*S, and λ*L), single-factor repeated measures ANOVAs were used to determine main effects differences across perturbation amplitudes separately for platform and visual perturbation trials. Pair-wise comparisons were performed using estimated marginal means with a Sidak correction. All statistical analyses were performed using SPSS 16 (SPSS Inc., Chicago, IL).

Results

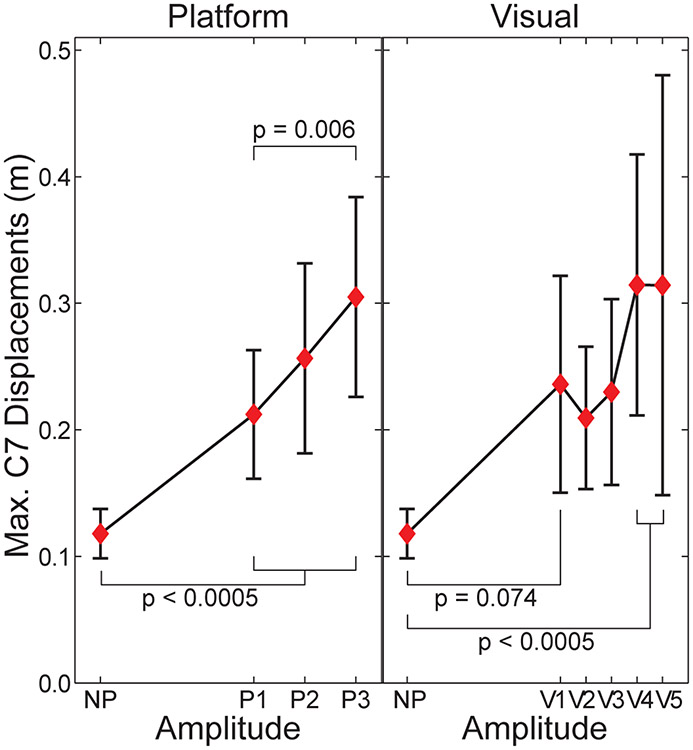
All subjects exhibited clear responses to the perturbations applied (Figs. 2 & 3), consistent with previous findings (McAndrew et al., 2010; 2011). Maximum peak-to-peak displacements of the C7 marker were significantly greater than NP for all 3 platform perturbation conditions and for the 2 largest visual perturbation amplitudes (Fig. 3). Maximum C7 displacements also tended to increase with increasing perturbation amplitudes (Fig. 3), especially for the platform perturbations (P3 > P1; p = 0.006).

Figure 3. Maximum Peak-to-Peak Displacements of the C7 Marker:

Figure 3.

Open in a new tab

Data are for the platform (P1-P3) and visual (V1-V5) perturbations, each relative to the no-perturbation (NP) condition. Horizontal axes are scaled to the amplitude weighting factors (Aw; Table 1) for each perturbation type. For platform perturbation trials, the platform displacements were first subtracted from the C7 marker displacements. Error bars indicate between-subject ± SD.

Subjects remained both orbitally stable (maxFM < 1; Figs. 4 & 6) and locally unstable (λ*S and λ*L > 0; Figs. 5 & 7) during all test conditions. This was consistent with previous experimental findings in humans (Dingwell and Kang, 2007) and predictions from dynamic walking models (Su and Dingwell, 2007; Roos and Dingwell, 2011).

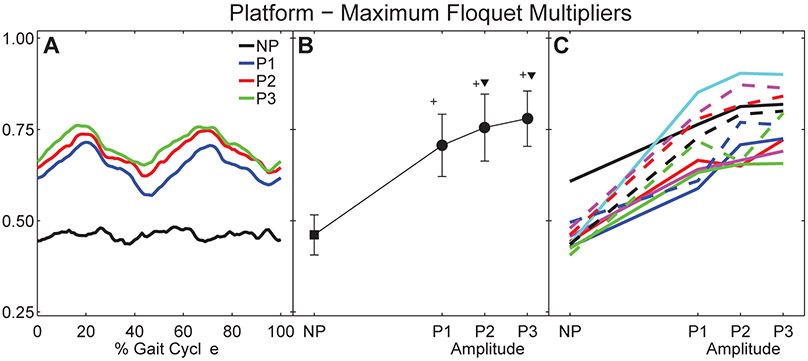
Figure 4. Orbital Dynamic Stability During Platform Perturbations:

Figure 4.

Open in a new tab

A) Average maximum Floquet multipliers for each percent gait cycle (0 – 100%) for all subjects. B) Mean maximum Floquet multipliers over entire gait cycle for all subjects. Error bars indicate between-subject ± SD. The ‘+’ symbols indicate significant differences from NP. The ‘▼’ symbols indicate significant differences from P1. C) Mean maximum Floquet multipliers for each individual subject. Each unique line and color combination represents one subject.

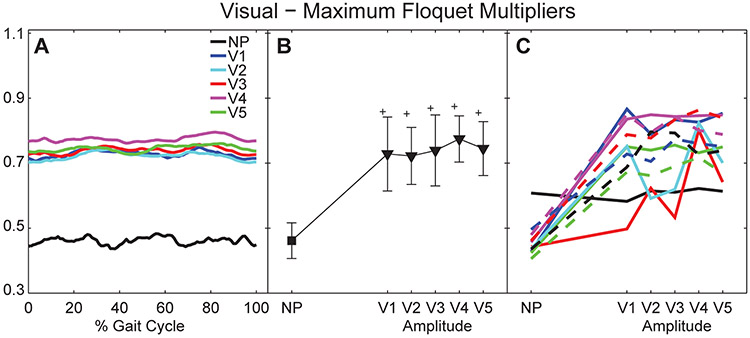
Figure 6. Orbital Dynamic Stability During Visual Perturbations:

Figure 6.

Open in a new tab

A) Average maximum Floquet multipliers for each percent gait cycle (0 – 100%) for all subjects. B) Mean maximum Floquet multipliers over entire gait cycle for all subjects. Error bars indicate between-subject ± SD. The ‘+’ symbols indicate significant differences from NP. C) Mean maximum Floquet multipliers for each individual subject. Each unique line and color combination represents one subject.

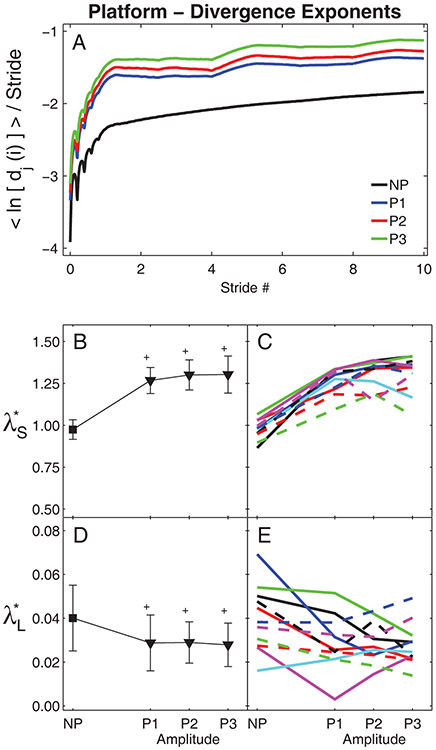
Figure 5. Local Dynamic Stability During Platform Perturbations:

Figure 5.

Open in a new tab

A) Average mean log divergence curves for all subjects. B) Group means for λ*S exponents. C) Mean λ*S exponents for individual subjects. D) Group means for λ*L exponents. E) Mean λ*L exponents for individual subjects. In (B) and (D), error bars indicate between-subject ±SD and the ‘+’ symbols indicate significant differences from NP. In (C) and (E), each unique line and color combination represents one subject.

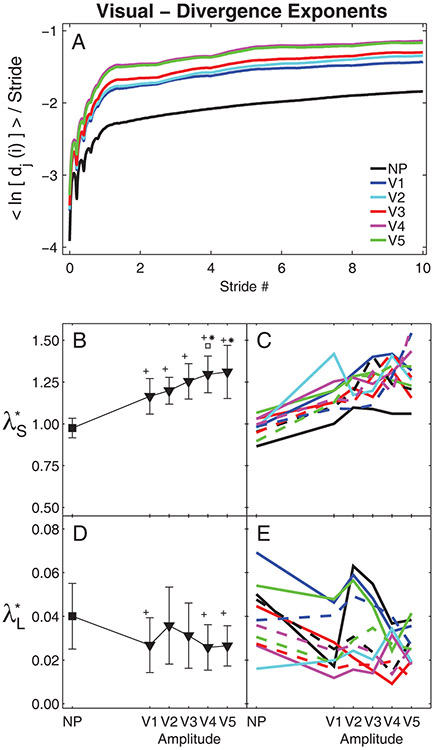
Figure 7. Local Dynamic Stability During Visual Perturbations:

Figure 7.

Open in a new tab

A) Average mean log divergence curves for all subjects. B) Group means for λ*S exponents. C) Mean λ*S exponents for individual subjects. D) Group means for λ*L exponents. E) Mean λ*L exponents for individual subjects. In (B) and (D), error bars indicate between-subject ±SD, the ‘+’ indicate significant differences from NP, the ‘*’ indicate significant differences from V1 and V2, and the ‘□’ indicates a significant difference from V2. In (C) and (E), each unique line and color combination represents one subject.

Platform Perturbations

During un-perturbed walking, maximum Floquet multipliers remained approximately constant across the entire gait cycle (Fig. 4A), consistent with previous findings (Dingwell and Kang, 2007). However, when the platform perturbations were imposed, the maximum Floquet multipliers varied systematically across the gait cycle (Fig. 4A). Here, they exhibited distinct peaks near the middle of each single limb stance phase (i.e., at ~20% and ~70% of the gait cycle). All subjects exhibited increased maxFM (p < 0.001; Fig. 4B) for all platform perturbation conditions relative to un-perturbed walking. MaxFM also increased significantly as perturbation amplitude increased from P1 to P3. MaxFM for P2 and P3 were both significantly greater than maxFM for P1 (p < 0.01). However, maxFM for P2 and P3 were not significantly different (p = 0.235). These increases in maxFM with increasing perturbation amplitude were highly consistent across subjects (Fig. 4C).

Subjects exhibited large increases in local divergence amplitudes during all platforms perturbation conditions (Fig. 5A). All subjects exhibited increased λ*S (p < 0.001; Fig. 5B), and decreased λ*L (p < 0.001; Fig. 5D) for all platform perturbation conditions relative to un-perturbed walking. However, increasing perturbation amplitude from P1 to P3 did not significantly change λ*S (p > 0.40; Fig. 5B) or λ*L (p > 0.90; Fig. 5D). Increases in λ*S were somewhat consistent across most subjects (Fig. 5C), but changes in λ*L were far less consistent across subjects (Fig. 5D).

Visual Perturbations

Contrary to the platform perturbations (Fig. 4A), during the visual perturbation conditions, subjects exhibited no systematic variations across the gait cycle in their maximum Floquet multipliers (Fig. 6A). However, all subjects exhibited increased maxFM (p < 0.001; Fig. 6B) for all visual perturbation conditions relative to un-perturbed walking. Also different from the platform perturbation conditions (Fig. 4B), increasing visual perturbation amplitude beyond V1 did not significantly change maxFM (p > 0.2; Fig. 6B). Changes in maxFM with varying visual perturbation amplitudes were also far less consistent across subjects (Fig. 6C).

Similar to the platform perturbations (Fig. 5A), subjects exhibited large increases in local divergence amplitudes during all visual perturbation conditions (Fig. 7A). Likewise, subjects exhibited increased λ*S (p < 0.001; Fig. 7B) for all visual perturbation conditions relative to un-perturbed walking. However, unlike the platform perturbations (Fig. 5B), changes in visual perturbation amplitudes did elicit changes in λ*S (Fig. 7B). Perturbation amplitude V4 elicited significantly greater λ*S than amplitudes V1 or V2 (p < 0.01) and perturbation amplitude V5 elicited significantly greater λ*S than amplitude V1 (p < 0.01). Post-hoc analyses revealed that only perturbation amplitudes V1, V4, and V5 elicited significantly decreased λ*L compared to un-perturbed walking (p < 0.04; Fig. 7D). Variations across visual perturbation amplitudes were less consistent across subjects for both λ*S (Fig. 7C) and λ*L (Figs. 7E) than variations across platform perturbation amplitudes (Fig. 5C & 5E).

Discussion

Quantifying dynamic stability while walking with varying perturbation amplitudes is critical to determining if dynamic stability metrics can adequately predict fall risk without having to make subjects fall. Here, we systematically varied the magnitudes of external perturbations imposed by the walking environment on the same subjects walking at the same speed. This is the first study to quantify how such experimental manipulations affect well-established measures of local dynamic stability. We applied both platform and visual perturbations in the mediolateral direction because mediolateral perturbations present the greatest challenge to stability during walking (Bauby and Kuo, 2000; Dean et al., 2007; McAndrew et al., 2010; McAndrew et al., 2011).

During both platform and visual perturbations, both maxFM and λ*S significantly increased, but λ*L significantly decreased, compared to un-perturbed walking. These findings were consistent with data from McAndrew et al. (2011) and indicate individuals were destabilized while walking in these environments. Van Schooten et al. (2011) also reported increased λ*S but decreased λ*L when healthy subjects walked at 1.53 m/s with galvanic vestibular stimulation. Generally, increases in λ*S or λ*L could indicate greater local instability. However, the local divergence curves (Figs. 5A & 7A) quantify real physical distances in state space. Because our subjects did not fall down, their movement trajectories remained bounded within a finite region in state space. In such cases, the local divergence curves cannot increase indefinitely (Rosenstein et al., 1993; McAndrew et al., 2011). Once the divergence reaches its natural maximum, these curves must become flat (i.e., λ*L → 0) (Rosenstein et al., 1993). This is seen directly in Figs 5A & 7A, where the perturbed divergence curves clearly rise more quickly (resulting in higher λ*S), but then also “flatten out” sooner (resulting in lower λ*L). Thus, it is more likely that the decreased λ*L observed here (as in McAndrew et al., 2011) indicate that subjects’ state trajectories approached their divergence limits more quickly and thus began to plateau sooner (Figs. 5A & 7A), and do not reflect any “improvement” in their long-term local dynamic stability (McAndrew et al., 2011). These results extend previous findings suggesting λ*L may not be a good predictor of instability or fall risk (Dingwell and Marin, 2006; Roos and Dingwell, 2011; van Schooten et al., 2011; Bruijn et al., 2012).

Both the maxFM and local divergence exponents easily detected differences between perturbed and un-perturbed walking for both platform (Figs. 4–5) and visual (Figs. 6–7) perturbations, consistent with previous experiments (McAndrew et al., 2011). However, whereas maxFM also distinguished differences between individual platform perturbation amplitudes (Fig. 4B), the local divergence exponents did not (Fig. 5B & 5D). This contrasts somewhat with previous modeling work (Su and Dingwell, 2007; Bruijn et al., 2011; Roos and Dingwell, 2011; Bruijn et al., 2012), where λ*S was more sensitive to changes in perturbation amplitudes than maxFM. However, there are many differences between those models and humans (e.g., degree of mechanical complexity, lack of neurophysiological control, differences in types and/or magnitude of perturbations applied, etc.) that might account for these differences. Conversely, for the visual perturbation conditions, λ*S distinguished differences between individual perturbation amplitudes (Fig. 7B), while maxFM did not (Fig. 6B). Thus, here, maxFM was more sensitive to changes in platform perturbation amplitudes and λ*S was more sensitive to changes in visual perturbation amplitudes.

Several previous modeling (Schwab and Wisse, 2001; Hobbelen and Wisse, 2007; Su and Dingwell, 2007; Bruijn et al., 2011) and experimental (Dingwell and Kang, 2007; Dingwell et al., 2007; van Schooten et al., 2011) studies found that maxFM was either not, or only minimally, sensitive to changes/differences in purported fall risk. The present results appear somewhat contrary to these findings. However, those previous efforts studied either un-perturbed or only minimally perturbed walking. Conversely, other studies found significantly greater maxFM for post-polio patients vs. healthy adults (Hurmuzlu et al., 1996), for healthy elderly vs. young (Kang and Dingwell, 2008), for elderly fallers vs. non-fallers (Granata and Lockhart, 2008; Hamacher et al., 2011), and for young healthy humans subjected to larger perturbations (McAndrew et al., 2011). These experimental findings are supported by recent modeling work (Roos and Dingwell, 2011) that showed increases in maxFM, but only for large perturbation amplitudes that induced high fall risk. Taken together, these findings suggest that while maxFM may exhibit less sensitivity to detect small/subtle changes in fall risk, this measure might exhibit greater specificity to detect more dramatic increases in fall risk.

Platform perturbations also elicited systematic variations in maxFM across the gait cycle (Fig. 4A), but visual perturbations did not (Fig. 6A). In theory, Floquet multipliers of periodic systems should be independent of the choice of Poincaré section (Nayfeh and Balachandran, 1995). We previously confirmed this to be true for un-perturbed walking in humans (Dingwell and Kang, 2007) and perturbed walking in models (Su and Dingwell, 2007). However, human walking is not strictly periodic. Especially here, continuously subjecting subjects to random perturbations further increases the aperiodicity of their walking. Floquet theory was not intended to apply to such stochastic systems. And yet, these systematic variations in maxFM (Fig. 4A) somehow arose from the interactions between our human subjects and the stochastic perturbations applied to them. It is possible they resulted from variations in local stability along the limit cycle (Ali and Menzinger, 1999), although we did not test this directly. In either case, this clearly indicates the need to quantify these maxFM measures across the entire gait cycle to obtain a comprehensive assessment of how subjects respond to these perturbations.

There were clear differences between how subjects responded to mechanical perturbations of different amplitudes and how they responded to visual perturbations of difference magnitudes (Fig. 3). Varying platform perturbation amplitudes elicited significant changes in maxFM (Fig. 4B), but not λ*S (Fig. 5B). Conversely, varying visual perturbation amplitudes elicited significant changes in λ*S (Fig. 7B), but not maxFM (Fig. 6B). Clearly, not all perturbations are equal. The mechanical perturbations of the moving platform imposed real physical forces on the body that subjects simply could not ignore. However, there were no physical penalties if subjects chose to “ignore” the visual perturbations. The “perturbations” imposed by the moving visual field were purely perceptual / cognitive. Thus, any movements made in response to the visual perturbations were entirely self-generated. Some subjects responded to these visual perturbations more than others. This was consistent with previous studies (Bardy et al., 1996; Warren et al., 2001) and contributed to the larger between-subject differences observed in response to the visual perturbations (Figs. 3, 6C, 7C, and 7E) than to the platform perturbations (Figs, 3, 4C, 5C, and 5E). Thus, this greater between-subject variability likely resulted from the self-generated nature of responses to visual stimuli that depend solely on each individual’s perception of the applied perturbations.

Both local and orbital dynamic stability metrics detected differences between un-perturbed and perturbed walking, but were less sensitive to the changes in perturbation amplitudes imposed in this study. As platform perturbation amplitudes increased (from P1 to P3), healthy individuals became more orbitally unstable (i.e., increased maxFM), but were not more locally unstable (λ*S and λ*L). Conversely, as visual perturbation amplitudes increased (from V1 to V5), these individuals were not more orbitally unstable (maxFM), but were more locally unstable (i.e., increased λ*S). Although statistically significant differences between perturbation amplitudes were found for maxFM for the platform perturbation trials (Fig. 4B) and for λ*S for the visual perturbation trials (Fig. 7B), the magnitudes of these changes were relatively small, especially compared to the differences between perturbed and un-perturbed values. It is possible we did not see larger changes in these stability metrics as perturbation amplitudes increased because the responses elicited at the lowest perturbation amplitudes we applied were already near the maximum responses these perturbations could produce. Had we tested perturbation amplitudes across a wider range in between NP and P1 or V1, we expect we might have seen larger effects of perturbation amplitude.

The present findings demonstrate that the type of perturbation applied is far more critical than perturbation magnitude in determining the nature of the response elicited. Importantly, while we assume the perturbations we applied increased our subjects’ risk of falling, we did not induce actual falls. Likewise, the metrics applied here quantify “local dynamic stability” during walking. This is qualitatively distinct from “global” stability (i.e., risk of falling). However, existing methods that estimate global stability (e.g., (Schwab and Wisse, 2001; Hobbelen and Wisse, 2007; Bruijn et al., 2012), provide only indirect estimates of fall risk, and cannot easily be implemented experimentally. To our knowledge, only Roos and Dingwell (2011) used local stability measures to directly predict actual fall risk, but that was in a model. Those findings are supported by indirect evidence in humans (Granata and Lockhart, 2008; Hamacher et al., 2011). Since the ultimate goal of these efforts is to identify measures that can predict fall risk in humans without having to induce actual falls, a critical need for future work will be to correlate these measures to actual risk of actual falls in humans. The present work provides a necessary foundation from which to do this.

Acknowledgements:

Support by National Institutes of Health (NIH) grant 1-R01-HD059844 (to JBD and JMW).

✰

The views expressed herein are those of the authors and do not reflect the official policy or position of Brooke Army Medical Center, the U.S. Army Medical Department, the U.S. Army Office of the Surgeon General, the Department of the Army, Department of Defense or the U.S. Government.

References:

  1. Ali F, Menzinger M, 1999. On the local stability of limit cycles. Chaos: An Interdisciplinary Journal of Nonlinear Science 9 (2), 348–356. [DOI] [PubMed] [Google Scholar]
  2. Bardy BG, Warren WH, Kay BA, 1996. Motion parallax is used to control postural sway during walking. Experimental Brain Research 111 (2), 271–282. [DOI] [PubMed] [Google Scholar]
  3. Bauby CE, Kuo AD, 2000. Active control of lateral balance in human walking. Journal of Biomechanics 33 (11), 1433–1440. [DOI] [PubMed] [Google Scholar]
  4. Bruijn SM, Bregman DJJ, Meijer OG, Beek PJ, van Dieën JH, 2011. The validity of stability measures: A modelling approach. Journal of Biomechanics 44 (13), 2401–2408. [DOI] [PubMed] [Google Scholar]
  5. Bruijn SM, Bregman DJJ, Meijer OG, Beek PJ, van Dieën JH, 2012. Maximum lyapunov exponents as predictors of global gait stability: A modelling approach. Medical Engineering & Physics 34 (4), 428–436. [DOI] [PubMed] [Google Scholar]
  6. Bruijn SM, van Dieën JH, Meijer OG, Beek PJ, 2009. Is slow walking more stable? Journal of Biomechanics 42 (10), 1506–1512. [DOI] [PubMed] [Google Scholar]
  7. Chang MD, Sejdić E, Wright V, Chau T, 2010. Measures of dynamic stability: Detecting differences between walking overground and on a compliant surface. Human Movement Science 29 (6), 977–986. [DOI] [PubMed] [Google Scholar]
  8. Dean JC, Alexander NB, Kuo AD, 2007. The effect of lateral stabilization on walking in young and old adults. IEEE Transactions on Biomedical Engineering 54 (11), 1919–1926. [DOI] [PubMed] [Google Scholar]
  9. Dingwell JB, Cusumano JP, 2000. Nonlinear time series analysis of normal and pathological human walking. Chaos: An Interdisciplinary Journal of Nonlinear Science 10 (4), 848–863. [DOI] [PubMed] [Google Scholar]
  10. Dingwell JB, Cusumano JP, Sternad D, Cavanagh PR, 2000. Slower speeds in neuropathic patients lead to improved local dynamic stability of continuous overground walking. Journal of Biomechanics 33 (10), 1269–1277. [DOI] [PubMed] [Google Scholar]
  11. Dingwell JB, Kang HG, 2007. Differences between local and orbital dynamic stability during human walking. Journal of Biomechanical Engineering 129 (4), 586–593. [DOI] [PubMed] [Google Scholar]
  12. Dingwell JB, Kang HG, Marin LC, 2007. The effects of sensory loss and walking speed on the orbital dynamic stability of human walking. Journal of Biomechanics 40 (8), 1723–1730. [DOI] [PubMed] [Google Scholar]
  13. Dingwell JB, Marin LC, 2006. Kinematic variability and local dynamic stability of upper body motions when walking at different speeds. Journal of Biomechanics 39 (3), 444–452. [DOI] [PubMed] [Google Scholar]
  14. Donelan JM, Shipman DW, Kram R, Kuo AD, 2004. Mechanical and metabolic requirements for active lateral stabilization in human walking. Journal of Biomechanics 37 (6), 827–835. [DOI] [PubMed] [Google Scholar]
  15. England SA, Granata KP, 2007. The influence of gait speed on local dynamic stability of walking. Gait & Posture 25 (2), 172–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Fraser AM, Swinney HL, 1986. Independent coordinates for strange attractors from mutual information. Physical Review A 33 (2), 1134–1140. [DOI] [PubMed] [Google Scholar]
  17. Gates DH, Dingwell JB, 2009. Comparison of different state space definitions for local dynamic stability analyses. Journal of Biomechanics 42 (9), 1345–1349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Gates DH, Wilken JM, Scott SJ, Sinitsky EH, Dingwell JB, 2012. Kinematic strategies for walking across a destabilizing rock surface. Gait & Posture 35 (1), 36–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Granata KP, Lockhart TE, 2008. Dynamic stability differences in fall-prone and healthy adults. Journal of Electromyography and Kinesiology 18 (2), 172–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Hamacher D, Singh NB, Van Dieën JH, Heller MO, Taylor WR, 2011. Kinematic measures for assessing gait stability in elderly individuals: A systematic review. Journal of The Royal Society Interface 8 (65), 1682–1698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Hobbelen DGE, Wisse M, 2007. A disturbance rejection measure for limit cycle walkers: The gait sensitivity norm. IEEE Transactions on Robotics 23 (6), 1213–1224. [Google Scholar]
  22. Hurmuzlu Y, Basdogan C, Stoianovici D, 1996. Kinematics and dynamic stability of the locomotion of post-polio patients. ASME Journal of Biomechanical Engineering 118 (3), 405–411. [DOI] [PubMed] [Google Scholar]
  23. Kang HG, Dingwell JB, 2008. The effects of walking speed, strength and range of motion on gait stability in healthy older adults. Journal of Biomechanics 41 (14), 2899–2905. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kang HG, Dingwell JB, 2008. Separating the effects of age and speed on gait variability during treadmill walking. Gait & Posture 27 (4), 572–577. [DOI] [PubMed] [Google Scholar]
  25. Kennel MB, Brown R, Abarbanel HDI, 1992. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Physical Review A 45 (6), 3403–3411. [DOI] [PubMed] [Google Scholar]
  26. Kuo AD, 1999. Stabilization of lateral motion in passive dynamic walking. The International Journal of Robotics Research 18 (9), 917–930. [Google Scholar]
  27. Manor B, Wolenski P, Li L, 2008. Faster walking speeds increase local instability among people with peripheral neuropathy. Journal of Biomechanics 41 (13), 2787–2792. [DOI] [PubMed] [Google Scholar]
  28. McAndrew PM, Dingwell JB, Wilken JM, 2010. Walking variability during continuous pseudo-random oscillations of the support surface and visual field. Journal of Biomechanics 43 (8), 1470–1475. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. McAndrew PM, Wilken JM, Dingwell JB, 2011. Dynamic stability of human walking in visually and mechanically destabilizing environments. Journal of Biomechanics 44 (4), 644–649. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Nayfeh AH, Balachandran B, 1995. Applied nonlinear dynamics: Analytical, computational, and experimental methods. John Wiley & Sons,, New York, New York. [Google Scholar]
  31. O'Connor SM, Kuo AD, 2009. Direction-dependent control of balance during walking and standing. Journal of Neurophysiology 102 (3), 1411–1419. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Roos PE, Dingwell JB, 2011. Influence of simulated neuromuscular noise on the dynamic stability and fall risk in a 3d dynamic walking model. Journal of Biomechanics 44 (8), 1514–1520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Rosenstein MT, Collins JJ, DeLuca CJ, 1993. A practical method for calculating largest lyapunov exponents from small data sets. Physica D: Nonlinear Phenomena 65, 117–134. [Google Scholar]
  34. Schwab AL, Wisse M, 2001. Basin of attraction of the simplest walking model (paper # detc01 / vib-21363). In. Proceedings of the 2001 asme design engineering technical conferences and computers and information in engineering conference. American Society for Mechanical Engineering, Pittsburgh, PA. [Google Scholar]
  35. Sloot L, van Schooten K, Bruijn S, Kingma H, Pijnappels M, van Dieën J, 2011. Sensitivity of local dynamic stability of over-ground walking to balance impairment due to galvanic vestibular stimulation. Annals of Biomedical Engineering 39 (5), 1563–1569. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Su JL, Dingwell JB, 2007. Dynamic stability of passive dynamic walking on an irregular surface. ASME Journal of Biomechanical Engineering 129 (6), 802–810. [DOI] [PubMed] [Google Scholar]
  37. van Schooten KS, Sloot LH, Bruijn SM, Kingma H, Meijer OG, Pijnappels M, van Dieën JH, 2011. Sensitivity of trunk variability and stability measures to balance impairments induced by galvanic vestibular stimulation during gait. Gait & Posture 33 (4), 656–660. [DOI] [PubMed] [Google Scholar]
  38. Vaughan CL, O'Malley MJ, 2005. Froude and the contribution of naval architecture to our understanding of bipedal locomotion. Gait & Posture 21 (3), 350–362. [DOI] [PubMed] [Google Scholar]
  39. Warren WH, Kay BA, Zosh WD, Duchon AP, Sahuc S, 2001. Optic flow is used to control human walking. Nature Neuroscience 4 (2), 213–216. [DOI] [PubMed] [Google Scholar]
  40. Yakhdani HRF, Bafghi HA, Meijer OG, Bruijn SM, van den Dikkenberg N, Stibbe AB, van Royen BJ, van Dieën JH, 2010. Stability and variability of knee kinematics during gait in knee osteoarthritis before and after replacement surgery. Clinical Biomechanics 25 (3), 230–236. [DOI] [PubMed] [Google Scholar]
  41. Zeni JA, Richards JG, Higginson JS, 2008. Two simple methods for determining gait events during treadmill and overground walking using kinematic data. Gait & Posture 27 (4), 710–714. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES