Summary:
Many studies have shown that the excitation and inhibition received by cortical neurons remain roughly balanced across many conditions. A key question for understanding the dynamical regime of cortex is the nature of this balancing. Theorists have shown that network dynamics can yield systematic cancellation of most of a neuron’s excitatory input by inhibition. We review a wide range of evidence pointing to this cancellation occurring in a regime in which the balance is loose, meaning that the net input remaining after cancellation of excitation and inhibition is comparable in size to the factors that cancel, rather than tight, meaning that the net input is very small relative to the cancelling factors. This choice of regime has important implications for cortical functional responses, as we describe: loose balance, but not tight balance, can yield many nonlinear population behaviors seen in sensory cortical neurons, allow the presence of correlated variability, and yield decrease of that variability with increasing external stimulus drive as observed across multiple cortical areas.
In what regime does cerebral cortex operate? This is a fundamental question for understanding cerebral cortical function. The concept of a “regime” can be defined in various ways. Here we will focus on a definition in terms of the balance of excitation and inhibition: how strong are the excitation and inhibition that cortical cells receive, and how tight is the balance between them? As we will see, the answers to these questions have important implications for the dynamical function of cortex.
We first consider several more fundamental distinctions in cortical regime. First, neurons may fire in a regular or irregular fashion, where regular firing refers to emitting spikes in a more clock-like manner, while irregular firing refers to emitting spikes in a more random manner, like a Poisson process. Cortex appears to be in an irregular regime (Softky and Koch, 1993; Shadlen and Newsome, 1998), though some areas are less irregular than others (Maimon and Assad, 2009). Second, neurons may fire in a synchronous regime, meaning with strong correlations between the firing of different neurons, or an asynchronous regime, meaning with weak (or no) correlations. Here there is varying evidence, which appears to depend on species, cortical area, and brain state. In the asleep or anesthetized condition, slow synchronous fluctuations are the norm (e.g., Stevens and Zador, 1998; Lampl et al., 1999; DeWeese and Zador, 2006; Ecker et al., 2014), with correlations decreased by stimulus drive (Churchland et al., 2010; Smith and Kohn, 2008). In the awake state, both asynchronous (Cohen and Kohn, 2011; Ecker et al., 2010, 2014; Doiron et al., 2016; Poulet and Petersen, 2008; Tan et al., 2014) and synchronous (DeWeese and Zador, 2006; Poulet and Petersen, 2008; Tan et al., 2014) firing regimes have been observed, with correlations decreased by stimulus drive (Churchland et al., 2010; Tan et al., 2014), arousal (including whisking and locomotion; Poulet and Petersen, 2008; McGinley et al., 2015; Vinck et al., 2015; Mccormick et al., 2015; Ferguson and Cardin, 2020) or attention (Cohen and Maunsell, 2009; Mitchell et al., 2009; Engel et al., 2016; Denfield et al., 2018). In our initial discussion we will take cortex to be in an asynchronous regime, as in much previous theoretical work and as seems to generally characterize the awake and stimulated or active state (but see DeWeese and Zador, 2006). Later we will consider mechanisms that suppress correlations with increasing drive. Brunel (2000) first defined conditions on networks of excitatory and inhibitory neurons that led them to operate in asynchronous or synchronous, and irregular or regular, regimes.
A third distinction is whether a network goes to a stable fixed rate of firing for a fixed input (with noisy fluctuations about that fixed rate given noisy inputs), or whether it shows more complex behaviors, such as movement between multiple fixed points, oscillations, or chaotic wandering of firing rates. We will focus on the case of a single stable fixed point, which seems likely to reasonably approximate at least awake sensory cortex (see discussion in Miller, 2016).
Finally, for a given fixed point, recurrent excitation may be strong enough to destabilize the fixed point in the absence of feedback inhibition; that is, if inhibitory firing were held frozen at its fixed point level, a small perturbation of excitatory firing rates would cause them to either grow very large or collapse to zero. In that case, the fixed point is stabilized by feedback inhibition, and the network is known as an inhibition-stabilized network (ISN). Alternatively, the recurrent excitation may be weak enough to remain stable even without feedback inhibition. A number of studies have found strong evidence that multiple cortical areas operate as ISNs, including primary visual, somatosensory, and motor/premotor cortices at spontaneous (Sanzeni et al., 2020a) and primary visual and auditory cortex at stimulus-driven (Ozeki et al., 2009; Kato et al., 2017; Adesnik, 2017) levels of activity.
Note that for some of the distinctions we describe between regimes, there is a sharp transition from one regime to the other, while for others the transition is gradual. We use the word “regime” in either case to describe qualitatively different network behaviors.
The assumption that cortex is in an irregularly-firing regime (as well as its operation as an ISN) strongly points to the need for some kind of balance between excitation and inhibition. Stochasticity of cellular and synaptic mechanisms (Mainen and Sejnowski, 1995; Schneidman et al., 1998; O’Donnell and van Rossum, 2014) and input correlations (Stevens and Zador, 1998; DeWeese and Zador, 2006) may contribute to irregular firing. However, a number of authors have argued that, assuming inputs are un- or weakly-correlated, then irregular firing will arise if the mean input to cortical cells is sub- or peri-threshold, so that firing is induced by fluctuations from the mean rather than by the mean itself (Tsodyks and Sejnowski, 1995; van Vreeswijk and Sompolinsky, 1996, 1998; Troyer and Miller, 1997; Amit and Brunel, 1997). This is referred to as the fluctuation-driven regime, as opposed to the mean-driven regime in which the mean input is strongly suprathreshold and spiking is largely driven by integration of this mean input. The fluctuation-driven regime yields random, Poisson-process-like firing, because fluctuations are equally likely to occur at any time, whereas the mean-driven regime yields regular firing.
Given the strength of inputs to cortex (to be discussed below), the mean excitation received by a strongly-responding cell is likely to be sufficient to drive the cell near or above threshold. Therefore, for the mean input to be subthreshold, the mean inhibition is likely to cancel a significant portion of the mean excitation; that is, the excitation and inhibition received by a cortical cell should be at least roughly balanced (Tsodyks and Sejnowski, 1995; van Vreeswijk and Sompolinsky, 1996, 1998). Consistent with the idea that inhibition balances excitation, many experimental investigations have suggested that cortical or hippocampal excitation and inhibition remain balanced or inhibition-dominated across varying activity levels (Galarreta and Hestrin, 1998; Anderson et al., 2000; Shu et al., 2003; Wehr and Zador, 2003; Marino et al., 2005; Wu et al., 2006; Moore et al., 2018; Haider et al., 2006; Higley and Contreras, 2006; Wu et al., 2008; Okun and Lampl, 2008; Atallah and Scanziani, 2009; Tan and Wehr, 2009; Yizhar et al., 2011; Graupner and Reyes, 2013; Haider et al., 2013; Zhou et al., 2014; Barral and Reyes, 2016; Dehghani et al., 2016; Bridi et al., 2020; Antoine et al., 2019; Dorrn et al., 2010; Sukenik et al., 2021).
Excitation and inhibition may be balanced in at least two ways. First, inhibitory and excitatory synaptic weights may be co-tuned, so that cells (Xue et al., 2014; Bhatia et al., 2019) and/or dendritic segments (Iascone et al., 2020; Liu, 2004) that receive more (or less) excitatory weight receive correspondingly more (or less) inhibitory weight. Plasticity rules have been identified that may help achieve such a balance (Froemke, 2015; Field et al., 2020; Chiu et al., 2018, 2019; Joseph and Turrigiano, 2017; Hennequin et al., 2017). However, this does not ensure balancing of excitation and inhibition received across varying patterns of activity. Second, given sufficiently strong feedback inhibitory weights, the network dynamics may ensure that the mean inhibition and mean excitation received by neurons remain balanced across patterns of activity, without requiring tuning of synaptic weights. Here, we will focus on this second, dynamic form of balancing.
As we will discuss, theorists have described mechanisms for such dynamic balancing of excitation and inhibition, keeping neurons in the fluctuation-driven regime, without any need for fine tuning of parameters such as synaptic weights. This dynamical balance can be a “tight balance”, which we define to mean that the excitation and inhibition that cancel are much larger than the residual input that remains after cancellation, or a “loose balance”, meaning that the canceling inputs are comparable in size to the remaining residual input (terms to describe balanced networks are not yet standardized; see Appendix 1 for comparison of our usage to other nomenclatures). An example of a tightly balanced network is shown in Fig. 1. The question of whether the balance is tight or loose has important implications for the behavior of the network. Here we will review these issues and argue that the evidence is most consistent with a loosely balanced regime.
Figure 1: Balance of excitation and inhibition.
A: a neuron receiving KE excitatory and KI inhibitory recurrent inputs with unitary strengths JE and Ji, respectively, and KX excitatory external inputs with unitary strength JX. B: Top: Spike rasters from a simulation of a network of spiking integrate-and-fire neurons in the asynchronous irregular regime. Spike trains of representative subpopulations of excitatory (red) and inhibitory (blue) cells are shown. The external input to the network is turned on at t = 0. Middle: The membrane voltage trajectory of a typical excitatory neuron in the network. Bottom: Inputs to the same neuron over time: recurrent excitatory (E) and external excitatory (X) inputs, which together provide the total excitatory input (red); inhibitory input (I, blue); and net inputs (yellow). The arrows show the steady-state means (μ) and standard deviations (σ) of the excitatory, inhibitory, and net inputs. The horizontal gray lines in middle and bottom plots show the spiking threshold. This network is in a regime of tight balance of excitation and inhibition: the net input, after cancellation of excitatory and inhibitory inputs, is much smaller than the factors that cancel.
A Theoretical Problem: How to Achieve Input Mean and Fluctuations That Are Both Comparable in Size to Threshold?
How do cortical neurons stay in the irregularly firing regime? There are two requirements to be in the fluctuation-driven regime, which yields irregular firing: (1) The mean input the neurons receive must be sub- or peri-threshold; (2) Input fluctuations must be sufficiently large to bring neuronal voltages to spiking threshold sufficiently often to create reasonable firing rates. We will measure the voltage effects of a neuron’s inputs in units of the voltage distance from the neuron’s rest to threshold; this distance, typically around 20 mV for a cortical cell (e.g., Constantinople and Bruno, 2013, Fig. 3K), is equal to 1 in these units. Thus, a necessary condition for being in the irregularly firing regime is that the voltage mean driven by the mean input (henceforth abbreviated to “the mean input”) should have order of magnitude 1, which we write as , or smaller. The second requirement above then dictates that the voltage fluctuations driven by the input fluctuations from the mean (henceforth abbreviated to “input fluctuations”) should also be . In particular, this means that the ratio of the mean input to the input fluctuations should be . (Note, we use the notation simply to indicate order of magnitude, and not in its more technical, asymptotic sense of the scaling with some parameter as that parameter goes to zero or infinity.)
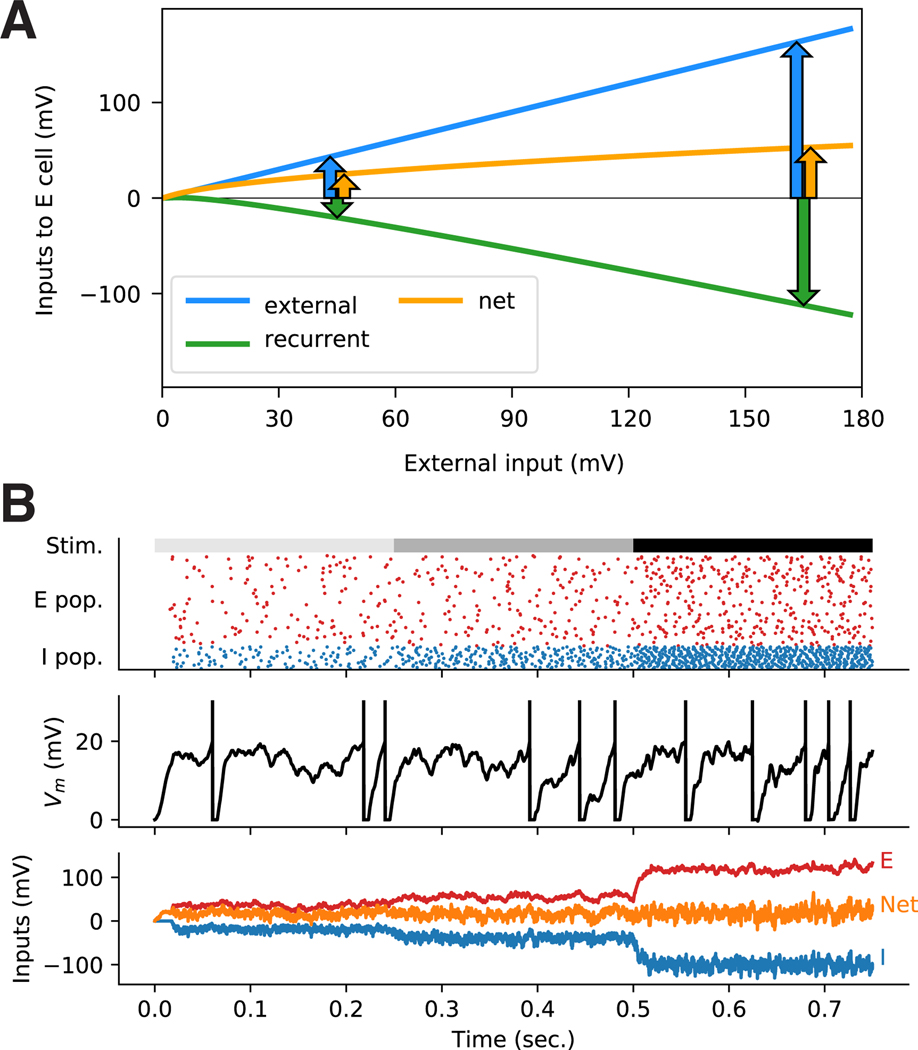
Figure 3: Loose vs. tight balance.
A. Simulation of a rate model, the Stabilized Supralinear Network (SSN). The plot shows the external input (blue), the recurrent or within-network input (green), and the net input (orange, equal to external plus recurrent) to the excitatory cell receiving the peak stimulus. At all biological ranges of external input (stimulus) strength, the balance is loose, as exhibited by the left set of three arrows (representing the external, recurrent, and net inputs): the net input is comparable in size to the other two. The balance systematically tightens with increasing external input (right set of arrows), as the net input grows only sublinearly with increasing external input strength. At high (possibly non-biological) levels of external input, the balance will become tight, with the net input much smaller in magnitude than the external and recurrent inputs. The neurons were arranged in a ring topology (there was an E/I neuronal pair at each position on the ring), with position on the ring corresponding e.g. to preferred direction, as in (Ahmadian et al., 2013; Rubin et al., 2015). The strength of synaptic connections decreased with distance over the ring, and external (stimulus-driven) input peaked at the stimulus direction. B. Simulations of a randomly-connected network of NE = 9600 excitatory and NI = 2400 inhibitory integrate-and-fire spiking neurons, in the asynchronous irregular regime, receiving increasing levels of external input. The network had ring topology, as in A, with probability rather than strength of connections decreasing with distance, Top: spike rasters of 80 excitatory and 20 inhibitory neurons (randomly chosen from the portion of the ring approximately tuned to the stimulus). The gray bars on top denote the three stages with different levels of external input, μX, which for the stimulus-tuned neurons were at 0.5, 1.5 and 4, in units of the rest-to-threshold distance (which was 20 mV), respectively (other key parameters: in same units, all KAB = 480 on average, and for existing connections , , , ). Middle: voltage trace of a randomly chosen E cell from the subpopulation shown in the top rasters. Bottom: E, I, and net input to the same cell. The balance tightens with growing external input strength; in the first two stages (up to t = 0.5 s) the network is in a loose balance regime , while in the last stage it is tightly balanced .
Several authors have considered the requirements for these conditions to be true (Tsodyks and Sejnowski, 1995; van Vreeswijk and Sompolinsky, 1996, 1998; Renart et al., 2010). Following these authors, we assume the network is composed of excitatory (E) and inhibitory (I) neuron populations, which receive excitatory inputs from an external (X) population. The latter could represent any cortical or subcortical neurons outside the local cortical network, for example, the thalamic input to an area of primary sensory cortex. As a simplified toy model of the assumption that the network is in the asynchronous irregular regime, we assume that the cortical cells fire as Poisson processes without any correlations between them, as do the cells in the external population.
Suppose that a neuron receives KE excitatory inputs. Suppose these inputs produce EPSPs that have an exponential time course, with mean amplitude JE and time constant τE, and have mean rate rE (Fig. 1A). Then the mean depolarization produced by these excitatory inputs is . Defining to be the mean number of spikes of an input in time τE, we find that the mean excitatory input to the neuron is
| (1) |
Let σE denote the standard deviation (SD) of fluctuations in this input. Assuming the spike counts of pre-synaptic neurons are uncorrelated, their spike count variances just add. Because they are firing as Poisson processes, the variance in a neuron’s spike count in time τE is equal to its mean spike count nE. Thus, the variance of input from one pre-synaptic neuron is and so the variance in the total input is and
| (2) |
Therefore the ratio of the mean to the SD of the neuron’s excitatory input is
| (3) |
independent of JE. Similar reasoning about the neuron’s inhibitory or external input leads to all the same expressions, except with E subscripts replaced with I or X subscripts to represent quantities describing the inhibitory or external input the cell receives.
Again assuming that the different populations are uncorrelated so that their contributed variances add, the total or net input the neuron receives has mean, μ, and standard deviation, σ, given by:
| (4) |
| (5) |
We imagine that KE and KI are the same order of magnitude, for some number n, and similarly nE and nI are for some number n. We also assume μX and σX are the same order of magnitude as μE or μI and σE or σI, respectively, or smaller. Then, if is , both μ and σ can simultaneously be made with suitable choice of the J’s (barring special cases in which the elements of μ precisely cancel). This means that the irregularly-firing regime is self-consistent: having assumed that neurons are in the irregularly-firing regime, we arrive at expressions for the mean and SD of their input that indeed can keep the network in this regime.
If K is very large, however – large enough that – then the ratio of the mean to the SD of each type of input, and hence of the net input, is much greater than 1. Van Vreeswijk and Sompolinsky (1996,1998) considered the case of such very large K and showed how the network could remain in the AI regime. They proposed choosing the J’s proportional to , so that the standard deviations σE and σI are (Eq. 2), but then by Eq. 3 the means μE and μI are large, . Then, for the neurons to be in the asynchronous irregular regime, inhibitory input, −μI, must cancel or “balance” a sufficient portion of the excitatory input, , so that the mean input, μ, is .
If a neuron’s mean excitatory and inhibitory inputs very precisely cancel each other, so that the mean net input μ is much smaller than either of these factors alone, we say there is tight balance. If the net input is more comparable in size to the factors that are cancelling, we call this loose balance. The two cases may be distinguished by the size of a dimensionless balance index β:
| (6) |
Note that, using the above analysis, in the limit of large K considered by Van Vreeswijk and Sompolinsky (1996,1998), . Tight balance means that the balance index is very small, ; in loose balance, the index is not so small, say , very roughly. As we will see, whether the network is in tight or loose balance has important implications for the network’s behavior and computational ability. (Note that, in general, the degree of balance can be different in different neurons in the same network. In the above discussion we assumed that different neurons of the same E / I type are statistically equivalent, e.g., in terms of the number and activity of presynaptic inputs; this is the case in the randomly connected network of Van Vreeswijk and Sompolinsky (1996,1998). In that case β would not vary systematically between neurons of the same type.)
The Tightly Balanced Solution
Van Vreeswijk and Sompolinsky (1996,1998) showed that, for very large K, and hence very large Kn, and all , the network dynamics would produce a tightly balanced solution provided only that some mild (inequality) conditions on the weights and external inputs are satisfied, without any requirements for fine tuning. This is known more generally as the “balanced network” solution (Fig. 1B). To understand this solution, we define the mean number of inputs, PSP amplitude, and time constant from population , to a neuron in population to be KAB, JAB and τAB respectively. We define the mean effective weight from population B to a neuron in population . Letting rB be the average firing rate of population B, then , the mean input from population B to population A. We assume that for all A, B. The requirements for balance are then that the mean net input to both excitatory and inhibitory cells, uE and uI respectively, are , where (from Eqs. 1,4),
| (7) |
| (8) |
If we define the external inputs to the network , then these equations can be written as the vector equation
| (9) |
where , and W is the weight matrix .
1The balanced network solution arises by noting that the left side of Eq. 9 is very small relative to the individual terms on the right . So we first find an approximate solution r0 to Eq. 9 in which the small left side is replaced by 0 to yield the equation for perfect balance, i.e. all inputs perfectly cancelling: , or , where W−1 is the matrix inverse of W. Note that r0 is , because the elements of W and I are all the same order of magnitude, so their ratio is generically . We can then write r as an expansion in powers of , , where r0, r1, … are all , to obtain a consistent solution: where the first term on the right is , as desired, and the remaining terms are very small ( or smaller). The authors showed that, with some mild general conditions on the weights W and inputs I, this tightly balanced solution would be the unique stable solution of the network dynamics. That is, for a given fixed input I, the network’s excitatory/inhibitory dynamics will lead it to flow to this balanced solution for the mean rates: .
We immediately see two points about the tightly balanced solution:
Mean population responses are linear in the inputs. is a linear function of the input I. Tight balance implies that nonlinear corrections to are very small relative to this linear term, so mean response r is for practical purposes a linear function of the input.
External input must be large relative to the net input and to the distance from rest to threshold. The external input I must have the same order of magnitude as the recurrent input Wr0, so that balance can occur, , with rates that are . If I were smaller, the firing rates would correspondingly be unrealistically small.
In the above treatment we focused on population-averaged responses, rE and rI. We emphasize that the balancing only applies to the mean input across neurons of each type, and leaves unaffected input components with mean of zero across a given type; while the mean input is very large in the tightly balanced regime, zero-mean input components can be and yet elicit responses in individual neurons (see e.g. (Hansel and van Vreeswijk, 2012; Pehlevan and Sompolinsky, 2014; Sadeh and Rotter, 2015)). Furthermore, even in the tightly balanced regime, individual neurons can exhibit nonlinearities in their responses, but these are washed out at the level of population-averaged responses. We also note that nonlinear population-averaged response properties can arise in the tightly balanced state due to synaptic nonlinearities, e.g. synaptic depression, which were neglected here (Mongillo et al., 2012), or due to stimuli that force some neural sub-populations to zero firing rate (Baker et al., 2020).
A Loosely Balanced Regime
As we have seen, if Kn is , the mean and the fluctuations of the input that neurons receive can both be without requiring any balancing. Given that there is both excitatory and inhibitory input, there will always be some input cancellation or ”balancing” – some portion of the input excitation will be cancelled by input inhibition, leaving some smaller net input. When Kn is , all of these quantities – the excitatory input, the inhibitory input, and the net input after cancellation – will generically be , and thus balancing is “loose” – the factors that cancel and the net input after cancellation are of comparable size, and the balance index β is not small.
However, the fact that there is some inhibition that cancels some excitation does not by itself imply interesting consequences for network behavior. We will use the term ”loosely balanced solution” to refer more specifically to a solution having two features: (1) the dynamics yields a systematic cancellation of excitation by inhibition like that in the tightly balanced solution. In particular, in the loosely balanced networks on which we will focus, a signature of this systematic cancellation is that the net input a neuron receives grows sublinearly as a function of its external input (as shown in Fig. 3A, and see below); (2) this cancellation is “loose”, as just described. As we will discuss, such a loosely balanced solution produces various specific nonlinear network behaviors that are observed in cortex.
Ahmadian et al. (2013) showed that such a loosely balanced solution would naturally arise from E/I dynamics for recurrent weights and external inputs that are not large, provided that the neuronal input/output function, determining firing rate vs. input level, is supralinear (having ever-increasing slope) over the neuron’s dynamic range. They modeled this supralinear input/output function as a power law with power greater than 1 (Fig. 2). Such a power-law input-output function is theoretically expected for a spiking neuron when firing is induced by input fluctuations rather than the input mean (Miller and Troyer, 2002; Hansel and van Vreeswijk, 2002), and is observed in intracellular recordings over the full dynamic range of neurons in primary visual cortex (V1) (Priebe and Ferster, 2008). Of course, a neuron’s input/output function must ultimately saturate but, at least in V1, the neurons do not reach the saturating portion of their input/output function under normal operation. For the loosely balanced solution to arise, some general conditions on the weight matrix and external inputs, similar to those for the tightly balanced network solution but less restrictive, must also be satisfied.
Figure 2: The supralinear (power-law) neuronal transfer function.
The transfer function of neurons in cat V1 is non-saturating in the natural dynamic range of their inputs and outputs, and is well fit by a supralinear rectified power-law with exponents empirically found to be in the range 2–5. Such a curve exhibits increasing input-output gain (i.e. slope, indicated by red lines) with growing inputs, or equivalently with increasing output firing rates. Gray points indicate a studied neuron’s average membrane potential and firing rate in 30ms bins; blue points are averages for different voltage bins; and black line is fit of power law, , where r is firing rate, V is voltage, otherwise; θ is a fitted threshold; and p, the fitted exponent, here is 2.79. Note that this shows that firing rate depends supralinearly on mean voltage, but the loosely balanced circuits described here rely on rate depending supralinearly on . The voltage may be sublinear in this quantity, due to synaptic depression of the recurrent inputs, spike-rate adaptation, post-spike reset, or input-induced conductance increases; it may be supralinear in this quantity, due to synaptic facilitation of recurrent inputs or dendritic excitability. The models rely on the assumption that any sublinearity in the net transformation from u to voltage is insufficient to undo the supralinear voltage-to-firing-rate transformation, yielding a net supralinear transformation from u to firing rate. Figure modified from Priebe et al. (2004).
In the presence of a supralinear input/output function, the loosely balanced solution arises as follows. Whereas previously we considered the effects of increasing K when recurrent and external inputs were all , now we consider the more biological case of increasing external input (i.e., stimulus) strength while recurrent weights are at some fixed level. The supralinear input/output function means that a neuron’s gain – its change in output for a given change in input – is continuously increasing with its activation level. This in turn means that effective synaptic strengths are increasing with increasing network activation. The effective synaptic strength measures the change in the postsynaptic cell’s firing rate per change in presynaptic firing rate. This is the product of the actual synaptic strength – the change in postsynaptic input induced by a change in presynaptic firing – and the postsynaptic neuron’s gain. Hence, the effective synaptic strengths increase with increasing gains.
The increasing effective synaptic strengths lead to two regimes of network operation. For very weak external drive and thus weak network activation, all effective synaptic strengths are very weak, for both externally-driven and network-driven synapses. External drive to a neuron is delivered monosynaptically, via the weak externally-driven synapses. In contrast, assuming that the network is inactive in the absence of external input, network drive involves a chain of two or more weak synapses: the weak externally driven synapses activate cortical cells, which then drive the weak network-driven synapses. From the same principle that when , the network drive is therefore much weaker than the external drive. Thus, the input to neurons is dominated by the external input, with only relatively small contributions from recurrent network input. In sum, in this weakly-activated regime, the neurons are weakly coupled, largely responding directly to their external input with little modification by the local network.
With increasing external (stimulus) drive and thus increasing network activation, the gains and thus the effective synaptic strengths grow. This causes the relative contribution of network drive to grow until the network drive is the dominant input. At some point, the effective connections become strong enough that the network would be prone to instability – a small upward fluctuation of excitatory activities would recruit sufficient recurrent excitation to drive excitatory rates still higher, which if unchecked would lead to runaway, epileptic activity (and to ever-growing effective synaptic strengths and thus ever-more-powerful instability). However, if feedback inhibition is strong and fast enough, the inhibition will stabilize the network, that is, it becomes an ISN. This stabilization is accompanied by a loose balancing of excitation and inhibition, as we will explain in more detail below. Thus, in this more strongly-activated regime, the neurons are strongly coupled and are loosely balanced. Note that the input driving spontaneous activity may already be strong enough to obscure the weakly coupled regime, as suggested by the finding that V1 under spontaneous activity is already an ISN (Sanzeni et al., 2020a). As in the tightly balanced network, the network’s excitatory/inhibitory dynamics lead it to flow to this loosely balanced solution, without any need for fine tuning of parameters. Because this mechanism involves stabilization, by inhibition, of the instability induced by the supralinear input/output function of individual neurons along with connections, it has been termed the Stabilized Supralinear Network (SSN) (Ahmadian et al., 2013; Rubin et al., 2015).
To describe the mathematics of this mechanism, we again consider an excitatory and an inhibitory population along with external input. We define the vectors r, u and I and the matrix W as before. Then the power-law input/output function means that the network’s steady state firing rate rSS for a steady input I satisfies
| (10) |
where is the vector v with negative elements set to zero, means raising each element of to the power p, p is a number greater than 1 (typically, 2 to 5, Priebe and Ferster, 2008), and k is a constant with units (and the units of W, r, and I are , Hz, and mV respectively).
If we let represent a norm of W (think of it as a typical total E or I recurrent weight received by a neuron), and similarly let represent a typical input strength, then it turns out the network regime is controlled by the dimensionless parameter
| (11) |
As we increase the strength of external drive and thus of network activation, c and thus α is increasing. When , the network is in the weakly coupled regime; for , the network is in the strongly coupled regime; and the transition between regimes generically occurs when α is (Ahmadian et al., 2013).
The loosely-balanced solution then turns out to be of the form
| (12) |
where r1 is dimensionless and , and the higher-order terms (indicated by …) involve higher powers of (see Appendix 2). Equation 12 is precisely the same equation as for the tightly balanced solution, in the case that the input/output function is a power law. In the tightly balanced network, ψ and c are both , so α is , i.e. very large, and the in the second term becomes , as expected. The loosely-balanced solution arises, however, when α is . In particular, in the biological case of fixed weights but increasing stimulus drive, and given the supralinear neuronal input/output functions, the same E/I dynamics that lead to the tightly balanced solution when inputs are very large will already yield a loosely balanced solution when inputs are . The conditions for this loosely balanced solution to arise are further discussed in Appendix 2.
The fact that the solution is loosely balanced can be seen by computing the balance index, β (Eq. 6). The network excitatory drive is , the external drive is , and because the first term on the right side of Eq. 12 cancels the external input, the net input after balancing is the product of W (which is ) and the 2nd term on the right side of Eq. 12, and thus . Since 1/p < 1, the net input thus grows sublinearly with growing external input strength, c, as illustrated in Fig. 3. Moreover, it follows that the balance index (Eq. 6) is which is (assuming the order of magnitude of the recurrent input, ψr, is the same as or smaller than that of the external input strength, c). Again, for the tightly balanced solution this is very small , but the loosely balanced solution arises when this is .
We noted that the requirements on the weights and external inputs for the loosely balanced solution to arise are less restrictive than those for the tightly balanced solution (further discussed in Appendix 2). When the conditions for the tightly balanced solution are met, then, mathematically, with increasing external input strength c, the loosely balanced solution evolves smoothly into the tightly balanced solution, as illustrated in Fig. 3. However, biologically, the entire dynamical range of c may lie within c the loosely balanced regime. Furthermore, firing rates scale as (Eq. 12; note that the scale of so that if firing rates are in a reasonable range in the loosely balanced regime, they may become unrealistically high if c is increased sufficiently to reach the tightly balanced regime.
In models involving many neurons with structured connectivity and stimulus selectivity, like those illustrated in Fig. 3, neurons that prefer stimuli far from that presented may have their firing rates pushed to zero. Then, because of the rectification in Eq. 10, Eq. 12 no longer describes the full solution. Nonetheless, loosely-balanced solutions still arise when α is . That is, in such cases the full nonlinear steady state equations, Eq. (10), can yield biologically plausible solutions, and when that happens the net inputs to activated neurons grow sublinearly with growing external input strength, and balance indices are (as illustrated in Fig. 3). The case of structured networks with stimulus selectivity is further discussed in Appendix 2.
We can now see that the loosely balanced regime differs from the tightly balanced in the two points summarized previously:
In the loosely balanced regime, mean population responses are nonlinear in the inputs. This is because, when balance is loose, the second term in Eq. 12, which is not linear in the input, cannot be neglected relative to the first, linear term. In particular, the nonlinear population behaviors observed in the loosely balanced regime with a supralinear input/output function closely match the specific nonlinear behaviors observed in sensory cortex (Rubin et al., 2015), as we will discuss below.
In the loosely balanced regime, external input can be comparable to the net input and to the distance from rest to threshold.
What Regime Do Experimental Measurements Suggest?
As we have seen above (Fig. 3), the same model can give a loosely balanced solution (Eq. 12) when α is (e.g., when c and ψ are both ), but give a tightly balanced solution when α is large (e.g., when c and ψ are both ). Which of these regimes is supported by experimental measurements?
Measurements of Biological Parameters
How large is We saw in Eq. 3 that the ratio of the mean to the standard deviation, , of the input of type received by a neuron is equal to where KY is the number of inputs of type Y a given neuron receives and nY is the average number of spikes one of these inputs fires in a PSP decay time (, where rY is the average firing rate of one of these inputs). Here we estimates .
Note that is actually an upper bound for the ratio for a given input type, because we have neglected a number of factors that would increase fluctuations for a given mean. These include (i) correlations among inputs which, even if weak, can significantly boost the input SD, σY, without altering input mean; (ii) variance in the weights, JY, which would increase the estimate of σY by a factor (where indicates the average value of x); and (iii) network effects that can amplify input variances by creating firing rate fluctuations, although this amplification may be small for strong stimuli (Hennequin et al., 2018). Furthermore, the ratio μ/σ of total input is expected to be smaller than the ratio for any single type. This is because σ2 involves the sum of three variances (Eq. 5), while μ involves a difference of one mean from the sum of two others (Eq. 4), representing the effect of loose balancing.
Given these considerations, we are primarily concerned with estimating the overall magnitude of rather than detailed values. If this magnitude is very much larger than the observed μ / σ ratio in vivo, then tight balancing may be needed to explain the in vivo ratio. To estimate the in vivo μ / σ ratio, we note that, in anesthetized cat V1, σ varies from 1 to 7 mV and μ ranges from 0 to 15 mV (20 mV in one case) for a strong stimulus (Finn et al., 2007; Sadagopan and Ferster, 2012). While these authors did not give the paired μ and σ values for individual cells, it seems reasonable to guess from these values that the value of μ / σ for the total input to these cells is generally in the range 0−15. Finn et al. (2007) also reported that, at the peak of a simple cell’s voltage modulation to a high-contrast drifting grating, the ratio σ / μ had an average value of about 0.15 (here, we are taking μ to be the mean voltage at the peak). This suggests that the average value of μ / σ at peak activation is around 1/ 0.15 = 6.7.
How large is In a study of input to excitatory cells in layer 4 of rat S1 (Schoonover et al., 2014), the EPSP decay time τE was around 20 ms. From 1800 to 4000 non-thalamic-recipient spines were found on studied cells which, with an estimated average of 3.4 synapses per connection between layer 4 cells (Feldmeyer et al., 1999), corresponds to a KE – the number of other cortical cells providing input to one cell – of 530 to 1200. If rE is expressed in Hz, then ranges from 3.3 . Thus, even if average input firing rates were 10 Hz, which would be very high for rodent S1 (Barth and Poulet, 2012) (note that the average is over all inputs, not just those that are well driven in a given situation, and so is likely far below the rate of a well-driven neuron), these ratios would be 10.4−15.5. For more realistic rates of 0.01−1Hz (Barth and Poulet, 2012; Brecht et al., 2003; Manns et al., 2004), these ratios would be 0.33−4.9. All of these are comparable in magnitude to observed in vivo levels of μ / σ.
More generally, estimates across species and cortical areas of the number of spines on excitatory cells, and thus of the number of excitatory synapses they receive, range from 700 to 16,000, with numbers increasing from primary sensory to higher sensory to frontal cortices (Elston, 2003; Elston and Manger, 2014; Elston and Fujita, 2014; Amatrudo et al., 2012). Estimates of the mean number of synapses per connection between excitatory cells range from 3.4 to 5.5 across different areas and layers studied (Fares and Stepanyants, 2009; Feldmeyer et al., 1999, 2002; Markram et al., 1997). These numbers yield a KE of 130 to 4700. In Table 1, we show the value of for KE ranging from 200 to 5000 (rounded upward to bias results most in favor of a need for tight balancing) and for rates rE of 0.1 to 10 Hz. The results are all comparable to the μ / σ’s observed in vivo, except for the most extreme case considered , and even that case is only off by a factor of 2. Thus, the numbers strongly argue that tight balancing is not needed for the ratio of voltage mean to variance to have values as observed in vivo.
Table 1:
Values of for varying KE and rE, for .
| KE = 200 | KE = 1000 | KE = 5000 | |
|---|---|---|---|
| rE = 0.1 Hz | 0.6 | 1.4 | 3.2 |
| rE = 1 Hz | 2.0 | 4.5 | 10.0 |
| rE = 10 Hz | 6.3 | 14.1 | 31.6 |
External input is comparable in strength to net input.
Several studies have silenced cortical firing while recording intracellularly to determine the strength of external input, with cortex silenced, relative to the net input with cortex intact. These find the external input to be comparable to the net input, consistent with the loose balance scenario, rather than much larger as the tight balance scenario requires.
Ferster et al. (1996) cooled V1 and surrounding V2 in anesthetized cats to block spiking of almost all cortical cells, both excitatory and inhibitory, leaving axonal transmission (e.g. of thalamic inputs) intact, though with weakened release. By measuring the size of EPSPs evoked by electrical stimulation of the thalamic lateral geniculate nucleus (LGN) in thalamic-recipient cells in layer 4 of V1, they could estimate the degree of voltage attenuation of EPSPs induced by cooling. Correcting for this attenuation, they estimated that the first harmonic voltage response to an optimal drifting luminance grating stimulus of a layer 4 V1 cell was, on average, about 1/3 as great with cortex cooled as with cortex intact, suggesting that the external input to cortex is smaller than the net input with cortex intact. Chung and Ferster (1998) and Finn et al. (2007) assayed the same question by using cortical shock to silence the local cortex for about 150 ms, during which time the voltage response to an optimal flashed grating was measured. They found that on average the transient voltage response in layer 4 cells with cortex silenced was about 1/2 the size of that with cortex intact (Chung and Ferster, 1998), and more generally ranged from 0% to 100% of the intact cortical response (Finn et al., 2007). This again suggests that the external input to cortex is smaller than the net input, i.e. the external input is , consistent with loose but not tight balance.
Total excitatory or inhibitory conductance is comparable to threshold.
The above results suggest that depolarization due to thalamus alone is less than that induced by the combination of thalamic and cortical excitation plus cortical inhibition, i.e. after cortical ”balancing” has occurred. One can also ask what proportion of the total excitation is provided by thalamus. This has been addressed in voltage-clamp recordings in anesthetized mice by silencing cortex through light activation of parvalbumin-expressing inhibitory cells expressing channelrhodopsin. In layer 4 cells of V1 (Lien and Scanziani, 2013; Li et al., 2013b) and primary auditory cortex (A1) (Li et al., 2013a), mean stimulus-evoked excitatory conductance with cortex silenced was estimated to be 30–40% of that with cortex intact.
This tells us that the external and cortical contributions to excitation are comparable. How large are they compared to the excitation needed to depolarize the cell from rest to threshold, which is typically a distance of about 20 mV (Constantinople and Bruno, 2013)? With cortical spiking intact, these authors (Lien and Scanziani, 2013; Li et al., 2013a) found mean stimulus-evoked peak excitatory currents ranging from 60 to 150pA for various stimuli. Even assuming a membrane resistance of 200 MΩ, which seems on the high end for in vivo recordings (Li et al. (2013a) reported input resistances of 150−200 MΩ ), these would induce depolarizations of 12 to 30 mV; that is, the total excitatory current is comparable to threshold, i.e. it is .
A similar result can be found from decomposition of excitatory and inhibitory conductances from current-clamp recordings at varying hyperpolarizing current levels. In neurons in anesthetized cat V1 for an optimal visual stimulus, peak excitatory and inhibitory stimulus-induced conductances, gE and gI, were typically <10 nS and almost always < 20 nS, on top of stimulus-independent conductances ( gL, for leak conductance) around 10nS (Anderson et al., 2000; Ozeki et al., 2009). A study of response to whisker stimulation in anesthetized rat barrel cortex found excitatory and inhibitory conductances of ≤ 5ns (Lankarany et al., 2016). The depolarization that the stimulus-induced excitatory conductance would induce by itself is , where VE is the driving potential of excitatory conductance, about 50 mV at spike threshold of around −50 mV (e.g. Wilent and Contreras, 2005). Using the cat V1 numbers, this means that the depolarization driven by excitatory conductance is typically < 25 mV and almost always < 33 mV. Hyperpolarization driven by the inhibitory conductance alone would be 0.4 to 0.6 times these values, given inhibitory driving force of −20 to −30 mV at spike threshold. These values are all quite comparable to the distance from rest to threshold, ~ 20 mV, that is, they are .
How large is the expected mean excitatory input?
We have seen that the expected mean depolarization induced by recurrent excitation is where JE is the mean EPSP amplitude. Based on the measurements of Lien and Scanziani (2013) and Li et al. (2013b), discussed above, total excitation may be about 1.5 times greater than recurrent excitation. JE can be difficult to estimate, because some of the KE anatomical synapses may be very weak and not sampled in physiology, and because synaptic failures, depression, or facilitation can alter average EPSP size relative to measured EPSP sizes. Furthermore, measurements are variable, for example JE for layer 4 to layer 4 connections in rodent barrel cortex has been estimated to be 1.6 mV in vitro (Feldmeyer et al., 1999) vs. 0.66 mV in vivo (Schoonover et al., 2014). If we assume typical values for JE of 0.5 1− mV, then would exceed 75 mV for and exceed 150 mV (compare values of in Table 1). We can very roughly guess that neural responses may become better described by tight rather than loose balance somewhere in this range of mean excitatory input (and corresponding ). While the measurements of excitatory currents and conductances described above argue that such a range is not reached in primary sensory cortex, it could conceivably be reached (Table 1) in areas with higher KE e.g. frontal cortex.
Nonlinear Behaviors
Sensory cortical neuronal responses display a variety of nonlinear behaviors that, as we will describe, are expected from the SSN loosely balanced regime but not from the tightly balanced regime. A number of these behaviors of the SSN model are shown in Fig. 4. Many of these nonlinearities are often summarized as “normalization” (Carandini and Heeger, 2012), meaning that responses can be fit by a phenomenological model of an unnormalized response that is divided by (normalized by) some function of all of the unnormalized responses of all the neurons within some region. To describe these nonlinear behaviors, we must first define the classical receptive field (CRF): the localized region of sensory space in which appropriate stimuli can drive a neuron’s response.
Figure 4: Nonlinear neural behaviors in the loosely balanced regime.
All panels are based on simulations of a Stabilized Supralinear Network (SSN). A,B: same ring model as in Fig. 3A. A) Three forms of response summation, for three levels of input (indicated by colors, corresponding to arrows in B): supralinear summation, for very weak stimuli (left); sublinear summation, for stronger stimuli yielding loose balance (middle); and approximately linear summation, for very strong stimuli yielding tight balance (right). The x-axis is position on the ring, unrolled into a line. Black line shows profile of responses across excitatory population to a 90° stimulus; response to a 270° stimulus is identical except shifted to peak at 270°. Green dotted lines show linear sum of responses to these two stimuli. Red lines show actual responses when the two stimuli are presented simultaneously. B): Additivity index is height of peak response to the two stimuli together (red lines in A), divided by peak height of the linear summation of responses to each stimulus (green dashed lines in A). Index is shown for excitatory population (red) and inhibitory population (blue). For very weak stimuli, summation is supralinear (index >1); for moderate stimuli yielding loose balance, summation is sublinear (index <1); and for very strong stimuli that ultimately yield tight balance, summation approaches linear (index =1). X-axis is identical to that of Fig. 3A, from which degree of balance for a given input strength can be seen. The inset is a blow-up of the same plot in the region of weak stimuli. The strength of supralinearity or sublinearity, and whether the model approaches tight balance and linear summation for sufficiently high stimulus strength, can vary considerably with parameters, see (Ahmadian et al., 2013). C, D: Dependence of surround suppression on stimulus strength. C: Response of an excitatory neuron to stimuli of different sizes, for increasing stimulus strength c. (Increasing stimulus strength corresponds to increasing stimulus contrast, as indicated qualitatively by example stimuli shown at right; the quantitative contrast levels illustrated are arbitrary.) With increasing stimulus strength, surround suppression of increasing strength is seen, and the summation field size – the size yielding peak response – decreases. D: Normalized summation field size (normalized to value for very large stimulus strength) vs. stimulus strength, for excitatory (red) and inhibitory (blue) cells, for same model as in C. Summation field size systematically shrinks with stimulus strength. E: with increasing input strength, the ratio of recurrent (network) excitatory input, En, to inhibitory input, I, decreases with increasing stimulus strength, as observed in (Shao et al., 2013; Adesnik, 2017). C, D, E all from Rubin et al. (2015), used by permission; E is from a ring model as in A,B but with different parameters, C,D are from a model of E and I neurons arranged on a line.
One nonlinear property is sublinear response summation: across many cortical areas, the response to two stimuli simultaneously presented in the CRF is less than the sum of the responses to the individual stimuli, and is often closer to the average than the sum of the individual responses (reviewed in Reynolds and Chelazzi, 2004; Carandini and Heeger, 2012). An additional nonlinearity is that the form of the summation changes with the strength of the stimulus: summation becomes linear for weaker stimuli (Heuer and Britten, 2002; Ohshiro et al., 2013). While the SSN shows supralinear summation for very weak stimuli (Fig. 4A-B), the circuits in multiple cortical areas during spontaneous activity are ISNs (Sanzeni et al., 2020a), indicating that the external input driving spontaneous is likely already strong enough to eliminate the weakly-coupled regime of the SSN, in which summation is supralinear. In experiments, it is often difficult to determine if such nonlinear behaviors are computed in the recorded area or involve changes in the inputs to that area. For example, cross-orientation suppression in V1 – suppression of response to a preferred-orientation grating by simultaneous presentation of an orthogonal grating – is largely (Priebe and Ferster, 2006; Li et al., 2006), but not entirely (Sengpiel and Vorobyov, 2005) mediated by changes in thalamic inputs to V1. However, some recent experiments studied summation of response to an optogenetic and a visual stimulus, a case in which the inputs driven by each stimulus should not alter those driven by the other. Sublinear summation of responses to these stimuli was found (Nassi et al., 2015; Wang et al., 2019, but see Histed, 2018), which became linear for weak stimuli (Wang et al., 2019).
Another set of nonlinearities involve interaction of a CRF stimulus and a “surround” stimulus, which is located outside the CRF. Across many cortical areas, surround stimuli can suppress response to a CRF stimulus (“surround suppression”; reviewed in Rubin et al., 2015; Angelucci et al., 2017), but this effect varies with stimulus strength. When the center stimulus is weak, a surround stimulus can facilitate rather than suppress response (Sengpiel et al., 1997; Polat et al., 1998; Ichida et al., 2007; Schwabe et al., 2010; Sato et al., 2014). In one study in V1 (Sato et al., 2014), the surround stimulus was added intracortically rather than by a visual stimulus, establishing that this computation took place in V1. Similarly, the summation field size – the size of a stimulus that elicits strongest response, before further expansion yields surround suppression – is largest for weak stimuli and shrinks with increasing stimulus strength (Anderson et al., 2001; Song and Li, 2008; Sceniak et al., 1999; Cavanaugh et al., 2002; Shushruth et al., 2009; Nienborg et al., 2013; Tsui and Pack, 2011) (illustrated for the SSN in Fig. 4C-D). The summation field size in feature space – the optimal range of simultaneously presented motion directions in monkey area MT – similarly shrinks with increasing stimulus strength (Liu et al., 2018).
Additional nonlinearities include a decrease, with increasing stimulus strength, in the ratio of excitation to inhibition received by neurons (Shao et al., 2013; Adesnik, 2017), shown for the SSN in Fig. 4E, and in the wavelength of a characteristic spatial oscillation of activity (Rubin et al., 2015). In addition, while multiple cortical areas are ISNs during spontaneous activity, they become non-ISNs with suppression to sub-spontaneous levels of activity by optogenetic activation of inhibitory neurons (Sanzeni et al., 2020a). As discussed above, this is expected in an SSN when activity suppression makes the effective excitatory connections sufficiently weak. However, this is not unique to the SSN; for example, in a rectified linear network, effective excitatory connections weaken as more excitatory neurons reach zero firing rate.
All of these nonlinear cortical response properties, and more, follow naturally (Ahmadian et al., 2013; Rubin et al., 2015) from the two regimes (i.e., weak activation/weak effective synaptic strengths vs. stronger activation/stronger effective synaptic strengths/loosely balanced regimes) of the scenario with a supralinear input/output function, along with simple assumptions on connectivity (e.g. that connections decrease in strength and/or probability with spatial distance, e.g. Markov et al., 2011, or with difference in preferred features, e.g. Ko et al., 2011; Cossell et al., 2015). In contrast, as described previously, the tightly balanced scenario causes population-averaged responses to be linear responses to the input (individual neurons, but not the population average, may have nonlinear behaviors), and thus appears inconsistent with these nonlinear cortical behaviors, which in most cases are consistent enough across neurons that they should characterize the mean population response. Synaptic nonlinearities can give nonlinear population-averaged behavior in the tightly balanced regime (Mongillo et al., 2012), as can rectification nonlinearities (Baker et al., 2020), but it has not been claimed or demonstrated that this could produce the specific nonlinearities we have discussed that are seen in cortical responses.
Correlations and Variability
Across many cortical systems, the correlated component of neuronal variability is decreased when a stimulus is given, with variability decrease seen both in neurons that respond to the stimulus and those that don’t respond (Churchland et al., 2010). This is also naturally explained by the loosely balanced SSN network (Hennequin et al., 2018). In the strongly coupled regime of the loosely balanced SSN network, increasing stimulus strength increases the strength with which correlated patterns of activity inhibit themselves, thus damping their responses to input fluctuations. The tightly balanced state represents the end state of this process – a fully asynchronous regime in which correlations are completely suppressed (van Vreeswijk and Sompolinsky, 1998; Renart et al., 2010; with dense connectivity, the mean correlation is proportional to 1/ K, and the standard deviation of the distribution of correlations is proportional to Renart et al. (2010); recall that K is meant to be a very large number to achieve the tightly balanced state). Thus, the tightly balanced state appears incompatible with the observed decrease in correlated variability induced by a stimulus, because the state has essentially no correlated variability. However, it should be noted that variants of the tightly balanced network involving structured connectivity can break the tight balance in structured ways that yield finite correlated variability among preferentially connected neurons (Rosenbaum et al., 2017; Litwin-Kumar et al., 2012).
Discussion
We have seen that many independent lines of evidence are all consistent with cortex being in a loosely balanced regime, and are inconsistent with tight balance. We define balance to mean that the dynamics yields a systematic cancellation of excitation by inhibition. A signature of this, for the loosely balanced scenario that we consider, is that the net input a neuron receives after cancellation grows sublinearly as a function of its external input. Loose balance means that the net input after cancellation is comparable in size to the factors that cancel, whereas tight balance means that the net input is very small relative to the cancelling factors. In both cases, the net input after cancellation is comparable in size to the distance from rest to threshold so that neuronal firing can be in the fluctuation-driven regime that produces irregular firing like that observed in cortex.
One line of evidence for loose balance involves a variety of measurements on the numbers and/or strengths of the inputs cells receive, including spine counts, strengths of external and total input, and strengths of excitatory and of inhibitory input. These measurements show that the expected ratio of mean to standard deviation of the network input before any tight balancing is already consistent with the ratios observed for a cell’s net input as judged by its voltage response. That is, tight cancellation is not needed to achieve the ratios observed. These measurements further show that external input and network input are comparable in size to the net input remaining after cancellation, and that they and the total excitatory and total inhibitory input are all comparable to the distance from rest to threshold, consistent with loose but not tight balancing. Other lines of evidence include a variety of nonlinear population response properties of sensory cortical neurons, as well as the presence of correlated variability in neural responses and its decrease upon presentation of a stimulus, all of which emerge naturally from loose balance with a supralinear input/output function, but appear largely incompatible with tight balance.
It should be emphasized that the number of excitatory synapses received by an excitatory cell, KE, increases from primary sensory to higher sensory to frontal cortex (e.g. Elston, 2003). Higher numbers are expected to push in the direction of tighter balance. The expected ratio of input mean to standard deviation and the expected size of the mean input both can become high enough to potentially yield tight balance for the highest KE ‘s, particularly if higher average firing rates rE are assumed (Table 1). Our other arguments depend largely, but not entirely, on measurements from sensory cortex. The measurements of net input and external input are all from primary sensory cortex. The studied nonlinear response properties are primarily from both lower and higher visual cortices (reviewed in Rubin et al., 2015). Suppression of correlated variability by a stimulus, however, has been observed in frontal and parietal as well as sensory cortex (Churchland et al., 2010). In sum, while the evidence strongly favors loose balance in sensory cortex, the evidence as to the regime of motor or frontal cortex is weaker.
All of our analysis has been done in the simplified framework of a single-compartment or “point” neuron, in which a neuron’s inputs simply add, so that excitation and inhibition cancel. This ignores nonlinear aspects of dendritic integration (Palmer et al., 2016; Spruston et al., 2016; Poirazi and Papoutsi, 2020). For example, summation may occur within individual dendritic branches, whose nonlinear outputs may then be summed in more proximal branches and ultimately in the soma. Furthermore, modulation of dendritic (Larkum et al., 2001) or somatic (Titley et al., 2017) excitability may greatly alter the influence of synaptic inputs on somatic voltage, so that synaptic input may be a poor predictor of spike output. As noted previously, the strengths of excitatory and inhibitory synapses appear to remain balanced on individual dendritic segments (Iascone et al., 2020; Liu, 2004). The mechanisms and functions of such local balancing remain important outstanding questions. However, theoretical study must abstract away some details to focus on others. The approach of simplifying a neuron to a single compartment to focus on the behavior of circuits of such neurons has been a very fruitful one for gaining theoretical insights that illuminate experiments, as exemplified by the studies discussed here. In addition to the theoretical utility of this simplification, it also receives empirical justification from a finding that, despite dendritic nonlinearities, linear summation gives a very good approximation of input integration in cortical pyramidal cells in vivo, capturing more than 90% of the variance of somatic membrane potential in experimental recordings (Ujfalussy et al., 2018).
We have studied a regime in which the dynamics is asynchronous and goes to a fixed point – a steady rate of firing – for a steady input. It has been argued that in awake rodent auditory cortex, spontaneous activity may be driven by correlated bursts or “bumps” of input on an otherwise quiet or far-from-threshold background (DeWeese and Zador, 2006; Hromádka et al., 2013; see also Tan et al., 2014). More generally, as discussed in the Introduction, both synchronous and asynchronous states are observed in spontaneous activity in awake cortex (e.g. Mccormick et al., 2015; Ferguson and Cardin, 2020). Stimulus-evoked responses to commonly used stimuli in both auditory (Hromadka et al., 2008) and somatosensory (Barth and Poulet, 2012) cortex tend to be very sparse, with neurons having low mean firing rates, although a given neuron may respond vigorously to particular stimuli. Very low firing rates may also suggest a regime sitting far from threshold with occasional input “bumps” driving occasional responses, although alternatively they may represent failure to find optimal stimuli for the cells. Finally, in both of these systems, natural stimuli and responses to them may be rapidly-changing rather than sustained, requiring analysis of time-dependent network dynamics rather than steady states. In the tightly balanced network, the mean population response follows the mean input close to instantaneously, although this could be changed by incorporating more biophysical details of cells and synapses. In the loosely balanced network, the population dynamics can be more complex and more model-dependent. It remains to be seen how useful the concepts discussed here will be for understanding cortical systems that are synchronously firing, driven by occasional synchronous inputs, or dynamically responding to dynamically changing stimuli.
The seminal discovery of the tightly balanced network (van Vreeswijk and Sompolinsky, 1996, 1998) solved a key problem in theoretical neuroscience: how can neurons remain in the fluctuation-driven regime, so that they have irregular firing with reasonable firing rates, without requiring fine tuning of parameters? The answer was that when external and network inputs were very large, the network’s dynamics could robustly tightly balance the excitation and inhibition that neurons receive, leaving a net mean input after cancellation that is negligibly small relative to the factors that cancel. This allows both the mean and standard deviation of the net input to be comparable to the distance from rest to threshold despite the very large size assumed for the factors that cancel, yielding the fluctuation-driven regime. This achievement along with the model’s mathematical tractability have made it a very influential model for the theoretical study of neural circuits. However, for all of the reasons stated above, the tightly balanced regime on which the work focused does not seem to match observations of at least sensory cortical anatomy and physiology.
The loosely balanced solution shows that, when neuronal input/output functions are supralinear, the same dynamical balancing can arise from network dynamics without fine tuning, but in a regime in which external and network inputs are not large. Instead, the balancing arises when these inputs, and the net input remaining after cancellation of excitatory and inhibitory input, are all comparable in size to one another and to the distance from rest to threshold. Furthermore, for weak inputs this same scenario produces a weakly-coupled, feedforward-driven regime which can explain the observation that network-level input summation changes from sublinear for stronger stimuli to linear or supralinear for weak inputs.
The tightly balanced network demonstrated that a network could self-consistently generate its own variability. As we showed in the section “How large is , the loosely balanced regime can also generate realistic levels of variability. However, biologically there is no need for the network to generate all of its own variability, as all inputs to cortex are noisy (and there are other sources of noise such as stochasticity of cellular and synaptic mechanisms (Mainen and Sejnowski, 1995; Schneidman et al., 1998; O’Donnell and van Rossum, 2014) and input correlations (Stevens and Zador, 1998; DeWeese and Zador, 2006)). In at least one case (Sadagopan and Ferster, 2012), the noise derived from the cortical area’s input was argued to be large enough to potentially fully account for the noise seen in the cortical neurons.
Very recently, other solutions have been proposed to the problem of having both the input mean and standard deviation be comparable to the distance from rest to threshold (Khajeh et al., 2021; Sanzeni et al., 2020b). Based on the evidence we have presented here, any such solution, to be compatible with biology, should be loosely rather than tightly balanced.
In conclusion, we believe that at least sensory, and perhaps all of, cortex operates in a regime in which the inhibition and excitation neurons receive are loosely balanced. This along with the supralinear input/output function of individual neurons and simple assumptions on connectivity explains a large set of cortical response properties. A key outstanding question is the computational function or functions of this loosely balanced state and the response properties it creates (e.g., see Echeveste et al., 2020; G. Barello and Y. Ahmadian, in preparation).
Acknowledgements
We thank Larry Abbott, Mario DiPoppa and Agostina Palmigiano for many helpful comments on the manuscript and David Hansel, Carl Van Vreeswijk, Gianluigi Mongillo and Alfonso Renart for many useful discussions. YA was supported by start-up funds from the University of Oregon. KDM is supported by NSF DBI-1707398, NIH U01NS108683, NIH R01EY029999, NIH U19NS107613, Simons Foundation award 543017, and the Gatsby Charitable Foundation.
Excitation and inhibition are balanced or cancel out in cerebral cortex. Ahmadian and Miller distinguish tight vs. loose balance, according to the size of the residual after cancellation. They show this critically affects cortical dynamics, and summarize evidence strongly supporting loose balance.
Appendix 1: Nomenclature for balanced solutions
There is no standard nomenclature for describing balanced solutions. Here we have used loose vs. tight balance to describe, given systematic cancellation, whether the remainder after cancellation is comparable to, or much smaller than, the factors that cancel.
Deneve and Machens (2016) used loose balance to mean that fast fluctuations of excitation and inhibition are uncorrelated, although they are balanced in the mean, as in the sparsely-connected network of van Vreeswijk and Sompolinsky (1996, 1998); and used tight balance to mean that fast fluctuations of excitation and inhibition are tightly correlated with a small temporal offset, as in the densely-connected network of Renart et al. (2010) and in the spiking networks of Deneve, Machens and colleagues in which recurrent connectivity has been optimized for efficient coding (Boerlin et al., 2013; Bourdoukan et al., 2012; Barrett et al., 2013). All of these networks are tightly balanced under our definition.
Hennequin et al. (2017) also defined balance to be tight if it occurs on fast timescales, and loose otherwise, but they implied that this is equivalent to our definition, that tight balance means the remainder is small compared to the factors that cancel, and loose balance means the remainder is comparable to the factors that cancel. The implied equivalence rests on the fact that tight balance under our definition produces very large (i.e., ) negative eigenvalues (in linearization about the fixed point) which means very fast dynamics, approaching instantaneous population response as K and hence negative eigenvalues go to infinity. We point out, however, that loose balance under our definition can produce negative eigenvalues large enough to produce quite fast dynamics, with effective time constants on the order of single neurons’ membrane time-constant, or even as small as a few milliseconds, depending on parameters.
An additional source of confusion is that there are two forms of fast fluctuations, with different behaviors. Fast fluctuations can be shared (correlated) across neurons, or they can be independent. The large negative eigenvalues in tightly balanced networks (in our definition) affect shared fluctuations corresponding to eigen-modes in which the activities of excitatory and inhibitory neurons fluctuate coherently. Thus, shared fluctuations are balanced on fast time scales. By contrast, spatial activity patterns in which neurons fluctuate independently are largely unaffected by those eigenvalues, and need not be balanced.
Fluctuations due to changes in population mean rates of the external input are shared, and so this form of fluctuation is followed on fast time scales in all balanced networks (at finite rates in loosely balanced networks, and approaching instantaneous following in tightly balanced networks). Fluctuations also arise from network and external neuronal spiking noise. In networks with sparse connectivity (van Vreeswijk and Sompolinsky, 1998), this yields independent fluctuations in different neurons, and thus independent fluctuations of excitation and inhibition on fast time scales (though their means are balanced). In networks with dense connectivity (Renart et al., 2010), these spiking fluctuations become shared fluctuations due to common inputs arising from the dense connectivity, and so in these networks excitation and inhibition are balanced on fast time scales. To summarize, all balanced networks will balance shared fluctuations, such as those due to changing external input rates, on fast time scales; but excitation and inhibition can nonetheless be unbalanced on fast time scales in sparse networks, due to independent fluctuations induced by spiking noise.
To conclude, we would argue for a future standardized terminology for dynamically-induced balancing of excitation and inhibition, in which “loose” vs. “tight” balance refer to our definition as to whether the remainder after cancellation is comparable to, or much smaller than, the factors that cancel. We suggest the use of “temporal” vs. “mean” balance to refer to whether or not excitation and inhibition are balanced on fast time scales, which depends on whether there are substantial shared input fluctuations across neurons. “Finite” vs. “instantaneous” time scales of balancing can distinguish whether relaxation rates – the rates of balancing shared fluctuations – are moderately-sized vs. very large.
Appendix 2: When do balanced solutions arise?
We consider a rate model in which the neuron’s input/output function is described by some function f (x), which is zero for x ≤ 0 and monotonically increasing for x ≥ 0. Then the network’s steady-state firing rate rSS for a steady input I is
| (13) |
where f acts element by element on its argument, that is, f (u) is a vector whose ith element is f (μi) (the f’s might differ for different neurons, which we neglect for simplicity). As before, we let . We define the dimensionless and matrix and vector , so that J and g represent the relative synaptic strengths and relative input strengths, respectively, while their overall magnitudes and dimensions are in ψ and c. Then, as in Ahmadian et al. (2013), we can define the dimensionless variable , and Eq. 13 can be rewritten
| (14) |
Note that this equation ensures that . Note also that, when , otherwise), then this equation can be rewritten where . This is the origin of the dimensionless constant α mentioned in the main text.
If we define , then because f is monotonically increasing for non-negative arguments, it is invertible over that range, i.e is defined for x ≥ 0. We can then rewrite Eq. 14 as
| (15) |
If we assume
| (16) |
that is, if for all i, then we can replace the right side of Eq. 15 with JySS + g (without the ( )+). This condition, Eq. 16, is a condition on the solution ySS, which we must check is self-consistently met for any solution we derive under this assumption. Note also that, from Eq. 14, the condition is met if and only if so if we find a solution ySS that has all positive elements, it will automatically satisfy Eq. 16. Given this assumption, a bit of further manipulation then yields
| (17) |
The first term , is the balancing term, which cancels the external input g, i.e. . If the second term becomes small relative to the first in some limit, then the tightly balanced solution, or equivalently , exists in that limit, while a loosely balanced solution (balance index ) arises when the 2nd term is comparable in size to the first. (More careful analysis is needed to ensure that this solution is stable, and that there are not also other solutions.) Note that Eq. 17 gives an equation of the form Eq. 12 when we (1) Take and (2) Multiply both sides of Eq. 17 by c/ψ to convert ySS to rSS.
Assuming all the elements of , a self-consistent solution in which the second term in Eq. 17 becomes small can be found in at least three cases:
If c and ψ are scaled by the same factor, which becomes arbitrarily large, then there is a self-consistent solution in which ySS is converging to . Then the factor is not changing (except for the small changes due to the changes in ySS as it converges), but it is multiplied by the factor which becomes arbitrarily small; thus the second term becomes arbitrarily small, regardless of the particular structure of f. This is the case studied for the tightly balanced solution, where both c and ψ are taken proportional to with K very large. (Note that the mean field equations derived in (van Vreeswijk and Sompolinsky, 1998) differ from the generic steady-state rate equations, Eq. (13), in that they also involve the self-consistently calculated input fluctuation strengths, σA; the scaling argument given here nevertheless holds in that case too.)
Suppose c is scaled for fixed ψ, which is the biological case in which synaptic strengths are fixed and the strength of the external input is varied from small to large. Then if grows more slowly than linearly in increasing x, then the factor shrinks faster than the term grows, so c again there is a self-consistent solution in which ySS is converging to and the second term becomes arbitrarily small with increasing c. This is the case studied for the loosely balanced solution in the SSN, in which f(x) grows supralinearly with x and therefore grows sublinearly with x.
We again suppose c is scaled for fixed ψ, but now imagine that grows faster than linearly in increasing x, i.e. f (x) is sublinear (for example, ). Then there is a self-consistent solution in which as , with the second term in Eq. 17 going to zero as . This case is the reverse of the SSN: the strongly coupled, balanced regime arises for , while the weakly coupled, feedforward-driven regime arises for large c.
In sum, if the elements of are positive, then a self-consistent tightly-balanced solution arises for any f if c and ψ are scaled together by an increasing factor; for supralinear f if c is scaled by an increasing factor; or for sublinear f if c is scaled by a decreasing factor. In all of these cases, for moderate sizes of the scaled parameter(s) (e.g., for the SSN, for ) such that the second term of Eq. 17 is comparable in size to the first, a loosely balanced solution should arise. Note that, since , then from Eq. 17 the net input after balancing should grow with increasing external input c as ; this is sublinear in c for the SSN case of supralinear f.
If one considers a two-population model – a population of E cells and a population of I cells, with each population’s average rate represented by a single variable – then conditions on J and g can be defined such that the elements of are positive and the balanced fixed point is stable and is the only fixed point (van Vreeswijk and Sompolinsky, 1998; Ahmadian et al., 2013; Kraynyukova and Tchumatchenko, 2018). On the other hand, when the E element of is negative, Eq. 17 cannot serve as a basis for an asymptotic expansion with the leading term , and the tightly balanced state does not exist. (Given , if the tightly balanced state existed – meaning that the second term of Eq. 17 becomes much smaller than the first while Eq. 17 is applicable – then ySS must have crossed zero to become negative, but once that has happened we could no longer proceed past Eq. 15 and Eq. 17 would no longer be applicable, which is a contradiction; hence the tightly balanced state cannot exist.) However, the loosely balanced state can still arise in this case in a broad parameter regime of J and g, and can be found as the fixed point of the iterative equation, , given appropriate initial conditions ySS (0); see Ahmadian et al. (2013). In this case, with increasing c, rE grows, but then saturates and starts decreasing, and eventually is pushed down to 0. However, if we assume that the maximal external input (i.e. the maximal c; for example, the maximal firing rate of the thalamic input to a primary sensory cortical area) can only drive rE to saturation or slightly beyond, this represents a viable model of cortical systems (Ahmadian et al., 2013; Rubin et al., 2015; Hennequin et al., 2018).
A two-population model accurately describes the behavior of an unstructured model with many E and I neurons, i.e. with random connectivity and with neurons in each population receiving comparable stimulus inputs. In some cases this model also can form a good approximation to the behavior of a multi-neuron circuit with structured connectivity and stimulus selectivity (Ahmadian et al., 2013). More generally, though, in such a structured circuit with localized connectivity, for larger/stronger localized stimuli, some set of neurons (e.g., neurons not selective for the stimulus) may eventually receive a net inhibition and become silent, meaning that the condition of Eq. 16 is not met and Eq. 17 does not apply. (However, if the connectivity is translation-invariant – the same at any position in the model – and the external input extends more narrowly than the network connections, then a balanced fixed point can still be attained, Rosenbaum and Doiron, 2014.) Nonetheless, we find in simulations (Ahmadian et al., 2013; Rubin et al., 2015; Hennequin et al., 2018) that for reasonable stimulus input strengths, SSN behavior is reasonably described by the two-population model, in that (1) there is a transition with increasing input strength from a weakly coupled, feedforward-driven regime to a strongly-coupled, loosely balanced regime in which the input to excited neurons grows sublinearly as a function of the external input strength; and (2) if we define the W and g of the two-population model as describing the net input received by a cell in the larger, structured model – e.g., WEE represents the mean summed synaptic strength from excitatory cells to a single excitatory cell, and gE represents the mean external input received by stimulus-selective excitatory cells – then reasonably good insight into the operating regime of the larger model can be obtained from the analysis of the two-population model presented here and, in much more detail, in Ahmadian et al. (2013); Kraynyukova and Tchumatchenko (2018).
We believe the same overall analysis of a transition from a weakly coupled regime to a strongly coupled, loosely balanced regime will apply to multi-population models incorporating multiple subtypes of inhibitory cells (e.g. Litwin-Kumar et al., 2016; Kuchibhotla et al., 2017; Garcia Del Molino et al., 2017), but more detailed aspects of the analysis of the two-population model (Ahmadian et al., 2013; Kraynyukova and Tchumatchenko, 2018) need to be generalized to that case.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Adesnik H. (2017). Synaptic Mechanisms of Feature Coding in the Visual Cortex of Awake Mice. Neuron, 95:1147–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ahmadian Y, Rubin DB, and Miller KD (2013). Analysis of the stabilized supralinear network. Neural Computation, 25:1994–2037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amatrudo JM, Weaver CM, Crimins JL, Hof PR, Rosene DL, and Luebke JI. (2012). Influence of highly distinctive structural properties on the excitability of pyramidal neurons in monkey visual and prefrontal cortices. J. Neurosci., 32(40):13644–13660. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amit D. and Brunel N. (1997). Dynamics of a recurrent network of spiking neurons before and following learning. Network: Comput. Neural Syst, 8:373–404. [Google Scholar]
- Anderson JS, Carandini M, and Ferster D. (2000). Orientation tuning of input conductance, excitation, and inhibition in cat primary visual cortex. J. Neurophysiol, 84:909–926. [DOI] [PubMed] [Google Scholar]
- Anderson JS, Lampl I, Gillespie DC, and Ferster D. (2001). Membrane potential and conductance changes underlying length tuning of cells in cat primary visual cortex. J. Neurosci, 21:2104–2112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelucci A, Bijanzadeh M, Nurminen L, Federer F, Merlin S, and Bressloff P. (2017). Circuits and mechanisms for surround modulation in visual cortex. Ann. Rev. Neurosci, 40:425–451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antoine MW, Langberg T, Schnepel P, and Feldman DE (2019). Increased Excitation-Inhibition Ratio Stabilizes Synapse and Circuit Excitability in Four Autism Mouse Models. Neuron, 101:648–661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atallah BV and Scanziani M. (2009). Instantaneous modulation of gamma oscillation frequency by balancing excitation with inhibition. Neuron, 62:566–577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker C, Zhu V, and Rosenbaum R. (2020). Nonlinear stimulus representations in neural circuits with approximate excitatory-inhibitory balance. PLoS Comput Biol, 16:e1008192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barral J. and Reyes A. (2016). Synaptic scaling rule preserves excitatory-inhibitory balance and salient neuronal network dynamics. Nat. Neurosci, 19:1690–1696. [DOI] [PubMed] [Google Scholar]
- Barrett D, Deneve S, and Machens C. (2013). Firing rate predictions in optimal balanced networks. In Pereira F, Burges C, Bottou L, and Weinberger K, editors, Advances in Neural Information Processing Systems, pages 1538–1546. MIT Press. [Google Scholar]
- Barth AL and Poulet JF (2012). Experimental evidence for sparse firing in the neocortex. Trends Neurosci., 35:345–355. [DOI] [PubMed] [Google Scholar]
- Bhatia A, Moza S, and Bhalla US (2019). Precise excitation-inhibition balance controls gain and timing in the hippocampus. Elife, 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boerlin M, Machens CK, and Deneve S. (2013). Predictive coding of dynamical variables in balanced spiking networks. PLoS Comput. Biol, 9(11):e1003258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourdoukan R, Barrett D, Deneve S, and Machens C. (2012). Learning optimal spike- based representations. In Pereira F, Burge C, Botto L, and Weinberge K, editors, Advances in Neural Information Processing Systems, pages 2285–2293. MIT Press. [Google Scholar]
- Brecht M, Roth A, and Sakmann B. (2003). Dynamic receptive fields of reconstructed pyramidal cells in layers 3 and 2 of rat somatosensory barrel cortex. J. Physiol. (Lond.), 553(Pt 1):243–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bridi MCD, Zong FJ, Min X, Luo N, Tran T, Qiu J, Severin D, Zhang XT, Wang G, Zhu ZJ, He KW, and Kirkwood A. (2020). Daily Oscillation of the Excitation-Inhibition Balance in Visual Cortical Circuits. Neuron, 105:621–629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunel N. (2000). Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comput Neurosci, 8:183–208. [DOI] [PubMed] [Google Scholar]
- Carandini M. and Heeger DJ (2012). Normalization as a canonical neural computation. Nat. Rev. Neurosci, 13:51–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavanaugh JR, Bair W, and Movshon JA (2002). Nature and interaction of signals from the receptive field center and surround in macaque V1 neurons. J. Neurophysiol, 88:2530–2546. [DOI] [PubMed] [Google Scholar]
- Chiu CQ, Barberis A, and Higley MJ (2019). Preserving the balance: diverse forms of longterm GABAergic synaptic plasticity. Nat Rev Neurosci, 20:272–281. [DOI] [PubMed] [Google Scholar]
- Chiu CQ, Martenson JS, Yamazaki M, Natsume R, Sakimura K, Tomita S, Tavalin SJ, and Higley MJ (2018). Input-Specific NMDAR-Dependent Potentiation of Dendritic GABAergic Inhibition. Neuron, 97:368–377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung S. and Ferster D. (1998). Strength and orientation tuning of the thalamic input to simple cells revealed by electrically evoked cortical suppression. Neuron, 20:1177–89. [DOI] [PubMed] [Google Scholar]
- Churchland MM, Yu BM, Cunningham JP, Sugrue LP, Cohen MR, Corrado GS, Newsome WT, Clark AM, Hosseini P, Scott BB, Bradley DC, Smith MA, Kohn A, Movshon JA, Armstrong KM, Moore T, Chang SW, Snyder LH, Lisberger SG, Priebe NJ, Finn IM, Ferster D, Ryu SI, Santhanam G, Sahani M, and Shenoy KV (2010). Stimulus onset quenches neural variability: a widespread cortical phenomenon. Nat. Neurosci, 13:369–378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR and Kohn A. (2011). Measuring and interpreting neuronal correlations. Nat. Neurosci, 14:811–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohen MR and Maunsell JH (2009). Attention improves performance primarily by reducing interneuronal correlations. Nat. Neurosci, 12:1594–1600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Constantinople CM and Bruno RM (2013). Deep cortical layers are activated directly by thalamus. Science, 340:1591–1594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cossell L, Iacaruso MF, Muir DR, Houlton R, Sader EN, Ko H, Hofe SB, and Mrsic-Flogel TD. (2015). Functional organization of excitatory synaptic strength in primary visual cortex. Nature, 518:399–403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehghani N, Peyrache A, Telenczuk B, Le Van Quyen M, Halgren E, Cash SS, Hatsopoulos NG, and Destexhe A. (2016). Dynamic Balance of Excitation and Inhibition in Human and Monkey Neocortex. Sci Rep, 6:23176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deneve S. and Machens CK (2016). Efficient codes and balanced networks. Nat. Neurosci, 19:375–382. [DOI] [PubMed] [Google Scholar]
- Denfield GH, Ecker AS, Shinn TJ, Bethge M, and Tolias AS (2018). Attentional fluctuations induce shared variability in macaque primary visual cortex. Nat Commun, 9:2654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWeese M. and Zador A. (2006). Non-Gaussian membrane potential dynamics imply sparse, synchronous activity in auditory cortex. J. Neurosci, 26:12206–12218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doiron B, Litwin-Kumar A, Rosenbaum R, Ocker GK, and Josic K. (2016). The mechanics of state-dependent neural correlations. Nat. Neurosci, 19:383–393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorrn AL, Yuan K, Barker AJ, Schreiner CE, and Froemke RC (2010). Developmental sensory experience balances cortical excitation and inhibition. Nature, 465:932–936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Echeveste R, Aitchison L, Hennequin G, and Lengyel M. (2020). Cortical-like dynamics in recurrent circuits optimized for sampling-based probabilistic inference. Nat Neurosci, 23:1138–1149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ecker AS, Berens P, Cotton RJ, Subramaniyan M, Denfield GH, Cadwell CR, Smirnakis SM, Bethge M, and Tolias AS (2014). State dependence of noise correlations in macaque primary visual cortex. Neuron, 82:235–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ecker AS, Berens P, Keliris GA, Bethge M, Logothetis NK, and Tolias AS (2010). Decorrelated neuronal firing in cortical microcircuits. Science, 327(5965):584–587. [DOI] [PubMed] [Google Scholar]
- Elston GN (2003). Cortex, cognition and the cell: new insights into the pyramidal neuron and prefrontal function. Cereb. Cortex, 13:1124–1138. [DOI] [PubMed] [Google Scholar]
- Elston GN and Fujita I. (2014). Pyramidal cell development: postnatal spinogenesis, dendritic growth, axon growth, and electrophysiology. Front Neuroanat, 8:78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elston GN and Manger P. (2014). Pyramidal cells in V1 of African rodents are bigger, more branched and more spiny than those in primates. Front Neuroanat, 8:4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel TA, Steinmetz NA, Gieselmann MA, Thiele A, Moore T, and Boahen K. (2016). Selective modulation of cortical state during spatial attention. Science, 354:1140–1144. [DOI] [PubMed] [Google Scholar]
- Fares T. and Stepanyants A. (2009). Cooperative synapse formation in the neocortex. Proc. Natl. Acad. Sci. U.S.A, 106(38):16463–16468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldmeyer D, Egger V, Lübke J, and Sakmann B. (1999). Reliable synaptic connections between pairs of excitatory layer 4 neurones within a single “barrel” of developing rat somatosensory cortex. J. Physiol., 521:169–190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldmeyer D, Lübke J, Silver RA, and Sakmann B. (2002). Synaptic connections between layer 4 spiny neurone-layer 2/3 pyramidal cell pairs in juvenile rat barrel cortex: physiology and anatomy of interlaminar signalling within a cortical column. J Physiol, 538:803–822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferguson KA and Cardin JA (2020). Mechanisms underlying gain modulation in the cortex. Nature Reviews Neuroscience, 21:80–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferster D, Chung S, and Wheat H. (1996). Orientation selectivity of thalamic input to simple cells of cat visual cortex. Nature, 380:249–252. [DOI] [PubMed] [Google Scholar]
- Field RE, D’amour JA, Tremblay R, Miehl C, Rudy B, Gjorgjieva J, and Froemke RC (2020). Heterosynaptic Plasticity Determines the Set Point for Cortical Excitatory-Inhibitory Balance. Neuron, 106:842–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finn IM, Priebe NJ, and Ferster D. (2007). The emergence of contrast-invariant orientation tuning in simple cells of cat visual cortex. Neuron, 54:137–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Froemke RC (2015). Plasticity of cortical excitatory-inhibitory balance. Annu Rev Neurosci, 38:195–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galarreta M. and Hestrin S. (1998). Frequency-dependent synaptic depression and the balance of excitation and inhibition in the neocortex. Nat. Neurosci, 1:587–594. [DOI] [PubMed] [Google Scholar]
- Garcia Del Molino LC, Yang GR, Mejias JF, and Wang XJ (2017). Paradoxical response reversal of top-down modulation in cortical circuits with three interneuron types. Elife, 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graupner M. and Reyes AD (2013). Synaptic input correlations leading to membrane potential decorrelation of spontaneous activity in cortex. J. Neurosci, 33:15075–15085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider B, Duque A, Hasenstaub AR, and McCormick DA (2006). Neocortical network activity in vivo is generated through a dynamic balance of excitation and inhibition. J. Neurosci, 26:4535–4545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider B, Hausser M, and Carandini M. (2013). Inhibition dominates sensory responses in the awake cortex. Nature, 493:97–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel D. and van Vreeswijk C. (2002). How noise contributes to contrast invariance of orientation tuning in cat visual cortex. J. Neurosci, 22:5118–5128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansel D. and van Vreeswijk C. (2012). The mechanism of orientation selectivity in primary visual cortex without a functional map. J. Neurosci, 32:4049–4064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hennequin G, Agnes EJ, and Vogels TP (2017). Inhibitory Plasticity: Balance, Control, and Codependence. Annu. Rev. Neurosci, 40:557–579. [DOI] [PubMed] [Google Scholar]
- Hennequin G, Ahmadian Y, Rubin DB, Lengyel M, and Miller KD (2018). The Dynamical Regime of Sensory Cortex: Stable Dynamics around a Single Stimulus-Tuned Attractor Account for Patterns of Noise Variability. Neuron, 98(4):846–860. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heuer HW and Britten KH (2002). Contrast dependence of response normalization in area MT of the rhesus macaque. J. Neurophysiol, 88:3398–3408. [DOI] [PubMed] [Google Scholar]
- Higley M. and Contreras D. (2006). Balanced excitation and inhibition determine spike timing during frequency adaptation. J. Neurosci, 26:448–457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Histed MH (2018). Feedforward Inhibition Allows Input Summation to Vary in Recurrent Cortical Networks. eNeuro, 5(1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hromadka T, Deweese MR, and Zador AM (2008). Sparse representation of sounds in the unanesthetized auditory cortex. PLoS Biol., 6(1):e16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hrom[start]Ã[end][start]¡[end]dka T, Zador AM, and DeWeese MR (2013). Up states are rare in awake auditory cortex. J Neurophysiol, 109:1989–1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iascone DM, Li Y, S[start]Ã[end][start]¼[end]mb[start]Ã[end][start]¼[end]l U, Doron M, Chen H, Andreu V, Goudy F, Blockus H, Abbott LF, Segev I, Peng H, and Polleux F. (2020). Whole-Neuron Synaptic Mapping Reveals Spatially Precise Excitatory/Inhibitory Balance Limiting Dendritic and Somatic Spiking. Neuron, 106:566–578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ichida JM, Schwabe L, Bressloff PC, and Angelucci A. (2007). Response facilitation from the ”suppressive” receptive field surround of macaque V1 neurons. J. Neurophysiol, 98:2168–2181. [DOI] [PubMed] [Google Scholar]
- Joseph A. and Turrigiano GG (2017). All for One But Not One for All: Excitatory Synaptic Scaling and Intrinsic Excitability Are Coregulated by CaMKIV, Whereas Inhibitory Synaptic Scaling Is Under Independent Control. J Neurosci, 37:6778–6785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kato HK, Asinof SK, and Isaacson JS (2017). Network-Level Control of Frequency Tuning in Auditory Cortex. Neuron, 95(2):412–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khajeh R, Fumarola F, and Abbott L. (2021). Sparse balance: excitatory-inhibitory networks with small bias currents and broadly distributed synaptic weights. biorxiv, 2021.02.26.433027; doi: 10.1101/2021.02.26.433027. [DOI] [PMC free article] [PubMed]
- Ko H, Hofer SB, Pichler B, Buchanan KA, Sjostrom PJ, and Mrsic-Flogel TD (2011). Functional specificity of local synaptic connections in neocortical networks. Nature, 473:87–91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kraynyukova N. and Tchumatchenko T. (2018). Stabilized supralinear network can give rise to bistable, oscillatory, and persistent activity. Proc. Natl. Acad. Sci. U.S.A, 115(13):3464–3469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuchibhotla KV, Gill JV, Lindsay GW, Papadoyannis ES, Field RE, Sten TA, Miller KD, and Froemke RC (2017). Parallel processing by cortical inhibition enables context-dependent behavior. Nat. Neurosci, 20:62–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lampl I, Reichova I, and Ferster D. (1999). Synchronous membrane potential fluctuations in neurons of the cet visual cortex. Neuron, 22:361–374. [DOI] [PubMed] [Google Scholar]
- Lankarany M, Heiss JE, Lampl I, and Toyoizumi T. (2016). Simultaneous Bayesian Estimation of Excitatory and Inhibitory Synaptic Conductances by Exploiting Multiple Recorded Trials. Front Comput Neurosci, 10:110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larkum ME, Zhu JJ, and Sakmann B. (2001). Dendritic mechanisms underlying the coupling of the dendritic with the axonal action potential initiation zone of adult rat layer 5 pyramidal neurons. J. Physiol. (Lond.), 533(Pt 2):447–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li B, Thompson JK, Duong T, Peterson MR, and Freeman RD (2006). Origins of cross-orientation suppression in the visual cortex. J. Neurophysiol, 96:1755–1764. [DOI] [PubMed] [Google Scholar]
- Li LY, Li YT, Zhou M, Tao HW, and Zhang LI (2013a). Intracortical multiplication of thalamocortical signals in mouse auditory cortex. Nat. Neurosci, 16:1179–1181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li YT, Ibrahim LA, Liu BH, Zhang LI, and Tao HW (2013b). Linear transformation of thalamocortical input by intracortical excitation. Nat. Neurosci, 16:1324–1330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lien AD. and Scanziani M. (2013). Tuned thalamic excitation is amplified by visual cortical circuits. Nat. Neurosci., 16:1315–1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litwin-Kumar A, Chacron MJ, and Doiron B. (2012). The spatial structure of stimuli shapes the timescale of correlations in population spiking activity. PLoS Comput. Biol, 8:e1002667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Litwin-Kumar A, Rosenbaum R, and Doiron B. (2016). Inhibitory stabilization and visual coding in cortical circuits with multiple interneuron subtypes. J. Neurophysiol, 115:1399–1409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu G. (2004). Local structural balance and functional interaction of excitatory and inhibitory synapses in hippocampal dendrites. Nat Neurosci, 7:373–379. [DOI] [PubMed] [Google Scholar]
- Liu LD, Miller KD, and Pack CC (2018). A Unifying Motif for Spatial and Directional Surround Suppression. J. Neurosci, 38(4):989–999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maimon G. and Assad JA (2009). Beyond Poisson: increased spike-time regularity across primate parietal cortex. Neuron, 62:426–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mainen ZF and Sejnowski TJ (1995). Reliability of spike timing in neocortical neurons. Science, 268:1503–1506. [DOI] [PubMed] [Google Scholar]
- Manns ID, Sakmann B, and Brecht M. (2004). Sub- and suprathreshold receptive field properties of pyramidal neurones in layers 5A and 5B of rat somatosensory barrel cortex. J. Physiol. (Lond.), 556(Pt 2):601–622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marino J, Schummers J, Lyon DC, Schwabe L, Beck O, Wiesing P, Obermayer K, and Sur M. (2005). Invariant computations in local cortical networks with balanced excitation and inhibition. Nature Neurosci., 8:194–201. [DOI] [PubMed] [Google Scholar]
- Markov NT, Misery P, Falchier A, Lamy C, Vezoli J, Quilodran R, Gariel MA, Giroud P, Ercsey-Ravasz M, Pilaz LJ, Huissoud C, Barone P, Dehay C, Toroczkai Z, Van Essen DC, Kennedy H, and Knoblauch K. (2011). Weight consistency specifies regularities of macaque cortical networks. Cereb. Cortex, 21(6):1254–1272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markram H, Lubke J, Frotscher M, Roth A, and Sakmann B. (1997). Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. J. Physiol. (Lond.), 500 ( Pt 2):409–440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mccormick DA, Mcginley MJ, and Salkoff DB (2015). Brain state dependent activity in the cortex and thalamus. Current Opinion in Neurobiology, 31:133–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGinley MJ, Vinck M, Reimer J, Batista-Brito R, Zagha E, Cadwell CR, Tolias AS, Cardin JA, and McCormick DA (2015). Waking State: Rapid Variations Modulate Neural and Behavioral Responses. Neuron, 87:1143–1161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KD (2016). Canonical computations of cerebral cortex. Curr. Opin. Neurobiol, 37:75–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KD and Troyer TW (2002). Neural noise can explain expansive, power-law nonlinearities in neural response functions. J. Neurophysiol, 87:653–659. [DOI] [PubMed] [Google Scholar]
- Mitchell JF, Sundberg KA, and Reynolds JH (2009). Spatial attention decorrelates intrinsic activity fluctuations in macaque area V4. Neuron, 63:879–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mongillo G, Hansel D, and van Vreeswijk C. (2012). Bistability and spatiotemporal irregularity in neuronal networks with nonlinear synaptic transmission. Phys. Rev. Lett, 108:158101. [DOI] [PubMed] [Google Scholar]
- Moore AK, Weible AP, Balmer TS, Trussell LO, and Wehr M. (2018). Rapid Rebalancing of Excitation and Inhibition by Cortical Circuitry. Neuron, 97:1341–1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassi JJ, Avery MC, Cetin AH, Roe AW, and Reynolds JH (2015). Optogenetic Activation of Normalization in Alert Macaque Visual Cortex. Neuron, 86:1504–1517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nienborg H, Hasenstaub A, Nauhaus I, Taniguchi H, Huang ZJ, and Callaway EM (2013). Contrast dependence and differential contributions from somatostatin- and parvalbumin-expressing neurons to spatial integration in mouse V1. J. Neurosci, 33:11145–11154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Donnell C. and van Rossum MC (2014). Systematic analysis of the contributions of stochastic voltage gated channels to neuronal noise. Front Comput Neurosci, 8:105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohshiro T, Angelaki DE, and DeAngelis G. (2013). A normalization model of multisensory integration accounts for distinct forms of cross-modal and within-modal cue integration by cortical neurons. Program No. 360.19. 2013 Neuroscience Meeting Planner. San Diego, CA: Society for Neuroscience, 2013. Online. [Google Scholar]
- Okun M. and Lampl I. (2008). Instantaneous correlation of excitation and inhibition during ongoing and sensory-evoked activities. Nat. Neurosci, 11:535–537. [DOI] [PubMed] [Google Scholar]
- Ozeki H, Finn IM, Schaffer ES, Miller KD, and Ferster D. (2009). Inhibitory stabilization of the cortical network underlies visual surround suppression. Neuron, 62:578–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer L, Murayama M, and Larkum M. (2016). Dendritic integration in vivo. In Stuart G, Spruston N, and Hausser M, editors, Dendrites, 3rd Edition, pages 399–428. Oxford University Press. [Google Scholar]
- Pehlevan C. and Sompolinsky H. (2014). Selectivity and sparseness in randomly connected balanced networks. PLoS ONE, 9:e89992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poirazi P. and Papoutsi A. (2020). Illuminating dendritic function with computational models. Nat Rev Neurosci, 21:303–321. [DOI] [PubMed] [Google Scholar]
- Polat U, Mizobe K, Pettet MW, Kasamatsu T, and Norcia AM (1998). Collinear stimuli regulate visual responses depending on cell’s contrast threshold. Nature, 391:580–584. [DOI] [PubMed] [Google Scholar]
- Poulet JF and Petersen CC (2008). Internal brain state regulates membrane potential synchrony in barrel cortex of behaving mice. Nature, 454:881–885. [DOI] [PubMed] [Google Scholar]
- Priebe N, Mechler F, Carandini M, and Ferster D. (2004). The contribution of spike threshold to the dichotomy of cortical simple and complex cells. Nat. Neurosci, 7:1113–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Priebe NJ and Ferster D. (2006). Mechanisms underlying cross-orientation supression in cat visual cortex. Nature Neurosci., 9:552–561. [DOI] [PubMed] [Google Scholar]
- Priebe NJ and Ferster D. (2008). Inhibition, spike threshold and stimulus selectivity in primary visual cortex. Neuron, 57:482–497. [DOI] [PubMed] [Google Scholar]
- Renart A, de la Rocha J, Bartho P, Hollender L, Parga N, Reyes A, and Harris KD (2010). The asynchronous state in cortical circuits. Science, 327:587–590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reynolds JH and Chelazzi L. (2004). Attentional modulation of visual processing. Annu. Rev. Neurosci, 27:611–647. [DOI] [PubMed] [Google Scholar]
- Rosenbaum R. and Doiron B. (2014). Balanced networks of spiking neurons with spatially dependent recurrent connections. Physical Review X, 4(2):021039. [Google Scholar]
- Rosenbaum R, Smith MA, Kohn A, Rubin JE, and Doiron B. (2017). The spatial structure of correlated neuronal variability. Nat. Neurosci, 20:107–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubin DB, Van Hooser SD, and Miller KD (2015). The stabilized supralinear network: A unifying circuit motif underlying multi-input integration in sensory cortex. Neuron, 85:402–417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadagopan S. and Ferster D. (2012). Feedforward origins of response variability underlying contrast invariant orientation tuning in cat visual cortex. Neuron, 74:911–923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadeh S. and Rotter S. (2015). Orientation selectivity in inhibition-dominated networks of spiking neurons: effect of single neuron properties and network dynamics. PLoS Comput. Biol, 11:e1004045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanzeni A, Akitake B, Goldbach HC, Leedy CE, Brunel N, and Histed MH (2020a). Inhibition stabilization is a widespread property of cortical networks. Elife, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanzeni A, Histed MH, and Brunel N. (2020b). Emergence of irregular activity in networks of strongly coupled conductance-based neurons. arXiv:2009.12023 [q-bio.NC]. [DOI] [PMC free article] [PubMed]
- Sato TK, Hausser M, and Carandini M. (2014). Distal connectivity causes summation and division across mouse visual cortex. Nat. Neurosci, 17:30–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sceniak M, Ringach DL, Hawken M, and Shapley R. (1999). Contrast’s effect on spatial summation by macaque v1 neurons. Nature Neurosci., 2:733–739. [DOI] [PubMed] [Google Scholar]
- Schneidman E, Freedman B, and Segev I. (1998). Ion channel stochasticity may be critical in determining the reliability and precision of spike timing. Neural Comput, 10:1679–1703. [DOI] [PubMed] [Google Scholar]
- Schoonover CE, Tapia JC, Schilling VC, Wimmer V, Blazeski R, Zhang W, Mason CA, and Bruno RM (2014). Comparative strength and dendritic organization of thalamocortical and corticocortical synapses onto excitatory layer 4 neurons. J. Neurosci, 34:6746–6758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwabe L, Ichida JM, Shushruth S, Mangapathy P, and Angelucci A. (2010). Contrast-dependence of surround suppression in Macaque V1: experimental testing of a recurrent network model. Neuroimage, 52:777–792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengpiel F, Blakemore C, and Sen A. (1997). Characteristics of surround inhibition in cat area 17. Exp. Brain Res, 116:216–228. [DOI] [PubMed] [Google Scholar]
- Sengpiel F. and Vorobyov V. (2005). Intracortical origins of interocular suppression in the visual cortex. J. Neurosci, 25:6394–6400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN and Newsome WT (1998). The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J. Neurosci, 18:3870–3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao YR, Isett BR, Miyashita T, Chung J, Pourzia O, Gasperini RJ, and Feldman DE (2013). Plasticity of recurrent l2/3 inhibition and gamma oscillations by whisker experience. Neuron, 80:210–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shu Y, Hasenstaub A, and McCormick DA (2003). Turning on and off recurrent balanced cortical activity. Nature, 423:288–293. [DOI] [PubMed] [Google Scholar]
- Shushruth S, Ichida JM, Levitt JB, and Angelucci A. (2009). Comparison of spatial summation properties of neurons in macaque V1 and V2. J. Neurophysiol, 102:2069–2083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA and Kohn A. (2008). Spatial and temporal scales of neuronal correlation in primary visual cortex. J Neurosci, 28:12591–12603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Softky W. and Koch C. (1993). The highly irregular firing of cortical-cells is inconsistent with temporal integration of random EPSPS. J. Neurosci, 13:334–350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song XM and Li CY (2008). Contrast-dependent and contrast-independent spatial summation of primary visual cortical neurons of the cat. Cerebral Cortex, 18:331–336. [DOI] [PubMed] [Google Scholar]
- Spruston N, Stuart G, and Hausser M. (2016). Principles of dendritic integration. In Stuart G, Spruston N, and Hausser M, editors, Dendrites, 3rd Edition, pages 351–398. Oxford University Press. [Google Scholar]
- Stevens C. and Zador A. (1998). Input synchrony and the irregular firing of cortical neurons. Nat. Neurosci, 1:210–217. [DOI] [PubMed] [Google Scholar]
- Sukenik N, Vinogradov O, Weinreb E, Segal M, Levina A, and Moses E. (2021). Neuronal circuits overcome imbalance in excitation and inhibition by adjusting connection numbers. Proc Natl Acad Sci U S A, 118:e2018459118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan AY, Chen Y, Scholl B, Seidemann E, and Priebe NJ (2014). Sensory stimulation shifts visual cortex from synchronous to asynchronous states. Nature, 509:226–229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tan AY and Wehr M. (2009). Balanced tone-evoked synaptic excitation and inhibition in mouse auditory cortex. Neuroscience, 163:1302–1315. [DOI] [PubMed] [Google Scholar]
- Titley HK, Brunel N, and Hansel C. (2017). Toward a Neurocentric View of Learning. Neuron, 95(1):19–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Troyer TW and Miller KD (1997). Physiological gain leads to high ISI variability in a simple model of a cortical regular spiking cell. Neural Comput., 9:971–983. [DOI] [PubMed] [Google Scholar]
- Tsodyks MV and Sejnowski T. (1995). Rapid state switching in balanced cortical network models. Network, 6:111–124. [Google Scholar]
- Tsui JM and Pack CC (2011). Contrast sensitivity of MT receptive field centers and surrounds. J. Neurophysiol, 106:1888–1900. [DOI] [PubMed] [Google Scholar]
- Ujfalussy BB, Makara JK, Lengyel M, and Branco T. (2018). Global and Multiplexed Dendritic Computations under In Vivo-like Conditions. Neuron, 100:579–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Vreeswijk C. and Sompolinsky H. (1996). Chaos in neuronal networks with balanced excitatory and inhibitory activity. Science, 274:1724–1726. [DOI] [PubMed] [Google Scholar]
- van Vreeswijk C. and Sompolinsky H. (1998). Chaotic balanced state in a model of cortical circuits. Neural Computation, 10:1321–1371. [DOI] [PubMed] [Google Scholar]
- Vinck M, Batista-Brito R, Knoblich U, and Cardin JA (2015). Arousal and locomotion make distinct contributions to cortical activity patterns and visual encoding. Neuron, 86:740–754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S, Miller KD, and van Hooser SB (2019). Combined visual and patterned optogenetic stimulation of ferret visual cortex reveals that cortical circuits respond to independent inputs in a sublinear manner. Cosyne Abstracts 2019, Lisbon, Portugal, (to appear):1–15. [Google Scholar]
- Wehr M. and Zador AM (2003). Balanced inhibition underlies tuning and sharpens spike timing in auditory cortex. Nature, 426:442–446. [DOI] [PubMed] [Google Scholar]
- Wilent WB and Contreras D. (2005). Stimulus-dependent changes in spike threshold enhance feature selectivity in rat barrel cortex neurons. J. Neurosci, 25:2983–2991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu GK, Arbuckle R, Liu BH, Tao HW, and Zhang LI (2008). Lateral sharpening of cortical frequency tuning by approximately balanced inhibition. Neuron, 58:132–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu GK, Li P, Tao HW, and Zhang LI (2006). Nonmonotonic synaptic excitation and imbalanced inhibition underlying cortical intensity tuning. Neuron, 52:705–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue M, Atallah BV, and Scanziani M. (2014). Equalizing excitation-inhibition ratios across visual cortical neurons. Nature, 511:596–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yizhar O, Fenno LE, Prigge M, Schneider F, Davidson TJ, O’Shea DJ, Sohal VS, Goshen I, Finkelstein J, Paz JT, Stehfest K, Fudim R, Ramakrishnan C, Huguenard JR, Hegemann P, and Deisseroth K. (2011). Neocortical excitation/inhibition balance in information processing and social dysfunction. Nature, 477:171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou M, Liang F, Xiong XR, Li L, Li H, Xiao Z, Tao HW, and Zhang LI (2014). Scaling down of balanced excitation and inhibition by active behavioral states in auditory cortex. Nat. Neurosci, 17:841–850. [DOI] [PMC free article] [PubMed] [Google Scholar]