Accounting for Space, Time, and Behavior Using GPS Derived Dynamic Measures of Environmental Exposure

Abstract

Time-weighted spatial averaging approaches (TWSA) are an increasingly utilized method for calculating exposure using global positioning system (GPS) mobility data for health-related research. They can provide a time-weighted measure of exposure, or dose, to various environments or health hazards. However, little work has been done to compare existing methodologies, nor to assess how sensitive these methods are to mobility data inputs (e.g., walking vs driving), the type of environmental data being assessed as the exposure (e.g., continuous surfaces vs points of interest), and underlying point-pattern clustering of participants (e.g., if a person is highly mobile vs predominantly stationary). Here we contrast three TWSA approaches that have been previously used or recently introduced in the literature: Kernel Density Estimation (KDE), Density Ranking (DR), and Point Overlay (PO). We feed GPS and accelerometer data from 602 participants through each method to derive time-weighted activity spaces, comparing four mobility behaviors: all movement, stationary time, walking time, and in-vehicle time. We then calculate exposure values derived from the various TWSA activity spaces with four environmental layer data types (point, line, area, surface). Similarities and differences across TWSA derived exposures for the sample and between individuals are explored, and we discuss interpretation of TWSA outputs providing recommendations for researchers seeking to apply these methods to health-related studies.

1. Introduction

Exposure science in public health has seen an increase in use of personalized global positioning systems (GPS) to measure human mobility. GPS devices are widely available, resulting data are increasingly easier to process, and there is increasing desire to better match dynamic human movement with exposure measures. The underlying promise of GPS data are more accurate and specific measures of where people go and spend time, and therefore more precise measures of what people are exposed to within their activity spaces (1). Theoretical underpinnings classify GPS data under dynamic conceptualization of exposure, which vary through space and over time (e.g. air pollution exposure over the course of the entire day of movement), rather than static ones that capture constant or single locations of exposure (e.g. poverty level in census tract of residence) (2–4). In parallel, several methodologies for calculating activity spaces and their resulting dynamic exposures using GPS data have been utilized in the health literature (as well as other topics) including buffers, convex hulls, domain-based alignment, trip calculation, standard deviation ellipses, and space-time prisms (5–7).

These methods are increasingly being applied to a variety of health-related research including air pollution effects on health (8), active living (9), obesity and food environment (10), addiction, impacts of noise pollution (11), and environmental effects on biomarker outcomes (12). A subset of activity space methods using GPS data are dubbed time-weighted spatial averaging (TWSA) approaches. Compared to domain based or spatial averaging approaches, TWSA uses time spent along the movement path to generate a time-weighted activity space for extracting exposure measures (13). TWSA methods are currently rarely utilized in health and exposure studies compared to non time-weighted measures, yet time-weighting may play an important role in understanding how much of an exposure, or dose, is accumulated through time spent in an environment and how that dose, in turn, relates to health outcomes.

Time-weighting is closely tied to behavior and context. For example, time accumulated sitting in an office can be compared to time accumulated sitting in a park, or even time accumulated sitting in a vehicle on a highway. Each example may provide important clues of dose-response to air pollution exposure. TWSA methods will likely continue to grow in applications where time-related dose may be important, as well as applications where minute-level exposure analytics may be necessary, e.g., just in time adaptive interventions (14). Yet currently there is a considerable gap in understanding of how TWSA methods generate time-weighted activity spaces, extract environmental exposures, their sensitivity to movement of participants and underlying environmental data structures, and how we interpret resulting exposure measures in the context of health and exposure studies. Better understanding of how different TWSA methods work, their intrinsic assumptions, and their sensitivity to data inputs will help researchers interested in time-weighting exposure measures to identify the approach that fits best with the theoretical space-time mechanism for a specific environmental health question under investigation.

1.1. TWSA as an extension of movement and time geography

TWSA methods draw from two fundamental research domains: movement and time geography. Time geography as originally conceived by Hägerstrand’s seminal 1970 work (15) outlines the joining of individual movement in space and time as constrained by people’s daily geographies. Interactions of humans and the environment are recognized as spatial processes. In the realm of human health, Rainham et al. (3) define these principles as a “healthscape” resulting from geographic properties that include attributes assigned to context, spatiotemporal relationships between people and their surroundings, and underlying characteristics of humans and their behaviors. A key crux of the time × movement relationship recognizes that specific types of movement can result in smaller or larger healthscapes (e.g., from walking vs. car riding), and consequently in diverse exposures depending on mobility patterns.

Research on movement is a larger field where the study of dynamic motion of any mobile object is the focus, however it is often closely coupled with time geography due to the fundamental question of what movement is probable and possible. Focusing on geography, Laube (16) recently described six semantic levels for quantifying movement ranging from instantaneous (e.g., fixes or vectors) to aggregations (e.g., areas and densities). In this semantic ordering, TWSA methods sit at the latter end of spectrum by offering aggregated surfaces not only of where an individual has gone, but how much time was spent there. Most developments of TWSA methods have evolved out of the animal tracking realm. There are few proposed extensions that have been adapted for human health research and specifically exposure science, and advances in time-weighted location detection using GPS data are prone to removing trip-related data (17,18). There is a need to better understand the application of TWSA methods to GPS data through a health and exposure science lens.

1.2. TWSA applications to health

In building movement and time geography theory into health exposure science, there must be a recognition that specific combinations of movement, time, and environment will result in distinct exposures, which may in turn have different implications for health. Should a researcher equally weigh 2 hours sitting in an office building with 2 hours of walking through a neighborhood? This will, of course, highly depend on the research question. In a study looking at relationships between built environment features and insulin resistance in a cohort of women at risk of breast cancer, time-weighted kernel density estimates (KDE) of exposures that used all GPS points of participants were not associated with insulin resistance. However, KDE exposures that only considered GPS points when a participant was walking or physically active did show significant associated with decreased insulin resistance (12). Without a better comprehension of how time-weighted methods estimate environmental exposure under diverse human mobility conditions, it will be difficult to explain the resulting exposure estimates’ association with health. We cannot ignore the fundamental role that movement plays in both exposure and access, and better understanding of the time × movement relationship in the context of environment and health will be an essential contribution to the field.

In this paper we explore and compare three TWSA approaches – kernel density estimation, point overlay, and density ranking – with the goal of digging into the methodological aspects that dictate how these methods generate time-weighted activity spaces and estimate environmental exposure. We specifically focus on nuances of the methods’ resulting exposure measures rather than their link to a health outcome to be able to provide recommendations and potential pitfalls for using TWSA across a variety of health-related studies. We assess TWSA sensitivity to types of mobility data inputs (e.g., walking vs in vehicle), types of environmental layer inputs (e.g., point patterns compared to continuous surfaces), and underlying point-pattern clustering of participants (e.g., if a person is highly mobile vs predominantly stationary). The introduction of the time dimension increases complexity for the measure of environmental exposure, therefor we believe it is necessary to better understand how these methods operationalize exposure so they can be appreciated in relationship to health. Our specific research questions are:

• RQ1: What are the similarities and differences across TWSA methods for representing time-weighted activity spaces and resulting environmental exposures?

• RQ2: What is the sensitivity of the TWSA methods’ exposure outcomes to different types of mobility and environmental inputs across the sample and within individuals?

2. Methodology

We apply three TWSA methods – point overlay (PO), kernel density estimation (KDE), and density ranking (DR) – to a set of real-world GPS tracks derived from a previously completed study of 602 individuals. To explore sensitivity to various mobility data inputs, GPS tracks were joined with accelerometer data to generate four mobility modalities: all points, stationary points, in-vehicle points, and walking points. These four mobility modalities were chosen as they are representative of a variety of common movement patterns, are of interest to several health outcomes including physical activity and air pollution, and are readily available to most researchers using GPS data inputs even without matched accelerometer data. We also explored sensitivity to environmental data representations including vector discrete spatial features (point, line, and polygon/area data) as well as continuous features (raster data). In testing the three TWSA methods across mobility data inputs × environmental data inputs, we can review the sensitivity of the methods to a variety of research data situations. Detailed description of GPS/accelerometer processing for mobility type and environmental layer generation are provided in Appendix A.1 and A.2 respectively. Here we focus on the TWSA methods, calculation of exposure, and analysis for sensitivity comparison.

2.1. Participant data

We chose a real-world dataset for experimentation to best demonstrate realistic data processing and analytic issues, as well as interpretability of exposure results. The Community of Mine study enrolled participants 35 and older in San Diego County, California from 2014 to 2017. The full study protocol and eligibility criteria are described elsewhere (19). A total of 602 individuals completed the study of average age 59, 42% Hispanic/Latino, and 56% female. Data for this study were generated from two sensors worn by participants on the hip during waking hours over a two-week period: a GT3X+ ActiGraph accelerometer (ActiGraph, LLC; Pensacola, FL) and a Qstarz GPS device (Qstarz International Co. Ltd, Taipei, Taiwan). Participants did not wear devices during sleep, and thus wear time represents times of the day the participant is active and awake. Valid days were defined as having at least 10 hours of overlapping GPS and accelerometer measured wear time after non-wear time was excluded using the validated Choi algorithm (20). Participants wore devices for an average of 13.7 valid days, and 3 participants were dropped from analysis due to not having any valid days resulting in a final sample of 599. All participants gave informed consent and study protocol was approved by the University of California San Diego Institutional Review Board (protocol #140510). A full description of accelerometer and GPS sensor processing can be found in the Appendix (A.1).

2.2. TWSA methods

Point Overlay (PO):

The simplest implementation of TWSA is a one-to-one point overlay (PO) of GPS data onto the exposure surface of interest. In this approach GPS point data is used to extract values from the underlying Geographic Information Systems (GIS) layer that represents the exposure. A drawback of PO is both types of spatial data (GPS and GIS) are susceptible to locational and content error, and therefore exact matching is likely to exacerbate error of exposure measures (21–23). Another problem is that the extent of exposure is limited to the exact location of the match, e.g., an individual in a fast-food outlet vs. an individual seeing a fast-food outlet 100m away. Some studies have addressed this issue by smoothing underlying GIS layers through rasterization or density estimation, making the extent of the exposure layer less reliant on exact locational match (24). Because PO does not perform any mathematical smoothing, each minute adds an equal amount to an individual’s exposure value.

Kernel Density Estimation (KDE):

The most common TWSA method is kernel density estimation (KDE) due to its ease of application, research into its statistical properties, existence of several tuning functions, and study of its applied use in a variety of settings. In an analysis of temporal stability and ability to capture exposure variability within and between participants, KDE was found to be a more reliable for measuring exposure compared to route buffers or convex hull measures (25). Using GPS point data, KDE generates a smoothed continuous surface that represents variation in the spatial density of events. A decay probability density function is applied to each GPS data point and assigned the values to the intersecting surrounding data points, where each value corresponds to the distance between the central and surrounding data points. Summing up all the values of each input data point, KDE generates a continuous probability surface with the estimated probability at each grid cell p(x,y) described as (26):

$$P\left(x,y\right)=\frac{1}{n{h}^2}\sum _{i=1}^{m}K\left(\underset{h}{di\left(x,y\right)}\right)$$

where h is the defined kernel size (or bandwidth); K is the kernel function; n is the number of observation data points; and di is the distance between the grid cell (x, y) and i-th data point. The selection of kernel size (h) reflects the maximum distance of spatial interaction between activity locations (27) and from the dynamic exposure point of view it is the extent where a person is being impacted by the environment.

KDE is both a nonparametric estimator allowing it to learn the shape of the density from the data automatically (28), and a local estimator based on a user defined set of neighbors (29). In terms of human mobility this translates to a surface of smoothed density estimates that highly weight places where an individual spends significant amounts of time compared to low weights for places where little time is spent. Overlaying this time-weighted activity space of GPS data onto GIS data allows us to calculate a time-weighted estimate of exposure.

Density Ranking (DR):

A recent addition to the TWSA literature for human-specific mobility is Density Ranking (DR) developed by Chen and Dobra (30) as an improvement to KDE. DR promotes recognition of high intensity grid cells along movement trajectories in GPS datasets, while also recognizing activity space around anchoring locations where the participant spends the most time. DR utilizes a probability-like density ranking function ordering KDE outputs from lowest to highest density. By ranking densities DR can reveal densities that may not show up well with KDE: this is particularly the case for curved structures such as movement trajectories, which have low dimensional structure and make the probability density function of KDE ill-defined. The DR formula is:

$$\widehat{\alpha }\left(x\right)=\frac{1}{n}\sum _{i=1}^n\text{I}\left(\widehat{p}\left(Xi\right)\le \widehat{p}\left(x\right)\right)$$

where $\widehat{p}\left(x\right)$ is the estimated probability at location x by the KDE; and $\widehat{\alpha }\left(x\right)$ represents a probability-like quantity α-function defined by (31) that takes values between 0 and 1. For a given location x, the α-function is the fraction of all observation data points from the mobility dataset whose estimated density is lower than the estimated density of point x.

2.3. Measuring environmental exposures

Figure 1 illustrates the analysis workflow for calculating exposures. Four mobility data inputs were used: Stationary, InVehicle, Walking, and the full data set dubbed AllPoints. The final number of participants for each mobility type varied, as some participants did not have data for certain mobilities. The four mobility data inputs were fed into the three TWSA methods generating twelve time-weighted activity spaces for each participant. Details of TWSA implementation decisions and software are in Appendix A.3. The four environmental layer data inputs were rasterized for ease of computation and multiplied with the twelve time-weighted activity spaces. The result was a series of 48 raster surfaces (3 TWSA methods * 4 mobility data inputs * 4 environmental layer inputs) for each participant. Cells with either no mobility or no environmental feature resulted in values of zero. To obtain final exposure measures, the mean and standard deviation was calculated over all non-zero values for each of the 48 raster surfaces. Mean provides an average time-weighted exposure across the participant’s activity space, and standard deviation assesses the variance and spread of time-weighted exposure. Sum of exposure was not examined as the length of days could vary among participants. The result is a set of 48 mean and 48 standard deviation time-weighted exposure values for each participant.

Figure 1.

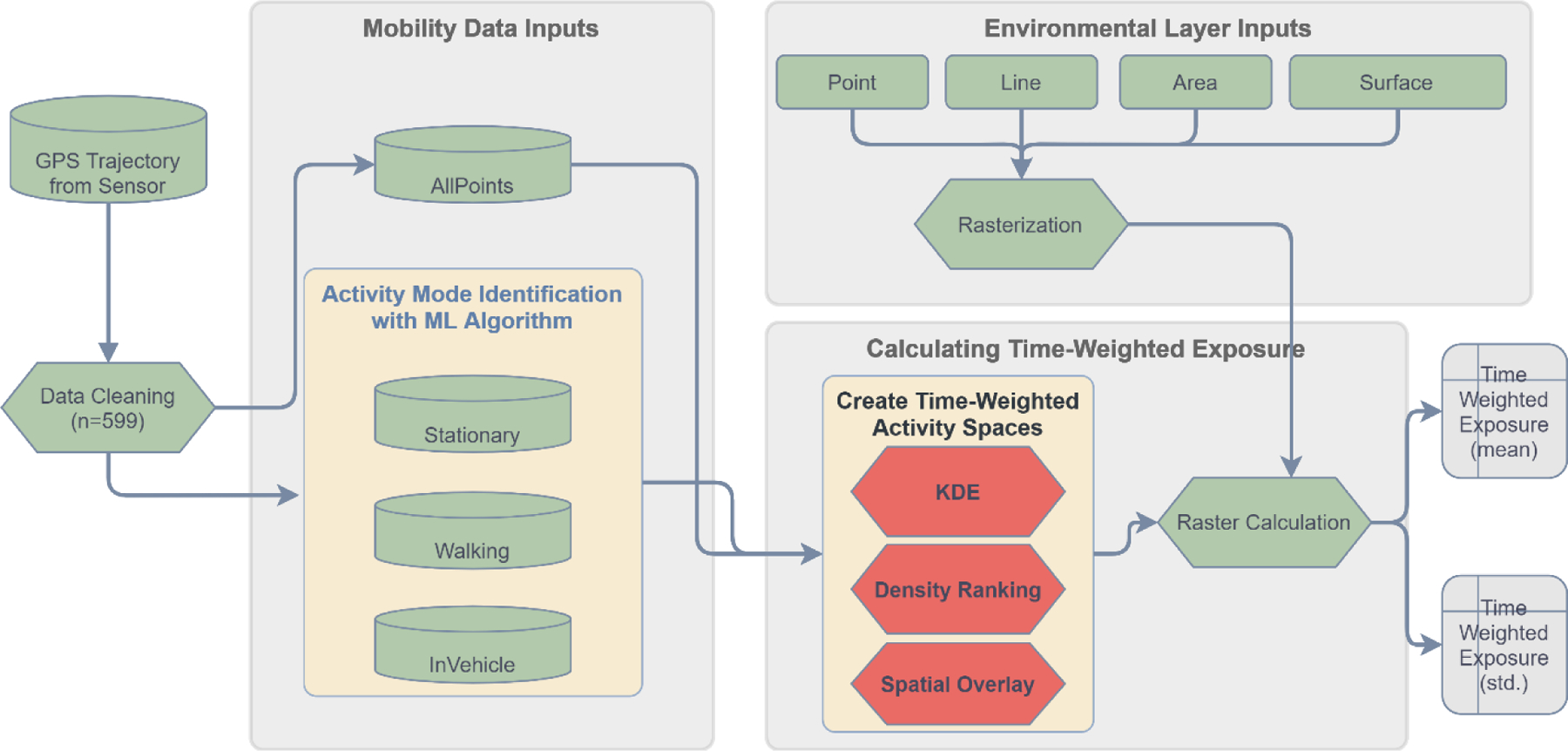
Analysis workflow for calculating time-weighted measures of environmental exposure across TWSA method, mobility data input, and environmental layer input.

2.4. Comparing TWSA exposure outputs

To answer RQ1, time-weighted activity spaces for each TWSA method*mobility data input were mapped in ArcGIS Pro 2.7 (ESRI, Redlands, California) allowing for visual comparison of the resulting time-weighted activity spaces. Overall similarity of exposure averages and standard deviations were assessed using Spearman correlations. One way analysis of variance (ANOVA) was used to assess differences between average and standard deviation exposure outputs across methods, with further Tukey Post hoc tests for significant ANOVA results to understand pairwise differences between the three TWSA methods. All statistical tests were considered significant at the 5% level and conducted in R using the stats package (32).

RQ2 was assessed using intraclass correlation coefficient (ICC) and multidimensional scaling (MDS). ICC estimates the proportion of the total variance in the TWSA exposure measures that are between participants compared to within participants. ICC was calculated using linear mixed models and the lme4 package in R (33). An ICC > 0.80 was considered as reliable across mobility inputs and environmental layers for differentiating participants with different mobilities or environmental attributes (e.g., participants that spend walking time in high vs. low feature areas). MDS is a statistical method that quantifies the (dis)similarity between data samples and is often used for dimension reduction. It is visual representation of the distances between observations, where participants that are closer together in the resulting graph are more similar to one another. MDS was represented using scatter plots of cosine distances between the vectors of 12 scenarios (3 activity input types * 4 exposure layers). The AllPoints data input was excluded to not double count exposures, as AllPoints is represented by the other three activity types. Because each activity data input had different numbers of participants, the common participant sample across all inputs of n=417 was used.

Additionally, the Nearest Neighbor Index (NNI) was calculated for the 417 participants to examine whether a given set of point features is dispersed, random, or clustered. An NNI value smaller than 1 means that the point pattern is more clustered than random, while NNI larger than 1 indicates a more dispersed point pattern. Integrating NNI with the MDS results allows us to investigate if some aspect of the GPS point pattern (e.g., clustered with an individual spending considerable time in one or few locations vs. dispersed with an individual moving throughout many locations and with several movement trajectories) can explain variability across three TWSA methods at the individual level. Another aspect of mobility, the proportion of non-stationary points (InVehicle and Walking) among all data points, was also examined with the MDS outputs to assess if TWSA methods were sensitive to participants with greater mobility.

3. Results

3.1. Visualizing time-weighted activity spaces

An example of time-weighted activity spaces of one participant generated from combinations of TWSA methods and mobility data inputs are presented in Figure 2. The KDE and PO outputs are most like one another. Both methods represent the entirety of the individual’s activity space, as can be seen in trailing lines of movement in the AllPoints and InVehicle data input maps. KDE includes a larger spatial extent of the surrounding environment than PO. This is because KDE applies the 200m bandwidth around each point, while PO assigns the point to a 200m cell regardless of where in that cell the point occurs and does not extend the boundary around the cell. KDE and PO include movement seen in the top right corner and the lower left section in AllPoints and InVehicle data input maps, but DR barely picks up this activity due to DR’s ranking function which downgrades areas with little to no time spent in them.

Figure 2.

Time-weighted activity space surface calculated for one participant. Rows represent different TWSA methods (KDE, DR, PO) and columns represent activity data inputs (AllPoints, Stationary, InVehicle, Walking). Areas with darker red indicate greater weighted time spent in location during the study period for a particular data type.

When inputting Stationary and Walking activity type data, differences between the three methods become much smaller and very similar regions of high time spent emerge. However, the areas where most time is spent in the DR map form a larger extent as more weights are given, and some regions are diminished due to very little time spent within the given data input sample. We see less coverage of the trajectory with DR resulting in more weight given to cells that are kept, a pattern seen in greater detail in Figure 3. Compared to KDE and PO, the DR method can capture finer details of the activity space in the AllPoints set where higher point density occurs. However, DR ranks the sparse points along the south-north direction highway (on the right side) relatively low and thus no activity space was created for those segments. For the InVehicle set, all three methods recognize similar activity intensity, however again DR does not include in-vehicle movement points along the highway.

Figure 3.

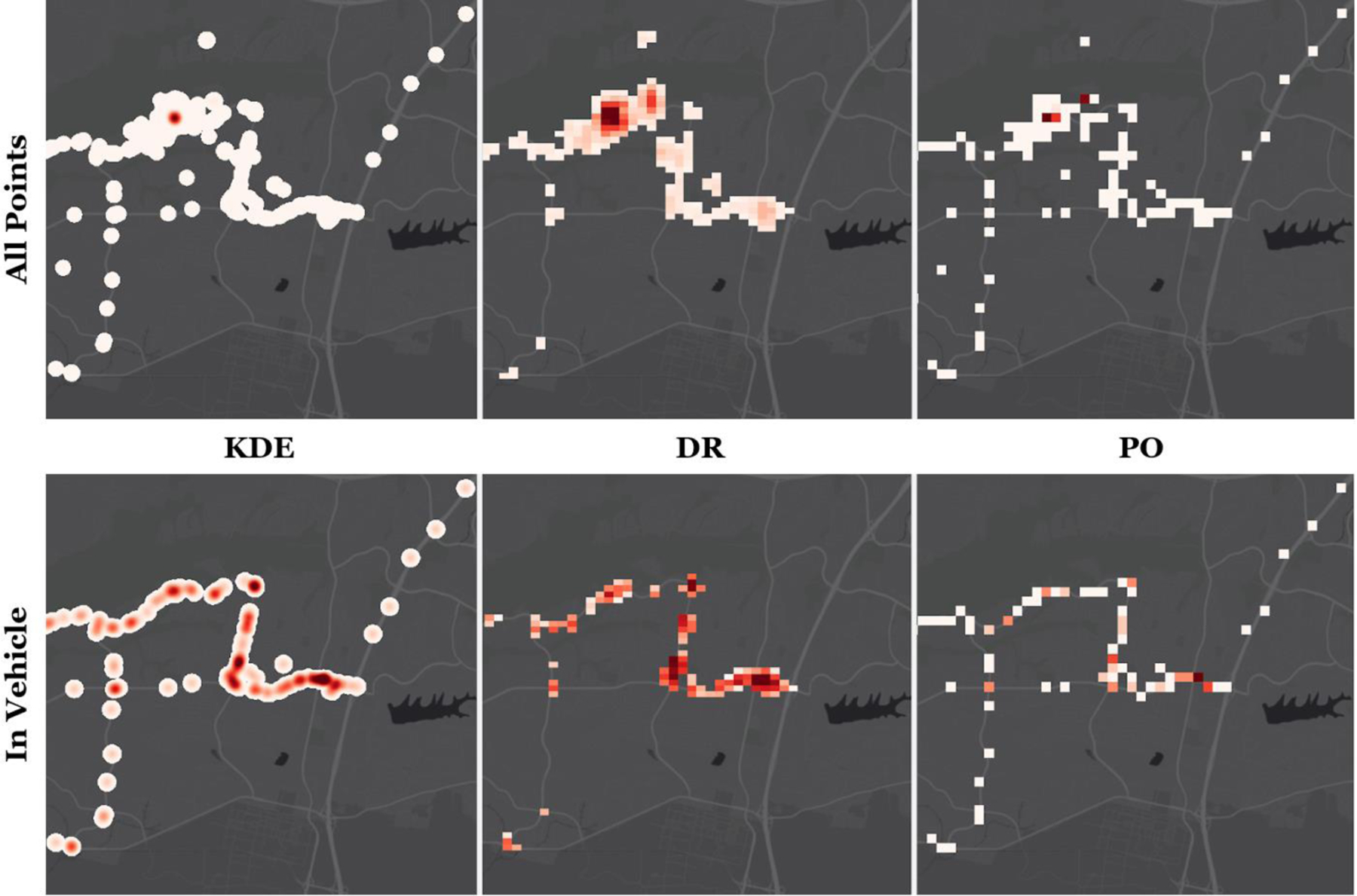
Zoomed-in time-weighted activity space surfaces of one participant with the AllPoints and InVehicle activity types. Cells with darker red indicate higher total exposure during the study period.

3.2. Exposure measurement comparison

When combining mobility data input and environmental data layers, several participants ended up not having valid data to contribute to analysis. Table 1 illustrates variation in participants who had exposure measures after processing ranging from 489 to 599 participants depending on TWSA method, mobility data input, and environmental data layer. Table 1 includes the sample mean and averaged standard deviation outputs from each input combination. For KDE and PO methods, we see the lowest mean and standard deviation exposures with AllPoints, followed by Stationary, InVehicle, and the highest exposures with Walking. In contrast for mean DR outputs, lowest values are for Stationary followed by AllPoints, Walking, and highest exposures for InVehicle. The same pattern is not followed by DR standard deviation outputs, which vary in magnitude order based on mobility data input. Overall, mean and standard deviation values are similar between PO and KDE methods for Point, Line, and Area exposure layers. The greatest differences are seen in the Walking data inputs across environmental data layers (0.055 difference for PO and KDE measured mean Area-Walking, 0.082 difference for PO and KDE measured standard deviation Point-Walking). DR results across all environmental data layers and mobility data inputs measure higher exposure means and standard deviations than PO and KDE results, except for standard deviation Walking exposures. These differences are greatest for mean Surface layer measures (DR measures 2.938 and 2.629 more exposure for Surface-InVehicle than KDE and PO respectively). Results for the Spearman correlations and ANOVA analysis between TWSA methods are presented in Appendix A.4.

Table 1.

Total valid participants for each combination of TWSA method, environmental data layer, and mobility data input. Mean and standard deviation exposure outputs across the samples.

		PO			KDE			DR
Enviro Data Layer	Mobility Data Input	N	Exposure (mean)	Exposure (std)	N	Exposure (mean)	Exposure (std)	N	Exposure (mean)	Exposure (std)
Point	AllPoints	599	0.011	0.083	599	0.007	0.075	599	0.203	0.103
	Stationary	584	0.025	0.106	588	0.01	0.025	589	0.098	0.118
	InVehicle	591	0.123	0.103	591	0.064	0.053	591	0.616	0.197
	Walking	569	0.159	0.231	583	0.077	0.104	582	0.228	0.184
Line	AllPoints	599	0.005	0.006	599	0.002	0.003	599	0.11	0.047
	Stationary	591	0.025	0.049	591	0.012	0.03	591	0.08	0.06
	InVehicle	591	0.061	0.046	591	0.033	0.03	591	0.361	0.092
	Walking	587	0.102	0.095	587	0.046	0.043	589	0.151	0.089
Area	AllPoints	596	0.007	0.024	598	0.003	0.006	593	0.125	0.071
	Stationary	536	0.029	0.086	567	0.01	0.025	557	0.088	0.104
	InVehicle	588	0.062	0.057	590	0.021	0.021	573	0.339	0.118
	Walking	489	0.106	0.138	544	0.051	0.073	500	0.167	0.154
Surface	AllPoints	599	0.052	0.039	599	0.027	0.019	599	1.048	0.478
	Stationary	591	0.289	0.408	591	0.152	0.285	591	0.796	0.515
	InVehicle	591	0.536	0.386	591	0.227	0.156	591	3.165	0.983
	Walking	587	1.012	0.827	587	0.465	0.363	590	1.468	0.878

3.3. Intraclass correlation

ICC results are presented in Figure 4. For ICC by mobility data input type, the standard deviation aggregations of exposure are consistently over 0.80 while mean values only approach or exceed 0.80 for DR AllPoints and InVehicle. PO and KDE mean results are like one another with InVehicle and Walking data inputs showing higher ICCs (between 0.50 and 0.56) compared to AllPoints and Stationary. Compared to mean PO and KDE exposure results, DR means show greater overall ICC for each mobility input with the highest for InVehicle (0.88). ICCs by environmental data layer are generally poor (no values over 0.80). For mean outcomes, PO and KDE results follow a similar pattern with Point and Area inputs seeing the lowest ICC (0.21 to 0.22). ICC results for PO Line (0.36) and Surface (0.40) are slightly higher than for KDE Line (0.30) and Surface (0.36). DR mean exposure estimates have larger ICC values across all environmental data layers, with the Line input reaching the highest value of 0.74. Standard deviation exposure values were low across all TWSA methods (<0.31) for Area and Line inputs. PO and KDE had low values for Point layer inputs, but ICC was higher (0.42) for the DR standard deviation. Surface layer exposure estimates saw the opposite pattern and were lower for DR and higher for PO (0.56) and KDE (0.54).

Figure 4.

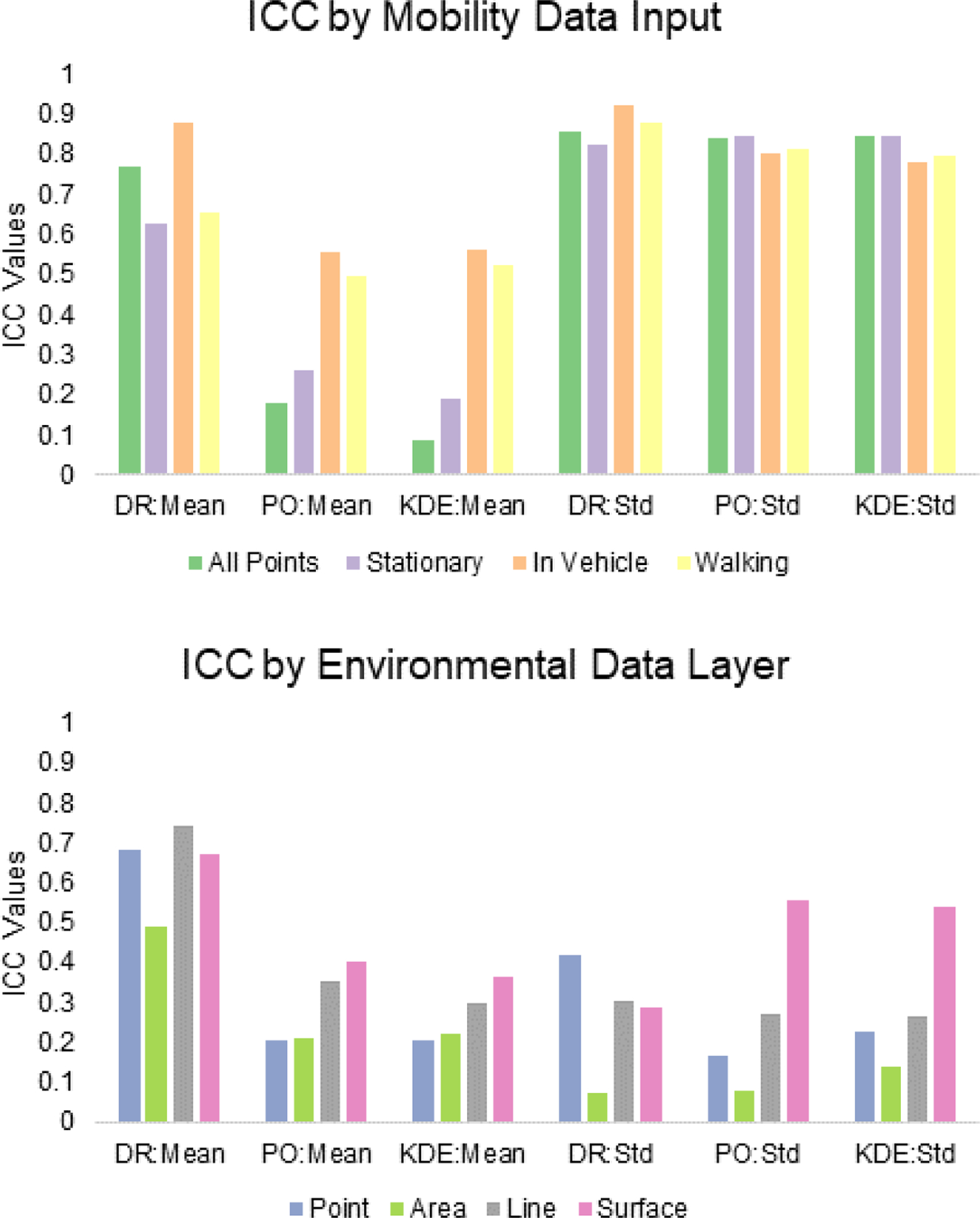
Intraclass correlation coefficient (ICC) values by TWSA method and mean/standard deviation by mobility data input type (top) and environmental data layer type (bottom).

3.4. Multidimensional scaling

Figure 5 displays MDS scatter plot results where tighter clusters of participants show exposure measures are more consistent across the mobility and environmental data input scenarios. Points that are further away from the main cluster illustrate participants that have dissimilar exposure metrics across scenarios. Among the MDS plots for mean values, KDE:mean results in a tight cluster with one participant pushed far away from others. In Appendix A.5 we perform further analysis on the 30 most distant participants. Besides this participant, the rest forms a loose cluster with sparse points away from the center. DR:mean is similar to PO:mean with a main loose cluster and minor clusters forming near the boundaries. In contrast to the mean results, plots for DR:std are more clustered than KDE or PO, showing fewer isolated points scattered outside the main cluster. Coloration of Figure 5 represents NNI results. If point-pattern clustering were playing a role in driving variance of exposure estimates between participants, we would expect to see progressive coloring of light yellow, to orange, to red moving from the inner cluster to the outer rings (or vice versa). There is no discernable pattern in any TWSA methods or exposure measures, suggesting that point-pattern clustering of participant data is playing a role in reliability of exposure estimates across mobility and environmental data inputs. Proportion of non-stationary activity points among all data points (as % non-stationary) are shown in Appendix A.5.

Figure 5.

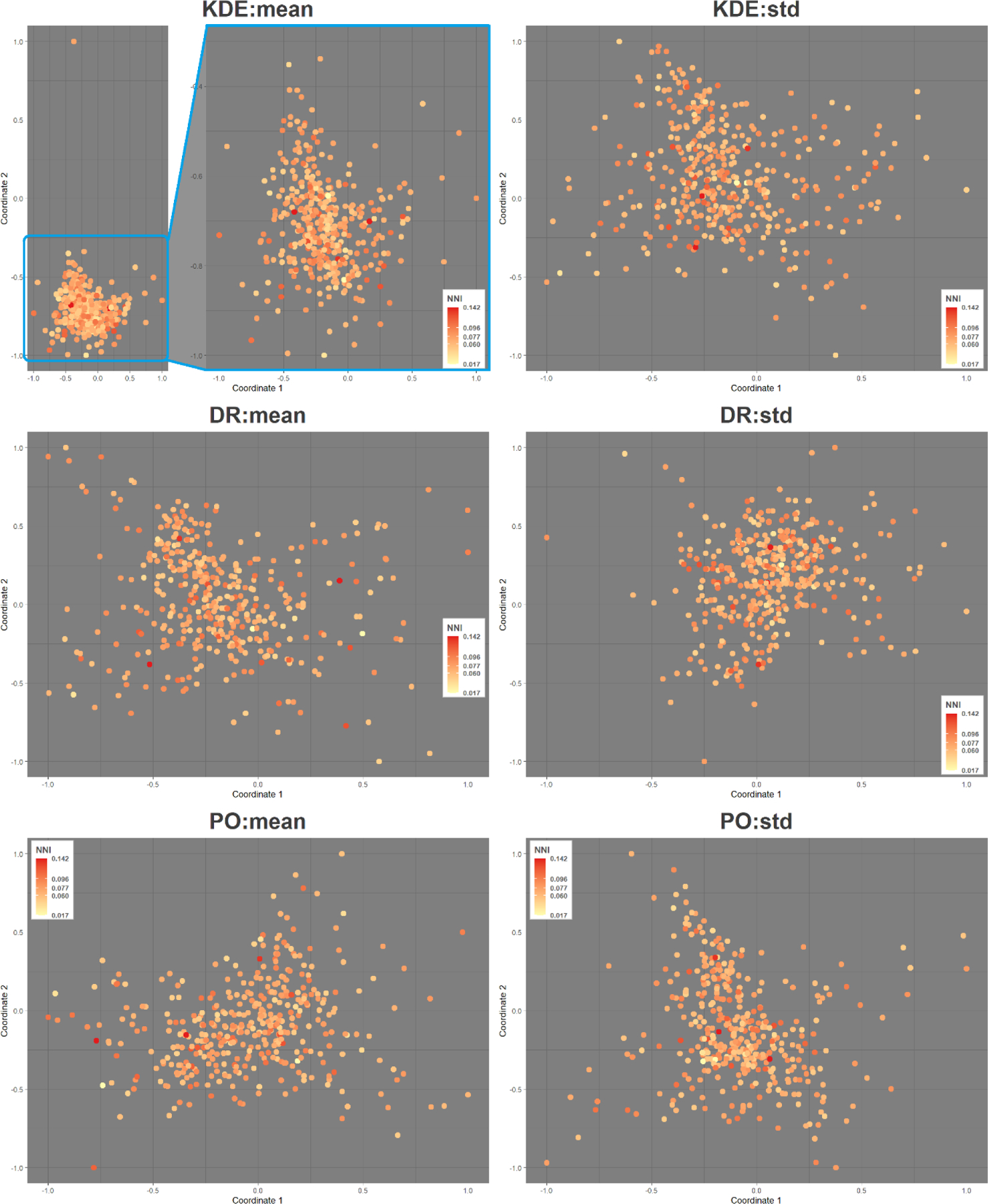
Multidimensional scaling of participants’ exposure based on the cosine similarity considering the 12 exposure scenarios (3 mobility data types * 4 environmental data layers). Each point in the scatter plot represents one participant and is colored by the nearest neighbor index (NNI). Colors range from GPS data being clustered on NNI index (yellow) to dispersed (red). For KDE:mean (top left), a zoom-in of the main cluster is shown.

4. Discussion

4.1. RQ1: Similarities and differences between TWSA methods

In answer to RQ1, we found that KDE and PO produced visually similar activity spaces, while DR varied from the other two methods. DR is designed to be better at capturing movement trajectories, however its ranking function will downgrade movement that does not occur often. Therefor trajectories that rarely occur (e.g., a weekend trip) will likely be reduced or eliminated from the overall time-weighted activity space. DR is an improvement to KDE and PO for generating overall multi-day or month time-weighted activity spaces but may not be a good choice for researchers seeking to capture all possible activity spaces including rarely utilized ones. In comparing exposure outputs KDE and PO values were similar across mobility and environmental data inputs, but larger differences between TWSA methods were seen for standard deviation values compared to means (Table 1). Again, DR tended to have exposure outputs that were quite different from KDE and PO, as would be expected due to the difference in generated activity space.

These results were supported by correlation results (Appendix A.4), where we found that KDE and PO values tended to significantly correlate with one another (Figures A.1 and A.2), but not for all layers (Area and Line mean values) or activity data inputs (Stationary and Walking mean values). Significant correlations of DR with KDE and PO were rarer. ANOVA and Tukey’s Post Hoc tests showed consistent significant differences for exposure estimates between DR and KDE and DR and PO, but fewer significant differences between exposure estimates for KDE and PO (further discussion in Appendix A.4). Generally, we recommend the use of KDE over PO due to the smoothing function of the method and reduction in potential spatial error matching. However, KDE is a more complex methodology to implement, and our results indicate that for researchers needing a simpler approach PO produces similar results to KDE.

4.2. RQ2: Sensitivity of TWSA methods to different types of mobility and environmental inputs across the sample and within individuals.

ANOVA and Tukey’s Post Hoc tests (Appendix Table A.1) indicate that for mobility data inputs that focus on movement (InVehicle and Walking), there are significant differences in mean exposures between all methods. Additionally, the Surface layer exposure showed higher exposure estimates and more similarity across TWSA measures and data input types than the Point, Line, and Area layers. This indicates that discrete spatial features exposure inputs may be more sensitive than continuous data to the TWSA method and activity data used. ICC outputs (Figure 4) show that reliability of exposure estimates within individuals varies by mobility data input type, environmental exposure layer type, and aggregation method (mean vs. standard deviation). Less variation was seen across mobility data input type, especially when exposures were aggregated by standard deviation. PO and KDE were more sensitive to mobility data input type when exposure was assessed by means compared to DR. Generally, the TWSA methods all saw low reliability across environmental exposure layer inputs, with DR exhibiting the most reliable results for mean aggregation values.

MDS results showed that with the exception of one extreme outlier in the KDE:mean plot, overall the methods had similar clustering patterns (one larger central cluster with outliers) indicating general consistency of between individual variability (Figure 5). Exploration of the one outlier from KDE:mean measures in Appendix Figure A.3 indicate this participant consistently was 40% above or below average mean exposures of the study population. Interestingly, we did not find that point-pattern clustering or mobility pattern (% non-stationary) helped to explained MDS results (Appendix Figure A.4). The underlying spatial pattern of data does not seem to have substantial influence on the ability of the TWSA methods to consistently measure exposure means and standard deviations. The only method that showed some reliance on point-pattern clustering and mobility was KDE when using standard deviation means, however the results are not compelling enough to warrant significant concern. Overall, this is a positive finding as it alleviates concerns that TWSA methods will work better for individuals with more mobility and less spatial clustering, and that time-weighted dynamic exposure estimates may introduce significant confounding into exposure models due to underlying individual behavioral patterns (34).

4.3. Analytic considerations

Because interpretation of direct results for each TWSA is challenging, we recommend weighting the TWSA generated activity space to allow for comparability between participants in the study. In our study we normalized the time-weighted activity space generated by each TWSA method within the participant. So, participant X’s area of greatest time-weighting (e.g., spending 90 minutes at home) is treated equally to participant Y’s place of greatest time-weighting (e.g. spending 200 minutes at work). This allows for comparison across each participant’s maximum and minimum time spent in locations. Another approach would be to normalize across the entire sample, however this approach would drive estimates toward the extremes of participants who spend large amounts of time in one location while potentially washing out other participants’ habits of spending small amounts of time in a diverse number of locations. Without normalization results may be a greater reflection of the underlying time-weighting due to device wear time than actual exposure. Interpretation also presents a challenge for comparison of TWSA exposures across studies, and future methods will need to develop dose measures for time-weighted exposure that are more easily comparable.

Time-weighting occurs according to the global input sample. Thus, by inputting different point samples (e.g., walking vs. stationary data, or daily vs. total mobility over several day period), different weighting will occur based on the high and lows of time spent in places. Our results reflect this with wide variation in exposure based on activity data input type with Allpoints and Stationary seeing lower exposure measures compared to InVehicle and Walking (Table 1). This variation does not necessarily mean that ‘more’ exposure occurs in walking compared to stationary behavior, but rather that being in a vehicle and walking are movement behaviors precluding large amounts of time being spent in one location. The TWSA methods will more equally weight all points in the movement datasets compared to downgrading movement in the stationary/all datasets because more time is spent in stationary locations. This effect is seen in Figures 1 and 2, where comparatively more weight is shown across data points in the InVehicle dataset. Datasets with significant walking, vehicle, or other movement time may need to carefully consider which TWSA method to use as well as which activity data type to input into the algorithm.

4.4. Interpreting exposure estimates for health studies

The method used to generate a time-weighted activity space plays a role in interpretation of results. PO is the simplest to understand, where each raster cell value is equivalent to the number of minutes spent in the cell and can be related as minutes/200m2. In contrast to PO, KDE and DR estimates are less straightforward to interpret as they do not directly quantify the time dimension (e.g., in minutes) regarding a given exposure of interest. Instead, KDE and DR use the time spent in each geographical location to proportionately weight places that were visited during the study period. Absolute estimated values of the KDE and DR methods cannot result in an absolute dose of time-weighted exposure, but instead should be used to assess dose exposure within and between a sample of participants. While PO can offer a more straightforward dose estimate (although still confusing – consider μg m−3*minute/200m2), outputs would need to be normalized by wear time or days to ensure comparability across participants making a direct dose measurement difficult.

Another interpretation decision a researcher must grapple with is the aggregation method for the final exposure measure. Mean exposure values can be interpreted as the spatially varying exposure weighted by time averaged across the participant’s mobility track. Standard deviation values are more indicative of the range of high and low time*exposure values a participant incurs. Sum values can also be used if there is control for variation in days of device wear across participants. Sum can be a useful measure in contexts where the total dose accumulated over time is of interest. A limitation in all aggregate measures is the erasure of local behavior and exposure interaction. For example, higher mean values may be indicative of fast-food outlets distributed across several places where the participant goes, or a high concentration of fast-food outlets centered in a location where the participant spends a great amount of time. If the specific behavior*exposure interaction is of interest (i.e., how and where the person is exposed) alternative activity space methods may be a better choice than TWSA such as trip vs. location analysis or domain-based approaches (13).

4.4. Opportunities for advancing TWSA for health and exposure assessment

KDE was not originally developed for trajectory-based data, which may violate assumptions of independence due to the highly spatiotemporal autocorrelation in the data. Individual trajectories present two autocorrelation problems: 1) high degree of spatiotemporal autocorrelation from one data point to the next (e.g., each point is highly predictive of the next consecutive point), and 2) high degree of autocorrelation in behavior over extended time (e.g., one individual will visit the same locations over and over). Solutions for dealing with directional KDE data (35) and time series data (36) have been discussed in mathematics. Animal tracking research of home range offers approaches that can help deal with issues such as time-geographic density estimation (29) and autocorrelated KDE (37). However, human mobility has unique criteria that incorporates elements of directionality (e.g., network path travel), high moment to moment spatiotemporal autocorrelation (previous point related to the last), and high spatiotemporal autocorrelation over extended periods of time (a person will visit the same places repeatedly). There is also evidence that this sort of autocorrelation may vary based on demographic characteristics (38). Implementation of approaches from other scientific branches into exposure-related research may be beneficial in developing newer TWSA methods that can offer better interpretability, address underlying statistical issues, and be tailored at measuring exposure*mobility rather than activity space alone.

One ‘low hanging fruit’ to consider is bandwidth selection and incorporating an adaptive bandwidth based on characteristics of the data and exposure of interest. Bandwidth selection in traditional KDE applications smooths data per an even distance setting, and adaptive bandwidths are meant to constrain or expand the original bandwidth based on an underlying factor like population density. However, in TWSA exposure approaches, the bandwidth is also meant to generate an area of exposure for the participant. It is likely that exposure does not always occur equally, nor does it need the same amount of space or time to occur. For example, a stationary individual inside is likely not being exposed to air pollution and therefor their exposure bandwidth should be small or nonexistent. Or certain exposures may be acute (e.g., the body stops producing Vitamin D after a certain amount of time outside) and need more fine-tuned temporal weighting compared to cumulative exposures. Behavior types can be generated from GPS and accelerometer data and combined with assumptions based on researcher experience, domain knowledge, and exposure application to generate equations for adaptive bandwidths as an individual moves through space and time. The incorporation of kinetics and behavior into animal movement models provides some examples of these types of applications (39,40), however models would need to be adapted to the human health exposure measurement context.

5. Conclusion

The introduction of mobility sensors into health-related research to understand the effects of context and environment on health has opened new possibilities for more accurate and specific definitions of exposure incorporating where an individual goes, how much time they spend there, and the types of behaviors they engage in during an exposure of interest. TWSA methods for extracting time-weighted exposure estimates are increasingly common in the literature, but to our knowledge this is the first study to contrast and compare several TWSA methods with real world data. We find that among the methods, DR provides an advance to KDE for generating time-weighted activity spaces and can provide more reliable estimates of exposure across data input types, however it may not be the best tool for researchers looking to account for environmental exposures in rarely visited places or short time intervals. PO may be a good option for researchers looking for a straightforward approach that is easier to interpret than DR or KDE, but it may be highly prone to spatial error. We found that discrete spatial feature exposure inputs as well as datasets with considerable walking, vehicle, or other movement time may be more sensitive to the specific TWSA methods used, and thus experimentation on the part of the researcher is warranted in these cases. While between individual variability of measures was relatively consistent, we did find several outlier participants for each method that had higher within person variability of exposure measures. These outliers were not found to be consistently related to mobility or point-pattern clustering, alleviating some concerns that TWSA methods introduce confounding into statistical models due to individual mobility patterns.

The TWSA approaches described in our study offer unique opportunities to measure spatiotemporal exposures while considering various time-weighted activity spaces, but we recommend careful consideration of method selection for each research question and conducting sensitivity analyses when possible as each approach relies on different assumptions and mathematical foundations. Furthermore, we recommend weighting TWSA generated activity spaces to allow for comparability between participants in a study, and to carefully consider which aggregation method to utilize for final exposure measures. Future research should focus on utilizing behavioral sensor data as well as the spatiotemporal nature of the exposure itself to better fine tune dynamic exposure measures.

Highlights.

• Time-weighted spatial averaging exposures vary with mobility and environmental data inputs.

• Kernel Density Estimation and Point Overlay methods result in similar mean and standard deviation exposure estimates.

• Density Ranking results in larger mean and lower standard deviation estimates compared to other methods.

• Density Ranking generally provides more reliable estimates of exposure within individuals

• Between individual variability is consistent between methods; point-pattern clustering of individual movement does not impact results.