Modeling explains prolonged SARS-CoV-2 nasal shedding relative to lung shedding in remdesivir-treated rhesus macaques

Summary

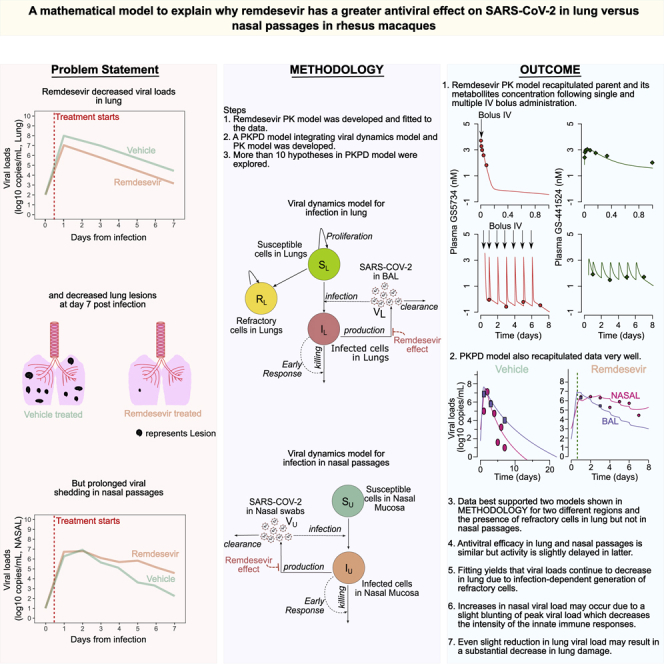
In clinical trials, remdesivir decreased recovery time in hospitalized patients with SARS- CoV-2 and prevented hospitalization when given early during infection, despite not reducing nasal viral loads. In rhesus macaques, early remdesivir prevented pneumonia and lowered lung viral loads, but viral loads increased in nasal passages after five days. We developed mathematical models to explain these results. Our model raises the following hypotheses: 1) in contrast to nasal passages, viral load monotonically decreases in lungs during therapy because of infection-dependent generation of refractory cells, 2) slight reduction in lung viral loads with an imperfect agent may result in a substantial decrease in lung damage, and 3) increases in nasal viral load may occur because of a blunting of peak viral load that decreases the intensity of the innate immune response. We demonstrate that a higher potency drug could lower viral loads in nasal passages and lungs.

Graphical abstract

Highlights

• •A math model captures viral load decrease in lungs during remdesivir treatment
• •The model predicts moderate antiviral potency sufficient to limit lung damage
• •Generation of refractory cells in lung may assist in limiting lung damage
• •The model explains the surprising increase in nasal viral load during treatment

Molecular modeling; Virology

Introduction

There is a desperate need for treatments for SARS-CoV-2, the virus which causes COVID-19 disease (Schiffer et al., 2020). One unmet need of antiviral therapy development is identification of virologic surrogates for clinically meaningful endpoints such as death or need for hospitalization. Viral load surrogate endpoints allow for much smaller and efficient clinical trials (Block et al., 2017; Chen et al., 2013; Duke et al., 2021; Murray et al., 1999; Natori et al., 2018). In the case of SARS-CoV-2- infected people, viral load can be routinely measured in nasal samples or saliva (Wölfel et al., 2020). However, the primary site of disease is lung tissue. Therefore, bronchoalveolar lavage (BAL) of lungs would be an ideal sample. However, BAL is usually not necessary for diagnosis, represents an infection risk to medical personnel and is rarely performed in the care of COVID-19 patients. When BAL does occur, it is often late during disease in critically ill patients rather than at early clinical presentation. In addition, BAL only samples select lobes of the lung and is not spatially comprehensive. Thus, the natural kinetics of SARS-CoV-2 in lungs is likely to remain unknown in humans.

In humans, a double-blind, randomized, placebo-controlled trial showed that the nucleoside analog remdesivir limited the duration of illness and approached statistical significance for reduction in mortality when given later in disease (Beigel et al., 2020). In a separate study with an overall later time of treatment initiation, remdesivir had no effect on viral load or clinical outcome (Wang et al., 2020b). A more recent trial showed that remdesivir given early during infection in the outpatient setting dramatically decreased the likelihood of hospitalization and/or death (https://www.gilead.com/news-and-press/press-room/press-releases/2021/9/veklury-remdesivir-significantly-reduced-risk-of-hospitalization-in-highrisk-patients-with-covid19). Surprisingly, nasal viral loads did not differ between the treatment and placebo arms in this study, raising the question of whether nasal viral loads could serve as a valid surrogate endpoint for remdesivir or other antiviral agents of interest. In contrast, molnupiravir, an agent which induces viral RNA copying errors, showed a reduction in viral loads in a similar study and has clinical benefit (Fischer et al., 2021), as did PF-07321332, a boosted protease inhibitor (https://www.pfizer.com/news/press-release/press-release-detail/pfizer-announces-additional-phase-23-study-results). Monoclonal antibody cocktails dosed early during infection also lower nasal viral loads and reduce hospitalization rates dramatically (Dougan et al., 2021; Weinreich et al., 2021).

Remdesivir was highly effective when initiated 12 h after infection in rhesus macaques (Williamson et al., 2020b). In this context, remdesivir prevented pneumonia and limited extent of clinical illness. Although there was an effect on viral shedding in serial BAL specimens, viral load in the nasal passage was unchanged relative to animals treated with a vehicle during the first several days of infection and was significantly higher starting at day 5.

Several mathematical models have been developed detailing SARS-CoV-2 viral kinetics in humans (Cao et al., 2021; Goyal et al., 2020; Ke et al., 2021a, 2021b; Kim et al., 2021a; Néant et al., 2021), nonhuman primates (Dobrovolny, 2020; Gonçalves et al., 2021; Kim et al., 2021b; Rodriguez and Dobrovolny, 2021), and ferrets (Vaidya et al., 2021). The general structure follows a target cell-limited model with or without innate and adaptive immune responses. In particular to modeling in nonhuman primates, Dobrovolny (2020) and Kim et al. (2021b) explained the observed prolonged viral shedding in nasal passages with early treatment with remdesivir. However, these studies did not provide an explanation for viral kinetics in the lung under treatment along with observed improved pathogenesis in treated animals. Here, we develop a mathematical model that recapitulates viral load trajectories in both anatomic compartments of the infected rhesus macaques and qualitatively describes the pulmonary pathology. The model explains these differences according to underlying distinct viral kinetics off-therapy in both compartments as well as differential drug potency in the nasal passage versus the lung compartment.

Results

Discrepant SARS-CoV-2 viral loads in lungs and nasal passages in response to remdesivir treatment in rhesus macaques

12 rhesus macaques were infected with 2.6 × 10⁶ TCID50 of SARS-CoV-2 strain nCoV-WA1-2020 via intranasal, oral, ocular, and intratracheal routes and then treated with either placebo or IV remdesivir (10 mg/kg loading dose followed by 5 days of 5 mg/kg) starting at 12 h post infection (Williamson et al., 2020b). Overall treatment resulted in reduced severity of clinical illness, less pronounced infiltrates on chest radiograph, lower viral load by nucleic acid, and viral titer measurement in bronchoalveolar lavage (BAL) fluid on days 1, 3, and 7 and decreased volume of lung lesions, lung weight, and inflammation on histologic postmortem exam (Williamson et al., 2020b).

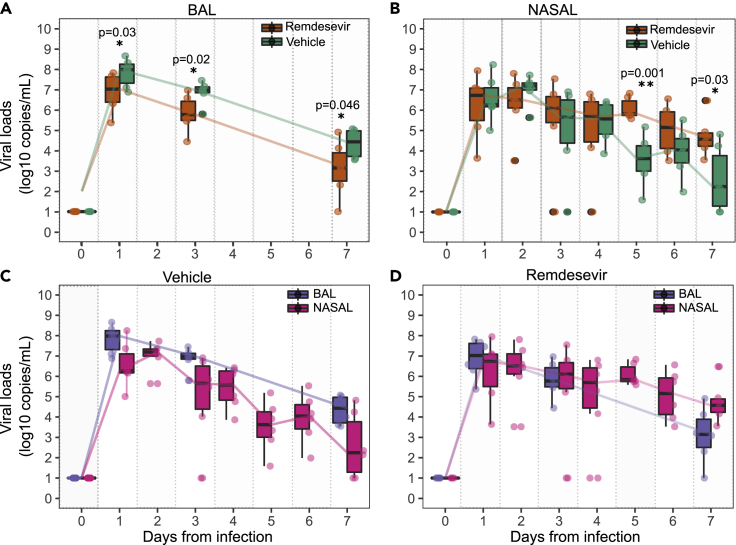
We reexamined viral loads in BAL and nasal specimens, and noted that at days 1, 3, and 7 postinfection BAL viral loads were lower in the remdesivir arm relative to the vehicle arm by approximately a single order of magnitude (Figure 1A). Similar results were observed when viral load was measured using viral culture (Williamson et al., 2020b). In nasal specimens, there was no observed difference in viral loads at days 1, 2, 3, and 4; on day 6, there was a trend toward higher viral loads in the remdesivir-treated arm; on day 5 and 7, nasal viral loads were statistically higher in the remdesivir-treated arm relative to vehicle (Figure 1B).

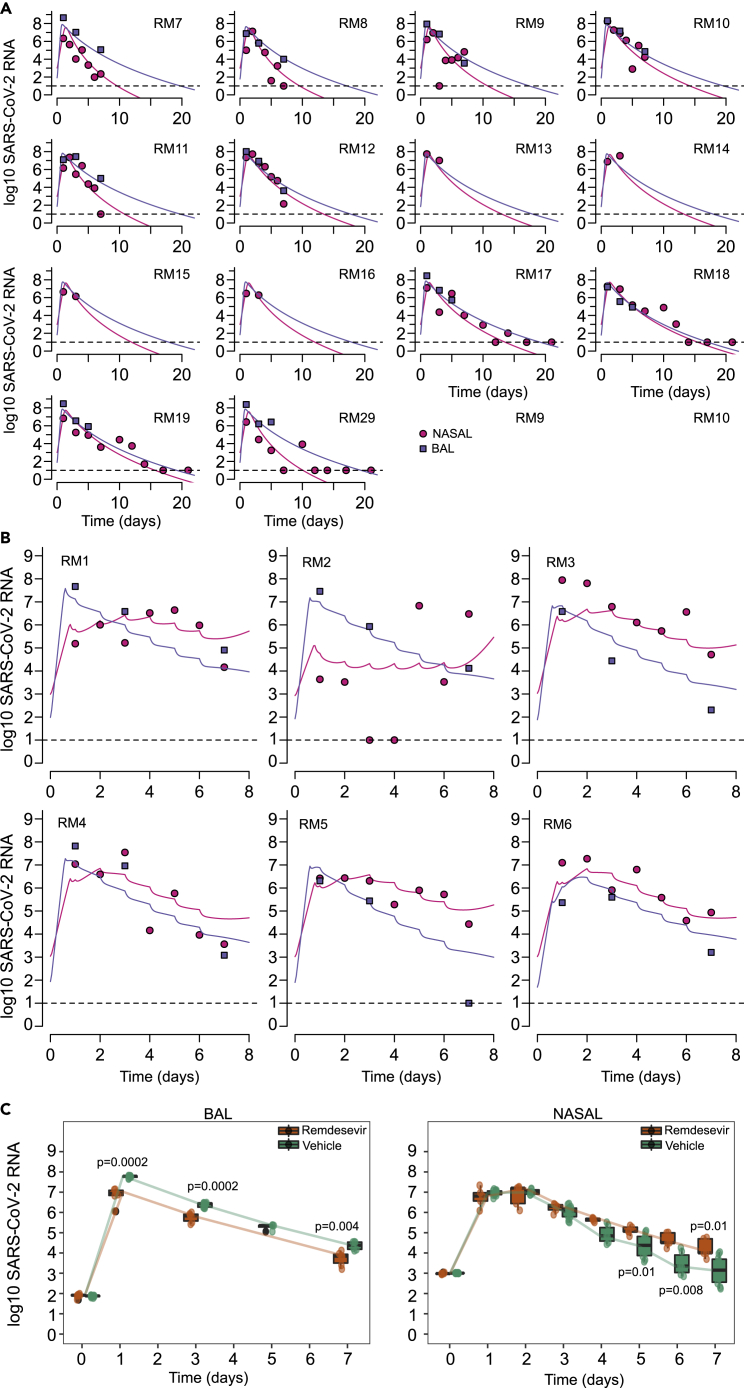
Figure 1.

Viral load kinetics following remdesivir treatment in 6 rhesus macaques

(A) Decreased bronchoalveolar lavage (BAL) viral loads in 6 remdesivir-treated animals versus 6 vehicle controls at all measured time points.

(B) Increased nasal viral loads in remdesivir-treated animals versus controls at day 5 and 7.

(C) BAL versus nasal viral loads in vehicle treated animals.

(D) BAL versus nasal viral loads in remdesivir-treated animals. The Wilcoxon rank sum test was employed to determine the differences in the median viral loads in treated and vehicle controls at different time points. p < 0.05 denotes statistical significance (∗); p < 0.01 is denoted ∗∗. The boxs represent the area of the interquartile range (IQR). Whiskers are the wdgsw of the box + 1.5 IQR. Dots are outliers.

When nasal viral loads were compared longitudinally to BAL viral loads in vehicle treated animals, viral loads were generally higher in BAL than in the nasal passages at days 1, 3, and 7 (Figure 1C); in the remdesivir-treated animals, viral loads were equivalent on days 1 and 3 but higher in nasal passages than BAL at day 7 (Figure 1D). Overall, these results suggest that remdesivir lowered viral load in the lung but had the opposite effect in nasal passages of rhesus macaques at late time points.

Dual compartment PK/PD model of remdesivir

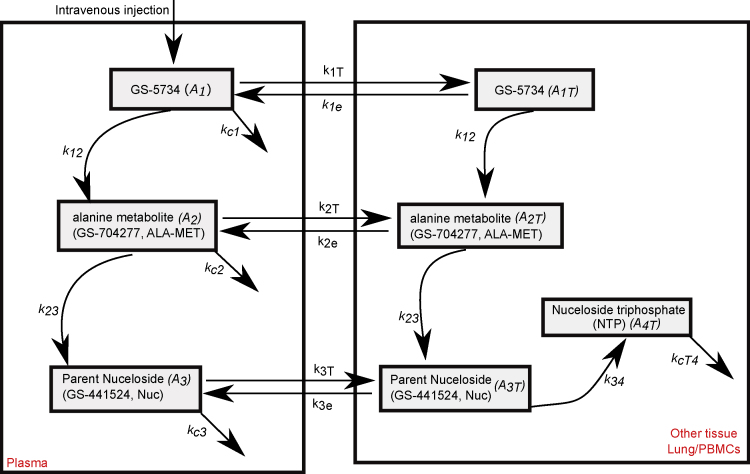
To explain the differential observations in lung and nasal passages of remdesivir-treated animals, we developed a mathematical model to capture drug pharmacokinetic (PK) and pharmacodynamics (PD), as well as viral and immune dynamics. The PK model is represented in Figure 2 with equations listed in the Methods. It captures the steps following intravenous injection of remdesivir (GS-5734), including conversion to an alanine metabolite (GS-704277) and then to the parent nucleoside GS-441524 (Nuc), the necessary phosphorylation of this molecule to achieve its active triphosphate form (NTP) as well as the distribution of these metabolites from plasma to tissue.

Figure 2.

Schematic of the remdesivir pharmacokinetic (PK) model

The model includes plasma and tissue levels of remdesivir GS-5734 (A₁, A_1T), the alanine metabolite GS-507277 (A₂, A_2T), and the parent nucleoside GS-441524 (A₃, A_3T) that is phosphorylated in tissue to the active nucleoside triphosphate form of the drug (A_4T). For remdesivir and the first two metabolites, we modeled the drug distribution from plasma to tissues.

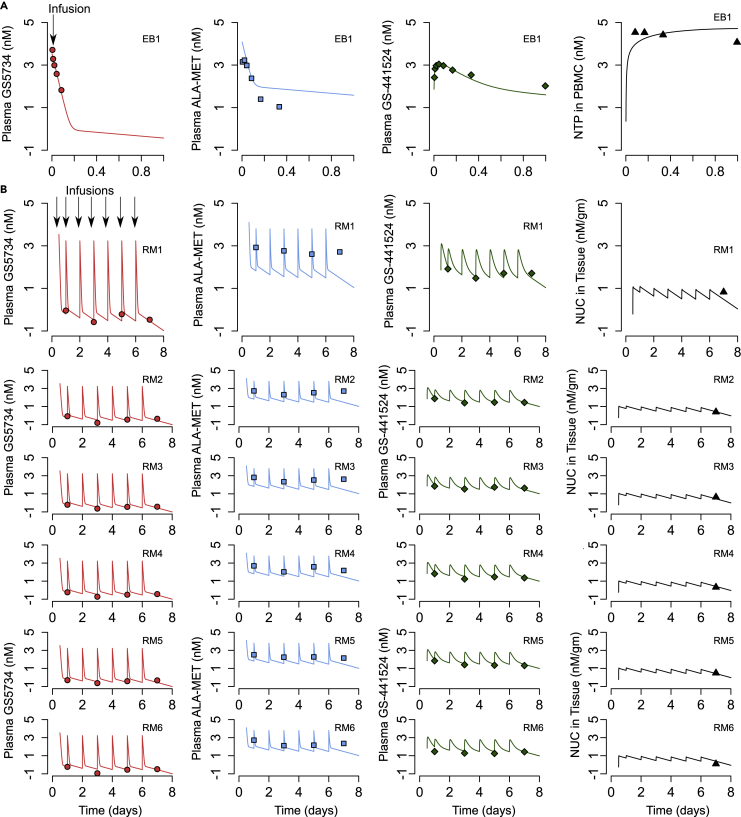
For single-dose PK, we fit the model to averaged data from three healthy rhesus macaques in which various intermediate metabolites were measured over time following a single injection of 10 mg/kg, including the levels of NTP is PBMCs (Figure 3A) (WHO, 2018; Warren et al., 2016). We also simultaneously fit the model to multidose drug and metabolite trough levels from the infected rhesus macaques (10 mg/kg at day 0.5 and thereafter, 5 mg/kg daily at days 2 till 6 postinfection), including a day 7 level of the Nuc in tissue at the time of necropsy on day 7 in Figure 3B (Williamson et al., 2020b). RDV PK parameters are listed in Tables S1 and S2. The model is able to recapitulate the averaged levels of remdesivir and its metabolites in healthy (Figure 3A) and infected rhesus macaques (Figure 3B); however, it is to be noted that all parameters in the model are not identifiable as discussed in the Methods and shown in Table S2.

Figure 3.

Remdesivir (RDV) pharmacokinetic (PK) model fits to data

(A) RDV PK model fits to data in rhesus macaques from a single dose of 10 mg/kg remdesevir at day 0.

(B) Fits of drug and intermediate levels from the rhesus macaques from the current COVID-19 study. Animals received 10 mg/kg remdesevir at day 0.5 and 5 mg/kg remdesevir at days 1, 2, 3, 4, 5, and 6.

The commonly used Emax PD model, evaluating the reduction in viral production as a function of the concentration of drug, should ideally use the concentration of active metabolite in tissue (NTP) to estimate EC₅₀ (the concentration of the drug in infected cells, at which viral replication is inhibited by 50%). However, such experimental data is unavailable because of rapid decay of the active metabolite in the lungs. To overcome this limitation, we followed the same strategy as in the experimental article and used the concentration of nucleoside GS-441524 ($A_{3T}$) in tissue as a surrogate for the concentration of active metabolite in tissue toward the calculation of EC₅₀. We also assumed equivalent levels of the metabolite in nasal passages and the lung. Overall, the viral production ${\pi }_i$ is assumed to be reduced by a factor $(1-\frac{A_{3T}}{A_{3T}+E{C}_{50i}})$, where $E{C}_{50i}$ is the in vivo EC₅₀ of the nucleoside GS-441524 in the respective compartment $i$.

Mathematical model of SARS-CoV-2 in lungs and nasal passages in rhesus macaques

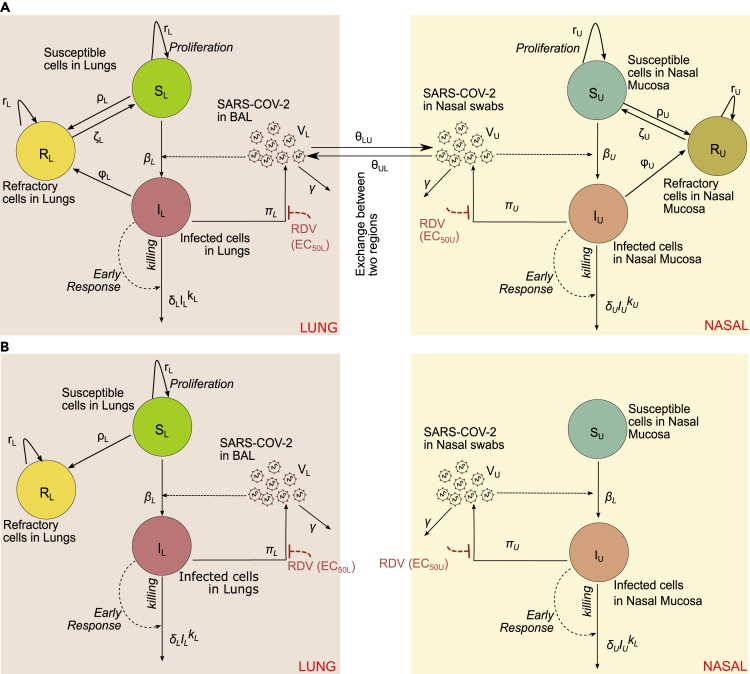
We developed a model of viral replication in the nasal passage and lungs that include multiple mechanisms that may occur following infection in lungs and nasal passages (Figure 4A). This model is an adaptation of our previous model of human COVID-19 infection (Goyal et al., 2020) and includes density-dependent death of infected cells as a proxy for an intensifying innate response to a higher burden of infection, delayed proliferation of susceptible epithelial cells, the possible conversion of susceptible and/or infected cells to an infection refractory state, the possible movement of the virus between nasal passages and the lung, and the possible delay in the antiviral activity of remdesivir in lungs and the nasal passages. We fit different versions of this model to the viral loads in nasal passages and lung from 6 infected, remdesivir-treated animals, 14 infected and untreated animals, including the 6 vehicle animals in the remdesivir protocol (RM7-12) (Williamson et al., 2020b), and 8 other animals infected using the same protocol (4 of that had extended nasal viral load measures through 21 days after infection) (Munster et al., 2020). Each model explored was a version of the full model in Figure 4A with individual components removed (Methods). An extended model proposed by Ke et al. (2021a) was also fit to the observed data in rhesus macaques. This model incorporated features such as refractory cells and immune-effector cells in nasal passages and in saliva to explain viral shedding in 60 individuals.

Figure 4.

Mathematical models of nasal and lung SARS-CoV-2 dynamics and remdesivir therapy

(A) Schematic of a comprehensive viral dynamics model inclusive of all possible compartments and assumptions.

(B) A reduced model that recapitulates the complete viral load data. Exclusions relative to the complete model include no refractory cell compartment in the nasal passage and no proliferation of susceptible cells in the nasal compartment.

Using model selection theory, we found that the model with minimal complexity necessary to explain the observed data in its entirety was the one in Figure 4B. In this model, infected cell death and viral production have different rates in the lung compared to the nasal passage (Tables S3 and S4). Furthermore, susceptible lung cells proliferate and become refractory to infection, but cells in the nasal passages do not (Table S5). This model also lacked viral interchange between lung and nasal passages (i.e., ${\theta }_{LU}=0$ and ${\theta }_{UL}=0$).

Ke et al.’s model (Ke et al., 2021a) performed statistically better than our best model (AIC = 565.4, i.e., lower AIC by ∼100 points) most likely by virtue of fewer unknown parameters. Overall fit to data was similar (Figure S1A) but this model did not produce the higher levels of late viral shedding in nasal passages in treated animals compared to untreated animals. This is because the depletion of target cells in nasal passages within a couple of days of infection does not allow prolonged viral shedding in the absence of active new cycles of infection (Figure S1B). Moreover, the same model did not capture faster recovery/lower lung damage in treated animals (Figure S1B). We believe that this is because this model does not allow regeneration of susceptible cells or the presence of refractory cells in the lung. Thus, the total epithelial cell population in the lung dies, presumably leading to profound tissue damage in simulations (Figure S1B).

Model fit to viral load data from untreated rhesus macaques

The best model recapitulated the observed trend of higher viral loads in BAL at late time points relative to the nasal passage in untreated macaques (Figure 5A). The model also closely captured the viral dynamics in BAL from untreated animals and mostly captured nasal viral loads as well, though outlier data points, mostly representing transient viral rebound compromised models fit somewhat in several animals.

Figure 5.

Mathematical model fits to viral load data

(A) Fits to untreated animals. RM 7-12 received a placebo vehicle in direct comparison to the remdesivir-treated animals. RM 13-20 are from different studies.

(B) Fits to 6 treated animals who received 10 mg/kg at day 0.5 and 5 mg/kg at days 1, 2, 3, 4, 5, and 6. Dots (pink = nasal swabs, purple = BAL) are datapoints and lines are model projections. Dots overlying the dotted line are below the limit of detection.

(C) Model simulated viral kinetics has similar statistical results as the raw data in Figures 1A and 1B. Time is in days from infection.

Infected cell death rates ($\delta$) and viral replication rates ($\pi$) were generally higher in the nasal passages relative to lungs in the untreated animals (Table S4). The density-dependent exponent had a similar value in both compartments (k = 0.09), consistent with predicted value in humans (Goyal et al., 2020), and led to a 2-2.5-fold increase in the overall death rate of infected cells at peak viral load.

Model fit to viral load data from remdesivir-treated rhesus macaques

The PK/PD model (the combination of the PK model in Figure 2 and the viral dynamics model shown in Figure 4B) recapitulated the observed trend of lower viral loads in BAL at late time points relative to the nasal passages (Figure 5B). The model also captured BAL viral loads on treatment accurately while reproducing nasal viral loads as well, though outlier data points again compromised the model fit somewhat in several animals. In particular, our model failed to capture the day ‘1’ viral load in the nasal compartment under a population-based fitting procedure (Figure 5B), which could be improved upon by performing data fitting for each animal separately assuming a constant efficacy of remdesivir (Figure S2). We also were not able to fit to the dramatically observed biphasic viral expansion in one animal (RM2). The model recapitulated the fact that BAL viral load was lower in treated animals at all-time points but that nasal viral loads was higher in treated animals at late time points (Figure 5C) closely approximating summary results in Figures 1A and 1B.

Remdesivir's antiviral potency in nasal and lung cells

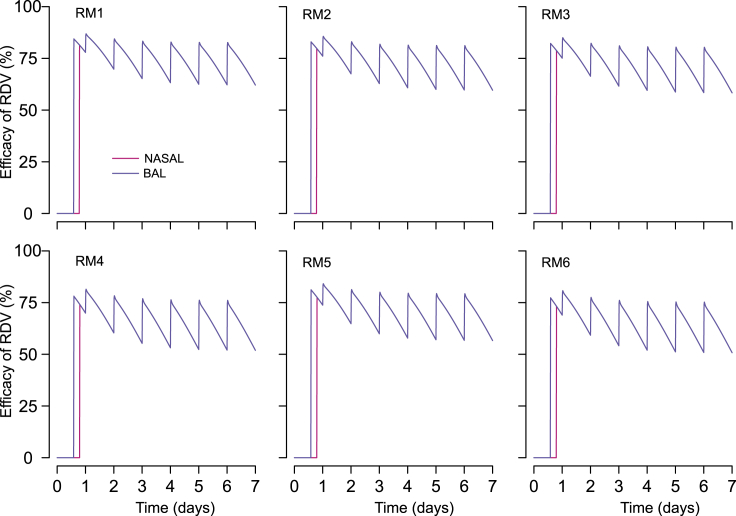
The estimated degree to which remdesivir suppressed viral replication varied somewhat across animals. Over the course of the treatment (from day 0.5 to day 7), the mean efficacy of the RDV treatment in nasal mucosa and lung cells was estimated to be ∼75%, ∼73%, 72%, 66%, 70, and 65% in RM1, RM2, RM3, RM4, RM5, and RM6, respectively (Figure 6). Brief reductions in RDV drug concentrations between doses related to lower active metabolite levels in cells and were associated with viral re-expansion after each dose (Figure 5B). Finally, we found that a model that ignores fluctuations in RDV PK and assumes that the drug efficacy is constant between 0.5 to 7 days does not fit observed data at the population level as well as the model that includes RDV PK ($\text{Δ}$ AIC∼21).

Figure 6.

Projected direct antiviral efficacy of RDV treatment (${\mathbf{\epsilon }}_{\mathbf{U}}$ and ${\mathbf{\epsilon }}_{\mathbf{L}}$) in nasal passages (pink line) and the lung (blue line)

Over the course of the treatment (from day 0.5 to day 7), the projected efficacy of remdesivir in nasal cell (pink, which is superimposed by the purple line) is same as in lung cells (purple). Projections are based on data from RM 1-6. Time is in days from infection.

The antiviral potency of remdesivir was estimated using “in vivo” EC₅₀. Although “in vitro” IC₅₀ estimates the antiviral concentration needed to inhibit 50% of viral replication based on in vitro experiments, we estimate EC₅₀ based on viral loads measured in vivo in animal or human experiments (Goyal et al., 2020). Estimates for in vivo EC₅₀ were the same in the lung and the nasal passages (Table S6). Variability in nasal viral load peak and contemporaneous viral loads between treated animals is generally related to difference in death rate of infected cells in nasal passages rather than EC₅₀. RM2 had complex kinetics with low peak viral load followed by viral rebound (which was not captured by the model and may represent a drug resistant variant) (Goyal et al., 2020) and was found to have the highest death rate of infected cells in nasal passages. One animal with accelerated viral elimination in the lung (RM5) was found to have a higher infected cell death rate in lung but EC₅₀ the same as the other 5 treated animals (Table S6).

Of note is that we estimate the drug potency (i.e., EC₅₀) to be the same in nasal passages and lungs assuming the same levels of the nucleoside GS-441524 in nasal passages and lungs. Differences in drug concentration in the two tissue compartments might yield differences in potency. This is because we require the same antiviral efficacy in two compartments to reproduce the observed data (Figure 6). The preservation of this relationship requires that the EC₅₀ increases (or decreases) if the drug concentration is higher (or lower) in nasal passages compared to lung because antiviral efficacy is inversely proportional to the ratio of drug concentration and EC₅₀. Our model also suggests that despite similar antiviral potency in the two compartments, the antiviral effects are delayed by ∼0.3 days from the time of first administration in nasal passages whereas it is relatively quicker in lungs with a shorter delay of ∼0.1 day.

Lack of viral rebound in the lung may be explained by infection-dependent generation of refractory cells

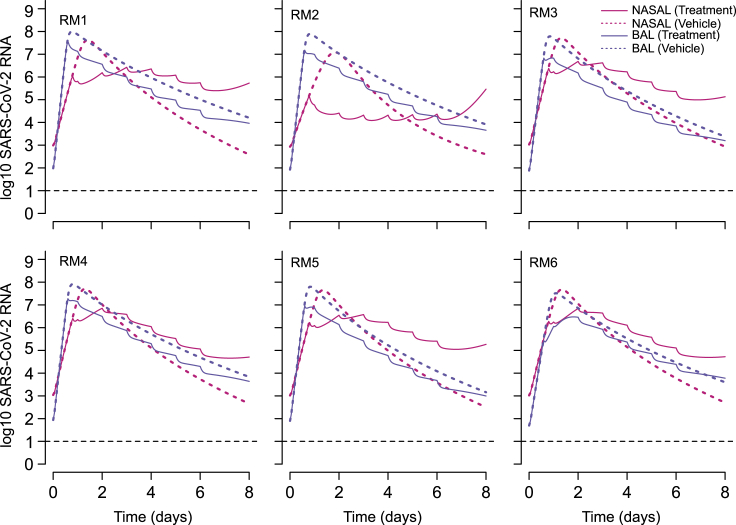
We next performed counterfactual simulations assuming the six treated animals did not receive treatment (${\mathrm{\epsilon }}_{\text{U}}$ =0 and ${\mathrm{\epsilon }}_{\text{L}}$ = 0). The viral load trajectories in these simulations (Figure 7) appear similar to those in untreated animals with BAL viral loads exceeding nasal viral loads at later time points (Figure 5A). Comparisons of the counterfactual viral load tracings to the treated animals suggests that a majority of viral load decrease in lungs is achieved following the first dose and is then carried forward throughout the duration of therapy with unchanged decay slopes. On the other hand, in nasal passages, viral load is decreased initially during therapy but then stabilizes or even increases, leading to higher viral loads than counterfactual projections (Figure 7).

Figure 7.

Projected impact of RDV treatment on viral dynamics in the nasal passages and lungs

Solid lines refer to the simulated viral loads under treatment and dotted lines are counterfactual simulations assuming no treatment. In the case of the lung (BAL specimens), therapy is projected to lead to consistently lower viral loads. In the case of nasal viral load, therapy temporarily lowers viral load, but viral load is predicted to ultimately persist at higher levels than in the absence of treatment. Simulations are based on data from RM 1-6. Time is in days from infection.

In the nasal cavity, somewhere between day 2 and 6 of therapy, the tracing cross and viral loads of the treated animals are predicted to exceed the counterfactual simulations of the same animals off therapy (Figure 7). The model projects that early treatment reduces viral load, thereby decreasing new early infection and preventing depletion of susceptible cells in the nasal passages (Figure S3). Even without assuming susceptible cell proliferation, there is an adequate population of these cells to establish a steady state of viral replication (Figure S3). In the lung, even with remdesivir moderate potency, initially susceptible cells rapidly become refractory to infection and treatment leads to a slower depletion of susceptible cells. These cells are nevertheless depleted in a nonlinear fashion as they convert to a refractory state (Figure S3). Inclusion of a refractory cell compartment is therefore necessary in our model to allow the elimination of virus from serial BAL samples.

Decreased cell death in the lungs of remdesivir-treated animals

We longitudinally assessed cell death over time in our counterfactual simulations as an approximation of total lung damage. In each case, therapy decreased the degree of peak cell death by 15–67% (Figure S4) and significantly decreased the cumulative number of dead cells over 7 days (p = 0.03, Wilcoxon rank-sum test). Although lung damage is multifactorial during COVID-19 and may involve immune-mediated destruction, this finding is qualitatively compatible with the observation that early remdesivir spared these 6 animals from severe clinical disease and abnormal lung histopathology.

Projected nasal and lung viral load trajectories at higher drug potency

Next, we performed sensitivity analyses in which we assumed a more potent antiviral effect, which could arise either from different dosing of remdesivir or a drug with a lower EC₅₀. In nasal passages (Figure S5A) and in lungs (Figure S5B), the impact of the first dose is more profound with higher potency leading to a more abrupt decline in viral load in both compartments.

We estimate that minimum drug efficacies of 99.0 and 99.9% would be required to drive the viral load below the detection limit (i.e., 100 copies/mL) in the nasal passages and lungs within 5 days of treatment initiation, when treatment is initiated 12 h postinfection. The need for such high potency reflects the lack of a concurrent immune response at this early stage of infection.

Projected impact of later therapy in nasal and lung viral load kinetics

We previously predicted in modeling of human infection that antiviral treatment with moderate potency would not clear viral infection in the nasal passage (or sputum) if dosed before the peak viral load but would clear infection if dose several days later (Goyal et al., 2020). Our simulations of the rhesus macaque data arrive at a similar conclusion in the nasal passage; paradoxically, later treatment with a moderate potency drug results in lower viral loads, whereas treatment started before peak results in increased late viral loads (Figure S6A). In contrast, in the lungs, later treatment at days 2 or 4 leads to a subsequent viral load trajectory similar to that of the earlier treated animals during the later stages of infection (Figure S6B).

We estimate that minimum drug efficacies of 70 and 99% would be required to drive the viral load below the detection limit (i.e., 100 copies/mL) in the nasal passages and lungs within 5 days of treatment initiation, when treatment is initiated 4 days postinfection. This result is because of the higher remaining viral load in the lungs of animals during the first untreated 4 days of infection.

Discussion

Viral load is a valid surrogate endpoint for treatment efficacy of several viruses including HIV, hepatitis B, hepatitis C, and cytomegalovirus (Block et al., 2017; Chen et al., 2013; Duke et al., 2021; Murray et al., 1999; Natori et al., 2018). It is plausible that SARS-CoV-2 lung viral load is also predictive of disease severity in humans. Viral loads from swabs of infected tissue provide an approximation of the number of infected cells at a given point in time, and therefore the surface area of infected tissue (Schiffer et al., 2010, 2013a). Unfortunately, it is less certain whether viral load measurements can be leveraged for SARS-CoV-2 treatment response in humans because BAL is required to measure lung viral load but these are never performed longitudinally in infected people as part of routine clinical care. Experience from other respiratory viruses suggests that viral load measures in the upper airway by nasal swab or saliva may or may not be representative of those in the lung (Seo et al., 2014).

Here, we apply mathematical models to remdesivir treatment data in rhesus macaques in which both lung and nasal viral load were measured. We believe that our model explains the observed data in its entirety and allows several testable hypotheses not generated by existing models (Gonçalves et al., 2021; Kim et al., 2021b; Rodriguez and Dobrovolny, 2021). Specifically, our model provides a plausible explanation for prolonged viral shedding in nasal passages in treated animals while also capturing lower lung viral load kinetics and limited pulmonary pathology in treated animals. We identify that the relationship between lung and nasal viral load in the context of antiviral treatment is complex and dependent on the potency and timing of therapy. With an assumed potency of ∼70% for remdesivir (consistent with estimates from (Kim et al., 2021b)), our model projects lower viral loads in the lung over the 7 days following infection, but viral loads in the nasal mucosa are only transiently lowered. Several days into treatment viral loads increased slightly and surpassed what might have occurred without treatment.

This result suggests that nasal viral load may not be an optimal surrogate for lung disease in the context of a partially effective antiviral therapy such as remdesivir at the doses used in this study. On the other hand, when we assume a more potent therapy with a lower in vivo EC₅₀, then nasal viral loads are predicted to decrease in an exponential manner, in lock step with lung viral loads, immediately after starting treatment. Therefore, nasal viral loads in humans — measured either by duration of shedding or viral decay slope — could be a viable surrogate endpoint for lung viral load and downstream lung damage but only in the context of a highly potent agent. This observation may explain the observed reduction in viral loads in trials for two other oral agents as well as monoclonal antibodies, which were given early during therapy and shown to also lower hospitalization rates (https://www.pfizer.com/news/press-release/press-release-detail/pfizer-announces-additional-phase-23-study-results; Dougan et al., 2021; Fischer et al., 2021; Weinreich et al., 2021).

The experimental results highlight inherent strengths and limitations of the rhesus macaque model. Nasal passage viral kinetics and histologic lung damage appear similar between humans and rhesus macaques (Goyal et al., 2020; Zhang et al., 2020). We are also encouraged by the fact that a nearly equivalent mathematical model with a similar parameter set explains nasal viral loads in humans and rhesus macaques during the first week of infection (Goyal et al., 2020), (though the acquired immune response is not modeled in the macaques because we do not observe complete viral elimination within the experimental time frame). Similarly, our modeling of human data led to the prediction that a semi-potent treatment given extremely early during infection might allow higher late nasal viral loads (Goyal et al., 2020), which was observed in the rhesus macaque experiments described herein.

On the other hand, in rhesus macaques, peak viral load, extensive lung damage, and clinic illness are observed within two days of infection, which is not in keeping with severe illness in humans which usually emerges at least a week after the initial phase of illness (Munster et al., 2020; Wang et al., 2020a; Williamson et al., 2020b). We hypothesize that direct intratracheal inoculation of macaques with a high viral titer results in more immediate infection of the lung and early peaking of viral load. In humans, respiratory viruses may start replicating in the upper airway and then transmit to the lungs in a second stage of infection (Chemaly et al., 2014). An alternative and not mutually exclusive explanation is that the degree of viral replication in the lung can also be established extremely early in humans, but that the more extensive immune-mediated damage which may be correlated with the extent of early viral replication occurs 1-2 weeks later. Had the rhesus macaques with the highest lung viral loads been followed for a longer time, it is possible that a more severe pneumonia would have developed at later time points. The observed differences in the pathology and viral kinetics between humans and rhesus macaques might also be one of the reasons for why our best model that is designed to explain data in rhesus macaques is structurally different to the model that describes human data (Ke et al., 2021a).

A counterintuitive result predicted by our model is that the activity of remdesivir is slightly more delayed in the nasal cavity than in the lung (assuming that drug levels are indeed equivalent in the two compartments). This could perhaps be because the distribution of the drug to one compartment takes less time than the other among other reasons. For example, highly perfused organs (including lung) will receive the drugs sooner than the slowly perfused organs in the body. Nevertheless, SARS-CoV-2 is not cleared in nasal passages as effectively as in the lungs while on treatment, because the effectiveness of antiviral therapies is never independent of the concurrent intensity of the immune response to infection (Schiffer et al., 2013b, 2016). We previously predicted that a more potent therapy is needed after 2 days of SARS-CoV-2 infection relative to >5 days after infection because there is little innate immune pressure against the virus during its early expansion phase (Goyal et al., 2020). As a result, despite a slight blunting of initial viral loads, the virus will rebound or stabilize and end up at a higher viral level in the nose than in the absence of treatment.

Here, we recapitulate this finding in the nasal passages, but also predict why this does not occur in the lungs of macaques. In the lung as in the nasal cavity, we assume density-dependent killing as a proxy for an intensifying innate response to a higher burden of infection. However, our model also suggests that ongoing infection drives a percentage of lung cells to become temporarily refractory to infection. Inclusion of this assumption is required to recapitulate lung viral load data and to explain the observation that lung damage is severely blunted in animals receiving treatment. This assumption is supported by modeling of influenza infection (Pawelek et al., 2012) but requires further experimental validation in human and nonhuman primate SARS-CoV-2 infection. Because rapid infection of all available lung cells is likely not compatible with survival, it is a priority to identify why much of the lung is spared from infection in most people infected with SARS-CoV-2.

In conclusion, we demonstrate that in rhesus macaques, the nonlinear forces governing SARS-CoV-2 viral load trajectories in the lung and nasal passages differ substantially in the presence of a partially effective antiviral therapy. To the extent that the rhesus macaque model approximates human infection, nasal viral load remains a promising surrogate endpoint marker but perhaps only in the context of a highly potent antiviral therapy.

Limitations of the study

There are several limitations of our approach. First, our approximation of lung damage is relatively coarse based on the complexity of this post-viral inflammatory process which may be mediated by factors other than number of infected cells. This is therefore a qualitative target of our modeling. Second, our fits to nasal viral load are imperfect which may be because of imprecision in viral load measurements or to missed components within the model. In the case of RM2, there is substantial viral rebound that may be because of incomplete innate responses to the first pulse of infection or to de novo drug resistance. Third, we only model early infection and therefore neglect the critical impact of the late acquired immune response (Braun et al., 2020; Suthar et al., 2020; Weiskopf et al., 2020). This may represent a fundamental shortcoming of the nonhuman primate model in which virus is cleared extremely rapidly. Fourth, although in vitro evidence supports the possibility of interferon mediated refractory target cells (Blanco-Melo et al., 2020; Sa Ribero et al., 2020), this model prediction is not yet experimentally verified. We support experiments assessing for upregulation of interferon-simulated genes in uninfected cells during natural SARS-CoV-2 infection. Fifth, although we can confidently conclude that compartmental drug potency is the same in nasal and lung sites, we cannot discriminate differences in active drug levels or intracellular drug potency in the upper versus lower airway. We start with the unverified assumption that nucleoside GS-441524 is at the same levels in nasal passages and lung and then solve for EC₅₀ which also ends up nearly the same in both locations. However, only the combination of these values is truly identifiable. Sixth, our PK model has parameters that are not fully identifiable. However, the goal of our modeling exercise in this case was just to reproduce drug and metabolite levels rather than identify a fully mechanistic PK model. Seventh, the viral inoculum in the animals is extremely high which may explain the peak in viral load at day 1 or 2 after infection, which is earlier than in humans. However, the upslope of viral expansion appears similar in humans and macaques. We surmise that lower inoculum in humans may prolong time to viral detection. Finally, the number of studied animals is small. Our results suggest that partially efficacious therapies may have differential effects on viral load in the upper versus the lungs. This result needs to be replicated in other animals to strengthen the veracity of our claims.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Other
All code and original data is available here: https://github.com/ashish2goyal/Simulating-remdesevir-effect-in-RMs

Resource availability

Lead contact

Further information and requests for resources including data and codes should be directed to and will be fulfilled by the lead contact, Joshua T Schiffer (jschiffe@fredhutch.org).

Materials availability

This study did not generate new unique reagents.

Method details

Experimental data

We analyzed viral load observations from nasal passages and BAL from 12 SARS-CoV-2-infected rhesus macaques in which 6 were treated with remdesivir and 6 received a vehicle control (Williamson et al., 2020b). Remdesivir was infused 12 h after infection at a dose 10 mg/kg with subsequent daily doses of 5 mg/kg until day 6, and remdesivir and its metabolites plasma concentrations were measured. We also added viral loads from nasal passages and BAL from 8 additional untreated animals (Munster et al., 2020). In both studies, rhesus macaques were infected with 2.6 × 10⁶ TCID50 of SARS-CoV-2 strain. Details about the infection and treatment protocol can be found in these two articles.

We also analyzed more frequently sampled observations of remdesivir and its metabolites averaged from three healthy animals after a single IV infusion of 10 mg/kg of remdesivir.

Remdesivir pharmacokinetics model

We used a compartmental and metabolism pharmacokinetics (PK) model for remdesivir. The goal of this model was to recapitulate the sparse data from remdesivir and its metabolites after several doses to the SARS-CoV-2-infected animals (Williamson et al., 2020b), along with the very frequently sampled data after a single dose in healthy animals (Warren et al., 2016). The PK model (depicted in Figure 2) describes the metabolism of remdesivir Prodrug GS-5734 (A₁), to the alanine metabolite GS-704277 (A₂) and subsequent parent Nucleoside GS-441524 (A₃) in serum and their distribution to other tissue (A_1T, A_2T, and A_3T in the same order). Metabolism rates from GS-5734 to GS-704277 and to GS-441524 are described by parameters k₁₂ and k₂₃. Drug distribution to other tissues and back to plasma are described by parameters k_1T, k_1e, k_2T, k_2e, k_3T and k_3e. We assumed that in other tissues the active triphosphate metabolite (A_4T) is metabolized from the parent nucleoside at rate k₃₄ and ignored the drug distribution of the active triphosphate metabolite between plasma and tissue compartments (Sun, 2020). We finally assumed all metabolites have clearance with rates k_c1, k_c2, k_c3 in serum and k_cT4 in tissue. These assumptions are captured by the differential equations below:

Plasma compartments:

$$\frac{d{A}_1}{dt}=-k_{c1}{A}_1-k_{12}{A}_1-k_{1T}{A}_1+k_{1e}{A}_{1T}(\text{Prodrug GS}-5734)$$

$$\frac{d{A}_2}{dt}=-k_{c2}{A}_2+k_{12}{A}_1-k_{23}{A}_2-k_{2T}{A}_2+k_{2e}{A}_{2T}(\text{Alanine metabolite GS}-704277)$$

$$\frac{d{A}_3}{dt}=-k_{c3}{A}_3+k_{23}{A}_2-k_{3T}{A}_3+k_{3e}{A}_{3T}(\text{Nucleoside GS}-441524)$$

Other tissue Compartments:

$$\frac{d{A}_{1T}}{dt}=k_{1T}{A}_1-k_{12}{A}_{1T}-k_{1e}{A}_{1T}(\text{Prodrug GS}-5734)$$

$$\frac{d{A}_{2T}}{dt}=k_{2T}{A}_2+k_{12}{A}_{1T}-k_{23}{A}_{2T}-k_{2e}{A}_{2T}(\text{Alanine metabolite GS}-704277)$$

$$\frac{d{A}_{3T}}{dt}=k_{3T}{A}_3+k_{23}{A}_{2T}-k_{34}{A}_{3T}-k_{3e}{A}_{3T}(\text{Nucleoside GS}-441524)$$

$$\frac{d{A}_{4T}}{dt}=k_{34}{A}_{3T}-k_{cT4}{A}_{4T}\left(\text{Active triphosphate metabolite}\right)$$

We further assumed that the volume of distribution of GS-5734 in plasma, GS-704277 in plasma, GS-441524 in plasma, GS-441524 in other tissue and NTP in PBMCs to be $V_1$, $V_2$, $V_3$, $V_{3T}$ and $V_{4T}$, respectively.

Pharmacokinetics model fitting

We used a mixed effects model to fit the PK model to the data from two data sources, namely, (i) averaged data from three healthy rhesus macaques in which various intermediate metabolites were measured over time following a single injection of 10 mg/kg, including the levels of NTP is PBMCs (Warren et al., 2016), and (ii) multi-dose drug and metabolite trough levels from the infected rhesus macaques (10 mg/kg at day 0.5 and thereafter, 5 mg/kg daily at days 2 till 6 post-infection), including a day 7 level of the Nuc in tissue at the time of necropsy on day 7 (Williamson et al., 2020a). The frequently sampled data in the ref (Warren et al., 2016) allowed us to estimate several key parameters such as $k_{1T}$, $k_{12}$ and $k_{1e}$.

As the data was limited, we first fixed the half-life of prodrug GS-5734 in blood ($\ln 2/k_{c1}$) to 1/24 days (or 1 h) (https://sidp.org/resources/Documents/COVID19/Matt%20Remdesivir%20Handouts%204.7.2020.pdf)[46][46], the half-life of alanine metabolite (GS-704277) in blood ($\ln 2/k_{c2}$) to 1 day (https://sidp.org/resources/Documents/COVID19/Matt%20Remdesivir%20Handouts%204.7.2020.pdf)[46][46], and the half-life of the active triphosphate metabolite in tissue ($\ln 2/k_{cT4}$) to 1 day (WHO, 2018; Sheahan et al., 2017; Warren et al., 2016). To avoid parameter identifiability issues in the absence of rich data, we further only estimated fixed effects of all parameters except $k_{23}$, $k_{34T}$, $V_1$, $V_2$, $V_3$, $V_{3T}$ and $V_{4T}$. It is to be noted that some parameters such as the rate at which active triphosphate metabolite is metabolized from the parent nucleoside ($k_{34}$) cannot be identified because there is very little to no data available of the amount of Nuc and NTP in other tissues.

Viral dynamics model

We extended our previous model of SARS-CoV-2 dynamics (Goyal et al., 2020) to include both the lung and nasal passages. In both compartments ($i\in [L,U]$, $L$ for lung and $U$ for NASAL), we assume that susceptible cells ($S_i$) are infected at rate ${\beta }_i{V}_i{S}_i$ by SARS-CoV-2 ($V_i$). SARS-CoV-2-infected cells ($I_i$) die with density dependent rate ${\delta }_i{I}_i{I}_i^{k_i}$, where $k_i$ describes by how much the first death rate depends on the infected cell density (Holte et al., 2006; Smith et al., 2018). This density dependent term represents a combined death of infected cells due to cytopathic effects of the virus and the killing of infected cells due to early immune responses. SARS-CoV-2 is produced at a rate ${\text{π}}_{\text{i}}$ and cleared with rate ${\text{γ}}_{\text{i}}$ (Pawelek et al., 2012). Free virus is allowed to be exchanged between the lungs and nasal passages and back at rates ${\theta }_{LU}$ and ${\theta }_{UL}$, respectively.

We also considered the possibility of the emergence of refractory cells. Due to antiviral actions of cytokines such as interferon responses ($F$), it has been experimentally demonstrated that uninfected lung airway cells may become refractory ($R_i$) at rate ${\rho }_i^{\prime }{S}_{i}F$ (Pawelek et al., 2012), and that infected cells may convert directly to refractory cells ($R_i$) at rate ${\phi }_i{I}_i$. Typically, the rate of change of interferon responses ($F$) in compartment ‘i is given by $\frac{d{F}_i}{dt}=s_{1i}{I}_i-s_2{F}_i$ (Ke et al., 2021a), where $s_{1i}$’s are the production rates of interferon in response to infection and $s_2$ is the clearance of interferon responses. However, to limit the number of unknown parameters (such as $s_{1i}$’s and $s_2$) in the model in the absence of relevant information, the interferon dynamics is assumed to be much faster than the dynamics of infected cells. This allows for the model simplification by replace $F_i=\frac{s_{1i}{I}_i}{s_2}$ and assuming ${\rho }_i=\frac{{\rho }_i^{\prime }{s}_{1i}}{s_2}$. Refractory cells may lose their refractory state and become susceptible at rate ${\zeta }_i$ (Pawelek et al., 2012). Since we are interested in the viral dynamics in a short span of ∼7 days (with or without treatment), we ignored the death rate of uninfected and refractory cells in the lung, that are usually long-lived.

We also included the possibility of regeneration of susceptible cells during infection. Innate immune cells eliminate virus but can also induce pulmonary tissue damage or endothelium damage as part of this process (Gorski et al., 2012; Newton et al., 2016). The restoration of the respiratory epithelial barrier after an injury happens within days after viral clearance (Fujino et al., 2019; Vaughan and Chapman, 2013; Yoo et al., 2013), depending on the severity of the infection and the extent of lung involvement. Indeed, the proliferation of epithetical cells and progenitor stem cells (or distal airway stem cells or DASCs) is critical for barrier repair following an inflammatory insult. Following lung injury, the tissue repair process is promoted by immune cells including macrophages (Hung et al., 2019). Epithelial restoration is initiated locally by proliferating alveolar type II (AT2) cells (Olajuyin et al., 2019). We modeled this restoration by adding a logistic proliferation of susceptible and refractory but not infected epithelial cells with maximum rate $r_i$ (Gibbs et al., 2009). We included the possibility that proliferation might be a delayed process and could happen after $\tau$ days post-infection (Yoo et al., 2013). All the previous mechanisms are modeled by the following differential equation system:

Nasal compartment:

$$\frac{d{S}_U}{dt}=r_U{S}_U\left(1-\frac{S_U+I_U+R_U}{N_U}\right)-{\beta }_U{V}_U{S}_U-{\rho }_U{S}_U{I}_U+{\zeta }_U{R}_U$$

$$\frac{d{I}_U}{dt}={\beta }_U{V}_U{S}_U-{\delta }_U{I}_U{I}_U^{k_U}-{\phi }_U{I}_U$$

$$\frac{d{V}_U}{dt}={\pi }_U{I}_U-{\gamma }_U{V}_U-{\theta }_{UL}{V}_U+{\theta }_{LU}{V}_L$$

$$\frac{d{R}_U}{dt}={\rho }_U{S}_U{I}_U+{\phi }_U{I}_U+r_U{R}_U\left(1-\frac{S_U+I_U+R_U}{N_U}\right)-{\zeta }_U{R}_U$$

Lung compartment (measured with BAL):

$$\frac{d{S}_L}{dt}=r_L{S}_L\left(1-\frac{S_L+I_L+R_L}{N_L}\right)-{\beta }_L{V}_L{S}_L-{\rho }_L{S}_L{I}_L+{\zeta }_L{R}_L$$

$$\frac{d{I}_L}{dt}={\beta }_L{V}_L{S}_L-{\delta }_L{I}_L{I}_L^{k_L}-{\phi }_L{I}_L$$

$$\frac{d{V}_L}{dt}={\pi }_L{I}_L-{\gamma }_L{V}_L-{\theta }_{LU}{V}_L+{\theta }_{UL}{V}_U$$

$$\frac{d{R}_L}{dt}={\rho }_L{S}_L{I}_L+{\phi }_L{I}_L+r_L{R}_L\left(1-\frac{S_L+I_L+R_L}{N_L}\right)-{\zeta }_L{R}_L$$

Here, $N_U$ and $N_L$ are the maximum carrying capacity of cells in respective compartments (assumed to be the total number of susceptible cells at the time of infection or t=0).

Model assumptions about lung lesion formation

Although the formation of lung lesions during viral respiratory infections is multi-factorial and complex, we assumed it is mainly related to the number of dying SARS-CoV-2-infected cells and the lungs ability regenerate the epithelium damaged to avoid pulmonary edema (Myers et al., 2019; Yoo et al., 2013). Thus, we modeled an informal surrogate for lesion damage $\left(G_L\right)$ with expansion kinetics equal to the total number of dying infected cells and shrinkage kinetics defined by the proliferation of susceptible and refractory cells reprsenting the recovery of the lung tissue damage (or the reduction of the area covered by virus-induced lesions). These dynamics can be represented by the following equation:

$$\frac{d{G}_L}{dt}={\delta }_L{I}_L{I}_L^{k_L}-r_L\left(S_L+R_L\right)\left(1-\frac{S_L+I_L+R_L}{N_L}\right)$$

Notice that this definition of $G_L$ is equivalent to $G_L=N_L-S_L-I_L-R_L$. Under this assumption, the fraction of the lung covered with dead cells would be: $\frac{G_L}{N_L}$.

Modeling remdesivir therapy

Here we assumed that RDV inhibits viral production (Cao et al., 2020; Tchesnokov et al., 2019). Thus, because of treatment, the viral production ${\pi }_i$ is reduced by a factor $(1-\frac{A_{3T}}{A_{3T}+E{C}_{50i}})$, where $E{C}_{50i}$ is the in vivo EC₅₀ of the nucleoside GS-441524 in the respective compartment $i$. To investigate whether the viral inhibition is independent of the drug concentration, we assumed a constant efficacy of the treatment during 0.5–7 days (${\epsilon }_i$) or in other words, we simply assume that the viral production ${\pi }_i$ is reduced by a factor ${\epsilon }_i$.

Viral dynamics model fitting and selection

To fit different versions of the virus dynamics model to the data we used a non-linear mixed effects approach (Chan et al., 2011; Karlsson et al., 2015). Briefly, in this approach observed viral load for animal $k$ at time $j$ is modeled as ${\log }_{10}{y}_{kj}=f_V\left(t_{kj},{\theta }_k\right)+{\epsilon }_V$ being $f_V$ the solution of model for the virus given the individual parameter vector ${\theta }_k$ and ${\epsilon }_V$ the measurement error. Here, the individual-parameter vector ${\theta }_k$ is drawn from a population probability distribution. We estimated population parameters using the Stochastic Approximation Expectation Maximization (SAEM) algorithm and the individual parameters using a Markov Chain Monte-Carlo (MCMC) algorithm based on the estimated population distributions. Both algorithms, SAEM and MCMC, were performed using the software Monolix.

We first fit models to nasal and BAL viral loads from untreated animals assuming absent of cell proliferation and refractory cells. Given the lack of observations for the viral load upslope in BAL, we assumed ${\beta }_L={\beta }_U$ (the heterogeneity in early viral dynamics in two regions can still be captured as it depends on the ratio $\frac{\beta {\pi }_i}{{\delta }_i\gamma }{N}_i$). We excluded treated animals in this fitting procedure as $\beta$, ${\pi }_i$ and $E{C}_{50i}$ cannot be estimated together. We assumed $t=0$ as the time of infection with initial values $V_i\left(0\right)=\frac{{\pi }_i{I}_i\left(0\right)}{{\gamma }_i}$ cps/swab, $S_L\left(0\right)=3.7\times {10}^8$ cells (based on 3.7×10⁹ cells in humans from (Crapo et al., 1982) and assumed ∼10-fold lower number of cells in rhesus macaques based on differences in weight), $S_U\left(0\right)=2.6\times {10}^6$ cells (Crapo et al., 1982; Zheng et al., 2000). We used the concept of multiplicity of infection (MOI) to that dictates that ∼ $1-e^{-m}$ fraction of susceptible cells becomes infected following an inoculation with an MOI of $m$ to obtain initial values of infected cells. For small values of MOI, this fraction is simply equal to $m$ and thus $I_U\left(0\right)=m{S}_U\left(0\right)$ cells and $I_L\left(0\right)=4m{S}_L\left(0\right)$ cells (because intratracheally, approximately dose of the virus was 4 times compared to intranasal challenge). We systematically search for the value of $\text{m}$ to calculate $I_i\left(0\right)$ and subsequently ${\text{V}}_{\text{i}}\left(0\right)$ while also estimating the other parameters in the model (Table S3). Our best estimate of $m={10}^{-5}$ suggests that upon inoculation, there are ∼26 infected cells in the nasal and ∼13,000 infected cells in the lung. This seems reasonable given that although animals are inoculated with high TCID50, their baseline nasal viral loads are below the detection limit (Munster et al., 2020). It is to be further noted that $m\ge {10}^{-4}$ achieves peak viral loads almost instantly due to large number of initially infected cell population (Table S3) which seems biologically unreasonable for any infection.

We also assumed a virus clearance rate to be the same in both compartments ${\gamma }_L={\gamma }_U=15$ /day along with $N_L=3.7\times {10}^8$ cells and $N_U=2.6\times {10}^6$ cells. We estimated the remaining parameters depending on each model assumptions. The explored competing models on this stage are listed in Table S3.

We next fit models to viral load and lung lesion observations from treated and untreated animals. Here, we explored different competing models listed in Table S5 and described below. We explored models that included cell proliferation and refractory cells in the lungs, fixing ${\rho }_U=0$ (Baccam et al., 2006), ${\phi }_U=0$ and ${\zeta }_U=0$. We explored the possibility that AT2 cells proliferate with maximum rate $r_L$ after some delay (Yoo et al., 2013), i.e. $r_L=0$ if $t<{\tau }_L$. Since we ignore the proliferation of cells in nasal passages, we also assume ${\tau }_U=0$. During the estimation procedure, we also assumed that the maximum possible value of $r_L$ to be 2/day, in between previous estimates 0.75/day (Quirouette et al., 2020) and 3.4/day for liver whose regeneration capability is no less than extraordinary for an organ (Goyal et al., 2017).

We also included models assuming that the antiviral activity of remdesivir in nasal passages and lungs occurs by a delay $\nu$ (or, ${\epsilon }_L=0$ if t < 0.5+ ${\nu }_L$ and otherwise, ${\epsilon }_L=(1-\frac{A_{3T}}{A_{3T}+E{C}_{50L}})$ but ${\epsilon }_U=0$ if t < 0.5+ ${\nu }_U$ and ${\epsilon }_U=(1-\frac{A_{3T}}{A_{3T}+E{C}_{50U}})$). For comprehensiveness, we checked two models where refractory cells emerged from susceptible cells in a linear fashion independent on the concentration of infected cells, i.e, with rate ${\rho }_i{S}_i$. We finally checked if refractory cells could lose their refractory state and become susceptible cells. In all models, we fixed parameters to the estimated value of the best model when fitting untreated animals and assumed remdesivir reduces viral production ${\pi }_i$ by a factor $(1-\frac{A_{3T}}{A_{3T}+E{C}_{50i}})$ in $i$ th compartment. Here, we also assumed $t=0$ as the time of infection with same initial values and fixed parameters ${\gamma }_L$, ${\gamma }_U$, $N_L$ and $N_U$ as before. We estimated the remaining parameters depending on each model assumptions (Table S5).

To determine the best and most parsimonious model among the instances above, we computed the log likelihood (log L) and the Akaike Information Criteria (AIC = −2log L+2m, where m is the number of parameters estimated). We assumed a model has similar support from the data if the difference between its AIC and the best model (lowest) AIC is less than two (Burnham and Anderson, 2002).

Quantification and statistical analysis

Statistical analyses were performed using Wilcoxon rank-sum test with multiple comparison (n = 6 for treatment group and n = 14 for untreated/vehicle group). For all tests, p values ≤0.05 were considered as statistically significant.

Published: June 17, 2022

Data and code availability

This paper analyzes existing, publicly available data. All data reported in this paper will be shared by the lead contact upon request. All original code has been deposited at https://github.com/ashish2goyal/Simulating-remdesevir-effect-in-RMs and is publicly available as of the date of publication. Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.