Pose Classification Using Three-Dimensional Atomic Structure-Based Neural Networks Applied to Ion Channel–Ligand Docking

Abstract

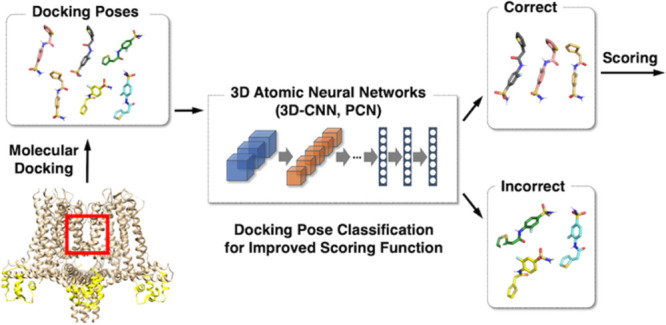
The identification of promising lead compounds showing pharmacological activities toward a biological target is essential in early stage drug discovery. With the recent increase in available small-molecule databases, virtual high-throughput screening using physics-based molecular docking has emerged as an essential tool in assisting fast and cost-efficient lead discovery and optimization. However, the best scored docking poses are often suboptimal, resulting in incorrect screening and chemical property calculation. We address the pose classification problem by leveraging data-driven machine learning approaches to identify correct docking poses from AutoDock Vina and Glide screens. To enable effective classification of docking poses, we present two convolutional neural network approaches: a three-dimensional convolutional neural network (3D-CNN) and an attention-based point cloud network (PCN) trained on the PDBbind refined set. We demonstrate the effectiveness of our proposed classifiers on multiple evaluation data sets including the standard PDBbind CASF-2016 benchmark data set and various compound libraries with structurally different protein targets including an ion channel data set extracted from Protein Data Bank (PDB) and an in-house KCa3.1 inhibitor data set. Our experiments show that excluding false positive docking poses using the proposed classifiers improves virtual high-throughput screening to identify novel molecules against each target protein compared to the initial screen based on the docking scores.

1. Introduction

The discovery of novel drugs is a highly complex, expensive, and time-consuming process. High-throughput screening (HTS) has been used to rapidly identify lead compounds by testing thousands to millions of compounds for biological activity at the model organism, cellular pathway, or molecular target protein level. However, due to the high-cost and time-consuming nature of HTS and the exponential rise in the number of viable novel drug targets, computational methodology, namely, virtual high-throughput screening (vHTS) is being increasingly applied to accelerate the drug discovery process. In particular, recent studies have shown that vHTS-based methods are capable of identifying small-molecule inhibitors against SARS-CoV-2.¹⁻³

To date, molecular docking is one of the most commonly used vHTS approaches for the calculation of protein–ligand binding activities, enabling virtual screening of massive compound databases. In general, there are three main traditional scoring functions for molecular docking: force field based, empirical, and knowledge based. The force field-based scoring function consists of a sum of physical interactions including van der Waals interactions, electrostatic interactions, and bond stretching/bending/torsional forces. However, this approach often suffers from speed and sampling limitations, due to the intensive computation and sampling insufficiency.⁴ The empirical scoring function utilizes a set of weighted different energy terms such as hydrogen bonds, van der Waals interactions, electrostatic energy, and hydrophobicity. The energy terms are manually selected and weighted based on experimental affinity data.⁵ The knowledge-based scoring function is based on statistical energy potentials that are derived from experimental structure data of protein–ligand complexes.⁶ Since the last two approaches rely on known ligand–protein structures and binding affinities, they are difficult to apply to targets and ligands that are structurally distinct from existing data.⁷

Molecular docking software tools such as AutoDock Vina (empirical and knowledge-based scoring functions)⁸ and Glide (empirical scoring function)⁹ compute the preferred poses of a ligand within the constraints of the protein’s binding pocket selected by users or based on the crystal structure of the receptor. The top-ranked pose of each ligand is then selected by the scoring function composed of multiple energetic factors, as described above. However, we often observe discrepancies between the top-ranked poses and conformations of crystal structures, resulting in low hit rates. According to a study by Irwin and Shoichet,¹⁰ the hit rate of top-rated compounds from virtual screening of molecular docking is only about 12%. It is not a trivial task to select the best poses since it cannot always be assumed that the pose of the ligand model with the lowest energy score represents the correct one (i.e., in validation with a cocrystal structure of the same protein–ligand). Table 1 shows docking poses of an exemplary protein–ligand complex, the enzyme carbonic anhydrase with a bound inhibitor (PDB ID: 3R17) from the refined PDBbind 2019 set,¹¹ and lists the Vina docking scores of the various poses together with the root-mean-square deviation (RMSD) compared to the crystal structure. RMSD is widely used as a measure of how different a calculated docking pose of a ligand is from its corresponding cocrystallized orientation in the same protein. Note that generally poses with an RMSD of less than 2 Å are considered correct, while poses with larger than 4 Å RMSD are considered incorrect.^12,13 As shown in Table 1, there is little correlation between the Vina score and RMSD values. For example, the RMSD of the top-ranked pose is 3.53 Å, whereas the pose with the best RMSD value (1.72 Å) is ranked in 12th place. Figure 1 visualizes the two poses, together with the crystal structure. The pose ranked in 12th (cyan) has the lowest RMSD with a more similar orientation to the crystal structure (black) compared to the top-ranked pose (magenta).

Table 1. List of Our Curated PDB Ion Channel Data Set.

PDB ID	Protein name
1J95	KCSA potassium channel with TBA (tetrabutylammonium) and potassium
2LY0	Membrane ion channel M2 solution NMR structure of the influenza A virus S31N mutant (19–49) in presence of drug M2WJ332
2RLF	Proton channel M2 from influenza A in complex with inhibitor rimantadine
3JAF	Structure of alpha-1 glycine receptor by single particle electron cryomicroscopy, glycine/ivermectin-bound state
4TNW	Avermectin-sensitive glutamate-gated chloride channel GluCl alpha
4XDK	Crystal structure of human two pore domain potassium ion channel TREK2 (K2P10.1) in complex with norfluoxetine
4XDL	Crystal structure of human two pore domain potassium ion channel TREK2 (K2P10.1) in complex with a brominated fluoxetine derivative
5EK0	Human Nav1.7-VSD4-NavAb in complex with GX-936
5IS0	Structure of TRPV1 in complex with capsazepine, determined in lipid nanodisc
5KLG	Structure of CavAb(W195Y) in complex with Br-dihydropyridine derivative UK-59811
5KMD	Structure of CavAb in complex with amlodipine
5KMF	Structure of CavAb in complex with nimodipine
5KMH	Structure of CavAb in complex with Br-verapamil
5OSC	GLIC-GABAAR alpha1 chimera crystallized in complex with pregnenolone sulfate
5VDH	Crystal structure of human glycine receptor alpha-3 bound to AM-3607, glycine, and ivermectin
5VDI	Crystal structure of human glycine receptor alpha-3 mutant N38Q bound to AM-3607, glycine, and ivermectin
6HUG	CryoEM structure of human full-length alpha1-beta3-gamma2L GABA(A)R in complex with picrotoxin and megabody Mb38
6JPA	Rabbit Cav1.1-verapamil complex
6JPB	Rabbit Cav1.1-Bay K8644 complex
6JUH	Structure of CavAb in complex with efonidipine
6KEB	Structure basis for Diltiazem block of a voltage-gated calcium channel
6LQA	Voltage-gated sodium channel Nav1.5 with quinidine
6MVX	NavAb voltage-gated sodium channel, I217C, in complex with Class 1C antiarrhythmic flecainide
6RV3	Crystal structure of the human two pore domain potassium ion channel TASK-1 (K2P3.1) in a closed conformation with a bound inhibitor BAY 1000493
6RV4	Crystal structure of the human two pore domain potassium ion channel TASK-1 (K2P3.1) in a closed conformation with a bound inhibitor BAY 2341237
6SXF	Crystal structure of the voltage-gated sodium channel NavMs (F208L) in complex with Tamoxifen
6UZ0	Cardiac sodium channel (Nav1.5) with flecainide
6WJ5	Structure of human TRPA1 in complex with inhibitor GDC-0334
6X40	Human GABAA receptor alpha1-beta2-gamma2 subtype in complex with GABA plus picrotoxin
6YSN	Human TRPC5 in complex with Pico145 (HC-608)
7BYM	Cryo-EM structure of human KCNQ4 with retigabine
7BYN	Cryo-EM structure of human KCNQ4 with linopirdine
7CR1	Human KCNQ2 in complex with ztz240
7D4P	Structure of human TRPC5 in complex with clemizole
7D4Q	Structure of human TRPC5 in complex with HC-070
7JUP	Structure of human TRPA1 in complex with antagonist compound 21
7LQZ	Structure of squirrel TRPV1 in complex with RTX
7MZC	Cryo-EM structure of minimal TRPV1 with RTX bound in C1 state
7MZD	Cryo-EM structure of minimal TRPV1 with RTX bound in C2 state
7RHJ	Cryo-EM structure of human rod CNGA1/B1 channel in l-cis-Diltiazem-blocked open state

Figure 1.

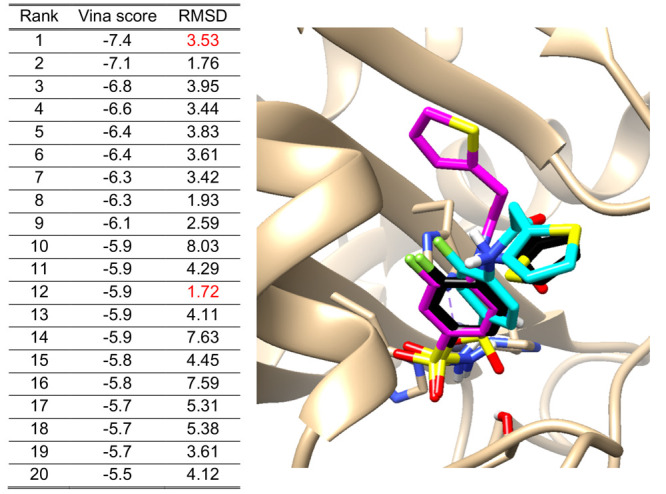
Example of 20 Vina docking scores with their RMSD values. They were calculated between each pose and the crystal structure of the 3R17 ligand (human carbonic anhydrase, hCA) from the PDBbind 2019 refined set.

Recently, data-driven machine learning (ML) approaches trained on three-dimensional (3D) structures of protein–ligand complexes have been proposed for the task of binding affinity prediction.^1,14−19 Most approaches in this category use PDBbind data sets for training and evaluation. These trained ML models can be used for virtual screening by predicting the binding affinity of each compound in a protein target (i.e., a complex structure). Since crystal structures of the protein–ligand complexes are not available in most screening applications, structure modeling-based docking tools are used to generate protein–ligand docking poses for their evaluation. However, due to the above-discussed deviations between the top-ranked poses and crystal structures, incorrect poses reduce prediction accuracy. To improve the prediction accuracy of protein–ligand interaction, robust pose classification filtering out incorrect protein–ligand poses is crucial.

To address these problems, several ML approaches have been recently applied to identify active compounds as well as to predict the binding affinity of ligands to protein. Durrant and McCammon developed one of the first neural network receptor–ligand scoring functions called NNScore.^20,21 McNutt et al. developed a ML-based molecular docking program called GNINA using an ensemble of convolutional neural networks (CNNs) as a scoring function.²² Aggarwal and Koes utilized a ML-based scoring function to predict the RMSD value of each pose to the true binding structure.²³ Francoeur et al. applied a grid-based CNN to predict binding affinity using a new data set called CrossDocked2022 with 22.5 million poses.¹⁹ Adeshina et al. used eight different machine learning classification algorithms to filter out false positive docking poses for AChE inhibitors: Gradient Boosting (GB), Extreme Gradient Boosting (XGB), Random Forest (RF), Extremely Randomized Trees (ET), Gaussian Naïve Bayes (GNB), k-Nearest Neighbor (kNN), Linear Discriminant Analysis (LDA), and Quadratic Discriminant Analysis (QDA). The authors found that most candidate inhibitors in a screen against acetylcholinesterase showed detectable activity, and 10 of the 23 identified inhibitors had IC₅₀ values less than 50 μM.²⁴ Ashtaway and Mahapartra explored a range of novel scores employing different ML approaches in conjunction with physicochemical and geometrical features characterizing protein–ligand complexes to predict the native or near-native pose of a ligand docked to a receptor protein’s binding site.²⁵ Boyles et al. proposed a method to predict the binding affinity of docking poses using a hybrid ML-based scoring function with structure- and ligand-based features. They showed that their method is comparable to other scoring approaches trained only on crystal structures. A random forest algorithm was then used for their machine learning method.²⁶ Bao et al. predicted RMSD of a ligand docking pose with reference to its native binding pose as a regression problem using a machine learning model called DeepBSP and evaluated their model on the PDBbind core set (CASF-2016).²⁷ Recently, Pei et al. proposed a Random Forest (RF)-based pose classification with physics-based energy scores as input features and evaluated their model on PDBbind CASF-2016 data set.²⁸

Although there have been many attempts using ML techniques to address binding affinity prediction and scoring functions, classification of molecular docking poses using deep neural networks, especially approaches using 3D atomic representations, have not been extensively studied. We here propose two machine learning approaches for the task of pose classification, 3D convolutional neural network (3D-CNN) and point cloud neural network (PCN), to improve the accuracy of protein–ligand binding affinity predictions and other vHTS tasks. 3D-CNN-based approaches have been extensively used to predict the binding affinity of complexes.^1,14 Unlike the previous approaches, we propose to employ it as a pose classifier to filter out false positive docking poses to improve the accuracy of virtual screening. Moreover, as an alternative to the 3D-CNN-based method, we present another neural network approach (PCN) that directly captures global information on 3D atom structures without voxelizing them into a 3D voxel grid. The proposed PCN is faster and has smaller memory footprint requirements compared to 3D-CNN. Our experiments show that the two proposed ML approaches effectively filter out incorrect poses, resulting in better binding affinity and other bioactivity predictions, than when using docking poses based solely on the scoring functions. We used the PDBbind 2019 crystal structures and their Vina docking poses for training and quantitative evaluation. To evaluate our methods with structurally different receptors and compounds (i.e., holdout set), we used ion channel complexes extracted from the Protein Data Bank (PDB) and data from our own work and literature for the calcium-activated potassium channel KCa3.1.

2. Data

For experiments and evaluations of the proposed pose classification, we used several data sets of protein–ligand complexes. First, we used the PDBbind database¹¹ for training and testing, as a standard data set. The PDBbind database is a collection of experimentally determined structures of cocrystallized protein–ligand complexes deposited in the PDB,²⁹ which has been widely used for protein–ligand binding affinity prediction.^14,15 The PDBbind database is composed of three subsets: general, refined, and CASF-2016 (also known as core set). The general set is the main body of the PDBbind database, consisting of the protein–ligand complexes with experimentally determined binding affinity data for the given complexes. The refined set is compiled to down-select the protein–ligand complexes with better resolution quality, less than 2.5 Å, out of the general set. CASF-2016 is a relatively small compilation of high-quality protein–ligand complexes for various docking scoring and ML studies. CASF-2016 (core set) has been used as the primary evaluation set in the comparative assessment of scoring functions (CASF) benchmark. In this study, we used the PDBbind 2019 edition: the refined set with 4,585 protein–ligand complexes for training and CASF-2016 with 285 complexes for evaluation. Note that there is no overlap between the refined and CASF-2016 sets, i.e., no duplicated PDB IDs between the two sets. Nevertheless, CASF-2016 is drawn from similar ligands and protein complexes where structural similarity to pockets in the refined set is still high. For further comprehensive evaluation of the proposed method, we used two additional holdout data sets that do not contain similar counterparts in the training data: (1) ion channel complexes selected from the PDB and (2) the KCa3.1 inhibitor data set published by our own group^30,31 and scientists from Bayer^32,33 and docked into the inner pore of the channel.

Ion channels are multipass membrane proteins that regulate the flux of anions and cations across cellular membranes in all organisms ranging from bacteria to humans. However, many ion channels are large multisubunit proteins that often “bury” between 50% and 85% of their amino acids in the lipid environment of the membrane making them challenging targets in structural biology³⁴⁻³⁶ because of technical difficulties in expressing, purifying, and crystallizing them. To date, there are more than 50,000 PDB entries in the Protein Data Bank (PDB) repository of protein structures, but less than 1% of these entries represent membrane proteins with ion channels constituting only a few dozen structural entries. There accordingly have not been many ML-based vHTS studies focusing on ion channels. Table 1 shows 40 ion channel complex data which were manually selected from the PDB. Note that five of the 40 complexes also appear in the PDBbind general set. However, those five complexes are not included in our training data set (refined set). In addition, most of the crystal structures in this ion channel data set have relatively low resolution compared to the refined set and CASF-2016 in the PDBbind data set.

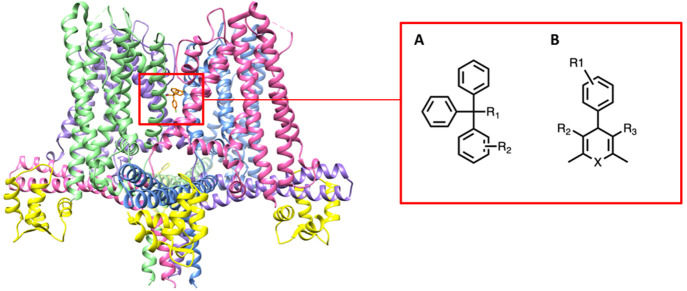
We further applied our method to the potassium channel KCa3.1. Currently, there is no cocrystal structure of the KCa3.1 channel with a ligand, but there are three structures of the channel: one structure in the closed state (PDB ID: 6CNM) and two open state structures (PDB IDs: 6CNN, 6CNO).³⁷ Except for the KCa3.1 channel data set, we use cocrystallized complex data with the RMSD calculations to validate and evaluate our method. For the KCa3.1 inhibitor data set, we calculated correlations between the experimental pIC50 values and docking scoring functions from poses obtained by docking various KCa3.1 inhibitors into a binding site identified in the inner pore by mutagenesis.^38,39Figure 2 shows the structure of KCa3.1 (PDB ID: 6CNM) and the general structures of triarylmethane and cyclohexadiene based KCa3.1 inhibitors. The structures of KCa3.1 inhibitors are provided in Figure S1 of the Supporting Information. Note that the diversity of the KCa3.1 compounds is somewhat limited since the experimental discovery work from our group and industry has largely focused on the two pharmacophores shown in Figure 2, whereas our curated PDB ion channel set includes a diverse collection of ligands for evaluation.

Figure 2.

(Left) Closed state of the KCa3.1 channel (PDB ID: 6CNM) and binding site of inhibitors (red box). (Right) General structures of KCa3.1 channel triarylmethane and cyclohexadiene based inhibitors. The four channel alpha subunits are rainbow colored; the channel associated with calmodulin is shown in yellow.

Both the ion channel and KCa3.1 data sets are considered holdout sets, also known as out-of-distribution (OOD) data sets, since there are only three ion channel structures in the PDBbind 2019 refined set used to train our models. The three ion channel structures in the refined set are not complete ion channels containing the transmembrane domain and the ion conducting pore. They are intracellular “pieces” of the channels that have been crystallized without the rest of the channel. PDB ID 3U10 is a tetramer of C-terminal domains of HCN1, and 4NVP is a similar tetramer of the C-terminal domains of HCN4, while 4MUV is the monomeric cyclic nucleotide binding domain of a bacterial potassium channel. Our ion channel data set from the PDB is hand curated and only contains ion channel structures that contain the ion-conducting transmembrane domains. Thus, we can conclude that there is no overlap between the training complexes and the ion channel holdout sets. Moreover, compared to enzyme proteins which make up the vast majority of the PDBbind complexes, ion channel proteins generally contain unique symmetric structures with a conduction pathway for ions, as shown in Figure 2. Thus, the holdout sets present a distinct structural motif compared to other structures included in the training set.

2.1. Preprocessing

The provided crystal structure data in the data sets described above were used as ground-truth correct poses. To generate more correct poses (positive examples) and a similar number of incorrect poses (negative examples), we performed AutoDock Vina docking with its scoring function. We then extracted 20 docking poses for each protein–ligand complex. In order to dock each ligand against the target protein using AutoDock Vina, all receptors and ligands were prepared in the pdbqt format using MGLtools.⁴⁰ In the preparation of receptor structures, charges were merged, and nonpolar hydrogen, lone pairs, waters, and nonstandard 20 amino acids were removed from the protein, which is the default setting of the MGLtools. For the ligand preparation, the default setting of the MGLtools was used as well. Feinstein and Brylinski⁴¹ demonstrated that docking results depend heavily on the choice of docking region size, as the docking poses are affected by the size of the search space. To increase the diversity and the number of poses for training and evaluation (i.e., data augmentation), docking for the refined set was performed twice with different grid sizes. The initial docking box was calculated based on the boundary coordinates of each ligand in the crystal structure, and the box dimensions in x, y, and z axes were increased by 8 and 4 Å, accordingly.⁴¹

The total number of poses for training is 82,591, where the number of correct and incorrect poses are 23,834 and 58,757, respectively. As described above, generally RMSDs of 2 and 4 Å were used as thresholds to determine correct and incorrect poses. In our experiment, however, we considered poses with an RMSD less than 2.5 Å as correct, while poses with greater than 6 Å RMSD were considered incorrect for two reasons. First, classifying docking poses using the thresholds of 2 and 4 Å results in a severe class imbalance problem (too fewer positive examples), which causes overclassification of the incorrect poses. To alleviate the problem, we used slightly higher RMSDs for thresholding poses. Second, the main goal of the proposed pose classification is to train the ML models to filter out “definite” incorrect poses to improve molecular docking processes for high-fidelity docking screening. We observed that the threshold of 2.5 and 6.0 Å provides a reasonable distinction between correct and incorrect poses. Even with the revised RMSD threshold, the number of incorrect poses is greater than that of correct poses in many cases. Thus, the crystal structures were added to the correct poses.

For featurization of complex data of each crystal and docking poses, we used a widely used atomic representation where each atom has its (x, y, z) coordinates and features. The atomic representation is comprised of 19 features, described in Jones et al.¹⁴ Optionally we incorporate four protein–ligand interaction features in addition to the 3D atomic representation. The interaction features include number of hydrogen bonds, number of hydrophobic contacts, number of pi stackings, and number of salt bridges extracted by using the interaction module in the Open Drug Discovery Toolkit (ODDT).⁴² The ODDT library is a modular and comprehensive toolkit written in Python (https://github.com/oddt/oddt). In ODDT, we used the oddt.interactions module to collect the interaction features between each ligand and protein receptor complex. We describe the use of these interaction features in the following section. For the KCa3.1 inhibitors evaluation, we used Glide in addition to AutoDock Vina. To run Glide, we converted all ligand structures in 2D SDF into 3D conformation format as preprocessing. We then performed LigPrep to prepare the ligands with Epik.⁴³ The protein structure was prepared using Schrödinger’s Protein Preparation Wizard, and the binding site of the protein was specified using Receptor Grid Generation. For the grid of the receptor, the inner box (a search space that indicates acceptable positions for the ligand center) was set to 10 Å × 10 Å × 10 Å, while the outer box (a search space that must contain all the ligand atoms) was set to 20 Å × 20 Å × 20 Å. The docking was carried out in standard precision (SP) mode.^9,44

3. 3D-CNN

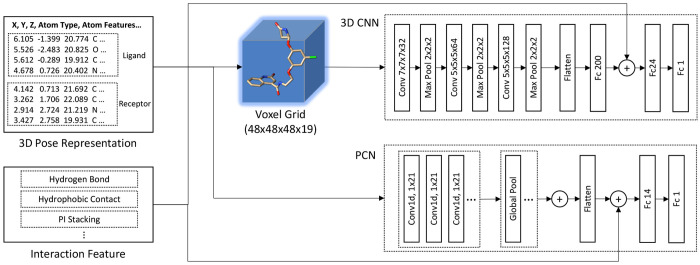
3D convolutional neural networks (3D-CNNs), widely used for a vast number of computer vision applications with 3D volumetric data, have been successfully applied to the prediction of protein–ligand binding affinity.^{1,14,18,19,22,23,35,45} We herein propose to use 3D-CNNs as a binary pose classifier to learn representation for 3D atomic structures of compound poses. Our 3D-CNN is composed of three convolutional layers and three fully connected layers, followed by a sigmoid activation. Each convolutional layer comes with ReLU activation for nonlinearity and batch normalization to normalize feature outputs across each mini-batch, followed by max pooling. The voxelization step for 3D-CNNs is similar to the work in Jones et al.¹⁴ The ligand and its surrounding pocket region within 8 Å are extracted from the protein–ligand complex structure, and all the atoms inside the region are assigned to voxels in a 48 × 48 × 48 voxel grid. To avoid too sparse representation in the voxel grid, we applied Gaussian smoothing so that the atom regions with their atomic features are propagated into its neighboring voxels. For this, we used the gaussian_filter function provided in Python’s SciPy library with sigma = 1 and truncate = 2.

The input volume dimension for each compound pose’s atomic representation is 48 × 48 × 48 × 19, where 48 is the voxel grid size in each axis and 19 is the number of atomic features. The dimension of 3D filters in the 3D convolutional layers is 7 × 7 × 7 for the first layer and 5 × 5 × 5 for the second and third layers. 3D convolutional layers capture spatial features and underlying patterns of the protein–ligand docking poses. The pooling layers select the most representative elements of the convolved features and give translational invariances. By following a series of 3D convolutional and max-pooling layers, the fully connected layers integrate spatial features of all positions in the docking poses generated by the convolutional layers to make a final prediction.

The final layer’s output activations are then passed through the sigmoid function to calculate the error of the prediction (loss). For the classification, we used the standard binary cross entropy (BCE) loss. Figure 3 (top) illustrates the overall layer structure of the 3DNN. For the pose classification, we used two slightly different versions of the 3D-CNN architecture. The first version uses a 3D atomic representation in a voxel grid, just like the previous 3D-CNN methods used for the binding affinity prediction.^14,17 The second version incorporates protein–ligand interaction features into the 3D-CNN inference model by concatenating the interaction features and the output activation of a fully connected layer, as shown in Figure 3.

Figure 3.

Overall network architecture of the proposed 3D-CNN and PCN. The input for the networks is 3D atomic structures with their features (3D pose representation). The PCN uses the input data directly, whereas the 3D-CNN uses their voxelized data. The optional interaction features are concatenated with one of the fully connected layer activations.

4. Point Cloud Network (PCN)

In addition to the 3D-CNN approach described above, we introduce a new deep neural network approach for the task of pose classification. Our proposed approach, called point cloud network (PCN), directly uses 3D atom coordinates with their associated features. It is inspired by the attention models for word–sentence inference in natural language processing.⁴⁶ The main motivation of the PCN approach is a more efficient inference model with small memory footprint requirements compared to the 3D-CNN which uses a 48 × 48 × 48 × 19 voxel grid per protein–ligand complex. Since the 3D atomic structure is an unordered list of atom positions (x, y, z) and their features, the data need to be interpreted without any order dependency. Moreover, the network should learn feature representations invariant to any geometric transformation. To this end, we propose to use a neural network that directly interprets the 3D atomic structure data as a point cloud by globally aggregating information across all the atom positions and features. The basic concept of the PCN is similar to that of PointNet⁴⁷ to classify and segment point cloud data. Unlike PointNet, the PCN incorporates atom positions and their features together, and the geometric transformation is performed outside the network as augmentation.

The detailed architecture of the PCN is as follows. The PCN utilizes 1D CNNs to interpret each atom position and its feature, followed by global max pooling to aggressively summarize the output feature map given each 1D filter by extracting the best feature response of the filter. All pooled features are then concatenated and flattened. Unlike the word–sentence models to highlight relevant features among words in a sequence, this PCN does not interpret the atom data (position with features) as a sequence because there is no order dependency in the atoms of ligands and proteins. Since the network directly reads atom (x, y, z) coordinates without any need for voxelization, it does not suffer from quantization errors unlike 3D-CNN. Moreover, it uses significantly less memory and GPU computation compared to a 3D-CNN. Figure 3 (bottom) illustrates the overall architecture of the proposed PCN. Like the 3D-CNN versions, we incorporate the protein–ligand interaction features by concatenating them and the fully connected layer’s activation.

5. Experimental Setup

To train both the 3D-CNN and PCN models, we used the refined data set of the PDBbind 2019 edition which is comprised of 4,585 cocrystal structures and their docking poses using AutoDock Vina. The cocrystal structures and docking poses whose RMSD is less than 2.5 Å were labeled as correct poses, whereas docking poses whose RMSD is greater than 6.0 Å were labeled as incorrect poses, as described earlier.

In training the proposed networks, we optionally applied 3D affine transformation to (x, y, z) coordinates of the input atom data to augment training sample sizes and to increase distributions of the spatial coordinates of the input atom data. The affine transformed data samples add variance of the 3D representation, which also reduces the risk of overfitting and improves overall accuracy. Note that we apply only rotation and translation to the 3D atom coordinates of the complex structures because other geometric transformations such as skewness and scaling break its 3D molecular conformation with important bonds and connectivity. In our experiment, we randomly rotated and translated (x, y, z) coordinates of atoms by up to 20° and 10 Å, respectively. We applied the random rotation in all three axes, which we observed is enough to provide significantly increased diversity of the same 3D structure.

Moreover, we optionally used interaction features between the ligand and protein which are concatenated with the output activations of the second last layer. Thus, seven different training strategies were used in our experiment: (1) 3D-CNN, (2) 3D-CNN with protein–ligand interaction features (3D-CNN_i), (3) 3D-CNN with affine transformation (3D-CNN_a), (4) 3D-CNN with both interaction features and affine transformation (3D-CNN_ia), (5) PCN, (6) PCN with affine transformation (PCN_a), and (7) PCN with both interaction features and affine transformation (PCN_ia).

All the proposed neural networks were implemented using PyTorch⁴⁸ and performed on an NVIDIA Tesla K80 GPU. All neural network models were trained using the commonly used BCE loss and optimized using Adam optimizer with learning rates of 0.0002 for 3D-CNNs and 0.001 for PCNs. Minibatch sizes for training both networks are 50, and the number of epochs is around 50, which were chosen based on the previous work.¹⁴

Although many shallow learner algorithms have been developed to score ligand–protein binding affinity, fewer shallow models are available for pose classification. Pei et al.’s pose classification model²⁸ was trained and tested exclusively on the CASF-2016 data set precluding direct comparison with our results. Instead, we include a baseline RF model (RF_i) using the calculated interaction features also considered in the Supporting Information to the deep learning models, in order to motivate the potential benefits of our proposed deep learning modeling with 3D atomic representations. The input of this RF baseline model is the same as the protein–ligand interaction features used in 3D-CNN and PCN. It was implemented using the scikit-learn Python library with the default parameters (number of trees = 100, minimum number of samples for split = 2, criterion = Gini impurity).

6. Results

We performed several evaluations to quantitatively measure the effectiveness of the proposed pose classification approaches. Our evaluation report includes (1) model performance, (2) speed (evaluation runtime) between 3D-CNN and PCN models, and (3) incorporation into Vina docking evaluation and screening. To address these evaluations, we used the CASF-2016 benchmark data set and two holdout sets, i.e., PDB ion channel data set and KCa3.1 channel inhibitor data set.

6.1. Pose Classification Model Performance

We first determined the performance of the proposed pose classifiers using accuracy, precision, recall, and F1 score. Accuracy is obtained by dividing the total number of correctly classified poses by the total number of predictions made for a data set

Precision is calculated as the number of true positives divided by the total number of true positives and false positives, whereas recall is calculated as the number of true positives divided by the total number of true positives and false negatives

The F1 score is calculated by multiplying the product of precision and recall by 2 and dividing it by the sum of precision and recall

We also analyzed our data with the area under the curve (AUC) and receiver operating characteristic (ROC) curve where 0.0 and 1.0 represent incorrect and correct poses, respectively. Table 2 summarizes the performance of our seven different models on the docking poses and crystal structures of CASF-2016 where there are 1,633 incorrect poses (RMSD is greater than 6) and 796 correct poses including crystal structures (RMSD is less than 2.5 Å).

Table 2. Prediction Performance of Proposed Pose Classification on CASF-2016^a.

		No. Poses	Accuracy (%)	Precision	Recall	F1 score
RF_i	incorrect	1633	69.9	0.70	0.96	0.81
	correct	796		0.68	0.16	0.26
3D-CNN	incorrect	1633	83.4	0.92	0.82	0.87
	correct	796		0.70	0.86	0.77
3D-CNN_i	incorrect	1633	83.7	0.84	0.93	0.88
	correct	796		0.82	0.65	0.72
3D-CNN_a	incorrect	1633	87.4%	0.87	0.96	0.91
	correct	796		0.89	0.71	0.79
3D-CNN_ia	incorrect	1633	88.4	0.93	0.89	0.91
	correct	796		0.80	0.87	0.83
PCN	incorrect	1633	81.4	0.86	0.86	0.86
	correct	796		0.71	0.72	0.72
PCN_a	incorrect	1633	82.1	0.89	0.84	0.86
	correct	796		0.70	0.79	0.74
PCN_ia	incorrect	1633	87.2	0.90	0.92	0.91
	correct	796		0.82	0.78	0.80

^aFrom top to bottom, Random Forest with protein–ligand interaction features (RF_i), 3D-CNN, 3D-CNN with protein–ligand interaction features (3D-CNN_i), 3D-CNN with affine transformation (3D-CNN_a), 3D-CNN with both interaction features and affine transformation (3D-CNN_ia), PCN, PCN with affine transformation (PCN_a), and PCN with both interaction features and affine transformation (PCN_ia).

All 3DCNN and PCN models show an accuracy of over 80%. Among the four 3D-CNN models, 3D-CNN with affine transformation and interaction features (3D-CNN_ia) shows the best accuracy of 88.4%. Among the three PCN models, the PCN with affine transformation and interaction features (PCN_ia) model shows the best accuracy of 87.2%. The accuracy difference between the best performing 3D-CNN with affine transformation and interaction features (3D-CNN_ia) and PCN with affine transformation and interaction features (PCN_ia) is somewhat negligible (1.2%). The results of this experiment show that affine and interaction features play an important role in the pose classification. Except for the PCN model, all methods in this setting achieve better than 0.9 area under curve (AUC) scores, as shown in Figure 4. The baseline RF_i model yields poor performance (accuracy, 69.9%; AUC, 0.554) compared to our proposed models.

Figure 4.

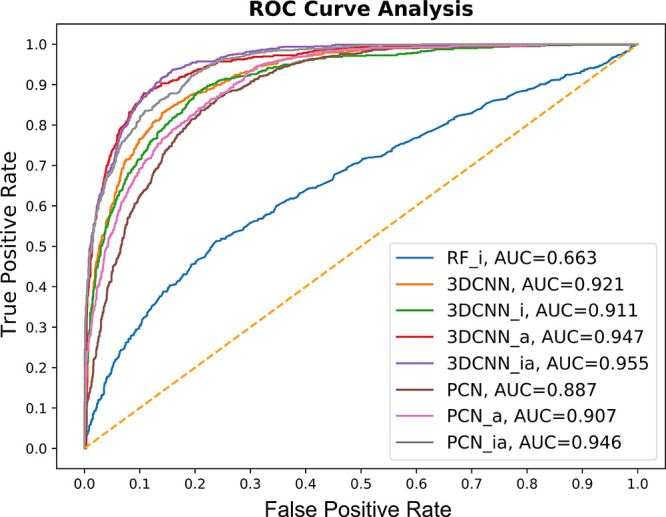
ROC curves of the pose classification models (3DCNN, 3DCNN_i, 3DCNN_a, 3DCNN_ia, PCN, PCN_a, PCN_ia, and RF_i) on CASF-2016.

Evaluating prediction performance on structurally different OOD data is crucial to demonstrate effectiveness of ML models. The evaluation data set (CASF-2016) includes representative protein families that are expected be similar to complexes in the training set (refined set). Thus, the measured accuracy reflects the case where the test set reflects complexes that are similar to those used for training (i.e., “in-distribution” prediction accuracy). Here, we evaluate the models on our curated PDB ion channel data set with its docking poses. This evaluation data set can be considered unseen data with structurally different novel targets (ion channels) compared to other protein targets in the training data set, as discussed earlier. Ion channels are typically membrane proteins consisting of three, four, or five subunits that are arranged around a central ion-conducting pore with 4-fold symmetry or pseudosymmetry, whose structures and conformations are significantly different from other types of proteins. See Table 1 for 40 complexes of the PDB ion channel data set used for evaluation. Using the ion channel complexes, 191 incorrect and 117 correct docking poses were used for evaluation. Overall, two PCN models outperform 3D-CNN models, as shown in Table 3 and Figure 5.

Table 3. Prediction Performance of the Proposed Pose Classification on PDB Ion Channel Data Set.

		No. Poses	Accuracy (%)	Precision	Recall	F1 score
RF_i	incorrect	191	62.0	0.62	1.00	0.77
	correct	117		1.00	0.01	0.02
3D-CNN	incorrect	191	74.4	0.77	0.84	0.80
	correct	117		0.69	0.59	0.64
3D-CNN_i	incorrect	191	70.5	0.69	0.94	0.80
	correct	117		0.77	0.32	0.45
3D-CNN_a	incorrect	191	62.7	0.63	0.99	0.77
	correct	117		0.67	0.03	0.07
3D-CNN_ia	incorrect	191	75.6	0.78	0.84	0.81
	correct	117		0.71	0.62	0.66
PCN	incorrect	191	76.6	0.82	0.80	0.81
	correct	117		0.68	0.72	0.70
PCN_a	incorrect	191	83.1	0.94	0.78	0.85
	correct	117		0.72	0.91	0.80
PCN_ia	incorrect	191	81.2	0.89	0.80	0.84
	correct	117		0.72	0.84	0.77

Figure 5.

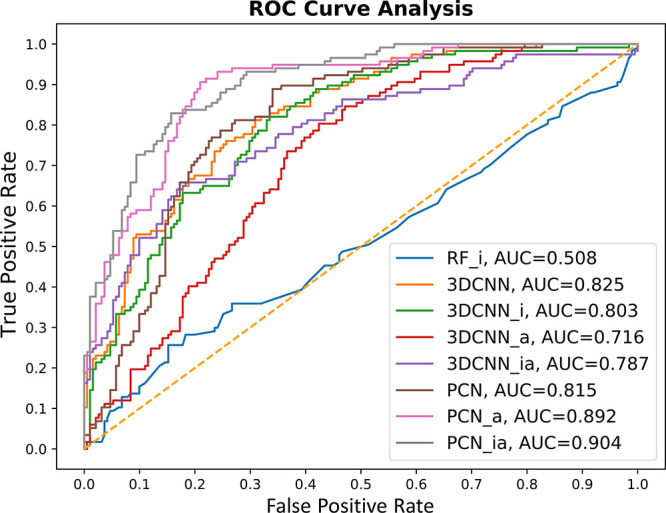
ROC curves of the pose classification models (3DCNN, 3DCNN_i, 3DCNN_a, 3DCNN_ia, PCN, PCN_a, PCN_ia, and RF_i) on PDB ion channel data set.

Unlike the CASF-2016 evaluation results, PCN with affine transformation (PCN_a) yields the best performance with an accuracy of 83.1%. The second-best performing model is PCN with affine transformation and interaction features (PCN_ia). Among the 3D-CNN models, 3D-CNN with affine transformation with interaction features performs best (accuracy of 75.6%) among the four different 3D-CNN models. The accuracy difference between the best performing 3D-CNN and PCN models is 7.5%. The AUC score evaluation in Figure 5 shows that the PCN_ia model achieves the highest scores among the seven models (0.904). Although most of the models have lower AUC scores than those in the PDBbind CASF-2016 evaluation, five models achieve better than 0.8. Like the previous evaluation, all our proposed models outperform the baseline RF_i model (accuracy, 62%; AUC, 0.508).

6.2. Speed Test on Pose Classifiers

We report computation speeds of the proposed pose classifier approaches. In the evaluation of CASF-2016 which contains 2,429 docking pose instances, the total evaluation runtime of 3D-CNN is 5 min 43 s, while that of PCN is 11 s, indicating that PCN is approximately 30 times faster than 3D-CNN. The runtimes were measured using an NVIDIA Tesla K80 GPU. The PCN architectures are significantly faster than 3D-CNN architectures, while achieving competitive performance in accuracy. According to the Vina docking evaluation described in Section 6.3, 3D-CNN models make slightly improved predictions.

6.3. Vina Docking Pose Evaluation with Pose Classification

Through evaluations on two data sets in Section 6.1, we have shown that the proposed 3D-CNN and PCN models can effectively classify correct or incorrect poses. In most real screening applications, however, the docking poses are used for evaluation, due to the lack of crystal structures. We now demonstrate the applicability of the proposed pose classification with molecular docking-based screening tasks. To this end, we used two different OOD data sets: PDB ion channel and in-house KCa3.1 data sets. Structure-based molecular docking processes such as AutoDock Vina, MOE-Dock,⁴⁹ and Glide⁵⁰ generate multiple poses with scores using their empirical scoring functions. The top-ranked poses based on their scores are then identified as correct ligand binding poses. However, as briefly discussed in the Introduction, the top-ranked poses are often misrepresented as correct poses, which results in incorrect compound screening. Nevertheless, structure-based molecular docking methods have been widely used as fast, efficient tools for large-scale vHTS, especially when crystal structures and other experiment information are unavailable.^8,51,52

In this evaluation, we show that the proposed pose classification method can supplement the structure-based docking process by vastly filtering out incorrect poses. We aim to show how the pose classifiers can filter out obviously incorrect poses (i.e., false positives of the molecular docking process) and weak-binding compounds which are miscalculated by docking programs as strong binders. In this section, we do not report RMSD values but correlation coefficients between experimentally measured binding affinities and negative Vina scores.

6.3.1. PDB Ion Channel Data Set: Correlation between Vina Scores and Affinity Values

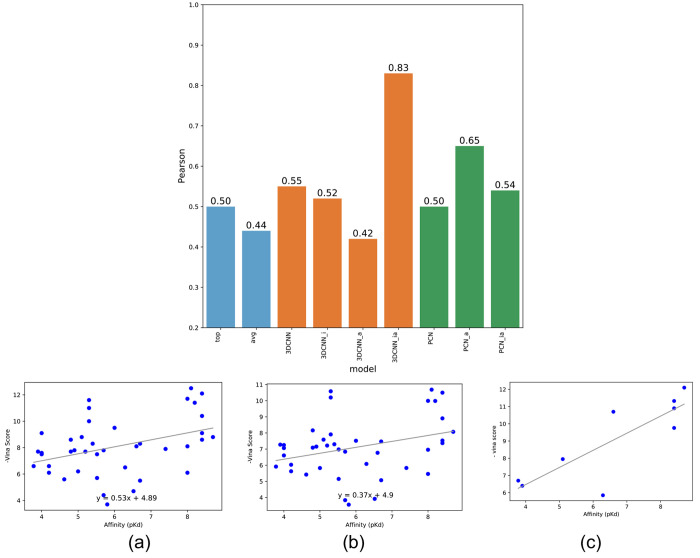
We first evaluated our curated PDB 40 ion channel complex data with Vina docking poses. We report (1) correlation between the actual binding affinity values and Vina scores of the top-ranked docking poses of each ligand, (2) correlation between the affinity values and the average Vina scores of all docking poses (light-blue bars in Figure 6), and (3) correlation between the affinity values and the average Vina scores of remaining docking poses filtered by four 3D-CNN models (orange bars in Figure 6) or three PCN models (green bars in Figure 6).

Figure 6.

Pearson correlations between docking scores and binding affinities using seven pose classification models for the PDB ion channel data set. (a) Vina scores of top-ranked poses, (b) average Vina scores of all docking poses, and (c) average Vina scores across correct poses filtered by the proposed pose classifier (3D-CNN_ia).

As shown in Figure 6, the Pearson coefficients between the affinity values and negative Vina scores without using any pose classifier are 0.5 and 0.44 for top-ranked scores and average scores, respectively. However, filtering out incorrect docking poses and compounds using one of the proposed 3D-CNN models (3D-CNN_ia) resulted in a significant increase in the Pearson correlation (0.83). With the massive number of compounds filtered out by the pose classifiers, this Pearson coefficient is higher than an averaged Pearson coefficient (0.48) of randomly selected sets of compounds of identical sample size (nine compounds in Figure 6C) in multiple trials.

Using two other 3D-CNN models marginally improved the Pearson coefficients (0.55 and 0.52 for 3D-CNN and 3D-CNN_i, respectively). However, filtering out using 3D-CNN_a resulted in a slight decrease in the Pearson coefficient (0.42). Using the PCN models marginally improved the Pearson coefficients (0.50, 0.65, and 0.54 for PCN, PCN_a, and PCN_ia, respectively). We also observed that large portions of the entire protein ligand complexes were filtered out since all the docking poses in those compounds were classified as incorrect by the pose classifiers, which increases the correlation between the binding affinity values and Vina scores. See Figure S2 in the Supporting Information for the analysis of the other pose classification models.

6.3.2. KCa3.1 Channel Inhibitor Data Set: Correlations between Binding Affinity and Docking Scores

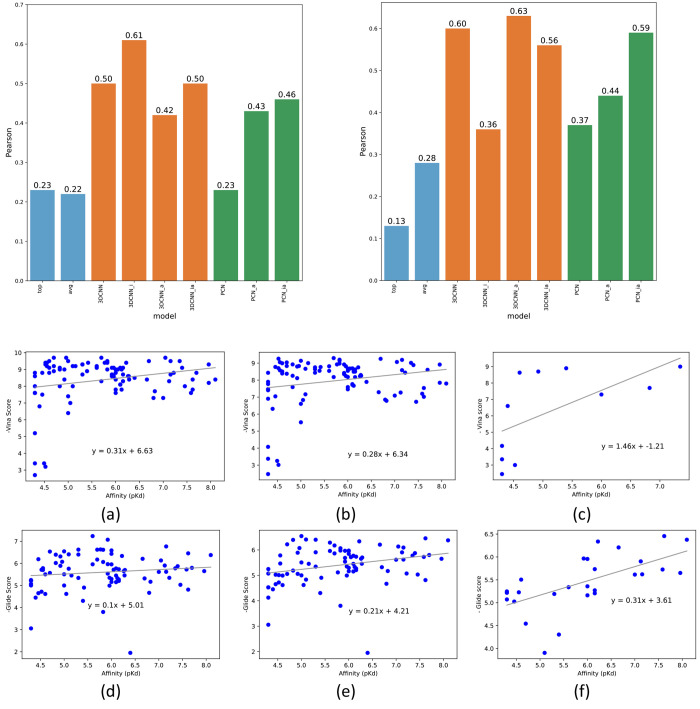
We next evaluated our models on a set of inhibitors for the calcium-activated potassium channel KCa3.1. This data set contains 95 KCa3.1 inhibitors developed by either our own group, scientists at NeuroSearch, or Urbahns and coworkers at Bayer.³⁰⁻³³Figure 7 shows correlations between the IC₅₀ values determined either by a whole-cell patch clamp or an ion flux assay (both techniques measuring inhibition of ion flux through the pore of the channel) and Vina or Glide scores with and without using the proposed pose classifiers. The Pearson correlations of Vina and Glide docking without using our ML models are 0.23, 0.22, 0.13, and 0.28 for the top-ranked Vina scores, averaged Vina scores, top-ranked Glide scores, and averaged Glide scores, respectively (light-blue bars in Figure 7). When the 3D-CNN models were applied to screen incorrect poses and ligands, the Pearson coefficients significantly increased from 0.23 to 0.61 with a p-value of 0.044 and from 0.13 to 0.63 with a p-value of 0.0003 for Vina and Glide docking, respectively (orange bars in Figure 7). The Pearson coefficients when using the PCN models also show improved Pearson coefficients (green bars in Figure 7). The complete listing of the correlation plots is provided in Figures S3 and S4 in the Supporting Information. Note that it is nontrivial to perform compound docking for multiple receptors due to nonautomatable preparation of each receptor structure with its grid. Thus, we did not perform a similar evaluation using Glide for the PDB ion channel data set.

Figure 7.

Pearson correlations between the docking scores and binding affinities using seven pose classification models for the KCa3.1 channel inhibitor data set (left, Vina; right, Glide). (a) Vina scores of top-ranked poses, (b) average Vina scores of all docking poses, (c) average Vina scores across correct poses filtered by the proposed pose classifier (3D-CNN_i), (d) Glide scores of top-ranked poses, (e) average Glide scores of all docking poses, and (f) average Glide scores across correct poses filtered by the proposed pose classifier (3D-CNN_a).

7. Discussion

Our proposed approaches based on convolutional neural networks have two distinct advantages over regular fully connected neural network architectures or other ML approaches. First, we use 3D spatial information to capture structural relationships between ligands and proteins to classify poses, and the convolution operation would be a better choice to interpret such 3D data. Second, our approaches use protein–ligand complex structures instead of ligand-only data, and they can be applied to other protein receptors directly, whereas ligand-only-based models (e.g., RF models using SMILES string data) need to be retrained for each receptor.

We used the refined set of the PDBbind 2019 edition to train the pose classifier models. For evaluation, we used the CASF-2016 data set which is widely used in the literature to evaluate ML models. However, the CASF-2016 set is not the best representative evaluation set, with respect to structural similarity of ligands and protein classes compared to those in the training data set since similar protein types appear in both sets. For that reason, other ML works such as Jones et al.¹⁴ defined another holdout set for further evaluation. To assess the model performance of the proposed pose classifiers across different protein structures, we evaluated our models on PDB ion channel and in-house KCa3.1 data sets as holdout sets (OOD data sets). Both data sets contain unique protein structures (Figure 2), which can be largely categorized as ion channel proteins and which are characterized by being multisubunit membrane proteins with typically a 4-fold or 5-fold symmetry and a conduction pathway for ions through the protein. Since only three ion channel receptors are present in the 2019 refined data set (training set), these two data sets are sufficient to be holdout sets to verify the accuracy.

The model performance evaluation (Section 6.1) shows that the proposed methods can effectively classify docking poses into correct or incorrect poses. The first observation is that the methods are more effective on the CASF-2016 benchmark data set (core set) where most AUCs are higher than 0.9. The prediction performance on the PDB ion channel data set is less effective since only PCN_a and PCN_ia yield close to 0.9 AUCs. The majority of the proteins in the training set (PDBbind refined set) are enzymes, and even CASF-2016 mostly consists of enzymes. It was anticipated to show favorable accuracy on the CASF-2016 evaluation. However, the protein types in the PDB ion channel data set are significantly different protein structures, and the performance decreases accordingly. Nevertheless, the models perform satisfactorily on this holdout set largely consisting of a different protein class (ion channels) than the training set (enzymes) demonstrating the usefulness of the classifiers. We also observed that applying affine transformation to the 3D atomic coordinates together with using the interaction features generally exhibits better overall performance on both 3D-CNN and PCN models (3D-CNN_a, 3D-CNN_ia, PCN_a, PCN_ia). The affine transformation provides a more diverse spatial conformation of the protein–ligand structures to learn geometrically invariant features. The PCN model without using affine transformation and interaction features renders the worst performance among the seven models. This is somewhat anticipated since it is difficult to capture invariant information without applying affine transformation when aggregating the unordered list of atom position data in the PCN architecture. Although the interaction features generally enrich the pose classification models, the models using those features sometimes perform slightly poorly compared to the ones without using them, because the calculation of the interaction features depends on the type of the complex structure such as ligand, receptor, and binding site. In addition, the baseline RF model using the interaction features does not perform well, resulting in low AUC values on both data sets. One can incorporate more sophisticated descriptors such as Pei et al.²⁸ into our classifiers to boost performance. Yet, our deep learning methods with automated feature learning from 3D spatial information are still effective.

The speed evaluation shows that the PCN models are significantly faster with competitive performance in accuracy compared to the 3D-CNN models. However, in the docking score evaluation in Section 6.3, the 3D-CNN models generally outperform the PCN models. Nonetheless, PCN would be a better option to facilitate rapid drug screening unless there is a specific need to use 3D-CNN architectures for a particular data set.

Through the docking evaluations in Section 6.3, 3D-CNN models yield a more reliable and stable prediction performance across multiple data sets. However, 3D-CNN models require larger memory footprints and more computation in the convolutional operations, due to the additional step to voxelizing the atomic representation. On the other hand, PCN models use much less memory and computation resources, processing 3D atomic coordinates directly. One of the disadvantages of the PCN models is the lack of more sophisticated spatial representations such as atom sizes using van der Waals radius or Gaussian blur-based atom propagation, which might cause slightly lower accuracy compared to the 3D-CNN models.

The evaluations in Section 6.3 show that the proposed methods can be effectively incorporated into docking-based screening processes. Compared to the Vina and Glide docking correlations without using the pose classification, the averaged docking scores across correctly classified poses only exhibit much higher Pearson correlations in both the PDB ion channel and our in-house KCa3.1 data sets. We observe that there are many compounds where all docking poses are filtered out by the classifiers so that the compounds are excluded in the correlation evaluation. As discussed earlier, previous studies show that the Vina scores are not strongly correlated with the experimentally measured binding affinities (i.e., moderate degree of correlation).^51,52 Nonetheless, these evaluations show that the pose classification can effectively assist the Vina and Glide docking pipelines in screening promising compounds by filtering out incorrect poses.

We observe inconsistency in the model performance between input from Vina and Glide docking poses. It is nontrivial to analyze the model behavior since the performance and accuracy depend on various factors such as training and evaluation data, network initialization, and other hyperparameter settings. One possible explanation is due to differences in the docking procedures of the two docking tools and the models being trained exclusively on Vina poses. Glide docking requires an additional protein preparation step, which is different from the preprocessing in the Vina docking process. Compared to the protein receptors processed by Vina docking, the protein coordinates slightly changed with different atomic configurations (e.g., additional hydrogens), which can result in differences in the interaction feature calculation of several compounds.

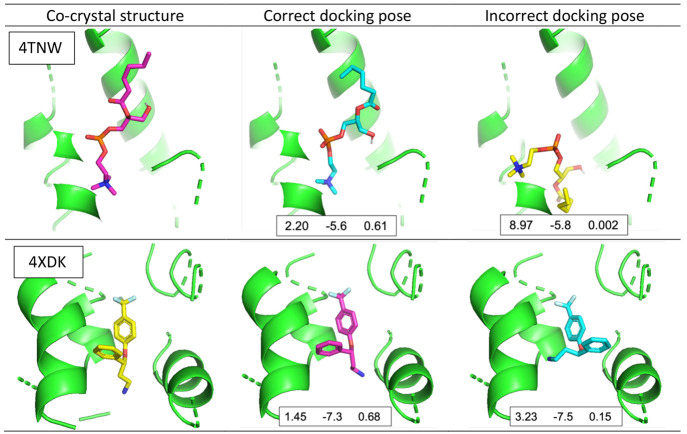
Figure 8 shows the effectiveness of the proposed pose classifiers with two examples from the PDB ion channel data set. In both cases, the Vina scores of the incorrect poses are lower (better) than those of the correct poses, whereas the confidence scores of the pose classifier provide correct information about the reliability of the poses. It shows that the proposed model accurately classified incorrect poses to improve docking scoring accuracy, which can ultimately improve screening by assisting in compound selection.

Figure 8.

Example of correct and incorrect docking poses in the PDB ion channel data set with pose classification results (4TNW, top; 4XDK, bottom). Each docking pose includes RMSD, Vina score, and model confidence of one of our pose classifiers (3D-CNN_ia), respectively. The model confidence can be [0, 1], where a number close to 0 indicates incorrect.

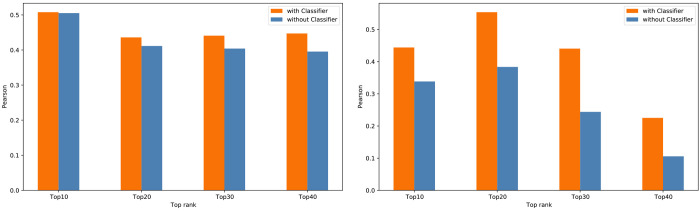
Evaluations in Figure 7 show correlation between the binding affinity and docking scores (Vina and Glide) after the proposed classifiers were applied and filtered out incorrect poses. However, there is a possibility that the correlation may increase as more compounds are filtered out. Alternatively, the confidence scores of the pose classifiers can be used to select the best pose for each compound, as shown in Figure 9. First, the best pose for each compound is selected using the confidence scores. Then, the top 10, 20, 30, and 40 compounds are selected based on the confidence score of the best poses, and the Pearson correlation is calculated between the corresponding docking score of the best confidence pose and binding affinity. The Pearson coefficient is compared with the Pearson between the lowest (best) docking score and binding affinity of the same compound. This result shows that best poses identified by our pose classifiers and their docking scores increase the correlation to the binding affinity values. More evaluation results with all pose classifier models are included in the Supporting Information (Figures S5 and S6).

Figure 9.

Pearson correlations between binding affinity and docking scores of the top 10, 20, 30, and 40 ranked compounds based on the confidence scores of our pose classifier models on the KCa3.1 channel inhibitor data set. 3D-CNN_i with Vina docking poses (left) and 3D-CNN_a with Glide docking poses (right).

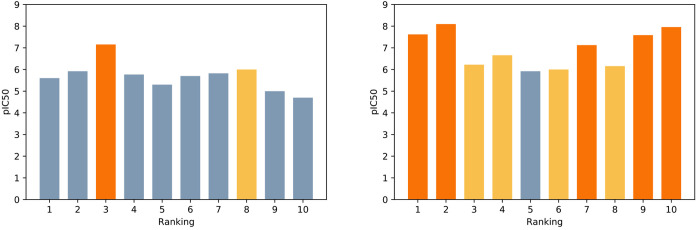
To understand the effectiveness of the pose classifiers especially in identifying compounds with good pIC50 values, we collected the top 10 compounds ranked by Glide’s scoring function, as shown in Figure 10. Among the original top 10 compounds, there is only one strong binder (Figure 10, left). However, using the best performing pose classifier (3D-CNN_a), the docking poses of 68 compounds out of 95 compounds were filtered out, resulting in five strong binders among top 10 compounds (Figure 10, right). For the evaluation of the best performing pose classifiers (3D-CNN_a, 3D-CNN_ia, PCN_a, PCN_ia), see Figure S7 in the Supporting Information.

Figure 10.

pIC50 of the top 10 ranked compounds in the KCa3.1 channel inhibitor data set without (left) and with the pose classifier (3D-CNN_a,right). The orange colors indicate strong binders (pIC50 ≥ 7). The yellow colors indicate compounds with 6 ≤ pIC50 < 7.

While this somewhat “drastic” filtering might result in the loss of some true positives, it lowers the false positive rate substantially and thus increases the hit rate, especially in large libraries where the main challenge for experimental follow-up is the large number of false positive predictions.

8. Conclusion

In this work, we showed that the pose classification approach using two convolutional neural networks improves molecular docking-based screening tools such as AutoDock Vina and Glide. We applied our pose classifiers to an experimental data set for KCa3.1, an example for a potassium channel, a target class which has not been well studied in the ML-based drug discovery community. We demonstrated that incorporating the proposed pose classification into the docking screening considerably improves the identification of compounds with activity against the KCa3.1 channel target.

We introduced a fast neural network approach, PCN, which learns feature representations from 3D atomic positions with their associated features without voxelizing them. This network has an advantage over 3D-CNN as it uses significantly less memory and GPU computations. We also highlighted that the use of affine transformation and ligand interaction features in the 3D-CNN and PCN has an advantage, exhibiting better performance in the accuracy prediction and ROC-AUCs presented here.

Importantly, our work showed that the pose classification improves overall screening in the docking process by filtering out many false positive poses and weak-binding compounds, resulting in enrichment of true positives in the top scoring compounds, although at the cost of filtering out some high affinity compounds. These evaluations allow us to conclude that our new approach ensures the improved results in a virtual screening process for docking.

Data and Software Availability

The implementation of the 3D-CNN and PCN models is freely available as open source (MIT license) on the author’s GitHub: https://github.com/heesung80/PECAN. The readme file of the repository provides a Google drive link for the model checkpoint files and the CASF-2016 data files. The PDB ion channel and KCa3.1 inhibitor data sets together with an evaluation tool for benchmarking will be provided as a separate paper soon, thus are available only upon request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.1c01510.

• All the compound structures of our in-house KCa3.1 inhibitor data sets. Correlations between the Vina docking scores and the binding affinities of the PDB ion channel complexes using all seven pose classification models. Correlations between the docking scores and the binding affinities of the KCa3.1 channel inhibitors complexes using all seven pose classification models. Pearson correlations between binding affinity and docking scores of the top 10, 20, 30, and 40 ranked compounds based on the confidence scores of our pose classifier models on the KCa3.1 channel inhibitor data set with Vina and Glide. Top 10 ranked compounds in the KCa3.1 channel inhibitor data set using the four best performing pose classifiers (3D-CNN_a, 3D-CNN_ia, PCN_a, PCN_ia). (PDF)

The authors declare no competing financial interest.