Skip to main content
PMC home page
JACS Au logoLink to JACS Au
. 2022 May 12;2(5):1223–1231. doi: 10.1021/jacsau.2c00204

Sabatier Principle for Rationalizing Enzymatic Hydrolysis of a Synthetic Polyester

Jenny Arnling Bååth †, Kenneth Jensen ‡, Kim Borch ‡, Peter Westh †,*, Jeppe Kari §,*
PMCID: PMC9131473  PMID: 35647598

Abstract

graphic file with name au2c00204_0008.jpg

Interfacial enzyme reactions are common in Nature and in industrial settings, including the enzymatic deconstruction of poly(ethylene terephthalate) (PET) waste. Kinetic descriptions of PET hydrolases are necessary for both comparative analyses, discussions of structure–function relations and rational optimization of technical processes. We investigated whether the Sabatier principle could be used for this purpose. Specifically, we compared the kinetics of two well-known PET hydrolases, leaf-branch compost cutinase (LCC) and a cutinase from the bacterium Thermobifida fusca (TfC), when adding different concentrations of the surfactant cetyltrimethylammonium bromide (CTAB). We found that CTAB consistently lowered the strength of enzyme–PET interactions, while its effect on enzymatic turnover was strongly biphasic. Thus, at gradually increasing CTAB concentrations, turnover was initially promoted and subsequently suppressed. This correlation with maximal turnover at an intermediate binding strength was in accordance with the Sabatier principle. One consequence of these results was that both enzymes had too strong intrinsic interaction with PET for optimal turnover, especially TfC, which showed a 20-fold improvement of kcat at the maximum. LCC on the other hand had an intrinsic substrate affinity closer to the Sabatier optimum, and the turnover rate was 5-fold improved at weakened substrate binding. Our results showed that the Sabatier principle may indeed rationalize enzymatic PET degradation and support process optimization. Finally, we suggest that future discovery efforts should consider enzymes with weakened substrate binding because strong adsorption seems to limit their catalytic performance.

Keywords: PET hydrolase, polyester degradation, enzyme kinetics, heterogeneous catalysis, Sabatier principle, volcano curve, enzyme affinity

Introduction

Enzymatic hydrolysis of poly(ethylene terephthalate) (PET) has been recognized as a potential technology for bioprocessing of some plastic waste streams.1 Several studies have reported promising enzyme candidates, including the PETase from Ideonella sakaiensis,2 the leaf-branch compost cutinase (LCC),3,4 and cutinases from various Thermobifida species.5−8 However, there is still a need to engineer better catalytic efficiency and improve reaction conditions on PET. Previous activity in this area has used strategies such as rational redesign of the active site,9,10 construction of chimeric enzymes with binding modules,11,12 and application of surfactants in the reaction medium.13,14

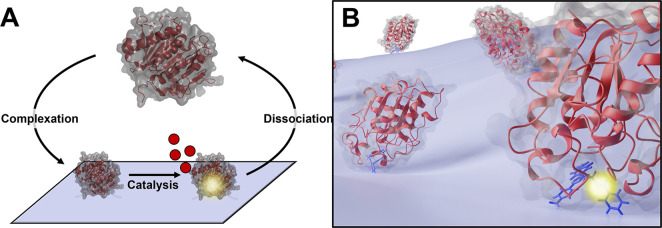
To optimize enzymes rationally, it is crucial to have a molecular-level understanding of structure–function relationships. The experimental input that links structure and function is typically kinetic data, but there is no general framework to rationalize the kinetics of these interfacial enzymes, and this has hampered fundamental and comparative descriptions of PET hydrolases. In lack of a detailed kinetic model, the PET hydrolase reaction may be coarsely described by its most basic steps; complexation, catalysis, and dissociation, as shown in Figure 1A. In this three-step model, the first involves enzyme adsorption on the substrate surface and transfer of a piece of the PET molecule into the enzyme’s active site. The second step encompasses the covalent changes of the hydrolytic reaction (catalysis), while the third delineates product release and the enzyme’s dissociation to the aqueous bulk. This model bears some resemblance to the classical Henri–Michaelis–Menten scheme, but as the substrate is insoluble, the complexation step differs fundamentally. Unlike enzymes acting in the bulk phase, interfacial enzymes such as PET hydrolases need to compete with attractive forces in the substrate matrix to make a productive enzyme–substrate complex15−17 (see Figure 1B). One consequence of this is that the effective substrate concentration in interfacial enzyme reactions may be correlated with ligand-binding strength. Thus, the tighter the binding, the more diverse polymer conformations on the surface could potentially be transferred to the active site.18−20 However, a high ligand-binding affinity may come at the cost of turnover speed.21 This type of tradeoff between binding strength and rate is well-known within inorganic, heterogeneous catalysis, and is originally coined as the Sabatier principle, which states that efficient catalysis occurs when the catalyst binds its reactant with intermediate strength.22,23 The Sabatier principle has recently been proven useful for predicting and rationalizing catalytic properties of cellulases24,25 and as a guide for computer-aided enzyme design and discovery.26

Figure 1.

Figure 1

Open in a new tab

(A) Simplified reaction scheme for enzymatic degradation of PET. PET hydrolase (red cartoon) binds to the PET surface and catalyzes the hydrolysis of ester bond(s), releasing soluble products (red disks), before enzyme and products dissociate into the solution. (B) Illustration of the enzyme–substrate complex at the solid–liquid interface. The enzyme needs to dislodge a small piece of the polymeric substrate from the matrix to access the scissile bond and make a productive enzyme–substrate complex.

In this study, we investigate whether the Sabatier principle could rationalize the kinetics of two well-known PET hydrolases; LCC and a cutinase from the thermophilic bacterium Thermobifida fusca (TfC). We used two types of steady-state measurements to assess kinetic parameters for the hydrolysis of suspended PET particles and tuned enzyme–substrate binding strength through the addition of the cationic surfactant cetyltrimethylammonium bromide (CTAB).

Results

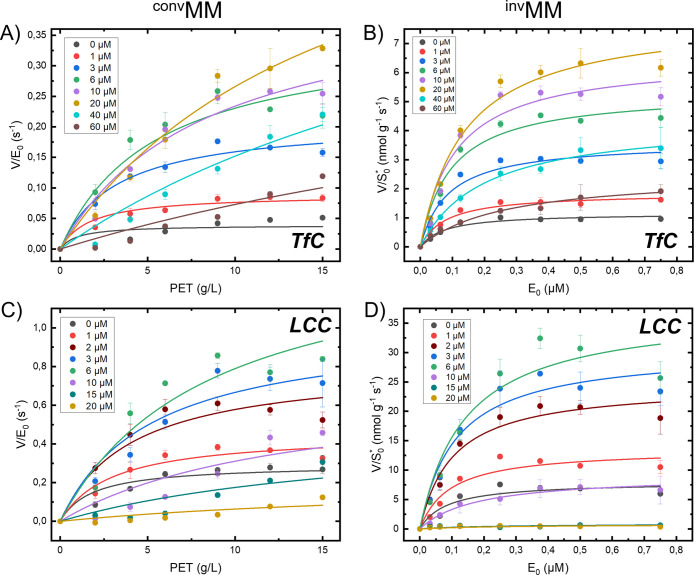
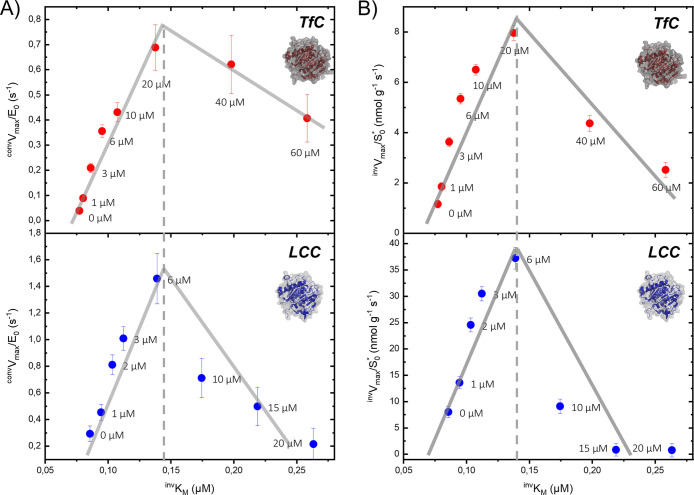
We have applied a modified Michaelis–Menten (MM) approach to assess the kinetics of two PET hydrolases, LCC and TfC. Specifically, we collected one set of data in the conventional way with substrate excess (convMM analysis), while another was made in the inverse concentration regime with enzyme excess (invMM analysis). We characterized both enzymes at different concentrations of the cationic surfactant CTAB, and derived kinetic parameters for both convMM and invMM by non-linear regression as described in the Experimental section and in the Supporting Information. Experimental data (circles) and the results of the regression analyses (lines) are illustrated in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Experimental data at 50 °C for conventional (panel A,C) and inverse (panel B,D) MM analysis. Measurements (circles) were conducted for both LCC and TfC in buffers supplemented with different concentrations of the cationic surfactant CTAB. The CTAB concentrations are indicated by color codes in each panel. The results were analyzed with respect to the conventional and inverse MM equation, eqs 3 and 5, see the Experimental section. Error bars represent standard deviations of triplicate measurements.

Experimental values for the kinetic parameters invKM, invVmax, convKM, and convVmax (defined in eqs 2–6, Experimental section) derived in Figure 2 are listed in Table S1 in the Supporting Information. Inspection of these numbers revealed systematic effects of the surfactant. In particular, we found that the maximal specific rate from both the conventional (convVmax/E0, eq 6) and inverse (invVmax/S0*, eq 4) analyses showed distinctive maxima at intermediate CTAB concentrations (Figure 3). To put these observations into perspective, we reiterate the meaning of the two parameters. convVmax/E0 is the usual maximal turnover (eq 6), which is experimentally observed when essentially all enzymes are complexed (when [ES] ∼ E0). The inverse parameter, invVmax/S0*, specifies the rate when all attack sites on the PET surface is covered with enzyme (eq 4). The effect of CTAB on these two parameters was distinctive and quite similar for both enzymes. Thus, for LCC both parameters increased approximately 5-fold between [CTAB] = 0 and the maximum at [CTAB] ∼ 6 μM (Figure 3). The analogous increment for TfC was up to 20-fold, and it follows that CTAB strongly lessened the difference in performance of a highly efficient (LCC) and a mediocre (TfC) PET hydrolase.

Figure 3.

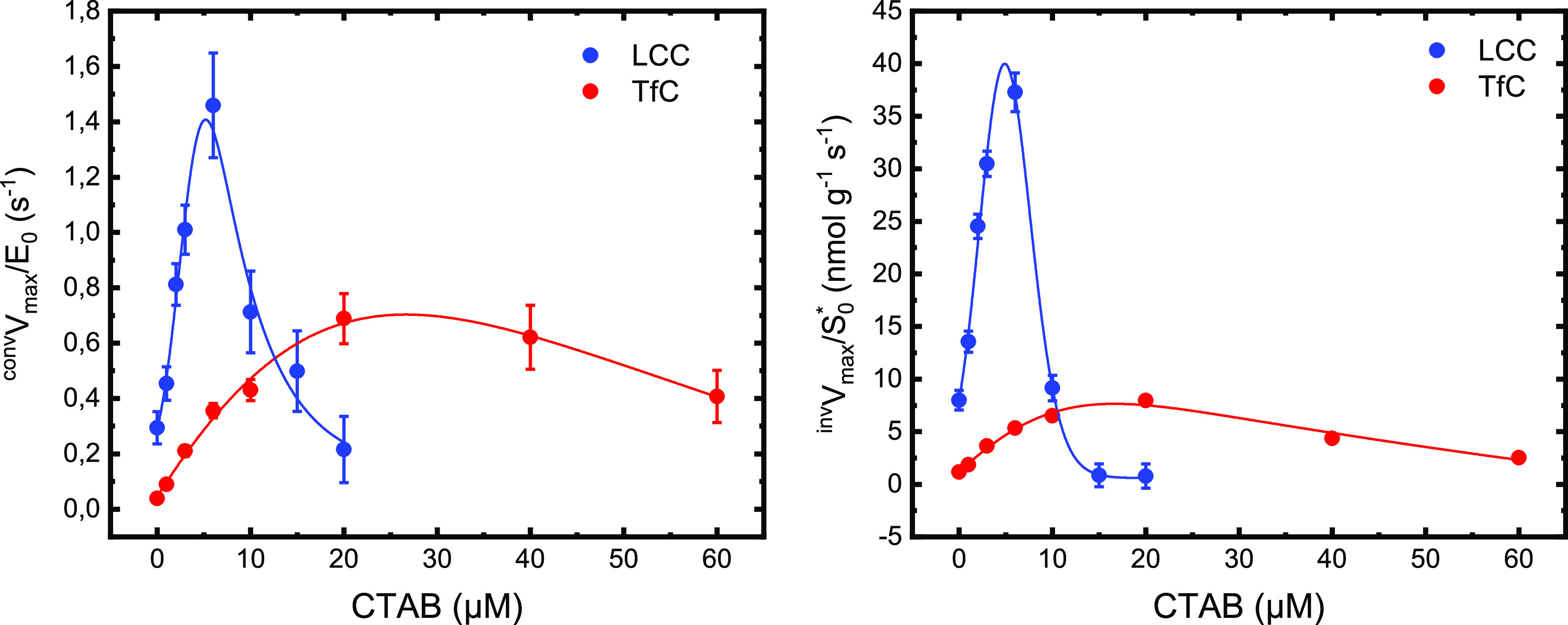
Figure 3

Open in a new tab

Maximal specific rates for conventional (convVmax/E0) and inverse (invVmax/S0*) MM analysis of LCC and TfC acting on PET particles at 50 °C. Symbols represent kinetic parameters obtained with different concentrations of the cationic surfactant CTAB (see Figure 2). Maximal specific rates from the two analyses showed distinctive optima at intermediate CTAB concentrations for both enzymes.

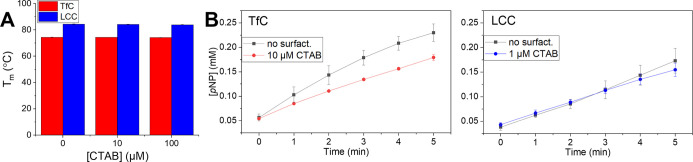
We conducted several experiments to explore possible origins of the biphasic curves in Figure 3. First, we found that at the concentrations used here, CTAB had no significant effect on the two enzymes’ thermostability, expressed as the apparent transition temperature, Tm, (Figure 4A). This figure also shows that Tm for LCC was the same (about 84 °C) as reported previously in calcium-free buffer.4 As a result, it was not deemed necessary to supplement the experiments (at 50 °C) with calcium although this has been shown to significantly improve thermal stability of LCC.4 We only found minor effects of CTAB on the catalytic performance against the small soluble substrate, 4-nitrophenyl butyrate (pNP-Bu). Specifically, when adding a (low) CTAB concentration corresponding to the ascending parts in Figure 3, we found no effect on the activity of LCC and a moderate inhibitory effect on TfC (Figure 4B). Hence, the large initial increments in Figure 3 could not be related to an intrinsic boost in enzyme activity generated by the surfactant. Finally, we assessed whether long-term exposure of the enzymes to high concentrations of CTAB, corresponding to the descending parts in Figure 3, resulted in a subsequent decrease in kinetic performance toward pNP-Bu. The results (Figure S3 in the Supporting Information) did not reveal any loss of enzyme activity, and we conclude that CTAB does not significantly influence the kinetic stability of the enzymes.

Figure 4.

Figure 4

Open in a new tab

(A) Apparent transition temperature, Tm, for LCC and TfC in the absence and presence of CTAB at 10 or 100 μM. (B) Progress curves for LCC and TfC acting on the soluble substrate pNP-Bu at no or a low concentration of CTAB. Experiments were conducted in duplicate, and standard errors represent the spread. CTAB had no considerable effect on either the thermostability of the enzymes or their catalytic performance on the small soluble pNP-substrate.

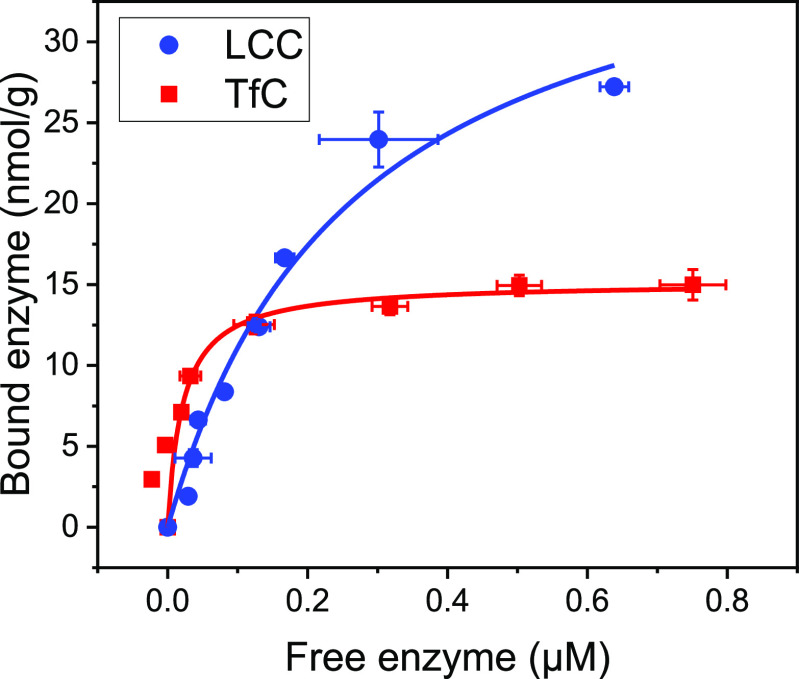
Figure 5 illustrates adsorption behavior of LCC and TfC on the insoluble PET substrate (in the absence of CTAB). We analyzed these measurements with respect to a simple Langmuir isotherm

graphic file with name au2c00204_m001.jpg 1

where Γ and Γmax are coverage and saturation coverage, respectively, in mol enzyme per g substrate, Efree is the molar concentration of free enzyme (unbound enzyme), and KD is the dissociation constant. Lines in Figure 5 represent the best fits of eq 1, and we found that TfC adsorbed more tightly (KD = 22 ± 1.9 nM) compared to LCC (KD = 260 ± 54 nM). However, saturation coverage was higher for LCC, 40 ± 4.1 nmol/g PET, compared to 15 ± 0.025 nmol/g for TfC.

Figure 5.

Figure 5

Open in a new tab

Enzyme adsorption on suspended PET particles (50 g/L) at 50 °C. Symbols represent the measured coverage, Γ, as a function of the free enzyme concentration, and lines are best fits of eq 1. Error bars represent standard deviations of triplicate measurements. TfC showed the tightest adsorption, whereas saturation coverage was substantially higher for LCC, when comparing the two enzymes.

Discussion

In recent years, gradually better PET degrading enzymes have been identified, and this has spurred optimism regarding bioprocessing of PET waste.27−31 However, continuous improvement of catalytic efficiency through engineering and discovery of novel enzymes will probably be necessary to make biological approaches viable contributions to a circular plastic economy. Progress in this field would benefit from a general framework to compare and rationalize the performance of different enzymes and conditions, and in the current work, we propose one potential approach to this. The two main elements in the suggested framework are a modified MM analysis (Figure 2) and the Sabatier principle.

Our results (see Figure 3) revealed that addition of the surfactant CTAB had a distinctive and biphasic effect on the catalytic performance of two PET hydrolases. Especially for TfC, moderate amounts of CTAB (20–30 μM) substantially accelerated the maximal rate for both conventional and inverse MM kinetics. This CTAB concentration is one or two orders of magnitude below the critical micelle concentration,32 and it did not exert any measurable reduction in the thermostability of the investigated enzymes (Figure 4A). Neither did it significantly alter the catalytic efficacy on a soluble substrate (Figures 4B and S3), and in light of this, we will test whether the biphasic behavior could reflect CTAB-induced alterations in the strength of interactions with the insoluble substrate.

This idea has been discussed before. In particular, Furukawa and co-workers reported a beneficial effect of charged surfactants on the enzymatic hydrolysis of PET films. They found that an anionic surfactant promoted activity of the positively charged PETase from I. sakaiensis,14 and that a cationic surfactant boosted activity of another PET hydrolase, which carried a net-negative charge at the experimental pH.13 These observations were collectively ascribed to enhanced enzyme adsorption driven by electrostatic interactions between enzyme and an oppositely charged surfactant that accumulated on the PET surface. However, this interpretation is not readily transferred to the current data. First, we observed both activating and inhibitory effects of the same surfactant (Figure 3). Second, the two investigated enzymes have pI values, respectively, above (LCC: pI 9.3) and below (TfC: pI 6.3) the experimental pH (pH 8.0). Nevertheless, the two enzymes responded analogously to the addition of CTAB and the concomitant buildup of positive charge on the PET surface.

In search of a more robust interpretation of the biphasic behavior in Figure 3, we note that the Michaelis constant may be used as a descriptor of substrate affinity.33,34 Thus, while not a true binding constant, the concentration required to reach half-saturation under different conditions provides some ranking of substrate interaction strength. As illustrated in Table S1A in the Supporting Information, we found that KM values increased regularly with the surfactant load throughout the investigated range. We conclude that CTAB consistently lowered the strength of enzyme–substrate interactions, and we will discuss the results in this perspective. We acknowledge that other more specific effects of CTAB may influence the maximal specific rates, and we will return to this in the concluding paragraph.

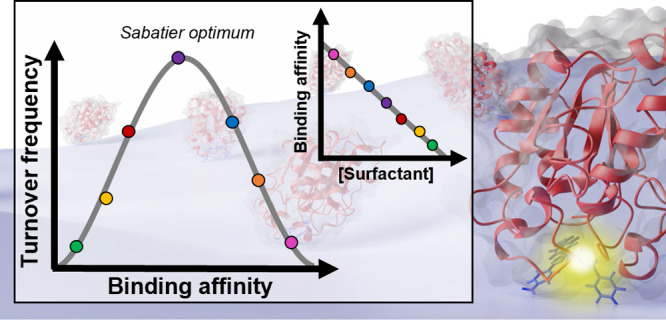
General relationships between binding strength and catalytic turnover can be expressed by the Sabatier principle,35 which states that catalysis is most effective when the interaction between a catalyst and reactants is intermediate in strength. The intuitive underpinning is that tight binding implies slow dissociation of stable enzyme–substrate intermediates, while weak binding is associated with low complex concentration. Both of these limiting cases lead to a poor overall rate, while an intermediate binding strength balances off the two effects and hence supports a faster turnover. The Sabatier principle has been widely employed within inorganic, heterogeneous catalysis,36 but it has also been applied to interfacial enzyme reactions.24,37 Experimentally, the principle can be illustrated in so-called volcano plots, which have a measure of catalytic efficacy such as turnover frequency on the ordinate and interaction strength on the abscissa. For the current systems, this implies plotting the maximal specific rate from either invMM or convMM as a function of binding strength expressed as a Michaelis constant. Figure 6 illustrates such plots, where we used invKM (i.e., the enzyme concentration required to reach half-saturation under conditions of enzyme excess) as a descriptor of binding strength. These plots clearly had volcano-like shapes and hence corroborated that intermediate binding strength provides the most efficient catalysis in accord with the Sabatier principle.

Figure 6.

Figure 6

Open in a new tab

Volcano plots for TfC and LCC acting on insoluble PET. The turnover frequency under (A) enzyme saturation condition (convVmax/E0) or (B) substrate saturation condition (invVmax/S0*) is plotted against the enzyme–substrate binding affinity (invKM) for different concentrations of CTAB in the background, as specified by the label in the plot. Symbols represent kinetic parameters, and solid lines are guide to the eye.

One consequence of data in Figure 6 is that LCC and particularly TfC bind their substrate too tightly for efficient catalysis. The tight binding of TfC was reflected both in a low invKM (77 ± 15 nM, Table S1) and the independently measured KD value (22 ± 1.9 nM, Figure 5). This strong substrate affinity occurred together with a slow maximal turnover of TfC (kcat ∼ 0.04 s–1), but when the interaction was weakened by CTAB to a level of invKM ∼ 140 nM, the turnover rose dramatically to about 0.8 s–1. Interestingly, an invKM of this magnitude also gave rise to the highest values of both kcat for LCC (1.6 s–1, Figure 6A) and maxima in the inverse specific rates for both enzymes (Figure 6B). Hence, it appears that a substrate affinity specified by invKM ∼ 140 nM represents the Sabatier optimum, where the lifetime of the enzyme–substrate complex attains a favorable, intermediate value. As the inherent substrate affinity measured without CTAB (see Figure 5) was lower for LCC compared to TfC, it required less CTAB to bring LCC to the Sabatier optimum (Figure 6). This implied that the inherent substrate affinity of LCC was closer to the Sabatier optimum, which explains the larger activity increment (Figure 6A) at the maximum of TfC (20-fold) compared to LCC (5-fold). The binding affinity of LCC appears to be better tuned for the substrate and hence there is less to gain for this enzyme.

Comparisons of LCC and TfC may be expanded by considering specific changes in invMM and convMM parameters, respectively. To this end, we already noted that the maximal turnover, kcat = convVmax/E0 (eq 6), at the Sabatier optimum was about twice as high for LCC than for TfC (Figure 6A). Comparisons of the inverse maximal rate invVmax/S0*, illustrated in Figure 6B, are more complicated as it reflects the product of kcat and Γmax (eq 4). From the binding isotherm in Figure 5, it can be seen that LCC had around two times more binding sites than TfC. As both kcat and Γmax were 2-fold higher for LCC, we would expect that this enzyme performed 4-fold better than TfC under the most favorable conditions (i.e., when the substrate is saturated with enzyme, and the binding strength is adjusted to the Sabatier optimum). This prediction is confirmed in Figure 6B, where direct and independent measurements of invVmax/S0 gave maximal values of about 9 and 40 nmol g–1 s–1 for TfC and LCC, respectively. This supports the conclusion that the superior performance of LCC on PET, which is widely recognized,3,4,28,38 reflects partly a low, nearly optimal substrate affinity (which is associated with a high kcat) and partly a high capacity of combining productively with different polymer conformations on the PET surface (high attack site density). If indeed so, it would be relevant to investigate other PET hydrolases with variable substrate affinity. So far, focus has been on high affinity,11,12,39−43 but the current work hints that this strategy may not always be fruitful. Hence, we suggest that future discovery campaigns consider enzymes with a broad spectrum of substrate-binding strengths.

In conclusion, we have found that effects of the cationic surfactant CTAB on the kinetics of two PET-hydrolases may be rationalized along the lines of the Sabatier principle. We hasten to say, that other, more specific effects of the surfactant cannot be ruled out by the current experiments. However, controls focusing on thermodynamic- and kinetic enzyme stability as well as the general catalytic performance against soluble substrate failed to explain the pronounced kinetic alterations observed on insoluble PET. Instead, we propose that the biphasic effect of CTAB on the enzymatic turnover reflected a continuous weakening in enzyme–substrate interactions as surfactant concentrations rose. This weakening initially promoted and subsequently suppressed enzyme activity as stipulated by the Sabatier principle. If indeed applicable, this principle may be useful both in discussions of structure–function relationship and for the optimization of technical PET degradation. Regarding the latter, we note that the current work only covered conditions of very low (<1%) degrees of PET conversion, where progress curves on the same substrate have previously been shown to be essentially linear.44 This is a formal prerequisite for the steady-state kinetic analysis performed here, but not for use of the Sabatier principle per se. Future experimental work may elucidate whether the principle can be applied to lengthy, industrially relevant reaction conditions and if so, it could become a valuable instrument within both enzyme discovery and optimization of reaction conditions for PET hydrolases.

Experimental Section

Enzymes

Two cutinases, LCC [PDB: 4EB0] and TfC from T. fusca [PDB: 5ZOA], were heterologously expressed in Bacillus subtilis and purified in a similar way as described previously.45,46 The two enzymes are of the same size (28 kDa) and have a sequence identity of approximately 60%. The production of LCC incorporated the following two modifications compared to the published procedures. The native signal peptide was replaced by the signal peptide from the B. licheniformis α-amylase AmyL (FJ556804.1), and a histidine tag (6xH) was added to the C-terminal. A small linker consisting of LE was inserted between the C-terminal and His-tag. The fermentation broth was sterile filtrated and 500 mM NaCl was added and adjusted to pH 7.5/NaOH. The sample was loaded onto a Ni-Sepharose six Fast Flow column (GE Healthcare, Piscataway, NJ, USA) equilibrated in 50 mM HEPES, pH 7.5 with 500 mM NaCl (buffer A). After loading, the column was washed with 10 column volumes of buffer A, and bound proteins were eluted with 500 mM imidazole in buffer A. The fractions containing the enzyme were pooled and applied to a Sephadex G-25 (medium) (GE Healthcare, Piscataway, NJ, USA) column equilibrated and eluted in 50 mM HEPES pH 7.5. Enzyme concentrations were determined by Abs280. Molar extinction coefficients and theoretical pI values were calculated using the protein identification and analysis tools in the ExPASy Server.47Tm of the enzymes was determined by differential scanning fluorimetry using a Nanotemper Prometheus Nt.48 (Nanotemper). Enzyme samples (in pure phosphate buffer or supplemented with 10 or 100 μM CTAB) were heated from 20 °C to 95 °C at 10% laser intensity and a rate of 1.5 °C/min.

Substrates and Chemicals

The PET substrate used was a semicrystalline PET powder purchased from Goodfellow Co. UK (Product number ES306031). The typical particle size was about 100 μm.48 This substrate has previously been characterized with a reported Mw of 33 kDa and % crystallinity of 38.49 The powder was suspended in 50 mM sodium phosphate (NaPi) buffer pH 8.0. The surfactant CTAB (57-09-0) and the substrate pNP-Bu(2635-84-9) were both purchased from Sigma.

Binding Isotherms

The adsorption of TfC and LCC to PET was determined using a PET concentration of 50 g/L and (total) enzyme concentrations ranging from 0–2 μM. Adsorption measurements used 1 h equilibration in a thermomixer operated at 1000 rpm at 50 °C, and non-binding microtiter plates (Greiner Bio-One) were used to reduce unproductive binding. Solids and liquids were separated by centrifugation in a temperature-controlled centrifuge, set to 50 °C. The protein content of the supernatant was determined using a micro bicinchoninic acid protein kit from Thermo Fischer scientific (product number 23225), as described previously.48 Standard curves of the two enzymes (ranging from 0–2 μM in concentration) were used to quantify the amount of free enzyme in the reactions (performed in triplicate). The bound enzyme population was calculated from the difference between the total and the free concentrations, and the bound fraction was used to assess binding parameters as described previously.48

Activity Assay with pNP-Bu

To investigate potential side effects of the surfactant CTAB on the two enzymes, not related to surface phenomena and the Sabatier principle, we investigated activity on a soluble pNP-substrate at different concentrations of CTAB. One set of experiments was performed in order to investigate if a long contact time with a high amount of CTAB present (concentrations that resulted in a decrease in PET activity) possibly resulted in (irreversible) enzyme denaturation. This control was performed in two steps, with the first involving incubation of the enzymes with either CTAB or in pure 50 mM NaPi buffer at 50 °C, shaking at 300 rpm. The samples were incubated in microtiter plates with 10 μM enzyme and 0, 10, or 40 μM CTAB (LCC) or 0, 40, or 80 μM CTAB (TfC). After 2 h, the samples were 1000-fold diluted to final enzyme concentrations of 10 nM. These enzyme dilutions were used in a second step, where enzyme activity was monitored on pNP-Bu. In a microtiter plate, 5 nM enzyme and 5 mM pNP-Bu were mixed, and the enzymatic release of pNP was monitored over 5 min in a plate reader at 405 nm at 25 °C. Reactions were performed in duplicate, and blank samples without enzymes were included. The concentration of released pNP was calculated from standards with known concentrations.

We also assessed possible effects of CTAB on progress curves, which used the soluble pNP substrate. In a volume of 100 μL, reactions with 50 mM buffer, 5 nM enzyme, and 5 mM pNP-Bu, either with or without CTAB (1 μM for LCC and 10 μM for TfC), were prepared, and the enzymatic release of pNP was monitored and analyzed as explained above. The CTAB concentrations were selected to match concentrations resulting in an increased catalytic rate in the activity measurement on the insoluble PET substrate.

Activity Assay for Solid PET Substrate and MM Analysis

For determination of PET hydrolase activity on insoluble PET, a plate reader-based assay (Abs240) adapted for initial rate kinetics was used, described in detail elsewhere.50 Enzyme reactions were performed at 50 °C, in 50 mM NaPi buffer pH 8, using non-binding microtiter plates (Greiner Bio-One), in an incubator operated at 450 rpm (KS 4000 ic control, IKA, Staufen, Germany). Initial activity measurements were performed in duplicate with a final volume of 250 μL. The load of PET was 10 g/L, enzyme concentrations were 0.10 μM, and the CTAB concentration range was from 0 to 100 μM. The contact times for these reactions were 2 h for TfC and 30 min for LCC. Enzymatic product formation was quantified as “bis(2-hydroxyethyl) terephthalate equivalents” (BHETeq), which were defined by the supernatant absorbance at 240 nm normalized against standard curves of BHET. Hence, the derived rates were based on soluble products only and this has previously been shown to be a good descriptor of the overall activity.50 The results from initial activity measurements are presented in Figure S4 in the Supporting Information.

For kinetic analysis, two sets of experiments (each performed in triplicates) were executed, either under conditions of enzyme saturation (convMM) or substrate saturation (invMM). Experiments under convMM used 0.1 μM enzyme and a PET load from 0–20 g/L, while invMM experiments used a fixed PET load of 10 g/L and enzyme concentrations from 0–1 μM. Both types of experiments were conducted in pure buffer and in buffers supplemented by CTAB at concentrations ranging from 1–60 μM (TfC) and 1–20 μM (LCC). Other assay conditions were similar as explained above.

Data Analysis

The steady-state kinetics of LCC and TfC was analyzed under convMM and invMM conditions. The former used a constant and low enzyme concentration (E0) and recorded initial rates for a number of substrate loads (S0*, specified below). These results were analyzed by the conventional MM equation (eq 5). For invMM experiments, we used a fixed substrate load and measured initial rates at gradually increasing enzyme concentrations, E0. These latter data were analyzed using the inverse MM equation (eq 3). Background, validity, and limitations of this approach have been discussed in detail elsewhere,51,52 but we briefly reiterate the key relationships that are needed for the current discussion. The pivot of the analysis is the assumption that the mass load of a substrate (S0) in g/L, which is known in kinetic experiments, can be converted to an apparent molar substrate concentration (S0) if one knows the density of accessible surface sites (in mol/g). This number can be approximated experimentally from a binding isotherm as the one shown in Figure 5, where the saturation coverage (Γmax) gives the number of accessible surface sites on 1 g PET substrate. We note that Γmax depends on both the enzyme and the physical properties (particularly surface area) of the insoluble substrate. The apparent molar concentration of the substrate may be written as

graphic file with name au2c00204_m002.jpg 2

Under the condition of enzyme excess, the steady-state rate may be described using a rate equation, which is symmetric to the MM equation (eq 5) and sometimes called the inverse MM equation.52

graphic file with name au2c00204_m003.jpg 3

with invVmax being the maximal rate at substrate saturation (i.e., the rate when all accessible surface sites are in complex with an enzyme). This may be expressed as

graphic file with name au2c00204_m004.jpg 4

The Michaelis constant in eq 3, invKM, is the molar enzyme concentration at the half-saturation point. The conventional MM equation (eq 5), which holds under conditions of substrate excess, may be expressed with KM in mass units (g/L) as discussed elsewhere.52

graphic file with name au2c00204_m005.jpg 5

In eq 5, convVmax is the maximal rate at enzyme saturation, defined in the usual way

graphic file with name au2c00204_m006.jpg 6

The Michaelis constant convKM in eq 5 has the unit of mass concentration (g/L), but can be converted to invKM using the relationship invKM = convKMΓmax. We used the two MM equations (eqs 3 and 5) to analyze the experimental data and the derived kinetic parameters to rationalize and compare the kinetics of LCC and TfC. Additional information on non-linear regression is described in detail in the Supporting Information.

Acknowledgments

The research was supported by the Independent Research Fund Denmark (grant number: 307 8022-00165B) and the Novo Nordisk foundation (grant number: NNFSA170028392). The authors acknowledge Kristina Mielec for technical assistance with laboratory experiments.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacsau.2c00204.

  • Detailed information on non-linear regression and global fit using competitive inhibition model with local Vmax; extracted kinetic parameters; results from control experiments with high concentration of CTAB; and initial activity measurements with increasing amount of CTAB (PDF)

The authors declare the following competing financial interest(s): K.B. and K.J. work for Novozymes A/S, a major enzyme producing company.

Supplementary Material

au2c00204_si_001.pdf (969.3KB, pdf)

References

  1. DeFrancesco L. Closing the Recycling Circle. Nat. Biotechnol. 2020, 38, 665–668. 10.1038/s41587-020-0541-0. [DOI] [PubMed] [Google Scholar]
  2. Yoshida S.; Hiraga K.; Takehana T.; Taniguchi I.; Yamaji H.; Maeda Y.; Toyohara K.; Miyamoto K.; Kimura Y.; Oda K. A Bacterium That Degrades and Assimilates Poly(Ethylene Terephthalate). Science 2016, 351, 1196–1199. 10.1126/science.aad6359. [DOI] [PubMed] [Google Scholar]
  3. Sulaiman S.; Yamato S.; Kanaya E.; Kim J.-J.; Koga Y.; Takano K.; Kanaya S. Isolation of a Novel Cutinase Homolog with Polyethylene Terephthalate-Degrading Activity from Leaf-Branch Compost by Using a Metagenomic Approach. Appl. Environ. Microbiol. 2012, 78, 1556–1562. 10.1128/AEM.06725-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Tournier V.; Topham C. M.; Gilles A.; David B.; Folgoas C.; Moya-Leclair E.; Kamionka E.; Desrousseaux M.-L.; Texier H.; Gavalda S.; Cot M.; Guémard E.; Dalibey M.; Nomme J.; Cioci G.; Barbe S.; Chateau M.; André I.; Duquesne S.; Marty A. An Engineered PET Depolymerase to Break down and Recycle Plastic Bottles. Nature 2020, 580, 216–219. 10.1038/s41586-020-2149-4. [DOI] [PubMed] [Google Scholar]
  5. Herrero Acero E.; Ribitsch D.; Steinkellner G.; Gruber K.; Greimel K.; Eiteljoerg I.; Trotscha E.; Wei R.; Zimmermann W.; Zinn M.; Cavaco-Paulo A.; Freddi G.; Schwab H.; Guebitz G. Enzymatic Surface Hydrolysis of PET: Effect of Structural Diversity on Kinetic Properties of Cutinases from Thermobifida. Macromolecules 2011, 44, 4632–4640. 10.1021/ma200949p. [DOI] [Google Scholar]
  6. Müller R.-J.; Schrader H.; Profe J.; Dresler K.; Deckwer W.-D. Enzymatic Degradation of Poly(ethylene terephthalate): Rapid Hydrolyse using a Hydrolase fromT. fusca. Macromol. Rapid Commun. 2005, 26, 1400–1405. 10.1002/marc.200500410. [DOI] [Google Scholar]
  7. Wei R.; Oeser T.; Barth M.; Weigl N.; Lübs A.; Schulz-Siegmund M.; Hacker M. C.; Zimmermann W. Turbidimetric Analysis of the Enzymatic Hydrolysis of Polyethylene Terephthalate Nanoparticles. J. Mol. Catal. B: Enzym. 2014, 103, 72–78. 10.1016/j.molcatb.2013.08.010. [DOI] [Google Scholar]
  8. Roth C.; Wei R.; Oeser T.; Then J.; Föllner C.; Zimmermann W.; Sträter N. Structural and Functional Studies on a Thermostable Polyethylene Terephthalate Degrading Hydrolase from Thermobifida Fusca. Appl. Microbiol. Biotechnol. 2014, 98, 7815–7823. 10.1007/s00253-014-5672-0. [DOI] [PubMed] [Google Scholar]
  9. Samak N. A.; Jia Y.; Sharshar M. M.; Mu T.; Yang M.; Peh S.; Xing J. Recent Advances in Biocatalysts Engineering for Polyethylene Terephthalate Plastic Waste Green Recycling. Environ. Int. 2020, 145, 106144. 10.1016/j.envint.2020.106144. [DOI] [PubMed] [Google Scholar]
  10. Gao R.; Pan H.; Lian J. Recent Advances in the Discovery, Characterization, and Engineering of Poly(Ethylene Terephthalate) (PET) Hydrolases. Enzyme Microb. Technol. 2021, 150, 109868. 10.1016/j.enzmictec.2021.109868. [DOI] [PubMed] [Google Scholar]
  11. Dai L.; Qu Y.; Huang J.-W.; Hu Y.; Hu H.; Li S.; Chen C.-C.; Guo R.-T. Enhancing PET hydrolytic enzyme activity by fusion of the cellulose-binding domain of cellobiohydrolase I from Trichoderma reesei. J. Biotechnol. 2021, 334, 47–50. 10.1016/j.jbiotec.2021.05.006. [DOI] [PubMed] [Google Scholar]
  12. Ribitsch D.; Yebra A. O.; Zitzenbacher S.; Wu J.; Nowitsch S.; Steinkellner G.; Greimel K.; Doliska A.; Oberdorfer G.; Gruber C. C.; Gruber K.; Schwab H.; Stana-Kleinschek K.; Acero E. H.; Guebitz G. M. Fusion of Binding Domains to Thermobifida Cellulosilytica Cutinase to Tune Sorption Characteristics and Enhancing PET Hydrolysis. Biomacromolecules 2013, 14, 1769–1776. 10.1021/bm400140u. [DOI] [PubMed] [Google Scholar]
  13. Furukawa M.; Kawakami N.; Tomizawa A.; Miyamoto K. Efficient Degradation of Poly(Ethylene Terephthalate) with Thermobifida Fusca Cutinase Exhibiting Improved Catalytic Activity Generated Using Mutagenesis and Additive-Based Approaches. Sci. Rep. 2019, 9, 1–9. 10.1038/s41598-019-52379-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Furukawa M.; Kawakami N.; Oda K.; Miyamoto K. Acceleration of Enzymatic Degradation of Poly(Ethylene Terephthalate) by Surface Coating with Anionic Surfactants. ChemSusChem 2018, 11, 4018–4025. 10.1002/cssc.201802096. [DOI] [PubMed] [Google Scholar]
  15. Wei R.; Breite D.; Song C.; Gräsing D.; Ploss T.; Hille P.; Schwerdtfeger R.; Matysik J.; Schulze A.; Zimmermann W. Biocatalytic Degradation Efficiency of Postconsumer Polyethylene Terephthalate Packaging Determined by Their Polymer Microstructures. Adv. Sci. 2019, 6, 1900491. 10.1002/advs.201900491. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Cho H. M.; Gross A. S.; Chu J.-W. Dissecting Force Interactions in Cellulose Deconstruction Reveals the Required Solvent Versatility for Overcoming Biomass Recalcitrance. J. Am. Chem. Soc. 2011, 133, 14033–14041. 10.1021/ja2046155. [DOI] [PubMed] [Google Scholar]
  17. Beckham G. T.; Matthews J. F.; Peters B.; Bomble Y. J.; Himmel M. E.; Crowley M. F. Molecular-Level Origins of Biomass Recalcitrance: Decrystallization Free Energies for Four Common Cellulose Polymorphs. J. Phys. Chem. B 2011, 115, 4118–4127. 10.1021/jp1106394. [DOI] [PubMed] [Google Scholar]
  18. Payne C. M.; Jiang W.; Shirts M. R.; Himmel M. E.; Crowley M. F.; Beckham G. T. Glycoside Hydrolase Processivity Is Directly Related to Oligosaccharide Binding Free Energy. J. Am. Chem. Soc. 2013, 135, 18831–18839. 10.1021/ja407287f. [DOI] [PubMed] [Google Scholar]
  19. Himmel M. E.; Ding S.-Y.; Johnson D. K.; Adney W. S.; Nimlos M. R.; Brady J. W.; Foust T. D. Biomass Recalcitrance: Engineering Plants and Enzymes for Biofuels Production. Science 2007, 315, 804–807. 10.1126/science.1137016. [DOI] [PubMed] [Google Scholar]
  20. Jeoh T.; Ishizawa C. I.; Davis M. F.; Himmel M. E.; Adney W. S.; Johnson D. K. Cellulase Digestibility of Pretreated Biomass Is Limited by Cellulose Accessibility. Biotechnol. Bioeng. 2007, 98, 112–122. 10.1002/bit.21408. [DOI] [PubMed] [Google Scholar]
  21. Fersht A.Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding, Series in Structural Biology; WORLD SCIENTIFIC, 2017; Vol. 9. [Google Scholar]
  22. Bligaard T.; Nørskov J. K.; Dahl S.; Matthiesen J.; Christensen C. H.; Sehested J. The Brønsted-Evans-Polanyi relation and the volcano curve in heterogeneous catalysis. J. Catal. 2004, 224, 206–217. 10.1016/j.jcat.2004.02.034. [DOI] [Google Scholar]
  23. Sabatier P.La Catalyse En Chimie Organique; Nouveau Monde, 2013. [Google Scholar]
  24. Kari J.; Olsen J. P.; Jensen K.; Badino S. F.; Krogh K. B. R. M.; Borch K.; Westh P. Sabatier Principle for Interfacial (Heterogeneous) Enzyme Catalysis. ACS Catal. 2018, 8, 11966–11972. 10.1021/acscatal.8b03547. [DOI] [Google Scholar]
  25. Kari J.; Molina G. A.; Schaller K. S.; Schiano-di-Cola C.; Christensen S. J.; Badino S. F.; Sørensen T. H.; Røjel N. S.; Keller M. B.; Sørensen N. R.; Kolaczkowski B.; Olsen J. P.; Krogh K. B. R. M.; Jensen K.; Cavaleiro A. M.; Peters G. H. J.; Spodsberg N.; Borch K.; Westh P. Physical Constraints and Functional Plasticity of Cellulases. Nat. Commun. 2021, 12, 3847. 10.1038/s41467-021-24075-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Schaller K. S.; Kari J.; Molina G. A.; Tidemand K. D.; Borch K.; Peters G. H. J.; Westh P. Computing Cellulase Kinetics with a Two-Domain Linear Interaction Energy Approach. ACS Omega 2021, 6, 1547–1555. 10.1021/acsomega.0c05361. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zhu B.; Wang D.; Wei N. Enzyme Discovery and Engineering for Sustainable Plastic Recycling. Trends Biotechnol. 2022, 40, 22–37. 10.1016/j.tibtech.2021.02.008. [DOI] [PubMed] [Google Scholar]
  28. Tiso T.; Narancic T.; Wei R.; Pollet E.; Beagan N.; Schröder K.; Honak A.; Jiang M.; Kenny S. T.; Wierckx N.; Perrin R.; Avérous L.; Zimmermann W.; O’Connor K.; Blank L. M. Towards Bio-Upcycling of Polyethylene Terephthalate. Metab. Eng. 2021, 66, 167–178. 10.1016/j.ymben.2021.03.011. [DOI] [PubMed] [Google Scholar]
  29. Singh A.; Rorrer N. A.; Nicholson S. R.; Erickson E.; DesVeaux J. S.; Avelino A. F. T.; Lamers P.; Bhatt A.; Zhang Y.; Avery G.; Tao L.; Pickford A. R.; Carpenter A. C.; McGeehan J. E.; Beckham G. T. Techno-Economic, Life-Cycle, and Socioeconomic Impact Analysis of Enzymatic Recycling of Poly(Ethylene Terephthalate). Joule 2021, 5, 2479–2503. 10.1016/j.joule.2021.06.015. [DOI] [Google Scholar]
  30. Maity W.; Maity S.; Bera S.; Roy A. Emerging Roles of PETase and MHETase in the Biodegradation of Plastic Wastes. Appl. Biochem. Biotechnol. 2021, 193, 2699–2716. 10.1007/s12010-021-03562-4. [DOI] [PubMed] [Google Scholar]
  31. Wei R.; von Haugwitz G.; Pfaff L.; Mican J.; Badenhorst C. P. S.; Liu W.; Weber G.; Austin H. P.; Bednar D.; Damborsky J.; Bornscheuer U. T. Mechanism-Based Design of Efficient PET Hydrolases. ACS Catal. 2022, 12, 3382–3396. 10.1021/acscatal.1c05856. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Alam M. S.; Mohammed Siddiq A.; Mythili V.; Priyadharshini M.; Kamely N.; Mandal A. B. Effect of Organic Additives and Temperature on the Micellization of Cationic Surfactant Cetyltrimethylammonium Chloride: Evaluation of Thermodynamics. J. Mol. Liq. 2014, 199, 511–517. 10.1016/j.molliq.2014.09.026. [DOI] [Google Scholar]
  33. Sousa S. F.; Calixto A. R.; Ferreira P.; Ramos M. J.; Lim C.; Fernandes P. A. Activation Free Energy, Substrate Binding Free Energy, and Enzyme Efficiency Fall in a Very Narrow Range of Values for Most Enzymes. ACS Catal. 2020, 10, 8444–8453. 10.1021/acscatal.0c01947. [DOI] [Google Scholar]
  34. Warshel A. Electrostatic Origin of the Catalytic Power of Enzymes and the Role of Preorganized Active Sites. J. Biol. Chem. 1998, 273, 27035–27038. 10.1074/jbc.273.42.27035. [DOI] [PubMed] [Google Scholar]
  35. Nørskov J. K.; Studt F.; Abild-Pedersen F.; Bligaard T.. Fundamental Concepts in Heterogeneous Catalysis. Fundamental Concepts in Heterogeneous Catalysis; John Wiley & Sons, Inc: Hoboken, NJ, USA, 2014. [Google Scholar]
  36. Nørskov J. K.; Bligaard T.; Rossmeisl J.; Christensen C. H. Towards the Computational Design of Solid Catalysts. Nat. Chem. 2009, 1, 37–46. 10.1038/nchem.121. [DOI] [PubMed] [Google Scholar]
  37. Lin J.-L.; Wheeldon I. Kinetic Enhancements in DNA-Enzyme Nanostructures Mimic the Sabatier Principle. ACS Catal. 2013, 3, 560–564. 10.1021/cs300766d. [DOI] [Google Scholar]
  38. Shirke A. N.; White C.; Englaender J. A.; Zwarycz A.; Butterfoss G. L.; Linhardt R. J.; Gross R. A. Stabilizing Leaf and Branch Compost Cutinase (LCC) with Glycosylation: Mechanism and Effect on PET Hydrolysis. Biochemistry 2018, 57, 1190–1200. 10.1021/acs.biochem.7b01189. [DOI] [PubMed] [Google Scholar]
  39. Xue R.; Chen Y.; Rong H.; Wei R.; Cui Z.; Zhou J.; Dong W.; Jiang M.. Fusion of Chitin-Binding Domain From Chitinolyticbacter Meiyuanensis SYBC-H1 to the Leaf-Branch Compost Cutinase for Enhanced PET Hydrolysis. Front. Bioeng. Biotechnol. 2021, 9. 10.3389/fbioe.2021.762854 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Ribitsch D.; Acero H.; Przylucka A.; Zitzenbacher S.; Marold A.; Gamerith C.; Tscheließnig R.; Jungbauer A.; Rennhofer H.; Lichtenegger H.; Amenitsch H.; Bonazza K.; Kubicek C. P.; Druzhinina I. S.; Guebitz G. M. Enhanced Cutinase-Catalyzed Hydrolysis of Polyethylene Terephthalate by Covalent Fusion to Hydrophobins. Appl. Environ. Microbiol. 2015, 81, 3586–3592. 10.1128/AEM.04111-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Zhang Y.; Wang L.; Chen J.; Wu J. Enhanced activity toward PET by site-directed mutagenesis of Thermobifida fusca cutinase-CBM fusion protein. Carbohydr. Polym. 2013, 97, 124–129. 10.1016/j.carbpol.2013.04.042. [DOI] [PubMed] [Google Scholar]
  42. Herrero Acero E.; Ribitsch D.; Dellacher A.; Zitzenbacher S.; Marold A.; Steinkellner G.; Gruber K.; Schwab H.; Guebitz G. M. Surface engineering of a cutinase fromThermobifida cellulosilytica for improved polyester hydrolysis. Biotechnol. Bioeng. 2013, 110, 2581–2590. 10.1002/bit.24930. [DOI] [PubMed] [Google Scholar]
  43. Biundo A.; Ribitsch D.; Guebitz G. M. Surface Engineering of Polyester-Degrading Enzymes to Improve Efficiency and Tune Specificity. Appl. Microbiol. Biotechnol. 2018, 102, 3551–3559. 10.1007/s00253-018-8850-7. [DOI] [PubMed] [Google Scholar]
  44. Arnling Bååth J.; Borch K.; Jensen K.; Brask J.; Westh P. Comparative Biochemistry of Four Polyester (PET) Hydrolases. ChemBioChem 2021, 22, 1627–1637. 10.1002/cbic.202000793. [DOI] [PubMed] [Google Scholar]
  45. Adams C.; Schmidt B.. Detergent Compositions Containing Thermobifida Fusca Lipase and Methods of Use Thereof. WO 2011084412 A1, 2011.
  46. Jensen K.; Oestergaard P. R.; Wilting R.; Lassen S. F. Identification and Characterization of a Bacterial Glutamic Peptidase. BMC Biochem. 2010, 11, 47. 10.1186/1471-2091-11-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Gasteiger E.; Hoogland C.; Gattiker A.; Duvaud S. e.; Wilkins M. R.; Appel R. D.; Bairoch A.. Protein Identification and Analysis Tools on the ExPASy Server. In The Proteomics Protocols Handbook; Walker J. M., Ed.; Humana Press: Totowa, NJ, 2005; pp 571–607. DOI: 10.1385/1592598900., [DOI] [Google Scholar]
  48. Badino S. F.; Bååth J. A.; Borch K.; Jensen K.; Westh P. Adsorption of Enzymes with Hydrolytic Activity on Polyethylene Terephthalate. Enzyme Microb. Technol. 2021, 152, 109937. 10.1016/j.enzmictec.2021.109937. [DOI] [PubMed] [Google Scholar]
  49. Erickson E.; Shakespeare T. J.; Bratti F.; Buss B. L.; Graham R.; Hawkins M. A.; König G.; Michener W. E.; Miscall J.; Ramirez K. J.; Rorrer N. A.; Zahn M.; Pickford A. R.; McGeehan J. E.; Beckham G. T. Comparative Performance of PETase as a Function of Reaction Conditions, Substrate Properties, and Product Accumulation. ChemSusChem 2022, 15, e202101932 10.1002/cssc.202101932. [DOI] [PubMed] [Google Scholar]
  50. Arnling Bååth J.; Borch K.; Westh P. A Suspension-Based Assay and Comparative Detection Methods for Characterization of Polyethylene Terephthalate Hydrolases. Anal. Biochem. 2020, 607, 113873. 10.1016/j.ab.2020.113873. [DOI] [PubMed] [Google Scholar]
  51. Andersen M.; Kari J.; Borch K.; Westh P. Michaelis-Menten equation for degradation of insoluble substrate. Math. Biosci. 2018, 296, 93–97. 10.1016/j.mbs.2017.11.011. [DOI] [PubMed] [Google Scholar]
  52. Kari J.; Andersen M.; Borch K.; Westh P. An Inverse Michaelis-Menten Approach for Interfacial Enzyme Kinetics. ACS Catal. 2017, 7, 4904–4914. 10.1021/acscatal.7b00838. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

au2c00204_si_001.pdf (969.3KB, pdf)

Articles from JACS Au are provided here courtesy of American Chemical Society

RESOURCES