Mapping Enzyme Landscapes by Time-resolved Crystallography with Synchrotron and XFEL light

Abstract

Directly observing enzyme catalysis in real-time at the molecular level has been a long-standing goal of structural enzymology. Time-resolved serial crystallography methods at synchrotron and X-ray free electron laser (XFEL) sources have enabled enzyme catalysis and other non-equilibrium events to be followed at ambient conditions with unprecedented time resolution. X-ray crystallography provides detailed information about conformational heterogeneity and protein dynamics, which is enhanced when time-resolved approaches are used. This review outlines the ways that information about the underlying energy landscape of a protein can be extracted from X-ray crystallographic data, with an emphasis on new developments in XFEL and synchrotron time-resolved crystallography. The emerging view of enzyme catalysis afforded by these techniques can be interpreted as enzymes moving on a time-dependent energy landscape. Some consequences of this view are discussed, including the proposal that irreversible enzymes or enzymes that use covalent catalytic mechanisms may commonly exhibit catalysis-activated motions.

1. Introduction

The conformational dynamics of proteins play a central role in their function. At equilibrium, proteins are driven by thermal energy to sample an ensemble of structures on a wide range of timescales (127). When perturbed from equilibrium (e.g. by the addition of substrate to an enzyme), proteins structural ensembles evolve in time as the macromolecule responds to the perturbation. The structural complexity of proteins ensures that these ensembles are unwieldy, not easily visualized, and challenging to experimentally characterize. Thus there are two intertwined challenges in protein dynamics that have informed one another: 1) developing theoretical tools of sufficient complexity to understand protein motions while retaining generality and 2) measuring the dynamics of proteins at sufficient temporal and spatial resolutions so that these motions can be related both to theory and to function.

In the 1990s, the theoretical challenge of understanding protein dynamics was met with the development of the energy landscape model of protein dynamics (8, 35). The energy landscape model replaced an older view of protein conformational change as being limited to the transitions among a few defined states with a richer view of proteins populating an ensemble of structures defined by the minima of a high dimensional energy landscape (29). This model was initially qualitative but has been developed in more quantitative detail through the use of computational approaches that are well-suited to representing transitions among states in a high-dimensional space that describes the macromolecular structure at any instant (47, 82).

The experimental challenge of characterizing protein dynamics has been addressed by a variety of biophysical methods, including the recent addition of a new generation of time-resolved X-ray crystallographic techniques. These new X-ray crystallographic techniques use third generation synchrotron (78) and X-ray free electron laser (XFEL) X-ray sources (7, 16, 18) to visualize protein conformational changes at the Ångstrom length-scale and picosecond-minutes time-scale resolutions. A critical advantage of time-resolved X-ray diffraction approaches is that they are able to study non-equilibrium conformational dynamics that are critical for the function of proteins in living systems. These methods add a temporal dimension to X-ray crystallography experiments and build upon the already large amount of information about averaged atomic disorder that is present in electron density maps, providing a view of proteins sampling different parts of an energy landscape.

In this review we will explore how new XFEL and synchrotron time-resolved X-ray crystallography approaches allow non-equilibrium protein dynamics to be viewed as excursions of the protein on an underlying energy landscape. Because there is an extensive and rapidly growing body of review literature on XFEL methods (15, 80, 84, 100), we describe only the most relevant aspects of these methods for structural enzymology while acknowledging that this is not a comprehensive treatment of XFEL crystallography. After an introduction to how X-ray crystallography reports on protein conformational dynamics, we focus on the new opportunities to use time-resolved synchrotron and XFEL sources to observe enzyme motion during catalysis.

2. The energy landscape model of protein dynamics

The energy landscape concept postulates that the dynamic behavior of a molecule can be understood as a diffusion process on a high-dimensional energy surface. Either a potential energy surface (PES) or a Gibbs free energy surface (FES) can be considered, and these have important differences that are discussed below. A PES is constructed by first specifying the structure of a protein as a single point in a configuration space where each dimension corresponds to a degree of freedom in the system. In the case of Cartesian space, each coordinate (X, Y, Z) for each atom constitutes a separate dimension. Therefore, the structure of a 1000 atom protein would be represented as a single point in a 3000-dimensional configuration space. At each point in this space (corresponding to a unique structure for the protein), the potential energy is evaluated and represented along a separate dimension, resulting in a landscape whose peaks and wells correspond to local maxima and minima of the potential energy function. Other critical points (defined as points where the first derivative of the potential energy with respect to each dimension is zero) on the PES correspond to saddle points. These saddle points are barriers that separate minima and thus represent transition states on the PES. In total, the PES describes every accessible conformation of a protein and all paths for interconverting between these conformations. With the PES formalism, protein dynamics is more akin to a meandering walk on rough terrain rather than a march through a linear progression of structural intermediates. There is an appealing intuitiveness to the resulting energy landscape, although it should be remembered that this landscape exists in a space of many thousands of dimensions. Intuition born of three dimensions can be unreliable in such spaces and thus quantitative tools to extract information from the PES are valuable.

The potential energy function for a macromolecule is constructed by quantifying the contributions from all physical interactions (e.g. covalent, electrostatic, dihedral, etc.) between its constituent atoms without reference to other thermodynamic state variables, which has several advantages. Chief among them is that the protein PES is a fundamental feature of the molecule from which thermodynamic properties such as the entropy, free energy, and the associated FES can be derived at a given temperature (21, 113). The explicit contribution of entropy and other thermodynamic state variables to the FES is an important distinction with the PES. At equilibrium, conformational substates observed in an experiment represent minima in the PES with populations given by the Boltzmann distribution, which can be grouped and related to minima in the FES in many cases, though this is not always straightforward. The PES is often more computationally accessible than the FES, as entropy does not need to be calculated to represent a PES (113). Perhaps most importantly, the PES can be used to describe both non-equilibrium and equilibrium behavior of proteins with comparable facility, in contrast to the FES, which is only rigorously defined at equilibrium. Both the PES and the FES have been used for explaining non-equilibrium biophysical phenomena, initially in foundational work by Frauenfelder, Sligar, and Wolynes (35) when they developed a hierarchical protein PES model to explain the temperature-dependent kinetics of CO photodissociation from myoglobin and by Wolynes, Onuchic, Dill, and coworkers (8, 29) when they used both the PES and the FES to explain protein folding kinetics. The protein folding “funnel” model that emerged from this work has provided a useful theoretical tool for understanding the competing effects of decreasing both energy and entropy on spontaneous protein folding kinetics (55). The PES is arguably more general and easier to apply to non-equilibrium interpretations of time-resolved X-ray crystallographic data, which is important because these experiments measure the structural response of proteins to perturbations that, by definition, take the molecule out of equilibrium. The distinction between these two hypersurfaces is important to consider, as different applications can require different surfaces.

3. Time-resolved X-ray crystallography and XFEL sources

Most biophysicists would not place X-ray crystallography at the top of their list of preferred techniques for studying protein dynamics. There are some good reasons for this as well as some problematic ones, which are often conflated in confusing ways. Conventional X-ray crystallography measures the diffraction from a single crystal over a period of minutes to hours, although much faster measurements are now possible, as discussed below. Therefore, a single conventionally collected diffraction dataset is both a time- and ensemble-average that provides no time-domain information. Compared to techniques like nuclear magnetic resonance spectroscopy and other spectroscopies that contain information regarding the molecular dynamical processes that govern relaxation of the spectroscopically excited system toward equilibrium, conventional X-ray crystallography does not report on macromolecular dynamics per se. However, the common emphasis on this limitation neglects the promise of time-resolved X-ray techniques and is often misconstrued as meaning that X-ray crystallography has nothing to offer with respect to characterizing protein dynamics. The most succinct and popular summary of this sentiment is that X-ray crystallography provides a “static snapshot” of proteins. This is false, as atomic mobility in proteins ensures that the time- and ensemble-averaged electron density map will contain a large amount of information about the average atomic displacements, which we discuss below (Section 4). Time- and ensemble-averaging of the electron density map in a conventional X-ray crystallography experiment results in “smearing” of the electron density that reports on averaged atomic displacements in the same way that a single long-exposure photograph allows the viewer to infer aspects of motion that occurred while the shutter was open. Direct information about the time evolution of a molecule when perturbed from equilibrium can be obtained using time-resolved crystallography, where multiple electron density maps are obtained at various time points after perturbation of the molecule. Each electron density map in a time-resolved X-ray crystallography experiment is still an ensemble average but is no longer a time average, similar to the individual frames of a movie. Therefore, while considerable information about the conformational heterogeneity of a protein can be extracted from conventional electron density maps, time-resolved techniques dramatically increase that information by adding a time dimension.

3.1. Methodological considerations for time-resolved crystallography

Time-resolved X-ray crystallography has been used to follow protein conformational dynamics under non-equilibrium conditions for several decades (88, 90, 105), although it has been a niche technique for most of its history. Part of the reason that it was not more widely used is that there are three stringent criteria that must be met for a successful time-resolved crystallography experiment: 1) the reaction must occur in the crystal 2) the crystal must not be damaged by reaction initiation or progress and 3) the reaction must proceed at experimentally accessible rates. Some reaction proceed slowly enough under selected experimental conditions that intermediates can be observed by traditional X-ray crystallography (43). The advent of cryocrystallography in the late 1970s and its increased use in the decades that followed allowed enzymes to be cryotrapped in key intermediate states, typically on the timescale of seconds (1, 39, 70, 91). The temporal resolution of this approach has been dramatically expanded recently using innovative cryocooling approaches that observed phosphoenolpyruvate carboxykinase (PEPCK) turnover on the millisecond timescale (23). For enzymes that catalyze freely reversible reactions, the position on the reaction coordinate can be tuned with substrate concentration (31), although this is not technically a time-resolved experiment.

With the advent of synchrotron radiation lightsources, faster non-equilibrium processes could be tracked using polychromatic Laue X-ray diffraction techniques (78). Laue crystallography can probe down to ~100 picosecond timescales for light-initiated reactions and has been successfully applied to various systems, (38, 49, 90, 95, 101, 104). A difficulty of Laue experiments that prevented it from being more widely adopted is that even modest-sized macromolecular crystals with a chromophore absorb nearly all of the light that is shined on them, and thus the diffraction data are a mixture of photoinitiated reactions at the surface of the crystal and non-reacting molecules in the “shaded” interior of the sample. Also, like all single crystal X-ray crystallography experiments, radiation damage can obscure time-dependent changes driven by the desired triggering event. An additional limitation is that the ~100–500 μm size of typical protein crystals means that diffusion of small molecule ligands or enzyme substrates happens much more slowly than the rate of most of the interesting structural changes and will be heterogeneous through the volume of the crystal over the timescale of the experiment, prohibiting most ligand-initiated Laue experiments.

3.2. XFEL sources permit new time-resolved crystallography experiments

The limitations of Laue-based methods are being addressed by new methods. Time-resolved crystallography is currently enjoying a renaissance owing to a combination of new X-ray free electron laser (XFEL) sources of exceptional brightness (7), fast detectors (26, 45), and serial crystallographic approaches that allow full datasets to be collected from a large number of small crystals (7, 18). These technical developments have been mutually reinforcing. The ultra-intense XFEL pulses of ~10–50 fs duration will destroy each illuminated crystal in ~100 fs, but the crystal diffracts in its native state for the duration of the brief XFEL pulse (81). This “diffraction-before-destruction” principle (5, 17) allows datasets with minimal radiation damage to be compiled from a large number of single crystal diffraction images, which is critical for extremely radiation-sensitive metalloprotein crystals such as photosystem II (59, 65, 106, 129), methane monooxygenase (102), cytochrome c oxidase (46, 51, 96), copper nitrite reductase (CuNiR) (89), cytochrome c peroxidase and ascorbate peroxidase (68), and p450 NO reductase (109). The fs pulse also allows for faster timescale events to be probed with XFEL radiation than other X-ray sources, opening up entirely new dynamical regimes to structural characterization.

Since each crystal is destroyed by the XFEL pulse, a large number of crystals are needed to collect a full serial crystallography dataset. Fortunately, the extreme intensity of an XFEL pulse delivers so many photons (~10¹²/pulse) that microcrystals (~0.5–50 μm) are sufficient to generate high-quality diffraction data (7, 18). Microcrystals help address two major limitations of the Laue technique: their small size is more uniformly illuminated if a reaction is initiated by light (42) and small molecules can diffuse throughout the microcrystal quickly if the reaction is initiated by introduction of a ligand (92, 118). This provides tighter control over the start of the reaction, both increasing the time resolution of the resulting experiment and producing higher quality data because the reaction is more homogeneous though the volume of the crystal. Serial diffraction from microcrystals means that irreversible reactions can be characterized more easily that with Laue approaches, which often required repeatedly cycling the reaction during data collection to obtain a complete dataset. Moreover, a suspension of micron-sized crystals in stabilizing solution has the consistency of a slurry and thus can be handled as a liquid (20), allowing mixing with substrates and delivery to the X-ray beam via a gas dynamic virtual nozzle (27), microfluidic mixing devices (14), lipidic cubic phase (LCP) jet (122), electrokinetic injector (97), acoustically-ejected droplet (37), or solid fixed target (48). In addition, microcrystals appear to be more tolerant of perturbations that would damage larger crystals. The physical explanation for this is still unclear but is likely due to diminished opportunity for strain to accumulate in the lattice of these small crystals. For example, microcrystals of the adenine riboswitch RNA aptamer underwent a change in spacegroup upon introduction of its cognate ligand yet, quite surprisingly, still diffracted well (103). While much of the initial development of time-resolved serial crystallography methods was driven by XFEL sources, these methods are now being applied at synchrotron beamlines as well (74, 75, 87). XFEL beamtime is scarce and competitive, which has limited the pace at which the field can grow. The larger number of synchrotron beamlines, the greater ease of beam delivery at these facilities, and automated sample handling tools will widen access to time-resolved crystallography equipment and expertise. The advent of megahertz repetition XFEL sources such as the European XFEL (41) and the planned LCLS-II upgrade will also help ameliorate the scarcity of XFEL beamtime and dramatically increase the speed with which time-resolved experiments can be performed. Considered in total, time-resolved serial X-ray crystallography methods have opened a new window into non-equilibrium structural biology and now permit experiments that will address questions involving intrinsically non-equilibrium events like enzyme catalysis.

4. The crystallographic view of protein dynamics

Achieving a non-equilibrium view of protein function from X-ray crystallography requires methods to extract relevant dynamical information from the diffraction data. The electron density map contains all of the information obtained in an X-ray crystallography experiment. Naturally, much of the information in a time-resolved experiment comes from a comparison of the electron density at various time points, which can be interpreted as the changes in the protein conformational ensemble in response to perturbation, as discussed below. However, the electron density map at each timepoint also contains information about ensemble-averaged atomic motions that relates to the underlying energy landscape.

4.1. The atomic displacement parameter and harmonic potential energy wells at equilibrium

X-ray diffraction data are related to the average electron density by a Fourier transformation as described in the structure factor. Because the average electron density is the integral of the product of the static electron density and the probability density function (p.d.f) for atomic displacements (i.e. a convolution), the structure factor equation contains a function called the Debye-Waller factor that is related to the Fourier transform of this p.d.f. (110, 124). The p.d.f. that defines the form of the Debye-Waller factor could have any physically plausible form. In the context of an energy landscape, the p.d.f. would correspond to the Boltzmann distribution for the underlying PES at equilibrium and thus have a complicated exponential functional form. For ease of modeling and refinement however, it is almost always assumed that atomic displacements from the mean position are normally (Gaussian) distributed. A normal distribution of atomic displacements corresponds to the Boltzmann distribution of positions for an atom moving in a harmonic potential energy well, connecting ADPs to assumptions about the underlying PES (Fig. 1). The harmonic assumption is always wrong for protein atoms, although it is adequate in many cases, particularly if the motion of interest is dominated by thermal motion confined to a single minimum in the PES.

Figure 1:

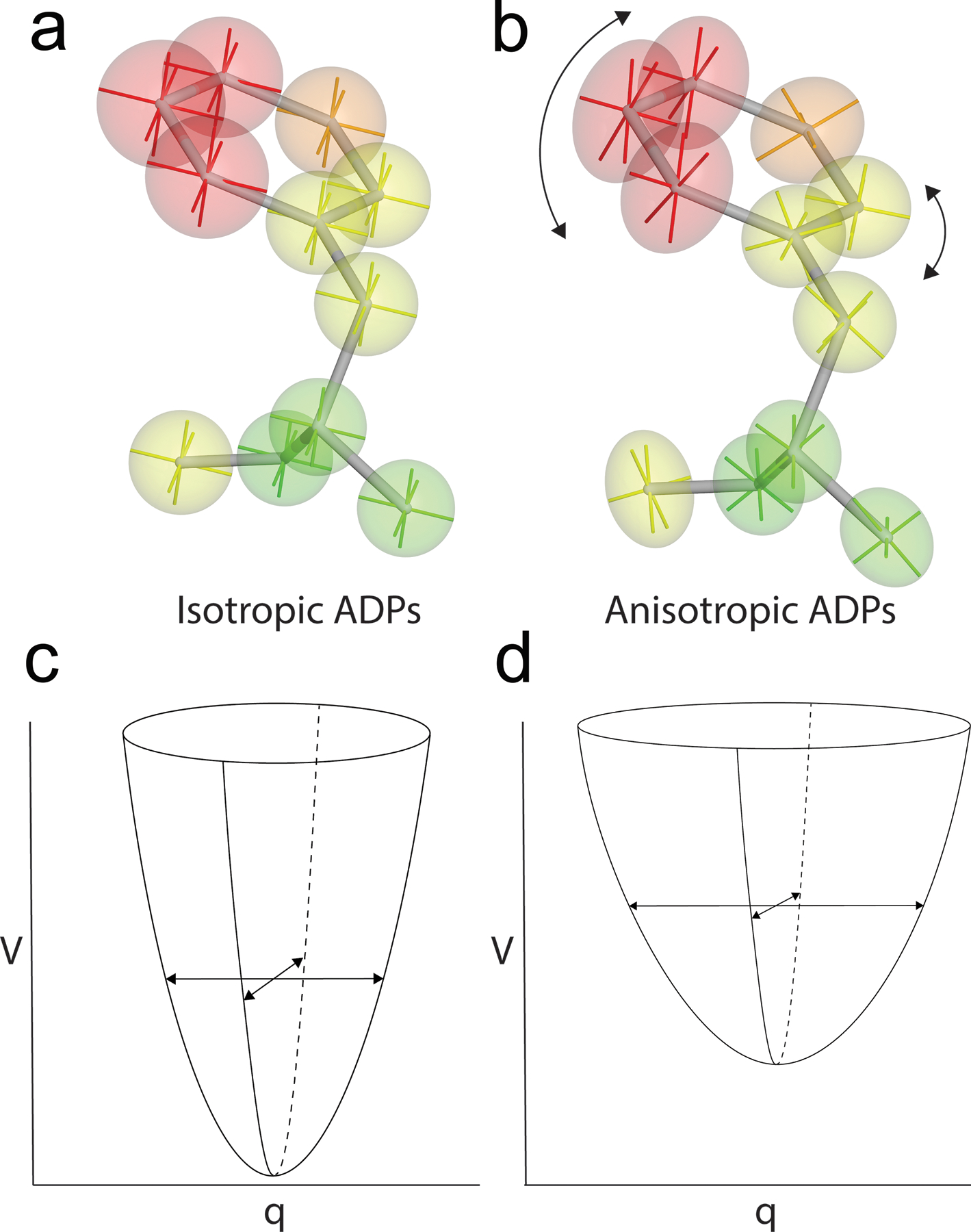
Anisotropic displacement parameters (ADPs) can provide detailed information about atomic motion. ADPs assume Gaussian-distributed displacements, consistent with Boltzmann-weighted motion in a harmonic well in the PES. Isotropic ADPs (a) show magnitude but not direction of atomic motion, while anisotropic ADPs (b) provide detailed information about both magnitude and preferred directions of atomic displacement. Isotropic ADPs correspond to motion in an isotropic PES well (c) , while anisotropic ADPs correspond to motion in a PES well with different widths in each direction (d). V is the potential energy, and q is the generalized coordinate.

The quantity in the Debye-Waller factor that is directly related to the atomic displacement is called variously the atomic displacement parameter (ADP), the B-factor, or the thermal factor. ADPs can either have one or six parameters to describe the variance of the underlying normal p.d.f. A single variance parameter ADP describes isotropic displacement from the mean position, while the six parameters of the anisotropic ADP describe the symmetric variance-covariance matrix of atomic displacements. Because of the increased number of free parameters in an anisotropic ADP, more experimental data (corresponding to high resolution diffraction) are needed to refine this type of model. Obtaining the resolution needed to refine anisotropic ADPs is often a limiting factor for macromolecular crystals, which is compounded by the room temperature conditions of most XFEL experiments. For the isotropic ADP, the harmonic potential well has equal widths in three spatial dimensions per atom and the isoprobability surface is spherical. For an anisotropic ADP, the harmonic well has different widths in each dimension and the isoprobability surface is ellipsoidal, indicating the directions of preferred atomic motion (Fig. 1). Therefore, even within a conventional time- and ensemble averaged crystallographic experiment, there a considerable amount of information about the magnitudes and directional preferences of atomic displacements that can be extracted if data quantity and quality permit.

4.2. Models of correlated atomic displacements in crystallography

The stubbornly persistent impression that crystallography provides a “static snapshot” is largely a consequence of the dominant approach to the modeling and refinement of X-ray crystal structures using a single conformation for each atom and an associated ADP. These refined ADPs are often treated as secondary model parameters that are not always analyzed. ADPs can underestimate atomic mobility, sometimes dramatically, as shown in a study using synthetic diffraction data calculated from molecular dynamics simulations where ground truth atomic displacements were known (67). Also, ADPs can contain contributions from model error as well as bona fide atomic displacements, and thus are often regarded with skepticism ranging from appropriate caution to outright dismissal. However, even for well-intentioned crystallographers aiming to responsibly extract the most information from their data, individual ADPs can be difficult to analyze. The central difficulty is that ADPs represent displacements for each atom, but atomic motion in proteins is correlated and those correlations are important for understanding how structure and dynamics are related. Some reduced parameter representations of anisotropic ADPs impose physically plausible models of correlated atomic displacements, including the translation-libration-screw (TLS) (94, 126) and normal mode approaches (19, 28, 61). TLS models treat a group of atoms as composing a rigid body whose harmonic translations and librations provide a parsimonious representation of anisotropic motion. Normal mode models use the lowest-frequency, most collective normal modes as a basis for representing the ADPs by assuming the entire protein is described by a harmonic potential. A shared limitation of both models is that they assume harmonicity in correlated atomic displacements along the relevant degrees of freedom. However, many correlated motions are likely to be strongly anharmonic because they represent transitions among minima of the PES. Such motions might correspond to the movement of a single amino acid sidechain, the shifting of a secondary structural element, or global changes in protein structure that affect most atoms. There is often evidence of these types of motions in the electron density map but extracting this information from the diffraction data remains a challenge that becomes more pressing once time-dependent changes are considered.

Anharmonic atomic displacements can be inferred from regions of multimodal electron density and are represented with alternate conformations for these regions of the atomic model. Multiple peaks in the electron density in vicinity of an atom is a direct visualization of the protein sampling distinct minima in the PES (98) (Fig. 2). At resolutions better than ~1.5 Å, individual amino acids are often modeled in two or more discrete conformations when the electron density map supports it (98, 107). Less commonly modeled, but not necessarily any rarer, are alternate conformations of the mainchain atoms (56). Most time-resolved crystallography experiments are performed at room temperature, and proteins have been shown to sample more conformational substates at these non-cryogenic temperatures (33, 34). The recent renaissance in room temperature data collection for traditional X-ray crystallography has permitted a fuller exploration of functionally important crystallographic disorder and conformational dynamics than was possible using prevailing cryo-crystallographic approaches at ~100 K (32, 33, 128). Cryocooling can suppress certain motions and redistribute the populations of conformational substates to favor low entropy, low enthalpy conformations that are not representative of the large number of substates populated at physiologically relevant temperatures (34, 44, 58). Moreover, the ways that these substates are populated as the temperature is increased reveals a complex set of transitions among multiple minima in the underlying PES that would not be easily inferred from inspection of electron density maps obtained at a single temperature (57). Extracting information about the collective character of various conformational transitions from electron density maps requires either the simultaneous refinement of multiple non-interacting copies of the entire protein (10, 11, 71, 125), automated multiconformer models of the regions that have the strongest evidence of multiple conformations (56, 111, 112), or time-averaged molecular dynamics (MD) refinement of the entire protein (12, 40), where structures from the MD trajectory compose the final ensemble model. Regardless of how they are created, these ensemble models often have correlations imposed by the physical constraints of the protein. For example, a stretch of residues might be presumed to move together because the entire backbone samples two conformations that can be modeled from the electron density. However, in many cases crystallographically-inferred correlated displacements must remain tentative because Bragg diffraction data do not contain direct information about correlated atomic displacements. That information is contained in the non-Bragg diffuse X-ray scattering data (22, 114, 115), whose collection and analysis has recently been revitalized (77, 116) and holds promise for improving models of collective atomic motion in crystals in both conventional and time-resolved experiments.

Figure 2:

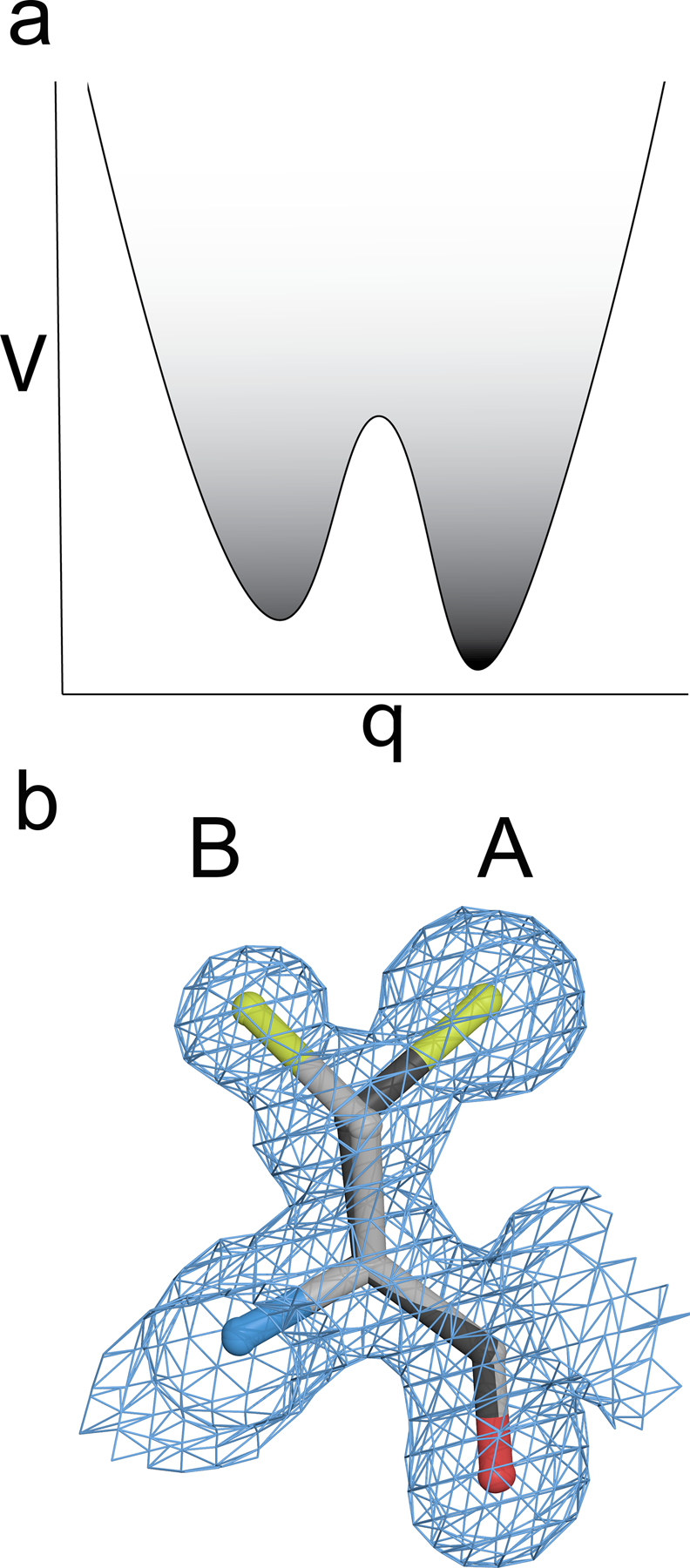
Electron density reports on multiple minima in the PES. An example of clearly multimodal density for two sidechain conformations of cysteine that indicates two distinct minima of the PES are occupied. The “A” conformer (darker line) has greater electron density, indicating that this conformer is more occupied. The greater occupancy corresponds to the “A” conformation being a deeper PES minimum, which is more darkly shaded. V is the potential energy, and q is the generalized coordinate.

5. Visualizing non-equilibrium enzyme dynamics using time-resolved X-ray crystallography

One of the most exciting applications of time-resolved crystallography experiments is to observe enzymes during catalysis. This achieves one of the foundational goals of enzymology-to watch an enzyme actively catalyze its reaction in real-time and at atomic resolution. When combined with the various methods discussed above that connect features of the electron density map to transitions among minima on the PES, it is now possible for structural enzymologists to map enzyme reaction dynamics to the structures populated in the underlying energy landscapes. As discussed above, there are two energy landscapes to consider: the PES and the FES (113). The FES is appropriate when considering kinetically distinct states of an enzyme (e.g. resting, bound to substrate, an intermediate, etc), and each minimum in the FES will subsume a number of minima in the PES (6). The distinct structures that contribute to the total electron density for a single state of the enzyme represent minima in the PES. The number of these PES minima and their widths in configuration space are related to the entropy of this enzyme state in the FES, which can be related to the thermodynamics and kinetics of the reaction (53).

5.1. Initiating enzyme catalysis with light and diffusion

Initiating enzyme catalysis for a time-resolved crystallography experiment requires synchronization of the reaction across many active sites in the crystal. Two major approaches have been used to achieve this: photoinitiation and diffusion. Reactions that involve light are obvious choices for photoinitiation. For example, the entire catalytic cycle of fatty acid photodecarboxylase (FAP) was characterized using time-resolved XFEL crystallography, computation, and spectroscopy, starting with a distorted flavin adenine dinucleotide (FAD) cofactor absorbing blue light and oxidatively decarboxylating the fatty acid substrate, followed by a radical FAD cofactor intermediate reducing the radical alkyl intermediate (99). Despite the power of photoinitiated enzymology exemplified by this study of FAP, very few enzymes are natively phototriggered. However, bright, pulsed, UV-visible-wavelength lasers allow for unparalleled control over the timing of reaction initiation (down to picoseconds), which can be especially important for fast enzymes (k_obs>~100 s⁻¹). Photocaged substrates can allow many enzymes to be made phototriggered by soaking inert caged substrates into the crystals prior to the experiment and then liberate the authentic substrate with a “pump” pulse from the UV-visible laser that breaks the chemical cage (104). This approach was used with microcrystals of fluoroacetate dehalogenase (76) and p450 NO reductase (109), allowing the formation of enzyme intermediates to be followed at millisecond time resolution. In some cases, a reaction can be triggered by X-rays of a different wavelength than the probe pulse used to collect diffraction data: these are examples of two-color experiments (72).

A second approach to initiate catalysis is by rapidly mixing substrate into the enzyme microcrystals and then deliver this mixture to the X-ray beam: a “mix-and-inject” serial crystallography (MISC) experiment (66, 83). One advantage of MISC is that the technique is applicable to many enzymes whose substrates are small enough to soak into a crystal, which includes a large number of candidate systems that cannot be phototriggered. MISC has been successfully used to observe catalysis in β-lactamase (83, 86), isocyanide hydratase (ICH) (25), and cytochrome c oxidase (CcO) (50). It is hoped that more enzyme MISC experiments are in progress at the time of this writing. Pioneering MISC XFEL experiments in β-lactamase permitted the visualization of a ring-opened catalytic intermediate derived from ceftriaxone in the enzyme active site and permitted correlations of the intermediates with the simulated kinetic profile of the enzyme (83). A general consideration for time-resolved studies that is especially pertinent for MISC structural enzymology is that a knowledge of the kinetics of the enzyme is always helpful and sometime necessary. Enzymes that exhibit burst kinetics, where formation of a key intermediate occurs markedly faster than subsequent rate-limiting steps, are particularly attractive targets for MISC experiments because the electron density is likely to unambiguously show the accumulated intermediate. Since diffusion time is related to molecular size via the diffusion coefficient in Fick’s Second Law, under ideal mixing cases, smaller molecules will provide more rapid and uniform reaction triggering in MISC (92). Therefore, enzymes that use gasses such as oxygen as a substrate provide especially promising targets for time-resolved MISC experiments, as was shown by characterization of the oxygen-bound intermediate of cytochrome c oxidase (50).

5.2. The isomorphous difference (F_o-F_o) electron density map and non-equilibrium conformational fluxes in proteins

As discussed in Section 4, a variety of tools can be used to analyze electron density maps for evidence of conformational heterogeneity resulting from protein dynamics. These can be applied to the study of individual time-points in a time-resolved X-ray crystallography experiment if data quality and resolution permit. However, the most important analytical tool in time-resolved crystallography is comparing electron density maps obtained at different times after the reaction is initiated. These comparisons are typically made using difference electron density maps, in particular the isomorphous difference (or F_o-F_o) map. The F_o-F_o map is so called because it is calculated by subtracting the observed set of observed structure factor amplitudes (F_o) at the initial time point from those in a subsequent dataset collected at a later time. The peaks in F_o-F_o maps represent areas where electron density is moving between timepoints and thus correspond to the non-equilibrium conformational fluxes on the underlying protein energy landscapes. Because of the centrality of the F_o-F_o electron density map for analysis of time-resolved experiments, several different approaches have been developed to interpret features in these maps. In some cases, the interpretation of the peaks is straightforward, such as in localized changes to chromophores during photoexcitation (24, 65, 79, 85) or the formation of enzyme intermediates (25, 76, 83, 99). However, in many other cases it can be challenging to determine the structural origin of F_o-F_o map peaks, particularly when they extend beyond the immediate vicinity of a mobile group or when they represent the ensemble average of different chemical species or conformational states. For example, in a time-resolved XFEL experiment with isocyanide hydratase (ICH), the structural explanation for positive difference peaks that appeared near a mobile helix would have been impossible to confidently provide without prior structures of ICH where this helix was in a shifted conformation (69) (Fig. 3a). In this case, combining information about structural heterogeneity obtained from electron density maps at equilibrium with difference maps obtained during catalysis was essential to interpret the experimental result and relate it to changes in the FES of the reaction (25). Owing to the importance and challenge of interpreting F_o-F_o electron density, methods such as the singular value decomposition (SVD) (60, 93), clustering analysis (64), and local map correlation (123) have been applied to extract information from F_o-F_o maps. The continued development of methods that can relate features in time-resolved difference electron density maps to protein structural changes is a key area for future development in time-resolved crystallography, especially because the number of timepoints (i.e. maps) per dataset is expected to increase substantially in the near future.

Figure 3:

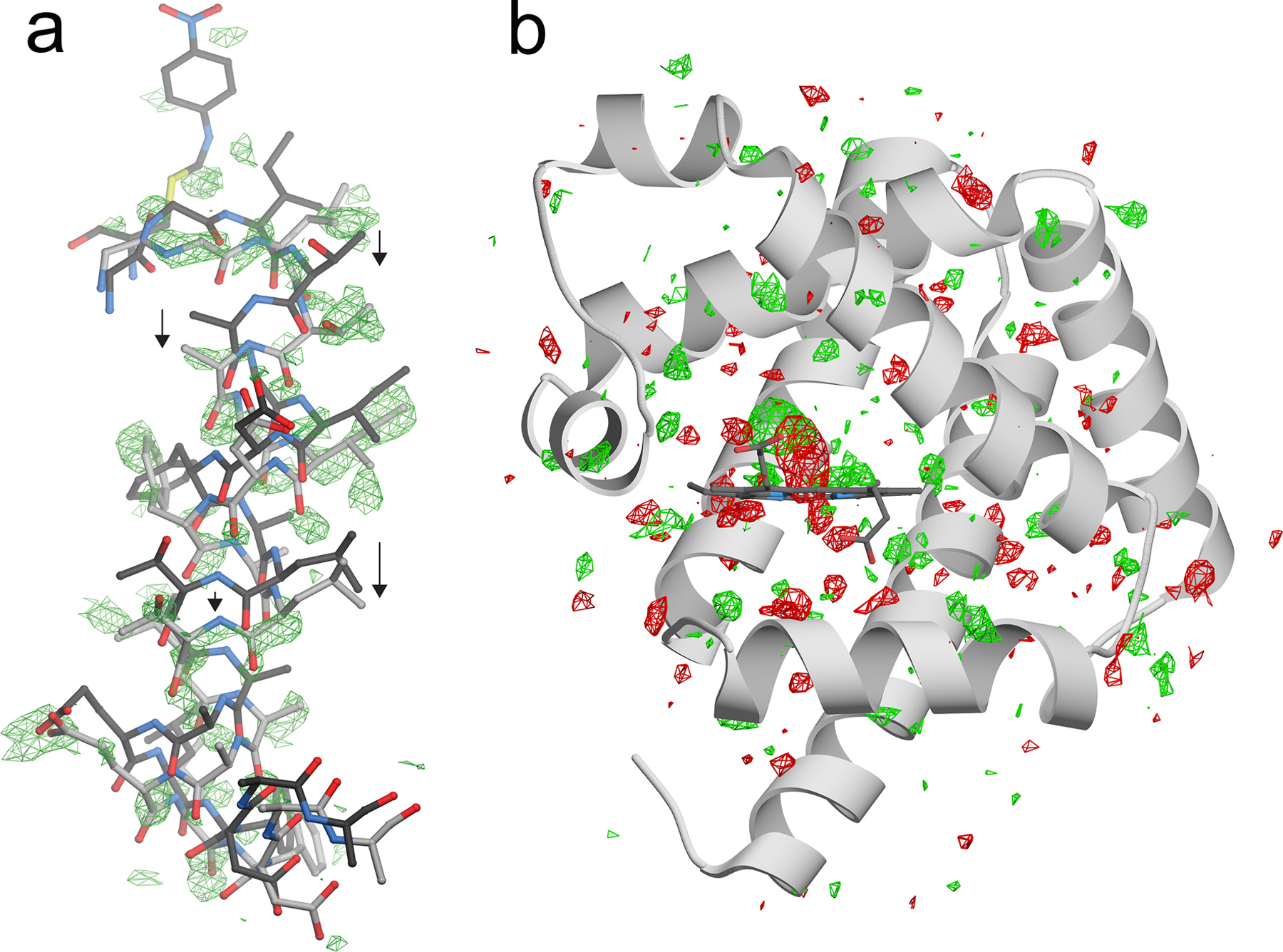
Isomorphous (F_o-F_o) difference electron density maps show distributed dynamical changes in proteins when perturbed from equilibrium. In (a), the mobile helix near the active site of ICH is shown with positive F_o(intermediate)-F_o(free) electron density in green at 2.7 σ. Intermediate formation results in a downward shift of the entire helix, shown with arrows and indicated in the lighter gray bonds. In (b) a F_o(0.5 ps)-F_o(dark) electron density map is shown for CO-myoglobin before (dark) and 0.5 ps after flash photolysis of the CO [4]. The “proteinquake” long proposed for flash photolysis of carboxymyoglobin is evident as positive (green) and negative (red) difference electron density at 2.7 σ radiating away from the heme group and throughout the protein.

In several time-resolved studies, the F_o-F_o peaks appear near the site of perturbation and then radiate outwards in later timepoints. In photoinitiated reactions of photoactive yellow protein (PYP) (108), reversible photoswitchable fluorescent protein rsEGFP2 (24), and carboxymyoglobin (4), the propagation of these motions throughout the protein was observed at ps time resolution using serial femtosecond XFEL crystallography. These propagating difference map peaks are a direct visualization of the “proteinquake” initially proposed in 1985 to explain the non-equilibrium response of myoglobin to a localized perturbation caused by photodissociation of carbon monoxide from the heme prosthetic group (2) (Fig. 3b). If the state change that gives rise to these F_o-F_o electron density features are irreversible, then these underlying motions are dissipative and increase the system entropy, corresponding to a decent into a basin in the FES. The extension of the theory of energy landscapes to far-from-equilibrium systems (119) including dissipative protein conformational changes (121) is relevant for interpreting future XFEL studies of enzymes as time-dependent conformational ensembles on an emergent, non-equilibrium PES.

The relationship between non-equilibrium catalytic motions of enzymes to their equilibrium dynamics can be complex. In the enzyme ICH, formation of a catalytic intermediate in the active site 15 seconds after mixing with substrate resulted in the appearance of F_o-F_o difference peaks distributed throughout the protein (25). Some of the F_o-F_o map peaks clustered in the same regions of the protein that showed evidence of conformational heterogeneity in electron density maps, MD simulations, and kinematic flexibility analysis (9) at equilibrium, qualitatively consistent with the fluctuation-dissipation relation (13). However, other F_o-F_o peaks that appeared upon formation of the intermediate were in previously well-ordered parts of the protein. The incomplete overlap in the areas that were observed to be mobile at equilibrium and those that were perturbed during catalysis suggests that the ICH ensemble (and underlying PES) changes during catalysis. These non-equilibrium dynamical changes resulting from intermediate formation facilitate subsequent, irreversible steps in ICH catalysis, including intermediate hydrolysis. Global changes in enzyme dynamics correlated with progress along the reaction coordinate have also been observed in a time-resolved study of fluoroacetate dehalogenase (FAcD), where four full catalytic cycles were mapped by millisecond time-resolved crystallography at a synchrotron (76). FAcD contracted and expanded during catalysis while the solvation of the enzyme reorganized in synchrony with these dynamical changes. These enzyme “breathing motions” are proposed to be generally important for allostery in proteins and may play a role in the dynamical symmetry-breaking that occurs in the FAcD dimer during catalysis (62).

5.3. Relating enzyme dynamics to catalysis using time-resolved crystallography

The role of protein dynamics in enzyme catalysis has been one of the more active and contentious fields in biophysics in the past two decades (30, 54). It is clear that enzymes, like all proteins, sample many distinct conformations. The kernel of the debate about enzyme dynamics has been ascribing a functional role to these motions, if any exists. Enzyme motions that promote substrate binding and product release are well-documented (3) and can contribute to entropic terms in these steps (36, 117), but the role of dynamics in transition state barrier crossing is contested (63, 120). Time-resolved crystallography can directly observe motions that arise from catalysis, and thus allows functional motions to be identified with greater confidence than is possible at equilibrium.

One of the most powerful applications of time-resolved crystallography is characterizing dynamics of transient states such as enzyme intermediates at room temperature. Because these species are fleeting, they are impossible to directly isolate and characterize, thus requiring time-resolved approaches. Using techniques described in Section 4, information about time-dependent conformational heterogeneity of ICH during catalysis was extracted from 1.55 Å resolution MISC XFEL data. Combining this crystallographic analysis with enzyme kinetics, mutational analysis, and computation revealed that catalysis activates motions in ICH that promote progress along the reaction coordinate (25). Although the mechanism of this activation involves specific changes in ICH active site electrostatics, it is possible that catalysis-activated motions are a more general enzymological phenomenon. Many enzymes are transiently modified during catalysis, which alters the underlying PES and thus changes the enzyme’s conformational ensemble in a time-dependent manner (Fig. 4). The resulting time-dependent enzyme ensemble is expected to be non-ergodic on relevant experimental timescales (i.e. the time-average and ensemble-averages will not converge), and thus the degrees of freedom that are most active at equilibrium are not necessarily the same ones that will dissipate the energy released by catalysis, violating both detailed balance and the classical fluctuation-dissipation relation (73). An interesting corollary of this is that it implies that the effective local temperature of an irreversible enzyme active site should increase during catalysis, which may contribute to the enhanced diffusion of catalytically active enzymes, although the physical origin of this effect is still debated (52). For ICH, detailed analysis of conformational heterogeneity was possible because the microcrystals diffracted to ~1.6 Å, where reduced parameter anisotropic ADPs and multiconformer models can be reliably refined. Most XFEL experiments are performed at room temperature using microcrystals, which tends to reduce the maximum resolution attainable and thus provides fewer data for analysis. Nevertheless, a direction for future growth in time-resolved structural enzymology is applying existing ensemble models and developing new types of analysis to interpret electron density map time series as non-equilibrium motions of enzymes on a dynamic, time-dependent PES. Although there are currently few published time-resolved XFEL crystallography studies of enzymes, there is good reason to believe that the field is on the cusp of a deluge of XFEL structural enzymology studies, providing the information-rich datasets from which generalizable themes in the relationship between enzyme dynamics can be discerned. Finally, a major challenge for every enzyme system studied will be determining if catalysis-activated motions are functionally important, which will require a battery of methods in addition to structural biology to be brought to bear on the system.

Figure 4:

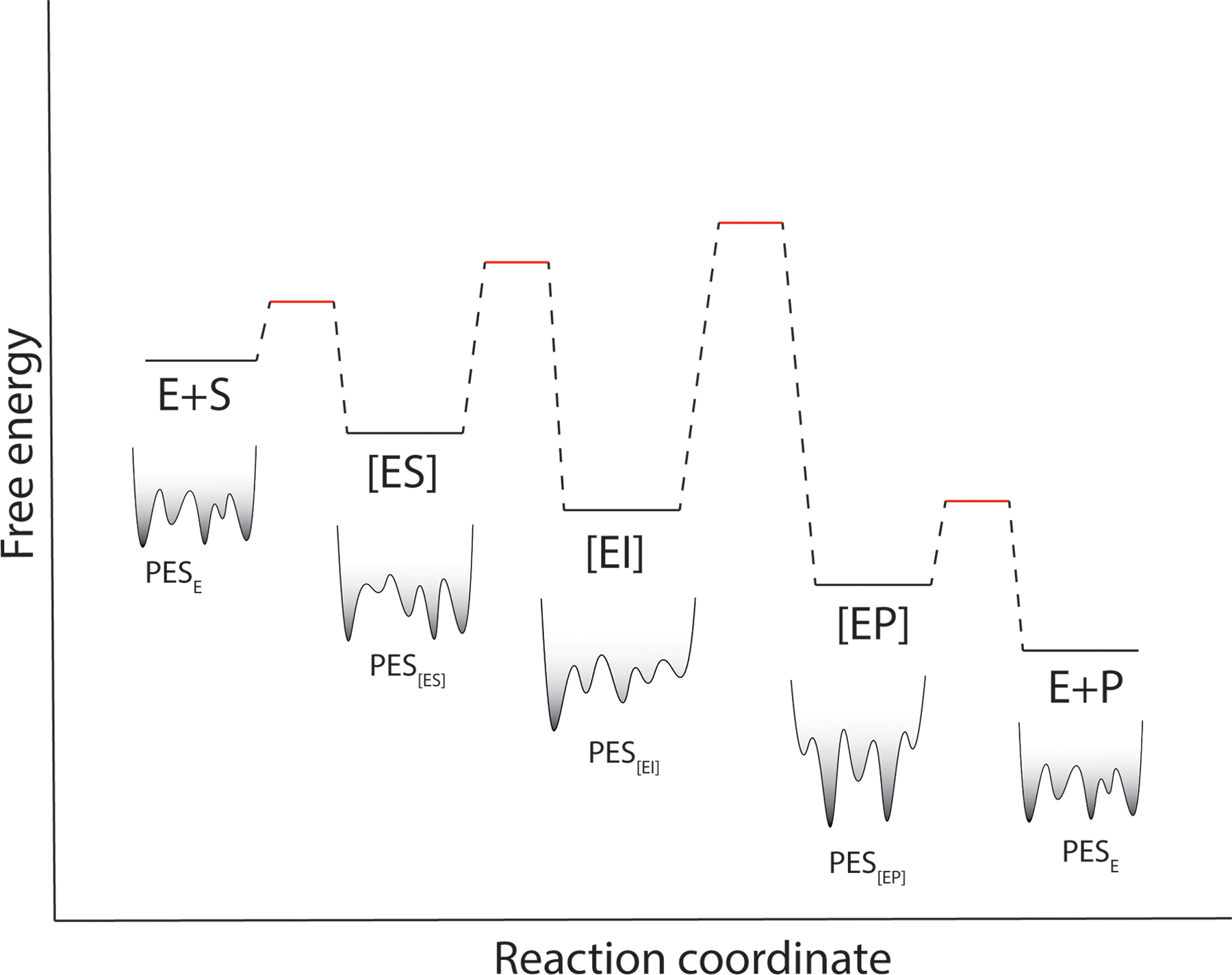
Enzyme conformational ensembles change during catalysis. A generic free energy diagram for an enzyme where substrate concentration is >> K_M. [ES] is the Michaelis complex, [EI] is a catalytic intermediate, and [EP] is the enzyme-product complex. Below each species is a stylized version of its potential energy surface (PES), which changes during catalysis. This time-dependent PES suggests that catalysis-activated (or suppressed) motions are likely to be generally observed in enzymes using time-resolved crystallography.

6. Conclusions

X-ray diffraction data offer a wealth of information about atomic displacements at equilibrium. A new generation of time-resolved experiments at synchrotrons and XFELs has expanded that information into the non-equilibrium domain, including enzyme catalysis. As the ability to rapidly collect X-ray diffraction datasets at many time points improves (86), the resulting time series of electron density maps will provide unprecedentedly detailed views of enzymes sampling non-equilibrium ensembles during catalysis. The future of time-resolved structural enzymology is closely tied to the rapidly evolving technical capabilities of synchrotron and XFEL lightsources as well as the continued development of analytical methods capable of parsing the complicated, time-dependent electron density maps that can now be generated. The compatibility of serial X-ray crystallography with spectroscopic techniques allows transient structural changes to be correlated with electronic and vibrational ones in the active site of enzymes. I propose that catalysis-activated enzyme dynamics may be a common consequence of time-dependent enzyme ensembles violating the fluctuation-dissipation relation and that evidence for this phenomenon will accumulate as more time-resolved crystallography studies of irreversible enzymes are performed. In total, the ability to directly observe enzyme catalysis in real-time and at atomic resolution will expand the frontiers of the emerging field of non-equilibrium structural biology in directions that are only just emerging.