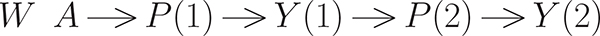Adjusting for Perception and Unmasking Effects in Longitudinal Clinical Trials

Abstract

A blinded clinical trial design requires masking of patients to prevent measurement of their outcome from being influenced by knowledge of treatment assignment. However, during the course of a trial, some patients may be practically unmasked either due to experiencing treatment related side effects in the treatment arm, or lack of efficacy in the placebo arm. In a recent paper, we introduced concepts of perception, unmasking, and placebo effects for point treatment studies. In this paper, we generalize these concepts to longitudinal studies, and use recent advancements in causal inference and semi-parametric efficient estimation to define and estimate perception and unmasking effects. This allows differentiation of the impact on measured outcomes of èarly’ versus `late’ unmasking. In particular, two semi-parametric, substitution methods, one based only on the prediction model (G-computation) and an augmented version of that model for targeted bias-reduction (Targeted Maximum Likelihood Estimation; TMLE), are used for estimation of perception and treatment effects. We motivate our discussion by analyzing data from a recent longitudinal study on the effect of gabapentin on pain among diabetic patients experiencing painful neuropathy.

1. Introduction

In masked clinical trials, treatment assignment is purposefully concealed to prevent patients’ outcomes from being influenced by biases due to knowledge of treatment assignment. Patients’ responses may also be affected by the unconscious biases on part of the investigator, and thus, in a double blinded trial, the investigators may also be masked in addition to the patients. However, during the course of a trial, some patients may be practically unmasked as a result of experiencing treatment related side effects in the treatment arm, or lack of efficacy (or side effects) in the placebo arm. Unmasking of patients may affect their response and thus distort measurements of the treatment effect; in such situations, investigators must account for unmasking of patients for a full interpretation of the findings.

Jamshidian et al. (2012) used a counterfactual framework from causal inference literature to formally define a placebo effect and some of its components such as unmasking and perception effects in a cross-sectional setting. There we defined direct effects of a treatment under hypothetical interventions on a patient’s masking and perception, for example, estimating the treatment effect had a patient remained masked throughout the trial, or had patient’s perception regarding treatment been kept at some other fixed level. This framework was applied to a pain trial in which occurrence of treatment-related side effects was used as a proxy for unmasking of the patients. Two semi-parametric, substitution estimators were implemented to obtain estimates of joint treatment and perception effects, one procedure based on a data-adaptive prediction model of the outcome given the variable(s) of interest and covariates, and one that uses an augmented version of the prediction model (Targeted Maximum Likelihood Estimation, or TMLE; van der Laan and Rubin (2006)).

In this paper, we generalize the concepts of perception and unmasking effects to longitudinal settings, where perception and unmasking of patients are measured as time dependent random variables. In section 2, we reassess the gabapentin trial (Backonja et al., 1998) for evaluation of the effect of gabapentin on pain among diabetic patients with painful neuropathy, now considering use of available longitudinal information on unmasking. This study was the motivating example in our previous paper for the cross-sectional setting, and we refer to it throughout the paper. In section 3, we present the statistical framework and estimation strategy, including a) the formal data structure and statistical model, b) parameters of interest that disentangle longitudinal masking effects from treatment effects, and c) substitution estimators. In section 4, we present estimation results using data from the gabapentin trial, and, in section 5, we discussed these results, and the extent to which this approach is well-suited to estimating unmasking effects given data practically available from clinical trials.

2. The Gabapentin Trial

About 45% of diabetic patients experience discomforting pain due to peripheral neuropathy (Pirart, 1978). A randomized double-blind study conducted by Backonja et al. (1998) evaluated the effectiveness of gabapentin (also referred to as neurontin) among Type I and Type II diabetic patients. The study consisted of a seven day screening phase during which baseline covariates including age, height, weight, race, sex, baseline pain and sleep scores were measured, followed by a double-blind phase. At the screening stage, eligible patients reporting an average pain score of at least four (on an 11-point Likert scale) were randomized. In total, 165 participants were randomly assigned to either treatment or placebo. The screening stage was followed by an eight-week double-blind phase, which was broken up into two dose periods: a four week dose titration period followed by a second four week fixed dose period. During the first four week dose titration period, patients assigned to the treatment group were administered gradually titrated dosages of gabapentin up to their tolerability level (with maximum of 3600 mg/d per week). During the second half of the eight week study, treatment patients received a fixed dosage for four weeks, which consisted of their maximum tolerability dosage. The primary outcome of the study was the severity of daily pain at the end of the eight week trial. Patients were instructed to record their pain level on an 11-point Likert scale (0–10) on daily diaries, 0 indicating no pain and 10 being the most severe pain. The primary endpoint was calculated using the mean score of the last seven recorded pain levels.

Backonja et al. (1998) explored the possibility that presence of side effects in the study might result in the unmasking of patients simply by deleting those with treatment related side effects from the analysis. Jamshidian et al. (2012), placed this approach on a solid causal footing that appropriately allowed for confounding effects on unmasking, showing that “adjusting” for indicators of side effects resulted in significantly different estimates of the treatment effect. There, and in this extended development, we reanalyze the gabapentin trial data by considering the occurrence of any treatment related side effect as a proxy for a patient’s perception being set at “believing she is on active treatment”. The main advance in the approach used here is to account for the time at which side effects occur. This is important to the extent to which it is possible that early onset of treatment related side effects might have a different impact on the primary outcome in contrast to later onset that is closer in time to measurement of the final pain scores. In addition, it is possibly to allow for the nuances of time-dependent confounding of intermediate pain scores in their relation to future unmasking–see Jewell et al. (2012) for a preliminary discussion.

Optimally, one would have available a quantitative recorded measure of a patients perception of which treatment they were on, so that one could define a patient’s perception towards his treatment as, for instance, the degree of certainty the patient feels about having received the active treatment (or placebo). A low level of such a variable would imply that the patient is leaning towards placebo with a high level reflecting perception that she thinks she is on treatment (Jamshidian et al., 2012). In longitudinal settings, a measure of patient’s perception regarding their treatment will likely vary over time. For instance, a patient might believe she is on placebo during the early stages of the trial (due to limited efficacy, say), but subsequently change perception later as a result of experiencing treatment related side effects. We refer to this time dependent random variable as a patient’s perception at time t. In general, P(t) = 1 indicates that a patient is certain that he has been assigned the active treatment at time t and, at the other end of the scale, P(t) = −1 indicates that a patient is certain that he is receiving the placebo at t; in the ‘middle’ P(t) = 0 would indicate that a patient has no leanings towards one treatment assignment or the other (the ideal masked situation). For the gabapentin trial there is no proxy for the state P(t) = 0, and so, for simplicity the states P(t) = 0 and P(t) = −1 are collapsed together as in Jamshidian et al. (2012) and referred to as P(t) = 0 for simplicity. That is, for the purposes of this paper, we will retain the simple definition that, P(t) = 1, if a patient reports side-effects at, or before time t (and thus the implication is they believe they are on treatment), and P(t) = 0 otherwise. We note here the limitation that this means that the perception variable is monotonic in that P(t) cannot move from 1 to 0 with this definition; that is, once unmasked, always unmasked.

3. Statistical Framework

3.1. Data Structure

As indicated we wish here to expand the cross-sectional treatment of perception described in Jamshidian et al. (2012) to allow for time-dependent measurement of perception and related confounding factors that might include intermediate pain scores. In principal, this could be achieved by allowing such variables to change each day over the eight week trial. For simplicity, we collapse this time period to two intervals, 0 to 4 weeks, and 4 weeks to 8 weeks. This will allow illustration of the principal issues introduced from moving from the cross-sectional setting previously considered. We return to further discussion of this point in Section 6.

Given this simplification, we create average pain scores for the screening week (baseline pain), and for week 4 and week 8 of the trial. If patients were missing pain scores for any days during week 4 or 8, the rest of the pain scores during that week were used to calculate the average, and only if a patient was missing all the seven pain scores did we consider their pain score to be missing. In addition to the pain variables, we created two variables for perception. The first variable was an indicator for presence of any treatment related side effects between randomization and the end of week 3, and the second variable was an indicator for presence of any treatment related side effects between randomization and the end of week 7. The set of baseline covariates used in our analysis included sex, race, height, weight, age, mean baseline pain score, and mean baseline sleep score.

The outcome process of interest consists of pain scores measured (as week averages) at two time (t) points: weeks 4 and 8. For ease we will now alter the definition of the time scale and refer to these measurements as taken at t = 1 and 2; randomization defines the baseline, or t = 0. Thus there are three pain scores used, denoted by Y (0) ∈ W,Y (1), and primary outcome, Y (2). As explained further below, our interventions of interest are defined as the combination of treatment given at baseline, side-effects (the proxy for perception) between baseline and the pain score at t = 1 (denoted by P(1), as well as the side effects measured between t = 1 and the last pain score at t = 2 (denoted by P(2)). As noted, P(1) is defined as an indicator of the presence of any treatment related side effects between randomization and the end of week 3, with P(2) similarly defined but dependent on treatment related side effects between randomization and the end of week 7. It is important to note that measurement of P(1) occurs before measurement of Y (1), that in turn occurs before the measurement of P(2), all prior to measurement of Y (2).

Before formally defining the observed data structure, we first discuss the so-called hypothetical “full” data that is used to motivate our parameters of interest, and to do so, we follow the counterfactual framework considered by Neyman (1990), Rubin (1978), Robins (1986), and Holland (1988). As exploited in Jamshidian et al. (2012), we focused on parameters of interest described in terms of (controlled) direct effects. We thus introduce a framework in which the observed data is regarded as a missing data structure on a full data consisting of all the potential counterfactuals for the intermediate variables and the outcome for every possible treatment (Robins and Greenland (1992), Pearl (2000), Robins (2003), Petersen et al. (2006),Rosenblum et al. (2009) ). Under this framework, the full data structure for the gabapentin trial would consist of all pain measurements for different hypothetical combinations of treatment and perception for each patient through time. Causal effects of interest may then be defined as differences in the counterfactual outcomes under different hypothetical treatment/perception patterns. Specifically, for the “intervention” variables of interest, there is binary treatment assigned at baseline and binary perception, P(t), measured at t = 1 and t = 2. Most generally, our parameters of interest are functions of the distributions of counterfactuals defined by theoretical rules on assigning treatment and longitudinal perception to the population. We will discuss only a simple subset of such rules, such as assigning all subjects fixed values of treatment (A = a), and perception (P(1) = p₁, P(2) = p₂, or $\overline{p}\equiv \left(p_1,p_2\right)$; we call the longitudinal rule, $d=(a,\overline{p})$, and the observed random set for a subject, D = (P(1), P(2), A) (where A = 1 if assigned to gabapentin, 0 if placebo). If we call the counterfactuals of interest, Y_d, it is not possible to observe counterfactuals of the type d = (a, 1, 0), so that there are 6 possible counterfactuals of interest to consider for defining parameters of interest.

Formally, we define the “full data” to be

$$X=\left\{W,Y_d(1),Y_d(2)\right\}~P_X;d\in \mathcal{D},$$

where W are the baseline covariates, Y_d(1), Y_d(2) are the 4-week and 8-week pain scores. Our our parameters of interest will be differences of the mean of the counterfactual 8-week pain scores based on the relevant set of rules, d, or simply E[Y_d(2)].

In reality, we only observe baseline covariates, random treatment assignment, and the resulting pain and perception processes. Thus, the observed data is (in the absence of missing data is):

$$O=\{W,A,P(1),Y(1),P(2),Y(2)\}=\{W,A,\overline{Y}(2),\overline{P}(2)\},$$

where the bar notation indicates history, or $\overline{Y}(t)\equiv (Y(u),u\le t)$. To accommodate missing data due to drop-out, which can occur before t = 1 or t = 2, the actual observed data becomes:

$$O=\{WA,C,\overline{Y}(C)\overline{P}(C)\}~P_0$$ (1)

where C is the time of drop-out. That is, we observe treatment and baseline covariates fully, and the perception and pain process up to the end of study or time C, whichever comes first. P₀ refers to the unknown true data-generating distribution.

3.2. Parameters of Interest

Analogous to our development in Jamshidian et al. (2012), we define the controlled direct effect of treatment (with the possible indirect effects through perception removed) using parameters:

$$\mathrm{\Psi }\left(d_1,d_0\right)\equiv E\left(Y_{d_1}-Y_{d_0}\right),$$ (2)

where we, for instance, compare the average final pain score of a population with universal application of treatment as compared to the same population with placebo, but for both experiments, now controlling perception at a fixed level, so $d_1=(0,\overline{p})$, $d_0=(1,\overline{p})$ (see Petersen et al. (2006)), for general definitions of direct effects). In general, we can examine different combinations of treatment and perception, or parameters of interest of the form comparing the mean outcomes of counterfactuals defined by different combinations of treatment assignment and longitudinal perception (side-effect) profiles.

As discussed in Jamshidian et al. (2012), we concentrate on controlled direct effects, rather than natural or pure direct effects, because (i) the estimate of the treatment effect at different set histories of perception, in particular at $\overline{p}=(0,0)$, is of primary interest, and (ii) the representation of the estimand of natural direct effect is a weighted average of the controlled direct effects across different set values of the intermediates as shown in Petersen and van der Laan (2008). Because this weighted average potentially obscures that the controlled direct effect could be different at different levels of the intermediate perception process (much like a summary odds ratio can obscure effect modification), we chose to report these different controlled direct effects rather than summarizing them as a specific weighted average. This also allows us to avoid making an extrapolation assumption necessary to interpret the final estimate as a direct effect estimate; see Tchetgen and VanderWeele (2012) and Zheng and van der Laan (2012) for further discussion of natural direct effects in longitudinal settings.

Defining the parameter of interest (2) as a function of only the data-generating distribution requires identifiability assumptions. First, one needs the longitudinal equivalent of no unmeasured confounding, sometimes called the sequential randomization assumption (SRA). This can be stated as a set of conditional independence assumptions, that themselves are implied by the appropriate (graphical) causal model. If the data, as represented in (1), is equivalent to a time ordering (so all variables have arrows into them from any variable in the past, with the possible exception that A is randomized and thus exogenous), then the additional assumption is simply that there are no unmeasured confounders. Let Parents(P(t)) be all parent nodes of P(t), then Figure 1, implies the following sequential randomization assumption (given that A is randomized):

$$Y_d(2)\perp P(t)\mid Parents(P(t))$$ (3)

In addition, Figure 1 also reflects the related time ordering assumption, or in this case, a patient’s pain measurement at some time point is not affected by his perception level after the pain measurement is recorded.

Figure 1:

Graph showing time-ordering for the gabapentin trial incorporating time of occurrence of treatment related side effects (all nodes presumed to have arrow into future nodes, with exception of W into A due to randomization)

Another necessary identifiability assumption concerns whether there is sufficient natural experimentation with regards to P(t) (for sub-groups of observations at each time point t, defined by the treatment, perception and pain history up to that point), so that the association of the outcome and P(t) within such sub-groups is possible. This is referred to as the “experimental treatment assignment” (ETA) or positivity assumption (Petersen et al., 2012). Specifically, for the parameters we discuss, the ETA is equivalent to:

$$0<P(P(t)=1\mid W,A,\overline{P}(t-1),\overline{Y}(t-1))<1,\text{for}t=1,2.$$

3.3. Semi-Parametric Estimation

3.3.1. G-computation

Various semi-parametric estimators have been suggested for estimation of causal effects under time dependent interventions, including inverse probability of treatment wighted estimators (IPTW; Robins (1999), Hernan et al. (2000), Robins (2000b)), Augmented IPTW (Robins and Rotnitzky (2001), Robins et al. (2000), Robins (2000a)), maximum likelihood (G-computation) estimators (Robins, 1986), and Targeted Maximum Likelihood Estimation (TMLE; van der Laan and Rubin (2006) and van der Laan and Rose (2011)). Here, we discuss two substitution estimators, (G-computation and the augmented TMLE version). Given the representation of the observed data (1) from the causal model described in Figure 1 in the gabapentin trial, the observed data likelihood is:

$$\begin{gathered} p(O)=P(A)P(W)\{\prod _{j=1}^{2}P[Y(j)\mid Parents(Y(j))]\}\{\prod _{j=1}^{2}P[P(j)\mid Parents(P(j))]\} \\ =P(A)P(W)\{\prod _{j=1}^2{Q}_{Y(j)}(Y(j)\mid \overline{P}(j),\overline{Y}(j-1),A,W)\} \\ *\{\prod _{j=1}^2{g}_{P(j)}(P(j)\mid \overline{Y}(j-1),\overline{P}(j-1),A,W)\}, \end{gathered}$$ (4)

where Q_{Y (j)} denotes the conditional distribution of Y (j), given parents of Y (j) in Figure 1 and g_P(j) denotes the conditional distribution of P(j), given the corresponding parents (note Y (0) is already included in W and P(0) is empty). Under SRA and positivity assumptions, we can define the rule-specific counterfactual distribution of interest via the so-called G-computation formula corresponding with intervention d = (a, p₁, p₂) as:

$$P^d(\overline{Y}=\overline{y},W=w)=\prod _{j=1}^2{Q}_{Y(j)}\left(Y(j)=y_j\mid P(j)={\overline{p}}_j,\overline{Y}(j-1)={\overline{y}}_{j-1},A=a,W=w\right)P(w),$$

where $\overline{y}=\left(y_1,y_2\right)$. This leads to the G-computation, substitutions estimator (Robins, 1986) which is derived by simulations from estimates of the ${\widehat{Q}}_{Y(j)}$, and the empirical distribution of W. For example, consider estimation the mean of the pain score at the end, for a scenario where everyone gets treatment, but no one experiences side-effects, that is, estimation of EY_d, d = (1, 0, 0). To do so, one would

1. obtain (regression) estimates ${\widehat{Q}}_{Y(1)}$, ${\widehat{Q}}_{Y(2)}$, (in our case, the intermediate pain score is binary, so that a regression model of Q_{Y (1)} defines the entire distribution, and we only need the predicted value, not the entire distribution, for the 8-week pain score, that is the predicted value from ${\widehat{Q}}_{Y(2)}$),

2. draw a large random sample with replacement from the empirical distribution of W,

3. draw a random sample of Y_d(1), using binary regression ${\widehat{Q}}_{Y(1)}(\cdot \mid P(1)=0,A=1,W)$ for each randomly drawn W, call these ${\widehat{Y}}_d(1)$,

4. derive the predictions, ${\widehat{Y}}_d(2)$, using ${\widehat{Q}}_{Y(2)}(\cdot \mid P(2)=0,Y_d(1)={\widehat{Y}}_d(1),P(1)=0,A=1,W)$,

5. average the ${\widehat{Y}}_d(2)$ across the randomly drawn W to get $\widehat{E}{Y}_d$, for the estimated mean pain score at 8-weeks had the population had treatment, but no side effects throughout the study.

Thus, the estimator is based on predictions derived from some regression estimator for the intermediate and final pain scores. Though any regression estimators could be used (from simple generalized linear models, to highly data adaptive procedures), theory exists to guide one on algorithms, which should have relative optimality with regards to some loss function (e.g., residual squared error). Specifically, each of the regressions (${\widehat{Q}}_{Y(1)}$ and ${\widehat{Q}}_{Y(2)}$), we used the so-called SuperLearning algorithm (van der Laan et al. (2007), chapter 3 in van der Laan and Rose (2011), and available as R package, Polley and van der Laan (2012)). The SuperLearner (SL) is defined in terms of a library of candidate estimators and it uses cross-validation (with non-negative least squares) to select a combination among these candidate estimators. The specific theorem, the Oracle Inequality, suggests that the SL estimator will asymptotically do as well (with regards to the expected loss, or risk) the so-called Oracle estimator (an algorithm based on knowing the true statistical model, and choosing the candidate that has smallest risk). The specific conditions of the theorem also suggest that that many algorithms should be tried, and because we wanted to allow for a broad range of functional forms for these regressions, we included both very parametric models (simple linear regressions) as well as very flexible, potentially arbitrary functional forms (e.g., neural nets). Thus, if one can do no better than a very smooth, simple model, we still attain good rates of convergence, whereas we are able to cover a very broad range of models, when, given the variance-bias trade-off, the best fitting model is quite complicated and “rough”.

3.3.2. Targeted Maximum Likelihood Estimation (TMLE)

Targeted Maximum Likelihood estimator is a two stage estimator that augments the estimated models that comprise the G-computation algorithm discussed above, which results in a targeted (to the parameter of interest) bias-reduction step, which will remove residual bias relative to the G-computation estimator if the treatment (censoring) mechanism can be estimated consistently (van der Laan and Rose, 2011). The estimation strategy reported here involves a clever representation of the parameter of interest, as desribed in van der Laan and Gruber (2011), one can use the iterative conditional expectation rule (tower rule), to represent E[Y_d] as an iterative conditional expectation. Thus, one virtue of the this TMLE approach is that it requires no density estimation (from which one could simulated random variables), for instance, intermediate pain nodes, and only on a set of sequential mean regressions.

• choose the treatment/perception rule of interest, say $d=(a,\overline{p})$, using the same example as above, or d = (1, 0, 0),

• estimate using the SL algorithm the model of the mean of the outcome given the past, which, in a slight abuse of notation, we will refer to as Q_{Y (2)}(p(2), y(1), p(1), a, w) ≡ E(Y (2) | (P(2) = p(2), Y (1) = y (1), P(1) = p(1),A = a, W = w).

• Predict the outcome for each observation, based on the desired time-dependent intervention, and the observed history of covariates, or get predictions for each observation from ${\widehat{Q}}_{Y(2)}(0,Y(1),0,1,W)$, say $Y_d^{*}(2)$ to distinguish it from predictions of counterfactual, ${\widehat{Y}}_d(2)$, discussed above.

• Regress (again using SL) $Y_d^{*}(2)$ against P(1), A, W for each observation to obtain an estimate of $Q_{Y(1)}^d(P(1),A,W)\equiv E(Y_d^{*}(2)\mid P(1),A,W)$. Use this model to predict again for each observation conditional on the desired rule, d, so in this case, A = 1, P(1) = 0, or ${\widehat{Q}}_{Y(1)}^d(0,1,W)$.

• Average these predictions, to get an estimate of mean of interest, or

$$\widehat{E}\left[Y_d\right]=\widehat{E}\left[Y_{(1,0,0)}\right]=\frac{1}{n}\sum _{i=1}^n{\widehat{Q}}_{Y(1)}^d\left(0,1,W_i\right).$$

This serves as the basis of an initial substitution estimator (and alternative to that described in the previous section). One can think of TMLE as a bias-reduction step, based on the fact that the loss-based estimation for estimating the data-generating distribution was for the individual regressions, not based on minimizing the expected loss w.r.t. the parameter of interest. The mechanics involve augmenting the initial fits of the regressions (in our case, ${\widehat{Q}}_{Y(2)}$, $Q_{Y(1)}^d$) by so-called clever covariates. The technical motivation for the form of these covariates is derived from attempting to minimize the sampling variability of the estimates of the relevant treatment/perception specific means in a semiparametric model, but can be heuristically justified in several related ways, including increased robustness to model misspecification, reduced residual confounding. The augmented, or updated models, are done in the same iterative algorithm as described above, or:

• linear regression of Y on covariate $I(A=a,\overline{P}=\overline{p})/g_{n;2}$,

  $$g_{n;J}=P_n(A)\prod ^J{\widehat{g}}_{P(j)}\left(P_j\mid \overline{Y}(j-1),\overline{P}(j-1),A,W\right),$$

  (where P_n refers to empirical distribution) treating the initial fit, ${\widehat{Q}}_{Y(2)}$ as an offset. This yields the TMLE ${\widehat{Q}}_{*Y(2)}$ of the last component. For estimating g_P(j), we used simple main terms logistic regression of the perception outcome at time j versus covariates (past perception, treatment, and baseline covariates),

• use this augmented model, as described above, to derive predictions, $Y_d^{*}(2)$.

• regression of $Y_d^{*}(2)$ on clever covariate, I(A = a, P(1) = p₁)/g_n;1 with the initial estimate ${\widehat{Q}}_{Y(1)}^d$ treated as an offset, resulting in the TMLE estimate of this second component, ${{\widehat{Q}}^{*}}_{Y(1)}^d$,

• derive the TMLE estimate as a simple average, or

$${\widehat{E}}^{*}\left[Y_d\right]={\widehat{E}}^{*}\left[Y_{(1,0,0)}\right]=\frac{1}{n}\sum _{i=1}^n{{\widehat{Q}}^{*}}_{Y(1)}^d(0,1,W_i)$$

One the important virtues of TMLE over the initial substitution estimator is that it reduces bias due to the fact that the original statistical models are chosen based on minimizing expected loss with regards to prediction of the outcomes (intermediate and final), and not with regards to minimizing the mean-squared-error of the estimate of the parameter of interest. Informally, the addition of the clever covariate can help to reduce any residual confounding in the original data-adaptive, SL fits of the pain prediction models. Relatedly, the TMLE estimate is consistent if either the Q or g models are consistently estimated, which defines the estimator as doubly-robust, and if they both are consistent, then the estimator is semi-parametrically (locally) efficient. Finally, the TMLE can be thought of a smoothing of the original substation estimator, and thus can have more predictable sampling distributional properties; it is an asymptotically linear estimator with a known influence function, and this can be used to derive robust asymptotic inference (see appendix in van der Laan and Rose (2011)).

4. Data Analysis

The data analysis was performed with the R statistical package for longitudinal TMLE (ltmle; Schwabb et al. (2012)), that provides three substitution estimators: one (naive) based on no adjustment for baseline covariates, one based on G-computation (G-comp), and one based on the augmented TMLE substitution estimator. For the estimation of the Q^Y(j), the library of learners used was generalized linear models, stepwise regression with only main effect terms based on AIC (stepAIC; Venables and Ripley (2002)) and the same procedure with all two-way multiplicative interaction terms, Bayesian glm (bayesglm; Gelman et al. (2012)), and neural nets, (nnet; Venables and Ripley (2002)). This library provides a very large, flexible statistical model. The g_A,P(t), used in the clever covariates was estimated with main terms logistic regression on covariates representing past (t−) treatment, perception and baseline covariates: average baseline sleep score, gender, race, age, height, weight, and average baseline pain score. Finally, the inference provided is based on the influence curve of the estimator (van der Laan and Gruber (2011)). It is important to note that for some rules, d, the number of observations following the rules was small (for d = (0, 1, 1), n = 7; d = (1, 0, 1), n = 6) and so the inference provided for parameters involving these patterns should be interpreted with great caution. Obviously, this problem becomes even worse if one were to use even finer time increments to define perception patterns within this study.

4.1. Results

The estimates of the treatment specific means, E[Y_d], for two of the perception patterns underlying our comparisons of interest are shown in Table 1, with the corresponding (nonaugmented) G-computation estimator, as well as the naive estimator, simply an average of the outcome in groups defined by the observed rule they followed, or averages of the Y (2) with groups defined by their observed rule, D = (A, P(1), P(2)); confidence intervals are provided only for the TMLE estimates. Results suggest similar mean pain scores for each combination of treatment and perception pattern, with the notable exception for a (counterfactual) population that are assigned treatment and also perceive that they have treatment (that is, report treatment related side-effects) at both time points t = 1, 2. The group that are unmasked at t = 1 are simply those individuals who experience treatment related side effects during the first three weeks of the trial and they are estimated to have significantly lower primary pain outcomes at the end of the trial. This is also reflected in the comparisons listed in Table 2 (that derive from these estimated treatment/perception specific means).

Table 1:

TMLE, G-computation, and Naive (unadjusted) estimates of treatment specific means

	TMLE	(95%CI)	G-comp	Naive
E(Y0,0,0)	4.75	(4.28, 5.22)	4.54	4.71
E(Y1,0,0)	4.43	(3.82, 5.05)	4.27	4.32
E(Y0,1,1)	4.80	(3.84, 5.77)	4.18	4.47
E(Y1,1,1)	3.02	(2.19, 3.85)	3.80	3.08
E(Y1,0,1)	1.25	(0.44, 2.07)	4.13	2.21

Table 2:

TMLE estimates of comparisons of various treatment/perception interventions

	TMLE	p-value	(95%CI)
E (Y0,0,0 − Y1,0,0)	0.32	0.43	(−0.46, 1.09)
E (Y0,1,1 − Y1,1,1)	1.78	0.01	( 0.51, 3.06)
E (Y0,0,0 − Y0,1,1)	−0.05	0.92	(−1.13, 1.02)
E (Y1,0,0 − Y1,1,1)	1.42	0.01	( 0.38, 2.45)
E (Y0,0,0 − Y1,0,0)	−1.76	0.003	( 0.60, 2.93)

The estimate of the difference in mean pain scores had no treatment related side effects occurred, comparing the treated to untreated (in Table 2), was only 0.32 points (on a 0–10 scale) with p=0.43. In other words, had no one experienced any treatment related side effects, the treatment effect is not statistically significantly different from 0. This is the causal treatment effect that the trial was designed to estimate. Conversely, the suggested reduction in mean pain score if everyone experienced treatment related side effects (i.e., all patients perceived they were on treatment) for both intermediate time points, is 1.78 (p = 0.01). We can also consider effects of differing perception patterns pattern, by considering rows in Table 2 where treatment is held constant. For example, if treatment is placebo, the estimated difference in average final pain scores between a population who experience no treatment related side effects (masking is maintained throughout) and a population who are unmasked early (both P(1) and P(2) set to 1) is −0.05 with p = 0.92. There thus appears to be no “perception” effect amongst a placebo population. The opposite is true for a population provided treatment where the same perception effect showed a significant reduction in average final pain score (estimated as 1.42, with p = 0.01).

In comparing the three estimators (G-computation without the bias-reduction step, a naive estimator assuming no confounding, and TMLE), we observe a sizable impact on the estimated treatment specific means as a consequence of the TMLE bias reduction step. This is most profound when comparing both the estimates of E(Y_1,1,1) and E(Y_0,1,1) in Table 1, where the TMLE estimate of the treatment impact (if unmasking is assumed throughout) is 1.78, much larger for the corresponding G-computation estimate of 4.18 – 3.89 = 0.29.

Interestingly, the smallest mean pain score appears to result from later reporting of side effects when in treatment group $(\widehat{E}\left(Y_{1,0,1}\right)=1.25)$, with a statistically significant reduced pain score from those that report earlier side effects $(\widehat{E}\left(Y_{1,0,1}-Y_{1,1,1}\right)=1.76,p=0.003)$. However, this should be interpreted with great caution given very few subjects had P(1) = 0, P(2) = 1 in the treatment arm (only 6). Though the equivalent comparison in the placebo group (not shown) had an estimate in the opposite direction (later reporting of symptoms resulted in higher average pain score at 8 weeks), the sample size of placebo subjects with P(1) = 0, P(2) = 1 was only 3, so obviously no meaningful conclusions can be made from this comparison.

Finally, for convenience, Table 3 reproduces analogous results from Jamshidian et al. (2012) that ignored the timing of the occurrence of treatment related side effects. Here, perception is defined as a single variable so that perception patterns of (0, 1) and (1, 1) are reduced to a single value P = 1 with perception (0, 0) simple P = 0. Comparing Tables 2 and 3, the results are very similar, suggesting that a more refined timing of perception as it relates to changing pain scores does not significantly change the conclusions made in our original paper, and serves to address an issue raised by Shrier (2012); see our response anticipating this paper (Jewell et al., 2012). The most relevant change is that the desired estimate of the causal treatment effect in a world where there is no unmasking is moved somewhat closer to zero (from 0.78 to 0.32), and is consequently even less significant from both a statistical and clinical point of view. From this perspective, the more nuanced consideration of the impact of time dependent occurrence of treatment related side effects is important as compared to the more static view considered in Jamshidian et al. (2012).

Table 3:

TMLE Estimates of effects of simultaneous treatment/perception interventions in original cross-section analysis, (Jamshidian et al., 2012)

	TMLE	p-value	(95%CI)
E(Y0,0 − Y1,0)	0.78	0.18	(−0.35, 1.91)
E(Y0,1 − Y1,1)	1.98	0.04	( 0.04, 3.91)
E(Y0,0 − Y0,1)	−0.07	0.93	(−1.64, 1.50)
E(Y1,1 − Y1,1)	1.12	0.07	(−0.09, 2.32)

5. Discussion

Using an intention-to-treat analysis, Backonja et al. (1998) reported a significantly lower (1.2 points, p = 0.001) average pain score for the gabapentin group as compared to placebo. Additionally, if patients who reported dizziness were excluded from the analysis, the estimated mean difference in pain scores between the treatment and placebo groups remained almost the same (1.19 points, p = 0.002). Separately, after excluding patients who experienced somnolence, the magnitude of the treatment effect decreased to 0.81, but the difference remained statistically significant (p = 0.03). Dizziness and somnolence were the two most frequently reported treatment related side effects. This analysis necessarily ignores confounding effects of covariates that are both related to the risk of a treatment related side effect and the final pain outcome, and does not deal with the two treatment side effects (and other less frequent) simultaneously.

However, treating the gabapentin trial as a cross-sectional study, Jamshidian et al. (2012) found different results from those obtained by Backonja et al. (1998) (see Table 3). Specifically, the treatment effect on average final pain scores was estimated to be reduced to 0.78 for a population where no unmasking occurred. This is further reduced here in a more complex longitudinal analysis to 0.32 and both of these results fail to achieve statistical significant differences from the null. There thus only appears to be any form of comparative effect for gabapentin patients who suffered treatment related side effects. As argued in Jamshidian et al. (2012), the data does not allow the separation of effects of potential unmasking from those of treatment efficacy. That is, it can be argued that the treatment is having a stronger effect on exactly those patients who experience treatment related side effects in the treatment arm (but are thus potentially unmasked with regard to their treatment assignment). This phenomenon is referred to as Philip’s paradox (Ney et al., 1986). The argument for a stronger treatment effect may be more reasonable for patients who experience side effects earlier in the trial during the titration period as the investigators try to find the maximum tolerable dosage. Yet, any treatment related side effects in the placebo arm cannot be definitively attributed to the active component and are plausibly due to the patient’s changing perception regarding his treatment. The last row of Table 2 (comparing, among the treatment group, those with early versus later reporting of first side-effect) possibly suggest the impact of unmasking rather than a true treatment effect causing side effects, although we have noted the small sample sizes underlying our estimates here. For further discussion of these topics, see Howick (2011) (especially Chapter 6).

In order to tease the chicken-vs-egg ordering of whether side-effects precede efficacy or efficacy precedes side-effects, one could argue for an analysis where the data of pain measurement and those of side-effects is done on an even finer scale, say weekly, or even daily. However, there is a trade-off, as was obvious even here. As the number of time points of monitoring (or analysis) increase, so do the number of potential patterns observed, and also thus the required sample size necessary to make strong inferences about how these longitudinal patterns affect pain score at the end of the trial (at least without assuming identical regression models for such effects which seems implausible even in our two time point analysis). As mentioned in the Results section, we could not meaningfully estimate the effect of late versus early first reported side-effects among the placebo group due to small cell sizes.

In the cross-sectional analysis we noted that using treatment related side effects as a proxy for a patient’s perception regarding treatment assignment results in an asymmetry in the analysis of the gabapentin trial (Jamshidian et al., 2012). Our analysis does not account for the possibility of a patient’s perception switching to placebo at a specific time point during the course of the trial. It is plausible that a patient may start believing that they are on placebo due to lack of efficacy of the administered treatment, biasing the patient’s subjective pain score upward. Depending on the treatment arm which the patient belongs to, this bias might result in either an increase or decrease in the estimated treatment effect. Unfortunately, it is impossible to determine the size of this bias in case of the gabapentin trial without additional information.

Issues with using side effects as a proxy for perception and Philip’s paradox highlight challenges for blinded comparative trials and suggest the possibility of collecting data (possibly longitudinally) on patients’ perception regarding their treatment in randomized clinical trials; the methods described here provide a methodology to use such data in estimating causal treatment effects that are not influenced by perception. In 2003, the Food and Drug Administration (FDA) noted that treatment related side effects have the potential to unmask subjects and investigators, and may bias subjective study end points (Office of Therapeutics). It should be noted, however, that questioning patients on their perception regarding their treatment arm during a trial might also affect their perception itself. For instance, patients who have no knowledge of their treatment assignment might reevaluate and change their perception if they are continuously asked to identify their treatment group.

Research and Review, Center for Biologics Evaluation and Research (FDA 2003) recommended that a questionnaire be administered at the completion of the study to investigate the effectiveness of blinding of the subjects and the investigators (Bang et al., 2010). In a home drinking water intervention trial for estimating rates of highly credible gastrointestinal illness, Colford et al. (2002) assessed whether participants could be successfully blinded to a sham or active water treatment device installed underneath the kitchen sink. They administered a questionnaire every 2 weeks for a 4 month period, and the participants were asked to rate their degree of certainty regarding having the active device. Blinding of the participants was assessed using a blinding index, and the investigators concluded that the participants were successfully blinded to their treatment assignment. James et al. (1996), Howard et al. (1982), and Bang et al. (2004) have introduced different indices for the degree of blinding in clinical trials. Although these indices tell the investigators whether blinding has been effective or not, they do not directly explore the effect of unmasking on the outcome of interest. In any case, these different measures could be incorporated into an analysis such as we present here, where explicit definitions of appropriate treatment effects are made in a counterfactual framework, and then estimated using these (locally) efficient, targeted maximum likelihood estimators.