Sample size estimation for modified Poisson analysis of cluster randomized trials with a binary outcome

Abstract

The modified Poisson regression coupled with a robust sandwich variance has become a viable alternative to log-binomial regression for estimating the marginal relative risk in cluster randomized trials. However, a corresponding sample size formula for relative risk regression via the modified Poisson model is currently not available for cluster randomized trials. Through analytical derivations, we show that there is no loss of asymptotic efficiency for estimating the marginal relative risk via the modified Poisson regression relative to the log-binomial regression. This finding holds both under the independence working correlation and under the exchangeable working correlation provided a simple modification is used to obtain the consistent intraclass correlation coefficient estimate. Therefore, the sample size formulas developed for log-binomial regression naturally apply to the modified Poisson regression in cluster randomized trials. We further extend the sample size formulas to accommodate variable cluster sizes. An extensive Monte Carlo simulation study is carried out to validate the proposed formulas. We find that the proposed formulas have satisfactory performance across a range of cluster size variability, as long as suitable finite-sample corrections are applied to the sandwich variance estimator and the number of clusters is at least 10. Our findings also suggest that the sample size estimate under the exchangeable working correlation is more robust to cluster size variability, and recommend the use of an exchangeable working correlation over an independence working correlation for both design and analysis. The proposed sample size formulas are illustrated using the Stop Colorectal Cancer (STOP CRC) trial.

1. Introduction

Cluster randomized trials (CRTs), or sometimes called group randomized trials, allocate entire groups of participants to interventions.^1,2 These trials have been frequently used in public health, epidemiology and medicine. Methods for the design and analysis of CRTs have been developed over the past few decades, and these developments were summarized in a pair of recent review articles.^3,4 Compared to individually randomized trials (IRTs), an important feature of CRTs is that observations taken from individual participants within the same cluster are often correlated, and therefore the intraclass correlation coefficient (ICC) must be accounted for in both the sample size calculation and the analysis.⁵ The ICC measures the degree of similarity between outcomes measured among participants in the same cluster and reflects extra variation attributed to each cluster. This extra variation inflates the required number of participants in an IRT to achieve a desired level of statistical power.

Binary outcomes are commonly reported in CRTs, especially in pragmatic trials that involve an implementation primary endpoint. For example, the Stop Colorectal Cancer (STOP CRC) trial is a pragmatic trial that randomizes 26 federally qualified health clinics to either active intervention designed to increase colorectal cancer screening or the usual care.⁶ The primary endpoint is the completion status of fecal immunochemical test (FIT) within one year since study initiation, and is a binary outcome measured at the participant level.⁷ Typical effect measures of binary outcomes are on the relative scale and include relative risk (or risk ratio) and odds ratio. While the odds ratio is commonly used perhaps due to its intrinsic connection to the canonical logistic regression, it is often misinterpreted as the relative risk and could over-state the magnitude of relative risk when the outcome is not rare.^8–10 There is also a consensus in the epidemiologic literature that relative risk is more interpretable and is preferred over odds ratio for most prospective studies.^11,12 For these reasons, relative risk regression has received increasing attention for analyzing binary data,¹³ and was recently extended to the analysis of CRTs.¹⁴

Although the log-binomial model is a natural choice for direct regression analysis of the relative risk, such a model could fail to report an estimate due to non-convergence.^15,16 In contrast, the modified Poisson regression uses the working Poisson variance to circumvent this convergence issue, and serves as a practical alternative to estimate the relative risk.¹³ The modified Poisson regression, proposed in Zou and Donner,¹⁴ further uses the robust sandwich variance to adjust for clustering as well as variance function misspecification. In the context of clustered binary outcomes, empirical simulation studies such as those in Zou and Donner¹⁴ and Yellend et al.¹⁷ indicate that the modified Poisson regression has adequate performance in terms of the type I error rate and coverage even with a limited number of clusters, as long as suitable finite-sample bias-corrections are applied to the sandwich variance estimator. Although the modified Poisson model has been suggested as a promising analytical approach for CRTs, the sample size requirement under such models remains unclear. In particular, the efficiency implication of misspecifying the variance function has not been formally explored, and a corresponding sample size formula for relative risk regression via the modified Poisson regression in CRTs is currently not available. Through an analytical exploration, we establish the asymptotic equivalence between the modified Poisson analysis and the log-binomial analysis of CRTs when the marginal mean model includes only the intervention indicator, and develop suitable sample size procedures for analyzing marginal relative risk in CRTs based on the method of generalized estimating equations (GEE).¹⁸

The remainder of this article is organized as follows. Section 2 briefly reviews the sample size equation for IRTs, introduces the modified Poisson regression in the context of CRTs, and develops corresponding closed-form sample size formulas accounting for both clustering and variable cluster sizes. A simulation study is carried out in Section 3 to investigate the accuracy of the proposed sample size formulas for relative risk regression in CRTs. In Section 4, we illustrate the proposed formulas using the STOP CRC pragmatic CRTs. Section 5 offers concluding remarks.

2. Statistical methods

2.1. Sample size formula for IRTs

To help clarify the key difference between sample size methods developed for IRTs and CRTs, we first briefly review the existing formula developed for IRTs. We focus on the relative risk as the effect measure. Assuming a two-arm IRT with πN patients (0 < π < 1) and (1 − π)N patients randomized to intervention and control, Blackwelder¹⁹ developed a normality-based sample size equation

$$N=\frac{{\left(z_{{ϵ}_1/2}+z_{{ϵ}_2}\right)}^2{\lambda }^2}{{\Delta }^2}$$ (1)

where Δ = logP₁ − logP₀ is the effect size on the log relative risk scale, P₁ and P₀ are the expected prevalence of outcome in the intervention and control groups, z_q is the qth quantile of the standard normal distribution, ϵ₁ and ϵ₂ are the nominal type I and type II error rates, and

$${\lambda }^2=\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}$$ (2)

Under equal randomization with π = 1/2, formula (1) becomes the special case introduced in Lemeshow et al.²⁰ While this formula is widely used in IRTs, it is inappropriate for designing CRTs as it has not accounted for the ICC. It is well known that failure to account for ICC will result in an unrealistically small sample size for CRTs and therefore lead to an underpowered study.^1,21,22

2.2. Modified Poisson analysis of CRTs

We now consider a parallel CRT with n clusters, where nπ clusters are randomized to intervention and the remaining n(1 − π) clusters to the usual care. Let Y_ij represent the binary outcome for participant j (j = 1, …, m_i) in cluster i (i = 1, …, n). The cluster sizes m_i are allowed to be variable, and the total sample size $N={\sum }_{i=1}^n{m}_i$. Write μ_ij = E(Y_ij) as the marginal mean, and the following log-linear model is often used to estimate the relative risk in a CRT

$$\text{log}\left({\mu }_{ij}\right)={\beta }_0+{\beta }_1{X}_i$$ (3)

where X_i = 1 indicates that cluster i receives intervention and X_i = 0 otherwise, β₀ is the grand mean, and β₁ is the marginal log relative risk parameter of interest. Write θ = (β₀, β₁)′, A_i = diag(ν_i1, …, ν_imi) where ν_ij is a working variance function, and R_i(α) is the common working correlation structure indexed by parameter α, and one could solve the following GEE to estimate θ

$$\sum _{i=1}^n{D}_i^{\prime }{A}_i^{-1/2}{R}_i^{-1}(\alpha )A_i^{-1/2}\left(Y_i-{\mu }_i\right)=0$$ (4)

where $Y_i={\left(Y_{i1},\dots ,Y_{i{m}_i}\right)}^{\prime }$ is the collection of outcomes in cluster i, ${\mu }_i={\left({\mu }_{i1},\dots ,{\mu }_{i{m}_i}\right)}^{\prime }$, and D_i = ∂μ_i/∂θ′ = (1, X_i) ⊗ μ_i. In CRTs, two typical choices of working correlation structure R_i(α) are the independence and exchangeable structure. The former assumes that $R_i(\alpha )=I_{m_i}$, i.e. the m_i × m_i identity matrix, while the latter assumes $R_i(\alpha )=(1-\alpha )I_{m_i}+\alpha J_{m_i}$ with $J_{m_i}$ defined as the m_i × m_i matrix of ones and α defined as the common ICC. These two working correlation structures are implemented in standard statistical software for fitting GEE models, such as the gee or geeglm package in R, PROC GENMOD or PROC GLIMMIX in SAS and xtgee module in Stata.

When the working variance function is correctly specified as the binomial variance function ν_ij = μ_ij(1 − μ_ij), model (3) is referred to as the log-binomial model with the estimating equations given by equation (4). Although this binomial variance function is a natural choice for binary data, the log-binomial regression frequently results in non-convergence, rendering this approach less attractive. Of note, an alternative approach to marginal model (3) is a log-binomial mixed-effects model, which similarly estimates the marginal relative risk due to collapsibility. However, the log-binomial mixed-effects model is also prone to non-convergence, especially with the addition of the random cluster effect. Zou et al.¹⁴ proposed the modified Poisson regression in the GEE framework for estimating relative risk that bypasses the convergence problem. The modified Poisson regression assumes the Poisson variance function ν_ij = μ_ij, under which case the estimating equation (4) can be further simplified. For example, under the independence working correlation, equation (4) becomes

$$\sum _{i=1}^n\left(\begin{array}{c}1\\ X_i\end{array}\right)\sum _{j=1}^{m_i}\left(Y_{ij}-{\mu }_{ij}\right)=0$$ (5)

Further, under the exchangeable working correlation, equation (4) becomes

$$\sum _{i=1}^n\left(\begin{array}{c}1\\ X_i\end{array}\right)\sum _{j=1}^{m_i}\frac{Y_{ij}-{\mu }_{ij}}{1+\left(m_i-1\right)\alpha }=0$$ (6)

In the latter case, the estimation of θ and α proceeds via a modified Fisher-scoring algorithm, and α is estimated by the all-available-pairs estimator by Liang and Zeger¹⁸

$$\widehat{\alpha }=\frac{{\sum }_{i=1}^n{\sum }_{j>j^{\prime }}\left(Y_{ij}-{\widehat{\mu }}_{ij}\right)\left(Y_{ij}-{\widehat{\mu }}_{i{j}^{\prime }}\right)/\sqrt{{\widehat{\mu }}_{ij}{\widehat{\mu }}_{i{j}^{\prime }}}}{{\sum }_{i=1}^n{m}_i\left(m_i-1\right)/2-2}$$ (7)

In the special case when the cluster sizes are all equal and m_i = m, it is easy to see that equations (5) and (6) become identical for solving θ, and therefore the point estimates for the marginal relative risk are numerically equivalent under either one of these two working correlation structures.

To simultaneously account for clustering and variance function misspecification, Zou et al.¹⁴ suggested using the robust sandwich variance to quantify the uncertainty of the GEE estimator $\widehat{\theta }$. Specifically, with a large number of clusters (usually n larger than 40), the variance of $\widehat{\theta }$ can be consistently estimated by ${\widehat{\Sigma }}_1^{-1}{\widehat{\Sigma }}_0{\widehat{\Sigma }}_1^{-1}$, where ${\widehat{\Sigma }}_1^{-1}={\left({\sum }_{i=1}^n{\widehat{D}}_i^{\prime }{\widehat{A}}_i^{-1/2}{R}_i^{-1}(\widehat{\alpha }){\widehat{A}}_i^{-1/2}{\widehat{D}}_i\right)}^{-1}$ is the model-based variance, and

$${\widehat{\Sigma }}_0=\sum _{i=1}^n{\widehat{D}}_i^{\prime }{\widehat{A}}_i^{-1/2}{R}_i^{-1}(\widehat{\alpha }){\widehat{A}}_i^{-1/2}\text{c}\widehat{\text{o}}\text{v}\left(Y_i\right){\widehat{A}}_i^{-1/2}{R}_i^{-1}(\widehat{\alpha }){\widehat{A}}_i^{-1/2}{\widehat{D}}_i$$ (8)

where $\text{c}\widehat{\text{o}}\text{v}\left(Y_i\right)=\left(Y_i-{\widehat{\mu }}_i\right){\left(Y_i-{\widehat{\mu }}_i\right)}^{\prime }$, and all components are evaluated at $\widehat{\theta }$ and $\widehat{\alpha }$. With a small number of clusters, the sandwich variance estimator tends to be biased towards zero, and so inflates the type I error rate of the test. To maintain the test size, finite-sample adjustments to the sandwich variance estimator such as those developed in Mancl and DeRouen,²³ Kauermann and Carroll,²⁴ and Fay and Graubard²⁵ could be considered in conjunction with the t-test with n − 2 degrees of freedom (the between-within degree of freedom²⁶). Explicit expressions of these bias-corrected sandwich variance estimators are provided in Section 3.1. Yelland et al.¹⁷ have demonstrated the adequacy of the bias-corrected sandwich variance estimators for modified Poisson analysis of clustered data in simulation studies with a small number of clusters. The t-test with such bias-corrected variance estimators has also been considered in GEE analysis of alternative cluster randomized designs and has demonstrated good finite-sample properties across a wide range of scenarios.^27–30

To summarize, the modified Poisson regression and the log-binomial regression assume the same marginal mean model. However, while the log-binomial regression assumes the binomial variance function in the GEE, the modified Poisson regression assumes a Poisson working variance function in the GEE to avoid convergence issues. Because the log-binomial model assumes the correct variance function, when the correlation model is also correctly specified, valid inference can proceed with the model-based variance. In contrast, because the Poisson working variance is misspecified for binary outcomes, inference under the modified Poisson regression should always use the robust sandwich variance estimator, regardless of the specification of the working correlation model.¹⁴

2.3. Sample size estimation based on modified Poisson analysis

For the general set up of sample size requirements, one would specify the hypothesis of interest as H₀ : β₁ = 0 versus H₁ : β₁ = Δ, when Δ is the effect size expressed in log relative risk. Given the pre-specified type I error rate ϵ₁, and type II error rate ϵ₂, the general sample size requirement based on a t-test is given by

$$n\ge \frac{{\left(t_{n-2,{ϵ}_1/2}+t_{n-2,{ϵ}_2}\right)}^2{\sigma }^2}{{\Delta }^2}$$ (9)

where t_n−2,q is the qth quantile of the t distribution with n − 2 degree of freedom, and ${\sigma }^2=n\text{var}\left({\widehat{\beta }}_1\right)$ is the asymptotic variance of the GEE estimator for β₁. We choose the t-test over the z-test because the former provides better control of empirical type I error rates in CRTs especially when the number of clusters n is not large.³¹ Operationally, a closed-form sample size formula thus critically depends on the expression of the variance σ².

With the knowledge of the potential variable cluster sizes m_i, we follow the approach outlined in Pan³² to derive the explicit form of σ² for the modified Poisson regression analysis. Denote $1_{m_i}$ as the m_i × 1 vector of ones, and R_i = R_i(α) is the working correlation, and we have

$${\Sigma }_1^{-1}={\left(\sum _{i=1}^n{\widehat{D}}_i^{\prime }{A}_i^{-1/2}{R}_i^{-1}{A}_i^{-1/2}{D}_i\right)}^{-1}={\left(\sum _{i=1}^n{1}_{m_i}^{\prime }{R}_i^{-1}{1}_{m_i}\right)}^{-1}{M}^{-1}$$ (10)

where

$$M^{-1}=\frac{1}{(1-\pi )P_0}\left(\begin{array}{cc}1& -1\\ -1& 1+\{(1-\pi )/\pi \}\left(P_0/P_1\right)\end{array}\right)$$

and $P_0=e^{{\beta }_0},P_1=e^{{\beta }_0+{\beta }_1}$ are the prevalence in the control and treatment arms, respectively. In addition, assume $R_i^{*}$ is the true correlation structure common to all clusters, and we have

$${\Sigma }_0=\sum _{i=1}^n{\widehat{D}}_i^{\prime }{A}_i^{-1/2}{R}_i^{-1}{A}_i^{-1/2}\text{cov}\left(Y_i\right)A_i^{-1/2}{R}_i^{-1}{A}_i^{-1/2}{D}_i=\left(\sum _{i=1}^n{1}_{m_i}^{\prime }{R}_i^{-1}{R}_i^{*}{R}_i^{-1}{1}_{m_i}\right)G$$ (11)

where $\text{cov}\left(Y_i\right)=A_i^{*,1/2}{R}_i^{*}{A}_i^{*,1/2},A_i^{*}=\text{diag}\left({\mu }_{i1}\left(1-{\mu }_{i1}\right),\dots ,{\mu }_{i{m}_i}\left(1-{\mu }_{i{m}_i}\right)\right)$ is the true variance structure, and hence

$$G=\left(\begin{array}{cc}\pi P_1\left(1-P_1\right)+(1-\pi )P_0\left(1-P_0\right)& \pi P_1\left(1-P_1\right)\\ \pi P_1\left(1-P_1\right)& \pi P_1\left(1-P_1\right)\end{array}\right)$$

These expressions allow us to obtain

$${\sigma }^2=\frac{n{\sum }_{i=1}^n{1}_{m_i}^{\prime }{R}_i^{-1}{R}_i^{*}{R}_i^{-1}{1}_{m_i}}{{\left({\sum }_{i=1}^n{1}_{m_i}^{\prime }{R}_i^{-1}{1}_{m_i}\right)}^2}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}$$ (12)

Throughout, we assume that the true correlation model is exchangeable with a common ICC parameter ρ. This is a typical assumption used in parallel CRTs,⁴ and under this assumption, the true correlation model is written as $R_i^{*}=(1-\rho )I_{m_i}+\rho J_{m_i}$. It is then straightforward to show that when the working correlation has the independence structure, we have

$${\sigma }_{\text{indep }}^2=\frac{n{\sum }_{i=1}^n{m}_i\left\{1+\left(m_i-1\right)\rho \right\}}{{\left({\sum }_{i=1}^n{m}_i\right)}^2}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}$$ (13)

After some algebra, we can also show that when the working correlation has the exchangeable structure

$${\sigma }_{\text{exch }}^2=\frac{n{\sum }_{i=1}^n{m}_i\left\{1+\left(m_i-1\right)\rho \right\}/{\left\{1+\left(m_i-1\right)\alpha \right\}}^2}{{\left({\sum }_{i=1}^n{m}_i/\left\{1+\left(m_i-1\right)\alpha \right\}\right)}^2}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}$$ (14)

In the special case when the cluster sizes are all equal such that m_i = m for all i, both variances simplify to

$${\sigma }_{\text{indep }}^2={\sigma }_{\text{exch }}^2=\frac{1+(m-1)\rho }{m}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}$$ (15)

which indicates that using an independence working structure does not lead to efficiency loss in estimating the relative risk with the modified Poisson regression. This finding is consistent with that of Pan³² for logistic GEE, and in fact analytically explain the simulation results of Zou and Donner,¹⁴ who showed almost identical finite-sample efficiency using these two working correlations when the cluster sizes vary only within a small range, i.e. Uniform(5, 10). Equation (15) also clearly explains the role of the ICC parameter in designing CRTs compared to designing IRTs. Because $m{\sigma }_{\text{indep }}^2=m{\sigma }_{\text{exch }}^2=\{1+(m-1)\rho \}{\lambda }^2$, where λ² is the variance parameter defined in Section 2.1 for IRTs, the factor {1 + (m − 1)ρ} is known as the design effect that inflates the variance of log relative risk due to cluster randomization.^1,5 The design effect increases when either the cluster size m or the ICC ρ increases. This connection suggests that, with equal cluster sizes, one could compute the sample size in a CRT by first using the formula developed under individual randomization, and then inflating the estimate by the usual design effect.

In the case when cluster sizes are known a priori, sample size estimation can proceed by combining equations (9) with equation (13) or (14). However, a particular issue with using variance expression (14) is that while ρ reflects the anticipated ICC for a binary outcome in the usual sense, α is defined as the probability limit of the correlation under the misspecified Poisson variance. Because α differs from the true ICC, a good estimate of α may not be available during the design stage, rendering expression (14) less useful, with one exception where the cluster sizes m_i’s are all large. With large cluster sizes (e.g. typically seen in pragmatic trials embedded in health care delivery systems), we have

$$\frac{n{\sum }_{i=1}^n{m}_i\left\{1+\left(m_i-1\right)\rho \right\}/{\left\{1+\left(m_i-1\right)\alpha \right\}}^2}{{\left({\sum }_{i=1}^n{m}_i/\left\{1+\left(m_i-1\right)\alpha \right\}\right)}^2}\approx \rho \approx {\left(\frac{1}{n}\sum _{i=1}^n\frac{m_i}{1+\left(m_i-1\right)\rho }\right)}^{-1}$$

thus removing the dependence of ${\sigma }_{\text{exch }}^2$ on the nuisance parameter α. In fact, such an approximation may not be required once a simple modification is provided to the correlation estimator under the exchangeable correlation structure, as we demonstrate in Section 2.4.

2.4. A simple modification and efficiency consideration

In CRTs, it is recommended practice to report the ICC parameter, which facilitates the design of future studies with similar endpoints.³³ However, with an exchangeable correlation, the default correlation estimator with the modified Poisson analysis is $\widehat{\alpha }$, which is a biased estimator of the true ICC ρ due to the misspecification of the variance function. This makes the estimated $\widehat{\alpha }$ difficult to interpret and as we explained before, specifying a reasonable value of α in ${\sigma }_{\text{exch }}^2$ for sample size estimation is challenging. Because μ_ij is in theory contained between zero and one, the Poisson variance function is larger than the true binomial variance, such that $\widehat{\alpha }$ has a positive bias for estimating ρ, namely, α ≥ ρ. However, if we replace equation (7) with a consistent estimator of ρ by using the correct binomial variance such as

$$\widehat{\alpha }=\frac{{\sum }_{i=1}^n{\sum }_{j>j^{\prime }}\left(Y_{ij}-{\widehat{\mu }}_{ij}\right)\left(Y_{ij}-{\widehat{\mu }}_{i{j}^{\prime }}\right)/\sqrt{{\widehat{\mu }}_{ij}{\widehat{\mu }}_{i{j}^{\prime }}\left(1-{\widehat{\mu }}_{ij}\right)\left(1-{\widehat{\mu }}_{i{j}^{\prime }}\right)}}{{\sum }_{i=1}^n{m}_i\left(m_i-1\right)/2-2}$$ (16)

then the variance of the marginal relative risk estimator (14) simplifies to

$${\tilde{\sigma }}_{\text{exch }}^2={\left(\frac{1}{n}\sum _{i=1}^n\frac{m_i}{1+\left(m_i-1\right)\rho }\right)}^{-1}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}$$ (17)

which becomes much easier to use as it no longer depends on the nuisance parameter α. Because of this convenience, we will work with the modified correlation estimator (16) throughout.

Through a simulation study with a single cluster-level exposure, Zou and Donner¹⁴ indicated that the modified Poisson regression has almost identical efficiency to the log-binomial regression for estimating relative risks. In fact, we can show analytically that the large-sample variances obtained under the modified Poisson regression, ${\sigma }_{\text{indep }}^2$ and ${\tilde{\sigma }}_{\text{exch }}^2$ (with the modified correlation estimator (16)), are identical to those obtained under the log-binomial regression, even when the cluster sizes are variable. In other words, using the misspecified Poisson variance can improve the convergence property but results in no loss of efficiency for estimating the marginal relative risk. To see why, we can repeat the derivation in Section 2.3 by assuming the correct binomial variance function. With the binomial variance used in the log-binomial regression, equation (10) becomes ${\Sigma }_1^{-1}={\left({\sum }_{i=1}^n{1}_{m_i}^{\prime }{R}_i^{-1}{1}_{m_i}\right)}^{-1}{L}^{-1}$, where

$$L^{-1}=\frac{1-P_0}{(1-\pi )P_0}\left(\begin{array}{cc}1& -1\\ -1& 1+\{(1-\pi )/\pi \}\{P_0\left(1-P_1\right)/\text{(}{P}_1\left(1-P_0\right)\}\end{array}\right)$$

Similarly, equation (11) becomes ${\Sigma }_0=\left({\sum }_{i=1}^n{1}_{m_i}^{\prime }{R}_i^{-1}{R}_i^{*}{R}_i^{-1}{1}_{m_i}\right)Q$ where

$$Q=\left(\begin{array}{cc}\pi P_1/\left(1-P_1\right)+(1-\pi )P_0/\left(1-P_0\right)& \pi P_1/\left(1-P_1\right)\\ \pi P_1/\left(1-P_1\right)& \pi P_1/\left(1-P_1\right)\end{array}\right)$$

Multiplying out the sandwich variance gives the general expression of ${\tau }^2=n\text{var}\left({\widehat{\beta }}_1\right)$ under the log-binomial model as

$${\tau }^2=\frac{n{\sum }_{i=1}^n{1_{m_i}}^{\prime }{R}_i^{-1}{R}_i^{*}{R}_i^{-1}{1}_{m_i}}{{\left({\sum }_{i=1}^n{1}_{m_i\prime }/R_i^{-1}{1}_{m_i}\right)}^2}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}={\sigma }^2$$ (18)

In other words, this suggests that under the independence working correlation

$${\tau }_{\text{indep }}^2=\frac{n{\sum }_{i=1}^n{m}_i\left\{1+\left(m_i-1\right)\rho \right\}}{{\left({\sum }_{i=1}^n{m}_i\right)}^2}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}={\sigma }_{\text{indep }}^2$$ (19)

and under the exchangeable working correlation

$${\tau }_{\text{exch}}^2={\left(\frac{1}{n}{\sum }_{i=1}^n\frac{m_i}{1+\left(m_i-1\right)\rho }\right)}^{-1}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}={\tilde{\sigma }}_{\text{exch }}^2$$ (20)

These results formally establish the asymptotic equivalence between the modified Poisson regression and log-binomial regression when a cluster-level treatment indicator is involved in the marginal mean model (provided a simple modification of the ICC estimator is used under the exchangeable working correlation structure).

2.5. Further approximations with unequal cluster sizes

Recall that the sample size formula critically depends on the variance expressions ${\sigma }_{\text{indep }}^2$ and ${\tilde{\sigma }}_{\text{exch }}^2$, which requires the exact information of cluster sizes m_i. Although the cluster sizes or estimates of them are available in some situations, estimates of the mean and standard deviation of cluster sizes may be more accessible in other cases. Therefore, it would be desirable to approximate the variance expressions of the marginal relative risk using the distributional characteristics of m_i.

For the variance expression derived under the independence correlation structure, we have

$$\begin{gathered} \frac{n{\sum }_{i=1}^n{m}_i\left\{1+\left(m_i-1\right)\rho \right\}}{{\left({\sum }_{i=1}^n{m}_i\right)}^2} \\ =\frac{n^{-1}\left\{{\sum }_{i=1}^n{m}_i(1-\rho )+{\sum }_{i=1}^n{m}_i^2\rho \right\}}{{\left({\sum }_{i=1}^n{n}^{-1}{m}_i\right)}^2} \\ \approx \frac{1+\left\{\left(1+{\text{CV}}^2\right)\overline{m}-1\right\}\rho }{\overline{m}} \end{gathered}$$

where $\overline{m}$ is the average cluster size, and CV is the coefficient of variation of the cluster sizes. Therefore, the variance becomes

$${\sigma }_{\text{indep }}^2\approx \frac{1+\left\{\left(1+{\text{CV}}^2\right)\overline{m}-1\right\}\rho }{\overline{m}}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}$$ (21)

Interestingly, $1+\left\{\left(1+{\text{CV}}^2\right)\overline{m}-1\right\}\rho$ is the design effect with variable cluster sizes previously derived for the weighted cluster-level analysis of continuous, binary and count outcomes.^21,34–37 The above approximation indicates that the same design effect applies to the individual-level modified Poisson analysis assuming an independence working correlation structure. Further, it is clear from equation (21) that the required sample size increases when either the ICC or the coefficient of variation of cluster sizes increases.

For the variance expression derived under the exchangeable correlation structure, recall that

$$\frac{1}{n}\sum _{i=1}^n\frac{m_i}{1+\left(m_i-1\right)\rho }\approx \frac{1}{\rho }E\left\{\frac{m_i}{m_i+(1-\rho )/\rho }\right\}$$

Based on the Taylor expansion results of van Breukelen et al.³⁸ and Candel and van Breukelen,³⁹ the second-order approximation of the above expression can be written as

$$E\left\{\frac{m_i}{m_i+(1-\rho )/\rho }\right\}\approx \left(\frac{\overline{m}}{\overline{m}+(1-\rho )/\rho }\right)\left\{1-{\text{CV}}^2\frac{\overline{m}(1-\rho )/\rho }{{\{\overline{m}+(1-\rho )/\rho \}}^2}\right\}$$

This provides an approximation of the variance expression so that

$${\tilde{\sigma }}_{\text{exch }}^2\approx {\left\{1-{\text{CV}}^2\frac{\overline{m}\rho (1-\rho )}{{\{1+(\overline{m}-1)\rho \}}^2}\right\}}^{-1}\frac{1+(\overline{m}-1)\rho }{\overline{m}}\left\{\frac{1-P_1}{\pi P_1}+\frac{1-P_0}{(1-\pi )P_0}\right\}$$ (22)

Expressions (21) and (22) require the average cluster size $\overline{m}$ and coefficient of variation of cluster sizes as key input parameters, which may be more convenient to obtain in the design stage. For ease of reference, Table 1 summarizes the various expressions of ${\sigma }^2=n\text{var}\left({\widehat{\beta }}_1\right)$, depending on the working correlation structure and the information of cluster sizes.

Table 1.

Summary of variance expressions of marginal relative risk with the modified Poisson regression.

Working correlation	mi = m?	Known mi	Expression of κ
Independence	Yes	–	$\frac{1+(m-1)\rho }{m}$
Independence	No	Yes	$\frac{n{\sum }_{i=1}^n{m}_i\left\{1+\left(m_i-1\right)\rho \right\}}{{\left({\sum }_{i=1}^n{m}_i\right)}^2}$
Independence	No	No	$\frac{1+\left\{\left(1+C{V}^2\right)\overline{m}-1\right\}\rho }{\overline{m}}$
Exchangeable	Yes	–	$\frac{1+(m-1)\rho }{m}$
Exchangeable	No	Yes	${\left(\frac{1}{n}\sum _{i=1}^n\frac{m_i}{1+\left(m_i-1\right)\rho }\right)}^{-1}$
Exchangeable	No	No	${\left(\frac{\overline{m}}{1+(\overline{m}-1)\rho )}\right)}^{-1}{\left\{1-{\text{CV}}^2\frac{\overline{m}\rho (1-\rho )}{{\left\{1+(\overline{m}-1)\rho \right\}}^2}\right\}}^{-1}$

Note: The general variance expression is σ² = κ × {(1 − P₁)/πP₁ + (1 − P₀)/(1 − π)P₀}.

The variance expressions (21) and (22) allow us to analytically explore the efficiency implications for the modified Poisson analysis of CRTs under variable cluster sizes. Equation (15) provides the variance expression of ${\widehat{\beta }}_1$ under both the independence and exchangeable working correlation models with equal cluster sizes, or equivalently when the CV parameter equals zero. We define the variance inflation factor (VIF) due to unequal cluster sizes as the ratio of variances obtained under unequal cluster sizes (CV > 0) and under equal cluster sizes (where $m_i=\overline{m}$), and plot the VIF in Figure 1. The upper panels of Figure 1 present the VIF

$${\text{VIF}}_{\text{indep }}\approx \frac{1+\left\{\left(1+{\text{CV}}^2\right)\overline{m}-1\right\}\rho }{1-(\overline{m}-1)\rho }$$ (23)

by values of the ICC (x-axis) and CV of cluster sizes (colored lines) under the independence working correlation. Because commonly reported ICC rarely exceeds 0.2,¹ we only vary ρ ∈ [0, 0.25) with the largest value representingm the extreme case. Three values of mean cluster sizes are considered, corresponding to small $(\overline{m}=20)$, moderate $(\overline{m}=50)$ and relatively large $(\overline{m}=100)$ average cluster sizes. It is evident that large values of the ICC, CV as well as large average cluster sizes lead to a more pronounced variance inflation. In particular, when the average cluster size is large $(\overline{m}=100)$ and the CV further deviates from zero, the variance inflation becomes very sensitive to even a slight change in ICC, highlighting the potential inefficiency of using an independence working correlation model in those scenarios.

Figure 1.

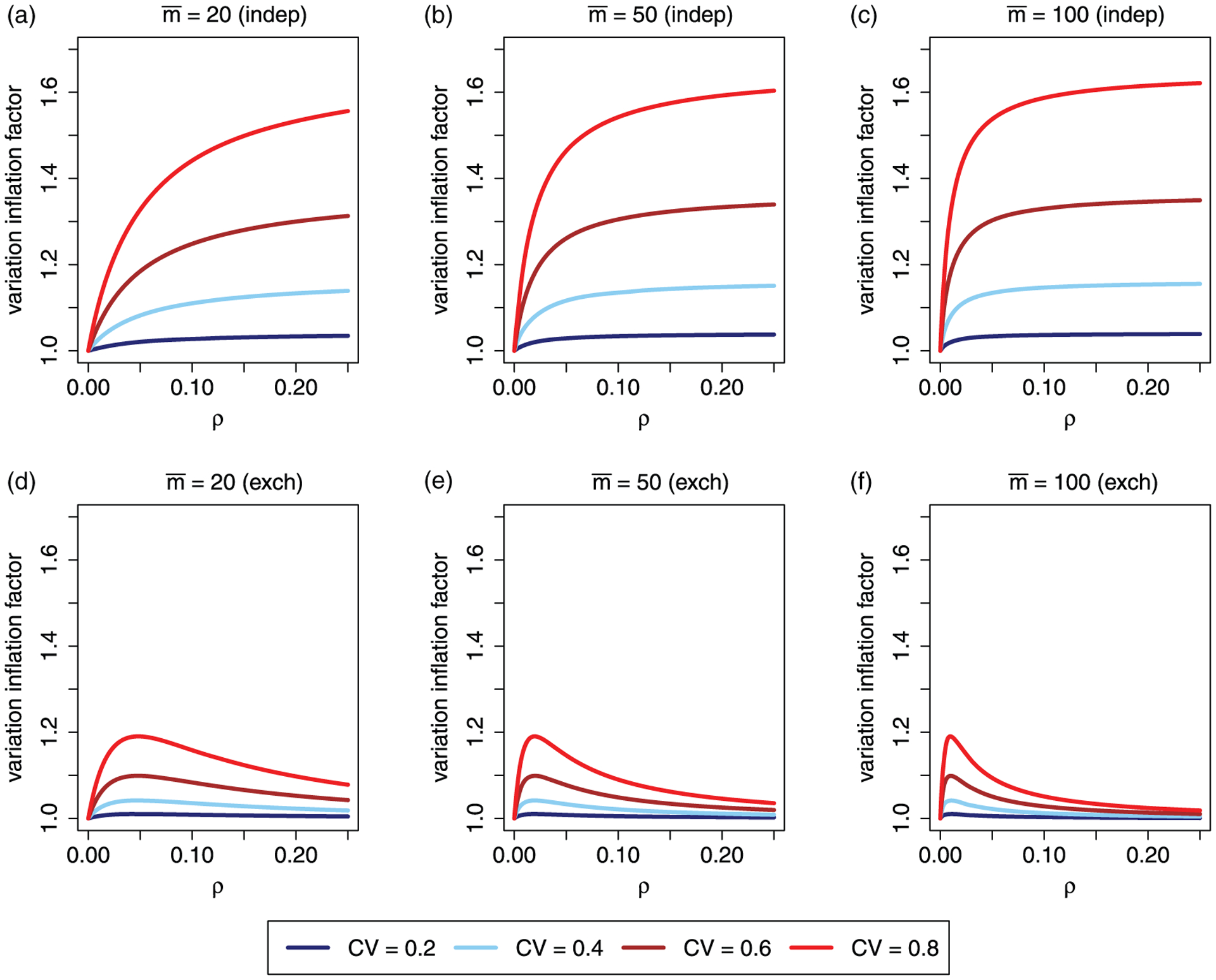
Variance inflation factor due to variable cluster sizes for modified Poisson regression under the independence working correlation (a–c) and under the exchangeable working correlation (d–f).

Under the exchangeable working correlation model, a similar variance inflation factor is defined as

$${\text{VIF}}_{\text{exch }}\approx {\left\{1-{\text{CV}}^2\frac{\overline{m}\rho (1-\rho )}{{\{1+(\overline{m}-1)\rho \}}^2}\right\}}^{-1}$$

which is plotted in the lower panels of Figure 1. Unlike the results under the independence correlation, the variance inflation under the exchangeable correlation structure due to cluster size variation is less sensitive, and exhibits a parabolic relationship with the ICC. Some algebra shows that VIF_exch reaches its maximum when the ICC $\tilde{\rho }=1/(\overline{m}+1)$,³⁸ and monotonically decreases towards 1 when ICC further increases. In sharp contrast with the results under independence correlation, the variance inflation under the exchangeable correlation is minimum when the average cluster size is larger and the ICC deviates from $1/(\overline{m}+1)$. Given that the asymptotic efficiency is identical between the independence and exchangeable working correlation models under equal cluster sizes (common denominator used when defining VIF_ind and VIF_exch), a direct comparison between the upper panels and lower panels in Figure 1 reveals the relative efficiency of modeling the correlation under variable cluster sizes. Importantly, when the average cluster size is large (typical in embedded pragmatic CRTs) and when the true correlation is farther away from zero, VIF_exch tends to converge to unity while VIF_indep diverges; this is the most typical scenario where employing the exchangeable correlation structure leads to efficiency gain for the modified Poisson analysis.

3. A simulation study

3.1. Simulation design

In this section, we investigate the accuracy of the sample size procedure for modified Poisson analysis of parallel CRTs. For simplicity, we focus on the scenario where the clusters are randomized in a 1:1 ratio so that π = 1/2. We consider two levels of baseline prevalence P₀ ∈ {0.15, 0.30}, with the former value resembling the STOP CRC study, and five levels of ICCs ρ ∈ {0.01, 0.05, 0.10, 0.15, 0.20}; these values are within the commonly reported range in CRTs.^1,40 Under the null, we set P₁ = P₀, and under the alternative, we consider P₁ = 0.3 when P₀ = 0.15 (relative risk = 2) and P₁ = 0.5 when P₀ = 0.3 (relative risk = 1.67). Two levels of mean cluster sizes $\overline{m}\in \{50,100\}$ are examined. We do not further examine $\overline{m}=20$ because under equal conditions, the required sample size may be much larger and becomes less practical for pragmatic CRTs. Five levels of CV of cluster sizes are considered with CV ∈ {0, 0.2, 0.4, 0.6, 0.8}, representing commonly used values used in simulations for CRTs.^31,38,41 Given each value of $\overline{m}$ and CV, the actual cluster size m_i~Gamma(a, b), where the shape parameter a = CV⁻² and the rate parameter $b={\overline{m}}^{-1}{\text{CV}}^{-2}$. We further round m_i to the nearest integer and ensure the minimum of m_i is at least 2 for computational stability. In total, we have a factorial design with 2 × 5 × 2 × 5 = 100 scenarios. Throughout, we fix the nominal type I error rate at 5%. For each scenario, we combine equation (9) with equation (21) or (22) to estimate the required number of clusters $\widehat{n}$ to achieve 80% power for a two-sided Wald t-test, under either the independence or exchangeable working correlation model. We then simulate 1000 data sets with correlated binary outcomes using the method of Qaqish⁴² based on $\widehat{n}$, the set of cluster sizes m_i, prevalence P₁, P₀ and the ICC ρ, and fit the modified Poisson analysis with either the independence or exchangeable working correlation model. Under the null such that P₁ = P₀, we report the empirical type I error rate of the Wald t-test as the proportion of false rejections over the 1000 simulations. Under the alternative, we report the empirical power of the Wald t-test, and the proposed sample size procedure is considered accurate if the empirical power agrees well with the nominal value 80%. Further, when using the exchangeable working correlation, we consider the modified correlation estimator (16) throughout the simulation.

As alluded to in Section 2.2, a complication in this empirical evaluation is that the Wald t-test with the original sandwich variance estimator of Liang and Zeger¹⁸ may be liberal when there is a limited number of clusters, and therefore modifications of the sandwich variance estimator are required to properly evaluate the empirical power. On the other hand, we wish to identify valid tests that carry the nominal type I error rate and have empirical power that agrees well with the prediction. For this reason, we consider three popular bias-corrections to the sandwich variance estimator. The Mancl and DeRouen (MD) variance estimator modifies equation (8) by setting $\text{c}\widehat{\text{o}}{\text{v}}_{\text{MD}}\left(Y_i\right)={\left(I-{\widehat{H}}_i\right)}^{-1}\left(Y_i-{\widehat{\mu }}_i\right){\left(Y_i-{\widehat{\mu }}_i\right)}^{\prime }{\left(I-{\widehat{H}}_i^{\prime }\right)}^{-1}$, where ${\widehat{H}}_i={\widehat{D}}_i{\widehat{\Sigma }}_1^{-1}{\widehat{D}}_i^{\prime }{\widehat{A}}_i^{-1/2}{R}_i^{-1}(\widehat{\alpha }){\widehat{A}}_i^{-1/2}$ is the cluster leverage matrix. Because the diagonal entries of the leverage matrix are between 0 and 1, the MD variance estimator inflates the robust sandwich variance estimator to reduce its negative bias in small samples.²³ The Kauermann and Carroll (KC) bias-correction corresponds to setting ${\text{c}\widehat{\text{o}}\text{v}}_{\text{KC}}\left(Y_i\right)={\left(I-{\widehat{H}}_i\right)}^{-1/2}\left(Y_i-{\widehat{\mu }}_i\right){\left(Y_i-{\widehat{\mu }}_i\right)}^{\prime }{\left(I-{\widehat{H}}_i^{\prime }\right)}^{-1/2}$ in equation (8) and has been shown to avoid the potential over-correction of the MD variance estimator.^24,43 The validity of these two bias-corrected variance estimators requires that the matrix inverses, ${\left(I-{\widehat{H}}_i\right)}^{-1}$ and ${\left(I-{\widehat{H}}_i\right)}^{-1/2}$, are well defined. The Fay and Graubard (FG) variance sets equation (8) as

$${\widehat{\Sigma }}_{0,\text{FG}}=\sum _{i=1}^n{\widehat{C}}_i{\widehat{D}}_i^{\prime }{\widehat{A}}_i^{-1/2}{R}_i^{-1}(\widehat{\alpha }){\widehat{A}}_i^{-1/2}\text{c}\widehat{\text{o}}\text{v}\left(Y_i\right){\widehat{A}}_i^{-1/2}{R}_i^{-1}(\widehat{\alpha }){\widehat{A}}_i^{-1/2}{\widehat{D}}_i{\widehat{C}}_i$$ (24)

where ${\widehat{C}}_i=\text{diag}\left\{{\left(1-\text{min}\left\{0.75,{\left[{\widehat{Q}}_i\right]}_{jj}\right\}\right)}^{-1/2}\right\}$ and ${\widehat{Q}}_i={\widehat{D}}_i^{\prime }{\widehat{A}}_i^{-1/2}{R}_i^{-1}(\widehat{\alpha }){\widehat{A}}_i^{-1/2}{\widehat{D}}_i{\widehat{\Sigma }}_1^{-1}$. Scott et al.⁴⁴ has shown that the KC variance estimator can be derived as a modified version of the FG variance estimator, which underlies their similarity in previous simulations with linear or logistic GEE^27–29; however, their performance could differ under variable cluster sizes, as shown in Li and Redden³¹ with logistic GEE. Although there are several other bias-corrected variance estimators available in the literature,^45–47 we mainly focus on the above three approaches because (i) they are readily implemented in SAS PROC GLIMMIX, the geesmv package in R,⁴⁸ and a Stata module xtgeebcv,⁴⁹ and (ii) the KC and FG variance estimators have been shown to perform adequately well in small samples with logistic GEE and correct variance and correlation specifications.^{27–29,31,43} Based on these three bias-corrections, we further examine three hybrid bias-corrected standard error estimators in constructing the Wald t-test: the average MD/KC standard error, the average MD/FG standard error and the average KC/FG standard error. Because the MD variance estimator tends to over-correct the bias, while the KC or FG variance estimators occasionally under-correct the bias, averaging two bias-corrected standard errors may lead to better finite-sample behavior. In fact, with logistic GEE and under the null hypothesis of no intervention effect, while Li and Redden³¹ recommended either KC or FG variance estimator depending on the CV of cluster sizes, Ford and Westgate⁴¹ showed that the average MD/KC standard error estimator has the best performance under variable cluster sizes over a range of CV. Our empirical validation of the sample size formula can help us assess the generalizability of these previous findings to modified Poisson regression, both under the null and the alternative. For fitting GEE with independence working correlation, we use our own R code to obtain the bias-corrected variance estimators. For fitting the GEE with exchangeable working correlation and the modified correlation estimator (16), we use our own R code to implement the modified Fisher-scoring algorithm and the bias-corrected variance estimators. The R code is provided in Web Appendix A.

3.2. Simulation results

Table 2 summarizes the empirical power and type I error rates (in parenthesis) for the modified Poisson regression under the independence working correlation when the mean cluster size is $\overline{m}=50$, the baseline prevalence P₀ = 0.15 and under five levels of the cluster size variability. Notably, the required sample size under the independence working correlation can be very sensitive to the change in CV of cluster sizes, especially when the ICC becomes large. For example, when ICC is 0.15, the required sample size $\widehat{n}=46$ when CV=0, but becomes $\widehat{n}=71$ when CV = 0.8. Further, it is clear that the t-test with the conventional robust sandwich standard error estimator has an inflated test size in almost all cases. Therefore, although the power of this test is consistently higher than nominal, the test is not appropriate due to its liberal size. Although the set of bias-corrected standard error estimators generally lead to more accurate test sizes, the t-test with the KC standard error or the average KC/FG standard error estimator occasionally lead to inflated type I error rate when the CV is large. Further, the t-test with the MD standard error estimator and the average MD/FG standard error estimator could occasionally lead to empirical power below 80%. These findings are consistent with previous observations with equal cluster sizes²⁷ and unequal cluster sizes³¹ under logistic GEE models. Across all tests, the t-test coupled with the FG standard error estimator or the average MD/KC standard error estimator has the best performance because they most frequently produce the closest nominal test size and maintain power close to prediction. This finding strengthens the previous recommendation in Ford and Westgate,⁴¹ by further showing that the t-test with the average MD/KC standard error estimator has adequate power (in addition to being valid) in the context of modified Poisson analysis.

Table 2.

Empirical power and type I error rates (in parentheses) for modified Poisson regression under independence working correlation when the mean cluster size is $\overline{m}=50$; P₀ = 0.15.

ρ	CV	$\widehat{n}$	Robust	MD	KC	FG	MD/KC	MD/FG	KC/FG
0.01	0	11	91.0(7.1)	79.7(3.4)	86.5(5.1)	83.3(4.0)	83.1(4.3)	82.2(3.7)	84.5(4.6)
	0.2	11	89.1(7.6)	77.2(3.2)	83.6(4.8)	80.9(3.6)	81.0(4.0)	79.3(3.3)	82.3(4.2)
	0. 4	11	89.2(10.0)	75.2(3.1)	83.1(5.7)	79.6(4.6)	79.0(4.2)	77.3(3.7)	81.4(5.1)
	0. 6	12	91.4(8.6)	77.5(3.5)	85.2(6.2)	81.3(4.4)	81.6(4.6)	79.2(3.9)	83.8(5.2)
	0. 8	12	89.3(10.9)	71.3(4.8)	82.0(7.5)	76.0(6.3)	76.1(6.0)	74.0(5.7)	79.2(6.6)
0.05	0	21	86.9(5.0)	82.1(3.3)	84.6(3.9)	83.5(3.7)	83.6(3.8)	82.7(3.4)	84.1(3.8)
	0. 2	21	84.8(5.9)	77.3(3.8)	81.5(4.8)	79.1(4.1)	79.5(4.2)	78.2(3.9)	80.6(4.3)
	0. 4	23	86.4(5.5)	80.4(3.4)	83.4(4.4)	81.6(4.0)	81.7(4.3)	81.0(3.8)	82.5(4.4)
	0. 6	25	85.5(6.3)	78.3(3.5)	82.3(4.8)	80.5(4.2)	80.5(4.2)	79.8(3.8)	81.4(4.4)
	0. 8	29	87.5(9.0)	80.4(5.8)	84.6(7.6)	82.2(6.5)	82.0(6.8)	81.5(6.1)	83.3(7.1)
0.10	0	33	84.3(6.3)	81.7(5.4)	82.9(5.8)	82.3(5.6)	82.1(5.5)	81.8(5.4)	82.5(5.6)
	0. 2	34	83.6(6.1)	80.4(4.5)	82.6(5.4)	81.7(4.8)	81.7(4.9)	81.1(4.6)	82.1(5.3)
	0. 4	38	85.0(7.2)	81.1(5.2)	83.3(6.2)	82.5(5.6)	82.5(5.7)	82.0(5.3)	83.0(5.8)
	0. 6	43	84.6(6.9)	81.3(6.0)	83.2(6.5)	82.4(6.3)	82.2(6.4)	81.6(6.3)	82.5(6.4)
	0. 8	50	89.3(8.2)	71.3(6.2)	82.0(7.2)	76.0(6.3)	76.1(6.5)	74.0(6.3)	79.2(6.9)
0.15	0	46	82.5(4.8)	79.8(3.7)	80.8(4.2)	80.2(3.8)	80.4(3.9)	80.1(3.7)	80.5(3.9)
	0. 2	48	82.5(6.9)	80.3(5.7)	81.3(6.2)	81.2(5.9)	81.0(6.2)	80.7(5.8)	81.2(6.2)
	0. 4	52	80.9(6.0)	78.2(5.1)	79.2(5.6)	79.0(5.5)	79.0(5.5)	78.8(5.3)	79.1(5.5)
	0. 6	60	84.1(6.1)	81.3(4.3)	82.8(5.1)	81.9(4.4)	82.0(4.6)	81.5(4.4)	82.4(4.6)
	0. 8	71	85.0(8.2)	80.5(6.3)	82.5(7.2)	81.4(6.7)	81.4(6.7)	81.1(6.6)	81.9(6.7)
0.20	0	59	83.6(6.4)	81.6(5.9)	82.7(6.1)	82.0(5.9)	82.1(6.0)	81.7(5.9)	82.2(6.1)
	0.2	61	82.9(6.1)	81.3(5.0)	82.0(5.7)	81.6(5.4)	81.6(5.5)	81.4(5.1)	81.8(5.7)
	0.4	67	83.4(6.4)	80.4(5.3)	82.0(5.8)	81.4(5.4)	81.3(5.4)	80.8(5.4)	81.7(5.4)
	0.6	78	84.5(7.1)	81.9(5.7)	83.1(6.4)	82.7(5.9)	82.5(6.0)	82.2(5.7)	82.9(6.2)
	0.8	92	83.9(7.4)	79.3(5.6)	80.8(6.4)	80.1(5.9)	79.8(6.1)	79.6(5.9)	80.4(6.3)

Note: Empirical type I error rate between 3.6% and 6.4% and empirical power between 77.5% and 82.5% are in bold font and considered close to nominal according to the margin of error under a binomial model with 1000 replications. ρ refers to ICC; CV refers to the coefficient of variation of cluster sizes; $\widehat{n}$ refers to the estimated number of clusters. Robust refers to the t-test with the uncorrected robust sandwich variance estimator; MD refers to the t-test with the bias-corrected sandwich variance estimator due to Mancl and DeRouen; KC refers to the t-test with the bias-corrected sandwich variance estimator due to Kauermann and Carroll; FG refers to the t-test with the bias-corrected sandwich variance estimator due to Fay and Graubard; MD/KC refers to the t-test with the average MD/KC standard error estimator; MD/FG refers to the t-test with the average MD/FG standard error estimator; KC/FG refers to the t-test with the average KC/FG standard error estimator.

Table 3 parallels Table 2 and summarizes the empirical power and type I error rates (in parentheses) for the modified Poisson regression with the exchangeable working correlation. With an exchangeable working correlation, the required number of clusters $\widehat{n}$ is relatively insensitive to cluster size variability. For example, when the ICC is 0.15, the required sample size $\widehat{n}=46$ when CV = 0, but becomes $\widehat{n}=49$ when CV = 0.8, suggesting that the additional number of clusters required to compensate unequal cluster sizes is much smaller than that using independence working correlation. This pattern confirms the analytical findings in Figure 1. On the other hand, findings concerning the validity and power of the t-test under the exchangeable working correlation largely agree with those under the independence working correlation. In particular, both the t-test with the FG standard error estimator and the t-test with the average MD/KC standard error estimator have optimal and comparable performance in terms of controlling for test size and providing adequate power. Interestingly, the performance of these two t-tests is also slightly improved under the exchangeable working correlation versus the independence working correlation. The similarity in the performance of these two tests suggests that either one could be used for the modified Poisson analysis with exchangeable correlation.

Table 3.

Empirical power and type I error rates (in parentheses) for modified Poisson regression under exchangeable working correlation when the mean cluster size is $\overline{m}=50$; P₀ = 0.15.

ρ	CV	$\widehat{n}$	Robust	MD	KC	FG	MD/KC	MD/FG	KC/FG
0.01	0	11	91.0(7.1)	79.7(3.4)	86.5(5.1)	83.3(4.0)	83.1(4.3)	82.2(3.7)	84.5(4.6)
	0.2	11	88.8(7.7)	78.1(3.5)	83.9(5.2)	81.1(4.0)	80.7(4.1)	79.6(3.4)	82.2(4.5)
	0.4	11	88.9(10.1)	75.1(3.9)	82.6(6.8)	79.3(5.4)	79.0(5.1)	77.1(4.4)	81.0(6.3)
	0.6	11	88.0(10.9)	73.1(4.0)	82.1(7.2)	78.4(5.8)	78.4(5.8)	75.4(4.8)	81.0(6.5)
	0.8	12	88.7(10.9)	71.2(3.6)	81.5(7.1)	77.8(5.8)	77.6(4.7)	75.0(4.1)	80.4(6.5)
0.05	0	21	86.9(5.0)	82.1(3.3)	84.6(3.9)	83.5(3.7)	83.6(3.8)	82.7(3.4)	74.1(3.8)
	0. 2	21	85.6(5.6)	78.7(3.7)	82.8(4.0)	80.4(3.8)	80.7(3.7)	79.6(3.7)	81.6(4.0)
	0. 4	21	85.3(5.9)	77.5(3.8)	81.5(4.4)	79.2(3.9)	78.9(4.1)	78.2(3.9)	80.3(4.1)
	0. 6	22	84.9(7.2)	80.1(5.3)	82.4(5.8)	81.6(5.5)	81.6(5.4)	81.0(5.4)	82.2(5.5)
	0. 8	23	85.5(7.3)	80.0(4.9)	83.4(6.2)	81.8(5.8)	81.8(5.6)	80.9(5.2)	82.3(6.0)
0.10	0	33	84.3(6.3)	81.7(5.4)	82.9(5.8)	82.3(5.6)	82.1(5.5)	81.8(5.4)	82.5(5.6)
	0. 2	34	84.9(5.9)	81.7(4.3)	83.5(5.2)	82.5(4.6)	82.6(4.7)	81.9(4.4)	82.7(4.9)
	0. 4	34	83.6(5.4)	80.2(4.7)	81.9(4.9)	81.3(4.7)	81.1(4.7)	80.7(4.7)	81.3(4.8)
	0. 6	35	83.8(5.9)	80.3(5.1)	82.2(5.4)	81.2(5.3)	81.3(5.2)	80.8(5.2)	81.7(5.3)
	0. 8	36	84.1(6.6)	81.2(5.1)	82.2(5.9)	81.8(5.4)	81.9(5.4)	81.5(5.1)	82.0(5.8)
0.15	0	46	82.5(4.8)	79.8(3.7)	80.8(4.2)	80.2(3.8)	80.4(3.9)	80.1(3.7)	80.5(3.9)
	0. 2	46	79.9(5.1)	78.4(4.5)	79.3(4.6)	79.0(4.6)	78.9(4.6)	78.7(4.6)	79.2(4.6)
	0. 4	47	84.3(6.0)	81.8(5.1)	83.2(5.7)	82.3(5.6)	82.3(5.3)	82.0(5.3)	83.0(5.6)
	0. 6	48	83.9(6.8)	81.6(5.3)	82.8(6.0)	82.2(5.5)	82.2(5.5)	81.8(5.4)	82.4(5.6)
	0. 8	49	84.0(6.2)	80.9(5.2)	82.5(5.6)	81.9(5.3)	82.0(5.3)	81.3(5.3)	82.1(5.4)
0.20	0	59	83.6(6.4)	81.6(5.9)	82.7(6.1)	82.0(5.9)	82.1(6.0)	81.7(5.9)	82.2(6.1)
	0. 2	59	85.2(5.9)	83.0(5.3)	84.0(5.4)	83.3(5.3)	83.3(5.3)	83.0(5.3)	83.5(5.4)
	0. 4	60	83.1(6.4)	81.7(5.4)	82.0(5.7)	81.8(5.6)	81.9(5.6)	81.7(5.6)	82.0(5.6)
	0. 6	60	82.4(5.6)	80.0(4.4)	81.3(5.0)	80.7(4.7)	80.8(4.6)	80.5(4.6)	81.1(4.8)
	0. 8	62	83.9(4.2)	81.7(3.8)	83.0(3.8)	82.4(3.8)	82.6(3.8)	82.2(3.8)	82.7(3.8)

Note: Empirical type I error rate between 3.6% and 6.4% and empirical power between 77.5% and 82.5% are in bold font and considered close to nominal according to the margin of error under a binomial model with 1000 replications. Robust refers to the t-test with the uncorrected robust sandwich variance estimator; MD refers to the t-test with the bias-corrected sandwich variance estimator due to Mancl and DeRouen; KC refers to the t-test with the bias-corrected sandwich variance estimator due to Kauermann and Carroll; FG refers to the t-test with the bias-corrected sandwich variance estimator due to Fay and Graubard; MD/KC refers to the t-test with the average MD/KC standard error estimator; MD/FG refers to the t-test with the average MD/FG standard error estimator; KC/FG refers to the t-test with the average KC/FG standard error estimator. ρ refers to ICC; CV refers to the coefficient of variation of cluster sizes; $\widehat{n}$ refers to the estimated number of clusters.

In our factorial simulation study design, we have additionally considered the baseline prevalence P₀ = 0.3 and mean cluster size $\overline{m}=100$; the corresponding results are summarized in Web Appendix B. Specifically, Web Tables 1 and 2 present the simulation results with P₀ = 0.3 and $\overline{m}=50$. The findings there are consistent with the results under P₀ = 0.15 and $\overline{m}=50$, suggesting the superior performance of t-tests coupled with the FG or the average MD/KC standard error estimator. However, these tests may be occasionally underpowered when the number of clusters is smaller than 10. Web Tables 3 to 6 present the simulation results with a larger mean cluster size $\overline{m}=100$, under both levels of baseline prevalence. When the mean cluster size is large, it is evident that the required sample size under the exchangeable working correlation is almost unaffected by CV of cluster sizes (no more than 2 additional clusters are required when CV increases from 0 to 0.8), whereas the required sample size under the independence working correlation is equally sensitive as the $\overline{m}=50$ scenario. The results of type I error and power under the $\overline{m}=100$ scenario further reveal that (i) the t-tests coupled with the FG or the average MD/KC standard error estimator have the best control of empirical test size throughout, and have power close to prediction when the number of clusters is at least 10; (ii) the performance of these two t-tests seems to be further improved in terms of type I error rate when the exchangeable correlation structure is used. In fact, across all scenarios, as long as the exchangeable working correlation structure is used, these two t-tests have rarely carried an inflated test size.

With an interest to further explore the implications of ignoring variable cluster sizes in the sample size calculation stage, we replicate the above simulation where $\widehat{n}$ is now estimated using the formula assuming equal cluster sizes $\overline{m}$. This is sometimes referred to as the “average cluster size method” by simply plugging in the average cluster size in formula (15). In this case, we have also shown that the sample size estimates are identical regardless of the use of the independence or exchangeable working correlation structure. Web Tables 7 to 10 summarize the corresponding results when $\overline{m}=50$. When the independence working correlation is used in fitting the modified Poisson GEE, the power of the t-test quickly declines when the CV of cluster size increases. In some cases, the largest power loss due to variable cluster sizes may be nearly 20%. However, under the exchangeable working correlation structure, the largest power loss due to variable cluster sizes is usually at most 5%, as long as the number of clusters is greater than 10. This clearly indicates that the power of modified Poisson analysis with exchangeable working correlation is generally insensitive to cluster size variability, whereas the modified Poisson analysis with independence working correlation can be subject to notable inefficiency under cluster size variability. In other words, ignoring cluster size variability has a substantially larger chance to result in an under powered study if the pre-specified analysis uses the independence working correlation, but is less likely to incur substantial power loss if the pre-specified analysis uses the exchangeable working correlation. The results for $\overline{m}=100$ are qualitatively similar and presented in Web Tables 11 to 14.

4. Illustrative calculation for the STOP CRC trial

We perform an illustrative sample size calculation based on the proposed formula, in the context of Stop Colorectal Cancer (STOP CRC) trial. As we mentioned in Section 1, the STOP CRC is a CRT that randomizes 26 federally qualified health clinics to an active intervention designed to increase colorectal cancer screening or usual care.⁶ The active intervention includes an automated, data-driven program embedded in EHR for mailing FIT kits with pictographic instructions to patients due for colorectal cancer screening. In the usual care arm, patients are only provided opportunistic colorectal cancer screening. Eligible patients are accrued in a comparable manner for intervention and control clinics over a one-year period and, once accrued, individuals are followed for 12 months to observe the completion of a CRC screening test. The primary outcome is the completion status of FIT at follow-up and is measured at the patient level. The actual sample size estimation is presented in Coronado et al.,⁶ from which the numbers will be drawn in this illustration. Suppose the primary analysis is the modified Poisson regression for the relative risk, and the FIT completion rate is P₀ = 0.15 under usual care. It was hypothesized that the effect size corresponds to a 10% increase in the completion rate, which corresponds to a marginal relative risk, e^Δ = 1.67. Although the original sample size estimation conservatively assumed an equal clinic size 450, the actual baseline statistics suggest that the clinic sizes vary from 461 to 3299, with mean $\overline{m}=1584$ and CV = 0.475. We will use this more accurate clinic size information to illustrate the implications of variable cluster sizes. Throughout, we consider a two-sided Wald t-test and fix the nominal type I error rate at 5%.

Assuming $m_i=\overline{m}=1584$ for each clinic i and no cluster size variability, the smallest n that ensures sample size equation holds with 80% power is $\widehat{n}=19$, which becomes 20 if rounded to the nearest even integer. Therefore, at least 10 clusters are required in each arm to ensure 80% power to detect the desired marginal relative risk. As we explained in Section 2.3, the sample size estimate is identical under either the independence or exchangeable working correlation if the clinic sizes are the same. Accounting for the variable cluster sizes through CV, we estimate the required number of clusters to be $\widehat{n}=22$ under the independence working correlation, and $\widehat{n}=19$ under the exchangeable working correlation. This suggests that at least two additional clusters would be required to power the study if the primary relative risk analysis is based on an independence working correlation, while the sample size estimate is virtually unaffected under the exchangeable working correlation. Next, we replicate the above calculation to achieve 90% power for the study. In this case, assuming equal cluster sizes, the required number of clusters is estimated as $\widehat{n}=24$ under either working correlation structure. When we take the cluster size variability into account, the required number of clusters is inflated to $\widehat{n}=29$ under the independence working correlation, while the required number of clusters remains unchanged $(\widehat{n}=24)$ under the exchangeable working correlation structure. Because the study can afford to randomize 26 clinics, the trial may be under powered if the primary analysis uses the modified Poisson regression coupled with the independence working correlation. Using an exchangeable working correlation, however, would adequately power the study based on the affordable number of clinics, regardless of whether CV is taken into account during sample size calculation.

While the above calculation focuses on determining the required number of clusters given full information of the cluster sizes, our sample size formula can also be used to jointly determine the required number of clusters and cluster sizes. Assuming an independence working correlation, panel (a) of Figure 2 plots the values of ($\overline{m}$, n) that ensure the STOP CRC trial has 80% power to detect a relative risk of 1.67 for five different levels of cluster size variability measured by CV. As the mean cluster size $\overline{m}$ increases from 50 to 2000, the required number of clusters decreases from 28 to 19 under equal cluster sizes (CV = 0). Given the same mean cluster size, increasing the CV of cluster sizes could substantially inflate the required number of clusters. For example, when the CV of cluster sizes becomes 0.8, the required number of clusters will decrease from 38 to 28 as the mean cluster size increases from 50 to 2000. On the other hand, the relationship between the required number of clusters and mean cluster size appears more robust to cluster size variability, under the exchangeable working correlation. In panel (b) of Figure 2, as long as the mean cluster sizes reaches 670, the required number of clusters will always be 19 for all CV ≤ 0.8, and increasing the CV of cluster sizes only affects the rate at which the required number of clusters reaches the minimum value, 19. These results further confirm that the loss of efficiency due to variable cluster sizes is much smaller when the correct correlation structure is considered in the analysis. Further, calculations such as those done in Figure 2 present a number of design options so that investigators could jointly decide the number of clusters and mean cluster sizes, after taking the logistical and financial factors into consideration.

Figure 2.

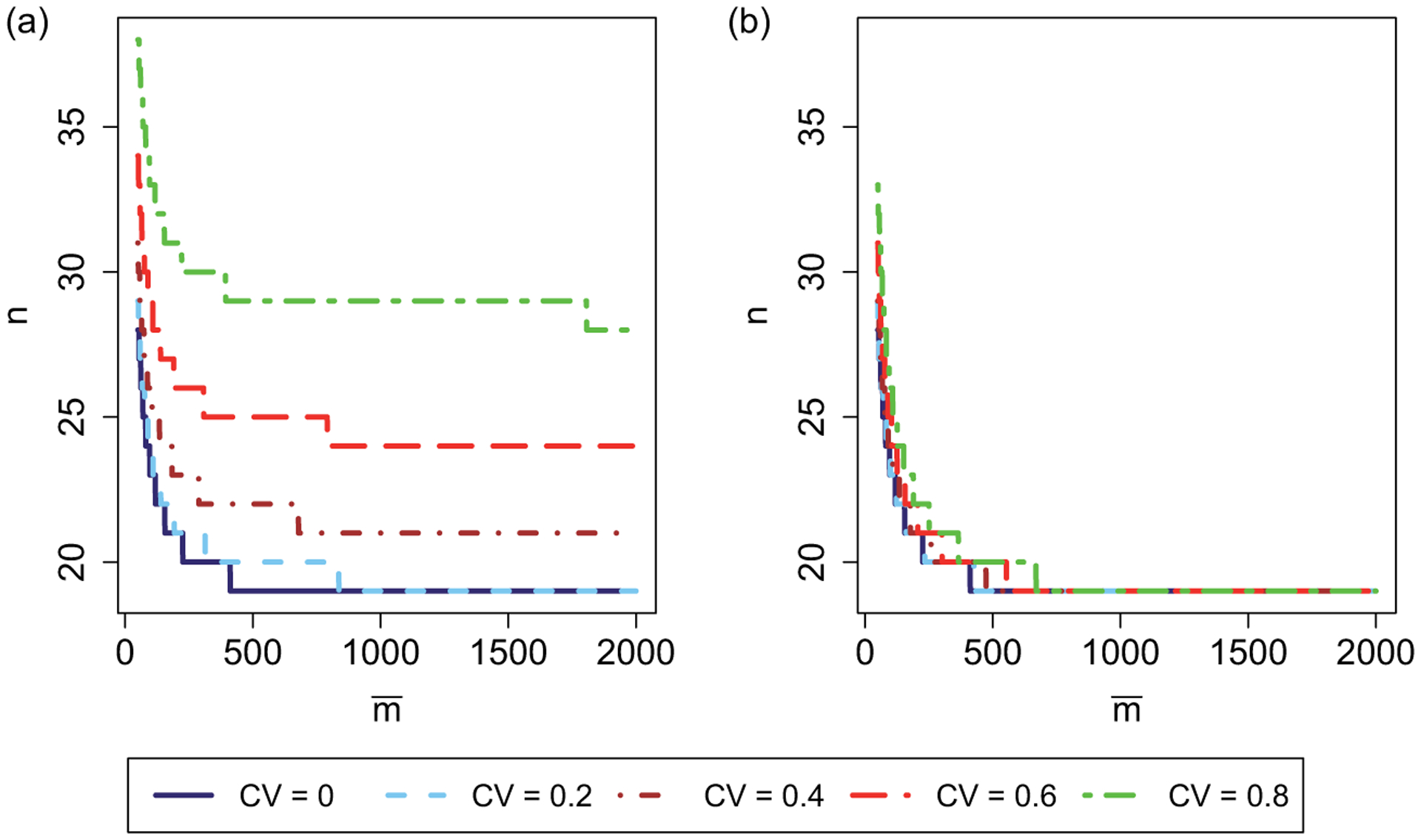
Required number of clusters n and average cluster sizes $\overline{m}$ to achieve 80% power across five levels of cluster size variability in the STOP CRC study. (a) Working independence and (b) working exchangeable.

5. Discussion

In this article, we have studied the sample size requirement for modified Poisson analysis of parallel CRTs, and proposed closed-form sample size formulas under both the independence and exchangeable working correlation structures. With an independence working correlation, we have shown that the asymptotic variance of the marginal relative risk estimator from the modified Poisson regression is identical to that from the log-binomial regression. This asymptotic equivalence also extends to the exchangeable working correlation, provided a simple modification is used to obtain a consistent estimate of the ICC parameter. From a design perspective, these results suggest that the sample size formula derived for log-binomial analysis of CRTs can be directly applied to modified Poisson analysis of CRTs. From a trial analysis perspective, the asymptotic results imply that the misspecification of the variance function does not lead to efficiency loss for estimating the marginal relative risk in CRTs and could have better convergence property¹⁴; this further supports the application of the modified Poisson model over log-binomial model in CRTs.

We have also clarified the implication of variable cluster sizes for modified Poisson analysis of CRTs by deriving the required sample size as a function of the CV of cluster sizes. The results, however, diverge between the independence and exchangeable working correlation structures. Interestingly, while the sample size requirement under the independence working correlation is quite sensitive to changes in CV of cluster sizes, the sample size requirement under the exchangeable working correlation is generally stable to the changes in CV of cluster sizes; see, for example, Figure 2 in our illustrative example. This finding shows that the impact of variable cluster sizes critically depends on whether the analytical strategy exploits the within-cluster correlation, an observation that is not explicitly emphasized in the current CRT literature. In fact, the expressions of the variance inflation factor, VIF_indep and VIF_exch themselves are not new, as they have been previously derived for cluster-level analysis,^21,34–37 as well as mixed-effects regression of CRTs.^38,39 The contribution of this article is then to connect these separate results under the same marginal modeling framework but allowing for differences in working correlations. From this perspective, the statements of van Breukelen et al.³⁸ that “the loss of efficiency due to variation in cluster sizes rarely exceed 10%” and of Liu and Colditz⁵⁰ that “the efficiency loss (due to unequal cluster sizes) could be approximately 14% in CRTs with large cluster sizes” would apply only to the modified Poisson analysis coupled with the exchangeable working correlation; the efficiency loss under the independence working correlation could easily exceed 14% even with a moderate CV. In fact, because the asymptotic variance of the intervention effect estimate under GEE analyses of CRTs shares a similar form for continuous, binary and count outcomes,^50,51 the expressions of VIF_indep and VIF_exch apply more generally to marginal analyses of CRTs with an arbitrary generalized linear mean model. To summarize, from a trial design perspective, while there is a deleterious consequence by ignoring cluster size variability in sample size estimation under an independence working correlation, the sample size estimate under the exchangeable working correlation should be more robust to cluster size variability. From an analytical perspective, we also recommend marginal analysis of CRTs that exploits within-cluster correlation (e.g. using an exchangeable working correlation), not only because it adheres to the recommendation of the CONSORT extension to CRTs³³ by offering a valid ICC estimate, but also because the efficiency of intervention effect estimator would be less affected by cluster size variability.

In an attempt to validate our sample size formula for modified Poisson analysis of CRTs, we carry out an extensive simulation study under various parameter constellations. Several key messages are clear from our simulation study. First, the Wald t-test with the original sandwich variance estimator carries an inflated type I error rate, even when the number of clusters is over 90 and an independence working correlation is used (Table 2). While all finite-sample bias-corrections generally improve the test size, the t-tests coupled with the FG standard error estimator²⁵ and the average MD/KC standard error estimator⁴¹ should be preferred due to their optimal control of type I error rate and close-to-nominal empirical power. However, these two tests may be occasionally under powered when no more than 10 clusters are randomized. Second, the additional simulation results in Web Appendix B further illustrates that ignoring cluster size variability in the design stage can result in a severely underpowered CRT, if the primary analysis uses the independence working correlation. Even when the number of clusters are larger than 50, the power loss due to unequal cluster sizes with an independence working correlation could frequently exceed 15%. In contrast, as long as more than 10 clusters are randomized, the power loss due to unequal cluster sizes with an exchangeable working correlation is usually controlled within 5%, suggesting the need to account for ICC when estimating the relative risk. Third, it is often the case that the t-test has improved control of empirical type I error rate once an exchangeable working correlation is used (compare to an independence working correlation), regardless of finite-sample bias-corrections of the variance estimators. This last finding enhances the recommendation that the modified Poisson analysis of CRTs should proceed with an exchangeable working correlation instead of assuming working independence. Finally, while finite-sample bias-corrections are considered in the sandwich variance estimators, they are not required for deriving the large-sample variance expressions in Table 1. This is because the true covariance cov(Y_i) is used in deriving the large-sample variance expressions, which are estimands rather than estimators and therefore have no “finite-sample bias” on their own.

While we have developed our sample size requirement based on the relative risk measure of the treatment effect in CRTs, there exist alternative sample size formulas based on the risk difference measure. For example, Cornfield⁵² discussed a variance expression based on the estimated risk difference under cluster randomization, and later Donner et al.⁵³ proposed an explicit sample size procedure based on the risk difference. In Web Appendix C, we show that the Cornfield formula and the Donner et al. formula are identical, and therefore lead to the same sample size estimate. We also numerically compared the estimated number of clusters using our formulas and the Cornfield/Donner formula across scenarios examined in Section 3, and observed that the Cornfield/Donner formula frequently led to a smaller number of clusters compared to ours. This comparison does not necessarily indicate one formula is always “better” than the other, but emphasizes the importance of consistent choices in the effect measure during the design and analysis stages. For example, if one uses the Cornfield/Donner formula to power the CRTs with an assumed risk difference, then the study can become underpowered when the analysis proceeds with the modified Poisson regression and estimates the relative risk. In addition, the Cornfield/Donner formula assumed equal randomization (π = 1/2) and equal cluster sizes, while our formulas have relaxed both assumptions to accommodate unequal randomization and variable cluster sizes.

One potential limitation of the current study is that we have limited our development to parallel CRTs. Because there is an increasing body of literature on alternative cluster randomized designs with more complex assignment of interventions, such as the cluster randomized crossover design²⁸ and the stepped wedge design,^27,28 it would be interesting to examine whether similar findings concerning modified Poisson regression extend to those alternative designs. One complication is that the intervention status varies within each cluster during each period, and therefore the derivation of sample size formula requires additional considerations. For example, Li et al.²⁸ proposed a sample size expression for log-binomial regression of the cluster randomized crossover design (Web Appendix F of Li et al.²⁸), which depends on the design parameters in a more complex fashion. It remains unknown whether misspecification of the variance function maintains the same efficiency in estimating the marginal relative risk as the log-binomial model. Another complication is that the true correlation structure usually deviates from the simple exchangeable structure as measurements are taken for each cluster during multiple periods.⁵⁴ Therefore, it would be relevant to study whether accounting for multilevel correlation structures would be less prone to efficiency loss compared to simply using working independence. The design and analysis of these alternative cluster randomized designs with a binary outcome under variable cluster sizes remain an active topic for statistical research, and we plan to pursue the extensions of modified Poisson regression under the cluster randomized crossover design and stepped wedge design in our future work.