Abstract
Scans without evidence of dopaminergic deficit (SWEDD) refers to patients who mimics motor and non-motor symptoms of Parkinson’s disease (PD) but showing integrity of dopaminergic system. For this reason, the differential diagnosis between SWEDD and PD patients is often not possible in absence of dopamine imaging. Machine Learning (ML) showed optimal performance in automatically distinguishing these two diseases from clinical and imaging data. However, the most common applied ML algorithms provide high accuracy at expense of findings intelligibility. In this work, a novel ML glass-box model, the Explainable Boosting Machine (EBM), based on Generalized Additive Models plus interactions (GA2Ms), was employed to obtain interpretability in classifying PD and SWEDD while still providing optimal performance. Dataset (168 healthy controls, HC; 396 PD; 58 SWEDD) was obtained from PPMI database and consisted of 178 among clinical and imaging features. Six binary EBM classifiers were trained on feature space with (SBR) and without (noSBR) dopaminergic striatal specific binding ratio: HC-PDSBR, HC-SWEDDSBR, PD-SWEDDSBR and HC-PDnoSBR, HC-SWEDDnoSBR, PD-SWEDDnoSBR. Excellent AUC-ROC (1) was reached in classifying HC from PD and SWEDD, both with and without SBR, and by PD-SWEDDSBR (0.986), while PD-SWEDDnoSBR showed lower AUC-ROC (0.882). Apart from optimal accuracies, EBM algorithm was able to provide global and local explanations, revealing that the presence of pairwise interactions between UPSIT Booklet #1 and Epworth Sleepiness Scale item 3 (ESS3), MDS-UPDRS-III pronation-supination movements right hand (NP3PRSPR) and MDS-UPDRS-III rigidity left upper limb (NP3RIGLU) could provide good performance in predicting PD and SWEDD also without imaging features.
Keywords: Explainable boosting machine, Interpretable machine learning, Parkinson’s disease, SWEDD, DaT-SPECT
Introduction
The Parkinson’s disease (PD) is the second most common neurodegenerative disease after Alzheimer’s disease (AD) (Amoroso et al., 2018) and it affects an important percentage of the elderly population (de Lau & Breteler, 2006). The degeneration of dopaminergic neurons in the substantia nigra is known as the cause of PD, which leads to motor symptoms such as the rigidity, tremor, akinesia, gait, and speech disturbance. Together with motor symptoms, the PD also presents alterations in non-motor functions, negatively affecting the daily activities of the patients (Vaccaro et al., 2021; Sarica, 2021a). The motor and non-motor impairment is usually quantified through several clinical scales, such as the commonly used Movement Disorder Society Unified Parkinson’s Disease Rating Scale (MDS-UPDRS) (Goetz et al., 2008). The Single-photon emission computed tomography (SPECT) with the DaTSCAN (123I-Ioflupane) is the most widely applied diagnostic technique for assessing the dopamine deficit in PD. The SPECT tracer binds to the dopamine transporters in the brain regions of caudate and putamen (the striatum). Such clinical and imaging evaluations are recognized as the main tools for the diagnosis of PD. However, in the 10% of clinically diagnosed PD patients, the dopaminergic functional imaging is negative, and these patients are classified as Scans without evidence of dopaminergic deficit (SWEDD) (Schwingenschuh et al., 2010). It has been hypothesized that SWEDD patients suffer from other neurological diseases, e.g. essential tremor or dystonia, which mimic PD and present overlapping motor and non-motor symptoms. For these reasons, the differential diagnosis of PD and SWEDD results to be still complex and challenging (Schwingenschuh et al., 2010).
Artificial Intelligence (AI) and Machine Learning (ML) are nowadays broadly applied for supporting the diagnosis of PD and Parkinsonisms (Vaccaro et al., 2021; Sarica, 2021a; Chien, 2021; Palumbo, 2014; Salvatore et al., 2014; Oliveira & Castelo-Branco, 2015; Yang et al., 2021), as well as for distinguishing between PD and SWEDD (Mabrouk et al., 2017; Mabrouk et al., 2019; Hirschauer et al., 2015; Prashanth et al., 2017) from clinical, neuropsychological and imaging features. Although the ML algorithms for the automatic prediction and the differential diagnosis of PD showed excellent performance (Vaccaro et al., 2021; Chien, 2021; Palumbo, 2014; Salvatore et al., 2014; Oliveira & Castelo-Branco, 2015; Mabrouk et al., 2017; Mabrouk et al., 2019; Hirschauer et al., 2015; Prashanth et al., 2017; Lei et al., 2019), the usually applied approaches are black-boxes, that is they are not able to provide a satisfactory interpretation of ML findings. It is indeed beyond doubt that the application of ML in the healthcare and neurological realm should provide an acceptable tradeoff between the accuracy and the interpretability (Ahmad et al., 2018; Sarica, 2022), and for this reason, a novel field of AI has been born very recently, the Explainable AI (XAI) (Arrieta et al., 2020). One of the interpretable ML algorithms that showed good performance on biomedical and clinical data is the Explainable Boosting Machine (EBM) (Lou et al., 2012), a glassbox model based on the Generalized Additive Models plus interactions (GA2Ms) (Hastie & Tibshirani, 1990; Lou et al., 2013). EBM showed comparable accuracy to the state-of-the-art ML methods, such as Random Forest (Breiman, 2001; Sarica et al., 2017) or XGBoost (Chen & Guestrin, 2016), and it has been successfully employed for the prediction of the Alzheimer’s disease from MRI data (Sarica et al., 2021b), for the assessment of the Pneumonia risk (Caruana et al., 2015) and of the COVID-19 risk (Magunia, 2021), and for supporting the optimal treatment of Kawasaki disease (Wang et al., 2020). Because of the extreme novelty, very few works assessed the reliability and utility of the XAI approaches for the early and/or differential diagnosis of PD (Ma et al., 2021; Magesh et al., 2020; Shahtalebi et al., 2021), and furthermore none of these studies applied EBM for the prediction of PD. Thus, the main contributions of the present work are: (i) to investigate the performance of the EBM algorithm for the prediction of PD; (ii) to evaluate the reliability of EBM in distinguishing between PD and SWEDD patients by using clinical scales and imaging features; (iii) to compare the performance of EBM classifiers trained with and without striatal DaTSCAN uptake; (iv) to assess the influence of the pairwise interactions on the EBM models performance; (v) to provide the interpretability and the feature contribution in the single prediction of PD.
Methods
Participants
Data used in the preparation of this article were obtained from the Parkinson’s Progression Markers Initiative (PPMI) database (www.ppmi-info.org/data). For up-to-date information on the study, visit www.ppmi-info.org. Table 1 reports the demographic, the clinical and imaging characteristics of the cohort, which consisted of 168 healthy controls (HC), 396 PD and 58 SWEDD. Only subjects without missing clinical and imaging features were considered and all data used for the analysis are acquired at the baseline visit.
Table 1.
Demographic, clinical and imaging data of the PPMI dataset (values are mean ± SD)
| HC (168) |
PD (396) |
SWEDD (58) |
#a | p-value ANOVA | Post-hocb | |
|---|---|---|---|---|---|---|
| Age | 61.1 ± 11.3 | 61.7 ± 9.65 | 60.6 ± 10 | - | 0.71 | N.A. |
| Gender (M/F) | 109/59 | 260/136 | 35/23 | - | N.A. | N.A. |
| H&Y | 0.005 ± 0.07 | 1.57 ± 0.51 | 1.41 ± 0.53 | - | < 0.0001 | PD > HC, SWEDD; SWEDD > HC |
| MDS-UPDRS-I | 2.89 ± 2.76 | 5.61 ± 4.12 | 8.24 ± 6.56 | 13 | < 0.0001 |
SWEDD > HC, PD; PD > HC |
| MDS-UPDRS-II | 0.35 ± 0.95 | 5.39 ± 4.14 | 5.02 ± 5.03 | 13 | < 0.0001 | HC < PD, SWEDD |
| MDS-UPDRS-III | 1.19 ± 2.06 | 20.9 ± 8.84 | 13.9 ± 9.31 | 33 | < 0.0001 |
PD > HC, SWEDD; SWEDD > HC |
| MoCA | 28.1 ± 1.09 | 26.9 ± 2.38 | 26.8 ± 2.57 | 26 | < 0.0001 | HC > PD, SWEDD |
| STAI | 47.7 ± 4.97 | 47.3 ± 5.32 | 46.7 ± 4.89 | 40 | 0.36 | N.A. |
| GDS | 5.17 ± 1.39 | 5.26 ± 1.45 | 5.71 ± 1.75 | 15 | 0.11 | N.A. |
| SCOPA-AUT | 5.11 ± 3.38 | 8.58 ± 6.51 | 12.1 ± 8.80 | 21 | < 0.0001 |
SWEDD > HC, PD; PD > HC |
| JLO | 13.1 ± 1.95 | 12.8 ± 2.1 | 12.7 ± 2.49 | 1 | 0.18 | N.A. |
| UPSIT | 34 ± 4.75 | 22.3 ± 8.34 | 31 ± 6.42 | 4 | < 0.0001 | PD < HC, SWEDD; SWEDD < HC |
| ESS | 5.66 ± 3.38 | 5.81 ± 3.42 | 8.24 ± 4.83 | 8 | 0.0009 | SWEDD > HC, PD |
| Left Caudate SBR | 3.0 ± 0.63 | 1.99 ± 0.59 | 2.86 ± 0.57 | 1 | < 0.0001 | PD < HC, SWEDD |
| Right Caudate SBR | 2.9 ± 0.61 | 1.98 ± 0.59 | 2.83 ± 0.59 | 1 | < 0.0001 | PD < HC, SWEDD |
| Left Putamen SBR | 2.14 ± 0.56 | 0.812 ± 0.35 | 2.05 ± 0.51 | 1 | < 0.0001 | PD < HC, SWEDD |
| Right Putamen SBR | 2.16 ± 0.58 | 0.843 ± 0.36 | 2.09 ± 0.51 | 1 | < 0.0001 | PD < HC, SWEDD |
| Tot | 178 |
Statistical results are also reported
a Number of items per test, i.e. number of features used for training EBM models. Age, gender and H&Y not included in the feature space
b Tukey’s correction (p < 0.05)
Abbreviations: HC, healthy control; PD, Parkinson’s disease; SWEDD, Scans without evidence of dopaminergic deficit; N.A., Not applicable
Motor and non-motor evaluation of PD was conducted through the Movement Disorder Society Unified Parkinson’s Disease Rating Scale (MDS-UPDRS) (Goetz et al., 2008), which consists of three parts: part I, non-motor experiences of daily living; part II, motor experiences of daily living; part III, motor examination; part IV, motor complications. Other important scales for the assessment of non-motor symptoms, are the Montreal Cognitive Assessment (MoCA, for detecting cognitive impairment), State-Trait Anxiety Inventory (STAI, for assessing the level of anxiety), Geriatric Depression Scale (GDS, for evaluating the depression in older adults), Scales for Outcomes in Parkinson’s Disease - Autonomic Dysfunction (SCOPA-AUT, for evaluating autonomic symptoms), Judgment of Line Orientation (JLO, for assessing the visuospatial skills), the University of Pennsylvania Smell Identification Test (UPSIT, for testing the function of the olfactory system) and the Epworth Sleepiness Scale (ESS, for assessing the daytime sleepiness). The Hoen and Yahr (H&Y) scale was also reported here, but it was not included in the training features set since it is used for assessing the stage of PD and not for diagnosis.
The dopamine transporter single-photon emission computed tomography (DaT-SPECT) is the neuroimaging approach usually applied for the diagnosis PD. The brain region of interest (ROI) investigated with the 123I-Ioflupane (DaTSCAN) and SPECT is the striatum, consisting of the caudate and the putamen. The specific binding ratio (SBR) of these two ROIs for each hemisphere is calculated from the count densities in the ROI masks, considering the occipital cortex as reference tissue.
The number of items per clinical assessment and the total number of features (178) used for training the ML models are reported in Table 1.
Statistical analysis
Statistical analyses were conducted for comparing demographic, clinical and imaging features among the three groups. One-way analysis of variance (ANOVA) was applied for assessing differences in age, MDS-UPDRS-I, MDS-UPDRS-II, MDS-UPDRS-III, H&Y, MoCA, STAI, GDS, SCOPA-AUT, JLO, UPSIT, ESS, and SBR of caudate and putamen, while differences in gender distributions were assessed with Chi-squared test (p < 0.05). Tukey’s method was employed for the multiple comparisons correction (p < 0.05).
Machine learning analysis
The EBM algorithm (Caruana et al., 2015) is based on standard Generalized Additive Models (GAMs) (Hastie & Tibshirani, 1990), which accuracy is improved by adding pairwise interactions (Lou et al., 2013), taking the name of GA2Ms and the form:
| 1 |
where is the feature vector with p features, the response, denotes the jth variable in the feature space, g is the link function that adapts the GAMs to regression (e.g., g = identity) or classification (e.g., g = logistic), is the intercept that adjusts the prediction from the model, and fj is the feature function, which could be plot for visualizing the contribution of each feature to the final prediction (Nori et al., 2019). The two-dimensional interaction fij(xi,xj) in Eq. 1 can be rendered as heatmap on a two-dimensional xi,xj-plane, thus still maintaining the intelligibility. The EBM improves the standard GA2Ms thanks to bagging and gradient boosting with shallow tree-like ensembles for mitigating the co-linearity and for avoiding overfitting (Lou et al., 2012, 2013; Caruana et al., 2015). The best feature function fj for each feature is learnt by training the model on one feature at a time, so to obtain its contribution to the prediction, which is then added and sent through the link function g to make single predictions (Nori et al., 2019). The concept of additivity and modularity of the contributions allows to rank and visualize which features have the higher impact on the individual prediction (Nori et al., 2019). In terms of predictive performance, EBM is comparable or in some cases better than the state-of-the-art algorithms (Nori et al., 2019), such as Random Forest (Breiman, 2001; Sarica et al., 2017) and XGBoost (Chen & Guestrin, 2016).
ML analysis was conducted with Python 3.7 and the package InterpretML 0.2.7 (Nori et al., 2019), which implements the EBM algorithm, on a MacOS 10.14.6 (2.9 GHz, 32GB of RAM). First, the dataset containing the three diagnostic classes, was randomly split with a static seed into training and test sets with a percentage respectively of 80% and 20% and maintaining the balance in the distribution of classes. Then, the training and test sets were split into three pairs of training/test sets, so to contain two diagnostic classes for each: HC (134/34) and PD (317/79), HC and SWEDD (46/12), and PD and SWEDD. The binary EBM classifiers were built on two different feature spaces, with and without the caudate and putamen SBR: HC-PDSBR, HC-SWEDDSBR, PD-SWEDDSBR and HC-PDnoSBR, HC-SWEDDnoSBR, PD-SWEDDnoSBR. With the aim of assessing the influence of the pairwise interactions on the model performance, their number was automatically varied in a range from zero (no interactions) to 20. Then, we searched for optimal number of pairs in term of the Area under the Curve of the Receiver Operating Characteristic (AUC-ROC), evaluated on test set. Only the best binary model with the highest AUC was considered for further analysis. In case there was an equal AUC-ROC value among different classifiers, the model with less interactions was preferred for minimizing the complexity. The AUC-ROC of each best model was also calculated by applying a stratified 5-fold cross-validation to prevent overfitting and to assess the stability and reliability of the classifiers (reported as mean ± standard deviation). Sensitivity and specificity of the best models were calculated from the confusion matrix for test sets, and furthermore, given the imbalance of classes (Magunia, 2021), Balanced accuracy (BA) and AUC of the Precision-Recall curve (AUC-PR) were also calculated.
For each best binary classifier, the overall importance ranking (global explanation) of features was obtained by ordering their average absolute contribution in predicting training data. The local explanation of test subjects was also assessed as the ranking of the most important features in the single prediction, calculated as logit of the probability (logarithm of the odds) from the logistic link function g (Eq. 1), where the logit of each feature is sum up for obtaining the final prediction (Lou et al., 2012, 2013).
Results
Demographic, clinical and imaging characteristics
No significant differences existed among the three groups in age, STAI, GDS, JLO and in gender distribution, while the remaining other twelve scales were significantly different among them (Table 1). Regarding the post-hoc, PD patients had higher values than HC in UPDRS-I, UPDRS-II, UPDRS-III and H&Y, and lower values than HC in MoCA, SCOPA-AUT, UPSIT, caudate and putamen SBR. SWEDD patients had higher values than HC in UPDRS-I, UPDRS-II, UPDRS-III, H&Y and ESS, and lower values than HC in MoCA, SCOPA-AUT and UPSIT. PD and SWEDD groups were different in UPDRS-I, UPDRS-III, H&Y, SCOPA-AUT, UPSIT, ESS, caudate and putamen SBR, as reported in Table 1.
Machine learning analysis
The results of EBM models are reported in Table 2. The two best classifiers HC-PDSBR (zero interactions) and HC-PDnoSBR (one pairwise interaction: NP3FACXPxNP3BRADY) reached both the maximum AUC-ROC of 1 and an AUC-PR of 0.999, while the BA was 1 and 0.987 respectively. The two best classifiers HC-SWEDDSBR and HC-SWEDDnoSBR showed both an AUC-ROC of 1, BA 0.97 and AUC-PR 1, with the same only interaction NP2HWRTxNP2TRMR. For distinguishing between PD and SWEDD patients, the best result (AUC-ROC 0.986, BA 0.75, AUC-PR 0.998) was obtained by the model PD-SWEDDSBR with one interaction (PUTAMEN_LxPUTAMEN_R). When the SBRs were dropped from the feature space, the AUC-ROC of the model PD-SWEDDnoSBR decreased to 0.882 (BA 0.625, AUC-PR 0.979), with a higher number of pairwise interactions (eleven).
Table 2.
Performance of the EBM binary models by varying the number of interactions
| AUC-ROC min/mean/maxa |
#intb | Sens-Spec | BAb | AUC-PRb | AUC-ROC 5-fold cvb |
||
|---|---|---|---|---|---|---|---|
|
HC-PD [neg-pos] |
SBR | 1/1/1 | 0 | 1–1 | 1 | 0.999 | 1 ± 0.0 |
| noSBR | 0.997/0.999/1 | 1 | 0.974-1 | 0.987 | 0.999 | 1 ± 0.0 | |
|
HC-SWEDD [neg-pos] |
SBR | 0.975/0.991/1 | 1 | 1-0.970 | 0.97 | 1 | 0.97 ± 0.02 |
| noSBR | 0.955/0.990/1 | 1 | 1-0.970 | 0.97 | 1 | 0.97 ± 0.02 | |
|
PD-SWEDD [pos-neg] |
SBR | 0.955/0.981/0.986 | 1 | 1-0.5 | 0.75 | 0.998 | 0.94 ± 0.03 |
| noSBR | 0.823/0.859/0.882 | 11 | 1-0.25 | 0.625 | 0.979 | 0.85 ± 0.06 |
The performance of the best models are also reported
a AUC-ROC values obtained by varying the number of pairwise interactions from 0 to 20 (21 iterations)
b Referred to the best EBM binary model, i.e. with max AUC-ROC on the test set and smaller number of pairwise interactions
Abbreviations: HC, healthy control; PD, Parkinson’s disease; SWEDD, Scans without evidence of dopaminergic deficit; SBR, Specific Binding Ratio; pos, positive class; neg, negative class; AUC-ROC, Area under the Curve of the Receiver Operating Characteristic; BA, Balanced Accuracy; AUC-PR, AUC of the Precision-Recall curve; int, interactions; Sens, Sensitivity; Spec, Specificity; cv, cross-validation
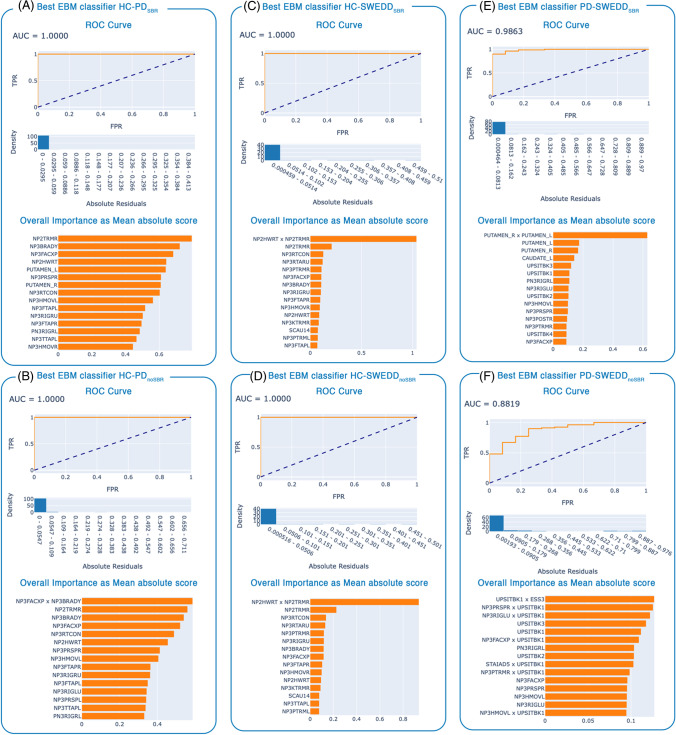
The ROC and the overall importance of the six best EBM models, with and without SBR, could be found in Fig. 1. The overall feature importance of the best model HC-PDSBR showed that the first three most important variables were NP2TRMR (MDS-UPDRS II Self-assessment of tremor, item 2.10), NP3BRADY (MDS-UPDRS III Global Spontaneity of movement, item 3.14) and NP3FACXP (MDS-UPDRS III Facial expression, item 3.2) (Fig. 1A). These three features were also the most predictive variables in the best model HC-PDnoSBR, except that they were outdated in importance by the pairwise interaction NP3FACXPxNP3BRADY (Fig. 1B). The features ranking of the two best models HC-SWEDDSBR and HC-SWEDDnoSBR showed that the most important variables for both classifiers were the interaction between NP2HWRT (MDS-UPDRS II Handwriting item 2.7) and NP2TRMR, followed by the two features NP2TRMR and NP3RTCON (MDS-UPDRS III Constancy of rest, item 3.18) (Fig. 1C-D). The best three variables in the model PD-SWEDDSBR were the interaction between the left putamen SBR and right putamen SBR, followed by the left putamen SBR and the right putamen SBR (Fig. 1E). When the SBRs were dropped from the feature space, the overall importance of the model PD-SWEDDnoSBR revealed that the most predictive variable were three interactions between UPISTBK1 (UPSIT Booklet #1) and ESS3 (Epworth Sleepiness Scale item 3, Sitting, inactive in a public space), between UPISTBK1 and NP3PRSPR (MDS-UPDRS-III pronation-supination movements right hand, item 3.6a), and between UPSITBK1 and NP3RIGLU (MDS-UPDRS-III rigidity left upper limb, item 3.3c).
Fig. 1.
Findings of the best EBM binary classifiers: (A) HC-PDSBR; (B) HC-PDnoSBR; (C) HC-SWEDDSBR; (D) HC-SWEDDnoSBR; (E) PD-SWEDDSBR; (F) PD-SWEDDnoSBR. Upper plots are the ROC Curves (on test set) and densities of the absolute residuals, bottom plots are the rankings of the overall feature importance (first fifteen features) as mean absolute score (on training set)
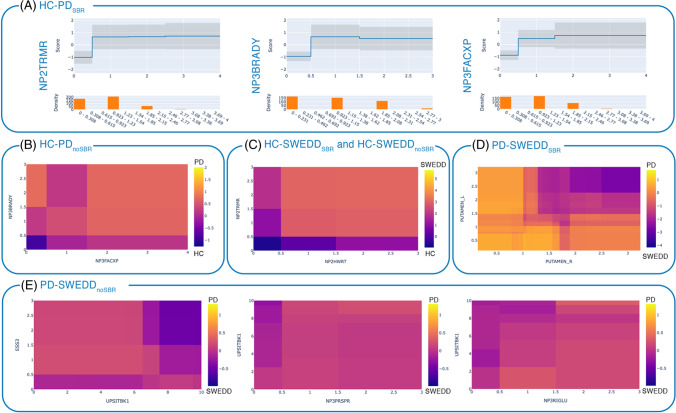
The global explanations of the six EBM models are reported in Fig. 2 and in particular, Fig. 2A depicts the plots of feature interpretability for the first three most important variables in the model HC-PDSBR (NP2TRMR, NP3BRADY and NP3FACXP). These plots of feature interpretability are in other words risk profiles, in which the risk score is reported in the vertical axis and the actual value of the feature is reported in the horizontal axis (upper graphs in Fig. 2A). Bottom graphs in Fig. 2A also reports the density/distribution of the feature. A feature risk score above zero represents a contribution to the classification towards the positive class (PD), while a score below zero denotes a contribution towards the negative class (HC). Looking at the plot of the variable NP2TRMR (Fig. 2A), it is possible to interpret that, actual values of this feature higher than 0.923 contribute to the diagnosis of PD, while values between 0 and 0.308 contribute to the prediction of HC. Similarly, the plot of interpretability of the feature NP3BRADY (Fig. 2A) shows that actual values between 0 and 0.5 contribute to the classification of HC, while values higher 0.5 contribute to the classification of PD.
Fig. 2.
Global explanation of the EBM models: (A) Plots of feature interpretability (risk profiles) for the first three most important variables in the model HC-PDSBR, where the upper graph reports the feature risk score, and the bottom graph depicts the feature distribution. Heatmaps of the pairwise interactions (B) NP3FACXPxNP3BRADY in the EBM models HC-PDnoSBR where HC is negative class (purple) and PD is positive class (yellow); (C) NP2HWRTxNP2TRMR in the EBM models HC-SWEDDSBR and HC-SWEDDnoSBR, where HC is negative class (purple) and SWEDD is positive class (yellow); (D) PUTAMEN_RxPUTAMEN_L in the EBM model PD-SWEDDSBR, where PD is positive class (yellow) and SWEDD is negative class (purple); (E) UPSITBK1xESS3, NP3PRSPRxUPSITBK1, NP3RIGLUxUPSITBK1 in the EBM model PD-SWEDDnoSBR, where PD is positive class (yellow) and SWEDD is negative class (purple). The risk scores are logits (log odds). NP2TRMR = MDS-UPDRS-II Tremor (item 2.10); NP2HWRT = MDS-UPDRS-II Handwriting (item 2.7); ESS3 = Epworth Sleepiness Scale item 3 (Sitting, inactive in a public space); UPSITBK1 = UPSIT Booklet #1; NP3PRSPR = MDS-UPDRS-III pronation-supination movements right hand (item 3.6a); NP3RIGLU = MDS-UPDRS-III rigidity left upper limb (item 3.3c)
For the EBM models in which the interactions resulted to be the most predictive features, we reported their heatmaps (Fig. 2B-E). In the model HC-PDnoSBR, the heatmap of the interaction NP3FACXPxNP3BRADY shows that having higher values of NP3FACXP and of NP3BRADY, or higher values of NP3BRADY and lower values of NP3FACXP, results to have higher risk of having a diagnosis of PD (areas in yellow/orange in Fig. 2B). The pairwise interaction NP2HWRTxNP2TRMR was the most important feature in both models HC-SWEDDSBR and HC-SWEDDnoSBR, where the higher risk to be diagnosed as SWEDD is obtained when these two features have both high values (yellow/orange area in the upper right corner of Fig. 2C). The heatmap of the pairwise interaction PUTAMEN_RxPUTAMEN_L - the most important feature in the model PD-SWEDDSBR – shows that higher risk to have a diagnosis of PD is when both putamina have lower SBR values (yellow area in the bottom left corner of Fig. 2D). Regarding the model PD-SWEDDnoSBR, the heatmaps of interactions (Fig. 2E) reveals that having lower values of UPSITBK1 accompanied by higher values of ESS3, NP3PRSPR and NP3RIGLU contributes to the prediction as PD (positive class in yellow).
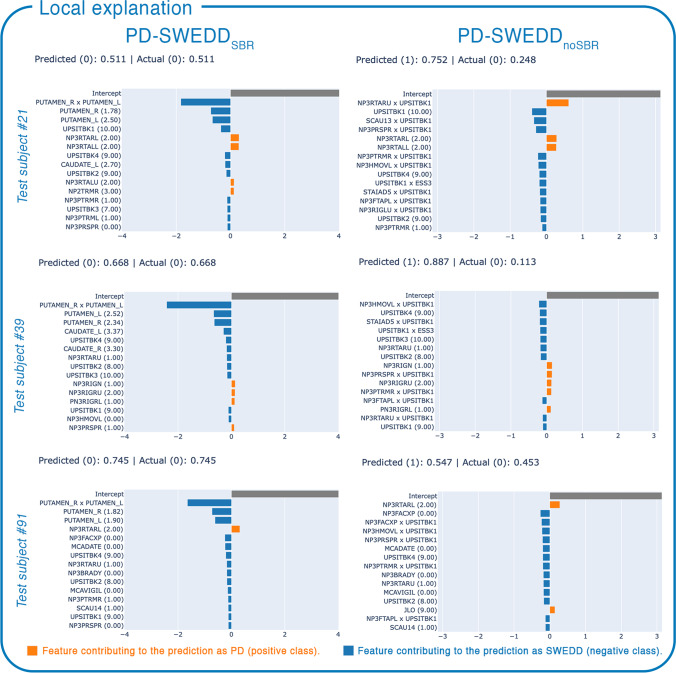
The local explanations were assessed on the three SWEDD test subjects (#21, #39, #91) who were misclassified as PD by the model PD-SWEDDnoSBR, but correctly classified by the model PD-SWEDDSBR. Figure 3 reports the contribution of each feature in the prediction of these three SWEDDs in both EBM classifiers, where feature scores below zero (in blue) contribute to the classification as SWEDD, while feature scores above zero (in orange) contribute to the classification as PD. In particular, the plots of the local interpretability in Fig. 3 show that the interaction PUTAMEN_RxPUTAMEN_L in the model PD-SWEDDSBR is primarily responsible for the correct classification of the three SWEDD subjects.
Fig. 3.
Local explanation of the three SWEDD test subjects (#21, #39, #91) misclassified as PD by the EBM binary model PD-SWEDDnoSBR, but correctly classified by the EBM model PD-SWEDDSBR. In round brackets the actual value of the feature. The local explanation scores are logits (log odds), where SWEDD is negative class (or class 0), and PD is positive class (or class 1). The probabilities of the predictions are also reported
Discussion
A highly intelligible ML approach, the EBM, was here applied for the differential diagnosis of PD and SWEDD through clinical and imaging features. The EBM models for distinguishing PD from HC, and SWEDD from HC, reached the maximum of accuracy (1), both with and without the striatum SBR as training feature. A slight decrease in the accuracy was obtained by the model for distinguishing PD from SWEDD with the SBR as feature (0.986), while the model without SBR had a greater decrease of the AUC-ROC (0.882). Our results improved the accuracies for the automatic diagnosis of PD and SWEDD provided by the literature (Chien 2021; Palumbo, 2014), in models trained on the same clinical and imaging features here used (Mabrouk et al., 2017; Hirschauer et al., 2015), as well as in other explainable ML approaches (Ma et al., 2021; Magesh et al., 2020).
It is noteworthy that the drop of the caudate and putamen SBR from the feature space, did not worse the performance of HC-PD and HC-SWEDD classifiers thanks to the presence of the pairwise interactions, thus providing an accurate model that do not require subjects to be acquired with an invasive and expensive SPECT imaging method (Hirschauer et al., 2015). In particular, we improved the accuracy of the previous literature (Mabrouk et al., 2019), where PDs were distinguished from HCs with an AUC-ROC of 88% by a K-NN classifier trained only on MoCA and UPSIT total scores. In another work (Hirschauer et al., 2015), for distinguishing PD and SWEDD from HC, classifiers were trained only on six clinical examinations (UPDRS-I, UPDRS-II, UPDRS-III, MoCA SCOPA-AUT, UPSIT) obtaining accuracies of 97.2%, and 93.6% for the binary problems HC-PD and HC-SWEDD respectively. With our AUC-ROC on test set of 1 and a mean AUC-ROC of 1 with the 5-fold cross-validation, we also outperformed the accuracies of explainable models recently applied for the detection of PD: the 95.2% obtained by an Explainable ML model applied on DaTSCAN images (Magesh et al., 2020), and the accuracy of 98.41% of an explainable deep learning approach trained on Gait data (Ma et al., 2021).
Regarding the more challenging classification of PD and SWEDD, we found that SBRs were still necessary as training features for reaching optimal accuracy, as in previous ML works (Chien, 2021; Palumbo, 2014; Oliveira & Castelo-Branco, 2015; Mabrouk et al., 2017, 2019; Hirschauer et al., 2015; Prashanth et al., 2017; Lei et al., 2019; Magesh et al., 2020), although no one until now evaluated and demonstrated the importance of left and right putamina pairwise interaction. The interaction PUTAMEN_RxPUTAMEN_L (Fig.2D) allowed us to obtain an AUC-ROC of 98.63% on the test set and a mean AUC-ROC with 5-fold cross validation of 94%, achieving similar or better performance than the literature. For example, in a study (Hirschauer et al., 2015) the classifier for distinguishing PD from SWEDD had an AUC-ROC of 95.3% with both SBRs and clinical data as training features, and an AUC-ROC of 93.7% with only putamen SBR (mean of the left and right putamen) as training feature. The importance of the striatum SBR was also confirmed when we looked at the local explanations of the misclassified SWEDD test subjects (Fig.3) provided by our PD-SWEDD classifiers. Although the model PD-SWEDDnoSBR showed worst performance than the PD-SWEDDSBR one, it had a good AUC-ROC (88.2%), which anyway improved the literature, as in comparison with Hirschauer et al. (2015), where, when the classifier was trained only on clinical examinations data, PD and SWEDD were distinguished with an accuracy of 86.8%.
Another important finding of the present work is that we demonstrated that one single pairwise interaction was enough for maximizing the accuracy in classifying HC-PD when SBRs was excluded from the feature space. We also found a stability of the results in the two best models HC-SWEDD, with and without SBRs, since they had the same and only interaction pair - NP2HWRTxNP2TRMR- that was also the most predictive variable. In other words, we confirmed the robustness to excess feature pairs of the EBM algorithm reported by Lou et al. (2013), demonstrating small variations in the range of accuracy when varying the number of interactions (Table 2). Although the model PD-SWEDDnoSBR showed this kind of stability too, a higher number of features pairs (11) was necessary for reaching the maximum performance. This could be due to the overlapping motor and non-motor symptoms between the two diseases, as well as to the heterogeneity of SWEDD patients, who can present a broad range of possible underlying diagnoses (Schwingenschuh et al., 2010), or to diagnostic uncertainty. Anyway, it is interesting to notice the predictive role of the UPSIT (Booklet #1) - a non-motor sign - in distinguishing SWEDD from PD, given its presence in the first three most important interactions (UPSITBK1xESS3, NP3PRSPRxUPSITBK1, NP3RIGLUxUPSITBK1, Fig. 1F). This result corroborates the previous literature that demonstrated that UPSIT best differentiated PD from SWEDD and proposed the UPSIT as an important indicator of the likelihood of SWEDD (Hirschauer et al., 2015).
Despite the promising findings, the present study has several limitations to be addressed. First of all, the low sample size, especially in the case of the SWEDD cohort, which could have limited the generalizability of the results, although it should be highlighted that the bagging and gradient boosting procedures of EBM may have been able to minimize this issue. Moreover, the imbalanced dataset may have allowed the majority class (PD) to have a larger weight than the minority (SWEDD) during the process of training, leading to a poor specificity on the test set. We cannot exclude that the bias introduced by the class imbalance of the binary problem PD-SWEDD led to build “unfair” classifiers (Amoroso et al., 2018; Wahlström et al., 2019; Zeng et al., 2022), which completely ignored the feature contribution of the minority class. Although we obtained good balanced accuracy (0.625) and optimal AUC-PR (0.979), future studies should investigate the ability of EBM algorithm to deal with imbalanced classes, or, from an algorithmic point of view, assess the EBM fairness through thresholding rules derived for example from Bayes-optimal classifiers (Amoroso et al., 2018; Wahlström et al., 2019; Zeng et al., 2022). Another limitation of this work is related to the possible presence of correlation among features, heavy multicollinearity and/or non-linearity around a prediction (Caruana et al., 2015), which may consider important interactions that are on the contrary spurious. Since we considered the subitem scores rather than the total score of the clinical assessments, the large feature space may have indeed introduced multicollinearity among features. Our choice relies on the complexity of the differential diagnosis of PD and SWEDD patients for which subtle differences between PD and SWEDD patients could be lost when only the total score is considered. Furthermore, the use of the subitems as training features could enhance the ability of EBM in providing interpretable findings and supporting the clinical decisions. Regarding the imaging feature, we considered only DaTSCAN since this is the gold standard for the PD diagnosis, and it is the most common imaging approach used in the clinical routine. Further works are needed to confirm our results on a larger cohort and with different features, for example MRI structural or diffusion metrics, especially to improve the diagnostic accuracy of the binary problem PD-SWEDD and to confirm the trustiness of the EBM global and local explanations.
Conclusions
In this study, a high intelligible ML approach, the EBM, was applied for the differential diagnosis of PD and SWEDD from clinical and imaging features obtaining excellent accuracies. We demonstrated that PD and SWEDD could be distinguished by the EBM algorithm with optimal performance (AUC-ROC 0.882) also without the striatal uptake from DaTSCAN, which is an invasive, time-consuming and expensive imaging technique. We showed that including the pairwise interactions between features increased the EBM models accuracy still maintaining high intelligibility of ML findings. Moreover, the visual analysis of the global and local explanations offered accurate information about the impact of each single feature around the prediction of PD and SWEDD, especially for understanding why a test subject was correctly or incorrectly classified.
Acknowledgements
PPMI – a public-private partnership – is funded by the Michael J. Fox Foundation for Parkinson’s Research funding partners 4D Pharma, Abbvie, Acurex Therapeutics, Allergan, Amathus Therapeutics, ASAP, Avid Radiopharmaceuticals, Bial Biotech, Biogen, BioLegend, Bristol-Myers Squibb, Calico, Celgene, Dacapo Brain Science, Denali, The Edmond J. Safra Foundaiton, GE Healthcare, Genentech, GlaxoSmithKline, Golub Capital, Handl Therapeutics, Insitro, Janssen Neuroscience, Lilly, Lundbeck, Merck, Meso Scale Discovery, Neurocrine Biosciences, Pfizer, Piramal, Prevail, Roche, Sanofi Genzyme, Servier, Takeda, Teva, UCB, Verily, and Voyager Therapeutics.
Author contributions
Author contributions included conception and study design (AS), data collection and acquisition (AS), statistical analysis (AS), interpretation of results (AS, AQ, AQ), drafting the manuscript (AS) and revising it critically for important intellectual content (AS, AQ, AQ), and approval of the final version to be published and agreement to be accountable for the integrity and accuracy of all aspects of the work (all authors).
Data availability
Data used in the preparation of this article were obtained from the Parkinson’s Progression Markers Initiative (PPMI) database (www.ppmi-info.org/data). For up-to-date information on the study, visit www.ppmi-info.org.
Declarations
Ethical approval
Not applicable.
Consent to participate
Not applicable.
Consent to publish
Not applicable.
Conflict of interest
Nothing to declare.
Footnotes
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Alessia Sarica and Andrea Quattrone contributed equally to this work.
References
- Ahmad, M. A., Eckert, C., & Teredesai, A. (2018). Interpretable machine learning in healthcare. Proceedings of the 2018 ACM international conference on bioinformatics, computational biology, and health informatics (pp. 559–560)
- Amoroso N, Rocca M, Bellotti R, Fanizzi A, Monaco A, Tangaro S. Alzheimer’s Disease Neuroimaging I: Alzheimer’s disease diagnosis based on the Hippocampal Unified Multi-Atlas Network (HUMAN) algorithm. Biomedical Engineering Online. 2018;17:6. doi: 10.1186/s12938-018-0439-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arrieta AB, Díaz-Rodríguez N, Del Ser J, Bennetot A, Tabik S, Barbado A, Benjamins R. Explainable Artificial Intelligence (XAI): Concepts, taxonomies, opportunities and challenges toward responsible AI. Information Fusion. 2020;58:82–115. doi: 10.1016/j.inffus.2019.12.012. [DOI] [Google Scholar]
- Breiman L. Random forests. Machine Learning. 2001;45:5–32. doi: 10.1023/A:1010933404324. [DOI] [Google Scholar]
- Caruana, R., Lou, Y., Gehrke, J., Koch, P., Sturm, M., & Elhadad, N. (2015). Intelligible models for healthcare: Predicting pneumonia risk and hospital 30-day readmission. Proceedings of the 21th ACM SIGKDD international conference on knowledge discovery and data mining (pp. 1721–1730)
- Chen, T., & Guestrin, C. (2016). Xgboost: A scalable tree boosting system. Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining (pp. 785–794)
- Chien, C. Y., Hsu, S. W., Lee, T. L., Sung, P. S., & Lin, C. C. (2021). Using artificial neural network to discriminate Parkinson’s Disease from other Parkinsonisms by focusing on putamen of dopamine transporter SPECT images. Biomedicines 9(1), 12 [DOI] [PMC free article] [PubMed]
- de Lau LML, Breteler MMB. Epidemiology of Parkinson’s disease. Lancet Neurology. 2006;5:525–535. doi: 10.1016/S1474-4422(06)70471-9. [DOI] [PubMed] [Google Scholar]
- Goetz CG, Tilley BC, Shaftman SR, Stebbins GT, Fahn S, Martinez-Martin P, LaPelle N. Movement disorder society URTF: Movement disorder society-sponsored revision of the Unified Parkinson’s Disease Rating Scale (MDS-UPDRS): scale presentation and clinimetric testing results. Movement Disorders. 2008;23:2129–2170. doi: 10.1002/mds.22340. [DOI] [PubMed] [Google Scholar]
- Hastie, T. J., & Tibshirani, R. J. (1990). Generalized additive models. CRC Press [DOI] [PubMed]
- Hirschauer, T. J., Adeli, H., & Buford, J. A. (2015). Computer-aided diagnosis of Parkinson’s disease using enhanced probabilistic neural network. Journal of Medical Systems, 39(11), 179 [DOI] [PubMed]
- Lei H, Huang Z, Zhou F, Elazab A, Tan EL, Li H, Lei B. Parkinson’s Disease diagnosis via joint learning from multiple modalities and relations. IEEE Journal of Biomedical and Health Informatics. 2019;23:1437–1449. doi: 10.1109/JBHI.2018.2868420. [DOI] [PubMed] [Google Scholar]
- Lou, Y., Caruana, R., & Gehrke, J. (2012). Intelligible models for classification and regression. Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 150–158)
- Lou, Y., Caruana, R., Gehrke, J., & Hooker, G. (2013). Accurate intelligible models with pairwise interactions. Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining (pp 623–631)
- Ma, Y. W., Chen, J. L., Chen, Y. J., & Lai, Y. H. (2021). Explainable deep learning architecture for early diagnosis of Parkinson’s disease. Soft Computing, 1–10
- Mabrouk, R., Chikhaoui, B., & Bentabet, L. (2017). Machine Learning Based Approaches for SWEDD diagnosis in DaTSCAN SPECT imaging. In 2017 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) (pp. 1–3). IEEE
- Mabrouk R, Chikhaoui B, Bentabet L. Machine learning based classification using clinical and DaTSCAN SPECT imaging features: A study on Parkinson’s Disease and SWEDD. IEEE Transactions on Radiation and Plasma. 2019;3:170–177. doi: 10.1109/TRPMS.2018.2877754. [DOI] [Google Scholar]
- Magesh, P. R., Myloth, R. D., & Tom, R. J. (2020). An explainable machine learning model for early detection of Parkinson’s Disease using LIME on DaTSCAN Imagery. Computers in Biology and Medicine, 126, 104041 [DOI] [PubMed]
- Magunia, H., Lederer, S., Verbuecheln, R., Gilot, B. J., Koeppen, M., Haeberle, H. A. … Rosenberger, P. (2021). Machine learning identifies ICU outcome predictors in a multicenter COVID-19 cohort. Critical Care, 25(1), 295 [DOI] [PMC free article] [PubMed]
- Nori, H., Jenkins, S., Koch, P., & Caruana, R. (2019). Interpretml: A unified framework for machine learning interpretability. arXiv preprint arXiv:190909223
- Oliveira, F. P. M., & Castelo-Branco, M. (2015). Computer-aided diagnosis of Parkinson’s disease based on [I-123]FP-CIT SPECT binding potential images, using the voxels-as-features approach and support vector machines. Journal of Neural Engineering, 12(2), 026008 [DOI] [PubMed]
- Palumbo, B., Fravolini, M. L., Buresta, T., Pompili, F., Forini, N., Nigro, P. … Tambasco, N. (2014). Diagnostic accuracy of Parkinson Disease by Support Vector Machine (SVM) analysis of I-123-FP-CIT Brain SPECT Data. Medicine 93(27), e228 [DOI] [PMC free article] [PubMed]
- Prashanth R, Roy SD, Mandal PK, Ghosh S. High-accuracy classification of Parkinson’s Disease through shape analysis and surface fitting in 123I-Ioflupane SPECT imaging. IEEE Journal of Biomedical and Health Informatics. 2017;21:794–802. doi: 10.1109/JBHI.2016.2547901. [DOI] [PubMed] [Google Scholar]
- Salvatore C, Cerasa A, Castiglioni I, Gallivanone F, Augimeri A, Lopez M, Quattrone A. Machine learning on brain MRI data for differential diagnosis of Parkinson’s disease and Progressive Supranuclear Palsy. Journal of Neuroscience Methods. 2014;222:230–237. doi: 10.1016/j.jneumeth.2013.11.016. [DOI] [PubMed] [Google Scholar]
- Sarica, A. (2022). Editorial for the special issue on “Machine Learning in Healthcare and Biomedical Application”, MDPI, 15, pp 97
- Sarica A, Cerasa A, Quattrone A. Random forest algorithm for the classification of neuroimaging data in Alzheimer’s disease: a systematic review. Frontiers in Aging Neuroscience. 2017;9:329. doi: 10.3389/fnagi.2017.00329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarica, A., Vaccaro, M. G., Quattrone, A., & Quattrone, A. (2021a). A novel approach for cognitive clustering of Parkinsonisms through affinity propagation. Algorithms, 14(2), 49
- Sarica, A., Quattrone, A., & Quattrone, A. (2021b). Explainable boosting machine for predicting Alzheimer’s Disease from MRI hippocampal subfields. International Conference on Brain Informatics (pp. 341–350). Springer
- Schwingenschuh P, Ruge D, Edwards MJ, Terranova C, Katschnig P, Carrillo F, Bhatia KP. Distinguishing SWEDDs patients with asymmetric resting tremor from Parkinson’s Disease: A clinical and electrophysiological study. Movement Disord. 2010;25:560–569. doi: 10.1002/mds.23019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shahtalebi, S., Atashzar, S. F., Patel, R. V., Jog, M. S., & Mohammadi, A. (2021). A deep explainable artificial intelligent framework for neurological disorders discrimination. Scientific Reports-UK, 11(1), 9630 [DOI] [PMC free article] [PubMed]
- Vaccaro MG, Sarica A, Quattrone A, Chiriaco C, Salsone M, Morelli M, Quattrone A. Neuropsychological assessment could distinguish among different clinical phenotypes of progressive supranuclear palsy: A machine learning approach. Journal of Neuropsychology. 2021;15:301–318. doi: 10.1111/jnp.12232. [DOI] [PubMed] [Google Scholar]
- Wahlström J, Skog I, Gustafsson F, Markham A, Trigoni N. Zero-velocity detection—A Bayesian approach to adaptive thresholding. IEEE Sensors Letters. 2019;3:1–4. doi: 10.1109/LSENS.2019.2917055. [DOI] [Google Scholar]
- Wang HL, Huang ZL, Zhang DF, Arief J, Lyu TW, Tian J. Integrating co-clustering and interpretable machine learning for the prediction of intravenous immunoglobulin resistance in Kawasaki Disease. IEEE Access. 2020;8:97064–97071. doi: 10.1109/ACCESS.2020.2996302. [DOI] [Google Scholar]
- Yang Y, Wei L, Hu Y, Wu Y, Hu L, Nie S. Classification of Parkinson’s disease based on multi-modal features and stacking ensemble learning. Journal Of Neuroscience Methods. 2021;350:109019. doi: 10.1016/j.jneumeth.2020.109019. [DOI] [PubMed] [Google Scholar]
- Zeng, X., Dobriban, E., & Cheng, G. (2022). Bayes-optimal classifiers under group fairness. arXiv preprint arXiv:220209724
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data used in the preparation of this article were obtained from the Parkinson’s Progression Markers Initiative (PPMI) database (www.ppmi-info.org/data). For up-to-date information on the study, visit www.ppmi-info.org.