In Vivo Development of Tissue Engineered Vascular Grafts: A Fluid-Solid-Growth Model

Abstract

Methods of tissue engineering continue to advance, and multiple clinical trials are underway evaluating tissue engineered vascular grafts (TEVGs). Whereas initial concerns focused on suture retention and burst pressure, there is now a pressing need to design grafts to have optimal performance, including an ability to grow and remodel in response to changing hemodynamic loads. Towards this end, there is similarly a need for computational methods that can describe and predict the evolution of TEVG geometry, composition, and material properties while accounting for changes in hemodynamics. Although the ultimate goal is a fluid-solid-growth (FSG) model incorporating fully 3D growth and remodeling and 3D hemodynamics, lower fidelity models having high computational efficiency promise to play important roles, especially in the design of candidate grafts. We introduce here an efficient FSG model of in vivo development of a TEVG based on two simplifying concepts: mechanobiologically equilibrated growth and remodeling of the graft and an embedded control volume analysis of the hemodynamics. Illustrative simulations for a model Fontan conduit reveal the utility of this approach, which promises to be particularly useful in initial design considerations involving formal methods of optimization which otherwise add considerably to the computational expense.

1. Introduction

Tissue engineering seeks to repair, replace, or regenerate tissues and organs, often using biodegradable polymeric constructs to guide cell-mediated neotissue formation. Now 20+ years later, its early promise to provide functional vascular conduits on demand (Niklason et al., 1999) is becoming a reality and multiple designs are under investigation via clinical trials (Hibino et al., 2010; Bockeria et al., 2020; Niklason and Lawson, 2020). With feasibility established, it is now time to advance from conceptualization and assessment to optimization. Although current achievements have been realized largely via trial-and-error empirical approaches, the current knowledge base provides data sufficient to inform computational models of neotissue formation having clinical utility (Drews et al., 2020; Blum et al., 2022), which in turn promise to enable formal optimization of both scaffold design (Szafron et al., 2019; Tamimi et al., 2019) and clinical use of implanted constructs (Yang et al., 2013).

Among others, we have shown that a constrained mixture theory (Humphrey and Rajagopal, 2002) can be used to model soft tissue growth and remodeling (G&R) and be specialized to describe (Miller et al., 2014) and predict (Khosravi et al., 2015) the long-term in vivo development of a functional tissue engineered vascular graft (TEVG). We have shown further that such models can be used to perform numerical parameter sensitivity studies (Miller et al., 2015) or combined with numerical optimization techniques (Szafron et al., 2019) to provide new insights into the design-driven natural history of TEVG geometry, composition, and material properties as it develops in vivo. Before optimization studies can reach their full potential, however, there remains a need for an additional theoretical advance – development of a fully 3D fluid-solid-growth (FSG) framework that accounts for the effects of hemodynamic changes as the TEVG develops, including possible transient luminal thrombus formation as well as local narrowing or dilatation of the graft. Notwithstanding the theoretical advantages of full constrained mixture models, which allow one to account for the separate rates of removal and production of different constituents having individually evolving natural configurations and material properties, the associated computational expense motivates the search for reduced models.

We thus introduce here a fast, efficient, reduced model for performing exploratory FSG simulations that can help focus the more computationally intensive simulations that will be needed for final design optimization. Advancing such a multi-fidelity modeling approach promises to be both time- and cost-efficient, with further promise of providing insight into the in vivo development of TEVGs that may be less evident in more complex simulations. Toward this end, we extend and couple a mechanobiologically equilibrated constrained mixture model of tissue G&R (Latorre and Humphrey, 2018, 2020a) with a control volume based analysis of luminal flow (Baek et al., 2007) which together enable the first simulations of in vivo TEVG development to include direct feedback from the changing hemodynamics. For completeness, we summarize key aspects of the framework and workflow in the next section.

2. A mechanobiologically equilibrated framework for in vivo TEVG development

2.1. Mass balance

In a continuum theory of constrained mixtures for G&R (Humphrey and Rajagopal, 2002), properties at a material point in configuration κ(s) are represented in a locally averaged sense in terms of multiple structurally significant constituents α = 1, …,N, to satisfy mass balance in spatial form $\partial {\rho }^{\alpha }/\partial s+\mathrm{div}\left({\rho }^{\alpha }{\mathbf{v}}^{\alpha }\right)={\overline{m}}^{\alpha }$, where ρ^α is the homogenized apparent mass density (mass of constituent α per unit current volume of mixture), s is the G&R time, v^α the velocity (constrained to equal the velocity v of the mixture), and ${\overline{m}}^{\alpha }$ the net rate of mass density production or removal, which must be prescribed constitutively. Let ${\overline{m}}^{\alpha }$ be defined in terms of true rates of mass density production m^α > 0 and removal n^α > 0 as ${\overline{m}}^{\alpha }=m^{\alpha }-n^{\alpha }$, both of which must be prescribed constitutively. Because div(ρ^αv^α) = ρ^α divv^α+v^α·gradρ^α, then $\partial {\rho }^{\alpha }/\partial s+{\mathbf{v}}^{\alpha }\cdot \mathrm{grad}{\rho }^{\alpha }={\dot{\rho }}^{\alpha }$, with ${\dot{\rho }}^{\alpha }$ the material time derivative of ρ^α, and $\mathrm{div}{\mathbf{v}}^{\alpha }=\mathrm{div}\mathbf{v}=\dot{J}/J$, with J =detF the Jacobian determinant of a deformation gradient F defined at the mixture level, which conveniently describes (measurable) deformations between an initial configuration κ_o:= κ(0) and current configuration κ(s). Mass balance can thus be written in terms of the referential mass density ${\rho }_{\text{R}}^{\alpha }=J{\rho }^{\alpha }$ (defined per unit reference volume of mixture) as

$$\frac{{\dot{\rho }}_{\text{R}}^{\alpha }}{J}\equiv {\dot{\rho }}^{\alpha }+{\rho }^{\alpha }\frac{\dot{J}}{J}=m^{\alpha }-n^{\alpha }.$$ (1)

Here, consider two types of load-bearing constituents, denoted by superscripts α = p (polymer) and α = c (collagen-dominated neotissue) within a TEVG that evolve differently for s > 0. The polymeric constituent p can only degrade, with half-lives on the order of weeks to years depending on the material, with its intermittent response described by hyperelasticity and possibly damage mechanics. In contrast, neotissue constituents c = 1,..,N^c (with 1 + N^c = N) can turnover continuously, thus contributing to local changes in mass and microstructure, with their response described herein by (rate-independent) G&R, examples of which are collagen fibers arising from inflammation-driven or mechano-mediated synthesis, which have a half-life of days to months.

2.1.1. Polymeric scaffold

With m^p = 0 and n^p > 0, we have

$$\frac{{\dot{\rho }}_{\text{R}}^p}{J}\equiv {\dot{\rho }}^p+{\rho }^p\frac{\dot{J}}{J}=-n^p.$$ (2)

2.1.2. Immuno-mechano-mediated neotissue

For collagen-dominated neotissue that turns over, it proves useful to define a stimulus function ϒ^c = m^c/n^c > 0, which enhances (ϒ^c − 1 > 0), reduces (ϒ^c − 1 < 0), or balances (ϒ^c − 1 = 0) mass production with respect to mass removal. Prescribing m^c and n^c is thus tantamount to prescribing n^c and ϒ^c, with

$$\frac{{\dot{\rho }}_{\text{R}}^c}{J}\equiv {\dot{\rho }}^c+{\rho }^c\frac{\dot{J}}{J}=m^c-n^c=n^c\left({\Upsilon }^c-1\right).$$ (3)

2.2. Linear momentum balance

For negligible body forces and (excess) exchanges of momentum, spatial linear momentum balance for constituent α, with vanishing interactive forces among constituents due to their constrained motion, can be written

$${\rho }^{\alpha }{\dot{\mathbf{v}}}^{\alpha }=\mathrm{div}{\mathit{\sigma }}_{\text{t}}^{\alpha }$$ (4)

where ${\mathit{\sigma }}_{\text{t}}^{\alpha }$ is the total Cauchy stress tensor (i.e., including a contribution σ^α derived from a strain energy function and others arising from kinematic constraints, such as transient incompressibility) for a constituent at the mixture level.

Summation of mass, Eqs. (2) and (3), and momentum, Eq. (4), balances over all α = polymer+neotissue constituents yields

$$\frac{{\dot{\rho }}_{\text{R}}}{J}\equiv \dot{\rho }+\rho \frac{\dot{J}}{J}=-n^p+\sum _{c=1}^{N^c}{n}^c\left({\Upsilon }^c-1\right)$$ (5)

and

$$\rho \dot{\mathbf{v}}=\mathrm{div}\mathit{\sigma }$$ (6)

where ${\rho }_{\text{R}}=\sum {\rho }_{\text{R}}^{\alpha }=J\sum {\rho }^{\alpha }=J\rho$ and $\mathit{\sigma }=\sum {\mathit{\sigma }}_{\text{t}}^{\alpha }$.

2.3. Mechanobiological (quasi-)equilibrium

We observe from Eqs. (2), (3) and (5) that a sufficient (hypothetical, purely mathematical) condition for a TEVG to be in mechanobiological equilibrium (to preserve its mixture mass, composition, and properties; Latorre and Humphrey, 2018) at G&R time s is n^p ≡ 0 (i.e., the polymer does not degrade) and ϒ^c ≡ 1 ∀c (i.e., production of neotissue precisely balances removal), whereby ${\dot{\rho }}_{\text{R}}^{\alpha }\equiv 0\forall \alpha$ and ${\dot{\rho }}_{\text{R}}=0$. Importantly, however, because the polymer degrades continuously until exhausted, and because this degradation may stimulate turnover of both immuno- and mechano-mediated neotissue, a suitable approximation for evolving, mechanobiologically quasi-equilibrated G&R processes is possible if

$$n^p>0\text{and}{\Upsilon }^c\simeq 1\forall c,$$ (7)

for which ${\dot{\rho }}_{\text{R}}>0$, which is most stringent, yields from Eq. (5)

$$\sum _{c=1}^{N^c}{n}^c\left({\Upsilon }^c-1\right)>n^p,$$ (8)

that is, if characteristic rates of turnover of neotissue are greater than rates of degradation of polymer (i.e., the “adaptation” timescale is shorter than the “stimulation” timescale). In particular, for N^c = 1, this last condition reduces to n^p/n^c < ϒ^c − 1 ≃ 0, which holds for n^c ≫ n^p. Note that if, as commonly assumed, degradation of neotissue constituents follows a first-order decay throughout the evolution (with n^c proportional to ρ^c), this condition would hardly hold at early times after implantation of the graft (when ρ^c ≪ ρ), suggesting that transient G&R effects could be important during an initial (typically short) phase, which this formulation disregards to a first approximation. Finally, quasistatic mechanical equilibrium in evolving in vivo states (pseudo-homeostatic, denoted by subscript h) additionally requires $\mathbf{0}\simeq \rho \dot{\mathbf{v}}=\mathrm{div}\mathit{\sigma }$ from Eq. (6), with F ≡ F_h describing deformations between configurations κ_o and κ_h, see Fig. 1.

Fig. 1.

Schematic representation of different configurations κ_i involved in mechanobiologically equilibrated TEVG G&R, with c ≡ collagen-dominated neotissue (including smooth muscle and collagen fibers) experiencing continuous turnover and p ≡ polymer only degrading over time. Note that κ_o (TEVG at s_h = 0, i.e., scaffold) and κ_h (TEVG at s_h > 0) are both “homeostatic”; all configurations are in vivo. Subscripts o and h denote original and evolved homeostatic; subscripts N and n denote Lagrangian and Eulerian natural configurations; subscript R denotes the (un)rotated current configuration of the TEVG.

2.4. Mechanobiologically equilibrated volume (and mass) fractions

Let constituents have different true mass densities ${\widehat{\rho }}^{\alpha }$ (i.e., current mass of constituent per unit current volume of constituent). We have shown previously (Latorre and Humphrey, 2018) that rule-of-mixture expressions are then given in terms of constituent-specific volume fractions Φ^α (i.e., current volume of constituent per unit current volume of mixture). Noting that ${\Phi }_o^c=0\forall c$ for a pure polymeric scaffold, the initial volume fraction ${\Phi }_o^p$ satisfies ${\Phi }_o^p+\sum {\Phi }_o^c={\Phi }_o^p=1$. Let also ${\widehat{\rho }}^{\alpha }$ remain constant, a plausible approximation for (highly hydrated) neotissue constituents and also polymeric scaffolds that degrade via surface erosion, though not necessarily for polymers undergoing bulk degradation (which, even if the present formulation could describe via evolving ${\widehat{\rho }}^p$ are not considered here due to a current lack of data). Because their differential production and removal contribute to changes in mass and volume of the mixture, both types of constituents can present evolved volume fractions ${\Phi }_h^p\ne {\Phi }_o^p$ and ${\Phi }_h^c\ne {\Phi }_o^c$ at any (new) equilibrium state κ_h, satisfying ${\Phi }_h^p+\sum {\Phi }_h^c=1$, with

$${\Phi }_o^{\alpha }=\frac{{\rho }_o^{\alpha }}{{\widehat{\rho }}^{\alpha }},{\Phi }_h^{\alpha }=\frac{{\rho }_h^{\alpha }}{{\widehat{\rho }}^{\alpha }}$$ (9)

for all constituents α = 1,…,1 + N^c, where ${\rho }_o^{\alpha }$ and ${\rho }_h^{\alpha }$ are equilibrated homogenized mass densities (defined locally as original o or updated h homeostatic, respectively). Mass (ϕ^α) and volume (Φ^α) fractions relate through

$${\varphi }_h^{\alpha }=\frac{{\rho }_h^{\alpha }}{{\rho }_h}={\Phi }_h^{\alpha }\frac{{\widehat{\rho }}^{\alpha }}{{\rho }_h}$$ (10)

where the, generally evolving, current mass density ρ_h of the overall tissue is

$${\rho }_h=\sum _{\alpha =1}^N{\rho }_h^{\alpha }=\sum _{\alpha =1}^N{\Phi }_h^{\alpha }{\widehat{\rho }}^{\alpha }$$ (11)

whereby ${\rho }_h=\left(\sum {\varphi }_h^{\alpha }\right){\rho }_h$, that is, $1=\sum {\varphi }_h^{\alpha }$. For the particular case ${\widehat{\rho }}^{\alpha }=\widehat{\rho }\forall \alpha$, then ${\rho }_h=\left(\sum {\Phi }_h^{\alpha }\right)\widehat{\rho }=\widehat{\rho }={\rho }_o$ remains constant and volume and mass fractions coincide (Latorre and Humphrey, 2018).

2.4.1. Polymeric scaffold

Based on our previous study (Drews et al., 2020), let the mass of polymer degrade via the following decay function

$$Q^p\left(s_h\right)=\frac{1+e^{-k^p{\chi }^p}}{1+e^{k^p\left(s_h-{\chi }^p\right)}}=:Q_h^p$$ (12)

where k^p and χ^p are associated rate and shape parameters. With ${\rho }_{\text{R}o}^p={\rho }_o^p={\Phi }_o^p{\widehat{\rho }}^p={\widehat{\rho }}^p$,

$${\rho }_{\text{R}h}^p={\rho }_{\text{R}o}^p{Q}_h^p={\widehat{\rho }}^p{Q}_h^p$$ (13)

and

$${\rho }_h^p=\frac{{\rho }_{\text{R}h}^p}{J_h}=\frac{{\widehat{\rho }}^p{Q}_h^p}{J_h}\Rightarrow {\Phi }_h^p\left(J_h\right)=\frac{Q_h^p}{J_h}.$$ (14)

Thus, the referential volume fraction of polymer ${\Phi }_{\text{R}h}^p=J_h{\Phi }_h^p$ (current volume of polymer per unit reference volume of mixture) equals the mass decay $Q_h^p$. Consistent with Eq. (2),

$$\begin{gathered} {\dot{\rho }}_{\text{R}h}^p={\widehat{\rho }}^p{\dot{Q}}_h^p=-\frac{k^p}{1+e^{-k^p\left(s_h-{\chi }^p\right)}}{\widehat{\rho }}^p{Q}_h^p \\ =-\frac{k^p}{1+e^{-k^p\left(s_h-{\chi }^p\right)}}{\rho }_{\text{R}h}^p=-n_{\text{R}h}^p \end{gathered}$$ (15)

where $n_{\text{R}h}^p=J{n}_h^p<0$. Note that the G&R time s_h plays the role of a parameter within this formulation; that is, one can compute an equilibrated state for each level of polymer degradation (or pseudo-time s_h).

2.4.2. Immuno-mechano-mediated neotissue

To delineate differential changes in mass of constituents c under mechanobiological equilibrium, one needs first to describe how they evolve with respect to each other under general G&R. For example, without explicitly prescribing n^c and ϒ^c in Eq. (3), let these constituents respond to changes in stimuli with proportional out-of-equilibrium stimulus functions and mass-specific rates for removal: ${\Upsilon }^i-1={\eta }_{\Upsilon }^{ij}\left({\Upsilon }^j-1\right)$ and $n^i/{\rho }^i={\eta }_{\text{q}}^{ij}{n}^j/{\rho }^j$ for $c=i\ne j=1,\dots ,N^c$, with ${\eta }_{\Upsilon }^{ij}$ and ${\eta }_{\mathrm{q}}^{ij}$ respective proportionality ratios. Then, from Eq. (3), local changes in mass of neotissue constituents per respective unit mass satisfy

$$\frac{{\dot{\rho }}_{\text{R}}^i}{{\rho }_{\text{R}}^i}={\eta }^{ij}\frac{{\dot{\rho }}_{\text{R}}^j}{{\rho }_{\text{R}}^j},c=i\ne j=1,\dots ,N^c$$ (16)

with ${\eta }^{ij}={\eta }_{\mathrm{q}}^{ij}{\eta }_{\Upsilon }^{ij}$ (no sum). Exact integration of Eqs. (16) from state κ_o (where ${\rho }_{\text{R}o}^c=J_o{\rho }_o^c={\rho }_o^c$ ) to κ_h (where ${\rho }_{\text{R}h}^c=J_h{\rho }_h^c$ ) yields N^c − 1 independent relations among the mass densities ${\rho }_h^c$

$$\frac{J_h{\rho }_h^i}{{\rho }_o^i}={\left(\frac{J_h{\rho }_h^j}{{\rho }_o^j}\right)}^{{\eta }^{ij}},c=i\ne j=1,\dots ,N^c$$ (17)

which, by noting that ${\rho }_o^c=0$, can be rewritten as

$$J_h{\Phi }_h^i={\Phi }_{\text{R}h}^i={\varrho }_o^{ij}{\left({\Phi }_{\text{R}h}^j\right)}^{{\eta }^{ij}}={\varrho }_o^{ij}{\left(J_h{\Phi }_h^j\right)}^{{\eta }^{ij}}$$ (18)

where we used Eqs. (9) and defined

$${\varrho }_o^{ij}:={\frac{{\Phi }_{\text{R}h}^i}{{\left({\Phi }_{\text{R}h}^j\right)}^{{\eta }^{ij}}}|}_{s_h\to 0^{+}}={\frac{{\Phi }_h^i}{{\left({\Phi }_h^j\right)}^{{\eta }^{ij}}}|}_{s_h\to 0^{+}}$$ (19)

which are parameters to be determined from experimental data. Eqs. (18) are similar to those obtained in Latorre and Humphrey (2018) between the two evolving constituents considered therein (smooth muscle cells “m” and collagen fibers “c”, with a single η = η_qη_ϒ). Finally, the constraint $\sum {\Phi }_h^{\alpha }=1$, with ${\Phi }_h^p\left(J_h\right)$ from Eq. (14), requires

$$\frac{Q_h^p}{J_h}+\sum _{c=1}^{N^c}{\Phi }_h^c=1$$ (20)

which, along with Eqs. (18), form a system of N^c independent equations that provide implicit expressions for ${\Phi }_h^c\left(J_h\right)={\rho }_h^c\left(J_h\right)/{\widehat{\rho }}^c$. If mass fractions ${\varphi }_h^{\alpha }={\Phi }_h^{\alpha }{\widehat{\rho }}^{\alpha }/{\rho }_h$ are needed, the evolving ρ_h is determined via Eq. (11), with $\widehat{\rho }:={\widehat{\rho }}^c\forall c$ and $\sum {\Phi }_h^c=1-\sum {\Phi }_h^p$,

$${\rho }_h\left(J_h\right)=\frac{Q_h^p}{J_h}{\widehat{\rho }}^p+\left(1-\frac{Q_h^p}{J_h}\right)\widehat{\rho }.$$ (21)

2.5. Mechanobiologically equilibrated deformation gradients

In a full constrained mixture theory, constituents are assumed to be deposited within the mixture at deposition time τ ≤ s in intermediate configurations, relative to their own possibly evolving natural configurations ${\kappa }_{\text{n}}^{\alpha }(\tau )$, via symmetric and volume-preserving deposition stretch tensors G^α (τ). Since the motion of each constituent, once deposited, equals that of the soft tissue, the deformation experienced by the material deposited at time τ that survives at s is ${\mathbf{F}}_{\text{n}(\tau )}^{\alpha }(s)=\mathbf{F}(s){\mathbf{F}}^{-1}(\tau ){\mathbf{G}}^{\alpha }(\tau )$ (Baek et al., 2007). Because newly deposited constituents at time τ satisfy ${\mathbf{F}}_{\text{n}(\tau )}^{\alpha }(\tau )={\mathbf{G}}^{\alpha }(\tau )$, one notices (Latorre and Humphrey, 2020a) that ${\kappa }_{\text{n}}^{\alpha }(\tau )$ can be interpreted as natural configurations that evolve with the configuration of the mixture κ(τ), with G^α playing the role of a (spatial) left (pre)stretch tensor when referred to a rotated natural configuration ${\kappa }_{\text{N}}^{\alpha }(\tau )$ that evolves while attached to the rotated configuration of the mixture κ_R (τ). In that case, let an associated deformation gradient

$${\mathbf{F}}_{\text{N}(\tau )}^{\alpha }(s)=\mathbf{F}(s){\mathbf{F}}^{-1}(\tau ){\mathbf{F}}_{\text{G}}^{\alpha }(\tau )$$ (22)

map line elements (fibers) from the rotated natural configuration ${\kappa }_{\text{N}}^{\alpha }(\tau )$ to the current configuration κ(s), where

$${\mathbf{F}}_{\text{G}}^{\alpha }(\tau ):={\mathbf{G}}^{\alpha }(\tau )\mathbf{R}(\tau )=\mathbf{R}(\tau ){\mathbf{G}}_{\text{N}}^{\alpha }(\tau )$$ (23)

is a constituent-specific deposition tensor at τ, with R the rotation tensor from a polar decomposition of F, thus

$${\mathbf{G}}_{\text{N}}^{\alpha }(\tau ):={\mathbf{R}}^{\text{T}}(\tau ){\mathbf{G}}^{\alpha }(\tau )\mathbf{R}(\tau )$$ (24)

is the associated (symmetric, volume-preserving) right (pre)stretch tensor defined in configuration ${\kappa }_{\text{N}}^{\alpha }(\tau )$. We then obtain mechanobiologically equilibrated deformation gradients for all constituents α from their respective equilibrated natural configurations to the equilibrated current configuration of the mixture κ_h, described by F(s) = F_h (see Fig. 1).

2.5.1. Polymeric scaffold

Constituents p are placed at τ = 0 and possibly pre-stretched with G^p (τ = 0) = G^p = const (indeed, depending on the fabrication process, residual stresses may exist in the scaffold prior to implantation). Hence, their natural configurations ${\kappa }_o^p:={\kappa }_{\text{n}}^p(0)={\kappa }_{\text{N}}^p(0)$ do not evolve over time, but are fixed and attached to the reference configuration for the mixture κ_o. Equation (22) specialized to a mechanobiologically equilibrated state, with F(τ = 0) = I, yields (see Fig. 1)

$${\mathbf{F}}_h^p:={\mathbf{F}}_{\text{N}h}^p={\mathbf{F}}_{\text{n}h}^p={\mathbf{F}}_h{\mathbf{G}}^p.$$ (25)

2.5.2. Immuno-mechano-mediated neotissue

Deposition stretches arise when synthetic cells act on the newly-secreted matrix via actomyosin activity, with magnitudes becoming constitutive parameters and so too the orientation of the new tissue when deposited (Valentín et al., 2013). We assume that the magnitude of ${\mathbf{G}}_{\text{N}}^c$ in Eqs. (22)–(24) remains constant over G&R time scales (including mechanobiologically equilibrated evolutions), but not its referential orientation (Latorre and Humphrey, 2020b). Furthermore, ${\mathbf{G}}_h^c={\mathbf{R}}_h{\mathbf{G}}_{\text{N}h}^c{\mathbf{R}}_h^{\text{T}}$ accounts for rotations that may arise as the TEVG evolves, particularly in cases of local narrowing. Equation (22) specialized for constituents that turnover within a “homeostatic” state, with F(τ) = F(s) = F_h ∀τ, yields (see Fig. 1)

$${\mathbf{F}}_{\text{N}h}^c={\mathbf{F}}_h{\mathbf{F}}_h^{-1}{\mathbf{F}}_{\text{G}h}^c={\mathbf{F}}_{\text{G}h}^c={\mathbf{R}}_h{\mathbf{G}}_{\text{N}h}^c,$$ (26)

which proves useful when computing mechanobiologically equilibrated (rotated) Cauchy stresses subject to material frame indifference (Latorre and Humphrey, 2020a).

2.6. Mechanobiologically equilibrated strain energy

2.6.1. Polymeric scaffold

Consider a strain energy function ${\widehat{W}}^p$ per unit reference volume of the natural configuration ${\kappa }_o^p$. Since polymeric constituent p is deposited within κ_o, but degrades over time, its contribution at the mixture level (per unit reference volume of mixture) is weighted directly by its respective evolved referential volume fraction ${\Phi }_{\text{R}h}^p$ as

$$W_{\text{R}h}^p={\Phi }_{\text{R}h}^p{\widehat{W}}_h^p$$ (27)

where ${\Phi }_{\text{R}h}^p=Q_h^p$ and ${\widehat{W}}_h^p={\widehat{W}}^p\left({\mathbf{C}}_h^p\right)$, which depends on the equilibrated polymeric constituent-specific right Cauchy–Green tensor ${\mathbf{C}}_h^p={\mathbf{F}}_h^{p\text{T}}{\mathbf{F}}_h^p={\mathbf{G}}^p{\mathbf{C}}_h{\mathbf{G}}^p$, from Eq. (25), with ${\mathbf{C}}_h={\mathbf{F}}_h^{\text{T}}{\mathbf{F}}_h$ the right Cauchy–Green tensor for the equilibrated mixture.

2.6.2. Immuno-mechano-mediated neotissue

Consider strain energy functions ${\widehat{W}}^c$ per unit reference volume of their natural configurations ${\kappa }_{\text{N}h}^c\equiv {\kappa }_{\text{N}}^c(s)$, with ${\kappa }_{\text{N}h}^c(s)\ne {\kappa }_{\text{n}h}^c(s)$ in general. Since neotissue constituents c are deposited within κ_h ≡ κ(s), contributions at the mixture level (per unit current volume of mixture) are weighted by evolved volume fractions ${\Phi }_h^c$ as $W^c={\Phi }_h^c{\widehat{W}}^c$, whereupon $W_{\text{R}}^c=J_h{W}^c=J_h{\Phi }_h^c{\widehat{W}}^c$, or

$$W_{\text{R}h}^c={\Phi }_{\text{R}h}^c{\widehat{W}}_h^c$$ (28)

where ${\Phi }_{\text{R}h}^c=J_h{\Phi }_h^c$ and ${\widehat{W}}_h^c={\widehat{W}}^c\left({\mathbf{C}}_{\text{N}h}^c\right)$ depends on the equilibrated neotissue constituent-specific right Cauchy–Green tensor ${\mathbf{C}}_{\text{N}h}^c={\mathbf{F}}_{\text{N}h}^{c\text{T}}{\mathbf{F}}_{\text{N}h}^c={\left({\mathbf{G}}_{\text{N}h}^c\right)}^2$, from Eq. (26).

2.6.3. Evolving TEVG

A rule-of-mixtures relation for W_Rh = J_hW_h, defined per unit volume in κ_o is

$$W_{\text{R}h}=\sum _{\alpha =1}^N{W}_{\text{R}h}^{\alpha }={\Phi }_{\text{R}h}^p{\widehat{W}}_h^p+\sum _{c=1}^{N^c}{\Phi }_{\text{R}h}^c{\widehat{W}}_h^c.$$ (29)

The mechanobiologically equilibrated strain energy for the TEVG (i.e., mixture) thus reads

$$W_{\text{R}}\left({\mathbf{C}}_h\right)=Q_h^p{\widehat{W}}^p\left({\mathbf{C}}_h^p\right)+\sum _{c=1}^{N^c}{\Phi }_{\text{R}h}^c\left(J_h\right){\widehat{W}}^c\left({\mathbf{C}}_{\text{N}h}^c\right)$$ (30)

with ${\Phi }_{\text{R}h}^c\left(J_h\right)$, c = 1, …, N^c, from Section 2.4.2. This energy defines that stored by the TEVG within its current, pre-stretched, mechanobiologically equilibrated in vivo state. An extension of Eq. (30) that allows computation of hyperelastic responses with respect to the configuration κ_h is given in Latorre and Humphrey (2020a).

2.7. Mechanobiologically equilibrated stresses

The second Piola–Kirchhoff stress for the mixture S during transient loading reads

$$\begin{gathered} \mathbf{S}=-J_{hp}{\mathbf{C}}^{-1}+{\mathbf{S}}^p+\sum _{c=1}^{N^c}{\mathbf{S}}^c \\ =-J_{hp}{\mathbf{C}}^{-1}+Q_h^p{\mathbf{G}}^p{\widehat{\mathbf{S}}}^p\left({\mathbf{C}}^p\right){\mathbf{G}}^p \\ +\sum _{c=1}^{N^c}{\Phi }_{\text{R}h}^c\left(J_h\right){\mathbf{U}}_h^{-1}{\mathbf{G}}_{\text{N}h}^c{\widehat{\mathbf{S}}}_{\text{N}}^c\left({\mathbf{C}}_{\text{N}}^c\right){\mathbf{G}}_{\text{N}h}^c{\mathbf{U}}_h^{-1} \end{gathered}$$ (31)

with U_h the equilibrated right stretch tensor and the appropriate C, C^p(C), and ${\mathbf{C}}_{\text{N}}^c(\mathbf{C})$ are given in Latorre and Humphrey (2020a). Note, too, that the mixture-level Lagrange multiplier p associates with the (inter-mittently imposed) constraint J = J_h, and

$${\widehat{\mathbf{S}}}^p\left({\mathbf{C}}^p\right)=2\frac{\partial {\widehat{W}}^p\left({\mathbf{C}}^p\right)}{\partial {\mathbf{C}}^p},{\widehat{\mathbf{S}}}_{\text{N}}^c\left({\mathbf{C}}_{\text{N}}^c\right)=2\frac{\partial {\widehat{W}}^c\left({\mathbf{C}}_{\text{N}}^c\right)}{\partial {\mathbf{C}}_{\text{N}}^c}$$ (32)

are second Piola–Kirchhoff stresses at the constituent level for both types of constituents. Straightforward specialization of these expressions to F = F_h provides mechanobiologically equilibrated stresses at the current in vivo state.

2.7.1. Polymeric scaffold

In the mechanobiologically equilibrated state, C^p reduces to ${\mathbf{C}}_h^p={\mathbf{G}}^p{\mathbf{C}}_h{\mathbf{G}}^p\ne \mathbf{const}$, ${\widehat{\mathbf{S}}}^p$ to ${\widehat{\mathbf{S}}}_h^p={\widehat{\mathbf{S}}}^p\left({\mathbf{C}}_h^p\right)\ne \mathbf{const}$ (in general), and S^p in Eq. (31) to

$${\mathbf{S}}_h^p=Q_h^p{\mathbf{G}}^p{\widehat{\mathbf{S}}}_h^p{\mathbf{G}}^p.$$ (33)

Associated equilibrated Cauchy stresses read

$${\mathit{\sigma }}_h^p=\frac{1}{J_h}{\mathbf{F}}_h{\mathbf{S}}_h^p{\mathbf{F}}_h^{\text{T}}={\Phi }_h^p{\mathbf{F}}_h^p{\widehat{\mathbf{S}}}_h^p{\mathbf{F}}_h^{p\text{T}},$$ (34)

where we used Eqs. (14) and (25) (see Fig. 1).

2.7.2. Immuno-mechano-mediated neotissue

Similarly, ${\mathbf{C}}_{\text{N}}^c$ reduces to ${\mathbf{C}}_{\text{N}h}^c={\mathbf{G}}_{\text{N}h}^{c2}\ne \mathbf{const}$, ${\widehat{\mathbf{S}}}_{\text{N}}^c$ to ${\widehat{\mathbf{S}}}_{\text{N}h}^c={\widehat{\mathbf{S}}}_{\text{N}}^c\left({\mathbf{C}}_{\text{N}h}^c\right)\ne \mathbf{const}$, and S^c in Eq. (31) to

$${\mathbf{S}}_h^c={\Phi }_{\text{R}h}^c{\mathbf{U}}_h^{-1}{\mathbf{G}}_{\text{N}h}^c{\widehat{\mathbf{S}}}_{\text{N}h}^c{\mathbf{G}}_{\text{N}h}^c{\mathbf{U}}_h^{-1}.$$ (35)

Associated equilibrated Cauchy stresses read

$${\mathit{\sigma }}_h^c=\frac{1}{J_h}{\mathbf{F}}_h{\mathbf{S}}_h^c{\mathbf{F}}_h^{\text{T}}={\Phi }_h^c{\mathbf{F}}_{\text{N}h}^c{\widehat{\mathbf{S}}}_{\text{N}h}^c{\mathbf{F}}_{\text{N}h}^{c\text{T}}={\Phi }_h^c{\mathbf{R}}_h{\widehat{\mathit{\sigma }}}_{\text{N}h}^c{\mathbf{R}}_h^{\text{T}}$$ (36)

where we used ${\mathbf{F}}_h{\mathbf{U}}_h^{-1}={\mathbf{R}}_h$, Eq. (26) (see Fig. 1), and a rotated Cauchy stress tensor for constituent c at the constituent level

$${\widehat{\mathit{\sigma }}}_{\text{N}h}^c={\mathbf{G}}_{\text{N}h}^c{\widehat{\mathbf{S}}}_{\text{N}h}^c{\mathbf{G}}_{\text{N}h}^c\ne \mathbf{const},$$ (37)

which may reorientate/adapt during mechanobiologically equilibrated evolutions (Latorre and Humphrey, 2020b).

2.7.3. Evolving TEVG

Hence, at current in vivo states F = F_h, equilibrated second Piola–Kirchhoff stresses for the mixture are

$${\mathbf{S}}_h=-J_h{p}_h{\mathbf{C}}_h^{-1}+{\mathbf{S}}_h^p+\sum _{c=1}^{N^c}{\mathbf{S}}_h^c$$ (38)

with ${\mathbf{S}}_h^p$ and ${\mathbf{S}}_h^c$ given in Eqs. (33) and (35), respectively. Associated Cauchy stresses specialize to the following evolved rule-of-mixtures relation

$$\begin{gathered} {\mathit{\sigma }}_h=\sum _{\alpha =1}^N{\mathit{\sigma }}_{\text{t}h}^{\alpha }=-p_h\mathbf{I}+{\mathit{\sigma }}_h^p+\sum _{c=1}^{N^c}{\mathit{\sigma }}_h^c \\ =-p_h\mathbf{I}+\frac{Q_h^p}{J_h}{\mathbf{F}}_h^p{\widehat{\mathbf{S}}}_h^p{\mathbf{F}}_h^{p\text{T}}+\sum _{c=1}^{N^c}{\Phi }_h^c{\mathbf{F}}_{\text{N}h}^c{\widehat{\mathbf{S}}}_{\text{N}h}^c{\mathbf{F}}_{\text{N}h}^{c\text{T}} \end{gathered}$$ (39)

with ${\mathit{\sigma }}_h^c$ given alternatively in terms of R_h and ${\widehat{\mathit{\sigma }}}_{\text{N}h}^c$ in Eq. (36). Note that ${\mathit{\sigma }}_{\text{t}h}^{\alpha }$ in Eq. (4) includes ${\mathit{\sigma }}_h^{\alpha }$, derived from the strain energy, and an associated reaction from the Lagrange multiplier −p_hI.

2.8. Mechanobiologically equilibrated stimulus function and Lagrange multiplier

The hyperelastic stresses ${\mathit{\sigma }}_h^p$ are computed from the equilibrated deformation gradient F_h, Jacobian-dependent volume fraction ${\Phi }^p\left(J_h\right)=Q_h^p/J_h$, and equilibrated stresses ${\widehat{\mathbf{S}}}_h^p={\widehat{\mathbf{S}}}^p\left({\mathbf{C}}_h^p\right)$, in Eq. (34); in contrast, ${\mathit{\sigma }}_h^c$, in Eq. (36), are computed from the unique equilibrated rotation R_h from F_h, Jacobian-dependent volume fraction Φ^c(J_h), in Section 2.4.2, and the tensor ${\widehat{\mathit{\sigma }}}_{\text{N}h}^c$, in Eq. (37). Hence, only the Lagrange multiplier p_h in Eq. (39) remains unknown at each s_h > 0, which one obtains by invoking mechanobiological equilibrium conditions.

Motivated by Fung’s call for mass-and-structure growth-stress relations (Fung, 1995), and consistent with previous constrained mixture models, let stimulus functions ϒ^c account for changes in collagen-dominated production in response to cell-perceived changes in stress relative to homeostatic baseline values. In particular, among other possible equilibrated stimuli, let ${\Upsilon }_h^c$ depend on a set of invariants ${\tilde{\sigma }}_h^i$ of the total Cauchy stress tensor σ_h, and perhaps structural tensors, that include the extent of p_h, that is ${\tilde{\sigma }}_h^i\left(p_h\right)$ from Eq. (39). Moreover, let the out-of-equilibrium stimulus functions ϒ^c−1 be proportional to each other, as in Section 2.4.2, so equilibrium conditions lead to a single nonlinear algebraic equation ϒ_h = 1 ∀c. Finally, let ${\mathbf{S}}_h^x:=\sum {\mathbf{S}}_h^{\alpha }={\mathbf{S}}_h^p+\sum {\mathbf{S}}_h^c$ be the total “extra”(Humphrey, 2002), with superscript x, second Piola–Kirchhoff stresses, with associated Cauchy stresses ${\mathit{\sigma }}_h^x=\frac{1}{J_h}{\mathbf{F}}_h{\mathbf{S}}_h^x{\mathbf{F}}_h^{\text{T}}$ given in Eq. (39), which allows invariants ${\tilde{\mathit{\sigma }}}_h^i$ to be expressed in terms of scalar products involving the second-order tensors C_h, ${\mathbf{S}}_h^x$, scalars J_h, p_h, and their couplings, that depend on C_h and p_h. Thus

$${\Upsilon }_h\left({\tilde{\sigma }}_h^1\left({\mathbf{C}}_h,p_h\right),\dots ,{\tilde{\sigma }}_h^I\left({\mathbf{C}}_h,p_h\right)\right)=1\Rightarrow p_h\left({\mathbf{C}}_h\right)$$ (40)

which is a generally implicit relation that yields the (a priori unknown) volumetric contribution to stress at the mixture level in Eq. (39). As noted in Latorre and Humphrey (2020a), the stress field for mechanobiologically equilibrated G&R given by Eq. (39), complemented by (40), depends only on the current state of deformation and, hence, is path-independent.

2.9. A stimulus function with mechano- and immuno-mediated contributions

In previous implementations of the concept of mechanobiologically equilibriated G&R including inflammatory effects, we analyzed G&R of uniform cylindrical arteries using stimulus functions for mass production

$${\Upsilon }_h^c=1+K_{\sigma }^c\Delta {\sigma }_h-K_{{\tau }_w}^c\Delta {\tau }_{wh}+K_{{\varrho }_{\phi }}^c\Delta {\varrho }_{\phi h}$$ (41)

where $\Delta {\sigma }_h=\left({\tilde{\sigma }}_h-{\tilde{\sigma }}_o\right)/{\tilde{\sigma }}_o$, $\Delta {\tau }_{wh}=\left({\tau }_{wh}-{\tau }_{wo}\right)/{\tau }_{wo}$, and $\Delta {\varrho }_{\phi h}=\left({\rho }_{\text{R}\phi h}-{\rho }_{\text{R}\phi o}\right)/{\rho }_{\text{R}\phi \max }$ x, with $\tilde{\sigma }={\sigma }_I=\mathrm{tr}\mathit{\sigma }\simeq {\sigma }_{\theta \theta }+{\sigma }_{zz}$ the first principal invariant of the mean wall stress (ignoring the radial component, which tends to be much less than in-plane components), τ_w = 4μQ/πa³ a measure of the wall shear stress over the endothelium for a fully developed Newtonian flow through a long cylindrical sector (with μ the viscosity of blood, Q the volumetric flow rate, and a the current luminal radius), and ρ_Rφh a characteristic measure for inflammatory cell density, with $K_{\mathit{\sigma }}^c$, $K_{{\tau }_w}^c$, and $K_{{\varrho }_{\phi }}^c$ associated gains.

While we easily compute $\tilde{\sigma }={\sigma }_I=\mathrm{tr}\mathit{\sigma }$ in the present case using 3D finite element methods given appropriate hemodynamic boundary conditions, with σ now defined pointwise through Eq. (39), local values of τ_w will need to be computed for more complex geometries, for which one could solve the Navier-Stokes equations for the luminal blood flow (Figueroa et al., 2009). In Latorre and Humphrey (2020a), however, we allowed τ_w = 4μQ/πa³ to locally approximate changes in flow-induced shear stress for axisymmetric arteries within a finite element G&R framework. Below, we introduce a control volume based method that estimates axial variations in blood pressure and mean flow in limited cases relevant to TEVGs. As in previous studies, the time course of inflammatory cell density (e.g., CD45+ staining) can be prescribed based on either direct experimental measurements or prior (indirect) determination via Eq. (41). In the latter case, assume a uniform narrowing of the TEVG and let deviations in pressure- and axial force-induced intramural stress and flow-induced shear stress be known from changes in inner radius and thickness. Then, an equilibrated ${\Upsilon }_h^c=1$ in Eq. (41) yields

$$\Delta {\varrho }_{\phi h}=-\frac{K_{\mathit{\sigma }}^c}{K_{{\varrho }_{\phi }}^c}\Delta {\sigma }_h+\frac{K_{{\tau }_w}^c}{K_{{\varrho }_{\phi }}^c}\Delta {\tau }_{wh}$$ (42)

which can be prescribed locally (at the integration point level) for the non-uniform finite element computations. Note that the ratios of gains can also be estimated using this last relation given (at least) two sets of values {Δσ_h,Δτ_wh,Δϱ_ϕh}.

3. Hemodynamic coupling

The control volume energy equation for steady flow between any two points, u (upstream) and d (downstream), in a tube states that the loss in total (i.e., static plus dynamic) pressure is given by viscous/fric8 tional and geometric/minor losses, that is

$$\begin{array}{l}\left(\frac{P_u}{{\rho }_f}+{\alpha }_f\frac{v_u^2}{2}\right)-\left(\frac{P_d}{{\rho }_f}+{\alpha }_f\frac{v_d^2}{2}\right)-\sum _e{F}_{fe}\frac{l_e}{a_e}\frac{v_e^2}{4}\\ +\sum _g{K}_{fg}\frac{v_g^2}{2}\end{array}$$ (43)

where P is blood pressure, v is mean blood velocity, ρ_f is blood mass density, α_f is a kinetic coefficient, l is axial length; moreover F_f and K_f are viscous and geometric loss coefficients, with the index e accounting for different characteristic regions along the tube and the index g representing different characteristic (typically local) changes in geometry along the tube. Variables with these subscripts represent characteristic magnitudes within their respective regions. With F_f = 64/Re = 32μ/ρ_fva for a laminar flow, P_u ≡ P (z = 0), and v = Q/πa², we can write, for each region z_E ≥ z₁ > 0

$$\begin{gathered} P\left(z_E\right)=P_1-\frac{{\alpha }_f{\rho }_f{Q}^2}{2{\pi }^2}\left(\frac{1}{a_E^4}-\frac{1}{a_1^4}\right) \\ -\frac{8\mu Q}{\pi }\sum _e^{z_e<z_E}\frac{l_e}{a_e^4}-\frac{{\rho }_f{Q}^2}{2{\pi }^2}\sum _g^{z_g<z_E}\frac{K_{fg}}{a_g^4} \end{gathered}$$ (44)

which, given the input venous pressure P_u ≃ P₁ and the value of the flow Q through the TEVG, depends on inner radii and lengths of these characteristic regions exclusively, which are not expected to change appreciably during a computation of the fluid mechanics given the extreme structural stiffness of the evolving TEVG and the modest changes in blood pressure within a Fontan conduit over a cardiac cycle (Blum et al., 2022; Schwarz et al., 2021). Hence, this last equation is discretized in terms of geometric factors that can be extracted from finite element simulations of the TEVG, with each element (e = 1,…,n_ez) and expansion/contraction regions (g = 1,…,n_gz) along the the axial direction interpreted as (local) characteristic regions. In particular, l_e = l/n_ez for a uniform discretization along the axial direction, thus

$$P\left(z_E\right)=P_1-A\left(\frac{1}{a_E^4}-\frac{1}{a_1^4}\right)-B\sum _e^{z_e<z_E}\frac{1}{a_e^4}-C\sum _g^{z_g<z_E}\frac{1}{a_g^4}$$ (45)

where A = α_fρ_fQ²/2π² (with α_f = 2 for a fully developed laminar flow), B = 8μQl/πn_ez, and C = K_fρ_fQ²/ 2π² are (dynamic, viscous, and geometric) parameters that, along with given axial distributions of elemental inner radii a_e and a_g, determine the elemental pressures P(z_E) acting on elemental faces that define the inner surface of the graft. With units of kg for mass, mm for length, and s for time, these parameters divided by a⁴ result in pressures in kPa.

Equation (44) (or (45)) is valid for quasi-steady-state, quasi-laminar (with possible secondary flow effects accounted for by the loss factors) flows, that is, generally non-turbulent flows for which the characteristic time for changes in flow properties is longer than the residence time of fluid particles within the tube. Assuming that the mean flow of blood is quasi-steady, with Q its net flow rate, is particularly relevant for flow in a Fontan conduit, for which the present derivation is intended (see Drews et al., 2020). Therefore, one can couple this equation with simultaneous mechanobiologically equilibrated G&R computations for the solid, leading to a simplified (1D fluid - 3D solid), fully rate-independent, FSG formulation. Under these conditions, and in particular for the present TEVG application, consider initially (iteration 0) a uniform distribution of blood pressure. Then, the following iterative procedure can be followed (see an extended flowchart in Fig. 2):

1. 3D solid computation: Given an axial distribution of pressure, compute the mechanobiologically equilibrated G&R evolution of the TEVG over a given number of load (pseudo-time) FE steps (including, in particular, flow-induced shear stress-dependent effects on the mechanobiology via Eq. (41)).

2. In postprocessing, extract the inner radius at each axial location (i.e., average elemental values) for each converged time step.

3. 1D fluid computation: Update the distribution of pressure for each time step via Eq. (44) (or (45)) (to modify, in particular, the pressure-induced intramural stresses to be re-computed in (I)) for given hemodynamic boundary conditions (see Remarks 1 and 2 below).

4. Repeat from (I) if the error for the input local pressure for (I) and the output pressure from (III), for any time step, is greater than a prescribed tolerance. Stop otherwise (the solution has converged).

Fig. 2.

Schematic of the work flow for the (1D) Fluid- (3D) Solid-Growth strategy (FSG). Note the direct embedding of the fluids within the solids code in Step I, with the (inner radius-dependent) wall shear stress τ_w = 4μQ/πa³ computed as part of the G&R FE solution to satisfy ϒ_h = 1 in Eq. (41) (Latorre and Humphrey, 2020a). Scaffold degradation, evolving neotissue parameters, and inflammatory cell density, for Step I, are previously obtained based on a uniform G&R description of the TEVG (see Section 4.3, Fig. 3, and Table 1). This framework allows one to prescribe evolving hemodynamic boundary conditions for the fluid pressure computation in Step III, which need not remain constant over TEVG development (Blum et al., 2022).

We have automated this procedure using Matlab scripts and functions that call a slightly modified version of the open source finite element code FEBio (Version 2.8.2¹; Maas et al., 2012) with the G&R model for the TEVG implemented via a material plugin (step I), postprocess output files (step II), re-compute pressures and their relative errors between consecutive iterations (step III), and write new input files for (I) until the FSG computation converges (step IV). For the current parameters, FE mesh (1512 3D quadratic elements), and load steps (20, converged to machine precision via global Newton–Raphson iterations showing an asymptotic rate of quadratic convergence, cf. Latorre and Humphrey, 2020a), four-to-five FSG iterations give a final (relative) local error in computed blood pressure over the whole (axial) fluid domain of ∼10⁻³ (∼0.5Pa), with a total elapsed time of ∼1 hour on a single processor Intel^® Xeon^® E5 at 3 GHz in a Workstation Dell Precision 5810 with 32GB RAM.

Remark 1:

Note that P₁ ≃ P_u (input venous pressure) and Q (flow rate through the TEVG) in Eq. (44), hence the parameters A, B, and C in Eq. (45), need not remain constant throughout TEVG development (Blum et al., 2022). To account for changes in both global and local hemodynamic conditions within the present FSG framework, evolving P_u(s_h) and Q(s_h) could be prescribed in step (III) via Eq. (44) for each (quasi-equilibrated) load step / pseudo-time s_h. Global changes in upstream pressure and mean flow would stimulate further G&R of the TEVG and, in particular, of its adjacent (host) venous segments.

Remark 2:

Alternatively, Eq. (43) can be solved for $P_d\equiv P(z=l)\simeq P_{n_{ez}}$ known, that is, for $z_E<z_{n_{ez}}<l$

$$P_E=P_{n_{ez}}-A\left(a_E^{-4}-a_{n_{ez}}^{-4}\right)+B\sum _e^{z_E\le z_e<z_{n_{ez}}}{a}_e^{-4}+C\sum _g^{z_E\le z_g<z_{n_{ez}}}{a}_g^{-4}$$ (46)

which, again, is particularly relevant for flow in a Fontan conduit, where $P_{n_{ez}}\simeq P_d$ (output venous pressure) remains nearly constant (Drews et al., 2020; Blum et al., 2022), as we consider below.

4. Uniform G&R computations of the TEVG

Consider first an analysis of G&R evolution using a uniform, thin-wall-equivalent, cylindrical model of the TEVG, details of which are given in Appendix A. The primary results from this simplified study prove very useful to inform the non-uniform FE simulations performed subsequently.

4.1. Native/host vessel

For the case of an interposition TEVG within the inferior vena cava (IVC), prior mechanical characterization of the native vessel is needed for two main reasons. First, recall that we assume that neotissue formation is driven by both mechano- and immuno-mediated mechanisms that seek to restore target stresses towards homeostatic (probably reset) values while the polymer degrades in the presence of inflammation, see Eq. (41); we thus define original homeostatic values from a native IVC under in vivo conditions of blood pressure, flow rate, axial stretch, and inflammation. Second, our FE model computes the in vivo development of a TEVG while it is attached to, and interacts with, the host IVC at both ends; the FE model/mesh thus includes two adjacent segments of the IVC, which we also let adapt in vivo in response to the altered hemodynamics and wall mechanics.

The passive mechanical behavior of the vein is described by a four-fiber-family constitutive relation (Lee et al., 2013; Sokolis, 2013; Miller et al., 2014; Szafron et al., 2018). This model considers different load-bearing constituents within the venous wall which, for simplicity, are lumped into three main groups: amorphous elastin matrix, circumferentially oriented smooth muscle, and circumferentially, axially, and diagonally oriented collagen fibers. The stored energy function for elastin has a neo-Hookean form whereas collagen and smooth muscle have a Fung-type exponential form. Parameters for this model of the native vein have been determined directly from experimental measurements (e.g., initial wall geometry and mass fractions) and nonlinear regressions from consistent biaxial mechanical data (including pressure-diameter and axial force-extension tests) and are listed in Table 1. Besides these parameters for the IVC (to perform G&R computations of the adjacent segments to the TEVG), we prescribe the associated in vivo blood pressure ( $P_o^{\text{IVC}}=4.4\text{mmHg}$ ) and axial force ( $f_{zo}^{\text{IVC}}=257\text{mN}$ ) as well as circumferential ( ${\sigma }_{\theta \theta o}^{\text{IVC}}=6.77\text{kPa}$ ) and axial ( ${\sigma }_{zzo}^{\text{IVC}}=6.16\text{kPa}$ ) stresses to initialize the TEVG computation for a model lamb implant (Drews et al., 2020; Blum et al., 2022).

Table 1.

Model parameters for the host thoracic IVC (adjacent segments to the TEVG) and the TEVG constituents: polymeric scaffold (initially present, then degrading; see Fig. 3, panel C) and collagen-dominated neotissue (initially absent, then produced / turning over). Baseline “native/host IVC” parameters are obtained/fitted for a representative lamb thoracic IVC (see Section 4.1); “polymeric scaffold” parameters are obtained from a representative biodegradable scaffold (Drews et al., 2020; Blum et al., 2022; see Sections 4.2 and 4.3); “neovessel” parameters (including evolving $c_1^c$, α₀ and inflammation $\Delta {\varrho }_{\phi h}$, shown in Fig. 3, panels D to F respectively) are determined from implanted TEVGs (Drews et al., 2020; Blum et al., 2022; see Section 4.3). In particular, deposition stretches of collagen fibers for both the IVC and the neovessel (higher than many reported for arteries, noting that the IVC has little elastin and so too the TEVG), have been estimated from (axial) in vivo stretches reported for these TEVGs (Table 1 in Blum et al., 2022) and then adjusted via a nonlinear regression to improve the fitting of data for the IVC. For the FE simulations, it is assumed that the initially loaded (pressurized and axially stretched) cross-section geometry (inner radius and thickness) of the scaffold precisely matches the initial in vivo cross-section geometry (a_o and h_o) of the host vessel. Also given are “blood” flow parameters required to perform FSG computations coupled via Eq. (46), with the narrowing-dependent geometric loss factor K_f varying gradually between K_f|min (no narrowing) and K_f|max (maximal narrowing); note that P_d = P_o = 4.4 mmHg, $Q=Q_o=v_o\pi a_o^2\approx 53.5\text{mL}{\text{s}}^{-1}$, and $\mathrm{R}\mathrm{e}=2{\rho }_f{v}_o{a}_o/\mu \approx 1125$, which qualifies as laminar flow in a tube (Re < 2100).

Native/Host Inferior Vena Cava
Inner Radius, Thickness, Length	ao, ho, lo	8.573 mm, 0.743 mm, 60 mm
Volume (≡mass) fractions	${\Phi }_o^e$, ${\Phi }_o^m$, ${\Phi }_o^c$	0.100, 0.081, 0.819
Collagen Fractions	βθ, βz, β d+ , βd−	0.017, 0.167, 0.408, 0.408
Diagonal Collagen Orientation	α 0	41.94°
Elastin Parameter	ce	9.913 kPa
Elastin Deposition Stretches	$G_r^e$, $G_{\theta }^e$, $G_z^e$	$1/G_{\theta }^e{G}_z^e$, 1.219, 1.428
Muscle Parameters	$c_1^m$, $c_2^m$	48.33 kPa, 1.02
Collagen Parameters	$c_1^{\theta }=c_1^z=c_1^d$, $c_2^{\theta }=c_2^z=c_2^d$	2.696 kPa, 14.92
Deposition Stretches	Gm, Gθ = Gz = Gd	1.200, 1.167
G&R Parameters	η, Kτw /Kσ, Kęφ /Kσ	1.0, 0.3, 0.0
Polymeric Scaffold
Neo-Hookean Parameter	cp	125.7 kPa
Pre-stretches	$G_r^p$, $G_{\theta }^p$, $G_z^p$	$1/G_{\theta }^p{G}_z^p$, 1.0103, 1.0079
Degradation Parameters	kp, χp	0.285 weeks−1, 15 weeks (Fig. 3 (C))
Neovessel
Muscle/Collagen Ratio	ϱo	0.1
Collagen Fractions	βθ, βz, β d+ , βd−	0.017, 0.167, 0.408, 0.408
Diagonal Collagen Orientation	α 0	Evolving (Fig. 3 (E))
Muscle Parameters	$c_1^m$, $c_2^m$	48.33 kPa, 1.02
Collagen Parameters	$c_1^{\theta }=c_1^z=c_1^d$, $c_2^{\theta }=c_2^z=c_2^d$	Evolving (Fig. 3 (D)), 14.92 · (sh/52)
Deposition Stretches	Gm, Gθ = Gz = Gd	1.200, 1.167
G&R Parameters	η, $K_{{\tau }_w}/K_{\sigma }$, $K_{{\varrho }_{\phi }}/K_{\sigma }$	1.0, 0.1, 0.89
Inflammation	$\Delta {\varrho }_{\phi h}$	Evolving (Fig. 3 (F))
Blood
Mass Density	ρf	1050 kg m−3
Dynamic Viscosity	μ	0.0037 kg m−1 s−1
Kinetic / Geometric Coefficients	αf, Kf|min, Kf|max	2, 0, 0.5
Mean Velocity	vo	0.232 m s−1

4.2. Initial equilibrium of the polymeric scaffold

Current grafts may be made up of several polymeric constituents. For the present study, however, we consider a single polymeric constituent that phenomenologically describes the combined response of a mixture of polymers to a first approximation. Its stored energy function ${\widehat{W}}^p\left({\mathbf{C}}_h^p\right)$ in Eq. (30) is described by a neo-Hookean form

$${\widehat{W}}^p\left({\mathbf{C}}_h^p\right)=\frac{c^p}{2}\left({\mathbf{C}}_h^p:\mathbf{I}-3\right)$$ (47)

where c^p is the associated shear modulus, which we estimate from experimental data. Noting that only one polymeric constituent is considered, the unloaded configuration coincides with the natural (stress-free) configuration of the scaffold, which is the reference configuration for ${\widehat{W}}^p$ in Eq. (47). Thus, let $\left\{{\lambda }_r^p,{\lambda }_{\theta }^p,{\lambda }_z^p\right\}=\left\{1/{\lambda }_{\theta }^p,{\lambda }_{\theta }^p,1\right\}$ be the radial (by incompressibility), circumferential (free), and axial (fixed) total stretches during a standard pressure-distension test (that is, without the need to specify the pre-stretch tensor G^p at this stage). For the in vivo value of blood pressure $P=P_o^{\text{IVC}}$, for example, ${\lambda }_{\theta }^p=1.0138$. Hence, with the associated Lagrange multiplier obtained from the radial equation ${\sigma }_{rr}^p\approx 0$, the circumferential (Laplace) stress at the experimentally loaded state under consideration is

$${\sigma }_{\theta \theta }^p=c^p\left({\lambda }_{\theta }^{p2}-\frac{1}{{\lambda }_{\theta }^{p2}}\right)=P{\lambda }_{\theta }^{p2}\frac{A}{H}$$ (48)

where A and H are the unloaded inner radius and thickness of the experimentally tested scaffold. With P and ${\lambda }_{\theta }^p$ known, this last equation serves to determine a representative value c^p = 125:7 kPa for the polymer, which we consider constant for all the computations in this work (i.e., losses of stiffness will be accounted for via losses in mass).

Next, the pre-stretch tensor G^p, see Eq. (25), is defined by two biaxial (circumferential $G_{\theta }^p$ and axial $G_z^p$ ) stretches that describe the in-plane stretching of the scaffold at the time of implantation (namely, accounting for the surgeon possibly stretching the scaffold axially when suturing the anastomoses plus the effect of pressurization when the distal and proximal cross-clamps are released and the scaffold is pressurized), with the stretch in the radial direction given by the incompressibility constraint $G_r^p{G}_{\theta }^p{G}_z^p=1$. We thus determine $G_{\theta }^p$ and $G_z^p$ by enforcing (ideal) equilibrium conditions upon implantation. To this end, let a polymeric scaffold, made of this material (i.e., neo-Hookean with a representative c^p = 125:7 kPa), be stretched and (ideally) implanted in vivo such that the circumferential and axial stresses equal the respective in vivo values of the host IVC. Since this Cauchy stress state corresponds to G&R time s_h = 0 for the TEVG, then F_h = F_o = I (i.e., J_h = J_o = 1), $Q_h^p=Q_o^p=1$ (i.e., ${\Phi }_h^p={\Phi }_o^p=1$ and ${\Phi }_h^c={\Phi }_o^c=0$ ), and ${\mathbf{F}}_h^p={\mathbf{F}}_o^p={\mathbf{G}}^p$ in Eq. (39), whose circumferential and axial components, with the Lagrange multiplier obtained again from the radial component, are

$${\sigma }_{\theta \theta o}^{\text{TEVG}}={\sigma }_{\theta \theta o}^p=c^p\left(G_{\theta }^{p2}-\frac{1}{G_{\theta }^{p2}{G}_z^{p2}}\right)={\sigma }_{\theta \theta o}^{\text{IVC}}$$ (49)

$${\sigma }_{zzo}^{\text{TEVG}}={\sigma }_{zzo}^p=c^p\left(G_z^{p2}-\frac{1}{G_{\theta }^{p2}{G}_z^{p2}}\right)={\sigma }_{zzo}^{\text{IVC}}$$ (50)

which serve in this case to determine the requisite pre-stretches $G_{\theta }^p=1.0103$ and $G_z^p=1.0079$. Note, from the values computed for c^p, $G_{\theta }^p$, and $G_z^p$ (compare to c^e, $G_{\theta }^e$, and $G_z^e$; Table 1), that the polymeric scaffold is much stiffer than the elastin within the native IVC. Albeit not required by our FE model below, the unloaded thickness, inner radius, and length of the particular graft being (ideally) implanted are $\left\{H^{\text{TEVG}},A^{\text{TEVG}},L^{\text{TEVG}}\right\}=\left\{h_o^{\text{IVC}}/G_r^p,a_o^{\text{IVC}}/G_{\theta }^p,l_o^{\text{IVC}}/G_z^p\right\}\approx \left\{h_o^{\text{IVC}},a_o^{\text{IVC}},l_o^{\text{IVC}}\right\}$, where $h_o^{\text{IVC}}$, $a_o^{\text{IVC}}$, and $l_o^{\text{IVC}}$ are the thickness, radius, and length of the portion of the IVC that is removed (which the graft replaces; note: $h_o^{\text{IVC}}$ and $a_o^{\text{IVC}}$ are, too, the thickness and radius of the host IVC adjacent to the TEVG).

4.3. Evolving TEVG

For the collagen-dominated neotissue that forms as the polymer degrades, we also consider a four-fiber-family model, with circumferential smooth muscle cells (c = m) and circumferential (c = θ), axial (c = z), and symmetric diagonal (c = d) collagen fibers described via Fung-type exponentials, which under mechanobiological equilibrium specialize to

$${\widehat{W}}^c\left(G^c\right)=\frac{c_1^c}{4c_2^c}\left(\exp \left(c_2^c{\left(G^{c2}-1\right)}^2\right)-1\right),$$ (51)

where $c_1^c$ (in kPa) and $c_2^c$ are material parameters. The turnover of these constituents is both mechano- and immuno-mediated. Noting that the neotissue properties need not remain constant throughout TEVG evolution, we allow some of the material parameters to evolve accordingly. In particular, we assign to neotissue constituents the same parameter values as for the native vessel, except for $c_1^{\theta }=c_1^z=c_1^d$ and the orientation angle α₀ at which diagonal fibers are deposited, which we let evolve to phenomenologically capture the evolving collagen fiber microstructure observed experimentally, see Table 1. Importantly, under these assumptions, these two evolving parameters can be uniquely determined from longitudinal experimental data as we explain next. Preliminary calculations showed, however, that assigning values for $c_2^{\theta }=c_2^z=c_2^d$ from native collagen gave rise to an excessively high biaxial stiffness during the evolution of the TEVG. Interestingly, letting them gradually increase over G&R time (from vanishing to native related values) yielded more realistic results, again reecting the evolving microstructure (Birk et al., 1995; Miller et al., 2014; Szafron et al., 2018).

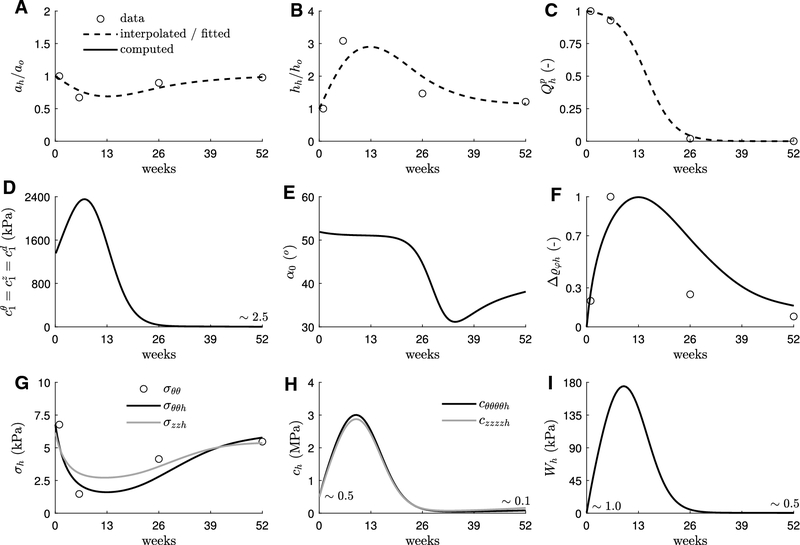
Figure 3 shows average values of inner radius a (panel A), wall thickness h (B), and polymer degradation Q^p (C) measured from implanted TEVGs at different times over the course of 52 weeks (Drews et al., 2020; Blum et al., 2022). From these data, we have adjusted the parameters in the degradation function for the polymer scaffold in Eq. (12), see Table 1, to yield the continuous function $Q_h^p$ shown in C. In addition, let the continuous curves (smooth interpolants) for a_h and h_h shown in A and B approximate the continuous evolution of inner radius and thickness. Based also on experimental observations at week 52, let %_o ≈ 0.1 and η = 1 approximate the evolution of the ratio between referential volume fractions of smooth muscle cells and collagen fibers in Eq. (18). Moreover, consider the stress- and inflammation-dominated set of gains $\left\{K_{\sigma }^c,K_{{\tau }_w}^c,K_{{\varrho }_{\phi }}^c\right\}=\text{{1.00,0.10,0.89}}$, noting that only their ratios (e.g., $K_{{\tau }_w}^c/K_{\sigma }^c$, $K_{Q_{\phi }}^c/K_{\sigma }^c$ ) are important for mechanobiologically equilibrated evolutions, with the former assumed to contribute to ${\Upsilon }_h^c$ less than normal (0.1 versus 0.3 for the native vein, see Table 1) and the latter scaled a posteriori to yield $\Delta {\varrho }_{\phi \max }=1$ (see panel F). Finally, let blood pressure $P_h=P_o=P_o^{\text{IVC}}$, volumetric flow rate ratio Q_h/Q_o = 1, axial stretch with respect to the initial in vivo reference state λ_zh = λ_zo = 1, and axial force $f_{zh}=f_{zo}=f_{zo}^{\text{IVC}}$ remain constant during the evolution of the TEVG (note that “experimental” values for axial length and force, the latter assumed constant owing to our current inability to measure it in vivo, can be simultaneously prescribed at this stage to determine yet unknown model parameters for the TEVG). Hence, let the evolution of the collagen-dominated parameters $c_1^{\theta }=c_1^z=c_1^d$ and α₀ as well as the inflammation $\Delta {\varrho }_{\phi h}$ be determined by enforcing a mechanobiologically quasi-equilibrated evolution (see expanded expressions in Appendix A)

$$\Delta {\sigma }_h-\frac{K_{{\tau }_w}^c}{K_{\sigma }^c}\Delta {\tau }_{wh}+\frac{K_{{\varrho }_{\phi }}^c}{K_{\sigma }^c}\Delta {\varrho }_{\phi h}=0$$ (52)

$$\sum _{\alpha =1}^N{\sigma }_{rrh}^{\alpha }-p_h=-\frac{P_h}{2}$$ (53)

$$\sum _{\alpha =1}^N{\sigma }_{\theta \theta h}^{\alpha }-p_h=\frac{P_h{a}_h}{h_h}$$ (54)

$$\sum _{\alpha =1}^N{\sigma }_{zzh}^{\alpha }-p_h=\frac{f_{zh}}{\pi \left(2a_h+h_h\right)h_h},$$ (55)

which, effectively, constitute a set of 4 equations with 4 unknowns $\left(c_1^{\theta }=c_1^z=c_1^d,{\alpha }_0,\Delta {\varrho }_{\phi h},p_h\right)$ for each level of polymer degradation $Q_h^p$ (or pseudo-time s_h; recall Section 2.4.1). The computed evolution for $c_1^{\theta }=c_1^z=c_1^d,{\alpha }_0$, and $\Delta {\varrho }_{\phi h}$ is shown in Fig. 3, panels D to F.

Fig. 3.

Inverse material characterization of an idealized geometrically and materially nonlinear but uniform TEVG that evolves subject to constant blood pressure, flow rate, in vivo length, and axial force. Dashed lines represent interpolated geometry (A,B) or fitted polymer degradation (C) from experimental data (open circles) collected at weeks 1, 6, 26, and 52 (Drews et al., 2020; Blum et al., 2022). These continuous curves informed our uniform G&R model to determine evolving parameters (solid lines) for newly produced collagen (D,E) and inflammation (F), with resulting circumferential and axial components of stress (G) and material stiffness (H) and stored energy per unit current volume (I). Properties at G&R time s_h = s_o = 0 associate with the polymeric scaffold whereas those at s_h = 52 weeks associate with the collagen-dominated neotissue (see panel C). IVC, scaffold, neotissue, and blood parameters in Table 1, complemented with the evolving (neotissue) parameters and inflammation in panels D to F, subsequently inform our nonuniform FSG FE model of the TEVG. Note the original homeostatic values for the IVC (i.e., at $s=s_o^{-}=0^{-}$, not shown): $c_1^{c\mid \text{IVC}}=2.696\text{kPa}$, ${\alpha }_0^{\text{IVC}}={41.94}^{°}$, ${\sigma }_{\theta {\theta }_o}^{\text{IVC}}=6.772\text{kPa}$, ${\sigma }_{zzo}^{\text{IVC}}=6.155\text{kPa}$, $c_{\theta \theta \theta \theta o}^{\text{IVC}}=0.094\text{MPa}$, $c_{zzzzo}^{\text{IVC}}=0.133\text{MPa}$, and $W_o^{\text{IVC}}=0.855\text{kPa}$.

Finally, panels G to I in Fig. 3 show biaxial (in-plane) components of stress and material stiffness as well as stored energy per unit current volume for the evolving TEVG. In particular, note the marked decrease in stresses, consistent with the luminal narrowing and marked thickening (under assumed constant pressure and axial force), but increased stored energy and biaxial stiffness, consistent with a degrading polymeric constituent being elastically deformed during the evolution of the TEVG and the computed peak in stiffness parameter $c_1^c$ for the continuously deposited (and removed) collagen. Indeed, stresses, computed directly from equilibrium, gradually return toward normal in parallel to the geometry, whereas elastic energy and stiffness, additionally depending on material properties and composition, do so only after the polymer completely degrades beyond week 26. Importantly, all the metrics defined at the tissue level (Fig. 3, panels A, B, F, G, H, and I) are respectively comparable (of the same order of magnitude) at initial (week 0) and final (week 52) times, despite the material composition of the TEVG being strikingly different, namely, an all-polymer scaffold (week 0) versus a neovessel mostly comprised of smooth muscle and collagen fibers (week 52).

5. Non-uniform FSG computations of the TEVG attached to the host IVC

In the previous Section we determined the requisite G&R model parameters from the available experimental data from a native IVC and evolving grafts. These parameters are either constant (Table 1) or evolve over G&R (pseudo)time s_h (for the neotissue, see Fig. 3, panels D and E). We let pressure and flow as well as axial length and force remain constant, but not inflammation, which was computed as part of the geometrically and materially uniform solution (Fig. 3, panel F). In this Section we perform FSG computations for an axially nonuniform, axisymmetric TEVG that evolves over time while attached to adjacent tissue (i.e., the host IVC) distally and proximally, for which we employ the 1D-fluid/3D-solid formulation detailed in the preceding Sections as follows.

5.1. Native/host vessel

Consider a 3D cylindrical mesh with dimensions corresponding to the IVC of a lamb: $a_o^{\text{IVC}}=8.573\text{mm}$, $h_o^{\text{IVC}}=0.743\text{mm}$, and an original IVC segment of total length $l_o^{\text{IVC}}=60\text{mm}$; see the left mesh in Figure 4. With the associated parameters in Table 1, we compute the original in vivo state of the IVC subject to uniform blood pressure $P_o^{\text{IVC}}=4.4\text{mmHg}$ and fixed axial displacements at both IVC ends, for which we follow the (hyperelastic solid) initialization phase referred to as “Stage I” in Latorre and Humphrey (2020a) (see Section 4 and Box III therein). Computed displacements yield no appreciable change in geometry; see the central, now pre-loaded, mesh in Figure 4. We associate this initially pre-stressed (circumferentially and axially, with collagen deposition stretches greater for a vein than an elastic artery, but also radially to a less extent) equilibrium state for the IVC, for which G&R or changing hemodynamics effects have not been yet considered, with $s_h=s_o^{-}=0^{-}$. As explained previously (Latorre and Humphrey, 2020a), original homeostatic values of target (volumetric) stress ${\tilde{\sigma }}_o={\sigma }_{vo}=\frac{1}{3}{\mathit{\sigma }}_o:\mathbf{I}$ are stored at the material points throughout the FE mesh, which, as assumed above for the uniform computations as well, will dictate, in part, the subsequent turnover of neotissue within the TEVG, now in the presence of axially nonuniform hemodynamics effects.

Fig. 4.

Initially unloaded (left) and pre-loaded (center) geometry and mesh (including n_r × n_θ × n_z = 1 × 22 × 60 3D quadratic elements with full 3 × 3 × 3 Gauss integration; see the expanded finite element on the left) for the initially cylindrical thoracic IVC segment into which the polymeric scaffold is subsequently pre-stretched biaxially and implanted (right; replacing a previously removed IVC central partial segment). Inner pressure P_o = 4.4 mmHg and axial force f_zo = 257 mN for all pre-loaded cross-sections, hence mean biaxial stresses ${\sigma }_{\theta \theta o}=6.772\text{kPa}$ and ${\sigma }_{zzo}=6.155\text{kPa}$ throughout, consistent with host vessel and scaffold parameters in Table 1. Shown in the central and right meshes is the combined volume fraction of collagen and smooth muscle, with the remaining amount up to 1.00 comprising elastin $\left({\Phi }_o^{\text{IVC}\mid e}=0.1\right)$ within the IVC segments and polymer alone $\left({\Phi }_o^{\text{TEVG}}\mid p=1.0\right)$ within the initial scaffold.

5.2. Initial equilibrium of the polymeric scaffold attached to both adjacent IVC segments

At s_h = s_o = 0, the TEVG (i.e., the polymeric scaffold) is elastically pre-stretched upon implantation (recall Section 4.2). To numerically simulate this (otherwise complex) process as ideally, yet realistically, as possible, we preserve the cylindrical FE mesh and change the IVC material parameters (i.e., a mixture of elastin, smooth muscle, and collagen, with respective volume fractions and deposition stretches) at material points between the axial locations z_o = l_o/4 and z_o = 3l_o/4 to those for the scaffold (i.e., a single polymeric constituent with $Q_o^p=1$ and associated pre-stretch G^p), whose initial in vivo dimensions are $[a_o^{\text{TEVG}},h_o^{\text{TEVG}}\text{,}{l}_o^{\text{TEVG}}]=\left[a_o^{\text{IVC}},h_o^{\text{IVC}},l_o^{\text{IVC}}/2\right]$; see the right, also pre-loaded, mesh in Figure 4. Let both IVC-TEVG (physical) interfaces be defined by elemental (mesh) interfaces. Indeed, following a mesh convergence study for the FSG solution, we employ a uniform mesh with 36 solid elements in the axial direction (i.e., 9(IVC)+ 18(TEVG)+9(IVC) to account for the proximal and distal host tissue), 42 in the circumferential direction, and 1 in the radial direction (the last capturing well, with full quadratic interpolation and full Gauss integration, the transmural gradient of stresses for a unilayered vessel with low thickness-to-radius ratio and nearly homogenized in-plane pre-stresses through the thickness; Latorre and Humphrey, 2020b).

For illustration, and to consider the ideal case, scaffold parameters are prescribed such that $\left[{\sigma }_{\theta \theta o}^{\text{TEVG}},{\sigma }_{zzo}^{\text{TEVG}}\right]=\left[{\sigma }_{\theta \theta o}^{\text{IVC}},{\sigma }_{zzo}^{\text{IVC}}\right]$, recall Eqs. (49) and (50), thus global (and local) mechanical equilibrium under in vivo pressure and fixed axial displacements at the FE model boundaries (i.e., z_o = 0 and z_o = 60 mm) is again easily enforced within our FE framework (including small radial variations) without appreciable changes in mesh dimensions (i.e., nodal displacements) or local stresses (e.g., σ_v ≈ σ_vo throughout both IVC and TEVG segments); compare different meshes in Figure 4.

Finally, let the IVC-scaffold-IVC model (i.e., with $Q_h^p=Q_o^p=1$ for the interposition TEVG) adapt to an initial axial pressure drop computed in a coupled fashion via the iterative FSG procedure in Section 3. For an initially straight cylindrical vessel (even if materially nonuniform), the 1D fluid computation induces only small variations in dynamic pressure and frictional losses (with K_f = 0 at this point), hence also small variations in pressure and G&R related deformations. This FSG solution (at s_h = s_o = 0), with both fluid and solid domains resolved and coupled, constitutes the starting point for all remaining FSG computations for the development of the IVC-TEVG-IVC segment as the polymer degrades and recruited cells synthesize neotissue (s_h > 0). In particular, to facilitate adaptations of newly produced collagen within the TEVG and both IVC segments, we let symmetric diagonal families locally reorient following a stretch-dependent adaptation based on the referential deposition stretch tensors present in Eq. (37), cf. Latorre and Humphrey (2020b).

5.3. Evolving TEVG attached to both adjacent IVC segments

For s_h > 0, we advance the mechanobiologically equilibrated solution of the structural IVC-TEVG-IVC model by prescribing $Q_h^p$, $c_1^{\theta }=c_1^z=c_1^d$, $c_2^{\theta }=c_2^z=c_2^d$, α₀, and $\Delta {\varrho }_{\phi h}$, as given in Fig. 3 and Table 1, throughout the TEVG segment, whose composition and 3D geometry evolve accordingly, whereas the adjacent IVC grows and remodels only as a reaction (computed via “Stage II” in Latorre and Humphrey, 2020a), both doing so in the presence of the changing hemodynamics (with $P_d=P_o^{\text{IVC}}$ and $Q=Q_o^{\text{IVC}}$ prescribed in Eq. (46)). Noting, however, the strong discontinuity at the IVC-TEVG interfaces in both wall properties (which evolve for the TEVG) and potentially evolving geometry (with a dramatic narrowing and thickening of the TEVG for s_h ~ [5, 25] weeks, see Fig. 3), it proves numerically convenient to prescribe different (less dramatic) evolutions from scaffold $\left(Q_h^p=1\right)$ to neovessel $\left(Q_h^p=0\right)$ properties for TEVG material points located within two short (6mm-long) axial transition regions at the ends of the TEVG mesh, for which uniform computations proved again useful. To do so, we computed different sets of evolving parameters $c_1^c$, α₀, and $\Delta {\varrho }_{\phi h}$ for the same $Q_h^p$ in Figure 3 but reduced deviations in both inner radius and thickness for the uniform model (i.e., gradually scaled between a minimal deviation, such that the TEVG cross-sections adjacent to the IVC potentially evolve with constant radius and thickness, and a nearly maximal (~70%) deviation, such that the associated TEVG cross-sections potentially experience substantial narrowing and thickening), which were then prescribed in the FE model to yield the desired smooth transition in cross-sectional geometry (i.e., computed as part of the FSG solution). Fig. 5 shows this particular (quasi-equilibrated mechanobiologically) progressive TEVG evolution due to the gradually increasing formation of collagen-dominated neotissue as the polymer degrades (cf. panel C in Fig. 3), with the maximal degree of computed narrowing for the lumen of the TEVG (relative to the proximal IVC) indicated between parentheses. Likewise, to facilitate convergence of the yet highly nonuniform (materially and geometrically, particularly at the IVC-TEVG interfaces) evolving structural model shown in Fig. 5, and owing to the rate- and path-independent nature of the present FSG method, we computed the TEVG evolution via a fictitious linear degradation profile $Q_h^{p\ast }$ $\left(s_h^{\ast }\right)$ and associated (re-computed, not shown) evolving parameters $c_1^{c\ast }$, ${\alpha }_0^{\ast }$, and $\Delta {\varrho }_{\phi h}^{\ast }$, with $s_h^{\ast }$ a computational (pseudo)time to drive the FE simulation. Lastly, converged results associated with an actual time s_h were identified from $Q_h^p\left(s_h\right)=Q_h^{p\ast }\left(s_h^{\ast }\right)$.

Fig. 5.

Mechanobiologically quasi-equilibrated, progressive development (clockwise from the upper right mesh) of the initially pre-loaded IVC-TEVG-IVC≡IVC-scaffold-IVC segment (0 weeks, right mesh in Fig. 4) with increasing degradation of the polymeric constituent (see panel C in Fig. 3), evolving properties of collagen and infiltration/clearance of inflammatory cells (see panels D to F in Fig. 3) in the presence of changing hemodynamic conditions computed with the present FSG formulation (see bottom row in Fig. 7). Shown in all meshes is the combined volume fraction of collagen and smooth muscle (elemental averages), with the remaining amount up to 1.00 comprising elastin $\left({\Phi }_h^{\text{IVC}\mid e}\approx 0.1\right)$ within the host IVC lateral segments and degrading polymer $\left({\Phi }_h^{\text{TEVG}}\mid p\to 0\right)$ within the central TEVG. The percentage between parentheses indicates the degree of maximal narrowing for the lumen of the TEVG (whose wall also thickens markedly), expressed as the percent reduction in luminal area relative to the proximal IVC. See the evolution of other metrics in Figs. 6 and 7.

Figs. 6 and 7 show associated regional values of evolving wall stretch, wall stress, material stiffness and stored energy, as well as inflammation and the axial distribution of blood pressure, at four representative times, all superimposed on the evolving IVC-TEVG-IVC segment (noting that blood pressure acts as a traction on the inner surface of the vessel only). Importantly, all of these metrics (except axial stretch and pressure) qualitatively follow the main temporal results, either prescribed or obtained, from the uniform computations shown in Fig. 3. Indeed, besides the appreciable thickening computed at week 12 (Fig. 6, second column, first row) and luminal narrowing (second row) of the TEVG, with associated decreases in mean circumferential (fourth row) and axial (fifth row) stresses and increase in inflammation (Fig. 7, fourth row), of particular interest is the additional prediction of a local axial shrinking of the TEVG (Fig. 6, third row; with an associated G&R-related lengthening of the adjacent IVC) as well as lower peaks in material stiffness (Fig. 7, first and second rows) and elastically stored energy (third row) relative to the uniform simulation with fixed TEVG length (cf. panels H and I in Fig. 3). The key difference between uniform G&R and non-uniform FSG is the ability of the latter to incorporate feedback from the changing hemodynamics conditions, especially axial variations in blood pressure (Fig. 7, fifth row) via Eq. (46) that further affect the remodeling through additional changes in intramural stresses (note that changes in flow-induced shear stress are predicted in both uniform / non-uniform solutions via the change in uniform / non-uniform inner radius). For blood flow properties given in Table 1, a maximal drop in static pressure of ~25% (~1.2mmHg) relative to upstream pressure is predicted within the TEVG segment at the time of maximal narrowing (second column), with the input venous pressure increasing ~15% (~0.6mmHg) relative to baseline due to the TEVG narrowing-induced viscous and geometric losses (i.e., an increased pressure gradient emerges as part of the FSG solution to overcome the increased resistance to flow; compare with the modest and gradual increase in upstream pressure for the initial and mostly cylindrical IVC-scaffold-IVC, first column, and the final but not yet fully resolved IVC-neovessel-IVC, fourth column). Consistent with the ~15% increase in upstream pressure, the proximal IVC segment wall thickens ~15%, tending to restore the local intramural stresses back to normal (for constant flow and in the absence of inflammation, as in certain cases of hypertension). Interestingly, this pressure gradient, predicted for the model lamb implant, reached a clinical definition for intervention (≥ 0.5mmHg, defined even more conservatively for greater reference venous pressures of ~13mmHg; Schwarz et al., 2021). Both experimental data and Computational Fluid Dynamics (CFD) simulations suggest, however, that grafts with even greater pressure gradients perform well within normal ranges for hemodynamic metrics (Schwarz et al., 2021; Blum et al., 2022). Indeed, using representative grown and remodeled IVC-TEVG-IVC geometries, extracted from the converged FSG solution at times s_h = 0 (initially cylindrical, first column) and s_h = 12 weeks (maximally stenosed, second column), we computed respective CFD solutions for steady 3D blood flow and rigid walls in the open source code SimVascular (Supplemental Figure S1; Updegrove et al., 2017), which confirmed the (favorable, almost uniform, and first favorable and then adverse, respectively) pressure gradients computed via Eq. (46), though with greater pressure gradients for the stenosed geometry. Importantly, more realistic 3D flow solutions of this type could alternatively be coupled to our 3D G&R formulation for TEVG development, which would require a different FSG strategy to (loosely) couple, especially, the wall shear stress (computed via CFD) to the G&R solution (informed via Eq. (41)), at the expense of a substantially higher computational cost (hours versus a fraction of a second) along with potential mesh adaptations for the flow simulations to converge (Supplemental Table S1). Considering the total cost of these different FSG approaches to perform, for example, optimization studies, ~50 1D-fluid/3D-solid FSG simulations (~1 hour each, where the G&R computation takes most of the wall time) could be run for each 3D-fluid/3D-solid FSG simulation (where the CFD computation takes most of the wall time). Finally, note that the IVC-neovessel-IVC segment (fourth column), for which inflammation has almost completely resolved, recovers nearly uniform properties throughout despite the lack of elastin (see s_h = 52 weeks in Fig. 4) and slightly different collagen properties (stiffness and orientation of diagonal fibers, recall Fig. 3) for the neovessel relative to the adjacent IVC.

Fig. 6.

Progressive, mechanobiologically quasi-equilibrated, development (left to right) of an interposition TEVG (central segment in all the meshes), attached to adjacent IVC segments (proximal and distal, which adapt to the changing environment via G&R as well), induced by the gradual degradation of the initially implanted polymeric scaffold (see Fig. 4, right panel, and Fig. 5), with evolving properties of neotissue in response to a gradual infiltration and then loss of inflammatory cells (see panels D to F in Fig. 3) as well as changing hemodynamics (computed by the FSG solution). Shown superimposed on the IVC-TEVG-IVC segment are the regional values (elemental averages, to facilitate comparisons with uniform results in Figure 3) of radial and biaxial stretches (first to third rows) as well as biaxial wall stresses (fourth and fifth rows). The G&R model predicted the experimentally observed thickening (radial stretch > 1), narrowing (circ. stretch < 1), and axial shrinking (axial stretch < 1) of the TEVG, along with the associated marked reductions in circumferential and axial stress, all followed by respective partial resolution of geometry and properties (see also Fig. 7).

Fig. 7.

As in Fig. 6, but showing regional values (elemental averages) of biaxial material stiffness (first and second rows), stored energy density (third row), inflammation (fourth row), and the axial distribution of blood pressure within the lumen (fifth row) resulting from the coupled FSG solution, with the output (downstream) venous pressure $P_d=P_o^{\text{IVC}}=4.4\text{mmHg}$ prescribed via Eq. (46).

Finally, because of the predicted axial shrinkage of the TEVG and associated lengthening of the host IVC, we repeated these simulations for an idealized case of a TEVG with an initial length:diameter ratio of 6.4 (Supplemental Figures S2–S4), in contrast to the actual (smaller) length:diameter ratio of 1.6 (Figures 5–7). As it can be seen in Supplemental Figures S2–S4, the overall predictions were similar, with nearly identical maximal narrowing in the central region, though with lower axial gradients predicted for the longer graft. Although there may be mechanical advantages to a longer graft, this must be contrasted with likely biological disadvantages, including the need to remove more native tissue and the need to endothelialize a larger luminal surface.

6. Discussion

As noted earlier, continuing advances in the development of novel biomaterials (Stowell and Wang, 2018) and methods of tissue engineering (Matsuzaki et al., 2019) have been spectacular, resulting in many viable approaches and multiple clinical trials of TEVGs (Syedain et al., 2017; Kirkton et al., 2019; Drews et al., 2020). Current research is thus turning towards the need to optimize the grafts, both the biomechanical design of the scaffold and the immuno-modulation (Harrison et al., 2016; Tamimi et al., 2019; Szafron et al., 2019; Wissing et al., 2020; Furdella et al., 2021). Computational models complement experimental investigations (Emmert et al., 2018; Drews et al., 2020; Loerakker and Ristori, 2020), promising to provide a path forward toward optimization.

Multiple approaches are available for modeling soft tissue G&R, with the two most common stemming from the theory of kinematic growth or the theory of constrained mixtures (Cyron and Humphrey, 2017; Ambrosi et al., 2019). Despite the computational efficiency of kinematic growth models, the composite nature of TEVGs – typically including multiple biodegradable polymeric constituents having different mechanical properties and degradation kinetics as well as diverse emerging extracellular matrix constituents – suggests that mixture-based models are both natural and essential. As noted earlier, full heredity integral-based constrained mixture models are often computationally expensive except for cases of membranes or axisymmetric bodies. Hence, reduced constrained mixture models have been derived, including temporally homogenized (rate-dependent) and mechanobiologically equilibrated (rate-independent) formulations (Cyron et al., 2016; Latorre and Humphrey, 2018). Given their increased computational efficiency, both are well suited for otherwise computationally intensive simulations, including fluid-solid-growth (FSG) and formal optimization. Herein, we presented a new FSG model based on the mechanobiologically equilibrated approach. This approximate method for computing evolving G&R within in vivo homeostatic configurations requires that the time scale for the adaptation must be less than the time scale for the stimulation. In the graft considered here, scaffold degradation has been shown to occur over periods in excess of 1 year (cf. Fig. 3 in Blum et al., 2022), while the half-life of collagenous neotissue is typically on the order of 1 to 3 months. Thus, this framework appears reasonable for our TEVG as well as for those cases of neovessel development where the polymeric scaffolds have relatively slow degradation profiles. Conceptually, of course, the present model can be extended to TEVGs having either more complex polymeric or biological scaffolds, with the primary need being identification of constituent-specific constitutive relations for mass production and removal as well as stored energy.

As seen in Table 1 and Figure 3, we were able to parameterize the model based on available data, including in vitro biaxial mechanical data for the native IVC and initial scaffold as well as in vivo measurements of evolving geometry (cf. Fig. 4 in Drews et al., 2020) and flow (cf. Fig. 6 in Blum et al., 2022) and preliminary immunohistological quantification of pan-leukocyte infiltration and resolution (cf. Fig. 4 in Blum et al., 2022). Although such data were sufficient, additional data, both in vivo and in vitro, will be needed to better inform the model, particularly during the period of rapid changes (2 to 20 weeks for this graft). There is similarly a need for more data on the possible G&R of the host tissue, proximal and distal IVC herein. Nevertheless, the model captured the data well (Figure 2), thus enabling the first FSG simulations of in vivo TEVG development. Most importantly, the model predicted the previously observed narrowing and spontaneous reversal of the TEVG, as seen in Figures 5–7. Whereas our uniform G&R model had similarly predicted a narrowing and spontaneous resolution (Drews et al., 2020), the present results provide the first spatio-temporal predictions, including G&R of the host IVC. Examining the host IVC response revealed persistent changes to the adjacent vessel segments, as the axial and circumferential stretches remain different from those in the homeostatic state after 52 weeks of remodeling (Figure 6), highlighting the need to consider the potential for TEVG effects on native tissue in designing scaffolds. Furthermore, the FSG model predicted axial shortening of the TEVG segment during the period of stenosis formation (Figure 6), which recapitulated the shortening observed experimentally (cf. Fig. 9 in Blum et al., 2022). This emerged naturally as a result of the problem setup. As such, the additional spatial information can allow better fidelity to the overall geometric changes observed in vivo and can facilitate predictions that are not possible in simulating simple cross-sections. Coupling of the hemodynamics to graft evolution similarly allows more realistic predictions; differences in upstream and downstream pressures were found to stimulate different adaptation processes by the adjacent IVCs on either side of the TEVG (Figures 6 and 7). In agreement with past work, we found a substantial increase in matrix stiffness during the period of immuno-driven neotissue formation that resolved with the depletion of the scaffold material (Szafron et al., 2018). Interestingly, the predicted narrowing occurred in the central region of the graft, which has been observed in vivo. Although the FSG model yielded coupled information on axial differences in blood pressure and flow, both the vein and TEVG are relative stiff when distended by venous pressures, and the pressure drop along the TEVG was a modest ~1mmHg. Unpredictable more distal or more proximal narrowing has also been observed in vivo; however, this does not appear to relate simply to the axial pressure gradient for the degree of narrowing observed here. Other factors, perhaps including details of the surgically created anastomosis, perivascular adhesions following surgery, differences in cellular infiltration rates along the graft length, or even graft imperfections may give rise to such spatial heterogeneities. We did not attempt to explore these possible factors parametrically given the lack of data.

In addition to the need for more data, there is clearly a need for a fully coupled 3D FSG model, one coupling a full constrained mixture model with full unsteady Navier-Stokes solutions to characterize graft behavior during the cardiac cycle, such as in exercise, as well as to capture transient remodeling behavior for promising polymer scaffolds that degrade rapidly (Wang et al., 2002). Such is not trivial (Figueroa et al., 2009), but there have been similar related advances, particularly in the study of aneurysms (Sheidaei et al., 2011; Wu and Shadden, 2015; Grytsan et al., 2015; Teixeira et al., 2020; Mousavi et al., 2021). Nevertheless, the high computational cost of such models suggests that multi-fidelity approaches, with many simulations using a lower cost algorithm, can guide parameter estimation or optimizations of a higher cost algorithm (Fleeter et al., 2020). Therefore, the present methods can also serve to accelerate simulations that use a fully coupled FSG framework. Additional limitations of the present model will also need to be addressed. We did not model expected platelet activation / adhesion to the luminal surface during the early post-operative period, which could stimulate the accumulation of a thin thrombus with attendant biological activity, including plasmin production (Wu et al., 2018; Reinhardt et al., 2019). We similarly did not model progressive endothelialization (Sánchez et al., 2018), which likely occurs from the proximal and distal ends of the graft toward the central region. A progressive development of a functional endothelium would not only prevent thrombus, it would also be expected to attenuate inflammation and eventually allow a flow-induced, paracrine control of smooth muscle cell function, both synthetic and contractile. Finally, we did not account for perivascular tissue, including fibrotic adhesions that arise post-operatively. Clearly, much remains to be understood and modeled in order to have a complete understanding of in vivo neovessel development.

Notwithstanding the ongoing lack of important experimental information and limitations to the computational models, we emphasize that multi-fidelity approaches can provide increased insight as well as computational advantages. Whereas there remains a need to couple full constrained mixture models with Navier-Stokes solvers and formal methods of optimization, the present reduced FSG model represents a fast, efficient model that can be used to perform initial optimization studies that include new functional targets, such as minimizing native vessel remodeling, and that can then be finalized via the more complete, but expensive, full simulations.

A Specialization: a thin-wall-equivalent TEVG

We reformulate and extend here the main algebraic equations derived in Latorre and Humphrey (2018) to show their consistency with the general boundary value formulation above. Indeed, one can alternatively solve an equivalent system of nonlinear algebraic equations formed by mechanobiological equilibrium ϒ_h = 1 plus mechanical equilibrium along the radial, circumferential, and axial directions, namely

$$\begin{gathered} {\Upsilon }_h=1+K_{\sigma }\left(\frac{{\sigma }_{rrh}+{\sigma }_{\theta \theta h}+{\sigma }_{zzh}}{{\sigma }_{rro}+{\sigma }_{\theta \theta o}+{\sigma }_{zzo}}-1\right) \\ -K_{{\tau }_w}\left(\frac{Q_h{a}_o^3}{Q_o{a}_h^3}-1\right)+K_{{\varrho }_{\phi }}\frac{{\rho }_{\text{R}\phi h}}{{\rho }_{\text{R}\phi \max }}=1 \end{gathered}$$ (56)

$${\sigma }_{rrh}=\sum _{\alpha =1}^N{\sigma }_{rrh}^{\alpha }-p_h=\frac{Q_h^p}{J_h}{\widehat{S}}_{rrh}^p{G}_r^{p2}{\lambda }_{rh}^2-p_h=-\frac{P_h}{2}$$ (57)

$$\begin{gathered} {\sigma }_{\theta \theta h}=\sum _{\alpha =1}^N{\sigma }_{\theta \theta h}^{\alpha }-p_h=\frac{Q_h^p}{J_h}{\widehat{S}}_{\theta \theta h}^p{G}_{\theta }^{p2}{\lambda }_{\theta h}^2 \\ +\sum _{c=1}^{N^c}{\Phi }_h^c{\widehat{\sigma }}_{\theta \theta }^c-p_h=\frac{P_h{a}_h}{h_h} \end{gathered}$$ (58)

$$\begin{gathered} {\sigma }_{zzh}=\sum _{\alpha =1}^N{\sigma }_{zzh}^{\alpha }-p_h=\frac{Q_h^p}{J_h}{\widehat{S}}_{zzh}^p{G}_z^{p2}{\lambda }_{zh}^2 \\ +\sum _{c=1}^{N^c}{\Phi }_h^c{\widehat{\sigma }}_{zz}^c-p_h=\frac{f_{zh}}{\pi h_h\left(2a_h+h_h\right)} \end{gathered}$$ (59)

where the primary unknowns are a_h, h_h, p_h, and f_zh, noting in Eqs. (56) and (57) the consideration of a mean radial stress −P_h/2 for more accurate comparisons with FE analyses. In particular, the evolved homeostatic Lagrange multiplier p_h can be obtained in this case from the mechanobiological equilibrium equation (recall Eq. (40)), which enables substitution of p_h in expressions for stresses (recall Eq. (39)), hence, representing a generalized (numerical) resolution procedure for a cylindrical TEVG consistent with the general formulation derived above.

To obtain analytical solutions, however, it may still be convenient to obtain p_h from the radial equilibrium equation (as in Latorre and Humphrey, 2018). Of particular interest here, with P_h = P_o and Q_h = Q_o, as well as ρ_Rφh → 0 and $Q_h^p\to 0$ for the TEVG at s_h ≫ 0, one gets for the neovessel

$$K_{\sigma }\left(\frac{{\sigma }_{rrh}+{\sigma }_{\theta \theta h}+{\sigma }_{zzh}}{{\sigma }_{rro}+{\sigma }_{\theta \theta o}+{\sigma }_{zzo}}-1\right)-K_{{\tau }_w}\left(\frac{a_o^3}{a_h^3}-1\right)=0$$

$${\sigma }_{rrh}=-p_h=-\frac{P_o}{2}={\sigma }_{rro}$$

$${\sigma }_{\theta \theta h}={\Phi }_h^m{\widehat{\sigma }}_{\theta \theta }^m+{\Phi }_h^{c_{\theta }}{\widehat{\sigma }}_{\theta \theta }^{c_{\theta }}+{\Phi }_h^{c_d^{+}}{\widehat{\sigma }}_{\theta \theta }^{c_d^{+}}+{\Phi }_h^{c_d^{-}}{\widehat{\sigma }}_{\theta \theta }^{c_d^{-}}-p_h=\frac{P_o{a}_h}{h_h}$$

$${\sigma }_{zzh}={\Phi }_h^{c_z}{\widehat{\sigma }}_{zz}^{c_z}+{\Phi }_h^{c_d^{+}}{\widehat{\sigma }}_{zz}^{c_d^{+}}+{\Phi }_h^{c_d^{-}}{\widehat{\sigma }}_{zz}^{c_d^{-}}-p_h=\frac{f_{zh}}{\pi h_h\left(2a_h+h_h\right)}$$

with ${\Phi }_h^m={\varrho }_o\left({\Phi }_h^{c_{\theta }}+{\Phi }_h^{c_z}+{\Phi }_h^{c_d}\right)$ and ${\Phi }_h^m+{\Phi }_h^{c_{\theta }}+{\Phi }_h^{c_z}+{\Phi }_h^{c_d}=1$ then ${\Phi }_h^{c_{\theta }}+{\Phi }_h^{c_z}+{\Phi }_h^{c_d}=1/\left(1+{\varrho }_o\right)$, ${\Phi }_h^m={\varrho }_o/\left(1+{\varrho }_o\right)$, and

$$K_{\sigma }\left(\frac{{\sigma }_{rro}+\frac{P_o{a}_h}{h_h}+\frac{f_{zh}}{\pi h_h\left(2a_h+h_h\right)}}{{\sigma }_{rro}+{\sigma }_{\theta \theta o}+{\sigma }_{zzo}}-1\right)=K_{{\tau }_w}\left(\frac{a_o^3}{a_h^3}-1\right)$$

$$\frac{1}{1+{\varrho }_o}\left({\varrho }_o{\widehat{\sigma }}^m+\left({\beta }^{\theta }+{\beta }^d{\sin }^2{\alpha }_0\right){\widehat{\sigma }}^c\right)+{\sigma }_{rro}=\frac{P_o{a}_h}{h_h}$$

$$\frac{1}{1+{\varrho }_o}\left({\beta }^z+{\beta }^d{\cos }^2{\alpha }_0\right){\widehat{\sigma }}^c+{\sigma }_{rro}=\frac{f_{zh}}{\pi h_h\left(2a_h+h_h\right)}$$

from which we obtain the final cylindrical geometry and axial force explicitly in terms of the material properties of smooth muscle and collagen fibers in the final state, namely: a_h(s_h ≫ 0) from

$$1+\frac{K_{\sigma }}{K_{{\tau }_w}}\left(\frac{3{\sigma }_{rro}+\frac{1}{1+{\varrho }_o}\left({\varrho }_o{\widehat{\sigma }}^m+{\widehat{\sigma }}^c\right)}{{\sigma }_{rro}+{\sigma }_{\theta \theta o}+{\sigma }_{zzo}}-1\right)=\frac{a_o^3}{a_h^3},$$ (60)

h_h(s_h ≫ 0) from

$$\frac{1}{1+{\varrho }_o}\left({\varrho }_o{\widehat{\sigma }}^m+\left({\beta }^{\theta }+{\beta }^d{\sin }^2{\alpha }_0\right){\widehat{\sigma }}^c\right)+{\sigma }_{rro}=\frac{P_o{a}_h}{h_h},$$ (61)

and f_zh(s_h ≫ 0) from

$$\frac{1}{1+{\varrho }_o}\left({\beta }^z+{\beta }^d{\cos }^2{\alpha }_0\right){\widehat{\sigma }}^c+{\sigma }_{rro}=\frac{f_{zh}}{\pi h_h\left(2a_h+h_h\right)}.$$ (62)