Linear Linking for Related Traits (LLRT): A novel method for the harmonization of cognitive domains with no or few common items

Abstract

Harmonization means to make data comparable. Recent efforts to generate comparable data on cognitive performance of older adults from many different countries around the world have presented challenges for direct comparison. Neuropsychological instruments vary in many respects, including language, administration techniques and cultural differences, which all present important obstacles to assumptions regarding the presence of linking items. Item response theory (IRT) methods have been previously used to harmonize cross-national data on cognition, but these methods rely on linking items to establish the shared metric. We introduce an alternative approach for linking cognitive performance across two (or more) groups when the fielded assessments contain no items that can be reasonably considered linking items: Linear Linking for Related Traits (LLRT). We demonstrate this methodological approach in a sample from a single United States study split by educational attainment, and in two sets of cross-national comparisons (United States to England, and United States to India). All data were collected as part of the Harmonized Cognitive Assessment Protocol (HCAP) and are publicly available. Our method relies upon strong assumptions, and we offer suggestions for how the method can be extended to relax those assumptions in future work.

1. Introduction

An estimated 70.5% of individuals living with dementia are anticipated to live in low and middle-income countries by 2050 [1]. However, to date, the majority of research on cognitive aging and dementia has been conducted in high-income countries [2]. To reach a more complete understanding of dementia and its sequelae, it is critical not only to conduct research in diverse settings, but also to be able to compare findings between settings. Differences or similarities identified across different settings can inform the implementation of targeted policies for preventing cognitive decline and dementia. Large differences in the distribution of exposures across geographic settings in cross-national research also provide an opportunity to characterize novel modifiable risk factors.

However, the comparison of cognitive measures across geographic settings is complicated by differences in cognitive batteries administered between countries due to changes needed to address linguistic and cultural differences [3-5]. Commonly used methods for summarizing and comparing cognitive test scores, such as the construction of z-scores, do not capture potential differences between samples, as scores are internally scaled to each setting seperately. Alternatively, item response theory (IRT) methods have been previously used to locate respondents along a common metric of cognitive functioning across studies with different cognitive test batteries while using all available information from questions (items) that are common as well as items that are different between surveys [6,7]. Recent work has shown these methods can be feasibly applied to link cognitive functioning across studies conducted in different geographic settings [8].

IRT methods rely on the presence of common or shared items, often referred to as linking items, between surveys. Linking items are used to create a shared metric between the studies, while other items contribute to the precision of the estimated ability for respondents in specific surveys [9]. However, IRT-based linking methods cannot be applied when there are no linking items, and can be unstable when the number of linking items is small [10]. Prior simulation studies have shown that having at least five linking items is optimal to ensuring accurate linking, although practical examples using fewer linking items exist [11,12].

Estimates of specific cognitive domains, such as memory, executive functioning, or visuospatial functioning, may be of interest in studies of cognitive aging, as different patterns of dysfunction in specific cognitive domains may indicate distinct pathological underpinnings [13-16]. While the cognitive batteries used across aging surveys often include linking items (i.e. items that are common) enabling the estimation of general cognitive functioning, linking items may not always exist to allow the linking of narrower cognitive domains. This is particularly true in cross-national research, where cultural and linguistic adaptations may lead to differences between items that would otherwise be considered to be common. An alternative solution is required to allow cross-national research of specific cognitive domains when there are few or no linking items available.

This paper aims to develop a novel method, Linear Linking for Related Traits (LLRT), to allow for the linking of cognitive domains where there are few or no linking items. We demonstrate this new method by equating executive functioning between individuals with low and high educational attainment in the United States, as well as between individuals in the United States, England, and India using data from the Harmonized Cognitive Assessment Protocol (HCAP) surveys.

2. Material and methods

The LLRT method harmonizes sub-domains of cognitive performance with few or no linking items by leveraging more reliable information on the relationship between samples from a subsuming domain. In this study, we sought to harmonize executive functioning (the subdomain). We used general cognitive functioning as the subsuming domain, or the related latent construct, for which adequate information exists to harmonize studies using conventional methods. The LLRT method has three steps:

1. Harmonization of the related latent construct (general cognitive function, which subsumes executive functioning and other cognitive domains) using IRT harmonization methods that leverage information from items that are common between the surveys. After this step, the subsuming domain is on the same metric across the samples.

2. Separate estimation of confirmatory factor analysis (CFA) models for the subdomain of interest (executive functioning) independently in each sample. These separately calibrated subdomain models are not directly comparable across samples because they are designed to have mean 0 and unit variance within each sample.

3. Linear equating to convert separately calibrated scores on the subdomain of interest to the metric of the subsuming domain or related construct.

LLRT assumes that the differences observed between the samples on the related latent construct are equivalent to the differences that would be observed between samples on the subdomain of interest. In our example, where the subdomain of interest is executive functioning and the related latent construct is general cognitive functioning, we assume that the difference in the distributions of executive functioning between our two samples is the same as the observed difference in the distributions of general cognitive functioning. While differences between specific individuals might vary when considering executive functioning versus general cognitive functioning, the overall differences in the population-level distributions are assumed to be equivalent. The analytic process is depicted in Figure 1. We will discuss each step in more detail in the sections to follow.

Figure 1.

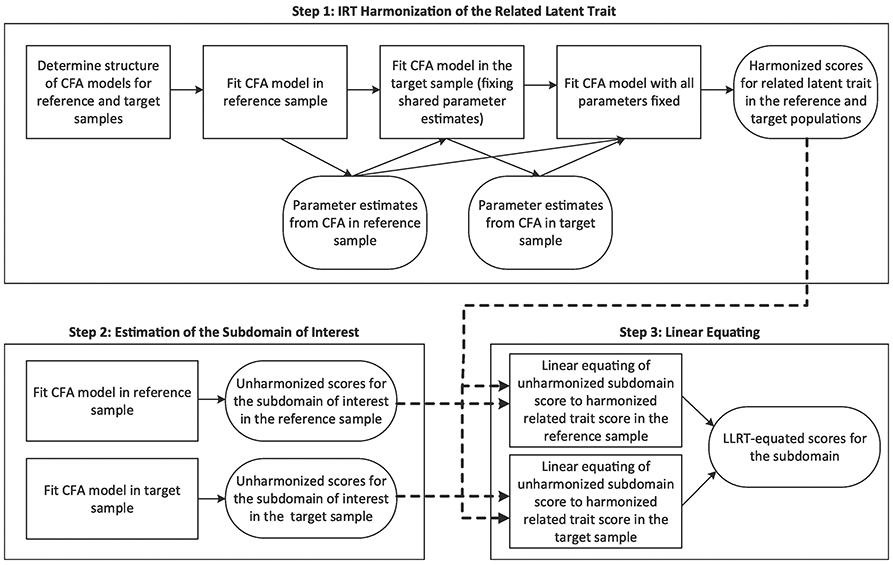
Flow diagram depicting the analytic steps used in Linear Linking for Related Traits (LLRT). Steps 1 (IRT harmonization of the related trait) and 2 (estimation of the subdomain of interest), provide inputs to Step 3 (linear equating).

2.1. Data sources

This study leveraged publicly available data from the HCAP studies conducted in the United States, England, and India [17-19]. The HCAP surveys were designed with the goal of implementing a consistent set of measures on cognition and functional limitations across different geographic locations to facilitate cross-national research on dementia. However, despite this goal, accommodations and adjustments were necessary to ensure that items were culturally and linguistically appropriate. In particular, many of the cognitive items within the executive functioning domain had to be adapted for use in India, leaving little overlap (1 item in common) in the items administered (Table 2). Therefore, we focused on the harmonization of executive functioning in the examples throughout this paper.

Table 2.

Overlap in cognitive test items assessing executive function administered in the United States (N = 3347), England (N= 1273), and Indian (N = 1777) HCAP samples

Cognitive Item	United States	England	India
	N	N	N
Executive Functioning Measure
Problem-solving test ‡			1015
Ravens progressive matrices ⊥	3303	1258	1777
Number series ⊥	2861	1153
Trail Making Test, Part B time ⊥	2860	1038
Similarities ‡			1777
Token Test ‡			1015
Go/No Go test ‡			1777
Digit Span Forward ⊥			1777
Digit Span Backward ⊥			1777
Trail Making Test, Part A time ⊥	3249	1209
Symbol Digit Modalities Test ⊥	3236	1196
Backward counting ⊥	3305	1253
Backward Day naming ‡			1777
Visual Scan (Symbol Cancellation Test) ⊥			1777
Spelling backwards ‡	3347
Serial 7s test ‡		1273	1624
Letter cancellation ⊥	3215	1273
Other Cognitive Measure
Orientation to time - Day of the month †	3249	1253	1777
Orientation to time – Month †	3321	1273	1777
Orientation to time – Year †	3302	1268	1777
Orientation to time - Day of the week †	3318	1269	1777
Orientation to time – Season †	3301	1270	1777
Orientation to place – Country †		1271
Orientation to place – State †	3325		1777
Orientation to place – County †	3274	1273
Orientation to place – City †	3326	1272	1777
Orientation to place - Floor of the building †	3329		1777
Orientation to place – Address †	3293		1777
Orientation to place - Name of place/hospital †		1273	1777
Orientation to place - Area of town/village or street name †		1271
Three word immediate recall ‡	3338	1268	1777
Three word delayed recall ‡	3305	1265	1777
CERAD word list immediate recall, sum of 3 trials ⊥	3343	1263
CERAD word list immediate recall, sum of 3 trials ⊥			1777
CERAD word list, delayed recall ⊥	3324
CERAD word list, delayed recall ⊥			1777
CERAD word list, delayed recall ⊥		1264
CERAD word list, recognition ⊥	3330
CERAD word list, recognition ⊥		1261	1777
Logical Memory, immediate recall ⊥	3306	1254	1777
Logical Memory, delayed recall ⊥	3253	1210	1777
Logical memory, recognition ⊥	3243	1222	1777
CERAD Constructional praxis (copy 4 figures), delayed recall ⊥	3303	1161	1777
East Boston Memory Test, immediate recall ⊥	3332	1264	1777
East Boston Memory Test, delayed recall ⊥	3496	1217	1777
Object naming by description (cactus) †	3344	1273
Object naming by description (coconut) †			1777
Object naming by description (scissors) †	3344	1273	1777
Object naming by description (elbow) †	3337	1273	1777
Object naming by description (hammer) (10/66 item) †	3340	1271	1777
Object identification (watch) †	3333		1777
Object identification (pencil) †	3337		1777
Animal fluency ⊥	3345	1270	1777
Write a sentence †	3240	1230	1741
Read and follow command †	3284	1260	1741
Repetition of phrase (e.g., no ifs, ands, or buts) †	3324	1265	1777
Following 2-step instruction (Point to window, then a door) †	3339	1272	1777
Where is the local market? (10/66 item) †	3338	1273	1777
Following 3-step instruction (paper, fold, floor) ‡	3317	1273	1777
CERAD constructional praxis (copy 4 figures), immediate ⊥	3308	1250	1777
Interlocking polygons †	3284		1777
Clock Drawing ‡			1777
Current President/Prime Minister †	3341	1273	1777

^*Numbers indicate the number of individuals with data on a given item for each survey location

^{† =}binary item

^{‡ =}ordinal item

^{⊥ =}continuous item

We used data from the baseline waves of the HCAP surveys in the United States (data collected 2016-2017, N = 3496), England (data collected 2018, N = 1273), and India (data collected 2017-2019, N = 4096). We excluded n = 149 individuals who did not complete the cognitive assessment United States HCAP sample. To account for high levels of illiteracy in the Indian population, some of the items administered in the Indian survey were different for literate versus illiterate participants. Therefore, the literate and illiterate populations need to be treated as two separate populations when conducting IRT harmonization. To simplify the examples presented in this paper, we excluded the n = 2317 illiterate participants from the India sample. We used the US HCAP survey stratified by level of educational attainment (12 or fewer years, n = 1578; more than 12 years, n = 1769) to illustrate our method via an example where we could be assured that the items used and context of assessment could be assumed to be equivalent.

2.2. Confirmatory factor analysis (CFA) models

Throughout the analysis, we used confirmatory factor analysis (CFA) to define a measurement model for cognitive data. The cognitive test items include a mix of binary, ordinal, and continuous items, and the CFA models were based on the correlation matrix of all items (including polychoric correlations between ordinal or binary items, polyserial correlations between an ordinal or binary item and a continuous item, and Pearson correlations between two continuous items). CFA of ordinal items on a polychoric correlation matrix is equivalent to a graded response IRT model and we refer to the use of these models for harmonization as IRT harmonization throughout the paper [20]. Parameter estimates from these models include the mean and variance of the latent trait, threshold and discrimination parameters for ordinal and binary items, and intercept and residual variance parameters for continuous items.

2.3. Harmonization of the subsuming domain: general cognitive functioning

In step 1 of the LLRT method, we developed harmonized scores of generalized cognitive functioning between samples using CFA as described above and an item banking approach [21]. The item banking approach involves first estimating a measurement model in a reference sample. Parameter estimates from this model are presumed to be population values. A second measurement model in a target sample is then used to obtain estimates for item parameters not in the item bank while constraining item parameters for items in the target sample data that do appear in the item bank to be equal to their presumed population values. Additional measurement models in other target samples can be added to this process to equate more than two samples. In our example, the United States was the reference sample, and England, followed by India, were the target samples.

The first step of this process was to evaluate the fit of CFA models independently to the target sample, and assess the need for methods factors to account for residual correlations among items with shared or similar content (e.g., items from the same cognitive test) [22]. Where the fit of the original CFA model was poor, methods factors were added where conceptually appropriate to improve model fit [8]. A list of the methods factors estimated in each sample is available in Appendix 1. Once we identified an appropriate set of methods factors for each sample, these were utilized in all subsequent CFA models for that sample.

Then, we estimated CFA models for the target samples. In our examples, the target samples were England and India (literate respondents only). In these CFA models, for all items that were shared between the reference and target sample (i.e., item parameters that were “in the bank” from the reference sample), we constrained item parameters to be identical to the item parameters estimated in the reference sample. For items that were not common between samples, we allowed item parameters to be freely estimated. We also freely estimated the mean and variance of the latent trait in the target sample, parameters that are identified as long as there is at least one mean or threshold and one measurement slope constrained to a banked parameter. As we moved on to additional target samples (e.g., India following England), we used item parameters estimated in the United States or England samples to serve as presumed known population values. As a final step, we estimated the mean and variance of the latent trait in the combined sample from a model with all item parameters fixed, and then obtained latent trait estimates from a model where all parameters were constrained based on prior models. The means and variances of the underlying trait are assumed to be equal to the estimated population values. By fixing the mean and variance of the latent trait in addition to all item parameters, we ensure that the generated factor scores are fixed for a given response pattern and not dependent upon the distributional properties of the analytic data file.

2.4. CFA models for the subdomain

We then ran CFA models separately for each of the samples to estimate executive function in each study. Methods factors were again included to capture residual covariation among items with shared content. Each model was internally scaled so that the latent trait had a mean of 0 and a standard deviation of 1 in each sample. All CFA models in this step and prior steps were estimated using a robust maximum likelihood estimator in Mplus version 8.

2.4. Linear equating of the subdomain to the subsuming domain

To transform internally scaled scores for the subdomain (e.g., executive functioning) within each study to the metric of the harmonized subsuming domain (e.g., general cognitive functioning), we used linear equating [9]. Linear equating is a method of linking two scales, which assumes that scores on one scale are a linear function of scores on the second scale. A transformation of person i’s score from the scale x (e.g., the subdomain score) to the scale y (e.g., the subsuming domain score) would therefore take the form:

$$scor{e}_y(x_i)={\mu }_y+\frac{{\sigma }_y}{{\sigma }_x}(x_i-{\mu }_x)$$

where score_y(x_i) is an individual’s subdomain (x) score re-expressed on the scale of the subsuming or related construct (y), σ_y and σ_x are the scale score means and standard deviations, μ_y, is the subsuming scale score mean, and μ_x is the subdomain mean. Estimated values are used in place of population parameters.

We conducted a linear equating procedure stratified by sample to translate scores from the scale of the internally scaled executive functioning score to the scale of the harmonized general cognitive functioning scores. By conducting stratified linear equating, we ensure that the mean difference between samples in LLRT-equated scores is equivalent to the mean difference between samples in the IRT-equated scores for the related latent construct. These equated executive functioning scores served as the final output of the LLRT method. Linear equating was conducted in R version 4.0.2 using the equate package [23]. To better enable comparisons, all cognitive scores have been rescaled such that the cognitive scores in the United States have a mean of 50 and standard deviation of 10 using the formula:

$$scor{e}_{itransformed}=50+\frac{10}{{\sigma }_{US}}\ast (scor{e}_i-{\mu }_{US})$$

Where μ_US and σ_US represent the mean and standard deviation of cognitive scores in the US sample. Example code is included in Appendix 2.

2.5. Comparisons of harmonization methods

For illustration, we conducted three sets of harmonizations. First, we linked executive functioning between individuals with low education and high education in the United States. For this comparison, we did not need to conduct an IRT harmonization of general cognitive functioning. Instead, we used scores from a single CFA model of general cognitive functioning in the United States. These scores are already on the same metric, as the two subpopulations are part of the same sample. Second, we linked executive functioning between the United States and England. We chose this comparison because the overlap in executive functioning items between these studies (7 items in common) gave us a reference standard (IRT-equated executive functioning) to compare with LLRT-equated executive functioning. Third, we linked executive functioning between the United States and India.

We evaluated the validity of the new harmonization method by comparing harmonized executive functioning scores derived using our new methodology with harmonized executive functioning scores based on standard methods. In the first comparison between individuals with high and low education in the United States, the comparison scores were estimated based on a single CFA model, including the entire sample. In the second, between the United States and England, and the third comparison, between the United States and India, the comparison scores were estimated based on an IRT item banking approach for the harmonization of executive function between samples. This approach is analogous to the approach described in Section 2.3 for the harmonization of general cognitive functioning. While we have confidence in the IRT-harmonized executive functioning scores linking the United States and England, IRT-harmonized executive functioning scores linking the United States and India may be unstable due to the presence of only 1 linking item [10]. For each of these comparisons, we assessed the Pearson’s correlation coefficient and compared the sample mean differences between the two methods of harmonization. Pearson’s correlation coefficients close to 1 and equivalent sample mean differences between the two methods of harmonization would indicate the two harmonization methods perform similarly.

3. Results

All data were collected between 2016 and 2019. The average age in the United States and England samples was about 75 years (range 64 to 102 years). The mean age was 68 years in India due to the inclusion of older adults as young as 60 years. Participants in the United States and England were mostly female (60% and 55%, respectively), but only 36% of Indian participants were female due to our restriction in that sample to literate respondents (Table 1).

Table 1.

Demographic characteristics and cognitive scores for individuals in the United States, England, and Indian HCAP samples

	United States			England	India
	Full Sample	High Education	Low Education
Years of Data Collection	2016-2017	2016-2017	2016-2017	2018	2017-2019
Number of Individuals	3347	1578	1769	1273	1777
Age (Mean [Range])	75.8 (64-102)	74.9 (64-101)	76.5 (64-102)	75.3 (65-89)	68.6 (60-100)
Percent Female	60.4%	57.2%	63.1%	55.0%	35.9%
Harmonized General Cognition (Mean [SD])	50.0 (10.0)	53.5 (8.7)	46.4 (9.0)	50.5 (10.1)	43.8 (8.0)
Unharmonized Executive Functioning (Mean [SD])	50.0 (10.0)	50.6 (9.6)	50.6 (9.6)	49.9 (9.9)	50.4 (8.8)

Harmonized scores for general cognitive functioning are comparable in the United States and England but about 0.7 standard deviations lower in India. There was also a corresponding difference of about 0.7 standard deviations between higher vs lower educated participants in the United States. Unharmonized factor scores for executive functioning were scaled to have a mean of 50 and standard deviation of 10 in each sample (Table 1). While there are plenty of overlapping items that can be used as linking items across the three studies when considering all cognitive domains, only one test overlaps within the domain of executive functioning between the United States and Indian surveys (Table 2). This scenario motivates our study.

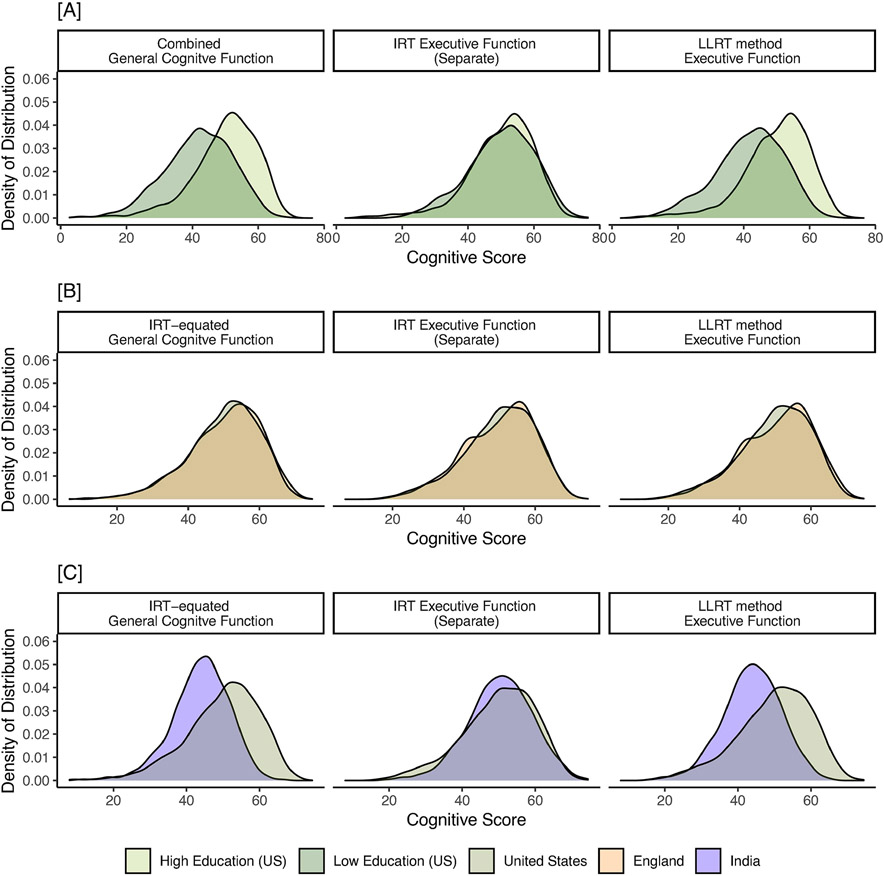
Figure 2 shows density plots of the various scores. The first column shows IRT-equated general cognitive factor scores, separated by low vs high education in the United States (Panel A), England vs United States (Panel B), and India vs United States (Panel C). The second column shows, for those same comparisons, distributions of internally-scaled factors for executive functioning, which are expected to mostly overlap. The third column shows LLRT-equated executive functioning scores, which represent transformations of scores in the second column based on the distribution of scores from the first column. For England, as expected, due to the small difference in distributions of general cognition (Panel B, column 1), LLRT-equating had minimal effect on the comparison of executive functioning scores (Panel B, column 3). The recovery of differences between samples using the LLRT method for the United States high vs low education contrast and for the United States vs India contrast is more apparent, given the larger differences in general cognitive performance between those groups.

Figure 2.

Distributions of equated cognitive functioning scores, separate executive functioning scores, and LLRT-equated executive functioning scores for [A] individuals with high and low education in the United States, [B] individuals from the United States and England samples, and [C] individuals from the United States and Indian samples.

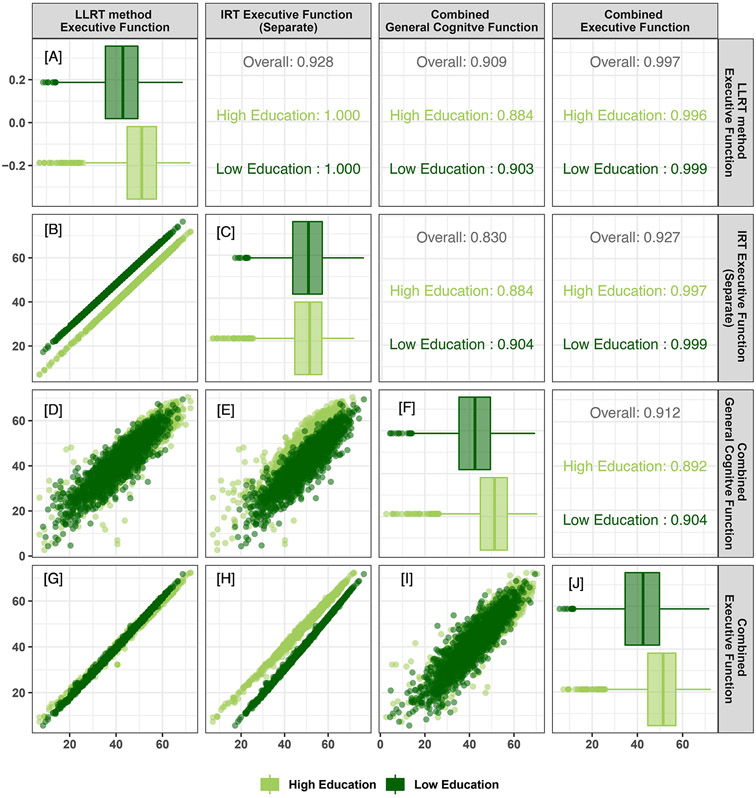
For the comparison between the high and low education groups within the United States sample (Figure 3), there was no need to harmonize the subsuming domain (general cognitive performance) or the subdomain (executive functioning), but to illustrate the LLRT method we separately estimated factor scores for executive functioning by education group. There was an 8.15-point difference in means between education groups in combined general cognitive functioning (Panel F) which was similar to the mean difference in the combined executive functioning score (Panel J; 8.41 points), but by design, there was no difference in means between education groups in separately-estimated executive functioning (Panel C). Upon application of the LLRT approach, LLRT-equated executive functioning means replicated the 8.15-point difference (Panel A), observed in the combined general cognitive functioning measure (Panel F). The LLRT scores also retained the rank order of scores estimated via the separate, internally-scaled executive functioning models (stratified r=1.000, Panel B). The high correlation (r=0.997) between the common executive functioning score and LLRT-equated executive functioning (Panel G) demonstrates the LLRT method recovered the sought-after distribution of the combined executive functioning scores, despite the latter not being used directly in the construction of the former.

Figure 3.

Correlation matrix for the correspondence between the distributions of combined executive functioning scores, combined general cognitive functioning scores, independent scores of executive functioning, and LLRT-equated scores of executive functioning for individuals with high and low educational attainment in the United States HCAP sample. The plots in the lower diagonal compare the distributions via scatterplots, while the upper diagonal displays corresponding Pearson correlation coefficients, both overall and stratified by subgroup. The plots on the diagonal show subgroup differences for each score examined.

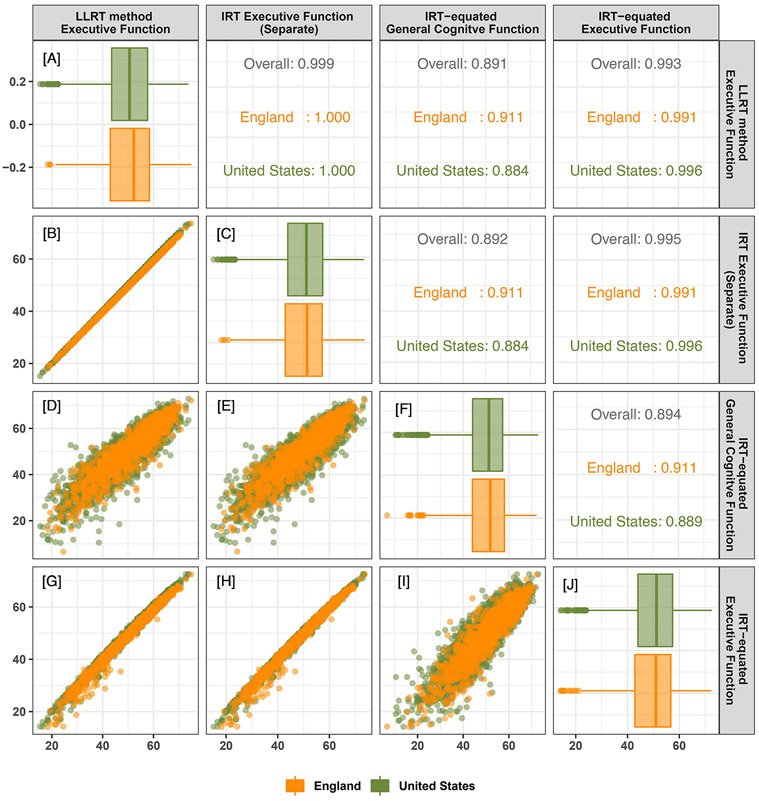
Figure 4 characterizes the contrast between the United States and England through the same assortment of scatterplots, boxplots and correlations used in Figure 3. The layout of Figure 4 is the same as in Figure 3, with the exception that for executive functioning, instead of a common score, we used the same item-banking approach to IRT harmonization described in Section 2.3 to equate this subdomain across studies. The United States and England had similar scores for general cognitive performance (Panel F) and IRT-equated executive functioning (Panel J). As with education groups within the US, the correlation of IRT-equated executive functioning and LLRT-equated executive functioning was high (r=0.989, Panel G), despite a lower correlation (r=0.903) between IRT-equated executive functioning and IRT-equated general cognitive functioning (Panel I).

Figure 4.

Correlation matrix for the correspondence between the distributions of IRT-equated executive functioning scores, IRT-equated general cognitive functioning scores, independent scores of executive functioning, and LLRT-equated scores of executive functioning for individuals in the United States and England HCAP samples. The plots in the lower diagonal compare the distributions via scatterplots, while the upper diagonal displays corresponding Pearson correlation coefficients, both overall and stratified by sample. The plots on the diagonal show sample differences for each score examined.

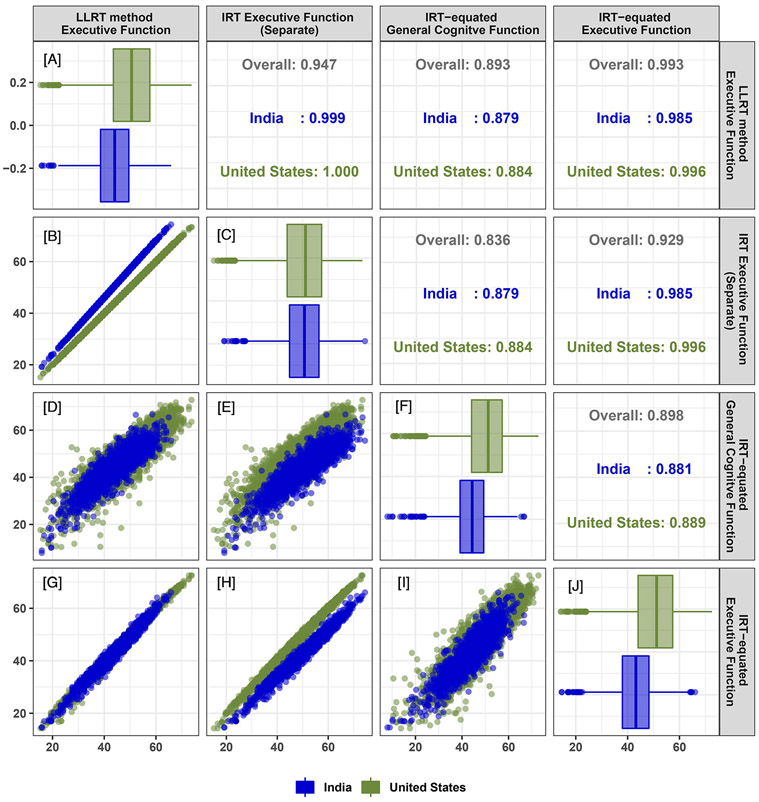
In the United States and India comparison (Figure 5), we consider the IRT-equated executive functioning score to be untrustworthy due to the availability of only 1 linking item between the United States and Indian surveys (Table 2). The LLRT-equated executive functioning score shows a 6.15-point difference between the United States and India (Panel A), which is extremely similar to the mean difference in IRT-equated general cognitive performance (6.16 points; Panel F). However, the LLRT scores preserve the rank order of scores as estimated in the separate, internally-scaled executive functioning models (stratified r=0.999,1.000, Panel B). The general cognitive performance score is similarly highly correlated with the LLRT-equated executive functioning score (r=0.905, Panel D).

Figure 5.

Correlation matrix for the correspondence between the distributions of IRT-equated executive functioning scores, IRT-equated general cognitive functioning scores, independent scores of executive functioning, and LLRT-equated scores of executive functioning for individuals in the United States and Indian HCAP samples. The plots in the lower diagonal compare the distributions via scatterplots, while the upper diagonal displays corresponding Pearson correlation coefficients, both overall and stratified by sample. The plots on the diagonal show sample differences for each score examined.

4. Discussion

We have demonstrated one approach for linking cognitive performance data across two groups when the fielded assessments contain few or no items that can be reasonably considered linking items (i.e., can be assumed to be equivalent across countries): Linear Linking for Related Traits (LLRT). We show in 2 examples (linking executive functioning between high and low education groups in the United States HCAP and the United States and England samples) that LLRT scores had high correspondence with gold-standard measures of executive functioning. In our third example linking executive function between the United States and India, we also found a high correlation between LLRT scores and IRT-equated executive functioning scores, even with only 1 linking item shared between the two surveys. Despite concerns about the reliability of IRT-equating methods in the presence of very small numbers of linking items, it is possible that the high quality and information content in the 1 available linking item (Raven’s progressive matrices) led to a more stable and reliable link in this example [24]. However, the LLRT method can also be used when there are no available linking items, or the few available linking items are of poor quality.

The LLRT method relies on linear equating, a well-known tool for equating incommensurate test forms, and a rather strict set of assumptions [25]. In addition to the usual assumptions of item response theory (unidimensionality, local independence, suitability of the item response function), we assume that the relative distribution of the subdomain matches that of a subsuming trait (e.g., general cognitive performance). In effect, the mean differences between groups for the subsuming trait serve as a spike prior on the differences for the subsuming domain (the related latent trait). Any external variables that may influence the distribution of the subdomain are also assumed to influence the distribution of the subsuming domain in the same manner. We acknowledge that this is a restrictive assumption, but also recognize that this assumption could be relaxed with further refinements of the approach, such as through the use of a hierarchical factor model and a less informative prior on the estimated latent trait location and variance parameters.

A further assumption is necessary to use the linked measures as comparable measures for group comparison activities: that the linked domains are vertical reflections of the reified domains of interest. At the extreme, the method we describe could be inappropriately applied to highly divergent domains (e.g. psychomotor speed and language) in different samples. Results from such an exercise would be meaningless. When applying the LLRT method without the presence of linking items, there will be no statistical evidence that the traits being linked are fundamentally incommensurate, and expert knowledge in the assessment of cognitive functioning and familiarity with the assessment items being used in the two group settings is required to adjudge the quality of the linked measures. It is possible that some applications of this method could allow for equality constraints in the measurement slopes (or factor loadings) for items that were of similar construction across countries. For example, both countries might have a category fluency task, one asking participants to name supermarket items, another asking participants to name animals. Constraints in the measurement slopes could arguably be allowed because the two items could be assumed to have the same correlation with the latent trait, although assuming the mean structure of the two items is identical across countries is untenable. However, without linking components in the mean structure (thresholds, intercepts), some method such as LLRT is necessary to place the estimates on a comparable metric.

The LLRT approach relies on well-known statistical tools for harmonization, linear equating and confirmatory factor analysis. As confirmatory factor analysis of ordinal items on a polychoric correlation matrix is equivalent to a graded response IRT model, we have used the more well-known term IRT harmonization methods to refer to these methods throughout this paper. The combination of both linear equating and IRT harmonization methods used in the LLRT method provides opportunities to increase the comparability of otherwise incomparable measures. A major assumption of our approach is that the relative distribution of the cognitive subdomain matches that of a subsuming trait (e.g., general cognitive performance). While a big assumption, it is reasonable. Empirically, general cognitive measures are constructed using items from various subdomains. Theoretically, general cognition is a gross summary of neuropsychological performance across several domains and should be correlated with a subdomain. Previous factor analytic studies have demonstrated high correlations between different subdomain factors as well as between general cognition and subdomain factors [26-28].

Cognition is a socially defined and shaped behavior, intrinsic to the local environment and context of the individual. Cognitive performance among older adults encompasses a lifetime of developmental and experiential factors [29,30]. It is unlikely that cognitive measures developed and/or refined in English speaking mass consumption economies will be able to return unbiased estimates of cognitive abilities in other contexts. Against this background, there is a desire among researchers and policy makers to understand differences in the distribution of cognitive performance across groups and countries as a foothold in understanding cross-national differences in the burden of dementing illnesses of later life. Despite the aforementioned issues with cross-national data on cognitive performance, in large epidemiologic field studies, it is customary to base dementia prevalence estimates on performance data (cognition, function) as detailed clinical evaluations and biomarker studies are infeasible. Until such time as a suitably efficient biomarker becomes available, researchers will use cognitive performance data as a key element in predicting levels of dementia in a population sample. Our method may help facilitate such cross-national comparisons.

Highlights.

• Cross-national harmonization of cognition is necessary for valid comparisons

• We introduce a new harmonization method when traditional approaches are infeasible

• Information from a subsuming cognitive domain informs linking of subdomains

• Strict but plausible assumptions are required for this novel method

Abrreviations:

IRT

Item response theory

LLRT

Linear linking for related traits

HCAP

Harmonized cognitive assessment protocol

CFA

confirmatory factor analysis