QQ-NET – using deep learning to solve quantitative susceptibility mapping and quantitative blood oxygen level dependent magnitude (QSM+qBOLD or QQ) based oxygen extraction fraction (OEF) mapping

Abstract

Purpose:

To improve accuracy and speed of quantitative susceptibility mapping plus quantitative blood oxygen level-dependent magnitude (QSM+qBOLD or QQ) -based oxygen extraction fraction (OEF) mapping using a deep neural network (QQ-NET).

Methods:

The 3D multi-echo gradient echo images were acquired in 34 ischemic stroke patients and 4 healthy subjects. Arterial spin labeling and diffusion weighted imaging (DWI) were also performed in the patients. NET was developed to solve the QQ model inversion problem based on Unet. QQ-based OEF maps were reconstructed with previously introduced temporal clustering, tissue composition, and total variation (CCTV) and NET. The results were compared in simulation, ischemic stroke patients, and healthy subjects using a two-sample Kolmogorov-Smirnov test.

Results:

In the simulation, QQ-NET provided more accurate and precise OEF maps than QQ-CCTV with 150 times faster reconstruction speed. In the subacute stroke patients, OEF from QQ-NET had greater contrast-to-noise ratio (CNR) between DWI-defined lesions and their unaffected contralateral normal tissue than with QQ-CCTV: 1.9 ± 1.3 vs 6.6 ± 10.7 (p = 0.03). In healthy subjects, both QQ-CCTV and QQ-NET provided uniform OEF maps.

Conclusion:

QQ-NET improves the accuracy of QQ-based OEF with faster reconstruction.

1 |. INTRODUCTION

Quantitative mapping of oxygen extraction fraction (OEF) and cerebral metabolic rate of oxygen (CMRO₂) is critical to evaluate brain tissue viability and function in stroke.^1–3 In MRI, quantitative models to investigate the effects of blood deoxyhemoglobin on the signal have fallen into two categories: (1) magnitude signal modeling methods such as T₂ based methods,^4–7 calibrated fMRI,^8–11 and quantitative blood oxygen level dependent magnitude (qBOLD);^12–14 and (2) phase signal modeling methods for whole brain OEF values^15–18 and voxel-wise quantitative susceptibility mapping (QSM)-based OEF methods.^19–21

Recently, an integrated model of QSM and qBOLD (QSM+qBOLD or QQ) has been introduced to consider the OEF effect on both magnitude and phase of a widely available multi-echo gradient echo (mGRE) data.²² QQ makes OEF mapping possible without clinically impractical vascular challenges. However, QQ-based OEF estimation remains challenging, because it is difficult to accurately disentangle the effect of venous oxygenation (Y) and venous blood volume (v) as its inversion is highly sensitive to noise.^13,23

The temporal clustering, tissue composition, and total variation (CCTV) algorithm has been proposed to over-come the noise sensitivity of QQ-based OEF by improving the effective signal-to-noise ratio (SNR).^24–29 Voxels with similar mGRE signal evolutions are grouped into the same cluster and assumed to have the same model parameter values. Averaging over many voxels in a cluster can substantially increase SNR in a cluster-wise inverse solution. Noise propagation on OEF is further suppressed by integrating tissue-type information into clustering and applying total variation.²⁵ However, inversion using gradient-based iterative solvers still depends on optimization details, e.g., initial guess and parameter scaling, and is time-consuming.

This study introduces a deep neural network (QQ-NET) to alleviate the dependency on optimization details and to improve the reconstruction speed in solving the QQ model. Deep neural networks have been applied as alternatives to the iterative method for solving inversion^30–37 as they can approximate any continuous function with a sufficient number of free parameters.³⁸ An established deep convolutional neural network architecture, Unet,^39,40 was used for the QQ model inversion (QQ-NET) and com- pared with QQ-CCTV in simulation, ischemic stroke patients, and healthy subjects.

2 |. METHODS

2.1 |. Data acquisition

This study was approved by the local Institutional Review Board. MRI was performed in 34 patients with ischemic stroke in a unilateral cerebral artery territory (6 hours to 42 days between stroke onset and MRI) on a clinical 3T scanner (GE MR Discovery 750) using a 32-channel brain receiver coil. The imaging protocol consisted of 3D ASL (24 cm field of view [FOV], 1.9 × 1.9 × 2.0 mm³ voxel size, 1500 ms labeling period, 1525 ms post-label delay, 976.6 Hz/pixel bandwidth, 68 axial slices, echo time [TE] = 14.6 ms, repetition time [TR] = 4787 ms, and three signal averages), 3D mGRE (0.47 × 0.47 × 2.0 mm³ voxel size, identical FOV to the 3D fast spin echo [FSE] arterial spin labeling [ASL] sequence, eight equally spaced echoes: TE₁/ΔTE/TE₈ = 4.5/5/39.5 ms, TR = 42.8 ms, band-width = 244.1 Hz/pixel, flip angle 20°, and scan time = 5 minutes 15 seconds), DWI (24 cm FOV, 0.94 × 0.94 × 3.2 mm³ voxel size, 1953.1 Hz/pixel bandwidth, 0, 1000 s/ mm² b-values, TE = 71 ms, TR = 3000 ms, and four signal averages), and a T1 weighted fluid attenuated inversion recovery sequence (24 cm FOV, 0.5 × 0.5 × 5 mm³ voxel size, TE = 23.4 ms, TR = 1750 ms).

Four healthy subjects (age 31 ± 6 y) were also scanned for QQ-NET performance testing on a 3T GE scanner using 3D mGRE with the same imaging parameters as the stroke patients (voxel size, TEs, bandwidth, flip angle, and scan time), but different resolution (0.86 × 0.86 × 1.2 mm³ voxel size, bandwidth 651.0 Hz/pixel, scan time = 5 min- utes 24 seconds) with all other parameters the same as in the stroke patients. The second scan was acquired after the first scan without delay.

2.2 |. Data processing: QSM and CBF

QSM reconstruction was performed by estimating the total field via a non-linear fit of the mGRE,⁴¹ obtaining the local field by the Projection onto Dipole Fields (PDF) method,⁴² and computing susceptibility with the Morphology Enabled Dipole Inversion with automatic uniform cerebrospinal fluid zero reference (MEDI+0) algorithm.^43–46 Cerebral blood flow (CBF) maps (mL/100g/min) were generated from the ASL data using FuncTool (GE Healthcare, Waukesha, WI, USA). All images were co-registered and interpolated to the resolution of the QSM maps using the FSL FLIRT algorithm.^47,48

2.3 |. QQ model

The QQ model combines QSM-based OEF method and qBOLD to estimate OEF, 1 − Y ∕Y_a with venous oxygenation (Y) and arterial oxygenation (Y_a = 0.98).²² The QSM-based model utilizes the mGRE phase and separates the estimated voxel-wise susceptibility $(\chi )$ into the contribution of deoxy-hemoglobin in venous blood, i.e., OEF effect, and non-blood neural tissue susceptibility$({\chi }_n)$.

$$\begin{gathered} \chi \left(Y,v,{\chi }_n\right)=\left[\frac{{\chi }_{ba}}{\alpha }+{\psi }_{Hb}\cdot \Delta {\chi }_{Hb}\cdot \left(-Y+\frac{1-(1-\alpha )\cdot Y_a}{\alpha }\right)\right] \\ \cdot v+\left(1-\frac{v}{\alpha }\right)\cdot {\chi }_n \end{gathered}$$ (1)

where ${\chi }_{ba}=-108.3$ ppb the fully oxygenated blood susceptibility assuming tissue hematocrit Hct = 0.357,²¹ α = 0.77 the ratio between the venous blood volume (v) and total blood volume,⁴⁹ ${\psi }_{Hb}=0.0909$ the hemoglobin volume fraction with setting $\text{Hct}=0.357{,}^{20,50-52}\Delta {\chi }_{Hb}=12522\text{ppb}$ the susceptibility difference between deoxy-and oxyhemoglobin.^19,53

The qBOLD models the OEF effect on the mGRE magnitude at TE, t²²:

$$S_{qBOLD}\left(S_0,R_2,Y,v,{\chi }_n,t\right)=S_0\cdot e^{-R_2\cdot t}\cdot F_{BOLD}\left(Y,v,{\chi }_n,t\right)\cdot G(t)$$ (2)

where S₀ is signal intensity at t = 0, R₂ is the transverse relaxation rate,$F_{BOLD}\left(Y,v,{\chi }_n,t\right)=\exp \left[-v\cdot f_s(\delta \omega \cdot t)\right]$ ¹³ where f_s is the signal decay by the presence of the blood vessel network $f_S(\delta \omega \cdot t)\approx \frac{3}{10}{(\delta \omega \cdot t)}^2$ for $t\ll 1/\delta \omega$ and $f_S(\delta \omega \cdot t)\approx \delta \omega \cdot t$ for t $\gg 1/\delta \omega$¹⁴ and δw is the characteristic frequency due to the susceptibility difference between deoxygenated blood and the surrounding tissue^{22$\delta \omega \left(Y,{\chi }_n\right)=\frac{1}{3}\cdot \gamma \cdot B_0\cdot \left[{\psi }_{Hb}\cdot \Delta {\chi }_{Hb}\cdot (1-Y)+{\chi }_{ba}-{\chi }_n\right]$} with γ = 267.51 rad s⁻¹ T⁻¹ the gyromagnetic ratio, and B₀ the main magnetic field strength. G(t) is the macroscopic field inhomogeneity contribution to mGRE signal decay estimated by the voxel spread function.²²

2.4 |. Deep neural network for QQ inversion (QQ-NET)

The fully convolutional neural network (QQ-NET) processing four-dimentional inputs (3D volumes with multiple channels) was based on an established architecture, U-net,^39,40 with three modifications: (1) Using zero-padding so that the output from each convolution layer has the same size as the input; (2) Setting the number of input channels and output channels for the network to nine (eight-echo mGRE magnitude signals and one QSM) and five (model parameters$({\text{S}}_0,R_2,Y,v,{\chi }_n)$), respectively; (3) Applying tanh function to the network output for setting the minimum (min) and maximum (max) values for the model parameters: [min, max] = [0.8, 2.5] for S₀, [2, 190] Hz for R₂, [0, 0.98] for Y, [0, 8]% for v, and [−1, 1.6] ppm for${\chi }_n$. Values were based on physiological expectations for Y (the Y range corresponds to 0~100% OEF) and v (PET and MRI literature v range 0.5~5.5%⁵⁴), and CCTV results for the other parameters. The network architecture of QQ-NET consisted of an encoding and decoding path (Supporting Information Figure S1, which is available on-line). The encoding path included four repeated groups. Each group consisted of two sets of convolution layers with a 3 × 3 × 3 kernel and ReLU activation and was connected by a max pooling layer (2 × 2 × 2). The decoding path was constructed similarly to the encoding path with four repeated groups. Each group additionally contained a feature map concatenation from the corresponding encoding path and was connected by a deconvolution layer (2 × 2 × 2). The last layer applied a convolution layer with a 1 × 1 × 1 kernel to obtain five channels (five model parameters) and an element-wise scaled tanh activation to set the min and max for each parameter.

For training data generation, (1) QQ-CCTV was performed in real 34 stroke patient cases to obtain model parameters$({\text{S}}_0,R_2,Y,v,{\chi }_n)$. The parameter average (μ), SD (σ), min, and max were S₀(1.09, 0.04, 1.04, 2.38), R2 (20.1, 7.2, 7.3, 189.3 Hz), Y (0.68, 0.10, 0.31, 0.98), v(1.8, 1.1, 0.3, 7.2 %), and${\chi }_n(-10.0,37.1,-910.0,160.7\text{ppb})$. S₀ was set such that the first echo magnitude signal was unity for input data normalization as used in a previous artificial neural network for QQ inversion.⁵⁵ (2) The resultant model parameter maps including OEF from QQ-CCTV were set as ground truth, and the QSM values and mGRE signals were simulated for each brain voxel using Equations 1 and 2, respectively. (3) Gaussian noise was added to the QSM and the mGRE signals to obtain SNR 100 at the first echo with a different noise instance for each training. In this way, the pairs of ground truth (QQ-CCTV results) and simulated measurements (QSM and mGRE signals) were acquired. For training, only the simulated datasets were used, not the real measurements. Among the 34 simulated datasets, 26/2/6 were used for training/validation/test, respectively.

For QQ-NET training, parameters were normalized to improve convergence behavior during network update with using z-score transformation. For R2, ${\chi }_n$, and S₀, $z_{R_2}=\frac{\nu -{\mu }_{R_2}}{{\sigma }_{R_2}},z_{{\chi }_n}=\frac{\nu -{\mu }_{X_n}}{{\sigma }_{{\chi }_n}}$, and$z_{S_0}=\frac{\nu -{\mu }_{S_0}}{{\sigma }_{S_0}}$. For Y$z_Y=\frac{Y-Y_{Ss}}{{\sigma }_Y}$where Y_ss is the venous oxygenation estimated from the susceptibility average of the straight sinus in each subject²⁴ to consider different global OEF averages in different subjects. For $z_v=\frac{v-{\mu }_v}{{\sigma }_v/2}$ to consider two peaks in vdistribution at 1.2% (white matter) and 3.5% (gray matter). Parameter normalization is a common practice in numerical optimization as it provides an improved convergence behavior with rescaling parameter space.^21,56–58 Parameter normalization using z-scores in this study is expected to result in that the different parameters in different scales and units, e.g., R2 in Hz and v in %, have similar scales (zero mean and unit SD), and their changes are weighed similarly in the loss function, analogous to z-score transformation for multiple parameters used in a previous QQ-NET for water/fat separation.⁵⁹ Due to memory constraints on the Graphic Processing Units (GPU), 4D patch (9 × 200 × 200 × 48) was used as the input, which includes an approximately entire brain. Batch size was chosen as 1 with patch center randomly located within a selected brain and repeated for all the training brains (1 epoch). Validation was then performed in the same way as training. Before each epoch, the order of the training brains was randomly shuffled.

The loss function was the weighted sum of three losses: (1) L1 difference between the normalized truth and the output of QQ-NET, $E_{L1}={\Vert Z_t-Z_o\Vert }_1$, where $Z_t=[Z_{S_0,t}{Z}_{R_2,t},Z_{Y,t},Z_{V,t},Z_{{\chi }_n,t}]$ and $Z_o=\left[Z_{S_0,o}{z}_{R_{2,o}},Z_{Y,o},z_{v,o},Z_{{\chi }_n,o}\right]$ where the subscript “t” and “o” indicate truth and output of network; (2) model loss to consider biophysics model consistency$E_{\text{Model}}=\Vert S_{qBOLD}\left(S_{0,t},R_{2,t},Y_t,v_t,{\chi }_{n,t}\right)-S_{qBOLD}(S_{0,o},R_{2,t\text{to}},Y_o,v_o,{\chi }_{n,o})\Vert {}_1+\Vert {\chi }_{QSM}\left(Y_t,v_t,{\chi }_{n,t}\right)-{\chi }_{QSM}\left(Y_o,v_o,{\chi }_{n,o}\right){\Vert }_1$; and (3) L1 difference of Y spatial gradient to prevent blurry OEF by preserving edge, $E_{Grad}={\Vert \nabla z_{Y,T}-\nabla z_{Y,o}\Vert }_1$The total loss (E) was set as$E=E_{L1}+w_1\cdot E_{Model}+w_2\cdot E_{Grand}$. where the weights were empirically determined: w₁ = 0.1 and w₂ = 1.

QQ-NET was implemented using Pytorch 1.4.0⁶⁰ and NVIDIA RTX 2080Ti GPU. Minimization was performed by ADAM⁶¹ with a learning rate of 10⁻⁴. Training was stopped at 420 epochs (~ 100 hours) as the validation loss became stable.

The trained QQ-NET was tested with three different datasets (Test Data 1, 2, and 3). Test Data 1: two additionally simulated stroke brains constructed in the same way as the training datasets (SNR 100): Case 1. Without OEF abnormality and Case 2. With low lesion OEF (Figure 1). The average of the CCTV and NET results from real stroke patients (18 hours and 7 days post onset for Cases 1 and 2) was used as the ground truth to minimize algorithm-dependent bias. For accuracy and precision measurements, the reconstruction was repeated five times with different instances of Gaussian noise. Additionally, to investigate the consequence of the noise level discrepancy between the training (SNR 100) and test datasets, Case 2 was repeated with SNR 50 and 20 (Supporting Information Figure S2). Test Data 2: 30 ischemic stroke patients, a subset of the 34 patients without hemorrhage transformation and reperfusion, were classified into two groups based on the time interval between stroke onset and MRI scan⁶²: acute (6–24 hours, N = 5) and subacute (1–14 days, N = 25) phase (Figures 2–4). To ensure that there was no overlap between training and test subjects, cross-validation was performed in which six real patient brains were chosen as test data, leaving the other 28 patients’ simulated dataset as training (N = 26) and validation (N = 2) data, resulting in five trained networks (6 test patients × 5 trials = 30 test patients). The network trained with the first 28 patients’ simulated dataset was applied to Test Data 1 and 3. Test Data 3: four healthy subjects acquired with the same imaging parameters including TE as used in training (Figure 5) to check if the network trained with simulated stroke brains can provide uniform OEF maps in healthy brains without severe false positives, e.g., low OEF values as in stroke lesions. Additionally, to check the robustness of the trained network against differences in resolution, a dataset with the same healthy subjects but with different resolution (0.86 × 0.86 × 1.2 mm³ voxel size) was also tested (Supporting Information Figure S3). In network testing, to make sure that the whole brain was fully covered, we used patch sliding with 30% overlap, generated multiple overlapped patches, and combined them into one whole brain after network inference.

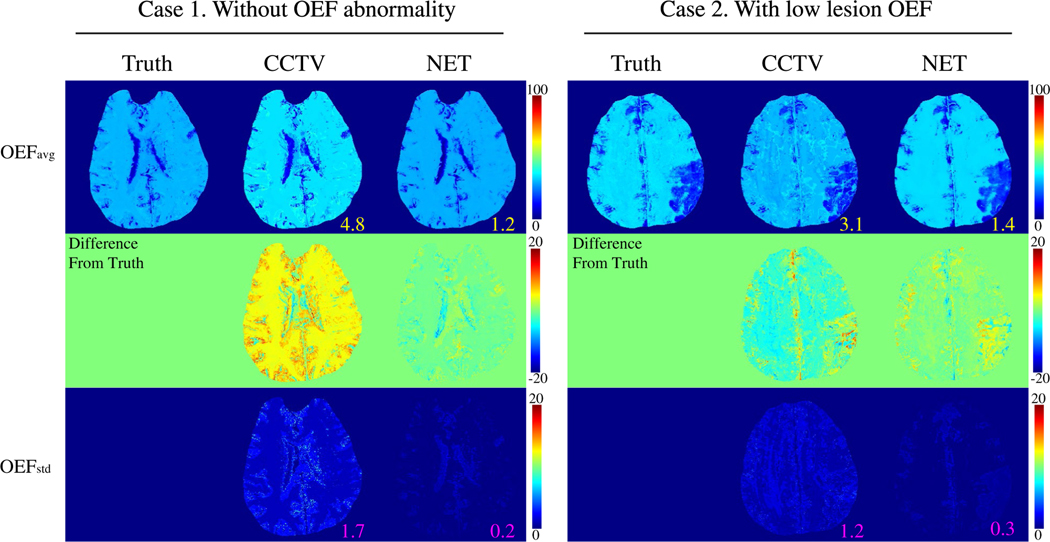
FIGURE 1.

Comparison between the OEFs obtained by CCTV and NET in two simulated brains (Test Data 1): Case 1. Without OEF abnormality and Case 2. With low lesion OEF. The numbers indicates MAE (yellow) and MSD (pink). NET provides greater accuracy (MAE: 4.8 vs. 1.2 % in Case 1 and 3.1 vs. 1.4 % in Case 2) and precision (MSD: 1.7 vs. 0.2 % in Case 1 and 1.2 vs. 0.3 % in Case 2). OEF_avg and OEF_std indicate the average and SD OEF maps, respectively, among five trials. OEF_avg and OEF_std are shown in the unit of [%]

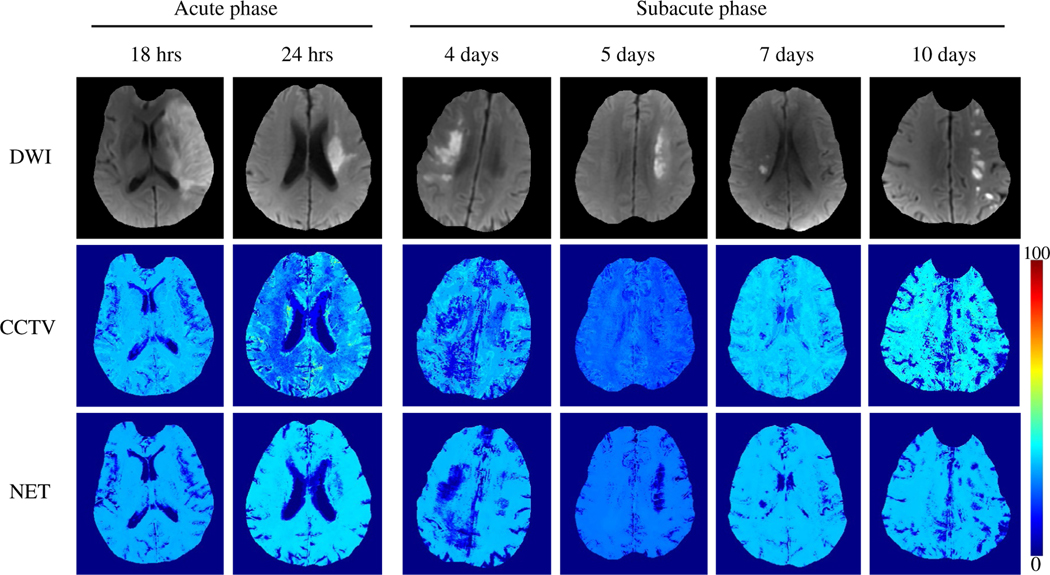
FIGURE 2.

Comparison between the OEFs obtained by QQ-CCTV and QQ-NET in six real ischemic stroke patients (Test Data 2). OEF maps from QQ-NET appear less noisy and have low OEF areas which agree better with DWI-lesions in the subacute phase

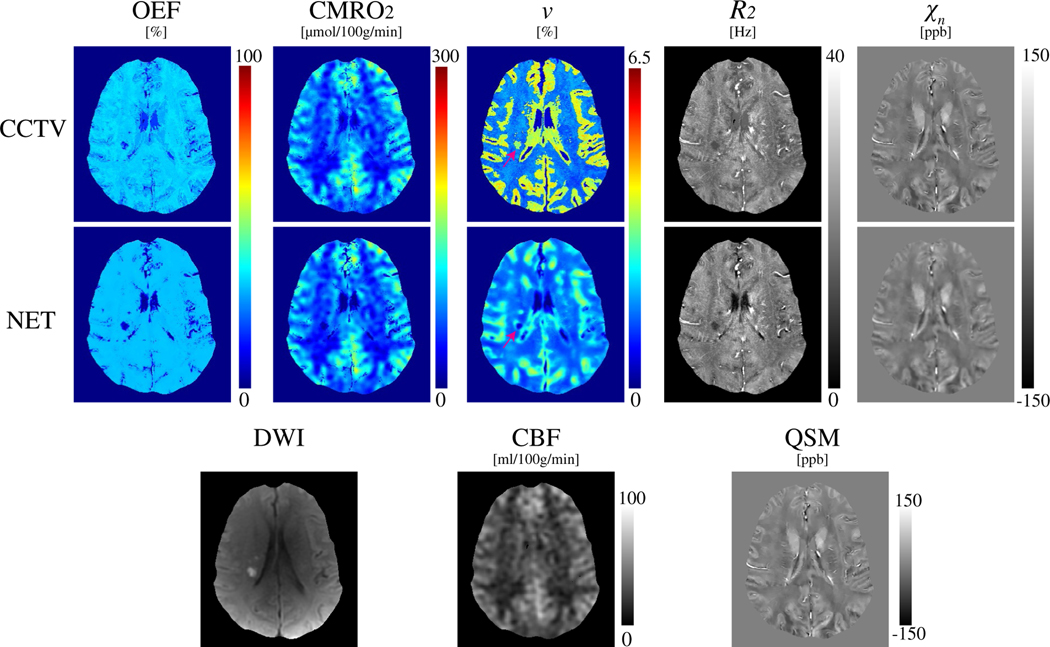
FIGURE 4.

Comparison of OEF, CMRO₂, v, R₂, and x_n maps between CCTV and NET in a stroke patient imaged 7 days post stroke onset (Test Data 2). NET provides less noisy OEF and low v values in DWI-defined lesions

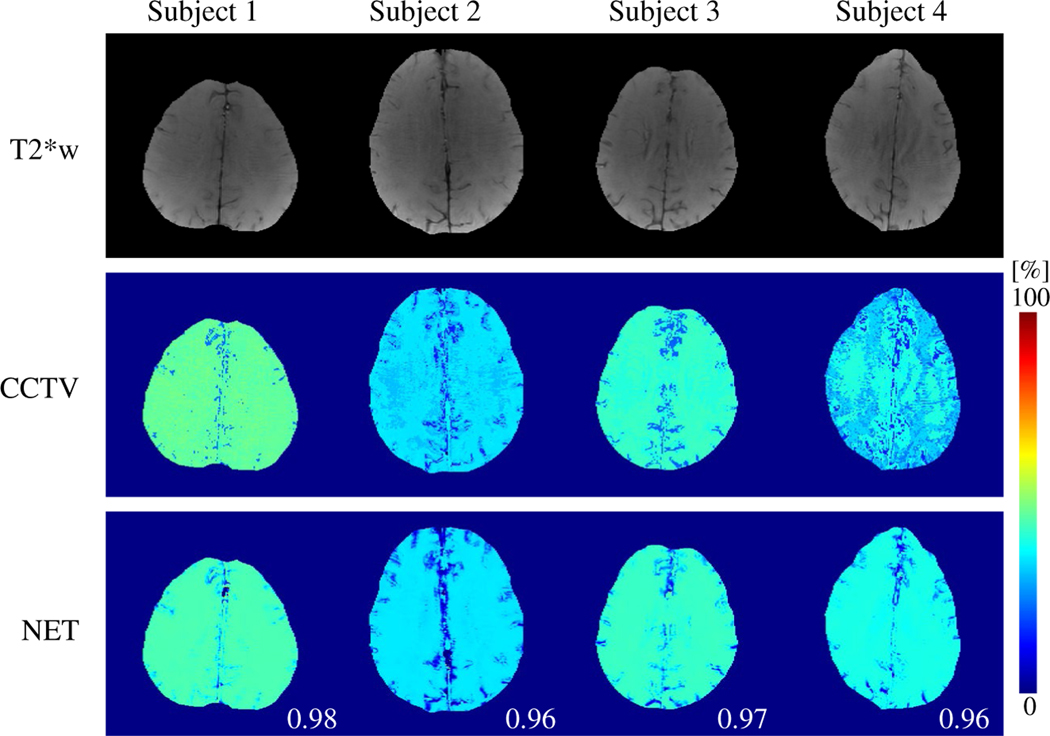
FIGURE 5.

Comparison between the OEFs obtained by QQ-CCTV and QQ-NET in four healthy subjects (Test Data 3). Numbers in white indicate SSIM. QQ-NET provides less noisy but similar OEF maps to QQ-CCTV with high SSIM values (≥ 0.96). T2*w indicates the echo-combined mGRE magnitude image

For comparison, QQ-CCTV was also performed on the test datasets with the same reconstruction as in Refs. [25,29] using Intel Xeon Gold 6130 CPU. First, temporal clustering was performed on voxel-wise$S_{qBOLD}/G$. Second, each cluster was further separated into gray matter/white matter/cerebrospinal fluid sub-clusters using segmentation obtained by FSL FAST algorithm⁶³ on T1-weighted images for stroke patients and echo-combined T2*-weighted images for healthy subjects. Last, cluster-based and voxel-wise optimization were performed sequentially with total variation regularization$(\Vert \nabla Y{\Vert }_1)$.⁶⁴

2.5 |. Statistical analysis

In the simulation (Test Data 1), accuracy and precision were calculated by mean absolute error (MAE) $(\text{MAE}\equiv \frac{1}{{\text{N}}_{\text{v}}}{\sum }_{i=1}^{N_v}\left|OE{F}_{truth}-OE{F}_{avg}\right|)$ and mean SD $(MSD\equiv \frac{1}{{\text{N}}_{\text{v}}}{\sum }_{i=1}^{N_v}OE{F}_{std})$ where$OE{F}_{avg}\equiv \frac{1}{{\text{N}}_{\text{t}}}{\sum }_{j=1}^{N_t}OE{F}_{i,j}$, $OE{F}_{std}\equiv \sqrt{\frac{1}{N_t}{\sum }_{j=1}^{N_t}{\left(OE{F}_{i,j}-\frac{1}{N}{\sum }_{j=1}^{N_t}OE{F}_{i,j}\right)}^2}$, i: the voxel index, j: the trial index, N_v: the number of voxels N_t: the number of trials.

In the stroke patients (Test Data 2), lesion ROIs were drawn based on DWI by an experienced neuroradiologist (S.J., 7 y of experience) and corresponding contralateral normal tissue masks were constructed by reflecting the lesion region of interest (ROI) to the other hemisphere and subsequently trimming by the same neuroradiologist. The detectability of lesion OEF abnormality was calculated by the contrast to noise ratio between the lesion and its contralateral normal tissue $(CNR\equiv \frac{\left|\overline{OE{F}_{lesion}}-\overline{OE{F}_{normaltissue}}\right|}{\sigma \left(OE{F}_{normaltissue}\right)})$ assuming that OEF variation within the contralateral normal tissue results from noise. CNR was compared between CCTV and NET using a two-sample Kolmogorov-Smirnov test. A p value less than .05 was considered significant.

In the healthy subjects (Test Data 3), OEF maps from CCTV and NET were compared with structural similarity index (SSIM).⁶⁵

3 |. RESULTS

Figure 1 shows the OEF comparison between CCTV and NET in the two simulated brains (Test Data 1). In both Cases 1 (Without OEF abnormality) and 2 (With low lesion OEF), NET provided higher accuracy (smaller MAE: 4.8 vs. 1.2 % in Case 1 and 3.1 vs. 1.4 % in Case 2) and higher precision (smaller MSD: 1.7 vs. 0.2 % in Case 1 and 1.2 vs. 0.3% in Case 2) than CCTV. The reconstruction speed of NET was 150 times faster than that of CCTV (1.4 ± 0.3 minutes vs. 212.8 ± 62.7 minutes).

Figure 2 shows representative OEF maps from QQ-CCTV and QQ-NET in the ischemic stroke patients (Test Data 2). Compared to QQ-CCTV, QQ-NET showed less noisy OEF maps with improved spatial overlap between low OEF regions and DWI-defined lesions in the subacute phase.

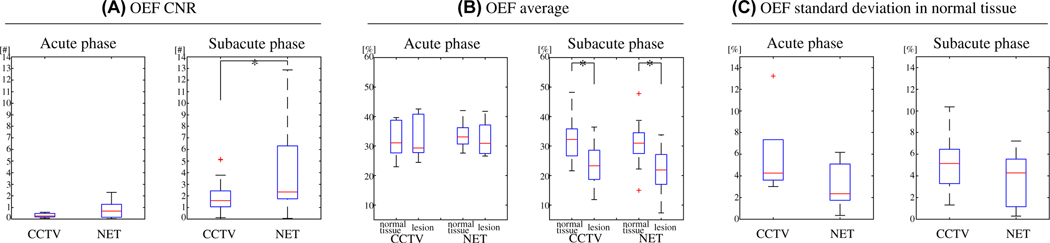
Figure 3 shows box plots of OEF-CNR between the lesion and its contralateral normal tissue (Figure 3A), OEF average in the lesion and the normal tissue (Figure 3B), and OEF SD in the normal tissue in the ischemic stroke patients (Figure 3C) (Test Data 2). Compared to CCTV, NET provided significantly higher CNR in the subacute phase, 1.9 ± 1.3 vs. 6.6 ± 10.7 (p = 0.03), but similar CNR in the acute phase, 0.3 ± 0.2 vs. 0.8 ± 0.9 (p = 0.2). In the subacute phase, both CCTV and NET provided significantly lower lesion OEF average compared to the contralateral normal tissue, 32.3 ± 7.3 vs. 23.9 ± 6.8% (p = 0.01) for CCTV and 31.0 ± 6.2 vs. 23.0 ± 7.2% (p = 0.0004) for NET, whereas both showed similar lesion OEF average as compared to the contralateral normal tissue OEF in the acute phase, 32.3 ± 6.9 vs. 33.1 ± 7.9% (p = 0.7) for CCTV and 33.7 ± 5.3 vs. 32.5 ± 6.3% (p = 0.7) for NET. NET pro-vided lower but not statistically significant OEF SD in the contralateral normal tissue than CCTV, 5.9 ± 4.2 vs. 3.2 ± 2.3% (p = 0.2) for the acute phase and 5.2 ± 2.4 vs. 3.5 ± 2.3% (p = 0.1) for the subacute phase.

FIGURE 3.

Box plots of OEF CNR between the lesion and its contralateral normal tissue (A), OEF average in the lesion and the normal tissue (B), and OEF SD in the normal tissue (C) in acute (6–24 hours post onset, N = 5) and subacute (1–14 days post onset, N = 25) ischemic stroke patients (Test Data 2). Red line, blue box, black whisker, and red cross indicate median, interquartile range, the range extending to 1.5 of the interquartile range, and outliers beyond the whisker range, respectively. Note that two outliers from NET in the subacute phase are not shown (34.8 and 45.1) in CNR. Asterisk (*) indicates a significant difference (p < 0.05, two-sample Kolmogorov-Smirnov test). Compared to CCTV, NET provided significantly greater CNR in the subacute phase, whereas the CNR was not significantly different in the acute phase

Figure 4 shows a comparison of QQ between CCTV and NET in a 7 days post-onset stroke patient. Compared to CCTV, NET showed a less noisy OEF map. In the v map, NET showed low v values in the DWI-defined lesion, whereas the lesion v from CCTV appeared higher than the v on the contralateral normal tissue (pink arrow).

Figure 5 shows the OEF maps with QQ-CCTV and QQ- NET in the four healthy subjects (Test Data 3). QQ-NET provided less noisy but similar OEF maps to QQ-CCTV (SSIM ≥ 0.96).

4 |. DISCUSSION

This study demonstrates the feasibility of a deep neural network, QQ-NET, for solving QSM+qBOLD (QQ) model inversion. Compared to a current inversion method, QQ-CCTV, QQ-NET provides improved accuracy and precision in simulations and better depicts OEF abnormalities in stroke patients. Therefore, the QQ-NET enables robust QQ-based OEF mapping from a conventional mGRE sequence with fast reconstruction.

The QQ model relies on the separation of deoxyheme in cylindrical geometries from other susceptibility sources diffusely distributed in tissue, based on their approximate 10% difference in TE-series signal.^14,66 Due to the poorly conditioned non-convex nature of QQ with this small difference, gradient-based iterative solver approaches are sensitive to noise and optimization details, e.g., initial guess and parameter scaling, and have slow reconstruction speeds, e.g., 0.5~3 hours.^22,24 Deep learning formulation can mitigate the dependency on optimization details and slow reconstruction speeds.^32,34

In the simulation (Figure 1), OEF maps obtained using the proposed QQ-NET show improved accuracy and precision when compared to QQ-CCTV. These findings are consistent with the less noisy OEF maps from QQ-NET (Figure 2) and smaller normal tissue OEF SD (Figure 3C) in the ischemic stroke patients. The suppressed noise propagation into OEF using NET is consistent with effective image denoising using convolutional neural network.⁶⁷

The network may learn noise specific features as well as the QQ model, e.g., additive Gaussian white noise used in the training,⁶⁸ as its training was supervised using noisy inputs and noise-free outputs. In this study, the network trained with SNR 100 datasets provided comparable OEF maps even when tested with more noisy data than the training, SNR 50 and 20 (Supporting Information Figure S2). This suggests that the network may learn Gaussian noise features that adapt to different noise levels, but the exact cause remains to be elucidated. Also, in Case 1, QQ-CCTV provided higher global OEF than the ground truth, which was accompanied with lower global v (Supporting Information Figure S4). To obtain the same QSM and qBOLD measurements, the higher OEF may result from the lower v (Equations 1 and 2). This suggests that CCTV could not decouple OEF and v perfectly. The decoupling between OEF and v has been an issue in qBOLD-based OEF methods including QQ in realistic SNR.¹³ Although CCTV alleviates the decoupling issue by temporal clustering, tissue composition, and total variation,²⁹ it is not still perfect. On the other hand, QQ-NET did not show severe global OEF bias, which suggests that the decoupling may be improved using NET. CNR estimation may not be sensitive to global OEF bias as global OEF bias may affect the difference in OEF average between a lesion and its contralateral normal tissue $\left(\left|\overline{{\text{OEF}}_{\text{lesion}}}-\overline{{\text{OEF}}_{\text{normal}\text{tissue}}}\right|\right)$ and the OEF SD in the normal tissue ${\chi }_n$ (OEFnormal tissue in a similar manner. For instance, in Case 1, where the OEF from CCTV was overestimated compared to the ground truth, CCTV also provided higher $\left(\left|\overline{{\text{OEF}}_{\text{lesion}}}-\overline{{\text{OEF}}_{\text{normal}\text{tissue}}}\right|\right)$ (0.1% vs. 0.08%) and higher $\sigma \left({\text{OEF}}_{\text{normal}\text{tissue}}\right)$ (7.1% vs 6.1%) than the ground truth. This led to CNR in CCTV that was similar to that of the ground truth (0.013 vs. 0.014) even with the OEF overestimation. In addition to the de- coupling issue between OEF and v, errors in other parameters that are affected by mGRE differences, e.g., R₂, may also contribute to OEF bias, which can be exacerbated by low SNR in the lesion, as QQ simultaneously estimates OEF, v, S₀, R₂, and${\chi }_n$.

In the subacute stroke patients (Figure 2), the low OEF regions from QQ-NET coincided substantially with the DWI-defined lesions, whereas QQ-CCTV did not depict the lesions clearly and/or showed noise and artifacts in the OEF maps. This agrees well with the significantly greater OEF CNR from NET than CCTV in the subacute phase, 1.9 ± 1.3 vs. 6.6 ± 10.7 (p = 0.03) (Figure 3A), which suggests improved detection of lesion OEF abnormality. A high OEF CNR in the subacute phase is expected based on the PET literature, e.g., a clear OEF contrast between lesion and its contralateral normal tissue was observed with relatively uniform OEF in normal tissue.⁶⁹ OEF CNR shows how much lesion OEF abnormality is highlighted compared to normal tissue, so it is expected to depend on the severity of tissue damage in the lesion, not directly on lesion location and/or size. Low OEF values in the subacute phase may indicate ischemic lesions with irreversible damage.⁷⁰ In the acute phase, lesion OEF values are heterogenous, which may suggest rapid lesion evolution within first few hours of stroke onset.⁷¹ In the 24 hours post-onset case, NET provides similar OEF to the contra- lateral normal tissue at the lesion center but low OEF at the boundary. That lesion OEF values are similar to the contralateral normal tissue may suggest salvageable lesion tissue.

Both QQ-CCTV and QQ-NET show uniform OEF maps in the healthy subjects (Figure 5); these findings are consistent with previous PET studies suggesting the presence of equilibrium between metabolic needs and blood flow in healthy tissue.^72,73

The low v within DWI-defined lesions from QQ-NET (Figure 4) agrees with a decrease in blood volume in ischemic stroke lesions,⁷⁴ and may be driven by a reliable Y and v decoupling. The high lesion v from QQ-CCTV may be caused by that lesion was mistakenly classified as gray matter. CCTV incorporates tissue type information into clustering by dividing temporal mGRE signal based clusters into gray matter/white matter/cerebrospinal fluid sub-clusters. For the stroke patients in this study, tissue segmentation was performed on T1-weighted images using a neuroimaging tool, FSL FAST.⁶³ As stroke lesions are sometimes dark on T1-weighted images, they may be mistakenly clustered as gray matter. This may lead to a poor v initialization for the lesion and subsequent problematic lesion v in CCTV (Supporting Information Figure S5), which may provide OEF bias in the lesion.

Despite of its advantage of more robust and faster reconstruction (1.4 vs. 212.8 minutes), the proposed neural network has limitations. First, it is less flexible. For instance, the network has to be re-trained for different TE sets (different qBOLD measurements), which is a critical limitation of the current network training scheme. Also, the network may need to be re-trained for different imaging resolutions or different SNRs. However, in this study, QQ-NET provided comparable OEF maps when tested with a different imaging parameter dataset (healthy subjects with lower resolution and higher band-width) (Supporting Information Figure S3) and with substantially lower SNR 50 and 20 (Supporting Information Figure S2). These results suggest that QQ-NET may not be sensitive to resolution or SNR. Second, for clinical implementation, the proposed QQ-NET should be tested extensively in various clinical scenarios, e.g., multiple sclerosis and brain tumor, to confirm its validity. Third, though the training of QQ-NET covered a wide physiological range for the model parameters, such as the entire possible range of OEF (0~100%) and v value range of 0~8% (which includes PET and MRI literature ranges of 0.5~5.5%⁵⁴), combinations of the parameter values in the training data may be limited using 26 simulated stroke datasets. Also, in this feasibility study, the four healthy subject datasets were only used to check if the network trained with simulated stroke datasets can produce reasonable uniform OEF maps without severe artifacts. QQ-NET performance can be further improved by training with more various parameter combinations of ground truth including various physiological brain datasets such as healthy subjects and patients with multiple sclerosis. Fourth, QSM values may depend on the dipole inversion algorithms used in reconstruction,^75,76 which may worsen QQ-based OEF precision. Using the phase signal of individual TEs instead of a QSM map may help the network provide a more reliable output without a dependency on the intermediate processing steps, e.g., QSM inversion. On the other hand, it may add complexity to the training. For instance, the training may involve learning both QSM (dipole inversion) and QQ processing, compared to the current learning for QQ inversion. Also, a more complex network architecture, e.g., a combined structure of two Unets (one for magnitude and the other for phase inputs), may be needed. The additional complexities may lead to challenges training the network. A comparison between the two different inputs (QSM vs. individual echo phases) should be conducted in a future study. Lastly, a validation study with the reference standard O¹⁵ PET remains to be performed.

In conclusion, with enhanced accuracy and fast reconstruction by using a deep neural network, the proposed QQ-NET may be useful to investigate tissue functions in brain pathologies, such as Alzheimer disease,^77,78 multiple sclerosis,⁷⁹ tumor,⁸⁰ and ischemic stroke.⁸¹

Supplementary Material

Supporting_material

FIGURE S1 Network structure of QQ-NET. A 3D Unet consists of an encoding and decoding path with 18 convolutional layers with 3 × 3 × 3 kernel (blue), 4 max pooling layers with 2 × 2 × 2 kernel (green), 4 deconvolution layers with 2 × 2 × 2 kernel (red), 4 feature concatenations (purple), 1 convolutional layer with 1 × 1 × 1 kernel (yellow), and element-wise Tanh function application for parameter boundary setting (cyan)

FIGURE S2 Comparison between the OEFs obtained by CCTV and NET at different SNRs (SNR 100, 50, and 20) in a simulated stroke brain (Case 2 in Test Data 1). Numbers indicate MAE (yellow) and MSD (pink). For both CCTV and NET, the lower SNR, the greater MAE and MSD. At all 3 SNRs, NET provides lower MAE and MSD than CCTV. Note that QQ-NET was trained with SNR 100 dataset and the trained network was tested on different SNR datasets. OEF_avg and OEF_std indicate the average and standard de- viation OEF maps among 5 trials. OEF_avg and OEF_std are shown in the unit of [%]

FIGURE S3 Comparison of the OEFs obtained by QQ-NET between 2 resolutions in the 4 healthy subjects shown in Figure 5. The network was trained by using simulated stroke brains with Resolution 1 (0.47 × 0.47 × 2.0 mm³) and tested with the 4 healthy subjects with Resolution 1 (as shown in Figure 5) and Resolution 2 (0.86 × 0.86 × 1.2 mm³). Numbers in white indicate SSIM, which was calculated after registering OEF maps from Resolution 1 to Resolution 2. NET provides comparable OEF maps between Resolutions 1 and 2 (SSIM ≥ 0.96)

FIGURE S4 Comparison between OEF and v obtained by CCTV and NET in 2 simulated brains (Test Data 1): Case 1. Without OEF abnormality and Case 2. With low lesion OEF. OEF_avg and v_avg indicate the average OEF and v maps, respectively, among 5 trials. OEF_avg and v_avg are shown in the unit of [%]. In Case 1, CCTV showed higher OEF_avg than the ground truth, which is accompanied with lower v_avg. NET did not show substantial OEF bias in both Case 1 and 2

FIGURE S5 xAn example of problematic tissue type incorporation in CCTV. DWI, T1-weighted image (T1w), tissue type, initial guess v for CCTV (v initial), and resultant v map from CCTV (v final) in the stroke patient shown in Figure 4 (7 days post onset) are shown. Tissue type (pink: gray matter, beige: white matter, green: cerebrospinal fluid) was constructed from T1w and used for v initial (gray matter/white matter/cerebrospinal fluid = 4/2/1%). Red arrow indicates the stroke lesion that was mistakenly segmented as gray matter which resulted in problematic v initial and v final in CCTV

DATA AVAILABILITY STATEMENT

The code and data that support the findings of this study are openly available in QQ-NET at https://github.com/jc2852/QQ-NET.