Characterization of Trabecular Bone Using the Backscattered Spectral Centroid Shift

Abstract

Ultrasonic attenuation in bone in vivo is generally measured using a through-transmission method at the calcaneus. Although attenuation in calcaneus has been demonstrated to be a useful predictor for osteoporotic fracture risk, measurements at other clinically important sites, such as hip and spine, could potentially contain additional useful diagnostic information. Through-transmission measurements may not be feasible at these sites due to complex bone shapes and the increased amount of intervening soft tissue. Centroid shift from the backscattered signal is an index of attenuation slope and has been previously used to characterize soft tissues. In this paper, centroid shift from signals backscattered from 30 trabecular bone samples in vitro were measured. Attenuation slope was also measured using a through-transmission method. The correlation coefficient between centroid shift and attenuation slope was −0.71. The 95% confidence interval was (−0.86, −0.47). These results suggest that the backscattered spectral centroid shift may contain useful diagnostic information potentially applicable to hip and spine.

Introduction

The diagnostic utility of ultrasound for osteoporosis detection is well documented [1]. Calcaneal broadband ultrasonic attenuation (BUA) and speed of sound (SOS) are highly correlated with calcaneal bone mineral density (BMD) [2–13] which is in turn an effective indicator of osteoporotic fracture risk in the hip [14]. Linear combinations of BUA and SOS have greater diagnostic capability than either parameter by itself and have been demonstrated to be predictive of hip and other fractures in women in prospective [15, 16] and retrospective [17–20] studies. Bone sonometry is less expensive, faster, simpler, and more portable than its x-ray counterparts: dual-energy x-ray absorptiometry (DEXA) and quantitative computed tomography (QCT). In addition, ultrasound produces no ionizing radiation.

Attenuation is generally measured using two broadband transducers in a through-transmission geometry around the calcaneus. Although measurements at the calcaneus provide useful information regarding general skeletal status, measurements at more clinically important sites such as hip and spine would be of greater interest. So far, practical methods for through-transmission measurements have not been developed at these sites, which exhibit more complex geometry and are surrounded by more intervening soft tissue than the calcaneus.

Many studies have shown that attenuation may be measured from backscattered signals from soft tissues [21]. This approach is less accurate than through-transmission methods but is generally required for in vivo applications in soft tissues. It has been shown that for a Gaussian spectrum propagating through a linearly attenuating medium, the spectral centroid shifts downward by an amount proportional to the product of the attenuation coefficient of the medium, the distance of propagation, and the square of the bandwidth [22,23]. The bandwidth of the Gaussian signal remains unchanged as it propagates.

Like soft tissues [21–33], bone exhibits approximately linear attenuation [2–13, 33–39]. Also like soft tissues, bone is quite inhomogeneous, making the analysis of backscattered signals difficult. Compared with soft tissue applications, the task of measuring attenuation, or some index of attenuation, in bone is easier in some respects but more challenging in others. The level of accuracy required for diagnostically useful measurements in bone is much less than that for soft tissue. In soft tissues, accuracies on the order of 0.1 dBcm⁻¹MHz⁻¹ are often required in order to separate normal from diseased cases [21]. In trabecular bone, attenuation coefficients have a tremendous range from about 5 to 30 dBcm⁻¹MHz⁻¹. In this case, a measurement with an accuracy of a few dBcm⁻¹MHz⁻¹ would still be useful. One complicating factor in the case of bone however is that tissue volumes are much smaller than those generally available in soft tissues such as liver. This leads to less data for averaging, resulting in increased measurement variance. Another factor that makes bone more difficult is that relatively high attenuation coefficients mandate the use of lower frequency transducers that have lower bandwidths. Since centroid shift is proportional to the square of the bandwidth (for Gaussian beams propagating through linearly attenuating media), it becomes necessary to measure smaller centroid shifts than would be the case with higher frequency transducers.

In this paper, the backscattered spectral centroid shift is proposed as an index to characterize bone. Since centroid shift is closely related to attenuation coefficient, it has potential to serve as a useful indicator of bone status. In order to evaluate this approach, through-transmission measurements of attenuation slope are compared with backscattered spectral centroid shifts from 30 human calcaneus samples in vitro.

Methods

Calcaneus Samples

Thirty human calcaneus samples (genders, ages unknown) were obtained. They were defatted using a trichloro-ethylene solution. Removal of fat decreases the risk of microorganism contamination of samples. Defatting was presumed not to significantly affect measurements since attenuation and speed of sound of defatted trabecular bone has been measured to be only slightly different from that of bone with marrow left intact [7, 40]. The cortical lateral layers were sliced off leaving two parallel surfaces with direct access to trabecular bone. (The angle between opposing planar surfaces was confirmed to be confined within ±0.2° by caliper measurements of thickness throughout each sample). The thicknesses of the samples varied from 16 to 21 mm. The other dimensions were approximately 35 mm X 70 mm.

In order to remove air bubbles, the samples were vacuum degassed underwater in a desiccator. After vacuum, samples were allowed to thermally equilibrate to room temperature prior to ultrasonic interrogation. Ultrasonic measurements were performed in distilled water at room temperature. The temperature was measured for each experiment and ranged between 19.1°C and 21.2°C. Attenuation in calcaneus is known to exhibit a slight temperature dependence [41–44]. The relative orientation between the ultrasound beam and the calcanea were the same as with in vivo measurements performed with commercial bone sonometers, in which sound propagates in the mediolateral (or lateromedial) direction.

Data Acquisition and Analysis

The experimental setup is shown in Figure 1. A Panametrics (Waltham, MA) 5800 pulser/receiver was used. Samples were interrogated in a water tank using a matched pair of coaxially-aligned Panametrics circular, focussed, broadband transducers. (Center frequency = 500 kHz, FWHM = 180 kHz, diameter = 1”, focal length = 1.5”). Received ultrasound signals were digitized (8 bit, 10 MHz) using a LeCroy (Chestnut Ridge, NY) 9310C Dual 400 MHz oscilloscope and stored on computer (via GPIB) for off-line analysis.

Figure 1.

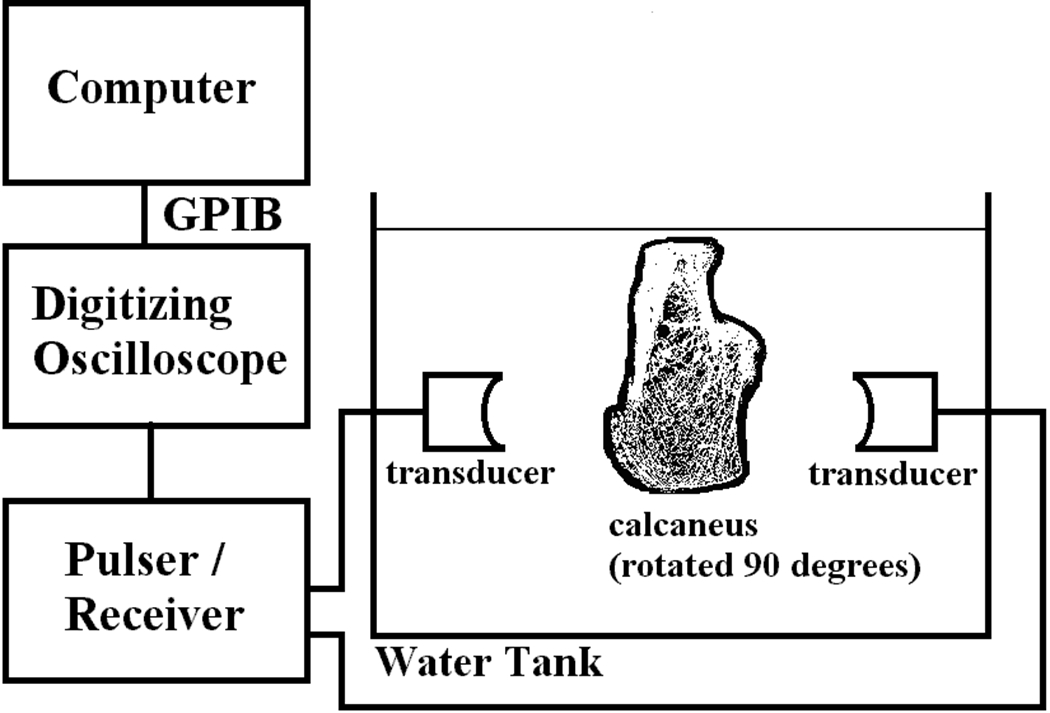
Experimental set up.

Attenuation was measured using a through-transmission method as follows. Using two opposing coaxially-aligned transducers (one transmitter and one receiver) separated by twice the focal length, transmitted signals were recorded both with and without the bone sample in the acoustic path. The bone samples were larger in cross-sectional area than the receiving transducer aperture. Eight attenuated signals were obtained for each sample by scanning across the calcaneal cross section. The eight corresponding power spectra (squared modulus of the Fast Fourier Transform) were averaged. Attenuation coefficient was then estimated using a log spectral difference technique [45]. A linear fit, α(f) = βf + α₀, was performed on the attenuation coefficient α, vs. frequency, f, data. There is abundant evidence to support this linear model in trabecular bone over a broad range of frequencies [38, 39]. The slope of the linear fit, β, is often referred to as normalized broadband ultrasonic attenuation (nBUA) [7] in the bone densitometry community and as attenuation slope in the biomedical ultrasound community [35–37]. In principle, the log spectral difference substitution technique can exhibit appreciable error if the speed of sound differs substantially between the sample and the reference [46]. However, one study suggests that this diffraction-related error is very small in calcaneus [47]. Apparently, the speed of sound in calcaneus (in the mediolateral orientation), approximately 1475 – 1650 m/s [47] is sufficiently close to that of distilled water at room temperature, 1487 m/s [48] that diffraction-related errors may be ignored.

For backscatter measurements, the same system was employed in pulse-echo mode using a single transducer. The diameter of the focal plane central diffraction lobe produced by the transducer (2.44 cz/fd where c is sound speed, z is focal depth, f is frequency, and d is transducer aperture diameter [49]) was 11.3 mm at 500 kHz. This width is safely less than the typical specimen width, which was about 35 mm, and allowed for multiple measurements (6–16) within each specimen, positioned at the focal plane. Each specimen was scanned as fully as possible. Each time domain RF signal was gated in order to isolate the region from 4 mm beyond the front surface (in order to exclude the specular reflection) to 16 mm beyond the front surface (gate length = 12 mm). Gated RF signals were zero-padded to 2048 points. Power spectra were estimated from the average squared modulus of the FFT. For each specimen, the centroid, $\overline{f}$, was measured from the average power spectrum, S(f).

$$\overline{f}=\frac{\sum _{i=i_1}^{i_2}{f}_{i}S(f_i)\Delta f}{\sum _{i=i_1}^{i_2}S(f_i)\Delta f}$$

where Δf = f_s / N, f_s = sampling rate = 10 MHz, N = digitized RF record length = 2048, f₁ = 400 kHz, f₂ = 800 kHz, i₁ = round(f₁ / Δf) and i₂ = round(f₂ / Δf) where round() rounds a real number to the nearest integer.

Reference spectra backscattered from a phantom were acquired along with bone measurements for two main reasons. First, this enabled computation of a centroid shift (between spectra backscattered from bone and phantom) which could be compared to numerical predictions based on experimental measurements from phantoms and an assumed model for the effect of attenuation on backscatter (see next section). Unlike some analytical approaches [23], this numerical approach does not require the assumption of Gaussian spectra. Second, a reference phantom method would be required to extend this method to the in vivo situation in which the distance between transducer and region of interest cannot be controlled so easily (as in the in vitro case).

The reference phantom was placed in the water tank at the same distance as for the bone samples (transducer focal distance). The same time gate was applied. The phantom consisted of glass spheres (size range: 212 – 250 microns) in agar with attenuation coefficient α_R(f)=0.124f^1.63 dB/cm, sound speed c = 1556 m/s, backscatter coefficient η_R(f) approximately equal to 0.0016f^3.75 cm⁻¹Sr⁻¹ over the range from 400 – 800 kHz. At least 20 RF lines were acquired for each calibration measurement. As with the bone data, power spectra were computed from the average squared modulus of the FFT. Calibration spectra were compensated for attenuation within the phantom.

Ideally, the frequency dependence of scattering from the reference phantom and bone would be equal so that centroid shifts could be solely attributed to attenuation within the bone. Scattering from bone at low frequencies may be approximated by a power law (proportional to fⁿ where n has been measured to be in the range of 3.2 from 300 – 700 kHz [50] to 3.4 from 400 kHz – 1.2 MHz [51]). In order to match the reference spectra to bone spectra with regard to frequency dependence of scattering, the former were multiplied by a scale factor of f^{3.2 – 3.75} = f ^−0.55. The purpose of this step was to minimize the component of centroid shift potentially attributable to discrepancy in frequency-dependent scattering.

Results

The attenuation coefficients of the 30 bone samples ranged from 0.1 to 22.8 dBcm⁻¹MHz⁻¹. The mean was 10.7 dBcm⁻¹MHz⁻¹. The standard deviation was 5.7 dBcm⁻¹MHz⁻¹.

In Figure 2, normalized average spectra (over all 30 samples) scattered from bone and the reference phantom are shown. The downshifted center frequency (centroid) correspond to data from bone may be seen. The average centroid shift was −18 kHz.

Figure 2.

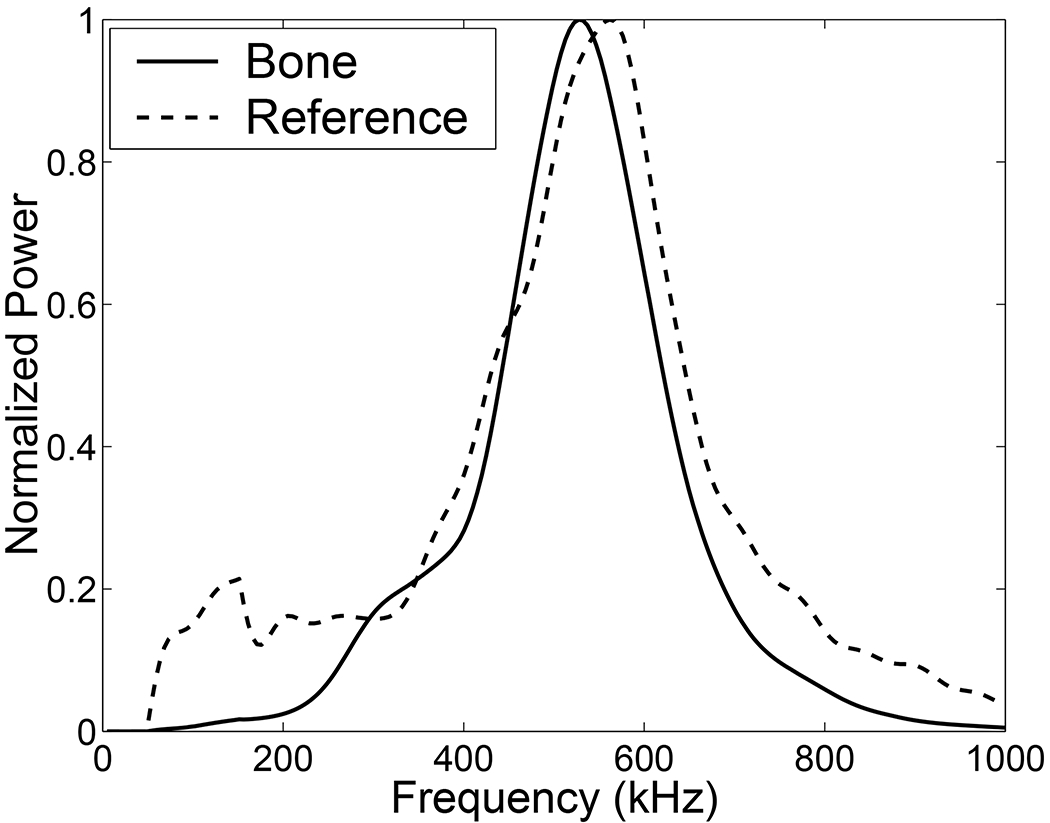
Normalized average spectra (over all 30 samples) scattered from bone and the reference phantom. The downshifted center frequency (centroid) corresponding to data from bone is clearly seen. The average centroid shift was −18 kHz.

Figure 3 shows a scatter plot of attenuation slope and centroid shift. As expected, greater attenuation slopes are associated with greater centroid downshifts. The solid curve in Figure 3 shows the theoretically expected centroid shift as a function of attenuation slope. This was obtained numerically by taking the average reference spectrum, correcting for the mismatch in frequency dependent scattering between the phantom and bone, applying a frequency-dependent attenuation correction function (Ref. [52], Equation 17), and computing the centroid shift. A linear relationship between attenuation and frequency, α(f) = βf + α₀, was assumed. (The constant term, α₀, was assumed to be zero as it has no effect on centroid shift). The theoretical curve in Figure 3 was obtained by repeating these steps for attenuation slopes ranging from 0 to 30 dBcm⁻¹MHz⁻¹. The dashed curve in Figure 3 corresponds to a power law fit to the data. This fit is reasonably close to the theoretically expected variation.

Figure 3.

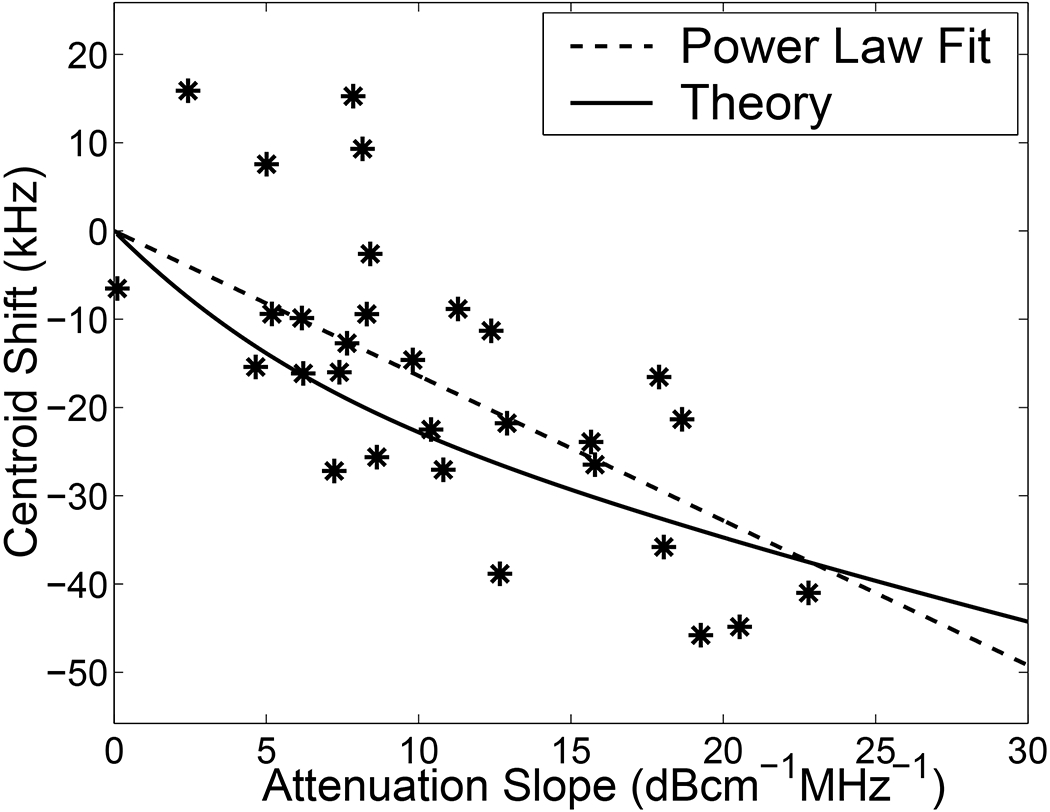
Scatter plot of attenuation slope (obtained from transmission measurements) and centroid shift (obtained from reflection measurements) for the 30 bone samples. The solid curve shows the theoretically expected centroid shift as a function of attenuation slope. The dashed curve corresponds to a power law fit to the data.

A linear least-squares to the data in Figure 3 yielded a correlation coefficient of R = −0.71. This value suggests that R² = 0.51 or 51% of variations in centroid shift were attributable to variations in attenuation slope among the bone samples. The 95% confidence interval for the estimate of R was (−0.86,−0.47).

The power law fit was inverted in order to predict attenuation slope based on centroid shift. Predicted attenuation slope is plotted versus measured attenuation slope (using the through-transmission method) for the thirty bone samples in Figure 4. The correlation between the two measurements was 0.75 (95% CI: 0.52 – 0.87).

Figure 4.

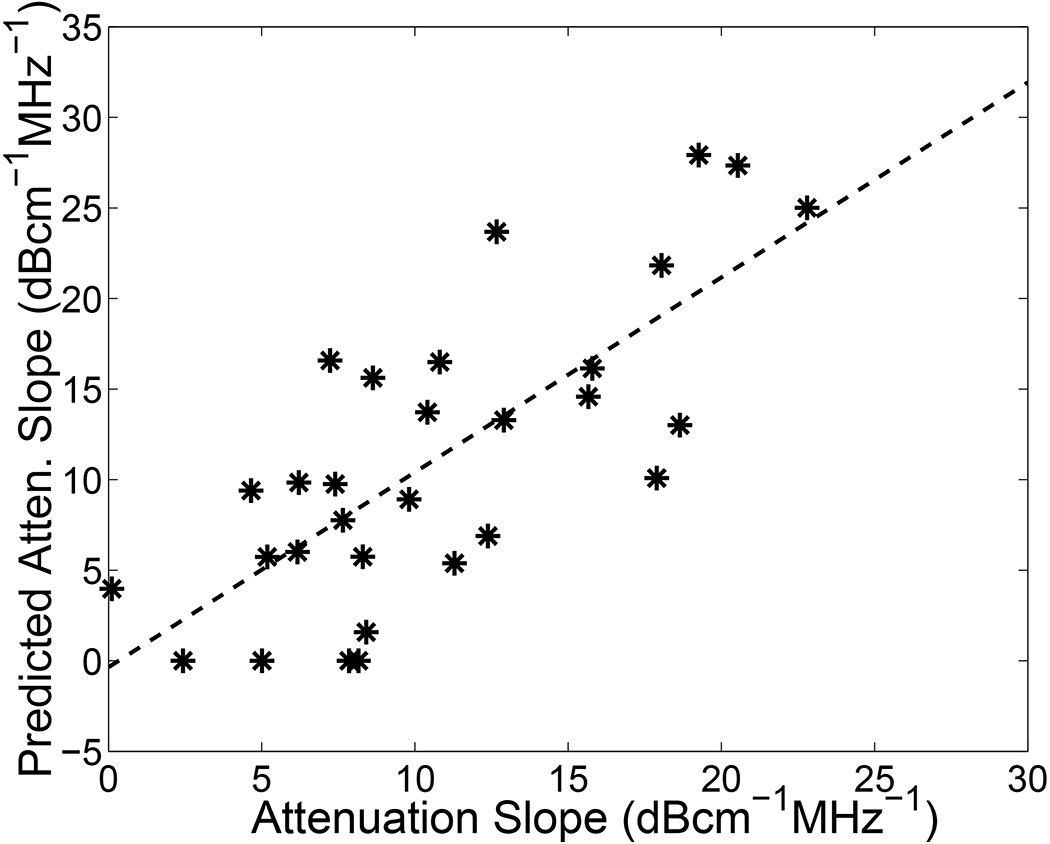
Predicted attenuation slope plotted versus measured attenuation slope (using the through-transmission method) for the 30 bone samples. The solid line is a linear least-squares fit to the data.

Discussion

Backscattered spectral centroid shift has been demonstrated here to exhibit moderate correlation with ultrasonic attenuation in trabecular bone samples in vitro. Compared with the standard through-transmission measurement of attenuation in the calcaneus in vivo, backscatter-based measurements have a greater potential for application at more clinically important sites such as hip and spine. The present study establishes some diagnostic potential for the backscattered spectral centroid shift.

The basic idea behind this measurement is that attenuation within the volume of interrogation produces downward shifts in the backscattered spectral centroid. The magnitude of that shift is roughly proportional to the attenuation coefficient. Thus, ideally, the centroid shift is an indirect index of attenuation.

One main limitation of this approach is as follows. The analysis algorithm assumes a fixed value for the frequency dependence of backscatter coefficient from bone (f ^3.2). However this frequency dependence can vary somewhat due to both biological variations in bone microarchitecture (e.g. trabecular thickness) as well as precision limitations of backscatter measurements. It has previously been shown that, in trabecular bone, speckle-related spectral uncertainty is the primary limitation of precision in estimates of frequency dependence of backscatter [53]. Although human calcaneal trabecular thickness exhibits substantial variation (mean: 127 microns; standard deviation: 17 microns [54]), it is always much smaller than the ultrasonic wavelength at 500 kHz (approximately 3 mm), so that the true backscatter coefficient always varies approximately as frequency cubed (as would be expected, say, from a thin cylinder). It is likely therefore that speckle-related precision limitations are the primary explanation why the correlation between centroid shift and attenuation slope was not found to be higher than reported here.

Additional limitations of this study include the facts that it was performed on defatted specimens with cortical plates removed. For in vivo applications, marrow and cortical plates will be present. Marrow in particular is known to have an effect on attenuation and backscattering properties [59]. One preliminary investigation in lumbar spine in vivo (7 normal subjects) does demonstrate that centroid shift exhibits a moderate correlation with BMD, even in the presence of these complicating factors [60].

Centroid shift is proportional to the square of the bandwidth (for a Gaussian spectrum anyway). Since bandwidth tends to scale with center frequency, higher frequency transducers would be expected to result in greater centroid shifts in spectra backscattered from bone. These greater shifts would likely be easier to measure, perhaps resulting in enhanced ability to assess attenuation. Although the present study was conducted using a transducer with a center frequency of 500 kHz, it has been previously shown however that it is feasible to acquire backscatter data from bone at frequencies as high as 1 MHz [55] and even 2.25 MHz [56].

Another backscatter-based measurement that has shown some promise for characterization of bone in vivo is the magnitude of the backscatter coefficient [55–58]. In order to convert measurements of apparent backscatter coefficient to backscatter coefficient, it is necessary to compensate for attenuation. In sites such as the hip and spine, where through-transmission measurements of attenuation are not feasible, centroid-shift based estimates could possibly be used for this conversion.

In addition to having merits on its own, backscattered spectral centroid shift may be a useful adjunct measurement in combination with others (e.g. X-ray based BMD and ultrasonic backscatter) for multi-feature characterization of bone.

Biography

Keith A. Wear graduated from the University of California at San Diego with a B.A. in Applied Physics in 1980. He received his M.S. and Ph.D. in Applied Physics with a Ph.D. minor in Electrical Engineering from Stanford University in 1982 and 1987.

He was a post-doctoral research fellow with the Physics department at Washington University, St. Louis from 1987–1989. He has been a research physicist at the FDA Center for Devices and Radiological Health since 1989. He has performed research in biomedical applications of ultrasound and magnetic resonance spectroscopy for 15 years. His research has included measurements of ultrasonic scattering properties from tissues, high-resolution spectral estimation, magnetic resonance spectroscopic image reconstruction methods, and analysis of statistical properties of ultrasonic echoes from tissues. He has become interested in applications with bone in the late 1990’s as FDA’s regulatory interest in bone sonometry has increased.

He is a senior member of IEEE and the American Institute of Ultrasound in Medicine (AIUM), a member of IEEE Ultrasonics Society, IEEE Signal Processing Society, IEEE Engineering in Medicine and Biology Society, AIUM Technical Standards Committee, and the American Society for Bone and Mineral Research. He is currently vice chairman of the AIUM Basic Sciences and Instrumentation Section.