Abstract

Magnetism in two-dimensional (2D) van der Waals (vdW) materials has recently emerged as one of the most promising areas in condensed matter research, with many exciting emerging properties and significant potential for applications ranging from topological magnonics to low-power spintronics, quantum computing, and optical communications. In the brief time after their discovery, 2D magnets have blossomed into a rich area for investigation, where fundamental concepts in magnetism are challenged by the behavior of spins that can develop at the single layer limit. However, much effort is still needed in multiple fronts before 2D magnets can be routinely used for practical implementations. In this comprehensive review, prominent authors with expertise in complementary fields of 2D magnetism (i.e., synthesis, device engineering, magneto-optics, imaging, transport, mechanics, spin excitations, and theory and simulations) have joined together to provide a genome of current knowledge and a guideline for future developments in 2D magnetic materials research.
Keywords: 2D magnetic materials, van der Waals, CrI3, magneto-optical effect, neutron scattering, Fe3GeTe2, magnetic genome, atomistic spin dynamics
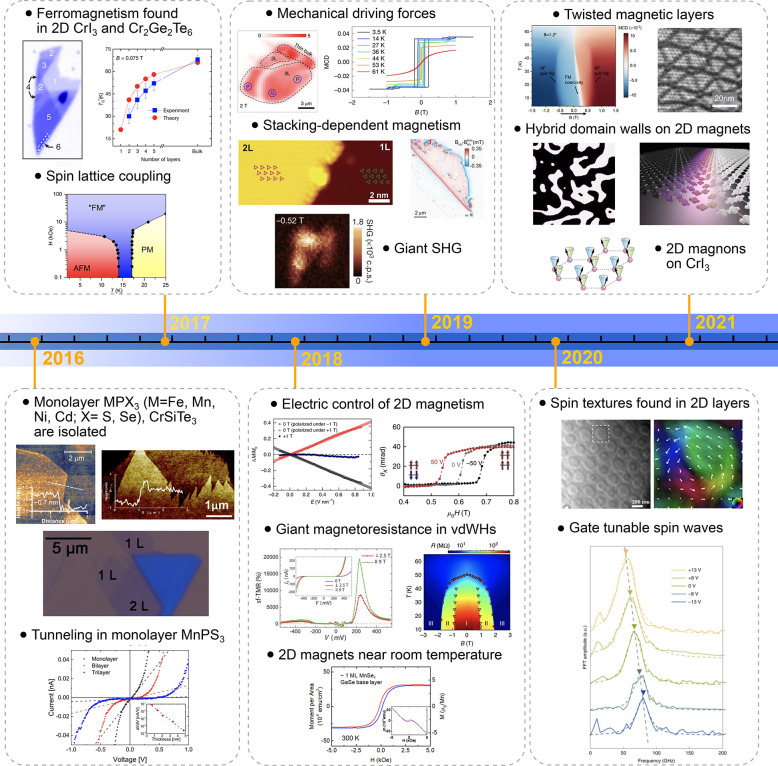
Two-dimensional (2D) materials have been the focus of intense and extensive research efforts around the world for the better of the past two decades, starting from the discovery of graphene and then rapidly expanding to an enormous variety of materials and properties. One of the most exciting recent developments in 2D materials has been the discovery of intrinsic long-range magnetic order in atomically thin layers. In Figure 1, we provide a timeline of the major discoveries in 2D magnets over the past few years. In a fairly short period of time, there have been significant advances in our knowledge of magnetic 2D materials, detailed characterization of magnetic states, and progress toward magnetic and spintronic devices with exceptional performance.
Figure 1.
Timeline of developments in 2D magnets. Since early 2016, a few results on monolayer phosphides MPX3 (M = Fe, Mn, Ni, Cd; X = S, Se)1,2 and CrSiTe33 appeared in the literature, with results on electron tunneling in MnPS3 also being reported.4 The conclusive measurements in 2017 of magnetism on CrI35 and Cr2Ge2Te66 sparked an increasing interest in several subjects involving magnetism in 2D. Results on spin–lattice coupling collected from CrCl37 also provided different mechanisms involving vibrations and spins in 2D. In 2018, the electric control of magnetism,8−12 giant magnetoresistance,13−16 and a potential 2D magnet (i.e., VSe2) displaying room-temperature magnetism17−19 attracted substantial interest in the community. In 2019, experimental evidence of stacking-dependent magnetic properties,20,21 pressure effects,22,23 and giant second-harmonic generation (SHG)24 drove the field toward intriguing magnetic properties. In 2020, spin-textures25−27 such as skyrmions, spirals, and spin-waves28 indicate that topologically nontrivial spins are a reality on 2D magnets. In 2021, a few reports on twisted magnetic layers,29,30 together with the hybrid character of narrow domain-walls31 on CrI3, raised possibilities for the angular control of magnetic features and domain-wall based applications (i.e., racetrack). All images adapted from the references cited above with permission as follows. Panels from (2016) reprinted with permission from ref (32), copyright 2016 American Chemical Society; ref (3), copyright 2016 Royal Society of Chemistry; ref (1), copyright 2016 American Chemical Society; and ref (4), copyright 2016 AIP Publishing and reprinted with permission under a Creative Commons Attribution (CC BY) license. Panels from (2017) reprinted with permission from ref (5), copyright 2017 Springer Nature; ref (6), copyright 2017 Springer Nature; and ref (7), copyright 2017 American Physical Society. Panels from (2018) reprinted with permission from ref (8), copyright 2018 Springer Nature; ref (9), copyright 2018 Springer Nature; ref (13), copyright 2018 AAAS; with permission under a Creative Commons CC by 4.0 license from ref (15), copyright 2018 Springer Nature; and ref (17), copyright 2018 American Chemical Society. Panels from (2019) reprinted with permission from ref (22), copyright 2019 Springer Nature; ref (23), copyright 2019 Springer Nature; ref (20), copyright 2019 AAAS; ref (21), copyright 2019 AAAS; and ref (24), copyright 2019 Springer Nature. Panels from (2020) reprinted with permission from ref (25), copyright 2020 American Chemical Society; and ref (28), copyright 2020 Springer Nature. Panels from (2021) reprinted with permission from ref (29), copyright 2021 Springer Nature; ref (30), copyright 2021 Springer Nature; and ref (31), copyright 2021 John Wiley and Sons.
The purpose of this review is to assemble a thorough genome of all aspects of 2D magnetic van der Waals (vdW) materials, and to provide a guideline for future directions. Throughout this work, we have drawn on the expertise of many key researchers in this exciting emerging field to summarize their most critical findings to date and to lay out the important upcoming challenges.
This review article is divided into the following sections:
Historical perspective: An overview of low-dimensional materials, models of how magnetic moments interact, and summary of key recent discoveries and developments in 2D magnets.
Device engineering: The main types of magnetic devices, e.g., magnetic tunnel junctions (MTJs), magnetoresistant lateral transport devices, and spin waves in tunnelling devices.
Magneto-optical phenomena: Characterization and study of 2D magnets by several magneto-optical spectroscopy methods including Kerr effect, circular dichroism, magneto-photoluminescence (PL), and magneto-Raman spectroscopy which can reveal spin-phonon effects.
Magnetic imaging: Magnetic force microscopy (MFM), nitrogen-vacancy center magnetometry (NV-center), nanosuperconducting quantum interference device (nanoSQUID), spin-polarized scanning transmission microscopy (SP-STM), and Lorentz transmission electron microscopy (Lorentz TEM or LTEM) are used to image magnetic domain features in 2D magnets.
Magnetic and electrical transport characterization: Magnetic critical behavior, magnetocaloric effect, magnetism in bulk and thin-layer vdW magnets of different electronic properties (i.e., insulator, metallic, semiconductor) via different techniques.
The role of defects and vacancies: Muon spin rotation (μSR) methods are used to investigate microscopic magnetic properties in the presence of defects.
Spintronics from fundamentals to devices: Basic magnetic properties of typical 2D magnets are described, followed by spintronic implementations and memory devices.
Magnetic-topological phases: Topological materials and transition-metal-based kagome lattice family of materials exhibit ferromagnetism and anomalous magnetization effects.
Synthesis and sample preparation: Methods of preparing samples of 2D magnets by top-down and bottom-up methods.
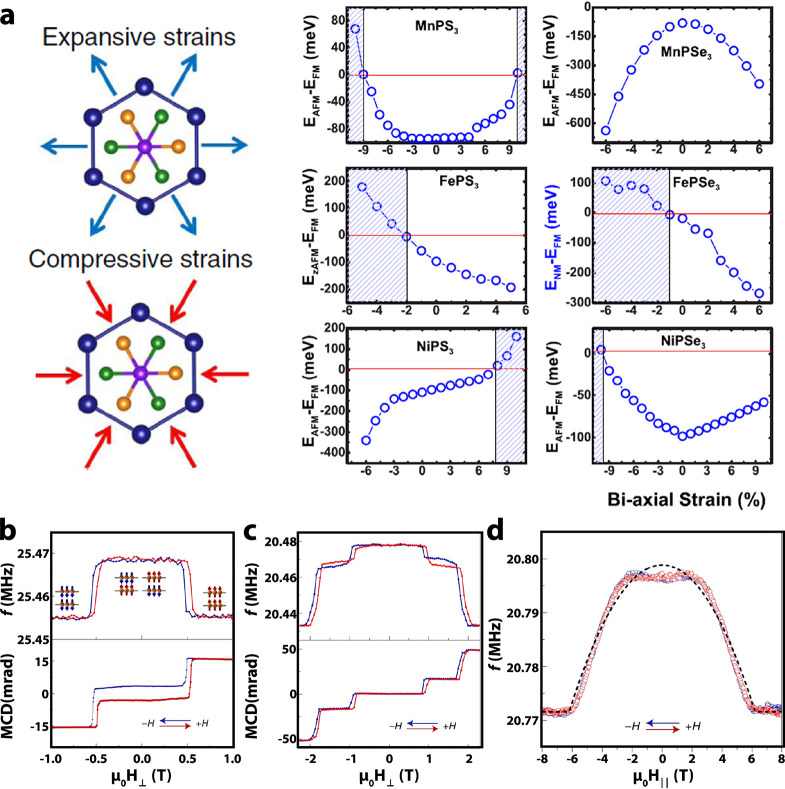
Mechanical properties and strain engineering: Description of mechanical properties 2D magnets, along with theoretical predictions, and how strain can induce further magnetic properties.
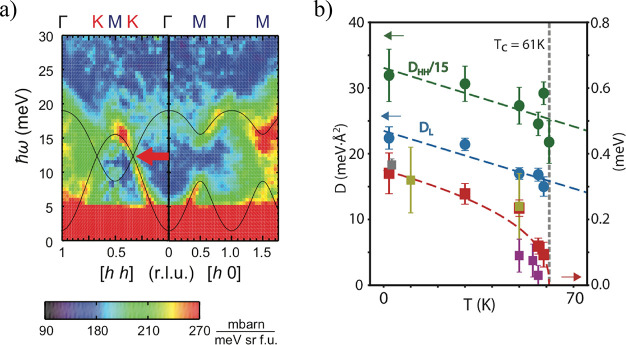
Spin excitations, topological properties: Measurement of collective excitations of electron spin states by neutron scattering, inelastic electron tunneling spectroscopy, and Raman spectroscopy.
Heterostructures, twisted layers, and interfaces: Stacking different 2D magnets together, generating exotic quantum phases, and how to integrate 2D magnets into broader device architectures.
Theory and simulations: Description of the underling theory, computational method and spin models to investigate 2D magnetic materials.
Perspectives and a forward-looking approach: The final key section is an overview of the major challenges and opportunities in the field and what we can expect research directions to focus on in the coming few years.
Historical Perspective
Since the 1970s, low-dimensional (low-d) physics has grown and matured into a major branch of science. In general, one can define a system with restricted dimensionality d as an object that is infinite only in one or two spatial directions (d = 1 and 2). Such a definition comprises, for example, isolated single chains or layers, in addition to fibers and thin layers (films) of varying but finite thicknesses. A multitude of physical phenomena, notably in solid-state physics, fall into the category of a low-d system. The study of such systems substantially advanced our fundamental knowledge of physics, but also led to relevant technological applications. No matter how widely different the many low-d physical systems may appear at first glance, there are several similarities and characteristics that they all share, which are inherent to their reduced dimensionality. It is for this very reason that one may consider low-d physics as a recognizable field of science on its own right. Within this larger field, the sub-branch of low-d magnetism played a quite important role from the outset. For example, theoretical work on magnetic chains and layers started as early as the twenties with the Ising chain,33 followed by studies of 2-d Ising magnets in the 1930s and 1940s.34 Systematic experimental studies on quasi low-d magnetic systems started in the 1940s and 1950s, but ultrathin magnetic films composed of just a few monolayers were studied in more recent past. These systems should be contrasted with the magnetic films used in thin-film technology, which have thicknesses ranging from 103 to 104 atomic layers.
Perhaps, one of the most important contributions of low-d magnetism to fundamental physics is in the subject of phase transitions and critical phenomena. The way in which cooperative phenomena are influenced by the crystal dimensionality, the symmetry of the interactions in the Hamiltonian, or the quantum-mechanical nature of the spin, led to such important concepts such as scaling, universality classes (models having the same set of critical exponents), and the renormalization group.35 This general theory of critical phenomena based upon the principles of quantum-field theory led to the Nobel prize granted to K. G. Wilson and is considered as a great advance in mathematical physics.35 Phase transitions are a very common phenomena that have a wide range of applicability, which explains the past interest in the study of low-d magnets. Most physical problems involving interacting elements that form a spatial array can be mapped into a magnetic language by describing the problem within a pseudospin formalism (e.g., structural or electric phase transitions).
Another unifying concept emerging from low-d magnetism is that of nonlinear excitations or domain walls such as solitons or kinks; excitations that can either be static (and topological) or dynamic. These occur when the ground state of the system is degenerate, as is the case for an Ising ferromagnet where the spin-up and -down ground states are distinct but have the same energy. Here, low-d magnets provided some of the simplest experimental systems to study these physical phenomena having very broad applicability. For instance, the absence of long-range magnetic order in an Ising ferromagnetic (FM) chain becomes immediately clear when one realizes that this system is unstable with respect to thermal excitations such as kinks, which are an effective means of destroying long-range correlations. For d ∼ 2 the analogue of the kink in Ising systems is the boundary around a droplet created, for example, by a fraction of up spins in a background sea of down spins. In summary, low-d magnetism has been characterized by a long-standing, strong interaction between theory and experiments, with both developing in parallel but with a continuous cross fertilization.
Historical Models of Interacting Magnetic Moments
The Ising Model
The Ising model corresponds to an ideal lattice of identical magnetic moments positioned at all lattice sites. For each elementary moment, or spin, only two states are possible (spin “up” and “down”). The lattice site r is associated with a variable σr whose two values ±1 corresponding to both spin orientations. The Hamiltonian:
| 1 |
is attributed to a fixed configuration of spins {σ}. Usually, only the nearest-neighbor interaction is considered, or J(r) = 0 for all r ≠ ai, where the ai’s are the basic vectors of a lattice. This is the simplest model for a highly anisotropic magnet. The J(r) are the exchange integrals and h is the magnetic field (in units of gμB). In the simplest scenario, the nonzero quantities J(r) are assumed to be independent of the direction of r. For h = 0, the Hamiltonian is invariant with respect to a change in the sign of the spins. This transformation together with its identical one forms the symmetry group Z2 for the Ising model. The Ising model was proposed by Lenz,36 but Ising33 presented the exact calculation of the partition function for the 1 – d case. A great success was achieved by Onsager,34 who calculated the partition function for the 2 – d case. Onsager demonstrated the existence of the second-order phase transition, and this stimulated intense subsequent theoretical and experimental investigations on critical phenomena.
The XY Model
Magnets with an easy plane of magnetic anisotropy can be described by the XY model which corresponds to a lattice of classical spins rotating in a plane and interacting with each other via the Hamiltonian:
| 2 |
The spins are fixed with respect to their angles of rotation ϕ(r). Their value S is assumed to be constant. The summation in eq 2 proceeds over the nearest-neighbor sites of the lattice. J is the exchange constant. The ground state is FM for J > 0 on an arbitrary lattice. In the opposite case J < 0, the ground state is antiferromagnetic (AF) if the lattice can be decomposed into two sublattices with the nearest-neighbor spins belonging to each sub-lattice. In the case of the triangular lattice with J < 0 the ground state consists of three sublattices with the spins in the different sublattices tilted at angles of ±120°. An external magnetic field fixes the orientation of the spins in ferromagnets and in antiferromagnets with two sublattices. In the last scenario, the spins are directed almost perpendicularly to the field direction. In the case of a three-sublattice antiferromagnet, the external magnetic field does not interfere with the freedom of spin rotation inherent to the ground state. The simplest excitations of a planar magnet, as described through the XY model, are spin-waves with a gapless spectrum, according to the Goldstone theorem. The static aspect of the Goldstone theorem implies an enhancement of the spin fluctuations at long wavelength, and this enhancement is precisely the starting point in the proof of the Landau-Peierls theorem37,38 stating that there is no long-range order in 2-d systems having a continuous symmetry. As discussed below, a rigorous proof for this theorem was given by Hohenberg39 for superfluids which have the same symmetry as a planar magnet, and by Mermin and Wagner40 for Heisenberg magnets. These proofs are based on the thermodynamic inequalities proposed by Bogolyubov.41
The Heisenberg Model
In the subsequent text, the symbol “d” is used for the dimensionality of the magnetic lattice, d = 1, 2, 3, corresponding to magnetic chains, magnetic layers, and three-dimensional (3D) arrays of magnetic moments, respectively. These three classes of magnetic systems may be further subdivided according to the type of magnetic interactions assumed to exist between the spins. If one restricts oneself only to interactions between nearest neighbors, one can write a generalized Heisenberg Hamiltonian that captures the essence of the several other historical models discussed below:
| 3 |
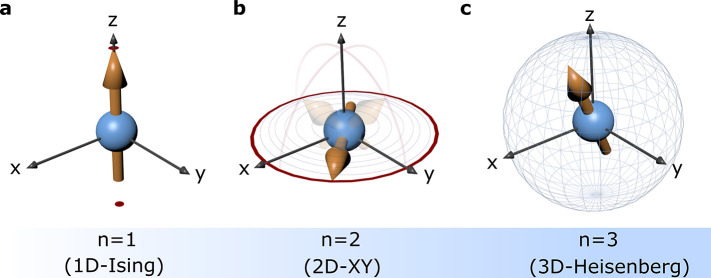
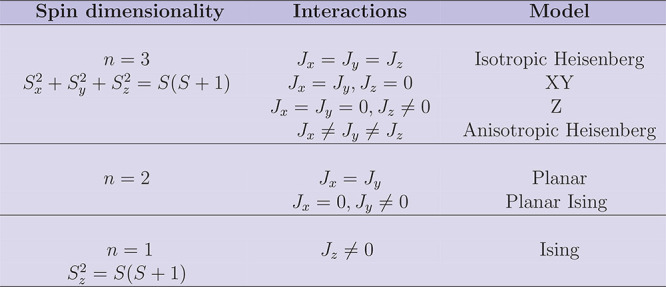
where the Js are the exchange couplings between spins Si and Sj on neighboring sites (with either FM, i.e., J > 0, or AF, J < 0, order), while Jz and D can, for a 2d system, be considered as the “on-site” and the “inter-site” magnetic anisotropies, respectively. In addition, depending on the number n of components (x, y, z) of the individual spins that are being considered, one has a one, two, or three component spin system. n is the spin-dimensionality (Figure 2), not to be confused with the lattice-dimensionality d. For a given n(>1), and for D = 0, one may in addition vary the number of interacting spin components by considering different combinations of Jx, Jy, and Jz as illustrated in Table 1.
Figure 2.
Role of spin dimensionality n on the 3D-axis. (a) n = 1; 1D Ising type, where spins point in either up or down along a given direction (e.g., easy axis). (b) n = 2; 2D XY type, where spins are constrained to a given plane (easy-plane anisotropy) without any restriction on which plane (e.g., XY, XZ, YZ). (c) n = 3; 3D isotropic Heisenberg type, where spins have no constraints on the direction assuming any position along the 3D sphere.
Table 1. Classification of model systems based on single-neighbor Heisenberg Hamiltonian including inter-site magnetic anisotropya.
Adapted with permission from ref (42). Copyright 1990 Springer.
This Hamiltonian can be further generalized by adding terms that describe exchange couplings with second, third, and more neighbors. The spin itself can also be varied by including quantum mechanical operators (S = 1/2, 1, 3/2, etc.) or classical spins (S = ∞).
Table 2 below conveys how past theoretical and experimental investigations on phase transitions revealed how the lattice-dimensionality d and the spin-dimensionality n influence the critical behavior of many-body systems.
Table 2. Either the absence (X) or the presence (checkmark symbol) of a phase-transition towards conventional long-range order at finite temperatures in model Hamiltoniansa.
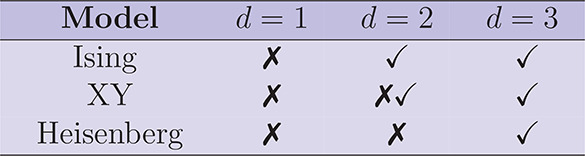
The simultaneous presence of both symbols in the 2d-XY model indicates the presence of quasi-long-range order characterized by a correlation function that falls off as power law below T = TKT. Adapted with permission from ref (42). Copyright 1990 Springer.
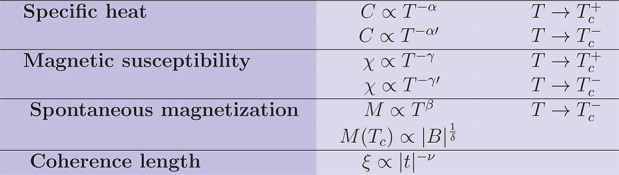
For systems displaying long-range order, mean-field (MF) theory becomes inadequate around the critical point; it cannot accurately describe the critical behavior, or the singularities occurring in the thermodynamic functions at the critical temperature Tc. The body of past experimental and theoretical studies established that in most cases the critical behavior of a thermodynamic function f(t) follows a power law in the reduced temperature t, where t = 1 – Tc/T for T > Tc and t = 1 – T/Tc for T < Tc. The critical exponents appearing in those power laws are defined as in Table 3.43
Table 3. Definition of the critical exponents associated to specific thermodynamic or physical variablesa.
Adapted with permission from ref (42). Copyright 1990 Springer.
The value of the critical exponents numerically extracted from the different models is displayed in Table 4.
Table 4. Comparison among the theoretical values for the critical exponents α, β, γ, δ, and ν according to the different models.
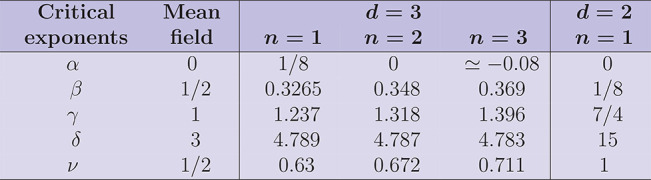
These critical exponents follow scaling relations such as α + 2β + γ = 2, or γ = β(δ – 1), or 2β + γ = dν, implying that only two of the exponents are independent, so that from the knowledge of two arbitrary indices, all the others can be derived (see Magnetic Critical Behavior section for additional discussion).44,45,47,48,49
Table 5. Critical temperature Tc for the different modelsa.

where C is a numerical coefficient, S is the spin on each site, and z and zL are the intra- and interlayer coordination numbers. Assuming in the 3D case a layered structure with |JL/J|≪ 1, where J and JL are the intralayer and the interlayer exchange couplings, respectively. In the case of the 2D Ising model (d = 2, n = 1), the reported expression refers to a square lattice.
Magnetic Critical Behavior
Critical Exponents and Magnetic Equation of State
We
start with descriptions of several standard critical exponents, and
we sketch the phenomenological scaling theory of critical behavior.50−53 Let us consider a ferromagnet in equilibrium at temperature T and in uniform magnetic field H. We use
the reduced temperature variable ε = (T – Tc)/Tc, where Tc is the critical temperature. We are interested in properties
as ε → 0 with H = 0. Near phase transition,
magnetic systems are characterized by power law behavior sufficiently
close to the critical point. Specific heat Cp, the spontaneous magnetization Ms, and the inverse initial magnetic susceptibility 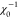 as well as the correlation length
ξ
can be described by Cp(T) ∝ (−ε)α, Ms(T) ∝ (−ε)β,
as well as the correlation length
ξ
can be described by Cp(T) ∝ (−ε)α, Ms(T) ∝ (−ε)β, 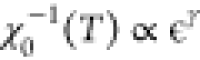 , M ∝ H1/δ, and ξ ∝ε–ν, where ε = (T – Tc)/Tc is the reduced temperature.54 Another
exponent η describes the spatial decay of the correlation function
at criticality Γ(r) ∝ r–d+2−η, where d denotes the spatial dimensionality of the system.55 As described above, the exponents α, β,
γ, δ, η, and ν are called critical exponents.
The phenomenological scaling theory predicts that the critical exponents
are connected by the scaling laws α + 2β + γ = 2
(Rushbrooke), γ = (2 – η)ν (Fisher), γ
= β(δ – 1) (Widom), 2 – α = νd (Josephson), and Δ = βδ = β + γ (Δ is the gap exponent).55−61 The existence of long-range magnetic order at finite temperature
in 2D vdW magnets heavily depends on the spin dimensionality n (n = 1, uniaxial or Ising spins; n = 2, XY or planar spins; n = 3, ordinary
or Heisenberg spins; Figure 2) and on the strength of magnetic anisotropy. The long-range
magnetic order in ideal Heisenberg 2D magnetic system is prevented
by thermal fluctuations based on Mermin-Wagner theorem.40 The presence of strong uniaxial anisotropy of
2D Ising type with n = 1 can open a gap in the spin-wave
spectrum, thus suppressing the effect of thermal fluctuations.62 When n = 2 with an easy-plane
anisotropy, a quasi-long-range topological magnetic order could be
established below the Berezinskii–Kosterlitz–Thouless
transition (TKT) that
is characterized by an algebraic decay of spin correlations and by
the presence of bound pairs of vortex and antivortex arrangement of
spins.62−64 Critical exponents for different theoretical models
in 2D and 3D are listed in Table 4.43,62,65,66
, M ∝ H1/δ, and ξ ∝ε–ν, where ε = (T – Tc)/Tc is the reduced temperature.54 Another
exponent η describes the spatial decay of the correlation function
at criticality Γ(r) ∝ r–d+2−η, where d denotes the spatial dimensionality of the system.55 As described above, the exponents α, β,
γ, δ, η, and ν are called critical exponents.
The phenomenological scaling theory predicts that the critical exponents
are connected by the scaling laws α + 2β + γ = 2
(Rushbrooke), γ = (2 – η)ν (Fisher), γ
= β(δ – 1) (Widom), 2 – α = νd (Josephson), and Δ = βδ = β + γ (Δ is the gap exponent).55−61 The existence of long-range magnetic order at finite temperature
in 2D vdW magnets heavily depends on the spin dimensionality n (n = 1, uniaxial or Ising spins; n = 2, XY or planar spins; n = 3, ordinary
or Heisenberg spins; Figure 2) and on the strength of magnetic anisotropy. The long-range
magnetic order in ideal Heisenberg 2D magnetic system is prevented
by thermal fluctuations based on Mermin-Wagner theorem.40 The presence of strong uniaxial anisotropy of
2D Ising type with n = 1 can open a gap in the spin-wave
spectrum, thus suppressing the effect of thermal fluctuations.62 When n = 2 with an easy-plane
anisotropy, a quasi-long-range topological magnetic order could be
established below the Berezinskii–Kosterlitz–Thouless
transition (TKT) that
is characterized by an algebraic decay of spin correlations and by
the presence of bound pairs of vortex and antivortex arrangement of
spins.62−64 Critical exponents for different theoretical models
in 2D and 3D are listed in Table 4.43,62,65,66
Besides a number of relations between critical exponents, scaling finds specific predictions on the magnetic equation of state: M(H, ε) = εβf±(H/εβ+γ). By using the scaled magnetization m ≡ ε–βM(H, ε) and field h ≡ ε–(β+γ)H, the magnetic equation of state takes the familiar form m = f±(h), where f+ for T > Tc and f– for T < Tc, respectively, are the regular functions. This relates M, H, and T, and it also implies that for the true scaling relations and for the right choice of β, γ, and δ values, scaled m and h will fall on universal curves above Tc and below Tc, respectively. Another commonly used form of the magnetic equation of state is H/Mδ = k(ε/H1/β), where k(x) is the scaling function. The scaled critical isotherms, MH–1/δversusεH–1/(βδ), will collapse into a single curve, and the Tc is located at the zero point of the horizontal axis.
Modified Arrott Plot, Kouvel–Fisher Plot, and Critical Isotherm
In the modified Arrot plot M1/βversus (H/M)1/γ based on the Arrot–Noaks equation of state67
the M(H, T) data taken in the critical region should fall on a set
of parallel straight-line isotherms with the one at T = Tc passing through
origin for a proper choice of the exponents β and γ. Values
β = 0.5 and γ = 1.0 describe the Arrot plot in the mean-field
approximation.68 Critical temperature can
be determined accurately since the isotherm at Tc will pass through the origin. Moreover,
this plot directly gives 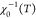 and Ms(T) as the
intercepts on the H/M axis and positive M2 axis, respectively. It is also applicable
to estimate the order
of magnetic transition through the slope of the straight line based
on Banerjee’s criterion.69 First-
(second-) order phase transition corresponds to a negative (positive)
slope.
and Ms(T) as the
intercepts on the H/M axis and positive M2 axis, respectively. It is also applicable
to estimate the order
of magnetic transition through the slope of the straight line based
on Banerjee’s criterion.69 First-
(second-) order phase transition corresponds to a negative (positive)
slope.
Once Ms(T) and 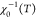 have been obtained
by the modified Arrott
plot, critical exponents β, γ, and Tc can be determined by the Kouvel–Fisher
analytical method with relatively high accuracy: Y(T) = Ms(T)/[dMs(T)/dT] = (T – Tc)/β and
have been obtained
by the modified Arrott
plot, critical exponents β, γ, and Tc can be determined by the Kouvel–Fisher
analytical method with relatively high accuracy: Y(T) = Ms(T)/[dMs(T)/dT] = (T – Tc)/β and 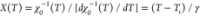 .70 The plots
of Y(T) and X(T) against T are straight lines with slopes
1/β and 1/γ, respectively. The most important advantage
of the Kouvel–Fisher plot is that no prior knowledge of Tc is needed, as the intercept
on the T-axis is at Tc. Both Y(T) versusT and X(T) versusT plots should
yield the same value of Tc which can be used for a precise determination of the exponents.
.70 The plots
of Y(T) and X(T) against T are straight lines with slopes
1/β and 1/γ, respectively. The most important advantage
of the Kouvel–Fisher plot is that no prior knowledge of Tc is needed, as the intercept
on the T-axis is at Tc. Both Y(T) versusT and X(T) versusT plots should
yield the same value of Tc which can be used for a precise determination of the exponents.
An iterative method can be used to obtain the most accurate values
of β, γ, and Tc.71 The linear extrapolation from
the high field region to the intercepts with the axis M1/β and (H/M)1/γ in the modified Arrott plot yields reliable values
of Ms(T) and 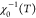 . A set of β
and γ can be obtained
by using the Kouvel–Fisher analytical method. The values of
these exponents are then used to reconstruct the modified Arrott
plot. Intercepts on the axes lead to an additional set of Ms(T) and
. A set of β
and γ can be obtained
by using the Kouvel–Fisher analytical method. The values of
these exponents are then used to reconstruct the modified Arrott
plot. Intercepts on the axes lead to an additional set of Ms(T) and  from which β
and γ values are
derived. This iteration procedure is continued until β and γ
are stable and unaltered by increasing number of iterations. Such
refining process converges very rapidly from a proper initial model
and yields the accurate exponent values β and γ. Another
exponent δ can be determined from the critical isotherm analysis
(M ∝ H1/δ at T = Tc) and the Widom scaling relation δ = 1 + γ/β.
from which β
and γ values are
derived. This iteration procedure is continued until β and γ
are stable and unaltered by increasing number of iterations. Such
refining process converges very rapidly from a proper initial model
and yields the accurate exponent values β and γ. Another
exponent δ can be determined from the critical isotherm analysis
(M ∝ H1/δ at T = Tc) and the Widom scaling relation δ = 1 + γ/β.
Absence of Magnetic Order in 2D: The Hohenberg, Mermin, and Wagner Theorem
Hohenberg published over 50 years ago a rigorous proof for the nonexistence of long-range order in a 2D superfluid or superconductor at finite temperatures.39 This proof was quickly extended by Mermin and Wagner to the Heisenberg Hamiltonian, in one and two dimensions for a Heisenberg ferromagnet (or antiferromagnet) with SU(2) symmetry, or a magnetic system with U(1) symmetry and an order parameter perpendicular to the symmetry axis.40 Soon thereafter, Mermin would prove the absence of translational long-range order in a two-dimensional (2D) crystal, whether in quantum or classical mechanics.72 Nevertheless, after the work by Berezinskii,73 Kosterlitz and Thouless,64,74 and Nelson and Kosterlitz,75 we now know that in two dimensions there will be a sharp transition temperature at a certain TKT, where for T > TKT the associated correlation function will fall off exponentially with the distance. For T < TKT the correlation function is expected to fall off as a power law, leading to what is commonly called as quasi-long-range order, with an exponent α ≥ 3. In contrast, for the Heisenberg model, the order-parameter correlation function decays exponentially with the distance at any nonzero temperature, and therefore there would be no phase transitions at finite temperatures.76 Nevertheless, the Hohenberg, Mermin, and Wagner (HMW) theorem sheds no light on whether quasi-long-range order can exist in any particular system. Hohenberg did note however that his theorem concerning the absence of long-range order for a 2D superfluid or superconductor would remain unaffected by the introduction of long-range interactions between the particles. In contrast, as discussed in ref (76), the absence of long-range order in the Heisenberg ferromagnet depends on the range of the interactions. Assuming J(r) to be the coupling constant between pairs of spins separated by a certain distance r, one can thus define a second magnetic moments as
| 4 |
where α and β denote both planar spatial directions. The absence of long-range magnetic order, as given by the Mermin–Wagner theorem, would require that the values of Kαβ remain finite. However, if the spins are allowed to rotate around an axis symmetry, one would define two coupling constants J∥(r) and J⊥(r) for spin components parallel and perpendicular to such axis of symmetry. Then, Mermin–Wagner would rule out long-range magnetic order for the spin components perpendicular to this axis of symmetry, provided that the second moments for J⊥ remain finite. Such condition is not required for J∥. For FM interactions decaying as r – (n < 4), Kαβ would diverge implying that long-range FM order should be possible in two dimensions, at small, but nonzero temperatures.44 However, it is important to state that the HMW theorem is unable to clarify the existence, or nonexistence, of long-range order in a quantum mechanical system in the limit T = 0 K. Yet, according to Halperin,76 nonrigorous arguments similar to those invoked at finite temperatures suggest that in many circumstances, long-range order would also be impossible at T = 0 K. In fact, in ref (76), Halperin provides a generalization of the HMW argument to rigorously rule out the possibility of ferromagnetism at T = 0 K for any 2D electron model that excludes spin–orbit coupling or magnetic dipole interactions.
Discovery of Magnetism in Exfoliated Monolayers
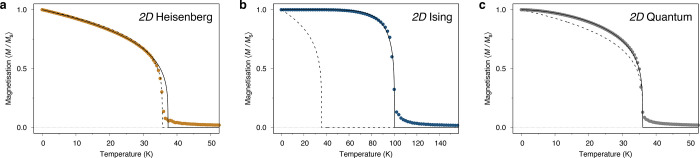
Therefore, it is in the context of the HMW that one should place the discovery of ferromagnetism in exfoliated monolayers of both CrI35 and Cr2Ge2Te66 through the magneto-optical Kerr effect (MOKE). For CrI3, the Curie temperature is found to decrease down to 41 K in the monolayer limit with respect to its bulk value of 61 K, which is a rather modest effect.5Tc in Cr2Ge2Te6 is found to decrease from ∼65 K in the bulk to approximately 30 K in bilayers.6 Interestingly, the nature of the FM order in CrI3 is highly sensitive to the number of layers in the system. In a bilayer, the remnant magnetization present in a single layer is suppressed and is consistent with each layer having oppositely oriented spins or with the material becoming an antiferromagnet. From a theoretical perspective, these results imply that these compounds cannot be described by an isotropic Heisenberg Hamiltonian but are subjected to magneto-crystalline anisotropy which in the case of Cr2Ge2Te6 is claimed to increase considerably upon the application of an external magnetic field. In the CrI3 case, it displays a substantial remnant magnetization in the absence of a magnetic field which is directed perpendicular to the plane of the lattice. Therefore, this magnetic system would be well described by the 2D Ising model.
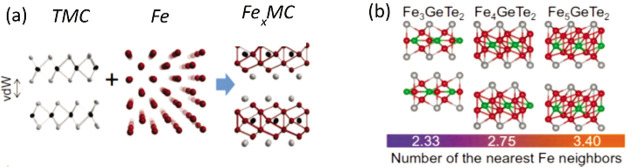
2D Magnets: Recent Progress and Current Challenges
Pioneering work establishing intrinsic ferromagnetism in two-dimensions has been performed on monolayer CrI3,5 Fe3GeTe2,77 and a few-layer Cr2Ge2Te6,6 which are considered now as prototypical 2D magnets. More recently, experimental studies on monolayer CrBr320 and CrCl378 and in few-layer V5Se8, CrTe2, and Cr2Te3 have also been reported.79−81 Whereas in the bulk and few-layer regime the Curie temperatures Tc approach room-temperature, in some of the systems such as in Fe3GeTe277 and CrTe2,81 this ordering is substantially suppressed in the strictly 2D limit, i.e., in the monolayer regime. For instance, exfoliated monolayers of CrBr3, CrI3, and Fe3GeTe2 display, through magnetization measurements, Tc values of 25 K,82 45 K,5 and 130 K,6 respectively, whereas monolayers of CrBr383 and CrCl378 prepared by molecular beam epitaxy (MBE) display Tc values of 16 and 13 K, respectively.78 In contrast, few-layer Cr2Ge2Te6 and V5Se8 are nearly ideal Heisenberg ferromagnets with Tc’s below 60 K, but with weak FM ordering in the truly 2D limit.6,79
The magnetic interactions in bilayer CrI3 and CrBr3 have been found to be highly dependent on the stacking order20 and can be tuned between antiferromagnetic (AF) and ferromagnetic (FM) with magnetic or electric fields8,9 and via applied mechanical pressure.22,23 There is currently a rich palette of 2D magnetic materials ranging from Ising, Heisenberg to XY behavior, and with a diversity of exchange interactions (itinerant, double-, or superexchange)62,84,85 which allow to tailor their magnetic properties on demand. There is no doubt that this enormous progress is of great fundamental interest, but the applications based upon 2D magnets remain limited due to two main current constraints: (i) the magnetic ordering temperature remains well below 300 K and (ii) the lack of synthesis methods that are scalable and produce homogeneous magnetic monolayers over large areas by bottom-up methods.
Enhancing the Magnetic Ordering Temperature in Two Dimensions
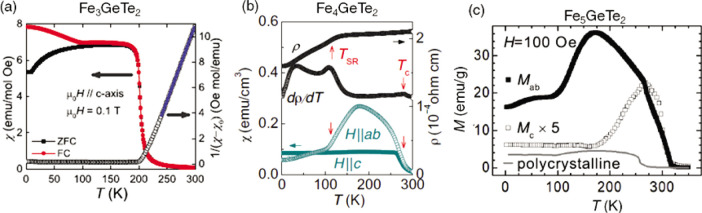
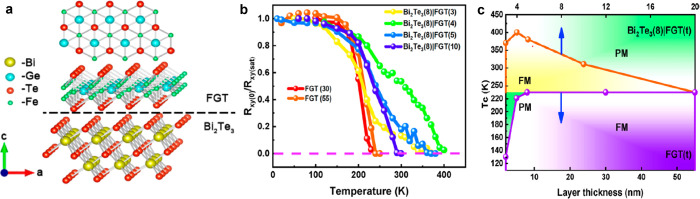
Efforts to achieve room-temperature ferromagnetism in some of these ultrathin layered magnets are currently being pursued. In semiconducting magnets, strong charge doping via ionic liquid gating has been shown to drastically increase the Curie temperature of Cr2Ge2Te6 from 60 K to nearly 200 K.86 In metallic systems such as Fe3GeTe2 (FGT), where electric gating is less efficient,12 alternative methods to increase the ordering temperature have been recently reported, such as changing the Fe stoichiometry in the lattice,87,88 by cobalt codoping89 or by bringing it in proximity to a topological insulator.90 In stoichiometry tuning studies, the composition is varied from FexGeTe2 (x ≃ 3–5), whereby the Tc increases with Fe content, up to 310 K.87,88 A partial substitution with Co-atoms (up to 26%) has been found to further increase the Tc to 328 K, while a further increase in Co-doping induces a concomitant structural and magnetic phase transition to an AF ground state.89 As for the Tc enhancement by proximity effect, an substantial improvement has been achieved in FGT/Bi2Te3 heterostructures, where a thickness dependent increase of the Tc up to 380 K (for FGT having a thickness of 4 nm) was reported.90 These intriguing results are not fully understood, especially whether effects such as strain or doping at the FGT/Bi2Te3 interface play a role in this observation, or if this can be attributed to the exotic topological character of Bi2Te3.
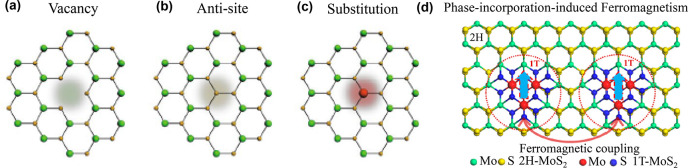
In another recent study, an anomalous enhancement of Tc in Cr2Te3 flakes was found as the thickness of the flake is decreased from 10 to 5.5 nm,80 behaving in an opposite way to nearly all other 2D magnets reported to date. This effect was attributed to doping and reconstruction at the surface of Cr2Te3, leading to a slightly different stoichiometry and interlayer distance. On another front, magnetic impurity doping and defect-induced magnetism of otherwise nonmagnetic transition-metal dichalcogenides (TMDs) is being attempted. Whereas defect-induced magnetism found in PtSe2 flakes91,92 results in a very low Curie temperature, transition-metal doping is found to boost the Tc as high as room temperature, as reported in V-doped WSe2 monolayers grown by a powder vaporization method.93 In another experimental study, room-temperature ferromagnetism was found in MoTe2 doped with a nonmagnetic element, i.e., Ta.94 This set of results coming from monolayers and nanosheets synthesized and doped through chemical vapor methods are quite intriguing and merit more experimental investigations. In this regard, it is also worth mentioning early works on room-temperature ferromagnetism in monolayer 1T-VSe218 and MnSe217, which could not be reproduced by other groups. Such systems have remained controversial as they relied mainly on volumetric magnetometry measurements of monolayers on large-volume substrates.
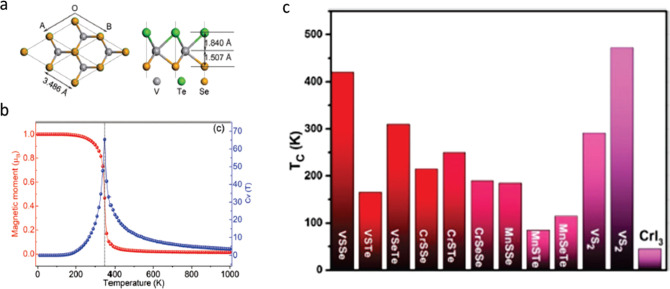
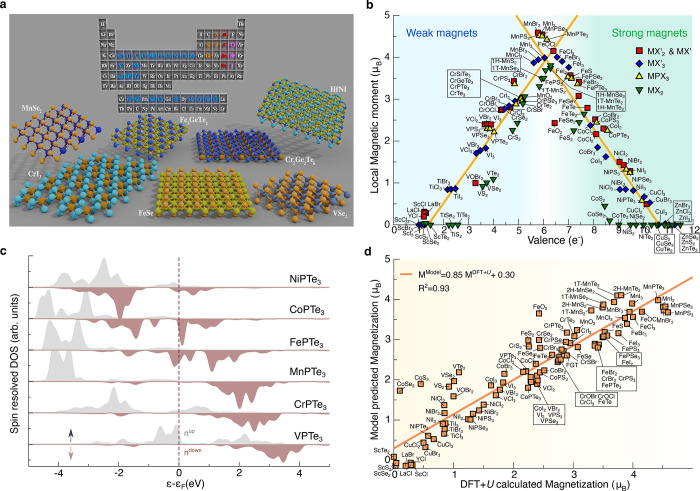
This urgent need for a room-temperature 2D magnet has recently caught the attention of many theoretical groups, from which a large number of high-Tc 2D magnetic materials has been predicted.95 For the sake of briefness, we are going to highlight only a couple of structural material families: (i) Janus monolayers of TMDs (MXY compounds, M: Cr, V, Mn and X, Y: Se, Te, S)96,97 and (ii) Cr-based III–V semiconducting layered compounds (CrP, CrAs),98 both of which have certain compounds in their structural families that reach well beyond room-temperature, at least from ab initio calculations. As for the TMD Janus systems, VSeS96 and VSeTe96,97 are the ones attaining a Tc above room temperature, with values of 420 K96 and 310 K96 (350 K),97 respectively, as shown in Figure 2. With regard to the III–V semiconducting compounds, CrP is found to order ferromagnetically up to 230 K,98 whereas calculations on CrAs show an easy-plane magnet behavior with an astonishingly high transition temperature of 855 K98 (albeit being expected to be of Berezinskii–Kosterlitz–Thouless type, or to display quasi-long-range order). These particular theoretical studies highlighted here are certainly going to trigger experimental investigations, given the ability to grow TMDs and III–V compounds by several bottom-up methods, such as MBE.
Toward the Fabrication of Scalable, Large-Area 2D Magnets
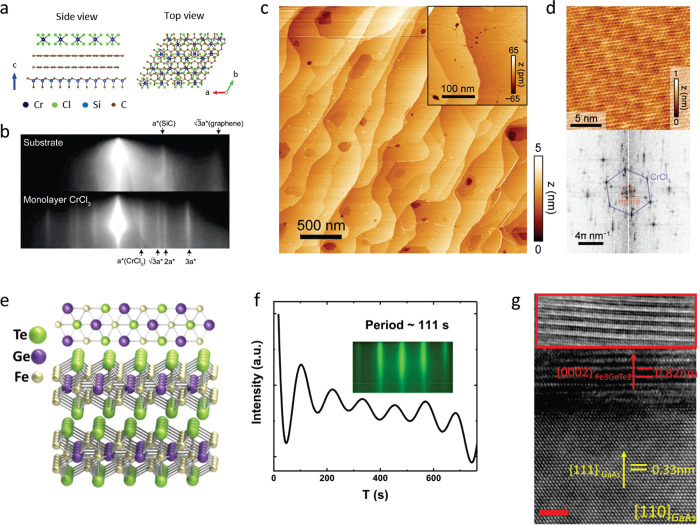
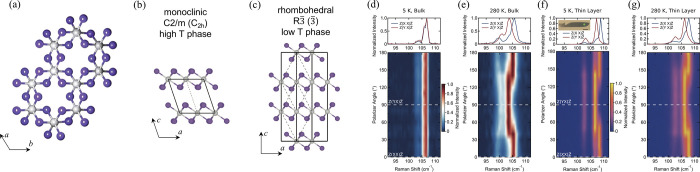
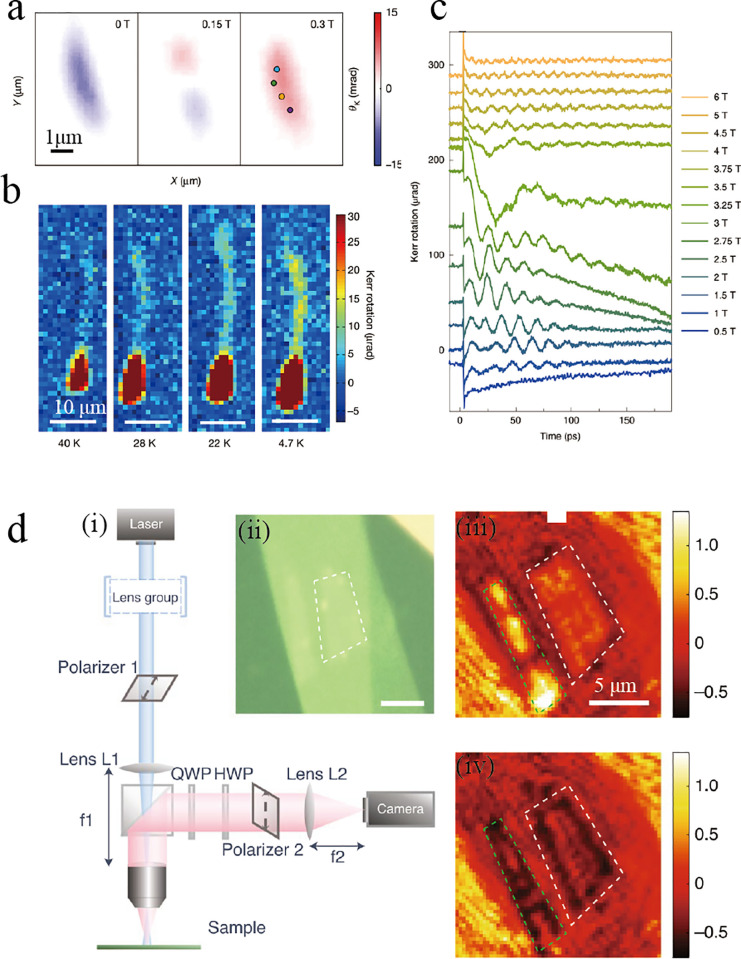
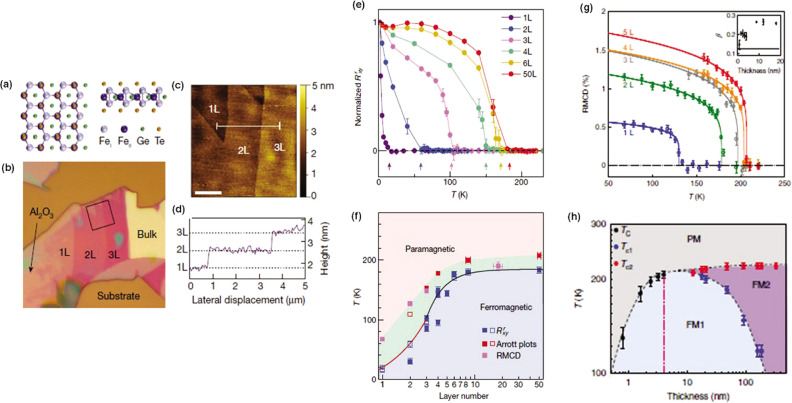
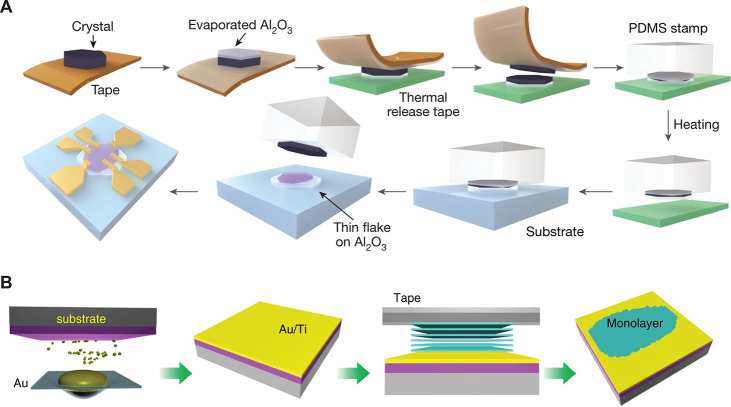
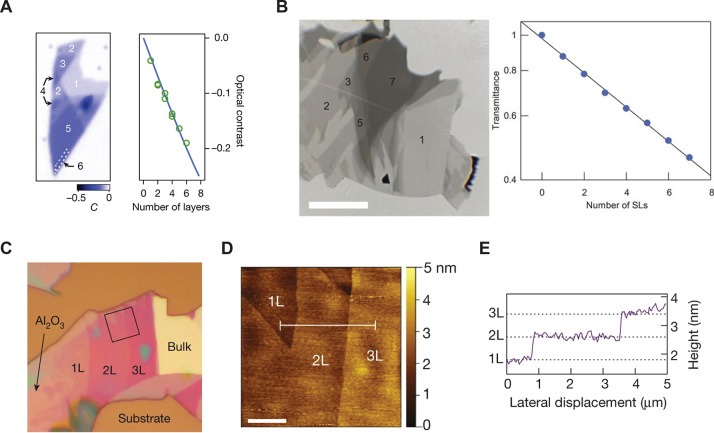
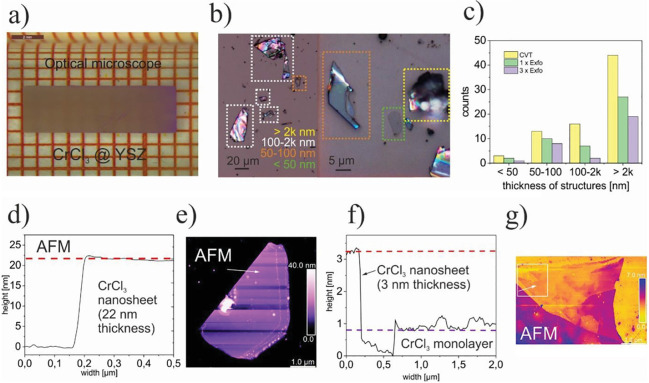
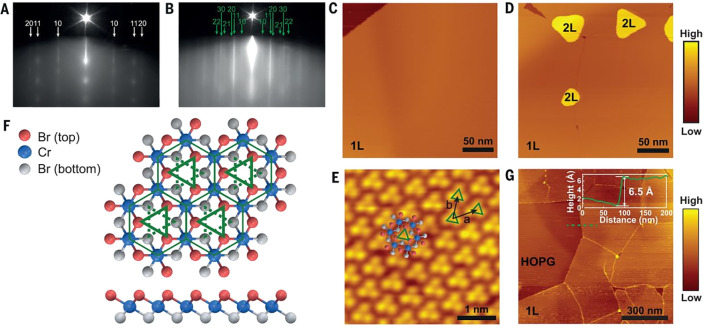
The synthesis of bulk layered magnets have a long history, but it is the recent technical breakthrough in exfoliation, isolation and encapsulation of 2D materials, that made possible to study magnetism in the truly 2D regime. Despite the enormous progress in preparing high-quality flakes and heterostructures of 2D materials, the exfoliated samples have dimensions of a few microns and frequently present an irregular shape, which represents a major limitation for their use in scalable device applications. An alternative fabrication strategy, which has been less popular than exfoliation due to its increased cost and the long material optimization process, is to use bottom up methods such as chemical vapor deposition (CVD) or MBE for the synthesis of 2D magnets. While the growth of only one family, that of doped (V- and Cr) TMDs, has been achieved by CVD so far,100 MBE has been successful in preparing a couple of 2D magnetic systems such as monolayered CrBr320,83 and CrCl378 and few-layer V5Se879 and Fe3GeTe290,99 with Curie temperatures lower than in their bulk counterparts (Figure 5). In the monolayer regime, the magnetism of CrBr3 was studied by local spin-polarized scanning tunneling microscopy (STM)20 and magneto-optical Kerr-effect (MOKE),83 the latter yielding a Tc of 20 K. In the case of CrCl3, a homogeneous monolayer coverage over large areas was achieved on Graphene/SiC(0001) substrates (see Figure 3), whereas the magnetic properties were evaluated via X-ray magnetic circular dichroism (XMCD) over larger areas, yielding a Tc of 13 K and a sizable easy-plane magnetic anisotropy.78 On top of the efforts to grow wafer scale 2D magnets by MBE (Figure 5), the selection and deposition of suitable capping layers to protect these materials from oxidation is a key step toward device processing.
Figure 5.
Examples of large-area 2D magnets grown by MBE. (a–d) Monolayer CrCl3 on Graphene/SiC(0001) and (e–g) few-layer Fe3GeTe2 on GaAs (111). (a) Schematic crystal structure of CrCl3/graphene/6H-SiC layers in top-down view and cross-section view. (b) In situ RHEED pattern of the substrate and monolayer CrCl3 grown by MBE, along Γ–M of graphene (Γ–K of SiC). Streaks from different high-symmetry directions of CrCl3 are observed, implying a twisted in-plane orientation of the grains. (c) STM topography of a monolayer CrCl3 grown on graphene/6H-SiC(0001), indicating a homogeneous coverage on long length scales. Inset: A magnified topography image, which reveals the grain boundaries. (d) Atom resolved image of the CrCl3 lattice featuring a moiré pattern (upper panel) and its Fourier transformed image (lower panel). Panels (a–d) adapted with permission from ref (78). Copyright 2021 AAAS. (e) Crystal structure of Fe3GeTe2. (f) RHEED oscillations indicating layer-by-layer growth of Fe3GeTe2 (0001) on GaAs (111), and the corresponding electron diffraction pattern (inset). The inferred growth rate is 111 s per monolayer. (g) Transmission electron microscopy of a Fe3GeTe2/GaAs cross-section, indicating the (111)/(0002) epitaxial relationship. Panels (e–g) adapted with permission under a Creative Commins CC BY license from ref (99). Copyright 2017 Springer Nature.
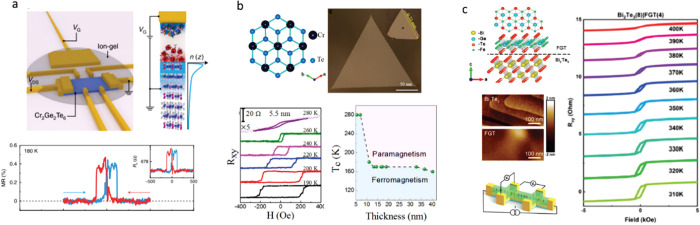
Figure 3.
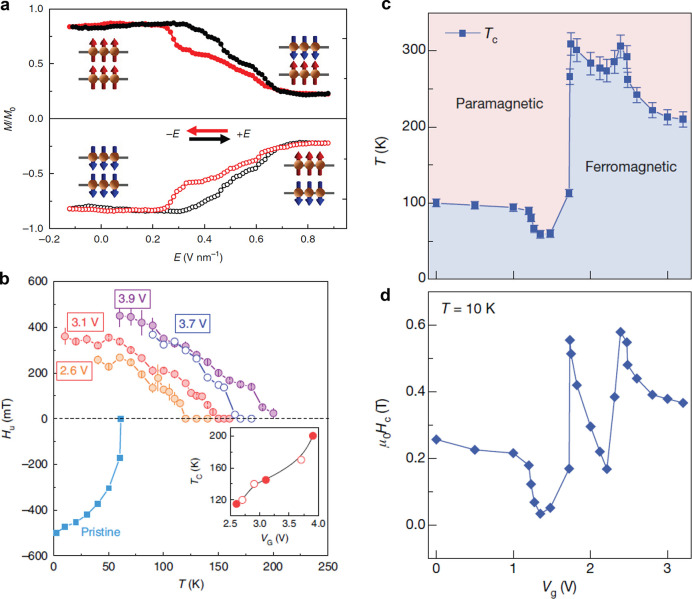
Routes toward room-temperature FM ordering in 2D layered materials by (a) electrostatic gating, (b) tuning dimensionality, and (c) proximity effect. Representative experimental examples include: (a) ionic liquid gating in Cr2Ge2Te6, achieving a dramatic increase from 60K to 180 K in the ordering temperature. Adapted with permission from ref (86). Copyright 2020 Springer Nature. (b) Substantial Tc enhancement in Cr2Te3 flakes as the thickness is reduced, measured by anomalous Hall effect. Adapted with permission from ref (80). Copyright 2020 American Chemical Society. (c) Persistent magnetic signals up to 380 K in 4 nm-thick Fe3GeTe2 interfaced with the topological insulator Bi2Te3. Adapted with permission from ref (90). Copyright 2020 American Chemical Society.
Figure 4.
Theoretical calculations for the Curie temperature in TMD Janus systems. (a) Diagram of the VSeTe crystal structure in top-down and cross-sectional views. (b) Temperature-dependent magnetic moment and specific heat of VSeTe, obtained via Monte Carlo simulations in a nearest-neighbor Heisenberg exchange model. Panels (a) and (b) reprinted with permission from ref (97). Copyright 2009 Royal Society of Chemistry. (c) Curie temperatures of V-, Cr- and Mn-based Janus TMDs, highlighting VSSe and VSeTe as the candidates with highest Tc. Adapted with permission from ref (96). Copyright 2018 Elsevier.
Device Implementations and Basic Concepts
Magnetoresistance
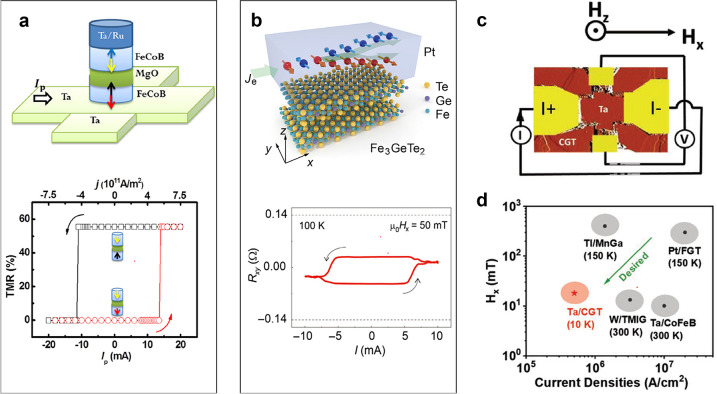
For spintronic device applications, a crucial material property is magnetoresistance—a dynamic and reversible change in sample resistance under varying magnetic field. Magnetic materials and their heterostructures can manifest exceptionally large switchable magnetoresistance due to a change in the magnetic structure or spin configuration upon the application of a magnetic field. There are two prominent strategies for exploiting magnetoresistance from magnetic compounds in functional electronics. One is engineering atypically large magnetoresistance through the fabrication of multilayer heterostructures such as MTJs. The concept was demonstrated independently by Baibich et al.101 and Binasch et al.,102 in which multilayer films consisting of adjacent FM electrodes leads to giant negative magnetoresistance when switching from an AF to FM configuration.101−103 Since then, MTJs have been further optimized to increase the magnetoresistance by changing the geometry to either two FM metals separated by an insulating barrier (conventional spin valves) or two nonmagnetic metals with an (anti)ferromagnetic barrier (less conventional spin filter). Despite numerous efforts to enhance the performance of MTJs over many decades, they still suffer from issues such as retaining the crystallinity and magnetization of ultrathin magnetic films and enlarging the tunnelling magnetoresistance (TMR) which prevent miniaturization of high-performance devices. The second approach is utilizing the high degree of electronic tunability of intrinsically magnetic 2D semiconductors (or 2D metals with high density ionic gates) to provide control over both charge and spin carriers, allowing for complete spin polarization of their conduction electrons. By exploiting the spins of electrons as information carriers, instead of their charge, these materials promise to improve the speed, density, and energy efficiency of electronic devices through single-spin transport.104−106 They are particularly attractive for device applications that utilize both the electronic tunability and spin-polarized transport in lateral MTJs and spin field effect transistors.107,108 The recent discovery of magnetism in atomically thin vdW materials, coupled with the diversity of their observed electronic properties including insulators (CrCl3, CrBr3, CrI3), semiconductors (CrSBr, Cr2Ge2Te6), and metals (Fe3GeTe2, Fe5GeTe2, CrTe2), makes vdW magnets exceptionally attractive for nanospintronic applications (see Spintronics: From Fundamentals to Devices section for details). An unusual property of 2D magnets is the abundant observation of strong intralayer magnetism with high magnetic anisotropy, which allows for the existence of magnetic order in the 2D limit, with weak interlayer coupling, which often results in layer-dependent spin ordering.5 These features, tied with the observed high crystallinity and low disorder characteristics of the parent compounds without forming dangling bonds in the 2D limit, make vdW magnets especially attractive for the fabrication of MTJs.13−16,109 The layered magnetic properties of vdW magnets also manifest as large intrinsic magnetoresistance in conducting vdW magnets,12,86,110,111 which, when paired with the high degree of electronic tunability obtained through electrostatic gating in the 2D limit, offers flexible control over both electronic and magnetic properties12,86,111 in transport devices fabricated with vdW magnets.
Spin Filtering Effect
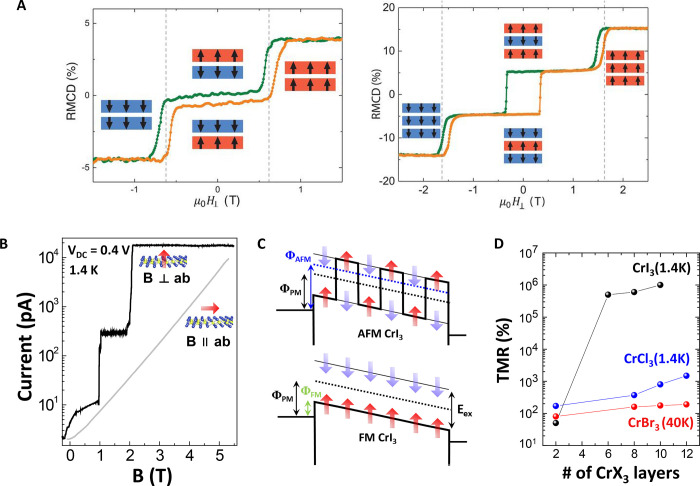
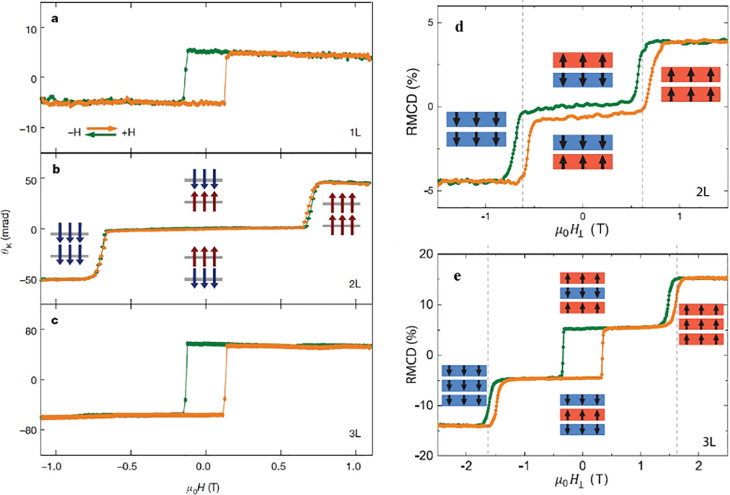
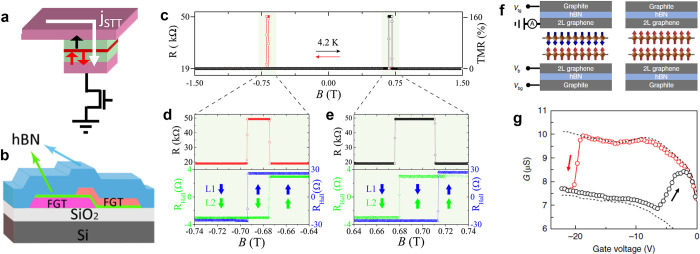
In fabricating MTJs from vdW materials, a particularly useful property is the existence of a layered AF ground state such as the one observed in CrI3, CrCl3, and CrSBr (Figure 6A for representative CrI3 case). It is worth noting that this layered AF structure is usually artificially made113,114 in traditional heterostructures, as it is rarely naturally occurring. Consequently, fabricating multiple-layered AF structures is prohibitively difficult with existing fabrication techniques. Although it is possible to realize the conventional spin-valve device using two FM metallic flakes separated by an insulating or semiconducting material109,115 (see Spintronics: From Fundamentals to Devices section for details), the exotic spin configuration of a layered AF ground state in 2D magnets gives rise to a substantial spin-filtering effect. From the point of view of MTJs, vdW magnets having layered AF structure are attractive as a tunnel barrier since the number of AF layers is determined purely by the thickness of the flakes and the naturally formed multiple antiparallel spin configurations can trigger enormous TMR values. Accordingly, several groups have reported TMR in vdW MTJ devices incorporating multilayer CrI3 as the insulating tunnel barrier sandwiched between graphene electrodes.13−16 The TMR at 1.4 K has been found to be as large as 106% under a 2T magnetic field as shown in Figure 6B, which is ∼103 times larger than a previous world record of giant magnetoresistance in a pseudospin-valve MTJ device with a MgO tunnel barrier.116
Figure 6.
Enormous TMR in vdW MTJs induced by layered antiferromagnetism. (A) Reflective magnetic circular dichroism (RMCD) of bilayer (left) and trilayer (right) CrI3 showing layer-dependent magnetism. Reproduced with permission from ref (13). Copyright 2018 AAAS. (B) Magnetic-field-dependent current change in a vdW MTJ incorporating magnetic CrI3. (C) Schematic energy diagrams of CrI3-based MTJs with AF barrier (top) and FM barrier (bottom). Panels (B and C) are adapted with permission from ref (16). Copyright 2018 American Chemical Society. (D) Summary of TMR values as a function of thickness. Reproduced from ref (112). Copyright 2019 American Chemical Society.
Given that the origin of the TMR value is due to the barrier height difference between the antiparallel and the parallel multistacks16 (which results in an exponential increase in TMR) as shown in Figure 6C, it is suspected that the performance could be enhanced further by finding materials with larger exchange splitting and lower barrier heights. Other chromium trihalides such as CrBr3 and CrCl3 have been studied, but CrI3-based MTJs still exhibit the highest TMR values due to the largest splitting combined with a narrow bandgap,112,117−120 as shown in Figure 6D. Another advantage of vdW MTJs is that the magnetic properties are easily tuned by external factors (electric fields,11 doping,8,9 and pressure22,23). Such a high degree of tunability can potentially give significant performance breakthroughs in future MTJ-based devices. Despite the promising possibilities of vdW MTJs, there are still myriad challenges remaining before vdW MTJs are useful for practical applications. These include finding higher Tc materials for room-temperature operation, developing nonvolatile functionality for memory applications, reducing the operation field for low power consumption, increasing the junction conductance while retaining high TMR, and enhancing the ambient/chemical stability for more reliable fabrication processes.
Lateral Transport Properties
A few conducting vdW magnets
manifest intrinsic magnetoresistance, including the semiconducting
CrSBr110 and Cr2Ge2Te6,86 the metallic Fe3GeTe2,12,77 and the topological
insulator MnBi2Te4.111 CrSBr and MnBi2Te4 are both vdW antiferromagnets
which manifest strong intraplanar ferromagnetism with weak layered
antiferromagnetism.110,121 CrSBr, a functional semiconductor
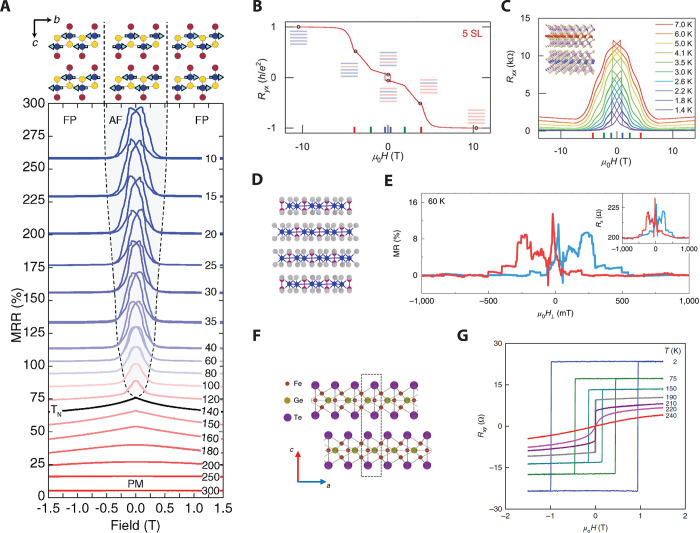
with an easy axis aligned parallel to the sample planes,110,122 exhibits a large negative magnetoresistance of ∼ −40%
at 10 K with a low saturation field of 0.5 T along the easy axis (Figure 7A).110 This behavior is attributed to the suppression of interlayer
tunnelling in the AF phase due to spins in adjacent planes having
opposite magnetization. In the fully polarized state (in which all
spins are aligned with an external magnetic field), interlayer tunnelling
is restored, leading to a decrease in the overall sample resistance.
In the few-layer limit, vdW materials with layered antiferromagnetism
have a layer-dependent ordering; odd layers functionally behave as
a ferromagnet due to a nonvanishing magnetic moment at zero magnetic
field.111 For example, a 5-layer flake
of MnBi2Te4 exhibits magnetic behavior reminiscent
of a ferromagnet at zero field followed by a series of magnetic states
due to the flipping of spins in adjacent layers upon the application
of an out-of-plane magnetic field. The various magnetic states manifest
as steps in the Hall resistance (Figure 7B). Due to the nontrivial band topology,
the Hall resistance quantizes to 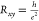 at the saturation field (∼6 T) from
the formation of quantum anomalous Hall states. Accompanying this
discovery was the observation of a giant negative magnetoresistance
in the longitudinal resistance (Figure 7C).111 In layered ferromagnets,
similar magnetoresistance features can be observed. In a 22 nm-thick
flake of Cr2Ge2Te6(Figure 7D), a sizable magnetoresistance
of ∼13% was observed in the longitudinal transport (Figure 7E) with a saturation
field <500 mT. Since the magnetoresistance displayed significant
hysteresis and the easy axis is out-of-plane, the large magnetoresistance
is credited to the spontaneous magnetization of magnetic domains characteristic
of ferromagnets. In metallic layered ferromagnets such as Fe3GeTe2 (Figure 7F),12 large magnetoresistance can
arise from the anomalous Hall effect;12,77,123 the Hall resistance displays a sharp switching hysteresis
at the saturation field (Figure 7G). Beyond the magnetoresistance behaviors observed
in vdW magnets with layered magnetic configurations, an advantage
of 2D vdW magnets is the observed sensitivity to electrostatic doping,12,86,111 which has demonstrated the ability
to increase the magnetic ordering temperature up to room temperature.12
at the saturation field (∼6 T) from
the formation of quantum anomalous Hall states. Accompanying this
discovery was the observation of a giant negative magnetoresistance
in the longitudinal resistance (Figure 7C).111 In layered ferromagnets,
similar magnetoresistance features can be observed. In a 22 nm-thick
flake of Cr2Ge2Te6(Figure 7D), a sizable magnetoresistance
of ∼13% was observed in the longitudinal transport (Figure 7E) with a saturation
field <500 mT. Since the magnetoresistance displayed significant
hysteresis and the easy axis is out-of-plane, the large magnetoresistance
is credited to the spontaneous magnetization of magnetic domains characteristic
of ferromagnets. In metallic layered ferromagnets such as Fe3GeTe2 (Figure 7F),12 large magnetoresistance can
arise from the anomalous Hall effect;12,77,123 the Hall resistance displays a sharp switching hysteresis
at the saturation field (Figure 7G). Beyond the magnetoresistance behaviors observed
in vdW magnets with layered magnetic configurations, an advantage
of 2D vdW magnets is the observed sensitivity to electrostatic doping,12,86,111 which has demonstrated the ability
to increase the magnetic ordering temperature up to room temperature.12
Figure 7.
Summary of intrinsic magnetoresistance in vdW magnets.
(A) Magnetoresistance
ratio MRR(B) 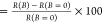 in bulk CrSBr versus magnetic
field (parallel to the b-axis) at various temperatures.
Each MRR curve is offset for clarity. The solid black line is an MRR
curve taken near the Néel temperature. The antiferromagnetic
(AF), fully polarized (FP), and paramagnetic (PM) phases are labeled,
and the phase boundary is denoted by dashed black lines. Schematics
showing the orientation of the spins in the AF and FP states are given
above the plot.110 Reproduced with permission
from ref (110). Copyright
2020 John Wiley and Sons. (B) Ryx of a 5-layer MnBi2Te4 sample as a function
of external magnetic field applied perpendicular to the sample plane
at T = 1.6 K. Data are symmetrized to remove the Rxx component.111 (C) Rxx of
a 5-layer MnBi2Te4 flake as a function of magnetic
field acquired at various temperatures. Data are symmetrized to remove
the Ryx component. Inset
shows the layered crystal structure of MnBi2Te4 in the AF state.111 Panels (B) and (C)
are reproduced with permission from ref (111). Copyright 2020 AAAS. (D) Ball and stick model
of the Cr2Ge2Te6 crystal structure.86 (E) Magnetoresistance
in bulk CrSBr versus magnetic
field (parallel to the b-axis) at various temperatures.
Each MRR curve is offset for clarity. The solid black line is an MRR
curve taken near the Néel temperature. The antiferromagnetic
(AF), fully polarized (FP), and paramagnetic (PM) phases are labeled,
and the phase boundary is denoted by dashed black lines. Schematics
showing the orientation of the spins in the AF and FP states are given
above the plot.110 Reproduced with permission
from ref (110). Copyright
2020 John Wiley and Sons. (B) Ryx of a 5-layer MnBi2Te4 sample as a function
of external magnetic field applied perpendicular to the sample plane
at T = 1.6 K. Data are symmetrized to remove the Rxx component.111 (C) Rxx of
a 5-layer MnBi2Te4 flake as a function of magnetic
field acquired at various temperatures. Data are symmetrized to remove
the Ryx component. Inset
shows the layered crystal structure of MnBi2Te4 in the AF state.111 Panels (B) and (C)
are reproduced with permission from ref (111). Copyright 2020 AAAS. (D) Ball and stick model
of the Cr2Ge2Te6 crystal structure.86 (E) Magnetoresistance 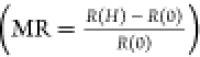 curves
for T = 60 K and
back-gate voltage of 3.9 V for a 22 nm-thick Cr2Ge2Te6 flake. The background is removed for clarity.
The magnetic field is applied in the out-of-plane direction. Unprocessed
data are shown in the inset.86 Panels (D)
and (E) are reproduced with permission from ref (86). Copyright 2020 Springer
Nature. (F) Side view of the atomic lattice of bilayer Fe3GeTe2. The dashed rectangular box denotes the crystal
unit cell.77 (G) Temperature-dependent
magnetic field (out-of-plane) sweeps of the Hall resistance measured
on a 12 nm thick Fe3GeTe2 flake.77 Panels (F) and (G) are reproduced with permission
from ref (77). Copyright
2018 Springer Nature.
curves
for T = 60 K and
back-gate voltage of 3.9 V for a 22 nm-thick Cr2Ge2Te6 flake. The background is removed for clarity.
The magnetic field is applied in the out-of-plane direction. Unprocessed
data are shown in the inset.86 Panels (D)
and (E) are reproduced with permission from ref (86). Copyright 2020 Springer
Nature. (F) Side view of the atomic lattice of bilayer Fe3GeTe2. The dashed rectangular box denotes the crystal
unit cell.77 (G) Temperature-dependent
magnetic field (out-of-plane) sweeps of the Hall resistance measured
on a 12 nm thick Fe3GeTe2 flake.77 Panels (F) and (G) are reproduced with permission
from ref (77). Copyright
2018 Springer Nature.
The Role of Spin Waves in Tunnelling Devices with Ferromagnetic Barriers
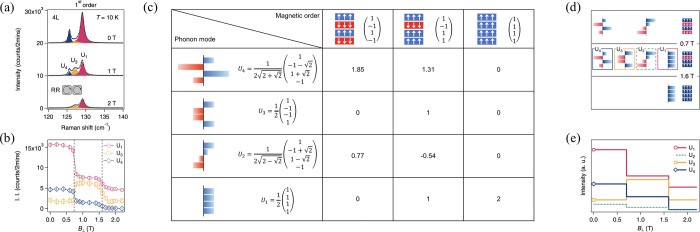
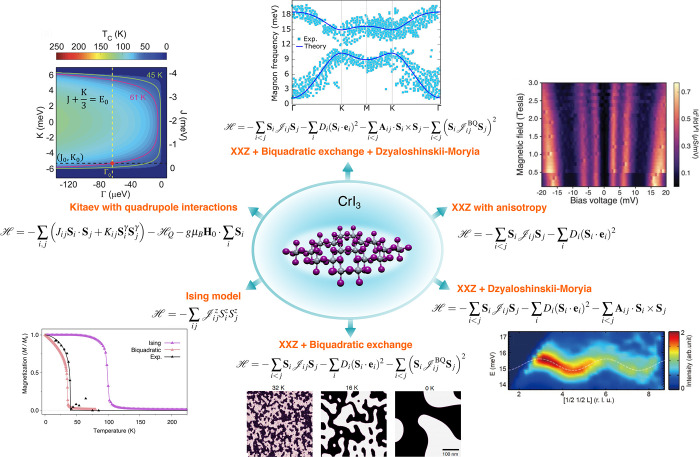
Spin waves play a crucial role in the perseverance of the alignment of magnetic moments in their 2D arrangements as described by the Mermin–Wagner theorem. As many other fundamental excitations, they exhibit wave-particle duality. The spin waves may be described as wave-like fluctuation of the spin state of the magnetic moments localized in a crystal lattice with a quantum of such excitation treated as a magnon quasiparticle. Akin to quanta of lattice vibrations (i.e., phonons), magnons can manifest naturally in inelastic scattering processes monitored, e.g., by optical or electrical methods. Therefore, Raman spectroscopy, neutron scattering,124,125 and/or tunnelling spectroscopy126−130 are common techniques used to get insight into the properties of magnons in solids exhibiting localized magnetic moments.
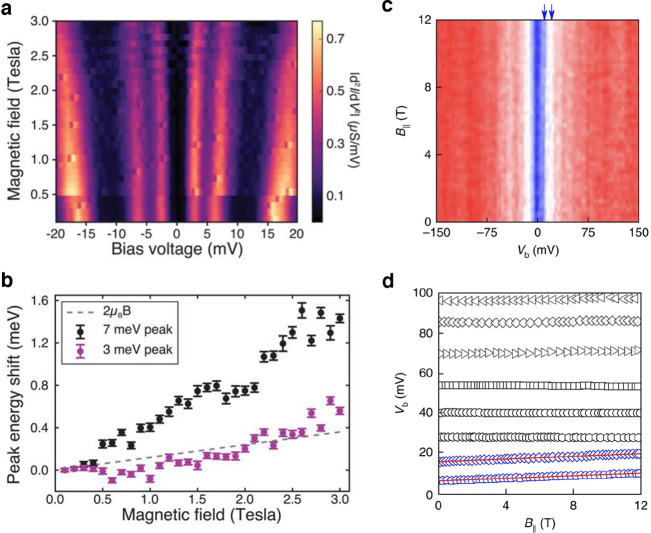
There are a few reports demonstrating the appearance of magnon resonances14,120,131 in 2D magnets, as seen in the conductance spectra in devices with graphene electrodes and magnetic barriers made of thin layers of CrI3,14,120,131 CrBr3,120,131 and CrCl3120 crystals. All three materials display evidence of magnon-assisted tunnelling processes in form of step-like features in the conductance spectra or narrow resonances in differential conductance spectra, as demonstrated in Figure 8. Characteristically for magnonic resonances, their energy is magnetic field dependent, and the observed slope ΔE/ΔB is indicative of the magnetic moment of the quasiparticles involved. Qualitatively, CrI3 and CrBr3 display two low energy resonances that are dispersive in magnetic field and may be associated with magnons. The tunnelling resonances in CrI3 occur at higher energy (3 and 7 meV) than those observed in CrBr3 (7.5 and 17 meV) as summarized in Table 6. The value of the ΔE/ΔB slope constitutes another differentiating factor between the two materials. The energies of the magnon resonances are consistent with the magnon density of states, calculated based on experimental values of the exchange integrals between the magnetic moments of Cr3+ ions in the lattice of CrI3 and CrBr3 crystals. However, the values of the ΔE/ΔB slope are more difficult to interpret.
Figure 8.
Comparison between tunnelling differential conductance spectra between Gr/CrI3/Gr and Gr/CrBr3/Gr devices in a magnetic field applied out-of-plane of the magnetic film for CrI3 sample and in-the-plane of the magnetic film for CrBr3 sample. For both materials, narrow low energy resonances appear, which are dispersive in the magnetic field. The color maps demonstrating the dependence of the differential conductance for (a, b) Gr/CrI3/Gr and (c) Gr/CrBr3/Gr devices illustrate the evolution of such resonances. The quantitative parameters describing the magnonic states, i.e., their zero-field energy and the slope ΔE/ΔB can be extracted based on the linear fits to the evolution of the energy of the resonances in the magnetic field (b, d). Panels (a) and (b) are adapted with permission from ref (14). Copyright 2018 AAAS. Panels (c) and (d) are adapted with permission from ref (131). Copyright 2018 Springer Nature.
Table 6. Zero-Field Energy and the ΔE/ΔB Slope Is Summarized for the Two Magnonic Resonances Observed in Gr/CrI3/Gr and Gr/CrBr3/Gr Devices, Based on the Evolution of the Differential Conductance Spectra in a Magnetic Field.
At the temperature of 0 K, the tunnelling processes are limited to those with an emission of a magnon quasiparticle, which arises from a spin flip mechanism within Cr3+ ions which gives rise to a quasiparticle characterized by a magnetic moment of 2.0 μB. At finite (low) temperatures, the magnon–magnon interactions provide additional contribution to the Zeeman term, leading to the increase of the magnetic moment. Self-consistent spin-wave calculations132 for CrBr3 predict a magnetic moment of 2.4 μB.131
The larger values of the experimentally observed ΔE/ΔB slopes in CrI3 and CrBr3 remain a puzzle; however, it is notable that the magnetic moment of magnons is strongly dependent on temperature, especially in the regime close to the critical Curie temperature (TC).133 First, the enhanced population of magnons at higher temperatures suppresses the short-range and long-range magnetic ordering. Second, the gap in the spin wave spectrum and interlayer exchange coupling (JL) suppresses the spin fluctuations (i.e., making the magnon excitations stiffer). Consequently, two regimes of magnetic coupling may be identified, with the transition between them defined by a condition 2 μBB ≈ JL, which differentiate the magnonic states by the value of their magnetic moment. Specifically, at low magnetic field and temperatures close to TC, the slope ΔE/ΔB for magnons in CrBr3 is predicted to be 4.5 μB and 7.1 μB for the lower energy and higher energy magnons, respectively.131
Except for modulating the ordering of magnetic moments in the crystal lattice, the presence of magnons can also mediate the inter-Landau level (LL) tunnelling processes. In experiments, where the magnetic field is applied perpendicularly to the graphene electrodes, Landau quantization occurs with the mutual alignment of the LLs in bottom and top graphene electrodes given by the applied bias. Example data are presented in Figure 9a,b. In such configuration, the LLs may be tuned in and out of resonance, favoring either an elastic tunnelling process directly between aligned LLs or an inelastic tunnelling process requiring an emission of a magnon as schematically illustrated in Figure 9a,b. These two tunnelling processes may be distinguished by changing the temperature and applying bias across both graphene electrodes. At low temperature, the inelastic tunnelling events with an emission of a magnon dominate the tunnelling spectra. With the increase of the temperature, two-magnon processes134 involving both absorption and emission of a magnon become more probable, due to enhanced population of magnons. Such processes contribute to the elastic scattering events, which can be further enhanced by spin disorder scattering135 for the temperatures close to TC.
Figure 9.
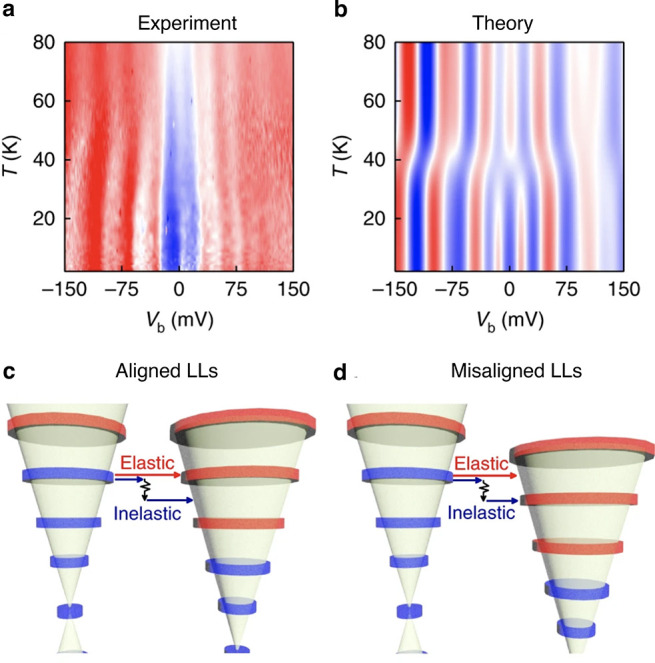
Temperature evolution of the differential conductance spectra in an out-of-plane magnetic field of 17.5 T is indicative of elastic and inelastic tunnelling processes mediated by magnons. The experimental data (a) shows qualitative agreement with theoretical predictions (b), which consider inelastic scattering processes with an emission of a magnon and elastic tunnelling processes involving two magnons. Both processes can be distinguished by applying a bias which shifts the mutual alignment of Landau levels (LLs) in the graphene electrodes (c, d). All panels adapted with permission from ref (131). Copyright 2018 Springer Nature.
Collectively, these observations provide evidence that spin waves participate actively in the magnetic properties of 2D magnetic materials. The magnon quasiparticles contribute to tunnelling spectroscopy by opening additional channels facilitating the tunnelling processes of charge carriers. As low-energy excitations, whose contribution to the tunnelling spectra can be tuned by electric and magnetic fields, magnons constitute a foundation for the principle of operation for devices relevant for spintronics applications.136 Particularly, the implementation of vdW magnets in unforeseen paradigms of magnon-based data processing137 and computing,138 utilizing selective spin-wave propagation to realize alternatives for commonly used logic gates,139 show promising avenues for investigations.
Magneto-Optical Phenomena
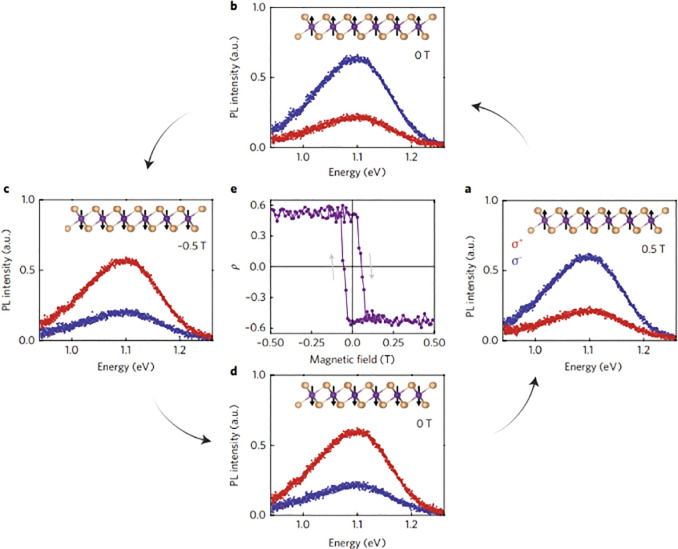
Magneto-optical phenomena develop when electromagnetic waves couple to the spin degree of freedom in solids because of spin–orbit-coupling. They have long been utilized in studying magnetic materials, more so in recent research of 2D magnetic crystals and moiré superlattices. In this section, we will review the recent progress on 2D magnetic phases in two important systems, 2D TMD heterostructures and 2D magnets (particularly, CrI3), studied by magneto-optical spectroscopy. Although TMDs are intrinsically nonmagnetic, magnetic states can be engineered in the strongly correlated regime in highly tunable moiré superlattices that compose of two stacked ML TMDs. In such systems, excitons in TMDs can be exploited as powerful optical probes of the emergent magnetic states or of nearby magnetic layers. On the other hand, 2D magnetic atomic layers isolated from bulk van der vdW magnetic crystals have formed another large pool of intrinsic 2D magnetic phases, of both fundamental scientific interest and potential for spintronic device applications. Static and dynamic magneto-optics (e.g., MOKE, magnetic circular dichroism (MCD), magneto-PL, and magneto-Raman spectroscopy) have been applied to reveal the underlying physics of 2D magnets.
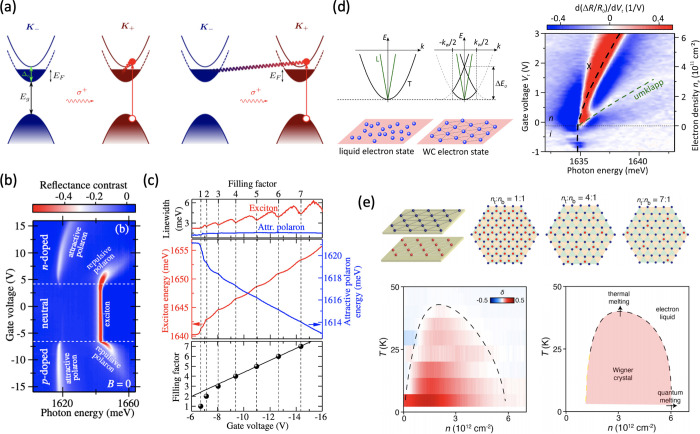
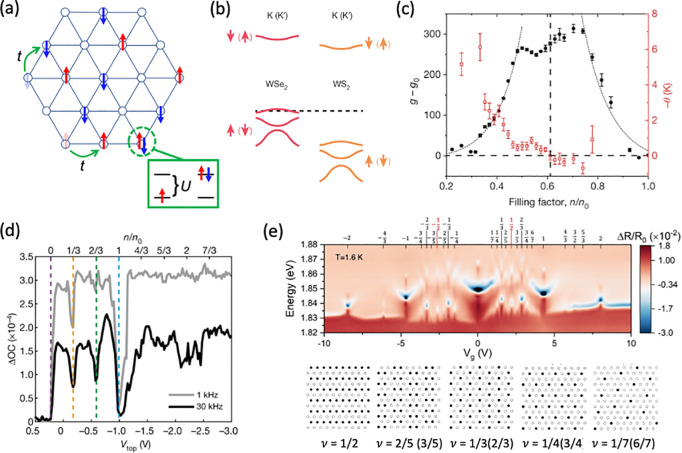
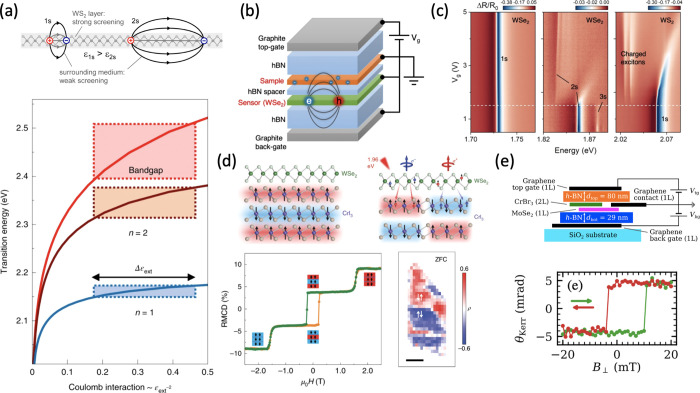
Excitons in TMDs: Optical Probes for Emergent Magnetic Phases in van der Waals Crystals and Heterostructures
Magnetism in Strongly Correlated TMD Heterostructures
Strongly correlated electron systems offer a fertile ground to discover, engineer, and probe emergent phases of matter, including distinct magnetic phases. Strong correlations among electrons arise when their mutual Coulomb interaction is similar or larger than their kinetic energy, and the delicate balance between these two energy scales determine the ground state of the system and its low-energy excitations. Strongly correlated electron systems exist in many well explored material families, e.g. transition metal oxides,140 cuprate high-Tc superconductors,141 and heavy Fermion materials.142 A general feature of these strongly correlated materials is that the relevant electron orbitals are typically d or f orbitals which, unlike s or p orbitals, have a degree of localization and thus lead to enhanced Coulomb interaction and reduced band widths. In this picture, at an appropriate Fermi energy, localized moments with large Coulomb interaction energies arise. While these “building blocks” of strongly correlated matter are well understood, many questions remain143 and the road to technological exploitation is onerous. Unfortunately, conventional quantum materials typically have strict limitations to engineering and probing strong correlations and their emergent phases.
Fortunately, the rise of 2D materials provides an ability to tune the two critical energy scales (Coulomb interaction and kinetic energies), and the Fermi energy, over several orders of magnitude, providing a solid-state quantum material platform with vast potential, as already demonstrated with twisted bilayer graphene heterostructures near the magic angle.144 In such twisted bilayer systems, a periodic potential landscape called a moiré superlattice arises, creating a means to engineer flat-bands and quench the kinetic energy. In the case of twisted bilayer graphene, the widely tunable parameters have given rise to a plethora of phases: Mott gap insulators, superconductivity, ferromagnetism, Chern insulators, and nematic ordering, among others; more are likely to be discovered.144 The scope for engineering the electron correlations in 2D materials rivals the impressive precision in cold-atom quantum simulators,145 but with very different energy scales. Beyond magic-angle graphene, TMD heterostructures present opportunities to create and probe highly tunable electron (or hole) correlations. Compared to graphene, monolayer TMDs have a much simpler band structure. Twisted bilayer graphene has 2-fold sublattice symmetry, 2-fold layer symmetry, and 2-fold time-reversal (spin) symmetry, leading to an 8-fold total degeneracy which puts strict limitations on the twist angle (∼1.05 ± 0.05°, the so-called “magic-angle” at which strong correlations arise).144 On-the other hand, in twisted TMDs, the sublattice and layer symmetries are broken, resulting in simple 2-fold total degeneracy. The impact of this is significant: The strong correlations are more robust in twisted TMDs; they can be realized over a wide range of twist angles, relaxing the demands on fabrication precision and setting possibilities for larger tunability of the correlations. Also, unlike graphene, TMDs have a finite energy gap which, at the monolayer limit, becomes direct in momentum space. Combined with strong spin–orbit coupling, TMDs present clean spin-resolved optical selection rules. Finally, electron–hole pairs form strongly bound excitons in TMDs due to their 2D nature, leading to the possibility to sensitively probe their environment. Altogether, in addition to engineering strongly correlated states in low-defect density TMDs and their heterostructures, these features suggest the probing and sensing of emergent magnetic phases within the TMD itself, or in nearby 2D materials, via optical spectroscopy. This is the motivation of our section review.
In the following, we will review how emergent states arise in a Fermi sea in a monolayer TMD or in a moiré heterostructure and how the exciton transitions in TMDs can act as sensitive probes of emergent states. We will first present a basic introduction into the fundamental magneto-optical properties of monolayer TMDs. Next we will introduce emergent magnetic phases that can arise due to strong correlations in Fermionic baths, why the properties of TMDs can promote additional investigations in these topics, and recent observations in this direction with a particular focus on the properties of an exciton–polaron, a bosonic impurity in a Fermi sea, in gated TMD devices. Following this, we will introduce the 2D Hubbard model and review the recent observations of strongly correlated states in moiré TMD heterostructures. Finally, we review how monolayer TMDs can act as sensitive probes of magnetic states in nearby 2D layers.
Magneto-Optical Properties of TMDs
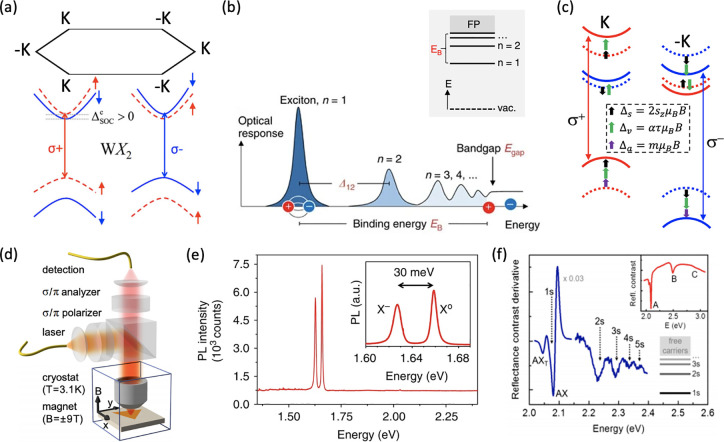
Among the plethora of vdW materials, 2D group-VIB TMDs such as MoS2, MoSe2, WS2, and WSe2 have emerged as a class of gapped semiconductors with appealing optoelectronic properties. In their monolayer forms, they present direct bandgaps with energies in the visible to near-infrared spectral range, with the band edges located at the degenerate but inequivalent corners of the hexagonal Brillouin zone (typically referred to as K and −K valleys, as shown in Figure 10a).146 The combination of a strong spin–orbit coupling and broken inversion symmetry in TMDs leads to an effective coupling between the carrier spin and the valley index of the electrons and holes at the ±K corners (see Figure 10a for a W-based TMD),152 which results in valley-dependent optical selection rules.153 After absorbing a σ±-polarized photon, a valence band electron at ±K can be promoted to the conduction band at ±K, leaving behind a hole in the corresponding valence band. The attractive Coulomb interaction between the conduction band electron and the valence band hole gives rise to the formation of a hydrogen-like state, known as exciton, in which the electron and hole are tightly bound together with a typical binding energy on the order of 0.5 eV.150,151,154
Figure 10.
(a) Schematic illustration in a single-particle picture of the direct band gap edge states for a W-based TMD (bottom) in the degenerate but inequivalent corners of the hexagonal Brillouin zone (top). The red dashed (blue solid) lines depict spin-up (down) band-edge states. Up (down) short arrows indicate spin-up (down) conduction band and valence band electrons. Long vertical arrows represent spin-allowed optical transitions with σ+ (red) and σ– (blue) polarization. Adapted with permission from ref (146). Copyright 2018 American Physical Society. (b) Schematic illustration of the optical response of an ideal 2D semiconductor, showing the exciton ground (n = 1) and excited state resonances (n = 2, 3, 4, ...) below the renormalized quasiparticle band gap. Adapted with permission under a Creative Commons CC BY 4.0 license from ref (147). Copyright 2017 Springer Nature. The top right inset shows the energy level scheme of the exciton states, designated by their principal quantum number n, with the binding energy of the exciton ground state below the free-particle (FP) band gap. Adapted with permission from ref (146). Copyright 2018 American Physical Society. (c) Schematic energy level diagram depicting the three contributions to the valley Zeeman shifts of the band-edge states: spin (black), valley (green) and atomic orbital (purple). The dashed (solid) lines represent the energies of the states before (after) applying a positive magnetic field perpendicular to the material interface. Adapted with permission from ref (148). Copyright 2015 Springer Nature. (d) Schematics of a typical microscope for optical spectroscopy of 2D materials in epifluorescence geometry. The 2D materials can be studied at temperatures T = 4–300 K by placing them on nonmagnetic nanopositioners inside a cryostat. A solenoid allows the application of magnetic fields (B) perpendicular to the crystal plane (Faraday geometry). The excitation and collection paths can feature several polarizing optical components for PL and reflectance experiments in circular (σ) and linear (π) bases. Adapted with permission from ref (149). Copyright 2017 Springer Nature. (e) PL spectrum of ML MoSe2 at T = 4 K under continuous-wave laser excitation with 2.33 eV. The spectrum shows the neutral exciton (X0) and the lower-energy negatively charged exciton (X–). The X– shows a binding energy of about 30 meV (see inset). Adapted with permission from ref (150). Copyright 2013 Springer Nature. (f) Derivative of the reflectance contrast spectrum (d/dE) (ΔR/R) for a WS2 monolayer (ML). The exciton states are labeled by their respective quantum numbers. The inset shows the as-measured reflectance contrast ΔR/R for comparison. Adapted with permission from ref (151). Copyright 2014 American Physical Society.
As a consequence of the large binding energy, excitons determine the fundamental optical properties of TMDs at both cryogenic and room temperatures. While the radii of 2D excitons in TMDs are small, their properties remain in the Wannier-Mott regime,146 resulting in a Rydberg series of excited states that resembles the physics of the hydrogen atom, although with a larger sensitivity to the surrounding dielectric environment151,154 (see Figure 10(b)). Moreover, the carrier spin, the valley index and the atomic orbital of the band edges involved in the optical excitonic transitions are associated with a magnetic moment.148 Such magnetic moments can couple to external magnetic fields and break the energy degeneracy between optical transitions at ± Kvia the Zeeman effect (see Figure 10(c)), endowing excitons in TMDs with a large sensitivity to external magnetic fields.
Therefore, properties such as the binding energy, oscillator strength, line width, polarization, and resonance energy of excitons in TMDs represent powerful optical probes to investigate emergent phases and magnetism in TMDs and adjacent vdW materials. Among the possible experimental techniques, optical spectroscopy represents the most powerful noninvasive technique to investigate the properties of excitons in 2D TMDs.155 It provides access to key properties of 2D TMDs such as the crystal quality, crystal orientation, the semiconductor band gap, the exciton binding energy and the absorption strength of the material.155 Moreover, when combined with a confocal microscope (see Figure 10(d)), it can also provide high spatial and polarization resolution, giving access to the spin and valley physics in TMDs. In this sense, PL spectroscopy has been largely employed to study the optical properties of neutral and charged excitons in TMDs at both room and cryogenic temperatures (see Figure 10e).150,152,154 However, PL emission tends to favor low-energy states (especially at low temperatures), limiting the access to excited exciton states. On the other hand, reflectance spectroscopy allows to characterize the energy, oscillator strength, and line width of the ground (n = 1s) and excited (n = 2s, 3s...) exciton states in TMDs. For example, one-photon reflectance contrast has been used to investigate the exciton Rydberg series in monolayer (ML) WS2 (see Figure 10f), revealing exciton resonances from the ground 1s state to the 5s excited state.
Emergent States in Fermion-Doped Monolayer TMDs
Strong
interactions in dilute electron systems can lead to emergent phases
and magnetism.156−158 At very low densities, Wigner predicted
that itinerant electrons will condense into an ordered array of electrons,156 while Bloch predicted that a paramagnetic Fermi
sea of electrons can spontaneously polarize into a FM state.158 To achieve strong correlations, the exchange
energy must dominate over kinetic energy. In an itinerant electron
system, the effective strength of the electron–electron interaction
is characterized by the Wigner–Seitz radius rs, which describes the average distance
between electrons measured in units of the effective Bohr radius.
In two-dimensions, 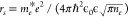 , where me* is the electron effective mass, ϵ is the dielectric
constant, and ne is the
electron density. The kinetic energy of an electron gas scales as
1/rs2
, where me* is the electron effective mass, ϵ is the dielectric
constant, and ne is the
electron density. The kinetic energy of an electron gas scales as
1/rs2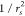 : At small rs (e.g., rs < 1), the kinetic energy of electrons exceeds
the Coulomb interaction energy and the properties of itinerant electrons
can be described by Fermi liquid theory. However, Monte Carlo calculations
reveal that when rs ≳
26, a two-dimensional electron system (2DES) becomes fully polarized,
while for rs ≳
30, the ground state of the 2DES is a Wigner crystal,159−161 a lattice of ordered electrons that forms to minimize the exchange
interaction energy.
: At small rs (e.g., rs < 1), the kinetic energy of electrons exceeds
the Coulomb interaction energy and the properties of itinerant electrons
can be described by Fermi liquid theory. However, Monte Carlo calculations
reveal that when rs ≳
26, a two-dimensional electron system (2DES) becomes fully polarized,
while for rs ≳
30, the ground state of the 2DES is a Wigner crystal,159−161 a lattice of ordered electrons that forms to minimize the exchange
interaction energy.
A simple analysis shows that for materials with large me* and modest ϵ, electrons in a 2DES should spontaneously arrange into a Wigner crystal at small ne. However, at small ne, carrier scattering due to intrinsic disorder in a material often dominates, making Wigner crystal formation elusive, especially in the absence of an external magnetic field (Landau quantization can also quench kinetic energy and lead to flat-bands). For example, in a 2DES in GaAs (me* = 0.067 and ϵ = 13), ne < 5 × 108 cm–2 for rs > 26, a huge challenge for defect densities in even the best MBE systems.162 Alternatively, 2D hole gases in GaAs (mh* = 0.4) offer better prospects, but still few reports exist and strong spin–orbit interaction complicates spin polarization measurements.163,164 In comparison, the weak dielectric screening (ϵ ∼ 10–30165,166) and large effective mass (me* 0.3–0.8)167,168 of TMDs offer renewed prospects.169
Gate-tunable 2D TMDs and related heterostructures represent an ideal material platform for exploring and controlling strongly correlated phenomena in a 2DES. In addition to exploring itinerant magnetic phases, gate-tunable TMDs provide a leap to investigate the many-body physics problem of a bosonic impurity interacting with a Fermionic sea. On the one hand, the Fermi energy (EF) in ML TMDs can be electrically tuned over a wide range simply by gating, enabling a precise control of the carrier density in the semiconductor. On the other hand, the large exciton binding energy (EX) of these materials (on the order of hundreds of meV150,151,154) allows one to reach the energy regime EX/EF ≫ 1, in which the excitons remain well-defined mobile atom-like particles (bosons) even in the presence of a substantial carrier Fermi energy. Moreover, the existence of positively and negatively charged exciton states with binding energies (ET) of a few tens of meV enables investigation of the strong coupling regime (EF/ET ∼ 1), where the trion binding energy competes with the kinetic energy of the excess electrons or holes in the Fermi reservoir.
The many-body phenomena resulting from the interaction between an exciton and a 2DES of excess carriers in the energy range EF ≤ ET ≪ EX can be understood in terms of Fermi polarons.174−178 In this framework, there are two types of exciton-electron interactions: electrons in the Fermi sea interact with excitons composed of electrons with antiparallel spin (singlet collisions) or parallel spin (triplet collisions).174,179 For ML TMDs doped with a 2DES with an EF much smaller than the conduction band spin–orbit splitting ΔCB, the photocreated exciton can interact with the electron gas either in the same valley (antiparallel spins) or in the opposite valley (parallel spins), as sketched in Figure 11a.170 For antiparallel spins, these interactions split the bare exciton resonance into two branches, a low-energy state interacting attractively with the bath of Fermions (attractive polaron), and a high-energy repulsive polaron (Figure 11b).171,175−177 The attractive-polaron resonance can be understood as a bound state of an exciton and a Fermi-sea electron, and it is normally identified as a trion branch. The repulsive exciton–polaron branch, normally identified as an exciton branch, stems from an exciton being dressed predominately by excitations of the Fermi sea, which leads to a repulsive blue-shift of the bare exciton resonance as the number of excess charge carriers increases. On the contrary, in parallel-spin collisions, there are no bound states of the exciton–electron interaction, and the spectrum only presents a repulsive polaron branch.174,179
Figure 11.
(a) Schematic band structure depicting intravalley (left) and intervalley (right) interactions between an exciton and a spin-polarized 2DES in a lightly doped W-based ML TMD. Adapted with permission from ref (170). Copyright 2020 AIP Publishing. (b) Voltage-gate-dependent color-scale map presenting reflectance contrast spectra measured in an hBN-encapsulated ML MoSe2. Attractive and repulsive exciton polarons are visible in both n- and p-doped regimes. Adapted with permission under a Creative Commons CC BY 4.0 license from ref (171). Copyright 2019 American Physical Society. (c) Gate-voltage dependencies of the line widths (top panel) and energies (middle panel) of the exciton (red) and attractive polaron (blue) resonances on the hole-doped side of an hBN-encapusulated ML MoSe2 at B = 16 T. Bottom panel: Gate voltages corresponding to integer filling factors determined based on the positions of the local minima of the exciton line width. Adapted with permission under a Creative Commons CC BY 4.0 license from ref (171). Copyright 2019 American Physical Society. (d) Gate-voltage-dependence derivative of the reflectance contrast spectrum with respect to the gate voltage of a charge-tunable, dual-graphene-gated, and fully hBN-encapsulated MoSe2 ML (right panel). The weak, higher-energy resonance is due to Umklapp scattering of the excitons off the electron Wigner crystal. Left panel: Schematics of the exciton dispersion in a ML TMD semiconductor hosting an electron system in various structural phases. The parabolic- and linear-in-momentum exciton branches arise from the splitting of the exciton branches due to the electron–hole exchange interaction, and correspond to the exciton dipole oriented along transverse (T) or longitudinal (L) directions with respect to the momentum vector, respectively. Adapted with permission from ref (172). Copyright 2021 Springer Nature. (e) Top panels: schematics of a Wigner crystal in a MoSe2 bilayer with an intercalated 1 nm thick layer of hBN (left). The top right panels show schematics of commensurate stacking in bilayer Wigner crystals with triangular lattices for filling ratios nt:nb of 1:1, 4:1, and 7:1, with nt and nb the carrier density in the top (blue dots) and bottom (red dots) MoSe2 layers. Bottom panels: 2D map of δ(nt, nb) as a function of total carrier density n and temperature T for nt:nb = 1:1 (right). The Wigner crystal forms in the region δ > 0 region. Theoretical schematic phase diagram of a bilayer Wigner crystal, showing both quantum and thermal phase transitions (left). Adapted with permission from ref (173). Copyright 2021 Springer Nature.
Experimental evidence of Fermi polarons in 2D semiconductors have recently been reported in the reflection and PL spectrum of intralayer excitons in gate-tunable ML TMDs.179−182 In addition to the formation of Fermi polarons, the strong interactions between tightly bound excitons and a dilute sea of carriers in gate-tunable TMDs have enabled the optical investigation of a wide variety of strongly correlated phenomena, including the interplay between LLs and many-body interactions in 2D semiconductors.171,182 For example, in ref (171), the authors carried out polarization-resolved resonant reflection spectroscopy in a gate-tunable ML MoSe2 hosting a dilute sea of fully spin- and valley-polarized holes in the presence of a strong magnetic field. Their results revealed filling-factor-dependent Shubnikov–de Haas-like oscillations in the energy and line width of the exciton–polaron transitions (see Figure 11c), which emerge as a consequence of the influence of Landau Level occupation on the strength of interactions between the excitons and the Fermi sea of holes. Exciton–polarons have also proved to be useful optical probes to explore interaction-induced magnetic phenomena in gate-tunable TMDs.179,181,183,184 In ref (181), a magnetic field of 7 T leads to a near-complete valley polarization of electrons in a gate-tunable ML MoSe2 with an electron density 1.6 × 1012 cm–2. By means of PL and resonant reflection measurements, they find that the Zeeman splitting of exciton–polarons can be strongly modified by interaction and phase-space filling effects, yielding effective exciton–polaron g factors as high as 18. These results suggest an interaction induced giant paramagnetic response of MoSe2. In addition to the paramagnetic phase observed for MoSe2, a FM ordering of 2D electrons was recently reported in gated ML MoS2 by optical spectroscopy measurements of exciton polarons.179 In ref (184), the same authors demonstrated that the magnetic phase of ML MoS2 can be controlled via the voltage applied to a gate electrode, leading to a fist-order magnetic phase transition between a FM phase at low electron density and a paramagnetic phase at high electron density.
Optical spectroscopy investigations of Fermi polarons in ML or weakly coupled BL MoSe2 have also recently enabled the demonstration of electronic Wigner crystallization in a 2D TMD semiconductor.172,173,185 As predicted theoretically,169 the large electron mass and reduced dielectric screening in these 2D semiconductors have led to the formation of Wigner crystals without the need of an applied external magnetic field.172,173,185 Moreover, even in the absence of an extrinsic periodic modulation of the band structure of the ML TMD, the charge order resulting from the Wigner crystal state gives rise to a periodic potential for the excitons in these 2D systems. In a charge-tunable ML MoSe2, the interaction between the periodic lattice of electrons and resonantly injected excitons has led to the emergence of resonances in the reduced excitonic Brillouin zone.172 The exciton resonances arise from Umklapp scattering of dark exciton states with momentum k = kW (where kW is the reciprocal lattice of the Wigner crystal), which folds the dark exciton states back to the light cone where they hybridize with the k = 0 exciton and thus can couple to photons (see left panel of Figure 11d). An example of these exciton resonances was observed in the high-energy side of the repulsive exciton polaron branch in a charge-tunable ML MoSe2 (see right panel of Figure 11d).172 Although both the repulsive polaron and the Umklapp resonance blue-shift upon electron doping, the energy splitting between these two resonances increases linearly with ne, in agreement with the reduction of the lattice constant of the Wigner crystal expected for increasing ne.172 Moreover, the same authors have shown that the application of a magnetic field further increases the stability of the Wigner crystal, since confinement of the electron motion into circular orbits partially suppresses its kinetic energy. Similar to ML MoSe2, resonant reflectance spectroscopy of a MoSe2 bilayer separated by hBN has also revealed the emergence of Umklapp exciton–polaron resonances due to spatially modulated interaction between excitons and electrons in an incompressible Wigner–Mott state.185 Finally, optical signatures of Wigner crystallization at cryogenic temperatures have also been observed in a nominally aligned MoSe2 bilayer separated by a 1 nm-thick hBN, in which robust correlated insulating states were formed at symmetric (1:1) and asymmetric (4:1 and 7:1) electron-doping ratios for the two MoSe2 layers (see top panel of Figure 11(e)).173 These bilayer Wigner crystal phases showed quantum and thermal melting transitions above a critical electron density of up to 6 × 1012 cm–2 and at temperatures of ∼40 K, as shown in the 2D plot of the dimensionless parameter δ(nt, nb) in the bottom right panel of Figure 11e for nt:nb = 1:1 (with δ(nt, nb) ≡ (I0(nt, nb) – It(nt)Ib(nb))/I0(0, 0), I0(nt, nb) the total exciton PL intensity and It(nt) (Ib(nb)) the PL intensity of the exciton from only the top (bottom) MoSe2 layer when its electron density is nt (nb)). The estimated phase boundary between an electron solid and a liquid, i.e., δ(nt, nb) = 0 (dashed line), resembles the theoretical melting curve calculated for a Wigner crystal (right panel of Figure 11e).173
Emergent States in Fermion-Doped TMD Moiré Heterostructures
A simple model to capture correlated electron phenomena in crystals
is to extend the tight-binding model, in which all electron hopping
processes have a kinetic energy −t, by introducing
an on-site Coulomb interaction energy U,186−188 as depicted in Figure 12a). This is the Hubbard model. The Hubbard Hamiltonian is 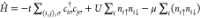 , with adjacent site indexes i and j, spin index σ,
, with adjacent site indexes i and j, spin index σ, 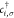 (ciσ) the operator to create (destroy)
an electron of spin σ
on lattice site i, and
(ciσ) the operator to create (destroy)
an electron of spin σ
on lattice site i, and 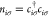 the number operator. The first
term describes
the kinetic energy, the second the interaction energy, and the third
the chemical potential which controls the filling factor (ν).
The situation where the filling is one electron per site is typically
refereed to as half-filling factor (ν = 1/2).
the number operator. The first
term describes
the kinetic energy, the second the interaction energy, and the third
the chemical potential which controls the filling factor (ν).
The situation where the filling is one electron per site is typically
refereed to as half-filling factor (ν = 1/2).
Figure 12.
(a) Schematic illustration of a 2D triangular moiré superlattice resulting from stacking two TMD MLs with different lattice constants and/or twist angle. The moiré potentials (empty blue circles) can be loaded with either electrons or holes with spin up (red arows) or down (blue arrows). The on-site Coulomb interaction energy U and hopping amplitude t between spins in the lattice is highly tunable by the stacking angle and choice of 2D materials, enabling the investigation of the Fermi–Hubbard model. (b) Sketch of the type-II band structure of a WSe2/WS2 heterobilayer, where K and K′ represent two valley degrees of freedom. Up (down) arrows denote the spin up (down) direction. (c) Dependence of the magnetic susceptibility χ ∝ g – g0 (left axis, black filled symbols) and Weiss constant θ (right axis, red empty symbols) on the filling factor of WSe2/WS2 at 1.65 K. Panels (b) and (c) adapted with permission from ref (197). Copyright 2020 Springer Nature. (d) Optically detected resistance and capacitance signal at 1 kHz (gray) and 30 kHz (black) from charge-neutral to moderate hole doping in WSe2/WS2, showing gap-like features at hole doping levels of n = n0/3 (orange dashed line), n = 2n0/3 (green dashed line) and n = n0 (blue dashed line). Adapted with permission from ref (198). Copyright 2020 Springer Nature. (e) Abundance of insulating states in WSe2/WS2 as revealed by the blue-shifts of the 2s exciton resonance in the reflectance contrast of a ML WSe2 sensor placed in close proximity to the heterobilayer (top panel). The top axis shows the proposed filling factor for the insulating states, with the corresponding configurations schematically shown in the bottom panels. Adapted with permission from ref (199). Copyright 2020 Springer Nature.
Similar to the emergence of strong correlations in a 2DES, the exchange interaction dominates over the kinetic energy, when U/t ≫ 1 strong correlations emerge in the Hubbard model. Because of the simplicity of the model, it provides valuable insights into emergent phases, including insulating, magnetic, and superconducting effects in quantum materials. For instance at ν = 1/2, it can be shown that a Mott insulator emerges, which is important in the context of high-temperature superconductors.143 This result is simple conceptually: at ν = 1/2 an electron can only hop to a site if it is already occupied. This costs an energy U. Hence, an energy gap U opens up at ν = 1/2, creating a Mott insulator. However, uncovering the magnetic phase of the Mott insulator becomes nontrivial. In general, the Hubbard model is nontrivial to solve in two- or three-dimensions, and a wide range of techniques (mean field or field theory approaches or numerical approaches such as diagonalization or quantum Monte Carlo) have been used. Experimentally probing the model is also challenging, due to the limited range of parameter control in conventional quantum materials. Motivated by this, quantum simulation of the Hubbard model with ultracold Fermions in optical lattices has materialized, with length scales on the order of 1 μm,189 compared to angstrom-scale length scales in the solid-state.
The 2D moiré superlattices formed by stacking two ML TMDs together provide an approach to create triangular Hubbard model simulators with an impressive range of tunability.190 The length scale, on the order of 10 nm, is precisely tunable by the combination of lattice mismatch and rotation angle between the two layers, while the filling factor can easily be tuned from ν < −1 to ν > 1 (hole-doping to electron doping), creating a straightforward means to tune U/t. Further, the choice of TMD material combinations (including homobilayers or heterobilayers) allows tuning the moiré potential depths, which can strongly affect the phase diagram. Theoretical work to understand the emergent phases and their dependence on the wide range of parameters is only just beginning.191−196
Equally, there has been an explosion in experimental efforts recently, with several early efforts investigating gated WSe2/WS2 moiré superlattices.197−201 In these initial works, the two TMD monolayers are closely aligned (∼0 or 60° relative twist), such that the moiré periodicity (∼8 nm) is largely determined by the lattice mismatch (∼4%). These heterostructures feature type II band-alignment and flat-bands (Figure 12b). With this system, Tang et al. characterized the phase diagram of strongly correlated holes as a function of ν, observing a Curie–Weiss behavior in the temperature dependence of the exciton Zeeman splitting (see Figure 12c). Interestingly, it was observed that the Weiss constant changes sign from negative to positive around ν = −0.6, consistent with a quantum phase transition from AF to FM ordering. Tang et al. also observed the Mott (or possibly charge transfer)191 insulating state at ν = 0.5 in a transport experiment and correlated this with an observation of signatures of charge-ordering in the differential reflectivity of the intralayer excitons as a function of ν.197 Regan et al. developed an optical technique to detect charge-ordered states in the flat valence-band at ν = −1/6, −1/3, and −1/2.198 The ν = −1/6 and −1/3 states likely represent Wigner crystals, while the ν = −1/2 state is the Mott or charge transfer insulator. Further, low-energy spin dynamics in the charge ordered states were observed using a pump–probe experiment to probe circular dichroism resulting from spin-ordering.198
Building on these initial observations, WSe2/WS2 moiré heterostructure device, with a nearby ML WSe2 sensor, was used to discover a number of correlated states at commensurate filling fractions. The charge ordering of these states is symmetric about ν = ± 1/4 and are proposed to range from generalized Wigner crystals to charge density waves (see Figure 12e).199 This stunning observation highlights the versatility to engineer and the power to optically probe emergent states in TMD moiré heterostructures. Jin et al. have recently characterized in-depth the properties of these strongly correlated states by combining optical anisotropy and electronic compressibility measurements.200 They find a strong electrical anisotropy, maximum at ν = 1/2, which is assigned to an insulating stripe phase. Further, wide-field imaging of the stripe phase domains reveals preferential alignment along the high-symmetry axis of the moiré superlattice. These results provide insight into the phase diagram of the extended triangular Hubbard model. Finally, recent results highlight the possibility to observe correlated states at fractional fillings in the PL emission of interlayer excitons.201 Interlayer excitons, Coulomb bound electrons and holes spatially separated in different monolayers, arise in TMD heterobilayers due to the type-II band alignment. In contrast to optical signatures of emergent phases in the reflectance contrast of intralayer moiré excitons, interlayer exciton PL provides access to the valley (K and −K) dynamics of excitonic states in the moiré superlattice. First indications are that the fractional states, with their insulating nature, can also enhance the intervalley scattering and suppress the valley polarization.201
TMDs as Sensors of Emergent States
The 2D nature of ML TMD semiconductors endows excitons in these systems with properties that differ fundamentally from those of the corresponding bulk semiconductor. A particular property of excitons in 2D semiconductors such as ML TMDs is that the electric field lines joining the bound electron–hole pairs (which are strongly confined to the plane of the atomically thin ML) extend outside the 2D semiconductor slab (see top panel of Figure 13a.151 This property makes excitonic transitions in ML TMDs very sensitive to their surroundings, since moderate changes of the local dielectric permittivity in the vicinity of the ML lead to dielectric-induced renormalizations of both the electronic band gap and the exciton binding energy by hundreds of meV.147 The bottom panel of Figure 13a summarizes these effects for ML WS2, a typical 2D TMD. The figure shows the theoretically calculated energies of the band gap and both the ground and first excited exciton states of ML WS2 (denoted by their principal quantum numbers of n = 1 and 2, respectively) as a function of the inverse squared external dielectric constant.202 Such sensitivity of excitonic transitions in 2D TMDs to their dielectric environment has been exploited to realize an in-plane dielectric heterostructure with a spatially dependent bandgap147 and to monitor the dielectric disorder in semiconducting nanostructures with micrometer spatial resolution.202
Figure 13.
(a) Top: Schematic illustration of electron–hole pairs forming 1s and 2s excitonic states in a 2D dielectric slab. Adapted with permission from ref (151). Copyright 2014 American Physical Society. Bottom: Theoretically calculated energies of the bandgap and exciton states in a WS2 ML as a function of inverse squared external dielectric constant. Shaded areas indicate fluctuations from variations of the external screening. Adapted with permission from ref (202). Copyright 2019 Springer Nature. (b) Schematic of a device heterostructure to demonstrate the sensing capabilities of excitons in ML WSe2. (c) Reflectance contrast of the 1s (left) and 2s and 3s (middle) excitonic transitions in the WSe2 sensor, and the 1s exciton in the WS2 sample as a function of the applied gate voltage (i.e., the electron concentration in WS2). (b) and (c) Adapted with permission from ref (199). Copyright 2020 Springer Nature. (d) Left: Reflective magneto-circular dichroism as a function of magnetic field (bottom) measured in a monolayer WSe2 and trilayer CrI3 heterostructure, depicted above schematically. Orange and green curves represent magnetic field sweeping up (increase) and down (decrease), respectively. Right: Schematic of a ML WSe2 and bilayer CrI3 heterostructure (top). The layered AF spatial domains that are indistinguishable by reflective magneto-circular dichroism can be resolved by circular polarization-resolved PL from WSe2 (bottom). Adapted with permission from ref (203). Copyright 2020 Springer Nature. (e) Measurement of the CrBr3 magnetization hysteresis using the MOKE (bottom) in a device like schematically shown on top. Adapted with permission under a Creative Commons CC BY 4.0 license from ref (204). Copyright 2020 American Physical Society.
In addition to the previously mentioned applications, the sensing capabilities of ML TMDs can also be harnessed to explore the emergence of correlated many-body states in vdW heterostructures. Xu et al. have recently unveiled an abundance of correlated insulating states at fractional fillings in a WSe2/WS2 moiré superlattice199 by optically probing the resonance energy and oscillator strength of the exciton excited states of a ML WSe2 sensor placed in close proximity to the TMD heterobilayer. Figure 13b shows a sketch of the device employed by Xu et al., in which a WSe2 ML was separated from a WSe2/WS2 heterobilayer by an hBN spacer with a thickness of 1 nm.199Figure 13c shows a proof-of-concept example of the sensing technique in a control device similar to the one depicted in Figure 13b, in which the TMD heterobilayer was replaced by a WS2 ML. This figure shows the reflectance contrast of the excitonic transitions of both the WSe2 sensor and the WS2 sample as a function of the applied gate voltage (i.e., the electron concentration in WS2). While the energy of the 1s excitonic transition in the WSe2 sensor shows negligible dependence with the applied gate voltage (left panel), the behavior of the 2s and 3s charged exciton states in the WSe2 sensor (middle panel) mirrors that of the 1s exciton in the WS2 sample (right panel). These results not only demonstrate the potential of the optical sensing technique enabled by excitons in TMDs but also highlight the further sensing capabilities of the exciton excited states (n = 2, 3) compared to the ground state (n = 1). The origin of the better sensing capabilities of the excited excitonic transitions is two-fold: First, the exciton excited states (2s, 3s, and so on) have Bohr radii many times the ML thickness, which allows them to sense the dielectric permittivity of nanostructures placed a few nm away from the layer. In contrast to the excited states, the Bohr radius of the ground exciton state is typically of the order of the ML thickness,168 which restricts the dielectric sensing to layers in direct contact with the sensor. Second, as shown in the bottom panel of Figure 13a for ML WS2, the excited-state excitonic resonances follow the external screening-induced variations of the band gap to a much larger extent,202 which results in a larger sensitivity to small variations of the local dielectric environment.
The potential of ML TMDs as atomically thin sensors for emergent correlated and magnetic phases in vdW materials and related heterostructures is not restricted to detecting variations in their dielectric surroundings. Both the proximity-induced exchange interaction and the charge transfer between vdW ferromagnets and ML TMD semiconductors can also be exploited to probe the magnetic phases of the atomically thin magnetic materials.203−205 An interface between a vdW ferromagnet such as CrI3 or CrBr3 and a TMD semiconductor, such as MoSe2 or WSe2, results in a type-II band structure alignment, where the lowest conduction band is in the magnetic material.203 Since the relevant conduction bands in CrI3 and CrBr3 are spin polarized, the type-II band structure leads to a spin-dependent charge transfer between the TMD and the 2D ferromagnet, resulting in a large spontaneous exciton valley-spin polarization in the TMD.203 The top left panel of Figure 13d shows the sketch of a ferromagnet/TMD vdW heterostructure in which a WSe2 ML was employed to monitor the layered antiferromagnetism of a trilayer CrI3.203 By measuring the reflective magneto-circular dichroism of ML WSe2 as a function of applied magnetic field at 15 K, the authors where able to observe three transitions in the magnetization of CrI3 (see bottom left panel of Figure 13d), with each transition corresponding to a flip in the magnetization of a single CrI3 layer. Moreover, the fast spin-polarized electron transfer between the CrI3 layer in contact with the WSe2 ML also enabled the use of WSe2 as a magnetic sensor to map out layered AF/FM spatial domains at zero magnetic field as well as at finite magnetic fields in bilayer CrI3/WSe2 heterostructure (see right panels of Figure 13d).
Finally, in 2D ferromagnet/TMD heterostructures, the 2D ferromagnet also induces a magnetic exchange field (proximity effect) in the adjacent TMD, which gives rise to a sizable valley Zeeman splitting for excitonic transitions in the TMD.204−207 Such proximity-induced magnetic effect has also been exploited to monitor the FM properties of CrBr3 (see Figure 13e).204,208
Raman Spectroscopy of 2D Magnetism: Exploring Lattice, Spin, and Charge Interactions
Magnetism in 2D Magnetic Atomic Crystals
Recently, a long-sought-after member of 2D material family, 2D magnetic atomic crystals, have been discovered in several mechanically exfoliated vdW magnetic materials, including both FM6,12,14,77,209 and AF32,210−212 ones.12,213,214 Among the 2D magnets revealed so far, CrI3 is of particular interest and extensively explored, because its layer-dependent magnetic states in ultrathin flakes can be controlled by external magnetic field,13−16,120 electric field,8,9 electrostatic doping,11 and hydrostatic pressure,22 which immediately triggered tremendous interest in employing 2D magnetism in spintronics applications such as spin filters13−16,120 and transistors.8,9,11
Optical spectroscopy has played an unmissable role in the discovery and exploration of 2D magnetism. MOKE and MCD have provided direct experimental evidence for 2D FM orders in mono- to few-layer CrI3,14 MnBi2Te4,209 Cr2Ge2Te6,6 and Fe3GeTe2.77 Spontaneous helical PL has shown the impact of FM on the electronic states in 2D magnetic semiconductors such as CrI3.215 Giant nonreciprocal second harmonic generation (SHG) has also shown the outstanding magnetic contribution to the nonlinear optical effects in noncentrosymmetric 2D magnetic states such as even number-of-layer CrI324 and MnPS3.216 Raman spectroscopy in fact has provided the earliest, although indirect, experimental signatures of zone-folded phonons in the search of 2D AF orders in (Fe, Mn, Ni)PS332,210−212 and has revealed the anomalous magneto-Raman effects in layered AF materials of CrI3217−224 and VI3.225
Comparing to the static optical probes of MOKE, MCD and magnetic SHG that primarily focus on the broken time-reversal and/or spatial point symmetries of magnetic orders, Raman spectroscopy takes the dynamic perspective in examining 2D magnetic materials, probing collective excitations including phonons in CrI3, VI3, Fe3GeTe2, Cr2Ge2Te6, and (Fe, Mn, Ni)PS3, magnons in CrI3, VI3, and (Fe, Mn, Ni)PS3, polarons in CrI3, etc., identifying the symmetry properties of both the crystallographic and magnetic structures, and resolving the coupling among lattice, charge, and spin degrees of freedom such as electron–phonon coupling and spin-phonon coupling. Comparing to the dynamic probe of helical PL that results from the carrier recombination across the semiconducting gaps (∼1 eV energy scale), Raman spectroscopy focuses on low-energy (∼2–3000 cm–1) collective excitations from the ordering of lattice, spin, and charge and works well for metallic, semiconducting, and insulating 2D magnetic materials.
In the following, we review three types of phonon-related collective excitations, using specific examples in bulk and few-layer CrI3. First, we look at the conventional phonons in CrI3 and show its evolution across the magnetic-field-induced magnetic phase transition. Second, we discuss the anomalous magneto-Raman effect reported in CrI3 by multiple groups217−224 and settle down its origin as the static layered AF order coupled with finite-momentum phonons. Third, we review the Raman scattering between phonon-dressed exciton states in CrI3 and show its response across thermal and magnetic-field-induced magnetic phase transitions. We have reserved the discussion on magnons in CrI3 for the Heterostructures, Twisted Layers, and Interfaces section.
Phonons and Structural Phase Transitions in CrI3
Figure 14a shows the top view of the CrI3 monolayer. The Cr3+ cations form a honeycomb structure with edge-sharing octahedral coordination formed by six I– anions. In bulk CrI3, the as-grown CrI3 single crystal has a monoclinic structure (space group C2/m, point group C2h) at room temperature, with the adjacent layers shifted along the a-axis direction by 1/3 lattice constant (Figure 14b), and undergoes a first-order structural phase transition to a rhombohedral structure (space group R3̅, point group C3i) at a critical temperature TC ∼ 200–220 K, with the layers stacked in the ABC sequence (Figure 14c). Unlike bulk CrI3, few-layer CrI3 does not experience such a structural phase transition even when the temperature is lowered to 5 K, suggesting that the monoclinic structure persists down to low temperature of 5 K.
Figure 14.
(a) Top view of CrI3 monolayer with gray and purple spheres representing Cr and I atoms. Adapted with permission from ref (5). Copyright 2017 Springer Nature. (b, c) Lateral view of bulk CrI3 in the monoclinic (b) and rhombohedral (c) phase. (d, e) Polarization resolved Raman spectra for bulk CrI3 taken at 5 K (d) and 280 K (e). (f, g) Polarization resolved Raman spectra for thin layer CrI3 taken at 5 K (f) and 280 K (g). Panels (b–g) adapted with permission under a Creative Commons CC BY license from ref (224). Copyright 2019 IOP Publishing.
Raman spectroscopy has been used to track the temperature dependent structural phase transition in bulk CrI3218,226 and to identify the monoclinic structure of few-layer CrI3.224 Below TS, the Raman scattering off the rhombohedral lattice (C3i) reveals phonon modes of Ag(C3i) and Eg(C3i) symmetries with corresponding Raman tensors of the form
 |
Above TS, the Raman active phonons of the monoclinic structure are of Ag(C2h) and Bg(C2h) with Raman tensors of the form
 |
The difference in the Raman response between the two phases contains two aspects. First, one would expect the selection rule difference in the Ag phonons which is isotropic and only present in the linearly parallel channel for Ag(C3i) but anisotropic and could appear in both linearly parallel and crossed channels for Ag(C2h). Second, one could observe the degeneracy lift from the doubly degenerated Eg(C3i) phonons into the nondegenerate Ag(C2h) and Bg(C2h) phonons. While the interlayer stacking induced phase transition is hardly reflected in the selection rule of Ag phonons, it is well captured by the degeneracy lift of the Eg(C3i) phonons. Figure 14d,e shows the polarization dependence of the Eg(C3i) modes at 5 K and the Ag(C2h) and Bg(C2h) phonons at 280 K in bulk CrI3, clearly showing the mode splitting and the selection rule symmetry reduction for the case at 280 K. Same polarization-dependent measurements on CrI3 thin flakes, however, show no distinct behaviors at 5 and 280 K (Figure 14f,g) and resemble that of bulk CrI3 in the monoclinic phase above TS (Figure 14e), which confirms the monoclinic structure down to the 5 K in few-layer CrI3.
In addition to the structural evolution as a function of the temperature and thickness, CrI3 undergoes a magnetic phase transition across a critical temperature of Tc,3D = 61 K for bulk CrI3 and Tc,2D ∼ 45 K for 2D flakes. The 2D magnetic phase in few-layer CrI3 has been shown to be a layered AF state where the S = 3/2 spins at the Cr3+ sites align ferromagnetically within the layers and antiferromagnetically between adjacent layers.14 The 3D bulk magnetic phase was believed to be a FM state within and across layers227 and has been recently revised to a hybrid surface layered AF and deep bulk FM state.218 The difference of the interlayer magnetic exchange coupling between few-layer 2D (and surface of 3D) and deep bulk 3D CrI3 has been attributed to the stacking difference, i.e., monoclinic for interlayer AF and rhombohedral for interlayer FM.228 When an external out-of-plane magnetic field is applied, a layered AF to FM phase transition across critical fields of Bc has been observed for both few-layer and bulk CrI3.14 One natural question would be how the crystal structure responds to this magnetic field-induced layered AF to FM magnetic phase transition, which can be addressed by tracking the magnetic field dependence of the phonon modes.
Figure 15a,c shows
Raman spectra in the circularly parallel (LL) and crossed (LR) channels
taken at 10 K and 0 and 7 T in bulk CrI3, with L(R) standing
for left-(right-)handed circularly polarized light. Consistent with
the Raman tensors of the rhombohedral crystal structure, Ag and Eg phonon modes at 0 T are observed exclusively in
the LL and LR channels, respectively, while another two time-reversal
symmetry broken modes (labeled as M) with antisymmetric Raman tensor
of the form 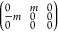 is only present in the LL channel. The
magnetic field dependence of Raman spectra in the LL channel is displayed
in the false color map in Figure 15b, showing abrupt changes in the phonon intensities
at a critical field Bc = 2 T corresponding to the surface layered AF to FM phase transition.
The phonon intensities can be extracted from the Raman spectra in
both channels and plotted against the applied external fields (Figure 15d–f). Three
types of phonon selection rule evolution support a monoclinic structural
distortion above Bc (shown
in Figure 15d–f).
The first type is the leakage of Ag phonons (e.g., at ∼129 cm–1) into the originally forbidden LR channel at B > Bc (Figure 15d), corresponding to the Raman tensor form
changing from
is only present in the LL channel. The
magnetic field dependence of Raman spectra in the LL channel is displayed
in the false color map in Figure 15b, showing abrupt changes in the phonon intensities
at a critical field Bc = 2 T corresponding to the surface layered AF to FM phase transition.
The phonon intensities can be extracted from the Raman spectra in
both channels and plotted against the applied external fields (Figure 15d–f). Three
types of phonon selection rule evolution support a monoclinic structural
distortion above Bc (shown
in Figure 15d–f).
The first type is the leakage of Ag phonons (e.g., at ∼129 cm–1) into the originally forbidden LR channel at B > Bc (Figure 15d), corresponding to the Raman tensor form
changing from 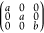 to
to 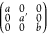 and corroborating
with the monoclinic structural
distortion. The second type corresponds to the appearance of Eg phonons (e.g., at ∼109 cm–1) in the LL channel at B > Bc (Figure 15e), reflecting
the evolution from Eg(C3i) into Ag(C2h) upon a monoclinic distortion. The third type features the Eg phonons remaining in its
original LR channel but experiencing an abrupt change in intensity
(Figure 15f), corresponding
to the transformation of Eg(C3i) into Bg(C2h) across a monoclinic structural phase transition
(Figure 15g).218
and corroborating
with the monoclinic structural
distortion. The second type corresponds to the appearance of Eg phonons (e.g., at ∼109 cm–1) in the LL channel at B > Bc (Figure 15e), reflecting
the evolution from Eg(C3i) into Ag(C2h) upon a monoclinic distortion. The third type features the Eg phonons remaining in its
original LR channel but experiencing an abrupt change in intensity
(Figure 15f), corresponding
to the transformation of Eg(C3i) into Bg(C2h) across a monoclinic structural phase transition
(Figure 15g).218
Figure 15.
(a) Raman spectra taken on bulk CrI3 in LL and LR channels at 10 K and 0 T. P(Ag), P(Eg), and M1,2 label phonon modes of Ag, Eg symmetry and coupled with layered magnetism, respectively. (b) Color map of magnetic field dependent Raman spectra taken in the LL channel. (c) Raman spectra taken on bulk CrI3 in LL and LR channels at 7 T. (d–f) Magnetic field dependence of selected Ag and Eg phonon modes. (g) A schematic illustration of the monoclinic distortion across the layered surface AF to FM transition. Adapted with permission under a Creative Commons CC BY 4.0 license from ref (218). Copyright 2020 American Physical Society.
It remains to be determined thus far whether this monoclinic structural distortion is also present in few-layer CrI3 and how to understand this structural monoclinicity in the magnetic field-induced FM state in the context of monoclinic structure leading to layered AF at zero field. Nonetheless, ordinary phonons probed by Raman spectroscopy are sensitive indicators of structural changes and can be exploited in studying lattice-magnetism coupling in 2D magnetic systems beyond CrI3.
Time-Reversal Symmetry Broken Static Layered Antiferromagnetic Coupled Phonons in CrI3
In few-layered CrI3, a time-reversal symmetry broken phonon mode with an antisymmetric Raman tensor has been observed in the close proximity to a fully symmetric Ag phonon mode at ∼129 cm–1. Moreover, it introduces exceptionally large polarization rotation in monolayer CrI3 (Figure 16a), shows distinct magnetic field dependence from the Ag phonon in bilayer (2L) CrI3 (Figure 16b,c), and exhibits more complex Raman spectral shape and magnetic field dependence in thicker CrI3 flakes (Figure 16d), therefore generally referred as anomalous magneto-Raman effect.221−223
Figure 16.
(a) Raman spectra taken in both linear parallel and crossed channels in monolayer CrI3 at 15 K and 0 T. Polar plots of polarization dependent Ag mode intensity (∼129 cm–1) at 60 and 15 K, above and below the magnetic onset temperature TC = 45 K, respectively. (b) Raman spectra of 2L CrI3 at 15 K and at 0 and 1.5 T in linearly parallel and crossed channels. Panels (a, b) adapted with permission from ref (221). Copyright 2020 Springer Nature. (c) Raman spectra of 2L CrI3 at 1.7 K and at 0 T and −1 T in linearly parallel and crossed channel. Adapted with permissions from ref (222). copyright 2020 American Chemical Society. (d) Raman spectra of 10L CrI3 at 9 K and at selected magnetic fields. Adapted with permission under a Creative Commons CC BY license from ref (223). Copyright 2020 Springer Nature.
A layered magnetism-coupled phonon scattering mechanism,
in combination
with Davydov splitting, is proposed to account for this observed anomalous
magneto-Raman effect in 2D CrI3 of arbitrary thickness. Figure 17a shows Raman spectra
taken on 1–4L CrI3 in both linearly parallel and
crossed channels at 10 K and 0 T. One can see three prominent features
in these layer-number dependent Raman spectra: First, the total number
of phonons increases proportionally to the number of layers; second,
the highest frequency remains constant while the lowest frequency
decreases monotonically at higher layer numbers; and third, the parallel
and crossed channels select the same (distinct) frequency mode(s)
in CrI3 with odd(even) number of layers. A simple linear
chain model of N-layer CrI3 of Hamiltonian, 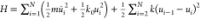 , is used to compute the Davydov splitting
of the single Ag phonon
mode into N phonon multiplets (i.e., N eigenvalues and N eigenvectors),
where ui represents the
displacement field in the ith layer, and k0 and k stand for the coupling
constant within each layer and between adjacent layers, respectively.
Among these N eigenvectors
, is used to compute the Davydov splitting
of the single Ag phonon
mode into N phonon multiplets (i.e., N eigenvalues and N eigenvectors),
where ui represents the
displacement field in the ith layer, and k0 and k stand for the coupling
constant within each layer and between adjacent layers, respectively.
Among these N eigenvectors 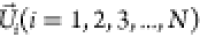 for N-layer CrI3, the highest frequency
mode
for N-layer CrI3, the highest frequency
mode 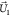 (i.e., i = 1) features the in-phase atomic displacement
of the Ag phonon of monolayer
across all N layers and is even under spatial inversion
symmetry operation
(i.e., parity even) whereas the lowest frequency
mode
(i.e., i = 1) features the in-phase atomic displacement
of the Ag phonon of monolayer
across all N layers and is even under spatial inversion
symmetry operation
(i.e., parity even) whereas the lowest frequency
mode 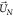 (i.e., i = N) has out-of-phase atomic
displacement between
adjacent layers and is parity even (odd) for odd (even) N (see Figure 17b).
For this, one would expect that the frequency of
(i.e., i = N) has out-of-phase atomic
displacement between
adjacent layers and is parity even (odd) for odd (even) N (see Figure 17b).
For this, one would expect that the frequency of 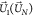 keeps unchanged (decreasing) with increasing N because
its in-phase (out-of-phase) atomic displacement
saves no (most) energy from the interlayer coupling.
keeps unchanged (decreasing) with increasing N because
its in-phase (out-of-phase) atomic displacement
saves no (most) energy from the interlayer coupling.
Figure 17.
(a) Raman spectra taken on 1–4L CrI3 in both linear parallel and crossed channels at 10 K and 0 T. Adapted with permission under a Creative Commons CC-BY license from ref (219). Copyright 2017 National Academy of Sciences. (b) A summary of linear chain model calculation results and selection rule analysis for 1–4L CrI3.
In the linearly parallel channel,
one expects the ordinary phonons
with symmetric Raman tensor (RS) of parity even Ag symmetry because N-layer CrI3 has centrosymmetric
crystal structures. These include every other phonon modes starting
from the highest frequency one (i.e., i = 1, 3, 5, ...), as is the case in Figure 17a that the linearly parallel channel picks 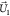 for 1L and 2L and
for 1L and 2L and 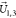 for 3L and 4L.219 In the linearly crossed
channel, the measured modes have antisymmetric
Raman tensors (RAS) and
therefore contains at least one copy of static layered magnetic order
contributing to the scattering process (
for 3L and 4L.219 In the linearly crossed
channel, the measured modes have antisymmetric
Raman tensors (RAS) and
therefore contains at least one copy of static layered magnetic order
contributing to the scattering process (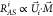 , where
, where 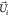 is the ith eigenvector
and
is the ith eigenvector
and 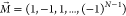 is the axial vector for the layered AF
order in N-layer CrI3). Because the layered
AF order is parity even (odd) for odd (even) N, it
should pair with the parity even (odd) phonon modes for odd (even) N to restore the centrosymmetry of the layered magnetism-phonon
coupled entity, leading to the crossed channeling selecting the modes
same as (complementary to) those in the parallel channel for odd (even) N.
is the axial vector for the layered AF
order in N-layer CrI3). Because the layered
AF order is parity even (odd) for odd (even) N, it
should pair with the parity even (odd) phonon modes for odd (even) N to restore the centrosymmetry of the layered magnetism-phonon
coupled entity, leading to the crossed channeling selecting the modes
same as (complementary to) those in the parallel channel for odd (even) N.
Based on this formalism of Davydov splitting and
layered magnetism-assisted
phonon scattering, the complex magnetic field dependence of thicker
CrI3 can be explained in a unified way as that of bilayer
CrI3. For every Davydov split mode  , its Raman tensor is
composed of the conventional
pure structural contribution of the symmetric Raman tensor
, its Raman tensor is
composed of the conventional
pure structural contribution of the symmetric Raman tensor  and the layered magnetism-coupled phonon
contribution of antisymmetric Raman tensor
and the layered magnetism-coupled phonon
contribution of antisymmetric Raman tensor  , i.e.,
, i.e., 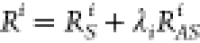 , where
, where 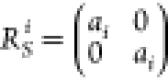 is magnetic field independent
and is only
present for parity-even modes,
is magnetic field independent
and is only
present for parity-even modes, 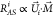 which changes across
the critical magnetic
fields Bc, and λi is ratio of the magnetic to structural contribution
for the ith mode that depends on microscopic parameters
such as spin–orbit-coupling. Taking 4L CrI3 as an
example, it undergoes two magnetic phase transitions at critical magnetic
fields of Bc1 = 0.7 T
and Bc2 = 1.6 T, across
which M⃗ changes from (1, −1, 1, −1)
to (1, −1, 1, 1) to (1, 1, 1, 1). Figure 18a shows selected Raman spectra taken on
4L CrI3 at 0 T (B < Bc1), 1 T (Bc1 < B < Bc2), and 2 T (B > Bc2) at 10 K in the circularly
parallel RR channel. Three (U1, U3, and U4) out of
four modes are resolved, as U2 is spectrally
very close to U1 and gets overwhelmed
by the much stronger U1. The Raman spectra
in three magnetic field ranges show clearly distinct spectral shape
that results from changes in the relative spectral intensity of the
three modes. Careful magnetic field dependent mode intensities are
shown in Figure 18b for the three observed modes, well capturing the critical fields
of Bc1 and Bc2 and displaying different field dependencies.
Looking at
which changes across
the critical magnetic
fields Bc, and λi is ratio of the magnetic to structural contribution
for the ith mode that depends on microscopic parameters
such as spin–orbit-coupling. Taking 4L CrI3 as an
example, it undergoes two magnetic phase transitions at critical magnetic
fields of Bc1 = 0.7 T
and Bc2 = 1.6 T, across
which M⃗ changes from (1, −1, 1, −1)
to (1, −1, 1, 1) to (1, 1, 1, 1). Figure 18a shows selected Raman spectra taken on
4L CrI3 at 0 T (B < Bc1), 1 T (Bc1 < B < Bc2), and 2 T (B > Bc2) at 10 K in the circularly
parallel RR channel. Three (U1, U3, and U4) out of
four modes are resolved, as U2 is spectrally
very close to U1 and gets overwhelmed
by the much stronger U1. The Raman spectra
in three magnetic field ranges show clearly distinct spectral shape
that results from changes in the relative spectral intensity of the
three modes. Careful magnetic field dependent mode intensities are
shown in Figure 18b for the three observed modes, well capturing the critical fields
of Bc1 and Bc2 and displaying different field dependencies.
Looking at 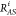 for different modes in different magnetic
field region (i.e., different M⃗) in Figure 18c,
one can see that
for different modes in different magnetic
field region (i.e., different M⃗) in Figure 18c,
one can see that 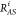 is nonzero for U2 and U4 at B < Bc1, for all four modes at Bc1 < B < Bc2, and for only U1 at B > Bc2 as summarized in Figure 18d. By just tuning the ratio λi and the overall intensity ai, the computed magnetic field dependence
of U1–4 in Figure 18e well matches the experimental data.
is nonzero for U2 and U4 at B < Bc1, for all four modes at Bc1 < B < Bc2, and for only U1 at B > Bc2 as summarized in Figure 18d. By just tuning the ratio λi and the overall intensity ai, the computed magnetic field dependence
of U1–4 in Figure 18e well matches the experimental data.
Figure 18.
(a) Raman spectra taken on 4L CrI3 in the RR channel at 10 K and at 0, 1, and 2 T, corresponding to the three magnetic field ranges B < Bc1, Bc1 < B < Bc2, and B > Bc2, respectively. (b) Magnetic field dependence of three modes U1,3,4. (c) A summary of the analysis of the layered magnetism-assisted Raman scattering for four phonon modes and three layered magnetic structures. (d) List of phonon modes in 4L CrI3 that contribute to the layered magnetism-assisted scattering channel with antisymmetric Raman tensors. (e) Calculated magnetic field dependence of the four phonons of 4L CrI3, U1–4, in the RR channel. Adapted with permission under a Creative Commons CC-BY license from ref (219). Copyright 2017 National Academy of Sciences.
The detection of this time-reversal symmetry broken layered magnetism-coupled phonon in few-layer CrI3 is a kind of phonon excitation found in such layered magnets. It distinguishes from the Davydov split in few-layer TMD semiconductors by having the magnetic contribution and also differentiates from the AF order-induced zone-folded time-reversal symmetric phonons in (Ni, Fe)PS3 by breaking the time-reversal symmetry.
Polaronic Effect of Excitons in CrI3
The PL spectra of monolayer CrI3 shows a large Stokes shift, broad line width, and skewed line shape, ascribed to the strong electron–phonon (e-ph) coupling present in 2D CrI3.215 Such strong e-ph coupling is further observed in wide-range (70–1100 cm–1) Raman spectra taken on 2L, as well as few-layer, CrI3, as a series of periodic broad modes up to the eighth order at low temperature.220
Absorption spectroscopy of 2L CrI3 features three prominent broad peaks at 1.51, 1.96, and 2.68 eV,220 whose line shape matches well with the reported differential reflectance spectroscopy in monolayer CrI3.215 These three peaks were originally assigned to be the ligand-field electronic transitions in the differential reflectance study and are revised to be bright exciton states by first principle GW and Bethe–Salpeter calculations.229 By choosing the Raman excitation energy matching the charge transfer exciton at 1.96 eV, a clear periodic modulation is observed in the low intensity part of the Raman spectra, which extends up to the eighth order at 10 K and sixth order at 70 K and spans a wide frequency range of 70–1100 cm–1 in 2L CrI3 (Figure 19a). Please note that the phonons and the layered magnetism coupled phonons reviewed in the two subsections above are all within the frequency range of 70–180 cm–1. By fitting the periodic modulation with broad Lorentzian profiles, the characteristic parameters, central frequency ωN, mode intensity AN, and line width ΓN, for the Nth mode can be extracted. A further linear fit of ωN as a function of N leads to the extracted periodicity of 120.6 ± 0.9 cm–1 whose energy matches that of the Eu LO phonon in the phonon calculations.230 The broadness of each mode in the periodic modulation precludes the phonon origins and instead suggests the electronic origin, for which the Nth mode is interpreted as Raman scattering off the exciton states dressed by N Eu LO phonons, with its energy agreeing with N times of the LO phonon energy and its line width dominated by the exciton line width. The existence of phonon dressed exciton states is a signature of the polaronic effect of charge transfer excitons in 2L CrI3 (as well as few-layer and bulk CrI3).
Figure 19.
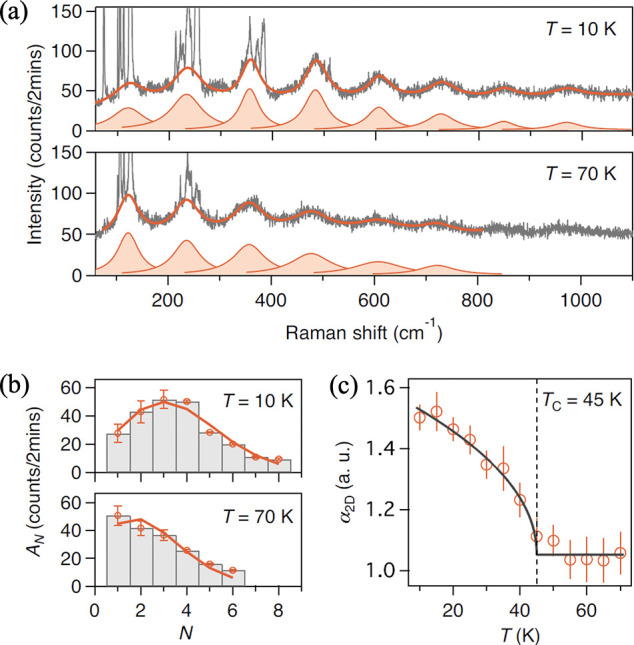
(a) Raman
spectra of 2L CrI3 taken at 10 and 70 K with
an excitation wavelength of 633 nm. Solid orange lines are fits to
the raw Raman spectra, using a sum of N Lorentzian
profiles and a constant background, 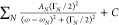 . (b) Histogram plot of
the fitted Lorentzian
mode intensity (AN) as
a function of N at 10 and 70 K. Solid curves are
fits of the peak intensity profiles to the Poisson distribution functions,
. (b) Histogram plot of
the fitted Lorentzian
mode intensity (AN) as
a function of N at 10 and 70 K. Solid curves are
fits of the peak intensity profiles to the Poisson distribution functions, 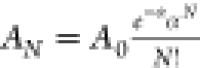 . (c)
Plot of 2D e-ph coupling constant
(α2D) as a function of temperature.
The dashed vertical line marks the magnetic onset TC = 45 K. Adapted with permission under
a Creative Commons CC BY license from ref (220). Copyright 2020 Springer Nature.
. (c)
Plot of 2D e-ph coupling constant
(α2D) as a function of temperature.
The dashed vertical line marks the magnetic onset TC = 45 K. Adapted with permission under
a Creative Commons CC BY license from ref (220). Copyright 2020 Springer Nature.
By taking careful temperature-dependent measurements of the
polaronic
effect, it is notable that the spectral weight shifts toward higher
order modes in the periodic modulation. To capture this phenomenon,
the fitted mode intensity AN at every temperature is fitted to a Poisson distribution function 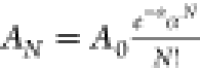 , where A0 is
the peak intensity of the original electronic band, AN is the peak intensity, and α
is the e-ph coupling in 3D (i.e., α3D) that can be scaled by a factor of 3π/4 for
2D (i.e., α2D)220 (Figure 19b). The temperature dependence of α2D shows a clear onset at the magnetic onset temperature TC = 45 K, and α2D at 10 K increases by nearly 50% from that above TC (Figure 19c). The significant enhancement of the e-ph
coupling in the magnetic state suggests an intimate coupling among
charge, lattice, and spin degrees of freedom.
, where A0 is
the peak intensity of the original electronic band, AN is the peak intensity, and α
is the e-ph coupling in 3D (i.e., α3D) that can be scaled by a factor of 3π/4 for
2D (i.e., α2D)220 (Figure 19b). The temperature dependence of α2D shows a clear onset at the magnetic onset temperature TC = 45 K, and α2D at 10 K increases by nearly 50% from that above TC (Figure 19c). The significant enhancement of the e-ph
coupling in the magnetic state suggests an intimate coupling among
charge, lattice, and spin degrees of freedom.
From the magnetic-field-dependent Raman measurements of the polaronic effect, one can see a spectral degeneracy in the two circularly parallel polarized channels (RR and LL) at 0 T, but a dramatic and opposite dichroism between RR and LL spectra at 1 T and −1 T (Figure 20a). By measuring the Raman spectra at fine steps of the magnetic field and fitting them with the Lorentzian profiles and then the Poisson distribution functions, the overall spectral intensity A0(B) in the RR and LL channels remains the same below Bc = ± 0.7 T and changes abruptly to different values above Bc with opposite relative strength under opposite magnetic field directions (Figure 20b). The magnetic field dependence of A0 well captures the layered AF to FM transition at Bc, and the dichroic behavior between RR and LL above Bc is consistent with the net magnetization present in the FM state. The e-ph coupling α2D however shows no observable magnetic field dependence (Figure 20c), suggesting that the interlayer magnetic order barely affects the e-ph coupling strength that contains the intralayer phonons and excitons.
Figure 20.
(a) Raman spectra of 2L CrI3 acquired at 10 K in the RR and LL polarization channels with an applied out-of-plane magnetic field (B⊥) of 1 T (top), 0 T (middle), and −1 T (bottom), respectively. (b, c) Plots of the Poisson fit amplitude A0 (b) and the 2D e-ph coupling strength α2D (c) as a function of the applied B⊥ in the RR (orange data points) and LL (blue) channels. Solid lines are step (orange and blue in b) and linear (gray in c) function fits to the magnetic field dependence of A0 and α2D, respectively. Adapted with permission under a Creative Commons CC BY license from ref (220). Copyright 2020 Springer Nature.
Although electronic Raman scattering often has a much weaker scattering cross section, it provides a perspective to see the electronic dynamics and its coupling to other collective excitations within the system. The polaronic effect in CrI3 reviewed here is the beginning of using electronic Raman scattering to study 2D materials.
Magnetic Birefringence and Photoluminescence Spectroscopy of 2D Magnetism
Magneto-optical characterization of atomically thin magnetic layers has proven to be a versatile tool for inspecting the magnetic interactions between localized magnetic moments in a crystal lattice. In a general view, nonzero net magnetization gives rise to birefringence effects when the magnetization impacts the polarization state of photons during reflection and/or transmission events. In a commonly used backscattering geometry, one can realize MOKE231 or refractive magnetic circular dichroism (RMCD) experiments to get insight into the arrangement of magnetic moments in single-layer (1L) or multilayer films. The MOKE technique relies on the observation that upon reflection from a layer, characterized by a finite net magnetization, additional phase arises between circularly polarized photons with left and right helicity, resulting in the rotation of a linear polarization axis between the incident and reflected photons. The RMCD technique is based on a difference in the absorption coefficient for circularly polarized photons with left and right helicity for a layer with a finite net magnetization, which creates nonzero circular polarization degree within reflected light beam.
Both types of experiments can demonstrate the existence of net magnetization in monolayer and multilayer films as illustrated in Figure 21 for CrI3 crystals. The evolution of the birefringence effects (Kerr rotation angle in MOKE experiments5 or circular polarization degree in RMCD experiments)77 with an external magnetic field applied perpendicularly to the plane of the magnetic layers, uncovers hysteric behavior characteristic of FM interactions for films with an odd number of layers (1L and 3L presented here). For bilayers and trilayers, an AF interlayer coupling is observed until a sufficient external magnetic field is applied to flip the orientation of magnetization in individual layer(s). A general view of magnetic interactions in thin films of CrI3, which arises from birefringence effects, is that individual atomic layers host magnetic moments that are coupled via in-plane FM interaction and that the character of the interlayer coupling in N-layers (N ≥ 2) depends on N. The type of interlayer coupling is likely determined by the different stacking displayed by thin and thick CrI3 films.232
Figure 21.
Birefringence effects in atomically thin CrI3. (a) The measurement of Kerr rotation angle in external magnetic field reveals finite magnetization in CrI3 monolayers.5 The inspection of CrI3 multilayers demonstrates AF interlayer coupling in (b) bilayers and (c) trilayers.5 Panels (a–c) adapted with permission from ref (5). Copyright 2017 by Springer Nature. (d, e) Qualitatively, the same behavior for atomically thin layers is observed when inspecting MCD.13 Adapted with permission from ref (13). Copyright 2018 AAAS.
Notably, the quantitative analysis of the relation between the birefringent effects and magnetization is more challenging in 2D magnets than in their 3D counterparts. For example, upon a single reflection from a surface of a 3D magnet, the Kerr rotation angle is proportional to the net magnetization (θK ∝ M) as a result of Maxwell’s equations. In case of 2D films, multiple reflections from individual layers combined with potential limitations to the applicability of Maxwell’s equations in atomic scale may lead to much more complex θK(M) functions.
An alternative probe into the magnetic effects related to the macroscopic alignment of magnetic moments comes from the inspection of magneto-PL.215 CrI3 crystals are formed via ionic bonds which lead to a band structure characterized by flat bands composed predominantly of Cr3+ ions’ d-orbitals.227,233−239 Consequently, the photoexcited electron–hole pairs are strongly localized in a way that the Bohr radius becomes comparable with the size of a unit cell in the crystal lattice. The PL response of CrI3 appears therefore, characteristically for molecular-like excitation, in form of broad emission bands originating from the coupling between the electronic states with vibrational motion of the crystal lattice. The observation of the circular polarization degree of the emitted light in external magnetic fields is consistent with the birefringence effects, as illustrated in Figure 22 for monolayer CrI3. Such finding is indicative of an efficient coupling between the band carriers with the localized magnetic moments of the Cr3+ ions.
Figure 22.
Photoluminescence bands in CrI3 monolayers below Curie temperature display large degree of circular polarization which can be linked to the emergence of magnetization. A rapid reorientation of magnetic moments leads to the change in the sign of the polarization degree combined with a hysteric behavior with a coercive field of about 0.1 T, in agreement with analogous observation by birefringence effects. Adapted with permission from ref (215). Copyright 2017 Springer Nature.
Challenges and Perspectives
Magneto-optical spectroscopy techniques have made significant contributions in revealing and investigating emergent 2D magnetic phases in both strongly correlated TMD heterostructures and natural 2D magnetic atomic crystals.
One the one hand, while TMD heterostructures have proven a rich test bed to optically explore emergent correlated phenomena in 2D systems, so far the material choices have been quite limited. This platform is ripe for many discoveries of unexplored phase diagrams of interacting electrons in tailored lattices. The robust excitons in TMDs present a large sensitivity to their surrounding magnetic and dielectric environment, which, together with their spin-selective coupling to photons, can help to probe and sense a variety of emergent magnetic phases either within the TMD themselves or in other nearby 2D vdW materials via optical spectroscopy. The ease of the “pick and place” stacking technique characteristic of 2D crystals offers further goals to engineer vdW heterostructures with enhanced sensing capabilities. For example, although vdW heterostructures consisting of a monolayer TMD semiconductor and a bilayer/trilayer ferromagnet have allowed to monitor the flip in the magnetization of an individual layer in the vdW ferromagnet, these heterostructures have not yet allowed to disentangle the layer responsible for the spin flip. Alternatively, a vdW heterostructure in which the bilayer/trilayer ferromagnet is encapsulated by TMDs monolayers with different energy band gaps would in principle allow to track down the individual layers responsible for the magnetization flips, providing further insight into the layered ferromagnetism of vdW crystals. Moreover, two of the current limitations of 2D TMD excitons as sensors of magnetic phenomena are their response to applied magnetic fields (i.e., the exciton g-factors) and the energy line widths of the exciton resonances. TMD excitons present typical g-factors of |g|∼ 4168 and transform-limited line widths down to 2–4 meV in the highest quality samples.240 Other excitonic species in TMDs which also exhibit spin-dependent optical selection rules, but present larger g-factors and narrower optical line widths, might naturally provide better sensitivity. For example, interlayer excitons localized in the moiré potential created by a TMD heterobilayer feature spin- and valley-dependent optical transitions with line widths below 100 μeV and g-factors as large as |g|∼ 16.207,241−245 These localized interlayer excitons and trions might prove useful to keep exploring the emerging field of magnetic phenomena in 2D vdW crystals.
On the other hand, 2D magnetic atomic crystals have shown a wealth of intriguing phenomena that stem out of the intimate interactions among the lattice, spin, and charge degrees of freedom, yet much effort so far has been focused on classical spin systems. Even though examples surveyed in this section focus on the archetype 2D magnet CrI3, it already presents interesting phenomena including magnetism-induced structural phase transitions and vice versa (spin–lattice coupling), time-reversal symmetry broken static magnetism-coupled phonon modes (spin-phonon coupling), and magnetism-enhanced exciton–polarons (spin-charge-lattice coupling). Looking at the much broader class of 2D magnets that have been and are to be discovered, ranging from Ising, XY, Heisenberg, and Kitaev-types to spin liquids, one can exploit 2D magnets of different kinds to explore interactions among multiple degrees of freedoms in the 2D limit that cannot be accessed previously in quasi-2D or 3D magnetic systems. One would also be driven to quest how the enhanced thermal and quantum fluctuations and the promoted instabilities, inherent to 2D, would impact the magnetic ground states, spin wave excitations, and the coupling of spin to other degrees of freedoms. Moreover, one would indeed be curious about how moiré superlattices would modulate the 2D magnetism in twisted 2D magnetic hetero- and homostructures. At the same time, the rich physics in 2D magnets naturally calls for sophisticated experimental tools to reveal, understand, and control them. Referring back to the research of quasi-2D and 3D magnets, a vast variety of optical, X-ray, neutron, and transport techniques have been exploited to uncover the nature of their magnetism. Due to the limitation from the sample size of 2D magnets, X-ray, neutron, and bulk transport probes become no longer feasible here, whereas the optical spectroscopy and nanotransport techniques remain active in the field. One may go well beyond the linear magneto-optical spectroscopy discussed here to apply nonlinear optical techniques such as multidimensional coherent spectroscopy that are suitable in capturing the spin, charge, and lattice degrees of freedom and disentangling their coupling in 2D magnets.
Magnetic Imaging
Magnetic imaging techniques play an important role in studying vdW magnetic materials. With optical, electron beam, and nanoscale physical probes, these techniques offer spatially resolved information on sample magnetization. The microscopic magnetic properties can be unambiguously determined from these measurements upon systematically varying conditions such as external magnetic field or temperature. In this section, we review magnetic imaging techniques that have been used to explore the vdW magnetic materials in the past few years. We briefly introduce the basic physics and applications of these techniques and discuss their strengths and limitations. Indeed, a comprehensive study of vdW magnets requires quantitative measurement at nanoscale and even atomic scale for both static and dynamic magnetization (up to THz). However, no single magnetic imaging technique can satisfy all these requirements. Multiple techniques are needed to obtain a complete understanding of materials.
Optical Detection Methods
Optical detection techniques using visible and UV light are most widely used in the primary characterization of vdW magnetic materials because they are easy to implement in ordinary laboratories and have nearly no limitation on work temperature and locally applied magnetic field. These methods are based on magnetization dependent response to light, for example, MOKE and MCD. MOKE is one of the magneto-optics effects, which is based on the effect that the polarization of reflected light changes as a function of sample magnetization. The case of transmitted light is called the Faraday effect, which is seldom used because it requires a transparent sample/substrate. MCD refers to the difference in absorption of left and right circularly polarized light by a material with a magnetization direction parallel to the light propagation direction. Actually, both MOKE and MCD originate from spin-dependent electronic states of the magnetic material, which results in an anisotropic optical permittivity. Both MOKE and MCD can be phenomenologically understood as a manifestation of imaginary and real parts of magnetization-dependent optical permittivity tensor.
With laser scanning MOKE, Huang et al. measured the magnetization of CrI3 and observed FM order in monolayer CrI3 and AF order in bilayer,5 and Gong et al. showed that Cr2Ge2Te6 remains a ferromagnet down to bilayers (Figure 23).6 The Curie temperatures of monolayer CrI3 (45 K) and Cr2Ge2Te6 (30 K) are lower than that of their bulk material, which are 60 and 70 K, respectively, indicating an enhanced spin fluctuation in intrinsic 2D systems. Later, electrical control of the magnetic order in atomically thin CrI3 has been demonstrated using MCD.8,9,11 A certain challenge for both techniques is that the MOKE and MCD signal level from vdW magnets only results in a relative change of the total detection signal in the order of 10–3 to 10–6. SiO2/Si substrates also contribute a disturbing background. The signal-to-noise ratio can be improved by using lock-in detection in laser scanning imaging setups.5,8,9,11 The laser scanning setup can be easily adapted to a femtosecond pump–probe scheme. This enables the observation of high-frequency magnetization dynamics, such as spin waves.28 The recent development of single photon level sensitivity electron-multiplying CCD cameras allows to reduce to laser power in the wide-field illumination MCD so that laser heating effects can be suppressed. Jin et al. imaged spin fluctuation in monolayer CrBr3 using a a wide-field MCD with time resolution of about 10 ms.246 They observed the usual strong critical slow down of spin fluctuation and demonstrated magnetic states switching using electrostatic gating .
Figure 23.
(a) MOKE maps of a CrI3 monolayer at external magnetic fields of 0, 0.15, and 0.3 T. Adapted with permission from ref (5). Copyright 2017 Springer Nature. (b) Kerr rotation signal for Cr2Ge2Te6 bilayer flake under 0.075 T as the temperature decreases from 40 to 4.7 K. The average background signal has been subtracted and the signals are truncated at 30 μrad. Adapted with permission from ref (6). Copyright 2017 Springer Nature. (c) Pump-induced Kerr rotation as a function of pump–probe delay time in bilayer CrI3 under different in-plane magnetic fields. Adapted with permission from ref (28). Copyright 2020 Springer Nature. (d) (iii) Illustration of the wide-field MCD experimental setup. Blue and red beams represent illumination light from the laser and scattered light from the sample with different effective numeric apertures. HWP: Half-wave plate. QWP: Quarter-wave plate. (ii–iv) Optical microscopy image (ii) and polarization-enhanced MCD image (iii, iv) of a monolayer CrBr3 (white dashed box). The MCD image shows giant optical contrast of ±60% for the positive (iii) and negative (iv) remnant magnetization. Adapted with permission from ref (246). Copyright 2020 Springer Nature.
Besides MOKE and MCD, SHG, Raman spectroscopy, and polarization resolved PL have also been used to probe the magnetic orders of chromium trihalides.24,203,247 All these techniques have been proved to be powerful tools to probe vdW magnets down to the monolayer with diffraction-limited spatial resolution.
A much higher spatial resolution can be achieved by using XMCD, which is based on measuring the asymmetry in X-ray absorption spectrum (XAS) upon exciting the atomic core levels with the left and right circular polarized X-rays. XMCD can be realized with many detection methods, for example, photoemission electron microscopy (PEEM) and scanning transmission X-ray microscopy (STXM) (Figure 24). Li et al. imaged the magnetic structure in Fe3GeTe2 flakes with PEEM and observed unconventional out-of-plane strip domains down to 14 nm-thick flakes. They found that patterned flakes show a transition to an in-plane vortex phase above the Curie temperature of the patterned flakes (230 K), which persists even at room temperature. Park et al. used STXM to observe the formation of Néel-type chiral magnetic skyrmions in thick Fe3GeTe2 flakes.26 They demonstrated that bipolar pulse injection can induce a transition from labyrinth random domain states into Néel-type magnetic skyrmion lattices. Further on, they imaged the current-driven motion of skyrmions. We note that the applications of magneto-optical sum rules allows for the separation and the determination of both spin and orbital magnetic moments of each constituent element in multicomponent systems . The limitation of XMCD is that it requires X-ray synchrotron radiation as a light source and samples should be prepared on special thin substrates (e.g.,100 nm-thick Si3N4 membrane substrate in ref (26)).
Figure 24.
(a) STXM images show the initial labyrinth domain states stabilized at 120 and 100 K transformed to the magnetic skyrmion lattices induced by bipolar pulse bursts. The other two images at Bz = 0 mT were acquired after removing the external fields. (b) Lorentz TEM images of magnetic skyrmion lattices taken at the sample tilting angle of −20° (left), 0° (middle) and 20° (right) with respect to x-axis as illustrated in the upper panels at Bz = −40 mT and 160 K, respectively. Panels (a) and (b) are adapted with permission from ref (26). Copyright 2021 American Physical Society. (c) (i) Overfocused Lorentz-TEM images of the skyrmion bubbles taken at 93 K and in zero-field. (ii) An enlarged in-plane magnetization distribution map obtained by transport of intensity equation analysis for a selected skyrmion bubble indicated by the white dotted box in (i). (iii) Simulation of skyrmion lattices at an out-of-plane field of 60 mT. Adapted with permission from ref (25). Copyright 2020 American Chemical Society. (d) Schematic diagram of a Néel-type skyrmion on a tilt sample for Lorentz TEM imaging (left). The orange and blue circles are for positive and negative magnetizations along z direction, respectively. Brown arrows indicate the in-plane magnetization component, while gray arrows indicate the Lorentz force. Lorentz TEM images (right) observation of skyrmion lattice from under focus to over focus on WTe2/40L Fe3GeTe2 samples at 180 K with a field of 51 mT. Adapted with permission under a Creative Commons CC BY license from ref (27). Copyright 2020 Springer Nature.
Electron Microscopy
Electron microscopy has high spatial resolution because the wavelength of an electron (0.037 Å for 100 keV,0.009 Å for 1 MeV) can be much smaller than atomic distances. Scanning electron microscopy (SEM) with polarization analysis can image the magnetic microstructure at nanometer scale by using the spin polarized secondary electrons emitted from the surface of a magnetic material when it is hit by a primary electron beam. Meijer et al. used this technique to observe Néel spin spirals at the surface of bulk Fe3GeTe2 and determined its periodicity to be 300 nm.248 The disadvantage of this technique is that it can only be applied to conducting magnets with clean surfaces and requires ultrahigh vacuum conditions to avoid degradation of electron polarization. The integration time of this technique is relatively long due to the low intensity and low efficiency polarization detectors.
LTEM generates magnetic images using the deflection of high-energy (100–1000 keV) electrons transmitted through the sample caused by the Lorentz force on its trajectory. The electron deflection forms an image contrast under certain experimental configurations, such as the conventional Fresnel and Foucault mode, electron holography, and the differential phase contrast mode. It has been shown that only the magnetization curl component parallel to the electron beam direction contributes to the magnetic contrast. Therefore, Néel-type domain walls or skyrmions can only be visualized by tilting the sample because of the lack of out-of-plane magnetization curl. This also makes Lorentz TEM a powerful tool to distinguish the Néel-type and Bloch-type magnetic textures. With this technique, three groups indecently reported topological magnetic textures observed in thick Fe3GeTe2 flakes.25,26,249 Park et al.26 determined the chirality of magnetic skyrmions observed via the STXM to be of Néel type and showed its origin to be the Dzyaloshinskii-Moriya interactions (DMI)250,251 induced at the oxidized Fe3GeTe2 interface. Wang et al.249 also observed Néel-type magnetic skyrmions but argued DMI in the Te/Fe3Ge/Te slabs as a source of spin chirality. Ding et al. showed the skyrmion bubbles form vortex-like domains with Bloch-type chirality which might be the result of competition between the perpendicular magnetic anisotropy and magnetic dipole–dipole interaction. We note that the mechanism that forms Skyrmions in thick Fe3GeTe2 flakes is still under debate.252 Wu et al. found that the DMI and topological spin textures can be induced by spin orbit coupling proximity at the Fe3GeTe2/WTe2 interface by transport experiments. They successfully imaged Néel-type magnetic skyrmions in thick Fe3GeTe2 and few-layer WTe2 heterostructures with Lorentz-TEM.27
Lorentz TEM suffers from a number of drawback. The electrons scattered by nuclei and the core electron of the sample generate a disturbing background, limiting the maximum sample thickness to be ∼100 nm. In addition, the ability to probe atomically thin vdW magnets has not been demonstrated yet. It is also challenging to apply high external magnetic fields. Both the stray magnetic field and the magnetic induction of the sample contribute to the electron deflection. In some cases, these contributions may cancel out each other and result in no net deflection. This also makes the interpretation of the magnetic image challenging.
Scanning Probe Microscopy
Scanning probe microscopy (SPM) is a family of surface analysis tools that form high-spatial-resolution images by scanning a physical probe over the sample. Spin-polarized scanning tunnelling microscopy (SP-STM) uses a magnetized tip, which results in a spin-dependent tunnelling probability. This technique allows both atomic scale imaging of the crystal structure and in situ determination of the magnetic order, which is crucial to investigate the stacking order dependent magnetism in chromium trihalides.228 With SP-STM, Chen et al. imaged the atomic structure in CrBr3 bilayer and found that the two layers can be aligned either parallel or antiparallel, and exhibit AF and FM order, respectively (Figure 25).20 In this work, they grow the CrBr3 film on freshly cleaved highly oriented pyrolytic graphite substrates by MBE. We note that the SP-STM usually works with a tip-to-sample distance of 1–2 nm or smaller and requires electrically conducting sample/substrate, i.e., it would be a challenge to probe vdW magnetic insulator with SP-STM.
Figure 25.
(a) STM images of a CrBr3 film with adjacent monolayer (1L) and bilayer (2L) regions and spin-polarized tunneling signals on the bilayer regions as a function of magnetic field. Adapted with permission from ref (20). Copyright 2019 AAAS. (b) Antiferromagnetic domain patterns in MnBi2Te4 measured with MFM. Adapted with permission from ref (253). Copyright 2020 American Chemical Society. (c) Schematic illustration of the pulled quartz tube with two Nb or Pb superconducting leads connected to Au electrodes and image of a Nb SQUID-on-tip device. Inset: Magnified view showing the superconducting loop on the apex of the tip. The bridges that reside in the gap regions between the leads form the two weak links of the SQUID. Adapted with permission from ref (254). Copyright 2013 Nature Springer. (d) Gradient magnetometry signal associated with the fully polarized twisted bilayer graphene device. Adapted with permission from ref (255). Copyright 2021 AAAS. (e–g) Magnetic images obtained with scanning NV magnetometry. (e) Magnetization image of bilayer/trilayer CrI3 adapted with permissions from ref (21). Copyright 2019 AAAS. (f) The magnetic domains in bilayer CrBr3 adapted with permission under a Creative Commons CC BY license from ref (256). Copyright 2021 Springer Nature. (g) Stray field map of a magnetic skyrmion in the CoFeB system adapted with permission under a Creative Commons CC BY license from ref (257). Copyright 2018 Springer Nature.
Magnetic force microscopy (MFM) is a variant of atomic force microscopy (AFM) for studying surface magnetic properties. It is based on the noncontact mode AFM while using a magnetized tip. The magnetic contrast is obtained by subtraction of images obtained in a dual-pass scan scheme: The surface topography is recorded by measuring the repulsive forces, and then in the second scan the repulsive forces are recorded with the tip lifted up by a constant distance above the previously measured surface profile. MFM has relative high spatial resolution determined by the tip geometry and lifted height (∼100 nm). Fei et al. directly imaged magnetic domains in a thick Fe3GeTe2 flake with MFM and recorded their evolution upon sweeping the magnetic field.77 These results can explain the sudden jump of MOKE signals in hysteresis measurements. Sass et al. showed that MFM can be used to directly image antiferromagnetic domain walls in the MnBi2Te4 family and the Dirac semimetal EuMnBi2.253 We note that MFM has also been used in other works and successfully revealed the domain structures in thick vdW magnets.81,258 However, MFM is an invasive probe because it relies on the interaction between the magnetic tip and the sample. The tip magnetization should be reduced to avoid disturbing the magnetic structure, at the expense of sensitivity. The electrostatic interaction between the tip and sample should also be minimized in magnetic imaging.253
In principle,
it is possible to obtain quantitative magnetic field
information in MFM measurement. But this requires a sophisticated
measurement process and system calibration. Scanning probe magnetometry
with nanoscale magnetometers is an elegant solution to directly measure
the magnetic field above the sample surface. Among all the traditional
magnetometers, the superconducting quantum interference device (SQUID)
offers the highest sensitivity. The recent progress in nano-SQUID
makes it possible to achieve high spatial resolution images in a scanning
probe geometry. The state-of-the-art nano-SQUID can achieve device
diameters down to about 50 nm, while still offering a magnetic field
sensitivity of sub-100 nT/  .254 This technique
has been used to observe the orbital FM order in twisted bilayer graphene255 and equilibrium currents of individual quantum
Hall edge states in graphene monolayers.259 The scanning nano-SQUID can work at sub-Kelvin temperatures and
in high magnetic fields of over 2.5 T. However, it is challenging
to use nano-SQUID at high temperature (>10K) limited by the low-temperature
superconducting material of the probe.
.254 This technique
has been used to observe the orbital FM order in twisted bilayer graphene255 and equilibrium currents of individual quantum
Hall edge states in graphene monolayers.259 The scanning nano-SQUID can work at sub-Kelvin temperatures and
in high magnetic fields of over 2.5 T. However, it is challenging
to use nano-SQUID at high temperature (>10K) limited by the low-temperature
superconducting material of the probe.
The nitrogen vacancy
(NV) center in diamond is a promising candidate
to realized nanoscale magnetometry.260 The
spin state of NV center can be easily initialized and readout with
a green laser and coherently manipulated with microwave fields. Interestingly,
the NV spin state has long relaxation and coherence time, and high
fidelity single spin control can be realized at temperatures from
cryogenic to room temperature. It has been demonstrated as a high
sensitivity magnetometer for magnetic field with frequency range from
DC to several GHz at a broad temperature range. Devices are operated
in a scanning probe geometry using a diamond probe with a single NV
center, which can simultaneously obtain the sample surface profile
and magnetic field information in a single scan. Thiel et
al. and Sun et al. independently studied
few-layer CrI3 and CrBr3 with cryogenic scanning
NV magnetometry.21,256 In both works, the stray magnetic
field is mapped by measuring the frequency shift of NV electron spin
resonance via the so-called optically detected magnetic
resonance, and the quantitative magnetization images are obtained
by reverse-propagation protocols. The spatial resolution achieved
in these works is about 50–80 nm, limited by the distance between
the NV center and the sample surface. Thiel et al. determined the magnetization of CrI3 to be about 16
μB/nm2 for odd number of layers while
vanishing for even number of layers. These results are consistent
with layer-number-dependent magnetism reported by Huang et
al.5 Moreover, by studying a sample
punctured unintentionally by a diamond tip, it was found that at structural
modifications can induce switching between FM and AF interlayer ordering.
Latter, Sun et al. determined the magnetization of
a CrBr3 bilayer to be about 26 μB/nm2 and imaged the magnetic domain structure formed in a thermally
demagnetized sample. They studied the domain evolution upon varying
the external magnetic field and directly imaged the domain wall pinning
at defect sites. The DC magnetic sensitivity achieved is about 300
nT/  . In the room-temperature measurement, Fabre et al. characterized the vdW magnet CrTe2 thin
flake and determined the magnetization to be ∼25 kA/m for a
20 nm-thick flake.261 These works highlighted
scanning NV magnetometry as a powerful tool to quantitatively study
static properties vdW magnets. A recent work by Vool et al.262,263 that studies the electron transport in WTe2 using echo magnetometry shows that it is feasible to study
the dynamic magnetization properties with scanning NV magnetometry.
. In the room-temperature measurement, Fabre et al. characterized the vdW magnet CrTe2 thin
flake and determined the magnetization to be ∼25 kA/m for a
20 nm-thick flake.261 These works highlighted
scanning NV magnetometry as a powerful tool to quantitatively study
static properties vdW magnets. A recent work by Vool et al.262,263 that studies the electron transport in WTe2 using echo magnetometry shows that it is feasible to study
the dynamic magnetization properties with scanning NV magnetometry.
Although scanning nano-SQUID and scanning NV magnetometry can provide quantitative information on the magnetism, it takes a long time to obtain a whole image. In the cases where the spatial resolution is not that crucial, NV microscopy based on ensemble NV centers implanted in a plane closed to the diamond surface can be used to reduce the measurement time.264 A common challenge for magnetic imaging techniques that probe magnetic field is the magnetization reconstruction problem. Generally, the solution of magnetization reconstruction does not result in a single solution. Dovzhenko et al. discussed this problem for scanning NV magnetometry and showed that arbitrariness of the solution can be attributed to gauge-like degree of freedom as in electromagnetism.257 They determined the magnetization distribution of magnetic skyrmions in a CoFeB system by fixing the gauge. In ref (21) and ref (256), the magnetization reconstruction is based on the out-of-plane spin assumption supported by previous studies. However, solutions for the general case are unexplored.
Magnetic and Electrical Transport Characterization
The discovery of intrinsic long-range magnetic order in atomic monolayer magnets has triggered significant interest in the fundamental 2D magnetism and spin-related applications. In order to understand the magnetic behavior in 2D thin samples and in nanostructures, it is necessary to probe the nature of magnetism in crystals and its influence on electrical transport properties. Here we survey the current status of magnetocaloric effect in the vicinity of magnetic transition temperature in 2D vdW magnetic crystals. We also present a review of electrical transport properties of the itinerant and exfoliable ferromagnet FenGeTe2.
Magnetocaloric Effect
The magnetocaloric effect discerned via adiabatic temperature change or isothermal magnetic entropy change ΔSM is an important property of ferromagnets that can be used for magnetic refrigeration, which is a promising and environmentally friendly energy conversion technology.265−268 The magnetic entropy change ΔSM is also correlated with the critical behavior of the phase transition via magnetization isotherms M(H) and specific heat Cp(T). The magnetic entropy change ΔSM(T, H) induced by the external field is
with the Maxwell’s relation [∂S(T,H)/∂H]T = [∂M(T,H)/∂T]H.269,270 In the case of magnetization measured at small discrete magnetic field and temperature intervals, ΔSM(T, H) could be practically approximated as
. The parameters of |ΔSM(T, H)| curves follow a series
of power laws dependent on the field as 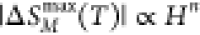 , δfwhm ∝ Hb, and RCP ∝ Hc, where
, δfwhm ∝ Hb, and RCP ∝ Hc, where 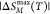 is the maximum of the |ΔSM(T, H)|, δfwhm is the full width at
half-maximum, and
is the maximum of the |ΔSM(T, H)|, δfwhm is the full width at
half-maximum, and 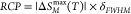 is relative cooling power.271,272 The magnetic entropy
change parameters directly fit critical exponents;
this can avoid the multistep nonlinear fitting induced deviation in
the modified Arrott plot and Kouvel–Fisher plot (see Magnetic Critical Behavior section for details).
The exponents n, b, and c are n = 1 + (β – 1)/(β
+ γ), b = 1/Δ, and c = 1 + 1/δ, respectively, where β, γ, δ,
and Δ are critical exponents; the reference temperature of the
peak entropy change should scale with 1/Δ.273Tc can be
obtained from the magnetic specific heat change ΔCp(T, H) = Cp(T, H) – Cp(T, 0) = T∂ΔSM(T, H)/∂T.274 With the decrease in temperature, ΔCp changes from positive in the paramagnetic
to negative in FM phase. At the critical point Tc, all ΔCp(T) curves cross over the zero point.
The entropy
is relative cooling power.271,272 The magnetic entropy
change parameters directly fit critical exponents;
this can avoid the multistep nonlinear fitting induced deviation in
the modified Arrott plot and Kouvel–Fisher plot (see Magnetic Critical Behavior section for details).
The exponents n, b, and c are n = 1 + (β – 1)/(β
+ γ), b = 1/Δ, and c = 1 + 1/δ, respectively, where β, γ, δ,
and Δ are critical exponents; the reference temperature of the
peak entropy change should scale with 1/Δ.273Tc can be
obtained from the magnetic specific heat change ΔCp(T, H) = Cp(T, H) – Cp(T, 0) = T∂ΔSM(T, H)/∂T.274 With the decrease in temperature, ΔCp changes from positive in the paramagnetic
to negative in FM phase. At the critical point Tc, all ΔCp(T) curves cross over the zero point.
The entropy 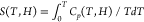 and the ΔSM induced by the external field should be ΔSM(T, H) = SM(T, H) – SM(T, 0). The adiabatic temperature
change ΔTad caused
by the field change can be indirectly determined, ΔTad(T, H) = T(S, H) – T(S, 0), where T(S, H) and T(S, 0) are the temperatures in the field H ≠
0 and H = 0, respectively, at constant total entropy S.
and the ΔSM induced by the external field should be ΔSM(T, H) = SM(T, H) – SM(T, 0). The adiabatic temperature
change ΔTad caused
by the field change can be indirectly determined, ΔTad(T, H) = T(S, H) – T(S, 0), where T(S, H) and T(S, 0) are the temperatures in the field H ≠
0 and H = 0, respectively, at constant total entropy S.
According to the principle of universality, ΔSM(T, H) can be scaled into a universal curve independent of the
external field.272 It is constructed by
normalizing all the −ΔSM curves against the respective maximum 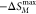 , namely,
, namely, 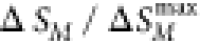 by rescaling the temperature θ defined
as θ– = (Tc – T)/(Tr1 – Tc), T < Tcand θ+ = (T – Tc)/(Tr2 – Tc), T > Tc, where Tr1 and Tr2 are
the temperatures of the two reference points below and above Tc, respectively. Here, Tr1 and Tr2 are defined as
by rescaling the temperature θ defined
as θ– = (Tc – T)/(Tr1 – Tc), T < Tcand θ+ = (T – Tc)/(Tr2 – Tc), T > Tc, where Tr1 and Tr2 are
the temperatures of the two reference points below and above Tc, respectively. Here, Tr1 and Tr2 are defined as 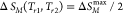 . A good scaling
and convergence of ΔSM(T, H) curves indicates that
the magnetic phase transition is
of a second-order type.275 Then, the ΔSM(T, H) curves should follow the scaling equation of state H/Mδ = f(ε/M1/β), where the ΔSM(T, H) can be rewritten in the form of ΔSM(T, H) = H(1−α)/Δg(ε/H1/Δ), where
critical exponents α and Δ can be obtained by Rushbrooke’s
law α = 2–2β – γ and Δ = βδ.
. A good scaling
and convergence of ΔSM(T, H) curves indicates that
the magnetic phase transition is
of a second-order type.275 Then, the ΔSM(T, H) curves should follow the scaling equation of state H/Mδ = f(ε/M1/β), where the ΔSM(T, H) can be rewritten in the form of ΔSM(T, H) = H(1−α)/Δg(ε/H1/Δ), where
critical exponents α and Δ can be obtained by Rushbrooke’s
law α = 2–2β – γ and Δ = βδ.
Magnetism in Bulk 2D vdW Magnets
Ferromagnetic order in ultrathin crystals was reported in a monolayer CrI3 and in a few-layer Cr2Ge2Te6.5,6 These discoveries were soon followed by many others including insulating CrCl3, CrBr3, VI3, MnPS3, FePS3 and conducting monolayers such as Fe3GeTe2 and CrTe2 exhibiting magnetic order close to or at the room temperature.12,32,119,120,212,234,276−278 Probing magnetic order in ultrathin crystals is beyond the reach of conventional magnetometry. Thus, several, mostly optical, methods have been used to probe the magnetic state in mono- and few-layer crystals such as MOKE, Raman, reflection MCD, polarization-resolved PL, and NV-center magnetometry (see Magnetic Imaging section). Here we summarize an extensive magnetization measurements used to investigate the critical behavior and magnetocaloric effect in 2D vdW crystals on the example of Cr2Ge2Te6. Estimate of universality class to which the material belongs gives an important starting point for the understanding of magnetic state in bulk and in nanofabricated crystals.
Cr2Ge2Te6 crystallizes in a quasi-2D layered structure
(Figure 26a), in which
the Cr ions are located at the centers of slightly distorted octahedra
of Te atoms.279,280 When compared to Cr2Si2Te6, Cr2Ge2Te6 features smaller vdW gap, larger cleavage energy and larger
in-plane nearest-neighbor Cr–Cr distance, which enhances the Tc from 32 K for Cr2Si2Te6 to 61 K for Cr2Ge2Te6 (Figure 26b). The isothermal data with 2D-Ising model (β = 0.125
and γ = 1.75) (Figure 26c) show a set of relatively parallel straight lines, in contrast
to different 3D models (not shown here). Figure 26d shows the final modified Arrott plot generated
by using β = 0.194 and γ = 1.36, rapidly converged by
a rigorous iterative method and with the adoption of 2D Ising model
as an initial model.269 The finally obtained Ms(T) and 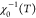 are plotted
as a function of T in Figure 26e. The
power law fit gives β = 0.196(3), Tc = 62.64(2) K for T < Tc and γ = 1.32(5), Tc = 62.66(9) K for T > Tc (Figure 26e), very close
to the values β = 0.200(3) with Tc = 62.65(7) K and γ = 1.28(3) with Tc = 62.75(6) K generated from
the Kouvel–Fisher plot (Figure 26f). The critical exponent δ = 7.96(1)
determined from the critical isotherm analysis at Tc = 62.7 K (Figure 26g), matches reasonably well with the calculated
values δ = 7.73(15)/7.40(5) by using the Widom relation δ
= 1 + γ/β with β and γ obtained from the modified
Arrott/Kouvel–Fisher plot. The scaled mversush well collapse into two separate
branches, one below Tc and another above Tc (Figure 26h), respectively,
as well as the MH–1/δversusεH–1/(βδ) which collapse into a single curve
(inset in Figure 26h). This clearly indicates that the interactions get properly renormalized
in a critical regime following the equation of state scaling.
are plotted
as a function of T in Figure 26e. The
power law fit gives β = 0.196(3), Tc = 62.64(2) K for T < Tc and γ = 1.32(5), Tc = 62.66(9) K for T > Tc (Figure 26e), very close
to the values β = 0.200(3) with Tc = 62.65(7) K and γ = 1.28(3) with Tc = 62.75(6) K generated from
the Kouvel–Fisher plot (Figure 26f). The critical exponent δ = 7.96(1)
determined from the critical isotherm analysis at Tc = 62.7 K (Figure 26g), matches reasonably well with the calculated
values δ = 7.73(15)/7.40(5) by using the Widom relation δ
= 1 + γ/β with β and γ obtained from the modified
Arrott/Kouvel–Fisher plot. The scaled mversush well collapse into two separate
branches, one below Tc and another above Tc (Figure 26h), respectively,
as well as the MH–1/δversusεH–1/(βδ) which collapse into a single curve
(inset in Figure 26h). This clearly indicates that the interactions get properly renormalized
in a critical regime following the equation of state scaling.
Figure 26.
(a) Crystal
structure of Cr2Ge2Te6. (b) Temperature
dependence of magnetization for Cr2Ge2Te6 measured in H = 1 kOe. Inset:
Field dependence of magnetization at T = 2 K. (c)
2D Ising model plot of isotherms around Tc. (d) Modified Arrott plot of M1/βversus (H/M)1/γ with β = 0.194 and γ
= 1.36. The straight line is the linear fit of isotherm at T = 62.5 K. (e) Temperature dependence of the spontaneous
magnetization Ms (left)
and the inverse initial susceptibility 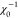 (right) with solid fitting curves.
(f)
Kouvel–Fisher plots of
(right) with solid fitting curves.
(f)
Kouvel–Fisher plots of 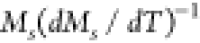 (left) and
(left) and 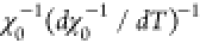 (right) with solid fitting curves. (g)
Isotherm MversusH plot collected at Tc = 62.7 K. Inset: The same plot in log–log scale with a solid
fitting curve. (h) Scaling plots of renormalized magnetization mversus renormalized field h below and above Tc for
Cr2Ge2Te6. Inset: The rescaling of
the M(H) curves by MH–1/δversus εH–1/(βδ).
All panels adapted with permission from ref (279). Copyright 2017 American
Physical Society.
(right) with solid fitting curves. (g)
Isotherm MversusH plot collected at Tc = 62.7 K. Inset: The same plot in log–log scale with a solid
fitting curve. (h) Scaling plots of renormalized magnetization mversus renormalized field h below and above Tc for
Cr2Ge2Te6. Inset: The rescaling of
the M(H) curves by MH–1/δversus εH–1/(βδ).
All panels adapted with permission from ref (279). Copyright 2017 American
Physical Society.
Considering the intrinsic
correlation between the magnetic entropy
change (|ΔSM|)
and critical behavior near the magnetic phase transition, the critical
exponents β, γ, δ, and Tc can also be deduced from the magnetic-field-dependent
|ΔSM(T, H)| without the use of any initial models. The
|ΔSM(T, H)| curves in different H are
depicted in Figure 27(a). The precise value of Tc = 66.7 K can be determined by the zero point of magnetic specific
heat change ΔCp (Figure 27b). The
field dependence of magnetocaloric effect parameters 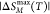 , δfwhm, and RCP are plotted in Figure 27c–e, where the power-law fitting
gives n = 0,575(9), b = 0.524(3),
and c = 1.902(1), respectively. Then the critical
exponents can be calculated as β = 0.177(9), γ = 1.746(8),
δ = 10.869(5), and Δ = 1.907(3), which avoids the multistep
nonlinear fitting described previously. The generated modified Arrott
plot illustrates the reliability of the obtained critical exponents,
in which the M1/βversus (H/M)1/γ curves
show a series of lines parallel to each other (Figure 27f). Good collapse and overlap of rescaled
curves around Tc further
confirms the reliability and validity of critical exponents obtained
by the magnetic entropy change method (Figure 27g,h). Critical exponents calculated by different
methods should agree with each other and show self-consistency for
a certain type of phase transition because the critical behavior is
independent of the microscopic details.
, δfwhm, and RCP are plotted in Figure 27c–e, where the power-law fitting
gives n = 0,575(9), b = 0.524(3),
and c = 1.902(1), respectively. Then the critical
exponents can be calculated as β = 0.177(9), γ = 1.746(8),
δ = 10.869(5), and Δ = 1.907(3), which avoids the multistep
nonlinear fitting described previously. The generated modified Arrott
plot illustrates the reliability of the obtained critical exponents,
in which the M1/βversus (H/M)1/γ curves
show a series of lines parallel to each other (Figure 27f). Good collapse and overlap of rescaled
curves around Tc further
confirms the reliability and validity of critical exponents obtained
by the magnetic entropy change method (Figure 27g,h). Critical exponents calculated by different
methods should agree with each other and show self-consistency for
a certain type of phase transition because the critical behavior is
independent of the microscopic details.
Figure 27.
Temperature dependence
of (a) |ΔSM| and
(b) ΔCp in different
fields with H ∥ c; Field
dependence of parameters from |ΔSM(T)| with the fitted
curves: (c) 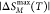 , (d) δTfwhm,
and (e) RCPversusH with the fitted curves; (f) Modified Arrott plot
based on the obtained critical exponents. Scaling of the |ΔSM(T, H)| curves: (g) normalized ΔSM(T, H)
as a function of θ (inset gives Tr1 and Tr2 as a function of H); (h) – ΔSM/H(1−α)/Δversus ε/H1/Δ. All panels adapted with permission from ref (280). Copyright 1998 American
Physical Society.
, (d) δTfwhm,
and (e) RCPversusH with the fitted curves; (f) Modified Arrott plot
based on the obtained critical exponents. Scaling of the |ΔSM(T, H)| curves: (g) normalized ΔSM(T, H)
as a function of θ (inset gives Tr1 and Tr2 as a function of H); (h) – ΔSM/H(1−α)/Δversus ε/H1/Δ. All panels adapted with permission from ref (280). Copyright 1998 American
Physical Society.
It is also important to understand the nature as well as the range of interactions in Cr2Ge2Te6. In renormalization group theory analysis the interaction decays with distance r as J(r) ≈ r–(d+σ), where σ is the range of interaction.281 According to this model, the range of spin interaction is long or short depending on the σ < 2 or σ > 2; and the mean-field model is satisfied when σ ≤ 3/2. The susceptibility exponent γ calculated from renormalization group approach is
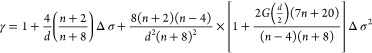 |
where 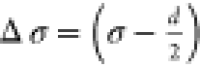 and
and 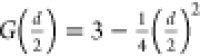 .282 To find
out the range of interaction σ as well as the dimensionality
of both lattice d and spin n in
Cr2Ge2Te6, the parameter σ
in above equation is adjusted for different set of {d:n} so that it yields a value for γ close
to that observed experimentally.282 Here
{d:n} = {2:1} and σ ≈
1.5–1.6 implies that the spin interaction in Cr2Ge2Te6 is of a 2D Ising type coupled with a
long-range interaction. This long-range interaction might be associated
with a non-negligible interlayer and strong spin–lattice coupling.283−286
.282 To find
out the range of interaction σ as well as the dimensionality
of both lattice d and spin n in
Cr2Ge2Te6, the parameter σ
in above equation is adjusted for different set of {d:n} so that it yields a value for γ close
to that observed experimentally.282 Here
{d:n} = {2:1} and σ ≈
1.5–1.6 implies that the spin interaction in Cr2Ge2Te6 is of a 2D Ising type coupled with a
long-range interaction. This long-range interaction might be associated
with a non-negligible interlayer and strong spin–lattice coupling.283−286
Critical exponents and magnetocaloric effect parameters obtained by different methods for related 2D vdW magnets are summarized in Table 7. In a comprehensive study of critical exponents for 2D magnets Taroni et al. concluded that the critical exponent β for a 2D magnet should be within a window ∼0.1 ≤ β ≤ 0.25.316 The critical exponents of Cr2Si2Te6 are close to those of Cr2Ge2Te6, indicating 2D Ising-like behavior coupled with a long-range interaction (Table 7). In contrast to Cr2(Si/Ge)2Te6, the critical exponents of bulk CrI3, Cr1–xTe, FeCr2Te4 and FenGeTe2 crystals exhibit 3D critical scaling since those compounds possess smaller vdW gaps, giving rise to much stronger interlayer coupling (Table 7). In CrX3 (X = Cl, Br, and I), the Cr–Cr distances increase with increasing halogen size, the direct exchange should weaken from Cl to Br to I. Therefore, the superexchange via Cr-X-Cr is expected to be FM and plays a more important role in magnetic interaction.235 Moving form Cl to Br to I, more covalent Cr–X bonds strengthen superexchange interactions and raise ordering temperatures. They also increase spin–orbit coupling, which may account for the large magnetic anisotropy.235 CrCl3 and VI3 are situated close to a 2D to 3D critical point (β ∼ 0.25). A similar critical phase transition crossover from 2D to 3D is also found in NiPS3 and MnPS3.317,318 Furthermore, a tunable Tc of 150–220 K for Fe3−δGeTe2 strongly depends on the Fe deficiency, suggesting the role of Fe occupancy in the magnetic exchange. However, the obtained critical exponents for this family show a robust 3D Heisenberg-type spins coupled with a long-range interaction; the range of interaction σ ranges from 1.6 to 1.89 with decrease in Fe content (Table 7). It is interesting that the Fe vacancy has small effect on the universality class of the critical behavior. Fe5GeTe2 also exhibits 3D Heisenberg-type magnetic exchange with long-range interaction decaying as J(r) ≈ r–4.916 (Table 7). In Mn3Si2Te6, a 3D analog of Cr2Si2Te6, some Mn atoms reside in the vdW gap, similar to intercalated TMDs.319,320 Such structure promises the robust interlayer coupling as well as a 3D long-range magnetic interaction.315 Further investigation on the size-dependent properties is of interest. In addition, we can take the dimensional crossover in the critical exponents from the values expected in 3D to those in 2D (see Table 4) to mark the transition from a 3D behavior to a truly 2D character, as for examples for CrI3 and Fe3GeTe2.321,322
Table 7. Comparison of magnetocaloric effect parameters and critical exponents of indicated vdW magnetic materialsa.
| materials | field | ref | technique | –ΔSMmax | RCP | ΔTad | α | β | γ | δ | Tc | J(r) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cr2Si2Te6 | H ∥ ab | (287) | MH | 4.9 | ||||||||
| H ∥ c | MH | 5.05 | 114 | |||||||||
| (288) | MAP | 0.170(8) | 1.532(1) | 10.01(5)cal | 30.95(20) | r–3.630 | ||||||
| KFP | 0.175(9) | 1.562(9) | 9.93(6)cal | 30.97(16) | ||||||||
| CI | 9.917(8) | 31 | ||||||||||
| (287) | MAP | 0.169(4) | 1.33(8) | 8.9(3)cal | 32.0(4) | |||||||
| KFP | 0.178(9) | 1.32(4) | 8.4(2)cal | 32.2(4) | ||||||||
| CI | 9.28(3) | 32 | ||||||||||
| Cr2Ge2Te6 | H ∥ ab | (287) | MH | 2.6 | ||||||||
| H ∥ c | MH | 2.64 | 87 | |||||||||
| (289) | MH | 3.21 | 94.3 | |||||||||
| (279) | MAP | 0.196(3) | 1.32(5) | 7.73(15)cal | 62.65(7) | r–3.52 | ||||||
| KFP | 0.200(3) | 1.28(3) | 7.40(5)cal | 62.70(12) | ||||||||
| CI | 7.96(1) | 62.7 | ||||||||||
| (280) | MEC | 0.177(9) | 1.746(8) | 10.869(5)cal | 66.4(3) | r–3.592 | ||||||
| (290) | MAP | 0.242(6) | 0.985(3) | 5.070(6)cal | 67.93(7) | |||||||
| KFP | 0.240(6) | 1.000(5) | 5.167(6)cal | 67.90(8) | ||||||||
| CI | 5.032(5) | 67.9 | ||||||||||
| (291) | AC | 0.35 | 1.43 | 5.24 | 62.84 | |||||||
| CrI3 | H ∥ ab | (292) | MH | 2.68 | ||||||||
| H ∥ c | MH | 4.24 | 122.6 | |||||||||
| SH | 5.65 | 2.34 | ||||||||||
| (293) | MAP | 0.284(3) | 1.146(11) | 5.04(1)cal | 60.42(8) | r–4.69 | ||||||
| KFP | 0.260(4) | 1.136(6) | 5.37(4)cal | 60.24(26) | ||||||||
| CI | 5.32(2) | 60 | ||||||||||
| (294) | MAP | 0.325(6) | 0.825(3) | 3.538(6)cal | 64.02(7) | |||||||
| KFP | 0.323(6) | 0.835(5) | 3.585(6)cal | 63.99(9) | ||||||||
| CI | 3.569(4) | 64 | ||||||||||
| SH | 0.11 | |||||||||||
| CrBr3 | H ∥ c | (295) | MH | 7.2 | 191.5 | |||||||
| SH | 6.91 | 2.37 | ||||||||||
| CrCl3 | H ∥ ab | (296) | MH | 14.6 | 340.3 | |||||||
| H ∥ c | MH | 13.8 | 317.3 | |||||||||
| H ∥ ab | (297) | MH | 19.8 | |||||||||
| H ∥ c | MH | 19.5 | ||||||||||
| SH | 6.8 | |||||||||||
| H ∥ ab | (296) | MAP | 0.26(1) | 0.86(1) | 4.31(9)cal | 19.11(10) | ||||||
| KFP | 0.28(1) | 0.89(1) | 4.18(8)cal | 19.18(37) | ||||||||
| CI | 4.6(1) | 19 | ||||||||||
| VI3 | H ∥ ab | (298) | MH | 2.27 | ||||||||
| H ∥ c | MH | 2.64 | ||||||||||
| SH | 2.80 | 0.96 | ||||||||||
| H ∥ ab | (299) | MH | 2 | |||||||||
| H ∥ c | MH | 3 | ||||||||||
| (298) | MAP | 0.244(5) | 1.03(1) | 5.21(4)cal | 50.04(10) | |||||||
| CI | 5.24(2) | 50 | ||||||||||
| (299) | MEC | 0.204(8) | 1.65(7) | 9.09(1)cal | ||||||||
| MAP | 0.155(7) | 1.04(2) | 7.70(9)cal | 45.31(13) | ||||||||
| KFP | 0.146(1) | 1.07(7) | 8.32(8)cal | 45.32(12) | ||||||||
| CI | 7.78(8) | 45 | ||||||||||
| AC | 0.12(3) | 0.92(4) | 8.30(4) | |||||||||
| Fe2.64GeTe2 | H ∥ ab | (300) | MH | 1.26 | ||||||||
| H ∥ c | MH | 1.44 | 113.3 | |||||||||
| SH | 1.20 | 0.66 | ||||||||||
| (301) | MAP | 0.374(1) | 1.273(8) | 4.404(12)cal | 151.27(1) | r–4.89 | ||||||
| KFP | 0.372(4) | 1.265(15) | 4.401(6)cal | 151.25(5) | ||||||||
| CI | 4.50(1) | 151 | ||||||||||
| Fe2.72GeTe2 | H ∥ c | (302) | MEC | 0.361(3) | 1.736(7) | 5.806(8) | 157.2(2) | |||||
| H ∥ ab | MEC | 0.714(3) | 1.243(7) | 2.741(1) | 158.5(2) | |||||||
| Fe2.85GeTe2 | H ∥ c | (303) | MAP | 0.361(2) | 1.225(2) | 4.39(1)cal | 193.68(26) | r–4.8 | ||||
| KFP | 0.363(4) | 1.228(4) | 4.38(3)cal | 193.77(11) | ||||||||
| CI | 4.41(3) | 194 | ||||||||||
| Fe3GeTe2 | H ∥ c | (304) | MAP | 0.327(3) | 1.079(5) | 4.30(5)cal | 215.13(8) | r–4.6 | ||||
| KFP | 0.322(4) | 1.063(8) | 4.30(7)cal | 215.15(21) | ||||||||
| CI | 4.261(9) | 215 | ||||||||||
| Fe5GeTe2 | H ∥ c | (305) | MAP | 0.351(1) | 1.413(5) | 5.02(6)cal | 273.82(10) | r–4.916 | ||||
| KFP | 0.346(4) | 1.364(9) | 4.94(0)cal | 273.86(19) | ||||||||
| CI | 5.02(1) | 274 | ||||||||||
| t-Cr5Te8 | H ∥ ab | (306) | MH | 1.39 | ||||||||
| H ∥ c | MH | 1.73 | 131.2 | |||||||||
| (307) | MAP | 0.314(7) | 1.83(2) | 6.83(7)cal | 230.76(9) | r–4.626 | ||||||
| KFP | 0.315(7) | 1.81(2) | 6.75(6)cal | 230.65(26) | ||||||||
| CI | 6.35(4) | 230 | ||||||||||
| (308) | MAP | 0.362 | 1.399 | 4.86cal | 220.1 | r–4.949 | ||||||
| CI | 4.83 | 220 | ||||||||||
| m-Cr5Te8 | H ∥ c | (309) | MAP | 0.327(4) | 1.26(1) | 4.9(1)cal | 221.82(44) | r–4.94 | ||||
| KFP | 0.321(7) | 1.27(2) | 4.9(2)cal | 221.7(7) | ||||||||
| CI | 4.86(4) | 222 | ||||||||||
| MH | 2.38 | 143 | ||||||||||
| Cr4Te5 | H ∥ c | (310) | MH | 2.42 | ||||||||
| H ∥ ab | MH | 2.58 | ||||||||||
| MAP | 0.388(4) | 1.290(8) | 4.32(3)cal | 318.88(24) | r–4.85 | |||||||
| KFP | 0.387(9) | 1.288(5) | 4.32(2)cal | 318.74(26) | ||||||||
| CI | 3.93(8) | 318.7 | ||||||||||
| FeCr2Te4 | H ∥ c | (311) | MH | 1.92 | ||||||||
| MAP | 0.33(2) | 1.20(1) | 4.6(2)cal | 122.8(4) | r–4.88 | |||||||
| KFP | 0.30(1) | 1.22(1) | 5.1(1)cal | 122.6(7) | ||||||||
| CI | 4.83(6) | 123 | ||||||||||
| Mn3Si2Te6 | H ∥ c | (312) | SH | 2.94 | 1.14 | |||||||
| H ∥ ab | MH | 2.53 | ||||||||||
| (312) | MAP | 0.41(1) | 1.25(1) | 4.05(5)cal | 74.23(4) | |||||||
| KFP | 0.41(1) | 1.21(2) | 3.95(2)cal | 74.27(15) | ||||||||
| CI | 4.29(5) | 74 | ||||||||||
| Cr0.33NbS2 | H ∥ c | (313) | MAP | 0.370(4) | 1.380(2) | 4.729(7)cal | 126.3(7) | r–4.9 | ||||
| CI | 4.853(6) | 126 | ||||||||||
| (314) | KFP | 0.346(40) | 1.344(2) | 4.88(44)cal | 130.78(8) | |||||||
| Fe0.26TaS2 | H ∥ c | (315) | MAP | 0.460(4) | 1.216(11) | 3.64(3)cal | 100.67(3) | r–4.71 | ||||
| KFP | 0.459(6) | 1.205(11) | 3.63(4)cal | 100.69(5) | ||||||||
| CI | 3.69(1) | 100.7 |
The MEC, SH, MAP, KFP, and CI represent the magnetic entropy change, specific heat, modified Arrott plot, Kouvel–Fisher plot, and critical isotherm, respectively.
Metallic vdW Ferromagnets
Here we discuss metallic, itinerant layered vdW ferromagnets87,88,323 which can be exfoliated and incorporated into heterostructures27,109,115,324,325 while presenting relatively high Curie temperatures.87,88,323 Such systems are also tunable via an external electric field12 or through microstructuring.326
So far, the most well studied compound
within this series is Fe3−δGeTe2 which displays comparatively high Tc, relative to the magnetic ordering temperature of
other 2D magnetic systems, i.e., ranging from 150
to 220 K depending on the Fe occupancy.99,323,328,329 Fe3GeTe2 can be understood as containing Fe3Ge slabs separated
by vdW-like bonded Te layers (Figure 28). An alternative way to understand its structure,
as discussed in ref.88 is to imagine a
scaffold with a lattice akin to that of the transition-metal dichalcogenides
(TMC2) but with the Fe atoms stuffed within
it. Its structure and the valence states of the constituent atoms
can be written as (Te2–) (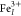 )[(
)[(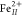 ) (Ge4–)](
) (Ge4–)](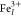 ) (Te2–) per formula unit
which leads to two inequivalent Fe sites,
) (Te2–) per formula unit
which leads to two inequivalent Fe sites, 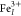 and
and 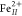 , within the
Fe3Ge slab.12,329 Partially filled Fe-d orbitals
dominate the band structure around
the Fermi level and give rise to itinerant ferromagnetism in bulk
Fe3GeTe2.6 Adjacent
monolayers are separated by a 2.95 Å vdW gap in bulk crystal.
As a result of the reduced crystal symmetry inherent to the layered
structure, bulk Fe3GeTe2 exhibits a strong magneto-crystalline
anisotropy.330 Such anisotropy would help
to stabilize long-range FM order in monolayer of this compound.
, within the
Fe3Ge slab.12,329 Partially filled Fe-d orbitals
dominate the band structure around
the Fermi level and give rise to itinerant ferromagnetism in bulk
Fe3GeTe2.6 Adjacent
monolayers are separated by a 2.95 Å vdW gap in bulk crystal.
As a result of the reduced crystal symmetry inherent to the layered
structure, bulk Fe3GeTe2 exhibits a strong magneto-crystalline
anisotropy.330 Such anisotropy would help
to stabilize long-range FM order in monolayer of this compound.
Figure 28.
(a) Schematics illustrating the combination of two structural motifs, i.e., that of transition-metal dichalcogenides TMC2 (TM, transition metal; C, chalcogen) together with that of body-centered cubic iron to form Fe-rich vdW coupled ferromagnets of composition FexGeC2. (b) Three stable structures within the FenGeTe2 series with the values n = 3, 4, and 5 which were previously identified through ab initio calculations. Fe–Fe dumbbells are the common structural units that form multiple-layer Fe-rich slabs stacked through vdW-like coupling. As n increases, the number of nearest Fe neighbors per Fe atom gradually increases, which is expected to enhance the pair exchange interaction and, thus, Tc. All panels are adapted with permission under a Creative Commons CC BY-NC 4.0 license from ref (88). Copyright 2020 AAAS.
One aspect of Fe3GeTe2 is
that its Curie–Weiss
susceptibility in the paramagnetic state yields effective moments
ranging from 3.9 to 4.9 μB/Fe for Fe fractions x ranging from 2.69 to 2.97, in contrast to neutron scattering
that finds values ranging from 1.4 to 2.18 μB/Fe
for x = 2.71 and 2.9, respectively.323 Magnetization measurements on the other hand, yield a saturation
of moment of ∼ (1.2 ± 1) μB/Fe (Figure 29).323,327 According to neutron scattering and magnetization measurements the
moments point along the c-axis forming a collinear
arrangement.323,327 The Rhodes–Wohlfarth
ratio (RWR), defined as Pc/Ps with Pc obtained from the effective moment 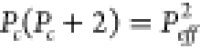 where Ps is the saturation moment obtained in
the ordered state331,332 is expected to be 1 for a localized
system and larger in an itinerant
system. Observed large values of RWR ∼ 3.3 in crystals with
Fe vacancies and ∼3.8 reported in CVT-grown single crystals
without Fe vacancy indicate a possible Kondo coupling, weak itinerant
character and/or strong spin fluctuations in the ground state.301,322,333
where Ps is the saturation moment obtained in
the ordered state331,332 is expected to be 1 for a localized
system and larger in an itinerant
system. Observed large values of RWR ∼ 3.3 in crystals with
Fe vacancies and ∼3.8 reported in CVT-grown single crystals
without Fe vacancy indicate a possible Kondo coupling, weak itinerant
character and/or strong spin fluctuations in the ground state.301,322,333
Figure 29.
(a) Magnetic susceptibility χ as a function of the temperature T for a Fe3GeTe2 single-crystal measured under zero field-cooled (black markers) and field cooled (red markers) conditions. Open markers correspond to the inverse of χ where the blue line is a linear fit. The Curie temperature exceeds 200 K. Adapted with permission from ref (327). Copyright 2017 American Physical Society. (b) χ as a function of T for a Fe4GeTe2 single-crystal and for fields along the c-axis (solid green makers) and the ab-plane (open green markers). Solid black markers depict both the resistivity and its derivative indicating a Tc of ∼270 K with another spin-reorientation transition above 100 K. Adapted with permission under a Creative Commons CC BY-NC 4.0 license from ref (88). Copyright 2020 AAAS. (c) Magnetization as a function of the temperature for Fe5GeTe2 for fields along the c-axis (open markers) and the ab-plane (solid markers) and also polycrystalline material (gray line). It displays a Tc in excess of 280 K. Adapted with permission from ref (87). Copyright 2019 American Chemical Society.
This collinear spin arrangement leads to stripe-like magnetic domains according to in situ LTEM.25,27,334 Interestingly, application of a magnetic field along the c-axis, induces the formation of magnetic bubbles or magnetic skyrmions as the domains having spins opposed to the field are suppressed by it.25,334 Skyrmions could result from the DMI since the inequivalent Fe sites form a lattice that lacks inversion symmetry.252 The size of these domains are susceptible to manipulation via electrical current pulses which seemingly can also induce skyrmion bubbles334 These observations suggest that this compound has a sizable potential for spintronic applications.
Yet another interesting aspect of Fe3GeTe2 is its very large anomalous Hall response claimed to result from the existence of a nodal line and its associated Berry curvature texture. This leads to very large anomalous Hall coefficients and anomalous Hall angles; the anomalous Hall coefficients is somewhat decreased in crystals Fe3−δGeTe2 crystals with Fe vacancies and smaller Tc.335,336 Therefore, Fe3GeTe2 would correspond to a rare example of a FM topological nodal line semimetallic system for which electronic correlations are claimed to be relevant.336,337
Perhaps more important is the fact that it was demonstrated that Fe3GeTe2 is exfoliable while still exhibiting robust ferromagnetism with a strong perpendicular anisotropy when thinned down to the monolayer limit.77 A study focused on layer-dependent properties reveals a crossover from 3D to 2D Ising ferromagnetism for thicknesses below 4 nm (five layers), which is accompanied by a fast drop of Tc from 207 to 130 K in the monolayer limit (Figure 30).77 For flakes thicker than ∼15 nm, a distinct magnetic behavior is emerges within an intermediate temperature range, due to formation of labyrinthine domain patterns.77 The persistence of itinerant ferromagnetism down to the monolayer limit is confirmed by ref.12 But upon exfoliation Tc is confirmed to be suppressed relative to the bulk Tc of 205 K in pristine bulk Fe3GeTe2.12 Utilization of solid ionic gating, however, raises Tc to room temperature, which is considerably higher than the bulk Tc. The gate-tunable room-temperature ferromagnetism in 2D Fe3GeTe2 is important for potential voltage-controlled magnetoelectronics based on atomically thin vdW crystals.8,10,14,338 This conclusion is particularly pertinent if one considers other members of this series, like Fe4GeTe2 and Fe5GeTe2 which can display Tcs as high as 280 and 310 K,88,339 respectively depending on the Fe content.
Figure 30.
(a) Atomic structure
of monolayer Fe3GeTe2. The left panel shows
the view along [001]; the right panel shows
the view along [010]. Bulk Fe3GeTe2 is a layered
crystal with an interlayer vdW gap of 2.95 Å. FeI and
FeII represent the two inequivalent Fe sites in the +3
and +2 oxidation states, respectively. (b) Optical image of typical
few-layer flakes exfoliated on an Al2O3 thin
film. (c) Atomic force microscopy image of the area marked by the
square in (b). Mono- and few-layer flakes are clearly visible. Scale
bar, 2 μm. (d) Cross-sectional profile of the Fe3GeTe2 flakes along the white line in (c). The steps are
0.8 nm in height, or consistent with the thickness (0.8 nm) of monolayer
(1L) Fe3GeTe2. (e) Normalized remanent anomalous
Hall resistance  as a function of temperature obtained from
Fe3GeTe2 thin-flake samples with varying numbers
of layers. Arrows mark the FM transition temperature Tc. (f) Phase diagram of Fe3GeTe2 as layer number and temperature are varied. Tc values are determined from
anomalous Hall effect, Arrott plots and RMCD are displayed in blue,
red and magenta, respectively. (g) Remanent RMCD signal as a function
of temperature for a sequence of selected few-layer flakes (1 L, monolayer;
2 L, bilayer; 3 L, trilayer; 4 L, four layers; 5 L, five layer). The
solid lines are least-squares criticality fits of the form α(1
– T/Tc)β. Inset: derived values of the exponent β plotted as a function
of thickness. (h) Thickness-temperature phase diagram. PM denotes
the region in which the flake is paramagnetic, FM1 that in which it
is FM with a single domain and FM2 that in which the flake exhibits
labyrinthine or stripe domains. The transition temperatures, Tc, Tc1, and Tc2, are based on the temperature-dependent RMCD or anomalous Hall effect
measurements for each flake thickness. The red dashed line denotes
the critical thickness at which a dimensional crossover occurs. All
panels are adapted with permission from ref (12). Copyright 2018 Springer
Nature.
as a function of temperature obtained from
Fe3GeTe2 thin-flake samples with varying numbers
of layers. Arrows mark the FM transition temperature Tc. (f) Phase diagram of Fe3GeTe2 as layer number and temperature are varied. Tc values are determined from
anomalous Hall effect, Arrott plots and RMCD are displayed in blue,
red and magenta, respectively. (g) Remanent RMCD signal as a function
of temperature for a sequence of selected few-layer flakes (1 L, monolayer;
2 L, bilayer; 3 L, trilayer; 4 L, four layers; 5 L, five layer). The
solid lines are least-squares criticality fits of the form α(1
– T/Tc)β. Inset: derived values of the exponent β plotted as a function
of thickness. (h) Thickness-temperature phase diagram. PM denotes
the region in which the flake is paramagnetic, FM1 that in which it
is FM with a single domain and FM2 that in which the flake exhibits
labyrinthine or stripe domains. The transition temperatures, Tc, Tc1, and Tc2, are based on the temperature-dependent RMCD or anomalous Hall effect
measurements for each flake thickness. The red dashed line denotes
the critical thickness at which a dimensional crossover occurs. All
panels are adapted with permission from ref (12). Copyright 2018 Springer
Nature.
Challenges and Perspectives
Persistence of magnetic order in nanofabricated monolayer and few-layer materials stems from magnetic anisotropy since rotational symmetry can not be spontaneously broken at finite temperature in an isotropic 2D system with short-range interactions, as formulated in the Mermin-Wagner theorem.40 Single-ion anisotropy and anisotropic exchange both could contribute to a spin wave gap which suppresses fluctuations and enables magnetic order in 2D limit.340 A promising direction for high-Tc 2D vdW insulating magnet design is a computational search with the spin wave gap in the magnon dispersion as a descriptor of magnetic state in 2D;341 the gap arises in the 2D vdW crystals due to magnetic anisotropy.235 In insulating magnetic hexagonal and honeycomb lattices high Curie temperatures are facilitated by the exchange anisotropy whereas the effects of single ion are similar except for S = 1/2 where an energy shift could be expected.342 Critical scaling behavior is a good and relatively rapid probe of the nature of the magnetic interaction and underlying anisotropy.
Whereas no predictive theory for metallic high-Tc 2D vdW magnets exists at the moment, it should be noted that in 2D metallic magnets with strong XY anisotropy, a quantum critical point is predicted by varying order/disorder in the lattice.343 Future materials in this class are likely to host a high proportion of magnetic atoms separated by a vdW gap and the theory should account for possibly complex magnetic sublattices. We note that spin density waves in metallic 2D vdW magnets might induce a periodic charge modulation, particularly at Fermi surfaces prone to nesting behavior.18,344,345 As seen on the example of Fe5GeTe2, critical behavior and scaling analysis should yield exponents consistent with 3D magnetic behavior for small vdW gaps (Table 7).
2D disordered Ising vdW magnets are also subjected to universal scaling behavior in the critical region of disorder-induced phase transition within the random field Ising model; the phase transition separates regions of smooth and step-like M(H).346 In the step-like M(H) region majority of spins flip in a single system-spanning avalanche. The scaling behavior, critical exponents and correlation length could give some insight into avalanche size distribution. The scaling also persists in variable thicknesses347 and it could be relevant in disordered 2D vdW magnetic crystals.
Probing the Magnetic Properties of Layered Materials via Elementary μ-Particles
Muon Spin Rotation (μSR)
The acronym μSR stands for muon spin rotation, or relaxation, or resonance, depending respectively on whether the muon spin motion is predominantly a rotation (more precisely a precession around a magnetic field), or a relaxation toward an equilibrium direction, or a more complex dynamics dictated by the addition of short radio frequency pulses.
Production of Spin Polarized Muon Beams and Parity Violating Decay
The muon is an elementary particle similar to the electron or positron, with a unitary positive or negative electric charge (±1) and a spin of 1/2.351 The muon is a particle belonging to the family of the leptons with an average lifetime of τμ = 2.2 μs. The muon mass is about one-ninth of the proton mass or, alternatively, about 200 times the electron mass.351 Note that for experiments in condensed matter physics mainly the positive muon is used. Beams of positive muons are artificially produced using proton accelerators. High energy proton beams are fired onto a target (usually graphite) to produce pions via the following process:
| 5 |
where p denotes the proton and n is a neutron. The pions π+ decay with a lifetime of τπ = 26 ns into muons:
| 6 |
where νμ is a muon neutrino. Lets consider pions which are produced at rest in the laboratory frame. According to the momentum conservation law, the muon μ+ and the neutrino νμ must have equal and opposite momentum. Since the pion π+ has zero spin the muon spin must be opposite to the neutrino spin. An interesting property of the neutrino is that its spin is aligned antiparallel to its momentum (it has negative helicity). This implies that the muon also has negative helicity. Thus, by selecting pions which stop in the target a beam of 100% spin-polarized muons is produced. This is the method most commonly used for producing muon beams for condensed matter physics research.352 Note that the muons produced by the above-mentioned way are called surface muons,353 and have a well-defined kinetic energy of 4.1 Mev and a corresponding momentum of 29.8 MeV/c.
When a beam of the spin polarized muons is implanted into a specimen of interest,354 the muons thermalize in the sample within typically 1 ns. Muons with positive charge stop at interstitial positions away from positively charged ions. In the presence of a magnetic field, the spin of the implanted muon precesses around the direction of the local magnetic field B with the Larmor frequency:
| 7 |
where γμ = 2π·135.5 MHz/T is the gyromagnetic ratio of the muon. An implanted μ+ in the sample will decay after a mean lifetime of τμ = 2.2 μs. The muon decay is a three body process:
| 8 |
where e+ denotes
the positron, νe the electron neutrino,
and  the muon antineutrino. The kinetic energy
of the emitted positron may vary continuously between zero and Emax = 52.3 MeV. Because of the parity violating
decay of the muon (the decay involves the weak interaction) the decay
positrons are emitted preferentially along the direction of muon spin.
By measuring the anisotropy of the decay positrons from a bunch of
muons, the statistical average direction of the spin polarization
of the muon ensemble is determined. This in turn reflects the spatial
and temporal distribution of magnetic fields at the muon site.
the muon antineutrino. The kinetic energy
of the emitted positron may vary continuously between zero and Emax = 52.3 MeV. Because of the parity violating
decay of the muon (the decay involves the weak interaction) the decay
positrons are emitted preferentially along the direction of muon spin.
By measuring the anisotropy of the decay positrons from a bunch of
muons, the statistical average direction of the spin polarization
of the muon ensemble is determined. This in turn reflects the spatial
and temporal distribution of magnetic fields at the muon site.
The μSR technique is made possible by the properties of the pion and the muon: (i) Due to parity violation in the decay of pions, surface muons are 100% spin polarized, (ii) the positron is preferentially emitted along the direction of the muon spin at decay time, and (iii) the muon has a magnetic moment and its spin precesses around a magnetic field with the Larmor frequency.
Due to the large magnetic moment of the muon, there is high sensitivity to extremely small magnetic moments (down to 10–3–10–4 μB) and the broad time window of 10–4 s to 10–11 s makes μSR a powerful tool to investigate magnetism in solid state physics.355−357 Moreover, the μSR technique has a time window for the study of magnetic fluctuations in materials, which is complementary to other experimental techniques such as neutron scattering, NMR or magnetic susceptibility. In addition to magnetism, this technique allows to study interesting problems related to superconductivity,358−370 chemical kinetics, diffusion, molecular dynamics, and semiconductor physics. One can also probe magnetic and superconducting properties at the surface of a superconductor using ultralow energy muons.361,371−373 In this chapter a brief introduction to the μSR technique and its applications to the study of magnetic materials are presented. A detailed description of the μSR technique can be found in textbooks374,375 or in review articles.351,355−357,376−379
Principle of a μSR Experiment
The μSR method is based on the observation of the time evolution of the spin polarization P⃗ (t) of the muon ensemble. A schematic layout of a μSR experiment is shown in Figure 31a. In a μSR experiments an intense beam (pμ = 29 MeV/c) of 100% spin-polarized muons is stopped in the sample (see Figure 31a). Currently available instruments allow essentially a background free μSR measurement at ambient conditions.377 The positively charged muons thermalize in the sample at interstitial lattice sites, where they act as magnetic microprobes. In a magnetic material the muons spin precesses in the local field Bμ at the muon site with the Larmor frequency νμ = γμ/(2π)Bμ (muon gyromagnetic ratio γμ/(2π) = 135.5 MHz T–1). The muons μ+ implanted into the sample will decay after a mean lifetime of τμ = 2.2 μs, emitting a fast positron e+ preferentially along their spin direction. Various detectors placed around the sample track the incoming μ+ and the outgoing e+ (see Figure 31a). When the muon detector records the arrival of a μ in the specimen, the electronic clock starts. The clock is stopped when the decay positron e+ is registered in one of the e+ detectors, and the measured time interval is stored in a histogramming memory. In this way a positron-count versus time histogram is formed (Figure 31b). A muon decay event requires that within a certain time interval after a μ+ has stopped in the sample a e+ is detected. This time interval extends usually over several muon lifetimes (e.g., 10 μs). After a number of muons has stopped in the sample, one obtains a histogram for the forward (Ne+F) and the backward Ne+B detectors as shown in Figure 31b, which in the ideal case has the following form:
| 9 |
Here, the
exponential factor accounts for
the radioactive muon decay. P⃗ (t) is the muon-spin polarization function with the unit vector 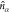 (α = F,B) with respect to the incoming muon
spin polarization. N0 is number of positrons
at the initial time t = 0. Nbgr is a background contribution
due to uncorrelated starts and stops. A0 is the initial asymmetry, depending on different experimental factors,
such as the detector solid angle, efficiency, absorption, and scattering
of positrons in the material. Typical values of A0 are between 0.2 and 0.3.
(α = F,B) with respect to the incoming muon
spin polarization. N0 is number of positrons
at the initial time t = 0. Nbgr is a background contribution
due to uncorrelated starts and stops. A0 is the initial asymmetry, depending on different experimental factors,
such as the detector solid angle, efficiency, absorption, and scattering
of positrons in the material. Typical values of A0 are between 0.2 and 0.3.
Figure 31.
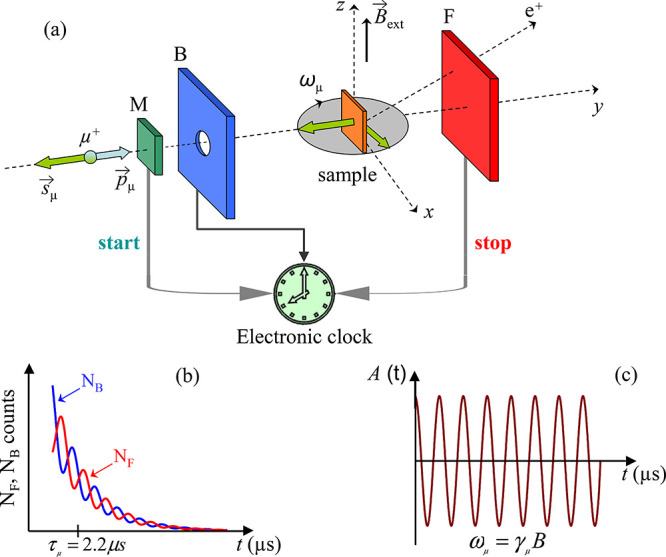
Principle of a μSR experiment. (a) Overview of the experimental setup. Spin polarized muons with spin Sμ antiparallel to the momentum pμ are implanted in the sample placed between the forward (F) and the backward (B) positron detectors. A clock is started at the time the muon goes through the muon detector (M) and is stopped as soon as the decay positron is detected in the detectors F or B. Adapted with permission from ref (348). Copyright Swiss Physical Society. (b) The number of detected positrons NF and NB as a function of time for the forward and backward detector, respectively. Reproduced with permissions from ref (349). Copyright University of Zurich. (c) The so-called asymmetry (or μSR) signal is obtained by essentially building the difference between NF and NB (eq 2). All panels are adapted with permission under a Creative Common CC BY license from ref (350). Copyright 2019 MDPI.
Since the positrons are emitted predominantly in the direction of the muon spin which precesses with ωμ, the forward and backward detectors will detect a signal oscillating with the same frequency. In order to remove the exponential decay due to the finite lifetime of the muon, the so-called asymmetry signal A(t) is calculated (see Figure 31c):
| 10 |
where, Ne+F(t) and Ne+B(t) are the number of positrons detected in the forward and backward detectors, respectively. The quantities A(t) and P(t) depend sensitively on the spatial distribution and dynamical fluctuations of the magnetic environment of the muons. Hence, these functions allow to study interesting physics of the investigated system.
Figure 32.
(a-c) Schematic illustration of the magnetically homogeneous (i.e., full volume magnetic) (d), inhomogeneous (full volume magnetic, but with domains) and phase separated (i.e., part of the volume magnetic and part paramagnetic) polycrystalline samples and the corresponding μSR spectra. The 1/3 nonoscillating μSR signal fraction originates from the spatial averaging in powder samples where 1/3 of the magnetic field components are parallel to the muon spin and do not cause muon spin precession. (d, e) Isotropic Gaussian field distribution for polycrystalline sample. Panels (a–c) adapted with permission under a Creative Common CC BY license from ref (350). Copyright 2019 MDPI.
In μSR experiments two different magnetic field configurations are used: (i) Transverse field (TF) μSR involves the application of an external field perpendicular to the initial direction of the muon spin polarization. The muon spin precesses around the transverse field, with a frequency that is proportional to the size of the field at the muon site in the material. (ii) In the longitudinal field (LF) configuration the magnetic field is applied parallel to the initial direction of the muon spin polarization. The time evolution of the muon spin polarization along its initial direction is measured in this configuration. Measurements are often carried out in the absence of external magnetic field, a configuration called zero-field (ZF) μSR. In this configuration the frequency of an obtained μSR signal is proportional to the internal magnetic field, from which the size of the ordered moment and thus the magnetic order parameter is calculated. The capability of studying materials in zero external field is a big advantage over other magnetic resonance techniques.
Applications of μSR in Magnetism
μSR has been widely applied to magnetic materials due to the high sensitivity of the muon to small fields and its capability to probe both static and dynamic local field distributions. ZF μSR is used to investigate microscopic magnetic properties of solids. If the local magnetic field B⃗ (r⃗) at the muon site is pointing under an angle θ with respect to the initial muon spin polarization, the decay positron asymmetry is given by351
| 11 |
where A0 is the maximal value of the asymmetry. Further assuming that the random fields are isotropic and each component can be represented by a Gaussian distribution of width Δ/γ, then a statistical average of this distribution yields
| 12 |
This function was obtained in a general stochastic treatment of Kubo and Toyabe.378 The form of the distribution of internal magnetic fields influences the form of the μSR signal.351,355,356 Thus, by analyzing the observed muon-spin time evolution, the magnetic field distribution inside the sample can be obtained. For clarity, the time traces in Figure 33a-c shows the expected time evolution of the muon spin polarization for three different cases of magnetically ordered polycrystalline sample: fully magnetic and magnetically homogeneous (a), full volume magnetic and inhomogeneous (b) and phase separation between magnetic and paramagnetic regions (c). The muons stopping in the homogeneous sample will sense the same magnetic field and their spin will precess around the internal field and the μSR signal is characterized by maximum amplitude and zero depolarization (Figure 33a). If there is an inhomogeneous static internal field in the sample, different muons will precess at slightly different frequencies. This leads to a progressive dephasing of the μSR signal, and the oscillations in the μSR time spectra will be damped (see Figure 33b). In some cases the signal is strongly damped, so that the oscillation will not be observed, and the resulting muon spin polarization will be averaged out to zero. Then, at a magnetic phase transition, if no wiggles are observed in the μSR signal, one expects a drop in the effective initial asymmetry from A0 in the paramagnetic state to A0 = 1/3 in the ordered state.355 However, this effect could also be due to fluctuations of the internal field. μSR is capable to distinguish between these two possibilities by performing a LF-μSR experiment. In a longitudinal field inhomogeneous line broadening and fluctuations lead to different μSR time spectra. Since muons stop uniformly throughout a sample, and the amplitudes of the μSR signals arising from the different regions of the sample are proportional to the volume of the sample occupied by a particular phase, the presence of paramagnetic regions will result in the reduction of the signal amplitude as shown in Figure 33c. This schematics is a simple illustration of the fact that μSR is capable to provide quantitative information on coexisting and competing phases in a material. We note that in a single crystal the amplitude of the oscillatory component depends not only on the ordered volume fraction but also on the angle between magnetic field and muon spin polarization. Thus, the amplitude indicates the direction of the internal field.
Figure 33.
Types of intrinsic disorder in TMDs: (a) vacancy, (b) antisite, (c) substitution. Panels (a–c) adapted with permission from ref (380). Copyright 2019 Springer Nature. (d) Schematic diagram of the phase incorporation strategy to achieve ferromagnetism of 2H-MoS2 nanosheets. Adapted with permission from ref (381). Copyright 2015 American Chemical Society.
Magnetism in Semiconducting vdW Materials
TMD systems have honeycomb layers of 2D sheets with the common formula MX2, where M is a transition metal (M = Ti, Zr, Hf, V, Nb, Ta, Mo, W or Re) and X is a chalcogen (X = S, Se, or Te). These compounds crystallize in different structural phases resulting from different stacking of the individual MX2 layers, with vdW bonding between them. The 2H forms of these compounds are semiconducting and can be mechanically exfoliated to a monolayer. In bulk form, 2H-MoTe2 has an indirect band gap of 0.88 eV. The properties of the TMDs, especially in the monolayer form, have triggered a great experience in device applications such as magnetoresistance and spintronics, high on/off ratio transistors, optoelectronics, valley-optoelectronics, superconductors and hydrogen storage. Many of these interesting properties arise due to the strong spin–orbit interaction present in these materials from the heavy metal ion. Until recently, the family of TMDs has been missing one crucial member: a magnetic semiconductor. The situation has changed over the past few years with the discovery of layered semiconducting magnetic crystals, like for example CrI35,62,227,383 and VI3.276,277,384 Unconventional magnetism in the semiconducting Mo-based TMD systems 2H-MoTe2 and 2H-MoSe2382 was also recently discovered. These observations suggest an importance of magnetic interactions in electronic structures of TMDs, and extend general commonalities of various unconventional superconductors to this important family of 2D conductor. This finding helps to study the interplay of 2D physics, semiconducting properties and magnetism in TMDs. It also provides a material platform to obtain tunable magnetic semiconductors, forming the basis for spintronics. To date, the origin and the nature of this magnetic order remains an unsolved issue. Thus, systematic magnetic, electronic and structural studies in the bulk and in thin films of semiconducting TMDs are essential. Here, we review recent experimental progress on magnetism of semiconducting TMDs with the emphasis on the results from the local-magnetic probe such as muon-spin rotation.
Magnetism and Intrinsic Defects in Mo-Based TMDs
While there are many studies focused on the spin–orbit coupling and the interesting consequences for electrical and optical properties in semiconducting TMDs, there are very limited, and mostly theoretical, studies on the intrinsic magnetism. Specifically, theoretical works show that the pristine lattice of 2H Mo- and W-based TMDs are nonmagnetic, because the Mo4+ ions are in a trigonal prismatic local coordination in which the two 4d electrons are spin-antiparallel and the net magnetic moment is zero. If the Mo4+ 4d electron configuration could be tuned to have nonzero magnetic moment, the 2H-, Mo-, and W-based TMDs could display magnetic properties. This can be achieved either by the presence of various intrinsic crystalline imperfections/disorder (Figure 33a–c) or using variety of external methods, including atomic doping, and phase incorporation (Figure 33d).
Intrinsic Defects
The types of defect observed in TMDs depends on the fabrication process.380 The most common experimental techniques used to produce large chunks of TMDs are mechanical exfoliation, CVD, and physical vapor deposition. Defects usually play an important role in tailoring electronic, optical and magnetic properties.91,380,386−388 It was found from first-principles calculations that (1) MoSe2, MoTe2, and WS2 exhibit surprising confinement-induced indirect–direct-gap crossover and (2) certain defects induce magnetism in TMDs. In particular, the Mo vacancy defect and the antisite defects in these materials can induce spin-polarization and long-range magnetic coupling. Certain TMDs was even shown to exhibit an exceptionally large magnetic moment due to these defects. The linear atomic doping386 of TMDs was also shown to give rise to nonlocalized defect states (similar to line vacancy defects) and to a long-range magnetism. For instance, F and Fe atoms linearly doped MoS2 was predicted to be FM semimetals, while Mn or Co atoms doped MoS2 are FM semiconductors.386 First-principles calculations also predicted that macroscopic ferromagnetism of MoS2 nanosheets could be introduced by biaxial strain.381 Applied strain was also shown to induce a transition from FM semiconductor to a half-metallic state in Mn or Co linear-doped MoS2.386
Atomic Doping
Different types of atoms have been used to initiate magnetism. On the basis of previous studies, transitional-metal (TM) atom doping can effectively induce magnetism into MoS2. For example, magnetism is observed for Mn,389−397 Fe,390,392−395 Co,390,392−395,398 Cr,390,393 Zn,392,393 Cd,393 and Hg393 doping, and the magnetic moment of the 3d TM-doped MoS2 increases with the d-band filling of the TM dopants.390 Additional, spin polarization was found in MoS2 with S atoms replaced by incomplete d-band atoms, such as Fe and V,396 and Group VA and III elements, such as N, P, As, B, Al, and Ga.395 Moreover, adsorption of various atoms, such as H, B, C, N, and F, is also effective to turn MoS2 from nonmagnetic to magnetism.397 H-absorbed WS2, MoSe2, and MoTe2 monolayers and F-adsorbed WS2 and MoSe2 monolayers show long-range AFM coupling between local moments even when their distance is as long as ∼12 Å. It is worth noting that no magnetism is observed in V-doped MoS2 based on ref (393), but according to refs (390) and (395), V doping induces more than 1 μB magnetic moments into monolayer MoS2. And based on the study of Lee et al.,392 the nonmagnetic element Cu doping brings strong magnetism into the doped MoS2. Calculations indicate that V and Mn are promising candidates for engineering and manipulating the magnetism of the 2D TMDs.
Phase Incorporation
It was anticipated381 that introducing the 1T phase into the 2H nanosheets could be an effective strategy for combining the semiconducting and magnetic features of TMDs. Within this framework, 1T-MoS2 phase was introduced into the matrix of 2H-MoS2 nanosheet and robust FM response with a magnetic moment of 0.25 μB/Mo at room temperature was observed.381 Since the crystal structures and the Mo atomic positions are identical in both 1T-MoS2 and 2H-MoS2, such an incorporation does not change the distributions of Mo ions in 2H-MoS2 and does not hamper its practical applications. It was further revealed that the interaction between the Mo 4d states of the 1T-MoS2 dopant and a bandgap energy state induced by sulfur vacancy is the origin of the ferromagnetism of the phase-incorporated MoS2 nanosheets. Such a phase-incorporation strategy can be also used for the bulk materials.
In the following, we will discuss the clearest evidence of involvement of magnetism in semiconducting TMDs 2H-MoTe2 and 2H-MoSe2 using local probe such as μSR. The muons in 2H-MoTe2 has one stable stopping site inside the Mo-layer and a metastable site in the vdW gap.399 It was observed that at low temperature, the spins of the implanted muons precess at an oscillating frequency (Figure 34) which correspond to an internal field μ0Hint = 200(2) mT at stable site inside the Mo-layer. There is a smooth increase of μ0Hint below TM ≃ 40 and 100 K for 2H-MoTe2 and 2H-MoSe2, respectively (Figure 34b). The observation of a spontaneous muon spin precession is a clear signature of the involvement of magnetism below TM ≃ 40 and 100 K in the bulk of MoTe2 and MoSe2, respectively.382 Moreover, we find that the bulk magnetic response observed with μSR in 2H-MoTe2 are robust and do not change in the near surface region of the crystals.399 This demonstrates potential applicability of 2H-MoTe2 for magnetic thin film heterostructures. We also find that the magnetic response is efficiently tuned by hydrostatic pressure.382
Figure 34.
(a) ZF μSR time spectra for the single crystal samples of Td-MoTe2 and 2H-MoTe2 recorded at T = 5 K. Adapted with permission under a Creative Common CC BY license from ref (350). Copyright 2019 MDPI. (b) Temperature dependence of the internal field Hint of 2H-MoTe2, 2H-MoSe2 as a function of temperature. Adapted with permission under a Creative Common CC BY-NC 4.0 license from refs (382). Copyright 2019 AAAS.
These results came as a surprise since the previous theoretical work400 and simple chemical bonding considerations indicate that the Mo atoms in these samples are in a nonmagnetic 4d2 configuration. The origin of this magnetism remains unclear. We note that in the same material intrinsic magnetic Mo antisite defects382 were observed by combination of the high-resolution STM401 and Hubbard corrected DFT+U calculations387 (Figure 35a–d). Namely, STM measurements demonstrate the presence of intrinsic dilute self-organized defects. Note that two major defects, i.e., metal-vacancies (Figure 35c) and chalcogen-antisites (Figure 35b) (where a molybdenum atom substitutes the Tellurium/Selenium atom) were found in these materials. In general, TMD crystals do not share the near-perfection of graphene. This is not surprising given that the formation energy for defects in TMDs is much lower than for similar defects in graphene (for example, 7–8 eV for a graphene vacancy versus 4.8 eV for a metal antisite defects in MoTe2). The defect concentration is small (∼0.5–1 %), but defects are found to have a large electronic impact. Moreover, DFT indicates that at finite values of U, a magnetic moment in the range of 0.9 to 2.8 μB is observed per chalcogen-antisite defect Mosub. But, the metal-vacancy defects Movac do not introduce a significant local moment. The Hubbard U value used in our simulations is in the range of 0.5 to 4.0 eV to account for strong on-site interactions at the defect. We calculated the local magnetization of the antisite defect as a function of U. The strong U dependence of moment is found as shown in Figure 36b. We have also explicitly calculated the magnitude of the Hubbard U using linear response theory as included in Figure 36a. The magnitude obtained is of ULR = 2.72 eV for the antisite defect (this value is marked as the dashed line in Figure 36b), which is within the limit of initial range calculated the magnetic properties of the defects. The calculation suggests that the Mosub defects are coupled antiferromagnetically to the nearest-neighbor Mo atoms, as shown in Figure 35d. The magnetic moments at the nearest-neighbor Mo atoms can reach 0.10 to 0.40 μB/atom, with smaller contributions for second and third neighbors (0.02 to 0.08 μB/atom).
Figure 35.
(a) Large-scale atomic-resolution STM topography (20 nm) of the 2H-MoTe2 surface. The image reveals an approximately uniform density of two types of defects over the entire surface. (b) DFT+U-optimized geometry for Mosub defect. (c) DFT+U-optimized geometry of the Mo vacancy Movac. (d) Magnetization density (0.001 electrons/bohr3) on the top surface of bulk 2H-MoTe2 in AF configuration. Spin-up and spin-down states are shown in faint blue and orange isosurfaces, respectively. Note that spins also couple antiferromagnetically at the local level between the Mo impurity and the nearest Mo atoms. All panels are adapted with permission under a Creative Common CC BY-NC 4.0 license from ref (382). Copyright 2019 AAAS.
Figure 36.
Calculated magnetization of the antisite defect. (a) Occupation
number versus rigid potential shifts α for
antisite defects for the bare, noninteracting potential χ0 and the interacting potential χ. From the angular coefficients
of both curves we can extract the optimum ULR for our system, ULR =  – χ–1.385 (b) Variation of the local magnetization
at
the defect antisite versus U. At U = 0, no magnetic moments are observed as the defect shows a symmetric
configuration at the Mo–Mo bonds. At U >
0.5
eV, this symmetry is broken and the defect develops an appreciable
magnetic moment that increases with U as a result
of the increased localization of the bands. All panels are adapted
with permission under a Creative Common CC BY-NC license from ref (382). Copyright 2019 AAAS.
– χ–1.385 (b) Variation of the local magnetization
at
the defect antisite versus U. At U = 0, no magnetic moments are observed as the defect shows a symmetric
configuration at the Mo–Mo bonds. At U >
0.5
eV, this symmetry is broken and the defect develops an appreciable
magnetic moment that increases with U as a result
of the increased localization of the bands. All panels are adapted
with permission under a Creative Common CC BY-NC license from ref (382). Copyright 2019 AAAS.
The Te atoms show negligible spin polarization. Although, DFT shows the magnetic defects in these systems, it is difficult to understand how the low-density of the chalcogen-antisite defects can give rise to homogeneous internal magnetic fields, observed in 2H-MoTe2 and 2H-MoSe2. This may be possible if these defects have electronic coupling to the semiconductor valence electrons. The presence of such spin-polarized itinerant electrons would imply that these materials are dilute magnetic semiconductors. This idea may be partly supported by the recent report on the observation of hidden spin-polarized states in the bulk MoTe2.388
Another possibility is that muons are trapped near the magnetic defect, senses the large dipolar field created by the defect and produces the coherent oscillations in the μSR signal. Although the exact link between μSR and STM/DFT results382 in 2H-MoTe2 and 2H-MoSe2 is not yet clear, both results together constitute a strong evidence concerning the relevance of magnetic order in the TMDs physics. Our observations also add to the growing evidence that defects in TMDs are important to understand their physical properties. Recently, there have been several reports on magnetism in Mo- and W-based TMDs from bulk magnetization measurements. Namely, the formation of ferromagnetism was reported for V-doped WS2402 and WSe293,403 monolayers with a small amount (∼0.5–4%) of V-content and the materials was classified as a dilute-magnetic semiconductor. Room-temperature hysteresis has been observed for small amounts of vanadium deposited on 2H-MoTe2. Defect induced, layer-modulated magnetism was recently reported for ultrathin metallic system PtSe2.91 Ferromagnetism has also been observed in metallic monolayer 1T-VSe2,18 which is different relative to semiconducting systems, i.e., 2H-MoTe2, 2H-MoSe2 and 2H-WSe2, 2H-VSe2.404 Thus, they raise opportunities to obtain tunable magnetic semiconductors, forming the basis for spintronics. Theoretical calculations also predict that apart from defects, hydrogen and transition metal dopants are able to induce spin polarization in MoTe2 in the monolayer limit. Since a muon can be considered a light hydrogen isotope, muon induced/enhanced399 magnetism has also been discussed. However, magnetic hysteresis is clearly seen in the macroscopic magnetization data of MoTe2 and MoSe2,382 which can be considered as additional, besides μSR, independent piece of evidence for the involvement of magnetism in TMDs.
Magnetic Phases in vdW Magnet CrI3
Besides Mo/W-based TMDs, very interesting magnetic semiconducting TMD system is CrI3. Although the experimental investigations of bulk CrI3 date back to the 1960s, the temperature-dependent magnetic and structural properties have only recently been reported.5,62,227 The presence of a heavy halide atom in CrI3 result in marked anisotropy constants and a clear deviations from the paramagnetic regime at relatively high temperatures. Standard bulk magnetization measurements provide clear signatures of long-range magnetic order and a consequent phase-transition at a nonzero temperature. However, they also fail to capture many fine details hidden at microscopic level. Such details are instrumental to distinguish macroscopic ground states with competing magnetic phases. It has recently been found that CrI3 exhibit both AF and FM orders in thin layers driven by hydrostatic pressure.22 These phases occurred at the same critical temperature with a spatial separation of few hundreds of nm and consequently no prelude of themally activated spin ordering. If competition occurs between phases it is largely unknown but these observations establish a much more intricate scenario than originally pictured for CrI3 with many hidden subtleties that have important implications in the ordering of the magnetic domains in the system. We recently reported results of high-resolution μSR spectroscopy, complemented by SQUID magnetometry and large scale micromagnetic simulations, to systematically study the thermal evolution of magnetic states in CrI3. This suite of techniques was essential to identify, characterize and understand distinct macroscopic ground states with any competing magnetic phases.
The temperature dependence of the total magnetic fraction Vm, determined from μSR experiments,383 is shown in Figure 37. The magnetic fraction Vm does not acquire full volume right below TC1 ≃ 62 K. Instead, it gradually increases below TC1 and reaches ≃80% at TC2 ≃ 50 K. Additional increase of Vm takes place below TC3 ≃ 25 K, at which the third strongly damped component appears and reaches nearly ≃100%. The volume wise evolution of magnetic order across TC1, TC2 and TC3 in CrI3 strongly suggests the presence of distinct magnetic states in the separate volumes of the sample. The experimental results are supported by macroscale micromagnetic simulations, which revealed three main phases emerged in CrI3 as a function of the temperature: disordered-I, ordered, and disordered-II. The main driving force for the formation of these three phases is the coexistence of different crystal structures (monoclinic and rhombohedral) on bulk CrI3.383
Figure 37.
Temperature dependence of the magnetic volume fraction for CrI3. Adapted with permission under a Creative Commons CC BY license from ref (383). Copyright 2021 Springer Nature.
Magnetic Transitions in vdW Magnet VI3
Ferromagnetism
below TC ≃ 50
K was also recently discovered in bulk single crystals of VI3.276,405 Similar to other transition-metal trihalides,
such as CrI3, VI3 consists of stacked layers
in which edgesharing VI6 octahedra form a honeycomb lattice.
This system VI3 was shown to undergo a structural transition
at Ts ≃ 78 K,
followed by two subsequent FM transitions at TC ≃ 50 K and  36 K upon cooling.405 Namely, using NMR,
two magnetically ordered V sites were
identified below
36 K upon cooling.405 Namely, using NMR,
two magnetically ordered V sites were
identified below  , whereas only one magnetically ordered
V site was observed for
, whereas only one magnetically ordered
V site was observed for  .405 We studied
the magnetism and its temperature dependence in VI3 using
the μSR technique.
.405 We studied
the magnetism and its temperature dependence in VI3 using
the μSR technique.
The temperature-dependent magnetic
fraction, shown in Figure 38a, shows a sharp transition from the paramagnetic to the magnetic
state with the coexistence of magnetic and paramagnetic regions in
the temperature interval 50–52 K, i.e., only
very close to the transition. In order to study the detailed temperature
evolution of the magnetic order parameter in VI3, zero-field
μSR measurements were carried out. The ZF-μSR spectra,
recorded at temperatures above and below TC (T = 60 and 5 K), is shown in Figure 38b. At T = 60 K, the entire sample is in the paramagnetic state as evidenced
by the weak μSR depolarization and its Gaussian functional form
arising from the interaction between the muon spin and randomly oriented
nuclear magnetic moments. At 5 K, five distinct precession frequencies
appear in the μSR spectra, which is most likely due to the presence
of magnetically inequivalent muon stopping sites, especially in the
condition of two magnetically ordered V sites. The temperature dependencies
of the internal fields for all the components are shown in Figure 38c. We find that
above  32 K, component III disappears as well
as components IV and V nearly merge. The decrease of number of components
above
32 K, component III disappears as well
as components IV and V nearly merge. The decrease of number of components
above  could be related to the fact that above
there is only one magnetically ordered V site, as shown by NMR measurements.
These data along with the previous NMR measurements405 point toward a complex temperature evolution of magnetic
structure in VI3 and call for a detailed understanding
of magnetic structures in this compound.
could be related to the fact that above
there is only one magnetically ordered V site, as shown by NMR measurements.
These data along with the previous NMR measurements405 point toward a complex temperature evolution of magnetic
structure in VI3 and call for a detailed understanding
of magnetic structures in this compound.
Figure 38.
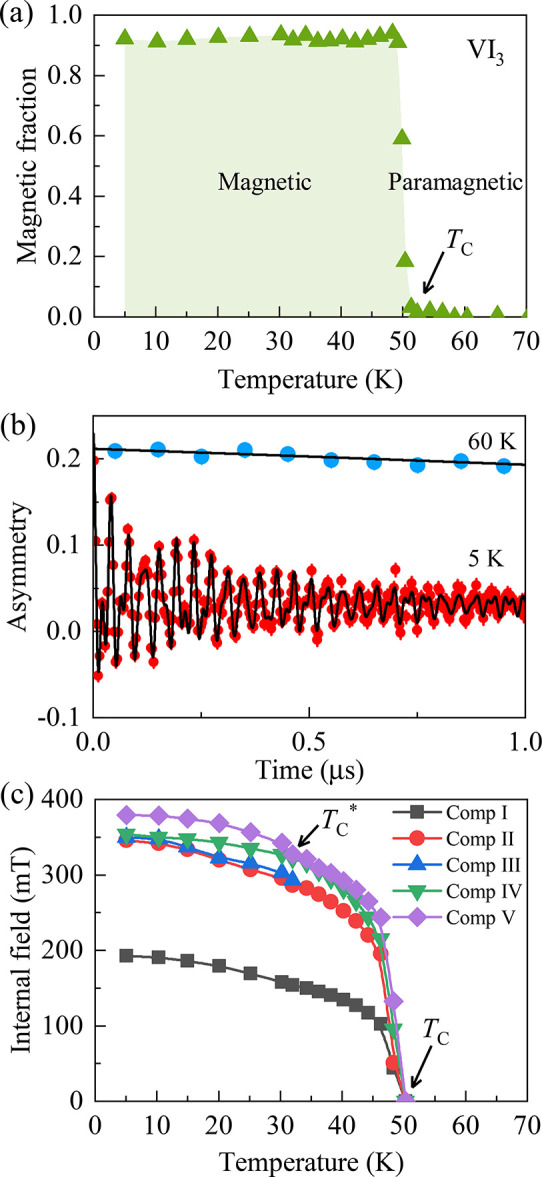
(a) Temperature dependence of the magnetic volume fraction for VI3, determined from weak transverse field μSR experiments. (b) Zero-field μSR spectra, recorded at T = 5 and 60 K. (c) The temperature dependence of the internal fields Hint for VI3. Original figure, no permissions needed.
Spintronics: From Fundamentals to Devices
General Introduction and Background
The ability to carry electron spin over long distances due to long relaxation times made graphene an excellent candidate for spin electronics giving rise to the emergence of graphene spintronics.406,407 Initially graphene, hexagonal boron nitride (hBN) and other vdW materials and heterostructures408 were explored as a spin transport channel in lateral geometry setups409−412 and/or as a tunnel barrier or part of vertical MTJs413−416 partially encouraged by theoretical predictions that they can serve as efficient spin filters.417,418 Since 2D materials were believed to be nonmagnetic, significant attention has been paid to induce magnetic moments and exchange splitting within graphene, for instance, via introducing defects (e.g., vacancies, adatoms,419,420 graphene nanomeshes421,422), or alternatively via proximity with magnetic insulators423−425 or with magnetic metals across a spacer made of 2D hBN.426,427
As already mentioned, the skepticism about the absence of standalone 2D materials with intrinsic magnetism was based on the Mermin–Wagner theorem40 stating that at any finite temperature no long-range magnetic order is possible due to massive gapless excitations of spin waves (magnons) that destroy it. The theorem was formulated for the case of isotropic Heisenberg model with finite-range interactions, leaving the opportunity to stabilize magnetic order in two dimensions. Indeed, it can be shown that the presence of uniaxial anisotropy (e.g., magnetocrystalline one caused by spin–orbit interaction) gives rise to a magnon excitation gap that quenches their impact on magnetic order lifting Mermin–Wagner restriction and thus resulting in finite Curie temperature (TC).213
As the system evolves from 2D toward 3D, the magnon spectrum behavior
softens with no anisotropy needed to preserve long-range magnetic
order at finite temperature.213 In this
case, the Curie temperature for systems comprising n monolayers, TC(n), should evolve according to finite-size scaling formula
representing its relative shift from its bulk value 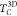 as
as 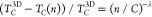 , where C represents characteristic
thickness for a given system and λ is the inverse of the bulk
correlation length exponent ν reflecting the appropriate universality
class.428−432 This formula is valid in case of thick layers and alternative expression
suitable for larger thickness range was suggested with the relative
shift in respect to TC(n) of the form
, where C represents characteristic
thickness for a given system and λ is the inverse of the bulk
correlation length exponent ν reflecting the appropriate universality
class.428−432 This formula is valid in case of thick layers and alternative expression
suitable for larger thickness range was suggested with the relative
shift in respect to TC(n) of the form 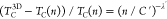 used, for instance, for studies of thin
transition metal433,434 or ferroelectric films.435 The problem is that λ′ disagrees
with λ and does not have a physical meaning, but such disagreement
seems to be resolved by taking into account spin–spin interactions
with its range parameter N0.432
used, for instance, for studies of thin
transition metal433,434 or ferroelectric films.435 The problem is that λ′ disagrees
with λ and does not have a physical meaning, but such disagreement
seems to be resolved by taking into account spin–spin interactions
with its range parameter N0.432
The scaling formula can then be written
for two distinct cases. TC scales according to the power
law in the case of thin films with n > N0 and follows the relationship 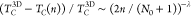 and, in the case of ultrathin films when n < N0, the scaling becomes
linear instead, yielding
and, in the case of ultrathin films when n < N0, the scaling becomes
linear instead, yielding 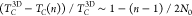 .432 Together
with other critical exponents, including those governing temperature
dependence behavior of magnetization (β), the scaling behavior
analysis provide powerful insights for identifying phase transitions
from 3D to 2D magnetism as demonstrated for thin transition metals
according to universality hypothesis436 and can be used to identify and describe 2D magnetism in vdW heterostructures.62
.432 Together
with other critical exponents, including those governing temperature
dependence behavior of magnetization (β), the scaling behavior
analysis provide powerful insights for identifying phase transitions
from 3D to 2D magnetism as demonstrated for thin transition metals
according to universality hypothesis436 and can be used to identify and describe 2D magnetism in vdW heterostructures.62
Indeed, TC behavior as a function of thickness of metallic exfoliated Fe3GeTe2 (FGT) nanoflakes was shown to follow the aforementioned power law with estimated λ and N0 values of the order 1.7 and 5 ML, respectively, corresponding to the Heisenberg ferromagnetism.123 Similar power law behavior was reported by Deng et al.,12 with smaller N0 ∼ 3 ML and larger estimated value of λ = 2.3 ± 0.8, more consistent with mean field behavior but also not excluding 3D Heisenberg magnetism. It is not surprising that it was harder to conclude on the type of magnetism since N0 indicating a boundary between 3D and 2D magnetism was smaller. It is interesting, however, that they were able to confirm the aforementioned linear scaling for thicknesses smaller than N0 pointing that they were able to reach ultrathin limit.12 A clear crossover from the bulk to 2D ferromagnetism in this vdW system of thickness less than 5 ML reaching 2D Ising model behavior for a FGT monolayer was demonstrated by Fei et al.(77) from the analysis of temperature dependence critical exponent β.
FGT has actually emerged as a higher TC alternative to a previously reported experiment with demonstration of 2D magnetism in Cr2Ge2Te6 (CGT) vdW semiconductors down to the bilayer limit with fine control of transition temperature with low applied magnetic fields.6 Another breakthrough experiment demonstrated intrinsic 2D magnetism down to the monolayer limit in insulating exfoliated CrI3.5 Interestingly, these vdW materials showed layer-dependent magnetism due to behavior alternating between FM and AF states as number of layer increases. Some TMDs, e.g., 1T-VSe218 and MnSe2,17 have been also reported being magnetic in some of their crystallographic phases or as a result of doping.437 Ising-type magnetic ordering has also been demonstrated in phosphorus-based insulating antiferromagnets, e.g., in FePS3.32
Actually, these studies triggered enormous interest in 2D vdW structures since they can be representing part of more general classes or families. For instance, CrI3 belongs to the family of chromium trihalides CrX3 with X = I, Br or Cl; CGT is part of Cr2X2Te6 with X = Si,Ge; TMD family can be written as MX2 with M being a transition metal and X = S,Se,Te; and phosphorus AF insulator 2D family formula is MPX3.
Such a vast number of atomically thin vdW magnets shows a wide variety of conduction and magnetic properties, ranging from FM semiconductors or metals to AF insulators. Due to their 2D character, they are much more sensitive to external stimuli allowing efficient control of their transport and magnetic properties. They can be naturally stacked together or with a wide range of vdW 2D or other 3D materials, forming heterostructures with properties induced via magnetic or spin–orbit proximity effects. Proximity can efficiently boost TC, alter interfacial spin polarization or introduce Rashba or Dzyaloshinskii–Moriya interactions. This implicates further exploration on spin–orbitronic and spin-caloritronic phenomena in nanostructures comprising vdW magnetic materials.
Voltage Control of Magnetism in 2D Magnets
The control of magnetism in a material with an electric field is raising a wide interest because the absence of heating by currents favors energy efficient writing in magnetic-based nonvolatile memories. Layered magnets are very promising, since the atomically thick materials have potential to be more sensitive to electric field than common thin films, with the possibility to obtain almost ideal interfaces when stacking them with other vdW materials. The electrical control of magnetism in a 2D magnet can occur via different mechanisms, such as linear magnetoelectric coupling or electrostatic doping.
The former mechanism requires the material to break simultaneously time-reversal symmetry and inversion symmetry, a condition fulfilled by bilayer CrI3 in the AF ground state, but not by the FM phase or by the monolayer CrI3, in which inversion symmetry is present. Jiang et al.8 measured the magnetoelectric response with MCD and using a dual gate structure to apply an electric field in order to take out the effect of doping. Interestingly, the magnetoelectric coupling was maximum around the spin-flip transition that occurs at ∼0.5 T. This allowed the authors to switch electrically bilayer CrI3 between the AF and FM states at a constant magnetic field (close to the spin-flip transition, see Figure 39a).
Figure 39.
Voltage control of the magnetic properties
of CrI3,
CGT and FGT. (a) Top: Normalized magnetization measured by MCD as
a function of the applied electric field (trace and retrace) at 4
K and fixed magnetic field (+0.44 T for top panel and −0.44
T for bottom panel), showing the electrical switching of the magnetic
order in bilayer CrI3. The insets represent the corresponding
magnetic states.8 Adapted with permission
from ref (8). Copyright
2018 Springer Nature. (b) Uniaxial magnetic anisotropy field 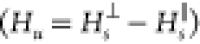 of multilayer CGT as a function of temperature
at different gate voltages and in the pristine case. Inset: The dependence
of TC on gate voltage.86 Adapted with permission from ref (86). Copyright 2020 Springer
Nature. (c) TC of a trilayer
FGT as a function of gate voltage.12 (d) HC of a trilayer FGT as a function
of gate voltage at 10 K.12 Panels (c) and
(d) are adapted with permission from ref (12). Copyright 2018 Springer Nature.
of multilayer CGT as a function of temperature
at different gate voltages and in the pristine case. Inset: The dependence
of TC on gate voltage.86 Adapted with permission from ref (86). Copyright 2020 Springer
Nature. (c) TC of a trilayer
FGT as a function of gate voltage.12 (d) HC of a trilayer FGT as a function
of gate voltage at 10 K.12 Panels (c) and
(d) are adapted with permission from ref (12). Copyright 2018 Springer Nature.
The control of magnetism is also possible via electrostatic doping in 2D magnets. The advantage is that this mechanism does not require the specific symmetry of the linear magnetoelectric coupling and, besides bilayer CrI3,9,11 is also possible in monolayer CrI311 and in CGT.10,86 In the case of monolayer CrI3,11 saturation magnetization (MS), coercive field (HC), and TC increase (decrease) with hole (electron) doping. In bilayer CrI3, electron doping (∼2.5 × 10 13 cm–2) reduces the spin flip transition almost to zero magnetic field.11 Although this should enable electrical switching of magnetization at zero field, a magnetic field close to the spin-flip transition still needs to be applied for fully reversible switches.9,11 Electrostatic doping using ionic liquid gating has also been reported in multilayer CGT.10,86 Wang et al.10 showed using MOKE measurements that saturation field (HS) decreases and MS increases as a function of doping levels (both electron and hole), while HC and TC are insensitive to doping. This behavior is tentatively attributed to a moment rebalance of the spin-polarized band structure while tuning its Fermi level. In contrast, Verzhbitskiy et al.86 report an enhancement of TC from ∼61 K to up to 200 K when an electron doping of ∼4 × 1014 cm–2 is applied, using magnetoresistance measurements. Interestingly, there is also a dramatic change in the magnetic anisotropy, which changes from perpendicular to in-plane (see Figure 39b). In this case, the effect is attributed to a double-exchange mechanism that is mediated by free carriers, which dominates over the superexchange mechanism of the original insulating state.
A different effect, reported in multilayer CrI3, is memristive switching at certain applied voltage, where the two resistive states are coupled to the magnetic phases.438 The mechanism here is thermally induced when current flows across CrI3.
Voltage control of magnetism has also been reported in FGT which, unlike the previous 2D magnets mentioned in this subsection, is metallic. Deng et al.12 use ionic gating to bring TC from ∼100 K up to ∼300 K in trilayer FGT (see Figure 39c), an important result since no pristine 2D magnet is FM at room temperature. HC roughly follows the variations in TC, as shown in Figure 39d. The large electron doping induced by the ionic gate (∼1014 cm–2 per layer) causes a substantial shift of the electronic bands of FGT. The large variation in the DOS at the Fermi level leads to appreciable modulation in the ferromagnetism, in agreement with the Stoner model for itinerant electrons.12,439 Finally, metallic ferromagnet Fe5GeTe2 has been electron doped with protonic gating, which can induce a transition to an AF phase at 2 K.440 Recently, room temperature ferromagnetism has been observed in MBE grown Fe5GeTe2 2D films.339
Manipulation of the Magnetization of 2D Magnets by Current-Induced Spin–Orbit Torque
The magnetization of 2D magnets can be manipulated by spin–orbit torques (SOTs) induced by spin-transfer from spin currents generated from charge currents by spin–orbit couplings (SOCs). The conversion of charge current into spin current can be obtained by spin Hall effect (SHE) in 3D materials of large SOC (e.g., heavy metals such as Pt) or by the Edelstein effect in 2D electron gas (2DEG) such as Rashba interface states or surface states of topological insulators.441 In the FGT/Pt bilayer of Figure 40a, a horizontal charge current in Pt is converted by SHE into a vertical spin current which is injected into FGT and generates the SOT on the FGT magnetization.442 The switching of the out-of-plane magnetization of FGT flake is detected by the transverse voltage induced by the anomalous Hall effect (AHE) in FGT, as shown in Figure 40b.442 This switching is observed only if an in-plane magnetic field (H0 in Figure 40a, 3, 6, or 9 kOe in Figure 40b) is also applied in the current direction, which is the usual symmetry breaking condition required in the experiments of magnetic switching in layers of 3D FM materials with out-of-plane magnetization.441 A similar experiment has been reported by Wang et al.443
Figure 40.
Current-induced magnetization switching of a FGT 2D magnet. (a) Schematic illustration of the current-induced switching of a FGT nanoflake by the spin current generated by SHE in the Pt layer deposited on FGT and injected into FGT to produce a SOT.442Jx is the current in Pt generating a downward spin current by SHE, H0 is the in-plane field tilting the magnetization M from its out-of-plane orientation at zero field, HDL is the damping-like (DL) component of the effective field expressing the action of the spin transfer torque. (b) Current-induced switching detected by the change of sign of the transverse voltage VH in panel (a) (RH ∼ VH/Jx).442 Panels (a) and (b) are adapted with permission from ref (442). Copyright 2019 American Chemical Society. (c) Schematic view of the CrI3/TaSe2 vdW heterostructure consisting of an insulating AF bilayer of CrI3 and a nonmagnetic metallic monolayer TMD TaSe2. The SOT on the magnetization of CrI3 is due to the charge-to-spin Edelstein conversion of the current flowing along the CrI3/TaSe2 interface. The resulting switching of m1 is indicated by arrows.444 Adapted with permission from ref (444). Copyright 2020 American Chemical Society.
Interestingly, similar experiments of switching by current-induced SOT have been performed with nonconducting 2D magnets, for example on bilayers of CGT and Pt or Ta.445−447 The SOT is detected by the Hall voltage ascribed to the introduction of spin polarization and AHE in Pt (Ta) by proximity with CGT. An alternative explanation is by the spin Hall magnetoresistance (SMR) associated with SOT, that is the dependence of the resistance of Pt (Ta) on the relative directions of the current and magnetization of CGT.445,447 SMR effects have been clearly observed in bilayers of the insulating 2D magnet Co-doped MoS2 and Ta.448
As mentioned above, the spin currents inducing SOT can be generated not only by the SHE of a 3D material as Pt but also from SOC effects in 2DEGs at interfaces or surfaces. An interesting example is given by the theory by Dolui et al.444 of the SOT acting on CrI3 in the bilayer CrI3/monolayer TaSe2 heterostructure shown in Figure 40c. A CrI3 bilayer is an antiferromagnet with opposite magnetizations of the two layers. The proximity of the bottom CrI3 layer with TaSe2 introduces interface states of large SOC and the current flowing in these states is converted by the Edelstein effect441 into a spin accumulation that is injected into the bottom CrI3 later and generates a SOT on its magnetization m1. An interesting result is that the SOT generated by current pulses in TaSe2 can reverse m1 and convert the CrI3 bilayer from antiferromagnet to ferromagnet with parallel magnetizations of the two layers. According to Dolui et al.,444 the transition should induce a change of resistance of 240% for a tunnel junction composed of a bilayer-CrI3/monolayer-TaSe2 between graphite/hBN electrodes.
Another example of interfacial SOT with 2D magnets is given by the SOT results on bilayers of the 3D ferromagnet NiFe and the 2D AF insulator NiPS3.449 As the large SOTs acting on NiFe include components of the different “damping-like” and “field-like” symmetries, they can be ascribed to interfacial SOT. The SOT increases below the Néel temperature of NiPS3 (170 K), pointing out a possible relation with magnetic ordering.
Proximity Effects
Atomically thin materials are expected to be very sensitive not only to electric fields but also to proximity effects. We first consider the proximity effects between 2D magnets and 3D materials and their potential to change the properties of the 2D magnets. A highly interesting example is the large increase of TC of the 2D magnet FGT when it is grown on the topological insulator (TI) Bi2Te3.90 The bilayer Bi2Te3/FGT is grown by MBE and its structure is displayed in Figure 41a. The magnetic properties are characterized by the AHE associated with the ferromagnetism of FGT. The plot of the AHE resistance as a function of temperature shown in Figure 41b demonstrates that TC of FGT is enhanced from about 230 K for pure FGT to 400 K in a Bi2Te3 (8 nm)/FGT(4 nm) heterostructure. TC decreases at increasing thickness of FGT but is still at about 300 K for Bi2Te3(8 nm)/FGT(10 nm).
Figure 41.
Structure and magnetic properties of Bi2Te3/FGT heterostructures. (a) Structure of Bi2Te3/FGT. (b) Anomalous Hall resistance Rxy as a function of temperature for FGT and Bi2Te3/FGT heterostructures. (c) Magnetic phase diagram of pure FGT and Bi2Te3/FGT heterostructures versus FGT layer thickness and temperature (FM for ferromagnetic, PM for paramagnetic). All panels are adapted with permission from ref (90). Copyright 2020 American Chemical Society.
A precise determination of TC in Bi2Te3(8 nm)/FGT(4 nm) heterostructures can be achieved by the classical Arrott plot and leads to the magnetic phase diagram of Bi2Te3/FGT versus layer thickness and temperature in Figure 41c. The decrease of TC with increasing FGT thickness is in favor of the general idea of interfacial effect. However, the role of the large SOC and spin-momentum locking in the surface states of TI is not well understood yet. It was suggested that the large SOC at the interface with Bi2Te3 could enhance the intralayer interactions in FGT.90 Anyhow, as it is extremely challenging to achieve room temperature 2D ferromagnets, the type of result described in the preceding lines is very promising for the future of the 2D magnets.
Proximity effects can also be used to introduce additional properties in vdW heterostructures involving 2D magnets. An example is the generation of magnetic skyrmions in FGT by the DMI introduced by an interface between FGT and the TMD WTe2.27 Another example is the introduction of magnetic proximity effect in graphene in combination with a 2D magnet. Karpiak et al.450 used ferromagnetic CGT on top of graphene and obtained an exchange field of few tens of mT using Hanle precession during spin transport, smaller than the one obtained by Tang et al.451 using CrBr3 and Zeeman spin Hall measurements (few T). Ghiasi et al.452 proximitized graphene with AF CrSBr. With this combination they obtained a conductivity spin polarization of 14%, corresponding to a much larger exchange field in graphene (∼170 T). These proximity-induced exchange fields are comparable with those obtained using magnetic insulators such as yttrium iron garnet (YIG)425,453,454 or bismuth ferrite (BFO)455 even though lower than theoretical predictions.456−459 This is an important addition to graphene functionalities for spintronics,406,407 besides long-distance spin transport460 and spin–orbit proximity effects.461 Beyond graphene, we refer to the examples of the proximity of CrI3 in inducing a zero-field Zeeman splitting in the valley states of WSe2.206,462
The properties of 3D materials can also be changed by proximity with a 2D material. We referred previously to the AHE or SMR effects induced in a Pt layer by proximity with the 2D magnet CGT and their use to detect the magnetic state of CGT.445−447 A proximity magnetoresistance in Pt has also been reported in combination with CrI3.463 In a similar way, the interfacial hybridization of magnetic Ni with graphene changes the effective spin polarization of its density of states, what has been used to obtain very large tunnel magnetoresistances.464 Similarly, proximity effects in Co/WSe2 bilayers change the sign and magnitude of the effective spin polarization of Co.465 The interfacial hybridization between Co and graphene orbitals can also explain strong enhancement of perpendicular magnetic anisotropy in Co films.466
Spin Seebeck Effect and Magnon Transport
The spin Seebeck effect (SSE) is the conversion of a temperature gradient into a voltage, mediated by spin currents, occurring in simple magnetic material/paramagnetic metal bilayers,469 with a potential to be used as thermoelectric conversion elements.470 In a structure similar to that of Figure 42b, a temperature gradient in the magnetic material along z creates a vertical magnon current that leads to magnon imbalance at the top interface. The angular momentum of the magnons (along x, the magnetization direction determined by the applied magnetic field H) is transferred via exchange coupling to the conduction electrons of the paramagnetic metal, generating a spin accumulation. This spin accumulation diffuses into the paramagnetic metal as a spin current along z, which is converted into a charge current along y via the inverse SHE.
Figure 42.
Spin Seebeck effect and magnon transport
with 2D magnets. (a) Crystal
structure of CGT and CST.467 (b) Schematic
of the longitudinal SSE measurements in CST/Pt or CGT/Pt bilayers. H denotes the external magnetic field and ΔT (∇T) the temperature difference
(gradient).467 (c, d) Normalized SSE voltage S = (V/∇T) (Lz/Ly) as a function of H in the (c)
CST/Pt and (d) CGT/Pt bilayers at selected temperatures.467 Panels (a–d) are adapted with permission
from ref (467). Copyright
2019 American Physical Society. (e) Schematic of the magnon generation,
transport, and detection in MnPS3.468 (f) Optical image of the device with the MnPS3 flake and Pt electrodes, including the measurement configuration
of the nonlocal SSE.468 (g) Normalized
nonlocal signal 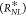 as a function of distance (d)
for selected temperatures in a 16 nm-thick MnPS3 flake.
The solid lines represent the best-fitting results based on a diffusion
equation.468 (h) Magnon diffusion length
as a function of MnPS3 thickness (t) for
selected temperatures.468 Panels (e–h)
are adapted with permission under a Creative Commons CC BY 4.0 license
from ref (468). Copyright
2019 American Physical Society.
as a function of distance (d)
for selected temperatures in a 16 nm-thick MnPS3 flake.
The solid lines represent the best-fitting results based on a diffusion
equation.468 (h) Magnon diffusion length
as a function of MnPS3 thickness (t) for
selected temperatures.468 Panels (e–h)
are adapted with permission under a Creative Commons CC BY 4.0 license
from ref (468). Copyright
2019 American Physical Society.
The SSE has been recently observed in 2D magnets. Ito et al.467 report SSE in FM insulators CGT and CST (CrSiTe3) covered by Pt (Figure 42a,b). In contrast to prototypical YIG, the SSE response persists above the critical temperatures in both 2D magnets (Figure 42c,d), which is attributed to exchange-dominated interlayer transport of in-plane paramagnetic moments reinforced by short-range FM correlations and strong Zeeman effects.
Furthermore, the SSE has been used to inject magnon currents in order to study magnon transport. By using a lateral structure, the magnon transport have been quantified in 3D insulating magnets such as ferrimagnetic YIG471,472 or AF α-Fe2O3.473 Xing et al.468 used such a nonlocal SSE to demonstrate magnon transport in 2D antiferromagnet MnPS3 (Figure 42e,f). Whereas the current injected in a Pt wire induces the temperature gradient to generate the magnon accumulation via the SSE, a second Pt wire detects the diffusing magnons as a voltage via the inverse SHE. The decay of this voltage with the distance (d) between Pt wires (Figure 42g) is used to extract the magnon diffusion length of MnPS3 (Figure 42h), which is of the order of the best 3D magnets471−473 and thus promising for magnonics. With the same approach, magnon transport induced by SSE has been reported in 2D FM insulator CrBr3 by Liu et al.(474)
Chiral Magnetic Structures: Skyrmions
The past decade has seen a substantial development of the research on chiral spin structures such as magnetic skyrmions or chiral domain walls. As represented in Figure 43a, skyrmions are small local whirls of the magnetization with a topology induced by chiral interactions between spins.475,476 These topological spin textures behave as nanoparticles that can be manipulated by electrical currents, which makes them suitable for important applications in information technologies. The skyrmions, in most cases, are induced by DMI.250,251 The DMI between spins S1 and S2 is of the form:
| 13 |
where D12 indicates the Dzyaloshinskii–Moriya vector. The DMIs are induced by SOC in systems without inversion symmetry, either in noncentrosymmetric lattices or when the inversion symmetry is broken by the presence of an interface. In recent years, most studies on chiral domain walls and skyrmions have been performed in systems with interface-induced DMI,477,478 as illustrated, for instance, in Figure 43b by a Pt/Co bilayer in which Pt brings its large SOC, while the inversion symmetry is broken by the presence of an interface. Large DMI can also be obtained in Co layers by their interface with graphene.479
Figure 43.
Skyrmions in 2D magnets. (a) Spin structure of a Néel skyrmion. (b) Pt/Co interface in which the absence of inversion symmetry generates DMI, HDMI = −(S1 × S2)·D12. (c) Side view of the crystal structure of the Janus TMD MnSTe in which the absence of inversion symmetry generates DMI.480 (d) DMI strength calculated for the Janus TMD MnSeTe, MnSTe, and MnSSe.480 (e) Skyrmions in MnSeTe (T = 10 K in applied field of 0.3 T) from DFT calculation of DMI and Monte Carlo simulations.480 Panels (c–e) are adapted with permission from ref (480). Copyright 2020 American Physical Society. (f) Side view of the crystal structure of WTe2 on FGT.27 (g) LTEM image of Néel skyrmion lattice at 180 K under 510 Oe in the sample 2L WTe2/40L FGT (L = layer) at tilt angle 30° and under focus. Scale bar: 500 nm.27 Panels (f) and (g) are adapted with permission under a Creative Commons CC BY license from ref (27). Copyright 2020 Springer Nature. (h) TEM image of Néel skyrmion lattice in an oxidized FGT flake (about 50 μm thick) at 160 K, tilt angle 20° and over focus.26 Adapted with permission from ref (26). Copyright 2021 American Physical Society. (i) Magnetization maps derived from analysis of LTEM image for Bloch bubbles in a CGT flake at 17 K in a field of 11.7 mT.481 Adapted with permission from ref (481). Copyright 2019 American Chemical Society.
For 2D magnets, the simplest situation for chiral magnetism is a structure with inherent inversion asymmetry and intrinsic DMI. The opportunity of this situation is given by the so-called Janus TMDs, which can be synthesized by controlling the reaction conditions.482−484 An example of Janus crystal structure is that of MnSTe shown in Figure 43c. First principles calculations based on density functional theory (DFT) have shown that single layers of the Janus TMD MnSeTe, MnSTe, and MnSSe are FM with Curie temperatures between 140 and 190 K, out of plane magnetizations and the DMI energies presented in Figure 43d.480 These DMIs are comparable to those generated by Pt/Co interface (Figure 43b) and other interfaces, which are routinely used for the generation of skyrmions.480,485 Monte Carlo simulations using the calculated exchange and DMI parameters find that the FM ground state of MnSeTe and MnSTe at zero field develops skyrmions by applying a magnetic field,480 see Figure 43e. The possibility of inducing skyrmions in Janus chromium chalcogenides,486 trihalides487 and in 2D multiferroics488 has been also recently reported.
In the general situation of 2D magnets with centrosymmetric structures, DMIs can be introduced by breaking their inversion symmetry by interfaces between different 2D materials. An example of interface induced DMI is the bilayer of Figure 43f in which the TMD WTe2 is deposited on a FGT layer. The LTEM images at tilt angle in Figure 43g, with black and with half-moons, are typical of Néel skyrmions, which have been ascribed to DMIs at the WTe2/FGT interface.27 However, DMIs at the single WTe2/FGT top interface are not expected to generate a skyrmionic texture extending to the bottom of the stack of 30 FGT monolayers. The authors have suggested a skyrmionic texture extending to only a certain depth, but its exact profile has not been determined.27 Néel skyrmions have been also clearly identified in LTEM images of similar FGT layers,26 as shown in Figure 43h. These skyrmions are ascribed to DMIs at the interface between top and bottom oxidized FGT layers and the nonoxidized central FGT. This interpretation is consistent with the absence of Néel skyrmions replaced by magnetic bubbles of Bloch type in FGT samples without oxidation.25,26 The pending question for the Néel skyrmions in the oxidized samples is again the exact profile of the skyrmions as a function of the depth in the 50-μm-thick FGT. Nevertheless, the promising result with the skyrmions in FGT of Figure 43h is that they can be moved by current pulses as classical Néel skyrmions in 3D materials.26
In the absence of DMI, 2D magnets with out-of-plane magnetization generally present spin textures of the magnetic bubble type, bubbles of reversed magnetization surrounded by a Bloch domain wall, as shown in Figure 43i for CGT481 and already mentioned above for nonoxidized FGT.26 The possibility of inducing skyrmions from mechanisms other than DMI such as dipole–dipole interactions in FGT on Co/Pd superlattices has also been reported.489 In addition, the skyrmion formation in 2D magnets using Moiré patterns in vdW heterostructures was also proposed.490
Spintronic Devices
2D magnets can be integrated into more complex structures to create spintronic devices that could present interesting advantages for rapidly emerging technologies. An example of such advantages is the possibility of obtaining almost ideal interfaces when stacking them with other vdW materials. The voltage control of magnetism present in atomically thin materials allows, in some cases, for extra functionalities beyond the classical spintronic devices.
The prototypical spintronic device is the spin valve, which consists of two different magnetic conducting layers sandwiching a nonmagnetic layer. The latter can be either a conductor or an insulator, giving rise to giant (GMR)101,102 or tunneling magnetoresistance (TMR),493,494 respectively, caused by the spin-dependent transport across the device. Since the 90s, the GMR has boosted the technologies of information storage, for example in the read heads of the hard disk drives.495 The TMR of MTJs is exploited today in nonvolatile magnetic random access memories (MRAM) (Figure 44a), and recent advances have been achieved in STT-MRAMs using magnetic layers with out-of-plane magnetization and spin-transfer torque (STT) for electrical switching.491,496 The advantages of the STT-MRAMs are nonvolatility, superior scaling properties, speed, and low energy consumption. They are presently commercialized as a replacement for SRAMs and eFlash in embedded cache memories.
Figure 44.
Toward MRAM with 2D magnets. (a) Schematic of STT-MRAM with 3D materials:491 information coded by the relative orientations of the magnetization of the two magnetic layers (green) separated by an insulating MgO layer (red), writing by current-induced STT and reading by TMR. Adapted with permission from ref (491). Copyright 2017 American Physical Society. (b) Schematic of the TMR device based on a FGT/hBN/FGT vertical stack used for the results shown in panels (c–e).109 (c) TMR measurement in a FGT/hBN/FGT vertical stack at 4.2 K. The swapped magnetic field is out of plane.109 (d, e) Magnified regions of the TMR measurement around the field range of antiparallel configuration (upper panels) and variation of the AHE resistance of the top (blue) and bottom (green) FGT electrodes in the same field range. Blue and green arrows indicate the successive orientations of the magnetizations.109 Panels (b–e) are adapted with permission from ref (109). Copyright 2018 American Chemical Society. (f) Schematic of the device combining a gate-controlled spin-flip transition in bilayer CrI3 and spin filtering in the tunnel junction. Arrows indicate the magnetic orientation of each layer.492 (g) Tunnel conductance of the device illustrated in panel f as a function of gate voltage (sweeping back and forth) under a constant magnetic field (0.76 T). The measured tunnel conductance changes when the magnetic order of bilayer CrI3 is switched by the gate.492 Panels (f) and (g) are adapted with permission from ref (492). Copyright 2019 Springer Nature.
MRAM technology could benefit from 2D magnets that present large magnetic anisotropy in atomically thick layers and can also be integrated with vdW heterostructures for a great variety of devices. An MTJ using 2D magnets was achieved by stacking two flakes of FM layered dichalcogenide Fe0.25TaS2, where native Ta2O5 oxide layer works as the spacing layer, reaching above 6% TMR ratios.497 Similar devices, replacing one of the magnetic layers with Cr0.33TaS2, yield up to 15% TMR.498 Taking advantage of vdW stacking, Wang et al.109 used atomically thin hBN as an insulating layer between two FGT flakes (Figure 44b), where a TMR up to 160% is observed (Figure 44c–e). This allowed the authors to determine a spin polarization of 0.66 for the density of states in FGT.109 Theoretical calculations predict that TMR ratios could exceed thousands of percent in such heterostructures.499 By replacing hBN with graphite, the observation of three resistance states is reported and attributed to spin-momentum locking at the FGT/graphite interface caused by the strong SOC in FGT.500 Furthermore, recent theoretical studies pointed out toward realization of four resistance states in vdW multiferroic tunnel junctions comprising FGT layers separated by 2D ferroelectric In2Se3 barrier layers.501 TMR up to 3.1% has been reported when using semiconducting MoS2 as a spacer, acting as a conductor rather than a tunnel barrier.115 The prediction of FeCl2, FeBr2, and FeI2 as half metals suggests these materials could further improve the figures for TMR.502 Beyond the standard spin valves, devices where the two magnetic layers do not conduct but spin-polarize the electrons of the nonmagnetic spacer by strong proximity effects have been theoretically proposed by Cardoso et al.,503 who model a bilayer graphene sandwiched by two CrI3 monolayers. A band gap opens at the Dirac point of graphene in the antiparallel configuration, whereas in the parallel configuration, the graphene bilayer remains conducting.
Large magnetoresistances are also achievable in devices where the magnetic and nonmagnetic layers are swapped, and two nonmagnetic conductors sandwich a magnetic insulator that acts as a spin filter. Altering the magnetic state of such spacer via applied magnetic field could lead to the large difference in the spin-dependent tunneling giving rise to enormous TMR values (see Spin Filtering Effect section for details). Taking advantage of the voltage control of magnetism present in these atomically thick materials, Song et al.504 and Jiang et al.492 combine the spin filtering in a graphene/CrI3/graphene heterostructure for reading the magnetic order of CrI3 with the electrical switching (“writing”) of such magnetic order via spin-flip transition (see Figure 44f). This device shows nonvolatility and a large conductance change between the different magnetic orders (Figure 44g), which could be an alternative in MRAM applications. For another CrI3 heterostructure, we have already mentioned a change of conductance induced by a spin-flip transition of a CrI3 bilayer.444
STT-MRAMs are expected to be ultimately limited in speed because of the relatively large switching latency of STT and high currents required to reach sub-ns switching times, which can damage the MTJ tunnel barrier. One of the most solid alternatives is the SOT-MRAM in which the magnetic state of an MTJ is switched by the SOT induced by the spin current generated by the Edelstein effect505 and/or the SHE in a material with large SOC.506−508 They offer unmatched switching speed and endurance compared to STT-MRAM. We present below the perspective with 2D magnet-based SOT-RAMs.
In the schematic of SOT-MRAM with 3D materials in Figure 45a, a horizontal current flowing in the Ta layer generates via SHE a vertical spin current injected into the bottom FeCoB layer of the MTJ to switch its magnetization by SOT.507Figure 45a also shows an example of the TMR signal reflecting the current-induced back and forth switching of the FeCoB/MgO/FeCoB MTJ.507 One can see a similar switching of the magnetization of a FGT layer by SOT for the device in Figure 45b reported by Wang et al.443 Here the SHE in the top platinum layer generates the vertical spin current injected into the FGT to reverse its magnetization that is detected by AHE resistance of FGT. The figure displays an example of back and forth switching of the magnetization of FGT similar to those in Figure 45a for FeCoB (in both cases, the switching requires an applied magnetic field along the current direction). The schematic in Figure 45c represents another example of device harnessing the SHE of Ta to switch the magnetization of the 2D magnet CGT.446 Actually, the performance of such SOT devices can be characterized by their requirement of small current density and small applied fields. Figure 45d compares the current densities and in-plane fields required for SOT switching in devices based on 3D magnetic layers (CoFeB, MnGa, TMIG) or 2D magnets (FGT, CGT). The comparison is at the advantage of 2D magnets, in particular Ta/CGT. However, the obvious disadvantage of 2D magnets is the low temperature that is required. They would be very promising for applications if their TC can be raised above room temperature, as it has been already achieved for FGT grown on Bi2Te390 or with electrostatic doping.12
Figure 45.
2D magnet-based SOT-MRAMs. (a) Top: Schematic of a SOT-MRAM based on 3D materials507 in which an electrical current in the heavy metal (Ta) of the bottom electrode generates by SHE the vertical spin current injected in the bottom FeCoB layer. This injection of spin current switches the magnetization of FeCoB by SOT (writing). The state of the memory is detected by the TMR of the FeCoB/MgO/FeCoB MTJ (reading). Bottom: Detection by TMR of the SOT-induced switching of the magnetization of the bottom FeCoB layer in the device of the schematic.507 Adapted with permission from ref (507). Copyright 2014 AIP Publishing. (b) Top: Schematic of a bilayer for SOT-MRAM in which the orientation of the out-of-plane magnetization of a FGT layer codes the information and is switched by the SOT generated by the SHE of the Pt layer.443 As shown in the bottom part of the figure, the switching is detected by the AHE resistance Rxy derived from the voltage between transverse contacts. Adapted with permission under a Creative Commons CC BY-NC 4.0 license from ref (443). Copyright 2019 AAAS. (c) Image of a heterostructure for SOT-MRAM in which the magnetic state of a CGT layer can be switched by the SHE of a Ta layer.446 (d) Comparison of the current densities and in-plane fields required for SOT switching in devices based on 3D magnetic layers (CoFeB, MnGa, thulium iron garnet (TmIG)) and 2D magnets (FGT, CGT). The best results so far are for Ta/CGT.446 Panels (c) and (d) are adapted with permission from ref (446). Copyright 2020 John Wiley and Sons.
Finally, recent results of skyrmions on 2D magnets may induce additional work on skyrmionic devices. The use of skyrmions for applications has already been put forward in several technologies, from devices for data storage to components for logic functions, neuromorphic or reservoir computing systems.509 The most prominent application of skyrmions is the racetrack device initially proposed for domain walls.510 Replacing domain walls with skyrmions has important advantages. A large number of recent papers have been devoted to several types of skyrmion-based racetrack memories based on the motion and manipulation of skyrmions in a track of magnetic material.476,509 Current-induced motions of skyrmions in 2D magnets have been already demonstrated, as in Figure 46a showing sequential images of the motion of skyrmions (with a diameter around 200 nm) induced by current pulses in a track of FGT.26 For 2D magnets, such results are an initial step toward the implementation of a skyrmion racetrack memory (Figure 46b) storing data by aligning objects like beads on an abacus and moving such a train of skyrmions from an injector of skyrmions to a detector to read the stored data.476,509 Up to now, the current-induced motion of skyrmions have been mainly studied in 3D layers of magnetic metals as Co or CoFeB in which the defects and roughness lead to pinning effects and finally to nonuniform velocities.511 The expected advantage of 2D magnets as the FGT of Figure 46a should be a lower density of defects and more uniform velocities. One can even see that the motion of skyrmions in FGT, Figure 46a, is almost uniform.
Figure 46.
Devices based on current-induced motion of skyrmions in 2D magnets. (a) Skyrmion motion induced by current pulses in a FGT track.26 Each STXM image is acquired after injecting five unipolar current pulses of 50 ns. Two individual Néel skyrmions are outlined in colored circled for clarity. The diameter of the skyrmions is about 200 nm, their velocity is around 1 m/s for a current density of 1.4 × 1011 A/m2 and the width of the track is 50 μm.26 Adapted with permission from ref (26). Copyright 2021 American Physical Society. (b) Schematic of racetrack memory storing data by aligning skyrmions like beads on an abacus and displacing them by current-induced SOT from write head to read head.476 Adapted with permission from ref (476). Copyright 2018 AIP Publishing. (c) Proposal of skyrmion-based racetrack memory based on the SOT-induced motion of antiferromagnetically-coupled skyrmions in two layers coupled by AF interactions.513 The left inset is a schematic of an antiferromagnetic (AFM or AF)-coupled nanotrack and the right inset represents AF-coupled skyrmions in Co/Ru/Co trilayers.512 As the AF-coupled skyrmions have the same chirality but opposite polarities, their motion has the advantage of being along the current direction (no Skyrmion Hall effect509,512,513). Note that the racetrack memory of the schematic includes not only injector and detector but also an update/delete/insert. Adapted with permission from ref (513). Copyright 2018 IEEE. (d) AF-coupled CrI3 layers in a CrI3 bilayer.9 Adapted with permission from ref (9). Copyright 2018 Springer Nature.
In addition, 2D magnets provide interesting opportunities beyond the usual scheme of skyrmion-based racetrack memory. A couple of recent works have been devoted to skyrmions in magnetic layers antiferromagnetically coupled by interlayer exchange interactions as for instance, Co layers separated by a layer of Ru, see right inset in Figure 46c.512 The resulting “AF skyrmions” have several advantages. The compensated magnetizations lead to a decrease of the dipolar fields and smaller interactions between skyrmions. In addition, for current-induced motion, there is a compensation of the transverse deflections of the skyrmions by the so-called skyrmion Hall effect and the motion is along the current direction (along the track). Figure 46c and right inset show schematics proposed for racetrack memory with AF skyrmions.513Figure 46d shows how this concept could be studied in a bilayer of CrI3 in which the magnetizations of the two layers are antiferromagnetically coupled.9
One of the most important current challenges in spintronics is the development of low-power components to reduce the continuous increase of energy consumption by information technologies. It is already starting with the massive production of low power STT-MRAMs for computers and smartphones. Devices based on 2D magnets can participate in the next generation with components harnessing commands by voltage or relativistic SOTs and concepts based on the topological properties of skyrmions for further reductions of energy consumption and faster speeds. We have shown that, in several types of these devices, the 2D magnets should have significant advantages over the 3D materials. However, the obvious bottleneck, as we have mentioned, is the excessively low ordering temperature of the 2D magnets. The challenge is increasing this temperature, and we have described some promising results on this problem. Putting the temperature issue aside, it turns out that 2D magnets, whether alone or integrated in vdW heterostructures, can improve the performance of several types of spintronic devices. It can be illustrated by the comparison between 3D and 2D SOT-MRAMs in Figure 45. In other domains of technology, 2D magnets provide a pathway to other device concepts. As scientists, we are happy to explore these intriguing roads in physics and technology.
Magnetic-Topological Phases
Insulators are known to be nonconducting because of a finite energy gap that separates the conduction and valence bands. Over the years, the differences between insulators have been considered only quantitatively, as for example the difference in the band dispersion and in the energy gap size. Over the past decade, however, it has been demonstrated that insulators can actually be further classified into different classes according to the topology of their band structures. For instance, the usual ordering conduction and valence bands of an ordinary insulator can be inverted by strong spin–orbital coupling, leading to a topological insulator (TI).517 The inverted bulk band structure topologically gives rise to metallic surface states. Therefore, a topological insulator is characterized by gapless surface states inside the bulk energy gap. These surface states commonly exhibit a Dirac cone-type dispersion in which spin and momentum are locked-up and perpendicular to each other. Topological insulators have been observed in many materials (e.g., ref (517) and references therein), such as HgTe and Bi2Se3.
Recently, a great interest has been triggered by the discovery of topologically nontrivial states in materials that are not insulators, such as topological metals and magnetic topological metals, involving Weyl and Dirac Fermions.518−520 While the existence of massless Fermions was demonstrated in 1929 by Hermann Weyl, Weyl Fermions have remained elusive until very recently with their discovery in condensed matter systems. In solid-state band structures, Weyl Fermions exist as low-energy excitations of the WSM, in which bands disperse linearly in 3D momentum space through a node termed a Weyl point. The whole ground state (surface and bulk) of Weyl metals are exotic, identified by topological Fermi arcs on the surface and chiral magnetic effects in the bulk. Thus, the topological metals have expanded the repertoire of exotic topological states, making unforeseen physics readily accessible and constitute a fascinating recent topic of modern quantum matter research.
Magnetic topological phases of quantum matter are an emerging frontier in physics and material science.514,516,517,521−527 Magnetic Weyl/Dirac semimetals are topological materials expected to host Weyl Fermions as emergent electronic quasiparticles and to display fascinating interplay between the topological invariants and the magnetic order. Theoretically, it is expected that in a magnetic topological system there is a wealth of topological phases associated with broken time-reversal symmetry.518,528 In addition, topological magnets may show the occurrence of intriguing topological phase transitions upon approaching the magnetic transition temperature. Also, the typical energy scale for spin–orbit coupling is only 0.1 eV, which has hindered the search for wide band gap topological insulators useful for technical applications. By contrast, magnetic exchange splitting is easily of the order of 1 eV, so that large and robust band inversions may be easier to produce through magnetism. For all these reasons, the study of magnets with topological band structure has emerged as an exciting research path. In our quest to find suitable systems to investigate the magnetic topological semimetals, we have identified a few systems that will be discussed in the following.
The interplay of symmetry, relativistic effects and the magnetic structure, in magnetic materials, allows for the realization of a wide variety of topological phases through Berry curvature design. Weyl points and other topological electronic bands can be manipulated by various external perturbations like temperature, magnetic fields and pressure, which results in exotic local properties such as the chiral or gravitational anomaly and large topological Hall effects, concepts which were developed in other fields of physics such as high energy physics and astrophysics.
One strategy to find FM Weyl semimetals is to look for materials that exhibit an anomalous Hall effect. The anomalous Hall effect can in part be attributed to scattering mechanisms, but there is also an intrinsic contribution arising from the Berry curvature of the band structure. Accordingly, being monopoles of Berry curvature, Weyl points (or topological nodal lines), as observed in magnetic topological semimetals, increase the anomalous Hall conductivity. Using this approach, several transition-metal-based kagome magnets were identified as ferro- or ferri-magnetic Weyl semimetal candidates, as they feature both large Berry curvature fields and unusual magnetic tunability.514−516,525,529−532 The kagome lattice is a 2D pattern of corner-sharing triangles. With this unusual symmetry and the associated geometrical frustration, the kagome lattice can host peculiar states including flat bands,516 Dirac Fermions525,529 and spin liquid phases.530,533 In the transition-metal based kagome family, the magnet Co3Sn2S2 (Figure 47a,d)515,531 is found to exhibit both the largest anomalous Hall effect (Figure 47e) and anomalous Hall angle.515 From the crystallographic point of view, Co3Sn2S2 has a layered structure with a CoSn kagome lattice (Figure 47b). Cleaving a sample at cryogenic temperatures often reveals Sn and S terminated surfaces as demonstrated by our recent STM study.516
Figure 47.
(a) Magnetic structure of Co3Sn2S2, showing a FM ground state with spins on Co atoms aligned along the c-axis. (b) Kagome lattice structure of the Co3Sn layer. (c) Topographic image of the CoSn surface. (d) A zoom-in image of the CoSn surface (left) that shows similar morphology with the FeSn surface (right) in Fe3Sn2. The inset illustrates the possible atomic assignment of the kagome lattice. Panels (a–d) are adapted with permission under a Creative Commons CC BY 4.0 license from ref (514). Copyright 2020 Springer Nature. (e) The temperature dependence of the intrinsic anomalous hall conductivity in Co3Sn2S2. (f) Left: linear band crossings form a nodal ring in the mirror plane. Right: Spin–orbit coupling breaks the nodal ring band structure into opened gaps and Weyl nodes. The Weyl nodes are located just 60 meV above the Fermi level, whereas the gapped nodal lines are distributed around the Fermi level. Panels (e) and (f) are adapted with permission from ref (515). Copyright 2018 Springer Nature.
In addition to these two dominant surfaces, we also rarely found CoSn surfaces (Figure 47c, left panel of (d)) which lies under the S surface. An enlarged view of this surface reveals a similar morphology similar to the FeSn surface (right panel of Figure 47d) in Fe3Sn2 at the atomic level, both of which are consistent with the transition metal based kagome lattice structure as seen in the STM images in Figure 47d. This material has a FM ground state (Curie temperature of TC = 177 K) with a magnetization arising mainly from the cobalt moments. Density functional theory (DFT) calculations have predicted 6 pairs of Weyl points located only 60 meV above the Fermi level515 (Figure 47f). Theoretical calculations show Fermi arcs, the protected topological surface states characterizing Weyl semimetals, below the Fermi level on the (001) surface. Moreover, using scanning tunneling spectroscopy, a pronounced peak at the Fermi level was observed, which was identified as arising from the kinetically frustrated kagome flat band.516 High-field STM experiments evince that state exhibits an anomalous magnetization polarized many-body Zeeman shift, dominated by an orbital moment that is opposite to the field direction. Such unusual negative magnetism (Figure 48a,b) is induced by spin–orbit coupling quantum phase effects tied to nontrivial flat band systems.516
Figure 48.
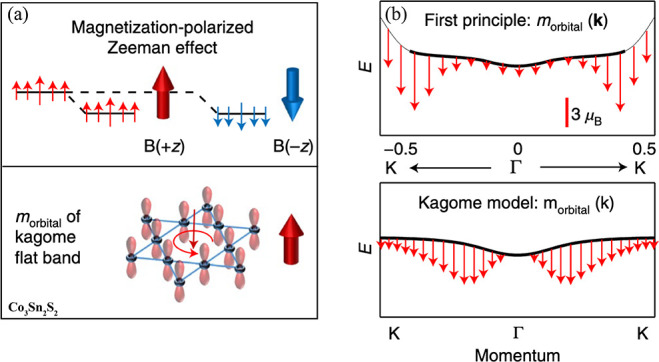
(a) Upper panel: Illustration of the magnetization-polarized Zeeman effect for Co3Sn2S2. Lower panel: illustration of the large negative orbital magnetism of the flat band in the kagome lattice. (b) Upper panel: Orbital magnetism for the flat band calculated from first principles. The magnetic moment (red arrows) is plotted along the flat band. The red bar marks the units of the magnetic moment value. Lower panel: Orbital magnetism from the magnetic kagome lattice model. The magnetic moment (red arrows, arbitrary unit) is plotted along the flat band. All panels adapted with permission from ref (516). Copyright 2019 Springer Nature.
Despite the knowledge of the occurrence of ferromagnetism below TC = 177 K515 with spins aligned along the c-axis (see Figure 47a) there was no report of its interplay with the topological band structure. We have carried out high-resolution ambient and high-pressure μSR370,377,534 and neutron diffraction, combined with first-principles calculations, muon stopping site calculations and group theoretical analysis, to systematically characterize the phase diagram of Co3Sn2S2.514 We found two magnetically ordered fractions in Co3Sn2S2 with different moment sizes: At low temperatures, the very homogeneous out-of-plane FM structure (top panel of Figure 49b) is dominant, and with increasing temperature, the fraction of the in-plane AF (bottom panel of Figure 49b) state grows and becomes the dominant component at 170 K. Both order parameters exhibits a monotonous decrease and clear separation with increasing temperature.
Figure 49.
(a) The temperature
dependence of the relative volume fractions
of the two magnetically ordered regions. Arrows mark the critical
temperatures TC1 and TC2 for FM and AF (or AFM) components,
respectively as well as the transition temperature  , below which only FM component is observed.
(b) Spin structures of Co3Sn2S2, i.e., the FM and the in-plane AF (or AFM) structures. (c)
The correlation plot of anomalous hall conductivity versus FM fraction.
(d) Calculated AHC for out-of-plane FM and in-plane AF structures.
The inset shows the calculated Berry curvature distribution in the
BZ at the FM phase. All panels are adapted with permission under a
Creative Commons CC BY 4.0 license from ref (514). Copyright 2020 Springer
Nature.
, below which only FM component is observed.
(b) Spin structures of Co3Sn2S2, i.e., the FM and the in-plane AF (or AFM) structures. (c)
The correlation plot of anomalous hall conductivity versus FM fraction.
(d) Calculated AHC for out-of-plane FM and in-plane AF structures.
The inset shows the calculated Berry curvature distribution in the
BZ at the FM phase. All panels are adapted with permission under a
Creative Commons CC BY 4.0 license from ref (514). Copyright 2020 Springer
Nature.
Figure 49a shows
the temperature dependence of the relative volume fractions of the
out-of-plane FM and in-plane AF ordered regions along with the total
magnetic fraction. Arrows mark the critical temperatures TC1 and TC2 for FM and AF components, respectively as well
as the transition temperature  , below which only FM component is observed.
It is clear that the volume of AF component develops at the cost of
the FM one. The key finding of our μSR experiments is the observation
of a phase separated ferromagnetically and antiferromagnetically ordered
regions in the large temperature range in the Weyl semimetal Co3Sn2S2 (Figure 49a).
, below which only FM component is observed.
It is clear that the volume of AF component develops at the cost of
the FM one. The key finding of our μSR experiments is the observation
of a phase separated ferromagnetically and antiferromagnetically ordered
regions in the large temperature range in the Weyl semimetal Co3Sn2S2 (Figure 49a).
We further show514 that the competition of these magnetic phases is tunable through applying either an external magnetic field or hydrostatic pressure. I note that although the measured moment size of Co is only of the order of 0.1 μB, using μSR, we were able to measure the whole temperature dependence of such a tiny moment as well as to determine the magnetic structure in Co3Sn2S2.514 High sensitivity of the μSR technique to extremely small moments is a tremendous advantage over other magnetic probes.
One of the most striking electronic effects in Co3Sn2S2 is a large intrinsic anomalous Hall conductivity and a giant anomalous Hall angle, due to the considerably enhanced Berry curvature arising from its topological band structure. Astonishingly, we found that the temperature dependence of the anomalous Hall conductivity very closely matches the volume fraction of the out-of-plane FM component, giving rise to an excellent linear correlation between these two quantities (Figure 49c).514 This is one of the rare examples of such a quantitative correlation between the magnetic volume fraction and the Berry curvature induced anomalous Hall conductivity (Figure 49c).
From first principles calculations,514 we concluded that the AHC is dominated by the c-axis FM structure (Figure 49d), providing an explanation for the reduction of the AHC when the ordered volume fraction of the out-of-plane FM state decreases. These results have strong impact since we establish Co3Sn2S2 as a material that hosts topological electronic states and frustrated magnetism. Our experiments suggest that the Co spins have both FM interactions along c-axis and AF interactions within the kagome plane, and there is a temperature dependent competition between these two ordering tendencies. The interplay between this intricate magnetism and the spin–orbit coupled band structure further induces nontrivial variations of its topological properties, which is characterized by a striking correlation between the giant anomalous Hall transport and the FM volume fraction. Our results demonstrate thermal tuning of Berry curvature effects mediated by changes in the frustrated magnetic structure. Our findings implicate control and manipulation of topological Fermions via thermodynamic and magnetic interactions. Moreover, the interplay between different magnetically ordered regions, each of which possesses distinct topological invariants, can possibly give rise to physical properties at the magnetic domain boundaries. Additionally, it enables the design of switchable magnetic materials with desired magneto-transport properties for potential technological applications.
Motivated by the scaling between AHC and the FM fraction in Co3Sn2S2, analytical model535 was built taking into account both localized electrons giving rise to a magnetic transition and conduction electrons producing topology of Bloch bands on the kagome lattice. Itinerant and localized electrons (the latter forming core spin-1/2’s on each atom) are coupled through a strong Hund’s FM mechanism. Hund’s coupling along z-direction, Mott physics and electron-mediated interactions between the half-filled orbitals was shown535 to reproduce the out-of-plane ferromagnetism and an AF transition with a 120° spin ordering in the xy plane, as we observed experimentally.514 Interestingly, it was shown that the (average) system’s magnetization in the z direction smoothly reduces to zero after the transition, producing the progressive canting of the spins, such that the statistically averaged Chern number follows the FM fraction (see Figure 50). This shows an excellent agreement with our experimentally obtained striking correlation between topological hall conductivity and the FM fraction.
Figure 50.
(a) Calculated fractions of the ferromagnetism F and antiferromagnetism (1 – F) in Co3Sn2S2 and (b) averaged Chern number as a function of the in-plane AF correlation Jxy, taking into account fluctuations in the Hund’s coupling. All panels are adapted with permission under a Creative Commons CC BY 4.0 license from ref (535). Copyright 2020 American Physical Society.
According to DFT calculations514 the energies of the out-of-plane FM and in-plane AF configurations are similar. It seems that temperature or In-doping affects536 this intricate balance, and tip it in favor of the in-plane magnetic structure. The hydrostatic pressure also causes a suppression of both FM and AF states,537 but a pressure as high as 20 GPa is needed at which both orders are suppressed simultaneously. In Co3Sn2–xInxS2 however, only small amount of In is sufficient to push the system toward the AF or helical state. Indium substitution introduces holes to the system and at the same time increases the separation of the kagome layers, while hydrostatic pressure shrinks the lattice and no doping is expected. This suggests that lattice expansion and/or hole doping disfavors the out-of-plane FM state. It was also recently shown that the coupling of this material’s topological properties to its magnetic texture leads to a strongly exchange biased anomalous Hall effect, which was argued to be likely caused by the coexistence or competition of two magnetic phases.538 The interplay between the competing magnetic states and the spin–orbit coupled band structure further seem to induce nontrivial variations of the topological properties of Co3Sn2–xInxS2, which is evidenced by a nonmonotonous In-doping dependence of the anomalous Hall conductivity.539 The AHC was also shown to be selectively tuned from 0 to a very large value 1600 Ω–1 cm–1 in magnetic Heusler compounds via suitable manipulations of the symmetries and band structures of the materials.540 A large AHC was also predicted and recently observed in noncollinear antiferromagnets such as Mn3Ge or Mn3Sn, in which the Berry curvature originates from the noncollinear spin structure.532,541,542
Topological electronic response was also found for the rare earth-transition metal based kagome system TbMn6Sn6. Namely, Shubnikov–de Haas quantum oscillations with nontrivial Berry phases from relatively low fields (∼7 T), a large AHC (0.14 e2/h per Mn kagome layer), arising from Berry curvature fields, and quasi-linear (∝ H1.1) magnetoresistance (MR) likely resulting from linearly dispersive electrons. Moreover, TbMn6Sn6 was found to demonstrate a bulk-boundary correspondence between the Chern gap and the topological edge state, as well as Berry curvature field correspondence of Chern-gapped Dirac Fermions.522,543 Thus, it is identified as a promising topological magnetic system.522,543 Using μSR, neutron diffraction and magnetization we identified the low-temperature magnetic state in TbMn6Sn6, which seems to be responsible for the low-T topological transport properties.544 A number of nontrivial magnetic phases and a large topological Hall effect was also observed in another rare earth-transition metal based system YMn6Sn6.527 A nematic chirality mechanism, which comes from frustrated interplanar exchange interactions that trigger strong magnetic fluctuations, was discussed as an origin of the topological Hall effect.
A giant AHC was also found in KV3Sb5, an exfoliable, highly conductive semimetal with Dirac quasiparticles and a vanadium kagome net. Even without report of long-range magnetic order, the anomalous Hall conductivity reaches 15507 Ω–1cm–1. It was theoretically suggested that the kagome sublattice in KV3Sb5 is acting as tilted dynamic spin clusters, giving rise to an enhanced skew scattering effect, responsible for large AHE. Charge-sensitive probes have suggested exotic charge order545 in the kagome superconductor KV3Sb5, which can lead to giant anomalous Hall effect. Using the μSR technique we provided systematic evidence for the existence of time-reversal symmetry-breaking by charge order.546 We showed that the breaking of time-reversal symmetry is spontaneous and that the magnetic response can be enhanced by external magnetic field. The time-reversal symmetry breaking charge order is indicative of extended Coulomb interactions, which would lead to correlated superconductivity. In the superconducting state, we find superconductivity of multigap nature and with a dilute superfluid (low density of Cooper pairs), indicating that the superconductivity is indeed correlated and unconventional.
Synthesis and Sample Preparation
In this section, we review the main methods of preparing atomically thin samples of vdW magnetic materials via exfoliation from larger bulk crystals (and the methods to grow the parent crystals), protecting sensitive samples from the environment, and bottom-up growth by vapor synthesis methods. Controlling sample quality and defects is also discussed.
Exfoliation of 2D Samples
Due to their weak interlayer interactions, magnetic vdW crystals can be readily cleaved to produce 2D flakes with thicknesses on the nanometer scale (<10 nm).547−549 The primary method for isolating such thin flakes from bulk magnetic vdW materials is through mechanical exfoliation, similar to other vdW 2D materials. This method involves physically cleaving layers from single crystals with adhesive polymers (such as commercially available tape or polydimethylsiloxane (PDMS)).548,550−552 The process flow is simple: place a single crystal on the adhesive polymer, fold and unfold the adhesive polymer several times, then transfer the polymer with exfoliated flakes onto the desired substrate (often quartz, sapphire, or SiO2).553−555 This process can be done within an inert environment (such as a glovebox) without exposing flakes to solvents, heat, or atmosphere, which is ideal for air- and moisture-sensitive vdW magnets. Liquid phase exfoliation (LPE), in which various mechanistic methods (such as ion intercalation, ion exchange, and sonication) are used to break single crystals into a solution of single-layer sheets, is an alternative exfoliation process554,556−560 implemented for select 2D magnets.561−564 Though highly scalable, flakes obtained through LPE are typically lower quality compared to those produced by mechanical exfoliation.559
Depending on the material, mechanical exfoliation with adhesive polymers can reliably yield flakes on the order of ∼10 μm × 10 μm in lateral dimensions,555 large enough for device fabrication and measurement. However, for especially difficult to exfoliate materials, film-assisted methods have been developed. These entail exfoliation with adhesive polymers followed by transfer to substrates with large adhesion compared to the interlayer binding energy of the crystal. For 2D magnets such as Fe3GeTe2 and MnBi2Te4, an Al2O3 assisted exfoliation was established (Figure 51A).12,111 It consists of covering a bulk surface with an Al2O3 thin film, exfoliating the stack onto thermal release tape, which is subsequently picked up and transferred onto a suitable substrate with PDMS. The increased yield of exfoliated flakes from the Al2O3 process is attributed to the increased contact area and affinity between the Al2O3 film and the target crystal.12 When exceptionally large 2D flakes are required, Au can be used as an exfoliation substrate to isolate millimeter-sized monolayers of a variety of 2D materials, including 2D magnets such as Fe3GeTe2 (Figure 51B).565−569 Though Au-assisted exfoliation is by far the most effective at isolating large monolayers, it necessarily requires a solvent to remove the Au layer before flakes can be utilized, which can damage especially sensitive 2D magnets. In contrast, the Al2O3 technique is solvent-free, allowing for feasible preparation of pristine sensitive flakes.
Figure 51.
Mechanical exfoliation methods. (A) Schematic of the Al2O3 film-assisted mechanical exfoliation.12 The strong adhesion between the crystal and the Al2O3 film makes it possible to exfoliate layered crystals that are otherwise difficult to cleave from SiO2 surfaces using conventional methods.12 Adapted with permission from ref (12). Copyright 2018 Springer Nature. (B) Schematic of the Au-assisted exfoliation process. First, a thin layer of Au is deposited onto a substrate, then a freshly cleaved bulk crystal is placed on the Au layer. The Au is then removed with a KI/I2 aqueous solution etchant.566 Adapted with permission under a Creative Commons CC BY license from ref (566). Copyright 2020 Springer Nature.
After exfoliated flakes are transferred onto a substrate, the universal method for identifying flake thickness is through optical contrast.5,6,12,111,122,552,570−574 As demonstrated by Novoselov et al.,552 single-layer flakes can be optically identified under a microscope if a suitable substrate is chosen. Light incident on the flake/substrate interface will interfere to generate an optical contrast that depends on flake thickness (Figure 52A–C), wavelength of the incident light and thickness of the substrate, and flake material (Figure 52A–C).571,575 Though optical contrast is an indirect measure of flake thickness, it can be combined with AFM imaging to map contrast to layer number (Figure 52D,E).5,6,12,122 AFM also screens for polymer or solvent residue introduced during the exfoliation process. In certain materials, Raman spectroscopy is used as a noninvasive probe to determine flake thickness by taking advantage of a systematic shift of particular Raman modes as a function of layer number in the few-layer limit.122,574,576
Figure 52.
Identification of exfoliated layer numbers. (A) Optical contrast map of a representative CrI3 flake (left) and the corresponding optical contrast per number of layers (right).5 Adapted with permission from ref (5). Copyright 2017 Springer Nature. (B) Left: Optical image of few-layer flakes of MnBi2Te4 exfoliated onto Al2O3. The corresponding layer number is labeled on selected flakes. The scale bar is 20 μm. Right: MnBi2Te4 transmittance versus layer number.111 Adapted with permission from ref (111). Copyright 2020 AAAS. (C) Optical image of few-layer Fe3GeTe2 flakes exfoliated onto Al2O3.12 (D) AFM image of the area in (C) marked by a solid black square.12 The scale bar is 2 μm. (E) Height profile plotted versus length along the white line in (D).12 Panels (C–E) are adapted with permission from ref (12). Copyright 2018 Springer Nature.
Protection of 2D Samples
Atomic-scale magnetic flakes are often extremely sensitive to the nanofabrication steps required to produce functional devices, including exposure to air, moisture, conventional polymer solvents, and heating. Therefore, preparing flakes for device fabrication and measurement requires careful encapsulation in an inert environment. To solve this problem, the dry-polymer-transfer technique577 is used to completely encapsulate flakes in hBN, which simultaneously protects the flake from degradation during fabrication578 and provides a high-quality dielectric substrate.579 This approach, combined with the ability to perform exfoliation and flake searching inside an inert environment (such as a glovebox),580 allows for the preparation of a wide array of high-quality magnetic 2D materials with diverse properties for measurements.
Crystal Growth and 2D Deposition
Currently, there are no scientific reports showing that monolayer or few-layer thick vdW magnetic crystals can be produced on large scales using commercially viable bottom-up synthesis techniques such as atomic layer deposition (ALD) or CVD. The lack of large-scale production methods stems from the limited environmental stability of many vdW magnetic crystals and/or a lack of knowledge surrounding surface chemistry that would enable the layer-by-layer deposition of vdW magnets in low dimensions, and for this reason, the scientific community is reliant on crystals produced by well-established bulk crystal synthesis routes. Additionally, bulk crystals produced from chemical vapor transport (CVT), sublimation, and flux zone growth techniques are highly crystalline and can be synthesized from precursors of the highest purity, rendering them free of magnetic impurities like Co, Fe, and Cr.
To produce these crystals, many different crystal growth techniques may be employed, but the most suitable technique can often be determined by considering the elemental precursors being used (chalcogen versus halogen) and by having a comprehensive understanding of the binary or ternary phase diagrams of the desired crystals. A survey of recent literature on vdW magnetic materials shows that chemical vapor transport (CVT), sublimation, and flux zone techniques are the most widely used. After these layered crystals are grown, a conventional mechanical exfoliation technique552 (as described above) can be used to obtain monolayer and few layer thick crystals on the desired substrate. While the previously mentioned techniques are currently the most common, recent studies are beginning to develop synthesis methods, which will expand our understanding of how to isolate low dimensional magnetic materials using bottom-up growth methods.
Bulk vdW Crystal Growth
Vapor Transport
CVT reactions were established in the 1930s, and over the decades has proven to be an incredibly reliable and effective route to synthesize high-quality, defect-free crystals, including many layered magnetic crystals.581−583 To achieve the highest quality impurity-free crystals by CVT, high purity (3N+) precursors are vacuum sealed in thick (1–2 mm) quartz ampules. In addition to having the utmost control over the environmental conditions for the growth, the vacuum sealing process is necessary to minimize the ambient pressure inside the ampule, as incredibly high pressures can build within the ampule due to the high temperature thermal processing required for crystal growth.
In a typical vapor transport reaction, precursor materials are transported from a source across a temperature gradient to a sink, where Le Chatelier’s principle governs the transport direction. Exothermic reactions transport from a cold zone to a hot zone, whereas endothermic reactions transport from a hot zone to a cold zone.584 To ensure that the precursor materials transport across the temperature gradient, they must achieve a gaseous state which is typically facilitated by a transport agent.585 To illustrate these points, halogen-assisted transport is usually required for the endothermic transport of elemental precursors for transition metal chalcogenides and transition metal phophosulfides/selenides (MnPSe3, CoPS3, and NiPS3),581 while additional transport agents are typically not required for the growth of transition metal halides (CrI3 and CrBr3), as the halogen is already contained within the crystal matrix.293
Similar to CVT, physical vapor transport (PVT) or direct sublimation of precursor compounds may also be used to reliably produce bulk high-quality, single crystals of vdW magnets.586,587 It has been established that direct sublimation is a low-cost and effective technique, where researchers do not need advanced vacuum manifolds or complex multizone furnaces that are requirements for chemical vapor transport reactions. However, vacuum sealing precursor compounds in quartz ampules may also be used to synthesize high-quality layered crystals.588 To synthesize transition metal halides such as CrCl3, commercially available polycrystalline powders are positioned inside of a cold, single-zone tube furnace in either an open-ended or vacuum-sealed quartz tube. The furnace is then heated to the desired temperature for sublimation, and the desired material transports, nucleates, and crystallizes in the cold zone of the furnace. Large, high-quality crystals grow directly on the quartz walls, and can be obtained with in shorter times (24–48 h) as compared to CVT.7
Flux Zone Growth
Melt-phase synthesis routes are a common technique for the synthesis of ternary tellurium based 2D magnets (Cr2Ge2Te3 and Fe3GeTe2),290,323,589 and unlike CVT, which can require a transport agent foreign to the crystal matrix, tellurium may be used as a solvent for the precursors, from which high-quality crystals will precipitate and grow out of the melt as the solution cools. To achieve the highest quality crystals, stoichiometric quantities of flux (solvent) and precursors (solute) are loaded into an inert crucible and vacuum sealed (∼10–5 Torr). Careful consideration when choosing a suitable crucible must be made to avoid undesired reactions between the crucible and flux. Much like CVT reactions, rather than a compatible transport agent, a suitable flux must be selected that is either part of the crystal matrix or has complete immiscibility with the elemental precursors at the required synthesis temperatures.
The sealed ampule containing the precursors and flux are first heated above their melting temperatures, and at this point the furnace temperature is held constant so the elemental precursors can completely mix into a homogeneous melt. The ampule is then slow cooled over a period of several days, and during the cooling process the desired material precipitates out of the melt, where spontaneous nucleation and crystallization occurs. It must be mentioned that the above process is highly governed by a material system’s respective phase diagram, and that growth parameters and optimization can be accelerated by having an intimate understanding the desired alloy’s binary or ternary phase diagram. However, a material system’s phase diagram is likely unknown; in which case these parameters must be empirically determined. After the growth has completed, the flux must be removed from the bulk crystals, where the most common technique to remove this flux is via a high temperature centrifugation process.590
Large-Scale Layer-by-Layer Deposition
While CVT, sublimation and flux methods are invaluable tools to discover and understand the novelties of champion material systems, these synthesis routes pose many challenges that make them unsuitable to be used in industrial manufacturing of thin films. The greatest challenge is that in order to isolate few-layer or monolayer thick sheets of vdW materials, they must first be exfoliated prior to being transferred onto a desired substrate. The most widely used technique for the exfoliation of vdW crystals being scotch-tape technique introduced by Novoselov552,591−593 and a more detailed review of this and other exfoliation techniques are covered (in the previous section). If these materials are ever to be considered viable options for future electronics applications, progress toward developing the fundamentals of bottom-up synthesis techniques of vdW magnetic materials must be made.
Vapor Deposition
Bottom-up synthesis of vdW magnets is still in its infancy, and researchers are just now beginning to unravel the fundamentals of how to synthesize the materials in their low-dimensional limits. It is no surprise that many of synthesized vdW magnets are chalcogen-based,95,594−598 as many CVD and PVD techniques have already been established for these material systems. As researchers begin to explore other classes of magnetic materials such as transition metal halides and ternary MPX3 materials (MnPS3, NiPS3, FePSe3) and MOHs (CrOCl), more experimental challenges present themselves as the growth dynamics become more complicated and as the precursors become more volatile and reactive. Recently, Grönke et al. produced thin flakes of a wide variety of vdW magnets using a modified CVT technique on different substrates (Figure 53).599−601 To achieve this, Grönke et al. computationally modeled the vapor transport reactions and determined several experimental parameters, such as precursor type, growth temperature, and transport rate of the desired materials. Furthermore, by predetermining the transport rates they were able to understand how growth times impact the thickness of the resultant films, which has enabled them to significantly accelerate their research efforts. They confirmed that CrX3 (X = I, Br, Cl) was successfully synthesized onto yttrium stabilized zirconia (YSZ) substrates (Figure 54), with only a small number of detectable impurities surficially incorporated into the crystal lattice (CrBr3) or adsorbed onto the surface of the crystals (CrI3 and CrCl3). While Grönke et al. showed that this technique may be applied to transition metal halides, it may have greater implications for other vdW magnetic crystals as researchers aim to better understand the surface/interface chemistry required to realize highly crystalline flakes in the monolayer or few-layer limit.
Figure 53.
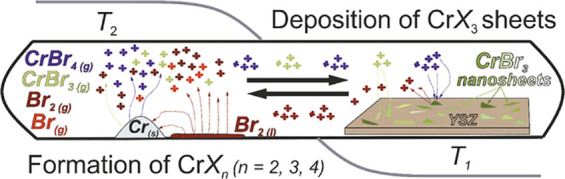
Scheme for the one-step synthesis and vapor transport of CrX3 (X = Br, I) micro- and nanosheets directly on YSZ substrates shown by the example of CrBr3. Prior to the CVT process for deposition of the respective nanolayers the introduction of chromium powder and bromine (Br2 in small sealed capillaries) lead to the formation of CrBr3 (solid) (Cr(s) + 1,5 Br2(l) → CrBr3(s)) and gaseous CrBrn(g) (n = 2, 3, 4) at T2. By application of a temperature gradient (T2 → T1) chemical vapor transport is achieved for deposition of CrBr3 micro- and nanosheets on YSZ substrates directly. The reaction course is similar for the formation of CrI3, while in contrast to this scheme CrCl3 is utilized as presynthesized compound, that is not introduced by mixture of the elements. Reproduced with permission from ref (600). Copyright 2019 John Wiley and Sons.
Figure 54.
Crystal growth by vapor transports of CrCl3 on YSZ substrates. (a) Optical microscopy of CrCl3 micro- and nanocrystals at YSZ substrate. (b) Optical microscope image of YSZ substrate surface with CrCl3 sheets with respective thicknesses in dotted boxes. (c) Distribution of thicknesses of CrCl3 structures on a YSZ substrate after CVT (yellow), after one time of exfoliation (green) and after three times of exfoliation (purple). (d) AFM measurement the height profile of a CrCl3 nanosheet. (e) Corresponding AFM image of measurement of (d) the white arrow is indicating the measurement. (f) AFM measurement of the height profile a CrCl3 ultrathin sheet (red line) and monolayer (purple line) after three repeats of exfoliation. (g) Corresponding AFM image of measurement of (f) the white line is indicating the monolayer AFM measurement. All panels are reproduced with permission from ref (600). Copyright 2019 John Wiley and Sons.
This method has also been expanded to dihalide systems, where earlier this year, Liu et al. synthesized thin flakes of NiI2 on hBN and Si/SiO2 using a conventional PVD, showing that a similar method used by Grönke et al. can be used to synthesize transition metal halides on more conventional substrates.602
Molecular Beam Epitaxy
The rebirth of studying layered vdW magnets has been sparked by the discovery of intrinsic ferromagnetism in monolayers of vdW systems, such as CrGeTe3 and chromium trihalides. Molecular beam epitaxy (MBE) is a very refined ultrahigh vacuum (UHV) bottom-up vacuum deposition technique enabling the layer-by-layer deposition of thin films, and naturally, MBE lends itself to the synthesis of layered vdW materials in their low dimensional limits.95,99 Being a UHV deposition method, it has become a fundamental tool for researchers and industry to control and study the impacts of precursor quality, interface and nucleation dynamics, in addition to the effects of alloying and doping of 2D materials at nanometer thicknesses.
While MBE has been heavily used for the synthesis of magnetic transition metal chalcogenides, recent reports show that transition metal halides may be synthesized at monolayer scales using this method.20,603 Weijong Chen et al. successfully synthesized CrBr3 at the monolayer limit by using compound source MBE, where CrBr3 powder was used as the source of Bromine. Growth dynamics for CrBr3 films were determined by in situ reflected high energy electron diffraction (RHEED) (Figure 55) and STM. While this is an isolated study on CrBr3, it will inevitably be a launchpad for future epitaxial growths of halide based vdW magnets at larger scales on more conventional substrates.
Figure 55.
(A, B) RHEED patterns with indicated diffraction orders of (A) the bare HOPG substrate and (B) the MBE-grown CrBr3 film. (C, D) STM images of (C) the CrBr3 monolayer with (D) bilayer islands. The scan parameters were as follows: Vb = 1.1 V, I = 100 pA, T = 5 K for (C) and Vb = 1.5 V, I = 100 pA, T = 5 K for (D). (E) Atomically resolved image of a monolayer CrBr3 with an overlaid atomic structure. The scan parameters were as follows: Vb = 1.5 V, I = 500 pA, T = 5 K. The lattice constants were determined to be 6.3 Å for the primitive vectors a and b, consistent with the bulk values. (F) Illustrations of the top and side views of the monolayer CrBr3 atomic structure. The Cr atoms form a honeycomb lattice sandwiched by Br atoms. Within the Cr honeycomb lattice, the top and bottom surfaces of Br atoms form single triangles but with opposite orientation, indicated by solid and dotted green lines, respectively. (G) AFM image of monolayer CrBr3 with partial coverage. A line-cut profile across the monolayer and bare substrate is shown with a monolayer height of 6.5 Å. All panels are adapted with permission from ref (20). Copyright 2019 AAAS.
Synthesis of CrSBr
Beyond prototypical 2D magnets such as Cr2Ge2Te6, Fe3GeTe2, and CrX3 (X = halide),5 ternary chromium sulfide bromide (CrSBr) has emerged as an exciting 2D material due to its magnetic structure in which each CrSBr layer is ferromagnetically ordered in-plane and coupled antiferromagnetically to adjacent layers.110 The synthesis of CrSBr requires advanced processes, combining both solid state and molecular chemistry. The primary reagent is disulfur dibromide (S2Br2), a highly air sensitive liquid prepared by heating a mixture of solid sulfur and liquid molecular bromine in a sealed pressure vessel, followed by vacuum distillation.604 Beyond this, CrSBr synthesis follows the canon model of CVT in a multizone furnace with a temperature gradient between 1223 and 1153 K,110,605 with S2Br2 acting as both reagent and CVT agent. Although not yet realized experimentally, other members of the chromium chalcogenide halide (CrEX, E = chalcogenide) family are predicted to have extremely high magnetic transition temperatures (e.g., CrSeBr with TN = 150 K), motivating the development of more controllable syntheses.606−608 A mixed halide compound CrSBr1–xClx (x = 0.33) with the same structure as CrSBr was previously reported, giving hope for the possibility of synthesizing additional compositions.609
Defect Studies in vdW Magnets
While defects are an inevitable part of synthesis, they can significantly alter the properties of materials. This effect is often magnified at the 2D limit.610−612 Defects have been explored in traditional 2D materials but they remain largely unexplored in 2D magnets.612−614 Two materials in which the effects of defects have been examined are Fe3GeTe2 and MnBi2Te4. Fe3GeTe2 is a 2D metal with a layered FM ordering and a high TC of 220 K decreasing to 130 K at the monolayer.333 It has received much attention due to the tunability of its TCvia electrostatic gating,12 its large anomalous Hall current,336 and its corresponding potential as a spintronic material.499 However, the origins of its bulk magnetic ordering have come to light only recently: Theory predicts an interlayer AF structure with intralayer FM ordering, but all experimental probes show that it has both interlayer and intralayer ferromagnetism. This discrepancy comes from defects in CVT-grown Fe3GeTe2. Theory calculations show that Fe defects are highly favorable. There are three incommensurate Fe sites (Figure 56A). The one which dominates interlayer AF interactions (FeI–FeI) is greatly decreased by defects and doping, while the two interactions (FeII–FeI and FeII–FeII) that contribute to interlayer FM ordering are increased (Figure 56B).615 Hence experimentally observed phases, such as Fe2.75GeTe2, are fully FM while completely stoichiometric Fe3GeTe2 is predicted to be AF between adjacent sheets.77 This demonstrates a clear opportunity for tuning bulk magnetic properties by controlling the number of Fe defects.
Figure 56.
(A, B) The structure and ground states of iron-deficient Fe3–xGeTe2. (A) Side view of stoichiometric Fe3GeTe2. FeI (red) and FeII (silver) are two inequivalent Fe sites with +3 and +2 formal charges, respectively. The FeI–FeI interactions are mostly responsible for interlayer AF ordering while FeI-FeII and FeII–FeII couplings are FM. With Fe defects or doping, FeI–FeII and FeII–FeII become dominant and push interlayer ordering into FM. (B) The calculated energy differences (ΔE) between interlayer AF and FM phases as a function of hole concentration. For ΔE > 0, FM is favored (between 0.2 and 0.6 holes per formula unit). Panels (A) and (B) are adapted with permission from ref (615). Copyright 2020 American Chemical Society. (C) The layered crystal structure of MBT. The red arrow indicates the Mn sites in which antisites have been identified. (D) STM of the surface of a cleaved MBT crystal; white spots show the presence of multiple antisite point defects. Panels (C) and (D) are adapted with permission from ref (616). Copyright 2020 American Chemical Society. (E) Crystal structure representation of the (MnBi2Te4)m(Bi2Te3)n series, ranging from AF to FM with various compositions derived from codepositional MBE. Here, we see that with the addition of Bi2Te3 layers, the MnBi2Te4 layers cannot be coupled together and the material becomes less AF. This is a prime example of an off-stoichiometry defect. Panel (E) adapted with permission from ref (617). Copyright 2020 AIP Publishing.
The relationship between defects and magnetic properties, and how they relate to the emergence of exotic insulating phenomena, has been thoroughly investigated in MnBi2Te4.616,618−621 By examining native Mn and Bi point defects (Figure 56D), Huang et al. quantified how Mn and Bi vacancies directly affect the local Fermi level by inducing localized defect states in the band gap.619 This work has led to further changes in the synthesis of MnBi2Te4 to either decrease defect concentration or control the electronic properties MnBi2Te4 through defect engineering. Controlling this system’s electronic states are critical for the observation of topological phenomena, such as the quantum anomalous Hall effect. In a different study, MBE was employed to produce off-stoichiometry phases by incorporating differing amounts of Bi2Te3 sub units (see Figure 56E); this off-stoichiometry leads to different stacking configurations of magnetic layers, resulting in modular magnetic ordering.617,622 Simultaneously, MBE was used to include point defects (Mn, Bi, Te vacancies), effectively chemically doping the system, to alter the Fermi level.616 By engineering stoichiometry and defect concentration through synthetic control, the electronic and magnetic state can be directly manipulated.616
Challenges and Perspectives
While well-established bulk crystal synthesis techniques outlined above are critical for researchers to identify champion material systems and probe their fundamental material properties, very little is currently understood about how different bulk synthesis techniques impact the magnetic properties of vdW magnets. This raises many questions about how thermal processing, precursor materials, flux and transport agents impact the magnetic character of these materials. Adding to the complexity of the current state of vdW magnets, even less is known about how defect density, magnetic impurities, and overall crystallinity impact the performance of these material systems, especially in their 2D limits where these factors will have even a greater impact on their quantum magnetic phenomena (e.g., skymionic effects). Commonly used chemical vapor transport samples are known to contain significant number of point defects and learning from our mistakes in diluted magnetic semiconductor will be essential to reaching reliable conclusions in these emerging fields. Initial reports in vdW materials show that flux growth is most suited to reduce these point defects but the question still remains if it can reach 6N or even higher purities. The purity is going to be a major challenge to overcome in order to reach quantum coherence in quantum devices involving 2D vdW magnets.
Another natural concern is around their material stability in air or ambient conditions. While it is true that some of the high-performance devices can operate under vacuum, it still raises questions about the photo degradation effects as well as long-term material stability. More studies are needed to clarify how one can improve the material stability through surface functionalization, encapsulation, or even curing chemically active defect sites without sacrificing the material properties.
Beyond the fundamental studies of these materials, the overarching aim is to bridge the gap between laboratory studies and the eventual development of next-generation technologies. To accomplish this, much work needs to be done to advance the large area (inch scale) synthesis and deposition of 2D vdW magnets, and researchers pushing the boundaries of layer-by-layer growths of these materials will need to overcome similar challenges that were paramount to producing large area TMD systems with high crystallinity and low defect densities. This gives a brief insight into the current state of vdW magnet synthesis and presents many exciting challenges and opportunities for scientists and engineers to solve which will establish the fundamentals and push the capabilities of vdW magnets from the lab and into cutting-edge quantum devices.
Key to understanding the role of defects in 2D magnets is to identify and quantify them both in the bulk and 2D regime. Methods of inspecting these features can be broadly divided by their spatial resolution and the directness by which they probe magnetic properties. The level of detail and resolution concerning magnetic properties obtained from various techniques is very often indirectly related to the feasibility of the experiment. On one hand, SQUID measurements give no microscopic details about spin configuration, but provide information about macroscopic magnetic properties and are widely available. On the other hand, spin-polarized STM can be used to gain electronic and magnetic information on the atomic scale but is prohibitively costly and time-consuming.623 Techniques such as Lorentz TEM624 and magnetic force microscopy625 can characterize magnetic domains between 2 and 20 nm,626 accessing the mesoscale, but also require expensive instrumentation and a high degree of training. To truly understand the magnetic effects of defects within a system, surveys utilizing a wide array of measurements are necessary. Crucial to improving our understanding of defects is making these myriad techniques widely available, or cultivating emerging atomic-level probes of magnetic defects such as nanopatterned SQUID,627 scanning SQUID,627 or NV-center magnetometry.21
Mechanical Properties and Strain Engineering
Mechanical properties play an important role in the applications of 2D magnets, such as strain engineering and flexible electronic devices. The thickness reduction of vdW materials to the atomic scale normally leads to mechanical enhancements. For example, graphene has an intrinsic Young’s modulus of ∼1 TPa and fracture strength of ∼120 GPa,628 about 1–2 orders larger than those measured from bulk graphite.629,630 The same phenomena have also been observed from many other 2D materials. Atomically thin hBN, an insulating 2D material, has a Young’s modulus (i.e., ∼865 GPa) and fracture strength (i.e., ∼70 GPa) comparable to those of graphene.631 Although TMDs have relatively weaker interaction between metal and chalcogen atoms, the Young’s moduli and strengths of 1L MoS2 (∼270 and 23 GPa, respectively),632 1L WS2 (302 and 47 GPa, respectively),633 and 1L WSe2 (258 and 38 GPa, respectively)633 are much higher than those of their bulk counterparts as well as most conventional materials. Two main reasons can be ascribed to this: a smaller probability of defects due to the dramatically decreased volume and less softening from the weak interlayer interactions at the atomic thicknesses.
Nevertheless, the mechanical properties of few-layer 2D materials are also subject to interlayer sliding. For example, although the in-plane covalent bonds in graphene are stronger than those in BN, the fracture strengths of 8–9L graphene and BN are close due to their different sliding tendencies under strain and compression, i.e., few-layer graphene spontaneously slides between layers under an in-plane strain and large compression, while few-layer BN has large positive sliding energies under the same conditions to prevent it from sliding.631 Similar interlayer sliding phenomena have also been found in few-layer WS2 and WSe2.633 The Young’s modulus and strength of 2D materials are mostly measured by nanoindentation methods,628,631−634 along with bulge method (Young’s modulus only)635,638 and microtensile tests636,637 (Figure 57).
Figure 57.
Common experimental techniques for measuring the Young’s modulus and strength of 2D materials. (a) Nanoindentation based on AFM.634 Adapted with permission under a Creative Commons CC BY license from ref (634). Copyright 2019 John Wiley and sons. (b) Bulge test involving interferometry and Raman spectroscopy.635 Adapted with permission from ref (635). Copyright 2017 American Physical Society. (c) Tensile testing push-to-pull micromechanical device controlled by an external pico-indenter in SEM, and the yellow arrow shows the loading direction. (d) Diagram showing the enlarged pink rectangle area in (c) with a suspended graphene sample after cutting by focused ion beam.636,637 Copyright 2009 Royal Society of Chemistry, copyright 2019 American Physical Society, copyright 2019 John Wiley and Sons, copyright 2017 American Physical Society, copyright 2020 Springer Nature, copyright 2014 Springer Nature. Panels (c) and (d) are adapted with permission under a Creative Commons CC BY 4.0 license from ref (636). Copyright 2020 Springer Nature.
AFMs are usually used for the indentation measurements. In particular, a sharp tip at the end of a cantilever indents at the center of suspended 2D materials, and the nonlinear elastic properties and strength can be derived from the force-displacement relation (Figure 57a).628,631−634 For accuracy, the 2D material should not slide on a substrate during indentation, and the tip should have a larger stiffness than the 2D nanosheets (e.g., diamond tip for graphene and BN). As atomically thin films, 2D materials are suitable for blister (bulge) tests, in which they are clamped over microholes and the stiffness can be calculated based on gas pressure-driven or electrostatically driven geometry changes (Figure 57b).635,638−642 In microtensile tests, suspended 2D materials of relatively large sizes are under uniform tensile stretch induced by special indentation-spring setups in scanning electron microscope (SEM), which is best at revealing the nonlocalized fracture strength and strain (Figure 57c).636,637 In addition to large Young’s modulus and strength, 2D materials also have extremely low bending moduli,643,644 strong adhesion to arbitrary surfaces,638,645 low fracture toughness,637,646 and increased friction coefficient.647 It should be emphasized that 2D materials are able to undertake large strains without failure,628,631,648 providing more opportunities for strain engineering. According to recent theoretical and experimental works, in-plane strain engineering can change the structural phase,649,650 electronic structure,651,652 and polarization653,654 of TMDs; strain can also induce pseudomagnetism in graphene.655,656
There have been few experimental studies of the mechanical properties of 2D magnets. Very recently, the intrinsic elasticity and strength of atomically thin chromium trihalides, i.e., CrX3 (X = Cl, I) mechanically exfoliated from their single crystals were measured by AFM-based nanoindentation at room temperature (Figure 58).657 The 2L CrI3 and CrCl3 had Young’s moduli of 62.1 ± 4.8 GPa and 43.4 ± 4.4 GPa, respectively, consistent with the theoretical predictions.234,237,657,658 Their fracture strengths were measured to be 3.6 ± 0.4 GPa and 2.2 ± 0.5 GPa, respectively; the maximum strains were in the range of ∼6.0–6.5%. The elasticity and strength of both materials decreased with increased layer thickness due to the high tendency of interlayer sliding, though this phenomenon was more prominent in CrCl3. The DFT calculations showed that CrCl3 and CrI3 had small sliding energy barriers in the equilibrium state and under in-plane strains.659 The interlayer sliding led to stress concentrations on the bottom layers during indentation, weakening the few-layer systems. This study indicates that atomically thin CrCl3 and CrI3 have one of the lowest elasticity and strength values among all 2D materials explored so far. The soft mechanical response and larger cleavage energy than shear (sliding) energy in the two materials give rise to the possibility of the superplastic phenomenon in their bulk crystals (Figure 58).
Figure 58.
Mechanical properties of CrCl3 and CrI3. (a) Optical microscopy images of 2L and few layers CrCl3 and Crl3 suspended over microwells (600 nm in diameter) on a SiO2/Si substrate. (b) Load–displacement curves and the corresponding fittings of 2L and 7L CrCl3 and CrI3. (c) Volumetric Young’s modulus and breaking strength of 2–10L CrCl3 and CrI3, along with dashed lines that show the linear fits. (d) Demonstration of the good plasticity of bulk CrCl3 and CrI3 crystals via folding them into rings. (e) Deformability factor versus Young modulus, where I, II, and III correspond to plastic-flexible, potentially deformable and brittle-rigid regions, respectively. The experiential results of CrCl3 and CrI3 are shown as red-filled circles, and the other layered vdW materials are shown as green filled circles. (f) Deformability factor versus bandgap for the same materials as in (e), and the materials that may show exceptional plastic behavior are shown in the dashed line encircled green area.659 All panels are adapted with permission from ref (659). Copyright 2021 American Chemical Society.
The number of theoretical investigations on the mechanical properties of 2D magnets is growing fast. The theoretical Young’s modulus (both 2D and 3D), fracture strength, Poisson’s ratio, and cleavage energy of monolayer magnets predicted so far are summarized in Table 8. Note that the fracture strength and strain of most 2D magnets have not been theoretically studied, except 2L CrCl3/CrI3659 and 1T VS2 and VSe2 along the zigzag direction.660
Table 8. DFT studies of the mechanical properties of 2D magnets.
| monolayer magnets | 2D Young’s modulus (N/m) | theoretical thickness (Å) | Young’s modulus (GPa) | fracture strength (N/m) | Poisson’s ratio | cleavage energy (J/m2) | ref |
|---|---|---|---|---|---|---|---|
| FePS3 | 65.98–119.7 | 6.42 | 102.8–186.4 | 0.304 | 0.265 | (1, 661, 662) | |
| FePSe3 | 67.9–90.2 | 6.61 | 102.7–136.5 | 0.312 | 0.37 | (1, 661, 662) | |
| MnPS3 | 55.1–107.7 | 6.49 | 84.9–165.9 | 0.327 | 0.26 | (1, 661, 662) | |
| MnPSe3 | 36–60.8 | 6.67 | 54.0–91.2 | 0.35 | 0.23–0.24 | (1, 661−663) | |
| NiPS3 | 80.9–106.8 | 6.34 | 127.6–168.5 | 0.265 | 0.21 | (1, 661, 662) | |
| NiPSe3 | 78.8 | ∼6.52 | 120.9 | 0.275 | (661) | ||
| CrSnTe3 | 64.8 | 0.283 | (664) | ||||
| CrSiTe3 | 40.8 | 6.86 | 59.5 | 0.35 | (663) | ||
| CrGeTe3 | 38.3 | 6.9 | 55.5 | 0.38 | (663) | ||
| K2CuF4 | 44.8 | 0.78 | (665) | ||||
| CrOCl | 38.39–46.83 | 0.208 | (666, 667) | ||||
| CrI3 | 22–28 | 6.62 | 33.2–42.3 | 2.3–3.6 (2L) | 0.253 | 0.155–0.28 | (234, 237, 657−659) |
| CrBr3 | 28–29.3 | 6.11 | 45.8–48.0 | 0.278 | 0.19–0.295 | (234, 658) | |
| CrCl3 | 31–34 | 5.80–6.10 | 53.4–55.7 | 3.9–4.9 (2L) | 0.297 | 0.13–0.3 | (234, 658, 659) |
| FeSe | 66.2–119.8 | 5.31–5.61 | 124.7–213.5 | 0.179–0.196 | (657, 668, 669) | ||
| Fe3GeTe2 | 134 (C11) | ∼0.01 | (330) | ||||
| VS2 | 85 | 5.71 | 148.9 | 12 (zz) | 0.16 | (660) | |
| VSe2 | 53.8–71 | 6.1–7.0 | 88.2–101.4 | 9.8(zz) | 0.18–0.229 5 | (660, 670) | |
| CrTe3 | 48–52 | 6.94 | 69.2–99.7 | 0.5 | (671, 672) | ||
| Mn3Se4 | 18.76–25.97 | 0.371 | 0.58 | (673) | |||
| Mn3Te4 | 22.6–29.42 | 0.293 | 0.53 | (673) | |||
| Fe2Si | 71 | 5.7 | 124.65 | (674) | |||
| CoAsS | 75.51 | 0.076 | (675) | ||||
| NiI2 | 45 | 6.54 | 68.8 | 0.26 | (676) | ||
| NiBr2 | 50 | 6.09 | 82.1 | 0.242 | (676) | ||
| NiCl2 | 54 | 5.8 | 93.1 | 0.223 | (676) | ||
| CrPbTe3 | 46.9 | 0.318 | (677) | ||||
| CrPS4 | 36.8–56.4 | 6.2 | 59.4–91.0 | 0.28–0.44 | (678, 679) |
Although 2D magnets have smaller Young’s moduli and strengths than most other 2D materials, they are stronger than their bulk counterparts and traditional magnetic thin films (Figure 59). For example, 1L FeSe has a theoretical Young’s modulus of 66.2–119.8 N/m (i.e., 124.7–213.5 GPa);657,668,669 in comparison, that of FeSe thin films is only 41 GPa determined by acoustical measurements.680 A 1 μm-thick SmCo5 deposited by RF magnetron sputtering on Si 100) substrate has a reduced modulus of 43.09 ± 1.60 GPa measured by indentation,681 smaller than that of most of the 2D magnets listed in Table 8. Magnetic thin films comprised of magnetic particles in polymer matrix normally have even smaller modulus values. Strontium ferrite particles (SrFe12O19) suspended in a benzophenone tetracarboxylic dianhydrideoxydianiline/metaphenylene diamine polyimide matrix had biaxial modulus values in the range of 6 to 17.8 GPa, measured by a modified in situ load/deflection technique.682 We can also compare the strength values of 2L CrCl3 (3.6 ± 0.4 GPa) and 2L CrI3 (2.2 ± 0.5 GPa) with the “so-called” ultrahigh strength value of 40–400 μm-thick Fe – Co – Ni-based maraging steel and 316L austenite stainless steel magnetic sheets (∼1.61 GPa).683
Figure 59.
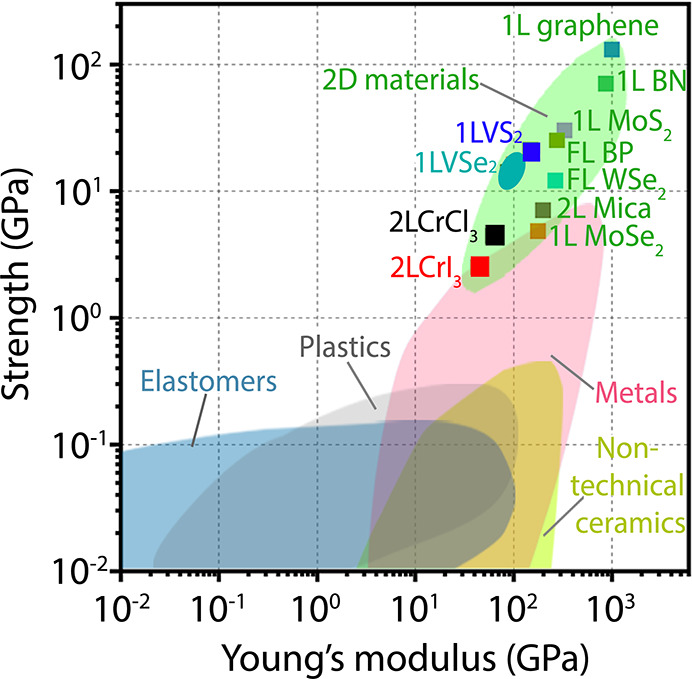
Modulus-strength graph. The Young’s modulus and fracture strength of 2D magnets are compared with those of conventional bulk materials and other 2D materials. Adapted with permission from ref (659). Copyright 2021 American Chemical Society.
Although traditional magnetic thin films show good susceptibility to external strain686,687 for sensing applications,688−690 strain engineering of 2D magnets could be conducted at higher strains and may lead to intriguing phenomena. Tensile strain can change the coupling between local spins, Curie temperature, and transitions between FM and AF phases of 2D magnets.234,330,657,666,667,677,678 For example, the strength of the exchange coupling and spin polarization of VZ2 (Z = S, Se, Te) monolayers are able to be altered via strain modulation (−5% to 5%) due to the effect on the ionic–covalent interactions between V and Z atomic pairs, where the increased unpaired electrons in the interacting atoms change the magnetic moments.691 Similar phenomena are observed in semiconducting or insulating 2D transition-metal trichalcogenides (MYX3), and the strain required for magnetic phase change is chemical composition-dependent. For FePS3, FePSe3, and VPTe3 monolayers, just 1% of tensile strain is adequate to trigger phase transition according to theoretical studies (Figure 60a).684 In the case of CrPS3 and NiPS3, the FM–AF magnetic phase transition happens at strains greater than 4%; while larger strain of ∼9% is needed to observe such transition in VPSe3 and MnPS3.684 Another FM semiconductor, chromium telluride compounds with metalloids as the middle element, i.e. CrYTe3 (Y = Si, Sn, Ge) show enhanced ferromagnetism and significant changes in their Curie temperature under moderate tensile strains of ∼4–5%.664,692−694 2D CrX3 (X = Cl, Br, I) also shows great potential in strain modulation under large strain,695 though it is not effective to modify their Curie temperatures.658 As shown by recent experiments, high-quality 2D CrX3 can sustain up to 6.0–6.5% strain without failure.659 Another experimentally strain-engineered 2D magnet is 1L FeSe, which could be stretched up to 5–6%.696,697 With their relatively low elasticity, 2D magnets should be highly sensitive to small stress variations. This great sensitivity to lattice deformation allows to experimentally detect one-step magnetization reversal, which has not been achieved in conventional magnetic materials.698 2D magnets also provide good platforms to study magnetostriction at the atomic thickness. Mechanical resonators based on few-layer CrI3 showed changed resonant frequency under external magnetic field due to competition between minimizing the elastic energy and internal magnetic interactions (Figure 60b).685 Magnetostriction is useful in sensing and producing ultrasonic vibration or waves. In addition to in-plane strain, it has also been demonstrated that the magnetic ground state and interlayer magnetic coupling of atomically thin CrI3 can be altered by out-of-plane hydrostatic pressure.22,23 The transition of magnetic phase under hydrostatic pressure relates to the varied stacking order in CrI3, and the same effect may exist in other 2D magnets.22
Figure 60.
Mechanical properties of ternary compounds. (a) Changes in the magnetic configurations of various MPX3 (M = Mn, Fe, Ni; X = S, Se) compounds at zero carrier density under in-plane biaxial compressive and expansive strains. Adapted with permission from ref (684). Copyright 2016 American Physical Society. (b) Magnetostriction in 2L CrI3 and (c) 6L CrI3 resonators under an out-of-plane magnetic field (μ0H⊥) and in (d) 6L CrI3 resonator under an in-plane magnetic field (μ0H∥). The resonance frequency (b–d) and MCD (b, c) of the membranes as a function of the magnetic field, where the red (blue) lines correspond to the measurement for the positive (negative) sweeping direction of the field. Panels (b–d) are adapted with permission from ref (685). Copyright 2020 Springer Nature.
Challenges
There are still many research gaps and opportunities in the mechanical properties of 2D magnets, such as (1) The intrinsic mechanical properties of most 2D magnets are still waiting for experimental investigations despite of the theoretical predictions. With the well-established experimental techniques for measuring the mechanical properties of other 2D materials, the difficulty mainly lies on the fabrication (e.g., by mechanical exfoliation) of suspended high-quality 2D magnets suitable for these tests. There could be additional technical challenges for dealing with 2D magnets that are not stable in air. (2) The large-scale synthesis of 2D magnets, such as by CVD and MBE are beneficial to their practical applications. However, based on the experience from other 2D materials, these 2D magnets could have lower than intrinsic mechanical strength and fracture strain due to the presence of large numbers of defects and grain boundaries, especially that the detrimental effect of vacancies on the strength of 2D materials is much more dramatic than that of bulk materials. Hence it is essential to study the mechanical properties of imperfect 2D magnets, which has not been theoretically and experimentally studied yet. (3) There are many exciting opportunities in the magneto-mechanical properties of 2D magnets. The aforementioned magnetostriction effect is one of them. Although the magnetostriction of CrI3 has been demonstrated, the magnetostrictive coefficient has not been quantified. Moreover, many applications of the magneto-mechanical coupling in 2D materials could be explored. The magneto-mechanical coupling in doping-enabled magnetism in intrinsically nonmagnetic 2D materials could be an interesting direction to explore as well.382,699 (4) Although the influence of strain on magnetic behaviors and other physical properties of 2D magnets has been extensively studied theoretically, there are just a few experimental studies so far. It is of particular interest to experimentally demonstrate one-step magnetization reversal in 2D magnets, as these effects are difficult to be achieved in conventional magnets because high tensile strain is normally required. The high strain susceptibility of the magnetic properties of 2D magnets offers great potential for various applications, such as in spintronics.
Spin Excitations and Topological Properties
Introduction
2D vdW magnetic materials have a long and distinct history.42 Compared with other 2D magnetic systems, including quasi-2D metallic magnetic materials, monolayer of magnetic ions on a substrate, monolayer organic molecules containing magnetic atoms deposited on a substrate via Langmuir–Blodgett technique, and 2D electron gases, one of the advantages of 2D vdW magnetic materials is that they can potentially be mechanically cleaved into a monolayer and therefore provide a platform to study fundamental physics without the influence of a substrate.62,84,700 Technologically, one can also develop spintronic devices with insulating thin 2D magnetic materials to avoid Ohmic heating.62 The field of 2D vdW magnetic materials took off a few years ago with the experimental demonstration of magnetic order in single atomic layer of several vdW 2D magnetic materials including FePS3,32,701 CrI3,5 Cr2Ge2Te6,6 VSe2,18 and MnSe2.17 While these developments are very exciting, they also call for a more detailed examination of the magnetic properties of these vdW materials, both in bulk form as well as with decreasing layer thickness.
For spin rotational invariant systems with short-range magnetic interactions describable by a Heisenberg Hamiltonian, it has been shown rigorously by Mermin and Wagner that there cannot be long-range FM or AF order at finite temperature in the 2D (monolayer) limit.40 This is because the continuous symmetry of the isotropic Heisenberg Hamiltonian leads to gapless long-wavelength (low-Q) spin waves that can be excited at any finite temperature, with detrimental effects on long-range magnetic order in low dimensions. However, when spin rotational invariance of the system is broken, say by anisotropic magnetic interactions in a 2D Ising model, long-range magnetic order can occur below a transition temperature when anisotropic interactions open a gap in the spin-wave spectrum and suppress the effect of thermal fluctuations.33,34 Finally, for the 2D XY model,702 there is no transition to a long-range magnetic order below a finite temperature where the magnetic susceptibility diverges. Instead, the diverging susceptibility is associated with the onset temperature of topological order, called Kosterlitz–Thouless temperature TKT below which spin correlations are characterized by an algebraic decay and the bound pairs of vortex and antivortex spins.64 In addition to the 1D Ising,33,34 2D XY,702 and 3D Heisenberg Hamiltonian,703 2D honeycomb lattice magnetic materials with spin S = 1/2 can be described by a Kitaev Hamiltonian, which is an exactly solvable model that can realize many emergent phenomena such as Z2 gauge field, quantum spin liquid (QSL) states, and topological order.704
2D vdW magnetic materials provide a broader and flexible approach for studying 2D magnetism, particularly in our ability to test different forms of spin Hamiltonian’s described above.84 In bulk crystal form, they exhibit highly anisotropic, quasi-2D electronic properties that are often qualitatively different from common 3D materials.705 To understand 2D magnetism,5 one must first determine the magnetic exchange couplings of these materials. In their bulk form, this can be achieved by neutron scattering, while Raman and tunneling spectroscopy can be used to understand the magnetic properties of thin flakes. Within the past two decades, the possibility of isolating a single molecular layer from cleavage has further led to numerous discoveries of unexpected 2D physics, such as Dirac Fermions in graphene.706,707 Recently, the discovery of FM order in ultrathin vdW films attracted considerable attention, as the interlayer coupling is eliminated in these clean 2D systems. These vdW magnetic materials not only allow experimental tests of magnetic theories, but also enable nanoscale spintronic devices more efficient than current transistor-based electronics.213 An advantage of 2D vdW films for fundamental research is their large and clean surface, which allows the manipulation of electronic states by gating and by the formation of heterostructures.708,709 For example, electrostatic doping was shown to switch net magnetization in bilayer CrI3.9,11 Moiré engineering, the formation of tunable superlattices by two misaligned vdW monolayers, has led to strongly correlated electronic and superconducting phases that are intimately related to magnetism.197,198,710
Compared with 3D magnetic materials, 2D magnetic interactions and frustrations play an important role in exotic phenomena like QSL711−714 and high-temperature superconductivity.715,716 The key to observable 2D long-range magnetic order is the presence of the anisotropic spin-exchange interaction, as it opens a gap for the low-energy spin excitations that allow the development of long-range magnetic order at finite temperature. In vdW magnetic materials with honeycomb, triangular, square, and kagome lattice structures, all four fundamental spin Hamiltonians (the Ising, XY, Heisenberg, and Kitaev) can be realized.84,211,665,717,718 The ground state of the system is sensitive to superexchange interaction and interlayer coupling.235 In many materials, the ground state may switch depending on lattice parameters.719 Therefore, for both fundamental understanding and practical applications of 2D magnetism,62,720 it is critical to study and control the spin Hamiltonian in these materials. In many cases, the spin anisotropy that controls the magnetic order of the system is determined by crystal field and/or SOC. By carefully measuring the magnetic order and spin excitations spectra in bulk and atomically thin crystals, one can model spin Hamiltonians of the system.
Neutrons—with their wavelengths comparable to atomic spacing and energies close to those of spin excitations in solids—have played a role in determining the lattice and magnetic properties of bulk vdW magnetic materials. Some of the reasons for this role are as follows: (1) A neutron carries a magnetic moment that interacts with localized magnetic ions and unpaired itinerant electrons in solids. (2) A neutron is a weak interacting probe. A neutron scattering cross section is determined by the static and dynamic correlation functions of the system, without the need for correcting the influence of the probe. (3) Neutrons are a highly penetrating bulk probe and therefore insensitive to surface imperfections, and therefore an ideal probe to study bulk magnetic properties of 2D vdW magnetic materials. (4) Neutron polarization analysis can determine magnetic anisotropy of the system, and therefore provide a way to directly probe the SOC-induced magnetic anisotropy of spin excitations and magnetic ordered moment direction.
Despite its advantages, neutron scattering is limited to bulk samples. In few-layer 2D flakes with lateral dimensions on the micron scale, or in systems where the surface exhibits different behavior than the bulk, it is necessary to utilize alternative probes. The purpose of this section of the review is to first discuss recent progress on understanding bulk magnetism and spin dynamics in vdW magnetic materials obtained by neutron scattering and muon spin relaxation (Figure 61). We shall then describe how inelastic tunneling spectroscopy (IETS) and Raman spectroscopy can be used to probe for magnetic excitations down to the 2D limit as well as on the surface of bulk crystals. Finally, we will also discuss possible future directions in these areas.
Figure 61.
Magnetic order and spin excitations in vdW magnetic materials with tunable fundamental spin Hamiltonian’s and structural parameters probed by neutron scattering methods. Adapted with permission from ref (84). Copyright 2018 Springer Nature.
Neutron Scattering in Bulk vdW Magnets
We begin by discussing layer transition metal (TM) thio(seleno) phosphate materials TMPS(Se)3 where TM = V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Pd, Ag, and Cd.721−723 For a subset of these materials with magnetic transition metal ions, magnetism can be described by 2D Ising (FePS3),32,724,725 2D Heisenberg (or possibly XY) (MnPS3),318,726,727 and 2D XY (NiPS3, CoPS3)317,728,729 Hamiltonian’s. While crystal structures of these materials are somewhat different, the transition metal magnetic ions all have a honeycomb lattice structure. Figure 62a–d shows magnetic structures of FePS3,724 MnPS3,318 NiPS3,317 CoPS3,729 respectively. In all cases, the systems order antiferromagnetically with different magnetic structures (Figure 62a–d). We first discuss FePS3, where the magnetic structure is collinear AF with moment perpendicular to the honeycomb lattice along the c-axis as shown in Figure 62a.724 There are three twinned domains rotated 120°, resulting in overlapping spin waves from different domains at the same reciprocal space point.725 Spin waves of FePS3 were measured by inelastic neutron scattering experiments and modeled via a Heisenberg Hamiltonian with single ion anisotropy and biquadratic exchange interaction.725 In most local moment systems, a Heisenberg Hamiltonian with single ion anisotropy should be able to describe spin waves. The biquadratic exchange interaction, originally proposed to explain spin waves in AF ordered parent compound of iron-based superconductors,730,731 is needed to understand spin wave deviations from Heisenberg Hamiltonian near the zone boundary.725 For AF MnPS3,721 neutron scattering experiments have studies magnetic order and spin waves of the system. Spin wave dispersions of MnPS3 can be well fitted by a Heisenberg Hamiltonian with first-, second-, and third-nearest in-plane neighbors magnetic exchange couplings.726 From neutron diffraction experiments, it was argued that the critical behavior of the material over most of the temperature range is more representative of an XY-like system instead of a classical Heisenberg system.727 For XY antiferromagnet NiPS3317 and CoPS3,729 their magnetic structures are rather similar except for the moment direction (Figure 62). Inelastic neutron scattering experiments were carried out on powder samples of NiPS3 and CoPS3 determined approximate magnetic exchange couplings.728,732 When NiPS3 was cleaved to monolayer, the AF order in bulk disappears consistent with the expectation of the XY magnetism in the atomically thin limit.211
Figure 62.
Magnetic structures of (a) FePS3.724 Adapted with permission from ref (724). Copyright 2016 American Physical Society. (b) MnPS3.318 adapted with permission from ref (318). Copyright 2006 American Physical Society. (c) NiPS3.317 adapted with permission from ref (317). Copyright 2015 American Physical Society. (d) CoPS3.729 adapted with permission from ref (729). Copyright 2017 IOP Publishing. All of these materials have honeycomb lattice structure and are antiferromagnetically ordered.
Next we discuss magnetic order and spin excitations in honeycomb lattice vdW magnetic materials, including semiconducting CrGeTe3,733 metallic Fe3GeTe2,323,333,734 and semiconducting chromium trihalides CrX3 where X = Cl, Br, I.735 In the monolayer limit, long-range FM order persists in some of these materials. There has been a huge amount of recent work on monolayer or few layers of these materials.62,700 For semiconducting FM CrGeTe3 with ordered moment direction along the c-axis below the Curie temperature TC,733 critical scattering measurements indicate that FM phase transition is second order in nature.279 Unfortunately, there are no inelastic neutron scattering experiments to determine spin waves and magnetic exchange couplings. For metallic FM Fe3GeTe2, it was found that Curie temperature of the system depends sensitively on the stoichiometry of the iron with reduced TC for iron deficient samples.323 Inelastic neutron scattering measurements on Fe2.75GeTe2 synthesized from flux method mapped out the spin excitations spectrum and found a spin gap of 3.7 meV at the Γ point, providing information of the magnetic exchange interactions and anisotropy.736 However, because of the Fe deficiency and the corresponding disorder, the excitations are rather broad and damped, precluding a detailed modeling of its spin Hamiltonian.
In the case of FM chromium trihalides with honeycomb lattice structure,735 while the role of the underlying structure in stabilizing the 2D ferromagnetism is under intense investigation,120,235 the honeycomb structure provides another interesting physics of massless magnetic Dirac particle analogous to the massless electrons near Dirac points in graphene.737−739 In this picture, magnons become massless at the Dirac K/K′ points with linear dispersions due to the exchange frustrations between two sublattices of the honeycomb lattice. The presence of these Dirac points are robust against finite next-nearest-neighbor exchanges, which will only shift positions of the Dirac points. The linear spin wave bands across the Dirac points have been experimentally observed in 2D ferromagnets CrBr3124 and Cr2Si2Te6.740 Similar magnon band crossings have also been observed in the 3D antiferromagnet Cu3TeO6.741,742 If the SOC induced antisymmetric DMI exists between the next-nearest neighbors in honeycomb lattice, a gap will appear in the spin wave spectra of the system at the Dirac K/K′ points, causing the magnon bands to become topological.743 For CrBr3, inelastic neutron scattering experiments found no evidence of a gap at the Dirac point,124 although these measurements were taken in 1971 and additional neutron time-of-flight measurements using spallation neutron source would be desirable. These results, if confirmed, would suggest that the SOC-induced DMI in CrBr3 is insufficient to induce topological spin excitations.
In the case of CrI3, which has larger SOC compared with CrBr3, neutron time-of-flight measurements of the magnon bands indeed reveal a spin gap at the Dirac points as shown in Figure 63.744 Although these results are interesting, the next-nearest neighbor DMI induced gap may not be the only interpretation of the data as Heisenberg–Kitaev Hamiltonian may also account for the observed spin gap near the Dirac points.746,747 In addition, the FM phase transition in CrI3 was found to be a weakly first order instead of second order in nature, and controlled by SOC instead of magnetic exchange couplings as in a conventional Heisenberg ferromagnet.748 Inelastic neutron scattering on different families of FM honeycomb lattice vdW materials should be able to test whether the microscopic origin of the observed 2D FM order is due to SOC-induced magnetic anisotropy,120,235 and determine if Heisenberg–Kitaev Hamiltonian is an appropriate description of the spin dynamical behavior in honeycomb lattice ferromagnets. By systematically tuning the strength of SOC in chromium trihalides,586,749 one can test if the observed spin-gap arises from SOC-induced DM effect or Kitaev interaction.746,747 Indeed, recently neutron scattering measurements suggest that the observed spin Dirac gap in CrI3 is induced by the next nearest neighbor DMIs.750,751
Figure 63.
(a) A spin gap at Dirac point in CrI3 suggests that spin excitations in this system can have chiral and topological edge mode. Adapted with permission under a Creative Commons CC BY 4.0 license from ref (744). Copyright 2018 American Physical Society. (b) The FM phase transition in CrI3 is weakly first-order and controlled by spin gap. Adapted with permission from ref (745). Copyright 2020 American Physical Society.
In addition to AF and FM order, geometric magnetic frustration in 2D materials can host a QSL phase, in which the spins of unpaired electrons in a solid are quantum entangled but do not show magnetic order in the zero-temperature limit.712−714 Because such a state may be important to the microscopic origin of high-Tc superconductivity716 and useful for quantum computation,704,754 experimental realization of QSL is a long-sought goal in modern condensed matter physics. Models supporting the existence of QSLs in 2D spin-1/2 kagome, triangular, honeycomb, and 3D pyrochlore lattice systems indicate that all QSLs share deconfined spinons, elementary excitations from the entangled ground state which carry spin S = 1/2 and thus are fractionalized quasiparticles, fundamentally different from the S = 1 spin waves in conventional 3D ordered magnets.714 In particular, honeycomb lattice magnetic materials are of interest because a QSL can arise from the exactly solvable Kitaev model with S = 1/2 Ising spins on a honeycomb lattice.704 Over the past several years, honeycomb lattice magnetic materials such as A2IrO3 (A = Cu, Li, or Na)755−758 and α-RuCl3718,753,759,760 have made considerable impact on the community and provided constraints on testing the Kitaev’s QSL Hamiltonian. However, all honeycomb lattice materials investigated so far have symmetric off-diagonal exchange interactions beyond Kitaev’s Hamiltonian (referred as the Γ term),747,761−764 and therefore induce long-range magnetic order. In the case of α-RuCl3, Ru spins order in zigzag AF structure with moment in the plane (see inset of Figure 64a).760 Upon application of an in-plane magnetic field above 7 T, the long-range magnetic order is suppressed and the system is believed to reach a field-induced Kitaev QSL state with half-integer thermal hall conductance plateau.752 Inelastic neutron scattering experiments reveal spin waves from the zigzag order coexisting a continuum of magnetic scattering center around the Γ point (Figure 64b). When an in-plane magnetic field of 8 T is applied, spin waves from the zigzag order are suppressed and the continuum of magnetic scattering, possibly arising from fractionalized quasiparticles of a Kitaev QSL, is still present (Figure 64c).753 In addition to neutron scattering experiments, recent resonant elastic X-ray scattering experiments on a single crystal α-RuCl3 using the Ru L2 and L3 edges (2838 and 2967 eV) established the Hamiltonian of the system, revealing that the Kitaev interaction is FM and the Γ term is AF comparable in size as the Kitaev interaction.765
Figure 64.
(a) The phase diagram of α-RuCl3 adapted with permission from ref (752). Copyright 2018 Springer Nature. At zero field, the system forms a zigzag magnetic structure as shown in the left inset. For in-plane magnetic field between 7 and 9 T, the system is believed to be in Kitaev QSL state. For fields above 9 T, the system becomes non topological from thermal transport measurements. (b) Wave vector/energy dependence of spin excitation of α-RuCl3 at 4 and 8 T, adapted with permission under a Creative Commons CC BY 4.0 from ref (753). Copyright 2018 Springer Nature. One can clearly see spin waves stemming from zigzag ordered wave vector (0.5, 0, 0) at 4 T. The scattering centered around Γ points is believed to arise from fractionalized excitations of a Kitaev QSL, which is enhanced upon suppression of spin waves with a 8 T in-plane magnetic field.
In addition to honeycomb lattices, 2D kagome lattices with arrangements of corner-sharing triangles and hexagons are incredible models with which to study magnetic frustration, electronic correlation, and topological electronic structures (Figure 65).530,767−771 Their competing spin interactions largely impede the development of a long-range magnetic order, frequently leading to the emergence of complex magnetic structures, interesting magnetic behaviors, and exotic states.772,773 For example, magnetic frustration in kagome lattice can lead to a QSL ground state.530 A kagome lattice ferromagnet can have topological magnon bands,767,768 leading to possible topological magnetic edge states.529 Topologically robust magnetic edge states are appealing for low-energy spending, fast spintronic devices, which would revolutionize modern-day technologies in applications such as sensing, information, and communication.774,775 It is predicted, taking SOC into account, that the kagome lattice can realize a 2D Chern insulating phase with quantized anomalous Hall conductance at 1/3 and 2/3 fillings.776 For real materials with three dimensions, the finite inter layer interaction may drive the mass gap to be closed and reopen along the c-axis, which is the case of 3D Weyl semimetal with broken time-reversal symmetry.777 Furthermore, the flat band also carries a finite Chern number that mimics the phenomenology of LLs, which further enrich the phase diagram that can be achieved in kagome lattices. Recently, ARPES experiments on kagome lattice antiferromagnet FeSn revealed the presence of an extremely flat electronic band about 0.23 eV below the Fermi level.766 Although a flat electronic band is expected in the single-orbital nearest-neighbor kagome model (Figure 66b), the microscopic origin of the observed flat band in FeSn remains a mystery.526 Since the presence of a flat band is extremely important to understanding the transport, electronic, magnetic, and superconducting properties of 2D magnetic vdW materials,84,778 it will be important to sort out structural and magnetic properties of kagome lattice materials.
Figure 65.
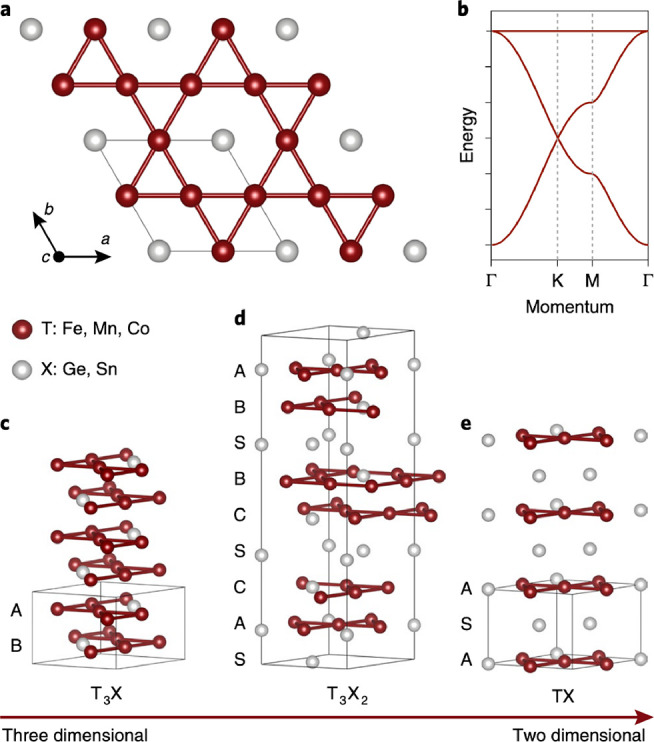
(a) The 2D kagome lattice structure. (b) Calculated electronic dispersion and flat band. (c, d, e) Crystal structures of T3X, T3X2, and TX, respectively, where T = Fe, Mn, Co, and X = Ge, Sn. All panels are adapted with permission from ref (766). Copyright 2019 Springer Nature.
Figure 66.
(a) Red arrows indicate in-plane spin directions at zero field. Black arrows indicate the moment direction in a c-axis aligned field. (b) Spin-wave branches for one acoustic and two optical bands. The middle and top green arrows indicate Dirac points and band top, respectively. (c) Nearest-neighbor DMI direction. (d) DMI induced spin gap at Dirac points. (e) Neutron scattering measured spin waves energy/moment map at (a) 0 T, (b) 2 T, (c) 7 T; (d) Calculated neutron spectra for 7 T. All panels are adapted with permission from ref (767). Copyright 2015 American Physical Society.
In the case of an insulating kagome lattice ferromagnet Cu(1,3-bcd), the FM moment direction is in the kagome lattice plane without external applied magnetic field (Figure 66a).767 Because there are three magnetic atoms per unit cell in a kagome lattice, one expects three spin wave branches including one acoustic and two optical modes with one of the optical band being flat in momentum space due to the geometry of the kagome lattice (Figure 66b). Spin waves from acoustic and first optical branches meet at the Dirac points as shown by the green arrows of Figure 66b. At zero field, there is no nearest-neighbor DMI since the ordered moment is in the plane. When a 7 T c-axis aligned magnetic field is applied, the moment is tuned along the c-axis, giving rise to finite nearest neighbor DMI that opens a gap at the Dirac points and induces topological spin excitations (Figure 66e(a–d)].767,768 It will certainly be interesting to carry out neutron scattering experiments on 2D kagome lattice magnetic materials such as T3X, T3X2, and TX where T= Fe, Mn, Co, and X = Ge, Sn. For example, FeSn is a metallic A-type antiferromagnet with interesting properties (Figure 67a).779 On the other hand, Mn3Ge are semimetallic antiferromagnets where Mn atoms form antichiral noncollinear spin structure [Figure 67(b)].745 For distorted kagome lattice magnets such as crystalline barlowite (Cu4(OH)6FBr), magnetic structures of the systems can be rather complicated as shown in Figure 67c, depending on the details of the lattice distortion.780 Another interesting kagome lattice magnet is YMn6Sn6, which exhibits helical spin structure at zero external magnetic field.781,782 Recently, it was found that application of an in-plane magnetic field can induce a topological Hall effect (THE) near room temperature,783 which is typically associated with a magnetic field-induced skyrmion lattice or noncollinear spin texture with nonzero scalar spin chirality that can induce nonzero Berry curvature acting as fictitious magnetic field for the conduction electrons to give rise to the THE.475,784−789 Neutron diffraction experiments reveal that an in-plane magnetic field can actually change the helical spin structure into a double fan spin structure with c-axis components,527 different from the skyrmion lattice786 and inhomogeneous magnetic domain formation.790
Figure 67.
(a) A-type AF structure of FeSn in 2D kagome lattice structure, adapted with permission from ref (779). Copyright 2019 American Physical Society. (b) The antichiral noncollinear structure of Mn3Ge, adapted with permission from ref (673). Copyright 2020 American Physical Society. (c, d) Complicated noncollinear magnetic structures of barlowite with proximate 2D kagome lattice structure, adapted with permission under a Creative Commons CC BY 4.0 license from ref (780). Copyright 2020 Springer Nature.
As we can see from these examples, magnetic structures of kagome lattice magnets can be quite different depending on details of the magnetic exchange interactions and subtle lattice distortions. Clearly, future inelastic neutron scattering experiments to sort out spin excitations in these materials are critical to understand their exotic magnetic interactions and resulting anomalous topological and transport properties.
Tunneling and Raman Spectroscopy of 2D Magnetic Layers and Surfaces
While neutron scattering can determine the full magnon dispersion relation in magnetic materials across the Brillouin zone, the technique is limited to bulk crystals. Below, we shall describe how IETS and Raman spectroscopy can be used to observe magnon behavior in layered magnets down to the 2D limit, as well as on the surfaces of bulk crystals. We shall focus on recent progress in the chromium trihalide family (CrX3, X = I, Cl, Br), although both techniques can be in principle generalized to other 2D magnets. By comparing with spin wave calculations for the honeycomb lattice, a simple spin Hamiltonian can be extracted for all three 2D systems, yielding information on the nearest neighbor exchange energy and anisotropy. In particular, strong easy-axis anisotropy in the direction perpendicular to the layers assists in stabilizing 2D ferromagnetism in monolayers. The surface layers of bulk CrI3 are further shown to host different magnetic order than those in the interior.
Electron tunneling is an old and established spectroscopic technique. The voltage V applied between two metal electrodes separated by a thin insulating barrier directly relates to the maximum energy of the tunneling electrons. While the overall current I is largely dominated by electrons that tunnel across the barrier elastically, when eV reaches the energy of an excitation within the barrier or at the interface, such as a phonon or magnon for magnetic insulators, electrons can lose energy to this excitation and tunnel inelastically. These two tunneling processes are shown schematically in the upper panel of Figure 68a. In particular, inelastic tunneling events open a secondary conduction channel and can be seen as either abrupt jumps in the differential conductance dI/dV at various V, or peaks in (d2I)/(dV2).791 Magnon excitations can often be distinguished from phonons by examining the evolution of the jumps or peaks with applied magnetic field.792
Figure 68.
(a) Top: Schematic illustrating IETS mechanism. Bottom: Color plot of IETS spectra (|(d2I)/(dV2)| versus V) taken on bilayer CrI3 as a function of out-of-plane magnetic field (easy axis) shows two dispersing magnon modes. Bottom panel adapted with permission from ref (120). Copyright 2019 National Academy of Sciences of the United States of America. (b) Top: Spin-wave calculations of magnon dispersion in 2D CrI3 from anisotropic Heisenberg model with nearest-neighbor interactions. Adapted with permission from 217. Copyright 2018 Springer Nature. Magnon energies are shown at high-symmetry Γ and M points as a function of nearest-neighbor exchange energy J and anisotropy α. Zoom-in of the acoustic branch at the Γ point shows an energy gap for α > 1. (c) Extracted J and α values for all three 2D chromium trihalides from IETS measurements.
One key advantage of the IETS technique is that the lateral size of the tunnel junction can be reduced to submicron dimensions using nanofabrication or, more recently, mechanical transfer techniques, making it a more localized probe of magnon behavior. Mechanical transfer is particularly suitable for exploring 2D magnets that are sensitive to air as vdW heterostructures can be fully assembled in inert gloveboxes.580 One drawback of IETS is that the tunneling process, unlike optical spectroscopy, does not obey rigorous selection rules. It therefore is not immediately apparent which momentum values correspond to the observed magnon energies, although positions with higher density of states are likely to contribute more strongly.126 As such, close comparison with spin wave theory is needed to obtain quantitative exchange parameters.
Recently, several groups have performed IETS on graphene tunnel junctions incorporating ultrathin layers of magnetic insulators CrX3.14,120,131 A schematic of the common device geometry is shown in Figure 71F. The lower panel of Figure 68a shows |(d2I)/(dV2)| versus V taken for bilayer CrI3 as a function of magnetic field applied along the easy axis (normal to the layers). The spectra are shown as a 2D color plot for clarity. As features at positive V are reproduced at negative V, only two modes are visible. The peaks shift toward higher energy with increasing magnetic field by the Zeeman energy with g-factor ∼2, indicating that they arise from magnons. Qualitatively similar features have also been observed for bilayer CrBr3 and CrCl3, although the peak positions are different due to different magnetic exchange parameters between the three materials.120
Figure 71.
Contact methods for exfoliated vdW magnets. (A) Schematic of a Cr2Ge2Te6 flake top contacted with metal electrodes under an ion-liquid gate.86 Adapted with permission from ref (86). Copyright 2020 Springer Nature. (B, C) Optical image of a 5.8 nm-thick Fe3GeTe2 (B)123 and a 28 nm-thick Fe5GeTe2 (C)87 flake contacted from the bottom with prepatterned metal electrodes. In (B) the red dashed line is the Fe3GeTe2 and the yellow dashed line is the hBN. The red scale bar is 10 μm.123 In (C) the scale bar is 20 μm.87 Panel (B) was adapted with permission from ref (123). Copyright 2018 Springer Nature. Panel (C) was adapted with permission from ref (87). Copyright 2019 American Chemical Society. (D–G) Schematics (D, F) and corresponding false-colored optical images (E, G) of CrI3 flakes contacted by graphene electrodes for lateral (D, E) and tunneling (F, G) transport measurements.15 In (E) and (G), the scale bars are both 5 μm.15 Panels (D–G) are reproduced with permission from ref (15). Copyright 2018 Springer Nature.
The magnon energies can be compared with linear spin wave
theory
for the 2D anisotropic Heisenberg model, whose Hamiltonian at zero
magnetic field can be written as  , where J > 0 is the FM
exchange coupling between spin components
, where J > 0 is the FM
exchange coupling between spin components 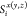 and
and 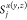 on nearest-neighboring
sites, and α
is the exchange anisotropy along the out-of-plane z direction. The calculated magnon dispersion is plotted in the upper
panel of Figure 68b for α = 1, which shows an acoustic (optical) branch at lower
(higher) energy, crossing at the K point due to inversion symmetry
of the underlying honeycomb lattice. The M point corresponds to a
van Hove singularity with high density of states, and so are most
likely to be seen in IETS, while photons can couple to Γ point
excitations with zero momentum. For an out-of-plane easy axis, as
in the case for CrI3, the energies at these specific momenta
are
on nearest-neighboring
sites, and α
is the exchange anisotropy along the out-of-plane z direction. The calculated magnon dispersion is plotted in the upper
panel of Figure 68b for α = 1, which shows an acoustic (optical) branch at lower
(higher) energy, crossing at the K point due to inversion symmetry
of the underlying honeycomb lattice. The M point corresponds to a
van Hove singularity with high density of states, and so are most
likely to be seen in IETS, while photons can couple to Γ point
excitations with zero momentum. For an out-of-plane easy axis, as
in the case for CrI3, the energies at these specific momenta
are 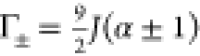 and
and 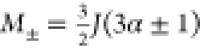 .120 In particular,
for α > 1, there is a gap for magnon excitations, as shown
in
the lower panel of Figure 68b. Identifying the momentum positions for the IETS peaks and
matching with the magnon dispersion thus allows for the exchange energy J and anisotropy α to be determined for 2D CrX3.
.120 In particular,
for α > 1, there is a gap for magnon excitations, as shown
in
the lower panel of Figure 68b. Identifying the momentum positions for the IETS peaks and
matching with the magnon dispersion thus allows for the exchange energy J and anisotropy α to be determined for 2D CrX3.
Based on full spin wave calculations with changing magnetic field, the strongest |(d2I)/(dV2)| peaks were assigned to be near the M point for CrI3. The extracted J and α values for all three 2D CrX3 are shown in the table in Figure 68c. Both quantities increase from CrCl3 to CrBr3 to CrI3. The evolution of J is consistent with that of the critical temperatures (Tc values) in the three bulk compounds.735 Upon reducing sample thickness from few layers to monolayer, Tc in CrBr3 is seen to decrease by 10 K,120 while Tc in CrI3 decreases only by 1 K.5,16 This can be attributed to the larger α in CrI3, which increases the magnon excitation gap and helps to stabilize ferromagnetism in the 2D limit.
While IETS is able to detect magnon modes at momenta with high density of states in CrX3, Raman spectroscopy specifically selects for zero-momentum excitations at the Γ point. The technique is most commonly used to probe for higher-energy phonon excitations; however, recent state-of-the-art methods have allowed modes to be resolved within a few wavenumber (or sub-meV) from the laser line.218 The upper left panel of Figure 69a shows ultralow energy Raman spectra taken on bulk CrI3 as a function of magnetic field. Negative wavenumbers correspond to anti-Stokes scattering.
Figure 69.
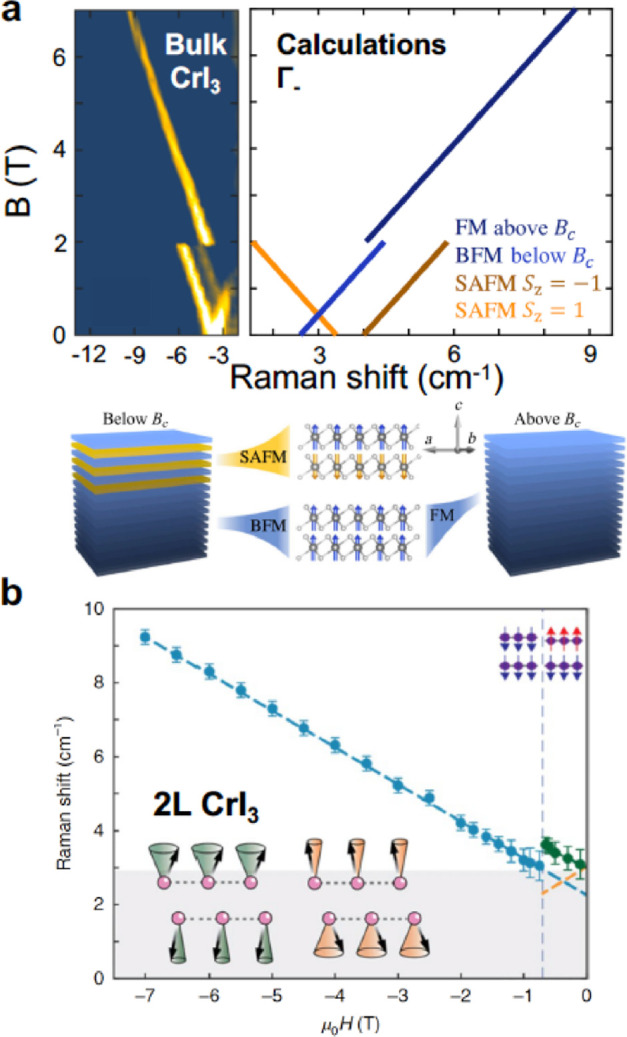
(a) Top: Experimental Raman spectra (left) and theoretical calculations (right) of magnon modes in bulk CrI3 as a function of out-of-plane magnetic field (easy axis). Above Bc ∼ 2 T, a single mode is observed as expected for a fully spin-polarized state for all layers. Below Bc, two additional modes are seen that disperse oppositely with field, corresponding to the layer-AF order on surface layers. Bottom: Schematic of spins in bulk CrI3 above and below Bc. Adapted with permission under a Creative Commons CC BY 4.0 license from ref (218). Copyright 2020 American Physical Society. (b) Field-dependent Raman spectra of bilayer CrI3. Only layer-AF magnons modes are obtained. Adapted with permission from ref (794). Copyright 2020 Springer Nature.
Above a critical out-of-plane magnetic field of Bc ∼ 2 T, a single peak is observed which blueshifts with increasing magnetic field by the Zeeman energy. This mode corresponds to the Γ point acoustic magnon in spin-polarized layers (layer-FM state), and extrapolation to zero field yields an energy of ∼2.5 cm–1 = 0.3 meV, close to that expected from the exchange parameters extracted from IETS. Below the critical field, this mode can still be seen, although there is a small discontinuity at the transition field. Interestingly, two additional modes appear in this region, which disperse in opposite directions with increasing field. These modes correspond to Γ point acoustic magnons in the layer-AF state—layers with spin direction aligned (antialigned) with the magnetic field yield increasing (decreasing) magnon energy with increasing magnetic field. Overall, these features compare well with the theoretical calculations shown in the upper right panel of Figure 69a.
Previously, bulk CrI3 was understood to be a ferromagnet,227,735 while ultrathin layers host a layered-AF ground state.5,16 These results show that even bulk CrI3 exhibits a mixed-phase structure with AF layers likely residing on the surface and FM layers in the interior (see the schematic shown in the lower panel of Figure 69a). Applying a field above Bc polarizes all of the spins, rendering a layered-FM state for both surface and bulk layers. In accordance with this picture, Raman spectra taken on ultrathin CrI3 (down to bilayer) only show Raman modes corresponding to the layered-AF state, as surface layers constitute the entire sample (see Figure 69b).218,794
These results highlight the importance of using microscopic probes to investigate magnetic excitations and interactions in 2D samples, as atomically thin samples or surfaces may exhibit different phenomena than their bulk counterparts. While we have focused on IETS and Raman measurements in this section of the review, we note that other techniques such as microwave absorption spectroscopy and pump–probe Kerr rotation have also been used to resolve Γ point magnons in CrX3.28,795 The latter study on bilayer CrI3 has further shown that the magnon frequency can be substantially tuned using an external gate, an opportunity unavailable for bulk crystals.
Future Challenges
While the field of vdW magnetism has seen immense progress in the past few years, there are still many hurdles to be overcome. A comprehensive investigation of magnetic excitations in atomically thin samples is especially challenging from a technical perspective. Currently, neutron scattering is one of the few techniques capable of determining the energy of magnons as a function of momentum. However, it is inherently a bulk probe and requires large crystals. On the other hand, while IETS, Raman, and other optical techniques can be applied to monolayers, they can only resolve magnons at select momenta, making it difficult to extract higher-order exchange terms in the spin Hamiltonian, such as the biquadratic exchange predicted for CrX3.796 This is particularly a concern if magnetic properties of thin samples or surfaces deviate from their bulk counterparts, in which case neutron scattering may no longer serve as an accurate reference.
In order to resolve the full magnon dispersion in magnetic insulator monolayers, it may be possible to use graphene with a well-defined relative twist angle as tunneling contacts. By systematically varying the twist angle, one may potentially be able to select for the momentum of the magnons that couple to electrons tunneling between the K points of the two graphene layers. In prior works that observe magnons in CrX3 using IETS,14,120,131 the relative twist angle of the graphene/graphite contacts have not been carefully controlled, which may partially explain the slightly different IETS peak positions observed across different devices incorporating the same magnetic insulator.
Finally, both IETS and Raman scattering have limitations in the energy range that can be accessed. Tunneling devices break down under large electric fields, and while arbitrarily small voltages can be applied to the junction, the lower energy limit is effectively set by the width of the IETS peak (∼meV).797 For Raman scattering, spectral leakage from the laser line prevents measurements down to arbitrarily low wavenumber. While recent work has demonstrated the ability to resolve Γ point magnons in CrI3 down to ∼3 cm–1 (∼0.4 meV), other systems such as CrCl3 possess a smaller anisotropy with low-energy magnons in the GHz range (μeV).795 Other techniques such as Brillouin scattering may be needed to access this energy window.
Another way to potentially resolve these difficulties in studying magnetism of thin films is to develop resonant inelastic/elastic X-ray scattering (RIXS/REXS).798 RIXS-based techniques may combine the advantages of a few existing methods to characterize 2D magnetism. On the high throughput end, optical imaging can detect strain-induced band gap changes or polarized refraction at video speed, but the spatial resolution is diffraction-limited to about 0.5 μm.246 Scanning-probe-based NV-center magnetometry recently demonstrated atomic resolution in 2D FM materials, but the speed is as low as a few seconds per pixel.21 Lorentz electron microscopy provides high speed and high resolution only for ferromagnetism and is not sensitive to spin orders without net magnetization.799 In addition, RIXS-based techniques can probe the spin dynamics of both ferromagnets as well as antiferromagnets, as long as kinematic scattering conditions are satisfied. Furthermore, RIXS/REXS can be element-selective, thus allowing experiments to be carried out if there is more than one magnetic ion in a 2D magnetic material. However, current RIXS also has drawbacks due to the trade-off among energy resolution, flux, and spatial resolution in synchrotron light sources, which are fundamentally limited by brilliance. RIXS has limited energy resolution of ∼10 meV (L-edge resonance) that only applies to materials with large magnetic exchange couplings.800,801 These wavelengths are too long to cover the entire Brillouin zone in the reciprocal space, for example, of iron based and cuprate superconductors.802 K-edge RIXS uses shorter wavelength, but the energy resolution is much worse.803 Even with these constraints, one can utilize RIXS/REXS to study magnetism of thin films of selected materials.
Heterostructures, Twisted Layers, and Interfaces
Introduction
A pivotal advancement in the 2D materials community was the development of techniques to fabricate vertical heterostructures—stacks consisting of multiple layers of different 2D materials.408,549,553,804−811 Such techniques are especially versatile since they only rely on vdW interactions to produce heterostructures, allowing for nearly infinite possibilities by combining vdW materials with different electronic, magnetic, or physical properties. With the recent discovery of 2D magnetism within the family of available vdW materials, opportunities have arisen for incorporating 2D magnetic layers within more complex heterostructures.62,213,809 Stacking 2D magnets into vdW heterostructures offers an alternative setup to create spin and pseudospin textures, topological superconductivity, and other exotic quantum phases.84,812 The potential of magnetic vdW devices in spintronics, optoelectronics, and quantum technology applications is invigorating for contemporary research. There are certain advantages arising from the atomic thickness of 2D materials compared to their bulk counterparts. These include the increased strength of exchange interactions, which fundamentally alters the electronic structure of proximitized 2D systems, and the inherent flexibility of 2D materials which enables precise fabrication of vdW heterostructures.
In this section, we will overview three areas of ongoing research in vdW heterostructures fabricated from magnetic materials. We will begin by introducing the techniques used to incorporate magnetic 2D materials into heterostructures followed by a discussion of how heterostructures can be used to investigate the fundamental properties of 2D magnetism under multiple external parameters including carrier doping, electric field, and isotropic pressure. We will then discuss how heterostructures incorporating 2D magnets can be used to engineer phenomena through the control of adjacent layer twist angle and the proximity effect, in which magnetization can be induced in a nonmagnetic layer from an adjacent 2D magnet. In this context, the weak vdW nature of interlayer interactions not only relaxes the need to consider lattice mismatch between contiguous 2D layers, but also makes interlayer twist angle and stacking order design ingredients for the bespoke magnetic systems.812 vdW heterostructures offer tunability of 2D magnetism. Some of the tuning mechanisms include built-in electric fields and charge transfer at interfaces between constituent 2D layers; strain, lattice reconstruction, and orbital hybridization at interfaces with moiré patterns due to lattice mismatch or twisting between layers; and band structure renormalization due to exchange interactions, dielectric screening and spin–orbit proximity coupling, to name a few.213
Heterostructure Fabrication
After 2D vdW crystals are isolated and identified on a suitable substrate (often SiO2/Si), the next step in fabricating a heterostructure is to remove the flakes from the substrate and prepare them for the incorporation of additional layers. Generally, this is accomplished by using an adhesive polymer (such as PMMA/PVA or PDMS/PPC/PC/PCL) that bonds to the flake more strongly than the flake bonds to the substrate.553,577,579,804,805,808,811 The primary method used for manipulating 2D magnets is the dry-polymer-transfer process in which a polymer is prepared on a glass slide which is then deterministically placed onto the desired 2D material.553,577,804 Once the flake is covered by the polymer, it can be slowly and controllably delaminated from the substrate by micromechanical manipulation or modulation of the sample temperature. This transfer process can be repeated with additional flakes to produce a multiple layer stack consisting of any number of desired 2D materials (typically limited to <10 flakes). Once the desired number of layers has been picked up, the entire heterostructure can be deposited onto a substrate by melting the transfer polymer (see Figure 70).
Figure 70.
Process flow for vdW heterostructure fabrication. Schematic of the dry-polymer-transfer process used to fully encapsulate a 2D flake with hBN (here, it is graphene).577 This process relies only on the vdW interactions between hBN and other 2D flakes and can be used to pick up and transfer a number of different 2D materials. Reproduced with permission from ref (577). Copyright 2013 AAAS.
Due to the extreme sensitivity of most known 2D magnets to air, water, and solvents,247,813,814 heterostructures and devices using magnetic flakes must be prepared under inert conditions.580 Therefore, heterostructures are assembled using the dry-polymer-transfer process inside a glovebox environment. To protect flakes during the nanofabrication steps needed to create devices and subsequent transfer into measurement systems, encapsulated heterostructures are fabricated which sandwich the 2D magnet between two layers of hBN.578,580,815 The hBN serves both as an effective protective coating578,580 as well as a high quality dielectric material579 for gated measurements.
Contact Methods
The variety of electronic properties observed in 2D magnetic compounds coupled with the differing sensitivities to air, water, and solvents has required the development of various contact methods for fabricating electronic transport devices. Certain less sensitive 2D magnets (such as multilayer Cr2Ge2Te6,10,86 Fe3GeTe2,12,77,109,123,500 Fe5GeTe2,816 Fe0.25TaS2,497 or MnBi2Te4111) can be directly contacted using lithography and metal deposition without an encapsulating layer (Figure 71A). However, in the few-layer limit, most 2D magnets require indirect contact techniques combined with protection by an hBN layer. This ranges from direct etching and deposition after encapsulation in an inert environment (such as metallic Fe4GeTe2)88 or prepatterned metal electrodes for metallic Fe3GeTe2,123 (Figure 71B), CrTe2,278 and Fe5GeTe2,87 (Figure 71C) to intermediate graphene contacts for the semiconductor Cr2Ge2Te6.10 For the most sensitive magnetic materials (CrX3 family), they cannot be exposed to ambient conditions at any stage of fabrication, necessitating full encapsulation with hBN and graphene intermediate contacts (Figure 71D–G for two different contact schemes).8,9,11,13−16,22,23,112,117−120,131,492,504 To date, most available 2D magnetic semiconductors have poor charge transport properties. As additional 2D magnets with functional semiconducting properties are identified, an upcoming challenge will be fabricating devices with low-resistance contacts. Many of the contact techniques used for nonmagnetic 2D semiconductors817−819 (such as lateral junctions or phase contact engineering) are currently not feasible. Significant progress can be made if contact geometries are developed (such as metal electrodes embedded in hBN for simultaneous contact and protection),820 more metallic 2D materials can be identified (for work function engineering), or if more stable 2D magnets can be discovered. A promising candidate for the latter is the CrEX family from which CrSBr (a layered AF semiconductor)110 has shown superior air-stability down to the monolayer limit.122
Overview of Heterostructures Based on Magnetic Materials
Utilizing the versatility of the vdW stacking process, a variety of heterostructures have been fabricated from 2D magnets to understand the nature of magnetism in the 2D limit and fabricate functional spintronics. One example is full hBN encapsulation with the incorporation of electrodes such as prepatterned metal electrodes (Fe5GeTe2,87 see Figure 71B) or graphene electrodes (Cr2Ge2Te6,10 or CrI315) (Figure 72A), which allows for the fabrication and measurement of lateral transport devices from conducting air-sensitive 2D magnets. The hBN has the additional advantage of being optically transparent, which allows for simultaneous characterization of the sample magnetization using optical probes.10,15
Figure 72.
Heterostructures fabricated from 2D vdW magnets. (A) Schematic of a Cr2Ge2Te6 flake fully encapsulated with hBN and contacted by graphene electrodes.10 Reproduced with permission from ref (10). Copyright 2018 Springer Nature. (B) Schematic (left) and corresponding optical image (right) of a MTJ fabricated from Fe3GeTe2 electrodes separated by an hBN barrier.109 In the right panel, the dotted lines outline the edges of the two Fe3GeTe2 flakes. The scale bar is 5 μm. Reproduced with permission from ref (109). Copyright 2018 American Chemical Society. (C) Optical image (left) and corresponding cartoon (right) of a spin-filter MTJ utilizing CrI3 as the tunnel barrier between graphene electrodes.14 Reproduced with permission from ref (14). Copyright 2018 AAAS. (D) Schematic (top) and a false-colored optical image (bottom) of a spin-field-effect transistor fabricated from 4-layer CrI3.504 Graphene acts as both transistor electrodes and local electrostatic gates. The scale bar is 5 μm. Reproduced with permission from ref (504). Copyright 2019 American Chemical Society. (E, F) Schematic (E) and false-colored optical image (F) of a heterostructure proximitizing CrI3 with WSe2.206 The scale bar in (F) is 5 μm. Panels (E, F) are reproduced with permission under Creative Commons CC BY-NC 4.0 license from ref (206). Copyright 2017 AAAS.
The second class of heterostructures are tunnel junctions fabricated from vdW magnets. Using layered FM 2D crystals, a heterostructure resembling a canonical MTJ can be fabricated from all vdW materials using either hBN, MoS2, or graphite (with Fe3GeTe2)109,115,500 or a naturally formed Ta2O5 surface (that forms upon the exposure of Fe0.25TaS2497 to ambient conditions) as the tunnel barrier (Figure 72B). The atomically sharp and clean interfaces naturally formed during stacking give rise to high quality tunneling interfaces. Due to the abundance of naturally layered AF vdW crystals, spin-filter MTJs can be easily created utilizing an AF 2D flake as the tunnel barrier between nonmagnetic metal electrodes (an alternative to the classical FM/I/FM MTJ structure). This concept has been demonstrated many times using the CrX3 compounds (CrI3,11,13−16,22,23,112,120,492,504 CrBr3,112,120,131 and CrCl3112,117−120), which boast exceptionally large on/off switching ratios upon a transition from an AF to a FM configuration, making them enticing for spintronic applications (Figure 72C).
Due to the aforementioned optical transparency of the constituent layers within the spin-filter-MTJ heterostructures, optical probes (such as Raman spectroscopy,23,118 MCD,8,13,22,504 and Kerr rotation9,15) are used to correlate tunneling measurements with direct measurements of the sample magnetization and structure, making these heterostructures a model system for investigating the nature of magnetism in the 2D limit. Toward this end, more complex heterostructures have been fabricated to include dual graphite gates (Figure 72D), which allows for the measurement of the magnetic properties (through either optics or tunneling transport) as a function of carrier doping or local electric field8,9,11,492,504 and hydrostatic pressure.22,23
Beyond studying the intrinsic properties of 2D magnets, heterostructures can be fabricated for the purpose of inducing magnetization in a nonmagnetic 2D layer through the proximity effect. For example, it was shown in a heterostructure consisting of CrI3 and WSe2 that the valley polarization in WSe2 was directly linked to the magnetization of the CrI3 and was tunable with an external magnetic field (Figure 72E,F).206
Band structure engineering can be used to induce magnetic response in nonmagnetic 2D materials. For instance, magnetism from itinerant electrons can be tuned by twistronics, where properties of vdW materials are controlled by changing twist angle between constituent 2D layers. With recent advances twistronics provides a strategy to reliably fabricate devices with arbitrary rotational order and in situ, thus significantly facilitating research in vdW heterostructures.821−823
In rotated graphene bilayers, a moiré superlattice results in the formation of moiré minibands which become particularly flat at specific magic angles.824 These flat minibands have vanishing Fermi velocity resulting in a large density of states which gives rise to electron–electron interactions. Recent experiments on magic-angle twisted bilayer graphene (MAG)710,824,825 triggered the use of twistronics for tuning interaction strength in 2D materials, where research on moiré superlattices in MAG revealed a score of correlated phases including ferromagnetism and quantum anomalous Hall state.700 For instance, at a fractional filling (3/4) of a moiré miniband, electronic interactions make MAG magnetic, as signified by a strong FM hysteresis and a strong anomalous Hall effect.826 Aligning MAG to a hBN substrate increases the strength of interactions and stabilizes magnetism, leading to a stronger orbital magnetization and a clear quantum anomalous Hall effect.255,827 This incipient magnetism could arise from strong interactions leading to spin-valley polarization of moiré minibands, characteristic for an orbital Chern insulator state. Notably, magnetic order of these MAG devices can be controlled by a nanoampere electrical current, showing potential for electrically controllable magnetic memory applications. Using twisted monolayer–bilayer graphene allows for the control of orbital Chern insulator magnetic states directly with electric fields (Figure 73A,D), which is crucial in designing reconfigurable circuits and ultralow-power magnetic memory828 for spintronics and multiferroics applications. Recently, spatially resolved measurements of the local electronic compressibility in MAG revealed a peculiar high-temperature state with a large spontaneous magnetization. From this broken spin-valley symmetry state, more fragile low-temperature correlated ground states stem.829 At quantizing magnetic fields, MAG devices demonstrate field-stabilized orbital magnetic states, demarcated by first-order phase transitions, and driven by the interplay of moiré periodicity and magnetic length scale.830,831
Figure 73.
2D magnetism controlled by twistronics and stacking order. (A) Variation of stacking order in small twist angle θ monolayer–bilayer graphene (tMBG).828 (B) Transverse resistance Ryx map measured versus total carrier density n and the magnetic field B at T = 6.4 K in a tMBG device with θ = 1.25° near ν = 3 orbital magnetic state presents a magnetization reversal driven by the change in n or B due to the non-negligible contribution from the topological edge states in large moiré unit cell area. ν = nA is the number of carriers n per moiré unit cell A.828 (C) In B-field, ν = 3 state switches between K and K′ valley polarization as doping level changes across the gap.828 (D) Nonvolatile switching between K and K′ valley-polarized magnetic states independently controlled by either n or B.828 Panels (A–D) reproduced with permission from ref (828). Copyright 2020 Springer Nature. (E) Temperature-dependent hysteresis (highlighted by colored areas) observed in magnetic field in rhombohedral graphite.832 (F) Phase diagram of the critical behavior in (E) characteristic to strongly correlated electronic systems.832 Panels (E, F) are reproduced with permission from ref (832). Copyright 2020 Springer Nature. (G) Scanning tunneling spectroscopy map of a small θ double bilayer graphene showing Bernal (black) and rhombohedral (white) stacking domains.833 Reproduced with permission under a Creatice Commons CC BY-NC 4.0 license from ref (833). Copyright 2021 National Academy of Sciences. (H–J) Rhombohedral (R) and monoclinic (M) stacking configuration and magnetic domains in a small θ twisted bilayer CrI3. (H) Three types of stacking domain walls in this system. Arrows represent the stacking vectors.834 (I) Sketch of the magnon network at θ = 0.1°.834 (J) Stacking and magnetic domain patterns of the gray rectangle area in (I). Red (blue) arrows represent stacking vectors for R (M) stacking. Red (cyan) lines represent the RR (MM) stacking domain walls.834 Panels (H–J) are reproduced with permission from ref (834). Copyright 2020 American Physical Society.
Another pure carbon material which exhibits emergent correlated phases is a multilayer rhombohedral graphene (RG), a simple material with flat electronic bands but without a moiré superlattice.832,833 VdW technology enabled the study of electronic transport in high-quality multilayer RG,835 which revealed strong correlations and behavior characteristic of multiferroic materials832 (shown in Figure 73E,F), while scanning tunneling spectroscopy revealed that tetralayer RG has a correlated many body broken symmetry state probably of an excitonic insulator or a ferrimagnet nature (Figure 73G).833
Twistronics in Ferromagnetic Materials
Twisting magnetic 2D materials could lead to an interesting interplay between magnetism and topology.700 For instance, tunable magnetic moiré skyrmions (topologically protected vortex-like magnetization textures) are predicted to form when a 2D ferromagnet is twisted on an AF substrate.490,836 A magnonic (spin wave) analogue of MAG is theorized in a simple twisted FM bilayer model without lattice relaxation; DMIs are predicted to result in a rich topological magnon band structure.837 By fully accounting for lattice relaxation, theoretical calculations of a twisted bilayer CrI3 predict stacking domain walls which would host stable 1D magnon channels (originating from Goldstone modes of the spin Hamiltonian) arranged into an interconnected moiré magnon network834 (Figure 73H–J). Recently developed general formalism of twisted (anti)ferromagnetic bilayers should stimulate further theoretical and experimental research in magnetic moiré heterostructures.778
Effects of Strain and Hydrostatic Pressure
Tuning material parameters such as interlayer separation or stacking order via the application of pressure or strain is an effective method for controlling magnetism in vdW materials.700 For instance, a hydrostatic pressure of 1 GPa significantly affects the Curie temperature of Cr2Ge2Te6,838 while higher pressures reorient its spins from out-of-plane to in-plane.283 Furthermore, interlayer exchange coupling depends on layer separation and stacking order which can both be tuned by hydrostatic pressure, as seen in hBN/graphene/CrI3/graphene/hBN heterostructures, pressure induces an AF-to-FM transition in bilayer CrI322,23 (Figure 74A,B). Nanoscale structural modifications also induce switching between FM and AF ordering, as was in the case of magnetic transition and enhanced magnetization observed in hBN- or graphene-encapsulated CrI3 flakes indented with a diamond scanning probe.21 Another possibility in controlling magnetism in vdW materials is through strain.700 A FM phase transition at room temperature is predicted in CrWI6 and CrWGe2Te6 monolayers subjected to an in-plane tensile strain,19 while monolayer chromium trihalides show AF phase transition upon a compressive strain.839
Figure 74.
Tuning magnetic vdW heterostructures. (A) Schematic of a high-pressure setup for a MTJ. Yellow line represents electrical leads.22 (B) Tunnel current It versus magnetic field H at pressures from 0 to 2.7 GPa in a bilayer CrI3 MTJ. Insets show spin alignments and optical image of the MTJ.22 Panels (A, (B) are reproduced with permission from ref (22). Copyright 2019 Springer Nature. (C) Proposed vdW heterostructure where exchange (EX) and spin–orbit (SO) coupling can be swapped by an electric field. Cr2Ge2Te6 magnetization is denoted by red arrows.840 Adapted with permission from ref (840). Copyright 2020 American Physical Society. (D, E) Dependence of RMCD on magnetic field in heterostructures of WSe2 and trilayer (D)/bilayer (E) CrI3 (shown in the insets).203 Panels (D, E) are reproduced with permission from ref (203). Copyright 2020 Springer Nature. (F–H) Photoemission and spin-dependent charge transfer in hBN encapsulated CrI3/WSe2 heterostructure. (F) A schematic of the heterostructure deposited on nanopillar array.841 (G) Spin-dependent charge transfer from spin-polarized states in WSe2 to CrI3 results in the highly p-doped WSe2, where an exciton can be turned into a localized charged trion (0D X+) via a hole capture process (H). Arrows in red and green (blue) denote the spin direction in WSe2 (CrI3).841 Panels (F–H) are reproduced with permission under a Creative Commons CC BY license from ref (841). Copyright 2020 Springer Nature.
Proximity Effects at vdW Interfaces
In atomically thin vdW materials, magnetic proximity effects become dominant, as even short-range effects exceed the thickness of contiguous 2D crystals.812 The proximity of 2D magnets can break time reversal symmetry in nonmagnetic 2D materials, leading to valley polarization in TMDs, quantum anomalous Hall effect in topological insulators, and other emerging phenomena including multiferroicity and topological superconductivity.213 For instance, FM exchange interactions from the 2D magnet Cr2Ge2Te6 induce an anisotropic spin texture in proximitized graphene.450 Similarly, the proximity of magnetic CrSBr to a bilayer graphene results in a large spin polarization of the graphene conductivity, making CrSBr/graphene heterostructure a promising system for spintronics applications.452Ab initio calculations for a Cr2Ge2Te6/PtSe2 heterobilayer suggest that 2D magnetism can be significantly enhanced by proximity of a 2D material with strong SOC.842 Another theoretical work predicts that the proximity of a bulk semiconductor substrate to a 2D CrI3 significantly increases its FM exchange interactions.843 Furthermore, in vdW moiré superlattices magnetic proximity effects can be tuned by twisting and/or strain between the vdW layers (Figure 74D,E).844 vdW engineering in combination with circular dichroism measurements demonstrate an interesting approach to control and probe a layer-dependent magnetic proximity effect between monolayer WSe2 and bi/trilayer CrI3, promising for spin- and valleytronics applications.203 The proximity of hBN encapsulated graphene to a 2D magnet allows for the detection of proximitized magnetic order via graphene-based ballistic Hall micromagnetometry.82
Combining a 2D ferromagnet and a superconductor into a vdW heterostructure provides a tunable route to the exotic state of a topological superconductor–a key element for topological quantum computing, due to the emergence of one-dimensional Majorana edge modes which are robust against disorder. MBE is a scalable approach to creating such designer topological heterostructures. For example, MBE was used to grow a 2D ferromagnet CrBr3 on the superconductor NbSe2, resulting in a high-quality interface in which signatures of Majorana modes were detected.83,845 This approach can be extended to other hybrid superconductor-magnet heterostructures, for example, NbSe2 and VSe2 give clean and atomically sharp interfaces, where a decrease in the superconducting gap of NbSe2 due to a magnetization of the VSe2 sheet was observed.846 Even more opportunities to study exotic strongly correlated behavior can be found in organic–inorganic heterostructures via molecular intercalation.847
Spin–Orbit Coupling and Optical Control of Magnetic Properties
Light–matter interactions provide an excellent opportunity to both probe and control magnetically ordered phases in vdW materials with considerable SOC.84 For instance, ferromagnetism in 2D materials can be directly probed using helicity-resolved Raman spectroscopy due to the spin angular momentum carried by circularly polarized light.225 Spin-dependent charge transfer between spin-split bands of WSe2 and CrI3 can be used to generate charged excitons, which can be arranged into large-scale deterministic arrays of quantum emitters via strain-inducing nanopillars841 (Figure 74F–H). Contributing to spin-photonics applications, room-temperature spin polarization can be achieved in heterostructures of monolayers of WS2 or WSe2 with PbI2, in which the spin polarization can be tuned by PbI2 layer thickness, temperature, or excitation energy.848 A theoretical proposal unites the fields of twistronics, spintronics, and many-body physics by engineering a heterostructure of a twisted WSe2 bilayer sandwiched between magnetic CrBr3.849 This moiré system features flat bands with tunable valley and spin ferromagnetism emerging from the interplay between twist engineering, SOC, and exchange proximity and provides a starting point to study strongly correlated systems tunable via exchange bias. Another theoretical work suggests that exchange and SOCs can be swapped by an applied electric field in a bilayer graphene (BLG) sandwiched between a 2D ferromagnet Cr2Ge2Te6 (CGT) and a monolayer WS2, where CGT provides proximity exchange coupling to the bottom layer of BLG, while WS2 induces a SOC to the top BLG layer (Figure 74C).840 This doubly proximitized BLG heterostructure can be further extended to systems comprising (anti)ferromagnets, ferroelectrics, topological insulators, and superconductors, and offers a platform to explore emergent spin physics.
Electrical Control of Magnetic Properties
Electrical control of 2D magnets offers another convenient tuning knob. In a bilayer CrI3 antiferromagnet, electric fields and electrostatic doping can affect the spin-flipping magnetic field, modulate the Curie temperature, and induce an AF-to-FM transition.8,9,11 The high quality of the interface in the MoSe2/CrBr3 heterostructure leads to a strong splitting of valley excitons in MoSe2 in zero magnetic field, with a distinct electric field dependence indicating a potential for electrical control of magnetization.204 vdW heterostructure multiferroics bring forward low-dimensional magnetoelectric physics and spintronic applications thanks to the increased efficiency of electrical control of magnetism enabled by their inherent coupling between magnetic and electric orders. Although some theoretical works predict single-phase 2D magnetoelectric multiferroics in CuMP2X6 (M = Cr, V; X = S, Se), CrN, and CrB2 systems,850,851 competing requirements of the orbital filling for ferroelectricity (empty d-orbitals) and ferromagnetism (filled d-orbitals) make these systems scarce. Another computational research circumvents this by suggesting multiferroics based on a 2D heterostructure comprised of FM Cr2Ge2Te6 and ferroelectric In2Se3, where the magnetism of Cr2Ge2Te6 switches following the polarization reversal of In2Se3 which in turn becomes a magnetic semiconductor due to the proximity effect.852
Conclusions and Outlook
The advent of techniques to fabricate heterostructures consisting of multiple layers of vertically stacked 2D vdW materials has allowed for the creation of myriad systems by combing materials with different electronic, magnetic, or other physical properties. With the recent surge of 2D magnetic materials, opportunities have emerged for fabricating heterostructures incorporating magnetic vdW materials. These magnetic heterostructures provide unparalleled access to a wide range of condensed matter systems with many exotic properties. Designer magnetic materials offer countless opportunities for engineering desired properties tunable by electrical, optical, mechanical, chemical, and other external stimuli, which could lead to hybrid artificial heterostructures with applications in spintronics, data storage, optical communications, and quantum computing.213 There are many challenges still present including developing more stable materials, tuning magnetic phases that exist at room temperature, optimizing fabrication techniques to more reliably fabricate heterostructures with multiple layers and various configurations, improving contacts to 2D magnets for functional electronics, and creating 2D magnets on a wafer scale for industrial processing.213
Theory and Simulations
Introduction
Experimental measurements present significant technical challenges in the area of 2D magnetic materials due their characteristically low magnetic ordering temperatures and general volatility. In contrast, simulation methods have advanced considerably in the past 20 years in terms of fundamental capabilities, accuracy and speed. Today it is possible to routinely perform magnetic first-principles and atomistic simulations with high accuracy and develop a deep and fundamental understanding of the underlying physical properties of 2D magnets. The broad availability of advanced simulation software and high performance computing facilities has pushed the frontier for 2D materials discovery from the lab to the desktop computer. Such a shift is important in the field of condensed matter and even at the birth of this exciting field it is clear that existing approaches are able to uncover a plethora of exciting magnetic phenomena with untold possible applications. In this section we aim to provide a basic framework in terms of fundamental theory and simulations techniques for exploration of 2D vdW magnetic materials in a feasible manner.
Theory
The general theory of magnetism is very well established and expressed in terms of a generalized spin Hamiltonian describing the magnetic interactions in the system. It is important to note the deliberate absence of nonmagnetic contributions to the Hamiltonian in this formalism. The effective parameters (i.e., exchange, single-ion anisotropy, magnetic moment) in the spin Hamiltonian are always computed ab initio with the full spin Hamiltonian including lattice, kinetic energy and relativistic contributions that are simply mapped to a set of magnetic interactions based on their symmetry and order. The general spin Hamiltonian is given by
| 14 |
where Si,j are unit vectors describing local
spin
directions, 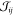 and
and 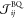 are the bilinear and
biquadratic exchange
tensors respectively, ku is the single-ion
uniaxial anisotropy constant, μs is the local spin
moment, and B = μ0H is
the externally applied magnetic (induction) field in tesla. The standard
bilinear exchange interaction is given by a summation of all pairwise
interactions for the index i < j to avoid double counting with the vector-tensor-vector multiplication:
are the bilinear and
biquadratic exchange
tensors respectively, ku is the single-ion
uniaxial anisotropy constant, μs is the local spin
moment, and B = μ0H is
the externally applied magnetic (induction) field in tesla. The standard
bilinear exchange interaction is given by a summation of all pairwise
interactions for the index i < j to avoid double counting with the vector-tensor-vector multiplication:
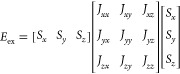 |
15 |
Here the exchange matrix includes three physical interactions in a compressed format for ease of computation and expressiveness. The tensor can be expanded in the following way:
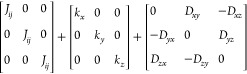 |
16 |
and includes isotropic exchange interactions Jij, 2-ion anisotropy kx, ky, kz, and Dzyaloshinskii–Moriya interactions D.744 In this form, the exchange tensor also encapsulates the Kitaev interaction704 and the XXZ model within a more general framework that extends beyond nearest neighbor interactions.853 The biquadratic exchange is a higher order exchange term that is an important correction for 2D magnets necessary to properly describe temperature dependent properties796 and spin waves.725
The principal assumption of the Heisenberg model is that of fixed length, localized magnetic moments, where the energy of the system is described purely in terms of coherent rotation of moments. This is generally a good approximation for bulk Fe, Co, and Mn, and less so for bulk Ni and Cr which have a more itinerant character. In 2D materials the validity of the local moment approximation is generally better than the bulk case796 due to the semiconducting character of the materials and enhanced electron localization. In the case of more itinerant-like spins longitudinal moment fluctuations can likely be represented by a Landau expansion of the Stoner model.854
The final
energetic contribution of importance is the dipole–dipole
field, or magnetostatics in bulk magnets. The dipole–dipole
interaction is long ranged and critically important for the magnetic
ground state spin orientation and the formation and evolution of magnetic
domain structures. Considering a localized magnetic moment mi = μiSi at position r, the field Bi from all
other dipoles mj = μjSj with position vector 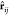 is given by
is given by
| 17 |
where δ(r) is the 3D Dirac δ-function and represents the self-field of the dipole. In conventional micromagnetic simulations, the magnetostatics are accounted for with the continuum approximation, but in 2D materials where the domain walls are exceptionally narrow, it is important to consider the effects of the lattice structure and thermal spin fluctuations on the dipole field.31 Direct calculations of the dipole–dipole field for large systems is computationally expensive but possible on large scale parallel computers. Other faster techniques such as fast Fourier transforms rely on translational invariance of the spins which is problematic for certain structures but in particular honeycomb lattices. Hierarchical approaches are promising in this regard, combining locally exact computations and far-field approximations for the ideal balance of accuracy and computational efficiency.
Monte Carlo Methods
The ab initio parameters
give important insight into the fundamental interactions in 2D materials,
but present only the case of fully ordered moments at zero temperature.
However, experimental measurements are always conducted at finite
temperature and so the temperature dependence of the properties is
an important component of validating simulations against experimental
data. Simple analytical approaches such as mean field and random phase
approximation855 allow the estimation of
Curie temperatures of magnetic materials, but today Monte Carlo Metropolis
methods provide a fast and efficient way of finding equilibrium thermodynamic
properties of a magnetic system.856 The
Metropolis algorithm857 takes a random
spin with direction Si and
changes its spin direction to a trial direction 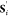 . The next step is to calculate the change
in energy between the initial and final states
. The next step is to calculate the change
in energy between the initial and final states 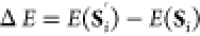 . The trial direction is either accepted
or rejected based on an acceptance probability (P):
. The trial direction is either accepted
or rejected based on an acceptance probability (P):
| 18 |
where kB is the Boltzmann constant and T is the absolute temperature. If the change in energy is less than zero then the probability is greater than one and the spin is automatically accepted. This is repeated N times with N corresponding to the number of atoms in the system, completing one Monte Carlo step.
An
important aspect of Monte Carlo Metropolis simulations is the sampling
method used to select trial spin positions 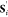 . Early models of 2D magnets assumed an
Ising model, conceived by Ernst Ising in 1925,33 where the spin system is evolved by spin flips
. Early models of 2D magnets assumed an
Ising model, conceived by Ernst Ising in 1925,33 where the spin system is evolved by spin flips 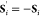 assuming a global quantization
axis, usually
defined by symmetry. As discussed later, this assumption leads to
artifacts and a significant overestimation of the Curie temperature
that are unrealistic. A natural extension of the Ising model is the
classical Heisenberg model in two and three dimensions. Note that
the dimensionality refers to the spatial dimensionality of the lattice
coordinates: The Heisenberg model explicitly describes an atomic spin
with the freedom to orientate anywhere in 3D space. Even though quantum
mechanical effects are neglected, the Heisenberg model is capable
of accurately modeling phase transitions, temperature dependent properties
and surface and finite size effects. In the Heisenberg model the random
spin positions must obey the principle of detailed balance.857 The simplest way of satisfying this is if the
moves are uniformly distributed over the unit sphere.
assuming a global quantization
axis, usually
defined by symmetry. As discussed later, this assumption leads to
artifacts and a significant overestimation of the Curie temperature
that are unrealistic. A natural extension of the Ising model is the
classical Heisenberg model in two and three dimensions. Note that
the dimensionality refers to the spatial dimensionality of the lattice
coordinates: The Heisenberg model explicitly describes an atomic spin
with the freedom to orientate anywhere in 3D space. Even though quantum
mechanical effects are neglected, the Heisenberg model is capable
of accurately modeling phase transitions, temperature dependent properties
and surface and finite size effects. In the Heisenberg model the random
spin positions must obey the principle of detailed balance.857 The simplest way of satisfying this is if the
moves are uniformly distributed over the unit sphere.
An efficient computational method for this was devised by Marsaglia858 and is known as the uniform method.856 This computational method is efficient at high temperatures, however is inefficient at low temperatures, since due to the exchange energy only moves with a small change in spin position will be accepted. Another possibility for sampling the surface is a Gaussian method, sampling a Gaussian distribution around the initial spin position the width of which is dependent on the temperature. This improves the acceptance rate (by sampling small spin moves) to achieve better computational efficiency but also presupposes that small moves are thermodynamically preferred, though in the case of exchange coupling this is a reasonable approximation. To ensure that all spin states are accessible, it is often beneficial to combine these Monte Carlo trial moves (spin-flip, random and Gaussian) into the sampling approach, found by Hinzke and Nowak.859 The three possibilities of trial moves allow the system to equilibrate quickly at any temperature by allowing large changes in the spin position at high temperatures using the uniform and spin flip sampling and smaller changes at low temperature using the Gaussian sampling. More recently an adaptive sampling algorithm for Heisenberg spin models was developed by Alzate-Cardona et al.860 which uses Gaussian sampling with a dynamically tunable width to achieve a constant acceptance rate of 50%, which was found to be more efficient at all temperatures compared to the previous approaches. In addition constrained Monte Carlo methods861 allow the determination of temperature dependent properties such as the effective exchange coupling862,863 and magnetic anisotropy864 though such properties are so far unexplored in 2D VdW materials.
Ising versus Heisenberg Descriptions of 2D Magnets
At this point it is useful to discuss the different Monte Carlo methods that have been used to describe the magnetism of 2D materials. Earlier works described the magnetism of perpendicularly magnetized 2D magnets as Ising-like,5,866 in reference to the simple model solved by Ernst Ising33 and used as a prototypical model for magnetic ordering. However, this classification is unhelpful as the global quantization axis for atomic spins in the Ising model leads to three erroneous physical effects that do not apply to real systems. First, the global quantization axis leads to an infinite magnetic anisotropy, preventing a coherent rotation of the system by an external magnetic field, such as seen for hysteresis measurements. Second, the existence of spin waves is completely forbidden as spins are only permitted to exist along a quantization axis. Third, the removal of infinitesimal spin rotations leads to an artificially flat temperature dependence of the magnetization at low temperatures, and an unrealistically high Curie temperature when considering realistic exchange parameters calculated ab initio using density functional theory. While the Ising model has its place in fundamental statistical physics, it is wholly inappropriate to model the temperature dependent properties of actual 2D magnetic materials. This has unfortunately led to the prediction of excessively large Curie temperatures in a number of studies.32,120,294,867−870
The 2D Heisenberg model, where spins are permitted to orientate anywhere in 3D space but sites are confined to two dimensions, provides a much better prediction of magnetic ordering temperatures that closely match the experimentally measured values31,796,871 of 2D magnets. To explore the qualitative and quantitative differences between the Heisenberg and Ising models, we consider calculations of the temperature dependent magnetization of CrI3 in Figure 75. Based on the ab initio parameters of Wahab et al.,31 the 2D Heisenberg model finds a Curie temperature of 36 K, which is close to the experimental value. The temperature dependence of magnetization m(T) of the 3D Heisenberg model is accurately described in the whole temperature865 by the equation
| 19 |
where T is the temperature, TC is the Curie temperature and β = 0.340 ± 0.001 is the critical exponent. In 2D materials of finite size there is a crossover in the critical exponent between the low temperature behavior and high temperature behavior, where small quantitative differences in the fitting function and the data appear. In our example in Figure 75a, fitting to the low temperature data up to T/TC = 0.9 yields a critical exponent of β = 0.2480 ± 0.0007 and a slight overestimation of the Curie temperature, while fitting to the high temperature regime T/TC > 0.9 yields an exponent of β = 0.212 ± 0.028 and an accurate estimate of the Curie temperature. We note that both of these exponents are substantially lower than the exponent β = 0.34 for the 3D Heisenberg model. Others have stated that critical exponents such as β are universal to particular classes of model279,294 but more recent data presents a more complicated story. First, the critical exponent for the 2D Heisenberg model of CrI3 with ab initio parameters is closer to 2.1 in the vicinity of the Curie temperature and significantly different from the exponent for the 3D case. Second, the exponent in reality depends on the different parameters in the Hamiltonian, particularly the presence of significant magnetic anisotropy and higher order exchange interactions. In particular a nearest neighbor exchange and uniaxial anisotropy for the 2D Heisenberg model yield an exponent of β = 0.34, identical to the case for the 3D Heisenberg model. At the time of writing there is little work on critical exponents in pure 2D Heisenberg systems, but this is likely to be an area of focus in the next few years and critically important for determining where universality does and does not apply in 2D magnetic systems.
Figure 75.
Comparison of different Monte Carlo models calculating the Curie temperature of CrI3. (a) Classical 2D Heisenberg. (b) Classical Ising model. (c) Quantum-like simulation with temperature rescaling. All panels are adapted with permission from ref (865). Copyright 2015 American Physical Society.
In Figure 75b, we show the simulated temperature dependent magnetization using an Ising Monte Carlo model for the same parameters, showing an unrealistically large predicted Curie temperature and essentially flat temperature dependent magnetization at low temperatures. The fit to the 2D Heisenberg model data in Figure 75a is shown for comparison. As previously noted, both of the main features of the Ising model are physically unrealistic and such simulations do not provide helpful comparisons to real 2D magnets, and as such should no longer be used. The final point to discuss is the disparity between experimentally measured temperature dependent magnetization curves and those obtained from a Heisenberg model, both in three865 and two31 dimensions. The main characteristic feature of Heisenberg models is the linear variation of the magnetization with temperature as T → 0. This is a consequence of the classical nature of the Heisenberg model, while the underlying heat bath responsible for spin fluctuations is quantum mechanical in nature.31,865 A relatively simple adaptation of the Heisenberg model is able to reproduce the quantum nature of the heat bath observed experimentally by fitting the temperature dependent magnetization to the Curie–Bloch equation865 which interpolates between the Bloch law behavior as T → 0 and Curie behavior as T → Tc:
| 20 |
where α is the Bloch exponent determining the shape of the magnetization curve as T → 0. The Curie–Bloch equation accurately describes the temperature dependence of the magnetization of 3D865 and 2D31 magnets in the full temperature range, while retaining a natural link to the critical behavior (with the same exponents) near the Curie temperature.865 The classical limit is recovered for α = 1. A convenient phenomenological extension to Heisenberg models is through spin temperature rescaling, which allows the direct mapping of the classical Heisenberg model onto the Curie–Bloch equation,865 as shown in Figure 75c. The rescaling mimics the effects of the quantum heat bath by reducing the strength of thermal fluctuations at low temperatures and allows for quantitatively accurate simulations of temperature dependent properties and dynamics of 2D magnets that are directly comparable to experiment. The full nature of the heat bath is a complex question and other approaches may reveal the microscopic details and interactions that will enable a fully ab initio description of the microscopic spin flip and spin scattering processes.872
Atomistic Spin Dynamics
Atomistic spin dynamics (ASD) is a more recently developed framework for simulating the dynamics of localized magnetic spin moments856,873,874 based on the atomistic Landau–Lifshitz–Gilbert equation (LLG).875 The LLG equation combines the quantum mechanical precession of atomic moments around an externally applied magnetic field with a phenomenological relaxation term that allows fro energy transfer from the spin system to the heat bath. Most studies of 2D magnets have so far focused on equilibrium properties computed using Monte Carlo Metropolis methods, but ASD enable an exciting class of dynamical simulations that have a correspondence to the time-dependent dynamics of materials.876 The time-dependent behavior described by the LLG equation is given by
| 21 |
where Si is a unit vector describing the direction of atomic spin moment i with an effective magnetic field (Beff). The effective field causes the atomic moments to precess around the field, where the frequency of precession is determined by the gyromagnetic ratio of an electron (γe = 1.76 × 1011 T–1 s–1), and λ is the microscopic Gilbert damping constant describing the coupling to the heat bath.875 The effective magnetic (induction) field is given by the first derivative of the spin Hamiltonian:
| 22 |
where μs is the
local spin moment and augmented by a stochastic thermal field.
In the LLG equation, the damping term λ models the energy dissipation
of the system, considering energy transfer to and from the lattice
and electron degrees of freedom. Formally the LLG equation does not
include any description of temperature and is only valid at 0 K, and
so to include the effects of temperature effects, we use Langevin
dynamics.877 The effect of temperature
is introduced by coupling the system to a heat bath in the form of
a fluctuating thermal field 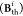 into the effective field873 described by
into the effective field873 described by
| 23 |
where Γ(t) is a Gaussian distributed random number in three dimensions and Δt is the integration time step. This formalism assumes a white noise approximation where the time correlation between the spin fluctuations induced by the thermal field must be shorter than the spin motion. This assumption is justified for metallic systems in that the time-scale of the electron heat bath is much faster than the spin system. For insulators and semiconductors the validity of this assumption is less clear and further work is needed to assess the noise correlations, for example through spin–lattice dynamics simulations.878
Codes for Atomistic Simulations
There are now a number of standard software packages available for computing temperature dependent magnetic properties using atomistic models including vampire,856uppasd,874spirit,879 and fidimag(880) which contain built-in and well-tested routines for computing basic properties such as the Curie temperature, spin dynamics and hysteresis loops. Different codes also implement energy minimization algorithms to determine energy barriers and temperature dependent magnetic properties such as the effective exchange coupling and anisotropy. Most of these packages support parallel simulations using multiple CPUs and GPUs that enable much faster calculations than available from typical serial codes, enabling much larger simulations of 2D materials over much longer time scales more readily comparable with experiment.
Electronic and Magnetic Structure
First-principles methods of different flavors are the most common approaches for the calculations of electronic and magnetic properties of 2D magnets. In particular, the development of spin DFT over the past two decades have allowed the fast exploration of spin-dependent properties. On the backbone of these approaches is the treatment of the underlying open-shell problem within nonrelativistic and the relativistic frameworks.881 Indeed, the development and improvement of DFT methods for open-shell (e.g., unpaired electrons) materials is currently one of the most important and challenging topics in theoretical chemistry/physics up to date.882 Several alternatives have been developed that may overcome this limitation.883
2D magnetic materials are not immune to such problems, which careful investigations are desired to address possible shortcomings. The majority of simulation results published so far have either undertaken vast amount of computations using plain DFT functionals (i.e., linear density approach (LDA), generalized gradient approach (GGA)),888,889 or used Hubbard-U approaches (i.e., DFT+U).341,890 A very few papers have been published using approaches beyond mean-field theory for magnetic layered materials (e.g., CrI3, VSe3)891,892 with conclusions slightly different from those by using standard DFT. On the current efforts to develop a critical mass of knowledge in a fast-pace field, DFT remains the low-cost choice for most of the research groups working on 2D materials. In particular, for high-throughput screening investigations where thousands of systems are explored systematically through different work-flows, it is paramount to use methods that provide reliable and prompt results even though they are not at high accuracy. For instance, this approach can be used to find materials with Curie temperatures at room temperature.
Another interesting problem is the organization of the different 2D magnets that may be discovered or already exist in terms of simple descriptors. One approach is to organize the layers via the magnetic moment M and the valence charge Z of the transition metal in a so-called Slater–Pauling curve.893,894 This plot was successfully used in the past to study the magnetic properties of pure metals and alloy compounds (i.e., Fe–V, Co–Cr, Fe–Pt)894 since it provides a generic picture in terms of a simple electron counting argument as discussed in the following. Moreover, in other fields such as in catalysis, the definition of volcano plots define species with high chemical activity for specific chemical reaction,895 which in the context of magnetism would be translated in compounds with high magnetic moments. Indeed, by using first-principle methods (see caption in Figure 76 for details) we show that despite of the crystal structure, elements considered and chemical formula (Figure 76a), the Slater–Pauling curve holds for 2D vdW magnetic materials (Figure 76b). The plot has two behaviors which can be used to distinguish the 2D magnets in two classes via the position of the ascending (positive slope) and descending (negative slope) branches:
weak magnets:
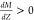 , ascending branch
, ascending branchstrong magnets:
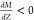 , descending branch
, descending branch
Figure 76.
Slater-Pauling or volcano plot for 2D magnets. (a) High-throughput screening undertook over several crystal structures and elements of the periodic table including formulas MX′2, MX, MX′3, MPX3, MX2, and CrFTe3 with M = Sc–Zn, La, Y; X′=Cl, Br, I; X=O, S, Se, Te; F=Si, Ge. The simulations included mainly transition metals with 3d electrons, but some with 4d and 5d were included for comparison. (b) Variation of the local magnetic moment M(μB) at the metal atom as function of its valence Z(e–). Bader charge analysis was used to extract Z for each metal atom at the compound. The solid lines show a fit to the data set on two different regimes according to the filling of the valence. The positive slope (weak magnets) can be fairly well fitted using M+ = 0.84Z – 1.15 (with a linear regression coefficient R2 = 0.96) and the negative (strong magnets) with M– = −0.87Z + 9.27 (R2 = 0.90). An electron counting argument can be used to explain both regimes as discussed in the text. (c) Spin resolved density of states (DOS) for monolayer MPTe3 (M = V, Cr, Mn, Fe, Co, Ni) as function of the energy ε displaying the spin up density nup (faint gray) and spin down ndown (faint brown) at opposite sides. The energy is shifted to the Fermi energy εF at zero. (d) Variation of the model predicted magnetization versus DFT + U calculated magnetization for the compounds showed in (a). Calculations were performed using the VASP code884 using a 21 × 21 × 1 k-sampling grid, the Dudarev (GGA+U) scheme885 with Hubbard U values following those in ref (341). The energy cutoff is set to 600 eV, the convergence criteria for energy to 10–7 eV and for the forces to 0.01 eV/Å. In order to avoid interactions between the layers, we applied periodic boundary conditions with a vacuum space of 25 Å. We used the projector augmented wave (PAW)886 methods with a plane wave basis. The Vosko–Wilk–Nusair modification scheme887 is applied for the spin-polarized calculations. All images in this figure are original, and no permissions are required.
The positive (+) and negative (−) slopes of M can be well fitted by
| 24 |
| 25 |
with a linear regression coefficient of R2 = 0.96 and R2 = 0.90, respectively.
One of the main reasons for the two different
gradients corresponds
to the amount of filling of the d-band following
the Hund’s first rule. The materials with  have their majority spin density
of states
(DOS) nup being filled
successively with the change of the metal atom until it is completely
full. In this process the magnetization increases linearly with the
additional charge reaching maximum values of M ∼
4.5 μB for Mn-based 2D materials (i.e., MnBr2, MnPX3 (X = S, Se, Te), MnI2). Once nup is filled,
the remaining electrons can only be added to minority spin states ndown leading to a decrease
of M or
have their majority spin density
of states
(DOS) nup being filled
successively with the change of the metal atom until it is completely
full. In this process the magnetization increases linearly with the
additional charge reaching maximum values of M ∼
4.5 μB for Mn-based 2D materials (i.e., MnBr2, MnPX3 (X = S, Se, Te), MnI2). Once nup is filled,
the remaining electrons can only be added to minority spin states ndown leading to a decrease
of M or 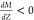 . A nonmagnetic state is obtained
as the
spin-down band is fully saturated. This effect can be seen systematically,
for instance, in MPTe3 (M = V, Cr, Mn, Fe, Co, Ni) compounds
as we computed the spin resolved DOS displayed in Figure 76c. The terms weak and strong
magnets are defined in terms of the filling of the 3d-band as the
latter represents those with a full nup, while the former corresponds to an empty ndown.
. A nonmagnetic state is obtained
as the
spin-down band is fully saturated. This effect can be seen systematically,
for instance, in MPTe3 (M = V, Cr, Mn, Fe, Co, Ni) compounds
as we computed the spin resolved DOS displayed in Figure 76c. The terms weak and strong
magnets are defined in terms of the filling of the 3d-band as the
latter represents those with a full nup, while the former corresponds to an empty ndown.
We also noticed that some compounds may have substantial charge transfer between the 3d-states at the transition metal and the sp electrons provided by the chalcogens or halides since the valence Z slightly shifted from the ideal valence for the 3d-shell atom. This indicates that depending on the nonmagnetic ion forming the 2D compound the local magnetization varies accordingly. However, by using eqs 24 and 25 we can still estimate with good accuracy relative to DFT+U calculations the value of the magnetization of any material just using Z as an input parameter (Figure 76d). We obtained an almost 1:1 comparison between model and DFT+U simulations (Mmodel = 0.85MDFT+U + 0.30, R2 = 0.93) when we considered all computed materials. A better estimation with angular coefficient roughly of 1 between Mmodel and MDFT+U can be extracted if the 2D magnets are separated by each corresponding families:
Mmodel = 0.94MDFT+U + 0.13, R2 = 0.98 for MX2 (M = V–Co; X = O, S, Se, Te).
Mmodel = 0.93MDFT+U + 0.20, R2 = 0.94 for MX2 (M = V, Mn, Fe, Co, Ni, Cu; X = Cl, Br, I).
Mmodel = 0.90MDFT+U + 0.27, R2 = 0.98 for MX3 (M = V–Cu; X = Cl, Br, I)
Mmodel = 1.00MDFT+U + 0.02, R2 = 0.98 for MPX3 (M = V–Ni; X = S, Se, Te)
It is worth mentioning that although the Slater–Pauling curve provides a simple but yet powerful tool to interpret a broad range of materials, the particular characteristics of each compound may influence its magnetic features. Such as whether a more itinerant component is present in which an atomic picture would be no longer valid. On that, additional theory in terms of the Stoner model896,897 or more sophisticated approaches would be required.854
Future Challenges and Outlook
The field of 2D magnets presents an exciting opportunity to probe magnetism down to the atomic scale and over the coming years will provide continuous challenges to our theoretical understanding of magnetism. The ability of first-principles methods to make quantitative predictions of the fundamental interactions in 2D magnets is a triumph of modern computational physics that will help to guide their future discovery.232,744,898−900 Despite this, many challenges still remain in developing a deeper understanding of 2D magnets. At the electronic level, ab initio approaches often rely on pseudopotentials that must be carefully parametrized or include the right amount of core-states to ensure accurate results. vdW interactions that dominate the interlayer magnetic properties present a particular difficulty and more accurate approaches such as the inclusion of vdW parametrization on hybrid functionals may assist in higher accuracy on the computation of magnetic properties and exchange parameters. These ingredients are critical in the search for high Curie temperature 2D magnets and predicting the properties of functionalized materials867,901 and heterostructures.868,902−904 High-throughput calculations796,890,905 allow for rapid identification of suitable 2D materials for different applications, while machine learning may also assist in the automated searching of larger parameter spaces. One of the most exciting aspects of 2D magnets is the crossover with spintronics, providing means to probe and manipulate electron spins at the nanoscale. Spintronics is a rapidly developing area in its own right, but understanding the interactions of electrical currents and magnetic textures in 2D materials is a significant challenge both fundamentally in terms of spin transport but also computationally in being able to model experimentally accessible time and length scales.
For elevated temperatures, the current atomistic approach used within the 2D Heisenberg model has some basic approximations assuming a fully classical heat bath865 and fully localized magnetic moments. While the latter approximation seems to be reasonable for a broad class of current 2D magnets,796 it may be necessary to introduce longitudinal spin fluctuations906−909 to better describe the itinerant characteristics of local moments. An outstanding problem common to both 3D and 2D magnetic materials is the nature of the heat bath that drives thermal spin fluctuations and allows for energy dissipation. In metallic systems the conduction electrons play a critical role in mediating spin–lattice energy transfer and is reasonably well described by Langevin dynamics.856 In insulating systems the spin and lattice systems are directly coupled, with recent developments allowing explicit treatment of coupled spin and lattice degrees of freedom.878 Several popular vdW systems are either insulators or semiconductors which present a particular challenge where the lattice and electron degrees of freedom are likely to be important to the resulting spin dynamics. The other component is that all these approaches are classical in nature, and neglect the quantum nature of the heat bath and localized spin flip (Elliott–Yafet) scattering events.910,911 Spin temperature rescaling31 is a phenomenological approach that gives better ensemble agreement with experimental data, but additional approaches founded in quantum thermodynamics are needed to better describe the nature of the heat bath in magnetic systems.872 On that, additional developments are needed together with efficient computer implementations.
The next few years will be groundbreaking in evolving our understanding of magnetism at the 2D limit, where computational methods will play a leading role in this endeavor. Experimental data will challenge theory and its underlying assumptions, while modeling can explore unexpected physics and materials at low cost and high speed to guide experiments toward the cutting edge at different forefronts. Such juxtapositions are rare in scientific discovery. It is undoubtedly an exciting time in determining the fundamental nature of magnetic materials that will lay the foundations of pioneering technologies into the future.
Perspectives and a Forward-Looking Approach
The last several years have seen significant advances in both the fundamental understanding and potential practical implementations of 2D magnetic materials on device platforms. It is important to recognize that this rapid development in science and engineering has been a driven by a focused effort by many research groups around the world. The result has been a flurry of science on the magnetism of atomically thin layers currently culminating in the emergence of truly transformational technologies with the potential to significantly alter the landscape for data storage, information processing and spintronics. A forward-looking approach to identify challenges to pursue and problems to solve will serve as a guideline for many scientists to enter the 2D world. In the following section, we have summarized some of the challenges discussed in this work that will help ensure fast progress of the field of 2D vdW magnetic materials.
Fundamental Aspects
The description of 2D magnets using different spin Hamiltonians is clearly one of the fundamental aspects to be addressed in the forthcoming years. Several models have been used to date to describe the spin interactions of layered materials (see previous section on Theory and Simulations for additional details). We use CrI3 as an example of how different spin Hamiltonians have been implemented by different research groups to understand its properties (Figure 77). The importance of such relies on the predictive power of unforeseen phenomena using an archetypal spin model as well as understanding measured properties. For instance, the spin gap observed at the Dirac point in bulk CrI3 has actively been modeled by different Hamiltonians744,745 without a more conclusive picture until very recently with more refined measurements.750 This suggests that instrumental resolution is a key feature for measurements of the topological properties of vdW materials, which then provides high-resolution data for modeling. It is also worth mentioning the large variation of magnetic parameters (e.g., exchange integrals, anisotropies, DMI, etc.) observed on the theoretical side. DFT of different varieties have been popular tools to compute them.85 However, most of the quantities important for parametrizing spin Hamiltonians are at the limit of the numerical libraries used to compile the software to carry out such tasks. That is, small variations on some input parameters (e.g., k-sampling, energy cutoff, basis set, pseudopotentials, functionals, Hubbard-U value) on the codes may have large implications on the calculated quantities. This calls for a more careful analysis of the approaches used to extract magnetic parameters for 2D magnets to ensure reproducibility and consistent data across different research groups. A successful case has been applied in other contexts,912 which provides ideas that could be applied toward the standardization of modeling approaches.
Figure 77.
Comparison of spin Hamiltonians used to model the magnetic properties of CrI3. The two most commonly used Hamiltonians in the literature have been the Ising and the Heisenberg (XXZ) models which also includes magnetic anisotropy. The latter was used to understand inelastic tunnelling spectra for MTJs.14 The former was initially assigned to CrI35 but its gross overestimation of the Curie temperature relative to experimental data made it unrealistic to account for the interactions in the system. Overall, depending on the property being measured, other alternatives have been considered: (i) for angle-dependent FM resonance measurements,746 the Kitaev model with quadrupole–quadrupole interactions and the Zeeman coupling was implemented; (ii) for inelastic neutron scattering to extract the magnon dispersion of bulk CrI3,744,745 the XXZ model either including DMI or adding biquadratic exchange with DMI796 have been proposed; and (iii) for the magnetic domains and domain walls on CrI3, a Hamiltonian taking into account biquadratic exchange was utilized.31 Starting with image at top, and going clockwise, panels adapted with permission under a Creative Commons CC BY license from refs (796). Copyright 2020 Springer Nature. Adapted with permission from ref (14). Copyright 2018 AAAS. Adapted with permission from ref (745). Copyright 2020 American Physical Society. Reproduce with permission from ref (31). Copyright 2021 John Wiley and Sons. Adapted with permission from ref (746). Copyright 2018 AAAs.
Furthermore, an important underlying aspect to be studied is the emergence of complex magnetic-field-induced spin textures such as skyrmions and merons in layered systems displaying high Curie temperatures including Fe3GeTe2,913,914 Fe5GeTe2,915 or Co-doped Fe5GeTe2. The goal is to evaluate their potential for applications in, for example, magnetic skyrmions race track memories.916,917 Fe3GeTe2 has already been grown via MBE, while Co-doped Fe5GeTe2 has shown Curie temperatures above room temperature, suggesting intriguing prospects for the development of such memories. Spin textures characterized by spin chirality were found to affect the Berry phase of the charge carriers leading to a type of topological transport even at room temperature. Such topological transport, emerging at relatively low magnetic fields, can yield a sizable Nernst response that could be explored for thermoelectric applications. Initial results on heterostructures combining these compounds with topological insulators indicate a pronounced enhancement of their Curie temperature, suggesting a promising path to improve their performance in similar applications.
Another interesting challenge to be addressed is the practical validity of the famous Mermin–Wagner theorem40,76 on vdW materials. Even though the theorem has been one of the cornerstones of the field, past experience on graphene918,919 has taught us the opposite. It is well accepted nowadays that finite size ripples (i.e., structural distortions) help to stabilize the intrinsic crystalline order at finite temperature in graphene. Similar arguments also apply for the majority of atomic layered materials found so far in the literature.920 However, if additional ingredients could be present to induce long-range magnetic order on 2D magnets without the need to fulfill the Mermin–Wagner theorem, i.e., the dependence on magnetic anisotropies, it would be certainly a step forward to unanticipated fundamental physics and practical applications. Indeed, recent theoretical results921 have demonstrated that the applicability of the Mermin–Wagner theorem is far more limited than initially predicted. That is, only for large length scales, i.e., near the diameter of the known universe (∼ 1025 m), 2D materials will display no net magnetic order at finite temperatures. This indicates that for implementations in real devices within the typical micrometer range, 2D magnets with no anisotropy constants could be used. Experimental validation of these predictions would be a leap forward for the exploration of a broad range of compounds with isotropic magnetic properties that potentially could be fabricated in 2D.
Devices, Synthesis and Related Challenges
Some of the main challenges are (i) to find 2D magnets with Tc at or above room temperature, (ii) to develop large-scale synthesis methods that are able to produce good quality atomic layers over large areas, (iii) refinements in device fabrication and integration in current technologies, and (iv) chemically stable materials under environment conditions.
For (i), a few materials have recently been found or predicted to hold magnetism at promising temperature ranges, e.g., 300–850 K. For (ii), two successful examples obtained by MBE growth78,83via MBE growth provide evidence that a pathway toward a bottom-up approach may be within reach in the lab. Moreover, CVD is a popular method that has been used for years to synthesize nonmagnetic 2D materials. Recent demonstrations on the synthesis of magnetic layers suggest that similar developments in CVD growth and fine-tuning of growth parameters to control material properties will be a crucial enabling step. Regarding (iii), the fabrication of devices with low-resistance contacts using device geometries needs to be developed for a broad usage of 2D magnets. Finally, for (iv), encapsulation via nonmagnetic materials (e.g., hBN, polymers) as well as substrate supports can reduce fast oxidation and preserve pristine properties long enough for use in practical applications. A critical development will be to find encapsulation materials that can simultaneously enhance magnetic properties and preserve chemical stability while being compatible with device fabrication and processing.
Magneto-Optics
A few challenges can be pointed out such as the relation between the birefringent effects and the total magnetization which is more challenging in 2D magnets than in their 3D counterparts (see Magneto-Optical Phenomena section). This calls for the combination of complementary techniques, e.g., magneto-PL, for a full characterization of the magnetic features. Raman spectroscopy is also a reliable technique for characterization of FM and AF samples. However, the rapid degradation of devices after a few days of environmental exposure suggests that additional improvements would be welcome. If sample conditions can be finely controlled in optical environments, several phenomena can experimentally be probed. For instance, dynamic magnetization processes can be induced by ultrafast laser excitations down to the 2D limit. It is unclear how atomically thin layers behave on read and write operations at times required by the industry. High-frequency signals within the terahertz (THz) regime is also one of the challenging issues in the field. The flexibility and control of the magnetic properties of vdW materials which can be mechanically manipulated with monolayer accuracy provide a horizon for device developments. Indeed, the fifth-generation of common wireless communication systems operates in frequencies on the order of hundreds of GHz up toward THz.922 Therefore, magnetic components for wireless networks would have to be adapted to a high-frequency domain. Investigations on 2D magnets that would result in compact, low-dissipation, low-cost THz spintronic devices may change our perspectives on information and communication technologies.
Imaging Approaches
In terms of techniques, two popular methods, MOKE and MCD, suffer of considerable signal-to-noise ratio. The signal level from vdW magnets typically results in low detection signal within the range of 10–3–10–6 (Magnetic Imaging section). The application of high magnetic fields on thin layers is also challenging due to interferences between the magnetic induction of the sample and stray fields which ramp up detection. Furthermore, SP-STM and MFM may need to be adapted to measure spin signals from magnetic insulating materials (Magnetic Imaging section). In terms of analysis, the image reconstruction for techniques that probe stray field maps (e.g., NV magnetometry) seems the one that stands out the most. A better description of algorithms that may take into account different components of the magnetic field in order to produce real-space magnetization images is worth exploring. A comparison with atomistic simulations helps to give hints about the sample magnetic structure. However, the dependence of stray fields with the tip–sample region puts limitations on the technique resolution and exploration of more fine features, such as domain walls or spin-textures (see Magnetic Imaging section).
Mechanical and Thermal Properties
The interplay between softness and magnetic properties still provides a substantial challenge on the measurements of mechanical and thermal features based conventional techniques such as using AFM to indent suspended 2D magnets (see Spin Excitations and Topological Properties section). Improving sample quality is a critical step in this goal since the presence of defects, grain-boundaries, and chemical stability all affect the properties. In addition, there is much room for exploration of magneto-mechanical phenomena that are largely unknown in 2D magnets. A number of opportunities in terms of (i) strain-induced magnetic phases, (ii) coupling between heat and magnetism via mechanical properties (e.g., magnetocaloric effect), and (iii) development of magnetic actuators and sensors. Indeed, central quantities in heat management such as the thermal conductivity and expansion coefficients are yet to be determined. These ingredients are critical in miniaturized modern devices where magnetic layers may be integrated and have an active role. In these applications, how spin effects may influence phononic thermal transport and what type of SOC may be present on different materials and interfaces are topics of increasing interest.
Spin Excitations and Topological Features
After the measurements of spin excitations on CrI3,744,745,750 and their implications on topological magnons on 2D vdW magnetic layers, several possibilities from a broad family of materials are potential candidates for exploration (see Heterostructures, Twisted Layers, and Interfaces section). Several difficulties need to be overcome, for example, quantum fluctuations in low dimensional magnets are particularly concerning since they may rule out the appearance of spin waves and obscure any topological behavior. Materials with spin-1/2 (e.g., α-RuCl3) would be avoided since they display large quantum fluctuations.
The hunt for topologically nontrivial spin textures in 2D magnets (e.g., skyrmions, merons, domain-walls, spirals, etc.) is also attracting substantial interest from both fundamental and applied directions (Figure 78). For the former, the stabilization of spin quasiparticles in strongly confined layers may provide the necessary platform for studying underlying interactions without disturbance from underlying substrates, such as in terms of two-body (Kijkl(Si·Sj)2), three-body (Kijk(Si·Sj)(Si·Sk)) and four-body coupling terms (Kijkl(Si·Sj)(Sk·Sl)), which may result in magnetic frustration, topological phases with anyonic excitations,923 and dynamics of rare quasiparticles.876,914 These phenomena can be studied at a level not yet achieved in more classical compounds. Furthermore, chiral magnetic interactions beyond DMI may lead to exotic noncollinear spin textures (i.e., hedgehog, monopole) as recently predicted.924 If information can be stored in such spin-polarized structures, it may also be controlled in racetrack platforms510 through electrical stimulus. The difficulties ahead would be to find vdW materials with such characteristics where high velocities for the spin quasiparticle at low currents and when negligible pinning or decoherence effects are present. In this context, high-throughput screening using multiscale complementary theoretical techniques31,925,926 will be crucial.
Figure 78.
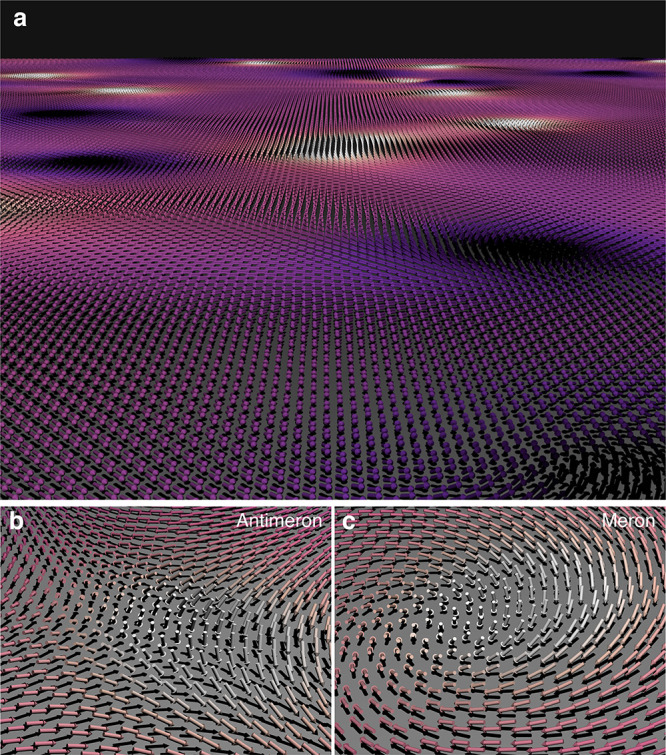
Merons and antimerons on 2D magnet CrCl3. (a) Artistic view of the presence of topologically nontrivial spin quasiparticles merons and antimerons on monolayer CrCl3.876 The different colors follow the orientation of the spins throughout the layer. (b, c) Local views of antimerons and merons, respectively, with their local spin configurations at Cr atoms.
Spintronics
Devices based on spin will be a key area for 2D vdW magnets particularly in the transition from fundamental research to applications. Several challenges have been in the field for decades, which may now find potential solutions in 2D vdW magnets, as was described in more detail in the earlier section on spintronics. For instance, reduced dimensionality, control of magnetism via electrical means, enhanced thermal stability, sharp interfaces and transfer of the magnetic layers on different substrates are milestones toward a generation of spintronic devices with low energy consumption. One of the key ingredients would be the reduction of critical currents (below 2.0× 106 A cm–2) in spin-transfer torque (STT) in information storage platforms, e.g. magnetic random-access memory (MRAM). At the moment little is known about STT phenomena in magnetic vdW layers and their interfaces. Currently, open questions in the field are surrounding (i) what substrates may enhance thermal stability and magnetic properties of 2D sheets, (ii) induce chiral interactions, and (iii) fast domain wall motion under STT current for high density memories and/or spin logic implementations. A few reports445,925 have appeared in the literature but additional exploration is urgently needed.
Acknowledgments
X.R., C.R.D., E.J.T., and A.H.D. acknowledge support from the Center for Precision Assembly of Superstratic and Superatomic Solids, a U.S. National Science Foundation (NSF) MRSEC (award nos. DMR-2011738 and DMR-1420634), the Air Force Office of Scientific Research (award no. FA9550-18-1-0020), and the Center on Programmable Quantum Materials, an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under award DE-SC0019443. H.H.K. acknowledges funding by the National Research Foundation of Korea Grant funded by the Korean Government (NRF-2021R1C1C1012394). This project was supported by the Ministry of Education (Singapore) through the Research Centre of Excellence program (grant EDUN C-33-18-279-V12, I-FIM). B.D.G., supported by a Wolfson Merit Award from the Royal Society and a Chair in Emerging Technology from the Royal Academy of Engineering, acknowledges the EPSRC (grant no. EP/P029892/1), the ERC (grant no. 725920), the EU Horizon 2020 research and innovation program under grant agreement no. 820423. M.B.-G. is supported by a University Research Fellowship from the Royal Society (ref URF/R1/211484). L.Z. acknowledges support by NSF CAREER grant no. DMR-174774 and AFOSR grant no. FA9550- 21-1-0065. J.W. acknowledges EU project ASTERIQS and European Research Council via SMeL DFG GRK 2642 and FOR 2724. A.Y. acknowledges support from the Army Research Office (ARO) through grant no. W911NF-17-1-0023, the Quantum Science Center (QSC), a National Quantum Information Science Research Center of the U.S. Department of Energy (DOE), the Gordon and Betty Moore Foundation through grant GBMF 9468, and the STC Center for Integrated Quantum Materials, NSF grant no. DMR-1231319. Y.L., L.B., and C.P. thank Milorad Milosevic for useful communication. Work at Brookhaven National Laboratory is supported by the Office of Basic Energy Sciences, Materials Sciences and Engineering Division, U.S. Department of Energy (DOE) under contract no. DE-SC0012704. L.B. is supported by the US-DOE through the BES program, award DE-SC0002613. The National High Magnetic Field Laboratory acknowledges support from the US-NSF Cooperative agreement Grant number DMR-1644779 and the state of Florida. The μSR experiments were carried out at the Swiss Muon Source (SμS) of the Paul Scherrer Institute using low background GPS (πM3 beamline)377 and high pressure GPD (μE1 beamline)534 instruments. The μSR time spectra were analysed using the free software package MUSRFIT.379 Z.G. gratefully acknowledges the financial support by the Swiss National Science Foundation (SNF fellowships P2ZHP2-161980 and P300P2-177832). A.F., F.C., and M.C. acknowledge European Union Horizon 2020 research and innovation programme under grant agreement no. 881603 (Graphene Flagship), Spanish MICINN under the Maria de Maeztu Units of Excellence Programme (no. MDM-2016–0618) and under project no. RTI2018-094861-B-100, French ANR MAGICVALLEY (ANR-18-CE24-0007) and discussions with P. Seneor, B. Dlubak, V. Cros, N. Reyren, H. X. Yang, A. Hallal, F. Ibrahim, F. Bonell, and M. Jamet. S.T. and M.B. acknowledge support from NSF DMR-1904716, NSF DMR-2111812, NSF ECCS-2052527, and DOE-SC0020653. The work on van der Waals materials at Rice University was supported by NSF DMR-1700081, DMR-2100741, and by the Robert A. Welch Foundation under grant no. C-1839 (P. D.). A.M. and Z.W. acknowledge the support of the EPSRC Early Career Fellowship (EP/N007131/1), the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement no. 865590), and the Royal Society International Exchanges 2019 Cost Share Program (IEC/R2/192001). S.J. acknowledges funding by the German Research Foundation (DFG) project no. 320163632 (EV 196/2). This project made use of of the viking cluster, a high performance computing facility provided by the University of York. R.F.L.E. gratefully acknowledges the financial support of ARCHER UK National Supercomputing Service via the embedded CSE programme (ecse1307). Q.H.W. acknowledges support from NSF grants QLCI-CG-1936882 and DMR-1906030. E.J.G.S. acknowledges computational resources through CIRRUS Tier-2 HPC Service (ec131 Cirrus Project) at EPCC (http://www.cirrus.ac.uk) funded by the University of Edinburgh and EPSRC (EP/P020267/1); ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) via Project d429. EJGS acknowledges the Spanish Ministry of Science’s grant program “Europa-Excelencia” under grant number EUR2020-112238, the EPSRC Early Career Fellowship (EP/T021578/1), and the University of Edinburgh for funding support. A.B.-P. acknowledges support by the Generalitat Valenciana (CIDEGENT/2021/005).
Glossary
Vocabulary
- 2D vdW magnets
a family of two-dimensional materials which display magnetic properties with a crystal structure of in-plane covalent bonding and weak interlayer (van der Waals) interactions
- Slater–Pauling curve or volcano plot for 2D vdW magnets
a linear scaling relationship between magnetization and atomic number via a simple counting argument through the filling of the valence of d-shell of the metallic atom composing the material. Such plot passes through a maximum and decreases at low/high electron valence with approximately triangle-shape profile similarly as a volcano
- Spin waves
collective excitations of the spin ordering which propagates along the magnetic lattice. Such excitations are incompatible with the Ising model given the continuous symmetry required. Spin waves are also known as magnons from a quasiparticle perspective
- 2D magnetic genome
a thorough revision of the state of the art achievements on the field of 2D magnetic materials providing a forward-looking approach on the main challenges to be delivered. Each included subject corresponds to a fundamental piece (“gene”) that would compose a large set of information (“genome”) needed to build that field and allow it to grow and develop promptly
- Meron
topological nontrivial spin textures with a topological charge 1/2, which is one of the fundamental solutions of the Yang–Mills field equations
- Ising model
simplistic spin model where only two discrete spin states (i.e., up or down) are considered throughout the magnetic ordering. The model is appropriate for spin systems where the energy is invariant to reflecting every spin to its opposite orientation
- Heisenberg model
continuous-symmetry-based spin model where spins can point anywhere in the unit sphere. In this model, the energy of a given spin configuration is invariant to rotating every spin in the same way around the unit sphere
Author Present Address
§ Los Alamos National Laboratory, Los Alamos, New Mexico 87545, United States
The authors declare no competing financial interest.
References
- Du K.-Z.; Wang X.-Z.; Liu Y.; Hu P.; Utama M. I. B.; Gan C. K.; Xiong Q.; Kloc C. Weak van der Waals Stacking, Wide-Range Band Gap, and Raman Study on Ultrathin Layers of Metal Phosphorus Trichalcogenides. ACS Nano 2016, 10, 1738–1743. 10.1021/acsnano.5b05927. [DOI] [PubMed] [Google Scholar]
- Kuo C.-T.; Neumann M.; Balamurugan K.; Park H. J.; Kang S.; Shiu H. W.; Kang J. H.; Hong B. H.; Han M.; Noh T. W.; Park J.-G. Exfoliation and Raman Spectroscopic Fingerprint of Few-Layer NiPS3 van der Waals Crystals. Sci. Rep. 2016, 6, 20904. 10.1038/srep20904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin M.-W.; Zhuang H. L.; Yan J.; Ward T. Z.; Puretzky A. A.; Rouleau C. M.; Gai Z.; Liang L.; Meunier V.; Sumpter B. G.; Ganesh P.; Kent P. R. C.; Geohegan D. B.; Mandrus D. G.; Xiao K. Ultrathin Nanosheets of CrSiTe3: A Semiconducting Two-Dimensional Ferromagnetic Material. J. Mater. Chem. C 2016, 4, 315–322. 10.1039/C5TC03463A. [DOI] [Google Scholar]
- Lee S.; Choi K.-Y.; Lee S.; Park B. H.; Park J.-G. Tunneling Transport of Mono- and Few-Layers Magnetic van der Waals MnPS3. APL Mater. 2016, 4, 086108. 10.1063/1.4961211. [DOI] [Google Scholar]
- Huang B.; Clark G.; Navarro-Moratalla E.; Klein D. R.; Cheng R.; Seyler K. L.; Zhong D.; Schmidgall E.; McGuire M. A.; Cobden D. H.; Yao W.; Xiao D.; Jarillo-Herrero P.; Xu X. Layer-Dependent Ferromagnetism in a van der Waals Crystal Down to the Monolayer Limit. Nature 2017, 546, 270–273. 10.1038/nature22391. [DOI] [PubMed] [Google Scholar]
- Gong C.; Li L.; Li Z.; Ji H.; Stern A.; Xia Y.; Cao T.; Bao W.; Wang C.; Wang Y.; Qiu Z. Q.; Cava R. J.; Louie S. G.; Xia J.; Zhang X. Discovery of Intrinsic Ferromagnetism in Two-Dimensional van der Waals Crystals. Nature 2017, 546, 265–269. 10.1038/nature22060. [DOI] [PubMed] [Google Scholar]
- McGuire M. A.; Clark G.; KC S.; Chance W. M.; Jellison G. E.; Cooper V. R.; Xu X.; Sales B. C. Magnetic Behavior and Spin-Lattice Coupling in Cleavable van der Waals Layered CrCl3 Crystals. Phys. Rev. Mater. 2017, 1, 014001. 10.1103/PhysRevMaterials.1.014001. [DOI] [Google Scholar]
- Jiang S.; Shan J.; Mak K. F. Electric-Field Switching of Two-Dimensional van der Waals Magnets. Nat. Mater. 2018, 17, 406–410. 10.1038/s41563-018-0040-6. [DOI] [PubMed] [Google Scholar]
- Huang B.; Clark G.; Klein D. R.; MacNeill D.; Navarro-Moratalla E.; Seyler K. L.; Wilson N.; McGuire M. A.; Cobden D. H.; Xiao D.; Yao W.; Jarillo-Herrero P.; Xu X. Electrical Control of 2D Magnetism in Bilayer CrI3. Nat. Nanotechnol. 2018, 13, 544–548. 10.1038/s41565-018-0121-3. [DOI] [PubMed] [Google Scholar]
- Wang Z.; Zhang T.; Ding M.; Dong B.; Li Y.; Chen M.; Li X.; Huang J.; Wang H.; Zhao X.; Li Y.; Li D.; Jia C.; Sun L.; Guo H.; Ye Y.; Sun D.; Chen Y.; Yang T.; Zhang J.; et al. Electric-Field Control of Magnetism in a Few-Layered van der Waals Ferromagnetic Semiconductor. Nat. Nanotechnol. 2018, 13, 554–559. 10.1038/s41565-018-0186-z. [DOI] [PubMed] [Google Scholar]
- Jiang S.; Li L.; Wang Z.; Mak K. F.; Shan J. Controlling Magnetism in 2D CrI3 by Electrostatic Doping. Nat. Nanotechnol. 2018, 13, 549–553. 10.1038/s41565-018-0135-x. [DOI] [PubMed] [Google Scholar]
- Deng Y.; Yu Y.; Song Y.; Zhang J.; Wang N. Z.; Sun Z.; Yi Y.; Wu Y. Z.; Wu S.; Zhu J.; Wang J.; Chen X. H.; Zhang Y. Gate-Tunable Room-Temperature Ferromagnetism in Two-Dimensional Fe3GeTe2. Nature 2018, 563, 94–99. 10.1038/s41586-018-0626-9. [DOI] [PubMed] [Google Scholar]
- Song T.; Cai X.; Tu M. W.-Y.; Zhang X.; Huang B.; Wilson N. P.; Seyler K. L.; Zhu L.; Taniguchi T.; Watanabe K.; McGuire M. A.; Cobden D. H.; Xiao D.; Yao W.; Xu X. Giant Tunneling Magnetoresistance in Spin-Filter van der Waals Heterostructures. Science 2018, 360, 1214–1218. 10.1126/science.aar4851. [DOI] [PubMed] [Google Scholar]
- Klein D. R.; MacNeill D.; Lado J. L.; Soriano D.; Navarro-Moratalla E.; Watanabe K.; Taniguchi T.; Manni S.; Canfield P.; Fernández-Rossier J.; Jarillo-Herrero P. Probing Magnetism in 2D van der Waals Crystalline Insulators via Electron Tunneling. Science 2018, 360, 1218–1222. 10.1126/science.aar3617. [DOI] [PubMed] [Google Scholar]
- Wang Z.; Gutiérrez-Lezama I.; Ubrig N.; Kroner M.; Gibertini M.; Taniguchi T.; Watanabe K.; Imamoğlu A.; Giannini E.; Morpurgo A. F. Very Large Tunneling Magnetoresistance in Layered Magnetic Semiconductor CrI3. Nat. Commun. 2018, 9, 2516. 10.1038/s41467-018-04953-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim H. H.; Yang B.; Patel T.; Sfigakis F.; Li C.; Tian S.; Lei H.; Tsen A. W. One Million Percent Tunnel Magnetoresistance in a Magnetic van der Waals Heterostructure. Nano Lett. 2018, 18, 4885–4890. 10.1021/acs.nanolett.8b01552. [DOI] [PubMed] [Google Scholar]
- O’Hara D. J.; Zhu T.; Trout A. H.; Ahmed A. S.; Luo Y. K.; Lee C. H.; Brenner M. R.; Rajan S.; Gupta J. A.; McComb D. W.; Kawakami R. K. Room Temperature Intrinsic Ferromagnetism in Epitaxial Manganese Selenide Films in the Monolayer Limit. Nano Lett. 2018, 18, 3125–3131. 10.1021/acs.nanolett.8b00683. [DOI] [PubMed] [Google Scholar]
- Bonilla M.; Kolekar S.; Ma Y.; Diaz H. C.; Kalappattil V.; Das R.; Eggers T.; Gutierrez H. R.; Phan M.-H.; Batzill M. Strong Room-Temperature Ferromagnetism in VSe2 Monolayers on van der Waals Substrates. Nat. Nanotechnol. 2018, 13, 289–293. 10.1038/s41565-018-0063-9. [DOI] [PubMed] [Google Scholar]
- Huang C.; Feng J.; Wu F.; Ahmed D.; Huang B.; Xiang H.; Deng K.; Kan E. Toward Intrinsic Room-Temperature Ferromagnetism in Two-Dimensional Semiconductors. J. Am. Chem. Soc. 2018, 140, 11519–11525. 10.1021/jacs.8b07879. [DOI] [PubMed] [Google Scholar]
- Chen W.; Sun Z.; Wang Z.; Gu L.; Xu X.; Wu S.; Gao C. Direct Observation of van der Waals Stacking-Dependent Interlayer Magnetism. Science 2019, 366, 983–987. 10.1126/science.aav1937. [DOI] [PubMed] [Google Scholar]
- Thiel L.; Wang Z.; Tschudin M. A.; Rohner D.; Gutiérrez-Lezama I.; Ubrig N.; Gibertini M.; Giannini E.; Morpurgo A. F.; Maletinsky P. Probing Magnetism in 2D Materials at the Nanoscale with Single-Spin Microscopy. Science 2019, 364, 973–976. 10.1126/science.aav6926. [DOI] [PubMed] [Google Scholar]
- Song T.; Fei Z.; Yankowitz M.; Lin Z.; Jiang Q.; Hwangbo K.; Zhang Q.; Sun B.; Taniguchi T.; Watanabe K.; McGuire M. A.; Graf D.; Cao T.; Chu J.-H.; Cobden D. H.; Dean C. R.; Xiao D.; Xu X. Switching 2D Magnetic States via Pressure Tuning of Layer Stacking. Nat. Mater. 2019, 18, 1298–1302. 10.1038/s41563-019-0505-2. [DOI] [PubMed] [Google Scholar]
- Li T.; Jiang S.; Sivadas N.; Wang Z.; Xu Y.; Weber D.; Goldberger J. E.; Watanabe K.; Taniguchi T.; Fennie C. J.; Fai Mak K.; Shan J. Pressure-Controlled Interlayer Magnetism in Atomically Thin CrI3. Nat. Mater. 2019, 18, 1303–1308. 10.1038/s41563-019-0506-1. [DOI] [PubMed] [Google Scholar]
- Sun Z.; Yi Y.; Song T.; Clark G.; Huang B.; Shan Y.; Wu S.; Huang D.; Gao C.; Chen Z.; McGuire M.; Cao T.; Xiao D.; Liu W.-T.; Yao W.; Xu X.; Wu S. Giant Nonreciprocal Second-Harmonic Generation from Antiferromagnetic Bilayer CrI3. Nature 2019, 572, 497–501. 10.1038/s41586-019-1445-3. [DOI] [PubMed] [Google Scholar]
- Ding B.; Li Z.; Xu G.; Li H.; Hou Z.; Liu E.; Xi X.; Xu F.; Yao Y.; Wang W. Observation of Magnetic Skyrmion Bubbles in a van der Waals Ferromagnet Fe3GeTe2. Nano Lett. 2020, 20, 868–873. 10.1021/acs.nanolett.9b03453. [DOI] [PubMed] [Google Scholar]
- Park T.-E.; Peng L.; Liang J.; Hallal A.; Yasin F. S.; Zhang X.; Song K. M.; Kim S. J.; Kim K.; Weigand M.; Schütz G.; Finizio S.; Raabe J.; Garcia K.; Xia J.; Zhou Y.; Ezawa M.; Liu X.; Chang J.; Koo H. C.; et al. Néel-Type Skyrmions and Their Current-Induced Motion in van der Waals Ferromagnet-Based Heterostructures. Phys. Rev. B 2021, 103, 104410. 10.1103/PhysRevB.103.104410. [DOI] [Google Scholar]
- Wu Y.; Zhang S.; Zhang J.; Wang W.; Zhu Y. L.; Hu J.; Yin G.; Wong K.; Fang C.; Wan C.; Han X.; Shao Q.; Taniguchi T.; Watanabe K.; Zang J.; Mao Z.; Zhang X.; Wang K. L. Néel-Type Skyrmion in WTe2/Fe3GeTe2 van der Waals Heterostructure. Nat. Commun. 2020, 11, 3860. 10.1038/s41467-020-17566-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang X.-X.; Li L.; Weber D.; Goldberger J.; Mak K. F.; Shan J. Gate-Tunable Spin Waves in Antiferromagnetic Atomic Bilayers. Nat. Mater. 2020, 19, 838–842. 10.1038/s41563-020-0713-9. [DOI] [PubMed] [Google Scholar]
- Xu Y.; Ray A.; Shao Y.-T.; Jiang S.; Lee K.; Weber D.; Goldberger J. E.; Watanabe K.; Taniguchi T.; Muller D. A.; Mak K. F.; Shan J. Coexisting Ferromagnetic–Antiferromagnetic State in Twisted Bilayer CrI3. Nat. Nanotechnol. 2022, 17, 143. 10.1038/s41565-021-01014-y. [DOI] [PubMed] [Google Scholar]
- Xie H.; Luo X.; Ye G.; Ye Z.; Ge H.; Sung S. H.; Rennich E.; Yan S.; Fu Y.; Tian S.; Lei H.; Hovden R.; Sun K.; He R.; Zhao L. Twist Engineering of the Two-Dimensional Magnetism in Double Bilayer Chromium Triiodide Homostructures. Nat. Phys. 2022, 18, 30–36. 10.1038/s41567-021-01408-8. [DOI] [Google Scholar]
- Wahab D. A.; Augustin M.; Valero S. M.; Kuang W.; Jenkins S.; Coronado E.; Grigorieva I. V.; Vera-Marun I. J.; Navarro-Moratalla E.; Evans R. F. L.; Novoselov K. S.; Santos E. J. G. Quantum Rescaling, Domain Metastability, and Hybrid Domain-Walls in 2D CrI3 Magnets. Adv. Mater. 2021, 33, 2004138. 10.1002/adma.202004138. [DOI] [PubMed] [Google Scholar]
- Lee J.-U.; Lee S.; Ryoo J. H.; Kang S.; Kim T. Y.; Kim P.; Park C.-H.; Park J.-G.; Cheong H. Ising-Type Magnetic Ordering in Atomically Thin FePS3. Nano Lett. 2016, 16, 7433–7438. 10.1021/acs.nanolett.6b03052. [DOI] [PubMed] [Google Scholar]
- Ising E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 1925, 31, 253–258. 10.1007/BF02980577. [DOI] [Google Scholar]
- Onsager L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. 10.1103/PhysRev.65.117. [DOI] [Google Scholar]
- Wilson K. G.; Kogut J. The Renormalization Group and the Epsilon-Expansion. Phys. Rep. 1974, 12, 75–199. 10.1016/0370-1573(74)90023-4. [DOI] [Google Scholar]
- Lenz W. Beitrag Zum Verständnis Der Magnetischen Erscheinungen in Festen Körpern. Z. Phys. 1920, 21, 613. [Google Scholar]
- Landau L. D. On the Theory of Phase Transitions. Zh. Eksp. Teor. Fiz. 1937, 7, 627. [Google Scholar]
- Peierls R. On Ising’s Model of Ferromagnetism. J. Proc. Cambridge-Philos. Soc. 1936, 32, 477–481. 10.1017/S0305004100019174. [DOI] [Google Scholar]
- Hohenberg P. C. Existence of Long-Range Order in 1 and 2 Dimensions. Phys. Rev. 1967, 158, 383–386. 10.1103/PhysRev.158.383. [DOI] [Google Scholar]
- Mermin N. D.; Wagner H. Absence of Ferromagnetism or Antiferromagnetism in One- or Two-Dimensional Isotropic Heisenberg Models. Phys. Rev. Lett. 1966, 17, 1133–1136. 10.1103/PhysRevLett.17.1133. [DOI] [Google Scholar]
- Bogolyubov N. N.Quantum Statistical Mechanics; World Scientific Publishing: Singapore, 2014; Chapter 2, pp 21–99. [Google Scholar]
- Magnetic Properties of Layered Transition Metal Compounds. Physics and Chemistry of Materials with Low-Dimensional Structures de Jongh L. J. E., Ed.; Springer: Netherlands, 1990; Vol. 9. [Google Scholar]
- Pelissetto A.; Vicari E. Critical Phenomena and Renormalization-Group Theory. Phys. Rep. 2002, 368, 549–727. 10.1016/S0370-1573(02)00219-3. [DOI] [Google Scholar]
- Stanley H. E. Scaling, Universality, and Renormalization: Three Pillars of Modern Critical Phenomena. Rev. Mod. Phys. 1999, 71, S358–S366. 10.1103/RevModPhys.71.S358. [DOI] [Google Scholar]
- Weiss P. J. L’hypothèse du Champ Moléculaire et la Propriété Ferromagnétique. Phys. Théor. Appl. 1907, 6, 661–690. 10.1051/jphystap:019070060066100. [DOI] [Google Scholar]
- Abe R. Some Remarks on Perturbation Theory and Phase Transition with an Application to Anisotropic Ising Model. Prog. Theor. Phys. 1970, 44, 339–347. 10.1143/PTP.44.339. [DOI] [Google Scholar]
- Hikami S.; Tsuneto T. Phase-Transition of Quasi-2 Dimensional Planar System. Prog. Theor. Phys. 1980, 63, 387–401. 10.1143/PTP.63.387. [DOI] [Google Scholar]
- Irkhin V. Y.; Katanin A. A.; Katsnelson M. I. Self-Consistent Spin-Wave Theory of Two-Dimensional Magnets with Impurities. Phys. Rev. B 1999, 60, 14779–14786. 10.1103/PhysRevB.60.14779. [DOI] [Google Scholar]
- Yasuda C.; Todo S.; Hukushima K.; Alet F.; Keller M.; Troyer M.; Takayama H. Néel Temperature of Quasi-Low-Dimensional Heisenberg Antiferromagnets. Phys. Rev. Lett. 2005, 94, 217201. 10.1103/PhysRevLett.94.217201. [DOI] [PubMed] [Google Scholar]
- Stanley H. E.Introduction to Phase Transitions and Critical Phenomena; Oxford University Publishing: London and New York, 1971. [Google Scholar]
- Milosevic S.; Stanley H. E. Calculation of the Scaling Function for the Heisenberg Model. Phys. Rev. B 1972, 5, 2526. 10.1103/PhysRevB.5.2526. [DOI] [Google Scholar]
- Milosevic S.; Stanley H. E. Equation of State Near the Critical Point. I. Calculation of the Scaling Function for S = ∞ Heisenberg Models Using High-Temperature Series Expansions. Phys. Rev. B 1972, 6, 986. 10.1103/PhysRevB.6.986. [DOI] [Google Scholar]
- Milosevic S.; Stanley H. E. Equation of State Near the Critical Point. II. Comparison with Experiment and Possible Universality with Respect to Lattice Structure and Spin Quantum Number. Phys. Rev. B 1972, 6, 1002. 10.1103/PhysRevB.6.1002. [DOI] [Google Scholar]
- Fisher M. E. The Theory of Equilibrium Critical Phenomena. Rep. Prog. Phys. 1967, 30, 615. 10.1088/0034-4885/30/2/306. [DOI] [Google Scholar]
- Lübeck S. Universal Scaling Behavior of Non-Equilibrium Phase Transitions. Int. J. Mod. Phys. B 2004, 18, 3977. 10.1142/S0217979204027748. [DOI] [Google Scholar]
- Essam J. W.; Fisher M. E. Padé Approximant Studies of Lattice Gas and Ising Ferromagnet Below Critical Point. J. Chem. Phys. 1963, 38, 802. 10.1063/1.1733766. [DOI] [Google Scholar]
- Domb C.; Hunter D. L. On Critical Behavior of Ferromagnets. P. Phys. Soc. London 1965, 86, 1147. 10.1088/0370-1328/86/5/127. [DOI] [Google Scholar]
- Widom B. Equation of State in the Neighborhood of the Critical Point. J. Chem. Phys. 1965, 43, 3898. 10.1063/1.1696618. [DOI] [Google Scholar]
- Kadanoff L. P. The Introduction of the Idea That Exponents Could Be Derived from Real-Space Scaling Arguments. Physics 1966, 2, 263. 10.1103/PhysicsPhysiqueFizika.2.263. [DOI] [Google Scholar]
- Patashinskii A. Z.; Pokrovskii V. L. Behavior of Ordered Systems Near Transition Point. Sov. Phys. JETP 1966, 23, 292. [Google Scholar]
- Griffiths R. B. Thermodynamic Functions for Fluids and Ferromagnets Near the Critical Point. Phys. Rev. 1967, 158, 176. 10.1103/PhysRev.158.176. [DOI] [Google Scholar]
- Gibertini M.; Koperski M.; Morpurgo A. F.; Novoselov K. S. Magnetic 2D Materials and Heterostructures. Nat. Nanotechnol. 2019, 14, 408–419. 10.1038/s41565-019-0438-6. [DOI] [PubMed] [Google Scholar]
- Berezinskii V. L. Destruction of Long-Range Order in One-Dimensional and Two-Dimensional Systems Having a Continuous Symmetry Group 1. Classical Systems. Sov. Phys. JETP 1971, 32, 493. [Google Scholar]
- Kosterlitz J. M.; Thouless D. J. Ordering, Metastability and Phase-Transitions in 2 Dimensional Systems. J. Phys. C: Solid State Phys. 1973, 6, 1181–1203. 10.1088/0022-3719/6/7/010. [DOI] [PubMed] [Google Scholar]
- Kaul S. Static Critical Phenomena in Ferromagnets with Quenched Disorder. J. Magn. Magn. Mater. 1985, 53, 5. 10.1016/0304-8853(85)90128-3. [DOI] [Google Scholar]
- LeGuillou J. C.; Zinn-Justin J. Critical Exponents from Field Theory. Phys. Rev. B 1980, 21, 3976. 10.1103/PhysRevB.21.3976. [DOI] [Google Scholar]
- Arrott A.; Noakes J. Approximate Equation of State for Nickel near Its Critical Temperature. Phys. Rev. Lett. 1967, 19, 786. 10.1103/PhysRevLett.19.786. [DOI] [Google Scholar]
- Arrott A. Criterion for Ferromagnetism from Observations of Magnetic Isotherms. Phys. Rev. B 1957, 108, 1394. 10.1103/PhysRev.108.1394. [DOI] [Google Scholar]
- Banerjee S. K. On a Generalised Approach to First and Second Order Magnetic Transitions. Phys. Lett. 1964, 12, 16. 10.1016/0031-9163(64)91158-8. [DOI] [Google Scholar]
- Kouvel J. S.; Fisher M. E. Detailed Magnetic Behavior of Nickel Near Its Curie Point. Phys. Rev. 1964, 136, A1626. 10.1103/PhysRev.136.A1626. [DOI] [Google Scholar]
- Pramanik A. K.; Banerjee A. Critical Behavior at Paramagnetic to Ferromagnetic Phase Transition in Pr0.5Sr0.5MnO3: A Bulk Magnetization Study. Phys. Rev. B 2009, 79, 214426. 10.1103/PhysRevB.79.214426. [DOI] [Google Scholar]
- Mermin N. D. Crystalline Order in 2 Dimensions. Phys. Rev. 1968, 176, 250–254. 10.1103/PhysRev.176.250. [DOI] [Google Scholar]
- Berezinskii V. L. Destruction of Long-Range Order in One-Dimensional and 2-Dimensional Systems Possessing a Continuous Symmetry Group. 2. Quantum Systems. Sov. Phys. JETP 1972, 34, 610–616. [Google Scholar]
- Kosterlitz J. M. Critical Properties of 2-Dimensional XY-Model. J. Phys. C: Solid State Phys. 1974, 7, 1046–1060. 10.1088/0022-3719/7/6/005. [DOI] [Google Scholar]
- Nelson D. R.; Kosterlitz J. M. Universal Jump in Superfluid Density of 2-Dimensional Superfluids. Phys. Rev. Lett. 1977, 39, 1201–1205. 10.1103/PhysRevLett.39.1201. [DOI] [Google Scholar]
- Halperin B. I. On the Hohenberg-Mermin-Wagner Theorem and Its Limitations. J. Stat. Phys. 2019, 175, 521–529. 10.1007/s10955-018-2202-y. [DOI] [Google Scholar]
- Fei Z.; Huang B.; Malinowski P.; Wang W.; Song T.; Sanchez J.; Yao W.; Xiao D.; Zhu X.; May A. F.; Wu W.; Cobden D. H.; Chu J. H.; Xu X. Two-Dimensional Itinerant Ferromagnetism in Atomically Thin Fe3GeTe2. Nat. Mater. 2018, 17, 778–782. 10.1038/s41563-018-0149-7. [DOI] [PubMed] [Google Scholar]
- Bedoya-Pinto A.; Ji J.-R.; Pandeya A. K.; Gargiani P.; Valvidares M.; Sessi P.; Taylor J. M.; Radu F.; Chang K.; Parkin S. S. P. Intrinsic 2D-XY Ferromagnetism in a van der Waals Monolayer. Science 2021, 374, 616–620. 10.1126/science.abd5146. [DOI] [PubMed] [Google Scholar]
- Nakano M.; Wang Y.; Yoshida S.; Matsuoka H.; Majima Y.; Ikeda K.; Hirata Y.; Takeda Y.; Wadati H.; Kohama Y.; Ohigashi Y.; Sakano M.; Ishizaka K.; Iwasa Y. Intrinsic 2D Ferromagnetism in V5Se8 Epitaxial Thin Films. Nano Lett. 2019, 19, 8806–8810. 10.1021/acs.nanolett.9b03614. [DOI] [PubMed] [Google Scholar]
- Wen Y.; Liu Z.; Zhang Y.; Xia C.; Zhai B.; Zhang X.; Zhai G.; Shen C.; He P.; Cheng R.; Yin L.; Yao Y.; Getaye Sendeku M.; Wang Z.; Ye X.; Liu C.; Jiang C.; Shan C.; Long Y.; He J. Tunable Room-Temperature Ferromagnetism in Two-Dimensional Cr2Te3. Nano Lett. 2020, 20, 3130–3139. 10.1021/acs.nanolett.9b05128. [DOI] [PubMed] [Google Scholar]
- Purbawati A.; Coraux J.; Vogel J.; Hadj-Azzem A.; Wu N.; Bendiab N.; Jegouso D.; Renard J.; Marty L.; Bouchiat V.; Sulpice A.; Aballe L.; Foerster M.; Genuzio F.; Locatelli A.; Mentes T. O.; Han Z. V.; Sun X.; Núñez Regueiro M.; Rougemaille N. In-Plane Magnetic Domains and Néel-like Domain Walls in Thin Flakes of the Room Temperature CrTe2 van der Waals Ferromagnet. ACS Appl. Mater. Interfaces 2020, 12, 30702–30710. 10.1021/acsami.0c07017. [DOI] [PubMed] [Google Scholar]
- Kim M.; Kumaravadivel P.; Birkbeck J.; Kuang W.; Xu S. G.; Hopkinson D. G.; Knolle J.; McClarty P. A.; Berdyugin A. I.; Ben Shalom M.; Gorbachev R. V.; Haigh S. J.; Liu S.; Edgar J. H.; Novoselov K. S.; Grigorieva I. V.; Geim A. K. Micromagnetometry of Two-Dimensional Ferromagnets. Nat. Electron. 2019, 2, 457–463. 10.1038/s41928-019-0302-6. [DOI] [Google Scholar]
- Kezilebieke S.; Silveira O. J.; Huda M. N.; Vaňo V.; Aapro M.; Ganguli S. C.; Lahtinen J.; Mansell R.; van Dijken S.; Foster A. S.; Liljeroth P. Electronic and Magnetic Characterization of Epitaxial CrBr3 Monolayers on a Superconducting Substrate. Adv. Mater. 2021, 33, 2006850. 10.1002/adma.202006850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burch K. S.; Mandrus D.; Park J.-G. Magnetism in Two-Dimensional van der Waals Materials. Nature 2018, 563, 47–52. 10.1038/s41586-018-0631-z. [DOI] [PubMed] [Google Scholar]
- Soriano D.; Katsnelson M. I.; Fernández-Rossier J. Magnetic Two-Dimensional Chromium Trihalides: A Theoretical Perspective. Nano Lett. 2020, 20, 6225–6234. 10.1021/acs.nanolett.0c02381. [DOI] [PubMed] [Google Scholar]
- Verzhbitskiy I. A.; Kurebayashi H.; Cheng H.; Zhou J.; Khan S.; Feng Y. P.; Eda G. Controlling the Magnetic Anisotropy in Cr2Ge2Te6 by Electrostatic Gating. Nat. Electron. 2020, 3, 460–465. 10.1038/s41928-020-0427-7. [DOI] [Google Scholar]
- May A. F.; Ovchinnikov D.; Zheng Q.; Hermann R.; Calder S.; Huang B.; Fei Z. Y.; Liu Y. H.; Xu X. D.; McGuire M. A. Ferromagnetism Near Room Temperature in the Cleavable van der Waals Crystal Fe5GeTe2. ACS Nano 2019, 13, 4436–4442. 10.1021/acsnano.8b09660. [DOI] [PubMed] [Google Scholar]
- Seo J.; Kim D. Y.; An E. S.; Kim K.; Kim G. Y.; Hwang S. Y.; Kim D. W.; Jang B. G.; Kim H.; Eom G.; Seo S. Y.; Stania R.; Muntwiler M.; Lee J.; Watanabe K.; Taniguchi T.; Jo Y. J.; Lee J.; Min B. I.; Jo M. H.; et al. Nearly Room Temperature Ferromagnetism in a Magnetic Metal-Rich van der Waals Metal. Sci. Adv. 2020, 6, eaay8912 10.1126/sciadv.aay8912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May A. F.; Du M.-H.; Cooper V. R.; McGuire M. A. Tuning Magnetic Order in the van der Waals Metal Fe5GeTe2 by Cobalt Substitution. Phys. Rev. Mater. 2020, 4, 074008. 10.1103/PhysRevMaterials.4.074008. [DOI] [Google Scholar]
- Wang H.; Liu Y.; Wu P.; Hou W.; Jiang Y.; Li X.; Pandey C.; Chen D.; Yang Q.; Wang H.; Wei D.; Lei N.; Kang W.; Wen L.; Nie T.; Zhao W.; Wang K. L. Above Room-Temperature Ferromagnetism in Wafer-Scale Two-Dimensional van der Waals Fe3GeTe2 Tailored by a Topological Insulator. ACS Nano 2020, 14, 10045–10053. 10.1021/acsnano.0c03152. [DOI] [PubMed] [Google Scholar]
- Avsar A.; Ciarrocchi A.; Pizzochero M.; Unuchek D.; Yazyev O. V.; Kis A. Defect Induced, Layer-Modulated Magnetism in Ultrathin Metallic PtSe2. Nat. Nanotechnol. 2019, 14, 674–678. 10.1038/s41565-019-0467-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avsar A.; Cheon C.-Y.; Pizzochero M.; Tripathi M.; Ciarrocchi A.; Yazyev O. V.; Kis A. Probing Magnetism in Atomically Thin Semiconducting PtSe2. Nat. Commun. 2020, 11, 4806. 10.1038/s41467-020-18521-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham Y. T. H.; Liu M.; Jimenez V. O.; Yu Z.; Kalappattil V.; Zhang F.; Wang K.; Williams T.; Terrones M.; Phan M.-H. Tunable Ferromagnetism and Thermally Induced Spin Flip in Vanadium-Doped Tungsten Diselenide Monolayers at Room Temperature. Adv. Mater. 2020, 32, 2003607. 10.1002/adma.202003607. [DOI] [PubMed] [Google Scholar]
- Yang L.; Wu H.; Zhang W.; Lou X.; Xie Z.; Yu X.; Liu Y.; Chang H. Ta Doping Enhanced Room-Temperature Ferromagnetism in 2D Semiconducting MoTe2 Nanosheets. Adv. Electron. Mater. 2019, 5, 1900552. 10.1002/aelm.201900552. [DOI] [Google Scholar]
- Wang M.-C.; Huang C.-C.; Cheung C.-H.; Chen C.-Y.; Tan S. G.; Huang T.-W.; Zhao Y.; Zhao Y.; Wu G.; Feng Y.-P.; et al. Prospects and Opportunities of 2D van der Waals Magnetic Systems. Ann. Phys. 2020, 532, 1900452. 10.1002/andp.201900452. [DOI] [Google Scholar]
- He J.; Li S. Two-Dimensional Janus Transition-Metal Dichalcogenides with Intrinsic Ferromagnetism and Half-Metallicity. Comput. Mater. Sci. 2018, 152, 151–157. 10.1016/j.commatsci.2018.05.049. [DOI] [Google Scholar]
- Guan Z.; Ni S. Predicted 2D Ferromagnetic Janus VSeTe Monolayer with High Curie Temperature, Large Valley Polarization and Magnetic Crystal Anisotropy. Nanoscale 2020, 12, 22735–22742. 10.1039/D0NR04837B. [DOI] [PubMed] [Google Scholar]
- Ma A.-N.; Wang P.-J.; Zhang C.-W. Intrinsic Ferromagnetism with High Temperature, Strong Anisotropy and Controllable Magnetization in the CrX (X = P, As) Monolayer. Nanoscale 2020, 12, 5464–5470. 10.1039/C9NR10322H. [DOI] [PubMed] [Google Scholar]
- Liu S.; Yuan X.; Zou Y.; Sheng Y.; Huang C.; Zhang E.; Ling J.; Liu Y.; Wang W.; Zhang C.; Zou J.; Wang K.; Xiu F. Wafer-Scale Two-Dimensional Ferromagnetic Fe3GeTe2 Thin Films Grown by Molecular Beam Epitaxy. npj 2D Mater. Appl. 2017, 1, 30. 10.1038/s41699-017-0033-3. [DOI] [Google Scholar]
- Och M.; Martin M.-B.; Dlubak B.; Seneor P.; Mattevi C. Synthesis of Emerging 2D Layered Magnetic Materials. Nanoscale 2021, 13, 2157–2180. 10.1039/D0NR07867K. [DOI] [PubMed] [Google Scholar]
- Baibich M. N.; Broto J. M.; Fert A.; Van Dau F. N.; Petroff F.; Etienne P.; Creuzet G.; Friederich A.; Chazelas J. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 1988, 61, 2472–2475. 10.1103/PhysRevLett.61.2472. [DOI] [PubMed] [Google Scholar]
- Binasch G.; Grünberg P.; Saurenbach F.; Zinn W. Enhanced Magnetoresistance in Layered Magnetic Structures with Antiferromagnetic Interlayer Exchange. Phys. Rev. B 1989, 39, 4828–4830. 10.1103/PhysRevB.39.4828. [DOI] [PubMed] [Google Scholar]
- Fert A.; Grunberg P.; Barthelemy A.; Petroff F.; Zinn W. Layered Magnetic Structures: Interlayer Exchange Coupling and Giant Magnetoresistance. J. Magn. Magn. Mater. 1995, 140–144, 1–8. 10.1016/0304-8853(94)00880-9. [DOI] [Google Scholar]
- Hoffmann A.; Bader S. D. Opportunities at the Frontiers of Spintronics. Phys. Rev. Applied 2015, 4, 047001. 10.1103/PhysRevApplied.4.047001. [DOI] [Google Scholar]
- Marrows C. Addressing an Antiferromagnetic Memory. Science 2016, 351, 558. 10.1126/science.aad8211. [DOI] [PubMed] [Google Scholar]
- Hirohata A.; Yamada K.; Nakatani Y.; Prejbeanu L.; Diény B.; Pirro P.; Hillebrands B. Review on Spintronics: Principles and Device Applications. J. Magn. Magn. Mater. 2020, 509, 166711. 10.1016/j.jmmm.2020.166711. [DOI] [Google Scholar]
- Datta S.; Das B. Electronic Analog of the Electro-Optic Modulator. Appl. Phys. Lett. 1990, 56, 665–667. 10.1063/1.102730. [DOI] [Google Scholar]
- Lou X.; Adelmann C.; Crooker S. A.; Garlid E. S.; Zhang J.; Reddy K. S.; Flexner S. D.; Palmstrøm C. J.; Crowell P. A. Electrical Detection of Spin Transport in Lateral Ferromagnet-Semiconductor Devices. Nat. Phys. 2007, 3, 197–202. 10.1038/nphys543. [DOI] [Google Scholar]
- Wang Z.; Sapkota D.; Taniguchi T.; Watanabe K.; Mandrus D.; Morpurgo A. F. Tunneling Spin Valves Based on Fe3GeTe2/hBN/Fe3GeTe2 van der Waals Heterostructures. Nano Lett. 2018, 18, 4303–4308. 10.1021/acs.nanolett.8b01278. [DOI] [PubMed] [Google Scholar]
- Telford E. J.; Dismukes A. H.; Lee K.; Cheng M.; Wieteska A.; Bartholomew A. K.; Chen Y. S.; Xu X.; Pasupathy A. N.; Zhu X.; Dean C. R.; Roy X. Layered Antiferromagnetism Induces Large Negative Magnetoresistance in the van der Waals Semiconductor CrSBr. Adv. Mater. 2020, 32, 2003240. 10.1002/adma.202003240. [DOI] [PubMed] [Google Scholar]
- Deng Y.; Yu Y.; Shi M. Z.; Guo Z.; Xu Z.; Wang J.; Chen X. H.; Zhang Y. Quantum Anomalous Hall Effect in Intrinsic Magnetic Topological Insulator MnBi2Te4. Science 2020, 367, 895–900. 10.1126/science.aax8156. [DOI] [PubMed] [Google Scholar]
- Kim H. H.; Yang B.; Tian S.; Li C.; Miao G. X.; Lei H.; Tsen A. W. Tailored Tunnel Magnetoresistance Response in Three Ultrathin Chromium Trihalides. Nano Lett. 2019, 19, 5739–5745. 10.1021/acs.nanolett.9b02357. [DOI] [PubMed] [Google Scholar]
- Chen B.; Xu H.; Ma C.; Mattauch S.; Lan D.; Jin F.; Guo Z.; Wan S.; Chen P.; Gao G.; Chen F.; Su Y.; Wu W. All-Oxide–Based Synthetic Antiferromagnets Exhibiting Layer-Resolved Magnetization Reversal. Science 2017, 357, 191–194. 10.1126/science.aak9717. [DOI] [PubMed] [Google Scholar]
- Miao G. X.; Müller M.; Moodera J. S. Magnetoresistance in Double Spin Filter Tunnel Junctions with Nonmagnetic Electrodes and Its Unconventional Bias Dependence. Phys. Rev. Lett. 2009, 102, 076601. 10.1103/PhysRevLett.102.076601. [DOI] [PubMed] [Google Scholar]
- Lin H.; Yan F.; Hu C.; Lv Q.; Zhu W.; Wang Z.; Wei Z.; Chang K.; Wang K. Spin-Valve Effect in Fe3GeTe2/MoS2/Fe3GeTe2 van der Waals Heterostructures. ACS Appl. Mater. Interfaces 2020, 12, 43921–43926. 10.1021/acsami.0c12483. [DOI] [PubMed] [Google Scholar]
- Lee Y. M.; Hayakawa J.; Ikeda S.; Matsukura F.; Ohno H. Effect of Electrode Composition on the Tunnel Magnetoresistance of Pseudo-Spin-Valve Magnetic Tunnel Junction with a MgO Tunnel Barrier. Appl. Phys. Lett. 2007, 90, 212507. 10.1063/1.2742576. [DOI] [Google Scholar]
- Wang Z.; Gibertini M.; Dumcenco D.; Taniguchi T.; Watanabe K.; Giannini E.; Morpurgo A. F. Determining the Phase Diagram of Atomically Thin Layered Antiferromagnet CrCl3. Nat. Nanotechnol. 2019, 14, 1116–1122. 10.1038/s41565-019-0565-0. [DOI] [PubMed] [Google Scholar]
- Klein D. R.; MacNeill D.; Song Q.; Larson D. T.; Fang S.; Xu M.; Ribeiro R. A.; Canfield P. C.; Kaxiras E.; Comin R.; Jarillo-Herrero P. Enhancement of Interlayer Exchange in an Ultrathin Two-Dimensional Magnet. Nat. Phys. 2019, 15, 1255–1260. 10.1038/s41567-019-0651-0. [DOI] [Google Scholar]
- Cai X.; Song T.; Wilson N. P.; Clark G.; He M.; Zhang X.; Taniguchi T.; Watanabe K.; Yao W.; Xiao D.; McGuire M. A.; Cobden D. H.; Xu X. Atomically Thin CrCl3: An In-Plane Layered Antiferromagnetic Insulator. Nano Lett. 2019, 19, 3993. 10.1021/acs.nanolett.9b01317. [DOI] [PubMed] [Google Scholar]
- Kim H. H.; Yang B.; Li S.; Jiang S.; Jin C.; Tao Z.; Nichols G.; Sfigakis F.; Zhong S.; Li C.; Tian S.; Cory D. G.; Miao G. X.; Shan J.; Mak K. F.; Lei H.; Sun K.; Zhao L.; Tsen A. W. Evolution of Interlayer and Intralayer Magnetism in Three Atomically Thin Chromium Trihalides. Proc. Natl. Acad. Sci. U. S. A. 2019, 116, 11131–11136. 10.1073/pnas.1902100116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu J.; Liu F.; Sasase M.; Ienaga K.; Obata Y.; Yukawa R.; Horiba K.; Kumigashira H.; Okuma S.; Inoshita T.; Hosono H. Natural van der Waals Heterostructural Single Crystals with Both Magnetic and Topological Properties. Sci. Adv. 2019, 5, eaax9989 10.1126/sciadv.aax9989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee K.; Dismukes A. H.; Telford E. J.; Wiscons R. A.; Wang J.; Xu X.; Nuckolls C.; Dean C. R.; Roy X.; Zhu X. Magnetic Order and Symmetry in the 2D Semiconductor CrSBr. Nano Lett. 2021, 21, 3511–3517. 10.1021/acs.nanolett.1c00219. [DOI] [PubMed] [Google Scholar]
- Tan C.; Lee J.; Jung S. G.; Park T.; Albarakati S.; Partridge J.; Field M. R.; McCulloch D. G.; Wang L.; Lee C. Hard Magnetic Properties in Nanoflake van der Waals Fe3GeTe2. Nat. Commun. 2018, 9, 1554. 10.1038/s41467-018-04018-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelsen E. J.; Silberglitt R.; Shirane G.; Remeika J. P. Spin Waves in Ferromagnetic CrBr3 Studied by Inelastic Neutron Scattering. Phys. Rev. B 1971, 3, 157–166. 10.1103/PhysRevB.3.157. [DOI] [Google Scholar]
- Yelon W. B.; Silberglitt R. Renormalization of Large-Wave-Vector Magnons in Ferromagnetic CrBr3 Studied by Inelastic Neutron Scattering: Spin-Wave Correlation Effects. Phys. Rev. B 1971, 4, 2280–2286. 10.1103/PhysRevB.4.2280. [DOI] [Google Scholar]
- Tsui D. C.; Dietz R. E.; Walker L. R. Multiple Magnon Excitation in NiO by Electron Tunneling. Phys. Rev. Lett. 1971, 27, 1729–1732. 10.1103/PhysRevLett.27.1729. [DOI] [Google Scholar]
- Yamaguchi K. Inelastic Electron Tunneling Due to Magnons and Phonons of Antiferromagnetic Layered MnPSe3 Semiconductors. Phys. Status Solidi B 2003, 236, 634–639. 10.1002/pssb.200301509. [DOI] [Google Scholar]
- Hirjibehedin C. F.; Lutz C. P.; Heinrich A. J. Spin Coupling in Engineered Atomic Structures. Science 2006, 312, 1021–1024. 10.1126/science.1125398. [DOI] [PubMed] [Google Scholar]
- Lee G.-H.; Yu Y.-J.; Lee C.; Dean C.; Shepard K. L.; Kim P.; Hone J. Electron Tunneling through Atomically Flat and Ultrathin Hexagonal Boron Nitride. Appl. Phys. Lett. 2011, 99, 243114. 10.1063/1.3662043. [DOI] [Google Scholar]
- Amet F.; Williams J. R.; Garcia A. G. F.; Yankowitz M.; Watanabe K.; Taniguchi T.; Goldhaber-Gordon D. Tunneling Spectroscopy of Graphene-Boron-Nitride Heterostructures. Phys. Rev. B 2012, 85, 073405. 10.1103/PhysRevB.85.073405. [DOI] [Google Scholar]
- Ghazaryan D.; Greenaway M. T.; Wang Z.; Guarochico-Moreira V. H.; Vera-Marun I. J.; Yin J.; Liao Y.; Morozov S. V.; Kristanovski O.; Lichtenstein A. I.; Katsnelson M. I.; Withers F.; Mishchenko A.; Eaves L.; Geim A. K.; Novoselov K. S.; Misra A. Magnon-Assisted Tunnelling in van der Waals Heterostructures Based on CrBr3. Nat. Electron. 2018, 1, 344–349. 10.1038/s41928-018-0087-z. [DOI] [Google Scholar]
- Irkhin V. Y.; Katanin A. A.; Katsnelson M. I. Self-Consistent Spin-Wave Theory of Layered Heisenberg Magnets. Phys. Rev. B 1999, 60, 1082–1099. 10.1103/PhysRevB.60.1082. [DOI] [Google Scholar]
- Ho J. T.; Litster J. D. Magnetic Equation of State of CrBr3 Near the Critical Point. Phys. Rev. Lett. 1969, 22, 603–606. 10.1103/PhysRevLett.22.603. [DOI] [Google Scholar]
- Woolsey R. B.; White R. M. Electron-Magnon Interaction in Ferromagnetic Semiconductors. Phys. Rev. B 1970, 1, 4474–4486. 10.1103/PhysRevB.1.4474. [DOI] [Google Scholar]
- Haas C. Spin-Disorder Scattering and Magnetoresistance of Magnetic Semiconductors. Phys. Rev. 1968, 168, 531–538. 10.1103/PhysRev.168.531. [DOI] [Google Scholar]
- Chumak A. V.; Vasyuchka V. I.; Serga A. A.; Hillebrands B. Magnon Spintronics. Nat. Phys. 2015, 11, 453–461. 10.1038/nphys3347. [DOI] [Google Scholar]
- Chumak A. V.; Serga A. A.; Hillebrands B. Magnon Transistor for All-Magnon Data Processing. Nat. Commun. 2014, 5, 4700. 10.1038/ncomms5700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahmoud A.; Ciubotaru F.; Vanderveken F.; Chumak A. V.; Hamdioui S.; Adelmann C.; Cotofana S. Introduction to Spin Wave Computing. J. Appl. Phys. 2020, 128, 161101. 10.1063/5.0019328. [DOI] [Google Scholar]
- Schneider T.; Serga A. A.; Leven B.; Hillebrands B.; Stamps R. L.; Kostylev M. P. Realization of Spin-Wave Logic Gates. Appl. Phys. Lett. 2008, 92, 022505. 10.1063/1.2834714. [DOI] [Google Scholar]
- Tokura Y.; Nagaosa N. Orbital Physics in Transition-Metal Oxides. Science 2000, 288, 462–468. 10.1126/science.288.5465.462. [DOI] [PubMed] [Google Scholar]
- Keimer B.; Kivelson S. A.; Norman M. R.; Uchida S.; Zaanen J. From Quantum Matter to High-Temperature Superconductivity in Copper Oxides. Nature 2015, 518, 179–186. 10.1038/nature14165. [DOI] [PubMed] [Google Scholar]
- Si Q.; Steglich F. Heavy Fermions and Quantum Phase Transitions. Science 2010, 329, 1161–1166. 10.1126/science.1191195. [DOI] [PubMed] [Google Scholar]
- Quintanilla J.; Hooley C. The Strong-Correlations Puzzle. Phys. World 2009, 22, 32. 10.1088/2058-7058/22/06/38. [DOI] [Google Scholar]
- Balents L.; Dean C. R.; Efetov D. K.; Young A. F. Superconductivity and Strong Correlations in Moiré Flat Bands. Nat. Phys. 2020, 16, 725–733. 10.1038/s41567-020-0906-9. [DOI] [Google Scholar]
- Gross C.; Bloch I. Quantum Simulations with Ultracold Atoms in Optical Lattices. Science 2017, 357, 995–1001. 10.1126/science.aal3837. [DOI] [PubMed] [Google Scholar]
- Wang G.; Chernikov A.; Glazov M. M.; Heinz T. F.; Marie X.; Amand T.; Urbaszek B. Colloquium: Excitons in Atomically Thin Transition Metal Dichalcogenides. Rev. Mod. Phys. 2018, 90, 021001. 10.1103/RevModPhys.90.021001. [DOI] [Google Scholar]
- Raja A.; Chaves A.; Yu J.; Arefe G.; Hill H. M.; Rigosi A. F.; Berkelbach T. C.; Nagler P.; Schüller C.; Korn T.; Nuckolls C.; Hone J.; Brus L. E.; Heinz T. F.; Reichman D. R.; Chernikov A. Coulomb Engineering of the Bandgap and Excitons in Two-Dimensional Materials. Nat. Commun. 2017, 8, 15251. 10.1038/ncomms15251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aivazian G.; Gong Z.; Jones A. M.; Chu R.-L.; Yan J.; Mandrus D. G.; Zhang C.; Cobden D.; Yao W.; Xu X. Magnetic Control of Valley Pseudospin in Monolayer WSe2. Nat. Phys. 2015, 11, 148–152. 10.1038/nphys3201. [DOI] [Google Scholar]
- Neumann A.; Lindlau J.; Colombier L.; Nutz M.; Najmaei S.; Lou J.; Mohite A. D.; Yamaguchi H.; Högele A. Opto-Valleytronic Imaging of Atomically Thin Semiconductors. Nat. Nanotechnol. 2017, 12, 329–334. 10.1038/nnano.2016.282. [DOI] [PubMed] [Google Scholar]
- Ross J. S.; Wu S.; Yu H.; Ghimire N. J.; Jones A. M.; Aivazian G.; Yan J.; Mandrus D. G.; Xiao D.; Yao W.; Xu X. Electrical Control of Neutral and Charged Excitons in a Monolayer Semiconductor. Nat. Commun. 2013, 4, 1474. 10.1038/ncomms2498. [DOI] [PubMed] [Google Scholar]
- Chernikov A.; Berkelbach T. C.; Hill H. M.; Rigosi A.; Li Y.; Aslan O. B.; Reichman D. R.; Hybertsen M. S.; Heinz T. F. Exciton Binding Energy and Nonhydrogenic Rydberg Series in Monolayer WS2. Phys. Rev. Lett. 2014, 113, 076802. 10.1103/PhysRevLett.113.076802. [DOI] [PubMed] [Google Scholar]
- Xiao D.; Liu G.-B.; Feng W.; Xu X.; Yao W. Coupled Spin and Valley Physics in Monolayers of MoS2 and Other Group-VI Dichalcogenides. Phys. Rev. Lett. 2012, 108, 196802. 10.1103/PhysRevLett.108.196802. [DOI] [PubMed] [Google Scholar]
- Xu X.; Yao W.; Xiao D.; Heinz T. F. Spin and Pseudospins in Layered Transition Metal Dichalcogenides. Nat. Phys. 2014, 10, 343–350. 10.1038/nphys2942. [DOI] [Google Scholar]
- He K.; Kumar N.; Zhao L.; Wang Z.; Mak K. F.; Zhao H.; Shan J. Tightly Bound Excitons in Monolayer WSe2. Phys. Rev. Lett. 2014, 113, 026803. 10.1103/PhysRevLett.113.026803. [DOI] [PubMed] [Google Scholar]
- Shree S.; Paradisanos I.; Marie X.; Robert C.; Urbaszek B. Guide to Optical Spectroscopy of Layered Semiconductors. Nat. Rev. Phys. 2021, 3, 39–54. 10.1038/s42254-020-00259-1. [DOI] [Google Scholar]
- Wigner E. On the Interaction of Electrons in Metals. Phys. Rev. 1934, 46, 1002. 10.1103/PhysRev.46.1002. [DOI] [Google Scholar]
- Stoner E. C. Ferromagnetism. Rep. Prog. Phys. 1947, 11, 43. 10.1088/0034-4885/11/1/304. [DOI] [Google Scholar]
- Bloch F. Bemerkung zur Elektronentheorie des Ferromagnetismus und der Elektrischen Leitfähigkeit. Z. Phys. 1929, 57, 545–555. 10.1007/BF01340281. [DOI] [Google Scholar]
- Attaccalite C.; Moroni S.; Gori-Giorgi P.; Bachelet G. B. Correlation Energy and Spin Polarization in the 2D Electron Gas. Phys. Rev. Lett. 2002, 88, 256601. 10.1103/PhysRevLett.88.256601. [DOI] [PubMed] [Google Scholar]
- Drummond N.; Needs R. Phase Diagram of the Low-Density Two-Dimensional Homogeneous Electron Gas. Phys. Rev. Lett. 2009, 102, 126402. 10.1103/PhysRevLett.102.126402. [DOI] [PubMed] [Google Scholar]
- Tanatar B.; Ceperley D. M. Ground State of the Two-Dimensional Electron Gas. Phys. Rev. B 1989, 39, 5005. 10.1103/PhysRevB.39.5005. [DOI] [PubMed] [Google Scholar]
- Zhu J.; Stormer H.; Pfeiffer L.; Baldwin K.; West K. Spin Susceptibility of an Ultra-Low-Density Two-Dimensional Electron System. Phys. Rev. Lett. 2003, 90, 056805. 10.1103/PhysRevLett.90.056805. [DOI] [PubMed] [Google Scholar]
- Yoon J.; Li C.; Shahar D.; Tsui D.; Shayegan M. Wigner Crystallization and Metal-Insulator Transition of Two-Dimensional Holes in GaAs at B = 0. Phys. Rev. Lett. 1999, 82, 1744. 10.1103/PhysRevLett.82.1744. [DOI] [Google Scholar]
- Hossain M. S.; Ma M.; Rosales K. V.; Chung Y.; Pfeiffer L.; West K.; Baldwin K.; Shayegan M. Observation of Spontaneous Ferromagnetism in a Two-Dimensional Electron System. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 32244–32250. 10.1073/pnas.2018248117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheiwchanchamnangij T.; Lambrecht W. R. Quasiparticle Band Structure Calculation of Monolayer, Bilayer, and Bulk MoS2. Phys. Rev. B 2012, 85, 205302. 10.1103/PhysRevB.85.205302. [DOI] [Google Scholar]
- Molina-Sánchez A.; Sangalli D.; Hummer K.; Marini A.; Wirtz L. Effect of Spin-Orbit Interaction on the Optical Spectra of Single-Layer, Double-Layer, and Bulk MoS2. Phys. Rev. B 2013, 88, 045412. 10.1103/PhysRevB.88.045412. [DOI] [Google Scholar]
- Kormányos A.; Burkard G.; Gmitra M.; Fabian J.; Zólyomi V.; Drummond N. D.; Fal’ko V. k·p Theory for Two-Dimensional Transition Metal Dichalcogenide Semiconductors. 2D Mater. 2015, 2, 022001. 10.1088/2053-1583/2/2/022001. [DOI] [Google Scholar]
- Goryca M.; Li J.; Stier A. V.; Taniguchi T.; Watanabe K.; Courtade E.; Shree S.; Robert C.; Urbaszek B.; Marie X.; Crooker S. A. Revealing Exciton Masses and Dielectric Properties of Monolayer Semiconductors with High Magnetic Fields. Nat. Commun. 2019, 10, 4172. 10.1038/s41467-019-12180-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarenia M.; Neilson D.; Partoens B.; Peeters F. Wigner Crystallization in Transition Metal Dichalcogenides: A New Approach to Correlation Energy. Phys. Rev. B 2017, 95, 115438. 10.1103/PhysRevB.95.115438. [DOI] [Google Scholar]
- Glazov M. Optical Properties of Charged Excitons in Two-Dimensional Semiconductors. J. Chem. Phys. 2020, 153, 034703. 10.1063/5.0012475. [DOI] [PubMed] [Google Scholar]
- Smoleński T.; Cotlet O.; Popert A.; Back P.; Shimazaki Y.; Knüppel P.; Dietler N.; Taniguchi T.; Watanabe K.; Kroner M.; Imamoglu A. Interaction-Induced Shubnikov–de Haas Oscillations in Optical Conductivity of Monolayer MoSe2. Phys. Rev. Lett. 2019, 123, 097403. 10.1103/PhysRevLett.123.097403. [DOI] [PubMed] [Google Scholar]
- Smoleński T.; Dolgirev P. E.; Kuhlenkamp C.; Popert A.; Shimazaki Y.; Back P.; Lu X.; Kroner M.; Watanabe K.; Taniguchi T.; Esterlis I.; Demler E.; Imamoğlu A. Signatures of Wigner Crystal of Electrons in a Monolayer Semiconductor. Nature 2021, 595, 53–57. 10.1038/s41586-021-03590-4. [DOI] [PubMed] [Google Scholar]
- Zhou Y.; Sung J.; Brutschea E.; Esterlis I.; Wang Y.; Scuri G.; Gelly R. J.; Heo H.; Taniguchi T.; Watanabe K.; Zaránd G.; Lukin M. D.; Kim P.; Demler E.; Park H. Bilayer Wigner Crystals in a Transition Metal Dichalcogenide Heterostructure. Nature 2021, 595, 48–52. 10.1038/s41586-021-03560-w. [DOI] [PubMed] [Google Scholar]
- Suris R. A.; Kochereshko V. P.; Astakhov G. V.; Yakovlev D. R.; Ossau W.; Nürnberger J.; Faschinger W.; Landwehr G.; Wojtowicz T.; Karczewski G.; Kossut J. Excitons and Trions Modified by Interaction with a Two-Dimensional Electron Gas. Phys. Status Solidi B 2001, 227, 343–352. . [DOI] [Google Scholar]
- Schmidt R.; Enss T.; Pietilä V.; Demler E. Fermi Polarons in Two Dimensions. Phys. Rev. A 2012, 85, 021602. 10.1103/PhysRevA.85.021602. [DOI] [Google Scholar]
- Massignan P.; Zaccanti M.; Bruun G. M. Polarons, Dressed Molecules and Itinerant Ferromagnetism in Ultracold Fermi Gases. Rep. Prog. Phys. 2014, 77, 034401. 10.1088/0034-4885/77/3/034401. [DOI] [PubMed] [Google Scholar]
- Efimkin D. K.; MacDonald A. H. Many-Body Theory of Trion Absorption Features in Two-Dimensional Semiconductors. Phys. Rev. B 2017, 95, 035417. 10.1103/PhysRevB.95.035417. [DOI] [Google Scholar]
- Fey C.; Schmelcher P.; Imamoglu A.; Schmidt R. Theory of Exciton-Electron Scattering in Atomically Thin Semiconductors. Phys. Rev. B 2020, 101, 195417. 10.1103/PhysRevB.101.195417. [DOI] [Google Scholar]
- Roch J. G.; Froehlicher G.; Leisgang N.; Makk P.; Watanabe K.; Taniguchi T.; Warburton R. J. Spin-Polarized Electrons in Monolayer MoS2. Nat. Nanotechnol. 2019, 14, 432–436. 10.1038/s41565-019-0397-y. [DOI] [PubMed] [Google Scholar]
- Sidler M.; Back P.; Cotlet O.; Srivastava A.; Fink T.; Kroner M.; Demler E.; Imamoglu A. Fermi Polaron-Polaritons in Charge-Tunable Atomically Thin Semiconductors. Nat. Phys. 2017, 13, 255–261. 10.1038/nphys3949. [DOI] [Google Scholar]
- Back P.; Sidler M.; Cotlet O.; Srivastava A.; Takemura N.; Kroner M.; Imamoğlu A. Giant Paramagnetism-Induced Valley Polarization of Electrons in Charge-Tunable Monolayer MoSe2. Phys. Rev. Lett. 2017, 118, 237404. 10.1103/PhysRevLett.118.237404. [DOI] [PubMed] [Google Scholar]
- Wang T.; Li Z.; Lu Z.; Li Y.; Miao S.; Lian Z.; Meng Y.; Blei M.; Taniguchi T.; Watanabe K.; Tongay S.; Yao W.; Smirnov D.; Zhang C.; Shi S.-F. Observation of Quantized Exciton Energies in Monolayer WSe2 Under a Strong Magnetic Field. Phys. Rev. X 2020, 10, 021024. 10.1103/PhysRevX.10.021024. [DOI] [Google Scholar]
- Wang Z.; Mak K. F.; Shan J. Strongly Interaction-Enhanced Valley Magnetic Response in Monolayer WSe2. Phys. Rev. Lett. 2018, 120, 066402. 10.1103/PhysRevLett.120.066402. [DOI] [PubMed] [Google Scholar]
- Roch J. G.; Miserev D.; Froehlicher G.; Leisgang N.; Sponfeldner L.; Watanabe K.; Taniguchi T.; Klinovaja J.; Loss D.; Warburton R. J. First-Order Magnetic Phase Transition of Mobile Electrons in Monolayer MoS2. Phys. Rev. Lett. 2020, 124, 187602. 10.1103/PhysRevLett.124.187602. [DOI] [PubMed] [Google Scholar]
- Shimazaki Y.; Kuhlenkamp C.; Schwartz I.; Smoleński T.; Watanabe K.; Taniguchi T.; Kroner M.; Schmidt R.; Knap M.; Imamoğlu A. Optical Signatures of Periodic Charge Distribution in a Mott-Like Correlated Insulator State. Phys. Rev. X 2021, 11, 021027. 10.1103/PhysRevX.11.021027. [DOI] [Google Scholar]
- Gutzwiller M. C. Effect of Correlation on the Ferromagnetism of Transition Metals. Phys. Rev. Lett. 1963, 10, 159. 10.1103/PhysRevLett.10.159. [DOI] [Google Scholar]
- Kanamori J. Electron Correlation and Ferromagnetism of Transition Metals. Prog. Theor. Phys. 1963, 30, 275–289. 10.1143/PTP.30.275. [DOI] [Google Scholar]
- Hubbard J. Electron Correlations in Narrow Energy Bands. Proc. R. Soc. London, Ser. A 1963, 276, 238–257. 10.1098/rspa.1963.0204. [DOI] [Google Scholar]
- Tarruell L.; Sanchez-Palencia L. Quantum Simulation of the Hubbard Model with Ultracold Fermions in Optical Lattices. C. R. Phys. 2018, 19, 365–393. 10.1016/j.crhy.2018.10.013. [DOI] [Google Scholar]
- Wu F.; Lovorn T.; Tutuc E.; MacDonald A. H. Hubbard Model Physics in Transition Metal Dichalcogenide Moiré Bands. Phys. Rev. Lett. 2018, 121, 026402. 10.1103/PhysRevLett.121.026402. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Yuan N. F.; Fu L. Moiré Quantum Chemistry: Charge Transfer in Transition Metal Dichalcogenide Superlattices. Phys. Rev. B 2020, 102, 201115. 10.1103/PhysRevB.102.201115. [DOI] [Google Scholar]
- Padhi B.; Chitra R.; Phillips P. W. Generalized Wigner Crystallization in Moiré Materials. Phys. Rev. B 2021, 103, 125146. 10.1103/PhysRevB.103.125146. [DOI] [Google Scholar]
- Slagle K.; Fu L. Charge Transfer Excitations, Pair Density Waves, and Superconductivity in Moiré Materials. Phys. Rev. B 2020, 102, 235423. 10.1103/PhysRevB.102.235423. [DOI] [Google Scholar]
- Zhan Z.; Zhang Y.; Lv P.; Zhong H.; Yu G.; Guinea F.; Silva-Guillén J. Á.; Yuan S. Tunability of Multiple Ultraflat Bands and Effect of Spin-Orbit Coupling in Twisted Bilayer Transition Metal Dichalcogenides. Phys. Rev. B 2020, 102, 241106. 10.1103/PhysRevB.102.241106. [DOI] [Google Scholar]
- Morales-Durán N.; MacDonald A. H.; Potasz P. Metal-Insulator Transition in Transition Metal Dichalcogenide Heterobilayer Moiré Superlattices. Phys. Rev. B 2021, 103, L241110. 10.1103/PhysRevB.103.L241110. [DOI] [Google Scholar]
- Xian L.; Claassen M.; Kiese D.; Scherer M. M.; Trebst S.; Kennes D. M.; Rubio A. Realization of Nearly Dispersionless Bands with Strong Orbital Anisotropy from Destructive Interference in Twisted Bilayer MoS2. Nat. Commun. 2021, 12, 5644. 10.1038/s41467-021-25922-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang Y.; Li L.; Li T.; Xu Y.; Liu S.; Barmak K.; Watanabe K.; Taniguchi T.; MacDonald A. H.; Shan J.; Mak K. F. Simulation of Hubbard Model Physics in WSe2/WS2 Moiré Superlattices. Nature 2020, 579, 353–358. 10.1038/s41586-020-2085-3. [DOI] [PubMed] [Google Scholar]
- Regan E. C.; Wang D.; Jin C.; Utama M. I. B.; Gao B.; Wei X.; Zhao S.; Zhao W.; Zhang Z.; Yumigeta K.; Blei M.; Carlström J. D.; Watanabe K.; Taniguchi T.; Tongay S.; Crommie M.; Zettl A.; Wang F. Mott and Generalized Wigner Crystal States in WSe2/WS2 Moiré Superlattices. Nature 2020, 579, 359–363. 10.1038/s41586-020-2092-4. [DOI] [PubMed] [Google Scholar]
- Xu Y.; Liu S.; Rhodes D. A.; Watanabe K.; Taniguchi T.; Hone J.; Elser V.; Mak K. F.; Shan J. Correlated Insulating States at Fractional Fillings of Moiré Superlattices. Nature 2020, 587, 214–218. 10.1038/s41586-020-2868-6. [DOI] [PubMed] [Google Scholar]
- Jin C.; Tao Z.; Li T.; Xu Y.; Tang Y.; Zhu J.; Liu S.; Watanabe K.; Taniguchi T.; Hone J. C.; Fu L.; Shan J.; Mak K. F. Stripe Phases in WSe2/WS2 Moiré Superlattices. Nat. Mater. 2021, 20, 940–944. 10.1038/s41563-021-00959-8. [DOI] [PubMed] [Google Scholar]
- Liu E.; Taniguchi T.; Watanabe K.; Gabor N. M.; Cui Y.-T.; Lui C. H. Excitonic and Valley-Polarization Signatures of Fractional Correlated Electronic Phases in a WSe2/WS2 Moiré Superlattice. Phys. Rev. Lett. 2021, 127, 037402. 10.1103/PhysRevLett.127.037402. [DOI] [PubMed] [Google Scholar]
- Raja A.; Waldecker L.; Zipfel J.; Cho Y.; Brem S.; Ziegler J. D.; Kulig M.; Taniguchi T.; Watanabe K.; Malic E.; Heinz T. F.; Berkelbach T. C.; Chernikov A. Dielectric Disorder in Two-Dimensional Materials. Nat. Nanotechnol. 2019, 14, 832–837. 10.1038/s41565-019-0520-0. [DOI] [PubMed] [Google Scholar]
- Zhong D.; Seyler K. L.; Linpeng X.; Wilson N. P.; Taniguchi T.; Watanabe K.; McGuire M. A.; Fu K. M. C.; Xiao D.; Yao W.; Xu X. Layer-Resolved Magnetic Proximity Effect in van der Waals Heterostructures. Nat. Nanotechnol. 2020, 15, 187–191. 10.1038/s41565-019-0629-1. [DOI] [PubMed] [Google Scholar]
- Ciorciaro L.; Kroner M.; Watanabe K.; Taniguchi T.; Imamoglu A. Observation of Magnetic Proximity Effect Using Resonant Optical Spectroscopy of an Electrically Tunable MoSe2/CrBr3 Heterostructure. Phys. Rev. Lett. 2020, 124, 197401. 10.1103/PhysRevLett.124.197401. [DOI] [PubMed] [Google Scholar]
- Lyons T. P.; Gillard D.; Molina-Sánchez A.; Misra A.; Withers F.; Keatley P. S.; Kozikov A.; Taniguchi T.; Watanabe K.; Novoselov K. S.; Fernández-Rossier J.; Tartakovskii A. I. Interplay Between Spin Proximity Effect and Charge-Dependent Exciton Dynamics in MoSe2/CrBr3 van der Waals Heterostructures. Nat. Commun. 2020, 11, 6021. 10.1038/s41467-020-19816-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong D.; Seyler K. L.; Linpeng X.; Cheng R.; Sivadas N.; Huang B.; Schmidgall E.; Taniguchi T.; Watanabe K.; McGuire M. A.; Yao W.; Xiao D.; Fu K.-M. C.; Xu X. Van der Waals Engineering of Ferromagnetic Semiconductor Heterostructures for Spin and Valleytronics. Sci. Adv. 2017, 3, e1603113 10.1126/sciadv.1603113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seyler K. L.; Zhong D.; Huang B.; Linpeng X.; Wilson N. P.; Taniguchi T.; Watanabe K.; Yao W.; Xiao D.; McGuire M. A.; Fu K.-M. C.; Xu X. Valley Manipulation by Optically Tuning the Magnetic Proximity Effect in WSe2/CrI3 Heterostructures. Nano Lett. 2018, 18, 3823–3828. 10.1021/acs.nanolett.8b01105. [DOI] [PubMed] [Google Scholar]
- Li J.; Goryca M.; Wilson N. P.; Stier A. V.; Xu X.; Crooker S. A. Spontaneous Valley Polarization of Interacting Carriers in a Monolayer Semiconductor. Phys. Rev. Lett. 2020, 125, 147602. 10.1103/PhysRevLett.125.147602. [DOI] [PubMed] [Google Scholar]
- Yang S.; Xu X.; Zhu Y.; Niu R.; Xu C.; Peng Y.; Cheng X.; Jia X.; Huang Y.; Xu X.; Lu J.; Ye Y. Odd-Even Layer-Number Effect and Layer-Dependent Magnetic Phase Diagrams in MnBi2Te4. Phys. Rev. X 2021, 11, 011003. 10.1103/PhysRevX.11.011003. [DOI] [Google Scholar]
- McCreary A.; Simpson J.; Mai T.; McMichael R.; Douglas J.; Butch N.; Dennis C.; Aguilar R. V.; Walker A. H.; et al. Quasi-Two-Dimensional Magnon Identification in Antiferromagnetic FePS3via Magneto-Raman Spectroscopy. Phys. Rev. B 2020, 101, 064416. 10.1103/PhysRevB.101.064416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim K.; Lim S. Y.; Lee J.-U.; Lee S.; Kim T. Y.; Park K.; Jeon G. S.; Park C.-H.; Park J.-G.; Cheong H. Suppression of Magnetic Ordering in XXZ-Type Antiferromagnetic Monolayer NiPS3. Nat. Commun. 2019, 10, 345. 10.1038/s41467-018-08284-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long G.; Henck H.; Gibertini M.; Dumcenco D.; Wang Z.; Taniguchi T.; Watanabe K.; Giannini E.; Morpurgo A. F. Persistence of Magnetism in Atomically Thin MnPS3 Crystals. Nano Lett. 2020, 20, 2452. 10.1021/acs.nanolett.9b05165. [DOI] [PubMed] [Google Scholar]
- Gong C.; Zhang X. Two-Dimensional Magnetic Crystals and Emergent Heterostructure Devices. Science 2019, 363, eaav4450 10.1126/science.aav4450. [DOI] [PubMed] [Google Scholar]
- Ningrum V. P.; Liu B.; Wang W.; Yin Y.; Cao Y.; Zha C.; Xie H.; Jiang X.; Sun Y.; Qin S.; Chen X.; Qin T.; Zhu C.; Wang L.; Huang W. Recent Advances in Two-Dimensional Magnets: Physics and Devices Towards Spintronic Applications. Research 2020, 2020, 1768918. 10.34133/2020/1768918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seyler K.; Zhong D.; Klein D.; Gao S.; Zhang X.; Huang B.; Navarro-Moratalla E.; Yang L.; Cobden D.; McGuire M.; Yao W.; Xiao D.; Jarillo-Herrero P.; Xu X. Ligand-Field Helical Luminescence in a 2D Ferromagnetic Insulator. Nat. Phys. 2018, 14, 277. 10.1038/s41567-017-0006-7. [DOI] [Google Scholar]
- Chu H.; Roh C.; Island J.; Li C.; Lee S.; Chen J.; Park J.-G.; Young A.; Lee J.; Hsieh D. Linear Magnetoelectric Phase in Ultrathin MnPS3 Probed by Optical Second Harmonic Generation. Phys. Rev. Lett. 2020, 124, 027601. 10.1103/PhysRevLett.124.027601. [DOI] [PubMed] [Google Scholar]
- Jin W.; Kim H.; Ye Z.; Li S.; Rezaie P.; Diaz F.; Siddiq S.; Wauer E.; Yang B.; Li C.; Tian S.; Sun K.; Lei H.; Tsen A.; Zhao L.; He R. Raman Fingerprint of Two Terahertz Spin Wave Branches in a Two-Dimensional Honeycomb Ising Ferromagnet. Nat. Commun. 2018, 9, 5122. 10.1038/s41467-018-07547-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S.; Ye Z.; Luo X.; Ye G.; Kim H. H.; Yang B.; Tian S.; Li C.; Lei H.; Tsen A. W.; Sun K.; He R.; Zhao L. Magnetic-Field-Induced Quantum Phase Transitions in a van der Waals Magnet. Phys. Rev. X 2020, 10, 011075. 10.1103/PhysRevX.10.011075. [DOI] [Google Scholar]
- Jin W.; Ye Z.; Luo X.; Yang B.; Ye G.; Yin F.; Kim H.; Rojas L.; Tian S.; Fu Y.; Yan S.; Lei H.; Sun K.; Tsen A.; He R.; Zhao L. Tunable Layered-Magnetism–Assisted Magneto-Raman Effect in a Two-Dimensional Magnet CrI3. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 24664. 10.1073/pnas.2012980117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin W.; Kim H.; Ye Z.; Ye G.; Rojas L.; Luo X.; Yang B.; Yin F.; Horng J.; Tian S.; Fu Y.; Xu G.; Deng H.; Lei H.; Tsen A.; Sun K.; He R.; Zhao L. Observation of the Polaronic Character of Excitons in a Two-Dimensional Semiconducting Magnet CrI3. Nat. Commun. 2020, 11, 4780. 10.1038/s41467-020-18627-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang B.; Cenker J.; Zhang X.; Ray E. L.; Song T.; Taniguchi T.; Watanabe K.; McGuire M. A.; Xiao D.; Xu X. Tuning Inelastic Light Scattering via Symmetry Control in the Two-Dimensional Magnet CrI3. Nat. Nanotechnol. 2020, 15, 212–216. 10.1038/s41565-019-0598-4. [DOI] [PubMed] [Google Scholar]
- Zhang Y.; Wu X.; Lyu B.; Wu M.; Zhao S.; Chen J.; Jia M.; Zhang C.; Wang L.; Wang X.; Chen Y.; Mei J.; Taniguchi T.; Watanabe K.; Yan H.; Liu Q.; Huang L.; Zhao Y.; Huang M. Magnetic Order-Induced Polarization Anomaly of Raman Scattering in 2D Magnet CrI3. Nano Lett. 2020, 20, 729. 10.1021/acs.nanolett.9b04634. [DOI] [PubMed] [Google Scholar]
- McCreary A.; Mai T.; Utermohlen F.; Simpson J.; Garrity K.; Feng X.; Shcherbakov D.; Zhu Y.; Hu J.; Weber D.; Watanabe K.; Taniguchi T.; Goldberger J.; Mao Z.; Lau C.; Lu Y.; Trivedi N.; Aguilar R. V.; Walker A. H.; et al. Distinct Magneto-Raman Signatures of Spin-Flip Phase Transitions in CrI3. Nat. Commun. 2020, 11, 3879. 10.1038/s41467-020-17320-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ubrig N.; Wang Z.; Teyssier J.; Taniguchi T.; Watanabe K.; Giannini E.; Morpurgo A.; Gibertini M. Low-Temperature Monoclinic Layer Stacking in Atomically Thin CrI3 Crystals. 2D Mater. 2020, 7, 015007. 10.1088/2053-1583/ab4c64. [DOI] [Google Scholar]
- Lyu B.; Gao Y.; Zhang Y.; Wang L.; Wu X.; Chen Y.; Zhang J.; Li G.; Huang Q.; Zhang N.; Chen Y.; Mei J.; Yan H.; Zhao Y.; Huang L.; Huang M. Probing the Ferromagnetism and Spin Wave Gap in VI3 by Helicity-Resolved Raman Spectroscopy. Nano Lett. 2020, 20, 6024–6031. 10.1021/acs.nanolett.0c02029. [DOI] [PubMed] [Google Scholar]
- Djurdjić-Mijin S.; Šolajić A.; Pešić J.; Šćepanović M.; Liu Y.; Baum A.; Petrovic C.; Lazarević N.; Popović Z. Lattice Dynamics and Phase Transition in CrI3 Single Crystals. Phys. Rev. B 2018, 98, 104307. 10.1103/PhysRevB.98.104307. [DOI] [Google Scholar]
- McGuire M. A.; Dixit H.; Cooper V. R.; Sales B. C. Coupling of Crystal Structure and Magnetism in the Layered, Ferromagnetic Insulator CrI3. Chem. Mater. 2015, 27, 612–620. 10.1021/cm504242t. [DOI] [Google Scholar]
- Sivadas N.; Okamoto S.; Xu X.; Fennie C. J.; Xiao Di Stacking-Dependent Magnetism in Bilayer CrI3. Nano Lett. 2018, 18, 7658–7664. 10.1021/acs.nanolett.8b03321. [DOI] [PubMed] [Google Scholar]
- Wu M.; Li Z.; Cao T.; Louie S. Physical Origin of Giant Excitonic and Magneto-Optical Responses in Two-Dimensional Ferromagnetic Insulators. Nat. Commun. 2019, 10, 2371. 10.1038/s41467-019-10325-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larson D.; Kaxiras E. Raman Spectrum of CrI3: An ab Initio Study. Phys. Rev. B 2018, 98, 085406. 10.1103/PhysRevB.98.085406. [DOI] [Google Scholar]
- Kerr J. X. On Rotation of the Plane of Polarization by Reflection from the Pole of a Magnet. London Edinb. Dublin Philos. Mag. J. Sci. 1877, 3, 321. 10.1080/14786447708639245. [DOI] [Google Scholar]
- Soriano D.; Cardoso C.; Fernández-Rossier J. Interplay Between Interlayer Exchange and Stacking in CrI3 Bilayers. Solid State Commun. 2019, 299, 113662. 10.1016/j.ssc.2019.113662. [DOI] [Google Scholar]
- Wang H.; Eyert V.; Schwingenschlögl U. Electronic Structure and Magnetic Ordering of the Semiconducting Chromium Trihalides CrCl3, CrBr3, and CrI3. J. Phys.: Condens. Matter 2011, 23, 116003. 10.1088/0953-8984/23/11/116003. [DOI] [PubMed] [Google Scholar]
- Zhang W.-B.; Qu Q.; Zhu P.; Lam C.-H. Robust Intrinsic Ferromagnetism and Half Semiconductivity in Stable Two-Dimensional Single-Layer Chromium Trihalides. J. Mater. Chem. C 2015, 3, 12457–12468. 10.1039/C5TC02840J. [DOI] [Google Scholar]
- Lado J.; Fernández-Rossier J. On the Origin of Magnetic Anisotropy in Two Dimensional CrI3. 2D Mater. 2017, 4, 035002. 10.1088/2053-1583/aa75ed. [DOI] [Google Scholar]
- Jiang P.; Li L.; Liao Z.; Zhao Y.; Zhong Z. Spin Direction-Controlled Electronic Band Structure in Two-Dimensional Ferromagnetic CrI3. Nano Lett. 2018, 18, 3844. 10.1021/acs.nanolett.8b01125. [DOI] [PubMed] [Google Scholar]
- Gao Y.; Wang J.; Li Z.; Yang J.; Xia M.; Hao X.; Xu Y.; Gao F. On the Ferromagnetism and Band Tailoring of CrI3 Single Layer. Phys. Status Solidi RRL 2019, 13, 1800410. 10.1002/pssr.201800410. [DOI] [Google Scholar]
- Kvashnin Y.; Bergman A.; Lichtenstein A.; Katsnelson M. Relativistic Exchange Interactions in CrX3 (X = Cl, Br, I) Monolayers. Phys. Rev. B 2020, 102, 115162. 10.1103/PhysRevB.102.115162. [DOI] [Google Scholar]
- Kim J.; Kim K.-W.; Kim B.; Kang C.-J.; Shin D.; Lee S.-H.; Min B.-C.; Park N. Exploitable Magnetic Anisotropy of the Two-Dimensional Magnet CrI3. Nano Lett. 2020, 20, 929. 10.1021/acs.nanolett.9b03815. [DOI] [PubMed] [Google Scholar]
- Cadiz F.; Courtade E.; Robert C.; Wang G.; Shen Y.; Cai H.; Taniguchi T.; Watanabe K.; Carrere H.; Lagarde D.; Manca M.; Amand T.; Renucci P.; Tongay S.; Marie X.; Urbaszek B. Excitonic Linewidth Approaching the Homogeneous Limit in MoS2-Based van der Waals Heterostructures. Phys. Rev. X 2017, 7, 021026. 10.1103/PhysRevX.7.021026. [DOI] [Google Scholar]
- Brotons-Gisbert M.; Baek H.; Molina-Sánchez A.; Campbell A.; Scerri E.; White D.; Watanabe K.; Taniguchi T.; Bonato C.; Gerardot B. D. Spin-Layer Locking of Interlayer Excitons Trapped in Moiré Potentials. Nat. Mater. 2020, 19, 630–636. 10.1038/s41563-020-0687-7. [DOI] [PubMed] [Google Scholar]
- Baek H.; Brotons-Gisbert M.; Koong Z.; Campbell A.; Rambach M.; Watanabe K.; Taniguchi T.; Gerardot B. Highly Energy-Tunable Quantum Light from Moiré-trapped Excitons. Sci. Adv. 2020, 6, eaba8526 10.1126/sciadv.aba8526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu E.; Barré E.; van Baren J.; Wilson M.; Taniguchi T.; Watanabe K.; Cui Y.-T.; Gabor N. M.; Heinz T. F.; Chang Y.-C.; Lui C. H. Signatures of Moiré Trions in WSe2/MoSe2 Heterobilayers. Nature 2021, 594, 46–50. 10.1038/s41586-021-03541-z. [DOI] [PubMed] [Google Scholar]
- Brotons-Gisbert M.; Baek H.; Campbell A.; Watanabe K.; Taniguchi T.; Gerardot B. D. Moiré-Trapped Interlayer Trions in a Charge-Tunable WSe2/MoSe2 Heterobilayer. Phys. Rev. X 2021, 11, 031033. 10.1103/PhysRevX.11.031033. [DOI] [Google Scholar]
- Baek H.; Brotons-Gisbert M.; Campbell A.; Vitale V.; Lischner J.; Watanabe K.; Taniguchi T.; Gerardot B. D. Optical Read-Out of Coulomb Staircases in a Moiré Superlattice via Trapped Interlayer Trions. Nat. Nanotechnol. 2021, 16, 1237–1243. 10.1038/s41565-021-00970-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin C.; Tao Z.; Kang K.; Watanabe K.; Taniguchi T.; Mak K. F.; Shan J. Imaging and Control of Critical Fluctuations in Two-Dimensional Magnets. Nat. Mater. 2020, 19, 1290–1294. 10.1038/s41563-020-0706-8. [DOI] [PubMed] [Google Scholar]
- Zhang Z.; Shang J.; Jiang C.; Rasmita A.; Gao W.; Yu T. Direct Photoluminescence Probing of Ferromagnetism in Monolayer Two-Dimensional CrBr3. Nano Lett. 2019, 19, 3138–3142. 10.1021/acs.nanolett.9b00553. [DOI] [PubMed] [Google Scholar]
- Meijer M. J.; Lucassen J.; Duine R. A.; Swagten H. J.; Koopmans B.; Lavrijsen R.; Guimarães M. H. D. Chiral Spin Spirals at the Surface of the van der Waals Ferromagnet Fe3GeTe2. Nano Lett. 2020, 20, 8563–8568. 10.1021/acs.nanolett.0c03111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H.; Wang C.; Li Z.-A.; Tian H.; Shi Y.; Yang H.; Li J. Characteristics and Temperature-Field-Thickness Evolutions of Magnetic Domain Structures in van der Waals Magnet Fe3GeTe2 Nanolayers. Appl. Phys. Lett. 2020, 116, 192403. 10.1063/5.0009484. [DOI] [Google Scholar]
- Dzyaloshinsky I. A. Thermodynamic Theory of “Weak” Ferromagnetism of Antiferromagnetics. J. Phys. Chem. Solids 1958, 4, 241–255. 10.1016/0022-3697(58)90076-3. [DOI] [Google Scholar]
- Moriya T. Anisotropic Superexchange Interaction and Weak Ferromagnetism. Phys. Rev. 1960, 120, 91–98. 10.1103/PhysRev.120.91. [DOI] [Google Scholar]
- Laref S.; Kim K. W.; Manchon A. Elusive Dzyaloshinskii-Moriya Interaction in Monolayer Fe3GeTe2. Phys. Rev. B 2020, 102, 060402(R) 10.1103/PhysRevB.102.060402. [DOI] [Google Scholar]
- Sass P. M.; Ge W.; Yan J.; Obeysekera D.; Yang J. J.; Wu W. Magnetic Imaging of Domain Walls in the Antiferromagnetic Topological Insulator MnBi2Te4. Nano Lett. 2020, 20, 2609–2614. 10.1021/acs.nanolett.0c00114. [DOI] [PubMed] [Google Scholar]
- Vasyukov D.; Anahory Y.; Embon L.; Halbertal D.; Cuppens J.; Neeman L.; Finkler A.; Segev Y.; Myasoedov Y.; Rappaport M. L.; Huber M. E.; Zeldov E. A Scanning Superconducting Quantum Interference Device with Single Electron Spin Sensitivity. Nat. Nanotechnol. 2013, 8, 639–644. 10.1038/nnano.2013.169. [DOI] [PubMed] [Google Scholar]
- Tschirhart C. L.; Serlin M.; Polshyn H.; Shragai A.; Xia Z.; Zhu J.; Zhang Y.; Watanabe K.; Taniguchi T.; Huber M. E.; Young A. F. Imaging Orbital Ferromagnetism in a Moiré Chern Insulator. Science 2021, 372, 1323–1327. 10.1126/science.abd3190. [DOI] [PubMed] [Google Scholar]
- Sun Q.-C.; Song T.; Anderson E.; Brunner A.; Förster J.; Shalomayeva T.; Taniguchi T.; Watanabe K.; Gräfe J.; Stöhr R.; Xu X.; Wrachtrup J. Magnetic Domains and Domain Wall Pinning in Atomically Thin CrBr3 Revealed by Nanoscale Imaging. Nat. Commun. 2021, 12, 1989. 10.1038/s41467-021-22239-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dovzhenko Y.; Casola F.; Schlotter S.; Zhou T. X.; Büttner F.; Walsworth R. L.; Beach G. S. D.; Yacoby A. Magnetostatic Twists in Room-Temperature Skyrmions Explored by Nitrogen-Vacancy Center Spin Texture Reconstruction. Nat. Commun. 2018, 9, 2712. 10.1038/s41467-018-05158-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Niu B.; Su T.; Francisco B. A.; Ghosh S.; Kargar F.; Huang X.; Lohmann M.; Li J.; Xu Y.; Taniguchi T.; Watanabe K.; Wu Di; Balandin A.; Shi J.; Cui Y.-T. Coexistence of Magnetic Orders in Two-Dimensional Magnet CrI3. Nano Lett. 2020, 20, 553–558. 10.1021/acs.nanolett.9b04282. [DOI] [PubMed] [Google Scholar]
- Uri A.; Grover S.; Cao Y.; Crosse J. A.; Bagani K.; Rodan-Legrain D.; Myasoedov Y.; Watanabe K.; Taniguchi T.; Moon P.; Koshino M.; Jarillo-Herrero P.; Zeldov E. Mapping the Twist-Angle Disorder and Landau Levels in Magic-Angle Graphene. Nature 2020, 581, 47–52. 10.1038/s41586-020-2255-3. [DOI] [PubMed] [Google Scholar]
- Casola F.; van der Sar T.; Yacoby A. Probing Condensed Matter Physics with Magnetometry Based on Nitrogen-Vacancy Centres in Diamond. Nat. Rev. Mater. 2018, 3, 17088. 10.1038/natrevmats.2017.88. [DOI] [Google Scholar]
- Fabre F.; Finco A.; Purbawati A.; Hadj-Azzem A.; Rougemaille N.; Coraux J.; Philip I.; Jacques V. Characterization of Room-Temperature In-Plane Magnetization in Thin Flakes of CrTe2 with a Single-Spin Magnetometer. Phys. Rev. Mater. 2021, 5, 034008. 10.1103/PhysRevMaterials.5.034008. [DOI] [Google Scholar]
- Ku M. J. H.; Zhou T. X.; Li Q.; Shin Y. J.; Shi J. K.; Burch C.; Anderson L. E.; Pierce A. T.; Xie Y.; Hamo A.; Vool U.; Zhang H.; Casola F.; Taniguchi T.; Watanabe K.; Fogler M. M.; Kim P.; Yacoby A.; Walsworth R. L. Imaging Viscous Flow of the Dirac Fluid in Graphene. Nature 2020, 583, 537–541. 10.1038/s41586-020-2507-2. [DOI] [PubMed] [Google Scholar]
- Vool U.; Hamo A.; Varnavides G.; Wang Y.; Zhou T. X.; Kumar N.; Dovzhenko Y.; Qiu Z.; Garcia C. A. C.; Pierce A. T.; Gooth J.; Anikeeva P.; Felser C.; Narang P.; Yacoby A. Imaging Phonon-Mediated Hydrodynamic Flow in WTe2. Nat. Phys. 2021, 17, 1216–1220. 10.1038/s41567-021-01341-w. [DOI] [Google Scholar]
- Broadway D. A.; Scholten S. C.; Tan C.; Dontschuk N.; Lillie S. E.; Johnson B. C.; Zheng G.; Wang Z.; Oganov A. R.; Tian S.; Li C.; Lei H.; Wang L.; Hollenberg L. C. L.; Tetienne J.-P. Imaging Domain Reversal in an Ultrathin van der Waals Ferromagnet. Adv. Mater. 2020, 32, 2003314 10.1002/adma.202003314. [DOI] [PubMed] [Google Scholar]
- Gschneidner K. A. Jr.; Pecharsky V. K.; Tsokol A. O. Recent Developments in Magnetocaloric Materials. Rep. Prog. Phys. 2005, 68, 1479. 10.1088/0034-4885/68/6/R04. [DOI] [Google Scholar]
- Smith A.; Bahl C. R. H.; Bjork R.; Engelbrecht K.; Nielsen K. K.; Pryds N. Materials Challenges for High Performance Magnetic Refrigeration Devices. Adv. Energy Matter. 2012, 2, 1288. 10.1002/aenm.201200167. [DOI] [Google Scholar]
- Kitanovski A. Energy Application of Magnetocaloric Materials. Adv. Energy Mater. 2020, 10, 1903741. 10.1002/aenm.201903741. [DOI] [Google Scholar]
- Lyubina J. Magnetocaloric Materials for Energy Efficient Cooling. J. Phys. D: Appl. Phys. 2017, 50, 053002. 10.1088/1361-6463/50/5/053002. [DOI] [Google Scholar]
- Pecharsky V.; Gscheidner K. A. Jr. Magnetocaloric Effect and Magnetic Refrigeration. J. Magn. Magn. Mater. 1999, 200, 44. 10.1016/S0304-8853(99)00397-2. [DOI] [Google Scholar]
- Griffiths D. J.Introduction to Electrodynamics, 3rd ed.; Prentice Hall Inc.: Upper Saddle River, NJ, 1999. [Google Scholar]
- Franco V.; Conde A.; Romero-Enrique J. M.; Blázquez J. S. A Universal Curve for the Magnetocaloric Effect: An Analysis Based on Scaling Relations. J. Phys.: Condens. Matter. 2008, 20, 285207. 10.1088/0953-8984/20/28/285207. [DOI] [Google Scholar]
- Franco V.; Blazquez J. S.; Conde A. Field Dependence of the Magnetocaloric Effect in Materials with a Second Order Phase Transition: A Master Curve for the Magnetic Entropy Change. Appl. Phys. Lett. 2006, 89, 222512. 10.1063/1.2399361. [DOI] [Google Scholar]
- Franco V.; Conde A. Scaling Laws for the Magnetocaloric Effect in Second Order Phase Transitions: From Physics to Applications for the Characterization of Materials. Int. J. Refrig. 2010, 33, 465. 10.1016/j.ijrefrig.2009.12.019. [DOI] [Google Scholar]
- Zhang X. X.; Wen G. H.; Wang F. W.; Wang W. H.; Yu C. H.; Wu G. H. Magnetic Entropy Change in Fe-Based Compound LaFe10.6Si2.4. Appl. Phys. Lett. 2000, 77, 3072. 10.1063/1.1323993. [DOI] [Google Scholar]
- Romero-Muniz C.; Tamura R.; Tanaka S.; Franco V. Applicability of Scaling Behavior and Power Laws in the Analysis of the Magnetocaloric Effect in Second-Order Phase Transition Materials. Phys. Rev. B 2016, 94, 134401. 10.1103/PhysRevB.94.134401. [DOI] [Google Scholar]
- Kong T.; Stolze K.; Timmons E. I.; Tao J.; Ni D.; Guo S.; Yang Z.; Prozorov R.; Cava R. J. VI3: New Layered Ferromagnetic Semiconductor. Adv. Mater. 2019, 31, 1970126. 10.1002/adma.201970126. [DOI] [PubMed] [Google Scholar]
- Tian S.; Zhang J.-F.; Li C.; Ying T.; Li S.; Zhang X.; Liu K.; Lei H. Ferromagnetic van der Waals Crystal VI3. J. Am. Chem. Soc. 2019, 141, 5326–5333. 10.1021/jacs.8b13584. [DOI] [PubMed] [Google Scholar]
- Sun X.; Li W.; Wang X.; Sui Q.; Zhang T.; Wang Z.; Liu L.; Li D.; Feng S.; Zhong S.; Wang H.; Bouchiat V.; Nunez Regueiro M.; Rougemaille N.; Coraux J.; Purbawati A.; Hadj-Azzem A.; Wang Z.; Dong B.; Wu X.; et al. Room Temperature Ferromagnetism in Ultra-Thin van der Waals Crystals of 1T-CrTe2. Nano Res. 2020, 13, 3358–3363. 10.1007/s12274-020-3021-4. [DOI] [Google Scholar]
- Liu Y.; Petrovic C. Critical Behavior of Quasi-Two-Dimensional Semiconducting Ferromagnet Cr2Ge2Te6. Phys. Rev. B 2017, 96, 054406. 10.1103/PhysRevB.96.054406. [DOI] [Google Scholar]
- Liu W.; Dai Y. H.; Yang Y. E.; Fan J. Y.; Pi L.; Zhang L.; Zhang Y. H. Critical Behavior of the Single-Crystalline van der Waals Bonded Ferromagnet Cr2Ge2Te6. Phys. Rev. B 2018, 98, 214420. 10.1103/PhysRevB.98.214420. [DOI] [Google Scholar]
- Fisher M. E.; Ma S. K.; Nickel B. G. Critical Exponents for Long-Range Interactions. Phys. Rev. Lett. 1972, 29, 917. 10.1103/PhysRevLett.29.917. [DOI] [Google Scholar]
- Fischer S. F.; Kaul S. N.; Kronmuller H. Critical Magnetic Properties of Disordered Polycrystalline Cr75Fe25 and Cr70Fe30 Alloys. Phys. Rev. B 2002, 65, 064443. 10.1103/PhysRevB.65.064443. [DOI] [Google Scholar]
- Lin Z.; Lohmann M.; Ali Z.; Tang C.; Li J.; Xing W.; Zhong J.; Jia S.; Han W.; Coh S.; Beyermann W.; Shi J. Pressure-Induced Spin Reorientation Transition in Layered Ferromagnetic Insulator Cr2Ge2Te6. Phys. Rev. Mater. 2018, 2, 051004. 10.1103/PhysRevMaterials.2.051004. [DOI] [Google Scholar]
- Li Z.; Cao T.; Louie S. G. Two-Dimensional Ferromagnetism in Few-Layer van der Waals Crystals: Renormalized Spin-Wave Theory and Calculations. J. Magn. Magn. Mater. 2018, 463, 28. 10.1016/j.jmmm.2018.04.064. [DOI] [Google Scholar]
- Casto L. D.; Clune A. J.; Yokosuk M. O.; Musfeldt J. L.; Williams T. J.; Zhuang H. L.; Lin M. W.; Xiao K.; Hennig R. G.; Sales B. C.; Yan J. Q.; Mandrus D. Strong Spin-Lattice Coupling in CrSiTe3. APL Mater. 2015, 3, 041515. 10.1063/1.4914134. [DOI] [Google Scholar]
- Carteaux V.; Moussa F.; Spiesser M. 2D Ising-Like Ferromagnetic Behaviour for the Lamellar Cr2Si2Te6 Compound: A Neutron Scattering Investigation. Europhys. Lett. 1995, 29, 251. 10.1209/0295-5075/29/3/011. [DOI] [Google Scholar]
- Liu Y.; Petrovic C. Anisotropic Magnetic Entropy Change in Cr2X2Te6 (X = Si and Ge). Phys. Rev. Mater. 2019, 3, 014001. 10.1103/PhysRevMaterials.3.014001. [DOI] [Google Scholar]
- Liu B. J.; Zou Y. M.; Zhang L.; Zhou S. M.; Wang Z.; Wang W. K.; Qu Z.; Zhang Y. H. Critical Behavior of the Quasi Two-Dimensional Semiconducting Ferromagnet CrSiTe3. Sci. Rep. 2016, 6, 33873. 10.1038/srep33873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y.; Luo X. Magnetic Entropy Scaling in Ferromagnetic Semiconductor CrGeTe3. Phys. Status Solidi B 2019, 256, 1900052. 10.1002/pssb.201900052. [DOI] [Google Scholar]
- Lin G.; Zhuang H.; Luo X.; Liu B.; Chen F.; Yan J.; Sun Y.; Zhou J.; Lu W.; Tong P.; Sheng Z. G.; Qu Z.; Song W. H.; Zhu X. B.; Sun Y. P. Tricritical Behavior of the Two-Dimensional Intrinsically Ferromagnetic Semiconductor CrGeTe3. Phys. Rev. B 2017, 95, 245212. 10.1103/PhysRevB.95.245212. [DOI] [Google Scholar]
- Sun Y.; Tong W.; Luo X. Possible Magnetic Correlation above the Ferromagnetic Phase Transition Temperature in Cr2Ge2Te6. Phys. Chem. Chem. Phys. 2019, 21, 25220. 10.1039/C9CP04685B. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Petrovic C. Anisotropic Magnetocaloric Effect in Single Crystals of CrI3. Phys. Rev. B 2018, 97, 174418. 10.1103/PhysRevB.97.174418. [DOI] [Google Scholar]
- Liu Y.; Petrovic C. Three-Dimensional Magnetic Critical Behavior in CrI3. Phys. Rev. B 2018, 97, 014420. 10.1103/PhysRevB.97.014420. [DOI] [Google Scholar]
- Lin G. T.; Luo X.; Chen F. C.; Yan J.; Gao J. J.; Sun Y.; Tong W.; Tong P.; Lu W. J.; Sheng Z. G.; Song W. H.; Zhu X. B.; Sun Y. P. Critical Behavior of Two-Dimensional Intrinsically Ferromagnetic Semiconductor CrI3. Appl. Phys. Lett. 2018, 112, 072405. 10.1063/1.5019286. [DOI] [Google Scholar]
- Yu X. Y.; Zhang X.; Shi Q.; Tian S. J.; Lei H. C.; Xu K.; Hosono H. Large Magnetocaloric Effect in van der Waals Crystal CrBr3. Front. Phys. 2019, 14, 43501. 10.1007/s11467-019-0883-6. [DOI] [Google Scholar]
- Liu Y.; Petrovic C. Anisotropic Magnetocaloric Effect and Critical Behavior in CrCl3. Phys. Rev. B 2020, 102, 014424. 10.1103/PhysRevB.102.014424. [DOI] [Google Scholar]
- Mondal S.; Midya A.; Patidar M. M.; Ganesan V.; Mandal P. Magnetic and Magnetocaloric Properties of Layered van der Waals CrCl3. Appl. Phys. Lett. 2020, 117, 092405. 10.1063/5.0019985. [DOI] [Google Scholar]
- Liu Y.; Abeykoon M.; Petrovic C. Critical Behavior and Magnetocaloric Effect in VI3. Phys. Rev. Res. 2020, 2, 013013. 10.1103/PhysRevResearch.2.013013. [DOI] [Google Scholar]
- Yan J.; Luo X.; Chen F. C.; Gao J. J.; Jiang Z. Z.; Zhao G. C.; Sun Y.; Lv H. Y.; Tian S. J.; Yin Q. W.; Lei H. C.; Lu W. J.; Tong P.; Song W. H.; Zhu X. B.; Sun Y. P. Anisotropic Magnetic Entropy Change in the Hard Ferromagnetic Semiconductor VI3. Phys. Rev. B 2019, 100, 094402. 10.1103/PhysRevB.100.094402. [DOI] [Google Scholar]
- Liu Y.; Li J.; Tao J.; Zhu Y. M.; Petrovic C. Anisotropic Magnetocaloric Cffect in Fe3–xGeTe2. Sci. Rep. 2019, 9, 13233. 10.1038/s41598-019-49654-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y.; Ivanovski V. N.; Petrovic C. Critical Behavior of the van der Waals Bonded Ferromagnet Fe3–xGeTe2. Phys. Rev. B 2017, 96, 144429. 10.1103/PhysRevB.96.144429. [DOI] [Google Scholar]
- Liu W.; Wang Y. M.; Fan J. Y.; Pi L.; Ge M.; Zhang L.; Zhang Y. H. Field-Dependent Anisotropic Magnetic Coupling in Layered Ferromagnetic Fe3–xGeTe2. Phys. Rev. B 2019, 100, 104403. 10.1103/PhysRevB.100.104403. [DOI] [Google Scholar]
- Mao Q. H.; Chen B.; Yang J. H.; Zhang Y. N.; Wang H. D.; Fang M. H. Critical Properties of the Quasi-Two-Dimensional Metallic Ferromagnet Fe2.85GeTe2. J. Phys.: Condens. Matter. 2018, 30, 345802. 10.1088/1361-648X/aad43b. [DOI] [PubMed] [Google Scholar]
- Liu B. J.; Zou Y. M.; Zhou S. M.; Zhang L.; Wang Z.; Li H. X.; Qu Z.; Zhang Y. H. Critical Behavior of the van der Waals Bonded High Tc Ferromagnet Fe3GeTe2. Sci. Rep. 2017, 7, 6184. 10.1038/s41598-017-06671-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Z. X.; Xia W.; Su H.; Yu Z. H.; Fu Y. P.; Chen L. M.; Wang X.; Yu N.; Zou Z. Q.; Guo Y. F. Magnetic Critical Behavior of the van der Waals Fe5GeTe2 Crystal with Near Room Temperature Ferromagnetism. Sci. Rep. 2020, 10, 15345. 10.1038/s41598-020-72203-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y.; Abeykoon M.; Stavitski E.; Attenkofer K.; Petrovic C. Magnetic Anisotropy and Entropy Change in Trigonal Cr5Te8. Phys. Rev. B 2019, 100, 245114. 10.1103/PhysRevB.100.245114. [DOI] [Google Scholar]
- Liu Y.; Petrovic C. Critical Behavior of the Quasi-Two-Dimensional Weak Itinerant Ferromagnet Trigonal Chromium Telluride Cr0.62Te. Phys. Rev. B 2017, 96, 134410. 10.1103/PhysRevB.96.134410. [DOI] [Google Scholar]
- Mondal R.; Kulkarni R.; Thamizhavel A. Anisotropic Magnetic Properties and Critical Behaviour Studies of Trigonal Cr5Te8 Single Crystal. J. Magn. Magn. Mater. 2019, 483, 27. 10.1016/j.jmmm.2019.02.082. [DOI] [Google Scholar]
- Zhang X.; Yu T.; Xue Q.; Lei M.; Jiao R. Critical Behavior and Magnetocaloric Effect in Monoclinic Cr5Te8. J. Alloys Compd. 2018, 750, 798. 10.1016/j.jallcom.2018.03.318. [DOI] [Google Scholar]
- Zhang L. Z.; Zhang A. L.; He X. D.; Ben X. W.; Xiao Q. L.; Lu W. L.; Chen F.; Feng Z. J.; Cao S. X.; Zhang J. C.; Ge J. Y. Critical Behavior and Magnetocaloric Effect of the Quasi-Two-Dimensional Room-Temperature Ferromagnet Cr4Te5. Phys. Rev. B 2020, 101, 214413. 10.1103/PhysRevB.101.214413. [DOI] [Google Scholar]
- Liu Y.; Koch R. J.; Hu Z.; Aryal N.; Stavitski E.; Tong X.; Attenkofer K.; Bozin E. S.; Yin W. G.; Petrovic C. Three-Dimensional Ising Ferrimagnetism of Cr-Fe-Cr Trimers in FeCr2Te4. Phys. Rev. B 2020, 102, 085158. 10.1103/PhysRevB.102.085158. [DOI] [Google Scholar]
- Liu Y.; Petrovic C. Critical Behavior and Magnetocaloric Effect in Mn3Si2Te6. Phys. Rev. B 2018, 98, 064423. 10.1103/PhysRevB.98.064423. [DOI] [Google Scholar]
- Han H.; Zhang L.; Sapkota D.; Hao N.; Ling L.; Du H.; Pi L.; Zhang C.; Mandrus D. G.; Zhang Y. Tricritical Point and Phase Diagram Based on Critical Scaling in the Monoaxial Chiral Helimagnet Cr0.33NbS2. Phys. Rev. B 2017, 96, 094439. 10.1103/PhysRevB.96.094439. [DOI] [Google Scholar]
- Clements E. M.; Das R.; Li L.; Lampen-Kelley P. J.; Phan M. H.; Keppens W.; Mandrus D.; Srikanth H. Critical Behavior and Macroscopic Phase Diagram of the Monoaxial Chiral Helimagnet Cr0.33NbS2. Sci. Rep. 2017, 7, 6545. 10.1038/s41598-017-06728-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C. H.; Yuan Y.; Wang M.; Li P.; Zhang J. W.; Wen Y.; Zhou S. Q.; Zhang X. X. Critical Behavior of Intercalated Quasi-van der Waals Ferromagnet Fe0.26TaS2. Phys. Rev. Mater. 2019, 3, 114403. 10.1103/PhysRevMaterials.3.114403. [DOI] [Google Scholar]
- Taroni A.; Bramwell S. T.; Holdsworth P. C. W. Universal Window for Two-Dimensional Critical Exponents. J. Phys.: Condens Matter. 2008, 20, 275233. 10.1088/0953-8984/20/27/275233. [DOI] [PubMed] [Google Scholar]
- Wildes A. R.; Simonet V.; Ressouche E.; McIntyre G. J.; Avdeev M.; Suard E.; Kimber S. A. J.; Lançon D.; Pepe G.; Moubaraki B.; Hicks T. J. Magnetic Structure of the Quasi-Two-Dimensional Antiferromagnet NiPS3. Phys. Rev. B 2015, 92, 224408. 10.1103/PhysRevB.92.224408. [DOI] [Google Scholar]
- Wildes A. R.; Roennow H. M.; Roessli B.; Harris M. J.; Godfrey K. W. Static and Dynamic Critical Properties of the Quasi-Two-Dimensional Antiferromagnet MnPS3. Phys. Rev. B 2006, 74, 094422. 10.1103/PhysRevB.74.094422. [DOI] [Google Scholar]
- Liu Y.; Hu Z.; Stavitski E.; Attenkofer K.; Petrovic C. Three-Dimensional Ferromagnetism and Magnetotransport in van der Waals Mn-Intercalated Tantalum Disufide. Phys. Rev. B 2021, 103, 144432. 10.1103/PhysRevB.103.144432. [DOI] [Google Scholar]
- Liu Y.; Hu Z.; Stavitski E.; Attenkofer K.; Petrovic C. Magnetic Critical Behavior and Anomalous Hall Effect in 2H-Co0.22TaS2 Single Crystals. Phys. Rev. Research 2021, 3, 023181. 10.1103/PhysRevResearch.3.023181. [DOI] [Google Scholar]
- Liu Y.; Wu L. J.; Tong X.; Li J.; Tao J.; Zhu Y. M.; Petrovic C. Thickness-Dependent Magnetic Order in CrI3 Single Crystals. Sci. Rep. 2019, 9, 13599. 10.1038/s41598-019-50000-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y.; Lu H.; Zhu X.; Tan S.; Feng W.; Liu Q.; Zhang W.; Chen Q.; Liu Y.; Luo X.; Xie D.; Luo L.; Zhang Z.; Lai X. Emergence of Kondo Lattice Behavior in a van der Waals Itinerant Ferromagnet, Fe3GeTe2. Sci. Adv. 2018, 4, eaao6791 10.1126/sciadv.aao6791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May A. F.; Calder S.; Cantoni C.; Cao H. B.; McGuire M. A. Magnetic Structure and Phase Stability of the van der Waals Bonded Ferromagnet Fe3–xGeTe2. Phys. Rev. B 2016, 93, 014411. 10.1103/PhysRevB.93.014411. [DOI] [Google Scholar]
- Shao Y.; Lv W.; Guo J.; Qi B.; Lv W.; Li S.; Guo G.; Zeng Z. The Current Modulation of Anomalous Hall Effect in van der Waals Fe3GeTe2/WTe2 Heterostructures. Appl. Phys. Lett. 2020, 116, 092401. 10.1063/1.5143323. [DOI] [Google Scholar]
- Zhu R.; Zhang W.; Shen W.; Wong P. K. J.; Wang Q. X.; Liang Q. J.; Tian Z.; Zhai Y.; Qiu C. W.; Wee A. T. S. Exchange Bias in van der Waals CrCl3/Fe3GeTe2 Heterostructures. Nano Lett. 2020, 20, 5030–5035. 10.1021/acs.nanolett.0c01149. [DOI] [PubMed] [Google Scholar]
- Li Q.; Yang M. M.; Gong C.; Chopdekar R. V.; N’Diaye A. T.; Turner J.; Chen G.; Schol A.; Shafer P.; Arenholz E.; Schmid A. K.; Wang S.; Liu K.; Gao N.; Admasu A. S.; Cheong S. W.; Hwang C. Y.; Li J.; Wang F.; Zhang X.; et al. Patterning-Induced Ferromagnetism of Fe3GeTe2 van der Waals Materials beyond Room Temperature. Nano Lett. 2018, 18, 5974–5980. 10.1021/acs.nanolett.8b02806. [DOI] [PubMed] [Google Scholar]
- Wang Y. H.; Xian C.; Wang J.; Liu B. J.; Ling L. S.; Zhang L.; Cao L.; Qu Z.; Xiong Y. M. Anisotropic Anomalous Hall Effect in Triangular Itinerant Ferromagnet Fe3GeTe2. Phys. Rev. B 2017, 96, 134428. 10.1103/PhysRevB.96.134428. [DOI] [Google Scholar]
- Abrikosov N. K.; Bagaeva L. A.; Dudkin L. D.; Petrova L. I.; Sokolova V. M. Phase-Equilibria in the Fe-Ge-Te System. Inorg. Mater. 1985, 21, 1467–1472. [Google Scholar]
- Deiseroth H. J.; Aleksandrov K.; Reiner C.; Kienle L.; Kremer R. K. Fe3GeTe2 and Ni3GeTe2 - Two New Layered Transition-Metal Compounds: Crystal Structures, HRTEM Investigations, and Magnetic and Electrical Properties. Eur. J. Inorg. Chem. 2006, 2006, 1561–1567. 10.1002/ejic.200501020. [DOI] [Google Scholar]
- Zhuang H. L.; Kent P. R. C.; Hennig R. G. Strong Anisotropy and Magnetostriction in the Two-Dimensional Stoner Ferromagnet Fe3GeTe2. Phys. Rev. B 2016, 93, 134407. 10.1103/PhysRevB.93.134407. [DOI] [Google Scholar]
- Wohlfarth E. P. Magnetic Properties of Crystalline and Amorphous Alloys: A Systematic Discussion Based on the Rhodes-Wohlfarth Plot. J. Magn. Magn. Mater. 1978, 7, 113–120. 10.1016/0304-8853(78)90163-4. [DOI] [Google Scholar]
- Moriya T. Recent Progress in the Theory of Itinerant Electron Magnetism. J. Magn. Magn. Mater. 1979, 14, 1–46. 10.1016/0304-8853(79)90201-4. [DOI] [Google Scholar]
- Chen B.; Yang J.; Wang H.; Imai M.; Ohta H.; Michioka C.; Yoshimura K.; Fang M. Magnetic Properties of Layered Itinerant Electron Ferromagnet Fe3GeTe2. J. Phys. Soc. Jpn. 2013, 82, 124711. 10.7566/JPSJ.82.124711. [DOI] [Google Scholar]
- Pei K.; Liu S. S.; Zhang E. Z.; Zhao X. B.; Yang L. T.; Ai L. F.; Li Z. H.; Xiu F. X.; Che R. C. Anomalous Spin Behavior in Fe3GeTe2 Driven by Current Pulses. ACS Nano 2020, 14, 9512–9520. 10.1021/acsnano.0c03269. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Stavitski E.; Attenkofer K.; Petrovic C. Anomalous Hall Effect in the van der Waals Bonded Ferromagnet Fe3–xGeTe2. Phys. Rev. B 2018, 97, 165415. 10.1103/PhysRevB.97.165415. [DOI] [Google Scholar]
- Kim K.; Seo J.; Lee E.; Ko K. T.; Kim B. S.; Jang B. G.; Ok J. M.; Lee J.; Jo Y. J.; Kang W.; Shim J. H.; Kim C.; Yeom H. W.; Il Min B.; Yang B. J.; Kim J. S. Large Anomalous Hall Current Induced by Topological Nodal Lines in a Ferromagnetic van der Waals Semimetal. Nat. Mater. 2018, 17, 794–799. 10.1038/s41563-018-0132-3. [DOI] [PubMed] [Google Scholar]
- Zhu J. X.; Janoschek M.; Chaves D. S.; Cezar J. C.; Durakiewicz T.; Ronning F.; Sassa Y.; Mansson M.; Scott B. L.; Wakeham N.; Bauer E. D.; Thompson J. D. Electronic Correlation and Magnetism in the Ferromagnetic Metal Fe3GeTe2. Phys. Rev. B 2016, 93, 144404. 10.1103/PhysRevB.93.144404. [DOI] [Google Scholar]
- Matsukura F.; Tokura Y.; Ohno H. Control of Magnetism by Electric Fields. Nat. Nanotechnol. 2015, 10, 209–220. 10.1038/nnano.2015.22. [DOI] [PubMed] [Google Scholar]
- Ribeiro M.; Gentile G.; Marty A.; Dosenovic D.; Okuno H.; Vergnaud C.; Jacquot J.-F.; Jalabert D.; Longo D.; Ohresser P.; Hallal A.; Chshiev M.; Boulle O.; Bonell F.; Jamet M. Large-Scale Epitaxy of Two-Dimensional van der Waals Room-Temperature Ferromagnet Fe5GeTe2. npj 2D Mater. Appl. 2022, 6, 10. 10.1038/s41699-022-00285-w. [DOI] [Google Scholar]
- Torelli D.; Olsen T. Calculating Critical Temperatures for Ferromagnetic Order in Two-Dimensional Materials. 2D Mater. 2019, 6, 015028. 10.1088/2053-1583/aaf06d. [DOI] [Google Scholar]
- Torelli D.; Thygesen K. S.; Olsen T. High Throughput Computational Screening for 2D Ferromagnetic Materials: The Critical Role of Anisotropy and Local Correlations. 2D Mater. 2019, 6, 045018. 10.1088/2053-1583/ab2c43. [DOI] [Google Scholar]
- Vanherck J.; Bacaksiz C.; Soree B.; Milosevic M. M.; Magnus W. 2D Ferromagnetism at Finite Temperatures Under Quantum Scrutiny. Appl. Phys. Lett. 2020, 117, 052401. 10.1063/5.0015619. [DOI] [Google Scholar]
- Zhu L.; Hou C.; Varma M. C. Quantum Criticality in the Two-Dimensional Dissipative Quantum XY Model. Phys. Rev. B 2016, 94, 235156. 10.1103/PhysRevB.94.235156. [DOI] [Google Scholar]
- Esters M.; Hennig R. G.; Johnson D. C. Dynamic Instabilities in Strongly Correlated VSe2 Monolayers and Bilayers. Phys. Rev. B 2017, 96, 235147. 10.1103/PhysRevB.96.235147. [DOI] [Google Scholar]
- Schlottmann P. Commensurate and Incommensurate Spin Density Waves in Heavy Electron Systems. AIP Adv. 2016, 6, 055701. 10.1063/1.4942549. [DOI] [Google Scholar]
- Spasojevic D.; Janicevic S.; Knezevic M. Numerical Evidence for Critical Behavior of the Two-Dimensional Nonequillibrium Zero-Temperature Random Field Ising Model. Phys. Rev. Lett. 2011, 106, 175701. 10.1103/PhysRevLett.106.175701. [DOI] [PubMed] [Google Scholar]
- Mijatovic S.; Jovkovic D.; Janicevic S.; Spasojevic D. Critical Disorder and Critical Magnetic Field of the Nonequillibrium Athermal Random-Field Ising Model in Thin Systems. Phys. Rev. B 2019, 100, 032113. 10.1103/PhysRevE.100.032113. [DOI] [PubMed] [Google Scholar]
- Guguchia Z.; Amato A. New Magnetic Two-Dimensional Semiconducting Layered Materials for Spintronic Applications. SPG Mitteilungen 2020, 60, 12–15. [Google Scholar]
- Guguchia Z.Investigations of Superconductivity and Magnetism in Iron-Based and Cuprate High-Temperature Superconductors. Ph.D. thesis, University of Zurich, Zurich, Switzerland, 2013. [Google Scholar]
- Guguchia Z. Unconventional Magnetism in Layered Transition Metal Dichalcogenides. Condens. Matter 2020, 5, 42. 10.3390/condmat5020042. [DOI] [Google Scholar]
- Blundell S. J. Spin-Polarized Muons in Condensed Matter Physics. Contemp. Phys. 1999, 40, 175–192. 10.1080/001075199181521. [DOI] [Google Scholar]
- Encyclopedia of Applied Physics; Wiley-VCH Verlag GmbH & Co KGaA: Weinheim, Germany, 2003; Chapter Muon Spin Rotation/Relaxation/Resonance. [Google Scholar]
- Pifer A.; Bowen T.; Kendall K. A High Stopping Density μ + Beam. Nucl. Instrum. Methods 1976, 135, 39–46. 10.1016/0029-554X(76)90823-5. [DOI] [Google Scholar]
- Ford G. W.; Mullin C. J. Scattering of Polarized Dirac Particles on Electrons. Phys. Rev. 1957, 108, 477–481. 10.1103/PhysRev.108.477. [DOI] [Google Scholar]
- de Réotier P. D.; Yaouanc A. Muon Spin Rotation and Relaxation in Magnetic Materials. J. Phys.: Condens. Matter 1997, 9, 9113–9166. 10.1088/0953-8984/9/43/002. [DOI] [Google Scholar]
- Amato A. Heavy-Fermion Systems Studied by μSR Technique. Rev. Mod. Phys. 1997, 69, 1119–1180. 10.1103/RevModPhys.69.1119. [DOI] [Google Scholar]
- Uemura Y. J.; Goko T.; Gat-Malureanu I. M.; Carlo J. P.; Russo P. L.; Savici A. T.; Aczel A.; MacDougall G. J.; Rodriguez J. A.; Luke G. M.; Dunsiger S. R.; McCollam A.; Arai J.; Pfleiderer C.; Böni P.; Yoshimura K.; Baggio-Saitovitch E.; Fontes M. B.; Larrea J.; Sushko Y. V.; et al. Phase Separation and Suppression of Critical Dynamics at Quantum Phase Transitions of MnSi and (Sr1–xCax)RuO3. Nat. Phys. 2007, 3, 29–35. 10.1038/nphys488. [DOI] [Google Scholar]
- Pümpin B.; Keller H.-J.; Kündig W.; Odermatt W.; Patterson B. D.; Schneider J. W.; Simmler H.; Conell S.; Müller K. A.; Bednorz J. G.; Morgenstern I. Internal Magnetic Fields in the High-Temperature Superconductor YBa2Cu3O7−δ from Muon Spin Rotation Experiments. Z. Phys. B: Condens. Matter 1988, 72, 175–180. 10.1007/BF01312133. [DOI] [Google Scholar]
- Keller H. In Earlier and Recent Aspects of Superconductivity, Springer Series in Solid-State Sciences; Bednorz J., Müller K., Eds.; Springer-Verlag: Heidelberg, Germany, 1990; Vol. 90; Chapter Muon Spin Rotation Experiments in High-Tc Superconductors, pp 222–239. [Google Scholar]
- Pümpin B.; Keller H.; Kündig W.; Odermatt W.; Savić I. M.; Schneider J. W.; Simmler H.; Zimmermann P.; Kaldis E.; Rusiecki S.; Maeno Y.; Rossel C. Muon-Spin-Rotation Measurements of the London Penetration Depths in YBa2Cu3O6.97. Phys. Rev. B 1990, 42, 8019–8029. 10.1103/PhysRevB.42.8019. [DOI] [PubMed] [Google Scholar]
- Morenzoni E.; Wojek B. M.; Suter A.; Prokscha T.; Logvenov G.; Božović I. The Meissner Effect in a Strongly Underdoped Cuprate above Its Critical Temperature. Nat. Commun. 2011, 2, 272. 10.1038/ncomms1273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uemura Y. J.; Luke G. M.; Sternlieb B. J.; Brewer J. H.; Carolan J. F.; Hardy W. N.; Kadono R.; Kempton J. R.; Kiefl R. F.; Kreitzman S. R.; Mulhern P.; Riseman T. M.; Williams D. L.; Yang B. X.; Uchida S.; Takagi H.; Gopalakrishnan J.; Sleight A. W.; Subramanian M. A.; Chien C. L.; et al. Universal Correlations Between Tc and ns/m* (Carrier Density over Effective Mass) in High-Tc Cuprate Superconductors. Phys. Rev. Lett. 1989, 62, 2317–2320. 10.1103/PhysRevLett.62.2317. [DOI] [PubMed] [Google Scholar]
- Sonier J. E.; Brewer J. H.; Kiefl R. F. μSR Studies of the Vortex State in Type-II Superconductors. Rev. Mod. Phys. 2000, 72, 769–811. 10.1103/RevModPhys.72.769. [DOI] [Google Scholar]
- Khasanov R.; Shengelaya A.; Maisuradze A.; Mattina F. L.; Bussmann-Holder A.; Keller H.; Müller K. A. Experimental Evidence for Two Gaps in the High-Temperature La1.83Sr0.17CuO4 Superconductor. Phys. Rev. Lett. 2007, 98, 057007. 10.1103/PhysRevLett.98.057007. [DOI] [PubMed] [Google Scholar]
- Keller H.; Bussmann-Holder A.; Müller K. A. Jahn-Teller Physics and High-Tc Superconductivity. Mater. Today 2008, 11, 38–46. 10.1016/S1369-7021(08)70178-0. [DOI] [Google Scholar]
- Uemura Y. J. Condensation, Excitation, Pairing, and Superfluid Density in High-Tc Superconductors: The Magnetic Resonance Mode As a Roton Analogue and a Possible Spin-Mediated Pairing. J. Phys.: Condens. Matter 2004, 16, S4515–S4540. 10.1088/0953-8984/16/40/007. [DOI] [Google Scholar]
- Bernhard C.; Drew A. J.; Schulz L.; Malik V. K.; Rössle M.; Niedermayer C.; Wolf T.; Varma G. D.; Mu G.; Wen H.-H.; Liu H.; Wu G.; Chen X. H. Muon Spin Rotation Study of Magnetism and Superconductivity in BaFe2–xCoxAs2 and Pr1–xSrxFeAsO. New J. Phys. 2009, 11, 055050. 10.1088/1367-2630/11/5/055050. [DOI] [Google Scholar]
- Luetkens H.; Klauss H.-H.; Kraken M.; Litterst F. J.; Dellmann T.; Klingeler R.; Hess C.; Khasanov R.; Amato A.; Baines C.; Kosmala M.; Schumann O. J.; Braden M.; Hamann-Borrero J.; Leps N.; Kondrat A.; Behr G.; Werner J.; Büchner B. The Electronic Phase Diagram of the LaO1–xFxFeAs Superconductor. Nat. Mater. 2009, 8, 305–309. 10.1038/nmat2397. [DOI] [PubMed] [Google Scholar]
- Luke G. M.; Fudamoto Y.; Kojima K. M.; Larkin M. I.; Merrin J.; Nachumi B.; Uemura Y. J.; Maeno Y.; Mao Z. Q.; Mori Y.; Nakamura H.; Sigrist M. Time-Reversal Symmetry-Breaking Superconductivity in Sr2RuO4. Nature 1998, 394, 558–561. 10.1038/29038. [DOI] [Google Scholar]
- Guguchia Z.; von Rohr F.; Shermadini Z.; Lee A. T.; Banerjee S.; Wieteska A. R.; Marianetti C. A.; Frandsen B. A.; Luetkens H.; Gong Z.; Cheung S. C.; Baines C.; Shengelaya A.; Taniashvili G.; Pasupathy A. N.; Morenzoni E.; Billinge S. J. L.; Amato A.; Cava R. J.; Khasanov R.; et al. Signatures of the Topological s+– Superconducting Order Parameter in the Type-II Weyl Semimetal Td-MoTe2. Nat. Commun. 2017, 8, 1082. 10.1038/s41467-017-01066-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jackson T. J.; Riseman T. M.; Forgan E. M.; Glückler H.; Prokscha T.; Morenzoni E.; Pleines M.; Niedermayer C.; Schatz G.; Luetkens H.; Litterst J. Depth-Resolved Profile of the Magnetic Field beneath the Surface of a Superconductor with a Few nm Resolution. Phys. Rev. Lett. 2000, 84, 4958–4961. 10.1103/PhysRevLett.84.4958. [DOI] [PubMed] [Google Scholar]
- Prokscha T.; Chow K. H.; Stilp E.; Suter A.; Luetkens H.; Morenzoni E.; Nieuwenhuys G. J.; Salman Z.; Scheuermann R. Photo-Induced Persistent Inversion of Germanium in a 200-nm-Deep Surface Region. Sci. Rep. 2013, 3, 2569. 10.1038/srep02569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salman Z.; Prokscha T.; Amato A.; Morenzoni E.; Scheuermann R.; Sedlak K.; Suter A. Direct Spectroscopic Observation of a Shallow Hydrogenlike Donor State in Insulating SrTiO3. Phys. Rev. Lett. 2014, 113, 156801. 10.1103/PhysRevLett.113.156801. [DOI] [PubMed] [Google Scholar]
- Schenck A.Muon Spin Rotation Spectroscopy: Principles and Applications in Solid State Physics; Taylor and Francis Inc: Philadelphia, PA, 1985. [Google Scholar]
- Yaouanc A.; de Réotier P. D.. Muon Spin Rotation Spectroscopy: Principles and Applications in Solid State Physics; Oxford University Press: Oxford, United Kingdom, 2011. [Google Scholar]
- Amato A.Physics with Muons: from Atomic Physics to Condensed Matter Physics. https://www.psi.ch/en/lmu/lectures (accessed 2021-12-07).
- Amato A.; Luetkens H.; Sedlak K.; Stoykov A.; Scheuermann R.; Elender M.; Raselli A.; Graf D. The New Versatile General Purpose Surface-Muon Instrument (GPS) Based on Silicon Photomultipliers for μSR Measurements on a Continuous-Wave Beam. Rev. Sci. Instrum. 2017, 88, 093301. 10.1063/1.4986045. [DOI] [PubMed] [Google Scholar]
- Kubo R.; Toyabe T. In Magnetic Resonance and Relaxation; Blinc R., Ed.; North-Holland: Amsterdam, The Netherlands, 1967; Chapter A Stochastic Model for Low Field Resonance and Relaxation, pp 810–823. [Google Scholar]
- Suter A.; Wojek B.M. Musrfit: A Free Platform-Independent Framework for μSR Data Analysis. Phys. Procedia 2012, 30, 69–73. 10.1016/j.phpro.2012.04.042. [DOI] [Google Scholar]
- Rhodes D.; Chae S. H.; Ribeiro-Palau R.; Hone J. Disorder in van der Waals Heterostructures of 2D Materials. Nat. Mater. 2019, 18, 541–549. 10.1038/s41563-019-0366-8. [DOI] [PubMed] [Google Scholar]
- Cai L.; He J.; Liu Q.; Yao T.; Chen L.; Yan W.; Hu F.; Jiang Y.; Zhao Y.; Hu T.; Sun Z.; Wei S. Vacancy-Induced Ferromagnetism of MoS2 Nanosheets. J. Am. Chem. Soc. 2015, 137, 2622–2627. 10.1021/ja5120908. [DOI] [PubMed] [Google Scholar]
- Guguchia Z.; Kerelsky A.; Edelberg D.; Banerjee S.; von Rohr F.; Scullion D.; Augustin M.; Scully M.; Rhodes D. A.; Shermadini Z.; Luetkens H.; Shengelaya A.; Baines C.; Morenzoni E.; Amato A.; Hone J. C.; Khasanov R.; Billinge S. J. L.; Santos E.; Pasupathy A. N. Magnetism in Semiconducting Molybdenum Dichalcogenides. Sci. Adv. 2018, 4, aat3672. 10.1126/sciadv.aat3672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meseguer-Sánchez J.; Popescu C.; García-Muñoz J.; Luetkens H.; Taniashvili G.; Navarro-Moratalla E.; Guguchia Z.; Santos E. J. G. Coexistence of Structural and Magnetic Phases in van der Waals Magnet CrI3. Nat. Commun. 2021, 12, 6265. 10.1038/s41467-021-26342-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Son S.; Coak M. J.; Lee N.; Kim J.; Kim T. Y.; Hamidov H.; Cho H.; Liu C.; Jarvis D. M.; Brown P. A. C.; Kim J. H.; Park C.-H.; Khomskii D. I.; Saxena S. S.; Park J.-G. Bulk Properties of the van der Waals Hard Ferromagnet VI3. Phys. Rev. B 2019, 99, 041402. 10.1103/PhysRevB.99.041402. [DOI] [Google Scholar]
- Cococcioni M.; de Gironcoli S. Linear Response Approach to the Calculation of the Effective Interaction Parameters in the LDA + U Method. Phys. Rev. B 2005, 71, 035105. 10.1103/PhysRevB.71.035105. [DOI] [Google Scholar]
- Zhang K.; Pan Y.; Wang L.; Mei W.-N.; Wu X. Extended 1D Defect Induced Magnetism in 2D MoS2 Crystal. J. Phys.: Condens. Matter 2020, 32, 215302. 10.1088/1361-648X/ab73a3. [DOI] [PubMed] [Google Scholar]
- Santos E. J. G.; Ayuela A.; Sánchez-Portal D. First-Principles Study of Substitutional Metal Impurities in Graphene: Structural, Electronic and Magnetic Properties. New J. Phys. 2010, 12, 053012. 10.1088/1367-2630/12/5/053012. [DOI] [Google Scholar]
- Oliva R.; Woźniak T.; Dybala F.; Kopaczek J.; Scharoch P.; Kudrawiec R. Hidden Spin-Polarized Bands in Semiconducting 2H-MoTe2. Mater. Res. Lett. 2020, 8, 75–81. 10.1080/21663831.2019.1702113. [DOI] [Google Scholar]
- Fan X.-L.; An Y.-R.; Guo W.-J. Ferromagnetism in Transitional Metal-Doped MoS2 Monolayer. Nanoscale Res. Lett. 2016, 11, 154. 10.1186/s11671-016-1376-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andriotis A. N.; Menon M. Tunable Magnetic Properties of Transition Metal Doped MoS2. Phys. Rev. B 2014, 90, 125304. 10.1103/PhysRevB.90.125304. [DOI] [Google Scholar]
- Ramasubramaniam A.; Naveh D. Mn-Doped Monolayer MoS2: An Atomically Thin Dilute Magnetic Semiconductor. Phys. Rev. B 2013, 87, 195201. 10.1103/PhysRevB.87.195201. [DOI] [Google Scholar]
- Yun W. S.; Lee J. D. Unexpected Strong Magnetism of Cu Doped Single-Layer MoS2 and Its Origin. Phys. Chem. Chem. Phys. 2014, 16, 8990–8996. 10.1039/C4CP00247D. [DOI] [PubMed] [Google Scholar]
- Cheng Y. C.; Zhu Z. Y.; Mi W. B.; Guo Z. B.; Schwingenschlögl U. Prediction of Two-Dimensional Diluted Magnetic Semiconductors: Doped Monolayer MoS2 Systems. Phys. Rev. B 2013, 87, 100401. 10.1103/PhysRevB.87.100401. [DOI] [Google Scholar]
- Mishra R.; Zhou W.; Pennycook S. J.; Pantelides S. T.; Idrobo J.-C. Long-Range Ferromagnetic Ordering in Manganese-Doped Two-Dimensional Dichalcogenides. Phys. Rev. B 2013, 88, 144409. 10.1103/PhysRevB.88.144409. [DOI] [Google Scholar]
- Lu S.-C.; Leburton J.-P. Electronic Structures of Defects and Magnetic Impurities in MoS2 Monolayers. Nanoscale Res. Lett. 2014, 9, 676. 10.1186/1556-276X-9-676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuhr J. D.; Saúl A.; Sofo J. O. Scanning Tunneling Microscopy Chemical Signature of Point Defects on the MoS2(0001) Surface. Phys. Rev. Lett. 2004, 92, 026802. 10.1103/PhysRevLett.92.026802. [DOI] [PubMed] [Google Scholar]
- He J.; Wu K.; Sa R.; Li Q.; Wei Y. Magnetic Properties of Nonmetal Atoms Absorbed MoS2 Monolayers. Appl. Phys. Lett. 2010, 96, 082504. 10.1063/1.3318254. [DOI] [Google Scholar]
- Xiang Z.; Zhang Z.; Xu X.; Zhang Q.; Wang Q.; Yuan C. Room-Temperature Ferromagnetism in Co Doped MoS2 Sheets. Phys. Chem. Chem. Phys. 2015, 17, 15822–15828. 10.1039/C5CP01509J. [DOI] [PubMed] [Google Scholar]
- Krieger J.Doping and Interface Effects in Topological Materials. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2020. [Google Scholar]
- Ataca C.; Şahin H.; Aktürk E.; Ciraci S. Mechanical and Electronic Properties of MoS2 Nanoribbons and Their Defects. J. Phys. Chem. C 2011, 115, 3934–3941. 10.1021/jp1115146. [DOI] [Google Scholar]
- Kerelsky A.; Nipane A.; Edelberg D.; Wang D.; Zhou X.; Motmaendadgar A.; Gao H.; Xie S.; Kang K.; Park J.; Teherani J.; Pasupathy A. Absence of a Band Gap at the Interface of a Metal and Highly Doped Monolayer MoS2. Nano Lett. 2017, 17, 5962–5968. 10.1021/acs.nanolett.7b01986. [DOI] [PubMed] [Google Scholar]
- Zhang F.; Zheng B.; Sebastian A.; Olson D. H.; Liu M.; Fujisawa K.; Pham Y. T. H.; Jimenez V. O.; Kalappattil V.; Miao L.; Zhang T.; Pendurthi R.; Lei Y.; Elías A. L.; Wang Y.; Alem N.; Hopkins P. E.; Das S.; Crespi V. H.; Phan M.-H.; et al. Monolayer Vanadium-Doped Tungsten Disulfide: A Room-Temperature Dilute Magnetic Semiconductor. Adv. Sci. 2020, 7, 2001174. 10.1002/advs.202001174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duong D. L.; Yun S. J.; Kim Y.; Kim S.-G.; Lee Y. H. Long-Range Ferromagnetic Ordering in Vanadium-Doped WSe2 Semiconductor. Appl. Phys. Lett. 2019, 115, 242406. 10.1063/1.5131566. [DOI] [Google Scholar]
- Wang X.; Li D.; Li Z.; Wu C.; Che C.-M.; Chen G.; Cui X. Ferromagnetism in 2D Vanadium Diselenide. ACS Nano 2021, 15, 16236–16241. 10.1021/acsnano.1c05232. [DOI] [PubMed] [Google Scholar]
- Gati E.; Inagaki Y.; Kong T.; Cava R. J.; Furukawa Y.; Canfield P. C.; Bud’ko S. L. Multiple Ferromagnetic Transitions and Structural Distortion in the van der Waals Ferromagnet VI3 at Ambient and Finite Pressures. Phys. Rev. B 2019, 100, 094408. 10.1103/PhysRevB.100.094408. [DOI] [Google Scholar]
- Han W.; Kawakami R. K.; Gmitra M.; Fabian J. Graphene Spintronics. Nat. Nanotechnol. 2014, 9, 794–807. 10.1038/nnano.2014.214. [DOI] [PubMed] [Google Scholar]
- Roche S.; Åkerman J.; Beschoten B.; Charlier J.-C.; Chshiev M.; Prasad Dash S.; Dlubak B.; Fabian J.; Fert A.; Guimarães M.; Guinea F.; Grigorieva I.; Schönenberger C.; Seneor P.; Stampfer C.; Valenzuela S. O.; Waintal X.; van Wees B. Graphene Spintronics: The European Flagship Perspective. 2D Mater. 2015, 2, 030202. 10.1088/2053-1583/2/3/030202. [DOI] [Google Scholar]
- Geim A. K.; Grigorieva I. V. der Waals Heterostructures. Nature 2013, 499, 419–425. 10.1038/nature12385. [DOI] [PubMed] [Google Scholar]
- Tombros N.; Jozsa C.; Popinciuc M.; Jonkman H. T.; van Wees B. J. Electronic Spin Transport and Spin Precession in Single Graphene Layers at Room Temperature. Nature 2007, 448, 571–574. 10.1038/nature06037. [DOI] [PubMed] [Google Scholar]
- Dlubak B.; Martin M.-B.; Deranlot C.; Servet B.; Xavier S.; Mattana R.; Sprinkle M.; Berger C.; De Heer W. A.; Petroff F.; Anane A.; Seneor P.; Fert A. Highly Efficient Spin Transport in Epitaxial Graphene on SiC. Nat. Phys. 2012, 8, 557–561. 10.1038/nphys2331. [DOI] [Google Scholar]
- Drögeler M.; Volmer F.; Wolter M.; Terrés B.; Watanabe K.; Taniguchi T.; Güntherodt G.; Stampfer C.; Beschoten B. Nanosecond Spin Lifetimes in Single- and Few-Layer Graphene–hBN Heterostructures at Room Temperature. Nano Lett. 2014, 14, 6050–6055. 10.1021/nl501278c. [DOI] [PubMed] [Google Scholar]
- Lin C.-C.; Penumatcha A. V.; Gao Y.; Diep V. Q.; Appenzeller J.; Chen Z. Spin Transfer Torque in a Graphene Lateral Spin Valve Assisted by an External Magnetic Field. Nano Lett. 2013, 13, 5177–5181. 10.1021/nl402547m. [DOI] [PubMed] [Google Scholar]
- Dlubak B.; Martin M.-B.; Weatherup R. S.; Yang H.; Deranlot C.; Blume R.; Schloegl R.; Fert A.; Anane A.; Hofmann S.; Seneor P.; Robertson J. Graphene-Passivated Nickel as an Oxidation-Resistant Electrode for Spintronics. ACS Nano 2012, 6, 10930–10934. 10.1021/nn304424x. [DOI] [PubMed] [Google Scholar]
- Cobas E.; Friedman A. L.; van’t Erve O. M. J.; Robinson J. T.; Jonker B. T. Graphene as a Tunnel Barrier: Graphene-Based Magnetic Tunnel Junctions. Nano Lett. 2012, 12, 3000–3004. 10.1021/nl3007616. [DOI] [PubMed] [Google Scholar]
- Martin M.-B.; Dlubak B.; Weatherup R. S.; Yang H.; Deranlot C.; Bouzehouane K.; Petroff F.; Anane A.; Hofmann S.; Robertson J.; Fert A.; Seneor P. Sub-Nanometer Atomic Layer Deposition for Spintronics in Magnetic Tunnel Junctions Based on Graphene Spin-Filtering Membranes. ACS Nano 2014, 8, 7890–7895. 10.1021/nn5017549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W.; Xue L.; Abruña H. D.; Ralph D. C. Magnetic Tunnel Junctions with Single-Layer-Graphene Tunnel Barriers. Phys. Rev. B 2014, 89, 184418. 10.1103/PhysRevB.89.184418. [DOI] [Google Scholar]
- Karpan V. M.; Giovannetti G.; Khomyakov P. A.; Talanana M.; Starikov A. A.; Zwierzycki M.; van den Brink J.; Brocks G.; Kelly P. J. Graphite and Graphene as Perfect Spin Filters. Phys. Rev. Lett. 2007, 99, 176602. 10.1103/PhysRevLett.99.176602. [DOI] [PubMed] [Google Scholar]
- Yazyev O. V.; Pasquarello A. Magnetoresistive Junctions Based on Epitaxial Graphene and Hexagonal Boron Nitride. Phys. Rev. B 2009, 80, 035408. 10.1103/PhysRevB.80.035408. [DOI] [Google Scholar]
- Yazyev O. V.; Helm L. Defect-Induced Magnetism in Graphene. Phys. Rev. B 2007, 75, 125408. 10.1103/PhysRevB.75.125408. [DOI] [Google Scholar]
- Nair R. R.; Sepioni M.; Tsai I.-L.; Lehtinen O.; Keinonen J.; Krasheninnikov A. V.; Thomson T.; Geim A. K.; Grigorieva I. V. Spin-Half Paramagnetism in Graphene Induced by Point Defects. Nat. Phys. 2012, 8, 199–202. 10.1038/nphys2183. [DOI] [Google Scholar]
- Fürst J. A.; Pedersen J. G.; Flindt C.; Mortensen N. A.; Brandbyge M.; Pedersen T. G.; Jauho A.-P. Electronic Properties of Graphene Antidot Lattices. New J. Phys. 2009, 11, 095020. 10.1088/1367-2630/11/9/095020. [DOI] [Google Scholar]
- Yang H.-X.; Chshiev M.; Boukhvalov D. W.; Waintal X.; Roche S. Inducing and Optimizing Magnetism in Graphene Nanomeshes. Phys. Rev. B 2011, 84, 214404. 10.1103/PhysRevB.84.214404. [DOI] [Google Scholar]
- Haugen H.; Huertas-Hernando D.; Brataas A. Spin Transport in Proximity-Induced Ferromagnetic Graphene. Phys. Rev. B 2008, 77, 115406. 10.1103/PhysRevB.77.115406. [DOI] [Google Scholar]
- Yang H. X.; Hallal A.; Terrade D.; Waintal X.; Roche S.; Chshiev M. Proximity Effects Induced in Graphene by Magnetic Insulators: First-Principles Calculations on Spin Filtering and Exchange-Splitting Gaps. Phys. Rev. Lett. 2013, 110, 046603. 10.1103/PhysRevLett.110.046603. [DOI] [PubMed] [Google Scholar]
- Wang Z.; Tang C.; Sachs R.; Barlas Y.; Shi J. Proximity-Induced Ferromagnetism in Graphene Revealed by the Anomalous Hall Effect. Phys. Rev. Lett. 2015, 114, 016603. 10.1103/PhysRevLett.114.016603. [DOI] [PubMed] [Google Scholar]
- Lazić P.; Belashchenko K. D.; Žutić I. Effective Gating and Tunable Magnetic Proximity Effects in Two-Dimensional Heterostructures. Phys. Rev. B 2016, 93, 241401. 10.1103/PhysRevB.93.241401. [DOI] [Google Scholar]
- Zollner K.; Gmitra M.; Frank T.; Fabian J. Theory of Proximity-Induced Exchange Coupling in Graphene on hBN/(Co, Ni). Phys. Rev. B 2016, 94, 155441. 10.1103/PhysRevB.94.155441. [DOI] [Google Scholar]
- Allan G. A. T. Critical Temperatures of Ising Lattice Films. Phys. Rev. B 1970, 1, 352–356. 10.1103/PhysRevB.1.352. [DOI] [Google Scholar]
- Fisher M. E.; Barber M. N. Scaling Theory for Finite-Size Effects in the Critical Region. Phys. Rev. Lett. 1972, 28, 1516–1519. 10.1103/PhysRevLett.28.1516. [DOI] [Google Scholar]
- Ritchie D. S.; Fisher M. E. Finite-Size and Surface Effects in Heisenberg Films. Phys. Rev. B 1973, 7, 480–494. 10.1103/PhysRevB.7.480. [DOI] [Google Scholar]
- Li Y.; Baberschke K. Dimensional Crossover in Ultrathin Ni(111) Films on W(110). Phys. Rev. Lett. 1992, 68, 1208–1211. 10.1103/PhysRevLett.68.1208. [DOI] [PubMed] [Google Scholar]
- Zhang R.; Willis R. F. Thickness-Dependent Curie Temperatures of Ultrathin Magnetic Films: Effect of the Range of Spin-Spin Interactions. Phys. Rev. Lett. 2001, 86, 2665–2668. 10.1103/PhysRevLett.86.2665. [DOI] [PubMed] [Google Scholar]
- Childress J. R.; Chien C. L.; Jankowski A. F. Magnetization, Curie Temperature, and Magnetic Anisotropy of Strained (111) Ni/Au Superlattices. Phys. Rev. B 1992, 45, 2855–2862. 10.1103/PhysRevB.45.2855. [DOI] [PubMed] [Google Scholar]
- Huang F.; Kief M. T.; Mankey G. J.; Willis R. F. Magnetism in the Few-Monolayers Limit: A Surface Magneto-Optic Kerr-Effect Study of the Magnetic Behavior of Ultrathin Films of Co, Ni, and Co-Ni Alloys on Cu(100) and Cu(111). Phys. Rev. B 1994, 49, 3962–3971. 10.1103/PhysRevB.49.3962. [DOI] [PubMed] [Google Scholar]
- Almahmoud E.; Kornev I.; Bellaiche L. Dependence of Curie Temperature on the Thickness of an Ultrathin Ferroelectric Film. Phys. Rev. B 2010, 81, 064105. 10.1103/PhysRevB.81.064105. [DOI] [Google Scholar]
- Back C. H.; Würsch C.; Vaterlaus A.; Ramsperger U.; Maier U.; Pescia D. Experimental Confirmation of Universality for a Phase Transition in Two Dimensions. Nature 1995, 378, 597–600. 10.1038/378597a0. [DOI] [Google Scholar]
- Vélez-Fort E.; Hallal A.; Sant R.; Guillet T.; Abdukayumov K.; Marty A.; Vergnaud C.; Jacquot J.-F.; Jalabert D.; Fujii J.; Vobornik I.; Rault J.; Brookes N. B.; Longo D.; Ohresser P.; Ouerghi A.; Veuillen J.-Y.; Mallet P.; Boukari H.; Okuno H. Ferromagnetism and Rashba Spin–Orbit Coupling in the Two-Dimensional (V,Pt)Se2. ACS Appl. Electron. Mater 2022, 4, 259. 10.1021/acsaelm.1c00992. [DOI] [Google Scholar]
- Kim H. H.; Jiang S.; Yang B.; Zhong S.; Tian S.; Li C.; Lei H.; Shan J.; Mak K. F.; Tsen A. W. Magneto-Memristive Switching in a 2D Layer Antiferromagnet. Adv. Mater. 2020, 32, 1905433. 10.1002/adma.201905433. [DOI] [PubMed] [Google Scholar]
- Wang Y.-P.; Chen X.-Y.; Long M.-Q. Modifications of Magnetic Anisotropy of Fe3GeTe2 by the Electric Field Effect. Appl. Phys. Lett. 2020, 116, 092404. 10.1063/1.5144032. [DOI] [Google Scholar]
- Tan C.; Xie W.-Q.; Zheng G.; Aloufi N.; Albarakati S.; Algarni M.; Li J.; Partridge J.; Culcer D.; Wang X.; Yi J. B.; Tian M.; Xiong Y.; Zhao Y.-J.; Wang L. Gate-Controlled Magnetic Phase Transition in a van der Waals Magnet Fe5GeTe2. Nano Lett. 2021, 21, 5599–5605. 10.1021/acs.nanolett.1c01108. [DOI] [PubMed] [Google Scholar]
- Manchon A.; Železný J.; Miron I. M.; Jungwirth T.; Sinova J.; Thiaville A.; Garello K.; Gambardella P. Current-Induced Spin-Orbit Torques in Ferromagnetic and Antiferromagnetic Systems. Rev. Mod. Phys. 2019, 91, 035004. 10.1103/RevModPhys.91.035004. [DOI] [Google Scholar]
- Alghamdi M.; Lohmann M.; Li J.; Jothi P. R.; Shao Q.; Aldosary M.; Su T.; Fokwa B. P. T.; Shi J. Highly Efficient Spin–Orbit Torque and Switching of Layered Ferromagnet Fe3GeTe2. Nano Lett. 2019, 19, 4400–4405. 10.1021/acs.nanolett.9b01043. [DOI] [PubMed] [Google Scholar]
- Wang X.; Tang J.; Xia X.; He C.; Zhang J.; Liu Y.; Wan C.; Fang C.; Guo C.; Yang W.; Guang Y.; Zhang X.; Xu H.; Wei J.; Liao M.; Lu X.; Feng J.; Li X.; Peng Y.; Wei H.; et al. Current-Driven Magnetization Switching in a van der Waals Ferromagnet Fe3GeTe2. Sci. Adv. 2019, 5, eaaw8904 10.1126/sciadv.aaw8904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dolui K.; Petrović M. D.; Zollner K.; Plecháč P.; Fabian J.; Nikolić B. K. Proximity Spin–Orbit Torque on a Two-Dimensional Magnet Within van der Waals Heterostructure: Current-Driven Antiferromagnet-to-Ferromagnet Reversible Nonequilibrium Phase Transition in Bilayer CrI3. Nano Lett. 2020, 20, 2288–2295. 10.1021/acs.nanolett.9b04556. [DOI] [PubMed] [Google Scholar]
- Gupta V.; Cham T. M.; Stiehl G. M.; Bose A.; Mittelstaedt J. A.; Kang K.; Jiang S.; Mak K. F.; Shan J.; Buhrman R. A.; Ralph D. C. Manipulation of the van der Waals Magnet Cr2Ge2Te6 by Spin–Orbit Torques. Nano Lett. 2020, 20, 7482–7488. 10.1021/acs.nanolett.0c02965. [DOI] [PubMed] [Google Scholar]
- Ostwal V.; Shen T.; Appenzeller J. Efficient Spin-Orbit Torque Switching of the Semiconducting van der Waals Ferromagnet Cr2Ge2Te6. Adv. Mater. 2020, 32, 1906021. 10.1002/adma.201906021. [DOI] [PubMed] [Google Scholar]
- Lohmann M.; Su T.; Niu B.; Hou Y.; Alghamdi M.; Aldosary M.; Xing W.; Zhong J.; Jia S.; Han W.; Wu R.; Cui Y.-T.; Shi J. Probing Magnetism in Insulating Cr2Ge2Te6 by Induced Anomalous Hall Effect in Pt. Nano Lett. 2019, 19, 2397–2403. 10.1021/acs.nanolett.8b05121. [DOI] [PubMed] [Google Scholar]
- Huang M.; Xiang J.; Feng C.; Huang H.; Liu P.; Wu Y.; N’Diaye A. T.; Chen G.; Liang J.; Yang H.; Liang J.; Cui X.; Zhang J.; Lu Y.; Liu K.; Hou D.; Liu L.; Xiang B. Direct Evidence of Spin Transfer Torque on Two-Dimensional Cobalt-Doped MoS2 Ferromagnetic Material. ACS Appl. Electron. Mater. 2020, 2, 1497–1504. 10.1021/acsaelm.0c00384. [DOI] [Google Scholar]
- Schippers C. F.; Swagten H. J. M.; Guimarães M. H. D. Large Interfacial Spin-Orbit Torques in Layered Antiferromagnetic Insulator NiPS3/Ferromagnet Bilayers. Phys. Rev. Mater. 2020, 4, 084007. 10.1103/PhysRevMaterials.4.084007. [DOI] [Google Scholar]
- Karpiak B.; Cummings A. W.; Zollner K.; Vila M.; Khokhriakov D.; Hoque A. M.; Dankert A.; Svedlindh P.; Fabian J.; Roche S.; Dash S. P. Magnetic Proximity in a van der Waals Heterostructure of Magnetic Insulator and Graphene. 2D Mater. 2020, 7, 015026. 10.1088/2053-1583/ab5915. [DOI] [Google Scholar]
- Tang C.; Zhang Z.; Lai S.; Tan Q.; Gao W.-B. Magnetic Proximity Effect in Graphene/CrBr3 van der Waals Heterostructures. Adv. Mater. 2020, 32, 1908498. 10.1002/adma.201908498. [DOI] [PubMed] [Google Scholar]
- Ghiasi T. S.; Kaverzin A. A.; Dismukes A. H.; de Wal D. K.; Roy X.; van Wees B. J. Electrical and Thermal Generation of Spin Currents by Magnetic Bilayer Graphene. Nat. Nanotechnol. 2021, 16, 788–794. 10.1038/s41565-021-00887-3. [DOI] [PubMed] [Google Scholar]
- Tang C.; Cheng B.; Aldosary M.; Wang Z.; Jiang Z.; Watanabe K.; Taniguchi T.; Bockrath M.; Shi J. Approaching Quantum Anomalous Hall Effect in Proximity-Coupled YIG/Graphene/h-BN Sandwich Structure. APL Mater. 2018, 6, 026401. 10.1063/1.5001318. [DOI] [Google Scholar]
- Leutenantsmeyer J. C.; Kaverzin A. A.; Wojtaszek M.; van Wees B. J. Proximity Induced Room Temperature Ferromagnetism in Graphene Probed with Spin Currents. 2D Mater. 2017, 4, 014001. 10.1088/2053-1583/4/1/014001. [DOI] [Google Scholar]
- Wu Y.-F.; Song H.-D.; Zhang L.; Yang X.; Ren Z.; Liu D.; Wu H.-C.; Wu J.; Li J.-G.; Jia Z.; Yan B.; Wu X.; Duan C.-G.; Han G.; Liao Z.-M.; Yu D. Magnetic Proximity Effect in Graphene Coupled to a BiFeO3 Nanoplate. Phys. Rev. B 2017, 95, 195426. 10.1103/PhysRevB.95.195426. [DOI] [Google Scholar]
- Qiao Z.; Ren W.; Chen H.; Bellaiche L.; Zhang Z.; MacDonald A. H.; Niu Q. Quantum Anomalous Hall Effect in Graphene Proximity Coupled to an Antiferromagnetic Insulator. Phys. Rev. Lett. 2014, 112, 116404. 10.1103/PhysRevLett.112.116404. [DOI] [PubMed] [Google Scholar]
- Hallal A.; Ibrahim F.; Yang H.; Roche S.; Chshiev M. Tailoring Magnetic Insulator Proximity Effects in Graphene: First-Principles Calculations. 2D Mater. 2017, 4, 025074. 10.1088/2053-1583/aa6663. [DOI] [PubMed] [Google Scholar]
- Ibrahim F.; Hallal A.; Lerma D. S.; Waintal X.; Tsymbal E. Y.; Chshiev M. Unveiling Multiferroic Proximity Effect in Graphene. 2D Mater. 2020, 7, 015020. 10.1088/2053-1583/ab5319. [DOI] [Google Scholar]
- Zanolli Z. Graphene-Multiferroic Interfaces for Spintronics Applications. Sci. Rep. 2016, 6, 31346. 10.1038/srep31346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingla-Aynés J.; Meijerink R. J.; van Wees B. J. Eighty-Eight Percent Directional Guiding of Spin Currents with 90 μm Relaxation Length in Bilayer Graphene Using Carrier Drift. Nano Lett. 2016, 16, 4825–4830. 10.1021/acs.nanolett.6b01004. [DOI] [PubMed] [Google Scholar]
- Safeer C. K.; Ingla-Aynés J.; Herling F.; Garcia J. H.; Vila M.; Ontoso N.; Calvo M. R.; Roche S.; Hueso L. E.; Casanova F. Room-Temperature Spin Hall Effect in Graphene/MoS2 van der Waals Heterostructures. Nano Lett. 2019, 19, 1074–1082. 10.1021/acs.nanolett.8b04368. [DOI] [PubMed] [Google Scholar]
- Li L.; Jiang S.; Wang Z.; Watanabe K.; Taniguchi T.; Shan J.; Mak K. F. Electrical Switching of Valley Polarization in Monolayer Semiconductors. Phys. Rev. Mater. 2020, 4, 104005. 10.1103/PhysRevMaterials.4.104005. [DOI] [Google Scholar]
- Su T.; Lohmann M.; Li J.; Xu Y.; Niu B.; Alghamdi M.; Zhou H.; Cui Y.; Cheng R.; Taniguchi T.; Watanabe K.; Shi J. Current-Induced CrI3 Surface Spin-Flop Transition Probed by Proximity Magnetoresistance in Pt. 2D Mater. 2020, 7, 045006. 10.1088/2053-1583/ab9dd5. [DOI] [Google Scholar]
- Piquemal-Banci M.; Galceran R.; Dubois S. M.-M.; Zatko V.; Galbiati M.; Godel F.; Martin M.-B.; Weatherup R. S.; Petroff F.; Fert A.; Charlier J.-C.; Robertson J.; Hofmann S.; Dlubak B.; Seneor P. Spin Filtering by Proximity Effects at Hybridized Interfaces in Spin-Valves with 2D Graphene Barriers. Nat. Commun. 2020, 11, 5670. 10.1038/s41467-020-19420-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zatko V.; Galbiati M.; Dubois S. M.-M.; Och M.; Palczynski P.; Mattevi C.; Brus P.; Bezencenet O.; Martin M.-B.; Servet B.; Charlier J.-C.; Godel F.; Vecchiola A.; Bouzehouane K.; Collin S.; Petroff F.; Dlubak B.; Seneor P. Band-Structure Spin-Filtering in Vertical Spin Valves Based on Chemical Vapor Deposited WS2. ACS Nano 2019, 13, 14468–14476. 10.1021/acsnano.9b08178. [DOI] [PubMed] [Google Scholar]
- Yang H.; Vu A. D.; Hallal A.; Rougemaille N.; Coraux J.; Chen G.; Schmid A. K.; Chshiev M. Anatomy and Giant Enhancement of the Perpendicular Magnetic Anisotropy of Cobalt–Graphene Heterostructures. Nano Lett. 2016, 16, 145–151. 10.1021/acs.nanolett.5b03392. [DOI] [PubMed] [Google Scholar]
- Ito N.; Kikkawa T.; Barker J.; Hirobe D.; Shiomi Y.; Saitoh E. Spin Seebeck Effect in the Layered Ferromagnetic Insulators CrSiTe3 and CrGeTe3. Phys. Rev. B 2019, 100, 060402. 10.1103/PhysRevB.100.060402. [DOI] [Google Scholar]
- Xing W.; Qiu L.; Wang X.; Yao Y.; Ma Y.; Cai R.; Jia S.; Xie X.; Han W. Magnon Transport in Quasi-Two-Dimensional van der Waals Antiferromagnets. Phys. Rev. X 2019, 9, 011026. 10.1103/PhysRevX.9.011026. [DOI] [Google Scholar]
- Uchida K.; Ishida M.; Kikkawa T.; Kirihara A.; Murakami T.; Saitoh E. Longitudinal Spin Seebeck Effect: From Fundamentals to Applications. J. Phys.: Condens. Matter 2014, 26, 343202. 10.1088/0953-8984/26/34/343202. [DOI] [PubMed] [Google Scholar]
- Kirihara A.; Uchida K.-i.; Kajiwara Y.; Ishida M.; Nakamura Y.; Manako T.; Saitoh E.; Yorozu S. Spin-Current-Driven Thermoelectric Coating. Nat. Mater. 2012, 11, 686–689. 10.1038/nmat3360. [DOI] [PubMed] [Google Scholar]
- Cornelissen L. J.; Liu J.; Duine R. A.; Youssef J. B.; van Wees B. J. Long-Distance Transport of Magnon Spin Information in a Magnetic Insulator at Room Temperature. Nat. Phys. 2015, 11, 1022–1026. 10.1038/nphys3465. [DOI] [Google Scholar]
- Gomez-Perez J. M.; Vélez S.; Hueso L. E.; Casanova F. Differences in the Magnon Diffusion Length for Electrically and Thermally Driven Magnon Currents in Y3Fe5O12. Phys. Rev. B 2020, 101, 184420. 10.1103/PhysRevB.101.184420. [DOI] [Google Scholar]
- Lebrun R.; Ross A.; Bender S. A.; Qaiumzadeh A.; Baldrati L.; Cramer J.; Brataas A.; Duine R. A.; Kläui M. Tunable Long-Distance Spin Transport in a Crystalline Antiferromagnetic Iron Oxide. Nature 2018, 561, 222–225. 10.1038/s41586-018-0490-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu T.; Peiro J.; de Wal D. K.; Leutenantsmeyer J. C.; Guimarães M. H. D.; van Wees B. J. Spin Caloritronics in a CrBr3-Based Magnetic van der Waals Heterostructure. Phys. Rev. B 2020, 101, 205407. 10.1103/PhysRevB.101.205407. [DOI] [Google Scholar]
- Fert A.; Reyren N.; Cros V. Magnetic Skyrmions: Advances in Physics and Potential Applications. Nat. Rev. Mater. 2017, 2, 17031. 10.1038/natrevmats.2017.31. [DOI] [Google Scholar]
- Everschor-Sitte K.; Masell J.; Reeve R. M.; Kläui M. Perspective: Magnetic Skyrmions—Overview of Recent Progress in an Active Research Field. J. Appl. Phys. 2018, 124, 240901. 10.1063/1.5048972. [DOI] [Google Scholar]
- Thiaville A.; Rohart S.; Jué É.; Cros V.; Fert A. Dynamics of Dzyaloshinskii Domain Walls in Ultrathin Magnetic Films. EPL 2012, 100, 57002. 10.1209/0295-5075/100/57002. [DOI] [Google Scholar]
- Yang H.; Thiaville A.; Rohart S.; Fert A.; Chshiev M. Anatomy of Dzyaloshinskii-Moriya Interaction at Co/Pt Interfaces. Phys. Rev. Lett. 2015, 115, 267210. 10.1103/PhysRevLett.115.267210. [DOI] [PubMed] [Google Scholar]
- Yang H.; Chen G.; Cotta A. A. C.; N’Diaye A. T.; Nikolaev S. A.; Soares E. A.; Macedo W. A. A.; Liu K.; Schmid A. K.; Fert A.; Chshiev M. Significant Dzyaloshinskii–Moriya Interaction at Graphene–Ferromagnet Interfaces Due to the Rashba Effect. Nat. Mater. 2018, 17, 605–609. 10.1038/s41563-018-0079-4. [DOI] [PubMed] [Google Scholar]
- Liang J.; Wang W.; Du H.; Hallal A.; Garcia K.; Chshiev M.; Fert A.; Yang H. Very Large Dzyaloshinskii-Moriya Interaction in Two-Dimensional Janus Manganese Dichalcogenides and Its Application to Realize Skyrmion States. Phys. Rev. B 2020, 101, 184401. 10.1103/PhysRevB.101.184401. [DOI] [Google Scholar]
- Han M.-G.; Garlow J. A.; Liu Y.; Zhang H.; Li J.; DiMarzio D.; Knight M. W.; Petrovic C.; Jariwala D.; Zhu Y. Topological Magnetic-Spin Textures in Two-Dimensional van der Waals Cr2Ge2Te6. Nano Lett. 2019, 19, 7859–7865. 10.1021/acs.nanolett.9b02849. [DOI] [PubMed] [Google Scholar]
- Lu A.-Y.; Zhu H.; Xiao J.; Chuu C.-P.; Han Y.; Chiu M.-H.; Cheng C.-C.; Yang C.-W.; Wei K.-H.; Yang Y.; Wang Y.; Sokaras D.; Nordlund D.; Yang P.; Muller D. A.; Chou M.-Y.; Zhang X.; Li L.-J. Janus Monolayers of Transition Metal Dichalcogenides. Nat. Nanotechnol. 2017, 12, 744–749. 10.1038/nnano.2017.100. [DOI] [PubMed] [Google Scholar]
- Zhang J.; Jia S.; Kholmanov I.; Dong L.; Er D.; Chen W.; Guo H.; Jin Z.; Shenoy V. B.; Shi L.; Lou J. Janus Monolayer Transition-Metal Dichalcogenides. ACS Nano 2017, 11, 8192–8198. 10.1021/acsnano.7b03186. [DOI] [PubMed] [Google Scholar]
- Sant R.; Gay M.; Marty A.; Lisi S.; Harrabi R.; Vergnaud C.; Dau M. T.; Weng X.; Coraux J.; Gauthier N.; Renault O.; Renaud G.; Jamet M. Synthesis of Epitaxial Monolayer Janus SPtSe. npj 2D Mater. Appl. 2020, 4, 41. 10.1038/s41699-020-00175-z. [DOI] [Google Scholar]
- Boulle O.; Vogel J.; Yang H.; Pizzini S.; de Souza Chaves D.; Locatelli A.; Menteş T. O.; Sala A.; Buda-Prejbeanu L. D.; Klein O.; Belmeguenai M.; Roussigné Y.; Stashkevich A.; Chérif S. M.; Aballe L.; Foerster M.; Chshiev M.; Auffret S.; Miron I. M.; Gaudin G. Room-Temperature Chiral Magnetic Skyrmions in Ultrathin Magnetic Nanostructures. Nat. Nanotechnol. 2016, 11, 449–454. 10.1038/nnano.2015.315. [DOI] [PubMed] [Google Scholar]
- Cui Q.; Liang J.; Shao Z.; Cui P.; Yang H. Strain-Tunable Ferromagnetism and Chiral Spin Textures in Two-Dimensional Janus Chromium Dichalcogenides. Phys. Rev. B 2020, 102, 094425. 10.1103/PhysRevB.102.094425. [DOI] [Google Scholar]
- Xu C.; Feng J.; Prokhorenko S.; Nahas Y.; Xiang H.; Bellaiche L. Topological Spin Texture in Janus Monolayers of the Chromium Trihalides Cr(I, X)3. Phys. Rev. B 2020, 101, 060404. 10.1103/PhysRevB.101.060404. [DOI] [Google Scholar]
- Liang J.; Cui Q.; Yang H. Electrically Switchable Rashba-Type Dzyaloshinskii-Moriya Interaction and Skyrmion in Two-Dimensional Magnetoelectric Multiferroics. Phys. Rev. B 2020, 102, 220409. 10.1103/PhysRevB.102.220409. [DOI] [Google Scholar]
- Yang M.; Li Q.; Chopdekar R. V.; Dhall R.; Turner J.; Carlström J. D.; Ophus C.; Klewe C.; Shafer P.; N’Diaye A. T.; Choi J. W.; Chen G.; Wu Y. Z.; Hwang C.; Wang F.; Qiu Z. Q. Creation of Skyrmions in van der Waals ferromagnet Fe3GeTe2 on (Co/Pd)n Superlattice. Sci. Adv. 2020, 6, eabb5157 10.1126/sciadv.abb5157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong Q.; Liu F.; Xiao J.; Yao W. Skyrmions in the Moiré of van der Waals 2D Magnets. Nano Lett. 2018, 18, 7194–7199. 10.1021/acs.nanolett.8b03315. [DOI] [PubMed] [Google Scholar]
- Dieny B.; Chshiev M. Perpendicular Magnetic Anisotropy at Transition Metal/Oxide Interfaces and Applications. Rev. Mod. Phys. 2017, 89, 025008. 10.1103/RevModPhys.89.025008. [DOI] [Google Scholar]
- Jiang S.; Li L.; Wang Z.; Shan J.; Mak K. F. Spin Tunnel Field-Effect Transistors Based on Two-Dimensional van der Waals Heterostructures. Nat. Electron. 2019, 2, 159–163. 10.1038/s41928-019-0232-3. [DOI] [Google Scholar]
- Moodera J. S.; Kinder L. R.; Wong T. M.; Meservey R. Large Magnetoresistance at Room Temperature in Ferromagnetic Thin Film Tunnel Junctions. Phys. Rev. Lett. 1995, 74, 3273–3276. 10.1103/PhysRevLett.74.3273. [DOI] [PubMed] [Google Scholar]
- Miyazaki T.; Tezuka N. Giant Magnetic Tunneling Effect in Fe/Al2O3/Fe Junction. J. Magn. Magn. Mater. 1995, 139, L231. 10.1016/0304-8853(95)90001-2. [DOI] [Google Scholar]
- Wolf S. A.; et al. Spintronics: A Spin-Based Electronics Vision for the Future. Science 2001, 294, 1488–1495. 10.1126/science.1065389. [DOI] [PubMed] [Google Scholar]
- Kent A. D.; Worledge D. C. A New Spin on Magnetic Memories. Nat. Nanotechnol. 2015, 10, 187–191. 10.1038/nnano.2015.24. [DOI] [PubMed] [Google Scholar]
- Arai M.; Moriya R.; Yabuki N.; Masubuchi S.; Ueno K.; Machida T. Construction of van der Waals Magnetic Tunnel Junction Using Ferromagnetic Layered Dichalcogenide. Appl. Phys. Lett. 2015, 107, 103107. 10.1063/1.4930311. [DOI] [Google Scholar]
- Yamasaki Y.; Moriya R.; Arai M.; Masubuchi S.; Pyon S.; Tamegai T.; Ueno K.; Machida T. Exfoliation and van der Waals Heterostructure Assembly of Intercalated Ferromagnet Cr1/3TaS2. 2D Mater. 2017, 4, 041007. 10.1088/2053-1583/aa8a2b. [DOI] [Google Scholar]
- Li X.; Lü J.-T.; Zhang J.; You L.; Su Y.; Tsymbal E. Y. Spin-Dependent Transport in van der Waals Magnetic Tunnel Junctions with Fe3GeTe2 Electrodes. Nano Lett. 2019, 19, 5133–5139. 10.1021/acs.nanolett.9b01506. [DOI] [PubMed] [Google Scholar]
- Albarakati S.; Tan C.; Chen Z.-J.; Partridge J. G.; Zheng G.; Farrar L.; Mayes E. L. H.; Field M. R.; Lee C.; Wang Y.; Xiong Y.; Tian M.; Xiang F.; Hamilton A. R.; Tretiakov O. A.; Culcer D.; Zhao Y.-J.; Wang L. Antisymmetric Magnetoresistance in van der Waals Fe3GeTe2/graphite/Fe3GeTe2 Trilayer Heterostructures. Sci. Adv. 2019, 5, eaaw0409 10.1126/sciadv.aaw0409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su Y.; Li X.; Zhu M.; Zhang J.; You L.; Tsymbal E. Y. Van der Waals Multiferroic Tunnel Junctions. Nano Lett. 2021, 21, 175–181. 10.1021/acs.nanolett.0c03452. [DOI] [PubMed] [Google Scholar]
- Ashton M.; Gluhovic D.; Sinnott S. B.; Guo J.; Stewart D. A.; Hennig R. G. Two-Dimensional Intrinsic Half-Metals With Large Spin Gaps. Nano Lett. 2017, 17, 5251–5257. 10.1021/acs.nanolett.7b01367. [DOI] [PubMed] [Google Scholar]
- Cardoso C.; Soriano D.; García-Martínez N.; Fernández-Rossier J. Van der Waals Spin Valves. Phys. Rev. Lett. 2018, 121, 067701. 10.1103/PhysRevLett.121.067701. [DOI] [PubMed] [Google Scholar]
- Song T.; Tu M. W. Y.; Carnahan C.; Cai X.; Taniguchi T.; Watanabe K.; McGuire M. A.; Cobden D. H.; Xiao D.; Yao W.; Xu X. Voltage Control of a van der Waals Spin-Filter Magnetic Tunnel Junction. Nano Lett. 2019, 19, 915. 10.1021/acs.nanolett.8b04160. [DOI] [PubMed] [Google Scholar]
- Miron I. M.; Garello K.; Gaudin G.; Zermatten P.-J.; Costache M. V.; Auffret S.; Bandiera S.; Rodmacq B.; Schuhl A.; Gambardella P. Perpendicular Switching of a Single Ferromagnetic Layer Induced by In-Plane Current Injection. Nature 2011, 476, 189–193. 10.1038/nature10309. [DOI] [PubMed] [Google Scholar]
- Yamanouchi M.; Chen L.; Kim J.; Hayashi M.; Sato H.; Fukami S.; Ikeda S.; Matsukura F.; Ohno H. Three Terminal Magnetic Tunnel Junction Utilizing the Spin Hall Effect of Iridium-Doped Copper. Appl. Phys. Lett. 2013, 102, 212408. 10.1063/1.4808033. [DOI] [Google Scholar]
- Cubukcu M.; Boulle O.; Drouard M.; Garello K.; Onur Avci C.; Mihai Miron I.; Langer J.; Ocker B.; Gambardella P.; Gaudin G. Spin-Orbit Torque Magnetization Switching of a Three-Terminal Perpendicular Magnetic Tunnel Junction. Appl. Phys. Lett. 2014, 104, 042406. 10.1063/1.4863407. [DOI] [Google Scholar]
- Liu L.; Pai C.-F.; Li Y.; Tseng H. W.; Ralph D. C.; Buhrman R. A. Spin-Torque Switching with the Giant Spin Hall Effect of Tantalum. Science 2012, 336, 555–558. 10.1126/science.1218197. [DOI] [PubMed] [Google Scholar]
- Back C.; Cros V.; Ebert H.; Everschor-Sitte K.; Fert A.; Garst M.; Ma T.; Mankovsky S.; Monchesky T. L.; Mostovoy M.; Nagaosa N.; Parkin S. S. P.; Pfleiderer C.; Reyren N.; Rosch A.; Taguchi Y.; Tokura Y.; von Bergmann K.; Zang J. The 2020 Skyrmionics Roadmap. J. Phys. D: Appl. Phys. 2020, 53, 363001. 10.1088/1361-6463/ab8418. [DOI] [Google Scholar]
- Parkin S. S. P.; Hayashi M.; Thomas L. Magnetic Domain-Wall Racetrack Memory. Science 2008, 320, 190–194. 10.1126/science.1145799. [DOI] [PubMed] [Google Scholar]
- Legrand W.; Maccariello D.; Reyren N.; Garcia K.; Moutafis C.; Moreau-Luchaire C.; Collin S.; Bouzehouane K.; Cros V.; Fert A. Room-Temperature Current-Induced Generation and Motion of Sub-100 nm Skyrmions. Nano Lett. 2017, 17, 2703–2712. 10.1021/acs.nanolett.7b00649. [DOI] [PubMed] [Google Scholar]
- Legrand W.; Maccariello D.; Ajejas F.; Collin S.; Vecchiola A.; Bouzehouane K.; Reyren N.; Cros V.; Fert A. Room-Temperature Stabilization of Antiferromagnetic Skyrmions in Synthetic Antiferromagnets. Nat. Mater. 2020, 19, 34–42. 10.1038/s41563-019-0468-3. [DOI] [PubMed] [Google Scholar]
- Zhu D.; Kang W.; Li S.; Huang Y.; Zhang X.; Zhou Y.; Zhao W. Skyrmion Racetrack Memory With Random Information Update/Deletion/Insertion. IEEE Trans. Electron Devices 2018, 65, 87–95. 10.1109/TED.2017.2769672. [DOI] [Google Scholar]
- Guguchia Z.; Verezhak J. A. T.; Gawryluk D. J.; Tsirkin S. S.; Yin J.-X.; Belopolski I.; Zhou H.; Simutis G.; Zhang S.-S.; Cochran T. A.; Chang G.; Pomjakushina E.; Keller L.; Skrzeczkowska Z.; Wang Q.; Lei H. C.; Khasanov R.; Amato A.; Jia S.; Neupert T.; et al. Tunable Anomalous Hall Conductivity Through Volume-Wise Magnetic Competition in a Topological Kagome Magnet. Nat. Commun. 2020, 11, 559. 10.1038/s41467-020-14325-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu E.; Sun Y.; Kumar N.; Muechler L.; Sun A.; Jiao L.; Yang S.-Y.; Liu D.; Liang A.; Xu Q.; Kroder J.; Süß V.; Borrmann H.; Shekhar C.; Wang Z.; Xi C.; Wang W.; Schnelle W.; Wirth S.; Chen Y.; et al. Giant Anomalous Hall Effect in a Ferromagnetic Kagome-Lattice Semimetal. Nat. Phys. 2018, 14, 1125–1131. 10.1038/s41567-018-0234-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin J.-X.; Zhang S. S.; Chang G.; Wang Q.; Tsirkin S. S.; Guguchia Z.; Lian B.; Zhou H.; Jiang K.; Belopolski I.; Shumiya N.; Multer D.; Litskevich M.; Cochran T. A.; Lin H.; Wang Z.; Neupert T.; Jia S.; Lei H.; Hasan M. Z. Negative Flat Band Magnetism in a Spin–Orbit-Coupled Correlated Kagome Magnet. Nat. Phys. 2019, 15, 443–448. 10.1038/s41567-019-0426-7. [DOI] [Google Scholar]
- Hasan M. Z.; Kane C. L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. 10.1103/RevModPhys.82.3045. [DOI] [Google Scholar]
- Hasan M. Z.; Xu S.-Y.; Belopolski I.; Huang S.-M. Discovery of Weyl Fermion Semimetals and Topological Fermi Arc States. Annu. Rev. Condens. Matter Phys. 2017, 8, 289–309. 10.1146/annurev-conmatphys-031016-025225. [DOI] [Google Scholar]
- Xu S.-Y.; Alidoust N.; Belopolski I.; Richardella A.; Liu C.; Neupane M.; Bian G.; Huang S.-H.; Sankar R.; Fang C.; Dellabetta B.; Dai W.; Li Q.; Gilbert M. J.; Chou F.; Samarth N.; Hasan M. Z. Momentum-Space Imaging of Cooper Pairing in a Half-Dirac-Gas Topological Superconductor. Nat. Phys. 2014, 10, 943–950. 10.1038/nphys3139. [DOI] [Google Scholar]
- Yan B.; Felser C. Topological Materials: Weyl Semimetals. Annu. Rev. Condens. Matter Phys. 2017, 8, 337–354. 10.1146/annurev-conmatphys-031016-025458. [DOI] [Google Scholar]
- Keimer B.; Moore J. E. The Physics of Quantum Materials. Nat. Phys. 2017, 13, 1045–1055. 10.1038/nphys4302. [DOI] [Google Scholar]
- Yin J.-X.; Ma W.; Cochran T. A.; Xu X.; Zhang S. S.; Tien H.-J.; Shumiya N.; Cheng G.; Jiang K.; Lian B.; Song Z.; Chang G.; Belopolski I.; Multer D.; Litskevich M.; Cheng Z.-J.; Yang X. P.; Swidler B.; Zhou H.; Lin H.; et al. Quantum-Limit Chern Topological Magnetism in TbMn6Sn6. Nature 2020, 583, 533–536. 10.1038/s41586-020-2482-7. [DOI] [PubMed] [Google Scholar]
- Wang J.; Zhang S.-C. Topological States of Condensed Matter. Nat. Mater. 2017, 16, 1062–1067. 10.1038/nmat5012. [DOI] [PubMed] [Google Scholar]
- Wen X.-G. Colloquium: Zoo of Quantum-Topological Phases of Matter. Rev. Mod. Phys. 2017, 89, 041004. 10.1103/RevModPhys.89.041004. [DOI] [Google Scholar]
- Yin J.-X.; Zhang S. S.; Li H.; Jiang K.; Chang G.; Zhang B.; Lian B.; Xiang C.; Belopolski I.; Zheng H.; Cochran T. A.; Xu S.-Y.; Bian G.; Liu K.; Chang T.-R.; Lin H.; Lu Z.-Y.; Wang Z.; Jia S.; Wang W.; et al. Giant and Anisotropic Many-Body Spin–Orbit Tunability in a Strongly Correlated Kagome Magnet. Nature 2018, 562, 91–95. 10.1038/s41586-018-0502-7. [DOI] [PubMed] [Google Scholar]
- Ghimire N. J.; Mazin I. I. Topology and Correlations on the Kagome Lattice. Nat. Mater. 2020, 19, 137–138. 10.1038/s41563-019-0589-8. [DOI] [PubMed] [Google Scholar]
- Ghimire N. J.; Dally R. L.; Poudel L.; Jones D. C.; Michel D.; Magar N. T.; Bleuel M.; McGuire M. A.; Jiang J. S.; Mitchell J. F.; Lynn J. W.; Mazin I. I. Competing Magnetic Phases and Fluctuation-Driven Scalar Spin Chirality in the Kagome Metal YMn6Sn6. Sci. Adv. 2020, 6, eabe2680 10.1126/sciadv.abe2680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnyder A. P.; Ryu S.; Furusaki A.; Ludwig A. W. W. Classification of Topological Insulators and Superconductors in Three Spatial Dimensions. Phys. Rev. B 2008, 78, 195125. 10.1103/PhysRevB.78.195125. [DOI] [Google Scholar]
- Ye L.; Kang M.; Liu J.; von Cube F.; Wicker C. R.; Suzuki T.; Jozwiak C.; Bostwick A.; Rotenberg E.; Bell D. C.; Fu L.; Comin R.; Checkelsky J. G. Massive Dirac Fermions in a Ferromagnetic Kagome Metal. Nature 2018, 555, 638–642. 10.1038/nature25987. [DOI] [PubMed] [Google Scholar]
- Han T.-H.; Helton J. S.; Chu S.; Nocera D. G.; Rodriguez-Rivera J. A.; Broholm C.; Lee Y. S. Fractionalized Excitations in the Spin-Liquid State of a Kagome-Lattice Antiferromagnet. Nature 2012, 492, 406–410. 10.1038/nature11659. [DOI] [PubMed] [Google Scholar]
- Wang Q.; Xu Y.; Lou R.; Liu Z.; Li M.; Huang Y.; Shen D.; Weng H.; Wang S.; Lei H. Large Intrinsic Anomalous Hall Effect in Half-Metallic Ferromagnet Co3Sn2S2 with Magnetic Weyl Fermions. Nat. Commun. 2018, 9, 3681. 10.1038/s41467-018-06088-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakatsuji S.; Kiyohara N.; Higo T. Large Anomalous Hall Effect in a Non-Collinear Antiferromagnet at Room Temperature. Nature 2016, 534, S5–S6. 10.1038/nature19416. [DOI] [PubMed] [Google Scholar]
- Yan S.; Huse D. A.; White S. R. Spin-Liquid Ground State of the S = 1/2 Kagome Heisenberg Antiferromagnet. Science 2011, 332, 1173–1176. 10.1126/science.1201080. [DOI] [PubMed] [Google Scholar]
- Khasanov R.; Guguchia Z.; Maisuradze A.; Andreica D.; Elender M.; Raselli A.; Shermadini Z.; Goko T.; Knecht F.; Morenzoni E.; Amato A. High Pressure Research Using Muons at the Paul Scherrer Institute. High Pressure Res. 2016, 36, 140–166. 10.1080/08957959.2016.1173690. [DOI] [Google Scholar]
- Legendre J.; Le Hur K. Magnetic Topological Kagome Systems. Phys. Rev. Research 2020, 2, 022043. 10.1103/PhysRevResearch.2.022043. [DOI] [Google Scholar]
- Guguchia Z.; Zhou H.; Wang C. N.; Yin J.-X.; Mielke C.; Tsirkin S. S.; Belopolski I.; Zhang S.-S.; Cochran T. A.; Neupert T.; Khasanov R.; Amato A.; Jia S.; Hasan M. Z.; Luetkens H. Multiple Quantum Phase Transitions of Different Nature in the Topological Kagome Magnet Co3Sn2–xInxS2. npj Quantum Mater. 2021, 6, 50. 10.1038/s41535-021-00352-3. [DOI] [Google Scholar]
- Chen X.; Wang M.; Gu C.; Wang S.; Zhou Y.; An C.; Zhou Y.; Zhang B.; Chen C.; Yuan Y.; Qi M.; Zhang L.; Zhou H.; Zhou J.; Yao Y.; Yang Z. Pressure-Tunable Large Anomalous Hall Effect of the Ferromagnetic Kagome-Lattice Weyl Semimetal Co3Sn2S2. Phys. Rev. B 2019, 100, 165145. 10.1103/PhysRevB.100.165145. [DOI] [Google Scholar]
- Lachman E.; Murphy R. A.; Maksimovic N.; Kealhofer R.; Haley S.; McDonald R. D.; Long J. R.; Analytis J. G. Exchange Biased Anomalous Hall Effect Driven by Frustration in a Magnetic Kagome Lattice. Nat. Commun. 2020, 11, 560. 10.1038/s41467-020-14326-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H.; Chang G.; Wang G.; Gui X.; Xu X.; Yin J.-X.; Guguchia Z.; Zhang S. S.; Chang T.-R.; Lin H.; Xie W.; Hasan M. Z.; Jia S. Enhanced Anomalous Hall Effect in the Magnetic Topological Semimetal Co3Sn2–xInxS2. Phys. Rev. B 2020, 101, 125121. 10.1103/PhysRevB.101.125121. [DOI] [Google Scholar]
- Manna K.; Muechler L.; Kao T.-H.; Stinshoff R.; Zhang Y.; Gooth J.; Kumar N.; Kreiner G.; Koepernik K.; Car R.; Kübler J.; Fecher G. H.; Shekhar C.; Sun Y.; Felser C. From Colossal to Zero: Controlling the Anomalous Hall Effect in Magnetic Heusler Compounds via Berry Curvature Design. Phys. Rev. X 2018, 8, 041045. 10.1103/PhysRevX.8.041045. [DOI] [Google Scholar]
- Nayak A. K.; Fischer J. E.; Sun Y.; Yan B.; Karel J.; Komarek A. C.; Shekhar C.; Kumar N.; Schnelle W.; Kübler J.; Felser C.; Parkin S. S. P. Large Anomalous Hall Effect Driven by a Nonvanishing Berry Curvature in the Noncolinear Antiferromagnet Mn3Ge. Sci. Adv. 2016, 2, e1501870 10.1126/sciadv.1501870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kübler J.; Felser C. Non-Collinear Antiferromagnets and the Anomalous Hall Effect. EPL (Europhysics Letters) 2014, 108, 67001. 10.1209/0295-5075/108/67001. [DOI] [Google Scholar]
- Ma W.; Xu X.; Yin J.-X.; Yang H.; Zhou H.; Cheng Z.-J.; Huang Y.; Qu Z.; Wang F.; Hasan M. Z.; Jia S. Rare Earth Engineering in RMn6Sn6 (R = Gd–Tm, Lu) Topological Kagome Magnets. Phys. Rev. Lett. 2021, 126, 246602. 10.1103/PhysRevLett.126.246602. [DOI] [PubMed] [Google Scholar]
- Mielke C. I.; Ma W.; Pomjakushin V.; Zaharko O.; Liu X.; Yin J. X.; Tsirkin S. S.; Cochran T. A.; Medarde M.; Poree V.; Das D.; Wang C. N.; Chang J.; Neupert T.; Amato A.; Jia S.; Hasan M. Z.; Luetkens H.; Guguchia Z.. Intriguing Magnetism of the Topological Kagome Magnet TbMn6Sn6. arXiv (Strongly Correlated Electrons), November 26, 2021, 2101.05763, ver. 2. https://arxiv.org/abs/2101.05763 (accessed 2021-12-07).
- Jiang Y.-X.; Yin J.-X.; Denner M. M.; Shumiya N.; Ortiz B. R.; Xu G.; Guguchia Z.; He J.; Hossain M. S.; Liu X.; Ruff J.; Kautzsch L.; Zhang S. S.; Chang G.; Belopolski I.; Zhang Q.; Cochran T. A.; Multer D.; Litskevich M.; Cheng Z.-J.; et al. Unconventional Chiral Charge Order in Kagome Superconductor KV3Sb5. Nat. Mater. 2021, 20, 1353–1357. 10.1038/s41563-021-01034-y. [DOI] [PubMed] [Google Scholar]
- Mielke C. I.; Das D.; Yin J.-X.; Liu H.; Gupta R.; Wang C. N.; Jiang Y.-X.; Medarde M.; Wu X.; Lei H. C.; Chang J. J.; Dai P.; Si Q.; Miao H.; Thomale R.; Neupert T.; Shi Y.; Khasanov R.; Hasan M. Z.; Luetkens H. Time-Reversal Symmetry-Breaking Charge Order in a Kagome Superconductor. Nature 2022, 602, 245–250. 10.1038/s41586-021-04327-z. [DOI] [PubMed] [Google Scholar]
- Ji L. J.; Qin Y.; Gui D.; Li W.; Li Y.; Li X.; Lu P. Quantifying the Exfoliation Ease Level of 2D Materials via Mechanical Anisotropy. Chem. Mater. 2018, 30, 8732–8738. 10.1021/acs.chemmater.8b01082. [DOI] [Google Scholar]
- Novoselov K. S.; Jiang D.; Schedin F.; Booth T. J.; Khotkevich V. V.; Morozov S. V.; Geim A. K. Two-Dimensional Atomic Crystals. Proc. Natl. Acad. Sci. U.S.A. 2005, 102, 10451–10453. 10.1073/pnas.0502848102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novoselov K. S.; Mishchenko A.; Carvalho A.; Neto A. H. C. 2D Materials and van der Waals Heterostructures. Science 2016, 353, aac9439. 10.1126/science.aac9439. [DOI] [PubMed] [Google Scholar]
- Budania P.; Baine P. T.; Montgomery J. H.; McNeill D. W.; Mitchell S. J.; Modreanu M.; Hurley P. K. Comparison Between Scotch Tape and Gel-Assisted Mechanical Exfoliation Techniques for Preparation of 2D Transition Metal Dichalcogenide Flakes. Micro. Nano. Lett. 2017, 12, 970–973. 10.1049/mnl.2017.0280. [DOI] [Google Scholar]
- Gao E.; Lin S. Z.; Qin Z.; Buehler M. J.; Feng X. Q.; Xu Z. Mechanical Exfoliation of Two-Dimensional Materials. J. Mech. Phys. Solids 2018, 115, 248–262. 10.1016/j.jmps.2018.03.014. [DOI] [Google Scholar]
- Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Zhang Y.; Dubonos S. V.; Grigorieva I. V.; Firsov A. A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. 10.1126/science.1102896. [DOI] [PubMed] [Google Scholar]
- Onodera M.; Masubuchi S.; Moriya R.; Machida T. Assembly of van der Waals Heterostructures: Exfoliation, Searching, and Stacking of 2D Materials. Jpn. J. Appl. Phys. 2020, 59, 010101. 10.7567/1347-4065/ab5ee0. [DOI] [Google Scholar]
- Yi M.; Shen Z. A Review on Mechanical Exfoliation for the Scalable Production of Graphene. J. Mater. Chem. A 2015, 3, 11700–11715. 10.1039/C5TA00252D. [DOI] [Google Scholar]
- Yuan L.; Ge J.; Peng X.; Zhang Q.; Wu Z.; Jian Y.; Xiong X.; Yin H.; Han J. A Reliable Way of Mechanical Exfoliation of Large Scale Two Dimensional Materials with High Quality. AIP Adv. 2016, 6, 125201. 10.1063/1.4967967. [DOI] [Google Scholar]
- Amiri A.; Naraghi M.; Ahmadi G.; Soleymaniha M.; Shanbedi M. A Review on Liquid-Phase Exfoliation for Scalable Production of Pure Graphene, Wrinkled, Crumpled and Functionalized Graphene and Challenges. FlatChem. 2018, 8, 40–71. 10.1016/j.flatc.2018.03.004. [DOI] [Google Scholar]
- Bonaccorso F.; Sun Z. Solution Processing of Graphene Topological Insulators and Other 2D Crystals for Ultrafast Photonics. Opt. Mater. Express 2014, 4, 63. 10.1364/OME.4.000063. [DOI] [Google Scholar]
- Cao W.; Wang J.; Ma M. Exfoliation of Two-Dimensional Materials: The Role of Entropy. J. Phys. Chem. Lett. 2019, 10, 981–986. 10.1021/acs.jpclett.9b00204. [DOI] [PubMed] [Google Scholar]
- Huo C.; Yan Z.; Song X.; Zeng H. 2D Materials via Liquid Exfoliation: A Review on Fabrication and Applications. Sci. Bull. 2015, 60, 1994–2008. 10.1007/s11434-015-0936-3. [DOI] [Google Scholar]
- Xu Y.; Cao H.; Xue Y.; Li B.; Cai W. Liquid-Phase Exfoliation of Graphene: An Overview on Exfoliation Media, Techniques, and Challenges. Nanomaterials 2018, 8, 942. 10.3390/nano8110942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Abhervé A.; Mañas-Valero S.; Clemente-León M.; Coronado E. Graphene Related Magnetic Materials: Micromechanical Exfoliation of 2D Layered Magnets Based on Bimetallic Anilate Complexes with Inserted [FeIII(acac2-trien)]+ and [FeIII(sal2-trien)]+ Molecules. Chem. Sci. 2015, 6, 4665–4673. 10.1039/C5SC00957J. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homkar S.; Chand B.; Rajput S. S.; Gorantla S.; Das T.; Babar R.; Patil S.; Klingeler R.; Nair S.; Kabir M.; Bajpai A. Few-Layer SrRu2O6 Nanosheets as Non-van der Waals Honeycomb Antiferromagnets: Implications for Two-Dimensional Spintronics. ACS Appl. Nano Mater. 2021, 4, 9313–9321. 10.1021/acsanm.1c01788. [DOI] [Google Scholar]
- León-Alcaide L.; López-Cabrelles J.; Mínguez Espallargas G.; Coronado E. 2D Magnetic MOFs with Micron-Lateral Size by Liquid Exfoliation. Chem. Commun. 2020, 56, 7657–7660. 10.1039/D0CC02982C. [DOI] [PubMed] [Google Scholar]
- Niu Y.; Villalva J.; Frisenda R.; Sanchez-Santolino G.; Ruiz-González L.; Pérez E. M.; García-Hernández M.; Burzurí E.; Castellanos-Gomez A. Mechanical and Liquid Phase Exfoliation of Cylindrite: A Natural van der Waals Superlattice with Intrinsic Magnetic Interactions. 2D Mater. 2019, 6, 035023. 10.1088/2053-1583/ab1a4c. [DOI] [Google Scholar]
- Heyl M.; Burmeister D.; Schultz T.; Pallasch S.; Ligorio G.; Koch N.; List-Kratochvil E. J. Thermally Activated Gold-Mediated Transition Metal Dichalcogenide Exfoliation and a Unique Gold-Mediated Transfer. Phys. Status Solidi RRL 2020, 14, 2000408. 10.1002/pssr.202000408. [DOI] [Google Scholar]
- Huang Y.; Pan Y.-H.; Yang R.; Bao L.-H.; Meng L.; Luo H.-L.; Cai Y.-Q.; Liu G.-D.; Zhao W.-J.; Zhou Z.; Wu L.-M.; Zhu Z.-L.; Huang M.; Liu L.-W.; Liu L.; Cheng P.; Wu K.-H.; Tian S.-B.; Gu C.-Z.; Shi Y.-G.; et al. Universal Mechanical Exfoliation of Large-Area 2D Crystals. Nat. Commun. 2020, 11, 2453–2453. 10.1038/s41467-020-16266-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F.; Wu W.; Bai Y.; Chae S. H.; Li Q.; Wang J.; Hone J.; Zhu X. Y. Disassembling 2D van der Waals Crystals into Macroscopic Monolayers and Reassembling into Artificial Lattices. Science 2020, 367, 903–906. 10.1126/science.aba1416. [DOI] [PubMed] [Google Scholar]
- Magda G. Z.; Petõ J.; Dobrik G.; Hwang C.; Biró L. P.; Tapasztó L. Exfoliation of Large-Area Transition Metal Chalcogenide Single Layers. Sci. Rep. 2015, 5, 3–7. 10.1038/srep14714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velický M.; Donnelly G. E.; Hendren W. R.; McFarland S.; Scullion D.; Debenedetti W. J.; Correa G. C.; Han Y.; Wain A. J.; Hines M. A.; Muller D. A.; Novoselov K. S.; Abruna H. D.; Bowman R. M.; Santos E. J.; Huang F. Mechanism of Gold-Assisted Exfoliation of Centimeter-Sized Transition-Metal Dichalcogenide Monolayers. ACS Nano 2018, 12, 10463–10472. 10.1021/acsnano.8b06101. [DOI] [PubMed] [Google Scholar]
- Benameur M. M.; Radisavljevic B.; Héron J. S.; Sahoo S.; Berger H.; Kis A. Visibility of Dichalcogenide Nanolayers. Nanotechnology 2011, 22, 125706. 10.1088/0957-4484/22/12/125706. [DOI] [PubMed] [Google Scholar]
- Bing D.; Wang Y.; Bai J.; Du R.; Wu G.; Liu L. Optical Contrast for Identifying the Thickness of Two-Dimensional Materials. Opt. Commun. 2018, 406, 128–138. 10.1016/j.optcom.2017.06.012. [DOI] [Google Scholar]
- Blake P.; Hill E. W.; Castro Neto A. H.; Novoselov K. S.; Jiang D.; Yang R.; Booth T. J.; Geim A. K. Making Graphene Visible. Appl. Phys. Lett. 2007, 91, 063124. 10.1063/1.2768624. [DOI] [Google Scholar]
- Castellanos-Gomez A; Agrait N; Rubio-Bollinger G Optical Identification of Atomically Thin Dichalcogenide Crystals. Appl. Phys. Lett. 2010, 96, 213116. 10.1063/1.3442495. [DOI] [Google Scholar]
- Gorbachev R. V.; Riaz I.; Nair R. R.; Jalil R.; Britnell L.; Belle B. D.; Hill E. W.; Novoselov K. S.; Watanabe K.; Taniguchi T.; Geim A. K.; Blake P. Hunting for Monolayer Boron Nitride: Optical and Raman Signatures. Small 2011, 7, 465–468. 10.1002/smll.201001628. [DOI] [PubMed] [Google Scholar]
- Wang Y. Y.; Gao R. X.; Ni Z. H.; He H.; Guo S. P.; Yang H. P.; Cong C. X.; Yu T. Thickness Identification of Two-Dimensional Materials by Optical Imaging. Nanotechnology 2012, 23, 495713. 10.1088/0957-4484/23/49/495713. [DOI] [PubMed] [Google Scholar]
- Ferrari A. C.; Meyer J. C.; Scardaci V.; Casiraghi C.; Lazzeri M.; Mauri F.; Piscanec S.; Jiang D.; Novoselov K. S.; Roth S.; Geim A. K. Raman Spectrum of Graphene and Graphene Layers. Phys. Rev. Lett. 2006, 97, 187401. 10.1103/PhysRevLett.97.187401. [DOI] [PubMed] [Google Scholar]
- Wang L.; Meric I.; Huang P. Y.; Gao Q.; Gao Y.; Tran H.; Taniguchi T.; Watanabe K.; Campos L. M.; Muller D. A.; Guo J.; Kim P.; Hone J.; Shepard K. L.; Dean C. R. One-Dimensional Electrical Contact to a Two-Dimensional Material. Science 2013, 342, 614–617. 10.1126/science.1244358. [DOI] [PubMed] [Google Scholar]
- Liu Z.; Gong Y.; Zhou W.; Ma L.; Yu J.; Idrobo J. C.; Jung J.; Macdonald A. H.; Vajtai R.; Lou J.; Ajayan P. M. Ultrathin High-Temperature Oxidation-Resistant Coatings of Hexagonal Boron Nitride. Nat. Commun. 2013, 4, 2541. 10.1038/ncomms3541. [DOI] [PubMed] [Google Scholar]
- Dean C. R.; Young A. F.; Meric I.; Lee C.; Wang L.; Sorgenfrei S.; Watanabe K.; Taniguchi T.; Kim P.; Shepard K. L.; Hone J. Boron Nitride Substrates for High-Quality Graphene Electronics. Nat. Nanotechnol. 2010, 5, 722–726. 10.1038/nnano.2010.172. [DOI] [PubMed] [Google Scholar]
- Cao Y.; Mishchenko A.; Yu G. L.; Khestanova E.; Rooney A. P.; Prestat E.; Kretinin A. V.; Blake P.; Shalom M. B.; Woods C.; Chapman J.; Balakrishnan G.; Grigorieva I. V.; Novoselov K. S.; Piot B. A.; Potemski M.; Watanabe K.; Taniguchi T.; Haigh S. J.; Geim A. K.; et al. Quality Heterostructures from Two-Dimensional Crystals Unstable in Air by Their Assembly in Inert Atmosphere. Nano Lett. 2015, 15, 4914–4921. 10.1021/acs.nanolett.5b00648. [DOI] [PubMed] [Google Scholar]
- Kim K.; Lim S. Y.; Kim J.; Lee J.-U.; Lee S.; Kim P.; Park K.; Son S.; Park C.-H.; Park J.-G.; Cheong H. Antiferromagnetic Ordering in van der Waals 2D Magnetic Material MnPS3 Probed by Raman Spectroscopy. 2D Mater. 2019, 6, 041001. 10.1088/2053-1583/ab27d5. [DOI] [Google Scholar]
- Nguyen G. D.; Lee J.; Berlijn T.; Zou Q.; Hus S. M.; Park J.; Gai Z.; Lee C.; Li A.-P. Visualization and Manipulation of Magnetic Domains in the Quasi-Two-Dimensional Material Fe3GeTe2. Phys. Rev. B 2018, 97, 014425. 10.1103/PhysRevB.97.014425. [DOI] [Google Scholar]
- Nikonov K.; Brekhovskikh M.; Egorysheva A.; Menshchikova T.; Fedorov V. Chemical Vapor Transport Growth of Vanadium (IV) Selenide and Vanadium (IV) Telluride Single Crystals. Inorg. Mater. 2017, 53, 1126–1130. 10.1134/S0020168517110061. [DOI] [Google Scholar]
- Binnewies M.; Glaum R.; Schmidt M.; Schmidt P.. Chemical Vapor Transport Reactions; Walter de Gruyter: Berlin, 2012. [Google Scholar]
- Binnewies M.; Schmidt M.; Schmidt P. Chemical Vapor Transport Reactions - Arguments for Choosing a Suitable Transport Agent. Z. Anorg. Allg. Chem. 2017, 643, 1295–1311. 10.1002/zaac.201700055. [DOI] [Google Scholar]
- Abramchuk M.; Jaszewski S.; Metz K. R.; Osterhoudt G. B.; Wang Y.; Burch K. S.; Tafti F. Controlling Magnetic and Optical Properties of the van der Waals Crystal CrCl3–xBrxvia Mixed Halide Chemistry. Adv. Mater. 2018, 30, 1801325. 10.1002/adma.201801325. [DOI] [PubMed] [Google Scholar]
- Kuhlow B. Magnetic Ordering in CrCl3 at the Phase Transition. Phys. Status Solidi A 1982, 72, 161–168. 10.1002/pssa.2210720116. [DOI] [Google Scholar]
- Atuchin V.; Gavrilova T.; Grigorieva T.; Kuratieva N.; Okotrub K.; Pervukhina N.; Surovtsev N. Sublimation Growth and Vibrational Microspectrometry of α-MoO3 Single Crystals. J. Cryst. Growth 2011, 318, 987–990. 10.1016/j.jcrysgro.2010.10.149. [DOI] [Google Scholar]
- Zhang X.; Zhao Y.; Song Q.; Jia S.; Shi J.; Han W. Magnetic Anisotropy of the Single-Crystalline Ferromagnetic Insulator Cr2Ge2Te6. Jpn. J. Appl. Phys. 2016, 55, 033001. 10.7567/JJAP.55.033001. [DOI] [Google Scholar]
- Fisk Z.; Remeika J. In Growth of Single Crystals from Molten Metal Fluxes; Handbook on the Physics and Chemistry of Rare Earths; Gschneidner K. A. Jr., Eyring L., Eds.; Elsevier: Amsterdam, The Netherlands, 1989; Vol. 12; pp 53–70. [Google Scholar]
- Lopez-Sanchez O.; Lembke D.; Kayci M.; Radenovic A.; Kis A. Ultrasensitive Photodetectors Based on Monolayer MoS2. Nat. Nanotechnol. 2013, 8, 497–501. 10.1038/nnano.2013.100. [DOI] [PubMed] [Google Scholar]
- Li H.; Wu J.; Yin Z.; Zhang H. Preparation and Applications of Mechanically Exfoliated Single-Layer and Multilayer MoS2 and WSe2 Nanosheets. Acc. Chem. Res. 2014, 47, 1067–1075. 10.1021/ar4002312. [DOI] [PubMed] [Google Scholar]
- Li H.; Lu G.; Wang Y.; Yin Z.; Cong C.; He Q.; Wang L.; Ding F.; Yu T.; Zhang H. Mechanical Exfoliation and Characterization of Single- and Few-Layer Nanosheets of WSe2, TaS2, and TaSe2. Small 2013, 9, 1974–1981. 10.1002/smll.201202919. [DOI] [PubMed] [Google Scholar]
- Jiang H.; Zhang P.; Wang X.; Gong Y. Synthesis of Magnetic Two-Dimensional Materials by Chemical Vapor Deposition. Nano Res. 2021, 14, 1789–1801. 10.1007/s12274-020-3020-5. [DOI] [Google Scholar]
- Gao T.; Zhang Q.; Li L.; Zhou X.; Li L.; Li H.; Zhai T. 2D Ternary Chalcogenides. Adv. Opt. Mater. 2018, 6, 1800058. 10.1002/adom.201800058. [DOI] [Google Scholar]
- Reale F.; Sharda K.; Mattevi C. From Bulk Crystals to Atomically Thin Layers of Group VI-Transition Metal Dichalcogenides Vapour Phase Synthesis. Appl. Mater. Today 2016, 3, 11–22. 10.1016/j.apmt.2015.12.003. [DOI] [Google Scholar]
- Cheng Z.; Sendeku M. G.; Liu Q. Layered Metal Phosphorous Trichalcogenides Nanosheets: Facile Synthesis and Photocatalytic Hydrogen Evolution. Nanotechnology 2020, 31, 135405. 10.1088/1361-6528/ab646d. [DOI] [PubMed] [Google Scholar]
- Shifa T. A.; Wang F.; Cheng Z.; He P.; Liu Y.; Jiang C.; Wang Z.; He J. High Crystal Quality 2D Manganese Phosphorus Trichalcogenide Nanosheets and Their Photocatalytic Activity. Adv. Funct. Mater. 2018, 28, 1800548. 10.1002/adfm.201800548. [DOI] [Google Scholar]
- Grönke M.; Schmidt P.; Valldor M.; Oswald S.; Wolf D.; Lubk A.; Büchner B.; Hampel S. Chemical Vapor Growth and Delamination of α-RuCl3 Nanosheets Down to the Monolayer Limit. Nanoscale 2018, 10, 19014–19022. 10.1039/C8NR04667K. [DOI] [PubMed] [Google Scholar]
- Grönke M.; Buschbeck B.; Schmidt P.; Valldor M.; Oswald S.; Hao Q.; Lubk A.; Wolf D.; Steiner U.; Büchner B.; et al. Chromium Trihalides CrX3 (X= Cl, Br, I): Direct Deposition of Micro- and Nanosheets on Substrates by Chemical Vapor Transport. Adv. Mater. Interfaces 2019, 6, 1901410. 10.1002/admi.201901410. [DOI] [Google Scholar]
- Grönke M.; Pohflepp D.; Schmidt P.; Valldor M.; Oswald S.; Wolf D.; Hao Q.; Steiner U.; Büchner B.; Hampel S. Simulation and Synthesis of α-MoCl3 Nanosheets on Substrates by Short Time Chemical Vapor Transport. Nano-Struct. Nano-Objects 2019, 19, 100324. 10.1016/j.nanoso.2019.100324. [DOI] [Google Scholar]
- Liu H.; Wang X.; Wu J.; Chen Y.; Wan J.; Wen R.; Yang J.; Liu Y.; Song Z.; Xie L. Vapor Deposition of Magnetic van der Waals NiI2 Crystals. ACS Nano 2020, 14, 10544–10551. 10.1021/acsnano.0c04499. [DOI] [PubMed] [Google Scholar]
- Li P.; Wang C.; Zhang J.; Chen S.; Guo D.; Ji W.; Zhong D. Single-Layer CrI3 Grown by Molecular Beam Epitaxy. Sci. Bull. 2020, 65, 1064–1071. 10.1016/j.scib.2020.03.031. [DOI] [PubMed] [Google Scholar]
- Fehér F. In Handbook of Preparative Inorganic Chemistry, 2nd ed.; Brauer G., Ed.; Academic Press: Cambridge, United States, 1963; pp 341–456. [Google Scholar]
- Beck J. Uber Chalkogenidehalide des Chroms. Synthese, Kristallstruktur und Magnetismus von Chromsulfidbromid, CrSBr. Z. Anorg. Allg. Chem. 1990, 585, 157–167. 10.1002/zaac.19905850118. [DOI] [Google Scholar]
- Katscher H.; Hahn H. Chalkogenidhalogenide des Dreiwertigen Chroms. Naturwissenschaften 1966, 53, 361–361. 10.1007/BF00621875.5993456 [DOI] [Google Scholar]
- Wang H.; Qi J.; Qian X. Electrically Tunable High Curie Temperature Two-Dimensional Ferromagnetism in van der Waals Layered Crystals. Appl. Phys. Lett. 2020, 117, 083102. 10.1063/5.0014865. [DOI] [Google Scholar]
- Han R.; Jiang Z.; Yan Y. Prediction of Novel 2D Intrinsic Ferromagnetic Materials with High Curie Temperature and Large Perpendicular Magnetic Anisotropy. J. Phys. Chem. C 2020, 124, 7956–7964. 10.1021/acs.jpcc.0c01307. [DOI] [Google Scholar]
- Saßmannshausen M.; Lutz H. D. Preparation and Crystal Structure of Quaternary Chromium Sulfide Halide CrSBr0.67Cl0.33. Mater. Res. Bull. 2000, 35, 2431–2436. 10.1016/S0025-5408(00)00433-5. [DOI] [Google Scholar]
- Krasheninnikov A. V. When Defects Are Not Defects. Nat. Mater. 2018, 17, 757–758. 10.1038/s41563-018-0153-y. [DOI] [PubMed] [Google Scholar]
- Terrones H.; Lv R.; Terrones M.; Dresselhaus M. S. The Role of Defects and Doping in 2D Graphene Sheets and 1D Nanoribbons. Rep. Prog. Phys. 2012, 75, 062501. 10.1088/0034-4885/75/6/062501. [DOI] [PubMed] [Google Scholar]
- Zou X.; Yakobson B. I. An Open Canvas - 2D Materials with Defects, Disorder, and Functionality. Acc. Chem. Res. 2015, 48, 73–80. 10.1021/ar500302q. [DOI] [PubMed] [Google Scholar]
- Hus S. M.; Li A. P. Spatially-Resolved Studies on the Role of Defects and Boundaries in Electronic Behavior of 2D Materials. Prog. Surf. Sci. 2017, 92, 176–201. 10.1016/j.progsurf.2017.07.001. [DOI] [Google Scholar]
- Wu Z.; Ni Z. Spectroscopic Investigation of Defects in Two-Dimensional Materials. Nanophotonics 2017, 6, 1219–1237. 10.1515/nanoph-2016-0151. [DOI] [Google Scholar]
- Jang S. W.; Yoon H.; Jeong M. Y.; Ryee S.; Kim H. S.; Han M. J. Origin of Ferromagnetism and the Effect of Doping on Fe3GeTe2. Nanoscale 2020, 12, 13501–13506. 10.1039/C9NR10171C. [DOI] [PubMed] [Google Scholar]
- Yuan Y.; Wang X.; Li H.; Li J.; Ji Y.; Hao Z.; Wu Y.; He K.; Wang Y.; Xu Y.; Duan W.; Li W.; Xue Q. K. Electronic States and Magnetic Response of MnBi2Te4 by Scanning Tunneling Microscopy and Spectroscopy. Nano Lett. 2020, 20, 3271–3277. 10.1021/acs.nanolett.0c00031. [DOI] [PubMed] [Google Scholar]
- Kagerer P.; Fornari C. I.; Buchberger S.; Morelhão S. L.; Vidal R. C.; Tcakaev A.; Zabolotnyy V.; Weschke E.; Hinkov V.; Kamp M.; Büchner B.; Isaeva A.; Bentmann H.; Reinert F. Molecular Beam Epitaxy of Antiferromagnetic (MnBi2Te4)(Bi2Te3) Thin Films on BaF2(111). J. Appl. Phys. 2020, 128, 135303. 10.1063/5.0025933. [DOI] [Google Scholar]
- Hu C.; Gordon K. N.; Liu P.; Liu J.; Zhou X.; Hao P.; Narayan D.; Emmanouilidou E.; Sun H.; Liu Y.; Brawer H.; Ramirez A. P.; Ding L.; Cao H.; Liu Q.; Dessau D.; Ni N. A van der Waals Antiferromagnetic Topological Insulator with Weak Interlayer Magnetic Coupling. Nat. Commun. 2020, 11, 97. 10.1038/s41467-019-13814-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Z.; Du M.-H.; Yan J.; Wu W. Native Defects in Antiferromagnetic Topological Insulator MnBi2Te4. Phys. Rev. Mater. 2020, 4, 121202. 10.1103/PhysRevMaterials.4.121202. [DOI] [Google Scholar]
- Lee S. H.; Zhu Y.; Wang Y.; Miao L.; Pillsbury T.; Yi H.; Kempinger S.; Hu J.; Heikes C. A.; Quarterman P.; Ratcliff W.; Borchers J. A.; Zhang H.; Ke X.; Graf D.; Alem N.; Chang C.-Z.; Samarth N.; Mao Z. Spin Scattering and Noncollinear Spin Structure-Induced Intrinsic Anomalous Hall Effect in Antiferromagnetic Topological Insulator MnBi2Te4. Phys. Rev. Research 2019, 1, 012011. 10.1103/PhysRevResearch.1.012011. [DOI] [Google Scholar]
- Liu C.; Wang Y.; Li H.; Wu Y.; Li Y.; Li J.; He K.; Xu Y.; Zhang J.; Wang Y. Robust Axion Insulator and Chern Insulator Phases in a Two-Dimensional Antiferromagnetic Topological Insulator. Nat. Mater. 2020, 19, 522–527. 10.1038/s41563-019-0573-3. [DOI] [PubMed] [Google Scholar]
- Lapano J.; Nuckols L.; Mazza A. R.; Pai Y. Y.; Zhang J.; Lawrie B.; Moore R. G.; Eres G.; Lee H. N.; Du M. H.; Ward T. Z.; Lee J. S.; Weber W. J.; Zhang Y.; Brahlek M. Adsorption-Controlled Growth of MnTe(Bi2Te3)n by Molecular Beam Epitaxy Exhibiting Stoichiometry-Controlled Magnetism. Phys. Rev. Mater. 2020, 4, 111201. 10.1103/PhysRevMaterials.4.111201. [DOI] [Google Scholar]
- Schneider L.; Beck P.; Wiebe J.; Wiesendanger R. Atomic-Scale Spin-Polarization Maps Using Functionalized Superconducting Probes. Sci. Adv. 2021, 7, eabd7302 10.1126/sciadv.abd7302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Möller M.; Gaida J. H.; Schäfer S.; Ropers C. Few-nm Tracking of Current-Driven Magnetic Vortex Orbits Using Ultrafast Lorentz Microscopy. Commun. Phys. 2020, 3, 36. 10.1038/s42005-020-0301-y. [DOI] [Google Scholar]
- Cao Y.; Zhao Y.; Tang J.; Du H.; Zhou Y.; Saito H. Direct Visualization of Magnetic Domain Wall Motion in Nd-Fe-B Magnets by Alternating Magnetic Force Microscopy Using Co-GdOx Superparamagnetic Tip. Ultramicroscopy 2020, 212, 112980. 10.1016/j.ultramic.2020.112980. [DOI] [PubMed] [Google Scholar]
- Kazakova O.; Puttock R.; Barton C.; Corte-León H.; Jaafar M.; Neu V.; Asenjo A. Frontiers of Magnetic Force Microscopy. J. Appl. Phys. 2019, 125, 060901. 10.1063/1.5050712. [DOI] [Google Scholar]
- Lin J.; Müller B.; Linek J.; Karrer M.; Wenzel M.; Martínez-Pérez M. J.; Kleiner R.; Koelle D. YBa2Cu3O7 Nano Superconducting Quantum Interference Devices on MgO Bicrystal Substrates. Nanoscale 2020, 12, 5658–5668. 10.1039/C9NR10506A. [DOI] [PubMed] [Google Scholar]
- Lee C.; Wei X.; Kysar J. W.; Hone J. Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene. Science 2008, 321, 385–388. 10.1126/science.1157996. [DOI] [PubMed] [Google Scholar]
- Cost J. R.; Janowski K. R.; Rossi R. C. Elastic Properties of Isotropic Graphite. Philos. Mag. 1968, 17, 851–854. 10.1080/14786436808223035. [DOI] [Google Scholar]
- Kim D. P.; Suhng Y.; Labes M. Mechanical Properties of Pyrolytic Graphite Flakes. Carbon 1992, 30, 729–737. 10.1016/0008-6223(92)90155-P. [DOI] [Google Scholar]
- Falin A.; Cai Q.; Santos E. J. G.; Scullion D.; Qian D.; Zhang R.; Yang Z.; Huang S.; Watanabe K.; Taniguchi T.; Barnett M. R.; Chen Y.; Ruoff R. S.; Li L. H. Mechanical Properties of Atomically Thin Boron Nitride and the Role of Interlayer Interactions. Nat. Commun. 2017, 8, 15815. 10.1038/ncomms15815. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertolazzi S.; Brivio J.; Kis A. Stretching and Breaking of Ultrathin Mos2. ACS Nano 2011, 5, 9703–9709. 10.1021/nn203879f. [DOI] [PubMed] [Google Scholar]
- Falin A.; Holwill M.; Lv H.; Gan W.; Cheng J.; Zhang R.; Qian D.; Barnett M. R.; Santos E. J. G.; Novoselov K. S.; Tao T.; Wu X.; Li L. H. Mechanical Properties of Atomically Thin Tungsten Dichalcogenides: WS2, WSe2, and WTe2. ACS Nano 2021, 15, 2600–2610. 10.1021/acsnano.0c07430. [DOI] [PubMed] [Google Scholar]
- Jiang H.; Zheng L.; Liu Z.; Wang X. Two-Dimensional Materials: From Mechanical Properties to Flexible Mechanical Sensors. InfoMat 2020, 2, 1077. 10.1002/inf2.12072. [DOI] [Google Scholar]
- Nicholl R. J. T.; Lavrik N. V.; Vlassiouk I.; Srijanto B. R.; Bolotin K. I. Hidden Area and Mechanical Nonlinearities in Freestanding Graphene. Phys. Rev. Lett. 2017, 118, 266101. 10.1103/PhysRevLett.118.266101. [DOI] [PubMed] [Google Scholar]
- Cao K.; Feng S.; Han Y.; Gao L.; Ly T. H.; Xu Z.; Lu Y. Elastic Straining of Free-Standing Monolayer Graphene. Nat. Commun. 2020, 11, 284. 10.1038/s41467-019-14130-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang P.; Ma L.; Fan F.; Zeng Z.; Peng C.; Loya P. E.; Liu Z.; Gong Y.; Zhang J.; Zhang X.; Ajayan P. M.; Zhu T.; Lou J. Fracture Toughness of Graphene. Nat. Commun. 2014, 5, 3782. 10.1038/ncomms4782. [DOI] [PubMed] [Google Scholar]
- Koenig S. P.; Boddeti N. G.; Dunn M. L.; Bunch J. S. Ultrastrong Adhesion of Graphene Membranes. Nat. Nanotechnol. 2011, 6, 543–546. 10.1038/nnano.2011.123. [DOI] [PubMed] [Google Scholar]
- Nicholl R. J. T.; Conley H. J.; Lavrik N. V.; Vlassiouk I.; Puzyrev Y. S.; Sreenivas V. P.; Pantelides S. T.; Bolotin K. I. The Effect of Intrinsic Crumpling on the Mechanics of Free-Standing Graphene. Nat. Commun. 2015, 6, 8789. 10.1038/ncomms9789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong C. L.; Annamalai M.; Wang Z. Q.; Palaniapan M. Characterization of Nanomechanical Graphene Drum Structures. J. Micromech. Microeng. 2010, 20, 115029. 10.1088/0960-1317/20/11/115029. [DOI] [Google Scholar]
- Lee J.-U.; Yoon D.; Cheong H. Estimation of Young’s Modulus of Graphene by Raman Spectroscopy. Nano Lett. 2012, 12, 4444–4448. 10.1021/nl301073q. [DOI] [PubMed] [Google Scholar]
- Hwangbo Y.; Lee C.-K.; Kim S.-M.; Kim J.-H.; Kim K.-S.; Jang B.; Lee H.-J.; Lee S.-K.; Kim S.-S.; Ahn J.-H.; et al. Fracture Characteristics of Monolayer CVD-Graphene. Sci. Rep. 2015, 4, 4439. 10.1038/srep04439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blees M. K.; Barnard A. W.; Rose P. A.; Roberts S. P.; McGill K. L.; Huang P. Y.; Ruyack A. R.; Kevek J. W.; Kobrin B.; Muller D. A.; et al. Graphene Kirigami. Nature 2015, 524, 204–207. 10.1038/nature14588. [DOI] [PubMed] [Google Scholar]
- Košmrlj A.; Nelson D. R. Response of Thermalized Ribbons to Pulling and Bending. Phys. Rev. B 2016, 93, 125431. 10.1103/PhysRevB.93.125431. [DOI] [Google Scholar]
- Zong Z.; Chen C.-L.; Dokmeci M. R.; Wan K.-T. Direct Measurement of Graphene Adhesion on Silicon Surface by Intercalation of Nanoparticles. J. Appl. Phys. 2010, 107, 026104. 10.1063/1.3294960. [DOI] [Google Scholar]
- Zhang T.; Li X.; Gao H. Fracture of Graphene: A Review. Int. J. Fract. 2015, 196, 1–31. 10.1007/s10704-015-0039-9. [DOI] [Google Scholar]
- Lee C.; Li Q.; Kalb W.; Liu X.-Z.; Berger H.; Carpick R. W.; Hone J. Frictional Characteristics of Atomically Thin Sheets. Science 2010, 328, 76–80. 10.1126/science.1184167. [DOI] [PubMed] [Google Scholar]
- Castellanos-Gomez A.; van Leeuwen R.; Buscema M.; van der Zant H. S. J.; Steele G. A.; Venstra W. J. Single-Layer MoS2 Mechanical Resonators. Adv. Mater. 2013, 25, 6719–6723. 10.1002/adma.201303569. [DOI] [PubMed] [Google Scholar]
- Duerloo K.-A. N.; Li Y.; Reed E. J. Structural Phase Transitions in Two-Dimensional Mo-and W-Dichalcogenide Monolayers. Nat. Commun. 2014, 5, 4214. 10.1038/ncomms5214. [DOI] [PubMed] [Google Scholar]
- Duerloo K.-A. N.; Reed E. J. Structural Phase Transitions by Design in Monolayer Alloys. ACS Nano 2016, 10, 289–297. 10.1021/acsnano.5b04359. [DOI] [PubMed] [Google Scholar]
- Nayak A. P.; Pandey T.; Voiry D.; Liu J.; Moran S. T.; Sharma A.; Tan C.; Chen C.-H.; Li L.-J.; Chhowalla M.; et al. Pressure-Dependent Optical and Vibrational Properties of Monolayer Molybdenum Disulfide. Nano Lett. 2015, 15, 346–353. 10.1021/nl5036397. [DOI] [PubMed] [Google Scholar]
- Pandey T.; Nayak A. P.; Liu J.; Moran S. T.; Kim J.; Li L.; Lin J.; Akinwande D.; Singh A. K. Pressure-Induced Charge Transfer Doping of Monolayer Graphene/MoS2 Heterostructure. Small 2016, 12, 4063–4069. 10.1002/smll.201600808. [DOI] [PubMed] [Google Scholar]
- Zelisko M.; Hanlumyuang Y.; Yang S.; Liu Y.; Lei C.; Li J.; Ajayan P. M.; Sharma P. Anomalous Piezoelectricity in Two-Dimensional Graphene Nitride Nanosheets. Nat. Commun. 2014, 5, 4284. 10.1038/ncomms5284. [DOI] [PubMed] [Google Scholar]
- Naumov I.; Bratkovsky A. M.; Ranjan V. Unusual Flexoelectric Effect in Two-Dimensional Noncentrosymmetric sp2-Bonded Crystals. Phys. Rev. Lett. 2009, 102, 217601. 10.1103/PhysRevLett.102.217601. [DOI] [PubMed] [Google Scholar]
- Levy N.; Burke S. A.; Meaker K. L.; Panlasigui M.; Zettl A.; Guinea F.; Neto A. H. C.; Crommie M. F. Strain-Induced Pseudo–Magnetic Fields Greater Than 300 T in Graphene Nanobubbles. Science 2010, 329, 544–547. 10.1126/science.1191700. [DOI] [PubMed] [Google Scholar]
- Klimov N. N.; Jung S.; Zhu S.; Li T.; Wright C. A.; Solares S. D.; Newell D. B.; Zhitenev N. B.; Stroscio J. A. Electromechanical Properties of Graphene Drumheads. Science 2012, 336, 1557–1561. 10.1126/science.1220335. [DOI] [PubMed] [Google Scholar]
- Zheng F.; Zhao J.; Liu Z.; Li M.; Zhou M.; Zhang S.; Zhang P. Tunable Spin States in the Two-Dimensional Magnet CrI3. Nanoscale 2018, 10, 14298–14303. 10.1039/C8NR03230K. [DOI] [PubMed] [Google Scholar]
- Liu J.; Sun Q.; Kawazoe Y.; Jena P. Exfoliating Biocompatible Ferromagnetic Cr-Trihalide Monolayers. Phys. Chem. Chem. Phys. 2016, 18, 8777–8784. 10.1039/C5CP04835D. [DOI] [PubMed] [Google Scholar]
- Cantos-Prieto F.; Falin A.; Alliati M.; Qian D.; Zhang R.; Tao T.; Barnett M. R.; Santos E. J. G.; Li L. H.; Navarro-Moratalla E. Layer-Dependent Mechanical Properties and Enhanced Plasticity in the van der Waals Chromium Trihalide Magnets. Nano Lett. 2021, 21, 3379–3385. 10.1021/acs.nanolett.0c04794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salavati M.; Rabczuk T. Application of Highly Stretchable and Conductive Two-Dimensional 1T VS2 and VSe2 as Anode Materials for Li-, Na-and Ca-Ion Storage. Comput. Mater. Sci. 2019, 160, 360–367. 10.1016/j.commatsci.2019.01.018. [DOI] [Google Scholar]
- Hashemi A.; Komsa H.-P.; Puska M.; Krasheninnikov A. V. Vibrational Properties of Metal Phosphorus Trichalcogenides from First-Principles Calculations. J. Phys. Chem. C 2017, 121, 27207–27217. 10.1021/acs.jpcc.7b09634. [DOI] [Google Scholar]
- Zhang X.; Zhao X.; Wu D.; Jing Y.; Zhou Z. MnPSe3 Monolayer: A Promising 2D Visible-Light Photohydrolytic Catalyst with High Carrier Mobility. Adv. Sci. 2016, 3, 1600062. 10.1002/advs.201600062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li X.; Wu X.; Yang J. Half-Metallicity in MnPSe3 Exfoliated Nanosheet with Carrier Doping. J. Am. Chem. Soc. 2014, 136, 11065–11069. 10.1021/ja505097m. [DOI] [PubMed] [Google Scholar]
- Zhuang H. L.; Xie Y.; Kent P. R. C.; Ganesh P. Computational Discovery of Ferromagnetic Semiconducting Single-Layer CrSnTe3. Phys. Rev. B 2015, 92, 035407. 10.1103/PhysRevB.92.035407. [DOI] [Google Scholar]
- Sachs B.; Wehling T. O.; Novoselov K. S.; Lichtenstein A. I.; Katsnelson M. I. Ferromagnetic Two-Dimensional Crystals: Single Layers of K2CuF4. Phys. Rev. B 2013, 88, 201402. 10.1103/PhysRevB.88.201402. [DOI] [Google Scholar]
- Miao N.; Xu B.; Zhu L.; Zhou J.; Sun Z. 2D Intrinsic Ferromagnets from van der Waals Antiferromagnets. J. Am. Chem. Soc. 2018, 140, 2417–2420. 10.1021/jacs.7b12976. [DOI] [PubMed] [Google Scholar]
- Rani S.; Nair A. K.; Kamalakar M. V.; Ray S. J. Spin-Selective Response Tunability in Two-Dimensional Nanomagnet. J. Phys.: Condens. Matter 2020, 32, 415301. 10.1088/1361-648X/ab8bf4. [DOI] [PubMed] [Google Scholar]
- Chowdhury U. K.; Rahman M. A.; Rahman M. A.; Bhuiyan M. T. H. Ab-Initio Study on Structural, Elastic, Electronic and Optical Properties of Iron-Based Superconductor. Cogent Phys. 2016, 3, 1265779. 10.1080/23311940.2016.1265779. [DOI] [Google Scholar]
- Chandra S.; Islam A. Elastic Properties of Mono- and Poly-Crystalline PbO-type FeSe1–xTex (x = 0 – 1.0): A First-Principles Study. Physica C: Supercond. 2010, 470, 2072–2075. 10.1016/j.physc.2010.10.001. [DOI] [Google Scholar]
- Rugut E. K.; Joubert D. P.; Jones G.. Numerical Simulation of Structural, Electronic and Optical Properties of Vanadium Diselenide (VSe2). Proceedings from the SAIP2017 South Africian Institute of Physics, July 3-7, 2017, Johannesburg, Africa; South Africian Institute of Physics: Pretoria, South Africa, 2017.
- McGuire M. A.; Garlea V. O.; Santosh K. C.; Cooper V. R.; Yan J.; Cao H.; Sales B. C. Antiferromagnetism in the van der Waals Layered Spin-Lozenge Semiconductor CrTe3. Phys. Rev. B 2017, 95, 144421. 10.1103/PhysRevB.95.144421. [DOI] [Google Scholar]
- Lu Z.-W.; Qiu S.-B.; Xie W.-Q.; Yang X.-B.; Zhao Y.-J. Theoretical Study of Strain Induced Magnetic Transition of Single-Layer CrTe3. J. Appl. Phys. 2020, 127, 033903. 10.1063/1.5126246. [DOI] [Google Scholar]
- Chen Z.; Fan X.; Shen Z.; Luo Z.; Yang D.; Ma S. Two-Dimensional Intrinsic Ferromagnetic Half-Metals: Monolayers Mn3X4 (X = Te, Se, S). J. Mater. Sci. 2020, 55, 7680–7690. 10.1007/s10853-020-04582-x. [DOI] [Google Scholar]
- Sun Y.; Zhuo Z.; Wu X.; Yang J. Room-Temperature Ferromagnetism in Two-Dimensional Fe2Si Nanosheet with Enhanced Spin-Polarization Ratio. Nano Lett. 2017, 17, 2771–2777. 10.1021/acs.nanolett.6b04884. [DOI] [PubMed] [Google Scholar]
- Liu L.; Zhuang H. L. Single-Layer Ferromagnetic and Piezoelectric CoAsS with Pentagonal Structure. APL Mater. 2019, 7, 011101. 10.1063/1.5079867. [DOI] [Google Scholar]
- Lu M.; Yao Q.; Xiao C.; Huang C.; Kan E. Mechanical, Electronic, and Magnetic Properties of NiX2 (X = Cl, Br, I) Layers. ACS Omega 2019, 4, 5714–5721. 10.1021/acsomega.9b00056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan I.; Hong J. High Curie Temperature and Strain-Induced Semiconductor-Metal Transition with Spin Reorientation Transition in 2D CrPbTe3 Monolayer. Nanotechnology 2020, 31, 195704. 10.1088/1361-6528/ab70fc. [DOI] [PubMed] [Google Scholar]
- Joe M.; Lee H.; Alyörük M. M.; Lee J.; Kim S. Y.; Lee C.; Lee J. H. A Comprehensive Study of Piezomagnetic Response in CrPS4 Monolayer: Mechanical, Electronic Properties and Magnetic Ordering under Strains. J. Phys.: Condens. Matter 2017, 29, 405801. 10.1088/1361-648X/aa80c5. [DOI] [PubMed] [Google Scholar]
- Lee J.; Ko T. Y.; Kim J. H.; Bark H.; Kang B.; Jung S.-G.; Park T.; Lee Z.; Ryu S.; Lee C. Structural and Optical Properties of Single- and Few-Layer Magnetic Semiconductor CrPS4. ACS Nano 2017, 11, 10935–10944. 10.1021/acsnano.7b04679. [DOI] [PubMed] [Google Scholar]
- Wen Y.-C.; Liao Y.-C.; Chang H.-H.; Mok B.-H.; Lee Y.-C.; Huang T.-W.; Yeh K.-W.; Luo J.-Y.; Wang M.-J.; Sun C.-K.; et al. Elastic Stiffness of Single-Crystalline FeSe Measured by Picosecond Ultrasonics. J. Appl. Phys. 2011, 110, 073505. 10.1063/1.3645058. [DOI] [Google Scholar]
- Kuru M.; Sahin O.; Ozarslan S.; Ozmetin A. E. Fabrication and Mechanical Characterization of Rare Earth Permanent Magnet SmCo5 Films. J. Alloys 2017, 694, 726–732. 10.1016/j.jallcom.2016.10.089. [DOI] [Google Scholar]
- Lagorce L. K.; Allen M. G. Magnetic and Mechanical Properties of Micromachined Strontium Ferrite/Polyimide Composites. J. Microelectromech. Syst. 1997, 6, 307–312. 10.1109/84.650127. [DOI] [Google Scholar]
- Zhang L.; Wang W.; Xiao X.; Shahzad M. B.; Shan Y.; Yang K. Ultra-Thin Laminated Metal Composites with Ultra-High Strength and Excellent Soft Magnetic Properties. Acta Metall. Sin.-Engl. 2020, 33, 385–390. 10.1007/s40195-019-00960-w. [DOI] [Google Scholar]
- Chittari B. L.; Park Y.; Lee D.; Han M.; MacDonald A. H.; Hwang E.; Jung J. Electronic and Magnetic Properties of Single-Layer MPX3 Metal Phosphorous Trichalcogenides. Phys. Rev. B 2016, 94, 184428. 10.1103/PhysRevB.94.184428. [DOI] [Google Scholar]
- Jiang S.; Xie H.; Shan J.; Mak K. F. Exchange Magnetostriction in Two-Dimensional Antiferromagnets. Nat. Mater. 2020, 19, 1295–1299. 10.1038/s41563-020-0712-x. [DOI] [PubMed] [Google Scholar]
- Heuver J. A.; Scaramucci A.; Blickenstorfer Y.; Matzen S.; Spaldin N. A.; Ederer C.; Noheda B. Strain-Induced Magnetic Anisotropy in Epitaxial Thin Films of the Spinel CoCr2O4. Phys. Rev. B 2015, 92, 214429. 10.1103/PhysRevB.92.214429. [DOI] [Google Scholar]
- Rajapitamahuni A.; Zhang L.; Koten M. A.; Singh V. R.; Burton J. D.; Tsymbal E. Y.; Shield J. E.; Hong X. Giant Enhancement of Magnetic Anisotropy in Ultrathin Manganite Films via Nanoscale 1D Periodic Depth Modulation. Phys. Rev. Lett. 2016, 116, 187201. 10.1103/PhysRevLett.116.187201. [DOI] [PubMed] [Google Scholar]
- Bieńkowski A.; Szewczyk R. The Possibility of Utilizing the High Permeability Magnetic Materials in Construction of Magnetoelastic Stress and Force Sensors. Sens. Actuators Phys. 2004, 113, 270–276. 10.1016/j.sna.2004.01.010. [DOI] [Google Scholar]
- Meydan T.; Oduncu H. Enhancement of Magnetorestrictive Properties of Amorphous Ribbons for a Biomedical Application. Sens. Actuators Phys. 1997, 59, 192–196. 10.1016/S0924-4247(97)80172-0. [DOI] [Google Scholar]
- Bieńkowski A.; Szewczyk R.; Salach J. Industrial Application of Magnetoelastic Force and Torque Sensors. Acta Phys. Polym., A 2010, 118, 1008–1009. 10.12693/APhysPolA.118.1008. [DOI] [Google Scholar]
- Ma Y.; Dai Y.; Guo M.; Niu C.; Zhu Y.; Huang B. Evidence of the Existence of Magnetism in Pristine VX2 Monolayers (X = S, Se) and Their Strain-Induced Tunable Magnetic Properties. ACS Nano 2012, 6, 1695–1701. 10.1021/nn204667z. [DOI] [PubMed] [Google Scholar]
- Li X.; Yang J. CrXTe3 (X= Si, Ge) Nanosheets: Two Dimensional Intrinsic Ferromagnetic Semiconductors. J. Mater. Chem. C 2014, 2, 7071–7076. 10.1039/C4TC01193G. [DOI] [Google Scholar]
- Chen X.; Qi J.; Shi D. Strain-Engineering of Magnetic Coupling in Two-Dimensional Magnetic Semiconductor CrSiTe3: Competition of Direct Exchange Interaction and Superexchange Interaction. Phys. Lett. A 2015, 379, 60–63. 10.1016/j.physleta.2014.10.042. [DOI] [Google Scholar]
- Sivadas N.; Daniels M. W.; Swendsen R. H.; Okamoto S.; Xiao D. Magnetic Ground State of Semiconducting Transition-Metal Trichalcogenide Monolayers. Phys. Rev. B 2015, 91, 235425. 10.1103/PhysRevB.91.235425. [DOI] [Google Scholar]
- Mukherjee T.; Chowdhury S.; Jana D.; Voon L. C. L. Y. Strain Induced Electronic and Magnetic Properties of 2D Magnet CrI3: A DFT Approach. J. Phys.: Condens. Matter 2019, 31, 335802. 10.1088/1361-648X/ab1fcf. [DOI] [PubMed] [Google Scholar]
- Peng R.; Xu H.; Tan S.; Cao H.; Xia M.; Shen X.; Huang Z.; Wen C.; Song Q.; Zhang T.; et al. Tuning the Band Structure and Superconductivity in Single-Layer FeSe by Interface Engineering. Nat. Commun. 2014, 5, 5044. 10.1038/ncomms6044. [DOI] [PubMed] [Google Scholar]
- Zhang P.; Peng X.-L.; Qian T.; Richard P.; Shi X.; Ma J.-Z.; Fu B.; Guo Y.-L.; Han Z.; Wang S.; et al. Observation of High-Tc Superconductivity in Rectangular FeSe/SrTiO3(110) Monolayers. Phys. Rev. B 2016, 94, 104510. 10.1103/PhysRevB.94.104510. [DOI] [Google Scholar]
- Wang Y.; Wang C.; Liang S.; Ma Z.; Xu K.; Liu X.; Zhang L.; Admasu A. S.; Cheong S.; Wang L.; et al. Strain-Sensitive Magnetization Reversal of a van der Waals Magnet. Adv. Mater. 2020, 32, 2004533. 10.1002/adma.202004533. [DOI] [PubMed] [Google Scholar]
- Edelberg D.; Rhodes D.; Kerelsky A.; Kim B.; Wang J.; Zangiabadi A.; Kim C.; Abhinandan A.; Ardelean J.; Scully M.; Scullion D.; Embon L.; Zu R.; Santos E. J. G.; Balicas L.; Marianetti C.; Barmak K.; Zhu X.; Hone J.; Pasupathy A. N. Approaching the Intrinsic Limit in Transition Metal Diselenides via Point Defect Control. Nano Lett. 2019, 19, 4371–4379. 10.1021/acs.nanolett.9b00985. [DOI] [PubMed] [Google Scholar]
- Huang B.; McGuire M. A.; May A. F.; Xiao D.; Jarillo-Herrero P.; Xu X. Emergent Phenomena and Proximity Effects in Two-Dimensional Magnets and Heterostructures. Nat. Mater. 2020, 19, 1276–1289. 10.1038/s41563-020-0791-8. [DOI] [PubMed] [Google Scholar]
- Wang X.; Du K.; Liu Y. Y. F.; Hu P.; Zhang J.; Zhang Q.; Owen M. H. S.; Lu X.; Gan C. K.; Sengupta P.; Kloc C.; Xiong Q. Raman Spectroscopy of Atomically Thin Two-Dimensional Magnetic Iron Phosphorus Trisulfide (FePS3) Crystals. 2D Mater. 2016, 3, 031009. 10.1088/2053-1583/3/3/031009. [DOI] [Google Scholar]
- Aizenman M.; Simon B. A Comparison of Plane Rotor and Ising Models. Phys. Lett. A 1980, 76, 281–282. 10.1016/0375-9601(80)90493-4. [DOI] [Google Scholar]
- Heisenberg W. Zur Theorie des Ferromagnetismus. Z. Phys. 1928, 49, 619–636. 10.1007/BF01328601. [DOI] [Google Scholar]
- Kitaev A. Anyons in an Exactly Solved Model and Beyond. Ann. Phys. 2006, 321, 2–111. 10.1016/j.aop.2005.10.005. [DOI] [Google Scholar]
- Wilson J. A.; Yoffe A. D. The Transition Metal Dichalcogenides Discussion and Interpretation of the Observed Optical, Electrical and Structural Properties. Adv. Phys. 1969, 18, 193–335. 10.1080/00018736900101307. [DOI] [Google Scholar]
- Geim A. K.; Novoselov K. S. The Rise of Graphene. Nat. Mater. 2007, 6, 183–191. 10.1038/nmat1849. [DOI] [PubMed] [Google Scholar]
- Novoselov K. S.; Geim A. K.; Morozov S. V.; Jiang D.; Katsnelson M. I.; Grigorieva I. V.; Dubonos S. V.; Firsov A. A. Two-Dimensional Gas of Massless Dirac Fermions in Graphene. Nature 2005, 438, 197–200. 10.1038/nature04233. [DOI] [PubMed] [Google Scholar]
- Hunt B.; Sanchez-Yamagishi J. D.; Young A. F.; Yankowitz M.; LeRoy B. J.; Watanabe K.; Taniguchi T.; Moon P.; Koshino M.; Jarillo-Herrero P.; Ashoori R. C. Massive Dirac Fermions and Hofstadter Butterfly in a van der Waals Heterostructure. Science 2013, 340, 1427–1430. 10.1126/science.1237240. [DOI] [PubMed] [Google Scholar]
- Ponomarenko L. A.; Gorbachev R. V.; Yu G. L.; Elias D. C.; Jalil R.; Patel A. A.; Mishchenko A.; Mayorov A. S.; Woods C. R.; Wallbank J. R.; Mucha-Kruczynski M.; Piot B. A.; Potemski M.; Grigorieva I. V.; Novoselov K. S.; Guinea F.; Fal’ko V. I.; Geim A. K. Cloning of Dirac Fermions in Graphene Superlattices. Nature 2013, 497, 594–597. 10.1038/nature12187. [DOI] [PubMed] [Google Scholar]
- Cao Y.; Fatemi V.; Demir A.; Fang S.; Tomarken S. L.; Luo J. Y.; Sanchez-Yamagishi J. D.; Watanabe K.; Taniguchi T.; Kaxiras E.; Ashoori R. C.; Jarillo-Herrero P. Correlated Insulator Behaviour at Half-Filling in Magic-Angle Graphene Superlattices. Nature 2018, 556, 80–84. 10.1038/nature26154. [DOI] [PubMed] [Google Scholar]
- Anderson P. W. Resonating Valence Bonds: A New Kind of Insulator?. Mater. Res. Bull. 1973, 8, 153–160. 10.1016/0025-5408(73)90167-0. [DOI] [Google Scholar]
- Balents L. Spin Liquids in Frustrated Magnets. Nature 2010, 464, 199–208. 10.1038/nature08917. [DOI] [PubMed] [Google Scholar]
- Broholm C.; Cava R. J.; Kivelson S. A.; Nocera D. G.; Norman M. R.; Senthil T. Quantum Spin Liquids. Science 2020, 367, eaay0668 10.1126/science.aay0668. [DOI] [PubMed] [Google Scholar]
- Savary L.; Balents L. Quantum Spin Liquids: A Review. Rep. Prog. Phys. 2017, 80, 016502. 10.1088/0034-4885/80/1/016502. [DOI] [PubMed] [Google Scholar]
- Anderson P. W. The Resonating Valence Bond State in La2CuO4 and Superconductivity. Science 1987, 235, 1196–1198. 10.1126/science.235.4793.1196. [DOI] [PubMed] [Google Scholar]
- Lee P. A.; Nagaosa N.; Wen X.-G. Doping a Mott Insulator: Physics of High-Temperature Superconductivity. Rev. Mod. Phys. 2006, 78, 17–85. 10.1103/RevModPhys.78.17. [DOI] [Google Scholar]
- Balz C.; Lampen-Kelley P.; Banerjee A.; Yan J.; Lu Z.; Hu X.; Yadav S. M.; Takano Y.; Liu Y.; Tennant D. A.; Lumsden M. D.; Mandrus D.; Nagler S. E. Finite Field Regime for a Quantum Spin Liquid in α-RuCl3. Phys. Rev. B 2019, 100, 060405. 10.1103/PhysRevB.100.060405. [DOI] [Google Scholar]
- Banerjee A.; Yan J.; Knolle J.; Bridges C. A.; Stone M. B.; Lumsden M. D.; Mandrus D. G.; Tennant D. A.; Moessner R.; Nagler S. E. Neutron Scattering in the Proximate Quantum Spin Liquid α-RuCl3. Science 2017, 356, 1055–1059. 10.1126/science.aah6015. [DOI] [PubMed] [Google Scholar]
- Jackeli G.; Khaliullin G. Mott Insulators in the Strong Spin-Orbit Coupling Limit: From Heisenberg to a Quantum Compass and Kitaev Models. Phys. Rev. Lett. 2009, 102, 017205. 10.1103/PhysRevLett.102.017205. [DOI] [PubMed] [Google Scholar]
- Avsar A.; Ochoa H.; Guinea F.; Ozyilmaz B.; van Wees B. J.; Vera-Marun I. J. Colloquium: Spintronics in Graphene and Other Two-Dimensional Materials. Rev. Mod. Phys. 2020, 92, 92. 10.1103/RevModPhys.92.021003. [DOI] [Google Scholar]
- Joy P. A.; Vasudevan S. Magnetism in the Layered Transition-Metal Thiophosphates MPS3 (M = Mn, Fe, and Ni). Phys. Rev. B 1992, 46, 5425–5433. 10.1103/PhysRevB.46.5425. [DOI] [PubMed] [Google Scholar]
- Park J.-G. Opportunities and Challenges of 2D Magnetic van der Waals Materials: Magnetic Graphene?. J. Phys.: Condens. Matter 2016, 28, 301001. 10.1088/0953-8984/28/30/301001. [DOI] [PubMed] [Google Scholar]
- Susner M. A.; Chyasnavichyus M.; McGuire M. A.; Ganesh P.; Maksymovych P. Metal Thio- and Selenophosphates as Multifunctional van der Waals Layered Materials. Adv. Mater. 2017, 29, 1602852. 10.1002/adma.201602852. [DOI] [PubMed] [Google Scholar]
- Lançon D.; Walker H. C.; Ressouche E.; Ouladdiaf B.; Rule K. C.; McIntyre G. J.; Hicks T. J.; Rønnow H. M.; Wildes A. R. Magnetic Structure and Magnon Dynamics of the Quasi-Two-Dimensional Antiferromagnet FePS3. Phys. Rev. B 2016, 94, 214407. 10.1103/PhysRevB.94.214407. [DOI] [Google Scholar]
- Wildes A. R.; Zhitomirsky M. E.; Ziman T.; Lançon D.; Walker H. C. Evidence for Biquadratic Exchange in the Quasi-Two-Dimensional Antiferromagnet FePS3. J. Appl. Phys. 2020, 127, 223903. 10.1063/5.0009114. [DOI] [Google Scholar]
- Wildes A. R.; Roessli B.; Lebech B.; Godfrey K. W. Spin Waves and the Critical Behaviour of the Magnetization in MnPS3. J. Phys.: Condens. Matter 1998, 10, 6417–6428. 10.1088/0953-8984/10/28/020. [DOI] [Google Scholar]
- Wildes A. R.; Roennow H. M.; Roessli B.; Harris M. J.; Godfrey K. W. Anisotropy and the Critical Behaviour of the Quasi-2D Antiferromagnet, MnPS3. J. Magn. Magn. Mater. 2007, 310, 1221–1223. 10.1016/j.jmmm.2006.10.347. [DOI] [Google Scholar]
- Lançon D.; Ewings R. A.; Guidi T.; Formisano F.; Wildes A. R. Magnetic Exchange Parameters and Anisotropy of the Quasi-Two-Dimensional Antiferromagnet NiPS3. Phys. Rev. B 2018, 98, 134414. 10.1103/PhysRevB.98.134414. [DOI] [Google Scholar]
- Wildes A. R.; Simonet V.; Ressouche E.; Ballou R.; McIntyre G. J. The Magnetic Properties and Structure of the Quasi-Two-Dimensional Antiferromagnet CoPS3. J. Phys.: Condens. Matter 2017, 29, 455801. 10.1088/1361-648X/aa8a43. [DOI] [PubMed] [Google Scholar]
- Wysocki A. L.; Belashchenko K. D.; Antropov V. P. Consistent Model of Magnetism in Ferropnictides. Nat. Phys. 2011, 7, 485–489. 10.1038/nphys1933. [DOI] [Google Scholar]
- Zhao J.; Adroja D. T.; Yao D. X.; Bewley R.; Li S. L.; Wang X. F.; Wu G.; Chen X. H.; Hu J. P.; Dai P. C. Spin Waves and Magnetic Exchange Interactions in CaFe2As2. Nat. Phys. 2009, 5, 555–560. 10.1038/nphys1336. [DOI] [Google Scholar]
- Kim C.; Jeong J.; Park P.; Masuda T.; Asai S.; Itoh S.; Kim H.-S.; Wildes A.; Park J.-G. Spin Waves in the Two-Dimensional Honeycomb Lattice XXZ-Type van der Waals Antiferromagnet CoPS3. Phys. Rev. B 2020, 102, 184429. 10.1103/PhysRevB.102.184429. [DOI] [Google Scholar]
- Carteaux V.; Brunet D.; Ouvrard G.; Andre G. Crystallographic, Magnetic and Electronic Structures of a New Layered Ferromagnetic Compound Cr2Ge2Te6. J. Phys.: Condens. Matter 1995, 7, 69–87. 10.1088/0953-8984/7/1/008. [DOI] [Google Scholar]
- Yi J.; Zhuang H.; Zou Q.; Wu Z.; Cao G.; Tang S.; Calder S. A.; Kent P. R. C.; Mandrus D.; Gai Z. Competing Antiferromagnetism in a Quasi-2D Itinerant Ferromagnet: Fe3GeTe2. 2D Mater. 2017, 4, 011005. 10.1088/2053-1583/4/1/011005. [DOI] [Google Scholar]
- McGuire M. A. Crystal and Magnetic Structures in Layered, Transition Metal Dihalides and Trihalides. Crystals 2017, 7, 121. 10.3390/cryst7050121. [DOI] [Google Scholar]
- Calder S.; Kolesnikov A. I.; May A. F. Magnetic Excitations in the Quasi-Two-Dimensional Ferromagnet Fe3–xGeTe2 Measured with Inelastic Neutron Scattering. Phys. Rev. B 2019, 99, 094423. 10.1103/PhysRevB.99.094423. [DOI] [Google Scholar]
- Haldane F. D. M. Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the “Parity Anomaly. Phys. Rev. Lett. 1988, 61, 2015–2018. 10.1103/PhysRevLett.61.2015. [DOI] [PubMed] [Google Scholar]
- Owerre S. A. A First Theoretical Realization of Honeycomb Topological Magnon Insulator. J. Phys.: Condens. Matter 2016, 28, 386001. 10.1088/0953-8984/28/38/386001. [DOI] [PubMed] [Google Scholar]
- Pershoguba S. S.; Banerjee S.; Lashley J. C.; Park J.; Ågren H.; Aeppli G.; Balatsky A. V. Dirac Magnons in Honeycomb Ferromagnets. Phys. Rev. X 2018, 8, 011010. 10.1103/PhysRevX.8.011010. [DOI] [Google Scholar]
- Williams T. J.; Aczel A. A.; Lumsden M. D.; Nagler S. E.; Stone M. B.; Yan J. Q.; Mandrus D. Magnetic Correlations in the Quasi-Two-Dimensional Semiconducting Ferromagnet CrSiTe3. Phys. Rev. B 2015, 92, 144404. 10.1103/PhysRevB.92.144404. [DOI] [Google Scholar]
- Bao S.; Wang J.; Wang W.; Cai Z.; Li S.; Ma Z.; Wang D.; Ran K.; Dong Z.-Y.; Abernathy D. L.; Yu S.-L.; Wan X.; Li J.-X.; Wen J. Discovery of Coexisting Dirac and Triply Degenerate Magnons in a Three-Dimensional Antiferromagnet. Nat. Commun. 2018, 9, 2591. 10.1038/s41467-018-05054-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yao W.; Li C.; Wang L.; Xue S.; Dan Y.; Iida K.; Kamazawa K.; Li K.; Fang C.; Li Y. Topological Spin Excitations in a Three-dimensional Antiferromagnet. Nat. Phys. 2018, 14, 1011–1015. 10.1038/s41567-018-0213-x. [DOI] [Google Scholar]
- Owerre S. A. Dirac Magnon Nodal Loops in Quasi-2D Quantum Magnets. Sci. Rep. 2017, 7, 9. 10.1038/s41598-017-07276-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L.; Chung J.-H.; Gao B.; Chen T.; Stone M. B.; Kolesnikov A. I.; Huang Q.; Dai P. Topological Spin Excitations in Honeycomb Ferromagnet CrI3. Phys. Rev. X 2018, 8, 041028. 10.1103/PhysRevX.8.041028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L.; Chung J.-H.; Chen T.; Duan C.; Schneidewind A.; Radelytskyi I.; Voneshen D. J.; Ewings R. A.; Stone M. B.; Kolesnikov A. I.; Winn B.; Chi S.; Mole R. A.; Yu D. H.; Gao B.; Dai P. Magnetic Anisotropy in Ferromagnetic CrI3. Phys. Rev. B 2020, 101, 134418. 10.1103/PhysRevB.101.134418. [DOI] [Google Scholar]
- Lee I.; Utermohlen F. G.; Weber D.; Hwang K.; Zhang C.; van Tol J.; Goldberger J. E.; Trivedi N.; Hammel P. C. Fundamental Spin Interactions Underlying the Magnetic Anisotropy in the Kitaev Ferromagnet CrI3. Phys. Rev. Lett. 2020, 124, 017201. 10.1103/PhysRevLett.124.017201. [DOI] [PubMed] [Google Scholar]
- Stavropoulos P. P.; Pereira D.; Kee H.-Y. Microscopic Mechanism for a Higher-Spin Kitaev Model. Phys. Rev. Lett. 2019, 123, 037203. 10.1103/PhysRevLett.123.037203. [DOI] [PubMed] [Google Scholar]
- Chen Y.; Gaudet J.; Dasgupta S.; Marcus G. G.; Lin J.; Chen T.; Tomita T.; Ikhlas M.; Zhao Y.; Chen W. C.; Stone M. B.; Tchernyshyov O.; Nakatsuji S.; Broholm C. Antichiral Spin Order, Its Soft Modes, and Their Hybridization with Phonons in the Topological Semimetal Mn3Ge. Phys. Rev. B 2020, 102, 054403. 10.1103/PhysRevB.102.054403. [DOI] [Google Scholar]
- Tartaglia T. A.; Tang J. N.; Lado J. L.; Bahrami F.; Abramchuk M.; McCandless G. T.; Doyle M. C.; Burch K. S.; Ran Y.; Chan J. Y.; Tafti F. Accessing New Magnetic Regimes by Tuning the Ligand Spin-Orbit Coupling in van der Waals Magnets. Sci. Adv. 2020, 6, eabb9379 10.1126/sciadv.abb9379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L.; Chung J.-H.; Stone M. B.; Kolesnikov A. I.; Winn B.; Garlea V. O.; Abernathy D. L.; Gao B.; Augustin M.; Santos E. J. G.; Dai P. Magnetic Field Effect on Topological Spin Excitations in CrI3. Phys. Rev. X 2021, 11, 031047. 10.1103/PhysRevX.11.031047. [DOI] [Google Scholar]
- Zhu F.; Zhang L.; Wang X.; dos Santos F. J.; Song J.; Mueller T.; Schmalzl K.; Schmidt W. F.; Ivanov A.; Park J. T.; Xu J.; Ma J.; Lounis S.; Blügel S.; Mokrousov Y.; Su Y.; Bruckel T. Topological Magnon Insulators in Two-Dimensional van der Waals Ferromagnets CrSiTe3 and CrGeTe3: Toward Intrinsic Gap-Tunability. Sci. Adv. 2021, 7, eabi7532 10.1126/sciadv.abi7532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasahara Y.; Ohnishi T.; Mizukami Y.; Tanaka O.; Ma S.; Sugii K.; Kurita N.; Tanaka H.; Nasu J.; Motome Y.; Shibauchi T.; Matsuda Y. Majorana Quantization and Half-Integer Thermal Quantum Hall Effect in a Kitaev Spin Liquid. Nature 2018, 559, 227–231. 10.1038/s41586-018-0274-0. [DOI] [PubMed] [Google Scholar]
- Banerjee A.; Lampen-Kelley P.; Knolle J.; Balz C.; Aczel A. A.; Winn B.; Liu Y.; Pajerowski D.; Yan J.; Bridges C. A.; Savici A. T.; Chakoumakos B. C.; Lumsden M. D.; Tennant D. A.; Moessner R.; Mandrus D. G.; Nagler S. E. Excitations in the Field-Induced Quantum Spin Liquid State of α-RuCl3. npj Quantum Mater. 2018, 3, 8. 10.1038/s41535-018-0079-2. [DOI] [Google Scholar]
- Takagi H.; Takayama T.; Jackeli G.; Khaliullin G.; Nagler S. E. Concept and Realization of Kitaev Quantum Spin Liquids. Nat. Rev. Phys. 2019, 1, 264–280. 10.1038/s42254-019-0038-2. [DOI] [Google Scholar]
- Kitagawa K.; Takayama T.; Matsumoto Y.; Kato A.; Takano R.; Kishimoto Y.; Bette S.; Dinnebier R.; Jackeli G.; Takagi H. A Spin–Orbital-Entangled Quantum Liquid on a Honeycomb Lattice. Nature 2018, 554, 341. 10.1038/nature25482. [DOI] [PubMed] [Google Scholar]
- Modic K. A.; Ramshaw B. J.; Betts J. B.; Breznay N. P.; Analytis J. G.; McDonald R. D.; Shekhter A. Robust Spin Correlations at High Magnetic Fields in the Harmonic Honeycomb Iridates. Nat. Commun. 2017, 8, 180. 10.1038/s41467-017-00264-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh Y.; Gegenwart P. Antiferromagnetic Mott Insulating State in Single Crystals of the Honeycomb Lattice Material Na2IrO3. Phys. Rev. B 2010, 82, 064412. 10.1103/PhysRevB.82.064412. [DOI] [Google Scholar]
- Takahashi S. K.; Wang J.; Arsenault A.; Imai T.; Abramchuk M.; Tafti F.; Singer P. M. Spin Excitations of a Proximate Kitaev Quantum Spin Liquid Realized in Cu2IrO3. Phys. Rev. X 2019, 9, 031047. 10.1103/PhysRevX.9.031047. [DOI] [Google Scholar]
- Banerjee A.; Bridges C. A.; Yan J. Q.; Aczel A. A.; Li L.; Stone M. B.; Granroth G. E.; Lumsden M. D.; Yiu Y.; Knolle J.; Bhattacharjee S.; Kovrizhin D. L.; Moessner R.; Tennant D. A.; Mandrus D. G.; Nagler S. E. Proximate Kitaev Quantum Spin Liquid Behaviour in a Honeycomb Magnet. Nat. Mater. 2016, 15, 733–740. 10.1038/nmat4604. [DOI] [PubMed] [Google Scholar]
- Plumb K. W.; Clancy J. P.; Sandilands L. J.; Shankar V. V.; Hu Y. F.; Burch K. S.; Kee H.-Y.; Kim Y.-J. α-RuCl3: A Spin-Orbit Assisted Mott Insulator on a Honeycomb Lattice. Phys. Rev. B 2014, 90, 041112. 10.1103/PhysRevB.90.041112. [DOI] [Google Scholar]
- Catuneanu A.; Yamaji Y.; Wachtel G.; Kim Y. B.; Kee H.-Y. Path to Stable Quantum Spin Liquids in Spin-Orbit Coupled Correlated Materials. npj Quantum Mater. 2018, 3, 23. 10.1038/s41535-018-0095-2. [DOI] [Google Scholar]
- Rau J. G.; Lee E. K. H.; Kee H. Y. In Annual Review of Condensed Matter Physics; Marchetti M. C., Sachdev S., Eds.; ; Annual Reviews: Palo Alto, 2016; Vol. 7; pp 195–221. [Google Scholar]
- Rau J. G.; Lee E. K.-H.; Kee H.-Y. Generic Spin Model for the Honeycomb Iridates Beyond the Kitaev Limit. Phys. Rev. Lett. 2014, 112, 077204. 10.1103/PhysRevLett.112.077204. [DOI] [PubMed] [Google Scholar]
- Winter S. M.; Riedl K.; Maksimov P. A.; Chernyshev A. L.; Honecker A.; Valentí R. Breakdown of Magnons in a Strongly Spin-Orbital Coupled Magnet. Nat. Commun. 2017, 8, 1152. 10.1038/s41467-017-01177-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sears J. A.; Chern L. E.; Kim S.; Bereciartua P. J.; Francoual S.; Kim Y. B.; Kim Y.-J. Ferromagnetic Kitaev Interaction and the Origin of Large Magnetic Anisotropy in α-RuCl3. Nat. Phys. 2020, 16, 837. 10.1038/s41567-020-0874-0. [DOI] [Google Scholar]
- Kang M.; Ye L.; Fang S.; You J.-S.; Levitan A.; Han M.; Facio J. I.; Jozwiak C.; Bostwick A.; Rotenberg E.; Chan M. K.; McDonald R. D.; Graf D.; Kaznatcheev K.; Vescovo E.; Bell D. C.; Kaxiras E.; van den Brink J.; Richter M.; Prasad Ghimire M.; et al. Dirac Fermions and Flat Bands in the Ideal Kagome Metal FeSn. Nat. Mater. 2020, 19, 163–169. 10.1038/s41563-019-0531-0. [DOI] [PubMed] [Google Scholar]
- Chisnell R.; Helton J. S.; Freedman D. E.; Singh D. K.; Bewley R. I.; Nocera D. G.; Lee Y. S. Topological Magnon Bands in a Kagome Lattice Ferromagnet. Phys. Rev. Lett. 2015, 115, 147201. 10.1103/PhysRevLett.115.147201. [DOI] [PubMed] [Google Scholar]
- Chisnell R.; Helton J. S.; Freedman D. E.; Singh D. K.; Demmel F.; Stock C.; Nocera D. G.; Lee Y. S. Magnetic Transitions in the Topological Magnon Insulator Cu(1,3-bdc). Phys. Rev. B 2016, 93, 214403. 10.1103/PhysRevB.93.214403. [DOI] [Google Scholar]
- de Vries M. A.; Kamenev K. V.; Kockelmann W. A.; Sanchez-Benitez J.; Harrison A. Magnetic Ground State of an Experimental S = 1/2 Kagome Antiferromagnet. Phys. Rev. Lett. 2008, 100, 157205. 10.1103/PhysRevLett.100.157205. [DOI] [PubMed] [Google Scholar]
- Fu M.; Imai T.; Han T.-H.; Lee Y. S. Evidence for a Gapped Spin-Liquid Ground State in a Kagome Heisenberg Antiferromagnet. Science 2015, 350, 655–658. 10.1126/science.aab2120. [DOI] [PubMed] [Google Scholar]
- Norman M. R. Colloquium: Herbertsmithite and the Search for the Quantum Spin Liquid. Rev. Mod. Phys. 2016, 88, 041002. 10.1103/RevModPhys.88.041002. [DOI] [Google Scholar]
- Gorbunov D. I.; Nomura T.; Ishii I.; Henriques M. S.; Andreev A. V.; Doerr M.; Stöter T.; Suzuki T.; Zherlitsyn S.; Wosnitza J. Crystal-Field Effects in the Kagome Antiferromagnet Ho3Ru4Al12. Phys. Rev. B 2018, 97, 184412. 10.1103/PhysRevB.97.184412. [DOI] [Google Scholar]
- Mazin I. I.; Jeschke H. O.; Lechermann F.; Lee H.; Fink M.; Thomale R.; Valenti R. Theoretical Prediction of a Strongly Correlated Dirac Metal. Nat. Commun. 2014, 5, 4261. 10.1038/ncomms5261. [DOI] [PubMed] [Google Scholar]
- Romhányi J. Multipolar Edge States in the Anisotropic Kagome Antiferromagnet. Phys. Rev. B 2019, 99, 014408. 10.1103/PhysRevB.99.014408. [DOI] [Google Scholar]
- Shabbir B.; Nadeem M.; Dai Z.; Fuhrer M. S.; Xue Q.-K.; Wang X.; Bao Q. Long Range Intrinsic Ferromagnetism in Two Dimensional Materials and Dissipationless Future Technologies. Appl. Phys. Rev. 2018, 5, 041105. 10.1063/1.5040694. [DOI] [Google Scholar]
- Xu G.; Lian B.; Zhang S.-C. Intrinsic Quantum Anomalous Hall Effect in the Kagome Lattice Cs2LiMn3F12. Phys. Rev. Lett. 2015, 115, 186802. 10.1103/PhysRevLett.115.186802. [DOI] [PubMed] [Google Scholar]
- Tang E.; Mei J.-W.; Wen X.-G. High-Temperature Fractional Quantum Hall States. Phys. Rev. Lett. 2011, 106, 236802. 10.1103/PhysRevLett.106.236802. [DOI] [PubMed] [Google Scholar]
- Hejazi K.; Luo Z.-X.; Balents L. Noncollinear Phases in Moiré Magnets. Proc. Natl. Acad. Sci. U. S. A. 2020, 117, 10721–10726. 10.1073/pnas.2000347117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sales B. C.; Yan J.; Meier W. R.; Christianson A. D.; Okamoto S.; McGuire M. A. Electronic, Magnetic, and Thermodynamic Properties of the Kagome Layer Compound FeSn. Phys. Rev. Mater. 2019, 3, 114203. 10.1103/PhysRevMaterials.3.114203. [DOI] [Google Scholar]
- Smaha R. W.; He W.; Jiang J. M.; Wen J.; Jiang Y.-F.; Sheckelton J. P.; Titus C. J.; Wang S. G.; Chen Y.-S.; Teat S. J.; Aczel A. A.; Zhao Y.; Xu G.; Lynn J. W.; Jiang H.-C.; Lee Y. S. Materializing Rival Ground States in the Barlowite Family of Kagome Magnets: Quantum Spin Liquid, Spin Ordered, and Valence Bond Crystal States. npj Quantum Mater. 2020, 5, 23. 10.1038/s41535-020-0222-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venturini G.; Fruchart D.; Malaman B. Incommensurate Magnetic Structures of RMn6Sn6 (R = Sc, Y, Lu) Compounds from Neutron Diffraction Study. J. Alloys 1996, 236, 102–110. 10.1016/0925-8388(95)01998-7. [DOI] [Google Scholar]
- Venturini G.; Idrissi B. C. E.; Malaman B. Magnetic Properties of RMn6Sn6 (R = Sc, Y, Gd-Tm, Lu) Compounds with HfFe6Ge6 Type Structure. J. Magn. Magn. Mater. 1991, 94, 35–42. 10.1016/0304-8853(91)90108-M. [DOI] [Google Scholar]
- Wang Q.; Neubauer K. J.; Duan C.; Yin Q.; Fujitsu S.; Hosono H.; Ye F.; Zhang R.; Chi S.; Krycka K.; Lei H.; Dai P. Field-Induced Topological Hall Effect and Double-Fan Spin Structure with a c-Axis Component in the Metallic Kagome Antiferromagnetic Compound YMn6Sn6. Phys. Rev. B 2021, 103, 014416. 10.1103/PhysRevB.103.014416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruno P.; Dugaev V. K.; Taillefumier M. Topological Hall Effect and Berry Phase in Magnetic Nanostructures. Phys. Rev. Lett. 2004, 93, 096806. 10.1103/PhysRevLett.93.096806. [DOI] [PubMed] [Google Scholar]
- Metalidis G.; Bruno P. Topological Hall Effect Studied in Simple Models. Phys. Rev. B 2006, 74, 045327. 10.1103/PhysRevB.74.045327. [DOI] [Google Scholar]
- Nagaosa N.; Tokura Y. Topological Properties and Dynamics of Magnetic Skyrmions. Nat. Nanotechnol. 2013, 8, 899–911. 10.1038/nnano.2013.243. [DOI] [PubMed] [Google Scholar]
- Onose Y.; Ideue T.; Katsura H.; Shiomi Y.; Nagaosa N.; Tokura Y. Observation of the Magnon Hall Effect. Science 2010, 329, 297–299. 10.1126/science.1188260. [DOI] [PubMed] [Google Scholar]
- Ueda K.; Iguchi S.; Suzuki T.; Ishiwata S.; Taguchi Y.; Tokura Y. Topological Hall Effect in Pyrochlore Lattice with Varying Density of Spin Chirality. Phys. Rev. Lett. 2012, 108, 156601. 10.1103/PhysRevLett.108.156601. [DOI] [PubMed] [Google Scholar]
- Ueland B. G.; Miclea C. F.; Kato Y.; Ayala-Valenzuela O.; McDonald R. D.; Okazaki R.; Tobash P. H.; Torrez M. A.; Ronning F.; Movshovich R.; Fisk Z.; Bauer E. D.; Martin I.; Thompson J. D. Controllable Chirality-Induced Geometrical Hall Effect in a Frustrated Highly Correlated Metal. Nat. Commun. 2012, 3, 1067. 10.1038/ncomms2075. [DOI] [PubMed] [Google Scholar]
- Bartram F. M.; Sorn S.; Li Z.; Hwangbo K.; Shen S.; Frontini F.; He L.; Yu P.; Paramekanti A.; Yang L. Anomalous Kerr Effect in SrRuO3 Thin Films. Phys. Rev. B 2020, 102, 140408. 10.1103/PhysRevB.102.140408. [DOI] [Google Scholar]
- Reed M. A. Inelastic Electron Tunneling Spectroscopy. Mater. Today 2008, 11, 46–50. 10.1016/S1369-7021(08)70238-4. [DOI] [Google Scholar]
- Fernández-Rossier J. Theory of Single-Spin Inelastic Tunneling Spectroscopy. Phys. Rev. Lett. 2009, 102, 256802. 10.1103/PhysRevLett.102.256802. [DOI] [PubMed] [Google Scholar]
- Cenker J.; Huang B.; Suri N.; Thijssen P.; Miller A.; Song T.; Taniguchi T.; Watanabe K.; McGuire M. A.; Xiao D.; Xu X. Direct Observation of Two-Dimensional Magnons in Atomically Thin CrI3. Nat. Phys. 2021, 17, 20–25. 10.1038/s41567-020-0999-1. [DOI] [Google Scholar]
- MacNeill D.; Hou J. T.; Klein D. R.; Zhang P.; Jarillo-Herrero P.; Liu L. Gigahertz Frequency Antiferromagnetic Resonance and Strong Magnon-Magnon Coupling in the Layered Crystal CrCl3. Phys. Rev. Lett. 2019, 123, 047204. 10.1103/PhysRevLett.123.047204. [DOI] [PubMed] [Google Scholar]
- Kartsev A.; Augustin M.; Evans R. F. L.; Novoselov K. S.; Santos E. J. G. Biquadratic Exchange Interactions in Two-Dimensional Magnets. npj Comput. Mater. 2020, 6, 150. 10.1038/s41524-020-00416-1. [DOI] [Google Scholar]
- Wang W.; Lee T.; Kretzschmar I.; Reed M. A. Inelastic Electron Tunneling Spectroscopy of an Alkanedithiol Self-Assembled Monolayer. Nano Lett. 2004, 4, 643–646. 10.1021/nl049870v. [DOI] [Google Scholar]
- Ament L. J. P.; van Veenendaal M.; Devereaux T. P.; Hill J. P.; van den Brink J. Resonant Inelastic X-Ray Scattering Studies of Elementary Excitations. Rev. Mod. Phys. 2011, 83, 705. 10.1103/RevModPhys.83.705. [DOI] [Google Scholar]
- Grundy P. J.; Tebble R. S. Lorentz Electron Microscopy. Adv. Phys. 1968, 17, 153–242. 10.1080/00018736800101286. [DOI] [Google Scholar]
- Dean M. P. M. Insights into the High Temperature Superconducting Cuprates from Resonant Inelastic X-Ray Scattering. J. Magn. Magn. Mater. 2015, 376, 3–13. 10.1016/j.jmmm.2014.03.057. [DOI] [Google Scholar]
- Kim Y.-J.; Hill J. P.; Kim J.; Casa D. Hard X-Ray Resonant Inelastic X-Ray Scattering at the Advanced Photon Source. Synchrotron Radiat. News 2012, 25, 3–8. 10.1080/08940886.2012.700841. [DOI] [Google Scholar]
- Dai P. Antiferromagnetic Order and Spin Dynamics in Iron-Based Superconductors. Rev. Mod. Phys. 2015, 87, 855–896. 10.1103/RevModPhys.87.855. [DOI] [Google Scholar]
- Hill J. P.; Blumberg G.; Kim Y.-J.; Ellis D. S.; Wakimoto S.; Birgeneau R. J.; Komiya S.; Ando Y.; Liang B.; Greene R. L.; Casa D.; Gog T. Observation of a 500 meV Collective Mode in La2–xSrxCuO4 and Nd2CuO4 Using Resonant Inelastic X-Ray Scattering. Phys. Rev. Lett. 2008, 100, 097001. 10.1103/PhysRevLett.100.097001. [DOI] [PubMed] [Google Scholar]
- Frisenda R.; Navarro-Moratalla E.; Gant P.; Pérez De Lara D.; Jarillo-Herrero P.; Gorbachev R. V.; Castellanos-Gomez A. Recent Progress in the Assembly of Nanodevices and van der Waals Heterostructures by Deterministic Placement of 2D Materials. Chem. Soc. Rev. 2018, 47, 53–68. 10.1039/C7CS00556C. [DOI] [PubMed] [Google Scholar]
- He J.; Wang C.; Zhou B.; Zhao Y.; Tao L.; Zhang H. 2D van der Waals Heterostructures: Processing, Optical Properties and Applications in Ultrafast Photonics. Mater. Horiz. 2020, 7, 2903–2921. 10.1039/D0MH00340A. [DOI] [Google Scholar]
- Huang Z.; Alharbi A.; Mayer W.; Cuniberto E.; Taniguchi T.; Watanabe K.; Shabani J.; Shahrjerdi D. Versatile Construction of van der Waals Heterostructures Using a Dual-Function Polymeric Film. Nat. Commun. 2020, 11, 3029. 10.1038/s41467-020-16817-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Y.; Herlinger P.; Taniguchi T.; Watanabe K.; Smet J. H. Reliable Postprocessing Improvement of van der Waals Heterostructures. ACS Nano 2019, 13, 14182–14190. 10.1021/acsnano.9b06992. [DOI] [PubMed] [Google Scholar]
- Kinoshita K.; Moriya R.; Onodera M.; Wakafuji Y.; Masubuchi S.; Watanabe K.; Taniguchi T.; Machida T. Dry Release Transfer of Graphene and Few-Layer h-BN by Utilizing Thermoplasticity of Polypropylene Carbonate. npj 2D Mater. Appl. 2019, 3, 4–6. 10.1038/s41699-019-0104-8. [DOI] [Google Scholar]
- Liang S. J.; Cheng B.; Cui X.; Miao F. Van der Waals Heterostructures for High-Performance Device Applications: Challenges and Opportunities. Adv. Mater. 2019, 32, 1903800. 10.1002/adma.201903800. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Weiss N. O.; Duan X.; Cheng H.-C.; Huang Y.; Duan X. Van der Waals Heterostructures and Devices. Nat. Rev. Mater. 2016, 1, 16042. 10.1038/natrevmats.2016.42. [DOI] [Google Scholar]
- Son S.; Shin Y. J.; Zhang K.; Shin J.; Lee S.; Idzuchi H.; Coak M. J.; Kim H.; Kim J.; Kim J. H.; Kim M.; Kim D.; Kim P.; Park J.-G. Strongly Adhesive Dry Transfer Technique for van der Waals Heterostructure. 2D Mater. 2020, 7, 041005. 10.1088/2053-1583/abad0b. [DOI] [Google Scholar]
- Huang P.; Zhang P.; Xu S.; Wang H.; Zhang X.; Zhang H. Recent Advances in Two-Dimensional Ferromagnetism: Materials Synthesis, Physical Properties and Device Applications. Nanoscale 2020, 12, 2309–2327. 10.1039/C9NR08890C. [DOI] [PubMed] [Google Scholar]
- Liu L.; Zhai K.; Nie A.; Lv W.; Yang B.; Mu C.; Xiang J.; Wen F.; Zhao Z.; Zeng Z.; Gong Y.; Tian Y.; Liu Z. Accelerated Degradation of CrCl3 Nanoflakes Induced by Metal Electrodes: Implications for Remediation in Nanodevice Fabrication. ACS Appl. Nano Mater. 2019, 2, 1597–1603. 10.1021/acsanm.9b00058. [DOI] [Google Scholar]
- Shcherbakov D.; Stepanov P.; Weber D.; Wang Y.; Hu J.; Zhu Y.; Watanabe K.; Taniguchi T.; Mao Z.; Windl W.; Goldberger J.; Bockrath M.; Lau C. N. Raman Spectroscopy, Photocatalytic Degradation, and Stabilization of Atomically Thin Chromium Tri-Iodide. Nano Lett. 2018, 18, 4214–4219. 10.1021/acs.nanolett.8b01131. [DOI] [PubMed] [Google Scholar]
- Li L. H.; Cervenka J.; Watanabe K.; Taniguchi T.; Chen Y. Strong Oxidation Resistance of Atomically Thin Boron Nitride Nanosheets. ACS Nano 2014, 8, 1457–1462. 10.1021/nn500059s. [DOI] [PubMed] [Google Scholar]
- Ohta T.; Tokuda M.; Iwakiri S.; Sakai K.; Driesen B.; Okada Y.; Kobayashi K.; Niimi Y. Butterfly-Shaped Magnetoresistance in van der Waals Ferromagnet Fe5GeTe2. AIP Adv. 2021, 11, 025014. 10.1063/9.0000067. [DOI] [Google Scholar]
- Allain A.; Kang J.; Banerjee K.; Kis A. Electrical Contacts to Two-Dimensional Semiconductors. Nat. Mater. 2015, 14, 1195–1205. 10.1038/nmat4452. [DOI] [PubMed] [Google Scholar]
- Schulman D. S.; Arnold A. J.; Das S. Contact Engineering for 2D Materials and Devices. Chem. Soc. Rev. 2018, 47, 3037–3058. 10.1039/C7CS00828G. [DOI] [PubMed] [Google Scholar]
- Xu Y.; Cheng C.; Du S.; Yang J.; Yu B.; Luo J.; Yin W.; Li E.; Dong S.; Ye P.; Duan X. Contacts Between Two- and Three-Dimensional Materials: Ohmic, Schottky, and p–n Heterojunctions. ACS Nano 2016, 10, 4895–4919. 10.1021/acsnano.6b01842. [DOI] [PubMed] [Google Scholar]
- Telford E. J.; Benyamini A.; Rhodes D.; Wang D.; Jung Y.; Zangiabadi A.; Watanabe K.; Taniguchi T.; Jia S.; Barmak K.; Pasupathy A. N.; Dean C. R.; Hone J. C. Via Method for Lithography Free Contact and Preservation of 2D Materials. Nano Lett. 2018, 18, 1416–1420. 10.1021/acs.nanolett.7b05161. [DOI] [PubMed] [Google Scholar]
- Ribeiro-Palau R.; Zhang C.; Watanabe K.; Taniguchi T.; Hone J.; Dean C. R. Twistable Electronics with Dynamically Rotatable Heterostructures. Science 2018, 361, 690–693. 10.1126/science.aat6981. [DOI] [Google Scholar]
- Wakafuji Y.; Moriya R.; Masubuchi S.; Watanabe K.; Taniguchi T.; MacHida T. 3D Manipulation of 2D Materials Using Microdome Polymer. Nano Lett. 2020, 20, 2486–2492. 10.1021/acs.nanolett.9b05228. [DOI] [PubMed] [Google Scholar]
- Yang Y.; Li J.; Yin J.; Xu S.; Mullan C.; Taniguchi T.; Watanabe K.; Geim A. K.; Novoselov K. S.; Mishchenko A. In Situ Manipulation of van der Waals Heterostructures for Twistronics. Sci. Adv. 2020, 6, eabd3655 10.1126/sciadv.abd3655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bistritzer R.; MacDonald A. H. Moiré Bands in Twisted Double-Layer Graphene. Proc. Natl. Acad. Sci. U.S.A. 2011, 108, 12233–12237. 10.1073/pnas.1108174108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao Y.; Fatemi V.; Fang S.; Watanabe K.; Taniguchi T.; Kaxiras E.; Jarillo-Herrero P. Unconventional Superconductivity in Magic-Angle Graphene Superlattices. Nature 2018, 556, 43–50. 10.1038/nature26160. [DOI] [PubMed] [Google Scholar]
- Sharpe A. L.; Fox E. J.; Barnard A. W.; Finney J.; Watanabe K.; Taniguchi T.; Kastner M. A.; Goldhaber-Gordon D. Emergent Ferromagnetism Near Three-Quarters Filling in Twisted Bilayer Graphene. Science 2019, 365, 605–608. 10.1126/science.aaw3780. [DOI] [PubMed] [Google Scholar]
- Serlin M.; Tschirhart C. L.; Polshyn H.; Zhang Y.; Zhu J.; Watanabe K.; Taniguchi T.; Balents L.; Young A. F. Intrinsic Quantized Anomalous Hall Effect in a Moiré Heterostructure. Science 2020, 367, 900–903. 10.1126/science.aay5533. [DOI] [PubMed] [Google Scholar]
- Polshyn H.; Zhu J.; Kumar M. A.; Zhang Y.; Yang F.; Tschirhart C. L.; Serlin M.; Watanabe K.; Taniguchi T.; MacDonald A. H.; Young A. F. Electrical Switching of Magnetic Order in an Orbital Chern Insulator. Nature 2020, 588, 66–70. 10.1038/s41586-020-2963-8. [DOI] [PubMed] [Google Scholar]
- Zondiner U.; Rozen A.; Rodan-Legrain D.; Cao Y.; Queiroz R.; Taniguchi T.; Watanabe K.; Oreg Y.; von Oppen F.; Stern A.; Berg E.; Jarillo-Herrero P.; Ilani S. Cascade of Phase Transitions and Dirac Revivals in Magic-Angle Graphene. Nature 2020, 582, 203–208. 10.1038/s41586-020-2373-y. [DOI] [PubMed] [Google Scholar]
- Lu X.; Stepanov P.; Yang W.; Xie M.; Aamir M. A.; Das I.; Urgell C.; Watanabe K.; Taniguchi T.; Zhang G.; Bachtold A.; MacDonald A. H.; Efetov D. K. Superconductors, Orbital Magnets and Correlated States in Magic-Angle Bilayer Graphene. Nature 2019, 574, 653–657. 10.1038/s41586-019-1695-0. [DOI] [PubMed] [Google Scholar]
- Saito Y.; Ge J.; Rademaker L.; Watanabe K.; Taniguchi T.; Abanin D. A.; Young A. F. Hofstadter Subband Ferromagnetism and Symmetry-Broken Chern Insulators in Twisted Bilayer Graphene. Nat. Phys. 2021, 17, 478–481. 10.1038/s41567-020-01129-4. [DOI] [Google Scholar]
- Shi Y.; Xu S.; Yang Y.; Slizovskiy S.; Morozov S. V.; Son S. K.; Ozdemir S.; Mullan C.; Barrier J.; Yin J.; Berdyugin A. I.; Piot B. A.; Taniguchi T.; Watanabe K.; Fal’ko V. I.; Novoselov K. S.; Geim A. K.; Mishchenko A. Electronic Phase Separation in Multilayer Rhombohedral Graphite. Nature 2020, 584, 210–214. 10.1038/s41586-020-2568-2. [DOI] [PubMed] [Google Scholar]
- Kerelsky A.; Rubio-Verdú C.; Xian L.; Kennes D. M.; Halbertal D.; Finney N.; Song L.; Turkel S.; Wang L.; Watanabe K.; Taniguchi T.; Hone J.; Dean C.; Basov D. N.; Rubio A.; Pasupathy A. N. Moiréless Correlations in ABCA Graphene. Proc. Natl. Acad. Sci. U. S. A. 2021, 118, e2017366118 10.1073/pnas.2017366118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.; Gao Y.; Lv H.; Xu X.; Xiao D. Stacking Domain Wall Magnons in Twisted van der Waals Magnets. Phys. Rev. Lett. 2020, 125, 247201. 10.1103/PhysRevLett.125.247201. [DOI] [PubMed] [Google Scholar]
- Yang Y.; Zou Y. C.; Woods C. R.; Shi Y.; Yin J.; Xu S.; Ozdemir S.; Taniguchi T.; Watanabe K.; Geim A. K.; Novoselov K. S.; Haigh S. J.; Mishchenko A. Stacking Order in Graphite Films Controlled by van der Waals Technology. Nano Lett. 2019, 19, 8526–8532. 10.1021/acs.nanolett.9b03014. [DOI] [PubMed] [Google Scholar]
- Akram M.; Erten O. Skyrmions in Twisted van der Waals Magnets. Phys. Rev. B 2021, 103, L140406. 10.1103/PhysRevB.103.L140406. [DOI] [Google Scholar]
- Ghader D. Magnon Magic Angles and Tunable Hall Conductivity in 2D Twisted Ferromagnetic Bilayers. Sci. Rep. 2020, 10, 15069. 10.1038/s41598-020-72000-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun Y.; Xiao R. C.; Lin G. T.; Zhang R. R.; Ling L. S.; Ma Z. W.; Luo X.; Lu W. J.; Sun Y. P.; Sheng Z. G. Effects of Hydrostatic Pressure on Spin-Lattice Coupling in Two-Dimensional Ferromagnetic Cr2Ge2Te6. Appl. Phys. Lett. 2018, 112, 072409. 10.1063/1.5016568. [DOI] [Google Scholar]
- Webster L.; Yan J. A. Strain-Tunable Magnetic Anisotropy in Monolayer CrCl3, CrBr3, and CrI3. Phys. Rev. B 2018, 98, 144411. 10.1103/PhysRevB.98.144411. [DOI] [Google Scholar]
- Zollner K.; Gmitra M.; Fabian J. Swapping Exchange and Spin-Orbit Coupling in 2D van der Waals Heterostructures. Phys. Rev. Lett. 2020, 125, 196402. 10.1103/PhysRevLett.125.196402. [DOI] [PubMed] [Google Scholar]
- Mukherjee A.; Shayan K.; Li L.; Shan J.; Mak K. F.; Vamivakas A. N. Observation of Site-Controlled Localized Charged Excitons in CrI3/WSe2 Heterostructures. Nat. Commun. 2020, 11, 5502. 10.1038/s41467-020-19262-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong X. J.; You J. Y.; Zhang Z.; Gu B.; Su G. Great Enhancement of Curie Temperature and Magnetic Anisotropy in Two-Dimensional van der Waals Magnetic Semiconductor Heterostructures. Phys. Rev. B 2020, 102, 144443. 10.1103/PhysRevB.102.144443. [DOI] [Google Scholar]
- Liu N.; Zhou S.; Zhao J. High-Curie-Temperature Ferromagnetism in Bilayer CrI3 on Bulk Semiconducting Substrates. Phys. Rev. Mater. 2020, 4, 094003. 10.1103/PhysRevMaterials.4.094003. [DOI] [Google Scholar]
- Tong Q.; Chen M.; Yao W. Magnetic Proximity Effect in a van der Waals Moiré Superlattice. Phys. Rev. Applied 2019, 12, 024031. 10.1103/PhysRevApplied.12.024031. [DOI] [Google Scholar]
- Kezilebieke S.; Huda M. N.; Vaňo V.; Aapro M.; Ganguli S. C.; Silveira O. J.; Głodzik S.; Foster A. S.; Ojanen T.; Liljeroth P. Topological Superconductivity in a van der Waals Heterostructure. Nature 2020, 588, 424–428. 10.1038/s41586-020-2989-y. [DOI] [PubMed] [Google Scholar]
- Kezilebieke S.; Huda M. N.; Dreher P.; Manninen I.; Zhou Y.; Sainio J.; Mansell R.; Ugeda M. M.; van Dijken S.; Komsa H. P.; Liljeroth P. Electronic and Magnetic Characterization of Epitaxial VSe2 Monolayers on Superconducting NbSe2. Commun. Phys. 2020, 3, 116. 10.1038/s42005-020-0377-4. [DOI] [Google Scholar]
- Huang Y.; Wolowiec C.; Zhu T.; Hu Y.; An L.; Li Z.; Grossman J. C.; Schuller I. K.; Ren S. Emerging Magnetic Interactions in van der Waals Heterostructures. Nano Lett. 2020, 20, 7852. 10.1021/acs.nanolett.0c02175. [DOI] [PubMed] [Google Scholar]
- Zhang D.; Liu Y.; He M.; Zhang A.; Chen S.; Tong Q.; Huang L.; Zhou Z.; Zheng W.; Chen M.; Braun K.; Meixner A. J.; Wang X.; Pan A. Room Temperature Near Unity Spin Polarization in 2D van der Waals Heterostructures. Nat. Commun. 2020, 11, 4442. 10.1038/s41467-020-18307-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soriano D.; Lado J. L. Exchange-Bias Controlled Correlations in Magnetically Encapsulated Twisted van der Waals Dichalcogenides. J. Phys. D: Appl. Phys. 2020, 53, 474001. 10.1088/1361-6463/abaa15. [DOI] [Google Scholar]
- Luo W.; Xu K.; Xiang H. Two-Dimensional Hyperferroelectric Metals: A Different Route to Ferromagnetic-Ferroelectric Multiferroics. Phys. Rev. B 2017, 96, 235415. 10.1103/PhysRevB.96.235415. [DOI] [Google Scholar]
- Qi J.; Wang H.; Chen X.; Qian X. Two-Dimensional Multiferroic Semiconductors with Coexisting Ferroelectricity and Ferromagnetism. Appl. Phys. Lett. 2018, 113, 043102. 10.1063/1.5038037. [DOI] [Google Scholar]
- Gong C.; Kim E. M.; Wang Y.; Lee G.; Zhang X. Multiferroicity in Atomic van der Waals Heterostructures. Nat. Commun. 2019, 10, 2657. 10.1038/s41467-019-10693-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu C.; Feng J.; Xiang H.; Bellaiche L. Interplay Between Kitaev Interaction and Single Ion Anisotropy in Ferromagnetic CrI3 and CrGeTe3 Monolayers. npj Comput. Mater. 2018, 4, 57. 10.1038/s41524-018-0115-6. [DOI] [Google Scholar]
- Mohn P.Magnetism in the Solid State: An Introduction; Springer-Verlag Berlin Heidelberg: Heidelberg, Germany, 2003; pp 139–145. [Google Scholar]
- Pajda M.; Kudrnovský J.; Turek I.; Drchal V.; Bruno P. Ab Initio Calculations of Exchange Interactions, Spin-Wave Stiffness Constants, and Curie Temperatures of Fe, Co, and Ni. Phys. Rev. B 2001, 64, 174402. 10.1103/PhysRevB.64.174402. [DOI] [Google Scholar]
- Evans R. F. L.; Fan W. J.; Chureemart P.; Ostler T. A.; Ellis M. O. A.; Chantrell R. W. Atomistic Spin Model Simulations of Magnetic Nanomaterials. J. Phys.: Condens. Matt. 2014, 26, 103202. 10.1088/0953-8984/26/10/103202. [DOI] [PubMed] [Google Scholar]
- Metropolis N.; Rosenbluth A. W.; Rosenbluth M. N.; Teller A. H.; Teller E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. 10.1063/1.1699114. [DOI] [Google Scholar]
- Marsaglia G. Choosing a Point from the Surface of a Sphere. Ann. Math. Stat. 1972, 43, 645–646. 10.1214/aoms/1177692644. [DOI] [Google Scholar]
- Nowak U.; Hinzke D. Magnetization Switching in Small Ferromagnetic Particles: Nucleation and Coherent Rotation. J. Appl. Phys. 1999, 85, 4337. 10.1063/1.370360. [DOI] [Google Scholar]
- Alzate-Cardona J. D.; Sabogal-Suárez D.; Evans R. F.; Restrepo-Parra E. Optimal Phase Space Sampling for Monte Carlo Simulations of Heisenberg Spin Systems. J. Phys.: Condens. Matter 2019, 31, 095802. 10.1088/1361-648X/aaf852. [DOI] [PubMed] [Google Scholar]
- Asselin P.; Evans R. F. L.; Barker J.; Chantrell R. W.; Yanes R.; Chubykalo-Fesenko O.; Hinzke D.; Nowak U. Constrained Monte Carlo Method and Calculation of the Temperature Dependence of Magnetic Anisotropy. Phys. Rev. B 2010, 82, 054415. 10.1103/PhysRevB.82.054415. [DOI] [Google Scholar]
- Atxitia U.; Hinzke D.; Chubykalo-Fesenko O.; Nowak U.; Kachkachi H.; Mryasov O. N.; Evans R. F.; Chantrell R. W. Multiscale Modeling of Magnetic Materials: Temperature Dependence of the Exchange Stiffness. Phys. Rev. B 2010, 82, 134440. 10.1103/PhysRevB.82.134440. [DOI] [Google Scholar]
- Moreno R.; Evans R. F. L.; Khmelevskyi S.; Muñoz M. C.; Chantrell R. W.; Chubykalo-Fesenko O. Temperature-Dependent Exchange Stiffness and Domain Wall Width in Co. Phys. Rev. B 2016, 94, 104433. 10.1103/PhysRevB.94.104433. [DOI] [Google Scholar]
- Evans R. F. L.; Rózsa L.; Jenkins S.; Atxitia U. Temperature Scaling of Two-Ion Anisotropy in Pure and Mixed Anisotropy Systems. Phys. Rev. B 2020, 102, 020412. 10.1103/PhysRevB.102.020412. [DOI] [Google Scholar]
- Evans R. F. L.; Atxitia U.; Chantrell R. W. Quantitative Simulation of Temperature-Dependent Magnetization Dynamics and Equilibrium Properties of Elemental Ferromagnets. Phys. Rev. B 2015, 91, 144425. 10.1103/PhysRevB.91.144425. [DOI] [Google Scholar]
- Hashmi A.; Nakanishi K.; Farooq M. U.; Ono T. Ising Ferromagnetism and Robust Half-Metallicity in Two-Dimensional Honeycomb-Kagome Cr2O3 Layer. npj 2D Mater. Appl. 2020, 4, 39. 10.1038/s41699-020-00174-0. [DOI] [Google Scholar]
- Rassekh M.; He J.; Shayesteh S. F.; Palacios J. J. Remarkably Enhanced Curie Temperature in Monolayer CrI3 by Hydrogen and Oxygen Adsorption: A First-Principles Calculations. Comput. Mater. Sci. 2020, 183, 109820. 10.1016/j.commatsci.2020.109820. [DOI] [Google Scholar]
- Chen S.; Huang C.; Sun H.; Ding J.; Jena P.; Kan E. Boosting the Curie Temperature of Two-Dimensional Semiconducting CrI3 Monolayer Through van der Waals Heterostructures. J. Phys. Chem. C 2019, 123, 17987–17993. 10.1021/acs.jpcc.9b04631. [DOI] [Google Scholar]
- Yang K.; Fan F.; Wang H.; Khomskii D. I.; Wu H. VI3: A Two-Dimensional Ising Ferromagnet. Phys. Rev. B 2020, 101, 100402. 10.1103/PhysRevB.101.100402. [DOI] [Google Scholar]
- Kulish V. V.; Huang W. Single-Layer Metal Halides MX2 (X = Cl, Br, I): Stability and Tunable Magnetism from First Principles and Monte Carlo Simulations. J. Mater. Chem. C 2017, 5, 8734–8741. 10.1039/C7TC02664A. [DOI] [Google Scholar]
- Lu X.; Fei R.; Yang L. Curie Temperature of Emerging Two-Dimensional Magnetic Structures. Phys. Rev. B 2019, 100, 205409. 10.1103/PhysRevB.100.205409. [DOI] [Google Scholar]
- Anders J.; Sait C. R. J.; Horsley S. A. R.. Versatile Three-Dimensional Quantum Spin Dynamics Equation with Guaranteed Fluctuation-Dissipation Link. arXiv (Quantum Physics), July 7, 2021, 2009.00600, ver. 2.https://arxiv.org/abs/2009.00600 (accessed 2021-12-07).
- Nowak U.Annual Reviews of Computational Physics IX; World Scientific: Singapore, 2001; pp 105–151. [Google Scholar]
- Skubic B.; Hellsvik J.; Nordström L.; Eriksson O. A Method for Atomistic Spin Dynamics Simulations: Implementation and Examples. J. Phys.: Condens. Matter 2008, 20, 315203. 10.1088/0953-8984/20/31/315203. [DOI] [Google Scholar]
- Ellis M. O. A.; Evans R. F. L.; Ostler T. A.; Barker J.; Atxitia U.; Chubykalo-Fesenko O.; Chantrell R. W. The Landau-Lifshitz Equation in Atomistic Models. Low Temp. Phys. 2015, 41, 705–712. 10.1063/1.4930971. [DOI] [Google Scholar]
- Augustin M.; Jenkins S.; Evans R. F. L.; Novoselov K. S.; Santos E. J. G. Properties and Dynamics of Meron Topological Spin Textures in the Two-Dimensional Magnet CrCl3. Nat. Commun. 2021, 12, 185. 10.1038/s41467-020-20497-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown W. Thermal Fluctuation of Fine Ferromagnetic Particles. IEEE Trans. Magn. 1979, 15, 1196–1208. 10.1109/TMAG.1979.1060329. [DOI] [Google Scholar]
- Strungaru M.; Ellis M. O. A.; Ruta S.; Chubykalo-Fesenko O.; Evans R. F. L.; Chantrell R. W. Spin-Lattice Dynamics Model with Angular Momentum Transfer for Canonical and Microcanonical Ensembles. Phys. Rev. B 2021, 103, 024429. 10.1103/PhysRevB.103.024429. [DOI] [Google Scholar]
- Müller G. P.; Hoffmann M.; Dißelkamp C.; Schürhoff D.; Mavros S.; Sallermann M.; Kiselev N. S.; Jónsson H.; Blügel S. Spirit: Multifunctional Framework for Atomistic Spin Simulations. Phys. Rev. B 2019, 99, 224414. 10.1103/PhysRevB.99.224414. [DOI] [Google Scholar]
- Bisotti M.-A.; Cortés-Ortuño D.; Pepper R.; Wang W.; Beg M.; Kluyver T.; Fangohr H. Fidimag – A Finite Difference Atomistic and Micromagnetic Simulation Package. J. Open Res. Softw. 2018, 6, 22. 10.5334/jors.223. [DOI] [Google Scholar]
- Jacob C. R.; Reiher M. Spin in Density-Functional Theory. Int. J. Quantum Chem. 2012, 112, 3661–3684. 10.1002/qua.24309. [DOI] [Google Scholar]
- Goodpaster J. D.; Barnes T. A.; Manby F. R.; Miller T. F. Density Functional Theory Embedding for Correlated Wavefunctions: Improved Methods for Open-Shell Systems and Transition Metal Complexes. J. Chem. Phys. 2012, 137, 224113. 10.1063/1.4770226. [DOI] [PubMed] [Google Scholar]
- Chong D.Recent Advances In Density Functional Methods, Part I; Recent Advances In Computational Chemistry; World Scientific Publishing Company: Singapore, 1995. [Google Scholar]
- Kresse G.; Furthmüller J. Efficient Iterative Schemes for ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Dudarev S. L.; Botton G. A.; Savrasov S. Y.; Humphreys C. J.; Sutton A. P. Electron-Energy-Loss Spectra and the Structural Stability of Nickel Oxide: An LSDA+U Study. Phys. Rev. B 1998, 57, 1505–1509. 10.1103/PhysRevB.57.1505. [DOI] [Google Scholar]
- Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
- Vosko S. H.; Wilk L.; Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
- Miyazato I.; Tanaka Y.; Takahashi K. Accelerating the Discovery of Hidden Two-Dimensional Magnets Using Machine Learning and First Principle Calculations. J. Phys.: Condens. Matter 2018, 30, 06LT01. 10.1088/1361-648X/aaa471. [DOI] [PubMed] [Google Scholar]
- Mounet N.; Gibertini M.; Schwaller P.; Campi D.; Merkys A.; Marrazzo A.; Sohier T.; Castelli I. E.; Cepellotti A.; Pizzi G.; Marzari N. Two-Dimensional Materials from High-Throughput Computational Exfoliation of Experimentally Known Compounds. Nat. Nanotechnol. 2018, 13, 246–252. 10.1038/s41565-017-0035-5. [DOI] [PubMed] [Google Scholar]
- Kabiraj A.; Kumar M.; Mahapatra S. High-Throughput Discovery of High Curie Point Two-Dimensional Ferromagnetic Materials. npj Comput. Mater. 2020, 6, 35. 10.1038/s41524-020-0300-2. [DOI] [Google Scholar]
- Ke L.; Katsnelson M. I. Electron Correlation Effects on Exchange Interactions and Spin Excitations in 2D van der Waals Materials. npj Comput. Mater. 2021, 7, 4. 10.1038/s41524-020-00469-2. [DOI] [Google Scholar]
- Kim T. J.; Ryee S.; Han M. J.; Choi S. Dynamical Mean-Field Study of Vanadium Diselenide Monolayer Ferromagnetism. 2D Mater. 2020, 7, 035023. 10.1088/2053-1583/ab8b48. [DOI] [Google Scholar]
- Pauling L. The Nature of the Interatomic Forces in Metals. Phys. Rev. 1938, 54, 899–904. 10.1103/PhysRev.54.899. [DOI] [Google Scholar]
- Slater J. C. The Ferromagnetism of Nickel. II. Temperature Effects. Phys. Rev. 1936, 49, 931–937. 10.1103/PhysRev.49.931. [DOI] [Google Scholar]
- Rothernberg G. In Catalysis; Rothernberg G., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2008; Chapter The Basics of Catalysis, pp 39–75. [Google Scholar]
- Stoner E. C.; Whiddington R. Collective Electron Specific Heat and Spin Paramagnetism in Metals. Proc. R. Soc. London, Ser. A 1936, 154, 656–678. [Google Scholar]
- Stoner E. C. Collective Electron Ferromagnetism. Proc. R. Soc. London, Ser. A 1938, 165, 372–414. 10.1098/rspa.1938.0066. [DOI] [Google Scholar]
- Vatansever E.; Sarikurt S.; Evans R. F. L. Hysteresis Features of the Transition-Metal Dichalcogenides VX2 (X = S, Se, and Te). Mater. Res. Express 2018, 5, 046108. 10.1088/2053-1591/aabca6. [DOI] [Google Scholar]
- Fuh H.-R.; Chang C.-R.; Wang Y.-K.; Evans R. F. L.; Chantrell R. W.; Jeng H.-T. Newtype Single-Layer Magnetic Semiconductor in Transition-Metal Dichalcogenides VX2 (X = S, Se and Te). Sci. Rep. 2016, 6, 32625. 10.1038/srep32625. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogulkoc A.; Modarresi M.; Rudenko A. N. Two-Dimensional Chromium Pnictides CrX (X = P, As, Sb): Half-Metallic Ferromagnets with High Curie Temperature. Phys. Rev. B 2020, 102, 024441. 10.1103/PhysRevB.102.024441. [DOI] [Google Scholar]
- Tang C.; Zhang L.; Du A. Tunable Magnetic Anisotropy in 2D Magnets via Molecular Adsorption. J. Mater. Chem. C 2020, 8, 14948–14953. 10.1039/D0TC04049E. [DOI] [Google Scholar]
- Li L. H.; Tian T.; Cai Q.; Shih C.-J.; Santos E. J. G. Asymmetric Electric Field Screening in van der Waals Heterostructures. Nat. Commun. 2018, 9, 1271. 10.1038/s41467-018-03592-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santos E. J. G. Carrier-Mediated Magnetoelectric Coupling in Functionalized Graphene. ACS Nano 2013, 7, 9927–9932. 10.1021/nn4037877. [DOI] [PubMed] [Google Scholar]
- Hong J.; Kim Y.; Liang J.; Chen H.; Park C.-Y.; Yang H.; Santos E. J. G.; Bokor J.; Hwang C.-C.; You L. Intrinsic Controllable Magnetism of Graphene Grown on Fe. J. Phys. Chem. C 2019, 123, 26870–26876. 10.1021/acs.jpcc.9b05886. [DOI] [Google Scholar]
- Tian T.; Scullion D.; Hughes D.; Li L. H.; Shih C.-J.; Coleman J.; Chhowalla M.; Santos E. J. G. Electronic Polarizability as the Fundamental Variable in the Dielectric Properties of Two-Dimensional Materials. Nano Lett. 2020, 20, 841–851. 10.1021/acs.nanolett.9b02982. [DOI] [PubMed] [Google Scholar]
- Ma P.-W.; Dudarev S. L. Longitudinal Magnetic Fluctuations in Langevin Spin Dynamics. Phys. Rev. B 2012, 86, 054416. 10.1103/PhysRevB.86.054416. [DOI] [Google Scholar]
- Pan F.; Chico J.; Delin A.; Bergman A.; Bergqvist L. Extended Spin Model in Atomistic Simulations of Alloys. Phys. Rev. B 2017, 95, 184432. 10.1103/PhysRevB.95.184432. [DOI] [Google Scholar]
- Khmelevskyi S. Longitudinal Integration Measure in Classical Spin Space and Its Application to First-Principle Based Simulations of Ferromagnetic Metals. J. Magn. Magn. Mater. 2018, 461, 14–18. 10.1016/j.jmmm.2018.04.023. [DOI] [Google Scholar]
- Ellis M. O. A.; Galante M.; Sanvito S. Role of Longitudinal Fluctuations in L10 FePt. Phys. Rev. B 2019, 100, 214434. 10.1103/PhysRevB.100.214434. [DOI] [Google Scholar]
- Elliott R. J. Theory of the Effect of Spin-Orbit Coupling on Magnetic Resonance in Some Semiconductors. Phys. Rev. 1954, 96, 266–279. 10.1103/PhysRev.96.266. [DOI] [Google Scholar]
- Yafet Y.Solid State Physics; Academic Press, Elsevier: New York, 1963; Chapter g Factors and Spin-Lattice Relaxation of Conduction Electrons, pp 1–98. [Google Scholar]
- Lejaeghere K.; Bihlmayer G.; Björkman T.; Blaha P.; Blügel S.; Blum V.; Caliste D.; Castelli I. E.; Clark S. J.; Corso A. D.; de Gironcoli S.; Deutsch T.; Dewhurst J. K.; Marco I. D.; Draxl C.; Dułak M.; Eriksson O.; Flores-Livas J. A.; Garrity K. F.; Genovese L.; et al. Reproducibility in Density Functional Theory Calculations of Solids. Science 2016, 351, aad3000. 10.1126/science.aad3000. [DOI] [PubMed] [Google Scholar]
- Peng L.; Yasin F. S.; Park T.-E.; Kim S. J.; Zhang X.; Nagai T.; Kimoto K.; Woo S.; Yu X. Tunable Néel–Bloch Magnetic Twists in Fe3GeTe2 with van der Waals Structure. Adv. Funct. Mater. 2021, 31, 2103583. 10.1002/adfm.202103583. [DOI] [Google Scholar]
- Macy J.; Ratkovski D.; Balakrishnan P. P.; Strungaru M.; Chiu Y.-C.; Flessa Savvidou A.; Moon A.; Zheng W.; Weiland A.; McCandless G. T.; Chan J. Y.; Kumar G. S.; Shatruk M.; Grutter A. J.; Borchers J. A.; Ratcliff W. D.; Choi E. S.; Santos E. J. G.; Balicas L. Magnetic Field-Induced Non-Trivial Electronic Topology in Fe3–xGeTe2. Appl. Phys. Rev. 2021, 8, 041401. 10.1063/5.0052952. [DOI] [Google Scholar]
- Gao Y.; Yin Q.; Wang Q.; Li Z.; Cai J.; Zhao T.; Lei H.; Wang S.; Zhang Y.; Shen B. Spontaneous (Anti)Meron Chains in the Domain Walls of van der Waals Ferromagnetic Fe5–xGeTe2. Adv. Mater. 2020, 32, 2005228. 10.1002/adma.202005228. [DOI] [PubMed] [Google Scholar]
- Romming N.; Hanneken C.; Menzel M.; Bickel J. E.; Wolter B.; von Bergmann K.; Kubetzka A.; Wiesendanger R. Writing and Deleting Single Magnetic Skyrmions. Science 2013, 341, 636–639. 10.1126/science.1240573. [DOI] [PubMed] [Google Scholar]
- Kang W.; Huang Y.; Zheng C.; Lv W.; Lei N.; Zhang Y.; Zhang X.; Zhou Y.; Zhao W. Voltage Controlled Magnetic Skyrmion Motion for Racetrack Memory. Sci. Rep. 2016, 6, 23164. 10.1038/srep23164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fasolino A.; Los J. H.; Katsnelson M. I. Intrinsic Ripples in Graphene. Nat. Mater. 2007, 6, 858–861. 10.1038/nmat2011. [DOI] [PubMed] [Google Scholar]
- Meyer J. C.; Geim A. K.; Katsnelson M. I.; Novoselov K. S.; Booth T. J.; Roth S. The Structure of Suspended Graphene Sheets. Nature 2007, 446, 60–63. 10.1038/nature05545. [DOI] [PubMed] [Google Scholar]
- Deng S.; Berry V. Wrinkled, Rippled and Crumpled Graphene: An Overview of Formation Mechanism, Electronic Properties, and Applications. Mater. Today 2016, 19, 197–212. 10.1016/j.mattod.2015.10.002. [DOI] [Google Scholar]
- Jenkins S.; Rózsa L.; Atxitia U.; Evans R. F. L.; Santos E. J. G.. Breaking through the Mermin-Wagner Limit in 2D van der Waals Magnets. 2022, under review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akpakwu G. A.; Silva B. J.; Hancke G. P.; Abu-Mahfouz A. M. A Survey on 5G Networks for the Internet of Things: Communication Technologies and Challenges. IEEE Access 2018, 6, 3619–3647. 10.1109/ACCESS.2017.2779844. [DOI] [Google Scholar]
- Wen X.-G.Quantum Field Theory of Many-Body Systems; Oxford University Press: New York, 2004. [Google Scholar]
- Grytsiuk S.; Hanke J. P.; Hoffmann M.; Bouaziz J.; Gomonay O.; Bihlmayer G.; Lounis S.; Mokrousov Y.; Blügel S. Topological–Chiral Magnetic Interactions Driven by Emergent Orbital Magnetism. Nat. Commun. 2020, 11, 511. 10.1038/s41467-019-14030-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alliati M.; Evans R. F. L.; Novoselov K. S.; Santos E. J. G. Relativistic Domain-Wall Dynamics in van der Waals Antiferromagnet MnPS3. npj Comput. Mater. 2022, 8, 3. 10.1038/s41524-021-00683-6. [DOI] [Google Scholar]
- Abdul-Wahab D.; Iacocca E.; Evans R. F. L.; Bedoya-Pinto A.; Parkin S.; Novoselov K. S.; Santos E. J. G. Domain Wall Dynamics in Two-Dimensional van der Waals Ferromagnets. Appl. Phys. Rev. 2021, 8, 041411. 10.1063/5.0062541. [DOI] [Google Scholar]