Wastewater-Based Estimation of the Effective Reproductive Number of SARS-CoV-2

Abstract

Background:

The effective reproductive number, $R_e$, is a critical indicator to monitor disease dynamics, inform regional and national policies, and estimate the effectiveness of interventions. It describes the average number of new infections caused by a single infectious person through time. To date, $R_e$ estimates are based on clinical data such as observed cases, hospitalizations, and/or deaths. These estimates are temporarily biased when clinical testing or reporting strategies change.

Objectives:

We show that the dynamics of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) RNA in wastewater can be used to estimate $R_e$ in near real time, independent of clinical data and without the associated biases.

Methods:

We collected longitudinal measurements of SARS-CoV-2 RNA in wastewater in Zurich, Switzerland, and San Jose, California, USA. We combined this data with information on the temporal dynamics of shedding (the shedding load distribution) to estimate a time series proportional to the daily COVID-19 infection incidence. We estimated a wastewater-based $R_e$ from this incidence.

Results:

The method to estimate $R_e$ from wastewater worked robustly on data from two different countries and two wastewater matrices. The resulting estimates were as similar to the $R_e$ estimates from case report data as $R_e$ estimates based on observed cases, hospitalizations, and deaths are among each other. We further provide details on the effect of sampling frequency and the shedding load distribution on the ability to infer $R_e$.

Discussion:

To our knowledge, this is the first time $R_e$ has been estimated from wastewater. This method provides a low-cost, rapid, and independent way to inform SARS-CoV-2 monitoring during the ongoing pandemic and is applicable to future wastewater-based epidemiology targeting other pathogens. https://doi.org/10.1289/EHP10050

Introduction

A critical quantity to monitor an ongoing epidemic is the effective reproductive number ($R_e$).^1–4 $R_e$ describes the time-varying average number of new infections caused by a single infectious person throughout the course of their infection. Typically, $R_e$ is estimated from case report data (hereafter referred to as $R_{cc}$), including the numbers of new clinical cases, hospitalizations, and deaths.^1,3–5 Here, we hypothesized that viral RNA concentrations measured in wastewater can also be used to estimate $R_e$ (hereafter referred to as $R_{ww}$). This independent data set complements existing $R_{cc}$ estimates to provide a more complete picture of transmission dynamics.

$R_e$ estimates for severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) are used to inform regional and national policies.^6,7 The $R_e$ changes through time and reflects changes in the immune status of the population, policy, climate, and/or individual behaviors.^1,2 It can thus be used to estimate the effectiveness of nonpharmaceutical interventions in disease control.^5,8–11 However, $R_{cc}$ estimates have some notable drawbacks. The most important aspect is that they depend on robust and accurate clinical case surveillance and reporting. Temporal changes in testing capacity, hospitalization criteria, or the definition of COVID-19-related deaths can bias the $R_{cc}$ estimates.^1,12 These estimates are also inferred with a delay: $R_{cc}$ is estimable once the infections occurring on that day tested positive and were reported as clinical cases.^1,2 The distribution of infection to reporting delays is necessary to accurately infer $R_{cc}$, yet differs through time and space, thus complicating the simultaneous computation of $R_{cc}$ across geographic regions. Wastewater data may provide an advantage over clinical case data in all these aspects.

SARS-CoV-2 RNA measurements in wastewater can be used to understand COVID-19 epidemiology because infected individuals shed the virus into the sewer system throughout their infection. During the COVID-19 pandemic, SARS-CoV-2 RNA has been repeatedly detected in wastewater and sewage sludge globally,^13–19 and measured RNA concentrations or loads correlate with clinical case data.^13–15,17 Detection of SARS-CoV-2 RNA in the wastewater implies that there is at least one actively shedding infected person in the catchment served by the sewer system. In comparison with clinical testing, substantially fewer wastewater samples are required to track changes in infection incidence at the community level.²⁰ Wastewater data have also been integrated into compartmental models of infectious disease transmission, allowing estimation of epidemiological parameters, including incidence and the basic reproductive number $R_0$ (which corresponds to the $R_e$ in a fully susceptible population at the start of an outbreak).^21,22 These model results are frequently validated against clinical case data, and the good correspondence between both supports the use of SARS-CoV-2 RNA measurements in wastewater to inform disease transmission dynamics. In addition, there are indications that the wastewater may track transmission dynamics more truthfully than cases, especially when test positivity is high.²³

Models relating SARS-CoV-2 RNA in wastewater to incidence or transmission rates are driven by assumptions of virus excretion rates into the sewer system. Excretion (whether via feces, saliva, or sputum) varies by individual and through time after infection. Generally, virus excretion can be described using a shedding load profile, which captures both the temporal dynamics of shedding [in the shedding load distribution (SLD)], and the total amount of virus shed by an infected individual. Clinical studies in various settings have measured shedding from symptom onset onward. Notable examples include Wölfel et al., who measured virus concentrations in the stool of hospitalized patients^22,24 and Han et al., who included symptomatic and asymptomatic children.²⁵ Benefield et al. combined such studies into a systematic review of SARS-CoV-2 viral loads.²⁶ However, little is known about shedding prior to symptom onset. Given uncertainty and variation in estimates of SLDs, modeling approaches to relate wastewater to transmission have varied. For example, Kaplan et al. used an infectivity profile (based on virus concentrations in the upper and lower respiratory tract from Li et al.²⁶) rather than information on gastrointestinal shedding to estimate the basic reproductive number $R_0$ from wastewater data.^21,27 More work is needed to determine both the SLD and the amount of virus shed during an infection to relate SARS-CoV-2 RNA measurements in wastewater to epidemiology.

We measured SARS-CoV-2 RNA in sewage sludge or wastewater from two distinct monitoring programs (Zurich, Switzerland, and San Jose, California, USA), used the measured RNA to estimate $R_{ww}$, and compared the estimates to $R_{cc}$ obtained from clinical case data. We further determined the SLD that optimized the fit between $R_{ww}$ and $R_{cc}$ and compared it to previously reported SLDs. To our knowledge, this is the first time $R_e$ has been estimated from pathogen concentrations in wastewater.

Methods

SARS-CoV-2 RNA Quantification in Wastewater and Primary Sludge

Overall approach.

Longitudinal samples of raw wastewater influent from Zurich and primary sludge from San Jose were collected over several weeks from late 2020 through early 2021. Samples were concentrated, viral RNA was extracted, and SARS-CoV-2 RNA markers as well as pepper mild mottle virus (PMMoV) RNA were quantified in each extract. PMMoV is a plant virus that is found in wastewater at high concentrations and in fairly constant loads and serves to detect anomalies in the collected sample or problems during concentration and extraction.²⁸

Sample collection and processing.

Zurich approach.

From 03 September 2020 to 19 January 2021, 24-h flow-proportional composite samples of raw influent (after fine screening) were collected from the Werdhölzli wastewater treatment plant (Zurich). Samples were collected twice per week (Thursdays, Sundays) until October 29; afterward, samples were collected almost daily. This change occurred due to increased availability of funding and prioritization of daily sampling over replication. Samples were collected in $500\text{-mL}$ polystyrene or polypropylene plastic bottles, shipped on ice, and stored at 4°C for up to 8 d before processing. Samples were processed following the protocol of Fernandez-Cassi et al. 2021.²³ Briefly, aliquots ($50\mathrm{mL}$) were stirred at room temperature for 30 min and then clarified by sequential filtration through $2\text{-}\mathrm{\mu }\mathrm{m}$ glass fiber prefilters (Merck) and $0.22\text{-}\mathrm{\mu }\mathrm{m}$ SteriCup filters (Merck). The filtrates were concentrated by centrifugation ($\mathrm{3,000}\times g$ for 30 min) using centrifugal filter units (10 kDa Centricon Plus-70; Millipore), followed by concentrate collection from the inverted filter during 3 min at $\mathrm{1,000}\times g$.

RNA was extracted from concentrates ($140–280\mathrm{\mu }\mathrm{L}$) using the QiaAmp Viral RNA MiniKit (Qiagen) according to the manufacturer’s instructions, using $80\mathrm{\mu }\mathrm{L}$ of eluate. Until 25 October, samples were processed in duplicate (biological replicates). After that date, we switched to daily sampling and processing of a single sample, because the variation between biological replicates was observed to be low. Samples were extracted once, and a negative extraction control using molecular grade water was run in parallel for every batch of extracted samples.

San Jose approach.

From 15 November 2020 to 19 March 2021, 125 settled solids samples (approximately $50\mathrm{mL}$) were collected and processed daily from the primary settling tank at the San Jose wastewater treatment plant (San Jose, California) using methods adapted from Graham et al. and described in published protocols.^15,29–31 Briefly, 24-h composite samples were collected in clean plastic containers, immediately stored at 4°C, and transported to the lab for initial processing within 6 h of collection. The solids were dewatered by centrifugation at $\mathrm{24,000}\times g$ for 30 min at 4°C. The supernatant was aspirated and discarded. A 0.5-g aliquot of the dewatered solids was dried at 110°C for 19–24 h to determine its dry weight. Dewatered solids were resuspended in Bovine Coronavirus (BCoV)-spiked DNA/RNA Shield (Zymo Research), to a concentration of $75\mathrm{mg}/\mathrm{mL}$. This concentration of solids represented a concentration at which the polymerase chain reaction (PCR) inhibition of the SARS-CoV-2 assays was minimized based on experiments with solutions containing varying concentrations of solids³² (see also Supplemental Material “Managing PCR inhibition in San Jose sludge samples” and Figure S1). BCoV was spiked as an external process control ($1.5\mathrm{\mu }\mathrm{L}$ rehydrated BCoV vaccine per milliliter of DNA/RNA shield). To homogenize samples, 5–10 5/32-in Stainless Steel Grinding Balls (OPS Diagnostics) were added to each sample before shaking with a Geno/Grinder 2010 (Spex SamplePrep). Samples were subsequently briefly centrifuged to remove air bubbles introduced during the homogenization process and then vortexed to remix the sample. Samples were either further processed immediately or stored at 4°C for processing within 7 d.

RNA was extracted from $300\mathrm{\mu }\mathrm{L}$ of homogenized sample using the Chemagic Viral DNA/RNA 300 Kit H96 for the Perkin Elmer Chemagic 360 into $60\mathrm{\mu }\mathrm{L}$ of eluent followed by PCR Inhibitor Removal with the Zymo OneStep-96 PCR Inhibitor Removal Kit.³⁰ Each sample was extracted 10 times. In addition, extraction negative and extraction positive controls, consisting of $\sim 500$ copies of SARS-CoV-2 genomic RNA (ATCC), were extracted using the same protocol as that used for homogenized samples in each batch of sample extraction.

Quantification of viral targets.

Zurich approach.

SARS-CoV-2 N gene markers N1 and N2 were quantified immediately or within 1 wk after RNA extraction (storage at $-80°\mathrm{C}$) using digital real-time polymerase chain reaction (RT-PCR) (RT-dPCR). RT-dPCR was performed on $5\mathrm{\mu }\mathrm{L}$ of extract containing RNA as template on either the Bio-Rad QX200 Droplet Digital (01 September 2020 to 7 October 2020) with the One-Step RT-ddPCR Advanced Kit for Probes (CN 1864021; Bio-Rad) or Crystal Digital PCR using the Naica System (Stilla Technologies; 8 October 2020 to 20 January 2021) with the qScript XLT 1-Step RT-PCR Kit (CN 95132-500; QuantaBio). SARS-CoV-2 N1 and N2 markers for the N gene were detected using the 2019-nCoV CDC ddPCR Triplex Probe Assay (Assay ID dEXD28563542; Bio-Rad) according to manufacturer’s instructions, with proprietary primer and probe concentrations. Primer and probe sequences are specified in Table S1, and further dPCR details in Excel Table S1.

For samples processed on the Bio-Rad QX200, $20\text{-}\mathrm{\mu }\mathrm{L}$ reaction volumes were prepared in a prereaction volume of $22\mathrm{\mu }\mathrm{L}$ consisting of $5.5\mathrm{\mu }\mathrm{L}$ of template, $5.5\mathrm{\mu }\mathrm{L}$ of Supermix, $2.2\mathrm{\mu }\mathrm{L}$ of Reverse Transcriptase, $1.1\mathrm{\mu }\mathrm{L}$ of Dithiothreitol (DTT), and $1.1\mathrm{\mu }\mathrm{L}$ of $20\times$ 2019-nCoV CDC ddPCR Triplex Probe Assay. Droplets were generated using the QX100 Droplet Generator (Bio-Rad). PCR was performed on the T100 Thermal Cycler (Bio-Rad) with the following protocol: hold at 25°C for 3 min, reverse transcription at 50°C for 60 min, enzyme activation at 95°C for 10 min, 40 cycles of denaturation at 95°C for 30 s, annealing and extension at 55°C for 1 min, enzyme deactivation at 98°C for 10 min, and an indefinite hold at 4°C. Ramp rate was 2°C/s, and the final hold at 4°C was at least 30 min to stabilize droplets. Droplets were analyzed using the QX200 Droplet Reader (Bio-Rad) and thresholding done on the QuantaSoft Analysis Pro Software (version 1.0; Bio-Rad).

For samples processed on the Crystal Digital PCR, $25\text{-}\mathrm{\mu }\mathrm{L}$ reactions were prepared in $27\mathrm{\mu }\mathrm{L}$ prereaction volumes for Sapphire Chips (CN C14012; Stilla Technologies) consisting of $5.4\mathrm{\mu }\mathrm{L}$ of template, $13.5\mathrm{\mu }\mathrm{L}$ of $2\times$ qScript XLT One-Step RT-PCR, and $1.35\mathrm{\mu }\mathrm{L}$ of $20\times$ 2019-nCov CDC ddPCR Triplex Probe Assay. Droplet production and PCR were performed on the Naica Geode with the following protocol: reverse transcription at 48°C for 50 min, denaturation at 94°C for 3 min, followed by 40 cycles of denaturation at 94°C for 30 s, annealing and extension at 57°C for 1 min. Chips were read and analyzed on the Naica Prism3 using the Crystal Reader and Crystal Miner software (Stilla Technologies).

For the Bio-Rad QX200, samples with more than 12,000 droplets with average partitioning volume of $1\text{\hspace{0.17em}nL}$ were deemed acceptable. For the Stilla Crystal Digital PCR, 15,000 droplets with average $0.8\text{\hspace{0.17em}nL}$ were deemed acceptable. The average [standard deviation (SD)] number of droplets observed in samples from QX200 was 15,000 (2,100) and for the Crystal Digital PCR excluding controls was 24,000 (2,000). Average copies per partition (relative uncertainty) was $8.7\times {10}^{-3}$ (54%). Technical replicate variability was, on average, $<20\%$. The variation among distinct RT-dPCR runs (interexperimental variation) was quantified as the coefficient of variation in the performance of a positive control [100 gene copies (gc)/reaction of synthetic SARS-CoV-2 RNA reference material; EURM-019, Joint Research Center] across 87 runs and was $<25\%$. Assays were only conducted in one laboratory, so reproducibility was not assessed. Example fluorescence plots are provided in Figures S2 and S3.

Samples were diluted 10-fold in a single step using molecular grade water before quantification in replicate wells. In addition, every thermal cycler run included one positive control and one no template control (NTC) consisting of RNAse/DNAse-free water. Thermal cycle runs and associated samples were deemed acceptable if the NTCs in the run contained two or fewer positive droplets and there was detectable SARS-CoV-2 RNA in the positive controls. All RT-dPCR runs fulfilled these criteria, with an average (SD) concentration of the positive controls of 101 (25) gc/reaction, in line with the target concentration. If the sample concentration was below the limit of quantification (LOQ), an undiluted sample was quantified. The limit of detection (LOD) and LOQ of the N1 and N2 markers were determined by processing 10 replicates of synthetic SARS-CoV-2 RNA reference material at target concentrations of 5, 8, 10, 25, 30, and 50 gc/reaction. The LOD was defined as the lowest sample concentration distinguishable from the no template control in at least 8 out of 10 replicates (3 or more positive droplets). At this concentration, there would be a $>95\%$ likelihood of detecting the target in at least one of the two technical replicates.³³ Using this criterion, LOD was determined to be 8 gc/reaction (equivalent to 2,560 gc/L wastewater).³³ LOQ was determined to be 25 gc/reaction (equivalent to 8,000 gc/L wastewater), which was the lowest concentration with coefficient of variation $<25\%$.³³ When sample concentrations were below the LOQ, samples were processed without dilution. Only one sample (20 September, replicate B) remained below LOQ in both dilute and undilute samples (22.5 gc/reaction). This sample was included in the analysis anyway, using the value returned.

To test PCR inhibition, the RT-dPCR was repeated using mastermix with a spiked internal positive control consisting of 800 gc/reaction of synthetic SARS-CoV-2 RNA reference material (EURM-019, Joint Research Center) so inhibition testing could be performed on the same assay used for quantification.³⁴ Samples were added to the mastermix with a spiked internal control at the same dilution used for quantification of the N1 and N2 markers. If either the observed N1 or N2 concentration in the samples analyzed in mastermix with synthetic SARS-CoV-2 RNA was 80% or less than the sum of the concentration of SARS-CoV–2 RNA in the samples (unspiked) plus the concentration in the sample-free, spiked internal positive control, then the samples were considered inhibited. Inhibited samples were diluted 1:10, retested for SARS-CoV-2 as well as inhibition, using the same spiked internal positive control. Dilution sufficiently reduced inhibition for all affected samples.

PMMoV was quantified by RT-qPCR using RNA UltraSense One-Step Quantitative RT-PCR System (CN 11732927; Applied Biosystems) on a LightCycler 480 instrument (Roche Life Science) using previously reported primers and probes (Microsynth AG; Table S1).^35,36 RNA extract aliquots that were separately stored at $-80°\mathrm{C}$ for $<3$ months were used as template. Samples were prepared in $25\text{-}\mathrm{\mu }\mathrm{L}$ reaction volumes consisting of $5\mathrm{\mu }\mathrm{L}$ of template, $5\mathrm{\mu }\mathrm{L}$ of $5\times$ Ultrasense Mix, $4\mathrm{\mu }\mathrm{L}$ of Bovine Serum Albumin (CN 05470-1G; Sigma-Aldrich) at $2\mathrm{mg}/\mathrm{mL}$ concentration, $1.25\mathrm{\mu }\mathrm{L}$ of Reverse Transcriptase, and $1\mathrm{\mu }\mathrm{L}$ of each primer at final concentrations of $400\text{\hspace{0.17em}nM}$ and $0.25\mathrm{\mu }\mathrm{L}$ of probe at a final concentration of $250\text{\hspace{0.17em}nM}$. The RT-qPCR was run with the following program: reverse transcription at 55°C for 60 min, denaturation at 95°C for 10 min, followed by 45 cycles of denaturation at 95°C for 15 s, and annealing and extension at 60°C for 1 min. PMMoV quantification was performed in six separate RT-qPCR runs by comparison to synthetic DNA standards (gBlock; IDT Technologies) run in duplicate at 10-fold dilutions between $5\times {10}^2$ (the lowest concentration measured) and $5\times {10}^7$ per $5\mathrm{\mu }\mathrm{L}$ reaction. All thermal cycler runs were pooled for analysis. The pooled standard curve had an amplification efficiency of 97.4% and a goodness-of-fit ($R^2$) of 0.997.

San Jose approach.

RNA extracts were used as template in RT-dPCR assays for SARS-CoV-2 N, S, and ORF1a RNA gene targets in a triplex assay and for PMMoV and BCoV in a duplex assay. All primers and probes are listed in Table S1. The SARS-CoV-2 assays were designed using Primer3Plus (https://primer3plus.com/) based on the genome of the SARS-CoV-2 isolate Wuhan-Hu-1 (Accession Number MN908947.3). The assay was designed to target product size range of 60–200 base pair (bp) at concentration of deoxynucleotide triphosphates (dNTPs) of $0.8\text{\hspace{0.17em}mM}$ and concentration of divalent cations of $3.8\text{\hspace{0.17em}mM}$, based on the following optimum [range] conditions: primer size: 20 bp [15 bp, 36 bp]; primer melting temperature 60°C [50°C, 65°C]; primer GC content: 50% [40%, 60%]; hydrolysis probe size 20 bp [15 bp, 27 bp]; hydrolysis probe melting temperature 63°C [62°C, 70°C]; hydrolysis probe GC content: 50% [30%, 80%]. The location (length) of the amplicons for N is 28,287–28,457 (171 bp), S is 23,591–23,665 (75 bp), and ORF1a is 12,885–13,063 (179 bp). Cross-reactivity was determined in silico using National Center for Biological Information Basic Local Alignment Search Tool (NCBI BLAST). The assays were optimized by varying annealing temperature and then benchmarked against a respiratory virus verification panel using extracted RNA. Limit of the blank was determined using negative nasal swab samples.

RT-dPCR was performed as previously described for the Bio-Rad QX200 analysis conducted in Zurich using the One-Step RT-ddPCR Advanced Kit for Probes (CN 1863021; Bio-Rad) with primers ($900\text{\hspace{0.17em}nM}$) and probes ($250\text{\hspace{0.17em}nM}$) targeting N, S, and ORF1a RNA. Droplets were generated using the AutoDG Automated Droplet Generator (Bio-Rad). PCR was performed using Mastercycler Pro with the following protocol: reverse transcription at 50°C for 60 min, enzyme activation at 95°C for 5 min, 40 cycles of denaturation at 95°C for 30 s and annealing and extension at either 59°C (for SARS-CoV-2 assay) or 56°C (for PMMoV/BCoV duplex assay) for 30 s, enzyme deactivation at 98°C for 10 min, and then an indefinite hold at 4°C. The ramp rate for temperature changes were set to 2°C/s, and the final hold at 4°C was performed for a minimum of 30 min to allow the droplets to stabilize.

Droplets were analyzed using the QX200 Droplet Reader (Bio-Rad), with thresholding done using QuantaSoft Analysis Pro Software (version 1.0.596; Bio-Rad). The average (SD) number of droplets in 10 merged wells determined from a random subset of 10 samples was 176,000 (14,500). Average (relative uncertainty) of the number of copies per partition in the same subset was $3.2\times {10}^{-3}$ (52%). As the samples were extracted 10 times and each extract analyzed in one well, technical replicate variability incorporated variation from both RNA extraction and RT-dPCR. Sample errors estimated from the merged wells were $<10\%$, in line with coefficient of variation estimates of $<8\%$ for all three targets (S, N, ORF1a) in an experiment of replicate ($n=97$) positive controls at target concentrations of 400 gc/reaction. Assays were conducted in only one lab, so reproducibility was not assessed. Example fluorescence plots are provided in the associated reference by Topol et al.³¹ All liquid transfers were performed using the Agilent Bravo (Agilent Technologies).

Undiluted extract was used for the SARS-CoV-2 assay template, and a 1:100 dilution of the extract ($2\mathrm{\mu }\mathrm{L}$ into $198\mathrm{\mu }\mathrm{L}$ molecular grade water) was used for the PMMoV and BCoV assay template. The 1:100 dilution was required because PMMoV was present in high concentrations, and it is important to be able to quantify the target and not saturate the number of positive partitions.

Each sample was run in 10 replicate wells, extraction negative controls were run in 7 wells, and extraction positive controls in 1 well. In addition, PCR-positive controls for SARS-CoV-2 RNA were run in 1 well, and NTC were run in 7 wells. Results from replicate wells were merged for analysis. Negative controls were required to have $<2$ droplets across all wells, PCR positive controls were required to have $\sim 200$ positive droplets, and PCR positive extraction controls were required to have $\sim 50$ positive droplets. If controls did not meet these acceptability criteria, then the samples included on that plate were reprocessed. Therefore, none of the samples included in this study had controls that failed these acceptability criteria.

Data Analysis and Exclusion Criteria

Zurich approach.

Concentrations of RNA targets were multiplied by the daily flow rate to estimate the total number of genome copies (gc) shed by people within the catchment per day (referred to as loads and reported as gene copies per day). Samples with PMMoV loads outside the mean plus or minus three times the SD were considered as inconsistent with respect to virus recovery and were excluded from further analysis. Inhibited samples were also removed from further analysis.

San Jose approach.

Concentrations of RNA targets were converted to concentrations per dry weight of solids in units of gene copies per gram dry weight. PMMoV was also used to monitor virus recovery in the San Jose samples, using the same criteria as those used for the Zurich samples. BCoV was used to assess virus recovery, and samples were removed from further analysis if the amount recovered was $<10\%$ of the amount added.

Deconvolution by the Shedding Load Distribution

To relate the viral RNA loads or concentrations measured in wastewater to the number of new infections per day, we used information on the profile of SARS-CoV-2 RNA shedding into the wastewater by an infected individual in days after infection or symptom onset. In general, this profile contains information about both the magnitude and timing of viral RNA shedding: a) the SLD ${\sum }_j{w}_j$ (a unitless distribution which sums to 1) describes the temporal dynamics of shedding, and b) a normalization factor N describes the total amount of virus shed by an infected individual during the course of infection (in units of gene copies per infection). After shedding, downstream processes further affect the total amount of viral RNA sampled per infected individual. We assume this does not affect the temporal dynamics and can be summarized into a second normalization factor M. In general, M will depend on the sewer system, the sampling point within the wastewater treatment plant, choice of sample matrix and processing pipeline. The units of M differ depending on the way viral concentrations were measured: in this study M is unitless for Zurich, and day per gram dry weight for San Jose.

With these definitions, the measurement $C_i$ of viral RNA in the wastewater on day i is related to the past incidence of infections $I_j$ on day j:

$$C_i=N\times M\sum _j{w}_{i-j}{I}_j,$$

i.e., the observed wastewater measurements are a convolution of the daily infection incidence with the SLD.

To obtain the infection incidence, we first filled gaps in the wastewater data through linear interpolation and smoothed it using local polynomial regression (LOESS) with first order polynomials and tricubic weights that take into account 21 d of data around each point. To deconvolve the resulting time series we used an expectation–maximization algorithm,² which iteratively determines the time series I(t) that maximizes the likelihood of the smoothed wastewater measurements $\overline{C}\left(t\right)$ (either in units of gene copies per day or gene copies per gram dry weight), given assumptions on N, M, and ${\sum }_j{w}_j$.

For the main analysis, we deconvolved by a SLD that was a combination of the incubation period (the time from infection to symptom onset) and the gastrointestinal SLD from Benefield et al. for the time from symptom onset to shedding.²⁶ Figure 3 from Benefield et al.²⁶ was digitized manually, and yielded a gamma distribution with mean 6.7 d and SD 7.0 d.²³ For the incubation period, we used the distribution of Linton et al.: a gamma distribution with mean 5.3 d and SD 3.2 d.³⁷ For additional comparisons, we exchanged the Benefield et al. distribution for the SLD upon symptom onset reported by Han et al. (gamma distributed with mean 4.7 d and SD 1.7 d),²⁵ or the symptom onset to death delay distribution from Linton et al. (gamma distributed with mean 15 d and SD 6.9 d).³⁷

Figure 3.

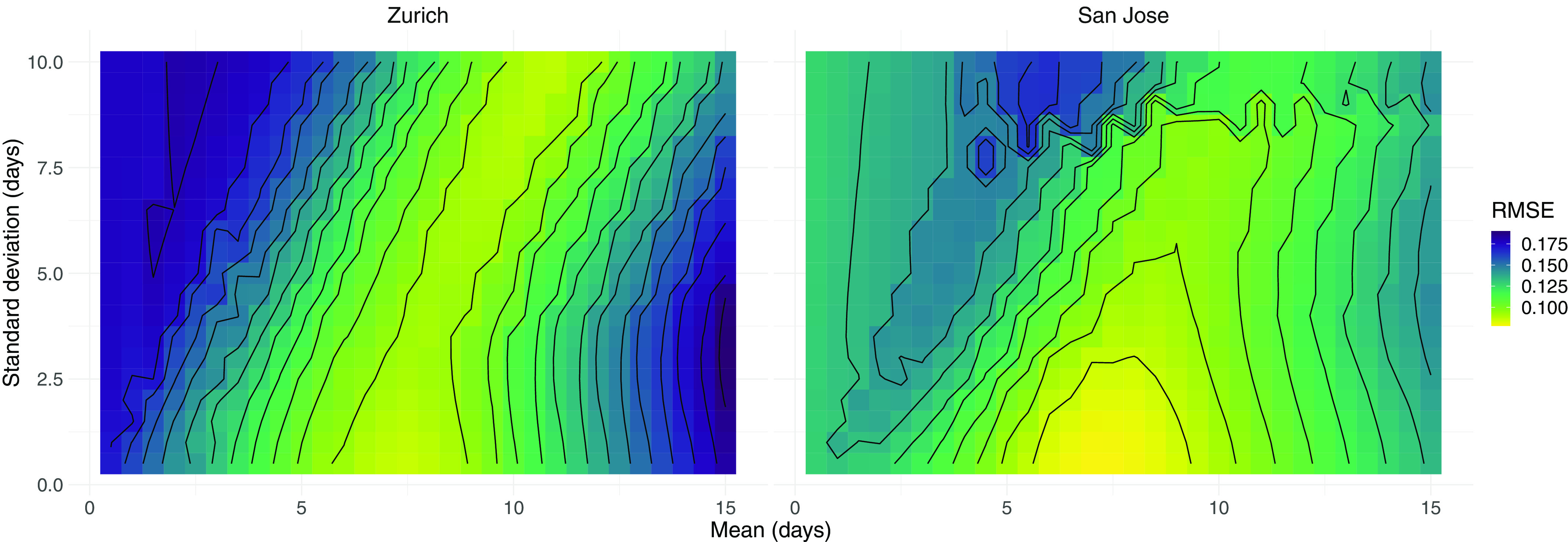
RMSE between case-based $R_{cc}$ and wastewater-based $R_{ww}$ for different SLDs. We scanned across different parameter pairs (mean, SD in days) for the SLD from time since infection. For the city of Zurich, the $R_{ww}$ from N1 marker loads in wastewater was compared to that of confirmed cases in the catchment. For San Jose, we compared S gene concentrations to confirmed cases in Santa Clara County. The contour lines show SLD parameter pairs with equal RMSE, in steps of 10% of the optimum value. The numeric data corresponding to this figure can be found in Excel Table S8. Note: $R_{cc}$, $R_e$ estimated from case report data; $R_e$, effective reproductive number; RMSE, root mean squared error; $R_{ww}$, $R_e$ estimated from viral RNA concentrations measured in wastewater; SD, standard deviation; SLD, shedding load distributions.

Because the normalization factors N and M are difficult to measure and only influence $R_{ww}$ point estimates when off by several orders of magnitude, we made a simplifying assumption. We assumed that the lowest measured RNA load (Zurich) or concentration (San Jose) represents the viral load or concentration from a single infection ($N\times M$). For the Zurich wastewater data, this was $1\times {10}^{12}$ gc per infection, and for the San Jose sewage sludge measurements this was 2,663.7 gc/g dry weight per infection per day.

To study the effect of less frequent sampling on the ability to estimate $R_{ww}$, we subsampled the wastewater measurements in Zurich and San Jose prior to estimating $R_e$. We varied the number of samples taken per week (1, 2, 3, 5), and the sampling schedule: daily (Monday–Sunday; 7 samples); working week (Monday–Friday; 5 samples); Monday, Wednesday, Friday (3 samples); Tuesday, Thursday, Saturday (3 samples); Monday, Thursday (2 samples); Tuesday, Friday (2 samples); only Monday; only Wednesday; only Friday. For Zurich, we restricted the analysis to the period with daily sampling (22 November 2020 to 11 January 2021).

$R_e$ Estimates

The $R_e$ was estimated from SARS-CoV-2 RNA loads in wastewater or concentrations in sewage sludge using the pipeline developed in Huisman et al.² In brief, we first transformed SARS-CoV-2 RNA measurements into a time series of infection incidence as described in the “Deconvolution” section above. Second, we used the R package EpiEstim to estimate the $R_e$ from this infection incidence.^4,38 The pipeline further accounts for noise in the observation process by bootstrapping the observations prior to smoothing and deconvolution. Specifically, we block-bootstrap the log-transformed residuals between the linear interpolated original observations and the smoothed value.²

To estimate $R_{cc}$ for Zurich, we obtained case data from the Health Department of Canton Zurich, restricted to cases in the catchment. We then used the pipeline from Huisman et al.,² where we deconvolved by a distribution specifying the delay from infection to case confirmation. This was parameterized as the sum of a gamma distributed incubation period with mean 5.3 d, SD 3.2 d³⁷; and a gamma distributed delay from symptom onset to case confirmation with mean 2.8 d, SD 3.0 d (estimated from line list data for Canton Zurich, September 2020–January 2021). The reported $R_{cc}$ values for confirmed cases, hospitalizations, and deaths at the cantonal level were taken from https://github.com/covid-19-Re/dailyRe-Data (based on Huisman et al.²). For the Swiss data, “case confirmation” refers to the earliest recorded date of either a positive test or case reporting.

To estimate $R_{cc}$ in San Jose, we downloaded COVID-19 case data for Santa Clara County from the California Health and Human Services Open Data portal.³⁹ The data included the reported cases, number of positive tests, and number of total tests in the county per day. The wastewater from Santa Clara County (population of $1.7\text{\hspace{0.17em}million}$) is nearly all treated at the San Jose wastewater treatment plant (catchment population of $1.5\text{\hspace{0.17em}million}$).³² We estimated $R_{cc}$ using the pipeline from Huisman et al.,² with the incubation period as before from Linton et al.,³⁷ and a gamma distributed symptom onset to case reporting delay distribution with a mean of 4.51 d and SD of 3.16 d (estimated from line list data for Santa Clara County in December; based on personal correspondence with the California Department of Public Health COVID-19 modeling team). During the study period, the mean of this distribution changed from 5.24 to 3.31 d, and the SD from 3.55 to 2.32 d. Negative numbers of cases reported (30 December) were set to zero for the main analysis and to 1,000 to test the impact of misreporting.

To estimate $R_e$ for the testing-adjusted cases in Santa Clara County, we extracted the daily number of positive tests per total number of tests, multiplied by the mean number of tests during the time period (14,960.3). This time series was then used to estimate $R_e$, similar to the confirmed cases (with the same delay distribution).² Technically, the tests are reported by testing date, which typically precedes the reporting date, so this approach constitutes a misspecification of the delay distribution. However, an analysis where the delay between symptom onset and testing was assumed zero did not yield qualitatively different results (Figure S4). We additionally compared our estimates to the $R_{cc}$ estimates for Santa Clara County from the California COVID assessment tool (https://calcat.covid19.ca.gov/cacovidmodels/).

Comparing $R_e$ Traces

We assessed how well the $R_e$ estimates from SARS-CoV-2 concentrations in wastewater ($R_{ww}$) match those estimated from case report data ($R_{cc}$) using several measures. First, we used the average root mean squared error between both point estimates across the time series (RMSE):

$$\sqrt{\frac{1}{K}{\sum }_{j=1}^K{(R_{ww,j}-R_{cc,j})}^2},$$

where j describes the date, and K the length of the time series. Second, we used the fraction of dates where the $R_{ww}$ point estimate was within the confidence interval of the $R_{cc}$ estimate (“coverage”). Third, we used the mean average percentage error between the time series (MAPE):

$$\frac{1}{K}{\sum }_{j=1}^K\left|\frac{R_{cc,j}-R_{ww,j}}{R_{cc,j}}\right|.$$

Scanning across Shedding Load Distributions

To investigate optimal parameters for the SLD, we conducted two separate scans. In the first scan, we varied the parameters of the SLD from infection. In the second scan, we estimated the parameters of the SLD from symptom onset onward. In the latter case, the delay sampled from the SLD was added to a second sampled delay corresponding to the incubation period (gamma distributed with mean 5.3 d and SD 3.2 d).³⁷ In both cases, we assumed the SLD was described by a gamma distribution and varied the mean $\mathrm{\mu }$ and SD σ on a grid ($\mathrm{\mu }\in \{\mathrm{0.5,1.0},\dots ,15\}$ and $\in \{\mathrm{0.5,1.0},\dots ,10\}$). The normalization factor ($N\times M$) was kept fixed to the location-specific value throughout. The $R_{ww}$ for the wastewater data was estimated across 50 bootstrap samples and compared to the $R_{cc}$ for the catchment.

Availability Statement

All code and underlying data are publicly available through the GitHub repository (https://github.com/JSHuisman/wastewaterRe). Wastewater measurements and daily flow rates for Zurich are available from the EAWAG open data repository.⁴⁰ Measurements from San Jose are available from the Stanford Data Repository (https://purl.stanford.edu/bx987vn9177),^32,41 and case data for Santa Clara County is available from the California Health and Human Services Open Data portal.³⁹

Approval

No ethics approval was required for this study because no humans or animals were involved.

Results

SARS-CoV-2 RNA in Wastewater

We tracked SARS-CoV-2 RNA concentrations in Zurich and San Jose during a rise and fall in clinical COVID-19 cases (Figure 1A,B; Figure 2A,B). Data from Zurich were used to develop and assess $R_{ww}$ estimates, and data from San Jose were used to assess the generalizability of the approach.

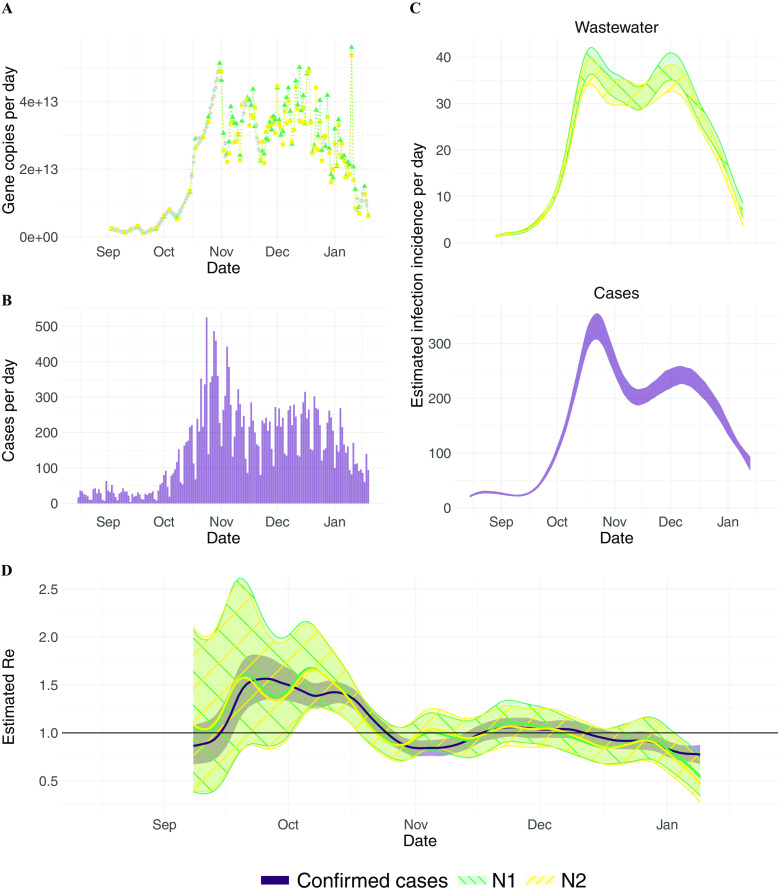
Figure 1.

$R_{ww}$ estimation from Zurich (Switzerland) wastewater measurements. (A) Measured RNA loads of the N1 and N2 markers (green triangles and yellow circles, respectively) between 1 September 2020 and 19 January 2021 (99 samples, of which 2 were excluded based on quality control). Linearly interpolated values are indicated in gray. (B) Confirmed cases (purple) in the catchment during the same time period. (C) The estimated infection incidence in the catchment per day from normalized RNA loads of the N1 and N2 markers (top; green\-hatched and yellow/-hatched bands respectively), and case reports (bottom; purple solid band). The measured loads were normalized by the lowest measured value ($N\times M=1\times {10}^{12}$ gene copies per infection). The ribbons indicate the $\text{mean}\pm \text{standard}$ deviation across 1,000 bootstrap replicates. (D) The estimated $R_{ww}$ compared to the $R_{cc}$ from confirmed cases. The colored line indicates the point estimate on the original data, and the ribbons the 95% CI across 1,000 bootstrap replicates. The N1- and N2-based CIs nearly completely overlap. The numeric data corresponding to this figure can be found in Excel Tables S2–S4. Note: CI, confidence interval; M, normalisation factor stemming from the virus recovery process; N, normalisation factor stemming from the total amount of virus shed per person; $R_{cc}$, $R_e$ estimated from case report data; $R_e$, effective reproductive number; $R_{ww}$, $R_e$ estimated from viral RNA concentrations measured in wastewater.

Figure 2.

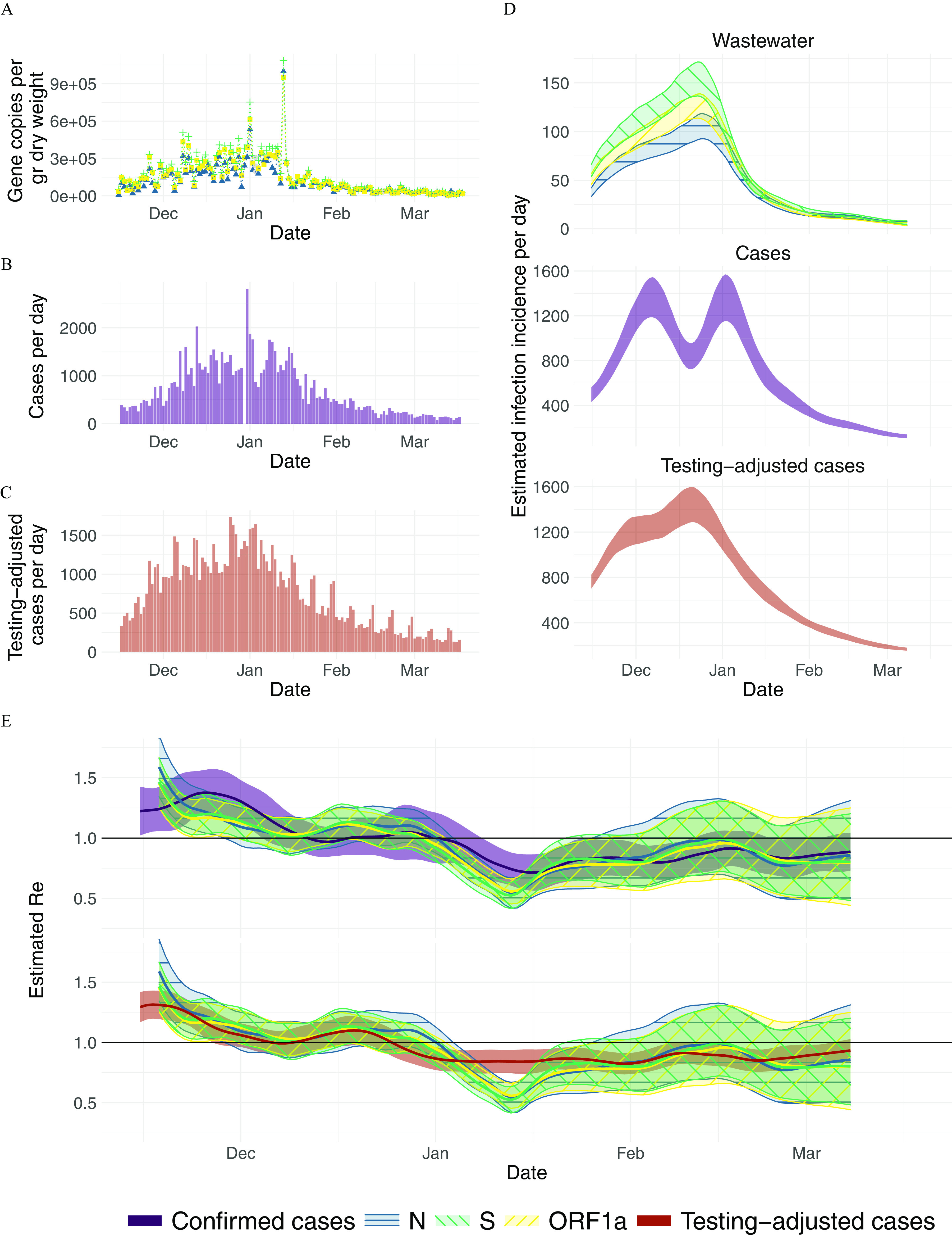
$R_{ww}$ estimation from San Jose, California sludge measurements: (A) Measured RNA concentrations of the N, S, and ORF1a genes (blue triangles, green plusses, yellow circles, respectively) between 15 November 2020 and 19 March 2021 (125 samples, of which 3 were excluded based on quality control). Linearly interpolated values are indicated in gray. (B,C) Confirmed cases and testing-adjusted cases in Santa Clara County (purple, red) during the same time period. The testing-adjusted cases describe the number of positive tests/total number of tests per day, normalized by the mean number of tests per day in Santa Clara County during the study period. (D) The estimated infection incidence per day from normalized RNA concentrations (top; the N, S, and ORF1a genes are indicated by blue horizontal-hatched, green\-hatched, and yellow/-hatched bands, respectively), case reports (middle), and testing-adjusted cases (bottom). The gene copies (gc) per gram dry weight were normalized by the lowest measured value ($N\times M=\mathrm{2,663.7}$ gc/g dry weight per infection/day). The ribbons indicate the $\text{mean}\pm \text{standard}$ deviation across 1,000 bootstrap replicates. (E) The estimated $R_{ww}$ compared to $R_{cc}$ from confirmed cases (top; purple solid band) and testing-adjusted cases (bottom; red solid band). The colored line indicates the point estimate on the original data, and the ribbons the 95% confidence interval across 1,000 bootstrap replicates. The numeric data corresponding to this figure can be found in Excel Tables S5–S7. Note: gc, gene copies; M, normalisation factor stemming from the virus recovery process; N, normalisation factor stemming from the total amount of virus shed per person; $R_{cc}$, $R_e$ estimated from case report data; $R_e$, effective reproductive number; $R_{ww}$, $R_e$ estimated from viral RNA concentrations measured in wastewater.

In Zurich, SARS-CoV-2 N1 and N2 markers of the N gene were detectable in the raw influent samples from the Zurich wastewater treatment plant between 1 September 2020 and 19 January 2021 in all 99 samples collected (Figure 1A). Of these, the average of the technical replicates was above the LOQ in 97, yielding median (range) loads of 13.4 [$<12$ (LOD), 13.7] ${\log }_{10}$ gc/d (Figure 1A).

Two samples (11 and 29 October 2020) were excluded based on quality control, which included monitoring sample inhibition and consistency of effluent PMMoV loads. One sample (11 October) was removed from analysis because the dilute sample (1:10) was below LOQ and the undiluted sample was inhibited, as defined by recovery of $<80\%$ of the synthetic SARS-CoV-2 RNA added in. PMMoV concentrations were obtained for all dates except 4 October. Mean (SD) PMMoV loads were 16.5 (0.12) ${\log }_{10}$ gc/d. All PMMoV loads fell within 3 standard deviations of the mean, consistent with a normal distribution, except on 29 October (16.1 ${\log }_{10}$ gc/d). The sample was subsequently removed from further analysis.

In San Jose, SARS-CoV-2 N, S, and ORF1a genes were quantifiable in the settled solids of the primary settling tank in all 125 samples collected between 15 November 2020 and 19 March 2021 (Figure 2A). The median [range] concentrations were 4.9 [3.4, 6.0], 5.0 [3.9, 6.0], and 5.0 [3.8, 6.0] ${\log }_{10}$ gc/g dry weight for N, S, and ORF1a genes, respectively (Figure 2A).

Three samples (03 January, 18 February, 19 March 2021) were excluded based on quality control using consistency of PMMoV concentrations. PMMoV concentrations were mean (SD) 8.9 (0.20) ${\log }_{10}$ gc/g dry weight. In two samples (03 January 2021, 18 February 2021), PMMoV concentrations exceeded the mean plus three times the SD. On one day (19 March 2021), PMMoV concentrations fell below the mean minus three times the SD. These three samples were excluded from further analysis. All samples met criteria for inclusion based on BCoV concentrations, which were all $>10\%$ of the expected concentrations based on the amount added.

Inferring the Infection Incidence Dynamics

Next, we related the RNA measurements in wastewater to the original infection incidence by applying a deconvolution with the SLD. SARS-CoV-2 wastewater measurements reflect the cumulative contributions of all infected individuals actively shedding virus into the wastewater. The amount of virus shed by each individual varies through time after infection and is captured in the shedding load profile. In general, this profile contains information about the timing of viral shedding—the SLD, which sums to 1—and the total amount of virus shed, captured by a normalization factor N. To estimate the true number of infections in the sewer shed, it is important to estimate the exact value of the normalization factor N, as well as a factor M describing losses along the way from shedding to sample processing. However, to estimate $R_e$ it suffices to know the temporal dynamics of shedding and infection (described in more detail in the “Methods” section). As a first approximation, we assumed individuals do not shed prior to symptom onset and thereafter shed according to the gastrointestinal SLD reported by Benefield et al.²⁶ With this assumption, we found that the dynamics of infection incidence inferred from wastewater measurements in Zurich are similar to the dynamics inferred from clinical case data (Figure 1C). In particular, both data sources show a steep increase starting from mid-September and capture two peaks (indicative of $R_e=1$) around late October and early December, each of which is followed by relatively rapid decline in daily case incidence. We later tested the sensitivity of our results to the assumed SLD and normalization.

Estimating the Effective Reproductive Number $R_{ww}$ from Wastewater Measurements

We used the inferred time series of infection incidence from SARS-CoV-2 RNA measured in wastewater to estimate $R_{ww}$ in Zurich (Figure 1D). The N1 and N2 markers resulted in nearly identical $R_{ww}$ estimates, and there is a good correspondence between $R_{ww}$ and $R_{cc}$. Both estimates showed a rapid increase up to $R_e=1$ in mid-September, a decline to below 1 in late October, followed by a period where $R_e$ was slightly above 1 until dropping more clearly below 1 from early December onward. $R_{ww}$ and $R_{cc}$ were changing in similar ways, with $R_{cc}$ lagging the $R_{ww}$ trajectory. Because both estimates describe the same underlying epidemic, this finding suggests that the wastewater measurements may be deconvolved too far back in time (the mean of the SLD is too high), or that the confirmed cases are not deconvolved back far enough (the mean of the delay distribution is too low).

Over the entire time period, the average RMSE between $R_{ww}$ and $R_{cc}$ is 0.11 and 0.12 for N1 and N2, respectively. This is smaller than the RMSE between the $R_e$ estimates based on different sources of case report data: 0.13 between confirmed cases and hospitalizations and 0.26 between confirmed cases and deaths (estimated on case report data from Canton Zurich, which has a population 3.4 times the size of the catchment, for the same time period as $R_{ww}$).

Application to an Independent Data Source and Different Wastewater Matrix

To assess whether these results could be generalized to different geographic locations and wastewater matrices, we analyzed daily sampled primary sewage sludge data from the San Jose wastewater treatment plant in California.

In San Jose, the inferred infection incidence curves between confirmed cases and wastewater data followed similar trends (Figure 2D). The inferred incidence from confirmed cases rose rapidly, reaching a maximum and fluctuating at a plateau throughout December. This fluctuation seems primarily caused by reporting errors on 30 December, because it fully disappeared when replacing the zero cases reported that day by 1,000 (Figure S5). Instead, wastewater estimates continued to rise more gradually throughout December, similar to the cases adjusted for test positivity. Starting in late December, all traces showed a similar decrease.

We found that $R_{ww}$ agreed with $R_{cc}$, although there was again some temporal lag between both, which seems more pronounced in November/December than in the second half of the time series (Figure 2D). The $R_e$ estimates based on the testing-adjusted cases are more comparable to $R_{ww}$, both in terms of slope (especially in December) and a more uniform delay throughout the entire time period. A comparison between $R_{cc}$ estimated using different methods (as reported on the website of the California State Department of Public Health) shows substantially larger differences than between the wastewater and the confirmed case estimates from the same pipeline (Figure S6).

Minimal Frequency of Wastewater Sampling Needed to Inform $R_{ww}$

When designing wastewater-based epidemiology studies, an important cost–benefit trade-off centers around the frequency of sampling. We subsampled the daily sampled wastewater measurements in Zurich and San Jose, prior to the $R_e$ estimation pipeline, to determine how this would affect the estimated $R_{ww}$. We assessed a range of sampling strategies that differed in the number and identity of the days sampled (e.g., Monday, Wednesday, and Friday or Monday–Friday). For Zurich, we restricted ourselves to the period with daily sampling (22 November 2020 to 11 January 2021). Using the RMSE to quantify the similarity between different $R_{ww}$ estimates, we found that subsampling down to three measurements per week still leads to results comparable to a daily sampling regime (Figure S7; Table S2 and Table S3). However, below this frequency the representativity of the $R_{ww}$ estimate started to depend on which days were sampled.

Susceptibility of $R_{ww}$ Estimates to the SLD

There is substantial variation between SLDs described in the literature, across patients, bodily fluids, and geographic locations.^20,24,25 We find that the shape of the used SLD, in particular the mean of the gamma distributions, affects the inferred timing of peak infection incidence (with larger means shifting the incidence further back in time; Figure S8). In our pipeline, we also observed that smaller normalization factors $N\times M$ increased the amplitude of the estimated $R_{ww}$, albeit only when misspecified by more than 5 orders of magnitude (Figure S9). In principle, the inference of the $R_e$ point estimate from an infection incidence is independent of the magnitude of this incidence.^2,4 However, the expectation maximization algorithm used for deconvolution in our pipeline was optimized for data on the scale of infections per day. Here, we have chosen to normalize the wastewater measurements such that the considered gene loads are on that same scale, because $R_{ww}$ otherwise reacts too strongly to changes in the daily incidence.

Estimating the SLD from the Fit between Clinical and Wastewater Data

Instead of assuming a single SLD and estimating $R_{ww}$ based only on that distribution, we also asked which SLD would maximize the similarity between the $R_{ww}$ and $R_{cc}$ estimates. We numerically scanned across different SLDs and quantified the resulting goodness of fit between the $R_{ww}$ and $R_{cc}$ for both Zurich and San Jose. We assumed the SLD is described by a single gamma distribution, starting at infection, and searched for the optimal fit on a grid of mean–SD parameter pairs (Table 1; Figure 3). The fit was quantified using the RMSE, coverage, and MAPE. Because the measurements of the different genetic markers followed nearly identical patterns in both locations (Figures 1 and 2), we conducted the SLD optimization analysis only for the N1 marker in Zurich and the S gene in San Jose.

Table 1.

Parameters of the optimal shedding distribution from infection.

Comparison method	Optimal pair (mean; SD)	Mean within 10% from the optimum	SD within 10% from the optimum
RMSE (Zurich)	(7.5; 0.5)	[6, 11.5]	[0.5, 10]
Coverage (Zurich)	(7.5; 0.5)	[6, 12.5]	[0.5, 10]
MAPE (Zurich)	(11; 9.5)	[6.5, 11]	[0.5, 10]
RMSE (San Jose)	(7.0; 0.5)	[6, 9]	[0.5, 3]
Coverage (San Jose)	(5; 0.5)	[1, 11]	[0.5, 10]
MAPE (San Jose)	(6; 0.5)	[5, 8]	[0.5, 2.5]

Note: We scanned across different (mean, SD) parameter pairs for the shedding load distribution from time since infection. For Zurich, the $R_{ww}$ from N1 loads in wastewater was compared to the $R_{cc}$ of confirmed cases in the catchment. For San Jose, we compared S gene concentrations to confirmed cases in Santa Clara County. For all values of the scan, see Figure 3 (RMSE), S10 (coverage), and S11 (MAPE). All parameters are in units of days. For the coverage, the 95% confidence intervals of $R_{cc}$ and $R_{ww}$ were based on 50 bootstrap replicates in each comparison. MAPE, mean average percentage error; RMSE, root mean squared error; SD, standard deviation.

The optimal fits based on these metrics suggest that the SLD has a mean between 7 and 11 d in Zurich and between 5 and 7 d in San Jose, with a very low SD of 0.5 d in both locations (Table 1). However, there is some nonidentifiability in our analysis, with most optimal value pairs lying along a ridge (Figure 3; repeated for coverage: Figure S10 and for MAPE: Figure S11). This ridge corresponds to SLDs with a similar median, which result in nearly indistinguishable $R_{ww}$ estimates (examples shown in Figure S12). If we consider the parameters yielding a fit within 10% from the optimum, the parameter ranges found in both locations are compatible and jointly suggest an SLD with mean between 6 and 9 d, and SD between 0.5 and 3 d. Longer time series and more locations would further constrain this distribution. In comparison with the delay between infection and case reporting, the SLD introduces a similar or lower mean delay to $R_{ww}$. For Zurich, the cases were delayed with respect to infection by 8.1 d on average, which is comparable to the 6–9 d for $R_{ww}$. For San Jose, instead, the delay distribution of the case report data had a mean of 9.8 d. There, the wastewater may lead the confirmed cases by 1–4 d, if the current testing and reporting regime is maintained.

To compare against published SLDs, which are frequently parameterized from symptom onset instead of infection, we conducted a second analysis. Here we assumed individuals do not shed during their incubation period and subsequently shed with a gamma distribution, starting at symptom onset. In this case, we found optimal SLDs with a mean between 0.5 and 3 d for San Jose and between 3.5 and 5.5 d for Zurich (Table S4; Figure S13). These optimal distributions have a lower mean than the SLD reported by Benefield et al.²⁶ (mean 6.7 d), and Han et al. (mean 4.7 d).²⁵ If we add the mean incubation period (5.3 d) to the results of this scan, we find that for both locations the mean delay between infection and shedding is comparable to the mean of the SLD we estimated from infection.

Discussion

We showed that regular measurements of SARS-CoV-2 concentrations in wastewater and settled solids can be used to estimate the effective reproductive number $R_e$. The difference between $R_e$ estimates from wastewater ($R_{ww}$) and from case report data ($R_{cc}$) was similar to the difference between $R_e$ estimates based on different types of case report data (clinical cases, hospitalizations, and deaths). This did not depend on which of the measured gene targets was used to estimate $R_{ww}$. We further showed wastewater samples should be collected at least three times per week to reliably estimate past $R_{ww}$, in line with analyses based on direct comparison of wastewater signals to clinical cases.^15,42 For real-time monitoring of $R_{ww}$, more frequent measurements may be preferable to ensure stable estimates when new data comes in.

Estimating $R_{ww}$ requires accurate characterization of the SLD, i.e., the temporal dynamics of shedding. In our primary analysis, we used the distribution for gastrointestinal shedding from Benefield et al.²⁶ In using this SLD, we implicitly assumed that fecal shedding dominates the viral load in wastewater. However, there is a wide range in published viral shedding loads, and it is unclear which—if any—accurately capture viral shedding dynamics of people within a catchment. Virus shed in saliva, sputum, and feces are possible contributors to the total amount of virus RNA in the wastewater.⁴³ Although upper respiratory tract swabs show peak viral loads around the day of symptom onset, there are indications that sputum samples peak a few days later, and feces even after that.^44–46 Studies differ in the inferred timing of peak viral load (even in the same bodily fluids), and there is a general lack of information to constrain dynamics prior to symptom onset.⁴⁷ Additionally, the duration and magnitude of viral shedding seem to differ within different populations (for example, due to age or severity of disease).^48,49 However, these individual differences will probably average out in a sufficiently large catchment, and better estimates of the SLD are likely to become available as prospective sampling studies report results.

We showed that the optimal SLD can also be inferred from the fit between $R_{ww}$ and $R_{cc}$. Once the SLD has been estimated from historic wastewater and case data, it may from then on provide a more accurate estimation of $R_{ww}$ than using one of the published SLDs. Indeed, here we show a range of gamma-distributed SLDs inferred from our wastewater data that generally align with but have lower means than published SLDs based on patient shedding profiles. Optimization based on alignment between $R_{ww}$ and $R_{cc}$ assumes accuracy of $R_{cc}$, which only holds when there is adequate clinical case surveillance. However, given widespread wastewater monitoring coincident to clinical case reporting, broader application of our methods would help constrain the SLD of SARS-CoV-2.

The utility of wastewater measurements for $R_e$ estimation is independent of the pipeline used to estimate $R_e$. Here, we report results obtained with the pipeline of Huisman et al.² However, many estimation methods exist, differing in assumptions on smoothing, deconvolution, and uncertainty quantification as well as the underlying method to estimate $R_e$ from infection incidence.^1,3,7,50,51 Although the $R_e$ point estimate is not affected by the absolute magnitude of the infection incidence (and thus comparable across wastewater treatment plants with differing sampling protocols), the rest of our pipeline (in particular the deconvolution) was originally developed specifically for use with clinical data. Thus, we had to normalize the measured wastewater concentrations to the same order of magnitude as the case data. Further development could make the method more specifically adapted to wastewater data and alleviate this dependence on the normalization.

Estimates of $R_{ww}$ are independent of biases influencing clinical case-based estimates. $R_{cc}$ estimates are based on only the subset of infections, hospitalizations, and/or deaths that are captured by surveillance within the health care system. If this subset changes (for instance, due to developments in testing or reporting policy), the resulting $R_{cc}$ estimates will be temporarily biased.^2,4 In Geneva, Switzerland, seroprevalence studies showed that the number of infections per reported case varied substantially, from an estimated 11.6 infections per reported case as of May 2020 to only 2.7 as of December 2020.^52,53 During that period, SARS-CoV-2 RNA concentrations in wastewater better reflected the dynamics than the clinical cases.²³

However, $R_{ww}$ estimates are also prone to biases. People’s behaviors, such as defecation timing outside of a daily routine⁵⁴ and/or movement into or out of the catchment⁵⁵ can influence $R_{ww}$ estimates, particularly when the number of infected individuals is low. RNA signals may also be impacted during sewer transport, with persistence influenced by environmental conditions (i.e., temperature) and/or sewage composition (i.e., solids content).^56–59 Furthermore, sample processing required to quantify SARS-CoV-2 RNA may introduce variation, as suggested by substantial day-to-day variation in measurements.^13,15,23,60 Finally, $R_{ww}$ estimates are informed by the number and proportion of infected and/or shedding people within the catchment: If there are too few active shedders, $R_{ww}$ may be very sensitive to the increased fluctuations in SARS-CoV-2 RNA concentrations.

To conclude, deriving $R_e$ from wastewater offers an independent method to track disease dynamics. Wastewater-based epidemiology is used globally to track the COVID-19 pandemic.^13–19,61 The data collected within these campaigns could be used to estimate $R_{ww}$ with a robust method that is not influenced by heterogeneous testing and reporting strategies, and hence the method would be more applicable across geographic areas. Additionally, $R_{ww}$ estimates could be derived for the transmission of SARS-CoV-2 variants and/or other pathogens for which SLDs are known. SARS-CoV-2 variants, including Variants of Concern (VOCs), are readily detectable in wastewater^62–64 as are other pathogens (e.g., norovirus, enterovirus, hepatitis A).^65–67 This could provide the temporal, quantitative wastewater measurements needed to estimate $R_{ww}$. Wastewater surveillance allows estimating $R_{ww}$ to track disease transmission dynamics in near real time, using low-cost, rapid, and geographically comparable methods, and such surveillance can be used when reporting clinical cases is not feasible, mandatory, or much delayed in comparison with infection and shedding.