Skip to main content
PMC home page
HHS Author Manuscripts logoLink to HHS Author Manuscripts
. Author manuscript; available in PMC: 2022 May 26.
Published in final edited form as: IEEE Trans Ultrason Ferroelectr Freq Control. 2000;47(4):777–780. doi: 10.1109/58.852057

The relationship between ultrasonic backscatter and bone mineral density in human calcaneus

Keith A Wear 1, David W Armstrong III 2
PMCID: PMC9135476  NIHMSID: NIHMS1808128  PMID: 18238608

Abstract

Backscatter and attenuation coefficients were measured from 24 human calcanei in vitro. The logarithm of the backscatter coefficient at 500 kHz showed moderate correlations with bone mineral density (r = 0.81, 95% confidence interval: 0.59 – 0.91) and attenuation (r = 0.79, 95% CI: 0.56 - 0.91). These results suggest that backscatter measurements may be useful in the diagnosis of osteoporosis.

Keywords: calcaneus, trabecular bone, cancellous bone, backscatter, osteoporosis

Introduction

Ultrasound has been demonstrated to be a powerful modality for prediction of osteoporotic fracture risk. Compared with traditional X-ray bone densitometry, ultrasound-based methods offer advantages including low cost, lack of ionizing radiation, speed, simplicity, and portability. Calcaneal broadband ultrasonic attenuation1–4 and speed of sound2,3,5–10 have been shown to correlate highly with calcaneal bone mineral density (BMD) which is in turn an indicator of osteoporotic fracture risk.11 Calcaneal ultrasonic measurements (broadband ultrasonic attenuation combined with sound speed) have been demonstrated to be predictive of fractures of the hip (generally the most debilitating kind of osteoporotic fracture) and other sites in women in prospective12,13 and retrospective14–17 studies.

The calcaneus is predominantly composed of trabecular bone and is surrounded by a thin cortical shell. The trabecular interior consists of a three dimensional lattice of branching spicules and plate-like structures. The spaces between the trabeculae are filled with marrow which consists of fat and cellular components of blood constituents. The interfaces between mineralized bone trabeculae and marrow (which have substantially different acoustic impedances) are likely candidates for the sources of ultrasonic scattering.

Measurements of ultrasonic backscattering properties may provide useful information regarding BMD and/or microarchitecture (another important determinant of osteoporotic fracture risk). For example, the aging process involves a reduction over time of the number and thicknesses of trabeculae. This would be expected to reduce backscatter. Diagnostic promise and clinical feasibility of the backscatter measurement have already been demonstrated.18–22 The purpose of this letter is to report an independent confirmation of an earlier experiment18 in which the correlation between backscatter and BMD was investigated using human calcaneus samples in vitro.

Experimental Methods

Preparation of Calcaneus Samples

Twenty four human calcaneus samples (genders and ages unknown) were defatted using a trichloro-ethylene solution. Defatting was presumed not to substantially alter measurements since attenuation and speed of sound of defatted trabecular bone have been found to be only slightly different from their counterparts obtained with marrow left intact.4,23,24 In addition, defatting may not have a profound effect on backscatter measurements provided that the acoustic properties of water (which fills spaces between trabeculae during the in vitro interrogation of defatted bone) and marrow (which normally fills the spaces between trabeculae) are much closer to each other than either is compared with the acoustic properties of mineralized bone trabeculae.

The lateral cortical layers were sliced off leaving two parallel surfaces with direct access to trabecular bone. The thicknesses of the samples varied from 12 to 21 mm. Prior to ultrasonic interrogation, samples were vacuum degassed underwater in a desiccator. Subsequently, samples were allowed to thermally equilibrate to room temperature. Ultrasonic measurements were performed in distilled water at room temperature. Temperature was measured for each experiment and ranged between 19.1°C and 21.2°C. The relative orientation between the ultrasound beam and the calcanei was the same as with in vivo measurements performed with commercial bone sonometers, in which sound propagates in the mediolateral (or lateromedial) direction.

BMD was measured using a Norland XR-26 dual energy x-ray absorptiometry (DEXA) system operating in single beam mode. The areal density (g/cm2) was divided by the thickness of each sample to give a true volumetric density (g/cm3). Apparent density was also measured by taking the ratio of the dry weight to the volume of each specimen. The volume was computed as the product of the thickness (the distance between the machine-cut planar surfaces, measured with calipers) and the cross-sectional area (measured using computer processing of scanned images of the samples). The cross-sectional areas of the samples were nearly, but not perfectly, uniform across each sample.

Ultrasonic Methods

Samples were interrogated in a water tank using a Panametrics (Waltham, MA) 5800 pulser/receiver and Panametrics 1.0” diameter, 1.5” focal length, broadband transducers with center frequencies of 500 kHz. Received signals were digitized (8 bit, 10 MHz) using a LeCroy (Chestnut Ridge, NY) 9310C Dual 400 MHz oscilloscope and stored on computer (via GPIB) for off-line analysis.

Backscatter coefficients were measured using a reference phantom method.22, 25 With this method, measurements are performed on the sample of interest (e.g. bone) and on a phantom with known frequency-dependent attenuation and backscatter coefficients. The backscatter coefficient of the sample may be computed from the ratio of attenuation-compensated backscattered power spectra and the known backscatter coefficient of the phantom.25 This technique suppresses any dependences of measurements on transducer electromechanical properties and diffraction (since both sample and phantom measurements are performed at the same distance from the transducer). Good agreement between experimental measurements using this method and theoretical predictions based on Faran’s26 theory of scattering from spheres for ultrasonic backscatter coefficients from phantoms has previously been reported by this laboratory.27 The backscatter coefficient vs. frequency data were least-squares fit to a power law relationship. The logarithm of the midband (500 kHz) value of the fit was used to characterize backscatter. Due to the high porosity of trabecular bone, the transmission coefficient at the water/bone interface was assumed to be one.30

Attenuation measurements were required in order to compensate signals prior to backscatter coefficient estimation. Using two opposing coaxially-aligned transducers (one transmitter and one receiver) separated by twice the focal length, transmitted signals were recorded both with and without the bone sample in the acoustic path. The bone samples were larger in cross-sectional area than the receiving transducer aperture. Attenuation coefficient was then estimated using a log spectral difference technique.28 Attenuation was characterized by the slope of a least-squares linear fit of attenuation coefficient vs. frequency. This parameter is often referred to as normalized broadband ultrasonic attenuation (nBUA)4 in the bone densitometry community and as attenuation slope in the biomedical ultrasound community. In principle, this substitution technique can exhibit appreciable error if the speed of sound differs substantially between the sample and the reference.29 However, one study indicates that this diffraction-related error is very small in calcaneus.30 Apparently, the speed of sound in calcaneus (in the mediolateral orientation), approximately 1475 – 1650 m/s,30 is sufficiently close to that of distilled water at room temperature, 1487 m/s,31 that diffraction-related errors may be ignored.

Results

DEXA BMD measurements of calcaneal samples (mean: 0.17 g/ml, standard devaiation: 0.06 g/ml) were roughly half as great as apparent densities (mean: 0.34 g/ml, standard deviation: 0.10 g/ml). This discrepancy was probably due to the exclusion of dense peripheral trabecular bone and thin but dense exterior cortical shells from DEXA regions of interest. The correlation between the two density measures was r = 0.90 (95% confidence interval: 0.78 – 0.96).

The logarithm of the midband backscatter coefficient is plotted as a function of BMD for the 24 calcaneus samples in Figure 1. The correlation coefficient from the least-squares linear fit was r = 0.81 (95% CI: 0.59 – 0.91). The correlation coefficient of the logarithm of the midband backscatter coefficient with apparent density was virtually identical: r = 0.80 (95% CI: 0.58 – 0.90).

Figure 1.

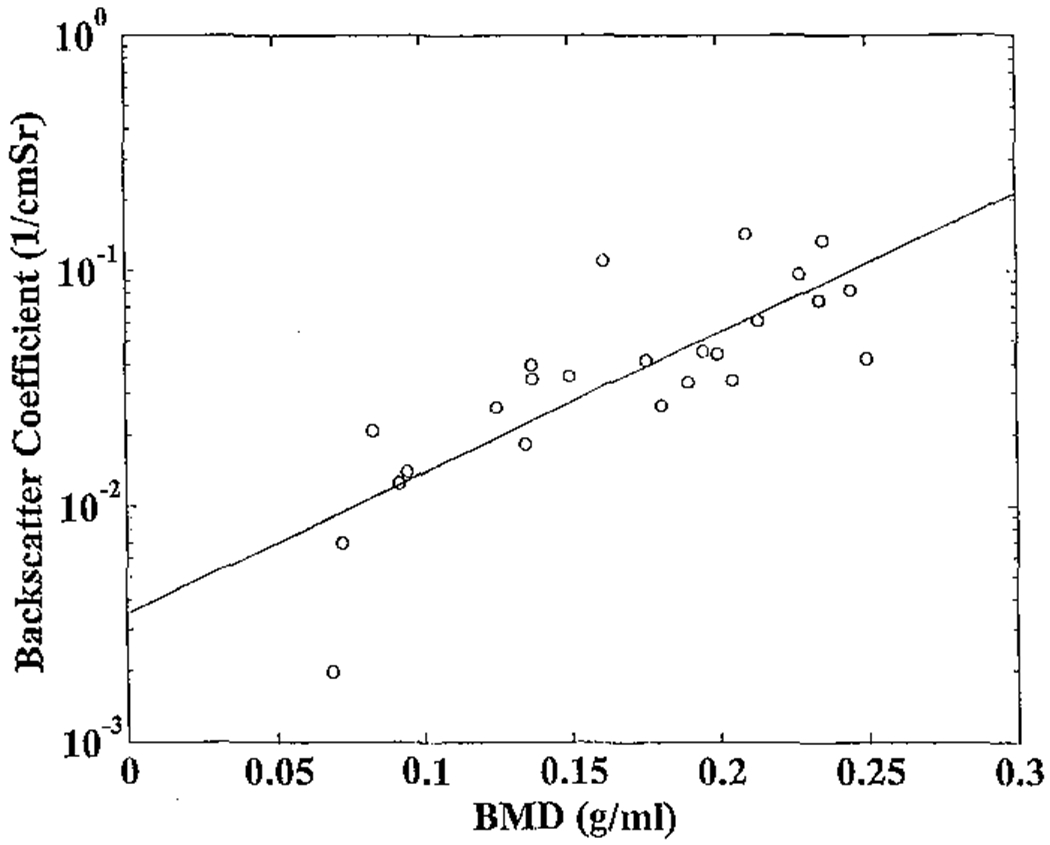
Figure 1.

Open in a new tab

The logarithm of the midband backscatter coefficient plotted as a function of bone mineral density (BMD) for the 24 bone samples. A least-squares linear fit is also shown.

The logarithm of the midband backscatter coefficient is plotted as a function of attenuation slope for the 24 calcaneus samples in Figure 2. The correlation coefficient from the least-squares linear fit was r = 0.79 (95% CI: 0.56 – 0.91). The magnitude of this correlation suggests that backscatter coefficient measurements may convey some information not already contained in attenuation measurements.

Figure 2.

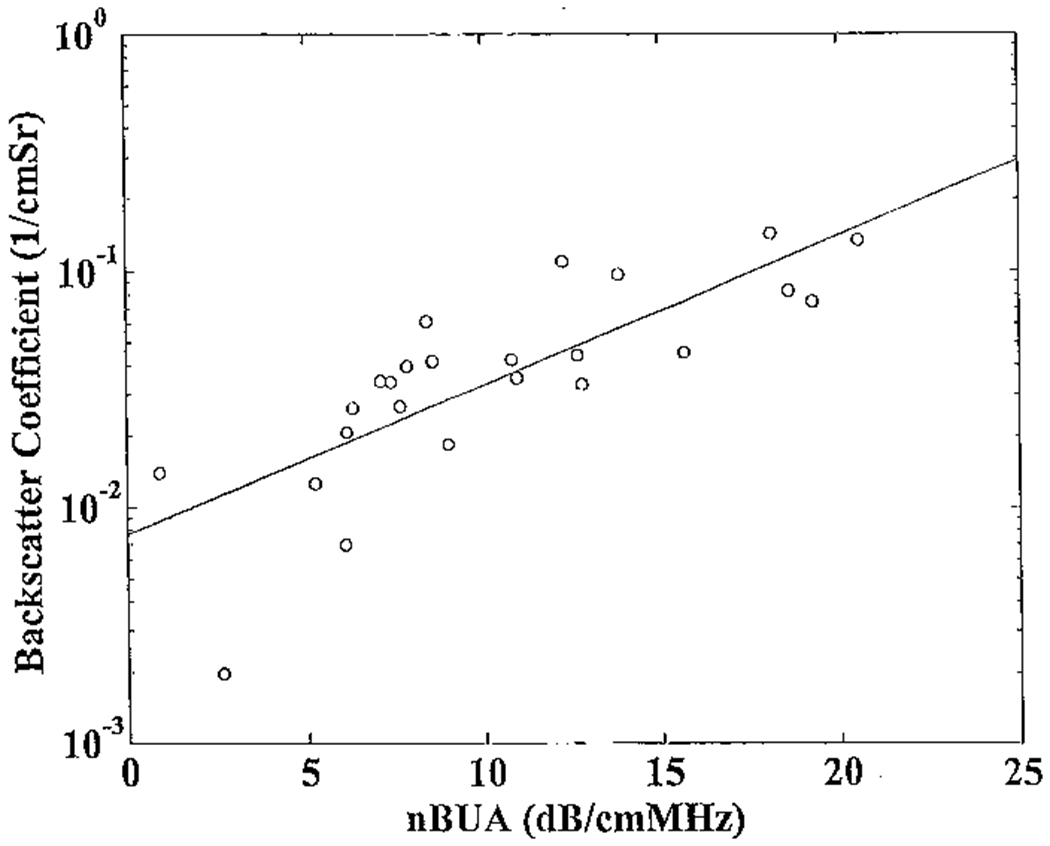
Figure 2.

Open in a new tab

The logarithm of the midband backscatter coefficient plotted versus attenuation slope (normalized broadband ultrasonic attenuation or nBUA) for the 24 bone samples. A least-squares linear fit is also shown.

The correlation between nBUA and BMD was 0.81 (95% CI: 0.59 – 0.91).

Discussion

One preliminary in vitro study18 and several preliminary in vivo studies19–21 have demonstrated that ultrasonic backscatter increases with BMD in human calcaneus. This letter reports a second in vitro study, in which ultrasonic measurements could be performed with greater accuracy and precision than in the in vivo cases, which was designed to independently confirm the findings of the first. The logarithm of the midband backscatter coefficient showed a moderate correlation with BMD. Variations in BMD accounted for 66% (comparable to 68% in the previous study18) of variations in the logarithm of the midband backscatter coefficient, suggesting that backscatter measurements give some indication of BMD, but also may convey some structural information not already contained in BMD measurements.

It should be acknowledged that possible partial (or alternative) explanations for the less-than-perfect correlation between the logarithm of the midband backscatter coefficient and BMD also include 1) inconsistency between analysis volumes for ultrasound and X-ray measurements, and 2) precision limitations of ultrasound and X-ray measurements. Due to the heterogeneity of calcaneus, the former issue is particularly important. In addition, while X-ray measurements are approximately uniformly weighted throughout the analysis volume, the ultrasound beam is most intense at the center and less intense at the periphery, leading to measurements which are essentially weighted averages of acoustic properties with central regions (within calcaneus samples) receiving relatively greater emphasis.

Several studies suggest that the commonly employed ultrasonic measurements in bone, broadband ultrasonic attenuation and speed of sound, provide rather limited additional information beyond that provided by BMD in predicting trabecular microstructural and elastic properties of bone.7–9 Generally speaking, it is well accepted that ultrasonic backscatter is highly dependent upon size, shape, number density, and elastic properties of scatterers.32 Whether backscatter can provide useful microarchitectural information beyond that provided by BMD in human trabecular bone is an important topic to be investigated.

Acknowledgements

The authors are grateful for funding provided by the US Food and Drug Administration Office of Women’s Health.

References

  • 1.Langton CM, Palmer SB, and Porter RW. The measurement of broadband ultrasonic attenuation in cancellous bone. Eng. in Med 13, 89–91, 1984. [DOI] [PubMed] [Google Scholar]
  • 2.Rossman P, Zagzebski J, Mesina C, Sorenson J, and Mazess R, “Comparison of Speed of Sound and Ultrasound Attenuation in the Os Calcis to Bone Density of the Radius, Femur and Lumbar Spine,” Clin. Phys. Physiol.Meas, 1989; 10:353–360. [DOI] [PubMed] [Google Scholar]
  • 3.Tavakoli MB and Evans JA. “Dependence of the velocity and attenuation of ultrasound in bone on the mineral content.” Phys. Med. Biol, 36, 1529–1537, (1991). [DOI] [PubMed] [Google Scholar]
  • 4.Langton CM, Njeh CF, Hodgskinson R, and Carrey JD, “Prediction of Mechanical Properties of the Human Calcaneus by Broadband Ultrasonic Attenuation,” Bone, 18, 495–503, (1996). [DOI] [PubMed] [Google Scholar]
  • 5.Zagzebski JA, Rossman PJ, Mesina C, Mazess RB, and Madsen EL. “Ultrasound transmission measurements through the os calcis.” Calcif Tissue Int. 49, 107–111, 1991. [DOI] [PubMed] [Google Scholar]
  • 6.Njeh CF, Hodgskinson R, Currey JD, and Langton CM. “Orthogonal relationships between ultrasonic velocity and material properties of bovine cancellous bone.” Med. Eng. Phys, 18, 373–381, 1996. [DOI] [PubMed] [Google Scholar]
  • 7.Laugier P, Droin P, Laval-Jeantet AM, and Berger G. “In vitro assessment of the relationship between acoustic properties and bone mass density of the calcaneus by comparison of ultrasound parametric imaging and quantitative computed tomography.” Bone, 20, 157–165, 1997. [DOI] [PubMed] [Google Scholar]
  • 8.Nicholson PHF, Muller R, Lowet G, Cheng XG, Hildebrand T, Ruegsegger P, Van Der Perre G, Dequeker J, and Boonen S. “Do quantitative ultrasound measurements reflect structure independently of density in human vertebral cancellous bone?” Bone. 23, 425–431, 1998. [DOI] [PubMed] [Google Scholar]
  • 9.Hans D, Wu C, Njeh CF, Zhao S, Augat P, Newitt D, Link T, Lu Y, Majumdar S, and Genant HK, “Ultasound velocity of trabecular cubes reflects mainly bone density and elasticity.” Calcif. Tissue Intl. 64, 18–23, 1999. [DOI] [PubMed] [Google Scholar]
  • 10.Trebacz H, and Natali A. “Ultrasound velocity and attenuation in cancellous bone samples from lumbar vertebra and calcaneus.” Osteo. Int’l, 9, 99–105, 1999. [DOI] [PubMed] [Google Scholar]
  • 11.Cummings SR, Black DM, Nevitt MC, Browner W, Cauley J, Ensrud K, Genant HK, Palermo L, Scott J, and Vogt TM, “Bone density at various sites for prediction of hip fractures.” Lancet, 341, 72–75, 1993. [DOI] [PubMed] [Google Scholar]
  • 12.Hans D, Dargent-Molina P, Schott AM, Sebert JL, Cormier C, Kotzki PO, Delmas PD, Pouilles JM, Breart G, and Meunier PJ, “Ultrasonographic heel measurements to predict hip fracture in elderly women: the EPIDOS prospective study,” Lancet, 348, 511–514, 1996. [DOI] [PubMed] [Google Scholar]
  • 13.Bauer DC, Glüer CC, Cauley JA, Vogt TM, Ensrud KE, Genant HK, and Black DM. “Broadband ultrasound attenuation predicts fractures strongly and independently of densitometry in older women,” Arch. Intern, Med. 157, 629–634 1997. [PubMed] [Google Scholar]
  • 14.Schott AM, Weill-Engerer S, Hans D, Duboeuf F, Delmas PD, and Meunier PJ, “Ultrasound discriminates patients with hip fracture equally well as dual energy X-ray absorptiometry and independently of bone mineral density.” J. Bone Min. Res, 10, 243–249 1995. [DOI] [PubMed] [Google Scholar]
  • 15.Turner CH, Peacock M, Timmerman L, Neal JM, and Johnston CC Jr., “Calcaneal ultrasonic measurements discriminate hip fracture independently of bone mass,” Osteo. International, 5, 130–135 1995. [DOI] [PubMed] [Google Scholar]
  • 16.Glüer CC, Cummings SR, Bauer DC, Stone K, Pressman A, Pressman A, Mathur A, and Genant HK, “Osteoporosis: Association of recent fractures with quantitative US findings”, Radiology, 199, 725–732 1996. [DOI] [PubMed] [Google Scholar]
  • 17.Thompson P, Taylor J, Fisher A, and Oliver R, “Quantitative heel ultrasound in 3180 women between 45 and 75 years of age: compliance, normal ranges and relationship to fracture history,” Osteo. Int’l, 8, 211–214, 1998. [DOI] [PubMed] [Google Scholar]
  • 18.Roberjot V, Laugier P, Droin P, Giat P, and Berger G. Meaurement of integrated backscatter coefficient of trabecular bone. Proc. 1996 IEEE Ultrason. Symp. Vol. 2, 1123–1126, 1996. [Google Scholar]
  • 19.Wear KA and Garra BS. Assessment of bone density using broadband ultrasonic backscatter, Proc. 22nd Int. Symp Ultrason. Imag. and Tissue Char., Washington, DC. 1997; 14 (Abstract). [Google Scholar]
  • 20.Giat P, Chappard C, Roux C, Laugier P, and Berger G. Preliminary clinical assessment of the backscatter coefficient in osteoporosis, Proc. 22nd Int. Symp Ultrason. Imag. and Tissue Char., Washington, DC, 1997, 16 (Abstract). [Google Scholar]
  • 21.Wear KA and Garra BS. Assessment of bone density using ultrasonic backscatter. Ultrason. Med. & Biol. 24, 689–695, 1998. [DOI] [PubMed] [Google Scholar]
  • 22.Wear KA. Frequency dependence of ultrasonic backscatter from human trabecular bone: theory and experiment. J. Acoust. Soc. Am 106, 3659–3664, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Alves JM, Ryaby JT, Kaufman JJ, Magee PP, and Siffert RS. Influence of marrow on ultrasounic velocity and attenuation in bovine trabecular bone. Calc. Tissue. Int, 58, 362–367, 1996. [DOI] [PubMed] [Google Scholar]
  • 24.Njeh CF and Langton CM. The effect of cortical endplates on ultrasound velocity through the calcaneus: an in vitro study. Brit. J. Radiol, 70, 504–510, 1997. [DOI] [PubMed] [Google Scholar]
  • 25.Zagzebski JA, Yao LX, Boote EJ, and Lu ZF. “Quantitative Backscatter Imaging” in Ultrasonic Scattering in Biological Tissues, edited by Shung KK and Thieme GA, CRC Press, Boca Raton, FL, 1993. [Google Scholar]
  • 26.Faran JJ, Sound scattering by solid cylinders and spheres, J. Acoust. Soc. Am, 23, 405–418, 1951. [Google Scholar]
  • 27.Wear KA, Garra BS, and Hall TJ, Measurements of ultrasonic backscatter coefficients in human liver and kidney in vivo, J. Acoust. Soc. Am, 98, 1852–1857, 1995. [DOI] [PubMed] [Google Scholar]
  • 28.Kuc R and Schwartz M. Estimating the acoustic attenuation coefficient slope for liver from reflected ultrasound signals. IEEE Trans. Son. Ultrason SU-26, 353–362, (1979). [Google Scholar]
  • 29.Xu W and Kaufman JJ. Diffraction correction methods for insertion ultrasound attenuation estimation. IEEE Trans. Biomed. Eng. 40, 563–570, (1993). [DOI] [PubMed] [Google Scholar]
  • 30.Droin P, Berger G, and Laugier P. Velocity dispersion of acoustic waves in cancellous bone. IEEE Trans. Ultrason. Ferro. Freq. Cont 45, 581–592 (1998) [DOI] [PubMed] [Google Scholar]
  • 31.Pierce D, Acoustics: An Introduction to Its Physical Principles and Applications (McGraw-Hill, New York, 1981), p. 31. [Google Scholar]
  • 32.Morse PM and Ingard KU, Theoretical Acoustics. Princeton, NJ, Princeton University Press, 1986, chapter 8. [Google Scholar]

RESOURCES