Graphical abstract
2000 MSC: 0000, 1111
Keywords: Simulations, Network sciences, Disease containment
Highlights
-
•
Paper discusses the relevance of the adoption of ad-hoc vaccination strategies.
-
•
Paper shows how to evaluate the impact of different vaccination strategy by considering network-based models.
-
•
Tailored interventions, e.g., vaccination, applied on central nodes of these networks may efficiently stop the propagation of an infection.
-
•
The way node "centrality" is defined is the key to curb infection spreading.
Abstract
The mitigation of an infectious disease spreading has recently gained considerable attention from the research community. It may be obtained by adopting sanitary measurements (e.g., vaccination, wearing masks), social rules (e.g., social distancing), together with an extensive vaccination campaign. Vaccination is currently the primary way for mitigating the Coronavirus Disease (COVID-19) outbreak without severe lockdown. Its effectiveness also depends on the number and timeliness of administrations and thus demands strict prioritization criteria. Almost all countries have prioritized similar classes of exposed workers: healthcare professionals and the elderly, obtaining to maximize the survival of patients and years of life saved. Nevertheless, the virus is currently spreading at high rates, and any prioritization criterion so far adopted did not account for the structural organization of the contact networks.
We reckon that a network where nodes are people while the edges represent their social contacts may efficiently model the virus’s spreading. It is known that tailored interventions (e.g., vaccination) on central nodes may efficiently stop the propagation, thereby eliminating the “bridge edges.” We then introduce such a model and consider both synthetic and real datasets. We present the benefits of a topology-aware versus an age-based vaccination strategy to mitigate the spreading of the virus. The code is available at https://github.com/mazzalab/playgrounds.
1. Introduction
Each successful outbreak containment strategy relies on three main pillars: detection (e.g., diagnostics tests), prevention (e.g., vaccines, containment), and cure (e.g., the existence of effective drugs). While the latter measure is effective when an outbreak has happened, appropriate detection and prevention strategies that may be used at every stage of an epidemic, from the detection to the resolution, are required. In particular, the development of effective diagnostic tests is technically challenging, which are helpful for detecting infected people but are applicable for spreading containment. It is thus evident that appropriate strategies for containment to ensure that future outbreaks can be more effectively contained are needed.
Containment strategies fall into two main categories, often interlaced: (i) social and sanitary containments, which are based on the limitation of contacts among people but require many social efforts (e.g. lockdown, change of behaviour, use of protective devices such as face masks); (ii) vaccination strategies, which tackle the spreading without imposing social limitations. For instance, for the SARS-CoV-2 pandemic [1], after initial containment measures, and the trial of different therapies, many research efforts led to the development of different vaccines [2], [3], [4], [5]. However, considering the spread of COVID-19 and the production rates, there is a need for developing ad hoc prioritization strategies [6] that are also effective for subsequent pandemics. Similarly, even in the presence of sufficient vaccines, it is important to consider the speed of spreading, which may be higher than the immunization rate, thus affecting the vaccination strategy. Unfortunately, this was clear only in the COVID-19 third wave. The availability of a vaccine prioritization strategy is then a crucial challenge in fighting COVID-19 and future pandemics. There is evidence that the production rate of vaccines may remain insufficient and that viruses may have different impacts and transmission rates in other social groups as demonstrated for SARS-CoV-2 [7], [8], [9], [10].
Considering that COVID-19 showed a higher fatality rate in older people [11], [12], and that healthcare workers showed a higher risk, many governments gave priority to such classes. As demonstrated by Goldstein et al. in [12], this strategy enabled to save both the most lives and most years of life. Common sense suggests that a good prioritization scheme should choose the best trade-off between saving the maximum number of lives and the most future life. The mathematical model developed by the authors demonstrated that giving priority to older adults may maximize both effects. Thus, this strategy is feasible. Older people’s prioritization was chosen as the main criterion in many countries such as Italy and the US. These countries also gave priority to healthcare professionals, teachers, and caregivers. Despite the effectiveness of this approach, it has been clear that a vaccine allocation strategy requires the incorporation of a model of transmission and the epidemiological characteristics of the disease among social groups [13], [14], [15]. For instance, Jentsch et al. [16] discussed the problem of the optimization of the strategy vaccination. They demonstrated that an approach based only on age is not optimal compared to a contact-based plans.
Consequently, some recent papers discussed the development and use of complex modeling strategies based on the integration of ordinary differential equations and network theory [17], [18], [19]. Such models enable the use of a large set of theoretical results related to the analysis of the influence of nodes connecting the characteristics of spreading processes and the network’s topology. It has been shown that the network evidences the presence of some nodes that have a relevant influence on spreading processes. Moreover, influent nodes have some topological characteristics related to centrality [20]. Chakrabarti et al., showed that there is a simple and effective mathematical relationship between the spreading and the magnitude of eigenvalues of the adjacency matrix [17]. In particular, the reduction of such magnitude may reduce its spreading.
The analysis of these approaches suggests, to the best of our knowledge, two primary considerations: (i) the optimization strategy depends on the desired goals, (ii) the integration of the characteristics of the modeling improves the performance, (iii) a dynamic strategy may outperform a static one. Despite this, we retain that modeling the spreading using a classical SEIR (Susceptible-Exposed-Infective-Recovered) model may not be the best choice since some parameters are considered at a global scale, while the spreading involves single contacts. In parallel, some previous studies, such as [21], [22], [23], [24], [25], [26], [27], have demonstrated that the use of a model coming from graph theory may be helpful to describe the spreading. Moreover, many works discussed the relevance of central nodes concerning diffusion processes in networks [28], [18]. These studies identify betweenness and eigenvalue centrality as representative measures of the influence of nodes [20]. In this way, comprehensive graphs may be derived using nodes, i.e., people, and edges, i.e., their contacts. Therefore, there is a need to introduce novel methods and supporting tools for the implementation of an optimal vaccination strategy.
Consequently, we propose a mixed framework for simulating the disease spreading on networks. As a first iteration, it was designed to model the number of (i) susceptible individuals, (ii) infected individuals, and (iii) recovered individuals. This so-called SIR model was tested on networks of increasing sizes, random and natural topology configurations, thereby mimicking the social contacts at most, and were subjected to vaccination in different instants of the infection to test the efficacy and timeliness of the implemented vaccination strategy. The way vaccination was mimicked deserves, in fact, particular attention. We propose removing, i.e., vaccine, the nodes with the highest topological centrality metrics within the network while controlling the consequent epidemic spreading reduction by a linear algebra formulation.
The application of this framework supports our initial hypothesis that any strategy of optimization that is unaware of the virus spreading topology without a severe lockdown may fail in virus circulation mitigation. This may favor the insurgence of novel virus variants during the vaccination that are not covered by existing vaccines [29].
2. Related work
2.1. Epidemics control on networks
Frameworks based on graph theory and network science are currently largely used for modeling and studying diffusion processes in several scenarios: ideas in social networks, objects in transport networks, and virus spreading. The COVID-19 outbreak has given researchers both an unprecedented source of data and a real application scenario. In [30], authors used a multiplex network and an SIR system [31] to model heterogeneous contacts among humans. They considered three kinds of contacts: a Household layer, a Work layer, and a Social layer. The SIR process mimicked the epidemic spreading. The framework’s objective was to compare partition strategies that model lockdown to evaluate the control of the epidemic outbreak and minimize the economic cost associated with the partial lockdown.
Similar to multiplex networks, temporal networks coupled to the SIR model have been used to model the infection spreading [32], [33], [34]. In [35], a temporal network implemented as a multiplex network with time-varying edges was used to model an epidemic. The authors also found a condition discriminating controlled/uncontrolled epidemics on the basis of the parameters of the SIR model and on the matrix, which describes the evolution of the SIR.
The spreading of information (or, more generally, the spreading itself) and the best conditions for spreading and the emergence of super-spreaders have been largely investigated in network science [36], [37]. These studies discussed the challenge of detecting and suppressing the spreading of dangerous viruses, pathogens, and misinformation or gossip. In [38], authors investigated the impact of the community structure of the network on percolation, simulating the spreading of an epidemic modeled through an SIR model. The authors concluded that spreading within communities is critically related to the network density [39], [40]. At the same time, the inter-community edges are the most critical factor in spreading an epidemic, regardless of community size and shape. In particular, in [41] a study of epidemic spreading using the adjacency matrix of a graph has been proposed. In this work, given a contact matrix (without any constraint on the structure of the matrix) and an epidemic modeled using an SIR model, which in turn was described by two parameters , i.e., the rate of novel infected, and , i.e., the rate of recovered, it has been demonstrated that an upper bound to the epidemic exists and it is given by the Eq. 1:
| (1) |
where is the largest eigenvalue of the adjacency matrix. Consequently, given the following property:
| (2) |
where and are the average and the maximum node degrees in a network, reducing would lead to a maximal network disconnection and, then, to the highest reduction in viral diffusion probability.
3. Results
3.1. Experiment on synthetic networks
Test graphs were generated randomly according to several well-known topology characteristics, as summarised in Table 1: Erdős Rényi, Random, Duplication Divergence, and Barabási-Albert. For each corresponding adjacency matrix, we calculated the largest eigenvalue.
Table 1.
Network Statistics.
| Graph Model | Nodes | Edges | Avg Density | Avg Clustering Coefficient |
|---|---|---|---|---|
| Erdős Rényi | 1000 | 199869 84 | 0.400 0.06 | 0.400 0.007 |
| 1000 | 199950 150 | 0.399 0.001 | 0.405 0.001 | |
| Duplication Divergence | 1000 | 2592 | 30 0.005 0.00002 | 0.002 0.00001 |
| Barabási-Albert | 1000 | 47500 | 0.095 0.001 | 0.17 0.002 |
Main statistics for the generated graphs. "Nodes" are the number of nodes for each graph. "Edges" are the average number of edges. "Density" and "Clustering Coefficients" were averaged for the generated graphs.
These were calculated for the same graphs but deprived of either k random nodes or k top-scored nodes according to the following topological metrics: degree, betweenness, or eigenvalue centrality. We then reported the reduction values obtained with both node elimination strategies and whether their differences were significant using a Student’s t-test. The normality of each distribution was tested using the Shapiro–Wilk test. Table 2 summarizes these results. The decrease obtained when removing the topologically central nodes was higher in all cases (Fig. 2). Therefore, the impact on the ratio was significantly higher.
Table 2.
Largest eigenvalues (expressed as mean and standard deviation), calculated for each graph model and centrality measure (CM), of the original graph (Original), the graph randomly deprived of k nodes (Random), and the graph deprived of the k most central nodes within the graph (Top-K). DC stands for degree centrality, BC for betweenees centrality, EC for eigenvalue centrality and CC for closeness centrality. A p-value lower than 0.05 means that the decrease in the distribution of the largest eigenvalue is significantly higher after deleting the Top-K central nodes.
| Graph Model | CM | Original | Top-K | Random | p-value |
|---|---|---|---|---|---|
| Erdős Rényi | DC | 400 0.51 | 351.2 0.65 | 368 0.7 | 0.01 |
| Erdős Rényi | BC | 400 0.51 | 354.2 0.65 | 365 0.7 | 0.01 |
| Erdős Rényi | EC | 400 0.51 | 351.4 0.21 | 367 0.92 | 0.01 |
| Random Graph | DC | 400.18 0.66 | 354.59 0.61 | 365.44 0,62 | 0.01 |
| Random Graph | BC | 400.18 0.66 | 357.79 0.61 | 368.44 0,62 | 0.01 |
| Random Graph | EC | 400.18 0.66 | 351.23 0.21 | 371.44 0.62 | 0.01 |
| Duplication Divergence | DC | 15.2 1.81 | 4.64 0.52 | 15.08 1.79 | 0.01 |
| Duplication Divergence | BC | 15.2 1.81 | 5.67 0.51 | 14.88 1.19 | 0.01 |
| Duplication Divergence | EC | 15.2 1.81 | 8.53 1.4 | 17.14 1.14 | 0.01 |
| Barabási-Albert | DC | 129.38 1.9 | 67.43 3.45 | 115.85 1.79 | 0.01 |
| Barabási-Albert | BC | 129.38 1.81 | 65.79 0.51 | 120.98 1.19 | 0.01 |
| Barabási-Albert | EC | 129.38 1.9 | 68.53 1.4 | 117.14 1.14 | 0.01 |
Fig. 2.
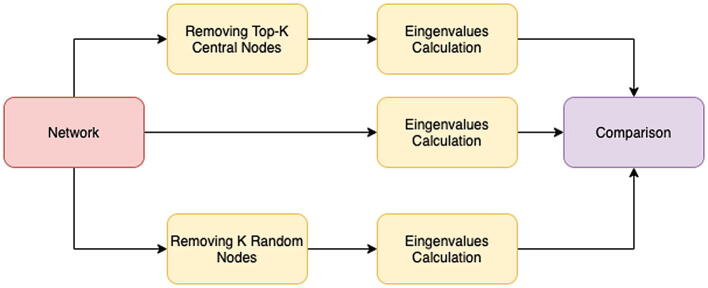
We initially built a test network. Next, we identified the k most central nodes. We built two networks: one in which we removed the top-k central nodes and a second one in which we removed k randomly selected node. We compared the spectra of the adjacency matrices of these two networks with respect to the spectrum of the input network. We noted that the largest eigenvalues of the adjacency matrix exhibited a greater decrease when considering the removal of central nodes.
3.2. Experiments on real networks
We considered the daily dynamic contact networks collected during the Infectious SocioPatterns event that took place at the Science Gallery in Dublin, Ireland, in 2009. The network consists of 77,602 contact events involving 242 individuals. We confirmed that eliminating the k most central nodes caused a superior reduction of than removing k random nodes. This held irrespective of the considered centrality metrics (Table 3).The significance of the difference has been verified using the Student’s t-test after that normality of the distribution was tested using the Shapiro–Wilk test.
Table 3.
Largest eigenvalues (expressed as mean and standard deviation), calculated for each graph model and centrality measure (CM), of the original graph (Original), the graph randomly deprived of k nodes (Random), and the graph deprived of the k most central nodes within the graph (Top-K).
| Graph | CM | Original | Top-K | Random | p-value |
|---|---|---|---|---|---|
| Infectious Graphs Dublin | DC | 23.0 0.21 | 14.35 0.0 | 23.36 0.7 | 0.01 |
| Infectious Graph Dublin | BC | 23.0 0.21 | 16.76 0.0 | 23.36 0.7 | 0.01 |
| Infectious Graph Dublin | EC | 23.0 0.21 | 16.88 0.0 | 23.36 0.7 | 0.01 |
3.3. Speeding-up herd immunity
Herd immunity is the Holy Grail of all the people who are fighting against COVID-19. Herd immunity is a type of indirect protection from an infectious disease that may occur when a significant fraction of the population has become immune to infection. Individuals become immune by recovering from an earlier infection or through vaccination.
For COVID-19, herd immunity was deeply investigated [42], [43], [44], focusing on effects that may hamper herd immunity, e.g., the number of infected people, time, and insurgence of variants that may disrupt the herd immunity equilibrium. Generally, all agreed that herd immunity can be reached when 60%-70% of people become immune.
When this study was conducted, the critical threshold was set to 70% (see, for instance https://www.mayoclinic.org/diseases-conditions/coronavirus/in-depth/herd-immunity-and-coronavirus/art-20486808). Unfortunately, recent studies have shown that reinfection is possible [45], after some times, so our analysis remains still valid considering the time in which people are immune.
Thus, supposing that people become immune only because of vaccination, we eliminated of nodes from our networks and calculated the largest eigenvalues, . We also calculated the number of central nodes that should be removed to obtain the same largest eigenvalues. We retain that the difference results in a lower time for reaching herd immunity, confirming the strength of the approach. As proof of concept, we also calculated the considering increasing values of equals 75%, 80%, and 85%. Results confirm that our approach requires the intervention of a lower number of nodes in all considered cases. Table 4 summarizes these results.
Table 4.
The number of people, , who should be vaccinated following the optimized strategy to reach herd immunity
| Graph Model | CM | ||
|---|---|---|---|
| Erdős Rényi | DC | 41.1% | 70% |
| Erdős Rényi | BC | 42.5% | 70% |
| Erdős Rényi | EC | 43.1% | 70% |
| Erdős Rényi | DC | 44.1% | 75% |
| Erdős Rényi | BC | 44.5% | 75% |
| Erdős Rényi | EC | 47.1% | 75% |
| Erdős Rényi | DC | 46.1% | 80% |
| Erdős Rényi | BC | 46.7% | 80% |
| Erdős Rényi | EC | 49.1% | 80% |
| Erdős Rényi | DC | 49.1% | 85% |
| Erdős Rényi | BC | 51.5% | 85% |
| Erdős Rényi | EC | 52.1% | 85% |
4. Discussion
The theoretical model we developed suggests that at least one rationale exists that can allow us to optimize the vaccination strategy against SARS-CoV-2. Before this study, several other independent studies have used mathematical modeling to explore new prioritization strategies. These models, as introduced before, vary widely in terms of considered populations, the model used, interventions, and assumptions [46], [47]. However, they all agreed that optimizing the vaccination strategy may positively impact the outcomes. We proposed designing an optimization strategy based on a topology model to accomplish this aim. It was based on the assumption that the contact network was trackable in time among people and then that the most “social” people were the first targets of a national vaccination campaign.
Our analysis was based on a simple graph-based model (SIR) built on the assumption that the perfect mixing strategy is too large since contacts among people generate a social network representable through models different from the perfect mixing. Contacts do not have geographical constraints and neglect any social aspect that may affect the network topology, in fact, locally. Moreover, we also assumed that vaccination could block both disease and transmission, even though some evidence seems to indicate that vaccines may have different efficacy in blocking transmission [48].
We are also aware that our model would benefit from the availability of contact tracing data. Nevertheless, such data poses many ethical issues beyond this paper’s scope, and many countries protect these data with strict privacy-preserving laws. Therefore, high-resolution mobility data are not currently available to the scientific community. From a computer science perspective, there is evidence of the introduction of technologies able to infer information about contacts that combine data gathered from phones in a privacy-preserving way [49], [50], [51]. If this was the case, note that our model would incredibly improve its performance by just enriching the edges of weights.
Our work showed how the implemented optimization strategy could provide good results for all centrality metrics and our network structure being studied. These results were significantly better than those obtained using the same methods and models but applying a random vaccination plan (an example in Fig. 3). Moreover, we showed how the largest eigenvalue could be effectively associated with topological metrics other than the node degree centrality. This leaves room for the possibility of improving vaccination performance further using slightly more complex, still intuitive, topological metrics, like Borgatti’s group centrality or the keyplayer matrics [52], [53], as implemented in Pyntacle [54].
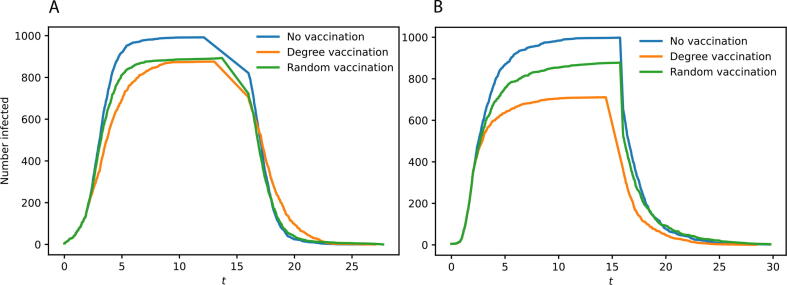
Fig. 3.
Impact of different vaccination strategies on the spreading of the infection using two different network models, the Erdős-Rényi graph (A) and the Duplication Divergence generative model (B). At the simulated time , both a random vaccination (green) and a degree-based vaccination (orange) strategies were applied, removing 100 random nodes and the 100 top-degree nodes, respectively. As a control, the spreading of the infection without any vaccination was simulated (in blue). We observed how removing the top-degree nodes from the graph results in a rapid decrease in infections compared to both control and random vaccination, especially in the Duplication Divergence Model network. At , we can observe the rapid decrease of the three lines, with a large part of the infected population starting to recover.
Herd immunity was considered achievable with at least 70% of the vaccinated people. In this simplified setting, we further showed how a vaccination strategy driven by a topological screening might help reach it in a shorter time.
5. Methods
We considered four different models of random networks: Erdős-Rényi, Duplication Divergence, Geometric-Random, and Barabási-Albert. We generated 100 randomized networks with the same degree distribution and shuffled edges for each network model. Main network statistics are reported in Table 1. For each node of the network, we calculated the degree, betweenness, closeness, and eigenvector centrality values, and, finally, the eigenvalues of the adjacency matrix. We removed the top 100 nodes having the highest value for each of these metrics and repeated the eigenvalues’ calculation. We also calculated the eigenvalues of the graph’s adjacency matrix obtained by removing 100 nodes selected at random to build a null model (Fig. 1).
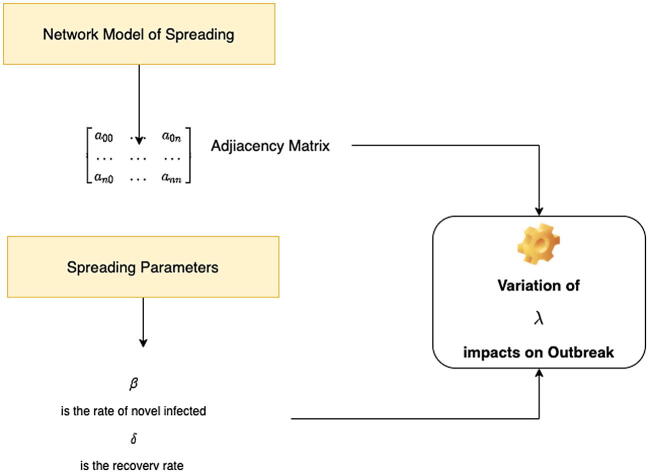
Fig. 1.
The rationale of the paper. The spreading of the SARS-CoV-2 may be modeled using a network whose nodes are people while edges are the contacts among them. The spreading may be summarized in an SIR model using two main parameters , and , representing the rate of novel infected people and the recovery rate. The network may be represented using the adjacency matrix of the resulting graph. Spreading may be contained when the following condition holds , where is the largest eigenvalue of the adjacency matrix. We hypothesize that an individual’s vaccination is equivalent to deleting a node (or equivalently to deleting the edge of the contacts).
5.1. Data
model. We generated a stochastic random graph, also known as binomial graph, using the fast generator provided by the Python NetworkX library [55]. We set the number of nodes equal to 1000 and a probability of having an edge connecting two nodes. Erdős-Rényi model. We generated an Erdős-Rényi graph having 1000 nodes and a probability of establishing an edge between two nodes [56].
Duplication Divergence model. We generated a random graph having the duplication divergence structure described by Ispolatov et al. in [57]. The library created a graph of 1000 nodes by duplicating the initial nodes and retaining edges incident to the original nodes with retention probability of .
Barabási-Albert model. We generated a Barabási-Albert graph, a random graph built according to the Barabási-Albert preferential attachment model [58]. A graph was grown by attaching new nodes, each with 50 edges, which were preferentially attached to existing high degree nodes.
Random Geometric model. We generated a random geometric graph, where 1000 nodes were placed uniformly at random in the unit cube. Two nodes were joined by an edge if their distance was at most radius [59].
5.2. Real networks
The dataset of real networks considered in this study was downloaded from the Network Repository [60]. It contained the daily dynamic contact networks collected during the Infectious SocioPatterns event that took held at the Science Gallery in Dublin, Ireland, in 2009 during the artscience exhibition INFECTIOUS: STAY AWAY. Each file in the downloadable package contains a tab-separated list representing the active contacts during 20-s intervals of one day of data collection.
5.3. Network centrality measures
As discussed before, a graph or network of n nodes can be represented as an adjacency matrix (), where each entry in the matrix indicates the existence of an edge between nodes i and j. In contrast, suggests the absence of an edge between the two nodes. A particular case of graphs, called edge-weighted graphs, is characterized by an adjacency matrix whose values are real-valued. The following discussion is focused on undirected, non-weighted graphs and may be easily extended to both ordered and edge-weighted graphs.
In the case of an unweighted network, a geodesic (or shortest path) from node to node is the path that involves the minimum number of edges. Consequently, we may define the distance between nodes and , where is the number of edges involved in a geodesic between and . Starting from the computation of distance, a set of centrality measures has been introduced. Such measures aim to evidence the relevance, or importance, of a node in a network by analyzing its local topology properties.
5.3.1. Degree centrality
The degree centrality of a node is the number of its adjacent nodes.
Sometimes, the degree centrality is normalized by the maximum degree possible of a node:
The degree centrality gives some information related to the immediate relevance of a node , but it misses some aspects of the entire structure of the network as well as the node’s position.
5.3.2. Closeness centralities
The closeness centrality considers the distance among the nodes. Formally, the closeness centrality of a node is the reciprocal of the average shortest path distance to overall reachable nodes, i.e.
where is the shortest distance among the considered pair.
5.3.3. Betweenness centrality
While closeness centrality indicates how close a node is to the others, betweenness centrality [61] evaluates how much a node stands between each other. For each node pair, and , in a network, it scores a node based on the number of shortest paths passing through it and all other geodesics connecting and not passing through it. Formally, the betweenness centrality of a node is calculated as:
where, is the total number of shortest paths from node to node and is the number of those paths that pass through i.
5.3.4. Eigenvector centrality
Eigenvector centrality [62] scores all nodes of a network on the assumption that connections to high-scoring nodes contribute more to the score of the node rather than connections to low-scoring nodes.
Given the adjacency matrix of a graph, the eigenvector centrality of a node v can be defined as:
Let be the eigenvector centrality of node , then is the solution of the equation , where is the greatest eigenvalue of to ensure that all values are positive [63] by the Perron-Frobenius theorem. The component of the related eigenvector will give the relative centrality score of the vertex v in the network.
5.4. Statistics
To assess the significance of the differences obtained using the two implemented vaccination policies, i.e., random, and based on the k top-central nodes, we resorted to the Student’s t-test for paired values. A p-value was considered significant if it was lower than 0.05.
5.5. Simulation framework implementation
As anticipated, in this work, we relied on the classical SIR model to spread disease. It is one of the simplest models for the epidemic spreading simulation, where each individual can be in a susceptible (S), infectious (I), or recovered (R) state. Once a susceptible individual comes into contact with an infected one, it gains a probability of becoming infectious. Each person can infect a susceptible neighbor and recover after a variable or fixed time span. Furthermore, recovered do not play any further role in the simulation and include both immune and deceased individuals.
To simulate the spreading of the SARS-CoV-2 virus, we implemented this model using the Python library Epidemics on Networks (EoN) [64]. We simulated each of the above-described networks ten times and then averaged the results. At the beginning of these runs, the entire population was in the S state, with an infected group composed of 5 individuals. Then, we set a constant transmission rate () with a fixed recovery time of 14 days to simulate the spreading.
To test our different vaccination approaches, we stopped the simulations at different simulated times and thus removed a constant fraction of S nodes based on topological considerations. As a control, we ran simulations with a random vaccination strategy, which drew 100 nodes randomly at a specific time t, and others without any vaccination strategy implemented. Finally, we restarted the simulations and evaluated the spreading of the infection by measuring the number of infected individuals over time.
6. Conclusion
Before COVID-19, pandemics were only an argument of study and organization, under the hypothesis that the probability of occurring was very low. Unfortunately, COVID-19 has shown that some worst scenarios may happen. Therefore, the scientific community should develop novel tools to support decision-makers in controlling and stop the virus from spreading. Current tools include sanitary measurements (e.g., vaccination, wearing masks), social rules (e.g., social distancing), and an extensive vaccination campaign.
The effectiveness of vaccination depends on the number and timeliness of administrations and thus demands strict prioritization criteria. Prioritization requires appropriate simulation models based on the joint use of network theory and mathematical modeling of spreading. We have shown that a network where nodes are people while the edges represent their social contacts may efficiently model the virus’s spreading. We presented some experimental evidence and a supporting tool that showed that spreading may be efficiently stopped by disconnecting such a network, i.e., by vaccinating the most central or relevant nodes, thereby eliminating the “bridge edges.”
This strategy has some limitations that mainly concern the realism of the resulting social model. The network described in this work hypothesizes that the contact number of an individual is constant over time. This may be roughly valid for some professional roles, such as the teachers, but not for others, such as the supermarkets’ staff. Moreover, more than one viral variant may coexist, each exhibiting a different infection rate and effect on people’s survival, thereby causing distorted spreading simulation results. Networks often present low-resolution contact data, which are difficult to obtain for evident and reasonable privacy-related considerations.
Data and Code Availability
Data and Codes are available at https://github.com/mazzalab/playgrounds
Author’s contributions
PHG. Conceived the experiments and drafted the manuscript; FP. Performed the simulations; TM analyzed the results and contributed to drafting the manuscript. All authors wrote, reviewed, and approved the manuscript.
CRediT authorship contribution statement
Francesco Petrizzelli: Conceptualization, Methodology, Software, Writing – original draft, Writing – review & editing. Pietro Hiram Guzzi: Conceptualization, Methodology, Software, Writing – original draft, Writing – review & editing. Tommaso Mazza: Conceptualization, Methodology, Software, Writing – original draft, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
Italian Ministry of Health (Ricerca Corrente 2022–2025); ‘5 1000’ voluntary contribution.
Footnotes
The paper was invited to be part of the 10th anniversary of the journal. It should be part of a celebration issue.
Contributor Information
Francesco Petrizzelli, Email: f.petrizzelli@css-mendel.it.
Pietro Hiram Guzzi, Email: hguzzi@unicz.it.
Tommaso Mazza, Email: t.mazza@css-mendel.it.
References
- 1.Gostin L.O. The coronavirus pandemic 1 year on–what went wrong? JAMA. 2021;325(12):1132–1133. doi: 10.1001/jama.2021.3207. [DOI] [PubMed] [Google Scholar]
- 2.Guo Y.-R., Cao Q.-D., Hong Z.-S., Tan Y.-Y., Chen S.-D., Jin H.-J., Tan K.-S., Wang D.-Y., Yan Y. The origin, transmission and clinical therapies on coronavirus disease 2019 (covid-19) outbreak–an update on the status. Military Med Res. 2020;7(1):1–10. [Google Scholar]
- 3.Le T.T., Andreadakis Z., Kumar A., Román R.G., Tollefsen S., Saville M., Mayhew S., et al. The covid-19 vaccine development landscape. Nat Rev Drug Discov. 2020;19(5):305–306. doi: 10.1038/d41573-020-00073-5. [DOI] [PubMed] [Google Scholar]
- 4.Kumar Das J., Tradigo G., Veltri P., Guzzi P.H., Roy S. Data science in unveiling covid-19 pathogenesis and diagnosis: evolutionary origin to drug repurposing. Briefings Bioinf. 2021;22(2):855–872. [Google Scholar]
- 5.Ortuso F., Mercatelli D., Guzzi P.H., Giorgi F.M. Structural genetics of circulating variants affecting the sars-cov-2 spike/human ace2 complex. J Biomol Struct Dyn. 2021:1–11. [Google Scholar]
- 6.Bubar K.M., Reinholt K., Kissler S.M., Lipsitch M., Cobey S., Grad Y.H., Larremore D.B. Model-informed covid-19 vaccine prioritization strategies by age and serostatus. Science. 2021;371(6532):916–921. doi: 10.1126/science.abe6959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Khamsi R. If a coronavirus vaccine arrives, can the world make enough. Nature. 2020;580(7805):578–580. doi: 10.1038/d41586-020-01063-8. [DOI] [PubMed] [Google Scholar]
- 8.Galicia J.C., Guzzi P.H., Giorgi F.M., Khan A.A. Predicting the response of the dental pulp to sars-cov2 infection: a transcriptome-wide effect cross-analysis. Genes Immun. 2020;21(5):360–363. doi: 10.1038/s41435-020-00112-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zucco C., Calabrese B., Agapito G., Guzzi P.H., Cannataro M. Sentiment analysis for mining texts and social networks data: Methods and tools. Wiley Interdiscip Rev: Data Min Knowl Discov. 2020;10(1) [Google Scholar]
- 10.Guzzi P.H., Mercatelli D., Ceraolo C., Giorgi F.M. Master regulator analysis of the sars-cov-2/human interactome. J Clin Med. 2020;9(4):982. [Google Scholar]
- 11.Cannistraci CV, Capua I. Age-adaptive and gender-balanced social interventions might be stepping stones to the next ‘new normal’ in covid-19 outbreak; 2020.
- 12.Goldstein J.R., Cassidy T., Wachter K.W. Vaccinating the oldest against covid-19 saves both the most lives and most years of life. Proc Natl Acad Sci. 2021;118(11) [Google Scholar]
- 13.Buckner J.H., Chowell G., Springborn M.R. Dynamic prioritization of covid-19 vaccines when social distancing is limited for essential workers. Proc Natl Acad Sci. 2021;118(16) [Google Scholar]
- 14.Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., Colaneri M. Modelling the covid-19 epidemic and implementation of population-wide interventions in italy. Nat Med. 2020;26(6):855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Maheshwari P., Albert R. Network model and analysis of the spread of covid-19 with social distancing. Appl Network Sci. 2020;5(1):1–13. [Google Scholar]
- 16.Jentsch P.C., Anand M., Bauch C.T. Prioritising covid-19 vaccination in changing social and epidemiological landscapes: a mathematical modelling study. Lancet Infect Dis. 2021 [Google Scholar]
- 17.Chakrabarti D., Wang Y., Wang C., Leskovec J., Faloutsos C. Epidemic thresholds in real networks. ACM Trans Inf Syst Secur. 2008;10(4):1–26. [Google Scholar]
- 18.Keeling M.J., Eames K.T. Networks and epidemic models. J R Soc Interface. 2005;2(4):295–307. doi: 10.1098/rsif.2005.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gu S., Jiang M., Guzzi P.H., Milenković T. Modeling multi-scale data via a network of networks. Bioinformatics. 2022;38(9):2544–2553. [Google Scholar]
- 20.Lawyer G. Understanding the influence of all nodes in a network. Scientific Rep. 2015;5(1):1–9. [Google Scholar]
- 21.Alguliyev R., Aliguliyev R., Yusifov F. Graph modelling for tracking the covid-19 pandemic spread. Infect Disease Model. 2021;6:112–122. doi: 10.1016/j.idm.2020.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.P. Bryant, A. Elofsson, Modelling the dispersion of sars-cov-2 on a dynamic network graph, medRxiv (2020).
- 23.Karaivanov A. A social network model of covid-19. Plos one. 2020;15(10) [Google Scholar]
- 24.Zaplotnik Ž., Gavrić A., Medic L. Simulation of the covid-19 epidemic on the social network of slovenia: Estimating the intrinsic forecast uncertainty. PloS one. 2020;15(8) [Google Scholar]
- 25.Cannataro M., Guzzi P.H., Sarica A. Data mining and life sciences applications on the grid, Wiley Interdisciplinary Reviews. Data Min Knowl Disc. 2013;3(3):216–238. [Google Scholar]
- 26.Das J.K., Roy S., Guzzi P.H. Analyzing host-viral interactome of sars-cov-2 for identifying vulnerable host proteins during covid-19 pathogenesis. Infect Genet Evol. 2021 [Google Scholar]
- 27.Patil R., Dave R., Patel H., Shah V.M., Chakrabarti D., Bhatia U. Assessing the interplay between travel patterns and sars-cov-2 outbreak in realistic urban setting. Appl Network Sci. 2021;6(1):1–19. [Google Scholar]
- 28.Ciaperoni M., Galimberti E., Bonchi F., Cattuto C., Gullo F., Barrat A. Relevance of temporal cores for epidemic spread in temporal networks. Scientific Rep. 2020;10(1):1–15. [Google Scholar]
- 29.Di Martino M.T., Scionti F., Sestito S., Nicoletti A., Arbitrio M., Guzzi P.H., Talarico V., Altomare F., Sanseviero M.T., Agapito G., et al. Genetic variants associated with gastrointestinal symptoms in fabry disease. Oncotarget. 2016;7(52):85895. doi: 10.18632/oncotarget.13135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Plazas A., Malvestio I., Starnini M., Díaz-Guilera A. Modeling partial lockdowns in multiplex networks using partition strategies. Appl Network Sci. 2021;6(1):1–15. [Google Scholar]
- 31.Boccaletti S., Bianconi G., Criado R., Del Genio C.I., Gómez-Gardenes J., Romance M., Sendina-Nadal I., Wang Z., Zanin M. The structure and dynamics of multilayer networks. Phys Rep. 2014;544(1):1–122. doi: 10.1016/j.physrep.2014.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Colizza V., Pastor-Satorras R., Vespignani A. Reaction–diffusion processes and metapopulation models in heterogeneous networks. Nat Phys. 2007;3(4):276–282. [Google Scholar]
- 33.Zhan X.-X., Li Z., Masuda N., Holme P., Wang H. Susceptible-infected-spreading-based network embedding in static and temporal networks. EPJ Data Sci. 2020;9(1):30. [Google Scholar]
- 34.Eskandarzade N., Ghorbani A., Samarfard S., Diaz J., Guzzi P.H., Fariborzi N., Tahmasebi A., Izadpanah K. Network for network concept offers new insights into host-sars-cov-2 protein interactions and potential novel targets for developing antiviral drugs. Comput Biol Med. 2022;105575 [Google Scholar]
- 35.Humphries R., Mulchrone K., Tratalos J., More S.J., Hövel P. A systematic framework of modelling epidemics on temporal networks. Appl Network Sci. 2021;6(1):1–19. [Google Scholar]
- 36.Paluch R., Lu X., Suchecki K., Szymański B.K., Hołyst J.A. Fast and accurate detection of spread source in large complex networks. Scientific Rep. 2018;8(1):1–10. [Google Scholar]
- 37.Ash C. Superspreaders are local and disproportionate. Science. 2017;355(6329):1036. [Google Scholar]
- 38.Stegehuis C., Van Der Hofstad R., Van Leeuwaarden J.S. Epidemic spreading on complex networks with community structures. Scientific Rep. 2016;6(1):1–7. [Google Scholar]
- 39.Menniti S., Castagna E., Mazza T. Estimating the global density of graphs by a sparseness index. Appl Math Comput. 2013;224:346–357. [Google Scholar]
- 40.Mazza T., Romanel A., Jordán F. Estimating the divisibility of complex biological networks by sparseness indices. Briefings Bioinf. 2010;11(3):364–374. [Google Scholar]
- 41.Wang Y, Chakrabarti D, Wang C, Faloutsos C. Epidemic spreading in real networks: An eigenvalue viewpoint. In 22nd International Symposium on Reliable Distributed Systems, 2003. Proceedings. IEEE; 2003. pp. 25–34.
- 42.Aschwanden C. Five reasons why covid herd immunity is probably impossible. Nature. 2021;591(7851):520–522. doi: 10.1038/d41586-021-00728-2. [DOI] [PubMed] [Google Scholar]
- 43.Fontanet A., Cauchemez S. Covid-19 herd immunity: where are we? Nat Rev Immunol. 2020;20(10):583–584. doi: 10.1038/s41577-020-00451-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Randolph H.E., Barreiro L.B. Herd immunity: understanding covid-19. Immunity. 2020;52(5):737–741. doi: 10.1016/j.immuni.2020.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kadkhoda K. Herd immunity to covid-19: alluring and elusive; 2021.
- 46.Medo M. Contact network models matching the dynamics of the covid-19 spreading. J Phys A: Math Theor. 2020;54(3) [Google Scholar]
- 47.Paré P.E., Beck C.L., Başar T. Modeling, estimation, and analysis of epidemics over networks: An overview. Annu Rev Control. 2020;50:345–360. [Google Scholar]
- 48.Mallapaty S. Can covid vaccines stop transmission? Scientists race to find answers. Nature. 2021 [Google Scholar]
- 49.Martín-Calvo D., Aleta A., Pentland A., Moreno Y., Moro E. Effectiveness of social distancing strategies for protecting a community from a pandemic with a data driven contact network based on census and real-world mobility data. Complex Dig. 2020 [Google Scholar]
- 50.Barrat A., Cattuto C., Kivelä M., Lehmann S., Saramäki J. Effect of manual and digital contact tracing on covid-19 outbreaks: a study on empirical contact data. J R Soc Interface. 2021;18(178):20201000. doi: 10.1098/rsif.2020.1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Cencetti G., Santin G., Longa A., Pigani E., Barrat A., Cattuto C., Lehmann S., Salathe M., Lepri B. Digital proximity tracing on empirical contact networks for pandemic control. Nat Commun. 2021;12(1):1–12. doi: 10.1038/s41467-020-20314-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Everett M., Borgatti S. The centrality of groups and classes. J Math Sociol. 1999;23(3):181–201. [Google Scholar]
- 53.Borgatti S. Identifying sets of key players in a social network. Comput Math Org Theor. 2006;12:21–34. [Google Scholar]
- 54.Parca L., Truglio M., Biagini T., Castellana S., Petrizzelli F., Capocefalo D., Jordán F., Carella M., Mazza T. Pyntacle: a parallel computing-enabled framework for large-scale network biology analysis. GigaScience. 2020;9(10):giaa115. doi: 10.1093/gigascience/giaa115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kumar R., Raghavan P., Rajagopalan S., Sivakumar D., Tomkins A., Upfal E. Proceedings 41st Annual Symposium on Foundations of Computer Science, IEEE. 2000. Stochastic models for the web graph; pp. 57–65. [Google Scholar]
- 56.Batagelj V., Brandes U. Efficient generation of large random networks. Phys Rev E. 2005;71(3) [Google Scholar]
- 57.Ispolatov I., Krapivsky P.L., Yuryev A. Duplication-divergence model of protein interaction network. Phys Rev E. 2005;71(6) [Google Scholar]
- 58.Barabási A.-L., Albert R. Emergence of scaling in random networks. Science. 1999;286(5439):509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 59.Penrose M., et al. vol. 5. Oxford University Press; 2003. (Random geometric graphs). [Google Scholar]
- 60.Rossi RA, Ahmed NK. The network data repository with interactive graph analytics and visualization. In AAAI; 2015. URL: http://networkrepository.com.
- 61.Brandes U., Pich C. Centrality estimation in large networks. Int J Bifurcation Chaos. 2007;17(07):2303–2318. [Google Scholar]
- 62.Bonacich P. Some unique properties of eigenvector centrality. Soc Networks. 2007;29(4):555–564. [Google Scholar]
- 63.Okamoto K., Chen W., Li X.-Y. International Workshop on Frontiers in Algorithmics. Springer; 2008. Ranking of closeness centrality for large-scale social networks; pp. 186–195. [Google Scholar]
- 64.Miller J.C., Ting T. Eon (epidemics on networks): a fast, flexible python package for simulation, analytic approximation, and analysis of epidemics on networks. J Open Source Software. 2019;4(44):1731. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data and Codes are available at https://github.com/mazzalab/playgrounds