Abstract
Missing data are ubiquitous in aging studies. Combining the National Health and Nutrition Examination Survey (NHANES) 2003/2004 and 2005/2006 cross-sectional aging studies (N = 9307), we investigated the effects of both real and simulated missing data on the Frailty Index (FI) and survival analysis, along with several mitigation strategies. We observed distinct block patterns of missing variables in the dataset. These blocks showed significant hazard rate (HR) differences when they were missing versus present, indicating that missingness cannot be simply ignored. Simulations of this patterned missingness produced a bias of 0.0112 ± 0.0008 to the mean FI when missing values were ignored, representing a change in hazard of 1.09 ± 0.01. A similar bias of 0.0106 ± 0.0001 was estimated in the real missingness. Imputation was able to correct the bias using the multivariate imputation by chained equations (MICE) method via the classification and regression tree (CART) prediction model together with rule-based imputation. Using auxiliary variables (CART+Aux) improved the performance of CART. Well-performing imputation models, especially CART+Aux, were able to increase the FI predictive power and the reliability of the HR estimates. In contrast, the default MICE models, predictive mean matching/logistic regression (PMM/logreg), caused even stronger biases to the FI. Our results demonstrate that calibration of the FI as a mortality predictor depends on how missing data are handled. Ignoring missing values when calculating the FI may be an acceptable strategy for clinical settings where the FI is used as a rough predictor of adverse outcomes. Where the FI is to be compared across studies or populations, judicious imputation — cognizant of the risks carried by poor imputation — should be used to ensure reliability and precision of statistical estimates and conclusions.
Electronic supplementary material
The online version of this article (10.1007/s11357-021-00489-w) contains supplementary material, which is available to authorized users.
Keywords: Imputation, Missing data, MICE, Frailty Index, Survival, CART
Introduction
Imputation uses statistical inference to estimate missing entries in recorded data. Imputation fills gaps that may interfere with or otherwise complicate data analysis. Often, analysis software silently excludes missing data, at times using only the complete cases. This approach can greatly reduce the amount of available data, and can bias statistical conclusions [1, 2]. Although imputation is not typically discussed in the Frailty Index (FI) literature, the most common approach of ignoring missing values is equivalent to individual (row)–mean imputation1.
For individuals admitted to hospital with an acute stroke, Deng et al. showed that complete-case analysis determined that none of the four individual history variables — including history of stroke — were significant determiners of the time-to-diagnosis proxy, whereas each of five imputation strategies showed that all variables were both significant and major predictors [3]. However, the choice of imputation strategy can be important. As discussed by Sterne et al., multiply imputed data in a cardiovascular risk study found that cholesterol was unrelated to risk when using initially imputed data, but was a risk factor either when using the available data or when using an improved imputation strategy [2].
Imputation is a valid statistical technique [4]: ideal (proper) imputation would introduce no bias and would not under-estimate uncertainties [5]. In contrast, poorly implemented imputation can worsen results [3, 6, 7]. Judiciously implemented imputation strategies, while typically not ideal, can often make significant gains compared to excluding or ignoring.
There are three canonical types of missing data (‘Missingness mechanisms’): missing completely at random (MCAR; independently missing), missing at random (MAR; due to covariates that are not missing), and missing not at random (MNAR; due to covariates that are missing, including the missing value itself) [1]. Higher-order missingness patterns may also be present [8].
Missing data in gerontology are distinctive for the high prevalence of MAR and MNAR missingness. Cognitive and functional deficits that can prevent data collection are common amongst older adults [9], even those dwelling in communities. For example, people living with frailty may be more likely to drop out of longitudinal studies, causing MAR and MNAR missingness in later waves to be more common amongst the frail [10]. Study designs may also neglect to ask young people about potential deficits that are only prevalent in older adults, a form of MAR missingness. Because of the prevalence of MAR and MNAR missingness, it is important to investigate potential biases when imputing gerontological data.
The FI operationalizes frailty [11] and is associated with adverse outcomes [12]. The FI is a number between 0 and 1 that is the average number of deficit health variables an individual has [12]. When calculating the FI, missing data treatment is typically not disclosed [13], and explicit imputation is seldom performed. Instead, the FI for each individual is typically computed by simply ignoring/dropping missing values, effectively replacing them with the average of the available variables. This is an implicit imputation strategy. A set of heuristics have built up around this ignoring strategy, such as inclusion criteria based on missingness: variables with more than 5% of individuals missing values may be excluded [14], as well as individuals with more than 20% of measurements missing [15, 16].
Per-individual and per-variable missingness can vary substantially between studies, as can the underlying missingness mechanism. As a result, heuristics that improve predictive performance of the FI in one study may affect another study differently. This heterogeneity is an impediment to translating quantitative heuristics between studies, and limits the development of the FI as a precision tool [17]. An attractive potential alternative is to identify good imputation methods that work for a variety of types and magnitudes of missingness. The Rotterdam study shows that explicit imputation models can improve FI predictive power of mortality [13]. We ask, what is the best available imputation model to use when calculating the FI? More generally, how does the choice of missing data strategy affect the FI?
Multivariate imputation by chained equations (MICE) is a popular multiple imputation (MI) method freely available in R [18]. The underlying engine of MICE is fully conditional specification (FCS), i.e. sequential regression or chained equations [19], which iteratively updates each missing variable or model parameter using the conditional distribution given all other variables and parameter estimates (i.e. Gibbs sampling) [4]. Multiple imputation generates a set of fully sized, completed datasets which allows estimation of both quantitative results of interest and the uncertainty in those results caused by imputed values.
MICE has been shown to outperform ignoring missing data [4], classical approaches including kNN (k-nearest neighbours) [20], and even deep learning methods [21, 22]. MICE is popular due to its flexibility, and availability in most statistical software (e.g. python [20, 23], R [18] and stata [7]).
Conversely, MICE can produce strong biases, putatively when too many variables/predictors are included [3, 24]. Since the underlying FCS approach is not theoretically grounded [19], all MICE models must be validated empirically. This may explain why the default MICE option in R for treating continuous-valued variables is predictive mean matching (PMM), an ad hoc model from the 1980s that has significant limitations [5, 25], but has been widely validated [5] (e.g. [20]).
Here we compare three MICE algorithms for gerontological data: Default (PMM for continuous variables and logistic regression for ordinal variables), CART (classification and regression tree) and RF (random forest) [18]. We also include two single-imputation strategies in our comparison: a classical de facto strategy, kNN [26], and a modern machine learning approach, missForest [27]. kNN is a popular, conventional approach that has been shown to outperform individual (row)-mean imputation for gene expression data [28]. In contrast, RF approaches are contemporary machine learning models that have been shown to modestly outperform kNN in numerous datasets [27, 29]. missForest is a variant of FCS that includes an automatic stopping strategy to prevent over-fitting and uses an RF prediction model.
The inclusion of a priori expert knowledge may enhance imputation, but presents a barrier-to-entry for non-experts. In the present study we tested inclusion of rule-based imputation (RI) for cases of study design–related missingness. Young, ostensibly healthy individuals were not asked questions specific to older and/or frailer individuals. In RI we assumed these missing values were optimally healthy. Only a subset of the missing values were missing due to study design, and therefore RI was always paired with another missing data handling strategy.
We do not consider other imputation models, including joint modelling, which conventionally requires the underlying distribution [18]. Other recent developments in imputation include tensor factorization [30], and deep learning [21, 22, 31–33].
We analysed the effects of missing data and imputation for the National Health and Nutrition Examination Survey (NHANES) cross-sectional data [34]. Our objective was to investigate the effects of missing data and imputation on estimating the FI values and subsequent survival prediction. First, we identified and grouped individuals by their patterns of missingness. We then used these observed patterns to artificially simulate missingness in order to test the performance of imputation strategies when the true values were known. We compared the FI-typical ignoring strategy to several versions of MICE and determined which strategy best reproduced the true FI and which gave the best mortality prediction. Using what we learned, we then applied the most promising imputation strategies to the naturally missing data.
Missingness mechanisms
There are three canonical missingness mechanisms: missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR) [1]. These can be defined in terms of [5],
| 1 |
where Yall is the matrix of all potentially measured values of interest, including all predictors and outcomes. Yobs are observed values and Ymis are missing. The missingness indicator is a matrix, M, with the same dimensions as Yall, where Mij = 1 indicates that variable j is missing for individual i.
By definition, values are MCAR if:
| 2 |
where Pr indicates the matrix of probabilities. For example, if you are interrupted while entering data and skip an arbitrary entry from an arbitrary individual, then that entry is MCAR. We expect that ignoring MCAR data will produce unbiased results [35].
MAR is defined by values for which:
| 3 |
For example, in the personal fitness questionnaire (PFQ) of NHANES 03/04 and 05/06 qualifying participants were asked PFQ061A: ‘how much difficulty {do you/does SP} have managing {your/his/her} money?’ These data are only present for participants who were aged 60 or older, or answered ‘yes’ to PFQ049, PFQ057 or PFQ059, therefore PFQ is MAR, so long as we know these (auxiliary) variables. When the data are MAR we may produce biases if we ignore the missingness, however, with a sufficiently powerful imputation model we can use Yobs and covariates to estimate the missing values.
Finally, MNAR is defined by:
| 4 |
For example, suppose an individual is left to fill out a survey on their own, they read VIQ071: ‘{have you/Has SP} ever had a cataract operation?’, but because they have never had problems with cataracts they skip the question entirely. If the data are MNAR then a proper treatment will require knowledge of the missingness mechanism since the dependence on Ymis could cause severe biases. Nevertheless, due to correlations in the data we may be able to achieve satisfactory results using an imputation model that assumes MAR, such as the imputation models we tested in this study.
Missingness patterns in the missingness matrix, M, may also cause problems. Missingness patterns are a higher-order statistic that represent whether variables tend to go missing together. Such patterns can apply to each of MCAR, MAR, and MNAR. For example, because of study design many of the variables in PFQ are often mutually missing. Similarly, individual limitations may prevent data collection of multiple related variables. In this paper we include a prefix ‘p’ to indicate the use of patterns (e.g. pMCAR) or ‘c’ to indicated conventional or cellwise missingness (e.g. cMCAR).
NHANES data
We used the combined 2003/04 and 2005/06 NHANES (National Health and Nutrition Examination Survey) cross-sectional study with public-use, linked mortality files from the National Death Index [16], with a total of N = 9307 individuals. Inclusion criteria were: over age 20 (N = 9816), available survival data (N = 9310), and survival at least one year post study date (N = 9307). We followed two analysis pipelines: first we investigated real missingness by analysing the entire, ‘Full’, dataset (N = 9307), and then we isolated the N = 1923 complete-case, ‘Complete’, dataset (individuals who had all 68 Frailty Index variables reported). The Complete dataset was used to test imputation strategies by simulated missingness together with ground truth (GT) values.
We calculated the combined lab plus self-reported (SR) FI using the methodology of Blodgett et al. [16]. We included 32 lab variables and 36 SR health variables to calculate the FIs (Supplemental Tables SXXIII and SXXIV, respectively). SR health variables were linearly scaled to the range [0,1], while the lab variables were defined as 0 if they were within sex-specific healthy ranges or 1 if they were outside of those ranges (Supplemental Table SXXIII). Lab variables were converted to binary scale after imputation to maximize the information available during imputation. SR variables were converted before imputation for coding convenience, but maintained their ordinal type. We used 100 additional variables to test the utility of auxiliary variables for improving imputation performance (detailed in Supplemental).
Demographic information is summarized in Table 1. Individuals in the complete-case dataset were older (p < 2.2 ⋅ 10− 16), frailer (p < 2.2 ⋅ 10− 16), died more often (p < 2.2 ⋅ 10− 16), and had a worse survival curve (p = 7.2 ⋅ 10− 4), relative to the Full dataset.
Table 1.
NHANES dataset summary
| Full | Complete1 | |
|---|---|---|
| N | 9307 | 1923 |
| Males | 4465 (48.0%) | 944 (49.1%) |
| Females | 4842 (52.0%) | 979 (50.9%) |
| Age [median (IQR)] | 48 (33–66) | 68 (62–76)∗∗∗ |
| Age 60+ | 3232 (34.7%) | 1635 (85.0%)∗∗∗ |
| Age under 60 | 6075 (65.3%) | 288 (15.0%)∗∗∗ |
| Frailty Index2 [mean (sd)] | 0.144 (0.078) | 0.176 (0.073)∗∗∗ |
| Deaths | 1016 (10.9%) | 379 (19.7%)∗∗∗ |
| Death age [median (IQR)]3 | 81.5 (80.7–82.7) | 81.2 (78.3–83.9)∗∗∗ |
| Missingness4 | 14.5% | 0%∗∗∗ |
| Aux5 missingness4 | 12.8% | 5.7%∗∗∗ |
1 Comparisons are between individuals in the Complete subset versus the remaining individuals
2 Using Ignore
3 Log-rank test
4 Cellwise missingness rate
5 Aux, auxiliary variables
Statistical significance is indicated with * p < 0.05, ** p < 0.01, or *** p < 0.001.
Methods
Real missingness
We directly analysed missingness of the 68 FI variables in the Full dataset, which we refer to as ‘real’ missingness. We used the md.pattern function in R [18] to estimate missingness patterns in the Full dataset.
Simulated missingness
The process of generating synthetic data with missing values is called ‘amputation’ [8]. Amputation should respect the missingness mechanism (MCAR, MAR, or MNAR) and any salient patterns. MICE incorporates a standardized amputation approach using missingness patterns [8], which we modified to handle larger quantities of data (see Supplemental). These patterns ensure that amputated data preserve missingness idiosyncrasies. For example, a pair of variables observed with 10% mutual-missingness are amputated together 10% of the time.
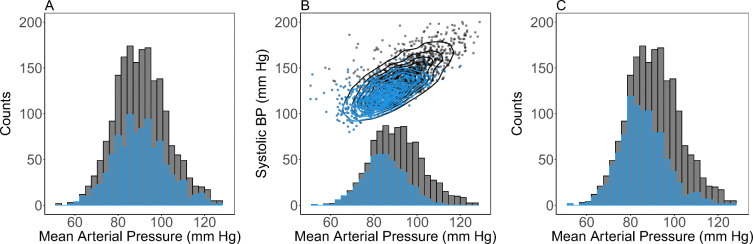
To simulate missingness, we took the Complete dataset and amputated values using the missingness patterns of the Full dataset. This generated a new dataset of the same size but with empty cells representing missing data. In contrast to real missingness, we retained the Complete dataset, providing us with a GT against which we compared our imputed values. Figure 1 illustrates missingness mechanisms and simulated missingness of mean arterial pressure when no higher-order missingness patterns are present.
Fig. 1.
Illustration of missingness mechanisms using complete-case NHANES blood pressure (BP) data. Black bars and points reflect the true distribution, blue bars and points are simulated distributions of observed values after applying different missingness mechanisms. (A) In missing completely at random (MCAR) the shape of the distribution is preserved but the total amount of data is reduced. (B) In missing at random (MAR) data are preferentially excluded according to other related variables. In this case, individuals with large values of systolic BP were preferentially set to missing (points), causing a small bias in the mean arterial pressure distribution (bars). (C) In missing not at random (MNAR) the value of missing variables affects the probability they are missing. In this example, we preferentially excluded high mean arterial pressure values
Amputation was performed using four missingness mechanisms: cellwise MCAR and MNAR (cMCAR and cMNAR, respectively), and patterned MCAR and MAR (pMCAR and pMAR, respectively). The patterns restricted our maximum simulated missingness to the same level as the real missingness; we chose rates of 5%, 10% and 15% (max). We used the same rates for cellwise missingness, but we were also able to simulate 25%, 50% and 75% missingness for both cMNAR and cMCAR. Selection data were normalized to a [0,1] deficit scale prior to amputation to prevent problems with the two-sided deficit rule for the lab variables (see Supplemental Table SXXIII). cMCAR randomly, and arbitrarily, selected data points to drop without any patterning. pMCAR and pMAR used the NHANES patterns determined from the Full dataset [8]. We confirmed the patterns were correctly reproduced in the simulated missingness — compare Supplemental Figures S1 versus S2. We used default settings for both pMCAR and pMAR, with a probabilistic linear decile exclusion rule [8]. cMNAR is a novel cellwise approach wherein we applied cuts directly to the pooled quantiles using the linear decile exclusion rule. Given that the amputation process is stochastic, we generated 10 datasets for each combination of missingness mechanism, patterns, and rate.
Imputation modelling
We performed imputation using the MICE package (version 3.10.0) [18] in R version 4.0.0 [36]. MICE uses FCS to iteratively impute missing data using a prediction model. We compared a representative sample of prediction models within MICE: logistic regression (logreg), predictive mean matching (PMM), classification and regression trees (CART), and random forest (RF). Logistic regression is the default for binary, ordinal and categorical data, whereas PMM is the default for continuous variables. CART is the special case of a RF with 1 tree — both accept mixed data types. We imputed the default number of times, m = 5, and combined results using Rubin’s rules [7], except when estimating predictive power (we used the average) and visualizing the FI distributions (we used all values).
Rubin’s rules describe how to properly aggregate multiple imputations to estimate both the expected effect (the average), and the uncertainty due to missing values, using an analysis of variance (ANOVA)–style decomposition of the between- and within-imputation variance. The recommended number of imputations is approximately equal to the percentage of missing data [7], but a smaller number has conventionally been regarded as sufficient [5]. As a sanity check, we have also included a CART m = 15 imputation for each of our ≤ 15% simulated missingness tests.
We also tested two single imputation (non-MICE) algorithms: kNN [26] and RF [27]. Our imputation models are summarized in Table 2.
Table 2.
Imputation model summary
| Name | Model(s) | MI1? | Note |
|---|---|---|---|
| RI2 | – | No | Imputed gated as 03 |
| Ignore | Row-mean4 | No | Typical approach |
| Ignore (weighted)5 | Row-mean4 | No | Linear weights |
| Ignore20 | Row-mean4 | No | 20% missingness cut |
| RF | RF | No | 100 trees |
| kNN | kNN | No | – |
| MICE Default | PMM/logreg6 | Yes | – |
| MICE CART | CART | Yes | 1 tree |
| MICE CART+Aux | CART | Yes | 100 auxiliary variables |
| MICE RF | RF | Yes | 10 trees |
1 MI, multiple imputations
2 RI, rule-based imputation
3 Gated variables were PFQ, RXD and VIQ blocks (Supplemental Table SV)
4 Mean value of the available deficit data for each individual
5 Results in Supplemental
6 PMM for continuous (lab) variables, logreg for ordinal/binary (self-reported) variables
A priori we know that the PFQ061 variables we used — the PFQ variable block (personal fitness, see Supplemental Table SV) — and the RXD variable block (prescription drugs) are all gated variables, meaning data are missing purposely as part of the study design. Individuals under age 60 who answered ‘no’ to PFQ049, PFQ057 and PFQ059 were not asked the PFQ block questions. The RXD block was not asked for individuals who answered ‘no’ to RXDUSE. In addition, the VIQ variable block was not asked for individuals under age 50 [34]. We considered RI (rule-based imputation) wherein all of the aforementioned types of missing values were assumed to be optimally healthy (0 deficit). We applied RI to the real missingness, supplemented by a variable secondary imputation strategy for the residual missingness. RI was not applied to the simulated missingness because it was based on the Complete dataset which has no missing values and therefore the conditions for RI are not satisfied by any individuals.
We also considered inclusion of 100 auxiliary variables to enhance results. Preliminary results indicated that CART was the best-performing, hence we tested auxiliary variables with CART+Aux.
The FI is typically calculated using available-case analysis, which uses all available data from included individuals [1]. We considered three versions of available-case analysis. In the first, typical, approach missing values were simply ignored when calculating the FI. Second, we considered Ignore20, which excluded individuals with over 20% missingness from analysis and ignored missing values for included individuals [16]. Finally, in the Supplemental, we considered weighting individuals in any analysis by the fraction of reported variables each individual has; statistics were only calculated when weighted models were readily available — excluding the area under the receiver operator characteristic curve (AUC) and the hazard rate/ratio (HR).
Statistical analysis
Our focus was on how imputation strategies affected the FI — including the mean, distribution and downstream measures calculated from it, such as the HR and AUC. Simulated missingness was compared to the GT (ground truth). For real missingness the GT was unknown and we had to infer imputation quality by comparing results to the simulated missingness and assessing survival predictive power.
Survival prediction was based on 4-year-survival using the AUC [37]. Four-year-survival was selected because almost all individuals (excluding 2 in the Full dataset: 1 in the Complete dataset) had survival followup for at least 4 years. Preliminary results showed identical trends using 1-, 2- or 4-year survival; final results were confirmed by comparing AUC to the C-index (Supplemental).
We calculated the age/sex-adjusted Cox proportional hazards model as was previously done after imputing the Rotterdam study [13]. Analysis of deviance was used to assess predictive power [38]. The FI was scaled by 100 such that the HR was the increase in hazard per 0.01 increase in FI, consistent with most FI survival studies [39]. Differences in survival were tested for using the log-rank test.
To summarize the measures of survival predictive power, we used the AUC, the HR, analysis of deviance and the C-index (Supplemental). The AUC [40] and the C-index [41, 42] are close-relatives, both are descendants of the Wilcoxon non-parametric statistic. The AUC estimates the probability that a metric will correctly rank the members of the affected group ahead of the members of the unaffected group [40] e.g. the probability that individuals who will die during the next 4 years currently have higher FIs than non-terminal individuals. The C-index estimates the probability that, for every possible pair of individuals, a metric will correctly rank which individual will be affected first, e.g. die first [42]. Analysis of deviance is a generalization of the residual sum of squares [43] and attributes dispersion (deviance) explained by each variable. The HR is a regression parameter [44] and depends on the quality/validity of the fit and the scale of the data; it is an estimate of the relative change in hazard due to a per unit increment in the predictor variable.
Multiply imputed FIs were aggregated by the mean for each individual when analysing survival predictive power to allow fair comparison to single imputation strategies, since the multiple imputations artificially increase variability in the FI, and therefore would likely reduce predictive power
FI distributions were compared using the Kolmogorov-Smirnov (KS) test. Binary group comparisons of continuous variables were made using Mann-Whitney test, avoiding the complication of pre-testing [45]. Categorical vs categorical comparisons used Pearson’s χ2 test. Survival curves were estimated using the Kaplan-Meier estimator with respect to age. AUCs were compared using the Delong test [46]. Note that the Delong test includes an additional 1/N term in the test statistic which allows significant p-values even when the standard errors overlap [46]. Generic tests for significance used the z-test. Statistical significance is indicated with *p < 0.05, **p < 0.01, or ***p < 0.001. All confidence intervals are 95%. Error bars are standard errors, error is reported in parenthesis from last digit, e.g. 0.0034(12) = 0.0034 ± 0.0012.
Results
Missingness patterns
As illustrated by Fig. 2, we observed substantial missingness. In the Full dataset we observed an overall missingness of 14.5% (91585 entries), the mean missingness per individual was 9.8 entries, with a median of 12 entries (17.6%) and an inter-quartile range (IQR) of 1 to 15 entries (1.5–22.1%). Individuals aged 60+ had significantly less missing data than individuals under 60 (p < 2.2 ⋅ 10− 16) and died more often (p < 2.2 ⋅ 10− 16). For individuals at least 60 years old, the mean missingness was 2.5 entries, with a median of 0 entries and an IQR of 0 to 1 entries (0–1.5%), with a death rate during followup of 26.7% versus 2.5% for people under 60. Considering the Full population, while 3606 (38.7%) of individuals were missing more than 20% of their entries only 203/3606 (5.6%) were at least 60 years old. This means that 3403/6075 (56.0%) of individuals under 60 did not pass the Ignore20 cut versus 203/3232 (6.3%) of individuals aged 60+, raising the prospect of age-related biases with Ignore20.
Fig. 2.
Mutual missingness histogram. Missingness fraction of NHANES variables for individuals: (A) under age 60 and (B) age 60+. These 2D histograms give the mutual missingness fraction for (row, column) pairs of variables with the diagonal corresponding to each variable’s overall missingness. We see a distinct block structure indicating groups of variables that are (almost) always missing together, for example the BPX (blood pressure) 5-variable group appears as a 5 × 5 block. The variables in each block are provided in Supplemental Table SV. Observe that in (B) the LB and BPX blocks dominate whereas the PFQ block is less often missing and contains unpatterned missingness (strong diagonal terms), in contrast to (A). Note the scale difference; older individuals had much less missing data. See Supplemental Figure S1 for the pooled young and old, and Figure S4 for the per-variable labeled result
Missingness was not independent across variables, with distinct blocks of missingness forming in the mutually missing histogram (Fig. 2, particularly for younger individuals (under 60). Following the NHANES naming convention, these blocks were the following: personal fitness questionnaire (PFQ), number of prescription drugs taken (RXD), vision questionnaire (VIQ), blood pressure measurement (BPX), lab measurements (LB) and miscellaneous (Misc). As shown in Fig. 2 the most commonly missing variables overall were the PFQ block of data, with an average cellwise missingness of 53.6% (80.7% for individuals under 60); at least one was missing 61.3% of the time (83.5% for individuals under 60). (See Supplemental Table SVI for block variable demographics.)
As shown in Fig. 2B, the missingness of older individuals (age 60+) was markedly different. We observed lower overall missingness, higher variance of cellwise missingness within blocks, and no visible block missingness for PFQ or VIQ. These are study-design effects: PFQ was not routinely collected for individuals under age 60, while VIQ was not routinely collected for individuals under age 50 [34].
Missingness-survival effects
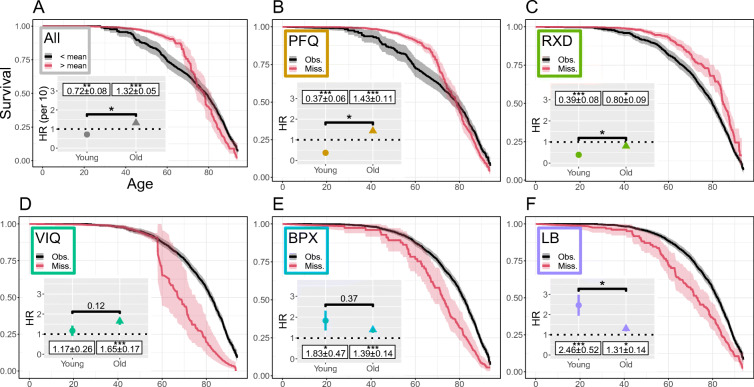
Kaplan-Meier survival curves showed that the variable blocks had heterogeneous effects on survival (Fig. 3). With some blocks of variables showing significantly better survival for unmeasured individuals while others showed significantly worse survival. The red curves represent individuals with any entry missing in that block whereas the black curves had all variables observed. The overall missingness (Fig. 3A) instead compared the individuals with above average missingness (red) vs below average missingness (black).
Fig. 3.
Survival and missingness. Survival curves conditioned on missingness show that the block patterns of missingness are strongly related to survival. (A) all variables, (B) personal fitness (PFQ), (C) prescription drugs (RXD), (D) vision (VIQ), (E) blood pressure (BPX), and (F) lab variables (LB). In (A) the black line indicates the Kaplain-Meier survival curve for the subpopulation of individuals missing less than the mean (9.8 variables), the red line indicates individuals missing more than the mean. In (B)–(F), black lines indicate subpopulations without any of the variables in the block missing, red lines have at least one variable in the block missing. Shaded regions indicate 95% confidence intervals. Insets: hazard ratios (HRs) for Cox survival model for individuals stratified by young (< 60) or old (≥ 60), conditioned on age and sex. In (A) the Cox model is HR per 10. In (B)–(F) each block Cox model was further conditioned on all other blocks (PFQ, RXD, VIQ, BPX and LB). Note the similarity of (B) PFQ and (A) all, reflecting that PFQ is a large block of variables and is the most commonly missing block. See Supplemental Figure S5 for age cut moved to 50, and Figure S6 for additional variables
Missing LB block meant poorer survival, as did VIQ — for older individuals, and BPX. Conversely, RXD indicated superior survival. The missing PFQ block had crossing survival curves, and was an excellent proxy for the full missingness, showing nearly identical trends for the survival curves. The overall missingness had a complicated effect on survival where missingness was advantageous at young ages but crossed to disadvantageous at older ages.
We also investigated hazard using a blockwise-missingness Cox model with important covariates (sex and age) (see the insets of Fig. 3). The HRs with respect to missingness qualitatively agree with the survival curves: PFQ missingness indicated good survival for the young and poor survival for the old, RXD missingness always indicated better survival but was less improved for the old, and VIQ indicated no change in survival for the young and poor survival for the old. BPX and LB missingness indicated worse survival, with missingness of LB for the young being significantly worse then the old. The overall missingness HR for the young (Fig. 3) was less significant than the PFQ, demonstrating that although the PFQ is a good proxy there is a reduction in the strength of the survival effect. In summary, the Cox models confirmed that the HRs were typically significantly different from unity, and differed between the young (< 60) versus old individuals (≥ 60).
Missingness biases the FI
As shown in Fig. 4, the blocks did not contribute equally to the FI — in particular the distributions of FI contributions from the blocks are distinct. This suggests that missing an entire block of variables, such as we observed with patterned missingness, will lead to biases in the FI if we simply ignore the missing values (effectively imputing the grey dashed line in Fig. 4).
Fig. 4.
The distribution of block-specific FIs for different variable blocks (labels and fill colours correspond to Figs. 2 and 3). Plotted values are the mean block FI across the population: bars indicate the histogram, lines indicate the cumulative distribution and filled circles indicate the median. y-axis grid lines indicate quartiles. The overall population mean FI, which is implicitly imputed by Ignore, is indicated by the dashed vertical grey line. Observe that the distributions vary considerably between blocks and the distributions are strongly skewed so that Ignore (dashed line) is typically well above the median. Plot is truncated at FI = 0.5 for visualization
This bias could be exacerbated by the Ignore20 exclusion rule. The block sizes were: 12 (PFQ), 1 (RXD), 3 (VIQ), 5 (BPX), and 27 (LB). For 68 variables, the Ignore20 exclusion rule cuts at N = 13.6, thus any individual missing the complete LB block would be excluded from analysis.
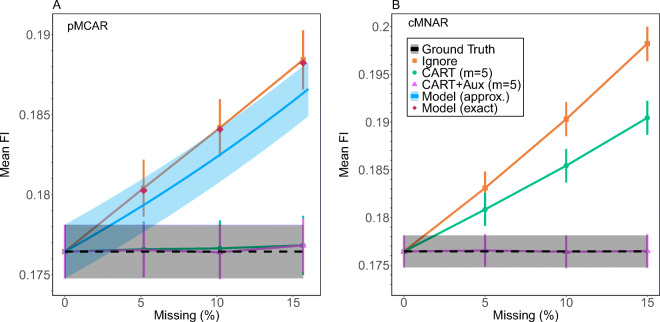
We can estimate potential bias by using simulated missingness. As shown in Fig. 5, we note significant and increasing biases of the FI (orange squares, with the implicit ignore imputation strategy) as compared to the ground truth (black dashed line) — for both pMCAR and cMNAR simulated missingness.
Fig. 5.
Missingness biases the FI. Using different percentages of simulated missingness of type (A) pMCAR or (B) cMNAR, we show the mean FI for different imputation strategies, as indicated by the legend. The typical, Ignore method (orange squares) shows the largest bias compared to the ground truth (black dashed), and for pMCAR the bias is captured by our approximate (blue line) and exact model (red diamonds), Equations A.3 and A.5, respectively. The bias is approximately linear in missingness. Our preferred imputation strategy, CART (green circles) eliminates the bias for pMCAR and reduces it for cMNAR. With the addition of auxiliary variables (pink triangles) CART eliminates the bias for both pMCAR and cMNAR. Error bars and intervals are standard errors. Complete plots for all types of simulated missingness and imputation are provided in Supplemental Figure S7
For the patterned missingness observed in the NHANES data, we developed a quantitative model of how pMCAR missingness biases the FI. The model details are presented in Appendix A. We see in Fig. 5A that the approximate model solution (blue line) as well as the more complex exact model solution (red points) agree with the observed FI bias with pMCAR.
Testing imputation with simulated missingness
Using simulated missingness, we explored how common imputation strategies affected the FI. Overall, we found that CART performed the best — and that using auxiliary variables further improved CART performance with no apparent downside. Under-performing imputation strategies, including Ignore, led to significant biases to both the mean and standard deviation (SD) of the FI distributions.
Figure 6 shows the distributions of FIs for representative imputation methods at 15% missingness. Imputation of pMCAR caused an increased skew of the FI distributions for both Ignore and Default, but no significant changes when CART or CART+Aux were used. The changes due to the Default (PMM/logreg) imputation were very significant. cMNAR showed a similar pattern, although CART also skewed significantly, and Default skewed less than Ignore. The FI distributions for other imputation strategies are shown in Supplemental Figure S12.
Fig. 6.
FI distributions by imputation type for simulated 15% missingness. (A) pMCAR, (B) cMNAR. Colours: quartiles. Vertical lines: GT quartiles. Stars: KS test significance (vs GT). Default was the least similar to the GT for pMCAR whereas Ignore was the least similar for cMNAR. See Supplemental Figure S12 for FI distributions of additional imputation methods. All values from the m = 5 multiple imputations are included for Default, CART and CART+Aux without aggregation
We generally found that the bias in the estimated mean FI was linear for smaller values of missingness (≤ 15%). This is illustrated in Fig. 5 for CART and Ignore; for other imputation methods see Supplemental Figure S7. Accordingly, we estimated the bias per unit missingness, i.e. the bias rate, using a linear zero-intercept regression model. We also calculated the HR and AUC for each imputed FI at 15% missingness. The results are summarized in Tables 3, 4, 5 and 6. Blockwise summaries and the C-index are provided in Supplemental Tables SVII to SXIV (bias) and Tables SXV to SXXII (predictive power).
Table 3.
Imputed FI statistics — cellwise simulated missingness
| Imputation | Type | Mean1 | Bias rate2,3 | SD1 | SD bias rate2,3 | HR1 | AUC1,4 |
|---|---|---|---|---|---|---|---|
| GT | – | 0.176 | 0.000(0) | 0.073 | 0.000(0) | 1.075(7) | 0.733(36) |
| Ignore | cMCAR | 0.176 | 0.000(1) | 0.076 | 0.014(1)∗∗∗ | 1.070(7) | 0.728(37) |
| Ignore20 | cMCAR | 0.176 | 0.000(1) | 0.075 | 0.013(1)∗∗∗ | 1.071(9) | 0.729(41) |
| Default (m = 5) | cMCAR | 0.193 | 0.109(1)∗∗∗ | 0.078 | 0.030(1)∗∗∗ | 1.071(7) | 0.734(37) |
| MICE RF (m = 5) | cMCAR | 0.188 | 0.073(1)∗∗∗ | 0.076 | 0.017(2)∗∗∗ | 1.073(7) | 0.734(37) |
| RF | cMCAR | 0.177 | 0.004(0)∗∗∗ | 0.074 | 0.006(0)∗∗∗ | 1.074(7) | 0.732(37) |
| kNN | cMCAR | 0.179 | 0.012(1)∗∗∗ | 0.072 | − 0.009(0)∗∗∗ | 1.076(7) | 0.730(37) |
| CART (m = 5) | cMCAR | 0.177 | 0.002(1)∗∗ | 0.073 | 0.002(1) | 1.075(8) | 0.732(37) |
| CART (m = 15) | cMCAR | 0.177 | 0.002(0)∗∗∗ | 0.074 | 0.004(1)∗∗∗ | 1.077(7) | 0.733(37) |
| CART+Aux (m = 5) | cMCAR | 0.177 | 0.000(1) | 0.074 | 0.004(1)∗ | 1.076(8) | 0.735(37) |
| Ignore | cMNAR | 0.198 | 0.142(1)∗∗∗ | 0.080 | 0.046(0)∗∗∗ | 1.069(7) | 0.732(37) |
| Ignore20 | cMNAR | 0.202 | 0.137(0)∗∗∗ | 0.081 | 0.050(1)∗∗∗ | 1.069(7) | 0.735(39) |
| Default (m = 5) | cMNAR | 0.193 | 0.109(1)∗∗∗ | 0.078 | 0.029(1)∗∗∗ | 1.071(7) | 0.733(37) |
| MICE RF (m = 5) | cMNAR | 0.188 | 0.074(1)∗∗∗ | 0.076 | 0.017(1)∗∗∗ | 1.073(7) | 0.734(37) |
| RF | cMNAR | 0.177 | 0.004(0)∗∗∗ | 0.074 | 0.006(0)∗∗∗ | 1.073(7) | 0.733(37) |
| kNN | cMNAR | 0.179 | 0.012(1)∗∗∗ | 0.072 | − 0.009(0)∗∗∗ | 1.076(7) | 0.730(37) |
| CART (m = 5) | cMNAR | 0.190 | 0.092(1)∗∗∗ | 0.077 | 0.025(1)∗∗∗ | 1.072(7) | 0.735(37) |
| CART (m = 15) | cMNAR | 0.190 | 0.092(1)∗∗∗ | 0.077 | 0.023(1)∗∗∗ | 1.074(7) | 0.735(37) |
| CART+Aux (m = 5) | cMNAR | 0.176 | 0.000(1) | 0.074 | 0.002(1) | 1.075(7) | 0.731(37) |
5,6
1 At 15% missingness
2 The bias rate is the theoretical bias at 100% missingness
3 p-value for t-test vs 0
4 p-value for vs Ignore; Ignore vs GT
5 See Supplemental Table SIII for additional results. See Supplemental Figure S8 for forest plot of HRs
6 Bold: noteworthy result
Statistical significance is indicated with * p < 0.05, ** p < 0.01, or *** p < 0.001.
Table 4.
Imputed FI statistics — patterned simulated missingness
| Imputation | Type | Mean1 | Bias rate2,3 | SD1 | SD bias rate2,3 | HR1 | AUC1,4 |
|---|---|---|---|---|---|---|---|
| GT | – | 0.176 | 0.000(0) | 0.073 | 0.000(0) | 1.075(7) | 0.733(36) |
| Ignore | pMCAR | 0.188 | 0.076(1)∗∗∗ | 0.078 | 0.029(1)∗∗∗ | 1.064(7) | 0.729(37) |
| Ignore20 | pMCAR | 0.181 | 0.031(1)∗∗∗ | 0.075 | 0.008(2)∗∗∗ | 1.073(12) | 0.733(50) |
| Default (m = 5) | pMCAR | 0.216 | 0.238(5)∗∗∗ | 0.133 | 0.388(24)∗∗∗ | 1.041(7) | 0.697(40)∗∗∗ |
| MICE RF (m = 5) | pMCAR | 0.168 | − 0.055(1)∗∗∗ | 0.068 | − 0.032(1)∗∗∗ | 1.078(8) | 0.732(37) |
| RF | pMCAR | 0.161 | − 0.101(1)∗∗∗ | 0.068 | − 0.035(1)∗∗∗ | 1.076(8) | 0.726(38) |
| kNN | pMCAR | 0.176 | 0.014(5)∗ | 0.072 | −0.002(2) | 1.071(8) | 0.722(38) |
| CART (m = 5) | pMCAR | 0.177 | 0.002(1)∗ | 0.073 | − 0.006(2)∗∗ | 1.075(8) | 0.733(37) |
| CART (m = 15) | pMCAR | 0.177 | 0.003(1)∗∗ | 0.072 | − 0.009(1)∗∗∗ | 1.080(8) | 0.733(37) |
| CART+Aux (m = 5) | pMCAR | 0.177 | 0.002(0)∗∗∗ | 0.073 | −0.002(1) | 1.076(8) | 0.733(37) |
| Ignore | pMAR | 0.187 | 0.067(1)∗∗∗ | 0.075 | 0.004(1)∗∗ | 1.070(8) | 0.732(37) |
| Ignore20 | pMAR | 0.191 | 0.029(1)∗∗∗ | 0.077 | 0.020(1)∗∗∗ | 1.078(10) | 0.742(47) |
| Default (m = 5) | pMAR | 0.216 | 0.244(5)∗∗∗ | 0.121 | 0.279(22)∗∗∗ | 1.046(7) | 0.697(41)∗∗∗ |
| MICE RF (m = 5) | pMAR | 0.169 | − 0.044(1)∗∗∗ | 0.071 | − 0.013(2)∗∗∗ | 1.074(8) | 0.732(37) |
| RF | pMAR | 0.162 | − 0.092(1)∗∗∗ | 0.072 | −0.004(2) | 1.070(7) | 0.728(38) |
| kNN | pMAR | 0.179 | 0.020(4)∗∗∗ | 0.074 | 0.002(1) | 1.071(7) | 0.721(38) |
| CART (m = 5) | pMAR | 0.178 | 0.013(1)∗∗∗ | 0.073 | − 0.004(2)∗∗ | 1.075(8) | 0.733(37) |
| CART (m = 15) | pMAR | 0.178 | 0.013(1)∗∗∗ | 0.073 | −0.002(2) | 1.078(8) | 0.735(37) |
| CART+Aux (m = 5) | pMAR | 0.177 | 0.005(1)∗∗∗ | 0.073 | − 0.002(1)∗ | 1.075(7) | 0.734(37) |
5,6
1 At 15% missingness
2 The bias rate is the theoretical bias at 100% missingness
3 p-value for t-test vs 0
4 p-values for vs Ignore; Ignore vs GT
5 See Supplemental Table SIV for additional results. See Supplemental Figure S8 for forest plot of HRs
6 Bold: noteworthy result
Statistical significance is indicated with * p < 0.05, ** p < 0.01, or *** p < 0.001
Table 5.
Imputed FI statistics for high simulated cMCAR missingness
| Imputation | Type | Mean1 | Bias rate2,3 | SD1 | SD bias rate2,3 | HR1 | AUC1,4 |
|---|---|---|---|---|---|---|---|
| GT | 0% | 0.176 | 0.000(0) | 0.073 | 0.000(0) | 1.075(7) | 0.733(36) |
| Ignore | 25% | 0.177 | 0.000(1) | 0.077 | 0.035(2)∗∗∗ | 1.068(7) | 0.723(38) |
| Ignore20 | 25% | 0.177 | 0.000(1) | 0.077 | 0.013(4)∗ | 1.079(27) | 0.741(101) |
| kNN | 25% | 0.153 | − 0.086(1)∗∗∗ | 0.061 | − 0.052(0)∗∗∗ | 1.084(9) | 0.716(38) |
| CART+Aux (m = 5) | 25% | 0.177 | 0.001(0)∗ | 0.073 | 0.013(4)∗∗∗ | 1.076(8) | 0.733(37) |
| Ignore | 50% | 0.177 | 0.000(1) | 0.085 | 0.035(2)∗∗∗ | 1.055(7) | 0.699(40)∗∗ |
| Ignore205 | 50% | – | – | – | – | – | – |
| kNN | 50% | 0.132 | − 0.086(1)∗∗∗ | 0.048 | − 0.052(0)∗∗∗ | 1.094(14) | 0.685(41) |
| CART+Aux (m = 5) | 50% | 0.176 | 0.001(0)∗ | 0.079 | 0.013(4)∗∗∗ | 1.074(9) | 0.729(37)∗∗∗ |
| Ignore | 75% | 0.176 | 0.000(1) | 0.106 | 0.035(2)∗∗∗ | 1.035(5) | 0.673(41)∗∗∗ |
| Ignore205 | 75% | – | – | – | – | – | – |
| kNN | 75% | 0.113 | − 0.086(1)∗∗∗ | 0.034 | − 0.052(0)∗∗∗ | 1.089(21) | 0.637(43)∗ |
| CART+Aux (m = 5) | 75% | 0.177 | 0.001(0)∗ | 0.085 | 0.013(4)∗∗∗ | 1.076(11) | 0.732(38)∗∗∗ |
6,7
1 At 15% missingness
2 The bias rate is the theoretical bias at 100% missingness
3 p-value for t-test vs 0
4 p-values for vs Ignore; Ignore vs GT
5 Insufficient data due to Ignore20 cutoff rule
6 See Supplemental Figure S9 for forest plot of HRs
7 Bold: noteworthy result
Statistical significance is indicated with * p < 0.05, ** p < 0.01, or *** p < 0.001
Table 6.
Imputed FI statistics for high simulated cMNAR missingness
| Imputation | Type | Mean1 | Bias rate2,3 | SD1 | SD bias rate2,3 | HR1 | AUC1,4 |
|---|---|---|---|---|---|---|---|
| GT | 0% | 0.176 | 0.000(0) | 0.073 | 0.000(0) | 1.075(7) | 0.733(36) |
| Ignore | 25% | 0.217 | 0.309(14)∗∗∗ | 0.086 | 0.078(2)∗∗∗ | 1.062(6) | 0.728(37) |
| Ignore20 | 25% | 0.252 | 0.127(1)∗∗∗ | 0.095 | 0.086(2)∗∗∗ | 1.068(17) | 0.762(72) |
| kNN | 25% | 0.183 | 0.141(12)∗∗∗ | 0.071 | − 0.013(0)∗∗∗ | 1.076(7) | 0.726(37) |
| CART+Aux (m = 5) | 25% | 0.200 | 0.205(11)∗∗∗ | 0.079 | 0.045(5)∗∗∗ | 1.071(7) | 0.736(37) |
| Ignore | 50% | 0.287 | 0.309(14)∗∗∗ | 0.106 | 0.078(2)∗∗∗ | 1.048(5) | 0.715(37)∗ |
| Ignore205 | 50% | – | – | – | – | – | – |
| kNN | 50% | 0.209 | 0.141(12)∗∗∗ | 0.067 | − 0.013(0)∗∗∗ | 1.078(8) | 0.713(38) |
| CART+Aux (m = 5) | 50% | 0.244 | 0.205(11)∗∗∗ | 0.088 | 0.045(5)∗∗∗ | 1.067(7) | 0.734(37)∗∗ |
| Ignore | 75% | 0.449 | 0.309(14)∗∗∗ | 0.138 | 0.078(2)∗∗∗ | 1.032(5) | 0.693(39)∗∗ |
| Ignore205 | 75% | – | – | – | – | – | – |
| kNN | 75% | 0.317 | 0.141(12)∗∗∗ | 0.064 | − 0.013(0)∗∗∗ | 1.063(10) | 0.668(44) |
| CART+Aux (m = 5) | 75% | 0.363 | 0.205(11)∗∗∗ | 0.115 | 0.045(5)∗∗∗ | 1.062(8) | 0.730(37)∗∗ |
6,7
1 At 15% missingness
2 The bias rate is the theoretical bias at 100% missingness
3 p-value for t-test vs 0
4 p-values for vs Ignore; Ignore vs GT
5 Insufficient data due to Ignore20 cutoff rule
6 See Supplemental Figure S10 for forest plot of HRs
7 Bold: noteworthy result
Statistical significance is indicated with * p < 0.05, ** p < 0.01, or *** p < 0.001
As shown in Table 3, for the simplest missingness type, cMCAR, all of the imputation strategies except for Ignore and CART+Aux had significant bias rates. Default MICE (PMM) and Mice RF had large biases: > 0.01 for 15% missingness. For cMNAR, all of the bias rates were significant except CART+Aux, although both kNN and RF were small (compared to the SD).
When missingness patterns from NHANES were used to generate either pMCAR or pMAR, they also caused a severe bias in the estimated Ignore FI and an even worse bias in the MICE default, as shown in Table 4. The bias rate was significant for all imputation methods including Ignore, but was relatively small for kNN, CART and CART+Aux. CART+Aux achieved a bias of only 2.7% of the SD at the theoretical limit of 100% missingness.
The SD of the FI was also significantly biased for most of the imputation strategies — including Ignore. CART had small bias rates, though still statistically significant, while kNN performed better than CART for cMNAR, pMCAR and pMAR, but worse for cMCAR. Overall, CART+Aux performed the best, having a consistently small bias rate.
Coverage is the probability that the true value of the mean FI was within the error interval of the imputed mean FI. CART+Aux had 100% coverage for missingness ≤ 15%, whereas kNN and the other imputation methods did not (see Supplemental Table SII). Excluding cMNAR, CART also had 100% coverage.
Increasing the number of imputations using CART from 5 to 15 made a trivial difference, yielding nearly identical results (see Tables 3 and 4). The bias rate of the mean did not change — nor did the coverage (Supplemental Table SII), while the changes to the bias rate of the SD appeared to be random and small.
In Table 5 we extended cMCAR to higher rates of missingness. We again observed that the ignore methods are unbiased estimators of the mean, as is CART+Aux. In contrast, kNN showed a large and significant bias rate. Furthermore the SD estimates were biased for all imputation methods. The smallest SD bias rate was observed for Ignore20 and CART+Aux — although Ignore20 excluded all of the data for missingness ≥ 50% and therefore could not be calculated. Interestingly, we saw significant reductions in HR and AUC at 50% and 75% missingness for the Ignore methods. Note the increasing HR for kNN likely masked the apparent drop in predictive power observed in the AUC. When 75% of data were missing, the mean FI decreased by 56% for kNN, the HR fit coefficient, , had to increase by 56% to compensate for the shrinking scale, resulting in an expected HR of 1.12 — larger than the observed HR of 1.089 ± 0.021. CART+Aux significantly outperformed Ignore for 50% and 75% missingness (AUC).
Finally, we investigated cMNAR with higher missingness in Table 6. We observed that all of the imputation strategies produced large biases in the mean FI, including CART+Aux, illustrating the difficulty of imputing cMNAR.
We found that when a relatively small fraction of data was missing, the HR of the FI did not substantially vary across most imputation methods — notably excluding Default, as shown in Tables 3, 4, 5 and 6, and Supplemental Figure S8. As such, biases in the FI affect the absolute but not relative risk assessed — comparing absolute FI between studies could cause discrepancies, but comparing relative FI within a study appears valid for most imputation strategies. Reinforcing this, the AUC was similar for most imputation strategies.
Imputation of real missingness
Given the success of CART when imputing against simulated missingness, we focused on testing this strategy with the observed (real) missingness. Ignore served as the de facto standard, and we included Default (PMM/logreg) and kNN for perspective. We also assessed RI as a prospective initial imputation step, which was paired with a subsequent model (Ignore, kNN, etc).
We observed a drop in FI with respect to Ignore for CART, CART+AUX and all of the RI-initialized methods (Table 7). In contrast, the FI for Ignore20 and kNN was greater than Ignore. We had no GT with which to directly observe whether the FI was biased for any particular imputation method. Using our quantitative model and assuming MCAR we estimated that the Ignore method should have a bias in the mean FI of 0.0028 using Eq. A.3 (approximate) or 0.0029 using Eq. A.5 (exact), both agree well with the difference between Ignore and CART or CART+Aux. Notably, this estimate is far smaller than the difference between Ignore and RI-initialized methods, which were all > 0.01.
Table 7.
Imputed FI statistics for real missingness
| Imputation | Mean | ‘Bias’1 | SD | SD ‘Bias’1 | HR2 | AUC3 |
|---|---|---|---|---|---|---|
| Ignore | 0.1442 | 0.0000(0) | 0.0782 | 0.0000 | 1.077(4) | 0.832(17) |
| Ignore204 | 0.1611 | − 0.0170(13)∗∗∗ | 0.0801 | − 0.0019 | 1.078(4) | 0.792(21)∗∗ |
| kNN | 0.1601 | − 0.0160(4)∗∗∗ | 0.0710 | 0.0071 | 1.073(4) | 0.773(21)∗∗∗ |
| Default (m = 5) | 0.1466 | − 0.0024(5)∗∗∗ | 0.0877 | − 0.0095 | 1.077(4) | 0.829(18) |
| CART (m = 5) | 0.1412 | 0.0029(4)∗∗∗ | 0.0816 | − 0.0034 | 1.079(4) | 0.839(17)∗∗∗ |
| CART+Aux (m = 5) | 0.1410 | 0.0031(3)∗∗∗ | 0.0784 | − 0.0003 | 1.079(4) | 0.841(17)∗∗∗ |
| Ignore + RI | 0.1330 | 0.0112(1)∗∗∗ | 0.0803 | − 0.0021 | 1.077(3) | 0.851(16)∗∗∗ |
| Ignore20 + RI5 | 0.1327 | 0.0108(1)∗∗∗ | 0.0774 | 0.0008 | 1.079(4) | 0.848(17) |
| kNN + RI | 0.1302 | 0.0140(2)∗∗∗ | 0.0771 | 0.0011 | 1.076(4) | 0.841(16)∗∗∗ |
| Default+RI (m = 5) | 0.1338 | 0.0104(2)∗∗∗ | 0.0790 | − 0.0009 | 1.077(4) | 0.850(16)∗∗∗ |
| CART+RI (m = 5) | 0.1336 | 0.0106(2)∗∗∗ | 0.0789 | − 0.0007 | 1.079(4) | 0.851(16)∗∗∗ |
| CART+Aux+RI (m = 5) | 0.1334 | 0.0107(2)∗∗∗ | 0.0786 | − 0.0005 | 1.079(4) | 0.852(16)∗∗∗ |
6,7
1 This is the bias proxy: Ignore − Value
2 HR per 0.01 increment in FI, conditioned on age and sex
3 p-value for vs Ignore
4 N = 5701 individuals
5 N = 8728 individuals
6 See Supplemental Tables SXXVIII, SXXIX and SSXXX for additional results
7 Bold: noteworthy result
Statistical significance is indicated with * p < 0.05, ** p < 0.01, or *** p < 0.001
Based on the observed missingness patterns, however, we suspected that the data were primarily MAR, and hence we also estimated the bias after RI, which should have removed the majority of MAR missingness. The bias in the mean FI for Ignore+RI was − 0.00059 (approximate) or − 0.00060 (exact), which agrees excellently with the differences between Ignore+RI and CART+RI (− 0.006 ± 0.002), and Ignore+RI and CART+Aux+RI (− 0.005 ± 0.002).
In summary, CART (with or without Aux) appeared to consistently refine Ignore or Ignore+RI, removing the residual pMCAR-related bias. Our best estimate for the bias in the Ignore mean FI was 0.0106 ± 0.0001, which we calculated by adding the estimated bias in Ignore+RI to the difference between Ignore and Ignore+RI. This effectively assumed MAR missingness was corrected by Ignore+RI and the residual missingness was MCAR and hence could be correctly calculated using our missingness models, Eq. A.3 and Eq. A.5. The estimate agrees well with the difference between the FI using Ignore versus either CART+RI or CART+Aux+RI.
In Table 8 we report the blockwise FIs for individuals under age 60, without RI. This was used to assess imputation quality. We observed that the blockwise FIs differed between imputation strategies. The qualitative survival effect of missingness (‘Survival Frailty’ column) was always the same direction as the CART and CART+Aux imputation strategies relative to Ignore, indicating good qualitative performance. For example, BPX missingness has a HR> 1 and CART imputations have higher BPX block FI averages than Ignore. RI agreed with the qualitative Survival Frailty for PFQ and RXD, but not VIQ. By design, RI imputed 0 for PFQ, VIQ and RXD, but only PFQ and RXD had HR ≤ 1. Note that it is possible that the correct (latent) values to impute were slightly larger than 0.
Table 8.
FI of real missingness imputation by blocks, under age 60
| Block | Ignore | Default | CART | CART+Aux | Survival frailty1 |
|---|---|---|---|---|---|
| All2 | 0.1218(8) | 0.1261(10) | 0.1179(8) | 0.1176(8) | Low |
| PFQ | 0.1151(8) | 0.1416(46) | 0.0876(32) | 0.0865(23) | Low |
| RXD | 0.1078(9) | 0.0941(18) | 0.0962(25) | 0.0909(14) | Low |
| VIQ | 0.1166(13) | 0.0966(34) | 0.0947(53) | 0.0801(33) | No effect |
| BPX | 0.1377(43) | 0.2454(222) | 0.2367(181) | 0.2291(148) | High |
| LB | 0.1232(33) | 0.1458(43) | 0.1449(46) | 0.1478(40) | High |
3
1 Frailty inferred from Cox model and Kaplan-Meier curves
2 All individuals under age 60
3 Bold: noteworthy result
In Table 9 we report the blockwise FIs for individuals age 60+, without RI. In contrast to Table 8, Ignore performed much better for the older individuals, with the FI in the same direction as the survival frailty in 2/5 blocks and for the overall FI, compared to CART and CART+Aux. Importantly, the Ignore strategy got the correct direction of the overall effect.
Table 9.
FI of real missingness imputation by blocks, age 60+
| Block | Ignore | Default | CART | CART+Aux | Survival frailty1 |
|---|---|---|---|---|---|
| All2 | 0.1862(15) | 0.1851(15) | 0.1850(15) | 0.1852(15) | High |
| PFQ | 0.2343(39) | 0.2072(84) | 0.2042(83) | 0.2060(81) | High |
| RXD | 0.1335(28) | 0.1123(53) | 0.1201(61) | 0.1302(73) | Low |
| VIQ | 0.2740(73) | 0.3580(181) | 0.3557(193) | 0.3732(214) | High |
| BPX | 0.2266(62) | 0.3290(240) | 0.3244(254) | 0.3260(245) | High |
| LB | 0.2097(62) | 0.1605(69) | 0.1610(70) | 0.1615(67) | High |
3
1 Frailty inferred from Cox model and Kaplan-Meier curves
2 All individuals age 60+
3 Bold: noteworthy result
The FI distributions are in Fig. 7. In Fig. 7A we observed that, excluding RI, the MICE default was the least similar to the surrogate GT (CART+Aux), as was the case with pMCAR simulation — though with less skew than in Fig. 6. The CART FI distribution was significantly different than CART+Aux, although the difference is not discernible by eye. Taken together, this suggests that the true missingness was somewhere between pMCAR and cMNAR, such as a combination of the two. This is at least partially consistent with our a priori expectations that PFQ, VIQ and RXD were pMAR, which was the foundation of our RI strategy.
Fig. 7.
FI distributions by imputation type for Full dataset (real missingness). (A) Without rule-based imputation (RI), (B) with RI. Observe that RI shifts the FI distribution to lower values (bottom row is duplicated from the other column for comparison). Colours: quartiles. Vertical lines are quantiles of CART+Aux (A) or CART+Aux+RI (B). Stars: KS test significance vs CART+Aux (A) or CART+Aux+RI (B). All values from the m = 5 multiple imputations are included for Default, CART and CART+Aux (including + RI) without aggregation
There was a large shift visible between Figs. 7A and B due to RI, as can be seen in the last row. In Fig. 7B we observed only small differences between the distributions after RI was performed, with only Ignore+RI being significantly different from CART+Aux+RI. It appears that the values imputed by RI were particularly difficult for Ignore and Default to handle, in the latter case we infer that, consistent with Fig. 6, patterned missingness — which RI imputes — seems to be especially difficult for Default to handle (see also Supplemental Figure S8).
The prediction accuracy for the real missingness is given in Table 7. We observed that, relative to Ignore, there was a significant increase in AUC for both CART (p = 1.7 ⋅ 10− 6) and CART+Aux (p = 5.6 ⋅ 10− 11) methods. The largest changes were significant decreases in AUC for the Ignore20 method (p = 0.0046, unpaired) and kNN (p < 2.2 ⋅ 10− 16). All of the RI-enhanced imputation strategies outperformed the Ignore method by AUC, except Ignore20+RI. The best AUC belonged to CART+Aux+RI, with an estimated bias of 0.0107 ± 0.0002 versus Ignore — in agreement with our calculated bias, and an HR of 1.079 ± 0.004, implying that the FI hazard would differ by 1.085 ± 0.005 between the two imputation strategies. The HRs are plotted in Supplemental Figure S11.
Investigating the effects of missingness via the Cox model, we confirmed that missingness is a significant predictor of mortality — with or without considering age and sex, and had a strong interaction effect at age 60 (Tables 10 and 11). The interaction term causes the direction of the hazard to change from protective (age < 60) to dangerous (age ≥ 60). We also considered changes due to the FI, and considered several imputation strategies (MIs were aggregated as mean). We observed similar results with and without RI.
Table 10.
Cox hazard analysis of deviance — FI first
| Model1 | Miss | Miss|Young2 | Deviance age | Sex | FI | |
|---|---|---|---|---|---|---|
| {1}. | Miss | 15(9)∗∗∗ | – | – | – | – |
| {2}. | {1}+Miss|Young | 15(9)∗∗∗ | 26(13)∗∗∗ | – | – | – |
| {3}. | RIDAGEYR+{2} | 15(9)∗∗∗ | 24(13)∗∗∗ | 7(6)∗∗ | – | – |
| {4}. | RIDAGEYR+RIAGENDR+{2} | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(5)∗∗ | 42(13)∗∗∗ | – |
| {5}. | FI(Ignore)+{4} | 3(5) | 7(7)∗∗ | 0(1) | 84(19)∗∗∗ | 406(43)∗∗∗ |
| {6}. | FI(Default)+{4} | 18(10)∗∗∗ | 12(9)∗∗∗ | 0(1) | 80(18)∗∗∗ | 399(43)∗∗∗ |
| {7}. | FI(CART)+{4} | 18(10)∗∗∗ | 12(8)∗∗∗ | 0(1) | 80(19)∗∗∗ | 405(43)∗∗∗ |
| {8}. | FI(CART+Aux)+{4} | 17(9)∗∗∗ | 12(8)∗∗∗ | 0(1) | 78(18)∗∗∗ | 402(44)∗∗∗ |
| {9}. | FI(Ignore+RI)+{4} | 5(6)∗ | 3(5) | 0(1) | 84(19)∗∗∗ | 416(42)∗∗∗ |
| {10}. | FI(Default+RI)+{4} | 16(9)∗∗∗ | 9(7)∗∗ | 0(1) | 79(18)∗∗∗ | 404(42)∗∗∗ |
| {11}. | FI(CART+RI)+{4} | 17(9)∗∗∗ | 8(7)∗∗ | 0(1) | 80(19)∗∗∗ | 409(44)∗∗∗ |
| {12}. | FI(CART+Aux+RI)+{4} | 19(10)∗∗∗ | 9(7)∗∗ | 0(1) | 78(18)∗∗∗ | 409(45)∗∗∗ |
3,4,5,6
1 Deviance was calculated sequentially
2 X|Y denotes an interaction between X and Y (‘X given Y’)
3 The null model had deviance (− 2 ⋅log-likelihood) 12480. Young (< age 60) was dropped (never significant)
4 p-value for z-test versus 0
5 Errors by bootstrapping N = 1000
6 Bold: noteworthy result
Statistical significance is indicated with * p < 0.05, ** p < 0.01, or *** p < 0.001
Table 11.
Cox hazard analysis of deviance — FI last
| Model1 | Miss | Miss|Young2 | Deviance age | Sex | FI | |
|---|---|---|---|---|---|---|
| {1}. | Miss | 15(9)∗∗∗ | – | – | – | – |
| {2}. | {1}+Miss|Young | 15(8)∗∗∗ | 26(14)∗∗∗ | – | – | – |
| {3}. | RIDAGEYR+{2} | 15(9)∗∗∗ | 24(13)∗∗∗ | 7(5)∗∗ | – | – |
| {4}. | RIDAGEYR+RIAGENDR+{2} | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(5)∗∗ | 42(13)∗∗∗ | – |
| {5}. | {4}+FI(Ignore) | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(6)∗∗ | 42(13)∗∗∗ | 405(44)∗∗∗ |
| {6}. | {4}+FI(Default) | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(6)∗∗ | 42(13)∗∗∗ | 413(43)∗∗∗ |
| {7}. | {4}+FI(CART) | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(5)∗∗ | 42(14)∗∗∗ | 419(42)∗∗∗ |
| {8}. | {4}+FI(CART+Aux) | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(5)∗∗ | 42(14)∗∗∗ | 413(44)∗∗∗ |
| {9}. | {4}+FI(Ignore+RI) | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(5)∗∗ | 42(14)∗∗∗ | 412(44)∗∗∗ |
| {10}. | {4}+FI(Default+RI) | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(5)∗∗ | 42(14)∗∗∗ | 412(43)∗∗∗ |
| {11}. | {4}+FI(CART+RI) | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(5)∗∗ | 42(13)∗∗∗ | 419(42)∗∗∗ |
| {12}. | {4}+FI(CART+Aux+RI) | 19(10)∗∗∗ | 27(13)∗∗∗ | 7(5)∗∗ | 42(13)∗∗∗ | 420(43)∗∗∗ |
3,4,5,6
1 Deviance was calculated sequentially
2 X|Y denotes an interaction between X and Y (‘X given Y’)
3 The null model had deviance (− 2 ⋅log-likelihood) 12480. Young (< age 60) was dropped (never significant)
4 p-value for z-test versus 0
5 Errors by bootstrapping N = 1000
6 Bold: noteworthy result
Statistical significance is indicated with * p < 0.05, ** p < 0.01, or *** p < 0.001
We observed a large drop in the predictive power of missingness when conditioned on the Ignore FI but not any other FI (Table 10), implying that the Ignore FI captured the missingness survival effect. For the other imputation strategies, the FI reduced the predictive power of missingness conditioned on being young. We saw no significant differences in predictive power of the FI between the different imputation methods. The deviance may be less sensitive to differences in predictive power than the AUC, because the deviance carries the underlying assumptions of the Cox model. Note that there was a clear FI position dependence in the predictive power of sex, probably due to sex differences in the FI (e.g. [47]), which appears to have bolstered the predictive power of the FI in Table 11, and which complicates direct comparison of the FI deviance between Tables 10 and 11.
Discussion
Deng et al. [3] and Sterne et al. [2] showed that either ignoring missing data or carelessly imputing values can adversely affect results. We investigated missingness with NHANES data to understand if and how the FI changes, and how well the commonly available imputation models perform. We considered both standard Ignore and Ignore20 approaches with the FI, together with a number of explicit imputation strategies including multiple imputation.
The powerful and commonly used imputation strategy, MICE via FCS, is not formally self-consistent. FCS builds predictive distributions for each variable conditioned on the other variables, typically using a modified prediction model. This approach does not represent a general factorization of the true joint distribution [4], and hence a stationary distribution may not exist. As a result, FCS may impute unrealistic values, which can become increasingly unrealistic as more variables are included. Complicating this issue is the underlying prediction model(s) needed by FCS which require separate validation for consistency across datasets. These concerns have been mostly ignored due to its satisfactory empirical performance [4, 19]. By including consistency checks on imputed FI distributions and by quantifying their predictive power we assessed the validity of several common MICE and other imputation models in our study.
Simulated missingness
We observed poor performance for both Default (PMM/logreg) and MICE RF, which both produced biased FI estimates for the simplest simulated missingness, cMCAR, even with ≤ 15% missingness. PMM has previously been shown to produce biased estimates when imputing MCAR data [24], reportedly because of high missingness and too many variables, which were tested up to 64% and 82, respectively. We observed a significant bias even with 15% missingness and 68 variables. MICE RF has also been shown to struggle with large numbers of variables (≥ 200) [3]. Our results indicate that 68 variables may still be too many for either Default or MICE RF.
Increasing cMCAR to 25%, 50%, and ultimately 75% simulated missingness, we also observed a breakdown of both Ignore and kNN. kNN produced a large, significant bias in estimating the mean FI and a drop in the AUC. Ignore showed unbiased estimates of the mean FI but showed a drop in the AUC and HR, with the HR reaching 1.055 for 50% missingness — the same approximate missingness as the PFQ block in the Full dataset, versus the GT value of 1.075 (Supplemental Figure S8). This change is likely due to a noisier FI, as indicated by the significant increase in the SD. Fewer values available to compute the FI should increase the SD by the Central Limit Theorem. Changes to the SD are important since they affect hypothesis testing, for example the t-test statistic is directly proportional to the inverse of the SD: if the SD is too large our p-values will also be too large (and vice versa). In contrast to Ignore and kNN, imputing with CART+Aux was robust even up to 75% missingness, showing no change in AUC or HR, a trivial change in estimated mean FI and the smallest change in the SD.
There was a significant bias in the Complete-case FI estimates using the Ignore method with NHANES missingness patterns (pMCAR). This bias was absent when the patterns were not used (cMCAR), implying the patterns were the cause. pMAR produced similar results. For 15% missingness, the pMCAR bias was small but visible in the FI distribution (Fig. 6). The bias was approximately 0.012, but represents a change in HR of 1.09. This suggests that the real missingness data may also produce biased FI estimates and risk assessment when using the Ignore method.
To confirm and better understand why the bias was present in pMCAR data, we modelled it as a consequence of two observations: (1) variables had different frequencies of missingness and (2) variable blocks had different distributions of deficit values (see Appendix A). For example, the PFQ block had the highest probability of missingness (Fig. 2) and the lowest median deficit/FI value (Fig. 4). Our calculation agreed perfectly with the observed bias. This confirmed that the pMCAR bias is due to a combination of differences between variables in their likelihood of being both deficit and missing; with a small additional bias due to mutual missingness patterns.
Real missingness
CART and CART+Aux imputed simulated missingness the best, and we have inferred that they also likely performed well with real missingness — and better than either Ignore or Default. The distributions of imputed FIs were very similar to simulated FIs (compare Fig. 6 vs Fig. 7) and showed a similar ordering of increasingly skewed FIs from CART+Aux to Default. Further, changes by variable block for younger individuals — representing 65% of our study population, matched changes expected based on survival, where an increased HR due to missingness — and therefore higher frailty [48], correlated perfectly with higher imputed FI values for CART and CART+Aux versus simply ignoring (see Tables 8 and 9). There was also a small, significant increase in the AUC of the FI for predicting 4-year-survival using CART or CART+Aux versus Ignore, implying these imputed FIs were better measures of frailty than the Ignore FI.
Notably, neither CART nor CART+Aux was able to fully compensate for missing expert knowledge regarding study design, as inferred from RI. In RI we assumed gated variables (PFQ, VIQ and RXD) were all optimally healthy, and in Table 7, saw a substantial increase in AUC: confirming RI. Validation of RI can be seen in the survival effects of PFQ and RXD for young people, which strongly imply the missing gated variables were healthy (Table 8). VIQ did not follow this trend, however, and therefore may have been better treated using a different imputation model such as CART. After RI was performed, we did observe that CART and CART+Aux appeared to correctly fine-tune the FI such that the residual bias, calculated using Eq. A.3 and Eq. A.5 was perfectly cancelled. Based on our results, there appears to be no downside to imputing using CART. The upsides include more accurate FI estimation and improved mortality prediction, especially when auxiliary variables are utilized. Imputing with CART is not a panacea: it did not obviate the need for RI, but it did improve upon it.
Investigating the underlying missingness mechanism, we observe that the real missingness is of mixed type. For example, for younger individuals PFQ was pMAR, since study design skipped those values when specific covariates were not deficits [34]. For older individuals PFQ was cMAR or cMNAR given the lack of patterning and strong relationship with survival (Figs. 2 and 3, respectively). The FI distributions (Fig. 7A) showed increasing skewness in the same order as the simulated pMCAR — from CART+Aux (least) to Default (most). But the Default distribution was less skewed than pMCAR, and there was a significant change in the distribution of CART vs CART+Aux. Given the similarities of pMCAR and pMAR in our simulations, the real missingness is a combination of patterned pMAR or pMNAR, and cellwise missingness cMAR or cMNAR.
Missingness and survival
What is the expected change in HR per 0.01 increase in FI [39]? This question cannot be answered precisely without good imputation practices since, as we have seen, both the FI and the HR depend on how missing data are handled [13]. High levels of missingness, even in the simplest case: cMCAR, can cause significant changes to the estimated HR. We also observed that patterned missingness can bias the FI on the scale of 0.01 in both our simulations and, ostensibly, in the real data. Our simulated patterns were handled well by CART, whereas the real patterns seemed to be better handled using RI then fine-tuning with CART; perhaps due to the increased heterogeneity of the Full population. In general, correct estimation of the HR and optimal reduction of FI bias require a robust imputation strategy such as CART.
We observed large differences in survival based on the missingness of variable blocks (Fig. 3). For example, individuals under 60 with the personal fitness (PFQ) block missing lived significantly longer than those with the variable reported — with a maximum difference of 17.6 years between the survival curves. In contrast, individuals missing the lab (LB) block tended to die younger than those with the variables reported. We observed heterogeneity between the variable blocks, with some blocks showing longer, shorter or equal survivals when absent, and often showing different survival effects for old versus young individuals.
Very high levels of missingness occur naturally. For example the PFQ block was missing at a rate of over 50% in the Full dataset, and over 80% for individuals under age 60. In the simulated cMNAR, 50% missingness led to a bias in the FI of 0.1110 ± 0.0030 and an HR estimate of 1.048 using Ignore versus 1.074 using CART+Aux (Supplemental Figure S9). Even the relatively benign cMCAR missingness caused the HR to drop to 1.055 at 50% missingness when using Ignore. We observed a decrease in the HR (per 0.01 increase in FI) estimate using Ignore, dropping continuously from the GT value of 1.075 to 1.032 at 75% cMNAR. This suggests that with a high missingness the Ignore method can cause large biases in the HR. No such bias was observed using CART+Aux.
Although the FI was systematically biased when ignoring simulated missing data, there was no significant change in either AUC or HR for ≤ 15% simulated missingness with either Ignore or CART. Increasing the missingness to a very high, 75% cMNAR, only reduced the AUC with Ignore by 1 error bar. Real missingness (at 14.5%) also showed a small effect on survival, although there was a significant increase in AUC when using CART versus Ignore, especially with inclusion of RI and auxiliary variables. The insensitivity of the AUC may be because it describes the predictive power of all possible FI risk thresholds, and therefore is not sensitive to a systematic bias, furthermore, the scale of the bias may have been too small to significantly change the mortality-risk dichotomization: it was typically much less than the between-individuals variability as measured by the SD. Instead, bias in the FI affects estimates of relative risk.
A previous meta-analysis of adjusted FI-HRs across multiple studies yielded an estimated HR of 1.04 (CI: 1.03–1.04) [39], while our age- and sex-adjusted FI-HR was 1.08 (Table 7). This unexpectedly high HR has previously been attributed to the use of both lab and clinical variables in constructing the FI [16], and is consistent with earlier work [49, 50]. We can speculate about the role of missingness in constructing the FI. The opposing survival effects of missing LB versus PFQ may have helped balance the adverse effects of Ignore. In general, selection bias due to missingness could either enhance or deteriorate the FI. This may help explain the heuristic rules-of-thumb to limit missing data of variables to < 5% and of individuals to < 20%. The latter could improve prediction of the Ignore FI by preferentially excluding young people, who tend to have bad imputations (Table 8). We observed in Table 10 that the Ignore FI usurped the predictive power of missingness, but this ability may depend on the variables used to construct the FI. The Ignore method pushed FI values higher for people with missing data, because values likely to be missing, e.g. PFQ, were almost always less than the individual-mean (Fig. 4). If the individual missing data was older than 60, they were at higher risk of death (Fig. 3), and therefore the Ignore, and especially Ignore20, methods would have incorporated this missingness-related-risk into the FI. This effect depends on the specific set of variables selected for the FI, and so may limit the utility of quantitative FI comparisons within and between studies.
Imputation strategies with the FI
We observed patterned missingness in the Full dataset with a wide range of missingness from 0 to over 50%. Variables often went missing together as nearly perfectly correlated blocks. We also observed unstructured missingness, particularly for older individuals.
Although the missing gated variables were best handled with RI, they also demonstrate clearly the utility of auxiliary variables. For example, the PFQ block was not reported for individuals under age 60 who reported ‘no’ to auxiliary variables PFQ049, PFQ057 and PFQ059. In this case these auxiliary variables are able to convert MNAR (for which there are no general imputation models) to MAR (which many imputation models address). Even with MNAR data, auxiliary variables may still be able to improve imputation by correlating with the latent cause(s) of missingness. With simulated missingness CART+Aux gave excellent performance for low levels of cMNAR missingness. Nevertheless, improvement from auxiliary variables was smaller with real missingness. This may be because simulated missingness was not applied to the auxiliary variables, leading to much lower auxiliary variable missingness in the Complete dataset (Table 1). Our simulations should be considered a best-case scenario for auxiliary variable performance.
We expected that RF models would perform well since they are powerful imputation models capable of handling mixed data with non-linearities and interactions between variables [29]. In the present study we compared 1 tree (CART) versus 10 trees (MICE RF) versus 100 trees (missForest). We found that using only one tree (CART) consistently performed the best, implying more trees caused over-fitting. Generally speaking, it is expected that more trees should reduce over-fitting [51], though the opposite has been reported for imputation [52]. Similarly, too many predictors can also lead to a biased MICE RF imputation [3]. Often, RFs are built by picking a random subset of input predictor variables for each node, i.e. ‘input selection’, whereas CART does not [53]. Input selection could greatly reduce fit quality if there are too many poor predictor variables, i.e. spurious covariates [54], since they dilute the pool of available features. This leads to poorly predicting trees and subsequently a poorly predicting forest. Input selection would then reduce accuracy, which could explain the superior performance of CART. A less likely potential source of over-fitting is tree depth [54].
Why do tree-based imputation methods perform better? Imputation strategies typically impute values by randomly drawing or combining ‘nearby’ observed values. For Ignore, nearby means other values of the same individual, while for other methods nearby is determined by a minimum distance. For PMM the distance is based on linear regression [25], whereas the distance in tree-based methods (CART and RF) is determined by iteratively partitioning the data. As a result, tree-based methods can automatically account for non-linearities, such as interactions between variables. Previous studies have demonstrated that tree-based methods perform well when interactions are present [52, 53, 55]. Non-linearities are expected in our data due to known interactions, such as the sex-frailty paradox [47], as well as the arbitrary scales used for questionnaire data and the presence of non-normally distributed lab data. These may explain the relatively poor behaviour of the default MICE method versus tree-based methods. Default struggled notably with patterned simulated missingness (pMCAR and pMAR), perhaps because finding a suitable donor (PMM) or set of predictors (logreg) was especially difficult due to the large blocks of mutually missing covariates.
CART was systematically biased high with cMNAR, along with most other strategies; although, CART was less biased than Ignore. kNN and missForest were both unbiased for 15% cMNAR, although missForest was consistently biased low and hence probably coincidentally biased in the correct direction for cMNAR. kNN performed relatively well with cMNAR but still struggled with ≥ 25% missingness. Our inability to successfully impute for cMNAR reflects the difficulty of the underlying problem, which in general requires knowledge of the biasing mechanism [19]. This may present an opportunity for imputation models designed specifically for aging data (e.g. [33]).
General thoughts
In our study, the 20% exclusion rule preferentially excluded young individuals (under age 60), removing 56% of young individuals versus 6% of older individuals. This radically altered our study population. Since young people had the least realistic blockwise imputation values using the Ignore method (Table 8) and Ignore generally imputed higher than the true missing values (Fig. 4), this suggests that the 20% rule might improve prediction by simply removing individuals for whom Ignore does not work well. In our study the 20% exclusion rule also excluded all individuals missing the lab block, which preferentially removed individuals with poor survival prognosis from the analysis (Fig. 3). The effect of 20% exclusion depends on the specific set of variables used to calculate the FI. If we had used 10 lab variables instead of 27, then the 20% cut would be ≥ 10.2, and only the PFQ block would be excluded, radically changing the survival effect of excluded individuals (Fig. 3). In the present study, survival prediction dropped significantly when the Ignore20 rule was used versus Ignore (Table 7). Given the superior performance of CART imputation, we see no reason to rely on heuristic rules such as the 20% rule — which biases the study population and could lead to unexpected effects.
Our primary source of error was differences between the Complete and Full datasets. We consistently observed that survival, frailty and missingness are interacting variables, and hence the Complete data had unavoidable differences in the overall FI, AUC, and mortality rates. Nevertheless, the qualitative results were similar between the simulated and real missingness. We consistently saw that the FI calculated using Default MICE or by ignoring missingness gave higher values than CART and CART+Aux. The latter two matched the GT distribution in the simulated missingness data, were consistent with our bias calculations for real and simulated missingness, and improved predictive power in the real missingness data.
We averaged together multiple imputations when estimating predictive power to estimate the maximum achievable predictive power versus single imputation strategies, but this neglected propagation of error due to imputation hence our confidence intervals were likely too small for the AUC and HR of the real missingness. The simulated missingness used Monte Carlo estimates for the error and therefore should be reliable. Recent results have implied that m = 5 imputations may be far too few for accurate estimation of statistical dispersion [56]; however, when we used the recommended m = 15 imputations [7] on the simulated data we saw only a small change in the estimated standard deviation, implying for our low levels of missingness m = 5 was sufficient.
In the future we would like to investigate missingness structures in other common aging studies. It will also be interesting to investigate the 5% missingness-by-variable cut-off that is commonly used in the literature [14]. Further investigation into MICE may prove worthwhile, such as the convergence properties (stability) of FCS and the effect of number of iterations. Tuning of MICE hyperparameters, notably of RF including depth, input selection and number of trees could enhance results, but would require a diverse set of gerontological studies to do reliably.
There is room for improvement from CART+Aux, which had poor performance for high levels of cMNAR, and struggled with the imputation of real missingness both for older individuals and for gated variables better handled using RI. This performance might be improved upon with deep learning models (e.g. [31, 33]), although scepticism is warranted regarding generalizability across datasets, as lightweight imputation models — including MICE via CART — have been shown to outperform deep learning in third-party comparison studies [21, 22]. Quantitative, stochastic modelling of aging naturally lends itself both to the development of new imputation strategies and to the ability to generate realistic datasets to validate imputation strategies. This synergy presents an opportunity for quantitative researchers to address a serious pragmatic issue endemic to aging studies: missing data.
Summary and conclusions
We considered several types of simulated missingness together with naturally missing data. Imputation of real missingness shared strong similarities with imputing the simulated missingness. Our results indicate that most imputation strategies, including Ignore and the MICE default, are weak against at least one type of missingness. Fortunately, MICE using CART appeared to be robust, and consistently improved estimation and predictive power over simply ignoring missing data.
We observed distinct missingness patterns that bias the standard Ignore (available-case) FI methodology, even when missing completely at random (pMCAR). Imputation with MICE using CART can remove this bias. We advise caution with other MICE models, especially with the default method (PMM/logreg) which made the bias even larger for our simulated missingness. The MICE RF model performed poorly and was unreliable — with performance dependent on the missingness mechanism, as were the popular single-imputation strategies of kNN and missForest. kNN did perform well for ≤ 15% missingness, but failed even the simplest test case — cMCAR, for ≥ 25% missingness, and had poor predictive power with the real missingness.
These same patterns of missing variable blocks have a significant effect in survival, with the missingness of some variables being predictive of poor survival, whereas others indicated better survival. These effects are evidence that missingness should not be ignored. The FI tended to cancel out survival effects when using the typical strategy of ignoring missing values, which may suggest an important cancellation in the choice of FI variables. For example, the self-reported and lab variables in this study tended to have opposing survival effects with missingness. What’s more, we observed that the heuristic 20% cutoff rule for individuals missing entries can partially compensate for the limitations of ignoring missingness in certain types of simulated missingness, but can also greatly bias the study population.
The FI prediction of mortality appeared to be robust to missingness, showing only a minor reduction in AUC even when 75% of the data were made missing, however, we observed large changes in the HR estimate for missingness ≥ 25% when missing values were simply ignored. Good HR estimation requires imputation. With inclusion of auxiliary variables, the CART+Aux imputation showed remarkable consistency in both AUC and HR estimation in the simulated missingness, even at 75% missingness. We also observed CART+Aux improved survival prediction (AUC) for the real missingness over ignoring the missing data.
Our observed improvement in survival prediction appears to be consistent with previous work using the Rotterdam study [13], although that study did not provide a direct measure of predictive power such as the AUC or C-index. That study also did not fully report their imputation model — only that they used MICE — but they found a similar bias in the median FI of the same scale, 0.01, and in the same direction as the Default MICE imputation in our study. In our study this was the same scale and opposite direction of CART and RI-based imputations, emphasizing the potential for differences between cohorts and the need for full disclosure of imputation models.
Our study indicates a hierarchy of increasingly complex missing data handling for increasingly precise estimation of the FI and subsequent HR. The simplest approach is to use the typical Ignore strategy. The Ignore-FI appears to be a simple, composite health measure of vulnerability to adverse outcomes, suitable for clinical situations. Unfortunately, ignoring missing data makes the FI prone to bias and hence inhibits quantitative FI comparisons across populations and studies. A large improvement in FI precision and predictive power follows if we apply RI. A smaller improvement to FI precision follows if CART is then used to impute remaining values. And finally, inclusion of auxiliary variables with CART can safeguard against low-levels of MNAR without serious risk of over-fitting. In situations where fewer rules are available for RI, imputing with CART using auxiliary variables becomes increasingly important.
Missing data handling can have a significant effect on the precision of the quantitative FI, HR estimate, and its mortality predictive power. A standardized approach for handling missingness is needed to achieve the increasingly high levels of precision desired in contemporary FI studies, and to facilitate comparisons between studies and translation across populations. Researchers should fully disclose their missing data handling methodology, including imputation model and number of imputations. Basic sanity checks on imputed values are advisable. It is still an open question what effect missingness has across studies and across sets of variables used for the FI. In the present NHANES-based study, imputation using the commonly available CART MICE consistently gave superior FI precision, HR estimation and mortality predictive power over simply ignoring missing values.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Acknowledgements
The authors wish to thank Dr. Joanna Blodgett (University College London) and Dr. Judith Godin (Dalhousie) for their helpful input.
: Appendix A. Missingness patterns bias the FI
The complete (binarized) data matrix B has true elements bij, where the rows i ∈{1, 2,...,N} are over N individuals and the columns j ∈{1, 2,...,Nb} are over Nb variables. The missingness matrix Mij = 1 if a given entry is missing, and 0 if it was observed. The overall missingness fraction is π = Nm/(NNb) where is the number of missing values in the dataset.
We define as the true average FI (Frailty Index) over the population, so . We define as the average observed FI, so . We define as the average FI of the missing values, so . We then have
| A.1 |
The true population average, , only coincides with the observed estimate, , when , otherwise there will be a bias (for π > 0).
To estimate the bias we assume that the distribution of missing data across individuals is Pi, across variables Pj, and across both Pi,j. We would have Pi,j = 〈Mij〉, where the angle brackets indicates an average over many missingness matrices. If we wanted the distribution of non-missing data , , and it would be just be Pc = 1 − P. Note that .
The bias, can be calculated using Bayes’ theorem as:
| A.2 |
We assume no individual-specific selection, i.e. Pi = 1/N. We can approximate the bias by assuming independence, , then we have:
| A.3 |
which is plotted as ‘Model (approx.)’ in Fig. 5. Note that requires knowledge of the grouth truth, unless the data are MCAR. Where and is:
| A.4 |
We have Mij directly from the data matrix. Note that if Pi,j = const. (cMCAR) then , in which case the Ignore method would be unbiased. The independence approximation is, in light of the strong missingness patterns (‘Missingness patterns’), unlikely to be exact. We can instead estimate by assuming independent, identically distributed individuals (pMCAR), as:
| A.5 |
which, after substitution into Eq. A.2, is plotted as ‘Model (exact)’ in Fig. 5. The key difference is that varies greatly for patterned missingness. The approximate model posits that the difference between FI contributions between variables and blocks causes a bias, whereas the exact model additionally posits that the specific patterns also contributeto the bias.
Footnotes
Suppose we measured N variables for an individual, , but M values are missing. The ignore FI is the mean, . Imputing fig for missing values also gives .
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Little RJ, Rubin DB. Statistical analysis with missing data. 3rd edn. Hoboken: Wiley; 2020. [Google Scholar]
- 2.Sterne JAC, White IR, Carlin JB, Spratt M, Royston P, Kenward MG, Wood AM, Carpenter JR. Multiple imputation for missing data in epidemiological and clinical research: potential and pitfalls. BMJ. 2009;338:2393. doi: 10.1136/bmj.b2393. [DOI] [Google Scholar]
- 3.Deng Y, Chang C, Ido MS, Long Q. Multiple imputation for general missing data patterns in the presence of high-dimensional data. Sci Rep. 2016;6:21689. doi: 10.1038/srep21689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Van Buuren S, Brand JP, Groothuis-Oudshoorn CG, Rubin DB. Fully conditional specification in multivariate imputation. J Stat Comput Simul. 2006;76(12):1049–64. doi: 10.1080/10629360600810434. [DOI] [Google Scholar]
- 5.Van Buuren S (2018) Flexible Imputation of Missing Data, 2nd edn. CRC press, Boca Raton. https://stefvanbuuren.name/fimd/
- 6.Allison PD. Multiple imputation for missing data: a cautionary tale. Sociol Methods Res. 2000;28(3):301–09. doi: 10.1177/0049124100028003003. [DOI] [Google Scholar]
- 7.White IR, Royston P, Wood AM. Multiple imputation using chained equations: issues and guidance for practice. Stat Med. 2011;30(4):377–99. doi: 10.1002/sim.4067. [DOI] [PubMed] [Google Scholar]
- 8.Schouten RM, Lugtig P, Vink G. Generating missing values for simulation purposes: a multivariate amputation procedure. J Stat Comput Simul. 2018;88(15):2909–30. doi: 10.1080/00949655.2018.1491577. [DOI] [Google Scholar]
- 9.Hardy SE, Allore H, Studenski SA. Missing data: a special challenge in aging research. J Am Geriatr Soc. 2009;57(4):722–29. doi: 10.1111/j.1532-5415.2008.02168.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.McCaul KA, Almeida OP, Norman PE, Yeap BB, Hankey GJ, Golledge J, Flicker L. How many older people are frail? Using multiple imputation to investigate frailty in the population. J Am Med Dir Assoc. 2015;16(5):439–17. doi: 10.1016/j.jamda.2015.02.003. [DOI] [PubMed] [Google Scholar]
- 11.Searle SD, Mitnitski A, Gahbauer EA, Gill TM, Rockwood K. A standard procedure for creating a frailty index. BMC Geriatr. 2008;8:24. doi: 10.1186/1471-2318-8-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rockwood K, Mitnitski A. Frailty in relation to the accumulation of deficits. J Gerontol A Biol Sci Med Sci. 2007;62(7):722–27. doi: 10.1093/gerona/62.7.722. [DOI] [PubMed] [Google Scholar]
- 13.Schoufour JD, Erler NS, Jaspers L, Kiefte-de Jong JC, Voortman T, Ziere G, Lindemans J, Klaver CC, Tiemeier H, Stricker B, Ikram AM, Laven JSE, Brusselle GGO, Rivadeneira F, Franco OH. Design of a frailty index among community living middle-aged and older people: the Rotterdam study. Maturitas. 2017;97:14–20. doi: 10.1016/j.maturitas.2016.12.002. [DOI] [PubMed] [Google Scholar]
- 14.Rockwood K, Song X, Mitnitski A. Changes in relative fitness and frailty across the adult lifespan: Evidence from the Canadian National Population Health Survey. CMAJ. 2011;183(8):487–94. doi: 10.1503/cmaj.101271. [DOI] [Google Scholar]
- 15.Peña FG, Theou O, Wallace L, Brothers TD, Gill TM, Gahbauer EA, Kirkland S, Mitnitski A, Rockwood K. Comparison of alternate scoring of variables on the performance of the frailty index. BMC Geriatr. 2014;14:25. doi: 10.1186/1471-2318-14-25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Blodgett JM, Theou O, Howlett SE, Rockwood K. A frailty index from common clinical and laboratory tests predicts increased risk of death across the life course. Geroscience. 2017;39(4):447–55. doi: 10.1007/s11357-017-9993-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Howlett SE, Rutenberg AD, Rockwood K. The degree of frailty as a translational measure of health in aging. Nature Aging. 2021;1(8):651–65. doi: 10.1038/s43587-021-00099-3. [DOI] [Google Scholar]
- 18.Buuren Sv, Groothuis-Oudshoorn K (2010) MICE: Multivariate imputation by chained equations in R. J Stat Softw 1–68
- 19.Murray JS. Multiple imputation: a review of practical and theoretical findings. Stat Sci. 2018;33(2):142–59. doi: 10.1214/18-STS644. [DOI] [Google Scholar]
- 20.Beaulieu-Jones BK, Lavage DR, Snyder JW, Moore JH, Pendergrass SA, Bauer CR. Characterizing and managing missing structured data in electronic health records: Data analysis. JMIR Med Inform. 2018;6(1):11. doi: 10.2196/medinform.8960. [DOI] [Google Scholar]
- 21.Jäger S, Allhorn A, Bießmann F. A benchmark for data imputation methods. Front Big Data. 2021;4:693674. doi: 10.3389/fdata.2021.693674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang Z, Akande O, Poulos J, Li F (2021) Are deep learning models superior for missing data imputation in large surveys? Evidence from an empirical comparison. arXiv:2103.09316
- 23.Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E. Scikit-learn: Machine learning in Python. J Mach Learn Res. 2011;12:2825–30. [Google Scholar]
- 24.Hardt J, Herke M, Leonhart R. Auxiliary variables in multiple imputation in regression with missing X: a warning against including too many in small sample research. BMC Med. Res Methodol. 2012;12:184. doi: 10.1186/1471-2288-12-184. [DOI] [Google Scholar]
- 25.Allison P (2015) Imputation by Predictive Mean Matching: promise & Peril. https://statisticalhorizons.com/predictive-mean-matching. Published: 05-03-2015. Accessed: 04-08-2020
- 26.Kowarik A, Templ M. Imputation with the R package VIM. J Stat Softw. 2016;74(7):1–16. doi: 10.18637/jss.v074.i07. [DOI] [Google Scholar]
- 27.Stekhoven DJ, Bühlmann P. Missforest—non-parametric missing value imputation for mixed-type data. Bioinformatics. 2011;28(1):112–18. doi: 10.1093/bioinformatics/btr597. [DOI] [PubMed] [Google Scholar]
- 28.Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, Botstein D, Altman RB. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17(6):520–25. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- 29.Tang F, Ishwaran H. Random forest missing data algorithms. Stat Anal Data Mining ASA Data Sci J. 2017;10(6):363–77. doi: 10.1002/sam.11348. [DOI] [Google Scholar]
- 30.Vazifehdan M, Moattar MH, Jalali M. A hybrid bayesian network and tensor factorization approach for missing value imputation to improve breast cancer recurrence prediction. J King Saud Univ Comput Inform Sci. 2019;31(2):175–84. [Google Scholar]
- 31.Gondara L, Wang K (2018) Mida: Multiple imputation using denoising autoencoders. In: Pacific-Asia Conference on Knowledge Discovery and Data Mining. Springer, pp 260–272
- 32.Qiu YL, Zheng H, Gevaert O (2020) Genomic data imputation with variational auto-encoders. Gigascience 9(8)
- 33.Farrell S, Mitnitski A, Rockwood K, Rutenberg A (2021) Interpretable machine learning for high-dimensional trajectories of aging health. arXiv:2105.03410, [q-bio.QM]
- 34.Centers for Disease Control and Prevention (CDC), & National Center for Health Statistics (NCHS) (2020) National Health and Nutrition Examination Survey Data. Available from: http://www.cdc.gov/nchs/nhanes.htm
- 35.Schafer JL, Graham JW. Missing data: our view of the state of the art. Psychol Methods. 2002;7(2):147. doi: 10.1037/1082-989X.7.2.147. [DOI] [PubMed] [Google Scholar]
- 36.R Core Team (2020) R: a Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. R Foundation for Statistical Computing. https://www.R-project.org/
- 37.Robin X, Turck N, Hainard A, Tiberti N, Lisacek F, Sanchez J-C, Müller M. Proc: an open-source package for r and s+ to analyze and compare roc curves. BMC Bioinforma. 2011;12:77. doi: 10.1186/1471-2105-12-77. [DOI] [Google Scholar]
- 38.Therneau TM (2020) A Package for Survival Analysis in R. R package version 3.1-12. https://CRAN.R-project.org/package=survival
- 39.Kojima G, Iliffe S, Walters K. Frailty index as a predictor of mortality: a systematic review and meta-analysis. Age Ageing. 2018;47(2):193–200. doi: 10.1093/ageing/afx162. [DOI] [PubMed] [Google Scholar]
- 40.Hanley JA, McNeil BJ. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology. 1982;143(1):29–36. doi: 10.1148/radiology.143.1.7063747. [DOI] [PubMed] [Google Scholar]
- 41.Brown BW Jr, Hollander M, Korwar RM (1973) Nonparametric tests of independence for censored data with application to heart transplant studies. Technical report, Florida State University
- 42.Harrell FEJr, Califf RM, Pryor DB, Lee KL, Rosati RA. Evaluating the yield of medical tests. JAMA. 1982;247(18):2543–46. doi: 10.1001/jama.1982.03320430047030. [DOI] [PubMed] [Google Scholar]
- 43.James G, Witten D, Hastie T, Tibshirani R. An introduction to statistical learning: with applications in R. New York: Springer; 2013. [Google Scholar]
- 44.Moore DF. Applied survival analysis using R. Switzerland: Springer; 2016. [Google Scholar]
- 45.Rochon J, Gondan M, Kieser M. To test or not to test: Preliminary assessment of normality when comparing two independent samples. BMC Med Res Methodol. 2012;12:81. doi: 10.1186/1471-2288-12-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics. 1988;44(3):837–45. doi: 10.2307/2531595. [DOI] [PubMed] [Google Scholar]
- 47.Hubbard RE. Sex differences in frailty. Interdiscip Top Gerontol Geriatr. 2015;41:41–53. doi: 10.1159/000381161. [DOI] [PubMed] [Google Scholar]
- 48.Dent E, Kowal P, Hoogendijk EO. Frailty measurement in research and clinical practice: a review. Eur J Intern Med. 2016;31:3–10. doi: 10.1016/j.ejim.2016.03.007. [DOI] [PubMed] [Google Scholar]
- 49.Blodgett JM, Theou O, Howlett SE, Wu FCW, Rockwood K. A frailty index based on laboratory deficits in community-dwelling men predicted their risk of adverse health outcomes. Age Ageing. 2016;45(4):463–68. doi: 10.1093/ageing/afw054. [DOI] [PubMed] [Google Scholar]
- 50.Howlett SE, Rockwood MRH, Mitnitski A, Rockwood K. Standard laboratory tests to identify older adults at increased risk of death. BMC Med. 2014;12:171. doi: 10.1186/s12916-014-0171-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mehta P, Bukov M, Wang C-H, Day AG, Richardson C, Fisher CK, Schwab DJ. A high-bias, low-variance introduction to machine learning for physicists. Phys Rep. 2019;810:1–124. doi: 10.1016/j.physrep.2019.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Shah AD, Bartlett JW, Carpenter J, Nicholas O, Hemingway H. Comparison of random forest and parametric imputation models for imputing missing data using MICE: a CALIBER study. Am J Epidemiol. 2014;179(6):764–74. doi: 10.1093/aje/kwt312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Doove LL, Van Buuren S, Dusseldorp E. Recursive partitioning for missing data imputation in the presence of interaction effects. Comput. Stat. Data Anal. 2014;72:92–104. doi: 10.1016/j.csda.2013.10.025. [DOI] [Google Scholar]
- 54.Friedman J, Hastie T, Tibshirani R. The elements of statistical learning, vol 1. New York: Springer; 2001. [Google Scholar]
- 55.Hong S, Lynn HS. Accuracy of random-forest-based imputation of missing data in the presence of non-normality, non-linearity, and interaction. BMC Med Res Methodol. 2020;20(1):199. doi: 10.1186/s12874-020-01080-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Bodner TE. What improves with increased missing data imputations? Struct Equ Modeling. 2008;15(4):651–75. doi: 10.1080/10705510802339072. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.