A Stratified Model to Predict Dispersion in Trabecular Bone

Abstract

Frequency-dependent phase velocity (dispersion) has previously been measured in trabecular bone by several groups. In contrast to most biologic tissues, phase velocity in trabecular bone tends to decrease with frequency. A stratified model, consisting of alternating layers of bone and marrow (in vivo) or water (in vitro), has been employed in an attempt to explain this phenomenon. Frequency-dependent phase velocity was measured from 300 kHz to 700 kHz in 1) phantoms consisting of regularly-spaced thin parallel layers of polystyrene sheets in water, and 2) thirty calcaneus samples in vitro. For the polystyrene phantoms, the agreement between theory and experiment was good. For the calcaneus samples, the model has some limited usefulness (error of about 5%) in predicting average phase velocity. More importantly, the model seems to perform consistently well for predicting the frequency dependence of phase velocity in calcaneus.

Introduction

Speed of sound (SOS) in calcaneus has been reported by numerous investigators to be predictive of osteoporotic fracture risk [1–23]. In addition, calcaneal SOS may provide some additional information regarding fracture risk independent of that provided by bone mineral density (BMD), the traditional measurement for diagnosis of osteoporosis [19].

Phase velocity in calcaneus has been reported by several groups to vary with ultrasonic frequency [8, 9, 16, 23]. In other words, calcaneus is dispersive. Dispersion can be positive (phase velocity increasing with frequency) or negative (phase velocity decreasing with frequency) in individual calcaneal samples. However, on the average, dispersion tends to be negative [8, 9, 16, 23]. This is rather unusual for biologic tissue and is contrary to what one might expect based on models relating frequency-dependent attenuation and frequency-dependent phase velocity [24, 25].

Negative dispersion has been reported in so-called stratified media. The simplest example of a stratified medium consists of alternating parallel layers of two materials. Fundamental theory regarding such media has been developed by Rytov [26], Bruggeman [27], Tarkov [28], Riznichenko [29], and Postma [30]. Brekhovskikh [31] has provided a nice summary. Plona and co-workers have demonstrated good agreement between theory and experiment for negative dispersion in aluminum/water and in plexiglass/water stratified media [32]. Hughes and co-workers have applied a stratified model to trabecular bone and have found it useful for predicting the angular dependence of fast and slow compressional waves [33].

The objective of this paper is to apply the stratified model to predict dispersion in trabecular bone. First, a brief summary of a stratified model is presented. Next, experimental methods are described for measurements of frequency-dependent phase velocity in phantoms and in calcaneus samples. Finally results are presented and discussed.

The Stratified Model

The stratified model is illustrated in Figure 1. Two homogeneous materials (1 and 2) are arranged in alternating layers. Each material is characterized by its density, ρ, and its first and second Lame’ constants, λ and μ. The widths of the alternating layers are denoted by h₁ and h₂. The width of the periodic unit is h = h₁ + h₂ and is assumed to be small relative to the wavelength. The periodic nature of the model imposes periodic conditions on the solution to the wave equation. Thus velocities and pressures at a location z are the same as those at z + nh where n is an integer. Continuity of velocities and pressures is also assumed at layer boundaries.

1.

Stratified Model. Two materials are arranged in alternating layers. Each material is characterized by its first and second Lame’ constants, λ, and μ, as well as its density, ρ. The thicknesses of the individual layers are given by h₁ and h₂. The period of the medium is h = h₁ + h₂. The wave is assumed to propagate in the z direction.

For plane wave propagation perpendicular to the planar interfaces between adjacent layers, the dispersion relation for the longitudinal wave is given by [31]

$$\cos \xi h=\cos k_1{h}_1\cos k_2{h}_2-[(1+s)/2s]\sin k_1{h}_1\sin k_2{h}_2$$ (1)

where k₁ = ω/c₁, k₂ = ω/c₂,

$$s=\frac{({\lambda }_2+2{\mu }_2)k_2}{({\lambda }_1+2{\mu }_1)k_1}$$ (2)

and the phase velocity of the longitudinal wave for propagation perpendicular to the layers is given by c_zz = ω/ξ where ω=2πf and f is the frequency of the wave. The right hand side of Equation (1) may computed from the material properties of the two media. After taking an inverse cosine and dividing by h, ξ is obtained. Phase velocity is then computed from c_zz = ω/ξ.

Experimental Methods

Biological Methods

Thirty human calcaneus samples (both genders, ages unknown) were obtained. They were defatted using a trichloro-ethylene solution. Defatting was presumed not to significantly affect measurements since speed of sound of defatted trabecular bone has been measured to be only slightly different from that of bone with marrow left intact [14, 34]. The cortical lateral layers were sliced off leaving two parallel surfaces with direct access to trabecular bone. The thicknesses of the samples varied from 12 to 21 mm. In order to remove air bubbles, the samples were vacuum degassed underwater in a desiccator. After vacuum, samples were allowed to thermally equilibrate to room temperature prior to ultrasonic interrogation. Ultrasonic measurements were performed in distilled water at room temperature. The temperature was measured for each experiment and ranged between 19°C and 22°C. The relative orientation between the ultrasound beam and the calcaneus samples was the same as with in vivo measurements performed with commercial bone sonometers, in which sound propagates in the mediolateral (or lateromedial) direction.

Ultrasonic Methods

The experimental setup is illustrated in Figure 2. A Panametrics (Waltham, MA) 5800 pulser/receiver was used. Samples were interrogated in a water tank using a pair of opposing coaxially-aligned Panametrics 1” (2.54 cm) diameter, 500 kHz center frequency, focussed (focal length = 1.5” or 3.81 cm), broadband transducers. Received ultrasound signals were digitized (8 bit, 10 MHz) using a LeCroy (Chestnut Ridge, NY) 9310C Dual 400 MHz oscilloscope and stored on computer (via GPIB) for off-line analysis.

2.

Experimental Setup. The calcaneus sample is shown rotated 90 degrees about a vertical axis.

Two phantoms consisting of polystyrene layers were constructed. One had 15 0.02” (0.051 cm) thick parallel layers. The other had 22 0.015” (0.0381 cm)thick parallel layers. In each case the spacing between layers was equal to the layer thickness. Water filled the spaces in between the layers. The layers were oriented perpendicular to the ultrasound propagation direction.

Phase velocity was computed using [23]

$$c_p(\omega )=\frac{c_w}{1+\frac{c_w\Delta \varphi (\omega )}{\omega d}}$$ (3)

where Δϕ(ω) is the difference in unwrapped phases of the received signals with and without the sample in the water path. The unwrapped phase difference, Δϕ(ω), was computed as follows. The received digitized signal was gated to isolate the main burst of ultrasound. (See Figure 3a). The dc component of this signal was subtracted out. The Fast Fourier Transform (FFT) of the signal was taken. The phase of the signal at each frequency was taken to be the inverse tangent of the ratio of the imaginary to real part of the FFT at that frequency. Since the inverse tangent function yields principal values between −π and π, the phase had to be unwrapped by adding an integer multiple of 2π to all frequencies above each frequency where a discontinuity appeared.

3.

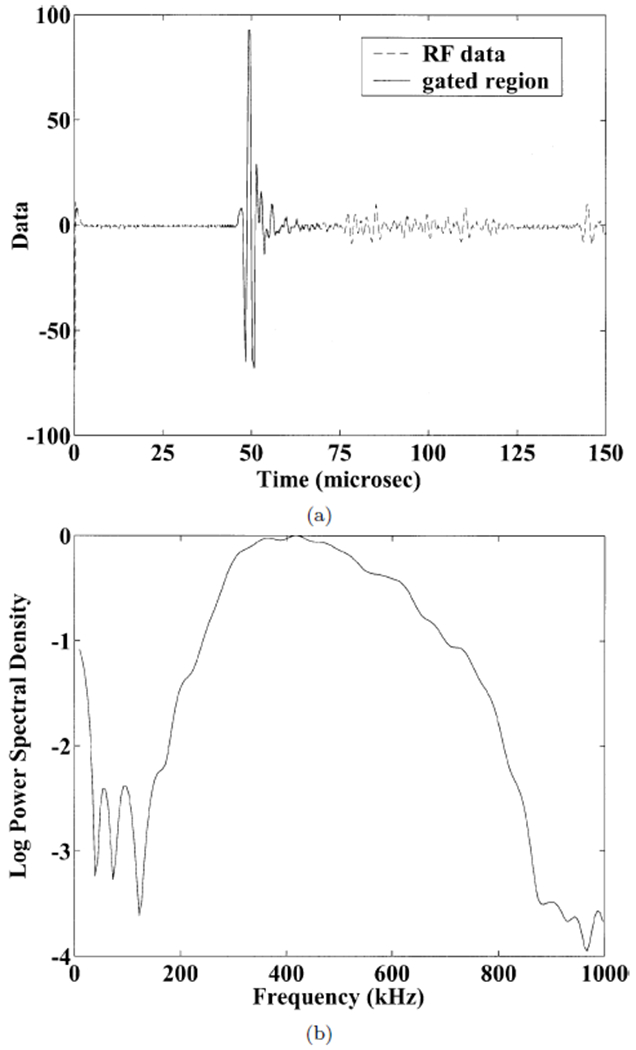
(a) Radio frequency data acquired through 0.02” thick polystyrene layers in water. The gated region used for analysis is shown by the solid line. (b) Power spectrum from data in (a). Multiple reverberations are apparent. The usable bandwidth was from 300 – 700 kHz.

The speed of sound in the calcaneus, approximately 1475 – 1650 m/s [16], is sufficiently close to that of distilled water at room temperature, 1490 m/s [35], that potential diffraction-related errors in this substitution method due to the disparity in sound speeds between the two media [36, 37] may be ignored [16].

Results

Figure 3 shows the radio-frequency data and the (normalized) logarithm of power spectral density corresponding to a signal that propagated through one of the polystyrene phantoms. Multiple reverberations are apparent. The usable bandwidth was taken to be from 300 to 700 kHz.

Figure 4 shows theoretical curves (Equation 1) and experimental data for frequency-dependent phase velocity for the polystyrene phantoms. The values assumed for the theoretical curves were longitudinal velocity = 2400 m/s, λ = 3271 MPa, μ = 1389 MPa, ρ = 1050 kg/m³ (polystyrene), and longitudinal velocity = 1490 m/s, λ = 2241 MPa, μ = 0 MPa, ρ = 1000 kg/m³ (water). The experimental data for the 0.015” thick polystyrene shows little if any dispersion, consistent with the gradually decreasing frequency-dependent phase velocity predicted by the theory. The experimental data for the 0.02” thick polystyrene shows a greater decline especially for frequencies between 600 and 700 kHz. A comparison of Figures 3 and 4 indicates that this rather precipitous decline is not attributable to inadequate signal-to-noise ratio for these frequencies. Although the theoretical and experimental dispersion curves for the 0.02” thick polystyrene show similar trends, the frequency at which rapid decline begins is lower for the theory than for the experimental data. This discrepancy may be attributable to some uncertainty regarding the true material properties for the specific samples of polystyrene investigated. Also, edge effects may have distorted measurements. The stratified model theory assumes an infinite medium. The 0.015” thick polystyrene phantom had 22 periods (one period corresponds to one layer of polystyrene plus one equally thick layer of water) and was about 17 mm across while the 0.02” thick polystyrene phantom had 15 periods and was about 15 mm across.

4.

Frequency-dependent phase velocity measured through 0.015” polystyrene and 0.02” polystyrene layers. Both theoretical (continuous curves) and experimental data are shown. Error bars denote standard deviations. The theoretical and experimental data corresponding to the 0.02” polystyrene show a rather sharp drop off for frequencies greater than about 500 or 600 kHz. The theoretical and experimental data corresponding to the 0.015” polystyrene show a much more gradual decline.

Figure 5 shows frequency-dependent measurements of phase velocity for the thirty calcaneus samples. The error bars denote standard errors of the estimates. A linear fit to the trend is shown by the dotted line. This negatively sloped trend has been reported previously by four groups [8, 9, 16, 23]. Also shown in Figure 5 are theoretical dispersion relations (Equation 1) based on material parameters reported for synthetic hydroxyapatite [38], powdered human femur [38], and cortical bone [39]. The absolute values of phase velocity for the three sets of assumed material parameters varies somewhat. However, the frequency dependence of phase velocity is quite similar for the three cases.

5.

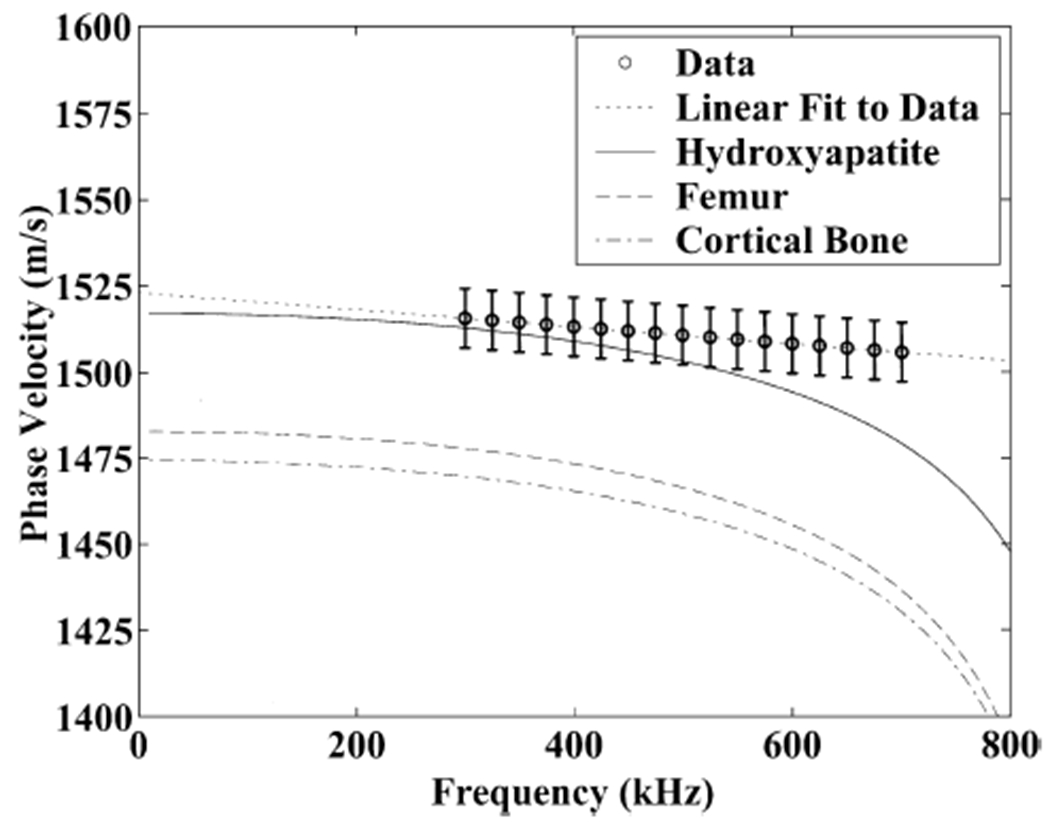
Frequency-dependent phase velocity measured in thirty calcaneus samples. Theoretical curves based on material parameters published for synthetic hydroxyapatite [38], powdered human femur [38], and cortical bone [39] are also shown. Error bars denote standard errors.

The parameter values assumed for the theoretical dispersion relations in Figure 5 were as follows. The material thicknesses, h₁ and h₂, were taken to be the average trabecular thickness (120 microns) and spacing (630 microns) of human calcaneus determined by histomorphometry [40]. As required by the theory, the sum of these values is small relative to the wavelength of ultrasound in water (about 3 mm at 500 kHz). The density of the bone was assumed to be 1850 kg/m³ [39]. The Lame’ constants were assumed to be λ = 15398 MPa, μ = 8000 MPa (synthetic hydroxyapatite [38]), λ = 58168 MPa, μ = 45500 MPa (powdered human femur [38]), and λ = 9306 MPa, μ = 3127 MPa (cortical bone [39]).

Discussion

Negative dispersion in trabecular bone has been reported by several groups [8, 9, 16, 23]. In this paper, a stratified model has been employed to predict frequency-dependent phase velocity in two-component media. The model performed well for phantoms consisting of alternating layers of polystyrene sheets and water. The absolute levels of phase velocity predicted by this model for calcaneus were fairly sensitive to the assumed values for material parameters. Hence the stratified model may not have more than a limited utility (error of about 5%) for prediction of average phase velocity. However, the frequency dependence of phase velocity (dispersion) seems to be relatively insensitive to the choices for material parameters. Moreover, the model predicts negative dispersion similar to the measurements reported here and elsewhere.

Although the experimental data for calcaneus presented here seem to vary approximately linearly with frequency between 300 and 700 kHz, the model predicts somewhat nonlinear behavior over this range with phase velocity curving increasingly downward at higher frequencies. (There may be a hint of the increasing rate of decline of phase velocity at higher frequencies in the data published by Nicholson and co-workers [9], Table 1). The measured rate of decline of phase velocity with frequency was somewhat less than that predicted by theory, particularly at high frequencies.

While the experimental data reported here were acquired with focussed transducers, the theory applies to plane waves propagating normally to the layer surfaces. The focussed beams used in the experiments had angular spectral content propagating at a range of angles about the normal direction. This difference may account for some of the discrepancy observed between theory and experiment for both the polystyrene and the calcaneus data.

Additional sources of disparity between predicted and measured phase velocity and dispersion in calcaneus may include the following. Trabecular bone consists of approximately cylindrically shaped rather than planar objects embedded within marrow (in vivo) or water (in vitro). In addition, the stratified model corresponds to an infinite medium. Edge-effects may have an effect in measurements in small samples containing roughly 16-27 cycles. Also, trabecular bone is not nearly so orderly as the stratified model. Also, although the material properties of trabecular bone have estimated in several indirect ways, substantial uncertainty remains regarding the true values. Finally, the assumption that h₁ + h₂ is much less than the wavelength becomes challenged at the high end of the frequency band of analysis.

Figure 3 illustrates potential diagnostic value in the dispersion measurement. The two phantoms investigated had precisely the same volumetric density. Specifically, their densities over any rectangular solid volume containing an equal number of polystyrene and water layers equals the arithmetic mean between the densities of water and polystyrene. However the structural (or microarchitectural) properties (layer thickness and spacing) of the two phantoms clearly differed. Hence, dispersion may contain useful diagnostic microarchitectural information not already contained in bone mineral density (BMD), the traditional measurement for diagnosis of osteoporosis. It is known that variations in BMD account for only 60 – 80% of variations in bone strength [12]. The remaining variations (20 – 40%) are thought to be due to variations in microarchitecture and elasticity.

Biography

Keith A. Wear graduated from the University of California at San Diego with a B.A. in Applied Physics in 1980. He received his M.S. and Ph.D. in Applied Physics with a Ph.D. minor in Electrical Engineering from Stanford University in 1982 and 1987.

He was a post-doctoral research fellow with the Physics department at Washington University, St. Louis from 1987-1989. He has been a research physicist at the FDA Center for Devices and Radiological Health since 1989. He has performed research in biomedical applications of ultrasound and magnetic resonance spectroscopy for 15 years. His research has included measurements of ultrasonic scattering properties from tissues, high-resolution spectral estimation, magnetic resonance spectroscopic image reconstruction methods, and analysis of statistical properties of ultrasonic echoes from tissues. He has become interested in applications with bone in the late 1990’s as FDA’s regulatory interest in bone sonometry has increased.

He is a senior member of IEEE, a member of IEEE Ultrasonics Society, IEEE Signal Processing Society, IEEE Engineering in Medicine and Biology Society, American Institute of Ultrasound in Medicine (AIUM), AIUM Technical Standards Committee, American Society for Testing of Materials, and the American Society for Bone and Mineral Research.