Abstract
Programmable shape morphing enables soft machines to safely and effectively interact with the environment. Stimuli-responsive materials can transform 2D sheets into 3D geometries. However, most solutions cannot hold their shape at zero power, are limited to predetermined configurations, or lack sufficient mechanical stiffness to manipulate common objects. We demonstrate here segmented soft electromagnetic actuators integrated with shape memory polymer (SMP) films, capable of deforming and latching into a broad range of configurations. The device consists of liquid metal (LM) coils in an elastomer shell, laminated between two SMP films. The coils are linked by narrow joints, on which stretchable heaters are patterned. Heating the SMP greatly reduces its stiffness. Driving current through an LM coil in the presence of a magnetic field then leads to large bending or twisting. Cooling the SMP locks in the shape, leading to load-bearing capacity. Complex shapes are obtained from an initially flat device.
Shape memory polymers are integrated with soft electromagnetic actuators for dynamic shape morphing and latching.
INTRODUCTION
Soft actuators with programmable shapes can perform complex tasks through morphological transformations. Soft devices that can change their geometries to achieve desired time-varying shapes have the potential to create mechanical functionalities beyond those of traditional machines (1, 2). Shape change using integrated actuators can be achieved based on different physical principles such as shape memory polymers (SMPs) (3), swelling hydrogels (4), liquid crystal elastomers (5), or dielectric elastomers (6). By generating local deformations using these actuation principles (7), it is possible to morph flat sheets into three-dimensional (3D) surfaces by bending (8), buckling (9), or folding (10). These techniques have been reported for a wide range of applications from microrobots that swim inside the body (11), to surfaces that respond to the environmental stimuli (12, 13), to soft robotic grippers (14). Developing on-demand shape morphing therefore has been a major goal of soft robotics because it enables key features such as a safe human-robot collaboration (15) and gentle manipulation of fragile objects (7). Research on shape programming has enabled the execution of tasks at multiple size scales (13, 16, 17) and bio-inspired systems that are getting better at mimicking their biological counterparts (18).
A common strategy for shape programming is to fabricate a 2D polymer sheet and morph it into 3D geometries (19). Numerous strategies have been demonstrated for complex shape transformations. Most of them switch from the as-fabricated state to a set predefined 3D geometry (19). For those systems, the final shape is usually determined at fabrication and cannot be reprogrammed (20). More recent studies have introduced devices that can be reconfigured to achieve a finite set of different geometries (21). Hajiesmaili and Clarke (6), for instance, have shown that multiple deformed states of a planar dielectric elastomer composite can be achieved by spatially varying the electric field in the elastomer sheet using a set of electrodes. Systems with multiple shape transformation can solve a broader range of robotic challenges.
Because of their compliant nature, soft systems exhibit large stimuli-induced shape transformations when driven by relatively small forces. These soft systems, however, cannot sustain large external loads. A main limitation of soft shape morphing systems is thus their low mechanical stiffness, which greatly limits applications. Variable-stiffness systems that can be soft during actuation and become rigid after the deformation have been developed (22, 23). These approaches generally combine a soft actuation mechanism with a stiffness tunable material such as bistable electroactive polymers (24), low-melting point alloys (25, 26), SMPs (27–29), and ionic electroactive polymers (30). Another limitation of soft shape-morphing designs is the need to continuously apply power to maintain the deformed shapes. In some actuator types, i.e., electromagnetic (EM) actuators, this leads to high energy consumption (31). The ideal shape morphing system can be reprogrammed repeatedly to reach a wide range of shapes, holds any position without any power consumption, has high load-bearing ability and variable stiffness, and can be rapidly and accurately deformed into arbitrary shapes. Although various designs have been developed to include some of these features in a single material design (32), a soft material system that combines all of these has not been developed.
We report a segmented EM beam with variable-stiffness joints that allows both control of shape transformation and shape fixation. By spatially tuning the stiffness of joints between the segments and by individually addressing the local EM actuators, we attain multiple distinct deformations that can be latched in zero-power states, as shown in Fig. 1. Because of the local stiffness control, large actuation deformation (in the soft state) and high blocking force (in the latched state) are achieved in the same device. In this study, we designed a device with three segments linked with three joints, representing a variable-stiffness robotic finger with multiple degrees of freedom. The number of the segments and joints can be scaled up to increase the complexity of the deformation or to develop a reconfigurable surface with 2D actuators array.
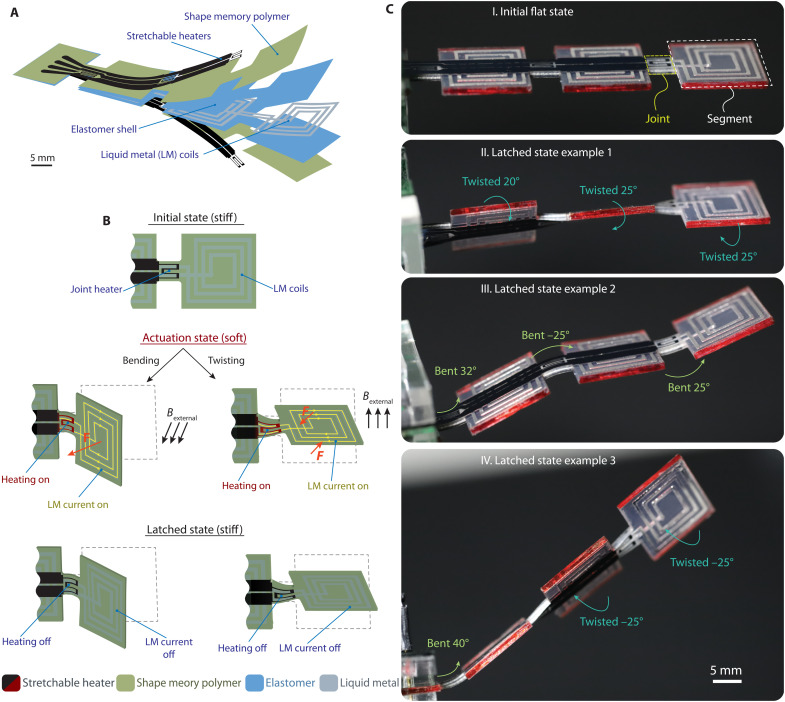
Fig. 1. Design of the multistable beam and examples of latched configurations.
(A) The device is composed of three square segments linked by three narrow joints. The segments consist of liquid metal (LM) coils in a silicone shell, covered on both top and bottom surfaces with a layer of a SMP. The joints have the same internal structure as the segments, but additionally have stretchable heaters on both sides. (B) The device is electromagnetically actuated by running current through one or several coils, generating a bending or a twisting force, depending on the orientation of the external magnetic field. When the hinges are cold (no current in the heaters), the SMP has a high stiffness, and the hinges do not deform. When the hinges are heated above the glass transition temperature of the SMP, the SMP rigidity drops by two orders of magnitude, and the Lorentz force allows for bending or twisting. Turning off the heating current then locks in the shape, allowing the coil current to be removed. (C) Photographs showing different latched states obtained from a series of bend-and-latch and twist-and-latch operations. By changing the order of the actuation and the type of the deformation of the joints, many distinct configurations can be reached.
RESULTS
Actuator design and operational principle
The device shown in Fig. 1 consists of three square “segments” linked by three narrow joints. The segments have a surface area of 15 mm by 15 mm and house the liquid metal (LM) coils, embedded in a silicone shell (see fig. S1). The silicone structure is sandwiched between two 60-μm-thick films of SMP. The coils and their electrical traces are made of eutectic gallium-indium (EGaIn) alloy, chosen because it is liquid at room temperature and can sustain large deformations (33, 34). The segments are electromagnetically actuated by running current through these LM coils, which generates a bending or a twisting force, depending on the direction of the external magnetic field, in our case from a permanent magnet.
The joints are the deformable narrow sections (less than 4.5 mm in width) of the device and have the same internal structure as the segments. However, they additionally have stretchable heaters on both sides. The heaters are made of carbon-loaded polyurethane (C-SMP), i.e., the SMP material mixed with carbon particles to make it electrically conductive. The heaters are used to control the temperature of the SMP and therefore to control the mechanical stiffness of the joints. These heaters are referred to as activators in this study, as they enable us to activate (Joule heating) or deactivate (cooling) the joints. During the actuation, the active joint deforms, whereas the deactivated joints do not undergo any deformation.
We use SMP layers in our device not only to fix the deformation (shape fixation) but also to recover the initial shape (shape recovery) (35). When the polyurethane SMP we use is heated above the glass transition temperature (Tg), its stiffness drops by more than a factor of 100 (see fig. S2): The SMP’s stiffness is 1.48 GPa at room temperature and drops down to below 10 MPa when the temperature is just above Tg. This temperature modulation changes the torsional and bending stiffness of the joints by more than 8 and 27 times, respectively (see fig. S3). This allows large deformation in activated (heated) joints, while the deactivated (unheated) joints remain nearly undeformed because they are one order of magnitude stiffer. The undeformed (initial) state of the joints can be recovered by simply reheating them to above Tg.
Cooling the SMP joints locks in the deformation and allows the coil current to be removed, leading to a zero-power load-bearing deformed state. The joints can be softened (activated) independently. The shape recovery and individual addressing enabled us to transform the device from its initial flat shape into various distinct configurations by changing the order, direction, and type of the joints’ deformation. Figure 1C shows the three latched states, among many configurations, obtained from a series of bend-and-latch and twist-and-latch operations. Because we have three joints that can be individually activated, three coils through which current can be driven independently in two directions, and because we can choose the direction of the external magnetic field and sequence of events, there is a very rich set of deformed states that can be reached.
A plate magnet with a radius of 35 mm and height of 35 mm is used to provide the external magnetic field (see fig. S8). By changing the position of the magnet relative to the LM coils, we can generate either a torque or a force. The right side of Fig. 1B (actuation state—twisting) illustrates a scenario where the direction of the magnetic field is orthogonal the LM coil. This generates a Lorentz force in the top and bottom sections (horizonal in the figure) of the coil. Because of the direction of the current, the bottom and top coil segments experience forces in opposite directions. These opposite forces create a torque on the segment and, hence, on any joint or segment that is located between the actuated LM coil and the clamp. However, this torque can only twist the soft (activated) joint, while the deactivated ones remain undeformed. The left-hand side of Fig. 1B depicts the magnet field–coil configuration for the bending case, where the magnet field and the axial direction of the LM coils are colinear. When a current is applied to the LM coil, the segment is attracted or repelled because of the interaction with the induced magnetic field (36). This configuration of the magnet and LM coils leads to bending in the soft joint.
The LM (EGaIn) coils have electrical resistance between 0.19 and 0.23 ohms. This allows us to drive up to 1.5 A through the coils without excessive heating. In our device, 1.5 A generates a torque of 140 mN·mm in twisting mode and a force of 67 mN in bending mode. The force and torque depend not only on the amplitudes of the current and of the magnetic field but also on the relative position of the magnet and the coil (distance and angle). Although higher currents can be driven in the LM coils to increase the force and torque, currents higher than 1.5 A heat the SMP past Tg, limiting shape fixation of the SMPs, as discussed in the following section.
Twisting and bending deformations in the soft (actuated) and stiff (latched) states
The device has four operating states for each joint: (i) actuated, (ii) shape fixing, (iii) latched, and (iv) recovery.
In the actuated state, the target joint is softened by Joule heating (activation), and the desired EM segments (which may be next to the joint but could also be further away) are bent or twisted by driving current in the selected LM coil or coils (actuation). In this actuated state, the soft (active) joints can deform in either twisting or bending mode as explained previously. The design parameters (film thickness, materials choice, etc.) are optimized to achieve higher deformation in this state.
Shape fixing is an intermediate state where the Joule heaters are turned off but LM current is still on. During this state, the temperature of the joints cools to below Tg, which allows the SMP layers to fix the deformation.
Once the joint is deactivated (cold), the LM current is turned off. We are then in the latched state. Because the joint deformation is locked, the device remains in the deformed configuration. The amount of the deformation that can be latched depends on the relative thickness of the SMP and elastic layers (i.e., the SMP must counteract the restoring force of the elastomer shell).
The final state is the recovery state, in which the joints go from their deformed configuration back to the undeformed state. The recovery is done by simply reheating the joints and using the memory effect of the SMP.
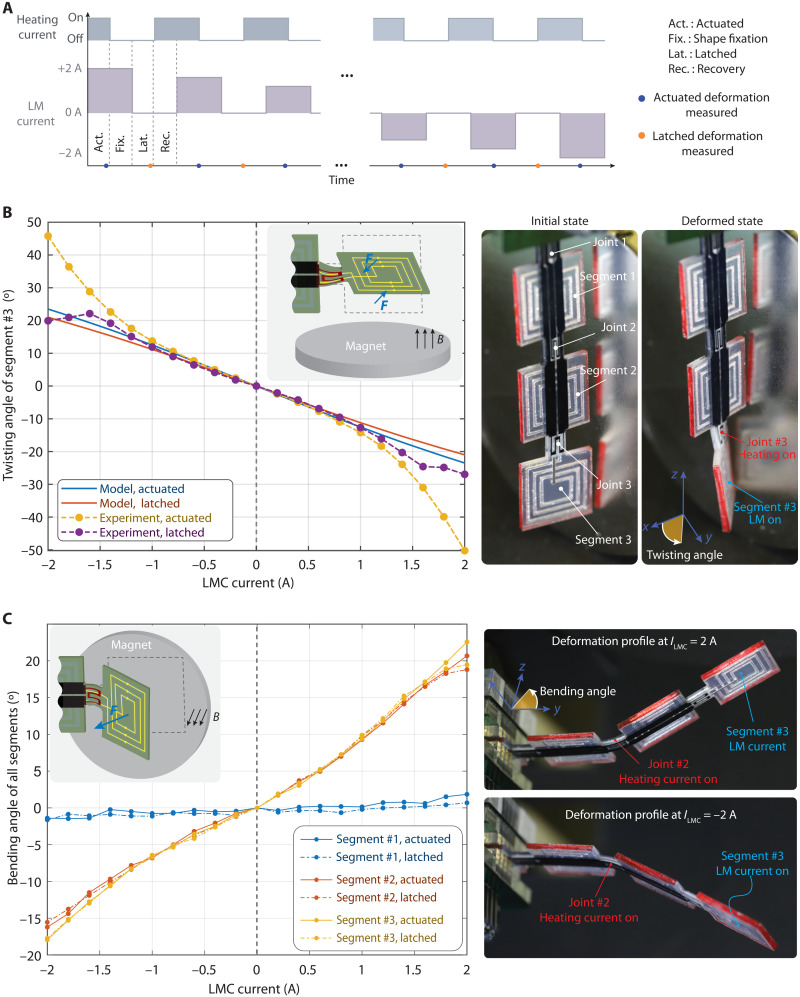
We first characterized the actuated and latched deformations of the joints in the twisting mode. We then performed the same measurements for the bending motion. For twisting, the segment is aligned perpendicularly to the magnet surface as shown in the right-hand side of Fig. 1B. When current flows through the LM coil, it generates a Lorentz force, proportional to the current, twisting in the activated joint. The joint deformation is determined by measuring the rotation of the tip segment. The segment rotation is captured for each current increment, and the image is processed to extract the twisting angle. Because the deactivated joints are 27 times stiffer than the active joints, the rotation of the segment corresponds nearly only to the twisting angle of the soft joints. The sequence of the activators (heaters) and actuator currents (LM current that generates the EM actuation) is shown in Fig. 2A. The deformation of the joints was measured at different LM currents, from −2 to +2 A, in increments of 0.2 A.
Fig. 2. Characterization of twisting and bending deformation and latching.
(A) Time sequence of the voltage applied to the heaters and of the current driven in the LM coils (LM current). For each LM current, the device is actuated, the shape is then fixed, and, lastly, the initial flat shape is recovered by heating the joint. (B) Measured and simulated twisting angle of the third joint versus LM current in the third segment, heating only the third joint. The initial and deformed states of the beam are shown on the right-hand side of the panel. The relative position of the magnet and segment is shown in the inset. The model predictions and the experimental data are in very good agreement for the LM current up to 1.5A. Above this current, heat from current in the LM coil softens the joint even when no heating voltage is applied. (C) Measured actuated and latched bending angles of all three segments, with heating applied only to the second joint and LM current only in the third segment. Because the joints between the holder and the first segments and between the second and third segments remain stiff during this test, segment 1 does not move, and segments 2 and 3 have the same bending angle.
A sample twisting deformation of the third joint is shown on the right-hand side of Fig. 2B. Because the third joint was activated, only this one twisted when the third segment was actuated. The relative position of the magnet and the segment to generate the twisting (torsional) motion is shown in the inset of Fig. 2B. In this configuration, the magnetic field is perpendicular to the surface normal of the segment (see left-hand side of Fig. 1B). The joint twists due to the torque created by the Lorentz forces acting in the opposite direction of the top and bottom segments of the LM coil. The dashed lines in Fig. 2B show the measured twisting of the joint in the actuated (orange) and latched states (purple). The actuation deformation increases linearly between 0 and 1.5 A of the LM current. When the LM current is above 1.5 A, the actuated deformation increases faster than linearly. This is due to heat flow from the actuated (third) segment to the joint. This cross-heating increases the joint temperature during the actuation, making it softer than it would be if heated only with the heating element.
For LM currents lower than 1.5 A, the latched deformation is nearly identical to the actuated deformation, because of the high shape fixation ratio of the SMP. For LM currents higher than 1.5 A, larger twisting is achieved during the actuation, as explained above. However, during the shape fixation state, this extra heat reduces the shape fixation ratio, because the joint is latched at an elevated temperature (see fig. S9). As a result, increasing the LM current above 1.5 A does not further increase the latched deformation. The thermal limitation of the LM current on the trade-off actuation and latching deformation, as well as on the choice of SMP material, is discussed in the Supplementary Materials and schematically illustrated in figs. S6 and S7.
Figure 2B also includes the modeling results of the joint deformation in the actuated and latched states. The model, presented in the optimization section below, is based on the analytical analysis of the beam deformation and shape memory effect (see the “Numerical analysis to achieve large actuation deformation and high mechanical stiffness” section for more details). It predicts very well the actuated and latched deformations at LM currents below 1.5 A. Because we neglect the effect of heat transfer from the EM coil to the joint, the modeled deformation deviates from the measured one at LM currents higher than 1.5 A. When the polarity of the LM current was reversed, the joint twists in the opposite direction (see Fig. 2A). Actuated and latched deformations in the reversed polarity follow a similar trend: The deformation is linear deformation below 1.5 A and is nonlinear above this current.
The actuated and latched deformations of the joints were then investigated in the bending mode. As shown in the inset of Fig. 2C, bending occurs when the external magnetic field is parallel to the surface normal of the segments. For the bending test, the second joint was activated, while the third segment was actuated. Photographs of the deformed device at 2 and − 2 A of LM currents are shown in Fig. 2C. When the LM current of the third segment was reversed, the second joint deformed in the opposite direction. As seen in the photographs, only the second (activated) joint deforms during the actuation, whereas the deactivated joints remain stiff and do not undergo visible deformation. The first segment thus has zero deformation, whereas the second and third segments move together with the same bending angle, as seen in Fig. 2C. The graph shows the bending angle of the segments in the actuated and latched states for different LM currents. In the bending mode, a positive LM current moves the segments toward to the magnet, whereas a negative LM current moves the segments away from the magnet. The bending angles of the moving segments are therefore higher in the approaching cases than in the moving-away, simply due to a higher magnetic field. As seen from the graph, almost all of the deformation achieved during the actuation is then locked in by the SMP layers once cooled. The same deformation analysis was carried out for the remaining joints, and the results are included in fig. S10.
In both bending and twisting scenarios, the activated joint deforms and latches independently of the deactivated ones, e.g., when the second joint is bent with an angle >20°, the unaddressed first joint has deformation of <2°. Because the deactivated joints are stiff (8 times stiffer in bending and 27 times stiffer in twisting), they hold their current state. The deformation achieved during the actuation is locked by the SMPs when cooled down below the glass transition temperature. To minimize unwanted heating, we chose to operate our devices at ±1.5A. In this region, we can achieve large deformation and also can lock it with high fixation ratio.
Complex shapes obtained by sequential deform-and-latch operations
The variable-stiffness beam can be transformed into complex shapes by controlling and locking the deformation of each joint. This is possible because the joints can be individually activated and the segments can be actuated independently. To demonstrate this ability, we deformed and latched the joints in different orders and directions to achieve multiple complex shape transformations.
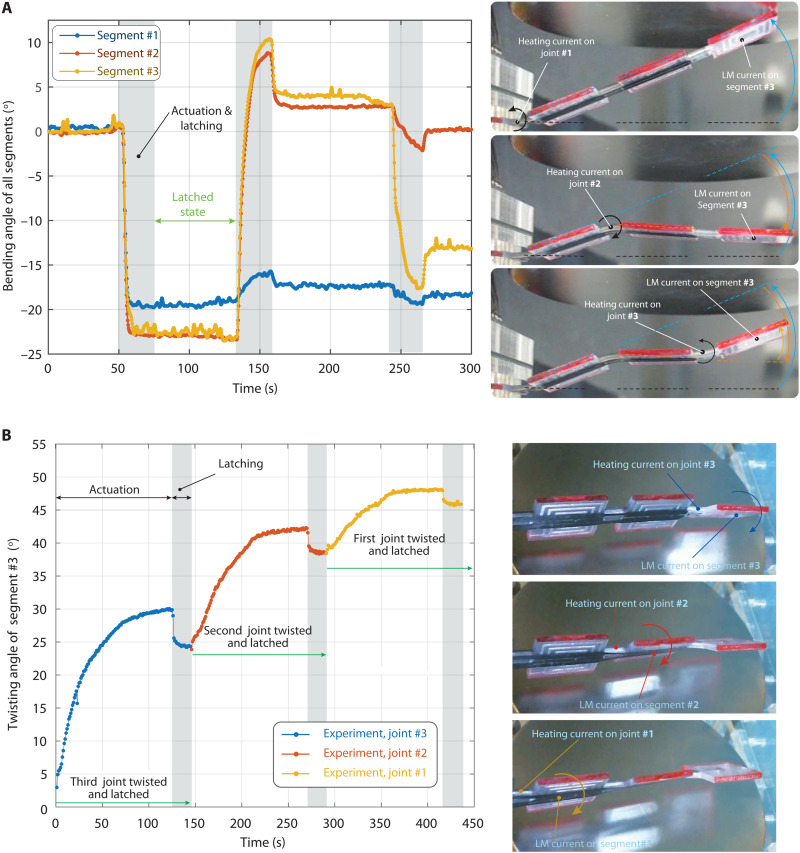
Figure 3A shows the sequential bending and latching of three joints. During the test, the first, second, and third joints were activated in sequence, with always only the third EM segment actuated. The initially flat device was first bent around the first joint, in the upward direction, by applying +1.5-A LM current. It was then latched (see the first photograph in Fig. 3A). Then, the second joint was softened and then bent in the downward direction using −1.5 A of LM current. After the second joint was latched in this position (second photograph in Fig. 3A), the third joint was deformed in the upward direction and latched (last photograph in Fig. 3A). The deflection angle of the segments during this shape transformation (extracted from the recorded video; see movie S1) is plotted in Fig. 3A. When the first joint is activated, all segments move together with the same angle because the joints (second and third) between them are stiff. Similarly, when the second joint is addressed, the second and third segments bend with the same angle and subsequently latch with small relaxation. When we compare the latching performance of the joints, a small difference is observed. As seen from Fig. 3A, the first joint has slightly better latching than the others. This is due to the long distance between the actuated segment (third) and the activated joint (first). The longer the distance between the actuated segment and the activated joint, the smaller the heat transfer, and thus the smaller the cross-heating, resulting in a latching angle closer to the actuation angle.
Fig. 3. Sequential actuation and latching of different joints, in bending and in twisting.
(A) Bending: Time evolution of the bending angle of the segments. The first, second, and third joints were softened, one after the other, while the third segment was actuated with +1.5 A of LM current when heating the first and third joints and with −1.5 A of LM current when heating the second joint. The first and third segments thus move in the same direction, and the second segment moves in the opposite direction. Between actuation steps, the joints were latched. (B) Twisting: Twisting angle of the tip segment is plotted as the joints were sequentially deformed in the same direction and latched. As expected, the narrowest joint (joint #3) has the highest twisting, whereas the widest joint (joint #1) has the smallest deformation. The model prediction for the actuation and latched states (only stationary analysis) agrees reasonably with the experimental results.
In Fig. 3B, we show an example of increasing the twisting angle of the tip segment by twisting and latching the joints in the same direction. The joints were sequentially activated, twisted, and locked into their deformed state. Photographs of the device after each joint deformation are shown in Fig. 3B. The graph plots the deflection angle of the bottom segment (tip segment) when the third, second, and first joints are twisted, one after the other. We observe that θjoint3 > θjoint2 > θjoint1. This is due to varying widths of the joints: wjoint1 > wjoint2 > wjoint3, given different twisting stiffness, and also due to the temperature uniformity of the joints, i.e., the first joint heaters provide more uniform temperature distribution compared with the third joint heaters. The section of the SMPs that is not sufficiently heated, e.g., if temperature is below Tg, significantly increases the overall joint stiffness in the actuated state. Joint stiffness as a function of the temperature is shown in fig. S3. Although our model only predicts the actuated and latched deformations in the static (stationary) mode, we include the model predictions on the graph of angle versus time (Fig. 3B) to compare the model with the measured final deformed state. The model accurately predicts the behavior of the joints during both actuated and latched states. The small difference between the model and experimental data is mainly attributed to the nonuniform temperature distribution in the joints and the inaccuracy in the temperature measurement of a stack structure using an infrared camera.
Different strategies can be used to improve the shape transformation, for example, obtaining larger deformation, faster deformation, creating more complex shapes, and lowering energy use. A combination of twisting and bending can be used to achieve more complex shapes; some examples of attainable shapes are shown in Fig. 1C. For instance, the last image of Fig. 1C was obtained by bending and latching of the first joint followed by twisting and latching of the second and third joints. Our approach gives the freedom to choose both the deformation type and the deformation location. Unlike the hierarchical shape transformation techniques (28, 37) where the order of the deformations is fixed, this technique provides higher degrees of freedom, thus more options of distinct and complex shapes.
When we do not use the latching function of the device, we can operate it in a dynamic mode, in which the desired joint is kept in the soft state and LM current is rapidly changed. This allows for much shorter response times. Movie S1 and fig. S11 show the dynamic response of soft and rigid joints at different actuation frequencies, up to 4 Hz. The bending angle versus time plot shows no reduction in amplitude at 4 Hz compared with lower actuation frequencies.
Shape morphing to match a target object
In this section, we show how the shape of the beam can be programmed to manipulate objects or to align its segments according to a slit in an object. The latching ability enables both the alignment of the device to the object and also firm holding.
Figure 4A shows frames from movie S2 starting with a straight beam. One segment is first twisted to match the slit orientation of the object in order to slide in. A further twisting motion is used to prevent extraction, allowing the now twisted beam to be used to pull on the object. The undeformed beam was initially positioned vertically, with an angle between the object entrance slit and the segments of 20°. To match the slit orientation, the first segment of the beam was twisted by −20° around the z axis and subsequently latched in this deformed configuration. Once latched, the device was lowered manually so the first segment fitted inside the object. Then, the second joint was activated and twisted in the opposite direction of the first rotation, with an angle of +20°. The second motion allowed to engage with a firm grip. Once the joint was latched in the final deformed state, the device was pulled up, taking the object with it. This latched state of the device is stable and robust enough to hold heavy weights, up to 2.5 N (see movie S2).
Fig. 4. Matching target shapes by a series of deform and latch operations.
(A) An initially flat beam is first deformed to match the slit orientation in the object and then further actuated to allow picking up the object. To match the slit orientation, the first segment of the beam is twisted and latched by −20° around the z axis. The device is then lowered so that the first segment is inside the object. The second joint then is softened and twisted to an angle of +20°, thus preventing the device from being pulled out, and hence allowing the object to be picked up. See movie S2. (B) In this example, bending on two axes is required to match the slit on the target. The slide on the green object is rotated by −25° and 25° with respect to the x and z axes. The beam was initially flat and was aligned with the z axis. The device was first bent and latched with an angle of 25° using the first joint and then twisted through the third joint with an angle of 25°. Throughout the second deformation, the first joint is locked and does not deform. Once the device configuration matched the object slit orientation, the device was lowered, slotting in as required. (C) Frames from movie S2 showing the insertion of an initially flat device through a series of differently oriented slits. The initially flat device successfully passed the apertures by performing a series of local twisting and shape fixation.
Figure 4B includes frames from movie S2, showing the deformation of the beam to match the slit orientation in a tip-tilt stage. The beam was initially flat (undeformed) and was placed longitudinally along the z axis (its surface normal was parallel to the y axis). The object was placed on the stage and was rotated with angles of −25° and 25° with respect to the x and z axes. For the beam to completely match the slit, it has to go through several deform and latch operations, where each operation needs to be independent from the others. A single bending or twisting deformation would not be sufficient for a perfect match. The device was first bent with an angle of 25° using the first joint and then latched. The device was then twisted through the third joint with an angle of 25°. Throughout the second deformation, the first joint was locked and does not deform. Once the device configuration matched with the slit orientation, the device was lowered down manually to demonstrate the fitting. We showed two sequential deform-and-latch operations using the first and the third joints. Multiple distinct deformations can be achieved by changing the sequence and the type of the deformation of each joint.
Figure 4C shows the frames from another demonstration where a sequence of twisting of three joints is required to allow the system to pass through a set of three slits. The initially flat device was inserted through the obstacles with actuate-and-latch operation for each aperture, flowed by a lowering step. To pass through all obstacles, the device had to go through a series of local deformation and shape fixation.
Numerical analysis to achieve large actuation deformation and high mechanical stiffness
We take advantage of the local stiffness tuning to achieve large deformations and use shape memory effect to fix the deformations into place. However, there is a trade-off between achieving large actuation deformation and high shape fixation. Using thin layers of SMP adds less stiffening, allowing larger deformations for a given EM force. However, very thin SMP layers cannot resist the elastic recovery forces of other layers, leading to low shape fixation. In addition, thin SMP layers cannot hold their shape under high external loads. We derive a numerical model to maximize the performance of the beams by getting the best trade-off between the stiffening and the shape fixation of SMPs.
On the basis of a model that we previously developed (38) for soft actuators combining SMP and dielectric elastomer actuators, we optimize the design parameters of the multistable soft EM actuators. As the joints are the deformable sections of the device, we optimize their geometries for both twisting and bending motions. Their widths are designed to be as small as possible to reduce the torsional stiffness (the torsional stiffness is proportional to the third power of the width). However, the heaters and their traces induce a constraint for the minimum width of each joint. Therefore, the joints along the beam have slight differences in their widths, from 4 to 4.5 mm, as those closer to the anchor have more traces leading to the heaters. Although the width of the beam varies along the longitudinal direction, the thickness of the layers is uniform everywhere in the device (see fig. S1). The silicone layer has a constant thickness of 1.30 mm, chosen to accommodate two layers of LM channels. The thickness of the SMP layers is the most crucial design parameter as it affects the amplitude of the actuation deformation and the load-bearing capacity of the beam. Therefore, the SMP thickness is optimized to achieve large deformation and high mechanical stiffness in both bending and twisting scenarios.
In the twisting mode, the LM coils are placed on a magnetic field that is perpendicular to the surface normal, as shown in Fig. 1B. When current flows in the LM coils, a torque is created by the Lorentz forces, given by
| (1) |
where Bz(zi) is the z component of the magnetic field at a distance of zi, I is the LM current, li is the length of the coil segment, and di is the distance between the coil segment and the center of the rotation (see fig. S4). Recall that zi and di depend on the angle of the twist (θact). These parameters can be written as di = di0 cos (θact) and zi = zi0 + di0(1 − cos (θact)), where subscript 0 refers to the initial (undeformed) state. For the sake of readability, we do not substitute these expansions for the following equations (the full expressions are included in the Supplementary Materials). The general formula of the twisting angle for the actuation can be written as
| (2) |
where T is the torque acting on the segment, Ljoint is the length of the joint (5 mm for all joints), and <GJ> is the equivalent torsional rigidity of the joint in the soft state. In this equation, G stands for the shear modulus of the materials, and J is their second moment of area. The details of the torsional rigidity calculation are provided in the Supplementary Materials.
Once actuation is achieved, the deformation is locked in by the SMP layers. In this latched state, the SMPs fix their deformation, whereas the silicone layer exerts an elastic force, given their deformation from the initial state. The equation of the torque equilibrium for the latched state can be written as
| (3) |
where θlatch is the angle of the twist in the latched state. Recall that, because the SMP layer already fixes its actuation deformation during the shape fixing step, the angle of the twist for this layer is θactuation − θlatch (not θlatch). In this equation, we use the shear moduli of the materials at the cold state because both SMP and silicone layers are at the room temperature.
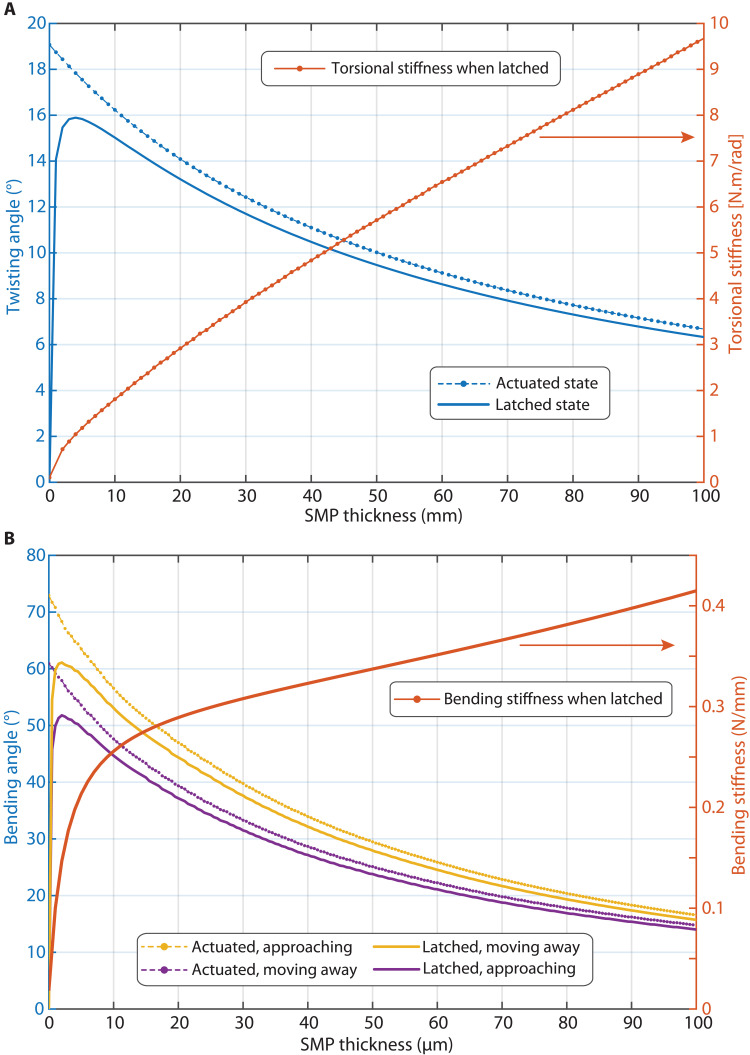
Figure 5A shows the computed actuation and the latched deformations of the third joint as a function of SMP thickness. The highest actuation deformation is obtained at tsmp = 0, and it decreases as the SMP thickness increases. At tsmp = 0, i.e., when there is no SMP, the joint is soft and is easy to deform. The SMP films on both sides of the silicone layer increase the torsional rigidity because of the stiffening of the SMPs, even in the hot state. As depicted in Fig. 5A, increasing the SMP thickness reduces the actuation deformation. Although the actuation deformation is high for thinner SMP layers (<5 μm), the latching is small because the thin SMP layers cannot counter the elastic restoring force of the polydimethylsiloxane layer, resulting in very large relaxation and hence small latched deformation. The maximum latched deformation takes place at around 10-μm SMP thickness. Above 10 μm, the latched deformation decreases as the SMP thickness increases, because of smaller actuation deformation.
Fig. 5. Optimization of the SMP thickness to achieve both large actuation deformation and high mechanical stiffness.
(A) The computed twisting angle plotted as a function of the SMP thickness for the actuated (SMP is hot, Y95°C = 7.6 MPa) and latched (SMP cold, Y25°C = 1.48 GPa) states. The actuation deformation is highest at tSMP = 0 because the stiffness of the SMP layer is then zero. At zero SMP thickness, however, the latched deformation is zero. Increasing SMP thickness increases latched deformation until a maximum is reached for an SMP thickness of 10 μm. Above this thickness, the actuation decreases because of higher stiffening effect of the hot-state SMP. (B) Computed bending angle of the joints as a function of the SMP thickness. When there is zero SMP thickness, the joint has the highest deformation. However, there is no shape fixation. We choose an SMP thickness of 50 μm to reach both large latched deformation (in both bending and twisting modes) and high mechanical stiffness. Some deformation range is sacrificed to increase the holding force.
To decide on the SMP thickness, we also need to take into account the mechanical stiffness of the devices, as a proxy for robustness under external loads. In addition, we need to perform the same analysis for the bending configuration as we did for twisting. We consider the mechanical stiffness as one of the important design criteria because we want devices with high load bearing ability when latched. The torsional stiffness in the latched state is plotted on Fig. 5A. It increases as the SMP thickness increases. There is a trade-off between the latched deformation and the mechanical stiffness. Higher mechanical stiffness comes at the price of lower deformation.
A similar analytical approach is also used to compute the bending deformation of the joints during the actuated and latched steps. In bending mode, it is difficult to numerically quantify the EM force between the LM coils and the magnet. We therefore used a finite element model (COMSOL) to determine the interaction force and then used Stoney’s equation to quantify the bending deformations (39). Details of this calculation can be found in the Supplementary Materials. Figure 5B shows the bending angles and bending stiffness as a function of SMP thickness. Unlike the twisting scenario, the distance between the magnet and the actuated segment changes between the negative and positive values of the LM currents. Because this distance differs in approaching the magnet and moving away from the magnet cases, the actuation deformation has different curves when approaching the magnet or moving away. When the segment approaches the magnet, it experiences a higher magnetic field than when it moves away from the magnet (see fig. S5) and therefore reaches a higher bending angle when approaching the magnet. Similar to the twisting analysis, larger bending deformation is attainable with thinner SMPs; however, the device then latches with a lower amplitude. Although thick SMPs provide a high fixation ratio, they reduce the actuation performance because of increased stiffening and result in small final latched deformation. The highest latched deformation is predicted for an SMP thickness of around 10 μm. When we choose SMP thickness, we however also consider the mechanical stiffness of the device at the latched state. As we want our device to be more robust against external loads, we choose SMP thickness of 50 μm, giving up some deformation to obtain a higher stiffness in the cold state.
The models shown here predict very well the behavior of the joints in bending and twisting modes. It also provides insights into the joint’s behavior for actuation and latched states. Figure 2B, for instance, compares the model prediction with experimental data, with a good agreement. At higher LM current (above 1.5 A), the device deforms more than predicted, because of heat transfer from the actuated segment, which is neglected in the modeling.
Stiffness of the joints in the actuated and latch states and their performance under cyclic loading
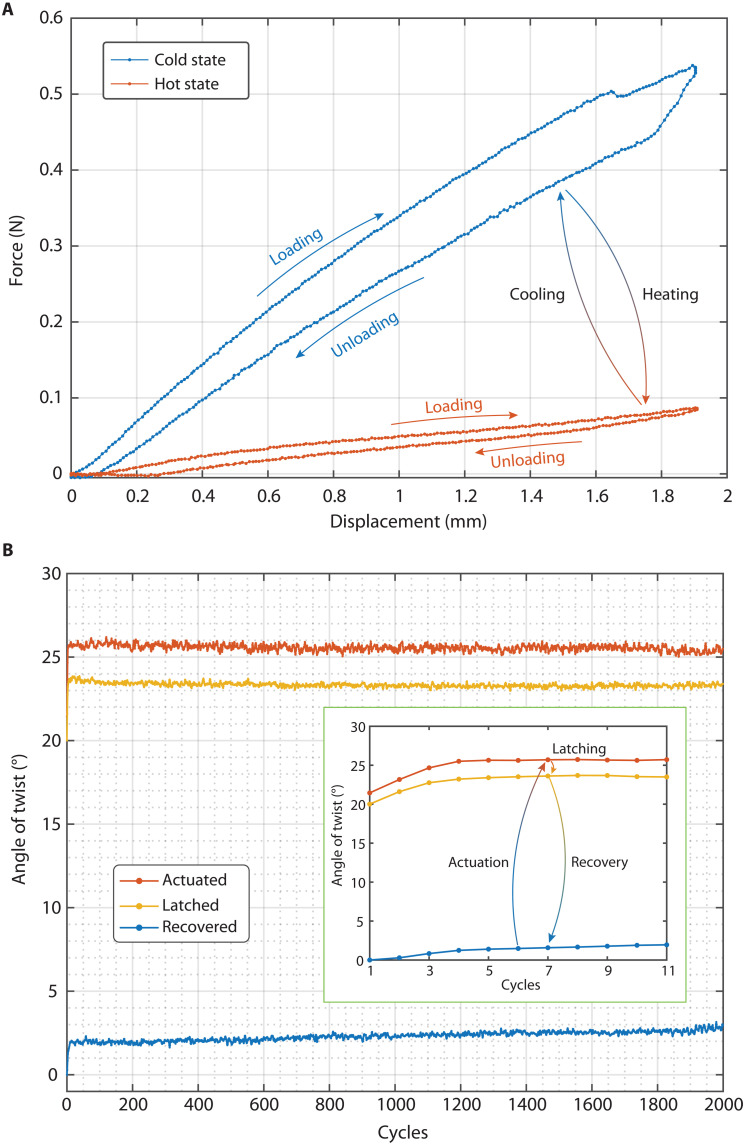
The bending stiffness of the joints was measured at 25° and 90°C, corresponding the temperature of the latched and actuated states. The joints were clamped at one end, and the load was applied to the other end (see fig. S12). Figure 6A plots force versus displacement of the one joint at both temperatures. The bending stiffness of the joints at room temperature is approximately seven times higher than the stiffness at 90°C, e.g., at room temperature, 340 mN of force is required to displace the joint by 1 mm, whereas in the hot state, only 49 mN of force is needed for the same displacement. More details on the measurement setup and on deformation of the joints at different temperature are shown in fig. S12.
Fig. 6. Bending stiffness of the joints in the actuated and latched states and their cyclic performance.
(A) Measured bending stiffness of a joint at 25° and 90°C, corresponding to the temperatures in the actuated and latched states. The bending stiffness of the joint at room temperature is approximately seven times higher than at 90°C. (B) Time evolution over 2000 cycles of the twisting angle of a joint cycling through the actuated, latched, and recovered states. The three angular positions remain nearly constant over the 33 hours of the test.
The time-dependent behavior of soft actuators under cyclic actuation is important for long-term applications. Soft and electroactive materials are often challenging because of their material nonlinearity and time-dependent viscoelastic behavior (40). We experimentally evaluated the performance of our devices for over 2000 cycles, using the third joint and third segment. For each cycle, the segment was first actuated, then latched, and, lastly, recovered. The joint was heated with a power of 500 mW, and the segment was actuated with 1.25 A of current. Figure 6B shows the time evolution of the twisting angle in these states for 2000 cycles. The first three cycles exhibit a small drift. This is the well-known creep behavior in elastomers and in SMPs, which occurs mostly in the first few cycles (41, 42). After the first three cycles, the device has almost constant deformation profiles, showing its suitability for cyclic operation.
DISCUSSION
This paper reports variable-stiffness EM actuators that are capable of performing adaptive shape morphing and latching. The devices provide versatile movements from planar shapes into distinct 3D configurations and latch in the deformed state, providing highly energy efficient systems with good load bearing. We show that the device is able to transform between a low-stiffness state for easy deformation and a high-stiffness state for robust holding.
Once softened by the Joule heaters (activated), the device achieves fast shape transformations thanks to the EM actuation of the LM coils. When stiff (deactivated, i.e., cooled), it forms a robust structure that can withstand large external loads, e.g., the joints are >7× stiffer in the cold state and then in the hot state. This technique holds a potential for reconfigurable systems where distinct and robust shapes are needed for long-period of time.
The current design leaves room for improvements. Here, we showed a proof of concept for a 1D array. A planar surface with 2D array of actuators could be developed for higher geometric complexity. The stretchable heaters, as another example of improvement, could be used as resistive sensors for positional feedback. This would allow for accurate shape control without external sensors.
We used thermoresponsive SMPs for shape fixation and Joule heating to stimulate them. While the EM actuation can be very fast (31), the heating and cooling times impose a limit on actuation and latching speeds. The actuation speed can be increased by using higher heating power in a shorter time. An active cooling system (instead of passive cooling) would accelerate the latching process. Another approach to accelerate the speed would be using an SMP with lower and sharper glass transition temperature region. This would allow for more quickly reaching a different state, but it would be more sensitive to undesired Joule heating from the LM current. Scaling down the size is another approach that reduces the response time and allows faster actuation and recovery.
In our design, a silicone layer is sandwiched between two SMP films. Having the SMPs on the outer sides increases the overall stiffness of the device at the cold state. Heating and cooling these SMP layers change the stiffness by 8 times in bending and 27 times in the torsional mode. The silicone layer could be replaced with the SMP to much increase the stiffness change between the cold and hot states. This requires the development of fabrication processes where the SMP is to be molded with microfluidic channels.
A plate magnet is used here to generate the external magnetic field. Although this greatly simplified our experimental setup, it is not suitable for portable or wearable devices, and it requires manual repositioning to obtain different types of motion. By replacing the permanent magnet with several electromagnets, the direction of the magnetic field can be rapidly changed, allowing for a quick switch between bending and twisting.
MATERIALS AND METHODS
Choice of the SMP material
Figure S7 shows the measured Young’s moduli of two different SMP materials are functions of temperature. MM4520 and MM7520 are thermoplastic polyurethanes with glass transition temperatures around 45° and 75°C. Figure S7b shows the calculated EM force of the segment and the simulated temperature of its adjacent joint as functions of the LM current. As depicted in the graph, using the SMP with higher glass transition temperature allows higher EM force before getting softened because of the Joule heating from the LM current. We therefore choose the SMP with high Tg (MM7520) for this study.
Thermomechanical characterization of SMP
The thermomechanical characterization of SMP (MM7520 from SMP technologies) is carried out using a dynamic mechanical analyzer (DM Q800). This enables us to measure the storage modulus (Y′) and loss modulus (Y″), and loss factor tan(delta) of the material as functions of the temperature. The measured data are shown in fig. S2. When the temperature is swept from 20° to 100°C, the modulus of the SMP reduces more than 100 times, where most of this stiffness change occurs in a narrow range around 80°C (the glass transition region).
The mechanical stiffness of the silicone layer sandwiched by two SMP layers strongly depends on temperature. The design of these joints and their bending and torsional stiffness as a function of temperature are shown in fig. S3. Both the bending and torsional stiffness decrease significantly when the temperature increases above 80°C.
Fabrication
The fabrication flow process of our device is summarized in fig. S13. The fabrication starts with the manufacturing of the conductive SMP (heaters) + SMP + PDMS composite. An A4-size polyethylene terephthalate (PET) sheet was used as the substrate layer. The surface of the PET was treated with oxygen plasma, followed by coating a thin layer of Teflon using a thin film applicator. The Teflon layer acts as a sacrificial layer and eases the release of the device layers.
To fabricate the conductive SMP, we dissolved MM7520 pellets in a glass container with dimethylformamide (DMF) at a weight ratio of 1:4 at 80°C for 12 hours. In another container, the carbon particles (Ketjenblack KB300) were ball mixed with DMF at a weight ratio of 1:20 at 2000 rpm for 5 min. The solutions in these two containers are then ball mixed together for another 5 min at 2000 rpm. This mixture was blade casted on the Teflon sacrificial layer. The DMF in this solution was evaporated on a hotplate at 80°C for 4 hours. Once the conductive SMP layer was cured, the layer was patterned using a laser cutter to define the local heaters. A bare SMP mixture was then casted on the heaters using the thin film applicator. The bare SMP solution was prepared by mixing the SMP pellets with DMF at a weight ratio of 1:4 and dissolved at 80°C for 12 hours. The final layer in this composite was the PDMS layer. For this layer, we used Sylgard 186 (from Dow Corning) with a ratio of 1:10 (curing agent: prepolymer) and casted it on the SMP layer. Last, the composite was put in the oven at 80°C for 1 hour. After this step, the composite is ready to bond with the microchanneled PDMS. These steps are schematically shown in fig. S13.
To fabricate the PDMS layer with the microfluidic channels, we used polymethyl methacrylate (PMMA) master molds. First, the mixture of Sylgard 186 was poured into the top and bottom PMMA molds. The air bubbles were removed using a desiccator. The bottom and the top were then aligned and clamped. The PDMS structure was cured in the oven at 80°C for 2 hours.
The final step of the device assembly was to bond the molded PDMS with the composite layers using an oxygen plasma treatment. Both surfaces of the molded PDMS and the PDMS side of the composite layers were treated with oxygen plasma. The PDMS was then sandwiched by the composite layers, forming the final device. This way, we had a symmetrical design with the heaters positioned on the exterior of the structure, allowing for easy electrical connections. The final step of the fabrication was to fill the silicone channels with LM. The channels were filled with EGaIn alloy using a syringe. After the electrical connection was made, the channels were sealed with a silicone glue.
Acknowledgments
We thank E. Leroy for help with the experimental setup.
Funding: This work was supported by the Swiss National Science Foundation, grant number 200020_184661.
Author contributions: Conceptualization: B.A. and H.S. Methodology: B.A. and H.S. Investigation: B.A. Visualization: B.A. and H.S. Supervision: H.S. Writing—original draft, review, and editing: B.A. and H.S.
Competing interests: The authors declare that they have no conflict of interest.
Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Raw data and analysis scripts are available from the Zenodo repository at https://doi.org/10.5281/zenodo.5802450.
Supplementary Materials
This PDF file includes:
Supplementary Text
Figs. S1 to S13
Tables S1 and S2
Other Supplementary Material for this manuscript includes the following:
Movies S1 and S2
REFERENCES AND NOTES
- 1.Rus D., Tolley M. T., Design, fabrication and control of soft robots. Nature 521, 467–475 (2015). [DOI] [PubMed] [Google Scholar]
- 2.van Manen T., Janbaz S., Zadpoor A. A., Programming the shape-shifting of flat soft matter. Mater. Today 21, 144–163 (2018). [Google Scholar]
- 3.Behl M., Kratz K., Zotzmann J., Nöchel U., Lendlein A., Reversible bidirectional shape-memory polymers. Adv. Mater. 25, 4466–4469 (2013). [DOI] [PubMed] [Google Scholar]
- 4.Le X., Lu W., Zhang J., Chen T., Recent progress in biomimetic anisotropic hydrogel actuators. Adv. Sci. 6, 1801584 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ware T. H., McConney M. E., Wie J. J., Tondiglia V. P., White T. J., Voxelated liquid crystal elastomers. Science 347, 982–984 (2015). [DOI] [PubMed] [Google Scholar]
- 6.Hajiesmaili E., Clarke D. R., Reconfigurable shape-morphing dielectric elastomers using spatially varying electric fields. Nat. Commun. 10, 183 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.McCracken J. M., Donovan B. R., White T. J., Materials as machines. Adv. Mater. 32, e1906564 (2020). [DOI] [PubMed] [Google Scholar]
- 8.Bauhofer A. A., Krödel S., Rys J., Bilal O. R., Constantinescu A., Daraio C., Harnessing photochemical shrinkage in direct laser writing for shape morphing of polymer sheets. Adv. Mater. 29, 1703024 (2017). [DOI] [PubMed] [Google Scholar]
- 9.Kim J., Hanna J. A., Byun M., Santangelo C. D., Hayward R. C., Designing responsive buckled surfaces by halftone gel lithography. Science 335, 1201–1205 (2012). [DOI] [PubMed] [Google Scholar]
- 10.Hawkes E., An B., Benbernou N. M., Tanaka H., Kim S., Demaine E. D., Rus D., Wood R. J., Programmable matter by folding. Proc. Natl. Acad. Sci. U.S.A. 107, 12441–12445 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang H. W., Sakar M. S., Petruska A. J., Pané S., Nelson B. J., Soft micromachines with programmable motility and morphology. Nat. Commun. 7, 12263 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Deng H., Zhang C., Su J. W., Xie Y., Zhang C., Lin J., Bioinspired multi-responsive soft actuators controlled by laser tailored graphene structures. J. Mater. Chem. B 6, 5415–5423 (2018). [DOI] [PubMed] [Google Scholar]
- 13.Cui J., Huang T. Y., Luo Z., Testa P., Gu H., Chen X. Z., Nelson B. J., Heyderman L. J., Nanomagnetic encoding of shape-morphing micromachines. Nature 575, 164–168 (2019). [DOI] [PubMed] [Google Scholar]
- 14.Shintake J., Cacucciolo V., Floreano D., Shea H., Soft robotic grippers. Adv. Mater. 30, 1707035 (2018). [DOI] [PubMed] [Google Scholar]
- 15.Park Y. L., Chen B. R., Wood R. J., Design and fabrication of soft artificial skin using embedded microchannels and liquid conductors. IEEE Sens. J. 12, 2711–2718 (2012). [Google Scholar]
- 16.Diller E., Sitti M., Three-dimensional programmable assembly by untethered magnetic robotic micro-grippers. Adv. Funct. Mater. 24, 4397–4404 (2014). [Google Scholar]
- 17.Ford M. J., Ambulo C. P., Kent T. A., Markvicka E. J., Pan C., Malen J., Ware T. H., Majidi C., A multifunctional shape-morphing elastomer with liquid metal inclusions. Proc. Natl. Acad. Sci. U.S.A. 116, 21438–21444 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Baek S. M., Yim S., Chae S. H., Lee D. Y., Cho K. J., Ladybird beetle-inspired compliant origami. Sci. Rob. 5, eaaz6262 (2020). [DOI] [PubMed] [Google Scholar]
- 19.Liu Y., Genzer J., Dickey M. D., “2D or not 2D”: Shape-programming polymer sheets. Prog. Polym. Sci. 52, 79–106 (2016). [Google Scholar]
- 20.Pikul J. H., Li S., Bai H., Hanlon R. T., Cohen I., Shepherd R. F., Stretchable surfaces with programmable 3D texture morphing for synthetic camouflaging skins. Science 358, 210–214 (2017). [DOI] [PubMed] [Google Scholar]
- 21.Nojoomi A., Arslan H., Lee K., Yum K., Bioinspired 3D structures with programmable morphologies and motions. Nat. Commun. 9, 3705 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang L., Yang Y., Chen Y., Majidi C., Iida F., Askounis E., Pei Q., Controllable and reversible tuning of material rigidity for robot applications. Mater. Today 21, 563–576 (2018). [Google Scholar]
- 23.Aksoy B., Besse N., Boom R. J., Hoogenberg B. J., Blom M., Shea H., Latchable microfluidic valve arrays based on shape memory polymer actuators. Lab Chip 19, 608–617 (2019). [DOI] [PubMed] [Google Scholar]
- 24.Y. Qiu, Z. Ren, W. Hu, C. Liu, Q. Pei, in Electroactive Polymer Actuators and Devices (EAPAD) 2016 (SPIE, 2016), vol. 9798, p. 97981U. [Google Scholar]
- 25.Piskarev Y., Shintake J., Ramachandran V., Baugh N., Dickey M. D., Floreano D., Lighter and stronger: Cofabricated electrodes and variable stiffness elements in dielectric actuators. Adv. Intell. Syst. 2, 2000069 (2020). [Google Scholar]
- 26.Shintake J., Schubert B., Rosset S., Shea H., Floreano D., Variable stiffness actuator for soft robotics using dielectric elastomer and low-melting-point alloy. Int. Conf. Intelli. Rob. Syst., 1097–1102 (2015). [Google Scholar]
- 27.Behl M., Razzaq M. Y., Lendlein A., Multifunctional shape-memory polymers. Adv. Mater. 22, 3388–3410 (2010). [DOI] [PubMed] [Google Scholar]
- 28.Ze Q., Kuang X., Wu S., Wong J., Montgomery S. M., Zhang R., Kovitz J. M., Yang F., Qi H. J., Zhao R., Magnetic shape memory polymers with integrated multifunctional shape manipulation. Adv. Mater. 32, e1906657 (2020). [DOI] [PubMed] [Google Scholar]
- 29.Chautems C., Tonazzini A., Boehler Q., Jeong S. H., Floreano D., Nelson B. J., Magnetic continuum device with variable stiffness for minimally invasive surgery. Adv. Intell. Syst. 2, 1900086 (2020). [Google Scholar]
- 30.Khaldi A., Elliott J. A., Smoukov S. K., Electro-mechanical actuator with muscle memory. J. Mater. Chem. C. 2, 8029–8034 (2014). [Google Scholar]
- 31.Mao G., Drack M., Karami-Mosammam M., Wirthl D., Stockinger T., Schwödiauer R., Kaltenbrunner M., Soft electromagnetic actuators. Sci. Adv. 6, eabc0251 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chen J., Huang J., Zhang H., Hu Y., A photoresponsive hydrogel with enhanced photoefficiency and the decoupled process of light activation and shape changing for precise geometric control. ACS Appl. Mater. Interfaces 12, 38647–38654 (2020). [DOI] [PubMed] [Google Scholar]
- 33.Park S., Shintake J., Piskarev E., Wei Y., Joshipura I., Frey E., Neumann T., Floreano D., Dickey M. D., Stretchable and soft electroadhesion using liquid-metal subsurface microelectrodes. Adv. Mater. Technol. 6, 2100263 (2021). [Google Scholar]
- 34.Dickey M. D., Stretchable and soft electronics using liquid metals. Adv. Mater. 29, 1606425 (2017). [DOI] [PubMed] [Google Scholar]
- 35.Behl M., Lendlein A., Shape-memory polymers. Mater. Today 10, 20–28 (2007). [Google Scholar]
- 36.Zárate J. J., Tosolini G., Petroni S., de Vittorio M., Shea H., Optimization of the force and power consumption of a microfabricated magnetic actuator. Sens. Actuators A Phys. 234, 57–64 (2015). [Google Scholar]
- 37.Cera L., Gonzalez G. M., Liu Q., Choi S., Chantre C. O., Lee J., Gabardi R., Choi M. C., Shin K., Parker K. K., A bioinspired and hierarchically structured shape-memory material. Nat. Mater. 20, 242–249 (2021). [DOI] [PubMed] [Google Scholar]
- 38.Aksoy B., Shea H., Reconfigurable and latchable shape-morphing dielectric elastomers based on local stiffness modulation. Adv. Funct. Mater. 30, 2001597 (2020). [Google Scholar]
- 39.Stoney G. G., The tension of metallic films deposited by electrolysis. Proc. R Soc. Lond. A Math. Phys. Sci. 82, 172–175 (1909). [Google Scholar]
- 40.Gu G. Y., Gupta U., Zhu J., Zhu L. M., Zhu X., Modeling of viscoelastic electromechanical behavior in a soft dielectric elastomer actuator. IEEE Trans. Robot. 33, 1263–1271 (2017). [Google Scholar]
- 41.D. Ponnamma, Y. M. H. El-Gawady, M. Rajan, S. Goutham, K. Venkateswara Rao, M. A.-A. Al-Maadeed, in Smart Polymer Nanocomposites (Springer, 2017), pp. 321–343. [Google Scholar]
- 42.R. Purwar, R. Sachan, in Advances in Functional and Protective Textiles (Elsevier, 2020), pp. 37–62. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Text
Figs. S1 to S13
Tables S1 and S2
Movies S1 and S2