Studying the mixed transmission in a community with age heterogeneity: COVID-19 as a case study

Abstract

COVID-19 has been prevalent worldwide for about 2 years now and has brought unprecedented challenges to our society. Before vaccines were available, the main disease intervention strategies were non-pharmaceutical. Starting December 2020, in Ontario, Canada, vaccines were approved for administering to vulnerable individuals and gradually expanded to all individuals above the age of 12. As the vaccine coverage reached a satisfactory level among the eligible population, normal social activities resumed and schools reopened starting September 2021. However, when schools reopen for in-person learning, children under the age of 12 are unvaccinated and are at higher risks of contracting the virus. We propose an age-stratified model based on the age and vaccine eligibility of the individuals. We fit our model to the data in Ontario, Canada and obtain a good fitting result. The results show that a relaxed between-group contact rate may trigger future epidemic waves more easily than an increased within-group contact rate. An increasing mixed contact rate of the older group quickly amplifies the daily incidence numbers for both groups whereas an increasing mixed contact rate of the younger group mainly leads to future waves in the younger group alone. The results indicate the importance of accelerating vaccine rollout for younger individuals in mitigating disease spread.

1. Introduction

COVID-19 has been prevalent worldwide for around 2 years now since the initial identification in Wuhan, China in December 2019. The global pandemic has caused more than 328,000,000 total infections and over 5,500,000 deaths worldwide (WHO Coronavirus, 2022). In Ontario, Canada alone, the total confirmed case number of COVID-19 surpassed 970,000 and more than 10,000 population deceased due to complications of COVID-19 infection (COVID-19 Data Repository by the).

The novel pneumonia disease can be transmitted via close contact between susceptible and infected populations, similar to other pneumonia diseases such as influenza. However, recent evidences show that the majority of COVID-19 transmission may be attributed to the aerosol droplets (Azimi et al., 2021; Wang et al., 2021). The transmission via aerosol implies that the spread of the disease may occur in a long-range, which signifies the difficulties of mitigating the disease spread.

In Ontario, before vaccines were approved, the main disease mitigation strategies were non-pharmaceutical, such as closing non-essential businesses, practising social distancing, setting limitations of indoor gathering size, requiring mandatory face-covering etc. The non-pharmaceutical strategies are effective in mitigating the disease spread but disrupt normal social activities and cause huge economic loss. Therefore, aggressive strategies can only be imposed in a short period and are not practical in long term. Progressing into the second year of the pandemic, vaccines were approved by Health Canada in December 2020 and quickly rolled out across the province.

In the initial stage of the vaccine rollout program, vaccines were administered to the senior population or other vulnerable individuals with underlying health conditions. Starting in late May 2021, Health Canada expanded the criteria so that all individuals above the age of 12 were eligible for receiving vaccines. The vaccine for children between the age of 5–11 was approved recently in late November 2021 but the rollout takes time and only 3.2% of the children in the age group are fully vaccinated up to now (Age stratified data of COVID, 2021).

Clinical trail evidences show that vaccines offer a high protection efficacy for vaccinated individuals that reduces the probability of infection to a large extent (WHO Coronavirus, 2022). As the vaccine coverage steadily increased and reached a satisfactory level among eligible individuals, the province lifted majority of the restrictive measures in July 2021. During this time, unvaccinated children were on the summer break and weren't on high risks of transmitting the disease because of limited contacts within the household.

Starting in September 2021, schools reopen and in-person learning resumes. In-person learning environment inevitably creates a larger social gathering size, larger contact numbers between the children, and a higher infection probability in the indoor setting. Evidences show that children are at a lower risk of developing serious symptoms after contracting the virus and therefore the within-group transmission may not raise serious concerns. However, children may transmit the disease to elder family members within the household after school. Infected elder individuals are more likely to develop serious symptoms and need medical attention, which causes stress on the provincial health system.

Mathematical models have been used extensively in studying COVID-19 since the initial emergence of the disease, see (He et al., 2020a; Iwata & Miyakoshi, 2020; Liu et al., 2020a, 2020b; Moyles et al., 2021; Ruan, 2020; Tang et al., 2020; Wang, 2020; Zhao & Feng, 2020) for example. The aforementioned studies focus on modeling the initial wave of the pandemic and provide valuable insights in short-term predictions and disease intervention strategies. Age-stratified models were proposed to study the heterogeneity in social contact patterns among a susceptible population in early stage of the disease (Davies et al., 2020; Fields et al., 2021; Gabriele-Rivet et al., 2021; McCarthy et al., 2020). Statistical analyses were applied in studying various aspects of the disease spread, such as identifying the impact of undiagnosed cases in COVID-19 (Hamadeh et al., 2021), the importance of household transmission (Paul et al., 2021), and suggestions for testing policy (Lawless & Yan, 2021). As the disease evolves, particularly with the rollout of vaccines and resumption of normal social activities, models need to be revisited to gain better understanding of the disease spread.

In this paper, we propose an age-stratified model where individuals in the older group are eligible for receiving vaccines while the individuals in the younger group are not. We fit the model to the COVID-19 data in Ontario, Canada for illustration. In Ontario, the schools reopen starting in September 2021 and the vaccines for children haven't been approved by then. The individuals above the age of 12 are eligible for receiving vaccines but breakthrough infections may occur due to relaxed social distancing. The main objective of this paper is to identify the relative importance of within-group transmission and between-group transmission and shed light on future disease mitigation strategies.

2. Methods

2.1. Data

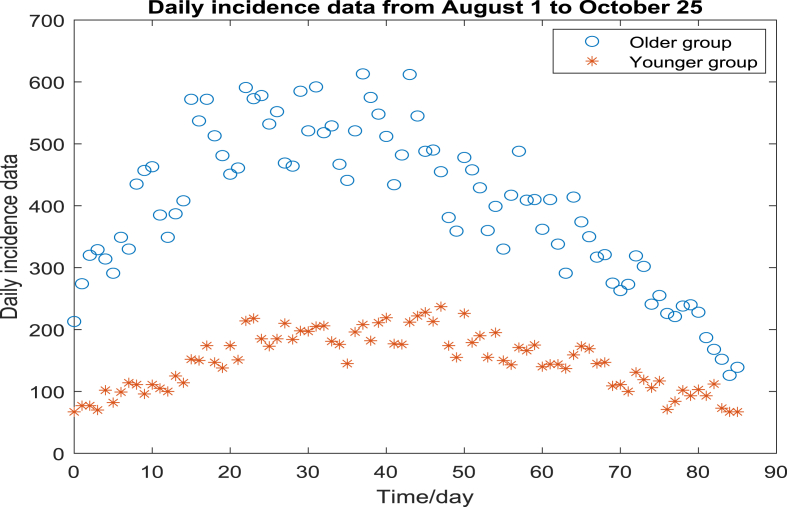
We accessed the COVID-19 data in Ontario from the online data catalogue in Ontario government (Status of COVID, 2021). The data contains demographic information of individuals who are confirmed of positive COVID-19 infection among all 34 health units across Ontario, such as age, sex, and location of the reporting health unit. Fig. 1 shows the daily incidence number between Aug. 1, 2021 and Oct. 25, 2021, based on the estimated symptom onset date recorded in (Status of COVID, 2021). In the aforementioned time window, individuals who are above the age of 12 are eligible for receiving vaccines but individuals who are below the age of 12 haven't been approved for receiving vaccines yet. Therefore, in this study, we divide the entire population in Ontario into two groups: the older group and the younger group, where individuals are above/below the age of 12 respectively. Fig. 1 demonstrates the daily incidence case number for each group separately.

Fig. 1.

The daily incidence number for older/younger group in Ontario between August 1, 2021 and October 25, 2021.

2.2. The model

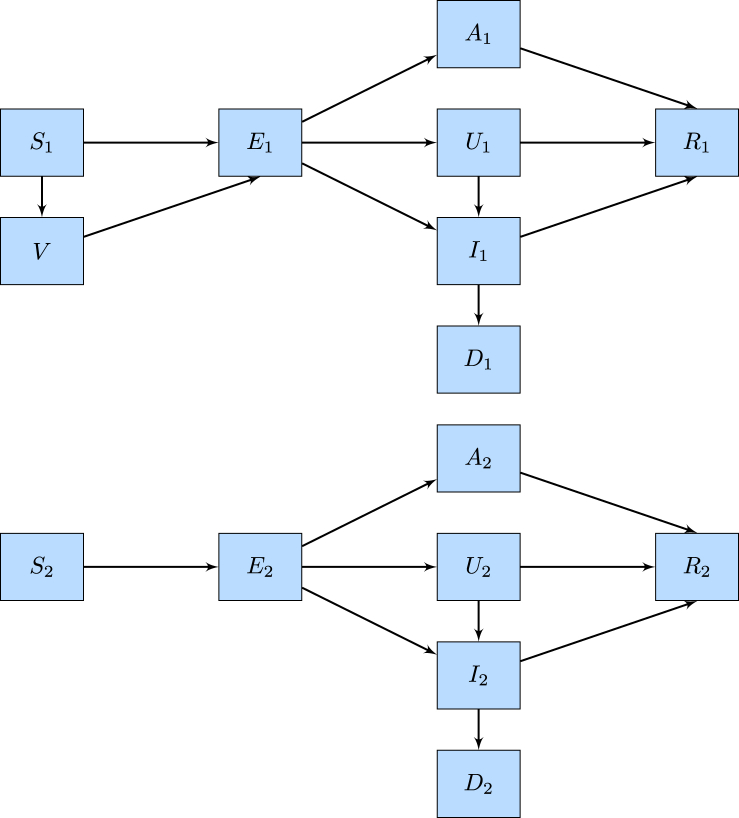
We propose a compartmental model that stratifies the entire population into the following compartments: susceptible class (S), vaccinated class (V), exposed class (E), asymptomatic class (A), unreported symptomatic class (U), confirmed infected class (I), recovered class (R), and the deceased class (D). Moreover, within each compartment, we further stratify individuals into the older group and the younger group, as denoted by S_i for i = 1, 2 for example. Fig. 2 demonstrates the flowchart of the model. Note that within the time window between August and October, the individuals below the age of 12 are not eligible for receiving vaccines and therefore, the compartment V comprises of vaccinated individuals of the older group only.

Fig. 2.

The flow chart for model.

In the model, individuals in the exposed class (E) are individuals who have been infected with the COVID-19 virus but are still in the incubation period and are not contagious yet. Vaccinated individuals are at a lower risk of contracting the virus but may still become infected because the vaccine efficacy is not 100%. Asymptomatic individuals in class (A) are those who are contagious but show no symptoms of infection. On the other hand, individuals in class (U) show mild symptoms and are also contagious but do not seek medical resources for diagnosis. Individuals in class (I) are those who are confirmed with the COVID-19 infection and are in quarantine at home if they experience mild to moderate symptoms or are in the hospital if they show severe symptoms. Because individuals in class (I) follow the public health protocols, we assume that they maintain a very low possibility of transmitting the disease. Individuals in all the asymptomatic classes, unreported symptomatic class, and reported infected class may recover and are no longer transmissible and therefore move to the recovered class (R).

Based on the aforementioned discussions, the model for the older group, where individuals are above the age of 12 and are eligible to be vaccinated is

$$\begin{array}{cc}& \frac{d{S}_1}{dt}=-{\mathrm{\Lambda }}_{11}-{\mathrm{\Lambda }}_{12}-\omega S_1,\\ & \frac{dV}{dt}=\omega S_1-{\mathrm{\Lambda }}_{11}^v-{\mathrm{\Lambda }}_{12}^v,\\ & \frac{d{E}_1}{dt}={\mathrm{\Lambda }}_{11}+{\mathrm{\Lambda }}_{12}+{\mathrm{\Lambda }}_{11}^v+{\mathrm{\Lambda }}_{12}^v-{\mu }_1{E}_1,\\ & \frac{d{A}_1}{dt}={\mu }_1{\rho }_1{E}_1-{\eta }_{11}{A}_1,\\ & \frac{d{U}_1}{dt}={\mu }_1{\rho }_2{E}_1-{\eta }_{12}{U}_1-{\tau }_1{U}_1,\\ & \frac{d{I}_1}{dt}={\mu }_1\left(1-{\rho }_1-{\rho }_2\right)E_1+{\tau }_1{U}_1-{\eta }_{13}{I}_1-{\delta }_1{I}_1,\\ & \frac{d{R}_1}{dt}={\eta }_{11}{A}_1+{\eta }_{12}{U}_1+{\eta }_{13}{I}_1,\\ & \frac{d{D}_1}{dt}={\delta }_1{I}_1.\end{array}$$ (2.1)

In (2.1), Λ₁₁ = β₁₁A₁S₁ + β₁₂U₁S₁ represents the within-group transmission of the susceptible population, where β₁₁, β₁₂ are the infectious contact rates between susceptible individuals and asymptomatic/unreported symptomatic individuals in the older group. Moreover, Λ₁₂ = β₁₃A₂S₁ + β₁₄U₂S₁ represents the between-group transmission, where β₁₃, β₁₄ are the contact rates between susceptible individuals in the older group and the asymptomatic/unreported infected individuals in the younger group.

Similarly, ${\mathrm{\Lambda }}_{11}^v={\beta }_{11}^v(1-\epsilon )A_{1}V+{\beta }_{12}^v(1-\epsilon )U_{1}V$ is the within-group transmission of the vaccinated individuals, where ${\beta }_{11}^v,{\beta }_{12}^v$ are the contact rates between vaccinated individuals and asymptomatic/unreported symptomatic individuals in the older group. Furthermore, ${\mathrm{\Lambda }}_{12}^v={\beta }_{13}^v(1-\epsilon )A_{2}V+{\beta }_{14}^v(1-\epsilon )U_{2}V$ is the between-group transmission of the vaccinated individuals, where ${\beta }_{13}^v,{\beta }_{14}^v$ are the contact rates between the vaccinated individuals and the asymptomatic/unreported symptomatic individuals in the younger group. Because vaccinated individuals are at lower risk of transmitting the disease, we introduce the factor (1 − ε) in ${\mathrm{\Lambda }}_{11}^v,{\mathrm{\Lambda }}_{12}^v$ to indicate the reduced probability of infection where ε is the vaccine efficacy and 0 < ε < 1.

The model for the younger group is similar but without the vaccinated compartment because individuals below the age of 12 are not eligible for receiving vaccines. The model is

$$\begin{array}{cc}& \frac{d{S}_2}{dt}=-{\mathrm{\Lambda }}_{21}-{\mathrm{\Lambda }}_{22},\\ & \frac{d{E}_2}{dt}={\mathrm{\Lambda }}_{21}+{\mathrm{\Lambda }}_{22}-{\mu }_2{E}_2,\\ & \frac{d{A}_2}{dt}={\mu }_2{\rho }_1{E}_2-{\eta }_{21}{A}_2,\\ & \frac{d{U}_2}{dt}={\mu }_2{\rho }_2{E}_2-{\eta }_{22}{U}_2-{\tau }_2{U}_2,\\ & \frac{d{I}_2}{dt}={\mu }_2\left(1-{\rho }_1-{\rho }_2\right)E_2+{\tau }_2{U}_2-{\eta }_{23}{I}_2-{\delta }_2{I}_2,\\ & \frac{d{R}_2}{dt}={\eta }_{21}{A}_2+{\eta }_{22}{U}_2+{\eta }_{23}{I}_2,\\ & \frac{d{D}_2}{dt}={\delta }_2{I}_2,\end{array}$$ (2.2)

where Λ₂₁ = β₂₁A₂S₂ + β₂₂U₂S₂ is the within-group transmission of the susceptible individuals, and Λ₂₂ = β₂₃A₁S₂ + β₂₄U₁S₂ is the between-group transmission of the susceptible individuals.

In (2.1), (2.2), ρ₁ is the proportion of the exposed individuals who move to the asymptomatic class and ρ₂ is the proportion of the exposed individuals who move to the unreported symptomatic class. This leaves 1 − ρ₁ − ρ₂ as the proportion of the exposed individuals who eventually move to the reported symptomatic class. We assume that ρ₁, ρ₂ are the same for both the older and the younger groups because there is no evidence so far that suggests the proportions of asymptomatic individuals and symptomatic individuals differ significantly among different age groups.

Susceptible individuals in the older group transfer to the vaccinated class at a rate of ω. The parameter ω will be estimated below from the data in Fig. 1. Exposed individuals in the older and the younger group move to either the asymptomatic class/unreported symptomatic class/reported infected class at a rate of μ_i for i = 1, 2 respectively. Based on (He et al., 2020b; Li et al., 2020), we fix μ_i = 1/3 for i = 1, 2 because evidence shows that individuals who have contracted the virus generally have an incubation period of 2–3 days before they become contagious.

Asymptomatic individuals in the older group and the younger group move to the recovered class at a rate of η₁₁ and η₂₁ respectively. Similarly, the unreported infected individuals and the confirmed infected individuals in the older/younger group recover from the infection at a rate of η_i2 and η_i3 for i = 1, 2. We assume that η_i,j = 1/7 where i = 1, 2, j = 1, 2, 3 based on (Liu et al., 2020a, 2020b), which indicates that in average, infected individuals may transmit the disease within a period of 7 days until they recover and are no longer contagious.

Unreported infected individuals may seek diagnosis from medical facilities if the symptoms persist or their heath deteriorates over time and therefore move to the reported infected class at a rate of τ. In (Li et al., 2020), the authors analyzed the patients’ data and recorded that infected individuals waited for an average of 4.6 days after observing symptoms before they sought diagnosis. Hence, in our study, we assume that τ_i = 1/4.6 for i = 1, 2. All the other parameters in model (2.1)–(2.2) are listed in Table 1 below and are either fitted via data or estimated via existing literature.

Table 1.

Parameter estimates for the COVID-19 epidemics in Ontario, Canada.

Parameter	Definition	Estimated Mean Value	Standard Deviation	Data Source
β11	Contact rate between S1 and A1	2.1772 × 10−8	1.708 × 10−9	Fitted
β13	Contact rate between S1 and A2	4.8079 × 10−7	3.5895 × 10−8	Fitted
ω	Transition rate from S1 to V	3.7286 × 10−2	4.3604 × 10−3	Fitted
${\beta }_{11}^v$	Contact rate between V and A1	5.5607 × 10−7	2.4585 × 10−8	Fitted
${\beta }_{13}^v$	Contact rate between V and A2	1.4986 × 10−8	1.1856 × 10−9	Fitted
ε	Contact rate reduction between V and Ai/Ui	0.96783	4.423 × 10−3	Fitted
μ1	Transition rate from E1 to A1/U1/I1	1/3	−	Li et al. (2020)
μ2	Transition rate from E2 to A2/U2/I2	1/3	−	Li et al. (2020)
ρ1	Proportionality of transferred Ei to Ai	0.3	−	Nishiura et al. (2020)
ρ2	Proportionality of transferred Ei to Ui	0.3	−	Nishiura et al. (2020)
ηi1	Recovery rate of Ai	1/7	−	Liu et al. (2020a, 2020b)
ηi2	Recovery rate of Ui	1/7	−	Liu et al. (2020a, 2020b)
ηi3	Recovery rate of Ii	1/7	−	Liu et al. (2020a, 2020b)
τi	Transition rate from Ui to Ii	0.21739	−	Liu et al. (2020a, 2020b)
δ1	Disease death rate of I1	1.0928 × 10−5	6.1912 × 10−7	Fitted
β21	Contact rate between S2 and A2	4.079 × 10−9	3.765 × 10−10	Fitted
β23	Contact rate between S2 and A1	7.0164 × 10−8	2.5621 × 10−9	Fitted
δ2	Disease death rate of I2	2.9753 × 10−6	4.1384 × 10−7	Fitted
Initial Value	Definition	Estimated Mean Value	Standard Deviation	Data Source
S1(0)	Initial susceptible population of group-1	2.5117 × 106	−	Age stratified data of COVID (2021)
V(0)	Initial vaccinated population	9.8651 × 106	−	Age stratified data of COVID (2021)
E1(0)	Initial exposed population of group-1	912.8571	−	Fitted
A1(0)	Initial asymptomatic population of group-1	678.83	63.497	Fitted
U1(0)	Initial unreported population of group-1	42.791	4.3679	Fitted
I1(0)	Initial reported case number of group-1	200	−	Age stratified data of COVID (2021)
S2(0)	Initial susceptible population of group-2	1.7513 × 106	−	Age stratified data of COVID (2021)
E2(0)	Initial exposed population of group-2	287.1429	−	Fitted
A2(0)	Initial asymptomatic population of group-2	165.88	15.296	Fitted
U2(0)	Initial unreported population of group-2	184.81	32.996	Fitted
I2(0)	Initial reported case number of group-2	18	−	Age stratified data of COVID (2021)

2.3. The reproduction number

We first calculate the basic reproduction number ${\mathcal{R}}_0$ for the age-structured model (2.1)–(2.2). Direct calculations show that

$$\frac{d(S_1+V+E_1+A_1+U_1+I_1+R_1+D_1)}{dt}=0,$$

which leads to the total population of the older group as a constant N₁. Similarly, the total population in the younger group also remains as a constant N₂. Hence, the disease-free equilibrium of (2.1), (2.2) is

$$\begin{array}{cc}& \left(S_1,V,E_1,A_1,U_1,I_1,R_1,D_1,S_2,E_2,A_2,U_2,I_2,R_2,D_2\right)\\ & =\left(0,N_1,0,0,0,0,0,0,N_2,0,0,0,0,0,0\right).\end{array}$$

Following the next generation matrix method for compartmental models in (Van den Driessche & Watmough, 2002), we obtain the new infection matrix

$$\mathcal{F}=\left(\begin{array}{cccccccc}0& F_{12}& F_{13}& 0& 0& F_{16}& F_{17}& 0\\ & {\text{0}}_{3\times 3}& & \cdots & \cdots & & {\text{0}}_{3\times 3}\\ 0& {\beta }_{23}{S}_2& {\beta }_{24}{S}_2& 0& 0& {\beta }_{21}{S}_2& {\beta }_{22}{S}_2& 0\\ & {\text{0}}_{3\times 3}& & \cdots & \cdots & & {\text{0}}_{3\times 3}\end{array}\right),$$

and the transition matrix

$$\mathcal{V}=\left(\begin{array}{cccc}{\mu }_1& 0& 0& 0\\ -{\mu }_1{\rho }_1& {\eta }_{11}& 0& 0& & {\text{0}}_{4\times 4}\\ -{\mu }_1{\rho }_2& 0& V_{33}& 0\\ V_{41}& 0& -{\tau }_1& V_{44}& \\ & & & & {\mu }_2& 0& 0& 0\\ & & & & -{\mu }_2{\rho }_1& {\eta }_{21}& 0& 0\\ & {\text{0}}_{4\times 4}& & & -{\mu }_2{\rho }_2& 0& V_{77}& 0\\ & & & & V_{85}& 0& -{\tau }_2& V_{88}\end{array}\right),$$

where F₁₂ = β₁₁S₁ + β_11v(1 − ε)V, F₁₃ = β₁₂S₁ + β_12v(1 − ε)V, F₁₆ = β₁₃S₁ + β_13v(1 − ε)V, F₁₇ = β₁₄S₁ + β_14v(1 − ε)V, V₃₃ = η₁₂ + τ₁, V₄₁ = −μ₁(1 − ρ₁ − ρ₂), V₄₄ = η₁₃ + δ₁, V₇₇ = η₂₂ + τ₂, V₈₅ = −μ₂(1 − ρ₁ − ρ₂), V₈₈ = η₂₃ + δ₂. It follows that

$${\mathcal{R}}_0=\rho (\mathcal{F}{\mathcal{V}}^{-1})=\frac{J_{11}+J_{55}+\sqrt{{(J_{11}+J_{55})}^2-4(J_{11}{J}_{55}-J_{15}{J}_{51})}}{2},$$ (2.3)

where

$$\begin{array}{cc}& J_{11}=\frac{{\beta }_{11}^v(1-\epsilon ){\rho }_1{N}_1}{{\eta }_{11}}+\frac{{\beta }_{12}^v(1-\epsilon ){\rho }_2{N}_1}{{\eta }_{12}+{\tau }_1},J_{15}=\frac{{\beta }_{13}^v(1-\epsilon ){\rho }_1{N}_1}{{\eta }_{21}}+\frac{{\beta }_{14}^v(1-\epsilon ){\rho }_2{N}_1}{{\eta }_{22}+{\tau }_2},\\ & J_{51}=\frac{{\beta }_{23}{\rho }_1{N}_2}{{\eta }_{11}}+\frac{{\beta }_{24}{\rho }_2{N}_2}{{\eta }_{12}+{\tau }_1},J_{55}=\frac{{\beta }_{21}{\rho }_1{N}_2}{{\eta }_{21}}+\frac{{\beta }_{22}{\rho }_2{N}_2}{{\eta }_{22}+{\tau }_2}.\end{array}$$

To predict the severity of the disease spread at an arbitrary time of the epidemics, we calculate the effective reproduction number ${\mathcal{R}}_t=(S_t/S_0){\mathcal{R}}_0$, where S_t is the total susceptible population at time t and S₀ is the total susceptible population at the initial time when the epidemic starts (Diekmann & Heesterbeek, 2000; Nishiura & Chowell, 2009). Biologically, the effective reproduction number implies that the disease persists if R_t > 1 and diminishes if R_t < 1.

2.4. Parameter estimation

Based on the census data in Ontario, the total population of the older group at the beginning of the pandemic is 12,932,471 and the total population of the younger group is 1,801,543. The number of cumulative infections until July 31, 2021 for the older group is 555,583 whereas the total infection case for the younger group is 50,156 (Age stratified data of COVID, 2021). The vaccine coverage data shows that a total number of 10,582,731 individuals received at least one dose and a total of 9,147,534 individuals are fully vaccinated with two doses. We average the data to obtain the estimated initial population of the vaccinated compartment V₀ = 9, 865, 132. It follows that the initial susceptible population for the older group is S₁(0) = 2, 511, 756. Similarly, the initial susceptible population for the younger group is S₂(0) = 1, 751, 387. On August 1, the reported infection number for the older group is 200 and the reported infection number for the younger group is 18, which leads to I₁(0) = 200 and I₂(0) = 18 respectively.

We fit the model (2.1), (2.2) to the daily incidence data in Fig. 1 by the Markov Chain Monte Carlo (MCMC) method and adopt the adaptive Metropolis-Hastings algorithm to carry out this approach (Haario et al., 2006). We run the algorithm for 10,000 iterations with a burn-in of the first 7000 iterations. Geweke convergence test is employed to diagnose the convergence of the Markov chains. The estimated parameters and the initial data are listed in Table 1.

3. Results

• (I)Fitting results

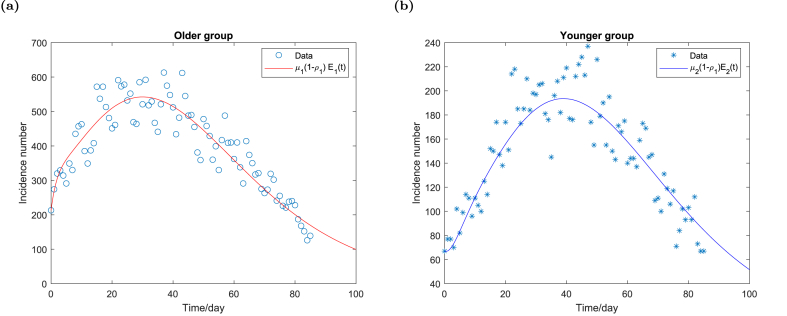
Fig. 3 shows the fitting result of the daily incidence data in Fig. 1 to the older group (2.1) and the younger group (2.2) respectively. As shown in Fig. 3, the daily incidence data increases initially but then declines. The data shows the fourth wave of COVID-19 in Ontario, which is before the new variant emerges in Canada. The initial increase of the daily incidence case number may be attributed to the reopening in August and September, when the vaccine program steadily rolls out. It is then followed by a gradual decline, which is due to a combination of a few factors, such as a high vaccine coverage among eligible individuals, implementation of health protocols etc. Fig. 3 indicates that the daily incidence data changes in the same pattern for both the older and the younger groups but the infected case number peaks slightly later in the younger group than the older group.

Fig. 3.

The fitting result of model (2.1)–(2.2) to the daily incidence data between August 1 and October 25 in Ontario, Canada. Fig. 3a shows the fitting of the daily incidence data to the older group. Fig. 3b shows the fitting of the daily incidence data to the younger group.

Under the current set of parameters in Table 1, the prediction of (2.1), (2.2) indicates that the disease dies out eventually. The prediction is confirmed by the effective reproduction number ${\mathcal{R}}_t=0.31727<1$ by substituting the parameter values in Table 1. However, starting in November and afterwards, vaccinated individuals may experience higher probabilities of infection because of the gradual decline of vaccine protection efficacy. Meanwhile, before December, individuals in the younger group are still not eligible for receiving vaccines but are at higher risks of infection. This is mainly because children stay indoors more often due to the weather condition and will contract the virus more easily if they follow the same health protocols as before. We will explore different scenarios below by increasing the within-group contact rate and the between-group contact rate.

• (II)Comparing the relative importance of the within-group and between-group transmission

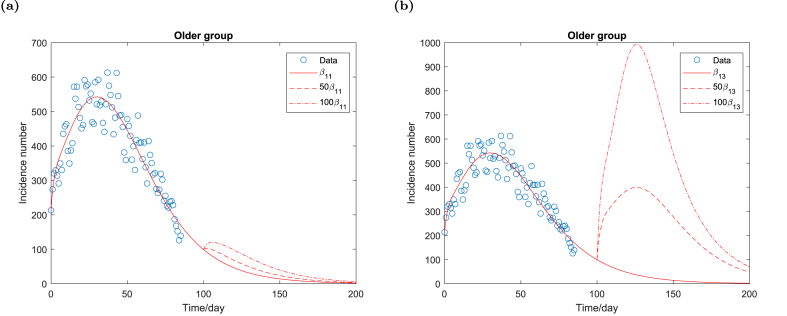
Next, we analyze the impact of β₁₁ and β₁₃ on future epidemic waves and compare the relative importance of the within-group contact rate and the between-group contact rate on the final epidemic size. By increasing the contact rate β₁₁ or β₁₃, we obtain a similar pattern of the future waves for both the older group and the younger group and hence show only the result of the older group.

Fig. 4a shows that the daily incidence number of the older group increases and initiates a further wave if the within-group contact rate β₁₁ increases. The further epidemic wave achieves a higher peak if the contact rate β₁₁ is larger. However, the peak size of epidemics is relatively small compared to the peak size of the fourth wave even if the contact rate is larger and is on an order of different magnitude.

Fig. 4.

Daily incidence number of the older group for different contact rate β₁₁ and β₁₃ respectively. All the parameters remain unchanged as shown in Table 1 except β₁₁ and β₁₃ respectively.

However, Fig. 4b shows that an increasing between-group contact rate β₁₃ triggers a future epidemic wave of a large size. The peak size of future epidemic waves possibly exceeds the peak size of the fourth wave if the between-group contact rate of the older group is sufficiently large. Fig. 4 shows that the between-group contact rate of the older group imposes a much larger impact on future epidemic waves compared to the within-group contact rate.

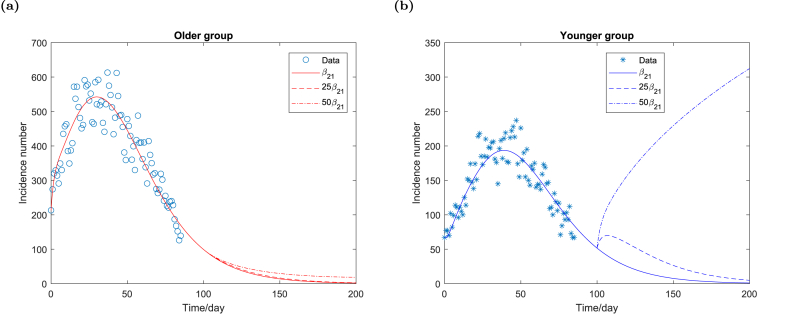
Next, we increase the within-group contact rate of the younger group β₂₁. Fig. 5a demonstrates that the daily incidence number of the older group declines monotonically even if β₂₁ increases significantly. However, the daily incidence number of the younger group shifts to a gradual increase from the original decline if β₂₁ increases, as shown in Figure Fig. 5b. More importantly, the daily incidence number of the younger group increases rapidly and forms a new epidemic wave of the size much larger than the fourth wave if β₂₁ is relatively large.

Fig. 5.

Daily incidence number of the older group and the younger group respectively for different contact rate β₂₁. All the parameters remain unchanged as shown in Table 1 except β₂₁.

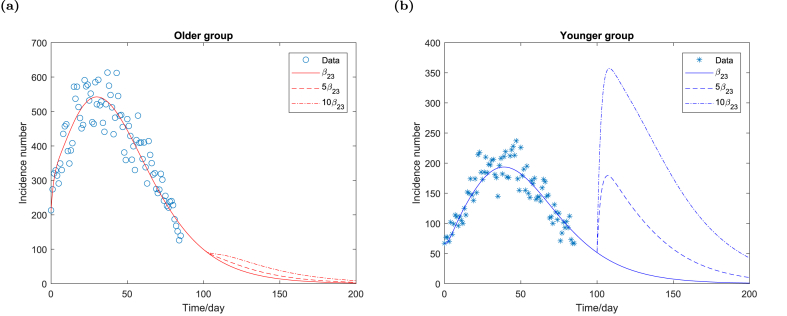
We also examine how the between-group contact rate of the younger group β₂₃ may trigger the future epidemic waves. Fig. 6a shows that the daily incidence number of the older group decreases monotonically if β₂₃ increases. However, by comparing Fig. 5a and Figure Fig. 6a, we observe that the daily incidence number of the older group is more sensitive to β₂₃ than β₂₁ even though a steady decline holds for both varying β₂₁ and β₂₃ in reasonable ranges. Fig. 6b indicates that an increasing between-group contact rate of the younger group leads to a rapid increase in the daily incidence number of the younger group. The new wave reaches the peak of a larger size than the fourth wave in a short time and then declines.

Fig. 6.

Daily incidence number of the older group and the younger group respectively for different contact rate β₂₃. All the parameters remain unchanged as shown in Table 1 except β₂₃.

Overall, Figs. 4, Figure 5, Fig. 6 demonstrate that an increasing between-group contact rate in either the older group or the younger group may trigger future epidemic waves. The difference is that an increasing between-group contact rate of the older group leads to rapid growths of the daily incidence numbers of both groups whereas an increasing between-group contact rate of the younger group impacts more heavily on the younger group alone. The results indicate that a mixed transmission in different age groups plays an important role in triggering future waves and hence confirms the importance of vaccinating the younger group. The results also shed light on the demographic structure among the infected individuals in future waves: reported cases in the younger group will constitute a heavier proportion in the total infected individuals.

• (III)Sensitivity analysis

In this section, we conduct sensitivity analysis to investigate the sensitivity of the total cumulative infection and infection number in each age-group on the estimated parameters. For each parameter, Latin Hypercube Sampling (Blower & Dowlatabadi, 1994; Helton et al., 2006) is adopted to generate parameter values with assumed ranges and distributions as specified in Table 2. We generate 3000 sets of parameter values for the analysis. By using these sets of values, partial rank correlation coefficients (PRCC) are calculated to determine the impact of varying parameters on the number of cumulative infections of COVID-19 between August and October 2021 (Hamby, 1994). The PRCC indices range between −1 and 1, with positive (negative) values indicating a positive (negative) relationship and magnitudes indicating the relative level of impact on the quantity of interest, with a magnitude of 0 having almost no impact and 1 having the most influential impact.

Table 2.

Parameter ranges and distributions for sensitivity analysis.

Parameter	Lower Bound	Upper Bound	Distribution
β11 = β12	0	10–5	T
β13 = β14	0	10–5	T
${\beta }_{11}^v={\beta }_{12}^v$	0	10–5	T
${\beta }_{13}^v={\beta }_{14}^v$	0	10–5	T
ε	0	1	T
β21 = β22	0	10–5	T
β23 = β24	0	10–5	T
ω	0	0.3	T
τ1	0	0.3	T
τ2	0	0.3	T

T indicates triangular distribution with its peak value from Table 1.

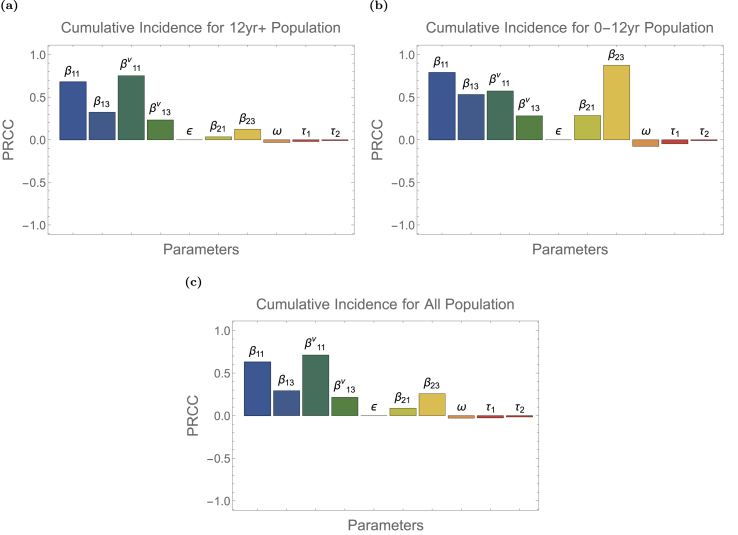
Fig. 7 shows the PRCC for cumulative incidence number of COVID-19 infection for the older group, the younger group, and the entire population in Ontario between August 1 and October 25, 2021. Fig. 7a, b, Fig. 7c demonstrate that the transition rate τ₁, τ₂ from unreported infected class to reported infected class in respective group and vaccination rate ω in the older group have negative impact on the number of cumulative infections. The result is not surprising because individuals in the reported infected class are excluded from social activities due to self-isolation or hospitalization and therefore unable to transmit the pathogen whereas vaccinated individuals gain immunity and become less susceptible to infection. Comparing τ₁, τ₂, ω, vaccination rate ω has a stronger influence than the reporting rates τ₁ and τ₂, which implies that vaccination is a more effective means to control the spread of disease than reporting infected cases. Moreover, reporting rate of the older group τ₁ has a relatively larger impact than reporting rate of the younger group τ₂ because the majority of infected population are adults.

Fig. 7.

Partial rank correlation coefficients (PRCC) calculated using parameter values from Latin Hypercube Sampling with respect to cumulative infections for population 12+ years of age, 0–12 years of age and all from Aug. 1, 2021 to Oct. 25, 2021 in Ontario, Canada.

4. Conclusion and discussion

Since the initial identification of COVID-19 in Wuhan, China, the transmissible disease quickly escalates and becomes a global pandemic for about 2 years up to now. In Ontario, Canada, during the first year of the disease prevalence, the main intervention strategies have been nonpharmaceutical, such as provincial-wise lock down, keeping social distancing etc. due to the lack of effective vaccines. Such interventions are effective in mitigating the disease spread but cause significant economic loss at the same time and therefore are not long-lasting.

Progressing to the second year of the pandemic, in Ontario, starting from December 2020, the vaccine program gradually rolls out. The initial phase of the vaccine rollout targets the seniors population or vulnerable individuals and then gradually expands to individuals who are above the age of 12. The vaccine for children between the age of 5–11 was approved by Health Canada in late November but the rollout takes time and only 3.2% of the children in the age of 5–11 are fully vaccinated by now (Age stratified data of COVID, 2021).

In this paper, we propose an age-stratified model that divides the entire population in Ontario into two groups: the older group where individuals are above the age of 12 and are eligible to receive vaccines and the younger group where individuals are below the age of 12 and are not eligible to receive vaccines. We fit the model to the daily incidence data of each group in Ontario between August 1, 2021 and October 25, 2021 and obtain a good fitting result.

The results demonstrate that between-group contact rate plays a more important role in triggering future waves than the within-group contact rate. The increasing between-group contact rate of the older group shifts the daily incidence number of either group from the decline to a rapid growth. However, an increasing between-group contact rate of the younger group mainly leads to a new epidemic wave in the younger group only. The results confirm the importance of achieving a high vaccine coverage in the younger group in order to mitigate the disease spread.

A new variant B.1.1.529 emerges in late November 2021 in multiple African countries and quickly spreads to Canada in December. Early data indicate that the new variant is highly transmissible compared to other variants. Moreover, data show that currently, vaccines offer a much lower protection efficacy for even fully vaccinated individuals. Our model can be extended to study the invasion of the new variant, which leaves as future work.

Declaration of competing interest

We declare that the authors have no conflict of interest.

Handling editor: Jianhong Wu