Agent-based computational modeling of glioblastoma predicts that stromal density is central to oncolytic virus efficacy

Summary

Oncolytic viruses (OVs) are emerging cancer immunotherapy. Despite notable successes in the treatment of some tumors, OV therapy for central nervous system cancers has failed to show efficacy. We used an ex vivo tumor model developed from human glioblastoma tissue to evaluate the infiltration of herpes simplex OV rQNestin (oHSV-1) into glioblastoma tumors. We next leveraged our data to develop a computational, model of glioblastoma dynamics that accounts for cellular interactions within the tumor. Using our computational model, we found that low stromal density was highly predictive of oHSV-1 therapeutic success, suggesting that the efficacy of oHSV-1 in glioblastoma may be determined by stromal-to-tumor cell regional density. We validated these findings in heterogenous patient samples from brain metastatic adenocarcinoma. Our integrated modeling strategy can be applied to suggest mechanisms of therapeutic responses for central nervous system cancers and to facilitate the successful translation of OVs into the clinic.

Graphical abstract

Highlights

• •Ex vivo human glioblastoma model tracks oncolytic herpes simplex virus-1 efficacy
• •Computational model predicts treatment efficacy in heterogeneous glioblastoma samples
• •Simulations show performance of treatment relies on tumor cell density
• •Findings validated in heterogeneous patient samples

Immunology; Computational bioinformatics; Cancer

Introduction

Brain cancers encompass a range of primary and metastatic diseases, with glioblastoma the most common and deadly primary brain tumor in adults (Alifieris and Trafalis, 2015). Standard-of-care for patients with glioblastoma integrates maximal surgical resection, radiation, and temozolomide (TMZ) chemotherapy with the goal of removing the bulk of tumor tissue and targeting remaining glioblastoma cells after surgery (De Vleeschouwer, 2017). Although treatment with TMZ extends progression-free survival (Stupp et al., 2005), nearly all glioblastomas will recur owing to TMZ resistance, and overall survival is limited to around 15 months (Fernandes et al., 2017). Solid tumors, such as glioblastomas, are composed of a variety of cell types including the stroma, which is a critical component of the tumor microenvironment (TME) and known to promote resistance (Valkenburg et al., 2018).

Glioblastomas in particular are known for their inter- and intratumoral heterogeneity (Gallaher et al., 2020; Puchalski et al., 2018). There is a lack of understanding of the mechanisms underlying drug efficacy and resistance in glioblastoma, owing to this extensive heterogeneity and the complex interactions between tumors and the brain’s unique microenvironment (Nguyen et al., 2018). In addition to primary disease and recurrence, the brain is also a site of secondary disease from metastasizing breast and other solid malignancies (Rostami et al., 2016). To improve therapeutic approaches in glioblastoma and other brain cancers, it is, therefore, crucial to consider how heterogeneity impacts treatment efficacy (Craig et al., 2019).

Oncolytic viruses (OVs) represent an exciting new treatment modality in brain tumors owing to their ability to kill cancer cells directly by infection (Heidbuechel et al., 2020; Xu et al., 2021) and indirectly by stimulating the immune system (Marelli et al., 2018). By expressing specific genes or receptors (Jhawar et al., 2017), OVs can be engineered to preferentially target and kill tumor cells through lysis, which releases tumor-specific antigens that stimulate the innate and adaptive immune systems, augmenting CD4⁺ and CD8⁺ T cell responses (Marelli et al., 2018). Talimogene laherparepvec (T-VEC), a genetically modified herpes-simplex virus (HSV), was the first OV to reach the western market and was approved in 2015 for the treatment of late-stage melanoma (Andtbacka et al., 2016; Cassidy and Craig, 2019). Despite these advances, early-phase clinical trials of OVs in gliomas exhibited limited therapeutic efficacy (Forsyth et al., 2008; Freeman et al., 2006). Oncolytic HSV in particular has not achieved expected levels of efficacy in glioma trials owing to limited viral distribution within the tumor tissue (Mi et al., 2020). Encouragingly, rQNestin34.5, a second-generation oncolytic HSV-1 currently in Phase I clinical trial for the treatment of recurrent glioblastoma, shows high efficacy in preclinical models (Nakashima et al., 2015; NCT03152318, 2017). Developing a quantitative picture of the effects of the TME and glioblastoma heterogeneity on rQNestin34.5 is an important component of its successful translation into the clinic.

Owing to the limited success of OVs in the treatment of glioblastoma and other cancers, it is crucial that we develop new tools for measuring and predicting therapeutic efficacy in preclinical studies. Mathematical and computational models are ideally situated to respond to preclinical drug development needs (Cassidy and Craig, 2019; Jenner et al., 2021). Many mathematical models of OVs have helped inform dosage protocols and delineate mechanisms of therapeutic efficacy (Cassidy and Craig, 2019; Heidbuechel et al., 2020; Jenner et al., 2020b; Jenner et al., 2021; Kim et al., 2019; Lee et al., 2020; Mahasa et al., 2020). Additionally, several models of glioma and glioblastoma growth and response to treatment have also been developed (Böttcher et al., 2018; Gallaher et al., 2020; Jacobs et al., 2019; Kim et al., 2019; Massey et al., 2012; Swan et al., 2018; Swanson et al., 2011; Yan et al., 2017). Despite these efforts, many mathematical models do not account for the roles of stroma and various immune cell subsets within the TME.

Computational agent-based models are particularly attractive modeling frameworks that support investigations into both temporal and spatial aspects of the many different cell types within tumors that may impact therapy (Cess and Finley, 2020; Fadai et al., 2019; Gallaher et al., 2020; Ghaffarizadeh et al., 2018; Jenner et al., 2020b; Metzcar et al., 2019; Norton et al., 2019), 2017; Ozik et al. (2018); Piretto et al. (2019); Rocha et al. (2021); Wang et al. (2021). These models account for stochasticity in single-cell and cell–cell mechanics using probabilistic rules that are based on kinetic rates of action between cells and substrates. Computational models of glioblastoma are becoming more widely used (Falco et al., 2021; Grimes et al., 2020; Randles et al., 2021; Scott et al., 2021), but none have considered the interplay between an OV, immune cells, and stroma and the role these entities play in the efficacy of oncolytic virotherapy.

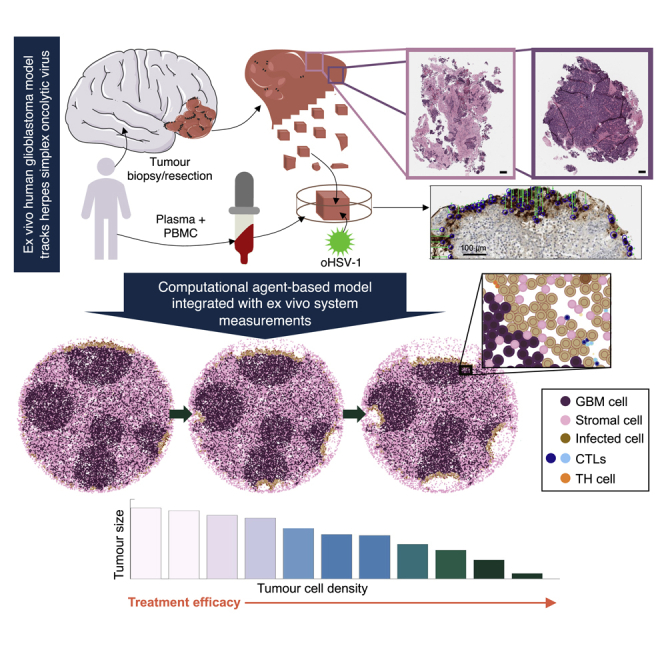
To investigate the roles of the stroma and inter- and intratumoral heterogeneity in the treatment of glioblastoma with oHSV-1, we developed an integrative framework combining an ex vivo 3D tumor ecosystem (Majumder et al., 2015) that recapitulates the TME and patient-specific immune characteristics (Figure 1) with an agent-based model that describes immune, glioblastoma, and stromal cell interactions with oHSV-1. Experimental data for oHSV-1 infiltration, immune composition, and stroma density from ex vivo patient glioblastoma samples were used to establish a hybrid discrete-continuous model in PhysiCell (Ghaffarizadeh et al., 2018). Our results suggest that directing OV injections to denser regions of the tumor could increase therapeutic efficacy, thereby providing measurable benefits to patients. These findings were further corroborated in a sample from a patient with a metastatic adenocarcinoma in the brain treated with rQNestin in our ex vivo system. The computational model established here can be easily translated to other therapeutic OV treatments or immunostimulatory treatments. Together, our theoretical platform represents a significant step forward in understanding tumor-immune interactions after oncolytic virotherapy and furthers the preclinical-to-clinical translation of oHSV-1 for glioblastoma treatment.

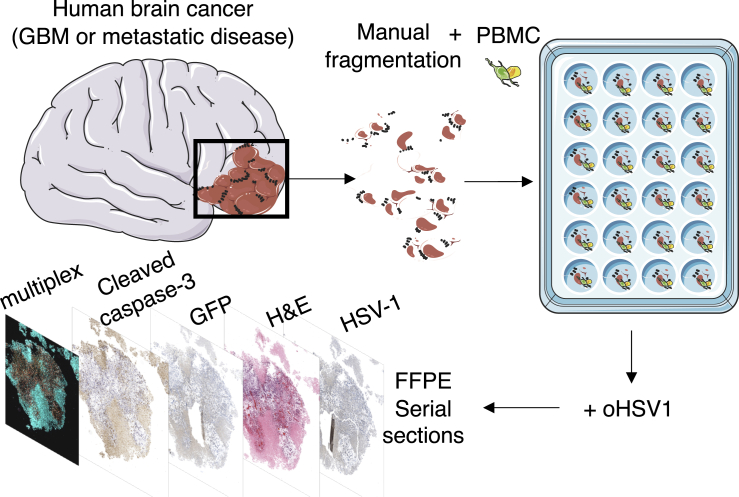
Figure 1.

Ex vivo tumor model

Patient biopsies or resections were manually cut and cultured with peripheral blood mononuclear cells (PBMCs) and grown in ex vivo tumor ecosystems (Majumder et al., 2015) in the presence of oHSV-1. Tumor tissue slices were then formalin-fixed and paraffin-embedded (FFPE), and serial sections were collected and stained for HSV-1, cleaved caspase-3, or with hemotoxylin and eosin (H&E). Multiplex immunohistochemistry (mIHC) was performed to investigate the impact of oHSV-1 on the spatial context and activity of the immune compartment in the glioblastoma TME ex vivo.

Results

Agent-based computational model of glioblastoma

We developed a computational representation of glioblastoma tumors based on our ex vivo patient samples, previous human studies, and experimental studies of glioblastoma using an agent-based model built-in PhysiCell (Ghaffarizadeh et al., 2018) to longitudinally predict approaches to optimize the efficacy of oHSV-1 against glioblastoma. PhysiCell is a physics- and agent-based modeling framework that provides a robust and scalable platform for biologically-realistic modeling of cell cycling, apoptosis, necrosis, cell volume changes, and phenotypic interactions (Ghaffarizadeh et al., 2018). The agent-based model is directly coupled with the biotransport solver BioFVM (Ghaffarizadeh et al., 2015) that simulates diffusing substrates and cell-secreted signals (here chemokine and free OV) in the microenvironment. BioFVM also allows cells to dynamically update their phenotypes based on microenvironmental conditions. For more information on PhysiCell see the STAR Methods, Figures S1–S3, and full algorithmic detail and test results in the PhysiCell method paper (Ghaffarizadeh et al., 2018).

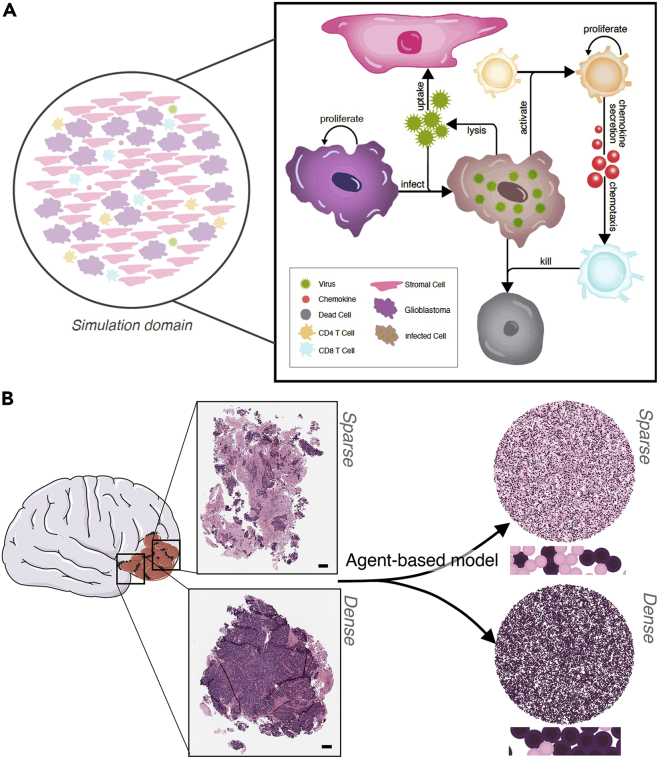
As in our experimental system, our computational model was built to describe the individual interactions between glioblastoma, stromal, CD4⁺, and CD8⁺ T cells (Figure 2A). Proliferating glioblastoma cells become infected by OV, changing phenotype to infected cells. CD4+T cells become activated by the presence of infected cells. To develop into effector populations that combat viral infections, naïve CD4⁺ T cells need to recognize viral antigens that are usually presented to them by virus-infected antigen-presenting cells (APCs) (Janeway et al., 2005; Juno et al., 2017; Swain et al., 2012). As we have no measurements for the APCs in the sample, we modeled the process of viral antigen presentation using viral-infected cancer cells as a proxy, as is common in immunovirological models (Cassidy and Craig, 2019; Jenner et al., 2020a; Myers et al., 2021). Once CD4⁺ T cells are primed, they begin to, and secrete chemokine which recruits CD8+T cells through chemotaxis. CD8+T cells then induce apoptosis in infected cells and/or tumor cells depending on their antigen specificity. Each cell was modeled as an agent and equipped with an independent state and set of rules dictating its behavior based on local environmental conditions (i.e., chemokine and virus concentrations) and cell-cell interactions (Table 1) with virus and chemokine modeled as diffusing fields (Equation 1, STAR Methods).

Figure 2.

Agent-based model of glioblastoma patient tumor tissue slices infected with oHSV-1

(A) Schematic describing the model agents: glioblastoma (GBM) cell, stromal cell, CD4⁺ T cell, and CD8⁺ T cell. Corresponding agent rules and cell–cell interactions are in Table 1. Glioblastoma (purple) and stromal (pink) cells were randomly distributed in a 2D domain inside a circle of radius $R$ with initial numbers depending on the stromal cell to glioblastoma cell ratio. oHSV-1 particles were modeled to diffuse through the domain (Equation 1, STAR Methods), bind, and become internalized by glioblastoma or stromal cells. In infected glioblastoma cells (brown cells), the virus then undergoes replication and eventually lyses the infected cell releasing new viral particles and killing the cell (black cell) (Figure S4). CD4⁺ T cells and CD8⁺ T cells are both present in the tissue and contribute to localized clearance of infected cells. Stromal cells act as virus sinks. Through contact with an infected tumor cell, a naïve CD4⁺ T cells (Th) will become activated and secrete chemokines which attract CD8⁺ T cells (CTL) through chemotaxis. CD8+T cells kill infected cells they encounter (Figure S5).

(B) A patient-derived resected glioblastoma was sub-sectioned into two smaller slices, which were then formalin-fixed, paraffin-embedded, sectioned onto slides, and stained with hematoxylin and eosin (H&E). A clinical pathologist scored the fraction of tumor cell, necrosis, immune cell, and stroma content (Table 2). Scale bar $=750\text{μm};$ further zoomed in inserts can be found in Figure S6. The two subsections were recreated in our agent-based model and designated as sparse (top) or dense (bottom) based on the pathology scores. Larger versions of the simulations can be found in Figure S7.

Table 1.

Agent phenotypes, rules, and cell–cell interactions

Phenotype	Cell rules	Cell–cell interactions
Uninfected (glioblastoma)	Migration: cells were designated either “stop” or “go” with a corresponding time in each respective phenotype. Cells designated as “go” moved with Brownian motion (MODELLING CELL MORPHOLOGY AND KINETICS, STAR Methods) Proliferation: If not too crowded, cells will proliferate with some probability (CELL PROLIFERATION MODEL, STAR Methods). Infection: Cells uptake new virions from the extracellular milieu (VIRUS MODEL, STAR Methods).	Glioblastoma cell apoptosis: CD8+T cells induce apoptosis in infected glioblastoma cells if we assume sensitivity to tumor-antigen (IMMUNE CELL MODEL, STAR Methods).
Infected (glioblastoma)	Migration: cells were designated either “stop” or “go” cell with a corresponding time in each respective phenotype. Cells designated as “go” moved with Brownian motion (MODELLING CELL MORPHOLOGY AND KINETICS, STAR Methods). Death through lysis: cells undergo lysis if the newly replicated virions exceed $\alpha$ (VIRUS MODEL, STAR Methods).	Infected-cell apoptosis: CD8+ T cells induce apoptosis in infected glioblastoma cells (IMMUNE CELL MODEL, STAR Methods).
Dead (glioblastoma)	Disintegration: cell volume reduces mimicking fluid loss as pre-defined in PhysiCell rules (Ghaffarizadeh et al., 2018) (MODELLING CELL MORPHOLOGY AND KINETICS, STAR Methods).
Stromal	Virus uptake: Cells uptake virions from the extracellular milieu, but the virus does not replicate, and the cells do not lyse (VIRUS MODEL, STAR Methods).
Inactive CD4+ T cell	Migration: cells chemotaxis up chemokine gradient (MODELLING CELL MORPHOLOGY AND KINETICS, STAR Methods).	Activate: become activated through contact with infected glioblastoma cells (IMMUNE CELL MODEL, STAR Methods)
Active CD4+ T cell	Proliferation: Cells will proliferate with some probability (IMMUNE CELL MODEL, STAR Methods). Chemokine secretion: Secrete chemokines (IMMUNE CELL MODEL, STAR Methods)
Active CD8+ T cell	Migration: cells chemotaxis up chemokine gradient (MODELLING CELL MORPHOLOGY AND KINETICS, STAR Methods). Proliferation: Cells will proliferate with some probability (CELL PROLIFERATION MODEL, STAR Methods). Chemokine secretion: Secrete chemokines (IMMUNE CELL MODEL, STAR Methods).	Infected-cell apoptosis: induce apoptosis in infected glioblastoma cells (IMMUNE CELL MODEL, STAR Methods). Glioblastoma -cell apoptosis: induce apoptosis in infected glioblastoma cells if we assume sensitivity to tumor-antigen (IMMUNE CELL MODEL, STAR Methods).

For each agent type (glioblastoma, stromal, CD4⁺ and CD8⁺ T cells), the cell rules and cell–cell interactions are listed. For a full summary of the model rules, see Figure 2B and the STAR Methods.

As glioblastomas are characterized by rapid cell proliferation, we assumed an exponential proliferation rate ($\beta$) for each tumor cell, with a minor fraction that might be quiescent at any one given time. To reproduce logistic growth, the probability an uninfected glioblastoma tumor cell might proliferate was also modeled to be dependent on the local cell density (sampled indirectly via the mechanical pressure). We assumed that cells under mechanical pressure from neighboring cells greater than some threshold $p_{max}$ would not proliferate, whereas cells whose pressure was under this threshold were proliferating at a rate $\beta$. In this way, we could simulate a carrying capacity density where the growth of cells slowed to a limiting value as an increasing number of cells reached the threshold pressure and were thus unable to proliferate.

Cell migration is an important process associated with cancer progression and was implemented by calculating a cell migration velocity ${\mathit{v}}_{mot}$ that was a combination of bias and random motion. To restrict cell migration to within the tumor boundary while still accounting for tumor expansion, we designated areas of the domain that were migratory or non-migratory, and expanded the area of the migratory domain according to the growth of glioblastoma tumors estimated using patient MRI scans for glioblastoma growth (Stensjøen et al., 2015, 2018) (Figure S8). Although glioblastoma growth can vary greatly depending on driver mutations, pressure, oxygen, nutrients and so forth, we choose not to model these factors specifically and assume they can be accounted for in the stochasticity of the model and by estimating the domain expansion from the average of patient MRI scans (Stensjøen et al., 2015, 2018).

Glioblastoma tumors in particular are comprised of highly migratory tumor cells that migrate in a “stop and go” fashion (Gallaher et al., 2020). To replicate this movement, each glioblastoma tumor cell agent was modeled as either migrating or at rest for a period of time (Gallaher et al., 2020). Rules governing individual glioblastoma tumor cell migration were implemented based on the hybrid mathematical and computational model of glioblastoma growth by Gallaher et al. (2020). By calibrating to serial magnetic resonance imaging and cell tracking data (Gallaher et al., 2020) derived frequencies for mean speeds and persistence times of glioblastoma cells. Based on their work, each cell in our model was initialized as either a “stop” or “go” cell with a corresponding time in each respective type (persistence time) sampled from their distribution (Figure S9). Cells designated as a “go” cell are then assigned a random direction and speed drawn from their distributions as well (Gallaher et al., 2020).

To replicate the dynamics of rQNestin, we modeled the extracellular and intracellular viral processes separately. We modeled oHSV-1 as a decaying diffusing infectious agent (Equation 1, STAR Methods) that was administered either at the periphery (i.e., homogeneous dosage at the exterior of the slice) or center of the tumor tissue domain. do Free virus was considered to decay (e.g., through loss back to circulation and phagocytic uptake) as it diffused within the TME. Free virus was also taken up by glioblastoma through association with receptors on the cells’ surfaces and released from glioblastoma cells as they undergo lysis (Figure S4).

Following viral entry into a glioblastoma cell, the intracellular dynamics of replication and eventual cell lysis were governed by a system of ordinary differential equations describing viral replication within the cell until the number of viral particles reaches the lysis-burst size $\alpha$, at which point the cell is killed causing it to release virus at a rate ${\delta }_V$. After a cell has undergone lysis, we initiate the cell death model in PhysiCell (called “apoptosis”) for that cell using the default PhysiCell parameteSTAR Methodsrs for cell volume change. In the “apoptosis” model, the cell that has died shrinks and eventually exits the system (see the STAR Methods for more details).

Glioblastoma stromal cells have been known to drive tumor resistance and malignancy, and be a major hindrance to the successful treatment of this cancer (Cai et al., 2021; Clavreul et al., 2014; Huang et al., 2020). Traditionally, tumor stroma is broadly viewed as the amalgam of non-cancer cells and the structural components that hold tumor tissues together. We model stromal cells as all non-cancer, non-immune cells. These include fibroblasts, glioblastoma-associated stromal cells, and any other parts of the structure of the tumor that might impede virus movement (Clavreul et al., 2014). Stromal cells were placed in and around glioblastoma cells to represent the tumor structure, with additional empty space between cancer and stromal cells representing regions of extracellular matrix (ECM) not considered within our model. Viral infiltration is known to be inhibited by the stroma and ECM, and interstitial structure is one of the major barriers to drug delivery in solid tumors Everts et al. (2020); Kim et al. (2006); Krol et al. (1999). As such, the stroma was modeled as individual cells able to uptake virus but unable to replicate virus, therefore acting as sinks that trap viral particles. Biologically, not all viruses will be taken up or inhibited by stroma, as virus particles can often be too small to be trapped by the ECM. We account for this within the model by modeling virus as a continuous density whose diffusion is unimpeded by the stroma or glioblastoma cells. In this way, the virus can diffuse past obstructions. We are therefore able to simulate virus that might escape “trapping” or stromal uptake.

The immune landscape of glioblastoma has been investigated extensively, and glioblastoma is well known as a highly immunosuppressive cancer (Pires-Afonso et al., 2020) with low numbers of lymphocytes in comparison to other tumors such as melanoma or lung cancers (Pires-Afonso et al., 2020). In our computational model, CD4⁺ T cells were all initially inactive and became activated through contact with oHSV-infected glioblastoma cells (Figure S5). It is well-established that chemokines produced upon antigen-specific interactions between dendritic and CD4⁺ T cells can actively attract CD8⁺ T cells (Rosendahl Huber et al., 2014; Swain et al., 2012). We, therefore, considered contact between infected and CD4⁺ T cells to cause CD4⁺ T cells to start secreting a diffusing chemokine (Equation 1, STAR Methods), mimicking cell-to-cell communication cascades. All T cells were modeled to chemotaxis up the chemokine gradient, i.e., the migration velocity vector ${\mathit{v}}_{mot}$ included a bias towards the chemokine gradient with bias constant $b=0.85.$ CD8+T cells attach to infected cells and induce their apoptosis. As such, glioblastoma cells could die either through virus-induced lysis (necrosis) or CD8⁺ T cell-induced apoptosis. The recruitment and expansion of CD8⁺ and CD4⁺ T cells lead to more effective antitumor immunity by increasing the likelihood of T cell-induced cancer cell apoptosis (Dummer et al., 2002; Kmiecik et al., 2013; Maimela et al., 2019; Stephan et al., 2015). To model the expansion of T cells within the tumor, both CD4⁺ and CD8⁺ T cells were considered capable of proliferation once activated after encountering an infected cancer cell (see supplementary information).

Further modeling details are in the STAR Methods with a summary of all parameters and variables provided in Table S2. All simulations were performed in PhysiCell, which is a cross-platform C++ codebase. Analysis of the simulations and the parallelization of multiple simulations were conducted in Matlab R2020b or Python.

Model parameterization

The model was parameterized and validated using our experimental data, data in the literature, and previously estimated values. There were 46 parameters in the model. Of these, 23 were fixed to previously determined values in the literature, thirteen were initialized using the data from the ex vivo tumor platform, and two were fit to the kinetic data produced from the ex vivo system ($\text{n}=13$ data points). Of the remaining parameters, three were fit to previously published experimental data ($\text{n}=4$ data points for one parameter and 16 data points for two parameters) and five were estimated using biological reasonable ranges. Full details are given in the STAR Methods, with a brief overview later in discussion.

For each ex vivo tumor slice, we determined a circular approximation using the 50 $\mu m$ wide-band areas from the automated image analysis and obtained an average slice radius of $1269.7\mu m$ (Figure S10). We fixed the domain size to the average slice radius as we assumed that the area of the fragment would not have a significant impact on the overall OV dynamics as we were only investigating treatment in a short time frame. We estimated cell morphology, such as size and volume kinetics using available data (Freitas, 1999; Gallaher et al., 2020; Kouwenberg et al., 2018; Oraiopoulou et al., 2017; Rossi et al., 2019; Tasnim et al., 2018; Wang et al., 2014).

Virus binding, internalization, and replication kinetics were modeled at the individual cellular level (Figure S4) and estimated based on measurements in the literature (Nakashima and Chiocca, 2018; Nicola and Straus, 2004). We leveraged in-built tracking capabilities to calculate the net total amount of bound and internalized substrates over the lifetime of the cell by defining functions describing the binding, replication, and secretion rates of cells. In particular, the binding rate for glioblastoma cells ($u_g$) was modulated by the intracellular amount of virus and was dependent on the concentration of virus outside the cell.

Virus-induced lysis and cell death rates were estimated from literature values (Lambright et al., 2000; Workenhe et al., 2014). The virus was modeled as replicating at a rate $\text{γ}$. We fixed the burst size to that of HSV-1716 which was estimated to be $\text{α}=$ 6600 virions in the human cell line mesothelioma REN (Lambright et al., 2000). Using this value and the assumption that viral replication occurs over $12$ hours (Nakashima and Chiocca, 2018), we estimated the viral replication rate to be $\gamma =0.4886/\text{min}$. Once the intracellular viral count exceeds $\alpha$, the cell lyses or bursts and releases the intracellular virions at a rate ${\delta }_V$. As mentioned above, viral infiltration is known to be inhibited by the ECM, and interstitial structure is one of the major barriers to drug delivery in solid tumors (Krol et al., 1999). As this has not been readily measured, we investigated this parameter in detail through changes to $u_S$. The base line value was set to $u_s=0.01/\text{min}$ to account for the fact it is known that ECM/stromal uptake is a hindrance to viral diffusion.

Complete details for the parameterization of cell characteristics and migration within the domain, cell placement and numbers, cellular proliferation, virus binding, internalization, replication, virus-induced lysis and cell death rates, and immune model dynamics are provided in the STAR Methods. Parameterization of initial cell numbers, viral diffusivity, and generation of spatial configurations is discussed in the Results. Unless specified, all data fitting was undertaken in Matlab R2020b using lsqnonlin. When fitting, we investigated multiple regions of the parameter space for initial parameter guesses. Four parameters were fit to more than six data points each. For the single parameter with only four data points, we used the standard deviation in the data to provide a weighting on the residual calculation while fitting to avoid issues with identifiability. It is also possible to overcome issues like these using mixed-effects models or multistart algorithms.

Initializing computational simulations: tumor to stroma ratio

To initialize each simulation, we used a patient-derived resected glioblastoma that had been sub-sectioned into two smaller slices and scored by a clinical pathologist for the proportion of tumor cells to stromal content (Figures 2B and S6). These two sections had significantly different compositions of tumor cells to stromal cells (Table 2) and we designated them dense (cancer cell-enriched sample) and sparse (stromal cell-enriched) tumor samples. Both dense and sparse samples were composed of tumor and stromal cells but in opposing ratios. To investigate the impact of varying glioblastoma tumor cell to stromal cell distributions on treatment outcomes, we generated tumor tissue configurations that consisted of different compositions of these dense (cancer cell enriched) and sparse (stromal cell enriched) areas denoted by the ratio dense:sparse (Figure S11). For example, 10:90 refers to a tumor tissue comprised of 10% dense (cancer cell-enriched region) and 90% sparse (stromal cell-enriched region) configuration. To generate these configurations, we initially generated a patchy configuration of 50:50 where 50% of the tumor was comprised of dense, cancer cell-enriched regions and the other 50% comprised of sparse stromal-cell enriched regions. Other compositions were then created from this base case. The 50:50 configuration was generated by first randomly assigning five points as the center of dense patches (Figure S12, see STAR Methods). The radius for these patches was then drawn from a distribution informed by the approximate semi-axis of dense regions in the patient-derived sparse tumor slices such that 50% of the tumor configuration consisted of dense and 50% of sparse areas (Figure 2B). To then generate different ratios of dense to sparse configurations, we scaled the radius of each patch by a constant $\kappa$ so that the area breakdown equaled the desired dense:sparse ratio (see Table S1 for the values of $\kappa$ for the different ratios). Further details on model parameterization can be found in the STAR Methods and in the Results.

Table 2.

Histology for patient-derived glioblastoma tumor slices in Figures 2B and S6

	Figure 2B (top), sparse	Figure 2B (bottom), dense
Histology	% of total H&E slide	% of total H&E slide
Tumor	40	90
Stroma	50	10
Necrosis	10	<5
Immune cells	10	<5
Stromal cells	40	<5

Qualitative scores from clinical pathology for each tumor slice by the total fraction of tumor stroma, necrosis, immune cell, and stromal cell content (i.e., non-cancer cells within the stroma vs tumor matrix). The fraction of stroma includes tumor matrix proteins (TMPs) as well as the stromal cells (e.g., fibroblasts). Stromal cell content is calculated separately, and can be extrapolated to determine the TMPs (e.g., collagen/fibronectin and so forth) vs. stromal, non-cancer cells.

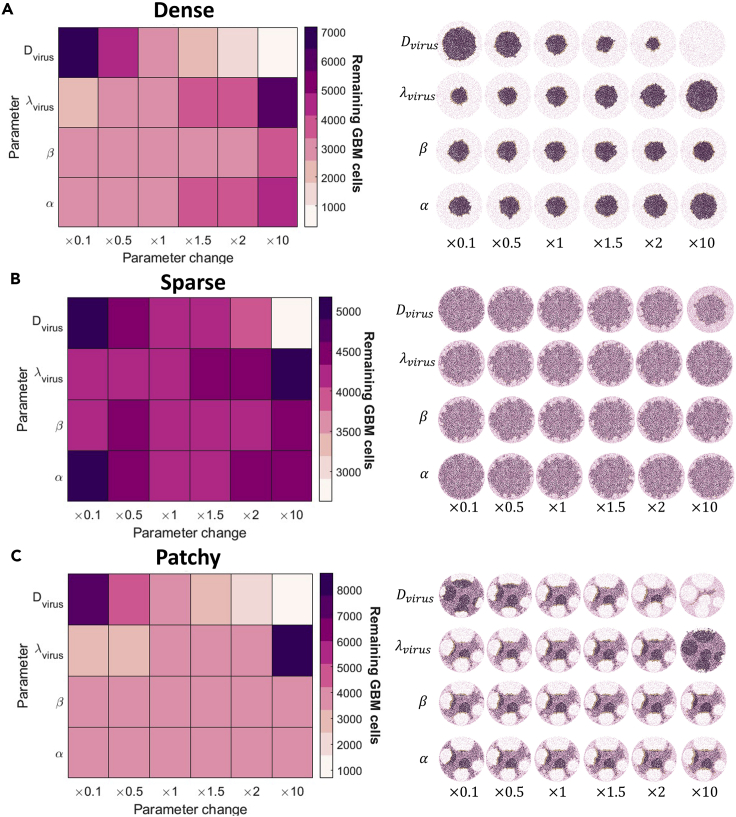
Parameter sensitivity analysis

Parameters were investigated for their sensitivity by a localized sensitivity analysis. We evaluated the sensitivity of the virus diffusion coefficient $D_{virus}$, the decay of the virus ${\lambda }_{virus}$, the infectivity of the virus $\beta ,$ and the lytic burst size $\alpha$. We chose these four parameters as they can be modulated when an OV is generated (through modification or encapsulation) or vary greatly between OV derivatives. Viral diffusion can be increased through the modification of the TME (Goradel et al., 2020), viral decay by the immune system can be decreased through encapsulation with shields (Shin et al., 2021), and viral infectivity and burst size can vary greatly between oncolytic derivatives (Macedo et al., 2020) and can also be modified through modifying viral receptor attachment (Cattaneo et al., 2008).

Each individual parameter was varied one at a time from its calibrated value and multiplied by a factor between 0.1 and 10 (i.e., $[0.1,0.5,1.5,2,10$]). This distribution of values near the base case was selected to generate a robust evaluation of sensitivity for parameter values that are most physically reasonable (Wells et al., 2015). The ensuing model predictions for each individual parameter perturbation were compared and the resulting remaining number of glioblastoma cells at 3 days was recorded for dense, sparse, and patchy tumor tissue types. Initially, we measured several metrics including the area under the curve for the number of infected cells, live cells, and dead cells. However, we found the number of glioblastoma cells at 3 days to capture all the information about the sensitivity of these parameters, and hence we used this as our metric for the sensitivity analysis presented in the results.

Computational model replicates ex vivo growth and treatment dynamics

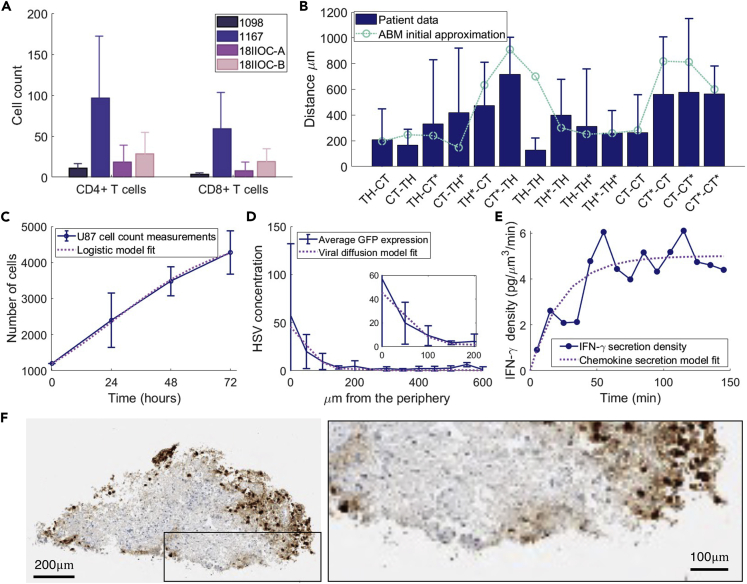
From our calculations (Smalley et al., 2019), there were on average approximately 9740 glioblastoma cells in a tumor slice. However, tumor density varied according to different experimental conditions, and we found a high degree of heterogeneity in the immune cell subset counts across the slices. In the computational model, the initial number of CD4⁺ and CD8⁺ T cells ($N_{CD4}$ and $N_{CD8}$, respectively) was determined by the average of the patient samples (Figure 3A). Taking the average area of the tumor slices to be 5.1 ${\text{mm}}^2$ resulted in an approximate density of $6.7\times {10}^{-6}\text{cells}/\text{μ}{\text{m}}^2$ for CD4⁺ T cells and $4.3\times {10}^{-6}\text{cells}/\text{μ}{\text{m}}^2$ for CD8⁺ T cells.

Figure 3.

Validation of the computational model to ex vivo, in vivo, and in vitro measurements

(A) The number of CD4⁺ and CD8+T cells in tumor slices (4 patients). Mean and standard deviation are given for the number of CD4+T cells (Th) cells and CD8⁺ T cells (CTLs) in each slice for patients 1098 (20 slices), 1167 (20 slices), 18IIOC-A (23 slices), and 18IIOC-B (28 slices).

(B) Nearest neighbor distances between CD4⁺ (TH) and CD8⁺ (CT) T cells averaged across patients 1098, 1167, 18IIOC-A, and 18IIOC-B. Ki67+ proliferative (∗) and Ki67-non-proliferative subsets of cells were noted and for each cell–cell pair relationship, the distance from a randomly chosen cell of the first type to its nearest neighbor of the second type was calculated. Error bars: standard deviation (individual patient data in Figure S13). The average minimum distance between each cell type TH, TH∗, CT, and CT∗ after a single simulation of the Hooke’s law simulation (Figure S14) is overlaid in green.

(C) To model glioblastoma cell proliferation, a logistic model was fit to in vitro cell counts for U87 cell (Mercurio et al., 2017) growth, the blue error bars are the mean and standard deviation of the cell count measurements and the black solid line is the logistic growth approximation (Figure S16).

(D) Average viral infiltration in 50 μm wide bands from the periphery of ex vivo tumor slices (n = 5) measured at 24 h with an initial 5 PFU per cell by the detection of GFP label (other PFU concentrations in Figure S15). Overlaid is the fit for viral diffusion.

(E) $S_{chemokine}$ and ${\rho }_{chemokine}^{\ast }$ were estimated from data from Gao et al. (Gao et al., 2014), who measured the density of IFN-$\gamma$ secreted from cells. Blue solid line and circles: data. Purple solid line: model fit.

(F) Example of high-grade glioma stained for HSV-1. Scale bars represent $200\text{μm}$ and $100\text{μm}$ in the left and right panels, respectively.

To initialize our simulations and placement of CD4⁺ and CD8⁺ T cells in our computational model, we leveraged their nearest neighbor measurements (Figures 3B and S13), and simulated Hooke’s law (Jenner et al., 2020) (Figure S14). Given an initial placement of CD4⁺ and CD8⁺ T cells in a tissue sample, we randomly picked a cell of a specific cell type (e.g., a Ki67 + CD4⁺ T cell) and calculated the distance to its nearest neighbor of a certain cell type (e.g., a Ki67- CD8⁺ T cell). This calculation was performed for samples from four patients (1098, 1167, 18IIOC-A, and 18IIOC-B; Figure S13). Averaging across all patient slices gave an average distance between cells of a given type (Figure 3B). We compared Hooke’s law simulation to random initial placement of immune cells and confirmed that the simulated Hooke’s law placement was able to qualitatively match the patient measurements better than simple random placement (Figure S9). It is worth noting that restricting immune cell placement as matching to the data in this way introduces bias in the initial placement of the immune cells towards that of the average nearest neighbor distances, as measured in our ex vivo data. Future work could attempt to match higher-order statistics as well, or use general adversarial networks (GANs) (Baniukiewicz et al., 2019; Han et al., 2018) to generate initial tissue geometries that mimic such subtle variations in cell distributions.

Cell count measurements for U-87MG cell proliferation in vitro (Mercurio et al., 2017) were used to estimate the glioblastoma cell replication rate of $\beta$ (Figure 3C) by fitting a logistic growth curve to the model. We introduced a threshold for cell proliferation based on the local pressure, which was determined using the initial density of cells in the sparse tumor slices (Figure 2B (top)). When local pressure exceeded ${\overline{p}}_{max}=217.8$ (dimensionless), glioblastoma cells were modeled as unable to divide. The stroma represents several cell types such as fibroblasts and endothelial cells, and we assumed that their proliferation rate is slower than tumor cells (Sahai et al., 2020).

We extracted parameters governing viral diffusivity and infiltration into the tumor tissue by tracking the presence of GFP. We estimated the diffusion coefficient for oHSV-1 (Equation 1, STAR Methods) by fitting infiltration measurements taken 24 h after exposure (Figures 3D and S15). We assumed negligible binding and release in the first 24 h (i.e., $S_{virus}=U_{virus}=0$). In other words, we assumed the primary process we could extract from the infiltration measurements in the first 24 h was the viral diffusivity, and that this parameter accounts for the limitation owing to stromal uptake. Viral dosages of 5 plaque-forming units (PFU) per cell were used to convert GFP expression to a concentration of virions $/\mu m^3$. Parameters for chemokine secretion by cells and the local voxel saturation density were obtained using cell secretion for IFN-$\gamma$ measurements (Gao et al., 2014) (Figure 3E, see STAR Methods).

To quantify the fraction of tumor cells, stroma, immune cells, and necrotic tissue, a clinical pathologist scored thin sections collected from two H&E patient-derived tumor slices (Figure 2B and Table 2). Based on this, we created realistic representations of these two patient-derived tumor slices denoted dense (90% tumor cells) and sparse (40% tumor cells) samples, where dense samples were defined to be glioblastoma cancer cell rich versus sparse samples that were made up of primarily stromal cells (Figures 2B and S11). The number of glioblastoma ($N_{GBM}$) and stromal cells ($N_{stromal}$) in the sparse and dense slices was calculated by assuming 100% of the surface area was covered by cells and then multiplying the ratio of total tissue area to cross-sectional area of a cell by the percentage of tumor cells in the tissue. For dense tumor tissue this gave $N_{GBM}=12556,$ $N_{stromal}=2861$, and for sparse tumor tissues $N_{GBM}=5580,N_{stromal}=14306$. Cells were then randomly placed in the domain by sampling an angle (${\theta }_{cell}\in \text{U}\left(0,2\pi \right)$) and radius ($d_i=\sqrt{\text{U}\left(0,1\right)}R$, where $d_i$ is the Euclidean distance ($\mu m$) from the center of the tumor slice to each individual cell, and $R$ is the total slice radius).

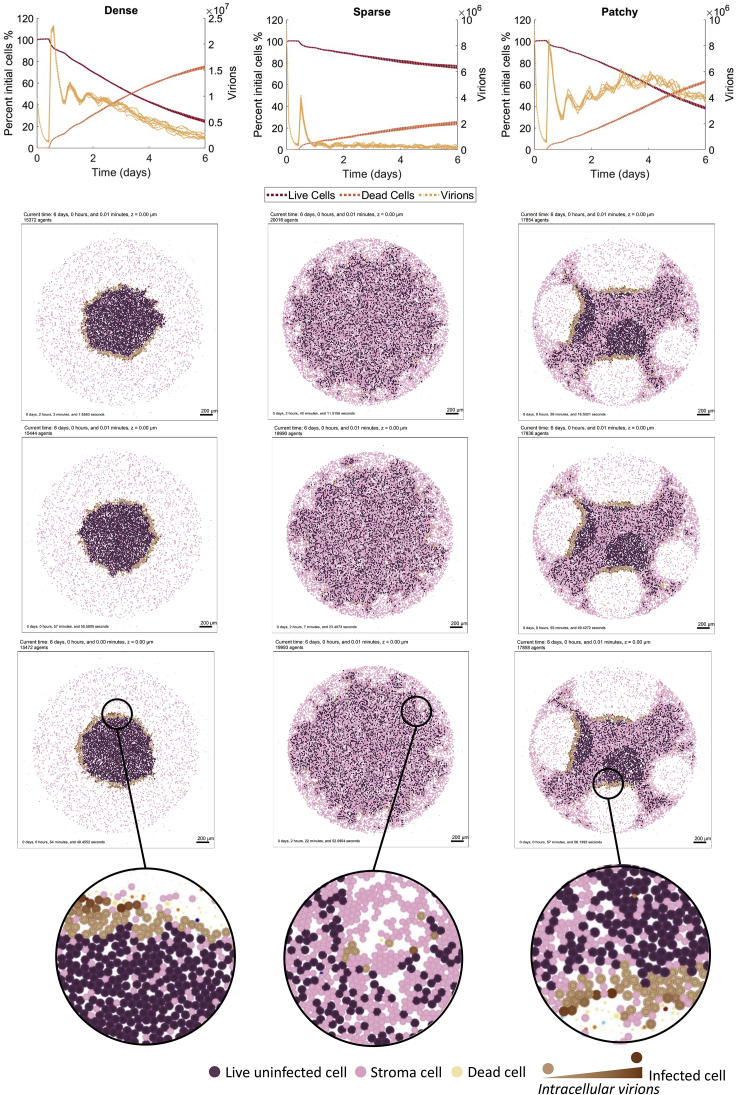
To confirm the model recapitulated our ex vivo experimental results, we simulated the computational model for tumor tissue comprising a fully dense composition (Figure 4A), full sparse composition (Figure 4B), and a patchy tumor tissue configuration consisting of 50% sparse and 50% dense regions (50:50, Figure 4C, see STAR Methods). To obtain inhomogeneous OV infiltration and match our ex vivo measurement (Figure 3F), it was sufficient to have infiltration measurements for regions of high and low glioblastoma tumor cell density (Figure 4). The simulated initial binding of virus and then slowly decline in OV concentration over time was found to be correlated to the simulated increase in chemokine concentrations. Simulated spatial configuration of viral and chemokine concentrations and immune cells numbers are found in Figure S17.

Figure 4.

Computational model predicts the ex vivo infiltration of oHSV-1 in glioblastoma tissue

Simulations of the computational model for fully dense sample 100:0 (first column), fully sparse sample 0:100 (second column), and patchy 50:50 dense to sparse (third column) tumor tissue configurations. The resulting viral infiltration in tumor tissue configurations at 6 days is given for three replicates of each tumor type. Uninfected glioblastoma cells (purple), infected glioblastoma tumor cells (brown), stromal cells (pink). See Figure S17 for corresponding spatial densities of chemokine and virus and total local density. The resulting % of live uninfected and infected cells relative to the total number of cells over time is plotted along with the total virion count (n = 9).

Changes to viral diffusivity and clearance are major drivers of final tumor size

In addition to rQNestin, there are other OV derivatives currently undergoing investigation in clinical trials for different cancers (e.g. Pexa-Vec NCT02562755, VSV-IFN $\beta$-NIS NCT03647193, MG1 NCT02285816) or under preclinical investigation (Oh et al., 2018; Xu et al., 2021) for the treatment of glioblastoma. These OVs are heterogeneous in their genome size, lytic activity, and features. This variability would be reflected in differences related to diffusivity, clearance, infectivity, and viral burst size in our model. Apart from varying viral derivatives with different characteristics, there are many strategies for enhancing the intratumorally spread, and hence diffusivity of OVs. These include ECM degradation enzymes, junction opening peptides, and fusogenic proteins (Goradel et al., 2020). Arming an OV with transgenes that degrade the ECM (Choi et al., 2010; Ganesh et al., 2008; Jung et al., 2017; Kim et al., 2006; Martinez-Quintanilla et al., 2015; Zhang et al., 2020) increases the viral diffusion by removing the barrier imposed by the ECM. Co-administration of OVs with junction opening peptides increases the spread of virus throughout the tumor by degrading the tight junctions that exist between cells (Yumul et al., 2016). Similarly, there are many strategies to circumvent antiviral immunity (Shin et al., 2021), and hence clearance of an OV. OVs can be shielded from the humoral immune responses through encapsulation in protective coatings and carriers. In particular, coatings, such as polyethylene glycol (Kim et al., 2011) or graphene oxide (Xia et al., 2019), protect the virus from detection by B cells, and antibodies, and increase the accumulation of virus at the tumor site.

Furthermore, patient-specific differences in tumor growth rates may also affect OV efficacy. To assess the sensitivity of our model’s predictions to these viral and tumor-specific characteristics, we performed a local parameter sensitivity analysis focused on the virus diffusion coefficient, $D_{virus}$, virus clearance rate, ${\lambda }_{virus}$, tumor cell proliferation, $\beta$, and viral burst size, $\alpha$ (Figure 5), as described in the STAR Methods.

Figure 5.

Systemic evaluation of parameter contributions to model behavior

Parameter sensitivity was evaluated by running simulations for perturbations in the parameters $D_{virus},{\lambda }_{virus},\beta ,$ and $\alpha$. Each parameter was perturbed by $\left[0.1,0.5,1,1.5,2,10\right]\times p$, where $p$ is the parameters original value (see Table S2). The average remaining glioblastoma cells on day 3 from 10 simulations are reported in the heatmaps (left). The corresponding model spatial tumor configuration for an instance of a parameter value is given in the heatmaps for (A) fully dense sample 100:0, (B) fully sparse sample 0:100, and (C) patchy 50:50 (dense:space).

We found that increasing viral diffusivity caused a significant decrease in the number of glioblastoma cells remaining, largely owing to the increased reach of the OV into the tumor tissue. Decreasing the clearance rate of the virus also caused a large drop in the number of glioblastoma cells remaining in the dense and patchy tumor tissues and, to a lesser extent, the sparse fragments. This suggests that extending overall OV exposure and increasing viral diffusivity produce similar effects. Interestingly, changes to the glioblastoma cell proliferation rate and viral burst size had a lesser effect on the glioblastoma tumor tissue, most likely owing to the controlled tumor expansion that limited the creation of new tumor cells and thus capping the extracellular virus density (Figure S18). Other patchy configurations were generated, and we found the overall sensitivity to changes in the parameters was conserved.

T cell recruitment and antigen-specificity are critical for therapeutic success

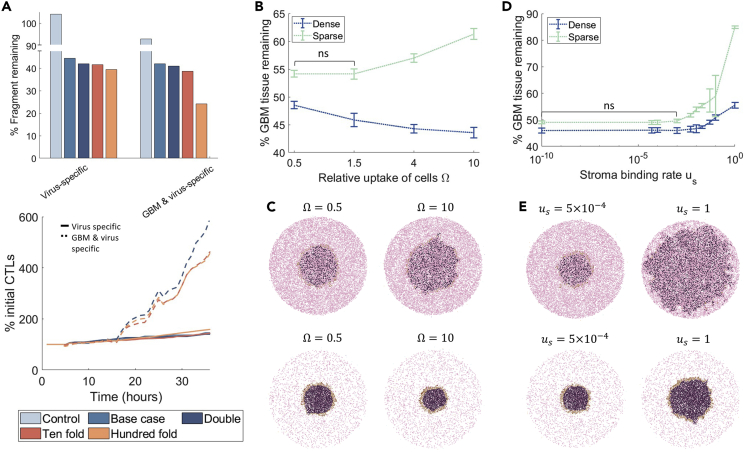
Glioblastoma treatment outcomes are also regulated, in part, by the presence of immune cells within the tumor. Though the glioblastoma TME is highly immunosuppressive, OVs can be used to drive antitumor immunity by harnessing the inflammatory responses to viral infection and the immune responses to OV-induced cancer cell death (Saha et al., 2018). To explore the significance of CD4⁺ and CD8⁺ T cells on oHSV-1 treatment efficacy, we next investigated the impact of the number of T cells recruited to the tumor tissue and the antigen-specificity of the T cells in the simulations of dense tumor slices. For this, we initialized the number of CD4⁺ and CD8⁺ T cells as 2-times, 10-times, and 100-times their base value (Table S2) and measured the percentage of the tumor tissue remaining. We considered two cases: 1) where there is a limited to no antitumor immune response (CD8⁺ T cells are virus-antigen specific i.e., CD8⁺ T cells induce apoptosis in infected glioblastoma tumor cells only) and 2) a strong antitumor immune response (CD8+T cells are both virus and tumor-antigen specific, i.e., able to induce apoptosis in both uninfected and infected tumor cells). The latter scenario was investigated to account for immunovirotherapies aimed at priming an anti-tumor immune response using OVs. We then compared these simulations to the control case with no OV to assess the role of CD8⁺ T cells within glioblastomas treated with and without oHSV-1.

In the case where there is no antitumor immune response (CD8+T cells are virus-specific only), increasing the number of T cells in our simulations had no major impact on the tumor cell burden remaining (Figure 6A). This is likely owing to the limited number of infected cells in the sample at any point in time, given that the efficacy of the treatment relies on virus survival. As the number of CD8⁺ T cells increases, there is more CD8⁺ T cell attachment and induction of infected cell apoptosis. However, if infected cells are apoptosed pre-maturely, the spread of the virus to neighboring cells is reduced thereby decreasing treatment efficacy. This trade-off between increasing the immune response without reducing the treatment spread has been previously noted in the literature (Aurelian, 2016; Filley and Dey, 2017; Goradel et al., 2021; Russell et al., 2019).

Figure 6.

Effect of T cell recruitment, antigen specificity, and virus binding rates of stromal and glioblastoma cells on oHSV-1 simulations

(A) The number of CD8⁺ and CD4⁺ T cells in the simulation was increased from the control and base case 2-times, 10-times, and 100-times. The control simulation considered no OV administration, whereas all other simulations included the OV. The percentage of tissue remaining at 72 h (top) and CD8⁺ T cell (CTL) percentage increase over time (bottom) were quantified for the different immune cell numbers considered (infected cells and CD4⁺ T cells (THs) over time are in Figure S22). In addition, we considered CD8⁺ T cells as either virus-specific (induce apoptosis in infected cells only) or glioblastoma and virus specific (induce apoptosis in both uninfected and infected cells).

(B) The percentage of the initial tissue remaining at 72 h for different glioblastoma and stromal cell relative binding rates $\text{Ω}$, where ${\text{u}}_{\text{s}}=0.01\times \text{Ω}$ and ${\text{u}}_{\text{g}}=0.002\times \text{Ω}$ in dense and sparse tissues is given as mean and standard deviation error bars (n = 3). p-value tests for significance ($p>0.05$) with not significant (ns) is noted.

(C) Simulation snapshots of (bottom) dense and (top) sparse tumor tissue at 144 h for the stromal cell relative binding rates $\text{Ω}$ of $\text{Ω}=0.5$ and $\text{Ω}=10$.

(D) The percentage of the initial tissue remaining at 72 h for different stromal binding rates (${\text{u}}_{\text{s}}$) in both dense and sparse tissues. Corresponding viral infiltration measurements are in Figure S19.

(E) Simulation snapshots of (bottom) dense and (top) sparse tumor tissue at 144 h for stromal cell-virus binding rate $u_s=5\times {10}^{-4}$ and $u_s=1$. Stromal cells (pink), glioblastoma cells (purple) and infected cells (brown).

In contrast, in the case of a strong antitumor immune response (CD8⁺ T cells that are both virus- and tumor-antigen specific), increasing CD8+T cells 100-times resulted in an additional 20% reduction in the tumor cell burden remaining. Interestingly, increasing the virus- and tumor-antigen specific CD8+T cells 100-times was the only condition that resulted in a significant increase in treatment efficacy, as we found that 2-times and 10-times increases were insufficient for reducing tumor cell numbers. Furthermore, we found that increases in the number of virus- and tumor-antigen specific CD8⁺ T cells correlate with an increase in OV efficacy, suggesting that there is a threshold number of CD8⁺ T cells necessary to provide a discernable treatment impact (Figure 6A).

Impact of the binding rate of stromal and glioblastoma tumor cells on oHSV-1 efficacy

We next interrogated how viral-specific properties affect oHSV-1 therapeutic efficacy, given that engineered modifications of OVs can increase their ability to bind and be internalized by cells (Jung et al., 2017). To investigate the impact of oHSV-1 binding and internalization kinetics in dense and sparse tumor tissue configurations, we measured the effect of various glioblastoma and stromal cell relative uptake rates $(\text{Ω}$) and different stromal binding rates ($u_s$) on tumor size 72 h after adding oHSV-1 to the periphery of the tumor tissue configuration (Figure 6B).

We tested relative binding rates by varying both $u_g$ and $u_s$ and setting $u_g=\text{Ω}\times 0.002$ and $u_s=\text{Ω }\times 0.1$, where $\text{Ω}=0.5,1.5,4,10$ is the relative binding rate. We found treatment to be most effective in dense tumor tissue configurations with larger values of $\text{Ω}$ (e.g., $\text{Ω}=10$) while treatment efficacy was highest in sparse tumor tissue when cell-binding rates were low ($\text{Ω}=0.5$ and $1.5$) (Figure 6C). This outcome is consistent with sparser tissues having fewer glioblastoma cells to drive viral replication, and high binding rates by stromal cells trapping virions and impeding oHSV-1 infiltration. The difference in oHSV-1 infiltration, and thus efficacy, between sparse and dense tumor tissue was further highlighted when the model was simulated for different viral replication rates and cell-binding rates (Figures S19 and S20). Overall, our predictions suggest that a small increase in the relative binding rate of $\text{Ω}=1.5$ would be best for both extreme tumor-stromal densities (i.e., fully dense and fully sparse tumors).

We also found that the stromal cell-virus binding rate had a significant effect on the fraction of the tumor cells remaining in sparse tissues, and that treatment in these tumors was especially hindered by stromal cell-virus binding rates above $0.01$ (Figures 6D–6E). Indeed, we found that as $u_S$ increased, the stromal cells trap an increasing number of oHSV-1 virions, thus reducing treatment efficacy. Consistent with our study of changes in the relative binding rate $\text{Ω}$, this effect was most pronounced for sparse tissue with less viral replication. Together, these simulations suggest a lack of treatment efficacy in sparse regions, which could be explained by the lack of infiltration (∼150 $\mu m$) seen in sparse tissues with a binding rate of $u_s=0.1$ (Figure S19). In comparison, the efficacy of oHSV-1 is significant for dense tumor tissues, reducing the tumor bulk by 47% to 57% (Figure 6B–6C) and infiltrating to a depth of 350–450 $\mu m$ from the periphery regardless of the stromal cell-binding rate (Figure S19). Hence, given unknown rates of stromal inhibition, dense areas of the tumor are better suited for OV treatment. This finding remains unchanged even when we considered the binding rates or viral replication rates to be heterogeneous parameters drawn from gamma distributions (Figures S20 and S21).

High stroma cell content limits oHSV-1 therapeutic efficacy

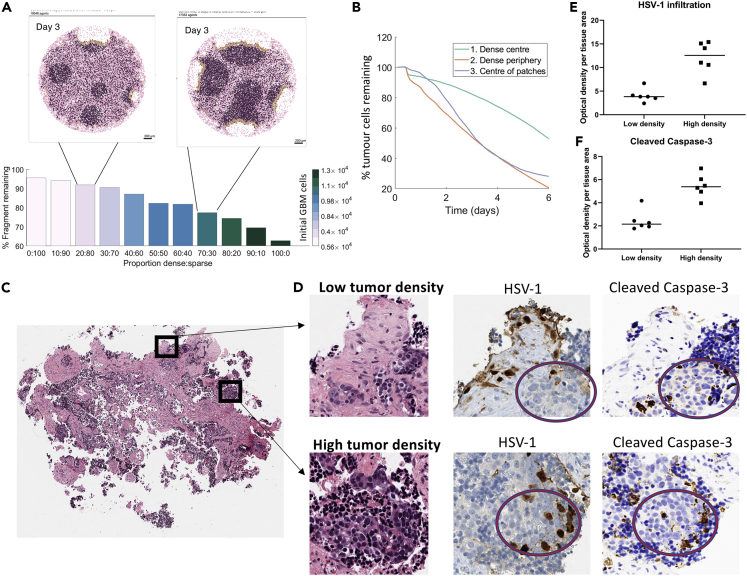
To further characterize the dependence of the therapeutic efficacy of oHSV-1 on tumor heterogeneity in our simulations, we tested a set of several tumors that displayed a wide range of tumor cell to stromal cell ratios (i.e., different dense:sparse tissues). Assuming a highly inhibitory stroma (i.e., $u_s=1$, the extreme case in Figure 6D), we measured the percentage of tissue remaining at 72 h given varying proportions of dense and sparse regions (Figure S11). We found that this fraction was directly dependent on the proportion of dense and sparse regions in the tissue configuration (Figure 7A), indicating poor oHSV-1 efficacy for tumors with expansive areas of low glioblastoma tumor cell density. Our simulations exhibited significant (>20%) tumor reduction only when dense regions comprised greater than 70% of the tumor.

Figure 7.

Tumor and stromal cell density determines oHSV-1 efficacy

(A) A range of tumor tissue configurations was generated with dense and sparse regions making up the proportion of total area denoted dense:sparse (Figure S11). In these simulations, the stromal binding rate was set at $u_s=1$. For different proportions of sparse and dense regions, the fraction of tumor tissue remaining was calculated at 72 h. The color of the bar represents the initial number of glioblastoma cells in that tumor tissue. For the 20:80 and 70:30 tumor configuration, the model snapshot is given on day 3. The corresponding time-evolution for 0:100, 50:50, and 100:0 tumors is in Figure 4.

(B) The percentage of glioblastoma tumor cells remaining over six days for three different administration protocols: a single injection into the center of the dense slice (green), a homogeneous administration of the OV on the periphery (orange), and six OV injections each into the center of dense patches for a 50:50 slice (blue). The total amount of virus administered was conserved across the protocols.

(C and D) Brain metastatic adenocarcinoma (N = 1) was isolated for ex vivo experiments and multiple independent biological replicates were then treated with oHSV1 at PFU = 5 per cell (N = 3). Following the sequential imaging strategy (described in STAR Methods), regions were characterized by clinical pathology as retaining “high” or “low” tumor cell density. Optical density of HSV-1 and caspase-3 immunostain was then quantified by automated image analysis and graphed as (E) HSV-1 expression or (F) cleaved caspase-3 per region of tissue area (${\text{mm}}^2$).

In previous simulations (Figure 3, Figure 4, Figure 5), oHSV-1 was applied to the surface or periphery of the tumor slice to mimic our ex vivo experimental conditions. However, rQNestin is currently being evaluated in clinical trials using direct injections of the OV into the tumor. To understand the dependence of the therapeutic efficacy of oHSV-1 on the virus administration method in our computational model, we simulated the injection of the same PFU per cell into the center of each of the five patches, as was conducted in our simulations at the periphery. This further highlighted the dependency of treatment efficacy on the dense region to sparse region ratio (Figure 7B). Our predictions showed that single-point injections have slower initial binding rates but exhibit more rapid tumor killing after 2 days. Our model predicted that the rate of tumor cell killing proceeded rapidly in the dense patches but slowed at the borders approaching sparse patches. Around day 4, the fraction of cells remaining after injections into the center of 50:50 patches equaled the efficacy of oHSV-1 application at the periphery of cancer cell dense tumors, suggesting that injections in these cancer cell dense patches or regions are optimal. Given that a dense region refers to a higher ratio of tumor cells to stromal cells and a sparse region refers to a higher ratio of stromal cells to tumor cells, we found that high stroma cell content reduces oHSV-1 efficacy.

To experimentally determine whether our model’s predictions held true for other types of brain cancer, we assessed tissue from a patient with metastatic adenocarcinoma to the brain. We used the ex vivo tumor model system to treat the manually cut tissue slices with oHSV-1 at 5PFU per cell for 48 h. Tissue was then formalin fixed, cut onto slides, and serial sections were stained with hematoxylin and eosin (H&E), or immunostained for HSV-1, or cleaved caspase- 3. Next we identified tumor-containing regions that were characterized as having a high stromal cell with low tumor cell density or a low stromal cell with a high tumor cell density (Figure 7C) that are qualitatively similar to the original dense and sparse samples (Figure 2B). Regions of high and low tumor cell density were then quantified for oHSV-1 or cleaved caspase-3 expression (Figures 7D–7F) based on optical density measurements from image analysis and normalized to the tissue area that was analyzed (see STAR Methods).

Across all samples we examined, we determined that regions with low tumor cell density but high stromal cell density had reduced oHSV-1 infiltration compared to regions with higher tumor cell density (Figure 7E). In addition, and consistent with the hypothesis from the computational simulations, we established that the induction of cell death, as determined by cleaved caspase-3 optical density per area (Figure 7F), trended much higher in the high tumor cell dense tissue regions.

Discussion

Oncolytic viruses (OVs) are a central avenue of investigation for improved cancer treatment and hold great promise for the treatment of particularly aggressive and deadly tumors, including glioblastoma. Their mechanism of action includes a lytic component, whereby the viral construct limits tumor cell replication and induces lysis in tumor cells, and an innate and adaptive immune component, in which immune cells are recruited to the site of infection and stimulate T cell-mediated tumor cell killing. Leveraging the oHSV-1 rQNestin treatment strategy with the preclinical glioblastoma ex vivo tumor ecosystem platform, we developed an agent-based computational framework to recapitulate this treatment and assess key viral- and tumor-specific characteristics determining oHSV-1 therapeutic efficacy. Using our computational model allowed us to generate hypotheses and investigate the key determinants of OV treatment success in these difficult-to-treat tumors in a robust preclinical platform. The platform developed here is flexible and can be applied to other oncolytic virotherapy treatment contexts. Our aim is to use our model complement to experimental and clinical studies in future studies.

Our model simulations suggest that viruses that can infiltrate deep into the tumor simply by diffusion are able to reduce tumor size significantly (Figure 5). In terms of immune kinetics, our simulations found that the efficacy of the immune response is a function of both the size of the recruited CD8⁺ T cell pool and antigen specificity (Figure 6A). Only with significantly large numbers of initial CD8+T cells that are both virus- and tumor antigen-specific did we see tumor reduction to ∼20% of the control size. Treatment efficacy of an OV requires a sufficiently robust CD8+T cell response for therapy to be most effective (Martikainen and Essand, 2019). In our simulations, with tumor-antigen specific T cells, the T cell efficacy was maximized at smaller T cell populations, as viral lysis was the primary cause of cell death. Comparing the number of CD8⁺ T cells over time for the different initial numbers of immune cells shows that the largest increase in CD8⁺ T cells is achieved with a 100-fold increase in the initial number. The dramatic increase in CD8⁺ T cells in this scenario is largely owing to the higher likelihood of a T cell encountering its complement antigen (i.e., virus-infected tumor cell). This suggests that CD8⁺ T cell proliferation can cause substantial cancer cell killing with sufficient initial numbers in the tumor. Our simulations showed that T cell recruitment and specificity play a major role in OV therapy, and point to the need for testing combinations of oHSV-1 and immunostimulatory agents (Andtbacka et al., 2016; Cassidy and Craig, 2019; Jenner et al., 2021) to overcome stromal inhibition.

The stroma can have a significant impact on the ability of treatments to reduce tumor size (Plava et al., 2019; Valkenburg et al., 2018), and our model supported this by predicting that strong stroma-virus binding rates negatively affected oHSV-1 therapeutic efficacy and rendered the OV ineffective in regions of the tumor with low glioblastoma tumor cell to stromal cell ratios (Figures 6B–6C). In contrast, our model predicted glioblastomas with high tumor cell content are likely to readily support oHSV-1 constructs designed to target and replicate in cancer cells. Although the dependence of oHSV-1 efficacy on high tumor cell content is not entirely surprising, there is minimal work in clinical trial settings that considers the impact of tumor and stromal cell density on the treatment outcome for patients. Introducing modifications to oHSV-1 kinetics that increase stromal and glioblastoma cell-binding rates would be most effective when the patient tumor stromal density is known, allowing treatment to be appropriately tailored.

Simulated perturbations in viral binding rates for all cells highlighted the trade-off in optimizing oHSV-1 for the treatment of tumors with different stromal cell contents (Figures 6D–6E). Indeed, we found that increasing glioblastoma and stromal cell-binding rates improve treatment efficacy in areas of high tumor cell density where viral replication in the glioblastoma cells can outpace binding by stromal cells. Conversely, high viral binding rates are counterproductive in areas of low glioblastoma tumor cell density where low levels of oHSV-1 replication are outpaced by high levels of stromal cell binding, thereby reducing overall viral infiltration. This phenomenon became readily apparent when stromal cell viral binding rates were high relative to glioblastoma tumor cell-binding rates. Designing OV constructs that are limited to replication in tumor cells meets important safety requirements but requires targeted application or injection of the virus into tumor compartments with high cancer cell content. Our model suggests that finding and mapping these regions of high content would help improve therapeutic efficacy. Increasing viral binding rates for tumor cells and decreasing binding rates for stromal cells might also boost efficacy.

Measuring the remaining tumor tissue in the slice after oHSV-1 treatment in simulations designed to compare efficacy in regions of low and high tumor cell content revealed that OV treatment success is determined by regional cancer cell density (Figure 7). This implies that a significant proportion of patients with low glioblastoma tumor cell density may not benefit from oncolytic virotherapy. As OVs require cancer cells to proliferate and with a reduction in the source of their proliferation, it is intuitive that the treatment efficacy would drop in regions of low density. Fortunately, OVs can be genetically modified to express proteins that result in the breakdown of the ECM (such as matrix metalloproteinase-1 and -8 (Cheng et al., 2007) and Relaxin (Jung et al., 2020). Although these sorts of modifications are under experimental investigation, the impact of the breakdown of human patient stroma or ECM constituents in the clinical setting is missing. Our model suggests that patients may benefit from these strategies and supports their clinical translation.

Ultimately, our simulations suggest that oncolytic viral therapies such as oHSV-1 may find their greatest success when used to debulk large tumors with high tumor cell content in combination with other OVs (Jenner et al., 2021) or tumor-targeted immunotherapies (e.g., CAR T cell therapies) that can increase innate and adaptive immune responses. Conversely, oHSV-1 may be less successful in maintaining remission in smaller tumors that lack sufficient cancer cell density to drive sustained viral replication. Our model predictions suggest that oHSV-1 would potentially fail as it currently stands as a treatment aimed at preventing recurrence, particularly after resection. Notwithstanding this, OVs hold promise owing to their multimodal mode of action and their possibility of arming with genes that improve replication and spread, decrease tumor vascularisation, and elicit strong antitumor immune responses. The approval of TVEC (Imlygic) for the treatment of melanoma and more recently teserpaturev for the treatment of glioma is further evidence of the potential effectiveness of this therapy (Kaufman et al., 2022; Yuan et al., 2022; Zeng et al., 2021).

For the most part, clinical trials for oncolytic HSV-1 derivatives to date have been targeted at patients with recurrent and/or malignant brain cancers (Markert et al., 2000, 2009, 2014; Rampling et al., 2000; Todo, 2019). A wide range of treatment options has been investigated in these clinical trials. These include inoculations before and after resection (Markert et al., 2009), oHSV-1 in combination with radiation (Markert et al., 2014), or with chemotherapy (Todo, 2019). In the case of the rQNestin34.5v2 clinical trial (NCT03152318), oHSV-1 was administered during biopsy surgery in recurrent high-grade glioma. Our computational model supports oHSV-1 as a late-stage therapy as it predicts that oHSV-1 must be administered in large dense tumors, such as those being considered in the clinical trials in patients with recurrent brain cancer to have optimal efficacy.

Throughout, our simulations showed that the ratio of tumor cell to stromal cell content determines oHSV-1 therapeutic efficacy. We reproduced this finding empirically by testing a brain metastatic adenocarcinoma patient sample in the ex vivo ecosystem platform, where we found that oHSV-1 infiltration and cell death were highest in the regions of high tumor cell content, as predicted by our computational model. Although these results represent a single patient sample, we were able to study multiple independent regions of tissue. More work should be conducted to understand whether these empirical results hold true for glioblastoma, particularly as the expression of the oHSV vector is not well studied in brain metastatic adenocarcinoma. Furthermore, fractal dimension analysis using a box-count method (or other related approaches) can be applied to tumor tissue fragments to measure the clustering of cancer cells over varying patient samples (Chan and Tuszynski, 2016; Cross and Cotton, 1992; Landini and Rippin, 1996; Sedivy, 1996), similar to previous works (Abduljabbar et al., 2021; Chiba et al., 1990; Grizzi et al., 2005; Lennon et al., 2015; Pleşea et al., 2019), to propose whether this is correlated with oncolytic virotherapy effectiveness.

In this work, we have developed a computational platform that was used to probe the treatment of glioblastoma with oHSV-1. As noted in Table 3, our simulations produce predictions and hypotheses that have already been validated experimentally and/or clinically. Importantly, our approach supports results in the literature and highlights avenues requiring further attention through a hypothesis-generation and prediction paradigm, suggesting key mechanisms as promising avenues of investigation. Most importantly, this integrated computational and experimental approach highlights how intuitive suggestions can be made that can easily be modified experimentally and result in a more effective treatment. We still do not have a good understanding of the myriad of ways in which virus might spread through a population of cancerous cells (Wodarz et al., 2012). In this work, we model cancer cells as having some motility based on previous work by Gallaher et al. (2020). As such, an infected cell can become infected and travel with the intracellular virus. As the time taken for a cell to leave its immediate neighborhood is sufficiently longer than the time taken for cell lysis or viral diffusion through that microenvironment, an infected cell carrying virus will not have a significant impact on the spread of virus. However, future extensions of the model could investigate this in more detail. For example, though not accounted for here, virus-induced syncytia have been known to be motile (Alzahrani et al., 2020; Sylwester et al., 1993). Recent agent-based modeling advances developed to investigate cellular fusion in SARS-CoV-2 (Risner et al., 2020) could potentially be adapted to investigate these effects.

Table 3.

Summary of model-generated hypotheses from examining different underlying effects/metrics with the computational model, along with possible experiments and evidence (where available) in the literature in agreement with prediction

Effect/metric examined	Model predicted effect on treatment efficacy	Hypothesis generated	Experimental and/or clinical evidence
T cell recruitment and antigen specificity (Figure 6A)	Increasing the virus- and tumor-antigen specific CD8+ T cells reduces the number of glioblastoma cells	Improvements to OV efficacy are only seen with large populations of virus- and antigen-specific CD8+ T cells	A study in 56 patients with small-cell lung carcinoma (SCLC) detected that a significantly low tumor size was associated with a high number of tumor-infiltrating T cells (Eerola et al., 2000). Staining for CD4+ and CD8+ T cells in 284 gliomas revealed that the number of CD8+ T cells was inversely correlated with tumor grade (Han et al., 2014).
Virus binding rates to stromal cells, $u_s$, and glioblastoma cells, $u_g,$ (Figure 6B–6E)	Increasing the virus binding of cells negatively affects sparse samples and positively affects dense samples	The loss of virus to stroma can significantly hinder OV efficacy	OV-expressed factors such as proteases (e.g. MMP9) have been shown to facilitate stroma degradation, and enhance HSV delivery, distribution, and oncolytic effect in mice bearing human brain tumors (Hong et al., 2010). An EGFR-retargeted HSV with MMP9, KMMP9 demonstrated selective infection and killing and improved viral penetration and survival in a glioblastoma multiforme xenograft model (Sette et al., 2019).
Viral diffusivity, $D_{virus}$, and clearance, ${\lambda }_{virus}$, (Figure 5)	Increased glioblastoma cell death with increases in $D_{virus}$ and decreases in ${\lambda }_{virus}$	Increasing the diffusivity of an OV and/or decreasing the clearance, will significantly improve treatment efficacy	Arming OVs with a transgene that degrades the ECM (e.g. hyaluronidase (Ganesh et al., 2008; Martinez-Quintanilla et al., 2015), decorin (Choi et al., 2010; Zhang et al., 2020) or relaxin ) improves viral spread and enhance viral potency. In glioblastoma, clearance of oHSV has been linked to (natural killer cells) NKs causing diminished OV-efficacy (Alvarez-Breckenridge et al., 2012). Combining TGF-$\text{β}$ with oHSV was shown to inhibit NK recruitment and increased viral efficacy (Han et al., 2015).
Injection location (Figure 7B)	OV administered on the tumor periphery is more effective at reducing the number of glioblastoma tumor cells than OV injected in the center	Intratumoral OV injections are not as effective as injections on the tumor periphery	While there is extensive discussion around the advantages and challenges of intratumoral injections compared with intravenous injections (Geletneky et al., 2017; Zamarin and Pesonen, 2015), experiments that compare administering treatment directly at the tumor periphery versus intratumorally are absent in the literature. Future work could investigate this with a tumor spheroid model.
Proportion of dense to sparse regions in tumor tissue (Figure 7A)	Increased glioblastoma cell death with increased proportion of dense tumor tissue (dense:sparse)	Glioblastoma cell density in the tumor is an indicator of OV efficacy and treatment success	Isolated brain metastatic adenocarcinoma treated with oHSV-1 showed higher HSV-1 infiltration and cleaved caspase-2 in areas of high tumor cell density compared to areas of low tumor cell density (Figures 7C–7F)

In summary, we developed a computational agent-based model for glioblastoma tumor tissue treated with an OV considering the presence of tumor-infiltrating CD4⁺ and CD8⁺ T cells. This work demonstrates how ex vivo measurements can be used to inform agent-based model development while also providing an open-source framework that can be extended by others to investigate alternate OV derivatives and glioblastoma treatments. Using the platform, we generated hypotheses (Table 3) that have support both from the literature and from data presented here using a metastatic adenocarcinoma sample. Together, this work has implications for the continued development of OVs for the treatment of brain tumors and ultimately allows for more personalized patient predictions and improved treatment outcomes. Importantly, our cross-disciplinary platform is an exciting addition to the study of oncolytic virotherapy for the treatment of glioblastoma and other brain cancers, and the field of cancer immunotherapies more broadly.

Limitations of the study

As with any ex vivo system or tissue culture model, there are limitations to our approach. In particular, viral infiltration beyond the periphery of the glioblastoma samples was significantly limited, although deeper infiltration was readily apparent in the metastatic adenocarcinoma sample. As the depth of viral infiltration was only calibrated to the first 24 h of measurements, we assumed the computational model to be independent of any artifacts of the ex vivo system that may arise after 24 h. Unfortunately, it is not possible to definitively conclude whether this is an artifact of the ex vivo system (e.g., sample preparation by manual cutting of thick slices, application of viral particles by dropping onto a partially submerged sample, and so forth), a limitation of the oHSV-1 construct rQNestin, which was designed to be replication-competent in malignant glioma cells, or owing to the tumor tissue composition itself. Fortunately, as we did not calibrate to measurements from our ex vivo system after 24 h, the computational model we developed was calibrated to be independent of these shortcomings, further highlighting the complementarity of experimental and theoretical approaches. In terms of the modeling assumptions, there are a few simplifying assumptions that introduce limitations to the work, for example we chose not to model explicitly the ECM fibers or tumor structure, we left “empty space” between cells in our simulations. In addition, it is worth noting that from a clinical standpoint, four patient biopsies of glioblastoma represent a small sample size. More should be conducted in future work to validate the findings in a larger number of patients.

STAR★Methods

Key resource table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
GFP antibody (clone 168AT1211)	Abgent	Cat 3 AM1009a; RRID:AB_352468
Bacterial and virus strains
rQnestin34.5v1	University of Pittsburgh	(137)
Critical commercial assays
Cleaved caspase-3	Cell signalling Tech	(138)
Hematoxylin and eosin (H&E)	Sigma Aldrich	(131)
mIHC	Roche	CD3 (anti- CD3 rabbit, Ventana, 790-4341) CD4 (anti-CD4 rabbit, Ventana, 790-4423) CD8 (anti-CD8 rabbit, Ventana, 790-4460) Ki67 (anti-Ki67 rabbit, Ventana, 790-4286) Pan-keratin (anti-pan-keratin mouse, Ventana, 760-2135)
Deposited data
rQnestin34.5v1 infiltration and mIHC data	N/A	https://github.com/adriannejnner/PhysiCell-GBM-oHSV1
Experimental models: Organisms/strains
Homo Sapiens/ tumor explants	Clinical samples	Human samples for ex vivo experiments were obtained from patients clinically diagnosed with primary or metastatic brain tumors and were collected by Farcast Biosciences under institutional review board (IRB) approval with written informed consent from each patient. Matched-patient non-heparinized blood (5–10 mL) was also collected at the time of biopsy in BD-Vacutainer tubes (Becton Dickinson) following published protocol and established quality control criteria. Tissue slices were maintained in customized tumor matrix protein (TMP) coated plates as described in prior report. Tissue fragments (approximately 300 μm - 2 mm in size) were treated with the indicated drugs for up to 72 h. Media alone or DMSO was used as a vehicle control.
Software and algorithms
HALO	Indica Labs, Corrales, NM, USA	H&E stains were annotated digitally by a clinical pathologist to designate tumor tissue, non-tumor tissue and stromal areas using the HALO™ digital image analysis software version 2.3.1.2089.70 (Indica Labs, Corrales, NM, USA) to establish ROI (regions of interest). HALO Spatial analysis (Indica Labs, Corrales, NM, USA) module was used for plotting data sets.
PhysiCell	(39)	http://physicell.org/
xml2jupyter	(139)	https://github.com/rheiland/xml2jupyter
nanoHUB platform	(140)	https://nanohub.org
Matlab	The MathWorks Inc.	https://au.mathworks.com/products/matlab.html
Other
Computational model in C++	This paper	https://github.com/adriannejnner/PhysiCell-GBM-oHSV1
Online interactive version of the model	This paper	https://nanohub.org/tools/ohsv1gbmapp

Resource availability

Lead contact

Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact Morgan Craig, PhD (morgan.craig@umontreal.ca).

Materials availability

This study did not generate new unique reagents.

Experimental models and subject details

Human subjects

Human samples for ex vivo experiments were obtained from a male patient in his 50s and three anonymous donors who were clinically diagnosed with brain cancers, including metastatic adenocarcinoma and glioblastoma, and were collected by Farcast Biosciences (formerly Mitra Biotech) under institutional review board approval with written informed consent from each patient. The study at the Swedish Neuroscience Institute was reviewed and approved by Western IRB (IRB20091563) in compliance with the ethical principles as set forth in the report of the National Commission for the Protection of Human Subjects of Biomedical and Behavioral Research entitled “Ethical Principles and Guidelines for the Protection of Human Subjects of Research (Belmont Report)”. The research protocol was also approved by the Swedish Neuroscience Institute research steering committee. All participants provided written informed consent according to IRB guidelines prior to participation. No consent was required for publication.

Viral constructs and tumour specimens

rQnestin34.5v1 (oHSV-1) was cultured and purified as previously described (Nakashima et al., 2015). Vero cell monolayers in 10-layer cell factories grown in DMEM-10%FBS at 37°C, were infected with virus (MOI = 0.005) in VP-SFM media. Once cells reached 90–100% CPE, NaCl was added to make the overall concentration 0.45 M and cells re-incubated at 33°C O/N. Cellular debris was removed by low-speed centrifugation, 2500 rpm, 5 min, 4°C), the supernatant containing virus filtered through a 0.8-micron vacuum CN filters. Virus was Benzonase-treated to remove extra-viral DNA and further purified by high-speed centrifugation (13,000 rpm, 90 min, 4°C), washed with PBS and re-suspended in PBS buffer (Goins et al., 2014). Once the pellet is completely re-suspended, sterile glycerol (0.22 μM filtered) is added to 10% of total volume, individual aliquots stored at −80°C. Aliquots were tittered in standard plaque assays and total viral genomes quantitated by qPCR (Uchida et al., 2013). Incorporation of green fluorescent protein (GFP) was used for tracking.

Glioblastoma ex vivo culture with rQNestin

To assimilate the effects of oHSV-1 on the tumour microenvironment (TME), we deployed an ex vivo human tumour model that retains the native, patient-autologous TME by incorporating peripheral blood mononucleated cells (Figure 1). We have previously deployed this platform for the quantification of spatial and phenotypic heterogeneity in a variety of heterogeneous cancers, including non-small cell lung cancer (Craig et al., 2019). Glioblastoma tissue (n = 4 patient samples) was cut manually into slices or fragments of various sizes up to 1 mm thick, and treated with rQNestin (0.1–5 PFU per cell, for 24 h) by adding the virus in a 100 $\text{μ}$ L drop of saline to the piece of tissue submerged in 400 $\text{μ}$ L of complete medium and incubated at 37$°C$ with 5% CO2 (Smalley et al., 2020). Using a “sequential imaging strategy”, which we described recently (Smalley et al., 2019), serial sections were then fixed and either stained with hematoxylin and eosin (H&E), or immunostained for HSV-1 (DAKO, B0114), GFP (GFP antibody CAT# AM1009a from Abgent, clone 168AT1211), or cleaved caspase-3 (Cell signaling Tech, for clone information see Goldman et al., 2015). The impact of rQNestin on the spatial context and activity of the immune compartment in the glioblastoma ex vivo slices was further assessed by multiplex immunohistochemistry (mIHC). The multiplex panel markers consisted of CD3 (anti- CD3 rabbit, Ventana, 790–4341), CD4 (anti-CD4 rabbit, Ventana, 790–4423), CD8 (anti-CD8 rabbit, Ventana, 790–4460), Ki67 (anti-Ki67 rabbit, Ventana, 790–4286) and Pan-keratin (anti-pan-keratin mouse, Ventana, 760–2135). Measurements for the fragment dimensions were carried out using the automated image analysis HALO (Akoya Biosciences: tissue classifier, high-plex analysis, and spatial analysis modules) software package. Tissue slices or fragments were defined as sequential bands $50\text{μm}$ in width beginning from the periphery and moving inwards (Figure S10). In addition, HALO was used to determine the number of CD4⁺ T cells (Th) and cytotoxic T lymphocytes (CD8⁺ T cells, or CTLs) in a slice or fragment and measure the distances between proliferating and non-proliferating immune cell subsets.

The HSV expression was measured within each band of the tissue slice 24 h after administering either 0.1 PFU, 0.5 PFU, 1 PFU or 5 PFU per cell into the ex vivo glioblastoma patient (n = 4) tissue samples. Immunohistochemical staining of infiltrating oHSV-1 (using anti-HSV-1 antibody) was used for the visualization of viral trafficking and inferred replication (Elliott and O’Hare, 1999; Lux et al., 2005).

Method details

General information about agent-based simulator physicell

Our computational model was implemented leveraging the previously developed PhysiCell (Ghaffarizadeh et al., 2018) (physics-based multicellular simulator), an agent-based simulator that models the interaction between cells and diffusing fields in dynamic tissue microenvironments. Below we provide a very brief overview of the PhysiCell software and direct the reader to physicell.org and the following publications for more information (Ghaffarizadeh et al., 2018; Ozik et al., 2018; Rocha et al., 2021; Wang et al., 2021).

BioFVM: Simulating diffusing entities

PhysiCell is directly coupled to a biotransport solver known as BioFVM (Ghaffarizadeh et al., 2015) that simulates many diffusing substrates and cell-secreted signals in the microenvironment, allowing cells to dynamically update their phenotype based on microenvironment conditions. Virus and chemokine extracellular dynamics in this model (Figure 2A, Main Text) are modelled in BioFVM by

$$\frac{\partial \mathit{\rho }}{dt}=\mathit{D}{\nabla }^2\mathit{\rho }-\mathit{\lambda }\mathit{\rho }+\mathit{S}\left({\mathit{\rho }}^{\ast }-\mathit{\rho }\right)-\mathit{U}\mathit{\rho }+\sum _{cellsk}\delta \left(\mathit{r}-{\mathit{r}}_k\right)V_k\left[{\mathit{S}}_k\left({\mathit{\rho }}^{\ast }-\mathit{\rho }\right)-{\mathit{U}}_k\mathit{p}\right]in\text{B}$$ (Equation 1)

where $\mathit{\rho }$ is the vector of virus and chemokine densities (i.e., $\mathit{\rho }=\left[{\rho }_{virus},{\rho }_{chemokine}\right]$), $\mathit{D}$ is the vector of diffusion coefficients (i.e., $\mathit{D}=\left[D_{virus},D_{chemokine}\right]$), $\mathit{\lambda }$ is the vector of decay rates (i.e., $\mathit{\lambda }=\left[{\lambda }_{virus},{\lambda }_{chemokine}\right]$), ${\mathit{\rho }}^{\text{∗}}$ is the vector of saturation densities (i.e., ${\mathit{\rho }}^{\ast }=\left[{\rho }_{virus},{\rho }_{chemokine}\right]$), $\mathit{U}$ is the vector of bulk uptake (binding) rates (i.e., $\mathit{U}=\left[U_{virus},U_{chemokine}\right]$) and $\mathit{S}$ is the vector of bulk source rate (i.e., $\mathit{S}=\left[S_{virus},S_{chemokine}\right]$).

Boundary conditions exist on $\delta \text{B}$, where $\text{B}$ is the computational domain. Here $\delta \left(x\right)$ is the Dirac delta function, ${\mathit{r}}_k$ is the $k$ th cell’s position, $V_k$ is its volume, ${\mathit{S}}_k$ is its vector of source rates and ${\mathit{U}}_k$ is its vector uptake (binding) rates. The expression ${\mathit{\rho }}^{\ast }-\mathit{\rho }$ in Equation (1) assumes that intracellular substrates (or molecules) are secreted at a rate proportional to the difference between the substrate directly outside the cell and the saturation density. The purpose of this term is to capture that the secretion rate of a cell will slow as the density of molecules outside reaches some equilibrium threshold. Equation (1) is solved using first order (stable) implicit operating splitting on a discretized grid of equal sized voxels. Computationally, the solver is first-order accurate and numerically stable and performs optimally when the computational voxels are comparable to the cells’ sizes or larger (Ghaffarizadeh et al., 2016, 2018). To satisfy this requirement, we set a voxel length of $\epsilon =20\text{μm}$ which is comparable to the glioblastoma cancer cell size. We implemented the default Dirichlet boundary conditions on the outer boundary $\delta B$.

Cell agents

PhysiCell is an agent-based simulation framework that simulates individual cells as software agents that ac within a simulated tissue environment (Metzcar et al., 2019). PhysiCell agents implement key cell-scale processes of cell-cycling and death, volume changes, mechanics, motility, and secretion and uptake of diffusible substrates in the tissue microenvironment. Individual cell agents record a variety of phenotypic parameters that regulate these processes, including position ${\mathbf{x}}_i$, volume (and sub-volumes), cell cycle or death status, secretion parameters, and mechanics (adhesive, deformation, and motility) parameters. Each agent’s inbuilt cell processes are controlled by modulating their corresponding phenotypic parameters with cell functions that implement our biological hypotheses on how each cell type responds to microenvironmental stimuli (See Figure S2 of the supplementary figures.). The underlying phenotypic rate parameters can either be set to default inbuilt values or can be user-defined. In this work, we tailor a large number of these properties; details on this can be found throughout the Main Text and STAR Methods. We also summarize these properties in Figure S2 of the Supplementary Figures.

In this work, there are four main cell types: cancer cell, stromal cell, CD4⁺ T cell and CD8⁺ T cell (see Table 1 in the Main Text). For different phenotype states in these cell types (e.g., active vs inactive, infected vs uninfected), different aspects of the cell phenotype are updated based on the characteristics in Table 1. Each cell type (cancer cell, stromal cell, CD4⁺ T cell and CD8⁺ T cells) is also associated with an independent cell function that can describe rules and behaviours of that particular cell. For example, a cancer cell function first evaluates whether the cell is infected and checks whether the cell might undergo lysis if sufficient replicated virus is contained within. Non-lysed cells continue viral replication. The description of each of these functions is provided in Figure S2 in the supplementary figures where each decision path for a cell type depicts a cell type function.

In PhysiCell, each cell tracks the total internalized substrates by calculating the net total amount of substrate uptaken and secreted over the cell, conserving mass with the uptake/secretion terms in Equation (1). In our model, we use this tracking to account for virus that is taken up and secreted by an individual cell. In this way, our model through Equation (1) automatically calculates the amount of virus internalized by a cell based on the uptake rate $U_k$ and/or secretion rate $S_k$ in a cell specific manner. We describe how these are used in more detail in VIRUS MODEL.

Time steps

PhysiCell uses three separate time step sizes, $\text{Δ}{t}_{diff},\text{Δ}{t}_{mech},\text{Δ}{t}_{cells}$, to account for the differences in the diffusive biotransport processes which occur relatively fast compared to the cell mechanics and the slower cell processes. We use these inbuilt time steps and their default values $\text{Δ}{t}_{diff}=0.01$ min, $\text{Δ}{t}_{mech}=0.1$ min and $\text{Δ}{t}_{cells}=6$ min to model diffusion of the virus and chemokine (which occurs on the diffusive time step $\text{Δ}{t}_{diff}$), cell movement (which occurs on the cell mechanics time step $\text{Δ}{t}_{mech}$) and cell functions (which occurs on the cell update time step $\text{Δ}{t}_{cells}$). A summary for the evaluation of the model and these timesteps is given in the supplementary information Figure S1–S3.

Agent hierarchy and heritage

For each of the four cell types, glioblastoma cancer cell, stromal cell, CD4⁺ T cell and CD8⁺ T cell, there is an initial state every cell starts its ‘lifetime’ in the simulation, before it then moves through the different cell states or phenotypes. Each glioblastoma cell starts its lifetime as an uninfected live glioblastoma cancer cell. It can then change state into an infected cancer cell if it becomes infected and then become a dead cell. It is possible for a cancer cell to transfer straight from uninfected to dead if a CD8⁺ T cell induces death in the scenario where immune cells are tumour antigen specific. A stromal cell has no state change or phenotype change. For the immune cells, CD4⁺ T cells start in an initial ‘inactive’ state. Once they recognize an infected cell by being in its neighborhood, they become an active CD4⁺ T cell. CD8⁺ T cells start in an ‘active’ state in the sense they are able to automatically attach to infected cells. After a CD8⁺ T cell has attached and then detached from at least 1 infected cell, it then increases its proliferation. The rules associated with each cells type is summarised in Table 1 in the Main Text and the hierarchy described here is summarized in supplementary information, Figure S3.

As cells move between the different cell types, they inherit the previous conditions from their previous cell type unless otherwise specified. For example, after an uninfected glioblastoma cancer cell becomes infected, it retains the motility from its previous type. In a similar manner, when a cell proliferates, its two daughters inherit its characteristics. This is a simplification in our model, and future work could consider resampling a new cell’s characteristic after it changes type.

Linking cell agents to substrate matrix and tumour microenvironment

Cells interact with the local tumour microenvironment through the substrate equations described by BioFVM (Equation 1) and through their movement in the domain. The ways cells integrate with the substrates (i.e., virus and chemokine) is through uptake and secretion. Cancer cells can uptake virus and CD4⁺ T cells secrete chemokine. We use the inbuilt models in PhysiCell for these functions and briefly describe their set-up here.

BioFVM divides the simulation domain into a collection of non-intersecting voxels, or volumetric pixels (Ghaffarizadeh et al., 2016). Each voxel has a unique position (centre) and volume. The uptake of virus and secretion of chemokine by cells is concentrated to a single voxel that contains its location using a Dirac delta function (Equation 1). The impact of the tumour microenvironment on cell movement is captured by the cell-drag forces modelled using the default settings in PhysiCell. These settings were originally estimated by Macklin et al. from modelling ductal carcinoma in situ (Macklin et al., 2012). CD8⁺ T cell movement is also impacted by the local environment depending on the concentration of chemokine by increasing the bias towards the chemokine gradient vector in the migration Equation (2).

Initial glioblastoma tumour domain size

The dimensions of our glioblastoma tumour tissue slice simulation were calibrated to those of an average ex vivo glioblastoma tumour slice from CANscript cultures containing tumour cells, stroma, and tumour infiltrating immune cells from patient tissue biopsies and resections (Smalley et al., 2019) (Figure 1, Main Text). Tissue slices were collected from these samples at the end of the experiment by slicing the cultured tumour into $5\text{μm}$ deep tumour tissues (Figure S10A). The total area of each slice was calculated by determining the areas of bands with width 50 $\text{μm}$ in from the periphery using the HALO software suite (https://indicalab.com/halo/). The area $A_i\left(\mu m^2\right)$ of the $i$ th band from the periphery of the slice was recorded using HALO and the sum of these areas gave the total slice area. To model these tumour slices in our agent-based model, we assumed that they were created from spherical tumours and were therefore circular (Figure S10B) which gave the area of the $i$ th band

$$A_i=\frac{\pi }{{10}^6}\left(R_i^2-{\left(R_i-50\right)}^2\right),$$

where $R_i\text{μm}$ is the radius at the outer edge of the $i$ th band in the slice (Figure S10B). From the area of each band, we can extrapolate the slice’s radius $R_1$ using

$$R_1=\frac{{10}^6{A}_i}{{10}^2\pi }+25+50\left(i-1\right).$$

Since each fragment was not perfectly circular (Figure S10A), this equation returns a distribution of $R_1$ values calculated from each band area $A_i$ of an individual fragment (Figures S10C–S10D).

We conducted a series of control experiments where CANscript ex vivo tissue samples were grown for 0, 24, 48 or 72 h and their band area calculated using HALO (Smalley et al., 2019). Two tumour slices from each patient (1098 and 1167) were analyzed with HALO at 0 h and the area of each band was calculated as $A_i\left(\text{μ}{\text{m}}^2\right)$. Using these measurements and the expression for $R_1$ gave a distribution of total radii (Figures S10C–S10D), where the periphery band is indexed as $i=1$ and the centre band by $i=N_b$ (with $N_b$ giving the total number of bands). We then calculated the approximate radius of each tumour slice at every time point (Figure S10E). The mean of all tumour slices (irrespective of time) gives an area of $A_{frag}=$ 5.0644 ${\text{mm}}^2$ (Figure S10F) and radius of $R=1269.7\text{ sμm}$.

Glioblastoma and stromal cell size and volume characteristics

Cellular solid and fluid volumes are part of the inbuilt PhysiCell agent environment (Ghaffarizadeh et al., 2018). Oraiopoulou et al. (2017) estimated the cell diameter of U87 cells to be 21.5 $\text{μm}$, similar to the diameter of $25\text{μm}$ used by Gallaher et al. (2020) in their agent-based model of glioblastoma. Approximating U87 cells as circular, we fixed the radius to be $10.75\text{μm}$, giving a total volume of $V=5203.7\text{μ}{\text{m}}^3$. Kouwenberg et al. (2018) measured the average nucleus volume of U87 cells to be $V_N=740\pm 150\text{μ}{\text{m}}^3$. This then gives a cytoplasmic volume of $V_C=4463.7\text{μ}{\text{m}}^3$ and a “target” cytoplasmic to nuclear volume ration of $f_{CN}=6.032$. To model the fluid fraction of a cell $f_F$, we assumed that the water mass fraction of a typical cell is 75% (Ghaffarizadeh et al., 2018). Moreover, we calculated the target nuclear solid volume as $V_{NS}^{\ast }=\left(1-f_F\right)V_N=185\text{μ}{\text{m}}^3$. The rate of water intake, cytoplasmic solid biomass creation and nuclear biomass creation were all fixed to the typical values determined by Ghaffarizadeh et al. (2018) To model the degradation of glioblastoma cells after lysis with oHSV-1, we used the previous calibrations by Ghaffarizadeh et al. (2018) for the rate of fluid removal from cells and cytoplasmic blebbing.

Tumour stroma is broadly defined as the non-cancer cell and non-immune cell components of tumours. Fibroblasts are the predominant cells in tumour stroma (Bhowmick et al., 2004; Tripathi et al., 2012). As such, we used fibroblasts as representative of stromal cell size and set the nuclear volume and the total diameter to be to 500 $\text{μ}{\text{m}}^3$ and $15\text{μm}$ based on previous measurements (Freitas, 1999). For simplicity, we assumed all other volume change characteristics were equivalent to glioblastoma, GBM, cells. That is that the fluid fraction of stromal cells, $f_F$, was the same and hence the target nuclear solid volume $V_{NS}^{\ast }$ was calculated in the same way.

CD4⁺ and CD8⁺ T cell size and volume characteristics

Rossi et al. (2019) found that unstimulated CD4⁺ and CD8⁺ T cells had diameters of $7.180\pm 0.109\text{μm}$ and $7.214\pm 0.175\text{μm}$, respectively, which is within the range of other measurements for naïve T cell diameters ($5-7\text{μm}$) (Du et al., 2017; Tasnim et al., 2018; Wang et al., 2014). We therefore set the cell radius for CD4⁺ and CD8⁺ T cells to be 3.6 $\text{μm}$. The nucleus-to-cytosol volume ratio was set to $0.95\pm 0.005$ for CD4⁺ cells and $0.97\pm 0.003$ for CD8⁺ cells, based on the experiments of Rossi et al. (2019). These ratios gave a cell diameter of $R_{cell}=7.2\text{μm}$ for CD4⁺ and CD8⁺ T cells and a volume of $V=195.43\text{μ}{\text{m}}^3$, with a nucleus volume of $V_N=185.66\text{μ}{\text{m}}^3$ for CD4⁺ T cells and $V_N=189.57\text{μ}{\text{m}}^3$ for CD8⁺ T cells. All remaining parameters were fixed to their value for the glioblastoma cells.

General cell migration

Cells in PhysiCell are designed to respond to forces through interactions with other cells and the basement membrane. To become motile, each cell has an additional net locomotive force (${\mathbf{F}}_{\text{loc}}$), e.g., in the case of chemotaxis, cells might respond to chemical stimuli and move up a particular gradient, which contributes a migrational component ${\mathit{v}}_{mot}$ to the cell’s velocity. Each cell can have its own migration speed ($\psi$), migration bias direction (${\mathit{d}}_{bias}$, a unit vector) and migration bias $b$, that ranges from 0 (Brownian motion) to 1 (deterministic motion along ${\mathit{d}}_{bias}$).

In PhysiCell the locomotive force is defined as.

$${\mathit{v}}_{mot}=\psi \frac{\left(1-b\right)\varphi +b{\mathit{d}}_{bias}}{\Vert \left(1-b\right)\varphi +b{\mathit{d}}_{bias}\Vert },$$ (Equation 2)

where ${\mathit{v}}_{mot}$ is also known as the cell’s migration speed and $\varphi$ is a random unit vector that is sampled each time a cell can change direction. When updating the cell’s overall velocity, its migration velocity ${\mathit{v}}_{mot}$ is added to the cell’s current velocity based on the cell mechanics and interactions with other cells and the basement membrane.

In this work, we only vary the bias of an individual cell to a given direction and the migration speed. Since glioblastoma and CD4⁺ T cells were modelled as having no migration bias (i.e., purely Brownian motion), we set $b=0$. Stromal cells do not move implying that $\psi =0$. CD8⁺ T cells chemotaxis up the chemokine gradient, so we set $b=0.85$ and ${\mathit{d}}_{bias}$ as the gradient vector of the chemokine at that cell’s position, i.e., for the $k$ th cell at position ${\mathit{r}}_k$, ${\mathit{d}}_{bias}=\nabla {\rho }_{chemokine}({\mathit{r}}_k$). In this way, a CD8⁺ T cell will sample the local gradient of chemokine and move up that gradient with some random motion (as $b<1$). More information can be found in Ghaffarizadeh et al. (2018).

Since the tumour tissue fragments our model is based upon are roughly circular, we assumed cells were only able to move within a circular domain of tissue of radius $R$. As such, cells were modelled as unable to migrate in the region outside the designated tumour radius (Figure S8). We achieved this non-migratory region by simply turning off cell migration (i.e., $\psi =0$) once the cell left the migratory region of tissue. As the glioblastoma tumour tissue grows, the area it occupies will also expand. Since we do not model connective tissue within the tumour, we approximated the expansion of the tumour region based on patient data, namely we used the rate of glioblastoma tumour expansion estimated by Stensjoen et al. (Stensjøen et al., 2018) and Stensjøen et al. (2015). These authors estimated the rate the volume of a glioblastoma tumour changes through matching longitudinal patient MRI scans to Gompertzian growth (Jenner et al., 2018a; Jenner et al., 2018b):

$$\frac{dV}{dt}=\beta log\left(\frac{K_V}{V}\right)V,V\left(0\right)=V_1,$$

where $\beta$ is the tumour growth rate and $K_V$ is the tumour volume carrying capacity. The authors obtained a growth parameter value of $\beta =5.239\times {10}^{-6}$/min and $K_V=1.5804\times {10}^{14}\text{μ}{\text{m}}^3$. Using their approximation, we calculated the time taken for the tumour radius to change by $10\text{μm}$ to be

$$t_{\text{Δ}r=10\mu m}=\frac{1}{\beta }\ln \left[\frac{\ln \left(\frac{1}{K_V}\left(\frac{4}{3}\pi R^3\right)\right)}{\ln \left(\frac{1}{K_V}\left(\frac{4}{3}\pi {\left(R+10\right)}^3\right)\right)}\right].$$

Thus, for each time point in our agent-based model simulation, we calculated $t_{\text{Δ}r=10\mu m}$ for each given radius of the tumour to update the tumour size and migratory domain.

Glioblastoma cell migration

In the “stop” or “go” model, moving glioblastoma cells have no directed motion and hence have a bias parameter $b=0$ (Equation 2) (Ghaffarizadeh et al., 2018). Migration speeds for glioblastoma cells range from 0.36 $\text{μm}/\text{min}-0.79\text{μm}/\text{min}$ (Diao et al., 2019; Gallaher et al., 2020; Kaphle et al., 2019). Following the method in Gallaher et al. (2020), where cells were randomly assigned a migration status (stop or go) sampled from the distribution of persistence times, we randomly sampled a persistence time (T) for each cell which represented the time a cell would spend either stopped or moving at its current angle and velocity (Figure S9A), similar to subdiffusive motion (Jenner et al., 2020). After exceeding its persistence time, a cell would then be assigned as either stopped or moving with probability 0.5. If the cell was designated a moving cell, then it was randomly assigned a speed (Figure S9B). Cells were modelled to remain in their type (going or stopping) for the duration of their persistence time, at the end of which the process would be restarted.

CD4⁺ and CD8⁺ T cell migration

The migration speed $\psi$ of CD4⁺ T cells and CD8⁺ T cells was based on leukocyte in vitro and in vivo chemotaxis speed observed to be $4\text{μm}/\text{min }$ (Trepat et al., 2012). Since CD4⁺ T cells did not undergo chemotaxis, CD4⁺ T cells were modelled as following Brownian motion. CD4⁺ T cell migration speed was therefore fixed to $\psi =$ 4$\text{μm}/\text{min}$ with a migration bias of $b=0$ (Equation 2). To model the rapid chemotaxis of CD8⁺ T cells up the chemokine gradient, we assumed CD8⁺ T cells modulate their speed based on the concentration of chemokine at their position, i.e., ${\rho }_{chemokine}\left({\mathit{r}}_k\right)$, where ${\mathit{r}}_k$ is the cell’s position. The speed of a CD8⁺ T cell is then

$$\psi =\nu +{\nu }_{max}\left(\frac{{\rho }_{chemokine}\left({\mathit{r}}_k\right)}{\frac{{\nu }^{\ast }}{2}+{\rho }_{chemokine}\left({\mathit{r}}_k\right)}\right),$$

where ${\nu }_{max}$ is the maximum speed a CD8⁺ T cell will reach during chemotaxis, $\nu$ is the base speed of the CD8⁺ T cell (which we set equal to CD4⁺ T cell speed (i.e., $\nu =$ 4$\text{μm}/\text{min}$)), ${\rho }_{chemokine}({\mathit{r}}_k$) is the chemokine concentration at the CD8⁺ T cell’s position ${\mathit{r}}_k$, and ${\nu }^{\ast }$ is the chemokine effective half-concentration. The expression in the brackets $(\dots )$ will vary between 0 and 1. As the local chemokine concentration increases above ${\nu }^{\ast }$, CD8⁺ T cell speed tends to $\psi =\nu +{\nu }_{max}$, whereas for low chemokine concentrations ${\rho }_{chemokine}\ll {\nu }^{\ast }/2$, the speed will tend to $\psi =\nu$. The idea of modulating the speed in this manner was first suggested by Ghaffarizadeh et al. (2018) Since IFN-$\gamma$ directly promotes CD8⁺ T cell motility (Bhat et al., 2017), we assumed a max-speed ${\nu }_{max}$ = 24.6$\text{μm}/\text{min}$ for CD8⁺ T cells based on the analysis of Bhat et al. (2017). We assumed that CD8⁺ T cells chemotaxis up chemokine gradients with bias parameter $b=0.85$ (Ghaffarizadeh et al., 2018). The introduction of the modulated migration speed for CD8⁺ T cells was also to avoid rapid CD8⁺ T cell chemotaxis along extremely low gradients of chemokines, as such we set the speed of chemotaxis to be proportional to the strength of the signal.

We also assumed stromal cells were moveable (Ghaffarizadeh et al., 2018) but not motile when force was applied to them by other cells in the domain.

Generation of dense and sparse stromal density configurations

To generate the dense regions of the patchy configuration, we first determined the centre of dense patches ($\hat{x},\hat{y}$) by sampling a distance of the patch centre from the centre of the tumour slice ($d_{patch}$) from a uniform distribution (i.e., $\left(R-20\right)\times \sqrt{U\left(\mathrm{0,1}\right)}$), and angle ${\theta }_{patch}$ from the uniform distribution $\left[\mathrm{0,2}\pi \right)$ giving patch centre coordinates: $\hat{x}=d_{patch}cos\theta ,\hat{y}=d_{patch}sin\theta .$ The radius $R_{patch}$ for the patch was then sampled from a normal distribution $N(\mu ,\sigma )$ where $\mu$ was chosen such that if patches were circular, they would take up 50% of the slice if there were five of them, i.e., $5\text{π}{R}_{patch}^2=0.5\text{π}{R}^2\iff R_{patch}=\sqrt{0.3162R^2}$, so $\mu =402$. The standard deviation $\sigma$ was chosen using $\sigma =0.4742\mu$ based on the relative standard deviation of the distribution of semi-axis regions approximated from the sparse slice (Figures S12A–S12B). We iterated through this process until five patch centres and radii had been found so that 50% of the slice was covered by dense areas and 50% by sparse areas (Figure S12C). Then, to generate different ratios of dense to sparse regions, we scaled the radius of each patch by a constant $\kappa$ so that the area breakdown equalled the desired dense:sparse ratio (see Table S1 for the values of $\kappa$ for the different breakdowns). As we generated it through randomly sampling based on the image in Figure S12C, the final patch configuration used in the main text (see Figures 4 and 5) is only one possible realization of a patchy tumour. There are many other possible realisations of a 50:50 dense:sparse patch that can be generated using the method described above.

Different dense:sparse configurations are plotted in Figure S5 Supplementary information. The dense:sparse ratio would result in different numbers of glioblastoma and stromal cells. This was due to these two cells having different sizes. The numbers of either cell type are listed in Table S1.

Initial CD4⁺ T cell and CD8⁺ T cell placement using Hooke’s law

Using the average distances between immune cell subtypes (Figure 3B), we generated an initial spatial distribution for CD4⁺ T cells (TH) and CD8⁺ T cells (CT) on the circular domain with radius $R.$ Given the total number of immune cells $N_{immune}=N_{CD4}+N_{CD8}$, we generated $N_{immune}$ points with coordinates $\left(x,y\right)$ in the same manner as the placement of glioblastoma and stromal cells. Each point was assigned either TH, TH∗, CT or CT∗, where ∗ denotes Ki67+, depending on how many cells of each type were required.

Let $\mathit{s}$ be the vector of distances between the immune types, (e.g., TH-CT). We simulated the movement of points through the domain using the force-balance equation for Hooke’s law (Jenner et al., 2020):

$${\mathit{r}}_k\left(t+\text{Δ}t\right)={\mathit{r}}_k\left(t\right)+\frac{c_s}{\eta }\sum _{j\in \Pi \left(k\right)}\frac{{\mathit{r}}_{k,i}\left(t\right)}{\left|\left|{\mathit{r}}_{k,i}\left(t\right)\right|\right|}\left(s_{k,i}\left(t\right)-\left|\left|{\mathit{r}}_{k,i}\left(t\right)\right|\right|\right),$$ (Equation 3)

where ${\mathit{r}}_k$ is the vector for the position of point $k,$ ${\mathit{r}}_{k,i}$ is the vector joining cell $k$ and $i$, $s_{k,i}$ is the equilibrium distance between $k$ and $i$ which is determined by the vector $\mathit{s}$ depending on the type of point ${\mathit{r}}_k$ and ${\mathit{r}}_i$, $c_s$ is the spring constant and $\eta$ is the velocity of proportionality. The set of points that interact with point $k,$ is denoted by $\text{Π}\left(k\right)$ and was determined by a Delaunay triangulation of the lattice of points (Jenner et al., 2020) (Figure S14A). Both $c_s$ and $\eta$ were initialized based on our previous Voronoi cell-based model simulation of tumour growth (Jenner et al., 2020).

To avoid points grouping on the boundary or exiting the boundary of the domain, we constructed an approximation for symmetric boundary conditions by determining the unit vector ${\hat{\mathit{r}}}_{centre}$ between each cell (${\mathit{r}}_i$) and the centre of the slice. We then created a set of new points $\left\{{\mathit{r}}_{sym}\in {\mathbb{R}}^2\right\}$ that were the duplicate of each point in the opposite direction at a distance $2R$ from its corresponding point, i.e.,

$${\mathit{r}}_{sym}={\mathit{r}}_i-2R{\hat{\mathit{r}}}_{centre}.$$

If the new position of a point, ${\mathit{r}}_k(t+\text{Δ}t)$ was outside the domain, the point was repositioned inside the domain along the diagonal through the centre of the circle at a distance $2R$ (Figure S14A). The simulation was run until the sum of the distances moved by all points in a single timestep $\text{Δ}t$ was less than $5\text{μm}$. Note that when the distance between two cells was $>\mathit{s}+50\text{μm}$ they were no longer considered within each other’s neighborhood. This was to avoid cells dragging each other long distances through the domain. The evolution of immune cell configuration is provided in Figure S14B.

To confirm the validity of Hooke’s law simulation strategy, we determined the average minimum distance between cell types (Figure S13C). In most cases, e.g., TH-TH, CT-TH, TH-TH∗, TH-CT and TH-CT∗, we obtained a good approximation to the initial spatial distribution of the immune cells (Figure 3B). Individual patient distances can be found in Figure S6 supplementary information.

Proliferation rate of U-87MG cells

The proliferation of glioblastoma cells is characterized by two factors, a baseline proliferation rate $\beta$ and the pressure felt by an individual cell. To first determine a deterministic approximation for glioblastoma cell growth we fit a logistic growth function to U-87MG cell growth. Logistic growth (de Pillis et al., 2005; Forys and Marciniak-Czochra, 2003; Ribba et al., 2011; Scott et al., 2013) is regularly used to model tumour growth.

$$\frac{d{N}_{GBM}}{dt}=\beta N_{GBM}\left(1-\frac{N_{GBM}}{K_C}\right),$$ (Equation 4)

where $N_{GBM}$ is the total number of cells, $\beta$ is the cell proliferation rate and $K_C$ is the population carrying capacity. Parameter values in Equation (4) were fit to the in vitro U87MG cell count measurements from Mercurio et al. (2017) (Figure 3C in the Main Text). Mercurio et al. (2017) measured cell counts using Trypan blue exclusion tests. Fixing the initial number of cells to their measurements (i.e., $N_{GBM}\left(0\right)\approx 1.2\times {10}^6$ cells), we obtained $\beta =7.35\times {10}^{-4}$/min and $K_C=4.76\times {10}^6$ cells.

To then approximate this growth stochastically in the ABM we used the inbuilt PhysiCell “Live” model which does not model individual cell cycle phases, but rather allows any live cell to stochastically divide based upon its individual division rate. Thus, in any given time step $[t+\text{Δ}t$] they have a division probability of

$$\text{Prob}\left(division\right)=1-\exp \left(-\beta \text{Δ}t\right)\approx \beta \text{Δ}t.$$

We fix $\beta$ to the value estimated by Equation (4), as logistic growth can approximate this stochastic exponential growth at early times, and then evaluate the probability above to determine whether a cell proliferates.

To account for the carrying capacity $K_C$, we introduced a hold on proliferation when individual cells were under too much pressure, in other words we used the pressure felt by individual cells to introduce a cap on cell proliferation. Neighboring cell pressure and a lack of available space are known to cause a decrease in tumour cell proliferation (DiResta et al., 2005; Indana and Chaudhuri, 2021; Levayer, 2020). To account for this, previous agent-based models or individual based models have implemented force-balance equations to calculate neighboring cell pressures and determine the likelihood of proliferation (Byrne and Drasdo, 2009; D’Antonio et al., 2013; Sadhukhan et al., 2021; Van Liedekerke et al., 2019). We chose to take advantage of PhysiCell’s inbuilt cell-cell pressure calculation to determine the mechanical pressure felt by an individual cell and then place a threshold on cell’s proliferating if under too much pressure. While there are other ways to model reduced proliferation based on pressure or even a lack of available ‘empty space’, we note that mechanical pressure is directly correlated to the local cell density and thus nearby empty space.

In PhysiCell, pressure on a given cell $i$ is modelled by

$$p_i=\frac{1}{A_{cell,i}}\sum _{j\in \text{Π}\left(i\right)}\left|{\mathbf{F}}_{ij}^{ccr}\right|,$$

where $\text{Π}\left(i\right)$ is the set of neighbor cells of cell $i$, $F_{ij}^{ccr}$ is the cell-cell repulsive force imparted on cell $i$ by its neighbors $j$, and $A_{cell,i}$ is the surface area of cell $i$. This formulation for pressure is equivalent to that used by Byrne and Drasdo (2009) and Schaller and Meyer-Hermann (2005) and assumes that the force felt by cell $i$ is a sum of the forces ${\mathbf{F}}_{ij}^{ccr}$ exerted on that cell by each of its neighbors $j,$ where ${\mathbf{F}}_{ij}^{ccr}$ comes from Newton’s section law balance equation and represents cell-cell repulsive forces. In the pressure calculation for cell $i$, the set of neighbors $\text{Π}\left(i\right)$ is determined in PhysiCell as the list of cells located in neighboring voxels (those that share an edge with the cell $i$’s current voxel) and the cells in cell $i$’s current voxel (see Ghaffarizadeh et al., 2018 for more details). The force ${\mathbf{F}}_{ij}^{ccr}$ between cell $i$ and cell $j$ was calculated using from the approximation

$${\mathbf{F}}_{ij}^{ccr}=c_j^{ccr}{\left(1-\frac{r_{ij}}{R_{cell,i}+R_{cell,j}}\right)}^2\frac{{\mathit{r}}_{ij}}{r_{ij}},$$

originally derived in Macklin et al. (2012) where ${\mathit{r}}_{ij}={\mathit{r}}_j-{\mathit{r}}_i$ and $r_{ij}=\left|{\mathit{r}}_{ij}\right|$ and $R_{cell,i}$ and $R_{cell,j}$ are the radius of cell $i$ and $j$, respectively, and $c_j^{ccr}$ is the cell-cell repulsive force coefficient (Macklin et al., 2012). This equation comes from modelling cell-cell interactions with potential functions. We note that the mechanical pressure experienced by a cell directly correlates with the local cell density and thus also with the nearby availability of empty space. See Macklin et al., 2012 and Byrne and Drasdo (2009) for a detailed discussion on modelling cell-cell interactions in this way.

To define a maximum proliferation pressure $p_{max}$, we calculated the pressure $p_i$ felt by cell $i$, when the system was at an equilibrium state, the total number of cells equalled the carrying capacity $K_C,$ and the cells were evenly spaced. In this scenario, we assumed all glioblastoma cells have equal radius $R_{cell}=R_{GBM}=10.75\mu m.$ Since cells are equally spaced they are at an equal distance apart, therefore $r_{ij}=s$ and $R_{cell,i}=R_{cell,j}$. The equilibrium spacing between cells, $s\text{μm}$, was obtained by converting the density of cells at this equilibrium carrying capacity ($\xi =K_C/A_{frag}$) to an equivalent regular hexagonal cell packing (see Macklin et al., 2012 and Hyun and Macklin, 2013 for more details) using

$$s=\sqrt{\frac{2}{\sqrt{3}\xi }}=\sqrt{\frac{2A_{frag}}{\sqrt{3}{K}_C}},$$

where $A_{frag}$ is the domain area and $K_C$ is the number of cells. The pressure at carrying capacity was then given by

$$\begin{array}{l}{p}_{max}=\frac{1}{A_{cell}}\sum _{j=1}^6\left|{\mathbf{F}}_{ij}^{ccr}\right|,=\frac{1}{A_{cell}}\sum _{j=1}^6\left|c_j^{ccr}{\left(1-\frac{s}{2R_{cell}}\right)}^2\frac{{\mathit{r}}_{ij}}{r_{ij}}\right|,=\frac{c_j^{ccr}}{A_{cell}}{\left(1-\frac{1}{2R_{cell}}\sqrt{\frac{2}{\sqrt{3}\xi }}\right)}^2\sum _{j=1}^6\left|\frac{{\mathit{r}}_{ij}}{r_{ij}}\right|,\\ =6\frac{c_j^{ccr}}{A_{cell}}{\left(1-\frac{1}{2R_{cell}}\sqrt{\frac{2A_{frag}}{\sqrt{3}{K}_C}}\right)}^2,\end{array}$$

where surface area is $A_{cell}=4\pi R_{cell}^2=1452.2\mu m^2$. We estimated $c_j^{ccr}$ by assuming the cell-cell repulsive forces were equal for all cells such that $c_j^{ccr}=c^{ccr}$ and then fixed $c^{ccr}=10\nu \text{μm}/\text{min}$ based on the estimate to ductal carcinoma in situ (Macklin et al., 2012).

We further non-dimensionalized $p_{max}$ by the pressure scale designated by Ghaffarizadeh et al. (2018), to convert to a “simple pressure” ${\overline{p}}_{max}$. “Simple pressure” is an analog for mechanical pressure nondimensionalized by a scale that is calculated automatically in PhysiCell for each cell (Ghaffarizadeh et al., 2018). We converted $p_{max}$ into its non-dimensional form using:

$${\overline{p}}_{max}=\frac{p_{max}}{{\overline{p}}_i}=\frac{p_{max}}{0.02729\frac{c_{ccr}^i}{{A_{cell}}_i}}.$$ (Equation 5)

Therefore, we defined the condition on the proliferation rate of cells to be

$$\{\begin{array}{l}\begin{array}{ll}\beta \hfill & {\overline{p_i}}^2\le p_{max}\hfill \end{array}\hfill \\ \begin{array}{ll}0\hfill & {\overline{p_i}}^2>p_{max}\hfill \end{array}\hfill \end{array},$$

where $\beta$ is the proliferation rate. The density $\xi$ used to calculate $p_{max}$ was determined as the combined total cells (stroma + glioblastoma) cells in the sparse fragments $K_C=19947$ cells divided by the area of the initial fragment $A_{frag}={1269.7}^2\pi \text{μ}{\text{m}}^2$ (Figure S16A). The estimate for the proliferation pressure was calculated using the approximate number of cells at carrying capacity from our data, their size and force equations already adopted for modelling cell-cell interactions.

Immune cell proliferation

To model immune cell proliferation, we used PhysiCell’s inbuilt Ki67 Basic model (Ghaffarizadeh et al., 2018). In this model, the cell cycle is divided into two phases: a non-proliferative $\left(\left[Ki67-\right]\right)$ and proliferative $\left(\left[Ki67+\right]\right)$ phase with associated transitions rates. Assuming cells transition from a non-proliferative state to proliferative state at a rate $r_{01}$, and a cell divides into a non-proliferative state at a rate $r_{10}$, then the two states in this model have transition rates $r_{01}$ and $r_{10}$ respectively (see Figure S16B). The deterministic ODEs describing this model are given by

$$\frac{d\left[Ki67-\right]}{dt}=-r_{01}\left[Ki67-\right]+2r_{10}\left[Ki67+\right],$$

$$\frac{d\left[Ki67+\right]}{dt}=r_{01}\left[Ki67\right]-r_{10}\left[Ki67+\right].$$

In PhysiCell, the process of proliferation modelled in the ODEs above is implemented stochastically. Consider the state of an individual cell $k$ at time $t$ is given by $X_k\left(t\right)$. In any time interval $\left[t,t+\text{Δ}t\right],$ if that cell is in state $[Ki67-]$, it has a probability of exiting that phase and entering the $[Ki67+]$ phase given by

$$\text{Prob}\left(X_k\left(t+\text{Δ}t\right)=\left[Ki67+\right]|X_k\left(t\right)=\left[Ki67-\right]\right)=1-\exp \left(-r_{01}\text{Δ}t\right)\approx r_{01}\text{Δt}.$$

The other transition rule where for a cell that moves from the proliferative to non-proliferative state can be derived in the same manner. In this way, immune cell proliferation can be modelled stochastically in our ABM.

To determine parameters governing these transition rates, we used the deterministic ODE version above. We fixed the cell cycle time to be 700 min based on the measurements by Kinjyo et al. (2015), giving $r_{10}=0.00143$/min. We then determined $r_{01}$ by requiring that the stable equilibrium ratio [Ki67+]/[Ki67-] needed to match the mIHC average ratio of CD4⁺ and CD8⁺ T cells Ki67+/Ki67-ratio, or $r_{01,CD4}=7.9026\times {10}^{-5}$ 1/min (Figure S16B). More detailed investigations into CD4⁺ T cell expansion in response to antigen stimulation can be found in De Boer and Perelson (2013). Once T cells became activated (Figure S2 supplementary information) their transition to proliferation increases $100$ x based on measurements showing the percentage of proliferating CD4+T cells increases from ∼10% to ∼80% after stimulation (Cronin et al., 2018).

Estimating OV-HSV-1 diffusion coefficient

Extracellular OV model parameters were estimated from the GFP infiltration measurements for HSV-1. Assuming the dominant process acting on the virus within 24 h is solely diffusion and decay reduces Equation (1) to

$$\frac{\partial {\rho }_{virus}}{\partial t}=D_{virus}{\nabla }^2{\rho }_{virus}-\lambda {\rho }_{virus}.$$ (Equation 6)

We assumed the initial expression of GFP (i.e., virus particles) at the periphery of the tumour slice was uniform and equal (${\rho }_{virus}\left(0\right)=V_0$) and that virus diffused homogeneously into the slice. We fit the initial GFP expression to be an increasing scalar of plaque forming units (PFU) and assumed ${\lambda }_{virus}$ and $D_{virus}$ were equivalent across experiments (Figure S15). Parameter values for $D_{virus}$ and ${\lambda }_{virus}$ are summarised in Table S2, with the different $V_0$ for 0.1 PFU, 0.5 PFU, 1 PFU and 5 PFU given by $1481$ GFP, $1482$ GFP, $2748$ GFP, and 4414 GFP respectively.

To convert PFU to a density, we assumed a one-to-one relationship between the number of virions and plaque forming units. Therefore, given 9740 cells initially, there were approximately 974, 4870, and 48700 viral particles in each experimental realization. Assuming virus was administered in a tight band of width $10\text{μm}$ around the initial tumour and imposing no-flux boundary conditions on the larger domain $\delta \text{B}$, the initial density of administered oHSV-1 is given by

$$V_0=\rho \left(0\right)=\frac{PFU\times 9740}{{10}^2+10R},$$ (Equation 7)

where $R$ is the radius of the slices, i.e., $R=1269.7\text{μm}$ and $\epsilon =20\text{μm}$ (voxel length). All simulations in the Main Text were undertaken for 5 PFU, or an initial density $V_0=3.028$ virions/$\text{μ}{\text{m}}^3$. The exponential viral clearance rate was set to be ${\lambda }_{virus}=0.0029{\text{min}}^{-1}$ based on the in vitro the half-life of HSV particles at 37 degrees in tumour cell conditioned media, which is approximately 4 hours (Mok et al., 2009).

To determine the saturation density of virus ${\rho }_{virus}^{\ast }$ (Equation 1), we followed the method of Krol et al. (1999) for estimating the available volume fraction in the extravascular space of slices that is accessible to therapeutic agents ($K_{AV}$). We approximated the value of $K_{AV}$ as in Dreher et al. (2006), who assumed that the $K_{AV}$ for 70-kDa and 2-MDa dextrans are approximately equal. As HSV-1 virions have a total molecular weight of approximately 3.2 MDA (Bowman et al., 2003), we assumed that the available volume fraction for 3.2 MDA was equivalent to 20,0000 kDA, giving an available volume fraction of 0.05. Given an approximate total domain size of ${1270}^2\pi \text{μ}{\text{m}}^2\times 10\text{μm}=5.0671\text{μ}{\text{m}}^3$, the virus fills up a volume of $2.535\times {10}^6\text{μ}{\text{m}}^3$. Assuming viruses take up a cube volume of $0.155\times 0.155\times 0.155$, we calculated the maximum number of viral particles in the available tumour volume to be $6.8\times {10}^8$. We assumed that the maximum density (or saturation density ${\rho }_{virus}^{\ast }$) was therefore given by $268.51\text{virions}/\text{μ}{\text{m}}^3$.

Virus receptor binding and uptake model

PhysiCell has inbuilt tracking for the cellular uptake and secretion of substrates. We took advantage of this to track the amount of internalized virus. Virus is internalized by cell $k$ at a rate $U_k$ (see Equation 1). For immune cells, this rate is set to zero as we assume they do not take up any virus. For stromal cells, this uptake rate is set as $U_k=u_s$. Glioblastoma cells were modelled to bind virus from the extracellular density of virus ${\rho }_{virus}$ at a rate $U_k=U_{virus}$, modulated by the intracellular amount of virus $m$, as cells will not bind an infinite amount of virus. Assume there is a maximum effective amount of virus that a cell will bind ${\rho }_{max}$. The binding rate of the cell is then

$$U_{virus}=u_g\frac{{\rho }_{virus}}{m_i/V_{voxel}+m_{1/2}/V_{voxel}},if{\rho }_{virus}<{\rho }_{max}$$ (Equation 8)

$$U_{virus}=u_g\frac{{\rho }_{max}^2/{\rho }_{V_i}}{m_i/V_{voxel}+m_{1/2}/V_{voxel}},if{\rho }_{virus}\ge {\rho }_{max}$$ (Equation 9)

where ${\rho }_{virus}$ is the local density of virus in the voxel where the cell is located, $m_i$ is the intracellular amount of virus in the $i$ th cell, $m_{1/2}$ is the half effect on the binding rate, and $u_g$ is the constant binding rate (rate per unit volume). To determine ${\rho }_{max}$, we assumed that the maximum number of viruses that can infect a cell at any given time is 100. As such, the maximal density that can influence a cell is ${\rho }_{max}=0.0125$ (since $V_{voxel}={20}^3$). Binding and internalization of intact, enveloped HSV from the.

Cell surface into endocytic vesicles is rapid (half-life t_1/2 of 8–9 min) and independent of the known cell surface glycoprotein D (gD) receptors (Nicola and Straus, 2004). Accordingly, we fixed $m_{1/2}=10$ virions, as we assumed that a cell would very quickly limit the number of new infections and reach its maximum infection rate. Figure S18 illustrates how $U_{virus}$ varies as a function of the intracellular amount of virus and the extracellular density. We fixed the virus-glioblastoma cell binding rate $u_g$ to be the equivalent to the loss of virus over the 24-period fit in Figure S15. The intracellular amount of virus taken up by the cell through receptor binding is automatically tracked in PhysiCell as the net total amount of virus, conserving mass with the uptake term in Equation (1).

Intracellular virus replication and secretion model

As viruses can replicate within glioblastoma cells, we then used the internalized amount of virus tracked within PhysiCell to determine exactly how much virus was in the cell at time $t$ after replication. For each timestep $\text{Δ}{t}_{cells}$, the intracellular amount of virus within the $i$ th cell was updated by

$$m_i\left(t+\text{Δ}{t}_{cells}\right)=m_i\left(t\right)+\gamma m_i\left(t\right)\text{Δ}{t}_{cells},$$ (Equation 10)

where $\gamma$ is the number of new viruses created at the rate of cell replication. In other words, for each cell $i$, we used a forward Euler approximation to calculate the number of new virions created in time step $\text{Δ}{t}_{cells}$ based on the number of intracellular virions $m_i$. We then updated the intracellular tracking of the internalized virions in PhysiCell so that it reflected the addition of the newly replicated virus particles.

Upon entry in tumour cells, the virus enters the lytic cycle, usually resulting in tumour cell lysis within 12–18 h (Nakashima and Chiocca, 2018). We varied the initial amount of taken-up virus and its replication rate to calculate the time to reach 6600 viruses (Figures S15B–S15C).The burst size of HSV-1716 was previously estimated to be 6600 in the human cell line mesothelioma REN (Lambright et al., 2000). Fixing the viral burst size to be $\alpha =$ 660, the number of viruses created through the cells replication rate is 6600 in 12 h, i.e., of at least 1 infected virus entering the cell. Given that that lysis occurs within 12 h (Nakashima and Chiocca, 2018) if the cell is replicating at its full capacity, then $\gamma =1/(18\times 60)\ln \left(6600\right)=0.4886$/min.

Once the cell reaches its lysis burst size $\alpha ,$ we modelled the cell to secrete its contents at rate ${\delta }_V$ proportional to the amount of virus inside $m_i$. We assumed that an infected cell would only secrete once $m_i\ge \alpha$. Thus, for $m_i<\alpha$, $S_k=0$ and for $m_i\ge \alpha ,S_k={\delta }_V$. We fixed ${\delta }_V$ such that all $\alpha$ virions were secreted within an hour (i.e., ${\delta }_V=\text{ln}(1/6600)$). Thus, the change in intracellular amount of virus is given by

$$S_{virus}{V}_{voxel}=\frac{d{m}_i}{dt}=-{\delta }_V{m}_i,$$ (Equation 11)

where $m_i$ is the amount of intracellular virus in cell $i$, $S_{virus}$ is the secretion rate from Equation (1). To approximate Equation (11) in the model, we simply used a forward Euler approximation and added the amount of virus secreted to the extracellular density of virus ${\rho }_{virus}$, i.e.,

$${\rho }_{virus,i}\left(t+\text{Δ}{t}_{cells}\right)={\rho }_{virus,i}\left(t\right)+\frac{{\delta }_V{\sum }_{\forall infectedcells}{m}_i\left(t\right)}{V_{Voxel}}\text{Δ}{t}_{cells}.$$ (Equation 12)

where ${\rho }_{virus,i}$ is the density of virus in voxel $i$. We tracked the intracellular change in virus (Equation 11) using the same forward Euler scheme as in Equation (10). All parameters relating to the intracellular virus model are summarized in Table S2 and the schematic for the intracellular model is depicted in Figure S1 supplementary information.

CD4⁺ T cell activation and chemokine section

CD4⁺ T cells, or helper T cells, are crucial for CD8⁺ T cell recruitment, activation and support (Alberts et al., 2002; Janeway et al., 2005; Juno et al., 2017; Melssen and Slingluff, 2017; Swain et al., 2012). When a CD4⁺ T cell comes into contact with their cognate antigen (in this scenario viral antigen) expressed by tumour cells or by antigen presenting cells, they produce IFN $\text{γ}$ (Janeway et al., 2005; Melssen and Slingluff, 2017). To model this activation, we assume CD4⁺ T cells become activated if there is an infected cell in its neighborhood, defined to be a circle of radius of $R_{TH}$ centered at the CD4⁺ T cell’s position (Figure S24). We set $R_{TH}=4R_{cell}$, where $R_{cell}$ is the average radius of a glioblastoma cell. We model activation as occurring as long as the infected cell is in some neighborhood, as opposed to cell boundaries touching, since cells are moving in the domain.

Once activated, CD4⁺ T cells secrete a chemokine at a rate $S_{chemokine}$ and this secreted substrate diffuses at a rate $D_{chemokine}.$ Activated CD4⁺ T cells will only be activated while in a neighborhood of an infected cell, outside of which they will stop producing chemokines and return to normal proliferation.

We adapted the estimated diffusion coefficient of chemokines from Matzavinos et al. (2004) to obtain $D_{chemokine}=8\times {10}^{-3}$ cm²/day by assuming the molecular mass of a typical chemokine to be 11 kDa, using the Stokes-Einstein formula. The half-life of cytokines and chemokines ranges anywhere from 30 min (Hillyer and Male, 2005) to 60 days (Reisenberger et al., 1996). As we are considering a local tumour model, we considered a chemokine half-life of 60 days which gave ${\lambda }_{chemokine}=1/\left(60\times 24\times 60\right)\times \ln 1/2=8.02\times {10}^{-6}{\text{min}}^{-1}$.

To estimate the secretion rate of chemokine by CD4⁺ T cells ($S_{chemokine})$ and the chemokine maximum density (${\rho }_{chemokine}^{\ast })$, we used measurements of the in vitro IFN $\text{γ}$ production by CD4⁺ T cells from Gao et al. (2014). where they measured the production of IFN $\text{γ }$ in vitro by CD4⁺ T cells. As their measurements did not include a spatial component and only captured the total concentration in the dish over time, we assumed the diffusion would be unnecessary to be able to match their experiments. In addition, as this was a controlled in vitro experiment for cell secretion, we assumed decay and cell uptake would be negligible. Reducing Equation (1) to consider only cell secretion, we have that.

$$\frac{\partial {\rho }_{chemokine}}{\partial t}=S_{chemokine}\left({\rho }_{chemokine}^{\ast }-{\rho }_{chemokine}\right).$$ (Equation 13)

Fitting $S_{chemokine}$ and ${\rho }_{chemokine}^{\text{∗}}$ to the secretion rate measured by Gao et al. (2014) gave the curve in Figure 3E and parameters in Table S2. Since all other cells did not secrete chemokine, $S_{chemokine}=0$ for these cells. Note, Equation (13) was only used for fitting to the experimental data, and the model was otherwise maintained in its original form given in Equation (1).

CD8⁺ T cell infected cell killing

We assumed that CD8⁺ T cells detect infected cells if the distance between each cell’s centre is within 50 $\mu m$. To induce apoptosis, the CD8⁺ T cell will then dock for a time $\tau$, after which the infected cell undergoes apoptosis. Direct observations of CD8⁺ T cell-target-cell interaction behaviour and quantification of target (virus infected)-cell fate have revealed that killed virus-infected cells experience a median of 3.5 distinct CD8⁺ T cell contacts, whereas surviving cells were rarely targeted (0 median contacts) (Halle et al., 2016). Killed targets experienced a cumulative median contact time of 50 min, with individual contacts between CD8⁺ T cells and surviving targets lasted 8.5 min, and individual contacts between CD8⁺ T cells and killed targets lasted for approximately 9.0 min (Halle et al., 2016). We therefore set $\tau =50$ min (Halle et al., 2016), assuming this is roughly the time taken for successful induction of apoptosis.

Quantification and statistical analysis

A two-sided t-test with a test significance $\text{α}=0.05$ was used in Figure 6 to evaluate the significance of varying stroma binding rates.

Additional resources

nanoHUB (Madhavan et al., 2013) (nanohub.org) is an open and free environment that offers several services aimed at the dissemination of science and engineering products. In particular, nanoHUB offers a toolkit for the development of GUIs that allow greater accessibility and reproducibility of software. The computational model developed here is available for simulation through the nanoHUB platform.

Published: June 17, 2022

Data and code availability

• •De-identified patient data have been deposited at https://github.com/adriannejnner/PhysiCell-GBM-oHSV1. They are publicly available as of the date of publication.
• •The source code is available as open source at https://github.com/adriannejnner/PhysiCell-GBM-oHSV1 (https://doi.org/10.5281/zenodo.6486572). An interactive, online version can be run at https://nanohub.org/tools/ohsv1gbmapp which is hosted on nanoHUB (Madhavan et al., 2013) using a Jupyter foundation (Heiland et al., 2019).
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.