Quantification of Chemotaxis to Naphthalene by Pseudomonas putida G7

Abstract

The capillary assay was used to quantify the chemotactic response of Pseudomonas putida G7 to naphthalene. Experiments were conducted in which the cell concentration in the assay chamber, the naphthalene concentration in the capillary, or the incubation time was varied. Data from these experiments were evaluated with a model that accounted for the effect of diffusion on the distribution of substrate and the transport of cells from the chamber through the capillary orifice. By fitting a numerical solution of this model to the data, it was possible to determine the chemotactic sensitivity coefficient, χ₀. The mean of the best-fit values for χ₀ from the three types of experiments was 7.2 × 10⁻⁵ cm²/s. A less computationally intensive model based on earlier approaches that ignore cell transport in the chamber resulted in χ₀ values that were approximately three times higher. The models evaluated in the present study could simulate the results of capillary assays only at low chamber cell concentrations, for which the effect of consumption on the distribution of substrate was negligible. Results from this work suggest that it is possible to use the capillary assay to quantify taxis towards environmentally relevant chemoeffectors that have low aqueous solubility.

The effect of bacterial motility on the bioremediation of contaminated subsurface environments is poorly understood. There has been speculation that motility might be required to ensure the proper distribution of the degrader organisms relative to the target pollutant (28), yet little evidence exists to support this hypothesis. Studies on the influence of chemotaxis (30) or random motility (5, 23, 26, 29, 34) on substrate utilization have focused on hydrophilic substrates not commonly considered to be pollutants. Recently Pseudomonas putida G7 was shown to be chemotactic to naphthalene (16), one of the most prevalent groundwater contaminants at sites contaminated with polycyclic aromatic hydrocarbons (9). However, a role for chemotaxis in the biodegradation of naphthalene or other substrates of limited aqueous solubility in contaminated environments has not been documented.

The positive effect of either type of bacterial motion is manifested as a bacterial flux, which serves to change the distribution of bacteria relative to substrate. In a one-dimensional system, the flux of bacteria due to chemotaxis and random motility can be represented as follows (22):

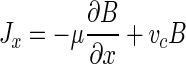1

where μ is the random motility sensitivity coefficient, B is the bacterial concentration, and v_c is the one-dimensional chemotactic velocity. The net effect of the chemotactic flux, v_cB, will be for bacteria to move closer to a chemoattractant, which should in turn permit a higher rate of chemoattractant utilization (17). The chemotactic velocity, v_c, has been shown to be a function of bacterial species-specific parameters, the chemoattractant concentration, and the chemoattractant concentration gradient (7, 31):

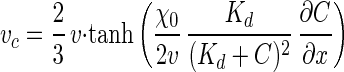2

where v is the three-dimensional cell swimming speed, χ₀ is the chemotactic sensitivity coefficient, C is the substrate concentration, and K_d is the dissociation constant for the chemoreceptor.

The influence of chemotaxis on pollutant biodegradation will depend on the value of χ₀ for a given organism relative to the value of μ, in addition to the distribution of substrate and bacteria (11, 12, 24, 25). However, there is a lack of data on the sensitivity coefficients for random motility and chemotaxis in systems of interest in bioremediation. In the few cases wherein these parameters have been determined, the organism was not a soil microorganism (10), the chemoattractant was not a pollutant (32), or the chemoattractant was not metabolized (3). Metabolism of the substrate of interest is important if the actual chemoeffectors are intermediates of the degradation pathway (18, 21) or central metabolism (4).

The standard capillary assay (2) has been used to quantify coefficients for random motility (22) and chemotactic sensitivity (13, 32). A complication in the use of the capillary assay with substrates of low aqueous solubility, such as naphthalene, is that chemotactic organisms may not respond to these attractants at all under some conditions (16). The solubility limit of poorly soluble substrates could constrain the magnitude and extent of substrate concentration gradients, which could in turn result in a chemotactic response that cannot be detected. In addition, constraints on substrate concentration gradients caused by low aqueous solubility can be exacerbated by consumption of the substrate. One approach to estimating χ₀ under such conditions is to account for the overall effect of consumption on the distribution of substrate in the capillary system (13). As the mathematical approximation used in this approach is difficult to verify, an alternative approach would be to render the level of consumption negligible by lowering the concentration of bacteria in the chamber surrounding the capillary mouth (32). Such a modification has been shown to increase the sensitivity of the capillary assay in other systems in which the chemoattractant is metabolized (2, 36).

The purpose of the work reported here was to evaluate the range of conditions and mathematical models for which the standard capillary assay could be used to quantify the sensitivity coefficients relevant to the chemotaxis of P. putida G7 to naphthalene. Since existing models (13, 32) include untested assumptions about the concentration of bacteria and substrate at the capillary mouth, we also evaluated an approach that incorporates a model of the chemoattractant concentration surrounding the capillary mouth (14) and the corresponding spatial distribution of bacteria in the chamber.

MATERIALS AND METHODS

Media.

Tryptone broth was made from 10 g of tryptone and 5 g of NaCl per liter of distilled water. For the growth of P. putida G7 on a single carbon source, a mineral salts buffer was used which contained 25 mM KH₂PO₄, 25 mM Na₂HPO₄, 0.1% (NH₄)₂SO₄, and 1% Hutner’s mineral base (15, 19). Phosphate buffer (pH 7.0) used for cell suspensions and the preparation of solutions used to fill the capillaries consisted of 25 mM KH₂PO₄, 25 mM K₂HPO₄, and 10 μM EDTA (2). CFU were enumerated on plates containing R2A agar (Difco Laboratories, Detroit, Mich.).

Saturated solutions of naphthalene in phosphate buffer were made by melting about 0.1 g of naphthalene (Aldrich, Milwaukee, Wis.) in a 16-by-125-mm test tube submerged in a boiling water bath. After the melted substrate recrystallized at room temperature, 5 ml of sterile phosphate buffer was added, and the tube was shaken on a wrist-action shaker for at least 12 h.

Culture conditions.

P. putida G7 was obtained from Caroline Harwood (University of Iowa). It is stored cryogenically (−80°C) in 1.5-ml aliquots of overnight cultures grown in tryptone broth subsequently supplemented with dimethyl sulfoxide to 10% (vol/vol).

Tryptone broth (5 ml) was inoculated from a stab of frozen culture. After 1 day, 1 ml of culture was centrifuged for 1 min, the supernatant was decanted, and the pellet was resuspended in 1 ml of mineral salts buffer containing 5 mM sodium salicylate. Approximately 5 μl of the suspension was diluted in 20 ml of mineral salts buffer containing 5 mM sodium salicylate and then placed on a rotary shaker (240 rpm) at 25°C and grown to an optical density at 590 nm (OD₅₉₀) of 0.2 to 0.3 (requiring 16 to 20 h). The cells were then centrifuged at 2,800 × g for 3 min, the supernatant was decanted, and the pellet was resuspended in phosphate buffer.

Cell swimming speed.

Cells were diluted to an OD₅₉₀ of 0.1 to 0.2 in phosphate buffer. A 10-μl drop of culture was placed on an uncovered microscope slide. Images of bacteria swimming along the plane of the slide were viewed with the 20× objective and projected onto a computer screen that was calibrated to convert screen distances to actual distances. The movements of several cells were tracked and analyzed simultaneously for 1 min by using a Hobson Tracker (Hobson Tracking Systems Ltd., Sheffield, England). Twenty-two 1-min segments, each tracking about 12 bacteria, were analyzed. The average speed determined for all of the runs was used for the cell swimming speed.

Diffusivity and solubility of naphthalene.

The diffusivity of naphthalene in aqueous solution was determined by using the Wilke-Chang equation (35). The solubility of naphthalene in phosphate buffer was determined by measuring the absorbance at 256 nm for a solution of phosphate buffer saturated with naphthalene and converting this absorbance into a concentration value with a standard curve.

Capillary assay.

Several minor modifications to the original procedure (2) were made to optimize reproducibility, convenience, and the plating conditions of P. putida G7. Multiple chamber assemblies were prepared on a 25-by-50-cm glass plate. Triplicate 1-μl capillaries for each experimental condition were prepared by moving the flame-sealed capillaries onto a glass petri dish. The dish was then placed on a hot stir plate for at least 15 min. Hot capillaries were then immersed, with the open side down, into the substrate solution. After a cooling period of 5 to 10 min, the capillaries were placed individually in the culture chambers. The glass plates with completed assemblies were incubated at 25°C for 60 min, unless stated otherwise. The capillaries were then removed, rinsed with deionized water, broken, and emptied into an aliquot of mineral salts buffer. The suspensions were diluted, if necessary, and plated onto R2A agar plates, which were counted after 20 to 30 h of incubation at 30°C.

Chemoreceptor constant.

The chemoreceptor half-saturation constant, K_d, was determined by using a capillary assay in which the concentration of naphthalene was varied in both the capillary and the chamber but in which the ratio between the two concentrations remained constant at 2. A sensitivity curve (6, 27) was fitted to the data from this experiment by using nonlinear regression (ProStat; Poly Software International, Salt Lake City, Utah), with K_d as the fitted parameter.

Random motility sensitivity coefficient.

The random motility coefficient was determined from data on bacterial accumulations in the capillary in the absence of chemoattractant (33):

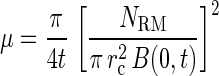3

where N_RM is the accumulation in the capillary containing phosphate buffer only, t is the time of capillary incubation in seconds, r_c is the radius of the capillary, and B(0,t) is the concentration of bacteria at the capillary mouth. The best-fit value of μ was determined by performing linear regression of N_RM² versus 4πr_c⁴[B(0,t)]²t, where B(0,t) is assumed to equal B_ch, the concentration of bacteria in the chamber, for experiments in which the capillary contained phosphate buffer only.

Modeling approach.

For assays in which capillaries contained naphthalene, the total accumulation, N, was due to both random motility and chemotaxis. The accumulation due to random motility was accounted for by differentiating equation 3 and expressing the result in finite-difference form:

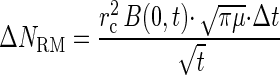4

An expression for the net accumulation of bacteria in the capillary due to chemotaxis (N − N_RM) is based on the chemotactic flux of cells (equation 1) across the entrance to the capillary (13). Shown in finite difference form:

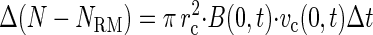5

The chemotactic velocity (v_c) is a function of the concentration and concentration gradient of chemoattractant at the entrance to the capillary (equation 2). To determine the distribution of chemoattractant, it is necessary to have a model that incorporates the geometry of the capillary assay system. In our system, the capillary lies flat on a glass surface, so diffusion in the chamber is predominantly hemispherical with the mouth of the capillary at the center and the glass plate forming the flat surface. Futrelle and Berg (14) proposed a model, which was substantiated experimentally, to account for the distribution of substrate near the mouth of the capillary tube in which diffusion in the capillary toward the mouth is linear, while diffusion away from the mouth is hemispherical. The resulting concentration and gradient at the mouth are as follows:

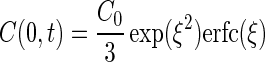6

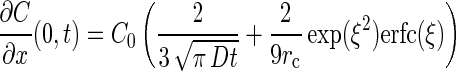7

where C₀ = C(x,0), ξ = 2√Dt/3r_c, and D is the diffusivity of the substrate. The corresponding solution for chemoattractant concentration in the chamber (14) is:

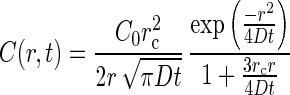8

As substrate diffuses from the capillary into the chamber, bacteria will swim towards the capillary mouth. To determine B(0,t), material balance equations for bacteria in a series of hemispherical shells radiating from the capillary mouth were solved in the radial direction for each time interval:

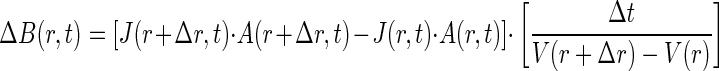9

where ΔB(r,t) is the change in bacterial concentration over the time interval, J(r,t) is the flux in the radial direction (similar to equation 1), A(r,t) is the surface area of the hemispherical shell, and V(r+Δr,t) − V(r,t) is the volume of the shell. The chemotactic velocity as a function of radial distance was determined by incorporating the attractant concentration (equation 8) and the concentration gradient, which was determined by linear interpolation of concentration between the nodes. By solving the sequence of mass balance equations for sequential time steps, it is possible to determine the concentration of bacteria at the mouth, B(0,t), for any time t. This approach is similar to that used in a previous study on the distribution of chemotactic bacteria within a system where the attractant concentration varied in one dimension (25).

Ford and Lauffenburger (13) suggested a simpler model to simulate the accumulation of chemotactic bacteria in a capillary tube that contains a chemoattractant. They assumed that B(0,t) is constant and equal to B_ch, the initial concentration of bacteria throughout the chamber, and that the concentration of substrate at the capillary mouth is constant with respect to time:

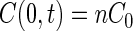10

where n is a number between 0 and 1. The corresponding one-dimensional substrate concentration gradient at the mouth of the capillary is (8):

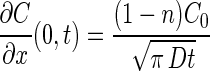11

The value of n in equations 10 and 11 was determined by solving equation 6 over a 1-h period. Although the concentration of substrate at the mouth is not constant with time, it was found that the average concentration was approximately 0.03 C₀. Thus, a value of n equal to 0.03 was used in simulations involving the Ford and Lauffenburger (F/L) model.

The model formulation that incorporated the method of Futrelle and Berg (14) for estimating conditions at the mouth of the capillary and in the chamber is referred to as the F/B model. The F/L formulation incorporated the assumptions of Ford and Lauffenburger (13) for conditions at the capillary mouth. To run either model, the chemotactic velocity [v_c(0,t)] and the bacterial concentration [B(0,t)] at the mouth were used to determine the accumulation due to random motility (equation 4) and chemotaxis (equation 5) as a function of time. Programs for both models were written in Visual Basic for Applications (Microsoft Corp., Redmond, Wash.). For the F/B model, equations 6 and 7 were first solved for each time interval by using MatLab (The Mathworks, Inc., Natick, Mass.). The resulting values of substrate concentration and its gradient at the mouth of the capillary were then imported into the Visual Basic model. The values of the biological and system parameters that were used in all computer simulations are shown in Table 1.

TABLE 1.

Parameter values used in the capillary assay simulations

Parameter	Value
v (cm/s)	4.8 × 10−3
Kd (g/cm3)	2.1 × 10−6
Csat (g/cm3)	2.1 × 10−5
D (cm2/s)	8.5 × 10−6
rc (cm)	1.0 × 10−2
n	0.03

Chemotactic sensitivity coefficient, χ₀.

The best-fit value of χ₀ was determined by running each model with a range of assumed χ₀ values. For each assumed value, the predicted and measured accumulations of cells in the capillary containing chemoattractant were compared. The best-fit χ₀ was that which resulted in the minimum sum-of-square errors between predicted and measured accumulations for all of the data within a given experiment. In all cases, the μ value determined from a given experiment was used in the models to estimate the value of χ₀ for the same experiment.

The discretization error of the mathematical models solved by numerical methods was evaluated by running the models with decreasing time intervals until the predicted accumulation did not change significantly. The simulations were tested with a reasonable χ₀ value and it was found, with both models, that time intervals of 10 s or less produced accumulation results which varied from each other by less than 1%. Time intervals of 1 s were used in the reported simulations. The radial discretization for the mass balance of cells in the chamber was 2r_c, so that the approximation of radial symmetry applies to the system (14).

RESULTS

In the capillary assay, there are several experimental variables that can be adjusted when designing an experiment. Among the readily controlled variables are the initial concentration of bacteria in the chamber, B_ch; the initial substrate concentration in the capillary, C₀; and the time of the assay, t. By designing each experiment around one of these three variables, it should be possible to discern how well the role of each is accounted for in each model.

Experimentally measured accumulations of cells, as well as predicted accumulations for the best-fit χ₀ values, are shown for the three different independent variables in Fig. 1, 2, and 3. The best-fit χ₀ values for each experiment are summarized in Table 2. In all three experiments, the χ₀ determined from the F/L model is between two and three times the value found according to the F/B model.

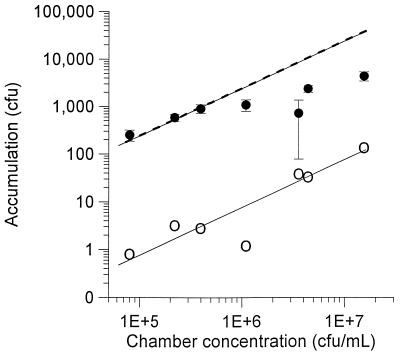
FIG. 1.

Effect of chamber cell concentration on the accumulation of P. putida G7 in the capillary assay. Solid circles represent data for accumulations in the capillaries containing phosphate buffer saturated with naphthalene, while the open circles represent data for accumulations in the capillaries that contained buffer only. The upper solid and dashed lines correspond to simulations of accumulation in the naphthalene capillaries based on the F/B and F/L models, respectively, using the best-fit values of χ₀ for each model. The lower, solid line is the best fit for accumulations in the capillaries that contain buffer only. Error bars represent the standard deviations for triplicate measurements; error bars for the blank capillaries are not shown for clarity.

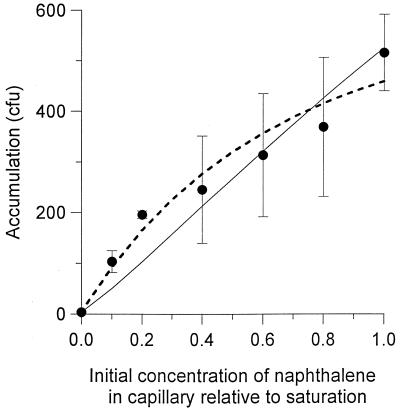
FIG. 2.

Effect of the initial naphthalene concentration in the capillary on the accumulation of P. putida G7. The concentration of bacteria in the chamber was 2.9 × 10⁵ CFU/ml. The solid line represents the simulation with the F/B model, while the dashed line represents the simulation with the F/L model.

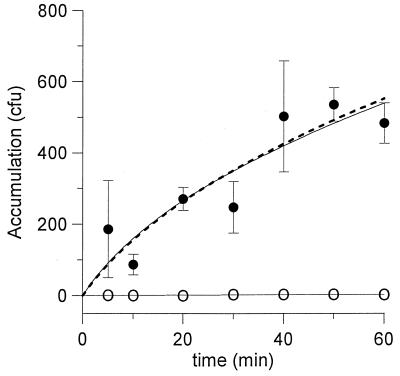
FIG. 3.

Accumulation of P. putida G7 in the capillary with time. The concentration of bacteria in the chamber was 3.2 × 10⁵ CFU/ml. Symbols and lines are as described for Fig. 1. Accumulations of cells in the capillaries containing buffer only were all below 10 CFU.

TABLE 2.

Best-fit sensitivity coefficients for different experiments

Variablea	μ (10−7 cm2/s)	χ0 (10−5 cm2/s)b
		F/B model	F/L model
Bch	1.3 ± 0.4c	8.8 (1.34)	27 (1.34)
C0	5.2 ± 2.6d	6.6 (1.50)	14 (1.31)
t	3.1 ± 0.5c	6.1 (2.17)	16 (2.16)
Avg	3.2	7.2 ± 1.4e	19 ± 7e

^aSimulations and data are compared in Fig. 1 to 3, respectively. 

^bNumbers in parentheses refer to sum-of-square errors in capillary accumulations between model simulations and the data (10⁵ CFU²). 

^cBest-fit and standard deviations as determined by regression analysis. 

^dMean and standard deviation of triplicate values calculated from the accumulations in the blank capillary. 

^eError ranges are standard deviations of fitted values. 

The accumulation of cells in the capillaries containing naphthalene was more easily distinguished from that in the blank capillaries as the initial concentration of cells in the chamber decreased (Fig. 1). From B_ch values of about 5 × 10⁵ CFU/ml to as low as 8 × 10⁴ CFU/ml, the experimental accumulation in the naphthalene capillary is parallel to the best-fit line for the accumulation in the blank capillary, representing the region for which N/N_RM is constant. Models that do not account for substrate consumption result in simulations wherein the ratio, N/N_RM, is not a function of B_ch (13). Therefore, experimental conditions in which the resulting N/N_RM is constant are indicative that substrate consumption could be ignored for modeling purposes. At concentrations of more than 5 × 10⁵ CFU/ml, N/N_RM decreases with increasing B_ch, so that the models for chemotaxis which ignore substrate consumption cannot be applied directly. Thus, only the first three data points were used in estimating a χ₀ value for the experiment illustrated in Fig. 1. Subsequent experiments used bacterial concentrations in the chamber of less than 5 × 10⁵ CFU/ml.

DISCUSSION

The capillary assay is a simple experimental system that can be used to study chemotaxis and to quantify chemotaxis parameters by fitting mathematical models to the experimental data. Previous models (13, 32) incorporated assumptions about the bacterial and substrate concentrations at the mouth that merit further examination. The F/L model (13) specified that the concentration of substrate at the capillary mouth in the absence of consumption is the average of the initial concentration of substrate in the chamber and the concentration of substrate in the solution used to fill the capillary tube. For instance, if the capillary tube were filled with phosphate buffer saturated with naphthalene and the concentration of naphthalene in the chamber were zero, the value of n in equations 10 and 11 would be 0.5. Using this value, we obtained χ₀ values which were at least 1 order of magnitude greater than previously reported values for P. putida (2) and simulations that did not match the trend in the data of Fig. 2 qualitatively. Several investigators have provided evidence that the relative substrate concentration at the mouth is much lower, on average, than 0.5. Weiss et al. (36) did a theoretical analysis under slightly different conditions in which the average concentration at the mouth (relative to the bulk capillary concentration) was predicted to be 0.02 to 0.01 for 20 to 60 min into the capillary assay. In an experimental analysis, Hazelbauer (20) was able to explain chemotactic responses of Escherichia coli to galactose in the capillary assay with the assumption that the relative substrate concentration at the mouth was, on average, ca. 0.01. We found that for the conditions in the present study, the average n over a 1-h experiment was approximately 0.03 with the F/B model. This value was used in simulations involving the F/L model.

Another assumption used in previous models (13, 32) is that the concentration of cells at the capillary mouth remains constant and is equal to the initial concentration in the chamber. While this condition may hold if the chamber is completely mixed, the experimental studies that accompanied these models did not incorporate mechanical mixing. Furthermore, mixing in the chamber would influence the motility of bacteria by creating advective currents, which are not accounted for in any model of the capillary assay.

Adler (1) has observed that E. coli cultures accumulate near the mouth of a capillary containing 2 mM aspartate. Our modeling approach also predicted a net accumulation of cells near the capillary mouth. For the experiments wherein the initial concentration of naphthalene in the capillary was at the aqueous saturation point, the predicted bacterial concentration at the mouth according to the F/B model ranged between two and three times the initial concentration throughout the chamber over a 1-h simulation (not shown).

The accumulation of cells at the capillary mouth predicted in the F/B model accounted for much of the difference between it and the F/L model. The predicted substrate concentration gradients for each model (equations 7 and 11) were nearly identical (not shown), and the chemotactic flux was not very sensitive to the time-dependent changes in the substrate concentration at the mouth, so these were not significant sources of the differences between the two models.

The two models provided similar fits to the experimental data both qualitatively (similar lines in Fig. 1 and 3) and quantitatively (sum-of-squares errors in Table 2). The greatest difference between the models was manifested for the dose-response experiment (Fig. 2). Although both models involve approximations and simplifying assumptions, we believe the model based on the work by Futrelle and Berg (14) is a more rigorous method for determining χ₀. The F/B model calculates substrate concentrations near the mouth of the capillary in a manner that was substantiated experimentally and accounts for accumulation of bacteria at the capillary mouth. However, the F/B model is also more computationally intensive than the F/L model and a simple analytic expression for χ₀ derived from it (13). The F/L models may be appropriate under conditions where it can be shown that the concentration of bacteria at the mouth does not change significantly. Such circumstances are predicted in the system we studied for naphthalene concentrations that are below 10% of the aqueous saturation point.

Significance of the χ₀ value for chemotaxis to naphthalene by P. putida G7.

The average χ₀ value of P. putida G7 for naphthalene determined from the three different experiments is 7.2 × 10⁻⁵ cm²/s. This is below the published values of E. coli for fucose, 8 × 10⁻⁵ cm²/s (10); E. coli for α-methyl aspartate, 7.5 × 10⁻⁴ cm²/s (32); and P. putida PRS 2000 for 3-chlorobenzoate, 1.9 × 10⁻⁴ cm²/s (3). However, the magnitude of the chemotactic sensitivity coefficient may not be as significant as its value relative to the random motility coefficient. Lauffenburger et al. (25) predicted that the relative growth of chemotactic bacteria compared to nonmotile bacteria is proportional to the ratio of chemotactic to random motility sensitivity coefficients, χ₀/μ. With a ratio greater than 1, the advantage of chemotaxis to growth is significant under a variety of conditions. For P. putida G7, with naphthalene as the chemoattractant, the ratio is approximately 225. The ratios for E. coli on fucose and methyl aspartate and for P. putida on 3-chlorobenzoate were 5 (10), 50 (32), and 7 (3) respectively.

Implications for quantifying chemotaxis to hydrophobic, metabolized substrates.

Data and simulations shown in Fig. 1 to 3 reveal possible strategies for detecting and studying chemotaxis to other poorly soluble, metabolized substrates. If the concentration of bacteria is sufficiently low so that the overall loss of substrate due to consumption is insignificant, the accumulations in the attractant capillary should parallel those in the blank capillary in a log-log plot against the concentration of cells in the chamber (Fig. 1). However, a model that accounts for substrate metabolism may be necessary to determine the χ₀ value in systems for which substrate consumption cannot be neglected. While a model has been proposed to account for the effect of metabolism on cell accumulation in the capillary (13), this model did not describe well the results of the capillary assays for P. putida G7 at higher cell concentrations in the chamber than those used to estimate χ₀ values in this work.

The data in Fig. 2 indicate that the peak chemotactic response to naphthalene occurs at or near its saturation concentration in phosphate buffer. For metabolizable chemoattractants that are less soluble than naphthalene, it would be more difficult to design experiments that preclude substantial effects of metabolism. Therefore, with poorly soluble chemoattractants, aqueous saturation conditions may be the most likely to allow quantification and detection of chemotaxis by the capillary assay.

The incubation time can also be adjusted to minimize the effects of chemoattractant metabolism (Fig. 3). Shorter experimental times will reduce the overall level of consumption, and such a strategy may also help define conditions for which the level of substrate consumption in the system is insignificant.

Quantification of the chemotactic sensitivity coefficient is essential to evaluating the potential role of chemotaxis in the biodegradation of pollutants in the environment. While the quantification of chemotactic sensitivity coefficients to hydrophobic, metabolized substrates by using the capillary assay may seem problematic, this study suggests that methods are available to achieve such quantification.