Deep Learning for Glaucoma Detection and Identification of Novel Diagnostic Areas in Diverse Real-World Datasets

Abstract

Purpose

To develop a three-dimensional (3D) deep learning algorithm to detect glaucoma using spectral-domain optical coherence tomography (SD-OCT) optic nerve head (ONH) cube scans and validate its performance on ethnically diverse real-world datasets and on cropped ONH scans.

Methods

In total, 2461 Cirrus SD-OCT ONH scans of 1012 eyes were obtained from the Glaucoma Clinic Imaging Database at the Byers Eye Institute, Stanford University, from March 2010 to December 2017. A 3D deep neural network was trained and tested on this unique raw OCT cube dataset to identify a multimodal definition of glaucoma excluding other concomitant retinal disease and optic neuropathies. A total of 1022 scans of 363 glaucomatous eyes (207 patients) and 542 scans of 291 normal eyes (167 patients) from Stanford were included in training, and 142 scans of 48 glaucomatous eyes (27 patients) and 61 scans of 39 normal eyes (23 patients) were included in the validation set. A total of 3371 scans (Cirrus SD-OCT) from four different countries were used for evaluation of the model: the non overlapping test dataset from Stanford (USA) consisted of 694 scans: 241 scans from 113 normal eyes of 66 patients and 453 scans of 157 glaucomatous eyes of 89 patients. The datasets from Hong Kong (total of 1625 scans; 666 OCT scans from 196 normal eyes of 99 patients and 959 scans of 277 glaucomatous eyes of 155 patients), India (total of 672 scans; 211 scans from 147 normal eyes of 98 patients and 461 scans from 171 glaucomatous eyes of 101 patients), and Nepal (total of 380 scans; 158 scans from 143 normal eyes of 89 patients and 222 scans from 174 glaucomatous eyes of 109 patients) were used for external evaluation. The performance of the model was then evaluated on manually cropped scans from Stanford using a new algorithm called DiagFind. The ONH region was cropped by identifying the appropriate zone of the image in the expected location relative to Bruch's Membrane Opening (BMO) using a commercially available imaging software. Subgroup analyses were performed in groups stratified by eyes, myopia severity of glaucoma, and on a set of glaucoma cases without field defects. Saliency maps were generated to highlight the areas the model used to make a prediction. The model's performance was compared to that of a glaucoma specialist using all available information on a subset of cases.

Results

The 3D deep learning system achieved area under the curve (AUC) values of 0.91 (95% CI, 0.90–0.92), 0.80 (95% CI, 0.78–0.82), 0.94 (95% CI, 0.93–0.96), and 0.87 (95% CI, 0.85–0.90) on Stanford, Hong Kong, India, and Nepal datasets, respectively, to detect perimetric glaucoma and AUC values of 0.99 (95% CI, 0.97–1.00), 0.96 (95% CI, 0.93–1.00), and 0.92 (95% CI, 0.89–0.95) on severe, moderate, and mild myopia cases, respectively, and an AUC of 0.77 on cropped scans. The model achieved an AUC value of 0.92 (95% CI, 0.90–0.93) versus that of the human grader with an AUC value of 0.91 on the same subset of scans ($P=0.99$). The performance of the model in terms of recall on glaucoma cases without field defects was found to be 0.76 (0.68–0.85). Saliency maps highlighted the lamina cribrosa in glaucomatous eyes versus superficial retina in normal eyes as the regions associated with classification.

Conclusions

A 3D convolutional neural network (CNN) trained on SD-OCT ONH cubes can distinguish glaucoma from normal cases in diverse datasets obtained from four different countries. The model trained on additional random cropping data augmentation performed reasonably on manually cropped scans, indicating the importance of lamina cribrosa in glaucoma detection.

Translational Relevance

A 3D CNN trained on SD-OCT ONH cubes was developed to detect glaucoma in diverse datasets obtained from four different countries and on cropped scans. The model identified lamina cribrosa as the region associated with glaucoma detection.

Introduction

Glaucoma, one of the leading causes of irreversible blindness, is a chronic progressive optic neuropathy with characteristic visual field (VF) defects matching structural changes, including nerve fiber layer thinning with ganglion cell loss and corresponding optic nerve neuroretinal rim reduction, known commonly as “cupping.”^1,2 Currently, the main modifiable risk factor is elevated intraocular pressure (IOP), which, in combination with structural and functioning longitudinal imaging, is one of the main parameters followed during treatment. Standardized pathologic glaucomatous structural changes include retinal nerve fiber layer (RNFL) and ganglion cell inner plexiform layer (GCIPL) thinning.

The normative database for the conventional Cirrus spectral-domain optical coherence tomography (SD-OCT) RNFL and optic nerve head (ONH) map consists of 284 healthy individuals with an age range between 18 and 84 years (mean age of 46.5 years). Ethnically, 43% were Caucasian, 24% were Asian, 18% were African American, 12% were Hispanic, 1% were Indian, and 6% were of mixed ethnicity. The refractive error ranged from −12.00D to +8.00D.³ Due to the relatively small normative database, there is a significant percentage of false positives from high myopia disc changes or thin RNFL from other nonglaucomatous or artifactual reasons.⁴ One of the difficulties in diagnosing glaucoma is that there is no single test with a high sensitivity and specificity to confirm the diagnosis, which is why OCT alone is not the best label to train a deep learning algorithm. Currently, clinicians incorporate the color scale OCT printouts but use a multimodal ground-truth label of glaucoma including risk factors, clinical examination of the fundus, IOP measurement, VF evaluation, treatment, and other relevant clinical history along with OCT RNFL and GCIPL maps to more accurately confirm glaucoma.

It is known that glaucoma changes extend deep into the ONH at the level of the lamina cribrosa (LC), a network of columns supporting the neuronal axon connections as they traverse from the surface of the retina to the visual cortex of the brain.⁵ However, only qualitative enhanced depth imaging (EDI) SD-OCT research protocols have been able to visualize these changes in the past, and no quantitative printouts exist.

Based on current understanding of high-pressure induced glaucoma, biomechanical deformation and remodeling of the ONH leads to posterior displacement of the LC relative to the sclera as well as progressive loss of ganglion cell axons and cell bodies, resulting in RNFL thinning.⁵ LC changes in glaucomatous eyes, including focal defects, thinning, and posterior displacement, have been previously reported.^6–8 Due to errors in manual measurements and lack of quantifiable LC morphology changes with normative values, it is presently not part of routine glaucoma evaluation in clinics.^9,10 Thus, it seems reasonable to hypothesize that there is additional information in a routinely captured SD-OCT ONH cube scan outside of the extracted RNFL that currently is not being tracked clinically but can be discovered through deep learning as a separate differentiator of glaucoma from normal. Despite multiple deep learning studies being designed for automated glaucoma detection,^11,12 since the real-world translational use rarely matches the curated datasets in these studies, the algorithms are often not generalizable and none have been cleared by regulatory Food and Drug Administration.^13,14 Ideally, the training datasets must reflect diverse population characteristics of the treatment population to be clinically useful.

Hence, this study concentrates on developing and validating a three-dimensional (3D) neural network to predict glaucoma based on better ground-truth definitions as determined by multiple data inputs from fundus photos, OCTs, visual fields, and clinical exam data over time instead of a single test. The algorithm excludes suspects and utilizes standard SD-OCT ONH cube scans obtained from diverse real-world datasets from four different countries. We attempt to understand the model better by utilizing additional cropping data augmentation and evaluate the model's performance on areas of interest on a subset of manually cropped scans to see if ONH was an important part of the algorithm performance versus nerve fiber layer.

Method

The study adhered to the tenets of the Declaration of Helsinki,¹⁵ and the protocols were approved by the respective institutional review boards of Stanford School of Medicine (United States), The Chinese University of Hong Kong (Hong Kong), Narayana Nethralaya Foundation (India), and Tilganga Institute of Ophthalmology (Nepal). Informed consent was waived based on the study's retrospective design, anonymized dataset of OCT images and test data, minimal risk, and confidentiality protections.

In this work, a 3D neural network is trained to detect glaucoma using unprocessed raw SD-OCT ONH cube (volume) scans retrospectively obtained from Byers Eye Institute, Stanford School of Medicine (USA). The performance of the model is evaluated on a separate nonoverlapping test dataset from Stanford and on three external datasets, each obtained from Hong Kong, India, and Nepal. Subsequent analyses are done in subgroups stratified by eyes (right versus left), myopia, and severity of glaucomatous optic neuropathy (mild versus moderate or severe). The performance of the model is also evaluated on glaucoma cases without visual field defects. The classification accuracy of this model is then compared with that of a glaucoma specialist on a subset of cases. Saliency maps are generated to highlight the areas the model attended to in order to make a prediction. The model's performance is further evaluated on partial ONH data on a subset of manually cropped scans. Further, the performance of the algorithm is evaluated across different severity levels of myopia cases on the cropped scans.

Data Source

The 3D SD-OCT ONH cube (volume) scans of the training, validation, test, and the external datasets used in our study were acquired using Cirrus HD-OCT (Carl Zeiss Meditec, Dublin, CA, USA) according to the optic disc cube scanning protocol. The 3D OCT cube (volume) ONH scans of 2202 eyes of 1253 patients evaluated at the Byers Eye Institute, Stanford School of Medicine, from March 2010 to December 2017, were extracted and used for the study. Prior to labeling as glaucoma versus normal, based on chart review, 749 eyes were excluded due to the presence of other ocular pathologies and 93 eyes were excluded due to the presence of OCT artifacts or due to signal strength being less than 3, as per exclusion criteria mentioned below. In total, 267 eyes diagnosed as suspects (high and low risk) were excluded based on chart review. Forty-two eyes were diagnosed as having glaucoma without visual field defects. Twenty eyes were excluded after arbitration as described below. Finally, 1012 eyes of 562 patients (2461 scans) were labeled and used for training, validation, and testing.

Ground-Truth Labeling

The inclusion criteria were (1) age equal to or older than 18 years, (2) reliable visual field (VF) tests, and (3) availability of one or more qualified SD-OCT optic disc scans.

Glaucoma was defined as those eyes with glaucomatous disc changes¹⁶ on fundus examination, with localized defects on OCT RNFL/GCIPL deviation or sector maps that correlated with the VF defect that fulfilled the minimum definition of Hodapp—Anderson—Parrish glaucomatous VF defect and had IOP lowering treatment as per chart review.¹⁷ Normal was defined as nonglaucomatous optic disc on fundus exam with no structural defects on OCT RNFL/GCIPL deviation or sector map and normal visual fields, as well as normal intraocular pressures. Glaucoma cases with structural defects alone (as defined by Supplementary Table S1) without visual field defects were not included in the training or validation dataset. More information about ground-truth labeling is provided in Supplementary Table S1. SD-OCT scans with signal strength less than 3 or any artifact obscuring imaging of the ONH, or any artifacts or missing data areas that prevented measuring the thickness of the RNFL at 3.4 mm diameter, were excluded from the study. A signal strength of ≥3 was included because the entire cube of data was being used and not the results from the machine's segmentation algorithm, which often fails at low signal strength.¹⁸ Eyes with nonglaucomatous ONH pathologies and retinal pathologies were carefully excluded. Further details of inclusion and exclusion criteria and grading of the SD-OCT scans are provided in Supplementary Section S4. The severity of myopia was defined by slightly modifying the Blue Mountain Eye Study (BMES).¹⁹ The BMES category of moderate to severe myopia (>−3D) was modified by further subdividing it into mild myopia (up to −3D), moderate myopia (−3D up to −6D), and severe myopia (>−6D), using cutoffs established in the Beijing Eye Study.²⁰ Furthermore, glaucoma cases were classified based on mean deviation (MD) values as severe (MD $\le -12$), moderate ($-12<\text{MD}\le -6$), and mild ($-6<\text{MD}$).

To compare the performance of the model to that of a human grader, a subset of 100 cases was randomly drawn from the Stanford test dataset for grading by a glaucoma fellowship-trained human grader (DC). The human grader had access to multiple screening data, including fundus images, OCT RNFL and GCIPL printouts, IOP values, visual field parameters, access to patient history and physical examination for grading the cases as glaucoma versus normal. The performance of the model was then evaluated on the same subset of cases.

Training and Validation

In total, from the Stanford dataset, 1022 optic nerve scans of 363 eyes from 207 patients with a diagnosis of glaucoma (eyes randomly chosen) and 542 scans of 291 eyes from 167 patients of definitive normal were included in the training set. A total of 142 scans of 48 eyes from 27 patients with a glaucoma annotation and 61 scans of 39 eyes from 23 patients with a normal annotation were included in the validation set.

The splitting of data into different sets was based on patients, to make sure that scans belonging to each patient are included in only one of the splits and there is no data leakage between different sets. Each OCT scan over the ONH is a 3D array of size $6\text{mm}\times 6\text{mm}\times 2\text{mm}$ divided into a cube of resolution of $200\times 200\times 1024$, with numbers representing the height, width, and depth of the array, respectively. For the dataset from Stanford, cases were labeled according to the criteria mentioned above by a glaucoma fellowship-trained ophthalmologist with more than 2 years’ experience (SSM) based on fundus images, VF, OCT RNFL, GCIPL parameters, and IOP-lowering treatment (based on chart review). In cases where labeling needed arbitration, a senior glaucoma specialist with more than 10 years of experience (RTC) reviewed the cases and his diagnoses were considered final. Twenty out of 36 conflicting cases were eliminated based on insufficient data on chart review. To compute intergrader agreement for diagnosis, a glaucoma fellowship-trained specialist (DC) adjudicated the labeling of randomly selected 50 glaucoma and 50 normal cases. Following this, Cohen's $k$ value was calculated. Intergrader agreement calculations resulted in a Light's $k$ (arithmetic mean of Cohen's $k$) of 0.8535, considered to represent almost perfect agreement.²¹

Test and External Validation Datasets

Data from four different countries were used in the evaluation of the model. The test dataset from Stanford is composed of 694 additional OCT 3D cube scans: 241 OCT 3D cube volumes from 113 eyes (of 66 patients) that were labeled as normal and 453 scans of 157 eyes (of 89 patients) labeled as glaucoma. There was no overlap of cases with this test set and that of cases in the training or validation data sets. Three external validation datasets consisted of data each obtained from single institutions in Hong Kong, India, and Nepal. The Hong Kong dataset consists of 1625 OCT 3D cube images from the Chinese University of Hong Kong, with 666 OCT 3D cubes of 196 eyes (of 99 patients) labeled as normal and 959 OCT 3D cubes of 277 eyes (of 155 patients) labeled as glaucoma. The India dataset is composed of 672 OCT 3D cube images of ONH from the Narayana Nethralaya Foundation, India. In total, 211 scans from 147 eyes of 98 patients were labeled as normal and 461 OCT 3D cubes from 171 eyes of 101 patients had a glaucoma annotation. Finally, the Nepal dataset contained 380 OCT 3D cube images of ONH from the Tilganga Institute of Ophthalmology, Nepal. In this dataset, 158 scans from 143 eyes of 89 patients were labeled as normal, and 222 scans from 174 eyes of 109 patients were labeled as glaucoma.

In the dataset from Hong Kong, glaucoma was defined as RNFL defects on thickness or deviation maps that correlated in position with the VF defect, which fulfilled the definition of glaucomatous VF defects.¹⁷ Two glaucoma specialists worked separately to label all the eyes with gradable SD-OCT scans into normal/glaucoma combined with VF results. An SD-OCT volumetric scan was labeled as gradable when signal strength was equal to or better than 5 without any artifacts or when the artifacts influenced <25 percentage peripheral area, excluding the measurement center.

For the datasets from India and Nepal, glaucoma specialists each with experience of more than 10 years in glaucoma practice labeled the cases into glaucoma and normal. The ground-truth labeling, inclusion criteria, exclusion criteria, visual field, and SD-OCT device used for the external validation datasets from India and Nepal were the same as those used for the training dataset from Stanford. Details of dataset labeling are given in Supplementary Table S1 and details of inclusion and exclusion criteria are provided in Supplementary Section S4. The splitting of data sets in terms of number of scans, eyes, and patients from each center is given in Supplementary Table S2. Even though glaucoma cases without visual field defects were not included in the training or validation dataset, we evaluated the performance of the model on a nonoverlapping set of these cases from Stanford. This included a separate data set of 169 scans of 42 eyes from 27 patients. These glaucoma cases were those with structural defects on OCT RNFL and/or GCIPL maps (thickness and/or deviation) and without any visual field defects.

Development of the Deep Learning Algorithm

Network Architecture

A 3D convolutional neural network (CNN) similar to the classification network of De Fauw et al.²² is used in our experiments (Supplementary Fig. S4). This network uses multiple layers of dense convolutional blocks.²³ Each dense convolutional block consists of one 3D spatial convolutional block (Fig. 1a) followed by a 3D depth-wise convolutional block (Fig. 1b). Each convolutional block applies a convolutional operation, followed by group normalization²⁴ and ReLU nonlinearity to the input, and the output is concatenated to the input of the convolutional block along the channel axis. The number of channels in a convolutional layer is defined as a multiple of $g$, which is called growth rate in the DenseNet²³ architecture. All convolutional layers have a stride of 1, and max pooling stride was set to 2 for dimensions that had a larger than 1 window size.

Figure 1.

Building blocks of the dense convolutional blocks used in the convolutional neural network.

To increase the amount of effective training data, random flipping and dense elastic deformations were used as data augmentation during training (see Supplementary Fig. S3). Adam optimizer with weight decay²⁵ was used for training. After training, model checkpoint with the best results on the validation set was selected as the final model.

Finding Areas of Interest

After training, to get better insight into the predictions of the model, we used saliency methods to try to interpret how the model made its predictions. For this purpose, the Grad-CAM saliency method²⁶ was used.

To test whether the ONH area of the scan contains any diagnostic information, a new experiment was devised. Manual cropping of the OCT images on a small subset of scans selected by random sampling was done by a glaucoma fellowship-trained ophthalmologist (SSM) to only include the ONH, creating a 3D mask for this area. For cropping the scans, we used a software known as 3D Slicer,²⁷ which is an open-source software platform for biomedical image informatics, image processing, and 3D visualization. The ONH region was cropped by identifying the appropriate zone of the image in the expected location relative to Bruch's Membrane Opening (BMO).

For a border of dark/light junction at the typical position of the anterior and posterior LC position identified by consolidating and connecting, as well as identified individual positions of likely target regions under additional 3D visualization of axial scans. Examples of cropped scans are shown in Supplementary Figure S2.

The novel method used for finding new areas in the OCT scans that contain useful diagnostic information has been termed DiagFind and is described in detail in the next section.

DiagFind

 .

  

Algorithm 1: DiagFind
1:	Train a neural network on a medical imagery classification task.
2:	Utilize saliency methods to find areas of potential sensitivity, and confirm these areas are useful by consulting a domain expert (e.g., a glaucomaspecialized ophthalmologist for this paper)
3:	Further refine these areas of sensitivity to those that correlate with a diagnostic label for which the model is being trained.
4:	Redo training, while utilizing a cropping data augmentation that crops the focus onto the areas of sensitivity.
5:	Manually crop a number of evaluation data points to the area of interest and evaluate and measure the performance of the model on the cropped data.
6:	If the resulting performance of the model is nontrivial, it shows that the identified area contains useful diagnostic information for the given medical imagery problem, since the model has no input other than the area of interest.

The DiagFind algorithm for finding new areas with diagnostic information consists of multiple steps that are described in Algorithm 1. Based on saliency map observations, we utilized DiagFind and retrained the model using additional random cropping data augmentation. In this data augmentation, we found a heuristic to select the subset of the scan that would contain the area of interest according to the observations from the saliency maps with a high probability. During training, the data augmentation would randomly select a subset of the scan cube and set all the values outside the selected cube as zero. Note that in this data augmentation, cube sampling was implemented in a way that the heuristically identified scan cube would be selected with a higher priority compared to other plausible subset cubes. If this area of sensitivity can be positively identified using DiagFind, it can be further analyzed to uncover any causal relations (stronger than the initial perceived correlation) between the model prediction and the newly identified area of interest.

Further, we also evaluated the performance of the algorithm across different severity levels of myopia cases on the cropped scans.

Statistical Analysis

Area under the (receiver operating) curve (AUC), sensitivity, specificity, and F1 scores have been used to quantify the performance of the models on the test sets.

The AUC summarizes the performance of the binary classifier for different values of discrimination threshold.

To compute sensitivity and specificity, we used a discrimination threshold from the validation set, such that the resulting predictions would have a maximum F2 score, giving more weight to recall than to precision, to have a smaller number of false-negative predictions. The statistical analysis for comparisons of numerical demographic data was performed with the MedCalc software (Version 19.4). Results are expressed as mean ($\pm$standard deviation). Independent two-sample t-test was used to evaluate the level of significance. A P value of 0.005 or less was considered significant. Chi-squared test was used for comparisons of categorical demographic data for proportions.

Results

Demographic and Clinical Background of the Datasets

Demographic background of the training, validation, and test sets along with mean deviation (MD) and mean refractive error values are presented in Supplementary Tables S3, S4, and S5, respectively. The demographic data include age, gender, and ethnicity distribution, as these are parameters known to affect the OCT cube tissue thicknesses independent of glaucoma. Note that for some patients, demographic data were incomplete, and therefore, aggregate numbers do not necessarily add up to the dataset size. Demographic information, MD, and mean refractive error values for Hong Kong, India, and Nepal are presented in Supplementary Tables S6, S7, and S8, respectively.

The training dataset included patients of Asian, Caucasian, African American, and Hispanic ethnicity while the external datasets from Hong Kong, India, and Nepal included cases belonging to Asian ethnicity only. There was a statistically significant difference in the female to male ratio between the training dataset (55:45) and the datasets from Hong Kong (67:33; $P<0.005$), India (40:60; $P<0.005$), and Nepal (40:60; $P<0.005$). There was no significant difference in the average age among the glaucoma cases in the training (age in years $\pm$ SD; 69.41 $\pm$ 14.70), validation (70.09 $\pm$ 10.37, $P=0.74$), and test set from Stanford (69.82 $\pm$ 16.15, $P=0.79$). The average age of patients labeled as having glaucoma in Hong Kong (age in years $\pm$ SD; 65.90 $\pm$ 9.30; $P<0.005$), India (63.84 $\pm$ 11.72, $P<0.005$) and Nepal (45.34 $\pm$ 17.08, $P<0.005$) datasets was significantly lower than that of the training dataset from Stanford (69.41 $\pm$ 14.70, $P<0.005$). There was a significant difference in the mean refractive error (in terms of spherical equivalent) between the glaucoma subsets in the training data (in diopters $\pm$ SD: −3.57 $\pm$ 3.37) compared to the data from Hong Kong (−0.85 $\pm$ 2.57, $P<0.005$), India (−0.48 $\pm$ 2.25, $P<0.005$), and Nepal (−1.38 $\pm$ 2.38, $P<0.005$). The distribution of cases in the datasets according to severity of refractive error is shown in Supplemetary Table S10. The glaucoma training dataset from Stanford had a higher percentage (8.88%) of cases with severe myopia compared to the datasets from Hong Kong (4.70%, $P=0.12$), India (0.0%, $P<0.005$), and Nepal (2.5%, $P<0.005$). Also there is a significantly higher percentage of severe myopia in the normal subset of the Stanford data compared to Hong Kong, India, and Nepal datasets ($P<0.005$). There was no significant difference in severity of glaucoma (in terms of mean deviation $\pm$ SD) between the training (−9.75 $\pm$ 7.50) validation sets (7.89 $\pm$ 4.17, $P=0.07$) and Stanford test set (−9.01 $\pm$ 7.52, $P=0.27$), Hong Kong dataset (−8.50 $\pm$ 6.81, $P=0.035$), and Nepal dataset (8.30 $\pm$ 7.04, $P=0.04$), while the mean deviation was significantly lower in the dataset from India (−12.74 $\pm$ 9.22, $P<0.005$). The percentage of severe glaucoma cases in the India dataset was significantly higher (44.80%, $P<0.005$) compared to the training (28.40%), Hong Kong (24.00%), and Nepal (21.10%) datasets. Severity distribution of datasets from Stanford, Hong Kong, India, and Nepal is shown in Supplementary Table S9. Details of additional clinical information such as cup-to-disc ratio, IOP, gender distribution, pattern standard deviation, and visual field index, along with statistical comparisons, are shown in Supplementary Table S11.

Performance in Detecting Glaucoma on Primary and External Datasets

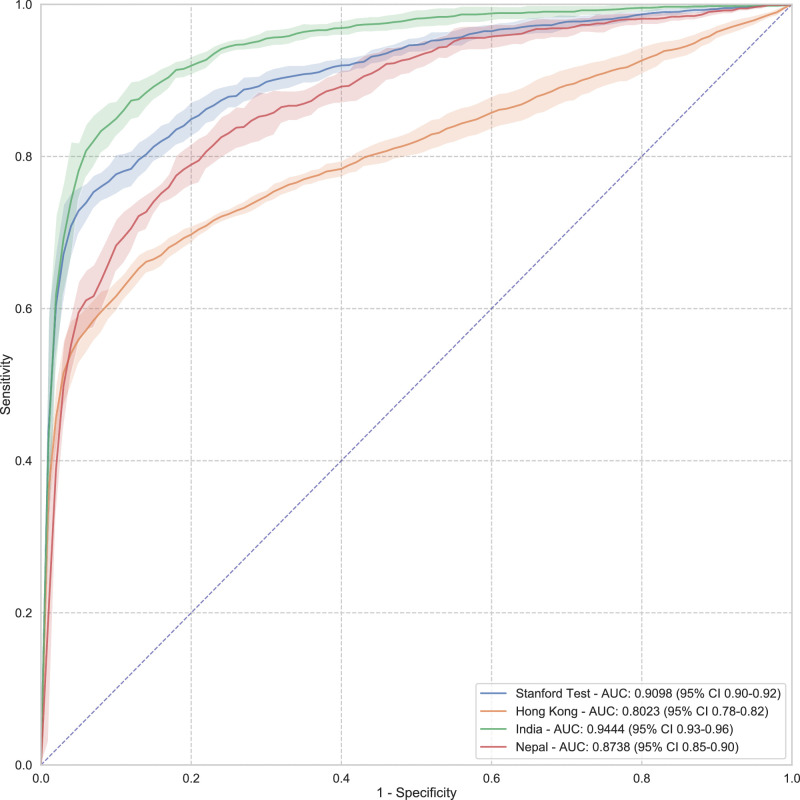
On the Stanford test set, our model was able to achieve an AUC value of 0.91 (95% CI, 0.90–0.92) with a sensitivity value of 0.86 (95% CI, 0.80–0.92), to differentiate between healthy and normal eyes. The model was able to achieve an AUC value of 0.80 (95% CI, 0.78–0.82) with a sensitivity value of 0.73 (95% CI, 0.67–0.79) on the Hong Kong dataset, an AUC value of 0.94 (95% CI, 0.93–0.96) on the India dataset with sensitivity of 0.93 (95% CI, 0.88–0.99) and an AUC of 0.87 (95% CI, 0.85–0.90) on the dataset from Nepal with a sensitivity of 0.79 (95% CI, 0.68–0.90). The complete results of the model are presented in Table 1. AUCs and sensitivities at fixed specificities (90% and 95%) are presented in Supplementary Table S12. AUCs for all the datasets, with standard deviations computed over five runs of the model to plot the shaded areas, are shown in Figure 2.

Table 1.

Results of the Proposed Model on the Stanford Test and External Data Sets

Dataset	AUC, 95% CI	Sensitivity, 95% CI	Specificity, 95% CI	F1 Score, 95% CI
Stanford	0.91 (0.90–0.92)	0.86 (0.80–0.92)	0.78 (0.68–0.88)	0.87 (0.86–0.89)
Hong Kong	0.80 (0.78–0.82)	0.73 (0.67–0.79)	0.73 (0.61–0.85)	0.76 (0.75–0.77)
India	0.94 (0.93–0.96)	0.93 (0.88–0.99)	0.71 (0.51–0.91)	0.91 (0.90–0.92)
Nepal	0.87 (0.85–0.90)	0.79 (0.68–0.90)	0.79 (0.66–0.92)	0.80 (0.78–0.83)

The 95% confidence intervals (CIs) are computed over five independent runs of the model.

Figure 2.

AUC for all the data sets, with standard deviations computed over five runs of the model to plot the shaded areas.

Performance in Comparison to Human Grader

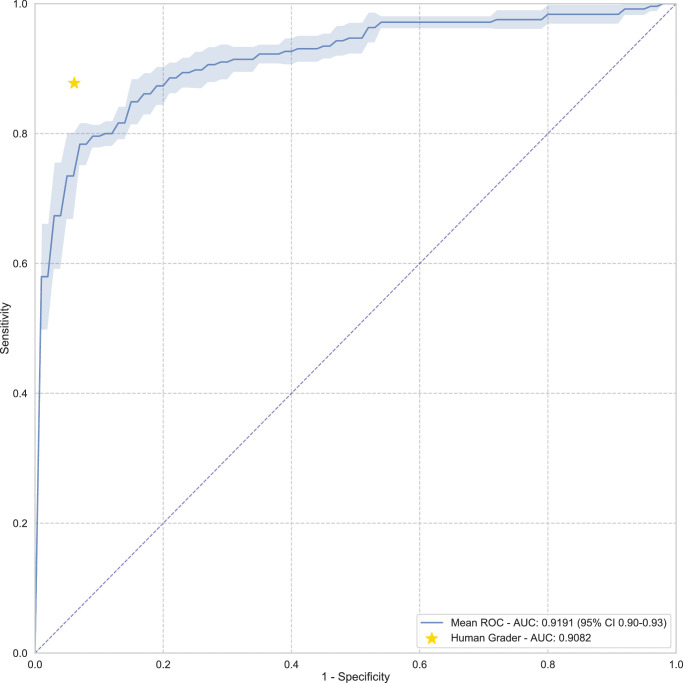
We also computed the performance of the human grader on a subset of scans from the Stanford test set, and the AUC value of the human grader was 0.91. Further, we also evaluated the sensitivity at matched specificity for human grading. On the same subset, our proposed model was able to achieve an average AUC value of 0.92 (95% CI, 0.90–0.94) (see Fig. 3). The difference between the performance of the human grader and the performance of the proposed model on the Stanford test set was not statistically significant ($P=0.99$).^28–31 From five runs of our model, the worst P value obtained was 0.367. At a matched specificity of 94%, the sensitivity of the human grader was 89.80% versus a sensitivity of 73.64% (95% CI, 69.86–77.43) of the model.

Figure 3.

AUC for the proposed model on the subset of the Stanford test set that was graded by a glaucoma fellowship-trained ophthalmologist, with standard deviations computed over five runs of the model to plot the shaded areas. To assign a ground-truth label, human grader had access to other screening data, including fundus images, OCT RNFL and GCIPL printouts, IOP values, and visual field parameters, and also had access to patient history and physical examination data, while the model only had access to the OCT scan cube.

Performance on Myopia

The model was able to achieve an F1 score of 0.97 (95% Cl, 0.96–0.98) and AUC of 0.99 (95% CI, 0.97–1.00) on severe myopia cases. The model was also able to achieve an F1 score of 0.91 (95% CI, 0.86–0.96) and AUC of 0.97 (95% CI, 0.93–1.00) on moderate myopia cases (Table 2). The model achieved an F1 score of 0.87 (95% CI, 0.84–0.91) and AUC of 0.92 (95% CI, 0.89–0.95) on mild myopia cases.

Table 2.

Results of the Proposed Model on the Stanford Test Set for Each Myopia Severity Level

Myopia Severity	Number of Scans (Eyes)	AUC, 95% CI	Sensitivity, 95% CI, %	Specificity, 95% CI, %	F1 Score, 95% CI
Mild	166 (67)	0.92 (0.89–0.95)	89.37 (84.53–94.21)	69.09 (59.78–78.40)	0.87 (0.84–0.91)
Moderate	52 (18)	0.96 (0.93–1.00)	91.43 (83.37–99.48)	89.17 (80.51–97.82)	0.91 (0.86–0.96)
Severe	51 (13)	0.99 (0.97–1.00)	94.47 (91.46–97.48)	90.00 (73.00–100.0)	0.97 (0.96–0.98)

The 95% confidence intervals (CIs) are computed over five independent runs of the model.

Performance on Different Severity of Glaucoma

Additionally, we evaluated the performance of our algorithm across different levels of glaucoma severity. The model was able to achieve recall values of 0.84 (95% CI, 0.74–0.94), 0.92 (95% CI, 0.89–0.95), and 0.99 (95% CI, 0.97–1.00), on mild, moderate, and severe glaucoma, respectively (see Table 4).

Table 4.

Results of the Proposed Model on the Stanford Test Set for Each Glaucoma Severity Level, for Scans Where We Have Glaucoma Severity Information

Glaucoma Severity	Number of Scans (Eyes)	Recall, 95% CI
Mild	225 (50)	0.84 (0.74–0.94)
Moderate	70 (20)	0.92 (0.89–0.95)
Severe	66 (29)	0.98 (0.97–1.00)

The 95% confidence intervals (CIs) are computed over five independent runs of the model.

Performance on Right Versus Left Eyes

Supplementary Table S13 shows the results of the subgroup analysis in right versus left eyes in all the test datasets. There was no significant difference in performance of the model in right versus left eyes in any of the test data sets ($P>0.005$).

Performance on Glaucoma Cases Without Visual Field Defects

We evaluated the performance of the model with a nonoverlapping set of glaucoma cases from Stanford, without any visual field defects. The performance of the model in terms of recall for these data was found to be 0.76 (95% CI, 0.68–0.85).

Analysis of False Predictions

False predictions were analyzed on the Stanford test set, as can be seen in Table 5. Among the 15 false-positive cases, age >70 years was observed to be a common association in 73.3% of cases. Severe myopia with tilted discs and large cup disc ratio (CD) (>0.7) were the other observed causes of false-positive results. Among the 34 cases identified as false negative by the model, 26 cases (76.47%) were mild glaucoma cases with mean deviation >−6. Small cup to disc ratio (<0.3) and age <50 were observed as other causes for false-negative predictions in less than 10% of cases. Examples of saliency visualizations with wrong predictions are shown in Supplementary Figure S1.

Table 5.

Observed Causes of False Predictions of Glaucoma Versus Normal on the Stanford Test Set

False Predictions		Number (%) of Eyes
False positives		15
	Age >70	11 (73.3)
	Severe myopia with tilted discs	2 (13.3)
	Large CD (>0.7)	1 (6.6)
	Causes unidentifiable	1 (6.6)
False negatives		34
	Mild glaucoma MD >6	26 (76.47)
	Small CD (<0.3)	3 (8.82)
	Age <50	3 (8.82)
	Causes unidentifiable	2 (5.88)

Results of Saliency Maps Analysis

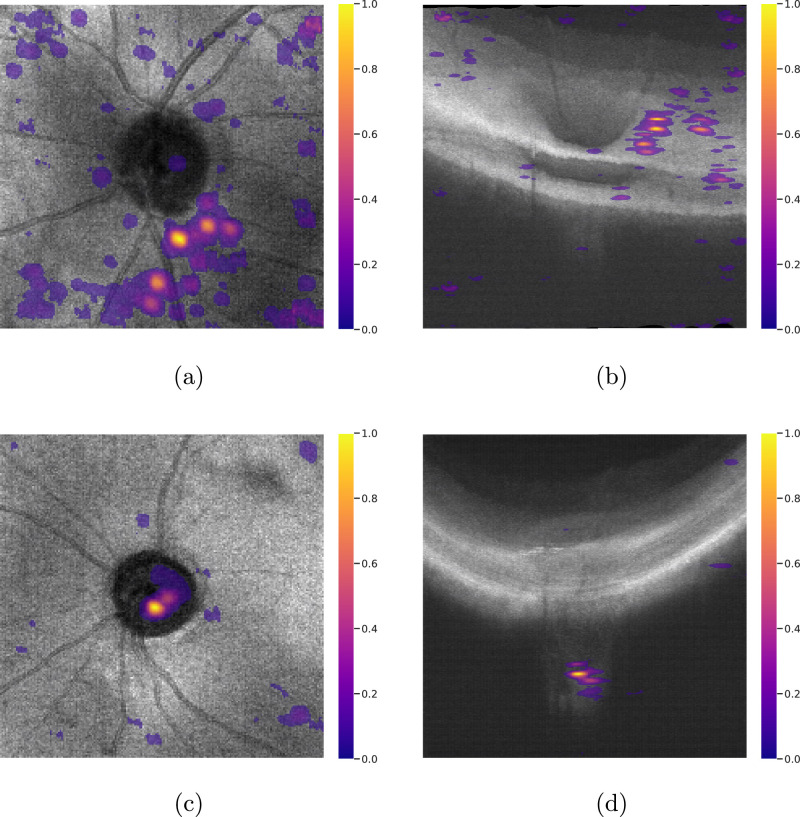
Saliency visualizations show that in most of the cases in which the model makes a glaucoma prediction, the LC is highlighted (see Figs. 4a, 4b). Out of the 156 cases predicted as glaucoma by the model on the Stanford test set, all the cases had LC highlighted on the saliency visualizations, with or without retina highlighting. However, when the prediction was normal, superficial retina was highlighted in a high number of cases (see Figs. 4c, 4d). Out of the 92 cases predicted as normal, 67.3% had superficial retina highlighting.

Figure 4.

Saliency visualizations for two cases from the Stanford Test set. (a) Top and (b) side view of saliency visualizations of a correctly classified normal eye. (c) Top and (d) side view of saliency visualizations of a correctly classified glaucomatous eye. As can be seen, in most of the cases, a highlight in the lamina cribrosa region is mostly correlated with Glaucoma prediction, while for cases with normal prediction, the retinal layer is mostly highlighted. Saliency visualization has been obtained with respect to the predicted class. Regions with a higher value are more salient for the model in making the final prediction.

Performance on Cropped Data Using the DiagFind Algorithm

The initial model (without random cropping data augmentation) was able to achieve an AUC value of 0.41 on the manually cropped test set. The model trained on the same data with the same hyperparameters, with the addition of the random cropping data augmentation, increased the AUC value to 0.69.

We also tried this experiment by utilizing more training data from each of the external test sets, in addition to the training set from Stanford. Twenty percent of the cases from each external test set were randomly selected. This resulted in 322 additional normal scans and 474 additional glaucoma scans. Using these additional data and retraining using the procedure described in the Algorithm 1, the AUC on the cropped scans increased to 0.77, which is a substantial relative increase, even though the difference is not statistically significant ($P=0.071$).^29–31 We evaluated the performance of the algorithm across different severity levels of myopia cases on the cropped scans (see Table 3). The algorithm performed with an AUC of 0.77, 0.75, and 1.00 on mild, moderate, and severe myopia cases, respectively.

Table 3.

Results of the Proposed Model Trained With the DiagFind Algorithm, on the Cropped Scans From the Stanford Test Set for Each Myopia Severity Level

Myopia Severity	Number of Scans (Eyes)	AUC	Sensitivity, %	Specificity, %	F1 Score
Mild	24 (24)	0.77	71.43	50.00	0.69
Moderate	7 (7)	0.75	75.00	66.67	0.75
Severe	4 (4)	1.00	100	100	1.00

The number of cropped scans with myopia severity information that have severe and moderate levels of myopia is very small.

Discussion

In this study, the authors developed and validated a 3D deep learning system using real-world raw OCT ONH volumes to detect manifest glaucoma as defined by multiple inputs. The proposed model performed well in both the Stanford test and external datasets, suggesting that automated detection of glaucoma using raw SD-OCT cube scans is feasible on diverse data sets using deep learning methods. This algorithm may provide new insights by going beyond solely looking at normative data of segmented RNFL, namely also the lamina.

The differences in the performance of the model on datasets from Hong Kong, India, and Nepal can be attributed to the variances in demographic and clinical characteristics. Apart from this, the difference in performance on the Hong Kong dataset may be due to the differences in labeling criteria, which defined structural changes in glaucoma based on RNFL maps alone. Although the latter cannot not be attributed to the lower performance, as per this definition, scans with glaucomatous changes only in the macula would be included in the normal category, which would have influenced the performance of the algorithm in this dataset. The higher performance of the model on the dataset from India can be attributed to a significantly higher percentage of eyes with severe disease in this dataset, which would likely be easier to differentiate from normal cases. The performance of the model on glaucoma cases without VF defects despite the model not being trained on this subtype of cases suggests that the model was not overfitted and that the model can generalize to unseen data.

The model performed slightly better compared to human grader in terms of AUC values (albeit statistically insignificant). But at matched specificity, the sensitivity of the human grader was higher than the sensitivity of the model. The human grader had access to multiple screening data, including fundus images, OCT RNFL and GCIPL printouts, IOP, VF parameters, access to patient history, and physical examination data, while the model used information from the OCT cube scans alone, which still attests to the strength of the model.

Myopic refractive error is known to impact RNFL and macular thickness measurements due to stretching and thinning of these layers and due to increased axial length and optical projection artifact of the scanning area,⁴ resulting in many false-positive diagnoses, also known as “red disease.” Using the entire cube and highlighting the LC may help researchers study this LC region more closely in myopes when trying to differentiate glaucoma from normal. The difference in the performance in the myopia subsets compared to the total dataset could be due to the fewer number of cases in each subgroup (Table 2). The assessment of false-positive predictions by the present model showed only 13.3% of cases to be associated with severe myopia, despite the fact that severe myopia is one of the most common reasons for misdiagnosis of glaucoma in clinical presentations.⁴ This suggests that by training the model on scans of eyes with high myopia, as long as there are no data loss artifacts in the scans, the training examples provide enough information within the volumes of slices for the model to avoid myopia from affecting the result. The performance of the model across different severity levels of myopia cases on cropped scans (see Table 3) points toward the possibility of utilization of diagnostic information at the LC level in different degrees of myopia in glaucoma diagnosis, especially as an alternative to unreliable RNFL parameters in severe myopia.⁴ This requires further evaluation due to the small data distribution of the present study.

The training dataset included cases with signal strength ≥3. This is because at times, clinicians do not have high-quality OCT images for diagnosis and evaluation of glaucoma, due to patient cooperation, medial opacity, tear film issues, small pupils, or other limitations. Furthermore, it has been reported that a signal strength of >3 is acceptable to obtain reproducible scanning images among patients with ocular media opacities.³² Since real-world data collection rarely matches the standards and quality control described in many deep learning studies, it is one of the reasons for variable performance of the algorithm in real-life settings.^13,14 Variances in SD-OCT raw images, such as differences in machine calibration and image intensity (e.g., background noise, brightness), could be contributing to the differences in performance among external datasets. The present study aimed to train the algorithm to be able to identify glaucoma even on low-quality images (without data loss), hence replicating real-world representations.

The saliency maps generated showed that for cases with normal prediction, the areas on superficial retina were mostly highlighted, and for glaucoma prediction, the LC region was highlighted. This agrees with the established clinical parameters for glaucoma diagnosis (e.g., cup diameter/volume and rim area/volume). Given that clinicians do not routinely review every single slice of the cube, and because current OCT RNFL and ONH printouts do not provide any diagnostic information based on LC, saliency visualization highlighting the LC region suggests that it should also be looked at closely by clinicians.

The present algorithm's ability to utilize the diagnostic information at the LC from the conventional scans (without EDI) using the DiagFind algorithm is a new insight since it does correspond with the disease process. In a recent study by Rahman et al.,³³ an automated system was constructed using 600 SD-OCT images (Heidelberg Engineering GmbH, Heidelberg, Germany) of 60 patients. The model was used to quantify the morphologic parameters of the LC, including depth, curve depth, and curve index from OCT images. The model consisted of a two-stage deep learning model, which was composed of the detection and the segmentation models as well as a quantification process with a postprocessing scheme. Similar to what our model discovered, this study proposes that incorporating these morphologic parameters in glaucoma detection can contribute to obtaining high-accuracy detection results for diagnosing glaucoma.³³

Recently, Maetschke et al.¹¹ employed a 3D CNN to detect glaucoma from raw, unsegmented Cirrus SD-OCT ONH volumes (total of 1110 scans split into 888 training, 112 validation, and 110 test samples) and achieved a substantially high AUC of 0.94. The neural network used in this work has a simpler architecture compared to the network used in our work. There is a higher probability that a larger network would perform better compared to a simpler network. However, to correctly compare their network and the network used in this work, and to prove this claim and measure the relative merit of the larger, more complex architecture, both should be trained on the same data with a large enough budget dedicated to hyperparameter search, to make sure that both networks are able to obtain their best results given the training data. Similar to the present study, for healthy eyes, the network in Maetschke et al.¹¹ tends to focus on a section across all layers and ignores the optic cup/rim and the lamina cribrosa. In contrast, for glaucomatous eyes, the optic disc cupping, neuroretinal rims, and the LC and its surrounding regions were highlighted.

In the recent study by Ran et al.,¹² a 3D deep learning system performed with an AUC of 0.97 to detect glaucoma. This study used 2926 raw unsegmented Cirrus SD-OCT ONH scans for training, 975 scans for testing, and 976 scans for primary validation.

Similar to our study, the heatmaps generated in their study showed neuroretinal rim and areas covering the LC to be highlighted in the detection of glaucoma. Apart from this, the RNFL and choroid were also potentially found to be related to the detection of glaucoma. The difference in their study from ours was in the definitions used for glaucomatous structural defect (which was based on OCT RNFL thickness and deviation maps alone) and inclusion of images with signal strength ≥5. Another difference was the distribution of ethnicity in their training set, which consisted exclusively of Chinese Asian eyes, while our training, validation, and test data from Stanford included subjects belonging to multiple ethnicities.

The present study has several strengths. Multiple international datasets provide diversity in our database for evaluation purposes, which is rare to have for glaucoma datasets. Fine-tuning the model on the external data sources would have probably resulted in increased accuracy on the external test sets, but this was not done due to the differences in ground-truth definitions among the datasets.

Another significant strength of our method was that the training dataset was not cleaned for this experiment to more closely follow the challenges that are faced in real-world clinical settings and included all ranges of myopia and disc sizes. One other major highlight of our study was that the ground-truth labeling included various multimodal evaluations, replicating real-world clinical settings. Additionally, using the DiagFind algorithm, the current study was able to show that the LC region in the routine SD-OCT scan, which is mostly not used by ophthalmologists, contains useful diagnostic information that can serve as an additional signal in the glaucoma diagnosis. Apart from this, the experiment with cropped scans had encouraging results for using the ONH region with a focus on LC in diagnosis of the disease, especially in high myopia and severe glaucoma, where conventional RNFL parameters have limitations.

On the other hand, our study has a few limitations. Despite using the term “real-world” dataset, due to the absence of acceptable consensus on the definition of glaucoma suspects among experts and incomplete records across countries, we did not include these cases in our study. Other cases that are difficult to be diagnosed by skilled clinicians have been excluded, including cases with concomitant retinal or optic nerve pathology. Second, even though we have not excluded any cases based on disc sizes or presence of myopic tilted discs in our dataset and have included cases with low signal strength, we have not looked into the performance of our model across subsets. Due to the unavailability of data on signal strength of individual scans (other than the information of it being >3), the present study is unable to analyze performance based on varying signal strength. Another possible drawback of our study is that during ground-truth labeling, some glaucoma cases that had focal defects that were only seen on the deviation map with an “all green” RNFL/GCIPL map might have been excluded as being classified as glaucomatous.

Going forward, we plan to develop a 3D deep learning algorithm using a wider range of data including high- and low-risk suspect cases that would help in identifying cases that require referral for management by glaucoma specialists. This would be based on acceptable definitions structured with inputs from multiple international experts. Second, we plan to compare the performance of our model with that of multiple human graders at various levels of expertise in glaucoma care. Finally, we plan to include raw OCT macula cube scans along with ONH scans for better algorithm correspondence.

Conclusion

Our 3D deep learning model was trained and tested using the largest OCT glaucoma dataset so far from multinational data sources, and it has been able to detect glaucoma from raw SD-OCT volumes across severity of myopia and severity of glaucoma. By using a multimodal definition of glaucoma, we could include more scans from the real world, including low signal strength, which are typically excluded from studies. The saliency visualizations highlighted the LC as an important component in the 3D ONH cube in differentiating glaucoma, which may be useful in high myopes who have thin RNFL. Based on this information, and using the DiagFind algorithm, we studied the performance of the model in the case that only the ONH crop of the full scan was given to the model. We observed that our model, trained with additional random cropping data augmentation, was able to detect glaucoma on the cropped scans.