Comparing Bayesian early stopping boundaries for phase II clinical trials

Summary

When designing phase II clinical trials, it is important to construct interim monitoring rules that achieve a balance between reliable early stopping for futility or safety and maintaining a high true positive probability (TPP), which is the probability of not stopping if the new treatment is truly safe and effective. We define and compare several methods for specifying early stopping boundaries as functions of interim sample size, rather than as fixed cut-offs, using Bayesian posterior probabilities as decision criteria. We consider boundaries with constant, linear, or exponential shapes. For design optimization criteria, we use the TPP and mean number of patients enrolled in the trial. Simulations to evaluate and compare the designs’ operating characteristics under a range of scenarios show that, while there is no uniformly optimal boundary, an appropriately calibrated exponential shape maintains high TPP while limiting the number of patients assigned to a treatment with an inferior response rate or an excessive toxicity rate.

1 |. INTRODUCTION

Before proceeding to a large-scale confirmatory phase III trial to compare a potential new anti-disease agent or combination treatment regimen, E, to standard treatment, S, pharmaceutical companies and medical research institutes usually conduct one or more single-agent phase II trials. The aim of phase II is to screen new treatments and identify promising candidates before investing the resources required by a phase III trial. In about two-thirds of phase II trials, E fails to achieve a pre-specified minimum level of efficacy. In many settings, a maximum tolerable dose (MTD) of a new agent first is chosen in a small phase I trial, hence at the start of phase II any estimate of the probability of toxicity has low reliability, and excessive toxicity at the MTD is not unlikely.¹ Phase II trial designs thus require carefully constructed monitoring rules for early stopping due to either futility or excessive toxicity.^2,3 There always is a tension between the goals of avoiding the waste of human and financial resources by continuing to give patients a new treatment E that is either ineffective or excessively toxic, and incorrectly discarding a truly effective and acceptably safe new treatment. Futility and safety stopping rules are especially important in phase oncology II trials, which may have small sample sizes of about 30 to 80 patients and slow patient accrual rates, often one to two patients per month. It is not uncommon for a single-arm phase II oncology trial to take 2 to 3 years to complete. Ethical concerns may make early stopping rules for futility especially important if fatal outcomes are likely for cancer patients who do not achieve early response because they are given an ineffective experimental treatment. Efficient monitoring rules can (a) reduce the number of patients who receive ineffective or unsafe treatments, (b) reduce the financial cost of the trial, and (c) save patients for enrollment in other competing trials.

Any early stopping rules for futility or safety unavoidably cause some reduction of the true positive probability (TPP), which is the probability that a design’s monitoring rules do not stop a trial of an agent E that is truly both effective and safe. A design’s TPP quantifies its potential benefit to future patients. A well-designed phase II trial should achieve a balance between reliably monitoring futility and safety, and retaining reasonably high TPP. While a phase II design’s TPP sometimes is referred to as its “power,” here we do not test hypotheses, and thus we will refer to TPP rather than abusing the conventional definition of power used in frequentist hypothesis testing.

Bayesian designs for phase II clinical trials facilitate formally incorporating historical data and expert experience, easy sequential updating, and they are practical with small sample sizes. These features make them useful in many settings, including early phase oncology trials with frequent monitoring. There is a rich literature on Bayesian clinical trial designs. Thall et al,^2,4–7 proposed a variety of Bayesian designs using posterior probabilities as criteria for interim monitoring of one or more outcomes. Tan and Machin⁸ proposed a Bayesian two-stage design in which the parameters are calibrated on the basis of posterior probabilities. Sambucini⁹ accounted for the uncertainty of future data. Heitjan¹⁰ developed flexible Bayesian phase II designs with continuous monitoring based on predictive probabilities. Wathen and Thall¹¹ proposed a Bayesian adaptive model selection method for optimizing the stopping boundary of a phase III group sequential trial with a time-to-event endpoint. There are numerous other publications dealing with Bayesian clinical trial designs,^12–14 that include early stopping rules.

As an illustrative example, we consider a single-arm phase II trial designed using the method of Thall et al,⁴ to construct futility and safety monitoring rules. This study¹⁵ aims to investigate the dose-adjusted EPOCH regimen in combination with ofatumumab as therapy for patients with newly diagnosed or relapsed/refractory Burkitt leukemia. The maximum sample size is 30, with monitoring done for cohorts of 5 patients. The trial will be stopped early if, with posterior probability 0.95 or higher, the response rate with the new treatment is not at least 14% higher than the historical response rate. The historical response rate was assumed to be beta(73, 27) based on historical data, and the prior distribution for the new treatment response rate was assumed to be beta(1.46, 0.54), which has the same mean as the historical response rate, but a much larger variance, so it may be considered non-informative. For toxicity monitoring, the trial will be stopped early if, with posterior probability 0.90 or higher, the toxicity rate with the experimental treatment is very likely to exceed 30%, based on a beta (0.6, 1.4) prior distribution. This Bayesian monitoring method gives the following stopping rules: stop for futility if [number of patients who respond to the new treatment]/[number of patients evaluated] is less than or equal to 2/5, 6/10, 10/15, 14/20 or 17/25; and stop for unacceptably high toxicity if [number of patients with toxicity]/[number of patients evaluated] is greater than or equal to 3/5, 5/10, 7/15, 9/20, or 11/25. This general methodology has been applied to design many other single-arm phase II trials.^16,17

In this paper, we consider designs for a single-arm phase II trial of E with frequent futility and toxicity monitoring, after successive cohorts of m = 1 or 5 patients. We characterize anti-disease effect by a binary “efficacy” variable, sometimes called response, and also characterize one or more severe adverse treatment effects collectively as a binary “toxicity” variable. Our primary aims are to compare early stopping boundaries for efficacy and toxicity monitoring that have different shapes as functions of interim sample size, n, and identify nearly optimal boundaries for use in practice. We use posterior probabilities as stopping criteria, and explore four different futility stopping rules, each defined in terms of boundary shape and starting point. The first rule uses a constant cutoff for all interim analyzes and the final analysis (constant stopping boundary, CSB). Motivated by the concern that applying a stopping rule based on a very small early sample has an unacceptably high risk of incorrectly stopping an effective treatment,¹⁸ the second monitoring rule is a modification of CSB that does the first interim analysis at 10 patients, rather than at m = 1 or m = 5 (constant stopping boundary with first analysis at n = 10, CSB10). The third rule uses a linearly increasing function of n, (linear stopping boundary, LSB). The fourth rule uses an exponential function of n (exponential stopping boundary, ESB). We do not include versions of LSB or ESB that are constrained to do the first interim analysis at 10 patients because these boundaries are highly unlikely to stop a trial before at least 10 patients have been evaluated. In order to focus on comparison of the three shapes CSB, LSB, and ESB, we use constant stopping boundaries for toxicity throughout. We consider two optimality criteria, TPP and the number of patients enrolled in the trial, which are both ethical and practical considerations.

There are several different types of ESBs, which at one extreme consists of no interim futility monitoring. We will show, by simulation, that the particular ESB we choose as best yields effective interim monitoring by stopping the trial with high probability if the agent is ineffective while maintaining good TPP, that is, minimizing loss due to early stopping for futility when an agent is truly effective and safe. The ethical goals are to maximize benefit for both the trial participants and future patients, in terms of TPP. To quantify how well a design performs for the trial participants, we also calculate the mean number of patients and percent responders for each stopping boundary. Our simulations will show that CSB, CSB10, LSB, and ESB yield designs with substantively different properties, especially compared with designs that have no futility monitoring.

To consider optimization of futility monitoring rules, one may define, for example, a quantitative risk-benefit trade-off between TPP and the False Positive Probability (FPP), which is the probability of not stopping a trial early for an E that does not provide an improvement over standard treatment, S. One also may evaluate designs in terms of the number of patients who receive an ineffective treatment. Unavoidably, defining and quantifying such a trade-off is subjective. A thorough exploration of this issue might consider the total number of future patients who may benefit from the current trial, the total number of competing new treatments, and distributions of the efficacy and toxicity probabilities of these new treatments. All of these factors change over time with ongoing medical advances. Despite these challenges, optimization of futility monitoring rule shapes, per se, still is a very important issue, considering the potential impact on clinical trials in oncology and other areas of medical research. Based on our simulations, we conclude that some of our newly proposed futility stopping boundaries are close to optimal, with small room for further improvement. However, an exact answer to the question of which design may be considered optimal still depends on the specific criteria listed above.

The rest of the paper is organized as follows. In section 2, we introduce Bayesian trial designs, including notation, posterior probabilities, and choice of prior distributions. In section 3, we consider futility monitoring only. We first propose phase II designs with futility stopping boundaries based on a Bayesian posterior probability as a function of the trial’s current sample size. We then show how to calibrate design parameters and compare the operating characteristics (OCs) of different futility stopping boundaries under a range of different practical scenarios, using simulation as a design tool. In section 4, we compare the OCs of the different boundaries in trials with both futility and toxicity monitoring. We close with a discussion in section 5.

2 |. BAYESIAN PHASE II TRIAL DESIGNS

The primary endpoint of a phase II trial is often a binary indicator of a “response” event, R, that corresponds to early treatment success (efficacy). To provide an initial efficacy assessment, a phase II trial often is designed as a single-arm, open-label study. Multi-stage designs with one or more monitoring rules applied after successive cohorts often are used so that the trial will be stopped early if the interim data show that the study drug is either inefficacious or too toxic. We compare E with a standard, S, using historical data to specify prior distributions for the response and toxicity probabilities of S.

Patients are enrolled into the trial sequentially, and we denote responses to E by Y_{R, 1}, Y_{R, 2}, …, where each Y_{R, i} = 1 if subject i has a response and 0 if not. Similarly, Y_{T, i} = 1 or 0 indicates whether or not subject i experiences severe toxicity, T. Denote the maximum number of patients by N. For the interim analysis after the n-th patient (n < N), the total number of responses is X_{R, n} = Y_{R, 1} + … + Y_{R, n}, and the total number of toxicities is X_{T, n} = Y_{T, 1} + … + Y_{T, n}. Denote treatment by Tr = E or S, and denote the joint probability θ_{k, ab} = Pr(Y_R = a, Y_T = b| Tr = k), for a, b ∈ {0, 1} and k ∈ {E, S}. The marginal probabilities of R and T for treatment k are

$${\pi }_{k,R}={\theta }_{k,10}+{\theta }_{k,11}\text{and}{\pi }_{k,T}={\theta }_{k,01}+{\theta }_{k,11}.$$

We use the following posterior probabilities as interim monitoring criteria, with Data_n denoting all observed data up to the n-th subject enrolled in the trial,

$${\varphi }_{n,R}=\mathrm{Pr}\left({\pi }_{E,R}>{\pi }_{S,R}+\delta \mid {\text{Data}}_n\right),$$ (1)

$${\varphi }_{n,T}=\mathrm{Pr}\left({\pi }_{E,T}>{\pi }_{S,T}\mid {\mathrm{Data}}_n\right),$$ (2)

where, δ is the targeted improvement in response probability for E over S. In our simulations, we use fixed δ = 0.2. We stop the trial for futility if ϕ_{n, R} is unacceptably small, specifically, if ϕ_{n, R} < b(n), where b(n) is a boundary function of one of the four forms CSB, CSB10, LSB, or ESB. In section 4, we also will include a rule to stop the trial if E is too toxic, specifically, if ϕ_{n, T} > t(n), where t(n) is a second boundary function used for toxicity monitoring. When two boundaries are used, the relevant OCs represent how these two rules work together.

Suppose that a historical data set of n_h patients is available, with n_{h, R} responders, and n_{h, T} experiencing severe toxicity. We specify distributions of π_{S, R} and π_{S, T} empirically as follows:

$${\pi }_{S,R}~\mathrm{beta}\left(\frac{n_{h,R}}{\kappa },\frac{n_h-n_{h,R}}{\kappa }\right),$$ (3)

$${\pi }_{S,T}~\mathrm{beta}\left(\frac{n_{h,T}}{\kappa },\frac{n_h-n_{h,T}}{\kappa }\right),$$ (4)

where the parameter κ ≥ 1 may be used to discount the historical information. This is based on the consideration that, over time, the patient population may have changed, so if S were administered to the current patient population, it may have somewhat different efficacy and toxicity profiles than seen in the historical data. Consequently, the parameter κ is used to decrease the amount of information by increasing the variances in the above distributions. Using κ = 2 discounts the historical data by 50%, while κ = 1 does not do any discountimg. Because larger κ reduces the informativeness of the distributions of π_{S, R} and π_{S, T}, it affects how the stopping rules behave.

In the next Section, we define and compare different boundaries for futility monitoring only. In section 4, we consider monitoring for both futility and toxicity.

3 |. COMPARING STOPPING BOUNDARIES FOR FUTILITY

3.1 |. Different shapes of futility stopping boundaries

We assume prior distribution π_{E, R}~ beta(α, β) having the same mean as π_{S, R}, but with a much smaller amount of information. To specify this, we set α/(α + β) = n_{h, R}/n_h, and α + β = 1, that is, a prior effective sample size of 1. After observing X_{R, n} = x_{R, n} successes out of the first n patients, the posterior of π_{E, R} is beta(α + x_{R, n}, β + n − x_{R, n}), which is used to compute the decision criterion

$${\varphi }_{n,R}=\mathrm{Pr}\left({\pi }_{E,R}>{\pi }_{S,R}+\delta \mid {\mathrm{Data}}_n\right)$$

with the distribution of π_{S, R} specified in (3).

A very commonly used early stopping criterion for futility is a CSB (“Method I”). This futility monitoring rule stops patient accrual at the n-th patient if

$${\varphi }_{n,R}<C_1,\text{with}n=m,2m,3m,\dots ,N,$$ (5)

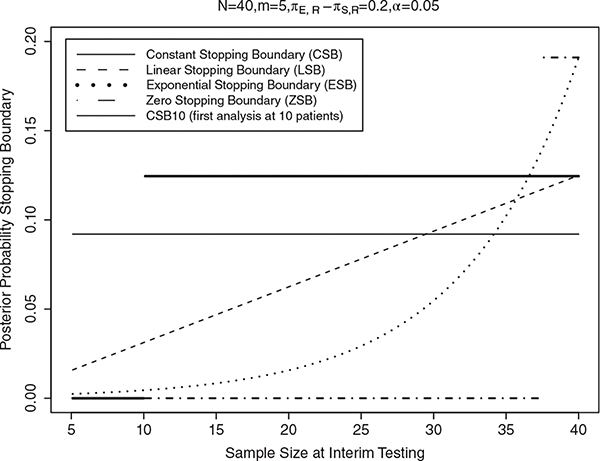
where C₁ is a fixed small number, usually in the range 0.01 to 0.20. In practice, the value of C₁ is calibrated by preliminary computer simulations to achieve a specified small false positive probability, FPP = probability of not stopping the trial early, if E does not provide an improvement over S. For example, in our simulation study given below, we consider a trial with π_{S, R} ~ beta(30, 70) and δ = 0.20, maximum sample size N = 40, and interim analyzes conducted after the outcomes of each cohort of m = 5 patients have been evaluated. We study the sensitivity of this rule to values of C₁ from 0.001 to 0.20 in increments of 0.001, and do 10,000 simulations for each value of C₁ in the setting where the fixed value ${\pi }_{E,R}^{\text{true}}=E\left({\pi }_{S,R}\right)=p_0$, to estimate the FPP with each C₁. We found that C₁ = 0.092 achieves FPP =0.05 when ${\pi }_{E,R}^{\text{true}}=p_0=0.30$. With this value C₁ = 0.092, the futility rule resulting from Equation (5) is to stop the trial if [number of successes]/[number of patients evaluated] is ≤1/5, 3/10, 4/15, 7/20, 9/25, 11/30, 13/35 or 15/40. This is shown as the thin solid line in Figure 1. R code to find C₁ (as well as C₂ to C₅, below) and accompanying documentation are provided as supplementary materials. If the trial is not stopped at any interim analyzes, E is regarded as promising, and the trial’s result is nominally “positive.” Otherwise, E is discarded and the trial is “negative.” We use these definitions of positive and negative trials in the calculations of the true positive and false positive probabilities, TPP and FPP, in the simulations, presented in the next Section. In addition, for practical application, we give the futility rules of each type of stopping boundary in terms of [number of successes]/[number of patients] in supplementary materials (Tables S1 and S2).

FIGURE 1.

Futility stopping boundaries at each interim analysis (n = 5, 10, …, 40) for the five designs: Constant stopping boundary (CSB, thin solid line), Constant stopping boundary with first interim at 10 (CSB10, thick solid line), linear stopping boundary (LSB, dashed line), exponential stopping boundary (ESB, dotted line), and no early stopping (or Zero Stopping Boundary, ZSB, dot-dashed line), respectively, under N = 40, m = 5, π_{S, R} = 0.30, δ = 0.2, α = 0.05

A major problem with the CSB futility monitoring rule is that it may be too likely to stop the trial early, when ϕ_{n, R} is most variable, resulting in a substantial loss of TPP. A simple way to address this problem is to do the first interim analysis at 10 patients, that is, change CSB to CSB10 (“Method II”), which stops the trial if

$${\varphi }_{n,R}<C_2,\text{for}n=10,10+m,\dots ,N,$$ (6)

where C₂ is calibrated in the same way as C₁.

A general way to re-define the stopping rules is to define boundaries that change over time as functions of current sample size, n, making it harder to stop at early stages and easier to stop at later stages. Our goal is to improve the design’s TPP, while still reliably stopping accrual for truly inefficacious or unsafe E. Motivated by these considerations, we propose two new designs, “Method III” and “Method IV”. Method III uses LSB, with a monitoring rule that stops accrual for futility if

$${\varphi }_{n,R}<\frac{n}{N}{C}_3,\text{for}n=m,2m,3m,\dots ,N,$$ (7)

where C₃ is calibrated similarly to C₁ and C₂. The LSB is less likely to stop at the early stages than the later stages of a trial, shown by the dashed line in Figure 1. This reduces the probability that the trial will be stopped prematurely based on limited information from only a few patients.

For Method IV, we define an ESB, which behaves more strictly at the early stages and more loosely at the later stages compared to the LSB. The ESB stops accrual for futility if

$${\varphi }_{n,R}<\exp \left(\frac{5n}{N}\right)C_4,\text{for}n=m,2m,3m,\dots ,N,$$ (8)

where C₄ is calibrated in the same way as C₁, C₂, and C₃. The ESB is represented by the dotted line in Figure 1.

We also consider a design without an early stopping rule. Since the interim stopping boundary is zero in this case, we call it the “zero stopping boundary (ZSB)” design. The ZSB is Method V, an extreme case where the trial will never be stopped early, and at the end one concludes futility if

$${\varphi }_{N,R}<C_5,$$ (9)

with C₅ calibrated to achieve a pre-specified FPP. The ZSB is represented by the dot-dashed line in Figure 1.

3.2 |. Comparisons between the stopping boundaries

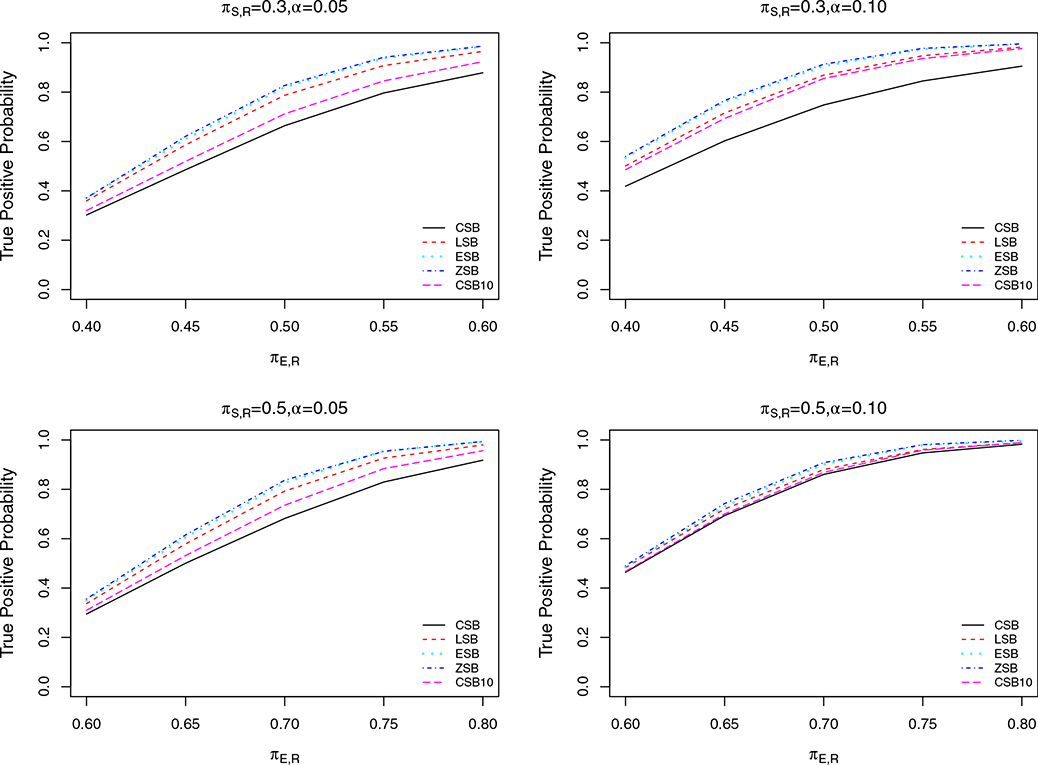
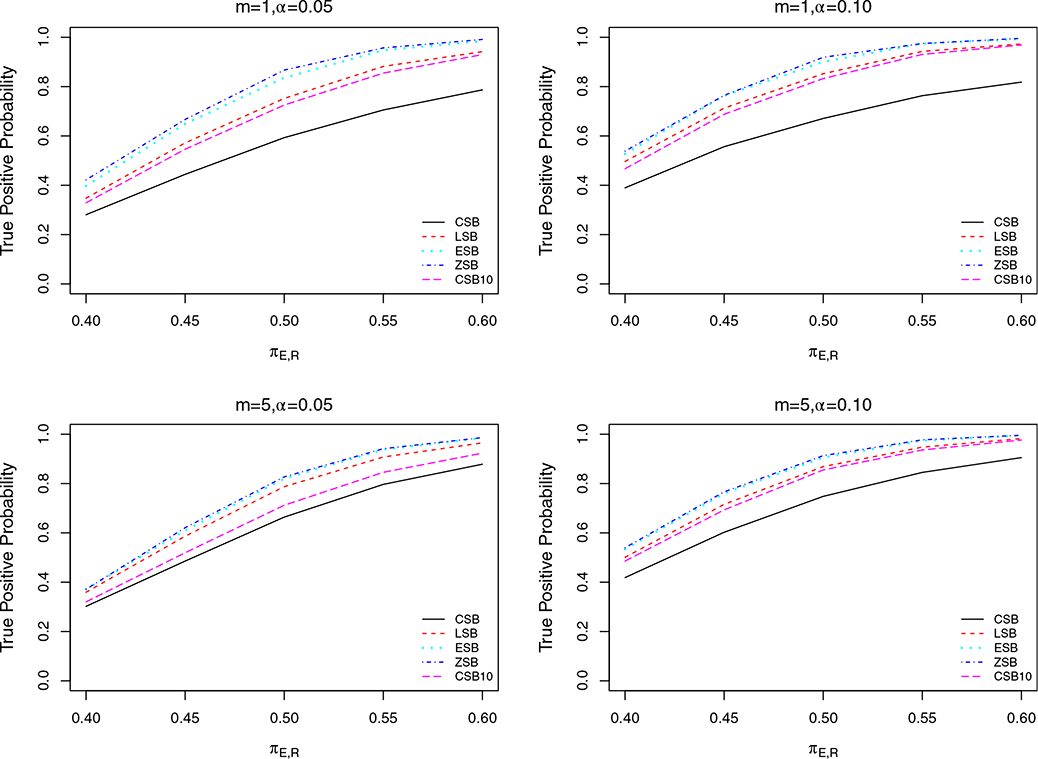
We first calibrated the parameters C₁, C₂, C₃, C₄ and C₅ to achieve the same FPP (denoted by α) for all designs, to ensure comparability. The resulting designs were used to simulate trials under a range of scenarios to estimate and compare the TPPs of CSB, CSB10, LSB, ESB and ZSB. We evaluated the futility rules under three scenarios for different values of N, m, α, and π_{S, R}, with TPP for given π_{E, R} the main quantity of interest used for comparison. We considered α = 0.05 and 0.10 in all three scenarios. In Scenario 1, we set N = 40 or 80, with fixed cohort size m = 5 and π_{S, R} = 0.3. In Scenario 2, we set m = 1 (continuous monitoring) or m = 5, with fixed N = 40 and π_{S, R} = 0.3. In scenario 3, we set π_{S, R} = 0.3 or 0.5, with fixed N = 40 and m = 5. We conducted 10,000 simulations of each case in each scenario. The results are displayed in Figures 2–4. In all of these plots, the TPP of the LSB is always substantially larger than that of CSB and CSB10, while the TPP levels of ESB and ZSB are slightly better than those of LSB. Although ZSB does not suffer from TPP loss due to early stopping, it can be seen from the plots that its gain in TPP over ESB is negligible. This indicates that the room for improvement over ESB on TPP is small. Thus, we conclude that ESB successfully maintains high TPP, with only a small TPP loss due to early futility stopping.

FIGURE 2.

Plots of TPP for designs with constant stopping boundary (CSB, solid line), constant stopping boundary with first interim look at 10 patients (CSB10, longdashed line), linear stopping boundary (LSB, dashed line), exponential stopping boundary (ESB, dotted line), and zero stopping boundary (ZSB, dot-dashed line), respectively, as functions of true ${\pi }_{E,R}^{\text{true}}$ changing from 0.40 to 0.60, for N = 40 or 80 with m = 5, ${\pi }_{S,R}^{\text{true}}=0.30$, α = 0.05 or 0.10

FIGURE 4.

Plots of TPP for designs with constant stopping boundary (CSB, solid line), constant stopping boundary with first interim at 10 (CSB10, long dashed line), linear stopping boundary (LSB, dashed line), exponential stopping boundary (ESB, dotted line), and zero stopping boundary (ZSB, dot-dashed line), respectively, as functions of ${\pi }_{E,R}^{\text{true}}$ changing from 0.40 to 0.60 or from 0.60 to 0.80, for ${\pi }_{S,R}^{\text{true}}=0.30$ or 0.50 with N = 40, m = 5, α = 0.05 or 0.10

The simulations show that, as the stopping boundary curve gets closer to the ZSB, that is, the stopping boundary becomes tighter, more TPP is gained. However, we also note that ZSB, which has no interim futility stopping, is a very undesirable design, because it provides no protection in the cases where E is not more efficacious than S, or has lower efficacy.

To provide some background, it is useful to consider what often occurs when evaluating new drugs. In practice, it very often turns out that a new E is no better than S, or has a lower response rate. To compare the five boundary shapes with this in mind, we performed simulations to examine the mean number of patients enrolled for different true π_{E, R}. In these simulations, we set N = 40 or 80, π_{S, R} = 0.30 or 0.5, m = 5 and control FPP = 0.05. In each simulated trial, we recorded the number of patients enrolled. Based on all simulated trials, we used the mean number of patients enrolled to compare the performances of the different futility stopping boundaries. In each case considered, ${\pi }_{E,R}^{\text{true}}$might be less than, equal to, or larger than π_{S, R}. Thus, this simulation study shows how reliably each design either correctly stops the trial when it should stop, that is, when $({\pi }_{E,R}^{\text{true}}\le {\pi }_{S,R})$, or correctly does not stop the trial when it should not stop, that is, when $({\pi }_{E,R}^{\text{true}}>{\pi }_{S,R})$, with performance evaluated in terms of the mean number of patients enrolled. The simulations show that, when E is worse than S (eg, ${\pi }_{E,R}^{\text{true}}=0.20$), as expected the ZSB (no interim futility stopping) gives the highest mean number of patients enrolled (see Figure 5). The other four designs, that include interim futility monitoring, result in substantially lower mean numbers of patients enrolled. For example, when N = 80, π_{S, R} = 0.3, π_{E, R} = 0.2, ZSB always enrolls all 80 patients, while all of the other four designs enroll less than 30 patients, on average, and thus prevent more than 50 patients from receiving an inferior treatment. This is a compelling reason for using futility monitoring rules. In all of the four scenarios in Figure 5, when the new drug is less efficacious than the standard drug by .10, ESB always enrolls on average about 20 patients, while the other three designs, CSB, CSB10, and LSB, may enroll about only 10 patients.

FIGURE 5.

Plots of mean number of patients enrolled for designs with constant stopping boundary (CSB, solid line), constant stopping boundary with first interim at 10 (CSB10, longdashed line), linear stopping boundary (LSB, dashed line), exponential stopping boundary (ESB, dotted line), and zero stopping boundary (ZSB, dot-dashed line), respectively, as functions of true ${\pi }_{E,R}^{\text{true}}$ changing from 0.20 to 0.60 or from 0.40 to 0.80, for N = 40 or 80, π_{S, R} = 0.30 or 0.50 with m = 5, α = 0.05

There are many other considerations when conducting a phase II trial, including patient heterogeneity, and comparability between current and historical patient populations. While more elaborate designs may address these issues, as the phase II design of Wathen et al¹¹ that accommodates heterogeneous patients, in general a trial should enroll a sufficient number of patients to reliably prevent premature early stopping. With this consideration in mind, the comparatively larger number of patients enrolled by ESB in such scenarios should be regarded as reasonably conservative and acceptable. In addition, we also calculated the percentage of responders for different true π_{S, R}, shown in supplementary materials (Table S3).

Considering the above simulations together shows that there is no uniformly optimal early stopping boundary. In general, if E has a higher true response rate than S, then LSB, ESB and ZSB have higher TPP than CSB and CSB10. On the other hand, if E has a lower true response rate than S, then CSB, CSB10, LSB, and ESB all are likely to stop assigning patients to such an ineffective treatment, and they all result in much lower numbers of patients enrolled than ZSB. Considering these optimistic and pessimistic cases together, we believe that both LSB and ESB provide a good balance between retaining large TPP and still preventing assignment of an unacceptably large number of patients to an inferior E. Overall, they are more ethically more desirable than ZSB. If one wishes to choose which of the two is closer to being optimal, it appears ESB is slightly better than LSB, considering all of the simulations.

To further evaluate the performance of ESB, we compared it with Simon’s optimal and minimax two-stage designs. The comparisons are summarized in Table 1. In the null scenario, where ${\pi }_{E,R}^{\text{true}}={\pi }_{S,R}$, calibrating the designs to have the same FPP for comparability, ESB has mean number of patients enrolled, E(N), very similar to Simon’s Optimal and MiniMax designs (25.2 vs 23.6 and 25.7), but ESB has a much higher probability of early termination (PET) (.875 vs .713 and .666), and a slightly higher TPP (.82 vs .80 and .80). These results demonstrate that the main advantage of ESB over Simon’s two-stage designs is its much larger PET when ${\pi }_{E,R}^{\text{true}}={\pi }_{S,R}$). This is due mainly to the fact that ESB has multiple interim analyzes while the Simon designs have only one interim analysis.

TABLE 1.

Comparison between ESB and Simon 2-stage design under null scenario with ${\pi }_{S,R}^{\text{true}}=0.30$ and ${\pi }_{E,R}^{\text{true}}=0.50$

Methods	FPP	TPP	N	E(N)	PET
Simon_Optimal	0.05	0.80	46	23.63	0.71
Simon_MiniMax	0.05	0.80	39	25.69	0.66
ESB	0.05	0.82	40	25.18	0.87

4 |. MONITORING FUTILITY AND TOXICITY SIMULTANEOUSLY

In this section, we consider designs with two monitoring rules, a safety rule for toxicity and a futility rule for efficacy. To focus on comparison of how the different boundary shapes behave in this more general setting, we use a CSB for the safety rule. As before, we use the priors given in section 3 for the response rates π_{S, R} and π_{E, R}. We also assume that prior distributions for the toxicity probabilities used by the different monitoring designs are identical, with π_{S, T}~ beta (30, 70) for S and π_{E, T}~ beta(0.30,0.70) for E. Thus, if X_{T, n} = x_{T, n} patients out of the first n experience toxicity, then the posterior distribution of π_{E, T} is beta(0.30 + x_{T, n},0.70 + n − x_{T, n}). For the toxicity rule criterion, we use the posterior probability ϕ_{n, T} = Pr(π_{E, T} > π_{S, T}| Data_n). If ϕ_{n, T} > C_T, then the trial is stopped for toxicity, where C_T is a constant. We set C_T = 0.85, which implies that the trial is stopped for toxicity if [the number of toxicities observed]/[number of patients evaluated] ≥ 3/5, 5/10, 7/15, 9/20, 11/25, 13/30, 14/35, or 16/40. The early toxicity stopping probability is high when the drug is excessively toxic, such as $p_{E,T}^{\text{true}}=0.50$. Temporarily ignoring the early stopping rule for futility, the early stopping probabilities due to toxicity for C_T = 0.85 considered per se are given in Table 2.

TABLE 2.

Operating characteristics under toxicity stopping boundary C_T = 0.85

Toxicity stopping boundary CT = 0.85, N = 40, m = 5
[Number of toxicities observed]/[Number of patients]≥3/5, 5/10, 7/15, 9/20, 11/25, 13/30, 14/35, 16/40
${\pi }_{E,T}^{\text{true}}$	Probability of early toxicity stopping	Sample size percentiles (10, 25, 50, 75, 90)
0.10	0.01	40	40	40	40	40
0.20	0.09	40	40	40	40	40
0.30	0.34	5	15	40	40	40
0.40	0.73	5	5	15	40	40
0.50	0.95	5	5	5	15	30

With two monitoring rules, a trial is considered a success only if it is not stopped by either the futility rule or the toxicity rule. We consider the previous five futility stopping boundaries, CSB, CSB10, LSB, ESB and ZSB, now applied with the above safety rule. We compare the five futility rules, each used with the CSB toxicity rule, for each of the three assumed true toxicity probabilities $p_{E,T}^{\text{true}}=0.10$, 0.30 and 0.50, which may be considered slight, moderate, and excessive toxicity. We use the calibrated futility boundaries in section 3 and toxicity boundary C_T = 0.85 in the simulations.

Table 3 shows the OCs of the four designs, evaluated under each of the following four scenarios of response and toxicity probabilities:

• In the first scenario, the response probabilities are low, such as 0.20, and the designs CSB, CSB10, LSB, and ESB all have the stopping probabilities above .09, regardless of $p_{E,T}^{\text{true}}$. However, unless E is excessively toxic with $p_{E,T}^{\text{true}}=0.50$, the probability of stopping under ZSB is very low. This shows the importance of including a futility monitoring rule.

• In the second scenario, where $p_{E,T}^{\text{true}}$ is as high as 0.50, the probabilities of stopping are all above .09 for all four designs, regardless of $p_{E,R}^{\text{true}}$. This illustrates the importance of including a safety monitoring rule.

• In the third scenario, E is desirable, with negligible toxicity $p_{E,T}^{\text{true}}=0.10$ and high $p_{E,R}^{\text{true}}=0.50$. The early stopping probabilities decrease in order for CSB, CSB10, LSB, ESB, and ZSB. This demonstrates the advantages of using LSB, ESB or ZSB over CSB or CSB10 in this scenario.

• In the fourth scenario, where the toxicity probability is relatively high, p_T = 0.30, and the response probability is low, p_E = 0.30, early stopping is desirable. In these scenarios, the probabilities of being stopped early by ESB, LSB, CSB10 or CSB are higher than that by ZSB, demonstrating advantages of these four boundaries over the ZSB in this scenario of an unfavorable E.

TABLE 3.

Operating characteristics of a design with joint monitoring of futility and toxicity: ${\pi }_{E,R}^{\text{true}}=0.2$ or 0.3 is too low, implying a need to stop

${\pi }_{E,R}^{\text{true}}$	${\pi }_{E,T}^{\text{true}}$	Probability of stopping
		CSB	CSB10	LSB	ESB	ZSB
0.20	0.10	1.00	1.00	1.00	1.00	0.01
	0.30	1.00	1.00	1.00	1.00	0.32
	0.50	1.00	1.00	1.00	1.00	0.95
0.30	0.10	0.94	0.93	0.91	0.88	0.01
	0.30	0.96	0.95	0.94	0.92	0.32
	0.50	1.00	1.00	0.99	0.99	0.95
0.40	0.10	0.68	0.65	0.55	0.46	0.01
	0.30	0.78	0.76	0.70	0.64	0.32
	0.50	0.98	0.98	0.98	0.97	0.95
0.50	0.10	0.34	0.29	0.18	0.11	0.01
	0.30	0.55	0.51	0.44	0.39	0.32
	0.50	0.96	0.96	0.96	0.95	0.95

Note: ${\pi }_{E,R}^{\text{true}}=0.4$ or 0.5 is good, implying no need to stop. ${\pi }_{E,T}^{\text{true}}=0.5$ is too toxic, implying a need to stop. ${\pi }_{E,T}^{\text{true}}=0.1$ is not bad, implying no need to stop. ${\pi }_{E,T}^{\text{true}}=0.3$ is borderline. Desirable clinical scenarios are highlighted in bold.

In summary, considering all of the above scenarios, ESB and LSB have desirable OCs in all scenarios, whereas the CSB, CSB10 and ZSB have very undesirable properties in some scenarios. Consequently, we recommend that ESB or LSB be used, since the differences between them are small. R code for simulating the designs is available at https://odin.mdacc.tmc.edu/~xhuang/.

5 |. DISCUSSION

For futility monitoring in single-arm phase II clinical trials, in addition to the commonly used constant stopping boundary (CSB) and constant stopping boundary with first interim look at 10 patients (CSB10), we have proposed two new Bayesian adaptive phase II designs for early futility stopping, using either a linear stopping boundary (LSB) or exponential stopping boundary (ESB). The LSB and ESB designs define the early stopping boundaries as functions of the number of patients enrolled. They are conservative in that they are unlikely to stop the trial in the early stages, but gradually relax as more patients are enrolled and more treatment outcome data accumulates. The LSB and ESB designs both reduce TPP loss due to early stopping compared to CSB or CSB10, and provide a good balance between frequently monitoring the trial for futility, and reducing the number of patients who receive ineffective treatments.

While we have used Bayesian designs for frequent monitoring, there is a rich literature on choosing the shape of futility monitoring boundaries¹⁹ for frequentist hypothesis test based designs. However, most of these methods are based on p-values derived from large sample approximations, which may be inappropriate for phase II trials with small to moderate sample sizes. Bayesian methods offer easy real-time computation for updating posterior probabilities, and thus make it easy to implement frequent trial monitoring rules.

Although the proposed designs can be applied to any single-arm phase II clinical trial with binary outcomes, they are especially appealing for oncology trials, which often have small sample sizes. This is because most cancers are highly heterogeneous, which effectively makes each cancer subtype a rare disease. Many cancer trials focus on a particular cancer subtype defined by tumor location, stage, number of previous treatments, and possibly molecular mutations or other biomarkers. Thus, many cancer trials evaluate a small patient subpopulation, and have slow patient accrual rates, which make it feasible to do frequent futility monitoring. The need to frequently monitor cancer trials often is motivated by potentially fatal outcomes for their participants and the large number of toxic oncology drugs with unknown anti-disease activity. Thus, it is ethically appealing to conduct futility and safety monitoring frequently, starting early in the trial with reasonably small cohort sizes, rather than starting only after a large number of patients have been enrolled. Bayesian designs are particularly appealing in such settings.

FIGURE 3.

Plots of TPP for designs with constant stopping boundary (CSB, solid line), constant stopping boundary with first interim at 10 (CSB10, longdashed line), linear stopping boundary (LSB, dashed line), exponential stopping boundary (ESB, dotted line), and zero stopping boundary (ZSB, dot-dashed line), respectively, as functions of true ${\pi }_{E,R}^{\text{true}}$ changing from 0.4 to 0.60, for m = 1 or 5 with N = 40, ${\pi }_{S,R}^{\text{true}}=0.30$, α = 0.05 or 0.10

DATA AVAILABILITY STATEMENT

There are no real data used in this article. All results are based on computer-simulated data. The R code for simulations is available at https://odin.mdacc.tmc.edu/~xhuang/.