Quantitative Structure–Activity Relationship (QSAR) Study Predicts Small-Molecule Binding to RNA Structure

Abstract

The diversity of RNA structural elements and their documented role in human diseases make RNA an attractive therapeutic target. However, progress in drug discovery and development has been hindered by challenges in the determination of high-resolution RNA structures and a limited understanding of the parameters that drive RNA recognition by small molecules, including a lack of validated quantitative structure–activity relationships (QSARs). Herein, we develop QSAR models that quantitatively predict both thermodynamic- and kinetic-based binding parameters of small molecules and the HIV-1 transactivation response (TAR) RNA model system. Small molecules bearing diverse scaffolds were screened against TAR using surface plasmon resonance. Multiple linear regression (MLR) combined with feature selection afforded robust models that allowed direct interpretation of the properties critical for both binding strength and kinetic rate constants. These models were validated with new molecules, and their accurate performance was confirmed via comparison to ensemble tree methods, supporting the general applicability of this platform.

Introduction

Initiated in 2003, the ENCODE project¹ revealed an unprecedented number of non-protein-coding RNAs (ncRNAs), and their roles in the regulation of transcription, translation, genetic modification, and RNA degradation have been the subject of intense study in relation to human diseases.² ncRNAs have been found to be abnormally expressed in multiple disease phenotypes, including neurodegenerative diseases and metastatic cancers.³⁻⁶ The implications of these RNAs in disease pathogenesis underscore their potential roles as drug targets. To date, small molecules have been used to target various ncRNAs from several different organisms, including mammals, viruses, bacteria, and fungi.⁷⁻¹⁸

While RNA is an attractive therapeutic target, some RNA properties pose intrinsic challenges, including (1) limited chemical diversity of RNA relative to proteins, (2) the highly negatively charged backbone of RNA, and (3) the dynamic nature of RNA, which allows it to sample a wide population of conformers. In particular, the diverse and complex conformational dynamics of RNA increase the complexity of RNA structural determination, including that of RNA:ligand structures, ultimately hindering the development of predictive binding models as well as our understanding of the drivers of small molecule:RNA recognition. The most successful discovery method for bioactive RNA-targeted small molecules has been focused screens, which require synthetic library curation based on prior knowledge of the biased chemical space of RNA-targeted small molecules.¹⁹ Additionally, the characterization of RNA-targeted small molecules often disregards binding kinetics, precluding a full understanding and optimization of the binding behaviors of a compound. Many protein-targeted drugs are characterized by slow dissociation processes and prolonged target occupancy, supporting the significance of binding kinetics for in vivo activity.²⁰ The design of compounds with kinetic selectivity will open a new avenue for RNA targeting and facilitate the hit-to-lead triage during hit optimization,^21,22 yet few studies have demonstrated how to intentionally optimize RNA binding kinetics.²³ Overall, there are clear unmet needs in identifying potential RNA-targeted chemical probes and rationally designing small molecules with desired binding behaviors, including appropriate binding kinetics.

To fully access the numerous potentially druggable RNA targets, a rational tool for ligand design and a comprehensive understanding of RNA:small-molecule binding details are required. Recently, machine learning-aided mechanistic studies and ligand predictions have shown success in multiple complex tasks, including the design of enantioselective catalysts in organic synthesis and bioactive ligands for kinase inhibition.²⁴⁻²⁷ Among multiple computational tools, quantitative structure–activity relationship (QSAR) studies can pinpoint guiding principles for a specific target by correlating the experimentally observed binding properties with the molecular descriptors of the ligands.²⁸⁻³⁰ A robust and predictive QSAR model has been proven to be an efficient tool to predict the activities of small-molecule candidates and to drive hit optimization. Despite its success in protein-based ligand design, however, a few QSAR studies have been conducted for identifying RNA-targeted small molecules.³¹⁻³⁴ While significant work has been done to explore key descriptors involved in RNA recognition,³⁵⁻³⁷ these existing data cannot be used as input for a QSAR approach targeting a specific RNA structure, as these data are derived from disparate methods and RNA targets.

Herein, we build a general workflow utilizing QSAR as a predictive platform to connect molecular descriptors of a given ligand with its binding profiles against a specific RNA. The activities, including binding affinity (K_D) and kinetic rate constants (k_on and k_off), were measured for molecules bearing multiple scaffolds via surface plasmon resonance (SPR). Model building was accomplished by combining representative data splitting, descriptor selection, and linear regression. Postmodeling assessment validated the statistical assumption for linear regression and defined the specific applicable domain for the QSAR model in future use. To the best of our knowledge, this constitutes the first example of a systematic empirical QSAR study conducted on various scaffolds against a specific RNA target. We anticipate that this framework can be readily extended to different RNA targets to facilitate the design and synthesis of novel RNA-targeted ligands. The workflow built in this study will contribute to improving the understanding of RNA:small-molecule binding mechanisms and provide an efficient tool to rationally design new ligands for a given RNA target.

Results and Discussion

Selection of RNA Target and Small-Molecule Training Set

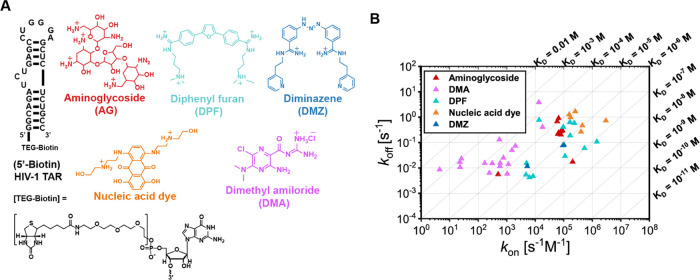
We chose the HIV-1 transactivation response (TAR) element (Figure 1a) as a suitable model system to develop our workflow as this well-validated antiviral target has been frequently screened against small molecules, providing us with numerous candidates for the training process.^12,38−40 In total, we selected 48 compounds in this study, including 29 reported TAR–ligands and 19 compounds with known RNA-targeted scaffolds. These ligands could be classified into five categories, namely, aminoglycosides (AGs), dimethyl amilorides^41,42 (DMAs), diphenyl furans^43,44 (DPFs), diminazenes⁴⁵ (DMZs), and nucleic acid dyes (Figure 1a). These ligands covered a range of binding behaviors with the aim of building a model that can be applied to the prediction of ligands with diverse chemical architectures.

Figure 1.

A. Sequence and structure of 5′ biotinylated HIV-1 TAR and representative chemical structures of the scaffolds used in this work. B. Kinetics map of 48 tested ligands, represented on 10-based logarithmic coordinates. The diagonal lines represent K_D values calculated from k_off/k_on. Units of three parameters are shown. The rest of the study used values based on these units.

Calculations of Molecular Descriptors

To begin, we obtained molecular information for each compound via quantitative calculation of their molecular descriptors. Each descriptor provides information on a physicochemical property of a compound, ranging from topological to electrostatic terms. For example, atomic connectivity, which represents topological connections within a molecule, was calculated using graph theory matrices,^46,47 which lays the foundation of many other descriptors including related adjacency distance matrices as well as surface properties. In addition, many QSAR expressions in previous reports suggest that ligand binding preferences originate from noncovalent interactions exerted in the microspace of the ligand.⁴⁸ Hence, conformation-dependent three-dimensional (3D) descriptors were included to account for the spatial environment of the ligands, such as partial charges and potential energy. In total, we calculated 435 descriptors of each ligand.

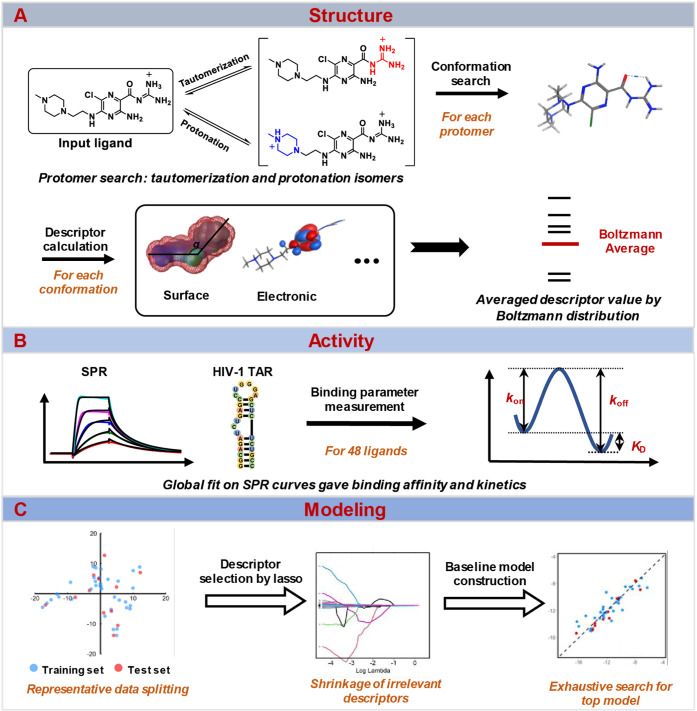
We also considered whether multiple species of a given molecule may exist under experimental conditions (panel A, Scheme 1). Specifically, we evaluated protonation and tautomerization states for each ligand by distribution ratio as their population representation. For each state, potential conformations within 3 kcal/mol of the lowest-energy conformation, as determined by the molecular operating environment (MOE) software, were selected. The descriptor value of a specific ligand state was determined as the Boltzmann-weighted average of these conformations. Finally, the descriptor value of each ligand is the weighted average of the results from multiple states based on the distribution ratio mentioned before. While the presence of multiple species and/or conformations is often overlooked due to computational cost, the accuracy of molecular descriptors is a prerequisite for reliable and robust QSAR models.

Scheme 1. QSAR Workflow.

A. Input molecules were searched for “protomers” and then searched on conformations of each protomer. Molecular descriptors were calculated for each conformation and averaged based on the Boltzmann distribution. B. Small molecules binding HIV-1 TAR were characterized via SPR, and parameters including K_D, k_on, and k_off were fitted globally. C. With representative data splitting and lasso-assisted model searching, the final model was selected based on the performance of the separate test set.

Measurement of Binding Parameters

To evaluate the binding parameters of the small molecules against HIV-1 TAR, we utilized SPR to measure the kinetic rate constants and binding affinities. Kinetic analyses for the observed SPR curves were performed globally for the entire concentration series (panel B, Scheme 1). The kinetics map summarizes the distribution of k_on, k_off, and K_D along logarithmic coordinates (Figure 1b). All three parameters have a wide range of values spanning at least 2 log units, supporting the appropriateness for reliable QSAR modeling from a response variable perspective.⁴⁹

We next compared our kinetics data to a previous survey, which showed that the RNA–ligand association was generally slower than that for protein.⁵⁰ The measured on- and off-rate values in our SPR data are similar in the order of magnitude to the RNA:ligand values previously reported (Table 1).⁵⁰ The overall association rate constant of an RNA–ligand pair for all three RNA–ligand sets listed in Table 1 (median: ∼10⁴ M^–1 s^–1) was not only far below the diffusion limit (centered at 10⁹ M^–1 s^–1) but also suggested a generally slower binding than protein–ligand pairs (median: 6.6 × 10⁶ M^–1 s^–1).⁵⁰ This slow RNA recognition was expected due to the existence of multiconformation distribution in unbound RNA states, though some variation was observed between ligand classes. Specifically, in our HIV-1 TAR–ligand set, most of the fast association rates were observed for aminoglycosides, nucleic acid dyes, and DPFs (k_on: 10⁴∼10⁵ M^–1 s^–1), probably due to their strong electrostatic (aminoglycosides) or topologically matched π–π stacking interactions (dyes, DPFs). As moderate and weak binders in this set, DMAs were characterized by fewer potential protonation sites or less planar structures than other molecules, leading to overall slower binding rates. Rates of dissociation were comparable among the three RNA–ligand sets, with median values around 10^–2 s^–1. Comparing binding strengths between sets in Table 1, it was expected that RNA–ligand pairs with in vitro-selected RNAs (e.g., aptamers) and naturally occurring RNAs that have evolved to bind small molecules (e.g., riboswitches and ribozyme) would have tighter binding than those in our data set (Table 1). In our QSAR study, we covered a range of binding affinities to achieve a generalizable scope and aid the discovery of decisive descriptors for the binding of diverse small molecules.

Table 1. Median Values of Binding Parameters from Three Sets of RNA–Ligand Interaction, Values for In Vitro-Selected, and Naturally Occurring RNA–Ligands from ref (50)^a.

	kon (M–1 s–1)	koff (s–1)	Kd (M)
RNA (in vitro-selected)–ligand (N = 13)50	8.1 × 104	6.3 × 10–2	4.3 × 10–7
RNA (naturally occurring)–ligand (N = 24)50	5.5 × 104	1.9 × 10–2	3.0 × 10–7
HIV-1 TAR–ligand (N = 48, used in this work)	3.8 × 104	7.9 × 10–2	5.0 × 10–6

^aAdapted with permission from ref (50). Copyright 2017/RNA Cold Spring Harbor Laboratory Press for the RNA Society/RNA.

QSAR Modeling: Baseline Model Construction

Data Refinement

We used the log-transformed versions of K_D, k_on, and k_off as our response variables, as the transformed versions yielded residuals that better satisfy the normality assumption of linear regression models. To mitigate the redundancy of constant and intercorrelated descriptors, a descriptor prereduction was applied. First, constant descriptors that have more than 80% compounds sharing the same value were deleted.⁵¹ Next, intercorrelation between every descriptor pair was calculated by Pearson correlation coefficient (ρ). High intercorrelation (ρ > 0.95 or ρ < −0.95) between descriptors can cause unstable estimation of regression coefficients, sign-change problems, and insignificance of regression coefficients.⁵² Therefore, multicollinearity (the occurrence of high intercorrelations among two or more descriptors) terms need to be deleted before multiple linear regression. Descriptors intercorrelated with multiple descriptors were deleted one by one based on the maximal number of multicollinearity terms. After several rounds, the maximal number of multicollinearity terms for any descriptor would be one, namely, only pairwise intercorrelations left. In the remaining pairwise intercorrelations, the term with a lower correlation to the response variable was deleted. The above procedure afforded 193 refined descriptors in the ln K_D and ln k_on data sets and 191 in the ln k_off data set.

Representative Data Splitting by the Kennard–Stone Algorithm

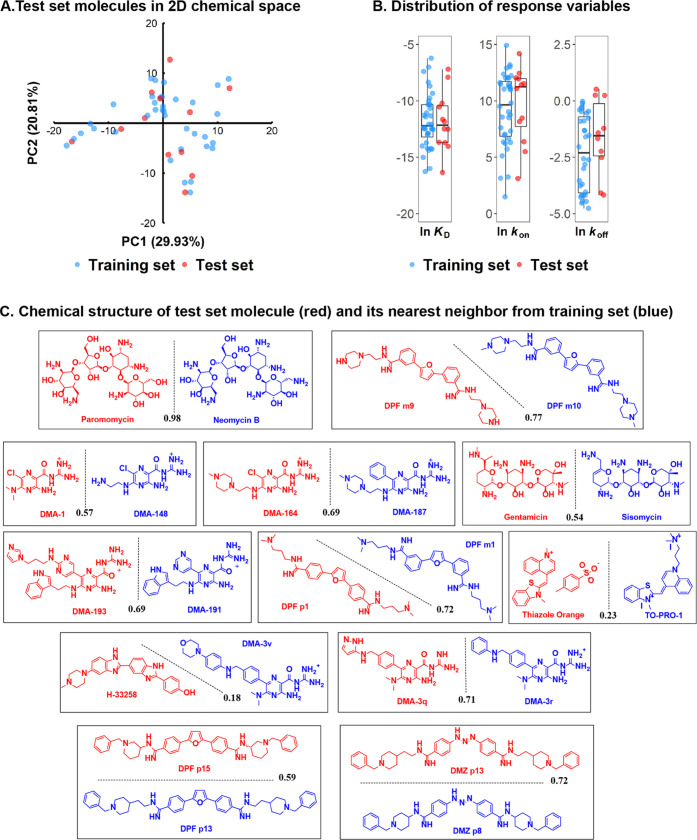
A key consideration for QSAR with diverse substrates is the continuity of the energy landscapes created by the ligands, i.e., whether gradual changes in ligand properties are smoothly plotted along the target activity function.^30,53 While QSAR has been classically applied to molecules from the same scaffold (congeneric sets) to alleviate these concerns, several studies have reported successful continuous fields even with the use of diverse scaffolds.⁵⁴⁻⁵⁶ Appropriate splitting of the training and test sets is critical to achieving a smooth landscape that avoids local minima where the model would explain only a subset of the compound pool.⁵⁷ For the model trained from the training set to be used to predict unseen data in the test set, the distribution of the training set and test set molecules must be representative of the entire sample. To this purpose, we first applied principal component analysis (PCA) to reduce the dimension of the descriptor space. Then, the Kennard–Stone algorithm⁵⁸ was utilized to maximize the representativeness of the selected sample with the whole data set, and the slightly different descriptor space between ln K_D/ln k_on and ln k_off data sets did not alter the sampling results. This specific sampling method rather than random splitting was applied here due to the small sample size (48), which can guarantee that representative small molecules are chosen to achieve a uniform representation of the descriptor space, giving more confidence in future predictions of test set molecules that come from the same distribution of the training set (Figure 2A). The distribution of corresponding response variables (ln K_D, ln k_on, and ln k_off) derived from SPR for training and test sets was visualized in a boxplot (Figure 2B). Sampling of ln K_D data set over descriptor space resulted in two subsets with the most representative distribution of the response variable, as seen by the similar range and median values. ln k_on has a moderately consistent distribution, while ln k_off poorly matched the distribution. This result indicated that the performance order of QSAR models might be ln K_D > ln k_on > ln k_off, given the QSAR assumption that gradual changes in the descriptor space lead to gradual changes in the response variable. Importantly, the unique test set selected by the Kennard–Stone algorithm contains diverse candidates from every scaffold (Figure 2C) and is thus a representative subset from the chemical structural perspective (Supporting information, Section A).

Figure 2.

A. Locations of test set molecules in the two-dimensional (2D) chemical space constructed from the first two principal components (29.9 and 20.8% of variances, respectively) of the whole data set. B. Distribution of response variables for the test and training set molecules. C. Chemical structures of the test set molecules (red) selected with the Kennard–Stone algorithm. The closest neighbor molecule in the training set (blue) is shown in pairs for comparison. The similarity was calculated as the Tanimoto coefficient (black) and is listed along the separation line.

QSAR Model Development and Interpretation

To obtain a predictive and interpretable model, we used multiple linear regression (MLR) in this QSAR study, followed by an assumption evaluation. Due to the limited observations but a large number of descriptors, the classical MLR could not afford a unique closed-form solution. To reduce the dimension of the data and find the most relevant descriptors, we applied the least absolute shrinkage and selection operator (lasso) for descriptor selection prior to MLR.⁵⁹ Lasso has been widely used in QSAR studies to control the model complexity and increase the performance by applying a penalty constraint to the loss function that needs to be minimized during modeling.^60,61 Specifically, a hyperparameter λ controls the model complexity as larger λ leads to more descriptor shrinkage. The operator can remove irrelevant descriptors by shrinking the regression coefficients to zero and keeping the most relevant ones. After descriptor selection by lasso, exhaustive searches for all combinations from selected descriptors using MLR were performed. The maximal number of descriptors in an MLR model was set as seven based on the Topliss rule,⁶² namely, that at least five compounds in the training set were required for adding an extra descriptor in the QSAR model. This exhaustive search afforded multiple model candidates, which were further screened by their performance on training and test sets, as well as the statistical significance (p-value) of each descriptor involved. Additionally, the principle of “Occam’s razor” was followed to choose the model with fewer descriptors if two have a similar level of performance.⁶³

In detail, for ln K_D modeling, lasso selection was applied to gradually shrink the size of the descriptor set, as hyperparameter λ increases (Figure 3A). The best λ was determined to be 0.01 as a result of 5-fold cross validation that aimed at minimizing the prediction biases or the mean cross-validated error. Using this λ value, the number of descriptors was shrunk to 35. These 35 descriptors formed the new descriptor space for exhaustive model search, from the simplest two-parameter linear model to the most complex seven-parameter linear model. These model candidates were first screened by their performance on the training and test sets (R² > 0.75, Q² > 0.75) and then the statistical significance of each descriptor for explaining the model (p-value < 0.05).

Figure 3.

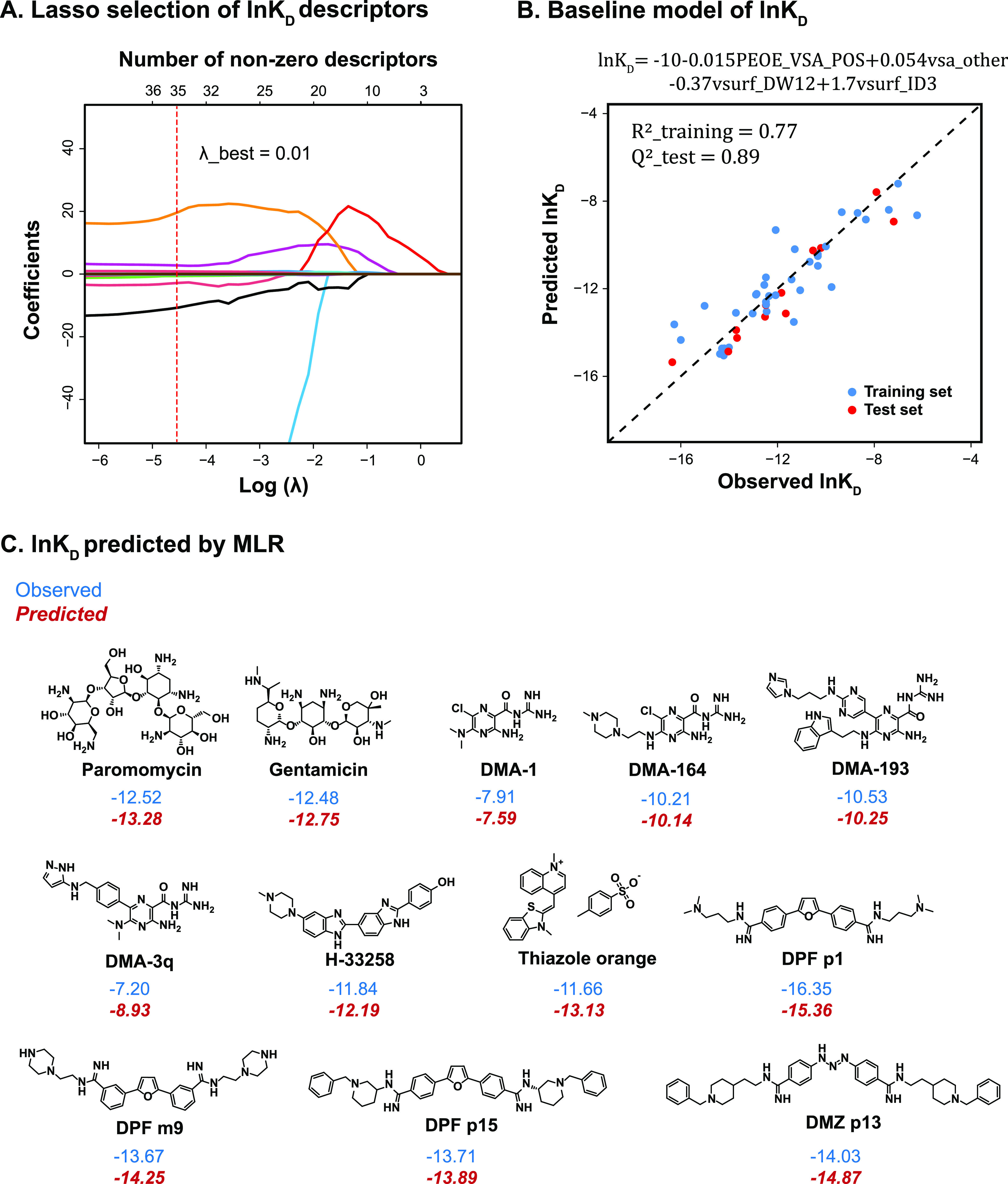
A. Coefficients of ln K_D descriptors were shrunk as λ increased using lasso regression; each curve with a different color represented a descriptor coefficient shrinkage; the top x-axis showed the number of descriptors with nonzero coefficients at a specific λ value that was indicated by the bottom x-axis. The best λ value (0.01) was determined by the 5-fold cross validation. B. Observed ln K_D (both training and test sets) was plotted with the value predicted by the MLR baseline model shown at the top. C. Small molecules from the test set were predicted by MLR of the ln K_D value (in red italics) versus the observed values (in blue).

The final model based on our selection process (Figure 3B) was found with the below expression, which predicted ln K_D values of our structurally diverse test molecules with high accuracy (Figure 3C)

The model included four physicochemical descriptors (PEOE_VSA_POS, vsa_other, vsurf_DW12, and vsurf_ID3) with their physical meaning shown in Table 2. The negative coefficient of PEOE_VSA_POS explicitly suggested that the non-negative electrostatic properties of the molecule helped to improve ln K_D, which is consistent with the fact that RNA is overall negatively charged. Additionally, vsa_other describes the sum of van der Waals surface area of atoms typed as “other”. These “other” atoms are not H-bond acceptors, H-bond donors, acidic, basic, polar, or hydrophobic residues, thus mostly referring to the surface area of carbon atoms near oxygen, nitrogen, and halide atoms.⁶⁴ According to the model, a decrease in vsa_other could favor tight binding for HIV-1 TAR. vsurf_DW12 is the contact distance between the physical location of the first two hydrophilic energy interaction minima when a hydrophilic probe (OH2) interacts with the target molecule. The negative correlation of this descriptor indicated that high-affinity ligands have energy minima that are relatively distant from each other in 3D space, which is also consistent with a previous report.⁶⁵ Interaction energy (integy) moment is a type of descriptor that resembles dipole moment, but instead of describing the separation of the partial charge, integy moments express the unbalance between the center of mass of a molecule and the barycenter of its hydrophilic or hydrophobic (vsurf_ID) regions. Specifically for vsurf_ID3, it is the vector pointing from the center of mass to the center of the hydrophobic regions that is calculated at -0.6 kcal/mol energy level.⁶⁶ The positive correlation of this descriptor to ln K_D suggested that tight binding could be achieved by small molecules that possess hydrophobic moieties that are either close to the center of mass or they balance at opposite ends of the molecule.

Table 2. Descriptors Involved in Three Models and Their Physical Meanings.

descriptor name	physical meaning
PEOE_VSA_POS	Total positive van der Waals surface area.
vsa_other	van der Waals surface area (Å2) of atoms typed as “other”. Other: not H-bond acceptors, H-bond donors, acidic, basic, polar, or hydrophobic residues.
vsurf_DW12	Contact distances of vsurf_EWmin1 and vsurf_EWmin2; vsurf_EWmin describes the lowest hydrophilic energy representing the distances between the best three local minima of interaction energy when a water probe (OH2) interacts with the target molecule.
vsurf_ID3	Hydrophobic integy moment calculated at −0.6 kcal/mol energy level.
GCUT_PEOE_0	The GCUT descriptors are calculated from the eigenvalues of a modified graph distance adjacency matrix. Each (i,j) entry of the adjacency matrix takes the value 1/sqr(dij), where dij is the (modified) graph distance between atoms i and j. The diagonal takes the value of the PEOE partial charges. The resulting eigenvalues are sorted, and the smallest (GCUT_PEOE_0), 1/3-ile, 2/3-ile, and the largest eigenvalues are reported.
vsurf_DD23	Contact distances of vsurf_EDmin2 and vsurf_EDmin3; vsurf_EDmin describes the lowest hydrophobic energy representing the distances between the best three local minima of interaction energy when a hydrophobic probe (DRY) interacts with the target molecule.
a_base	Number of basic atoms.
a_nN	Number of nitrogen atoms.
vsurf_DD13	Contact distances of vsurf_EDmin1 and vsurf_EDmin3.

To investigate how molecular descriptors quantitatively impact the association process of HIV-1 TAR–ligands, we performed ln k_on modeling. Similarly, lasso selection afforded 16 descriptors after the regression coefficient shrinkage with optimized λ equaled to 0.22 (Figure S2A). A further model search led to the identification of the model below (Figure S2B)

This model included four physicochemical descriptors, namely, GCUT_PEOE_0, vsa_other, vsurf_DD23, and vsurf_DW12 (Table 2). Two of them (vsa_other and vsurf_DW12) also appeared in the ln K_D model, consistent with the correlation between ln K_D and ln k_on (ρ ln K_D, ln k_on = −0.82). GCUT_PEOE_0 encodes information of partial charge and atomic connectivity, supporting an important role for partial charge distribution on on-rate constants, though it is hard to directly deduce chemically intuitive information as it is the mathematical representation of atomic partial charge calculated from the partial equalization of orbital electronegativity (PEOE) method combining atomic connectivity. The negative coefficient of this descriptor suggested that a decreased value of GCUT_PEOE_0 could accelerate the association process. The contribution of vsa_other and vsurf_DW12 followed the same trend identified in ln K_D model, namely, lower van der Waals surface area for atoms typed as “other” and more distant distribution of hydrophilic interaction energy minima would benefit fast association, thus favoring tighter binding. Finally, vsurf_DD23 is another surface property descriptor, describing the physical distance between the location of the second-lowest and third-lowest hydrophobic energy interactions that were measured by a specific hydrophobic probe (DRY).⁶⁷ The positive coefficient of this descriptor signified that by increasing the distance between these energy minima sites, the compounds were predicted to have faster association processes.

We next assessed whether the above workflow could afford a predictive ln k_off model. In this case, lasso selection refined the descriptor set to only four descriptors, using the cross-validated best λ value (λ = 0.50). This shrinkage appeared to be too stringent as lasso regression equally penalized all of the descriptor coefficients and suffered from biased estimates in this situation, namely, descriptors with large coefficients were overpenalized and descriptors with small coefficients were not detected.⁶⁸ Specifically, the combination of these four features poorly explained the data (R_training² = 0.43, Q_test = 0.38). We adjusted the λ value (λ = e^–2 ∼ e^–4) as a less stringent shrinkage to include more descriptors (Figure S2C) and found that when the descriptor vsurf_DD13 was included, the model performance could be greatly enhanced. The final model (Figure S2D) we found for explaining ln k_off is shown as follows

This model matched that from an exhaustive search result using all 191 descriptors, suggesting that lasso was able to pick significant variables but sometimes needs fine tuning of the hyperparameter λ. In this model, the negative correlation between the number of basic atoms (a_base) and the dissociation rate constants suggested that increased electrostatic interactions can slow ligand dissociation. Introduction of nitrogen-containing groups may also increase the retention time as a negative correlation was found between the number of nitrogen atoms (a_nN) and the dissociation rate constants. The correlation between these two descriptors was low (ρ_{abase,a_nN} = 0.23), indicating that they contribute to the rate constant differently, probably through electrostatic interactions (a_base) and π–π stacking from nitrogen-containing heterocyclic rings (a_nN). Additionally, vsurf_DD13 positively correlated with the off-rate constant, suggesting that decreasing the physical distance between the lowest and third-lowest hydrophobic energy interaction sites will slow dissociation. Overall, however, regressions using ln k_off data could not afford a baseline model with comparable performance as the above two models. This might be caused by a number of factors, including the poor representativeness of the selected subset in terms of the response variable distribution (Figure 2B) and the larger measurement variance as seen from different SPR replicates. Larger data sets are likely needed to precisely model the off-rate constants.

Nonetheless, these data did show that QSAR can yield a promising model for understanding the dissociation process of HIV-1 TAR: small-molecule recognition, assisting the design of ligands with prolonged retention time over the target. The success of training a predictive and interpretable QSAR model for explaining different binding parameters of HIV-1 TAR–ligands suggested that the QSAR study could be a lens to investigate the complicated macromolecular binding event and a guide for molecular design with a specific response property.

Comparison with Nonparametric Ensemble Tree Methods

To further evaluate the performance of MLR baseline models, we compared them to models constructed by ensemble tree methods, such as bagging and boosting. Tree methods use a flow-chart-like structure to make predictions (leaf) based on the outcomes (branch) of the tests (nodes).⁶⁹ By combining multiple decision tree models and making predictions from the averaged results, ensemble tree methods have been identified to improve the model performance and/or overcome the variance-bias trade-off in prediction.⁷⁰ However, the ensemble process increases the difficulty of explicit model interpretation when compared to the single parametric model such as that given by MLR due to its aggregated model complexity.

We started our comparison by building a single decision tree, which was the foundation of other ensemble-based models. Unlike MLR that needs a normality assumption to explain the randomness of the error (see the Model Assessment and Applicable Domain section), decision tree is a nonparametric method that can avoid the risk of mis-specifying these preassumptions and probability distributions. The complexity of the decision tree was controlled by the cross-validated error, which afforded us the best number of terminal nodes in the pruned tree. Decision trees trained on ln K_D and ln k_on training sets gave satisfactory predictions on the corresponding test set (Table 3). This result suggested that different scaffolds have distinct binding affinities and association rate constants that can be revealed by the splitting nodes using existing descriptors. Meanwhile, the poor fitting on the dissociation rate constant indicated that more decisive descriptors were needed to explain the observations. Parallel training of multiple decision trees over a subset of training data that was generated by bootstrapping (sampling with replacement) gave us bagging models. The optimized number of trees was determined based on the averaged error of samples that were not included in training or out-of-bag samples. Random forest is a special scenario of bagging that in addition to using bootstrapping samples, only a subset of descriptor space will be used for the training of each individual tree. Figure 4A shows that when training on ln K_D data, the out-of-bag error was gradually converged as the number of trees increased. Figure 4B shows the random forest model trained for ln K_D using 400 trees. Boosting, however, is a sequential training process that the current model trains on the residuals from the last model by adding weight to the poorly predicted data point. Similarly, Figure 4C shows that the loss function (squared error) decreased as the number of above sequential iterations increased, where the optimal iterations (990) could be found by looking at the cross-validated error. An out-of-bag error was also plotted. The discrepancy between these two errors suggested the heterogeneity of the data set. Figure 4D represents the final boosting model trained for ln K_D using 990 iterations.

Table 3. Comparison of Model Performance Built by Different Methods.

	ln KD		ln kon		ln koff
	train	test	train	test	train	test
decision tree	0.90	0.78	0.87	0.86	0.73	–0.1
decision tree bagging	0.91	0.89	0.83	0.71	0.94	0.21
random forest	0.90	0.87	0.90	0.70	0.89	0.39
boosting	0.92	0.87	0.92	0.73	0.90	0.25
MLR	0.77	0.89	0.77	0.77	0.64	0.61

Figure 4.

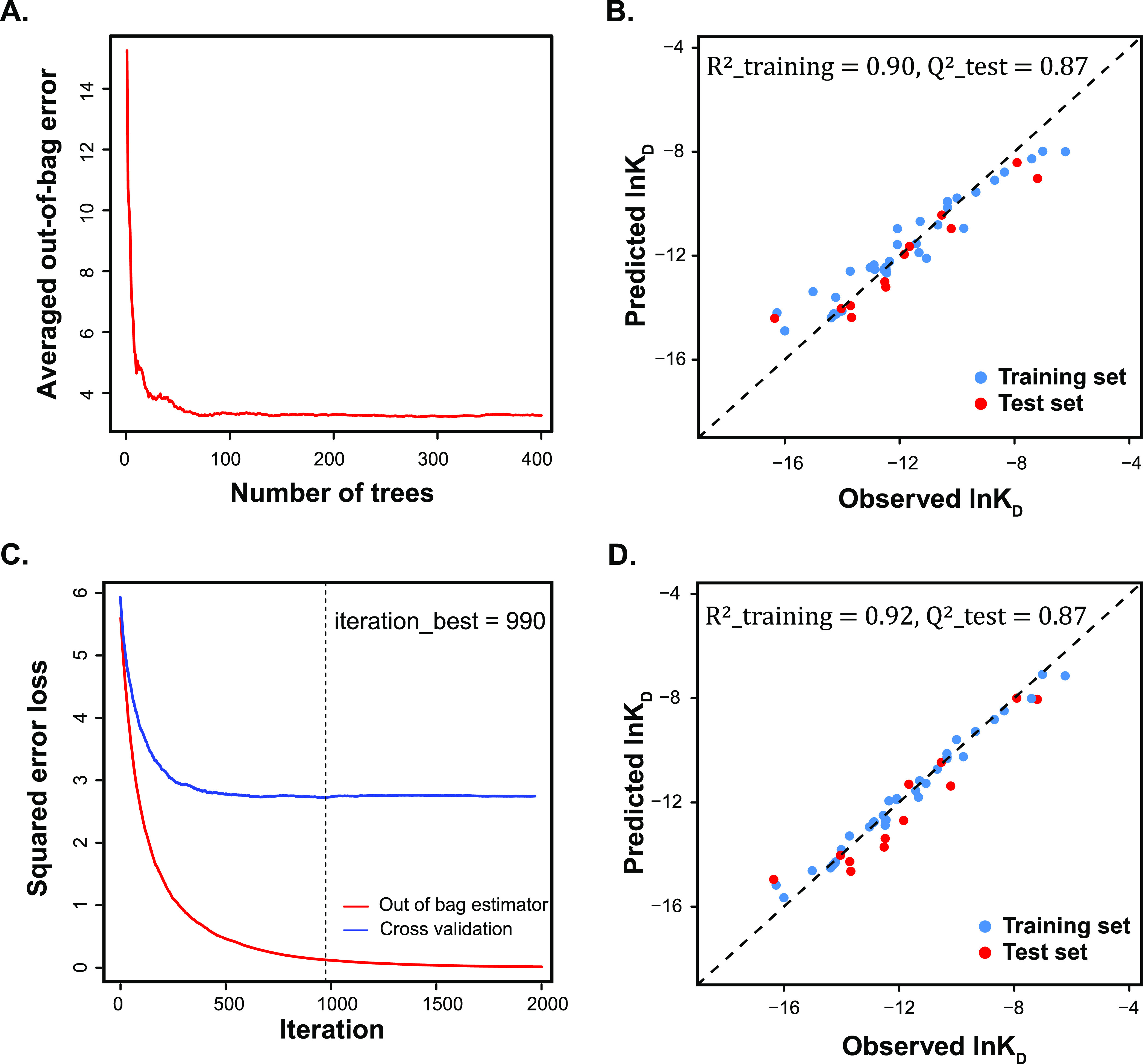
A. Out-of-bag error of random forest model vs number of trees. B. Random forest model of ln K_D built with 400 decision trees. C. Squared error loss vs number of iterations in boosting; two methods (out-of-bag method and cross-validation method) were used to determine the best iteration number. D. Boosting model of ln K_D.

Overall, models trained by the above methods with different response variables behaved with the same trend as in MLR, namely, their performance order is ln K_D models > ln k_on models > ln k_off models (Table 3). ln K_D models showed significant enhancement after the ensemble learning, namely, aggregation of multiple weak learners led to a stronger learner, and the prediction accuracy on the test set was comparable to the MLR model. For ln k_on, it was interesting that the single decision tree with six nodes achieved both high training efficiency and prediction accuracy. Further application of the ensemble learning seemed to overfit the data as performance discrepancy between the training set and test set data was observed. For this data set, ensemble learning failed to push the predictivity of the model to a higher level when compared to the MLR baseline model. For all ln k_off models, the prediction on the test set was not satisfactory, probably due to the lack of decisive descriptors or the poor representativeness of the test set to the training set, as seen from the ln k_off distribution (Figure 2B).

Model Assessment and Applicable Domain

To validate the main regression assumption, namely, that standardized residuals of MLR follow a normal distribution, we plotted quantile–quantile (Q–Q) graphs. The Q–Q plot is commonly used to compare the distribution of two data sets. Herein, we plot the standard quantiles of the normal distribution on the x-axis and the standardized residuals from MLR on the y-axis for comparison. Q–Q plots of all three MLR models (Figures 5A and S3A) showed that residuals from linear regression lined around the 45-degree reference line, indicating the validity of the normality assumption. For the linearity assumption check, we plotted residuals against each descriptor (Figure S4). In such plots, we found that residuals were randomly distributed around zero and no obvious trend could be observed, suggesting that no additional relationship with the corresponding descriptor remained in residuals. For the independence and equal variance check, we plotted residuals against the fitted values (Figure S5). Similarly, the residuals were located randomly along zero with equal variance, suggesting the validity of the linear regression.

Figure 5.

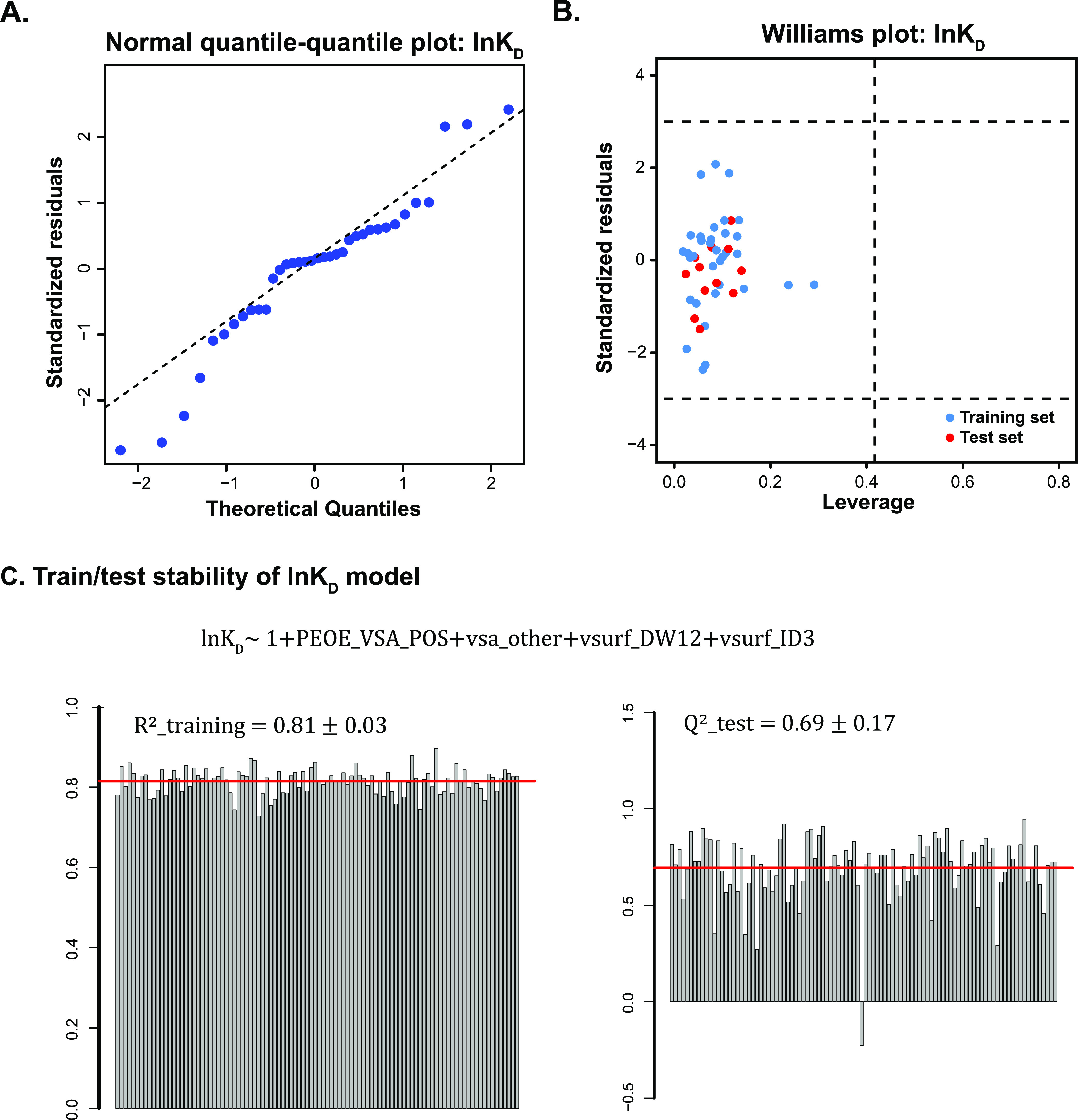
A. Normal quantile–quantile plots of ln K_D model. B. Williams plot showed the applicable domain of ln K_D model with training and test sets. C. Model stability test on ln K_D data using the formula: ln K_D ∼ 1 + PEOE_VSA_POS + vsa_other + vsurf_DW12 + vsruf_ID3. The training and prediction stability are shown on the left and right, respectively. Each bar represented the result from a random sampling, totally 100 times.

To further evaluate the MLR model for future predictions, we defined a proper range of small molecules that can be applied to the models or the applicable domain. Y-outliers represent data points that have significant deviations on response values that do not follow the general trend of the rest of the data, while influential compounds are those that have a large impact on the regression and usually have extreme descriptor values or leverage values (a scoring metric between 0 and 1; large values represent far away the values of the predictor variables for the observation from those of other observations). We generated a Williams plot to identify outliers from the response variable perspective, as well as influential points from the descriptor perspective (Figures 5B and S3B). In this plot, the leverage value of each compound was plotted against its standardized residuals and y-outliers could be detected if the standardized residuals were higher than the ±3 limit. Potential influential points that have extreme descriptor values could be found by checking leverage values, whereas the threshold was set as 3(p + 1)/n (p is the number of descriptors in the MLR model and n is the number of data points). In these three Williams plots, we did not observe any outliers from the view of the response variable. There is one compound, DMZ-p8, that has high leverage values from the training set of ln k_off model. However, the fitting on this compound did not further support this as an influential point. Meanwhile, by looking through the Williams plot, we could find potential inaccurately measured data points. For instance, the Williams plot of ln k_off model found that two compounds (DMA-1 and DMA-3k) have large fitting residuals but shared similar descriptor space as their leverage values were both low. In fact, both compounds were measured with much larger dissociation rate constants than other DMAs, indicating potential measurement error. Removal of DMA-3k in the training and DMA-1 in the test set would increase the R²(training) from 0.64 to 0.71 and prediction accuracy from 0.61 to 0.70 of the ln k_off MLR model.

To evaluate the robustness of the model constructed by the above descriptors, a training/prediction stability test was performed for each MLR model. In this stability test, a set of 36 molecules were randomly selected as the training set, and then an MLR model was trained using the same descriptors found before on the training set. The prediction accuracy was calculated using the remaining 12 compounds in the test set. By repeating this process, we can test the robustness of identified descriptors for building a well-performed MLR model. In Figures 5C and S6, the 100 random samplings gave distinctive training/test sets, but models trained with the same set of descriptors afforded high and stable training efficiency and were consistent with the original MLR model. In terms of the prediction accuracy on test sets, we still see overall high Q² scores for all three data sets but with higher variance, which might be caused by the extremely unrepresentative data splitting.

Conclusions

Discovery of novel RNA-targeted chemical probes is pivotal for connecting the basic understanding of RNA regulation in biology and its potential therapeutic application. Numerous ncRNAs have been discovered as potential drug targets following the RNA revolution. However, difficulties in obtaining accurate 3D structures and conformational landscapes for RNA hinder the rational design of RNA-targeted ligands from a structure-based approach. Additionally, the lack of appreciation of binding kinetics in hit discovery compromised an alternative path toward ligand optimization via kinetic selectivity. Consequently, a novel method that can bypass the structural information and comprehensively evaluate binding parameters, from affinities to kinetics, is greatly needed. To this aim, a systematic QSAR workflow for RNA–ligand discovery was built using HIV-1 TAR as a model system to demonstrate the application of this method on a broad scope of ligands. To the best of our knowledge, this is the first time that 2D-QSAR has been used to predict binding parameters of RNA-targeted ligands with diverse scaffolds.

By applying a representative data splitting, we trained models from 36 small molecules derived from five structural classes (DMZ, DMA, DPF, AG, nucleic acid dyes) as the basis of our understanding of RNA–ligand chemical space. The trained models afforded satisfactory explanations for both binding affinities and kinetics data empirically gathered via SPR. The subsequent prediction of 12 previously untested compounds revealed similar or even higher precision as compared to the well-established ensemble learning-based methods, supporting the power of MLR models to inform compound design. Notably, the accurate prediction of the binding affinity and kinetics of 12 structurally diverse small molecules not present in the training set underscored the breadth of application of the method to a general small-molecule library. The detailed analysis of the descriptor space highlighted by the best models revealed important roles of the ligand surface properties and potential charge in RNA recognition of small molecules. Moreover, the MLR model provided quantitative information on how the modification of these descriptors can better aid molecular design and lead optimization. Further evaluation of the applicable domain informed the proper range of future small molecules that can be appropriately predicted using these models. Limitations of the current model are the small number of training molecules that limit the chemical space explored, from which the applicable domain was derived. As in all QSAR models, this model is specific to the test conditions employed, including environmental factors like buffer and dimethyl sulfoxide (DMSO) content. Additionally, the statistical nature of the QSAR method cannot yield a detailed description of the microscopic interactions involved, such as induced-fit or conformational selection. The impact of each of these limitations is being addressed in the ongoing work.

We anticipate that the method applied here will be an efficient tool in hit identification and lead optimization for a wide range of specific RNA targets. The knowledge gained from known ligands during training can now be efficiently transformed into quantitative models for generalization, i.e., prediction of binding affinity and kinetics. Additionally, this proof-of-concept study could be feasibly extended to other biomacromolecule targets with little structural characterization, including other ncRNAs and proteins. We anticipate the workflow set forth here to significantly facilitate rational decision-making in medicinal chemistry, overcoming one of the current bottlenecks in RNA-targeted small-molecule development.

Experimental Section

Materials and Methods

Reagents were purchased from commercial suppliers and were used without further purification. DMA-1–DMA-164 are from ref (41), DMA-180–DMA-194 are from ref (42), DMA compounds are from ref (71), DPF x1–DPF x10 are from ref (43) (x = m or p), and DPF p13 and p15 are from ref (44). DMZs were synthesized as below. The rest of compounds tested in the SPR are commercially available. The above 36 compounds from the training set and 12 compounds in the test set were examined through PAINS filter via SwissADME.⁷² The results showed two alerts for mitoxantrone (anthranil_one_A, quinone_A), one alert for DMA-3v (anil_di_alk_A), one alert for thiazole orange (het_pyridiniums_A), one alert for DMZ-m3 (azo_A), one alert for DMZ-p8 (azo_A), and one alert for DMZ-p13 (azo_A). All solvents were ACS grade or better and were used without further purification. Anhydrous toluene was obtained by storing ACS-grade toluene over 4 Å molecular sieves, while anhydrous tetrahydrofuran (THF) was dispensed from VWR SureSeal bottles and kept under argon. All microwave reactions were run on a Biotage Initiator+ reactor from Biotage Inc. and under an argon inert atmosphere. All chromatographic purifications were conducted via flash chromatography using ultrapure silica gel (230–400 mesh, 60 Å) purchased from Silicycle as the stationary phase. Thin-layer chromatography was performed with glass-backed silica gel plates purchased from VWR and visualized with 254 nm UV light. All deuterated solvents for NMR experiments were purchased from Cambridge Isotope Laboratories. All ¹H NMR and ¹³C NMR spectra were recorded using a 500 MHz Bruker spectrometer. The corresponding ¹³C resonance frequencies were 100 and 125 MHz, respectively. Chemical shifts are expressed as parts per million from tetramethylsilane. ¹H chemical shifts were referenced with that of the solvent (7.26 for CDCl₃, 3.31 for CD₃OD, and 4.87 for D₂O), and coupling constants (J values) are reported in units of Hertz (Hz). Splitting patterns have been designated as follows: s (singlet), d (doublet), t (triplet), m (multiplet), and br (broad). Low- and high-resolution electrospray ionization (ESI) and mass spectra were recorded on an Agilent MSD-trap spectrometer at Duke University. High-performance liquid chromatography (HPLC) spectra were recorded using a Shimadzu SIL-20AHT Prominence instrument. All HPLC experiments were run at room temperature using gradients or isocratic mixtures of 0.1% trifluoroacetic acid (TFA) in water and acetonitrile as solvents A and B, respectively. Yields refer to ≥95% spectroscopically and chromatographically pure compounds. SPR experiments were performed with a four-channel Biacore T200 system (GE Healthcare Life Sciences) at 25 °C. Molecular descriptors were calculated on molecular operating environment (MOE, Chemical Computing Group, 2018.01). Descriptor refinement was performed on MATLAB (R2020a). Representative data splitting by the Kennard–Stone algorithm, PCA, lasso regression, tree-based ensemble modeling, model assessment, and prediction stability test was performed on RStudio v1.4.1717; see detailed packages and codes in SI.

Synthesis and Characterization

The compound structures and reaction schemes can be found in the Supporting Information. ¹H NMR spectra and ¹³C NMR spectra and MS of compounds are shown in the Supporting Information. The purity of all target compounds was >95% by HPLC analysis in the Supporting Information.

Bis-cyanide Scaffold (2a–c)

4-(1a), 3-(1b), or 2-Aminobenzonitrile (1c) (16.9 mmol) was dissolved in 0.5 M HCl (80 mL) in a 200 mL round-bottom flask and cooled to 0 °C on an ice bath. Upon complete dissolution of the aniline, 2 mL of a 4.5 M solution of sodium nitrite was added dropwise. A precipitate formed immediately, and each coupling was allowed to react to room temperature until a dense solution formed. The reaction was then filtered through a fritz funnel, and the solid was washed with ice-cold deuterated water. The precipitate was left to dry overnight under vacuum and used in the scaffold decoration (the procedure was adapted from the previous methodology).⁷³

(E)-4,4′-(Triaz-1-ene-1,3-diyl)dibenzonitrile (2a)

Bright yellow solid; yield = 88%; ¹H NMR (500 MHz, D₂O) δ 13.28 (s, 1H), 7.97–7.54 (m, 9H). ¹³C NMR (126 MHz, D₂O) δ 134.90, 133.58, 119.47. Calcd for C₁₄H₉N₅ ([M + H]⁺): 248.0; found: 247.1 (±2.1 ppm).

(E)-3,3′-(Triaz-1-ene-1,3-diyl)dibenzonitrile (2b)

Pale beige solid; yield = 53%; ¹H NMR (500 MHz, DMSO-d₆) δ 12.98 (s, 1H), 7.96 (s, 1H), 7.79 (d, J = 8.3 Hz, 2H), 7.61 (q, J = 8.7, 7.5 Hz, 4H), 6.88–6.82 (m, 1H). ¹³C NMR (126 MHz, DMSO) δ 132.03, 130.50, 119.09, 112.76. Calcd for C₁₄H₉N₅ ([M + H]⁺): 248.0; found: 249.1 (±1.8 ppm).

(E)-2,2′-(Triaz-1-ene-1,3-diyl)dibenzonitrile (2c)

Bright yellow solid; yield = 74%; ¹H NMR (500 MHz, DMSO-d₆) δ 13.41 (s, 1H), 7.96 (d, J = 8.2 Hz, 1H), 7.82 (dd, J = 37.5, 8.0 Hz, 2H), 7.69 (dt, J = 21.9, 8.5 Hz, 2H), 7.48–7.40 (m, 2H), 7.27–7.19 (m, 1H). ¹³C NMR (126 MHz, DMSO) δ 152.05–151.93, 142.93, 135.56–132.83, 128.36, 124.26, 119.00–108.57, 98.40, 93.96, 55.32, 40.50–39.50, 29.99. Calcd for C₁₄H₉N₅ ([M + H]⁺): 248.0; found: 248.1 (±1.6 ppm).

Amidine Formation

2a–c (0.41 mmol) and DABAL-Me₃ (1.2 mmol) were added to a 5 mL over-dried pressure vial under argon. The solids were dissolved in anhydrous THF or toluene (2.5 mL), and a primary amine (1 mmol) was added dropwise in a 5 mL over-dried pressure vial under argon and heated to 105 °C for 4.5 h. After running, the reaction was diluted in dichloromethane and quenched with acetonitrile dropwise while stirring. The solution was then evaporated under vacuo. The solid was redissolved in methanol, and a 5:1 ratio of celite: starting material was added. Compounds were purified using silica column chromatography in a gradient 95:4:1 DCM:MeOH:NH₄OH to 85:14:1 DCM:MeOH:NH₄OH to yield the final compounds. The procedure was adapted from the previously published synthesis.⁷⁴

(E)-3,3′-(Triaz-1-ene-1,3-diyl)bis(N-(2-(pyridin-3-yl)ethyl)benzimidamide) (DMZ-M3)

¹H NMR (500 MHz, methanol-d₄) δ 8.39 (s, 2H), 8.29 (d, J = 4.7 Hz, 2H), 7.73 (d, J = 7.8 Hz, 2H), 7.61 (s, 2H), 7.53 (d, J = 8.1 Hz, 2H), 7.39 (t, J = 7.9 Hz, 2H), 7.28 (dd, J = 7.9, 4.2 Hz, 4H), 3.54 (t, J = 7.3 Hz, 4H), 2.97 (t, J = 7.2 Hz, 4H). ¹³C NMR (126 MHz, MeOD) δ 163.53, 149.17, 146.83, 137.45, 135.55, 134.73, 129.57, 123.89, 123.11, 120.60, 116.07, 47.62, 47.45, 47.28, 47.11, 43.96, 31.37. HRMS-ESI (m/z) calcd for C₂₈H₂₉N₉ ([M + H]⁺): 492.6; found: 246.3 (±1.1 ppm) for 1/2 [M + H]⁺.

(E)-4,4′-(Triaz-1-ene-1,3-diyl)bis(N-(1-benzylpiperidin-4-yl)benzimidamide) (DMZ-P8)

¹H NMR (500 MHz, methanol-d₄) δ 7.63–7.55 (m, 4H), 7.51–7.37 (m, 4H), 7.42–6.82 (m, 10H), 3.55 (tt, J = 14.0, 5.6 Hz, 2H), 3.47 (s, 4H), 2.97–2.71 (m, 4H), 2.12 (td, J = 12.0, 2.5 Hz, 4H), 1.99–1.75 (m, 4H), 1.61 (qd, J = 12.1, 3.5 Hz, 4H). ¹³C NMR (126 MHz, MeOD) δ 129.23, 127.98, 127.11, 62.39, 51.48, 48.12, 47.60, 47.43, 47.26, 47.09, 30.01. HRMS-ESI (m/z) calcd for C₃₈H₄₅N₉ ([M + H]⁺): 628.4; found: 628.4 (±1.0 ppm).

(E)-4,4′-(Triaz-1-ene-1,3-diyl)bis(N-(2-(1-benzylpiperidin-4-yl)ethyl)benzimidamide) (DMZ-P13)

¹H NMR (500 MHz, methanol-d₄) δ 7.82 (d, J = 8.3 Hz, 4H), 7.68 (d, J = 8.3 Hz, 4H), 7.55–7.45 (m, 10H), 4.28 (s, 4H), 3.56–3.44 (m, 8H), 3.00 (t, J = 12.6 Hz, 4H), 2.04 (d, J = 14.1 Hz, 4H), 1.78 (q, J = 6.5 Hz, 6H), 1.59 (q, J = 11.6, 10.9 Hz, 4H). ¹³C NMR (126 MHz, MeOD) δ 163.89, 161.77, 161.49, 130.85, 129.61, 129.13, 128.87, 118.03, 115.70, 51.89, 47.45, 47.28, 47.11, 40.34, 32.75, 31.15, 28.66. HRMS-ESI (m/z) calcd for C₄₂H₅₃N₉ ([M + H]⁺): 684.45; found: 684.45 (±3.3 ppm).

Surface Plasmon Resonance

RNA Immobilization

Followed a recently published protocol from ref (75), the entire system was washed with 50% (v/v) RNase Zap (Invitrogen by ThermoFisher Scientific) three times and then manually ran it (flow rate of 25 μL/min) in RNase-free water for more than 14 h to make sure no more RNase Zap was left in the system. A series S CM5 sensor chip (GE Healthcare Bio-science Corp, Marlborough, MA) was used for RNA immobilization in HBS buffer (10 mM HEPES, 150 mM NaCl, 3 mM EDTA, 0.05% (v/v) P20, pH 7.4). In the manual run mode, two cells (either cell 4&3 or cell 2&1) from a sensor chip were selected and the immobilization began when the system reached a stable baseline (the difference in RU over a period of time (ΔRU) <1 for at least 60 s) with a flow rate of 5 μL/min. First, 80 μL of 11.5 mg/mL N-hydroxysuccinimide (NHS) and 75.0 mg/mL of N-ethyl-N′-(dimethylaminopropyl) carbodiimide (EDC) from Amine Coupling Kit (GE Healthcare) were mixed just prior to the injection to take advantage of the best activation time window. The injection of EDC/NHS (flow rate of 5 μL/min) took 720 s to reach 100–200 ΔRU. Streptavidin (Sigma-Aldrich) was diluted to 300 μg/mL in immobilization buffer (10 mM sodium acetate pH 4.5) beforehand and then was injected (flow rate of 5 μL/min) right after EDC/NHS activation. The injection of streptavidin took ∼2000 s to reach 4000–6000 RU increase of the sensorgram. Afterward, 1.0 M ethanolamine hydrochloride (pH 8.5) was injected (flow rate of 5 μL/min) for 600 s to deactivate the surface of the sensor chip. The system was primed several times to obtain a stable baseline.

Before RNA immobilization, the surface was activated by injecting 75 μL of 1 M NaCl (prepared in RNase-free water) at a 25 μL/min flow rate 5 times. The stabilization of the baseline was waited for at least 1 h. The flow rate was changed to 1 μL/min for RNA immobilization, and the flow path was switched to the working cell (cell 4 or cell 2) only. Biotinylated HIV-1 TAR (5′-TEG-biotin-GGCAGAUCUGAGCCUGGGAGCUCUCUGCC-3′, Integrated DNA Technologies) was annealed beforehand by diluting to 50 μM in DEPC-treated water and then heating to 95 °C and cooling on ice for 30 min. RNA was diluted to 250 nM in HBS buffer and injected under a manual run for 100–600 s to achieve a 200–500 increase of RU. After RNA immobilization, the HBS buffer was replaced by a running buffer (50 mM tris–HCl, 50 mM KCl, 5% DMSO, 0.01% Triton-X-100, pH 7.4) and primed 3 times before measurements.

Binding Measurements

Ligand solutions were prepared with an SPR running buffer by serial dilutions from concentrated stock solutions. Typically, a series of different ligand concentrations (at least five nonzero concentrations; the range depends on binding affinity, e.g., DPFs from 50 to 1000 nM, DMAs from 1 to 200 μM) were injected over the sensor chip at a flow rate of 50 μL/min for 60 s, followed by buffer flow for ligand dissociation for 120 s. After each cycle, the sensor chip surface was regenerated with a 1 M NaCl solution for 60 s. A zero-concentration injection was placed at the very beginning for each ligand for blank subtraction. The injection with the middle concentration was repeated finally to check the stability of the instrument’s behavior. Kinetic analyses were performed by fitting curves from the entire concentration series using a 1:1 Langmuir binding equation via BIAevaluation software.

Similarity Calculation

Tanimoto coefficient was used here to compare the shared portion of substructures between two molecules. The Morgan fingerprints (calculated using RDkit package) were obtained by calling the “GetMorganFingerprintAsBitVect” function, using the radius of 2 and 2048-bit vector. Then, the similarity index between two compounds was calculated as the Tanimoto coefficient by calling the “DataStructs.TanimotoSimilarity” function. The values calculated are between 0 and 1, and a higher value suggests a higher similarity between the two.

Descriptor Calculation

Before calculation, all of the ligands were tuned to the correct protonation and tautomerization states using molecular operating environment (MOE, Chemical Computing Group, 2018.01). Each of the protonation and tautomerization states was sent to conformational search individually to account for the flexibility of the ligand. Low-energy conformations of each molecule were calculated using the conformation search algorithm in MOE. The conformation search function was performed using the stochastic method with the MMFF94 force field and the generalized Born solvation model. The input for each parameter is listed in Table S1, and the following options were checked: hydrogens. The 3 kcal/mol energy window was selected to survey the biologically relevant conformation space and to obtain a representative population of conformers at equilibrium (>99%), as described in eq S1. After the conformation search was complete, the 435 descriptors, ranging from the electrostatic properties to topological terms, were calculated for each conformation and averaged using the Boltzmann-weighted equation (eq S2). The final descriptor set of each molecule was obtained by further averaging based on the distribution of the protonation and tautomerization states. In total, we calculated 435 descriptors of each ligand.

QSAR Modeling

Descriptor Refinement

The descriptors were first refined based on the constant terms. A descriptor was deleted if it has more than 80% entries sharing the same values. Then, the left descriptors were calculated on their correlation coefficients using the corrcoef function in MATLAB. The descriptor has a maximum number of correlated descriptors (abs(rho) > 0.95) that were deleted. If the target descriptor was found to be more than one, the first appeared one was deleted. Then, the left descriptors were calculated on their correlation coefficients again and the descriptor has a maximum number of correlated descriptors (abs(rho) > 0.95) that were deleted. After several rounds, the left descriptors have at most one multicorrelations. In a pair of multicorrelations, the one with the lower correlation coefficient with y variable was deleted.

Representative Data Splitting by the Kennard–Stone Algorithm and PCA

Data splitting was performed using the “prospectr” package in RStudio (v1.4.1717). The 48 data points were divided into 36 ones as the training set and 12 ones as the test set. The distance metric used in the Kennard–Stone algorithm was the mahalanobis distance, where 99% data variance was explained by the principal components. PCA was performed using the “prcomp” function to visualize the distribution of the training set and test set molecules in the PCA space.

Descriptor Selection by Lasso and Model Selection

Lasso regression was performed using the “glmnet” package in RStudio (v1.4.1717). Random seed was set before the cross-validation process. A range of lambda values were tested to find the best lambda with the lowest mean-squared error from cross validation. The selected descriptors formed the new feature space for the following exhaustive model search.

Tree-Based Ensemble Models

Decision tree, bagging, random forest, and gradient boost machine were performed in RStudio (v1.4.1717) using “tree”, “randomForest”, “randomForest”, and “gbm” packages, respectively. Random seed was set before all of the cross-validation process for selecting optimized hyperparameters.

Glossary

Abbreviations Used

AG

aminoglycoside

DMA

dimethyl amiloride

DMZ

diminazene

DPF

diphenyl furan

DRY

hydrophobic probe

Integy

interaction energy

lasso

least absolute shrinkage and selection operator

MLR

multiple linear regression

MOE

molecular operating environment

ncRNA

noncoding RNA

OH2

hydrophilic probe

PCA

principal component analysis

PEOE

partial equalization of orbital electronegativities

Q–Q

quantile–quantile

QSAR

quantitative structure–activity relationship

SPR

surface plasmon resonance

TAR

transactivation response element

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jmedchem.2c00254.

• SMILES molecular formula strings, original SPR data, and molecular descriptor values (CSV)

• Synthesis scheme, mass spectrometric analysis, HPLC assessment of diminazene compounds,¹H and ¹³C NMR spectra, surface plasmon resonance sensorgrams, QSAR modeling packages and scripts, and supplementary figures/tables/equations (PDF)

Accession Codes

Source code and original data files in this GitHub repository: https://github.com/hargrove-lab/QSAR.

The authors declare no competing financial interest.