The effect of Wolbachia on dengue dynamics in the presence of two serotypes of dengue: symmetric and asymmetric epidemiological characteristics

SUMMARY

An innovative strategy to reduce dengue transmission uses the bacterium Wolbachia. We analysed the effects of Wolbachia on dengue transmission dynamics in the presence of two serotypes of dengue using a mathematical model, allowing for differences in the epidemiological characteristics of the serotypes. We found that Wolbachia has a greater effect on secondary infections than on primary infections across a range of epidemiological characteristics. If one serotype is more transmissible than the other, it will dominate primary infections and Wolbachia will be less effective at reducing secondary infections of either serotype. Differences in the antibody-dependent enhancement of the two serotypes have considerably less effect on the benefits of Wolbachia than differences in transmission probability. Even if the antibody-dependent enhancement rate is high, Wolbachia is still effective in reducing dengue. Our findings suggest that Wolbachia will be effective in the presence of more than one serotype of dengue; however, a better understanding of serotype-specific differences in transmission probability may be needed to optimize delivery of a Wolbachia intervention.

INTRODUCTION

The increasing number of dengue cases worldwide and its re-appearance in dengue-free countries demonstrate the global threat it poses. Recent estimates are that dengue results in 390 million individuals infected annually [1].

Dengue, which is transmitted mainly by Aedes aegypti mosquitoes, is caused by four different virus serotypes. Individuals obtain lifelong immunity to the serotype they are infected with, but do not have immunity to other serotypes. When infected by a second serotype, individuals are at greater risk of severe forms of dengue, such as dengue haemorrhagic fever (DHF) and dengue shock syndrome (DSS) [2]. Patients with DHF have viral levels 100–1000 times that of non-DHF patients [3]. This higher viral load is due to a phenomenon known as antibody-dependent enhancement (ADE), and is associated with higher transmissibility. In the majority of dengue endemic regions, more than one dengue serotype circulates, with dominant serotypes varying over time [4], thus increasing the opportunity for individuals to develop DHF or DSS.

Traditional strategies for dengue control such as insecticides have been found to be unsustainable [5] particularly in the developing world, and thus an innovative biological strategy against dengue has been proposed using the Wolbachia bacterium [6–10]. Mosquitoes carrying Wolbachia have lower levels of dengue virus in their salivary glands, and thus are less likely to transmit the virus to humans [6, 10]. Wolbachia also reduces the mosquito's lifespan [6], and hence mosquitoes have less time to transmit dengue. Additionally, the bacterium also reduces the reproductive rate of mosquitoes [6] and causes an effect called bendy proboscis which results in a reduced biting rate [11]. Mosquitoes carrying the bacterium are still viable in the wild, since Wolbachia gives female mosquitoes a reproductive advantage known as cytoplasmic incompatibility, whereby Wolbachia-carrying females can reproduce with non-Wolbachia or Wolbachia-carrying males, but non-Wolbachia females can only reproduce successfully when mating with non-Wolbachia males. Because Wolbachia in male mosquitoes modifies the sperm of their host, a pairing between a non-Wolbachia female and a Wolbachia-carrying male may not result in embryonic development [6, 12]. The results from mathematical models have shown that Wolbachia-carrying mosquitoes are likely to persist in the wild [13–16], and field experiments have confirmed that Wolbachia-carrying mosquitoes persist and can become established [7, 8].

Modelling studies suggest that Wolbachia may reduce dengue by 50–90%, with greater effects if the reproduction number is not large [14, 17]. These studies did not consider the effect of Wolbachia on dengue transmission dynamics in the presence of more than one serotype of dengue. The effect of multiple serotypes may be of importance because interactions between serotypes of dengue may affect dengue transmission dynamics. Disease severity is known to differ between serotypes [3], although estimates of the basic reproduction number from serological data showed relatively little difference between serotypes [18, 19].

Here we develop a two-serotype mathematical model of dengue transmission and explore symmetric and asymmetric epidemiological characteristics between serotypes. That is, when serotypes exhibit the same epidemiological parameter values, and when there are differences. We focus in particular on the ADE factor and the transmission probability (TP), and compare the effect of Wolbachia on both primary and secondary infections. Our model provides insights into the effectiveness of the Wolbachia intervention on dengue dynamics when more than one serotype of dengue is circulating in the population.

METHODS

There are two aspects to our methods, the mathematical model and how we measure the effectiveness of the Wolbachia intervention. Throughout the paper, serotypes 1 and 2 refer to two different dengue serotypes but do not specifically refer to the DEN1 and DEN2 viruses.

Mathematical model

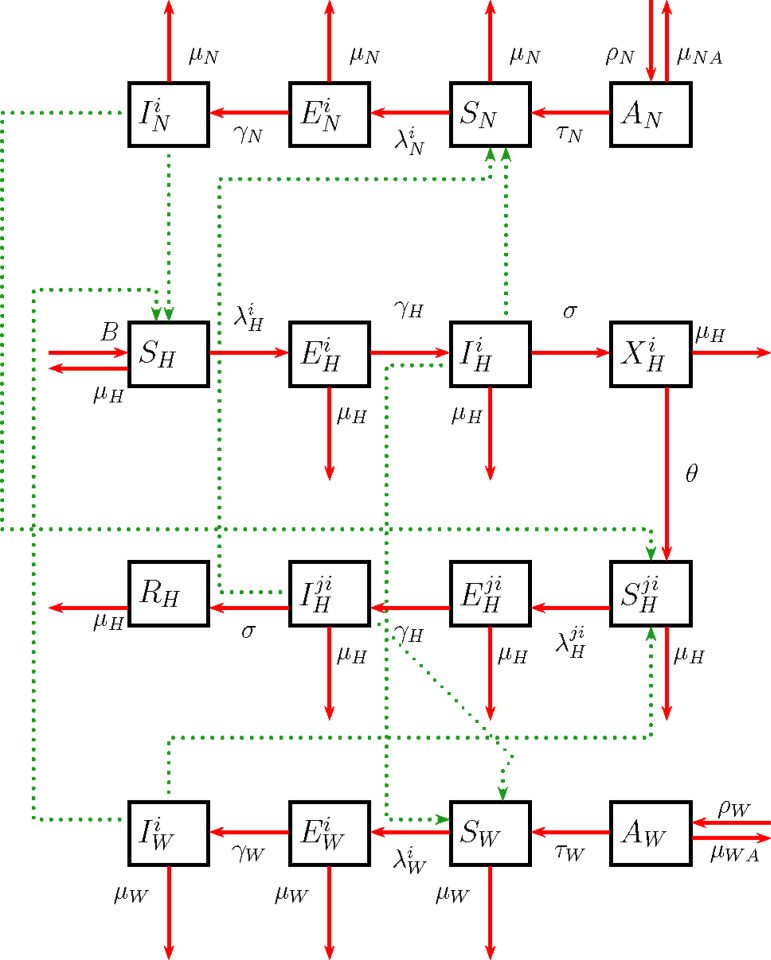
The dynamics of two serotypes of dengue in the presence of Wolbachia were studied using a deterministic SEIR mathematical model that builds on the model by Ndii et al. [14]. As we are particularly interested in determining the efficacy of Wolbachia once mosquitoes carrying Wolbachia establish and persist in the wild [7, 8], we do not consider the transmission dynamics of dengue during transient periods as Wolbachia becomes established. Full details of the model and parameters are given in the Supplementary material, and a diagram showing states and transitions in the model is provided in Figure 1.

Fig. 1.

Flowchart for the two-serotype dengue transmission model in the presence of Wolbachia-carrying mosquitoes. Solid lines denote progression between states, dashed lines denote transmission routes. Subscripts H, N, and W represent human, non-Wolbachia and Wolbachia-carrying mosquitoes, respectively, with categories of Susceptible (S), Exposed (E), and Infectious (I) for both mosquitoes and humans, aquatic stage for mosquitoes, and Recovered (R) and temporarily immune (X) for humans. Parameters in the diagram are described in detail in Supplementary Table S1.

Human disease states in the model include Susceptible, Exposed, Infectious and Recovered, and we also include a temporary immunity class, X, following primary infection, where individuals have a short period of temporary immunity to all serotypes before being susceptible to the serotypes that they have not previously been infected with. The period of temporary immunity is taken to be 6 months [20]. We assume a constant human population of 150 000, which approximates that of Cairns, Australia, which was used in our parameter estimation [14], and also assume no deaths due to dengue, so that the birth and death rates of humans are the same.

Mosquito states in the model include an aquatic stage as well as Susceptible, Exposed and Infectious adult mosquitoes, with subscripts N and W indicating non-Wolbachia and Wolbachia mosquitoes. Although many parameters describing mosquito behaviour may depend on seasonality, in earlier work we found that the mosquito death rate is the most influential parameter [14] and hence this is the only parameter that is seasonally forced.

We simulate the model without dengue using initial conditions S_H0 = 150000, A_N0 = S_N0 = 3 × S_H0 and S_W0 = 2 × S_N until the mosquito population reaches a stable state, and then use those mosquito populations as new initial conditions for our simulations including dengue. To ensure that the epidemics do not occur when the infected population is <1 individual, the infected population is set to zero if it falls below a threshold of 0·5 individuals. This is a deterministic proxy for stochastic fade out.

Measurement of Wolbachia performance and dengue introduction scenarios

The performance of Wolbachia is assessed by comparing the relative difference between the outbreak size in the absence and presence of Wolbachia-carrying mosquitoes. Because only one dengue serotype generally dominates a yearly outbreak [4], humans carrying dengue serotype 1 are introduced weekly into the population for a 1-year period, and then individuals carrying serotype 2 are introduced weekly into the population in the subsequent year. Since we assume a constant human population, when the infected individuals are introduced through importation, the same numbers of individuals are subtracted from the susceptible population. The introduction process is repeated until the human infected populations remain the same for 75 years. Epidemiological characteristics of interest are the ADE factor and TP. We investigate their effect on outbreak sizes, separately and together, assuming they have the same values for both serotypes. Then we investigate the case where serotype 2 has a higher TP or a higher ADE level. As ADE results in higher viral load [3], it increases the TP. Although they are related, we vary these two parameters independently to explore their effects on primary and secondary infections.

RESULTS

The results below are divided into those for symmetric epidemiological characteristics between the two dengue serotypes, and the results where epidemiological characteristics differ (the asymmetric case).

Symmetric epidemiological characteristics

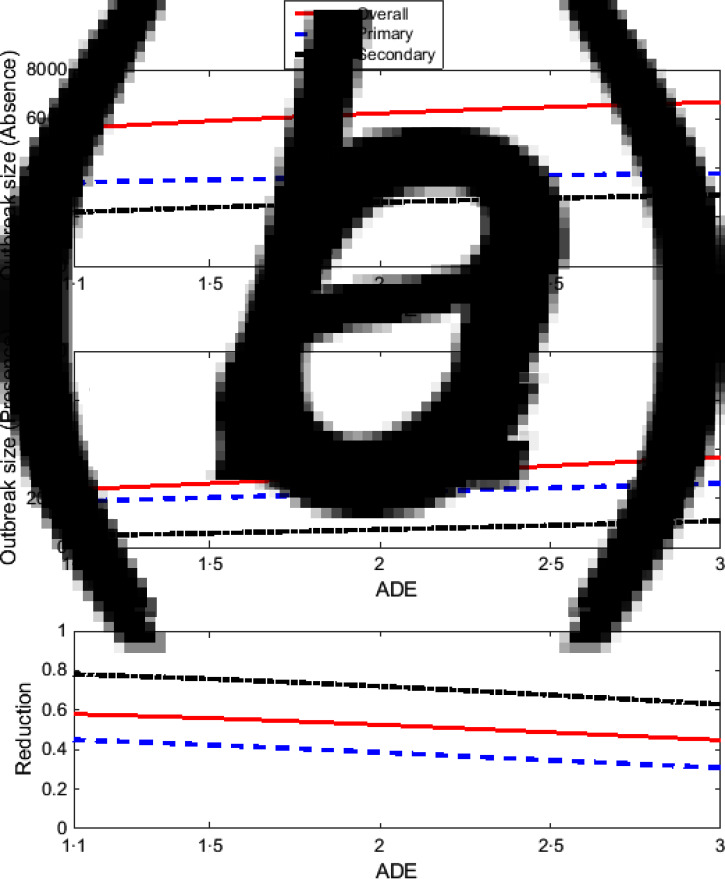
Figure 2 presents the effect of Wolbachia on the outbreak size due to primary and secondary infections when both serotypes have the same epidemiological characteristics. The overall outbreak size is simply the sum of the outbreak sizes due to primary and secondary infections. As expected, the outbreak size in the absence of Wolbachia-carrying mosquitoes is always higher than in the presence of Wolbachia-carrying mosquitoes.

Fig. 2.

The effect of changes in the antibody-dependent enhancement (ADE) factor for both dengue serotypes under the first scenario of dengue introduction. All plots show overall (solid red lines), primary (blue dashed line) and secondary (black dash-dot line) infections. Plots (a) and (b) show the outbreak size in the absence and presence of Wolbachia-carrying mosquitoes, respectively. Plot (c) shows the proportional reduction in dengue due to Wolbachia.

As the ADE rate increases, the outbreak sizes in the absence and presence of Wolbachia-carrying mosquitoes also increase, while the proportional reduction in dengue due to Wolbachia decreases (Fig. 2). The reduction in secondary infections is higher than that of primary infections, with up to 78% reduction in secondary infections compared to ≈45% in primary infections.

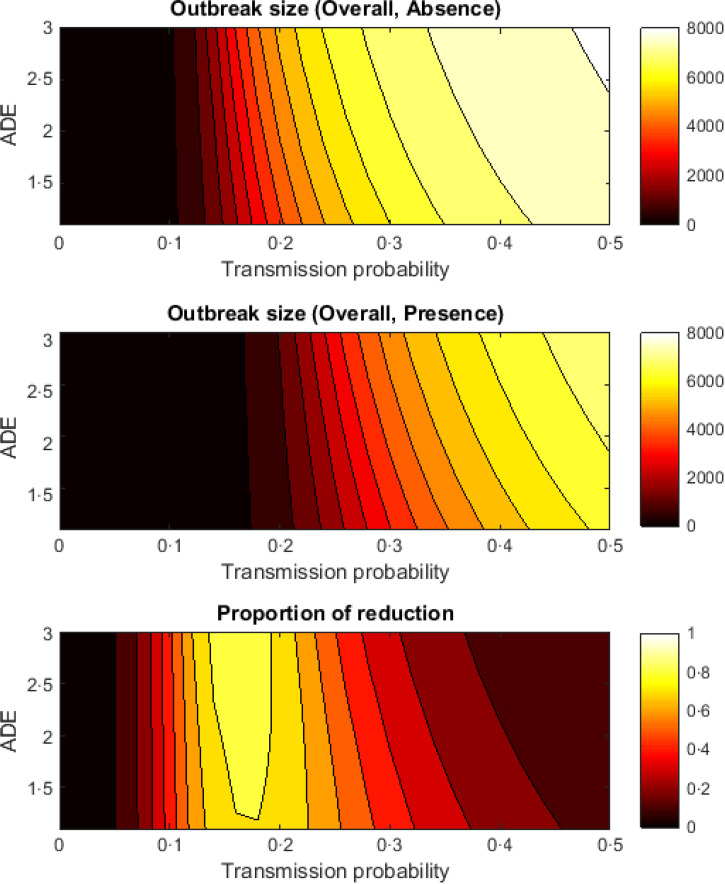
When both ADE and TP are varied (Fig. 3), in the absence of Wolbachia-carrying mosquitoes, epidemics do not occur when TP is low (between 0 and 0·1). ADE has relatively little effect on the reduction in dengue due to Wolbachia. In the presence of Wolbachia-carrying mosquitoes, epidemics do not occur unless TP > 0·18. This means that the presence of Wolbachia-carrying mosquitoes raises the threshold value of TP at which epidemics occur. The maximum reduction in dengue due to Wolbachia is around 70–80% which occurs when TP is between 0·16 and 0·23. If TP is high (>0·23), Wolbachia becomes less effective in reducing dengue. Qualitatively similar results are obtained when considering primary and secondary infections (Supplementary Figs S1 and S2), although there is potential for greater reduction in secondary infections than primary infections.

Fig. 3.

Contour plot showing simultaneous changes to the antibody-dependent enhancement (ADE) factor and transmission probability. The top and middle plots give the outbreak size in the absence and presence of Wolbachia-carrying mosquitoes. The bottom plot shows the proportional reduction in dengue due to Wolbachia.

Asymmetric epidemiological characteristics

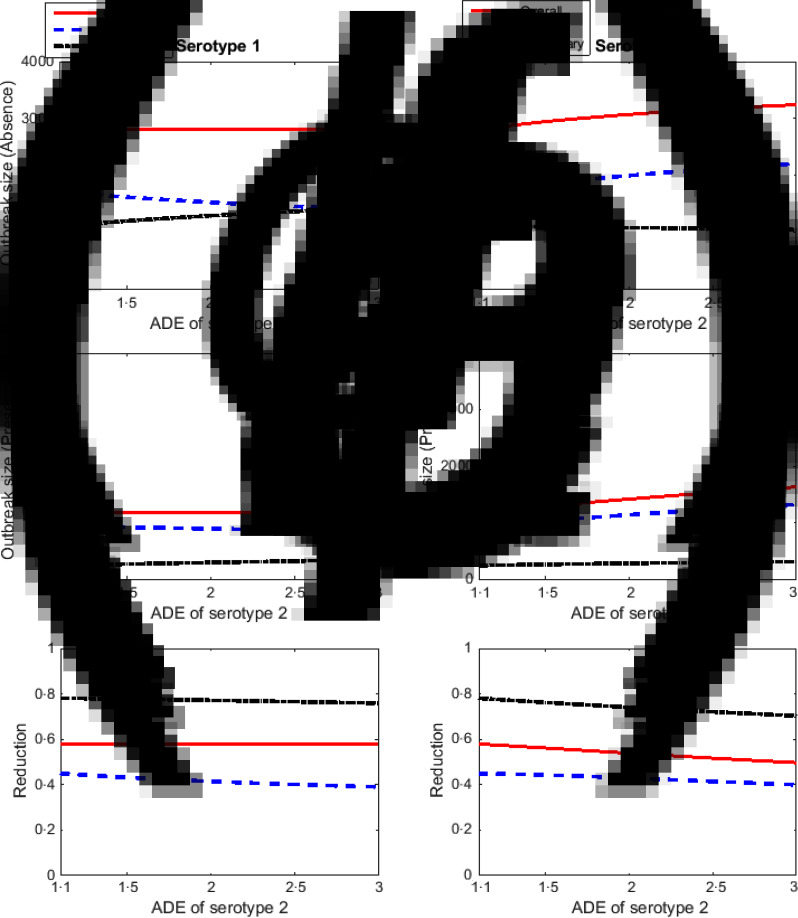
As the ADE factor of serotype 2 increases relative to that of serotype 1, primary infections due to serotype 2 increase and there is a slight decline in secondary infections (Fig. 4) in the absence of Wolbachia-carrying mosquitoes. The same behaviour is found in the presence of Wolbachia-carrying mosquitoes, except that the outbreak size for secondary infections with serotype 2 slightly increases. In contrast, primary infections due to serotype 1 decrease and secondary infections increase.

Fig. 4.

The effect of changes in the antibody-dependent enhancement (ADE) factor for serotype 2 when the ADE for serotype 1 is fixed. All plots show overall (solid red lines), primary (dashed blue lines) and secondary (dash-dot black lines) infections. Plots show the outbreak size in the absence (a, d) and presence (b, e) of Wolbachia-carrying mosquitoes. Plots (c) and (f) show the proportional reduction in dengue incidence due to Wolbachia. The left-hand plots (a–c) show serotype 1 and the right-hand plots (d–f) show serotype 2.

Interestingly, the overall effect is of similar total case numbers due to serotype 1 as the ADE of serotype 2 increases, because the decrease in primary infections is offset by an increase in secondary infections. The performance of Wolbachia in reducing primary infections of serotype 2 varies between 40% and 45% and that of serotype 1 between 39% and 45%. The number of secondary infections of serotype 2 is reduced by 70–78% and that of serotype 1 is reduced by 76–78%. The upper bounds in the reduction in the number of dengue cases due to Wolbachia are the same for both serotypes because the maximum reduction in dengue cases occurs when the ADE factor of both serotypes are equal. Again, it is clear that the reduction in secondary cases due to Wolbachia is higher than that of primary cases.

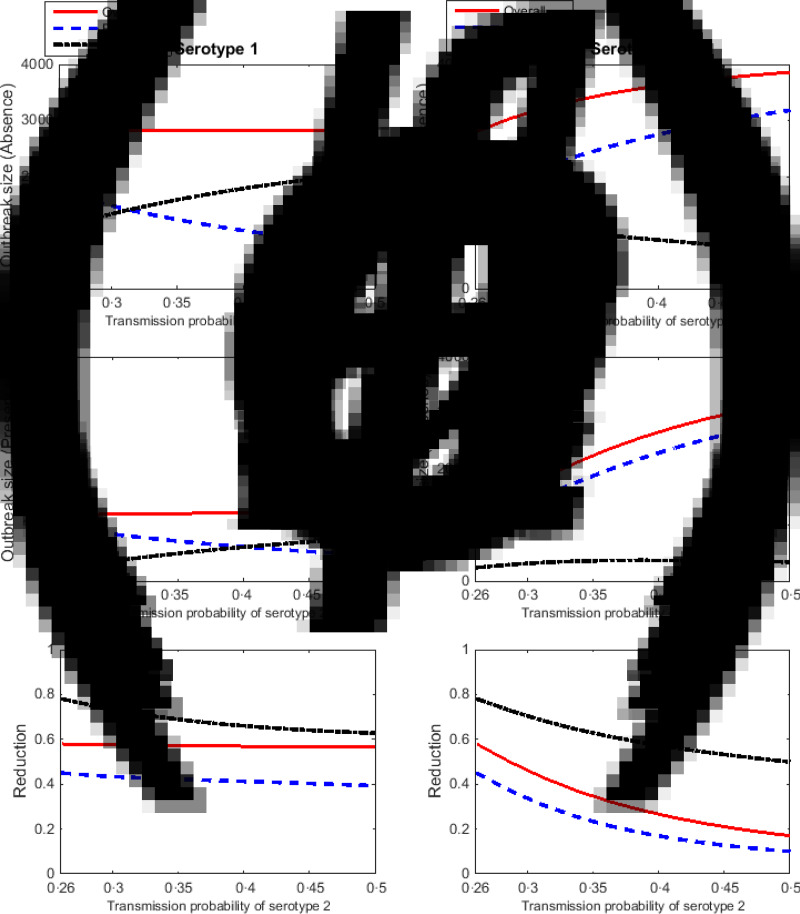
If the TP of serotype 2 increases relative to that of serotype 1, the number of primary infections it causes increases greatly (Fig. 5). As the TP of serotype 2 increases, the number of primary infections due to serotype 1 decreases, while that of secondary infections increases. The overall outbreak size due to serotype 1 remains constant as the TP of serotype 2 increases because the increase in secondary infections due to serotype 1 is balanced by a decrease in primary infections due to this serotype. Interestingly, in the presence of Wolbachia-carrying mosquitoes, although the number of primary infections due to serotype 1 decreases, the number of secondary infections due to serotype 2 slightly increases, but the latter is still lower than the former. The proportional reduction of primary infections of serotype 2 due to Wolbachia varies between 7% and 45%, and that of secondary infections varies between 47% and 78%. The overall reduction of dengue infections caused by serotype 2 varies between 13% and 58%. Although serotype 1 is less transmissible, an increase in TP of serotype 2 results in a decline in Wolbachia performance in reducing secondary infections caused by serotype 1. The presence of Wolbachia-carrying mosquitoes still reduces secondary infections caused by serotype 1 by >60%, although Wolbachia reduces primary infections due to serotype 1 by only around 38–45%.

Fig. 5.

The effect of changes in the transmission probability of serotype 2 while the transmission probability of serotype 1 is fixed. All plots show the overall (solid red lines), primary (dashed blue lines) and secondary (dash-dot black lines) infections. Plots show the outbreak size in the absence (a, d) and presence (b, e) of Wolbachia-carrying mosquitoes. Plots (c) and (f) show the proportional reduction in dengue incidence due to Wolbachia. The left-hand plots (a–c) show serotype 1 and the right-hand plots (d–f) show serotype 2.

DISCUSSION AND CONCLUSIONS

The key results of this paper are that Wolbachia can reduce primary and secondary dengue infections, although the effects decline if one serotype is significantly more transmissible than the other. In particular, a significant reduction in secondary infections of up to 78% can be achieved using the Wolbachia intervention. This is of great importance for public health as secondary infections have a higher risk of developing the more severe forms of dengue. Although the potential for higher transmissibility of secondary dengue cases due to ADE influences the effectiveness of Wolbachia, the TP remains the key parameter affecting dengue transmission dynamics.

When dengue subtypes have the same epidemiological characteristics, we find that the ADE factor does not noticeably affect the effectiveness of Wolbachia except where TP is high. When TP < 0·14, an outbreak does not take off, so that the number of infectious humans is dominated by imported cases. When TP ⩾ 0·14, an outbreak will take off. The maximum reduction in dengue cases is obtained for TPs in the range 0·14–0·22, and considerable reductions in secondary infections of 60–80% are achieved. This implies Wolbachia will be most effective in reducing dengue transmission if dengue serotypes are not strongly transmissible, which is similar to the findings of Ndii et al. [14] for a single serotype. TP is one of the parameters that regulate the basic reproduction number, which means that a higher TP typically indicates a higher reproduction number. Hence, our result is consistent with the finding by Hughes & Britton [21] and Ferguson et al. [17] that Wolbachia will be effective if the basic reproduction number is not too high.

When the epidemiological characteristics of dengue serotypes differ, we find a shift towards greater numbers of primary infections of the subtype with the higher enhancement rate or higher TP. Where only the ADE factor differs between serotypes, we find relatively little decline in the effectiveness of Wolbachia. However, if one serotype is more transmissible than the other, the effectiveness of Wolbachia against this serotype can drop below 20%, while still reducing dengue due the other serotype by ≈60%. Thus, Wolbachia may be less effective in reducing secondary infections if the TP of one of the serotypes is noticeably higher than that of the other.

If there are two serotypes circulating in the population and more individuals have primary infections with one of the serotypes, then it is likely that more individuals have secondary infections with the other serotype. Interestingly, we find that although the number of primary infections due to serotype 1 decreases in the presence of Wolbachia-carrying mosquitoes, the number of secondary infections caused by serotype 2 increases slightly. However, the number of secondary infections caused by serotype 2 is still lower than the number of primary infections caused by serotype 1. This may be for the following reasons. As ADE of serotype 2 increases, there are more individuals primarily infected with serotype 2 than serotype 1. The higher number of primary infections with serotype 2 affects the force of infection, resulting in a greater likelihood of secondary infection with serotype 2 for individuals previously infected with serotype 1. Hence, as ADE for serotype 2 increases, the number of secondary infections caused by serotype 2 increases. This implies that there is a complex interaction between variables regulating the force of infection. Note that similar behaviour is also found when varying the TP of serotype 2.

Our results imply that the introduction of Wolbachia-carrying mosquitoes into the population can potentially reduce dengue transmission. In particular, a greater reduction in secondary infections can be obtained. However, the effectiveness of Wolbachia in reducing dengue transmission may be lower when TP is higher. This finding suggests that this intervention may only be effective in regions with lower transmission strength. There are complex interactions between variables regulating the force of infection. These include the mosquito biting rate and TP. Further analysis of the effects of Wolbachia on these variables is required to enhance our understanding of Wolbachia effectiveness. Specific variables of interest include the mosquito biting rate and the level of virus in mosquitoes in particular when they are released into the field.

In this paper, we used a deterministic model which is appropriate for a large population such as that considered here. Consideration of stochastic effects may be important for investigating small infected populations. We have also assumed a fairly simple serotype introduction pattern, with two serotypes dominating in alternate years. While our model simplifies the typical pattern of serotype introductions [22], it captures yearly variation in serotype introductions. We also tested other introduction patterns – including one in which one serotype is introduced more often than the other – and found broadly similar results. Our finding that differences in the ADE factor between serotypes has much less effect on dengue dynamics than differences in TP indicates that a better understanding of serotype-specific TPs may be needed to optimize delivery of Wolbachia interventions.

DECLARATION OF INTEREST

None.