A gyrification analysis approach based on Laplace Beltrami eigenfunction level sets

Abstract

An accurate measure of the complexity of patterns of cortical folding or gyrification is necessary for understanding normal brain development and neurodevelopmental disorders. Conventional gyrification indices (GIs) are calculated based on surface curvature (curvature-based GI) or an outer hull surface of the cortex (outer surface-based GI). The latter is dependent on the definition of the outer hull surface and a corresponding function between surfaces. In the present study, we propose the Laplace Beltrami-based gyrification index (LB-GI). This is a new curvature-based local GI computed using the first three Laplace Beltrami eigenfunction level sets. As with outer surface-based GI methods, this method is based on the hypothesis that gyrification stems from a flat surface during development. However, instead of quantifying gyrification with reference to corresponding points on an outer hull surface, LB-GI quantifies the gyrification at each point on the cortical surface with reference to their surrounding gyral points, overcoming several shortcomings of existing methods. The LB-GI was applied to investigate the cortical maturation profile of the human brain from preschool to early adulthood using the PING database. The results revealed more detail in patterns of cortical folding than conventional curvature-based methods, especially on frontal and posterior tips of the brain, such as the frontal pole, lateral occipital, lateral cuneus, and lingual Negative associations of cortical folding with age were observed at cortical regions, including bilateral lingual lateral occipital, precentral gyrus, postcentral gyrus, and superior frontal gyrus. The results also indicated positive significant associations between age and the LB-GI of bilateral insula, the medial orbitofrontal, frontal pole and rostral anterior cingulate regions. It is anticipated that the LB-GI will be advantageous in providing further insights in the understanding of brain development and degeneration in large clinical neuroimaging studies.

1. Introduction

Accurate and robust methods for tracking and quantifying cortical folding complexity are critical in the study of both normal brain development and neurodevelopmental disorders (Lebed et al., 2013; Tan et al., 2020). A gyrification index (GI) is a metric encapsulating the degree of folded-ness of the cortex. The first such measure, proposed by Zilles et al. (1988), computed the ratio of the length of the cortical surface to the perimeter of the exposed outer surface of the brain. The length of the cortical surface was computed on manually delineated 2D sections. This method did not consider the intrinsic 3D structure of the brain, and therefore, the GI values could vary depending on the orientation and thickness of the slicing. As the spatial resolution of MRI improved, new GIs were proposed to automatically quantify the degree of cortical folding using the reconstructed 3D surface of the brain (Lebed et al., 2013; Schaer et al., 2008; Luders et al., 2006a; Kao et al., 2007; Batchelor et al., 2002; Su et al., 2013; Rabiei et al., 2017; Lyu et al., 2018).

There are two main categories of automated 3D GI methods. The first category uses an outer hull surface of the brain, which bridges the sulcal regions and tightly wraps the gyral surface of the brain. These methods hypothesize that the cortical surface is convoluted from a flat surface during development. We refer to these methods as outer surface-based GI since the GI values are dependent on the definition of the outer hull surface and the correspondence function between the cortex and its hull surfaces. An example of a local outer surface-based GI is that proposed by Schaer et al. (2008). In this approach, after computing the outer hull surface, for each point on the hull a region of interest is defined as the intersected patch of the hull surface and a sphere of a fixed radius centered at that point. By finding the closest points on the cortical surface to each point on the selected patch on the hull, the corresponding region of interest is characterized. They defined localized GI as the ratio of the perimeter of the corresponding region of the interest to the perimeter of the region of the interest on the hull surface. Other studies, such as Lebed et al. (2013), extended Schaer’s GI by proposing a new mathematical definition for computation of the outer hull surface. They noted that computing the outer surface using a surface smoothing approach would automatically find the correspondence points on the cortical surface. Lyu et al. (2018) recently proposed computing surface-based local gyrification within an anisotropic patch (kernel) instead of the traditional disc patch (Schaer et al., 2008) and used a Laplace-based method to find the correspondence between points on the cortical surface and the outer hull surface. The proposed anisotropic patch was created by performing wavefront propagation over a tensor field computed from a travel-time map. Travel-time maps were computed as the geodesic distances between the sulcal and gyral regions. These regions were segmented using sulcal and gyral curves automatically extracted from the cortex (Lyu et al., 2017; Lyu et al., 2015). Sulcal and gyral points forming the curve were detected from candidate sulcal points (the vertices with positive maximum curvatures) using a line simplification method based on two dimensional cutting planes creating contours at a given candidate point (Lyu et al., 2017; Lyu et al., 2015). The results presented by Lyu et al. (2018) rendered a more localized measure of gyrification along sulcal fundi compared to Schaer’s method (Schaer et al., 2008). However, GI values computed by both the Lebed and Lyu techniques still depend on the construction of an outer surface, and the values are ratios between the surface area of the cortical surface and that of the outer surface. Another disadvantage of outer surface-based methods is that they assign equal GI values to two cortical regions with equal sur- face areas, one formed by highly curved gyral and sulcal points and the other one with smoother curvature at sulcal and gyral points. Moreover, these methods are unable to distinguish between deep and complex folds (with a high variation of cortical mean curvature) with equal surface area (Rabiei et al., 2017). Therefore, there is a need for GI methods that are independent of any outer surface reconstruction and that are sensitive to geometric characterizations of cortical morphology such as depth and curvature.

The second category of GIs is based on cortical surface curvature, namely curvature-based GI. The curvature of a 2D surface is an important geometrical feature that quantifies its variation from a flat sur- face. The methods in this class of GI capture the local geometry of each point on the cortical surface, independent of any outer hull surface construction. Unfortunately, this very localized measure of the surface can be very sensitive to image acquisition and surface reconstruction artifacts. To tackle this problem, Luders et al. (2006a) proposed a method which computes mean 3D curvature at each point on the surface and then smooths the absolute values using a heat kernel. The method was applied to show cortical gyrification associations with mindfulness practices (Luders et al., 2012) and intelligence (Luders et al., 2009). However, as pointed out in Lyu et al. (2018), the smoothing of the curvature values have a blurring effect and reduces the ability to identify fine folding details of sulcal and gyral shape.

In this paper, we propose the use of mean curvature and the Laplace Beltrami (LB) operator for extracting intrinsic geometric features of the cortical surface. Rather than computing a local GI for each point on a triangulated cortical surface using corresponding points on the constructed outer hull, as in Lebed et al. (2013) and Schaer et al. (2008), we propose computation of a local Laplace Beltrami-based GI, hereafter termed the LB-GI, using the positions of gyri on the level sets of LB eigenfunction of the brain surface. The method inherits the biological intuition of outer surface-based GI that quantifies cortical gyrification as the degree of convolution from a flat surface, however, the LB-GI values at each point on the cortex are calculated with reference to their surrounding gyral points instead of the corresponding points on an outer hull surface.

We extend our previous work (Shishegar et al., 2015) using a new gyrification index derived from level sets of the first Laplace Beltrami eigenfunction. Previously the approach was applied to the study of cortical folding development on fetal sheep brains. However, this approach would not be able to fully capture the complex patterns of convoluted adult human cortex, as some level sets may lie parallel to the sulcal lines of the cortex. Consequently, the LB-GI values computed using these particular level sets would not necessarily reflect the neighboring geometry (Lombaert et al., 2013). Moreover, irrespective of the chosen eigenfunction or the number of level sets used for the LB-GI computation, the level sets of a single eigenfunction could not follow the highly convoluted patterns of the human cortex near the Laplace Beltrami eigenfunction extrema points. Our current work overcomes these limitations by using level sets of the first three Laplace Beltrami eigenfunctions instead of only the first (Shishegar et al., 2015). Although using three level sets increases the computational cost, the new approach reflects the 3D na- ture of the folded cortical surface more accurately. In the current paper, the utility of the Laplace Beltrami gyrification index in application to highly convoluted brains was investigated in human brain development from preschool into young adulthood and compared against conven- tional curvature-based indices.

2. Methods

2.1. LB eigenspectrum

The Laplace Beltrami (LB) operator and its eigenspectrum are isometric invariant and the values are independent of the Euclidean space embedding the shape (Reuter et al., 2009) which allows for image analysis with minimal required pre-processing. The operator has recently become popular in neuroimaging studies. It has been applied in several applications, such as shape registration (Lefèvre and Auzias, 2015), surface matching (Lombaert et al., 2013; Lombaert et al., 2012), analysis of gyrification (Germanaud et al., 2012; Rabiei et al., 2017, 2019), shape classification (Lai et al., 2009; Wachinger et al., 2015), and segmentation of cortical surfaces (Lefèvre et al., 2018). Lombaert et al. (2012) proposed an LB spectral embedding approach that learns fast and accurate mappings between surfaces and showed that using additional geometric information such as sulcal depth and cortical curvature in the spectral embedding improves the brain surface matching precision.

The LB operator of a smooth function ƒ on a Riemannian manifold M is given by

$${\text{Δ}}_{M}f=di{v}_M\left({\nabla }_M\text{f}\right)$$ (1)

where div_M and ∇_M are divergence and gradient operators on the Riemannian manifold M, respectively.

In local coordinates, such as a local surface parameterization, $\psi :R^2\to R^3$, if the metric is given by g_ij, then the LB operator of a function is computed by

$$\text{Δ}f=\frac{1}{W}{\sum }_{ij}{\partial }_i\left(g_{ij}W{\partial }_{j}f\right)$$ (2)

where

$$g_{ij}=\langle {\partial }_i\psi ,{\partial }_j\psi \rangle ,G=\left(g_{ij}\right),W=\sqrt{\det G},\left(g_{ij}\right):G^{-1}$$ (3)

The LB operator has a discrete non-negative spectrum diverging to infinity, $0\le {\lambda }_1\le {\lambda }_2\le \dots \uparrow$, and the multiplicity of each eigenvalue is finite. The Laplacian eigenvalue problem is

$${\text{Δ}}_{M}f=-\lambda f$$ (4)

Solving (4) on each brain’s triangulated surface generates eigenvalues and corresponding eigenfunctions. This processing can be achieved using the software ShapeDNA-tria ( http://reuter.mit.edu/software/ shapedna ), which implements the cubic finite element (FE) approximations as proposed in Reuter et al. (2009). Computational details can be found in Reuter et al. (2006, 2009).

After computing the eigenfunctions of the triangular surface mesh of the brain, the LB-GI is calculated by the following steps: a) computing the level sets of the first, second and third non-constant Laplace Beltrami eigenfunction; b) estimating mean curvature of the cortical surface; c) automatically detecting gyral points on each level set; d) computing LB-GI on each point on each level set as the relative curvature with reference to the neighboring gyri points, and e) mapping the values to the triangulated surface.

2.2. Computation of level sets

LB eigenfunctions are real-valued functions calculated for each vertex on a triangular mesh. As shown in Reuter et al. (2009), LB eigenfunctions with lower frequencies are stable across the surfaces and provide an “indirect registration ” between the cortical surfaces. However due to the high dimension of LB eigenfunctions, topological methods, such as the extraction of level sets of eigenfunctions, are performed to compute simpler local shape descriptors (Reuter et al., 2009). Reuter et al. (2009) showed that these shape descriptors, e.g. level sets, are localized at similar locations for heterogeneous shapes.

Here, we expand the original idea of gyrification index proposed by Zilles et al. (1988) by obtaining curved slices of the brain following LB eigenfunctions level set. Instead of slicing the brain in Cartesian coordinates along the anterior/posterior axis, the LB-GI computations employ the level sets of the first, second and third LB eigenfunctions to provide an intrinsic topological shape descriptor. As we illustrate in Fig. 1, these three level sets provide us with the anterior/posterior, superior/inferior and medial/lateral structure of the cortical surface (Shi et al., 2009).

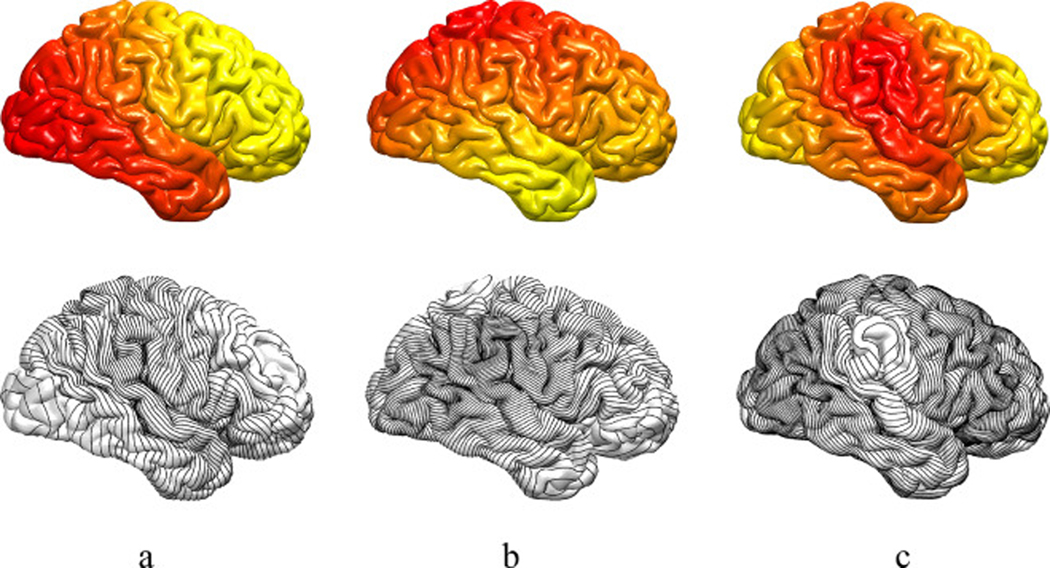
Fig. 1.

First row: The cortical surface of an exemplar human brain is color coded by the first (a), the second (b) and the third (c) LB eigenfunctions. Second row: Black curves represent the corresponding level sets of the three LB eigenfunctions.

For the real valued function $f:M\to R$, level set L_k is defined as the set of points with similar eigenfunction values (Reuter, 2010). In order for the number of level sets for each shape to be consistent, the eigenfunctions are normalized by their maximum and minimum. The N level sets are defined as

$$\begin{array}{c}{L}_k=\left\{x\in M:f(x)=f_m+k\left(f_M-f_m\right)/N\right\},\\ k=1,2,\dots ,N\end{array}$$ (5)

where f_M and f_m are maximum and minimum values respectively. The automated procedure for level set curve construction starts at the intersection of an edge and a desired eigenfunction level set line and continues by finding the two other edges in the triangle and choosing the one which the level set passes through. The procedure continues until returning to the initial point. The constructed level sets are closed polyhedral (i.e. discrete) curves in 3D space. Fig. 1 depicts the first three LB eigenfunctions and their corresponding level sets for an adult human brain extracted from MRI. We calculated N = 199 level sets for each eigenfunction which provides 200 slices in each direction (anterior/posterior, superior/inferior and medial/lateral). The number of level sets was chosen to provide a dense mesh structure, formed from closed level set curves, which fully covers and accurately follows the complex cortical folding pattern of the cortical surface. In our previous study of cortical development in fetal sheep brains (Shishegar, 2017), we showed that 99 level sets provided a dense mesh and accurate measurement of cortical folding in fetal sheep brains with a relatively smaller size and less complexity compared to human brains. For the adult human brain data considered in this paper, the new mesh structure has edge length varying from 0.1 mm to 1 mm, comparable with the original triangulated mesh with edge length between 0.05 mm and 3.5 mm.

The application of level sets of multiple Laplace Beltrami eigenfunctions has been previously reported for remeshing algorithms in the computer graphics literature (Dong et al., 2005; Lévy, 2006) and spherical parameterization of the brain surface (Lefèvre and Auzias, 2015). Shi et al. (2009) proposed a new feature space using the first three eigenfunctions. They showed that this feature space characterizes the cortical geometry, and provides meaningful anatomical features of the cortex (e.g. applicable to automatically extract primary sulcal paths). We have previously shown that by using the level sets of the first three Laplace Beltrami eigenfunctions instead of only the first eigenfunction, higher robustness is achieved in the presence of segmentation and slice artifact (Shishegar, 2017).

2.3. Gyri detection on level sets

Estimation of the mean curvature (MC) at each point on a discrete 2D surface, defined as in Luders et al. (2006a) and MacDonald (1997), is computed as the angular deviation from a flat surface. As proposed by Luders et al. (2006a), the computed mean curvature values are averaged within a distance of 3 mm on the surface in order to increase the signal to noise ratio for the curvature. Note that the definition of curvature used in this method is one way to calculate the mean curvature on a discrete surface, but there are different estimation approaches in the literature (Meyer et al., 2003; Magid et al., 2007). To make the computational steps comparable with MC and the Luders’ GI values calculated with CAT toolbox, which have been widely used in neuroimage analysis applications (Luders et al., 2006b, 2012; Gaser et al., 2006; Spalthoff et al., 2018; Hedderich et al., 2019; Evermann et al., 2020), a similar definition was used in our analysis. The MC metric can be expressed in degrees (Luders et al., 2006b, 2012; MacDonald, 1997; Gaser et al., 2006), ranging between −180 ° and 180°, which is positive for gyri and negative for sulci. While Luders et al. (2006a) smoothed the MC values with a heat kernel filter of 25 mm full width at half maximum (FWHM) to have a less spatially detailed index, hereafter termed Luders’ GI, we take a different approach explained below. They choose the FWHM based on the sulcus– gyrus pattern (20–30 mm distance between sulci and gyri). The computation of MC values and Luders’ GI can be achieved using the Computational Anatomy Toolbox (CAT; http://dbm.neuro.uni-jena.de/cat/).

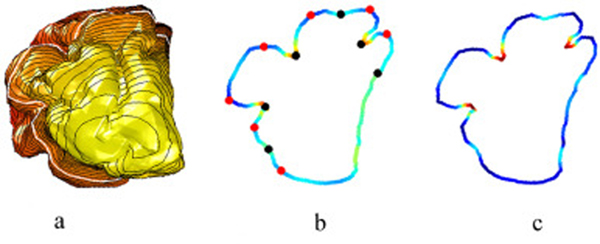
After the computation of MC, as depicted in Fig. 2 (recreated from Shishegar et al., 2016), using a fetal sheep brain at 90 day of gestational age (dga) which has less convoluted cortical folding patterns compared to adult human brain, gyral ridge points are detected along each constructed LB eigenfunction level sets. For this purpose, the surface MC is mapped to each point x _ik on kth level set, C _ik. Then, using C _ik, local maxima and minima of the curvature along the level set are detected. The indices of local maxima of the curvature of the kth level set, [ g_1k, g_2k, …], form the sequence of gyri locations for that level set. Similarly, the local minima of mean curvature form the sulci index sequence on the kth level set, [s_1k, s_2K, …].

Fig. 2.

Computation of LB-GI on an exemplar level set of a fetal sheep brain at 90 days gestational age: (a) First LB eigenfunction color encoded on triangulated cortical surface, depicting level sets (closed black curves), with a level set highlighted in white. (b) Measure of mean curvature, C, along the selected level set. Automatically detected gyri (sulci) positions are represented by red (black) bullets. (c) Illustration of LB-GI based on mean curvature at each point on the level set (figure recreated from Shishegar et al., 2016).

To suppress local optima we use the concepts from persistent homology (Biasotti et al., 2008; Edelsbrunner and Harer, 2010) as suggested in Reuter (2010) and Reuter et al. (2009). We define two concepts of topological persistence to apply to potential sulcal fundus and gyral ridge points: firstly, the absolute difference in curvature, C_xgik – C_xsik, and secondly, the distance between points on the level set, dist ( x_gik, x_gik ). This introduces two tuning parameters, C _thr and d_thr, chosen to be C_thr = 10° and d_thr = 20 mm for human brain. Pairs with a small persistence are cancelled, and a global set of gyral ridge and sulcal fundus points remains. We repeated this step by finding the new pairs in remaining set and iterated until all pairs with small persistence are cancelled. The selection of the tuning parameters was driven by human cortical morphology, and defined to cancel local minimum-maximum pairs caused by segmentation error and topological artifacts. Human gyral ridge-sulcal fundus pairs have distance between 20 and 30 mm (Im et al., 2008; Luders et al., 2006b) and show changes in curvature more than 10°, compared to maximum–minimum pairs caused by topological artifacts. A manual quality check confirmed the appropriate detection of gyral and sulcal points for the experimental data. Note that the tuning parameters directly impact the detected gyral and sulcal points and should be chosen to cancel local minimum-maximum pairs caused by topological artifacts but select the gyral ridge-sulcal fundus pairs (Fig. 2). Shishegar et al. (2016) used a similar procedure to detect sulcal fundus positions to extract sulcal lines using minima and maxima of the surface mean curvature along the LB level sets.

2.4. Computation of LB-GI

The positions of the gyri, $\left[x_{g_1},x_{g_2},\dots ,x_{g_G}\right]$, are used to define the LB-GI value at each point on a level set curve. Each point x_i lies between two gyral index locations, $x_{g_j}$ and $x_{g_j+1}$. The localized LB-GI is computed as the mean curvature, $C_{x_i}$, with reference to the mean curvature of the neighboring gyri, $x_{g_j}$, $x_{g_{j+1}}$. This results in assignation of the minimal value (zero) to gyral positions (ridge points) and maximal LB-GI values to sulcal positions. In order to render the LB-GI dependent on sulcal geometry, not just curvature, the signed curvature values are normalized by the distance of position x_i to the neighboring gyri positions along the level set curve. Let relative distance, $\omega \left(x_i\right)$, be such a weighting function,

$$\omega \left(x_i\right)=\frac{dist\left(x_i,x_{g_j}\right)}{dist\left(x_i,x_{g_j}\right)+dist\left(x_i,x_{g_{j+1}}\right)}$$ (6)

where $dist\left(x_i,x_{g_j}\right)$is the distance between points $x_i$and $x_{g_j}$on level set.

Note the difference between curvatures is computed as relative MC:$\varphi \left(x_i,x_j\right)=C_{x_i}-C_{x_j}$.

The LB-GI is then defined by

$$LB-GI\left(x_i\right)=\left(1-\omega \left(x_i\right)\right)\varphi \left(x_i,x_{g_j}\right)+\omega \left(x_i\right)\varphi \left(x_i,x_{g_j}\right)$$ (7)

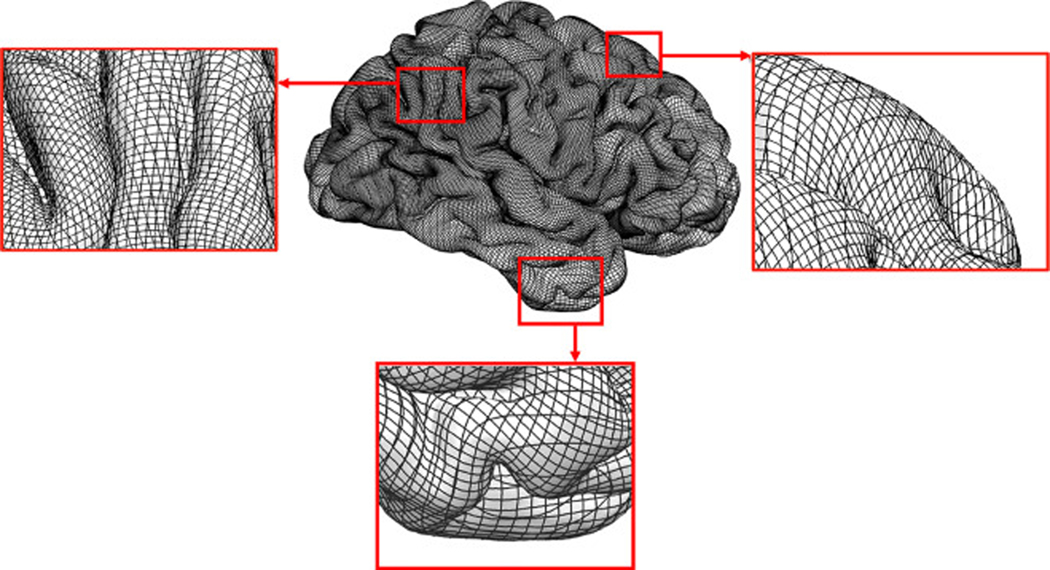
To avoid the aforementioned limitations of calculating LB-GI measure as originally proposed by Shishegar et al. (2015), we use the first three Laplace Beltrami eigenfunctions instead of only the first eigenfunction. As illustrated in Fig. 3, where one set of level sets is parallel to a sulcal line, we observe that additional level sets are oblique or perpendicular to the sulcal lines, thus allowing calculation of the relative curvature at each vertex with reference to its surrounding gyral points. Moreover, the use of three level sets creates a new, dense mesh at all regions of the cortical surface in particular at each eigenfunction extrema. Figs. 1 and 3 show that around the extrema of each eigenfunction, the level sets of the other two eigenfunctions form a mesh that provides a well-sampled coverage of the region. For instance, an extremum of the second LB eigenfunction is positioned on the temporal pole, and the first and the third level sets form the mesh around this extremum (Fig. 3).

Fig. 3.

Illustration of the first three LB eigenfunctions level sets overlaid on an exemplar cortical pial surface. The zoomed in view of three boxed areas of the pial surface show a dense mesh structure which fully covers and accurately follows the complex cortical folding pattern of the pial surface.

Finally, the LB-GI of each level set is mapped to the triangulated surface by averaging between the LB-GIs of the ten closest neighboring points calculated from different level sets. The number of closest neighboring points was chosen as a trade-off to have at least one or two points of each level set while having minimal computational cost. The LB-GI can be calculated on either the pial or white matter cortical surface. Note that the LB-GI calculates changes in the curvature weighted by distance between the position of each point to the neighboring gyri positions along the level set and therefore the values are weighted by the relative distance. The aforementioned characteristic of the LB-GI values calculated along the level sets and the dense mesh structure formed by the level sets (Fig. 3) makes the method less sensitive to the number of closest neighboring points selected for averaging.

2.5. Synthetic data

In order to compare LB-GI, Luders’ GI and mean curvature maps, we calculated the GI values on simple synthetic surfaces of the brains at different stages of development. The simulation of the brain folding process was performed using a brain longitudinal growth model proposed by Wang et al. (2019). Synthetic cortical surfaces at different stages of development (34, 38 and 42 weeks gestation) were generated from a sphere. Details about analysis and generation of the synthetic data are presented in the supplementary materials.

2.6. Experimental data and pre-processing

The applicability of the LB-GI to investigate the cortical development of the human brain from preschool to early adulthood was examined. Subjects were part of the Pediatric Imaging, Neurocognition, and Genetics (PING) Study. The study scanned approximately 1400 typically developing individuals between the ages of 3–21 years to estimate trajectories of normal brain development. A subset of the PING data was used in this study ( n = 791, age = 14.2 ± 4.3 [3–21], 48% female). The 3T, T1-weighted structural images were collected across multiple sites in a multi-modal brain imaging, behavioral and genetics study (for further information on the dataset see Jernigan et al., 2016). Participants were excluded from our study due to missing neuroimaging and demographic data, and segmentation errors caused by imaging artifacts ( n = 18). The latter was automatically detected by LB- GI algorithm. Preprocessed data, including the pial and white matter cortical surfaces and vertex-wise maps of cortical thickness, was made available as part of the publicly available dataset and used in this study ( http://ping.chd.ucsd.edu/).

2.7. Statistical analysis

In order to find vertex-to-vertex correspondence between cortical surfaces of all subjects, the multimodal surface matching (MSM) toolbox was used (Robinson et al., 2014). The surfaces registrations were driven by sulc which is a measure calculated by FreeSurfer and is a measure of sulcal depth. The target surface was the FreeSurfer’s spherical atlas namely fsaverage (Fischl et al., 1999; Yeo et al., 2010 ). To increase signal to noise ratio in group comparison tests, the GI maps were smoothed on the cortical surface using a heat kernel smoothing method based on Laplace Beltrami operator (Chung et al., 2005). To have comparable levels of smoothing with Luders’ GI, the kernel bandwidth and iterations were chosen to be $\delta =1$ and $\text{iter}=144$ respectively, equivalent to Gaussian kernel smoothing of 26 mm FWHM.

A linear model was employed at each vertex to analyze the effects of age on the degree of cortical folding. Multiple comparisons were corrected using random field theory. Vertex level p values (statistical threshold p < 0.05 corrected) were used to extract clusters of statistically significant age dependent gyrification. These analyses were performed using SurfStat toolbox ( www.math.mcgill.ca/keith/surfstat/).

We further examined the efficiency of the GI techniques for tracking cortical surface maturation. Firstly, the regions showing significant association with age were extracted and assigned to each gyral-based Desikan-Killiany parcel. The regional GI were then calculated as the mean GI across all vertices within each parcel with significant association with age. Lastly, partial correlations between age and regional GI were performed. Both vertex-wise and regional analyses were corrected for gender.

3. Results: application to study gyrification maturation with age

3.1. Gyrification maps: synthetic data

Supplementary Fig. S1 illustrates the gyrification maps of simple synthetic surfaces of the brains at age 34, 38 and 42 weeks gestation. GI maps are calculated using three different curvature-based gyrification indices, namely LB-GI, Luders’ GI and MC. Supplementary Figs. S2 and S3 present the quantitative comparison between these three GI measures.

3.2. Gyrification maps: experimental data

The gyrification maps of the white matter surface of a randomly selected 20 year old subject from the PING dataset are presented in Fig. 4. The maps are calculated using curvature-based gyrification indices, LB-GI, Luders’ GI and MC.

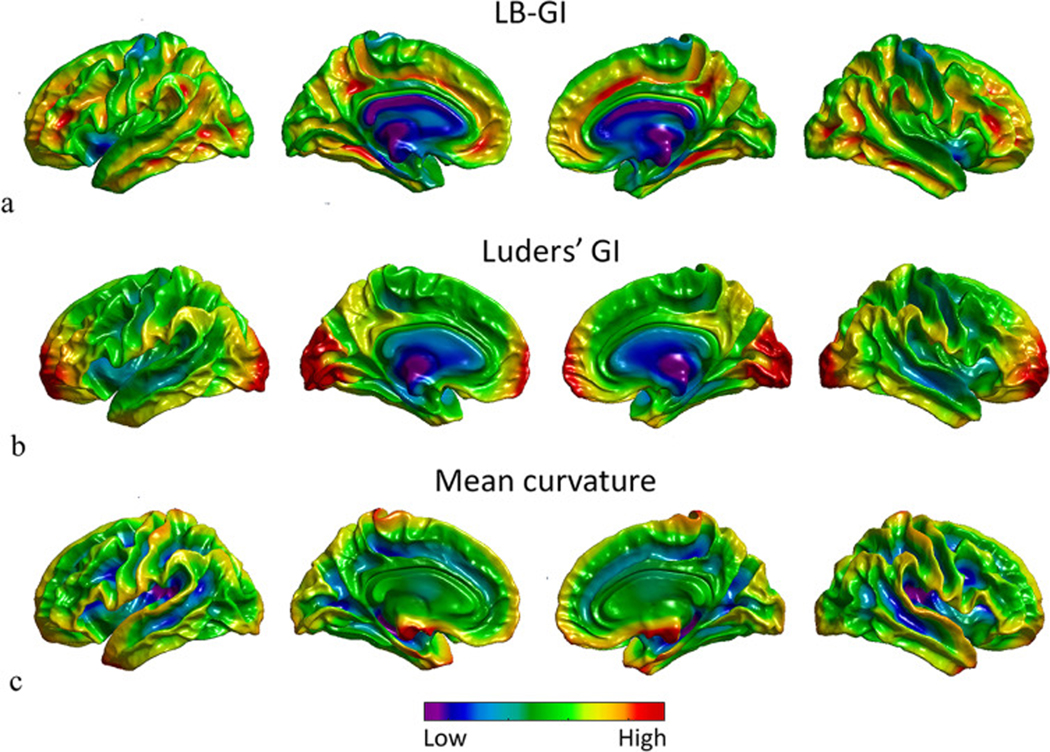
Fig. 4.

Local gyrification maps of the white matter surface of a randomly selected, 20 year old subject from the PING dataset, projected on left lateral view, medial view of left hemisphere, medial view of right hemisphere, and right lateral view respectively from left to right. (a) LB-GI values color coded on the white matter surface of both hemispheres. Note that LB-GI is a measure of weighted curvature in degrees. (b) Luders’ GI values calculated on the white matter surface values, calculated by the CAT toolbox in degrees. (c) Mean curvature of the white matter surface values, calculated by FreeSurfer in mm⁻¹. The cool and warm colors encode low and high degrees of folding respectively.

Fig. 4a illustrates LB-GI values of the white matter surface. The high values (warm colors) highlight the walls of sulcal regions reaching the maximum value at the deep highly curved sulcal basins, while low values reveal ridges of gyral regions. LB-GI is a measure of relative curvature weighted by relative distance ranging from 0° to 180° and represents both depth and curvature, resulting in a consistent assignment of minimal values (cool colors) to all gyral ridge points, not just sharply curved gyri. Fig. 4b depicts Luders’ GI values, ranging from 0° to 180°. The gyrification maps estimated by Luders’ GI are heavily smoothed and the fine details of cortical folding are absent from individual sulcal regions. Fig. 4c highlights the MC values ranging from −1 to 1 (mm ⁻¹ ), as calculated by FreeSurfer. MC assigns minimal values (cool colors) to highly curved gyral points and the maximal values (warm colors) to highly curved sulcal points. As shown by the several jagged points on the white matter surface of the brain in Fig. 4c, MC also assigns minimal values to highly curved topological defects, which may be caused by segmentation error (Reuter, 2010). This is due to the sensitivity of the measure to local curvature. In summary, the LB-GI method enables greater detection of regional cortical folding and differences along and between sulci on each individual brain compared to Luders’ and MC method.

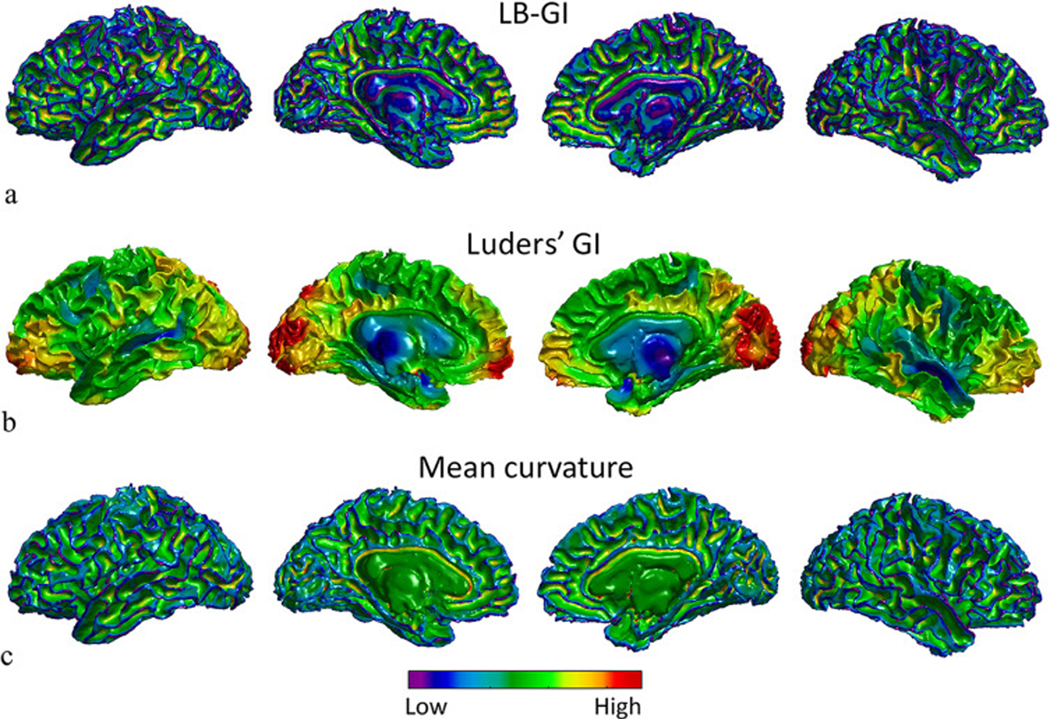
Fig. 5 illustrates the smoothed and averaged GI values of white mater surface across all 791 subjects rendered on an average atlas ( fsaverage ). Smoothing the results and averaging across all subjects presents the general features of cortical folding of the cortical surface highlighted by these three methods. Fig. 5a illustrates that even after smoothing and averaging across the subject, LB-GI highlights distinct sulcal and gyral regions. The averaged measurements of the LB-GI method also indicates most consistent gyral points across all ages and across all subjects, which are the postcentral and precentral gyri. Fig. 5b shows regions with a high degree of cortical folding based solely on curvature (Luders’ GI) but missing details at the sulcal and gyral level. Notably, some cortical regions (e.g. temporal and frontal lobes) have a higher degree of curvature compared to other cortical regions, however, these differences are not captured along the sulcal and gyral regions (e.g. the parieto occipital fissure and the occipitotemporal lateral sulcus). Fig. 5c depicts that as a result of MC measuring only curvature, the GI values may be sensitive to segmentation discrepancies. This is evidenced by high curvature around parts of hypothalamus and pituitary gland forming a sharp corner on the medial side of the brain.

Fig. 5.

Average of local gyrification values of the white matter surface of all 791 subjects rendered on of an averaged atlas (fsaverage): (a) LB-GI, (b) Luders’ GI, and (c) Mean curvature. The cool and warm colors encode low and high degrees of folding respectively.

3.3. Brain maturation with age from preschool to early adulthood

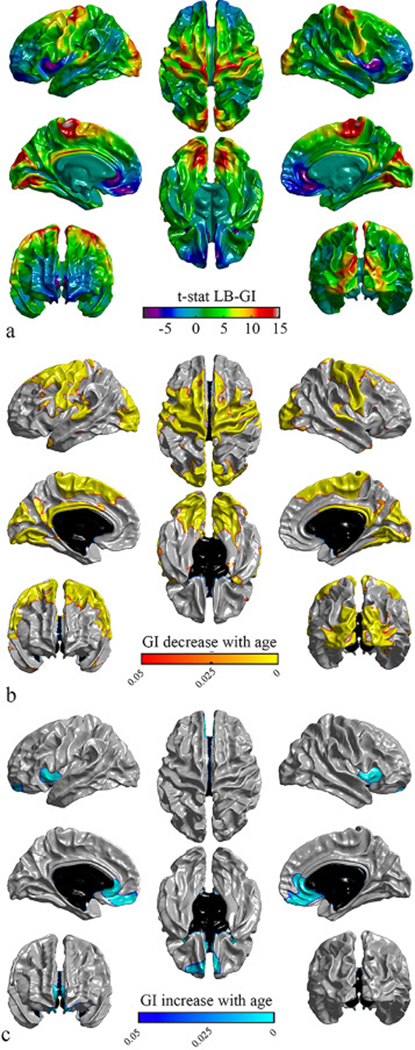
Fig. 6 illustrates the significance of cortical folding association with age for LB-GI across the cortex. There were bilateral significant negative associations with age in the precentral gyrus, the postcentral gyrus, the paracentral lobule, the cuneus, the lateral occipital sulcus, the isthmus cingulate and the lingual regions and portions of the superior frontal gyrus, the superior parietal gyrus, the precuneus, the superior temporal gyrus, the pars opercularis, the caudal anterior cingulate, the caudal middle frontal, the inferior parietal and temporal pole regions as visualized in Fig. 6b. Bilateral significant positive associations were observed in the insula, the medial orbitofrontal, frontal pole and rostral anterior cingulate regions (Fig. 6c).

Fig. 6.

Statistical maps of gyrification values for LB-GI, projected on different views of the brain. Left panel: left lateral view (top), medial view of left hemisphere (middle), anterior view (bottom). Middle panel: superior view (top), inferior view (bottom). Right panel: right lateral view (top), medial view of right hemisphere (middle), posterior view (bottom). a) T -statistic maps for an age effect on decrease in gyrification. b) Illustration of the regions of significantly decreased gyrification with age (warm colors). c) The regions of significantly increased gyrification with age (cool colors). Vertex level p -values ( p < 0.05) are corrected for multiple comparisons using random field theory; vertices surviving correction are highlighted. Non-cortical regions are colored black.

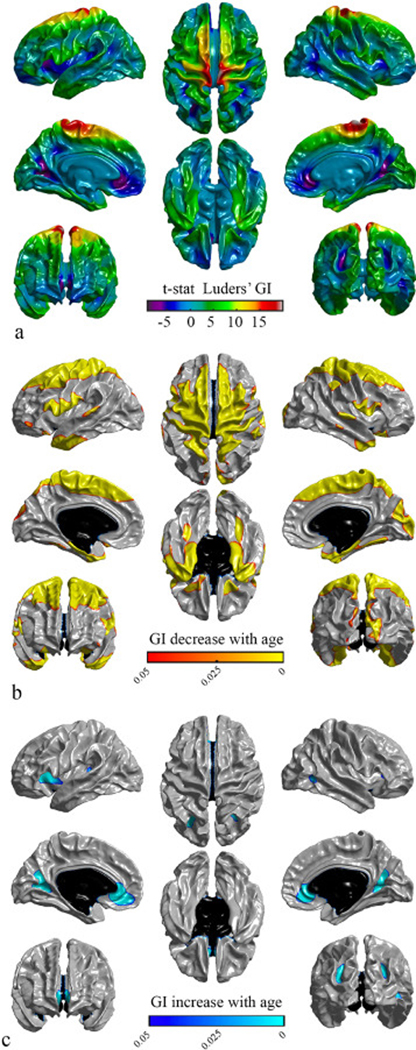
Fig. 7 shows the significance of cortical folding association with age for Luders’ GI. Bilaterally, regions with significant negative associations with age included the paracentral lobule, the entorhinal, the parahip-pocampal, the pars opercularis and the temporal pole regions and portions of the precentral gyrus, the postcentral gyrus, the superior frontal gyrus, the superior parietal gyrus, the precuneus, the superior temporal gyrus, the caudal middle frontal, the middle temporal gyrus and the inferior temporal (Fig. 7b). Lateral significant negative associations with age were shown in the right cuneus and portions of the right lateral occipital sulcus, the right lateral orbito-frontal, the right pericalcarine and the left pars orbitalis regions (Fig. 7b). Also, a significant positive association with age was present bilaterally in portions of the lingual, portions of the pre-cuneus, the medial orbitofrontal regions, and intra- parietal gyrus, and laterally in the left insula and portions of right middle temporal gyrus (Fig. 7c).

Fig. 7.

Statistical maps of gyrification values for Luders’ GI, projected on different views of the brain. Left panel: left lateral view (top), medial view of left hemisphere (middle), anterior view (bottom). Middle panel: superior view (top), inferior view (bottom). Right panel: right lateral view (top), medial view of right hemisphere (middle), posterior view (bottom). a) T -statistic maps for an age effect on decrease in gyrification. b) Illustration of the regions of significantly decreased gyrification with age (warm colors). c) The regions of significantly increased gyrification with age (cool colors). Vertex level p -values ( p < 0.05) are corrected for multiple comparisons using random field theory. Non-cortical regions are represented black.

While Figs. 6 and 7 demonstrate a large proportion of overlap between age-dependent LB-GI and Luders’ GI significant maps, there are nonetheless areas of variability between the maps. This is illustrated in the Luders’ GI results which present more lateralized significant age- dependent findings compared to the LB-GI results.

For further comparison between GI techniques, we examined the correlation between age and the regional LB-GI and Luders’ GI for selected regions. The LB-GI and Luders’ GI significance maps were mapped to a gyral-based regional parcellation, resulting in 30 regions identified that showed significant associations with age. Table 1 lists the aforementioned significant parcels and shows their association with age. Fig. S2 in Supplementary material plots the relationship between age and regional GI for the right hemisphere of each subject at each selected region. Significant correlations between age and regional LB-GI, but not with regional Luders’ GI measures, were found for a number of the selected regions.

Table 1.

Regional GI correlations with age. Reported cortical parcels were found to have significant vertex-wise association with age.

Region of interest	Left hemisphere		Right hemisphere
	LB-GI	Luders’GI	LB-GI	Luders’GI
Banks of the superior temporal sulcus	− 3.29 **	− 2.46 *	− 4.57 ***	− 1.89
Caudal anterior cingulate	− 4.27 ***	− 0.87	− 2.83 **	− 0.33
Caudal middle frontal	− 10.65 ***	− 7.46 ***	− 8.21 ***	− 5.50 ***
Cuneus	− 11.84 ***	− 1.09	− 12.73 ***	− 4.02 ***
Entorhinal	− 3.32 **	− 6.25 ***	− 4.51 ***	− 7.82 ***
Inferior parietal	− 2.04 *	− 0.09	− 3.00 **	1.18
Inferior temporal	− 1.92	− 3.47 **	− 2.18 *	− 1.65
Isthmus	− 9.34 ***	1.52	− 8.20 ***	1.80
Lateral occipital	− 14.62 ***	− 2.59 *	− 12.62 ***	− 1.84
Lateral orbitofrontal	1.65	− 1.85	1.17	− 2.74 **
Lingual	− 13.43 ***	0.92	− 11.25 ***	− 0.50
Medial orbitofrontal	5.86 ***	1.86	7.30 ***	1.16
Middle temporal	− 2.28 *	− 3.28 **	− 3.99 ***	− 2.55 *
Parahippocampal	− 4.41 ***	− 4.77 ***	− 4.00 ***	− 4.96 ***
Paracentral	− 16.83 ***	− 11.66 ***	− 16.55 ***	− 11.94 ***
Pars opercularis	− 6.28 ***	− 5.04 ***	− 3.37 **	− 3.68 ***
Pars orbitalis	− 1.67	− 3.20 **	− 2.91 **	0.06
Pericalcarine	− 3.02 **	0.61	− 4.68 ***	− 3.13 **
Postcentral	− 12.77 ***	− 9.03 ***	− 11.44 ***	− 8.41 ***
Posterior cingulate	− 8.90 ***	− 1.48	− 7.03 ***	− 0.79
Precentral	− 17.11 ***	− 10.40 ***	− 16.18 ***	− 9.25 ***
Precuneus	− 5.91 ***	− 0.55	− 6.72 ***	− 1.08
Rostral anterior cingulate	6.57 ***	5.87 ***	7.980 ***	5.45 ***
Superior frontal	− 11.21 ***	− 11.13 ***	− 7.67 ***	− 9.17 ***
Superior parietal	− 6.45 ***	− 3.39 **	− 5.52 ***	− 5.03 ***
Superior temporal	− 4.71 ***	− 1.590	− 5.13 ***	− 2.85 **
Supramarginal	− 4.61 ***	− 1.89	− 3.88 ***	− 2.40
Frontal pole	3.66 ***	1.94	4.21 ***	0.89
Temporal pole	− 2.62 **	− 5.37 ***	− 4.00 ***	− 6.11 ***
Insula	3.26 **	3.18 **	3.91 ***	1.08

^*T -statistics with p < 0.05.

^**T -statistics with p < 0.01.

^***T -statistics with p < 0.001.

4. Discussion

The present work introduces a new gyrification index, the Laplace Beltrami gyrification index (LB-GI), which combines the advantages of outer surface-based and curvature-based measures. The index employs a measurement of curvature along the level sets of the first, second and third Laplace Beltrami eigenfunctions. The method, like outer surface-based methods, provides a GI that is reflective of features of the neighboring cortical surface morphology. The LB-GI method computes weighted curvature relative to the geometry of neighboring gyral ridge points without the need to define a hull outer surface, which is a characteristic previously attributed only to curvature-based methods.

By using points exclusively on the brain surface, rather than using corresponding points on the constructed outer hull, as in (Schaer et al., 2008; Lebed et al., 2013), the LB-GI values are independent of any outer surface reconstruction. A further advantage of the approach compared to the outer surface-based GI methods (Kao et al., 2007; Lebed et al., 2013; Schaer et al., 2008; Su et al., 2013) is that the LB-GI method more accurately reflects subtle aspects of sulcal geometry. In particular, the outer surface-based GIs, which compute sulcal depth (Kao et al., 2007), do not readily differentiate between narrow and wide sulci of similar depth, which is a desired feature of a metric to distinguish between highly folded and less folded brains. Moreover, outer surface-based methods that are defined as a ratio between the area of a region of interest of the cortical surface and an outer hull surface of the cortex, are unable to distinguish between deep and complex folds (with a high variation of cortical mean curvature) as they have the same surface area (Rabiei et al., 2017). These methods are also unable to distinguish between two cortical regions with equal surface area, one containing sulcal and gyral regions with larger curvature and the other one containing regions with smaller curvature. Such geometrical characteristics of the cortical surface are important for the study of cortical morphology in neurodevelopmental and neurogenerative diseases (Im et al., 2008; Nopoulos et al., 2007; Shishegar et al., 2019). For instance, Nopoulos et al. (2007) re- ported significant lower curvature at gyral ridge and sulcal fundus points in individuals with preclinical Huntington’s disease compared to controls. The study by Im et al. (2008) reported significant decreases in mean curvature and sulcal depth in subjects with Alzheimer’s disease and Mild Cognitive Impairment compared to controls.

In contrast to our method, a number of curvature-based GI’s such as MC or derivatives of MC (Shimony et al., 2016) only provide localized measures of cortical folding (Rabiei et al., 2017). The mean curvature methods assign minimal and maximal values to highly curved gyral and sulcal points, respectively, independent of their neighboring geometry. This limitation has been overcome by proposing a local GI based on Laplace Beltrami eigenfunction level sets that provides a measure reflective of features of the neighboring environment. Other studies (e.g. Luders et al., 2006a) have circumvented this drawback by smoothing ab- solute values of the MC using a heat kernel function. However, analysis of the experimental data revealed that the LB-GI method provides more detailed results than Luders’ GI which excessively smooths the cortical folding details at the subject level. Rabiei et al. (2017) proposed two interesting and novel mathematical measures to compute local GI using curvature. Rabiei’s approach defines a mesh windowed Fourier transform using LB eigenfunctions and calculates the surface complexity by applying the mesh windowed Fourier transform to the surface mean curvature. This approach shares a common idea with the LB-GI method, i.e. to use cortical curvature as a strong geometrical measure of cortical folding, and the Laplace Beltrami eigenfunctions to model the intrinsic topology and geometry of the cortical surface (Lévy, 2006). However, as the LB-GI method calculates weighted curvature relative to the geometry of neighboring gyral ridge points, based on the hypothesis that cortical surfaces are deformed from a flat form, compared to Rabiei’s approach, the LB-GI method has the advantage of being intuitive and biologically interpretable which, in our opinion, is important when applied to neuroscience studies.

The proposed LB-GI measure was shown to be effective in characterizing associations between cortical gyrification and age. Overall, region-specific local gyrification associations with age demonstrated consistent results with other studies on human cortical development (Gogtay et al., 2004; Klein et al., 2014; Li et al., 2014; Lyu et al., 2018; Remer et al., 2017). The majority of these studies show an overall age-related increase in cortical folding and cortical thickness, during gestation and early childhood, and then a decrease from childhood to adolescence (Gogtay et al., 2004; Klein et al., 2014; Li et al., 2014). However, recent studies have revealed subtle variability between brain regions, reporting both negative and positive associations between age and both cortical folding and thickness from childhood to adolescence. In a detailed analysis of cortical folding, Lyu et al. (2018) observed decreases in the cortical folding of several regions of the cortex (e.g. cingulate sulci and central motor regions) during early childhood (0 to 2 years). In contrast, Remer et al. (2017) showed a significant increase in curvature in the insula between 1 and 5 years of age.

Cumulatively, our findings illustrate more areas of the brain showing negative than positive significant associations between age and cortical folding while the brain is developing from preschool to early adulthood. The observed bilateral positive significant association between age and the LB-GI of the insula, the medial orbitofrontal, frontal pole and rostral anterior cingulate regions may relate to the known maturation of higher-order cognitive areas in early adulthood. The lack of consistency in this pattern over the whole frontal cortex is not wholly surprising.

Higher-order cognitive regions process information from lower-order sensorimotor areas and the time course of maturation between higher and lower-order areas may differ (Gogtay et al., 2004), which is consistent with our observations of both negative and positive associations between gyrification and age. We observed slight differences in results between our method and Luders’ GI, which appear to be driven by methodological differences. For instance, both Schaer’s outer surface-based GI and Luders’ curvature-based GI fail to distinguish some fine details of the cortical folding due to computing the GI values at the subject level within a disc patch or using a heat kernel smoothing function, respectively.

Although the regions where age and gyrification are significantly correlated are comparable for both LB-GI and Luders’ GI measures, analysis in using the average GI maps from cortical regions derived from FreeSurfer reveal higher reliability to detect associations between age and cortical folding of developing brains for LB-GI compared to Luders’ MC-based GI. This is due to the ability of Luders’ GI measure to capture the overall patterns of folding, but not the detailed gyral cortical folding caused by the impact of smoothing. Losing detailed information of folding due to smoothing is more highlighted on frontal and posterior tips of the brain such as frontal pole, lateral orbitofrontal, lateral occipital, lateral cuneus, and lingual (Fig. 5, Table 1). The associations between age and gyrification in these regions has been reported in a number of studies (Lamballais et al., 2020; Kelly et al., 2013; Mallela et al., 2020). Due to the smoothing, Luders’ GI at each point quantifies the gyrification in a neighboring cortical region. Thus the average Luders’ GI across a gyral-based parcel (Desikan-Killiany atlas) also reflects the gyrification in surrounding parcels. Consequently, the proposed method also works better in the smaller Desikan-Killiany parcelles, especially regions hidden and further away from the scalp such as insula and Pericalcarine.

The main limitation of the proposed local GI is high computational complexity. The algorithm run-time per hemisphere for a convoluted adult human brain is about 10 h on a standard desktop computer. The largest computation proportion of the proposed analysis belongs to the detection of gyral points on each level set. As this step is independent for each level set, simultaneously running the iterations using array jobs on separate allocated CPU cores can reduce the computation time. For instance, splitting the iterations into a 10-element array requires 10 CPU cores, with 8 GB RAM, and reduces the running time to less than 2 h. While our method is advantageous over other more geometrically simple methods, because it incorporates curvature and depth along both sulcal and gyral regions, the utility of the measure is dependent on the research question. For example, if one was only interested in depth, the use of such a computationally complex approach may be unnecessary. Further analyses of the nonlinear effects of ageing using the LB-GI method would be beneficial for the investigation of brain maturation trajectories from early childhood to adolescence.

5. Conclusion

In this study, we proposed a new gyrification index derived from the level sets of Laplace Beltrami eigenfunctions and mean curvature, referred to as LB-GI. The proposed index requires neither definition of an outer hull surface nor correspondence between the cortical surface and outer hull, both of which are required by outer surface-based methods. The use of change in curvature along the LB eigenfunction level sets embodies traditional sulcal geometry characterizations such as depth together with a measure of sulcal curvature. The LB-GI method demonstrates more localized details of cortical folding along sulcal and gyral regions compared to Luders’ mean curvature-based index. The LB-GI method can track age-related brain development and adolescent brain maturation. Future applications of the method will be to investigate the patterns of cortical folding changes over time in neurodegenerative diseases (e.g., Huntington’s disease) using large clinical neuroimaging datasets.