Use of random forest to estimate population attributable fractions from a case-control study of Salmonella enterica serotype Enteritidis infections

SUMMARY

To design effective food safety programmes we need to estimate how many sporadic foodborne illnesses are caused by specific food sources based on case-control studies. Logistic regression has substantive limitations for analysing structured questionnaire data with numerous exposures and missing values. We adapted random forest to analyse data of a case-control study of Salmonella enterica serotype Enteritidis illness for source attribution. For estimation of summary population attributable fractions (PAFs) of exposures grouped into transmission routes, we devised a counterfactual estimator to predict reductions in illness associated with removing grouped exposures. For the purpose of comparison, we fitted the data using logistic regression models with stepwise forward and backward variable selection. Our results show that the forward and backward variable selection of logistic regression models were not consistent for parameter estimation, with different significant exposures identified. By contrast, the random forest model produced estimated PAFs of grouped exposures consistent in rank order with results obtained from outbreak data, with egg-related exposures having the highest estimated PAF (22·1%, 95% confidence interval 8·5–31·8). Random forest might be structurally more coherent and efficient than logistic regression models for attributing Salmonella illnesses to sources involving many causal pathways.

INTRODUCTION

Each year, about 9 million people in the United States become sick from known foodborne pathogens, resulting in more than 120 000 estimated hospitalizations and 3000 deaths [1, 2]. To prevent foodborne illness, we need reliable estimates of the percentages of illness attributable to specific foods so that targeted food safety interventions can be designed. Finding the sources of foodborne illnesses is challenging because causal pathways for most individual illnesses are unknown. Data from case-control studies of sporadic infections are used to estimate population attributable fractions (PAFs), defined as the proportion of cases over a specified period that would be prevented if the causal exposure was removed from the population [3, 4]. Such estimates are needed by food safety regulatory and public health agencies to assess the likely effect of interventions.

Causal pathways of sporadic enteric diseases are complex, in part because the sources may or may not be foodborne. Causality may vary geographically, demographically, and socially. As a result, the questionnaires of case-control studies often include hundreds of plausible food and non-food exposures and exposure modifiers such as food processing, handling and preparation techniques, and consumption settings. Exposure data collected by study questionnaires are hierarchically structured to ascertain broad categories of exposure (e.g. consumption of beef) and also be specific to measure levels of exposure risk (e.g. consumption of undercooked vs. well-cooked ground beef). With the limitation of mathematical tractability, analysis of study data using conventional logistic regression is challenging because of the difficulty in capturing mixed and conditional causality of numerous exposures. Another difficulty is missing data (caused by non-response), which might bias the estimation of exposure–disease relationships [5]. Furthermore, whereas study questionnaires often explore the relationships between illness and individual exposures, summary estimates are needed for groups of exposures related to the same food category. It is difficult to estimate summary PAFs for groups of exposures using a logistic regression model because individual exposures may be overlapped [6, 7]. Therefore, new approaches are needed to analyse complex causal relationships in case-control studies of infetions transmitted commonly by food.

Random forest is a powerful machine learning tool that has been successfully used to analyse high-dimensional biomedical datasets [8, 9]. Unlike logistic regression, which requires assumptions of functional forms and interactions, random forest can learn nonlinear relationships and interactions from data [10]. This is especially useful for studies with more than 20 variables of interest because it is difficult to specify a logistic regression model with appropriate biologically relevant functional forms and all plausible interactions. Although random forest is a popular tool for data mining, its application in causal inference based on observational epidemiological studies is lacking. Random forest does not produce risk estimates that allow straightforward epidemiological interpretation. For causal estimation, we developed a counterfactual random forest to estimate PAFs for grouped exposures using data from a case-control study of Salmonella enterica serotype Enteritidis (SE) infections [11]. SE is one of the most common serotypes of Salmonella bacteria reported worldwide and is a common cause of foodborne outbreaks [12].

MATERIAL AND METHODS

Case-control study data

The Foodborne Diseases Active Surveillance Network (FoodNet) is a collaborative programme between CDC, 10 state health departments, the U.S. Department of Agriculture's Food Safety and Inspection Service, and the U.S. Food and Drug Administration. Since 1996, FoodNet has conducted active, population-based surveillance of laboratory-confirmed infections caused by pathogens transmitted commonly by food [13], which provides a foundation for food safety policy and prevention efforts.

In 2002, FoodNet sites conducted a year-long case-control study of sporadic laboratory-confirmed SE infections and reported the results based on logistic regression analyses [11]. Enrolled cases were aged at least 1 year, were not known to be associated with an outbreak, and did not report contact with a household member with diarrhoea before illness began. Controls were aged at least 1 year and resided in the same FoodNet surveillance site as the cases; at least 10 controls were enrolled each month of the study. The study included 218 cases and 742 healthy controls. We restricted our analyses to 127 cases and 681 controls aged at least 5 years with no history of international travel in the 5 days before they became ill and assumed all illnesses in our study were acquired in the United States. We excluded participants aged <5 years because illnesses in young children might have causal pathways distinct from adults.

The original study questionnaire had 278 questions about food and non-food exposures, locations where the exposures occurred, and food handling practices. We restricted our analysis to six demographic variables and 66 individual exposures that were considered epidemiologically relevant and also had complete data for at least 50% of study participants. The exposures were grouped into seven transmission routes (egg, chicken, beef, other meat, dairy, produce, animal contact) for estimation of PAF (see Supplementary Appendix).

Data analyses

Random forest model

A random forest is an ensemble of decision trees based on bootstrap samples of data. Each tree is fully grown by recursively splitting a parent node, resulting in increased homogeneity of cases or controls in daughter nodes until a node could not be split further (terminal nodes). For each split, the splitting variable is selected from a random set of original variables to reduce between-tree correlation. For each tree built, about one-third of unused samples, called out-of-bag (OOB) samples, are used to assess prediction accuracy. A proximity matrix is calculated to measure closeness between observations by scoring frequencies of two observations falling into the same terminal node in all trees. The proximity matrix is used to impute missing values of a covariate based on observed values of the covariate in other observations weighted by their proximities [14].

In random forest, a permutation method is commonly used to assess the importance of variables in influencing prediction accuracy (i.e. to correctly classify observations as cases or controls). After the variable being studied in the OOB samples is permuted, its prediction accuracy is compared with that of the original prediction. Permutation importance is the difference between correct classifications before and after the variable is permutated. If the variable is important, permutation will distort the relationship and reduce prediction accuracy, whereas permutation of unimportant variables will scarcely influence prediction accuracy. Permutation importance is not straightforward for epidemiological interpretation because permutation can change exposure status in either direction (i.e. exposed to unexposed or unexposed to exposed). Consequently, permutation importance is not equivalent to an effect measure of the exposure on health outcome – we were interested only in the effect of removing exposures.

We developed a random forest model of 1000 trees based on the SE case-control study data using the random forest package [15] in R [16]. Missing values of predictors were imputed using the rfImpute function with 800 trees and five iterations. Because only 16% of enrollees in the original dataset were case-patients, we took subsamples of healthy controls to increase the case proportion to 33% for each tree built. To adapt the random forest model to causal estimation, we developed a counterfactual method to quantify the influence of reduced levels of exposures on predicted illnesses. We did this by changing the exposure status in the original dataset from exposed to unexposed according to a pre-specified probability, a, reflecting the level of reduced exposure (from 0 for no change to 1 for complete removal of exposure). Then we reran the random forest model on the altered data to calculate the change in the number of predicted cases compared to the prediction of the original data. For example, for a = 0·8, we generated a random number for each study participant from a uniform distribution (ranging from 0 to 1). If the random number was smaller than 0·8, then the status of the person was changed from exposed to unexposed; otherwise, the exposure status remained unchanged. We estimated the predicted percentage reduction in illnesses associated with the probability of reduced exposure a:

where N_ori is the number of correctly predicted cases in the original data, and N_a is the number of correctly predicted cases when exposures were reduced by a. The PAF was the predicted percentage reduction in illnesses when a = 1.

To estimate PAFs for grouped exposures, we simultaneously applied the same a value to all exposures in a transmission category. For example, all exposures that a study participant was exposed to in the egg group were subject to the same probabilistic change (a) in exposure to calculate the changes in predicted cases.

For simulation, we generated 500 a values in the range of 0–1, and calculated the reduction rate of predicted illness. We obtained a summary PAF for grouped exposures by calculating the ratio of reduced illnesses to the original number after removing the group's exposures (a = 1) from the study population. We calculated confidence intervals (CIs) by bootstrap sampling the data and building random forest models. For each sample we removed grouped exposures (a = 1) and calculated the percentage reduction in illnesses compared with the original samples. The 2·5 and 97·5 percentiles of the predicted percentage reduction in illness in 1000 bootstrap samples provided the estimated 95% CIs.

Logistic regression model

For comparison, we developed logistic regression models on the original study data using three variable selection methods: (1) a full model including all predictors and possible confounders; (2) forward, and (3) backward variable selection models based on Akaike's Information Criterion (AIC) using stepAIC (MASS package) in R [16]. We did not include interactions. We filled missing values with the variable mean (continuous variables) or mode (categorical variables) values before model fitting. We did not subsample healthy controls for model building because parameter estimation of logistic regression is robust for unbalanced data [17].

To compare the predictive ability of random forest and logistic regression, we examined each model's performance using a fourfold cross-validation method. We measured model performance based on the area under the curve (AUC) of the receiver-operating characteristic. For cross-validation, the data were randomly partitioned into four subsets. We then fitted models to 75% of the data. We applied the fitted models to the remaining 25% of the data and calculated the resulting AUC. We did this four times so that each of the four subsets served as a validation set for calculating AUC, and then we averaged the results.

RESULTS

All exposures were missing some values; this occurred more frequently in cases (1·6–15·7% for each exposure) than controls (0–1·6%) (Table 1). Furthermore, differential missingness between cases and controls was relatively frequent in variables with low exposure frequencies, such as living with a dog or cat having diarrhoea or consumption of poached eggs inside or outside the home.

Table 1.

Percentage of missing data and estimated odds ratios of significant exposures identified by different variable selection methods of logistic regression

	No. of missingness (%)		Estimated OR (95% CI)
Exposure	Cases	Controls	Full model†	Backward variable selection	Forward variable selection
Direct contact with birds	3 (2·4)	0 (0)	3·4 (1·3–8·4)	3·2 (1·4–7·1)	2·7 (1·1–6·1)
Direct contact with snakes	2 (1·6)	0 (0)	4·3 (0·9–18·7)	3·7 (1–13·4)	3·9 (1·0–14·6)
Direct contact with a gecko*	2 (1·6)	0 (0)	4·6 (0·8–30·5)	4·0 (0·9–20·5)	6·2 (1·3–34·2)
Living with dog having diarrhoea*	20 (15·7)	1 (0·1)	3·3 (0·5–16·1)		10·4 (3·3–33·4)
Living with cat having diarrhoea*	16 (12·6)	6 (0·9)	2·8 (0·3–18·5)		7·0 (2·0–25·2)
Visit pond or lake	2 (1·6)	0 (0)	0·3 (0·1–0·7)	0·3 (0·1–0·6)	0·2 (0·1–0·5)
Consumption of
Uncooked chicken	5 (3·9)	3 (0·4)	1·4 (0·8–2·5)	1·6 (0·9–2·6)
Any food containing chicken	10 (7·9)	8 (1·2)	2·6 (1·1–6·2)	2·7 (1·5–5)
Chicken cooked at home	13 (10·2)	9 (1·3)	0·5 (0·2–1)	0·4 (0·2–0·8)
Chicken cooked outside home	15 (11·8)	11 (1·6)	1·1 (0·6–2·2)		2·1 (1·3–3·3)
Uncooked ground beef*	4 (3·1)	0 (0)	109·9 (8·6–3142·3)	97·9 (9·2–2350·2)	112·5 (13·1–2611·3)
Steak	7 (5·5)	5 (0·7)	1·2 (0·7–2·1)		1·8 (1–2·9)
Roast beef	7 (5·5)	2 (0·3)	0·5 (0·2–1·1)	0·6 (0·3–1·1)
Ground beef in spaghetti sauce, tacos	14 (11)	4 (0·6)	0·5 (0·3–0·8)	0·5 (0·3–0·8)	0·6 (0·3–1)
Burger cooked at home	19 (15)	10 (1·5)	1·0 (0·3–2·9)		1·7 (1–3·1)
Pasteurized milk	3 (2·4)	2 (0·3)	0·6 (0·4–1·1)		0·6 (0·3–0·9)
Eggs	10 (7·9)	3 (0·4)	6·5 (2·5–17·4)	4·5 (2·2–9·4)
Eggs cooked at home	11 (8·7)	4 (0·6)	0·2 (0·1–0·8)	0·2 (0·1–0·5)
Scrambled eggs at home	12 (9·4)	4 (0·6)	0·5 (0·2–1·3)		0·6 (0·3–1·1)
Boiled eggs at home	13 (10·2)	4 (0·6)	1·5 (0·5–4·1)		2·0 (0·9–4·2)
Poached eggs at home*	13 (10·2)	4 (0·6)	2·7 (0·5–13·4)		6·3 (2–19·5)
Scrambled eggs outside home	13 (10·2)	6 (0·9)	0·2 (0–1·4)	0·5 (0·2–1·2)
Poached eggs outside home*	13 (10·2)	6 (0·9)	0·1 (0–3211·9)		5·8 (1·3–24·5)
Cookie dough with raw egg	2 (1·6)	0 (0)	0·2 (0–1·4)	0·2 (0–1·0)	0·2 (0–1·4)
Alfalfa sprouts	6 (4·7)	3 (0·4)	0·4 (0–2·9)	0·3 (0–1·4)
Uncooked carrots	9 (7·1)	2 (0·3)	0·5 (0·2–0·8)	0·5 (0·3–0·8)	0·5 (0·3–0·8)
Cantaloupe	6 (4·7)	1 (0·1)	0·3 (0·1–0·8)	0·5 (0·2–0·9)	0·5 (0·2–1·0)
Watermelon	5 (3·9)	1 (0·1)	2·1 (1·1–4·1)	2·4 (1·3–4·3)	2·4 (1·3–4·5)
Other melon	5 (3·9)	1 (0·1)	1·2 (0–24·6)		9·9 (1·1–76·7)
Grapes	13 (10·2)	2 (0·3)	1·4 (0·8–2·4)		1·5 (0·9–2·4)
Other pork	9 (7·1)	1 (0·1)	0·5 (0·2–1·1)	0·5 (0·3–1·0)	0·4 (0·2–0·8)
Lamb	1 (0·8)	0 (0)	0·1 (0–0·9)	0·2 (0–1·0)	0·2 (0–1·0)
Fish	9 (7·1)	2 (0·3)	0·6 (0·3–1·1)		0·6 (0·4–1·1)

OR, Odds ratio; CI, confidence interval.

^*Top ranked six exposures for permutation variable importance by random forest.

^†Estimates for the full model include only variables identified as significant by either the backward or the forward selection methods.

Variable importance of individual exposures

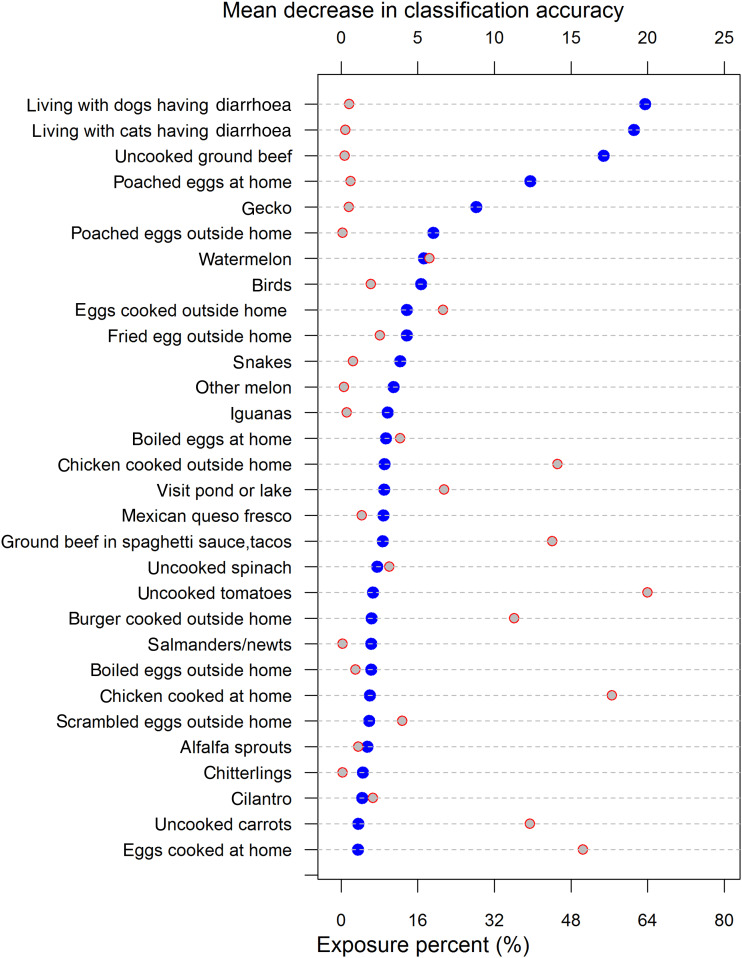
The six top-ranked variables based on random forest permutation importance (three animal-related, one beef-related, two egg-related) had low frequencies (<5%) of exposure (Fig. 1). Similarly, these six variables had high estimated odds ratios (ORs) (⩾5·8) by the forward logistic regression model (Table 1). In the three logistic regression models, estimated ORs were relatively consistent between the full and the forward selection models, but the backward selection identified different sets of significant exposures. For example, living with a dog or cat having diarrhoea were significant exposures in the forward logistic regression model, but not in the backward logistic regression model (Table 1).

Fig. 1.

Permutation importance (blue circles) by mean decrease in classification accuracy of the random forest model [normalized by the standard deviation of the differences in classification accuracy of pre- and post-permutation out-of-bag (unused) data] and exposure frequency in cases (red-grey circles) of individual exposures measured.

Estimates of summary PAFs for grouped exposures

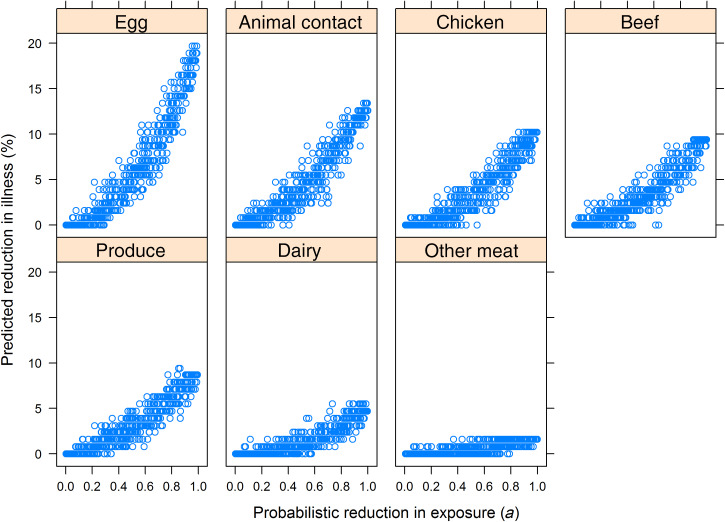
The numbers of individual exposures ascertained varied in transmission pathways. There were more exposures to eggs (12 exposures), animals (13 exposures), and produce (12 exposures) ascertained than for other transmission routes (Table 2). Exposure to eggs had the highest summary PAF by random forest (22·1%, 95% CI 8·5–31·8), followed by animal contact (12·6%, 95% CI 2·7–19·2), exposure to chicken (11·0%, 95% CI 1·5–24·8), and exposure to beef (9·4%, 95% CI 1·9–17·6). Counterfactual random forest showed that estimated reductions in SE infections appeared linearly related to exposure reductions after 20–40% of exposures in a transmission pathway were removed; the exception, however, was the dairy transmission pathway, which showed little change (Fig. 2). We observed considerable variability in the estimated reductions in illnesses associated with a given reduction in exposure; for example, hypothetical interventions reducing exposures to contaminated eggs by 0·8 reduced illnesses 9–16% (Fig. 2).

Table 2.

Estimated summary population attributable fractions for grouped exposures obtained by random forest model based on the Salmonella Enteritidis case-control study data collected by the FoodNet in 2002

Grouped exposures	Exposures in transmission category (n)	PAF (95% CI)
Exposure to eggs	12	22·1 (8·5–31·8)
Direct contact with animals	13	12·6 (2·7–19·2)
Exposure to chicken	4	11·0 (1·5–24·8)
Exposure to beef	8	9·4 (1·9–17·6)
Exposure to produce	12	9·4 (2·6–15·3)
Exposure to dairy products	9	6·3 (1·3–11·6)
Exposure to other meat (turkey, deli meat, sausage, lamb and fish)	8	3·1 (0–7·4)

PAF, Population-attributable fraction; CI, confidence interval.

Fig. 2.

Predicted percentage reduction of illness as a function of probabilistic reduction in grouped exposures based on counterfactual modelling of hypothetical interventions.

Model comparison by cross-validation

An AUC comparison showed logistic regression models were modestly predictive (68–70%) and that the approach used to select variables made little difference in predictability. The random forest model was slightly more predictive (73%).

DISCUSSION

Although random forest is increasingly being used to assess the importance of genetic markers in high-dimensional genomic data [9, 18–20], we are unaware of its application analysing epidemiological data for causal inference. In this study, we adapted random forest to model exposures ascertained in a hierarchically structured questionnaire in a case-control study of SE infections. We devised counterfactual random forest for causal estimation. Our results showed random forest could be used to analyse complex causal relationships with numerous exposures and missing values. Estimates of summary PAFs using random forest were highest for egg-related exposures, which is consistent with attributable fraction estimates for SE from outbreak surveillance data [12]. Additionally, our approach provided estimated percentages of illnesses that could be reduced by incrementally decreasing the frequency of risk exposure.

Logistic regression is widely used in epidemiological studies for causal inference. With a relatively limited number of variables (e.g. <20), it provides estimates of ORs and PAFs. [21, 22] However, its limitations become apparent when analysing datasets with a high number of relevant exposures and multiple interactions. Interactions are fundamental to the analysis of diseases with complex causality because the exposure–disease relationship may differ between groups or may be affected by modifiers in different ways in different groups. Rarely is sufficient information about interactions available to include all in a model; for example, specifying all interactions for the 72 predictors in our SE data would be nearly impossible. Because estimated ORs vary depending on other variables in the model, logistic regression estimation can be unstable for complex data. For example, consumption of poached eggs cooked outside the home was not associated with risk (OR 0·0) in the full logistic regression model but was highly risky (OR 5·8) in the forward variable selection model. In addition, the three logistic regression models appeared to identify many ‘protective’ exposures (OR <1), such as consumption of roast beef, eggs cooked at home, and alfalfa sprouts, which were likely artifacts because those estimates were dependent on the other predictors in the models.

Another limitation of logistic regression is that it implies parallel proximity of causality (i.e. each exposure has the same proximity to the risk of disease) [23]. However, when exposures belonging to the same transmission pathway are nested, the exposure on top of the nest might be distant causally in the chain of the exposures. For example, three of the four chicken-related exposures (consuming uncooked chicken, consuming chicken cooked at home, consuming chicken cooked outside the home) retained in at least one of the logistic regression models were nested in a fourth exposure (consuming any food containing chicken). The fourth exposure, at the top of the nest, might be related to illness conditional on the nested exposures below. An estimated PAF that does not properly account for chained causality tends to neglect or underestimate the distant causality [23]. Therefore, logistic regression models can be inadequate for reliable causal inference or estimation of summary PAFs [23].

By contrast, random forest is not compromised by a high number of predictors because interactions and nonlinearity are learned from the data [10]. Tree-based models are structurally accommodating of conditional causality in which an exposure higher on a tree is related to the disease risk through exposures down the tree. Empirical and theoretical studies demonstrate the superiority of random forest for model prediction and evaluation of variables [24, 25]. The epidemiology of sporadic enteric illnesses such as SE infection entails multifactorial causality that varies over large geographical areas and includes diverse social and demographic characteristics. Therefore, the causality of SE illness might be context-dependent and locally defined. Random forest provides a reliable mechanism to derive exposure–risk relationships in diverse and complex contexts, including interactions [26].

Another advantage of random forest is that it imputes missing covariates based on a proximity matrix, which uses weighted averages of observed values from similar cases. This approach may be more reasonable than complete case analysis or filling missing data with the mean or mode, as is frequently done in logistic regression. In this SE case-control study, filling missing data with the most common value was a concern because the effect of low-frequency risky exposures might be underestimated if many of the missing values were filled as unexposed. This was especially problematic in our study because many cases had missing values, and simple filling would bias the exposure status downward compared with controls. For example, 17 values were missing in our data for the variable ‘consuming poached egg in home’ (13 cases, four controls). Random forest imputed 11 missing values (seven cases, four controls) as exposed and six (all cases) as unexposed, whereas simple filling with the variable mean or mode set all 17 missing variables as unexposed.

For counterfactual modelling, we did not differentiate exposures based on their manipulability to intervention. For example, chicken consumers were counterfactually changed into a subpopulation that did not consume chicken during the 5 days before the onset of illness. Our interpretation of the counterfactual modelling is that simulated reduction or removal of chicken consumption serves as a proxy for different hypothetical food safety interventions such as reducing contamination in chicken products or improving chicken handling and preparation practices. We assumed that the multitude of trees approximated complex causal pathways of sporadic illness to the extent that the average effect of exposure removal on predicted illness across all trees would estimate the summary PAF for the target population.

A limitation of random forest for causal inference is the opaqueness of tree assembly, which prevents interpretation of individual trees. Random forest was introduced as a predictive tool that used the black-box approach for mapping input variables and predicting values of a response variable, and permutation variable importance was biased toward correlated predictors [27]. For observational epidemiological studies, the focus is on causal inference rather than prediction. We adapted random forest for causal inference because of its ability to account for complex data structures inherent to many case-control studies of enteric disease. By estimating the PAF of grouped rather than individual exposures, we minimized the inherent bias of variable importance in correlated exposures in the same transmission route. Overall, random forest has distinct advantages over logistic regression models: flexible functional forms, better ability to model interactions between variables, and imputation of missing data. Coupled with the counterfactual estimation method that we propose that random forest can provide a meaningful estimation of PAFs to estimate the sources of foodborne illnesses.

DECLARATION OF INTEREST

None.