SUMMARY
A randomized control trial on verocytotoxigenic Escherichia coli (VTEC)-infected farms found evidence that: (1) keeping animals in the same group; (2) maintaining dry bedding; (3) preventing direct contact with neighbouring cattle; and (4) maintaining a closed herd, were associated with a reduced risk of infection in youngstock aged 3–18 months. This study evaluated these interventions using a cost-effectiveness framework for UK dairy farms. Keeping animals in the same group was considered to have negligible cost and was feasible for herds containing over 77 dairy cows. Assuming equal efficacy of the remaining interventions, preventing direct contact between neighbouring cattle is most cost-effective with a median annual cost of £2.76 per cow. This compares to £4.18 for maintaining dry bedding and £17.42 for maintaining a closed herd using quarantine procedures. Further model validation and exploration of other potential benefits are required before making policy decisions on VTEC control.
Key words: Cost-effectiveness study, Escherichia coli (E. coli), zoonoses
INTRODUCTION
Verocytotoxigenic Escherichia coli (or VTEC) O157:H7 is a bacterial zoonosis that can cause severe disease in humans but is asymptomatic in the animal host. Although isolated from a variety of species, ruminants are the usual source in human outbreaks. Transmission to humans is usually through contaminated food, which can be controlled through abattoir and pasteurization measures. However, foodborne outbreaks continue to occur and a significant proportion of human infections occur through contact with animal faeces and contaminated water [1]. Although measures such as hand washing are considered effective in decreasing the risk of transmission in some circumstances, they may be practically difficult to implement particularly in groups at high risk of infection like young children [2]. Therefore measures that reduce the prevalence of animals shedding the pathogen are important in managing the risk associated with zoonotic transmission. Research in this area was highlighted in the report produced in the aftermath of the Godstone Farm outbreak in Surrey 2009, the largest disease outbreak in the UK associated with an open farm [3].
Few established measures have been identified to reduce the prevalence of infection on farms. Vaccinating cattle has shown some efficacy in experimental trials [4] but is some way off being a commercially available licensed product. Studies have shown that prevalence of shedding is higher in youngstock [5] and risk-factor studies have identified a number of management factors associated with an increased prevalence in this group such as being housed rather than at pasture, spreading slurry on land rather than manure, feeding straw when housed, and poor bedding management [6, 7]. With this knowledge, a randomized control trial (RCT) was performed to assess a variety of potential intervention measures to reduce the prevalence of VTEC in youngstock [8]. This study provided evidence of a reduced prevalence associated with keeping animals in the same group; maintaining dry bedding; having no direct contact with other cattle; and no new animals being introduced into the herd unless under quarantine.
Who pays for the control of zoonotic disease requires an assessment of public and private benefits [9], which is of importance for diseases such as VTEC as there are no tangible farm-level benefits, only human health benefits. A discussion on this is beyond the scope of the current study, which will focus on the cost-effectiveness of interventions, an important aspect for guiding decision making. A previous cost-effectiveness analysis of measures in the beef supply chain using transmission models found slaughterhouse-based control measures to be more cost-effective than farm-level interventions [10]. However, reducing the prevalence on farms has implications for other routes (direct contact with cattle or contact with contaminated farm environment) of transmission to humans. The current study is a cost-effectiveness analysis of the control measures found in the RCT to reduce the prevalence of VTEC as applied to a UK dairy herd [8] and therefore informs assessment of feasibility of these on-farm measures to minimize the risk of human infection. The study hypothesis is that the control measures described by Ellis-Iversen et al. [8] provide a cost-effective approach to reducing VTEC prevalence in UK dairy youngstock in a variety of farm settings.
MATERIALS AND METHODS
Trial description
The original trial was performed between October 2003 and November 2004. Farms were initially identified and recruited with the inclusion criteria of having at least 60 cattle (including 20 youngstock); negative test results for tuberculosis; and not having any public access enterprise on the farm [6]. One or more positive cultures from 20 faecal samples from weaned youngstock aged 3–18 months were used to define VTEC-positive farms and eligibility for trial recruitment. Farms were randomly allocated to four groups including one control and three intervention packages (Table 1). Four farm visits were conducted 4–6 weeks apart where a single group of youngstock aged between 3 and 18 months was monitored. Visits comprised of taking faecal samples from the monitored group and assessing compliance to the individual measures within the assigned intervention package. Farms that applied a measure for at least 75% of the time were considered to have implemented it in the analysis. Risk ratios were calculated for each group compared to the control using generalized estimating equations that accounted for repeated measurements on the same group. Intention-to-treat analysis, adjusted for actual compliance with the individual measures, revealed good evidence of a reduction in VTEC prevalence only with package ‘A’ (Table 1). Stepwise removal of individual measures within the superior package revealed evidence that the effect was associated with keeping animals in the same groups (P = 0·01), maintaining dry bedding (P = 0·01), having no direct contact with other cattle (P = 0·07) and no new animals being introduced into the herd (P = 0·07). The cost-effectiveness analysis in this study only focuses on the effects seen in package A and assumes these four measures alone to be causing the reduced VTEC prevalence observed.
Table 1.
Control package interventions and their measures of effect from intention-to-treat analysis adjusted for compliance to the individual intervention measure (adapted from [ 8])
| Interventions allocated | A | B | C | Control |
|---|---|---|---|---|
| None | ✓ | |||
| No new animals brought in | ✓ | ✓ | ✓ | |
| No contact with other cattle | ✓ | ✓ | ✓ | |
| No shared water sources | ✓ | ✓ | ✓ | |
| Keep bedding dry | ✓ | ✓ | ||
| Keep animals clean | ✓ | ✓ | ||
| Maintain closed group | ✓ | ✓ | ||
| Use boot-dip | ✓ | ✓ | ||
| Use overcoat | ✓ | ✓ | ||
| Clean water troughs weekly | ✓ | ✓ | ||
| Empty water troughs weekly | ✓ | ✓ | ||
| Risk ratio (95% CI) | 0·14 (0·02–0·84) | 0·80 (0·20–3·10) | 0·77 (0·14–4·34) | |
| P value | 0·032 | 0·744 | 0·768 |
CI, Confidence interval.
Model approach and description
The approach taken in the analysis was to create and parameterize cost models of four independently implemented interventions on UK dairy farms. In order to account for the variability in farm types and the uncertainty in some parameters, a stochastic approach was taken where appropriate. Interventions were defined in accordance with those used by the authors of the original trial [8]. Significant capital expenditure, such as the cost of new buildings, was not considered and interventions were assumed to be implementable within the farm's pre-existing structure without such investment. All models were developed using an Excel spread sheet and Monte Carlo simulation was performed using stochastic modelling add-in software (@Risk 5.7, Palisade Corporation, USA) and Latin Hypercube sampling.
Advice on assumptions related to management practices was gained through an interview conducted with the farm manager at the Royal Veterinary College dairy unit. Generation of the cost models identified data requirements that were gathered through a combination of a literature search, primary data collection and contacts within industry. Some data were included based on the primary author's experience of dairy farm practice. Where original data were available, continuous data distributions were fitted using the Kolmogorov–Smirnov goodness-of-fit statistic. For primary data collection, veterinary surgeons in farm animal practices were contacted in Somerset, Wales and South East England and asked to identify farms that carried out the relevant measures. The objective was to get a minimum of five farms to participate with the extreme values from these farms forming the upper and lower limits of a uniform distribution in the model.
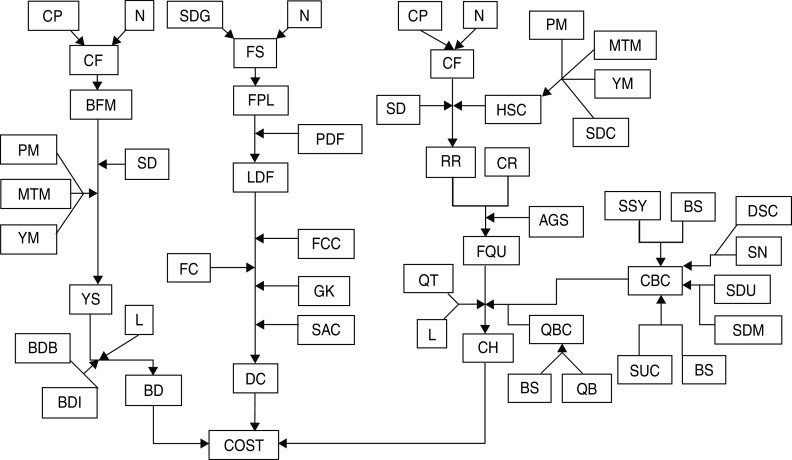
For keeping animals in the same groups and maintaining dry bedding, the interventions were only applied to youngstock aged 3–18 months and it was assumed they would be housed for the entire period. Within all models the number of breeding cows is kept constant, all dairy heifers produced are retained as replacements with any surplus sold as in-calf heifers over the age of 18 months, and all non-dairy heifers/ bull calves are sold/culled before the age of 3 months. Any purchased replacements are aged >18 months and quarantined prior to entry. All additional labour is based on the extra time an employee would have to be paid rather than the farmer accruing additional duties. Further details of intervention cost models are outlined below and represented in Figure 1. Accompanying abbreviations, equations and input parameters are shown in Tables 2–4.
Fig. 1.
Flowchart of model inputs in relation to overall cost output (for explanation of abbreviations see Table 2).
Table 2.
Description of symbols used in model diagram
| Symbol | Parameter | Symbol | Parameter | Symbol | Parameter |
|---|---|---|---|---|---|
| AGS | Average group size purchased | FC | Fencing cost (consumables and labour) | QBC | Bedding cost in quarantine |
| BD | Cost of keeping bedding dry | FCC | Fencing construction cost | QT | Extra labour in quarantine |
| BDI | Time for keeping bedding dry – intervention | FPL | Farm perimeter length | RR | Herd self-replacement rate |
| BDB | Time for keeping bedding dry – baseline | FQU | Frequency of quarantine use | SAC | Cost of maintaining land for set aside |
| BFM | Number of youngstock born in a 15-month period | FS | Farm size | SD | Proportion of cows served to dairy semen |
| BS | Cost of barley straw | GK | Cost of grass keep | SDC | Proportion of heifers aged >18 months that calve |
| CBC | Combined main herd bedding cost | HSC | Proportion of heifers born that survive and conceive | SDG | Pasture stocking density |
| CF | Calving frequency | L | Labour cost | SDM | Amount of sawdust used on mattresses |
| CH | Cost of maintaining a closed herd using quarantine | LDF | Length of double fencing | SDU | Sawdust cost |
| COST | Combined cost of interventions | MTM | Mortality rate (age 24 h to 3 months) | SN | Sand cost |
| CP | Proportion of cows calving per year | N | Number of dairy cows in herd | SSY | Amount of straw used in straw yards |
| CR | Culling rate | Proportion of perimeter double-fenced | SUC | Amount of straw used on cubicles | |
| DC | Cost of preventing direct contact between cattle | PM | Perinatal mortality (birth to 24 h) | YM | Mortality rate (age 3–18 months) |
| DSC | Amount of sand used in deep sand cubicles | QB | Bedding use in quarantine | YS | Average number of youngstock (age 3–18 months) |
Table 3.
Calculated values not included in the main text
| Parameter | Symbol* | Calculation | Units |
|---|---|---|---|
| Keep bedding dry | |||
| Calving frequency | CF | (N × CP)/365 | Births/day |
| Births in a 15-month period | BFM | 456·25 × CF | Number |
| No direct contact with other cattle | |||
| Farm size | FS | SDG × N | Hectares |
| Fencing perimeter length | FPL | 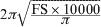 |
Metres |
| Length of double fencing | LDF | FPL × PDF | Metres |
| No new animals being brought into the herd | |||
| Proportion of heifers born that survive and conceive | HSC | (1 – PM) × (1 – MTM) × (1 – YM) × SDC | Proportion |
| Self-replacement rate | RR | 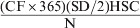 |
Proportion/year |
| Frequency of quarantine use | FQU | 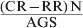 |
Number |
| Combined bedding cost | CBC | Discrete({SSY × BS, DSC × SN, SDU × SDM, SUC × BS}, {0·25, 0·25, 0·25, 0·25}) | £/day |
For explanation of symbols see Table 2.
Table 4.
Model inputs and distributions used in the stochastic model
| Parameter | Symbol* | Value and distribution | Unit | Source |
|---|---|---|---|---|
| Global parameters (affecting more than one intervention cost) | ||||
| Average number of breeding cows in herd† | N | Gamma (2·84, 53·9) | Number | National Milk Records, 2011 |
| Proportion of cows calving per year† | CP | Gamma (2·64, 0·142) | Proportion | National Milk Records, 2011 |
| Perinatal mortality (birth to 24 h)† | PM | Pearson 5 (4·52, 0·295) | Proportion | [11] |
| Young stock mortality (age 24 h to 3 months)† | MTM | Exponential (0·0215) | Proportion | [11] |
| Young stock mortality rate (age 3–18 months)† | YM | Exponential (0·0402) | Proportion | [11] |
| Proportion served to dairy | SD | Varied in scenario modelling | n.a. | |
| Labour cost | L | Constant (13·08) | £/hour | [12] |
| Keeping bedding dry (BD) | ||||
| Time for keeping bedding dry (baseline) | BDB | Uniform (0·66, 1·0) equivalent to 2–3 min every 3 days | Minutes/animal/day | User defined estimate |
| Time for keeping bedding dry (intervention) | BDI | Uniform (1·0, 2·0) | Minutes/animal/day | User defined estimate |
| No direct contact with other cattle (DC) | ||||
| Stocking density (grazing)† | SDG | Gamma (12·0, 0·198) | Cows/ha | Promar, 2011 |
| Fencing cost (consumables and labour) | FC | Uniform (0·0098, 0·32) | £/metre | Primary data collection |
| Fencing construction cost | FCC | Constant (3·45) | £/metre | [12] |
| Grass keep | GK | Constant (110·0) | £/ha/year | [12] |
| Set aside variable cost | SAC | Constant (20·0) | £/ha/year | [13] |
| Proportion of perimeter double fenced | Varied in scenario modelling | n.a. | ||
| No new animals being brought into the herd (CH) | ||||
| Extra labour in quarantine | QT | Uniform (0·0, 1·52) | Hours/day | Primary data collection |
| Bedding use in quarantine | QB | Uniform (0·0, 58·0) | Kg/cow/day | Primary data collection |
| Culling rate† | CR | Gamma (4·12, 0·080) | Proportion/year | National milk records, 2011 |
| Proportion that calve after reaching age 18 months† | SDC | Exponential (0·045) | Proportion | [11] |
| Barley straw† | BS | Logistic (58·4, 1·90) | £/tonne | [20] |
| Sand cost | SN | Constant (15·0) | £/tonne | Cardigan Sand and Gravel Ltd, 2011 |
| Sawdust cost | SDU | Uniform (45·0, 90·0) | £/tonne | NW Resources Ltd, 2011 |
| Main herd bedding (straw yards) | SSY | Constant (5·48) | Kg/cow/day | [12] |
| Main herd bedding (deep sand cubicles) | DSC | Uniform (7·5, 10·0) | Kg/cow/day | [14] |
| Main herd bedding (sawdust on mattresses) | SDM | Uniform (0·75, 1·0) | Kg/cow/day | [14] |
| Main herd bedding (straw on cubicles) | SUC | Uniform (2·5, 4·0) | Kg/cow/day | [14] |
| Average group size purchased | AGS | Varied in scenario modelling | n.a. | |
n.a., Not applicable.
For explanation of symbols see Table 2.
Parameters fitted to original data using @Risk 5.5 (Palisade Corporation, USA).
Keep animals in the same group (‘SG’)
The intervention ‘SG’ is defined as maintaining animals in the same group and not adding animals once the group has been constructed. In the RCT, these groups were formed after weaning and the age range was 3–18 months. The cost of ‘SG’ is assumed to be negligible. However, the measure will only be feasible on farms above a certain size that produce sufficient calves to form a management group between weaning and age 3 months. Assuming an all year around calving pattern, the number of calves available to form a group will depend upon the calving frequency (estimated from the number of breeding cows/calving interval), weaning age and minimum group size. From this information, Goal Seek Analysis in Excel was used to estimate the minimum feasible herd size for this intervention.
Maintain dry bedding (‘BD’)
The ‘BD’ intervention ensures that bedding is kept at a level so animals remain clean and dry and do not become contaminated when lying down. Daily assessments are made by pressing the bedding with the heel of the boot and more material added if the bedding ‘squelches’. The assumed baseline measure is performing the same task every 3 days. Potential inputs considered include extra labour and bedding, together with the total number of youngstock aged between 3 and 18 months.
On an individual farm, the absolute amount of bedding required will depend upon factors such as stocking density, ventilation, diet, age of animals and water trough position. However, the use of extra bedding is considered negligible because when bedding is applied less frequently, relatively more is applied. Therefore the marginal cost is assumed to only depend upon extra labour which itself is dependent on the number of youngstock present.
The number of youngstock on the farm aged between 3 and 18 months will vary according to the farm's replacement policy (self-replacement or buying in), the frequency of births and the timing of any purchases or sales. With the assumption that herds sell/cull all beef and male dairy calves at birth and no replacement purchases are made of cattle aged <18 months, the average number of youngstock present between the ages of 3 and 18 months will depend upon: the number of births in a 15-month period; the proportion of animals served to dairy semen (i.e. potential replacements); the proportion of animals reaching the age of 3 months and the youngstock mortality rate between the age of 3 and 18 months so that
| (1) |
where YS = average number of youngstock on farm aged between 3 and 18 months, BFM = number of youngstock born in a 15-month period, SD = proportion of cows served to dairy semen, PM = perinatal mortality (within first 24 h of birth), MTM = mortality rate from age at 24 h to 3 months, and YM = mortality rate from age 3 to 18 months.
This calculation assumes all dairy heifers born are retained in the herd, there is a linear mortality rate from age 3 to 18 months, and there is no change in overall herd size. The calculation also assumes that the mortality rates are independently consistent with the source study findings [11].
The overall annual cost for the intervention can be represented as
| (2) |
where BD = annual cost of keeping bedding dry compared to baseline (£/year), YS = average number of youngstock on farm aged between 3 and 18 months, BDI = time for keeping bedding dry – intervention (minutes/animal/day), BDB = time for keeping bedding dry – baseline (minutes/animal/day), and L = labour cost (£/hour).
No direct contact with other cattle (‘DC’)
The ‘DC’ intervention is focused upon limiting nose-to-nose contact between livestock on bordering units. Double fencing may be used but is not necessarily required, such as when there are no neighbouring units, neighbourly agreements not to graze in adjacent fields or when physical barriers prevent contact (e.g. roads, rivers). The only costs for this intervention are assumed to be associated with any double fencing required. The baseline scenario is that double fencing is not present and direct contact with neighbouring cattle is possible.
A secure outer perimeter fence is assumed to be present on all farms to prevent stock escaping and therefore not an intervention cost. Farmers using double fencing were contacted and asked to estimate the amount of labour and consumable cost required each year for maintaining the extra fence above the normal cost for the outer perimeter. Farmers were then asked to estimate how much of the land was double fenced so that a cost per metre could be calculated. When double-fencing length was unknown, the farmer estimated the proportion of the perimeter that was double fenced and the total perimeter was estimated from the land area, assuming the farmland was circular. Both beef and dairy farmers were considered appropriate for contact.
For the stochastic model, farm perimeter length can be estimated from knowledge of the number of breeding cattle and published pasture stocking densities assuming a circular perimeter (Table 3). The proportion of the perimeter requiring double fencing will vary and therefore this was evaluated through scenario simulations. Assuming a fence lifetime of 10 years, the average yearly cost is assumed to be one tenth of the total construction cost. Limited information on maintenance costs are available so primary data collection was performed. The area of land within the double-fence boundary will not be available for grazing and is assumed to have a cost from forgone revenue equivalent to potential earnings from leasing the area for grass keep. This area of land also has a maintenance cost considered equivalent to the variable costs associated with set aside land. Double-fencing width is assumed to be 3 metres, which is consistent with industry recommendations [15].
The overall cost for this intervention for a 1-year period is
| (3) |
where DC = annual cost of having double fencing (£/year), FC = fencing cost (consumables and labour) (£/m), FCC = fencing construction cost (£/m), LDF = length of double fencing (m), GK = cost of grass keep (£/ha/year), SAC = cost of maintaining land for set aside (£/ha/year).
No new animals being brought into the herd (‘CH’)
The ‘CH’ intervention is defined as the farm being closed with any new cattle introduced being from another closed unit owned by the farmer or born on the farm. Where being closed is impossible from required replacements, the use of a quarantine area or pen must be used for a 3-week period. The costs associated with this measure are the extra labour and bedding when a cow is in quarantine above that incurred if the cow were in the main herd enclosures. It is assumed that cows are housed when quarantined and bedded on barley straw. Feed costs are assumed to be identical. Dairy farmers were contacted and asked to estimate the daily labour and bedding required for a single lactating cow. In the model, a 0·1 compounding factor is incorporated for each additional cow simultaneously quarantined to account for extra labour and bedding. Labour cost when a cow is in the main herd is assumed negligible and not considered in the analysis. The extra bedding cost is compared with four bedding scenarios: (a) straw yards, (b) deep sand cubicles, (c) sawdust on mattresses, (d) straw on cubicles. The four scenarios are combined into a single discrete distribution representing the variability in costs in the population assuming an equal probability of each bedding type (Table 3).
The frequency of quarantine use depends on the number of replacements required and the average group size purchased. Assuming a constant herd size, the self-replacement rate can be estimated from the number of calves born per year, the proportion of the herd served to dairy semen that produces heifers and the proportion of heifers that survive, conceive and enter lactation (Table 3). To maintain herd size, any deficit in replacement rate relative to the culling rate necessitates purchased replacements with a frequency of quarantine use being derived from the average batch size purchased.
The overall annual cost of maintaining a closed herd, assuming a 21-day quarantine period for any purchases, can be estimated as
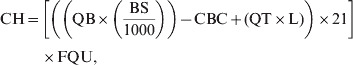 |
(4) |
where CH = annual cost of maintaining a closed herd (£/year), QB = bedding use in quarantine (kg/cow/day), BS = cost of barley straw (£/tonne), CBC = combined main herd bedding cost (£/day), QT = extra labour in quarantine (hours/day), L = labour cost (£/hour), and FQU = frequency of quarantine use (number/year).
This equation assumes any surplus heifers are sold as in-calf heifers to maintain a constant number of breeding cows in the herd.
Outputs
Risk ratios were the measures of effect used in the RCT. The non-intervention baseline scenario is equivalent to a risk ratio of 1·0 (i.e. no increase or decrease in the farm prevalence of VTEC in youngstock). The four parameters together were assumed to be associated with a risk ratio of 0·14 and therefore an attributable fraction of 0·86 (1 – risk ratio). The attributable fraction is the proportional reduction in the prevalence of VTEC if the intervention measure(s) are implemented (i.e. there is an 86% reduction in the prevalence of VTEC with implementation of all four measures). Individual measures of effect for the four interventions were not available so assumptions of equal effects were made so that each individual measure's effect is equivalent to 25% of the total attributable fraction (equal to 0·215). All costs generated from the equations are expressed on a per cow basis with cost-effectiveness calculated as the intervention cost per dairy cow divided by the attributable fraction. Where more than one intervention measure is employed, the attributable fraction is additive (i.e. two measures’ effect are equivalent to an attributable fraction of 0·215 × 2=0·43). The assumption of equal measures of effect was explored using sensitivity analysis.
Scenarios
Scenarios were considered for variables where data were not readily available. These included the proportion of perimeter that had to be double fenced, the proportion of breeding animals served to dairy semen and the average group size purchased that enter quarantine. For each scenario, individual interventions were considered alone, and in combination, assuming an equal effect associated with each intervention. Due to no cost being associated with keeping animals in the same group, this intervention was assumed to occur in all scenarios.
Sensitivity analysis
As part of the cost-effectiveness analysis, various sensitivity analyses were conducted. A one-way sensitivity analysis was performed to explore the assumption of equal effect associated with each intervention. For the four individual cost models, important inputs were established using non-parametric Spearman's rank-order correlations generated using @Risk software. All sensitivity analyses were performed keeping proportion of perimeter double fenced, proportion of cows served to dairy semen, and average group size purchased constant and the model was run for 10 000 iterations (see Table 2 for abbreviations). Correlation values less than a quarter of the maximum correlation were considered insignificant [16].
RESULTS
The feasibility of keeping animals within the same group was considered negligible, and the estimated minimum herd size intervention feasibility is based on assumptions of an average calving interval of 428 days (National Milk Records, 2011), a minimum group size of five and a weaning age of 8 weeks. In this scenario, for sufficient calves to be present by the age of 12 weeks to form a viable group, the minimum herd size would have to be 77 cows (milking and dry). In herds smaller than this, the intervention is unlikely to be feasible.
Analysis of intervention costs
The median annual cost of maintaining dry bedding, restricting direct contact with neighbouring cattle, and maintaining a closed herd through using quarantine was £4.18 (5th and 95th percentile: £0.75, £14.23), £2.76 (5th and 95th percentile: £1.54, £5.53) and £17.42 (5th and 95th percentile: £1.57, £47.63) per cow respectively (Fig. 2 a–c). For all three interventions combined, the median annual cost was £25.99 per cow (5th and 95th percentile: £10.55, £55.86).
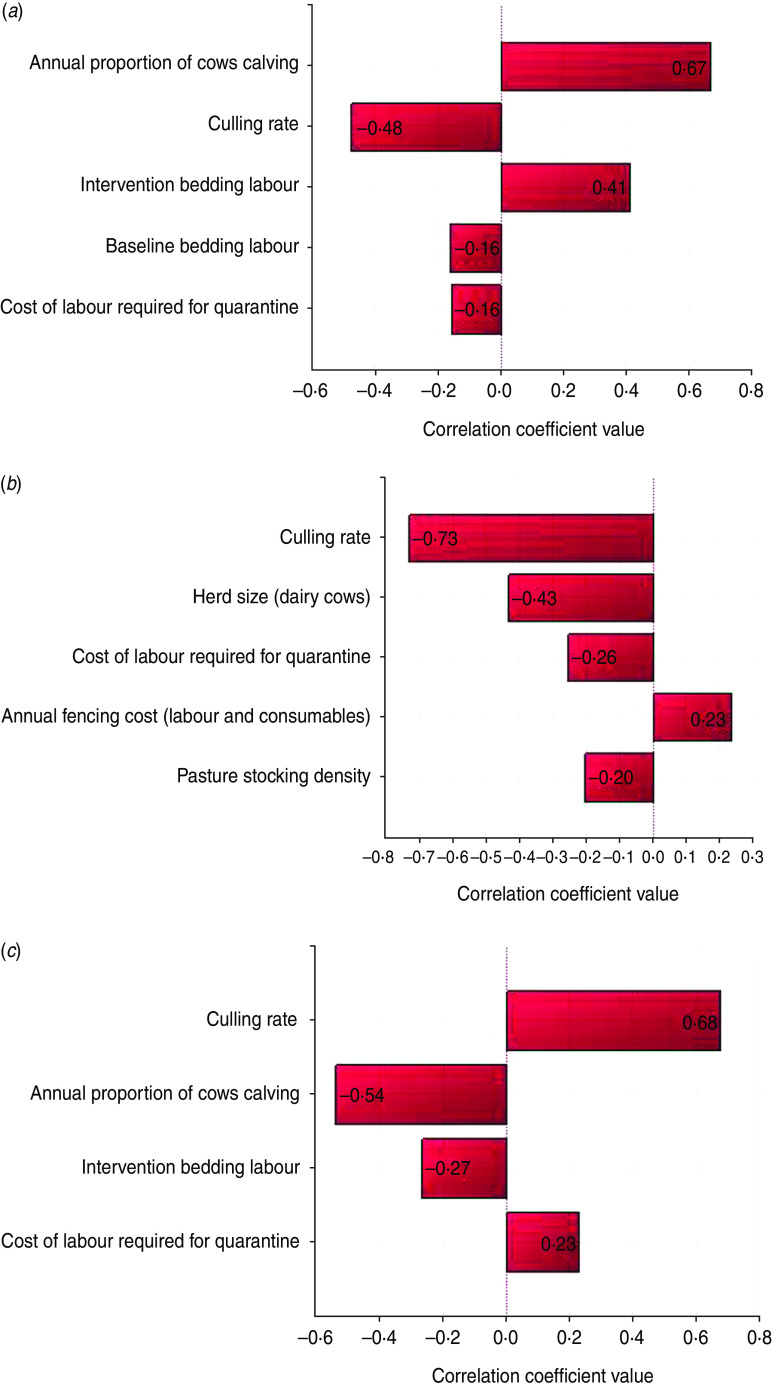
Fig. 2.
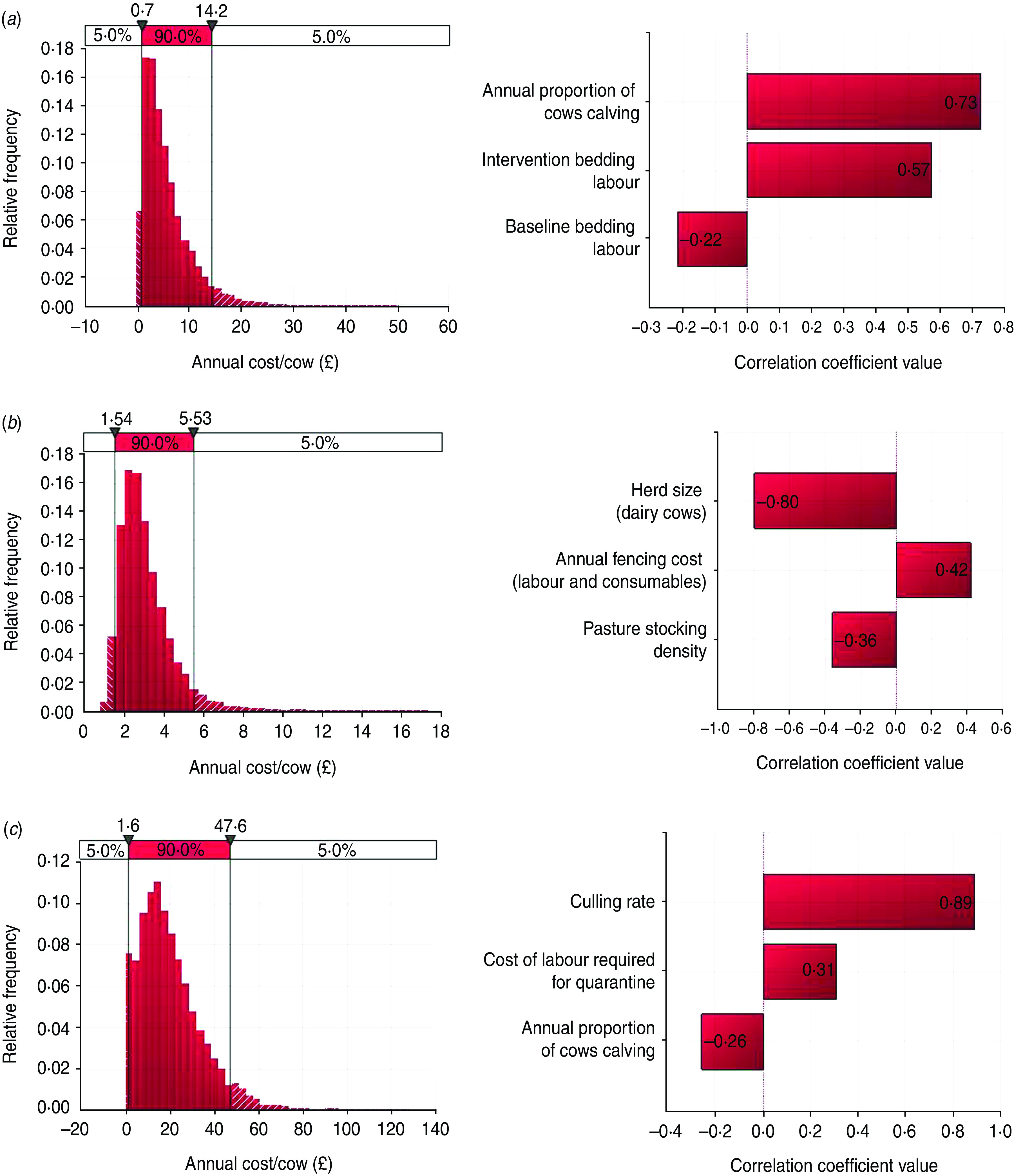
[colour online]. Relative frequencies for each intervention costs and their associated sensitivity analyses using Spearman's rank-order correlations. The parameters proportion of cows served to dairy semen, proportion of perimeter double fenced, and average group size purchased were fixed at 50%, 25% and 5%, respectively. (a) Maintaining dry bedding (median £4.18; 5th and 95th percentiles £0.75, 14.23). (b) Preventing direct contact (median £2.75; 5th and 95th percentiles £1.54, £5.53). (c) Closed herd using quarantine (median £17.42; 5th and 95th percentiles £1.57, £47.63).
Sensitivity analysis of the individual measures shows the proportion of cows calving annually to have the greatest impact on keeping bedding dry through an associated increase in number of farm youngstock (Fig. 2 a). The uncertainty around the time required per animal in the baseline and intervention scenarios also has a significant impact on the measure's cost. For preventing direct contact, herd size has the greatest influence with larger farms having less cost associated with the intervention (Fig. 2 b). Culling rate has the greatest impact on the cost of quarantine (Fig. 2 c), due to an associated increase in the number of purchased replacements required.
When all four measures were considered in combination, on average the quarantine component was the largest proportion of the total cost at a median of 70·2% (5th and 95th percentile: 12·0%, 90·4%). This compares with preventing direct contact at 11·2% (5th and 95th percentile: 4·2%, 29·9%) and maintaining dry bedding at 16·6% (5th and 95th percentile: 2·6%, 64·5%). However, the cost of maintaining a closed herd was the most variable, with sensitivity analysis showing the intervention to be most influenced by the cost of labour in quarantine and farm culling rate with high values leading to a higher proportion of cost associated with this intervention (Fig. 3 a–c). The influence of these parameters is strong enough to have a significant negative influence on the proportion of cost attributable to maintaining dry bedding and preventing direct contact with other cattle.
Fig. 3.
[colour online]. Sensitivity analysis using Spearman's rank-order correlations for the proportion each of the three interventions contributes to the total cost if all are implemented. The parameters proportion of cows served to dairy semen, proportion of perimeter double fenced, and average group size purchased were fixed at 50%, 25% and 5%, respectively. (a) Maintaining dry bedding. (b) Preventing direct contact. (c) Closed herd using quarantine.
Intervention scenarios
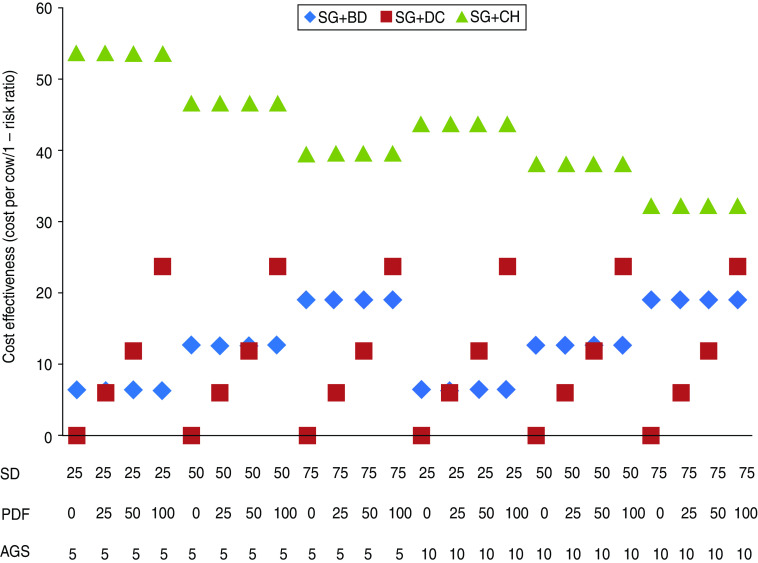
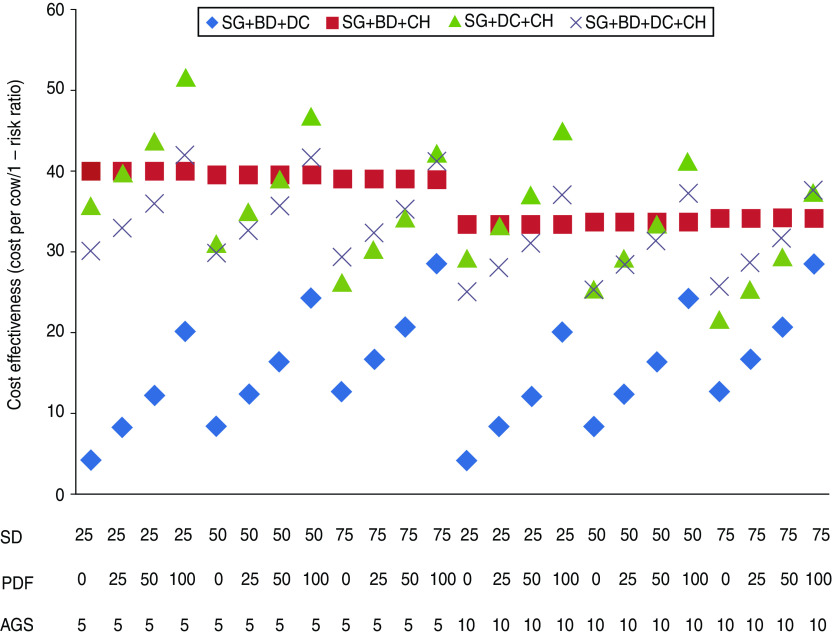
The results of the different intervention scenarios considered are presented in figures 4 and 5. A decrease in cost-effectiveness is shown through an increase in the cost for the proportional reduction in the prevalence of VTEC (1 – risk ratio; attributable fraction). As expected, as farms serve more cows to dairy semen it becomes less cost-effective to implement the dry-bedding intervention due to more youngstock aged between 3 and 18 months being present on the farm (with the assumption that all non-replacement stock are sold before age 3 months). However, this also reduces the quarantine requirement since fewer replacement purchases are required as shown by the stepwise decrease in cost for maintaining a closed herd (Fig. 4; SG + CH). These conflicting costs are balanced out when the two interventions are combined with only a very minor difference in cost-effectiveness with an increase in proportion of cows served to dairy semen (Fig. 5; SG + BD + CH).
Fig. 4.
[colour online]. Mean cost-effectiveness of combinations of two interventions for different herd scenarios. X-axis values refer to SD and PDF percentage and AGS number in each scenario. SD = Percentage of cows served to dairy semen; PDF = percentage of perimeter requiring double fencing; AGS = average group size purchased/quarantined; SG = keeping animals in the same group; BD = keeping bedding dry; DC = limiting direct contact of animals between neighbouring farms. CH = maintaining a closed herd through the use of quarantine.
Fig. 5.
[colour online]. Mean cost-effectiveness of combinations of more than two interventions for different herd scenarios. X-axis values refer to SD and PDF percentage and AGS number in each scenario. SD = Percentage of cows served to dairy semen; PDF = percentage of perimeter requiring double fencing; AGS = average group size purchased/quarantined; SG = keeping animals in the same group; BD = keeping bedding dry; DC = limiting direct contact of animals between neighbouring farms; CH = maintaining a closed herd through the use of quarantine.
It is also expected that the cost-effectiveness of preventing direct contact will decrease as the requirement for double fencing increases (Fig. 4; SG + DC). The intervention scenarios show that the most cost-effective scenario is where farms can restrict nose-to-nose contact with neighbouring stock without the need for double fencing, alongside maintaining animals in the same group (zero cost, attributable fraction 0·43; Fig. 4). However, increasing the perimeter proportion required to be double fenced (PDF) has a large impact on the cost-effectiveness as evidenced by the sharp increase seen in all scenarios (Figs 4, 5). Where considering implementing a single measure in addition to maintaining animals in the same group, the least cost-effective approach in all scenarios is maintaining a closed herd through quarantine shown through the high cost for the proportional reduction in VTEC prevalence (Fig. 4; SG + CH).
Variation of measures of effect
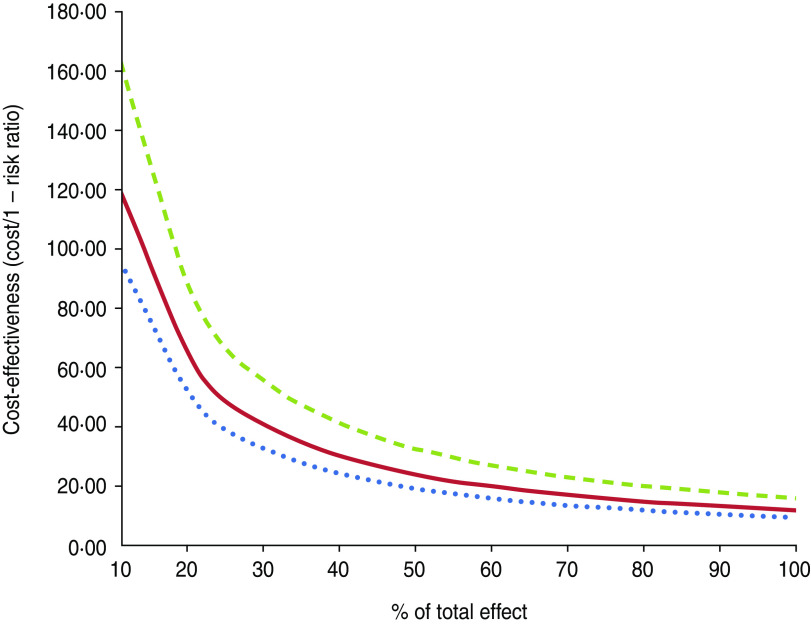
In order to explore the assumption of equal measures of effect with each intervention, a one-way sensitivity analysis was performed whereby the cost-effectiveness was calculated for each intervention with its measure of effect varying between 10% and 100% of the total attributable fraction (Fig. 6). This is equivalent to varying the attributable fraction between 0·086 to 0·86. As expected, the cost-effectiveness increases as the intervention becomes more effective in reducing VTEC prevalence. Figure 6 demonstrates that the impact of the assumed effectiveness is potentially large in particular for intervention ‘CH’ with most variation occurring when the percentage is between 10% and 30% of the total effect.
Fig. 6.
[colour online]. One-way sensitivity analysis showing variation in the cost-effectiveness of individual interventions when their measure of effect is allowed to vary between 10% and 100% of the total effect (equivalent to attributable fraction 0·086–0·86). Top, middle and bottom lines represent maintaining dry bedding (– – –), preventing direct contact (——), and maintaining a closed herd using quarantine (⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅), respectively. Percentage of cows served to dairy semen (50%), percentage of perimeter requiring double fencing (25%), average group size purchased/quarantined (5%).
DISCUSSION
The objective of this study was to develop an economic model to assess the cost-effectiveness of measures to reduce VTEC prevalence on UK dairy farms. Of all the interventions tested, keeping youngstock in the same group was the most cost-effective measure as no cost was associated with this practice, although it was estimated to be unfeasible for a unit size of less than 77 dairy cows (22·4% of dairy farms from July 2011, National Milk Records data). Maintaining a closed herd by using quarantine was the most expensive and least cost-effective measure, with its inclusion in any farm scenario being the least cost-effective option. The model showed double fencing to be the least variable cost for an individual farm but scenario analysis showed the cost-effectiveness to vary sharply with the proportion of the perimeter requiring double fencing. The potentially large impact of the assumption of equal measures of effect makes expanding the original epidemiological analysis to obtain specific intervention risk ratios worthwhile.
This analysis shows that an intervention's cost-effectiveness has a high level of variability and specific interventions are more cost-effective in particular farm situations. The impact of variability associated with maintaining dry bedding is mostly ascribed to the proportion of cows calving annually, indicating the number of youngstock present on the farm to be the most important determinant of the implementation's cost. Therefore farms that retain more youngstock may find this a suboptimal measure. The degree of spread of the input distribution used for time associated with bedding calves is based on uncertainty, and these also have a large impact suggesting a primary data collection exercise would be worthwhile. Preventing direct contact between cattle is strongly influenced by herd size, with smaller herds tending to find this measure less cost-effective. Maintaining a closed herd through using quarantine is less likely to be cost-effective in herds with a high culling rate although the strong influence of labour cost may offer a way to subsidize this intervention, especially where implementing other measures is not possible. However, this analysis does not consider the other likely benefits these interventions may have in controlling other infectious diseases, many of which may impact upon cattle productivity and would have more direct economic impact on the farmer. Although maintaining a closed herd using quarantine is the least cost-effective strategy, of the two measures directed at inter-farm spread of infection, it is arguably the measure that has the most potential to limit other diseases entering the farm. Whereas limiting direct contact between farms will tend to prevent spread of communicable diseases present locally (e.g. tuberculosis in South West England), purchasing cattle has the potential to introduce disease less spatially restricted. Other economic analyses would be useful to quantify other benefits before considering subsidizing for societal gain. However, necessary monitoring of compliance with the subsidized interventions to ensure prudent spending of public funds may make them unmanageable at the farm level.
This economic model is mostly based on secondary data with assumptions made on the intervention's measure of effect and related farming practices. To validate the model, primary data collection from real-life implementation of the interventions is required. Ideally, economic data would have been collected during the original RCT on which this analysis was based. Further analysis of the RCT is also needed to establish risk ratios associated with the four specified measures. In a recent study, Cross et al. [2] evaluated expert opinion regarding the effectiveness of interventions for VTEC. This scored keeping animals in the same group and maintaining dry bedding as approximately equal but limiting direct contact between cattle as relatively ineffective (maintaining a closed herd was not included). However, in the context of this cost-effectiveness analysis, the RCT results would provide a more objective and valid approach. Validating the model will allow much greater confidence in its interpretation regarding allocation of resources and policy formation. The model would also be strengthened by adapting it to other cattle farming systems (e.g. beef suckler), extending the impact of farm measures to human disease incidence as part of a cost-utility analysis, and considering in more detail the cost of the farmer's time as opposed to an employee's.
It is important to consider the outcomes of the model within the limitations of the assumptions made. The model assumed that livestock are housed all year. Although farms may have a period of grazing for livestock between the ages of 3 and 18 months, this system was considered to represent a worse case scenario for cost. Assumptions were also made that interventions could be made within the farm's pre-existing infrastructure without the need for capital costs. This means the cost of implementing interventions on farms where this assumption is invalid may be substantially different to those estimated. Therefore the output of this model should only be considered for farms where this assumption is valid.
The interventions in the original trial were implemented on farms that had previously been confirmed positive for VTEC with the ascribed interventions being associated with a reduction in the risk of shedding in youngstock. The initial costs associated with confirming farms as VTEC positive would include taking and processing samples and utilizing not routinely used diagnostic tests. For a national control programme, costs associated with screening farms for the presence of infection would have to be considered as well as monitoring of the programme's effectiveness on a subset of farms. The RCT gave good evidence of the effectiveness of the interventions on VTEC-positive farms so repeated sampling was not considered necessary in this analysis for a farm already confirmed positive.
A farmer's decision-making process regarding disease control is complex and may include economic and non-economic factors. Habits may be difficult to break even if there is strong evidence that a costly measure is ineffective [17]. Measures that are practically easier to implement may be more likely to be used and therefore affect compliance. In other work by Cross [18], farmer opinion was used to assess practicalities of VTEC interventions, which assigned maintaining dry bedding, preventing direct contact and keeping animals in the same group relatively low practicality scores (closed herd was not included). However, financial gain can also be an important motivator. For an infection like VTEC where the only ill effects are seen through human infection, farmers usually feel a social responsibility in contributing to its control but are less willing to finance the necessary interventions [19]. Therefore, until market signals indicate a favourable climate to motivate compliance, farmers are unlikely to implement necessary measures. Alternatively, government funding targeted at cost-effective interventions may be needed for the desired societal gains from reduced VTEC prevalence with the results of this work used to create a decision framework for determining the most cost-effective intervention on individual farms.
CONCLUSION
This study demonstrates that keeping youngstock in the same groups, maintaining dry bedding, preventing direct contact with neighbouring cattle and maintaining a closed herd by using quarantine may offer a cost-effective approach to reduce the prevalence of VTEC in youngstock on UK dairy farms. However, inter-farm variation creates large variances in the cost-effectiveness. Further work on other potential benefits of the interventions, such as reduction of other infectious diseases, together with clear market signals, are likely to be required before farmers begin complying with the necessary changes.
ACKNOWLEDGEMENTS
The authors thank Johanne Ellis-Iversen (AHVLA), Malla Hovi (AHVLA), Sheila Millington (Promar), John Wall (NMR), Paddy Gordon (Shepton Veterinary Group), Alex Mastin (RVC), Hannah Bishop (RVC) and Paul Christian (RVC) for their assistance. Thanks are also due to the vets and farmers that assisted with data collection and to Dr Solenne Costard and Dr Andrew Hill for advice on aspects of stochastic modelling. This project was completed as part of Nick Lyons’ M.Sc. in Veterinary Epidemiology made possible by a BBSRC scholarship.
DECLARATION OF INTEREST
None.
REFERENCES
- 1.Snedeker KG, et al. Primary and secondary cases in Escherichia coli O157 outbreaks: a statistical analysis. BMC Infectious Diseases 2009; 9: 144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cross P, Rigby D, Edwards-Jones G. Eliciting expert opinion on the effectiveness and practicality of interventions in the farm and rural environment to reduce human exposure to Escherichia coli O157. Epidemiology and Infection 2012; 140: 643–654. [DOI] [PubMed] [Google Scholar]
- 3.Griffin G. Review of the major outbreak of E. coli O157 in Surrey, 2009. Report of the Independent Investigation Committee, June. 2010.
- 4.McNeilly TN, et al. Immunization of cattle with a combination of purified intimin-531, EspA and Tir significantly reduces shedding of Escherichia coli O157:H7 following oral challenge. Vaccine 2010; 28: 1422–1428. [DOI] [PubMed] [Google Scholar]
- 5.Paiba GA, et al. Prevalence of faecal excretion of verocytotoxigenic Escherichia coli O157 in cattle in England and Wales. Veterinary Record 2003; 153: 347–353. [DOI] [PubMed] [Google Scholar]
- 6.Ellis-Iversen J, et al. Identification of management risk factors for VTEC O157 in young-stock in England and Wales. Preventive Veterinary Medicine 2007; 82: 29–41. [DOI] [PubMed] [Google Scholar]
- 7.Gunn GJ, et al. An investigation of factors associated with the prevalence of verocytotoxin producing Escherichia coli O157 shedding in Scottish beef cattle. Veterinary Journal 2007; 174: 554–564. [DOI] [PubMed] [Google Scholar]
- 8.Ellis-Iversen J, et al. Farm practices to control E. coli O157 in young cattle – a randomised controlled trial. Veterinary Research 2008; 39: 3. [DOI] [PubMed] [Google Scholar]
- 9.Shaw APM. The Economics of zoonoses and their control. In: Rushton J, ed. The Economics of Animal Health and Production. CAB International, 2009, pp. 161–167. [Google Scholar]
- 10.Vosough Ahmadi B. Cost-effectiveness of Escherichia coli O157: H7 control in the beef chain (Ph.D. thesis). Wageningen, The Netherlands: Wageningen University, 2007, pp. 91–111. [Google Scholar]
- 11.Brickell JS, et al. Mortality in Holstein-Friesian calves and replacement heifers, in relation to body weight and IGF-I concentration, on 19 farms in England. Animal 2009; 3: 1175–1182. [DOI] [PubMed] [Google Scholar]
- 12.Nix J. The John Nix Farm Management Pocketbook, 41st edn. Melton Mowbray, UK, 2011. [Google Scholar]
- 13.Agro Business Consultants. The Agricultural Budgeting and Costing Book, 70th edn. Melton Mowbray, UK, 2010. [Google Scholar]
- 14.Yeates M. Is there an optimum cubicle system for mastitis control? British Mastitis Conference. Stoneleigh, UK, 2008, pp. 29–39. [Google Scholar]
- 15.Cattle Health Certification Standards. Incorporating Rules for cattle health schemes (technical document), 2011.
- 16.Vose D. Understanding and using the results of a risk analysis. In: Risk analysis: A Quantitative Guide. Hoboken, NJ: Wiley; Chichester: John Wiley (distributor) 2008, pp. xiv, 735 pp. [Google Scholar]
- 17.Ellis-Iversen J.Control of VTEC O157 and Campylobacter jejuni/coli on cattle farms – effective interventions and implementation (Ph.D. thesis). Utrecht, The Netherlands: Utrecht University, 2009, chapter 6. [Google Scholar]
- 18.Cross P. Estimating the best way forward: expert and farmer evaluations of environmental interventions to reduce human exposure to E. coli O157. Zoonoses in a Changing Socioeconomic Environment. University of Liverpool, Leahurst, 2011.
- 19.Ellis-Iversen J, et al. Perceptions, circumstances and motivators that influence implementation of zoonotic control programs on cattle farms. Preventive Veterinary Medicine 2010; 93: 276–285. [DOI] [PubMed] [Google Scholar]
- 20.Defra. Commodity prices (http://www.defra.gov.uk/statistics/foodfarm/farmgate/commodity/). Accessed July 2011.