A Novel Method for Adult Height Prediction in Children With Idiopathic Short Stature Derived From a German-Dutch Cohort

Abstract

Context

Prediction of adult height (AH) is important in clinical management of short children. The conventional methods of Bayley-Pinneau (BP) or Roche-Wainer-Thissen (RWT) have limitations.

Objective

We aimed to develop a set of algorithms for AH prediction in patients with idiopathic short stature (ISS) which are specific for combinations of predicting variables.

Methods

Demographic and auxologic data were collected in childhood (1980s) and at AH (1990s). Data were collected by Dutch and German referral centers for pediatric endocrinology. A total of 292 subjects with ISS (219 male, 73 female) were enrolled. The population was randomly split into modeling (n = 235) and validation (n = 57) cohorts. Linear multi-regression analysis was performed with predicted AH (PAH) as response variable and combinations of chronological age (CA), baseline height, parental heights, relative bone age (BA/CA), birth weight, and sex as exploratory variables.

Results

Ten models including different exploratory variables were selected with adjusted R² ranging from 0.84 to 0.78 and prediction errors from 3.16 to 3.68 cm. Applied to the validation cohort, mean residuals (PAH minus observed AH) ranged from −0.29 to −0.82 cm, while the conventional methods showed some overprediction (BP: +0.53 cm; RWT: +1.33 cm; projected AH: +3.81 cm). There was no significant trend of residuals with PAH or any exploratory variables, in contrast to BP and projected AH.

Conclusion

This set of 10 multi-regression algorithms, developed specifically for children with ISS, provides a flexible tool for AH prediction with better accuracy than the conventional methods.

Predicting adult height (AH) in growing children or adolescents has been a scientific objective for many decades. Such predictions are useful in daily clinical practice, but are also required in clinical research, for instance, to estimate the gain in height due to a growth-promoting therapy. A priori, any method to predict AH should meet the following requirements: (i) it should include only variables that are available at the time of initial presentation of the patient; (ii) the variables used for prediction should be easily accessible; (iii) the prediction should be sufficiently accurate to draw conclusions for individual patients; (iv) predictions should be free from systematic errors with respect to the predicting variables; and (v) prediction methods should be applicable in different regions and different ethnicities.

To date, a number of methods are available, of which the tables of Bayley-Pinneau (BP) [1], Roche-Wainer-Thissen (RWT) [2], and Tanner-Whitehouse (TW) [3] are most commonly used. All 3 methods share the feature of having been developed several decades ago in populations of normally growing children. In clinical practice, however, the relevant question is usually whether a short child will finally attain a normal AH, and it is unclear whether the growth pattern of short children can adequately be modeled by the growth pattern of children with normal height. These commonly used methods result in systematic deviations of predicted AH (PAH) from actually observed AH when applied to short children [4]. Although it is believed that the most widely used method of BP is the most robust in “pathological conditions” [4], it overestimates AH in males, in particular if bone age (BA) is retarded [5, 6] and underestimates AH in females with idiopathic short stature (ISS) [7-12].

Therefore, we set out to develop AH prediction models based on subjects with ISS in order to improve height predictions in such patients. This is clinically relevant, because recombinant human growth hormone (rhGH) treatment for children with ISS is only indicated if AH is predicted to be low [13]. The newly developed models were compared with the conventional methods of BP [1], RWT [2], and the projected AH to judge whether they can improve AH prediction.

Methods

Subjects

Patients from 3 German centers (Giessen, Leipzig and Tübingen) and patients participating in a Dutch nationwide study coordinated in Leiden (The Netherlands) who had sought advice from a pediatric endocrinologist because of short stature (height below the tenth percentile) were invited to return to the hospitals at adult age for a height measurement. The study was conducted in accordance with the Declaration of Helsinki. Institutional review board approvals were obtained, and regulatory requirements as requested at the time were followed. Written consent for data collection and anonymized data processing was provided by the patients.

The diagnoses at initial presentation were ISS, familial short stature (FSS, 26%), constitutional delay of growth and puberty (CDGP), a combination of these or other synonym diagnoses (non-FSS, 73%). According to the consensus definition of ISS, all these diagnostic labels fall under the umbrella of ISS [14, 15]. The data from the Dutch cohort were previously used for reports on spontaneous growth in ISS [16-18] and for comparison with growth hormone (GH)-treated children [5].

Subjects were included in the analysis, if the following variables were available: sex, birth year and month, chronological age (CA), bone age (BA) and height at baseline (H0), CA at AH measurement, and AH. The last measured height was accepted as AH, if CA was ≥ 18 years or if BA was ≥ 16 years in males or ≥ 14 years in females, alike the criteria of the BP and RWT methods [1, 2]. Subjects were excluded if any of the following criteria applied: born small for gestational age with birth weight < −2 SDs according to the tables of Usher and McLean [19], gestational age < 36 weeks, GH deficiency, skeletal dysplasia, defined clinical syndrome, or any other known cause or therapy that interferes with growth. The initial population consisted of 354 patients, of whom 62 were excluded because they did not comply with the inclusion criteria. The final study population comprised 292 subjects (51 from Giessen, 55 from Leipzig, 56 from the Netherlands, and 130 from Tübingen).

Methods

Height was measured with precision stadiometers with an accuracy of 0.1 cm. For conversion of height (cm) to standard deviation scores (SDS), the reference data of the Zürich Longitudinal Study [20] were used, applying linear interpolation of data between chronological age boundaries. The parents’ heights were measured whenever possible, otherwise reported actual heights were used. Target height (TH; sex-corrected mid-parental height) was calculated using the method of Tanner [21]. Weight was measured with precision scales at an accuracy of 0.1 kg. Body mass index (BMI) was calculated by weight (kg)/height (m)² and expressed as SDS [22].

BA was assessed locally by the method of Greulich-Pyle (BAGP) [23]. In some patients, BA had been determined by the TW radio ulna and short bones (RUS) method (BARUS) [24]. These values were converted to Greulich-Pyle (GP) equivalent values using previously reported formulas [25]. BAGP values were converted to SDS [(BA − CA)/SD] using the reference values given in the Greulich-Pyle atlas [23]. BA delay was defined as BA minus CA, and relative bone age as BA/CA.

Subjects were considered prepubertal, if the testicular volume on both sides was < 4 mL in boys or if breast stage according to Tanner was 1 in girls. Male subjects were considered pubertal, if the testicular volume on one side was ≥ 4 mL, or, if testicular volume was not available, the stage of pubic hair was ≥ 2 according to Tanner and BA at baseline was ≥ 12 years. Females were considered pubertal if breast stage was ≥ 2. If none of these criteria were reported or if available information was equivocal, no assignment regarding puberty was made. Subjects were considered to have FSS, if their H0 SDS minus TH SDS (Tanner) was greater than −1.28 [11].

For prediction of AH by conventional methods, the tables of BP [1], and the method of RWT [2] were applied. In addition, projected AH (ProjAH) was calculated by converting the height SDS for BA (according to GP) at baseline to height (cm) at 18 years according to the Zürich reference values.

Statistics

The total study population (N = 292) was stratified by sex and age and randomly split into a modeling cohort (n = 235) and a validation cohort (n = 57). In order to identify variables suitable for developing linear multi-regression models with AH (cm) or AH SDS as response variables, factor structure analysis was performed with the modeling cohort. This method provides groups (“factors”) of closely correlated variables. Ideally, prediction models should include variables from different factors to take maximum advantage of the information provided by the dataset. Factor structure was optimized by rotating the variables space using the “Varimax” procedure (SAS). Exploratory variables selected on the basis of factor structure were included in multi-regression models applying the C_p selection procedure using least squares (LS). The preferred models were selected on the basis of following criteria: (i) low Mallow’s C_p value, (ii) high adjusted R², (iii) low root mean square error (RMSE), (iv) absence of a trend of residuals (PAH minus observed AH) vs PAH, (v) minimal skewness as suggested by visual inspection of QQ-normal plots, (vi) robustness of the LS method confirmed by the MM robust method, and (vii) availability of variables in clinical practice. The finally selected models were applied to the validation cohort to get an impression of their performance. Analyses were conducted using SAS software (SAS Institute Inc., Cary, NC). The values of descriptive statistics of continuous variables are presented as mean ± SD (range) unless otherwise specified. The significance of differences between subgroups was tested by the 2-sided Student’s t test. A 2-sided P value of less than 0.05 was considered statistically significant.

Results

Clinical Data at Baseline and at Follow-Up

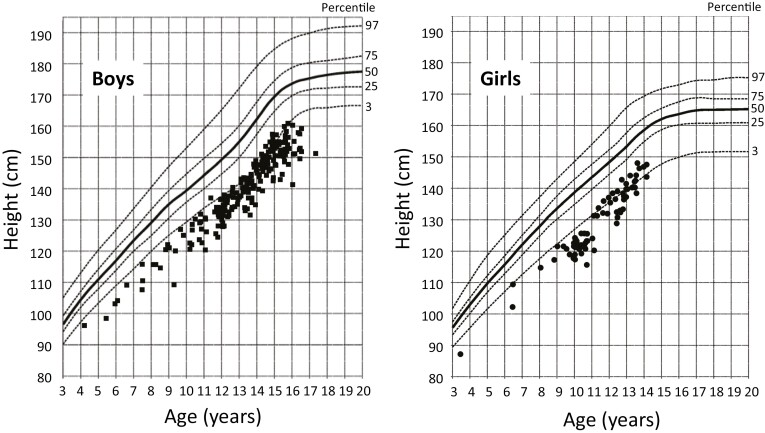
Figure 1 illustrates the distribution of baseline height (H0) vs CA in boys (n = 219) and girls (n = 73) of the total study population (N = 292) against the background of the reference ranges of the Zürich Longitudinal Study. Demographic and auxologic characteristics at initial presentation and at AH measurement are presented in Table 1. The mean CA at AH was 20.5 ± 2.3 years with 8 patients of less than 18 years, 2 male and 6 female. All patients had retarded BA (BA − CA) with the great majority (93%) below −1 year. The modeling cohort (n = 235) and the validation cohort (n = 57) did not significantly differ in any of the variables (Table 1). Both cohorts were further split by sex. The proportion of males was 3 times greater in both cohorts than that of females (176 vs 59 and 43 vs 14). As expected, a number of sex-dependent variables were different between sexes such as CA, BA, H0, and AH. Although some BA-related variables were slightly different between sexes, relative BA (BA/CA) was not.

Figure 1.

Baseline height of all subjects vs the normal reference ranges of the Zürich Longitudinal Study.

Table 1.

Demographic and auxologic characteristics of the study population at first and last presentation. Splitting of the study population in a modeling and a validation cohort and further splitting by sex

Variable	Total study population	Modeling cohort				Validation cohort
		All	Male	Female	P a	All	Male	Female	P b	P c
N (%)	292 (100%)	235 (80.5%)	176 (60.3%)	59 (20.2%)		57 (19.5%)	43 (19.5%)	14 (4.8%)
Baseline (first determination at diagnosis)
Birth year	1974.9 ± 6.4 (1963; 1985)	1974.9 ± 6.4 (1963; 1985)	1974.9 ± 6.5 (1963; 1985)	1974 ± 6.2 (1964; 1985)	0.987	1974.0 ± 6.3 (1967; 1985)	1973.4 ± 6.3 (1967; 1985)	1975.9 ± 6.3 (1969; 1985)	0.204	0.336
Birth weight (BiWt), kg	3.23 ± 0.46 (1.99; 4.90)	3.2 ± 0.4 (2.0; 4.9)	3.3 ± 0.4 (2.0; 4.5)	3.1 ± 0.5 (2.0; 4.9)	< 0.001	3.2 ± 0.5 (2.2; 4.5)	3.3 ± 0.5 (2.2; 4.5)	3.1 ± 0.4 (2.3; 4.0)	0.150	0.919
Birth weight SDS	-0.31 ± 0.96 (-1.99; 3.12)	-0.31 ± 0.98 (-1.99; 3.12)	-0.21 ± 0.97 (-1.99; 3.12)	-0.55 ± 0.99 (-1.97; 3.09)	0.044	-0.31 ± 0.86 (-1.58; 2.22)	-0.12 ± 0.93 (-1.36; 2.22)	-0.76 ± 0.46 (-1.58; -0.06)	0.030	0.982
Chronological age (CA), y	12.7 ± 2.4 (3.4; 17.3)	12.7 ± 2.4 (3.4; 17.3)	13.2 ± 2.3 (4.2; 17.3)	11.2 ± 1.9 (3.4; 14.0)	< 0.001	12.7 ± 2.3 (6.3; 16.4)	13.3 ± 2.2 (6.6; 16.4)	10.9 ± 1.9 (6.3; 13.4)	< 0.001	0.949
Bone age (BA), y	10.4 ± 2.4 (1.8; 14.0)	10.4 ± 2.3 (1.8; 14.0)	10.9 ± 2.3 (2.7; 14.0)	9.1 ± 2.1 (1.8; 12.5)	< 0.001	10.4 ± 2.7 (2.5; 13.8)	11.0 ± 2.5 (3.0; 13.8)	8.7 ± 2.4 (2.5; 11.5)	< 0.001	0.971
Bone age delay (BA-CA), y	-2.3 ± 1.1 (-5.6; +0.6)	-2.3 ± 1.0 (-5.6; +0.6)	-2.4 ± 1.0 (-5.6; +0.6)	-2.1 ± 1.1 (-4.7; 0.0)	0.024	-2.3 ± 1.1 (-5.6; -0.3)	-2.3 ± 1.2 (-5.6; -0.3)	-2.3 ± 1.1 (-4.1; -0.9)	0.920	0.951
Relative bone age (BA/CA)	0.81 ± 0.09 (0.39; 1.05)	0.81 ± 0.09 (0.49; 1.05)	0.81 ± 0.08 (0.49; 1.05)	0.81 ± 0.10 (0.55; 1.00)	0.976	0.81 ± 0.12 (0.39; 0.97)	0.82 ± 0.11 (0.45; 0.97)	0.78 ± 0.14 (0.39; 0.91)	0.259	0.642
Bone age SDS	-2.37 ± 1.11 (-6.36; +0.62)	-2.36 ± 1.06 (-5.48; +0.62)	-2.45 ± 1.04 (-5.48; +0.62)	-2.09 ± 1.07 (-4.36; 0.00)	0.025	-2.40 ± 1.33 (-6.36; -0.37)	-2.40 ± 1.32 (-6.36; -0.37)	-2.43 ± 1.39 (-5.24; -1.03)	0.937	0.796
Estimated time to grow, y	5.1 ± 2.3 (1.5; 13.3)	5.1 ± 2.2 (1.5; 13.3)	5.2 ± 2.2 (2.0; 13.3)	4.9 ± 1.9 (1.5; 12.2)	0.337	5.1 ± 2.5 (2.3; 13.0)	5.0 ± 2.5 (2.3; 13.0)	5.3 ± 2.4 (2.5; 11.5)	0.690	0.942
Height (H0), cm	138.5 ± 13.2 (88.0; 162.0)	138.4 ± 13.2 (88.0; 162.0)	141.2 ± 12.6 (97.0; 162.0)	130.0 ± 11.3 (88.0; 148.8)	< 0.001	138.7 ± 13.2 (103.0; 161.4)	141.8 ± 12.6 (110.0; 161.4)	129.1 ± 10.1 (103.0; 144.8)	0.001	0.885
Height SDS	-2.35 ± 0.57 (-4.61; -1.29)	-2.36 ± 0.57 (-4.61; -1.32)	-2.29 ± 0.56 (-4.61; -1.32)	-2.56 ± 0.59 (-4.20; -1.48)	< 0.001	-2.31 ± 0.55 (-3.64; -1.29)	-2.25 ± 0.55 (-3.64; -1.29)	-2.49 ± 0.55 (-3.42; -1.58)	0.155	0.553
Target height SDS	-0.64 ± 0.74 (-3.08; +1.49)	-0.68 ± 0.74 (-3.08; +1.07)	-0.68 ± 0.75 (-3.08; +1.07)	-0.67 ± 0.71 (-2.10; +1.02)	0.924	-0.50 ± 0.71 (-2.22; +1.49)	-0.53 ± 0.64 (-2.22; +1.49)	-0.44 ± 0.94 (-1.92; +1.27)	0.694	0.118
Height SDS—target height SDS	-1.71 ± 0.72 (-3.70; +0.49)	-1.68 ± 0.71 (-3.65; +0.49)	-1.61 ± 0.72 (-3.65; +0.49)	-1.89 ± 0.66 (-3.61; -0.66)	< 0.001	-1.81 ± 0.75 (-3.70; -0.38)	-1.73 ± 0.70 (-3.33; -0.38)	-2.06 ± 0.87 (-3.70; -0.57)	0.154	0.250
Body mass index SDS	-0.59 ± 1.08 (-3.62; +2.74)	-0.56 ± 1.07 (-3.62; +2.74)	-0.55 ± 1.10 (-3.62; +2.74)	-0.58 ± 0.96 (-2.06; +2.37)	0.893	-0.70 ± 1.10 (-2.80; +1.97)	-0.67 ± 1.10 (-2.80; +1.97)	-0.84 ± 1.12 (-2.22; +1.33)	0.695	0.452
At adult age (last determination)
Age at adult height, y	20.5 ± 2.3 (13.8; 32.8)	20.5 ± 2.4 (13.8; 32.8)	20.4 ± 2.2 (16.7; 32.8)	20.8 ± 3.0 (13.8; 31.5)	0.271	20.5 ± 2.1 (17.0; 26.8)	20.7 ± 2.0 (17.0; 26.8)	19.7 ± 2.1 (17.1;24.5)	0.095	0.980
Adult height (AH), cm	166.2 ± 7.8 (138.2; 183.0)	166.0 ± 7.8 (138.2; 183.0)	169.2 ± 5.5 (154.9; 183.0)	156.4 ± 5.2 (138.2; 165.8)	< 0.001	167.0 ± 8.0 (148.0; 179.5)	170.3 ± 6.0 (156.1; 179.5)	157.2 ± 4.5 (148.0; 164.5)	< 0.001	0.370
Adult height SDS	-1.25 ± 0.82 (-4.46; +0.79)	-1.28 ± 0.82 (-4.46; +0.79)	-1.25 ± 0.80 (-3.34; +0.79)	-1.37 ± 0.86 (-4.46; +0.23)	0.323	-1.14 ± 0.83 (-3.17; +0.21)	-1.11 ± 0.86 (-3.17; +0.21)	-1.24 ± 0.77 (-2.81; -0.02)	0.608	0.263
Adult height SDS—target height SDS	-0.62 ± 0.69 (-2.58; +0.89)	-0.61 ± 0.68 (-2.58; +0.87)	-0.58 ± 0.67 (-2.54; +0.87)	-0.73 ± 0.70 (-2.58; +0.70)	0.144	-0.64 ± 0.72 (-2.30; +0.89)	-0.58 ± 0.74 (-2.18; +0.89)	-0.80 ± 0.67 (-2.30; +0.06)	0.325	0.832
Adult height SDS—cond. target height SDS	-0.80 ± 0.65 (-3.11; +0.85)	-0.80 ± 0.64 (-3.11; +0.85)	-0.77 ± 0.63 (-2.74; +0.85)	-0.92 ± 0.68 (-3.11; +0.56)	0.129	-0.78 ± 0.68 (-2.31; +0.59)	-0.73 ± 0.72 (-2.31; +0.59)	-0.93 ± 0.56 (-1.94; +0.04)	0.355	0.788
Adult height SDS—baseline height SDS	+1.10 ± 0.68 (-0.58; +3.42)	+1.08 ± 0.68 (-0.54; +2.76)	+1.05 ± 0.68 (-0.54; +2.66;	+1.19 ± 0.66 (-0.26; +2.76)	0.172	+1.17 ± 0.72 (-0.58; +3.42)	+1.14 ± 0.74 (-0.58; +3.42)	+1.25 ± 0.67 (-0.40; +2.21)	0.625	0.389

Values are given as mean ± SD (minimum; maximum). Comparisons were made by 2-sided Student’s t test.

Abbreviations: SDS, standard deviation score; bone age delay = bone age minus chronological age; relative bone age = bone age/chronological age; estimated time to grow: 16 y—bone age in males and 14 y—bone age in females.

P

^a for comparison of males and females in the modeling cohort, P

^b in the validation cohort. P

^c comparison of the total modeling vs validation cohort. Bone age according to Greulich-Pyle.

Model Development

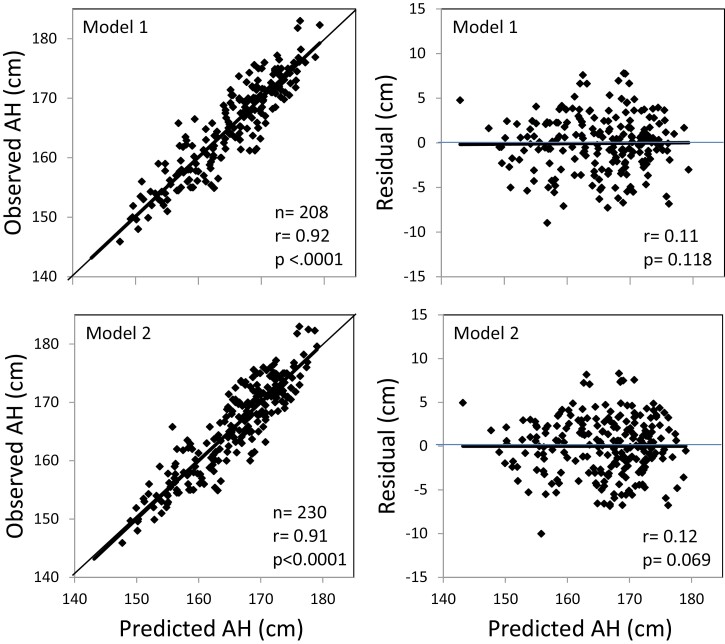
Table 2 shows the 10 models that were finally selected on the basis of statistical characteristics and practical aspects such as ready availability of clinical variables. It also exhibits the variables included in the various models starting with model 1 with the greatest number of variables: CA, H0, TH requiring mother’s height and father’s height, BA/CA, birth weight (BiWt) and sex. Adjusted R² was highest in this model (0.84) and the prediction error (RMSE) was smallest (3.16 cm). According to the QQ plots, the residuals of all models did not indicate skewness (not shown). Along with increasing numbers of missing variables, adjusted R² decreased from 0.84 to 0.78 in model 9 and RMSE increased from 3.16 cm to 3.68 cm. The R² of 0.79 obtained in model 10 with no information on parental heights shows that even in such a situation, the accuracy is close to the other models. All models were highly significant (P < 0.0001). Figure 2 illustrates the correlation between observed AH and PAH in the modeling cohort for models 1 and 2 and of the corresponding residuals as examples.

Table 2.

Finally selected models for adult height (cm) prediction based on statistical characteristics and practical aspects

Model	Parameter estimatesa									Model characteristics
	Intercept (cm)	CA (y)	H0 (cm)	TH (cm)	MoH (cm)	FaH (cm)	BA/CA	BiWt (kg)	Sex (M = 1, F = 2)	N	Adj R2	P b value	RMSE (cm)
1	63.3339	-2.9595	+0.7256	+0.3173			-13.0399	+1.2695c	-6.2213	205	0.84	< 0.0001	3.16
2	62.1795	-2.9892	+0.7328	+0.3442			-12.6821		-6.3021	229	0.82	< 0.0001	3.30
3	50.3654	-2.6372	+0.6408	+0.3986					-5.9171	229	0.81	< 0.0001	3.46
4	80.3645	-3.4309	+0.8241		+0.2242		-15.1678	+1.2688d	-10.2474	207	0.84	< 0.0001	3.20
5	83.4866	-3.4717	+0.8374		+0.2234		-14.7156		-10.6257	231	0.82	< 0.0001	3.36
6	75.8792	-3.1944	+0.7581		+0.2449				-10.9519	231	0.79	< 0.0001	3.57
7	93.2475	-3.4020	+0.8239			+0.1203	-14.2739	+1.6156e	-10.0340	205	0.82	< 0.0001	3.34
8	94.2381	-3.5784	+0.8759			+0.1348	-14.2476		-10.5319	229	0.80	< 0.0001	3.49
9	84.3600	-3.2207	+0.7623			+0.1775			-10.8759	229	0.78	< 0.0001	3.68
10	110.8863	-4.1250	+0.9661				-16.0541		-10.4331	234	0.79	< 0.0001	3.58

Abbreviations: Adj R², R² adjusted for number of exploratory variables; BA/CA, bone age/ chronological age; BiWt, birth weight; CA, chronological age; F, female; FaH, father’s height; H0, height at baseline; M, male; MoH, mother’s height; N, total of subjects included in modeling; TH, target height (Tanner); RMSE, root mean square error.

The significance of models was tested by analysis of variance (ANOVA) (P

^b). The significance of parameter estimates was tested by two-sided t test: P

^a < 0.0001 for all parameter estimates except for BiWt (

^c0.0192,

^d0.0198,

^e0.0046). Empty fields indicate missing variables except for MoH and FaH in models 1 to 3 where they were combined in TH.

Figure 2.

Observed adult height (AH) and residuals (predicted—observed AH) vs predicted AH of models 1 (M1) and 2 (M2) of the modeling cohort. Regression lines in bold.

Calculation of Predicted Adult Height

The use of this system of equations (models) for calculating PAH may be illustrated by the following fictive example: A boy, 10.0 years of age (CA), height (H0) 123.0 cm, mother’s height 167.5 cm and father’s height 180.5 cm (→ target height [TH] 174.0 cm), BA 8.0 y (→ relative BA [BA/CA] 0.80). All variables are available except BiWt. Therefore, model 2 (M2) should be applied: PAH = (intercept −2.9892*CA + 0.7328*H0 + 0.3442*TH −12.6821*BA/CA −6.3021*Sex) cm = (62.1795 −2.9892*10.0 + 0.7328*123.0 + 0.3442* 174.0 −12.6821*0.80 -6.3021*1) cm = 165.9 cm. If both BiWt and father’s height (FaH) are missing but mother’s height (MoH) is available, TH cannot be calculated and one should apply M5 yielding a PAH of 166.8 cm. If MoH is missing but FaH is available, one should apply model 8 yielding a PAH of 168.6 cm. If neither MoH nor FaH are available, one should apply model 10, yielding a PAH of 165.2 cm.

Validation of the Models

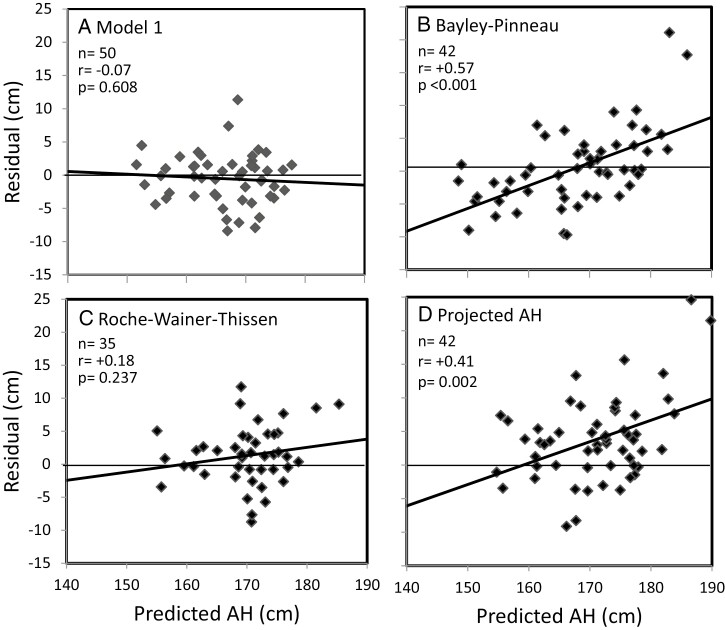
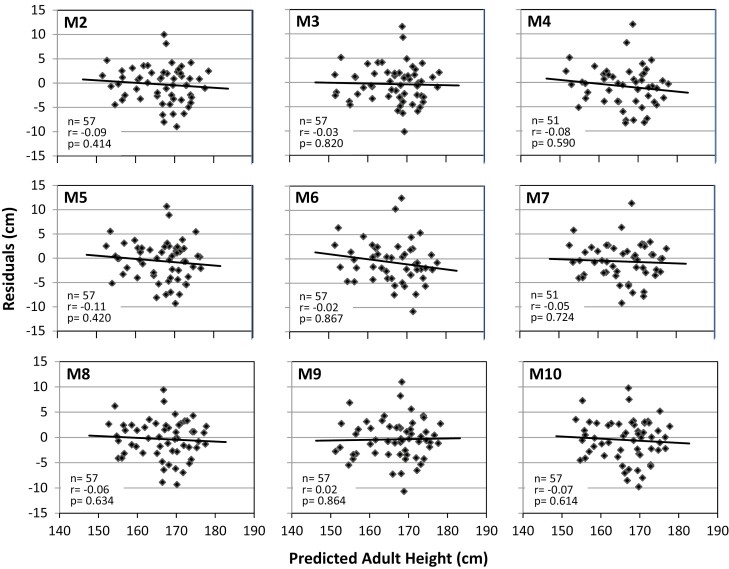
The models developed with the modeling cohort were applied to the independent validation cohort to test whether PAHs by the various models are meaningful and consistent. The mean PAH by models M1 to M10 of cohorts including both sexes ranged from 166.1 to 166.8 cm. Residuals were within an acceptable range without a significant trend vs PAH. Figure 3a for M1 and Fig. 4 for M2 to M10 visualize the relationship between the residuals and PAHs for all 10 models. There was a slight negative, nonsignificant trend of the regression lines. Table 3 shows numerical data that underline these findings for M1 to M10.

Figure 3.

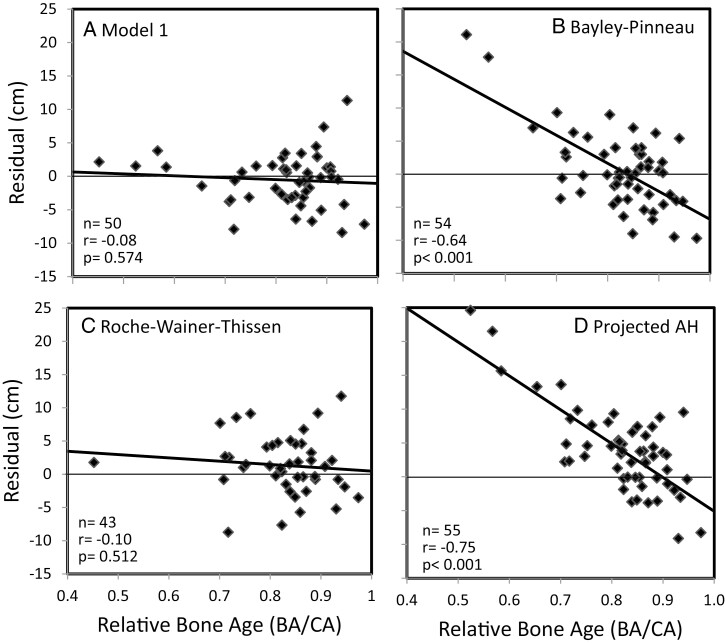
Residuals (predicted AH—observed AH) vs predicted AH in the validation cohort. AH prediction by a) model 1, b) Bayley-Pinneau, c) Roche-Wainer-Thissen, d) projected AH. Regression lines in bold.

Figure 4.

Residuals (predicted − observed AH) vs predicted AH by models 2 to 10 (M2 to M10) in the validation cohort and regression lines. None of the regressions was statistically significant.

Table 3.

Applying models 1 to 10 (M1 to M10) and the conventional methods of Bayley-Pinneau, Roche-Wainer-Thissen, and the bone-age-based projected adult height to the validation cohort: means, SD, and 95% CI of residuals and correlations between residuals and predicted adult height

Method	Included variables	N	Residuals (cm)			Residuals vs PAH
			Mean	SD	95% CI	r (Pearson)	P value
M1	CA, H0, TH, sex, BA/CA, BiWt	50	-0.53	3.76	-1.50 to 0.43	-0.07	0.608
M2	CA, H0, TH, sex, BA/CA	57	-0.29	3.70	-1.25 to 0.67	-0.09	0.414
M3	CA, H0, TH, sex	57	-0.34	3.78	-1.30 to 0.62	-0.03	0.820
M4	CA, H0, MoH, sex, BA/CA, BiWt	51	-0.82	4.04	-1.78 to 0.14	-0.08	0.590
M5	CA, H0, MoH, sex, BA/CA	57	-0.57	4.00	-1.53 to 0.39	-0.11	0.420
M6	CA, H0, MoH, sex	57	-0.71	4.19	-1.67 to 0.25	-0.02	0.867
M7	CA, H0, FaH, sex, BA/CA, BiWt	51	-0.66	3.79	-1.63 to 0.30	-0.05	0.723
M8	CA, H0, FaH, sex, BA/CA	57	-0.33	3.78	-1.29 to 0.63	-0.06	0.634
M9	CA, H0, FaH, sex	57	-0.38	3.90	-1.34 to 0.58	+0.02	0.864
M10	CA, H0, sex, BA/CA	57	-0.52	4.04	-1.48 to 0.44	-0.07	0.614
BP	H0, sex, BA, (CA)	42	+0.53	5.81	-1.23 to 2.29	+0.57	< 0.001
RWT	H0, TH, sex, BA, Wt	35	+1.33	4.37	-0.12 to 2.78	+0.18	0.237
ProjAH	H0, sex, BA	42	+3.81	6.21	+1.93 to 5.69	+0.41	0.002

Abbreviations: BA, bone age; BA/CA, relative BA; BiWt, birth weight (kg); BP, Bayley-Pinneau; CA, chronological age (y); FaH, father’s height (cm); H0, baseline height (cm); MoH, mother’s height (cm); PAH, predicted adult height; ProjAH, projected adult height; RWT, Roche-Wainer-Thissen; TH, target height (cm) according to Tanner; Wt, baseline weight (kg). For BP, CA was included in parentheses (CA), because this method uses retarded, normal, or accelerated BA referring to CA as a categorical variable.

We tested further whether there were significant trends between residuals and any of the exploratory variables included in the models or in clinical subgroups. Figure 5a visualizes the relationship between the residuals of M1 vs BA/CA with a minimal nonsignificant negative trend. Overall, correlations between the residuals of any model and the exploratory variables did not reach statistical significance. The means of residuals by model were lower in males than in females with sex differences varying from −0.99 cm to +0.21 cm without statistical significance. The numbers of prepubertal and pubertal subjects in the validation cohort by model (M1 to M10) were similar, varying from 25 to 27 and from 25 to 30. The means of residuals varied from −0.49 to −0.94 cm in the prepubertal group vs from −0.10 to −0.66 cm in the pubertal group without statistically significant differences. There was no significant correlation between residuals of models and H0 SDS minus TH SDS.

Figure 5.

Residuals (predicted AH − observed AH) vs relative bone age (BA/CA) in the validation cohort. AH prediction by a) model 1, b) Bayley-Pinneau, c) Roche-Wainer-Thissen, d) projected AH.

Comparison With Conventional AH Prediction Methods

We compared the models of this study with the “classic” methods of BP, RWT, and ProjAH applying those also to the validation cohort. Table 3 shows the means, SD and 95% CI of the residuals for each method. While the residuals of the new models were slightly negative (means between −0.82 and −0.29 cm), the conventional methods overestimated AH (BP: +0.53 ± 5.81 cm; RWT: +1.33 ± 4.37 cm; ProjAH: +3.81 ± 6.21 cm). Moreover, the SD values of the new models (between 3.70 and 4.19 cm) were smaller than those of the conventional methods. The correlations between residuals and PAH were not significant except for BP (r = 0.57, P < 0.001) and ProjAH (r = 0.41, P = 0.002). These findings are illustrated in Fig. 3. Similarly, correlations between residuals of the new models and any of the exploratory variables in this study were not significant. In contrast, residuals by BP or ProjAH correlated significantly with BA/CA (r = −0.64, P < 0.001; r = −0.75, P < 0.001) (Fig. 5) and by ProjAH with H0 (r = −0.27, P = 0.045). When the conventional methods were applied to the total study population, no significant correlations between residuals and the exploratory variables were found for the RWT method in contrast to the BP method (N = 281, CA: r = 0.27; H0: r = 0.23; TH: r = 0.20; BA/CA: r = −0.59 with P < 0.001 for all; MoH: −0.13, P = 0.031) and the ProjAH method (N = 288; H0: r = −0.13, P < 0.027; MoH: −0.15, P = 0.009; BA/CA: −0.76, P < 0.001).

Discussion

Pediatric research made efforts for more than 70 years to develop methods for predicting AH [1-3]. The basis of these methods was normally growing children; however, these methods are mostly applied to abnormally growing short or tall children. Therefore, we decided to develop AH prediction models in subjects with ISS, who account for 60% to 80% of short children [26, 27]. According to 2 subsequent consensus meetings [14, 15], confirmed by the International Classification of Pediatric Endocrine Diagnoses (www.icped.org) [28], the diagnosis of ISS includes familial and non-familial ISS, and CDGP. As expected, patients with FSS and non-FSS differed in variables related to parental heights, but in none of the other exploratory variables. Consequently, we neglected the category FSS as an independent variable because this was mirrored by TH. Moreover, because of the variability of pubertal stage assignment and high collinearity between pubertal stage and CA or BA/CA, pubertal stage was not included as an exploratory variable. This decision was corroborated by the studies of Thodberg et al [29]. Sex was included as an exploratory nominal variable aiming at development of regression models that can be applied independently of sex.

The birth year of the patients was around 1975 and the time of baseline assessment was on average in the mid-1980s. AH was assessed on average in the 1990s (Table 1). One may wonder whether such a “historical” population would still be appropriate for AH prediction today and whether the secular trend of height and pubertal development would influence the prediction. While the secular trend has significantly slowed down in Western countries, it is still present in other regions [30-32]. Since most patients in this study were Caucasian of Western/Central European origin, the question may be raised whether the models can also be applied in other ethnic populations. In the absence of such data, we hypothesize that this is possible, because growth patterns are similar in different ethnicities [33].

Linear multi-regression models of this study were developed with PAH (cm) or PAH SDS as the response variables and a multitude of combinations of exploratory variables including absolute values or values after conversion to SDS such as H0 SDS, TH SDS, MoH SDS and FaH SDS, and BMI SDS. Although the use of SDS is common practice in pediatrics, we finally refrained from including SDS values in the models for the following reasons: First, the use of prediction models is more practical, if simply the directly measured data such as H0 (cm) are included. Second, using regional- and ethnic-specific SDS values would require local reference ranges, which often do not exist, and models based on local SDS values. This would limit the usability of this AH prediction tool. Third, the use of SDS often neglects a fundamental problem which can become an additional source of error: The distribution of a variable outside the normal range is a speculative extrapolation of the distribution of the normal range, because the number of subjects for establishing the empirical distribution there is very small. The authors of the CDC reference ranges explicitly pointed out this limitation [34]. In fact, the majority of subjects in this study had heights below the normal range. Fourth, SDS-based models were statistically not superior to models based on absolute values in our analysis (data not shown).

Most patients with ISS have retarded BA. However, BA retardation of 1 year at the age of 5 years may impact further growth differently than at the age of 13 years. Therefore, we included BA/CA as an exploratory variable. Although other variables such as baseline weight, used in the RWT method [2], or BMI were also statistically significant predictors of AH, their contribution was minor and they worsened model quality criteria such as QQ plots. A weak inverse association between childhood BMI and AH was also observed by others [29, 35]. Therefore, we focused on the variables listed in Table 2. In certain situations, however, the height of one or both biological parents, such as in an adopted child, or BA may be unknown, while the parents insist on AH prediction. Therefore, we developed models specific for such situations.

Validation of the models was performed using the validation cohort. Because there were no differences of residuals between the subgroups FSS vs non-FSS, and prepubertal vs pubertal, we believe that neglecting these categories is a valid approach. Residuals of all models scattered symmetrically around the zero-line (Figs. 3 and 4). The means and 95% CI of residuals and correlations between residuals and PAH were not significantly different across models (Table 3) and regression lines were slightly, nonsignificantly descending along the zero-line except with M9. These findings indicate that all 10 models show similar prediction characteristics, although the parameter estimates for the various algorithms are greatly different.

Substantive prediction errors around ± 10 cm were consistently observed in the same few patients across all models. Scrutinized review of these patients did not reveal obvious reasons for such deviations. Since ISS is a diagnostic pool of short children with unknown etiology [15, 26, 27, 36], growth of patients with certain rare unrevealed etiologies may not follow the growth pattern of the majority of patients, and individual AH prediction errors may therefore be substantial. Identifying such etiologies, for example, by genetic techniques, is possible nowadays in many cases.

To further evaluate the performance of the new AH prediction algorithms, they were compared with the methods of BP, RWT, and ProjAH, applying those also to the validation cohort. These 3 methods were chosen because they are the most frequently used methods and because they also use manually rated BA by the GP method [23], which has not only been appraised to be more convenient in daily practice [37], but also to yield acceptable AH prediction results [7, 37-40]. While the new models use CA, H0, sex, and flexibly parental heights, BA/CA and BiWt, the number of predicting variables with the conventional methods is smaller (Table 3). The BP method uses H0, sex, BA, and implicitly CA by differentiating between retarded, normal, and accelerated BA. It is limited to patients with BA greater than 6 years if BA is retarded, as in the vast majority of patients with ISS, or greater than 7 years in boys with normal BA [1]. The RWT method uses H0, sex, TH, BA, and in addition, body weight [2]. BA-based ProjAH, also called “index of potential height”, uses H0, sex, and BA [38, 41].

While all new models slightly underestimated AH on average by −0.5 cm, the conventional methods overestimated AH by +0.5 cm (BP) up to +3.8 cm (ProjAH). All residual SD values and 95% CI of the new models were smaller than those of the conventional methods (Table 3), suggesting that the new models predict AH more accurately in patients with ISS. Reports on AH prediction by BP in comparable cohorts with ISS corroborate these findings (Table 4) [7-12, 20, 42, 43]. While residuals of the new models and of the RWT method did not significantly correlate with PAH in the validation cohort, residuals of the BP and ProjAH methods did (Table 3). They showed a significant positive trend meaning that greater PAHs are associated with a greater prediction error. Moreover, there were also no significant correlations between the residuals of the new models or the RWT method with any of the exploratory variables listed in Table 2. In contrast, the BP method showed a significant positive trend with CA, H0, and TH and a negative trend with MoH and BA/CA. This means that the BP method tends to overestimate AH in children with ISS who are at baseline older, taller, have greater TH, and more retarded BA. The latter has also been observed in other studies [5, 6, 44]. Marginally significant negative trends were obtained between ProjAH residuals and H0 or MoH, whereas the negative association with BA/CA was even greater than with the BP method. While the validation cohort was the only independent basis for testing the new models, the total study population could be used as an independent cohort for the BP, RWT, and ProjAH methods. Applying them to this large population confirmed the findings with the validation cohort. Overall, the new models were somewhat more accurate than the RWT method while the BP method was clearly inferior. Comparisons between the RWT and BP methods in other studies support these findings [7, 38, 39, 45, 46], although not in all [37]. Comparisons between the RWT and TW methods yielded inconclusive results [7, 38, 45]. ProjAH was clearly less accurate than the new models and the BP or RWT methods [38] and should therefore be used at best for getting a quick impression of potential AH by simple inspection of growth charts.

Table 4.

Residuals (predicted AH − observed AH) in this study using model 1 (M1) compared to published studies using the Bayley-Pinneau method. Data of this study refer to the validation cohort

Study	Reference	Method	Diagnosis	Males				Females
				N	Age (y)	Height SDS	Residuals (cm)	N	Age (y)	Height SDS	Residuals (cm)
This study		M1	ISS	37	13.3	-2.3a	-0.7	13	10.9	-2.5a	-0.1
Brämswig et al.	7	BP	ISS	42	14.8	-2.2b	+5.3	33	12.9	-2.1b	+2.9
LaFranchi et al.	8	BP	CDGP	29	13.3	<-2c	+1.9	13	12.3	<-2c	-0.8
Sperlich et al.	10	BP	CDGP	49	13.3	-2.3a	+0.2
Ranke et al.	11	BP	ISS	146	12.6	-2.2b	+4.8d	40	11.1	-2.2b	-0.1d
Buchlis et al.	12	BP	ISS	41	12.7	-2.9c	+1.7	17	12.2	-3.0c	-0.4

Data are shown as means.

Abbreviations: AH, adult height; BP, Bayley-Pinneau; CDGP, constitutional delay of growth and puberty; ISS, idiopathic short stature; SDS, standard deviation score;

Height SDS at baseline according to

^aPrader et al [20],

^bTanner et al [42],

^cHamill et al [43].

^dResiduals provided as SDS were converted to cm using the data of the Tanner standards.

Although in daily practice, the tables of BP [1, 47] and the algorithms of RWT [2] are the most frequently used tools for predicting AH, their reliability is limited. Therefore, attempts were made to improve their quality by first better statistical models and second better methods for assessment of the key variable BA. For instance, the RWT method was improved through mathematical refinement [39, 46]. Improvement of AH predictions by BP in short normal boys and by TWII in girls using “correction factors” was suggested by Maes et al [37]. A recent report by Reinehr et al proposed modified BP tables for improvement of AH prediction in boys with CDGP [6]. Regarding BA, accurate assessment is important. In practice, manually rated BA by the GP method is most widely used because of convenience. However, manual BAGP rating depends much on the experience of the assessor [48] and is quite subjective. Significant progress has been achieved by automated BA reading (BoneXpert) eliminating subjective bias and improving AH prediction [40, 49-51]. Most recent approaches for improvement of AH prediction utilize modern machine learning [52].

ISS is a diagnosis by exclusion made at the end of a series of diagnostic procedures [15, 26, 27]. Therefore, AH should be predicted at this final stage rather than at the beginning. The purpose of AH prediction is 2-fold. First, in general, patients and parents wish to know which height they can expect. In this context, height can be a limiting criterion for many occupations and therefore, AH prediction may influence future career aspirations. Although the AH prediction algorithms provide numbers which appear to be precise, it needs to be communicated that there is an inherent error in the order of about ± 4 cm. Second, recombinant human GH (rhGH) treatment of patients with ISS to increase AH has been approved in various countries including the USA. According to the regulations there, expected AH should be subnormal [13]. Therefore, AH prediction, preferably with the most accurate methods, is required to qualify for rhGH therapy. The model with the greatest number of available variables should be used, because this promises to yield the most accurate result. Due to the simplicity of the linear multi-regression models, calculation of PAH can be done with a calculator; however, computer programs may be developed for daily practice.

The authors are aware of weaknesses of the study. Data on ethnicity were not collected at the time, but we believe that the vast majority of the study population was Caucasian of Western/Central European origin mirroring the ethnic composition of the populations in Germany and The Netherlands in the 1980s. Therefore, validation of the algorithms in modern societies with greater diversity and in different ethnic groups is required. Further, the subjects of the study population were born about 40 to 50 years before the patients for whom we propose to apply the algorithms today. Depending on the regional secular trend, this aspect may be important in some countries [30, 53]. In addition, BA was not assessed centrally, although BA assessment may differ between assessors. However, this reflects the real-world situation, which we believe is a strength. Finally, in the last 15 years, DNA sequencing has made significant progress and it is likely that several patients included in the study population would no longer be diagnosed with ISS today, if up-to-date genetic diagnosis was performed, for example using targeted genome-based gene panels [36, 54, 55].

On the other hand, there are also strengths: 1) The algorithms were developed in the targeted population of patients with ISS. 2) The algorithms are simple linear equations including sex, but not pubertal development and FSS. 3) Only variables which are readily available at first visit were chosen for modeling. 4) BA and CA were used as continuous independent variables in contrast to BP and other BP-derived methods which use these as categorical variables. 5) Specific algorithms were developed accounting for situations in which parents’ heights or BA are missing, making this AH prediction tool flexible. We wish to emphasize that the algorithms should not be applied to normally growing or tall children unless their performance has been studied in such individuals in the future.

In conclusion, this study collected demographic and auxologic data of patients with ISS in childhood and adulthood. In retrospective studies and in clinical practice, variables required for AH prediction with a given method are often missing, for example, BA or either parent’s height. Therefore, a series of algorithms was developed by linear multi-regression analysis. Finally, 10 models were selected on the basis of their statistical characteristics and availability of variables in clinical practice: sex, chronological age (CA), baseline height (H0; cm), target height (TH; cm), mother’s height (MoH; cm), father’s height (FaH; cm), relative bone age (BA/CA), and birth weight (BiWt; kg). AH prediction in an independent validation cohort yielded similar results across all 10 models. There were no significant trends of prediction error vs PAH or any other applied independent variables. Comparison of the new models with conventional methods such as Bayley-Pinneau, Roche-Wainer-Thissen, and projected AH showed a better performance of the new models. On these grounds, the authors believe that this new tool for AH prediction in patients with ISS provides improved accuracy and flexibility, and they recommend using these new models to see whether this approach will stand the test of time.

Glossary

Abbreviations

AH

adult height

BA

bone age

BAGP

bone age by Greulich-Pyle method

BiWt

birth weight

BMI

body mass index

BP

Bayley-Pinneau

CA

chronological age

CDGP

constitutional delay of growth and puberty

FaH

father’s height

FSS

familial short stature

GH

growth hormone

GP

Greulich-Pyle

H0

height at baseline

ISS

idiopathic short stature

MoH

mother’s height

PAH

predicted adult height

ProjAH

projected adult height

rhGH

recombinant human growth hormone

RMSE

root mean square error

RWT

Roche-Wainer-Thissen

SDS

standard deviation score

TH

target height

TW

Tanner-Whitehouse

Financial Support

Publication fees are paid by Division of Pediatric Endocrinology & Diabetology, Center of Child and Adolescent Medicine, Justus-Liebig University, Giessen, Germany, and Willem-Alexander Children’s Hospital, Department of Pediatrics, Leiden University Medical Center, Leiden, The Netherlands

Disclosures

W.F.B. is a non-equity holding consultant to Lumos Pharma, and a former employee and current stockholder of Eli Lilly and Company. M.B.R. received lecture fees from Merck, Sandoz, Pfizer, and Mediagnost. J.M.W. received honoraria for advisory board (Merck, Aeterna Zentaris, Agios, Lumos) and lecture fees (Pfizer, Sandoz, Merck, Novo Nordisk). E.K., A.K., S.B., C.d.B., and S.A.W. have nothing to disclose.

Data Availability

Some or all datasets generated during and/or analyzed during the current study are not publicly available but are available from the corresponding author on reasonable request.