Optimizing a Deep Residual Neural Network with Genetic Algorithm for Acute Lymphoblastic Leukemia Classification

Abstract

Acute lymphoblastic leukemia (ALL) is the most common childhood cancer worldwide, and it is characterized by the production of immature malignant cells in the bone marrow. Computer vision techniques provide automated analysis that can help specialists diagnose this disease. Microscopy image analysis is the most economical method for the initial screening of patients with ALL, but this task is subjective and time-consuming. In this study, we propose a hybrid model using a genetic algorithm (GA) and a residual convolutional neural network (CNN), ResNet-50V2, to predict ALL using microscopy images available in ALL-IDB dataset. However, accurate prediction requires suitable hyperparameters setup, and tuning these values manually still poses challenges. Hence, this paper uses GA to find the best hyperparameters that lead to the highest accuracy rate in the models. Also, we compare the performance of GA hyperparameter optimization with Random Search and Bayesian optimization methods. The results show that GA optimization improves the accuracy of the classifier, obtaining 98.46% in terms of accuracy. Additionally, our approach sheds new perspectives on identifying leukemia based on computer vision strategies, which could be an alternative for applications in a real-world scenario.

Introduction

Acute lymphoblastic leukemia (ALL) is a type of cancer caused by immature lymphocytes in bone marrow [1]. It is the most common childhood cancer worldwide and accounts for 80% of all childhood leukemia [2–4]. ALL can be diagnosed through a variety of tests, such as physical examinations, blood tests, blood counts, myelogram, lumbar punctures, and bone marrow biopsies [5].

Visual analysis in microscopy images is the most economical method for the initial screening of patients with ALL. However, it is a very subjective and time-consuming task [1]. Leukocytes are detected by their dark purple-like appearance, but the analysis and further processing become very complicated due to their variability in shape and texture. Also, significant changes in the morphology of the cells are found in severe cases of the disease.

To overcome these limitations, computer-aided diagnosis systems based on image processing and machine learning techniques are essential and widely applied in several fields of medicine [6–10]. Moreover, these techniques are financially attractive, especially for developing countries [11].

Following the advances of computational resources, deep convolutional neural networks (CNNs) have been significantly outperforming approaches based on handcrafted features. This strategy provides an automatic feature extraction from input images and demonstrates effective results in visual recognition tasks in many areas [12, 13].

In this study, we explore the classification of ALL using microscopy images and deep learning. Our main goal is to improve the identification rate among immature lymphocytes and healthy lymphocytes, thus helping in the diagnosis of ALL in the early stages. Our deep learning approach used a ResNet-50 V2 [14] CNN architecture, and we evaluated its performance using a k-fold cross-validation procedure over the training set and validated the overall results in using the and test sets.

Finding the optimal hyperparameters to train a deep CNN is crucial because there is no optimum method for selecting hyperparameters. In machine learning, for example, grid search (equivalent to brute force), random search, Bayesian optimization, and GA are common approaches used for hyperparameter optimization [15–18]. However, the computational cost of grid search is too high, while random and Bayesian approaches are limited to the search space distribution [19].

To address this challenge, we innovate with a method to find a suitable setup for hyperparameter optimization using genetic algorithm (GA). Hyperparameters are a set of variables to be tuned before applying the learning algorithm to the dataset. These hyperparameters directly affect the learning speed, the convergence of the cost function, and the classification performance [20].

Our results suggest that hyperparameter optimization combined with fine-tuning training tends to be the best performing strategy. Our results demonstrate the suitability and performance score of hyperparameter optimization based on GA, and the best result achieved an accuracy of 98.46% in ALL classification.

Moreover, as far as we know, our result is the best obtained for ALL classification in microscopy images using the dataset evaluated in this study. We believe that our proposed method can contribute to future research intended to help healthcare workers to identify leukemia and manage patients’ conditions.

The remaining of this paper is organized as follows: "Related Work" surveys related work. "Materials and Methods" describes the material and methods. "Experimental Protocol" presents the experimental procedure. "Results and Discussion" presents and discusses the results. Finally, conclusion and future work are presented in "Conclusions".

Related Work

Leukemia identification using microscopy images is a field of intense research, with many approaches being developed over the years. Piuri and Scotti [21] were among the first to propose an automatic system for classifying leukocytes from other blood components such as red blood cells, platelets, and plasma in microscopy images. After, Scotti [22] proposed another system that uses shape features to identify ALL from microscopic images. According to their experiments, morphological features allowed the white blood characterization.

Several studies have been proposed for classifying ALL in microscopy images with hand-crafted feature extraction (i.e., using a non-automated user-based process). Mohapatra et al. [23] proposed leukocytes classification by using a support vector machine (SVM) with shape, texture, and color features. After, [24] proposed an approach based on shape and color features and an ensemble of classifiers.

Khashman et al. [25] applied Otsu’s threshold method, median filtering, Canny edge detection, and pattern averaging kernel to process 80 images from ALL-IDB2 dataset. They conducted experiments with different ratios of training and test sets and used a multi-layer perceptron for classification.

Putzu et al. [26] proposed an approach based on shape, color, and texture analysis for ALL identification in 245 sub-images obtained from ALL-IDB dataset. Bhattacharjee and Saini [27] used morphological operations, SVM, K-NN, and K-means clustering. Singhal and Singh [28] classified ALL using a SVM classifier with local binary patterns (LBP) and gray-level co-occurrence matrix (GLCM).

Rodrigues et al. [29] converted RGB images to HSV color space and extracted and converted V channel into binary. They analyzed morphological features and performed the classification with four different classifiers. Sus and Oliveira [30] extracted B and S channels, obtained from RGB and HSV color models, respectively. Segmentation methods, morphological analysis, and several classifiers were used to classify leukocytes in microscopy images. The approaches seen in [29] and [30] consider all 260 images from ALL-IDB2 dataset, and these authors reported difficulties in the segmentation stage due to problems intensity variations in the images.

Faria et al. [31] presented a simple and efficient combination of SIFT and SURF descriptors, stacking the descriptors of key points into a single matrix and evaluated two classifiers. Sahlol et al. [32] segmented each cell with Zack’s threshold method and optimized a feed-forward neural network with elephant herd optimization (EHO) algorithm, which updates the weights and the biases of the network to classify ALL. In another study, Sahlol et al. [33] applied a bio-inspired meta-heuristic method called social spider optimization algorithm (SSOA) and tested several types of classifiers such as K-NN and SVM.

Although most of the previous works achieve an accuracy rate above 90%, they depend on the use of a proper segmentation process and handcrafted feature extraction. To overcome this limitation, strategies based on deep learning, specifically convolutional neural networks (CNNs), have been proposed to classify ALL in microscopy images and produce better results than all classical techniques [34–37].

Vogado et al. [38] proposed a method to identify leukemia using a hybrid-Leukocyte database and transfer learning strategy. Three CNNs architectures were used for feature extraction, and the gain ratio method was applied for feature selection. Further, the features selected were used as input to the SVM classifier.

Sipes and Li [39] developed a simple sequential CNN and compared it with conventional classifiers to classify the ALL in microscopy images. They evaluated the classifiers with training from scratch and tuned some hyperparameters empirically. However, to deal with small datasets, training based on transfer learning is most suitable [40].

Claro et al. [41] proposed a method for the automatic classification of two leukemia types and healthy cells in microscopy images using a CNN called AlertNet that shares the basic architecture of AlexNet [42] and uses a residual structure similar to ResNet [43]. In addition, they overcome overfitting using different data augmentation strategies and transfer learning.

Sahlol et al. [44] extracted features from lymphocytes images using VGG architecture and reducing the features extracted using a statistically enhanced salp swarm algorithm (SESSA). The training of VGG considered transfer learning, and six conventional classifiers received as input the features extracted by VGG architecture and reduced by SESSA algorithm.

Most recently, Das and Meher [45] proposed a hybrid transfer learning approach that ensembles MobilenetV2 and ResNet18 architectures. They considered the training based on transfer learning but did not exploit data augmentation techniques to deal with a small number of training images.

Automatic feature extraction is the main strength of previous studies based on deep CNNs. However, these studies do not investigate the appropriate choice of training-relevant hyperparameters, which can also significantly affect classification performance. Thus, to overcome this problem, we propose an approach based on GA to identify the optimal hyperparameters in a broad search space that considers a uniform distribution, data augmentation strategy, and training based on fine-tuning. Also, our method does not need the segmentation process, it is more robust to the intensity variations in the images, and it is also suitable to deal with the lack of training data for approaches based on deep learning.

Material and Methods

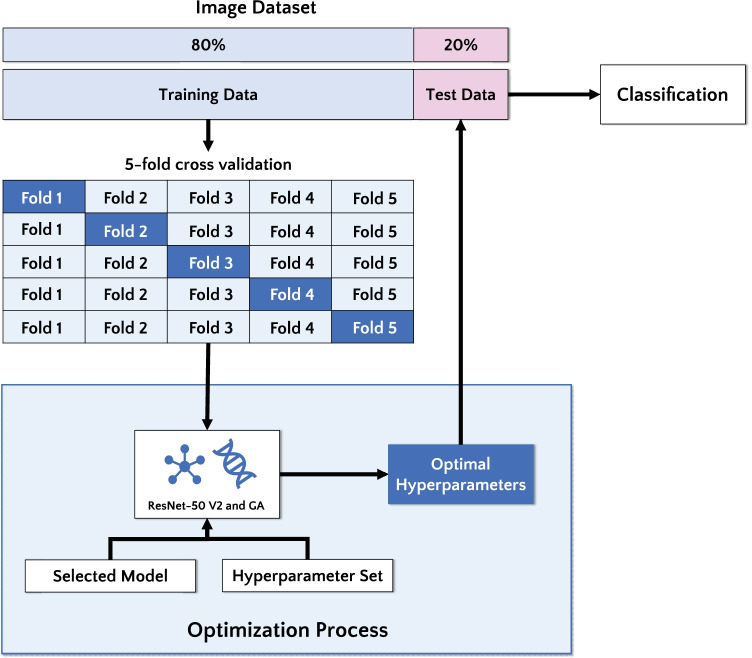
To fill the state-of-the-art gap concerning the best hyperparameters setup [46], we developed a novel approach based on GA. The main goal of this paper is to evaluate the performance of a deep residual CNN architecture to classify ALL in microscopy images. More precisely, we find the best hyperparameter combination and improve classification performance. Figure 1 illustrates the steps of the methodology adopted here.

Fig. 1.

Flowchart of the proposed approach

Image dataset

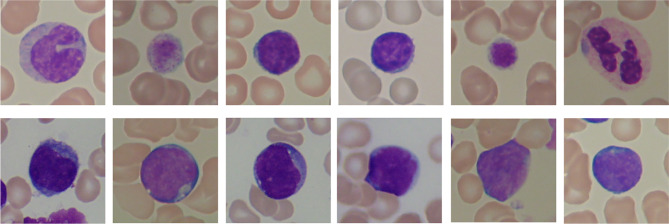
The images used in this work were obtained from ALL-IDB2 dataset¹ provided by Department of Information Technology - Universitá degli Studi di Milano [47]. It contains 260 images, each with a single, centered cell in evidence, categorized into two classes: healthy (130 images) and immature (130 images). All images are in JPG format with 24 bit color depth and $2592\times 1944$ pixels size. Figure 2 shows some images from the dataset for both classes, healthy and immature.

Fig. 2.

Image instances from the ALL-IDB2 dataset showing healthy (top) and immature (bottom) lymphocytes

Deep Residual Network

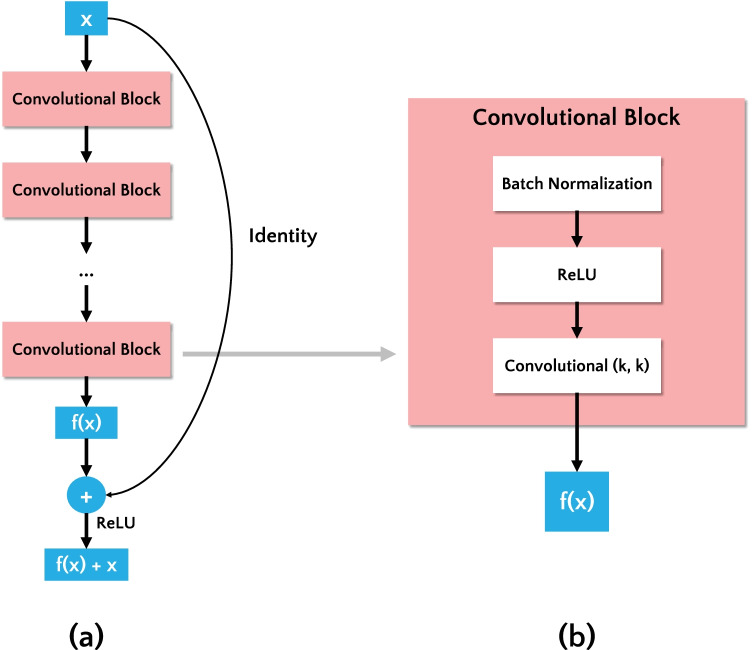
Convolutional neural networks (CNNs) are the state-of-the-art in image classification tasks, designed to extract visual patterns from input images directly, without requiring handcrafted feature extraction [12]. In CNNs, the classification performance increases as the number of deep layers increases. However, as the number of layers increases, the accuracy tends to saturate and eventually degrade [48]. To overcome this problem, a residual network (ResNet) [43] was proposed. It uses residual blocks to address the gradient degradation in the training step and each residual block is composed of several stacked convolutional layers. Thus, the residual block adds a shortcut connection summing the input feature map (x) and the output of convolutional blocks (f(x)), as shown in Fig. 3(a).

Fig. 3.

(a) Residual block. (b) Detail of a convolutional block inside the Residual Block

In this study, we evaluated a deep residual network named ResNet-50 V2 [14]. ResNet-50 V2 is the enhanced version of ResNet-50 [43] that won the ILSVRC 2015 challenge [49]. The authors of [14] refined the residual block using a pre-activation variant of residual block, in which the gradients can flow through the shortcut connections to any other earlier layer unimpeded. The convolutional block is illustrated in Fig. 3(b), and it is composed of following layers: batch normalization, rectified linear unit (ReLU), and convolutional with a kernel of size k.

Hyperparameter Optimization

Hyperparameters define the optimization algorithms used, details of training, architecture, and topology of the CNN [20]. The choice of their values is essential to the performance of the CNN, although there is no optimum method for their selection. This choice may be performed empirically by evaluating different values until the algorithm provides satisfactory performance. However, the optimal values are unknown, and any definition of satisfaction degree is subjective.

Alternatively, the choice of hyperparameter values can be modeled as an optimization problem, where the hyperparameters are defined as decision variables, and the objective function minimizes the loss function. The fine-tuned hyperparameters in this study are as follows:

• Dropout (d): dropout is a technique to deal with overfitting. It is based on the random dropping of neurons during the training process, i.e., a unit out is temporarily removed from the network, along with all its incoming and outgoing connections [50].

• Learning rate (l): the learning rate is the main tuning parameter, being responsible for improving the stochastic gradient descent (SGD) [51] optimizer runtime. It defines the level of adjustment of weight connections and network topology applied at each training epoch. A high learning rate may sacrifice accuracy due to a lack of precision in the adjustments. On the other hand, a low learning rate requires more training epochs and longer processing time [20].

• Momentum ($\mu$): the momentum coefficient [52] is responsible for reducing oscillations in the high-curvature regions of the loss function generated by the SGD. By default, its value is set to 1, but fine-tuning this hyperparameter may lead to improved results [13].

Proposed Genetic Algorithm

Genetic algorithm (GA) [53] is inspired by the natural biological evolution, and it is a type of evolutionary algorithm. Usually, a GA is composed of a population with n individuals and a series of bio-inspired operations, such as selection, crossover, and mutation.

GA is suitable for combinatorial optimization problems, and the quality of the solution obtained by GA suggests that it is better than simulated annealing or tabu search algorithms [54]. We choose GA over other heuristic algorithms for hyperparameter CNN evolution because the GA can incorporate domain-specific knowledge in all optimization phases [54], which is essential for hyperparameter combination in deep learning.

The conventional GA includes three main steps, as shown in Algorithm 1 and explained in the next subsections. Initially, n chromosomes are randomly generated according to the specific encoding method. Then, new offspring are continuously generated from the existing population and combined with the older generation to form a new generation. Finally, there is a population evolution process in which all individuals enter an iterative competition generating a new population composed of the survivors generated from the crossover of survivors and mutation operation.

Population Initialization

Initialization is the process of randomly selecting candidate solutions in the search space. In this study, we defined the search space size as an input from the hyperparameter set. Also, we use a uniform distribution to ensure the random distribution of candidates in the search space. There is a particular interval for all hyperparameters in which the gene can assume values within the defined range, limiting the search space of the GA.

During population initialization, hyperparameters are defined, and a random value is chosen within the pre-defined interval to encode the chromosome. We must include the information of dropout, learning rate, and momentum coefficient for the chromosome encoding in an array. Each chromosome is composed of three genes, and each gene encodes a real value for its respective hyperparameter. The structure of the chromosome is shown in Fig. 4.

Fig. 4.

Chromosome representation for hyperparameter optimization

Selection

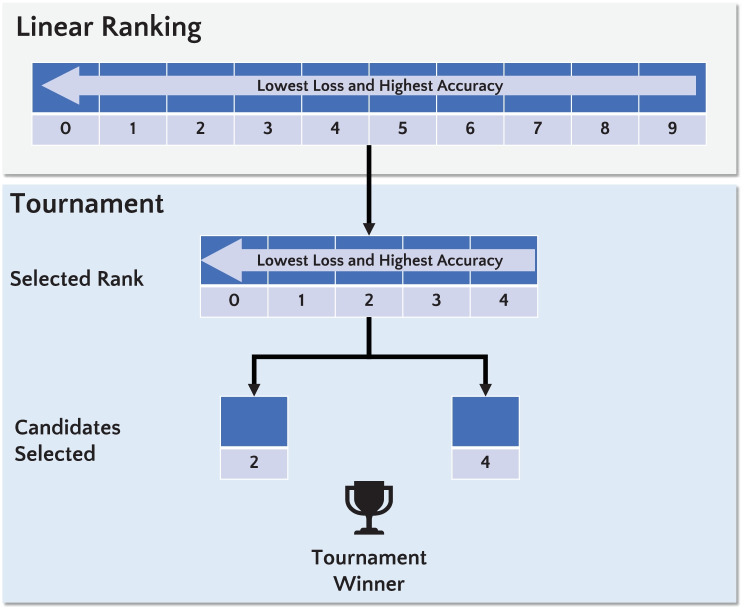
The selection is based on fitness, i.e., the fittest individual is selected to participate in the reproduction process. In this operator, the current generation members with the highest fitness values are the most likely to generate the next population. In this study, we applied linear ranking with tournament selection.

• Linear Ranking: It is based on the classification of individuals according to fitness, being the probability of selecting an individual depends solely on fitness. For this, the worst individual gets a rating of 1; the second-worst individual gets a rating of 2. This idea repeats successively until the best individual receives a rating of n (corresponding to the number of chromosomes in the population). Thus, based on their rating ($ran{k}_i$), each individual i has the probability $P_i$ to be selected from a population of n individuals, as defined in Eq. 1 [55].

  $$\begin{array}{c}\hfill P_i=\frac{ran{k}_i}{n\times (n-1)}\end{array}$$ 1
• Tournament: The tournament selection [56] aims to select a set of k individuals randomly, which will be sorted according to their relative fitness. Afterward, the fittest individual is chosen for reproduction. This process is repeated several times for the entire population, and the probability $P_i$ of each individual being selected is expressed in Eq. 2.

  $$\begin{array}{c}\hfill P_i=\left\{\begin{array}{cc}{C}_{n-1}^{k-1}& ,ifi\in [1,n-k-1]\\ 0& ,ifi\in [n-k,1]\end{array}\right)\end{array}$$ 2

Figure 5 shows the selection method based on linear ranking and tournament applied in this study. All individuals are ranked, and half of the best chromosomes will be selected for the tournament. After, a tournament ($t=2$) is performed considering the best-ranked chromosomes. Afterward, the winner of the tournament will be selected for the reproduction process.

Fig. 5.

Selection based on linear ranking and tournament. The linear ranking is applied to select half of the best chromosomes, sorting the highest accuracy and lowest loss at the top of the population. Then, the selection with a tournament ($t=2$) is performed considering the best-ranked chromosomes

Crossover and Mutation

The crossover operator is used to generate new individuals by recombining the genes of parent chromosomes. In this study, we used a single-point crossover. For each iteration in the GA process, one point was randomly selected. For example, as illustrated in Fig. 6, to generate a “child 1”, the random crossover point is index 1. Thus, index 0 and 1 from “parent 1” will be selected as head, and index 2 from “parent 2” will be chosen as tail. After, a similar process occurs to generate a “child 2”.

Fig. 6.

Example of single-point crossover

Also, we applied the mutation operator, which is initiated after the crossover process by randomly modifying one bit of an individual’s chromosome to generate a child.

Fitness Evaluation

In this paper, we considered the objective function as the loss-function defined by $\mathcal{L}(W)$. Eq. 3 show that $\mathcal{L}(W)$ is computed over a set of training samples $X_j$ considering the tuned weights W, parameters $f(x_j)$, and the known classes $y_j$, where j represents the classes lymphocytes immature and healthy.

$$\begin{array}{c}\hfill \mathcal{L}(W)=\frac{1}{n}\sum _{j=1}^N\ell (y_j,f(x_j;W))\end{array}$$ 3

In this way, to minimize $\mathcal{L}(W)$, we applied the stochastic gradient descent (SGD) [51] optimization algorithm with hyperparameters (dropout, learning rate, and momentum) optimized through GA. Consequently, when we minimize the loss-function, the accuracy (Eq. 4) is maximized.

Experimental Protocol

Firstly, we have to adapt the image size in the dataset for the input of the ResNet-50 V2. All images were resized to 224 $\times$ 224 pixels size using bilinear interpolation.

We arranged the dataset into training and test sets: 80% for training (further split into 80% for training and 20% for internal validation using stratified fivefold cross-validation method [57]) and 20% for testing (external validation). We applied fivefold internal cross-validation to all experiments, reporting the results on the external test set.

Neural networks like ResNet generally require a large amount of data during the training in order to avoid overfitting. Given the reduced number of images in the dataset, we used data augmentation and transfer learning techniques to improve the training of the networks [40, 41]. Data augmentation enables to increase the training set artificially by generating new samples of a given image under different variations, without introducing labeling costs [42]. In our experiments, we performed the data augmentation using only vertical and horizontal flips.

Additionally, we applied transfer learning, i.e., we used the pre-trained 2012 ImageNet weights to initialize the network [49]. This strategy enables to use low-level features learned in larger datasets, which are better in comparison to the ones learned using a network trained from scratch in a smaller dataset. For comparison, ImageNet data set contains approximately 1.2 million images divided into 1000 classes. In the sequence, we used our small dataset to fine-tune the network weights to our problem, i.e., we initialized all convolutional layers with weights from the pre-trained model, and the fine-tuning was performed only in the deeper layers [13].

We report our results in terms of average accuracy, precision, recall, and F1-score [58], averaged over the fivefold:

• Accuracy: is the ratio between the correct classifications and total samples (Eq. 4).

  $$\begin{array}{c}\hfill Accuracy=\frac{TP+TN}{TP+TN+FP+FN}\end{array}$$ 4
• Precision: is the ratio between TP and the total of positives classification (Eq. 5).

  $$\begin{array}{c}\hfill Precision=\frac{\mathit{TP}}{TP+FP}\end{array}$$ 5
• Recall: is the proportion of TP correctly classified (Eq. 6).

  $$\begin{array}{c}\hfill Recall=\frac{\mathit{TP}}{TP+FN}\end{array}$$ 6
• F1-Score: is the harmonic average of the precision and recall (Eq. 7).

  $$\begin{array}{c}\hfill F1-Score=2\times \frac{Precision\times Recall}{Precision+Recall}\end{array}$$ 7

where TP is true positive, TN is true negative, FP is false positive and FN is false negative. For a given fold, we obtain these metrics and then we compute the average metrics among the folders.

All experiments were conducted using the Google Colaboratory cloud service with a machine Intel(R) Xeon(R) 2.20GHz processor, 12 GB RAM, and a GPU NVIDIA Tesla T4. The experiments were programmed using Python (version 3.6) and Keras 2.0 [59] deep learning framework. The hyperparameter optimization algorithms random search and Bayesian optimization were drawn from the KerasTuner library [60], version 1.1.0.

Results and Discussion

We propose experiments aiming to answer the following questions:

• What are the best values of hyperparameters (dropout, learning rate, and momentum coefficient), which bring the highest classification performance?

• How much does the hyperparameter optimization increase the performance of ResNet-50 V2, considering fine-tuning approach?

• Considering metrics derived from confusion matrix, what is the most suitable approach for leukocytes image classification: training without GA or with GA?

• In terms of consumed time for training and the classification performance, considering GA, random search, and Bayesian optimal parameter finding methods, which one is the best approach?

Classification Without Hyperparameter Optimization

Aiming to assess the impact of the training without hyperparameter optimization, we analyze the classification performance according to metrics of accuracy, precision, recall and F1-score. We trained the CNN SGD optimizer with a learning rate of 0.01, momentum of 1.0, batch size of eight, and 100 epochs. The values of learning rate and momentum were defined according to the literature [13].

Regarding the classification performance, Table 1 present the result obtained for the test set. Results show that using the default values generates poor results, indicating that these hyperparameters need to be well adjusted in order to the CNN to achieve a good performance.

Table 1.

Classification results considering training without GA using the test set

Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)
50.00	25.00	50.00	33.00

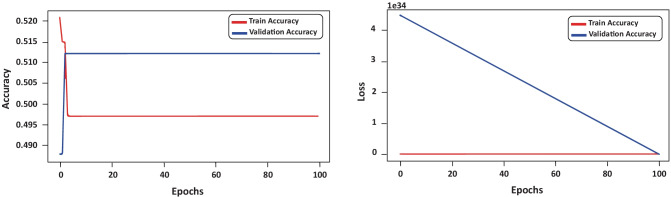
In order to assess the values of accuracy and loss during the training phase, the evolution of these values is presented in Fig. 7, considering the fifth iteration of the k-fold. Throughout the training, the behavior of the accuracy and loss function generated noise values resulting in underfitting.

Fig. 7.

Evolution of accuracy and loss values considering the training and validation set

Evaluating the Impact of GA Optimization

This experiment aimed to demonstrate that proper hyperparameter tuning improves the performance of the ResNet-50 V2 deep CNN. The selection of hyperparameter values was carried out as an optimization problem, as described in "Hyperparameter Optimization".

We applied the GA to optimize the fine-tune values, namely the dropout, learning rate, and momentum coefficient in pre-trained ResNet-50 V2. The hyperparameter optimization process for each fold took about 78 minutes to complete. The GA setting considered a mutation rate of 30%, population size of ten, and five generations. For each generation, the CNN was trained for 20 epochs. Usually, a larger population size and larger maximal generation number results in better performance, but this is time-consuming and requires more computational resources. To overcome this limitation, we applied the same setting adopted by [61] to optimize a deep CNN with GA.

Table 2 presents the hyperparameter space search evaluated in this study. All hyperparameters are searched considering a uniform distribution. Besides, Table 3 presents the best values for each hyperparameter returned by the GA.

Table 2.

Hyperparameter search space used for optimization

Hyperparameter	Value
Dropout	x $\in$ [0.0, 0.5]
Learning Rate	x $\in$ [0.005, 0.01]
Momentum	x $\in$ [0.0, 1.0]

Table 3.

Hyperparameter optimized with GA

		Hyperparameter
Fold	Dropout	Learning Rate	Momentum
1	0.01326	0.00179	0.15547
2	0.01489	0.00187	0.15547
3	0.01326	0.00187	0.15547
4	0.01489	0.00187	0.09274
5	0.01326	0.00179	0.15547

For all analyses, we consider “HS” as the abbreviation of the hyperparameter setting, which is obtained from fivefold internal cross-validation. Given the results obtained by GA, we trained the ResNet-50 V2 using the optimized hyperparameters with 100 epochs.

As shown in Table 4, the GA hyperparameter optimization improved the classification performance significantly. When we compare the results obtained with and without GA, it is possible to observe that optimization generated an accuracy enhancement of 48.46 percentage points (accuracy increased from 50.00% to 98.46%).

Table 4.

Classification results considering training with five different hyperparameters setting from Table 3 applied on the test set

HS	Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)
1	100.00	100.00	100.00	100.00
2	98.08	98.15	98.08	98.08
3	96.15	96.43	96.15	96.15
4	100.00	100.00	100.00	100.00
5	98.08	98.15	98.08	98.08
Average	98.46 ± 0.01	98.55 ± 0.01	98.46 ± 0.01	98.46 ± 0.01

The results suggest that our hyperparameter optimization based on GA is superior in all evaluated metrics over the strategy without automatic optimization. This implies that defining optimal hyperparameters requires lots of domain expertise, and manually pre-configurations limit the feasible solution space to miss out on the better set of hyperparameters. It is a relief that GA can automatically search for the optimal solution in a large space without a manual setting. Thus, the automatic selection by GA reduces the domain expertise requirements in deep learning for researchers and helps some non-expert researchers to define the best hyperparameters obtaining high-performance classifiers.

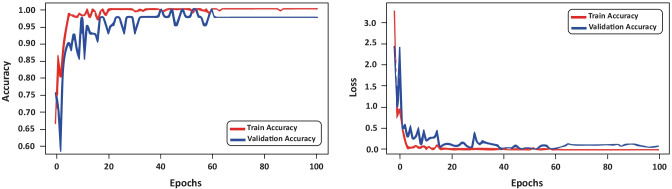
As a check on the learning behavior of the training step, Fig. 8 shows the loss and accuracy values considering the second iteration of the k-fold. It is important to note the low values of the loss function. This behavior suggests that the training did not overfit the data, thus retaining the generalization property of the deep residual CNN.

Fig. 8.

Evolution of accuracy and loss values considering the training and validation set and GA hyperparameter optimization

The proposed model optimized by GA has further exploited the potential of ResNet-50 V2 and improved the acute lymphoblastic leukemia detection performance. In summary, the proposed model shows better and more balanced performance compared with conventional ResNet-50 V2, without GA optimization.

Figure 9 shows the feature map acquired in selected convolutional layers of the ResNet-50 V2 optimized by GA. The filters embedded in the convolutional layers shows that most of the features behaved as texture extractors and edge detectors, preserving the leukocyte cell spatial information. The results demonstrate that our approach does not need the segmentation process and it is more robust to deal with the different leukocyte features.

Fig. 9.

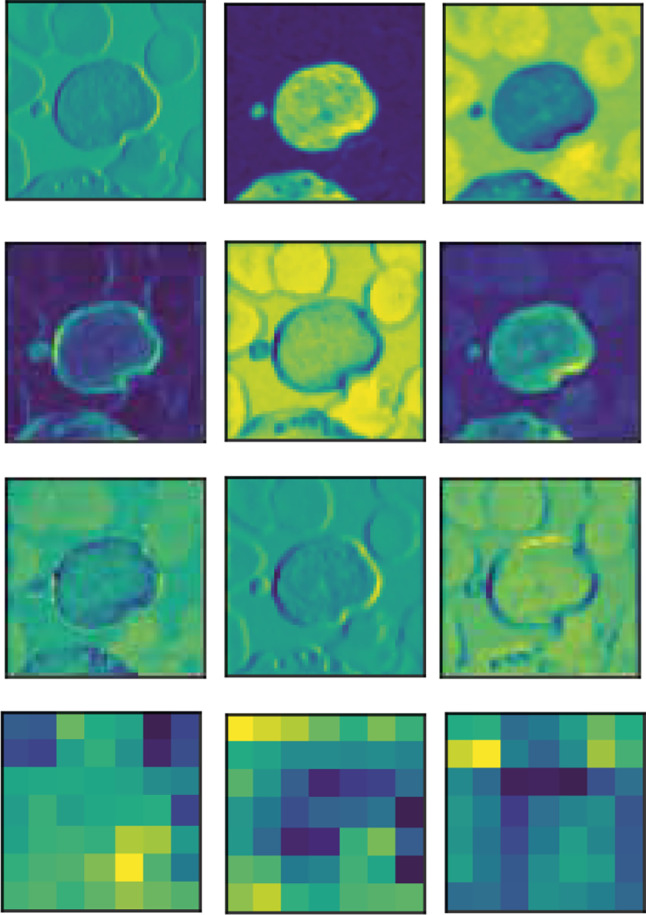
Feature maps obtained for some of the convolutional layers of the ResNet-50 V2 optimized by GA

Table 5 presents the confusion matrix for ResNet-50 V2 optimized by GA, and it shows the aspects of the classification problem investigated in this study. It can be seen that our approach classifies 97.69% of leukemia images correctly and does not require preprocessing or segmentation process (commonly used in state-of-the-art techniques).

Table 5.

Confusion matrix for ResNet-50 V2 optimized with GA averaged over the five hyperparameters

	Healthy	Leukemia
Healthy	99.23%	0.77%
Leukemia	2.31%	97.69%

Comparison of Different Hyperparameter Optimization Approaches

In addition to optimizing with GA, we also evaluated the impact of optimization using random search and Bayesian optimization approaches to compare their performance. We choose these approaches because they are widely used in CNN hyperparameter optimization [17, 62–67].

Random search [68] is a method that selects a suitable set of optimal hyperparameter configurations by testing random combinations of hyperparameters. However, the method is entirely random and uses no intelligence in selecting the trial points resulting in a non-adaptive approach. On the other hand, Bayesian optimization [69] finds the value that minimizes the objective function by building a probability model (using the Gaussian process) based on the previous evaluation results of the target.

For a fair comparison, we considered the same search space evaluated in GA hyperparameter optimization (see Table 2). The relevant hyperparameters obtained for each fold with random search and Bayesian optimization are presented in Tables 6 and 7, respectively.

Table 6.

Hyperparameter optimized with random search

	Hyperparameter
Fold	Dropout	Learning Rate	Momentum
1	0.31971	0.00519	0.40853
2	0.31971	0.00519	0.40853
3	0.31971	0.00519	0.40853
4	0.27407	0.00533	0.49753
5	0.31971	0.00519	0.40853

Table 7.

Hyperparameter optimized with Bayesian optimization

	Hyperparameter
Fold	Dropout	Learning Rate	Momentum
1	0.0	0.005	0.0
2	0.00624	0.005	0.0
3	0.00610	0.005	0.0
4	0.86178	0.00944	0.35184
5	0.5	0.005	0.0

By comparing the values returned by the two optimizers, we observed that the Bayesian optimization better explored the search space by finding different possible optimal solutions.

Given the optimized hyperparameters obtained by random search and Bayesian optimization, we trained the ResNet-50 V2 with 100 epochs. As shown in Table 8, the random search optimization allowed to achieve an accuracy of 62.31%. However, this result is only better than classification without hyperparameter optimization (as presented in "Classification Without Hyperparameter Optimization"). In contrast, Bayesian optimization performed better than random search obtained an accuracy of 80.39% as shown in Table 9. Furthermore, when considering the results obtained in hyperparameter setting 2 and 3, we observed that the accuracy is very close to the results obtained with the GA.

Table 8.

Classification results on the test set considering training with five different hyperparameters setting obtained from random search

HS	Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)
1	71.15	71.44	71.15	71.06
2	51.92	75.49	51.92	37.47
3	50.00	25.00	50.00	33.00
4	71.15	71.97	71.15	70.88
5	67.31	80.23	67.31	63.40
Average	62.31 ± 0.10	64.83 ± 0.22	62.31 ± 0.10	55.16 ± 0.18

Table 9.

Classification results on the test set considering training with five different hyperparameters setting obtained from Bayesian optimization

HS	Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)
1	92.31	92.56	92.31	92.30
2	98.08	98.15	98.08	98.08
3	98.08	98.15	98.08	98.08
4	57.69	68.84	57.69	50.35
5	55.77	76.53	55.77	45.01
Average	80.39 ± 0.21	86.85 ± 0.13	80.39 ± 0.21	76.76 ± 0.26

In order to compare the hyperparameter optimization methods, Table 10 shows the classification performance metrics and optimization time. It is important to note that the GA improved leukemia image classification significantly, although it requires more time to perform the optimization. This result demonstrates that random search and Bayesian optimization approaches don’t explore the search space distribution as well as the GA. At the same time, GA can incorporate domain-specific knowledge in all optimization phases, guaranteeing gains in all classification performance metrics. Also, once GA obtains the best hyperparameters, the training time becomes similar to training with manual configuration, taking around 10 minutes.

Table 10.

Average classification and optimization time for each optimization method

Method	Accuracy (%)	Precision (%)	Recall (%)	F1-Score (%)	Optimization Time
Random Search	62.31	64.83	62.31	55.16	22min 10s
Bayesian Optimization	80.39	86.85	80.39	76.76	22min 36s
Genetic Algorithm	98.46	98.55	98.46	98.46	78min 45s

Comparison With Literature

We also compared the best result achieved in this study in terms of accuracy with other state-of-art work in the literature. The best result in our work was obtained with GA hyperparameter optimization, which scored 98.46% of accuracy (as shown in Table 4). The best results reported in the literature are presented in Table 11 for the same ALL-IDB2 dataset. It can be seen that our best score is upper to the best state-of-the-art technique reported in the literature.

Table 11.

Highest accuracy of other classification methods using the ALL-IDB2 dataset

Method	Accuracy (%)
Rodrigues et al. [29]	85.00
Singhal and Singh [28]	93.84
Sahlol et al. [32]	91.80
Sus and Oliveira [30]	94.60
Faria et al. [31]	97.22
Sahlol et al. [33]	95.23
Sahlol et al. [44]	96.11
Das and Meher [45]	97.18
Our proposal (2022)	98.46

Conclusion

The results presented in this paper point to a promising use of deep CNN with hyperparameter optimization to classify ALL cases based on microscopy images. We compared the performance of ResNet-50 V2 optimized with GA, trained with transfer learning and data augmentation approaches. Our best result of 98.46% was upper to the highest accuracy score presented in the literature.

Additionally, we demonstrated that hyperparameter tuning with GA leads CNN to achieve higher performance rates against approaches without optimization and optimization using random search and Bayesian algorithms, answering the raised questions regarding classification performance. Besides, we found, quantified, and presented the hyperparameters and measured the improvement they promoted in the performance of ResNet-50 V2 over the dataset evaluated.

Moreover, the transfer learning strategy helped to reduce the training time, enabling us to evaluate the hyperparameter optimization and the use of k-fold cross-validation. Our dataset partitioning complies with the state of the art once our experimental protocol avoids biased model and abnormal CNN behaviors.

The presented results open new opportunities towards better machine learning based on deep CNN for automated detection of leukemia and the development of new computer-aided diagnosis applications. We believe that hyperparameter optimization using GA and other evolutionary approaches is an alternative to overcome challenges in deep CNNs.

As future work, we intend to evaluate other CNN architectures, different data augmentation strategies, and different settings for GA with a more extensive set of hyperparameters. Also, we plan to test the proposed method with other datasets of images containing lymphocytes and other types of cells to verify that our findings hold for similar datasets.