A practical introduction to EEG Time-Frequency Principal Components Analysis (TF-PCA)

Abstract

This EEG methods tutorial provides both a conceptual and practical introduction to a promising data reduction approach for time-frequency representations of EEG data: Time-Frequency Principal Components Analysis (TF-PCA). Briefly, the unique value of TF-PCA is that it provides a data-reduction approach that does not rely on strong a priori constraints regarding the specific timing or frequency boundaries for an effect of interest. Given that the time-frequency characteristics of various neurocognitive process are known to change across development, the TF-PCA approach is thus particularly well suited for the analysis of developmental TF data. This tutorial provides the background knowledge, theory, and practical information needed to allow individuals with basic EEG experience to begin applying the TF-PCA approach to their own data. Crucially, this tutorial article is accompanied by a companion GitHub repository that contains example code, data, and a step-by-step guide of how to perform TF-PCA: https://github.com/NDCLab/tfpca-tutorial. Although this tutorial is framed in terms of the utility of TF-PCA for developmental data, the theory, protocols and code covered in this tutorial article and companion GitHub repository can be applied more broadly across populations of interest.

1. Introduction

1.1. Motivation and background

Electroencephalography (EEG) affords many strengths as a tool for the developmental cognitive neurosciences. EEG reflects the direct readout of neural activity with millisecond precision and provides a non-invasive means of measuring neural oscillations (Nunez et al., 2006). At the same time, EEG is relatively inexpensive and easy to collect, both in and outside the lab, and is generally well-tolerated across the lifespan. At the analysis stage, time-domain EEG data can be transformed into time-frequency (TF) representations reflecting dynamic changes within particular frequency bands in response to events of interest (Cohen, 2014). TF approaches can reveal neurocognitive phenomena missed by more traditional EEG analysis techniques (e.g., Event-related-potentials; ERPs). However, decomposing EEG data into TF representations also exponentially increases the multiple comparisons problem, necessitating appropriate data reduction methods. With a focus on developmental cognitive neuroscience, the current article provides both a conceptual and practical introduction to a promising data reduction approach for TF data: Time-Frequency Principal Components Analysis (TF-PCA). Briefly, the unique value of TF-PCA, compared to other data reduction approaches, is that it provides a data-reduction approach that does not rely on strong a priori constraints regarding the specific timing or frequency band of interest (Bernat et al., 2005). Given that the time and frequency characteristics of neurocognitive process are known to change across development, we believe that TF-PCA may be a particularly powerful, yet currently underutilized, approach for the analyses of developmental TF data.

1.2. Brief introduction to EEG time-frequency (TF) representations

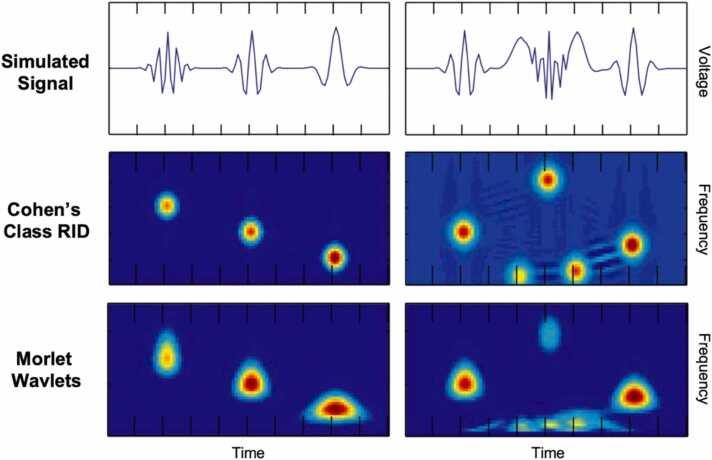
A TF representation depicts a time-varying signal, such as an EEG waveform, in terms of frequency-specific activity (e.g., power magnitude) as a function of time. A TF representation can be plotted as a spectrogram, with two spatial dimensions (the x and y axes) and a third, non-spatial dimension that is mapped to color values (see Fig. 1). In this case, the x-axis delineates time in sample points (relative to an event of interest), the y-axis delineates frequency in bins, and the activity of interest at each point in the TF representation is represented by color along the non-spatial z-dimension. There are multiple approaches for decomposing time domain EEG signals into TF representations, but the most common approach is a continuous wavelet transform (CWT) using Morlet wavelets (Cohen, 2014). The CWT/Morlet approach has several advantages and is widely used, and moreover, we recommend the CWT/Morlet approach as a useful analysis approach. At the same time, it is important to note that one of the major drawbacks of this approach is that it tends to produce “smearing” across time in lower frequencies and smearing across frequencies in higher frequencies (see Fig. 1 in this article, as well as Bernat et al., 2005). If a researcher has strong prior knowledge about the exact frequency boundaries for an effect of interest, then parameters governing the CWT/Morlet approach (i.e., the number of cycles in the mother wavelet) can be modified to yield improved time-frequency resolution for a particular frequency band (Cohen, 2014). Unfortunately, it is often the case in developmental research that the exact frequency boundaries of a given effect are unknown or not well-characterized a priori. As a result, researchers employing the CWT/Morlet approach are often left with TF representations that contain substantial smearing in time and frequency.

Fig. 1.

Comparison of time-frequency representations produced using Morlet wavelets vs. Cohen’s Class Reduced Interference Distributions (RID).

This figure was created using a subset of the original figures (with modification) appearing in Bernat et. al. (2005).

In contrast to CWT with Morlet wavelets, the Cohen’s Class Reduced Interference Distribution (RID) approach is able to produce relatively higher resolution in both the time and frequency domains, simultaneously across all frequency bands (see Fig. 1; Bernat et al., 2005). Thus, the Cohen’s Class RID approach is less reliant on prior knowledge about the exact frequency boundaries for a given effect, making this approach well-suited for developmental contexts in which such a priori knowledge is lacking. As a pre-processing step for TF-PCA, the Cohen’s Class RID approach offers several advantages relative to CWT, including uniform time-frequency resolution, global features (e.g. harmonics), time-frequency shift and shape invariance, among others (Bernat et al., 2005). Nonetheless, while our work, and the examples in this paper, are focused on RIDs, the core logic of the TF-PCA is applied as readily to any TF transform approach, including CWT with Morlet wavelets.

1.3. Data reduction approaches for TF representations of EEG

Regardless of the method used to compute TF representations, a difficulty that naturally arises is how to statistically analyze TF representations of EEG data, or more specifically, how to prepare data for statistical analyses. There are near infinite possible ways to deal with such a problem, and a complete review of all existing methods is beyond the scope of this article. However, before turning to TF-PCA, the focus of this article, we first overview a necessarily incomplete subset of all possible approaches to the problem of how to statistically analyze TF representations of EEG data and/or how to prepare data for statistical analyses.

One set of approaches involves largely avoiding data reduction techniques, instead subjecting all points in the TF representation (and/or all electrode locations) to statistical analysis and to correct for the large number of multiple comparisons in some way (e.g., via the LIMO Toolbox; Pernet et al., 2011). Such approaches can be particularly useful for detecting effects of interest that exhibit effect sizes large enough to withstand the necessary correction for multiple comparisons. However, it is often beneficial to perform data reduction prior to statistical analysis, in order to maximize statistical power to detect more subtle effects. One of the most common approaches to TF data reduction is to define a rectangular “region of interest” (ROI), in both time and frequency, and then compute the average value within this ROI (Cohen, 2014). This approach can work well in situations where the researcher has prior knowledge about the time-frequency boundaries for the effect of interest. However, as previously noted, such a priori knowledge is often lacking in developmental contexts.

There are alternatives to the standard ROI approach for TF data reduction. For example, one promising method is to define the frequency boundaries of the ROI using a data-driven method (Cohen, 2021). Alternatively, Independent Components Analysis (ICA) can be employed as a preprocessing step, prior to computing TF representations. Briefly, ICA involves computing a set of spatial weighting matrices to separate the raw EEG signal into a set of mutually independent (non-gaussian) components (Delorme & Makeig, 2004). Each independent component (IC) is defined by its spatial weighting matrix, which reflects the relative contribution of each electrode to the IC. When this IC weighting matrix is multiplied by the raw EEG, this allows for recovering the component activations (temporal activity) of a given IC, which can, in turn, be converted into a TF representation. To this end, ICA provides a data-driven method of isolating independent sources of scalp-recorded neural activity, each of which is associated with a TF representation for the activity of interest (e.g., power magnitude). However, this still leaves the researcher with a full TF surface to statistically analyze, often requiring the additional application of a multiple comparison correction approach. Note that it is possible to apply ICA to a TF representation itself (Inuso et al., 2007, Mika et al., 2020), which may reflect a promising new direction in the use of ICA for data reduction in the context of TF analyses. It is also possible to apply ICA at the rotation step in TF-PCA, following similar logic as that described for time domain analyses (ERPs; (Dien, 2010)). However, to our knowledge, applying ICA to the TF representation is, at least currently, primarily employed only for artifact removal purposes in the EEG literature (Inuso et al., 2007) and applying ICA at the rotation step in TF-PCA has not been widely explored. Similarly, although it is possible to perform group-level EEG ICA (Eichele et al., 2011), at least currently, EEG ICA is most commonly applied at the individual level for EEG data. As a result, a more general drawback of standard EEG ICA pipelines is that, because they are typically performed at the participant level, there is an inherent difficulty associated with determining how to relate (i.e. cluster) unique ICA components across participants for group-level statistics.

TF-PCA represents a data-driven data reduction approach, allowing researchers to move from the complete set of points in the TF representation to a substantially reduced set of principal components (Bernat et al., 2005). Thus, unlike the standard EEG ICA approach that still requires multiple comparisons testing for each component’s TF representation, TF-PCA reduces the TF representation down to a small number of principal components (often in the range of ~1–5 components) that can be statistically compared across participants or conditions. Relatedly, because TF-PCA is computed using the TF representation, and reflects a weighting across all TF points, it obviates the need to define an explicit ROI in time and frequency dimensions. Instead, the effective boundaries of a given principal component are defined in a data-driven manner, in both the time and frequency dimensions, reflected in the component weighting matrix (Bernat et al., 2005). As previously mentioned, it is possible to also apply ICA to a TF representation itself (Inuso et al., 2007, Mika et al., 2020), which would yield similar benefits to TF-PCA in this domain, although (to our knowledge) applying ICA to EEG TF representations is currently used primarily for artifact removal purposes (Inuso et al., 2007). In situations where TF-PCA is run on data from all participants at once, this approach also obviates the issue of relating components across participants (Bernat et al., 2005). Here again, it is also possible to run ICA at the group level (Eichele et al., 2011), although this is not a commonly used approach in the EEG literature to date. Although, it is worth noting that further work is needed to more rigorously define recommendations for when it is, and is not, appropriate to apply TF-PCA across participant groups, as discussed further in the sections entitled, “Common questions and practical considerations” and “Developmental utility of the TF-PCA approach”.

1.4. Scope of this article

The goal of this tutorial article is to provide enough background knowledge, theory, and practical information to allow individuals with basic EEG experience to apply the TF-PCA approach to their own data. The remainder of this article provides a brief introduction to principal components analysis, a detailed walk-through of how to apply PCA to TF representations of EEG data, a discussion of practical considerations, and examples of using TF-PCA for developmental data. Crucially, this tutorial article is accompanied by a companion GitHub repository that contains example code, data, and a step-by-step guide of how to perform TF-PCA. The companion GitHub repository is located here: https://github.com/NDCLab/tfpca-tutorial.

Although the current tutorial is framed in terms of the utility of TF-PCA within developmental contexts, all theory, protocols and code contained in this tutorial article and companion GitHub repository can readily be applied more broadly across populations of interest. The majority of published work using the TF-PCA method has been performed using adult samples (Bernat et al., 2007a, Bernat et al., 2011, Harper et al., 2014) with only more recent applications of the method to developmental data collected from child or adolescent samples. Finally, it is important to note that, although TF-PCA is the focus of the current article, we do not view TF-PCA as the ideal EEG analysis approach in all contexts (or even in the majority of contexts). As noted in the prior section, entitled “Data reduction approaches for TF representations of EEG”, there are cases where alternative data-reduction approaches are better suited, or, situations in which a data reduction approach should be avoided altogether. In addition to the preceding section, the reader should also refer to later sections, entitled “Common questions and practical considerations”, and “Developmental utility of the TF-PCA approach” for examples of when and why TF-PCA may or may not be a useful method for one’s own data. Similarly, there may be cases where alternative methods for TF decomposition are preferred (e.g., Morlet vs. Cohen’s Class RID). Nonetheless, we argue that TF-PCA (and our associated recommendations for Cohen’s Class RID) is one of several useful tools available to developmental EEG researchers and we hope this tutorial will help facilitate wider application of the method.

2. Introduction to TF-PCA for EEG

2.1. Brief introduction to principal components analysis (PCA)

While an in-depth introduction to PCA is beyond the scope of this article, we orient readers by beginning with a basic introduction to PCA. Briefly, the goal of PCA is to reduce a larger set of observed variables (points on the TF representation in the case of TF-PCA) into a smaller set of “components” that explain a majority of the variance present in the original set of variables (Hotelling, 1933, Jolliffe and Cadima, 2016, Pearson, 1901). Towards this end, PCA involves performing eigendecomposition on either the correlation or covariance matrix associated with a set of variables. Eigendecomposition returns as many eigenvectors (components) as variables submitted to PCA, and the length of each eigenvector is equal to the number of variables in the original correlation/covariance matrix. Each eigenvector serves to project the data into a new feature space, and the eigenvalue associated with a given eigenvector describes the magnitude within this new feature space. The eigenvalue for a given component can also be used to identify the amount of information retained (variance explained) by a given eigenvector (component). Finally, multiplying a component’s eigenvector by the square root of its eigenvalue will yield a set of loadings for a given component.

The purpose of PCA is data reduction, and thus, it is necessary to not retain all eigenvectors (components) produced by eigendecomposition. There are multiple approaches for determining how many eigenvectors (components) to retain. For example, one approach is to use an a priori determination of the cumulative amount of variance that should be explained by the retained eigenvectors (e.g., a cutoff of 60% or 80% of the variance explained) (Hair, 2006). Relatedly, one can employ an a priori rule to retain all components above a given eigenvalue; for example, Kaiser’s rule of retaining all components with an eigen value greater than one (Kaiser, 1960), or performing Horn’s parallel analysis (HPA; Horn, 1965) to identify the a priori eigenvalue cutoffs to use. A major strength of basing component selection on a priori cutoffs is that such approaches provide an objective decision rule to base component selection on. However, these approaches are not without issue, as they may fail to identify the most parsimonious solution in some cases, or result in the exclusion of crucial variance of interest. Thus, an alternative—albeit subjective—approach involves combing multiple sources of information, including the evaluation of a scree plot and consideration of domain-specific knowledge. Briefly, a scree plot depicts eigenvalues in descending order, which can facilitate selecting a cut point (or “elbow”) where the change in eigenvalues begins to flatten out. In practice, there are typically multiple elbows (potential cut points) present in a given scree plot, and thus, the user must consider a number of factors to make a subjective determination as to which cut point to use (e.g., see Fig. 2). Although this alternative approach is inherently subjective, in practice it often leads to the most parsimonious solution that also retains the variance of interest. Once a given component solution has been selected, an analytic rotation (either orthogonal or oblique) is typically applied to produce a set of loadings (“weights”) in a format that is easier to interpret and relate back to the original data.

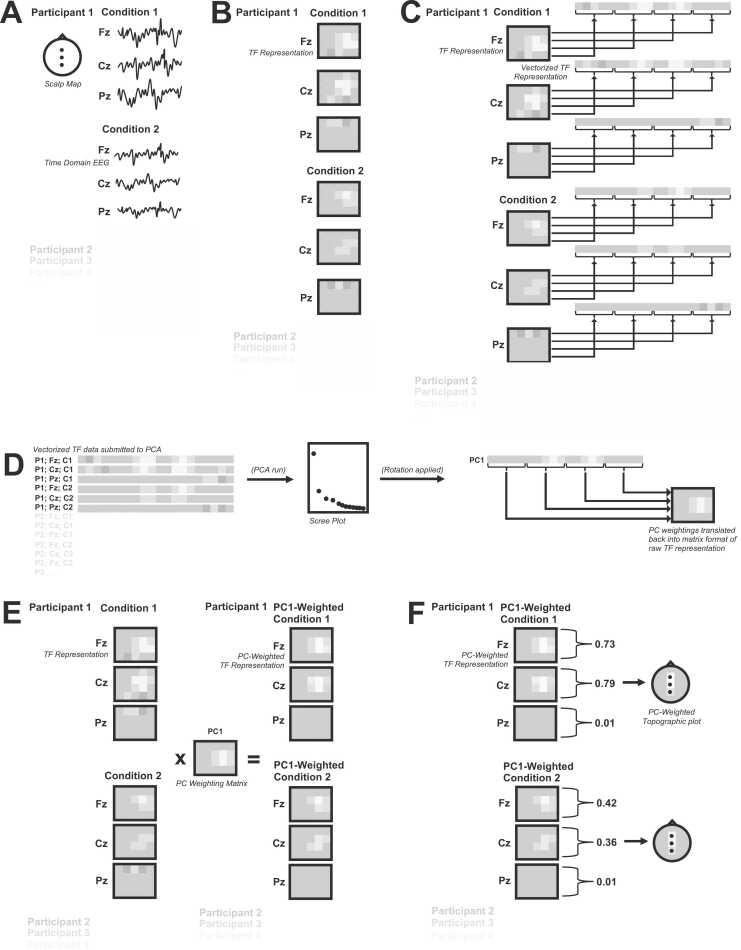
Fig. 2.

Conceptual overview of steps involved in TF-PCA. A) For all conditions/channels of interest, for all participants, preprocessed/epoched data is required. B) TF representations are computed for each channel, for each condition of interest, for each participant. C) Each TF representation is transformed from its native matrix organization into a vector by concatenating each row in each TF representation (corresponding to change over time for a single frequency bin) end-to-end. D). The Vectorized TF representations are “stacked” across conditions, channels, and participants to create a matrix of data submitted to PCA. A factor solution is chosen, and analytic rotation applied, yielding a single vector of weights for each PC. This vector of PC weights is transformed back into the native matrix format of the original TF representation, yielding a PC weighting matrix. E) The same PC weighting matrix is multiplied by the original TF representations for each channel, for each condition of interest, for each participant, resulting in a set of PC-weighted TF representations. F) For each PC-weighted TF representation of interest, the mean of all TF points within a given TF representation is taken. These mean values can then be plotted topographically and statistically compared across conditions.

It is important to note that PCA ultimately involves several choices on the part of the user, and thus, there is no one single method of performing PCA. PCA requires a choice in terms of whether to perform eigendecomposition on the correlation matrix or the covariance matrix, a choice of the number of components to extract, and finally, a choice of the type of analytic rotation to apply. Similarly, while there is no one single TF-PCA approach for EEG data, throughout this article we provide recommendations and/or a description of the steps and decisions that have most commonly been leveraged for TF-PCA of EEG data. In line with prior EEG work (Donchin & Heffley, 1978), TF-PCA for EEG data is typically performed via eigendecomposition on the covariance matrix (to retain the influence of amplitude, i.e. relative to the correlation matrix), and after selecting the appropriate component solution, an orthogonal rotation method (Varimax) is typically applied (to maximize TF separation of the resulting PCs). However, in terms of choosing the appropriate component solution, this depends entirely on the question of interest, and we devote more in depth discussion of this issue in the section entitled, “common questions and practical considerations”.

2.2. Overview of the TF-PCA approach

Having provided a relatively brief, domain-general introduction to PCA, we turn now to a more conceptual, and practical introduction to PCA in the context of TF-PCA for EEG data. As previously mentioned, there is no one single TF-PCA approach. However, the approach can broadly be described in terms of five steps (see B-F in Fig. 2). First, a TF representation must be computed for each channel, for each condition of interest (Fig. 2B). Second, each TF representation must be transformed from its native matrix organization into a vector by concatenating each row in each TF representation (corresponding to change over time for a single frequency bin) end-to-end (Fig. 2C). This transformation yields one long vector for each TF representation, and eigendecomposition is then applied to these vectorized TF representations. Third, an appropriate PCA component solution must be selected and a Varimax rotation applied, yielding a vector of weights (loadings) for each extracted component (Fig. 2D). Each vector of component weights is then transformed back into the native matrix organization corresponding to the dimensions of the original TF representations. Fourth, for each extracted component of interest, the matrix of component weights is multiplied by the original TF representation (or a related TF representation) to isolate the TF-PCA component of interest (Fig. 2E). Fifth, the extracted TF-PCA components are analyzed in a manner similar to traditional TF data and subjected to statistical analyses (Fig. 2F). Collectively, these five steps describe the TF-PCA approach. In the following sections, we walk through each of these steps in further detail.

2.3. Detailed walk-through of steps involved in TF-PCA

2.3.1. Step 1: Compute TF representations

The first step of TF-PCA is to compute TF representations from conventional time domain signals. An initial choice is whether to compute TF representations at the trial level, or at the condition-averaged level (i.e. the condition-averaged signals used to compute ERP component analyses.). This choice produces TF representations indexing either “average power” (phase-locked power; also sometimes referred to in the literatures as “evoked power”) or “total power” (comprised of both phase-locked and non-phase-locked power; sometimes referred to as “evoked and induced power”), respectively. Averaged power often yields a more parsimonious component structure that consists of temporally discrete components when compared to total power. That is, TF-PCA applied to average power is more likely to produce a satisfactory component solution that contains one or more components of interest without needing to extract a large number of components (see section entitled, “moving beyond average (phase-locked) power” for further details). In order to compute average power, the EEG data must first be averaged across trials (in the time domain; i.e., to compute ERPs). Average power is then computed, for each participant, for each channel, for each condition of interest, using the Cohen’s Class RID approach (Bernat et al., 2005). Note that while a traditional TF baseline correction (e.g., dB-power relative to baseline) can be performed prior to performing TF-PCA, to date, it has been less common to perform a TF baseline correction (beyond an initial subtraction of the baseline mean in the time domain, before a TF transform is applied) when performing TF-PCA. This is because PCA can provide an alternative method of distinguishing pre- and post-event TF dynamics in the absence of a TF baseline correction (e.g., Buzzell et al., 2019). However, it is possible to perform a TF baseline correction before the application of TF-PCA. It is also worth noting that any established method for decomposing time-domain EEG data into a TF representation can be employed (e.g., the commonly used CWT using Morlet wavelets), but traditionally, Cohen’s Class RID is used to compute the TF representation of average power, given its improved resolution in both time and frequency across the entirety of the TF representation (Bernat et al., 2005).

For additional details on the distinction between different measures of power (e.g., average vs. total) see the paper by Buzzell and colleagues (2019), or a more thorough treatment of these concepts in the book by Cohen (2014). Note that it is possible to apply TF-PCA to TF representations of total power, however, given the potential drawbacks of this approach, a complementary method is to first run TF-PCA on TF representations of average power and then apply the resulting PCA weights to TF representations of total power. Additional details and instructions for performing the average/total power hybrid approach are presented later, in the section entitled, “Moving beyond average (phase-locked) power”. However, before describing this average/total power hybrid approach, we first continue walking through the steps involved in the basic TF-PCA approach when working only with average (phase-locked) power.

2.3.2. Step 2: Reorganize TF representations into vectors and perform Eigendecomposition

Having computed TF representations of average power, each TF representation must now be transformed from its native matrix organization into a vector; this is done by concatenating each row in a given TF representation (each row corresponding to a single frequency bin) end-to-end. Following this set of transformations, there should now be a vectorized TF representation for each participant, for each channel, for each condition. For the purposes of PCA, each vector reflects a single “observation” whereas the vector indices, each of which corresponds to a specific point in the TF representation, reflect the “variables”. Note that it is not necessary to transform and submit the entire TF representation to PCA. Instead, the user is free to choose (based on theoretical and/or practical considerations) a subset of the entire TF representation on which to reorganize into vectors and submit to PCA; this issue is further discussed in the section entitled, “common questions and practical considerations”. Finally, Eigendecomposition is applied to the covariance matrix of the TF points (variables) across all observations (participants x conditions x channels). Note that it is not inherently necessary to run TF-PCA in the manner described above, whereby the intersection of each participant, channel, and condition reflects a unique “observation” supplied to PCA. However, this approach has most commonly been followed in order to ensure an adequate ratio of “observations” to “variables”, at least when condition-averaged (as opposed to trial-level) TF representations are being used (Bernat et al., 2005), and it is therefore the method described throughout this article. However, this issue is further discussed in the section entitled, “common questions and practical considerations”.

2.3.3. Step 3: Component selection, rotation, and reorganization of TF representations

TF-PCA does not automatically return the “best” component solution for the data, and the decision of how many components to extract is left up to the user. Moreover, it is worth noting that the process of choosing the appropriate PCA solution in TF-PCA is essentially the same as the process employed in other domains. Thus, at this step in TF-PCA, the user is free to employ any appropriate PCA component selection method that they are familiar with. However, to aid new users in component selection within the context of TF-PCA we provide a detailed description of our typical process and general recommendations for component selection in the section entitled, “common questions and practical considerations”. Once a given component solution has been selected, an analytic rotation is applied (typically Varimax in TF-PCA) to produce a vector of component loadings (weights). Finally, each vector of component weights is transformed back into the native matrix organization corresponding to the dimensions of the original TF representations.

2.3.4. Step 4: Weighting of TF representations by component weighting matrices

At this point, for each component of interest, a weighting matrix (component loadings) has been created with the same dimensions as the original TF representations. Thus, in order to extract a TF-PCA component of interest, one can multiply the corresponding component matrix weights by the original TF representations (or related TF representations). Note that although a separate TF representation for each participant, for each channel, for each condition was submitted to TF-PCA, only a single weighting matrix is produced for each component of interest. Thus, in order to isolate a given TF-PCA component of interest in the original data, the original TF representations for each participant, for each channel, for each condition, are each multiplied by the same component weighting matrix associated with the TF-PCA component of interest. Ultimately, this process converts the original TF representations into PC-weighted (or TF-PCA filtered) TF representations that can be plotted topographically and analyzed statistically.

Although it is the PC-weighted TF representations (for each participant, channel, and condition) that are the primary focus of TF-PCA, it can also be informative to plot and explore the component weighting matrices on their own. However, note that because only a single weighting matrix is produced for each component, it is not possible to plot the component weights topographically. Instead, it is only possible to produce topographical plots of the PC-weighted TF representations (across channels).

2.3.5. Step 5: Exporting TF-PCA data for further statistical analysis

Having created PC-weighted TF representations that isolate components of interest, it is now possible to export summary statistics for the purpose of conducting further (inferential) statistical analyses. Here, there are multiple options available to the researcher, and the appropriate method depends on the scientific question of interest. The most common approach is to compute the average of the PC-weighted TF representation, either at a single channel (or at a single cluster of channels), or to compute this average across all channels. If computing the average for a single channel (or cluster) then the decision of how to select this channel can be made a priori (based on prior literature) or determined in a data-driven manner based on topographic plots of the PC-weighted data. Of course, if using a data-driven approach, then the researcher needs to consider the inferential statistics that will ultimately be performed on the data and ensure that the selection of channel(s) is performed on a contrast that does not bias the inferential statistics that will ultimately be computed. Regardless of how the channel(s) are selected, the average should then be computed across all TF points within the PC-weighted TF representation, for the selected channel(s) of interest, and further averaged across channels if more than one channel is being combined (e.g., in the case of computing a channel cluster or averaging across all channels). This procedure yields a single summary statistic (average) for each participant, for each condition of interest. These summary statistics can then be subjected to further statistical analyses to compare condition differences and/or to evaluate individual differences in a given TF-PCA component.

Note that it is possible to compute additional summary statistics for the PC-weighted TF representations. For example one can compute either the peak frequency or peak latency for a given component (at a single channel, cluster of channels, or across all channels). However, this tutorial focuses on computing average values and alternative analyses of peak frequency/latency are not discussed further. Moreover, for all examples reviewed in the section entitled, “Developmental utility of the TF-PCA approach”, average values were of interest and computed.

2.4. Moving beyond average (phase-locked) power

The previous section provided a thorough overview of the most commonly performed set of steps involved in the TF-PCA approach, at least as it applies to TF representations of average (phase-locked) power. In part, a majority of work with the TF-PCA approach has focused on average power in order to facilitate more direct comparisons and connections with decades of conventional ERP research characterizing more conventional time domain components (e.g., see Bernat et al., 2007b; Bowers et al., 2018b; Harper et al., 2014, Harper et al., 2016). However, it is worth noting that the broader EEG TF literature (e.g., see Cohen, 2014) more commonly focuses on total power, and, the set of steps described above can also be applied to other TF representations. TF-PCA can be applied directly to TF representations of total power (comprised of both phase-locked and non-phase locked power), as well as TF representations of phase-based metrics (e.g., phase synchrony metrics computed within or across electrodes), among others. To this end, TF-PCA has been demonstrated to produce interesting and parallel results when applied to averaged and total power in at least some contexts (Bernat et al., 2007a, Bernat et al., 2007b). Yet, perhaps unsurprisingly, TF-PCA solutions derived from different types of TF representations can produce results differing in important ways. For example, when TF-PCA is applied directly to TF representations of total power, the resulting components tend to be less temporally discrete, or “smeared in time”, (compared to components derived from a TF representation of average power), and TF-PCA applied to TF representations of phase can often lack a gaussian structure. However, given that much less work has been published on TF-PCA applied directly to TF representation of total power or phase, more work in this domain would be beneficial.

Given the considerations outlined above, one efficient, “hybrid” approach to analyzing TF representations of total power (and/or phase) is to identify a single set of TF-PCA components for a given data set, and then apply these components across different TF representations (e.g., average power, total power) generated from the same data set. To this end, the most common approach to date has been to perform TF-PCA on TF representations of average power, and then apply the TF-PCs to total power and phase representations (e.g., see Buzzell et al., 2019). Broadly, this hybrid approach, which differs from deriving separate TF-PCs for each TF representation of interest, involves three steps. First, TF representations of average power are computed and then decomposed into a set of TF-PCA weighting matrices for the components of interest. Second, within the same dataset, and using the exact same trials, channels, conditions, and participants, TF representations of total power (and/or phase) are computed. Third, the TF-PCA weighting matrices for the components of interest, derived from the TF representations of average power, are applied to the TF representations of total power (and/or phase) instead of generating new TF-PCs based on the TF representations of total power (and/or phase). The end result of this procedure is a set of PC-weighted TF representations for average power, as well as total power (and/or phase), which can then be plotted and analyzed statistically, and otherwise compared.

When using the hybrid approach of applying TF-PCA component weighting matrices derived from average power to other TF representations (e.g., total power), it is important to understand exactly what the resulting PC-weighted TF representations reflect, as well as when they can be useful and their relations to other derived EEG/ERP measures. In terms of usefulness, one benefit is that centering TF-PCA analyses around TF representations of average power, via the hybrid approach, allows for contextualizing results within decades of conventional time-domain average ERP work, notwithstanding additional phenomena of interest present in TF representations of total power (e.g., see Bernat et al., 2007b; Bowers et al., 2018b; Harper et al., 2014, Harper et al., 2016). Another important benefit of the hybrid approach is that it allows researchers to isolate temporally discrete components within a TF representation that is composed of both phase and non-phase locked data (and/or TF representation of phase). That is, this approach can be particularly useful in contexts where the researcher is interested in studying TF representations of total power while also retaining a relatively high degree of temporal precision from the phase-locked activity. As described in the section entitled, “Developmental utility of the TF-PCA approach”, we have previously used this approach to help disentangle overlapping, but functionally distinct, total power dynamics (e.g., see Buzzell et al., 2019). Researchers using these methods should also understand the inherent differences in data derived from the hybrid approach of applying TF-PCs of average power to other TF representations (e.g., to total power), TF-PCA analyses applied separately to TF representations of average and total power, and associations with more traditional analyses of TF representations and related ERPs. Building on prior published work (e.g., see Bernat et al., 2007b; Bowers et al., 2018b; Harper et al., 2014, Harper et al., 2016), the supplement includes an exploration of similarities and differences between the data derived using these complementary analytic approaches.

3. Common questions and practical considerations

Having provided an introduction to the TF-PCA approach, we turn now to several common questions and practical considerations that researchers should consider when employing TF-PCA. We also provide some discussion of possible variations on the most commonly performed TF-PCA steps (described above), which may be of interest to some researchers. As previously noted, while TF-PCA can be a useful approach, it may not be the most appropriate method to employ in all cases. Thus, this section, and the one that follows, also provides initial recommendations for when (and why) TF-PCA may or may not be the most appropriate method to use for a given dataset.

3.1. Do I have enough data for TF-PCA?

As with any analysis, it is important to ensure that there is an adequate amount of data for performing PCA. Unfortunately, while there is no universal rule for determining the amount of data needed for PCA, the same general guidelines that have been used to determine the amount of data needed to perform PCA in other domains likely apply in the same way to TF-PCA. For example, a common heuristic is that at least 5 observations are required per variable, as a lower limit for determining the amount of data required (Gorsuch, 1983), however, more sparse data representations (as TF representations tend to be) may be able to tolerate less. Regardless of the exact set of guidelines used to determine the amount of data required, it is important that researchers are aware of exactly what constitutes a “variable” and an “observation” in TF-PCA. As mentioned previously, for the most common method of performing TF-PCA on EEG data, the number of variables is equal to the number of points in the TF representation submitted to eigendecomposition, whereas the number of observations is determined by the number of participants, conditions, and channels (participants x conditions x channels = total number of observations). If TF-PCA is performed in this way, and if we assume that the number of participants, conditions and channels are relatively fixed for a (previously collected) dataset, then the important consideration for TF-PCA is ultimately the number of points in the TF representations submitted to PCA. Thus, to increase the ratio of observations (fixed number of participants x conditions x channels) to variables (TF points), one option is to reduce the resolution of the original TF representations by either reducing the number of sample points (via down sampling), reducing the number of frequency bins in the computed TF representation, or both. For example, if a researcher’s data is natively sampled at 500 Hz, but the researcher is only interested in time-frequency dynamics below ~9 Hz, then the researcher could down sample their data considerably (e.g. to 32 Hz) in order to substantially increase the ratio of observations to variables (by a factor of ~15) while not impacting the ability to resolve frequencies of interest (i.e., at 32 Hz, Nyquist frequency = 16 Hz). Alternatively, the researcher could choose to leave the resolution of the original TF representation unchanged, but instead select a sub-window within the full TF representation on which to run TF-PCA. For example, although one’s data might be epoched from − 1000 ms to + 1000 ms, if the researcher is really only interested in the period from − 500 to + 500 ms, then they could choose to submit only this sub-window to TF-PCA and increase the ratio of observations to variables (by a factor of ~2). In practice, it is common to use a combination of both of these approaches in order to increase the ratio of observations to variables when performing TF-PCA.

It is also worth noting, that although it is most common (at least to date) to perform TF-PCA such that the number of “variables” is equal to the number of points in the TF representation, and the number of “observations” reflects the number of participants, conditions, and channels (participants x conditions x channels = total number of observations), alternatives to this approach are possible (assuming the ratio of observations to variables remains sufficiently high)(Bernat et al., 2005). For example, it is valid to perform TF-PCA for only a single channel, or cluster of channels. Similarly, it is also valid to leverage trial-level data when performing TF-PCA, such that the number of observations is reflected in the number of participants, conditions, channels, and trials (participants x conditions x channels x trials = total number of observations). In sum, it is valid to perform TF-PCA using one of multiple combinations of observations and variables, so long as the data being used is of sufficient quality (i.e., single trial data may be more or less appropriate, pending the quality of the single-trial data being used), and as long as there is a sufficient ratio of observations to variables.

Above, we address general guidelines for the amount of data needed to perform TF-PCA, focusing on the ratio of “observations” to “variables” submitted to PCA. However, a related question is the number of trials per condition that are recommended for TF-PCA (either for condition-averaged or trial-level data). Here, it is important to note that, similar to traditional ERP or TF analyses, TF-PCA can be used to target a wide variety of components of interest that vary in their underlying signal-to-noise ratios. Thus, we do not suggest any broad recommendations specific to TF-PCA. Rather, we suggest that current recommendations for ERP and TF literature are an appropriate starting point (e.g. Psychophysiology guidelines for ERP and TF, respectively; (Picton et al., 2000, Keil et al., 2022)), as well as work relevant for the focus of activity on a given project (e.g. P300, or other components). Stated broadly, we support the view that the recommended minimum number of trials will depend on the specific component(s) of interest being targeted, and the specific context in which they are measured (similar to how the minimum number of trials recommended for reliable measurement of a given ERP component is unique to that ERP component and context of assessment) (Clayson and Miller, 2017b, Clayson and Miller, 2017a).

3.2. How do I determine the appropriate PCA factor solution for TF-PCA?

The appropriate method to use when choosing the optimal component solution entirely depends on whether prior knowledge is available, and whether plots and statistical comparisons can be performed to determine the optimal component solution without biasing subsequent inferential statistics for the scientific question(s) of interest. In the absence of prior knowledge that can be used to guide component selection, or in situations where use of prior knowledge would bias subsequent inferential statistics, we strongly recommend the use of purely objective approaches. For example, one could base component selection on a predetermined eigenvalue cutoff or the total amount of variance to be explained.

When prior knowledge is available to guide component selection, it can be helpful to examine plots of the PC-weighed TF representations and related topographic plots. These plots can be computed for particular conditions and/or as a difference between specific conditions. However, it is critical that during this stage of component selection the researcher is careful not to base component selection on specific conditions/contrasts that would bias subsequent inferential statistics for the study. For example, if a researcher was conducting a study to determine whether error and correct trials differ in theta power over mediofrontal cortex, then it would be appropriate to base component selection on plots that collapse across error and correct trials. In contrast, it would lead to biased inferential statistics if the researcher also considered plots of condition differences (error vs. correct trials) when determining the component solution. An alternative scenario might be that a second researcher is primarily interested not in error vs. correct differences per se, but has instead designed a study to determine whether previously published error vs. correct correlate with psychopathology symptoms. In this case, it would be appropriate for the researcher to also consider difference plots (error vs. correct) during component selection in order to identify the solution that maximizes this difference. Nonetheless, and regardless of the approach used by the researcher during component selection, it is crucial that the details and rationale for the component selection procedure be reported in any publication of the results.

3.3. How to deal with saturation of the TF-PCA solution by low-frequency data

A practical issue that often arises in TF-PCA is that when low-frequency (delta) oscillations are present in the TF representation, they often tend to dominate the majority of components in the TF-PCA solution. This occurs, at least in part, due to the 1/f scaling of TF EEG data (i.e. lower frequencies tend to exhibit much greater magnitudes; Nunez et al., 2006). This is problematic if the user is interested in identifying PCA components above the delta band (e.g., theta and alpha oscillations), when using a covariance matrix (which retains the influence of amplitude). Relatedly, if researchers are interested only in a particular frequency band (e.g., ~4–7 Hz theta oscillations), then the presence of higher frequency (~8–12 Hz) alpha oscillations in the TF-PCA solution may also be unwanted, as it will reduce the parsimony of the solution to account for components that are not of theoretical interest. However, in these cases, there are three options available to the user, which we describe in relation to a study in which the researcher is primarily interested in measuring oscillations within the theta band (typically ~4–7 Hz in healthy adult populations) and leverage the same dataset used in the step-by-step walkthrough found in the supplement. The first option, is to select a component solution that contains a relatively large number of components to ensure that at least some of the components capture the frequency dynamics of interest (within the range of theta). However, this is typically not a practical approach, as more parsimonious component solutions are preferred in most cases. The second option, is to apply filters to the data to remove activity within unwanted frequency bands prior decomposing TF representations and subsequent TF-PCA. For example, applying a high pass filter to remove delta oscillations and/or an additional low pass filter to remove alpha (and higher frequency) oscillations. Here, the filters applied can be relatively modest (e.g., a high pass filter that removes < 2 Hz activity), or more restrictive (e.g., a bandpass filter that isolates 4–7 Hz activity). Finally, the third option is to not directly filter the data prior to decomposing a TF representation, but instead, to restrict the window on which TF-PCA is run so that lower frequency (and/or higher frequency) data is not included in the PCA. Again, this method can apply relatively modest in the restrictions placed on the frequency window being submitted to PCA (e.g., submitting all data within the 3–9 Hz range), or more restrictive (e.g., submitting only data within the 4–7 Hz range).

In approaching this problem, it is important to keep in mind that the goal of TF-PCA is to leverage a data-driven method for identifying TF dynamics of interest, especially in situations where the exact frequency boundaries of interest are not known a priori. Thus, while a restrictive approach can be used to isolate a given frequency band of interest (e.g., 4–7 Hz theta oscillations; see Supplemental Fig. S2B), this comes at the cost of imposing strong a priori constraints on the TF-PCA solution. At the same time, if no constraints are introduced prior to running TF-PCA, a less parsimonious solution must be dealt with. In practice, we have found that a compromise can be found by employing a combination of options 2 and 3, but using relatively weak constraints on the data submitted to TF-PCA. For example, when targeting theta oscillations, instead of employing a strict 4–7 Hz cutoff for the TF window and/or a strict band pass filter to isolate 4–7 Hz activity, a modest high pass filter (e.g., 2 Hz) combined with relatively wider cutoffs for the TF window (e.g., 3–9 Hz) can be used to produce a parsimonious TF-PCA solution for theta component(s). The supplement provides an illustration of this approach (Fig. S2C), in contrast to more restrictive approaches on the one hand (Fig. S2B) or completely unbiased approaches on the other (Fig. S2A).

3.4. The assumption of time-frequency stationarity

It is important to note that one of the underlying assumptions of TF-PCA is that of TF stationarity (Bernat et al., 2005). Specifically, TF-PCA assumes that while the magnitude of individual components may vary across observations, the overall “structure” of the TF representation remains largely similar. In practice, TF-PCA is robust to moderate variation in the timing or frequency response of individual components across observations, although such variation will lead to more dispersed components either in the time or frequency dimensions, respectively. However, more substantial variation in individual components, across observations, will typically produce suboptimal TF-PCA solutions. That is, if the goal of TF-PCA is to define one or more components, and then to compare the magnitude of those components across conditions (i.e., experimental conditions, assessment timepoints, sample groups, etc.) then it is problematic if the TF representations (and associated TF-PCA components) fundamentally differ. The difficulty here arises from uncertainty over whether any apparent differences in the magnitude of PCA-weighted data across conditions are the result of true changes in magnitude alone, as opposed to a combination of changes in magnitude and/or changes in the underlying component structure across conditions (i.e., a lack of structural invariance). To this end, if there is reason to believe that there may be substantial differences in the TF representations (and in turn, component structures) across conditions of interest, then it is prudent to also test for structural invariance in the underlying component structure across conditions, in order to facilitate proper interpretation of any condition differences. At the same time, researchers may also be interested in testing the degree of structural invariance across conditions as the hypothesis of interest in itself. In both cases, a formal statistical test of how similar component structures are across conditions (structural invariance) would be particularly useful. For a treatment of these concepts within the context of longitudinal change, see: Malone et al. (2021).

Prior literature providing explicit recommendations for how to formally test for structural invariance (a specific subset of the broader topic of measurement invariance), in the context of EEG TF-PCA, is limited. While the development and validation of a formal testing procedure for structural invariance in the context of EEG TF-PCA is beyond the scope of this introductory tutorial, here, we draw on prior measurement invariance literature in other domains (Fischer & Karl, 2019) and suggest that an orthogonal Procrustes rotation (McCrae et al., 1996, Schönemann, 1966) followed by calculating Tucker’s Φ (Fischer and Karl, 2019, Lorenzo-Seva and ten Berge, 2006, ten Berge, 1986) can be used as a formal test of structural invariance in TF-PCA applied to EEG data. For a similar emerging approach, see: Malone et al. (2021). While further testing and validation in this domain are needed, we tentatively suggest that the following procedure can be followed to test for structural invariance across conditions. First, one of the two conditions (i.e., experimental conditions, assessment timepoints, sample groups, etc.) that is to be compared must be chosen as the “reference group”. Second, TF-PCA is applied to the reference group, and standard procedures are followed for identifying the optimal component solution and extracting the weighting matrix (component loadings) following Varimax rotation. Third, the same number of components are extracted from the second condition (and a Varimax rotation applied). Fourth, an orthogonal Procrustes rotation is applied in order to rotate the weighting matrix from the second condition towards the weighting matrix of the reference group. Fifth, Tucker’s Φ is computed in order to provide a metric of structural invariance across the two conditions. Tucker’s Φ ranges from 0 to 1, with prior work in other domains suggesting that Φ > 0.95 reflects equivalent component structure across the two conditions (structural invariance),.95 > Φ > 0.85 reflects a moderate level of structural invariance, and Φ < 0.85 reflects a lack of structural invariance (Fischer and Karl, 2019, Lorenzo-Seva and ten Berge, 2006, ten Berge, 1986). Further work is needed to fully validate the use of Procrustes rotation and Tucker’s Φ in the context of EEG TF-PCA, to include possible revisions to the recommended cutoff values for Tucker’s Φ. Nonetheless, given that the use of Procrustes rotation and Tucker’s Φ has been established in other domains (Fischer & Karl, 2019), and the current lack of a comparable structural invariance test for EEG TF-PCA (but see Malone et al., 2021), we currently suggest the procedure outlined above as a means to formally test for structural invariance in the context of EEG TF-PCA.

4. Developmental utility of the TF-PCA approach

Having introduced the TF-PCA technique and practical considerations for its use, we turn now to several concrete examples of the utility of this approach within a developmental context. In particular, we draw on previously published work from our group investigating theta dynamics related to cognitive control in children and adolescents.

4.1. Detecting cross-sectional differences missed by other approaches

One example of leveraging TF-PCA within a developmental context is provided by the cross-sectional study investigating feedback processing by Bowers et al. (2018a). Briefly, prior work reported mixed findings in terms of whether feedback processing differs across childhood and adolescence when studied using the feedback-related negativity (FRN) ERP component (Miltner et al., 1997; note that the FRN can also be inversely quantified as the Reward Positivity, RewP; (Holroyd et al., 2008; Proudfit, 2015)). In the study by Bowers et al. (2018a), we were able to identify the presence of a significant FRN ERP, but in line with at least some prior work (Larson et al., 2011, Lukie et al., 2014), we did not identify significant changes in this component across age. However, when employing TF-PCA to analyze the same dataset, robust age-related changes in both theta and delta TF-PCA components were revealed. Moreover, these theta and delta components shared a similar timing and topography with the FRN/RewP, and subsequent regression analyses demonstrated how these components related to the FRN/RewP. Finally, we were also able to demonstrate further age-related changes in a TF-PCA component reflecting synchrony within the theta band, consistent with other emerging work in this domain (Crowley et al., 2014). Collectively, this study provides an example of how TF-PCA can be leveraged to provide sensitive indices of neurocognitive changes across age that might be missed by more traditional EEG analysis techniques.

4.2. A data driven method for isolating effects of interest

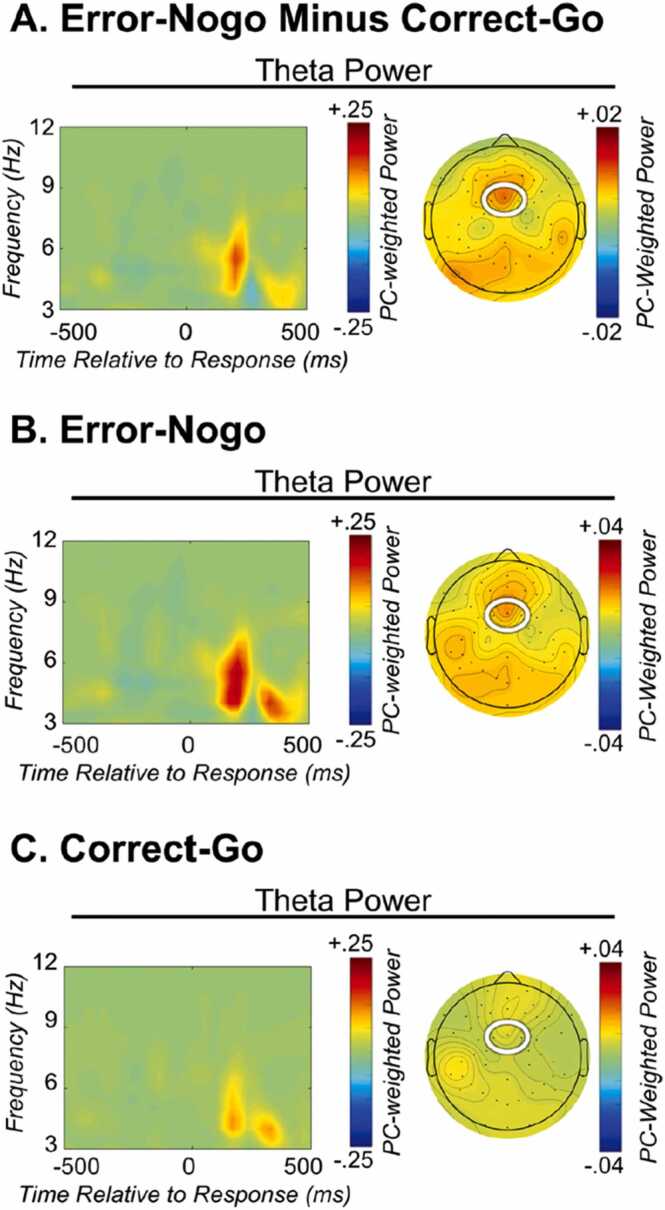
TF-PCA can be useful not only to identify neurocognitive dynamics missed by other approaches, but can also be used to optimize the analysis of known TF effects in situations where the exact timing or frequency boundaries are uncertain. For example, it is fairly well established, at least in adults, that responses on error trials (relative to correct responses) are associated with an increase in theta power over mediofrontal cortex (Cavanagh et al., 2009, Cavanagh and Frank, 2014). Given that this effect is fairly well characterized in adults, both in terms of its timing and approximate frequency boundaries, it is possible to define a TF ROI when studying such error-related effects in healthy adult populations. However, if a developmental researcher is interested in studying similar error-related effects within a given developmental window, it might be problematic to approach this problem using a TF ROI, given that a lack of established studies in developmental samples makes it unclear whether this effect would manifest at a similar point in the TF representation. The study by Kim et al. (2020) provides an example of how TF-PCA can be useful in such contexts. In this study, we were interested in studying error-related theta dynamics in a sample of young children with autism. We were able to draw on prior adult work suggesting that: (1) errors would likely be associated with an increase in theta power, and (2) such error-related theta dynamics would most likely arise over mediofrontal scalp locations. However, given a lack of prior studies investigating error-related theta in similar clinical/demographic samples, we did not have strong a priori knowledge regarding the exact timing or frequency boundaries for such an effect. Thus, we used the TF-PCA approach, loosely guided by prior (adult) knowledge of approximate timing, frequency band, and topography, to identify an error-related mediofrontal theta TF-PCA component in this sample. Having isolated our effect of interest, we were then able to perform inferential, statistics testing how this effect related to other factors in the sample (e.g., behavior and academic abilities). Crucially, the timing of the error-related theta component identified was at least 100 ms later than what one might have predicted (see Fig. 3), based on prior adult work, and therefore, we might have missed this robust effect if we were to have employed a more traditional, ROI-based analysis of the TF representation. Collectively, this study provides an example of how TF-PCA can be used to isolate a given effect of interest in situations where there may be some prior knowledge to guide analyses (e.g., based on prior work in adults or a distinct developmental window), but the exact timing, frequency boundaries, or topography remain uncertain for the specific sample of interest. Crucially, such situations are quite common in developmental cognitive neuroscience research, and therefore, we believe that this reflects a prime example of the utility of TF-PCA for developmental research in particular.

Fig. 3.

Error vs. correct theta isolated using TF-PCA. PC-weighted TF representations of response-locked average power for (A) the error-correct difference, (B) Error-nogo trials, and (C) Error-go trials. Note that the timing of the error-related theta component identified is > 100 ms later than similar effects observed in healthy adults; without employing a TF-PCA approach, this effect of interest might have been missed.

Figure reprinted from Kim et al. (2020).

4.3. Disentangling overlapping neurocognitive dynamics

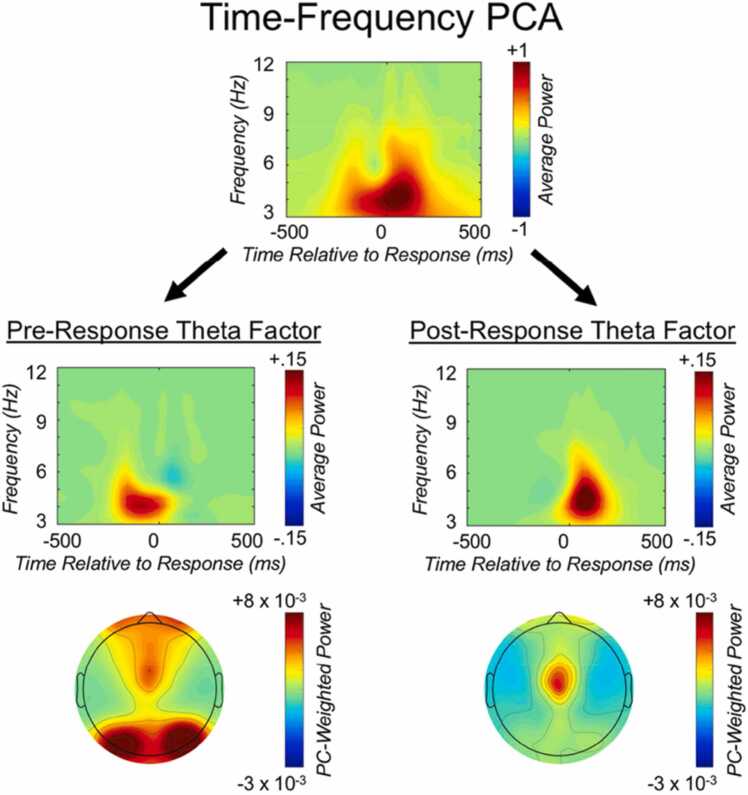
In addition to facilitating the isolation of a single effect of interest within a given TF representation, a major strength of the TF-PCA approach is that it also provides a framework for isolating and distinguishing overlapping effects of interest within a given TF representation. For example, the study by Buzzell et al. (2019) provides an example of how TF-PCA can be used to disentangle overlapping, yet functionally distinct, TF dynamics. That is, while error responses and conflicting stimuli are both known to elicit mediofrontal theta oscillations (Cavanagh & Frank, 2014), these neurocognitive processes have traditionally been studied in isolation from one another. Nearly all prior research investigating conflict-related theta has been performed on stimulus-locked TF representations alone, and error-related theta almost always studied in separate, response-locked TF representations. The problem with this approach is that it does not account for the potential for conflict-related theta to confound error-related theta, or vice-versa. Nonetheless, at least in principle, it should be possible to extract conflict- and error-related theta dynamics from the same TF representation and to demonstrate that they are functionally distinct (differentially relating to trial types and behavior). In the study by Buzzell et al. (2019), we showed how the TF-PCA approach can be used to disentangle distinct components reflecting pre-response theta (which is more sensitive to stimulus conflict) and post-response theta (which more sensitive to error commission) within the same TF representation (see Fig. 4). Specifically, in this paper we employed the method of applying TF-PCA weights between average and total power to isolate a pre-response total power component and a post-response total power component. Moreover, we extended this hybrid method of applying TF-PCA weights to additionally extract pre- and post-response measures of phase synchrony across frontal electrodes. Crucially, we were able to functionally distinguish pre- and post-response theta, in terms of their relations to stimulus conflict, current trial accuracy, and next trial behavioral performance. Collectively, this study illustrates how TF-PCA can provide a useful framework for disentangling specific subprocesses present in a single TF representation.

Fig. 4.

Example of time-frequency principal components analysis (TF-PCA) applied to EEG data. Isolation of separate pre- and post-response theta factors by applying time-frequency principal component analysis (PCA) to average power data. The top panel reflects the unweighted average power time-frequency distribution over medial-frontal cortex (MFC), collapsed across all conditions of interest. The second row depicts the same average power distribution weighted by the pre- and post-response theta factors, respectively; the third row displays the corresponding topographic plots.

Reprinted from NeuroImage, Vol 198, Buzzell et al. (2019), Copyright (2019), with permission from Elsevier.

4.4. Studying longitudinal change

As previously discussed, TF-PCA relies on the assumption of at least moderate TF stationarity, and, if this assumption is not violated, then the TF-PCA method can be used to assess developmental changes in the magnitude of a given component of interest. For example, the study by Buzzell et al. (2020) provides an illustration of one way in which TF-PCA can be used to study longitudinal change in a given TF component. In this study, we were interested in testing whether the magnitude of error-related mediofrontal theta changes across early- to mid-adolescence. Thus, we first conducted TF-PCA on the later adolescent time point alone, in order to extract a TF-PCA weighting matrix capturing error-related mediofrontal theta. We then applied the same weighting matrix to the original TF representations for both timepoints in order to extract the same error-related mediofrontal theta component at each timepoint. From here, we were able to statistically test for the presence of longitudinal change in this error-related mediofrontal theta component, finding significant changes over time. Moreover, such developmental changes in the mediofrontal theta component were also predictive of longitudinal changes in psychopathology symptoms across the same developmental window.

It is important to note that the method employed in the study by Buzzell et al. (2020), reflects only one approach to using TF-PCA to assess longitudinal change, and moreover, there is an inherent limitation in the approach used. Specifically, the study by Buzzell et al. (2020) employed the method of copying PCA weights from one age to another in order to extract components of interest, and did not explicitly test for structural invariance across ages. As a result, it is difficult to draw conclusions as to whether age-related changes in the PC-weighted data reflect changes in magnitude per se, as opposed to changes in component structure (or a combination of both). Depending on the hypothesis of interest, specificity at the level of changes in magnitude vs changes in component structure may be more or less important. For example, the study by Buzzell et al. (2020) definitively shows that developmental change (across early-to-mid adolescence) in an error-related mediofrontal theta component (which is present by mid-adolescence) is predictive of the psychopathology. This represents a developmental and clinically meaningful conclusion that can be drawn from the analyses performed. Yet, at the same time, without first testing for measurement invariance across ages, it is not possible to more precisely infer whether the observed changes reflect changes in component magnitude/structure. Thus, we recommend that future work explicitly perform tests of measurement invariance whenever possible, in order to allow more precise conclusions to be drawn from TF-PCA applied to EEG data. For further details, please refer to the section entitled, “Common questions and practical considerations”.

5. Tutorial walk-through using example code and data

Part five of this article consists of a detailed, step-by-step walk-through of how to apply TF-PCA to a publicly available data set. This walk-through, and all required data, code, and examples of the output generated, can be found in the supplement, as well as within the companion (open source) GitHub repository: https://github.com/NDCLab/tfpca-tutorial. Whether your goal is to only gain a more intuitive understanding of the TF-PCA approach, or if you wish to perform TF-PCA analyses on your own data, we highly encourage all readers of this tutorial article to also read the step-by-step walkthrough located in the supplement and companion GitHub repository. However, while users can follow these steps via the supplement, we strongly recommend that users refer to the online version of this content, and in particular, the ‘README.md’ and ‘step-by-step Walk Through.md’ files located in the online GitHub repository. Moreover, given the open source nature of the companion GitHub repository, we encourage other researchers to contribute additional examples and related code to the repository.

6. Conclusions

The unique value of TF-PCA is that it provides a data-reduction approach that does not rely on strong a priori constraints regarding the specific timing or frequency boundaries for effects of interest. This strength of the TF-PCA approach makes it particularly well suited for the analysis of developmental TF data in which strong a priori knowledge regarding the time-frequency boundaries of an effect is often lacking. In order to facilitate more widespread use of the TF-PCA approach, particularly among developmental cognitive neuroscientists, the current tutorial was designed to provide researchers with the background knowledge, theory, and practical information needed to fully understand the TF-PCA approach. Moreover, the step-by-step tutorial located in the supplement and the companion GitHub repository (https://github.com/NDCLab/tfpca-tutorial) provides readers with the code needed to run similar analyses on their own data. Despite the promise of TF-PCA for developmental EEG research, this method is currently underutilized by the field. Thus, we hope that this tutorial article and companion GitHub repository will make it easier for more developmental scientists to apply this method in future studies. Moreover, we encourage contributions to the companion GitHub repository to further extend TF-PCA tools and tutorials for the field of developmental cognitive neuroscience.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary material

Supplementary material.

.