Sensitivity analysis on a network model of glymphatic flow

Abstract

Intracranial cerebrospinal and interstitial fluid (ISF) flow and solute transport have important clinical implications, but limited in vivo access to the brain interior leaves gaping holes in human understanding of the nature of these neurophysiological phenomena. Models can address some gaps, but only insofar as model inputs are accurate. We perform a sensitivity analysis using a Monte Carlo approach on a lumped-parameter network model of cerebrospinal and ISF in perivascular and extracellular spaces in the murine brain. We place bounds on model predictions given the uncertainty in input parameters. Péclet numbers for transport in penetrating perivascular spaces (PVSs) and within the parenchyma are separated by at least two orders of magnitude. Low permeability in penetrating PVSs requires unrealistically large driving pressure and/or results in poor perfusion and are deemed unlikely. The model is most sensitive to the permeability of penetrating PVSs, a parameter whose value is largely unknown, highlighting an important direction for future experiments. Until the value of the permeability of penetrating PVSs is more accurately measured, the uncertainty of any model that includes flow in penetrating PVSs is so large that absolute numbers have little meaning and practical application is limited.

1. Introduction

Flow of cerebrospinal fluid (CSF) and interstitial fluid (ISF) in the brain has significant implications for waste clearance and drug and nutrient delivery, the failure of which leads to devastating clinical consequences and has been linked to ageing and neurodegenerative disease [1–5]. The glymphatic model describes a system where annular perivascular spaces (PVSs) surrounding arterial blood vessels provide low resistance pathways that carry CSF into the brain interior where it mixes with ISF in the parenchyma, delivering nutrients and picking up waste that is then transported out of the brain via other low-resistance pathways, such as venous PVSs, lymphatic vessels and white matter tracts [6,7].

Experimental measurements, including two-photon imaging [6,8–10], transcranial imaging [11], magnetic resonance imaging [12–16] and real-time iontophoresis [17–20], provide insight regarding glymphatic flow and transport and form the basis for the glymphatic model; however, each of these measurement techniques provides only limited access to these flows, leaving gaps in our understanding and limiting our ability to prevent and treat related pathological conditions. Mathematical models provide valuable insight into the mechanisms that drive glymphatic flows and point out the most important unknown aspects. In particular, reduced-order network models [21–25] provide insight into how the flows vary across different parts of system or under different conditions.

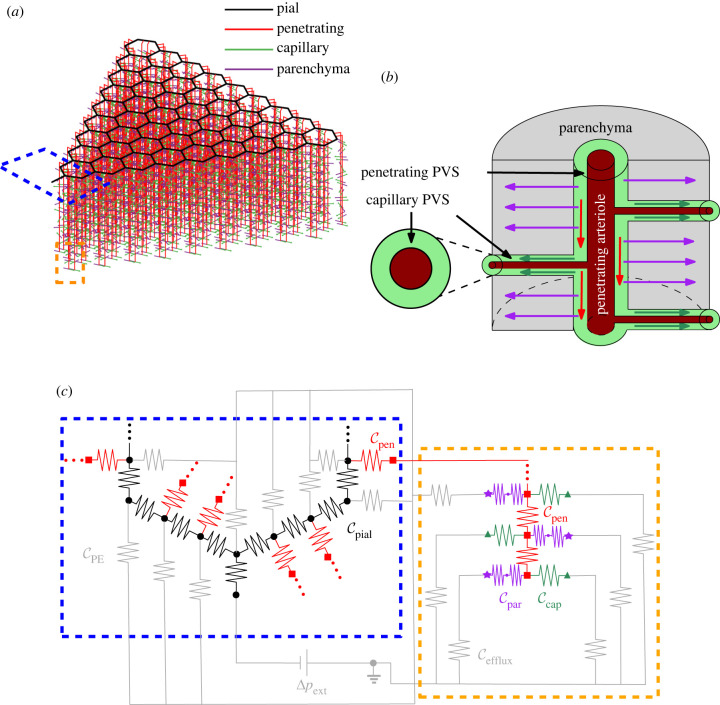
Tithof et al. [24] recently developed a network model of the murine glymphatic system based on experimental measurements. The model, depicted in part in figure 1a, is composed of a hexagonal lattice of annular channels representing pial PVSs on the surface of the cortex, with penetrating arteriole PVSs branching from the pial PVSs and descending into the cortex. Each penetrating arteriole PVS is connected to network elements representing lumped resistance to flow through capillary PVSs and the parenchyma. The capillary and parenchymal elements are modelled as parallel routes, as illustrated in figure 1b,c. The route representing flow through the parenchyma consists of two elements in series, accounting for the resistance to flow through gaps in the astrocyte endfeet that form the outer boundary of the penetrating PVS and the lumped resistance to flow through the parenchyma, which is modelled as a porous medium.

Figure 1.

(a) Schematic of the model, including a network of perivascular spaces (PVSs). (b) Schematic of the portion of the model inside the orange dashed box, showing the direction of flow in the penetrating (red arrows) and capillary PVSs (dark green arrows) and in the parenchyma (purple arrows). PVSs are annular spaces surrounding blood vessels. (c) Circuit schematic of the regions indicated by the blue and orange dashed boxes in (a). The grey resistors connected to the pial PVSs inside the blue dashed box represent the conductance of the pial efflux routes C_PE, while the grey resistors connected to the parenchymal and capillary routes in the dashed orange box represent the conductance of the other efflux routes, C_efflux. C_efflux is typically much higher than C_PE. C_par is the combined conductance of flow through the astrocyte endfeet gaps and the parenchyma, as described by Tithof et al. [24], and is thus represented by two resistors in series in the schematic. C_cap, C_pen, C_pial are the conductances through capillary, pial and penetrating PVSs.

The model involves 23 parameters representing geometrical and material properties of the network. While Tithof et al. validated many aspects of the model, including their idealization of the vascular geometry, several parameters are largely unknown. They explored eight scenarios, involving different combinations of the five parameters with the largest uncertainties, and determined the most likely parameter regime. However, their eight scenarios are based on various combinations of approximate extrema for these five parameters. With only eight scenarios, it is difficult to know how the uncertain values interact. Additionally, the parameter values are based on median or mean values, but all of the parameters have some degree of natural variation that further complicates their interactions. In this work, we perform a comprehensive sensitivity analysis to identify the model parameters whose variations most strongly affect the results. Our analysis provides insight into how the different model parameters affect glymphatic flow and points to the parameters whose accurate future measurement is most important.

2. Methods

The model in this work is similar to that described by Tithof et al. [24] with two adjustments. First, in the version described by Tithof et al. all of the flow in the pial PVSs enters the penetrating PVSs and exits through either the parenchyma or the capillary PVSs. However, it is possible that there is some efflux from pial PVSs to other routes; for example, flow could enter venous pial PVSs directly, bypassing the parenchyma [26–28], or flow could leak out of pial PVSs into the subarachnoid space through stomata in the PVS walls [29,30] and exit through the cribriform plate and other perineural routes to reach the lymphatic system [26]. In order to simulate the effect of pial PVS efflux, we add an additional exit pathway to each pial node. Since the potential pial PVS efflux routes are not well defined, we use the same conductance for all pial efflux pathways. We choose a fraction of the total flow which will exit through pial efflux routes, then set the corresponding conductance, C_PE, which is determined iteratively: C_PE is adjusted until the target fraction of pial flow E_pial exits through the pial efflux pathways.

We impose the limit E_pial ≤ 0.8 based on the observation by Lee et al. [31] that 20% of a tracer injected into the cisterna magna reached the parenchyma. This limit should be thought of as an absolute upper bound because not all tracer injected into the cisterna magna will enter pial PVSs (instead, some directly exits the skull [2,32–34]), so it is likely that a portion of the 80% of tracer that did not reach the parenchyma never even entered pial PVSs (this may be a very substantial proportion). It is also important to point out that the fraction of tracer transported (as reported by Lee et al. ) does not precisely reflect the fraction of fluid transport; however, if we assume that solute transport prior to delivery to the parenchyma is dominated by bulk fluid flow, the fraction of fluid delivered will approximately match the fraction of solute delivered. Solute transport is clearly dominated by advection due to unidirectional bulk flow [35,36] (as opposed to transport induced by oscillatory net zero flow and/or diffusion) in pial PVSs and probably in penetrating PVSs as well [16,37]. Of course, this bound is only valid for the conditions in Lee et al. [31]: rats anaesthetized with dexmedetomidine (0.015–0.020 mg⁻¹ kg⁻¹ h⁻¹) supplemented with 0.5–0.8% isoflurane. For other anaesthetics or states of arousal the relative resistance of both the pathways leading to the parenchyma and other efflux routes are likely to change, leading to a different amount of tracer entering the parenchyma from the cisterna magna [18,21,38,39]. The efflux fraction from pial PVSs may also be different in mice than in rats; we hope future experimental measurements will provide additional information.

The second adjustment we make to the model is that we use the expression Schreder et al. [40] calculate for resistance to flow in the murine parenchyma through an array of arterioles and venules

$$R_{\mathrm{par}}=0.9563\cdot \frac{\mu }{{\kappa }_{\mathrm{par}}}\cdot \frac{n}{l_{\mathrm{pen}}},$$ 2.1

where μ is the viscosity, l_pen = 1000 μm is the total length of the penetrating arteriole and n = 11 is the number of parenchymal segments. CSF is well-modelled as Newtonian [41], and the value we use for viscosity is the same used in the original model, 7 × 10⁻⁴ Pa · s.

In this analysis, we vary 11 of the model parameters, which are listed and defined in table 1 with the range of values we consider. We chose to vary these parameters because their values are uncertain (E_pial, Γ_pen, κ_pen, L, r, Γ_cap, κ_cap, κ_par, T, F_c) and/or the values are expected to vary significantly with arousal state and with location (Γ_pial, Γ_pen). All other model parameters are fixed and are the same as described by Tithof et al. [24]. We use a Monte Carlo approach as the basis for the analysis. We create 1000 different instances of the model using Latin hypercube sampling (using the built-in MATLAB function lhsdesign). For each instance, the 11 input parameters are randomly sampled from distribution that spans the range in table 1. The distribution is uniform for parameters with a range that spans less than one order of magnitude, and the distribution is log-uniform if the range spans more than an order of magnitude (κ_pen, κ_par, κ_cap and F_c). We solve for the volume flow rates and pressures in each instance of the model in MATLAB, as described by Tithof et al. [24]. As in their work, the total model driving pressure is set so that the median pial PVS velocity is 18.7 μm s⁻¹ for each instance of the model, matching experimental measurements [9]. This results in similar total volumetric flow rates for all of the models. For the sensitivity analysis, we focus on how varying the input parameters changes the total model conductance, C, which is the inverse of the total model resistance, i.e. C = 1/R.

Table 1.

Parameters and the range of values included in the sensitivity analysis.

input parameters (Xi)			lower (li)	upper (ui)	ref.
pial	fraction pial efflux	Epial	0	0.8	[31]
	pial area ratio	Γpial	0.5	2	[9]
penetrating	penetrating area ratio	Γpen	0.5	2	[9]
	penetrating PVS permeability (m2)	κpen	4.50 × 10−15	3.71 × 10−12	[16,42]
capillary	capillary effective length (m)	L	5.00 × 10−5	4.00 × 10−4	[24]
	capillary radius (m)	r	1.50 × 10−6	4.50 × 10−6	[43]
	capillary area ratio	Γcap	0.07	0.36	[44,45]
	capillary PVS permeability (m2)	κcap	2.25 × 10−18	4.66 × 10−14	[22,46]
parenchymal	parenchymal permeability (m2)	κpar	1.20 × 10−17	4.50 × 10−15	[42,47]
	endfoot wall thickness (m)	T	2.00 × 10−7	1.00 × 10−6	[48]
	endfoot cavity fraction	Fc	0.003	0.37	[48,49]

It is unknown whether the penetrating and capillary PVSs are open or porous; therefore, the permeability of those spaces ranges between a lower bound (provided in table 1) and a value for permeability that produces a resistance equivalent to flow through an open (non-porous) PVS, as described by Tithof et al. [24] in their electronic supplementary material. It is important to note that a permeability value larger than this bound is non-physical, as it corresponds to a scenario in which the presence of obstructions (the solid porous media phase) increase flow speed compared to that of an open, unobstructed space. Since the permeability corresponding to an open space depends on the vessel radius and area ratio, the upper bound listed in table 1 is the effective permeability for the upper bound on vessel radius and area ratio. For each of the 1000 instances of the model, if the permeability assigned in the initial Latin hypercube sampling is larger than the permeability equivalent to an open space for the vessel radius and area ratio of that instance, the permeability is reduced to the open-space-equivalent permeability.

2.1. Proportional reduction of error

In order to quantify the effect of each input parameter on the total model conductance, C, we calculate the proportional reduction of error for a linear regression fit of the total conductance as a function of the 11 varying input parameters. We centre C by subtracting the C value calculated with the midpoint of the range for every input parameter, which we denote C_m

$${\hat{C}}_j=C_j-C_{\mathrm{m}},$$ 2.2

where j ∈ {1, 2, …, 1000} indicates the simulation number. We denote an arbitrary input parameter as X_i,j, where i ∈ {1, 2, …, 11} indicates the variable. We scale the input parameters so they vary from zero to one; for the linearly distributed variables,

$${\hat{X}}_{i,j}=\frac{X_{i,j}-l_i}{u_i-l_i},$$ 2.3

and for the logarithmically distributed variables,

$${\hat{X}}_{i,j}=\frac{{\log }_{10}(X_{i,j})-{\log }_{10}(l_i)}{{\log }_{10}(u_i)-{\log }_{10}(l_i)},$$ 2.4

where l_i are the lower bounds of the ranges and u_i are the upper bounds, all provided in table 1. It is also useful to name the input parameter values at the midpoints of their ranges, which for linearly distributed variables are

$$X_{i,\mathrm{m}}=0.5(u_i+l_i),$$ 2.5

and for logarithmically distributed variables are

$$X_{i,\mathrm{m}}={10}^{0.5({\log }_{10}(u_i)-{\log }_{10}(l_i))+{\log }_{10}(l_i)}.$$ 2.6

We calculate the summed squared error, SSE_none, for the linear regression fit of ${\hat{C}}_j({\hat{X}}_{i,j}$), with all variables included. We then exclude one variable ${\hat{X}}_{i,j}$ from the fit and calculate the new summed squared error, SSE_i. The proportional reduction of error,

$${\mathrm{PRE}}_i=\frac{{\mathrm{SSE}}_i-{\mathrm{SSE}}_{\mathrm{none}}}{{\mathrm{SSE}}_{\mathrm{none}}},$$ 2.7

indicates, with a single number, how dependent a linear regression fit of C is on the input parameters across the entire parameter space.

2.2. Local sensitivity analysis

In order to determine how the sensitivity varies across the parameter space, we also calculate the local sensitivity for each of the 1000 instances of the model. We do this using a forward difference approach, where we perturb the value of each input parameter one at a time while holding all other parameters constant, then divide the amount C changes by the perturbation amount. We use two different measures of local sensitivity: we perturb the input parameters by increasing them by either 5% of the range (range sensitivity) or 5% of the value of the parameter (value sensitivity). We normalize the change in total model conductance ΔC_i,j by the total model conductance C_j for the jth instance of the model, and we normalize the change in the variable ΔX_i,j by either the range (indicated by subscript r) or the value of the parameter (indicated by subscript v):

$${\left(\frac{\mathrm{\partial }C}{\mathrm{\partial }{X}_i}\right)}_r=\frac{\mathrm{\Delta }{C}_{i,j}/C_j}{\mathrm{\Delta }{X}_{i,j}/(u_i-l_i)},$$ 2.8

and

$${\left(\frac{\mathrm{\partial }C}{\mathrm{\partial }{X}_i}\right)}_v=\frac{\mathrm{\Delta }{C}_{i,j}/C_j}{\mathrm{\Delta }{X}_{i,j}/X_{i,j}}.$$ 2.9

These two different measures of local sensitivity offer different, complementary insights into the model. Perturbing and normalizing by a fraction of the range (range sensitivity (∂C/∂X_i)_r) elucidates how the size of the range, or the uncertainty of each parameter, affects the output. The range sensitivity indicates how changing an input variable by 5% of the range changes the output, C. If we do not know the value of a parameter very precisely (a large input range), a variation of 5% of the range will result in large changes in the output, C. In standard uncertainty theory, the uncertainty of a parameter can be estimated using the Taylor Series method, where uncertainty due to each component is calculated by the change in the output parameter with respect to the input parameter multiplied by the uncertainty of that component, i.e. $U_C^2=\sum _i{(\mathrm{\partial }C/\mathrm{\partial }{X}_i)}^2{U}_{X_i}^2$ where U is the uncertainty. If we consider the range to be the uncertainty of each input parameter, then normalizing the perturbation amount ΔX_i,j (in the denominator) by dividing by the range is equivalent to multiplying ∂C/∂X_i by the uncertainty. Therefore, the range sensitivity can be considered an estimate of the uncertainty in C due to each input parameter.

However, if we are less concerned with the uncertainty in a parameter or are not confident in the range, we can perturb and normalize by a per cent of the parameter value (value sensitivity, (∂C/∂X_i)_v). The value sensitivity tells us how much changing the input by 5% changes the output, C, and is independent of the range. This is a useful feature if we do not have high confidence in the range or if we know the value more precisely than indicated by the range (e.g. if future experimental measurements estimate the unknown value with greater precision). To summarize, the range sensitivity provides a practical indication of how the uncertainty in each input parameter affects the model, while the value sensitivity indicates how sensitive the model is to each input parameter, independent of its range.

2.3. Speed and Péclet number

We calculate the flow speed u by dividing the absolute value of the volume flow rate in each segment by the area, u = |Q|/A. For the penetrating and capillary segments, the area A is the PVS cross-sectional area. For the parenchymal segments, A is the surface area through which fluid entering the parenchyma exits the penetrating PVS, i.e. $A=\pi {\mathrm{d}}_{\mathrm{pen}}\left(\sqrt{{\Gamma }_{\mathrm{pen}}+1}\right)(l_{\mathrm{pen}}/n)$, where ${\mathrm{d}}_{\mathrm{pen}}\sqrt{{\Gamma }_{\mathrm{pen}}+1}$ is the diameter of the penetrating PVS outer wall and l_pen/n is the length of each penetrating PVS segment. Note that since parenchymal flow is modelled as planar and flows radially outward from the penetrating PVS in the transverse plane, this is the maximum velocity in the parenchyma. We report the median speed for each type of segment.

We define the Péclet number for each type of segment as

$$Pe=\frac{\mathcal{U}\mathcal{L}}{D_{\mathrm{eff}}},$$ 2.10

where $\mathcal{U}$ is the median velocity for each segment type as described above, $\mathcal{L}$ is the characteristic length of the segment and D_eff is the effective diffusivity. We use the median velocity to calculate Pe, but the velocity for each segment type varies widely, with velocity generally decreasing with depth into the parenchyma as more fluid exits through other pathways. However, the median velocity is a convenient measure to provide a general estimate of the relative importance of advection and diffusion. The characteristic lengths are $\mathcal{L}=1000\hspace{0.17em}\mu \mathrm{m}$ for the penetrating PVSs, $\mathcal{L}=L$ for the capillary PVSs, and $\mathcal{L}=128\hspace{0.17em}\mu \mathrm{m}$ for the parenchymal segments, which is the average nearest-neighbour distance between murine arterioles and venules in data provided by Blinder et al. [40,50].

We calculate Pe for monomeric amyloid-β, for which the free diffusion coefficient is D = 1.35 × 10⁻¹⁰ m² s⁻¹ [51]. For flow through the parenchyma, we calculate the effective diffusivity, D_eff, by dividing D by the square of the tortuosity, which accounts for the fact that the diffusion occurs in a porous medium

$$D_{\mathrm{eff}}=\frac{D}{{\lambda }^2},$$ 2.11

where the tortuosity λ = 1.6 [52]. Ray et al. estimated that λ = 1.85 [17], which would make Pe 30% higher. It is unclear whether penetrating and capillary PVSs are open or porous: if they are porous, the tortuosity would likely be different from that of parenchymal brain tissue. Here, we use D_eff = D for the penetrating and capillary PVSs, assuming them to be open, but if they are porous, Pe would be greater: for tortuosities of 1.6 or 1.85, Pe would increase by a factor of 2.6 or 3.4, respectively.

2.4. Exclusion criteria

Some combinations of variables in the parameter space result in scenarios that behave unrealistically; we can eliminate those scenarios, further narrowing the parameter space. For example, some combinations of variables require driving pressures that are unreasonably large. The network model is based on conductance of the various segments and therefore is independent of the driving mechanism, but it is unlikely that any mechanism will produce a pressure drop larger than 1 mmHg across the entire network model. Another requirement of the glymphatic model is that flow must reach the deeper levels of the cortex, producing reasonably uniform CSF perfusion. We expect reasonably uniform perfusion based on evidence of tracer penetration into the cortex and evidence that flow is important for metabolic waste removal, as suggested by Tithof et al. [6,12,14,18,24,53–58]. Therefore, we suggest that scenarios in which more than 50% of the flow that enters penetrating PVSs exits the cortex in the first 90 μm below the surface (ϕ₉₀ > 0.5) are unlikely. We calculate ϕ₉₀ as

$${\varphi }_{90}=\frac{Q_{\mathrm{cap},90}+Q_{\mathrm{par},90}}{Q_{\mathrm{PVS}}},$$ 2.12

where Q_PVS is the total flow into the penetrating PVS and Q_cap,90 and Q_par,90 are the total flow that enters the capillary and parenchymal routes in the first 90 μm below the surface. In some of the results discussed below, we use these two requirements, a driving pressure drop greater than 1 mmHg or more than 50% of the flow exiting by the first 90 μm below the surface, to identify combinations of parameters that behave unrealistically, thus narrowing the parameter space.

3. Results

3.1. Proportional reduction of error

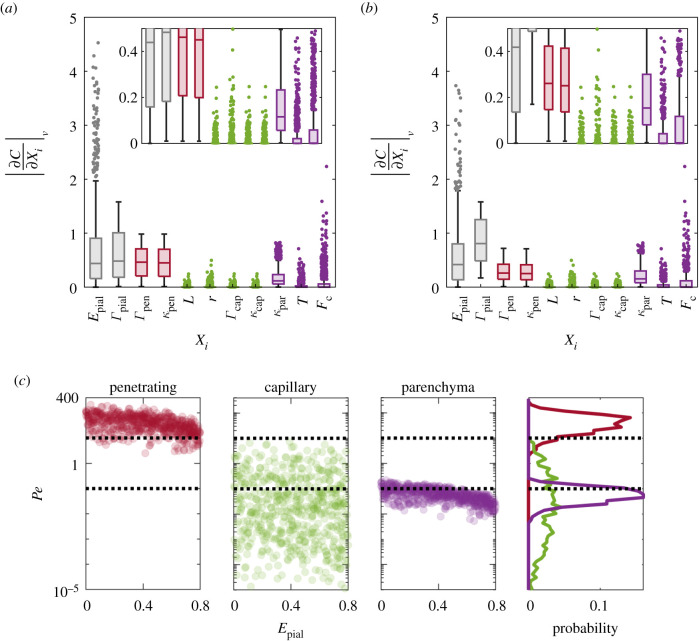
We show the proportional reduction of error for a linear regression fit of total model conductance in figure 2a. The proportional reduction of error indicates how much excluding a variable impacts the goodness of a linear regression fit of total model conductance, C, as a function of the input parameters. Across the parameter space, the parenchymal permeability κ_pen has the largest influence on the fit of C. When κ_pen is excluded from the linear regression, the sum squared error is more than 50% larger. The large influence of κ_pen is due in part to the fact that the range of values of κ_pen in the Monte Carlo simulation spans almost three orders of magnitude. Other input parameters, such as the capillary PVS permeability and the parenchymal permeability, also have large ranges of possible values, but the flow that passes through the penetrating PVSs is split between the capillary PVSs and parenchyma. In other words, the resistances to flow in the parenchyma and capillary PVSs are connected in parallel with each other but connected in series with the resistance to flow in the penetrating PVSs, so capillary/parenchymal resistances and their associated parameters have less influence those of the penetrating PVSs. Relative to the other parameters, the parenchymal permeability is also important, as is the fraction pial efflux.

Figure 2.

(a) The proportional reduction of error (PRE) for a linear regression fit of total model conductance, showing that across the entire parameter space, the model is most sensitive to the penetrating PVS permeability, κ_pen. (b) Box plots indicating the median, interquartile range, full range and outliers of the local range sensitivities. The penetrating PVS permeability is not only the most sensitive input parameter, but it is relatively sensitive across all instances of the model, covering a large parameter space. (c) Box plots of the local value sensitivities. When not accounting for the large uncertainty associated with penetrating permeability, other parameters are also important. (d) The distribution of capillary flow fractions across the 1000 instances of the model. Regardless of which (range or value) sensitivity is used, capillary PVS flow variables have relatively little influence on the total conductance because parenchymal conductance always dominates, so the majority of the flow passes through the parenchyma.

The simplicity of the proportional reduction of error makes this approach a convenient way to estimate model sensitivity. However, it is an indirect measure of the single-parameter sensitivity, because it indicates how excluding each parameter affects the linear regression fit, rather than how each parameter contributes to C directly. Furthermore, because the fit covers the entire parameter space, it does not capture how the sensitivity varies across the parameter space.

3.2. Local sensitivity

In order to demonstrate how the sensitivity varies across the parameter space, we show the local sensitivity for all 1000 instances of the model in figure 2b,c. Figure 2b shows box plots of the local range sensitivities for all 1000 instances of the model. The range sensitivity shows how much perturbing each input variable with respect to its range changes the total model conductance; for example, a sensitivity of 10 indicates that changing X_i by 1% of its range results in a 10% change in C. When considering the range sensitivity, κ_pen is not only the most sensitive parameter overall, as indicated by the PRE analysis, but it is also very sensitive in most of the 1000 instances of the model, meaning it is important at most points in the parameter space. Though the sensitivity varies widely across the parameter space, the median sensitivity is 280, i.e. a variation in κ_pen of 1% of its range changes C by 280%; thus, we can have little confidence in C without greater confidence in κ_pen. This result highlights the need to reduce the uncertainty in κ_pen in order to accurately model glymphatic flows. Normal physiological changes and the uncertainty associated with other parameters have relatively little influence on C when compared with the influence of κ_pen. C is also moderately sensitive to parenchymal permeability κ_par, and the pial efflux fraction E_pial is consistently sensitive across the entire parameter space.

It is also instructive to determine how the local sensitivity changes when normalized with respect to the value of each variable (i.e. the value sensitivity), rather than its range. Calculating sensitivity in this manner shows how perturbing a given input parameter affects the total model conductance; for example, a sensitivity of two indicates that changing X_i by 1% of its value will result in a 2% change in C. In figure 2c, we show that, when considering the value sensitivity, κ_par is still important, but the penetrating PVS area ratio Γ_pen is also important. The total conductance is also relatively sensitive to the pial efflux fraction, and in some cases it is very sensitive, with sensitivities as high as 3 and 4. This occurs in cases where the pial efflux fraction is large, meaning a larger fraction of the flow is exiting the pial PVS and not entering the penetrating PVS, and the resistance through other pathways is relatively low, requiring an extremely high pial efflux conductance in order to draw the flow.

The total model conductance is relatively insensitive to changes in parameters related to capillary PVS flow for both the range and value sensitivity. This is because in 80% of the cases simulated, less than 1% of the flow in the penetrating PVS exits through the capillary PVSs, as we show in figure 2d. In the network model, flow through the parenchyma and capillary PVS routes are in parallel, so the capillary PVS flow fraction is exactly related to a ratio of the capillary PVS conductance and the sum of the capillary PVS and parenchymal conductances

$$\frac{Q_{\mathrm{cap}}}{Q_{\mathrm{par}}+Q_{\mathrm{cap}}}=\frac{C_{\mathrm{cap}}}{C_{\mathrm{par}}+C_{\mathrm{cap}}}.$$ 3.1

Across the large parameter space, we are investigating, most of the flow exits through the parenchyma rather than the capillary PVSs, and the parenchymal conductance dominates the equivalent conductance of the parallel exit routes, so changes in capillary conductance have little impact on the overall conductance.

In order to gain more insight into the relative importance of the different model parameters, we rank their local per cent sensitivities for each of the 1000 cases we simulate. In figure 3a, we show for which fraction of the simulations each variable is the most sensitive (based on the value sensitivity). No variable is the most sensitive in the majority of cases. The pial efflux fraction and penetrating area ratio are each the most sensitive in about one-third of the cases. Interestingly, κ_pen is never the most sensitive variable, although it is often the second most sensitive, as demonstrated in figure 3b, which shows the distribution of rank for each variable. The sensitivity of the penetrating PVS conductance to κ_pen is identical to the sensitivity to Γ_pen, but Γ_pen also appears in the expression for the conductance through the endfeet gaps, and thus the total model conductance is always more sensitive to Γ_pen than κ_pen.

Figure 3.

For the 1000 instances of the model, we rank the variables by local value sensitivity and show (a) the frequency with which each variable is most sensitive and (b) the frequency of rank for each variable.

Which variable is most sensitive depends on where the model lies within the parameter space. For several of the parameters, particularly the highly uncertain ones, the sensitivity is strongly dependent on the value of the parameter; they are highly nonlinear since their first derivatives change across their ranges. For example, as we show in figure 4,κ_pen, κ_par and F_c are very sensitive near their lower bounds but relatively insensitive near their upper bounds, while E_pial is more sensitive as it approaches its upper bound but less sensitive near its lower bound. As these variables approach the ends of their range, they often become the crucial factor that dominates the total conductance, making them the most sensitive variable. Experiments that narrow the range of uncertainty of these four variables would greatly improve the accuracy of the network model or any model of CSF flow in the cortex that includes these properties.

Figure 4.

The local value sensitivity as a function of each parameter.

The area ratios Γ_pial and Γ_pen do not change sensitivity systematically across the range. The noisy plots of the value sensitivities shown in figure 4 suggest that they have strong interactions with other variables. The remaining parameters (L, r, Γ_cap, κ_cap and T) have low sensitivities across their ranges.

3.3. Speed and Péclet number

The median speed for each segment type is shown in figure 5a. Though the speeds vary widely due to the large ranges of the input parameters, the majority of the simulations predict significant differences in speeds between penetrating PVSs and the parenchyma. Speed generally decreases with increasing pial efflux fraction, as less fluid enters the penetrating PVSs, and yet even when 80% of the fluid is exiting at the pial level and not entering the penetrating PVS, the speeds predicted in the penetrating PVSs and parenchyma are not negligible. Speeds in penetrating and capillary PVSs have not been measured directly, so models such as this one provide useful predictions, and the range of speeds can be narrowed as the uncertainty of the input parameters is reduced. We plot flow speeds predicted in previous studies with dashed lines for comparison, and we discuss the comparison further in the Discussion.

Figure 5.

(a) The median flow speed for each segment type in each of the 1000 different simulations. The black dashed line indicates the speed estimated by Ray et al. for brain tissue (3 μm s⁻¹), which lumps together the penetrating and capillary PVSs and parenchymal tissue [16]. The dark blue dashed line marks the interstitial fluid velocity estimated by Ray et al. (0.1 μm s⁻¹) [17]. The cyan dashed line marks the velocity estimated by Holter et al. near the outer wall of the PVS (0.035 μm s⁻¹) [47]. (b) The corresponding Péclet number in each of the 1000 different simulations. Dashed lines indicate Pe = 0.1 and 10, the range where both diffusion and advection play an important role in transport.

We show the Péclet number, Pe, for penetrating, capillary and parenchymal segments of the network for all 1000 simulations in figure 5b. When Pe ≫ 1, we expect amyloid-β monomers to be transported primarily by advection, whereas when Pe ≪ 1, we expect transport to be primarily by diffusion. For reference, the Péclet number in pial PVSs is 72 for all simulations (using a characteristic length of 525 μm, the length of pial PVS segments in our model) since the median velocity in the pial PVSs is always 18.7 μm s⁻¹. Given the large uncertainty associated with the parameters, it is not possible to rule out either advection or diffusion as a potentially significant contributor to mass transport in the penetrating PVSs because in approximately a quarter of the simulations, 0.1 < Pe < 10, indicating that both modes of transport are significant. However, even with the large uncertainty, across the large parameter space we explore, 90% of simulations have Pe > 0.1 in the penetrating PVSs, indicating that advection likely plays a significant role in mass transport in the penetrating PVSs, even if it is not the dominant mode. The finding that advection plays a significant role in transport in penetrating PVSs is consistent with work from Iliff et al. who found that molecules of very different sizes (less than 1 kDa and approx. 200 kDa) had similar rates of transport, which suggests that advection, rather than diffusion, is dominating transport [37]. Fewer than 1% of the capillary PVSs and none of the parenchymal spaces have Pe > 10, indicating that diffusion most likely plays the dominant role in mass transport in capillary PVSs and the parenchyma, at least for amyloid-β monomers. Thirteen per cent of the simulations have parenchymal Pe > 0.1, and none have Pe > 1, so while bulk flow likely exists in the parenchyma, advection likely plays a smaller role than diffusion in transport of amyloid-β-sized molecules and smaller. This agrees with Koundal et al. [55], who found evidence that diffusion plays a significant role in transport in the brain parenchyma.

3.4. Exclusion criteria

The amount of fluid that reaches the deeper levels of the cortex and the uniformity of perfusion along the cortical depth is determined by the ratio of the conductance in the penetrating PVS (into the cortex) and the combined conductance of transverse routes (capillary PVSs and parenchyma). In the network model, the segments of penetrating PVS, capillary PVS, or parenchyma are identical, so even though the flow rate in each penetrating PVS is different, the fraction of transverse to penetrating flow at each level of the cortex is identical and depends explicitly on the ratio between the combined conductance $C_{\mathrm{b}}=C_{\mathrm{cap}}+C_{\mathrm{par}}$ and the penetrating PVS conductance C_pen. We show the cumulative flow fraction, or total amount of fluid that exits penetrating PVSs within a given cortical depth, as a function of the ratio $C_{\mathrm{b}}/C_{\mathrm{pen}}$ in figure 7a. When the penetrating PVS conductance C_pen is large relative to the combined conductance of parenchymal and capillary segments $C_{\mathrm{b}}$, the amounts of fluid that enter the capillary and parenchymal routes at each level of the cortex approach equality. As $C_{\mathrm{b}}/C_{\mathrm{pen}}$ approaches zero, the perfusion becomes perfectly uniform, with the same amount of fluid perfusing into capillary PVSs and/or parenchyma at every level of the cortex.

Figure 7.

The local sensitivity analysis (a) shown in figure 2c, duplicated for comparison and (b) without the excluded simulations. (c) Péclet number without the excluded simulations.

To this point, the results have included all 1000 scenarios. However, some combinations of variables result in scenarios that behave unrealistically, requiring large pressure drops or exhibiting non-uniform perfusion. Of the 1000 different scenarios we simulated, 550 meet the requirements of a total driving pressure drop less than 1 mmHg and less than 50% of the flow exiting in the first 90 μm of the cortex. We can exclude the remainder and thereby narrow the parameter space. One straightforward requirement is that $C_{\mathrm{b}}/C_{\mathrm{pen}}<5.5$, which can be obtained from the plot of $C_{\mathrm{b}}/C_{\mathrm{pen}}$ in figure 6a, as indicated by the dashed vertical line. However, since C_pen and C_b both involve several variables, this does not provide much insight. In figure 6b, we show the scenarios that meet the criteria in blue and those that do not in red. No scenario with a parenchymal permeability less than 1 × 10⁻¹⁴ met the inclusion criteria. Also, as the pial efflux fraction decreases, the minimum viable permeability also increases. The dashed line approximately delineates the region containing scenarios that are never viable.

Figure 6.

(a) The cumulative fraction of flow in penetrating PVSs that exits at different cortical depths z. Perfectly uniform perfusion occurs when $C_{\mathrm{b}}/C_{\mathrm{pen}}=0$. The horizontal dashed line indicates the cumulative flow fraction threshold 0.5, and the vertical dashed line indicates where the threshold intersects the line corresponding to z = 90 μm. Simulations to the right of the vertical dashed line are excluded. (b) Excluded variables based on pressure and perfusion. The region to the left of the dashed line indicates a portion of the parameter space where all simulations are excluded.

In figure 7a,b, we show the box plot of the local sensitivities with and without the excluded scenarios, for comparison. The overall distribution of sensitivities is not significantly different, so the points raised in relation to figure 2c are still applicable. However, there are some noteworthy differences. First, the median sensitivities for both Γ_pen and κ_pen are lower because simulations with small κ_pen are excluded and, as we show in figure 4, C is most sensitive to κ_pen when it is small. When κ_pen is small, the conductance in the penetrating vessels dominates the total conductance, and κ_pen and Γ_pen become the most important. By eliminating scenarios where the penetrating PVS conductance dominates (which leads to large pressure drops and large perfusion), the median sensitivity of κ_pen and Γ_pen is reduced. This line of reasoning leads to an important conclusion: if κ_pen is closer to the high end of its range, e.g. if the penetrating PVS is an open space, the penetrating PVS conductance would not dominate and κ_pen and Γ_pen would not be the most sensitive parameters.

Second, Γ_pial κ_par, T and F_c have higher median sensitivities. The sensitivity of C to other parameters is low when the penetrating PVS conductance dominates C, so by eliminating those simulations, we increase the median sensitivities of the other parameters. The increase in median sensitivity is most dramatic for Γ_pial, which now becomes the most sensitive parameter in most cases.

We also show spread of the Péclet number Pe, after imposing exclusion criteria, in figure 7c. The simulations with very low Pe are eliminated, and the conclusion about the relative importance of advection and diffusion in the penetrating PVSs is strengthened: in penetrating PVSs, Pe > 1 in all of the simulations and Pe > 10 in 91% of the simulations, suggesting advection likely dominates transport there. In the capillary PVSs and parenchyma, we find 0.1 < Pe < 10 in 29% and 17% of the simulations, respectively, so we cannot say that diffusion dominates, nor can we say that advection does not play a role, nor can we very decisively say that they both play a role.

4. Discussion

The proportional reduction of error and the range sensitivity indicate how the input parameter ranges, which reflect their uncertainty or natural variation, affect the total model conductance. Both the proportional reduction of error and the range sensitivity clearly show that the variations in κ_pen with respect to its range have the largest impact on C. Without narrowing the range of possible values for κ_pen, we can have little confidence in C. Variations and uncertainty in other parameters are relatively unimportant in the face of the uncertainty in κ_pen, which must be reduced in order to accurately model glymphatic flows.

Since one of the primary conclusions of this work is the importance of reducing the uncertainty associated with κ_pen, we describe here the work that has already been done to estimate κ_pen and how more accurate measurements might be obtained in the future. The true value of κ_pen was suggested to be approximately that of the upper bound by Tithof et al. [24] based on the following reasoning. Basser et al. [42] performed experiments that estimated the parenchymal (not penetrating PVS) permeability at 4.5 × 10⁻¹⁵ m², but Holter et al. [47] estimated the parenchymal permeability as 1.2 × 10⁻¹⁷ m² based on a numerical reconstruction of the neuropil, and they speculated that the discrepancy with the findings of Basser and other experimental studies could be attributed to fluid escaping to high-permeability pathways such as penetrating PVSs in those experiments. Tithof et al. supposed that the value of 4.5 × 10⁻¹⁵ m² from Basser et al. [42] accurately represents the penetrating PVS permeability and used that as their lower bound. The upper bound is based on the possibility that penetrating PVSs are open—as pial PVSs have been shown to be [59]—rather than porous. Ray et al. conducted a quantitative analysis of murine DCE-MRI data to estimate the relative contributions of advection and diffusion, determining that the large transport rates they observed suggest that the large penetrating PVSs are open [16]. Others that have estimated penetrating PVS permeability have used values that fall in between these upper and lower bounds [22,60]. Reliable permeability measurements are challenging to obtain. Permeability values based on ex vivo measurements are questionable due to the changes in the extracellular space that occur after death and during fixation; consequently, permeability can only be estimated using numerical reconstructions such as those of Holter et al. [47] or Jin et al. [61]. Both groups used the same ex vivo data from Kinney et al. [62] but implemented different approaches, obtaining permeability estimates that differed by a factor of 72. Mestre et al. [9] provided strong evidence that perfusion fixation dramatically alters the size of PVSs, so estimates of penetrating PVS permeability based on ex vivo measurements would be highly unreliable. Estimating the permeability using this approach in vivo is challenging due to the high-spatial-resolution required. Though estimates of permeability based on ex vivo samples would not be reliable, examining ex vivo samples of penetrating PVSs might offer insight into whether the spaces are open or porous, narrowing the uncertainty associated with κ_pen. Another method for measuring the permeability would be to track particles in the penetrating PVS: this method could also at least determine whether penetrating PVSs are open or porous, as described by Min Rivas et al. [59], narrowing the uncertainty associated with κ_pen. However, the 1 μm particles they used do not enter penetrating PVSs, which may indicate that the penetrating PVSs are porous, and if so, smaller particles would be required. Another exciting possibility is the approach of Ray et al. [16], who used in vivo MRI to estimate effective diffusivities in different regions of the brain and from that inferred velocities and Pe. Their approach could potentially be refined to narrow the possible range of penetrating PVS permeability.

This sensitivity analysis is based on the model described by Tithof et al. [24]. However, given the uncertainty surrounding several of the geometrical and material properties governing flow of CSF in the cortex, it is important to perform a rigorous sensitivity analysis on any model of glymphatic flow. Some of the conclusions from the sensitivity analysis presented here also apply to other models. For example, the impact of the uncertainty in κ_pen is applicable to any model that includes flow in the penetrating PVSs. Faghih & Sharp [25] use a reduced-order approach to model flow in PVSs, although they did not distinguish between pial and penetrating PVSs and used a branching network, in contrast to our hexagonal lattice with branching penetrating PVSs. They modelled both open and porous PVSs and also found a large difference (a factor of 667) in the required driving pressure when using a permeability of 1.8 × 10⁻¹⁴ m², supporting the conclusion that reducing the uncertainty of the PVS permeability is critical for modelling glymphatic flows. Though some of the conclusions from the sensitivity analysis presented here are specific to this model, they illustrate the importance of performing rigorous uncertainty analysis on any model.

We can use the value sensitivity to consider how temporal changes in model parameters, such as those that occur with changes in arousal state or pathological conditions, affect C. Glymphatic clearance is known to change with arousal and anaesthetic state [11,15,18,39,63]. Xie et al. [18] showed that the parenchymal permeability changes with arousal state, but it has been hypothesized that other parameters may also change. From figure 2c, we can see how changes in these parameters would affect glymphatic flow and speculate about their potential for driving the changes observed between sleep and wake. It has been shown that the gaps in the astrocytic endfeet may change in space and hypothesized that the gaps may also change in time as a means of regulating glymphatic flow [64], and indeed, the endfoot cavity fraction F_c, which is related to the endfoot gap size, is very sensitive for scenarios where the gap size is very small. In these cases, the endfoot gap conductance is very small and dominates the total conductance, precisely controlling glymphatic flow. However, this level of sensitivity occurs only for relatively small gaps in the endfeet; if the gap size is large, as estimated by Korogod et al. [49] (who fixed their samples by snap freezing rather than by chemical fixation), the endfoot gap conductance is large and C is relatively insensitive to changes in F_c. Another intriguing possibility is that Γ_pen changes with arousal state. For most scenarios modelled, C is considerably more sensitive to changes in Γ_pen than κ_par. In contrast to measuring changes in endfoot gap size T, which is challenging to image in vivo because the gaps are so small, measuring how Γ_pen changes with arousal state is relatively straightforward and can be accomplished with two-photon imaging.

It is noteworthy that even when 80% of the fluid is exiting at the pial level, there are many simulations where Pe > 0.1 in the penetrating PVS, indicating flow is sufficiently fast such that advection plays a significant role in transport, and there are some simulations where Pe > 10, indicating that advection dominates transport. The presence of significant pial efflux does not eliminate the possibility that flow in the penetrating PVSs plays an important role in transport. Ray et al. also find that advection plays a role in transport of gadoteridol (which has a similar diffusivity to monomeric amyloid-β [16]) in brain tissue, which includes the penetrating PVSs. We report Pe for monomeric amyloid-β, but Pe for other substances will scale linearly with the diffusivity. Pe will be reduced for smaller solvents (e.g. sucrose) and increased for larger solvents (e.g. tau). The diffusion coefficient for the 1 μm tracer particles often used to measure CSF speeds is D = 6.55 × 10⁻¹³ m² s⁻¹ [9], which would result in Pe values 200 times larger than in figure 5.

In this work, we focus on the sensitivity of the total model conductance, C, to the various input parameters because C provides a single number related to overall glymphatic flow and is directly related to the total driving pressure. However, the sensitivity of other output variables could also be considered. We calculated the sensitivity of penetrating PVS flow fraction that exits in the first 90 μm of the cortex (ϕ₉₀). Since ϕ is the penetrating PVS flow fraction, the parameters related to flow in pial spaces, E_pial and Γ_pial have no impact on ϕ₉₀. The relative sensitivities to the other parameters are similar to that for C.

In our analysis, the range over which we vary the parameters in some cases, like κ_pen, represents the large uncertainty in the value of the parameter, while in other cases, like Γ_pial, the average value of the parameter is relatively well quantified and the range represents the degree of natural variation expected. Our different simulations characterize the impact of changing the average value of each parameter, not the effect of different distributions of each parameter throughout space. Indeed, in our model, the segment types (pial, penetrating, capillary and parenchymal) are homogeneous throughout the network. In reality, many parameters likely vary throughout the cortex, such as the penetrating vessel diameter (which narrows with cortical depth). Including variation in the model by assigning the parameters according to a statistical distribution, for example, is not expected to significantly change total model quantities like pressure or conductance, but the variation in pressure, flow, velocity and Pe between different segments of the model would be larger. Exploring the impact of spatially varying parameter values throughout the model, particularly for parameters for which we show conductance is especially sensitive, would be valuable future work. Wang et al. [64] show that astrocyte endfeet vary with vessel diameter, and they suggest, based on their modelling, that the variation in endfoot size leads to uniform perivascular–interstitial flux, as mentioned above. It would also be interesting to explore how varying the astrocyte size affects flows in this model.

Ray et al. [16] analysed the in vivo spread of contrast in a murine brain based on DCE-MRI and estimated a velocity of 3.3 μm s⁻¹ for regions of tissue that include both the parenchyma and microvessels, which correspond to the penetrating and capillary PVSs and brain parenchyma in our model. In their analysis, they lumped parenchymal tissue and small PVSs together because the spatial resolution did not enable differentiation. Across the wide parameter space, none of the simulations in our analysis have parenchymal velocities as large as the 3.3 μm s⁻¹, while many of the simulations have penetrating PVS speeds around 3.3 μm s⁻¹, supporting their inference that the rapid transport they observed comes from flow in penetrating PVSs. The parenchymal flow speeds agree well with estimates from both a separate study by Ray et al. [17] and one by Holter et al. [47] (see velocity estimates near the PVS wall in their figure 3).

The parameter values in the hydraulic network model are based on the murine brain, for which measurements of anatomy and material properties are more readily available, but the parameter values, including the number of pial generations, could be adjusted to model flow in a human brain. Adjusting the model would be challenging because it is unclear how the parameters scale between species. Even without knowing how the parameters scale, one conclusion from the sensitivity analysis still applies: it is critical to determine the nature of penetrating PVSs (open or porous, and if porous, the permeability) in order to accurately model glymphatic flow. A model for flow in the human brain could offer valuable insight into important clinical applications, such as drug delivery, and how glymphatic transport is affected by changes in the brain, whether normal (e.g. sleep, ageing) or pathological (e.g. Alzheimer’s disease, traumatic brain injury).

5. Conclusion

Based on a Monte Carlo sensitivity analysis for 11 of the 23 parameters in a network model of glymphatic flow, we identify the parameters that have the greatest influence on total model conductance, C. From the proportional reduction of error (PRE), we show that across the large parameter space we explore, C is most sensitive to the penetrating PVS permeability, κ_pen. We also calculate the local sensitivity for each parameter and show that not only is penetrating PVS permeability the most sensitive overall, it is sensitive across the entire parameter space, indicating that it is important regardless of the value of the uncertain parameters. The high sensitivity of C to κ_pen is due to the large uncertainty associated with κ_pen and indicates that κ_pen is the most important parameter to measure experimentally in order to improve the accuracy of the glymphatic network model. Without more accurate measurements of κ_pen, the uncertainty of model predictions is so large that absolute numbers have little meaning, limiting the practical utility of this and any model that includes flow in penetrating PVSs.

We also calculate the local value sensitivity, which is independent of the parameter range. Calculating the sensitivity in this way shows how much changing each parameter value changes the total conductance. When defining the sensitivity in this way, κ_pen is still important, but the penetrating PVS area ratio Γ_pen also has a large influence, and for some instances of the model (those with large pial efflux), the pial efflux fraction also has a large influence. Regardless of how the sensitivity is calculated, variables related to capillary flow have very little influence on the conductance because the capillary PVS flow is parallel to the parenchymal flow, and the latter route almost always dominates. Ranking the local value sensitivity for each variable shows that the pial efflux fraction and Γ_pen are each the most sensitive parameter in about one-third of the cases.

We calculate the median Péclet number in the penetrating and capillary PVSs and parenchyma, and show that advection likely dominates transport of monomeric amyloid-β in penetrating PVSs, but advection plays a much smaller role in transport in the parenchyma since Péclet numbers in the parenchyma are more generally at least two orders of magnitude lower than Péclet numbers in the penetrating PVSs. We show that approximately half of the simulated cases require driving pressures that are unrealistically large or do not permit perfusion of tissue deep in the cortex. Penetrating PVS permeability κ_pen < 1 × 10⁻¹⁴ m² and the combination of small κ_pen and low E_pial are unlikely because they would require unrealistically large pressure drops and would not permit good perfusion, thereby narrowing the large parameter space. Other (or more restrictive) exclusion criteria could be used to reduce the parameter space even more.

Data accessibility

Simulation codes for the model on which this work is based are available at https://doi.org/10.5281/zenodo.5644079.

Authors' contributions

K.A.S.B.: conceptualization, methodology, visualization, writing—original draft, writing—review and editing; J.T.: conceptualization, visualization, writing—review and editing; D.D.C.: conceptualization, writing—review and editing; J.H.T.: supervision, writing—review and editing; D.H.K.: supervision, writing—review and editing.

All authors gave final approval for publication and agreed to be held accountable for the work performed therein.

Conflict of interest declaration

The authors declare that they have no competing interests.

Funding

This work was supported by the NIH National Institute on Aging through grant no. RF1AG057575 and by the Army Research Office through grant no. MURI W911NF1910280. J.T. is supported by a Career Award at the Scientific Interface from Burroughs Wellcome Fund.