Abstract
In photoacoustic tomography (PAT) systems, the tangential resolution decreases due to the finite size of the transducer as the off-center distance increases. To address this problem, we propose a multi-angle detection approach in which the transducer used for data acquisition rotates around its center (with specific angles) as well as around the scanning center. The angles are calculated based on the central frequency and diameter of the transducer and the radius of the region-of-interest (ROI). Simulations with point-like absorbers (for point-spread-function evaluation) and a vasculature phantom (for quality assessment), and experiments with ten 0.5 mm-diameter pencil leads and a leaf skeleton phantom are used for evaluation of the proposed approach. The results show that a location-independent tangential resolution is achieved with 150 spatial sampling and central rotations with angles of ±8°/±16°. With further developments, the proposed detection strategy can replace the conventional detection (rotating a transducer around ROI) in PAT.
Keywords: Finite transducer size, Photoacoustic tomography, Virtual source, Tangential resolution, Artifacts reduction
1. Introduction
Photoacoustic tomography (PAT) is a promising imaging modality with many preclinical/clinical applications [1], such as imaging from breast [2], palm and forearm [3], animal whole-body [4], [5], brain [6], [7] and rheumatoid arthritis diagnosis [8], [9]. It combines the contrast of optical and resolution of ultrasound imaging modalities [10] and is safe and relatively inexpensive compared to MRI/CT scans [2], [11]. First, a short laser excitation induces photoacoustic (PA) waves (due to photoacoustic effect). Then, Ultrasound transducers record the PA waves, and finally mathematical algorithms are used to reconstruct an image which represents the optical absorption distribution [12].
PAT systems are based on cylindrical [13], [14], [15], spherical [16] and planar [17] detection geometries, each of which has its own (dis) advantages [18]. For image reconstruction, it is generally assumed that point-like ultrasound detectors continuously enclose the medium. Point-like detectors record PA waves from a large acceptance angle (i.e., a wide mainlobe in the directivity pattern), which results in a location-independent axial/tangential resolution [19]. However, (1) there is no point-like ultrasound transducer (i.e., transducers have limited angular view), and (2) the spatial sampling (positioning of the transducers) is limited; of course a small transducer can mimic a point-like transducer, but the small active area causes a high noise and reduced sensitivity [20]. These two factors cause artifacts in the reconstructed image and limit the location-independent resolution of the imaging system in the cylindrical geometry; the resolution degrades as off-center distance increases [21].
There are methods reported before for improving the tangential resolution and keeping its uniformity in the ROI by compensating the effects of the finite-size transducer; mainly categorized into two groups: (a) developing advanced image reconstruction algorithms, and (b) developing new imaging set-ups.
Yuan, et al. [22] used a deconvolution with respect to the finite size of the detector in an exact frequency-domain reconstruction formula to compensate the blurring effect and resolution in a planar detection geometry. Kalva and Pramanik [23], [24] proposed the modified delay-and-sum (MDAS) algorithm for a circular detection geometry. Each photoacoustic RF signal received by the ultrasound transducer was back-projected from multiple points within the transducer surface (more than 100 points). Xiao, et al. [25] also proposed an improved version of MDAS by combining it with a sensitivity weighting factor. While promising results were achieved, MDAS and its improved version are computationally expensive (due to the multi back-projection procedure) and still suffer from a limited detection view and blurring once the detection radius is selected such that the whole ROI stays in the Fraunhofer zone of the transducer. Wang, et al. [26] proposed an approximate back-projection method by compensating the time-delay and directivity pattern of the finite-size transducer in a circular geometry. As the ROI enlarges (to a radius of 5–6 cm), this method becomes very time/cost consuming (5 min was taken for processing a ROI with a radius of 15 mm) due to a considerable growth in the size of the system matrix. Model-based (MB) reconstruction algorithms have also been extensively used in PAT [27], [28], [29], [30]. The MB methods are less sensitive to noise and better suppress artifacts than Back-projection-based (BPB) methods [28], especially when limited-view occurs [31]. Although the computational cost of MB algorithms is high, real-time imaging was realized by parallelizing on a graphics processing unit (GPU) [27]. Combining MB methods with total impulse response (TIR), spatial impulse response (SIR), and electrical impulse response (EIR) of the imaging system further improves the image quality [32], [33]. Yet, due to limited field-of-view of transducers in conventional structure, missed data could not be compensated even by MB method and needs structural modification.
Schwarz, et al. [34] placed two linear arrays perpendicular to each other (called bi-directional scanning geometry). This detection geometry imposes the limited-view issue [35] and loses most of the spatial frequencies. Li and Wang [36] used both positive and negative lab-made focused transducers with a large numerical aperture (NA) in a small ROI (2.5–3 cm diameter) to mimic a virtual point detector with a wide directivity pattern. Still, since the sensitivity of focused transducers is much less than the flat transducers in out-of-focus regions, more streak artifacts have appeared in the images compared to when a flat transducer is used. Li, et al. [36], Pramanik, et al. [20] and Nie, et al. [37] used an acoustic lens attached to the transducer to mimic a virtual point-like detector. However, this technique reduces the sensitivity (due to acoustic mismatch and manufacturing difficulties) and quality of the reconstructed images (due to the different speed of sound in the lens and the imaging medium).
In this study, we propose a multi-angle PAT (MA-PAT) system for compensating the finite size of the ultrasound transducer in 2D circular detection geometry. While a transducer is rotated around the region of interest (ROI) to record the PA waves needed for image reconstruction (Fig. 1(c)) this structure is called the conventional system throughout this paper, we additionally use central rotations (rotating the transducer around its center) with certain angles at each spatial sample (Fig. 2); The combination of all transducers with different central rotations and non-central rotated at each location mimics a virtual point detector with a large angular view (Fig. 2(a, b)). Spatial samples in this paper refer to the location of the virtual point detectors in the proposed structure and the location of transducers in the conventional structure. This is feasible with motor-based PAT detection systems by tilting the transducer at the beginning of data acquisition for each angle. The angles are calculated based on the impulse response, the diameter of the transducer and the radius of detection surface so that each point source in the ROI is within the field of view (FOV) of either the transducer or its rotations. In this way, a uniform spatial frequency spectrum would be captured from all the absorbers in the ROI. The point spread function (PSF) is evaluated through simulations and experiments, with the conventional and proposed detection geometries. The results indicate that the proposed approach provides a location-independent resolution and more structural information.
Fig. 1.
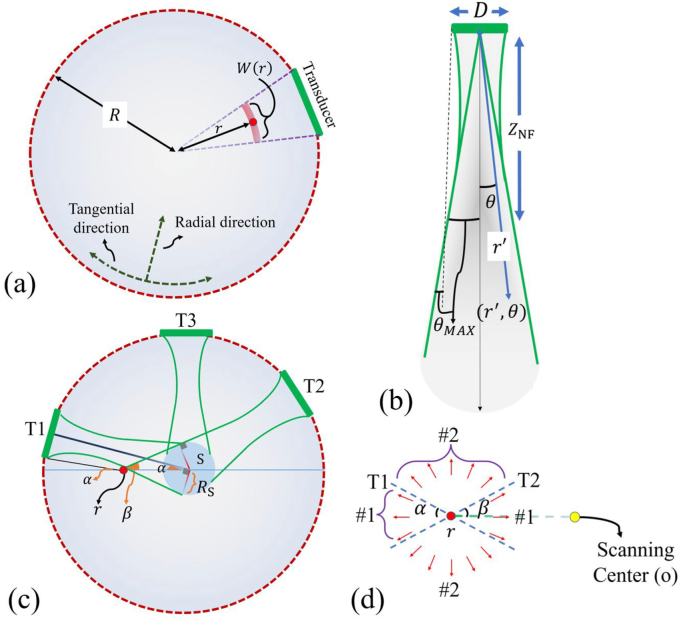
(a) The schematic of a conventional 2D PAT system. is the distance from the center of each point-absorber in ROI, is the scanning radius, red circle is a random point-absorber, and is the PSF extension of the red circle. (b) The schematic of the directivity pattern of a flat finite-size transducer with a diameter of . is the divergence angle, is the Fraunhofer zone. (c) The schematic of a conventional circular scanning PAT system where S is the area (with a radius of ) that stays in the FOV of all the transducers. The transducers between position T1 and T2 (for example T3) do not see the absorbing point (shown in red) in their main lobe. and are the angles of edges of the directivity pattern of transducer T1 and T2 connecting the absorber with respect to the horizon line passing through the red absorber, respectively. (d) The and generated ultrasound waves of the red circle in (c) can and cannot be fully captured with the conventional detection approach, respectively.
Fig. 2.
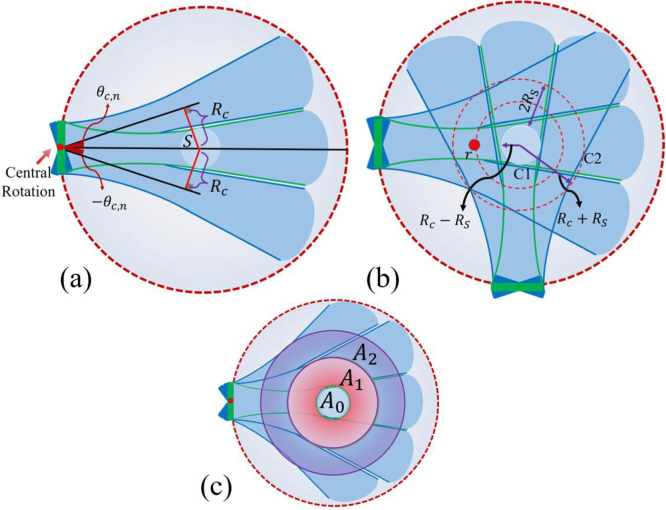
(a) A representation of the pressure field of a single element transducer with a central rotation 0° (green) and central rotation (blue). (b) The area between C1 and C2 stays in the FOV of all the tilted transducers, and the thickness of this area is . (c) Each area () stays in the FOV of the tilted transducers with a central rotation of .
2. Materials and methods
2.1. Effects of finite-size transducer on radial/tangential resolution in PAT
In a circular scanning geometry, typically a single-element transducer is rotated around the scanning center. ROI must be located in the far-field of the ultrasound transducer (Fraunhofer zone), where the pressure field changes are predictable and is convenient for imaging. The exact image reconstruction algorithm for this detection geometry is reported in [38]. Based on the finite-size transducer effect, in a circular arrangement, the PSF of a random point-absorber positioned at radial location of , extends along the tangential direction (see the arc around the point absorber in Fig. 1(a)) with the following amount (see supplement 1 for detail):
| (1) |
where, is the radius of the detection system, and is diameter of the transducer. Eq. (1) indicates that the PSF extension in the tangential direction is directly proportional to the distance from the center and transducer diameter, and inversely proportional to the scanning radius. Therefore, (1) the PSF extends along the tangential direction (degrading the tangential resolution) as the off-center distance, , increases, furthermore (2) the tangential resolution degrades faster with a larger transducer diameter. In general, for a limited size transducer, not all angular views of each arbitrary absorber in the ROI would be captured which results in tangential resolution degradation. This results in the appearance of blind angles (discussed in Section 2.2.) for some absorbing points in the ROI. To extract the range of these blind angles the concept of spatial frequency for each absorbing point and its relation to the transducers’ directivity pattern and beam-width should be first defined. These definitions are given in Section 2.
2.2. Blind angles and reconstruction range calculation in PAT
2.2.1. Directivity pattern
2D schematic of the directivity pattern of a flat disc transducer with a diameter (, where is the radius) is shown in Fig. 1(b). where is the radial distance of each point relative to the center of the transducer, and is the divergence angle. The pressure field of a disc transducer in is given by [39]:
| (2) |
where is the wave-number, is the angular-frequency, is a constant which defines the reference amplitude at the reference distance (i.e., the surface of the transducer). The Bessel function () in (2) describes the directivity of the transducer. The edge of the mainlobe can be calculated as follows:
| (3) |
Where, is a constant and is the wavelength. based on −6 dB, −10 dB and the extreme edge of the beam criteria, is 0.56, 0.9 and 1.22, respectively. Therefore, the smaller the transducer diameter, the larger the transducer FOV () would become; assuming the same wavelength in (3).
2.2.2. Spatial frequency components
Each point-absorber in the 2D ROI generates a circular wave once excited with the laser beam. This circular wave can be considered as a superposition of plane waves propagating in different directions (the range of is 0 to ) each with a specific spatial frequency component along tangential direction where is measured with respect to the radius that passes through this point. is received if all of these spatial frequency components, or in other words, all the generated rays, are captured by the detectors arranged around the ROI. The lower the range of the spatial frequency vectors of each point-absorber captured by the detectors, the lower the tangential spatial frequency range () becomes which results in the reduction of angular/tangential resolution () [40].
The blue circle in Fig. 1(c) stays in the FOV of all the transducers. As a result, the photoacoustic radiated k-vectors (spatial frequency components) of an absorber inside region S are fully captured by the detectors. The radius of region S is calculated as:
| (4) |
In Fig. 1(c), if we move from a specific transducer in the clockwise direction, the transducers between position T1 and T2 do not see the point absorber (the red circle in Fig. 1(c)) due to their limited mainlobe.
By assuming that the edges of the directivity pattern of transducer T1 are parallel with T1 bisector (see dashed-line in Fig. 1(b)), due to the small value of in large aperture transducer, and considering the angles specified in Fig. 1(c) (where and are the angles of the line connecting the absorber and T1 and T2, respectively with respect to the horizon line passing through the point absorber), we will find that the angles between and in the upper and lower sides of the source are blind angles for the photoacoustic source, which is shown in Fig. 1(d) (see regions). The other angles along which the k-vectors are received are called acceptance angles for that source. The total acceptance angle for each pixel based on its distance from the scanning center () is given as:
| (5) |
Dividing by (5) gives the ratio of the range of frequency components captured by transducers to the range of frequency components produced by a photoacoustic source as:
| (6) |
Eq. (6) indicates that as the off-center distance increases, the captured spatial frequency range by the finite-size transducers decreases.
2.3. Proposed method: Multi-angle detection geometry
A schematic of the proposed method is given in Fig. 2(a). The single transducer is initially centrally-rotated before circular scanning around the ROI by a step-motor. The FOV of the transducer at each central angle () captures specific spatial frequency components that were not captured by the non-centrally-rotated () case where is the number of required central rotations which will be calculated later. For a scanning radius of , consider the transducer is centrally rotated with degrees. The perpendicular line from the central point of the ROI to the tilted transducer beam bisector is (see Fig. 2(a)):
| (7) |
The overlap of the mainlobe of all the centrally-rotated transducers act like an area with an inner and outer radius of and , respectively (see Fig. 2(b)):
| (8) |
If a source is located in this area, all its spatial frequencies are fully captured by either transducer’s positions or its central rotations.
The radial range of the areas produced by each pair of symmetrical () central rotations is . Eq. (9) represents the number of required areas () with radius to cover a ROI of radius . An example with two areas is shown in Fig. 2(c).
| (9) |
If ROI radius () is different from chamber radius (), is equal to .
In order to find the values of , rings with a thickness of should be considered for each pair of symmetric central rotations. Ideally, the total number of required rings (i.e., the number of required ), is . Therefore, based on (7) the variable is ideally given by (10):
| (10) |
where, the value of , which is considered for central rotation, is from 0 to . Based on this, the maximum value of () which can be calculated by substituting the maximum value of in (10) is .
2.3.1. Tangential resolution analysis of the proposed approach
The combination of all transducer with different central rotations and non-centrally rotated mimic a new virtual detector with a wide main-lobe and a maximum angular width of :
| (11) |
For , (3) could be rewritten as follows:
| (12) |
By substituting (3), (11) in (12), the active diameter of the new virtual detector () can be extracted:
| (13) |
By substituting the value of with from (13), in (1), the PSF extension achieved by the proposed approach, , will be obtained as follows:
| (14) |
which is apparently smaller than the PSF width of the conventional structure given in (7). This reduction in PSF width and thus tangential resolution improvement will be validated via experimental measurements in Section 3.
2.3.2. Angular weighing in back-projection
In this work, a modified version of the Universal back-projection (UBP) algorithm is used for reconstruction [18] where the RF data is back-projected with a weighting factor. This weighting factor consists of two factors; (1) a binary directivity factor which refers to the transducer directivity pattern. (2) a solid-angle weighting factor that is considered in the back-projection formula (see Figs. 1 and 2 in [18]). In the solid-angle weighting, the value of the weighting factor in each region is inversely proportional to the distance from the transducer. To minimize the number of required central rotations for covering the entire ROI, the width of the mainlobe of the transducer at −10 dB is considered as the edge of the binary weighting factor.
2.3.3. Minimum number of spatial sampling for the proposed approach
In conventional PAT systems, the minimum number of spatial samples (assuming point-like transducers) [41]; where is the wavelength corresponding to the high cut-off frequency of the transducer bandwidth, and is the radius at which the photoacoustic absorber is placed.
In MA-PAT, for each central rotation, the RF data is back-projected considering the transducer directivity pattern to reduce the number of spatial samples, clutter artifacts and aliasing [42]. Therefore, the virtual detector (resembling the combination of all central rotations around the axis of the transducer at a spatial sample) is called a directional virtual detector in our study. Given that in the proposed approach, at each spatial sample, the total number of required central rotation angles and non-central rotation angle () is . Therefore, the number of spatial samples for our detection approach () would be as follows:
| (15) |
which is lower than the required number of spatial samples in the conventional structure by a factor of . Therefore, the total number of central rotation and non-central rotation angles would be same in the conventional and proposed structure. The numerical and experimental results of the effect of different numbers of spatial samples on the image quality of the proposed approach are given in Section 3.3.
2.4. Numerical and experimental study
2.4.1. Numerical study
The k-Wave toolbox [43] was used to synthesize the numerical data in 2D. Two synthetic phantoms were used: one with point absorbers to evaluate point spread function (see Fig. 4) and one to mimic vasculature (Fig. 5(a, b)). A flat transducer with a diameter, central frequency and bandwidth of 13 mm, of 2.25 MHz and 67% was used, respectively; properties of Olympus NDT, V306-SU transducer. The medium and grid size were 25 cm and 0.1 mm at both directions (2500 × 2500 grids), respectively. The speed of sound and sampling frequency were 1500 m/s and 25 MHz, respectively. The scanning radius (the yellow circle in Fig. 5(a)) was 12 cm. The imaging ROI (the dashed circle in Fig. 5(a)) was within a radius of 5.5 cm. The size of the point absorbers was equal to the grid size. Point detectors in our study are modeled as a one-grid detector. The PA signals recorded by many point detectors at the surface of a transducer are averaged to model a PA signal recorded by a finite-size transducer. In the conventional method, a finite-size transducer rotates around the imaging region and captures PA waves (see Fig. 1(c)).
Fig. 4.
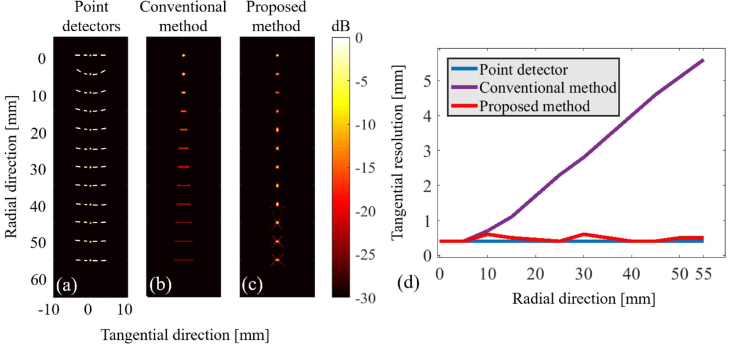
The numerical results using point absorbers. (a) The reconstructed image with point-like detectors. The reconstructed images with (b) the conventional and (c) proposed methods, respectively. (d) The tangential resolution. The image intensities on dashed-arc passing through the reconstructed absorber are used for calculating the tangential resolution.
Fig. 5.
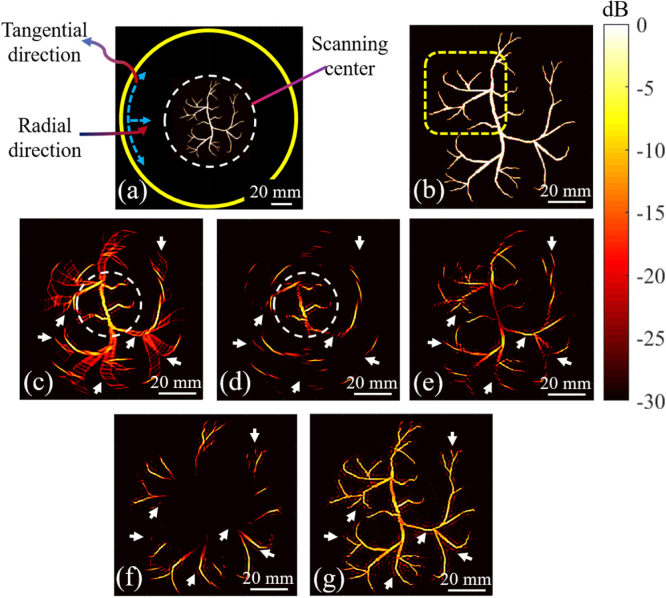
The numerical results using the vasculature phantom. In (a), the vasculature phantom, the ROI (dashed white circle) and the scanning trajectory (yellow circle) are shown. (b) The zoomed version of the ROI. (c) and (d) show the reconstructed images with the conventional method where 750 and 150 spatial samples are used, respectively. (e) and (f) show reconstructed images with 150 spatial samples and a central rotation of and , respectively. (g) shows the reconstructed image with the proposed detection approach after coherent summation of the images generated with all the angles (shown by d–f). The white arrows show the structure that are not detectable with the conventional detection geometry.
By substituting the transducer properties and ROI in (7, 8), we calculated and . By substituting , , and transducer properties in (3, 9–12), respectively, and , other variables for the proposed detection approach were calculated and reported in Table 1.
Table 1.
The properties of the MA-PAT system.
| 750 | 150 | 2.6 |
2.4.2. Experimental study
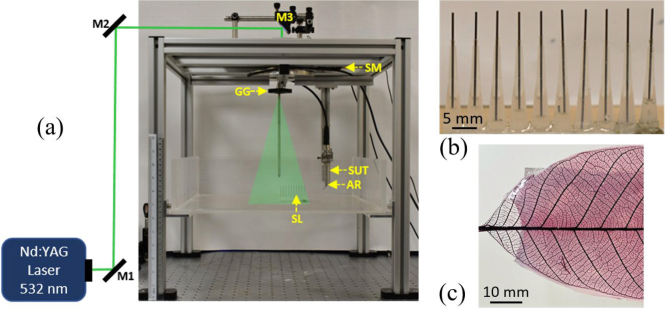
Two experimental studies were conducted to evaluate the performance of the proposed method. (1) pencil leads with 0.5 mm diameter to mimic point absorbers (see Fig. 3(b)) and (2) complex leaf skeleton phantom (see Fig. 3(c)). The photograph of the experimental set-up is shown in Fig. 3(a). A Q-switched Nd: YAG laser delivering 532 nm at 5 ns pulse width at 10 Hz was used as the excitation source. An unfocused single ultrasound transducer (SUT) of 2.25 MHz (Olympus NDT, V306-SU) fitted with an acoustic reflector (F102, Olympus NDT) was rotated around the region of interest to acquire the PA waves. The transducer is used in the vertical mode and the acoustic reflector is used to deflect the photoacoustic waves from the sample towards the ultrasound detector. The phantom is oriented perpendicular to the laser illumination and is placed at the scanning center for imaging (see Fig. 3). The PA signals were amplified by a low signal noise amplifier (Olympus-NDT, 5072PR) and stored in a desktop computer (IntelXeon, 3.7 GHz 64-bit processor, 16 GB RAM) equipped with a data acquisition (DAQ) card (GaGe, compuscope 4227).
Fig. 3.
(a) Photograph of the Nd:YAG laser photoacoustic tomography system; SM, stepper motor; GG, ground glass diffuser; SUT, single-element ultrasound transducer; AR, Acoustic reflector; SL, sample; M1, M2, M3, mirror. (b) Ten pencil leads are used to mimic point absorbers. (c) Complex leaf skeleton phantom.
2.4.3. Comparison with previous studies
The existing techniques to tackle the finite size transducer issue are categorized into developing advanced image reconstruction algorithms and new data acquisition set-ups. For comparison, we selected works representing each category. For data acquisition set-ups category, a comparison was conducted with Pramanik, et al. [20] which improved the tangential resolution using a negative acoustic lens, and Nie, et al. [37] which improved the tangential resolution by a convex/concave transducer. For the reconstruction category, three methods were selected: Wang, et al. [26] which compensated the time-delay and directivity pattern, Kalva and Pramanik [23] which proposed the modified delay-and-sum (MDAS) algorithm and Chowdhury, et al. [32] which combined a MB method with TIR. Two metrics were used for quantification: (1) region-of-interest (ROI) radius to difference between the tangential resolution of the outmost to the central absorber in the ROI (): The metric indicates the slope of tangential resolution increment to the off-center distance increment. The smaller the , the lower the dependence of the tangential resolution on the location. (2) Resolution improvement of the outmost absorber obtained by the proposed method compared to that obtained by the conventional detection (IPC; this metric is reported in percent ()).
3. Results
3.1. Numerical results
Fig. 4(a) indicates that a location-independent tangential resolution (limited to the half of the wavelength at the central frequency) is indeed achievable with a point-like transducer. The full width at half maximum (FWHM) of the image intensities on an arc passing through the maximum of each reconstructed absorber (see dashed lines in Fig. 4(a)) are used for calculating the tangential resolution. In the conventional detection geometry, as the radial distance increases, the PSF extends (Fig. 4(b)), and the resolution degrades (Fig. 4(d)) along the tangential direction. At a distance of 55 mm from the scanning center, the tangential resolution reaches 5.6 mm, which is about 10-times the tangential resolution of the scanning center. This is due to the limited FOV of the transducer and causes image blurring (see arrows in Fig. 5(c)). The proposed detection geometry addresses this issue (see Fig. 4(c) and Fig. 5(g)), and the resolution obtained in different radial distances follows that obtained with the point-like detector (see Fig. 4(c, d)). In the proposed detection geometry, the tangential resolution reaches 0.65 mm at a distance of 55 mm from the scanning center which, compared to the conventional structure, is improved by 88%.
The quality of the reconstructed images by the conventional (Fig. 5(c)) and the proposed approach with (Fig. 5(d)) is close in the center of the ROI (see the white dashed circle in Fig. 5(c, d)) while only 150 spatial samples were used in Fig. 5(d). This is due to having a large enough spatial samples (150) to capture all the information needed to do reconstruction within a limited central region (the region inside the white dashed circle in Fig. 5(c, d) is covered by the in Fig. 2(c)). To compare the reconstructed regions corresponding to each central rotation, same colormap is applied to all reconstructed image (see Fig. 5(c–f)). At each central rotation, the transducers capture more solid angles of PA waves generating from specific regions in the ROI than others. Therefore, the reconstructed image corresponding to each central rotation, provides visualization of different regions and certain regions are better reconstructed (compare areas shown by white arrows in Fig. 5(d–f)). Coherent summation of the reconstructed images at each rotation angle results in a final high-quality image which is our main goal (see Fig. 5(g)). Furthermore, the sensitivity of our approach in the off-center regions is higher than the conventional method (see Fig. 5(c, g)). The peak-signal-to-noise ratio (PSNR) and structural similarity index metric (SSIM) were measured in yellow dashed area (indicated in Fig. 5(b)). A PSNR and SSIM of 12.5/19.2 dB and 0.57/0.85 were obtained for the conventional/proposed method, respectively. Therefore, our approach increases the similarity to the phantom (SSIM) by 28% and PSNR by 6.7 dB.
3.2. Experimental results
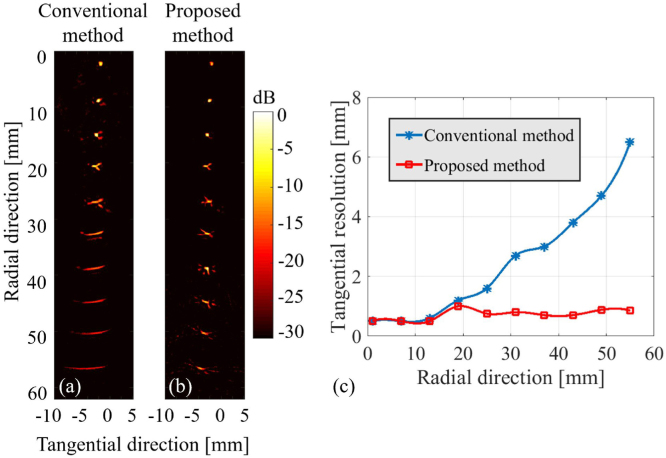
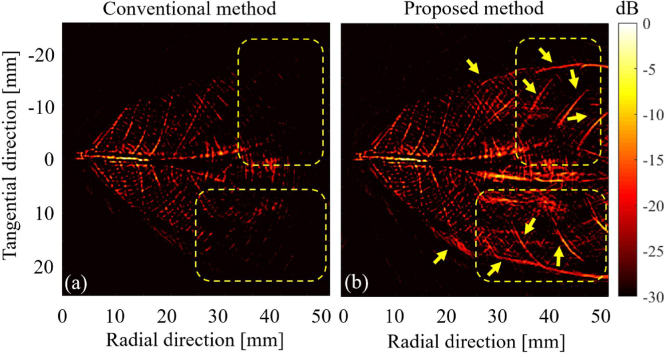
The results of pencil lead targets (Fig. 6(a)) show that the conventional method extends the PSF when the radial distance increases and the resolution rapidly degrades after a radial distance of 20 mm (Fig. 6(b)). The tangential resolution of 0.5 mm pencil lead absorber reaches 3/6.4 mm in the radial distance of 37 mm and 55 mm, respectively (see Fig. 6(c)). However, the proposed approach prevents the PSF extension (Fig. 6(b)) and maintains the tangential resolution as the radial distance increases Fig. 6(c). The tangential resolution in the proposed method in radial distances of 37- and 55 mm reaches 0.6 and 0.8 mm, respectively, which is of about 86% improvement compared to the conventional method (Fig. 6(c)). For the leaf skeleton phantom experiment, the edges of the phantom are reconstructed well in the proposed method. But due to the limited FOV of the conventional method, edges of the leaf phantom are blurred in the conventional method (see yellow arrows in Fig. 7(a, b)). The significant parts of the leaf phantom are reconstructed well in the results from the proposed method and are blurred in the conventional method images (see yellow arrows in Fig. 7(a, b)). Comparing the yellow dashed rectangle in Fig. 7(a, b) shows that the proposed method provides more structural information than the conventional method. Moreover, based on the directional back-projection of the proposed method (considering the transducer field of view in the back-projection of the RF data), artifacts and blurred areas are suppressed in the reconstructed image.
Fig. 6.
Experimental evaluation of the point spread function (PSF). (a, b) show the reconstructed images with the conventional method (750 spatial samples) and the proposed method (150 spatial samples), respectively. The tangential resolution obtained by the conventional and proposed methods are shown in (c).
Fig. 7.
The experimental results using the complex leaf skeleton phantom. The reconstructed images with (a) the conventional method and (b) the proposed method, respectively. The yellow arrows and dashed-rectangles show the structure that are not detectable with the conventional detection geometry.
3.3. Effects of number of spatial samples
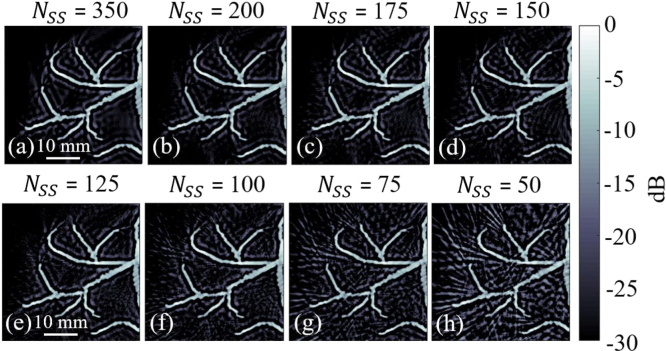
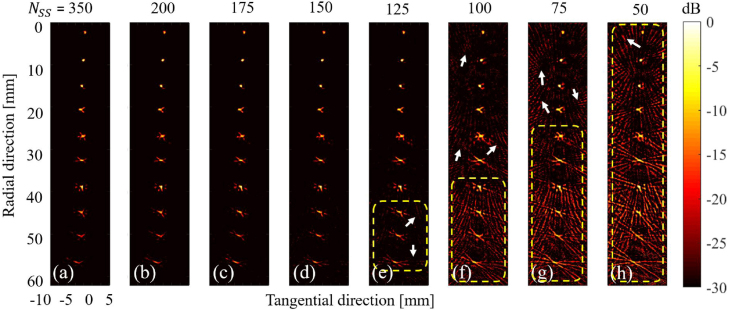
Fig. 8 indicates that with a number of spatial sampling () less than 150, the streak artifacts increase while there is no change in the image quality with a higher than 150. This agrees with the experimental results (see Fig. 9 with severe artifacts in (h) while degraded from (e) to (h)) and (15) where is calculated. As can be seen from Fig. 9, by decreasing the number of spatial samples from 150 to 50 with step size of 25 in the proposed approach, streak artifacts increase (see white arrows and yellow dashed-rectangle in Fig. 9(e–h)).
Fig. 8.
The numerical results of evaluation of the effects of the number of spatial samples () used in the proposed approach. These images are corresponding to the region inside the yellow dashed rectangle in Fig. 5(b).
Fig. 9.
The experimental results of evaluation of the effects of the number of spatial samples () used in the proposed approach.
3.4. Comparison with previous works
The comparison of our method (MA-PAT) with five existing is given in Table 2.
Table 2.
Comparison to existing works.
indicates that our method has the lowest dependence of the tangential resolution on the location. Based on the IPC metric, our method improves the tangential resolution of the outmost absorber in the ROI by 88%, which is more than other techniques presented in Table 2.
4. Discussion
4.1. Overview
In circular geometry PAT, usually, a large aperture single element transducer is rotated around a region of interest (ROI) of scanning radius . As the off-center distance increases, the captured spatial frequency range by the finite-size transducer decreases due to the limited main lobe of the transducer, and the point spread function (PSF) width extends along the tangential direction. Consequently, the tangential resolution degrades in off-center regions as given by (1). In case of using an ideal point-like detector (with a wide main lobe), the whole range of generated spatial frequency vectors are captured given that the entire ROI fall in the field-of-view (FOV) of detector. This leads to a location-independent tangential resolution. Yet, point-like transducers are hard/expensive to manufacture and suffer from a low sensitivity, which makes them impractical for photoacoustic tomography systems. In this work, we introduced a multi-angle photoacoustic tomography system in which a directional virtual detector with a wide detection angle (coming from combining the transducer directivity pattern at each central rotation with an angle of () is developed. With our detection approach, the entire spatial frequencies of each pixel are captured independent from its radial location and a location-independent tangential resolution is achieved. The proposed approach could be useful for human brain/breast imaging [6], [16] and whole-body small animal imaging [44] where a large ROI (10 cm diameter) should be covered.
It should be noted that a new detection strategy (which allows capturing high spatial frequency components missed by the conventional data acquisition) was proposed in this work, but not a reconstruction technique. While we used the back-projection, other reconstruction techniques (e.g., model-based techniques) could also be used.
4.2. Limitations of the proposed data acquisition approach
Sources with the same size and absorption coefficient might appear with different values after reconstructing with our approach. The difference is expected to be minor though. This is because the captured waves are back-projected to the regions inside the −10 dB of the directivity pattern of the transducer (either tilted or non-tilted)
Placing the transducer exactly at the central rotation angle may be problematic in practice. Yet, since these angles are approximately calculated, a small amount of alignment error ( degree) slightly induces artifacts to the reconstructed images. This could explain the artifacts seen in Fig. 9(d) after a depth of 25 mm.
Applying the central rotation is time consuming and the main drawback of our method. Currently, it is not possible to use this method for imaging live animals. There are studies that used lab-made ring array transducers with small-size elements [13], [14]. Video-rate imaging can be achieved using ring arrays, but spatial aliasing and arc artifacts may occur due to the pitch size (the spacing between the array elements); the pitch must be lower than half of the wavelength at the central frequency of the array [45]. This necessitates a very large number of elements, read-out circuits and cables, which impose manufacturing difficulties and setup complexities [42], [46], [47], [48]. Further development of our data acquisition strategy in combination with ring arrays could remove the rotation step in our approach and possibly mitigate the effects of aliasing and arc artifacts caused by the large pitch size of the current ring arrays [13], [14]. GPU parallel programming can also be used to reconstruct images of each angle simultaneously, allowing real-time imaging [49].
5. Conclusion
In this work, we proposed a multi-angle detection approach for circular photoacoustic tomography systems to compensate the effects of finite transducer size. The novelty of our approach lies in the fact that the transducer rotates around its center (for limited number of angles) as well as rotating around the region of interest with a stepper motor to record the photoacoustic waves. The numerical and experimental results showed that the proposed approach allowing capturing the entire spatial frequencies of the photoacoustic waves mimics a directional point-like transducer with a large angular view and provides a location-independent tangential resolution. The proposed approach could replace the conventional detection geometry due to structural simplicity and low processing cost.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgment
MP would like to acknowledge the support by the Tier 1 Grant funded by the Ministry of Education in Singapore (RG30/21, RT16/19).
Biographies

Soheil HakakZadeh was born in 1997. He received B.Sc. degree from Faculty of Electrical Engineering, Khaje Nasir Toosi University of Technology, Tehran, Iran, and M.Sc. degree from Faculty of Electrical Engineering, Sharif University of Technology, Tehran, Iran, in 2019 and 2021, respectively. Currently, he is a Ph.D. student in Electrical Engineering at the Sharif University of Technology. His research interests include Photoacoustic/ultrasound imaging, Deep learning, image reconstruction.

Moein Mozaffarzadeh received his B.Sc. degree in electrical engineering from Babol Noshirvani University of Technology, Mazandaran, Iran, in 2015, and his M.Sc. degree in biomedical–bioelectric engineering from Tarbiat Modares University, Tehran, Iran, in 2017. He is currently a Ph.D. student in the Laboratory of Medical Imaging, Department of Imaging Physics, Delft University of Technology. His research interests include photoacoustic/ultrasound imaging, acoustic beamforming and medical ultrasound transducer design.

Seyed Masood Mostafavi received his B.Sc. degree from Isfahan University of Technology, Isfahan, Iran and M.Sc. degree from Sharif University of Technology. He is now studying a Ph.D. degree in Sharif University of Technology. His Ph.D. thesis is in the field of Photoacoustic imaging.

Zahra Kavehvash received her B.Sc., M.Sc. and Ph.D. degrees all from Sharif University of Technology, Tehran, Iran. In September 2014 she joined sharif University of Technology as a faculty member. She is now an Associate professor at EE department working in the field of optical and ultrasonic imaging systems, optical holography, millimeter-wave holography and optical signal processing.

Praveenbalaji Rajendran is currently a Ph.D. student in the School of Chemical and Biomedical Engineering, Nanyang Technological University (NTU), Singapore. He received his M.Tech in biomedical engineering from the Indian Institute of Technology, Hyderabad. His research interests include Photoacoustic imaging; Deep learning; image reconstruction, image processing, Machine vision, and molecular imaging.

Martin D. Verweij (M’10) received the M.Sc. (cum laude) and Ph.D. degrees in electrical engineering from Delft University of Technology, Delft, The Netherlands, in 1988 and 1992, respectively. From 1993 to 1997, he was a Research Fellow with the Prestigious Royal Netherlands Academy of Arts and Sciences, Amsterdam, The Netherlands. In 1995 and 1997, he was a Visiting Scientist at Schlumberger Cambridge Research, Cambridge, U.K. In 1998, he became an Assistant Professor, and later an Associate Professor, with the Laboratory of Electromagnetic Research, Delft University of Technology, where he switched to the Laboratory of Acoustical Wavefield Imaging in 2011. Since 2015, he also has a part-time position at the Biomedical Engineering Group, Erasmus Medical Centre, Rotterdam, The Netherlands. His research interests include dedicated transducer design, beamforming algorithms, and the theoretical modeling and numerical simulation of medical ultrasound. He is the originator of the iterative nonlinear contrast source method for the computation of nonlinear ultrasound fields.
Dr. Verweij is a Research Leader of the Dutch Technology Foundation (STW) on projects involving transducer design, beamforming, and imaging. He was elected as the Best Teacher of the Electrical Engineering Curriculum in the academic year from 2001 to 2002. He is an Associate Editor of the Journal of the Acoustical Society of America, and a Treasurer of the Dutch Society for Medical Ultrasound.

Nico de Jong, (A’97–M’09) graduated from the Delft University of Technology, Delft, The Netherlands, in 1978. He received the M.Sc. degree in physics (specialized in the field of pattern recognition) from the Delft University of Technology, and the Ph.D. degree from the Erasmus Medical Center, Rotterdam, The Netherlands, in 1993. His Ph.D. dissertation was on acoustic properties of ultrasound contrast agents. Since 1980, he has been a Staff Member at the Thorax enter, Erasmus Medical Center. In 2003, he was a part-time Professor at the Physics of Fluids Group, University of Twente, Enschede, The Netherlands. He teaches on technical universities and the Erasmus Medical Center. He has been a Promotor of 35 Ph.D. students and is currently supervising 11 Ph.D. students. Since 2011, he has been a Professor in Molecular Ultrasonic Imaging and Therapy at the Erasmus Medical Center and Delft University of Technology.
Dr. de Jong is the Organizer of the Annual European Symposium on Ultrasound Contrast Imaging, held in Rotterdam and attended by approximately 175 scientists from universities and industries all over the world. He is on the safety committee of the World Federation of Ultrasound in Medicine and Biology. Over the last five years, he has given more than 30 invited lectures and has given numerous scientific presentations for international industries. He has been a guest editor for special issues of different journals. He is an Associate Editor of Ultrasound in Medicine and Biology.

Manojit Pramanik is currently an Associate Professor in the School of Chemical and Biomedical Engineering, Nanyang Technological University (NTU), Singapore. He received his Ph.D. in biomedical engineering from Washington University in St. Louis, Missouri. His research interests include the development of photoacoustic/thermoacoustic imaging systems; image reconstruction, machine learning, medical image processing, contrast agents and molecular imaging, and Monte Carlo simulation of light–tissue interaction.
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.pacs.2022.100373.
Contributor Information
Zahra Kavehvash, Email: kavehvash@sharif.edu, http://ee.sharif.edu/~kavehvash.
Manojit Pramanik, Email: manojit@ntu.edu.sg, http://www.bilab2012.com.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
.
References
- 1.Das D., Sharma A., Rajendran P., Pramanik M. Another decade of photoacoustic imaging. Phys. Med. Biol. 2021;66(5):05TR01. doi: 10.1088/1361-6560/abd669. [DOI] [PubMed] [Google Scholar]
- 2.Rao A.P., Bokde N., Sinha S. Photoacoustic imaging for management of breast cancer: A literature review and future perspectives. Appl. Sci. 2020;10(3):767. [Google Scholar]
- 3.Wray P., Lin L., Hu P., Wang L.V. Photoacoustic computed tomography of human extremities. J. Biomed. Opt. 2019;24(2) doi: 10.1117/1.JBO.24.2.026003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhang Y., Wang L. Video-rate ring-array ultrasound and photoacoustic tomography. IEEE Trans. Med. Imaging. 2020;39(12):4369–4375. doi: 10.1109/TMI.2020.3017815. [DOI] [PubMed] [Google Scholar]
- 5.Cai C., Wang X., Si K., Qian J., Luo J., Ma C. Feature coupling photoacoustic computed tomography for joint reconstruction of initial pressure and sound speed in vivo. Biomed. Opt. Express. 2019;10(7):3447–3462. doi: 10.1364/BOE.10.003447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Na S., Russin J.J., Lin L., Yuan X., Hu P., Jann K.B., Yan L., Maslov K., Shi J., Wang D.J., et al. Massively parallel functional photoacoustic computed tomography of the human brain. Nat. Biomed. Eng. 2021:1–9. doi: 10.1038/s41551-021-00735-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Rajendran P., Sahu S., Dienzo R.A., Pramanik M. In vivo detection of venous sinus distension due to intracranial hypotension in small animal using pulsed-laser-diode photoacoustic tomography. J. Biophotonics. 2020;13(6) doi: 10.1002/jbio.201960162. [DOI] [PubMed] [Google Scholar]
- 8.Nishiyama M., Namita T., Kondo K., Yamakawa M., Shiina T. Ring-array photoacoustic tomography for imaging human finger vasculature. J. Biomed. Opt. 2019;24(9) doi: 10.1117/1.JBO.24.9.096005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ermilov S., Su R., Zamora M., Hernandez T., Nadvoretsky V., Oraevsky A. Photons Plus Ultrasound: Imaging and Sensing 2012, vol. 8223. International Society for Optics and Photonics; 2012. Optoacoustic angiography of peripheral vasculature; p. 82230D. [Google Scholar]
- 10.Zackrisson S., Van De Ven S.M.W.Y., Gambhir S.S. Light in and sound out: Emerging translational strategies for photoacoustic imaging. Cancer Res. 2014;74(4):979–1004. doi: 10.1158/0008-5472.CAN-13-2387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Toi M., Asao Y., Matsumoto Y., Sekiguchi H., Yoshikawa A., Takada M., Kataoka M., Endo T., Kawaguchi-Sakita N., Kawashima M., et al. Visualization of tumor-related blood vessels in human breast by photoacoustic imaging system with a hemispherical detector array. Sci. Rep. 2017;7(1):1–11. doi: 10.1038/srep41970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Xu M., Wang L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006;77(4) [Google Scholar]
- 13.Lin L., Hu P., Shi J., Appleton C.M., Maslov K., Li L., Zhang R., Wang L.V. Single-breath-hold photoacoustic computed tomography of the breast. Nature Commun. 2018;9(1):1–9. doi: 10.1038/s41467-018-04576-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Li L., Zhu L., Ma C., Lin L., Yao J., Wang L., Maslov K., Zhang R., Chen W., Shi J., et al. Single-impulse panoramic photoacoustic computed tomography of small-animal whole-body dynamics at high spatiotemporal resolution. Nat. Biomed. Eng. 2017;1(5):1–11. doi: 10.1038/s41551-017-0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brecht H.-P.F., Su R., Fronheiser M.P., Ermilov S.A., Conjusteau A., Oraevsky A.A. Whole-body three-dimensional optoacoustic tomography system for small animals. J. Biomed. Opt. 2009;14(6) doi: 10.1117/1.3259361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kruger R.A., Lam R.B., Reinecke D.R., Del Rio S.P., Doyle R.P. Photoacoustic angiography of the breast. Med. Phys. 2010;37(11):6096–6100. doi: 10.1118/1.3497677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang Y., Guo Z., Wang L.V., Erpelding T.N., Jankovic L., Robert J.-L., David G. In vivo three-dimensional photoacoustic imaging based on a clinical matrix array ultrasound probe. J. Biomed. Opt. 2012;17(6) doi: 10.1117/1.JBO.17.6.061208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Xu M., Wang L.V. Universal back-projection algorithm for photoacoustic computed tomography. Phys. Rev. E. 2005;71(1) doi: 10.1103/PhysRevE.71.016706. [DOI] [PubMed] [Google Scholar]
- 19.Xu M., Wang L.V. Analytic explanation of spatial resolution related to bandwidth and detector aperture size in thermoacoustic or photoacoustic reconstruction. Phys. Rev. E. 2003;67(5) doi: 10.1103/PhysRevE.67.056605. [DOI] [PubMed] [Google Scholar]
- 20.Pramanik M., Ku G., Wang L.V. Tangential resolution improvement in thermoacoustic and photoacoustic tomography using a negative acoustic lens. J. Biomed. Opt. 2009;14(2) doi: 10.1117/1.3103778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Xu M., Wang L.V. Pulsed-microwave-induced thermoacoustic tomography: Filtered backprojection in a circular measurement configuration. Med. Phys. 2002;29(8):1661–1669. doi: 10.1118/1.1493778. [DOI] [PubMed] [Google Scholar]
- 22.Xu Y., Feng D., Wang L.V. Exact frequency-domain reconstruction for thermoacoustic tomography. I. Planar geometry. IEEE Trans. Med. Imaging. 2002;21(7):823–828. doi: 10.1109/tmi.2002.801172. [DOI] [PubMed] [Google Scholar]
- 23.Kalva S.K., Pramanik M. Experimental validation of tangential resolution improvement in photoacoustic tomography using modified delay-and-sum reconstruction algorithm. J. Biomed. Opt. 2016;21(8) doi: 10.1117/1.JBO.21.8.086011. [DOI] [PubMed] [Google Scholar]
- 24.Pramanik M. Improving tangential resolution with a modified delay-and-sum reconstruction algorithm in photoacoustic and thermoacoustic tomography. J. Opt. Soc. Amer. A. 2014;31(3):621–627. doi: 10.1364/JOSAA.31.000621. [DOI] [PubMed] [Google Scholar]
- 25.Xiao J., Luo X., Peng K., Wang B. Improved back-projection method for circular-scanning-based photoacoustic tomography with improved tangential resolution. Appl. Opt. 2017;56(32):8983–8990. doi: 10.1364/AO.56.008983. [DOI] [PubMed] [Google Scholar]
- 26.Wang B., Ye T., Wang G., Guo L., Xiao J. Approximate back-projection method for improving lateral resolution in circular-scanning-based photoacoustic tomography. Med. Phys. 2021;48(6):3011–3021. doi: 10.1002/mp.14880. [DOI] [PubMed] [Google Scholar]
- 27.Ding L., Deán-Ben X.L., Razansky D. Real-time model-based inversion in cross-sectional optoacoustic tomography. IEEE Trans. Med. Imaging. 2016;35(8):1883–1891. doi: 10.1109/TMI.2016.2536779. [DOI] [PubMed] [Google Scholar]
- 28.Caballero M.A.A., Gateau J., Déan-Ben X.-L., Ntziachristos V. Model-based optoacoustic image reconstruction of large three-dimensional tomographic datasets acquired with an array of directional detectors. IEEE Trans. Med. Imaging. 2013;33(2):433–443. doi: 10.1109/TMI.2013.2286546. [DOI] [PubMed] [Google Scholar]
- 29.Ding L., Razansky D., Deán-Ben X.L. Model-based reconstruction of large three-dimensional optoacoustic datasets. IEEE Trans. Med. Imaging. 2020;39(9):2931–2940. doi: 10.1109/TMI.2020.2981835. [DOI] [PubMed] [Google Scholar]
- 30.Ding L., Deán-Ben X.L., Razansky D. Efficient 3-D model-based reconstruction scheme for arbitrary optoacoustic acquisition geometries. IEEE Trans. Med. Imaging. 2017;36(9):1858–1867. doi: 10.1109/TMI.2017.2704019. [DOI] [PubMed] [Google Scholar]
- 31.Prakash J., Kalva S.K., Pramanik M., Yalavarthy P.K. Binary photoacoustic tomography for improved vasculature imaging. J. Biomed. Opt. 2021;26(8) doi: 10.1117/1.JBO.26.8.086004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chowdhury K.B., Prakash J., Karlas A., Jüstel D., Ntziachristos V. A synthetic total impulse response characterization method for correction of hand-held optoacoustic images. IEEE Trans. Med. Imaging. 2020;39(10):3218–3230. doi: 10.1109/TMI.2020.2989236. [DOI] [PubMed] [Google Scholar]
- 33.Queirós D., Déan-Ben X.L., Buehler A., Razansky D., Rosenthal A., Ntziachristos V. Modeling the shape of cylindrically focused transducers in three-dimensional optoacoustic tomography. J. Biomed. Opt. 2013;18(7) doi: 10.1117/1.JBO.18.7.076014. [DOI] [PubMed] [Google Scholar]
- 34.Schwarz M., Buehler A., Ntziachristos V. Isotropic high resolution optoacoustic imaging with linear detector arrays in bi-directional scanning. J. Biophotonics. 2015;8(1–2):60–70. doi: 10.1002/jbio.201400021. [DOI] [PubMed] [Google Scholar]
- 35.Hakakzadeh S., Kavehvash Z. Blind angle and angular range detection in planar and limited-view geometries for photoacoustic tomography. 2021 29th Iranian Conference on Electrical Engineering; ICEE; IEEE; 2021. pp. 922–926. [Google Scholar]
- 36.Li C., Ku G., Wang L.V. Negative lens concept for photoacoustic tomography. Phys. Rev. E. 2008;78(2) doi: 10.1103/PhysRevE.78.021901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nie L., Guo Z., Wang L.V. Photoacoustic tomography of monkey brain using virtual point ultrasonic transducers. J. Biomed. Opt. 2011;16(7) doi: 10.1117/1.3595842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Xu M., Wang L.V. Analytic explanation of spatial resolution related to bandwidth and detector aperture size in thermoacoustic or photoacoustic reconstruction. Phys. Rev. E. 2003;67(5) doi: 10.1103/PhysRevE.67.056605. [DOI] [PubMed] [Google Scholar]
- 39.Azhari H. John Wiley & Sons; 2010. Basics of Biomedical Ultrasound for Engineers. [Google Scholar]
- 40.Kazemi M., Kavehvash Z., Shabany M. K-space aware multi-static millimeter-wave imaging. IEEE Trans. Image Process. 2019;28(7):3613–3623. doi: 10.1109/TIP.2019.2900588. [DOI] [PubMed] [Google Scholar]
- 41.Xu Y., Xu M., Wang L.V. Exact frequency-domain reconstruction for thermoacoustic tomography. II. Cylindrical geometry. IEEE Trans. Med. Imaging. 2002;21(7):829–833. doi: 10.1109/TMI.2002.801171. [DOI] [PubMed] [Google Scholar]
- 42.Mozaffarzadeh M., Soozande M., Fool F., Pertijs M.A.P., Vos H.J., Verweij M.D., Bosch J.G., de Jong N. Receive/transmit aperture selection for 3D ultrasound imaging with a 2D matrix transducer. Appl. Sci. 2020;10(15):5300. [Google Scholar]
- 43.Treeby B.E., Cox B.T. K-wave: MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. J. Biomed. Opt. 2010;15(2) doi: 10.1117/1.3360308. [DOI] [PubMed] [Google Scholar]
- 44.Brecht H.-P.F., Su R., Fronheiser M.P., Ermilov S.A., Conjusteau A., Oraevsky A.A. Whole-body three-dimensional optoacoustic tomography system for small animals. J. Biomed. Opt. 2009;14(6) doi: 10.1117/1.3259361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cobbold R.S.C. Oxford University Press; 2006. Foundations of Biomedical Ultrasound. [Google Scholar]
- 46.van Willigen D.M., Kang E., Janjic J., Noothout E., Chang Z.-Y., Verweij M.D., De Jong N., Pertijs M.A.P. A transceiver ASIC for a single-cable 64-element intra-vascular ultrasound probe. IEEE J. Solid-State Circuits. 2021;56(10):3157–3166. [Google Scholar]
- 47.Van Willigen D., Mozaffarzadeh M., Noothout E., Verweij M., De Jong N., Pertijs M., Daeichin V. Fabrication and characterization of a prototype forward-looking single-cable 64-element intra-vascular ultrasound probe. 2019 IEEE International Ultrasonics Symposium; IUS; IEEE; 2019. pp. 978–980. [Google Scholar]
- 48.Chen C., Chen Z., Bera D., Noothout E., Chang Z.-Y., Tan M., Vos H.J., Bosch J.G., Verweij M.D., de Jong N., et al. A pitch-matched front-end ASIC with integrated subarray beamforming ADC for miniature 3-D ultrasound probes. IEEE J. Solid-State Circuits. 2018;53(11):3050–3064. [Google Scholar]
- 49.Miri Rostami S.R., Mozaffarzadeh M., Ghaffari-Miab M., Hariri A., Jokerst J. GPU-accelerated double-stage delay-multiply-and-sum algorithm for fast photoacoustic tomography using LED excitation and linear arrays. Ultrason. Imaging. 2019;41(5):301–316. doi: 10.1177/0161734619862488. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
.