Electromechanical characterization of biomimetic membranes using electrodeformation of vesicles

Abstract

We describe a facile method to simultaneously measure the bending rigidity and capacitance of biomimetic lipid bilayers. Our approach utilizes the ellipsoidal deformation of quasi-spherical giant unilamellar vesicles induced by a uniform AC electric field. Vesicle shape depends on the electric field frequency and amplitude. Membrane bending rigidity can be obtained from the variation of the vesicle elongation on either field amplitude at fixed frequency or frequency at fixed field amplitude. Membrane capacitance is determined from the frequency at which the vesicle shape changes from prolate to oblate ellipsoid as the frequency is increased at a given field amplitude.

1. INTRODUCTION

Cells and their internal organelles are enveloped by thin sheets made of lipid bilayers. Mechanical properties of these lipid membrane such as the bending rigidity regulate many cell biological processes, e.g., membrane fusion and fission [1], mechanosensing [2–4], and cell motility [5, 6], to name a few. An electric potential difference across the plasma membrane exists in living cells, and electrical properties such as capacitance play crucial role in the propagation of action potentials in neurons [7, 8], electromotility of outer hair cells in hearing [9], and cardiomyocyte contractions in heart beating [10].

In vitro membrane system such as the giant unilamellar vesicle (GUV), which is a cell-sized sac of closed lipid bilayer (typical radius of 10 μm), provides a well-defined model to assay membrane properties and investigate the electromechanics of membranes at a fundamental level [11–13]. Several experimental methods are widely used to measure bending rigidity and tension using GUVs [14]. Fluctuation spectroscopy analyses the thermally-driven membrane undulations with micron and sub-micron wavelength recorded with optical microscopy [15–21]. Tension and bending rigidity control the dynamics of the long and short wavelength undulations, respectively. The method works best if membrane tension is very low ~ 10⁻⁹ N/m in order to to resolve enough wavelengths for good statistics. GUVs can be analyzed by micropipette aspiration [22, 23] and electrodeformation [24–26]. These methods analyze macroscale vesicle deformation (on the scale of the vesicle radius) induced by either pressure or electric field. The latter approach is particularly appealing because of its easy implementation and versatility - in addition to membrane elastic properties, it can be utilized to obtain membrane capacitance [27] and viscosity [28, 29].

In this paper, we provide the theoretical foundations of the electrodefomation method and show how to utilize it to simultaneously measure bending rigidity, tension and capacitance of lipid bilayer membranes.

2. MATERIALS AND METHODS

2.1. The electrodeformation method

The method relies on the entropic elasticity of lipid bilayers. Lipid bilayers are very soft and thermal fluctuations cause membrane undulations that store area. Application of electric stress causes vesicle deformation and the vesicle apparent area A increases due to flattening of the thermally-driven suboptical membrane undulations, see Figure 1. Restricting the fluctuations raises the membrane tension [22, 30]

$$\sigma ={\sigma }_0\exp \left[\frac{8\pi \kappa }{k_{B}T}\alpha \right],\alpha =\frac{A-A_0}{A_0}$$ (1)

FIG. 1.

An initially spherical vesicle deforms into an ellipsoid and its apparent area increase when a uniform AC electric field is applied. The conductivity conditions inside and outside the vesicle correspond to λ_in = 25 μS/m (0.2 mM NaCl) and λ_ex = 3 μS/m (0 mM NaCl). The conductivity ratio is Λ = 8.33. The AC field frequency is 10 kHz. Images are obtained with phase contrast microscopy.

where σ₀ and A₀ = 4πR² are the membrane tension and vesicle area in absence of applied stress. Eq. 1 can be used to obtain the membrane bending rigidity κ if the area increase and tension can be measured independently. Next, we show how the tension can be calculated from the applied electric field.

2.2. Theoretical model of vesicle electrodeformation

Let us consider a vesicle made of a charge-free lipid bilayer membrane with bending rigidity κ, tension σ, capacitance C_m. The vesicle is suspended in a solution with conductivity λ_ex and permittivity ε_ex, and filled with a different solution characterized by λ_in and ε_in.

A uniform AC electric field with amplitude E₀ and frequency ω, $E=E_0\cos \left(\omega t\right)\widehat{z}$, deforms the vesicle into a spheroid with symmetry axis aligned with the field direction. The spheroid aspect ratio is ν = a/b, where a is the length of the symmetry axis and b is the length of the axis perpendicular to the symmetry axis, see sketch in Figure 1. For small deformations, $\nu \lesssim 1.3$, the shape is well approximated by

$$r_s\left(\theta \right)=R\left(1+\frac{s}{2}\left(1+3\cos 2\theta \right)\right),$$ (2)

where r_s is the position of the surface, R is the initial radius of the vesicle, s is the deformation parameter, and θ is the angle with the applied field direction; θ = 0 and π/2 correspond to the pole and the equator, respectively. The ellipsoid aspect ratio is related to the deformation parameter by $\nu =\left(1+s\right)/\left(1-2s\right)$. The theory developed by Vlahovska et al. [25, 31–33] predicts that the steady deformation parameter is given by the balance of electric and membrane stresses

$$s={\epsilon }_{ex}{E}_0^2{R}^3\frac{p^{\mathrm{el}}\left(\omega \right)}{6\kappa +\sigma R^2}.$$ (3)

The frequency dependence of the electric stress is given by

$$p^{\mathrm{el}}=\frac{1}{48}\left(4\left(1-P_{\text{ex}}^r\right)+P_{\text{ex}}^2-4S{P}_{\text{in}}^2\right)$$ (4)

where

$$P_{\text{ex}}=\frac{K_{\text{ex}}+K_{\text{in}}\left(V_m-1\right)}{K_{\text{in}}+2K_{\text{ex}}},P_{\text{in}}=\frac{K_{\text{ex}}\left(3-2V_m\right)}{K_{\text{in}}+2K_{\text{ex}}},V_m=\frac{3K_{\text{in}}{K}_{\text{ex}}}{2K_{\text{in}}{K}_{\text{ex}}+i{C}_{\text{m}}\left(K_{\text{in}}+2K_{\text{ex}}\right)\overline{\omega }}$$ (5)

Here $\overline{\omega }=\omega {\epsilon }_{\text{ex}}/{\lambda }_{\text{ex}}$ and ${\overline{C}}_{\text{m}}=C_{\text{m}}R/{\epsilon }_{\text{ex}}$ are the dimensionless frequency and membrane capacitance. $K_{\text{in}}=1+i\overline{\omega }$ and $K_{\text{ex}}=\Lambda +i\overline{\omega }S$ are the dimensionless complex permittivities. $S={\epsilon }_{\text{in}}/{\epsilon }_{\text{ex}}$ and $\Lambda ={\lambda }_{\text{in}}/{\lambda }_{\text{ex}}$ are the ratios of permittivities and conductivities of the fluids interior and exterior to the vesicle. P^r is the real part of P, and $P^2=P{P}^{*}$, where the superscript * denotes complex conjugate.

Typically, both the inner and outer fluids are aqueous solutions with similar permittivities, ${\epsilon }_{\text{in}}\approx {\epsilon }_{\text{ex}}=\epsilon$, hence S can be set to 1. In this case Eq. 3 reduces to

$$s\left(\overline{\omega }\right)=\frac{\epsilon E_0^2{R}^3}{\kappa \left(6+\overline{\sigma }\right)}\frac{3\left[{\overline{\omega }}^2\left({\overline{C}}_{\text{m}}^2{\left(\Lambda +2\right)}^2\left(\Lambda -1\right)\left(\Lambda +3\right)+2{\overline{C}}_{\text{m}}\Lambda \left({\Lambda }^2+\Lambda -2\right)+9{\Lambda }^2\right)+{\Lambda }^2{\left(\Lambda +2\right)}^2\right]}{16\left({\left(\Lambda +2\right)}^2+9{\overline{\omega }}^2\right)\left({\overline{C}}_{\text{m}}^2{\left(\Lambda +2\right)}^2{\overline{\omega }}^2+4{\Lambda }^2\right)},$$ (6)

where $\overline{\sigma }=\sigma R^2/\kappa$. For a given vesicle with specified Λ and C_m, the aspect ratio can be modulated by varying either the electric field amplitude at fixed frequency or the field frequency at a given field strength. These two modalities of electrodeformation can be utilized to yield the vesicle electromechanical properties: bending rigidity, tension and capacitance. The details of the implementation of the two approaches are discussed in Sections 3.1 and 3.2.

2.3. Vesicle Preparation

Giant unilamellar vesicles are formed from the lipid palmitoyloleoylphosphatidylcholine (POPC), dipalmitoylphosphatidylcholine (DPPC) and Cholesterol (Chol) which are purchased from Avanti Polar Lipids (Alabaster, AL). The vesicles were produced using the electroformation method [34]. The stock solutions of 12 mM lipid in choloroform are diluted to 4 mM from which 8 μl of the solution is spread on the conductive sides of the ITO slides (PGO, Germany). The slides are stored in vacuum for 2 hours to evaporate all the organic solvents. The two slides are then sandwiched with a 2 mm thick teflon spacer and the electroformation chamber is filled with 40 mM sucrose solution in 0.1-1 mM of NaCl. The chamber is connected to a signal generator (Agilent, USA) for 2 hours at 50 Hz and from Teflon with two 92 μm cylindrical voltage 1.5 V_p (voltage amplitude). The harvested vesicles are diluted in isotonic glucose solution in 0.1-1 mM NaCl. Solutions conductivities were measured with S47 Mettler Toledo conductivity meter (USA).

2.4. Electrodeformation

The electrodeformation experiments are conducted in the electrofusion chamber (Eppendorf, Germany). The chamber is made from Teflon with two 92 μm cylindrical platinum parallel electrodes 500 μm apart. The field is applied using a function generator (Agilent 3320A, USA). The function generator is controlled using a custom built MATLAB (Mathworks, USA) program. This gives a precise control over the strength and duration of applied electric fields.

2.5. Optical Microscopy and Imaging

The vesicles are visualized using a phase contrast microscope (A1 Axio Observer, Zeiss, Germany) with 63x objective 0.75 NA (air). Imaging is performed using Photron SA1.1 camera. The image acquisition rate for electrodeformation recordings is kept to a constant of 60 fps for lipid vesicles and the shutter speed is fixed to 300 μs. The time evolution of the vesicle is analyzed using a home-made image analysis software. The software uses a Fourier series to fit around the vesicle contour, $r_s={\sum }_{n=0}^{\infty }{c}_n\cos \left(n\theta \right)+d_n\sin \left(n\theta \right)$, where r_s is the vesicle contour radius at the azimuthal angle θ, c_n and d_n are the amplitude of the mode number n. The second mode in the series is used to determine the major and minor axis, a and b, of the deformed vesicles to evaluate $\nu =\left(1+c_2\right)/\left(1-c_2\right)$ [18, 20, 21].

3. RESULTS AND DISCUSSION

3.1. Tension–area strain curve from increasing field amplitude yields bending rigidity

If tension is much stronger than bending rigidity forces, $\overline{\sigma }\gg 1$, then we can use Eq. 3 to determine the tension as a function of area strain.

$$\sigma \left(s,E_0\right)=\frac{\epsilon E_0^{2}R{p}^{\mathrm{el}}\left(\omega \right)}{s}.$$ (7)

In terms of the deformation parameter, the area strain $\alpha \approx 8s^2/5$ [35]. Substituting in Eq. 1, using the expressions in terms of the deformation parameter, we obtain

$$\ln \frac{\epsilon R{p}^{\mathrm{el}}\left(\omega \right)}{{\sigma }_0}+\ln \frac{E_0^2}{s}=\frac{8\pi \kappa }{k_{B}T}\left(\frac{8s^2}{5}\right)$$ (8)

The bending rigidity is thus determined from the slope of the linear fit of s² as a function of ln $E_0^2/s$. Figure 2 illustrates the use of method.

FIG. 2.

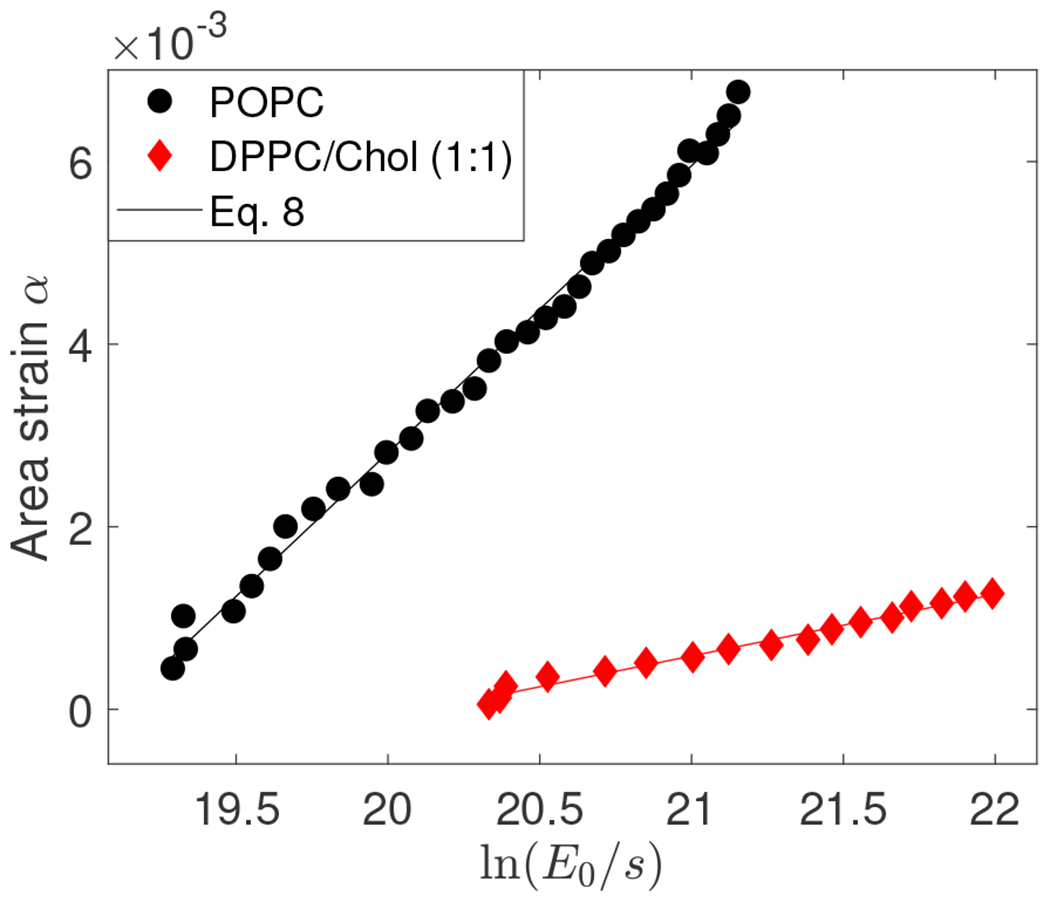
Area strain α = 8s²/5 vs $\ln \left(E_0^2/s\right)$ for POPC and DPPC/Chol (1:1) vesicle. For POPC, R = 26 μm, λ_in = 42 μS/m (0.5 mM NaCl) and λ_ex = 107 μS/m (0.8 mM NaCl). Electric field amplitude was increased from 2 to 10 kV/m at increments of 0.25 kV/m. The AC field frequency is 0.2 kHz. The bending rigidity determined from the slope is 12.67 k_BT and the tension obtained from the intercept is 1.76× 10⁻⁷ N/m with R-squared value of 0.994. For DPPC/Chol (1:1), R = 21.2 μm, λ_in = 3 μS/m (0 mM NaCl) and λ_ex = 120 μS/m (1 mM NaCl). Electric field amplitude was increased from 2 to 10 kV/m at increments of 0.5 kV/m. The AC field frequency is 1 kHz. The bending rigidity determined from the slope is 58.01 k_BT with R-squared value of 0.983.

In the original implementation [24], the tension was computed assuming low frequency $\left(\overline{\omega }\to 0\right)$

$$\sigma =\frac{9\epsilon E_0^{2}R}{16}{\left(H\left(0\right)-H\left(\pi /2\right)\right)}^{-1},$$ (9)

where H(θ) is the mean curvature of the ellipsoid

$$H\left(\theta \right)=\frac{a\left(a^2+3b^2+\left(b^2-a^2\right)\cos 2\theta \right)}{\sqrt{2}b{\left(a^2+b^2+\left(b^2-a^2\right)\cos 2\theta \right)}^{3/2}}$$ (10)

For small aspect ratios, in terms of the deformation parameter, $H\left(\theta \right)\approx 1+s\left(1+3\cos 2\theta \right)$ and the above formula reduces to Eq. 3 with $\overline{\omega }=0$. The area strain is computed from the aspect ratio and for a prolate ellipsoid (ν > 1) it is

$$\alpha =\frac{1}{2}{\upsilon }^{-2/3}\left(1+\upsilon \frac{\arcsin \left(e\right)}{e}\right),e=\sqrt{1-{\upsilon }^{-1/2}}.$$ (11)

Setting a = 1 + s and b = 1 − 2s and expanding for small s, recovers the area strain in terms of the deformation parameter, $\alpha \approx 8s^2/5$.

The electrodeformation method for measuring the bending rigidity was originally developed assuming low frequencies, $\overline{\omega }\to 0$. However, as seen from Eq. 8 the method can be performed at any frequency because the frequency-dependent prefactor $p^{\mathrm{el}}\left(\omega \right)$ is absorbed in the intercept and does not affect the slope. Figure 3 shows that the bending rigidity is indeed independent of the frequency. Furthermore, the values for the bending rigidity in Figure 3 and obtained from Figure 2, which were done with different NaCl concentration in the suspending solution, are similar thus suggesting that the bending rigidity is insensitive to the salt conditions at such low concentrations.

FIG. 3.

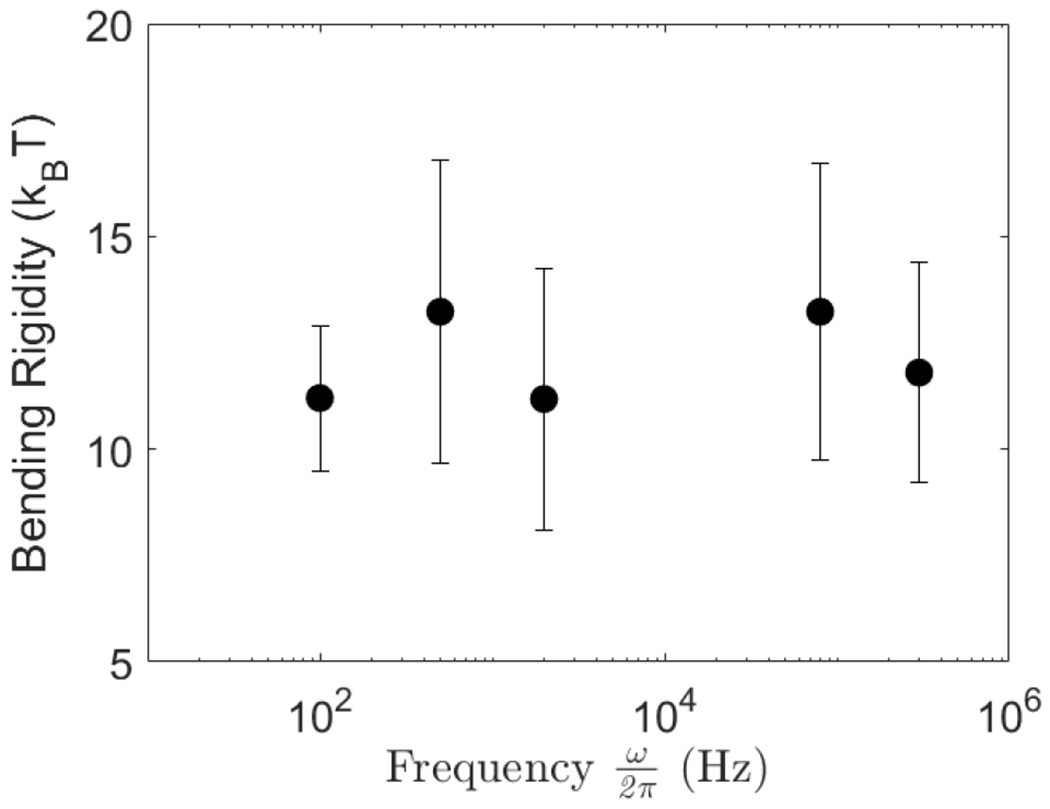
Bending rigidity of a POPC lipid bilayer membrane measured at different field frequencies. Solutions contain 0.2 mM NaCl inside (λ_in = 42 μS/cm) and no salt outside (λ_ex = 2 μS/cm). Values obtained from population averages over 12-15 vesicles. Field amplitude is increased from 2 to 10 kV/m with steps of 0.5 kV/m.

3.2. Frequency-dependent vesicle shape yields capacitance and bending rigidity

Vesicle deformation depends not only on field strength but also on field frequency [36]. Figure 4 shows the variation of the aspect ratio with applied field frequency and summarizes the physical mechanisms underlying the observed shape changes.

FIG. 4.

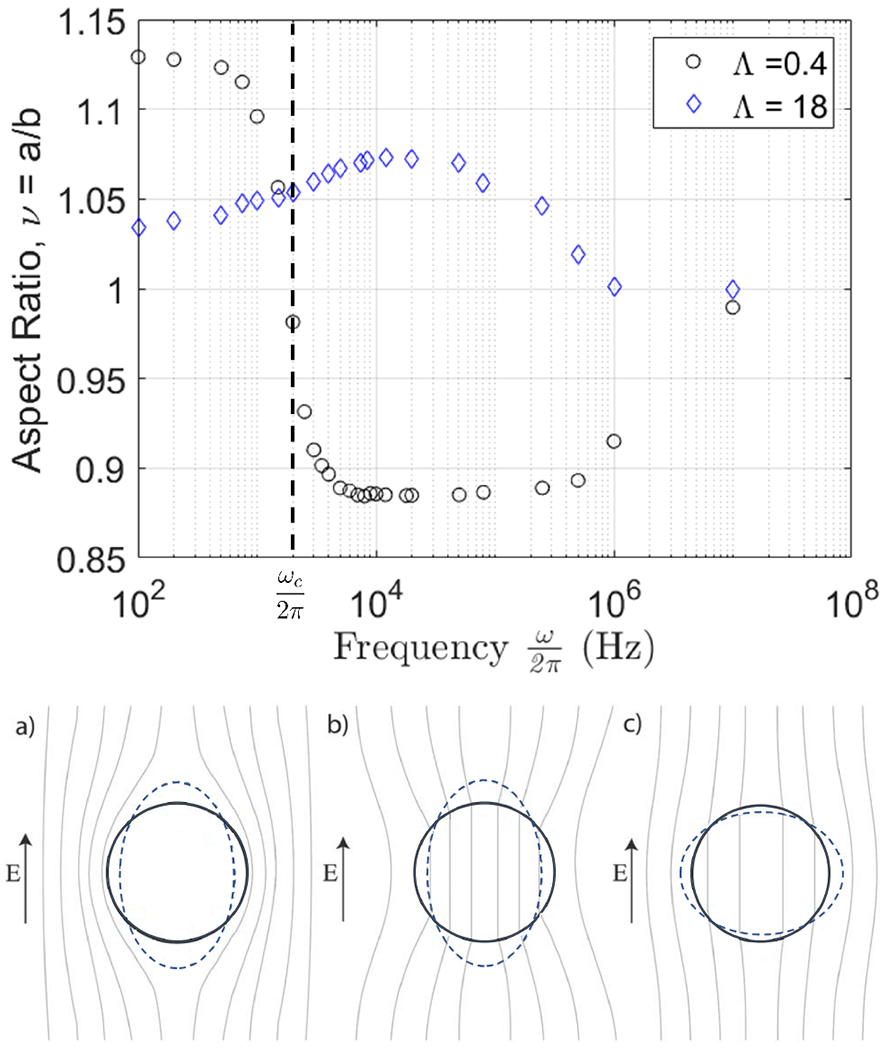
(top) Deformation of two POPC GUVs in a uniform AC electric field with amplitude 6 kV/m at different field frequencies in Hz at different conductivity ratios. (bottom) Physical mechanisms of the frequency-dependent vesicle shape in an applied uniform AC field. The lines correspond to constant electric field. (a) At low frequencies, $\omega \ll {\omega }_c$, the membrane capacitor is fully charged and the electric field inside the vesicle is zero. (b) and (c) At intermediate frequencies, $\omega >{\omega }_c$, it is short-circuited. (b) If the enclosed solution is more conducting than the suspending medium, Λ > 1, vesicle is pulled into an prolate ellipsoid. (c) The polarization is reversed in the opposite case Λ < 1 and the vesicle deforms into an oblate ellipsoid.

While the shape of vesicles with conductivity ratio Λ > 1 is always prolate, if Λ < 1, i.e., the vesicle is filled with a solution less conducting than the suspending one, the deformation parameter s (ω) is positive at low frequencies indicating prolate deformation, which decreases with frequency and becomes zero at a certain frequency. Above this critical frequency, the shape becomes oblate. For ${\overline{C}}_m\gg 1$, a condition that is typically satisfied for membranes, the critical frequency can be approximated as [37]

$${\omega }_c=\frac{{\lambda }_{\text{in}}}{R{C}_{\text{m}}}\frac{1}{\sqrt{\left(1-\Lambda \right)\left(3+\Lambda \right)}}$$ (12)

Thus, the membrane capacitance can be obtained from the experimentally measured critical frequency for prolate-oblate transition [27, 38]. The frequency-dependent shape is described by

$$s\left(\overline{\omega }\right)]=\frac{\epsilon E_0^{2}R}{{\sigma }_0}\frac{p^{\mathrm{el}}\left(\overline{\omega }\right)}{\exp \left(\frac{64\kappa }{5k_{B}T}{s}^2\left(\overline{\omega }\right)\right)}.$$ (13)

Figure 5 shows frequency-sweep experimental data for the same vesicle analyzed in Figure 2. The theoretical curve is obtained by using κ deduced from the classical electrodeformation method discussed in Section 3.1. Thus, the frequency sweep confirms the results from the field-amplitude-sweep. Furthermore, the frequency-sweep itself can be used to obtain the bending rigidity. Eq. 13 can be recast in a form analogous to Eq. 8

$$\ln \frac{\epsilon R{E}_0^2}{{\sigma }_0}+\ln \frac{p^{\mathrm{el}}\left(\omega \right)}{s}=\frac{8\pi \kappa }{k_{B}T}\left(\frac{8s^2}{5}\right)$$ (14)

FIG. 5.

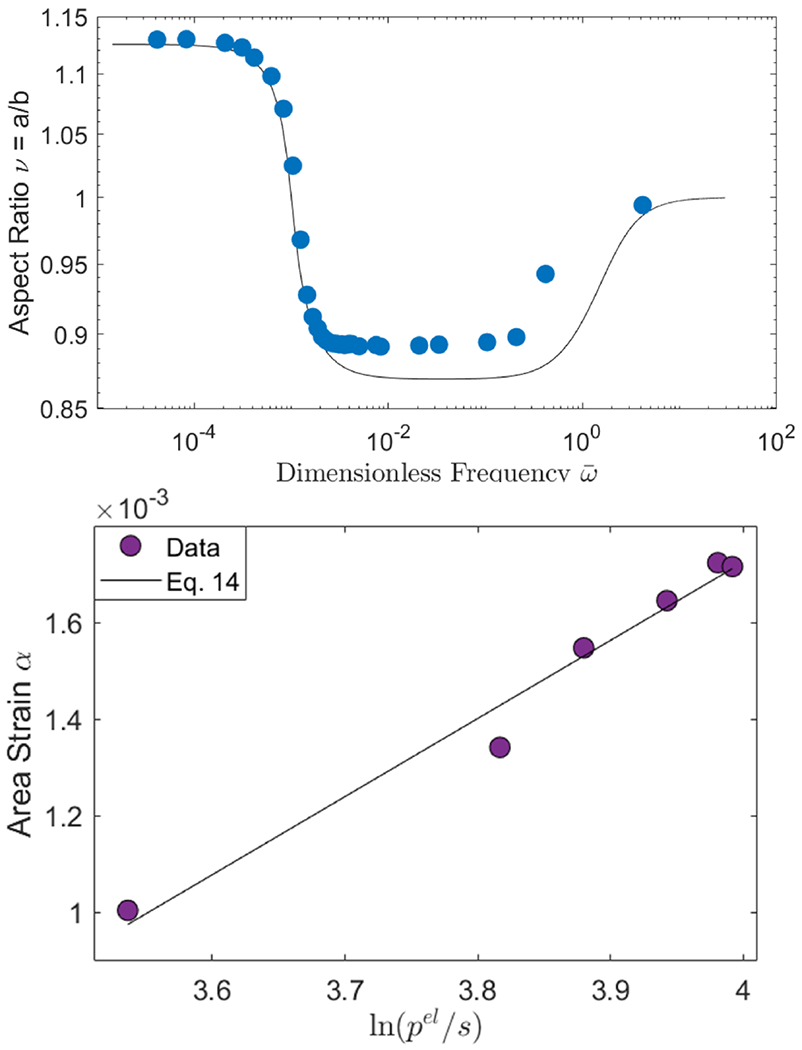
(top) Frequency dependence of the aspect ratio of the same POPC vesicle as in Figure 2 at E₀ = 6 kV/m. The solid line is Eq. 13 with the κ = 12.67 k_BT obtained by the classical electrodeformation method and σ₀ = 3.53 × 10⁻⁷ N/m. (bottom) The fit of frequency-sweep data at ω < ω_c yields κ = 14.97 k_BT with R-squared=0.975.

Fitting the data in the prolate deformation regime $\left(\omega <{\omega }_c\right)$ yields a similar value of the bending rigidity as in Figure 2. Note that using the whole frequency range is not convenient because vesicle shape changes from a prolate to an oblate ellipsoid. We also observe that the tension σ₀ needed to describe the frequency-sweep data is twice the one obtained from the intercept of the linear fit in Figure 2. The origin of this increase is currently being investigated. The membrane capacitance obtained from the the critical frequency ω_c is 0.72±0.04 μFcm⁻² from measurements of 13 vesicles. The value is consistent with the previously reported data by Salipante et al. [27]. Note that the capacitance is obtained independently of bending rigidity and tension.

3.3. Apparent bending rigidity of membranes with tubes

Biological membranes are inherently asymmetric [39]. Different lipid compositions in the two leaflets and proteins [40–42], or difference in cytosolic and periplasmic buffer conditions [43], can lead to membrane curvature resulting in formation defects such as tubes [44]. Here we illustrate the utility of the electrodeformation method to measure the bending rigidity and membrane tension of such membranes, as these are difficult to characterize using conventional methods such as flickering spectroscopy [21].

We observe that vesicles with large difference in the the salt concentrations inside and outside (filled with 0.5mM Na Cl and suspended in no salt solution) have many tubes with diameter 1-2 μm, see Figure 6. The formation of the tubes is likely due to spontaneous curvature arising from asymmetry in the electric double layers adjacent to the membrane. The Debye length (calculated for a 1:1 electrolyte from κ_D = 0.303c^−1/2 nm, where c is the electrolyte concentration in M) is 14 nm for the inner and 78 nm for the outer double layer in the asymmetric case, while in the symmetric case the outer double layer is 10 nm. For the salt-free solution, the procedure to estimate the Debye layer thickness is given in [20].

FIG. 6.

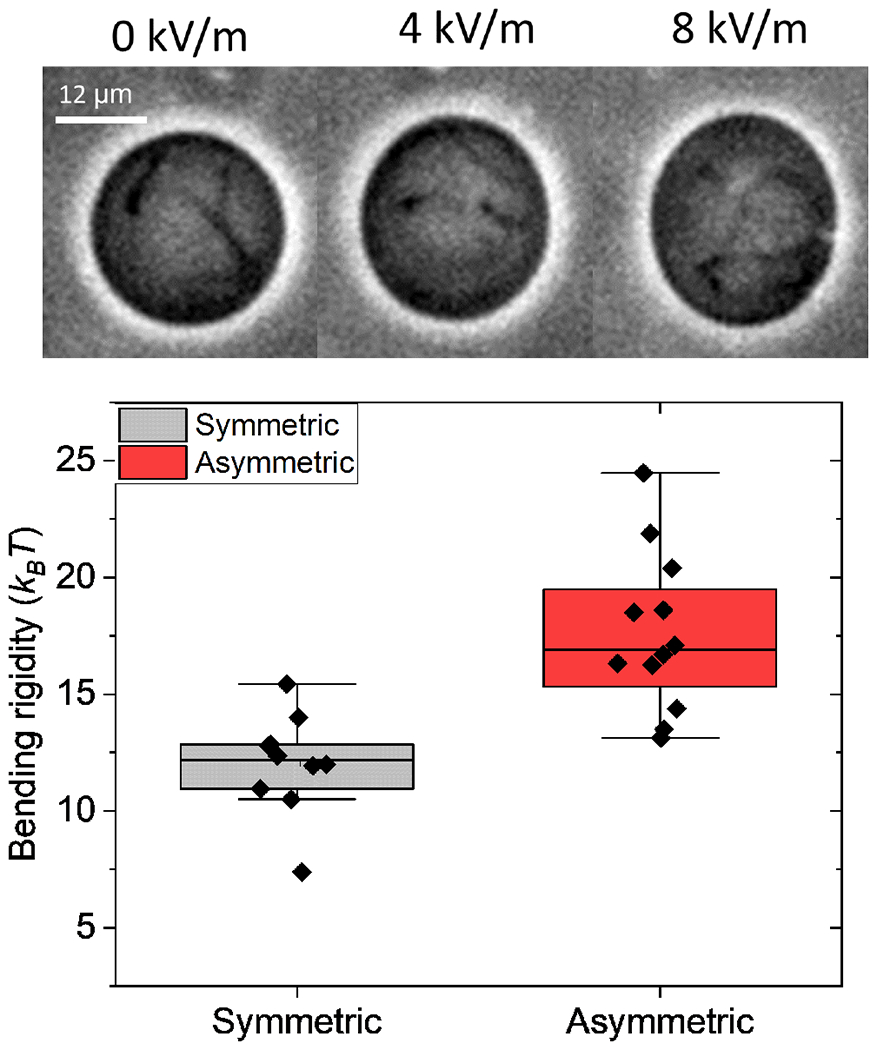
(top) Snapshots of GUV showing tubes. 0.5 mM NaCl inside and no salt outside. (bottom) Membrane bending rigidity obtained for asymmetric (0.5 mM NaCl and no salt outside) and symmetric (0.5 mM NaCl inside and 0.8 mM NaCl outside) membranes.

We measured the bending rigidity using the electrodeformation method and found membranes with tubes to be more rigid (17.4 ± 3.3 k_BT) compared to symmetric membranes (12.0 ± 2.2 k_BT) as shown in Figure 6.

4. CONCLUSIONS

We describe a method to characterize the electric and mechanical properties of biomimetic membranes using a uniform AC electric field. The approach relies on the analysis of the variation of the equilibrium shapes of giant unilamellar vesicles with electric field amplitude and frequency. Using the theory developed in [25], we derive the theoretical foundations for the method originally proposed by Kummrow and Helfrich [24], which utilizes the variation of the area strain on electric field amplitude at fixed field frequency. We show that fitting the dependence of the area strain on either the field amplitude or frequency yields similar values for the bending rigidity and tension. The frequency sweep, however, also provides the membrane capacitance. The latter is obtained from the frequency at which the vesicle shape changes from prolate to oblate ellipsoid as the frequency is increased. We demonstrate the utility of the method by measuring the mechanical properties of membranes with tubes, which so far could only be analyzed using more complex methods such as micropipette aspiration. Our method can be applied to a variety of membrane compositions, including multicomponent systems containing cholesterol, block-copolymers, and asymmetric membranes. The method should even work with membranes containing charged lipids since in AC electric field the charged species do not undergo electrophoresis. The extension of the method to such systems will be investigated in near future.

7. DATA AVAILABILITY

All the data is available upon a reasonable request.